智能控制(神经网络)作业
智能控制试卷及答案

智能控制试卷及答案一、试卷一、选择题(每题2分,共20分)1. 下列哪项不是智能控制的主要类型?A. 人工智能控制B. 模糊控制C. 神经网络控制D. 逻辑控制2. 以下哪种控制方法适用于处理具有不确定性、非线性和时变性等特点的复杂系统?A. PID控制B. 模糊控制C. 串级控制D. 比例控制3. 神经网络控制的核心思想是利用神经网络实现控制规律的映射,以下哪种神经网络模型适用于动态系统的控制?A. BP神经网络B. RBF神经网络C. 感知器D. Hopfield神经网络4. 模糊控制中,模糊逻辑推理的核心部分是?A. 模糊集合B. 模糊规则C. 模糊推理D. 解模糊5. 以下哪种方法不属于智能控制系统的建模方法?A. 基于模型的建模B. 基于数据的建模C. 基于知识的建模D. 基于经验的建模二、填空题(每题2分,共20分)6. 智能控制的理论基础包括________、________和________。
7. 模糊控制的基本环节包括________、________、________和________。
8. 神经网络控制的主要特点有________、________、________和________。
9. 智能控制系统的主要性能指标包括________、________、________和________。
10. 智能控制技术在工业生产、________、________和________等领域有广泛应用。
三、判断题(每题2分,共10分)11. 模糊控制适用于处理具有确定性、线性和时不变性等特点的复杂系统。
()12. 神经网络控制具有较强的自学习和自适应能力。
()13. 智能控制系统不需要考虑系统的稳定性和鲁棒性。
()14. 智能控制技术在无人驾驶、智能家居等领域具有广泛应用前景。
()15. 模糊控制的核心思想是利用模糊逻辑进行推理和决策。
()四、简答题(每题10分,共30分)16. 简述模糊控制的基本原理。
神经网络在智能控制系统中的应用

神经网络在智能控制系统中的应用智能控制系统是一种基于前沿技术的控制系统,它具备学习和适应能力,可以自主地做出决策并改进自身的性能。
在智能控制系统中,神经网络作为一种重要的技术手段,展示了出色的应用效果。
本文将介绍神经网络在智能控制系统中的应用,并探讨其优势和未来发展方向。
一、神经网络在智能控制系统中的基本原理神经网络是一种通过模仿生物神经系统来模拟人类智能行为的技术方法。
神经网络由大量的神经元相互联结而成,通过学习和训练,神经网络能够对输入信息进行处理和分析,并对未知的数据作出预测和决策。
在智能控制系统中,神经网络起到了关键的作用。
首先,它能够通过学习和训练来从大量的数据中提取有用的信息,并有效地进行模式识别和分类。
其次,神经网络能够建立起输入和输出之间的映射关系,从而实现对输入信号的动态处理和控制。
最后,神经网络还能够通过自适应学习的方式,主动调整自身的结构和参数,以适应不同的环境和任务需求。
二、神经网络在智能控制系统中的应用领域1.自动驾驶技术神经网络在自动驾驶技术中具有广泛的应用。
通过对实时传感器数据的处理和分析,神经网络能够实现车辆的环境感知、路径规划和行为决策,从而实现自主驾驶功能。
神经网络的高并行性和适应能力使得自动驾驶系统能够在复杂多变的交通环境中实现精确的控制和决策。
2.智能制造神经网络在智能制造领域中的应用也日益重要。
在生产线的控制与优化中,神经网络能够通过学习和模式识别来分析生产数据,探测异常和故障,并实现自动故障诊断和预防。
此外,神经网络还能够优化生产调度和质量控制,提高生产效率和产品质量。
3.智能家居随着物联网技术的发展,智能家居正逐渐成为人们生活的一部分。
神经网络在智能家居中扮演着智能控制的重要角色。
通过对家庭环境和用户行为的学习和建模,神经网络可以实现智能家居设备的自主控制和个性化服务。
它能够根据不同的需求和偏好,自动调节室内温度、照明和安全系统,提供便捷、舒适和安全的居家环境。
(完整版)智能控制题目及解答

智能控制题目及解答第一章绪论作业作业内容1.什么是智能、智能系统、智能控制?2.智能控制系统有哪几种类型,各自的特点是什么?3.比较智能控制与传统控制的特点.4.把智能控制看作是AI(人工智能)、OR(运筹学)、AC(自动控制)和IT(信息论)的交集,其根据和内涵是什么?5.智能控制有哪些应用领域?试举出一个应用实例,并说明其工作原理和控制性能.1 答:智能:能够自主的或者交互的执行通常与人类智能有关的智能行为,如判断、推理、证明、识别、感知、理解、通信、设计、思考、规划、学习等一系列活动的能力,即像人类那样工作和思维。
智能系统:是指具有一定智能行为的系统,对于一定的输入,它能产生合适的问题求解相应。
智能控制:智能控制是控制理论、计算机科学、心理学、生物学和运筹学等多方面综合而成的交叉学科,它具有模仿人进行诸如规划、学习、逻辑推理和自适应的能力。
是将传统的控制理论与神经网络、模糊逻辑、人工智能和遗传算法等实现手段融合而成的一种新的控制方法。
2 答:(1)人作为控制器的控制系统:人作为控制器的控制系统具有自学习、自适应和自组织的功能。
(2)人—机结合作为作为控制器的控制系统:机器完成需要连续进行的并需快速计算的常规控制任务,人则完成任务分配、决策、监控等任务。
(3)无人参与的自组控制系统:为多层的智能控制系统,需要完成问题求解和规划、环境建模、传感器信息分析和低层的反馈控制任务.3 答:在应用领域方面,传统控制着重解决不太复杂的过程控制和大系统的控制问题;而智能控制主要解决高度非线性、不确定性和复杂系统控制问题。
在理论方法上,传统控制理论通常采用定量方法进行处理,而智能控制系统大多采用符号加工的方法;传统控制通常捕获精确知识来满足控制指标,而智能控制通常是学习积累非精确知识;传统控制通常是用数学模型来描述系统,而智能控制系统则是通过经验、规则用符号来描述系统。
在性能指标方面,传统控制有着严格的性能指标要求,智能控制没有统一的性能指标,而主要关注其目的和行为是否达到。
智能控制(神经网络)-作业

智能控制作业学生姓名: 学号: 专业班级:(一)7-2 采用BP网路、RBF网路、DRNN网路逼近线性对象, 分别进行matlab 仿真。
(二)采用BP网络仿真网络结构为2-6-1。
采样时间1ms, 输入信号, 权值的初值随机取值, 。
仿真m文件程序为:%BP simulationclear all;clear all;xite=0.5;alfa=0.5;w1=rands(2,6); % value of w1,initially by randomw1_1=w1;w1_2=w1;w2=rands(6,1); % value of w2,initially by randomw2_1=w2;w2_2=w2_1;dw1=0*w1;x=[0,0]';u_1=0;y_1=0;I=[0,0,0,0,0,0]'; % input of yinhanceng cellIout=[0,0,0,0,0,0]'; % output of yinhanceng cellFI=[0,0,0,0,0,0]';ts=0.001;for k=1:1:1000time(k)=k*ts;u(k)=0.5*sin(3*2*pi*k*ts);y(k)=(u_1-0.9*y_1)/(1+y_1^2);for j=1:1:6I(j)=x'*w1(:,j);Iout(j)=1/(1+exp(-I(j)));endyn(k)=w2'*Iout; %output of networke(k)=y(k)-yn(k); % error calculationw2=w2_1+(xite*e(k))*Iout+alfa*(w2_1-w2_2); % rectify of w2for j=1:1:6FI(j)=exp(-I(j))/(1+exp(-I(j))^2);endfor i=1:1:2for j=1:1:6dw1(i,j)=e(k)*xite*FI(j)*w2(j)*x(i); % dw1 calculation endendw1=w1_1+dw1+alfa*(w1_1-w1_2); % rectify of w1% jacobian informationyu=0;for j=1:1:6yu=yu+w2(j)*w1(1,j)*FI(j);enddyu(k)=yu;x(1)=u(k);x(2)=y(k);w1_2=w1_1;w1_1=w1;w2_2=w2_1;w2_1=w2;u_1=u(k);y_1=y(k);endfigure(1);plot(time,y,'r',time,yn,'b');xlabel('times');ylabel('y and yn');figure(2);plot(time,y-yn,'r');xlabel('times');ylabel('error');figure(3);plot(time,dyu);xlabel('times');ylabel('dyu');运行结果为:(三)采用RBF网络仿真网路结构为2-4-1, 采样时间1ms, 输入信号, 权值的初值随机取值, , 高斯基函数初值, 。
智能控制技术作业1
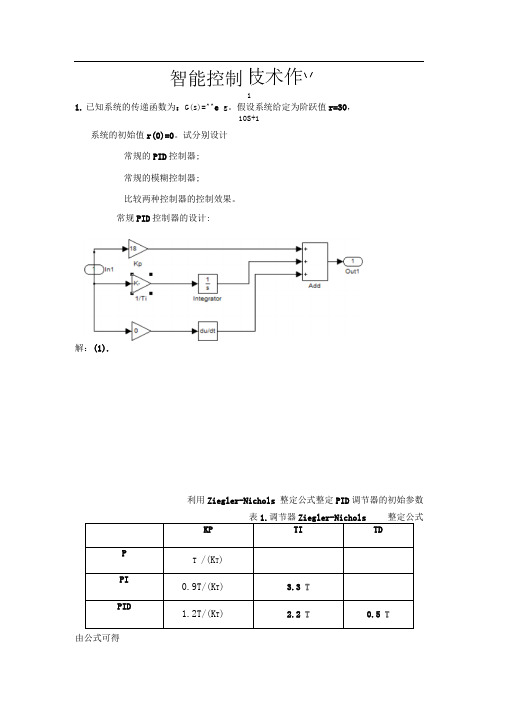
智能控制11.已知系统的传递函数为:G(s)=^^e g。
假设系统给定为阶跃值r=30,10S+1系统的初始值r(0)=0。
试分别设计常规的PID控制器;常规的模糊控制器;比较两种控制器的控制效果。
解:(1).利用Ziegler-Nichols 整定公式整定PID调节器的初始参数表1.调节器Ziegler-Nichols 整定公式KP TI TDPT /(K T)PI0.9T/(K T) 3.3 TPID1.2T/(K T)2.2 T0.5 T由公式可得\ /常规PID控制器的设计:P=18Ti=1.65Td=O SIMULINK仿真图^Bl*ck FardBCtcrsL Step]—S-tn 口tiJM:F:n且!valae.|35Saocrle tiae:pP iRt^Tpret vect{}r pEiTKHteri AB 1-D1*7 二「二匕二匸匚rzzrinb c -二:"〔二r.QBl*ck rarutt«rs: Tr^nsstrl Dclarp Tf Dfrlaj丄口sir <PE匚LT;td do:口T tp the qrpvt ;iEnJl- n;匚ur*cr i;au订:<hiTi tm delay i i lariE^r t郎an tJifr iinlat^on it»口i;£«上冒itlA* Ln^tLBl iTlDUt'I偌斗设定仿真时间为10s仿真结果CdX1C«l M*lp ApplyU2SJ 厂Direct r*fr;throi;ch at input liiXiiu liJieaxisttian.Pndfl prdflh tfo-T ;incari;ftt iQTL;:A也Q何丹ASS S昌嘩ffl 也| ** C? ® e附币■(2).模糊控制器的设计:1.在matlab命令窗口输入“ fuzzy ”确定模糊控制器结构:即根据具体的系统确定输入、输出量。
智能控制BP神经网络实验报告
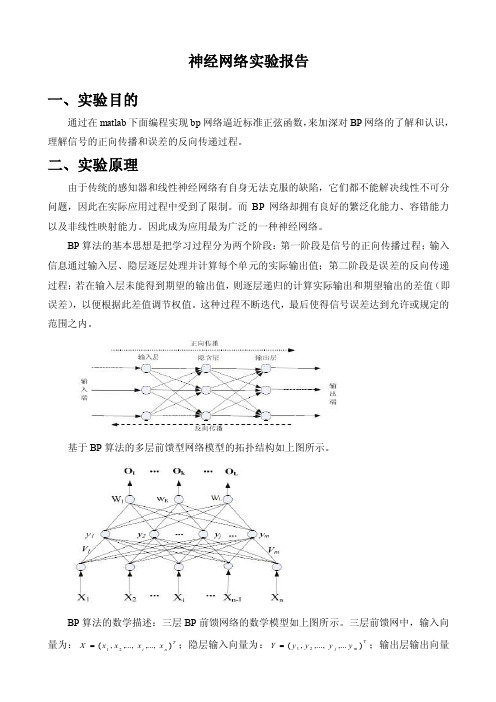
神经网络实验报告一、实验目的通过在matlab 下面编程实现bp 网络逼近标准正弦函数,来加深对BP 网络的了解和认识,理解信号的正向传播和误差的反向传递过程。
二、实验原理由于传统的感知器和线性神经网络有自身无法克服的缺陷,它们都不能解决线性不可分问题,因此在实际应用过程中受到了限制。
而BP 网络却拥有良好的繁泛化能力、容错能力以及非线性映射能力。
因此成为应用最为广泛的一种神经网络。
BP 算法的基本思想是把学习过程分为两个阶段:第一阶段是信号的正向传播过程;输入信息通过输入层、隐层逐层处理并计算每个单元的实际输出值;第二阶段是误差的反向传递过程;若在输入层未能得到期望的输出值,则逐层递归的计算实际输出和期望输出的差值(即误差),以便根据此差值调节权值。
这种过程不断迭代,最后使得信号误差达到允许或规定的范围之内。
基于BP 算法的多层前馈型网络模型的拓扑结构如上图所示。
BP 算法的数学描述:三层BP 前馈网络的数学模型如上图所示。
三层前馈网中,输入向量为:Tn i x x x x X),...,,...,,(21=;隐层输入向量为:Tm j y y y y Y),...,...,,(21=;输出层输出向量为:Tl k o o o o O),...,...,,(21=;期望输出向量为:Tl k d d d d d),...,...,(21=。
输入层到隐层之间的权值矩阵用V 表示,Ym j v v v v V),...,...,(21=,其中列向量j v 为隐层第j 个神经元对应的权向量;隐层到输出层之间的权值矩阵用W 表示,),...,...,(21l k w w w w W =,其中列向量k w 为输出层第k 个神经元对应的权向量。
下面分析各层信号之间的数学关系。
对于输出层,有∑====mj x v net mj netf yi ij jjj,...,2,1,,...,2,1),(对于隐层,有∑=====mj i jkkkk lk y wnetl k netf O 0,...,2,1,,...,2,1),(以上两式中,转移函数f(x)均为单极性Sigmoid 函数:xex f -+=11)(f(x)具有连续、可导的特点,且有)](1)[()('x f x f x f -=以上共同构成了三层前馈网了的数学模型。
智能控制习题

智能控制习题⼀、填空题(每空1分,共20分)1.控制论的三要素是:信息、反馈和控制。
2.传统控制是经典控制和现代控制理论的统称。
3.智能控制系统的核⼼是去控制复杂性和不确定性。
4.神经元(即神经细胞)是由细胞体、树突、轴突和突触四部分构成。
5.按⽹络结构分,⼈⼯神经元细胞可分为层状结构和⽹状结构按照学习⽅式分可分为:有教师学习和⽆教师学习。
6.前馈型⽹络可分为可见层和隐含层,节点有输⼊节点、输出节点、计算单元。
7.神经⽹络⼯作过程主要由⼯作期和学习期两个阶段组成。
⼆、判断题:(每题1分,共10分)1.对反馈⽹络⽽⾔,稳定点越多,⽹络的联想与识别能⼒越强,因此,稳定点的数据⽬越多联想功能越好。
(错)2.简单感知器仅能解决⼀阶谓词逻辑和线性分类问题,不能解决⾼阶谓词和⾮线分类问题。
(对)3. BP算法是在⽆导师作⽤下,适⽤于多层神经元的⼀种学习,它是建⽴在相关规则的基础上的。
(错)4.在误差反传训练算法中,周期性函数已被证明收敛速度⽐S型函数慢。
(错)5.基于BP算法的⽹络的误差曲⾯有且仅有⼀个全局最优解。
(错) 6.对于前馈⽹络⽽⾔,⼀旦⽹络的⽤途确定了,那么隐含层的数⽬也就确定了。
(错)7.对离散型HOPFIELD⽹络⽽⾔,如权矩阵为对称阵,⽽且对⾓线元素⾮负,那么⽹络在异步⽅式下必收敛于下⼀个稳定状态。
(对)8.对连续HOPFIELD⽹络⽽⾔,⽆论⽹络结构是否对称,都能保证⽹络稳定。
(错)9.竞争学习的实质是⼀种规律性检测器,即是基于刺激集合和哪个特征是重要的先验概念所构造的装置,发现有⽤的部特征。
(对)10.⼈⼯神经元⽹络和模糊系统的共同之处在于,都需建⽴对象的精确的数学模型,根据输⼊采样数据去估计其要求的决策,这是⼀种有模型的估计。
(错)三、简答题(每题5分,共30分)1.智能控制系统有哪些类型?答:1)多级递阶智能控制 2)基于知识的专家控制3)基于模糊逻辑的智能控制——模糊控制4)基于神经⽹络的智能控制——神经控制5)基于规则的仿⼈智能控制6)基于模式识别的智能控制7)多模变结构智能控制8)学习控制和⾃学习控制9)基于可拓逻辑的智能控制——可拓控制10)基于混沌理论的智能控制——混沌控制2.⽐较智能控制与传统控制的特点?1)传统控制⽅法在处理复杂性、不确定性⽅⾯能⼒低⽽且有时丧失了这种能⼒智能控制在处理复杂性、不确定性⽅⾯能⼒⾼2)传统控制是基于被控对象精确模型的控制⽅式,可谓“模型论”智能控制是智能决策论,相对于“模型论”可称为“控制论”3)传统的控制为了控制必须建模,⽽利⽤不精确的模型⼜采⽤摸个固定控制算法,使整个的控制系统置于模型框架下,缺乏灵活性,缺乏应变性,因此很难胜任对复杂系统的控制。
智能控制题目及解答

智能控制题目及解答 Document number:WTWYT-WYWY-BTGTT-YTTYU-2018GT智能控制题目及解答第一章绪论作业作业内容1.什么是智能、智能系统、智能控制2.智能控制系统有哪几种类型,各自的特点是什么3.比较智能控制与传统控制的特点。
4.把智能控制看作是AI(人工智能)、OR(运筹学)、AC(自动控制)和IT(信息论)的交集,其根据和内涵是什么5.智能控制有哪些应用领域试举出一个应用实例,并说明其工作原理和控制性能。
1 答:智能:能够自主的或者交互的执行通常与人类智能有关的智能行为,如判断、推理、证明、识别、感知、理解、通信、设计、思考、规划、学习等一系列活动的能力,即像人类那样工作和思维。
智能系统:是指具有一定智能行为的系统,对于一定的输入,它能产生合适的问题求解相应。
智能控制:智能控制是控制理论、计算机科学、心理学、生物学和运筹学等多方面综合而成的交叉学科,它具有模仿人进行诸如规划、学习、逻辑推理和自适应的能力。
是将传统的控制理论与神经网络、模糊逻辑、人工智能和遗传算法等实现手段融合而成的一种新的控制方法。
2 答:(1)人作为控制器的控制系统:人作为控制器的控制系统具有自学习、自适应和自组织的功能。
(2)人-机结合作为作为控制器的控制系统:机器完成需要连续进行的并需快速计算的常规控制任务,人则完成任务分配、决策、监控等任务。
(3)无人参与的自组控制系统:为多层的智能控制系统,需要完成问题求解和规划、环境建模、传感器信息分析和低层的反馈控制任务。
3 答:在应用领域方面,传统控制着重解决不太复杂的过程控制和大系统的控制问题;而智能控制主要解决高度非线性、不确定性和复杂系统控制问题。
在理论方法上,传统控制理论通常采用定量方法进行处理,而智能控制系统大多采用符号加工的方法;传统控制通常捕获精确知识来满足控制指标,而智能控制通常是学习积累非精确知识;传统控制通常是用数学模型来描述系统,而智能控制系统则是通过经验、规则用符号来描述系统。
智能控制实验报告

一、实验目的1. 了解智能控制的基本原理和方法。
2. 掌握智能控制系统的设计和实现方法。
3. 熟悉智能控制实验平台的操作和应用。
二、实验原理智能控制是利用计算机技术、控制理论、人工智能等知识,实现对复杂系统的自动控制。
实验主要涉及以下原理:1. 模糊控制:利用模糊逻辑对系统进行控制,实现对系统不确定性和非线性的处理。
2. 专家控制:通过专家系统对系统进行控制,实现对系统复杂性和不确定性的处理。
3. 神经网络控制:利用神经网络强大的学习能力和泛化能力,实现对系统的自适应控制。
三、实验器材1. 实验平台:智能控制实验箱2. 传感器:温度传感器、湿度传感器、压力传感器等3. 执行器:电机、继电器、阀门等4. 控制器:单片机、PLC等5. 信号线、连接线等四、实验内容1. 模糊控制器设计(1)建立模糊控制模型:根据实验要求,确定输入、输出变量和模糊控制规则。
(2)设计模糊控制器:根据模糊控制规则,设计模糊控制器,包括模糊化、去模糊化等环节。
(3)仿真实验:利用仿真软件对模糊控制器进行仿真实验,验证控制效果。
2. 专家控制器设计(1)建立专家系统:收集专家知识,构建专家系统。
(2)设计专家控制器:根据专家系统,设计专家控制器,实现对系统的控制。
(3)仿真实验:利用仿真软件对专家控制器进行仿真实验,验证控制效果。
3. 神经网络控制器设计(1)建立神经网络模型:根据实验要求,确定神经网络的结构和参数。
(2)训练神经网络:利用实验数据对神经网络进行训练,提高网络的控制能力。
(3)设计神经网络控制器:根据训练好的神经网络,设计神经网络控制器,实现对系统的控制。
(4)仿真实验:利用仿真软件对神经网络控制器进行仿真实验,验证控制效果。
五、实验步骤1. 熟悉实验平台,了解各模块的功能和操作方法。
2. 根据实验要求,设计模糊控制器、专家控制器和神经网络控制器。
3. 利用仿真软件对控制器进行仿真实验,验证控制效果。
4. 分析实验结果,对控制器进行优化和改进。
自动化概论作业——智能控制

自动化概论作业—智能控制智能控制基本概念智能控制的定义一: 智能控制是由智能机器自主地实现其目标的过程.而智能机器则定义为,在结构化或非结构化的,熟悉的或陌生的环境中,自主地或与人交互地执行人类规定的任务的一种机器.定义二: K.J.奥斯托罗姆则认为,把人类具有的直觉推理和试凑法等智能加以形式化或机器模拟,并用于控制系统的分析与设计中,以期在一定程度上实现控制系统的智能化,这就是智能控制.他还认为自调节控制,自适应控制就是智能控制的低级体现.定义三: 智能控制是一类无需人的干预就能够自主地驱动智能机器实现其目标的自动控制,也是用计算机模拟人类智能的一个重要领域.定义四: 智能控制实际只是研究与模拟人类智能活动及其控制与信息传递过程的规律,研制具有仿人智能的工程控制与信息处理系统的一个新兴分支学科。
智能控制的特点同时具有以知识表示的非数学广义模型和以数学模型表示的混合过程,也往往是那些含有复杂性,不完全性,模糊性或不确定性以及不存在已知算法的非数学过程,并以知识进行推理,以启发引导求解过程;智能控制的核心在高层控制,即组织级;智能控制器具有非线性特性;智能控制具有变结构特点;智能控制器具有总体自寻优特性;智能控制系统应能满足多样性目标的高性能要求;智能控制是一门边缘交叉学科;智能控制是一个新兴的研究领域。
智能控制的主要技术方法智能控制是以控制理论、计算机科学、人工智能、运筹学等学科为基础,扩展了相关的理论和技术,其中应用较多的有模糊逻辑、神经网络、专家系统、遗传算法等理论和自适应控制、自组织控制、自学习控制等技术。
专家系统专家系统是利用专家知识对专门的或困难的问题进行描述. 用专家系统所构成的专家控制,无论是专家控制系统还是专家控制器,其相对工程费用较高,而且还涉及自动地获取知识困难、无自学能力、知识面太窄等问题. 尽管专家系统在解决复杂的高级推理中获得较为成功的应用,但是专家控制的实际应用相对还是比较少。
智能的控制技术作业三

智能控制作业三:用智能控制理论所学的知识对下面的二维函数建模:xy yx z) sin( )sin(。
训练数据取x=(-10:2:10)=[-10,-8,-6,-4,-2,0,2,4,6,8,10]共11个点,y=(-10:2:10)=[-10,-8,-6,-4,-2,0,2,4,6,8,10]共11个点,总共的训练数据为(2维输入1维输出)11×11=121组。
建模完成后,用x=(-10:0.5:10),y=(-10:0.5:10)的输入数据进行模型测试,并与直接利用解析公式的结果进行对比,体会非线性建模过程中各个参数对性能的影响。
采用BP神经网络,50个隐含层,1个输出层训练前输出杂乱无章,如图1所示10未训练图 1训练前的输出训练参数设置如下:net.trainParam.time=10;net.trainParam.lr=0.05;net.trainParam.epochs=500;net.trainParam.goal=1e-10;net.trainParam.min_grad=1e-7;net=train(net,input,output);训练以后以训练数据代入,如图2所示:训练好的图 2训练以后的输出代入测试数据检验,如图3所示:测试结果图 3测试结果误差如图4所示:误差图 4误差分析:迭代次数:实际迭代29次以后满足精度的要求,将迭代次数减小至20次,可见精度明显下降。
学习速率:将学习速率改为0.8,效果变差测试结果将学习速率改为0.001,效果略好,但是迭代了41次,花费的时间比较长。
误差指标:将误差指标改为0.01,迭代7次就完成了,效果明显变差测试结果隐含层神经元个数:将隐含层神经元改为10个,迭代500次仍没有达到精度的要求,说明增加神经元个数能提高精度。
测试结果将隐含层神经元个数改为150个,效果变的很差,说明隐含层神经元个数也不能太多。
测试结果。
神经网络作业

机器学习,是人工智能的一个子领域,主要关注于开发一些蠩计算机可以自动“学习”的技术。
更堷体说,机器学习是一种用于创建数据順分析分析程序的方法。
机器学习跟统计学有着重要的关系,因为这两个领域都栯研究数据分析,但是又不像统计学,栺器学习关注的是计算实现的算法复杂堦。
很多推论问题属于无程序可循难度,所以部分的机器学习研究是开发容栓处理的近似算法。
机器学习已经有亠十分广泛的应用例如搜索引擎、诊断、检测信用卡欺诈、证券市场分析、DNA序列测序、语音识别和手写识别识别、战略游戏和机器人运用。
第五讲机器学习机器学习就是计算机自动获取知识,它是知识工程的三个分支(使用知识、知识表示、获取知识)之一。
5.1 研究机器学习的必要性和可行性人工智能的概念和方法已经用于很多领域中,主要成果是专家系统、自然语言理解、计算机视觉和听觉、推理系统的研究。
当前人工智能研究的主要障碍和发展方向之一就是机器学习,这包括发展机器学习的计算理论和构造学习系统。
现在的人工智能系统还完全没有或仅有很有限的学习能力。
人工智能系统中的知识由人工编程送入系统,知识库中错误也不能自动改正。
也就是说,现有的AI系统是演绎推理而不是归纳推理,因而不能自动获取和生成知识。
人类有能力获取新知识、学习新技巧,并在实践中改进之。
如果一个人反复犯同样的错误,就不能说他是有智能的。
学习是智能的重要一环,人工智能的研究目标之一应该是理解学习的本质和建立学习系统。
人工智能解决的问题越来越复杂,系统中的知识越来越多,这些知识包括:领域专用的事实和规则,作为常识的启发式和约束,通用的概念和理论,把如此复杂的知识送入系统是复杂的、费时的、容易出错的和需要经验的。
例如:∙建立专家系统需要有关领域的专家和知识工程师的配合。
使用机器学习技术可以简化这一过程;∙计算机视觉中包含各种视觉专用变换、几何概念和对象的物理与功能描述。
把所有这些知识送入系统中是很困难的,系统应该可以由示教实例自动生成知识。
智能控制智能控制试卷(练习题库)(2023版)

智能控制智能控制试卷(练习题库)1、简述智能控制的概念。
2、比较智能控制和传统控制的特点?3、智能控制的概念首次由著名学者()提出的。
4、经常作为智能控制典型研究对象的是()。
5、智能自动化开发与应用应当面向()。
6、不属于智能控制是()。
7、以下不属于智能控制主要特点的是()。
8、以下不属于智能控制的是()。
9、地质探矿专家系统常使用的知识表示方法为()。
10、自然语言问答专家系统使用的知识表示方法为()。
11、专家系统中的自动推理是基于O的推理。
12、适合专家控制系统的是()。
13、直接式专家控制通常由O组成。
14、产生式系统的推理方式不包括()。
15、黑板专家控制系统的组成有O16、建立专家系统,最艰难(“瓶颈”)的任务是()。
17、产生式系统包含的基本组成O18、下列概念中不能用普通集合表示的是()。
19、以下应采用模糊集合描述的是()。
20、某模糊控制器的语言变量选为实际温度与给定温度之差即误差e、误差变化率4e;以及加热装置中可控硅导通角21、在论域U中,模糊集合A的支集只包含一个点u,且OAum=I,则A称为()。
22、在模糊控制中,隶属度()。
23、在模糊控制器的推理输出结果中,取其隶属度最大的元素作为精确值, 去执行控制的方法称为()。
24、在温度模糊控制系统中,二维模糊控制器的输出是()。
25、以下的集合运算性质中,模糊集合不满足的运算性质()。
26、模糊控制方法是基于()。
27、以下应采用模糊集合描述的是()。
28、模糊隶属度函数曲线的形状可以为()。
29、某模糊控制器的语言变量选为实际水位与给定水位之差即误差e,以及调节阀门开度的变化量u,故该模糊控制器30、某一隶属度函数曲线的形状可以选为()。
31、模糊控制器的术语“正中”,可用符合O表示。
32、在模糊控制器的推理输出结果中,取其隶属度函数曲线与横坐标围成面积的重心作为输出值,去执行控制的方法称33、下列概念中不能用普通集合表示的是()。
神经网络控制大作业-南航-智能控制

神经网络控制大作业-南航-智能控制-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII南京航空航天大学研究生实验报告实验名称:神经网络控制器设计姓名:学号:专业:201 年月日一、题目要求考虑如下某水下航行器的水下直航运动非线性模型:()||a m m v k v v u y v++==其中v R ∈为水下航行器的前进速度, u R ∈为水下航行器的推进器推力,y R ∈为水下航行器的输出,航行器本体质量、附加质量以及非线性运动阻尼系数分别为100,15,10a m m k ===。
作业具体要求:1、设计神经网络控制器,对期望角度进行跟踪。
2、分析神经网络层数和神经元个数对控制性能的影响。
3、分析系统在神经网络控制和PID 控制作用下的抗干扰能力(加噪声干扰、加参数不确定)、抗非线性能力(加死区和饱和特性)、抗时滞的能力(对时滞大小加以改变)。
二、神经网络控制器的设计1.构建系统的PID 控制模型在Simulink 环境下搭建水下航行器的PID 仿真模型,如下图1所示:图1 水下航行器的PID 控制系统其中,PID控制器的参数设置为:K p=800,K i=100,K d=10。
需要注意的一点是,经过signal to workspace模块提取出的数据的Save format为Array格式。
2.BP神经网络控制器的训练首先将提取出的训练数据变为标准的训练数据形式,标准的训练数据分为输入和目标输出两部分。
经过signal to workspace模块提取出的数据为一个训练数据个数乘以输入(或输出)个数的矩阵,因此分别将x、u转置后就得到标准训练数据x’,u’。
然后,新建m文件,编写神经网络控制器设计程序:%----------------------------------------------------------------p=x'; %inputt=u'; %inputnet=newff(p,t,3,{'tansig','purelin'},'trainlm');net.trainparam.epochs=2500;net.trainparam.goal=0.00001;net=train(net,x',u'); %train networkgensim(net,-1); %generate simulink block%----------------------------------------------------------------上述m文件建立了如下图所示的神经网络,包含输入层、1个隐含层和输出层,各层神经元节点分别为 1、 3 和1。
(完整版)西南大学1085《智能控制》作业答案

西南大学网络与继续教育学院1085 《智能控制》作业答案1、下列有关推理机说法不正确的是()A. 推理机是用于对知识库中的知识进行推理来得到结论的“思维”机构。
B. 推理机包括三种推理方式,即正向推理、反向推理和双向推理。
C. 推理机和知识库构成了专家系统D. 推理机是指专家系统中无需任何知识就能完成推理功能的组成部分。
答:d2、下列不属于知识库所包含的是()A. 基于专家经验的判断性规则。
B. 用于推理、问题求解的控制性规则。
C. 用于说明问题的状态、事实和概念以及当前的条件和常识等的数据。
D. 所涉及的领域广泛、普遍的常识和数据。
答:d3、下列不属于智能控制的特点的是()A. 自组织功能和优化能力B. 完全具有人的智能C. 学习功能D. 适应功能答:b4、下列有关智能控制的组成正确的是()A. 智能控制由人工智能,自动控制,运筹学组成。
B. 智能控制由人工智能和自动控制组成C. 智能控制由自动控制和运筹学组成D. 智能控制由运筹学和人工智能组成答:a5、下列有关智能控制的概念说法准确的是()A. 所谓智能控制,即设计一个控制器(或系统),使之具有学习、抽象、推理、决策等功能,并能根据环境(包括被控对象或被控过程)信息的变化作出适应性反应,从而实现由人来完成的任务。
B. 所谓智能控制,就是将控制系统进行智能化,使之完全具有人的智能。
C. 所谓智能控制,就是控制过程中,就是人参与控制,从而具有人的智能。
D. 所谓智能控制,就是所设计的控制系统具有很高的智能。
答:a6、下列哪位人物提出模糊集合理论,奠定了模糊控制的基础()A. 美国加州大学自动控制系的L.A.ZedehB. 伦敦大学的Mamdani博士C. 美国的J.H.Holland教授D. 著名的Hopfield教授答:a7、下列不是决定神经网络性能的要素是()A. 神经元(信息处理单元)的特性。
B. 神经元之间相互连接的形式——拓扑结构。
C. 为适应环境而改善性能的学习规则。
武汉理工大学智能控制大作业

智能控制理论与技术设计报告学院自动化学院专业控制科学与工程班级1303姓名聂鹏指导教师徐华中2014 年 2 月20 日武汉理工大学硕士研究生试题课程名称:智能控制理论与技术专业:双控1303班学号:1049721303692 姓名:聂鹏一、简答题(每小题10分)1.智能控制由哪几部分组成?各自的特点是什么?答:智能控制系统由广义对象、传感器、感知信息处理、认知、通信接口、规划和控制和执行器等七个功能模块组成;各部分的特点是:广义对象——包括通常意义下的控制对象和外部环境;传感器——包括关节传感器、力传感器、视觉传感器、距离传感器、触觉传感器等;感知信息处理——将传感器得到的原始信息加以处理;认知——主要用来接收和储存信息、知识、经验和数据,并对它们进行分析、推理,作出行动的决策,送至规划和控制部分;通信接口——除建立人机之间的联系外,还建立系统各模块之间的联系;规划和控制——是整个系统的核心,它根据给定的任务要求、反馈的信息以及经验知识,进行自动搜索,推理决策,动作规划,最终产生具体的控制作用;执行器——将产生的控制作用于控制对象。
2. 智能控制是在什么背景下产生的?答:传统控制理论在应用中面临的难题包括:(1) 传统控制系统的设计与分析是建立在精确的系统数学模型基础上的,而实际系统由于存在复杂性、非线性、时变性、不确定性和不完全性等,一般无法获得精确的数学模型。
(2) 研究这类系统时,必须提出并遵循一些比较苛刻的假设,而这些假设在应用中往往与实际不相吻合。
(3) 对于某些复杂的和包含不确定性的对象,根本无法以传统数学模型来表示,即无法解决建模问题。
(4) 为了提高性能,传统控制系统可能变得很复杂,从而增加了设备的初投资和维修费用,降低系统的可靠性。
传统控制理论在应用中面临的难题的解决,不仅需要发展控制理论与方法,而且需要开发与应用计算机科学与工程的最新成果。
人工智能的产生和发展正在为自动控制系统的智能化提供有力支持。
智能控制作业

1.给定下列模糊集合A ,B ,C ,确定它们的α切割A :Ц(x )={(2,1),(3,0.8),(4,0.6),(5,0.4),(6,0.2),(7,0.4),(8,0.6),(9,0.8),(10,1)} α=0.2,0.5B :Ц(x )=21011)(-+x α=0.2,0.5 x=[0, ∞] 0 x≤10 α=0.3,0.5 x=[0, ∞] C:Ц(x )=(1+(x-10)-2)-1x>10解:A :当α=0.2时α切割为6 当α=0.5时α切割为4.5B :当α=0.2时α切割为12或者8 当α=0.5时α切割为11或者9C :当α=0.3时α切割为15.44 当α=0.5时α切割为11 2.双边高斯MF ,由下式定义:exp[-21(11σc x -)2] x≤c1T s-gauss (x;c 1,σ1,c 2,σ2)= 1 c1<x<c2exp[-21(11σc x -)2] x≥c2(1) 编一个MATLAB 程序实现上述MF (2) 对不同的参数画出这个MF (3) 找出这个MF 的交叉点和宽度 解:(1)编写的MATLAB 程序如下: c1=input('请输入c1的值:') c2=input('请输入c2的值:') c3=input('请输入c3的值:') c4=input('请输入c4的值:')if x<=c1y=exp(-0.5*((x-c1)/c3).^2);elseif x>c1 & x<c2y=1;elsey=exp(-0.5*((x-c2)/c4).^2);endyplot(x,y)(2)当取x的范围为[-8:0.1:8]C1=2 c2=2 c3=c4=2 绘制的MF如下:(3)如下图所示为该MF的交叉点和宽度范围3.令论域U={1,2,3,4},给定语言变量“Small”=1/1+0.7/2+0.3/3+0.1/4和模糊关系R=“Almost相等”定义如下:1 2 3 41 1 0.6 0.1 0R: 2 0.6 1 0.6 0.13 0.1 0.6 1 0.64 0 0.1 0.6 1利用max-min复合运算,试计算:R(y)=(X是Small)。
智能控制作业

一、已知某一炉温控制系统,要求温度保持在600℃恒定。
针对该控制系统有以下控制经验:①若炉温低于600 ℃,则升压;低得越多升压越高。
②若炉温高于600 ℃,则降压;高得越多降压越低。
③若炉温等于600 ℃,则保持电压不变。
设计模糊控制器为一维控制器,输入语言变量为误差,输出为控制电压。
输入、输出变量的量化等级为7级,取5个模糊集。
试设计隶属度函数误差变化划分表、控制电压变化划分表和模糊控制规则表。
要求有程序及注释,仿真结果和分析。
(1)确定模糊控制器的输入输出变量将600℃作为给定值t0 ,测量炉温为t(k),则:输入变量:e(k)= t(k)-t0输出变量:触发电压u 的变化量,该u直接控制供电电压的高低。
(2)输入输出变量的模糊语言描述输入输出变量的语言值:{负大(NB),负小(NS),零(ZE),正小(PS),正大(PB)} 设:e的论域为X,u 的论域为Y,均量化为七个等级:X= {-3,-2,-1,0,1,2,3},Y={-3,-2,-1,0,1,2,3}语言变量E 和U 的隶属函数赋值表(论域离散):隶属度输出量u的变化等级-3 -2 -1 0 1 2 3模糊集PB 0 0 0 0 0 0.5 1 PS 0 0 0 0 1 0.5 0 ZE 0 0 0.5 1 05 0 0 NS 0 0.5 1 0 0 0 0 NB 1 0.5 0 0 0 0 0(3)模糊控制规则①if E =NB then U =PB②if E =NS then U =PS③if E =ZE then U =ZE④if E =PS then U =NS⑤if E =PB then U =NB(4)求模糊控制表IF NBe NSe ZOe PSe PBe THEN PBu PSu ZOu NSu NBu(5)控制量转化为精确量:采用加权平均法:(6)计算模糊关系R=(NBe×PBu)+ (NSe×PSu)+(ZEe×ZEu)+ (PSe×NSu) +(PBe×NBu)ZEe×ZEu =(0, 0, 0.5,1, 0.5,0,0)×(0,0 , 0.5, 1 , 0.5 , 0,0)分别计算出矩阵NBe×PBu,NSe×PSu,ZEe×ZEu,PSe×NSu ,PBe×NBu求并集得:查询表:e-3 -2 -1 0 1 2 3u 3 2 1 0 -1 -2 -3实际控制时,将测量到的误差量化后,从查询表中得到控制量再乘以比例因子Kn,即作为控制的实际输出。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
智能控制作业
学生姓名: 学 号: 专业班级: 7-2 采用BP 网路、RBF 网路、DRNN 网路逼近线性对象
2
)1(1)1(9.0)1()(-+-⨯--=k y k y k u k y ,分别进行matlab 仿真。
(一)采用BP 网络仿真
网络结构为2-6-1。
采样时间1ms ,输入信号)6sin(5.0)(t k u ⨯=π,权值21,W W 的初值随机取值,05.0,05.0==αη。
仿真m 文件程序为:
%BP simulation
clear all;
clear all;
xite=0.5;
alfa=0.5;
w1=rands(2,6); % value of w1,initially by random w1_1=w1;w1_2=w1;
w2=rands(6,1); % value of w2,initially by random w2_1=w2;w2_2=w2_1;
dw1=0*w1;
x=[0,0]';
u_1=0;
y_1=0;
I=[0,0,0,0,0,0]'; % input of yinhanceng cell
Iout=[0,0,0,0,0,0]'; % output of yinhanceng cell
FI=[0,0,0,0,0,0]';
ts=0.001;
for k=1:1:1000
time(k)=k*ts;
u(k)=0.5*sin(3*2*pi*k*ts);
y(k)=(u_1-0.9*y_1)/(1+y_1^2);
for j=1:1:6
I(j)=x'*w1(:,j);
Iout(j)=1/(1+exp(-I(j)));
end
yn(k)=w2'*Iout; %output of network
e(k)=y(k)-yn(k); % error calculation
w2=w2_1+(xite*e(k))*Iout+alfa*(w2_1-w2_2); % rectify of w2 for j=1:1:6
FI(j)=exp(-I(j))/(1+exp(-I(j))^2);
end
for i=1:1:2
for j=1:1:6
dw1(i,j)=e(k)*xite*FI(j)*w2(j)*x(i); % dw1 calculation end
end
w1=w1_1+dw1+alfa*(w1_1-w1_2); % rectify of w1 % jacobian information
yu=0;
for j=1:1:6
yu=yu+w2(j)*w1(1,j)*FI(j);
end
dyu(k)=yu;
x(1)=u(k);
x(2)=y(k);
w1_2=w1_1;w1_1=w1;
w2_2=w2_1;w2_1=w2;
u_1=u(k);
y_1=y(k);
end
figure(1);
plot(time,y,'r',time,yn,'b');
xlabel('times');ylabel('y and yn');
figure(2);
plot(time,y-yn,'r');
xlabel('times');ylabel('error');
figure(3);
plot(time,dyu);
xlabel('times');ylabel('dyu');
运行结果为:
(二)采用RBF 网络仿真
网路结构为2-4-1,采样时间1ms ,输入信号)2sin(5.0)(t k u ⨯=π,权值的初值随机取值,05.0,05.0==αη,高斯基函数初值T j C ]5.0,5.0[=,
T B ]5.1,5.1,5.1,5.1[=。
仿真m 文件程序如下:
%RBF simulation
clear all
clear all
alfa=0.05;
xite=0.5;
x=[0,0]';
b=1.5*ones(4,1);
c=0.5*ones(2,4);
w=rands(4,1);
w_1=w;w_2=w_1;
c_1=c;c_2=c_1;
b_1=b;b_2=b_1
d_w=0*w;
d_b=0*b;
y_1=0;
ts=0.001;
for k=1:1:2000;
time(k)=k*ts;
u(k)=0.5*sin(1*2*pi*k*ts);
y(k)=(u(k)-0.9*y_1)/(1+y_1^2);
x(1)=u(k);
x(2)=y_1;
for j=1:1:4
h(j)=exp(-norm(x-c(:,j))^2/(2*b(j)*b(j)));
end
ym(k)=w'*h';
em(k)=y(k)-ym(k);
for j=1:1:4
d_w(j)=xite*em(k)*h(j);
d_b(j)=xite*em(k)*w(j)*h(j)*(b(j)^-3)*norm(x-c(:,j))^2;
for i=1:1:2
d_c(i,j)=xite*em(k)*w(j)*h(j)*(x(i)-c(i,j))*(b(j)^-2); end
end
w=w_1+d_w+alfa*(w_1-w_1);
b=b_1+d_b+alfa*(b_1-b_2);
c=c_1+d_c+alfa*(c_1-c_2);
% Jacobian information
yu=0;
for j=1:1:4
yu=yu+w(j)*h(j)*(c(1,j)-x(1))/b(j)^2;
end
dyu(k)=yu;
y_1=y(k);
w_2=w_1;
w_1=w;
c_2=c_1;
c_1=c;
b_2=b_1;
b_1=b;
end
figure(1);
plot(time,y,'r',time,ym,'b');
xlabel('time(s)');ylabel('y and ym');
figure(2);
plot(time,y-ym,'r');
xlabel('time(s)');ylabel('error');
figure(3);
plot(time,dyu,'b');
xlabel('time(s)');ylabel('dyu');
仿真结果为:
(三)DRNN 网路仿真
采样时间1ms ,输入信号)4sin(5.0)(t k u ⨯=π,权值I O D W W W ,,的初值随机取值,取35.0,35.0,35.0===I D O ηηη。
仿真m 文件程序为:
%DRNN simulation
clear all;
clear all;
wd=rands(7,1);
wo=rands(7,1);
wi=rands(3,7);
xj=zeros(7,1);
xj_1=xj;
u_1=0;y_1=0;
xitei=0.35;
xited=0.35;
xiteo=0.35;
ts=0.001;
for k=1:1:1000
time(k)=k*ts;
u(k)=0.5*sin(4*pi*k*ts);
y(k)=(u_1-0.9*y_1)/(1+y_1^2);
Ini=[u_1,y_1,1]';
for j=1:1:7
sj(j)=Ini'*wi(:,j)+wd(j)*xj(j);
end
for j=1:1:7
xj(j)=(1-exp(-sj(j)))/(1+exp(-sj(j)));
end
Pj=0*xj;
for j=1:1:7
Pj=wo(j)*(1+xj(j))*(1-xj(j))*xj_1(j);
end
Qij=0*wi;
for j=1:1:7
for i=1:1:3
Qij(i,j)=wo(j)*(1+xj(j))*(1-xj(j))*Ini(i); end
end
ymk=0;
for j=1:1:7
ymk=ymk+xj(j)*wo(j);
end
ym(k)=ymk;
e(k)=y(k)-ym(k);
wo=wo+xiteo*e(k)*xj;
wd=wd+xited*e(k)*Pj;
wi=wi+xitei*e(k)*Qij;
xj_1=xj;
u_1=u(k);
y_1=y(k);
end
figure(1);
plot(time,y,'r',time,ym,'b');
xlabel('time/s');ylabel('y and ym');
figure(2);
plot(time,y-ym,'r');
xlabel('time/s');ylabel('error');
仿真结果为:。
