20140506 计算机数值方法习题集(学生)
计算机数值方法试题集

P3 ( x) = N 3 ( x) = 2 + 2( x − 1) − ( x − 1)( x − 3) +
f (2) ≈ P3 (2) = 5.5
⎧ y′ = 2x + 3 y ⎨ (0 ≤ x ≤ 1) 4、取步长 h = 0.2 ,用预估-校正法解常微分方程初值问题 ⎩ y (0) = 1
3
求按五位有效数字计算). 1、迭代格式
⎧ ( k +1) 1 (k ) (k ) = (11 − 2 x 2 − x3 ) ⎪ x1 4 ⎪ ⎪ ( k +1) 1 (k ) = (18 − x1( k +1) − 2 x3 ) ⎨ x2 4 ⎪ ⎪ ( k +1) 1 ( k +1) = (22 − 2 x1( k +1) − x 2 ) ⎪ x3 5 ⎩
∫
1
数精度为 3。
∫1
2
1 1 8 1 1 1 t =2x −3 1 1 1 + + ] dx = ∫ dt ≈ [ ]+ [ −1 t + 3 x 9 − 1 + 3 1 + 3 9 − 1/ 2 + 3 1 2 + 3 = 97 ≈ 0.69286 140
3. 已知分别用拉格朗日插值法和牛顿插值法求 f ( x ) 的三次插值多项式 P3 ( x) ,并求
)。
M <1
B.
ρ ( A) < 1
C.
ρ(M ) < 1
D.
ρ (M ) < 1
三、计算题: 1、为了使 20 的近似值的相对误差限小于 0.1%,要取几位有效数字? 1、解:设 20 有 n 位有效数字,由 令
(完整word版)计算方法习题集及答案.doc

习题一1.什么叫数值方法?数值方法的基本思想及其优劣的评价标准如何?数值方法是利用计算机求解数学问题近似解的方法xmax x i , x ( x 1 , x 2 , x n ) T R n 及 A nR n n .2.试证明maxa ij , A ( a ij )1 in1 i n1j证明:( 1)令 x rmaxxi1 i nnp 1/ pnx ip1/ pnx r p 1/ p1/ pxlim(x i lim x r [( ]lim x r [limx r))() ]x r npi 1pi 1 x rpi 1 xrp即 xx rnp1/ pnp 1/ p又 lim(lim(x rx i)x r)pi 1pi 1即 xx rxx r⑵ 设 x(x 1,... x n )0 ,不妨设 A 0 ,nnnn令maxaijAxmaxaijx jmaxa ij xjmax x i maxaijx1 i nj 11 i nj 11 i nj 11 i n1 i nj 1即对任意非零 xR n,有Axx下面证明存在向量 x 00 ,使得Ax 0,x 0n( x 1,... x n )T 。
其中 x j设j a i 0 j ,取向量 x 0sign(a i 0 j )( j 1,2,..., n) 。
1nn显然x 01 且 Ax 0 任意分量为ai 0 jx jai 0 j,i 1i1nn故有Ax 0maxaijx jai 0 j即证。
ii 1j 13. 古代数学家祖冲之曾以355作为圆周率的近似值,问此近似值具有多少位有效数字?113解: x325 &0.314159292 101133xx355 0.266 10 6 0.5 101 7 该近似值具有 7 为有效数字。
4. 若 T(h)逼近其精确值T 的截断误差为R(T ) : T (h) T A i h2 ii 1T0 ( h) T (h) 其中,系数 A i与h无关。
计算机数值方法测试题二

计算机数值方法测试题二Company number【1089WT-1898YT-1W8CB-9UUT-92108】《计算机数值方法》测试题一.判断题(1分×10=10分)(对打√,错打×)1.数值方法是指解数值问题的计算机上可执行的系列计算公式。
( ) 2.……计算R=e-2.71828≈0.00000182是截断误差。
( )3.不同的矩阵三角分解对应着不同的解法,但在本质上,都是经过A=LU 的分解计算,再解Ly=b和Ux=y的线性方程组。
( )4.一般不用n次多项式做插值函数。
( )5.Runge现象说明并非插值多项式的次数越高其精度就越高。
( )6.Romberg算法是利用加速技术建立的。
( )7.从复合求积的余项表达式看,计算值的精度与步长无关。
( )8.可用待定系数法和函数值或公式的线性组合构造新的数值函数求解微分方程。
( )9.局部截断误差e k(h)与y(x k)的计算值y k有关。
( )10.对大型线性方程组和非线性方程采用逐次逼近更为合适。
( )二.填空题(2分×5=10分)1.设x∈[a,b],x≠x0,则一阶均差f(x)= 。
2.矩阵A的F-范数||A||F= 。
3. Euler公式为。
4.矩阵 A的条件数Cond(A)∞= 。
5. 设x 为准确值,x *为x 的一个近似值,近似值x *的相对误差E r (x *)= 。
三.选择题(2分×5=10分)1.设x=Pi ;则x *=3.1415有( )位有效数字。
(A) 4位 (B)5位 (C)6位2.顺序主元a ii ≠0(i=1,2……k )的充要条件是A 的顺序主子式D i(i=1,2……n-1)( )。
(A) 不全为0 (B) 全不为0 (C) 全为03.若存在实数P ≥1和c >0,则迭代为P 阶收敛的条件是( )。
(A) ∞−→−k limp k k e e ||||1+=c (B) O(h p ) (C) O(h p+1) 4.方程x 3-x 2-1=0在x 0=1.5附近有根,则迭代格式x k+1=在x 0=1.5附近( )。
数值计算方法总结计划试卷试题集及答案

一、选择题(每题2分,共20分)1.数值计算的基本思想是()。
A.精确求解B.近似求解C.解析表达D.图像显示2.下列哪种方法不属于数值计算方法?()A.有限差分法B.有限元法C.插值法D.微积分3.在数值计算中,为避免数值计算误差,通常采用()方法。
A.精确计算B.误差分析C.误差校正D.舍入运算4.下列哪种数值方法适用于求解偏微分方程?()A.欧拉法B.龙格-库塔法C.有限差分法D.牛顿法5.下列哪种方法不属于求解线性方程组的数值方法?()A.高斯消元法B.追赶法C.迭代法D.矩阵分解法二、填空题(每题2分,共20分)6.数值计算方法是利用计算机求解科学和工程问题的_______方法。
7.数值计算的主要目的是将_______问题转化为_______问题。
8.在数值计算中,通常需要对实际问题进行_______,以简化计算过程。
9.有限差分法的核心思想是将偏微分方程转化为_______方程。
10.牛顿法是一种_______方法,适用于求解非线性方程组。
三、判断题(每题2分,共20分)11.数值计算方法只能解决线性问题。
()12.在数值计算中,误差只能通过增加计算精度来减小。
()13.迭代法求解线性方程组时,需要预先知道方程组的解。
()14.数值计算方法在实际应用中具有较高的可靠性。
()15.有限元法适用于求解所有类型的偏微分方程。
()四、简答题(每题10分,共30分)16.请简要说明数值计算的基本思想及其应用范围。
17.请简要介绍有限差分法的原理及应用。
18.请简要说明牛顿法求解非线性方程组的原理。
五、计算题(每题10分,共50分)2x+3yz=14xy+5z=2-x+2y+z=3y'=-y+e^x,初始条件y(0)=1答案:一、选择题1.B2.D3.B4.C5.A二、填空题6.近似7.连续离散8.简化9.差分10.迭代三、判断题11.×12.×13.×14.√15.×四、简答题16.数值计算的基本思想是将实际问题转化为数学问题,再通过计算机求解。
计算机数值方法试题

一、填空(共20分,每题2分)1、设,取5位有效数字,则所得的近似值x=_____.2、设一阶差商,则二阶差商3、数值微分中,已知等距节点的函数值则由三点的求导公式,有4、求方程的近似根,用迭代公式,取初始值,那么5、解初始值问题近似解的梯形公式是6、,则A的谱半径=,A的=7、设,则=和=8、若线性代数方程组AX=b 的系数矩阵A为严格对角占优阵,则雅可比迭代和高斯-塞德尔迭代都_____9、解常微分方程初值问题的欧拉(Euler)方法的局部截断误差为_____10、设,当时,必有分解式,其中L为下三角阵,当其对角线元素足条件时,这种分解是唯一的。
二、计算题(共60 分,每题15分)1、设(1)试求在上的三次Hermite插值多项式H(x)使满足 H(x)以升幂形式给出。
(2)写出余项的表达式2、已知的满足,试问如何利用构造一个收敛的简单迭代函数,使0,1…收敛?3、试确定常数A,B,C和,使得数值积分公式有尽可能高的代数精度。
试问所得的数值积分公式代数精度是多少?它是否为Gauss型的?4、推导常微分方程的初值问题的数值解公式:三、证明题1、设(1)写出解的Newton迭代格式(2)证明此迭代格式是线性收敛的2、设R=I-CA,如果,证明:(1)A、C都是非奇异的矩阵(2)参考答案:一、填空题1、2、3、4、5、6、7、8、收敛9、O(h)10、二、计算题1、1、(1)(2)2、由,可得因故故,k=0,1,…收敛。
3、,该数值求积公式具有5次代数精确度,它是Gauss型的4、数值积分方法构造该数值解公式:对方程在区间上积分,得,记步长为h,对积分用Simpson求积公式得所以得数值解公式:三、证明题1、证明:(1)因,故,由Newton迭代公式:n=0,1,…得,n=0,1,…(2)因迭代函数,而,又,则故此迭代格式是线性收敛的。
2、证明:(1)因,所以I–R非奇异,因I–R=CA,所以C,A都是非奇异矩阵 (2) 故则有()因CA=I–R,所以C=(I–R)A-1,即A-1=(I–R)-1C又RA-1=A-1–C,故由(这里用到了教材98页引理的结论)移项得结合()、两式,得模拟试题一、填空题(每空2分,共20分)1、解非线性方程f(x)=0的牛顿迭代法具有_______收敛2、迭代过程(k=1,2,…)收敛的充要条件是___3、已知数 e=...,取近似值 x=,那麽x具有的有效数字是___4、高斯--塞尔德迭代法解线性方程组的迭代格式中求______________5、通过四个互异节点的插值多项式p(x),只要满足_______,则p(x)是不超过二次的多项式6、对于n+1个节点的插值求积公式至少具有___次代数精度.7、插值型求积公式的求积系数之和___8、 ,为使A可分解为A=LL T, 其中L为对角线元素为正的下三角形,a的取值范围_9、若则矩阵A的谱半径(A)=___10、解常微分方程初值问题的梯形格式是___阶方法二、计算题(每小题15分,共60分)1、用列主元消去法解线性方程组2、已知y=f(x)的数据如下求二次插值多项式及f()3、用牛顿法导出计算的公式,并计算,要求迭代误差不超过。
计算机数值方法试题

标准适用数值计算方法试题一、填空(共 20 分,每题 2 分)1、设,取5位有效数字,则所得的近似值x=_____.2、设一阶差商,则二阶差商3、数值微分中,已知等距节点的函数值则由三点的求导公式,有4、求方程的近似根,用迭代公式,取初始值,那么5、解初始值问题近似解的梯形公式是6、,则A的谱半径=,A的=7、设,则=和=8、若线性代数方程组AX=b 的系数矩阵 A 为严格对角占优阵,则雅可比迭代和高斯 - 塞德尔迭代都 _____9、解常微分方程初值问题的欧拉(Euler )方法的局部截断偏差为_____10、设,当时,必有分解式,此中L为下三角阵,当其对角线元素足条件时,这类分解是独一的。
标准适用二、计算题(共 60 分,每题 15 分)1、设(1)试求在上的三次Hermite插值多项式H(x)使知足H( x)以升幂形式给出。
(2)写出余项的表达式2、已知的足,怎样利用结构一个收的迭代函数,使0, 1⋯收?3、试确立常数 A, B, C和,使得数值积分公式有尽可能高的代数精度。
试问所得的数值积分公式代数精度是多少?它能否为Gauss型的?4、推常微分方程的初值问题的数值解公式:三、证明题1、设(1)写出解的 Newton 迭代格式(2)证明此迭代格式是线性收敛的2、R=I - CA,假如,明:(1)A、C 都是非奇怪的矩阵(2)参照答案:一、填空题1、2、3、4、5、6、7、8、收敛9、O(h)10、二、计算题1、1、(1)(2)2、由,可得因故故, k=0,1, ⋯收。
3、,数求公式拥有 5 次代数精准度,它是Gauss型的4、数分方法结构数解公式:方程在区上分,得,步 h, 分用 Simpson 求公式得因此得数解公式:三、明1、明:( 1)因,故,由Newton迭代公式:n=0,1, ⋯得, n=0,1, ⋯( 2)因迭代函数,而,又,故此迭代格式是性收的。
2、明:( 1)因,因此I–R非奇怪,因I–R=CA,因此C,A都是非奇怪矩(2)故有( 2.1 )因 CA=I–R,因此 C=( I – R) A-1,即 A-1 =(I –R)-1 C-1-1又 RA =A –C,故由(里用到了教材98 引理的)移得(2.2)合( 2.1 )、 (2.2) 两式,得模拟试题一、填空题(每空 2 分,共 20 分)1、解非线性方程f(x)=0的牛顿迭代法拥有_______收敛2、迭代过程(k=1,2, ⋯)收的充要条件是___3、已知数 e=2.718281828...,取近似值 x=2.7182,那麽 x 拥有的有效数字是___4、高斯 -- 塞尔德迭代法解线性方程组的迭代格式中求______________5、经过四个互异节点的插值多项式p(x), 只需知足_______,则 p(x) 是不超出二次的多项式6、对于 n+1 个节点的插值求积公式起码拥有___次代数精度 .7、插值型求积公式的求积系数之和___8、, 为使 A 可分解为 A=LL T,此中L为对角线元素为正的下三角形, a 的取值范围_9、若则矩阵A的谱半径(A)=___10 、解常微分方程初值问题的梯形格式是___阶方法二、计算题(每题15 分,共 60 分)1、用列主元消去法解线性方程组2、已知y=f(x)的数据以下x023f (x)132求二次插值多项式及 f ( 2.5 )3、用牛顿法导出计算的公式,并计算,要求迭代偏差不超出。
《计算机数值方法》测试题四

《计算机数值方法》测试题一.判断题(1分×10=10分)(对打√,错打×)1. 计算机上的算法,按面向求解问题的不同,可分为数值算法和非数值算法。
( )2. 已知e=2.71828182……计算R=2.71828-9.2100≈-6.49172是截断误差。
( )3. 如果矩阵A 非奇异,总可以通过带有行交换或不带行交换的消元过程,将A 化为非奇异上三角形矩阵A (n )。
( )4. n 次多项式只能写成一种形式。
( )5. 用Newton 插值法应当避免使用高次插值多项式。
( )6. Newton —Cotes 公式是利用等距节点的Lagrange 插值多项式建立的。
( )7. 利用Lagrange 插值多项式导出的数值微分公式可求任意节点上的导数。
( )8. e i (h) 的大小都与h 有关。
( )9. 隐式R —K 法比显示方法好,但是每步要解非线性代数方程。
( )10. 逐次逼近法涉及两个元素的逼近问题。
( )二.填空题(2分×5=10分)1. 表示f (x )在x 0及x 1两点的一阶差商f[x 0,x 1]= 。
2. 矩阵A 的行范数||A||∞= 。
3.设区间[a ,b]上x 0,x 1为给定的互异的结点及函数值y 0,y 1则Lagrange 线性插 值的余项R 1(x )= 。
4.设x *为准确值x 的一个近似值,ε为x *的绝对误差限,相对误差限ε*(x)= 。
5. 复合梯形公式的余项近似值表达式I-T n ≈ 。
三.选择题(2分×5=10分)1.设准确值为x=5.73446;则x *=5.7344有( )位有效数字。
(A) 4位 (B)5位 (C)6位2.下面哪个公式的局部截断误差为O (h 3)。
( )(A )Euler 公式 (B )Simpson 公式 (C )梯形公式3.求积公式具有m 次代数精度的充要条件是( )。
(A) x i (i=1,2……m )准确成立,x m+1不能准确成立 (B)f (m+1)(ξ)=0 (C)e(h)=O(h m+1)4.A 为( )矩阵,则必存在排列矩阵P 以及单位下三角矩阵L 和非奇异上三角矩阵U 使PA=LU 。
计算机数值方法 第四章作业

n −1 b−a T8 = f ( a ) + 2∑ f ( xi ) + f (b) 2n i =1
1 = 0 + 2∑ f ( xi ) + 0.679570 ≈ 0.358726 16 i =1
7
习题4(P162):用复合梯形公式和复合 用复合梯形公式和复合simpson公式计算定积分 习题 公式计算定积分
若要该计算式具有2价代数精度,则必须有: 若要该计算式具有 价代数精度,则必须有: 价代数精度
1 2 2 2 (1+ 2α + 3β ) = 3 3
α β
= 1 − 5 6 6
(2) )
= 1 + 5 6 6
至此, )、(2)两式,可求出α 至此,由(1)、( )两式,可求出α、β: )、(
1
α β
解:
xe x = 。 I =∫ dx ,n=8。 0 (1 + x ) 2
1
i+1/2 1/2 3/2 5/2 7/2 复合 1/16 3/16 5/16 7/16 Simpson Xi+1/2 f (xi+1/2 ) 0.058934 0.160385 0.247952 0.327919 公式 i 9/2 11/2 13/2 15/2 xi 9/16 11/16 13/16 15/16 f (xi ) 0.404365 0.480134 0.557355 0.637733
I − Tn = − 8−2 2 1 1 1 h ( × 2η −3 ) ≤ 4 h 2 ≤ 10−5 12 2 2 2
8
1 计算ln2时,若采用复合 时 d x = 2 ln 2 计算 x
b−a 2 I − Tn = − h f "(η ) 12
计算机数值方法习题解答
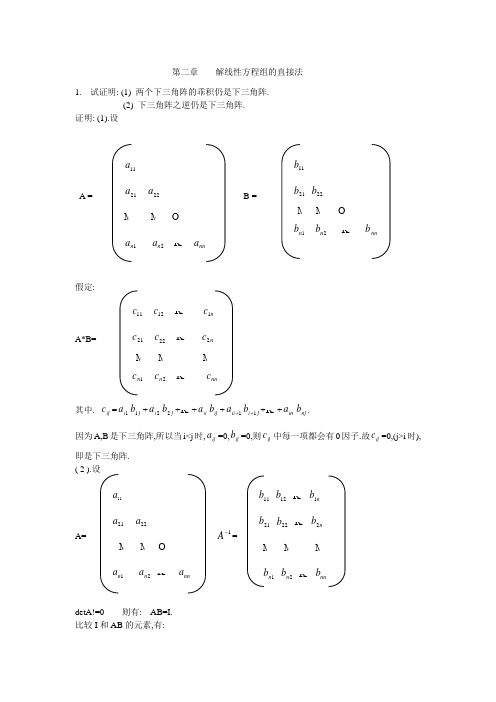
第二章 解线性方程组的直接法1. 试证明: (1) 两个下三角阵的乖积仍是下三角阵. (2) 下三角阵之逆仍是下三角阵. 证明: (1).设A =B =假定:A*B=其中.ij c =1i a j b 1+2i a j b 2+K +ii a ij b +1+ii a j i b 1++K +in a nj b .因为A,B 是下三角阵,所以当i<j 时,ij a =0,ij b =0,则ij c 中每一项都会有0因子.故ij c =0,(j>i 时),即是下三角阵.( 2 ).设A=1-A =detA!=0 则有: AB=I. 比较I 和AB 的元素,有:11a21a 22aMM O 1n a 2n a K nn a11b21b 22bM M O1n b 2n b K nn b11c 12c K n c 1 21c 22c K n c 2 M M M1n c 2n c K nn c 11a 21a 22aM M O 1n a 2n a K nn a 11b 12b K n b 1 21b 22b K n b 2MMM 1n b 2n b K nn b1=n b a b a b a b a 1111311121111110,,0,0,===K K 因为detA!=0, 可得0!,,0!,0!2211===nn a a a K 所以.0,,0,011312===n b b b K 依此类推下去,对其它行,当i<j 时,都是0=ij b . 故B 是下三角阵.2. 用Gauss 消去法求解方程组. 1x + 2x -44x =1 -1x + 2x + 3x +34x =-2 1x +32x +53x -44x =-4 2x -4x =-2 解: 消元过程:回代过程可得:4x =0,3x =-1,2x =0,1x =1.1 1 0 -4 1 -1 1 1 3 -2 13 5 -4 -4 0 1 2 -1 -2 1 1 0 -4 1 0 2 1 -1 -1 0 25 0 -5 0 1 2 -1 -21 1 0 -4 1 02 1 -1 -1 0 0 4 1 -4 0 0 1.5 0.5 -1.5 1 1 0 -4 1 0 2 1 -1 -1 0 0 4 1 -4 0 0 0 0.125 03.试写Gauss 消去法的算法:解: Gauss 消去法算法分为消元过程和回代过程,其中: 对k=1,2,K ,n-1 i=k+1,k+2,K ,n n x =n b /nn a消 ik m =ik a /kk a 回对i=n-1,n-2,K ,1 元 j=k+1,k+2,K ,n代i x =(i b -∑ijaxj)/ii a过 ij a =ija -ik m kj a 程 i b=i b -ik m k b4,用Gauss 列主元素消去法解方程组.=解:1 2 1 -2 -1 2 5 3 -2 3 2 5 3 -2 3 0 3 6 3 18 -2 -2 3 5 15 0 -0.5 -0.5 -1 -2.5 1 3 2 5 9 0 0.5 0.5 6 7.5 2 5 3 -2 3 交换1,2行 2 5 3 -2 3 1 2 1 -2 -1 Gauss 消去 0 3 6 3 18 -2 -2 3 5 15 一步 0 0 0.5 -0.5 0.5 1 3 2 5 9 0 0 -0.5 5.5 4.5 2 5 3 -2 3 2 5 3 -2 3 0 -0.5 -0.5 -1 -2.5 交换2,3行. 0 3 6 3 18 0 3 6 3 18 Gauss 消去一步 0 0 0.5 -0.5 0.5 0 0.5 0.5 6 7.5 0 0 0 5 5 回代求解得:.3,1,2,11234-====x x x x1 2 1 -2 2 5 3 -2 -2 -2 3 5 1 3 2 5 4321x x x x-13 15 95.某一装置运动轨迹为一圆锥曲线2x +bxy+c 2y +dx+ey+f=0在运动轨上测得5个不同点:1c :(14.38,3.94),2c :(11.38,2.79),)59.2,81.8(:),11.5,38.6(:),07.3,42.7(:543c c c 试写出b,c,d,e,f 所满足的方程,并用列主元素消去法求出b,c,d,e,f 的近似值. 解:依题义得方程组: 祥见教材第270页.6.设A=n n ij a *)(是实对称阵,且ii a !=0.经过Gauss 消去法一步后,A 约化为 .其中,是阶方阵.证明是对称阵. 证明:A== ;而=11aα0 2A11a 12a 13a K n a 121a 22a 23a K n a 231a 32a 33a K n a 3 M M M1n a 2n a 3n a K a 11a 12a 13a K n a 10 )2(22a )2(23a K )2(2n aMM M M 0 )2(2n a )2(3n a K )2(nn a11a α0 2A1-1121a a1 M O -11a a nnK 1 11a 12a K n a 121a 22a K n a 2M M M1n a 2n a K nn a=其中:1111)2(a a a a a j i ij ij -=,i,j=2,3,K ,n.A=T A ,ji ij a a =,i,j=1,2,K ,n..,,3,2,,)2(11111111)2(n j i a a a a a a a a a aji j i ji j i ij ijK ==-=-=亦得证2A 是对称的. 7.证明: (1) k L =的逆阵:(2)11a 12a K n a 10 11122122a a a a -K 111212a a a a n n - M M M 0 111212a a a a n n -K 1111a aa a n n nn - 1 O1k k l ,1+- 1 M O k n l ,- k1 O1k k l ,1+ 1MO nk l 1121l 131l 32l 1 M O1n l 2n l 3n l K 1=----111211n L L L K证明:(1)直接验证I L L k k =-1.=-1k k L L= I.(2).用有限归纳法证明:I n L L L L L L n n )2(111211111211--+++=--------K K .1),当k=2时.=--1211L L==I L L )12(1211-++--2),假若k=m 时成立,要让k=m+1时成立mIL L L L L m mI mL L L L L m L L L L L L L I m L L L L L L L I m L L L L L L m m m m m m m m m m m m m m m m +++++=---++++=--+++=--+++=--+++=------+-+----+-+--+--+--+----+---------1111211111112111111111121111111121111112111121111211)1()1(])1([)1(ΛK K K K K K .所以结论成立.8设nn a A ij )(=实方阵,若对i=1,2,K n.∑==>nij j ijii aa !1成立,则称A(行)严格对角占优.试证明:若严格对角占优,则A 非奇异.1 O1k k l ,1+- 1M O k n l ,- 11 O 1k k l ,1+ 1M Ok n l , 11 21l 1 31l 0 1M M O1n l 0 K 111 32l 1MO 2n l 1121l 1 31l 32l 1M M O1n l2n l证明:A 严格对角占优,所以0211>=>∑=nj ijaaGauss 消去一步得:, 且有严格对角化.n i a a a a a a a a nij j i ij j i ii ,,3,2.,2!11111111K =->-∑= 1111,2!111,2!,2!1111,2!,2!1111?a a a a a a a a a a a a a aj i nij j nij ijnij j i nij ij ni j j i ij-+=+≤-∑∑∑∑∑=====111111111111,1!1111,2!?a a a a a a a a a a a a a a a a j i ii j i ii j i nij ij j i nij ij -≤-<-=-+<∑∑==由2A 严格对角占优0!)2(22=a ,Gauss 消去法一步类似的证3A 严格对角优化.0!)3(33=a 仿此做下去可推得:0!)(=n nn a 又由0!det )()3(33)2(2211==n nn a a a a A K 亦得证A 严格对角占优.则非奇异9.设Ax= b,其中.A=b=用Dollitle 方法解此方程组.解:先求A=LU 分解,由Dolittle 分解算法.L= U== 得y=11a α 0 2A5 7 9 106 8 10 97 1089 5 7 6 5 2618 22 911.2 11.4 -0.5 11 0 0.6 15 7 9 10-0.4 -0.8 -3 -5 -6.5 -1.111.2 1 1.4-0.5 11 0 0.6 1 4321y y y y 26 18 22 926 -13.2 -21 -4.4=得x=10.用追赶法解三对角方程组AX=F,其中:A= ,F=解:先求三角分解:=由公式(6.6),(6.8)解得i i i y ,,βα)3,2,1()4,3,2(,)4,3,2(111===-====-i c i a b b i a ii i i i i i i i αββααγ (6.6)(6.8)i i α i β i γ 1 2 1/2 -3/2 2 7/2 2/7 15/7 3 26/7 7/26 83/26 4 45/25 -35 7 9 10-0.4 -0.8 -3-5 -6.5 -1.1 4321x x x x 26 -13.2 -21 -4.4 -8 5 -1 42 1 0 0 1 4 1 0 0 1 4 1 0 0 1 2 -3 6 14 -2 1b 1c 2a 2b 2c 3a 3b 3c 4a 4b1α 2γ 2α3γ 3α4λ 4α1 1β1 2β 1 3β 1)4,3,2(1111=-==-i y a f y f y ii i i i αα再公式(6.10)44y x =1+-=i i i i x y x β i=3,2,1 (6.10)得到: 2,1,4,31234-===-=x x x x。
计算方法习题集及答案

得:
当方法为零稳定时 ,从而 ,故方法是二阶收敛的。
6.给出题(6.5)题中 时的公式的绝对稳定域.
解:
6.5中当 时,即为方法
其相应的差分方程的多项式为
令 ,
即方法的绝对稳定域为
7.指出Heun方法
0
0
0
0
1/3
1/3
0
0
2/3
0
2/3
0
1/4
0
3/4
的相容阶,并给出由该方法以步长h计算初值问题(6.45)的步骤.
即
取 。即
满足上述条件的多步方法即为一类三步四阶显示方法,令 可得
方法即为
3.形如
的k阶方法称为Gear方法,试确定一个三步Gear方法,并给出其截断误差主项。
解:线性k步公式为
由Gear法的定义知,三步Gear法满足
方法为 阶,故有
得:
取 得
得三步Gear方法:
其中
4.试用显式Euler法及改进的Euler法
证明:
且
即 为 的二阶零点
设
令
易知
又
由微分中值定理(Rolle定理) ,使得
进而 有三个零点, 有两个零点, 有一个零点,
即 使得
得
8.设 是Lagrange基函数,则 。
9.求一个次数不超过4次的多项式 ,使它满足
,并写出其余项表达式。
10.求一个四次插值多项式 ,使 时, ;而 时, ,并写出插值余项的表达式。
练习
班级
学号
姓名
1.试构造迭代收敛的公式求解下列方程:
(1) ; (2) 。
解:
(1)迭代公式 , 公式收敛
k
数值计算方法习题答案(习题3-习题6)

习题三 2 解:()()2112230.2()10.210.80.80.20.80.20.80.61440.4613n n n n n y y y x y y y y +=+--=+⨯-==+⨯--⨯==同理,7. 解:()()()22212111,0.1(2)11,0.1(2)112pn n n n n nc n n n n p n n p c y y hf x y y y x y y hf x y y y x y y y +++⎧=+=+⨯-⎪+⎪⎪=+=+⨯-⎨+⎪⎪=+⎪⎩111230.1,0.097,0.09850.1913,0.2737p c y y y y y =====同理,11. 解:()112341213243123412340.2226833830.223830.228330.21, 1.4, 1.58, 1.05,(0.2) 2.30041.0986,0.7692,0.8681,0.5780,(0.4)2.4654n n nn n n y y k k k k k y k y k k y k k y k k k k k y k k k k y +⎧=+⨯+++⎪⎪=-⎪⎪⎪=--⨯⨯⎨⎪⎪=--⨯⨯⎪⎪=--⨯⨯⎪⎩==========同理,13. 解:()()[]()[]()110.220.22321,00,(0.2)0.181(0.4)(0.2)3(0.2)10.1810.1310.18110.3267(0.6)(0.4)3(0.4)(0.2)0.32670.1310.3267(10.181)0.4468n n nn hy y y y y y y y y y y y y y y +-''=+-'=-=='=+-=+⨯⨯--=⎡⎤⎣⎦''=+-=+⨯⨯---=⎡⎤⎣⎦(0.8)0.5454,(1)0.6265y y ==同理,习题四),(,121)('sin 21)('cos 21)(.2∞-∞∈<≤-==x x xx x x ϕϕϕ证明:迭代函数所以在均收敛。
《数值计算方法》试题集及答案(1-6) 2-推荐下载

18、 设 f (1)=1, f(2)=2,f (3)=0,用三点式求 f (1) ( 2.5 )。
19、如果用二分法求方程 x3 x 4 0 在区间[1,2]内的根精确到三位小数,需对分( 10 )次。
20、已知
S(x)
x3
1 2
(
x
1)3
a =( 3 ), b =( 3 ), c =( 1
一、填空题:
《计算方法》期中复习试题
1、已知 f (1) 1.0, f (2) 1.2, f (3) 1.3,则用辛普生(辛卜生)公式计算求得
3
1
f
( x )dx
答案:2.367,0.25
_________
,用三点式求得
2、 f (1) 1, f (2) 2, f (3) 1,则过这三点的二次插值多项式中 x2 的系数为
答案:-1,
,拉格朗日插值多项式为
L2 (x)
1 2
(x
2)(x
3、近似值 x* 0.231 关于真值 x 0.229 有( 2 )位有效数字;
4、设 f (x) 可微,求方程 x f (x) 的牛顿迭代格式是(
答案
x n 1
xn
xn 1 f
f (xn ) (xn )
2)
。
);
f(
3 1)] 23
0.15 );
),代数精
1
2001 1999 改写为
2 2001 1999 。
13、 用二分法求方程 f (x) x3 x 1 0 在区间[0,1]内的根,进行一步后根的所在区间
(完整版),数值计算方法试题及答案,推荐文档

1
0
e
x
dx
时,
(1) (1) 试用余项估计其误差。
(2)用 n 8 的复化梯形公式(或复化 Simpson 公式)计算出该积
分的近似值。
四、1、(15 分)方程 x3 x 1 0 在 x 1.5 附近有根,把方程写成三种
不同的等价形式(1) x 3 x 1 对应迭代格式 xn1 3 xn 1 ;(2)
-1.75 -1
0.25 2
4.25
所确定的插值多项式的次数是( )。
(1)二次; (2)三次; (3)四次; (4)五次
4、若用二阶中点公式
y n 1
yn
hf
(xn
h, 2
yn
h 4
f
(xn , yn )) 求解初值问题
y 2y, y(0) 1,试问为保证该公式绝对稳定,步长 h 的取值范围为
数 ,使其代数精确度尽量高,并指出其代数精确度的次数。
五、(8 分)已知求 a (a 0) 的迭代公式为:
xk 1
1 2 (xk
a xk
)
x0 0 k 0,1,2
证明:对一切 k 1,2,, xk a ,且序列xk 是单调递减的,
从而迭代过程收敛。
六、(9
3
分)数值求积公式 0
f
( x)dx
六、(下列 2 题任选一题,4 分)
1、 1、 数值积分公式形如
1
xf
( x)dx
S(x)
Af
(0)
Bf
(1)
Cf
(0)
Df
(1)
0
(1)(1) 试确定参数 A, B,C, D 使公式代数精度尽量高;
1
(2)设 f (x) C 4[0,1] ,推导余项公式 R(x) 0 xf (x)dx S(x) ,
《数值计算方法》试题集及答案资料

《数值计算方法》复习试题一、填空题:1、⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=410141014A ,则A 的LU 分解为A ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦。
答案:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=15561415014115401411A 3、1)3(,2)2(,1)1(==-=f f f ,则过这三点的二次插值多项式中2x 的系数为 ,拉格朗日插值多项式为 。
答案:-1,)2)(1(21)3)(1(2)3)(2(21)(2--------=x x x x x x x L4、近似值*0.231x =关于真值229.0=x 有( 2 )位有效数字;5、设)(x f 可微,求方程)(x f x =的牛顿迭代格式是( );答案)(1)(1n n n n n x f x f x x x '---=+6、对1)(3++=x x x f ,差商=]3,2,1,0[f ( 1 ),=]4,3,2,1,0[f ( 0 );7、计算方法主要研究( 截断 )误差和( 舍入 )误差;8、用二分法求非线性方程 f (x )=0在区间(a ,b )内的根时,二分n 次后的误差限为( 12+-n a b );10、已知f (1)=2,f (2)=3,f (4)=5.9,则二次Newton 插值多项式中x 2系数为( 0.15 ); 11、 解线性方程组A x =b 的高斯顺序消元法满足的充要条件为(A 的各阶顺序主子式均不为零)。
12、 为了使计算32)1(6)1(41310---+-+=x x x y 的乘除法次数尽量地少,应将该表达式改写为11,))64(3(10-=-++=x t t t t y ,为了减少舍入误差,应将表达式19992001-改写为199920012+ 。
13、 用二分法求方程01)(3=-+=x x x f 在区间[0,1]内的根,进行一步后根的所在区间为 0.5,1 ,进行两步后根的所在区间为 0.5,0.75 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(A) (B) (C) (D)
已知 ,则 为(D)
(A) 0(B) 1(C)2(D)4
已知 且 , ; , 用拉格朗日线性插值求 的近似值,并估计截断误差。
解:
即
余项估计 ,其中
9.已知 ,求 及 的值。(8分)
A、牛顿(Newton)法B、迭代法C、消去法D、二分法
下面程序实现的公式是(D)
for(k=1;k<=n;k++)
for(j=1;j<=n;j++)
{
if(j==k) continue;
a[k][j]=a0[k][j]/a0[k][k];
}
A. B.
C. D.
1.试用c程序实现下面公式。
定义a[k][j]为本次计算所得数组a的结果;a0[k][j]为上一次计算所得数组a的结果。
for(k=1;k<=n;k++)
for(j=1;j<=n;j++)
{
if(j==k) continue;
a[k][j]=a0[k][j]/a0[k][k];
}
要使 的近似值的相对误差不超过0.1%,应取几位有效数字。
第
若f(x)再[a,b]上连续,且f(a)f(b)<0,则方程f(x)=0在[a,b]内至少有一个根。
二分法只能用于求实函数的实根
求解方程 ,若 可以表成 ,则用简单迭代法求根,那么 满足 ,近似根序列 一定收敛。
2.用迭代法求方程 的正根,下面有三种迭代格式:
xi
yi
xi2
xi3
xi4
xiyi
xi2yi
0
-2
0.2
4
-8
16
-0.4
0.8
1
-1
0.8
1
-1
1
-0.8
0.8
2
0
2
0
0
0
0
0
3
1
3
1
1
1
3
3
4
2
4
4
8
16
8
16
∑
0
10
10
0
34
9.8
20.6
(5分)
求解可得:
所以,拟合函数为: (5分)
其
(B)是用某种收敛于所给问题的精确解的极限过程,来逐步逼近的一种计算方法。
(3)有好的计算复杂性,时间复杂性和空间复杂性。
(4)要有数值实验,通过数值试验证明是可行的。
简述计算机中数系的特点。
在计算机数系中,数的个数有限,数系中的每一个数都是有理数;从整体看,数系中的数分布很不均匀;从局部看,阶数相同的数,又以相等的距离,分布在数轴的某一段上;所以计算机数系是由一些残缺不全,分布不均匀的数组成,如果运算超出了计算机数系的范围,则产生溢出
测得平行四边形的底 的值为 ,高 的值为 ,已知 , ,试求平行四边形的面积 的绝对误差限和相对误差限。
解:因为 , , 则
由于 , , , ,于是绝对误差限
简述数值计算方法的特点。
(1)面向计算机,算法只能包括加、减、乘、除运算和逻辑运算
(2)有可靠的理论分析,能任意逼近并达到精度要求,保证收敛性和数值稳定性,对误差进行分析。
1.用牛顿法求 在 附近的实根,使用小数点后3位进行计算。(7分)
解:令 ,则
由 有 (4分)
; ; ,所以 (3分)
用牛顿法计算 ,精确到2位小数。
解:令 则
, , ,
所以
第
求解线性方程组的数值方法大致可分为两类直接法和迭代法
使用列主元素消元法代替高斯消元法的目的是为了控制舍入误差。
对矩阵 进行A=LU分解,则L=( ),U=( )。
解:由已知条件可得: ; (4分)
则有 ; (4分)
第
2.求下列超定方程组的最小二乘解(8分)
解:方程组写成矩阵形式为:
(2分)
正规方程为:
(2分)
即: (2分)解得: (2分)
已知下列数据
xi
-2
-1
0
1
2
yi
0.2
0.8
2
3
4
试用二次代数多项式对其进行拟合(进行3位小数的运算)。(10分)
解:
i
用列主元素消元法解下列线性方程组。
解:
6.用完全主元素消元法解下列线性方程组(按三位小数计算)。(10分)
解:
,
求解可得:
用雅可比迭代法求解方程组 时的迭代公式为:(D)
(A) (B)
(C) (D)
用高斯-塞德尔迭代法求解方程组 时的迭代公式为:(B)
(A) (B)
(C) (D)
已知 ,求A的∞范数,1范数,2范数, (A)以及条件数cond2(A)(10分)。
计算机数值方法
习题集
2014/5/6
太原理工大学 计算机科学与技术学院
王峥
第
计算机解决科学计算问题的一般过程,可概括为:实际问题→数学模型→计算方法→程序设计→上机计算
某电压为228.3657V,测量结果为228.3104V,则测量结果的绝对误差为:(-0.0553V)相对误差为(-0.00011)
误差的来源主要包括:模型误差、观测误差、截断误差、舍入误差。
浮点数分为尾数和阶数两部分。
用1+x近似表示ex产生的误差是(截断)误差。
将 转换为 进行计算是为了避免两相近数相减。
设 =0.03000为 =0.0300211的近似值,则 的有效数字的位数是___3位______.
十进制数0.003012的规格化的浮点数为0.3012×10-2;二进制数1001.101的规格化的浮点数为0.1001101×24。
① ;② ;③
(1)判定此三种迭代格式在 附近的收敛情况。(9分)
(2)指出此三种迭代格式中,哪一种迭代格式收敛最快,为什么。(3分)
( )
解:(1)由 则 ,
当 时, 不收敛;(3分)
(2)由 则 ,
当 时, 收敛;(3分)
(3)由 则 ,
当 时, 收敛;(3分)
(4)因为
所以,此三种迭代格式中,第二种迭代格式收敛最快。(3分)
(2分); (2分);
;
;
∴
∴ (2分);
∴
(2分)
(2分)
已知x= ,则 =________, =________. =________.
第
幂法是一种求任意矩阵A的按模最大特征值及其对应特征向量的迭代算法;反幂法是一种求任意矩阵A的按模最小特征值及其对应特征向量的迭代算法。
当给出特征值 的一个近似值p时,可通过()求对应于 的特征向量。
