二元一次方程练习题及答案
二元一次方程练习题及答案百度文库

二元一次方程练习题及答案百度文库8.1二元一次方程组一、填空题1、二元一次方程4x-3y=12,当x=0,1,2,3时,y=____2、在x+3y=3中,若用x表示y,则y表示x,则x=3、已知方程x2+x+y=k+2,当k=______时,方程为一元一次方程;当k=______时,方程为二元一次方程。
4、对二元一次方程2-3=10,当x=0时,则y=____;当y=0时,则x=____。
5、方程2x+y=5的正整数解是______。
6、若2+|2y+1|=0,则?x?2?x?y?a7、方程组?的一个解为?,那么这个方程组的另一个解是。
y?3xy?b??8、若x?1时,关于x、y的二元一次方程组2?ax?2y?1的解互为倒数,则??x?by?2a?2b?二、选择题1、方程2x-3y=5,xy=3,x?二元一次方程的有个。
A、1B、2C、3D、42、方程2x+y=9在正整数范围内的解有A、1个B、2个C、3个D、4个3、与已知二元一次方程5x-y=2组成的方程组有无数多个解的方程是A、10x+2y=B、4x-y=C、20x-4y=D、15x-3y=64、若是5x2ym与4xn?m?1y2n?2同类项,则m2?n的值为A、1B、-1C、-D、以上答案都不对5、在方程x2+x+y+3k=0中,若此方程为二元一次方程,则k值为?3,3x-y+2z=0,x2?y?6中是yA、2B、-C、2或-D、以上答案都不对.6、若??x?2是二元一次方程组的解,则这个方程组是 ?y??1?x?3y?5?y?x?3?2x?y?5?x?2yA、? B、? C、?D、?x?y?5y?2x?5x?y?1x?3y?17、在方程2?3?3中,用含x的代数式表示y,则A、y?5x?B、y??x?C、y?5x?D、y??5x?38、已知x=3-k,y=k+2,则y与x的关系是A、x+y=5B、x+y=1C、x-y=1D、y=x-19、下列说法正确的是A、二元一次方程只有一个解B、二元一次方程组有无数个解C、二元一次方程组的解必是它所含的二元一次方程的解D、三元一次方程组一定由三个三元一次方程组成?3x?5y?610、若方程组? 的解也是方程3x+ky=10的解,则k的值是x?15y?16?A、k=6= B、k=10C、k=9D、k=三、解答题1、解关于x的方程x?a?22、已知方程组?1 10?x?y?7,试确定a、c的值,使方程组:?ax?2y?c有一个解;有无数解;没有解3、关于x、y的方程3kx?2y?6k?3,对于任何k的值都有相同的解,试求它的解。
二元一次方程计算题含答案

二元一次方程组解法练习题精选一.解答题(共16小题)1.求适合的x,y的值.2.解下列方程组(1)(2)(3)(4).3方程组:4.解方程组:5.解方程组:6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?7.解方程组:(1);(2).8.解方程组:9.解方程组:10.解下列方程组:(1)(2)11.解方程组:(1)(2)12.解二元一次方程组:(1);(2)13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.14.15.解下列方程组:(1)(2).16.解下列方程组:(1)(2)二元一次方程组解法练习题精选(含答案)参考答案与试题解析一.解答题(共16小题)1.求适合的x,y的值.,得到一组新的方程,然后在用加减消元法消,,x=(1)(2)(3)(4).故原方程组的解为故原方程组的解为)原方程组可化为,.所以原方程组的解为,,代入×﹣.所以原方程组的解为3.解方程组:解:原方程组可化为所以方程组的解为4.解方程组:)原方程组化为,.所以原方程组的解为5.解方程组:,.所以方程组的解为6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.的二元一次方程组)依题意得:k=b=x+y=x+(1);(2).)原方程组可化为,;)原方程可化为.8.解方程组:解:原方程组可化为则原方程组的解为9.解方程组:解:原方程变形为:..10.解下列方程组:(1)(2))﹣=所以原方程组的解为)原方程组整理为,所以原方程组的解为(1)(2))原方程组可化简为∴原方程组可化为,∴原方程组的解为(1);(2).;)此方程组通过化简可得:,.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?)把代入方程组.代入方程组.∴方程组为则原方程组的解是14.(,∴原方程组的解为(1);(2).)化简整理为故原方程组的解为)化简整理为故原方程组的解为16.解下列方程组:(1)(2)∴原方程组的解为)原方程组可化为,∴原方程组的解为。
二元一次方程计算题含答案

二元一次方程组解法练习题精选一.解答题(共16小题)1.求适合的x,y的值.2.解下列方程组(1)(2)(3)(4).3方程组:4.解方程组:5.解方程组:6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?7.解方程组:(1);(2).8.解方程组:9.解方程组:10.解下列方程组:(1)(2)11.解方程组:(1)(2)12.解二元一次方程组:(1);(2)13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.14.15.解下列方程组:(1)(2).16.解下列方程组:(1)(2)二元一次方程组解法练习题精选(含答案)参考答案与试题解析一.解答题(共16小题)1.求适合的x,y的值.,得到一组新的方程,然后在用加减消元法消,,x=2.解下列方程组(1)(2)(3)(4).故原方程组的解为故原方程组的解为)原方程组可化为,.所以原方程组的解为,,代入×﹣.所以原方程组的解为3.解方程组:解:原方程组可化为所以方程组的解为4.解方程组:)原方程组化为,.所以原方程组的解为5.解方程组:,.所以方程组的解为6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?的二元一次方程组)依题意得:k=b=x+y=x+7.解方程组:(1);(2).)原方程组可化为,;)原方程可化为.8.解方程组:解:原方程组可化为则原方程组的解为9.解方程组:解:原方程变形为:..10.解下列方程组:(1)(2))﹣=所以原方程组的解为)原方程组整理为,所以原方程组的解为11.解方程组:(1)(2))原方程组可化简为∴原方程组可化为,∴原方程组的解为12.解二元一次方程组:(1);(2).;)此方程组通过化简可得:,.13.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的b,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解.)把代入方程组.代入方程组.∴方程组为则原方程组的解是14.(,∴原方程组的解为15.解下列方程组:(1);(2).)化简整理为故原方程组的解为)化简整理为故原方程组的解为16.解下列方程组:(1)(2)∴原方程组的解为)原方程组可化为,∴原方程组的解为。
二元一次方程组计算题20道带答案

二元一次方程组计算题20道带答案1.求解下列二元一次方程组:–3x - 2y = 7–2x + 4y = 10答案: x = 3, y = -12.解方程组:–2x + 5y = 11–3x - 7y = 8答案: x = 3, y = 13.求解二元方程组:–x + 2y = 9–3x - y = 3答案: x = 3, y = 34.解下列方程组:–4x + 2y = 10–2x - y = 9答案: x = 2, y = -55.解方程组:–5x - 3y = 4–x + 4y = 7答案: x = 2, y = 16.求解以下方程组:–8x + 3y = 21–2x - 5y = 7答案: x = 3, y = -37.解二元一次方程组:–3x + 2y = 13–4x - y = 6答案: x = 2, y = 58.解下列方程组:–7x + 3y = 17–5x - 2y = 11答案: x = 2, y = 39.求解二元方程组:–2x + 3y = 10–3x - y = 1答案: x = 2, y = 210.解方程组:–6x - 4y = 8–3x + 7y = 10答案: x = 2, y = 111.求解下列二元一次方程组:–5x + 2y = 11–x - 3y = 4答案: x = 2, y = 112.解方程组:–4x - 2y = 8–2x + 5y = 9答案: x = 2, y = 113.求解二元方程组:–x + 4y = 7–3x - y = 4答案: x = 2, y = 114.解下列方程组:–2x + 3y = 13–4x - y = 3答案: x = 2, y = 315.解方程组:–5x + 2y = 14–2x - 3y = 4答案: x = 2, y = 316.求解以下方程组:–3x - y = 4–5x + 2y = 11答案: x = 1, y = 117.解二元一次方程组:–4x + y = 9–x - 5y = -5答案: x = 2, y = 118.解下列方程组:–3x + 5y = 19–7x - 2y = 11答案: x = 2, y = 319.求解二元方程组:–2x - y = 1–3x + 4y = 11答案: x = 2, y = 320.解方程组:–4x - 3y = 5–x + 6y = 10答案: x = 2, y = 2以上为二元一次方程组计算题,每道题都已附有详细答案。
初中数学二元一次方程组经典练习题(含答案)

初中数学二元一次方程组经典练习题(含答案)解下列二元一次方程组:1. {x +y = 2 3x +7y =10;2.{x +3y = 810x −y =18;3.{3x +2y =1364x −3y =1;4.{ x+52+y−43=2x+20.3−y+70.4= −10 ;5.{ 4x −3y =−1 x 5=y 7 ;6. {3(x +2)=2(y +3)4(x −2)=3(y −3);7.{ x 5+y 7=10 x 3−y 4=3;8.{x 2+y 3=42x +7y =50 ;9.{12(x +3)+13(y −4)=52(x −3)+5(y +4)=70 ;10.{0.2x +0.5y =9x+22+y+105=15 ;11.{4(x −1) +3(y +1) =320%(x +1)+80%(y −1)=−3;12.{x+2y 2 +x−2y 3 = 113(x +2y )−4(x −2y )=30 ;参考答案1. {x +y = 23x +7y =10 ;解: {x +y = 2−−−−−−①3x +7y =10−−−−②①×3,得3x+3y=6-------③②-③,得4y=4,即y=1将y=1代入①,解得x=1故原方程组的解是: {x =1y =12.{x +3y = 810x −y =18; 解:{x +3y = 8−−−−−−−①10x −y =18−−−−−−②②×3,得 30x-3y=54----③①+③,得31x=62,即x=2将x=2代入①,得2+3y=8,y=2故原方程组的解是: {x =2y =23.{3x +2y =1364x −3y =1; 解:{3x +2y =136−−−−−−①4x −3y =1−−−−−−② ①×3,得9x+6y= 132------③ ②×2,得8x-6y=2-----④③+④,得17x= 172 ,x= 12 将x= 12代入②,2-3y=1,y= 13 故原方程组的解是: {x = 12y = 134.{ x+52+y−43=2 x+20.3−y+70.4= −10; 解:{ x+52+y−43=2 −−−−−−−① x+20.3−y+70.4= −10−−−−−−②①等号两边同时乘以6,得3(x+5)+2(y-4)=123x+15+2y-8=12整理,得3x+2y=5----------③②等号两边同时乘以0.3×0.4,得0.4(x+2)-0.3(y+7)=-1.2两边同时乘以10,得4(x+2)-3(y+7)=-124x+8-3y-21=-12整理,得4x-3y=1--------④③×3,得9x+6y=15------⑤④×2,得8x-6y=2-------⑥⑤+⑥,得17x=17,即x=1将x=1代入③,得3+2y=5,y=1故原方程组的解是: {x =1y =15.{ 4x −3y =−1 x 5=y 7 ; 解:{ 4x −3y =−1 −−−−−−−−−−−① x 5=y 7−−−−−−−−−−−−−−−② ②变化为x= 57 y--------------③ 将③代入①,得4×57y -3y=-1 20−217 y =-1,整理得y=7将y=7代入③,得x= 57 ×7,x=5 故原方程组的解是: {x =5y =76. {3(x +2)=2(y +3)4(x −2)=3(y −3); 解:{3(x +2)=2(y +3)4(x −2)=3(y −3)方程组去括号,得{3x +6=2y +64x −8=3y −9整理得{3x −2y =0−−−−①4x −3y +1=0−−②①×3,得9x-6y=0--------③②×2, 得8x-6y+2=0------④③-④,得x-2=0,即x=2将x=2代入①,得6-2y=0,y=3故原方程组的解是: {x =2y =37.{ x 5+y 7=10 x 3−y 4=3; 解:{ x 5+y 7=10 x 3−y 4=3 方程组去分母,得{ 7x +5y =350−−−−−−①4x −3y =36−−−−−−−②①×3,得21x+15y=1050---③②×5,得20x-15y=180----④③+④,得41x=1230,即x=30将x=30代入①,得210+5y=350,y=28故原方程组的解是: {x =30y =288.{x 2+y 3=4 2x +7y =50; 解:{x 2+y 3=4 2x +7y =50方程组去分母,得{3x +2y =24−−−−−−−① 2x +7y =50−−−−−−−②①×2,得6x+4y=48-----③②×3,得6x+21y=150---④④-③,得17y=102,即y=6将y=6代入① ,得3x+12=24,x=4故原方程组的解是: {x =4y =69.{12(x +3)+13(y −4)=52(x −3)+5(y +4)=70 ; 解:{12(x +3)+13(y −4)=5−−−−① 2(x −3)+5(y +4)=70−−−②①去分母,得3(x+3)+2(y-4)=30去括号,得3x+9+2y-8=30整理,得3x+2y-29=0-----------③②去括号,得2x-6+5y+20=70整理,得2x+5y-56=0-----------④③×2,得6x+4y-58=0------------⑤④×3,得6x+15y-168=0----------⑥⑥-⑤,得11y-110=0,即y=10将y=10代入③,得3x+20-29=0,x=3故原方程组的解是:{x=3 y=1010.{0.2x+0.5y=9x+2 2+y+105=15 ;解:{0.2x+0.5y=9−−−−−①x+22+y+105=15−−−−−−②①等号两边同时乘以10,得2x+5y=90------------------③②去分母,得5(x+2)+2(y+10)=150去括号,整理得5x+2y=120---④③×5,得10x+25y=450------⑤④×2,得10x+4y=240-------⑥⑤-⑥,得21y=210,即y=10将y=10代入③,得2x+50=90,x=20故原方程组的解是:{x=20 y=1011.{4(x −1) +3(y +1) =320%(x +1)+80%(y −1)=−3; 解:{4(x −1) +3(y +1) =3−−−−−−−−−①20%(x +1)+80%(y −1)=−3−−−−−−② ①去括号,得4x-4+3y+3=3,整理得4x+3y=4-----③ ②去百分号,得0.2(x+1)+0.8(y-1)=-3等号两边同时乘以10,得2(x+1)+8(y-1)=-30 去括号,得2x+2+8y-8=-30,整理得x+4y=-12----④ ④×4,得4x+16y=-48------------------------⑤ ⑤-③,得13y=-52,即y=-4将y=-4代入④,得x-16=-12,x=4故原方程组的解是: {x =4y =−412.{x+2y 2 +x−2y 3 = 11 3(x +2y )−4(x −2y )=30; 解:{x+2y 2 +x−2y 3 = 11 −−−−−−−−−−−−−−① 3(x +2y )−4(x −2y )=30−−−−−−② ①×6,得3(x+2y )+2(x-2y )=66----------------③③-②,得6(x-2y )=36,即x-2y= 6 -------④①×12,得6(x+2y )+4(x-2y )=132---------------⑤⑤+②,得9(x+2y)=162,即x+2y=18---⑥④+⑥,得2x=24,即x=12④-⑥,得-4y=-12,即y=3故原方程组的解是:{x=12 y=3。
二元一次方程练习题及答案

二元一次方程1、一个两位数,比它十位上的数与个位上的数的和大9;如果交换十位上的数与个位上的数,所得两位数比原两位数大27,求这个两位数.2、一件商品如果按定价打九折出售可以盈利20%;如果打八折出售可以盈利10元,问此商品的定价是多少?3、某厂共有120名生产工人,每个工人每天可生产螺栓25个或螺母20个,如果一个螺栓与两个螺母配成一套,那么每天安排多名工人生产螺栓,多少名工人生产螺母,才能使每天生产出来的产品配成最多套?4、在某条高速公路上依次排列着A、B、C三个加油站,A到B的距离为120千米,B到C 的距离也是120千米.分别在A、C两个加油站实施抢劫的两个犯罪团伙作案后同时以相同的速度驾车沿高速公路逃离现场,正在B站待命的两辆巡逻车接到指挥中心的命令后立即以相同的速度分别往A、C两个加油站驶去,结果往B站驶来的团伙在1小时后就被其中一辆迎面而上的巡逻车堵截住,而另一团伙经过3小时后才被另一辆巡逻车追赶上.问巡逻车和犯罪团伙的车的速度各是多少?5、某船的载重量为300吨,容积为1200立方米,现有甲、乙两种货物要运,其中甲种货物每吨体积为6立方米,乙种货物每吨的体积为2立方米,要充分利用这艘船的载重和容积,甲、乙两重货物应各装多少吨?6、某服装厂接到生产一种工作服的订货任务,要求在规定期限内完成,按照这个服装厂原来的生产能力,每天可生产这种服装150套,按这样的生产进度在客户要求的期限内只能完成订货的45;现在工厂改进了人员组织结构和生产流程,每天可生产这种工作服200套,这样不仅比规定时间少用1天,而且比订货量多生产25套,求订做的工作服是几套?要求的期限是几天?7、某停车场的收费标准如下:中型汽车的停车费为6元/辆,小型汽车的停车费为4元/辆.现在停车场有50辆中、小型汽车,这些车共缴纳停车费230元,问中、小型汽车各有多少辆?8、某蔬菜公司收购蔬菜进行销售的获利情况如下表所示:销售方式直接销售粗加工后销售精加工后销售每吨获利(元)100 250 450现在该公司收购了140吨蔬菜,已知该公司每天能精加工蔬菜6吨或粗加工蔬菜16吨(两种加工不能同时进行).(1)如果要求在18天内全部销售完这140吨蔬菜,请完成下列表格:销售方式全部直接销售全部粗加工后销售尽量精加工,剩余部分直接销售获利(元)(2)如果先进行精加工,然后进行粗加工,要求在15天内刚好加工完140吨蔬菜,则应如何分配加工时间?9、为满足市民对优质教育的需求,某中学决定改变办学条件,计划拆除一部分旧校舍,建造新校舍,拆除旧校舍每平方米需80元,建新校舍每平方米需700元. 计划在年内拆除旧校舍与建造新校舍共7200平方米,在实施中为扩大绿地面积,新建校舍只完成了计划的80%,而拆除旧校舍则超过了计划的10%,结果恰好完成了原计划的拆、建总面积.(1)求:原计划拆、建面积各是多少平方米?(2)若绿化1平方米需200元,那么在实际完成的拆、建工程中节余的资金用来绿化大约是多少平方米?答案:1、分析:设这个两位数十位上的数为x ,个位上的数为y ,则这个两位数及新两位数及其之间的关系可用下表表示:解方程组109101027x y x y y x x y +=++⎧⎨+=++⎩,得14x y =⎧⎨=⎩,因此,所求的两位数是14.2、分析:商品的利润涉及到进价、定价和卖出价,因此,设此商品的定价为x 元,进价为y 元,则打九折时的卖出价为0.9x 元,获利(0.9x-y)元,因此得方程0.9x-y=20%y ;打八折时的卖出价为0.8x 元,获利(0.8x-y)元,可得方程0.8x-y=10. 商品价格(x ) 进价 卖出价打九折盈利 y 0.9x 0.9x-y=20%y 打八折盈利y0.8x0.8x-y=10解方程组0.920%0.810x y y x y -=⎧⎨-=⎩,解得200150x y =⎧⎨=⎩,因此,此商品定价为200元.3、分析:要使生产出来的产品配成最多套,只须生产出来的螺栓和螺母全部配上套,根据题意,每天生产的螺栓与螺母应满足关系式:每天生产的螺栓数×2=每天生产的螺母数×1.因此,设安排x人生产螺栓,y人生产螺母,则每天可生产螺栓25x个,螺母20y个,依题意,得120502201x y x y +=⎧⎨⨯=⨯⎩,解之,得20100x y =⎧⎨=⎩. 故应安排20人生产螺栓,100人生产螺母.4、【分析】设巡逻车、犯罪团伙的车的速度分别为x 、y 千米/时,则()3120120x y x y -=⎧⎪⎨+=⎪⎩,整理,得40120x y x y -=⎧⎨+=⎩,解得8040x y =⎧⎨=⎩, 十位上的数个位上的数对应的两位数相等关系 原两位数 x y 10x+y 10x+y=x+y+9 新两位数yx10y+x10y+x=10x+y+27因此,巡逻车的速度是80千米/时,犯罪团伙的车的速度是40千米/时.5、分析:“充分利用这艘船的载重和容积”的意思是“货物的总重量等于船的载重量”且“货物的体积等于船的容积”.设甲种货物装x 吨,乙种货物装y 吨,则300621200x y x y +=⎧⎨+=⎩,整理,得3003600x y x y +=⎧⎨+=⎩,解得150150x y =⎧⎨=⎩, 因此,甲、乙两重货物应各装150吨.6、分析:设订做的工作服是x 套,要求的期限是y 天,依题意,得()41505200125y x y x ⎧=⎪⎨⎪-=+⎩,解得337518x y =⎧⎨=⎩. 因此,工作服有3375套。
二元一次方程组经典练习题+答案解析100道

二元一次方程组经典练习题+答案解析100道二元一次方程组练题100道(卷一)1、判断1、方程组xy526的解是()。
解:这不是一个完整的方程组,缺少另一个方程,无法判断解。
2、方程组1是方程组yx3 2的解是方程3x-2y=13的一个解()。
解:将方程组代入3x-2y=13中,得到3x-2(-x/3-1/2)=13,化简得到x=5,y=-4,代入方程组可验证是解,因此选(√)。
3、由两个二元一次方程组成方程组一定是二元一次方程组()。
解:不一定,例如x+y=1和2x+2y=2就不是二元一次方程组。
4、方程组x3y 573x2y12235 3可以转化为方程组解:将第一个方程移项得到x+3y=2,代入第二个方程中消去x得到-7y=-18,解得y=18/7,代入第一个方程得到x=-41/7,因此可以转化为方程组5x-6y=-27和2y-3x+4=2,选(√)。
5、若(a-1)x+(a-1)x+(2a-3)y=0是二元一次方程,则a的值为±1()。
解:将XXX提取出来得到(a-1)(x+y)+(2a-3)y=0,因此x+y=-2a+3y/y-2,这是一个关于a的一次函数,当a=±1时,x+y=±1,此时方程组化为x+y=±1和-2x-2y=0,是二元一次方程组,因此选(√)。
6、若x+y=0,且|x|=2,则y的值为2()。
解:由x+y=0得到y=-x,代入|x|=2中得到|x|=|x+y|=|-x+y|=2,解得x=±1,因此y=±1,不等于2,选(×)。
7、方程组mx my m3x4x10y8有唯一的解,那么m的值为m≠-5()。
解:将第一个方程移项得到(m+3)x+my=m,代入第二个方程中消去x得到(3m+2)y=8-m,因为有唯一解,所以3m+2≠0,即m≠-2/3,代入方程组中验证,当m≠-5时,有唯一解,因此选(√)。
8、方程组1x y 233有无数多个解()。
二元一次方程组练习题(含答案)

二元一次方程组练习题(含答案) 二元一次方程组练题一.解答题(共16小题)1.解下列方程组:1)x+2y-1=23x-2y=52)1-yx+2/3=1/22y+3=3x3)5x+2y=11a4x-4y=6a4)2x+3y=73x-2y=15)2x-3y=75x+4y=176)2x+3y=13x-2y=57)3x-4y=-12x+5y=138)x(y+1)+y(1-x)=2x(x+1)-y-x^2=09)3x+y=72x-3y=-810)x^2+xy=2y-x+2=02.求适合的x,y的值。
已知关于x,y的二元一次方程y=kx+b的解有和。
1)求k,b的值。
2)当x=2时,y的值。
3)当y=3时,x的值为多少?解答:1.1)将第二个方程变形得到y=(3x-5)/2,代入第一个方程中,得到x=3,y=-2.2)将第一个方程变形得到y=(1/2-1+xy)/x,代入第二个方程中,得到x=3,y=-1.3)将第二个方程变形得到y=x-3/2,代入第一个方程中,得到x=2,y=1.4)将第二个方程变形得到y=(3x-1)/2,代入第一个方程中,得到x=2,y=1.5)将第一个方程变形得到y=(2x-7)/3,代入第二个方程中,得到x=1,y=-1.6)将第二个方程变形得到y=(3x-5)/2,代入第一个方程中,得到x=1,y=-1.7)将第二个方程变形得到y=(3x+1)/4,代入第一个方程中,得到x=5,y=2.8)将第一个方程变形得到y=(2-x^2)/(1-x),代入第二个方程中,得到x=1,y=1.9)将第二个方程变形得到y=(2x+8)/3,代入第一个方程中,得到x=1,y=1.10)将第一个方程变形得到y=2/x-x,代入第二个方程中,得到x=1,y=0.2.1)由于y=kx+b,所以当x=1时,y=k+b;当x=2时,y=2k+b。
又因为已知y=3时,x的值为多少,所以将y=kx+b代入得到kx+b=3,解得x=(3-b)/k。
二元一次方程及答案

1) 66x+17y=3967 25x+y=1200答案:x=48 y=47 (2) 18x+23y=2303 74x-y=1998答案:x=27 y=79 (3) 44x+90y=7796 44x+y=3476答案:x=79 y=48 (4) 76x-66y=4082 30x-y=2940答案:x=98 y=51 (5) 67x+54y=8546 71x-y=5680答案:x=80 y=59 (6) 42x-95y=-1410 21x-y=1575答案:x=75 y=48 (7) 47x-40y=85334x-y=2006答案:x=59 y=48 (8) 19x-32y=-1786 75x+y=4950答案:x=66 y=95 (9) 97x+24y=7202 58x-y=2900答案:x=50 y=98 (10) 42x+85y=6362 63x-y=1638答案:x=26 y=62 (11) 85x-92y=-2518 27x-y=486答案:x=18 y=44 (12) 79x+40y=2419 56x-y=1176答案:x=21 y=19 (13) 80x-87y=2156 22x-y=880答案:x=40 y=12 (14) 32x+62y=5134 57x+y=2850答案:x=50 y=57(15) 83x-49y=8259x+y=2183答案:x=37 y=61 (16) 91x+70y=5845 95x-y=4275答案:x=45 y=25 (17) 29x+44y=5281 88x-y=3608答案:x=41 y=93 (18) 25x-95y=-4355 40x-y=2000答案:x=50 y=59 (19) 54x+68y=3284 78x+y=1404答案:x=18 y=34 (20) 70x+13y=3520 52x+y=2132答案:x=41 y=50 (21) 48x-54y=-3186 24x+y=1080答案:x=45 y=99 (22) 36x+77y=7619 47x-y=799答案:x=17 y=91 (23) 13x-42y=-2717 31x-y=1333答案:x=43 y=78 (24) 28x+28y=3332 52x-y=4628答案:x=89 y=30 (25) 62x-98y=-2564 46x-y=2024答案:x=44 y=54 (26) 79x-76y=-4388 26x-y=832答案:x=32 y=91 (27) 63x-40y=-821 42x-y=546答案:x=13 y=41 (28) 69x-96y=-1209 42x+y=3822答案:x=91 y=78(29) 85x+67y=7338 11x+y=308答案:x=28 y=74 (30) 78x+74y=12928 14x+y=1218答案:x=87 y=83 (31) 39x+42y=5331 59x-y=5841答案:x=99 y=35 (32) 29x+18y=1916 58x+y=2320答案:x=40 y=42 (33) 40x+31y=6043 45x-y=3555答案:x=79 y=93 (34) 47x+50y=8598 45x+y=3780答案:x=84 y=93 (35) 45x-30y=-1455 29x-y=725答案:x=25 y=86 (36) 11x-43y=-1361 47x+y=799答案:x=17 y=36 (37) 33x+59y=3254 94x+y=1034答案:x=11 y=49 (38) 89x-74y=-2735 68x+y=1020答案:x=15 y=55 (39) 94x+71y=7517 78x+y=3822答案:x=49 y=41 (40) 28x-62y=-4934 46x+y=552答案:x=12 y=85 (41) 75x+43y=8472 17x-y=1394答案:x=82 y=54 (42) 41x-38y=-1180 29x+y=1450答案:x=50 y=85(43) 22x-59y=824 63x+y=4725答案:x=75 y=14 (44) 95x-56y=-401 90x+y=1530答案:x=17 y=36 (45) 93x-52y=-852 29x+y=464答案:x=16 y=45 (46) 93x+12y=8823 54x+y=4914答案:x=91 y=30 (47) 21x-63y=8420x+y=1880答案:x=94 y=30 (48) 48x+93y=9756 38x-y=950答案:x=25 y=92 (49) 99x-67y=4011 75x-y=5475答案:x=73 y=48 (50) 83x+64y=9291 90x-y=3690答案:x=41 y=92(51) 17x+62y=3216 75x-y=7350答案:x=98 y=25 (52) 77x+67y=2739 14x-y=364答案:x=26 y=11 (53) 20x-68y=-4596 14x-y=924答案:x=66 y=87 (54) 23x+87y=4110 83x-y=5727答案:x=69 y=29 (55) 22x-38y=804 86x+y=6708答案:x=78 y=24 (56) 20x-45y=-3520 56x+y=728(57) 46x+37y=7085 61x-y=4636答案:x=76 y=97 (58) 17x+61y=4088 71x+y=5609答案:x=79 y=45 (59) 51x-61y=-1907 89x-y=2314答案:x=26 y=53 (60) 69x-98y=-2404 21x+y=1386答案:x=66 y=71 (61) 15x-41y=754 74x-y=6956答案:x=94 y=16 (62) 78x-55y=656 89x+y=5518答案:x=62 y=76 (63) 29x+21y=1633 31x-y=713答案:x=23 y=46 (64) 58x-28y=2724 35x+y=3080答案:x=88 y=85 (65) 28x-63y=-2254 88x-y=2024答案:x=23 y=46 (66) 43x+50y=7064 85x+y=8330答案:x=98 y=57 (67) 58x-77y=1170 38x-y=2280答案:x=60 y=30 (68) 92x+83y=11586 43x+y=3010答案:x=70 y=62 (69) 99x+82y=6055 52x-y=1716答案:x=33 y=34 (70) 15x+26y=1729 94x+y=8554(71) 64x+32y=3552 56x-y=2296答案:x=41 y=29 (72) 94x+66y=10524 84x-y=7812答案:x=93 y=27 (73) 65x-79y=-5815 89x+y=2314答案:x=26 y=95 (74) 96x+54y=6216 63x-y=1953答案:x=31 y=60 (75) 60x-44y=-352 33x-y=1452答案:x=44 y=68 (76) 79x-45y=510 14x-y=840答案:x=60 y=94 (77) 29x-35y=-218 59x-y=4897答案:x=83 y=75 (78) 33x-24y=1905 30x+y=2670答案:x=89 y=43 (79) 61x+94y=11800 93x+y=5952答案:x=64 y=84 (80) 61x+90y=5001 48x+y=2448答案:x=51 y=21 (81) 93x-19y=286x-y=1548答案:x=18 y=88 (82) 19x-96y=-5910 30x-y=2340答案:x=78 y=77 (83) 80x+74y=8088 96x-y=8640答案:x=90 y=12 (84) 53x-94y=1946 45x+y=2610(85) 93x+12y=9117 28x-y=2492答案:x=89 y=70 (86) 66x-71y=-1673 99x-y=7821答案:x=79 y=97 (87) 43x-52y=-1742 76x+y=1976答案:x=26 y=55 (88) 70x+35y=8295 40x+y=2920答案:x=73 y=91 (89) 43x+82y=4757 11x+y=231答案:x=21 y=47 (90) 12x-19y=236 95x-y=7885答案:x=83 y=40 (91) 51x+99y=8031 71x-y=2911答案:x=41 y=60 (92) 37x+74y=4403 69x-y=6003答案:x=87 y=16 (93) 46x+34y=4820 71x-y=5183答案:x=73 y=43 (94) 47x+98y=5861 55x-y=4565答案:x=83 y=20 (95) 30x-17y=239 28x+y=1064答案:x=38 y=53 (96) 55x-12y=4112 79x-y=7268答案:x=92 y=79 (97) 27x-24y=-450 67x-y=3886答案:x=58 y=84 (98) 97x+23y=8119 14x+y=966(99) 84x+53y=11275 70x+y=6790答案:x=97 y=59 (100) 51x-97y=297 19x-y=1520答案:x=80 y=39。
二元一次方程组(例题、解方程组、练习及答案)
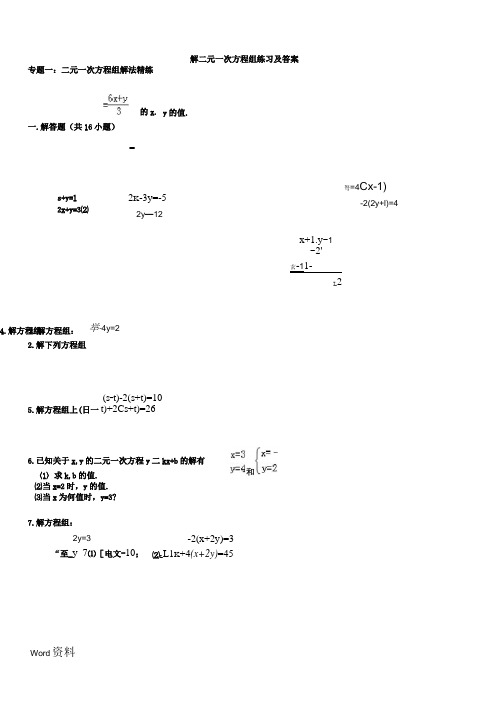
的x. y 的值.s+y=l 2x+y=3⑵2K -3y=-52y —12弩=4Cx-1)-2(2y+l)=43.解方程组:举-4y=24.解方程组: x+1.y~1 ~2'玄-11-L 2-2(x+2y)=3⑵L L1K +4(x+2y)=45解二元一次方程组练习及答案专题一:二元一次方程组解法精练一.解答题(共16小题)2.解下列方程组(s _t)-2(s+t)=10 5.解方程组上(日一t)+2Cs+t)=266.已知关于x,y 的二元一次方程y 二kx+b 的解有 (1)求k,b 的值. ⑵当x=2时,y 的值. ⑶当x 为何值时,y=3?7.解方程组:2y=3“至_y_7⑴[电文-10;=13_X "12,乙看错了方程组中的b.蓋二- £时,由于粗心,甲看错了方程组中的a,而得解为 (沪5而得解为尸°.(1)甲把a 看成了什么,乙把b 看成了什么? (2)求出原方程组的正确解.亠一空二5 14.I X0.315.解下列方程组:8.解方程组:卩(旳)(K -3y)=159.解方程组:10.解下列方程组: fs-y=4 ⑴4贵 11.解方程组: "T⑵[4(葢十7)-5(K-y)=212.解二元一次方程组: f 9s+2y=20(1).办十4尸10;乜(K -1)-4(y-4)=0⑵占〔厂"二3匕+5)鮎曲+5尸1013.在解方程组(1) 匹站3y=15 “x+1_y+4 ⑵f2x+y=4 16.解下列方程组:(1)时戈产5 p+y=l(2)■20^1+30^25^X2专题二:方程组解法强化训练 ■>二1+尸j3^-2/=6 2(右十为*175x+y+z=145 15 3.x+y —2z-5 仝%+4®二1124.5. 17 r0.25x+3ty+3)=156.匚(工十1)—1.5(^十刀二35 r 3(x-y 十E 二0'mJ4耳+2了+£=3i4 l 税25t+5v+z=6O 盲8.9.—2 4 J2 3 XH -/=60 J y +z =40 x+i=50 10. H 十JJ-H-Z=11<3A +J 二25z=4^11.L》+z -了工二号 5-3^+4-7y=1121」心+5我彳z +z-3j=5 13.乐十》)-4&p )二4土+二=118.21. fi-2j=7y x+1—二36y-1=3fx+|)16.y—1x二y-I2_y+2.2x=+13T" 33(x-0=4(卩一4)17.+500,[60%^+80%-7=500x72%.19.宝”一1)=3(兀+5)20.卜223A-3J-9=^±13r2(z+^+3(x-y)=1322.j-2z+3y=1123.尸(*)亠4决2刃=8724. 25. 弘+»=198jc-3y=6727. =-1=4IZ尹-1=128.30. SI兰工_气2十3-5巧P=〔23-_答案专题一1.x=6"X=1 「K=3、「K=3「⑵•卄8•解万程组:9•解方程组:1歼-1(y=0\y=0工二3114V——3⑷•y=-3•解方程组fl4•解方程组:鳥I尸4,尸亍6••(1)求k,b的值.k二言,b二号•7⑵当x=2时,y的值•把x=2代入,得y=p•(3)当x为何值时,y=3?把y=3代入,得x=1 7•解方程组:10•解下列方程组:17 \=60:'尸-2411•解方程组:⑴12⑵¥二广1712•解二元一次方程组:13.(1)甲把a看成了什么,乙把b看成了什么?fa=-2 [b=6(2)求出原方程组的正确解.P=152•解下列方程组专题二:=50rz=4rz=5K=5[75rz=-70rA=61.2.3.4.5.6.g1715•解下列方程组:⑴16•解下列方程组:⑴rx=-2cm =49.严=35L=2510.厂=30 12.J=_10 严=-17/4K=_19/413r=_5厂=17/15 厂1=714."11⑴15.J=-316.=1厂=20017.J=300 18. J -A =-1/4丫尹=3/819.29/6 -7/422. 23.CI ;rz =2324.f A =-11/2 25.f A =826.5=-127.rz=428.J -A =4.5 29.rz=6.530.。
初二数学二元一次方程练习题及答案

初二数学二元一次方程练习题及答案一、选择题1、下列方程中,是二元一次方程的是()A 3x 2y = 4zB 6xy + 9 = 0C 1/x + 4y = 6D 4x = y 2答案:D解析:A 选项中有三个未知数,不是二元一次方程;B 选项中未知数的最高次数是 2 ,不是一次方程;C 选项中 1/x 不是整式,不是二元一次方程;D 选项符合二元一次方程的定义。
2、二元一次方程 5a 11b = 21 ()A 有且只有一解B 有无数解C 无解D 有且只有两解答案:B解析:对于二元一次方程,只要给定一个 a 的值,就可以求出对应的 b 的值,所以有无数组解。
3、方程组{x + y = 3 ,x y =-1} 的解是()A {x = 1 ,y = 2}B {x = 1 ,y =-2}C {x = 2 ,y = 1}D {x = 0 ,y =-1}答案:C解析:将两个方程相加,可得 2x = 2 ,解得 x = 1 ;将两个方程相减,可得 2y = 4 ,解得 y = 2 ,所以方程组的解是{x = 1 ,y =2} 。
二、填空题1、已知方程 2x + 3y 4 = 0 ,用含 x 的代数式表示 y 为:y =____________。
答案:y =(4 2x) / 3解析:首先将方程移项可得 3y = 4 2x ,然后两边同时除以 3 ,得到 y =(4 2x) / 3 。
2、在二元一次方程-1/2 x + 3y = 2 中,当 x = 4 时,y =____________。
答案:y = 10 / 3解析:将 x = 4 代入方程-1/2 x + 3y = 2 中,可得-1/2 × 4 +3y = 2 ,即-2 + 3y = 2 ,解得 3y = 4 ,y = 4 / 3 。
3、若方程 x²m 1 + 5y³n 2 = 7 是关于 x 、y 的二元一次方程,则m =____________ ,n =____________ 。
二元一次方程练习题及答案

二元一次方程练习题及答案一、选择题:1.下列方程中,是二元一次方程的是()A.3x-2y=4z B.6xy+9=0 C.1x+4y=6 D.4x=24y2.下列方程组中,是二元一次方程组的是()A.228 423119 (23754624)x yx y a b xB C Dx y b c y x x y3.二元一次方程5a-11b=21 ()A.有且只有一解B.有无数解C.无解D.有且只有两解4.方程y=1-x与3x+2y=5的公共解是()A.3333 ...2422 x x x xB C Dy y y y5.若│x-2│+(3y+2)2=0,则的值是()A.-1 B.-2 C.-3 D.3 26.方程组43235x y kx y的解与x与y的值相等,则k等于()7.下列各式,属于二元一次方程的个数有()①xy+2x-y=7;②4x+1=x-y;③1x+y=5;④x=y;⑤x2-y2=2⑥6x-2y ⑦x+y+z=1 ⑧y(y-1)=2y2-y2+xA.1 B.2 C.3 D.48.某年级学生共有246人,其中男生人数y比女生人数x的2倍少2人,?则下面所列的方程组中符合题意的有()A.246246216246 ...22222222 x y x y x y x yB C Dy x x y y x y x二、填空题9.已知方程2x+3y-4=0,用含x的代数式表示y为:y=_______;用含y的代数式表示x 为:x=________.10.在二元一次方程-12x+3y=2中,当x=4时,y=_______;当y=-1时,x=______.11.若x3m-3-2y n-1=5是二元一次方程,则m=_____,n=______.12.已知2,3xy是方程x-ky=1的解,那么k=_______.13.已知│x-1│+(2y+1)2=0,且2x-ky=4,则k=_____.14.二元一次方程x+y=5的正整数解有______________.15.以57xy为解的一个二元一次方程是_________.16.已知2316x mx yy x ny是方程组的解,则m=_______,n=______.三、解答题17.当y=-3时,二元一次方程3x+5y=-3和3y-2ax=a+2(关于x,y的方程)?有相同的解,求a的值.18.如果(a-2)x+(b+1)y=13是关于x,y的二元一次方程,则a,b满足什么条件?19.二元一次方程组437(1)3x ykx k y的解x,y的值相等,求k.20.已知x,y是有理数,且(│x│-1)2+(2y+1)2=0,则x-y的值是多少?21.已知方程12x+3y=5,请你写出一个二元一次方程,?使它与已知方程所组成的方程组的解为41 xy.22.根据题意列出方程组:(1)明明到邮局买0.8元与2元的邮票共13枚,共花去20元钱,?问明明两种邮票各买了多少枚?(2)将若干只鸡放入若干笼中,若每个笼中放4只,则有一鸡无笼可放;?若每个笼里放5只,则有一笼无鸡可放,问有多少只鸡,多少个笼?23.方程组2528x yx y的解是否满足2x-y=8?满足2x-y=8的一对x,y的值是否是方程组2528x yx y的解?24.(开放题)是否存在整数m,使关于x的方程2x+9=2-(m-2)x在整数范围内有解,你能找到几个m的值?你能求出相应的x的解吗?答案:一、选择题1.D 解析:掌握判断二元一次方程的三个必需条件:①含有两个未知数;②含有未知数的项的次数是1;③等式两边都是整式.2.A 解析:二元一次方程组的三个必需条件:①含有两个未知数,②每个含未知数的项次数为1;③每个方程都是整式方程.3.B 解析:不加限制条件时,一个二元一次方程有无数个解.4.C 解析:用排除法,逐个代入验证.5.C 解析:利用非负数的性质.6.B7.C 解析:根据二元一次方程的定义来判定,?含有两个未知数且未知数的次数不超过1次的整式方程叫二元一次方程,注意⑧整理后是二元一次方程.8.B二、填空题9.424332x y10.43-1011.43,2 解析:令3m-3=1,n-1=1,∴m=43,n=2.12.-1 解析:把2,3xy代入方程x-ky=1中,得-2-3k=1,∴k=-1.13.4 解析:由已知得x-1=0,2y+1=0,∴x=1,y=-12,把112xy代入方程2x-ky=4中,2+12k=4,∴k=1.14.解:12344321 x x x xy y y y解析:∵x+y=5,∴y=5-x,又∵x,y均为正整数,∴x为小于5的正整数.当x=1时,y=4;当x=2时,y=3;当x=3,y=2;当x=4时,y=1.∴x+y=5的正整数解为12344321 x x x xy y y y15.x+y=12 解析:以x与y的数量关系组建方程,如2x+y=17,2x-y=3等,此题答案不唯一.16.1 4 解析:将2316x mx yy x ny代入方程组中进行求解.三、解答题17.解:∵y=-3时,3x+5y=-3,∴3x+5×(-3)=-3,∴x=4,∵方程3x+5y=?-?3?和3x-2ax=a+2有相同的解,∴3×(-3)-2a×4=a+2,∴a=-11 9.18.解:∵(a-2)x+(b+1)y=13是关于x,y的二元一次方程,∴a-2≠0,b+1≠0,?∴a≠2,b≠-1解析:此题中,若要满足含有两个未知数,需使未知数的系数不为0.(?若系数为0,则该项就是0)19.解:由题意可知x=y,∴4x+3y=7可化为4x+3x=7,∴x=1,y=1.将x=1,y=?1?代入kx+(k-1)y=3中得k+k-1=3,∴k=2 解析:由两个未知数的特殊关系,可将一个未知数用含另一个未知数的代数式代替,化“二元”为“一元”,从而求得两未知数的值.20.解:由(│x│-1)2+(2y+1)2=0,可得│x│-1=0且2y+1=0,∴x=±1,y=-12.当x=1,y=-12时,x-y=1+12=32;当x=-1,y=-12时,x-y=-1+12=-12.解析:任何有理数的平方都是非负数,且题中两非负数之和为0,则这两非负数(│x│-1)2与(2y+1)2都等于0,从而得到│x│-1=0,2y+1=0.21.解:经验算41xy是方程12x+3y=5的解,再写一个方程,如x-y=3.22.(1)解:设0.8元的邮票买了x枚,2元的邮票买了y枚,根据题意得130.8220 x yx y.(2)解:设有x只鸡,y个笼,根据题意得415(1)y xy x.23.解:满足,不一定.解析:∵2528x yx y的解既是方程x+y=25的解,也满足2x-y=8,?∴方程组的解一定满足其中的任一个方程,但方程2x-y=8的解有无数组,如x=10,y=12,不满足方程组25 28x yx y.24.解:存在,四组.∵原方程可变形为-mx=7,∴当m=1时,x=-7;m=-1时,x=7;m=?7时,x=-1;m=-7时x=1.。
二元一次方程专题(内含答案详解)

二元一次方程专题一.选择题(共12小题)1.已知是关于x、y的方程4kx﹣3y=﹣1的一个解,则k的值为()A.1 B.﹣1 C.2 D.﹣22.已知与是二元一次方程mx+ny=5的两组解,则m+n的值为()A.1 B.2 C.3 D.43.下列方程中,是二元一次方程的是()A.8x2+1=y B.y=8x+1 C.y= D.xy=14.在方程﹣=5中,用关于x的代数式表示y,正确的是()A.x=y﹣10 B.x=y+10 C.y=x﹣15 D.y=y+155.已知甲、乙两种商品的进价和为100元,为了促销而打折销售,若甲商品打八折,乙商品打六折,则可赚50元,若甲商品打六折,乙商品打八折,则可赚30元,甲、乙两种商品的定价分别为()A.50元、150元B.50元、100元C.100元、50元D.150元、50元6.若关于x,y的方程x m+2﹣y n﹣1=5是二元一次方程,则m+n的值为()A.1 B.﹣1 C.3 D.﹣37.将方程x+y=1中的x的系数化为整数,则下列结果正确的是()A.﹣x+y=1 B.x﹣2y=﹣2 C.﹣x+y=2 D.x﹣y=28.已知x和y满足2x+3y=5,则当x=4时,代数式3x2+12xy+y2的值是()A.4 B.3 C.2 D.19.若x、y满足方程组,则x﹣y的值等于()A.﹣1 B.1 C.﹣2 D.210.若方程组的解满足x+y=0,则k的值为()A.﹣1 B.1 C.0 D.不能确定11.一个长方形的长的2倍比宽的5倍还多1cm,宽的3倍又比长多1cm,求这个长方形的长与宽.设长为xcm,宽为ycm,则下列方程组中正确的是()A.B.C.D.12.小明的储钱罐有5角和1元的硬币共100枚,币值共有68元.求5角、1元硬币各有多少枚?设小明有5角硬币x枚,有1元硬币y枚,则可列出方程组为()A. B.C. D.二.填空题(共6小题)13.一个两位数的数字和为14,若调换个位数字与十位数字,新数比原数小36,则这个两位数是.14.有一些苹果及苹果箱,若每箱装25千克,则剩余40千克无处装,如每箱装30千克则余20只空箱,则共有千克苹果,个苹果箱.15.一次智力竞赛有20题选择题,每答对一道题得5分,答错一道题扣2分,不答题不给分也不扣,小亮答完全部测试题共得65分,那么他答错了道题.16.把面值20元的纸币换成1元和5元的两种纸币,则共有种换法.17.某同学家离学校12千米,每天骑自行车上学和放学,有一天上学时顺风,从家到学校共用30分钟,放学时逆风,从学校回家共用时40分钟,已知该同学在无风时骑自行车的速度为x千米/时,风速为y千米/时,则根据题意可列方程组.18.某校在春节运动会比赛中,七年级一班和二班的实力相当,关于比赛结果,甲同学说:一班与二班的得分比为4:3,乙同学说:一班得分比五班得分的2倍少40分.若设一班得x分,二班得y分,则根据题意可列方程组.三.解答题(共6小题)19.解下列方程或方程组:(1)3(2x﹣1)=2(1﹣x)﹣1(2)20.“中国制造”是世界上认知度最高的标签之一,因此,我县越来越多的群众选择购买国产空调,已知购买1台A型号的空调比1台B型号的空调少200元,购买2台A型号的空调与3台B型号的空调共需11200元,求A、B两种型号的空调的购买价各是多少元?21.机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,2个大齿轮和3个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大小齿轮刚好配套?22.甲、乙两人相距50千米,若同向而行,乙10小时追上甲;若相向而行,2小时两人相遇.求甲、乙两人每小时各行多少千米?23.某市一种出租车的起步价为10元,两位乘客分别乘这种出租车走了10km 和14km,车费分别为21.2元和27.6元,假设一路顺利,没有停车等候,且不考虑计程器计费的某些特殊规定.请你算出这种出租车起步价所允许行驶的最远路程;并算出超过起步路程但行驶不到15km时,超过部分每千米车费为多少元?24.一个被滴上墨水的方程组如下,小明回忆到:这个方程组的解为,而我求出的解是,经检查后发现,我的错误是由于看错了第二个方程中的x的系数所致,请你根据小明的回忆,把原方程还原出来.二元一次方程专题参考答案与试题解析一.选择题(共12小题)1.已知是关于x、y的方程4kx﹣3y=﹣1的一个解,则k的值为()A.1 B.﹣1 C.2 D.﹣2【分析】把代入方程4kx﹣3y=﹣1,即可得出一个关于k的方程,求出方程的解即可.【解答】解:∵是关于x、y的方程4kx﹣3y=﹣1的一个解,∴代入得:8k﹣9=﹣1,解得:k=1,故选:A.【点评】本题考查了二元一次方程的解和解一元一次方程,能根据题意得出关于k的方程是解此题的关键.2.已知与是二元一次方程mx+ny=5的两组解,则m+n的值为()A.1 B.2 C.3 D.4【分析】代入后得出关于m、n的方程组,两方程相加即可求出答案.【解答】解:∵与是二元一次方程mx+ny=5的两组解,∴代入得:①+②得:5m+5n=10,m+n=2,故选:B.【点评】本题考查了解二元一次方程组和二元一次方程组的解,能根据题意得出关于m、n的方程组是解此题的关键.3.下列方程中,是二元一次方程的是()A.8x2+1=y B.y=8x+1 C.y= D.xy=1【分析】根据二元一次方程的定义求解即可.【解答】解:A、是一元二次方程,故A不符合题意;B、是二元一次方程,故B符合题意;C、是分式方程,故C不符合题意;D、是二元二次方程,故D不符合题意;故选:B.【点评】本题考查了二元一次方程,二元一次方程必须符合以下三个条件:方程中只含有2个未知数;含未知数项的最高次数为一次;方程是整式方程.4.在方程﹣=5中,用关于x的代数式表示y,正确的是()A.x=y﹣10 B.x=y+10 C.y=x﹣15 D.y=y+15【分析】把x看做已知数表示出y即可.【解答】解:方程﹣=5,整理得:y==x﹣15,故选:C.【点评】此题考查了解二元一次方程,解题的关键是将x看做已知数求出y.5.已知甲、乙两种商品的进价和为100元,为了促销而打折销售,若甲商品打八折,乙商品打六折,则可赚50元,若甲商品打六折,乙商品打八折,则可赚30元,甲、乙两种商品的定价分别为()A.50元、150元B.50元、100元C.100元、50元D.150元、50元【分析】设甲种商品的定价分别为x元,则乙种商品的定价分别为y元,根据“若甲商品打八折,乙商品打六折,则可赚50元,若甲商品打六折,乙商品打八折,则可赚30元”可得出关于x、y的二元一次方程组,解方程组即可得出结论.【解答】解:设甲种商品的定价分别为x元,则乙种商品的定价分别为y元,根据题意得:,解得:.故选:D.【点评】本题考查了解二元一次方程组,根据数量关系列出二元一次方程组是解题的关键.6.若关于x,y的方程x m+2﹣y n﹣1=5是二元一次方程,则m+n的值为()A.1 B.﹣1 C.3 D.﹣3【分析】(方法一)根据二元一次方程的定义,即可得出关于m、n的二元一次方程组,解之即可得出m、n的值,将其相加即可得出结论;(方法二)根据二元一次方程的定义,即可得出m+2=1、n﹣1=1,将其相加即可得出m+n的值.【解答】解:(方法一)∵关于x,y的方程x m+2﹣y n﹣1=5是二元一次方程,∴,解得:,∴m+n=1.故选A.(方法二)∵关于x,y的方程x m+2﹣y n﹣1=5是二元一次方程,∴m+2=1,n﹣1=1,∴m+2+n﹣1=2,∴m+n=1.故选:A.【点评】本题考查了二元一次方程的定义以及解二元一次方程组,熟练掌握二元一次方程的定义是解题的关键.7.将方程x+y=1中的x的系数化为整数,则下列结果正确的是()A.﹣x+y=1 B.x﹣2y=﹣2 C.﹣x+y=2 D.x﹣y=2【分析】方程两边乘以2变形即可得到结果.【解答】解:方程左右两边乘以2得:﹣x+2y=2,即x﹣2y=﹣2.故选:B.【点评】此题考查了解二元一次方程,熟练掌握等式的性质是解本题的关键.8.已知x和y满足2x+3y=5,则当x=4时,代数式3x2+12xy+y2的值是()A.4 B.3 C.2 D.1【分析】根据题意先把x=4代入2x+3y=5求出y的值,然后把x、y的值代入代数式3x2+12xy+y2即可求得.【解答】解:把x=4代入2x+3y=5得:y=﹣1,把x=4,y=1代入3x2+12xy+y2得:3×16+12×4×(﹣1)+1=1,故选:D.【点评】本题考查了二元一次方程的解法,主要运用了代入法,难度适中.9.若x、y满足方程组,则x﹣y的值等于()A.﹣1 B.1 C.﹣2 D.2【分析】方程组的两个方程相减,即可求出答案.【解答】解:,②﹣①得:x﹣y=﹣2,故选:C.【点评】本题考查了解二元一次方程组,能选择适当的方法求解是解此题的关键.10.若方程组的解满足x+y=0,则k的值为()A.﹣1 B.1 C.0 D.不能确定【分析】根据等式的性质,可得答案.【解答】解:①+②,得3(x+y)=3﹣3k,由x+y=0,得3﹣3k=0,解得k=1,故选:B.【点评】本题考查了二元一次方程组的解,利用等式的性质是解题关键.11.一个长方形的长的2倍比宽的5倍还多1cm,宽的3倍又比长多1cm,求这个长方形的长与宽.设长为xcm,宽为ycm,则下列方程组中正确的是()A.B.C.D.【分析】由题意,得长的2倍比宽的5倍还多1cm可得方程2x﹣5y=1;宽的3倍又比长多1cm可得方程3y﹣x=1,即可得方程组.【解答】解:根据题意,得方程组.故选:C.【点评】根据实际问题中的条件列方程组时,要注意抓住题目中的一些关键性词语,找出等量关系,列出方程组.12.小明的储钱罐有5角和1元的硬币共100枚,币值共有68元.求5角、1元硬币各有多少枚?设小明有5角硬币x枚,有1元硬币y枚,则可列出方程组为()A. B.C. D.【分析】根据:①5角钱的枚数+1元钱的枚数=100、②5角的总钱数+1元的总钱数=68元,据此可得方程组.【解答】解:设小明有5角硬币x枚,有1元硬币y枚,则可列出方程组为,故选:C.【点评】本题主要考查由实际问题抽象出二元一次方程组,解题的关键是理解题意找到题目蕴含的相等关系.二.填空题(共6小题)13.一个两位数的数字和为14,若调换个位数字与十位数字,新数比原数小36,则这个两位数是95.【分析】设原来十位上数字为x,个位上的数字为y,分别表示出调换前后的两位数,根据题意列方程组求解.【解答】解:设原来十位上数字为x,个位上的数字为y,由题意得,,解得:,故这个两位数为95.故答案为;95.【点评】本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.14.有一些苹果及苹果箱,若每箱装25千克,则剩余40千克无处装,如每箱装30千克则余20只空箱,则共有3240千克苹果,128个苹果箱.【分析】设共有x千克苹果,y个苹果箱.等量关系:①每箱装25千克,则剩余40千克无处装;②每箱装30千克则余20只空箱.【解答】解:设共有x千克苹果,y个苹果箱.根据题意,得,解,得.则共有3240千克苹果,128个苹果箱.【点评】正确找到等量关系是列方程(组)解应用题的关键.15.一次智力竞赛有20题选择题,每答对一道题得5分,答错一道题扣2分,不答题不给分也不扣,小亮答完全部测试题共得65分,那么他答错了5道题.【分析】设答对x道题,答错了y道题,根据对1题给5分,错1题扣2分,不答题不给分也不扣分,总分为65分和有20题选择题可分别列等式求解.【解答】解:设答对x道题,答错了y道题,根据题意可得:,解得:,故他答错了5道题.故答案为:5.【点评】此题主要考查了二元一次方程组的应用,根据题意利用所得分数以及有20题选择题分别得出等式是解题关键.16.把面值20元的纸币换成1元和5元的两种纸币,则共有3种换法.【分析】设1元和5元的纸币各x张、y张,根据题意列出方程,求出方程的正整数解即可.【解答】解:设1元和5元的纸币各x张、y张,根据题意得:x+5y=20,整理得:x=20﹣5y,当x=1,y=15;x=2,y=10;x=3,y=5,则共有3种换法,故答案为:3【点评】此题考查了二元一次方程的应用,弄清题意是解本题的关键.17.某同学家离学校12千米,每天骑自行车上学和放学,有一天上学时顺风,从家到学校共用30分钟,放学时逆风,从学校回家共用时40分钟,已知该同学在无风时骑自行车的速度为x千米/时,风速为y千米/时,则根据题意可列方程组.【分析】由题意可知:顺风速度=无风时速度+风速,逆风速度=无风时速度﹣风速,根据家与学校之间的距离=顺风速度×顺风时间=逆风速度×逆风时间,列出方程组解答即可.【解答】解:30分钟=小时40分钟=小时设该同学在无风时骑自行车的速度为x千米/时,风速为y千米/时,则该同学在顺风时骑自行车的速度为(x+y)千米/小时,逆风时骑自行车的速度为(x﹣y)千米/小时,由题意得.故答案为:.【点评】此题考查由实际问题抽象出二元一次方程组,掌握顺风速度、逆风速度、无风时速度、风速之间的关系是解决问题的关键.18.某校在春节运动会比赛中,七年级一班和二班的实力相当,关于比赛结果,甲同学说:一班与二班的得分比为4:3,乙同学说:一班得分比五班得分的2倍少40分.若设一班得x分,二班得y分,则根据题意可列方程组.【分析】根据题意可得等量关系:①一班得分×3=二班的得分×4;②一班得分=五班得分×2﹣40,根据等量关系列出方程组即可.【解答】解:设一班得x分,二班得y分,由题意得:,故答案为:.【点评】此题主要考查了由实际问题抽象出二元一次方程组,关键是正确理解题意,找出题目中的等量关系.三.解答题(共6小题)19.解下列方程或方程组:(1)3(2x﹣1)=2(1﹣x)﹣1(2)【分析】(1)方程去括号,移项合并,把x系数化为1,即可求出解;(2)方程组整理后,利用加减消元法求出解即可.【解答】解:(1)3(2x﹣1)=2(1﹣x)﹣1,6x﹣3=2﹣2x﹣1,x=,(2),整理得:,②﹣①得:﹣x=1,x=﹣1,把x=﹣1代入①中得:y=5,∴方程组的解为:.【点评】此题考查了解二元一次方程组和一元一次方程,熟练掌握运算法则是解本题的关键.20.“中国制造”是世界上认知度最高的标签之一,因此,我县越来越多的群众选择购买国产空调,已知购买1台A型号的空调比1台B型号的空调少200元,购买2台A型号的空调与3台B型号的空调共需11200元,求A、B两种型号的空调的购买价各是多少元?【分析】设A型号的空调购买价为x元,B型号的空调购买价为y元,根据“购买1台A型号的空调比1台B型号的空调少200元,购买2台A型号的空调与3台B型号的空调共需11200元”,即可得出关于x、y的二元一次方程组,解之即可得出结论.【解答】解:设A型号的空调购买价为x元,B型号的空调购买价为y元,依题意得:,解得:.答:A型号的空调购买价为2120元,B型号的空调购买价为2320元.【点评】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.21.机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,2个大齿轮和3个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大小齿轮刚好配套?【分析】设需安排x名工人加工大齿轮,安排y名工人加工小齿轮,根据平均每人每天加工大齿轮16个或小齿轮10个,2个大齿轮和3个小齿轮配成一套,可列成方程组求解.【解答】解:设需安排x名工人加工大齿轮,安排y名工人加工小齿轮,,解得:.答:需安排25名工人加工大齿轮,安排60名工人加工小齿轮.【点评】本题考查理解题意能力,关键是能准确2个大齿轮和3个小齿轮配成一套,根据此正确列出方程.22.甲、乙两人相距50千米,若同向而行,乙10小时追上甲;若相向而行,2小时两人相遇.求甲、乙两人每小时各行多少千米?【分析】根据题目中的关键句子:“同向而行,乙10小时可追上甲;若相向而行,2小时两人相遇”找到两个等量关系后列出方程组即可.【解答】解:设甲每小时行x千米,乙每小时行y千米,则可列方程组为,解得,答:甲每小时行10千米,乙每小时行15千米.【点评】本题考查了二元一次方程组的应用的知识,解题的关键是根据题意找到两个等量关系,难度不大.23.某市一种出租车的起步价为10元,两位乘客分别乘这种出租车走了10km 和14km,车费分别为21.2元和27.6元,假设一路顺利,没有停车等候,且不考虑计程器计费的某些特殊规定.请你算出这种出租车起步价所允许行驶的最远路程;并算出超过起步路程但行驶不到15km时,超过部分每千米车费为多少元?【分析】设起步价允许行驶的最远路程是xkm,超过部分每千米车费是y元,关键描述语:出租车的起步价为10元,两位乘客分别乘这种出租车走了10km和14km,车费分别为21.2元和27.6元.【解答】解:设起步价允许行驶的最远路程是xkm,超过部分每千米车费是y元,则,解得:,答:起步价允许行驶的最远路程是3km,超过部分每千米车费是1.6元.【点评】本题考查了二元一次方程组的应用.解题关键是弄清题意,合适的等量关系,列出方程组.24.一个被滴上墨水的方程组如下,小明回忆到:这个方程组的解为,而我求出的解是,经检查后发现,我的错误是由于看错了第二个方程中的x的系数所致,请你根据小明的回忆,把原方程还原出来.【分析】由题意可知是方程组的解,是方程△x+口y=2的解,然后代入求解即可.【解答】解:∵是方程组的解,∴3○+14=8,3△﹣2□=2①,∴○=﹣2.∵是方程△x+口y=2的解,∴﹣2△+2口=2②.将①和②联立得:,解得:△=4,□=5(3分),∴原方程组为.【点评】本题主要考查的是二元一次方程组的解,依据方程组的解得概念列出方程或方程组是解题的关键.。
二元一次方程组 习题及答案100道解析

二元一次方程组习题及答案100道1.2x+9y=813x+y=342.9x+4y=358x+3y=303.7x+2y=527x+4y=624.4x+6y=549x+2y=875.2x+y=72x+5y=196.x+2y=213x+5y=567.5x+7y=525x+2y=228.5x+5y=657x+7y=2039.8x+4y=56x+4y=2110.5x+7y=415x+8y=4411.7x+5y=543x+4y=3812.x+8y=154x+y=299x+5y=46 14.9x+2y=62 4x+3y=36 15.9x+4y=46 7x+4y=42 16.9x+7y=135 4x+y=41 17.3x+8y=51 x+6y=27 18.9x+3y=99 4x+7y=95 19.9x+2y=38 3x+6y=18 20.5x+5y=45 7x+9y=69 21.8x+2y=28 7x+8y=62 22.x+6y=14 3x+3y=27 23.7x+4y=67 2x+8y=26 24.5x+4y=52 7x+6y=74 25.7x+y=926.6x+6y=486x+3y=4227.8x+2y=167x+y=1128.4x+9y=778x+6y=9429.6x+8y=687x+6y=6630.2x+2y=227x+2y=471) 66x+17y=3967 25x+y=1200答案:x=48 y=47 (2) 18x+23y=2303 74x-y=1998答案:x=27 y=79 (3) 44x+90y=7796 44x+y=3476答案:x=79 y=48 (4) 76x-66y=4082 30x-y=2940答案:x=98 y=51 (5) 67x+54y=8546 71x-y=5680答案:x=80 y=59 (6) 42x-95y=-1410 21x-y=1575答案:x=75 y=48 (7) 47x-40y=853 34x-y=2006答案:x=59 y=48 (8) 19x-32y=-1786 75x+y=4950答案:x=66 y=95 (9) 97x+24y=7202 58x-y=2900答案:x=50 y=98 (10) 42x+85y=6362 63x-y=1638答案:x=26 y=62 (11) 85x-92y=-2518 27x-y=486答案:x=18 y=44 (12) 79x+40y=2419 56x-y=1176答案:x=21 y=19 (13) 80x-87y=2156 22x-y=880答案:x=40 y=12(14) 32x+62y=5134 57x+y=2850答案:x=50 y=57 (15) 83x-49y=82 59x+y=2183答案:x=37 y=61 (16) 91x+70y=5845 95x-y=4275答案:x=45 y=25 (17) 29x+44y=5281 88x-y=3608答案:x=41 y=93 (18) 25x-95y=-4355 40x-y=2000答案:x=50 y=59 (19) 54x+68y=3284 78x+y=1404答案:x=18 y=34 (20) 70x+13y=3520 52x+y=2132答案:x=41 y=50 (21) 48x-54y=-3186 24x+y=1080答案:x=45 y=99 (22) 36x+77y=761947x-y=799答案:x=17 y=91 (23) 13x-42y=-2717 31x-y=1333答案:x=43 y=78 (24) 28x+28y=3332 52x-y=4628答案:x=89 y=30 (25) 62x-98y=-2564 46x-y=2024答案:x=44 y=54 (26) 79x-76y=-4388 26x-y=832答案:x=32 y=91 (27) 63x-40y=-821 42x-y=546答案:x=13 y=41 (28) 69x-96y=-1209 42x+y=3822答案:x=91 y=78 (29) 85x+67y=7338 11x+y=308答案:x=28 y=74 (30) 78x+74y=12928 14x+y=1218答案:x=87 y=83 (31) 39x+42y=5331 59x-y=5841答案:x=99 y=35 (32) 29x+18y=1916 58x+y=2320答案:x=40 y=42 (33) 40x+31y=6043 45x-y=3555答案:x=79 y=93 (34) 47x+50y=8598 45x+y=3780答案:x=84 y=93 (35) 45x-30y=-1455 29x-y=725答案:x=25 y=86 (36) 11x-43y=-1361 47x+y=799答案:x=17 y=36 (37) 33x+59y=3254 94x+y=1034答案:x=11 y=49 (38) 89x-74y=-2735 68x+y=1020答案:x=15 y=55(39) 94x+71y=7517 78x+y=3822答案:x=49 y=41 (40) 28x-62y=-4934 46x+y=552答案:x=12 y=85 (41) 75x+43y=8472 17x-y=1394答案:x=82 y=54 (42) 41x-38y=-1180 29x+y=1450答案:x=50 y=85 (43) 22x-59y=824 63x+y=4725答案:x=75 y=14 (44) 95x-56y=-401 90x+y=1530答案:x=17 y=36 (45) 93x-52y=-852 29x+y=464答案:x=16 y=45 (46) 93x+12y=8823 54x+y=4914答案:x=91 y=30 (47) 21x-63y=8420x+y=1880答案:x=94 y=30 (48) 48x+93y=9756 38x-y=950答案:x=25 y=92 (49) 99x-67y=4011 75x-y=5475答案:x=73 y=48 (50) 83x+64y=9291 90x-y=3690答案:x=41 y=92 (51) 17x+62y=3216 75x-y=7350答案:x=98 y=25 (52) 77x+67y=2739 14x-y=364答案:x=26 y=11 (53) 20x-68y=-4596 14x-y=924答案:x=66 y=87 (54) 23x+87y=4110 83x-y=5727答案:x=69 y=29 (55) 22x-38y=804 86x+y=6708答案:x=78 y=24 (56) 20x-45y=-3520 56x+y=728答案:x=13 y=84 (57) 46x+37y=7085 61x-y=4636答案:x=76 y=97 (58) 17x+61y=4088 71x+y=5609答案:x=79 y=45 (59) 51x-61y=-1907 89x-y=2314答案:x=26 y=53 (60) 69x-98y=-2404 21x+y=1386答案:x=66 y=71 (61) 15x-41y=754 74x-y=6956答案:x=94 y=16 (62) 78x-55y=656 89x+y=5518答案:x=62 y=76 (63) 29x+21y=1633 31x-y=713答案:x=23 y=46(64) 58x-28y=2724 35x+y=3080答案:x=88 y=85 (65) 28x-63y=-2254 88x-y=2024答案:x=23 y=46 (66) 43x+50y=7064 85x+y=8330答案:x=98 y=57 (67) 58x-77y=1170 38x-y=2280答案:x=60 y=30 (68) 92x+83y=11586 43x+y=3010答案:x=70 y=62 (69) 99x+82y=6055 52x-y=1716答案:x=33 y=34 (70) 15x+26y=1729 94x+y=8554答案:x=91 y=14 (71) 64x+32y=3552 56x-y=2296答案:x=41 y=29 (72) 94x+66y=1052484x-y=7812答案:x=93 y=27 (73) 65x-79y=-5815 89x+y=2314答案:x=26 y=95 (74) 96x+54y=6216 63x-y=1953答案:x=31 y=60 (75) 60x-44y=-352 33x-y=1452答案:x=44 y=68 (76) 79x-45y=510 14x-y=840答案:x=60 y=94 (77) 29x-35y=-218 59x-y=4897答案:x=83 y=75 (78) 33x-24y=1905 30x+y=2670答案:x=89 y=43 (79) 61x+94y=11800 93x+y=5952答案:x=64 y=84 (80) 61x+90y=5001 48x+y=2448答案:x=51 y=21 (81) 93x-19y=286x-y=1548答案:x=18 y=88 (82) 19x-96y=-5910 30x-y=2340答案:x=78 y=77 (83) 80x+74y=8088 96x-y=8640答案:x=90 y=12 (84) 53x-94y=1946 45x+y=2610答案:x=58 y=12 (85) 93x+12y=9117 28x-y=2492答案:x=89 y=70 (86) 66x-71y=-1673 99x-y=7821答案:x=79 y=97 (87) 43x-52y=-1742 76x+y=1976答案:x=26 y=55 (88) 70x+35y=8295 40x+y=2920答案:x=73 y=91(89) 43x+82y=4757 11x+y=231答案:x=21 y=47 (90) 12x-19y=236 95x-y=7885答案:x=83 y=40 (91) 51x+99y=8031 71x-y=2911答案:x=41 y=60 (92) 37x+74y=4403 69x-y=6003答案:x=87 y=16 (93) 46x+34y=4820 71x-y=5183答案:x=73 y=43 (94) 47x+98y=5861 55x-y=4565答案:x=83 y=20 (95) 30x-17y=239 28x+y=1064答案:x=38 y=53 (96) 55x-12y=4112 79x-y=7268答案:x=92 y=79 (97) 27x-24y=-45067x-y=3886答案:x=58 y=84 (98) 97x+23y=8119 14x+y=966答案:x=69 y=62 (99) 84x+53y=11275 70x+y=6790答案:x=97 y=59 (100) 51x-97y=297 19x-y=1520答案:x=80 y=39。
二元一次方程组经典练习题+答案解析100道(可编辑修改word版)

)
4
二、选择:
1、任何一个二元一次方程都有( )
(A)一个解;
(B)两个解;
(C)三个解;
(D)无数多个解;
2、如果
x y 3x 2 y
a
4
的解都是正数,那么
a
的取值范围是(
)
(A)a<2;
(B) a 4 ; (C) 2 a 4 ; (D) a 4 ;
3
3
3
3、关于
x、y
的方程组
x
y
பைடு நூலகம்
81 76 17 19
,若两人的计算都准确无误,请写出这个方程组,并求
出此方程组的解;
2、使 x+4y=|a|成立的 x、y 的值,满足(2x+y-1)2+|3y-x|=0,又|a|+a=0,求 a 的值;
3、要使下列三个方程组成的方程组有解,求常数 a 的值。 2x+3y=6-6a,3x+7y=6-15a,4x+4y=9a+9
2、某班学生到农村劳动,一名男生因病不能参加,另有三名男生体质较弱,教师安排他们与女生 一起抬土,两人抬一筐土,其余男生全部挑土(一根扁担,两只筐),这样安排劳动时恰需筐 68 个, 扁担 40 根,问这个班的男女生各有多少人?
3、甲、乙两人练习赛跑,如果甲让乙先跑 10 米,那么甲跑 5 秒钟就可以追上乙;如果甲让乙先跑 2 秒钟,那么甲跑 4 秒钟就能追上乙,求两人每秒钟各跑多少米?
x x
2 y
y 3m 9m
的解是方程
3x+2y=34
的一组解,那么
m
的值是(
)
(A)2;
(B)-1;
二元一次方程组练习题(含答案)

二元一次方程组练习题(含答案)1.解下列方程组:1) 5x + 2y = 11a,-4y = 6a;2) 4x + 3y - 1 = 0,2x + y - 2 = 0;3) x + 2y/3 - 1/3 = 2,x/3 + 1 - y/2 = 1/2;4) x - y/2 = 1,x + y/2 = 3.2.求解以下方程组:1) 2x + 3y = 7,x - y = 1;2) x + 2y = 5,2x + y = 7;3) 3x + 2y = 8,4x - 3y = -11.3.已知二元一次方程y = kx + b的解有(2,5)和(-1,0)。
1) 求k,b的值;2) 当x = 2时,y的值;3) 当y = 3/5时,x的值。
4.在解方程组2x + y = 5,x - y = 1时,甲看错了方程组中的a,而得到解x = 2,y = 1.乙看错了方程组中的b,而得到解x = 3,y = -1.1) 甲把a看成了什么,乙把b看成了什么?2) 求出原方程组的正确解。
参考答案与解析:1.解下列方程组:1) 5x + 2y = 11a,-4y = 6a。
将第二个方程式化简为y = -3/2a,代入第一个方程式中得到5x + 2(-3/2a) = 11a,化简得到x = (23/10)a,y = (-9/5)a。
2) 4x + 3y - 1 = 0,2x + y - 2 = 0.将第二个方程式中的y用第一个方程式中的x表示,得到y = 2 - 2x,代入第一个方程式中得到4x + 3(2 - 2x) - 1 = 0,化简得到x = 1/2,y = 1.3) x + 2y/3 - 1/3 = 2,x/3 + 1 - y/2 = 1/2.将第二个方程式中的x用第一个方程式中的y表示,得到x = 6 - 2y,代入第一个方程式中得到6 - 4y/3 = 2,化简得到y = 3/2,x = 0.4) x - y/2 = 1,x + y/2 = 3.将两个方程式相加得到2x = 4,化简得到x = 2,代入第一个方程式中得到y = 2.2.求解以下方程组:1) 2x + 3y = 7,x - y = 1.将第二个方程式中的x用第一个方程式中的y表示,得到x = y + 1,代入第一个方程式中得到2(y + 1) + 3y = 7,化简得到y = 1,x = 2.2) x + 2y = 5,2x + y = 7.将第一个方程式中的x用第二个方程式中的y表示,得到x = (7 - y)/2,代入第一个方程式中得到(7 - y)/2 + 2y = 5,化简得到y = 1,x = 2.3) 3x + 2y = 8,4x - 3y = -11.将第一个方程式中的x用第二个方程式中的y表示,得到x = (3y - 11)/4,代入第一个方程式中得到3(3y - 11)/4 + 2y = 8,化简得到y = 1,x = 1.3.已知二元一次方程y = kx + b的解有(2,5)和(-1,0)。
二元一次方程组经典练习题+答案解析100道.doc

二元一次方程组练习题100道(卷一)(范围:代数: 二元一次方程组)一、判断1、⎪⎩⎪⎨⎧-==312y x 是方程组⎪⎪⎩⎪⎪⎨⎧=-=-910326523y x y x 的解 …………( ) 2、方程组⎩⎨⎧=+-=5231y x x y 的解是方程3x -2y =13的一个解( )3、由两个二元一次方程组成方程组一定是二元一次方程组( )4、方程组⎪⎪⎩⎪⎪⎨⎧=-++=+++25323473523y x y x ,可以转化为⎩⎨⎧-=--=+27651223y x y x ( ) 5、若(a 2-1)x 2+(a -1)x +(2a -3)y =0是二元一次方程,则a 的值为±1( )6、若x +y =0,且|x |=2,则y 的值为2 …………( )7、方程组⎩⎨⎧=+-=+81043y x x m my mx 有唯一的解,那么m 的值为m ≠-5 …………( ) 8、方程组⎪⎩⎪⎨⎧=+=+623131y x y x 有无数多个解 …………( ) 9、x +y =5且x ,y 的绝对值都小于5的整数解共有5组 …………( )10、方程组⎩⎨⎧=+=-3513y x y x 的解是方程x +5y =3的解,反过来方程x +5y =3的解也是方程组⎩⎨⎧=+=-3513y x y x 的解 ………( )11、若|a +5|=5,a +b =1则32-的值为b a ………( )12、在方程4x -3y =7里,如果用x 的代数式表示y ,则437y x +=( ) 二、选择:13、任何一个二元一次方程都有( )(A )一个解; (B )两个解;(C )三个解; (D )无数多个解;14、一个两位数,它的个位数字与十位数字之和为6,那么符合条件的两位数的个数有( )(A )5个 (B )6个 (C )7个 (D )8个15、如果⎩⎨⎧=+=-423y x a y x 的解都是正数,那么a 的取值范围是( ) (A )a <2; (B )34->a ; (C )342<<-a ; (D )34-<a ;16、关于x 、y 的方程组⎩⎨⎧=-=+m y x m y x 932的解是方程3x +2y =34的一组解,那么m 的值是( ) (A )2; (B )-1; (C )1;(D )-2; 17、在下列方程中,只有一个解的是( )(A )⎩⎨⎧=+=+0331y x y x (B )⎩⎨⎧-=+=+2330y x y x (C )⎩⎨⎧=-=+4331y x y x (D )⎩⎨⎧=+=+3331y x y x 18、与已知二元一次方程5x -y =2组成的方程组有无数多个解的方程是( )(A )15x -3y =6 (B )4x -y =7 (C )10x +2y =4 (D )20x -4y =319、下列方程组中,是二元一次方程组的是( )(A )⎪⎩⎪⎨⎧=+=+9114y x y x (B )⎩⎨⎧=+=+75z y y x (C )⎩⎨⎧=-=6231y x x (D )⎩⎨⎧=-=-1y x xy y x 20、已知方程组⎩⎨⎧-=+=-135b y ax y x 有无数多个解,则a 、b 的值等于( )(A )a =-3,b =-14(B )a =3,b =-7 (C )a =-1,b =9 (D )a =-3,b =1421、若5x -6y =0,且xy ≠0,则yx y x 3545--的值等于( ) (A )32 (B )23 (C )1 (D )-122、若x 、y 均为非负数,则方程6x =-7y 的解的情况是( )(A )无解 (B )有唯一一个解(C )有无数多个解 (D )不能确定23、(A )14 (B )-4 (C )-12 (D )1224、已知⎩⎨⎧-==24y x 与⎩⎨⎧-=-=52y x 都是方程y =kx +b 的解,则k 与b 的值为( ) (A )21=k ,b =-4 (B )21-=k ,b =4 (C )21=k ,b =4 (D )21-=k ,b =-4 三、填空:25、在方程3x +4y =16中,当x =3时,y =________,当y =-2时,x =_______若x 、y 都是正整数,那么这个方程的解为___________;26、27、如果0.4x -0.5y =1.2,那么用含有y 的代数式表示的代数式是_____________;28、29、方程|a |+|b |=2的自然数解是_____________;30、如果x =1,y =2满足方程141=+y ax ,那么a =____________; 31、已知方程组⎩⎨⎧-=+=+m y x ay x 26432有无数多解,则a =______,m =______; 32、若方程x -2y +3z =0,且当x =1时,y =2,则z =______;33、34、若x +y =a ,x -y =1同时成立,且x 、y 都是正整数,则a 的值为________;35、从方程组)0(030334≠⎩⎨⎧=+-=--xyz z y x z y x 中可以知道,x :z =_______;y :z =________; 36、四、解方程组五、解答题:47、甲、乙两人在解方程组 时,甲看错了①式中的x 的系数,解得⎪⎪⎩⎪⎪⎨⎧==475847107y x ;乙看错了方程②中的y 的系数,解得⎪⎪⎩⎪⎪⎨⎧==19177681y x ,若两人的计算都准确无误,请写出这个方程组,并求出此方程组的解;48、使x +4y =|a |成立的x 、y 的值,满足(2x +y -1)2+|3y -x |=0,又|a |+a =0,求a 的值;49、代数式ax 2+bx +c 中,当x =1时的值是0,在x =2时的值是3,在x =3时的值是28,试求出这个代数式;50、要使下列三个方程组成的方程组有解,求常数a 的值。
二元一次方程专项练习60题+解析答案

一元二次方程专练60题一.解答题(共60小题)1.解二元一次方程组.(1);(2).2.解下列方程组:(1);(2).3.解方程组:(1);(2).4.解方程组.(1);(2).5.解方程组:(1);(2).6.解下列方程组:(1);(2).7.解方程组:(1);(2).8.解二元一次方程组:(1);(2).9.按要求解下列方程组:(1)(用代入消元法);(2)(用加减消元法).10.解方程组:(1);(2).11.解下列方程组:(1)(代入消元法);(2)(加减消元法).12.解下列方程组:(1);(2).13.用指定的方法解下列方程组:(1)(代入法);(2)(加减法).14.解下列方程组.(1);(2).15.解方程组:(1);(2).16.解下列方程组:(1);(2).17.解二元一次方程组:(1).(2).18.解方程组:(1);(2).19.解方程组:(1);(2).20.用适当的方法解下列方程组:(1)(2).21.解方程组:(1);(2).22.解二元一次方程组:(1);(2).23.解二元一次方程组:(1);(2).24.解方程组:(1);(2).25.解方程组:(1);(2).26.解方程组:(1);(2).27.解方程组:(1);(2).28.解方程组:(1);(2).29.解方程组:(1);(2).30.解方程组:(1);(2).31.解方程组:(1);(2).32.解方程组:(1);(2).33.用适当的方法解方程组:(1);(2).34.解下列方程组:(1);(2).35.解方程组:(1);(2).36.解方程组:(1);(2).37.解方程组:(1);38.解方程组:(1);(2).39.解方程组:(1);(2).40.解下列方程组:(1);41.解下列方程组:(1);(2).42.用加减消元法解方程:(1);(2).43.解二元一次方程组:(1);44.解方程组:(1);(2).45.解方程:(1);(2).46.用适当的方法解下列方程组:(1);47.解方程组:(1);(2).48.解方程组:(1);(2).49.解方程组:(1);(2).50.解方程组:(1);(2).51.阅读以下材料:解方程组:;小亮在解决这个问题时,发现了一种新的方法,他把这种方法叫做“整体代入法”,解题过程如下:解:由①得x﹣y=1③,将③代入②得:(1)请你替小亮补全完整的解题过程;(2)请你用这种方法解方程组:.52.已知关于x、y的方程组的解满足x+y =﹣10,求代数式m2﹣2m+1的值.53.在解方程组时,由于粗心,甲看错了方程组中的a,得解为;乙看错了方程组中的b,得解为.(1)甲把a错看成了什么?乙把b错看成了什么?(2)求出原方程组的正确解.54.已知方程组和方程组的解相同求a、b的值.55.甲和乙两人同解方程组甲因抄错了a,解得,乙因抄错了b,解得,求5a﹣2b 的值.56.对于实数x、y,定义新运算:x*y=ax+by;其中a、b是常数,等式右边是通常的加法和乘法运算,已知1*2=1,(﹣3)*3=6.(1)分别求出a、b的值;(2)根据上述定义新运算,试求2*(﹣4)的值.57.甲、乙两位同学在解方程组时,甲把字母a看错了得到方程组的解为;乙把字母b看错了得到方程组的解为.(1)求a,b的正确值;(2)求原方程组的解.58.定义一种新运算“※”:规定m※n=am+bn﹣mn,其中a,b为常数,且6※15=270,8※10=360,求﹣2※1的值.59.若关于x,y的方程组与方程组的解相同.(1)求两个方程组的相同解;(2)求(3a﹣b)2023的值.60.已知方程组和有相同的解,求a﹣2b的值.一元二次方程专练60题参考答案与试题解析一.解答题(共60小题)1.解二元一次方程组.(1);(2).【解答】解:(1)①+②,得4x=12,∴x=3.把x=3代入②,得3+2y=3,解得y=0所以原方程组的解为;(2),②化简得:2(x﹣2)﹣3(y﹣2)=6,即2x﹣3y=4③,①+③得:3x=18,解得:x=6,将x=6代入①得:6+3y=14,解得:y=,∴原方程组的解为:.2.解下列方程组:(1);(2).【解答】解:(1),由①得,3x+2y=12③,②×③﹣③×2,得5y=60,解得y=12,将y=12代入③,得3x+24=12,解得x=﹣4,∴原方程组的解为;(2),由①得x+1=5y+10,∴x=5y+9③,由②得6x﹣15﹣12y﹣16=5,整理,得6x﹣12y=36,∴x﹣2y=6④,将③代入④,得5y+9﹣2y=6,解得y=﹣1,将y=﹣1代入③,得x=﹣5+9=4,∴原方程组的解为.3.解方程组:(1);(2).【解答】解:(1),把①代入②,得3x+4x=7,解得x=1,把x=1代入①,得y=2,故原方程组的解为;(2),①+②,得6x=24,解得x=4,把x=4代入②,得y=5,故原方程组的解为.4.解方程组.(1);(2).【解答】解:(1),①﹣②得:9y=18,解得:y=2,把y=2代入①中得:3x+10=5,解得:x=﹣,∴原方程组的解为:;(2)将原方程组化简整理得:,①×3得:24u+27v=36③,③﹣②得:2v=22,解得:v=11,把v=11代入①中得:8u+99=12,解得:u=﹣,∴原方程组的解为:.5.解方程组:(1);(2).【解答】解:(1),①×2﹣②得:5x=﹣5,解得:x=﹣1,将x=﹣1代入①得:﹣3﹣y=﹣4,解得:y=1,故原方程组的解为;(2),①×5+②×3得:19x=19,解得:x=1,将x=1代入①得:2+3y=8,解得:y=2,故原方程组的解为.6.解下列方程组:(1);(2).【解答】解:(1),把②代入①得,6y﹣7﹣y=13,解得y=4;把y=4代入②得,x=6×4﹣7=17,故方程组的解为;(2),①×3﹣②×2得,6x+15y﹣6x﹣4y=24﹣10,解得y=,把y=代入②得,3x+2×=5,解得x=,故方程组的解为.7.解方程组:(1);(2).【解答】解:(1),①+②×2,得11x=33,解得:x=3,把x=3代入①,得9+2y=7,解得:y=﹣1,所以方程组的解是;(2)整理得:,①×2+②,得5x=15,解得:x=3,把x=3代入①,得3+2y=7,解得:y=2,所以方程组的解是.8.解二元一次方程组:(1);(2).【解答】解:(1),①﹣②×2,得7y=﹣14,解得y=﹣2,将y=﹣2代入①,得2x﹣2=2,解得x=2,∴原方程组的解为;(2),由①得,3x+4y=36③,由②得3x﹣2y=9④,③﹣④,得6y=27,解得y=,将y=代入④,得3x﹣9=9,解得x=6,∴原方程组的解为.9.按要求解下列方程组:(1)(用代入消元法);(2)(用加减消元法).【解答】解:(1),由②,得y=5﹣3x③,把③代入①,得3x+2(5﹣3x)=7,解得x=1,把x=1代入①,得y=2,故原方程组的解为;(2),①+②×2,得7x=21,解得x=3,把x=3代入②,得y=5,故原方程组的解为.10.解方程组:(1);(2).【解答】解:(1),①×4得:8x﹣4y=20③,②+③得:11x=22,解得:x=2,把x=2代入①得:4﹣y=5,解得:y=﹣1,故原方程组的解是:;(2),整理得:,①+②得:8y=24,解得:y=3,把y=3代入②得:x+15=10,解得:x=﹣5,故原方程组的解是:.11.解下列方程组:(1)(代入消元法);(2)(加减消元法).【解答】解:(1),由①得:x=1+2y③,把③代入②,得4(1+2 y)+3y=26,解得:y=2,把y=2代入③,得x=1+2×2=5,所以;(2),由①+②,得7x=21,解得:x=3,把x=3代入①,得2×3+3y=3,解得:y=﹣1,所以.12.解下列方程组:(1);(2).【解答】解:(1)将原方程组化简整理得:,②×4得:8x+20y=28③,③﹣①得:27y=27,解得:y=1,把y=1代入②中得:2x+5=7,解得:x=1,∴原方程组的解为:;(2)将原方程组化简整理得:,①×3得:9x﹣12y=﹣21③,②×4得:8x+12y=4④,③+④得:17x=﹣17,解得:x=﹣1,把x=﹣1代入②中得:﹣2+3y=1,解得:y=1,∴原方程组的解为:.13.用指定的方法解下列方程组:(1)(代入法);(2)(加减法).【解答】解:(1),把①代入②得:4x+3(2x﹣2)=5,解得x=,把x=代入①得:y=2×﹣2=,∴方程组的解为;(2),①×3得:3x+9y=﹣3③,③﹣②得:11y=﹣11,解得:y=﹣1,把y=﹣1代入①得:x﹣3=﹣1,解得:x=2,∴方程组的解为.14.解下列方程组.(1);(2).【解答】解:(1),由①+②得,5x=﹣5,解得x=﹣1,将x=﹣1代入①,得﹣2+5y=8,解得y=2,∴方程组的解为;(2),由①×3,②×2得:,由③+④得,13x=26,解得:x=2,把x=2代入①,得y=4,所以方程组的解为:.15.解方程组:(1);(2).【解答】解:(1),由①得,x=1+2y③,把③代入②,得3(1+2y)﹣y=3,解得y=0,把y=0代入③,得x=1,所以原方程组的解为:;(2)原方程组可化为,①+②得,4x=24,解得x=6,①﹣②得,6y=﹣6,解得y=﹣1,所以原方程组的解为:.16.解下列方程组:(1);(2).【解答】解:(1),①+②,得2x=12,解得x=6,将x=6代入①,得6﹣y=5,解得y=1,∴原方程组的解为;(2)原方程组化为,①﹣②,得25y=10,解得y=,将y=代入①,得5x+6=6,解得x=0,∴原方程组的解为.17.解二元一次方程组:(1).(2).【解答】解:(1),②﹣①×2得:x=6,把x=6代入①得:6+2y=0,解得y=﹣3.∴方程组的解是.(2),①×2+②×3得:13x=65,解得x=5.把x=5代入①得:10+3y=16,解得y=2.∴方程组的解是.18.解方程组:(1);(2).【解答】解:(1)对于方程组,①×2得:4x﹣10y=24③,②﹣③得:﹣13y=26,∴y=﹣2,将y=﹣2代入①得:x=1,∴原方程组的解为:.(2)对于方程组,将①代入②得:2×2y+y=5,∴y=1,将y=1代入①得:x=2,∴原方程组的解为:.19.解方程组:(1);(2).【解答】解:(1),①+②得4x=8,∴x=2,把x=2代入①得2+2y=3,,∴原方程组的解是.(2),整理得:,由①得:s=﹣2t③,把③代入②得:t=﹣2;把t=﹣2 代入③得:s=4,∴原方程组的解是.20.用适当的方法解下列方程组:(1)(2).【解答】解:(1),①+②得:6x=18,解得:x=3,把x=3代入①得:y=﹣4,则方程组的解为;(2),把①代入②得:4x﹣14=2,解得:x=4,把x=4代入①得:y=3,则方程组的解为.21.解方程组:(1);(2).【解答】解:(1),原方程可化为:,①+②×5得:46y=46,∴y=1,将y=1代入①得:x=7,∴原方程组得解为:;(2),原方程可化为:,①×4+②得:19x=57,∴x=3,将x=3代入①得:y=0,∴原方程组得解为:.22.解二元一次方程组:(1);(2).【解答】解:(1),②﹣①,得y=1,把y=1代入①,得x=2,故原方程组的解为;(2)原方程组整理,得,②﹣①×2,得7y=7,解得y=1,把y=1代入①,得x=5.故原方程组的解为.23.解二元一次方程组:(1);(2).【解答】解:(1),由②得y=13﹣2x③,把③代入①,得4x﹣3(13﹣2x)=11,解得x=5,把x=5代入③,得y=3,∴这个方程组的解是;(2),①×2﹣②×3,得﹣19y=19,解得y=﹣1.把y=﹣1代入①,得3x+2=5,解得x=1,∴这个方程组的解为.24.解方程组:(1);(2).【解答】解:(1),把①代入②,得3x﹣8(x﹣3)=14,解得x=2,把x=2代入①,得y=﹣1,故原方程组的解为;(2),①×2﹣②,得7x=35,解得x=5,把x=5代入①,得y=0,故原方程组的解为.25.解方程组:(1);(2).【解答】解:(1),由①+②得:4x=8,解得:x=2,将x=2代入①得:2﹣2y=1,解得:y=,∴方程组的解为:;(2),由①可得:x=3﹣2y③,将③代入②得:3(3﹣2y)﹣4y=4,解得:y=,将y=代入③得:x=3﹣2×,解得:x=2,∴原方程组的解为:.26.解方程组:(1);(2).【解答】解:(1),①×2得:4x﹣2y=0③,②+③得:5x=5,解得:x=1,把x=1代入①中得:y=2,∴原方程组的解为:.(2),②×2,8x﹣2y=6③,①+③得:11x=11,解得:x=1,把x=1代入②,得4﹣y=3,解得:y=1,∴原方程组的解为:.27.解方程组:(1);(2).【解答】解:(1),①+②,得7x=35,解得:x=5,把x=5代入①,得10﹣3y=﹣2,解得:y=4,所以方程组的解是;(2),①+②×2,得11x=11,解得:x=1,把x=1代入②,得4﹣y=3,解得:y=1,所以方程组的解是.28.解方程组:(1);(2).【解答】解:(1),把②代入①得y﹣9+3y=7,解得y=4,把y=4代入②得x=4﹣9=﹣5,所以方程组的解为;(2),①×2+②得10x+3x=34+5,解得x=3,把x=3代入②得9+4y=5,解得y=﹣1,所以方程组的解为.29.解方程组:(1);(2).【解答】解:(1),①+②得:4x=8,解得:x=2,把x=2代入①得:2+2y=﹣1,解得:,∴方程组的解为;(2),由②得:y=2x﹣2,把y=2x﹣2代入①得:4x﹣3(2x﹣2)=5,解得:,把代入y=2x﹣2得:,∴方程组的解为.30.解方程组:(1);(2).【解答】解:(1),将①代入②,可得:3x+2x+3=18,解得x=3,把x=3代入①,可得:y=9,∴原方程组的解是.(2),①×2﹣②,可得7y=35,解得y=5,把y=5代入①,可得:x=0,∴原方程组的解是.31.解方程组:(1);(2).【解答】解:(1),把①代入②得:3x+2(2x﹣1)=5,解得:x=1,把x=1代入①得:y=2﹣1=1,故原方程组的解是:;(2),①+②得:3m=6,解得:m=2,把m=2代入①得:2+3n=5,解得:n=1,故原方程组的解是:.32.解方程组:(1);(2).【解答】解:(1)把②代入①中,得3x+2(2x﹣8)=5.解得x=3.把x=3代入②中,得y=2×3﹣8解得y=﹣2.∴这个方程组的解为;(2)①﹣②,得﹣4y=8.解得y=﹣2.把y=﹣2代入①中,得2x+2=10.解得x=4.∴这个方程组的解为.33.用适当的方法解方程组:(1);(2).【解答】解:(1),②﹣①×3得:x=1,把x=1代入①中,解得:y=1,∴这个方程组的解为;(2)方程组整理为:,②×2+①得:5x=30,解得:x=6,把x=6代入②中,解得:y=9,∴这个方程组的解为.34.解下列方程组:(1);(2).【解答】解:(1),将①代入②,得:3x﹣2(2x+1)=2,解得:x=﹣4,把x=﹣4代入①得:y=﹣7,∴方程组的解为:;(2)①×2+②,得:5x=10,解得:x=2,把x=2代入①,得:4+y=1,解得:y=﹣3,∴方程组的解为:.35.解方程组:(1);(2).【解答】解:(1),①+②得,7x=14,解得x=2,把x=2代入①得,3×2+7y=9,解得y=,∴方程组的解是;(2),①×3得,15x+6y=12③,②×2得,16x+6y=14④,④﹣③得,x=2,把x=2代入①得,y=﹣3,∴方程组的解是.36.解方程组:(1);(2).【解答】解:(1),②﹣①得:y=2,把y=2代入①得:,∴方程组的解为:;(2),由③得:y=3﹣2x,把y=3﹣2x代入④得:3x﹣5(3﹣2x)=11,3x﹣15+10x=11,13x=26,x=2,把x=2代入y=3﹣2x得:y=﹣1,∴方程组的解为:.37.解方程组:(1);(2).【解答】解:(1),①×3得:3x﹣15y=0③,②﹣③得:17y=17,解得:y=1,把y=1代入①得:x﹣5=0,解得:x=5,∴原方程组的解为:;(2),把①代入②得:y﹣13﹣6y=7,解得:y=﹣4,把y=﹣4代入①得:x=﹣4﹣13=﹣17,∴原方程组的解为:.38.解方程组:(1);(2).【解答】解:(1),①+②得:5x=25,解得:x=5,把x=5代入①得:5﹣3y=10,解得:y=﹣,故原方程组的解是:;(2),由①得:3x﹣2y=8③,②+③得:6x=12,解得:x=2,把x=2代入②得:6+2y=4,解得:y=﹣1,故原方程组的解是:.39.解方程组:(1);(2).【解答】解:(1),①+②得:3x=12,解得:x=4,把x=4代入①得:4﹣y=2,解得:y=2,则方程组的解为;(2)方程组整理得:,①×4﹣②×3得:﹣7x=﹣14,解得:x=2,把x=2代入①得:4﹣3y=1,解得:y=1,则方程组的解为.40.解下列方程组:(1);(2).【解答】解:(1),由①,得x=y+3③,把③代入②,得3y+9﹣8y=14,解得y=﹣1,把y=﹣1代入①,得x=2,故原方程组的解为;(2),①×2+②,得11x=11,解得x=1,把x=1代入①,得x=﹣2,故原方程组的解为.41.解下列方程组:(1);(2).【解答】解:(1),②代入①,可得x+2x﹣1=2,解得,x=1,将x=1代入②,可得y=1,故方程组的解为.(2),②﹣①,可得,解得,x=3,将x=3代入①,可得y=2,故方程组的解为.42.用加减消元法解方程:(1);(2).【解答】解:(1),①﹣②得:12y=﹣36,即y=﹣3,把y=﹣3代入①得:x=,则方程组的解为;(2)方程组整理得:,①﹣②得:4y=28,即y=7,把y=7代入①得:x=5,则方程组的解为.43.解二元一次方程组:(1);(2).【解答】解:(1)方程整理得,由①+②得:5a+5b=﹣5,即a+b=﹣1③,由①﹣③×2得:b=1,把b=1代入③得:a+1=﹣1,解得a=﹣2,∴方程组的解是.(2),由②得:x=3y﹣2③,把③代入①得:9(3y﹣2)﹣7y﹣12=0,解得y=,把y=代入③得x=﹣2=,∴方程组的解是.44.解方程组:(1);(2).【解答】解:(1),解:①+②得3x=33,解得x=11,把x=11代入①得y=14,∴方程组的解是;(2),解:原方程组可化为,①﹣②得6x=6,解得x=1,把x=1代入①得,∴方程组的解是.45.解方程:(1);(2).【解答】解:(1),①代入②得,2x+(3x+1)=﹣9,解得:x=﹣2,将x=﹣2代入①得,y=﹣5,∴方程组的解为:;(2),①×2+②得,6x+x=14,解得:x=2,将x=2代入①得6﹣2y=5,解得:,∴方程组的解为:.46.用适当的方法解下列方程组:(1);(2).【解答】解:(1),由①﹣②×2得:3y﹣(﹣2y)=1﹣5×2,解得:,将代入②得:,解得:,∴原方程组的解为;(2),由①×2+②得:7x=14,解得:x=2,把x=2代入①得:2×2+y=2,解得:y=﹣2,∴原方程组的解为.47.解方程组:(1);(2).【解答】解:(1),①×3+②得:7y=28,解得:y=4,将y=4代入①得:x=1,∴方程组的解为:;(2)整理得:,①+②×5得:23y=23,解得y=1,把y=1代入①得:5x﹣2=﹣12,解得x=﹣2,∴方程组的解为.48.解方程组:(1);(2).【解答】解:(1),①+②得,2x=6,解得:x=3,把x=3代入①得y=﹣1,∴方程组的解为;(2),①×2,得10x+4y=50③,③﹣②,得7x=35,解得:x=5,把x=5代入①得,25+2y=25,解得:y=0,所以方程组的解为.49.解方程组:(1);(2).【解答】解:(1),整理得:,由①﹣②得:4y=28,解得:y=7,把y=7代入①得:3x﹣7=8,解得:x=5,∴原方程组的解为:;(2),由②﹣①得:5x=15,解得:x=3,把x=3代入①得:y﹣2×3=0,解得:y=6,∴原方程组的解为.50.解方程组:(1);(2).【解答】解:(1),②×3得:15x+3y=21③,①+③得:19x=38,解得:x=2,把x=2代入②得:10+y=7,解得:y=﹣3,故原方程组的解是:;(2),①×2得:2x﹣4y=16③,②+③得:5x=10,解得:x=2,把x=2代入①得:2﹣2y=8,解得:y=﹣3,故原方程组的解是:.51.阅读以下材料:解方程组:;小亮在解决这个问题时,发现了一种新的方法,他把这种方法叫做“整体代入法”,解题过程如下:解:由①得x﹣y=1③,将③代入②得:(1)请你替小亮补全完整的解题过程;(2)请你用这种方法解方程组:.【解答】解:(1)由①得x﹣y=1③,将③代入②得:4×1﹣y=0,解得y=4,把y=4代入①得:x﹣4﹣1=0,解得x=5,故原方程组的解是:;(2),整理得:,把③代入④得:2×2+1+15y=50,解得y=3,把y=3代入①得:3x﹣3﹣2=0,解得x=,故原方程组的解是:.52.已知关于x、y的方程组的解满足x+y =﹣10,求代数式m2﹣2m+1的值.【解答】解:,①×2﹣②×3得:y=4﹣m,把y=4﹣m代入②得:x=2m﹣6,代入x+y=﹣10得:4﹣m+2m﹣6=﹣10,解得:m=﹣8,则原式=(m﹣1)2=81.53.在解方程组时,由于粗心,甲看错了方程组中的a,得解为;乙看错了方程组中的b,得解为.(1)甲把a错看成了什么?乙把b错看成了什么?(2)求出原方程组的正确解.【解答】解:(1)将x=,y=﹣2代入方程组得:,解得:,将x=3,y=﹣7代入方程组得:,解得:,则甲把a错看成了1;乙把b错看成了1;(2)根据(1)得正确的a=2,b=3,则方程组为,解得:.54.已知方程组和方程组的解相同求a、b的值.【解答】解:方程组的解为,由于方程组和方程组的解相同,所以,解得.55.甲和乙两人同解方程组甲因抄错了a,解得,乙因抄错了b,解得,求5a﹣2b的值.【解答】解:由题意,是bx+y=12的解得5b+2=12,解得b=2.又是x+ay=5的解得3+2a=5,解得a=1,∴5a﹣2b=5×1﹣2×2=1.56.对于实数x、y,定义新运算:x*y=ax+by;其中a、b是常数,等式右边是通常的加法和乘法运算,已知1*2=1,(﹣3)*3=6.(1)分别求出a、b的值;(2)根据上述定义新运算,试求2*(﹣4)的值.【解答】解:(1)根据题中的新定义化简得:,解得:;(2)根据题中的新定义得:原式=2×(﹣1)+(﹣4)×1=﹣2﹣4=﹣6.57.甲、乙两位同学在解方程组时,甲把字母a看错了得到方程组的解为;乙把字母b看错了得到方程组的解为.(1)求a,b的正确值;(2)求原方程组的解.【解答】解:(1)由题意,将代入bx﹣4y=4,得4b﹣4=4,∴b=2,将代入ax+3y=9,得3a+6=9,∴a=1;(2),①×2﹣②,得y=1.4,将y=1.4代入①得,x=4.8,∴方程组的解为.58.定义一种新运算“※”:规定m※n=am+bn﹣mn,其中a,b为常数,且6※15=270,8※10=360,求﹣2※1的值.【解答】解:∵6※15=270,8※10=360,∴,解得:,∴﹣2※1=﹣100+4﹣(﹣2)×1=﹣94.59.若关于x,y的方程组与方程组的解相同.(1)求两个方程组的相同解;(2)求(3a﹣b)2023的值.【解答】解:(1)两方程组化简可得,,∵两方程组同解,∴①×2+②得:7x=21,解得:x=3,把x=3代入①式得:y=1,∴两个方程组的相同解为;(2)把代入方程组可得:①﹣②式得:2a=﹣4,解得:a=﹣2,把a=﹣2代入②式得:b=﹣5,∴(3a﹣b)2023=(﹣6+5)2023=﹣1.60.已知方程组和有相同的解,求a﹣2b的值.【解答】解:联立得:,①×2+②得:11x=11,解得:x=1,把x=1代入②得:y=﹣2,把代入,得,解得:,则a﹣2b=14﹣4=10.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二元一次方程练习题及答案
A .
B. C. D. 2
x y 4
2x 3y 7
5b 4c 6
y
2x
3. 二兀 次方程 5a — 11b=21 ()
A . 有且只有 一解
B . 有无数解
C . 无解
D. 有且只有两解
4.方程 y=1 — x 与3x+2y=5的公共解是(
)
x 3 x 3
x 3
x
3 A .
B.
C.
D.
y 2
y 4
y
2
y
2
5.若丨 x — 2 | +
(3y+2) 2=0, 则的值是(
)
3 A . —1
B . — 2
C .- -3
D . —
2
6.方程组 3y k
的解与
x 与y 的值相等, 则k 等于 ()
2.
2
2a 1
1
2x
7.
)
)
F 列方程组中,是二
元 x y 4 次方程组的是(
3b 3y 5
F 列各式,属于二元一次方程的个数
有
1. 、选择题:
下列方程中,是二元一次方程的是(
A . 3x — 2y=4z
B . 6xy+9=0
1 +4y=6 x
D . 4x=--
4
① xy+2x — y=7 ; ② 4x+1=x — y ;
⑥ 6x — 2y
A . 1
B . 2 某年级学生共有 246人, 方程组中符合题意的有 x y 246
A .
2y x 2
⑦x+y+z=1 C . 3
其中男生人数 )
x y 246 2x y 2 B.
二、填空题
9 .已知方程 2x+3y —
4=0 , 为:x= __ . 1
③一+y=5 ;④ x=y ;
x
⑧y (y — 1) =2y 2— y 2+x
D . 4
y 比女生人数
x y C . y y 2x
x 的2倍少 216 D.
⑤ x 2—y 2=2
2人,?则下面所列的
x y 246 2y x 2
用含x 的代数式表示y 为:y= ;用含y 的代数式表示x
一 1
10. 在二兀一次方程— 一
2
11. 若 x 3m 3 — 2y n 1=5 是二元一次方程,则 m= ______ , n=
x+3y=2 中,当 x=4 时,y= ;当 y= — 1 时,x=
x 2
12.已知
'是方程x — ky=1的解,那么k= _______ .
y 3
13 .已知 |x — 1 | + ( 2y+1 ) 2=0,且 2x — ky=4,贝U k=__ . 14. 二元一次方程 x+y=5的正整数解有 _________________ .
x 5
一
15.
以 _________________________________ 为解的一个二兀一次方程是 .
y 7
16. 已知 %
2
是方程组
mx y 3
的解,贝V m= _________ , n= ______ .
y 1
x ny 6
三、解答题
17. 当y= — 3时,二元一次方程 3x+5y= — 3和3y — 2ax=a+2 (关于x , y 的方程)?有相同
的解,求a 的值.
20 .已知x , y 是有理数,且(|x | — 1) 2+ (2y+1) 2=0,贝U x — y 的值是多少?
1&如果(a — 2) x+ (b+1) y=13是关于x , y 的二元一次方程,则 a , b 满足什么条件?
19 .二兀一次方程组
4x 3y 7
的解x
kx (k 1)y 3
y 的值相等,求 k .
21. 已知方程-x+3y=5,请你写出一个二元一次方程,?使它与已知方程所组成的方程组2
的解为
22. 根据题意列出方程组:
(1)明明到邮局买0.8元与2元的邮票共13枚,共花去20元钱,?问明明两种邮票各买了多少枚?
(2)将若干只鸡放入若干笼中,若每个笼中放4只,则有一鸡无笼可放; 里放5只,则有一笼无鸡可放,问有多少只鸡,多少个笼?
x y25 、23.方程组的解是否满足2x—y=8 ?满足2x —y=8的一对x, y的值是否是方
2x y8
x y25
程组的解?
2x y8
24.(开放题)是否存在整数m,使关于x的方程2x+9=2 —(m —2) x在整数范围内有解, 你能找
到几个m的值?你能求出相应的x的解吗?
答案: 一、选择题
1. D 解析:掌握判断二元一次方程的三个必需条件:①含有两个未知数;②含有未知数 的项
的次数是1;③等式两边都是整式. 2. A 解析:二元一次方程组的三个必需条件:①含有两个未知数,②每个含未知数的项 次数
为1 ;③每个方程都是整式方程. 3. B 解析:不加限制条件时,一个二元一次方程有无数个解. 4. C 解析:用排除法,逐个代入验证. 5. C 解析:利用非负数的性质. 6. B
7. C 解析:根据二元一次方程的定义来判定,
?含有两个未知数且未知数的次数不超过
1次的整式方程叫二元一次方程,注意⑧整理后是二元一次方程. & B 二、填空题 2
'代入方程 x — ky=1 中,得一2— 3k=1,二 k= — 1.
3
13. 4 解析:由已知得 x —仁0, 2y+仁0,
x 1
1
把 1 • x=1 , y=—
1
代入方程 2x — ky=4 中,2+ k=4 , • 2
y
2
2
x 1
x 2
x 3
x 4 14.解:
y 4 y 3 y 2
y 1
解析:••• x+y=5 , •
■- y=5 — x , 又 •/ x , y 均为正整数, ••• x 为小于5的正整数.当 x=1时,y=4 ;当x=2时,y=3; 当 x=3 , y=2 ;当 x=4 时,
y=1 .
,+… x 1 x 2
x 3 x+y=5的正整数解为
y 4
y 3
y 2
15.
x+y=12 解析:以x 与y 的数量关系组建方程,如 2x+y=17 , 2x — y=3等, 此题答
案不唯一. x 2 八、、十小 mx y 3亠―” 16. 1 4解析:将 代入万程组 中进行求解.
y 1 x ny 6
三、解答题
9.
4 2x 11.
4 3y 4
10. — —10
2
3
4
解析:令 3m — 3=1, n — 1=1,「. m= — , n=2 .
x 12.— 1 解析:把
y
y= —3 时,3x+5y= —3 ,• 3x+5 x( —3) = —3 ,• x=4 , 17.解:
0.
•••方程 3x+5y=? — ?3?和 3x — 2ax=a+2 有相同的解, 11 --3 x( — 3) — 2a x 4=a+2,…a=—
9
18. 解:T( a — 2) x+ (b+1) y=13是关于x , y 的二元一次方程,
•- a — 2工 0, b+1 工 0, ? • a H 2, b 工一1
解析:此题中,若要满足含有两个未知数,需使未知数的系数不为 (?若系数为0,则该项就是0)
19 .解:由题意可知 x=y , • 4x+3y=7可化为4x+3x=7 ,
• x=1 , y=1 .将 x=1 , y=?1?代入 kx+ (k — 1) y=3 中得 k+k — 1=3 ,
• k=2解析:由两个未知数的特殊关系,可将一个未知数用含另一个未知数的代数式 代替,化“二元”为“一元”,从而求得两未知数的值. 1
—仁0 且 2y+ 仁0 , /• x= ± 1, y=—
2
、「, 1 z
1 3
当 x=1 , y= 一 时,x 一 y=1+
= ;
2 2 2 七
1评
1
1
当 x= — 1, y=— 时,x — y= — 1+
=—
.
2 2 2
解析:任何有理数的平方都是非负数,且题中两非负数之和为 则这两非负数(| x 21.解:经验算
y 22.( 1)解:设0. 8元的邮票买了 x 枚, 2元的邮票买了 y 枚,根据题意得
4y 1 x (2 )解:设有x 只鸡,y 个笼,根据题意得5(y 1) x
23. 解:满足,不一定.
x y 25
、
解析:T
的解既是方程x+y=25的解,也满足2x — y=8, ?
2x y 8
•••方程组的解一定满足其中的任一个方程,
X
如x=10, y=12,不满足方程组
2x 24. 解:存在,四组.•••原方程可变形为— •••当 m=1 时,x= — 7; m= — 1 时,x=7 ;
20.解:由(|x
—1) 2
+ (2y+1 ) 2
=0,可得 |
x | — 1) 2与(2y+1) 2都等于0,从而得到丨 4
、
1
是方程 x+3y=5的解,再写一个方程,如
x — y=3 .
1 2
0, x | — 1=0,
x y 13 0.8x 2y 20
2x — y=8的解有无数组,
但方程
y 25 y 8
mx=7 ,
m=?7 时,x= — 1; m= — 7 时
x=1 .。
