三角形连接与星行连接
电机的星形连接、角形连接

三相电机有三组绕组,一般在接入三相电源时,有三角形连接(△连接)和星形连接(Y连接)两种方式。
星形连接(Y连接)就是将三组线圈顶点接在一起,然后把三组线圈另三个顶点接到电源的三根线上(下图图加电源接在U1,V1,W1即可),交换其中任意两根一次,转向会改变一次。
下面给一个星形连接和三角形连接的示意图:星形连接的线电压是相电压的1.732倍(线电流等于相电流),三角形的线电压等于相电压(线电流是相电流的1.732倍),在电机设计阶段,都会折算成等效三个等效单相,因为三相电机的等效电路是等效成单相的。
对于一个输入线电压为380V的电机而言,如果设计成星形,那么就按220V计算单相电路,如果设计成角形,那么就按380V计算单相电路,但相电流减小。
星形电机内部不会产生环流,理论上比三角形好,因为实际上三相绕组不可能绝对平衡,三相电压总有微小差异,这样在三角形内部会形成环流造成发热和效率降低(当然这个影响实际上很小)。
做成三角形连接是有历史原因的,那就是没有变频器的时候,电机启动时可以利用接触开关改变连接,将其接成星形,这样每个绕组的电压由380降低为220,大大减小了启动冲击电流,待启动后切换成三角形。
这就是所谓的星-三角启动。
星-三角启动可以成比例降低启动电流,但是会成平方降低启动转矩,所以只能用在轻载或空载启动。
大家看到的风机、水泵用星-三角启动没问题,但是起重机上肯定没有用星-三角启动的,起重机都是用绕线转子串电阻启动。
区别三角形连接和星形连接从电机外部看是没有任何区别的,你可以把电机看成一个黑盒子,外面看就是三根进线,通以互差120度的电流。
要说到电机三角形连接和星形连接的区别,只是在电机本体设计的时候会关注,我们知道,教科书上写星形连接的线电压是相电压的1.732倍,三角形的线电压等于相电压,在电机设计阶段,都会折算成等效三个等效单相,因为三相电机的等效电路是等效成单相的。
对于一个输入线电压为380V的电机而言,如果设计成星形,那么就按220V计算单相电路,如果设计成角形,那么就按380V计算单相电路,但相电流减小。
电阻星形连接与三角形连接的等效变换

公正处法人授权委托书范本一、前言为了明确公正处法人的授权范围和内容,确保代理人能够合法、合规地代表法人行事,特制定本授权委托书。
本授权委托书旨在规范法人授权行为,保障法人及其代理人的合法权益,维护社会经济秩序。
二、授权主体1. 授权单位:×××公正处2. 法定代表人:×××3. 授权人:×××三、授权范围1. 代理人代表公正处参加各类法律诉讼活动,包括但不限于起诉、应诉、举证、质证、调解、和解等。
2. 代理人代表公正处与各类当事人进行法律事务谈判、协商,并签署相关法律文件。
3. 代理人代表公正处处理各类法律事务,包括但不限于合同审查、起草、签订、变更、解除等。
4. 代理人代表公正处参加各类行政复议、行政诉讼活动,维护公正处的合法权益。
5. 代理人代表公正处处理各类法律咨询、法律培训、法律宣传等活动。
6. 代理人代表公正处与各类政府部门、企事业单位、社会团体等进行法律事务往来。
7. 代理人代表公正处处理其他各类法律事务,包括但不限于知识产权、劳动关系、交通事故等。
四、授权期限本授权委托书的有效期为自授权人之签名或盖章之日起至法定代表人书面声明本授权作废之日止。
五、授权方式1. 法定代表人签字或盖章。
2. 公正处盖章。
六、注意事项1. 代理人应当在授权范围内行事,不得超出授权范围进行任何活动。
2. 代理人不得转委托授权,不得将授权事项转让给他人。
3. 代理人不得以公正处名义从事任何非法活动,不得损害公正处的合法权益。
4. 代理人应当严格遵守国家法律法规,合规行事。
5. 代理人应当保持与当事人的良好沟通,确保授权事项的顺利进行。
6. 代理人应当及时向法定代表人报告授权事项的进展情况。
七、法律后果1. 代理人依据本授权委托书行事,其法律后果由公正处承担。
2. 代理人超出授权范围行事,其法律后果由代理人自行承担。
3. 代理人违反国家法律法规、本授权委托书约定,给公正处造成损失的,应当承担赔偿责任。
星形接法和三角形接法的区别

星形接法和三角形接法的区别三角形接法,可以比作一个三角形,分三个点,每个点均为火线,火火之间,为380V。
星形接法,可以比作三条线连接在一个公共点上,而公共点则是零,火零之间,为220V.星形接法启动电流较小,三角形接法启动电流大。
现在一般都是变频器,星三角转换很少了。
三相交流电有两种连接方式,星形连接和角形连接星形连接——就是把三相负载的3个末端连接在一起作为公共端,由3个首端引出3条火线的连接方式。
(如A相负载用Ax表示,B相负载用By表示,C相负载用Cz表示,那就是x和y和z连一起,引出A、B、C三根线)负载每相线圈承受的电压是相电压220伏,即火线与零线(中性线)间的电压是220V。
角形连接——就是把三相负载的每一相的始末端依次相接的连接方式。
(如A相负载用Ax表示,B相负载用By表示,C相负载用Cz 表示,那就是x和B相连,y和C相连,z和A相连,引出的三根线为Bx、Cy、Az)每相负载承受的电压是线电压380伏,即火线与火线间的电压。
相电压——每相绕组两端的电压,叫相电压。
线电压——任意两根火线之间的电压叫线电压。
相电流——流过每相负载的电流叫相电流。
线电流——流过每相线的电流叫线电流。
星形连接中:U相=1.732U线 I相=I线三角形连接:三角形连接中 U相=U线 I线=1.732I相1、绕组的区别星形接法和三角形接法都是指电机本身的绕组接法,星形接法指将电机绕组三相末端接在一起,三相首端为电源端;三角形接法指将三相绕组首尾互相连接,三个端点为电源端。
2、功率的区别星形接法由于起输出功率小,常用于小功率,大扭矩电机,或功率较大的电机起步时候用,这样对机器损耗较小,正常工作后再换用三角形接法。
3、电压方面的区别星形接法与三角形接法输出的相电压分别为220V与380V。
4、常见接法。
星形接法和三角接法区别

星形接法和三角接法区别-CAL-FENGHAI.-(YICAI)-Company One1星形接法基本简介把三相电源三个绕组的末端、X、Y、Z连接在一起,成为一公共点O,从始端A、B、C引出三条端线,这种接法称为“星形接法”又称“Y形接法”。
三相电源是由频率相同、振幅相等而相位依次相差120°的三个正弦电源以一定方式连接向外供电的系统。
三相电源的联接方式有Y形和△形两种。
星形接法三相电的星形接法是将三相电源绕组或负载的一端都接在一起构成中性线,由于均衡的三相电的中性线中电流为零,故也叫零线:三相电源绕组或负载的另一端的引出线,分别为三相电的三个相线。
远程输电时,只使用三根相线,形成三相三线制。
到达用户的电路,往往涉及220V 和380V两种电压,需三根相线和一根零线,形成三相四线制。
用户为避免漏电形成的触电事故,还要添加一根地线,这时就有三根相线,一根零线和一根地线,故也有三相五线制的说法。
2常用的接法编辑对称三相四线Y-Y系统是常见常用的系统,有三条火线、一条中线。
星形接法的三相电,线电压是相电压的根号3倍,而线电流等于相电流。
当三相负载平衡时,即使连接中性线,其上也没有电流流过。
三相负载不平衡时,应当连接中性线,否则各相负载将分压不等。
星形接法主要应用在高压大型或中型容量的电动机中,定子绕组只引出三根线。
对于星形接法,各相负载平衡,则任何时刻流经三相的电流矢量和等于零。
星形(Y)接法和三角形(△)接法关系密切,其负载相电压、相电流与对称三相线电压、线电流关系如下:星形接法和三角形接法星形接法I线=I相,U线=√3×U相,P相=U相×I相,P=3P相=√3×U线×I相=√3×U线×I线;三角接法I线=√3×I相,U线=U相,P相=I相×U相,P=3P相=√3×I线×U相=√3×I线×U线。
三角形接法与星形

三角形接法.
还有电压方面的区别:星形接法与三角形接法输出的相电压分别为220V与380V
星形连接的三个绕组,每一端接三相电压的一相,另一端接在一起,不接任何一相电,也可不接零线,这样每个绕组的电压是相电压,也就是每相对地的电压,也就是通常指的220V。
同一电机三角形接法功率是星形接法的三倍
星型接法的运转电流要比三角形接法的高
就是说马达启动时绕组为Y连接,待转速增加到一定程度是再转换为三角连接。
这种启动方法可使每相定子绕组所受的电压再启动时降低到电路电压的1/根号3(不会打根号了),其电流为直接启动时的1/3。
由于启动电流的减小,启动转矩也同时减小到直接启动时的1/3。
三相星形接法电动机的每相绕组只能承受220V电压.他们接为星形后适合380V电压.三相角接电动机的每相绕组能直接承受380V电压,他们接为星形后适合660V电压.一般不能改变电动机的接线方式.只有电动机绕组为角接功率较大时(大于14KW)时需要用星形接法启动.减小启动电流和导线截面.
1、 同样一台电机,可以安装绕成Y型绕组,也可以安装绕成△型绕组;
三相电机星形和三角形两种接法是设计时固定的接法形式,不能随便更改的。例如三相380V星形接法改为三角形接法,其适应电压是三相220V的。三角形接法改为星形接法,其适应电压是660V的。电动机是大功率的,为避免起动电流过大对线路产生冲击,一般是将三角形接法改为星形接法启动,起动后转换回三角形接法运行的。Y系列电机3KW以下均是星形接法,4KW以上均是三角形接法。
5、Y型绕组在三相对称性不好、电源对称性不高时,不会出现环流,但会出现零点飘移,三相工作严重不对称;
电阻网络中的星形三角形变换分析

电阻网络中的星形三角形变换分析在电阻网络中,星形和三角形连接是常见的连接方式。
这两种连接方式在电路分析和设计中具有重要的作用。
本文将对电阻网络中的星形三角形变换进行详细分析,以帮助读者更好地理解和应用这一概念。
一、星形连接和三角形连接简介1. 星形连接在电路中,星形连接是指将三个或更多的电阻连接在一起,其中一个节点连接到电源正极,其余节点连接到电源负极。
这种连接方式常用于电路中需要提供共地或共点的情况。
2. 三角形连接三角形连接是指将三个电阻以闭合的三角形连接方式相连。
三角形连接常用于电路中需要提供平衡电路或无共地的情况。
二、星形三角形变换原理星形三角形变换是一种将一个电路转换为与它等效的另一个电路的方法。
通过执行星形三角形变换,可以简化电路的分析和计算。
具体变换原理如下:1. 星型到三角形变换将星形连接的电阻网络转换为等效的三角形连接网络。
设星形连接的电阻为R1,R2,R3,其中节点A连接到电源正极,节点B和C连接到电源负极。
则等效的三角形连接电阻可表示为:RT = R1 * R2 / (R1 + R2 + R3)RA = R1 * R3 / (R1 + R2 + R3)RB = R2 * R3 / (R1 + R2 + R3)2. 三角形到星形变换将三角形连接的电阻网络转换为等效的星形连接网络。
设三角形连接的电阻为RT,RA,RB,其中节点A、B、C两两相连,形成闭合的三角形。
则等效的星形连接电阻可表示为:R1 = RA * RB / (RA + RB + RT)R2 = RA * RT / (RA + RB + RT)R3 = RB * RT / (RA + RB + RT)三、星形三角形变换的应用星形三角形变换在电路分析和设计中具有广泛应用,其中包括但不限于以下几个方面:1. 简化电路分析和计算通过执行星形三角形变换,可以将复杂的电路转换为等效的简化电路,从而简化电路的分析和计算。
这种方法尤其适用于涉及大量电阻和复杂连接的电路。
电动机三角形接法和星形接法有什么区别

电动机三角形接法和星形接法有什么区别Hessen was revised in January 2021电动机三角形接法和星形接法有什么区别三角形接线时,三相电机每一个绕组承受线电压(380V),而星形接线时,电机每一承受相电压(220V)。
在电机功率相同的情况,角线电机的绕组电流较星接电机电流小。
当电机接成Y型运行时起动转矩仅是三角形接法的一半,但电流仅仅是三角形起动的三分之一左右。
三角形起动时电流是额定电流的4-7倍,但转矩大。
转速是一样的,但转矩不一样。
三角形接法电机的三角形接法是将各相绕组依次首尾相连,并将每个相连的点引出,作为三相电的三个相线。
三角形接法时电机相电压等于线电压;线电流等于根号3倍的相电流。
星形接法电机的星形接法是将各相绕组的一端都接在一点上,而它们的另一端作为引出线,分别为三个相线。
星形接时,线电压是相电压的根号3倍,而线电流等于相电流。
星形接法由于起输出功率小,常用于小功率,大扭矩电机,或功率较大的电机起步时候用,这样对机器损耗较小,正常工作后再换用三角形接法。
这就是常常说到的星——三角启动。
电动机接法选择是三相电机,单相电机没有以上两种接法的说法。
一般3KW以下的电动机星型接法的较多,3千瓦以上的电动机一般都角型接法。
按规定,大于15kw的电动机需要星型启动角型运行,以降低启动电流。
还有小型电动机角型启动的,如果要接在三相220V电源电压上,必须接成星型。
电机接线盒连接从电机接线盒里可以看出:三个进线接线端子U1、V1、W1的另一端U2、V2、W2如用同一铁片短接,那就是星形(Y)接法,三个进线接线端子U1和W2短接、V1和U2短接、W1和V2短接、那就是三角形接法(接线盒里三根平形铁条),星接时线电压等于相电压的倍,相电流等于线电流,角接时相电压等于线电压,线电流等于相电流的倍采用什么接法是和工作电流有关的,内部的截面积一定的情况下,电压高用,电压低用。
一般情况下大功率电机都是采用的,因为可以降低。
星形连接、三角形连接
IB
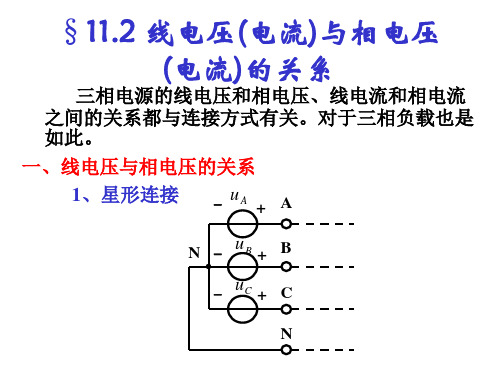
线电流与对称的三角形负载相电流之间的关系 可以用图示电流正三角形说明, 相电流对称时,线电流也一定对称,
线电流是相电流的 3倍,
依次滞后相应相电流的相位为30°。
实际计算时,只要算出一相就可以依序写出其 余两相。
_
UA
+ A
IA
Zl Zl Zl Z Z
A’
I A'B '
N
_
_
UB
+ B
线电压是相电压的 3倍,
依次超前相应相电压的相位为30°。
实际计算时,只要算出一相就可以依序写出其 余两相。
N -
uA
uB
+ A + B + C
uC
N
U AB U A - U B (1 ) U A 3 U A / 30
2
U BC U B - U C (1 ) U B 3 U B / 30
2
U CA U C - U A (1 ) U C 3 U C / 30
2
2、三角形电源
A +
uA
B C
uC
+
uB
+
U AB U A
U BC U B
U CA U C
3、对称星形负载和三角形负载
以上有关线电压和相电压的关系同样适用。
二、线电流和相电流的关系
+ C
IB
星形连接和三角形连接

在三相电路中,三相电源及三相负载都有两种连接方式:星形连接和三角形连接。
8.2.1星形连接在图8.3所示的三相电路中,三相电压源及三相负载都是星形连接的。
各相电压源的负 极性端连接在一起,称为三根电源的中点或零点,用N 表示。
各相电压源的正极性端A 、B 、 C 引出,以便与负载相连。
这就是星形连接方式,或称Y 形连接方式。
三相负载Z,、兀 Z 。
也是星形连接的。
各相负载的一端连接在一起,称为负载的中点或零点,用N'表示。
各相负载的另一端A'、B'、C'弓I 出后与电源连接。
电源与负载相应各相的连接线小'、 BB'、CC'称为端线。
电源中点与负载中点的连线NN'称为中线或零线。
具有三根端线 及一根中线的三相电路称为三相四线制电路;如果只接三根端线而不接中线,则称为三相三0 0 0 □ 0电压,畑、7站、7册为负载相电压。
端线之间的电压称为线电压。
例如7心、7处、 0 ODD卩蚀是电源的线电压,卩血、卩刼、卩必是负载的线电压。
流过电源或负载各相的电流称 为相电流。
流过各端线的电流称为线电流,流过中线的电流称为中线电流。
当电源或负载为星形连接时,线电压等于两个相应的相电压之差,例如在电源侧,各线 电压为□ 0 □VJLS 二/血一 V 刖□□ □ V }£: = V 附一 V 刖•□ 00 V CA 二 7饵一 7册(8.5)□ , □ □ , 0卩倒=a 丫测,卩抑=僅丫⑶则式(8・5)成为 0 0 □ S- C ? V M =辰30° 匚如 0 DV £>C=V 酬一 Q(8.6)在三相电站中,电源或负载各相的电压称为相电压。
例如卩洌、$刖、厂⑶为电源相如果相电压是三项对称的,□訂线电压与相电压的相長图如S 8.4a或图8•斗b所示。
由于在复平面上相長可以平移,所以这两种表示方法是一致的。
由式(8.6)71相長图可见,如果相电压是三相对称的,则线电压也是三相对称的。
三相交流电路星形连接和三角形连接

星形连接的优点
星形连接可以减小中性线电流, 从而减小了线路的损耗和电压 降。
在星形连接中,当一相绕组短 路时,其他绕组仍可正常运行, 提高了电路的可靠性。
星形连接可以方便地实现三相 平衡,从而减小了不平衡电流 对设备的影响。
星形和三角形连接的概述
星形连接
三相交流电路的各相绕组的一端连接在一起,另一端分别接入三相电源,形成 星形(Y)结构。
三角形连接
三相交流电路的各相绕组首尾相连,形成一个闭合回路,然后从三个连接点接 入三相电源,形成三角形(△)结构。
02
三相交流电路基础知识
三相交流电的产生
旋转磁场
当三相交流发电机定子绕组中的电流 发生变化时,会产生旋转磁场,进而 驱动转子旋转。
工业供电
三相交流电被广泛应用于工业供电领域,如电动机、加热器等设备的驱动和控制 。
家庭供电
家庭用电也采用三相交流电,通过变压器将高压电转换为低压电,以满足家庭用 电需求。
03
三相交流电路星形连接
星形连接的定义
星形连接是指将三相交流电源的三个 绕组末端连接在一起,作为公共点, 而每个绕组的始端分别作为独立的输 出端。
浪费。
THANKS
感谢观看
三相交流电路星形连 接和三角形连接
目录
• 引言 • 三相交流电路基础知识 • 三相交流电路星形连接 • 三相交流电路三角形连接 • 星形与三角形连接的比较 • 实际应用与案例分析
01
引言
主题介绍
01
三相交流电路是电力系统中的重 要组成部分,其星形和三角形连 接方式是常见的两种接线方式。
02
三角形连接和星形连接变换公式

三角形连接和星形连接变换公式一、三角形连接的变换公式:1.三角形连接的公式一:设三角形ABC、ADE、EFG均为等边三角形,且ADE与EFG的边DE和EF相互平行,连接三角形ABC和EFG的相应边AE、BF、CG,则所得到的图形是一个三角形。
且连接线段AE、BF、CG相互平行。
2.三角形连接的公式二:设三角形ABC、DBE、EFC均为等边三角形,连接三角形ABC和EFC的相应边AC、BE,则所得到的图形是一个四边形。
且连接线段AC、BE相互平行。
二、星形连接的变换公式:星形连接是指将若干个星形的顶点连接在一起形成一个新的图形。
这种变换常见于几何图形的构建和绘制过程中。
具体来说,星形连接的变换公式如下:1.星形连接的公式一:设星形A、B、C、D、E均为五角星形,连接星形A、C、E的顶点成線段,则所得到的图形是一个五边形。
且连接线段AC、CE相互平行。
2.星形连接的公式二:设星形A、B、C、D、E均为五边形,连接星形A、C、E的底部边AD、BD、ED,则所得到的图形是一个五角星形。
且连接线段AC、CE相互平行。
上述公式是对三角形连接和星形连接常见情况的描述,具体变换公式还可以根据实际情况进行推导和应用。
这些变换公式展示了三角形连接和星形连接的一般规律,为进行相关图形变换提供了指导。
除了上述变换公式,还可以通过其他方法进行三角形连接和星形连接的变换。
例如,可以使用平移、旋转、反射和缩放等变换操作来完成。
这些变换操作可以通过矩阵运算或几何变换公式来实现,达到构建和绘制出新的三角形连接和星形连接的图形。
这些方法在图形学和几何学中都有广泛的应用。
总结起来,通过三角形连接和星形连接的变换公式,可以在数学和几何学中进行复杂图形的构建和绘制。
这些公式和方法为我们理解和应用三角形连接和星形连接提供了重要的数学基础。
通过深入研究和探索,我们可以更好地理解和应用这些图形变换,创造出更加丰富多样的几何图形。
星形连接三角形连接计算及含义

星形连接三角形连接计算及含义星形连接和三角形连接是两种常见的网络拓扑结构,用于描述计算机网络中不同设备之间的连接方式。
下面将分别介绍这两种连接方式的计算方法及其含义。
一、星形连接星形连接是一种将所有设备连接到一个中心节点(通常是一个交换机或路由器)的网络布局。
中心节点负责转发数据包并协调各个设备之间的通信。
这种连接方式常见于局域网(LAN)中,优点是易于管理和维护,且具有高可靠性和可扩展性。
在星形连接中,中心节点和每个设备之间都有一条独立的连接。
当需要计算星形连接中的总连接数时,可以使用以下方法:设网络中有n个设备,则总连接数为n。
例如,一个局域网中有10台计算机连接到一个交换机,那么总连接数为10。
星形连接的含义是中心节点充当数据流的分发器,所有设备之间的通信都通过中心节点进行。
这意味着,如果中心节点出现故障,整个网络将无法正常工作。
因此,在设计星形连接网络时,需要确保中心节点具备高可靠性和冗余机制。
二、三角形连接三角形连接是一种将三个设备依次连接起来的网络布局,形状类似一个倒置的三角形。
三个设备之间的连接通常是点对点的,即每个设备只与相邻的两个设备直接连接。
这种连接方式常见于WAN(广域网)或点对点连接的场景中。
三角形连接的计算方式如下:设网络中有n个设备,则总连接数为n-1例如,一个由5台路由器组成的广域网,路由器之间的连接方式为三角形连接。
那么总连接数为5-1=4三角形连接的含义是每个设备只与其相邻的两个设备直接连接。
这种连接方式通常用于需要点对点传输的场景,如远程办公或跨地域数据传输。
综上所述,星形连接和三角形连接是两种常见的网络拓扑结构。
星形连接将所有设备连接到一个中心节点,适用于局域网环境,易于管理。
三角形连接是将三个设备依次连接起来的网络布局,适用于点对点传输的场景。
计算星形连接的总连接数只需统计设备数量,而计算三角形连接的总连接数需要减去一个设备数量。
电机三角形连接和星形连接的区别

电机三角形连接和星形连接的区别三角形连接和星形连接从电机外部看是没有任何区别的,你可以把电机看成一个黑盒子,外面看就是三根进线,通以互差120度的电流。
要说到电机三角形连接和星形连接的区别,只是在电机本体设计的时候会关注,我们知道,教科书上写星形连接的线电压是相电压的1."732倍,三角形的线电压等于相电压,在电机设计阶段,都会折算成等效三个等效单相,因为三相电机的等效电路是等效成单相的。
对于一个输入线电压为380V的电机而言,如果设计成星形,那么就按220V计算单相电路,如果设计成角形,那么就按380V计算单相电路,但相电流减小。
这个时候体现在电机上就是三角形的线用得长些细些,星形的线短些粗些,但理论上用的材料是一样多。
一旦电机做好后,从外部看,理论上三角形连接和星形连接是没区别的,你也没有办法单纯从外部三根线去区分二者的区别。
这里可能有同学想问,为什么电机要分成三角形和星形连接这么麻烦。
原则上讲,星形电机内部不会产生环流,理论上比三角形好,因为实际上三相绕组不可能绝对平衡,三相电压总有微小差异,这样在三角形内部会形成环流造成发热和效率降低(当然这个影响实际上很小)。
做成三角形连接是有历史原因的,那就是没有变频器的时候,电机启动时可以利用接触开关改变连接,将其接成星形,这样每个绕组的电压由380将为220,大大减小了启动冲击电流,待启动后切换成三角形。
这就是所谓的星-三角启动。
星-三角启动可以成比例降低启动电流,但是会成平方降低启动转矩,所以只能用在轻载或空载启动。
大家看到的风机水泵用星-三角启动没问题,但是起重机上肯定没有用星-三角启动的,起重机都是用绕线转子串电阻启动,为什么搞这么麻烦,都是有原因的。
电动机连接组别:1.当三相电机的三相绕组按△方式接线时,即绕组按U1-W2、"U2-V1、"V2-W1顺序连接后,引出线U1 V1 W1接于三相电源,此时每相绕组U1-U2 V1-V2 W1-W2上承受的是三相电源的线电压也就是380V.这样的接法使得电机的输出转矩较大。
三角形接法和星形接法的字母

三角形接法和星形接法的字母
在电力系统和电机学中,三角接法和星形接法通常用于三相交流电的接线方式。
三角接法,也被称为Δ接法,用字母Δ表示。
在这种接法中,三个相位的线直接相互连接,形成一个闭合的三角形。
星形接法,也被称为Y接法,用字母Y表示。
在这种接法中,三个相位是各自独立、相互分离的,并且在顶部通过一个共同的节点连接在一起。
这两种接法的主要区别在于电流的流向和电压的相位。
在三角接法中,每个线圈承受线电压,而在星形接法中,每个线圈承受相电压。
三角形和星形接法电压电流关系

三角形和星形接法电压电流关系
三角形和星形是指在三相电路中连接电阻或电感的方式。
在三
相电路中,可以使用三角形连接或星形连接来连接电阻或电感。
这
两种连接方式会影响电压和电流的关系。
首先,让我们讨论三角形连接。
在三角形连接中,每个元件
(电阻或电感)的一个端子连接到另一个元件的另一个端子,形成
一个类似于三角形的连接。
在这种连接方式下,电压和电流之间的
关系是复杂的。
如果我们考虑理想的情况,其中电阻或电感的值相等,那么在三角形连接中,线电压和相电压之间的关系是根号3倍。
也就是说,线电压是相电压的根号3倍。
而在电流方面,线电流和
相电流的大小是相等的。
接下来,我们来讨论星形连接。
在星形连接中,每个元件的一
个端子连接到一个公共的节点,形成一个类似于星形的连接。
在星
形连接中,线电压和相电压的关系是相等的,也就是说,线电压等
于相电压。
而在电流方面,线电流和相电流之间的关系是根号3倍。
换句话说,线电流是相电流的根号3倍。
总的来说,三角形连接和星形连接对电压和电流的关系有不同
的影响。
在三角形连接中,线电压是相电压的根号3倍,而线电流和相电流的大小是相等的。
而在星形连接中,线电压等于相电压,而线电流是相电流的根号3倍。
这些关系在三相电路中的电压和电流分析中起着重要的作用,工程师需要根据具体的电路情况选择合适的连接方式来进行设计和分析。
三角形联结与星形联结的关系

三角形联结与星形联结的关系
三角形联结与星形联结是数学中常见的两种场景,它们具有很强
的联系和相互依存关系。
首先来看三角形联结。
三角形联结是指三个点通过线段连接而构
成的三角形。
在几何学和计算机图形学中,三角形联结是一种非常基
本的图形联结方式。
它可以用来展示空间中任意一个平面图形,并且
可以用于执行图形处理操作。
三角形联结在计算机游戏中应用广泛,
因为它们占用空间小、计算速度快。
此外,三角形联结还可以用于处
理多边形检测、体积数据表示和地球仪表面三角化等方面。
接下来看星形联结。
星形联结是指将多个三角形联结在一起,以
中心点为基准,为每个三角形共享一条边并连成一个整体。
这种联结
方式得名于星形图形的形状,因为多个三角形联结起来后,形成的图
形就像一颗星。
星形联结在计算机图形学领域中应用广泛,因为它可
以构建出复杂的三维模型,并且可以更好地处理形态变换和纹理贴图
等复杂操作。
三角形联结与星形联结的关系可以简单地概括为:星形联结由多
个三角形联结而成,而三角形联结构成了星形联结的基本单元。
因此,理解和掌握三角形联结对于学习和应用星形联结非常重要。
总之,三角形联结和星形联结都是计算机图形学中非常重要的概念。
对于初学者来说,首先要掌握三角形联结的基本原理和应用,然
后再深入学习星形联结。
只有掌握了三角形联结这一基本技能,才能
更好地理解星形联结,并灵活地运用它们来进行图形处理和模型构建。
电阻的星形和三角形连接的等效变换
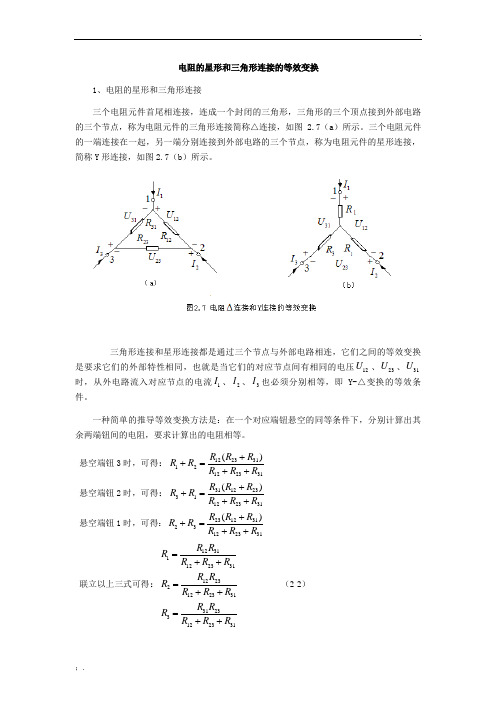
电阻的星形和三角形连接的等效变换1、电阻的星形和三角形连接三个电阻元件首尾相连接,连成一个封闭的三角形,三角形的三个顶点接到外部电路的三个节点,称为电阻元件的三角形连接简称△连接,如图 2.7(a)所示。
三个电阻元件的一端连接在一起,另一端分别连接到外部电路的三个节点,称为电阻元件的星形连接,简称Y形连接,如图2.7(b)所示。
三角形连接和星形连接都是通过三个节点与外部电路相连,它们之间的等效变换是要求它们的外部特性相同,也就是当它们的对应节点间有相同的电压12U、23U、31U时,从外电路流入对应节点的电流1I、2I、3I也必须分别相等,即Y-△变换的等效条件。
一种简单的推导等效变换方法是:在一个对应端钮悬空的同等条件下,分别计算出其余两端钮间的电阻,要求计算出的电阻相等。
悬空端钮3时,可得:12233112122331()R R RR RR R R++=++悬空端钮2时,可得:31122331122331()R R RR RR R R++=++悬空端钮1时,可得:23123123122331()R R RR RR R R++=++联立以上三式可得:123111223311223212233131233122331R RRR R RR RRR R RR RRR R R=++=++=++(2-2)式(2-2)是已知三角形连接的三个电阻求等效星形连接的三个电阻的公式。
从式(2-2)可解的:121212323232313131312R R R R R R R R R R R R R R R R R R =++=++=++ (2-3)以上互换公式可归纳为:=Y ∆∆形相邻电阻的乘积形电阻形电阻之和=Y ∆形电阻两两乘积之和形电阻Y 形不相邻电阻 当Y 形连接的三个电阻相等时,即123Y R R R R ===,则等效△形连接的三个电阻也相等,它们等于1223313Y R R R R R ∆==== 或1=3Y R R ∆ (2-4)。
