信息论试卷题目及答案
信息论试卷含答案资料讲解
《信息论基础》参考答案一、填空题（共15分，每空1分）1、信源编码的主要目的是提高有效性，信道编码的主要目的是提高可靠性。
2、信源的剩余度主要来自两个方面，一是信源符号间的相关性，二是信源符号的统计不均匀性。
3、三进制信源的最小熵为0，最大熵为32log bit/符号。
4、无失真信源编码的平均码长最小理论极限制为信源熵（或H(S)/logr= H r (S)）。
5、当R=C 或（信道剩余度为0）时，信源与信道达到匹配。
6、根据信道特性是否随时间变化，信道可以分为恒参信道和随参信道。
7、根据是否允许失真，信源编码可分为无失真信源编码和限失真信源编码。
8、若连续信源输出信号的平均功率为2σ，则输出信号幅度的概率密度是高斯分布或正态分布或()222x f x σ-=时，信源具有最大熵，其值为值21log 22e πσ。
9、在下面空格中选择填入数学符号“,,,=≥≤〉”或“〈”（1）当X 和Y 相互独立时，H （XY ）=H(X)+H(X/Y)=H(Y)+H(X)。
（2）()()1222H X X H X =≥()()12333H X X X H X = （3）假设信道输入用X 表示，信道输出用Y 表示。
在无噪有损信道中，H(X/Y)> 0, H(Y/X)=0,I(X;Y)<H(X)。
二、（6分）若连续信源输出的幅度被限定在【2,6】区域内，当输出信号的概率密度是均匀分布时，计算该信源的相对熵，并说明该信源的绝对熵为多少。
()1,2640,x f x ⎧≤≤⎪=⎨⎪⎩Q 其它()()()62log f x f x dx ∴=-⎰相对熵h x=2bit/自由度该信源的绝对熵为无穷大。
三、（16分）已知信源1234560.20.20.20.20.10.1S s s s s s s P ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦（1）用霍夫曼编码法编成二进制变长码；（6分） （2）计算平均码长L ;（4分）（3）计算编码信息率R ';（2分）（4）计算编码后信息传输率R ;（2分） （5）计算编码效率η。
信息论基础理论与应用考试题及答案
信息论基础理论与应用考试题一﹑填空题（每题2分，共20分）1.信息论研究的目的就是要找到信息传输过程的共同规律，以提高信息传输的 （可靠性）﹑（有效性）﹑XX 性和认证性，使信息传输系统达到最优化。
（考点：信息论的研究目的）2.电视屏上约有500×600=3×510个格点，按每点有10个不同的灰度等级考虑，则可组成531010⨯个不同的画面。
按等概计算，平均每个画面可提供的信息量约为（610bit /画面）。
（考点：信息量的概念与计算）3.按噪声对信号的作用功能来分类信道可分为 （加性信道）和 （乘性信道）。
（考点：信道按噪声统计特性的分类）4.英文电报有32个符号（26个英文字母加上6个字符），即q=32。
若r=2，N=1，即对信源S 的逐个符号进行二元编码，则每个英文电报符号至少要用 （5）位二元符号编码才行。
（考点：等长码编码位数的计算）5.如果采用这样一种译码函数，它对于每一个输出符号均译成具有最大后验概率的那个输入符号，则信道的错误概率最小，这种译码规则称为（最大后验概率准则）或（最小错误概率准则）。
（考点：错误概率和译码准则的概念）6.按码的结构中对信息序列处理方式不同，可将纠错码分为（分组码）和（卷积码）。
（考点：纠错码的分类）7.码C=｛（0，0，0，0），（0，1，0，1），（0，1，1，0），（0，0，1，1）｝是（（4，2））线性分组码。
（考点：线性分组码的基本概念）8.定义自信息的数学期望为信源的平均自信息量，即（11()log ()log ()()q i i i i H X E P a P a P a =⎡⎤==-⎢⎥⎣⎦∑）。
（考点：平均信息量的定义）9.对于一个（n,k）分组码，其最小距离为d，那么，若能纠正t个随机错误，同时能检测e（e≥t）个随机错误，则要求（d≥t+e+1）。
（考点：线性分组码的纠检错能力概念）10.和离散信道一样，对于固定的连续信道和波形信道都有一个最大的信息传输速率，称之为（信道容量）。
最新《信息论》试题及答案
期终练习一、某地区的人群中，10％是胖子，80％不胖不瘦，10％是瘦子。
已知胖子得高血压的概率是15％，不胖不瘦者得高血压的概率是10％，瘦子得高血压的概率是5％，则“该地区的某一位高血压者是胖子”这句话包含了多少信息量。
解：设事件A ：某人是胖子； B ：某人是不胖不瘦 C ：某人是瘦子 D ：某人是高血压者根据题意，可知：P （A ）=0.1 P （B ）=0.8 P （C ）=0.1 P （D|A ）=0.15 P （D|B ）=0.1 P （D|C ）=0.05而“该地区的某一位高血压者是胖子” 这一消息表明在D 事件发生的条件下，A 事件的发生，故其概率为P （A|D ）根据贝叶斯定律，可得：P （D ）＝P （A ）* P （D|A ）＋P （B ）* P （D|B ）＋P （C ）* P （D|C ）＝0.1 P （A|D ）＝P （AD ）/P （D ）＝P （D|A ）*P （A ）/ P （D ）＝0.15*0.1/0.1＝0.15 故得知“该地区的某一位高血压者是胖子”这一消息获得的多少信息量为： I （A|D ） = - logP （A|D ）=log （0.15）≈2.73 （bit ） 二、设有一个马尔可夫信源，它的状态集为{S 1，S 2，S 3}，符号集为{a 1，a 2，a 3}，以及在某状态下发出符号集的概率是(|)k i p a s （i ，k=1，2，3），如图所示（1）求图中马尔可夫信源的状态极限概率并找出符号的极限概率（2）计算信源处在某一状态下输出符号的条件熵H(X|S=j) (j=s 1，s 2，s 3) （3）求出马尔可夫信源熵H ∞解：（1）该信源达到平稳后，有以下关系成立：13212312123()()31()()()4211()()()42()()()1Q E Q E Q E Q E Q E Q E Q E Q E Q E Q E Q E =⎧⎪⎪=+⎪⎨⎪=+⎪⎪++=⎩可得1232()73()72()7Q E Q E Q E ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩3111322133313()()(|)72()()(|)73()()(|)7i i i i i i i i i p a Q E p a E p a Q E p a E p a Q E p a E =========∑∑∑（2）311113222133331(|)(|)log (|) 1.5bit/(|)(|)log (|)1bit/(|)(|)log (|)0bit/k k k kk k k k k H X S p a S p a S H X S p aS p a S H X S p a S p a S ====-==-==-=∑∑∑（符号）（符号）（符号）（3）31()(|)2/7*3/23/7*12/7*06/7iii H Q E H X E ∞==⨯=++=∑（比特/符号）三、二元对称信道的传递矩阵为0.60.40.40.6⎡⎤⎢⎥⎣⎦（1）若P(0)=3/4，P(1)=1/4，求H （X ），H （X|Y ）和I （X ；Y ）（2）求该信道的信道容量及其最大信道容量对应的最佳输入分布 解：⑴()H X =21()log ()iii p x p x ==-∑=0.75log 750.25log 25--≈0.811(比特/符号)1111212()()(|)()(|)p y p x p y x p x p y x =+=0.75*0.6+0.25*0.4=0.55 2121222()()(|)()(|)p y p x p y x p x p y x =+=0.75*0.4+0.25*0.6=0.45()0.55log0.550.45log0.45H Y =--=≈0.992(比特/符号)122(|)()(|)()(|)0.75(0.6,0.4)0.25(0.4,0.6)(0.6log 0.60.4log 0.4)0.971/H Y X p x H Y x p x H Y x H H =+=⨯+⨯=-+≈（比特符号）(|)()()()(|)()H X Y H XY H Y H X H Y X H Y =-=+-≈0.811+0.971-0.992=0.79 (比特/符号)I (X ;Y )=H (X )-H (X =0.811-0.79=0.021(比特/符号)（2）此信道为二元对称信道，所以信道容量为C=1-H(p)=1-H(0.6)=1-0.971=0.029(比特/符号) 当输入等概分布时达到信道容量四、求信道22042240p p p p εεεεεε⎡⎤-- ⎢⎥-- ⎢⎥⎣⎦的信道容量，其中1p p =-。
《信息论》期末考试试题( 卷)标准答案
2．（共 10 分）有两枚硬币，第一枚是正常的硬币，它的一面是国徽，另一面是 面值；第二枚是不正常的硬币，它的两面都是面值。现随机地抽取一枚硬币，进 行 2 次抛掷试验，观察硬币朝上的一面，其结果为：面值、面值。
1）求该试验结果与事件“取出的是第一枚硬币”之间的互信息；（4 分）
=
E( XS + αS 2 ) σ SσU
=
αQ σ SσU
I (U ; S) = H (U ) + H (S ) − H (US )
=
1 2
log
2πe σ
2 U
+
1 2
log
2πeσ
2 S
+
log 2πeσUσ S
1− ρ2
=
1 2
log
σ
σ σ2 2
SU
σ2 2
US
− (αQ)
2
=
1 log P + α 2Q
2 1 d = 1 0 7）若失真矩阵为 3 1 ，输入等概，则 Dmin = 2/3 ， Dmax = 2/3 。
三、简答题（6 分）
1．仙农第二定理指出了“高效率、高可靠性”的信道编码存在性，
1）“高效率”的含义是什么？
（1 分）
2）“高可靠性” 的含义是什么？
（1 分）
3）存在这种信道编码的必要条件是什么？
1− ρ2
=
1 log
σ
2 U
σ
2 Y
2
σ
2 U
σ
2 Y
−
(P
+ αQ)2
=
1 log
(P + Q + N )(P + α 2Q)
信息论试卷及解答
=
log 2 −
1+ε 2 2
log(1+ ε
2)
− εε
log ε
−ε
log ε
I (X
; Y1Y2
)
=
H
(X
)
+
H (Y1Y2
)
−
H ( XY1Y2
)
=
log
2
−
1+ε 2
2
log(1 +
ε
2
)
−
ε
(2
−
ε
) log ε
其中ε = 1 − ε
5
五、（22 分）一离散无记忆信道如图 3 所示：
1/2
01
10
0
0
εε 2
P y1 y2 (01)=
εε 2
εε 2
P y1 y2 (10)=
εε 2
11
0
ε2 2
P y1 y2 (11)=
ε2 2
∴ H (XY1Y2 ) = log 2 − ε 2 log ε − εε log εε − ε 2 log ε = log 2 + H (ε ) ；
H (Y1Y2 )
信息量为：
I(z
=
1/
x
=
0)
=
− log2
2 9
=
2.170
比特
（2） p(x = 1/ z = 0) = p(x = 1) p(z = 0 / x = 1) p(z = 0)
1
=
p( x = 1) p(z = 0 / x = 1)
p(x = 0) p(z = 0 / x = 0) + p(x = 1) p(z = 0 / x = 1)
信息论典型试题及答案
第五章
5.1将下表所列的信源进行六种不同的二进制编码。
（1）求这些码中哪些是惟一可译码。
（2）哪些码是非延长码
（3）对所有惟一可译码求出其平均码长 。
消息
C1
C2
C3
C4
C5
C6
1/2
000
0
0
0
0
0
1/4
001
01
10
10
10
100
1/16
010
011
110
110
1100
101
27.能够描述无失真信源编码定理
例1：.黑白气象传真图的消息只有黑色和白色两种，求：
1）黑色出现的概率为0.3，白色出现的概率为0.7。给出这个只有两个符号的信源X的数学模型。假设图上黑白消息出现前后没有关联，求熵H(X)；
2）假设黑白消息出现前后有关联，其依赖关系为：P(白/白)=0.9，P(黑/白)＝0.1，P(白/黑)＝0.2，P(黑/黑)＝0.8，求其熵H2(X)；
10.互信息的性质是什么？
11.熵的表达式、单位、含义是什么？
12.单符号离散信源最大熵是多少？信源概率如何分布时能达到？
13.熵的性质是什么？
14.联合熵、条件熵和熵的关系。
15.平均互信息的定义是什么？平均互信息的表达式怎么推导？
16.平均互信息的含义？
17.信道疑义度、损失熵和噪声熵的含义？
18.平均互信息的性质？（能够证明，并说明每个性质的含义）
解：
由题意可知该二元信道的转移概率矩阵为：
为一个BSC信道
所以由BSC信道的信道容量计算公式得到：
3.14电视图像编码中，若每帧为500行，每行划分为600个像素，每个像素采用8电平量化，且每秒传送30帧图像。试求所需的信息速率(bit/s)。
信息论考试卷及答案
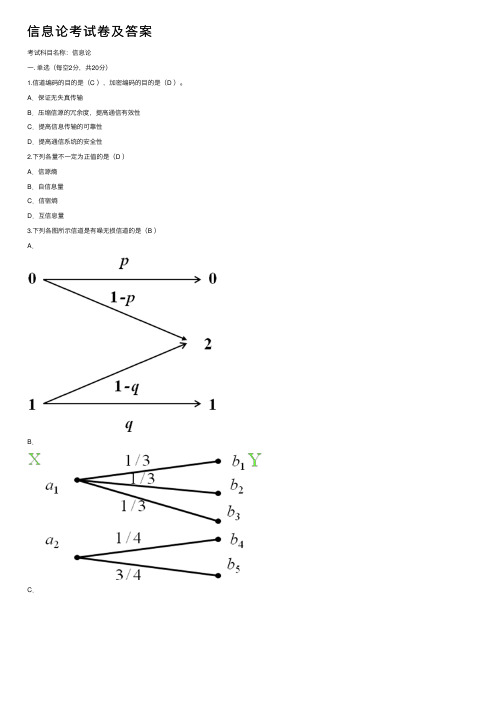
信息论考试卷及答案考试科⽬名称：信息论⼀. 单选（每空2分，共20分）1.信道编码的⽬的是（C ），加密编码的⽬的是（D ）。
A．保证⽆失真传输B．压缩信源的冗余度，提⾼通信有效性C．提⾼信息传输的可靠性D．提⾼通信系统的安全性2.下列各量不⼀定为正值的是（D ）A．信源熵B．⾃信息量C．信宿熵D．互信息量3.下列各图所⽰信道是有噪⽆损信道的是（B ）A．B．C．D．4.下表中符合等长编码的是（ A ）5.联合熵H（XY）与熵H（X）及条件熵H（X/Y）之间存在关系正确的是（A ）A．H（XY）＝H（X）＋H（Y／X）B．H（XY）＝H（X）＋H（X／Y）C．H（XY）＝H（Y）＋H（X）D．若X和Y相互独⽴，H（Y）=H（YX）6.⼀个n位的⼆进制数，该数的每⼀位可从等概率出现的⼆进制码元（0，1）中任取⼀个，这个n位的⼆进制数的⾃信息量为（C ）A．n2B．1 bitC．n bitnD．27.已知发送26个英⽂字母和空格，其最⼤信源熵为H0 = log27 = 4.76⽐特/符号；在字母发送概率不等时，其信源熵为H1 = 4.03⽐特/符号；考虑字母之间相关性时，其信源熵为H2 = 3.32⽐特/符号；以此类推，极限熵H=1.5⽐特/符号。
问若⽤⼀般传送⽅式，冗余度为（ B ）∞A．0.32B．0.68C ．0.63D ．0.378. 某对称离散信道的信道矩阵为，信道容量为（ B ）A ．)61,61,31,31(24log H C -= B ．)61,61,31,31(4log H C -= C ．)61,61,31,31(2log H C -= D ．)61,31(2log H C -= 9. 下⾯不属于最佳变长编码的是（ D ）A ．⾹农编码和哈夫曼编码B ．费诺编码和哈夫曼编码C ．费诺编码和⾹农编码D ．算术编码和游程编码⼆. 综合（共80分）1. （10分）试写出信源编码的分类，并叙述各种分类编码的概念和特性。
信息论复习题期末答案
信息论复习题期末答案1. 信息论的创始人是谁？答案：信息论的创始人是克劳德·香农。
2. 信息熵的概念是什么？答案：信息熵是衡量信息量的一个指标，它描述了信息的不确定性或随机性。
在信息论中，熵越高，信息的不确定性越大。
3. 请简述信源编码定理。
答案：信源编码定理指出，对于一个具有确定概率分布的离散无记忆信源，存在一种编码方式，使得信源的平均编码长度接近信源熵的值，且当信源长度趋于无穷大时，编码长度与信源熵之间的差距趋于零。
4. 什么是信道容量？答案：信道容量是指在特定的通信信道中，能够以任意小的错误概率传输信息的最大速率。
它是信道的最大信息传输率，通常用比特每秒（bps）来表示。
5. 香农公式是如何定义信道容量的？答案：香农公式定义信道容量为信道输入和输出之间的互信息量的最大值，可以表示为C = B log2(1 + S/N)，其中C是信道容量，B是信道带宽，S是信号功率，N是噪声功率。
6. 差错控制编码的目的是什么？答案：差错控制编码的目的是为了检测和纠正在数据传输过程中可能发生的错误，以提高数据传输的可靠性。
7. 什么是线性码？答案：线性码是一种特殊的编码方式，其中任意两个合法编码的线性组合仍然是一个合法编码。
线性码通常可以用生成矩阵和校验矩阵来表示。
8. 卷积码和块码有什么区别？答案：卷积码和块码都是差错控制编码的类型，但它们的主要区别在于编码的结构和处理方式。
卷积码是连续的，其编码过程是按时间序列进行的，而块码是离散的，其编码过程是针对数据块进行的。
9. 什么是信道编码定理？答案：信道编码定理指出，对于任何给定的信道和任何小于信道容量的错误概率，都存在一种编码方式，可以使得错误概率趋近于零。
10. 请解释什么是信道编码的译码算法。
答案：信道编码的译码算法是一种用于从接收到的编码信号中恢复原始信息的方法。
常见的译码算法包括维特比算法、最大似然译码和最小均方误差译码等。
这些算法旨在最小化译码错误的概率。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
中国海洋大学2008—2009学年第一学期
一、填空题（每空2分，共20分）
1、1948年，美国数学家 香农 发表了题为“通信的数学理论”的长篇论文，从而创立了信息论。
2、信源编码的目的是提高通信的有效性。
信道编码的最终目的是提高信号传输的可靠性。
3、离散平稳无记忆信源X 的N 次扩展信源的熵等于离散信源X 的熵的N 倍。
4、对于香农编码、费诺编码和哈夫曼编码，编码方法惟一的是香农编码。
5、信道输入与输出间的平均互信息是信道转移概率的 下凸 函数，是输入概率的 上凸 函数。
6、信道矩阵⎥⎦⎤⎢⎣⎡10002/12/1代表的信道的信道容量C=符号/1bit ，达到信道容量的条件是输入符号等概分布。
7、 设某二进制码｛00011，10110，01101，11000，10010，10001｝，则码的最小距离是2 ，假设码字等概分布，则该码的码率为 0.517比特/符号 ，这时若通过二元对称信道接收码字为01100和00110时，应译为01101 ， 10110 。
二、判断题（每题2分，共10分）
1、必然事件和不可能事件的自信息量都是0 。
（错）
2、最大后验概率准则与最大似然准则是等价的。
（错）
3、如果信息传输速率大于信道容量，就不存在使传输差错率任意小的信道编码。
（对）
4、连续信源和离散信源的熵都具有非负性。
（错）
5、相同功率的噪声中，高斯噪声使信道容量最小。
（对） 三、简答题（第1、2题各6分，第三题10分，共22分）
1、简述最大离散熵定理。
对于一个有m 个符号的离散信源，其最大熵是什么？ 答：最大离散熵定理为：离散无记忆信源，等概率分布时熵最大。
(3分) 最大熵值为
m
H 2max log = (3分)
2、对于任意概率事件集X 、Y 、Z ，证明下述三角不等式成立()()()Z X H Z Y H X H ≥+ 证：因为)|()|(Y X H YZ X H ≤ ，(3分) 所以：
)
|()|()|()
|,()
|()|()|()|(Z Y H XZ Y H Z Y H Z Y X I YZ X H Z X H Y X H Z X H ≤-==-≤-(3分)
所以原命题得证。
3、什么是保真度准则？对二元信源()⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡ωω110u p u ，其失真矩阵⎥
⎦⎤
⎢⎣⎡=00ααD ，求0>α时率失真函数的min D 和max D ？
答：1)保真度准则为：平均失真度不大于允许的失真度。
（3分）
2)因为失真矩阵中每行都有一个0，所以有0min =D （2分），
而(){}()⎪⎩
⎪⎨⎧<
≥-=-=21
211,1min max
ωωαωαωωααωD 。
（5分）
四、计算题（第1、2、3题每题15分，第4题10分，共55分）
1、黑白气象传真图的消息只有黑色和白色两种，求：（1）黑色出现的概率为0.3，白色出现的概率为0.7。
给出这个只有两个符号的信源X 的数学模型，假设图上黑白消息出现前后没有关联，求熵
()X H ；（2）假设黑白消息出现前后有关联，其依赖关系为：P(白/白)=0.9，P(黑/白)=0.1，P(白/
黑)=0.2，P(黑/黑)=0.8，求其熵()X H 2。
答：（1）信源模型为()⎥⎦⎤
⎢⎣⎡===⎥
⎦⎤⎢⎣⎡7.03
.021白黑x x x p X (5分) ()()()符号/881.07.0log 7.03.0log 3.0log 2
1bit x p x p X H i i i =--=-=∑=(5分)
（2）由()()()()()⎪⎩⎪⎨⎧
=+=∑=1
21
2
1
x P x P x x P x P x P j j i j i （2,1=i ）(3分) 可得()()()()()()()()⎪⎩⎪⎨⎧=++=+=1
9.02.01.08.021212211x P x P x P x P x P x P x P x P 得⎪⎪⎩
⎪⎪⎨⎧====32)(3
1)(11白黑x P x P (3分)
则()()()
[][]符号
/5533.09.0log 9.01.0log 1.032
1.0log 1.08.0log 8.031log )(2212
1
2bit x x P x x P x P X H i j i j i j i =⨯+⨯⨯-⨯+⨯⨯-=-=∑∑== (4分)
2、设有一离散信道，其信道矩阵为⎥
⎦
⎤
⎢⎣⎡=7.01.02.02.01.07.0p ，求（1）最佳概率分布？（2）当()7.01=x P ，()3.02=x P 时，求平均互信息()Y X I ;和信道疑义度()Y X H /；（3）输入为等概分布时，试写出一译码
规则，使平均译码错误率E p 最小，并求此E p 。
答：（1）是准对称信道，因此其最佳输入概率分布为()()5.021==x p x p (2分) (2)由已知的输入概率空间和信道转移概率，可求得输出概率
()()()∑==2
1i i j i j x y p x p y p (2分)
()()()55.02.03.07.07.021
11=⨯+⨯==∑=i i i x y p x p y p
()()()1
.01.03.01.07.02
122=⨯+⨯==∑=i i i x y p x p y p
()()()35
.07.03.02.07.02
1
33=⨯+⨯==∑=i i i x y p x p y p
(2分)
()()()
符号/3367.135.0log 35.01.0log 1.055.0log 55.0log 3
1
bit y p y p Y H j j j =⨯-⨯-⨯-=-=∑=(2分)
()()()()
()
()符号
/1569.17.0log 7.01.0log 1.02.0log 2.03.02.0log 2.01.0log 1.07.0log 7.07.0log 3
1
2
1
bit x y p x y p x p X Y H j i i i i i i =⨯+⨯+⨯⨯-⨯+⨯+⨯⨯-=-=∑∑==(2分)
平均互信息()()()符号/1798.01569.13367.1;bit X Y H Y H Y X I =-=-=(2分)
()()()符号/8813.07.0log 7.03.0log 3.0log 2
1bit x p x p X H i i i =⨯-⨯-=-=∑=(2分)
信道疑义度()()()符号/7015.01798.08813.0;bit Y X I X H Y X H =-=-=(2分) (3)此时可用最大似然译码准则，译码规则为
()11x y F =，()212x x y F 或=，()23x y F = (2分)
平均译码错误率
()[]
()()25.02.01.02.02
1
18,=++⨯==
=∑-a X Y i j j E a b p r y e p E p (2分) 3、（共20分）某离散无记忆信源符号集为 ，所对应的概率分别为：0.4，0.2，0.1，0.1，
0.07，0.05，0.05，0.02，0.01，码符号集为{0，1，2，3}。
1） 求信源的熵H (X )及信源剩余度 ；（2+2＝4分）
信源的熵：
（2分）信源剩余度：（2分）
2）对其进行四元Huffman编码；（5分）
，其中，若取，可得大于9但与9最接近的正整数10，因此在Huffman 编码是加入一个零概率符号。
编码为332；编码为331；编码为330；编码为32；编码为31；编码为30；编码为2；
编码为1；编码为0
3）求平均码长，编码效率及编码器输出的信息传输率（码率）R。
平均码长：
码元/信息符号（2分）编码效率：0.9194（2分）
信息传输速率： 1.8388比特/符号（2分）
4、已知加性高斯白噪声(AWGN，Add itiveWhite Gaussian Noise)信道，信号的带宽范围为300～3400Hz，信号与噪声功率比为26 dB，（1）计算该信道的最大信息传输速率；（2）若信号与噪声功率比降到10dB，且保持信道最大信息传输速率不变，则信道带宽应该变为多少？
解：（1）计算该信道的最大信息传输速率；（5分）
W=3400-300=3100Hz
SNR=26dB=398
（2）若信号与噪声功率比降到10dB，且保持信道最大信息传输速率不变，则信道带宽应该变为多少？（5分）
SNR=10dB=10。