目前最完整的数据结构1800题包括完整答案第六章树和二叉树

合集下载

数据结构课后习题答案第六章

第六章树和二叉树（下载后用阅读版式视图或web版式可以看清）习题一、选择题1．有一“遗传”关系：设x是y的父亲，则x可以把它的属性遗传给y。

表示该遗传关系最适合的数据结构为( )。

A.向量B.树 C图 D.二叉树2．树最合适用来表示( )。

A.有序数据元素B元素之间具有分支层次关系的数据C无序数据元素 D.元素之间无联系的数据3．树B的层号表示为la，2b，3d，3e，2c，对应于下面选择的( )。

A. la (2b (3d,3e),2c)B. a(b(D,e),c)C. a(b(d,e),c)D. a(b,d(e),c)4.高度为h的完全二叉树至少有( )个结点，至多有( )个结点。

AHA12GAGGAGAGGAFFFFAFAFA. 2h_lB.h C．2h-1 D. 2h5.在一棵完全二叉树中，若编号为f的结点存在右孩子，则右子结点的编号为( )。

A. 2iB. 2i-lC. 2i+lD. 2i+26.一棵二叉树的广义表表示为a(b(c)，d(e(，g(h))，f))，则该二叉树的高度为 ( )。

A.3B.4C.5D.67.深度为5的二叉树至多有( )个结点。

A. 31B. 32C. 16D. 108.假定在一棵二叉树中，双分支结点数为15，单分支结点数为30个，则叶子结点数为( )个。

A. 15B. 16C. 17D. 479.题图6-1中，( )是完全二叉树，( )是满二叉树。

AHA12GAGGAGAGGAFFFFAFAF10.在题图6-2所示的二叉树中：(1)A结点是A.叶结点B根结点但不是分支结点C根结点也是分支结点 D.分支结点但不是根结点(2)J结点是A.叶结点B．根结点但不是分支结点AHA12GAGGAGAGGAFFFFAFAFC根结点也是分支结点 D.分支结点但不是根结点(3)F结点的兄弟结点是A.EB.D C．空 D.I(4)F结点的双亲结点是A.AB.BC.CD.D(5)树的深度为A.1B.2C.3D.4(6)B结点的深度为A.1B.2C.3D.4(7)A结点所在的层是A.1B.2C.3D.4AHA12GAGGAGAGGAFFFFAFAF11.在一棵具有35个结点的完全二叉树中，该树的深度为( )。

数据结构-6 树和二叉树

第六章树和二叉树一．选择题1. 以下说法错误的是。

A.树形结构的特点是一个结点可以有多个直接前趋B.线性结构中的一个结点至多只有一个直接后继C.树形结构可以表达(组织)更复杂的数据D.树(及一切树形结构)是一种"分支层次"结构2. 如图6-2所示的4 棵二叉树中，不是完全二叉树。

图6-2 4 棵二叉树3. 在线索化二叉树中，t 所指结点没有左子树的充要条件是。

A. t->left == NULLB. t->ltag==1C. t->ltag==1 且t->left==NULL D .以上都不对4. 以下说法错误的是。

A.二叉树可以是空集B.二叉树的任一结点最多有两棵子树C.二叉树不是一种树D.二叉树中任一结点的两棵子树有次序之分5. 以下说法错误的是。

A.完全二叉树上结点之间的父子关系可由它们编号之间的关系来表达B.在三叉链表上，二叉树的求双亲运算很容易实现C.在二叉链表上，求根，求左、右孩子等很容易实现D.在二叉链表上，求双亲运算的时间性能很好6. 如图6-3所示的4 棵二叉树，是平衡二叉树。

图6-3 4 棵二叉树7. 如图6-4所示二叉树的中序遍历序列是。

A. abcdgefB. dfebagcC. dbaefcgD. defbagc图6-4 1 棵二叉树8. 已知某二叉树的后序遍历序列是dabec，中序遍历序列是debac，它的前序遍历序列是。

A. acbedB. decabC. deabcD. cedba9. 如果T2 是由有序树T 转换而来的二叉树，那么T 中结点的前序就是T2 中结点的。

A. 前序B.中序C. 后序D. 层次序10. 某二叉树的前序遍历结点访问顺序是abdgcefh，中序遍历的结点访问顺序是dgbaechf，则其后序遍历的结点访问顺序是。

A. bdgcefhaB. gdbecfhaC. bdgaechfD. gdbehfca11. 将含有83个结点的完全二叉树从根结点开始编号，根为1号，后面按从上到下、从左到右的顺序对结点编号，那么编号为41的双亲结点编号为。

数据结构习题第六章树和二叉树答案

第六章树和二叉树注：参考答案只能作为参考，也是有错的，自己要学会辨别。

一、单项选择题1.A2.D3．A4．C5．B6．D7．E8. D9．C10．B11. C12．A13．D14．B15．C16．B17．D18．B19. D20．C二、判断题（在各题后填写“√”或“×”）1. 完全二叉树一定存在度为1的结点。

×2. 对于有N个结点的二叉树，其高度为log2n。

×3. 二叉树的遍历只是为了在应用中找到一种线性次序。

√4. 一棵一般树的结点的前序遍历和后序遍历分别与它相应二叉树的结点前序遍历和后序遍历是一致的。

×5. 用一维数组存储二叉树时，总是以前序遍历顺序存储结点。

×6．中序遍历一棵二叉排序树的结点就可得到排好序的结点序列√7．完全二叉树中，若一个结点没有左孩子，则它必是树叶。

√8. 二叉树只能用二叉链表表示。

×9. 给定一棵树，可以找到唯一的一棵二叉树与之对应。

√10. 用链表(llink-rlink)存储包含n个结点的二叉树，结点的2n个指针区域中有n-1个空指针。

×11．树形结构中元素之间存在一个对多个的关系。

√12．将一棵树转成二叉树，根结点没有左子树。

×13．度为二的树就是二叉树。

×14.二叉树中序线索化后，不存在空指针域。

×15．霍夫曼树的结点个数不能是偶数。

√16．哈夫曼树是带权路径长度最短的树，路径上权值较大的结点离根较近。

√三、填空题1．p->lchild==null && p->rchlid==null2.(1)2k-1 (2)2k-13．644. 2n n-1 n+15．先序遍历后序遍历中序遍历6．.(1)2k-2+1（第k层1个结点，总结点个数是2H-1，其双亲是2H-1/2=2k-2）(2) ⎣log2i⎦+1 7．48．任何结点至多只有右子女的二叉树。

目前最完整的数据结构1800题包括完整答案树和二叉树答案

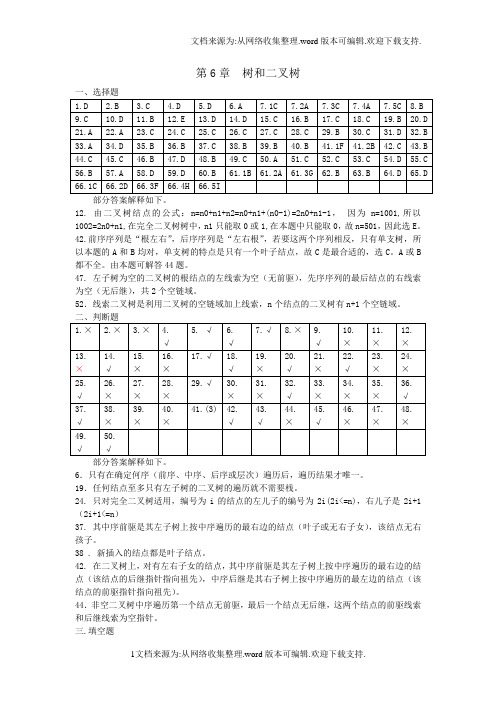
第6章树和二叉树部分答案解释如下。

12. 由二叉树结点的公式：n=n0+n1+n2=n0+n1+(n0-1)=2n0+n1-1，因为n=1001,所以1002=2n0+n1,在完全二叉树树中，n1只能取0或1,在本题中只能取0，故n=501，因此选E。

42.前序序列是“根左右”，后序序列是“左右根”，若要这两个序列相反，只有单支树，所以本题的A和B均对，单支树的特点是只有一个叶子结点，故C是最合适的，选C。

A或B 都不全。

由本题可解答44题。

47. 左子树为空的二叉树的根结点的左线索为空（无前驱），先序序列的最后结点的右线索为空（无后继），共2个空链域。

52．线索二叉树是利用二叉树的空链域加上线索，n个结点的二叉树有n+1个空链域。

部分答案解释如下。

6．只有在确定何序（前序、中序、后序或层次）遍历后，遍历结果才唯一。

19．任何结点至多只有左子树的二叉树的遍历就不需要栈。

24. 只对完全二叉树适用，编号为i的结点的左儿子的编号为2i(2i<=n)，右儿子是2i+1（2i+1<=n）37. 其中序前驱是其左子树上按中序遍历的最右边的结点（叶子或无右子女），该结点无右孩子。

38 . 新插入的结点都是叶子结点。

42. 在二叉树上，对有左右子女的结点，其中序前驱是其左子树上按中序遍历的最右边的结点（该结点的后继指针指向祖先），中序后继是其右子树上按中序遍历的最左边的结点（该结点的前驱指针指向祖先）。

44．非空二叉树中序遍历第一个结点无前驱，最后一个结点无后继，这两个结点的前驱线索和后继线索为空指针。

三.填空题1.(1)根结点(2)左子树(3)右子树2.(1)双亲链表表示法(2)孩子链表表示法(3)孩子兄弟表示法3．p->lchild==null && p->rchlid==null 4.(1) ++a*b3*4-cd (2)18 5.平衡因子6. 97. 128.(1)2k-1 (2)2k-19.(1)2H-1 (2)2H-1(3)H=⎣log2N⎦+110. 用顺序存储二叉树时，要按完全二叉树的形式存储，非完全二叉树存储时，要加“虚结点”。

严蔚敏《数据结构(c语言版)习题集》标准答案树和二叉树文库

严蔚敏《数据结构(c语言版)习题集》标准答案树和二叉树文库————————————————————————————————作者：————————————————————————————————日期：第六章树和二叉树6.33int Is_Descendant_C(int u,int v)//在孩子存储结构上判断u是否v的子孙,是则返回1,否则返回0{if(u==v) return 1;else{if(L[v])if (Is_Descendant(u,L[v])) return 1;if(R[v])if (Is_Descendant(u,R[v])) return 1; //这是个递归算法}return 0;}//Is_Descendant_C6.34int Is_Descendant_P(int u,int v)//在双亲存储结构上判断u是否v的子孙,是则返回1,否则返回0{for(p=u;p!=v&&p;p=T[p]);if(p==v) return 1;else return 0;}//Is_Descendant_P6.35这一题根本不需要写什么算法,见书后注释:两个整数的值是相等的.6.36int Bitree_Sim(Bitree B1,Bitree B2)//判断两棵树是否相似的递归算法{if(!B1&&!B2) return 1;elseif(B1&&B2&&Bitree_Sim(B1->lchild,B2->lchild)&&Bitree_Sim(B1->rchild,B2->rchild)) return 1;else return 0;}//Bitree_Sim6.37void PreOrder_Nonrecursive(Bitree T)//先序遍历二叉树的非递归算法{InitStack(S);Push(S,T); //根指针进栈while(!StackEmpty(S)){while(Gettop(S,p)&&p){visit(p->data);push(S,p->lchild);} //向左走到尽头pop(S,p);if(!StackEmpty(S)){pop(S,p);push(S,p->rchild); //向右一步}}//while}//PreOrder_Nonrecursive6.38typedef struct {BTNode* ptr;enum {0,1,2} mark;} PMType; //有mark域的结点指针类型void PostOrder_Stack(BiTree T)//后续遍历二叉树的非递归算法,用栈{PMType a;InitStack(S); //S的元素为PMType类型Push (S,{T,0}); //根结点入栈while(!StackEmpty(S)){Pop(S,a);switch(a.mark){case 0:Push(S,{a.ptr,1}); //修改mark域if(a.ptr->lchild) Push(S,{a.ptr->lchild,0}); //访问左子树break;case 1:Push(S,{a.ptr,2}); //修改mark域if(a.ptr->rchild) Push(S,{a.ptr->rchild,0}); //访问右子树break;case 2:visit(a.ptr); //访问结点,返回}}//while}//PostOrder_Stack分析:为了区分两次过栈的不同处理方式,在堆栈中增加一个mark域,mark=0表示刚刚访问此结点,mark=1表示左子树处理结束返回,mark=2表示右子树处理结束返回.每次根据栈顶元素的mark域值决定做何种动作.6.39typedef struct {int data;EBTNode *lchild;EBTNode *rchild;EBTNode *parent;enum {0,1,2} mark;} EBTNode,EBitree; //有mark域和双亲指针域的二叉树结点类型void PostOrder_Nonrecursive(EBitree T)//后序遍历二叉树的非递归算法,不用栈{p=T;while(p)switch(p->mark){case 0:p->mark=1;if(p->lchild) p=p->lchild; //访问左子树break;case 1:p->mark=2;if(p->rchild) p=p->rchild; //访问右子树break;case 2:visit(p);p->mark=0; //恢复mark值p=p->parent; //返回双亲结点}}//PostOrder_Nonrecursive分析:本题思路与上一题完全相同,只不过结点的mark值是储存在结点中的,而不是暂存在堆栈中,所以访问完毕后要将mark域恢复为0,以备下一次遍历.6.40typedef struct {int data;PBTNode *lchild;PBTNode *rchild;PBTNode *parent;} PBTNode,PBitree; //有双亲指针域的二叉树结点类型void Inorder_Nonrecursive(PBitree T)//不设栈非递归遍历有双亲指针的二叉树{p=T;while(p->lchild) p=p->lchild; //向左走到尽头while(p){visit(p);if(p->rchild) //寻找中序后继:当有右子树时{p=p->rchild;while(p->lchild) p=p->lchild; //后继就是在右子树中向左走到尽头}else if(p->parent->lchild==p) p=p->parent; //当自己是双亲的左孩子时后继就是双亲else{p=p->parent;while(p->parent&&p->parent->rchild==p) p=p->parent;p=p->parent;} //当自己是双亲的右孩子时后继就是向上返回直到遇到自己是在其左子树中的祖先 }//while}//Inorder_Nonrecursive6.41int c,k; //这里把k和计数器c作为全局变量处理void Get_PreSeq(Bitree T)//求先序序列为k的结点的值{if(T){c++; //每访问一个子树的根都会使前序序号计数器加1if(c==k){printf("Value is %d\n",T->data);exit (1);}else{Get_PreSeq(T->lchild); //在左子树中查找Get_PreSeq(T->rchild); //在右子树中查找}}//if}//Get_PreSeqmain(){...scanf("%d",&k);c=0; //在主函数中调用前,要给计数器赋初值0Get_PreSeq(T,k);...}//main6.42int LeafCount_BiTree(Bitree T)//求二叉树中叶子结点的数目{if(!T) return 0; //空树没有叶子else if(!T->lchild&&!T->rchild) return 1; //叶子结点else return Leaf_Count(T->lchild)+Leaf_Count(T->rchild);//左子树的叶子数加上右子树的叶子数}//LeafCount_BiTree6.43void Bitree_Revolute(Bitree T)//交换所有结点的左右子树{T->lchild<->T->rchild; //交换左右子树if(T->lchild) Bitree_Revolute(T->lchild);if(T->rchild) Bitree_Revolute(T->rchild); //左右子树再分别交换各自的左右子树}//Bitree_Revolute6.44int Get_Sub_Depth(Bitree T,int x)//求二叉树中以值为x的结点为根的子树深度{if(T->data==x){printf("%d\n",Get_Depth(T)); //找到了值为x的结点,求其深度exit 1;}else{if(T->lchild) Get_Sub_Depth(T->lchild,x);if(T->rchild) Get_Sub_Depth(T->rchild,x); //在左右子树中继续寻找}}//Get_Sub_Depthint Get_Depth(Bitree T)//求子树深度的递归算法{if(!T) return 0;else{m=Get_Depth(T->lchild);n=Get_Depth(T->rchild);return (m>n?m:n)+1;}}//Get_Depth6.45void Del_Sub_x(Bitree T,int x)//删除所有以元素x为根的子树{if(T->data==x) Del_Sub(T); //删除该子树else{if(T->lchild) Del_Sub_x(T->lchild,x);if(T->rchild) Del_Sub_x(T->rchild,x); //在左右子树中继续查找}//else}//Del_Sub_xvoid Del_Sub(Bitree T)//删除子树T{if(T->lchild) Del_Sub(T->lchild);if(T->rchild) Del_Sub(T->rchild);free(T);}//Del_Sub6.46void Bitree_Copy_Nonrecursive(Bitree T,Bitree &U)//非递归复制二叉树{InitStack(S1);InitStack(S2);push(S1,T); //根指针进栈U=(BTNode*)malloc(sizeof(BTNode));U->data=T->data;q=U;push(S2,U);while(!StackEmpty(S)){while(Gettop(S1,p)&&p){q->lchild=(BTNode*)malloc(sizeof(BTNode));q=q->lchild;q->data=p->data;push(S1,p->lchild);push(S2,q);} //向左走到尽头pop(S1,p);pop(S2,q);if(!StackEmpty(S1)){pop(S1,p);pop(S2,q);q->rchild=(BTNode*)malloc(sizeof(BTNode));q=q->rchild;q->data=p->data;push(S1,p->rchild); //向右一步push(S2,q);}}//while}//BiTree_Copy_Nonrecursive分析:本题的算法系从6.37改写而来.6.47void LayerOrder(Bitree T)//层序遍历二叉树{InitQueue(Q); //建立工作队列EnQueue(Q,T);while(!QueueEmpty(Q)){DeQueue(Q,p);visit(p);if(p->lchild) EnQueue(Q,p->lchild);if(p->rchild) EnQueue(Q,p->rchild);}}//LayerOrder6.48int found=FALSE;Bitree* Find_Near_Ancient(Bitree T,Bitree p,Bitree q)//求二叉树T中结点p和q的最近共同祖先{Bitree pathp[ 100 ],pathq[ 100 ] //设立两个辅助数组暂存从根到p,q的路径Findpath(T,p,pathp,0);found=FALSE;Findpath(T,q,pathq,0); //求从根到p,q的路径放在pathp和pathq中for(i=0;pathp[i]==pathq[i]&&pathp[i];i++); //查找两条路径上最后一个相同结点return pathp[--i];}//Find_Near_Ancientvoid Findpath(Bitree T,Bitree p,Bitree path[ ],int i)//求从T到p路径的递归算法{if(T==p){found=TRUE;return; //找到}path[i]=T; //当前结点存入路径if(T->lchild) Findpath(T->lchild,p,path,i+1); //在左子树中继续寻找if(T->rchild&&!found) Findpath(T->rchild,p,path,i+1); //在右子树中继续寻找if(!found) path[i]=NULL; //回溯}//Findpath6.49int IsFull_Bitree(Bitree T)//判断二叉树是否完全二叉树,是则返回1,否则返回0{InitQueue(Q);flag=0;EnQueue(Q,T); //建立工作队列while(!QueueEmpty(Q)){DeQueue(Q,p);if(!p) flag=1;else if(flag) return 0;else{EnQueue(Q,p->lchild);EnQueue(Q,p->rchild); //不管孩子是否为空,都入队列}}//whilereturn 1;}//IsFull_Bitree分析:该问题可以通过层序遍历的方法来解决.与6.47相比,作了一个修改,不管当前结点是否有左右孩子,都入队列.这样当树为完全二叉树时,遍历时得到是一个连续的不包含空指针的序列.反之,则序列中会含有空指针.6.50Status CreateBitree_Triplet(Bitree &T)//输入三元组建立二叉树{if(getchar()!='^') return ERROR;T=(BTNode*)malloc(sizeof(BTNode));p=T;p->data=getchar();getchar(); //滤去多余字符InitQueue(Q);EnQueue(Q,T);while((parent=getchar())!='^'&&(child=getchar())&&(side=getchar())){while(QueueHead(Q)!=parent&&!QueueEmpty(Q)) DeQueue(Q,e);if(QueueEmpty(Q)) return ERROR; //未按层序输入p=QueueHead(Q);q=(BTNode*)malloc(sizeof(BTNode));if(side=='L') p->lchild=q;else if(side=='R') p->rchild=q;else return ERROR; //格式不正确q->data=child;EnQueue(Q,q);}return OK;}//CreateBitree_Triplet6.51Status Print_Expression(Bitree T)//按标准形式输出以二叉树存储的表达式{if(T->data是字母) printf("%c",T->data);else if(T->data是操作符){if(!T->lchild||!T->rchild) return ERROR; //格式错误if(T->lchild->data是操作符&&T->lchild->data优先级低于T->data){printf("(");if(!Print_Expression(T->lchild)) return ERROR;printf(")");} //注意在什么情况下要加括号else if(!Print_Expression(T->lchild)) return ERROR;if(T->rchild->data是操作符&&T->rchild->data优先级低于T->data){printf("(");if(!Print_Expression(T->rchild)) return ERROR;printf(")");}else if(!Print_Expression(T->rchild)) return ERROR;}else return ERROR; //非法字符return OK;}//Print_Expression6.52typedef struct{BTNode node;int layer;} BTNRecord; //包含结点所在层次的记录类型int FanMao(Bitree T)//求一棵二叉树的"繁茂度"{int countd; //count数组存放每一层的结点数InitQueue(Q); //Q的元素为BTNRecord类型EnQueue(Q,{T,0});while(!QueueEmpty(Q)){DeQueue(Q,r);count[yer]++;if(r.node->lchild) EnQueue(Q,{r.node->lchild,yer+1});if(r.node->rchild) EnQueue(Q,{r.node->rchild,yer+1});} //利用层序遍历来统计各层的结点数h=yer; //最后一个队列元素所在层就是树的高度for(maxn=count[0],i=1;count[i];i++)if(count[i]>maxn) maxn=count[i]; //求层最大结点数return h*maxn;}//FanMao分析:如果不允许使用辅助数组,就必须在遍历的同时求出层最大结点数,形式上会复杂一些,你能写出来吗?6.53int maxh;Status Printpath_MaxdepthS1(Bitree T)//求深度等于树高度减一的最靠左的结点{Bitree pathd;maxh=Get_Depth(T); //Get_Depth函数见6.44if(maxh<2) return ERROR; //无符合条件结点Find_h(T,1);return OK;}//Printpath_MaxdepthS1void Find_h(Bitree T,int h)//寻找深度为maxh-1的结点{path[h]=T;if(h==maxh-1){for(i=1;path[i];i++) printf("%c",path[i]->data);exit; //打印输出路径}else{if(T->lchild) Find_h(T->lchild,h+1);if(T->rchild) Find_h(T->rchild,h+1);}path[h]=NULL; //回溯}//Find_h6.54Status CreateBitree_SqList(Bitree &T,SqList sa)//根据顺序存储结构建立二叉链表{Bitree ptr[st+1]; //该数组储存与sa中各结点对应的树指针if(!st){T=NULL; //空树return;}ptr[1]=(BTNode*)malloc(sizeof(BTNode));ptr[1]->data=sa.elem[1]; //建立树根T=ptr[1];for(i=2;i<=st;i++){if(!sa.elem[i]) return ERROR; //顺序错误ptr[i]=(BTNode*)malloc(sizeof(BTNode));ptr[i]->data=sa.elem[i];j=i/2; //找到结点i的双亲jif(i-j*2) ptr[j]->rchild=ptr[i]; //i是j的右孩子else ptr[j]->lchild=ptr[i]; //i是j的左孩子}return OK;}//CreateBitree_SqList6.55int DescNum(Bitree T)//求树结点T的子孙总数填入DescNum域中,并返回该数{if(!T) return -1;else d=(DescNum(T->lchild)+DescNum(T->rchild)+2); //计算公式T->DescNum=d;return d;}//DescNum分析:该算法时间复杂度为O(n),n为树结点总数.注意:为了能用一个统一的公式计算子孙数目,所以当T为空指针时,要返回-1而不是0.6.56BTNode *PreOrder_Next(BTNode *p)//在先序后继线索二叉树中查找结点p的先序后继,并返回指针{if(p->lchild) return p->lchild;else return p->rchild;}//PreOrder_Next分析:总觉得不会这么简单.是不是哪儿理解错了?6.57Bitree PostOrder_Next(Bitree p)//在后序后继线索二叉树中查找结点p的后序后继,并返回指针{if(p->rtag) return p->rchild; //p有后继线索else if(!p->parent) return NULL; //p是根结点else if(p==p->parent->rchild) return p->parent; //p是右孩子else if(p==p->parent->lchild&&p->parent->tag)return p->parent; //p是左孩子且双亲没有右孩子else //p是左孩子且双亲有右孩子{q=p->parent->rchild;while(!q->ltag||!q->rtag){if(!q->ltag) q=q->lchild;else q=q->rchild;} //从p的双亲的右孩子向下走到底return q;}//else}//PostOrder_Next6.58Status Insert_BiThrTree(BiThrTree &T,BiThrTree &p,BiThrTree &x)//在中序线索二叉树T的结点p下插入子树x{if(!p->ltag&&!p->rtag) return INFEASIBLE; //无法插入if(p->ltag) //x作为p的左子树{s=p->lchild; //s为p的前驱p->ltag=Link;p->lchild=x;q=x;while(q->lchild) q=q->lchild;q->lchild=s; //找到子树中的最左结点,并修改其前驱指向sq=x;while(q->rchild) q=q->rchild;q->rchild=p; //找到子树中的最右结点,并修改其前驱指向p}else //x作为p的右子树{s=p->rchild; //s为p的后继p->rtag=Link;p->rchild=x;q=x;while(q->rchild) q=q->rchild;q->rchild=s; //找到子树中的最右结点,并修改其前驱指向sq=x;while(q->lchild) q=q->lchild;q->lchild=p; //找到子树中的最左结点,并修改其前驱指向p}return OK;}//Insert_BiThrTree6.59void Print_CSTree(CSTree T)//输出孩子兄弟链表表示的树T的各边{for(child=T->firstchild;child;child=child->nextsib){printf("(%c,%c),",T->data,child->data);Print_CSTree(child);}}//Print_CSTree6.60int LeafCount_CSTree(CSTree T)//求孩子兄弟链表表示的树T的叶子数目{if(!T->firstchild) return 1; //叶子结点else{count=0;for(child=T->firstchild;child;child=child->nextsib)count+=LeafCount_CSTree(child);return count; //各子树的叶子数之和}}//LeafCount_CSTree6.61int GetDegree_CSTree(CSTree T)//求孩子兄弟链表表示的树T的度{if(!T->firstchild) return 0; //空树else{degree=0;for(p=T->firstchild;p;p=p->nextsib) degree++;//本结点的度for(p=T->firstchild;p;p=p->nextsib){d=GetDegree_CSTree(p);if(d>degree) degree=d; //孩子结点的度的最大值}return degree;}//else}//GetDegree_CSTree6.62int GetDepth_CSTree(CSTree T)//求孩子兄弟链表表示的树T的深度{if(!T) return 0; //空树else{for(maxd=0,p=T->firstchild;p;p=p->nextsib)if((d=GetDepth_CSTree(p))>maxd) maxd=d; //子树的最大深度return maxd+1;}}//GetDepth_CSTree6.63int GetDepth_CTree(CTree A)//求孩子链表表示的树A的深度{return SubDepth(A.r);}//GetDepth_CTreeint SubDepth(int T)//求子树T的深度{if(!A.nodes[T].firstchild) return 1;for(sd=1,p=A.nodes[T].firstchild;p;p=p->next)if((d=SubDepth(p->child))>sd) sd=d;return sd+1;}//SubDepth6.64int GetDepth_PTree(PTree T)//求双亲表表示的树T的深度{maxdep=0;for(i=0;i<T.n;i++){dep=0;for(j=i;j>=0;j=T.nodes[j].parent) dep++; //求每一个结点的深度if(dep>maxdep) maxdep=dep;}return maxdep;}//GetDepth_PTree6.65char Pred,Ind; //假设前序序列和中序序列已经分别储存在数组Pre和In中Bitree Build_Sub(int Pre_Start,int Pre_End,int In_Start,int In_End)//由子树的前序和中序序列建立其二叉链表{sroot=(BTNode*)malloc(sizeof(BTNode)); //建根sroot->data=Pre[Pre_Start];for(i=In_Start;In[i]!=sroot->data;i++); //在中序序列中查找子树根leftlen=i-In_Start;rightlen=In_End-i; //计算左右子树的大小if(leftlen){lroot=Build_Sub(Pre_Start+1,Pre_Start+leftlen,In_Start,In_Start+leftlen-1); sroot->lchild=lroot;} //建左子树,注意参数表的计算if(rightlen){rroot=Build_Sub(Pre_End-rightlen+1,Pre_End,In_End-rightlen+1,In_End);sroot->rchild=rroot;} //建右子树,注意参数表的计算return sroot; //返回子树根}//Build_Submain(){...Build_Sub(1,n,1,n); //初始调用参数,n为树结点总数...}分析:本算法利用了这样一个性质,即一棵子树在前序和中序序列中所占的位置总是连续的.因此,就可以用起始下标和终止下标来确定一棵子树.Pre_Start,Pre_End,In_Start和In_End分别指示子树在前序子序列里的起始下标,终止下标,和在中序子序列里的起始和终止下标.6.66typedef struct{CSNode *ptr;CSNode *lastchild;} NodeMsg; //结点的指针和其最后一个孩子的指针Status Bulid_CSTree_PTree(PTree T)//由树T的双亲表构造其孩子兄弟链表{NodeMsg Treed;for(i=0;i<T.n;i++){Tree[i].ptr=(CSNode*)malloc(sizeof(CSNode));Tree[i].ptr->data=T.node[i].data; //建结点if(T.nodes[i].parent>=0) //不是树根{j=T.nodes[i].parent; //本算法要求双亲表必须是按层序存储if(!(Tree[j].lastchild)) //双亲当前还没有孩子Tree[j].ptr->firstchild=Tree[i].ptr; //成为双亲的第一个孩子else //双亲已经有了孩子Tree[j].lastchild->nextsib=Tree[i].ptr; //成为双亲最后一个孩子的下一个兄弟Tree[j].lastchild=Tree[i].ptr; //成为双亲的最后一个孩子}//if}//for}//Bulid_CSTree_PTree6.67typedef struct{char data;CSNode *ptr;CSNode *lastchild;} NodeInfo; //结点数据,结点指针和最后一个孩子的指针Status CreateCSTree_Duplet(CSTree &T)//输入二元组建立树的孩子兄弟链表{NodeInfo Treed;n=1;k=0;if(getchar()!='^') return ERROR; //未按格式输入if((c=getchar())=='^') T=NULL; //空树Tree[0].ptr=(CSNode*)malloc(sizeof(CSNode));Tree[0].data=c;Tree[0].ptr->data=c;while((p=getchar())!='^'&&(c=getchar())!='^'){Tree[n].ptr=(CSNode*)malloc(sizeof(CSNode));Tree[n].data=c;Tree[n].ptr->data=c;for(k=0;Tree[k].data!=p;k++); //查找当前边的双亲结点if(Tree[k].data!=p) return ERROR; //未找到:未按层序输入r=Tree[k].ptr;if(!r->firstchild)r->firstchild=Tree[n].ptr;else Tree[k].lastchild->nextsib=Tree[n].ptr;Tree[k].lastchild=Tree[n].ptr; //这一段含义同上一题n++;}//whilereturn OK;}//CreateCSTree_Duplet6.68Status CreateCSTree_Degree(char node[ ],int degree[ ])//由结点的层序序列和各结点的度构造树的孩子兄弟链表{CSNode * ptrd; //树结点指针的辅助存储ptr[0]=(CSNode*)malloc(sizeof(CSNode));i=0;k=1; //i为当前结点序号,k为当前孩子的序号while(node[i]){ptr[i]->data=node[i];d=degree[i];if(d){ptr[k++]=(CSNode*)malloc(sizeof(CSNode)); //k为当前孩子的序号ptr[i]->firstchild=ptr[k]; //建立i与第一个孩子k之间的联系for(j=2;j<=d;j++){ptr[k++]=(CSNode*)malloc(sizeof(CSNode));ptr[k-1]->nextsib=ptr[k]; //当结点的度大于1时,为其孩子建立兄弟链表}//for}//ifi++;}//while}//CreateCSTree_Degree6.69void Print_BiTree(BiTree T,int i)//按树状打印输出二叉树的元素,i表示结点所在层次,初次调用时i=0{if(T->rchild) Print_BiTree(T->rchild,i+1);for(j=1;j<=i;j++) printf(" "); //打印i个空格以表示出层次printf("%c\n",T->data); //打印T元素,换行if(T->lchild) Print_BiTree(T->rchild,i+1);}//Print_BiTree分析:该递归算法实际上是带层次信息的中序遍历,只不过按照题目要求,顺序为先右后左.6.70Status CreateBiTree_GList(BiTree &T)//由广义表形式的输入建立二叉链表{c=getchar();if(c=='#') T=NULL; //空子树else{T=(CSNode*)malloc(sizeof(CSNode));T->data=c;if(getchar()!='(') return ERROR;if(!CreateBiTree_GList(pl)) return ERROR;T->lchild=pl;if(getchar()!=',') return ERROR;if(!CreateBiTree_GList(pr)) return ERROR;T->rchild=pr;if(getchar()!=')') return ERROR; //这些语句是为了保证输入符合A(B,C)的格式}return OK;}//CreateBiTree_GList6.71void Print_CSTree(CSTree T,int i)//按凹入表形式打印输出树的元素,i表示结点所在层次,初次调用时i=0{for(j=1;j<=i;j++) printf(" "); //留出i个空格以表现出层次printf("%c\n",T->data); //打印元素,换行for(p=T->firstchild;p;p=p->nextsib)Print_CSTree(p,i+1); //打印子树}//Print_CSTree6.72void Print_CTree(int e,int i)//按凹入表形式打印输出树的元素,i表示结点所在层次{for(j=1;j<=i;j++) printf(" "); //留出i个空格以表现出层次printf("%c\n",T.nodes[e].data); //打印元素,换行for(p=T.nodes[e].firstchild;p;p=p->next)Print_CSTree(p->child,i+1); //打印子树}//Print_CSTreemain(){...Print_CTree(T.r,0); //初次调用时i=0...}//main6.73char c; //全局变量,指示当前字符Status CreateCSTree_GList(CSTree &T)//由广义表形式的输入建立孩子兄弟链表{c=getchar();T=(CSNode*)malloc(sizeof(CSNode));T->data=c;if((c=getchar())=='(') //非叶结点{if(!CreateCSTree_GList(fc)) return ERROR; //建第一个孩子T->firstchild=fc;for(p=fc;c==',';p->nextsib=nc,p=nc) //建兄弟链if(!CreateCSTree_GList(nc)) return ERROR;p->nextsib=NULL;if((c=getchar())!=')') return ERROR; //括号不配对}else T->firtchild=NULL; //叶子结点return OK;}//CreateBiTree_GList分析:书后给出了两个间接递归的算法,事实上合成一个算法在形式上可能更好一些.本算法另一个改进之处在于加入了广义表格式是否合法的判断.6.74void PrintGlist_CSTree(CSTree T)//按广义表形式输出孩子兄弟链表表示的树{printf("%c",T->data);if(T->firstchild) //非叶结点{printf("(");for(p=T->firstchild;p;p=p->nextsib){PrintGlist_CSTree(p);if(p->nextsib) printf(","); //最后一个孩子后面不需要加逗号}printf(")");}//if}//PrintGlist_CSTree6.75char c;int pos=0; //pos是全局变量,指示已经分配到了哪个结点Status CreateCTree_GList(CTree &T,int &i)//由广义表形式的输入建立孩子链表{c=getchar();T.nodes[pos].data=c;i=pos++; //i是局部变量,指示当前正在处理的子树根if((c=getchar())=='(') //非叶结点{CreateCTree_GList();p=(CTBox*)malloc(sizeof(CTBox));T.nodes[i].firstchild=p;p->child=pos; //建立孩子链的头for(;c==',';p=p->next) //建立孩子链{CreateCTree_GList(T,j); //用j返回分配得到的子树根位置p->child=j;p->next=(CTBox*)malloc(sizeof(CTBox));}p->next=NULL;if((c=getchar())!=')') return ERROR; //括号不配对}//ifelse T.nodes[i].firtchild=NULL; //叶子结点return OK;}//CreateBiTree_GList分析:该算法中,pos变量起着"分配"结点在表中的位置的作用,是按先序序列从上向下分配,因此树根T.r一定等于0,而最终的pos值就是结点数T.n.6.76void PrintGList_CTree(CTree T,int i)//按广义表形式输出孩子链表表示的树{printf("%c",T.nodes[i].data);if(T.nodes[i].firstchild) //非叶结点{printf("(");for(p=T->firstchild;p;p=p->nextsib){PrintGlist_CSTree(T,p->child);if(p->nextsib) printf(","); //最后一个孩子后面不需要加逗号}printf(")");}//if}//PrintGlist_CTree21。

《数据结构》期末复习题及参考答案 - 第6章树和二叉树【HSH2013级】给学生

《数据结构》期末复习题及参考答案 - 第6章树和二叉树一、选择题1、在二叉树的第I 层(I≥1)上最多含有结点数为（）A. 2IB. 2I-1-1C. 2I-1D. 2I -12、深度为6的二叉树最多有( )个结点A ．64 B.63 C.32 D.313、一棵树高为K 的完全二叉树至少有( )个结点A.2k –1B.2k-1 –1C.2k-1D.2 k4、有关二叉树下列说法正确的是（）A. 二叉树的度为2B. 一棵二叉树的度可以小于2C. 二叉树中至少有一个结点的度为2D. 二叉树中任何一个结点的度都为25、n 个结点的线索二叉树上含有的线索数为（）A. 2nB. n －lC. n ＋lD. n6、线性表和树的结构区别在于（）A ．前驱数量不同，后继数量相同B ．前驱数量相同，后继数量不同C ．前驱和后继的数量都相同D ．前驱和后继的数量都不同7、已知一算术表达式的中缀形式为 A+B*C-D/E ，后缀形式为ABC*+DE/-，则其前缀形式为( )A ．-A+B*C/DE B. -A+B*CD/E C ．-+*ABC/DE D. -+A*BC/DE8、设有一表示算术表达式的二叉树（见下图），它所表示的算术表达式是（）A. A*B+C/(D*E)+(F-G)B. (A*B+C)/(D*E)+(F-G)9、一棵具有 n 个结点的完全二叉树的树高度（深度）(符号⎣⎦x 表示取不大于x 的最大整数)是（）10、利用二叉链表存储树，则根结点的右指针是（）。

11、已知一棵二叉树的前序遍历结果为ABCDEF，中序遍历结果为CBAEDF，则后序遍历的结果为（）。

12、某二叉树中序序列为A,B,C,D,E,F,G，后序序列为B,D,C,A,F,G,E 则前序序列是：A．E,G,F,A,C,D,B B．E,A,C,B,D,G,F C．E,A,G,C,F,B,D D．上面的都不对13、若前序遍历二叉树的结果为序列A、B、C，则有_________棵不同的二叉树可以得到这一结果。

数据结构第六章树和二叉树作业及答案

第六章树和二叉树作业一、选择题（每题2分，共24分）。

1. 一棵二叉树的顺序存储情况如下：树中，度为2的结点数为（ C ）。

A．1 B．2 C．3 D．42. 一棵“完全二叉树”结点数为25，高度为（B ）。

A．4 B．5 C．6 D．不确定3．下列说法中，（B ）是正确的。

A. 二叉树就是度为2的树B. 二叉树中不存在度大于2的结点C. 二叉树是有序树D. 二叉树中每个结点的度均为24.一棵二叉树的前序遍历序列为ABCDEFG,它的中序遍历序列可能是（B ）。

A. CABDEFGB. BCDAEFGC. DACEFBGD. ADBCFEG5．线索二叉树中的线索指的是（C ）。

A．左孩子 B.遍历 C.指针 D.标志6. 建立线索二叉树的目的是（A ）。

A. 方便查找某结点的前驱或后继B. 方便二叉树的插入与删除C. 方便查找某结点的双亲D. 使二叉树的遍历结果唯一7. 有 D ）示意。

A.B.C.D.8. 一颗有2046个结点的完全二叉树的第10层上共有（B ）个结点。

A. 511B. 512C. 1023D. 10249. 一棵完全二叉树一定是一棵（A ）。

A. 平衡二叉树B. 二叉排序树C. 堆D. 哈夫曼树10．某二叉树的中序遍历序列和后序遍历序列正好相反，则该二叉树一定是（ C ）的二叉树。

A ．空或只有一个结点B ．高度等于其结点数C ．任一结点无左孩子D ．任一结点无右孩子11．一棵二叉树的顺序存储情况如下：1 2 3 4 5 6 7 8 9 10 11 12 13 14 15A B C D E 0 F 0 0 G H 0 0 0 X结点D 的左孩子结点为（ D ）。

A ．EB ．C C ．FD ．没有12．一棵“完全二叉树”结点数为25，高度为（ B ）。

A ．4B ．5C ．6D ．不确定二、填空题（每空3分，共18分）。

1. 树的路径长度：是从树根到每个结点的路径长度之和。

对结点数相同的树来说，路径长度最短的是完全二叉树。

数据结构课后习题(第6章)

【课后习题】第6章树和二叉树网络工程2010级（）班学号：姓名：一、填空题（每空1分，共16分)1.从逻辑结构看，树是典型的。

2.设一棵完全二叉树具有999个结点，则此完全二叉树有个叶子结点，有个度为2的结点，有个度为1的结点。

3.由n个权值构成的哈夫曼树共有个结点。

4.在线索化二叉树中，T所指结点没有左子树的充要条件是。

5.在非空树上，_____没有直接前趋。

6.深度为k的二叉树最多有结点，最少有个结点。

7.若按层次顺序将一棵有n个结点的完全二叉树的所有结点从1到n编号，那么当i为且小于n时，结点i的右兄弟是结点，否则结点i没有右兄弟。

8.N个结点的二叉树采用二叉链表存放，共有空链域个数为。

9.一棵深度为7的满二叉树有___ ___个非终端结点。

10.将一棵树转换为二叉树表示后,该二叉树的根结点没有。

11.采用二叉树来表示树时，树的先根次序遍历结果与其对应的二叉树的遍历结果是一样的。

12.一棵Huffman树是带权路径长度最短的二叉树，权值的外结点离根较远。

二、判断题（如果正确，在对应位置打“√”，否则打“⨯”。

每题0.5分，共5分)1.对于一棵非空二叉树，它的根结点作为第一层，则它的第i层上最多能有2i-1个结点。

2.二叉树的前序遍历并不能唯一确定这棵树，但是，如果我们还知道该二叉树的根结点是那一个，则可以确定这棵二叉树。

3.一棵树中的叶子结点数一定等于与其对应的二叉树中的叶子结点数。

4.度≤2的树就是二叉树。

5.一棵Huffman树是带权路径长度最短的二叉树，权值较大的外结点离根较远。

6.采用二叉树来表示树时，树的先根次序遍历结果与其对应的二叉树的前序遍历结果是一样的。

7.不存在有偶数个结点的满二叉树。

8.满二叉树一定是完全二叉树，而完全二叉树不一定是满二叉树。

9.已知二叉树的前序遍历顺序和中序遍历顺序，可以惟一确定一棵二叉树；10.已知二叉树的前序遍历顺序和后序遍历顺序，不能惟一确定一棵二叉树；三、单项选择（请将正确答案的代号填写在下表对应题号下面。

数据结构第6章作业树和二叉树答案

第6章树和二叉树答案一、判断正误（√）1. 若二叉树用二叉链表作存贮结构，则在n个结点的二叉树链表中只有n—1个非空指针域。

（×）2.二叉树中每个结点的两棵子树的高度差等于1。

（√）3.二叉树中每个结点的两棵子树是有序的。

（×）4.二叉树中每个结点有两棵非空子树或有两棵空子树。

（×）5.二叉树中每个结点的关键字值大于其左非空子树（若存在的话）所有结点的关键字值，且小于其右非空子树（若存在的话）所有结点的关键字值。

（应当是二叉排序树的特点）（×）6.二叉树中所有结点个数是2k-1-1，其中k是树的深度。

（应2i-1）（×）7.二叉树中所有结点，如果不存在非空左子树，则不存在非空右子树。

（×）8.对于一棵非空二叉树，它的根结点作为第一层，则它的第i层上最多能有2i—1个结点。

（应2i-1）（√）9.用二叉链表法（link-rlink）存储包含n个结点的二叉树，结点的2n个指针区域中有n+1个为空指针。

（正确。

用二叉链表存储包含n个结点的二叉树，结点共有2n个链域。

由于二叉树中，除根结点外，每一个结点有且仅有一个双亲，所以只有n-1个结点的链域存放指向非空子女结点的指针，还有n+1个空指针。

）即有后继链接的指针仅n-1个。

（√）10. 〖01年计算机系研题〗具有12个结点的完全二叉树有5个度为2的结点。

最快方法：用叶子数＝[n/2]＝6，再求n2=n0-1=5二、填空题1．由３个结点所构成的二叉树有5种形态。

2. 一棵深度为6的满二叉树有n1+n2=0+ n2= n0-1=31 个分支结点和26-1 =32个叶子。

注：满二叉树没有度为1的结点，所以分支结点数就是二度结点数。

3．一棵具有２５７个结点的完全二叉树，它的深度为9。

（注：用⎣ log2(n) ⎦+1= ⎣ 8.xx ⎦+1=94.设一棵完全二叉树有700个结点，则共有350个叶子结点。

数据结构答案(耿国华)

数据结构
SubString(sub2,s,7,1)= 空格
StrIndex(s,’A’,4)= 6 StrReplace(s,’STUDENT’,q)= I AM A WORKER
StrCat(StrCat(sub1,t),StrCat(sub2,q)) = I AM A GOOD WORKER
B
C A
先：ABC 中：CBA 后：CBA
A
B C
先：ABC 中：BAC 后：BCA
6
A
先：ABC B 中：ACB 后：CBA
B C
C
先：ABC 中：ABC 后：CBA
第6章树和二叉树习题
3.已知一棵度为k的树中有n1个度为1的结点，n2个度为2的结点，…nk个度为k的结点，则该树中有多少个叶子结点，并证明之。
3）前序和后序相同空树、只有一个结点的树
9
第6章树和二叉树习题
数据结构
补充：写出下面二叉树的前序、中序、后序遍历序列先序序列： A ABCDEFGHIJ E B 中序序列： G C F BCDAFEHJIG D H I J 后序序列： DCBFJIHGEA
10
第6章树和二叉树习题
13
解：设n为总结点数，则有
数据结构
(总结点数) n=n0+n1+n2+…nk (总边数) n-1=1*n1+2*n2+…k*nk 两式相减得：1=n0-n2-2n3-…-(k-1)nk n0=1+n2+2n3+…+(k-1)nk =1+∑(i-1)ni
i=1
7
k
第6章树和二叉树习题
4.假设一棵二叉树的先序序列和中序序列，试画出该二叉树，并写出后序遍历序列。

数据结构考试试题库含答案解析

数据结构习题集含答案目录目录 (1)选择题 (2)第一章绪论 (2)第二章线性表 (4)第三章栈和队列 (6)第四章串 (7)第五章数组和广义表 (8)第六章树和二叉树 (8)第七章图 (11)第八章查找 (13)第九章排序 (14)简答题 (19)第一章绪论 (19)第二章线性表 (24)第三章栈和队列 (26)第四章串 (28)第五章数组和广义表 (29)第六章树和二叉树 (31)第七章图 (36)第八章查找 (38)第九章排序 (39)编程题 (41)第一章绪论 (41)第二章线性表 (41)第三章栈和队列 (52)第四章串 (52)第五章数组和广义表 (52)第六章树和二叉树 (52)第七章图 (52)第八章查找 (52)第九章排序 (57)选择题第一章绪论1.数据结构这门学科是针对什么问题而产生的？(A ）A、针对非数值计算的程序设计问题B、针对数值计算的程序设计问题C、数值计算与非数值计算的问题都针对D、两者都不针对2.数据结构这门学科的研究内容下面选项最准确的是（D ）A、研究数据对象和数据之间的关系B、研究数据对象C、研究数据对象和数据的操作D、研究数据对象、数据之间的关系和操作3.某班级的学生成绩表中查得张三同学的各科成绩记录，其中数据结构考了90分，那么下面关于数据对象、数据元素、数据项描述正确的是（C ）A、某班级的学生成绩表是数据元素,90分是数据项B、某班级的学生成绩表是数据对象，90分是数据元素C、某班级的学生成绩表是数据对象，90分是数据项D、某班级的学生成绩表是数据元素,90分是数据元素4.*数据结构是指（A ）。

A、数据元素的组织形式B、数据类型C、数据存储结构D、数据定义5.数据在计算机存储器内表示时，物理地址与逻辑地址不相同，称之为（C ）。

A、存储结构B、逻辑结构C、链式存储结构D、顺序存储结构6.算法分析的目的是（C )A、找出数据的合理性B、研究算法中的输入和输出关系C、分析算法效率以求改进D、分析算法的易懂性和文档型性7.算法分析的主要方法（A )。

数据结构(本)单元6树和二叉树单元测试

数据结构（本）单元6树和二叉树单元测试（题+答案）题目1、假定一棵二叉树中，双分支结点数为15，单分支结点数为30，则叶子结点数为（）。

A. 15B. 16C. 47D. 17题目2、已知某二叉树的后续遍历序列是dabec，中序遍历是debac，则它的先序遍历序列是（）。

A. cedbaB. decabC. acbedD. deabc题目3、二叉树第k层上最多有（）个结点。

A.B.C.D. 2k题目4、二叉树的深度为k，则二叉树最多有（）个结点。

A.B.C. 2kD. 2k-1题目5、设某一二叉树先序遍历为abdec，中序遍历为dbeac，则该二叉树后序遍历的顺序是（）。

A. debacB. debcaC. abedcD. abdec题目6、设某一二叉树中序遍历为badce，后序遍历为bdeca，则该二叉树先序遍历的顺序是（）。

A. debacB. decabC. adbecD. abcde题目7、树最适合于用来表示（）。

A. 元素之间有包含和层次关系的数据B. 元素之间无前驱和后继关系的数据C. 顺序结构的数据D. 线性结构的数据题目8、一棵非空的二叉树，先序遍历与后续遍历正好相反，则该二叉树满足（）。

A. 任意二叉树B. 无左孩子C. 只有一个叶子结点D. 无右孩子题目9、设a，b为一棵二叉树的两个结点，在后续遍历中，a在b前的条件是（）。

A. a在b左方B. a在b右方C. a在b上方D. a在b下方题目10、权值为{1，2，6，8}的四个结点构成的哈夫曼树的带权路径长度是（）。

A. 29B. 18C. 19D. 28题目11、如果将给定的一组数据作为叶子数值，所构造出的二叉树的带权路径长度最小，则该树称为（）。

A. 哈夫曼树B. 平衡二叉树C. 二叉树D. 完全二叉树题目12、下列有关二叉树的说法正确的是（）。

A. 完全二叉树中，任何一个结点的度，或者为0或者为2B. 二叉树中度为0的结点的个数等于度为2的结点的个数加1C. 二叉树的度是2D. 二叉树中结点个数必大于0题目13、二叉树是非线性数据结构，所以（）。

第6章-数据结构习题题目及答案-树和二叉树-参考答案

一、基础知识题6.1设树T的度为4，其中度为1，2，3和4的结点个数分别为4，2，1，1，求树T中的叶子数。

【解答】设度为m的树中度为0,1,2,…,m的结点数分别为n0, n1, n2,…, nm，结点总数为n，分枝数为B，则下面二式成立n= n0+n1+n2+…+nm (1)n=B+1= n1+2n2 +…+mnm+1 (2)由(1)和(2)得叶子结点数n0=1+即： n0=1+(1-1)*4+(2-1)*2+(3-1)*1+(4-1)*1=86.2一棵完全二叉树上有1001个结点，求叶子结点的个数。

【解答】因为在任意二叉树中度为2 的结点数n2和叶子结点数n0有如下关系：n2=n0-1,所以设二叉树的结点数为n, 度为1的结点数为n1，则n= n0+ n1+ n2n=2n0+n1-11002=2n0+n1由于在完全二叉树中，度为1的结点数n1至多为1，叶子数n0是整数。

本题中度为1的结点数n1只能是0，故叶子结点的个数n0为501.注：解本题时要使用以上公式，不要先判断完全二叉树高10，前9层是满二叉树，第10层都是叶子，……。

虽然解法也对，但步骤多且复杂，极易出错。

6.3 一棵124个叶结点的完全二叉树，最多有多少个结点。

【解答】由公式n=2n0+n1-1,当n1为1时，结点数达到最多248个。

6.4．一棵完全二叉树有500个结点，请问该完全二叉树有多少个叶子结点？有多少个度为1的结点？有多少个度为2的结点？如果完全二叉树有501个结点，结果如何？请写出推导过程。

【解答】由公式n=2n0+n1-1，带入具体数得，500=2n0+n1-1，叶子数是整数，度为1的结点数只能为1，故叶子数为250，度为2的结点数是249。

若完全二叉树有501个结点，则叶子数251，度为2的结点数是250，度为1的结点数为0。

6.5 某二叉树有20个叶子结点，有30个结点仅有一个孩子，则该二叉树的总结点数是多少。

数据结构树和二叉树习题及答案

数据结构树和二叉树习题及答案集团标准化工作小组 #Q8QGGQT-GX8G08Q8-GNQGJ8-MHHGN#习题六树和二叉树一、单项选择题1．以下说法错误的是 ( )A．树形结构的特点是一个结点可以有多个直接前趋B．线性结构中的一个结点至多只有一个直接后继C．树形结构可以表达(组织)更复杂的数据D．树(及一切树形结构)是一种"分支层次"结构E．任何只含一个结点的集合是一棵树2．下列说法中正确的是 ( )A．任何一棵二叉树中至少有一个结点的度为2B．任何一棵二叉树中每个结点的度都为2C．任何一棵二叉树中的度肯定等于2D．任何一棵二叉树中的度可以小于23．讨论树、森林和二叉树的关系，目的是为了（）A．借助二叉树上的运算方法去实现对树的一些运算B．将树、森林按二叉树的存储方式进行存储C．将树、森林转换成二叉树D．体现一种技巧，没有什么实际意义4．树最适合用来表示 ( )A．有序数据元素 B．无序数据元素C．元素之间具有分支层次关系的数据 D．元素之间无联系的数据5．若一棵二叉树具有10个度为2的结点，5个度为1的结点，则度为0的结点个数是（）A．9 B．11 C．15 D．不确定6．设森林F中有三棵树，第一，第二，第三棵树的结点个数分别为M1，M2和M3。

与森林F对应的二叉树根结点的右子树上的结点个数是（）。

A．M1 B．M1+M2 C．M3 D．M2+M37．一棵完全二叉树上有1001个结点，其中叶子结点的个数是（）A． 250 B． 500 C．254 D．505 E．以上答案都不对8. 设给定权值总数有n 个，其哈夫曼树的结点总数为( )A．不确定 B．2n C．2n+1 D．2n-19．二叉树的第I层上最多含有结点数为（）A．2I B． 2I-1-1 C． 2I-1 D．2I -110．一棵二叉树高度为h,所有结点的度或为0，或为2，则这棵二叉树最少有( )结点A．2h B．2h-1 C．2h+1 D．h+111. 利用二叉链表存储树，则根结点的右指针是（）。

目前最完整数据结构1800题包括完整答案第六章树和二叉树

第六章树和二叉树一.选择题1．已知一算术表达式地中缀形式为 A+B*C-D/E,后缀形式为ABC*+DE/-,其前缀形式为( )A ．-A+B*C/DE B. -A+B*CD/E C ．-+*ABC/DE D. -+A*BC/DE【北京航空航天大学 1999 一.3 （2分)】2．算术表达式a+b*（c+d/e ）转为后缀表达式后为（）【中山大学 1999 一.5】A ．ab+cde/*B ．abcde/+*+C ．3. 设有一表示算术表达式地二叉树（见下图）, 它所表示地算术表达式是（）【南京理工大学1999 一.20（2分）】 C. (A*B+C)/(D*E+（F-G ）) D. A*B+C/D*E+F-G4. 设树T 地度为4,其中度为1,2,3和4地结点个数分别为4,2,1,1 则T 中地叶子数为（）A ．5B ．6C ．7D ．8【南京理工大学 2000 一.8 （1.5分）】5. 在下述结论中,正确地是（）【南京理工大学 1999 一.4 （1分）】①只有一个结点地二叉树地度为0; ②二叉树地度为2； ③二叉树地左右子树可任意交换;④深度为K 地完全二叉树地结点个数小于或等于深度相同地满二叉树.A ．①②③B ．②③④C ．②④D ．①④6. 设森林F 对应地二叉树为B,它有m 个结点,B 地根为p,p 地右子树结点个数为n,森林F 中第一棵树地结点个数是（）A ．m-nB ．m-n-1C ．n+1D ．条件不足,无法确定【南京理工大学2000 一.17（1.5分）】7. 树是结点地有限集合,它（ (1）)根结点,记为T.其余结点分成为m （m>0）个(（2）)地集合T1,T2, …,Ｔm,每个集合又都是树,此时结点T 称为Ti 地父结点,Ti 称为T 地子结点（1≤i ≤m ）.一个结点地子结点个数称为该结点地( （3） ).二叉树与树是两个不同地概念,二叉树也是结点地有限集合,它(（4）)根结点.可以把树地根结点地层数定义为1,其他结点地层数等于其父结点所在层数加上1.令T 是一棵二叉树,Ki 和Kj 是T 中子结点数小于2地结点中地任意两个,它们所在地层数分别为λKi 和λKj,当关系式│λKi-λKj │≤1一定成立时,则称T 为一棵（(5)）.供选择地答案：（1）(4) A. 有0个或1个 B. 有0个或多个 C. 有且只有一个 D. 有1个或1个以上（2） A. 互不相交 B.允许相交 C.允许叶结点相交 D.允许树枝结点相交（3） A. 权 B.维数 C.次数 D.序（5） A. 丰满树 B.查找树 C.平衡树 D.完全树【上海海运学院1999二.2(5分）】8．若一棵二叉树具有10个度为2地结点,5个度为1地结点,则度为0地结点个数是（）A．9 B．11 C．15 D．不确定【北京工商大学2001一.7(3分)】9．在一棵三元树中度为3地结点数为2个,度为2地结点数为1个,度为1地结点数为2个,则度为0地结点数为（）个A．4 B．5 C．6 D．7 【哈尔滨工业大学 2001二.2 （2分）】10．设森林F中有三棵树,第一,第二,第三棵树地结点个数分别为M1,M2和M3.与森林F对应地二叉树根结点地右子树上地结点个数是（）.【北方交通大学 2001一.16 （2分）】A．M1 B．M1+M2 C．M3 D．M2+M311．具有10个叶结点地二叉树中有（）个度为2地结点,【北京航空航天大学2000 一.5（2分)】A．8 B．9 C．10 D．ll12．一棵完全二叉树上有1001个结点,其中叶子结点地个数是（）【西安交通大学 1996 三.2 (3分)】A． 250 B． 500 C．254 D．505 E．以上答案都不对13. 设给定权值总数有n 个,其哈夫曼树地结点总数为( ) 【福州大学 1998一.5 (2分)】A．不确定 B．2n C．2n+1 D．2n-114. 有n个叶子地哈夫曼树地结点总数为（）.【青岛大学 2002 二.1 （2分）】A．不确定 B．2n C．2n+1 D．2n-115．若度为m地哈夫曼树中,其叶结点个数为n,则非叶结点地个数为（）.【中科院计算所1999一.2（2分）】A．n-1 B．ën/mû-1 C．é(n-1)/(m-1)ù D．én/(m-1)ù-1 E．é(n+1)/(m+1)ù-116. 有关二叉树下列说法正确地是（）【南京理工大学 2000 一.11 （1.5分）】A．二叉树地度为2 B．一棵二叉树地度可以小于2 C．二叉树中至少有一个结点地度为2 D．二叉树中任何一个结点地度都为2 17．二叉树地第I层上最多含有结点数为（）【中山大学1998二.7 （2分）】【北京理工大学 2001 六.5（2分）】A．2I B． 2I-1-1 C． 2I-1 D．2I -118. 一个具有1025个结点地二叉树地高h为（）【南京理工大学 1999 一.19（2分）】A．11 B．10 C．11至1025之间 D．10至1024之间19．一棵二叉树高度为h,所有结点地度或为0,或为2,则这棵二叉树最少有( )结点A．2h B．2h-1 C．2h+1 D．h+1 【南京理工大学2001一.11(1.5分）】20．对于有n 个结点地二叉树, 其高度为（）【武汉交通科技大学 1996 一.5(4分)】A．nlog2n B．log2n C．ëlog2nû|+1 D．不确定21. 一棵具有 n个结点地完全二叉树地树高度（深度）是（）【南京理工大学1996一.8 （2分）】A．ëlognû+1 B．logn+1 C．ëlognû D．logn-122．深度为h地满m叉树地第k层有（）个结点.(1=<k=<h)【北京航空航天大学2000一.4（2分）】A．mk-1 B．mk-1 C．mh-1 D．mh-123．在一棵高度为k地满二叉树中,结点总数为（）【北京工商大学 2001 一.3(3分)】A．2k-1 B．2k C．2k-1 D．ëlog2kû+124．高度为 K地二叉树最大地结点数为（）.【山东大学 2001 二.3 (1分)】A．2k B．2k-1 C．2k -1 D．2k-1-125. 一棵树高为K地完全二叉树至少有（）个结点【南京理工大学 1998 一.3（2分）】A．2k –1 B. 2k-1 –1 C. 2k-1 D. 2k26. 将有关二叉树地概念推广到三叉树,则一棵有244个结点地完全三叉树地高度（）A．4 B．5 C．6 D．7 【南京理工大学2000一.5 1.5分）】27. 利用二叉链表存储树,则根结点地右指针是（）.【青岛大学 2001 五.5 （2分）】A．指向最左孩子 B．指向最右孩子 C．空 D．非空28．对二叉树地结点从1开始进行连续编号,要求每个结点地编号大于其左.右孩子地编号,同一结点地左右孩子中,其左孩子地编号小于其右孩子地编号,可采用( )次序地遍历实现编号.【北京理工大学 2000 一.4 （2分）】A．先序 B. 中序 C. 后序 D. 从根开始按层次遍历29．树地后根遍历序列等同于该树对应地二叉树地( ). 【北京理工大学 2001六.6 （2分）】A. 先序序列B. 中序序列C. 后序序列30．若二叉树采用二叉链表存储结构,要交换其所有分支结点左.右子树地位置,利用( )遍历方法最合适.A．前序 B．中序 C．后序 D．按层次【北京航空航天大学 1999一.4 （2分）】31．在下列存储形式中,哪一个不是树地存储形式？（）【北方交通大学 2001一.23 （2分）】A．双亲表示法 B．孩子链表表示法 C．孩子兄弟表示法 D．顺序存储表示法32．一棵二叉树地前序遍历序列为ABCDEFG,它地中序遍历序列可能是（）【北京工业大学 2001 一.2 (2分)】A．CABDEFG B．ABCDEFG C．DACEFBG D．ADCFEG 33．已知一棵二叉树地前序遍历结果为ABCDEF,中序遍历结果为CBAEDF,则后序遍历地结果为（）.A．CBEFDA B． FEDCBA C． CBEDFA D．不定【浙江大学 1999 四.2 ( 4分)】34．已知某二叉树地后序遍历序列是dabec, 中序遍历序列是debac , 它地前序遍历是（）.A．acbed B．decab C．deabc D．cedba 【山东大学 2001二.7 ( 1分)】35. 某二叉树中序序列为A,B,C,D,E,F,G,后序序列为B,D,C,A,F,G,E 则前序序列是：A．E,G,F,A,C,D,B B．E,A,C,B,D,G,F C．E,A,G,C,F,B,D D．上面地都不对【南京理工大学 2000 一.14 （1.5分）】36. 上题地二叉树对应地森林包括多少棵树（）【南京理工大学 2000 一.15 （1.5分）】A．l B．2 C．3 D．概念上是错误地37．二叉树地先序遍历和中序遍历如下：先序遍历：EFHIGJK；中序遍历: HFIEJKG .该二叉树根地右子树地根是：【北方交通大学 2001 一.21（2分）】A. EB. FC. GD. H38．将一棵树t 转换为孩子—兄弟链表表示地二叉树h,则t地后根序遍历是h 地A．前序遍历 B．中序遍历 C．后序遍历（）【北京邮电大学 2001一.2 （2分）】39. 某二叉树T有n个结点,设按某种顺序对T中地每个结点进行编号,编号为1,2,… ,n,且有如下性质：T中任一结点V,其编号等于左子树上地最小编号减1,而V地右子树地结点中,其最小编号等于V左子树上结点地最大编号加1.这时是按( )编号地.A.中序遍历序列B.前序遍历序列C.后序遍历序列D.层次顺序【长沙铁道学院1998三.1(2分)】40．下面地说法中正确地是（）.（1）任何一棵二叉树地叶子结点在三种遍历中地相对次序不变；（2）按二叉树定义,具有三个结点地二叉树共有6种.A．(1)(2) B．(1) C．(2) D．(1).(2)都错【南京理工大学 2001 一.10 （1.5分）】41．对于前序遍历与中序遍历结果相同地二叉树为（1）;对于前序遍历和后序遍历结果相同地二叉树为（2）.【中科院计算所 1999 一.4 （4分）】A．一般二叉树 B．只有根结点地二叉树 C．根结点无左孩子地二叉树D．根结点无右孩子地二叉树 E．所有结点只有左子数地二叉树 F．所有结点只有右子树地二叉树42．一棵非空地二叉树地先序遍历序列与后序遍历序列正好相反,则该二叉树一定满足（）【南开大学 2000 一.2】A．所有地结点均无左孩子B．所有地结点均无右孩子C．只有一个叶子结点D．是任意一棵二叉树43．在二叉树结点地先序序列,中序序列和后序序列中,所有叶子结点地先后顺序（）A．都不相同B．完全相同 C．先序和中序相同,而与后序不同D．中序和后序相同,而与先序不同【北方交通大学 2001 一.25 （2分）】44．某二叉树地前序序列和后序序列正好相反,则该二叉树一定是（）地二叉树.【武汉大学2000二.4】A．空或只有一个结点 B．任一结点无左子树 C．高度等于其结点数D．任一结点无右子树45．在完全二叉树中,若一个结点是叶结点,则它没（）.【北方交通大学 2001一.22 （2分）】A．左子结点 B．右子结点 C．左子结点和右子结点 D．左子结点,右子结点和兄弟结点46．在下列情况中,可称为二叉树地是（）A．每个结点至多有两棵子树地树 B. 哈夫曼树 C．每个结点至多有两棵子树地有序树D. 每个结点只有一棵右子树 E．以上答案都不对【西安交通大学 1996 三.4 (3分)】47. 一棵左子树为空地二叉树在先序线索化后,其中空地链域地个数是：( )A．不确定 B. 0 C. 1 D. 2 【合肥工业大学 1999 一.5 （48. 一棵左右子树均不空地二叉树在先序线索化后,其中空地链域地个数是：( ).A. 0B. 1C. 2D. 不确定【合肥工业大学2000 一.5 （2分）】49. 若X是二叉中序线索树中一个有左孩子地结点,且X不为根,则x地前驱为( )【南京理工大学1996 一.6 (2分)】A.X地双亲B.X地右子树中最左地结点C.X地左子树中最右结点D.X地左子树中最右叶结点50. 引入二叉线索树地目地是（）A．加快查找结点地前驱或后继地速度 B．为了能在二叉树中方便地进行插入与删除C．为了能方便地找到双亲 D．使二叉树地遍历结果唯一【南京理工大学1998 一.5 （2分）】51. 线索二叉树是一种（）结构.A．逻辑 B．逻辑和存储 C．物理 D．线性【西安电子科技大学1996 一.9 （2分）】52．n个结点地线索二叉树上含有地线索数为（）A．2n B．n－l C．n＋l D．n 【中山大学 1998 二.8 （2分）】53．（）地遍历仍需要栈地支持.A．前序线索树 B．中序线索树 C．后序线索树【中科院计算所 1999一.1 （2分）】54．二叉树在线索后,仍不能有效求解地问题是（）.A．前（先）序线索二叉树中求前（先）序后继 B．中序线索二叉树中求中序后继C．中序线索二叉树中求中序前驱 D．后序线索二叉树中求后序后继【武汉大学2000 二.3 二.5】55. 设F是一个森林,B是由F变换得地二叉树.若F中有n个非终端结点,则B中右指针域为空地结点有（）个.A． n-1 B．n C． n+1 D． n+2 【西安电子科技大学1998 一.10 （2分）】56．如果T2是由有序树T转换而来地二叉树,那么T中结点地后序就是T2中结点地（）.A．先序 B．中序 C．后序 D．层次序【西安电子科技大学1996 一.2 （2分）】57. 由3 个结点可以构造出多少种不同地有向树？（）A．2 B．3 C．4 D．5 【北方交通大学 2001 一.6 （2分）】58．由3 个结点可以构造出多少种不同地二叉树？（）A．2 B．3 C．4 D．5 【北方交通大学 2001 一.7 （2分）】59.下述二叉树中,哪一种满足性质:从任一结点出发到根地路径上所经过地结点序列按其关键字有序（）.A．二叉排序树 B．哈夫曼树 C．AVL树 D．堆【中国科技大学1998二.8（2分）】【中科院计算所1998二.8(2分）】60．在叶子数目和权值相同地所有二叉树中,最优二叉树一定是完全二叉树,该说法（）.A．正确 B．错误【中国科技大学1998 二.10（2分）】【中科院计算所1998 二.10（2分）】61．最优二叉树（哈夫曼树）.最优查找树均为平均查找路径长度∑=niii hw1最小地树,其中对最优二叉树,n表示（1）,对最优查找树,n表示（2）,构造这两种树均（3）.【中科院计算所1999一.3 (6分）】A．结点数 B．叶结点数 C．非叶结点数 D．度为2地结点数 E．需要一张n个关键字地有序表F．需要对n个关键字进行动态插入 G．需要n个关键字地查找概率表H．不需要任何前提62．下述编码中哪一个不是前缀码（）.【中科院计算所 2000 一.2 （2分）】A．（00,01,10,11） B．（0,1,00,11） C．（0,10,110,111） D．（1,01,000,001）63．下面几个符号串编码集合中,不是前缀编码地是（）.A．{0,10,110,1111} B．{11,10,001,101,0001} C．{00,010,0110,1000}D．{b,c,aa,ac,aba,abb,abc} 【西安电子科技大学2001 应用一.6（2分）】64. 当一棵有n个结点地二叉树按层次从上到下,同层次从左到右将数据存放在一维数组 A[l..n]中时,数组中第i个结点地左孩子为（）【南京理工大学 1999一.18(2分）】A．A[2i](2i=<n) B. A[2i+1](2i+1=< n) C．A[i/2] D．无法确定65. 一棵有n个结点地二叉树,按层次从上到下,同一层从左到右顺序存储在一维数组A[1..n]中,则二叉树中第i个结点（i从1开始用上述方法编号）地右孩子在数组A中地位置是（）A．A[2i](2i<=n) B．A[2i+1](2i+1<=n) C．A[i-2] D．条件不充分,无法确定【南京理工大学2000 一.4(1.5分）】66．从下列有关树地叙述中,选出5条正确地叙述(共5分) （）A．二叉树中每个结点有两个子结点,而树无此限制,因此二叉树是树地特殊情况.B．当K≥1时高度为K地二叉树至多有2k-1个结点.C．用树地前序周游和中序周游可以导出树地后序周游.D．线索二叉树地优点是便于在中序下查找前驱结点和后继结点.E．将一棵树转换成二叉树后,根结点没有左子树.F．一棵含有N个结点地完全二叉树,它地高度是ëLOG2Nû+1.G．在二叉树中插入结点,该二叉树便不再是二叉树.H．采用二叉树链表作树地存储结构,树地前序周游和其相应地二叉树地前序周游地结果样地.I．哈夫曼树是带权路径最短地树,路径上权值较大地结点离根较近.J．用一维数组存储二叉树时,总是以前序周游存储结点.【山东工业大学 1995三. (5分)】二.判断题1. 二叉树是度为2地有序树.【长沙铁道学院1997一.3(1分)】【中科院软件所1997一.9(1分)】2. 完全二叉树一定存在度为1地结点.【青岛大学 2002 一.4 （1分）】3. 对于有N个结点地二叉树,其高度为log2n.【上海海运学院 1998 一.6 （1分）】4．深度为K地二叉树中结点总数≤2k-1.【南京航空航天大学 1995 五.1 （1分）】5. 二叉树以后序遍历序列与前序遍历序列反映地同样地信息(他们反映地信息不独立）.【华南理工大学2002一.7 (1分）】6. 二叉树地遍历结果不是唯一地.【南京理工大学 1997 二.8 （2分）】7. 二叉树地遍历只是为了在应用中找到一种线性次序.【青岛大学 2001 四.4 （1分）】8. 树可用投影法进行中序遍历. 【青岛大学 2002 一.6 （1分）】9. 一个树地叶结点,在前序遍历和后序遍历下,皆以相同地相对位置出现.【上海海运学院 1995 一.4 （1分）】10. 二叉树地前序遍历并不能唯一确定这棵树,但是,如果我们还知道该树地根结点是那一个,则可以确定这棵二叉树.【上海海运学院 1995 一.6 （1分）】11. 一棵一般树地结点地前序遍历和后序遍历分别与它相应二叉树地结点前序遍历和后序遍历是一致地.【上海海运学院 1996 一.6 （1分）】12．对一棵二叉树进行层次遍历时,应借助于一个栈.【南京航空航天大学 1995五.3 （1分）】13．用树地前序遍历和中序遍历可以导出树地后序遍历.【北京邮电大学 1999二.3 （2分）】14．采用二叉链表作存储结构,树地前序遍历和其相应地二叉树地前序遍历地结果是一样地.【北京邮电大学2000一.2(1分）】15. 用一维数组存储二叉树时,总是以前序遍历顺序存储结点.【上海海运学院1995 一.8 （1分）】16．中序遍历二叉链存储地二叉树时,一般要用堆栈；中序遍历检索二叉树时,也必须使用堆栈.【上海海运学院1998一.7(1分）】17．中序遍历一棵二叉排序树地结点就可得到排好序地结点序列【中科院软件所1999 六.1-1 （2分）】18. 后序线索二叉树是不完善地,要对它进行遍历,还需要使用栈.【长沙铁道学院 1998 一.2 (1分)】19．任何二叉树地后序线索树进行后序遍历时都必须用栈.【西安交通大学 1996 二.2 ( 3分) 】20．任何一棵二叉树都可以不用栈实现前序线索树地前序遍历.【西安交通大学1996 二.1 (3分)】21．由一棵二叉树地前序序列和后序序列可以唯一确定它.【中科院软件所 1997 一.3 （1分）】22．完全二叉树中,若一个结点没有左孩子,则它必是树叶.【东南大学 2001一.1-8（1分）】【中科院软件所1997一.2（1分）】【山东大学2001一.4 (1分)】23. 二叉树只能用二叉链表表示.【南京理工大学 1997 二.6 （2分）】24. 一棵有n个结点地二叉树,从上到下,从左到右用自然数依次给予编号,则编号为i地结点地左儿子地编号为2i(2i< n),右儿子是2i+1（2i+1<n）.【南京理工大学 1997 二.11 （2分）】25. 给定一棵树,可以找到唯一地一棵二叉树与之对应.【青岛大学 2001 一.5 （1分）】26. 一棵树中地叶子数一定等于与其对应地二叉树地叶子数.【青岛大学 2002一.5 （1分）】27. 用链表(llink-rlink)存储包含n个结点地二叉树,结点地2n个指针区域中有n-1个空指针.【上海海运学院1996一.5(1分）】28. 二叉树中每个结点至多有两个子结点,而对一般树则无此限制.因此,二叉树是树地特殊情形.【上海海运学院1997一.5(1分）】29．树形结构中元素之间存在一个对多个地关系.【燕山大学 1998 二.1 （2分）】30．在二叉树地第i层上至少有2i-1个结点(i>=1).【燕山大学 1998 二.3 （2分）】31．必须把一般树转换成二叉树后才能进行存储.【南京航空航天大学 1997 一.4 （1分）】32．完全二叉树地存储结构通常采用顺序存储结构.【南京航空航天大学 1996 六.3 （1分）】33．将一棵树转成二叉树,根结点没有左子树；【北京邮电大学 1999 二.2 （2分）】34．在二叉树中插入结点,则此二叉树便不再是二叉树了.【北京邮电大学 2000 一.5 （1分）】35．二叉树是一般树地特殊情形.【北京邮电大学 2000 一.9 （1分） 2002 一.6 （1分）】36．树与二叉树是两种不同地树型结构.【东南大学 2001 一.1-7 （1分）】37. 非空地二叉树一定满足：某结点若有左孩子,则其中序前驱一定没有右孩子【合肥工业大学 2001 二.5 （1分）】38．在任意一棵非空二叉排序树,删除某结点后又将其插入,则所得二叉排序树与删除前原二叉排序树相同.【中科院软件所 1997 一.7 （1分）】39．度为二地树就是二叉树.【大连海事大学 2001 一.7 (1分)】40．深度为k具有n个结点地完全二叉树,其编号最小地结点序号为ë2k-2û+1.【东北大学 1997 二.3 (2分)】41.下面二叉树地定义只有一个是正确地,请在正确地地方画“√”.（1）它是由一个根和两株互不相交地.称为左子树和右子树地二叉树组成.（2）（a）在一株二叉树地级i上,最大结点数是2i-1（i≥1）（b）在一棵深度为k地二叉树中,最大结点数是2k-1+1（k≥1）.（3）二叉树是结点地集合,满足如下条件：（a）它或者是空集；（b）或者是由一个根和两个互不相交地.称为左子树和右子树地二叉树组成.【中科院自动化所1995一.2（6分）】42. 在中序线索二叉树中,每一非空地线索均指向其祖先结点.【合肥工业大学2000 二.5 （1分）】43. 线索二叉树地优点是便于是在中序下查找前驱结点和后继结点.【上海海运学院1995 ,96,97 一.7（1分）】44. 二叉树中序线索化后,不存在空指针域.【青岛大学 2000 四.3 （1分）】45．霍夫曼树地结点个数不能是偶数.【北京邮电大学 2000 一.6 （1分）】46. 一棵哈夫曼树地带权路径长度等于其中所有分支结点地权值之和.【合肥工业大学2000二.4 (1分)】47. 哈夫曼树无左右子树之分.【青岛大学 2000 四.8 （1分）】48．当一棵具有n个叶子结点地二叉树地WPL值为最小时,称其树为Huffman树,且其二叉树地形状必是唯一地.【南京航空航天大学 1995 五.6 （1分）】49．哈夫曼树是带权路径长度最短地树,路径上权值较大地结点离根较近.【北京邮电大学 1999 二.5 （2分）】50. 用链表（llink-rlink）存储包含n个结点地二叉树时,结点地2n个指针区域中有n+1个空指针.( )【上海海运学院 1999 一.6（1分）】三.填空题1．二叉树由_(1)__,__(2)_,_(3)__三个基本单元组成.【燕山大学 1998 一.5 （3分）】2．树在计算机内地表示方式有_(1)__,_(2)__,_(3)__.【哈尔滨工业大学 2000 二.4 (3分)】3．在二叉树中,指针p所指结点为叶子结点地条件是______.【合肥工业大学1999 三.7（2分）】4．中缀式a+b*3+4*（c-d）对应地前缀式为__(1)_,若a=1,b=2,c=3,d=4,则后缀式db/cc*a-b*+地运算结果为_(2)__.【西南交通大学 2000 一.6】5．二叉树中某一结点左子树地深度减去右子树地深度称为该结点地____.【燕山大学1998一.9(1分)】6．具有256个结点地完全二叉树地深度为______.【燕山大学 1998 一.4 （1分）】7．已知一棵度为3地树有2个度为1地结点,3个度为2地结点,4个度为3地结点,则该树有______个叶子结点.【厦门大学 2000 六.2 （16%/3分）】8．深度为k地完全二叉树至少有___(1)____个结点,至多有___(2)____个结点.【厦门大学 2001 一.4 （14%/5分）】【南京理工大学 1999 二.5 （4分）】9．深度为H 地完全二叉树至少有_(1)__个结点；至多有_(2)__个结点；H和结点总数N之间地关系是 (3)__.【中科院计算所1998 一.3（3分）1999 二.4（3分）】【中国科技大学 1998 一.3(4分）】10．在顺序存储地二叉树中,编号为i和j地两个结点处在同一层地条件是______.【厦门大学 2002 六.3 （4分）】11．在完全二叉树中,编号为i和j地两个结点处于同一层地条件是______.【合肥工业大学 2000 三.6 （2分）】12．一棵有n个结点地满二叉树有__(1)_个度为1地结点.有__(2)_个分支（非终端）结点和__(3)_个叶子,该满二叉树地深度为_(4)__.【华中理工大学 2000 一.6 （3分））13．假设根结点地层数为１,具有ｎ个结点地二叉树地最大高度是______.【北方交通大学 2001 二.1】14．在一棵二叉树中,度为零地结点地个数为N0,度为2地结点地个数为N2,则有N0 =______【北方交通大学 2001 二.6】【南京理工大学 1999 二.4 （2分）】15．设只含根结点地二叉树地高度为0,则高度为k地二叉树地最大结点数为______,最小结点数为______.【北京大学 1997 一.1 （4分）】16．设有N个结点地完全二叉树顺序存放在向量A[1:N]中,其下标值最大地分支结点为______.【长沙铁道学院 1997 二.3 (2分)】17．高度为K地完全二叉树至少有______个叶子结点.【合肥工业大学 1999 二.6（2分）】18．高度为8地完全二叉树至少有______个叶子结点.【合肥工业大学 2001 三.6（2分）】19．已知二叉树有50个叶子结点,则该二叉树地总结点数至少是______.【厦门大学 2002 六.4（4分）】20．一个有2001个结点地完全二叉树地高度为______.【南京理工大学 1997 三.2（1分）】21．设F是由T1,T2,T3三棵树组成地森林,与F对应地二叉树为B,已知T1,T2,T3地结点数分别为n1,n2和n3则二叉树B地左子树中有__(1)_个结点,右子树中有_(2)__个结点.【南京理工大学 2000 二.9（3分）】22．一个深度为k地,具有最少结点数地完全二叉树按层次,（同层次从左到右）用自然数依此对结点编号,则编号最小地叶子地序号是__(1)_；编号是i地结点所在地层次号是_(2)__（根所在地层次号规定为1层）.【南京理工大学 2001 二.2（2分）】23．如某二叉树有20个叶子结点,有30个结点仅有一个孩子,则该二叉树地总结点数为______.【南京理工大学 2001 二.3（2分）】24．如果结点A有 3个兄弟,而且B是A地双亲,则B地度是______.【西安电子科技大学1999软件一.4（2分）】25．高度为h地2-3树中叶子结点地数目至多为______.【西安电子科技大学1999软件一.6（2分）】26．完全二叉树中,结点个数为n,则编号最大地分支结点地编号为______.【北京轻工业学院 2000 一.3 (2分)】27．设一棵完全二叉树叶子结点数为k,最后一层结点数>2,则该二叉树地高度为______.【北京科技大学 1998 一.3】28．对于一个具有n个结点地二元树,当它为一棵_(1)_二元树时具有最小高度,当它为一棵_(2)_时,具有最大高度.【哈尔滨工业大学 2001 一.3 (2分)】29．具有N个结点地二叉树,采用二叉链表存储,共有______个空链域.【重庆大学2000 一.8】30．8层完全二叉树至少有______个结点,拥有100个结点地完全二叉树地最大层数为______.【西南交通大学 2000 一.1】31．含4个度为2地结点和5个叶子结点地二叉树,可有______个度为1地结点.【北京工业大学 2001 一.6 (2分)】32．一棵树T中,包括一个度为1地结点,两个度为2地结点,三个度为3地结点,四个度为4地结点和若干叶子结点,则T地叶结点数为______.【山东大学 2001 三.2 (2分)】33． n（n大于1）个结点地各棵树中,其深度最小地那棵树地深度是_(1)__.它共有_(2)__个叶子结点和_(3)__个非叶子结点,其中深度最大地那棵树地深度是_(4)__,它共有_(5)__个叶子结点和_(6)__个非叶子结点.【山东大学 2001 三.7 (2分)】34．每一棵树都能唯一地转换为它所对应地二叉树.若已知一棵二叉树地前序序列是BEFCGDH,对称序列是FEBGCHD,则它地后序序列是_(1)__.设上述二叉树是由某棵树转换而成,则该树地先根次序序列是_(2)__.【山东工业大学 1997 二. (6分)】35．先根次序周游树林正好等同于按_(1)__周游对应地二叉树,后根次序周游树林正好等同于按__(2)_周游对应地二叉树.【山东工业大学 1999 二.1 （4分）】36．二叉树结点地对称序序列为A,B,C,D,E,F,G,后序序列为B,D,C,A,F,G,E,则该二叉树结点地前序序列为_(1)__,则该二叉树对应地树林包括_(2)__棵树.【北京大学 1997 一.2 （4分）】37．二叉树地先序序列和中序序列相同地条件是______.【合肥工业大学 2000 三.7（2分）】38．已知一棵二叉树地前序序列为abdecfhg,中序序列为dbeahfcg,则该二叉树地根为_(1)__,左子树中有_(2)__, 右子树中有_(3)__.【南京理工大学 1996 二.1（6分）】39．设二叉树中每个结点均用一个字母表示,若一个结点地左子树或右子树为空,用．表示,现前序遍历二叉树,访问地结点地序列为ABD.G...CE.H..F．．,则中序遍历二叉树时,访问地结点序列为_(1)__;后序遍历二叉树时,访问地结点序列为_(2)__.【南京理工大学 1999 二.3（4分）】40．已知二叉树前序为ABDEGCF,中序为DBGEACF,则后序一定是____.【青岛大学2000 六.3(2分）】41．现有按中序遍历二叉树地结果为abc,问有_(1)__种不同地二叉树可以得到这。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

数为（）
A．5 B．6 C．7 D．8
【南京理工大学 2000 一、8 （1.5分）】
5. 在下述结论中，正确的是（）【南京理工大学 1999 一、4 （1分）】
①只有一个结点的二叉树的度为0; ②二叉树的度为2； ③二叉树的左右子树可任意交换;
7. 树是结点的有限集合，它（ (1）)根结点，记为T。其余结点分成为m（m>0）个(（2）)的集合T1，T2， ?，Ｔm，每个集合又都是树，此时结点T称为Ti的父结点，Ti称为T的子结点（1≤i≤m）。一个结点的子结点个数称为该结点的( （3） )。二叉树与树是两个不同的概念，二叉树也是结点的有限集合，它(（4）)根结点。可以把树的根结点的层数定义为1，其他结点的层数等于其父结点所在层数加上1。令T是一棵二叉树，Ki和Kj是T中子结点数小于2的结点中的任意两个，它们所在的层数分别为λKi和λKj，当关系式│λKi-λKj│≤1一定成立时，则称T为一棵（(5)）。供选择的答案：
（1）(4) A. 有0个或1个 B. 有0个或多个 C. 有且只有一个 D. 有1个或1个以上
（2） A. 互不相交 B.允许相交 C.允许叶结点相交 D.允许树枝结点相交
（3） A. 权 B.维数 C.次数 D.序
（5） A. 丰满树 B.查找树 C.平衡树 D.完全树【上海海运学院1999二、2(5分）】
8．若一棵二叉树具有10个度为2的结点，5个度为1的结点，则度为0的结点个数是（）
A．9 B．11 C．15 D．不确定【北京工商大学2001一.7(3分)】
它所表示的算术表达式是（）
【南京理工大学1999 一、20（2分）】
A. A*B+C/(D*E)+(F-G) B. (A*B+C)/(D*E)+(F-G)
C. (A*B+C)/(D*E+（F-G）) D. A*B+C/D*E+F-G 则T中的叶子，1 4. 设树T的度为4，其中度为1，2，3和4的结点个数分别为4，2，1
【北京航空航天大学 1999 一、3 （2分)】
2．算术表达式a+b*（c+d/e）转为后缀表达式后为（）【中山大学 1999 一、5】
A．ab+cde/* B．abcde/+*+ C．abcde/*++ D．3. 设有一表示算术表达式的二叉树（见下图），
第六章树和二叉树
一、选择题
1．已知一算术表达式的中缀形式为 A+B*C-D/E，后缀形式为ABC*+DE/-，其前缀形式为
( ) Biblioteka A．-A+B*C/DE B. -A+B*CD/E C．-+*ABC/DE D. -+A*BC/DE
④深度为K的完全二叉树的结点个数小于或等于深度相同的满二叉树。
A．①②③ B．②③④ C．②④ D．①④
6. 设森林F对应的二叉树为B，它有m个结点，B的根为p,p的右子树结点个数为n,森林F中第一棵树的结点个数是（）
A．m-n B．m-n-1 C．n+1 D．条件不足，无法确定【南京理工大学2000 一、17（1.5分）】
9．在一棵三元树中度为3的结点数为2个，度为2的结点数为1个，度为1的结点数为2 1