Matlab课程Simulink基础实例
matlab simulink案例

matlab simulink案例1. 电机传动系统模拟在这个案例中,我们将使用Simulink来模拟一个简单的电机传动系统。
我们将建立一个由电机、负载和控制器组成的系统,并使用Simulink来模拟系统的动态行为。
通过调整输入信号和控制器参数,我们可以观察系统的响应,并优化控制器的性能。
2. PID控制器设计在这个案例中,我们将使用Simulink来设计一个PID控制器,并将其应用于一个简单的控制系统。
我们将建立一个由传感器、控制器和执行器组成的系统,并使用Simulink来模拟系统的动态行为。
通过调整PID控制器的参数,我们可以观察系统的响应,并优化控制器的性能。
3. 机器人路径规划在这个案例中,我们将使用Simulink来进行机器人的路径规划。
我们将建立一个由传感器、路径规划器和执行器组成的系统,并使用Simulink来模拟机器人在不同环境中的路径规划行为。
通过调整路径规划器的算法和参数,我们可以优化机器人的路径规划性能。
4. 电力系统稳定性分析在这个案例中,我们将使用Simulink来进行电力系统的稳定性分析。
我们将建立一个由发电机、负载和传输线路组成的电力系统,并使用Simulink来模拟系统的动态行为。
通过调整系统的参数和控制策略,我们可以评估系统的稳定性,并优化系统的运行性能。
5. 汽车动力学模拟在这个案例中,我们将使用Simulink来进行汽车的动力学模拟。
我们将建立一个由车辆、发动机和传动系统组成的模型,并使用Simulink来模拟车辆在不同驾驶条件下的动力学行为。
通过调整车辆参数和控制策略,我们可以评估车辆的性能,并优化驾驶体验。
6. 无人机飞行控制在这个案例中,我们将使用Simulink来进行无人机的飞行控制。
我们将建立一个由无人机、传感器和控制器组成的系统,并使用Simulink来模拟无人机在不同飞行任务下的控制行为。
通过调整控制器的参数和飞行任务的要求,我们可以优化无人机的飞行性能。
第三讲MatlabSimulink入门——离散系统仿真实例

第三讲MatlabSimulink ⼊门——离散系统仿真实例第三讲 Matlab/Simulink ⼊门——离散系统仿真实例1、离散系统基本概念1.1 离散系统 离散系统: 是指系统的输⼊和输出仅在离散的时间上取值,⽽且离散的时间具有相同的时间间隔,与连续的概念相反。
设系统输⼊变量为,其中为系统的采样时间,为采样时刻。
由于为⼀固定值,因此系统输⼊,常简记为。
设输出系统为,简记为。
于是,离散系统的数学表达为:1.2线性离散系统 线性离散系统: 是离散系统的⼀种特殊形式,需要同时满⾜(1)、(2)两个条件,即 (1)、齐次性: 对于离散系统,如果对任意的输⼊与给定的常数,下⾯的式⼦总成⽴:则称系统满⾜齐次性。
(2)、叠加性: 对于系统对于输出和,输出分别为 和,总有下⾯的式⼦成⽴:则称系统满⾜叠加性。
对于线性离散系统,其⼀般数学描述为:⽤差分⽅程描述为:状态⽅程:输出⽅程:1.3 Z 变换u (nT ),n =s 0,1,2...T s n T s u (nT )s u (n )y (nT )s y (n )y (n )=f (u (n ),u (n −1),...;y (n −1),y (n −2))T {αu (n )+1βu (n )}=2αT {u (n )}+1βT {u (n )}2y (n )=T {u (n )},n =0,1,2...u (n )αT {αu (n )}=αT {u (n )}u (n )1u (n )2y (n )1y (n )2T {u (n )+1u (n )}=2T {u (n )}+1T {u (n )}2y (n )=f (u (n ),u (n −1),...;y (n −1),y (n −2))x (n +1)=f (x (n ),u (n ),n )y (n )=g (x (n ),u (n ),n ) 变换: 对于⼀个离散信号,其变换为。
⼀般来说离散信号的起始时间往往⼤于零,这时它的变换为,可简记为。
Matlab系列之Simulink仿真教程

交互式仿真
Simulink支持交互式 仿真,用户可以在仿 真运行过程中进行实 时的分析和调试。
可扩展性
Simulink具有开放式 架构,可以与其他 MATLAB工具箱无缝 集成,从而扩展其功 能。
Simulink的应用领域
指数运算模块
用于实现信号的指数运算。
减法器
用于实现两个信号的减法 运算。
除法器
用于实现两个信号的除法 运算。
对数运算模块
用于实现信号的对数运算。
输出模块
模拟输出模块
用于将模拟信号输出 到外部设备或传感器。
数字输出模块
用于将数字信号输出 到外部设备或传感器。
频谱分析仪
用于分析信号的频谱 特性。
波形显示器
控制工程
Simulink在控制工程领域 中应用广泛,可用于设计 和分析各种控制系统。
信号处理
Simulink中的信号处理模 块可用于实现各种信号处 理算法,如滤波器设计、 频谱分析等。
通信系统
Simulink可以用于设计和 仿真通信系统,如调制解 调、信道编码等。
图像处理
Simulink中的图像处理模 块可用于实现各种图像处 理算法,如图像滤波、边 缘检测等。
用于将时域信号转换为频域信号,如傅里叶变换、 拉普拉斯变换等。
03 时域变换模块
用于将频域信号转换为时域信号,如逆傅里叶变 换、逆拉普拉斯变换等。
04
仿真过程设置
仿真时间的设置
仿真起始时间
设置仿真的起始时间,通 常为0秒。
步长模式
选择固定步长或变步长模 式,以满足不同的仿真需 求。
大学Matlab课程 第4讲 Simulink

• 改变大小:选中模块,对模块出现的4个黑色标记进行
拖曳即可。
• 模块命名:先用鼠标在需要更改的名称上单击一下,然
后直接更改即可。名称在功能模块上的位置也可以变换 180度,可以用Format菜单中的Flip Name来实现,也可 以直接通过鼠标进行拖曳。Hide Name可以隐藏模块名称。
<
>
主菜单
• • •
2.4 Math(数学模块)
• Logical Operator:逻辑运算 • Relational Operator:关系运算 • Complex to Magnitude-Angle:由复数转为幅值和相 角输出 • Magnitude-Angle to Complex:由幅值和相角合成复 数输出 • Complex to Real-Imag:由复数转为实部和虚部输出 • Real-Imag to Complex:由实部和虚部合成复数输出
2.4 Math(数学模块)
• • • • • • Sum:加减运算 Product:乘运算 Dot Product:点乘运算 Gain:比例运算 Math Function:包括指数函数、对数函数、求平方、 开根号等常用数学函数 Trigonometric Function:三角函数,包括正弦、余弦、 正切等 MinMax:最值运算 Abs:取绝对值 Sign:符号函数
1、Solver页
此页可以进行的设置有:选择仿真开始和结束的时间;选择解 法器,并设定它的参数;选择输出项。 1) 仿真时间:注意这里的时间概念与真实的时间并不一样,只是 计算机仿真中对时间的一种表示,比如10秒的仿真时间,如果 采样步长定为0.1,则需要执行100步,若把步长减小,则采样点 数增加,那么实际的执行时间就会增加。一般仿真开始时间设 为0,而结束时间视不同的因素而选择。总的说来,执行一次仿 真要耗费的时间依赖于很多因素,包括模型的复杂程度、解法 器及其步长的选择、计算机时钟的速度等等。 2) 仿真步长模式:用户在Type后面的第一个下拉选项框中指定仿 真的步长选取方式,可供选择的有Variable-step(变步长)和 Fixed-step(固定步长)方式。变步长模式可以在仿真的过程中 改变步长,提供误差控制和过零检测。固定步长模式在仿真过 程中提供固定的步长,不提供误差控制和过零检测。用户还可 以在第二个下拉选项框中选择对应模式下仿真所采用的算法。
MATLAB-SIMULINK讲解完整版

点击图3-2中“树状结构目录窗口”中各模块库名前带 “+”的小方块可展开二级子模块库的目录。“模块窗口” 中显示的是用户在“树状结构目录窗口”中选中的模块库所 包含的模块图标。如果显示的模块图标前带“+”的小方块, 表明该图标下还有三级目录,直接点击该图标可在该窗口中 展现三级目录下的模块图标。
为了叙述方便,本书将模块库中以图标形式表示的典型 环节称为模块,将用典型环节模块组成的系统仿真模型简称 为模型。
在SIMULINK中创建子系统一般有两种方法。
1) 通过“子系统”模块的方法 该方法要求在用户的模型里添加一个称为Subsystem的 子系统模块,然后再往该模块里加入组成子系统的各种模块。 这种方法适合于采用自上而下设计方式的用户,具体实现步 骤如下: (1) 新建一个空白模型。 (2) 打开“端口和子系统”(Ports&Subsystems)模块库, 选取其中的“子系统”(Subsystem)模块并把它复制到新建的 仿真平台窗口中。
第3章 SIMULINK应用基础
3.1 SIMULINK仿真环境 3.2 SIMULINK的基本操作 3.3 SIMULINK系统建模 3.4 SIMULINK运行仿真 3.5 SIMULINK模块库 3.6 SIMULINK系统仿真应用 习题
3.1 SIMULINK仿真环境 SIMULINK是MATLAB的一个分支产品,主要用来实 现对工程问题的模型化及动态仿真。SIMULINK体现了模块 化设计和系统级仿真的思想,采用模块组合的方法使用户能 够快速、准确地创建动态系统的计算机模型,使得建模仿真 如同搭积木一样简单。SIMULINK现已成为仿真领域首选的 计算机环境。
单击模块,拖曳模块到合适的位置,松开鼠标按键
方法 1:选中模块,选择菜单命令[Format>Rotate Block], 模块顺时针旋转 90°;选择菜单命令[Format>Flip Block],
2010课程设计simulink_(MATLAB 基础)

3. 举例分析
【例2.4】 求多项式的根。 解:在MATLAB的命令窗口中依次输入以下命令, 即可求出其根。 >> p=[3 0 2 3];
>>rootp=roots(p)
>>rootp = 0.3911 + 1.0609i 0.3911 - 1.0609i -0.7822
% rootp为多项式的根
例如,矩阵
4 列向量,在MATLAB中可以分别表示为 C 5 5 >>A=[1 2 3; 46 6]
1 2 3 A ,行向量 4 5 6
,
>>B=[1 2 3] >>C=[4; 5; 6]
注意:(1) MATLAB中所有的矩阵与向量均包含在中括号[]之中。 如果矩阵的大小为1×1,则它表示一个标量,如
(2) conv(p,q):表示多项式p,q的乘积,一般也指p, q的卷积。
(3) poly(A):计算矩阵A的特征多项式向量。 (4) poly(p):由长度为n的向量中的元素为根建立的 多项式,结果是长度为n+1的向量。 (5) polyval(p,x):若x为一数值,则计算多项式在x 处的值;若x为向量,则计算多项式在x中每一元素处 的值。
p a n a n1 a 2 a1 a0
a (其中) n 0
注意,多项式中系数为0的项不能忽略,p中相应 元素应置为0。如多项式在MATLAB中应表示为 >>p=[3 0 2 3]
2. MATLAB中多项式操作函数简介
(1) roots(p):长度为n的向量,表示n阶多项式的根, 即方程p(x)=0的根,可以为复数。
部分内容仅作简单介绍,感兴趣的读者可以参考任何
MATLAB-Simulink的基础应用..

第3节 仿真模型的搭建方法与步骤
3.1 传感器输出特性仿真
例:已知某直流比较仪的输出特性曲线表达式为: I1=kI2+I0 式中I1和I2分别是一次电流和二次电流,I0为比较 仪的偏置系数,k为比较仪的灵敏度,已知k=114和 I0=110mA,试用Simulink绘制该比较仪的输出特性曲 线。 1. 调用功能模块 确定需要哪些功能模块,并找到所在的模块库。需 要以下模块:Ramp、Constant、Gain、sum、scope。
2
第2节 Simulink的操作方法
2.1 Simulink的运行操作
1、运行Simulink的方法 在MATLAB的命令窗口直接键入“simulink”; 利用MATLAB工具条上的Simulink快捷键图标; 在MATLAB菜单中,选择“File-New-Model” 2、打开已存在的模型文件 在MATLAB主窗口中直接键入文件名(不加扩展 名); 在MATLAB菜单中,选择“File-Open-Model” 利用MATLAB工具条上的“打开”图标。
13
4. 由功能模块组合成子系统 将现有的多个功能模块组合起来,形成新的功能模块。 例:构建下图所示的子系统
14
第4节 电力系统仿真初探
4.1 电力系统元件库简介
4.1.1 启动电力系统元件库 1. 利用指令窗口启动 在指令窗口中输入以下指令即可。 >> powerlib 2. 利用“开始”导航区启动 Start→Simulink →SimPowerSystem →Block Library 8.1.2 退出电力系统元件库 1. 单击“电力系统元件库”对话框中的File菜单,激活Exit Matlab命令即可; 2. 单击“电力系统元件库”对话框右上角上的“×”按钮即 15 可完成退出。
MATLABSimulink建模与仿真基础 ppt课件

Simulink建模与仿真基础
MATLABSimulink建模与仿真基础
MATLABSimulink建模与仿真基础
MATLABSimulink建模与仿真基础
MATLABSimulink建模与仿真基础
MATLABSimulink建模与仿真基础
MATLABSimulink建模与仿真 基础
2、打开文件 打开仿真模型文件主要有以下几种方式:
★ 在Matlab命令窗口输入不加扩展名的文件名
★ 在Matlab命令窗口选择“File”“Open”
★ 在Simulink模块库浏览器窗口选择 “File”“Open”
★ 在Simulink模型窗口选择“File”“Open”
MATLABSimulink建模与仿真 基础
◆ 信号线分支:将光标指向信号线的分支点上,按 住鼠标右键,光标变为十字,拖动鼠标直到分支线 的终点,释放鼠标。
虚线,因为终端 没有连接到模块
◆ 信号线文本注释,在信号线中插入模块,略……
MATLABSimulink建模与仿真 基础
1、基本模块
Simulink 基本模块
Simulink模块库 包含各种功能模块,如:放大器、 微分器、积分器、各种信号源等。
MATLABSimulink建模与仿真 基础
Simulink模型的文件为MDL模型文件,扩展名 为.mdl,以ASCII码形式存储。
1、新建文件 新建仿真模型文件主要有以下几种方式:
★ 在Matlab命令窗口选择 “File”“New”“Model” ★ 在命令窗口运行simulink命令,在弹出的模块库 浏览器窗口中选择“File”“New”“Model” ★在Simulink模型窗口中选择 “File”“New”“Model”
simulink入门及仿真实例

17
结果如下:上图为v(t), 下图为h(t).
18
r1 r2 1, n1 n2 100, s1 0.5, s2 2, x0 y0 10.
对x(t), y(t)进行模拟, 研究其发展趋势.
16
例3 弹跳的皮球(help/demos/simulink中的一个例子):
v(t) 15 tgdt, g 9.81, 0 t 数学模型:h(t) 10 0 v(t)dt, when h 0, v 0.8v.
4
子库 Continuous和 Discrete分别存放连续 和离散的函数, 如连续函数有Derivative(求导 数), Integrator(积分器), State-Space(状态空间), Transfer Fcn( 传 递 函 数 ) 等 等 , 离 散 的 有 Discrete Transfer Fcn(离散传递函数), Discrete Filter(离散滤波器), Discrete State-Space(离散 状态空间)等等. 在Simulink Library Browser窗口中, 建立 一个新模型(new model), 即打开一个新的空 白模型窗口, 用鼠标左键点取所需要的模块 拖到模型窗口中, 用鼠标左键在模块间建立 连接线(若在已有连接线上分叉则用右键)即 可.
Simulink入门
什么是Simulink? Simulink是MATLAB提供的实现动态 系统建模和仿真的一个软件包. 它让用户 把精力从编程转向模型的构造. Simulink一个很大的优点是为用户省 去了许多重复的代码编写工作,
1
Simulink的启动
首先须确定MATLAB已安装了Simulink工 具箱. 在工具栏点击Simulink图标:
matlab simulink仿真基础与工程应用实例

Singletasking: b) Singletasking:这种模式不检查模块间的 速率转换, 速率转换,它在建立单任务系统模型时非 常有用, 常有用,在这种系统就不存在任务同步问 题。 Auto:这种模式,simulink会根据模型中 c) Auto:这种模式,simulink会根据模型中 模块的采样速率是否一致, 模块的采样速率是否一致,自动决定切换 multitasking和singletasking。 到multitasking和singletasking。
Simulink 基础及应用
1
目
录
第一章:概 第一章: 述 第二章: 第二章:基本知识 第三章:实例分析 第三章:
第一章 概述
simulink是Mathworks公司开发的另一个 simulink是Mathworks公司开发的另一个 著名的动态仿真系统,它是Matlab Matlab的一个 著名的动态仿真系统,它是Matlab的一个 附加组件, 附加组件,为用户提供了一个建模与仿真 的工作平台。 的工作平台。 它能够实现动态系统建模与仿真的环境集 且可以根据设计及使用的要求, 成,且可以根据设计及使用的要求,对系 统进行修改与优化, 统进行修改与优化,以提高系统工作的性 能,实现高效开发系统的目的
1 Gain
1 Slider Gain |u| Product Divide eu Math Function t Sine Wave Function Product of Elem ents floor Rounding Function
f (z)
Dot Product P(u) O(P) = 5 Polynomial
4
第二章 基本知识
一.启动关闭 启动关闭
matlab simulink例子

matlab simulink例子
以下是一个简单的 MATLAB Simulink 的例子:
1. 首先,在 MATLAB 命令窗口中输入 `simulink` 打开Simulink 编辑器。
2. 在 Simulink 编辑器中,选择 File -> New -> Model,创建一个新的模型。
3. 在模型中添加一个 Constant 模块,这个模块将输出一个常数。
4. 添加一个 Scope 模块,用于显示模拟结果。
5. 连接 Constant 模块的输出到 Scope 模块的输入。
6. 在右上角的模型名称旁边的按钮上点击 Run 按钮,开始模拟。
7. 在模拟过程中,Scope 窗口将显示 Constant 模块输出的常数值。
这是一个非常简单的例子,但它演示了如何在 Simulink 中创建一个简单的模型,如何添加模块以及如何查看模拟结果。
你可以根据你的需求添加更多模块和功能来创建更复杂的模型。
matlabsimulink初级教程
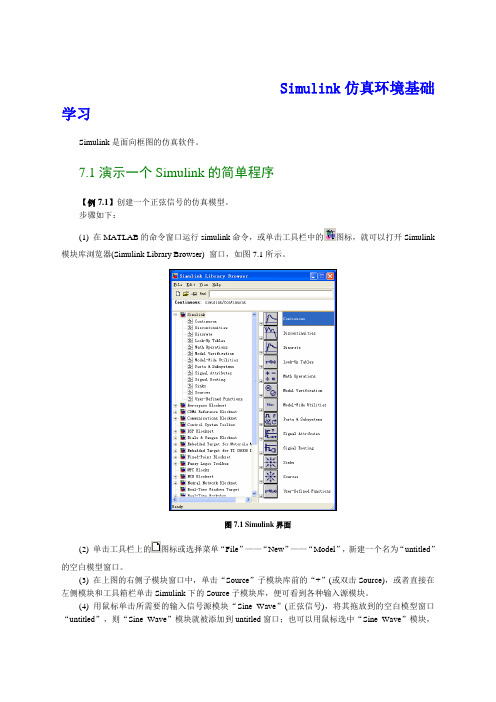
Simulink 仿真环境基础学习Simulink 是面向框图的仿真软件。
7.1演示一个Simulink 的简单程序【例7.1】创建一个正弦信号的仿真模型。
步骤如下:(1) 在MATLAB 的命令窗口运行simulink 命令,或单击工具栏中的图标,就可以打开Simulink模块库浏览器(Simulink Library Browser) 窗口,如图7.1所示。
(2) 单击工具栏上的图标或选择菜单“File ”——“New ”——“Model ”,新建一个名为“untitled ”的空白模型窗口。
(3) 在上图的右侧子模块窗口中,单击“Source ”子模块库前的“+”(或双击Source),或者直接在左侧模块和工具箱栏单击Simulink 下的Source 子模块库,便可看到各种输入源模块。
(4) 用鼠标单击所需要的输入信号源模块“Sine Wave ”(正弦信号),将其拖放到的空白模型窗口“untitled ”,则“Sine Wave ”模块就被添加到untitled 窗口;也可以用鼠标选中“Sine Wave”模块,图7.1 Simulink 界面单击鼠标右键,在快捷菜单中选择“add to 'untitled'”命令,就可以将“Sine Wave ”模块添加到untitled 窗口,如图7.2所示。
(5) 用同样的方法打开接收模块库“Sinks ”,选择其中的“Scope ”模块(示波器)拖放到“untitled ”窗口中。
(6) 在“untitled ”窗口中,用鼠标指向“Sine Wave ”右侧的输出端,当光标变为十字符时,按住鼠标拖向“Scope ”模块的输入端,松开鼠标按键,就完成了两个模块间的信号线连接,一个简单模型已经建成。
如图7.3所示。
(7) 开始仿真,单击“untitled ”模型窗口中“开始仿真”图标,或者选择菜单“Simulink ”——“Start ”,则仿真开始。
matlab 第9章 Simulink基础-王文杰

HYIT
41
几种常用仿真软件
PSPICE、ORCAD:通用的电子电路仿真软件,适 合于元件级仿真。 SYSTEM VIEW:系统级的电路动态仿真软件
MATLAB:具有强大的数值计算能力,包含各种工 具箱,其程序不能脱离MATLAB环境而运行,所以严 格讲,MATLAB不是一种计算机语言,而是一种高级 的科学分析与计算软件。
HYIT
29
参数设定:用鼠标双击模块,就可以进入 模块的参数设定窗口。参数设定窗口包含了该 模块的基本功能帮助,点击help按钮可获得更 详尽的帮助。
HYIT
30
属性设定:选中模块,打开Edit菜单的 Block Properties可以对模块进行属性设定。
HYIT
31
模块的输入输出信号:模块处理的信号包
HYIT
25
模块的创建及编辑
模块的基本操作,包括模块的移动、复制、删 除、转向、改变大小、模块命名、颜色设定、 参数设定、属性设定、模块输入输出信号等。
创建模块
在模块库浏览器列表中单击所需模块,拖曳 到模型窗口
HYIT
26
模块的编辑
模块选择:点击模块,则会显示出该模块被
选中的状态。
HYIT
5
开关
② ①
③
数学抽象
简单的手电筒电路
系统分析
S
US R RS 电源的模型 手电筒的电路图
计算机仿真
U=I*(R+RS)
计算机语言
Us I ( R RS )
HYIT
6
系统
数学抽象
系统分析 计算机仿真
数学 模型
计算机语言
计算机 模型
MATLAB—SIMULINK用法例题

将T1、T2、T3系统的阶跃响应图在同一Scope中显示。
仿真方块图
阶跃响应图:
练习6-2典型二阶欠阻尼系统的传递函数为:
第一问:设ωa=1,σ=0.5,1,5 ,求阶跃响应,(用同一Scope显示);
仿真方块图
阶跃响应图
第二问:设σ=1 ,ωa=0.5,1,5,求阶跃响应在(用同一Scope显示);
仿真方块图
阶跃响应图
第三问:求阶跃响应在(用同一Scope显示);
仿真方块图
阶跃响应图
实验报告
实验名称SIMULINK基本用法
系
控制工程
专业
班
姓名
学号
授课老师
预定时间
实பைடு நூலகம்时间
2013-4-16
实验台号
一、目的要求
1.学习SIMULINK软件工具的使用方法;
2.用SIMULINK仿真线性系统;
二、仪器设备
PC机一台,MATLAB软件
课堂练习:
仿真方块图:
阶跃响应图:
三、程序以及运行结果
matlabsimulink例题

matlabsimulink例题
当涉及到MATLAB Simulink的例题时,通常会涉及到控制系统、信号处理、通信系统等方面的建模和仿真。
下面我将以一个简单的
控制系统示例为例来说明。
假设我们要设计一个简单的PID控制器来控制一个直流电机的
转速。
首先,我们需要建立直流电机的数学模型,包括电机的转动
惯量、电磁转矩等参数。
然后,我们可以在Simulink中建立一个模型,包括输入端(期望转速)、控制器、电机模型和反馈回路。
我
们可以使用PID控制器模块来实现控制器部分,并将其参数进行调
整以达到期望的性能指标。
在Simulink中,我们可以使用Scope模块来实时监测电机的转
速响应,也可以使用Step模块来输入期望转速信号。
通过仿真我们
可以观察到实际转速与期望转速的差异,并根据需要对PID控制器
参数进行调整,直到达到满意的控制效果。
此外,Simulink还可以用于建模和仿真其他类型的系统,比如
通信系统、信号处理系统等。
例如,我们可以建立一个简单的调制
解调模型来演示数字通信系统的工作原理,或者建立一个滤波器模
型来演示信号处理系统的频率响应。
总之,MATLAB Simulink提供了一个强大的工具来进行系统建模和仿真,可以帮助工程师和研究人员快速有效地验证他们的设计和算法。
希望这个简单的例子可以帮助你更好地理解MATLAB Simulink的应用。
matlab实验六、SIMULINK基本用法
三、自定义功能模块的封装 exp5_7.mdl exp5_8.mdl exp5_9.mdl exp5_10.mdl
上面提到的两种方法都只是创建一个功能模块而已,如果要命名该 自定义功能模块、对功能模块进行说明、选定模块外观、设定输入 数据窗口,则需要对其进行封装处理。
首先选中Subsystem功能模块,再打开Edit菜单中的Mask Subsystem 进入mask的编辑窗口,可以看出有3个标签页。 1) Icon:设定功能模块的外观。 2) Initialization:设定输入数据窗口(Prompt List)。
d) dpoly(num,den,’z’):按z次数的降幂排序,在功能模块上显示离散的 传递函数。
用户还可以设置一些参数来控制图标的属性,这些属性在Icon页右下 端的下拉式列表中进行选择。 a) Icon frame:Visible 显示外框线;Invisible:隐藏外框线。
b) Icon Transparency:Opaque 隐藏输入输出的标签;Transparent:显示 输入输出的标签。 c) Icon Rotation:旋转模块。
3) Documentation:设计该功能模块的文字说明。
1、Icon标签页
此页最重要的部分是Drawing Commands,在该区域内可以用disp指 令设定功能模块的文字名称,用plot指令画线,用dpoly指令画转换函 数。
注意,尽管这些命令在名字上和以前讲的MATLAB函数相同,但它 们在功能上却不完全相同,因此不能随便套用以前所讲的格式。
例exp5_2.mdl
exp5_3.mdl
第四节 SIMULINK自定义功能模块
自定义功能模块有两种方法,一种方法是采用Signal&Systems 模块库 中的Subsystem功能模块,利用其编辑区设计组合新的功能模块;另一 种方法是将现有的多个功能模块组合起来,形成新的功能模块。对于 很大的SIMULINK模型,通过自定义功能模块可以简化图形,减少功 能模块的个数,有利于模型的分层构建。 一、方法1 exp5_5.mdl
MATLAB 第七章 SIMULINK基础PPT课件

SIMULINK仿真的运行
启动仿真
▪ 设置仿真参数和选择解法器之后,就可以启动仿真而运行。 ▪ 选择Simulink菜单下的start选项来启动仿真,如果模型中有些参数没有
定义,则会出现错误信息提示框。如果一切设置无误,则开始仿真运 行,结束时系统会发出一鸣叫声。 ▪ 除了直接在SIMULINK环境下启动仿真外,还可以在MATLAB命令窗 口中通过函数进行,格式如下:
– Real-Imag to Complex:由实部和虚部输入合成复数输出
12
7、Sinks(接收器模块)
– Scope:示波器 – XY Graph:显示二维图形 – To Workspace:将输出写入MATLAB的工作空间 – To File(.mat):将输出写入数据文件 – Terminator:连接到没有连接到的输出端
▪ SIMULINK是MATLAB软件的扩展,它是实现动态系统建模和仿真的 一个软件包,它与MATLAB语言的主要区别在于,其与用户交互接口 是基于Windows的模型化图形输入,其结果是使得用户可以把更多的 精力投入到系统模型的构建,而非语言的编程上。
▪ 所谓模型化图形输入是指SIMULINK提供了一些按功能分类的基本的 系统模块,用户只需要知道这些模块的输入输出及模块的功能,而不 必考察模块内部是如何实现的,通过对这些基本模块的调用,再将它 们连接起来就可以构成所需要的系统模型(以.mdl文件进行存取), 进而进行仿真与分析。
① Start time 和 Stop time 栏目分别允许用户填写仿真的起始 时间和结束时间。
② Solver options 的 Type 栏目有两个选项,允许用户选择定 步长和变步长算法。
③仿真精度控制有 Relative Tolerance 选项、Absolute Tolerance 等,其中相对误差限的默认值设置为 1e-3,该值在实 际仿真中显得偏大,建议选择 1e-6 和 1e-7。值得指出的是,由 于采用的变步长仿真算法,所以将误差限设置到这样小的值也 不会增加太大的运算量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二 Simulink 基 础
一·实验目的
1.熟练运用simulink 为函数建模
2.完成simulink 搭建模型的仿真过程
二.实验内容
【例1-2-1】对书上第35页图1-2-21所示系统,取fixed-step(固定步长)模式进行系统的单位阶跃响应过程仿真。
解:(1)步长类型选fixed-step,解法器算法odel(Euler),仿真步长取0.05;仿真曲线如图(a )所示。
由图(a )可见,其阶跃响应曲线是发散的。
因为系统本身是稳定的,不应该发散,所以此仿真曲线与实际不符。
原因是所取仿真步长偏大,致使仿真误差过大。
(2)步长类型选fixed-step,解法器算法odel(Euler),仿真步长取0.01;仿真曲线如图(b )所示。
由图(b )可见,仿真步长取下后的阶跃响应曲线就正确了。
图(a ) 图(b )
【例1-2-2】对系统4
4)(2++=s s s G ,试求单位阶跃仿真响应,用varible-step 模式。
解 首先在Simulink 下搭建系统的仿真模型,结构如图所示。
然后设置步长类型为varible-step ,解法器算法为ode45,仿真得到的响应曲线如图(a )所示。
由(a )可见,其响应曲线不够光滑,在最大峰值点处出现折线响应,这是仿真误差偏大的表现。
为此,应当减小solver 选项中relative tolerance (相对误差)的值,默认值为1e-3(即3
10-)修改为1e-6,运算所得的阶跃响应曲线如图(b )所示。
图(a ) 图(b )
课内练习
【1.2.1】已知一单位反馈系统的开环传递函数为)
4(16)(0+=s s s G ,试搭建Simulink 模型并进行该闭环系统的阶跃响应和斜坡响应实验。
解:分别选用信号源后,按照如下图所示构建模型,选择合适参数后,运行结果如下。
【1.2.2】已知系统的闭环传递函数为)2)(3(16
)(++=s s s G ,试分别用定步长和变步长的方
法求其单位阶跃响应,并讨论不同解法器的选用区别。
解:
选用定步长时,参数按下图设置,得到运行结果。
选用变步长时,参数按下图设置,得到运行结果。
课外实验
【1.2.1】用Simulink 仿真一个正弦信号和一个余弦信号相加,即计算)5cos()2sin(2)(t t t x +=。
在sources 库中找到sin wave ,并改变其参数使得符合题意,得此建模图,并设置如下图参数,得到运行结果。
【1.2.2】已知一个单位反馈系统的闭环传递函数为20116209)(232+++++=s s s s s s G ,试
搭建Simulink 模型并进行该系统的单位阶跃响应试验,找出最合适的仿真时间、仿真步长(定步长时)或Relative tolerance(相对误差)(变步长时)以及响应的解法器。
解:同上述步骤一样首先实现下图中的模型,然后在simulation 菜单下改为定步长,设置步长,直至合适的结果:
在定步长情况下,仿真时间为8秒,仿真步长为0.01(见图1)
在变步长的情况下,相对误差为le-3,解法器为ode45(见图2)
图(1)
图(2)。
