2015年南京邮电大学数据结构
南邮数据结构实验一

实验报告(2014 / 2015 学年第一学期)课程名称数据结构实验名称二叉树基本操作以及哈夫曼编码译码系统实验时间年月日指导单位指导教师学生姓名班级学号学院(系) 专业二叉树的基本运算:一、问题描述1.设计递归算法,实现二叉树的运算:删除一棵二叉树,求一棵二叉树的高度,求一棵二叉树中叶子节点数,复制一棵二叉树,交换一棵二叉树的左右子树2.设计算法,自上而下,自左向右即按层次遍历一棵二叉树3.设计main函数,测试上述每个运算二、系统分析和概要设计首先用maketree构造一棵二叉树,然后遍历二叉树,然后交换每个结点的左右子树,接着算出输得高度和叶子节点,最后删除。
三、详细设计2. 核心算法建立二叉树的void MakeTree(const T& x,BinaryTree<T>& left,BinaryTree<T>& right)和计算叶子节点的int Size();3. 算法分析删除一棵二叉树,求一棵二叉树的高度,求一棵二叉树中叶子节点数,复制一棵二叉树等都是用递归的方法实现。
四、程序代码流程图#include<iostream.h>template<class T>struct BTNode{BTNode(){lChild=rChild=NULL;}BTNode(const T &x){element=x;lChild=rChild=NULL;}BTNode(const T &x,BTNode<T>* l,BTNode<T>* r){element=x;lChild=l;rChild=r;}T element;BTNode<T>* lChild,* rChild;};template<class T>class BinaryTree{public:BinaryTree(){root=NULL;}~BinaryTree(){Clear();}void Copy(BinaryTree<T> &r) const;bool IsEmpty()const{return root == NULL;}void Clear();void Exchange();bool Root(T& x)const;int GetHeight();void MakeTree(const T& x,BinaryTree<T>& left,BinaryTree<T>& right);void BreakTree(T& x,BinaryTree<T>& left,BinaryTree<T>& right);void PreOrder(void (*Visit)(T &x));void LevelOrder(void (*Visit)(T& x));int Size();BinaryTree<T>(BinaryTree<T> &t)root=Copy(t.root);}// void InOrder(void (*Visit)(T &x));// void PostOrder(void (*Visit)(T &x));BTNode<T>* Copy(BTNode<T>* t);protected:BTNode<T> * root;private:static int number;void Clear(BTNode<T>* &t);void Exchange(BTNode<T>* t);int GetHeight(BTNode<T>* t);int Size(BTNode<T>* t);void PreOrder(void (*Visit)(T &x),BTNode<T>* t);void LevelOrder(void (*Visit)(T& x),BTNode<T>* t); // void InOrder(void (*Visit)(T &x),BTNode<T>* t);// void PostOrder(void (*Visit)(T &x),BTNode<T>* t); };template <class T>bool BinaryTree<T>::Root(T &x)const{if(root){x=root->element;return true;}elsereturn false;}template <class T>void BinaryTree<T>::Clear(){Clear(root);}template <class T>void BinaryTree<T>::Clear(BTNode<T>* &t){if(t)Clear(t->lChild);Clear(t->rChild);delete t;t=NULL;}}template <class T>void BinaryTree<T>::MakeTree(const T& x,BinaryTree<T>& left,BinaryTree<T>& right) {if(root||&left==&right)return;root=new BTNode <T>(x,left.root,right.root);left.root=right.root=NULL;}template <class T>void BinaryTree<T>::BreakTree(T& x,BinaryTree<T>& left,BinaryTree<T>& right) {if(!root||&left==&right||left.root||right.root)return;x=root->element;left.root=root->lChild;right.root=root->rChild;delete root;root=NULL;}template <class T>BTNode<T>* BinaryTree<T>::Copy(BTNode<T>* t){if(!t)return NULL;BTNode<T>*q=new BTNode<T>(t->element);q->lChild=Copy(t->lChild);q->rChild=Copy(t->rChild);return q;}template <class T>void Visit(T &x){cout<<x<<" ";}template <class T>void BinaryTree<T>::PreOrder(void (*Visit)(T& x)){PreOrder(Visit,root);}template <class T>void BinaryTree<T>::PreOrder(void (*Visit)(T& x),BTNode<T>* t) {if(t){Visit(t->element);PreOrder(Visit,t->lChild);PreOrder(Visit,t->rChild);}}template <class T>void BinaryTree<T>::Exchange(){Exchange(root);}template <class T>void BinaryTree<T>::Exchange(BTNode<T>* t){if(!t)return;BTNode<T>* temp;temp=t->lChild;t->lChild=t->rChild;t->rChild=temp;Exchange(t->lChild);Exchange(t->rChild);}template <class T>int BinaryTree<T>::GetHeight(){return GetHeight(root);}int BinaryTree<T>::GetHeight(BTNode<T>* t){int templ;int tempr;if(!t)return 0;templ=GetHeight(t->lChild);tempr=GetHeight(t->rChild);if(templ++>tempr++)return templ;elsereturn tempr;}template <class T>int BinaryTree<T>::number=0;template <class T>int BinaryTree<T>::Size(){Size(root);return number;}template <class T>int BinaryTree<T>::Size(BTNode<T>* t){if(t!=NULL){Size(t->lChild);if(t->lChild ==NULL&&t->rChild ==NULL)number++;Size(t->rChild);}return number;}template <class T>void BinaryTree<T>::LevelOrder(void (*Visit)(T& x)) {PreOrder(Visit,root);}void BinaryTree<T>::LevelOrder(void (*Visit)(T& x),BTNode<T>* t) {BTNode *quene[50],*p;int pre=1,rear=1;quene[++pre]=t;while(pre!=0){p=quene[++rear];cout<<p->element<<" ";if(p->lChild !=NULL)quene[++pre]=p->rChild ;if(p->rChild !=NULL)quene[++pre]=p->lChild ;}}void main(){BinaryTree <char> a,b,x,y,z;y.MakeTree('E',a,b);z.MakeTree('F',a,b);x.MakeTree('C',y,z);y.MakeTree('D',a,b);z.MakeTree('B',y,x);cout<<"二叉树z的先序遍历:"<<endl;z.PreOrder(Visit);cout<<endl;cout<<"层次遍历二叉树:";z.LevelOrder(Visit);cout<<endl;BinaryTree<char> q(z);cout<<"复制的二叉树q的先序遍历:"<<endl;q.PreOrder(Visit);cout<<endl;cout<<"树的高度:";cout<<z.GetHeight()<<endl;cout<<"叶子节点数量:";cout<<z.Size()<<endl;z.Exchange();cout<<"二叉树左右子树交换后的先序遍历:"<<endl;z.PreOrder(Visit);cout<<endl;}五、测试用例和运行结果测试用例如main函数中所示,结果如下图所示。
南邮数据结构实验一

实验报告(2014 / 2015 学年第二学期)课程名称数据结构实验名称线性表的基本运算及多项式的算术运算实验时间2015 年9 月28 日指导单位计算机科学与技术系指导教师黄海平学生姓名陈明阳班级学号Q学院(系) 贝尔英才专业信息科技强化班实验报告~SeqList() { delete[] elements; }bool IsEmpty() const;int Length() const;bool Find(int i, T& x) const;int Search(T x) const;bool Insert(int i, T x);bool Delete(int i);bool Update(int i, T x);void Output(ostream& out)const;private:int maxLength;T *elements;};template<class T>SeqList<T>::SeqList(int mSize){maxLength = mSize;elements = new T[maxLength];n = 0;}template<class T>bool SeqList<T>::IsEmpty() const{return n == 0;}template<class T>int SeqList<T>::Length()const{return n;}template<class T>bool SeqList<T>::Find(int i, T& x)const{if (i<0 || i>n - 1){cout <<"out of bounds"<< endl; return false;}x = elements[i];return true;}template<class T>int SeqList<T>::Search(T x)const{for (int j = 0; j < n; j++)if (elements[j] == x)return j;return -1;}template<class T>bool SeqList<T>::Insert(int i, T x){if (i<-1 || i>n - 1){cout <<"out of bounds"<< endl;return false;}if (n == maxLength){cout <<"over flow"<< endl;return false;}for (int j = n - 1; j > i; j--)elements[j + 1] = elements[j];elements[i + 1] = x;n++;return true;}template<class T>bool SeqList<T>::Delete(int i){if (i<0 || i>n - 1){cout <<"out of bounds"<< endl;return false;}if (!n){cout <<"over flow"<< endl;return false;}for (int j = i+1; j <n; j--)elements[j -1] = elements[j];n--;return true;}template<class T>bool SeqList<T>::Update(int i, T x){if (i<0 || i>n - 1){cout <<"out of bounds"<< endl;return false;}elements[i] = x;return true;}template<class T>void SeqList<T>::Output(ostream& out)const{for (int i = 0; i < n; i++)out << elements[i] << " ";out<< endl;}源.cpp:#include"seqlist.h"const int SIZE = 20;void main(){SeqList<int> LA(SIZE);int i = 0;for (i = 0; i<5; i++) LA.Insert(i - 1, i);LA.Insert(-1, 10);LA.Output(cout);}实现在线性表LA中插入0-4然后在一开始插入10 运行截图如下:多项式实验:定义类如下重构函数如下:源码:#include<iostream>using namespace std;class Term{public:Term(int c, int e);Term(int c, int e, Term* nxt);Term* InsertAfter(int c, int e);private:int coef;int exp;Term* link;friend ostream& operator<<(ostream &, const Term &);friend class Polynominal;};Term::Term(int c, int e) :coef(c), exp(e){link = 0;}Term::Term(int c, int e, Term *nxt) : coef(c), exp(e) {link = nxt;}Term* Term::InsertAfter(int c, int e){link = new Term(c, e, link);return link;}ostream& operator<<(ostream& out, const Term& val){if (0 == val.coef)return out;if (1!= val.coef)out<<val.coef;switch (val.exp){case 0:break;case 1:out<<"X"; break;default:out<<"X^"<<val.exp; break;}return out;}class Polynominal{public:Polynominal();~Polynominal();void AddTerms(istream& in);void Output(ostream& out)const;void PolyAdd(Polynominal& r);void PolyMul(Polynominal& r);private:Term* theList;friend ostream& operator<<(ostream &, const Polynominal &);friend istream& operator>>(istream&, Polynominal &);friend Polynominal& operator+(Polynominal &, Polynominal &);friend Polynominal& operator*(Polynominal &, Polynominal &); };Polynominal::Polynominal(){theList = new Term(0, -1); //头结点theList->link = NULL; //单链表尾结点指针域为空}Polynominal::~Polynominal(){Term* p = theList->link;while (p != NULL){theList->link = p->link;delete p;p = theList->link;}delete theList;}void Polynominal::AddTerms(istream & in){Term* q = theList;int c, e;for (;;){cout <<"Input a term(coef,exp):\n"<< endl;cin >> c >> e;q = q->InsertAfter(c, e);if (0 >= e) break;}}void Polynominal::Output(ostream& out)const{int first = 1;Term *p = theList->link;for (; p != NULL && p->exp >= 0; p = p->link){if (!first && (p->coef>0)) out<<"+";first = 0;out<< *p;}cout << endl;}void Polynominal::PolyAdd(Polynominal& r){Term *q, *q1 = theList, *p; //q1指向表头结点p = r.theList->link; //p指向第一个要处理的结点q = q1->link; //q1是q的前驱,p和q就指向两个当前进行比较的项while (p != NULL && p->exp >= 0)//对r的单循环链表遍历,知道全部结点都处理完{while (p->exp < q->exp) //跳过q->exp大的项{q1 = q;q = q->link;}if (p->exp == q->exp) //当指数相等时,系数相加{q->coef = q->coef + p->coef;if (q->coef == 0) //若相加后系数为0,则删除q{q1->link = q->link;delete(q);q = q1->link; //重置q指针}else{q1 = q; //若相加后系数不为0,则移动q1和qq = q->link;}}else//p>exp>q->exp的情况q1 = q1->InsertAfter(p->coef, p->exp); //以p的系数和指数生成新结点,插入q1后 p = p->link;}}void Polynominal::PolyMul(Polynominal& r){Polynominal result; //定义相乘后的数据Term *n = result.theList; //n指向result的头结点n = n->InsertAfter(0, 0); //在result的头结点后插入新结点,系数指数均为0 Term *p = r.theList->link; //p指向第一个要处理的结点while(p->exp >= 0) //对r的单循环链表遍历{Polynominal tmp; //存储某段相乘后的数据Term *m = tmp.theList; //m指向tmp的头结点Term *q = theList->link; //q指向表头结点的后继结点while(q->exp >= 0) //对当前对象的单循环环链表遍历{m = m->InsertAfter((p->coef)*(q->coef), (p->exp) + (q->exp)); //生成新结点插入n后 q = q->link;}result.PolyAdd(tmp); //将temp加到result上p = p->link;}Term *q = theList->link; //q指向表头结点的后继结点while(q != NULL) //删除原对象的所有数据{theList->link = q->link;delete q;q = theList->link;}q = theList;q = q->InsertAfter(0, 0);PolyAdd(result); //将result加到当前对象上}ostream &operator<<(ostream& out, const Polynominal& x){x.Output(out);return out;}istream &operator>>(istream& in, Polynominal &x){x.AddTerms(in);return in;}Polynominal & operator + (Polynominal &a, Polynominal &b){a.PolyAdd(b);return a;}Polynominal & operator * (Polynominal &a, Polynominal &b){a.PolyMul(b);return a;}int main()实验报告文档来源为:从网络收集整理.word版本可编辑.欢迎下载支持.。
南京邮电大学考研数据结构(811)00-09年真题和答案
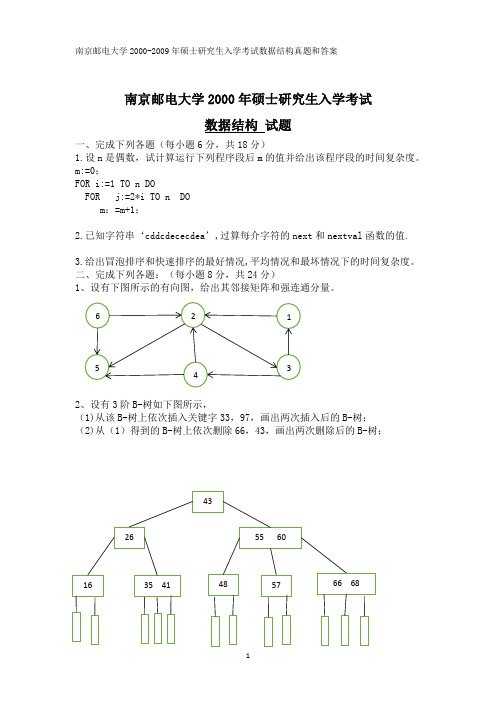
南京邮电大学2000年硕士研究生入学考试数据结构试题一、完成下列各题(每小题6分,共18分)1.设n是偶数,试计算运行下列程序段后m的值并给出该程序段的时间复杂度。
m:=0;FOR i:=1 TO n DOFOR j:=2*i TO n DOm:=m+1;2.已知字符串‘cddcdececd ea’,过算每介字符的next和nextval函数的值.3.给出冒泡排序和快速排序的最好情况,平均情况和最坏情况下的时间复杂度。
二、完成下列各题:(每小题8分,共24分)1、设有下图所示的有向图,给出其邻接矩阵和强连通分量。
2、设有3阶B-树如下图所示,(1)从该B-树上依次插入关键字33,97,画出两次插入后的B-树;(2)从(1)得到的B-树上依次删除66,43,画出两次删除后的B-树;(1)画出据此构造的败选择树(2)画出输出一个记录后的败方树三、阅读下列二叉树算法,每个结点三个域:lchild,element,rchild。
(10分)(1)X(p)对以p为根的二叉树执行什么功能?(2)以下图所示的二叉树调用此算法,则X(p)的执行结果是什么?(3)执行中,栈s中元素个数最多时为多少?给出该时栈中元素的情况。
void X(BinTree *t){struct Stack s;BinTnode *qPush(s,NUL1)While(*p){q=(*p)->lchild(*p)->1child=(*p)->rchild(*p)->rchild=qIf((*p)->lchild)Push(s,(*p)->1child);If((*p)->rchild)Push(s,(*p)->rchild);else(*p)=Pop(s)}}四、阅读下列要求每对顶点之间的最短路径的Floyd算法。
(16分)(1)若对下图所示的有向图执行此算法,写出对k为1到n的各步中,二维数组a和path的值。
南邮_数据结构课后习题答案讲解

?
?
?1 4 7 ?
?
?
?4 4 9 ?
?4 4 9 ?
4.7 求对题图4-1的稀疏矩阵执行矩阵转置时数组
num[]和k[]的值。
col
0
1
2
3
4
num[col] 1
0
2
1
2
k[col]
0
1
1
3
4
2020/2/8
14
第六章 习题讲解
6-2. 对于三个结点 A,B和C,可分别组成多少不同 的无序树、有序树和二叉树?
int i,j,sum=0;
for (i=0;temp[i]<x&&i<n;i++); //找到首个大于等于 x的元素位置 i
if(i>n-1) return; //没有符合条件的元素
ffoorr ((jj==ii;;ljs<tn[j;]<) =y&&j<n;j++); if (lst[j]>y//)找到首个//大大于于yy的的元元素素前位移置 j
?0 0 ???3 0
6 0
0 0
0? 7??
行三元组:???10
2 0
6 ?列三元组:?1
? 3??
??0
0 2
?3?
6
? ?
? 0 0 0 0 0?
?1 4 7 ?
?3 2 ?8?
? ?
0
0 ? 8 10 0??
??3 2 ?8??
??3
3
10
? ?
?? 0 0 0 0 9??
?3 3 10 ?
(2)void Search_Delete(List *lst, T x,T y)
南京邮电大学《811数据结构》历年考研真题汇总

目录
2006年南京邮电大学811数据结构考研真题 (5)
2005年南京邮电大学811数据结构考研真题 (9)
2004年南京邮电大学811数据结构考研真题 (13)
2003年南京邮电大学811数据结构考研真题 (17)
2002年南京邮电大学811数据结构考研真题 (21)
2001年南京邮电大学811数据结构考研真题 (25)
2000年南京邮电大学811数据结构考研真题 (27)
2006年南京邮电大学811数据结构考研真题
2005年南京邮电大学811数据结构考研真题
2004年南京邮电大学811数据结构考研真题
2003年南京邮电大学811数据结构考研真题
2002年南京邮电大学811数据结构考研真题
2001年南京邮电大学811数据结构考研真题
2000年南京邮电大学811数据结构考研真题。
【源版】南京邮电大学数据结构A第4章

4.1 数组
4.1.3 一维数组的C++类 1. 构造函数
size =3
elements = 0x0012FF7C
11 0 23 1 33 2
Array <int> A(3); A 的结构如图所示。
private: int size; T *elements;
};
4.1 数组
4.1.3 一维数组的C++类
1. 构造函数
template <class T> Array1D<T>::Array1D(int sz) { //创建动态一维数组
assert(sz>=0); //越界检查 size=sz; elements=new T[sz]; }
4.1 数组
4.1.2 数组的顺序表示 1. 一维数组的顺序表示
设第一个数组元素a[0]的地址是loc(a[0]),若已知每个元素 占k个存储单元,则a[i]的地址loc(a[i])为
loc(a[i])=loc(a[0])+i*k (i=0,1,2,…,n-1)。
2. 二维数组的顺序表示
二维数组a[m][n]映射到一维的存储空间时有两种顺序:
4.1 数组
4.1.2 数组的顺序表示
数组通常采用顺序表示: 1. 一维数组的顺序表示 2. 二维数组的顺序表示 3. 多维数组的顺序表示
课堂提要
第4章 数组和字符串 4.1 数组 4.1.1 数组抽象数据类型 4.1.2 数组的顺序表示 4.1.3 一维数组的C++类 4.2 特殊矩阵 4.3 稀疏矩阵 4.4 字符串
南邮数据结构

数据结构的宏观把握:数据结构学两个东西,一个是逻辑结构,一个是存储结构(他们两个的定义背下来,14年考了)这两个东西到现在你肯定已经能背下来了。
然后,看看这本书:1、第一章是绪论,这一章的重点在上面的概念,和算法的特点等这几个小概念,稍微背一下就行了。
还有最有一节,算法的渐进复杂度,有可能会考到一个选择或者填空题或者大题目的一个小问,分不多,说实话我也不会,考试的时候凭平时做题的感觉做出来的;2、第二、三、四章,可以把它归成一类!没错,就是逻辑结构中的线性结构!而线性表讲到了五个东西,线性表、链表、数组、堆栈和队列;(1)线性表(这是线性结构的顺序存储结构):掌握插入、删除、搜索的代码,能够自己算出(不是背下来的)插入和删除一个元素最好最坏和平均情况下需要移动的元素个数;(2)链表(这是线性结构的链式存储结构):掌握单链表,代表头链表,循环链表以及双循环链表的插入、删除、搜索的代码,并且知道什么情况下用哪个链表能满足题目要求(这一点说的有点抽象,真题有体现)还要掌握建立新节点的代码Node *p=(Node*)malloc(sizeof(Node));对于链表这边,还要强调下,要非常熟练掌握链表的插入删除!后期很多大程序都是以这个为基础;(3)数组这边只要掌握二维数组的那个位置的公式,然后会做关于这个公式应用的题目,这种题目应该做过很多了我就不赘述了,这一个知识点百分之九十九考!绝对不能失分;(4)堆栈这一章不难,关键掌握它的先进后出的特点,会画堆栈解决题目,比如说表达式的题目(中缀和后缀的相互转换),会做例如进栈序列为abcde,那么出站序列可能是_____(选择题)。
另外记住,空栈的时候s.top==-1而不是0,并且知道进栈和出站的代码,会判断栈空和栈满的代码,这些在后面图那一章会用到;(5)队列这一章也不难,知道为什么要循环队列?因为假溢出,什么是假溢出?不会来问我;循环队列会判断空队列、满队列、进队、出队的代码(都只有一句话),知道循环队列也会有假溢出现象,不能完全杜绝假溢出(因为q.r队尾指针始终要指向一个空的存储空间);还要会构造循环队列,这个很简单,只要你把之前的空满进出四个程序掌握了,马上就知道了;还有就是链式队列,最好了解一下,程序能看懂,不要求你背,至少能懂思想。
数据结构(陈慧南编 C++描述)南京邮电大学 课后答案 DS习题答案01

www.khd课后a答w案.网com
bool LinkedStack<T>::Push(const T x) {
Node <T> *q=new Node<T>; q->data=x; q->link=top; top=q; return true; }
template <class T> bool LinkedStack<T>::Pop() {
Node<T> *q; while (top){
q=top->link; delete top; top=q; } }
第四章 数组与字符串
1. 给出三维数组元素 A[i][j][k]的存储地址 loc(A[i][j][k])。 答: 设有三维数组声明为 A[n1][n2][n3],每个元素占 k 个存储单元,则
Node<T> *q; while (top){
q=top->link; delete top; top=q; } }
template <class T> bool LinkedStack<T>::IsEmpty() const {
return !top; }
template <class T> bool LinkedStack<T>::IsFull() const {
www.khd课后a答w案.网com
第一章 绪论
1.( 第 18页,第(5)题) 确定下列各程序段的程序步,确定划线语句的执行次数,计算它们的渐近时间复杂度。
(1) i=1; k=0; do { k=k+10*i; i++; } while(i<=n-1) 划线语句的执行次数为 n-1 。
【真题】2015年南京邮电大学数据结构初试真题

【真题】2015年南京邮电⼤学数据结构初试真题【真题】2015年南京邮电⼤学数据结构初试真题判断题(共15题*2分)1.消除递归不⼀定需要使⽤栈,此说法2.稀疏矩阵压缩存储后,必会失去随机存取功能3.完全⼆叉树中,若⼀个结点没有左孩⼦,则它必是树叶4.连通分量是⽆向图的极⼤强连通⼦图5.在9阶B-树中,除叶⼦以外的任意结点的分⽀数介于5 和9 之间6.在平衡⼆叉树中,向某个平衡因⼦不为零的结点的树中插⼊⼀新结点,必引起平衡旋转选择题(共15题*2分)1.以下属于逻辑结构的是()。
A.顺序表 B. 哈希表 C.有序表 D. 单链表2.下列数据中,()是⾮线性数据结构。
A.栈 B. 队列 C. 完全⼆叉树 D. 堆3.某线性表中最常⽤的操作是在最后⼀个元素之后插⼊⼀个元素和删除第⼀个元素,则采⽤()储⽅式最节省运算时间。
A.单链表B.仅有头指针的单循环链表C.双链表D.仅有尾指针的单循环链表4.循环队列存储在数组A[0..m]中,则⼊队时的操作为()。
A. rear=rear+1B. rear=(rear+1) mod (m-1)C. rear=(rear+1) mod mD. rear=(rear+1)mod(m+1)5.⼆叉树在线索后,仍不能有效求解的问题是()。
A.前(先)序线索⼆叉树中求前(先)序后继B.中序线索⼆叉树中求中序后继C.中序线索⼆叉树中求中序前驱D.后序线索⼆叉树中求后序后继6.下⾯⼏个符号串编码集合中,不是前缀编码的是()。
A.{0,10,110,1111} B.{11,10,001,101,0001} C.{00,010,0110,1000}D.{b,c,aa,ac,aba,abb,abc}7.⽤有向⽆环图描述表达式(A+B)*((A+B)/A),⾄少需要顶点的数⽬为( )。
A.5 B.6 C.8 D.98.下列关于AOE ⽹的叙述中,不正确的是()。
A.关键活动不按期完成就会影响整个⼯程的完成时间B.任何⼀个关键活动提前完成,那么整个⼯程将会提前完成C.所有的关键活动提前完成,那么整个⼯程将会提前完成D.某些关键活动提前完成,那么整个⼯程将会提前完成9.m 阶B-树是⼀棵( )A. m 叉排序树B. m 叉平衡排序树C. m-1 叉平衡排序树D. m+1 叉平衡排序树10.关于杂凑查找说法不正确的有⼏个( ) 【南京理⼯⼤学 2000 ⼀、16 (1.5 分)】A. 采⽤链地址法解决冲突时,查找⼀个元素的时间是相同的B. 采⽤链地址法解决冲突时,若插⼊规定总是在链⾸,则插⼊任⼀个元素的时间是相同的C. ⽤链地址法解决冲不易引起聚集现象D. 再哈希法不易产⽣聚集11.在下列排序算法中,哪⼀个算法⼀趟不能确定⼀个元素的最终位置()。
南京邮电大学数据结构A第3章

3.1 堆栈
3.1.1 堆栈抽象数据类型 3. 栈的C++模板抽象类
程序3-1 堆栈的C++类
#include <iostream.h> template <class T> class Stack { public: virtual bool IsEmpty() const=0; virtual bool IsFull() const=0; virtual bool Top(T &x) const=0; virtual bool Push(T x)=0; virtual bool Pop()=0; virtual void Clear()=0; };
3.2 队列
3.2.1 队列抽象数据类型 3. 队列的C++模板抽象类
template <class T> class Queue { public:
Queue(){};
~Queue(){}; virtual bool EnQueue(const T x)=0;
virtual bool DeQueue()=0;
出栈操作Pop() Node<T> *q = top; top = top->link; delete q;
top
an-1
an-2
an-3
…
a0
∧
图3-3 链式栈
3.2 队列
3.1.3 栈的链接表示 队列的示意图
Q=(a0,a1,…,an-1)
入队 课堂提要
第3章 堆栈和队列 3.1 堆栈 3.2 队列 3.2.1 队列抽象数据类型 3.2.2 队列的顺序表示 3.2.3 队列的链接表示 3.3 表达式的计算 3.4 递归
数据结构A第1章(南邮)

程序步数为2n+3。
41
1.5.3 渐近时间复杂度
渐近时间复杂度
使用大 O 记号表示的算法的时间复杂性,称为算法的渐
近时间复杂度,简称时间复杂度。
大O记号 如果存在两个正常数 c 和 n0 ,使得对所有的 n , nn0 ,有 f(n) c g(n) 则有 f(n)=O(g(n))。
42
渐近时间复杂度 使用大 O 记号表示的算法的时间复杂性,称为算法的渐
结点存储块分成两部分,元素本身和该元素后继元素所 在结点的存储地址。
Data
Link
20
小结
逻辑结构 概念
面向 关系
存储结构 数据及其关系在计 算机内的组织方式 面向计算机
数据元素之间逻 辑关系的描述 面向应用问题
存储结构是逻辑结构在计算机内的映像
21
1.2.4 数据结构的运算
• 数据结构最常见的运算 创建运算:创建一个数据结构; 清除运算:删除数据结构中的全部元素; 插入运算:在数据结构的指定位置上插入一 个新元素; 删除运算:将数据结构中的某个元素删除; ……
2.
数据类型 一个数据类型定义了一个值的集合以及作 用于该值集的操作的集合。 即一组值和一组操作。
26
3.抽象数据类型 抽象数据类型( Abstract Data Type, ADT )是一个 数据类型,其主要特征是该类型的对象及其操作的规 范 , 与该类型对象的表示和操作的实现分离,实行封 装和信息隐蔽,即使用和实现分离。 使用和实现分离:使用者通过规范使用该类型的数据,
南京邮电大学数据结构A第6章

(21,25,28,33,36,45) 33 搜索成功!
35 (21,25,28,33,36,45) 搜索失败!
6.2 顺序搜索
6.2.2 有序表的顺序搜索
程序6.4 顺序搜索有序表 const int Infinity = 1000; template <class T> ResultCode ListSet<T>::Search(T& x)const { l[n] = Infinity; for (int i=0;l[i]<x;i++) ; //当list[i]的关键字值大于等于 // x的关键字值时,退出循环 if (l[i]==x) { return Success; //搜索成功 } return NotPresent; //搜索失败 }
template<class K, class D> Struct E { operator K() const{return key;} //使元素间的比较视为关键字间的比较 K key; D data; };
其中,K称为关键字类型,应为可比较大小的类型。 key为关键字:用来标识一个数据元素的某个数据项。
6.3 二分搜索
6.3.2 对半搜索
由分割点的不同,可以得到不同的二分搜索方法。如:对 半搜索、一致对半搜索、斐波那契搜索和插值搜索等。
对半搜索是二分搜索中的一种,分割点为表的中点元素。
若当前搜索的子表为 (alow,alow+1,…,ahigh) 则 i=(low+high)/2 其中,i、low 和 high均为元素在表中的序号,low表示表的左 端,high表示表的右端。
6.3 二分搜索
6.3.2 对半搜索 对半搜索的例子 (1) key=66
南邮数据结构实验三

实验报告(2015 / 2016 学年第一学期)课程名称数据结构实验名称图的基本运算及飞机换乘次数最少问题实验时间2015 年12 月 4 日指导单位计算机科学与技术系指导教师黄海平学生姓名陈明阳班级学号Q14010119 学院(系)贝尔英才专业信息科技强化班实验报告实验名称图的基本运算及飞机换乘次数最少问题指导教师黄海平实验类型验证实验学时 4 实验时间12。
4一、实验目的和要求飞机最少换乘次数问题。
(1)设有n个城市,编号为0~n-1,m条航线的起点和终点由用户输入提供。
寻找一条换乘次数最少的线路方案。
(2)参考:可以使用有向图表示城市间的航线;只要两城市间有航班,则图中这两点间存在一条权值为1的边;可以使用Dijkstra算法实现。
二、实验环境(实验设备)VSUAL STUDIO2015三、实验原理及内容对象视图:源代码:Graph。
h#include<iostream>#include<string.h〉using namespace std;const int INF = 2147483647;enum ResultCode { Underflow,Duplicate,Failure,Success, NotPresent,OutOfBounds};template <class T〉class Graph//抽象类{public:virtual ResultCode Insert(int u, int v,T w) = 0;virtual ResultCode Remove(int u, int v) = 0;virtual bool Exist(int u, int v)const = 0;protected:int n, e;};template <class T>class MGraph :public Graph〈T> //邻接矩阵类{public:MGraph(int mSize, const T noedg);~MGraph();ResultCode Insert(int u,int v,T w);ResultCode Remove(int u,int v);bool Exist(int u,int v)const;int Choose(int*d, bool *s);void Dijkstra(int v,T *d, int*path);protected:T **a;T noEdge;};template〈class T〉MGraph〈T>::MGraph(int mSize, const T noedg){n = mSize;e = 0;noEdge = noedg;a = new T*[n];for(int i = 0; i〈n; i++){a[i] = new T[n];for(int j = 0; j〈n; j++)a[i][j] = noEdge;a[i][i] = 0;}}template〈class T>MGraph〈T>::~MGraph(){for (int i = 0; i〈n; i++)delete[]a[i];delete[]a;}template <class T〉ResultCode MGraph〈T>::Insert(int u, int v,T w){if (u<0 || v〈0 ||u>n — 1 || v〉n — 1 ||u == v)return Failure;if(a[u][v] != noEdge)return Duplicate;a[u][v] = w;a[v][u] = w;e++;return Success;}template〈class T〉ResultCode MGraph<T>::Remove(int u, int v){if(u<0 ||v〈0 ||u〉n — 1 ||v〉n - 1 ||u == v)return Failure;if (a[u][v] == noEdge)return NotPresent;a[u][v] = noEdge;a[v][u] = noEdge;e—-;return Success;}template〈class T〉bool MGraph〈T〉::Exist(int u,int v)const{if(u<0 || v<0 || u>n - 1 || v>n - 1 || u == v|| a[u][v] == noEdge) return false;return true;}template <class T>int MGraph<T>::Choose(int*d,bool *s) //求最小d[i]{int i, minpos;T min;min = INF;minpos = -1;for(i = 0; i<n; i++)if(d[i]〈= min&&!s[i]){min = d[i];minpos = i;}return minpos;}template <class T〉void MGraph〈T>::Dijkstra(int v,T*d,int *path)//迪杰斯特拉算法{int i, k, w;if (v〈0 ||v〉n — 1)throw OutOfBounds;bool *s = new bool[n];for(i = 0; i<n; i++){s[i] = false;d[i] = a[v][i];if(i != v&&d[i]<INF)path[i] = v;elsepath[i] = -1;}s[v] = true;d[v] = 0;for (i = 1; i〈n; i++){k = Choose(d, s);s[k] = true;for(w = 0; w<n; w++)if (!s[w]&& (d[k] + a[k][w])<d[w]){d[w] = d[k] + a[k][w];path[w] = k;}}}源.cpp#include<iostream〉#include<string。
南邮通达大数据结构B期中模拟试卷及问题详解

南京邮电大学通达学院 2014/2015学年第一学期《数据结构A》期中模拟试卷本试卷共4页;考试时间100分钟;院(系) 班级学号姓名一、填空题(每题4分,共5题)1.四种基本的数据逻辑结构是:___________、___________、___________、___________2.在数据结构中,数据的逻辑结构分线性结构和___________ 。
3.对于栈只能在_______插入和删除元素。
4.数组A中,每个元素的长度为3个字节,行下标i从1到8,列下标j从1到10,从首地址SA开始连续存放的存储器内,该数组按行存放,元素A[5][8]的地址为。
5.若一课二叉树的前序遍历和中序遍历分别为ABDEGCFH和DBGEACHF,则该二叉树的后序遍历为_________________二、选择题(每题4分,共5题)1.设有一个栈,元素的进栈次序为A,B,C,D,E,下列__________是不可能的出栈序列。
A. E,A,B,C,DB. B,C,D,E,AC. A,B,C,D,ED. E,D,C,B,A2.在深度为5的满二叉树中,叶子节点的个数为__________A.32B.31C.16D.153.已知一棵二叉树的前序遍历结果为ABCDEF,中序遍历结果为CBAEDF,则后序遍历的结果为.A.CBEFDA B. FEDCBA C. CBEDFA D.不定4.已知中缀表达式为a*(b+c)-d/e,请问下列哪个为正确的后缀表达式__________A.abc+*de/-B.bc+a*de/-C.bc+*a/de-D.abc+*de/-5.一棵具有n个结点的完全二叉树的树高度(深度)是()A.⎣logn⎦+1 B.logn+1 C.⎣logn⎦ D.logn-1三、简答题(每题10分,共6题)1.下图所示的森林:(1)求树(a)的先根序列和后根序列;(2)求森林先序序列和中序序列;(3)将此森林转换为相应的二叉树;(a)(b)2.设有正文AADBAACACCDACACAAD,字符集为A,B,C,D,设计一套二进制编码,使得上述正文的编码最短。
南京邮电大学数据结构A第10章

10.2 简单排序算法
本节介绍三种简单的排序算法: 简单选择排序 冒泡排序 直接插入排序 它们的时间复杂度在最坏情 况下均为O(n2)。 虽然这些算法对数据量较大的情况 不大实用, 但仍然可从中体验排序 课堂提要
第10章 内排序 10.1 排序的基本概念 10.2 简单排序算法 10.2.1 简单选择排序 10.2.2 直接插入排序 10.2.3 冒泡排序 10.3 快速排序 10.4 2路合并排序
48 48 48 48 72 (72 68) 68
02) 48) 48) 48) 48) 68 ) (72) 72)
(02)(36 12 12 12 12 12
12) (68
48) (68
排序结果: (02
图10-1 简单选择排序示意图
10.2 简单排序算法
10.2.1 简单选择排序
程序 10-1 简单选择排序 template <class T> void SelectSort(T A[], int n) { int small; for (int i=0; i<n-1; i++ ) { // n-1趟 small=i; for (int j=i+1; j<n; j++) if (A[j]<A[small]) small=j; Swap(A[i],A[small]); } //endfor } //函数Swap(T &a, T &b)交换两个元素 时间复杂度按比较次数衡量为O(n2)。
…, p(n-1),使得序列按 Kp(0) Kp(1)…Kp(n-1) (非递减) 或 Kp(0)Kp(1)…Kp(n-1) (非递增) 的次序排列为: (Rp(0),Rp(1),…,Rp(n-1))
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年南京邮电大学数据结构考研初试题目
判断题(共15题*2分)
1.消除递归不一定需要使用栈,此说法()
2.稀疏矩阵压缩存储后,必会失去随机存取功能()
3.完全二叉树中,若一个结点没有左孩子,则它必是叶结点()
4.连通分量是无向图的极大强连通子图()
5.在9阶B-树中,除叶子以外的任意结点的分支数介于5和9之间()
6.在平衡二叉树中,向某个平衡因子不为零的结点的树中插入一新结点,必引起平衡旋转()
7.10个叶子结点的哈弗曼树,其高度最小为58.队列和栈不可以使用散列存储()
选择题(共15题*2分)
1.以下属于逻辑结构的是()。
A.顺序表
B.哈希表
C.有序表
D.单链表
2.下列数据中,()是非线性数据结构。
A.栈 B.队列 C.完全二叉树 D.堆
3.某线性表中最常用的操作是在最后一个元素之后插入一个元素和删除第一个元素,则采用()储方式最节省运算时间。
A.单链表B.仅有头指针的单循环链表C.双链表D.仅有尾指针的单循环链表
4.循环队列存储在数组A[0..m]中,则入队时的操作为()。
A.rear=rear+1
B.rear=(rear+1)mod(m-1)
C.rear=(rear+1)mod m
D.rear=(rear+1)mod(m+1)
5.二叉树在线索后,仍不能有效求解的问题是()。
A.先序线索二叉树中求先序后继B.中序线索二叉树中求中序后继
C.中序线索二叉树中求中序前驱D.后序线索二叉树中求后序后继
6.下面几个符号串编码集合中,不是前缀编码的是()。
A.{0,10,110,1111}B.{11,10,001,101,0001}C.{00,010,0110,1000}D.{b,c,aa,ac,aba,abb,abc}
7.用有向无环图描述表达式(A+B)*((A+B)/A),至少需要顶点的数目为()。
A.5B.6C.8D.9
8.下列关于AOE网的叙述中,不正确的是()。
A.关键活动不按期完成就会影响整个工程的完成时间
B.任何一个关键活动提前完成,那么整个工程将会提前完成
C.所有的关键活动提前完成,那么整个工程将会提前完成
D.某些关键活动提前完成,那么整个工程将会提前完成
9.m阶B-树是一棵()
A.m叉排序树
B.m叉平衡排序树
C.m-1叉平衡排序树
D.m+1叉平衡排序树
10.关于杂凑查找说法不正确的有几个()
A.采用链地址法解决冲突时,查找一个元素的时间是相同的
B.采用链地址法解决冲突时,若插入规定总是在链首,则插入任一个元素的时间是相同的
C.用链地址法解决冲不易引起聚集现象
D.再哈希法不易产生聚集
11.在下列排序算法中,哪一个算法一趟不能确定一个元素的最终位置()。
A.直接插入 B.冒泡排序 C.快速排序 D.简单选择排序
简答题(共5题*10分)
1.举例说明顺序队的“假溢出”现象,并给出解决方案。
2.什么是算法?算法有哪些特征?
在程序设计算法中引入“程序步”,是不是"程序步"越少执行效率越高?
3.设T是具有n个内结点的扩充二叉树,I是它的内路径长度,E是它的外路径长度。
(1)试利用归纳法证明E=I+2n,n>=0.
(2)利用(1)的结果试说明:成功查找的平均比较次数s与不成功查找的平均比较次数u 之间的关系可用公式表示s=(1+1/n)u-1,n>=1。
4.一个图有0,1,2,3,4,5共6个结点,插入边(1,0)(1,3)(2,1)(2,3)(3,0)(3,2)(3,4)(4,1)(4,5)(1)画出对应的邻接矩阵
(2)写出所有强连通分量
5.试画出从空树开始,由字符序列(t,d,e,s,u,g,b,j,a,k)构成的二叉平衡树,并为每一次的平衡处理指明旋转类型。
再次插入字符a,画出此时的平衡二叉树
编程题(共4题*10分)
1.实现利用队列将栈中元素逆置并说明算法
2.已知无向图采用邻接表存储方式,试写出删除边(i,j)的算法。
3.有线性表(a1,a2,…,an),采用单链表存储,头指针为H,每个结点中存放线性表中一个元素,现查找某个元素值等于X的结点。
分别写出下面三种情况的查找语句。
要求时间尽量少。
(1)线性表中元素无序。
(2)线性表中元素按递增有序。
(3)线性表中元素按递减有序。
4.给定集合S,S的幂集是指以集合S的所有子集为元素构成的集合,利用递归算法编程求集合S的幂集。
