逢山开路模型
国赛历届数学建模赛题题目与解题方法

历届数学建模题目浏览:1992--20091992年 (A) 施肥效果分析问题(北京理工大学:叶其孝)(B) 实验数据分解问题(华东理工大学:俞文此; 复旦大学:谭永基)1993年 (A) 非线性交调的频率设计问题(北京大学:谢衷洁)(B) 足球排名次问题(清华大学:蔡大用)1994年 (A) 逢山开路问题(西安电子科技大学:何大可)(B) 锁具装箱问题(复旦大学:谭永基,华东理工大学:俞文此)1995年 (A) 飞行管理问题(复旦大学:谭永基,华东理工大学:俞文此)(B) 天车与冶炼炉的作业调度问题(浙江大学:刘祥官,李吉鸾)1996年 (A) 最优捕鱼策略问题(北京师范大学:刘来福)(B) 节水洗衣机问题(重庆大学:付鹂)1997年 (A) 零件参数设计问题(清华大学:姜启源)(B) 截断切割问题(复旦大学:谭永基,华东理工大学:俞文此)1998年 (A) 投资的收益和风险问题(浙江大学:陈淑平)(B) 灾情巡视路线问题(上海海运学院:丁颂康)1999年 (A) 自动化车床管理问题(北京大学:孙山泽)(B) 钻井布局问题(郑州大学:林诒勋)1999年(C) 煤矸石堆积问题(太原理工大学:贾晓峰)(D) 钻井布局问题(郑州大学:林诒勋)2000年 (A) DNA序列分类问题(北京工业大学:孟大志)(B) 钢管订购和运输问题(武汉大学:费甫生)(C) 飞越北极问题(复旦大学:谭永基)(D) 空洞探测问题(东北电力学院:关信)2001年 (A) 血管的三维重建问题(浙江大学:汪国昭)(B) 公交车调度问题(清华大学:谭泽光)(C) 基金使用计划问题(东南大学:陈恩水)(D) 公交车调度问题(清华大学:谭泽光)2002年 (A) 车灯线光源的优化设计问题(复旦大学:谭永基,华东理工大学:俞文此)(B) 彩票中的数学问题(解放军信息工程大学:韩中庚)(C) 车灯线光源的优化设计问题(复旦大学:谭永基,华东理工大学:俞文此)(D) 赛程安排问题(清华大学:姜启源)2003年 (A) SARS的传播问题(组委会)(B) 露天矿生产的车辆安排问题(吉林大学:方沛辰)(C) SARS的传播问题(组委会)(D) 抢渡长江问题(华中农业大学:殷建肃)2004年 (A) 奥运会临时超市网点设计问题(北京工业大学:孟大志)(B) 电力市场的输电阻塞管理问题(浙江大学:刘康生)(C) 酒后开车问题(清华大学:姜启源)(D) 招聘公务员问题(解放军信息工程大学:韩中庚)2005年 (A) 长江水质的评价和预测问题(解放军信息工程大学:韩中庚)(B) DVD在线租赁问题(清华大学:谢金星等)(C) 雨量预报方法的评价问题(复旦大学:谭永基)(D) DVD在线租赁问题(清华大学:谢金星等)2006年 (A) 出版社的资源配置问题(北京工业大学:孟大志)(B) 艾滋病疗法的评价及疗效的预测问题(天津大学:边馥萍)(C) 易拉罐的优化设计问题(北京理工大学:叶其孝)(D) 煤矿瓦斯和煤尘的监测与控制问题(解放军信息工程大学:韩中庚)2007年 (A) 中国人口增长预测(B) 乘公交,看奥运(C) 手机“套餐”优惠几何(D) 体能测试时间安排2008年(A)数码相机定位,(B)高等教育学费标准探讨,(C)地面搜索,(D)NBA赛程的分析与评价2009年(A)制动器试验台的控制方法分析(B)眼科病床的合理安排(C)卫星和飞船的跟踪测控(D)会议筹备历年全国数学建模试题及解法归纳赛题解法93A非线性交调的频率设计拟合、规划93B足球队排名图论、层次分析、整数规划94A逢山开路图论、插值、动态规划94B锁具装箱问题图论、组合数学95A飞行管理问题非线性规划、线性规划95B天车与冶炼炉的作业调度动态规划、排队论、图论96A最优捕鱼策略微分方程、优化96B节水洗衣机非线性规划97A零件的参数设计非线性规划97B截断切割的最优排列随机模拟、图论98A一类投资组合问题多目标优化、非线性规划98B灾情巡视的最佳路线图论、组合优化99A自动化车床管理随机优化、计算机模拟99B钻井布局 0-1规划、图论00A DNA序列分类模式识别、Fisher判别、人工神经网络00B钢管订购和运输组合优化、运输问题01A血管三维重建曲线拟合、曲面重建赛题解法01B 公交车调度问题多目标规划02A车灯线光源的优化非线性规划02B彩票问题单目标决策03A SARS的传播微分方程、差分方程03B 露天矿生产的车辆安排整数规划、运输问题04A奥运会临时超市网点设计统计分析、数据处理、优化04B电力市场的输电阻塞管理数据拟合、优化05A长江水质的评价和预测预测评价、数据处理05B DVD在线租赁随机规划、整数规划06A出版社书号问题整数规划、数据处理、优化06B Hiv病毒问题线性规划、回归分析07A 人口问题微分方程、数据处理、优化07B 公交车问题多目标规划、动态规划、图论、0-1规划08A 照相机问题非线性方程组、优化08B 大学学费问题数据收集和处理、统计分析、回归分析赛题发展的特点:1. 对选手的计算机能力提出了更高的要求:赛题的解决依赖计算机,题目的数据较多,手工计算不能完成,如03B,某些问题需要使用计算机软件,01A。
04年数学建模竞赛试题《逢山开路》

伍微 贺思三 杜琳琳 国防科学技术大学
摘要
这是一个规划问题。本文针对给定的三个控制点,采用动态规划的方法,分 别对起点到居民点、居民点到矿区进行定线。具体实现时,提出了两种方案: ① 用 Dijkstra 算法求两点间的最短路,与边界搜索结合,得到一条最佳路 线,由于实测数据间距较大,本文将网格逐步细化为 200m× 200m , 100m× 100m 的细网格,以获得较精确的路线; ② 逐步定线法,以局部最优为准则,逐步逼近目标点,得到较优解。 在对公路、桥梁、隧道这三种道路形式进行选择时,详细划分了每种道路在 不同情况下应满足的坡度条件,在此基础上确定不同道路的权值。
分析一:不同的地形造成道路选择方式不同 由 f 1 、 f 2 的表达式可知,不同的道路形式具有不同的权值。山区地形 复杂,设计线路要综合考虑山脉、湖泊、溪流以及地形起伏的影响。故对不 同的地形应有不同的道路形式 1. 公路 由于公路的修建成本远小于桥梁和隧道,所以在 >0.125 的情况下可以 考虑修建“Z”形路。 “Z”形路的每一段的斜率都为 0.125,所以, “Z”形 路的总长度为 L≈8△h。
图1 2. 隧道 在坡度较大的情况下,可以修建“Z”形路或隧道,而修建隧道的成本较高, 只有在坡度满足一定条件(见下面说明)时,修隧道比修“Z”形路节省资金。 当隧道垂直穿过山脉,即 =90(见图 2)时,隧道长度最短 ,我们按这种 方式修建隧道 。 1)隧道长度<300 米 修建隧道的条件为: 1500×(+)<300×16h
(从到,经过溪流)
(2)
f 1l1g, l1q =300×l1g +2000×l1q
l 2 g, l 2 s
(从到,经过山脉)
逢山开路

摘要A 题要求,在一山区修建一条公路,而公路要求穿过y=3200米处的东西走向的山峰和一条西北-东西走向的山谷,根据我们的分析,在地里条件有限制的条件下,我们需要根据不用的地理环境采用不同的修建方式。
具体如下图一;图一、工程平面解析图到坡度0=α处架桥。
而到达矿区就必须经过山顶,但是跨过山顶工程量大,并且很难实现,所以我们在E 到F 处开采隧道来代替跨越山顶。
对于AC 段、DE 段和FG 段我们打算修建一般的公路,经过我们查阅资料了解到在等高线上修建公路的工程量最小,并且工程成本比较低,所以我们将沿着等高线对一般的路线进行修建。
我们为了在满足题目要求的前提下节约工程成本,我们将沿着900米的等高线修建一般公路;对于不能沿等高线修建的公路的AB 段,我们按照坡度125.0<α的要求对AB 段进行曲线拟合,求出拟合的曲线方程,在利用曲线积分求出曲线长度,而BC 段和DE 段我们利用比例法,所谓的比例法就是用细线沿着曲线的延伸方向描绘出曲线的图示长度,再根据比例关系换算出曲线的实际长度,所以我们根据等高线图示的比例关系,我们利用细线沿着等高线的延伸路线进行延伸,然后利用刻度尺测出细线的长度,在根据比例关系计算出线路的长度。
但是GH 段既不能沿等高线又不能用曲线拟合来求其长度,但是GH 段的路程对总体的影响可以忽略,所以我们利用两点间的距离公式进行计算,并求出其长度。
从总体上看我们的模型,总的工程造价为5736197.26元,这对于一条含有隧道和桥梁长度为12420.6242米的山路来说比较符合实际情况。
关键字: 等高线 隧道 桥梁 曲线积分根据题目中的条件及我们对数据的分析,我们可以知道要想到达居民区就要跨过山谷,所以我们欲从C 到D 跨过山谷的地方找目录一、问题重述 (3)二、符号说明 (3)三、模型分析 (3)四、模型假设 (5)五、问题一模型建立及求解 (6)5.1、桥梁模型 (6)5.1.1、模型建立及求解 (6)5.2 、隧道模型 (7)5.2.1、隧道模型的建立及求解 (7)5.3、一般公路模型 (8)5.3.1、模型的建立 (8)5.3.2、模型求解 (9)六、问题二模型建立 (10)七、模型优缺点分析 (10)参考文献 (11)程序附录 (12)一、问题重述要在一个山区修条盘山公路,首先要测得不同地点的高度,由于山的不同地点的高度不同,并且要修路的山体上有湖泊和山谷,并且湖泊在雨季的时候会在山谷中形成一条小溪流,雨量最大的时候形成小溪的水面会变宽,其与溪流最深出的 x 坐标的关系可以近似表为()()()3424005240040002x w x x -=+≤≤ ① 在修路时由于要求此路要通过坐标为(4000,2000)的居民区后再到达坐标为(2000,4000)的矿区,我们要所修的道路中可以包含一般路段,桥梁和隧道,但是所设计的架起桥梁和开隧道方案必须满足两者对坡度的要求。
数学建模中常见的十大模型

数学建模常用的十大算法==转(2011-07-24 16:13:14)转载▼1. 蒙特卡罗算法。
该算法又称随机性模拟算法,是通过计算机仿真来解决问题的算法,同时可以通过模拟来检验自己模型的正确性,几乎是比赛时必用的方法。
2. 数据拟合、参数估计、插值等数据处理算法。
比赛中通常会遇到大量的数据需要处理,而处理数据的关键就在于这些算法,通常使用MATLAB 作为工具。
3. 线性规划、整数规划、多元规划、二次规划等规划类算法。
建模竞赛大多数问题属于最优化问题,很多时候这些问题可以用数学规划算法来描述,通常使用Lindo、Lingo 软件求解。
4. 图论算法。
这类算法可以分为很多种,包括最短路、网络流、二分图等算法,涉及到图论的问题可以用这些方法解决,需要认真准备。
5. 动态规划、回溯搜索、分治算法、分支定界等计算机算法。
这些算法是算法设计中比较常用的方法,竞赛中很多场合会用到。
6. 最优化理论的三大非经典算法:模拟退火算法、神经网络算法、遗传算法。
这些问题是用来解决一些较困难的最优化问题的,对于有些问题非常有帮助,但是算法的实现比较困难,需慎重使用。
7. 网格算法和穷举法。
两者都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具。
8. 一些连续数据离散化方法。
很多问题都是实际来的,数据可以是连续的,而计算机只能处理离散的数据,因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的。
9. 数值分析算法。
如果在比赛中采用高级语言进行编程的话,那些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用。
10. 图象处理算法。
赛题中有一类问题与图形有关,即使问题与图形无关,论文中也会需要图片来说明问题,这些图形如何展示以及如何处理就是需要解决的问题,通常使用MATLAB 进行处理。
数学建模中常见的十大模型

数学建模中常见的十大模型集团标准化工作小组 #Q8QGGQT-GX8G08Q8-GNQGJ8-MHHGN#数学建模常用的十大算法==转(2011-07-24 16:13:14)1. 蒙特卡罗算法。
该算法又称随机性模拟算法,是通过计算机仿真来解决问题的算法,同时可以通过模拟来检验自己模型的正确性,几乎是比赛时必用的方法。
2. 数据拟合、参数估计、插值等数据处理算法。
比赛中通常会遇到大量的数据需要处理,而处理数据的关键就在于这些算法,通常使用MATLAB 作为工具。
3. 线性规划、整数规划、多元规划、二次规划等规划类算法。
建模竞赛大多数问题属于最优化问题,很多时候这些问题可以用数学规划算法来描述,通常使用Lindo、Lingo 软件求解。
4. 图论算法。
这类算法可以分为很多种,包括最短路、网络流、二分图等算法,涉及到图论的问题可以用这些方法解决,需要认真准备。
5. 动态规划、回溯搜索、分治算法、分支定界等计算机算法。
这些算法是算法设计中比较常用的方法,竞赛中很多场合会用到。
6. 最优化理论的三大非经典算法:模拟退火算法、神经网络算法、遗传算法。
这些问题是用来解决一些较困难的最优化问题的,对于有些问题非常有帮助,但是算法的实现比较困难,需慎重使用。
7. 网格算法和穷举法。
两者都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具。
8. 一些连续数据离散化方法。
很多问题都是实际来的,数据可以是连续的,而计算机只能处理离散的数据,因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的。
9. 数值分析算法。
如果在比赛中采用高级语言进行编程的话,那些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用。
10. 图象处理算法。
赛题中有一类问题与图形有关,即使问题与图形无关,论文中也会需要图片来说明问题,这些图形如何展示以及如何处理就是需要解决的问题,通常使用MATLAB 进行处理。
优化模型举例

一单位实物 行走时间(分钟) 捕获时间(分钟) 热量(焦耳)
X
2
2
25
Y
3
1
30
假设捕食者每天能得到 x 单位的食物 X 和
y 单位的食物 Y ,则每天获得的热量值为
max u 25x 30 y 2x 3y 120
s.t 2x y 80 x 0, y 0.
2020/7/1
2020/7/1
收点
发点
B1
B2
…. Bn
A1X11 X12….. X1na1
A2
X21 X22
…. X2n
a2
….. …..
Am
Xm1
Xm2 ….. Xmn
am
b1 b2
….
bn
2020/7/1
A1的总费用
A1 ~ B j
n
C11x11 C12 x12 ... C1n x1n C1 j x1 j j 1
2020/7/1
03年B题:“露天矿生产的车辆安排”,非线性 规划模型。 04年B题:“电力市场的输电阻塞管理”,双目
标线性规划模型。 05年B题:“DVD在现租赁”,0-1规划模型。 06年A题:“出版社的资源优化配置”,线性规 划模型。
2020/7/1
(一)优化模型的数学描述
将一个优化问题用数学式子来描述,即求函数
2.根据设计变量的性质 静态问题和动态问题。
3.根据目标函数和约束条件表达式的性质 线性规划,非线性规划,二次规划,多目标规划等。
2020/7/1
(1)非线性规划
目标函数和约束条件中,至少有一个非线性函数。
min u f (x) x
s. t. hi ( x) 0,i 1,2,..., m. gi ( x) 0(gi ( x) 0), i 1,2,..., p.
逢山开路遇水搭桥的数学道理

逢山开路遇水搭桥的数学道理全文共四篇示例,供读者参考第一篇示例:逢山开路遇水搭桥,这是一句源自中国传统文化的谚语,意思是面对困难和挑战时,要有创新和智慧,找到突破的方法。
这句话深刻体现了中国人在面对困境时的乐观和智慧。
在数学中,逢山开路遇水搭桥的道理同样能够得到应用,让我们来探讨一下。
在数学中,遇到困难和挑战是难免的。
有时候我们会遇到难以解决的问题,数学难题如同一座高山,笔者无法攀登,这时我们就需要思考逢山开路的方法。
比如遇到一个难题,我们可以先从简单的例子入手,通过观察和总结找到规律,然后逐步深入,逢山开路,逐渐攻克难题。
逢山开路还可以理解为数学问题的化整为零。
有时候一个复杂的数学问题,我们无法一次性解决,但我们可以通过分解问题,逐步解决每一个小问题,最终达到解决整个问题的目的。
这就好比在山上修路,我们不可能一次性修好整条路,但可以逐步修筑,最终连成一片。
在数学中,逢山开路还可以理解为破除传统的思维定势。
有时候我们会受到传统的思维定势的束缚,无法突破。
但是如果我们能够打破自己的思维定势,寻找新的思路和方法,就能够以不变应万变,解决问题。
就像在山上修路,如果我们只顾着沿着一条已经有的路修,可能并不能达到最好的效果,但是如果我们能够打破传统思维,开辟新的道路,就能够顺利地修好一条畅通无阻的山路。
逢山开路遇水搭桥,也可以理解为遇到阻碍和挑战时,要有勇气和决心,不畏困难,勇往直前。
数学中也是如此,遇到困难和挑战时,我们要有坚韧不拔的毅力和勇气,不畏困难,不退缩。
只有勇往直前,才能够攻克难题,得到胜利。
逢山开路遇水搭桥的数学道理告诉我们,面对数学困难和挑战时,我们要有创新和智慧,找到突破的方法。
要化整为零,分而治之,打破传统思维定势,勇往直前。
只有如此,我们才能够攻克难题,取得成功。
逢山开路遇水搭桥,不仅仅是一句谚语,更是一种智慧和勇气的体现。
希望我们在数学的学习中,能够牢记这个道理,勇敢面对困难,不断前行,最终取得成功。
机理分析和测试分析

模型的修改: 修改后的模型与数据产生偏移。所以,模型和数据 拟合的不太好。是不是可以改进模型呢?
可以考虑更一般的模型:
dy dt
ry
1
y N
y(0) 566
问题:这个方程的解比较复杂,难以写成解析形式。
那么,如何对解
y y(t, N, r, )
m dv Sv mg v(0) 0
dt
解得:
v
mg
S
1
S t
em
由
dx v(t) x(0) 0 dt
解得
x
mg
S
t
m
S
St e m
1
下面先确定空气阻尼系数。代入m=300, S=2r3/3=18得到
机理分析:基于问题的特点,建立数学模型来揭 示问题的内在规律和本质。 例:经典力学的Newton定律,万有引力定律,光 的折射定律,计算体积的微积分方法等。
机理分析的基本工具: 微分方程 差分方程 数学规划 图与网络的方法 概率的方法 随机过程 ….
测试分析的基本工具: 函数插值 最小二乘拟合 随机模拟 统计分析如数据的分布等…
x
50g
3
t
50
3
3 e 50
t
1
利用最小二乘拟合函数lsqcurvefit来确定参数。 其中数据为
t(s) 0 3 6 9 12 15 18 21 24 27 30
X(m) 500 470 425 372 317 264 215 160 108 55 1
例2:逢山开路(全国大学生数学建模竞赛题)
数学建模基础(入门必备)

一、数学模型的定义现在数学模型还没有一个统一的准确的定义,因为站在不同的角度可以有不同的定义。
不过我们可以给出如下定义:“数学模型是关于部分现实世界和为一种特殊目的而作的一个抽象的、简化的结构。
”具体来说,数学模型就是为了某种目的,用字母、数学及其它数学符号建立起来的等式或不等式以及图表、图象、框图等描述客观事物的特征及其内在联系的数学结构表达式。
一般来说数学建模过程可用如下框图来表明:数学是在实际应用的需求中产生的,要解决实际问题就必需建立数学模型,从此意义上讲数学建模和数学一样有古老历史。
例如,欧几里德几何就是一个古老的数学模型,牛顿万有引力定律也是数学建模的一个光辉典范。
今天,数学以空前的广度和深度向其它科学技术领域渗透,过去很少应用数学的领域现在迅速走向定量化,数量化,需建立大量的数学模型。
特别是新技术、新工艺蓬勃兴起,计算机的普及和广泛应用,数学在许多高新技术上起着十分关键的作用。
因此数学建模被时代赋予更为重要的意义。
二、建立数学模型的方法和步骤1. 模型准备要了解问题的实际背景,明确建模目的,搜集必需的各种信息,尽量弄清对象的特征。
2. 模型假设根据对象的特征和建模目的,对问题进行必要的、合理的简化,用精确的语言作出假设,是建模至关重要的一步。
如果对问题的所有因素一概考虑,无疑是一种有勇气但方法欠佳的行为,所以高超的建模者能充分发挥想象力、洞察力和判断力,善于辨别主次,而且为了使处理方法简单,应尽量使问题线性化、均匀化。
3. 模型构成根据所作的假设分析对象的因果关系,利用对象的内在规律和适当的数学工具,构造各个量间的等式关系或其它数学结构。
这时,我们便会进入一个广阔的应用数学天地,这里在高数、概率老人的膝下,有许多可爱的孩子们,他们是图论、排队论、线性规划、对策论等许多许多,真是泱泱大国,别有洞天。
不过我们应当牢记,建立数学模型是为了让更多的人明了并能加以应用,因此工具愈简单愈有价值。
十大经典数学模型

十大经典数学模型1、蒙特卡罗算法(该算法又称随机性模拟算法,是通过计算机仿真来解决问题的算法,同时可以通过模拟来检验自己模型的正确性,是比赛时必用的方法)2、数据拟合、参数估计、插值等数据处理算法(比赛中通常会遇到大量的数据需要处理,而处理数据的关键就在于这些算法,通常使用Matlab作为工具)3、线性规划、整数规划、多元规划、二次规划等规划类问题(建模竞赛大多数问题属于最优化问题,很多时候这些问题可以用数学规划算法来描述,通常使用Lindo、Lingo软件实现)4、图论算法(这类算法可以分为很多种,包括最短路、网络流、二分图等算法,涉及到图论的问题可以用这些方法解决,需要认真准备)5、动态规划、回溯搜索、分支定界等计算机算法(这些算法是算法设计中比较常用的方法,很多场合可以用到竞赛中)6、最优化理论的三大非经典算法:模拟退火法、神经网络、遗传算法(这些问题是用来解决一些较困难的最优化问题的算法,对于有些问题非常有帮助,但是算法的实现比较困难,需慎重使用)7、网格算法和穷举法(网格算法和穷举法都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具)8、一些连续离散化方法(很多问题都是实际来的,数据可以是连续的,而计算机只认的是离散的数据,因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的)9、数值分析算法(如果在比赛中采用高级语言进行编程的话,那一些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用)10、图象处理算法(赛题中有一类问题与图形有关,即使与图形无关,论文中也应该要不乏图片的,这些图形如何展示以及如何处理就是需要解决的问题,通常使用Matlab进行处理)1、蒙特卡罗方法(MC)(Monte Carlo):蒙特卡罗(Monte Carlo)方法,或称计算机随机模拟方法,是一种基于“随机数”的计算方法。
2023年运筹学模型与数学建模竞赛

运筹学模型与数学建模竞赛一、引言一般来说,大学生数学建模竞赛所涉及到的运筹学模型涉及数学规划(线性规划和非线性规划),网络优化(含网络计划技术),排队模型,动态规划等,请看下表注:从1999年起,全国大学生数学建模竞赛开始设立专供大专院校学生做的C ,D 题。
下面重点介绍运筹学模型的数学规划。
二、数学规划的一般形式))(m ax ()(m in x f or x f⎪⎩⎪⎨⎧≤≤=≤==ub x lb m j x g li x h t s j i ,,2,1,0)(,,2,1,0)(.. 线性规划: 整数规划: 非线性规划:三、数学规划问题举例1 下料问题现要用100×50厘米的板料裁剪出规格分别为40×40 厘米与50×20厘米的零件,前者需要25件,后者需要30件。
问如何裁剪,才干最省料?解:先设计几个裁剪方案记 A---------40×40;B-----------50×20注:尚有别的方案吗?显然,若只用其中一个方案,都不是最省料的方法。
最佳方法应是三个方案的优化组合。
设方案i 使用原材料x i 件(i =1,2,3)。
共用原材料f 件。
则根据题意,可用如下数学式子表达:⎪⎩⎪⎨⎧=≥≥++≥+++=)3,2,1(03053252..min 32121321j x x x x x x t s x x x f j,整数 这是一个整数线性规划模型。
2 运送问题现要从两个仓库(发点)运送库存原棉来满足三个纺织厂(收点)的需要,数据如下表,方案1方案2方案3试问在保证各纺织厂的需求都得到满足的条件下应采用哪个运送方案,才干使总运费达成最小?(运价(元/吨)如下表)解:题意即要拟定从i 号仓库运到j 号工厂的原棉数量。
故设ij x 表达从i 号仓运到j 号工厂的原棉数量(吨)f 表达总运费.则运送模型为:⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥⎪⎭⎪⎬⎫=+=+=+⎭⎬⎫≤++≤+++++++=运输量非负约束;需求量约束运出量受存量约束),,j ,i (x x x x x x x x x x x x x .t .s x x x x x x f min ij 321210251540305042232231322122111232221131211232221131211 一般地,对于有m 个发点和n 个收点的运送模型为⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧==≥===≤=∑∑∑∑====),...2,1;,...2,1(0)...2,1(),...3,2,1(..min 1111n j m i x n j b x m i a x t s x c f ij mi j ij nj i ij m i nj ijij 其中a i 为i 号发点的运出量,b j 为j 号收点的需求量,c ij 为从i 号发点到j 号收点的单位运价。
matlab数学建模30个案例分析

案例4:基于微分方程的最优捕鱼策略
为了保护人类赖以生存的自然环境,可再生资源(如渔业、林业资源)的开发必须适度,一种合理、简化的策略是,在实现可持续收获的前提下,追求最大产量或最佳效益。考虑对某种鱼的最优捕鱼策略:假设这种鱼分4个年龄组:称1龄鱼,…,4龄组,各年龄组每条鱼的平均重量分别为5.07,11.55,17.86,22.99(克)各年龄组鱼的自然死亡率均为0.8(1/年)这种鱼为季节性集中产卵繁殖,平均每条4龄鱼的产卵量为1.109× 个,3龄鱼的产卵量为这个数的一半,2龄鱼和1龄鱼不产卵 产卵和孵化期为每年的最后4个月,卵孵化并成活为1龄鱼,成活率(1龄鱼条数与产卵总量n之比)为1.22 × /1.22× +n)
案例12:基于主成分分析的长江水质的评价和预测模型
运用主成分分析法对长江流域主要城市水质检测报告进行分析,选取主成分,并把主成分得分按方差贡献率加权求和,得出每个地区的污染综合评价指数,进而可以计算每个月长江流域的污染综合评价指数。
第三部分 优化问题
案例13:基于线性规划求解飞行管理模型
第二部分 评价问题
案例7:基于层次分析法的高考志愿选择策略
一年一度的高考结束后,许多考生面临估分后填写志愿的决策过程。这个决策关系重大,请你建立一个数学模型,帮考生考虑到各种决策因素使之能轻松应对这一重大决策。成都丙、重庆丁四所大学。
现有某市直属单位因工作需要,拟向社会公开招聘8名公务员。该单位拟将录用的8名公务员安排到所属的7个部门,并且要求每个部门至少安排一名公务员。这7个部门按工作性质可分为四类:(1)行政管理、 (2)技术管理、(3)行政执法、(4)公共事业。
招聘领导小组在确定录用名单的过程中,本着公平、公开的原则,同时考虑录用人员的合理分配和使用,有利于发挥个人的特长和能力。招聘领导小组将7个用人单位的基本情况(包括福利待遇、工作条件、劳动强度、晋升机会和学习深造机会等)和四类工作对聘用公务员的具体条件的希望达到的要求都向所有应聘人员公布。每一位参加面试人员都可以申报两个自己的工作类别志愿。
数学模型与大学生数学建模简介

运营调度要求,乘客候车时间一般不要超过10分钟,早高峰
时一般不要超过5分钟,车辆满载率不应超过 120%,一般也
不要低于50%。
试根据这些资料和要求,为该线路设计一个便于操作的全天
(工作日)的公交车调度方案,包括两个起点站的发车时刻
表;一共需要多少辆车;这个方案以怎样的程度照顾到了乘
客和公交公司双方的利益大家;好 等等。
看到,它们对数学知识要求不深,一般没有事先设定的
标准答案,但留有充分余地供参赛者发挥其聪明才智和
创造精神。
大家好
2
全国大学生数学建模竞赛
• 1992年由中国工业与应用数学学会(CSIAM)组织第一次竞赛
大家好
3
美国大学生数学建模竞赛
• 1985年开始举办数学建模竞赛(MCM) •1999年开始增办交叉学科竞赛(ICM).
一.
大家好
17
模型分析
对所得的结果进行数学上的分析,能否对 模型结果作出细致精当的分析,决定了你的模 型能否达到更高的档次。要记住,不论那种情 况都需进行误差分析,数据稳定性分析。
大家好
18
模型检验
将模型分析结果与实际情形进行比较, 以此来验证模型的准确性、合理性和适用性。 如果模型与实际较吻合,则要对计算结果给 出其实际含义,并进行解释。如果模型与实 际吻合较差,则应该修改假设,再次重复建模 过程。
2. 请你设计MS类型(可以分两种大小不同规模), 在20个商区内的分布(每个商区内不同类型MS的 个数),以满足“题目描述”中的三个基本要求。
3.阐明你的方法的科大家学好 性和结果是贴近实际的31 。
说明: 1.商业上用“商圈”来描述商店的覆盖范围。影响商店选址的主要因素是商圈内 的人流量,以及购物欲望。2.为简化,假定鸟巢(国家体育场)容量10万人,水立方 (国家游泳中心)容纳4万人,国家体育馆可容纳6万人。每个看台容1万人,出口对准一 个商区,各商区面积相同,图中白色为人行道路。
1994年A题逢山开路问题
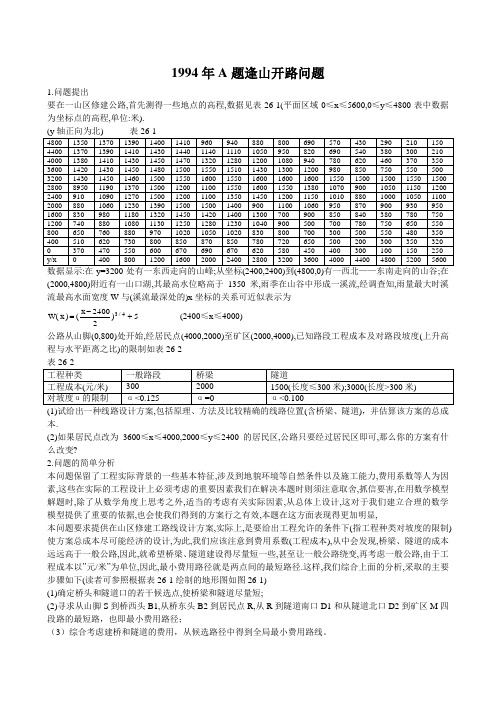
1994年A 题逢山开路问题1.问题提出要在一山区修建公路,首先测得一些地点的高程,数据见表26-1(平面区域0≤x ≤5600,0≤y ≤4800表中数据为坐标点的高程,单位:米).(2000,4800)附近有一山口湖,其最高水位略高于1350米,雨季在山谷中形成一溪流,经调查知,雨量最大时溪流最高水面宽度W 与(溪流最深处的)x 坐标的关系可近似表示为5)22400x ()x (W 4/3+-= (2400≤x ≤4000) 公路从山脚(0,800)处开始,经居民点(4000,2000)至矿区(2000,4000),已知路段工程成本及对路段坡度(上升高程与水平距离之比)的限制如表26-2(1)试给出一种线路设计方案,包括原理、方法及比较精确的线路位置(含桥梁、隧道),并估算该方案的总成本.(2)如果居民点改为3600≤x ≤4000,2000≤y ≤2400的居民区,公路只要经过居民区即可,那么你的方案有什么改变?2.问题的简单分析本问题保留了工程实际背景的一些基本特征,涉及到地貌环境等自然条件以及施工能力,费用系数等人为因素,这些在实际的工程设计上必须考虑的重要因素我们在解决本题时则须注意取舍,抓信要害,在用数学模型解题时,除了从数学角度上思考之外,适当的考虑有关实际因素,从总体上设计,这对于我们建立合理的数学模型提供了重要的依据,也会使我们得到的方案行之有效,本题在这方面表现得更加明显,本问题要求提供在山区修建工路线设计方案,实际上,是要给出工程允许的条件下(指工程种类对坡度的限制)使方案总成本尽可能经济的设计,为此,我们应该注意到费用系数(工程成本),从中会发现,桥梁、隧道的成本远远高于一般公路,因此,就希望桥梁、隧道建设得尽量短一些,甚至让一般公路绕变,再考虑一般公路,由于工程成本以”元/米”为单位,因此,最小费用路径就是两点间的最短路径.这样,我们综合上面的分析,采取的主要步骤如下(读者可参照根据表26-1绘制的地形图如图26-1) (1)确定桥头和隧道口的若干候选点,使桥梁和隧道尽量短;(2)寻求从山脚S 到桥西头B1,从桥东头B2到居民点R,从R 到隧道南口D1和从隧道北口D2到矿区M 四段路的最短路,也即最小费用路径;(3)综合考虑建桥和隧道的费用,从候选路径中得到全局最小费用路线。
1994年全国大学生数学建模逢山开路问题

1994年全国⼤学⽣数学建模逢⼭开路问题The 2ed homework of mathematical modelingTEAM:14#304 dormitoryPersons: 04231107 Fan Jingjing 04231114 Jiang Lan 04231115 Li Linjian 04231116 Li XiaMarch 21,2006Collage of Mathematical Science ,BNUModeling in construction Mathematical ModelingFor: Prof. Zeng and TA Lee.逢⼭修路问题⼀,摘要本题旨在通过对复杂地形的探索与分析,以及对资⾦费⽤的考虑,探索出⼀条逢⼭开路的最佳路线。
最终找到⼀条最优路线建设⽅案,使花费最低。
我们的主要思路如下:从⼭脚经居民点到矿区,需要经过⼀个峡⾕,并且有⼀条⼩溪,到达居民区,之后经过⼀条⼭脉到矿区。
经过⼩溪的地⽅我们要修桥,因为考虑到⼭的坡度问题以及修桥的⾼价费⽤问题,我们需要寻找⼀条最适路线,由于公路有坡度的限制(125α),我们必须选择可⾏的⼀条道路通向⼭⾕,并且尽量花费.0<最少。
修桥的地⽅我们也要考虑到坡度的可⾏性,以及结合⽔⾯最宽处与峡⾕深度的那个函数,找出河⾯⽐较窄的点来修桥达到资⾦花费最少。
之后考虑⼭峰修⼀条隧道,由已知条件,我们应尽量控制隧道长度在300⽶以内,因为超过300⽶花费就是⼀倍!通过对隧道长度,公路坡度,以及矿区⾼程的因素的考虑,我们选定了⼀条路线通过修隧道过⼭峰,再⾄矿区。
最后,我们通过⽤matlab作图,拟合函数计算路线长度,以及应⽤公路学以及城市规划的⼀些原理分析,提出了⼀种花费最⼩化的可⾏做法。
关键词:隧道,桥,⾼程,坡度,资费⼆,模型假设我们认为逢⼭开路主要从路线及价钱考虑,寻找⼀种可⾏的路线同时⼜较为省钱,为这个问题的最佳⽅案。
逢山开路的数学模型

作者: 孙长银;杨峤;黄琼
作者机构: 四川大学
出版物刊名: 三峡大学学报:人文社会科学版
页码: 25-28页
主题词: 插值;控制点;深度搜索
摘要: 在修建公路中,线路设计是首要的问题,对于具体的地形和必经之点.要做出最合理的工程成本最低的线路,是一个重要问题.本文用拉格朗日二元三点插值进行数据处理.以此为基础建立了两个模型:①用等高线方法,依着路线的总体方向,用解析法和目估法画出直观的路线(包括一般路段、桥梁、隧道).②用深度搜索法,在每一格点自动确定下一方向,然后利用函数的递归凋用,给出一条路线.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
逢山开路模型小组成员:李莉 朱国斌 景建岗摘要:在本问题的求解中,修桥和挖隧道是两个相类似的求解过程,我们将求解过程分为两个部分:第一、对河岸边一固定点'P ,将桥修在'P 处时,求解由起始点O 到经固定点'P 到居民点R 的最短路线。
第二、如何确定'P 的位置,使得总路线的费用最小。
我们分别用了两个模型来进行这两部分内容的求解。
模型一、针对坡度的限制,利用小区域内的局部最优来达到全局最优。
模型二、列出点'P 有一定的位移时,可以减少的费用Q 的函数方程,然后利用河岸附近等高线较紧密,公路不能沿偏离等高线方向前进的特性,求出减少的费用Q 的条件极值,从而确定最佳修桥地点0P 。
最后,我们利用模型一、二的原理对隧道部分的公路做了同样的优化设计,然后得出总的修路费用估计为324万元,较合理。
最后,我们对整个做法的误差及合理性做了分析。
一、 问题的提出要在山区修建公路,首先测得该地区的一系列的点的高程,数据显示:在Y=3200处有一条东西走向的山峰;从坐标(2400,2400)到(4800,0)有一西北——东南走向的山谷;在(2000,2800)附近有一山口湖,其最高水位略高于1350m ,雨季在山谷形成一溪流,经调查知,雨量最大时溪流的水面宽度W 于(溪流最深处)X 坐标的关系可近似表示为:34x-2400W(x)=()5,240040002x +≤≤路段工程成本及路段坡度α的限制已知。
要解决以下问题:(1)如何安排公路的设计路线,使得从山脚的(0,800)处开始,经居民点(4000,2000)至矿区(2000,4000)的总成本最低。
(2)如果居民点改为36004000x ≤≤,20002400y ≤≤的居民区,而公路只需经过居民区即可,设计方案应如何变动?二、问题的假设1、认为地貌基本上是平稳变化的,即不存在悬崖、断层、地堑等地形;2、不计岩石、地层等建筑因素,认为任何一处的地面由于修建公路的没有差别;3、不计修路过程中的交通费用,成本只与路面的长度有关;4、修桥和挖隧道时,不存在人任何技术问题,从任何一点均可以打通隧道,在任何一点都可以搭起桥梁;5、修路时,不计路面的宽度,不计横向坡度对路面的影响;6、在问题的分析中,我们需要对已知的数据做插值计算,建议采用三次样条插值,因为三次样条插值可以保证路面基本光滑。
但是三次样条插值的运算量十分大。
而且本题中的数据量比较大,所以我们在解决问题时可以采用线性插值法来进行插值,关于线性插值法的优缺点我们在最后的误差分析中在进一步讨论。
三、问题的分析首先我们由已知的高程画出该地区等高线示意图和地貌图,(见图一和图二),图中X轴和Y轴的一个单位代表400m。
图一:等高线分布图图二:地貌图在这个问题中最主要的问题就是确定桥梁和隧道的位置。
由于,桥梁和隧道的修建费用远远高于普通道路的修建费用,所以我们要尽量减少桥梁和隧道的长度。
我们采用逐步细化的方法。
我们首先来设计从起始点到居民点的路线。
为了减少桥梁的建设费用,我们设定桥梁的宽度刚好使得每年的水量最大时不致淹没桥梁。
即桥宽等于水量最大时的水面宽度。
观察我们所绘的地形地貌图,我们认为,在溪流的两侧的地形基本对称,所以我们依据溪流的方程及水面宽度函数可得方程:溪流的西面方程为:48004800(),2400480022x y x y x x +---=-≤≤溪流的东面方程为:48004800(),240048002x y x y x x +-+-=-≤≤为了尽量减少桥宽,我们应使桥建立在尽可能高的地方,例如图中的A1的位置。
我们把问题分为两个:1、何设计从起点到A1的路线使得普通公路的修建费用最低。
2、如何设计从A1点到居民点的路线使得普通公路的修建费用最低。
3、如何修正A1点的位置使得从起始点到居民点的总费用最低。
对于这个问题,我们考虑由于由A1点向上的等高线十分紧密,不适合修建上下坡的。
所以我们假设,公路到了A1点之后如果公路沿着河岸再修一段路,这时修建普通公路增加的费用和修桥减少的费用在何处达到平衡,这个平衡点就是桥应该选取的位置。
这是从起始点到居民点的总费用最少。
图三:对等高图标记模型一:我们首先研究由起始点到A1的普通公路的修建费用。
我们使用以下模型进行计算:在上图中,对任意的起点和终点,我们要使得从起点O到终点P的距离最短,起点O附近区域的高程已知。
不计路面状况的话两点间的直线距离最短,由于坡度的限制,这时我们就要考察由起点O到交点B的坡度 是否符合道路的修建要求,如果符合的话,就选交点B为新的起点,如果不符合坡度的要求,就在该区域的边界上对B做一个移动,使得移动后的点'B符合要求,如果'B的选取不唯一,就要利用直观分析法,选取最适合实际情况的点'B。
一旦选定新的起点(点B 或点'B ),设为1B ,然后对点1B 到终点P 按照原来的方法进行同样的分析。
这样做下去,就可以得到一条由起始点O 到终点P 的最优路线。
经计算,所得数据如下表:这样就可得到由起始点到桥梁的路线安排。
路线可见最后总图。
由上表,我们计算时采用的终点是点P ,但是实际上点P 处于溪流的中心位置。
通过解溪流的西岸方程,我们可以得到我们要找的实际的终点'(2800,1830.98)P 。
可以验证:从点9B 向实际终点'P 的直线段满足坡度的要求。
所以我们从起点O 到溪流的岸边一点'P 的最优路线可以确定为:129'O B B B P →→→→→然后,我们可以确定于点'P 对应的溪流另一侧的一点''P 的坐标为:(2969.02,2000)同理,我们可以得到由点''P 到居民点R 的一条最优路线。
解得的数据见下表:模型二:由于在溪流的河岸附近,等高线十分紧密,不适宜修建上下坡的道路,所以我们在点'P 做优化,求得一个最优的桥梁位置0P (在溪流的西岸),然后只需从点'P 到0P 修一条路,这就是最终所得的从起始点O 到居民点R 的最优路线了。
我们设最优点0P 的坐标为:00(,)x y ,则与之对应的点0'P 的坐标为:00(4800,4800)y x --。
两点之间的距离由距离公式为:BridgeWidth =由我们原来假设的终点'P 到最优点0P 的路线应沿着溪流的西岸方向。
观察西岸的方程,其函数形式为隐性函数,不易通过弧长公式对其进行计算,它的函数形式虽然十分复杂,但是它的线性性非常好,对这个函数进行线性二次拟和,所得的拟和二次函数的二次项系数的数量级为610-,可以看成一次式,它的一次拟和函数形式为:4767.65 - 1.0536x 。
所以'P 到最优点0P 的距离可以看成是直线距离:tan Dis ce =由于修建费用的要求,我们令:Q =-当Q 取最大值时,我们所得的0P 刚好满足从'P 到0P 由于桥梁宽度减少而减少的修桥费用与由于公路长度增加而增加的费用之差最大。
即总费用达到最小。
又0x 、0y 满足溪流西岸的方程,利用最优化的知识可求得Q 的极值为:42280.4,取极值时0P 的坐标为:(2792.2,1825.82)。
所以桥梁的最佳位置在(2792.2,1825.82)处,此时的修建费用与在原来的点'P 修桥可以节约42280.4元。
模型三:在修建隧道时,由于隧道长度大于300m 时修建的费用增长了一倍,我们优先考虑隧道长度小于300m 的隧道是否可行,如果可行,就不必考虑隧道长度大于300m 的情况了。
否则,在进一步分析隧道长度大于300m 的隧道应该如何修建。
我们首先考虑隧道水平的情况。
要想使隧道的长度300m ,就应该使普通路面修到尽可能的高的地方。
观察等高线示意图,可以发现,横坐标X 4400≥时,山脉非常陡峭,等高线分布也十分紧密。
取X 4400=的截面,由已知高程计算可知要使隧道的长度小于300m ,至少需要将公路修到300*(1500850)15001266(1500850)400400*(1500900)H -=-=-+-,利用线性插值,算得1266H =时,400*(15001266)320030441500900y -=-=-。
我们采取和寻找桥梁一样的方法来确定隧道的位置,首先选取一个点(4400,3044)L 作为隧道的位置来修建普通公路,然后在对L 进行修正,使得总的修建费用最低。
普通公路的路线采用模型一的方式来进行,我们从点L 进行逆向推导(数据见下表)。
值得一提的是,在图中观察我们推导出的路线,可以发现,这条路线可以很方便的和从桥上修过来的公路相交,为了节省修建费用,利用原来已经修好的公路就可以通向居民点了。
所以我们的线路数据没有到达居民点R ,而是到达与原来修好的公路很近的一点5D 。
考度为1266300*0.11296H =+=,所以隧道另一端的出口'L 的纵坐标为:400*(15001296)32003325.541500850Y -=+=-。
同理,我们可以对隧道的另一端进行分对隧道的位置的优化,同桥梁的优化相同。
我们可以近似的认为山峰的两侧都是线性增高的。
总可以找到一种路线使得公路沿着山峰的外侧一边增高一边向X轴正向前进。
这时的隧道的宽度由于修建高度的增加会减少,我们可以类似的求出它的最优值。
经过我们的计算,隧道位置的改变对总费用的影响不是很大,再此不加以说明。
图四:公路路线设计图经过我们以上的分析,我们可以得出总运费的估计值。
桥宽:66.4051m桥的费用:132810元隧道长度:300m隧道费用:447752元普通路面长度:8863.27m普通路面费用:2658982元总费用:3239544元总费用大约324万元。
四、模型的优缺点分析本模型主要是在线性插值的基础上进行数值计算的,由于本模型中需要使用的数据量比较大,线性插值就可以很快的提供解题思路,并且给出了较好的答案,最后得到的路线直观看来,大部分路线沿着等高线的走势前进,也比较符合工程实际。
最后,关于桥梁和隧道部分宽度基本上比较符合要求,估计的总费用也比较合理。
但是本模型仍然存在一些缺点,例如由局部最优求全局最优时,简单的认为两点之间直线的距离最短,没有详细的说明高程的差距如何影响极小值的选取。
另外,对于山脉来说,利用线性插值带来的误差应该比较大,最好可以采用三次样条插值来分析,应该可以得到更精确的值。
