AMC美国数学竞赛真题及解答

合集下载

amc考试题及答案

amc考试题及答案1. 题目：一个圆的半径是5厘米，求这个圆的面积。

答案：圆的面积公式为 $ A = \pi r^2 $，其中 $ r $ 是圆的半径。

将半径 $ r = 5 $ 厘米代入公式，得到 $ A = \pi \times5^2 = 25\pi $ 平方厘米。

2. 题目：如果一个数列的前三项是2，4，8，求这个数列的第四项。

答案：这个数列是一个等比数列，公比为2（因为 $ 4/2 = 2 $ 和$ 8/4 = 2 $）。

所以第四项是 $ 8 \times 2 = 16 $。

3. 题目：一个长方体的长、宽、高分别是10厘米、8厘米和6厘米，求这个长方体的体积。

答案：长方体的体积公式为 $ V = l \times w \times h $，其中$ l $ 是长，$ w $ 是宽，$ h $ 是高。

将长 $ l = 10 $厘米、宽 $ w = 8 $ 厘米、高 $ h = 6 $ 厘米代入公式，得到$ V = 10 \times 8 \times 6 = 480 $ 立方厘米。

4. 题目：一个等差数列的前两项分别是3和7，求这个数列的第五项。

答案：等差数列的公差 $ d $ 可以通过第二项减去第一项得到，即$ d = 7 - 3 = 4 $。

等差数列的第 $ n $ 项公式为 $ a_n =a_1 + (n-1)d $，其中 $ a_1 $ 是第一项。

将 $ n = 5 $，$ a_1 = 3 $，$ d = 4 $ 代入公式，得到 $ a_5 = 3 + (5-1)\times 4 = 3 + 16 = 19 $。

5. 题目：如果一个函数 $ f(x) = 2x^2 - 3x + 5 $，求 $ f(2) $ 的值。

答案：将 $ x = 2 $ 代入函数 $ f(x) = 2x^2 - 3x + 5 $，得到 $ f(2) = 2 \times 2^2 - 3 \times 2 + 5 = 8 - 6 + 5 = 7 $。

amc10英语真题及答案新课标

amc10英语真题及答案新课标AMC10是美国数学竞赛（American Mathematics Competitions）的10年级级别，面向10年级及以下的学生。

以下是一套模拟的AMC10英语真题及答案，请注意，这只是一个示例，并非真实的AMC10题目。

AMC10 英语真题及答案Part 1: Multiple Choice1. The word "innovate" is most closely related to which of the following?A. InnovatorB. InventionC. InventionistD. InnovatoryAnswer: D. Innovatory2. Which of the following is the correct spelling of the word meaning "to make something new"?A. InnovateB. InnovateC. InnovateD. InnovateAnswer: A. Innovate3. The phrase "a leap of faith" is used to describe:A. A large jumpB. A risky decisionC. A new religionD. A sudden increaseAnswer: B. A risky decision4. In the sentence "The company is looking to streamline its operations," the word "streamline" means:A. To make more expensiveB. To make more efficientC. To make more complicatedD. To make more visibleAnswer: B. To make more efficient5. The word "altruistic" is an antonym for:A. SelfishB. AltruismC. AltruisticallyD. AltruistAnswer: A. SelfishPart 2: Fill in the Blanks6. The scientist was awarded the Nobel Prize for his _______ contributions to the field of physics.Answer: innovative7. The _______ of the old building was a significantachievement for the preservation society.Answer: renovation8. The _______ of the new policy was met with mixed reactions from the public.Answer: implementation9. The _______ of the company's profits was due to a series of successful marketing campaigns.Answer: increase10. The _______ of the ancient ruins provided valuable insights into the history of the civilization.Answer: excavationPart 3: Reading ComprehensionRead the following passage and answer the questions that follow.Passage:In recent years, there has been a significant increase in the number of people who are interested in sustainable living. This trend has led to the development of various eco-friendly products and practices. One such practice is the use of solar panels to generate electricity. Solar panels are becoming more popular due to their ability to harness the power of the sun and convert it into usable energy.Questions:11. What is the main topic of the passage?Answer: Sustainable living and the use of solar panels.12. Why are solar panels becoming more popular?Answer: Because they can harness the power of the sun and convert it into usable energy.13. What is the trend mentioned in the passage?Answer: An increase in the number of people interested in sustainable living.Part 4: Vocabulary in Context14. The _______ of the old factory was a major concern for the environmentalists.Answer: pollution15. The _______ of the new technology was celebrated by the scientific community.Answer: advancement16. The _______ of the endangered species was a top priority for the conservation organization.Answer: preservation17. The _______ of the ancient artifact provided evidence ofa previously unknown civilization.Answer: discovery18. The _______ of the new policy was met with skepticism by some members of the community.Answer: enforcement请注意，AMC10是一个数学竞赛，通常不包含英语题目。

2023年AMC10美国数学竞赛A卷附中文翻译和答案

2023AMC10美国数学竞赛A卷1. A cell phone plan costs $20 each month, plus 5¢ per text message sent, plus 10¢ for each minute used over 30 hours. In January Michelle sent 100 text messages and talked for 30.5 hours. How much did she have to pay?(A) $24.00 (B) $24.50 (C) $25.50 (D) $28.00 (E) $30.002. A small bottle of shampoo can hold 35 milliliters of shampoo, Whereas a large bottle can hold 500 milliliters of shampoo. Jasmine wants to buy the minimum number of small bottles necessary to completely fill a large bottle. How many bottles must she buy?(A) 11 (B) 12 (C) 13 (D) 14 (E) 153. Suppose [a b] denotes the average of a and b, and {a b c} denotes the average of a, b, and c. What is {{1 1 0} [0 1] 0}?(A) (B)(C)(D) (E)4. Let X and Y be the following sums of arithmetic sequences:X= 10 + 12 + 14 + …+ 100.Y= 12 + 14 + 16 + …+ 102.What is the value of(A) 92 (B) 98 (C) 100 (D) 102 (E) 1125. At an elementary school, the students in third grade, fourth grade, and fifth grade run an average of 12, 15, and 10 minutes per day, respectively. There are twice as many third graders as fourth graders, and twice as many fourth graders as fifth graders. What is the average number of minutes run per day by these students?(A) 12 (B) (C) (D) 13 (E) 146. Set A has 20 elements, and set B has 15 elements. What is the smallest possible number of elements in A∪B, the union of A and B?(A) 5 (B) 15 (C) 20 (D) 35 (E) 3007. Which of the following equations does NOT have a solution?(A) (B) (C)(D) (E)8. Last summer 30% of the birds living on Town Lake were geese, 25% were swans, 10% were herons, and 35% were ducks. What percent of the birds that were not swans were geese?(A) 20 (B) 30 (C) 40 (D) 50 (E) 609. A rectangular region is bounded by the graphs of the equations y=a, y=-b, x=-c, and x=d, where a, b, c, and d are all positive numbers. Which of the following represents the area of this region?(A) ac + ad + bc + bd (B) ac – ad + bc – bd (C) ac + ad – bc – bd(D) –ac –ad + bc + bd (E) ac – ad – bc + bd10. A majority of the 20 students in Ms. Deameanor’s class bought pencils at the school bookstore. Each of these students bought the same number of pencils, and this number was greater than 1. The cost of a pencil in cents was greater than the number of pencils each student bought, and the total cost of all the pencils was $17.71. What was the cost of a pencil in cents?(A) 7 (B) 11 (C) 17 (D) 23 (E) 7711. Square EFGH has one vertex on each side of square ABCD. Point E is on AB with AE=7·EB. What is the ratio of the area of EFGH to the area of ABCD?(A) (B)(C)(D) (E)12. The players on a basketball team made some three-point shots, some two-point shots, some one-point free throws. They scored as many points with two-point shots as with three-point shots. Their number of successful free throws was one more than their number of successful two-point shots. The team’s total score was 61 points. How many free throws did they make?(A) 13 (B) 14 (C) 15 (D) 16 (E) 1713. How many even integers are there between 200 and 700 whose digits are alldifferent and come from the set {1, 2, 5, 7, 8, 9}?(A) 12 (B)20 (C)72 (D) 120 (E) 20014. A pair of standard 6-sided fair dice is rolled once. The sum of the numbers rolled determines the diameter of a circle. What is the probability that the numerical value of the area of the circle is less than the numerical value of the circle’s circumference?(A) (B)(C)(D) (E)15. Roy bought a new battery-gasoline hybrid car. On a trip the car ran exclusively on its battery for the first 40 miles, then ran exclusively on gasoline for the rest of the trip, using gasoline at a rate of 0.02 gallons per mile. On the whole trip he averaged55 miles per gallon. How long was the trip in miles?(A) 140 (B) 240 (C) 440 (D) 640 (E) 84016. Which of the following in equal to(A) (B) (C) (D) (E)17. In the eight-term sequence A, B, C, D, E, F, G, H, the value of C is 5 and the sum of any three consecutive terms is 30. What is A + H?(A) 17 (B) 18 (C) 25 (D) 26 (E) 4318. Circles A, B, and C each have radius 1. Circles A and B share one point of tangency. Circle C has a point of tangency with the midpoint of AB. What is the area inside Circle C but outside Circle A and Circle B?(B) (C) (D) (E)(A)19. In 1991 the population of a town was a perfect square. Ten years later, after an increase of 150 people, the population was 9 more than a perfect square. Now, in 2023, with an increase of another 150 people, the population is once again a perfect square. Which of the following is closest to the percent growth of the town’s popu lation during this twenty-year period?(A) 42 (B) 47 (C) 52 (D) 57 (E) 6220. Two points on the circumference of a circle of radius r are selected independently and at random. From each point a chord of length r is drawn in a clockwise direction. What is the probability that the two chords intersect?(A) (B) (C) (D) (E)21. Two counterfeit coins of equal weight are mixed with 8 identical genuine coins. The weight of each of the counterfeit coins is different from the weight of each of the genuine coins. A pair of coins is selected at random without replacement from the 10 coins. A second pair is selected at random without replacement from the remaining 8coins. The combined weight of the first pair is equal to the combined weight of the second pair. What is the probability that all 4 selected coins are genuine?(A) (B) (C) (D) (E)22. Each vertex of convex pentagon ABCDE is to be assigned a color. There are 6 colors to choose from, and the ends of each diagonal must have different colors. How many different colorings are possible?(A) 2500 (B) 2880 (C) 3120 (D) 3250 (E) 375023. Seven students count from 1 to 1000 as follows:·Alice says all the numbers, except she skips the middle number in each consecutive group of thre e numbers. That is Alice says 1, 3, 4, 6, 7, 9, …, 997, 999, 1000.·Barbara says all of the numbers that Alice doesn’t say, except she also skips the middle number in each consecutive grope of three numbers.·Candice says all of the numbers that neither Alice nor Barbara says, except she also skips the middle number in each consecutive group of three numbers. ·Debbie, Eliza, and Fatima say all of the numbers that none of the students with the first names beginning before theirs in the alphabet say, except each also skips the middle number in each of her consecutive groups of three numbers.·Finally, George says the only number that no one else says.What number does George say?(A) 37 (B) 242 (C) 365 (D) 728 (E) 99824. Two distinct regular tetrahedra have all their vertices among the vertices of the same unit cube. What is the volume of the region formed by the intersection of the tetrahedra?(A) (B) (C) (D) (E)an integer. A point X in the interior of R is25. Let R be a square region andcalled n-ray partitional if there are n rays emanating from X that divide R into N triangles of equal area. How many points are 100-ray partitional but not 60-ray partitional?(A) 1500 (B) 1560 (C) 2320 (D) 2480 (E) 25002023AMC10美国数学竞赛A卷1. 某通讯公司手机每月基本费为20美元, 每传送一则简讯收 5美分（一美元=100 美分）。

AMC美国数学竞赛AMC.B 试题及答案解析

2003A M C10 B 1、Which of the following is the same asSolution2、Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pink pill, and Al’s pills cost a total of for the two weeks. How much does one green pill costSolution3、The sum of 5 consecutive even integers is less than the sum of the rst consecutive odd counting numbers. What is the smallest of the even integersSolution4、Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the gure. She plants one flower per square foot in each region. Asters cost 1 each, begonias 1.50 each, cannas 2 each, dahlias 2.50 each, and Easter lilies 3 each. What is the least possible cost, in dollars, for her gardenSolution5、Moe uses a mower to cut his rectangular -foot by -foot lawn. The swath he cuts is inches wide, but he overlaps each cut by inches tomake sure that no grass is missed. He walks at the rate of feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow his lawnSolution.6、Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length of a “-inch” television screen is closest, in inches, to which of the followingSolution7、The symbolism denotes the largest integer not exceeding . For example. , and . ComputeSolution.8、The second and fourth terms of a geometric sequence are and . Which of the following is a possible first termSolution9、Find the value of that satisfies the equationSolution10、Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of three letters followed by three digits. By how many times is the number of possible license plates increasedSolution11、A line with slope intersects a line with slope at the point . What is the distance between the -intercepts of these two linesSolution12、Al, Betty, and Clare split among them to be invested in different ways. Each begins with a different amount. At the end of one year they have a total of . Betty and Clare have both doubled their money, whereas Al has managed to lose . What was Al’s original portionSolution.13、Let denote the sum of the digits of the positive integer . For example, and . For how many two-digit values of isSolution14、Given that , where both and are positive integers, find the smallest possible value for .Solution15、There are players in a singles tennis tournament. The tournament is single elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest players are given a bye, and the remaining players are paired off to play. After each round, the remaining players play in the next round. The match continues until only one player remains unbeaten. The total number of matches played isSolution16、A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that the restaurant should offer so that a customer could have a different dinner each night in the yearSolution.17、An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly ll the cone. Assume that the melted ice cream occupies of the volume of the frozen ice cream. What is the ratio of the cone’s height to its radiusSolution18、What is the largest integer that is a divisor offor all positive even integersSolution19、Three semicircles of radius are constructed on diameter of a semicircle of radius . The centers of the small semicircles divide into four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicirclesSolution20、In rectangle , and . Points and are on so that and . Lines and intersect at . Find the area of .Solution21、A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardless of the color you pulled out. What is the probability that all beads in the bag are red after three such replacementsSolution22、A clock chimes once at minutes past each hour and chimes on the hour according to the hour. For example, at 1 PM there is one chime and at noon and midnight there are twelve chimes. Starting at 11:15 AM on February , , on what date will the chime occurSolution23、A regular octagon has an area of one square unit. What is the area of the rectangleSolution24、The rst four terms in an arithmetic sequence are , , , and, in that order. What is the fth termSolution25、How many distinct four-digit numbers are divisible by and have as their last two digitsSolution。

AMC8(美国数学竞赛)历年真题、答案及中英文解析

AMC8（美国数学竞赛）历年真题、答案及中英文解析艾蕾特教育的AMC8 美国数学竞赛考试历年真题、答案及中英文解析：AMC8-2020年：真题 --- 答案---解析（英文解析+中文解析）AMC8 - 2019年：真题----答案----解析（英文解析+中文解析）AMC8 - 2018年：真题----答案----解析（英文解析+中文解析）AMC8 - 2017年：真题----答案----解析（英文解析+中文解析）AMC8 - 2016年：真题----答案----解析（英文解析+中文解析）AMC8 - 2015年：真题----答案----解析（英文解析+中文解析）AMC8 - 2014年：真题----答案----解析（英文解析+中文解析）AMC8 - 2013年：真题----答案----解析（英文解析+中文解析）AMC8 - 2012年：真题----答案----解析（英文解析+中文解析）析）AMC8 - 2010年：真题----答案----解析（英文解析+中文解析）AMC8 - 2009年：真题----答案----解析（英文解析+中文解析）AMC8 - 2008年：真题----答案----解析（英文解析+中文解析）AMC8 - 2007年：真题----答案----解析（英文解析+中文解析）AMC8 - 2006年：真题----答案----解析（英文解析+中文解析）AMC8 - 2005年：真题----答案----解析（英文解析+中文解析）AMC8 - 2004年：真题----答案----解析（英文解析+中文解析）AMC8 - 2003年：真题----答案----解析（英文解析+中文解析）AMC8 - 2002年：真题----答案----解析（英文解析+中文解析）AMC8 - 2001年：真题----答案----解析（英文解析+中文解析）AMC8 - 2000年：真题----答案----解析（英文解析+中文解析）析）AMC8 - 1998年：真题----答案----解析（英文解析+中文解析）AMC8 - 1997年：真题----答案----解析（英文解析+中文解析）AMC8 - 1996年：真题----答案----解析（英文解析+中文解析）AMC8 - 1995年：真题----答案----解析（英文解析+中文解析）AMC8 - 1994年：真题----答案----解析（英文解析+中文解析）AMC8 - 1993年：真题----答案----解析（英文解析+中文解析）AMC8 - 1992年：真题----答案----解析（英文解析+中文解析）AMC8 - 1991年：真题----答案----解析（英文解析+中文解析）AMC8 - 1990年：真题----答案----解析（英文解析+中文解析）AMC8 - 1989年：真题----答案----解析（英文解析+中文解析）AMC8 - 1988年：真题----答案----解析（英文解析+中文解析）析）AMC8 - 1986年：真题----答案----解析（英文解析+中文解析）AMC8 - 1985年：真题----答案----解析（英文解析+中文解析）◆AMC介绍◆AMC（American Mathematics Competitions) 由美国数学协会（MAA）组织的数学竞赛，分为 AMC8 、 AMC10、 AMC12 。

amc 美国数学竞赛 amc 10b 试题及答案解析

2004 AMC 10BProblem 1Each row of the Misty Moon Amphitheater has 33 seats. Rows 12 through 22 are reserved for a youth club. How many seats are reserved for this club?There are rows of seats, giving seats.Problem 2How many two-digit positive integers have at least one 7 as a digit?Ten numbers () have as the tens digit. Nine numbers () have it as the ones digit. Number is in both sets.Thus the result is .Problem 3At each basketball practice last week, Jenny made twice as many free throws as she made at the previous practice. At her fifth practice she made48 free throws. How many free throws did she make at the first practice?At the fourth practice she made throws, at the third one it was , then we get throws for the second practice, and finally throws at the first one.Problem 4A standard six-sided die is rolled, and P is the product of the five numbers that are visible. What is the largest number that is certain to divide P?Solution 1The product of all six numbers is . The products of numbers that can be visible are , , ..., . The answer to this problem is their greatest common divisor -- which is , where is the least common multiple of . Clearly and the answer is .Solution 2Clearly, can not have a prime factor other than , and .We can not guarantee that the product will be divisible by , as the number can end on the bottom.We can guarantee that the product will be divisible by (one of and will always be visible), but not by .Finally, there are three even numbers, hence two of them are always visible and thus the product is divisible by . This is the most we can guarantee, as when the is on the bottom side, the two visible even numbers are and , and their product is not divisible by .Hence .Problem 5In the expression , the values of , , , and are , , , and , although not necessarily in that order. What is the maximum possible value of the result?If or , the expression evaluates to .If , the expression evaluates to .Case remains.In that case, we want to maximize where .Trying out the six possibilities we get that the best one is, where .Problem 6Which of the following numbers is a perfect square?Using the fact that , we can write:▪▪▪▪▪Clearly is a square, and as , , and are primes, none of the other four are squares.Problem 7On a trip from the United States to Canada, Isabella took U.S. dollars. At the border she exchanged them all, receiving Canadian dollars for every U.S. dollars. After spending Canadian dollars, she had Canadian dollars left. What is the sum of the digits of ?Solution 1Isabella had Canadian dollars. Setting up an equation we get, which solves to , and the sum of digits of isSolution 2Each time Isabelle exchanges U.S. dollars, she gets Canadian dollars and Canadian dollars extra. Isabelle received a total of Canadian dollars extra, therefore she exchanged U.S. dollars times. Thus .Problem 8Minneapolis-St. Paul International Airport is 8 miles southwest of downtown St. Paul and 10 miles southeast of downtown Minneapolis. Which of the following is closest to the number of miles between downtown St. Paul and downtown Minneapolis?The directions "southwest" and "southeast" are orthogonal. Thus the described situation is a right triangle with legs 8 miles and 10 mileslong. The hypotenuse length is , and thus the answer is .Without a calculator one can note that . Problem 9A square has sides of length 10, and a circle centered at one of its vertices has radius 10. What is the area of the union of the regions enclosed by the square and the circle?The area of the circle is , the area of the square is . Exactly of the circle lies inside the square. Thus the total area is.Problem 10A grocer makes a display of cans in which the top row has one can and each lower row has two more cans than the row above it. If the display contains cans, how many rows does it contain?The sum of the first odd numbers is . As in our case , we have .Problem 11Two eight-sided dice each have faces numbered 1 through 8. When the dice are rolled, each face has an equal probability of appearing on the top. What is the probability that the product of the two top numbers is greater than their sum?Solution 1We have , hence if at least one of the numbers is , the sum is larger. There such possibilities.We have .For we already have , hence all other cases are good.Out of the possible cases, we found that in the sum is greater than or equal to the product, hence in it is smaller. Therefore the answer is .Solution 2Let the two rolls be , and .From the restriction:Since and are non-negative integers between and , either , , orif and only if or .There are ordered pairs with , ordered pairs with , and ordered pair with and . So, there areordered pairs such that .if and only if and or equivalently and . This gives ordered pair .So, there are a total of ordered pairs with .Since there are a total of ordered pairs , there are ordered pairs with .Thus, the desired probability is .Problem 12An annulus is the region between two concentric circles. The concentric circles in the ﬁgure have radii and , with . Let be a radius of the larger circle, let be tangent to the smaller circle at , and let be the radius of the larger circle that contains . Let , , and . What is the area of the annulus?The area of the large circle is , the area of the small one is , hence the shaded area is .From the for the right triangle we have , hence and thus the shaded area is .Problem 13In the United States, coins have the following thicknesses: penny, mm; nickel, mm; dime, mm; quarter, mm. If a stack of these coins is exactly mm high, how many coins are in the stack?All numbers in this solution will be in hundreds of a millimeter.The thinnest coin is the dime, with thickness . A stack of dimes has height .The other three coin types have thicknesses , , and . By replacing some of the dimes in our stack by other, thicker coins, we can clearly create exactly all heights in the set.If we take an odd , then all the possible heights will be odd, and thus none of them will be . Hence is even.If the stack will be too low and if it will be too high. Thus we are left with cases and .If the possible stack heights are , with the remaining ones exceeding .Therefore there are coins in the stack.Using the above observation we can easily construct such a stack. A stack of dimes would have height , thus we need to add . This can be done for example by replacing five dimes by nickels (for ), and one dime by a penny (for ).Problem 14A bag initially contains red marbles and blue marbles only, with moreblue than red. Red marbles are added to the bag until only of the marbles in the bag are blue. Then yellow marbles are added to the baguntil only of the marbles in the bag are blue. Finally, the number of blue marbles in the bag is doubled. What fraction of the marbles now in the bag are blue?We can ignore most of the problem statement. The only important information is that immediately before the last step blue marbles formed of the marbles in the bag. This means that there were blue and other marbles, for some . When we double the number of blue marbles, there will be blue and other marbles, hence bluemarbles now form of all marbles in the bag.Problem 15Patty has coins consisting of nickels and dimes. If her nickels were dimes and her dimes were nickels, she would have cents more. How much are her coins worth?Solution 1She has nickels and dimes. Their total cost iscents. If the dimes were nickels and vice versa, she would havecents. This value should be cents more than the previous one. We get , which solves to . Her coins are worth .Solution 2Changing a nickel into a dime increases the sum by cents, and changing a dime into a nickel decreases it by the same amount. As the sum increased by cents, there are more nickels than dimes. As the total count is , this means that there are nickels and dimes.Problem 16Three circles of radius are externally tangent to each other and internally tangent to a larger circle. What is the radius of the large circle?The situation in shown in the picture below. The radius we seek is . Clearly . The point is clearly the center of the equilateral triangle , thus is of the altitude of this triangle. We get that . Therefore the radius we seek is.WARNING. Note that the answer does not correspond to any of the five options. Most probably there is a typo in option D.Problem 17The two digits in Jack's age are the same as the digits in Bill's age, but in reverse order. In five years Jack will be twice as old as Bill will be then. What is the difference in their current ages?Solution 1If Jack's current age is , then Bill's current age is .In five years, Jack's age will be and Bill's age will be .We are given that . Thus .For we get . For and the value is not an integer, and for it is more than . Thus the only solution is , and the difference in ages is .Solution 2Age difference does not change in time. Thus in five years Bill's age will be equal to their age difference.The age difference is , hence it is a multiple of . Thus Bill's current age modulo must be .Thus Bill's age is in the set .As Jack is older, we only need to consider the cases where the tens digit of Bill's age is smaller than the ones digit. This leaves us with the options .Checking each of them, we see that only works, and gives the solution .Problem 18In the right triangle , we have , , and . Points , , and are located on , , and , respectively, so that , , and . What is the ratio of the area of to that of ?First of all, note that , and therefore.Draw the height from onto as in the picture below:Now consider the area of . Clearly the triangles and are similar, as they have all angles equal. Their ratio is ,hence . Now the area of can be computed as= . Similarly we can find that as well.Hence , and the answer is .Problem 19In the sequence , , , , each term after the third is found by subtracting the previous term from the sum of the two terms that precede that term. For example, the fourth term is. What is the term in this sequence?Solution 1We already know that , , , and . Let's compute the next few terms to get the idea how the sequence behaves. We get ,, , and so on.We can now discover the following pattern: and . This is easily proved by induction. It follows that.Solution 2Note that the recurrence can be rewritten as.Hence we get that and alsoFrom the values given in the problem statement we see that .From we get that .From we get that .Following this pattern, we get.Problem 20In points and lie on and , respectively. If and intersect at so that and , what is ?Solution (Triangle Areas)We use the square bracket notation to denote area.Without loss of generality, we can assume . Then , and . We have , so we need to find the area of quadrilateral .Draw the line segment to form the two triangles and . Let , and . By considering trianglesand , we obtain , and by considering triangles and , we obtain . Solving, we get , , so the area of quadrilateral is .ThereforeSolution (Mass points)The presence of only ratios in the problem essentially cries out for mass points.As per the problem, we assign a mass of to point , and a mass of to . Then, to balance and on , has a mass of .Now, were we to assign a mass of to and a mass of to , we'd have . Scaling this down by (to get , which puts and in terms of the masses of and ), we assign a mass of to and a mass of to .Now, to balance and on , we must give a mass of . Finally, the ratio of to is given by the ratio of the mass of tothe mass of , which is .Solution (Coordinates)Affine transformations preserve ratios of distances, and for any pair of triangles there is an affine transformation that maps the first one onto the second one. This is why the answer is the same for any , and we just need to compute it for any single triangle.We can choose the points , , and . This way we will have , and . The situation is shown in the picture below:The point is the intersection of the lines and . The points on the first line have the form , the points on the second line have the form . Solving for we get , hence.The ratio can now be computed simply by observing the coordinates of , , and :Problem 21Let ; ; and ; ; be two arithmetic progressions. The set is the union of the first terms of each sequence. How many distinct numbers are in ?The two sets of terms are and.Now . We can compute. We will now find .Consider the numbers in . We want to find out how many of them lie in . In other words, we need to find out the number of valid values of for which .The fact "" can be rewritten as ", and ".The first condition gives , the second one gives .Thus the good values of are , and their count is .Therefore , and thus .Problem 22A triangle with sides of 5, 12, and 13 has both an inscribed and a circumscribed circle. What is the distance between the centers of those circles?This is obviously a right triangle. Pick a coordinate system so that the right angle is at and the other two vertices are at and .As this is a right triangle, the center of the circumcircle is in the middle of the hypotenuse, at .The radius of the inscribed circle can be computed using the well-known identity , where is the area of the triangle and its perimeter. In our case, and , thus . As the inscribed circle touches both legs, its center must be at .The distance of these two points is then.Problem 23Each face of a cube is painted either red or blue, each with probability 1/2. The color of each face is determined independently. What is the probability that the painted cube can be placed on a horizontal surface so that the four vertical faces are all the same color?Label the six sides of the cube by numbers to as on a classic dice. Then the "four vertical faces" can be: , , or .Let be the set of colorings where are all of the same color, similarly let and be the sets of good colorings for the other two sets of faces.There are possible colorings, and there are goodcolorings. Thus the result is . We need to compute .Using the we can writeClearly , as we have two possibilities for the common color of the four vertical faces, and two possibilities for each of the horizontal faces.What is ? The faces must have the same color, and at the same time faces must have the same color. It turns out thatthe set containing just the two cubes where all six faces have the same color.Therefore , and the result is .Problem 24In we have , , and . Point is on the circumscribed circle of the triangle so that bisects . What is the value of ?Problem 25A circle of radius is internally tangent to two circles of radius at points and , where is a diameter of the smaller circle. What is the area of the region, shaded in the picture, that is outside the smaller circle and inside each of the two larger circles?The area of the small circle is . We can add it to the shaded region, compute the area of the new region, and then subtract the area of the small circle from the result.Let and be the intersections of the two large circles. Connect them to and to get the picture below:Now obviously the triangles and are equilateral with side .Take a look at the bottom circle. The angle is , hence the sector is of the circle. The same is true for the sector of the bottom circle, and sectors and of the top circle.If we now sum the areas of these four sectors, we will almost get the area of the new shaded region - except that each of the two equilateral triangles will be counted twice.Hence the area of the new shaded region is, and the area of the original shared region is .。

amc 美国数学竞赛 00 amc 0b 试题及答案解析

2003 AMC 10B1、Which of the following is the same asSolution2、Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pinkpill, and Al’s pills cost a total of for the two weeks. How much doesone green pill cost?Solution3、The sum of 5 consecutive even integers is less than the sum of theﬁrst consecutive odd counting numbers. What is the smallest of theeven integers?Solution4、Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the ﬁgure. She plants one flower per square foot in each region. Asters cost 1 each,begonias 1.50 each, cannas 2 each, dahlias 2.50 each, and Easterlilies 3 each. What is the least possible cost, in dollars, for hergarden?Solution5、Moe uses a mower to cut his rectangular -foot by -foot lawn.The swath he cuts is inches wide, but he overlaps each cut byinches to make sure that no grass is missed. He walks at the rate of feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow his lawn?Solution.6、Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length ofa “-inch” television screen is closest, in inches, to which of thefollowing?Solution7、The symbolism denotes the largest integer not exceeding . Forexample. , and . ComputeSolution.8、The second and fourth terms of a geometric sequence are and .Which of the following is a possible first term?Solution9、Find the value of that satisfies the equationSolution10、Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of three letters followed by three digits. By how many times is the number of possible license plates increased?Solution11、A line with slope intersects a line with slope at the point .What is the distance between the -intercepts of these two lines?Solution12、Al, Betty, and Clare split among them to be invested indifferent ways. Each begins with a different amount. At the end of one year they have a total of . Betty and Clare have both doubledtheir money, whereas Al has managed to lose . What was Al’soriginal portion?Solution.13、Let denote the sum of the digits of the positive integer . Forexample, and . For how many two-digitvalues of is ?Solution14、Given that , where both and are positive integers,find the smallest possible value for .Solution15、There are players in a singles tennis tournament. Thetournament is single elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest players aregiven a bye, and the remaining players are paired off to play. Aftereach round, the remaining players play in the next round. The match continues until only one player remains unbeaten. The total number of matches played isSolution16、A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that the restaurant should offer so that a customer could have a different dinner each night in the year ?Solution.17、An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly ﬁll the cone. Assume that the melted ice cream occupies of the volume of the frozen ice cream. What is theratio of the cone’s height to its radius?Solution18、What is the largest integer that is a divisor offor all positive even integers ?Solution19、Three semicircles of radius are constructed on diameter of asemicircle of radius . The centers of the small semicircles divideinto four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside thesmaller semicircles?Solution20、In rectangle , and . Points and are onso that and . Lines and intersect at . Findthe area of .Solution21、A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardless of the color you pulled out. What is the probability that all beads in the bag are red after three such replacements?22、A clock chimes once at minutes past each hour and chimes onthe hour according to the hour. For example, at 1 PM there is one chime and at noon and midnight there are twelve chimes. Starting at11:15 AM on February , , on what date will the chimeoccur?Solution23、A regular octagon has an area of one square unit.What is the area of the rectangle ?Solution24、The ﬁrst four terms in an arithmetic sequence are , , ,and , in that order. What is the ﬁfth term?Solution25、How many distinct four-digit numbers are divisible by and haveas their last two digits?Solution。

美国AMC10中文版试题及答案

2000到20XX年AMC10美国数学竞赛0 0P 0 A 0 B 0 C 0D 0 全美中学数学分级能力测验(AMC 10)2000年第01届美国AMC10 (2000年2月日时间75分钟)1. 国际数学奥林匹亚将于在美国举办，假设I 、M 、O 分别表示不同的正整数，且满足I ⨯M ⨯O =2001，则试问I +M +O 之最大值为。

(A) 23 (B) 55 (C) 99 (D) 111 (E) 6712. 2000(20002000)为。

(A) 40 (B) 50 (C) 55 (D) 60 (E) 754. Candra 每月要付给网络公司固定的月租费及上网的拨接费，已知她12月的账单为12.48元，而她1月的账单为17.54元，若她1月的上网时间是12月的两倍，试问月租费是元。

(A) 2.53 (B) 5.06 (C) 6.24 (D) 7.42 (E) 8.775. 如图M ，N 分别为PA 与PB 之中点，试问当P 在一条平行AB 的直在线移动时，下列各数值有项会变动。

(a) MN 长 (b) △P AB 之周长 (c) △P AB 之面积 (d) ABNM 之面积(A) 0项 (B) 1项 (C) 2项 (D) 3项 (E) 4项 6. 费氏数列是以两个1开始，接下来各项均为前两项之和，试问在费氏数列各项的个位数字中，最后出现的阿拉伯数字为。

(A) 0 (B) 4 (C) 6 (D) 7 (E) 97. 如图，矩形ABCD 中，AD =1，P 在AB 上，且DP 与DB 三等分∠ADC ，试问△BDP 之周长为。

2021年美国数学竞赛AMC12A 真题加答案解析

2021 AMC 12A Peeyush Pandaya et al.February 20211 Answer1.B2. D3. D4.D5.E Key6.C7.D8.C9.C10.E11.C12.A13.B14.E15. D16.C17.D18.E19.C20.B21.A22.D23.D24.D25.E2 Problems and SolutionsProblem 1. What is the value of21+2+3- (2¹+2²+23)?(A)0 (B)50 (C)52 (D)54 (E)57Solution.2⁶-(2¹+2²+23)=64-(2+4+8)=64-14=(B)50Problem 2.Under what conditionsisva²+62=a+btrue,whereaand bare real numbers?(A)It is never true(B) It is true if and only ifab=0(C) It is true if and only ifa+b≥0(D)It is true ifandonlyifab=0anda+b≥0(E)It is always trueSolution. It is clear that both sides of the equation must be nonnegative.Squaring,a²+b²=a²+2ab+b2→ab=0The answer is (D)Problem 3.The sum of two natural numbers is 17,402.One of the two numbers is divisible by 10.If the units digit of that number is erased, the other number is obtained. What is the difference of these two numbers?(A)10,272 (B)11,700 (C)13,362 (D)14,238 (E)15,426Solution. Let the first number mentioned be 10n;the second is n. Then10n+n=17,402,from which it follows thatProblem 4. Tom has a collection of 13 snakes,4 of which are purple and 5 of which are happy. He observes that●all of his happy snakes can add,·none of his purple snakes can subtract●all of his snakes that can't subtract also can't add.Which of these conclusions can be drawn about Tom's snakes?Solution. Together, the second and third conditions imply that none of Tom's purple snakes can add.Thus,(D) is correct: happy snakes are not purple.Problem 5.When a student multiplied the number 66 by the repeating decimal,where a and b are digits, he did not notice the notation and just multiplied 66 times 1.ab. Later he found that his answer is 0.5 less than the correct answer. What is the 2-digit integer gb? (A)15 (B)30 (C)45 (D)60 (E)75Solution. The student computed 66 ; the correct answer is 66 . Thus,Problem 6.A deck of cards has only red cards and black cards. The probability of a randomly chosen card being red is . When 4 black cards are added to the deck, the probability of choosing red becomes . How many cards were in the deck originally?(A)6 (B)9 (C) 12 (D)15 (E)18Solution. If the deck begins with x red cards and 3x cards in total, thenProblem 7.What is the least possible value of(ry- 1)²+(x+y)2 for real numbersa and y?Solution. We have(ry- 1)2+(x+y)2=(ry)2-2ry+1+x²+2ry+v²=x2v²+z²+y2+1= (r²+1)(y²+1),which achieves a minimum of (D)1 atx=y=0.D Do D ₁ D ₂D ₃ D ₁ D ₅D ₆ D ₇ D ₈ D, D1o Problem 8.A sequence of numbers isdefinedbyDo=0,D ₁=0,Dz=1,andDn=Dn- 1+Dn-3 forn≥3.What are the parities(evenness oroddness)of the triple of numbers(D2021,D2022,D2023), whereE denotes even and O denotes odd?Solution.0/10 01 D2+Do=1+0=1 D ₃+Di=1+0=1D ₄+Dz=1+1=0 Ds+D ₃=0+1=1D ₆+D4=1+1=0D-+Ds=0+0=0D ₈+D ₆=0+1=1Dg+D ₇=1+0=1We can see that the pattern repeats in cycles of length7.and as 2021=5 mod7,we have D2021= Ds,D2022=D6,D2023=D7→(C)(E,O,E) Problem 9.Which of the following is equivalent to(2+3)(2²+3²)(2⁴+34)(2⁸+3⁸)(216+316)(2³²+3³2)(264+364)?(A)3127+2127 (B)3127+2127+2.363+3.263 (C)3128-2128 (D)3128+2128 (E)5127Solution.(3-2)(2+3)(2²+3²)(2⁴+3⁴)(2⁸+3⁸)(216+316)(2³²+3³2)(264+364)=(3²-2²)(2²+3²)(2⁴+3⁴)(2⁸+3⁸)(216+316)(232+3³2)(264+364)=(3⁴-2⁴)(2⁸+3⁸)(216+316)(232+332)(264+364)=(C)3128-2129=(364-264)(264+364)Problem 10.Two right circular cones with vertices facing down as shown in the figure below contain the same amount of liquid. The radii of the tops of the liquid surfaces are 3cm and 6cm. Into each cone is dropped a spherical marble of radius lcm, which sinks to the bottom and is completely submerged without spilling any liquid. What is the ratio of the rise of the liquid level the narrow cone to the rise of the liquid level in the wide cone?(A)1:1 (B)47:43 (C) 2:1 (D)40:13 (E)4:1Solution. The two cones have equal volume, so the height of the first is times that of the second. Since the volumes increase by equal proportions, the heights increase by equal proportions. Thus, the ratio of the rise in liquid levels is (E)4:1Problem 11.A laser is placed at the point(3,5). The laser beam travels in a straight rry wants the beam to hit and bounce off the y-axis, then hit and bounce off the x-axis,then hit the point (7,5). What is the total distance the beam will travel along this path?(A)2√10 (B)5√2(C)10√2(D)15√2 (E)10√5Solution. Reflect about the y-axis then the z-axis. It is well-known that the image under the two reflections must be a straight line.The answer isv(3-(-7))²+(5-(-5)= (C) 10√2Problem 12.All the roots of polynomialz6- 10z ⁵+Az ⁴+Bz³+Cz²+Dz+16are positiveintegers, possibly repeated. What is the value of B?(A)-88 (B)-80 (C)-64 (D)-41 (E)-40Solution. By Vieta's,the sum of the 6 roots is 10 and the product is 16,hence they are all powers of 2. It is not hard to find that the only working unordered sextuple is(2,2,2,2,1,1). As(z-2)4=24-8z3+24z2-32z+16 and(z- 1)2=z2-2z+1.the z3 coefficient is -8.1+24 · (-2)+(-32) · 1= (B)-88Problem 13.Of the following complex numbers z, which has the property that z5 has the greatest real part?(A)-2 (B)-√3+i (C)-√2+√2i Solution. The magnitude of each complex number is the same, so it suffices to look at the argu- ment. The angles are π, ,and ,which after raising to the 5th power give π, and . We seek the angle that reaches farthest to the right(smallest argument),which is . Thus, our answer is (B)-√3+iProblem 14.What is the value of(A)21 (B)100logs3 (C)200log35 (D)2,200 (E)21,000Solution.And,Therefore, their product is210logs3.100log35=(E)21,000(D)- 1+√3i (E)2iProblem 15.A choir director must select a group of singers from among his 6 tenors and 8 basses. The only requirements are that the difference between the numbers of tenors and basses must be a multiple of 4,and the group must have at least one singer.Let be the number of groups that could be selected. What is the remainder when N is divided by 100?(A)47 (B)48 (C)83 (D)95 (E)96Solution. Suppose we mark down(1) the tenors that are in the group,and(2)the basses that aren't in the group. Then we necessarily mark down a number of people that is a multiple of 4. This is also sufficient; we mark down some people numbering a multiple of 4, then select the marked tenors and unmarked basses to form our choir. Clearly, we just mark down at least one person. The answer is thus(D)95Problem 16.In the following list of numbers, the integer n appears times in the list for l≤n≤200.1,2,2,3,3,3,4,4,4,4,.…,200,200,...200.What is the median of the numbers in this list?(A)100.5 (B)134 (C)142 (D)150.5 (E)167Solution.For general n, we have numbers. We want to approximate a such that is close to . Since the formula is a quadratic in n and we are halving this value,we can find that a is approximately .Plugging in n = 200,this is about 100√2,or 141.Of the answer choices, (C)142 is the closest, and indeed it is our answer.To verify, we can see that and ), so clearly 142 works.Problem 17.Trapezoid ABCD has ABICD,BC=CD=43,and AD1BD.Let O be the intersection of the diagonals AC and BD,and let P be the midpoint of BD.Given that OP=11, the length AD can be written in the form myn,where m and n are positive integers and n is not divisible by the square of any prime. What is m+n?(A)65 (B)132 (C)157 (D)194 (E)215Solution. Let M be the intersection of CPand AB.Since DCBMisakite,andCMIBD,we have MP1PB,and by considering the homothethy taking △MBD to △ABD with scale factor 2,we can see that M is the midpoint of AB.In particular,we haveSince AD 1BD,we have AD1DOandthusZADO=90°,andasCD=CB,wehaveCP1BD and ZCPD=2CPO=90°.Also,ZAOD=ZCOP,so △AOD~ △COP.Therefore,so DO=22.Thus,AD=√AB²-BD²=√86²-66²=4√ 190→m+n= (D)194The desired answer isProblem 18.Let f be afunction defined on the set of positive rational numbers with the property that f(a ·b)=f(a)+f(b)for all positive rational numbersa and b.Suppose that falso has the property that f(p)= pfor every prime numberp.For which of the following numbers zis f(x)<0?(A)整(B) (C) (D) (E) 51Solution. Note that f(a ·1)=f(a)+f(1)= f(1)=0,andIn particular, it follows by induction that f(p*)= kp for each k ∈Z.Thus,(A) f(2-5. 17)=-5·2+17=7(B) f(2-4. 11)=-4·2+11=3(C) f(3-2.7)=-2.3+7=1(D)f(2- 1.3- 1.7)=- 1.2+(- 1) ·3+7=2(E)f(52.11- 1)=2.5- 11=- 125The answer is (E)11Problem 19.How many solutions does the equation sinclosed interval [0,π]?(A)0 (B)1 (C) 2 (D) 3 (E)4Solution. Note on the interval , the left-hand side is negative while the right-hand side is positive.We thus restrict our attention to ]. The arguments cosx and sz are both between 0 and .ForsinA=cosBinA,B ∈[0,],we must have . This implies sinz+cosz=1,hence . There are (C) 2 solutions.Problem 20.Suppose that on a parabola with vertexV and focus F there exists a point Asuch that AF=20 and AV=21.What is the sum of all possible values of the length FV?(A)13 (B) 40 (C) (D)14 (E)Solution. Let the directrix be the x-axis,F=(0,2d),V=(0,d),A=(x,y),andB=(0,y)for some d>0.By the definition of a parabola,y=20.We compute x in two ways:x²=AF²-BF²=20²-|20-2d|2=AV²-BV²=21²-|20-d²Subtracting,O=20²-21²+(20-d)²-(20-2d)2=3d²-40d+41.The sum of all possible values ofProblem 21.The five solutions to the equation(z- 1)(z²+2z+4)(z²+4z+6)=0may be written in theformzk+ykiforl≤k≤5,where xk and yk are real.Let E be the unique ellipse that passes through the points(Ti,yi),(x2,32),(r3,Y3),(x4,y4)and(xs,ys).The eccentricity ofE can be written in the form ,where m and n are relatively prime positive integers. What is m+n?(Recall that the eccentrictiy of an ellipse E is the ratio,where 2a is the length of the major axis ofE and 2c is the distance between its two foci.)(A)7 (B)9 (C)11 (D)13 (E)15Solution. The roots of the polynomial arez=1,z=- 1±i√3,andz=-2±i√2,hence the five points onE are(1,0),( - 1,土√3),( - 2,±√2) .By symmetry through the x-axis, the ellipse is of the formE: a(x-r)²+by²=1.We then have the relationsa(1-r)²=1a(1+r)²+3b=1a(2+r)²+2b=1.Eliminating b from the latter two,1=3[a(2+r)²+2]-2[a(1+r)²+36]=a(r²+8r+10),henceit follows that and so the eccentricity is 1/√6. The requested sum is1+6= (A)7Problem 22.Suppose that the roots of the polynomialP(x)=x³+ax²+bx+care cos 2π,COS 47 and cos ,where angles are in radians. What is abc?(C) (D) (E)Solution. Recall1+e2m/7+ …+e12mi/7=0→e2mi/7+e4xi/7+e6mi/7=- 1/2,and in particular caNote are solutions to the equation cosb+cos28+cos30=- 1/2,so lettingx=co sθimplies thathas roots ,COS 4π7Thus, the polynomial in question is and the requested answer isRemark. Perhaps it is easier to motivate the solution as follows.Lett=e2mi/7andx=t+t- 1= 2cos2π/7.Thenx²-2=t²+t-2andx³-3x=t³+t-3.Moreover,t⁶+t⁵+ …+1=0impliest³+t²+t+t- 1+t-2+t-3=- 1,i.e.x+(x²-2)+(r³-3r) has root 2cos2π/7.It certainly seems logical that the Galois conjugates of 2cos would be 2cos and 2cos (especially given the phrasing of the problem),so simply replacex → to get the desired polynomial form.Let w = e2ix/7.Note thatLet these be r,s,t respectively. By Vieta's formulas, note that the desired quantity is(-rst)(rs+st+tr)(-r-s-t)=(r+s+t)(rs+st+tr)(rst).Note that 1+w+ …+w⁶=0.We haveThen,FinallyMultiplying yields the answer of (D)1 32Solution Manual 2021AMC12AProblem 23.Frieda the frog begins a sequence of hops on a 3×3 grid of squares,moving one square on each hop and choosing at random the direction of each hop up,down, left,or right. She does not hop diagonally. When the direction of a hop would take Frieda off the grid,she ”wraps around”and jumps to the opposite edge.For example if Frieda begins in the center square and makes two hops ”up”,the first hop would place her in the top row middle square, and the second hop would cause Frieda to jump to the opposite edge,landing in the bottom row middle square.Suppose Frieda starts from the center square, makes at most four hops at random,and stops hopping if she lands on a corner square. What is the probability that she reaches a corner square on one of the four hops?(A)G (B) (D)强(E)8Solution. We complementary count,and determine the probability we never reach a corner square. Denote by A the center,and B a square adjacent to the center. Then the first hop lands on B.● If the second hop lands on A(with probability ,then the third hop lands on B always,andthere is a chance the fourth hop lands on a non-corner square. The probability in this case is● If the second hop lands on B, then there is a chance the third hop lands on A,and achance the third hop lands on B.In the former subcase, the fourth hop always lands on a non-corner square, and in the latter subcase, there is a chance the fourth hop lands on a non-corner square. The probability in this case isThe requested probability isProblem 24.SemicircleT has diameter AB of length14.Circle Ωlies tangent to AB at a point P and intersectsI at pointsQandR.IfQR=3√3and ZQPR=60°,then the area of △PQR is ,where a and c are relatively prime positive integers, and b is a positive integer not divisible by the square of any prime. What isa+b+c?(A)110 (B)114 (C)118 (D)122 (E)126Solution. First, by Extended Law of Sines,we have that the radius of Q is .Let M be the midpoint of QR,O be the center ofT,and X be the center of 2.Since △OQR is isosceles, OM is perpendicular to QR. Thus we have that X lies on OM since it is the circumcenter of △puting lengths, we hav thagorean theorem on △ORM andfrom isosceles triangle XQR. Thus and OP=4 from Pythagorean theorem on △OXP.To find [PQR],we will find the height from P to QR.Let the foot of the perpendicular fromX to the P-altitude be D. Since PDⅡOM,we know that △XDP~△OPX.This means that . Now note that the bottom portion of the P-altitude after subtractingPD is equal to XM,so the height of the triangle is . The area is simply2021 AMC 12A11 Solution ManualProblem 25.Let d(n)denote the number of positive integers that divide n,including l and n. For example,d(1)=1,d(2)=2,and d(12)=6.(This function is known as the divisor function.) LetThere is a unique positive integer N such that f(N)> f(n)for all positive integers n≠N.What is the sum of the digits of N?(A)5 (B)6 (C)7 (D)8 (E) 9Solution. Letn=II;p',wherepi=2,Pz=3,etc.are the primes in increasing order and e; are nonnegative integers. ThenIt is equivalent to maximize Thus, it remains to find the optimal e; for each i. We go term-by-term, noting that it is only necessary to check until the expression first decreases, as exponentials increase more quickly than polynomials.ei 0 1 2 3 4 0 1 2 3 0 1 2 0 1 2 ((ez+1)3)/p⁸1³/20=1 23/2¹=433/2²=6.25 4³/2³=85³/2⁴<8 13/3⁰=1 23/31≈2.67 3³/32=3 43/3³<3 13/5⁰=1 2³/5¹=1.6 3³/5²=1.08 13/70=1 23/71≈1.14 3³/7²<1Note that we do not need to check p≥11,ase;=1yields which is suboptimal.Thus,the answer isN=23.32.5.7=2520,which has a Remark:It is sufficient to stop at p=3,for 3²|Nleaves N among the answer choices.digit sum of (E)9only one possibility for the digit sum ofi 1 1 1 1 1 2 2 2 2 3 3 3 4 4 4。

美国中学数学竞赛(AMC12-12级)(附答案)

2004 AMC12 试题1. 爱丽每小时的工资为美金20元，其中的1.45%要缴地方税，试问爱丽每小时的工资中要付地方税美金多少分？(美金1元二美金100分)(A) 0.0029 (B) 0.029 (C) 0.29 (D) 2.9 (E) 292. 于AMC2的测验中，每答对一题可得6分，答错可得0分，未作答可得2.5分.假设凯琳在25题中有8题未作答，她至少要答对几题，总分才会不低于100 分？(A) 11(B) 13(C) 14(D) 16(E) 173.滿足x 2y100的正整数序对(x, y)有多少組？(A) 33(B) 49(C) 50(D) 99(E) 1004.白婆婆有6个女儿、没有儿子，有些女儿也恰有6个女儿，其他的女儿没有孩子. 白婆婆有女儿及外孙女共30位，没有外曾孙女. 试问白婆婆的女儿及外孙女中有多少位没有女儿？(A) 22 (B) 23 (C) 24 (D) 25 (E) 265.直线y mx(A) mb 1 (B) 1 mb 0 (C) mb 0 (D) 0 mb 1 (E) mb 16.设u 2 20042005, V 20042005, W 2003 20042004, X 2 20042004Y 20042004, Z 20042003.試问以下何者值最大？(A) U V (B) V W (C) W X (D) X Y (E) Y Z7. 一种代币的游戏，其规那么如下：每回持有最多代币者须分给其他每一位参与游戏者一枚代币，并放一枚代币於回收桶中；当有一位游戏参与者没有代币时，那么游戏结束.假设A、B C三人玩此游戏，在游戏开始时分别持有15、14及13枚代币.试问游戏从开始到结束，共进行了多少回？(A) 36 (B) 37 (C) 38 (D) 39 (E) 409. 有一个将花生酱装在圆桶状瓶子内出售的公司 .市场研究建议瓶子较粗时可增加销售量.假设瓶子的直径增加25%,而体积仍维持不变，那么瓶子的高度应减少百分之多少？(A) 10(B) 25(C) 36(D) 50(E) 6010. 有49个连续整数，它的和为75,則它们排在最中间的数为何？(A) 7(B) 72(C) 73(D) 74(E) 7511. 某国的硬币中有1分、5分、10分及25分四种，在保拉的皮包內硬币的平均值为20分.假设再增加一枚25分的硬币，平均值則增为 21分.試问她的皮包內有多少枚10分的硬币？(A) 0(B) 1(C) 2(D) 3(E) 412. 设A (0, 9) , B (0,12).点A 、B 在直线y x 上, 且AA 与BB 交于点 C (2,8).試问AB的长度是多少？(A) 2(B) 2 2(C) 3(D) 22(E) 3“13. 以S 表示坐标平面上所有的点(a,b)所形成的集合，其中a,b 等于1, 0,或1.試问有多少条相异的直线至少通过集合 S 中的两个点？(A) 8(B) 20(C) 24(D) 27(E) 3614. 三个实数的数列形成一个等差数列，首项是9.假设将第二项加2、第三项加20可使得这三个数变为等比数列，那么这个等比数列中第三项最小可能是多少？(A) 1(B) 4(C) 36(D) 49(E) 8115.小美与小雯在一个圆形的跑道上向相反的方向跑，开始两人分别从8.如下图EAB 及 ABC 为直角，厢 4 , BC 6 , AE 8, AC 与BE 交于D 点.試问差为多少？(A) 2(B) 4(C) 5 (D) 8 (E) 9ADE 与BDC 面积之圆形跑道直径的两端起跑.小美跑了 100公尺时她们第一次相遇；在第一次相遇后小雯跑了 150公尺时她们第二次相遇.假设她们跑的速度都分别维持固定不变，试问此圆形跑道的长度是多少公尺？(A) 250(B) 300(C) 350(D) 400(E) 50016.使函数 log 2004{log 2003{log 2002{log 2001 X}}}有定义的集合为之值是多少？(A) 0(B) 20012002(C) 20022003(D) 20032004{xx c}.試问 c(E) 20012°°丹317.函数f 满足以下性质： (i) f(1) 1,且(ii)对任意的正整数n ,f(2n) n f(n).试问f(2100)之值为何？(A) 1(B) 299(C) 2100(D) 24950 18.如下图，ABCD 是边长2的正方形.在正方形的内部作一个以AB 为直径的半圆，且自C 点引此半圆的切线交AD 边于E 点•试问CE 的长度是多少？(E) 5 ■.5(E) 29999(B) 5 (C) 6 (D)?19.如下图，A B C 三圆彼此外切且均内切于圆等，圆A 的半径1且通过圆D 的圆心.试问圆B 的半径是多少?D.B 、C 两圆相(A)3(B)于(C) 土 (D) |20.从0与1之间的数，随机独立取出两实数a 与b,并将a, b 之和记作c.分别以A, B, C 表示最接近a, b, c 的整数.试问的机率为何？(A) 1(B) !(C) 1(D) 2(E) 443 23421.假设n 02nCOS5,那么Cos2之值是多少？(A) 15 (B) I (C) ±55(D) ?(E)上5522.三个半径为1的球彼此外切且放置在一水平面上，一个半径为2 的大球放在它们的上面 .试问大球的最高点至平面的距离是多少？C 2004 0,且 P (x)=0 有 2004个复数根 z a k b k i , 20042004b k 为实数，a ib i 0,且a kb k .k 1k 1试问以下哪一项可能不是 0 ?2004(A) C 0(B)C2003(C) b z b s L b s 004 (D)a kk 124. 设A 、B 为平面上的两点，其中AB 1.令S 为平面上所有半径是1且能盖住线段AB 之圆的并集，則S 的面积是多少？(A) 2.3(B) -(C) 33(D)卫 3(E) 4 2 33 2325. 对每一个整数n 4,令a n 表示n 进位的循环小数0.133n .把乘积a 4a 5L a 99写成—的形式，其中m P 为正整数，且p 尽可能小.试问mp!之值是多少？(A) 98(B) 101(C) 132(D) 798(E) 962Q屈o J123 52(A) 3(B) 3 -(C) 3 -(D)2349(E) 3 2、223.多项式P(x) GX C 0 ,的系数都是实数, 1 k 2004,其中 a k ,2004(E)C kk 12004C 2004X 2003C 2003XL答案:1 ( E )2 ( C )3 ( B )4 ( E )5 ( B )6 ( A )7 ( B )8 ( B )9 ( C )10 ( C ) 11 ( A )12 ( B )13 ( B )14 ( A )15 ( C ) 16 ( B )17 ( D )18 ( D )19 ( D )20( E ) 21 ( D )22 ( B )23 ( E )24 ( C )25 ( E )。

美国数学竞赛AMC题目及答案

2.3.Whatisthevalueof4.5.Hammieisinthegradeandweighs106pounds.Hisquadrupletsistersaretinybabiesandweigh5,5,6,and8pounds.W hichisgreater,theaverage(mean)weightofthesefivechildrenorthemedianweight,andbyhowman ypounds6.Thenumberineachboxbelowistheproductofthenumbersinthetwoboxesthattouchitintherowab ove.Forexample,.Whatisthemissingnumberinthetoprow7.8.Afaircoinistossed3times.Whatistheprobabilityofatleasttwoconsecutiveheads9.TheIncredibleHulkcandoublethedistancehejumpswitheachsucceedingjump.Ifhisfirstjumpis1 meter,thesecondjumpis2meters,thethirdjumpis4meters,andsoon,thenonwhichjumpwillhefirst beabletojumpmorethan1kilometer10.Whatistheratiooftheleastcommonmultipleof180and594tothegreatestcommonfactorof180a nd59411.12.Atthe2013WinnebagoCountyFairavendorisofferinga"fairspecial"onsandals.Ifyoubuyonepai rofsandalsattheregularpriceof$50,yougetasecondpairata40%discount,andathirdpairathalfthe regularprice.Javiertookadvantageofthe"fairspecial"tobuythreepairsofsandals.Whatpercentag eofthe$150regularpricedidhesave13.WhenClaratotaledherscores,sheinadvertentlyreversedtheunitsdigitandthetensdigitofones core.Bywhichofthefollowingmightherincorrectsumhavedifferedfromthecorrectone14.Letthetwodigitsbe and.Thecorrectscorewas.Claramisinterpreteditas.Thedifferencebetweenthetwoiswhichfactorsinto.Therefore,sincethedifferenceisamultipleof9,theonlyanswerchoicethatisamultipleof9 is.15.If,,and,whatistheproductof,,and16.AnumberofstudentsfromFibonacciMiddleSchoolaretakingpartinacommunityserviceproject.Theratioof-gradersto-gradersis,andthetheratioof-gradersto-gradersis .Whatisthesmallestnumberofstudentsthatcouldbeparticipatingintheproject17.Thesumofsixconsecutivepositiveintegersis2013.Whatisthelargestofthesesixintegers18.--Arpanliku16:22,27November2013(EST)Courtesyof19.Bridget,Cassie,andHannaharediscussingtheresultsoftheirlastmathtest.HannahshowsBridg etandCassiehertest,butBridgetandCassiedon'tshowtheirstoanyone.Cassiesays,'Ididn'tgetthel owestscoreinourclass,'andBridgetadds,'Ididn'tgetthehighestscore.'Whatistherankingofthethr eegirlsfromhighesttolowest20.Arectangleisinscribedinasemicirclewithlongersideonthediameter.Whatistheareaofthesemicircle21.22.Toothpicksareusedtomakeagridthatis60toothpickslongand32toothpickswide.Howmanytoo thpicksareusedaltogether23.Angle of isarightangle.Thesidesofarethediametersofsemicirclesasshown.Theareaofthesemicircleon equals,andthearcofthesemicircleon haslength.Whatistheradiusofthesemicircleon24.Squares,,and areequalinarea.Points andarethemidpointsofsides and,respectively.Whatistheratiooftheareaoftheshadedpentagontothesumoftheareasofthethreesquares25.Aballwithdiameter4inchesstartsatpointAtorollalongthetrackshown.Thetrackiscomprisedof3semicirculararcswhoseradiiare inches,inches,and1.2.The50%offpriceofhalfapoundoffishis$3,sothe100%,ortheregularprice,ofahalfpoundoffishis$6.Consequently,ifhalfapoundoffishcosts$6,thenawholepoundoffishis dollars.3.Noticethatwecanpairupeverytwonumberstomakeasumof1:Therefore,theansweris.4.Eachofhersevenfriendspaid tocoverJudi'sportion.Therefore,Judi'sportionmustbe.SinceJudiwassupposedtopay ofthetotalbill,thetotalbillmustbe.5.Themedianhereisobviouslylessthanthemean,sooption(A)and(B)areout. Liningupthenumbers(5,5,6,8,106),weseethatthemedianweightis6pounds.Theaverageweightofthefivekidsis.Therefore,theaverageweightisbigger,by pounds,makingtheanswer.6.Solution1:WorkingBackwardsLetthevalueintheemptyboxinthemiddlerowbe,andthevalueintheemptyboxinthetoprowbe. istheanswerwe'relookingfor.Weseethat,making.Itfollowsthat,so.Solution2:JumpingBacktotheStartAnotherwaytodothisproblemistorealizewhatmakesupthebottommostnumber.Thismethoddoes n'tworkquiteaswellforthisproblem,butinalargertree,itmightbefaster.(Inthiscase,Solution1wou ldbefastersincethere'sonlytwomissingnumbers.)Again,letthevalueintheemptyboxinthemiddlerowbe,andthevalueintheemptyboxinthetoprowbe.istheanswerwe'relookingfor. Wecanwritesomeequations: Nowwecansubstituteintothefirstequationusingthetwoothers:7.IfTreysaw,thenhesaw.2minutesand45secondscanalsobeexpressedas seconds.Trey'srateofseeingcars,,canbemultipliedbyonthetopandbottom(andpreservethesamerate):.Itfollowsthatthemostlikelynumberofcarsis. Solution2minutesand secondsisequalto.SinceTreyprobablycountsaround carsevery seconds,thereare groupsofcarsthatTreymostlikelycounts.Since,theclosestanswerchoiceis.8.First,thereare waystoflipthecoins,inorder. ThewaystogettwoconsecutiveheadsareHHT andTHH. ThewaytogetthreeconsecutiveheadsisHHH.Therefore,theprobabilityofflippingatleasttwoconsecutiveheadsis.9.Thisisageometricsequenceinwhichthecommonratiois2.Tofindthejumpthatwouldbeovera1000meters,wenotethat.However,becausethefirsttermis andnot,thesolutiontotheproblemis10.TofindeithertheLCMortheGCFoftwonumbers,alwaysprimefactorizefirst. Theprimefactorizationof.Theprimefactorizationof.Then,findthegreatestpowerofallthenumbersthereare;ifonenumberisonebutnottheother,useit(t hisis).Multiplyallofthesetoget5940.FortheGCFof180and594,usetheleastpowerofallofthenumbersthatareinbothfactorizationsandmultiply.=18.Thustheanswer==. Westartoffwithasimilarapproachastheoriginalsolution.Fromtheprimefactorizations,theGCFis .Itisawellknownfactthat.Sowehave,.Dividingby yields.Therefore,.11.Weusethatfactthat.Letd=distance,r=rateorspeed,andt=time.Inthiscase,letrepresentthetime.OnMonday,hewasatarateof.So,.ForWednesday,hewalkedatarateof.Therefore,.OnFriday,hewalkedatarateof.So,.Addingupthehoursyields++=.WenowfindtheamountoftimeGrandfatherwouldhavetakenifhewalkedatperday.Setuptheequation,.Tofindtheamountoftimesaved,subtractthetwoamounts:-=.Toconvertthistominutes,wemultiplyby.Thus,thesolutiontothisproblemis12.First,findtheamountofmoneyonewillpayforthreesandalswithoutthediscount.Wehave.Then,findtheamountofmoneyusingthediscount:.Findingthepercentageyields.Tofindthepercentsaved,wehave13.Letthetwodigitsbe and.Thecorrectscorewas.Claramisinterpreteditas.Thedifferencebetweenthetwoiswhichfactorsinto.Therefore,sincethedifferenceisamultipleof9,theonlyanswerchoicethatisamultipleof9is.14.Theprobabilitythatbothshowagreenbeanis.Theprobabilitythatbothshowaredbeanis.Thereforetheprobabilityis15.Therefore,.Therefore,.Tomostpeople,itwouldnotbeimmediatelyevidentthat,sowecanmultiply6'suntilwegetthedesirednumber:,so.Thereforetheansweris.16.Solution1:AlgebraWemultiplythefirstratioby8onbothsides,andthesecondratioby5togetthesamenumberfor8thgra ders,inorderthatwecanputthetworatiostogether:Therefore,theratioof8thgradersto7thgradersto6thgradersis.Sincetheratioisinlowestterms,thesmallestnumberofstudentsparticipatingintheprojectis.Solution2:FakesolvingThenumberof8thgradershastobeamultipleof8and5,soassumeitis40(thesmallestpossibility).Thenthereare6thgradersand7thgraders.Thenumbersofstudentsis17.Solution1Themeanofthesenumbersis.Thereforethenumbersare,sotheanswerisSolution2Letthe numberbe.Thenourdesirednumberis.Ourintegersare,sowehavethat.Solution3Letthefirsttermbe.Ourintegersare.Wehave,18.Solution1Therearecubesonthebaseofthebox.Then,foreachofthe4layersabovethebottom(assinceeachcubeis1foot by1footby1footandtheboxis5feettall,thereare4feetleft),therearecubes.Hence,theansweris.Solution2Wecanjustcalculatethevolumeoftheprismthatwascutoutoftheoriginalbox.Eachinteriorsideofthefortwillbe feetshorterthaneachsideoftheoutside.Sincethefloorisfoot,theheightwillbe feet.Sothevolumeoftheinteriorboxis.Thevolumeoftheoriginalboxis.Therefore,thenumberofblockscontainedinthefortis.19.IfHannahdidbetterthanCassie,therewouldbenowayshecouldknowforsurethatshedidn'tgett helowestscoreintheclass.Therefore,HannahdidworsethanCassie.Similarly,ifHannahdidworseth anBridget,thereisnowayBridgetcouldhaveknownthatshedidn'tgetthehighestintheclass.Therefore,HannahdidbetterthanBridget,soourorderis.20.Asemicirclehassymmetry,sothecenterisexactlyatthemidpointofthe2sideontherectangle,makingtheradius,bythePythagoreanTheorem,.Theareais.21.ThenumberofwaystogetfromSamantha'shousetoCityParkis,andthenumberofwaystogetfromCityParktoschoolis.Sincethere'sonewaytogothroughCityPark(justwalkingstraightthrough),thenumberofdifferentwaystogofromSamantha'shousetoCityParktoschool.22.Thereare verticalcolumnswithalengthof toothpicks,andthereare horizontalrowswithalengthof toothpicks.Aneffectivewaytoverifythisistotryasmallcase,i.e.agridoftoothpicks.Thus,ouransweris.23.Solution1.Solution2WegoasinSolution1,findingthediameterofthecircleonACandAB.Then,anextendedversionofthet heoremsaysthatthesumofthesemicirclesontheleftisequaltothebiggestone,sotheareaofthelargestis,andthemiddleoneis,sotheradiusis.24.Firstlet(where isthesidelengthofthesquares)forsimplicity.Wecanextenduntilithitstheextensionof.Callthispoint.Theareaoftriangle thenis Theareaofrectangle is.Thus,ourdesiredareais.Now,theratiooftheshadedareatothecombinedareaofthethreesquaresis.Solution2Letthesidelengthofeachsquarebe.Lettheintersectionof and be.Since,.Since andareverticalangles,theyarecongruent.Wealsohave bydefinition.Sowehave by congruence.Therefore,.Since and aremidpointsofsides,.Thiscombinedwith yields.Theareaoftrapezoid is.Theareaoftriangle is.Sotheareaofthepentagon is.Theareaofthe squaresis.Therefore,.Solution3Lettheintersectionof and be.Nowwehave and.Becausebothtriangleshasasideoncongruentsquarestherefore.Because and areverticalangles.Alsoboth and arerightanglesso.ThereforebyAAS(Angle,Angle,Side).Thentranslating/rotatingtheshaded intothepositionofSotheshadedareanowcompletelycoversthesquareSettheareaofasquareasTherefore,.25.Solution1Theradiusoftheballis2inches.Ifyouthinkabouttheballrollingordrawapathfortheball(seefigurebelow),youseethatinAandCitloses inches,anditgains inchesonB.So,thedeparturefromthelengthofthetrackmeansthattheansweris.Solution2Thetotallengthofallofthearcsis.Sincewewantthepathfromthecenter,theactualdistancewillbeshorter.Therefore,theonlyanswerchoicelessthan is.Thissolutionmaybeinvalidbecausetheactualdistancecanbelongerifthepaththecent ertravelsisontheoutsideofthecurve,asitisinthemiddlebump.。

AMC10美国数学竞赛A卷附中文翻译和答案

AMC10 美国数学竞赛 A 卷附中文翻译和答案简介AMC10 是美国的一项全国性数学竞赛，主要面向高中学生。

此文档提供了 AMC10 美国数学竞赛 A 卷的问题、答案及中文翻译，帮助考生更好地理解和准备竞赛。

问题和答案问题 1让我们从一个整数开始，每一步都按照以下规则进行操作：如果当前的数是偶数，将它除以 2；如果当前的数是奇数，将它乘以 3 并加 1。

通过这样的操作，我们可以生成一个数列，例如，从 9 开始的数列如下所示：9，28，14，7，22，11，34，...。

显然，这个数列最终会包含两个连续的 1。

以下哪个数开始操作后会生成包含两个连续的 1？$\\textbf{(A)}\\ 111 \\qquad \\textbf{(B)}\\ 120 \\qquad \\textbf{(C)}\\ 125 \\qquad \\textbf{(D)}\\ 130 \\qquad\\textbf{(E)}\\ 139$$\\textbf{(D)}\\ 130$问题 2如果 $2^x \\times 5^y = 5000000$，那么x+x的值是多少？$\\textbf{(A)}\\ 6 \\qquad \\textbf{(B)}\\ 7 \\qquad\\textbf{(C)}\\ 10 \\qquad \\textbf{(D)}\\ 12 \\qquad\\textbf{(E)}\\ 15$答案 2$\\textbf{(C)}\\ 10$问题 3数轴上三个数x、x、x的平均值是 6。

给定x−x=8，x−x=12，那么x的值是多少？$\\textbf{(A)}\\ -10 \\qquad \\textbf{(B)}\\ -6 \\qquad \\textbf{(C)}\\ 0 \\qquad \\textbf{(D)}\\ 6 \\qquad\\textbf{(E)}\\ 10$答案 3$\\textbf{(B)}\\ -6$某菜市场的一个南瓜重 100 磅，其中 99% 的重量是水分。

美国数学竞赛AMC题目及答案

2.3.What is the value of ?4.Eight friends ate at a restaurant and agreed to share the bill equally. Because Judi forgot her money, each of her seven friends paid an extra $2.50 to cover her portion of the total bill. What was the total bill?5.Hammie is in the grade and weighs 106 pounds. His quadruplet sisters are tiny babies and weigh 5, 5, 6, and 8 pounds. Which is greater, the average (mean) weight of these five children or the median weight, and by how many pounds?6.The number in each box below is the product of the numbers in the two boxes that touch it in the row above. For example, . What is the missing number in the top row?7.Trey and his mom stopped at a railroad crossing to let a train pass. As the train began to pass, Trey counted 6 cars in the first 10 seconds. It took the train 2 minutes and 45 seconds to clear the crossing at a constant speed. Which of the following was the most likely number of cars in the train?8.A fair coin is tossed 3 times. What is the probability of at least two consecutive heads?9.The Incredible Hulk can double the distance he jumps with each succeeding jump. If his first jump is 1 meter, the second jump is 2 meters, the third jump is 4 meters, and so on, then on which jump will he first be able to jump more than 1 kilometer?10.What is the ratio of the least common multiple of 180 and 594 to the greatest common factor of 180 and 594?11. Ted's grandfather used his treadmill on 3 days this week. He went 2 miles each day. On Monday he jogged at a speed of 5 miles per hour. He walked at the rate of 3 miles per hour on Wednesday and at 4 miles per hour on Friday. If Grandfather had always walked at 4 miles per hour, he would have spent less time on the treadmill. How many minutes less?12. At the 2013 Winnebago County Fair a vendor is offering a "fair special" on sandals. If you buy one pair of sandals at the regular price of $50, you get a second pair at a 40% discount, and a third pair at half the regular price. Javier took advantage of the "fair special" to buy three pairs of sandals. What percentage of the $150 regular price did he save?13. When Clara totaled her scores, she inadvertently reversed the units digit and the tens digit of one score. By which of the following might her incorrect sum have differed from the correct one?14. Let the two digits be and .The correct score was . Clara misinterpreted it as . The difference between the two is which factors into . Therefore, since the difference is a multiple of 9, the only answerchoice that is a multiple of 9 is .15. If , , and , what is the product of , , and ?16. A number of students from Fibonacci Middle School are taking part in a community service project. The ratio of -graders to -graders is , and the the ratio of -graders to -graders is . What is the smallest number of students that could be participating in the project?17. The sum of six consecutive positive integers is 2013. What is the largest of these six integers?18. Isabella uses one-foot cubical blocks to build a rectangular fort that is 12 feet long, 10 feet wide, and 5 feet high. The floor and the four walls are all one foot thick. How many blocks does the fort contain?--Arpanliku 16:22, 27 November 2013 (EST) Courtesy of Lord.of.AMC19. Bridget, Cassie, and Hannah are discussing the results of their last math test. Hannah shows Bridget and Cassie her test, but Bridget and Cassie don't show theirs to anyone. Cassie says, 'I didn't get the lowest score in our class,' and Bridget adds, 'I didn't get the highest score.' What is the ranking of the three girls from highest to lowest?20. A rectangle is inscribed in a semicircle with longer side on the diameter. What is the area of the semicircle?21. Samantha lives 2 blocks west and 1 block south of the southwest corner of City Park. Her school is 2 blocks east and 2 blocks north of the northeast corner of City Park. On school days she bikes on streets to the southwest corner of City Park, then takes a diagonal path through the park to the northeast corner, and then bikes on streets to school. If her route is as short as possible, how many different routes can she take?22. Toothpicks are used to make a grid that is 60 toothpicks long and 32 toothpicks wide. How many toothpicks are used altogether?23. Angle of is a right angle. The sides of are the diameters of semicircles as shown. The area of the semicircle on equals , and the arc of the semicircle on has length .What is the radius of the semicircle on ?24. Squares , , and are equal in area. Points and are the midpoints of sidesand , respectively. What is the ratio of the area of the shaded pentagon to the sum of the areas of the three squares?25. A ball with diameter 4 inches starts at point A to roll along the track shown. The track is comprised of 3 semicircular arcs whose radii are inches, inches, and inches, respectively. The ball always remains in contact with the track and does not slip. What is the distance the center of theball travels over the course from A to B?1.2.The 50% off price of half a pound of fish is $3, so the 100%, or the regular price, of a half pound of fish is $6. Consequently, if half a pound of fish costs $6, then a whole pound of fish is dollars.3.Notice that we can pair up every two numbers to make a sum of 1:Therefore, the answer is .4.Each of her seven friends paid to cover Judi's portion. Therefore, Judi's portion must be . Since Judi was supposed to pay of the total bill, the total bill must be .5.The median here is obviously less than the mean, so option (A) and (B) are out.Lining up the numbers (5, 5, 6, 8, 106), we see that the median weight is 6 pounds.The average weight of the five kids is .Therefore, the average weight is bigger, by pounds, making the answer.6.Solution 1: Working BackwardsLet the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.We see that , making .It follows that , so .Solution 2: Jumping Back to the StartAnother way to do this problem is to realize what makes up the bottommost number. This method doesn't work quite as well for this problem, but in a larger tree, it might be faster. (In this case, Solution 1 would be faster since there's only two missing numbers.)Again, let the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.We can write some equations:Now we can substitute into the first equation using the two others:7.If Trey saw , then he saw .2 minutes and 45 seconds can also be expressed as seconds.Trey's rate of seeing cars, , can be multiplied by on the top and bottom (and preserve the same rate):. It follows that the most likely number of cars is . Solution 2minutes and seconds is equal to .Since Trey probably counts around cars every seconds, there are groups of cars that Trey most likely counts. Since , the closest answer choice is .8.First, there are ways to flip the coins, in order.The ways to get two consecutive heads are HHT and THH.The way to get three consecutive heads is HHH.Therefore, the probability of flipping at least two consecutive heads is .9.This is a geometric sequence in which the common ratio is 2. To find the jump that would be over a 1000 meters, we note that .However, because the first term is and not , the solution to the problem is10. To find either the LCM or the GCF of two numbers, always prime factorize first.The prime factorization of .The prime factorization of .Then, find the greatest power of all the numbers there are; if one number is one but not the other, use it (this is ). Multiply all of these to get 5940.For the GCF of 180 and 594, use the least power of all of the numbers that are in both factorizations and multiply. = 18.Thus the answer = = .We start off with a similar approach as the original solution. From the prime factorizations, the GCF is .It is a well known fact that . So we have,.Dividing by yields .Therefore, .11. We use that fact that . Let d= distance, r= rate or speed, and t=time. In this case, let represent the time.On Monday, he was at a rate of . So, .For Wednesday, he walked at a rate of . Therefore, .On Friday, he walked at a rate of . So, .Adding up the hours yields + + = .We now find the amount of time Grandfather would have taken if he walked at per day. Set up the equation, .To find the amount of time saved, subtract the two amounts: - = . To convert this to minutes, we multiply by .Thus, the solution to this problem is12. First, find the amount of money one will pay for three sandals without the discount. We have.Then, find the amount of money using the discount: .Finding the percentage yields .To find the percent saved, we have13. Let the two digits be and .The correct score was . Clara misinterpreted it as . The difference between the two is which factors into . Therefore, since the difference is a multiple of 9, the only answerchoice that is a multiple of 9 is .14. The probability that both show a green bean is . The probability that both show a red bean is . Therefore the probability is15.Therefore, .Therefore, .To most people, it would not be immediately evident that , so we can multiply 6's until we get the desired number:, so .Therefore the answer is .16. Solution 1: AlgebraWe multiply the first ratio by 8 on both sides, and the second ratio by 5 to get the same number for 8th graders, in order that we can put the two ratios together:Therefore, the ratio of 8th graders to 7th graders to 6th graders is . Since the ratio is in lowest terms, the smallest number of students participating in the project is .Solution 2: FakesolvingThe number of 8th graders has to be a multiple of 8 and 5, so assume it is 40 (the smallest possibility). Then there are 6th graders and 7th graders. The numbers of students is17. Solution 1The mean of these numbers is . Therefore the numbers are, so the answer isSolution 2Let the number be . Then our desired number is .Our integers are , so we have that.Solution 3Let the first term be . Our integers are . We have,18. Solution 1There are cubes on the base of the box. Then, for each of the 4 layers above the bottom (as since each cube is 1 foot by 1 foot by 1 foot and the box is 5 feet tall, there are 4 feet left), there arecubes. Hence, the answer is .Solution 2We can just calculate the volume of the prism that was cut out of the original box. Each interior side of the fort will be feet shorter than each side of the outside. Since the floor is foot, the height will be feet. So the volume of the interior box is .The volume of the original box is . Therefore, the number of blocks contained inthe fort is .19. If Hannah did better than Cassie, there would be no way she could know for sure that she didn't get the lowest score in the class. Therefore, Hannah did worse than Cassie. Similarly, if Hannah did worse than Bridget, there is no way Bridget could have known that she didn't get the highest in the class.Therefore, Hannah did better than Bridget, so our order is .20.A semicircle has symmetry, so the center is exactly at the midpoint of the 2 side on the rectangle, making the radius, by the Pythagorean Theorem, . The area is .21.The number of ways to get from Samantha's house to City Park is , and the number of ways toget from City Park to school is . Since there's one way to go through City Park (just walking straight through), the number of different ways to go from Samantha's house to City Park to school .22. There are vertical columns with a length of toothpicks, and there are horizontal rows with a length of toothpicks. An effective way to verify this is to try a small case, i.e. a grid of toothpicks.Thus, our answer is .23. Solution 1If the semicircle on AB were a full circle, the area would be 16pi. Therefore the diameter of the first circle is 8. The arc of the largest semicircle would normally have a complete diameter of 17. The Pythagoreantheorem says that the other side has length 15, so the radius is .Solution 2We go as in Solution 1, finding the diameter of the circle on AC and AB. Then, an extended version of the theorem says that the sum of the semicircles on the left is equal to the biggest one, so the area of thelargest is , and the middle one is , so the radius is .24.First let (where is the side length of the squares) for simplicity. We can extend until it hits theextension of . Call this point . The area of triangle then is The area of rectangle is . Thus, our desired area is . Now, the ratio of the shaded area to thecombined area of the three squares is .Let the side length of each square be .Let the intersection of and be .Since , . Since and are vertical angles, they are congruent. We also have by definition.So we have by congruence. Therefore, .Since and are midpoints of sides, . This combined with yields.The area of trapezoid is .The area of triangle is .So the area of the pentagon is .The area of the squares is .Therefore, .Let the intersection of and be .Now we have and .Because both triangles has a side on congruent squares therefore .Because and are vertical angles .Also both and are right angles so .Therefore by AAS(Angle, Angle, Side) .Then translating/rotating the shaded into the position ofSo the shaded area now completely covers the squareSet the area of a square asTherefore, .25. Solution 1The radius of the ball is 2 inches. If you think about the ball rolling or draw a path for the ball (see figure below), you see that in A and C it loses inches, and it gains inches on B.So, the departure from the length of the track means that the answer is . Solution 2The total length of all of the arcs is . Since we want the path from the center, the actual distance will be shorter. Therefore, the only answer choice less than is . Thissolution may be invalid because the actual distance can be longer if the path the center travels is on the outside of the curve, as it is in the middle bump.古希腊哲学大师亚里士多德说：人有两种，一种即“吃饭是为了活着”,一种是“活着是为了吃饭”.一个人之所以伟大，首先是因为他有超于常人的心。

AMC_美国数学竞赛_2000_AMC_10__试题及答案解析

USA AMC 10 20001In the year , the United States will host the International Mathematical Olympiad. Let , , and be distinct positive integers such that the product . What's the largest possible value of the sum ?SolutionThe sum is the highest if two factors are the lowest.So, and .2Solution.3Each day, Jenny ate of the jellybeans that were in her jar at the beginning of the day. At the end of the second day, remained. How many jellybeans were in the jar originally?Solution4Chandra pays an online service provider a fixed monthly fee plus an hourly charge for connect time. Her December bill was , but in January her bill was because she used twice as much connect time as in December. What is the fixxed monthly fee?SolutionLet be the fixed fee, and be the amount she pays for the minutes she used in the first month.We want the fixed fee, which is5Points and are the midpoints of sides and of . As moves along a line that is parallel to side , how many of the four quantities listed below change?(a) the length of the segment(b) the perimeter of(c) the area of(d) the area of trapezoidSolution(a) Clearly does not change, and , so doesn't change either.(b) Obviously, the perimeter changes.(c) The area clearly doesn't change, as both the base and its corresponding height remain the same.(d) The bases and do not change, and neither does the height, so the trapezoid remains the same.Only quantity changes, so the correct answer is .6The Fibonacci Sequence starts with two 1s and each term afterwards is the sum of its predecessors. Which one of the ten digits is the last to appear in thet units position of a number in the Fibonacci Sequence?SolutionThe pattern of the units digits areIn order of appearance:.is the last.7In rectangle , , is on , and and trisect . What is the perimeter of ?Solution.Since is trisected, .Thus,.Adding, .8At Olympic High School, of the freshmen and of the sophomores took the AMC-10. Given that the number of freshmen and sophomore contestants was the same, which of the following must be true?There are five times as many sophomores as freshmen.There are twice as many sophomores as freshmen.There are as many freshmen as sophomores.There are twice as many freshmen as sophomores.There are five times as many freshmen as sophomores.SolutionLet be the number of freshman and be the number of sophomores.There are twice as many freshmen as sophomores.9If , where , thenSolution, so ...10The sides of a triangle with positive area have lengths , , and . The sides of a second triangle with positive area have lengths , , and . What is the smallest positive number that is not a possible value of ?SolutionFrom the triangle inequality, and . The smallest positive number not possible is , which is .11Two different prime numbers between and are chosen. When their sum is subtracted from their product, which of the following numbers could be obtained?SolutionTwo prime numbers between and are both odd.Thus, we can discard the even choices.Both and are even, so one more than is a multiple of four.is the only possible choice.satisfy this, .12Figures , , , and consist of , , , and nonoverlapping unit squares, respectively. If the pattern were continued, how many nonoverlapping unit squares would there be in figure 100?SolutionSolution 1We have a recursion:.I.E. we add increasing multiples of each time we go up a figure. So, to go from Figure 0 to 100, we add.Solution 2We can divide up figure to get the sum of the sum of the first odd numbers and the sum of the first odd numbers. If you do not see this, here is the example for :The sum of the first odd numbers is , so for figure , there are unit squares. We plug in to get , which is choice13There are 5 yellow pegs, 4 red pegs, 3 green pegs, 2 blue pegs, and 1 orange peg to be placed on a triangular peg board. In how many ways can the pegs be placed so that no (horizontal) row or (vertical) column contains two pegs of the same color?SolutionIn each column there must be one yellow peg. In particular, in the rightmost column, there is only one peg spot, therefore a yellow peg must go there.In the second column from the right, there are two spaces for pegs. One of them is in the same row as the corner peg, so there is only one remaining choice left for the yellow peg in this column.By similar logic, we can fill in the yellow pegs as shown:After this we can proceed to fill in the whole pegboard, so there is only arrangement of the pegs. The answer is14Mrs. Walter gave an exam in a mathematics class of five students. She entered the scores in random order into a spreadsheet, which recalculated the class average after each score was entered. Mrs. Walter noticed that after each score was entered, the average was always an integer. The scores (listed in ascending order) were , , , , and . What was the last score Mrs. Walter entered?SolutionThe sum of the first scores must be even, so we must choose evens or the odds to be the first two scores.Let us look at the numbers in mod .If we choose the two odds, the next number must be a multiple of , of which there is none.Similarly, if we choose or , the next number must be a multiple of , of which there is none.So we choose first.The next number must be 1 in mod 3, of which only remains.The sum of the first three scores is . This is equivalent to in mod .Thus, we need to choose one number that is in mod . is the only one that works.Thus, is the last score entered.15Two non-zero real numbers, and , satisfy . Which of the following is a possible value of ?SolutionSubstituting , we get16The diagram shows lattice points, each one unit from its nearest neighbors. Segment meets segment at . Find the length of segment .SolutionSolution 1Let be the line containing and and let be the line containing and . If we set the bottom left point at , then , , , and .The line is given by the equation . The -intercept is , so . We are given two points on , hence we cancompute the slope, to be , so is the lineSimilarly, is given by . The slope in this case is , so . Plugging in the point gives us , so is the line .At , the intersection point, both of the equations must be true, soWe have the coordinates of and , so we can use the distance formula here:which is answer choiceSolution 2Draw the perpendiculars from and to , respectively. As it turns out, . Let be the point on for which ., and , so by AA similarity,By the Pythagorean Theorem, we have ,, and . Let , so , thenThis is answer choiceAlso, you could extend CD to the end of the box and create two similar triangles. Then use ratios and find that the distance is 5/9 of the diagonal AB. Thus, the answer is B.17Boris has an incredible coin changing machine. When he puts in a quarter, it returns five nickels; when he puts in a nickel, it returns five pennies; and when he puts in a penny, it returns five quarters. Boris starts with just one penny. Which of the following amounts could Boris have after using the machine repeatedly?SolutionConsider what happens each time he puts a coin in. If he puts in a quarter, he gets five nickels back, so the amount of money he has doesn't change. Similarly, if he puts a nickel in the machine, he gets five pennies back and the money value doesn't change. However, if he puts a penny in, he gets five quarters back, increasing the amount of money he has by cents.This implies that the only possible values, in cents, he can have are the ones one more than a multiple of . Of the choices given, the only one is18Charlyn walks completely around the boundary of a square whose sides are each km long. From any point on her path she can see exactly km horizontally in all directions. What is the area of the region consisting of all points Charlyn can see during her walk, expressed in square kilometers and rounded to the nearest whole number?SolutionThe area she sees looks at follows:The part inside the walk has area . The part outside the walk consists of four rectangles, and four arcs. Each of the rectangles has area . The four arcs together form a circle with radius . Therefore the total area she can see is, which rounded to the nearest integer is .19Through a point on the hypotenuse of a right triangle, lines are drawn parallel to the legs of the triangle so that the trangle is divided into a square and two smaller right triangles. The area of one of the two small right triangles is times the area of the square. The ratio of the area of the other small right triangle to the area of the square isSolutionLet the square have area , then it follows that the altitude of one of the triangles is . The area of the other triangle is .By similar triangles, we haveThis is choice(Note that this approach is enough to get the correct answer in the contest. However, if we wanted a completely correct solution, we should also note that scaling the given triangle times changes each of the areas times, and therefore it does not influence the ratio of any two areas. This is why we can pick the side of the square.)20Let , , and be nonnegative integers such that . What is the maximum value of ?SolutionThe trick is to realize that the sum is similar to the product .If we multiply , we get.We know that , therefore.Therefore the maximum value of is equal to the maximum value of . Now we will find this maximum.Suppose that some two of , , and differ by at least . Then this triple is surely not optimal.Proof: WLOG let . We can then increase the value ofby changing and .Therefore the maximum is achieved in the cases where is a rotation of . The value of in this case is . And thus the maximum of is.21If all alligators are ferocious creatures and some creepy crawlers are alligators, which statement(s) must be true?I. All alligators are creepy crawlers.II. Some ferocious creatures are creepy crawlers.III. Some alligators are not creepy crawlers.SolutionWe interpret the problem statement as a query about three abstract concepts denoted as "alligators", "creepy crawlers" and "ferocious creatures". In answering the question, we may NOT refer to reality -- for example to the fact that alligators do exist.To make more clear that we are not using anything outside the problem statement, let's rename the three concepts as , , and .We got the following information:▪If is an , then is an .▪There is some that is a and at the same time an .We CAN NOT conclude that the first statement is true. For example, the situation "Johnny and Freddy are s, but only Johnny is a "meets both conditions, but the first statement is false.We CAN conclude that the second statement is true. We know that there is some that is a and at the same time an . Pick one such and call it Bobby. Additionally, we know that if is an , then is an. Bobby is an , therefore Bobby is an . And this is enough to prove the second statement -- Bobby is an that is also a .We CAN NOT conclude that the third statement is true. For example, consider the situation when , and are equivalent (represent the same set of objects). In such case both conditions are satisfied, but the third statement is false.Therefore the answer is .22One morning each member of Angela's family drank an -ounce mixture of coffee with milk. The amounts of coffee and milk varied from cup to cup, but were never zero. Angela drank a quarter of the total amount of milk and a sixth of the total amount of coffee. How many people are in the family?SolutionThe exact value "8 ounces" is not important. We will only use the fact that each member of the family drank the same amount.Let be the total number of ounces of milk drank by the family and the total number of ounces of coffee. Thus the whole family drank a total of ounces of fluids.Let be the number of family members. Then each family member drank ounces of fluids.We know that Angela drank ounces of fluids.As Angela is a family member, we have .Multiply both sides by to get .If , we have .If , we have .Therefore the only remaining option is .23When the mean, median, and mode of the list are arranged in increasing order, they form a non-constant arithmetic progression. What is the sum of all possible real values of ?SolutionAs occurs three times and each of the three other values just once, regardless of what we choose the mode will always be .The sum of all numbers is , therefore the mean is .The six known values, in sorted order, are . From this sequence we conclude: If , the median will be . If , the median will be . Finally, if , the median will be .We will now examine each of these three cases separately.In the case , both the median and the mode are 2, therefore we can not get any non-constant arithmetic progression.In the case we have , because. Therefore our three values inorder are . We want this to be an arithmetic progression. From the first two terms the difference must be . Therefore thethird term must be .Solving we get the only solution for this case: . The case remains. Once again, we have ,therefore the order is . The only solution is when , i. e., .The sum of all solutions is therefore .24Let be a function for which . Find the sum of all values of for which .SolutionIn the definition of , let . We get: . Aswe have , we must have , in other words .One can now either explicitly compute the roots, or use Vieta's formulas. According to them, the sum of the roots of is . In our case this is .(Note that for the above approach to be completely correct, we should additionally verify that there actually are two distinct real roots. This is, for example, obvious from the facts that and .)25In year , the day of the year is a Tuesday. In year , the day is also a Tuesday. On what day of the week did the of year occur?SolutionClearly, identifying what of these years may/must/may not be a leap year will be key in solving the problem.Let be the day of year , the day of year and the day of year .If year is not a leap year, the day will bedays after . As , that would be a Monday.Therefore year must be a leap year. (Then is days after .) As there can not be two leap years after each other, is not a leap year. Therefore day is days after . We have . Therefore is weekdays before , i.e., is a.(Note that the situation described by the problem statement indeed occurs in our calendar. For example, for we have =Tuesday, October 26th 2004, =Tuesday, July 19th, 2005 and =Thursday, April 10th 2003.)。

AMC美国数学竞赛AMC.B 试题及答案解析

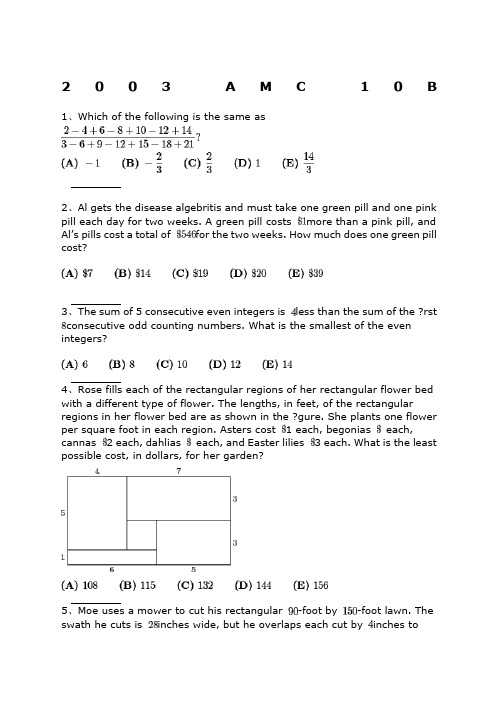
2003A M C10 B 1、Which of the following is the same as2、Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pink pill, and Al’s pills cost a total of for the two weeks. How much does one green pill cost?3、The sum of 5 consecutive even integers is less than the sum of the ?rst consecutive odd counting numbers. What is the smallest of the even integers?4、Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the ?gure. She plants one flower per square foot in each region. Asters cost 1 each, begonias each, cannas 2 each, dahlias each, and Easter lilies 3 each. What is the least possible cost, in dollars, for her garden?5、Moe uses a mower to cut his rectangular -foot by -foot lawn. The swath he cuts is inches wide, but he overlaps each cut by inches tomake sure that no grass is missed. He walks at the rate of feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow his lawn?.6、Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length of a “-inch” television screen is closest, in inches, to which of the following?7、The symbolism denotes the largest integer not exceeding . For example. , and . Compute.8、The second and fourth terms of a geometric sequence are and . Which of the following is a possible first term?9、Find the value of that satisfies the equation10、Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of three letters followed by three digits. By how many times is the number of possible license plates increased?11、A line with slope intersects a line with slope at the point . What is the distance between the -intercepts of these two lines?12、Al, Betty, and Clare split among them to be invested in different ways. Each begins with a different amount. At the end of one year they have a total of . Betty and Clare have both doubled their money, whereas Al has managed to lose . What was Al’s origin al portion?.13、Let denote the sum of the digits of the positive integer . For example, and . For how many two-digit values of is ?14、Given that , where both and are positive integers, find the smallest possible value for .15、There are players in a singles tennis tournament. The tournament is single elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest players are given a bye, and the remaining players are paired off to play. After each round, the remaining players play in the next round. The match continues until only one player remains unbeaten. The total number of matches played is16、A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that the restaurant should offer so that a customer could have a different dinner each night in the year ?.17、An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly ?ll the cone. Assume that the melted ice cream occupies of the volume of the frozen ice cream. What is the ratio of the cone’s height to its radius?18、What is the largest integer that is a divisor offor all positive even integers ?19、Three semicircles of radius are constructed on diameter of a semicircle of radius . The centers of the small semicircles divide into four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicircles?20、In rectangle , and . Points and are on so that and . Lines and intersect at . Find the area of .21、A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardless of the color you pulled out. What is the probability that all beads in the bag are red after three such replacements?22、A clock chimes once at minutes past each hour and chimes on the hour according to the hour. For example, at 1 PM there is one chime and at noon and midnight there are twelve chimes. Starting at 11:15 AM on February , , on what date will the chime occur?23、A regular octagon has an area of one square unit. What is the area of the rectangle ?24、The ?rst four terms in an arithmetic sequence are , , , and, in that order. What is the ?fth term?25、How many distinct four-digit numbers are divisible by and have as their last two digits?。