AMC美国数学竞赛AMCB试题及答案解析

合集下载

2019年美国数学竞赛(AMC10B)的试题与解答

这时第二个容器里充满了 3 的水. 问小容器与大容器的容积 4
之比是多少?
解: 设第一、二个容器的容积分别为 V1 和 V2, 依题意有
5 6 V1 =
3 4 V2,
从而
V1 V2
=
3 4 5 6
=
9 , 故 (D) 正确. 10
2. Consider the statement, ”If n is not prime, then n − 2 is
√ 由垂线段最短知, m2 + n2
|√am + bn|
=
√ 5.
当且仅当
a2 + b2
OA 与直线 ax + by = 5 垂直即 an = bm 时取最小值.
解法 2 由柯西不等式, (a2 +b2)(m2 +n2) (am+bn)2,
即 5(m2 + n2) 等号成立.
√ 25, m2 + n2
6 ter and the second was empty. She poured all the water from the
first container into the second container, at which point the sec3
ond container was full of water. What is the ratio of the volume 4
解: 反例是指符合命题的条件但不符合命题的结论的例
子, 即满足“若 n 不是素数, 则 n − 2 是素数. ”选项中只有 27
满足, 故 (E) 正确.
评注运用柯西不等式关键是“配凑”形式, 充分利用已
知条件. 当出现分式和的形式时, 一般构造分式分母和作为

美国数学竞赛AMC题目及答案

2.3.Whatisthevalueof4.5.Hammieisinthegradeandweighs106pounds.Hisquadrupletsistersaretinybabiesandweigh5,5,6,and8pounds.W hichisgreater,theaverage(mean)weightofthesefivechildrenorthemedianweight,andbyhowman ypounds6.Thenumberineachboxbelowistheproductofthenumbersinthetwoboxesthattouchitintherowab ove.Forexample,.Whatisthemissingnumberinthetoprow7.8.Afaircoinistossed3times.Whatistheprobabilityofatleasttwoconsecutiveheads9.TheIncredibleHulkcandoublethedistancehejumpswitheachsucceedingjump.Ifhisfirstjumpis1 meter,thesecondjumpis2meters,thethirdjumpis4meters,andsoon,thenonwhichjumpwillhefirst beabletojumpmorethan1kilometer10.Whatistheratiooftheleastcommonmultipleof180and594tothegreatestcommonfactorof180a nd59411.12.Atthe2013WinnebagoCountyFairavendorisofferinga"fairspecial"onsandals.Ifyoubuyonepai rofsandalsattheregularpriceof$50,yougetasecondpairata40%discount,andathirdpairathalfthe regularprice.Javiertookadvantageofthe"fairspecial"tobuythreepairsofsandals.Whatpercentag eofthe$150regularpricedidhesave13.WhenClaratotaledherscores,sheinadvertentlyreversedtheunitsdigitandthetensdigitofones core.Bywhichofthefollowingmightherincorrectsumhavedifferedfromthecorrectone14.Letthetwodigitsbe and.Thecorrectscorewas.Claramisinterpreteditas.Thedifferencebetweenthetwoiswhichfactorsinto.Therefore,sincethedifferenceisamultipleof9,theonlyanswerchoicethatisamultipleof9 is.15.If,,and,whatistheproductof,,and16.AnumberofstudentsfromFibonacciMiddleSchoolaretakingpartinacommunityserviceproject.Theratioof-gradersto-gradersis,andthetheratioof-gradersto-gradersis .Whatisthesmallestnumberofstudentsthatcouldbeparticipatingintheproject17.Thesumofsixconsecutivepositiveintegersis2013.Whatisthelargestofthesesixintegers18.--Arpanliku16:22,27November2013(EST)Courtesyof19.Bridget,Cassie,andHannaharediscussingtheresultsoftheirlastmathtest.HannahshowsBridg etandCassiehertest,butBridgetandCassiedon'tshowtheirstoanyone.Cassiesays,'Ididn'tgetthel owestscoreinourclass,'andBridgetadds,'Ididn'tgetthehighestscore.'Whatistherankingofthethr eegirlsfromhighesttolowest20.Arectangleisinscribedinasemicirclewithlongersideonthediameter.Whatistheareaofthesemicircle21.22.Toothpicksareusedtomakeagridthatis60toothpickslongand32toothpickswide.Howmanytoo thpicksareusedaltogether23.Angle of isarightangle.Thesidesofarethediametersofsemicirclesasshown.Theareaofthesemicircleon equals,andthearcofthesemicircleon haslength.Whatistheradiusofthesemicircleon24.Squares,,and areequalinarea.Points andarethemidpointsofsides and,respectively.Whatistheratiooftheareaoftheshadedpentagontothesumoftheareasofthethreesquares25.Aballwithdiameter4inchesstartsatpointAtorollalongthetrackshown.Thetrackiscomprisedof3semicirculararcswhoseradiiare inches,inches,and1.2.The50%offpriceofhalfapoundoffishis$3,sothe100%,ortheregularprice,ofahalfpoundoffishis$6.Consequently,ifhalfapoundoffishcosts$6,thenawholepoundoffishis dollars.3.Noticethatwecanpairupeverytwonumberstomakeasumof1:Therefore,theansweris.4.Eachofhersevenfriendspaid tocoverJudi'sportion.Therefore,Judi'sportionmustbe.SinceJudiwassupposedtopay ofthetotalbill,thetotalbillmustbe.5.Themedianhereisobviouslylessthanthemean,sooption(A)and(B)areout. Liningupthenumbers(5,5,6,8,106),weseethatthemedianweightis6pounds.Theaverageweightofthefivekidsis.Therefore,theaverageweightisbigger,by pounds,makingtheanswer.6.Solution1:WorkingBackwardsLetthevalueintheemptyboxinthemiddlerowbe,andthevalueintheemptyboxinthetoprowbe. istheanswerwe'relookingfor.Weseethat,making.Itfollowsthat,so.Solution2:JumpingBacktotheStartAnotherwaytodothisproblemistorealizewhatmakesupthebottommostnumber.Thismethoddoes n'tworkquiteaswellforthisproblem,butinalargertree,itmightbefaster.(Inthiscase,Solution1wou ldbefastersincethere'sonlytwomissingnumbers.)Again,letthevalueintheemptyboxinthemiddlerowbe,andthevalueintheemptyboxinthetoprowbe.istheanswerwe'relookingfor. Wecanwritesomeequations: Nowwecansubstituteintothefirstequationusingthetwoothers:7.IfTreysaw,thenhesaw.2minutesand45secondscanalsobeexpressedas seconds.Trey'srateofseeingcars,,canbemultipliedbyonthetopandbottom(andpreservethesamerate):.Itfollowsthatthemostlikelynumberofcarsis. Solution2minutesand secondsisequalto.SinceTreyprobablycountsaround carsevery seconds,thereare groupsofcarsthatTreymostlikelycounts.Since,theclosestanswerchoiceis.8.First,thereare waystoflipthecoins,inorder. ThewaystogettwoconsecutiveheadsareHHT andTHH. ThewaytogetthreeconsecutiveheadsisHHH.Therefore,theprobabilityofflippingatleasttwoconsecutiveheadsis.9.Thisisageometricsequenceinwhichthecommonratiois2.Tofindthejumpthatwouldbeovera1000meters,wenotethat.However,becausethefirsttermis andnot,thesolutiontotheproblemis10.TofindeithertheLCMortheGCFoftwonumbers,alwaysprimefactorizefirst. Theprimefactorizationof.Theprimefactorizationof.Then,findthegreatestpowerofallthenumbersthereare;ifonenumberisonebutnottheother,useit(t hisis).Multiplyallofthesetoget5940.FortheGCFof180and594,usetheleastpowerofallofthenumbersthatareinbothfactorizationsandmultiply.=18.Thustheanswer==. Westartoffwithasimilarapproachastheoriginalsolution.Fromtheprimefactorizations,theGCFis .Itisawellknownfactthat.Sowehave,.Dividingby yields.Therefore,.11.Weusethatfactthat.Letd=distance,r=rateorspeed,andt=time.Inthiscase,letrepresentthetime.OnMonday,hewasatarateof.So,.ForWednesday,hewalkedatarateof.Therefore,.OnFriday,hewalkedatarateof.So,.Addingupthehoursyields++=.WenowfindtheamountoftimeGrandfatherwouldhavetakenifhewalkedatperday.Setuptheequation,.Tofindtheamountoftimesaved,subtractthetwoamounts:-=.Toconvertthistominutes,wemultiplyby.Thus,thesolutiontothisproblemis12.First,findtheamountofmoneyonewillpayforthreesandalswithoutthediscount.Wehave.Then,findtheamountofmoneyusingthediscount:.Findingthepercentageyields.Tofindthepercentsaved,wehave13.Letthetwodigitsbe and.Thecorrectscorewas.Claramisinterpreteditas.Thedifferencebetweenthetwoiswhichfactorsinto.Therefore,sincethedifferenceisamultipleof9,theonlyanswerchoicethatisamultipleof9is.14.Theprobabilitythatbothshowagreenbeanis.Theprobabilitythatbothshowaredbeanis.Thereforetheprobabilityis15.Therefore,.Therefore,.Tomostpeople,itwouldnotbeimmediatelyevidentthat,sowecanmultiply6'suntilwegetthedesirednumber:,so.Thereforetheansweris.16.Solution1:AlgebraWemultiplythefirstratioby8onbothsides,andthesecondratioby5togetthesamenumberfor8thgra ders,inorderthatwecanputthetworatiostogether:Therefore,theratioof8thgradersto7thgradersto6thgradersis.Sincetheratioisinlowestterms,thesmallestnumberofstudentsparticipatingintheprojectis.Solution2:FakesolvingThenumberof8thgradershastobeamultipleof8and5,soassumeitis40(thesmallestpossibility).Thenthereare6thgradersand7thgraders.Thenumbersofstudentsis17.Solution1Themeanofthesenumbersis.Thereforethenumbersare,sotheanswerisSolution2Letthe numberbe.Thenourdesirednumberis.Ourintegersare,sowehavethat.Solution3Letthefirsttermbe.Ourintegersare.Wehave,18.Solution1Therearecubesonthebaseofthebox.Then,foreachofthe4layersabovethebottom(assinceeachcubeis1foot by1footby1footandtheboxis5feettall,thereare4feetleft),therearecubes.Hence,theansweris.Solution2Wecanjustcalculatethevolumeoftheprismthatwascutoutoftheoriginalbox.Eachinteriorsideofthefortwillbe feetshorterthaneachsideoftheoutside.Sincethefloorisfoot,theheightwillbe feet.Sothevolumeoftheinteriorboxis.Thevolumeoftheoriginalboxis.Therefore,thenumberofblockscontainedinthefortis.19.IfHannahdidbetterthanCassie,therewouldbenowayshecouldknowforsurethatshedidn'tgett helowestscoreintheclass.Therefore,HannahdidworsethanCassie.Similarly,ifHannahdidworseth anBridget,thereisnowayBridgetcouldhaveknownthatshedidn'tgetthehighestintheclass.Therefore,HannahdidbetterthanBridget,soourorderis.20.Asemicirclehassymmetry,sothecenterisexactlyatthemidpointofthe2sideontherectangle,makingtheradius,bythePythagoreanTheorem,.Theareais.21.ThenumberofwaystogetfromSamantha'shousetoCityParkis,andthenumberofwaystogetfromCityParktoschoolis.Sincethere'sonewaytogothroughCityPark(justwalkingstraightthrough),thenumberofdifferentwaystogofromSamantha'shousetoCityParktoschool.22.Thereare verticalcolumnswithalengthof toothpicks,andthereare horizontalrowswithalengthof toothpicks.Aneffectivewaytoverifythisistotryasmallcase,i.e.agridoftoothpicks.Thus,ouransweris.23.Solution1.Solution2WegoasinSolution1,findingthediameterofthecircleonACandAB.Then,anextendedversionofthet heoremsaysthatthesumofthesemicirclesontheleftisequaltothebiggestone,sotheareaofthelargestis,andthemiddleoneis,sotheradiusis.24.Firstlet(where isthesidelengthofthesquares)forsimplicity.Wecanextenduntilithitstheextensionof.Callthispoint.Theareaoftriangle thenis Theareaofrectangle is.Thus,ourdesiredareais.Now,theratiooftheshadedareatothecombinedareaofthethreesquaresis.Solution2Letthesidelengthofeachsquarebe.Lettheintersectionof and be.Since,.Since andareverticalangles,theyarecongruent.Wealsohave bydefinition.Sowehave by congruence.Therefore,.Since and aremidpointsofsides,.Thiscombinedwith yields.Theareaoftrapezoid is.Theareaoftriangle is.Sotheareaofthepentagon is.Theareaofthe squaresis.Therefore,.Solution3Lettheintersectionof and be.Nowwehave and.Becausebothtriangleshasasideoncongruentsquarestherefore.Because and areverticalangles.Alsoboth and arerightanglesso.ThereforebyAAS(Angle,Angle,Side).Thentranslating/rotatingtheshaded intothepositionofSotheshadedareanowcompletelycoversthesquareSettheareaofasquareasTherefore,.25.Solution1Theradiusoftheballis2inches.Ifyouthinkabouttheballrollingordrawapathfortheball(seefigurebelow),youseethatinAandCitloses inches,anditgains inchesonB.So,thedeparturefromthelengthofthetrackmeansthattheansweris.Solution2Thetotallengthofallofthearcsis.Sincewewantthepathfromthecenter,theactualdistancewillbeshorter.Therefore,theonlyanswerchoicelessthan is.Thissolutionmaybeinvalidbecausetheactualdistancecanbelongerifthepaththecent ertravelsisontheoutsideofthecurve,asitisinthemiddlebump.。

AMC美国数学竞赛AMC.B 试题及答案解析

2003A M C10 B 1、Which of the following is the same asSolution2、Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pink pill, and Al’s pills cost a total of for the two weeks. How much does one green pill costSolution3、The sum of 5 consecutive even integers is less than the sum of the rst consecutive odd counting numbers. What is the smallest of the even integersSolution4、Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the gure. She plants one flower per square foot in each region. Asters cost 1 each, begonias 1.50 each, cannas 2 each, dahlias 2.50 each, and Easter lilies 3 each. What is the least possible cost, in dollars, for her gardenSolution5、Moe uses a mower to cut his rectangular -foot by -foot lawn. The swath he cuts is inches wide, but he overlaps each cut by inches tomake sure that no grass is missed. He walks at the rate of feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow his lawnSolution.6、Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length of a “-inch” television screen is closest, in inches, to which of the followingSolution7、The symbolism denotes the largest integer not exceeding . For example. , and . ComputeSolution.8、The second and fourth terms of a geometric sequence are and . Which of the following is a possible first termSolution9、Find the value of that satisfies the equationSolution10、Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of three letters followed by three digits. By how many times is the number of possible license plates increasedSolution11、A line with slope intersects a line with slope at the point . What is the distance between the -intercepts of these two linesSolution12、Al, Betty, and Clare split among them to be invested in different ways. Each begins with a different amount. At the end of one year they have a total of . Betty and Clare have both doubled their money, whereas Al has managed to lose . What was Al’s original portionSolution.13、Let denote the sum of the digits of the positive integer . For example, and . For how many two-digit values of isSolution14、Given that , where both and are positive integers, find the smallest possible value for .Solution15、There are players in a singles tennis tournament. The tournament is single elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest players are given a bye, and the remaining players are paired off to play. After each round, the remaining players play in the next round. The match continues until only one player remains unbeaten. The total number of matches played isSolution16、A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that the restaurant should offer so that a customer could have a different dinner each night in the yearSolution.17、An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly ll the cone. Assume that the melted ice cream occupies of the volume of the frozen ice cream. What is the ratio of the cone’s height to its radiusSolution18、What is the largest integer that is a divisor offor all positive even integersSolution19、Three semicircles of radius are constructed on diameter of a semicircle of radius . The centers of the small semicircles divide into four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicirclesSolution20、In rectangle , and . Points and are on so that and . Lines and intersect at . Find the area of .Solution21、A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardless of the color you pulled out. What is the probability that all beads in the bag are red after three such replacementsSolution22、A clock chimes once at minutes past each hour and chimes on the hour according to the hour. For example, at 1 PM there is one chime and at noon and midnight there are twelve chimes. Starting at 11:15 AM on February , , on what date will the chime occurSolution23、A regular octagon has an area of one square unit. What is the area of the rectangleSolution24、The rst four terms in an arithmetic sequence are , , , and, in that order. What is the fth termSolution25、How many distinct four-digit numbers are divisible by and have as their last two digitsSolution。

amc 美国数学竞赛 amc 10b 试题及答案解析

2004 AMC 10BProblem 1Each row of the Misty Moon Amphitheater has 33 seats. Rows 12 through 22 are reserved for a youth club. How many seats are reserved for this club?There are rows of seats, giving seats.Problem 2How many two-digit positive integers have at least one 7 as a digit?Ten numbers () have as the tens digit. Nine numbers () have it as the ones digit. Number is in both sets.Thus the result is .Problem 3At each basketball practice last week, Jenny made twice as many free throws as she made at the previous practice. At her fifth practice she made48 free throws. How many free throws did she make at the first practice?At the fourth practice she made throws, at the third one it was , then we get throws for the second practice, and finally throws at the first one.Problem 4A standard six-sided die is rolled, and P is the product of the five numbers that are visible. What is the largest number that is certain to divide P?Solution 1The product of all six numbers is . The products of numbers that can be visible are , , ..., . The answer to this problem is their greatest common divisor -- which is , where is the least common multiple of . Clearly and the answer is .Solution 2Clearly, can not have a prime factor other than , and .We can not guarantee that the product will be divisible by , as the number can end on the bottom.We can guarantee that the product will be divisible by (one of and will always be visible), but not by .Finally, there are three even numbers, hence two of them are always visible and thus the product is divisible by . This is the most we can guarantee, as when the is on the bottom side, the two visible even numbers are and , and their product is not divisible by .Hence .Problem 5In the expression , the values of , , , and are , , , and , although not necessarily in that order. What is the maximum possible value of the result?If or , the expression evaluates to .If , the expression evaluates to .Case remains.In that case, we want to maximize where .Trying out the six possibilities we get that the best one is, where .Problem 6Which of the following numbers is a perfect square?Using the fact that , we can write:▪▪▪▪▪Clearly is a square, and as , , and are primes, none of the other four are squares.Problem 7On a trip from the United States to Canada, Isabella took U.S. dollars. At the border she exchanged them all, receiving Canadian dollars for every U.S. dollars. After spending Canadian dollars, she had Canadian dollars left. What is the sum of the digits of ?Solution 1Isabella had Canadian dollars. Setting up an equation we get, which solves to , and the sum of digits of isSolution 2Each time Isabelle exchanges U.S. dollars, she gets Canadian dollars and Canadian dollars extra. Isabelle received a total of Canadian dollars extra, therefore she exchanged U.S. dollars times. Thus .Problem 8Minneapolis-St. Paul International Airport is 8 miles southwest of downtown St. Paul and 10 miles southeast of downtown Minneapolis. Which of the following is closest to the number of miles between downtown St. Paul and downtown Minneapolis?The directions "southwest" and "southeast" are orthogonal. Thus the described situation is a right triangle with legs 8 miles and 10 mileslong. The hypotenuse length is , and thus the answer is .Without a calculator one can note that . Problem 9A square has sides of length 10, and a circle centered at one of its vertices has radius 10. What is the area of the union of the regions enclosed by the square and the circle?The area of the circle is , the area of the square is . Exactly of the circle lies inside the square. Thus the total area is.Problem 10A grocer makes a display of cans in which the top row has one can and each lower row has two more cans than the row above it. If the display contains cans, how many rows does it contain?The sum of the first odd numbers is . As in our case , we have .Problem 11Two eight-sided dice each have faces numbered 1 through 8. When the dice are rolled, each face has an equal probability of appearing on the top. What is the probability that the product of the two top numbers is greater than their sum?Solution 1We have , hence if at least one of the numbers is , the sum is larger. There such possibilities.We have .For we already have , hence all other cases are good.Out of the possible cases, we found that in the sum is greater than or equal to the product, hence in it is smaller. Therefore the answer is .Solution 2Let the two rolls be , and .From the restriction:Since and are non-negative integers between and , either , , orif and only if or .There are ordered pairs with , ordered pairs with , and ordered pair with and . So, there areordered pairs such that .if and only if and or equivalently and . This gives ordered pair .So, there are a total of ordered pairs with .Since there are a total of ordered pairs , there are ordered pairs with .Thus, the desired probability is .Problem 12An annulus is the region between two concentric circles. The concentric circles in the ﬁgure have radii and , with . Let be a radius of the larger circle, let be tangent to the smaller circle at , and let be the radius of the larger circle that contains . Let , , and . What is the area of the annulus?The area of the large circle is , the area of the small one is , hence the shaded area is .From the for the right triangle we have , hence and thus the shaded area is .Problem 13In the United States, coins have the following thicknesses: penny, mm; nickel, mm; dime, mm; quarter, mm. If a stack of these coins is exactly mm high, how many coins are in the stack?All numbers in this solution will be in hundreds of a millimeter.The thinnest coin is the dime, with thickness . A stack of dimes has height .The other three coin types have thicknesses , , and . By replacing some of the dimes in our stack by other, thicker coins, we can clearly create exactly all heights in the set.If we take an odd , then all the possible heights will be odd, and thus none of them will be . Hence is even.If the stack will be too low and if it will be too high. Thus we are left with cases and .If the possible stack heights are , with the remaining ones exceeding .Therefore there are coins in the stack.Using the above observation we can easily construct such a stack. A stack of dimes would have height , thus we need to add . This can be done for example by replacing five dimes by nickels (for ), and one dime by a penny (for ).Problem 14A bag initially contains red marbles and blue marbles only, with moreblue than red. Red marbles are added to the bag until only of the marbles in the bag are blue. Then yellow marbles are added to the baguntil only of the marbles in the bag are blue. Finally, the number of blue marbles in the bag is doubled. What fraction of the marbles now in the bag are blue?We can ignore most of the problem statement. The only important information is that immediately before the last step blue marbles formed of the marbles in the bag. This means that there were blue and other marbles, for some . When we double the number of blue marbles, there will be blue and other marbles, hence bluemarbles now form of all marbles in the bag.Problem 15Patty has coins consisting of nickels and dimes. If her nickels were dimes and her dimes were nickels, she would have cents more. How much are her coins worth?Solution 1She has nickels and dimes. Their total cost iscents. If the dimes were nickels and vice versa, she would havecents. This value should be cents more than the previous one. We get , which solves to . Her coins are worth .Solution 2Changing a nickel into a dime increases the sum by cents, and changing a dime into a nickel decreases it by the same amount. As the sum increased by cents, there are more nickels than dimes. As the total count is , this means that there are nickels and dimes.Problem 16Three circles of radius are externally tangent to each other and internally tangent to a larger circle. What is the radius of the large circle?The situation in shown in the picture below. The radius we seek is . Clearly . The point is clearly the center of the equilateral triangle , thus is of the altitude of this triangle. We get that . Therefore the radius we seek is.WARNING. Note that the answer does not correspond to any of the five options. Most probably there is a typo in option D.Problem 17The two digits in Jack's age are the same as the digits in Bill's age, but in reverse order. In five years Jack will be twice as old as Bill will be then. What is the difference in their current ages?Solution 1If Jack's current age is , then Bill's current age is .In five years, Jack's age will be and Bill's age will be .We are given that . Thus .For we get . For and the value is not an integer, and for it is more than . Thus the only solution is , and the difference in ages is .Solution 2Age difference does not change in time. Thus in five years Bill's age will be equal to their age difference.The age difference is , hence it is a multiple of . Thus Bill's current age modulo must be .Thus Bill's age is in the set .As Jack is older, we only need to consider the cases where the tens digit of Bill's age is smaller than the ones digit. This leaves us with the options .Checking each of them, we see that only works, and gives the solution .Problem 18In the right triangle , we have , , and . Points , , and are located on , , and , respectively, so that , , and . What is the ratio of the area of to that of ?First of all, note that , and therefore.Draw the height from onto as in the picture below:Now consider the area of . Clearly the triangles and are similar, as they have all angles equal. Their ratio is ,hence . Now the area of can be computed as= . Similarly we can find that as well.Hence , and the answer is .Problem 19In the sequence , , , , each term after the third is found by subtracting the previous term from the sum of the two terms that precede that term. For example, the fourth term is. What is the term in this sequence?Solution 1We already know that , , , and . Let's compute the next few terms to get the idea how the sequence behaves. We get ,, , and so on.We can now discover the following pattern: and . This is easily proved by induction. It follows that.Solution 2Note that the recurrence can be rewritten as.Hence we get that and alsoFrom the values given in the problem statement we see that .From we get that .From we get that .Following this pattern, we get.Problem 20In points and lie on and , respectively. If and intersect at so that and , what is ?Solution (Triangle Areas)We use the square bracket notation to denote area.Without loss of generality, we can assume . Then , and . We have , so we need to find the area of quadrilateral .Draw the line segment to form the two triangles and . Let , and . By considering trianglesand , we obtain , and by considering triangles and , we obtain . Solving, we get , , so the area of quadrilateral is .ThereforeSolution (Mass points)The presence of only ratios in the problem essentially cries out for mass points.As per the problem, we assign a mass of to point , and a mass of to . Then, to balance and on , has a mass of .Now, were we to assign a mass of to and a mass of to , we'd have . Scaling this down by (to get , which puts and in terms of the masses of and ), we assign a mass of to and a mass of to .Now, to balance and on , we must give a mass of . Finally, the ratio of to is given by the ratio of the mass of tothe mass of , which is .Solution (Coordinates)Affine transformations preserve ratios of distances, and for any pair of triangles there is an affine transformation that maps the first one onto the second one. This is why the answer is the same for any , and we just need to compute it for any single triangle.We can choose the points , , and . This way we will have , and . The situation is shown in the picture below:The point is the intersection of the lines and . The points on the first line have the form , the points on the second line have the form . Solving for we get , hence.The ratio can now be computed simply by observing the coordinates of , , and :Problem 21Let ; ; and ; ; be two arithmetic progressions. The set is the union of the first terms of each sequence. How many distinct numbers are in ?The two sets of terms are and.Now . We can compute. We will now find .Consider the numbers in . We want to find out how many of them lie in . In other words, we need to find out the number of valid values of for which .The fact "" can be rewritten as ", and ".The first condition gives , the second one gives .Thus the good values of are , and their count is .Therefore , and thus .Problem 22A triangle with sides of 5, 12, and 13 has both an inscribed and a circumscribed circle. What is the distance between the centers of those circles?This is obviously a right triangle. Pick a coordinate system so that the right angle is at and the other two vertices are at and .As this is a right triangle, the center of the circumcircle is in the middle of the hypotenuse, at .The radius of the inscribed circle can be computed using the well-known identity , where is the area of the triangle and its perimeter. In our case, and , thus . As the inscribed circle touches both legs, its center must be at .The distance of these two points is then.Problem 23Each face of a cube is painted either red or blue, each with probability 1/2. The color of each face is determined independently. What is the probability that the painted cube can be placed on a horizontal surface so that the four vertical faces are all the same color?Label the six sides of the cube by numbers to as on a classic dice. Then the "four vertical faces" can be: , , or .Let be the set of colorings where are all of the same color, similarly let and be the sets of good colorings for the other two sets of faces.There are possible colorings, and there are goodcolorings. Thus the result is . We need to compute .Using the we can writeClearly , as we have two possibilities for the common color of the four vertical faces, and two possibilities for each of the horizontal faces.What is ? The faces must have the same color, and at the same time faces must have the same color. It turns out thatthe set containing just the two cubes where all six faces have the same color.Therefore , and the result is .Problem 24In we have , , and . Point is on the circumscribed circle of the triangle so that bisects . What is the value of ?Problem 25A circle of radius is internally tangent to two circles of radius at points and , where is a diameter of the smaller circle. What is the area of the region, shaded in the picture, that is outside the smaller circle and inside each of the two larger circles?The area of the small circle is . We can add it to the shaded region, compute the area of the new region, and then subtract the area of the small circle from the result.Let and be the intersections of the two large circles. Connect them to and to get the picture below:Now obviously the triangles and are equilateral with side .Take a look at the bottom circle. The angle is , hence the sector is of the circle. The same is true for the sector of the bottom circle, and sectors and of the top circle.If we now sum the areas of these four sectors, we will almost get the area of the new shaded region - except that each of the two equilateral triangles will be counted twice.Hence the area of the new shaded region is, and the area of the original shared region is .。

amc 美国数学竞赛 00 amc 0b 试题及答案解析

2003 AMC 10B1、Which of the following is the same asSolution2、Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pinkpill, and Al’s pills cost a total of for the two weeks. How much doesone green pill cost?Solution3、The sum of 5 consecutive even integers is less than the sum of theﬁrst consecutive odd counting numbers. What is the smallest of theeven integers?Solution4、Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the ﬁgure. She plants one flower per square foot in each region. Asters cost 1 each,begonias 1.50 each, cannas 2 each, dahlias 2.50 each, and Easterlilies 3 each. What is the least possible cost, in dollars, for hergarden?Solution5、Moe uses a mower to cut his rectangular -foot by -foot lawn.The swath he cuts is inches wide, but he overlaps each cut byinches to make sure that no grass is missed. He walks at the rate of feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow his lawn?Solution.6、Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length ofa “-inch” television screen is closest, in inches, to which of thefollowing?Solution7、The symbolism denotes the largest integer not exceeding . Forexample. , and . ComputeSolution.8、The second and fourth terms of a geometric sequence are and .Which of the following is a possible first term?Solution9、Find the value of that satisfies the equationSolution10、Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of three letters followed by three digits. By how many times is the number of possible license plates increased?Solution11、A line with slope intersects a line with slope at the point .What is the distance between the -intercepts of these two lines?Solution12、Al, Betty, and Clare split among them to be invested indifferent ways. Each begins with a different amount. At the end of one year they have a total of . Betty and Clare have both doubledtheir money, whereas Al has managed to lose . What was Al’soriginal portion?Solution.13、Let denote the sum of the digits of the positive integer . Forexample, and . For how many two-digitvalues of is ?Solution14、Given that , where both and are positive integers,find the smallest possible value for .Solution15、There are players in a singles tennis tournament. Thetournament is single elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest players aregiven a bye, and the remaining players are paired off to play. Aftereach round, the remaining players play in the next round. The match continues until only one player remains unbeaten. The total number of matches played isSolution16、A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that the restaurant should offer so that a customer could have a different dinner each night in the year ?Solution.17、An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly ﬁll the cone. Assume that the melted ice cream occupies of the volume of the frozen ice cream. What is theratio of the cone’s height to its radius?Solution18、What is the largest integer that is a divisor offor all positive even integers ?Solution19、Three semicircles of radius are constructed on diameter of asemicircle of radius . The centers of the small semicircles divideinto four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside thesmaller semicircles?Solution20、In rectangle , and . Points and are onso that and . Lines and intersect at . Findthe area of .Solution21、A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardless of the color you pulled out. What is the probability that all beads in the bag are red after three such replacements?22、A clock chimes once at minutes past each hour and chimes onthe hour according to the hour. For example, at 1 PM there is one chime and at noon and midnight there are twelve chimes. Starting at11:15 AM on February , , on what date will the chimeoccur?Solution23、A regular octagon has an area of one square unit.What is the area of the rectangle ?Solution24、The ﬁrst four terms in an arithmetic sequence are , , ,and , in that order. What is the ﬁfth term?Solution25、How many distinct four-digit numbers are divisible by and haveas their last two digits?Solution。

2017amc10b解析

2017amc10b解析摘要：一、引言二、2017 AMC 10 B 的概述1.考试日期和时间2.考试地点3.考试难度和题型三、2017 AMC 10 B 的题目解析1.题目一a.题目内容b.解题思路c.答案及解析2.题目二a.题目内容b.解题思路c.答案及解析3.题目三a.题目内容b.解题思路c.答案及解析4.题目四a.题目内容b.解题思路c.答案及解析5.题目五a.题目内容b.解题思路c.答案及解析四、2017 AMC 10 B 的备考建议1.提前规划备考时间2.熟悉题型和难度3.加强解题技巧和方法4.参加模拟考试和培训课程五、结论正文：一、引言2017 AMC 10 B（American Mathematics Competition 10 级别B 组）是美国数学竞赛的一个级别，面向十年级及以下的学生。

本篇文章将对2017 年的AMC 10 B 竞赛进行解析，帮助大家更好地了解该次竞赛的情况，并提供一些备考建议。

二、2017 AMC 10 B 的概述1.考试日期和时间2017 AMC 10 B 竞赛的考试日期为某年某月某日，考试时长为25 分钟。

2.考试地点本次竞赛在全国各大城市设立了考点，考生可以根据自己的地理位置选择最近的考点参加考试。

3.考试难度和题型2017 AMC 10 B 竞赛的题目难度适中，题型包括选择题和填空题。

竞赛内容涵盖了代数、几何、组合、数论和概率等领域，全面考察学生的数学能力。

三、2017 AMC 10 B 的题目解析1.题目一题目内容：某正方体的体积为V，已知它的表面积是S，求V/S 的值。

解题思路：根据正方体的表面积和体积公式，可以得到V=S^3。

将V/S 表示为S^2，可得V/S=S^2。

答案及解析：V/S=S^2。

2.题目二题目内容：已知某等差数列的前n 项和为Sn，其中S10=20，S20=60，求该等差数列的通项公式。

解题思路：利用等差数列的求和公式，可以得到S10=10a1+45d=20，S20=20a1+190d=60。

2020 AMC 10B (美国数学竞赛)真题加详解

2020 AMC 10B Solution Problem1What is the value ofSolutionWe know that when we subtract negative numbers, .The equation becomesProblem2Carl has cubes each having side length , and Kate has cubes each having side length . What is the total volume of these cubes?SolutionA cube with side length has volume , so of these will have a total volume of .A cube with side length has volume , so of these will have a total volume of .~quacker88Problem 3The ratio of to is , the ratio of to is , and the ratioof to is . What is the ratio of toSolution 1WLOG, let and .Since the ratio of to is , we can substitute in the value of toget .The ratio of to is , so .The ratio of to is then so our answeris ~quacker88Solution 2We need to somehow link all three of the ratios together. We can start by connecting the last two ratios together by multiplying the last ratio by two., and since , we can link themtogether to get .Finally, since , we can link this again to get: ,so ~quacker88Problem4The acute angles of a right triangle are and , where andboth and are prime numbers. What is the least possible value of ?SolutionSince the three angles of a triangle add up to and one of the anglesis because it's a right triangle, .The greatest prime number less than is . If ,then , which is not prime.The next greatest prime number less than is . If ,then , which IS prime, so we have our answer ~quacker88 Solution 2Looking at the answer choices, only and are coprime to . Testing , the smaller angle, makes the other angle which is prime, therefore our answerisProblem5How many distinguishable arrangements are there of 1 brown tile, 1 purple tile, 2 green tiles, and 3 yellow tiles in a row from left to right? (Tiles of the same color are indistinguishable.)SolutionLet's first find how many possibilities there would be if they were all distinguishable, then divide out the ones we overcounted.There are ways to order objects. However, since there's ways to switch the yellow tiles around without changing anything (since they're indistinguishable) and ways to order the green tiles, we have to divide out these possibilities.~quacker88SolutionWe can repeat chooses extensively to find the answer. Thereare choose ways to arrange the brown tiles which is . Then from the remaining tiles there are choose ways to arrange the red tiles. And now from the remaining two tiles and two slots we can see there are two ways to arrange the purple and brown tiles, giving us an answerofProblem6Driving along a highway, Megan noticed that her odometershowed (miles). This number is a palindrome-it reads the same forward and backward. Then hours later, the odometer displayed the next higher palindrome. What was her average speed, in miles per hour, during this -hour period?SolutionIn order to get the smallest palindrome greater than , we need to raise the middle digit. If we were to raise any of the digits after the middle, we would be forced to also raise a digit before the middle to keep it a palindrome, making it unnecessarily larger.So we raise to the next largest value, , but obviously, that's not how place value works, so we're in the s now. To keep this a palindrome, our number is now .So Megan drove miles. Since this happened over hours, she drove at mph. ~quacker88 Problem7How many positive even multiples of less than are perfect squares?SolutionAny even multiple of is a multiple of , so we need to find multiples of that are perfect squares and less than . Any solution that we want will be in theform , where is a positive integer. The smallest possible value isat , and the largest is at (where the expression equals ). Therefore, there are a total of possible numbers.-PCChess Problem8Points and lie in a plane with . How many locations forpoint in this plane are there such that the triangle with vertices , ,and is a right triangle with area square units?Solution 1There are options here:1. is the right angle.It's clear that there are points that fit this, one that's directly to the rightof and one that's directly to the left. We don't need to find the length, we just need to know that it is possible, which it is.2. is the right angle.Using the exact same reasoning, there are also solutions for this one.3. The new point is the right angle.(Diagram temporarily removed due to asymptote error)The diagram looks something like this. We know that the altitude tobase must be since the area is . From here, we must see if there are valid triangles that satisfy the necessary requirements.First of all, because of the area.Next, from the Pythagorean Theorem.From here, we must look to see if there are valid solutions. There are multiple ways to do this:We know that the minimum value of iswhen . In this case, the equationbecomes , which is LESSthan . . The equationbecomes , which is obviously greater than . We canconclude that there are values for and in between that satisfy the Pythagorean Theorem.And since , the triangle is not isoceles, meaning we could reflectit over and/or the line perpendicular to for a total of triangles this case.Solution 2Note that line segment can either be the shorter leg, longer leg or thehypotenuse. If it is the shorter leg, there are two possible points for that cansatisfy the requirements - that being above or below . As such, thereare ways for this case. Similarly, one can find that there are also ways for point to lie if is the longer leg. If it is a hypotenuse, then thereare possible points because the arrangement of the shorter and longer legs can be switched, and can be either above or below the line segment. Therefore, the answer is .Problem9How many ordered pairs of integers satisfy theequationSolutionRearranging the terms and and completing the square for yields theresult . Then, notice that can onlybe , and because any value of that is greater than 1 will causethe term to be less than , which is impossible as must be real. Therefore, plugging in the above values for gives the orderedpairs , , , and gives a totalof ordered pairs.Solution 2Bringing all of the terms to the LHS, we see a quadraticequation in terms of . Applying the quadratic formula, weget In order for to be real, which it must be given the stipulation that we are seekingintegral answers, we know that the discriminant, must benonnegative. Therefore, Here, we see that we must split the inequality into a compound, resultingin .The only integers that satisfy this are . Plugging thesevalues back into the quadratic equation, we see that both produce a discriminant of , meaning that there is only 1 solution for .If , then the discriminant is nonzero, therefore resulting in two solutions for .Thus, the answer is .~TiblisSolution 3, x firstSet it up as a quadratic in terms of y:Then the discriminant is This will clearly only yield real solutionswhen , because it is always positive. Then . Checking each one: and are the same when raised to the 2020th power:This has only has solutions , so are solutions. Next, if :Which has 2 solutions, so andThese are the only 4 solutions, soSolution 4, y firstMove the term to the other side toget . Because for all , then . If or , the right side is and therefore . When , the right side become , therefore . Our solutions are , , , . There are solutions, so the answer is - wwt7535Problem 10A three-quarter sector of a circle of radius inches together with its interior can be rolled up to form the lateral surface area of a right circular cone by taping together along the two radii shown. What is the volume of the cone in cubicinches?SolutionNotice that when the cone is created, the radius of the circle will become the slant height of the cone and the intact circumference of the circle will become the circumference of the base of the cone.We can calculate that the intact circumference of the circle is . Since that is also equal to the circumference of the cone, the radius of the cone is . We also have that the slant height of the cone is . Therefore, we use the Pythagorean Theorem to calculate that the height of the coneis . The volume of the coneis -PCChessSolution 2 (Last Resort/Cheap)Using a ruler, measure a circle of radius 4 and cut out the circle and then the quarter missing. Then, fold it into a cone and measure the diameter to be 6cm . You can form a right triangle with sides 3, 4, and then through the Pythagorean theorem the height is found tobe . The volume of a cone is . Plugging in we findProblem11Ms. Carr asks her students to read any 5 of the 10 books on a reading list. Harold randomly selects 5 books from this list, and Betty does the same. What is the probability that there are exactly 2 books that they both select?SolutionWe don't care about which books Harold selects. We just care that Bettypicks books from Harold's list and that aren't on Harold's list.The total amount of combinations of books that Betty can selectis .There are ways for Betty to choose of the books that are on Harold's list.From the remaining books that aren't on Harold's list, thereare ways to choose of them.~quacker88Problem12The decimal representation of consists of a string of zeros after the decimal point, followed by a and then several more digits. How many zeros are in that initial string of zeros after the decimal point?Solution 1Now we do some estimation. Notice that , which meansthat is a little more than . Multiplying itwith , we get that the denominator is about . Notice that whenwe divide by an digit number, there are zeros before the first nonzero digit. This means that when we divide by the digitinteger , there are zeros in the initial string after the decimal point. -PCChessSolution 2First rewrite as . Then, we know that when we write this in decimal form, there will be 40 digits after the decimal point. Therefore, we just have to findthe number of digits in .and memming (alternatively use the factthat ),digits.Our answer is .Solution 3 (Brute Force)Just as in Solution we rewrite as We thencalculate entirely by hand, first doing then multiplying that product by itself, resulting in Because this is digits,after dividing this number by fourteen times, the decimal point is beforethe Dividing the number again by twenty-six more times allows a stringof zeroes to be formed. -OreoChocolateSolution 4 (Smarter Brute Force)Just as in Solutions and we rewrite as We can then look at the number of digits in powersof . , , , , ,, and so on. We notice after a few iterations that every power of five with an exponent of , the number of digits doesn't increase. This means should have digits since thereare numbers which are from to , or digits total. This means our expression can be written as , where is in therange . Canceling gives , or zeroes before the since the number should start on where the one would be in . ~aop2014 Solution 5 (Logarithms)Problem13Andy the Ant lives on a coordinate plane and is currently at facingeast (that is, in the positive -direction). Andy moves unit and thenturns degrees left. From there, Andy moves units (north) and thenturns degrees left. He then moves units (west) and againturns degrees left. Andy continues his progress, increasing his distance each time by unit and always turning left. What is the location of the point at which Andy makes the th leftturn?Solution 1You can find that every four moves both coordinates decrease by 2. Therefore, both coordinates need to decrease by two 505 times. You subtract, giving you theanswer of ~happykeeperProblem14As shown in the figure below, six semicircles lie in the interior of a regular hexagon with side length 2 so that the diameters of the semicircles coincide with the sides of the hexagon. What is the area of the shaded region — inside the hexagon but outside all of the semicircles?Solution 1Let point A be a vertex of the regular hexagon, let point B be the midpoint of the line connecting point A and a neighboring vertex, and let point C be the second intersection of the two semicircles that pass through point A. Then, , since B is the center of the semicircle with radius 1 that C lies on, , since B is the center of the semicircle with radius 1 that A lies on,and , as a regular hexagon has angles of 120,and is half of any angle in this hexagon. Now, using the sinelaw, , so . Since the angles in a triangle sum to 180, is also 60. Therefore, is an equilateral triangle with side lengths of 1.Since the area of a regular hexagon can be found with the formula , where is the side length of the hexagon, the area of this hexagonis . Since the area of an equilateral triangle can be foundwith the formula , where is the side length of the equilateral triangle,the area of an equilateral triangle with side lengths of 1 is . Since the area of a circle can be found with the formula , the area of a sixthof a circle with radius 1 is . In each sixth of the hexagon, thereare two equilateral triangles colored white, each with an area of , and onesixth of a circle with radius 1 colored white, with an area of . The rest of the sixth is colored gray. Therefore, the total area that is colored white in each sixthof the hexagon is , which equals , and the total areacolored white is , which equals . Since the area colored gray equals the total area of the hexagon minus the area colored white,the area colored gray is , whichequals .Solution 2First, subdivide the hexagon into 24 equilateral triangles with side length1:Now note that the entire shadedregion is just 6 times this part:The entire rhombus is just 2 equilatrial triangles with side lengths of 1, so it has an area of:The arc that is not included has an area of:Hence, the area ofthe shaded region in that section is For a final areaof:Problem15Steve wrote the digits , , , , and in order repeatedly from left to right, forming a list of digits, beginning He thenerased every third digit from his list (that is, the rd, th, th, digits from the left), then erased every fourth digit from the resulting list (that is, the th, th, th, digits from the left in what remained), and then erased every fifth digit from what remained at that point. What is the sum of the three digits that were then in the positions ?Solution 1After erasing every third digit, the list becomes repeated. After erasing every fourth digit from this list, the listbecomes repeated. Finally, after erasing every fifth digit from this list, the list becomes repeated. Since this list repeats every digits andsince are respectively in we have that the th, th, and st digits are the rd, th, and thdigits respectively. It follows that the answer is~dolphin7Problem16Bela and Jenn play the following game on the closed interval of the real number line, where is a fixed integer greater than . They take turns playing, with Bela going first. At his first turn, Bela chooses any real number in theinterval . Thereafter, the player whose turn it is chooses a real numberthat is more than one unit away from all numbers previously chosen by either player. A player unable to choose such a number loses. Using optimal strategy, which player will win the game?SolutionNotice that to use the optimal strategy to win the game, Bela must select themiddle number in the range and then mirror whatever number Jennselects. Therefore, if Jenn can select a number within the range, so can Bela. Jenn will always be the first person to run out of a number to choose, so theanswer is .Solution 2 (Guessing)First of all, realize that the value of should have no effect on the strategy at all. This is because they can choose real numbers, not integers, so even if is odd, for example, they can still go halfway. Similarly, there is no reason the strategy would change when .So we are left with (A) and (B). From here it is best to try out random numbers and try to find the strategy that will let Bela win, but if you can't find it, realize thatit is more likely the answer is since Bela has the first move and thus has more control.Problem17There are people standing equally spaced around a circle. Each person knows exactly of the other people: the people standing next to her or him, as well as the person directly across the circle. How many ways are there forthe people to split up into pairs so that the members of each pair know each other?SolutionLet us use casework on the number of diagonals.Case 1: diagonals There are ways: either pairs with , pairs with , and so on or pairs with , pairs with , etc.Case 2: diagonal There are possible diagonals to draw (everyone else pairs with the person next to them.Note that there cannot be 2 diagonals.Case 3: diagonalsNote that there cannot be a case with 4 diagonals because then there would have to be 5 diagonals for the two remaining people, thus a contradiction.Case 4: diagonals There is way to do this.Thus, in total there are possible ways. Problem18An urn contains one red ball and one blue ball. A box of extra red and blue balls lie nearby. George performs the following operation four times: he draws a ball from the urn at random and then takes a ball of the same color from the box and returns those two matching balls to the urn. After the four iterations the urn contains six balls. What is the probability that the urn contains three balls of each color?SolutionLet denote that George selects a red ball and that he selects a blue one. Now, in order to get balls of each color, he needs more of both and .There are 6cases:(wecan confirm that there are only since ). However we canclump , ,and together since they are equivalent by symmetry.andLet's find the probability that he picks the balls in the order of .The probability that the first ball he picks is red is .Now there are reds and blue in the urn. The probability that he picks red again is now .There are reds and blue now. The probability that he picks a blue is .Finally, there are reds and blues. The probability that he picks a blue is . So the probability that the case happensis . However, since the case is the exactsame by symmetry, case 1 has a probability of chance of happening.andLet's find the probability that he picks the balls in the order of .The probability that the first ball he picks is red is .Now there are reds and blue in the urn. The probability that he picks blue is .There are reds and blues now. The probability that he picks a red is . Finally, there are reds and blues. The probability that he picks a blue is .So the probability that the case happensis . However, since the case is the exactsame by symmetry, case 2 has a probability of chance of happening.andLet's find the probability that he picks the balls in the order of .The probability that the first ball he picks is red is .Now there are reds and blue in the urn. The probability that he picks blueis .There are reds and blues now. The probability that he picks a blue is .Finally, there are reds and blues. The probability that he picks a red is .So the probability that the case happensis . However, since the case is the exactsame by symmetry, case 3 has a probability of chance of happening.Adding up the cases, we have ~quacker88 Solution 2We know that we need to find the probability of adding 2 red and 2 blue balls insome order. There are 6 ways to do this, since there are ways to arrange in some order. We will show that the probability for each of these 6 ways is the same.We first note that the denominators should be counted by the same number. This number is . This is because 2, 3, 4, and 5 represent how many choices there are for the four steps. No matter what the stepinvolves numbers to choose from.The numerators are the number of successful operations. No matter the order, the first time a red is added will come from 1 choice and the second time will come from 2 choices, since that is how many reds are in the urn originally. Thesame goes for the blue ones. The numerator must equal . Therefore, the probability for each of the orderingsof is . There are 6 of these, so the total probabilityis .Solution 3First, notice that when George chooses a ball he just adds another ball of the same color. On George's first move, he either chooses the red or the blue witha chance each. We can assume he chooses Red(chance ), and then multiply the final answer by two for symmetry. Now, there are two red balls andone blue ball in the urn. Then, he can either choose another Red(chance ), in which case he must choose two blues to get three of each, withprobability or a blue for two blue and two red in the urn, withchance . If he chooses blue next, he can either choose a red then a blue, or ablue then a red. Each of these has a for total of . The total probability that he ends up with three red and three blueis . ~aop2014 Solution 4Let the probability that the urn ends up with more red balls be denoted . Since this is equal to the probability there are more blue balls, the probabilitythere are equal amounts is . the probability no more blues are chosen plus the probability only 1 more blue is chosen. The firstcase, .The second case, . Thus,the answer is .~JHawk0224Solution 5By conditional probability after 4 rounds we have 5 cases: RRRBBB, RRRRBB,RRBBBB, RRRRRB and RBBBBB. Thus the probability is . Put .~FANYUCHEN20020715Edited by KinglogicSolution 6Here X stands for R or B, and Y for the remaining color. After 3 rounds one can either have a 4+1 configuration (XXXXY), or 3+2 configuration (XXXYY). Theprobability of getting to XXXYYY from XXXYY is . Observe that the probability of arriving to 4+1 configuration is ( to get from XXY toXXXY, to get from XXXY to XXXXY). Thus the probability of arriving to 3+2configuration is also , and the answer isSolution 7We can try to use dynamic programming to solve this problem. (Informatics Olympiad hahaha)We let be the probability that we end up with red balls and blue balls. Notice that there are only two ways that we can end up with red balls and blue balls: one is by fetching a red ball from the urn when wehave red balls and blue balls and the other is by fetching a blue ball from the urn when we have red balls and blue balls.Then wehaveThen we start can with and try to compute .The answer is .Problem19In a certain card game, a player is dealt a hand of cards from a deckof distinct cards. The number of distinct (unordered) hands that can be dealt to the player can be written as . What is the digit ?Solution 1We're looking for the amount of ways we can get cards from a deck of ,which is represented by .We need to get rid of the multiples of , which will subsequently get rid of the multiples of (if we didn't, the zeroes would mess with the equation since you can't divide by 0), , leaves us with 17.Converting these into, we have~quacker88 Solution 2Since this number is divisible by but not , the last digits must be divisible by but the last digits cannot be divisible by . This narrows the options down to and .Also, the number cannot be divisible by . Adding up the digits, weget . If , then the expression equals , a multiple of . This would mean that the entire number would be divisible by , which is not what we want. Therefore, the only option is -PCChessSolution 3It is not hard to check that divides thenumber,As , using wehave .Thus , implying so the answer is .Solution 4As mentioned above,We can divide both sidesof by 10 to obtain which means is simply the units digit of the left-hand side. This valueisProblem20Let be a right rectangular prism (box) with edges lengths and ,together with its interior. For real , let be the set of points in -dimensional space that lie within a distance of some point . The volumeof can be expressed as ,where and are positive real numbers. What isSolutionSplit into 4 regions:1. The rectangular prism itself2. The extensions of the faces of3. The quarter cylinders at each edge of4. The one-eighth spheres at each corner ofRegion 1: The volume of is 12, soRegion 2: The volume is equal to the surface area of times . The surfacearea can be computed to be ,so .Region 3: The volume of each quarter cylinder is equal to . The sum of all such cylinders must equal times the sum of the edge lengths. This can be computed as , so the sum of the volumes of the quarter cylinders is , soRegion 4: There is an eighth of a sphere of radius at each corner. Since there are 8 corners, these add up to one full sphere of radius . The volume of thissphere is , so .Using these values,Problem21In square , points and lie on and , respectively, so that Points and lie on and , respectively, and points and lie on so that and . See the figure below. Triangle , quadrilateral ,quadrilateral , and pentagon each has area Whatis ?SolutionSince the total area is , the side length of square is . We see that since triangle is a right isosceles triangle with area 1, we can determinesides and both to be . Now, considerextending and until they intersect. Let the point of intersection be .We note that is also a right isosceles triangle with side and find it's area to be . Now, we notice that is also a rightisosceles triangle and find it's area to be . This is also equalto or . Since we are looking for , we want two times this. That gives .~TLiuSolution 2Since this is a geometry problem involving sides, and we know that is , we can use our ruler and find the ratio between and . Measuring(on the booklet), we get that is about inches and isabout inches. Thus, we can then multiply the length of by the ratioof of which we then get We take the square of that andget and the closest answer to that is . ~Celloboy (Note that this is just a strategy I happened to use that worked. Do not press your luck with this strategy, for it was a lucky guess)Solution 3Draw the auxiliary line . Denote by the point it intersects with , and by the point it intersects with . Last, denote by the segment , and by the segment . We will find two equations for and , and then solve for .Since the overall area of is ,and . In addition, the areaof .The two equations for and are then:Lengthof :Area of CMIF: .Substituting the first into the second,yieldsSolving for gives ~DrBSolution 4Plot a point such that and are collinear and extend line topoint such that forms a square. Extend line to meetline and point is the intersection of the two. The area of this square is equivalent to . We see that the area of square is , meaning each side is of length 2. The area of the pentagon is .Length , thus . Triangle is isosceles, and the area of this triangleis . Adding these two areas, we get . --OGBooger Solution 5 (HARD Calculation)We can easily observe that the area of square is 4 and its side length is 2 since all four regions that build up the square has area 1. Extend and let the intersection with be . Connect , and let the intersectionof and be . Notice that since the area of triangle is 1and , ,therefore . Let ,。

AMC美国数学竞赛AMC.B 试题及答案解析

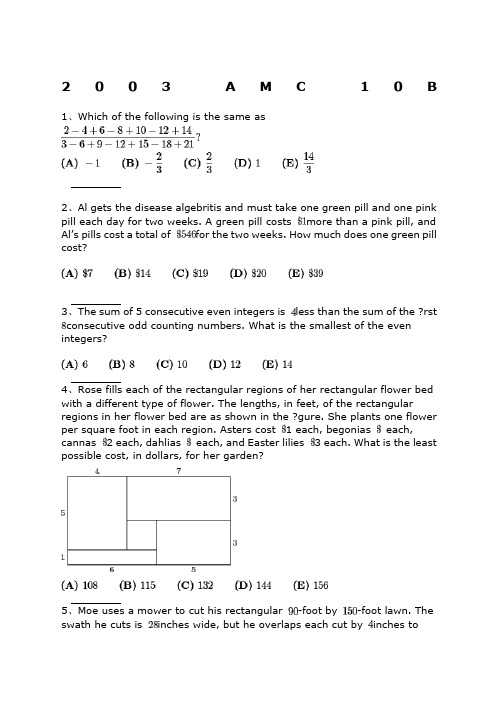
2003A M C10 B 1、Which of the following is the same as2、Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pink pill, and Al’s pills cost a total of for the two weeks. How much does one green pill cost?3、The sum of 5 consecutive even integers is less than the sum of the ?rst consecutive odd counting numbers. What is the smallest of the even integers?4、Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the ?gure. She plants one flower per square foot in each region. Asters cost 1 each, begonias each, cannas 2 each, dahlias each, and Easter lilies 3 each. What is the least possible cost, in dollars, for her garden?5、Moe uses a mower to cut his rectangular -foot by -foot lawn. The swath he cuts is inches wide, but he overlaps each cut by inches tomake sure that no grass is missed. He walks at the rate of feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow his lawn?.6、Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length of a “-inch” television screen is closest, in inches, to which of the following?7、The symbolism denotes the largest integer not exceeding . For example. , and . Compute.8、The second and fourth terms of a geometric sequence are and . Which of the following is a possible first term?9、Find the value of that satisfies the equation10、Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of three letters followed by three digits. By how many times is the number of possible license plates increased?11、A line with slope intersects a line with slope at the point . What is the distance between the -intercepts of these two lines?12、Al, Betty, and Clare split among them to be invested in different ways. Each begins with a different amount. At the end of one year they have a total of . Betty and Clare have both doubled their money, whereas Al has managed to lose . What was Al’s origin al portion?.13、Let denote the sum of the digits of the positive integer . For example, and . For how many two-digit values of is ?14、Given that , where both and are positive integers, find the smallest possible value for .15、There are players in a singles tennis tournament. The tournament is single elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest players are given a bye, and the remaining players are paired off to play. After each round, the remaining players play in the next round. The match continues until only one player remains unbeaten. The total number of matches played is16、A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that the restaurant should offer so that a customer could have a different dinner each night in the year ?.17、An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly ?ll the cone. Assume that the melted ice cream occupies of the volume of the frozen ice cream. What is the ratio of the cone’s height to its radius?18、What is the largest integer that is a divisor offor all positive even integers ?19、Three semicircles of radius are constructed on diameter of a semicircle of radius . The centers of the small semicircles divide into four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicircles?20、In rectangle , and . Points and are on so that and . Lines and intersect at . Find the area of .21、A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardless of the color you pulled out. What is the probability that all beads in the bag are red after three such replacements?22、A clock chimes once at minutes past each hour and chimes on the hour according to the hour. For example, at 1 PM there is one chime and at noon and midnight there are twelve chimes. Starting at 11:15 AM on February , , on what date will the chime occur?23、A regular octagon has an area of one square unit. What is the area of the rectangle ?24、The ?rst four terms in an arithmetic sequence are , , , and, in that order. What is the ?fth term?25、How many distinct four-digit numbers are divisible by and have as their last two digits?。

2013amc10b解析

2013 AMC 10B 题解AMC（American Mathematics Competitions）是美国数学竞赛的官方组织，每年举办一系列的数学竞赛。

AMC 10是其中面向高中生的一项竞赛，题目涵盖了代数、几何、概率等多个数学领域。

本文将详细解析2013年AMC 10B的题目。

## 题目1 一个正方形的时钟以每分钟1单位的速度运行。

它在12:00时指向12，那么在以下几个时间点它会指向3： - A. 3:00 - B. 3:05 - C. 3:10 - D. 3:15 - E. 3:20解析：一个圆周的周长是360度，而时钟在12小时内转了720度。

所以每分钟转动的角度是720/60=12度。

因为一个正方形有4个直角，所以时钟指向3点的时候，它转过的角度是3个直角=3*90=270度。

所以，它在12:00时指向12的话，在12:00 + 270/12分钟时会指向3。

计算这个时间是12:00 + 22.5分钟=12:00 + 22分30秒。

所以答案是B. 3:05。

题目2x和y是两个不为1的整数，满足xx−1=yy−1. 如果x+y=1242，那么x的值是多少？解析：我们可以通过代数运算来解决这个问题。

首先我们将等式两边都乘以(x−1)(y−1)，得到x(y−1)=y(x−1)。

然后展开并整理得到xy−x=xy−y。

消去xy的项得到−x=−y，进一步化简得到x=y。

我们已知x+y=1242，所以x+x=2x=1242。

解得x=12422=621。

所以答案是621。

题目3一个20个球的集合，其中有2个红球和18个蓝球。

抽取这些球中的3个，不放回，求恰好抽取到2个红球的概率。

解析：抽取到2个红球的概率等于抽取到2个红球和1个蓝球的概率。

首先，从2个红球中选择2个的概率是C(2,2)C(20,3)，其中C(n,m)表示从n个不同的元素中选择m个的组合数。

然后，从18个蓝球中选择1个的概率是C(18,1)C(20,3)。