美国数学竞赛AMC题目及答案
美国AMC8数学竞赛试题(含答案)

2001 年 美国AMC8 (2001年 月 日 时间40分钟)1. 卡西的商店正在制作一个高尔夫球奖品。
他必须给一颗高尔夫球面上的300个小凹洞着色, 如果他每着色一个小凹洞需要2秒钟,试问共需多 分钟才能完成他的工作。
(A) 4 (B) 6 (C) 8 (D) 10 (E) 12 。
2. 我正在思考两个正整数,它们的乘积是24且它们的和是11,试问这两个数中较大的数是什 么 。
(A) 3 (B) 4 (C) 6 (D) 8 (E) 12 。
3. 史密斯有63元,艾伯特比安加多2元,而安加所有的钱是史密斯的三分之一,试问艾伯特 有 元。
(A) 17 (B) 18 (C) 19 (D) 21 (E) 23 。
4. 在每个数字只能使用一次的情形下,将1,2,3,4及9作成最小的五位数,且此五位数为 偶数,则其十位数字为 。
(A) 1 (B) 2 (C) 3 (D) 4 (E) 9 。
5. 在一个暴风雨的黑夜里,史努比突然看见一道闪光。
10秒钟后,他听到打雷声音。
声音的速 率是每秒1088呎,但1哩是5280呎。
若以哩为单位的条件下,估计史努比离闪电处的距离 最接近下列何者 。
(A) 1 (B) 121 (C) 2 (D) 221 (E) 3 。
6. 在一笔直道路的一旁有等间隔的6棵树。
第1棵树与第4棵树之间的距离是60呎。
试问第1 棵树到最后一棵树之间的距离是 呎。
(A) 90 (B) 100 (C) 105 (D) 120 (E) 140 。
问题7、8、9请参考下列叙述:主题:竞赛场所上的风筝展览7. 葛妮芙为提升她的学校年度风筝奥林匹亚竞赛的质量,制作了一个小风筝与一个大风筝,并陈列在公告栏展览,这两个风筝都如同图中的形状,葛妮芙将小风筝张贴在单位长为一吋(即每两点距离一吋)的格子板上,并将大风筝张贴在单位长三吋(即每两点距离三吋)的格子板上。
试问小风筝的面积是 平方吋。
(A) 21 (B) 22 (C) 23 (D) 24 (E) 25 。
美国数学竞赛AMC题目及答案

2.3.What is the value of ?4.Eight friends ate at a restaurant and agreed to share the bill equally. Because Judi forgot her money, each of her seven friends paid an extra $2.50 to cover her portion of the total bill. What was the total bill?5.Hammie is in the grade and weighs 106 pounds. His quadruplet sisters are tiny babies and weigh 5, 5, 6, and 8 pounds. Which is greater, the average (mean) weight of these five children or the median weight, and by how many pounds?6.The number in each box below is the product of the numbers in the two boxes that touch it in the row above. For example, . What is the missing number in the top row?7.Trey and his mom stopped at a railroad crossing to let a train pass. As the train began to pass, Trey counted 6 cars in the first 10 seconds. It took the train 2 minutes and 45 seconds to clear the crossing at a constant speed. Which of the following was the most likely number of cars in the train?8.A fair coin is tossed 3 times. What is the probability of at least two consecutive heads?9.The Incredible Hulk can double the distance he jumps with each succeeding jump. If his first jump is 1 meter, the second jump is 2 meters, the third jump is 4 meters, and so on, then on which jump will he first be able to jump more than 1 kilometer?10.What is the ratio of the least common multiple of 180 and 594 to the greatest common factor of 180 and 594?11. Ted's grandfather used his treadmill on 3 days this week. He went 2 miles each day. On Monday he jogged at a speed of 5 miles per hour. He walked at the rate of 3 miles per hour on Wednesday and at 4 miles per hour on Friday. If Grandfather had always walked at 4 miles per hour, he would have spent less time on the treadmill. How many minutes less?12. At the 2013 Winnebago County Fair a vendor is offering a "fair special" on sandals. If you buy one pair of sandals at the regular price of $50, you get a second pair at a 40% discount, and a third pair at half the regular price. Javier took advantage of the "fair special" to buy three pairs of sandals. What percentage of the $150 regular price did he save?13. When Clara totaled her scores, she inadvertently reversed the units digit and the tens digit of one score. By which of the following might her incorrect sum have differed from the correct one?14. Let the two digits be and .The correct score was . Clara misinterpreted it as . The difference between the two is which factors into . Therefore, since the difference is a multiple of 9, the only answerchoice that is a multiple of 9 is .15. If , , and , what is the product of , , and ?16. A number of students from Fibonacci Middle School are taking part in a community service project. The ratio of -graders to -graders is , and the the ratio of -graders to -graders is . What is the smallest number of students that could be participating in the project?17. The sum of six consecutive positive integers is 2013. What is the largest of these six integers?18. Isabella uses one-foot cubical blocks to build a rectangular fort that is 12 feet long, 10 feet wide, and 5 feet high. The floor and the four walls are all one foot thick. How many blocks does the fort contain?--Arpanliku 16:22, 27 November 2013 (EST) Courtesy of Lord.of.AMC19. Bridget, Cassie, and Hannah are discussing the results of their last math test. Hannah shows Bridget and Cassie her test, but Bridget and Cassie don't show theirs to anyone. Cassie says, 'I didn't get the lowest score in our class,' and Bridget adds, 'I didn't get the highest score.' What is the ranking of the three girls from highest to lowest?20. A rectangle is inscribed in a semicircle with longer side on the diameter. What is the area of the semicircle?21. Samantha lives 2 blocks west and 1 block south of the southwest corner of City Park. Her school is 2 blocks east and 2 blocks north of the northeast corner of City Park. On school days she bikes on streets to the southwest corner of City Park, then takes a diagonal path through the park to the northeast corner, and then bikes on streets to school. If her route is as short as possible, how many different routes can she take?22. Toothpicks are used to make a grid that is 60 toothpicks long and 32 toothpicks wide. How many toothpicks are used altogether?23. Angle of is a right angle. The sides of are the diameters of semicircles as shown. The area of the semicircle on equals , and the arc of the semicircle on has length .What is the radius of the semicircle on ?24. Squares , , and are equal in area. Points and are the midpoints of sidesand , respectively. What is the ratio of the area of the shaded pentagon to the sum of the areas of the three squares?25. A ball with diameter 4 inches starts at point A to roll along the track shown. The track is comprised of 3 semicircular arcs whose radii are inches, inches, and inches, respectively. The ball always remains in contact with the track and does not slip. What is the distance the center of theball travels over the course from A to B?1.2.The 50% off price of half a pound of fish is $3, so the 100%, or the regular price, of a half pound of fish is $6. Consequently, if half a pound of fish costs $6, then a whole pound of fish is dollars.3.Notice that we can pair up every two numbers to make a sum of 1:Therefore, the answer is .4.Each of her seven friends paid to cover Judi's portion. Therefore, Judi's portion must be . Since Judi was supposed to pay of the total bill, the total bill must be .5.The median here is obviously less than the mean, so option (A) and (B) are out.Lining up the numbers (5, 5, 6, 8, 106), we see that the median weight is 6 pounds.The average weight of the five kids is .Therefore, the average weight is bigger, by pounds, making the answer.6.Solution 1: Working BackwardsLet the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.We see that , making .It follows that , so .Solution 2: Jumping Back to the StartAnother way to do this problem is to realize what makes up the bottommost number. This method doesn't work quite as well for this problem, but in a larger tree, it might be faster. (In this case, Solution 1 would be faster since there's only two missing numbers.)Again, let the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.We can write some equations:Now we can substitute into the first equation using the two others:7.If Trey saw , then he saw .2 minutes and 45 seconds can also be expressed as seconds.Trey's rate of seeing cars, , can be multiplied by on the top and bottom (and preserve the same rate):. It follows that the most likely number of cars is . Solution 2minutes and seconds is equal to .Since Trey probably counts around cars every seconds, there are groups of cars that Trey most likely counts. Since , the closest answer choice is .8.First, there are ways to flip the coins, in order.The ways to get two consecutive heads are HHT and THH.The way to get three consecutive heads is HHH.Therefore, the probability of flipping at least two consecutive heads is .9.This is a geometric sequence in which the common ratio is 2. To find the jump that would be over a 1000 meters, we note that .However, because the first term is and not , the solution to the problem is10. To find either the LCM or the GCF of two numbers, always prime factorize first.The prime factorization of .The prime factorization of .Then, find the greatest power of all the numbers there are; if one number is one but not the other, use it (this is ). Multiply all of these to get 5940.For the GCF of 180 and 594, use the least power of all of the numbers that are in both factorizations and multiply. = 18.Thus the answer = = .We start off with a similar approach as the original solution. From the prime factorizations, the GCF is .It is a well known fact that . So we have,.Dividing by yields .Therefore, .11. We use that fact that . Let d= distance, r= rate or speed, and t=time. In this case, let represent the time.On Monday, he was at a rate of . So, .For Wednesday, he walked at a rate of . Therefore, .On Friday, he walked at a rate of . So, .Adding up the hours yields + + = .We now find the amount of time Grandfather would have taken if he walked at per day. Set up the equation, .To find the amount of time saved, subtract the two amounts: - = . To convert this to minutes, we multiply by .Thus, the solution to this problem is12. First, find the amount of money one will pay for three sandals without the discount. We have.Then, find the amount of money using the discount: .Finding the percentage yields .To find the percent saved, we have13. Let the two digits be and .The correct score was . Clara misinterpreted it as . The difference between the two is which factors into . Therefore, since the difference is a multiple of 9, the only answerchoice that is a multiple of 9 is .14. The probability that both show a green bean is . The probability that both show a red bean is . Therefore the probability is15.Therefore, .Therefore, .To most people, it would not be immediately evident that , so we can multiply 6's until we get the desired number:, so .Therefore the answer is .16. Solution 1: AlgebraWe multiply the first ratio by 8 on both sides, and the second ratio by 5 to get the same number for 8th graders, in order that we can put the two ratios together:Therefore, the ratio of 8th graders to 7th graders to 6th graders is . Since the ratio is in lowest terms, the smallest number of students participating in the project is .Solution 2: FakesolvingThe number of 8th graders has to be a multiple of 8 and 5, so assume it is 40 (the smallest possibility). Then there are 6th graders and 7th graders. The numbers of students is17. Solution 1The mean of these numbers is . Therefore the numbers are, so the answer isSolution 2Let the number be . Then our desired number is .Our integers are , so we have that.Solution 3Let the first term be . Our integers are . We have,18. Solution 1There are cubes on the base of the box. Then, for each of the 4 layers above the bottom (as since each cube is 1 foot by 1 foot by 1 foot and the box is 5 feet tall, there are 4 feet left), there arecubes. Hence, the answer is .Solution 2We can just calculate the volume of the prism that was cut out of the original box. Each interior side of the fort will be feet shorter than each side of the outside. Since the floor is foot, the height will be feet. So the volume of the interior box is .The volume of the original box is . Therefore, the number of blocks contained inthe fort is .19. If Hannah did better than Cassie, there would be no way she could know for sure that she didn't get the lowest score in the class. Therefore, Hannah did worse than Cassie. Similarly, if Hannah did worse than Bridget, there is no way Bridget could have known that she didn't get the highest in the class.Therefore, Hannah did better than Bridget, so our order is .20.A semicircle has symmetry, so the center is exactly at the midpoint of the 2 side on the rectangle, making the radius, by the Pythagorean Theorem, . The area is .21.The number of ways to get from Samantha's house to City Park is , and the number of ways toget from City Park to school is . Since there's one way to go through City Park (just walking straight through), the number of different ways to go from Samantha's house to City Park to school .22. There are vertical columns with a length of toothpicks, and there are horizontal rows with a length of toothpicks. An effective way to verify this is to try a small case, i.e. a grid of toothpicks.Thus, our answer is .23. Solution 1If the semicircle on AB were a full circle, the area would be 16pi. Therefore the diameter of the first circle is 8. The arc of the largest semicircle would normally have a complete diameter of 17. The Pythagoreantheorem says that the other side has length 15, so the radius is .Solution 2We go as in Solution 1, finding the diameter of the circle on AC and AB. Then, an extended version of the theorem says that the sum of the semicircles on the left is equal to the biggest one, so the area of thelargest is , and the middle one is , so the radius is .24.First let (where is the side length of the squares) for simplicity. We can extend until it hits theextension of . Call this point . The area of triangle then is The area of rectangle is . Thus, our desired area is . Now, the ratio of the shaded area to thecombined area of the three squares is .Let the side length of each square be .Let the intersection of and be .Since , . Since and are vertical angles, they are congruent. We also have by definition.So we have by congruence. Therefore, .Since and are midpoints of sides, . This combined with yields.The area of trapezoid is .The area of triangle is .So the area of the pentagon is .The area of the squares is .Therefore, .Let the intersection of and be .Now we have and .Because both triangles has a side on congruent squares therefore .Because and are vertical angles .Also both and are right angles so .Therefore by AAS(Angle, Angle, Side) .Then translating/rotating the shaded into the position ofSo the shaded area now completely covers the squareSet the area of a square asTherefore, .25. Solution 1The radius of the ball is 2 inches. If you think about the ball rolling or draw a path for the ball (see figure below), you see that in A and C it loses inches, and it gains inches on B.So, the departure from the length of the track means that the answer is . Solution 2The total length of all of the arcs is . Since we want the path from the center, the actual distance will be shorter. Therefore, the only answer choice less than is . Thissolution may be invalid because the actual distance can be longer if the path the center travels is on the outside of the curve, as it is in the middle bump.古希腊哲学大师亚里士多德说:人有两种,一种即“吃饭是为了活着”,一种是“活着是为了吃饭”.一个人之所以伟大,首先是因为他有超于常人的心。
amc试题及答案

amc试题及答案1. 问题:已知函数 \( f(x) = 3x^2 - 2x + 5 \),求 \( f(2) \) 的值。
答案:将 \( x = 2 \) 代入函数 \( f(x) \) 中,得到 \( f(2) = 3(2)^2 - 2(2) + 5 = 12 - 4 + 5 = 13 \)。
2. 问题:解方程 \( 2x - 5 = 9 \)。
答案:首先将方程两边同时加5,得到 \( 2x = 14 \),然后除以2,得到 \( x = 7 \)。
3. 问题:如果一个圆的直径是10厘米,那么它的半径是多少?答案:圆的半径是直径的一半,所以半径 \( r = \frac{10}{2} = 5 \) 厘米。
4. 问题:计算 \( \sqrt{49} \)。
答案:\( \sqrt{49} = 7 \)。
5. 问题:一个班级有30名学生,其中20名是男生。
这个班级的男生比例是多少?答案:男生比例是 \( \frac{20}{30} = \frac{2}{3} \)。
6. 问题:如果一个三角形的两个内角分别是 \( 45^\circ \) 和\( 60^\circ \),那么第三个角是多少度?答案:三角形的内角和为 \( 180^\circ \),所以第三个角是\( 180^\circ - 45^\circ - 60^\circ = 75^\circ \)。
7. 问题:计算 \( 2^3 \)。
答案:\( 2^3 = 2 \times 2 \times 2 = 8 \)。
8. 问题:一个数的平方根是4,这个数是多少?答案:这个数是 \( 4^2 = 16 \)。
9. 问题:如果一个数的两倍加上3等于15,求这个数。
答案:设这个数为 \( x \),那么 \( 2x + 3 = 15 \)。
解这个方程,得到 \( 2x = 12 \),所以 \( x = 6 \)。
10. 问题:一个长方形的长是10厘米,宽是5厘米,求它的周长。
2023年AMC10美国数学竞赛A卷附中文翻译和答案

2023AMC10美国数学竞赛A卷1. A cell phone plan costs $20 each month, plus 5¢ per text message sent, plus 10¢ for each minute used over 30 hours. In January Michelle sent 100 text messages and talked for 30.5 hours. How much did she have to pay?(A) $24.00 (B) $24.50 (C) $25.50 (D) $28.00 (E) $30.002. A small bottle of shampoo can hold 35 milliliters of shampoo, Whereas a large bottle can hold 500 milliliters of shampoo. Jasmine wants to buy the minimum number of small bottles necessary to completely fill a large bottle. How many bottles must she buy?(A) 11 (B) 12 (C) 13 (D) 14 (E) 153. Suppose [a b] denotes the average of a and b, and {a b c} denotes the average of a, b, and c. What is {{1 1 0} [0 1] 0}?(A) (B)(C)(D) (E)4. Let X and Y be the following sums of arithmetic sequences:X= 10 + 12 + 14 + …+ 100.Y= 12 + 14 + 16 + …+ 102.What is the value of(A) 92 (B) 98 (C) 100 (D) 102 (E) 1125. At an elementary school, the students in third grade, fourth grade, and fifth grade run an average of 12, 15, and 10 minutes per day, respectively. There are twice as many third graders as fourth graders, and twice as many fourth graders as fifth graders. What is the average number of minutes run per day by these students?(A) 12 (B) (C) (D) 13 (E) 146. Set A has 20 elements, and set B has 15 elements. What is the smallest possible number of elements in A∪B, the union of A and B?(A) 5 (B) 15 (C) 20 (D) 35 (E) 3007. Which of the following equations does NOT have a solution?(A) (B) (C)(D) (E)8. Last summer 30% of the birds living on Town Lake were geese, 25% were swans, 10% were herons, and 35% were ducks. What percent of the birds that were not swans were geese?(A) 20 (B) 30 (C) 40 (D) 50 (E) 609. A rectangular region is bounded by the graphs of the equations y=a, y=-b, x=-c, and x=d, where a, b, c, and d are all positive numbers. Which of the following represents the area of this region?(A) ac + ad + bc + bd (B) ac – ad + bc – bd (C) ac + ad – bc – bd(D) –ac –ad + bc + bd (E) ac – ad – bc + bd10. A majority of the 20 students in Ms. Deameanor’s class bought pencils at the school bookstore. Each of these students bought the same number of pencils, and this number was greater than 1. The cost of a pencil in cents was greater than the number of pencils each student bought, and the total cost of all the pencils was $17.71. What was the cost of a pencil in cents?(A) 7 (B) 11 (C) 17 (D) 23 (E) 7711. Square EFGH has one vertex on each side of square ABCD. Point E is on AB with AE=7·EB. What is the ratio of the area of EFGH to the area of ABCD?(A) (B)(C)(D) (E)12. The players on a basketball team made some three-point shots, some two-point shots, some one-point free throws. They scored as many points with two-point shots as with three-point shots. Their number of successful free throws was one more than their number of successful two-point shots. The team’s total score was 61 points. How many free throws did they make?(A) 13 (B) 14 (C) 15 (D) 16 (E) 1713. How many even integers are there between 200 and 700 whose digits are alldifferent and come from the set {1, 2, 5, 7, 8, 9}?(A) 12 (B)20 (C)72 (D) 120 (E) 20014. A pair of standard 6-sided fair dice is rolled once. The sum of the numbers rolled determines the diameter of a circle. What is the probability that the numerical value of the area of the circle is less than the numerical value of the circle’s circumference?(A) (B)(C)(D) (E)15. Roy bought a new battery-gasoline hybrid car. On a trip the car ran exclusively on its battery for the first 40 miles, then ran exclusively on gasoline for the rest of the trip, using gasoline at a rate of 0.02 gallons per mile. On the whole trip he averaged55 miles per gallon. How long was the trip in miles?(A) 140 (B) 240 (C) 440 (D) 640 (E) 84016. Which of the following in equal to(A) (B) (C) (D) (E)17. In the eight-term sequence A, B, C, D, E, F, G, H, the value of C is 5 and the sum of any three consecutive terms is 30. What is A + H?(A) 17 (B) 18 (C) 25 (D) 26 (E) 4318. Circles A, B, and C each have radius 1. Circles A and B share one point of tangency. Circle C has a point of tangency with the midpoint of AB. What is the area inside Circle C but outside Circle A and Circle B?(B) (C) (D) (E)(A)19. In 1991 the population of a town was a perfect square. Ten years later, after an increase of 150 people, the population was 9 more than a perfect square. Now, in 2023, with an increase of another 150 people, the population is once again a perfect square. Which of the following is closest to the percent growth of the town’s popu lation during this twenty-year period?(A) 42 (B) 47 (C) 52 (D) 57 (E) 6220. Two points on the circumference of a circle of radius r are selected independently and at random. From each point a chord of length r is drawn in a clockwise direction. What is the probability that the two chords intersect?(A) (B) (C) (D) (E)21. Two counterfeit coins of equal weight are mixed with 8 identical genuine coins. The weight of each of the counterfeit coins is different from the weight of each of the genuine coins. A pair of coins is selected at random without replacement from the 10 coins. A second pair is selected at random without replacement from the remaining 8coins. The combined weight of the first pair is equal to the combined weight of the second pair. What is the probability that all 4 selected coins are genuine?(A) (B) (C) (D) (E)22. Each vertex of convex pentagon ABCDE is to be assigned a color. There are 6 colors to choose from, and the ends of each diagonal must have different colors. How many different colorings are possible?(A) 2500 (B) 2880 (C) 3120 (D) 3250 (E) 375023. Seven students count from 1 to 1000 as follows:·Alice says all the numbers, except she skips the middle number in each consecutive group of thre e numbers. That is Alice says 1, 3, 4, 6, 7, 9, …, 997, 999, 1000.·Barbara says all of the numbers that Alice doesn’t say, except she also skips the middle number in each consecutive grope of three numbers.·Candice says all of the numbers that neither Alice nor Barbara says, except she also skips the middle number in each consecutive group of three numbers. ·Debbie, Eliza, and Fatima say all of the numbers that none of the students with the first names beginning before theirs in the alphabet say, except each also skips the middle number in each of her consecutive groups of three numbers.·Finally, George says the only number that no one else says.What number does George say?(A) 37 (B) 242 (C) 365 (D) 728 (E) 99824. Two distinct regular tetrahedra have all their vertices among the vertices of the same unit cube. What is the volume of the region formed by the intersection of the tetrahedra?(A) (B) (C) (D) (E)an integer. A point X in the interior of R is25. Let R be a square region andcalled n-ray partitional if there are n rays emanating from X that divide R into N triangles of equal area. How many points are 100-ray partitional but not 60-ray partitional?(A) 1500 (B) 1560 (C) 2320 (D) 2480 (E) 25002023AMC10美国数学竞赛A卷1. 某通讯公司手机每月基本费为20美元, 每传送一则简讯收 5美分(一美元=100 美分)。
美国AMC10中文版试题及答案

2000到20XX年AMC10美国数学竞赛0 0P 0 A 0 B 0 C 0D 0 全美中学数学分级能力测验(AMC 10)2000年 第01届 美国AMC10 (2000年2月 日 时间75分钟)1. 国际数学奥林匹亚将于 在美国举办,假设I 、M 、O 分别表示不同的正整数,且满足I ⨯M ⨯O =2001,则试问I +M +O 之最大值为 。
(A) 23 (B) 55 (C) 99 (D) 111 (E) 6712. 2000(20002000)为 。
(A) 20002001 (B) 40002000 (C) 20004000 (D) 40000002000 (E) 200040000003. Jenny 每天早上都会吃掉她所剩下的聪明豆的20%,今知在第二天结束时,有32颗剩下,试问一开始聪明豆有 颗。
(A) 40 (B) 50 (C) 55 (D) 60 (E) 754. Candra 每月要付给网络公司固定的月租费及上网的拨接费,已知她12月的账单为12.48元,而她1月的账单为17.54元,若她1月的上网时间是12月的两倍,试问月租费是 元。
(A) 2.53 (B) 5.06 (C) 6.24 (D) 7.42 (E) 8.775. 如图M ,N 分别为PA 与PB 之中点,试问当P 在一条平行AB 的直 在线移动时,下列各数值有 项会变动。
(a) MN 长 (b) △P AB 之周长 (c) △P AB 之面积 (d) ABNM 之面积(A) 0项 (B) 1项 (C) 2项 (D) 3项 (E) 4项 6. 费氏数列是以两个1开始,接下来各项均为前两项之和,试问在费氏数列各项的个位数字中, 最后出现的阿拉伯数字为 。
(A) 0 (B) 4 (C) 6 (D) 7 (E) 97. 如图,矩形ABCD 中,AD =1,P 在AB 上,且DP 与DB 三等分∠ADC ,试问△BDP 之周长为 。
美国AMC10中文版试题及答案

2000到20XX年AMC10美国数学竞赛0 0P 0 A 0 B 0 C 0D 0 全美中学数学分级能力测验(AMC 10)2000年 第01届 美国AMC10 (2000年2月 日 时间75分钟)1. 国际数学奥林匹亚将于 在美国举办,假设I 、M 、O 分别表示不同的正整数,且满足I ⨯M ⨯O =2001,则试问I +M +O 之最大值为 。
(A) 23 (B) 55 (C) 99 (D) 111 (E) 6712. 2000(20002000)为 。
(A) 20002001 (B) 40002000 (C) 20004000 (D) 40000002000 (E) 200040000003. Jenny 每天早上都会吃掉她所剩下的聪明豆的20%,今知在第二天结束时,有32颗剩下,试问一开始聪明豆有 颗。
(A) 40 (B) 50 (C) 55 (D) 60 (E) 754. Candra 每月要付给网络公司固定的月租费及上网的拨接费,已知她12月的账单为12.48元,而她1月的账单为17.54元,若她1月的上网时间是12月的两倍,试问月租费是 元。
(A) 2.53 (B) 5.06 (C) 6.24 (D) 7.42 (E) 8.775. 如图M ,N 分别为PA 与PB 之中点,试问当P 在一条平行AB 的直 在线移动时,下列各数值有 项会变动。
(a) MN 长 (b) △P AB 之周长 (c) △P AB 之面积 (d) ABNM 之面积(A) 0项 (B) 1项 (C) 2项 (D) 3项 (E) 4项 6. 费氏数列是以两个1开始,接下来各项均为前两项之和,试问在费氏数列各项的个位数字中, 最后出现的阿拉伯数字为 。
(A) 0 (B) 4 (C) 6 (D) 7 (E) 97. 如图,矩形ABCD 中,AD =1,P 在AB 上,且DP 与DB 三等分∠ADC ,试问△BDP 之周长为 。
美国数学竞赛 美国高中数学竞赛 AMC 10 试题及答案 2000年-2015年

2000 AMC 10 ProblemsProblem 1In the year 2001, the United States will host the International Mathematical Olympiad. Let , , and be distinct positive integers such that the product 2001=••O M I . What is the largest possible value of the sum O M I ++ ?(A )23 (B )55 (C )99 (D )111 (E )671Problem 22000 (20002000)=(A )20012000 (B )20004000 (C )40002000 (D )2000000,000,4 (E )000,000,42000Problem 3Each day, Jenny ate 20% of the jellybeans that were in her jar at the beginning of that day. At the end of the second day, 32 remained. How many jellybeans were in the jar originally?(A )40 (B )50 (C )55 (D )60 (E )75Problem 4Chandra pays an on-line service provider a fixed monthly fee plus an hourly charge for connect time. Her December bill was , but in January her bill was because she used twice as much connect time as in December. What is the fixed monthly fee?(A )2.53 (B )5.06 (C )6.24 (D )7.42 (E )8.77Problem 5Points M and N are the midpoints of sides PA and PB of △PAB. As P moves along a line that is parallel to side AB, how many of the four quantities listed below change? (a) the length of the segment MN (b) the perimeter of △PAB(c) the area of △PAB (d) the area of trapezoid ABNM(A )0 (B )1 (C )2 (D )3 (E )4Problem 6The Fibonacci sequence 1,1,2,3,5,8,13,21,…… starts with two s, and each term afterwards is the sum of its two predecessors. Which one of the ten digits is the last to appear in the units position of a number in the Fibonacci sequence?(A )0 (B )4 (C )6 (D )7 (E )9Problem 7 In rectangle , , is on , and and trisect .What is the perimeter of ?(A )333+ (B )3342+ (C )222+ (D )2533+ (E )3352+ Problem 8At Olympic High School, 52 of the freshmen and 54 of the sophomores took the AMC-10. Given that the number of freshmen and sophomore contestants was the same, which of the following must be true?(A )There are five times as many sophomores as freshmen.(B )There are twice as many sophomores as freshmen.(C )There are as many freshmen as sophomores.(D )There are twice as many freshmen as sophomores.(E )There are five times as many freshmen as sophomores.Problem 9If , where , then(A )-2 (B )2 (C )2-2p (D )2p-2 (E )|2p-2|Problem 10The sides of a triangle with positive area have lengths , , and . The sides of a second triangle with positive area have lengths , , and . What is the smallest positive number that is not a possible value of |x-y |?(A )2 (B )4 (C )6 (D )8 (E )10Problem 11Two different prime numbers between 4 and 18 are chosen. When their sum is subtracted from their product, which of the following numbers could be obtained?(A )21 (B )60 (C )119 (D )180 (E )231Problem 12Figures 0, 1, 2 and 3 consist of 1, 5, 13, and 25 nonoverlapping unit squares, respectively. If the pattern were continued, how many nonoverlapping unit squares would there be infigure 100?Figure 0 Figure 1 Figure 2 Figure 3(A )10401 (B )19801 (C )20201 (D )39801 (E )40801 Problem 13There are 5 yellow pegs, 4 red pegs, 3 green pegs, 2 blue pegs, and 1 orange peg to be placed on a triangular peg board. In how many ways can the pegs be placed so that no (horizontal) row or (vertical) column contains two pegs of the same color?Problem 14Mrs. Walter gave an exam in a mathematics class of five students. She entered the scores in random order into a spreadsheet, which recalculated the class average after each score was entered. Mrs. Walter noticed that after each score was entered, the average was always an integer. The scores (listed in ascending order) were 71, 76, 80, 82, and 91. What was the last score Mrs. Walter entered?(A )71 (B )76 (C )80 (D )82 (E )91Problem 15Two non-zero real numbers, and , satisfy. Find a possible value of ab ab b a -+ . (A )-2 (B )-21 (C )31 (D )21 (E )2 Problem 16The diagram shows 28 lattice points, each one unit from its nearest neighbors. Segment AB meets segment CD at E. Find the length of segment AE.(A )354 (B )355 (C )7512 (D )52 (E )9565Boris has an incredible coin changing machine. When he puts in a quarter, it returns five nickels; when he puts in a nickel, it returns five pennies; and when he puts in a penny, it returns five quarters. Boris starts with just one penny. Which of the following amounts could Boris have after using the machine repeatedly?(A )<dollar/>3.63 (B )<dollar/>5.13 (C )<dollar/>6.30 (D )<dollar/>7.45 (E )<dollar/>9.07Problem 18Charlyn walks completely around the boundary of a square whose sides are each 5 km long. From any point on her path she can see exactly km horizontally in all directions. What is the area of the region consisting of all points Charlyn can see during her walk, expressed in square kilometers and rounded to the nearest whole number?(A )24 (B )27 (C )39 (D )40 (E )42Problem 19Through a point on the hypotenuse of a right triangle, lines are drawn parallel to the legs of the triangle so that the triangle is divided into a square and two smaller right triangles. The area of one of the two small right triangles is times the area of the square. The ratio of the area of the other small right triangle to the area of the square is(A )121 m (B )m (C )1-m (D )m 41 (E )281mProblem 20Let A, M, and C be nonnegative integers such that A+M+C=10. What is the maximum value of A ·M ·C + A ·M + M ·C +C ·A?(A )49 (B )59 (C )69 (D )79 (E )89Problem 21If all alligators are ferocious creatures and some creepy crawlers are alligators, which statement(s) must be true?I. All alligators are creepy crawlers.II. Some ferocious creatures are creepy crawlers.III. Some alligators are not creepy crawlers.(A )I only (B )II only (C )III only (D )II and III only (E )None must be true Problem 22One morning each member of Angela's family drank an 8-ounce mixture of coffee with milk. The amounts of coffee and milk varied from cup to cup, but were never zero. Angela drank a quarter of the total amount of milk and a sixth of the total amount of coffee. How many people are in the family?(A )3 (B )4 (C )5 (D )6 (E )7When the mean, median, and mode of the list 10, 2, 5, 2, 4, 2, x are arranged in increasing order, they form a non-constant arithmetic progression. What is the sum of all possible real values of ? (A )3 (B )6 (C )9 (D )17 (E )20Problem 24Let be a function for which. Find the sum of all values of for which. (A )-31 (B )-91 (C )0 (D )95 (E )35 Problem 25In year , the day of the year is a Tuesday. In year, the day is also a Tuesday. On what day of the week did the day of year occur?2000 AMC 10 SolutionProblem 1 The following problem is from both the 2000 AMC 12 #1 and 2000 AMC 10 #1, so both problems redirect to this page.The sum is the highest if two factors are the lowest.So, 1·3·776=2001 and 1+3+667=671 (E)Problem 2 The following problem is from both the 2000 AMC 12 #2 and 2000 AMC 10 #2, so both problems redirect to this page.2000 (20002000)=12000(20002000)=20012000 (A)Problem 3 The following problem is from both the 2000 AMC 12 #3 and 2000 AMC 10 #3, so both problems redirect to this pageSince Jenny eats 20% of her jelly beans per day, 80%=4/5 of her jelly beans remain after one day. Let be the number of jelly beans in the jar originally.325454=••x x=50 (B) Problem 4Let be the fixed fee, and be the amount she pays for the minutes she used in the first month.x+y=12.48 x+2y=17.54 y=5.06 x=7.42 We want the fixed fee, which is (D) Problem 5(a) Clearly AB does not change, and MN=0.5AB, so MN doesn't change either. (b) Obviously, the perimeter changes.(c) The area clearly doesn't change, as both the base AB and its corresponding height remain the same.(d) The bases AB and MN do not change, and neither does the height, so the area of the trapezoid remains the same.Only quantity changes, so the correct answer is .Problem 6 The following problem is from both the 2000 AMC 12 #4 and 2000 AMC 10 #6, so both problems redirect to this page.Note that any digits other than the units digit will not affect the answer. So to make computation quicker, we can just look at the Fibonacci sequence in :The last digit to appear in the units position of a number in the Fibonacci sequence is 6 (C).Problem 7AD=1 Since ∠ADC is trisected, ∠ADP=∠PDB=∠BDC=30º Thus, PD=332 BD=2 BP=332333=- Adding, 3342+Problem 8Let be the number of freshman and be the number of sophomores.s f 5452= f=2s There are twice as many freshmen as sophomores. Problem 9 The following problem is from both the 2000 AMC 12 #5 and 2000 AMC 10 #9, so both problems redirect to this page.When x<2, x-2 is negative so ∣x -2∣=2-x =p and x=2-pThus x-p=(2-p)-p=2-2p (C)Problem10From the triangle inequality, 2<x <10 and 2<y <10. The smallest positive number not possible is 10-2, which is . (D)Problem 11 The following problem is from both the 2000 AMC 12 #6 and 2000 AMC 10 #11, so both problems redirect to this page.All prime numbers between 4 and 18 have an odd product and an even sum. Any odd number minus an even number is an odd number, so we can eliminate B andD. Since the highest two prime numbers we can pick are 13 and 17, the highest number we can make is (13) (17) – (13+17) = 221-30=191. Thus, we can eliminateE. Similarly, the two lowest prime numbers we can pick are 5 and 7, so the lowest number we can make is (5) (7) – (5+7) =23. Therefore, A cannot be an answer. So, the answer must be .Problem 12 The following problem is from both the 2000 AMC 12 #8 and 2000 AMC 10 #12, so both problems redirect to this page.Solution 1We have a recursion: .I.E. we add increasing multiples of each time we go up a figure. So, to go from Figure 0 to 100, we addWe then add to the number of squares in Figure 0 to get, which ischoice Solution 2We can divide up figure to get the sum of the sum of the first odd numbers and the sum of the first odd numbers. If you do not see this, here is the example for :The sum of the first odd numbers is 2n , so for figure , thereare 22)1(n n ++ unit squares. We plug in n=100 to get 20201, which is choice Solution 3Using the recursion from solution 1, we see that the first differences of 4,8,12, … form an arithmetic progression, and consequently that the second differences are constant and all equal to . Thus, the original sequence can be generated from a quadratic function.If c bn an n f ++=2)(, and f(0)=1, f(1)=5, and f(2)=13, we get a system of three equations in three variables:f(0)=1 gives c=1; f(1)=5 gives a+b+c=5; f(2)=13 gives 4a+2b+c=13 Plugging in into the last two equations gives a+b=4 4a+2b=12 Dividing the second equation by 2 gives the system: a+b=4 2a+b=6Subtracting the first equation from the second gives , and hence . Thus, our quadratic function is: 122)(2++=n n n fCalculating the answer to our problem, f(100)=20201Problem 13In each column there must be one yellow peg. In particular, in the rightmost column, there is only one peg spot, therefore a yellow peg must go there.In the second column from the right, there are two spaces for pegs. One of them is in the same row as the corner peg, so there is only one remaining choice left forthe yellow peg in this column.By similar logic, we can fill in the yellow pegs as shown:After this we can proceed to fill in the whole pegboard, so there is only arrangement of the pegs. The answer is (B)Problem 14 The following problem is from both the 2000 AMC 12 #9 and 2000 AMC 10 #14, so both problems redirect to this page.Solution 1The first number is divisible by 1.The sum of the first two numbers is even.The sum of the first three numbers is divisible by 3.The sum of the first four numbers is divisible by 4.The sum of the first five numbers is 400.Since 400 is divisible by 4, the last score must also be divisible by 4. Therefore, the last score is either 76 or 80.Case 1: 76 is the last number entered.Since 400≡76≡1 (mod 3), the fourth number must be divisible by 3, but none of the scores are divisible by 3. Case 2: 80 is the last number entered. Since 80≡2 (mod 3), the fourth number must be 2 (mod 3). Thatnumber is 71 and only 71. The next number must be 91, since the sum of the first two numbers is even.So the only arrangement of the scores 76, 82, 91,71,80Solution 2We know the first sum of the first three numbers must be divisible by 3, so we write out all 5 numbers (mod 3), which gives 2,1,2,1,1, respectively. Clearly the only way to get a number divisible by 3 by adding three of these is by adding the three ones. So those must go first. Now we have an odd sum, and since the next average must be divisible by 4, 71 must be next. That leaves 80 for last, so the answer is .Problem 15 The following problem is from both the 2000 AMC 12 #11 and 2000 AMC 10 #15, so both problems redirect to this page.22)()()(22222=-=----+=--+=-+ba ab b a b a b a b a b a ab b a ab a b b a (E)Alternatively, we could test simple values, like )21,1(),(=b a , which would yield 2=-+ab ab b a Another way is to solve the equation for giving 1+=a a b , then substituting this into the expression and simplifying gives the answer ofProblem 16Solution 1Let be the line containing A and B and let be the line containing C and D. If we set the bottom left point at (0,0), then A=(0,3), B=(6,0), C=(4,2), and D=(2,0) . The line is given by the equation 11b x m y +=. The -intercept is A=(0,3), so 1b =3. We are given two points on , hence we can compute the slope, to be 210630-=-- , so is the line 321+-=x y Similarly, is given by 22b x m y +=. The slope in this case is 12402=--, so 2b x y +=. Plugging in the point (2,0) gives us 2b =-2, so is the line 2-=x y . At E, the intersection point, both of the equations must be true,2-=x y , 321+-=x y so 3212+-=-x x SO 310=x 34=y We have the coordinates of and , so we can use the distance formula here: 355)334()0310(22=-+- which is answer choiceSolution 2Draw the perpendiculars from andto , respectively. As it turns out, . Let be the point onfor which . , and, so by AA similarity,By the Pythagorean Theorem, wehave, ,。
AMC8(美国数学竞赛)历年真题、答案及中英文解析

AMC8(美国数学竞赛)历年真题、答案及中英文解析艾蕾特教育的AMC8 美国数学竞赛考试历年真题、答案及中英文解析:AMC8-2020年:真题 --- 答案---解析(英文解析+中文解析)AMC8 - 2019年:真题----答案----解析(英文解析+中文解析)AMC8 - 2018年:真题----答案----解析(英文解析+中文解析)AMC8 - 2017年:真题----答案----解析(英文解析+中文解析)AMC8 - 2016年:真题----答案----解析(英文解析+中文解析)AMC8 - 2015年:真题----答案----解析(英文解析+中文解析)AMC8 - 2014年:真题----答案----解析(英文解析+中文解析)AMC8 - 2013年:真题----答案----解析(英文解析+中文解析)AMC8 - 2012年:真题----答案----解析(英文解析+中文解析)析)AMC8 - 2010年:真题----答案----解析(英文解析+中文解析)AMC8 - 2009年:真题----答案----解析(英文解析+中文解析)AMC8 - 2008年:真题----答案----解析(英文解析+中文解析)AMC8 - 2007年:真题----答案----解析(英文解析+中文解析)AMC8 - 2006年:真题----答案----解析(英文解析+中文解析)AMC8 - 2005年:真题----答案----解析(英文解析+中文解析)AMC8 - 2004年:真题----答案----解析(英文解析+中文解析)AMC8 - 2003年:真题----答案----解析(英文解析+中文解析)AMC8 - 2002年:真题----答案----解析(英文解析+中文解析)AMC8 - 2001年:真题----答案----解析(英文解析+中文解析)AMC8 - 2000年:真题----答案----解析(英文解析+中文解析)析)AMC8 - 1998年:真题----答案----解析(英文解析+中文解析)AMC8 - 1997年:真题----答案----解析(英文解析+中文解析)AMC8 - 1996年:真题----答案----解析(英文解析+中文解析)AMC8 - 1995年:真题----答案----解析(英文解析+中文解析)AMC8 - 1994年:真题----答案----解析(英文解析+中文解析)AMC8 - 1993年:真题----答案----解析(英文解析+中文解析)AMC8 - 1992年:真题----答案----解析(英文解析+中文解析)AMC8 - 1991年:真题----答案----解析(英文解析+中文解析)AMC8 - 1990年:真题----答案----解析(英文解析+中文解析)AMC8 - 1989年:真题----答案----解析(英文解析+中文解析)AMC8 - 1988年:真题----答案----解析(英文解析+中文解析)析)AMC8 - 1986年:真题----答案----解析(英文解析+中文解析)AMC8 - 1985年:真题----答案----解析(英文解析+中文解析)◆AMC介绍◆AMC(American Mathematics Competitions) 由美国数学协会(MAA)组织的数学竞赛,分为 AMC8 、 AMC10、 AMC12 。
美国数学竞赛AMC8 -- 2006年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 – 2006年真题解析(英文解析+中文解析) \Problem 1Answer: DSolution:The three prices round to $2, $5, and $10, which has a sum of 17.中文解析:三件商品价格先近似取整,然后求和:2+5+10=17. 答案是D。
Problem 2Answer: CSolution:As the AMC 8 only rewards 1 point for each correct answer, everything is irrelevant except the number Billy answered correctly,13.中文解析:正确的题目每题1分,错误或没做的题目都是0分,做对13题的得分应该是13. 答案是C。
Problem 3Answer: ASolution:When Elisa started, she finished a lap in 25/10=2.5 minutes. Now, she finishes a lap is 24/12=2 minutes. The difference is 2.5-2=0.5中文解析:开始25分钟游10圈,平均2.5分钟游1圈。
后来24分钟游12圈,平均2分钟游1圈。
速度从2.5分钟提高到2分钟,提高了0.5分钟,即1/2 分钟。
答案是A。
Problem 4Answer: BSolution:If the spinner goes clockwise 2+1/4 revolutions and then counterclockwise 3+3/4 revolutions, it ultimately goes counterclockwise 1+1/2 which brings the spinner pointing east.中文解析:最初方向指向西,转整数圈不改变指针方向。
美国数学竞赛AMC题目及答案

2.3.Whatisthevalueof4.5.Hammieisinthegradeandweighs106pounds.Hisquadrupletsistersaretinybabiesandweigh5,5,6,and8pounds.W hichisgreater,theaverage(mean)weightofthesefivechildrenorthemedianweight,andbyhowman ypounds6.Thenumberineachboxbelowistheproductofthenumbersinthetwoboxesthattouchitintherowab ove.Forexample,.Whatisthemissingnumberinthetoprow7.8.Afaircoinistossed3times.Whatistheprobabilityofatleasttwoconsecutiveheads9.TheIncredibleHulkcandoublethedistancehejumpswitheachsucceedingjump.Ifhisfirstjumpis1 meter,thesecondjumpis2meters,thethirdjumpis4meters,andsoon,thenonwhichjumpwillhefirst beabletojumpmorethan1kilometer10.Whatistheratiooftheleastcommonmultipleof180and594tothegreatestcommonfactorof180a nd59411.12.Atthe2013WinnebagoCountyFairavendorisofferinga"fairspecial"onsandals.Ifyoubuyonepai rofsandalsattheregularpriceof$50,yougetasecondpairata40%discount,andathirdpairathalfthe regularprice.Javiertookadvantageofthe"fairspecial"tobuythreepairsofsandals.Whatpercentag eofthe$150regularpricedidhesave13.WhenClaratotaledherscores,sheinadvertentlyreversedtheunitsdigitandthetensdigitofones core.Bywhichofthefollowingmightherincorrectsumhavedifferedfromthecorrectone14.Letthetwodigitsbe and.Thecorrectscorewas.Claramisinterpreteditas.Thedifferencebetweenthetwoiswhichfactorsinto.Therefore,sincethedifferenceisamultipleof9,theonlyanswerchoicethatisamultipleof9 is.15.If,,and,whatistheproductof,,and16.AnumberofstudentsfromFibonacciMiddleSchoolaretakingpartinacommunityserviceproject.Theratioof-gradersto-gradersis,andthetheratioof-gradersto-gradersis .Whatisthesmallestnumberofstudentsthatcouldbeparticipatingintheproject17.Thesumofsixconsecutivepositiveintegersis2013.Whatisthelargestofthesesixintegers18.--Arpanliku16:22,27November2013(EST)Courtesyof19.Bridget,Cassie,andHannaharediscussingtheresultsoftheirlastmathtest.HannahshowsBridg etandCassiehertest,butBridgetandCassiedon'tshowtheirstoanyone.Cassiesays,'Ididn'tgetthel owestscoreinourclass,'andBridgetadds,'Ididn'tgetthehighestscore.'Whatistherankingofthethr eegirlsfromhighesttolowest20.Arectangleisinscribedinasemicirclewithlongersideonthediameter.Whatistheareaofthesemicircle21.22.Toothpicksareusedtomakeagridthatis60toothpickslongand32toothpickswide.Howmanytoo thpicksareusedaltogether23.Angle of isarightangle.Thesidesofarethediametersofsemicirclesasshown.Theareaofthesemicircleon equals,andthearcofthesemicircleon haslength.Whatistheradiusofthesemicircleon24.Squares,,and areequalinarea.Points andarethemidpointsofsides and,respectively.Whatistheratiooftheareaoftheshadedpentagontothesumoftheareasofthethreesquares25.Aballwithdiameter4inchesstartsatpointAtorollalongthetrackshown.Thetrackiscomprisedof3semicirculararcswhoseradiiare inches,inches,and1.2.The50%offpriceofhalfapoundoffishis$3,sothe100%,ortheregularprice,ofahalfpoundoffishis$6.Consequently,ifhalfapoundoffishcosts$6,thenawholepoundoffishis dollars.3.Noticethatwecanpairupeverytwonumberstomakeasumof1:Therefore,theansweris.4.Eachofhersevenfriendspaid tocoverJudi'sportion.Therefore,Judi'sportionmustbe.SinceJudiwassupposedtopay ofthetotalbill,thetotalbillmustbe.5.Themedianhereisobviouslylessthanthemean,sooption(A)and(B)areout. Liningupthenumbers(5,5,6,8,106),weseethatthemedianweightis6pounds.Theaverageweightofthefivekidsis.Therefore,theaverageweightisbigger,by pounds,makingtheanswer.6.Solution1:WorkingBackwardsLetthevalueintheemptyboxinthemiddlerowbe,andthevalueintheemptyboxinthetoprowbe. istheanswerwe'relookingfor.Weseethat,making.Itfollowsthat,so.Solution2:JumpingBacktotheStartAnotherwaytodothisproblemistorealizewhatmakesupthebottommostnumber.Thismethoddoes n'tworkquiteaswellforthisproblem,butinalargertree,itmightbefaster.(Inthiscase,Solution1wou ldbefastersincethere'sonlytwomissingnumbers.)Again,letthevalueintheemptyboxinthemiddlerowbe,andthevalueintheemptyboxinthetoprowbe.istheanswerwe'relookingfor. Wecanwritesomeequations: Nowwecansubstituteintothefirstequationusingthetwoothers:7.IfTreysaw,thenhesaw.2minutesand45secondscanalsobeexpressedas seconds.Trey'srateofseeingcars,,canbemultipliedbyonthetopandbottom(andpreservethesamerate):.Itfollowsthatthemostlikelynumberofcarsis. Solution2minutesand secondsisequalto.SinceTreyprobablycountsaround carsevery seconds,thereare groupsofcarsthatTreymostlikelycounts.Since,theclosestanswerchoiceis.8.First,thereare waystoflipthecoins,inorder. ThewaystogettwoconsecutiveheadsareHHT andTHH. ThewaytogetthreeconsecutiveheadsisHHH.Therefore,theprobabilityofflippingatleasttwoconsecutiveheadsis.9.Thisisageometricsequenceinwhichthecommonratiois2.Tofindthejumpthatwouldbeovera1000meters,wenotethat.However,becausethefirsttermis andnot,thesolutiontotheproblemis10.TofindeithertheLCMortheGCFoftwonumbers,alwaysprimefactorizefirst. Theprimefactorizationof.Theprimefactorizationof.Then,findthegreatestpowerofallthenumbersthereare;ifonenumberisonebutnottheother,useit(t hisis).Multiplyallofthesetoget5940.FortheGCFof180and594,usetheleastpowerofallofthenumbersthatareinbothfactorizationsandmultiply.=18.Thustheanswer==. Westartoffwithasimilarapproachastheoriginalsolution.Fromtheprimefactorizations,theGCFis .Itisawellknownfactthat.Sowehave,.Dividingby yields.Therefore,.11.Weusethatfactthat.Letd=distance,r=rateorspeed,andt=time.Inthiscase,letrepresentthetime.OnMonday,hewasatarateof.So,.ForWednesday,hewalkedatarateof.Therefore,.OnFriday,hewalkedatarateof.So,.Addingupthehoursyields++=.WenowfindtheamountoftimeGrandfatherwouldhavetakenifhewalkedatperday.Setuptheequation,.Tofindtheamountoftimesaved,subtractthetwoamounts:-=.Toconvertthistominutes,wemultiplyby.Thus,thesolutiontothisproblemis12.First,findtheamountofmoneyonewillpayforthreesandalswithoutthediscount.Wehave.Then,findtheamountofmoneyusingthediscount:.Findingthepercentageyields.Tofindthepercentsaved,wehave13.Letthetwodigitsbe and.Thecorrectscorewas.Claramisinterpreteditas.Thedifferencebetweenthetwoiswhichfactorsinto.Therefore,sincethedifferenceisamultipleof9,theonlyanswerchoicethatisamultipleof9is.14.Theprobabilitythatbothshowagreenbeanis.Theprobabilitythatbothshowaredbeanis.Thereforetheprobabilityis15.Therefore,.Therefore,.Tomostpeople,itwouldnotbeimmediatelyevidentthat,sowecanmultiply6'suntilwegetthedesirednumber:,so.Thereforetheansweris.16.Solution1:AlgebraWemultiplythefirstratioby8onbothsides,andthesecondratioby5togetthesamenumberfor8thgra ders,inorderthatwecanputthetworatiostogether:Therefore,theratioof8thgradersto7thgradersto6thgradersis.Sincetheratioisinlowestterms,thesmallestnumberofstudentsparticipatingintheprojectis.Solution2:FakesolvingThenumberof8thgradershastobeamultipleof8and5,soassumeitis40(thesmallestpossibility).Thenthereare6thgradersand7thgraders.Thenumbersofstudentsis17.Solution1Themeanofthesenumbersis.Thereforethenumbersare,sotheanswerisSolution2Letthe numberbe.Thenourdesirednumberis.Ourintegersare,sowehavethat.Solution3Letthefirsttermbe.Ourintegersare.Wehave,18.Solution1Therearecubesonthebaseofthebox.Then,foreachofthe4layersabovethebottom(assinceeachcubeis1foot by1footby1footandtheboxis5feettall,thereare4feetleft),therearecubes.Hence,theansweris.Solution2Wecanjustcalculatethevolumeoftheprismthatwascutoutoftheoriginalbox.Eachinteriorsideofthefortwillbe feetshorterthaneachsideoftheoutside.Sincethefloorisfoot,theheightwillbe feet.Sothevolumeoftheinteriorboxis.Thevolumeoftheoriginalboxis.Therefore,thenumberofblockscontainedinthefortis.19.IfHannahdidbetterthanCassie,therewouldbenowayshecouldknowforsurethatshedidn'tgett helowestscoreintheclass.Therefore,HannahdidworsethanCassie.Similarly,ifHannahdidworseth anBridget,thereisnowayBridgetcouldhaveknownthatshedidn'tgetthehighestintheclass.Therefore,HannahdidbetterthanBridget,soourorderis.20.Asemicirclehassymmetry,sothecenterisexactlyatthemidpointofthe2sideontherectangle,makingtheradius,bythePythagoreanTheorem,.Theareais.21.ThenumberofwaystogetfromSamantha'shousetoCityParkis,andthenumberofwaystogetfromCityParktoschoolis.Sincethere'sonewaytogothroughCityPark(justwalkingstraightthrough),thenumberofdifferentwaystogofromSamantha'shousetoCityParktoschool.22.Thereare verticalcolumnswithalengthof toothpicks,andthereare horizontalrowswithalengthof toothpicks.Aneffectivewaytoverifythisistotryasmallcase,i.e.agridoftoothpicks.Thus,ouransweris.23.Solution1.Solution2WegoasinSolution1,findingthediameterofthecircleonACandAB.Then,anextendedversionofthet heoremsaysthatthesumofthesemicirclesontheleftisequaltothebiggestone,sotheareaofthelargestis,andthemiddleoneis,sotheradiusis.24.Firstlet(where isthesidelengthofthesquares)forsimplicity.Wecanextenduntilithitstheextensionof.Callthispoint.Theareaoftriangle thenis Theareaofrectangle is.Thus,ourdesiredareais.Now,theratiooftheshadedareatothecombinedareaofthethreesquaresis.Solution2Letthesidelengthofeachsquarebe.Lettheintersectionof and be.Since,.Since andareverticalangles,theyarecongruent.Wealsohave bydefinition.Sowehave by congruence.Therefore,.Since and aremidpointsofsides,.Thiscombinedwith yields.Theareaoftrapezoid is.Theareaoftriangle is.Sotheareaofthepentagon is.Theareaofthe squaresis.Therefore,.Solution3Lettheintersectionof and be.Nowwehave and.Becausebothtriangleshasasideoncongruentsquarestherefore.Because and areverticalangles.Alsoboth and arerightanglesso.ThereforebyAAS(Angle,Angle,Side).Thentranslating/rotatingtheshaded intothepositionofSotheshadedareanowcompletelycoversthesquareSettheareaofasquareasTherefore,.25.Solution1Theradiusoftheballis2inches.Ifyouthinkabouttheballrollingordrawapathfortheball(seefigurebelow),youseethatinAandCitloses inches,anditgains inchesonB.So,thedeparturefromthelengthofthetrackmeansthattheansweris.Solution2Thetotallengthofallofthearcsis.Sincewewantthepathfromthecenter,theactualdistancewillbeshorter.Therefore,theonlyanswerchoicelessthan is.Thissolutionmaybeinvalidbecausetheactualdistancecanbelongerifthepaththecent ertravelsisontheoutsideofthecurve,asitisinthemiddlebump.。
美国数学竞赛AMC题目及答案

2.3.What is the value of ?4.Eight friends ate at a restaurant and agreed to share the bill equally. Because Judi forgot her money, each of her seven friends paid an extra $2.50 to cover her portion of the total bill. What was the total bill?5.Hammie is in the grade and weighs 106 pounds. His quadruplet sisters are tiny babies and weigh 5, 5, 6, and 8 pounds. Which is greater, the average (mean) weight of these five children or the median weight, and by how many pounds?6.The number in each box below is the product of the numbers in the two boxes that touch it in the row above. For example, . What is the missing number in the top row?7.Trey and his mom stopped at a railroad crossing to let a train pass. As the train began to pass, Trey counted 6 cars in the first 10 seconds. It took the train 2 minutes and 45 seconds to clear the crossing at a constant speed. Which of the following was the most likely number of cars in the train?8.A fair coin is tossed 3 times. What is the probability of at least two consecutive heads?9.The Incredible Hulk can double the distance he jumps with each succeeding jump. If his first jump is 1 meter, the second jump is 2 meters, the third jump is 4 meters, and so on, then on which jump will he first be able to jump more than 1 kilometer?10.What is the ratio of the least common multiple of 180 and 594 to the greatest common factor of 180 and 594?11. Ted's grandfather used his treadmill on 3 days this week. He went 2 miles each day. On Monday he jogged at a speed of 5 miles per hour. He walked at the rate of 3 miles per hour on Wednesday and at 4 miles per hour on Friday. If Grandfather had always walked at 4 miles per hour, he would have spent less time on the treadmill. How many minutes less?12. At the 2013 Winnebago County Fair a vendor is offering a "fair special" on sandals. If you buy one pair of sandals at the regular price of $50, you get a second pair at a 40% discount, and a third pair at half the regular price. Javier took advantage of the "fair special" to buy three pairs of sandals. What percentage of the $150 regular price did he save?13. When Clara totaled her scores, she inadvertently reversed the units digit and the tens digit of one score. By which of the following might her incorrect sum have differed from the correct one?14. Let the two digits be and .The correct score was . Clara misinterpreted it as . The difference between the two is which factors into . Therefore, since the difference is a multiple of 9, the only answerchoice that is a multiple of 9 is .15. If , , and , what is the product of , , and ?16. A number of students from Fibonacci Middle School are taking part in a community service project. The ratio of -graders to -graders is , and the the ratio of -graders to -graders is . What is the smallest number of students that could be participating in the project?17. The sum of six consecutive positive integers is 2013. What is the largest of these six integers?18. Isabella uses one-foot cubical blocks to build a rectangular fort that is 12 feet long, 10 feet wide, and 5 feet high. The floor and the four walls are all one foot thick. How many blocks does the fort contain?--Arpanliku 16:22, 27 November 2013 (EST) Courtesy of Lord.of.AMC19. Bridget, Cassie, and Hannah are discussing the results of their last math test. Hannah shows Bridget and Cassie her test, but Bridget and Cassie don't show theirs to anyone. Cassie says, 'I didn't get the lowest score in our class,' and Bridget adds, 'I didn't get the highest score.' What is the ranking of the three girls from highest to lowest?20. A rectangle is inscribed in a semicircle with longer side on the diameter. What is the area of the semicircle?21. Samantha lives 2 blocks west and 1 block south of the southwest corner of City Park. Her school is 2 blocks east and 2 blocks north of the northeast corner of City Park. On school days she bikes on streets to the southwest corner of City Park, then takes a diagonal path through the park to the northeast corner, and then bikes on streets to school. If her route is as short as possible, how many different routes can she take?22. Toothpicks are used to make a grid that is 60 toothpicks long and 32 toothpicks wide. How many toothpicks are used altogether?23. Angle of is a right angle. The sides of are the diameters of semicircles as shown. The area of the semicircle on equals , and the arc of the semicircle on has length .What is the radius of the semicircle on ?24. Squares , , and are equal in area. Points and are the midpoints of sidesand , respectively. What is the ratio of the area of the shaded pentagon to the sum of the areas of the three squares?25. A ball with diameter 4 inches starts at point A to roll along the track shown. The track is comprised of 3 semicircular arcs whose radii are inches, inches, and inches, respectively. The ball always remains in contact with the track and does not slip. What is the distance the center of theball travels over the course from A to B?1.2.The 50% off price of half a pound of fish is $3, so the 100%, or the regular price, of a half pound of fish is $6. Consequently, if half a pound of fish costs $6, then a whole pound of fish is dollars.3.Notice that we can pair up every two numbers to make a sum of 1:Therefore, the answer is .4.Each of her seven friends paid to cover Judi's portion. Therefore, Judi's portion must be . Since Judi was supposed to pay of the total bill, the total bill must be .5.The median here is obviously less than the mean, so option (A) and (B) are out.Lining up the numbers (5, 5, 6, 8, 106), we see that the median weight is 6 pounds.The average weight of the five kids is .Therefore, the average weight is bigger, by pounds, making the answer.6.Solution 1: Working BackwardsLet the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.We see that , making .It follows that , so .Solution 2: Jumping Back to the StartAnother way to do this problem is to realize what makes up the bottommost number. This method doesn't work quite as well for this problem, but in a larger tree, it might be faster. (In this case, Solution 1 would be faster since there's only two missing numbers.)Again, let the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.We can write some equations:Now we can substitute into the first equation using the two others:7.If Trey saw , then he saw .2 minutes and 45 seconds can also be expressed as seconds.Trey's rate of seeing cars, , can be multiplied by on the top and bottom (and preserve the same rate):. It follows that the most likely number of cars is . Solution 2minutes and seconds is equal to .Since Trey probably counts around cars every seconds, there are groups of cars that Trey most likely counts. Since , the closest answer choice is .8.First, there are ways to flip the coins, in order.The ways to get two consecutive heads are HHT and THH.The way to get three consecutive heads is HHH.Therefore, the probability of flipping at least two consecutive heads is .9.This is a geometric sequence in which the common ratio is 2. To find the jump that would be over a 1000 meters, we note that .However, because the first term is and not , the solution to the problem is10. To find either the LCM or the GCF of two numbers, always prime factorize first.The prime factorization of .The prime factorization of .Then, find the greatest power of all the numbers there are; if one number is one but not the other, use it (this is ). Multiply all of these to get 5940.For the GCF of 180 and 594, use the least power of all of the numbers that are in both factorizations and multiply. = 18.Thus the answer = = .We start off with a similar approach as the original solution. From the prime factorizations, the GCF is .It is a well known fact that . So we have,.Dividing by yields .Therefore, .11. We use that fact that . Let d= distance, r= rate or speed, and t=time. In this case, let represent the time.On Monday, he was at a rate of . So, .For Wednesday, he walked at a rate of . Therefore, .On Friday, he walked at a rate of . So, .Adding up the hours yields + + = .We now find the amount of time Grandfather would have taken if he walked at per day. Set up the equation, .To find the amount of time saved, subtract the two amounts: - = . To convert this to minutes, we multiply by .Thus, the solution to this problem is12. First, find the amount of money one will pay for three sandals without the discount. We have.Then, find the amount of money using the discount: .Finding the percentage yields .To find the percent saved, we have13. Let the two digits be and .The correct score was . Clara misinterpreted it as . The difference between the two is which factors into . Therefore, since the difference is a multiple of 9, the only answerchoice that is a multiple of 9 is .14. The probability that both show a green bean is . The probability that both show a red bean is . Therefore the probability is15.Therefore, .Therefore, .To most people, it would not be immediately evident that , so we can multiply 6's until we get the desired number:, so .Therefore the answer is .16. Solution 1: AlgebraWe multiply the first ratio by 8 on both sides, and the second ratio by 5 to get the same number for 8th graders, in order that we can put the two ratios together:Therefore, the ratio of 8th graders to 7th graders to 6th graders is . Since the ratio is in lowest terms, the smallest number of students participating in the project is .Solution 2: FakesolvingThe number of 8th graders has to be a multiple of 8 and 5, so assume it is 40 (the smallest possibility). Then there are 6th graders and 7th graders. The numbers of students is17. Solution 1The mean of these numbers is . Therefore the numbers are, so the answer isSolution 2Let the number be . Then our desired number is .Our integers are , so we have that.Solution 3Let the first term be . Our integers are . We have,18. Solution 1There are cubes on the base of the box. Then, for each of the 4 layers above the bottom (as since each cube is 1 foot by 1 foot by 1 foot and the box is 5 feet tall, there are 4 feet left), there arecubes. Hence, the answer is .Solution 2We can just calculate the volume of the prism that was cut out of the original box. Each interior side of the fort will be feet shorter than each side of the outside. Since the floor is foot, the height will be feet. So the volume of the interior box is .The volume of the original box is . Therefore, the number of blocks contained inthe fort is .19. If Hannah did better than Cassie, there would be no way she could know for sure that she didn't get the lowest score in the class. Therefore, Hannah did worse than Cassie. Similarly, if Hannah did worse than Bridget, there is no way Bridget could have known that she didn't get the highest in the class.Therefore, Hannah did better than Bridget, so our order is .20.A semicircle has symmetry, so the center is exactly at the midpoint of the 2 side on the rectangle, making the radius, by the Pythagorean Theorem, . The area is .21.The number of ways to get from Samantha's house to City Park is , and the number of ways toget from City Park to school is . Since there's one way to go through City Park (just walking straight through), the number of different ways to go from Samantha's house to City Park to school .22. There are vertical columns with a length of toothpicks, and there are horizontal rows with a length of toothpicks. An effective way to verify this is to try a small case, i.e. a grid of toothpicks.Thus, our answer is .23. Solution 1If the semicircle on AB were a full circle, the area would be 16pi. Therefore the diameter of the first circle is 8. The arc of the largest semicircle would normally have a complete diameter of 17. The Pythagoreantheorem says that the other side has length 15, so the radius is .Solution 2We go as in Solution 1, finding the diameter of the circle on AC and AB. Then, an extended version of the theorem says that the sum of the semicircles on the left is equal to the biggest one, so the area of thelargest is , and the middle one is , so the radius is .24.First let (where is the side length of the squares) for simplicity. We can extend until it hits theextension of . Call this point . The area of triangle then is The area of rectangle is . Thus, our desired area is . Now, the ratio of the shaded area to thecombined area of the three squares is .Let the side length of each square be .Let the intersection of and be .Since , . Since and are vertical angles, they are congruent. We also have by definition.So we have by congruence. Therefore, .Since and are midpoints of sides, . This combined with yields.The area of trapezoid is .The area of triangle is .So the area of the pentagon is .The area of the squares is .Therefore, .Let the intersection of and be .Now we have and .Because both triangles has a side on congruent squares therefore .Because and are vertical angles .Also both and are right angles so .Therefore by AAS(Angle, Angle, Side) .Then translating/rotating the shaded into the position ofSo the shaded area now completely covers the squareSet the area of a square asTherefore, .25. Solution 1The radius of the ball is 2 inches. If you think about the ball rolling or draw a path for the ball (see figure below), you see that in A and C it loses inches, and it gains inches on B.So, the departure from the length of the track means that the answer is . Solution 2The total length of all of the arcs is . Since we want the path from the center, the actual distance will be shorter. Therefore, the only answer choice less than is . Thissolution may be invalid because the actual distance can be longer if the path the center travels is on the outside of the curve, as it is in the middle bump.古希腊哲学大师亚里士多德说:人有两种,一种即“吃饭是为了活着”,一种是“活着是为了吃饭”.一个人之所以伟大,首先是因为他有超于常人的心。
美国数学竞赛AMC8 -- 2005年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 – 2005年真题解析(英文解析+中文解析)Problem 1Answer: BSolution:If x is the number, then 2x=60 and x=30. Dividing the number by 2 yields 15.中文解析:按照Connie的计算,这个数乘以2是60,可知这个数是30. 应该做的计算是30除以2,因而正确答案应该是15. 答案是B。
Problem 2Answer: CSolution:Karl paid 5*2.5=$12.5. 20% of this cost that he saved is 12.5*0.2=$2.5.中文解析:Karl按原价买了5个文件夹,支付的费用是:2.5*5=12.5. 折扣价是:1.25*0.8=10。
如果Karl 等一天,可以省2.5元。
答案是C.Problem 3Answer: DSolution:Rotating square ABCD counterclockwise 45° so that the line of symmetry BD is a vertical line makes it easier to see that 4 squares need to be colored to match its corresponding square.中文解析:如上图所示,以BD为对称轴,标蓝色的方块需要涂黑。
共4块,答案是D。
Problem 4Answer: CSolution:The perimeter of the triangle is 6.1+8.2+9.7=24cm. A square's perimeter is four times its side length, since all its side lengths are equal. If the square's perimeter is 24, the side length is24/4=6, and the area is 6*6=36.中文解析:三角形的周长是:6.1+8.2+9.7=24. 正方形的周长和三角形相等,也是24,则其边长是24/4=6. 其面积是:6*6=36. 答案是C。
AMC美国数学竞赛AMC.B 试题及答案解析
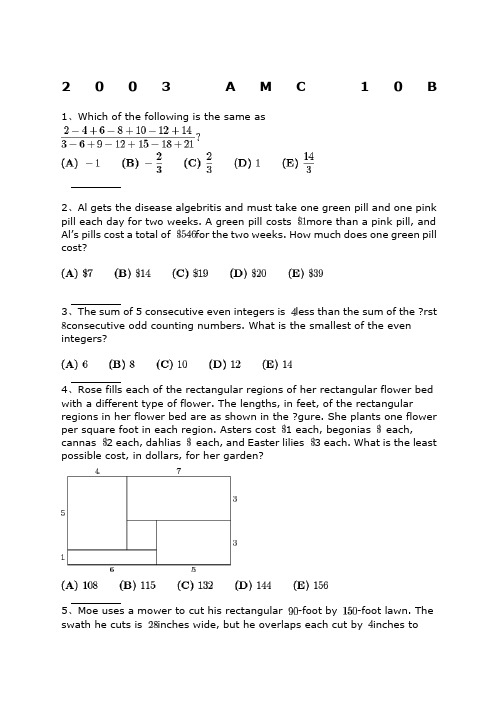
2003A M C10 B 1、Which of the following is the same as2、Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pink pill, and Al’s pills cost a total of for the two weeks. How much does one green pill cost?3、The sum of 5 consecutive even integers is less than the sum of the ?rst consecutive odd counting numbers. What is the smallest of the even integers?4、Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the ?gure. She plants one flower per square foot in each region. Asters cost 1 each, begonias each, cannas 2 each, dahlias each, and Easter lilies 3 each. What is the least possible cost, in dollars, for her garden?5、Moe uses a mower to cut his rectangular -foot by -foot lawn. The swath he cuts is inches wide, but he overlaps each cut by inches tomake sure that no grass is missed. He walks at the rate of feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow his lawn?.6、Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length of a “-inch” television screen is closest, in inches, to which of the following?7、The symbolism denotes the largest integer not exceeding . For example. , and . Compute.8、The second and fourth terms of a geometric sequence are and . Which of the following is a possible first term?9、Find the value of that satisfies the equation10、Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of three letters followed by three digits. By how many times is the number of possible license plates increased?11、A line with slope intersects a line with slope at the point . What is the distance between the -intercepts of these two lines?12、Al, Betty, and Clare split among them to be invested in different ways. Each begins with a different amount. At the end of one year they have a total of . Betty and Clare have both doubled their money, whereas Al has managed to lose . What was Al’s origin al portion?.13、Let denote the sum of the digits of the positive integer . For example, and . For how many two-digit values of is ?14、Given that , where both and are positive integers, find the smallest possible value for .15、There are players in a singles tennis tournament. The tournament is single elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest players are given a bye, and the remaining players are paired off to play. After each round, the remaining players play in the next round. The match continues until only one player remains unbeaten. The total number of matches played is16、A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that the restaurant should offer so that a customer could have a different dinner each night in the year ?.17、An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly ?ll the cone. Assume that the melted ice cream occupies of the volume of the frozen ice cream. What is the ratio of the cone’s height to its radius?18、What is the largest integer that is a divisor offor all positive even integers ?19、Three semicircles of radius are constructed on diameter of a semicircle of radius . The centers of the small semicircles divide into four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicircles?20、In rectangle , and . Points and are on so that and . Lines and intersect at . Find the area of .21、A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardless of the color you pulled out. What is the probability that all beads in the bag are red after three such replacements?22、A clock chimes once at minutes past each hour and chimes on the hour according to the hour. For example, at 1 PM there is one chime and at noon and midnight there are twelve chimes. Starting at 11:15 AM on February , , on what date will the chime occur?23、A regular octagon has an area of one square unit. What is the area of the rectangle ?24、The ?rst four terms in an arithmetic sequence are , , , and, in that order. What is the ?fth term?25、How many distinct four-digit numbers are divisible by and have as their last two digits?。
数学amc竞赛题目

数学amc竞赛题目以下是三道数学AMC竞赛题目:1. 某机场定期有两架航班从A地和B地往返。
一天结束时,发现从A出发的航班都准时到达了B,而从B出发的航班都晚点了15分钟到达A。
如果考虑时差,两架航班往返所需的总时间相差多少分钟?A. 0B. 15C. 30D. 45E. 602. 若$x,y$为正整数,满足$(x+y)^2+(x-y)^2=2(x^2+y^2)$,则$x$与$y$的比是?A. $1:1$B. $2:1$C. $1:2$D. $3:5$E. $5:3$3. 在坐标平面上,三角形ABC的顶点为A(1,4),B(5,4),C(5,2)。
目标是通过将三角形ABC旋转180度,在新位置上形成三角形A'B'C',使得$A'B'$与$AB$平行并且$A'C'$与$AC$垂直。
新三角形的顶点是?A. $A'(-3,-4), B'(-7,-4), C'(-7,-6)$B. $A'(-3,-4), B'(1,-4), C'(1,-6)$C. $A'(5,6), B'(1,6), C'(-3,4)$D. $A'(-3,-4), B'(-7,-4), C'(1,-6)$E. 不存在这样的三角形。
答案:1. C,两架航班的往返总时间相差30分钟。
2. B,$x:y=2:1$。
3. A,三角形A'B'C'的顶点为$A'(-3,-4), B'(-7,-4), C'(-7,-6)$。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.is the value offriends ate at a restaurant and agreed to share the bill equally. Because Judi forgot her money, each of her seven friends paid an extra $ to cover her portion of the total bill. What was the total billis in the grade and weighs 106 pounds. His quadruplet sisters are tiny babies and weigh 5, 5, 6, and 8 pounds. Which is greater, the average (mean) weight of these five children or the median weight, and by how many poundsnumber in each box below is the product of the numbers in the two boxes that touch it in the row above. For example, . What is the missing number in the top rowand his mom stopped at a railroad crossing to let a train pass. As the train began to pass, Trey counted 6 cars in the first 10 seconds. It took the train 2 minutes and 45 seconds to clear the crossing at a constant speed. Which of the following was the most likely number of cars in the trainfair coin is tossed 3 times. What is the probability of at least two consecutive headsIncredible Hulk can double the distance he jumps with each succeeding jump. If his first jump is 1 meter, the second jump is 2 meters, the third jump is 4 meters, and so on, then on which jump will he first be able to jump more than 1 kilometeris the ratio of the least common multiple of 180 and 594 to the greatest common factor of 180 and 59411. Ted's grandfather used his treadmill on 3 days this week. He went 2 miles each day. On Monday he jogged at a speed of 5 miles per hour. He walked at the rate of 3 miles per hour on Wednesday and at 4 miles per hour on Friday. If Grandfather had always walked at 4 miles per hour, he would have spent less time on the treadmill. How many minutes less12. At the 2013 Winnebago County Fair a vendor is offering a "fair special" on sandals. If you buy one pair of sandals at the regular price of $50, you get a second pair at a 40% discount, and a third pair at half the regular price. Javier took advantage of the "fair special" to buy three pairs of sandals. What percentage of the $150 regular price did he save13.When Clara totaled her scores, she inadvertently reversed the units digit and the tens digit of one score. By which of the following might her incorrect sum have differed from the correct one14. Let the two digits be and .The correct score was . Clara misinterpreted it as . The difference between the two is which factors into . Therefore, since the difference is a multiple of 9, the only answer choice that is a multiple of 9 is .15. If , , and , what is the product of , , and16. A number of students from Fibonacci Middle School are taking part in a community service project. The ratio of -graders to -graders is , and the the ratio of -graders to -graders is . What is the smallest number of students that could be participating in the project17. The sum of six consecutive positive integers is 2013. What is the largest of these six integers18. Isabella uses one-foot cubical blocks to build a rectangular fort that is 12 feet long, 10 feet wide, and 5 feet high. The floor and the four walls are all one foot thick. How many blocks does the fort contain--Arpanliku 16:22, 27 November 2013 (EST) Courtesy of19. Bridget, Cassie, and Hannah are discussing the results of their last math test. Hannah shows Bridget and Cassie her test, but Bridget and Cassie don't show theirs to anyone. Cassie says, 'I didn't get the lowest score in our class,' and Bridget adds, 'I didn't get the highest score.' What is the ranking of the three girls from highest to lowest20. A rectangle is inscribed in a semicircle with longer side on the diameter. What is the area of the semicircle21.Samantha lives 2 blocks west and 1 block south of the southwest corner of City Park. Her school is 2 blocks east and 2 blocks north of the northeast corner of City Park. On school days she bikes on streets to the southwest corner of City Park, then takes a diagonal path through the park to the northeast corner, and then bikes on streets to school. If her route is as short as possible, how many different routes can she take22.Toothpicks are used to make a grid that is 60 toothpicks long and 32 toothpicks wide. How many toothpicks are used altogether23.Angle of is a right angle. The sides of are the diameters of semicircles as shown. The area of the semicircle on equals , and the arc of the semicircle on has length . What isthe radius of the semicircle on24. Squares , , and are equal in area. Points and are the midpoints of sidesand , respectively. What is the ratio of the area of the shaded pentagon to the sum of the areas of the three squares25. A ball with diameter 4 inches starts at point A to roll along the track shown. The track is comprised of 3 semicircular arcs whose radii are inches, inches, and inches, respectively. The ball always remains in contact with the track and does not slip. What is the distance the center of theball travels over the course from A to B1.50% off price of half a pound of fish is $3, so the 100%, or the regular price, of a half pound of fish is $6. Consequently, if half a pound of fish costs $6, then a whole pound of fish is dollars.that we can pair up every two numbers to make a sum of 1:Therefore, the answer is .of her seven friends paid to cover Judi's portion. Therefore, Judi's portion must be . Since Judi was supposed to pay of the total bill, the total bill must be .median here is obviously less than the mean, so option (A) and (B) are out.Lining up the numbers (5, 5, 6, 8, 106), we see that the median weight is 6 pounds.The average weight of the five kids is .Therefore, the average weight is bigger, by pounds, making the answer .1: Working BackwardsLet the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.We see that , making .It follows that , so .Solution 2: Jumping Back to the StartAnother way to do this problem is to realize what makes up the bottommost number. This method doesn't work quite as well for this problem, but in a larger tree, it might be faster. (In this case, Solution 1 would be faster since there's only two missing numbers.)Again, let the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.We can write some equations:Now we can substitute into the first equation using the two others:Trey saw , then he saw .2 minutes and 45 seconds can also be expressed as seconds.Trey's rate of seeing cars, , can be multiplied by on the top and bottom (and preserve the same rate):. It follows that the most likely number of cars is . Solution 2minutes and seconds is equal to .Since Trey probably counts around cars every seconds, there are groups of cars that Trey most likely counts. Since , the closest answer choice is ., there are ways to flip the coins, in order.The ways to get two consecutive heads are HHT and THH.The way to get three consecutive heads is HHH.Therefore, the probability of flipping at least two consecutive heads is .is a geometric sequence in which the common ratio is 2. To find the jump that would be over a 1000 meters, we note that .However, because the first term is and not , the solution to the problem is10. To find either the LCM or the GCF of two numbers, always prime factorize first.The prime factorization of .The prime factorization of .Then, find the greatest power of all the numbers there are; if one number is one but not the other, use it (this is ). Multiply all of these to get 5940.For the GCF of 180 and 594, use the least power of all of the numbers that are in both factorizations and multiply. = 18.Thus the answer = = .We start off with a similar approach as the original solution. From the prime factorizations, the GCF is .It is a well known fact that . So we have,.Dividing by yields .Therefore, .11.We use that fact that . Let d= distance, r= rate or speed, and t=time. In this case, let represent the time.On Monday, he was at a rate of . So, .For Wednesday, he walked at a rate of . Therefore, .On Friday, he walked at a rate of . So, .Adding up the hours yields + + = .We now find the amount of time Grandfather would have taken if he walked at per day. Set up the equation,.To find the amount of time saved, subtract the two amounts: - = . To convert this to minutes, we multiply by .Thus, the solution to this problem is12. First, find the amount of money one will pay for three sandals without the discount. We have.Then, find the amount of money using the discount: .Finding the percentage yields .To find the percent saved, we have13. Let the two digits be and .The correct score was . Clara misinterpreted it as . The difference between the two is which factors into . Therefore, since the difference is a multiple of 9, the only answer choice that is a multiple of 9 is .14. The probability that both show a green bean is . The probability that both show a red bean is . Therefore the probability is15.Therefore, .Therefore, .To most people, it would not be immediately evident that , so we can multiply 6's until we get the desired number:, so .Therefore the answer is .16. Solution 1: AlgebraWe multiply the first ratio by 8 on both sides, and the second ratio by 5 to get the same number for 8th graders, in order that we can put the two ratios together:Therefore, the ratio of 8th graders to 7th graders to 6th graders is . Since the ratio is in lowest terms, the smallest number of students participating in the project is .Solution 2: FakesolvingThe number of 8th graders has to be a multiple of 8 and 5, so assume it is 40 (the smallest possibility). Then there are 6th graders and 7th graders. The numbers of students is17. Solution 1The mean of these numbers is . Therefore the numbers are , so the answer isSolution 2Let the number be . Then our desired number is .Our integers are , so we have that.Solution 3Let the first term be . Our integers are . We have,18. Solution 1There are cubes on the base of the box. Then, for each of the 4 layers above the bottom (as since each cube is 1 foot by 1 foot by 1 foot and the box is 5 feet tall, there are 4 feet left), there are cubes. Hence, the answer is .Solution 2We can just calculate the volume of the prism that was cut out of the original box. Each interior side of the fort will be feet shorter than each side of the outside. Since the floor is foot, the height will be feet. So the volume of the interior box is .The volume of the original box is . Therefore, the number of blocks contained in the fort is .19. If Hannah did better than Cassie, there would be no way she could know for sure that she didn't get the lowest score in the class. Therefore, Hannah did worse than Cassie. Similarly, if Hannah did worse than Bridget, there is no way Bridget could have known that she didn't get the highest in the class. Therefore, Hannah did better than Bridget, so our order is .20.A semicircle has symmetry, so the center is exactly at the midpoint of the 2 side on the rectangle, making the radius, by the Pythagorean Theorem, . The area is .21.The number of ways to get from Samantha's house to City Park is , and the number of ways to get from City Park to school is . Since there's one way to go through City Park (just walking straight through), the number of different ways to go from Samantha's house to City Park to school .22.There are vertical columns with a length of toothpicks, and there are horizontal rows with a length of toothpicks. An effective way to verify this is to try a small case, . a grid of toothpicks. Thus, our answer is .23. Solution 1If the semicircle on AB were a full circle, the area would be 16pi. Therefore the diameter of the first circle is 8. The arc of the largest semicircle would normally have a complete diameter of 17. The Pythagorean theorem says that the other side has length 15, so the radius is .Solution 2We go as in Solution 1, finding the diameter of the circle on AC and AB. Then, an extended version of the theorem says that the sum of the semicircles on the left is equal to the biggest one, so the area of the largestis , and the middle one is , so the radius is .24.First let (where is the side length of the squares) for simplicity. We can extend until it hits the extension of . Call this point . The area of triangle then is The area of rectangle is . Thus, our desired area is . Now, the ratio of the shaded area to the combinedarea of the three squares is .Solution 2Let the side length of each square be .Let the intersection of and be .Since , . Since and are vertical angles, they are congruent. We also have by definition.So we have by congruence. Therefore, .Since and are midpoints of sides, . This combined with yields.The area of trapezoid is .The area of triangle is .So the area of the pentagon is .The area of the squares is .Therefore, .Solution 3Let the intersection of and be .Now we have and .Because both triangles has a side on congruent squares therefore .Because and are vertical angles .Also both and are right angles so .Therefore by AAS(Angle, Angle, Side) .Then translating/rotating the shaded into the position ofSo the shaded area now completely covers the squareSet the area of a square asTherefore, .25. Solution 1The radius of the ball is 2 inches. If you think about the ball rolling or draw a path for the ball (see figure below), you see that in A and C it loses inches, and it gains inches on B.So, the departure from the length of the track means that the answer is . Solution 2The total length of all of the arcs is . Since we want the path from the center, the actual distance will be shorter. Therefore, the only answer choice less than is . This solution may be invalid because the actual distance can be longer if the path the center travels is on the outside of the curve, as it is in the middle bump.。
