密码学实验
现代密码学实验报告

现代密码学实验报告学生姓名学号专业班级指导教师学院完成时间实验一对称密码算法实验[实验目的]1.掌握密码学中经典的对称密码算法DES、AES、RC4的算法原理。
2.掌握DES、AES、RC4的算法流程和实现方法。
[实验内容]1. 分析DES、AES、RC4、SHA的实现过程。
2. 用程序设计语言将算法过程编程实现。
3. 完成字符串数据的加密运算和解密运算输入明文:Idolikethisbook输入密钥:cryption[实验步骤]一、DES算法1、DES算法及原理DES算法为密码体制中的对称密码体制,又被称为美国数据加密标准,是1972年美国IBM公司研制的对称密码体制加密算法。
明文按64位进行分组,密钥长64位,密钥事实上是56位参与DES运算(第8、16、24、32、40、48、56、64位是校验位,使得每个密钥都有奇数个1)分组后的明文组和56位的密钥按位替代或交换的方法形成密文组的加密方法。
2、DES算法加解密过程(1) DES算法加密过程如下:a.初始置换。
DES的第一阶段包括64位分组的置换,改变每个分组中位的顺序。
术语置换使用其严格的数学意义;只改变了顺序。
这64位数据现在被分成两半:L0(左半部分)和R0(右半部分)。
下标0说明是原始的数据。
在DES算法第二阶段的每次循环后,这些下标加1。
b.循环移位(16次)一种根据密钥,并且依赖于表格的算法。
这种操作通常被称为数据移位。
这个算法要重复16次,但由于每次移位都使用密钥的不同子分组,因此每次移位的操作各不相同。
密钥的子分组由另一组表格和表格的移位算法来确定。
在每次循环以后,L(左半部分)和R(右半部分)的下标依次加一。
第16次循环的结果被称为预输出。
c.逆置换DES的最后一个阶段包括64位分组的置换,改变每个分组中位的顺序,这与第1阶段的操作类似。
这次置换的输出结果就是密文。
(2)解密过程DES的解密过程和加密过程相同,只是在解密过程中将子密钥的使用顺序颠倒。
密码学案例实验报告书

一、实验背景随着信息技术的飞速发展,信息安全问题日益突出。
密码学作为保障信息安全的核心技术,在数据加密、身份认证、数字签名等领域发挥着重要作用。
为了加深对密码学原理的理解,提高实际应用能力,我们开展了本次密码学案例实验。
二、实验目的1. 掌握DES加密算法的基本原理和操作步骤。
2. 熟悉RSA加密算法的原理和应用。
3. 学习数字签名技术的应用。
4. 培养动手实践能力,提高解决实际问题的能力。
三、实验内容1. DES加密算法(1)实验目的:了解DES加密算法的基本原理,掌握DES加密和解密过程。
(2)实验内容:① 设计一个简单的DES加密程序,实现明文到密文的转换。
② 设计一个简单的DES解密程序,实现密文到明文的转换。
(3)实验步骤:① 编写DES加密程序,输入明文和密钥,输出密文。
② 编写DES解密程序,输入密文和密钥,输出明文。
2. RSA加密算法(1)实验目的:了解RSA加密算法的基本原理,掌握RSA加密和解密过程。
(2)实验内容:① 设计一个简单的RSA加密程序,实现明文到密文的转换。
② 设计一个简单的RSA解密程序,实现密文到明文的转换。
(3)实验步骤:① 编写RSA加密程序,输入明文和密钥对,输出密文。
② 编写RSA解密程序,输入密文和私钥,输出明文。
3. 数字签名技术(1)实验目的:了解数字签名技术的基本原理,掌握数字签名的生成和验证过程。
(2)实验内容:① 设计一个简单的数字签名程序,实现签名生成和验证。
(3)实验步骤:① 编写数字签名程序,输入明文、私钥和签名算法,输出签名。
② 编写数字签名验证程序,输入明文、公钥和签名,验证签名是否正确。
四、实验结果与分析1. DES加密算法实验结果通过编写DES加密和解密程序,成功实现了明文到密文和密文到明文的转换。
实验结果表明,DES加密算法在保证数据安全的同时,具有较高的效率。
2. RSA加密算法实验结果通过编写RSA加密和解密程序,成功实现了明文到密文和密文到明文的转换。
维吉尼亚密码学实验报告

一、实验目的1. 理解维吉尼亚密码的原理和加密解密过程。
2. 掌握维吉尼亚密码的编程实现。
3. 破解维吉尼亚密码,提高密码学应用能力。
二、实验原理维吉尼亚密码是一种多表密码,它通过将明文与密钥进行组合,实现字符的替换加密。
加密过程中,密钥的长度决定了密钥表的大小,密钥表中的每一行对应一个密钥,加密时按照密钥表中的行进行替换。
解密过程则是加密过程的逆过程。
三、实验内容1. 维吉尼亚密码的加密与解密实现(1)加密① 创建密钥表:根据密钥长度生成密钥表,密钥表中每一行对应一个密钥,密钥长度等于明文长度。
② 对明文进行加密:将明文中的每个字符按照密钥表中的行进行替换,得到密文。
(2)解密① 创建密钥表:根据密钥长度生成密钥表。
② 对密文进行解密:将密文中的每个字符按照密钥表中的行进行替换,得到明文。
2. 维吉尼亚密码的破解(1)重合指数法① 计算密文的重合指数:将密文与英文常见单词的重合指数进行比较,选择重合指数最高的密钥长度。
② 遍历密钥长度:对于每个密钥长度,遍历26个可能的偏移量,计算重合指数,选择重合指数最高的偏移量。
③ 解密密文:根据密钥长度和偏移量,对密文进行解密,得到可能的明文。
(2)暴力破解法① 遍历密钥长度:遍历所有可能的密钥长度。
② 遍历密钥:对于每个密钥长度,遍历所有可能的密钥。
③ 解密密文:根据密钥长度和密钥,对密文进行解密,得到可能的明文。
四、实验步骤1. 创建密钥表根据密钥长度生成密钥表,密钥表中每一行对应一个密钥。
2. 加密明文将明文中的每个字符按照密钥表中的行进行替换,得到密文。
3. 解密密文将密文中的每个字符按照密钥表中的行进行替换,得到明文。
4. 破解密文(1)重合指数法① 计算密文的重合指数。
② 遍历密钥长度。
③ 遍历密钥。
④ 解密密文。
(2)暴力破解法① 遍历密钥长度。
② 遍历密钥。
③ 解密密文。
五、实验结果与分析1. 加密与解密实验结果表明,维吉尼亚密码的加密和解密过程能够正确实现,密文与明文能够成功还原。
现代密码算法实验报告(3篇)

第1篇一、实验目的1. 了解现代密码学的基本原理和数论基础知识;2. 掌握非对称密码体制的著名代表RSA加密算法的工作原理和流程;3. 设计实现一个简单的密钥系统;4. 掌握常用加密算法AES和DES的原理及实现。
二、实验内容1. RSA加密算法实验2. AES加密算法实验3. DES加密算法实验三、实验原理1. RSA加密算法RSA算法是一种非对称加密算法,由罗纳德·李维斯特、阿迪·沙米尔和伦纳德·阿德曼三位密码学家于1977年提出。
其基本原理是选择两个大质数p和q,计算它们的乘积n=pq,并计算欧拉函数φ(n)=(p-1)(q-1)。
选择一个整数e,满足1<e<φ(n)且e与φ(n)互质。
计算e关于φ(n)的模逆元d。
公开密钥为(e,n),私有密钥为(d,n)。
加密过程为C=Me mod n,解密过程为M=Cd mod n。
2. AES加密算法AES(Advanced Encryption Standard)是一种分组加密算法,采用128位分组大小和128、192或256位密钥长度。
AES算法主要分为四个阶段:初始轮、密钥扩展、中间轮和最终轮。
每个轮包括字节替换、行移位、列混淆和轮密钥加。
3. DES加密算法DES(Data Encryption Standard)是一种分组加密算法,采用64位分组大小和56位密钥长度。
DES算法主要分为16轮,每轮包括置换、置换-置换、S盒替换和密钥加。
四、实验步骤及内容1. RSA加密算法实验(1)选择两个大质数p和q,计算n=pq和φ(n)=(p-1)(q-1);(2)选择一个整数e,满足1<e<φ(n)且e与φ(n)互质,计算e关于φ(n)的模逆元d;(3)生成公开密钥(e,n)和私有密钥(d,n);(4)用公钥对明文进行加密,用私钥对密文进行解密。
2. AES加密算法实验(1)选择一个128、192或256位密钥;(2)初始化初始轮密钥;(3)进行16轮加密操作,包括字节替换、行移位、列混淆和轮密钥加;(4)输出加密后的密文。
经典密码学实验报告

一、实验目的1. 了解经典密码学的基本原理和算法;2. 掌握古典密码的加密和解密方法;3. 通过编程实现古典密码的加密和解密过程;4. 体验古典密码的破解过程,加深对密码学原理的理解。
二、实验环境1. 操作系统:Windows 102. 编程语言:Python3.73. 开发工具:PyCharm三、实验内容本次实验主要涉及以下几种古典密码:1. 仿射密码2. 单表代替密码3. 维吉尼亚密码4. 移位密码1. 仿射密码(1)原理简介:仿射密码是一种单字母替换密码,加密公式为:Ci = (a pi + b) mod 26,其中,Ci 为密文,pi 为明文,a 和 b 为密钥。
(2)加密和解密代码实现:```pythondef encrypt(plain_text, a, b):cipher_text = ''for char in plain_text:if char.isalpha():cipher_text += chr(((ord(char.upper()) - ord('A') + a b) % 26) + ord('A'))else:cipher_text += charreturn cipher_textdef decrypt(cipher_text, a, b):plain_text = ''for char in cipher_text:if char.isalpha():plain_text += chr(((ord(char.upper()) - ord('A') - a b) % 26) + ord('A'))else:plain_text += charreturn plain_text```2. 单表代替密码(1)原理简介:单表代替密码是一种将明文中的每个字符映射到密文的密码,加密和解密过程是相反的。
密码学实验报告

密码学实验报告中文汉字的密码化实验1. 实验简介本实验旨在通过对中文汉字的密码化实验,探究密码学在信息安全领域中的应用。
在本实验中,我们将使用替换密码技术对中文汉字进行加密和解密,并评估其安全性和实用性。
2. 实验步骤2.1 选择密钥在开始实验之前,我们需要选择一个密钥。
密钥是密码算法的关键,它用于对明文进行加密和解密。
在本实验中,我们选择一个包含所有中文汉字的密钥表。
该密钥表将用于替换明文中的汉字,从而实现密码化。
2.2 加密过程加密过程涉及将明文中的汉字替换为对应的密钥表中的汉字。
我们将使用一种称为替换密码的技术来实现加密。
具体步骤如下:步骤一:准备明文 - 选择一段中文汉字作为明文。
步骤二:选择密钥表 - 使用预先准备好的密钥表,其中包含了所有中文汉字的替换映射关系。
步骤三:替换汉字 - 将明文中的每个汉字根据密钥表中的映射进行替换。
步骤四:生成密文 - 将替换后的汉字按照顺序组成密文。
2.3 解密过程解密过程即将密文还原为明文。
在我们的实验中,解密过程与加密过程密切相关,因为它需要使用相同的密钥表进行替换。
具体步骤如下:步骤一:准备密文 - 选择加密过程生成的密文作为输入。
步骤二:选择密钥表 - 使用和加密过程相同的密钥表。
步骤三:替换汉字 - 将密文中的每个汉字根据密钥表中的映射进行替换。
步骤四:生成明文 - 将替换后的汉字按照顺序组成明文。
3. 实验结果与讨论在本实验中,我们选择了一段中文汉字作为明文,并使用已准备好的密钥表进行加密和解密操作。
经过多次实验,我们得到了一些实验结果和相应的讨论。
3.1 加密结果经过加密过程,我们得到了一段由密文组成的结果。
加密后的密文将替换明文中的汉字,使其具有一定的保密性。
然而,我们也发现了一些问题:问题一:密文长度增加 - 密文的长度通常会大于明文的长度,这可能导致在传输和存储过程中的一些问题。
问题二:密钥表可预测 - 由于我们使用了固定的密钥表,攻击者有可能通过分析密文和明文之间的关系来推断出密钥表的内容。
密码学实验报告

密码学实验报告信息安全实验报告学号:学生姓名:班级:实验三密码学实验一、古典密码算法实验一、实验目的通过编程实现替代密码算法和置换密码算法,加深对古典密码体制的了解,为深入学习密码学奠定基础。
二、编译环境运行windows 或linux 操作系统的PC 机,具有gcc、VC 等C语言编译环境。
三、实验原理古典密码算法历史上曾被广泛应用,大都比较简单,使用手工和机械操作来实现加密和解密。
它的主要应用对象是文字信息,利用密码算法实现文字信息的加密和解密。
下面介绍两种常见的具有代表性的古典密码算法,以帮助读者对密码算法建立一个初步的印象。
1.替代密码替代密码算法的原理是使用替代法进行加密,就是将明文中的字符用其它字符替代后形成密文。
例如:明文字母a、b、c、d ,用D、E、F、G做对应替换后形成密文。
替代密码包括多种类型,如单表替代密码、多明码替代密码、多字母替代密码、多表替代密码等。
下面我们介绍一种典型的单表替代密码,恺撒密码,又叫循环移位密码。
它的加密方法,就是将明文中的每个字母用此字符在字母表中后面第k个字母替代。
它的加密过程可以表示为下面的函数:E= mod n其中:m 为明文字母在字母表中的位置数;n 为字母表中的字母个数;k 为密钥;E为密文字母在字母表中对应的位置数。
例如,对于明文字母H,其在字母表中的位置数为8,设k=4,则按照上式计算出来的密文为L:E = mod n = mod 26 = 12 = L2.置换密码置换密码算法的原理是不改变明文字符,只将字符在明文中的排列顺序改变,从而实现明文信息的加密。
置换密码有时又称为换位密码。
矩阵换位法是实现置换密码的一种常用方法。
它将明文中的字母按照给的顺序安排在一个矩阵中,然后用根据密钥提供的顺序重新组合矩阵中字母,从而形成密文。
例如,明文为attack begins at five,密钥为cipher,将明文按照每行6 列的形式排在矩阵中,形成如下形式: a ttack b e gins a tfive根据密钥cipher中各字母在字母表中出现的先后顺序,给定一个置换: 1 2 3 4 5 6 f =1 4 5 32 6根据上面的置换,将原有矩阵中的字母按照第 1 列,第 4 列,第5 列,第 3 列,第2列,第 6 列的顺序排列,则有下面形式: a a c t tk b i n g e s a I v f te从而得到密文:abatgftetcnvaiikse其解密的过程是根据密钥的字母数作为列数,将密文按照列、行的顺序写出,再根据由密钥给出的矩阵置换产生新的矩阵,从而恢复明文。
密码学实验报告

密码学实验报告摘要:本实验旨在通过实践掌握基本密码学算法的原理和应用。
在本次实验中我们完成了Caesar密码、仿射密码、VIC密码和Hill密码的加密和解密过程,并进行了相应的分析和评价。
实验结果表明,不同的密码算法有各自的优缺点,应根据具体需求进行选择。
一、实验目的1.了解基本密码学算法的原理和应用。
2.通过实践掌握Caesar密码、仿射密码、VIC密码和Hill密码的加密和解密过程。
3.分析和评价各个密码算法的优缺点。
二、实验原理Caesar密码:是一种非常简单的单字母替换密码。
按照字母表上旋转的位置,每个字母都用它在字母表中的下一个字母替代。
仿射密码:通过将明文中的每个字母转换为另一个字母,实现加密。
明文中的每个字母通过使用一组固定的数学函数进行加密。
随机选择这些函数,并按正确的顺序应用它们。
VIC密码:将某些字母替换为其他字母组合的运算称为置换。
VIC密码使用10个钥匙,其中每个钥匙是一个置换。
通过使用不同的键,VIC密码可以很容易地产生四十亿多个不同的密码。
Hill密码:是一种基于线性代数理论的密码算法。
对于一个给定的矩阵α,Hill密码通过将明文划分为每个字母,然后将其与矩阵α乘法来加密,最后将结果映射回字母表中的字母。
三、实验过程1.实现Caesar密码的加密和解密。
2.实现仿射密码的加密和解密。
3.实现VIC密码的加密和解密。
4.实现Hill密码的加密和解密。
5.对各个密码算法进行分析和评价。
四、实验结果1.在Caesar密码中,明文是将每个字母按照一定的步长向右或向左移动来进行加密。
由于其简单性,Caesar密码的加密和解密都很容易,但安全性较低。
2.仿射密码是Caesar密码的扩展版本。
通过随机选择两个数字,仿射密码在加密的过程中使用模运算和线性函数组合对明文进行加密。
由于消息加密和解密都使用数学功能进行计算,因此密钥空间大于Caesar,也比较安全。
3.VIC密码使用多个置换键(通常为10),交替使用它们来完成加密和解密过程。
实验吧_密码学实验报告(3篇)

第1篇一、实验背景密码学是一门研究信息加密与解密的学科,它广泛应用于信息安全领域。
为了更好地理解密码学的基本原理和算法,我们选择了实验吧平台上的密码学实验进行学习。
本次实验旨在通过实际操作,加深对古典密码、对称密码和不对称密码等密码学基本概念的理解,提高密码学应用能力。
二、实验目的1. 理解并掌握古典密码的基本原理和算法;2. 掌握对称密码和不对称密码的基本原理和算法;3. 通过实验操作,提高密码学应用能力;4. 培养团队协作和解决问题的能力。
三、实验内容1. 古典密码实验(1)仿射密码原理:仿射密码是一种单字母替换密码,加密公式为:C = (aP + b) mod 26,其中C为密文字母,P为明文字母,a和b为密钥。
操作步骤:1)编写加密函数encrypt,实现仿射密码加密;2)编写解密函数decrypt,实现仿射密码解密;3)测试加密和解密函数,验证其正确性。
(2)单表代替密码原理:单表代替密码是一种将明文字符映射到密文字符的替换密码。
操作步骤:1)编写加密函数subencrypt,实现单表代替密码加密;2)编写解密函数subdecrypt,实现单表代替密码解密;3)测试加密和解密函数,验证其正确性。
(3)维吉尼亚密码原理:维吉尼亚密码是一种多字母替换密码,加密公式为:C = (P + K[i]) mod 26,其中C为密文字母,P为明文字母,K为密钥,i为索引。
操作步骤:1)编写加密函数vigenereencrypt,实现维吉尼亚密码加密;2)编写解密函数vigeneredecrypt,实现维吉尼亚密码解密;3)测试加密和解密函数,验证其正确性。
2. 对称密码实验(1)DES加密算法原理:DES(Data Encryption Standard)是一种分组加密算法,采用56位密钥,64位分组。
操作步骤:1)编写DES加密函数desencrypt,实现DES加密;2)编写DES解密函数desdecrypt,实现DES解密;3)测试加密和解密函数,验证其正确性。
密码学相关实验报告

一、实验目的1. 理解并掌握常见的加密算法和密码体制的基本原理。
2. 学会使用密码学工具进行加密和解密操作。
3. 增强网络安全意识,提高对密码学在实际应用中的认识。
二、实验内容1. 仿射密码2. 单表代替密码3. 维吉尼亚密码4. AES加密算法三、实验原理1. 仿射密码:加密原理为将明文进行0~25字母编码,按照加密公式计算出密文对应位置的字母编码,最后从密文的字母编码还原出密文对应位置的字母。
解密原理与加密原理相反。
2. 单表代替密码:加密原理为利用代替表,将明文中的每个字符映射到密文。
解密原理为对代替表进行反向查找,由密文映射回明文。
3. 维吉尼亚密码:加密原理为通过加密方程Ci (pi k(i mod m)) mod 26,由明文得到密文。
解密原理为解密过程是加密过程的逆过程,通过解密方程pi (Cik(i mod m)) mod 26。
4. AES加密算法:是一种分组加密算法,将128位明文分为128位的数据块,使用密钥进行加密,得到128位的密文。
解密过程与加密过程相反。
四、实验步骤1. 仿射密码(1)选择明文:选择一段英文或数字,例如:"Hello World!"(2)选择密钥:选择一个密钥a和模数m,例如:a=5,m=26。
(3)加密:将明文进行0~25字母编码,按照加密公式计算出密文对应位置的字母编码,最后从密文的字母编码还原出密文对应位置的字母。
(4)解密:将密文进行0~25字母编码,按照解密公式计算出明文对应位置的字母编码,最后从明文的字母编码还原出明文对应位置的字母。
2. 单表代替密码(1)构造代替表:选择一个代替表,将明文中的每个字符映射到密文。
(2)加密:将明文中的每个字符按照代替表进行映射,得到密文。
(3)解密:将密文中的每个字符按照代替表的逆映射,得到明文。
3. 维吉尼亚密码(1)选择密钥:选择一个密钥,例如:"KEY"(2)加密:将明文和密钥进行异或操作,得到密文。
密码学实验——精选推荐
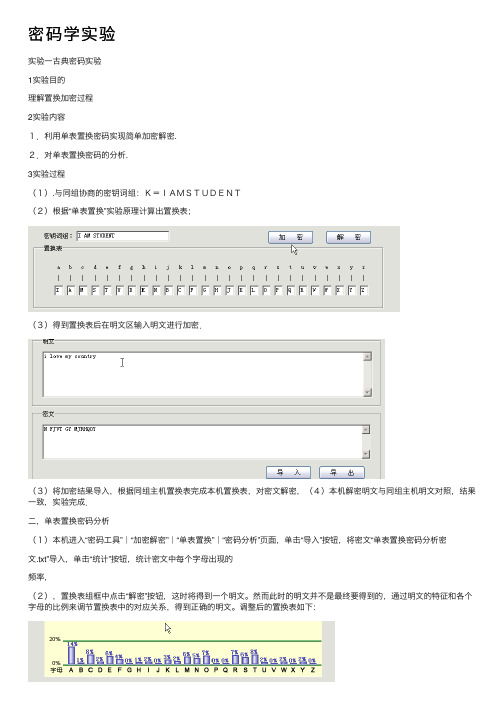
密码学实验实验⼀古典密码实验1实验⽬的理解置换加密过程2实验内容1.利⽤单表置换密码实现简单加密解密.2.对单表置换密码的分析.3实验过程(1).与同组协商的密钥词组:K=IAMSTUDENT(2)根据“单表置换”实验原理计算出置换表;(3)得到置换表后在明⽂区输⼊明⽂进⾏加密.(3)将加密结果导⼊,根据同组主机置换表完成本机置换表,对密⽂解密,(4)本机解密明⽂与同组主机明⽂对照,结果⼀致,实验完成.⼆,单表置换密码分析(1)本机进⼊“密码⼯具”|“加密解密”|“单表置换”|“密码分析”页⾯,单击“导⼊”按钮,将密⽂“单表置换密码分析密⽂.txt”导⼊,单击“统计”按钮,统计密⽂中每个字母出现的频率,(2),置换表组框中点击“解密”按钮,这时将得到⼀个明⽂。
然⽽此时的明⽂并不是最终要得到的,通过明⽂的特征和各个字母的⽐例来调节置换表中的对应关系,得到正确的明⽂。
调整后的置换表如下:(3)对密⽂解密如下:4结论通过将解密后的明⽂和同组主机记录的明⽂对照,得到相同结果,说明成功。
古典密码学中的单表置换在算法上简洁明了,易懂,并对明⽂进⾏⼀定的加密,然⽽通过对单表置换密码的分析,通过统计规律,我们可以通过英⽂字母出现的频率来破解密⽂,这样看来其实并不是完全安全的,实验⼆分组密码实验1实验⽬的1.理解对称加密算法的原理和特点2.理解DES算法的加密原理3理解AES算法的加密原理2实验内容1.进⾏简单的DES加密解密.2.利⽤AES原理实现加密解密,3实验过程⼀.进⼊“密码⼯具”|“加密解密”|“AES加密算法”|“加密/解密”页签,在明⽂输⼊区输⼊明⽂⼆.(1) 本机进⼊“密码⼯具”|“加密解密”|“AES加密算法”|“加密/解密”页签,在明⽂输⼊区输⼊明⽂:。
本机进⼊“密码⼯具”|“加密解密”|“AES加密算法”|“加密/解密”页签,在明⽂输⼊区输⼊明⽂(2)在密钥窗⼝输⼊16(128位)个字符的密钥k,要记住这个密钥以⽤于解密,密钥k= 。
密码学的实验报告

一、实验目的1. 了解密码学的基本概念和原理;2. 掌握常用的加密算法和解密算法;3. 学会使用密码学工具进行加密和解密操作;4. 培养学生的实践能力和创新思维。
二、实验环境1. 操作系统:Windows 102. 编程语言:Python3.83. 密码学库:PyCryptodome三、实验内容1. 加密算法实验1.1 实现DES加密算法1.2 实现AES加密算法1.3 实现RSA加密算法2. 解密算法实验2.1 使用DES解密算法解密加密数据2.2 使用AES解密算法解密加密数据2.3 使用RSA解密算法解密加密数据3. 密钥管理实验3.1 生成DES密钥3.2 生成AES密钥3.3 生成RSA密钥对4. 密码学工具使用实验4.1 使用PyCryptodome库进行加密和解密操作4.2 使用在线加密工具进行加密和解密操作四、实验步骤1. 加密算法实验1.1 实现DES加密算法1.1.1 导入PyCryptodome库中的DES模块;1.1.2 生成DES密钥;1.1.3 使用DES密钥对明文进行加密;1.1.4 输出加密后的密文。
1.2 实现AES加密算法1.2.1 导入PyCryptodome库中的AES模块;1.2.2 生成AES密钥;1.2.3 使用AES密钥对明文进行加密;1.2.4 输出加密后的密文。
1.3 实现RSA加密算法1.3.1 导入PyCryptodome库中的RSA模块;1.3.2 生成RSA密钥对;1.3.3 使用公钥对明文进行加密;1.3.4 输出加密后的密文。
2. 解密算法实验2.1 使用DES解密算法解密加密数据2.1.1 导入PyCryptodome库中的DES模块;2.1.2 使用DES密钥对密文进行解密;2.1.3 输出解密后的明文。
2.2 使用AES解密算法解密加密数据2.2.1 导入PyCryptodome库中的AES模块;2.2.2 使用AES密钥对密文进行解密;2.2.3 输出解密后的明文。
《密码学》课程设计实验报告-数字签名

《密码学》课程设计实验报告实验序号:06 实验项目名称:数字签名RSA签名RSA签名核心代码说明由于在实验报告5中已经对RSA的相关代码进行了分析,这里主要给出签名和验签的代码。
在对某个二进制文件进行签名之前,我们首先需要计算其数据摘要,这里我们采用md5哈希算法,其对应的代码如下md5哈希算法在RSA的签名中,其实就是用私钥进行解密的过程,其对应的代码如下RSA签名其中解密对应的代码如下,pow函数提供了快速幂的功能RSA解密在RSA验签的过程中,其实就是用公钥进行加密的过程,其对应的代码如下RSA验签其中加密对应的算法如下RSA加密RSA签名实验结果演示首先是计算待签名文件的md5值md5结果对得到的md5值进行签名,可以得到如下的结果RSA签名结果对签名进行验签,可以发现成功验证签名验证签名ECC签名代码整体说明相关文件(ecc.py)由于在前面的ECC加解密(实验报告5)中已经对ECC的相关接口进行了介绍,这里我们不再重复。
这里主要给出签名和验签的主要流程签名的主要流程如下1.选择一个随机数k,k∈{1,2,⋯,n−1}2.计算点R(x R,y R)=kG,并记r=x R3.利用保密的解密钥d计算s=(Hasℎ(m)−dr)k−1 (mod n)4.以<r,s>作为消息m的签名,并以<m,r,s>的形式传输或者存储验签的主要流程如下1.计算s−1 (mod n)2.利用公开的加密钥Q计算U(x U,y U)=s−1(Hasℎ(m)G−rQ)3.如果x U=r,则<r,s>是用户A对m的签名ECC签名核心代码说明由于在实验报告5中已经对ECC的相关代码进行了分析,这里主要给出签名和验签的代码。
进行签名的代码主要如下,可以发现和我们上面提到的签名步骤是一一对应的ECC签名进行验签的代码如下,和上述我们提到的验签步骤也是一一对应的ECC验签ECC签名实验结果演示同RSA签名一样,我们首先需要计算文件对应的数据摘要,这里我们使用md5哈希算法md5数据摘要接着对数据摘要进行签名,得到如下的签名结果ECC签名结果对得到的签名进行验签,可以发现成功验证ECC验签五、分析与讨论1)与ECC的签名相比,RSA的签名和验签显得更为优雅,即解密对应签名,加密对应验签2)和RSA签名相比,ECC引入了随机数k,使得即使对同一个数据进行签名,产生的结果也可能不一样,这在一定程度上增加了ECC签名的安全性3)与传统的分组密码相比,使用公钥密码实现数字签名非常方便且更加安全。
现代密码学实验报告

一、实验目的通过本次实验,了解现代密码学的基本原理和方法,掌握密码学在通信与网络安全中的应用,提高对密码算法的分析和设计能力。
二、实验内容1. 理解密码学的基本概念和原理;2. 掌握对称加密算法和非对称加密算法的基本原理;3. 实现DES、AES、RSA等常用密码算法;4. 分析和比较不同密码算法的性能;5. 设计简单的密码系统。
三、实验步骤1. 理解密码学的基本概念和原理密码学是研究保护信息安全的一门学科,主要包括加密、解密、认证和密钥管理等。
密码学的基本原理包括:保密性、完整性、可用性和抗抵赖性。
2. 掌握对称加密算法和非对称加密算法的基本原理(1)对称加密算法:加密和解密使用相同的密钥,如DES、AES等。
其优点是加密速度快,但密钥分发和管理困难。
(2)非对称加密算法:加密和解密使用不同的密钥,如RSA、ECC等。
其优点是密钥分发和管理简单,但加密速度较慢。
3. 实现DES、AES、RSA等常用密码算法(1)DES算法:本实验使用Python语言实现DES算法的加解密过程。
首先,构造DES密钥,然后对明文进行加密和解密。
(2)AES算法:本实验使用Python语言实现AES算法的加解密过程。
首先,构造AES密钥,然后对明文进行加密和解密。
(3)RSA算法:本实验使用Python语言实现RSA算法的加解密过程。
首先,生成公钥和私钥,然后使用公钥加密明文,使用私钥解密密文。
4. 分析和比较不同密码算法的性能通过对DES、AES、RSA等密码算法的实验,分析不同算法在加密速度、安全性、密钥长度等方面的差异,为实际应用提供参考。
5. 设计简单的密码系统结合所学知识,设计一个简单的密码系统,包括密钥生成、加密、解密和认证等功能。
四、实验结果与分析1. DES算法(1)加密速度:DES算法的加密速度较快,适合对速度要求较高的场合。
(2)安全性:DES算法的密钥长度为56位,相对较短,安全性较低。
2. AES算法(1)加密速度:AES算法的加密速度较快,适合对速度要求较高的场合。
密码学实验报告

一、实验目的1. 理解密码学的基本概念和原理。
2. 掌握常见的加密算法和解密算法。
3. 熟悉密码学的实际应用。
4. 培养实际操作能力和问题解决能力。
二、实验内容1. 古典密码学(1)单表替换密码实验内容:使用单表替换密码对一段明文进行加密和解密。
实验步骤:1)创建一个字符替换表;2)将明文中的每个字符替换为替换表中的对应字符;3)将替换后的字符拼接成密文;4)使用相同的替换表将密文解密,还原为明文。
(2)维吉尼亚密码实验内容:使用维吉尼亚密码对一段明文进行加密和解密。
实验步骤:1)确定密钥;2)按照密钥的长度将明文分成多个部分;3)对每个部分使用单表替换密码进行加密;4)将加密后的部分拼接成密文;5)使用相同的密钥和解密步骤将密文解密,还原为明文。
2. 现代密码学(1)DES加密算法实验内容:使用DES加密算法对一段明文进行加密和解密。
实验步骤:1)生成DES密钥;2)将明文分割成64位的数据块;3)对每个数据块进行加密,得到密文;4)使用相同的密钥和解密步骤将密文解密,还原为明文。
(2)AES加密算法实验内容:使用AES加密算法对一段明文进行加密和解密。
实验步骤:1)生成AES密钥;2)将明文分割成128位的数据块;3)对每个数据块进行加密,得到密文;4)使用相同的密钥和解密步骤将密文解密,还原为明文。
三、实验结果与分析1. 古典密码学实验结果单表替换密码和维吉尼亚密码的加密和解密效果良好,能够成功将明文加密为密文,再解密为明文。
2. 现代密码学实验结果DES和AES加密算法的加密和解密效果良好,能够成功将明文加密为密文,再解密为明文。
四、实验总结1. 通过本次实验,掌握了密码学的基本概念和原理。
2. 熟悉了常见的加密算法和解密算法,包括古典密码学和现代密码学。
3. 提高了实际操作能力和问题解决能力。
五、实验拓展1. 研究不同加密算法的优缺点,了解其在实际应用中的适用场景。
2. 学习更多密码学相关知识,如量子密码学、区块链密码学等。
密码学实验报告

目录AES加密算法实现 (2)一.实验目的 (2)二.实验原理 (2)三.实验步骤 (2)四.实验结果 (6)五.实验心得 (7)六.源代码: (8)RSA加解密算法实现 (17)一.实验目的: (17)二.实验要求: (17)三.RSA函数主要代码 (17)四.运算结果显示: (20)五.实验心得 (20)AES加密算法实现一.实验目的1.深入理解AES加密/解密算法理论的基础上,设计一个AES加密/解密软件系统;2.完成一个明文分组的加解密,明文和密钥是十六进制,长度都为128比特(32个16进制数),输入明文和密钥,输出密文,进行加密后,能够进行正确的解密;二.实验原理AES的区块长度固定为128 比特,密钥长度则可以是128,192或256比特;大多数AES计算是在一个特别的有限域完成的。
AES加密过程是在一个4×4的字节矩阵上运作,这个矩阵又称为“状态矩阵”,其初值就是一个明文区块(矩阵中一个元素大小就是明文区块中的一个Byte)。
加密时,各轮AES加密循环(除最后一轮外)均包含4个步骤:1.SubBytes —通过一个非线性的替换函数,用查找表的方式把每个字节替换成对应的字节。
2.ShiftRows —将矩阵中的每个行进行循环式移位。
3.MixColumns —列混淆。
这个步骤使用线性转换来混合每列的四个字节。
4.AddRoundKey —矩阵中的每一个字节都与该次回合轮密钥(round key)做XOR运算;每个子密钥由密钥生成方案产生。
三.实验步骤(一)加密1.密钥生成void keyexpansion(unsigned char S_BOX[][16],unsigned char keys[][44]){unsigned char Rcon[11] = {0,1,2,4,8,16,32,64,128,27,54};unsigned char past[4];register int i,j;//打开密钥文件if((fp=fopen("Key.txt","r"))==NULL){printf("CAN NOT OPEN THE FILE!\n");return ;}printf("\n请输入密钥!\n");for(i = 0;i <= 3;i ++)for(j = 0;j <= 3;j ++){fscanf(fp,"%02x",&keys[j][i]);printf("%02x ",keys[j][i]);}for(i = 4;i <= 43;i ++){ //make the other 40 keys if(i % 4 == 0){ //如果能被4整除,特殊处理for(j = 1;j <= 4;j ++) //把前一个密钥移位赋值给数组past[j - 1] = keys[j % 4][i -1];for(j = 0;j <= 3;j ++){if(j == 0)keys[j][i] = S_BOX[past[j] / 16][past[j] % 16] ^ Rcon[i / 4] ^ keys[j][i - 4];elsekeys[j][i] = S_BOX[past[j] / 16][past[j] % 16] ^ keys[j][i - 4];}}else{for(j = 0;j <= 3;j ++){keys[j][i] = keys[j][i - 4] ^ keys[j][i - 1];}}}}2.字节变换void bytesub(unsigned char S_BOX[][16],unsigned char B[][4]){register int i,j;for(i = 0;i <= 3;i ++)for(j = 0;j <= 3;j ++)B[i][j] = S_BOX[B[i][j] / 16][B[i][j] % 16];}3. 行移位void shiftrow(unsigned char B[][4]){int i,temp;temp = B[1][0];for(i = 0;i <= 2;i ++)B[1][i] = B[1][i + 1];B[1][3] = temp;for(i = 0;i <= 1;i ++){temp = B[2][i];B[2][i] = B[2][i + 2];B[2][i + 2] = temp;}temp = B[3][3];for(i = 3;i >=1;i --)B[3][i] = B[3][i - 1];B[3][0] = temp;}4. 列混合运算unsigned char xtime (unsigned char input){ // x乘法('02'乘法)int temp;temp = input<<1;if(input & 0x80){temp ^= 0x1b;}return temp;}void mixcolumn(unsigned char input[][4]){ //列混合int i, j;unsigned char output[4][4];for(j = 0;j <= 3;j++)for(i = 0;i <= 3;i++)output[i][j] = xtime(input[i%4][j]) //0x02乘法^ ( input[ ( i + 1 ) % 4][j] ^ xtime( input[ ( i + 1 ) % 4][j] ) ) //0x03乘法^ input[ ( i + 2 ) % 4][j] //0x01乘法^ input[ ( i + 3 ) % 4][j]; //0x01乘法for(i = 0;i <= 3;i ++)for(j = 0;j <= 3;j ++)input[i][j] = output[i][j];}(二)解密运算1.逆行移位void invshiftrow(unsigned char B[][4]){int i,temp;temp = B[1][3];for(i = 3;i >= 1;i --)B[1][i] = B[1][i - 1];B[1][0] = temp;for(i = 0;i <= 1;i ++){temp = B[2][i];B[2][i] = B[2][i + 2];B[2][i + 2] = temp;}temp = B[3][0];for(i = 0;i <= 2;i ++)B[3][i] = B[3][i + 1];B[3][3] = temp;}2.逆列混合运算void invmixcolum(unsigned char input[][4]){int i, j;unsigned char output[4][4];for(j=0; j< 4; j++)for(i=0; i<4; i++)output[i][j] = (xtime(xtime(xtime(input[i % 4][j]))) ^ xtime(xtime(input[i % 4][j]))^xtime(input[i % 4][j])) //0x0E乘法^ (xtime(xtime(xtime(input[ ( i + 1 ) % 4][j]))) ^ xtime(input[ ( i + 1 ) % 4][j]) ^ input[ ( i + 1 ) % 4][j]) //0x0B乘法^ (xtime(xtime(xtime(input[ ( i + 2 ) % 4][j]))) ^ xtime(xtime(input[ ( i + 2 ) % 4][j])) ^ input[ ( i + 2 ) % 4][j]) //0x0D 乘法^ (xtime(xtime(xtime(input[ ( i + 3 ) % 4][j]))) ^ input[ ( i + 3 ) % 4][j]); //0x09乘法for(i = 0;i <= 3;i ++)for(j = 0;j <= 3;j ++)input[i][j] = output[i][j];}3.逆字节变换void invbytesub(unsigned char N_S_BOX[][16],unsigned char B[][4]){register int i,j;for(i = 0;i <= 3;i ++)for(j = 0;j <= 3;j ++)B[i][j] = N_S_BOX[B[i][j] / 16][B[i][j] % 16];}四.实验结果我将明文设为13 43 67 69 88 d5 f6 8d 64 23 90 a2 e0 f5 b4 34,密钥设为23 43 45 78 28 af cd ab f7 d4 88 09 c3 4f 3c 57,运行结果如下:五.实验心得本程序是处理的AES分组大小和密钥长度都为128位,迭代轮数为10轮。
实验报告_密码学(二)2024

实验报告_密码学(二)引言概述:密码学是一门研究如何保护信息安全的学科,它的应用广泛涵盖了数据加密、数据完整性校验和身份认证等方面。
本实验报告旨在深入探讨密码学的相关知识,包括对称密码学、非对称密码学、哈希函数和数字签名的原理与应用等内容。
正文:1. 对称密码学- 原理:对称密码学采用相同的密钥对数据进行加密和解密,常用的算法有DES、AES等。
- 分组加密:将数据按固定长度进行分组加密,提高数据的安全性。
- 工作模式:常用的工作模式有电子密码本模式、密码分组链接模式等,用于提供更高的安全性和数据完整性。
- 密钥管理:讨论密钥的生成、分发和保护,包括密钥的更新和撤销等问题。
2. 非对称密码学- 原理:非对称密码学采用不同的密钥对数据进行加密和解密,常用的算法有RSA、DSA等。
- 公钥密码算法:介绍公钥密码算法的加密流程和解密过程,讨论公钥和私钥的生成和管理。
- 数字证书:介绍数字证书的概念和作用,讨论数字证书的颁发和验证过程。
- 密钥交换:讨论密钥交换协议,如Diffie-Hellman密钥交换协议,用于实现安全的密钥交换。
3. 哈希函数- 原理:哈希函数将任意长度的数据转换为固定长度的哈希值,常用的算法有MD5、SHA-1等。
- 安全性分析:讨论哈希函数的安全性,包括抗碰撞性、抗第二原像性和抗预像性等。
- 应用场景:介绍哈希函数在数字签名、消息认证码和数据完整性校验等方面的应用。
4. 数字签名- 原理:数字签名是利用非对称密码学中的私钥对消息进行加密,用于验证消息的真实性和完整性。
- 数字签名算法:介绍常用的数字签名算法,如RSA数字签名算法、DSA数字签名算法等。
- 数字证书:讨论数字证书在数字签名中的作用,以及数字证书颁发和验证的过程。
- 权威性和不可否认性:讨论数字签名的权威性和不可否认性,保证消息的信任和可靠性。
5. 密码学应用- 加密通信:介绍密码学在网络通信中的应用,如SSL/TLS协议和VPN等。
密码学实验报告-DES

密码学应用与实践课程实验报告实验1:实现DES密码体制2)子密钥的生成64比特的密钥生成16个48比特的子密钥。
其生成过程见图:3)解密DES的解密过程和DES的加密过程完全类似,只不过将16圈的子密钥序列K1,K2……K16的顺序倒过来。
即第一圈用第16个子密钥K16,第二圈用K15,其余类推。
第一圈:加密后的结果L=R15, R=L15⊕f(R15,K16)⊕f(R15,K16)=L15同理R15=L14⊕f(R14,K15), L15=R14。
同理类推:得 L=R0, R=L0。
3.密钥生成(1)取得密钥从用户处取得一个64位(本文如未特指,均指二进制位))长的密码key ,去除64位密码中作为奇偶校验位的第8、16、24、32、40、48、56、64位,剩下的56位作为有效输入密钥.(2)等分密钥(3)密钥移位DES算法的密钥是经过16次迭代得到一组密钥的,把在1.1.2步中生成的A,B视为迭代的起始密钥. 比如在第1次迭代时密钥循环左移1位,第3次迭代时密钥循环左移2位. 第9次迭代时密钥循环左移1位,第14次迭代时密钥循环左移2位.第一次迭代:A(1) = ǿ(1) AB(1) = ǿ(1) B第i次迭代:A(i) = ǿ(i) A(i-1)B(i) = ǿ(i) B(i-1)(4)密钥的选取在(3)步中第i次迭代生成的两个28位长的密钥为把合并按照表4所示k的第一位为56位密钥的第14位,k的第2位为56位密钥的第17位,...,依此类推,k的最后一位最后一位是56位密钥的第32位。
生成与进行第i次迭代加密的数据进行按位异或的48位使用密钥:(5)迭代DES算法密钥生成需要进行16次迭代,在完成16次迭代前,循环执行(3)(4)步.最终形成16套加密密钥:key[0] , key[1] , key[2] ,…. key[14] , key[15] .(1)取得数据把明文数据分成64位的数据块,不够64位的数据块以适当的方式补足。
密码学案例实验报告

一、实验背景随着信息技术的飞速发展,网络安全问题日益突出,加密技术作为保障信息安全的重要手段,在各个领域都得到了广泛应用。
本实验报告旨在通过实际操作,加深对密码学原理和算法的理解,提高加密和解密的能力。
二、实验目的1. 了解密码学的基本概念和分类;2. 掌握DES、AES等常用加密算法的原理和流程;3. 能够运用密码学工具进行加密和解密操作;4. 分析密码破解技术,提高安全意识。
三、实验内容1. 实验一:DES加密算法(1)实验原理DES(Data Encryption Standard)是一种经典的对称加密算法,它采用64位密钥和64位明文,经过16轮加密操作,生成64位密文。
(2)实验步骤① 编写程序实现DES加密算法的加解密功能;② 使用密钥对一段英文文本进行加密和解密;③ 分析加密和解密结果,验证算法的正确性。
2. 实验二:AES加密算法(1)实验原理AES(Advanced Encryption Standard)是一种广泛使用的对称加密算法,它支持128位、192位和256位密钥长度,具有速度快、安全性高等优点。
(2)实验步骤① 编写程序实现AES加密算法的加解密功能;② 使用不同长度的密钥对一段英文文本进行加密和解密;③ 分析加密和解密结果,验证算法的正确性。
3. 实验三:密码破解技术(1)实验原理密码破解技术是指通过尝试各种可能的密钥,来破解加密信息的技术。
常见的密码破解方法有穷举攻击、字典攻击、暴力破解等。
(2)实验步骤① 使用密码破解工具对加密文本进行破解;② 分析破解结果,了解不同破解方法的特点和适用场景;③ 提高安全意识,防范密码破解攻击。
四、实验结果与分析1. 实验一和实验二的结果表明,DES和AES加密算法能够正确地对文本进行加密和解密,验证了算法的正确性。
2. 通过实验三,我们了解到密码破解技术的种类和特点,提高了安全意识。
在实际应用中,应选择合适的加密算法和密钥长度,以提高安全性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一古典密码实验1实验目的理解置换加密过程2实验内容1.利用单表置换密码实现简单加密解密.2.对单表置换密码的分析.3实验过程(1).与同组协商的密钥词组:K=IAMSTUDENT(2)根据“单表置换”实验原理计算出置换表;(3)得到置换表后在明文区输入明文进行加密.(3)将加密结果导入,根据同组主机置换表完成本机置换表,对密文解密,(4)本机解密明文与同组主机明文对照,结果一致,实验完成.二,单表置换密码分析(1)本机进入“密码工具”|“加密解密”|“单表置换”|“密码分析”页面,单击“导入”按钮,将密文“单表置换密码分析密文.txt”导入,单击“统计”按钮,统计密文中每个字母出现的频率,(2),置换表组框中点击“解密”按钮,这时将得到一个明文。
然而此时的明文并不是最终要得到的,通过明文的特征和各个字母的比例来调节置换表中的对应关系,得到正确的明文。
调整后的置换表如下:(3)对密文解密如下:4结论通过将解密后的明文和同组主机记录的明文对照,得到相同结果,说明成功。
古典密码学中的单表置换在算法上简洁明了,易懂,并对明文进行一定的加密,然而通过对单表置换密码的分析,通过统计规律,我们可以通过英文字母出现的频率来破解密文,这样看来其实并不是完全安全的,实验二分组密码实验1实验目的1.理解对称加密算法的原理和特点2.理解DES算法的加密原理3理解AES算法的加密原理2实验内容1.进行简单的DES加密解密.2.利用AES原理实现加密解密,3实验过程一.进入“密码工具”|“加密解密”|“AES加密算法”|“加密/解密”页签,在明文输入区输入明文二.(1) 本机进入“密码工具”|“加密解密”|“AES加密算法”|“加密/解密”页签,在明文输入区输入明文:。
本机进入“密码工具”|“加密解密”|“AES加密算法”|“加密/解密”页签,在明文输入区输入明文(2)在密钥窗口输入16(128位)个字符的密钥k,要记住这个密钥以用于解密,密钥k= 。
单击“加密”按钮,将密文导出到AES文件夹(D:\Work\Encryption\AES\)中,通告同组主机获取密文,并将密钥k告诉同组主机。
(3)单击“导入”按钮,从同组主机的AES共享文件夹中将密文导入,然后在密钥窗口输入被同组主机通告的密钥k,点击“解密”按钮进行AES解密。
(4)将破解后的明文与同组主机记录的明文比较。
4结论通过这次的实验让我对对称密码中分组密码的DES和AES两种算法有了一定的了解,在算法上两种密码都有各自的密钥生成器,更加确保的密钥的可抗性,相对于古典密码,无论从算法上还是加密的过程都是更加的精密,安全性仅依赖于密钥,不依赖于算法。
分组密码体系是一种区别于古典密码体系的加密思路,当今绝大多数的分组密码都是乘积密码。
乘积密码就是以某种方式连续执行两个或多个密码,以使得所得到的最后结果或乘积比其任意一个组成密码都强。
在安全性上,分组密码比古典密码强的多,并且安全性仅依赖与密钥,不依赖于算法,而且算法完全确定,易于理解。
当然其缺点也是有的,例如密钥位数不够长,造成密文被破译等。
实验三公钥密码实验1实验目的1.了解非对称加密机制2.理解RSA算法的加密原理2实验内容(1)练习模拟RSA加密解密流程.(2)进行RSA加密解密简单应用(3).原理:所谓非对称密钥加密是指每个实体都有自己的公钥和私钥两个密钥,用其中的一个密钥对明文进行加密,都只能用另一个密钥才能解开,并且从其中的一个密钥推导出另一个密钥在计算上都是困难的。
非对称密码算法解决了对称密码体制中密钥管理的难题,并提供了对信息发送人的身份进行验证的手段,是现代密码学最重要的发明。
在公钥密码系统中每个实体都有自己的公钥和相应的私钥。
公钥密码系统的加密变换和解密变换分别用E和D表示。
任何实体B要向实体A发送信息m的步骤如下:实体B首先获得实体A的真实公钥的拷贝(eA),实体B使用eA计算密文c=E(m)并发送给实体A,实体A使用自己的私钥dA,计算m=D(c)解密密文,恢复出明文m。
这里公钥不需要保密,但要保证它的真实性,即eA 确实是实体A掌握的私钥dA所对应的公钥。
提供真实的公钥比安全地分配密钥实现起来要容易得多。
这也是公钥密码系统的主要优点之一。
公钥密码系统的主要目的是提供保密性,它不能提供数据源认证(data origin authentication)和数据完整性(data integrity)。
1.3实验过程(1)本机进入“密码工具”|“加密解密”|“RSA加密算法”|“公私钥”页签,在生成公私钥区输入素数p和素数q,这里要求p和q不能相等(因为很容易开平方求出p与q的值)并且p与q的乘积也不能小于127(因为小于127不能包括所有的ASCII码,导致加密失败)4结论RSA的安全性是基于分解大整数的困难性假定,一般不能直接用RSA进行加解密,因为它是一种决定性算法,相同的明文始终会给出相同的密文.大型网络中的每个用户需要的密钥数量少。
对管理公钥的可信第三方的信任程度要求不高而且是离线的。
只有私钥是保密的,而公钥只要保证它的真实性。
多数公钥加密比对称密钥加密的速度要慢几个数量级。
公钥加密方案的密钥长度比对称加密的密钥要长。
公钥加密方案没有被证明是安全的。
实验四Hash函数实验1实验目的1.理解SHA1函数的计算原理和特点2.理解SHA1算法原理2实验内容(1)了解SHA!原理:信息安全的核心技术是应用密码技术。
密码技术的应用远不止局限于提供机密性服务,密码技术也提供数据完整性服务。
密码学上的散列函数(Hash Functions)就是能提供数据完整性保障的一个重要工具。
密码学哈希函数(cryptography hash function,简称为哈希函数)在现代密码学中起着重要的作用,主要用于数据完整性认证和消息认证。
哈希函数的基本思想是对数据进行运算得到一个摘要,运算过程满足:压缩性:任意长度的数据,算出的摘要长度都固定。
容易计算:从原数据容易计算出摘要。
抗修改性:对原数据进行任何改动,哪怕只修改1个字节,所得到的摘要都有很大区别。
弱抗碰撞:已知原数据和其摘要,想找到一个具有相同摘要的数据(即伪造数据),在计算上是困难的。
强抗碰撞:想找到两个不同的数据,使它们具有相同的摘要,在计算上是困难的。
(2)利用SHA1算法进行加密解密.3实验过程(1)本机进入“密码工具”|“加密解密”|“SHA1哈希函数”|“生成摘要”页面,在明文框中编辑文本内容:。
单击“生成摘要”按钮,生成文本摘要:。
单击“导出”按钮,将摘要导出到SHA1共享文件夹(D:\Work\Encryption\SHA1\)中,并通告同组主机获取摘要。
(2)单击“导入”按钮,从同组主机的SHA1共享文件夹中将摘要导入:在文本框中输入同组主机编辑过的文本内容,单击“生成摘要”按钮,将新生成的摘要与导入的摘要进行比较,验证相同文本会产生相同的摘要。
(3)对同组主机编辑过的文本内容做很小的改动,再次生成摘要,与导入的摘要进行对比,验证SHA1算法的抗修改性:4结论散列函数是一个函数,它以一个变长的报文作为输入,并产生一个定长的散列码,有时也称为报文摘要,作为函数的输出。
散列函数最主要的作用是用于鉴别,鉴别在网络安全中起到举足轻重的地位。
鉴别的目的有以下两个:第一,验证信息的发送者不是冒充的,同时发信息者也不能抵赖,此为信源识别;第二,验证信息完整性,在传递或存储过程中未被篡改,重放或延迟等。
实验五数字签名实验1实验目的1.掌握安全通信中常用的加密算法2.掌握数字签名过程3.掌握安全文件传输基本步骤2实验内容一.假设一个要进行网络通信的两个终端(A和B)所处的环境A和B要进行通信但终端A和B相距很远,但是可以通过网络进行通信.在通信过程中,不能通过其他方式.(如:电话,传真等)二.保证通信安全性.(1)A的信息要加密通信给B(保密要求),(2)B能对发送方身份认证(认证要求),(3)B收到的信息没有被篡改(数据完整性要求),(4)事后A不能否认曾把信息传递给B.(不可否认要求).3实验过程(1).终端A与B先协商好所使用到的对称加密算法,非对称加密算法和哈希函数,采用对称加密算法对传输信息进行加密得到密文(会话秘钥),确保传输保密性。
(2)使用B的公钥对会话秘钥进行加密,确保传输信息的保密性以及接收方的不可否认性(3)采用哈希函数(生成摘要)确保信息传输的完整性病使用自己的私钥对文件摘要加密(得到数字签名)(4)将密文。
加密后的会话秘钥和数字签名封装到一起后,通过网络传输到终端B。
(5)终端B与终端A协商好所使用的同样的加密算法(6)使用自己的私钥对A的会话秘钥进行解密,得到准会话秘钥,使用准会话秘钥对的得到的密文进行解密,得到准明文;使用A的公钥对得到的数字签名进行签名验证,得到准明文摘要。
(7)使用哈希函数计算得到准明文摘要(8)将得到的摘要与准明文进行比较,若相同则表明文件实现安全传输。
4结论通过这次在文件传输中对数字签名的应用可以看出密码学的发展,为数字签名这项技术的实现提供了基础,利用数字签名技术来保证信息传输过程中的数据完整性以及提供对信息发送者身份的认证和不可抵赖性。
