灰狼算法和粒子群算法
粒子群算法原理

粒子群算法原理粒子群算法(ParticleSwarmOptimization,简称PSO)是一种基于群体智能的启发式算法,它由Ken Kennedy和James Kennedy在1995年发明,其目的是模拟物种在搜寻食物路线的过程。
PSO的思路同于生物群体中存在的社会行为,它根据所有参与计算的粒子(即搜索者)以及它们的历史经验进行搜索,以寻找最优解。
在这里,最优解是指可以满足我们的要求的最佳结果(给定的目标函数的最小值)。
PSO把一个群体看成一组搜索者,每个搜索者搜索有一个动态位置,每一步采用一个较优位置取代先前的位置,称之为粒子。
每个粒子都具有一个当前位置,一个速度,一个粒子最佳位置(全局最佳位置)和一个全局最佳位置(群体最佳位置)。
粒子群算法是一种迭代优化算法,它由以下4个步骤组成:1.始化粒子群:在此步骤中,使用随机算法给每个粒子分配初始位置和速度,通常使用均匀分布。
2.解目标函数:计算每个粒子的位置对应的目标函数值,并记录每个粒子的最佳位置以及群体最佳位置。
3.新粒子位置:根据群体最佳位置和每个粒子的最佳位置,更新每个粒子的位置以及速度,它们的新的位置和速度可以使用如下公式来计算:V(t+1)=V(t)+C1*rand(1)*(Pbest(t)-X(t))+C2*rand(2)*(Gbest(t) -X(t))X(t+1)=X(t)+V(t+1)其中,C1和C2是可调的引力系数,rand(1)和rand(2)是随机数,Pbest(t)和Gbest(t)分别表示每个粒子和群体中最佳位置。
4.复步骤2和3,直到收敛或者达到最大迭代次数。
由于粒子群算法有效而且简单,它已经在许多领域应用,比如多目标优化、复杂系统建模、神经网络训练等。
尽管PSO有许多优点,但它也有一些不足,比如,它可能不能收敛到全局最优解,可能会被局部最优解所困扰。
另外,由于其简单的搜索过程,它的计算速度很快,但是它的搜索效率可能不太高。
基于IAOA-PNN模型的天然气压缩因子计算方法研究

采输技术DOI :10.3969/j.issn.1001-2206.2023.06.012基于IAOA-PNN 模型的天然气压缩因子计算方法研究孙玮中国石油华北油田分公司检验检测中心,河北任丘062552摘要:针对部分压气站未设置气相色谱分析仪,无法获取天然气压缩因子的现状,通过拉丁超立方抽样获取虚拟天然气组分样本,随后以准确度较高的GERG-2008方程为基础,计算天然气密度、热值和压缩因子,形成具有热力学性质的天然气数据库,最后搭建概率神经网络(PNN)模型用于数据的训练、验证和预测,并对预测模型结果进行现场验证。
结果表明,IAOA 算法在收敛速度、训练精度和稳定性上优于AOA 算法、PSO 算法和GWO 算法,证明了算法从种群初始化和密度因子方面进行优化的有效性和科学性;现场校验时本文模型的相对误差维持在-1%~2%之间,且对于组分含量和工况的变化不敏感,可适用于大部分管输气的工况条件;密度是影响算法精度的重要参数,在参数缺失的情况下,应优先保证现场具有监测温度、压力和密度的仪器设备。
关键词:压缩因子;AOA;PNN;GERG-2008方程;相对误差Research on the calculation method of natural gas compression factor based on IAOA-PNN modelSUN WeiInspection and Testing Center of Petrochina Huabei Oilfield Company,Renqiu 062552,ChinaAbstract:In response to the situation where some pressurized gas stations do not have gas chromatography analyzers and cannot obtain natural gas compression factors,this study used Latin hypercube sampling to obtain virtual natural gas component samples.Subsequently,based on the highly accurate GERG-2008equation,natural gas density,calorific value and compression factor of natural gas were calculated to create a thermodynamic natural gas database.Finally,a probabilistic neural network (PNN)model was built for data training,verification and prediction,and the results of the prediction model are verified on site.The results show that IAOA algorithm is superior to AOA algorithm,PSO algorithm and GWO algorithm in convergence speed,training accuracy and stability,which proves that the algorithm is effective and scientific in population initialization and density factor optimization.The relative error of this model is between -1%and 2%,and it is not sensitive to the change of component content and working conditions,making it suitable for most gas transmission conditions.Density is an important parameter that affects the accuracy of the algorithm,and in cases of missing parameters,it is important to prioritize the presence of equipment and instruments for monitoring temperature,pressure,and density on-site.Keywords:compression factor;AOA;PNN;GERG-2008equation;relative error天然气作为清洁能源,在我国实现“碳达峰”“碳中和”的目标中占有重要地位[1]。
基于粒子群灰狼混合算法的多目标约束优化问题求解

基于粒子群灰狼混合算法的多目标约束优化问题求解
黄星;卢宇;申亮;林兵
【期刊名称】《小型微型计算机系统》
【年(卷),期】2023(44)2
【摘要】近年来,多目标优化问题引起了广泛关注,其求解目标多、目标函数复杂,当前方法通常将所有目标加权后求解,但这些方法会造成解集缺乏准确性.针对上述情况,本文首先根据目标分解的框架:辅助目标和等价目标约束优化框架,该框架是将约束优化的问题分解为辅助目标和等价目标相结合的优化问题,同时动态调整所分解出的对应子问题的权值,使分解出的子问题求解趋向于等价目标求解.其次基于粒子群优化算法和灰狼优化算法的各自优势,提出参数自适应的粒子群灰狼混合算法,混合算法的优势集合了粒子群算法的收敛性快和灰狼算法的搜索过程多样性,从而提高粒子进化过程的准确性.通过IEEE CEC2017数据集测试的结果表明:在调参合适的情况下,获得的函数最优值个数多于乌鸦搜索、受约束的模拟退火、带约束的水循环等经典算法,在10D情况下,28个测试函数中11个测试函数表现最佳;在30D的情况下,12个测试函数表现最佳.
【总页数】12页(P288-299)
【作者】黄星;卢宇;申亮;林兵
【作者单位】福建师范大学物理与能源学院;福建师范大学协和学院;福建商学院;福建省信息网络重点实验室
【正文语种】中文
【中图分类】TP18
【相关文献】
1.基于混合粒子群优化算法的旅行商问题求解
2.基于改进粒子群优化算法的约束多目标优化
3.基于文化粒子群算法的约束优化问题求解
4.用于约束多目标优化问题的混合粒子群算法
5.基于灰狼粒子群混合算法的相机标定优化方法
因版权原因,仅展示原文概要,查看原文内容请购买。
一种求解最优潮流的改进灰狼优化算法

第14卷㊀第3期Vol.14No.3㊀㊀智㊀能㊀计㊀算㊀机㊀与㊀应㊀用IntelligentComputerandApplications㊀㊀2024年3月㊀Mar.2024㊀㊀㊀㊀㊀㊀文章编号:2095-2163(2024)03-0046-08中图分类号:TE341文献标志码:A一种求解最优潮流的改进灰狼优化算法王㊀恒,杨㊀婷(铜仁职业技术学院信息工程学院,贵州铜仁554300)摘㊀要:最优潮流是电力系统最关键的问题之一,本文采用一种求解最优潮流的改进灰狼优化算法(LMGWO)求解最优潮流(OPF)问题,该算法引入算术优化算法(ArithmeticOptimizationAlgorithm,AOA)中的乘除算子,利用带透镜成像的反向学习策略增强最优个体的多样性,提高算法跳出局部最优的能力㊂通过与几种常用的算法进行对比实验表明:本文提出的LWG⁃WO算法是有竞争力的,总体上优于对比算法;LMGWO算法在最小化燃料成本㊁有功输电损耗和改善电压偏差方面更有效地找到了最优潮流(OPF)问题的最优解㊂关键词:灰狼优化算法;最优潮流;算术优化算法;燃料成本;有功输电损耗AnimprovedgreywolfoptimizationalgorithmforsolvingoptimalpowerflowWANGHeng,YANGTing(SchoolofInformationEngineering,TongrenPolytechnicCollege,Tongren554300,Guizhou,China)Abstract:Optimalpowerflowisoneofthemostcriticalproblemsinpowersystem.Inthispaper,animprovedGreyWolfOptimizationAlgorithm(LMGWO)isusedtosolvetheoptimalpowerflow(OPF)problem.Inthisalgorithm,multiplicationanddivisionoperatorsintheArithmeticOptimizationAlgorithm(AOA)areintroduced.Thereverselearningstrategywithlensimagingisusedtoenhancethediversityofoptimalindividualsandimprovetheabilityofthealgorithmtojumpoutofthelocaloptimal.Throughcomparativeexperimentalanalysisofseveralcommonlyusedalgorithms,theproposedLWGWOalgorithmiscompetitiveandgenerallysuperiortorecentalgorithms.TheexperimentalresultsshowthatLMGWOalgorithmcanfindtheoptimalsolutionofOPFproblemmoreeffectivelyintermsofminimizingfuelcost,activepowertransmissionlossandimprovingvoltagedeviation.Keywords:greywolfoptimizationalgorithm;optimalpowerflow;arithmeticoptimizationalgorithm;fuelcost;activepowertransmissionloss基金项目:铜仁市科学技术局基础科学研究项目(铜市科研(2022)72号)㊂作者简介:王㊀恒(1985-),男,博士研究生,讲师,主要研究方向:智能计算与混合系统㊁人工智能㊁故障诊断研究等㊂Email:wangheng_trzy@foxmail.com收稿日期:2023-06-160㊀引㊀言最优潮流(OPF)问题是电力系统运行过程中备受关注的焦点问题,旨在找到最优的运行方式,使得电力系统的运行成本最低,同时满足安全㊁稳定和环保等约束条件㊂OPF问题的求解是在满足一系列物理㊁环境㊁实际和运行的约束条件下,通过优化特定的目标来确定电力系统的运行状态㊂在此之前,许多传统的优化技术的应用已获成功,包括基于梯度的方法㊁牛顿法㊁单纯形法㊁序列线性规划和内点法[1-5]㊂由于OPF问题本质上是一个多极㊁多约束㊁非凸的复杂优化问题,使用传统的数值方法来求解,过程复杂㊁耗时且精度较差㊂近年来,元启发式算法的快速发展为解决OPF问题提供了更多的选择㊂元启发式算法具有参数少㊁易于操作㊁不需要梯度信息等优点,能够在合理的时间内和高度复杂的约束条件下找到复杂问题的最优解㊂刘自发等学者[6]提出了一种基于混沌粒子群优化方法的电力系统无功最优潮流(OPF)问题㊂Farhat等学者[7]提出了一种基于邻域维度学习搜索策略的增强型黏液霉菌算法(enhancedslimemouldalgorithm,ESMA)用于求解最优潮流(OPF)问题等等㊂越来越多的元启发式算法被广泛用于解决电力系统优化相关问题[8-13]㊂灰狼优化算法(greywolfoptimizer,GWO)是由Mirjalili等学者[14]在2014年上提出的一种新的元启发式算法㊂灰狼优化算法(GWO)原理简单㊁编程容易㊁需要调整的参数少,现已陆续应用于电力系统㊁自动控制㊁能源市场战略招标等领域[15-17]㊂然而,与许多元启发式优化算法一样,灰狼优化算法(GWO)在求解复杂的非线性问题时容易陷入局部最优且收敛速度慢㊂针对原有灰狼优化算法在求解最优潮流(OPF)问题时存在的不足,提出了一种改进的灰狼优化算法(LMGWO算法)㊂基于镜头成像学习和乘除算子策略对原灰狼优化算法(GWO)进行改进,主要有2点改进:(1)为了增强算法的全局探索能力,引入乘除算子策略,提高算法的收敛速度;(2)为增强最优个体的多样性,引入透镜成像修正反向学习策略,提高算法跳出局部最优的能力㊂1㊀最优潮流公式最优潮流(OPF)问题是典型的多变量㊁多约束的非线性组合优化问题㊂最优潮流(OPF)问题的求解过程是通过寻找最优的控制变量来获得最小的目标函数㊂数学模型定义如下:minF(u,x)s.t.g(u,x)=0h(u,x)ɤ0{㊀㊀其中,F表示目标函数;x表示控制变量;u表示状态变量;g(u,x)=0是等式约束;h(u,x)ɤ0是不等式约束㊂1.1㊀控制变量和状态变量最优潮流(OPF)问题公式中的控制变量集合为:㊀㊀x=[PG2, ,PGNG,VG1, ,VGNG,T1, ,TNT,QC1, ,QCNC](1)其中,PG2, ,PGNG为系统除松弛母线外的有功发电量;VG1, ,VGNG为系统的电压幅值;T1, ,TNT为变压器分接设定值;QC1, ,QCNC为并联无功补偿;NG㊁NT㊁NC分别为发电机个数㊁调节变压器个数㊁无功补偿器个数㊂最优潮流(OPF)问题表述的状态变量集合为:u=[PG1,VL1, ,VLNL,QG1, ,QGNG,Sl1, ,Slnl](2)其中,PG为空闲母线输出有功功率;VL为负载母线电压幅值;QG为各发电机组输出无功功率;Sl为输电线路负载㊂1.2㊀目标函数将燃油成本㊁有源输电损耗和电压偏差作为最优潮流(OPF)问题的目标函数㊂各目标函数的数学模型定义如下㊂(1)燃料成本(FC)㊂描述发电成本的目标函数,可得数学建模如下:F1(x,u)=ðNgi=1(ai+biPGi+ciP2Gi)(3)㊀㊀其中,Ng为发电机个数;ai,bi,ci为第i台发电机组的燃料成本系数;PGi为第i台发电机组的实际发电量㊂(2)有功输电损耗(APL)㊂传输线的APL可表示为:㊀F2(x,u)=ði,jɪNlGijV2i+V2j-2ViVjcos(θij)()(4)㊀㊀其中,Nl为输电线路数;Gij为线路ij的传递电导;Vi为第i根母线的电压幅值;Vj为第j根母线的电压幅值;θij为母线i与j之间的电压相角之差㊂1.3㊀约束条件在最优潮流(OPF)问题中,等式约束和不等式约束是电力系统需要满足的约束,通常是每个节点的功率平衡约束,可以通过式(5)和式(6)进行定义:PGi-PDi=ViðNi,j=1Vj(Gijcos(δi-δj)+Bijsin(δi-δj))(5)QGi-QDi=ViðNi,j=1Vj(Gijsin(δi-δj)-Bijcos(δi-δj))(6)其中,PDi㊁QDi分别为第i台母线的有功㊁无功功率;PGi和QGi为第i台发电机的无功发电量;N为母线个数;Gij和Bij分别为母线i和j之间的电导和电纳;Vi和Vj分别为母线i和j的电压幅值㊂2㊀改进的灰狼优化算法2.1㊀灰狼优化算法灰狼优化算法(GWO)是模仿自然界灰狼群体社会等级和捕食行为而衍生的一种元启发式算法[14]㊂灰狼群体的社会等级为α狼㊁β狼㊁δ狼和ω狼㊂狼的狩猎行为分为跟踪㊁包围和攻击猎物三个步骤㊂狼群包围猎物的数学模型定义为:X=Xα(t)-A㊃|C㊃Xα(t)-X(t)|(7)㊀㊀其中,X和Xα分别表示狼个体和猎物个体的位置向量,t表示当前迭代次数㊂系数向量A和C定义为:A=2a㊃r1-a(8)C=2㊃r2(9)㊀㊀其中,r1和r2是[0,1]之间的随机向量,a从2线性递减到0,其数学模型定义为:74第3期王恒,等:一种求解最优潮流的改进灰狼优化算法a=2-2㊃tTmax(10)㊀㊀其中,Tmax为最大迭代次数㊂包围猎物后,β狼和δ狼在α狼的带领下追捕猎物㊂在追捕过程中,狼群的个体位置会随着猎物的逃跑而发生变化㊂因此,灰狼群可以根据α㊁β㊁δ的位置Xα,Xβ,Xδ更新灰狼的位置:X1=Xα(t)-A1㊃|C1㊃Xα(t)-X(t)|(11)X2=Xβ(t)-A2㊃|C2㊃Xβ(t)-X(t)|(12)X3=Xδ(t)-A3㊃|C3㊃Xδ(t)-X(t)|(13)X(t+1)=X1+X2+X33(14)㊀㊀其中,X(t+1)是当前个体的位置㊂2.2㊀改进GWO算法的思路和策略2.2.1㊀算术乘除运算符策略2021年,Abualigah等学者[18]提出的一种新的元启发式算法,即算术优化算法(ArithmeticOptimizationAlgorithm,AOA),主要利用数学中的乘㊁除运算符以及加㊁减运算符四种混合运算㊂AOA中的乘除算子具有较强的全局探索能力㊂灰狼种群在更新位置时侧重使用α狼㊁β狼和δ狼作为精英来引导搜索,具有较强的局部开发能力㊂引入算术乘除算子策略,提高GWO算法的全局探索能力㊂算术乘除算子策略的数学模型定义为:Xji(t+1)=Xjbestː(MOP+ε)㊃[(ubj-lbj)㊃μ+lbj],㊀r3ɤ0.5XjbestˑMOP㊃[(ubj-lbj)㊃μ+lbj],㊀㊀㊀㊀r3>0.5{(15)㊀㊀其中,Xjbest表示当前最优解的第j个位置;r3表示介于[0,1]之间的随机数;ε表示防止分母为0的整数;μ表示调节搜索过程的控制参数,μ的值在基本AOA中为0.5;ubj和lbj分别表示第i个位置的上下界㊂MOP为概率函数,其数学模型描述为:MOP=1-t1τT1τmax(16)㊀㊀其中,τ=5是一个敏感因子,定义了迭代的搜索精度㊂由式(15)可知,AOA可以带来高分布,借助乘除算子实现位置更新,可以大大提高算法的全局探索能力㊂本文设置阈值为0.3㊂2.2.2㊀基于透镜成像的反向学习策略根据灰狼的位置更新公式,由α狼㊁β狼和δ狼带领群体中的其他狼进行位置更新㊂如果α狼㊁β狼和δ狼都处于局部最优,则整个群体会聚集在局部最优区域,导致种群陷入局部最优㊂针对该问题,本文提出一种基于透镜成像原理的反向学习方法,将对立个体与当前最优个体相结合,生成新个体㊂假设在一维空间中,在轴区间[lb,ub]上有一个高度为H的个体P,其在x轴上的投影为X(X为全局最优个体)㊂将焦距为F的镜头放置在基点位置O上(本文取基点位置为(lb+ub/2))㊂个体P通过透镜,以获得高度为H的倒置图像P∗,在这点上,第一个倒置的个体x通过透镜成像在X轴上产生㊂镜头图像的反向学习策略如图1所示㊂㊀㊀在图1中,全局最优个体X以O为基点找到其对应的逆个体X∗㊂因此,可以从透镜成像原理推导出数学模型,推得的公式为:(ub+lb)/2-XX∗-(ub+lb)/2=hh∗(17)㊀㊀设h/h∗=k,k表示拉伸因子㊂通过推导式(17),可以得到反转点X∗的计算公式:X∗=ub+lb2+ub+lb2k-Xk(18)xOh PXl bu b h*X *P*yF图1㊀基于镜头图像的反向学习策略Fig.1㊀Reverselearningstrategybasedonlensimage㊀㊀在算法搜索解时,使用拉伸因子k作为微观调节因子,增强算法的局部开发能力㊂然而,在基本的透镜成像逆学习策略中,拉伸因子一般作为固定值使用,不允许算法探索解空间的全范围㊂为此,本文提出一种基于非线性动态递减的伸缩因子策略,在算法迭代初期可以得到较大的值,有助于算法在不同维度的区域进行更大范围的搜索,以提高种群的多样性㊂非线性动态拉伸因子定义为:㊀k=kmax-(kmax-kmin)㊃[1-cos(πt2Tmax)](19)㊀㊀其中,kmax和kmin分别表示最大和最小拉伸因子,Tmax表示最大迭代次数㊂可以将式(18)扩展到D-维搜索空间,得到数学模型为:84智㊀能㊀计㊀算㊀机㊀与㊀应㊀用㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀第14卷㊀X∗j=ubj+lbj2+ubj+lbj2k-Xjk(20)㊀㊀其中,Xj和X∗j分别表示X和X∗的的第j维向量,ubj和lbj分别表示决策变量的第j维向量㊂基于透镜的反向学习策略虽然极大地提高了算法的求解精度,但无法直接判断生成的新反向个体是否优于原始个体㊂因此,本文引入贪心机制来比较新旧个体适应度值,从而筛选出最优个体㊂该方法不断获得更好的解,提高了算法的寻优能力㊂贪婪机制的数学模型描述如下:Xnew(t)=X∗,㊀f(X)>f(X∗)X,㊀f(X)ɤf(X∗){(21)2.2.3㊀LMGWO算法实现过程LMGWO算法实现流程如图2所示㊂计算每只狼的适应度,从狼群中选出α狼、β狼和δ狼开始初始化狼群的位置t =t +1i f t <T m a x 结束运行式(19)~(22)执行基于透镜成像的反向学习策略i f r <0.3通过式(17)、式(18)执行算术乘除运算符策略通过式(13)~(16)更新狼群的位置计算适应度值更新向量α狼、β狼和δ狼图2㊀LMGWO算法流程图Fig.2㊀FlowchartofLMGWOalgorithm3㊀实验3.1㊀实验环境及参数设置在Intel(R)Core(TM)i7-i7-6500UCPU㊁2.50GHz频率㊁8GB内存㊁Windows10(64bit)操作系统上进行仿真实验,编程软件为MatlabR2018a㊂采用9个基准测试函数,包括5个单峰函数F1 F5和4个非线性多峰函数F6 F9,见表1㊂参与对比的灰狼优化算法(GWO)[14]㊁算术优化算法(AOA)[18]㊁正弦余弦算法(SCA)[19]㊁猩猩优化算法(ChOA)[20]㊁鲸鱼优化算法(WOA)[21]㊁LMGWO的参数设置见表2㊂表1㊀基准测试函数Table1Benchmarkfunctions函数编号名称维度范围最优值F1Sphere30[-100,100]0F2Schwefel.2.2230[-10,10]0F3Schwefel.1.230[-100,100]0F4Schwefel.2.2130[-100,100]0F5Quartic30[-1.28,1.28]0F6Rastrigin30[-5.12,5.12]0F7Ackley30[-32,32]0F8Criewank30[-600,600]0F9Apline30[-10,10]094第3期王恒,等:一种求解最优潮流的改进灰狼优化算法表2㊀算法参数设置Table2㊀Parametersettingsofalgorithms算法名称参数设置SCA[19]M=2ChOA[20]fmax=2.5,fmin=0WOA[21]amax=2,amin=0,b=1AOA[18]MOP_Max=1,MOP_Min=0.2,α=5,μ=0.499GWO[14]amax=2,amin=0LMGWOamax=2,amin=03.2㊀算法性能对比分析为了验证了LMGWO算法的有效性和优越性,将LMGWO算法与灰狼优化算法(GWO)[14]㊁算术优化算法(AOA)[18]㊁正弦余弦算法(SCA)[19]㊁猩猩优化算法(ChOA)[20]㊁鲸鱼优化算法(WOA)[21]在9个不同特性的基准测试函数上进行仿真实验㊂在各个算法的测试环境相同的条件下,种群规模N=30,空间维度Dim=30,最大迭代次数Tmax=500㊂采用均值和标准差作为实验的评价指标,均值和标准差越小,表明算法的性能越好㊂6种算法对9个基准函数的求解结果见表3㊂表3㊀各算法在基准函数上的优化性能比较Table3㊀Optimizationperformancecomparisonofeachalgorithmonthebenchmarkfunction函数编号指标SCAChOAWOAAOAGWOLMGWOF1Mean均值2.82ˑ1015.45ˑ10-62.20ˑ10-721.57ˑ10-71.84ˑ10-270Std标准差7.15ˑ1013.34ˑ10-61.34ˑ10-714.36ˑ10-72.35ˑ10-280F2Mean均值6.48ˑ10-25.48ˑ10-55.55ˑ10-514.081.02ˑ10-160Std标准差3.45ˑ10-25.02ˑ10-59.54ˑ10-515.114.61ˑ10-170F3Mean均值1.25ˑ1046.45ˑ1021.02ˑ1049.61ˑ1035.21ˑ10-50Std标准差3.16ˑ1038.64ˑ1026.32ˑ1043.22ˑ1021.17ˑ10-40F4Mean均值2.77ˑ1019.15ˑ10-14.11ˑ1011.211.04ˑ10-60Std标准差5.68ˑ1015.47ˑ10-12.19ˑ1011.391.47ˑ10-60F5Mean均值3.27ˑ10-27.64ˑ10-32.45ˑ10-35.13ˑ10-12.30ˑ10-32.45ˑ10-5Std标准差5.98ˑ10-25.16ˑ10-33.09ˑ10-33.18ˑ10-21.70ˑ10-32.04ˑ10-5F6Mean均值3.02ˑ1018.99ˑ1016.11ˑ10-154.67ˑ1014.280Std标准差6.48ˑ1011.02ˑ1011.98ˑ10-142.13ˑ1015.440F7Mean均值5.514.07ˑ1011.11ˑ10-152.45ˑ10-12.05ˑ10-138.88ˑ10-16Std标准差1.845.11ˑ10-27.16ˑ10-154.411.17ˑ10-140F8Mean均值3.653.47ˑ10-26.39ˑ10-22.58ˑ10-24.68ˑ10-30Std标准差2.00ˑ10-15.19ˑ10-24.77ˑ10-28.12ˑ10-27.55ˑ10-30F9Mean均值4.55ˑ10-25.40ˑ10-35.49ˑ10-394.11ˑ106.79ˑ10-40Std标准差1.36ˑ10-21.24ˑ10-22.33ˑ10-382.28ˑ101.17ˑ10-40㊀㊀由表3可以看出,在基准测试中,对于F1 F4㊁F6㊁F8和F9函数,对比算法均未能找到最优解,而LMGWO算法达到100%的求解精度㊂在求解F5和F8函数时,LMGWO的求解精度优于其他5种对比算法,但也与其他算法一样容易陷入局部最优㊂基于以上分析说明LMGWO算法比其他算法具有更高的求解精度和稳定性,证明了其有效性和优越性㊂3.3㊀LMGWO算法在高维条件的性能分析为了进一步验证LMGWO求解高维优化问题的性能,以算法解的均值和平均变化率为评价指标,对9个函数在100 500维增量下进行测试,将本文提出的LMGWO算法与原始GWO算法独立运行30次,并记录其均值,实验结果见表4㊂由表4可知,随着维数的增加,LMGWO的均值基本保持不变,F1㊁F2㊁F3㊁F4㊁F6㊁F9函数的LMGWO均值保持为0㊂随着维数的增加,GWO均值呈现增加趋势㊂在测试函数F5上,LMGWO算法的均值基本保持不变,而GWO算法的均值变化明显大于LMGWO算法;在测试函数F8上,LMGWO算法的平均变化率均为0,远低于GWO算法的平均变化率㊂05智㊀能㊀计㊀算㊀机㊀与㊀应㊀用㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀第14卷㊀表4㊀LMGWO与GWO在不同维度下优化函数均值的比较Table4㊀ComparisonofLMGWOandGWOoptimizationfunctionmeanvaluesindifferentdimensions函数编号算法名称维数100200300400500平均变化率/%F1GWO1.46ˑ10-121.43ˑ10-75.79ˑ10-58.08ˑ10-41.79ˑ10-34.48ˑ10-4LMGWO000000F2GWO5.35ˑ10-83.25ˑ10-56.79ˑ10-43.34ˑ10-31.12ˑ10-22.80ˑ10-3LMGWO000000F3GWO7.31ˑ1022.02ˑ1049.11ˑ1041.94ˑ1053.09ˑ1057.71ˑ104LMGWO000000F4GWO8.82ˑ10-12.61ˑ1014.71ˑ1016.03ˑ1016.48ˑ1011.60ˑ101LMGWO000000F5GWO7.03ˑ10-31.26ˑ10-23.49ˑ10-26.63ˑ10-29.46ˑ10-22.19ˑ10-2LMGWO3.41ˑ10-53.87ˑ10-54.05ˑ10-54.72ˑ10-56.39ˑ10-57.45ˑ10-6F6GWO9.292.42ˑ1013.91ˑ1015.02ˑ1017.20ˑ1011.57ˑ101LMGWO000000F7GWO6.77ˑ10-72.22ˑ10-55.74ˑ10-49.09ˑ10-42.02ˑ10-35.05ˑ10-4LMGWO8.88ˑ10-168.88ˑ10-168.88ˑ10-168.88ˑ10-168.88ˑ10-160F8GWO8.05ˑ10-31.45ˑ10-22.14ˑ10-27.53ˑ10-29.46ˑ10-22.16ˑ10-2LMGWO000000F9GWO2.81ˑ10-31.13ˑ10-22.59ˑ10-24.54ˑ10-21.69ˑ10-14.15ˑ10-2LMGWO000000㊀㊀2种算法在不同维度下均值的变化情况如图3所示㊂在9个函数中,GWO的均值随着维度变大而显著增加,LMGWO的均值保持不变㊂这表明维数的不断增加对LMGWO的寻优能力影响不大,与GWO相比寻优性能更加突出,进一步验证了本文所提算法的优越性㊂1.61.41.21.00.80.60.40.20100150200250300350400450500F u n c t i o n d i m e n s i o nA v e r a g e o p t i m i z a t i o n v a l u e /10-3G WO L M G WO(a )F 1变化曲线605040302010100150200250300350400450500F u n c t i o n d i m e n s i o nA v e r a g e o p t i m i z a t i o n v a l u eG WOL M G WO(d )F 4变化曲线2.01.81.61.41.21.00.80.60.40.20100150200250300350400450500F u n c t i o n d i m e n s i o nA v e r a g e o p t i m i z a t i o n v a l u e /10-3G WO L M G WO(g )F 7变化曲线100150200250300350400450500F u n c t i o n d i m e n s i o nA v e r a g e o p t i m i z a t i o n v a l u e G WOL M G WO(h )F 8变化曲线0.090.080.070.060.050.040.030.020.01100150200250300350400450500F u n c t i o n d i m e n s i o nA v e r a g e o p t i m i z a t i o n v a l u eG WOL M G WO(e )F 5变化曲线0.0100.0080.0060.0040.002100150200250300350400450500F u n c t i o n d i m e n s i o nA v e r a g e o p t i m i z a t i o n v a l u eG WOL M G WO(b )F 2变化曲线0.090.080.070.060.050.040.030.020.01100150200250300350400450500F u n c t i o n d i m e n s i o nA v e r a g e o p t i m i z a t i o n v a l u eG WOL M G WO (i )F 9变化曲线0.160.140.120.100.080.060.040.020100150200250300350400450500F u n c t i o n d i m e n s i o nA v e r a g e o p t i m i z a t i o n v a l u eG WOL M G WO (f )F 6变化曲线706050403020100100150200250300350400450500F u n c t i o n d i m e n s i o nA v e r a g e o p t i m i z a t i o n v a l u e /105G WOL M G WO(c )F 3变化曲线3.02.52.01.51.00.5图3㊀基于函数维数变化曲线的函数优化Fig.3㊀Functionoptimizationbasedonthecurveoffunctiondimensionchange15第3期王恒,等:一种求解最优潮流的改进灰狼优化算法4㊀求解最优潮流(OPF)问题为了验证LMGWO算法的有效性和可行性,在标准IEEE-30总线测试系统模型上对算法进行了测试㊂该系统包括6台发电机㊁4台变压器㊁9台分流器和41条支路㊂IEEE30母线系统单线如图4所示㊂图4中母线1为平衡母线,母线2㊁5㊁8㊁11㊁13为电压控制(VoltageControl)和无功功率(ReactivePower)母线,其余为有功功率(ActivePower)和无功功率(ReactivePower)母线㊂本文假设变压器比及无功补偿输出为连续变量,最大迭代次数设置为200次,种群规模为40,OPF问题维度为24㊂231314121615181920212210911262524292730286431257817图4㊀IEEE30总线测试系统单线图Fig.4㊀SinglelinediagramofIEEE30bustestsystem4.1㊀案例1:燃料成本(FC)最小化最小化燃料成本是指通过各种手段和方法,将燃料成本控制在最低水平,以提高经济效益,同时也能够减少对环境的影响㊂将LMGWO算法与灰狼优化算法(GWO)[14]㊁算术优化算法(AOA)[18]㊁正弦余弦算法(SCA)[19]㊁猩猩优化算法(ChOA)[20]㊁鲸鱼优化算法(WOA)[21]算法进行对比实验,实验结果见表5㊂由表5可知,优化后的LMGWO算法燃油成本为799.3944Ɣ/H㊂与初始情况相比,燃料成本降低了11.37%,具有更加优越的性能㊂表5㊀不同算法在案例1上的比较结果Table5㊀ComparisonresultsofdifferentalgorithmsinCase1算法名称燃油成本/(Ɣ㊃h-1)GWO799.9624AOA799.9217SCA801.9700ChOA800.1853WOA800.1018LMGWO799.39444.2㊀案例2:有功功率损耗(APL)最小化有功功率损耗(APL)是指电路中有功电流通过负载时所产生的功率损耗㊂有功功率损耗会导致电能转换效率降低,增加能源消耗和运营成本㊂因此,对于电力系统设计和运行来说,减小有功功率损耗是非常重要的㊂将LMGWO算法与灰狼优化算法(GWO)[14]㊁算术优化算法(AOA)[18]㊁正弦余弦算法(SCA)[19]㊁猩猩优化算法(ChOA)[20]㊁鲸鱼优化算法(WOA)[21]算法进行对比实验,实验结果见表6㊂根据表6的实验结果,本文提出的LMGWO算法以有功功率损耗(APL)最小为目标,优于其他用于求解最优潮流(OPF)问题的对比算法㊂表6㊀不同算法在案例2上的比较结果Table6㊀ComparisonresultsofdifferentalgorithmsinCase2算法名称有功功率损耗/MWGWO3.0264AOA3.1232SCA3.8239ChOA3.1600WOA3.5165LMGWO2.96915㊀结束语本文提出了一种改进的灰狼优化算法(LMGWO),针对原始GWO算法在求解OPF问题时的性能进行了2方面的改进㊂将修正反向学习策略与透镜成像学习策略和乘除算子策略相结合,对9个具有不同特性的基准函数进行测试,并与现有元启发式算法进行对比实验㊂实验结果表明,LMGWO比其他算法具有更好的稳定性和寻优性能㊂在实际应用案例中,将LMGWO算法和其他对比算法在IEEE30节点标准测试系统模型上进行对比测试㊂实验结果表明,LMGWO算法具有较好的性能㊂在未来的工作中,将使用LMGWO算法解决更困难的最优潮流(OPF)问题㊂参考文献[1]SALGADOR,BRAMELLERA,AITCHISONP.Optimalpowerflowsolutionsusingthegradientprojectionmethod.Part1:Theoreticalbasis[J].IETProceedingsC(Generation,TransmissionandDistribution),1990,137(6):424-428.[2]TINNEYWF,HARTCE.PowerflowsolutionbyNewtonᶄsmethod[J].IEEETransactionsonPowerApparatusandSystems,1967(11):1449-1460.[3]LEVIVA,NEDICDP.Applicationoftheoptimalpowerflowmodelinpowersystemeducation[J].IEEETransactionsonPower25智㊀能㊀计㊀算㊀机㊀与㊀应㊀用㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀第14卷㊀Systems,2001,16(4):572-580.[4]OLOFSSONM,ANDERSSONG,SÖDERL.Linearprogrammingbasedoptimalpowerflowusingsecondordersensitivities[J].IEEETransactionsonPowerSystem,1995,10:1691-1697.[5]DINGXiaoying,WANGXifan,SONGYonghua,etal.Theinteriorpointbranchandcutmethodforoptimalpowerflow[C]//ProceedingsofInternationalConferenceonPowerSystemTechnology.Kunming,China:IEEE,2002,1:651-655.[6]刘自发,葛少云,余贻鑫.基于混沌粒子群优化方法的电力系统无功最优潮流[J].电力系统自动化,2005,29(7):53-57.[7]FARHATM,KAMELS,ATALLAHAM,etal.ESMA-OPF:Enhancedslimemouldalgorithmforsolvingoptimalpowerflowproblem[J].Sustainability,2022,14(4):2305.[8]AttiaAF,ElSehiemyRA,HasanienHM.OptimalpowerflowsolutioninpowersystemsusinganovelSine-Cosinealgorithm[J].InternationalJournalofElectricalPower&EnergySystems,2018,99:331-343.[9]WARIDW.OptimalpowerflowusingtheAMTPG-Jayaalgorithm[J].AppliedSoftComputing,2020,91:106252.[10]WARIDW,HIZAMH,MARIUNN,etal.OptimalpowerflowusingtheJayaalgorithm[J].Energies,2016,9(9):678.[11]ABDES,KAMELS,EBEEDM,etal.Animprovedversionofsalpswarmalgorithmforsolvingoptimalpowerflowproblem[J].SoftComputing,2021,25:4027-4052.[12]NGUYENTT.Ahighperformancesocialspideroptimizationalgorithmforoptimalpowerflowsolutionwithsingleobjectiveoptimization[J].Energy,2019,171:218-240.[13]ABDEL-RAHIMAMM,SHAABANSA,RAGLENDIJ.Optimalpowerflowusingatomsearchoptimization[C]//2019InnovationsinPowerandAdvancedComputingTechnologies(i-PACT).Vellore,India:IEEE,2019,1:1-4.[14]MIRJALILIS,MIRJALILISM,LewisA.Greywolfoptimizer[J].AdvancesinEngineeringSoftware,2014,69:46-61.[15]NUAEKAEWK,ARTRITP,PHOLDEEN,etal.Optimalreactivepowerdispatchproblemusingatwo-archivemulti-objectivegreywolfoptimizer[J].ExpertSystemswithApplications,2017,87:79-89.[16]PRECUPRE,DAVIDRC,PETRIUEM.Greywolfoptimizeralgorithm-basedtuningoffuzzycontrolsystemswithreducedparametricsensitivity[J].IEEETransactionsonIndustrialElectronics,2017,64(1):527-534.[17]SAXENAA,KUMARR,DASS.β-chaoticmapenabledgreywolfoptimizer[J].AppliedSoftComputing,2019,75:84-105.[18]ABUALIGAHL,DIABATA,MIRJALILIS,etal.Thearithmeticoptimizationalgorithm[J].ComputerMethodsinAppliedMechanicsandEngineering,2021,376:113609.[19]MIRJALILIS.SCA:Asinecosinealgorithmforsolvingoptimizationproblems[J].Knowledge-basedSystems,2016,96:120-133.[20]KHISHEM,MOSAVIMR.Chimpoptimizationalgorithm[J].ExpertSystemswithApplications,2020,149:113338.[21]MIRJALILIS,LEWISA.Thewhaleoptimizationalgorithm[J].AdvancesinEngineeringSoftware,2016,95:51-67.35第3期王恒,等:一种求解最优潮流的改进灰狼优化算法。
粒子群算法

智能优化计算
1 粒子群算法的基本原理
1.1 粒子群算法的提出 ➢ 五年后,在国际上逐步被接受,并有大批不同 领域的学者投入该算法相关研究,目前已经成 为智能优化领域研究的热门
➢ 2003年,《控制与决策》第二期刊登国内第一篇 PSO论文——综述文章
8
历年发表论文的数目
2500
2328
2000
1500
xikd
)
c2 ra n d( ) ( p gbest
xikd )
xk 1 id
xikd
vk 1 id
i 1,2,, m; d 1,2,, D
惯性权重(续)
通过调节w值,可以控制PSO的全局探索和局部开发能力:
• w≥1:微粒速度随迭代次数的增加而增加,微粒发散。
• 0<w<1 :微粒减速,算法的收敛性依靠惯性权重c1和 c2 。
共性
(1)都属于仿生算法; (2)都属于全局优化方法; (3)都属于随机搜索算法; (4)都隐含并行性; (5)根据个体的适配信息进行搜索,因此不受函 数约束条件的限制,如连续性、可导性等; (6)对高维复杂问题,往往会遇到早熟收敛和收 敛性能差的缺点,都无法保证收敛到最优点。
PSO就是对鸟群或鱼群寻找食物这种群体行为的模拟。
单个鸟 整个鸟群
单个微粒
由多个微粒组 成的微粒群
一个微粒代表问题 的一个解
每个微粒都有一个 由被优化函数值决 定的适应值
鸟群寻找食 物的飞行策 略
鸟群行为
微粒位置和速 度的更新策略
PSO
13
每个微粒通过跟踪 自身找到的最好位 置以及邻域内其它 微粒找到的最好位 置,完成对整个搜 索空间的搜索
最大化问题
自动驾驶汽车路径规划算法研究

自动驾驶汽车路径规划算法研究摘要:路径规划是自动驾驶汽车的重要研究内容,也是当前自动驾驶汽车领域研究的热点之一,其目的是在一定场景下利用所选定的评价指标获得一条连接起始点与目标点的最优无碰撞路径。
将当前常用的路径规划算法分为传统算法、智能仿生学算法、强化学习算法3类,按照路径规划算法的不同类别,对各类算法在路径规划领域中的应用进行了阐述,可为研究者提供一定的参考和借鉴。
关键词:自动驾驶汽车;路径规划;智能仿生学算法;强化学习算法引言自动驾驶汽车使用传感器感知环境,并依照合理的算法在复杂环境中实现自主运动,使其能在道路上安全、高校地行驶。
作为自动驾驶汽车研究地一个重要环节,路径规划就是根据给定地环境模型,在一定地约束条件下,利用路径规划算法规划出一条连接车辆当前位置和目标位置的无碰撞路径。
1路径规划算法分类自动驾驶汽车的路径规划问题,基于研究对象对所行驶环境信息掌握程度的不同,可分为2类。
第1类是已知行驶环境信息的全局路径规划,属于静态规划;第2类是利用车载传感器实时获取环境信息的局部路径规划。
全局路径规划问题实质上是在已掌握的所有环境信息的前提下,规划出从起点到目标点的路径生成问题。
通常是基于数字地图,根据周围环境的路网模型来选择路径。
当因环境或者其他因素导致规划的路径无法继续通行时,则需要重新启动全局规划,以得到更新后的可行路径。
局部路径规划需要车载传感器实时采集车辆周围的环境信息,充分了解周围环境地图信息以准确定位出车辆当前位置及周围障碍物分布,从而顺利规划出从当前节点到下一子目标节点的最优路径。
2路径规划算法传统路径规划算法包括A*算法、人工势场法、模糊逻辑算法、禁忌搜索算法等。
文章仅对最常见的前两种算法做详细说明。
2.1.1 A*算法A*算法[1]是一种典型的启发式搜索算法,它也是静态路网中求解最短路径最有效的直接搜索算法。
A*算法通过一个估价函数来引导和决定搜索方向,从起点开始向周围进行扩展搜索,利用估价函数来获取周围每个节点的价值,并从获取的周围节点中选择代价最小的节点作为下一个扩展节点,不断循环重复这一过程直到到达目标点,结束搜索,从而生成最终路径。
粒子群算法基本原理

粒子群算法基本原理粒子群算法(Particle Swarm Optimization, PSO)是一种基于群体智能的优化算法,模拟了鸟群或鱼群等生物群体在自然界中求解问题的行为。
粒子群算法是一种无约束优化算法,可以用于求解各种优化问题。
粒子群算法的基本原理是通过模拟粒子在解空间中的过程来寻找最优解。
每个粒子表示了一个潜在的解,其位置和速度表示了解的状态和速度。
整个粒子群可以看作是一个多维解空间中的群体,每个粒子都具有一个解向量和速度向量,通过不断调整速度和位置来寻找最优解。
1.初始化粒子群:根据问题的维度和约束条件,随机初始化粒子的位置和速度。
其中位置表示解向量,速度表示方向和速度。
2.计算粒子适应度:根据问题的定义,计算每个粒子的适应度。
适应度函数根据问题的不同而变化,可以是目标函数的取值或其他综合评价指标。
3.更新粒子速度和位置:通过利用粒子当前的位置、速度和历史最优解来更新粒子的速度和位置。
速度的更新过程包括两部分,第一部分是加速度项,其大小与粒子所处位置与个体最优解、群体最优解的距离有关;第二部分是惯性项,保持原有的速度方向并控制的范围。
位置的更新通过当前位置和速度得到新的位置。
4.更新个体最优解和群体最优解:将每个粒子的适应度与其历史最优解进行比较并更新。
个体最优解是粒子自身到的最优解,群体最优解是所有粒子中的最优解。
5.判断停止条件:根据预定的停止条件判断是否终止算法。
停止条件可以是达到最大迭代次数、适应度值达到一定阈值或范围满足一定条件等。
6.返回最优解:将群体最优解或个体最优解作为最终结果返回。
粒子群算法通过不断地更新粒子的速度和位置,通过粒子之间的信息交流和协作来找到最优解。
在算法的早期阶段,粒子的范围较大,有较高的探索性;随着的进行,粒子逐渐聚集在最优解周围,并逐渐减小范围,增强了局部的能力。
这种全局和局部的结合使得粒子群算法能够更好地求解多峰优化问题。
粒子群算法的优点是简单易实现、全局能力强,对于非线性、非凸性、多峰性问题有很好的适应性。
AI人工智能的几种常用算法概念

一、粒子群算法粒子群算法,也称粒子群优化算法(Particle Swarm Optimization),缩写为PSO,是近年来发展起来的一种新的进化算法((Evolu2tionary Algorithm - EA)。
PSO 算法属于进化算法的一种,和遗传算法相似,它也是从随机解出发,通过迭代寻找最优解,它也是通过适应度来评价解的品质,但它比遗传算法规则更为简单,它没有遗传算法的交叉(Crossover) 和变异(Mutation) 操作,它通过追随当前搜索到的最优值来寻找全局最优。
这种算法以其实现容易、精度高、收敛快等优点引起了学术界的重视,并且在解决实际问题中展示了其优越性。
优化问题是工业设计中经常遇到的问题,许多问题最后都可以归结为优化问题.为了解决各种各样的优化问题,人们提出了许多优化算法,比较著名的有爬山法、遗传算法等.优化问题有两个主要问题:一是要求寻找全局最小点,二是要求有较高的收敛速度.爬山法精度较高,但是易于陷入局部极小.遗传算法属于进化算法(EvolutionaryAlgorithms)的一种,它通过模仿自然界的选择与遗传的机理来寻找最优解.遗传算法有三个基本算子:选择、交叉和变异.但是遗传算法的编程实现比较复杂,首先需要对问题进行编码,找到最优解之后还需要对问题进行解码,另外三个算子的实现也有许多参数,如交叉率和变异率,并且这些参数的选择严重影响解的品质,而目前这些参数的选择大部分是依靠经验.1995年Eberhart博士和kennedy博士提出了一种新的算法;粒子群优化(ParticalSwarmOptimization-PSO)算法.这种算法以其实现容易、精度高、收敛快等优点引起了学术界的重视,并且在解决实际问题中展示了其优越性.粒子群优化(ParticalSwarmOptimization-PSO)算法是近年来发展起来的一种新的进化算法(Evolu2tionaryAlgorithm-EA).PSO算法属于进化算法的一种,和遗传算法相似,它也是从随机解出发,通过迭代寻找最优解,它也是通过适应度来评价解的品质.但是它比遗传算法规则更为简单,它没有遗传算法的交叉(Crossover)和变异(Mutation)操作.它通过追随当前搜索到的最优值来寻找全局最优二、遗传算法遗传算法是计算数学中用于解决最佳化的,是进化算法的一种。
探讨灰狼优化算法的应用研究及实践。

探讨灰狼优化算法的应用研究及实践。
前言1.1 选题的目的和意义本次论文题目需要我们深度学习灰狼优化算法的知识,探讨优化算法的实际内容。
并基于该算法的基础,并进行一些简单的应用研究及实践。
在实际应用中,根据灰狼优化算法的原理以及理论依据,实现求解连续函数的最优值问题,并且根据算法中存在的一些缺陷,针对性的进行研究与改进。
提出改进后的算法。
并结合原始的基础GWO算法,与改进算法的优化能力进行比较,实现算法对函数优化过程的对比,证明改进算法的意义。
GWO算法国内外的研究在国外,众多学者对GWO算法进行了研究与改进。
2014年,song等引入GWO来解决电力系统中的联合经济排放调度问题(CEED)。
结果于其他优化技术进行比较,以观察GWO的有效性。
2015年,Sulaiman等用GWO解决最优无功率电镀(ORPD)问题,采用IEEE30总线系统和IEEE118总线系统两个案列来现实GWO技术的有效性。
2016年,Medjahed等提出一种新的基于灰狼优化算法的框架,以降低高光谱图像的维度。
结果分析证明,所提出的方法可以有限的研究光谱波段选择问题,并通过使用少数样本训练提供分类准确率。
2017年,Katarya和Verma提供了一个基于电影的合作推荐系统,它利用灰狼优化算法和模糊C均值(FCM)具类技术,并基于他的历史数据预测特定用户的电影评分和用户的相似性。
推荐系统的实验结果表明,与以前的工作相比,效率和性能得到增强,并提供更好的建议。
国内近些年来,也有许多学者根据理论依据以及现实中存在的问题,对GWO算法进行了深度的研究。
2015年,龙文等提出一种改进的灰狼优化(IGWO)算法用于求解约束优化问题。
6个标准的约束优化测试结果表明该算法不仅克服了基本GWO的缺点,并且性能优于差分进化和粒子群优化算法。
2016年,龙文等提出一种基于混沌和精英反向学习的混合灰狼优化算法以解决高维优化问题,结果表明,混合灰狼优化算法在求解精度以及收敛速度指标上,均明显优于对比算法。
微震震源定位方法研究综述

微震震源定位方法研究综述摘要:微震震源定位方法研究是微震监测中的研究重点,定位的精确度直接影响微震的分析结果,是评价微震监测效果的重要指标。
随着微震监测技术的深入发展,学者们提出了不同的微震震源定位方法,针对不同的应用领域,这些定位方法各有所长。
通过分析研究国内外学者提出的比较有代表性的震源定位方法,包括混合优化法、速度模型法、无需预先测速法和群智能优化法,并讨论这些方法的优缺点。
关键词:微震震源定位;混合优化法;速度模型法;无需预先测速法;群智能优化法1引言微震震源定位是微震监测技术中的核心部分,震源时间和空间数据是微震监测技术中的重要参数。
对震源定位方法、定位精度和算法稳定性方面的研究是微震监测技术的研究重点。
1912年Geiger提出的经典定位算法为后续算法打下坚实基础,林峰等[1]提出了线性定位和Geiger定位相结合的联合定位方法,董陇军等[2]提出的无需预先测速的定位方法,李楠等[3]提出的采用单纯形法求解震源位置的定位方法。
随着群智能优化算法的迅速发展,也被用来求解微震源定位问题,如粒子群算法、灰狼算法和海鸥算法等,微震震源定位方法因此做出了从“数学模型”到“仿生模型”的转变。
文本将已有的具有代表性的算法进行归类,分为混合优化法、速度模型法、无需预先测速法和群智能优化法,分析每种算法的特点,并提出未来的发展方向。
2震源定位算法介绍虽然Geiger定位算法应用广泛,但是针对微震信号微弱、信噪比低、波速难以确定和到时提取不准确等问题,微震定位算法一直在进行改进优化。
下面阐述几种比较有代表性的定位算法。
2.1混合优化法取两种或两种以上算法的优点,将其结合在一起的方式称为混合优化算法。
例如Geiger定位算法与线性定位算法结合、多目标粒子群和模拟退火算法结合、模拟退算法和单纯形法结合等。
林峰等[1]提出了线性定位和Geiger定位相结合的联合定位方法,首先利用线性定位进行初步定位,再用线性定位的解作为Geiger定位算法的迭代初值进行求解,加快了收敛速度,避免陷入局部最优。
粒子群算法粒子群算法简介
粒子群算法(1)----粒子群算法简介二、粒子群算法的具体表述上面罗嗦了半天,那些都是科研工作者写论文的语气,不过,PSO的历史就像上面说的那样。
下面通俗的解释PSO算法。
PSO算法就是模拟一群鸟寻找食物的过程,每个鸟就是PSO中的粒子,也就是我们需要求解问题的可能解,这些鸟在寻找食物的过程中,不停改变自己在空中飞行的位置与速度。
大家也可以观察一下,鸟群在寻找食物的过程中,开始鸟群比较分散,逐渐这些鸟就会聚成一群,这个群忽高忽低、忽左忽右,直到最后找到食物。
这个过程我们转化为一个数学问题。
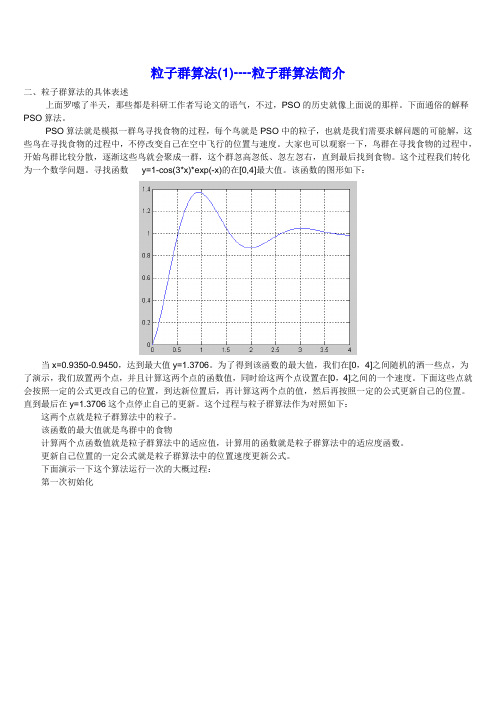
寻找函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
该函数的图形如下:当x=0.9350-0.9450,达到最大值y=1.3706。
为了得到该函数的最大值,我们在[0,4]之间随机的洒一些点,为了演示,我们放置两个点,并且计算这两个点的函数值,同时给这两个点设置在[0,4]之间的一个速度。
下面这些点就会按照一定的公式更改自己的位置,到达新位置后,再计算这两个点的值,然后再按照一定的公式更新自己的位置。
直到最后在y=1.3706这个点停止自己的更新。
这个过程与粒子群算法作为对照如下:这两个点就是粒子群算法中的粒子。
该函数的最大值就是鸟群中的食物计算两个点函数值就是粒子群算法中的适应值,计算用的函数就是粒子群算法中的适应度函数。
更新自己位置的一定公式就是粒子群算法中的位置速度更新公式。
下面演示一下这个算法运行一次的大概过程:第一次初始化第一次更新位置第二次更新位置第21次更新最后的结果(30次迭代)最后所有的点都集中在最大值的地方。
粒子群算法(2)----标准的粒子群算法在上一节的叙述中,唯一没有给大家介绍的就是函数的这些随机的点(粒子)是如何运动的,只是说按照一定的公式更新。
这个公式就是粒子群算法中的位置速度更新公式。
下面就介绍这个公式是什么。
在上一节中我们求取函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
基于社会等级淘汰机制的GWO_PSO算法

第45卷第2期2021年4月南京理工大学学报JournalofNanjingUniversityofScienceandTechnologyVol.45No.2Apr.2021㊀收稿日期:2020-08-27㊀㊀修回日期:2021-01-08㊀基金项目:国家自然科学基金(61673004)ꎻ中央高校基本科研业务费专项基金(XK1802-4)㊀作者简介:张子豪(1996-)ꎬ男ꎬ硕士生ꎬ主要研究方向:智能优化算法与先进控制ꎬE ̄mail:351125274@qq.comꎻ通讯作者:靳其兵(1971-)ꎬ男ꎬ教授ꎬ博士生导师ꎬ主要研究方向:先进控制ꎬE ̄mail:jinqb@mail.buct.edu.cnꎮ㊀引文格式:张子豪ꎬ靳其兵.基于社会等级淘汰机制的GWO_PSO算法[J].南京理工大学学报ꎬ2021ꎬ45(2):164-170.㊀投稿网址:http://zrxuebao.njust.edu.cn基于社会等级淘汰机制的GWO_PSO算法张子豪ꎬ靳其兵(北京化工大学信息科学与技术学院ꎬ北京100029)摘㊀要:灰狼优化(GreywolfoptimizerꎬGWO)算法是一种近年提出的新的群智能优化算法ꎬ为了解决其寻优精度低以及收敛速度慢的缺点ꎬ该文提出一种灰狼-粒子群智能优化(Greywolfoptimizer_particleswarmoptimizationꎬGWO_PSO)算法ꎮ采用混沌算法中的Logistic混沌映射初始化种群ꎬ使狼群种群开始分布更加趋于随机ꎻ提出一种繁衍淘汰机制ꎬ等级不同的灰狼对于下一代灰狼产生不同的权重ꎬ并且对狼群中最差的一批灰狼予以淘汰ꎬ根据繁衍机制生成新的种群ꎻ采用粒子群优化算法的速度矢量ꎬ为狼群狩猎提供方向ꎮ根据仿真实验ꎬGWO_PSO算法的收敛速度和精度相较与粒子群优化(ParticleswarmoptimizationꎬPSO)和GWO都有了极大的提高ꎬ相较于其他的改进灰狼算法ꎬGWO_PSO表现出不错的寻优能力ꎮ关键词:社会等级ꎻ淘汰机制ꎻ灰狼优化算法ꎻ粒子群优化算法ꎻ混沌映射ꎻ群智能优化中图分类号:TP301.6㊀㊀文章编号:1005-9830(2021)02-0164-07DOI:10.14177/j.cnki.32-1397n.2021.45.02.005GWO_PSOalgorithmbasedonsocialrankeliminationmechanismZhangZihaoꎬJinQibin(CollegeofInformationScienceandTechnologyꎬBeijingUniversityofChemicalTechnologyꎬBeijing100029ꎬChina)Abstract:Greywolfoptimizer(GWO)isanewswarmintelligenceoptimizationalgorithmproposedinrecentyears.Inordertosolvethedefectsoflowoptimizationaccuracyandslowconvergencespeedꎬagreywolfoptimizer_particleswarmoptimization(GWO_PSO)algorithmisproposed.FirstlyꎬtheLogisticchaoticmapisusedtoinitializethepopulationꎬwhichmakesthedistributionofwolfpopula ̄tionmorerandom.Secondlyꎬabreedingeliminationmechanismisproposedꎬinwhichgreywolvesofdifferentgradeshavedifferentweightsforthenextgenerationofgreywolvesꎬandtheworstgroupofwolvesinthepopulationareeliminatedtogeneratenewpopulationsaccordingtothereproductionmechanism.Finallyꎬthevelocityvectorofparticleswarmoptimizationalgorithmisusedtoprovide总第237期张子豪㊀靳其兵㊀基于社会等级淘汰机制的GWO_PSO算法㊀㊀directionforwolves hunting.Accordingtothesimulationexperimentꎬcomparedwithpartideswarmoptimization(PSO)andGWOꎬtheconvergencespeedandaccuracyofGWO_PSOalgorithmaregreatlyimproved.ComparedwithotherimprovedgreywolfalgorithmꎬGWO_PSOshowsgoodoptimizationability.Keywords:socialranksꎻeliminationmechanismꎻgreywolfoptimizeralgorithmꎻparticleswarmoptimizationalgorithmꎻchaoticmapsꎻswarmintelligenceoptimization㊀㊀群智能优化算法是一种由自然界中ꎬ群体动物的活动启发而产生的全局优化算法ꎮ典型的智能优化算法包括粒子群优化(ParticleswarmoptimizationꎬPSO)[1]算法ꎬ差分进化(DifferentialevolutionꎬDE)[2]算法ꎬ鲸鱼优化算法(WhaleoptimizationalgorithmꎬWOA)[3]ꎬ人工蜂群(ArtificialbeecolonyꎬABC)[4]算法ꎬ布谷鸟(CuckoosearchꎬCS)[5]算法等ꎮ智能优化算法在机器学习算法[6-8]㊁系统辨识[9ꎬ10]以及PID控制方面[11]也有很多的应用ꎮMirjalili等[12]由灰狼猎食以及灰狼种群中的等级制度得到启发ꎬ于2014年提出灰狼优化(GreywolfoptimizerꎬGWO)算法ꎬ其结构简单ꎬ参数少ꎬ易于编程ꎬ寻优性能较好ꎬ但其自身仍然存在收敛精度不足的问题ꎮ近年来ꎬ对此有很多学者提出了对灰狼算法的改进方法ꎬ文献[13]通过加入混沌策略和对收敛因子加入自适应策略ꎬ使算法精度和稳定性都有了一定的提高ꎻ文献[14]通过改进收敛因子的方法ꎬ使其不易陷入局部最优ꎻ文献[15]引入PSO的最优解记忆思想ꎬ采用佳点集策略和改进收敛因子的策略ꎬ提升了算法的性能ꎻ文献[16]引入差分进化算法的和灰狼算法混合的策略和优胜劣汰法则ꎬ改进了灰狼算法的寻优能力ꎮ1㊀GWO算法原理灰狼算法是受到灰狼狩猎觅食这一自然现象启发ꎬ而提出的群智能优化算法ꎬ灰狼优化算法在设计中考虑了狼群中的社会等级ꎬ模仿狼群寻找㊁包围㊁攻击猎物的狩猎模式ꎮ(1)社会等级(Socialhierarchy)ꎮ该算法设计了3种统治阶级的狼和普通的狼ꎬ统治阶级的狼分为α狼㊁β狼㊁δ狼ꎬ组成狼群的普通狼为ω狼ꎬ其分别对应的是最优解㊁次优解㊁第三优解和候选解[17]ꎮ(2)围猎(Encirclingprey)ꎮ灰狼在搜索猎物的过程中ꎬ会逐渐地接近猎物并包围它ꎬ该行为的数学模型如下㊀D=|C Xp(t)-X(t)|ꎬX(t+1)=Xp(t)-A D(1)式中:t指当前时刻ꎬA和C是协同系数ꎬXp是头狼的位置ꎬX是指灰狼ω狼群的位置ꎮ协同系数A㊁C分别为㊀A=2a r1-aꎬC=2 r2ꎬa=2-2∗(t/tmax)(2)式中:a由2线性衰减到0ꎬr1和r2是[0ꎬ1]之间的随机数ꎮ(3)狩猎(Hunting)ꎮ在每次迭代过程中ꎬ保留当前种群中的最优的3只灰狼ꎬ即适应度值最优的3个解ꎬα狼㊁β狼㊁δ狼ꎬ头狼根据他们自身所在位置ꎬ判断狼群与自己的距离ꎬ并通过商议ꎬ得出狼群所需移动的距离ꎮ该行为的数学模型可表示为㊀Dα=C1 Xα-XꎬDβ=C2 Xβ-Xꎬ㊀㊀Dδ=C3 Xδ-X(3)㊀X1=Xα-A1 (Dα)ꎬX2=Xβ-A2 (Dβ)ꎬ㊀㊀X3=Xδ-A3 (Dδ)(4)㊀X(t+1)=(X1+X2+X3)/3(5)式中:Dα㊁Dβ㊁Dδ分别表示3种头狼与猎物之间的距离ꎬX1㊁X2㊁X3分别表示α狼㊁β狼㊁δ狼的位置ꎬ式(5)表示ω狼根据α狼㊁β狼㊁δ狼的位置更新整个狼群的位置ꎮ2㊀PSO算法原理PSO算法是Kennedy和Eberhart提出的一种群智能优化算法ꎮ粒子群优化算法的基本思想是利用种群中不同粒子之间的信息共享ꎬ使群体由随机分布到有序分布ꎬ其速度向量的思想ꎬ对于群智能优化算法来讲是有开创意义的ꎮ粒子群优化算法将每一个粒子随机分布在解域空间内ꎬ设粒子的位置为Xꎬ根据适应度值设置局部最优Xpbest和全局最优XgbestꎬXpbest表示当561南京理工大学学报第45卷第2期前代适应度值最优的粒子ꎬXgbest表示历史代到目前最优的粒子ꎮ根据局部最优和全局最优可以得到一个速度矢量Vꎬ其公式为㊀V(t+1)=ωV(t)+c1r1(Xpbest(t)-X(t))+㊀㊀c2r2(Xgbest(t)-X(t))(6)式中:c1=2ꎬc2=2ꎬω表示惯性因子ꎬ通常由大到小线性收敛ꎬ值大时主要进行全局搜索ꎬ值小时进行局部搜索ꎮ其更新公式为㊀ω(t)=ωmax-(ωmax-ωmin)∗t/tmax(7)式中:tmax表示迭代的最大代数ꎬ通常ωmax=0.9ꎬωmin=0.4ꎮ根据得到的速度向量V更新粒子群中的每一个粒子ꎬ其表达式为㊀X(t+1)=X(t)+V(t+1)(8)3㊀灰狼_粒子群智能优化算法针对灰狼算法中仍然存在寻优精度低ꎬ收敛速度慢的问题ꎬ本文提出了一种灰狼_粒子群智能优化(Greywolfoptimizer_particleswarmoptimiza ̄tionꎬGWO_PSO)算法ꎮ3.1㊀GWO_PSO算法改进思路(1)混沌映射ꎮ混沌映射具有随机性㊁周期性的特点ꎮ在许多智能优化算法中ꎬ混沌映射都起到了很好的效果ꎬ如文献[18]采用了Iterative映射的方法初始化狼群ꎮLogistic映射通过迭代的方式产生ꎬ是一种具有确定性㊁类似随机性㊁非周期的㊁收敛性的伪随机序列ꎬ其分布均匀ꎮ为使灰狼狼群更随机地分布ꎬ引入Logistic映射对灰狼狼群进行初始化ꎮLogistic映射的公式为㊀uk+1=auk(1-uk)(9)从图1中可以看出ꎬ当a=4时ꎬLogistic在[0ꎬ1]分布最广ꎬ其中uk∉{0ꎬ0.25ꎬ0.5ꎬ0.75ꎬ1}ꎮ如图2所示ꎬLogistic映射的分布更加随机ꎬ因此选用Logistic映射用于初始化灰狼种群ꎮ(2)等级制度ꎮ灰狼算法中提出的等级制度没有体现出3只头狼的优先级的差别ꎬ容易偏离目标值ꎬ导致精度不足ꎮ为了凸显灰狼算法的等级制度ꎬ提出灰狼算法的等级制度思想ꎬ其基本思想就是在更新灰狼位置时ꎬ加上一个等级权重ꎬ分别为η1㊁η2㊁η3ꎬ三者的关系为㊀η1ʒη2ʒη3=4ʒ3ʒ2(10)通常取η1=2㊁η2=1.5㊁η3=1ꎮ图1㊀参数a对应的Logistic映射图2㊀两种混沌映射的分布(3)速度向量ꎮ灰狼算法中的位置更新只体现了灰狼和猎物之间的距离ꎬ并没有体现出灰狼寻优的方向ꎬ其对于解的判定只有位置信息而没有方向矢量信息ꎬ其优化能力还有一定地提升空间ꎮ受粒子群优化算法中速度向量V的启发ꎬ根据式(3)㊁(4)㊁(5)计算得到头狼及狼群的位置ꎬ引入速度向量Vꎬ其更新公式为㊀V(t+1)=ω∗V(t)+ð3i=1(ηi∗k∗(Xi-X(t)))(11)式中:ω为惯性因子ꎬηi为等级权重ꎬk为协同系数ꎮ通常ωmax=0.6ꎬωmin=0ꎬω的选择对于寻优效果有着重要影响ꎬ其更新公式为式(7)ꎮ协同系数k的公式为㊀k=0.1∗rand(12)灰狼狼群的位置更新公式为式(8)ꎮ通过引入速度向量ꎬ增加了寻优方向矢量信661总第237期张子豪㊀靳其兵㊀基于社会等级淘汰机制的GWO_PSO算法㊀㊀息ꎬ提高了收敛速度和收敛精度ꎮ(4)淘汰机制ꎮ一个灰狼种群中ꎬ存在一些老弱病残的灰狼ꎬ随着自然选择ꎬ会被新生的狼群代替ꎬ同时统治阶级的狼有更多的繁衍机会ꎮ在每一代ω狼中ꎬ选取适应度值在排在后三分之一的灰狼予以淘汰ꎬ同时由新一代的灰狼替代被淘汰的老弱病残ꎬ其更新公式为㊀Xnew=0.5∗Xold+1ð3i=1ηi∗ð3i=1(ηi∗Xi)(13)式中:η1㊁η2㊁η3为等级权重ꎮ淘汰机制的主要流程为:(1)根据适应度值排序ω狼ꎬ并对适应度值排后三分之一的灰狼Xold予以淘汰ꎮ(2)根据式(13)得到Xnewꎬ替换Xoldꎬ与之前的灰狼形成新的种群ꎮ淘汰机制强化了等级制度在灰狼算法中的作用ꎬ使算法的精度和收敛速度有所提高ꎮ3.2㊀GWO_PSO算法流程通过以上改进ꎬ提高了灰狼算法的精度和收敛速度ꎬ经过总结ꎬ可以将其归纳成如下步骤:步骤1㊀初始化ꎮ采用Logistic混沌映射ꎬ初始化灰狼种群Xꎬ并初始化参数ꎻ步骤2㊀计算适应度值ꎮ计算灰狼狼群X的适应度值ꎬ根据适应度值设α狼㊁β狼㊁δ狼ꎬ其包含的猎物信息分别是Xα㊁Xβ㊁Xδꎬ通过式(3)和式(4)得到X1㊁X2㊁X3ꎻ步骤3㊀根据式(5)获取ω狼群的猎物信息ꎻ步骤4㊀根据式(11)计算速度向量Vꎬ并将其代入式(8)更新种群位置ꎻ㊀㊀步骤5㊀淘汰机制ꎮ根据步骤2所计算的适应度值ꎬ进行排序ꎬ淘汰后三分之一的灰狼Xoldꎬ并根据式(13)得到Xnewꎻ步骤6㊀计算灰狼适应度值ꎬ和上一代迭代的值比较ꎬ根据适应度值选择新的α狼㊁β狼㊁δ狼ꎬ得到X1㊁X2㊁X3ꎻ步骤7㊀判断Xα的适应度值是否达到结束条件ꎬ若满足条件ꎬ则最优值为Xαꎻ若不满足条件ꎬ则重复步骤4-7ꎮGWO_PSO优化算法流程如图3所示ꎮ图3㊀GWO_PSO算法流程图4㊀函数优化实验及结果分析为测试GWO_PSO算法的有效性ꎬ本文采用12个经典的测试函数ꎬ其表达式如表1所示ꎮ表1㊀12个测试函数表函数n范围最优解F1(x)=ðni=1x2i100[-ɕꎬ+ɕ]0F2(x)=ðni=1|xi|+ᵑni=1|xi|100[-100ꎬ+100]0F3(x)=ðni=1ix4i+rand[0ꎬ1)100[-1.28ꎬ+1.28]0F4(x)=ðni=1sin2(xi)[]eðni=1sin2(|xi|){}100[-20ꎬ+20]0F5(x)=ðni=1ðni=1xj()2100[-100ꎬ+100]0761南京理工大学学报第45卷第2期续表1函数n范围最优解F6(x)=maxi(|xi|)100[-100ꎬ+100]0F7(x)=-20e-0.21nx2i-e-0.21nðni=1cos(2πxi)+20+e100[-32ꎬ+32]0F8(x)=ðni=1[x2i-10cos(2πxi)+10]100[-5.12ꎬ+5.12]0F9(xꎬy)=0.26∗(x2+y2)-0.48xy2-10<xꎬy<100F10(x)=14000ðni=1x2i-ᵑni=1cosxiiæèçöø÷+1100[-50ꎬ+50]0F11(x)=ðni=1ðnj=1jx2j100[-100ꎬ+100]0F12(x)=0.1sin2(3πxi)+ðni=1(xi-1)2[1+sin2(3πxi+1)]+㊀㊀{㊀㊀(xn-1)2[1+sin2(2πxn)]}+ðni=1u(xiꎬ5ꎬ100ꎬ4)u(xꎬaꎬkꎬm)=k(xi-a)ma<xi0-a<xi<ak(-xi-a)mxi<-aìîíïïï100[-50ꎬ+50]0㊀㊀为了体现本文所提算法对灰狼优化算法的改进效果ꎬ本节将对GWO_PSO算法与其他改进灰狼算法进行比较ꎬ分别选取F1~F12函数比较ꎬ测试函数F9为2维ꎬ其余函数为30维ꎮ将GWO_PSO与LGWO[19]㊁HGWO[20]㊁PGWO[21]㊁CGWO[22]比较ꎬ运算500次得到的平均值及标准差ꎬ其结果如表2所示ꎮ部分函数适应度收敛曲线如图4-6所示ꎮ表2㊀GWO_PSO与4种灰狼算法的寻优效果比较函数IndexGWO_PSOLGWOHGWOPGWOCGWOF1MeanStd001.18E-196.45E-191.12E-322.32E-324.63E-593.16E-591.51E-273.59E-27F2MeanStd9.62E-18901.75E-139.58E-139.33E-206.92E-201.44E-395.18E-391.16E-211.98E-22F3MeanStd6.60E-056.45E-057.77E-046.72E-043.18E-086.55E-082.22E-088.49E-051.32E-062.05E-05F4MeanStd1.55E-422.65E-439.96E-139.63E-126.29E-135.85E-131.29E-114.78E-135.57E-133.76E-12F5MeanStd004.59E-212.52E-203.18E-086.55E-081.22E-634.86E-633.17E-421.04E-41F6MeanStd9.51E-18801.97E-169.27E-164.17E-084.56E-084.31E-314.51E-301.02E-221.93E-23F7MeanStd-8.88E-16020.89780.0765573624.27E-144.37E-151.18E-172.12E-17-1403.21E-11F8MeanStd002.6985339173.8780127562.27E-019.20E-014.16E-221.53E-2200F9MeanStd001.97E-221.88E-222.72E-995.90E-981.40E-19101.49E-973.30E-96F10MeanStd000.0037543940.0084533591.37E-039.20E-019.31E-143.22E-1400F11MeanStd008.05E-141.37E-141.86E-253.20E-251.63E-571.20E-561.20E-252.79E-25F12MeanStd1.25E-018.76E-020.6933237220.226958843.44E-011.48E-012.6584235120.0885389314.97E-121.09E-11861总第237期张子豪㊀靳其兵㊀基于社会等级淘汰机制的GWO_PSO算法㊀㊀图4㊀F1函数收敛曲线图5㊀F2函数收敛曲线图6㊀F6函数收敛曲线5㊀结论本文提出了一种基于淘汰机制的GWO_PSO算法ꎬ引入了Logistic混沌映射策略初始化种群ꎬ使初始种群分布更加均匀ꎻ提出等级制度ꎬ突出了GWO算法中狼群的等级机制ꎻ引入速度向量思想ꎬ提高收敛精度及速度ꎻ提出了狼群中的淘汰机制ꎬ剔除了狼群中的 害群之马 ꎮ同时根据狼群社会中的等级制度ꎬ让狼群中等级更高的狼拥有繁衍权ꎬ提高了算法的精确度ꎬ提高了算法的收敛速度ꎮ在系统辨识问题中ꎬ该算法取得了很好的应用效果ꎮ参考文献:[1]㊀KennedyJꎬEberhartR.Particleswarmoptimization[C]//ProceedingsofICNN 95 ̄InternationalConfere ̄nceonNeuralNetworks.PerthꎬAustralia:IEEEꎬ1995:1942-1948.[2]张文丽ꎬ郭俊文ꎬ曲俊海ꎬ等.基于自适应差分进化算法的武器稳定系统参数辨识[J].火力与指挥控制ꎬ2020ꎬ45(5):119-124.ZhangWenliꎬGuoJunwenꎬQuJunhaiꎬetal.Parameteridentificationofweaponstabilitysystembasedonadap ̄tivedifferentialevolutionalgorithm[J].FireControl&CommandControlꎬ2020ꎬ45(5):119-124.[3]MirjaliliSꎬLewisA.Thewhaleoptimizationalgorithm[J].AdvancesinEngineeringSoftwareꎬ2016ꎬ95:51-67.[4]KarabogaDꎬBasturkB.Apowerfulandefficientalgorithmfornumericalfunctionoptimization:Artificialbeecolony(ABC)algorithm[J].JournalofGlobalOptimizationꎬ2007ꎬ39(3):459-471.[5]YangXinsheꎬDebS.Cuckoosearchvialévyflights[C]//2009WorldCongressonNature&BiologicallyInspiredComputing(NaBIC).CoimbatoreꎬIndia:IEEEꎬ2009:210-214.[6]张文宇ꎬ张茜ꎬ杨媛ꎬ等.基于改进GWO ̄CV优化的K-调和均值聚类算法[J].统计与决策ꎬ2020ꎬ36(16):9-13.ZhangWenyuꎬZhangXiꎬYangYuanꎬetal.K ̄harmonicmeanclusteringalgorithmbasedonimprovedGWO ̄CVoptimization[J].Statistics&Decisionꎬ2020ꎬ36(16):9-13.[7]潘成胜ꎬ张斌ꎬ吕亚娜ꎬ等.改进灰狼优化算法的K ̄means文本聚类[J].计算机工程与应用ꎬ2021ꎬ57(1):188-193.PanChengshengꎬZhangBinꎬLyuYanaꎬetal.K ̄meanstextclusteringbasedonimprovedgraywolfoptimizationalgorithm[J].ComputerEngineeringandApplicationsꎬ2021ꎬ57(1):188-193.[8]沈葛亮ꎬ顾斌杰ꎬ潘丰.基于灰狼优化算法的孪生支持向量回归机[J].南京理工大学学报ꎬ2020ꎬ44(2):202-208.ShenGeliangꎬGuBinjieꎬPanFeng.Twinsupportvectorregressionbasedongreywolfoptimizationalgo ̄rithm[J].JournalofNanjingUniversityofScienceandTechnologyꎬ2020ꎬ44(2):202-208.[9]王晨.基于智能计算的重尾噪声干扰下Hammers ̄tein模型参数辨识研究[D].北京:北京化工大学ꎬ2019.[10]王芷馨ꎬ王冬青ꎬ韩增亮ꎬ等.基于粒子群优化算法的非线性系统辨识[J].自动化与仪器仪表ꎬ2020(5):8-12.WangZhixinꎬWangDongqingꎬHanZengliangꎬetal.961南京理工大学学报第45卷第2期Nonlinearsystemidentificationbasedonparticleswarmoptimization[J].Automation&Instrumentationꎬ2020(5):8-12.[11]李书霞.改进群智能算法及其在PID控制器参数整定中的应用[D].鞍山:辽宁科技大学ꎬ2016. [12]MirjaliliSꎬMirjaliliSMꎬLewisA.Greywolfoptimizer[J].AdvancesinEngineeringSoftwareꎬ2014ꎬ69:46-61.[13]张悦ꎬ孙惠香ꎬ魏政磊ꎬ等.具有自适应调整策略的混沌灰狼优化算法[J].计算机科学ꎬ2017ꎬ44(S2):119-122ꎬ159.ZhangYueꎬSunHuixiangꎬWeiZhengleiꎬetal.Chaoticgraywolfoptimizationalgorithmwithadaptiveadjustmentstrategy[J].ComputerScienceꎬ2017ꎬ44(S2):119-122ꎬ159.[14]伍铁斌ꎬ桂卫华ꎬ阳春华ꎬ等.用对数函数描述收敛因子的改进灰狼优化算法及其应用[J].中南大学学报(自然科学版)ꎬ2018ꎬ49(4):857-864.WuTiebinꎬGuiWeihuaꎬYangChunhuaꎬetal.Improvedgreywolfoptimizationalgorithmwithlogarithmfunctiondescribingconvergencefactoranditsapplication[J].JournalofCentralSouthUniversity(ScienceandTechnology)ꎬ2018ꎬ49(4):857-864. [15]龙文ꎬ伍铁斌.协调探索和开发能力的改进灰狼优化算法[J].控制与决策ꎬ2017ꎬ32(10):1749-1757.LongWenꎬWuTiebin.Improvedgreywolfoptimizationalgorithmcoordinatingtheabilityofexplorationandexploitation[J].ControlandDecisionꎬ2017ꎬ32(10):1749-1757.[16]朱海波ꎬ张勇.基于差分进化与优胜劣汰策略的灰狼优化算法[J].南京理工大学学报ꎬ2018ꎬ42(6):678-686.ZhuHaiboꎬZhangYong.Graywolfoptimizationalgorithmbasedondifferentialevolutionandsurvivaloffitnessstrategy[J].JournalofNanjingUniversityofScienceandTechnologyꎬ2018ꎬ42(6):678-686. [17]吕新桥ꎬ廖天龙.基于灰狼优化算法的置换流水线车间调度[J].武汉理工大学学报ꎬ2015ꎬ37(5):111-116.LyuXinqiaoꎬLiaoTianlong.Permutationflow ̄shopschedulingbasedonthegreywolfoptimizer[J].JournalofWuhanUniversityofTechnologyꎬ2015ꎬ37(5):111-116.[18]王梦娜ꎬ王秋萍ꎬ王晓峰.基于Iterative映射和单纯形法的改进灰狼优化算法[J].计算机应用ꎬ2018ꎬ38(S2):16-20ꎬ54.WangMengnaꎬWangQiupingꎬWangXiaofeng.Improvedgreywolfoptimizationalgorithmbasedoniterativemappingandsimplexmethod[J].JournalofComputerApplicationsꎬ2018ꎬ38(S2):16-20ꎬ54. [19]凌颖ꎬ杨春燕ꎬ黎新ꎬ等.改进灰狼优化算法的研究[J].科学技术创新ꎬ2020(16):61-63.LingYingꎬYangChunyanꎬLiXinꎬetal.Researchonimprovedgraywolfoptimizationalgorithm[J].ScientificandTechnologicalInnovationꎬ2020(16):61-63.[20]ZhuAijunꎬXuChuanpeiꎬLiZhiꎬetal.Hybridizinggreywolfoptimizationwithdifferentialevolutionforglobaloptimizationandtestschedulingfor3DstackedSoC[J].JournalofSystemsEngineeringandElectron ̄icsꎬ2015ꎬ26(2):317-328.[21]滕志军ꎬ吕金玲ꎬ郭力文ꎬ等.一种基于Tent映射的混合灰狼优化的改进算法[J].哈尔滨工业大学学报ꎬ2018ꎬ50(11):40-49.TengZhijunꎬLüJinlingꎬGuoLiwenꎬetal.AnimprovedhybridgreywolfoptimizationalgorithmbasedonTentmapping[J].JournalofHarbinInstituteofTechnologyꎬ2018ꎬ50(11):40-49.[22]张铸ꎬ饶盛华ꎬ张仕杰.基于自适应正态云模型的灰狼优化算法[J/OL].控制与决策:1-6.https://doi.org/10.13195/j.kzyjc.2020.0233ꎬ2020-07-03.ZhangZhuꎬRaoShenghuaꎬZhangShijie.GreyWolfOptimizationAlgorithmBasedonAdaptiveNormalCloudModel[J/OL].ControlandDecision:1-6.https://doi.org/10.13195/j.kzyjc.2020.0233ꎬ2020-07-03.071。
群体进化优化算法有哪些

群体进化优化算法有哪些
群体进化优化算法有粒子群优化算法(PSO)、蚁群优化算法(ACO)、人工蜂群优化算法(ABC)、差分进化算法(DE)、引力搜索算法(GSA)、萤火虫算法(FA)、蝙蝠算法(BA)、布谷鸟优化算法(COA)、灰狼优化算法(GWO)、鲸鱼优化算法(WOA)和Salp群算法(SSA)等等。
群体智能优化算法是计算智能中的一种常用算法,其基本理论是模拟自然界中鱼群、鸟群、蜂群、狼群和细菌群等动物群体的行为,利用群体间的信息交流与合作,通过简单有限的个体间互动来达到优化的目的。
群体智能由Gerardo Beni和Jing Wang于1989年首次提出,是研究由大量简单个体构成的群体系统的学科。
与个体的智能相比,这些群体系统往往并没有复杂精细的内部设计,但基于简单的个体与规则,它们具有更强的鲁棒性、稳定性和适应性。
群体智能方法处理的最典型问题就是优化问题。
优化问题的基础性能够较为直观地体现群体方法的理论特性,辅助其理论研究,同时也具有重要的应用价值,进一步推动了群体智能算法的发展。
与传统的优化算法相比,基于仿生学的群体智能优化算法本质上是一种概率并行搜索算法。
其寻优速度更快,能更有效地搜索复杂优化问题的全局最优解。
1。
基于GWO和PSO协同优化的DV-Hop定位算法

基于GWO和PSO协同优化的DV-Hop定位算法作者:朱子行陈辉来源:《现代信息科技》2022年第03期摘要:無线传感器网络具有感知和处理信息的能力,只有当被测网络内节点的位置已知时,节点传递给用户的信息才有意义。
针对DV-Hop定位中传统最小二乘法不可避免的精度低的缺点,引入粒子群算法(PSO)和灰狼优化器(GWO)来估计未知节点位置。
粒子群算法具有个体记忆的特点,采用粒子位置更新代替灰狼个体位置更新,使灰狼算法在优化上具有可记忆性。
仿真数据表明,改进后的算法可以有效降低节点定位误差,实现更高的定位精度。
关键词:无线传感器网络;DV-Hop;灰狼优化器;粒子群算法中图分类号:TN934 文献标识码:A文章编号:2096-4706(2022)03-0088-04DV-Hop Positioning Algorithm Based on GWO and PSO Collaborative OptimizationZHU Zihang, CHEN Hui(Anhui University of Science & Technology, Huainan 232001, China)Abstract: Wireless sensor networks have the ability to sense and process information, and the information passed by the nodes to the user is meaningful only when the location of the nodes within the network under test is known. In view of the inevitable shortcoming of low precision of the traditional least squares method in DV-Hop (distance vector-hop) localization, the Particle Swarm optimization (PSO) and the Gray Wolf Optimizer (GWO) are introduced to estimate unknown node positions. The Particle Swarm optimization has the characteristics of individual memory, and the particle position update is used to replace the gray wolf individual position update, so that the gray wolf algorithm has memory in optimization. The simulation data show that the improved algorithm can effectively reduce the node positioning error and achieve higher positioning accuracy.Keywords: wireless sensor network; DV-Hop; Grey Wolf Optimizer; Particle Swarm optimization0 引言无线传感器网络(Wireless Sensor Network, WSN)作为信息获取的重要技术随着网络信息的快速发展得到了广泛使用[1]。
改进灰狼算法在搬运机器人轨迹规划中的应用

改进灰狼算法在搬运机器人轨迹规划中的应用
张攀;刘雨晗;张威
【期刊名称】《机械科学与技术》
【年(卷),期】2024(43)3
【摘要】为提高托盘式搬运机器人的运行稳定性,提出一种基于改进灰狼算法的机器人加速度最优轨迹规划方法。
针对灰狼算法局部收敛、寻优性能不足等问题,引入Logistic-Tent混沌映射,优化初始种群;引入差分优化算法,提高全局搜索能力;引入淘汰进化机制,优化种群结构,从而全面提升优化性能。
仿真结果表明,对比标准灰狼算法和粒子群算法,改进灰狼算法在不同类型的测试函数中具有更好的收敛速度和算法精度;在搬运机器人轨迹规划的应用中,经过该算法优化后的机器人最大关节角加速度下降了44.11%,大幅提高了运行稳定性。
【总页数】8页(P394-401)
【作者】张攀;刘雨晗;张威
【作者单位】中国民航大学航空工程学院;民航航空公司人工智能重点实验室;中国民航大学安全科学与工程学院;中国民航航空地面特种设备研究基地
【正文语种】中文
【中图分类】TP242;V354
【相关文献】
1.基于改进灰狼算法的机器人激励轨迹优化
2.粒子群算法改进灰狼算法的机器人路径规划
3.基于多目标灰狼优化算法的工业机器人最优轨迹规划
4.改进灰狼算法在焊接机器人路径规划的应用
5.一种改进RRT算法在机器人轨迹规划中的应用
因版权原因,仅展示原文概要,查看原文内容请购买。
粒子群算法简介优缺点及其应用

10
式(1)的第一部分称为动量部分,表示粒子对当前自身运动状 态的信任,为粒子提供了一个必要动量,使其依据自身速度进 行惯性运动;
第二部分称为个体认知部分,代表了粒子自身的思考行为,鼓 励粒子飞向自身曾经发现的最优位置;
第三部分称为社会认知部分,表示粒子间的信息共享与合作, 它引导粒子飞向粒子群中的最优位置。
粒子群算法(Particle Swarm Optimization,简称PSO),是一 种基于群体智能的进化计算方法。PSO由Kennedy和Eberhart博 士于1995年提出。
粒子群算法源于复杂适应系统(Complex Adaptive System,CAS)。CAS理论于1994年正式提出,CAS中的成员称 为主体。比如研究鸟群系统,每个鸟在这个系统中就称为主 体。主体有适应性,它能够与环境及其他的主体进行交流, 并且根据交流的过程“学习”或“积累经验”改变自身结构 与行为。整个系统的演变或进化包括:新层次的产生(小鸟 的出生);分化和多样性的出现(鸟群中的鸟分成许多小的 群);新的主题的出现(鸟寻找食物过程中,不断发现新的 食物)。
改变这些常数会改变系统的“张力”,较低的c1 和 c2值使得 粒子徘徊在远离目标的区域,较高的c1 和 c2值产生陡峭的运 动或越过目标区域。
Shi和Eberhart建议,为了平衡随机因素的作用,一般情况下 设置c1 = c2,大部分算法都采用这个建议。
2021/3/22
13
(4)粒子的最大速度vmax :粒子的速度在空间中的每一维上都 有一个最大速度限制值vdmax ,用来对粒子的速度进行钳制,使 速度控制在范围[-vdmax,+vdmax ]内,这决定问题空间搜索的 力度,该值一般由用户自己设定。
19
灰狼算法原理

灰狼算法原理灰狼算法是一种基于自然界中灰狼群体行为的优化算法,它是由伊朗研究人员Mirjalili等人于2014年提出的。
灰狼算法的原理是通过模拟灰狼群体的行为,来寻找最优解。
灰狼算法具有收敛速度快、全局搜索能力强等优点,被广泛应用于各种优化问题中。
灰狼算法的基本原理是模拟灰狼群体的行为,灰狼群体中的每只狼都有自己的位置和适应度值。
在灰狼算法中,每只狼的位置表示解空间中的一个解,适应度值表示该解的优劣程度。
灰狼算法的目标是找到适应度值最优的解。
灰狼算法的具体实现过程如下:1. 初始化灰狼群体在灰狼算法中,需要初始化一定数量的灰狼,每只灰狼的位置是随机生成的。
灰狼的数量越多,算法的搜索能力越强,但是计算时间也会增加。
2. 计算适应度值对于每只灰狼,需要计算其适应度值。
适应度值越高,表示该灰狼的位置越优秀。
3. 确定灰狼等级根据灰狼的适应度值,可以确定其在灰狼群体中的等级。
适应度值越高的灰狼,等级越高。
4. 确定灰狼领袖在灰狼群体中,适应度值最高的灰狼被称为灰狼领袖。
灰狼领袖的位置是当前最优解。
5. 更新灰狼位置根据灰狼群体中每只灰狼的等级和灰狼领袖的位置,可以更新每只灰狼的位置。
更新公式如下:D_alpha = abs(C1 * X_alpha - X_i)X1 = X_alpha - A * D_alphaD_beta = abs(C2 * X_beta - X_i)X2 = X_beta - A * D_betaD_delta = abs(C3 * X_delta - X_i)X3 = X_delta - A * D_delta其中,X_alpha、X_beta、X_delta分别表示灰狼群体中适应度值最高的三只灰狼的位置,C1、C2、C3是常数,A是控制步长的参数。
6. 更新适应度值根据更新后的灰狼位置,需要重新计算每只灰狼的适应度值。
7. 判断终止条件在灰狼算法中,需要设置终止条件。
当达到终止条件时,算法停止运行,输出最优解。
灰狼算法和粒子群算法

灰狼算法和粒子群算法
【最新版】
目录
1.灰狼算法和粒子群算法的概述
2.灰狼算法的基本思想和应用领域
3.粒子群算法的基本思想和应用领域
4.灰狼算法和粒子群算法的优缺点比较
5.灰狼算法和粒子群算法在我国的研究现状和前景
正文
一、灰狼算法和粒子群算法的概述
灰狼算法和粒子群算法都是近年来受到广泛关注的智能优化算法。
它们各自具有独特的特点和优势,分别在解决不同类型的问题中表现出色。
二、灰狼算法的基本思想和应用领域
灰狼算法是一种基于狼群捕猎行为的优化算法。
它模仿狼群在捕猎过程中对猎物的追踪和围攻,达到快速找到最优解的目的。
灰狼算法主要应用于组合优化问题、机器学习、信号处理等领域。
三、粒子群算法的基本思想和应用领域
粒子群算法是一种基于群体智能的优化算法。
它模拟鸟群在寻找食物过程中的协同搜索行为,通过粒子间的信息共享和个体的随机搜索,达到全局最优解。
粒子群算法主要应用于解决复杂系统的优化问题,如物流、生产调度、机器学习等。
四、灰狼算法和粒子群算法的优缺点比较
灰狼算法和粒子群算法各自具有一定的优点和缺点。
灰狼算法在解决大规模问题时具有较高的计算速度,但其全局搜索能力较弱;粒子群算法
具有较强的全局搜索能力,但计算复杂度较高,容易出现早熟现象。
五、灰狼算法和粒子群算法在我国的研究现状和前景
近年来,我国对灰狼算法和粒子群算法的研究取得了显著成果。
许多学者针对这两种算法的局限性,提出了一系列改进算法,提高了算法的性能。
在我国,灰狼算法和粒子群算法在多个领域得到了广泛应用,如物流、生产调度、机器学习等。
多目标灰狼优化算法的改进策略研究

多目标灰狼优化算法的改进策略研究崔明朗;杜海文;魏政磊;李聪【摘要】为了解决多目标灰狼优化算法(MOGWO)易陷入局部最优,稳定性差等缺点,基于对算法寻优时灰狼个体运动情况的分析,提出了两条改进策略:一是通过引入"观察"策略赋予灰狼个体自主探索的能力,以提高算法的优化效率和跳出局部最优的能力;二是改进控制参数调整策略,选用幂函数取代线性函数以提高算法的稳定性.然后对两条改进策略进行了可行性分析,提出了带观察策略的多目标灰狼算法并进行了算法复杂度分析.最后通过对6个不同特点测试函数的多次重复实验,结合GD 与IGD两种通用评价指标,对原算法、改进后算法和多目标粒子群算法进行比较,从算法效率、寻优能力和稳定性等方面综合验证了算法改进的有效性和优越性.%For the problems of easily falling into local optimum and poor stability of the Multi-Objective Grey Wolf Optimizer(MOGWO),two improvement strategies are put forward by studying the movement of grey wolf individual at algorithm optimization process:One is adding the"survey process",the grey wolf individual is endowed with the ability to explore independently and both the efficiency of algorithm and the ability of jumping out the local optimum solution are improved;the other is improving the adjustment strategy of control parameter.The power function is used to replace the linear function to improve the stability of the algorithm.Based on two universal evaluation methods of multi-objective optimization(Generational Distance and Inverted Generational Distance),6 different test functions and 3 different algo-rithms(the original algorithm,the improved algorithm and the Multi-Objective Particle SwarmOptimization algorithm) are compared with the repeat experiments. The experimental results show the effectiveness and feasibility of the AS-MOGWO from efficiency,ability and stability.【期刊名称】《计算机工程与应用》【年(卷),期】2018(054)005【总页数】9页(P156-164)【关键词】多目标灰狼算法;观察策略;控制参数;Pareto边界;多目标优化评价方法【作者】崔明朗;杜海文;魏政磊;李聪【作者单位】空军工程大学航空航天工程学院,西安710038;空军工程大学航空航天工程学院,西安710038;空军工程大学航空航天工程学院,西安710038;空军工程大学航空航天工程学院,西安710038【正文语种】中文【中图分类】TP3101 引言近年来,随着技术的发展,生物优化算法以其结构简单,求解效率高等特点被广泛应用在较为复杂的优化问题上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
灰狼算法和粒子群算法
灰狼算法和粒子群算法是两种常用的进化计算算法,它们在优化问题中具有广泛的应用。
本文将分别介绍灰狼算法和粒子群算法的原理和特点,并通过比较它们的优缺点,探讨其适用的场景。
1. 灰狼算法
灰狼算法是由灰狼群体的行为和特性启发而来的一种群体智能算法。
灰狼群体中的每只狼都有一个适应度值,适应度值越高表示狼的位置越好。
算法的核心思想是模拟灰狼群体中的寻食行为,通过迭代更新每只狼的位置,最终找到最优解。
灰狼算法的具体步骤如下:
1)初始化灰狼群体的位置和适应度值;
2)通过适应度值的大小确定群体中的Alpha狼、Beta狼和Delta 狼;
3)根据Alpha狼的位置和其他狼的位置,更新每只狼的位置;
4)更新每只狼的适应度值;
5)重复步骤3和4,直到满足停止条件。
灰狼算法的优点是简单易实现,收敛速度快,适用于解决复杂的非线性优化问题。
然而,灰狼算法在处理高维优化问题时,容易陷入局部最优解。
2. 粒子群算法
粒子群算法是一种模拟鸟群觅食行为的群体智能算法。
算法中的每个粒子都有一个位置和速度,通过更新粒子的速度和位置,最终找到最优解。
粒子群算法的核心思想是通过个体和群体的交互合作来搜索最优解。
粒子群算法的具体步骤如下:
1)初始化粒子群体的位置和速度;
2)根据粒子的适应度值,更新局部最优解;
3)根据局部最优解和全局最优解,更新粒子的速度和位置;
4)更新粒子的适应度值;
5)重复步骤2、3和4,直到满足停止条件。
粒子群算法的优点是容易实现,具有较好的全局搜索能力,适用于解决多峰优化问题。
然而,粒子群算法在处理高维优化问题时,易陷入局部最优解。
3. 算法比较与适用场景
灰狼算法和粒子群算法都是基于群体智能的优化算法,它们在某些方面具有相似之处,但也存在一些差异。
灰狼算法与粒子群算法相比,优点是收敛速度快,适用于解决复杂的非线性优化问题;缺点是在处理高维优化问题时,容易陷入局部最优解。
粒子群算法与灰狼算法相比,优点是具有较好的全局搜索
能力,适用于解决多峰优化问题;缺点是在处理高维优化问题时,易陷入局部最优解。
根据算法的特点和适用场景,我们可以选择合适的算法来解决不同类型的优化问题。
如果问题比较复杂,且维度较低,可以选择灰狼算法;如果问题具有多个局部最优解,或者维度较高,可以选择粒子群算法。
灰狼算法和粒子群算法都是常用的进化计算算法,在优化问题中具有广泛的应用。
通过对比它们的原理和特点,我们可以根据问题的类型和要求选择合适的算法,从而得到更好的优化结果。
