企业所得税季度申报表A类的25%是怎么算的营业收入,营业成本,利润总额及以下的累计金额怎么填

合集下载

聚四氟乙烯性能参数

1．聚四氟乙烯聚四氟乙烯是用于密封的氟塑料之一。

聚四氟乙烯以碳原子为骨架，氟原子对称而均匀地分布在它的周围，构成严密的屏障，使它具有非常宝贵的综合物理机械性能(表14—9)。

聚四氟乙烯对强酸、强碱、强氧化剂有很高的抗蚀性，即使温度较高，也不会发生作用，其耐腐蚀性能甚至超过玻璃、陶瓷、不锈钢以至金、铂，所以，素有“塑料王”之称。

除某些芳烃化合物能使聚四氟乙烯有轻微的溶胀外，对酮类、醇类等有机溶剂均有耐蚀性。

只有熔融态的碱金属及元素氟等在高温下才能对它起作用。

聚四氟乙烯的介电性能优异，绝缘强度及抗电弧性能也很突出，介质损耗角正切值很低，但抗电晕性能不好。

聚四氟乙烯不吸水、不受氧气、紫外线作用、耐候性好，在户外暴露3年，抗拉强度几乎保持不变，仅伸长率有所下降。

聚四氟乙烯薄膜与涂层由于有细孔，故能透过水和气体。

聚四氟乙烯在200℃以上，开始极微量的裂解，即使升温到结晶体熔点327℃，仍裂解很少，每小时失重为万分之二。

但加热至400℃以上热裂解速度逐渐加快，产生有毒气体，因此，聚四氟乙烯烧结温度一般控制在375～380℃。

聚四氟乙烯分子间的范德华引力小，容易产生键间滑动，故聚四氟乙烯具有很低的摩擦系数及不粘性，摩擦系数在已知固体材料中是最低的。

聚四氟乙烯的导热系数小，该性能对其成型工艺及应用影响较大。

其不但导热性差，且线膨胀系数较大，加入填充剂可适当降低线膨胀系数。

在负荷下会发生蠕变现象，亦称作“冷流”，加入填充剂可减轻蠕变程度。

聚四氟乙烯可以添加不同的填充剂，选择的填充剂应基本满足下述要求：能耐380℃高温即四氟制品的烧结温度；与接触的介质不发生反应；与四氟树脂有良好的混入性；能改善四氟制品的耐磨性、冷流性、导热性及线膨胀系数等。

常用的填充剂有无碱无蜡玻璃纤维、石墨、碳纤维、MoS2、A123、CaF2、焦炭粉及各种金属粉。

如填充玻璃纤维或石墨，可提高四氟制品的耐磨、耐冷流性，填充MoS2可提高其润滑性，填充青铜、钼、镍、铝、银、钨、铁等，可改善导热性，填充聚酰亚胺或聚苯酯，可提高耐磨性，填充聚苯硫醚后能提高抗蠕变能力，保证尺寸稳定等。

C#编码规范

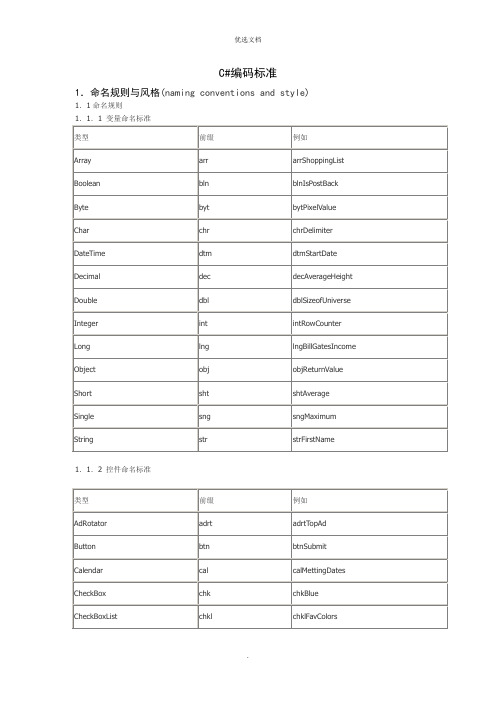
C#编码标准1．命名规则与风格(naming conventions and style) 1．1命名规则1．1．1 变量命名标准1．1．2 控件命名标准1．1．3 控件命名标准Form frmClass cls/CModule modGroupBox grpPictureBox picComboBox cboTreeView tvwListView lvwTabControl tabDateTimePicker dtpTimer tmrSplitter splProgressBar pbarRichTextBox rtfImageList imglToolBar tlbMenuItem mnuDate datStructure udtCrystal Report rpt1．1．5 事件处理子程序The name of an event-handling subroutine will consist of the ID of the control that rasied the event followed by the type of event being handled. For example, a subroutine named btnSubmit_Click handles the Click event of a Button control named btnSubmit.When a control that raises an event is not assigned an ID, the type of the control is used instead of the ID. For example, the subroutine named Button_Click handles the Click event of a Button control without an ID.1．2．编码风格1 用pascal规则来命名方法和类型.public class TextBox{public void DataBind(){}}2 用camel规则来命名局部变量和方法的参数.string userName;public AddUser(string userId, byte[] password);3 全部的成员变量前加前缀 _public class Database{private string _connectionString;}4 接口的名称加前缀 I.interface ICompare{int compare();}5 自定义的属性以Attribute结尾public class AuthorAttribute : Attribute{}6 自定义的异常以Exception结尾public class AppException : Exception{}7 方法的命名.一般将其命名为动宾短语.ShowDialog()CreateFile()GetPath()8 代码的缩进.要用Tab，而不要用space，保持严格的缩进：●对缩进使用3个空格位●绝不使用不标准的缩进,如1,2或4个空格位9 局部变量的名称要有意义.不要用x，y，z等等(除用于For循环变量中可使用i,j,k,l,m,n).string userName10.建议局部变量在最接近使用它时再声明.11 全部的成员变量声明在类的顶端，用一个换行把它和方法分开.public class MyClass{int_intNumber;string_strName;public void SomeMethodl(){}public void SomeMethod2(){}}12.用有意义的名字命名namespace，如：产品名、公司名.13.防止使用命名空间的完整限定名称,应使用using声明替代14.防止using声明放置在命名空间内部15.将全部的框架命名空间分组,将用户或第三方命名空间放置在其下using System;using System.Collections;using ponentModel;using System.Data;using MyCompany;using MyControls;16.使用某个控件的值时，尽量命名局部变量.17.文件名要能反响类的内容，最好是和类同名，一个文件中一个类或一组关连类.18.大括号"{"要新起一行.public class AuthorAttribute : Attribute{}19.用C#预定义的类名，而不要用在System空间内别名.object而不是System.0bjectstring 而不是System.Stringint 而不是System.Int3220.一行不要超过80个字符.21.尽量不要手工更改机器生成的代码，假设必须更改，肯定要改成和机器生成的代码风格一样.22.关键的语句(包含声明关键的变量)必需要写注释.23.将注释缩拍在与代码缩进同等级的位置上24.全部的注释应该通过拼写检查.拼错的注释将预示冗余的开发25.文字常量和数字常量不要硬编码，应该用常量类或枚举代替.26.不准使用goto系列语句.27.不要声明public和protected的成员变量，应用property.28.不要声明public的event，而应使用事件访问器.public class Source{private EventHandler _NumberChangeEvent;public event EventHandler NumberChangeEvent{add{_NumberChangeEvent += value;}remove{_NumberChangeEvent -= value;}}}29.类型转换的使用规则.Animal animal = new Dog();Dog dog = animal as Dog;if (dog != null){}30.生成和构建一个长的字符串时，肯定要使用StringBuilder，而不用string.31.始终使用"{ }"包含if下的语句，即使只有一条语句.32.switch语句肯定要有default来处理意外情况.33.尽量少使用三目运算符 ? : ，而要使用if语句.34.尽量不用使用this引用，除非是要调用类中的另一个Constructor.public class Person{private string _strName;public Person(string name){_strName=name;}public Person() : this("Jim"){}}35.使用易描述的变量名称●防止使用单一字符描述变量名称,如i或t.应使用index或temp替代●对public以及protected成员防止使用匈牙利命名法则●尽量不使用缩写字符,如使用num代替number36. 对于泛型,类型使用大写字母,当处理.NET格式Type时使用Type后缀//Correct:public class LinkedList<K, T>{..}//Avoid:public class LinkedList<KeyType,DataType>{..}37. 使用托付引用代替显式的托付实例(好似只有C#2.0才能这样用)delegate void SomeDelegate();public void SomeMethod(){..}SomeDelegate someDelegate=SomeMethod;38. 当使用partial类并将其分配给每个文件一局部时,对每个文件命名使用后缀P并附带一个额外的数字//In MyClassP1.cspublic partial class MyClass{..}// In MyClassP2.cspublic partial class MyClass{..}39. 对于匿名方法参照有规律的代码规划,其缩进应与匿名托付声明对齐delegate void SomeDelegate (string someString);//Correct:public void InvokeMethod(){SomeDelegate someDelegate=delegate (string name){MessageBox.Show(name);};someDelegate ("Juval");}//Avoidpublic void InvokeMethod(){SomeDelegate someDelegate=delegate (string name){MessageBox.Show(name);};someDelegate(〞Juval");}40. 对于匿名缺省参数的方法,应该使用空括号表示.delegate void SomeDelegate();//CorrectSomeDelegate someDelegate1=delegate(){MessageBox.Show("Hello");};//AvoidSomeDelegate someDelegate1=delegate{MessageBox.Show("Hello");};2．编码惯例(coding practices)1. 防止在一个文件中放多个类。

C# 中的常用正则表达式总结

(?:pattern)
匹配 pattern 但不获取匹配结果，也就是说这是一个非获取匹配，不进行存储供以后使用。这在使用 "或" 字符 (|) 来组合一个模式的各个部分是很有用。例如， ’industr(?:y|ies) 就是一个比 ’industry|industries’ 更简略的表达式。
{n,m}
m 和 n 均为非负整数，其中n <= m。最少匹配 n 次且最多匹配 m 次。例如，"o{1,3}" 将匹配 "fooooood" 中的前三个 o。’o{0,1}’ 等价于 ’o?’。请注意在逗号和两个数之间不能有空格。
?
当该字符紧跟在任何一个其他限制符 (*, +, ?, {n}, {n,}, {n,m}) 后面时，匹配模式是非贪婪的。非贪婪模式尽可能少的匹配所搜索的字符串，而默认的贪婪模式则尽可能多的匹配所搜索的字符串。例如，对于字符串 "oooo"，’o+?’ 将匹配单个 "o"，而 ’o+’ 将匹配所有 ’o’。
验证一年的12个月："^(0?[1-9]|1[0-2])$"正确格式为："01"～"09"和"1"～"12"。
验证一个月的31天："^((0?[1-9])|((1|2)[0-9])|30|31)$"正确格式为;"01"～"09"和"1"～"31"。
利用正则表达式限制网页表单里的文本框输入内容：
只能输入m~n位的数字：。"^\d{m,n}$"

2020考研数一真题答案及详细解析

一、选择题(1)【答案】D【解析】（方法一）利用结论：若f(x)和g(x)在x=O某邻域内连续，且当x-o时，f位）～g(x)'则J勹(t)dt �r g(t)dt.(A)『(/-l)dt� 『t 2dt =气3(B)『ln(l +万）dt �rt 令dt=气5(C) f"工s int 2dt �厂r t 2dt�f c 2d t =丘。

3(D)J :-co sx /忒臣了d t -I -c os rt i d t �I :''l令d t=岊（占）寺x故应选CD).（方法二）设J(x)和<p (x)在x =O某邻域内连续，且当x-0时，f(x)和<p (x)分别是x 的m阶和n阶无穷小，则『(,-)J(t)dt 是x -0时的n(m+ 1)阶无穷小．。

CA)r C / -1) d t , m = 2 , n = 1 , 则n(m+ 1) = 3. 。

ln(l + #)dt,m =立，n= 1, 则n(m+l)=立。

2 2.CC)厂sint 2dt, m =2, n =1 , 则n(m+ 1)=3.。

1一cos,·3叫产t,m=一，n= 2, 则n(m+l)=5.。

2故应选(D).(2)【答案】C【解析】（方法一）直接法若f(x)在x=O处可导，则f(x)在x=O处连续，且f(O)=lim f(x) = 0.工-o故应选(C).f(x) -f(O) = limf(x)j'(O) = Jim;-0X—r•OXf(x)f(x) lim=lim ——•X =j'(0)• 0 = 0工-o,/了.,·-oX�（方法二）排除法取f (x)= {X3, X # 0，则l im f位）=o ,且1,X= 0J-0 x 3f(x ) x 3lim·f(x)=lim _。

J了工-o�= O ,lim 一=lim —=22 工-oXr--0 X但f(x)在x=O处不可导，因为f(x)在X = 0处不连续，则排除选项(A),CB).若取f(x)= x , 则lim f(x)= 0, 且f(x)在x =O处可导，但J-0• 5 •叫排除CD )'故应选CC).(3)【答案】A2 ,·-·OX.r-0 X.r -•O X【解析】利用函数z = .I 一位，y)在(x 。

数列-2024高考数学压轴小题(解析版)

数列-2024高考压轴小题一．选择题（共13小题）1．数列{a n}中，＞1(∈∗)，点（a n，a n+1）在双曲线2y2﹣x2＝1上．若a n+2﹣a n+1＞λ（a n+1﹣a n）恒成立，则实数λ的取值范围为（）A．[12，+∞)B．(12，+∞)C．+∞)D．（1，+∞）2．已知等比数列{a n}的公比为−13，其前n项和为S n，且a1，2+43，a3成等差数列，若对任意的n∈N*，均有≤−2≤恒成立，则B﹣A的最小值为（）A．2B．76C．103D．53 3．已知数列{a n}满足1=13，r1=(r1)+，1+12+⋯+12⋯＜o∈p恒成立，则m的最小值为（）A．1B．2C．3D．54．已知数列{a n}满足a1+2a2+…+2n﹣1a n＝n•2n，记数列{a n﹣tn}的前n项和为S n，若S n≤S10对任意的n∈N*恒成立，则实数t的取值范围是（）A．[1211，1110]B．(1211，1110]C．[1110，109]D．(1110，109) 5．已知数列{142+4K3}的前n项和为T n，若对任意的n∈N*，不等式12T n＜3a2﹣a恒成立，则实数a的取值范围是（）A．[−1，43]B．[−43，1] C．(−∞，−1]∪[43，+∞)D．(−∞，−43]∪[1，+∞)6．设S n是一个无穷数列{a n}的前n项和，若一个数列满足对任意的正整数n，不等式＜r1r1恒成立，则称数列{a n}为和谐数列，有下列3个命题：①若对任意的正整数n均有a n＜a n+1，则{a n}为和谐数列；②若等差数列{a n}是和谐数列，则S n一定存在最小值；③若{a n}的首项小于零，则一定存在公比为负数的一个等比数列是和谐数列．以上3个命题中真命题的个数有（）个．A．0B．1C．2D．37．已知数列{a n}的前n项和为S n，a1＝2，且满足S n+1＝2S n+2n+1，若存在实数λ，使不等式λa n≤（n﹣19）S n对任意n∈N*恒成立，则λ的最大值为（）A．﹣24B．﹣18C．−683D．−703 8．已知等比数列{a n}的首项为2，公比为−13，其前n项和记为S n，若对任意的n∈N*，均有A≤3S n−1≤B恒成立，则B﹣A的最小值为（）A．72B．94C．114D．1369．已知等差数列{a n}满足a2＝2，a3+a6＝1+a8，数列{b n}满足b n a n+1a n＝a n+1﹣a n，记{b n}的前n项和为S n，若对于任意的a∈[﹣2，2]，n∈N*，不等式＜22+B−3恒成立，则实数t的取值范围为（）A．（﹣∞，﹣2]∪[2，+∞）B．（﹣∞，﹣2]∪[1，+∞）C．（﹣∞，﹣1]∪[2，+∞）D．[﹣2，2]10．已知数列{a n}的首项是a1＝1，前n项和为S n，且S n+1＝2S n+3n+1（n∈N*），设c n＝log2（a n+3）．若存在常数k，使得不等式k≥−1(r16)(∈∗)恒成立，则k的取值范围为（）A．[19，+∞）B．[116，+∞)C．[125，+∞)D．[136，+∞) 11．已知数列{a n}满足1=3，r1=+2−1，记数列{|a n﹣2|}的前n项和为S n，设集合={125，6225，4517，3512}，N＝{λ∈M|λ＞S n对n∈N*恒成立}，则集合N的元素个数是（）A．1B．2C．3D．4 12．设S n是数列{a n}的前n项和，=32−3r1，若不等式≥n∈N+恒成A．13B．16C．19D．13613．S n为数列{a n}的前n项和，a1＝2，a2＝5，a3＝10，a4＝17，对任意大于2的正整数n，有S n+1﹣3S n+3S n﹣1﹣S n﹣2+m＝0恒成立，则使得12−2+13−2+⋯+1K1−2+1−2≥2542成立的正整数k的最小值为（）A．7B．6C．5D．4二．多选题（共5小题）（多选）14．已知数列{a n}满足a1＝2，a n+1a n＝2a n﹣1（n∈N*），b1＝20a4，b n+1＝a n b n（n∈N •），数列{b n}的前n项和为T n，且对∀n∈N*，2T n+400≥λn恒成立，则（）A．a4=45B．数列{1−1}为等差数列C．b n＝16n D．λ的最大值为225（多选）15．设等差数列{a n}的前n项和为S n，且4=235，S7＝28，记T n为数列{1}的前n项和，若T n＜λ恒成立，则λ的值可以是（）A．1B．2C．3D．4（多选）16．已知数列{a n}满足：a1＝2，=2−1K1，n＝2，3，4，…，则下列说法正确的是（）A．5=65B．对任意n∈N*，a n+1＜a n恒成立C．不存在正整数p，q，r使a p，a r，a q成等差数列D．数列{1−1}为等差数列（多选）17．已知数列{a n}满足a1＝1，a n+1=(r1)+2，对于任意n∈N*，a∈[﹣2，2]，不等式3⋅2＜2t2+at﹣1恒成立，则t的取值可以是（）A．1B．2C．32D．4（多选）18．已知数列{a n}中，a1＝1，a n+1−1=(1+1)，n∈N*．若对于任意的t∈[1，2]，不等式＜−22−(+1)+2−a+2恒成立，则实数a可能为（）A．﹣4B．﹣2C．0D．22024高考压轴练--数列小题参考答案与试题解析一．选择题（共13小题）1．数列{a n }中，＞1(∈∗)，点（a n ，a n +1）在双曲线2y 2﹣x 2＝1上．若a n +2﹣a n +1＞λ（a n +1﹣a n ）恒成立，则实数λ的取值范围为（）A ．[12，+∞)B ．(12，+∞)C ．+∞)D ．（1，+∞）【解答】解：由题意可知：双曲线2y 2﹣x 2＝1的渐近线方程为，因为点（a n ，a n +1）在双曲线2y 2﹣x 2＝1上，则2r12−2=1，且＞1(∈∗)，可得r12−2=1−r12＜0，可知{2}为递减数列，且＞1(∈∗)，则{a n }为递减数列，可得a n +1﹣a n ＜0，且a n +2﹣a n +1＞λ（a n +1﹣a n ），可得＞r2−r1r1−，记点A n （a n ，a n +1），则r2−r1r1−为直线A n A n +1的斜率，记=r2−r1r1−，由双曲线的性质以及{a n }为递减数列可知，直线A n A n +1的斜率{k n }为递减数列，即k n ≤k 1，且随着a 1增大，直线A 1A 2越接近渐近线=，故k 1接近于22，所以则≥故选：C ．2．已知等比数列{a n }的公比为−13，其前n 项和为S n ，且a 1，2+43，a 3成等差数列，若对任意的n ∈N *，均有≤−2≤恒成立，则B ﹣A 的最小值为（）A ．2B ．76C ．103D ．53【解答】解：等比数列{a n}的公比为−13，因为a1，2+43，a3成等差数列，所以2×−131+43= 1+191，解得a1＝2，所以=2[1−(−13)]1−(−13)=32−32⋅(−13)，当n为奇数时，=32+32⋅(13)，易得S n单调递减，且32+32⋅(13)＞32，所以32＜≤1=2；当n为偶数时，=32−32⋅(13)，易得S n单调递增，且32−32⋅(13)＜32，所以43=2≤＜32．所以S n的最大值与最小值分别为2，43．函数=−2在（0，+∞）上单调递增，所以≤(−2)m=43−243=−16．≥(−2)B=2−22=1．所以B﹣A的最小值1−(−16)=76．故选：B．3．已知数列{a n}满足1=13，r1=(r1)+，1+12+⋯+12⋯＜o∈p恒成立，则m的最小值为（）A．1B．2C．3D．5【解答】解：依题意，a n≠0，由r1=(r1)+，得1r1=+(r1)，即r1r1=+1，因此数列{}是首项11=3，公差d＝1的等差数列，则=11+o−1)=+2，即=r2，则当n≥2时，12⋯=13⋅24⋅35⋅⋯⋅r2=2(r1)(r2)=2(1r1−1r2)，1=13= 22×3也符合上式，1+12+⋯+12⋯=2(12−13+13−14+⋯+1r1−1r2)=1−2r2＜1，所以m≥1，即m的最小值为1．故选：A．4．已知数列{a n}满足a1+2a2+…+2n﹣1a n＝n•2n，记数列{a n﹣tn}的前n项和为S n，若S n≤S10对任意的n∈N*恒成立，则实数t的取值范围是（）A．[1211，1110]B．(1211，1110]C．[1110，109]D．(1110，109)【解答】解：由1+22+⋯+2K1=⋅2①，当n＝1时，a1＝2，当n≥2时，1+22+⋯+2K2K1=(−1)⋅2K1②，①﹣②可得a n＝n+1（n≥2），又a1也符合上式，∴a n＝n+1，令b n＝a n﹣tn＝n+1﹣tn＝（1﹣t）n+1，∴b n+1﹣b n＝（1﹣t）（n+1）+1﹣[（1﹣t）n+1]＝1﹣t为常数，∴数列{b n}是等差数列，首项b1＝2﹣t，∴=2−r(1−pr12×=1−22+3−2，其对称轴为=−3−21−=−3−2−2，∵S n≤S10对任意的n∈N*恒成立，3−2−2≤10.5，解得1211≤≤1110，∴t的取值范围是[1211，1110]．故选：A．5．已知数列{142+4K3}的前n项和为T n，若对任意的n∈N*，不等式12T n＜3a2﹣a恒成立，则实数a的取值范围是（）A．[−1，43]B．[−43，1] C．(−∞，−1]∪[43，+∞)D．(−∞，−43]∪[1，+∞)【解答】解：由142+4K3=1(2r3)(2K1)=14（12K1−12r3），可得T n=14（1−15+13−17+15−19+...+12K3−12r1+12K1−12r3）=14（1+13−12r1−12r3）＜14×43=13．由对任意的n∈N*，不等式12T n＜3a2﹣a恒成立，可得3a2﹣a≥12×13，解得a≥43或a≤﹣1．故选：C．6．设S n是一个无穷数列{a n}的前n项和，若一个数列满足对任意的正整数n，不等式＜r1r1恒成立，则称数列{a n}为和谐数列，有下列3个命题：①若对任意的正整数n均有a n＜a n+1，则{a n}为和谐数列；②若等差数列{a n}是和谐数列，则S n一定存在最小值；③若{a n}的首项小于零，则一定存在公比为负数的一个等比数列是和谐数列．以上3个命题中真命题的个数有（）个．A．0B．1C．2D．3【解答】解：对于①，由＜r1r1，可得（n+1）S n＜nS n+1，则S n＜n（S n+1﹣S n），即S n＜na n+1，若a n＜a n+1，则S n＜na n＜na n+1，故①正确；对于②，设等差数列{a n}的公差为d，则=22+(1−)，则=2+1−2，即{}为公差为2的等差数列，若{a n}为和谐数列，即＜r1r1，则2＞0，所以关于n的二次函数=22+(1−)开口向上，则在n∈N•上一定存在最小值，故②正确；对于③，取1＜0，=−14，则=11−⋅(1−)=451[1−(−14)]，B r1=B1⋅(−14)，下面证明S n＜na n+1，即说明存在公比为负数的一个等比数列是和谐数列，即证451[1−(−14)]＜B1(−14)，即证45[1−(−14)]＞o−14)，即证(+45)(−14)＜45，当n＝2k+1，k∈N时，上式左边为负数，显然成立；当n＝2k，k∈N•时，即证(2+45)⋅116＜45，即证16−52−1＞0(⋅)，设op=16−52−1，′(p=16B16−52＞B16−52＞0，则f（k）＞f（1）＞0，即（*）式成立，故③正确．故选：D．7．已知数列{a n}的前n项和为S n，a1＝2，且满足S n+1＝2S n+2n+1，若存在实数λ，使不等式λa n≤（n﹣19）S n对任意n∈N*恒成立，则λ的最大值为（）A．﹣24B．﹣18C．−683D．−703【解答】解：由S n+1＝2S n+2n+1，得r12r1−2=1，∵S1＝a1＝2，∴121=1，∴{2}是首项为1，公差为1的等差数列，则2=1+1×（n﹣1）＝n，即S n＝n•2n，∴当n≥2时，a n＝S n﹣S n﹣1＝n•2n﹣（n﹣1）•2n﹣1＝（n+1）•2n﹣1，验证n＝1也满足，∴a n＝（n+1）•2n﹣1，由λa n≤（n﹣19）S n，得λ（n+1）•2n﹣1≤（n﹣19）•n•2n，即λ≤2oK19)r1．令f（n）=2oK19)r1，则f（n+1）﹣f（n）=2(r1)(K18)r2−2oK19)r1=2(2+3K18)(r1)(r2)= 2(K3)(r6)(r1)(r2)，可得f（1）＞f（2）＞f（3）＝f（4）＜f（5）＜…，∴f（n）min＝f（3）＝f（4）＝﹣24，而λ≤2oK19)r1，∴λ≤﹣24，得λ的最大值为﹣24．故选：A．8．已知等比数列{a n}的首项为2，公比为−13，其前n项和记为S n，若对任意的n∈N*，均有A≤3S n−1≤B恒成立，则B﹣A的最小值为（）A．72B．94C．114D．136【解答】解：S n=2[1−(−13)]1−(−13)=32−32•(−13)，①n为奇数时，S n=32+32•(13)，可知：S n单调递减，且m m∞=32，∴32＜S n≤S1＝2；②n为偶数时，S n=32−32•(13)，可知：S n单调递增，且m m∞=43，∴43=S2≤S n＜32．∴S n的最大值与最小值分别为：2，43．考虑到函数y＝3t−1在（0，+∞）上单调递增，∴A≤(3−1)m=3×43−143=134．B≥(3−1)B=3×2−12=112．∴B﹣A的最小值=112−134=94．故选：B．9．已知等差数列{a n}满足a2＝2，a3+a6＝1+a8，数列{b n}满足b n a n+1a n＝a n+1﹣a n，记{b n}的前n项和为S n，若对于任意的a∈[﹣2，2]，n∈N*，不等式＜22+B−3恒成立，则实数t的取值范围为（）A．（﹣∞，﹣2]∪[2，+∞）B．（﹣∞，﹣2]∪[1，+∞）C．（﹣∞，﹣1]∪[2，+∞）D．[﹣2，2]【解答】解：由等差数列的性质知a3+a6＝a8+a1＝a8+1，则a1＝1，又a2＝2，则等差数列{a n}的公差d＝a2﹣a1＝1，∴a n＝1+（n﹣1）＝n．由b n a n+1a n＝a n+1﹣a n，得=1−1r1=1−1r1，∴=(1−12)+(12−13)+(13−14)+⋯+(1K1−1)+(1−1r1)=1−1r1，则不等式＜22+B−3恒成立等价于1−1r1＜22+B−3恒成立，而1−1r1＜1，∴问题等价于对任意的a∈[﹣2，2]，n∈N*，2t2+at﹣4≥0恒成立．设f（a）＝2t2+at﹣4，a∈[﹣2，2]，则o2)≥0o−2)≥0，即2+−2≥02−−2≥0，解得：t≥2或t≤﹣2．故选：A．10．已知数列{a n}的首项是a1＝1，前n项和为S n，且S n+1＝2S n+3n+1（n∈N*），设c n＝log2（a n+3）．若存在常数k，使得不等式k≥−1(r16)(∈∗)恒成立，则k的取值范围为（）A．[19，+∞）B．[116，+∞)C．[125，+∞)D．[136，+∞)【解答】解：因为S n+1＝2S n+3n+1，所以当n≥2时，S n＝2S n﹣1+3（n﹣1）+1，两式相减，得a n+1＝2a n+3，所以a n+1+3＝2（a n+3），又a1+3＝4，a1+a2＝S2＝2S1+3×1+1＝6，所以a2＝5，a2+3＝2（a1+3），所以数列{a n+3}是以4为首项、2为公比的等比数列，所以+3=4×2K1=2r1，所以c n＝log2（a n+3）＝n+1，所以−1(r16)=(r16)(r1)=2+17r16=1r16+17≤18+17=125，当且仅当n＝4时等号成立，所以≥125，所以k的取值范围为[125，+∞)．故选：C．11．已知数列{a n}满足1=3，r1=+2−1，记数列{|a n﹣2|}的前n项和为S n，设集合={125，6225，4517，3512}，N＝{λ∈M|λ＞S n对n∈N*恒成立}，则集合N的元素个数是（）A．1B．2C．3D．4【解答】解：令r1=+2−1=，解得a n＝2，即数列{a n}的不动点为2，其生成函数为=+2−1，所以，作出函数=+2−1与函数y＝x的图像如图：故由上图：2＜a n+1＜a n≤3，∴13≤1＜12，∴r1=22−1+1=2(1−14)2+78∈[89，1)，即89≤r1＜，又∵r1−=2−1=2−，∴a n﹣2＝a n（a n﹣a n+1），一方面，由r1≥89得+r1≥179，∴≤917(+r1)，−2=(−K1)≤917(2−r12)，∴=(1−2)+(2−2)+⋯(−2)≤917[(12−22)+(22−32)+⋯+(2−r12)]=917(9−r12)∵a n+1＞2，且当n→+∞，a n+1→2，∴＜917(9−4)=4517，∵4517≥4517，3512＞4517，∴4517，3512∈，另一方面，由r1−2=(−2)(−1)，2＜≤3，得r1−2−2=1−1＞12，又∵1−2=1，2−2=23，3−2=512，∴=(1−2)+(2−2)+⋯(−2)≥1+23+512+512⋅12+⋯+512⋅(12)K3=52−53⋅2K1，又当→+∞，52−53⋅2K1→52，∴λ必须大于等于52，∵125＜52，6225＜52，∴125，6225∉，所以集合N的元素个数是2，故选：B．12．设S n是数列{a n}的前n项和，=32−3r1，若不等式≥n∈N+恒成A．13B．16C．19D．136【解答】解：当n＝1时，1=321−32，所以a1＝18，由=32−3r1，当n≥2时，K1=32K1−3，所以=−K1=32−3r1−32K1+2，所以=3K1+4⋅3，两边同除以3n，所以3=K13K1+4，所以数列{3}是以6为首项，以4为公差的等差数列，所以34(−1)=4+2，所以=(4+2)，由≥n∈N+恒成立，即2(2+1)⋅3≥所以≥2⋅3，设=2⋅3，则r1=r12⋅3r12⋅3=r13=13+13＜1，所以数列{c n}为递减数列，所以≥12×3=16，所以≥136，所以k的最小值为136，故选：D．13．S n为数列{a n}的前n项和，a1＝2，a2＝5，a3＝10，a4＝17，对任意大于2的正整数n，有S n+1﹣3S n+3S n﹣1﹣S n﹣2+m＝0恒成立，则使得12−2+13−2+⋯+1K1−2+1−2≥2542成立的正整数k的最小值为（）A．7B．6C．5D．4【解答】解：依题意知：当n＝3时有S4﹣3S3+3S2﹣S1+m＝0＝a4﹣2a3+a2+m，∵a2＝5，a3＝10，a4＝17，∴m＝﹣2，S n+1﹣3S n+3S n﹣1﹣S n﹣2﹣2＝0，即（S n+1﹣S n）﹣2（S n﹣S n﹣1）+（S n﹣1﹣S n）﹣2＝0，﹣2∴a n+1﹣2a n+a n﹣1﹣2＝0，即（a n+1﹣a n）﹣（a n﹣a n﹣1）＝2，n≥3，又a2﹣a1＝3，a3﹣a2＝5，（a3﹣a2）﹣（a2﹣a1）＝2，∴数列{a n+1﹣a n}是以3为首项，2为公差的等差数列，∴a n+1﹣a n＝2n+1，故a2﹣a1＝3，a3﹣a2＝5，a4﹣a3＝7，…，a n﹣a n﹣1＝2n﹣1（n≥2），由上面的式子累加可得：a n ﹣2=(K1)(3+2K1)2=（n ﹣1）•（n +1），n ≥2，∴1−2=1(K1)(r1)=12（1K1−1r1），n ≥2．由12−2+13−2+⋯+1K1−2+1−2≥2542可得：12[（11−13）+（12−14）+（13−15）+…+（1K1−1r1）]=12（1+12−1−1r1）≥2542，整理得1+1r1≤1342，∵k ∈N *且k ≥2，∴解得：k ≥6．所以k 的最小值为6．故选：B ．二．多选题（共5小题）（多选）14．已知数列{a n }满足a 1＝2，a n +1a n ＝2a n ﹣1（n ∈N *），b 1＝20a 4，b n +1＝a n b n （n ∈N •），数列{b n }的前n 项和为T n ，且对∀n ∈N *，2T n +400≥λn 恒成立，则（）A ．a 4=45B ．数列{1−1}为等差数列C ．b n ＝16n D ．λ的最大值为225【解答】解：∵数列{a n }满足a 1＝2，a n +1a n ＝2a n ﹣1，∴r1=2−1，∴r1−1=−1，∴1r1−1=−1=1−1+1，∴1r1−1−1−1=1，又11−1=12−1=1，∴{1−1}是以1为首项，公差为1的等差数列，∴B 选项正确；∴1−1=，∴=r1，∴4=54，∴A 选项错误；∴1=20×54=25，∴r1=(r1)，∴r1=r1，∴21=21，32=32，•••，K1=K1，累乘可得：21⋅32⋅⋅⋅⋅⋅K1=21×32×⋅⋅⋅×K1，∴1=，∴b n ＝b 1n ＝25n ，∴C 选项错误，∴=(25+25p2，又对∀n ∈N *，2T n +400≥λn ，∴对∀n ∈N *，25n 2+25n +400≥λn ，∴对∀n∈N*，λ≤25+400+25，又25+400+25≥225×400+25=225，当且仅当25=400，即n＝4时，等号成立，∴λ≤225，∴λ的最大值为225，∴D选项正确．故选：BD．（多选）15．设等差数列{a n}的前n项和为S n，且4=235，S7＝28，记T n为数列{1}的前n项和，若T n＜λ恒成立，则λ的值可以是（）A．1B．2C．3D．4【解答】解：∵4=235，∴41+4×32=23（51+5×42），整理得12a1+18d＝10a1+20d，即a1＝d，由S7＝28，可得71+7×62=28，即a1+3d＝4，∴a1＝d＝1，∴=+oK1)2=or1)2，1=2or1)=2(1−1r1)，∴=11+12+...+1=2(1−12+12−13+...+1−1r1)=2(1−1r1)=2−2r1．∵T n＜λ恒成立，∴λ≥2．结合选项可知，λ的值可以是2或3或4．故选：BCD．（多选）16．已知数列{a n}满足：a1＝2，=2−1K1，n＝2，3，4，…，则下列说法正确的是（）A．5=65B．对任意n∈N*，a n+1＜a n恒成立C．不存在正整数p，q，r使a p，a r，a q成等差数列D．数列{1−1}为等差数列【解答】解：∵=2−1K1，（n≥2，n∈N*），∴r1=2−1，（n∈N*），∴r1−1=1−1，又a1﹣1＝1≠0，∴1r1−1=11−1=−1=1−1+1，∴1r1−1−1−1=1，且11−1=1，∴数列{1−1}是以首项为1，公差为1的等差数列，∴1−1=，∴=1+1，∴D正确；对A，∵5=1+15=65，∴A正确；对B，∵r1−=(1+1r1)−(1+1)=−1or1)＜0，∴a n+1＜a n，∴B正确；对C，若存在正整数p，q，r使a p，a r，a q成等差数列，则2a r＝a p+a q，∴2+2=2+1+1，∴2=1+1，令p＝3，r＝4，q＝6，满足等式，∴C错误；故选：ABD．（多选）17．已知数列{a n}满足a1＝1，a n+1=(r1)+2，对于任意n∈N*，a∈[﹣2，2]，不等式3⋅2＜2t2+at﹣1恒成立，则t的取值可以是（）A．1B．2C．32D．4【解答】解：根据题意，r1=(r1)+2，两边同时取倒数可得，r1r1=1+2，即得r1r1+1=2(+1)，由此可得数列{1+}是首项为2，公比为2的等比数列，所以1+=2⇒=2−1，∴3⋅2=3(2−1)2=3−32＜3，∴2t2+at﹣1≥3，又因为at+2t2﹣4≥0在a∈[﹣2，2]上恒成立，所以−2+22−4≥02+22−4≥0⇒t∈（﹣∞，﹣2]∪[2，+∞）．故选：BD．（多选）18．已知数列{a n}中，a1＝1，a n+1−1=(1+1)，n∈N*．若对于任意的t∈[1，2]，不等式＜−22−(+1)+2−a+2恒成立，则实数a可能为（）A．﹣4B．﹣2C．0D．2【解答】解：由a n+1−1=(1+1)，得a n+1−1=r1，∴r1r1−=1or1)=1−1r1，∴=(−K1K1)+(K1K1−K2K2)+⋯+⋯+（a2﹣a1）+a1，＝（1K1−1）+（1K2−1K1）+…+（1−12）+1＝2−1＜2，∵不等式＜−22−(+1)+2−a+2恒成立，∴2≤﹣2t2﹣（a+1）t+a2﹣a+2，∴2t2+（a+1）t﹣a2+a≤0，在t∈[1，2]上恒成立，设f（t）＝2t2+（a+1）t﹣a2+a，t∈[1，2]，∴o1)=2++1−2+≤0o2)=8+2(+1)−2+≤0，解得a≤﹣2或a≥5，∴实数a可能为﹣4，﹣2．故选：AB．。

2023初中数学培优竞赛例题+练习专题36 全国初中数学竞赛分类汇编卷(七)三角形(提优)

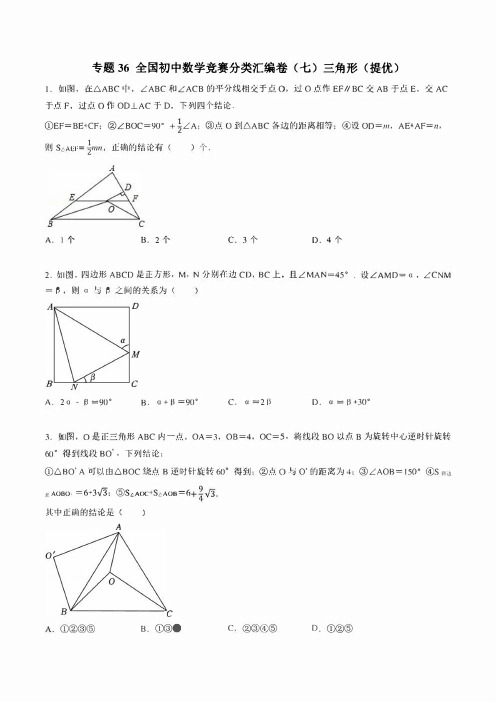
专题36全国初中数学竞赛分类汇编卷〈七〉三角形〈提优〉I.如｜蜀，在.6.ABC中，LABC和ζACB的平分线相交子点。

，过0点作EF//BC交AB子点E，交AC 于点F，过点。

你OD_l_AC于D，下列四个结论．1①EF=BE+CF：②LBOC=90。

＋2LA；＠点O itl.6.ABC各边的距离相等；④设OD=m,AE+AF=n, 则S c,A EF=�mn，正确的结论有（）个AB cA.l个B.2个 c.3个。

.4个2.如图，四边形ABCD是正方形，M,N分别在边CD,BC上，且LMAN=45。

．设LAMD＝口，ζCNM ＝白，则。

与自之间的关系为（〉DcNA.2 a －白＝90。

B.a+fJ=90。

C.a =2日。

.a＝自＋30。

3.如图，0是正三角形ABC内一点，OA=3,08=4, OC=S，将线段BO以点B为旋转中心逆时针旋转60。

得到线段BO’，下列结论：①.6.BO' A司以由.6.BOC绕点B逆时针旋转60。

得到；②点。

与O’的距离为4；③LAOB=l50。

④s P.!I地11;AOBO ＝削σ；⑤S叫＋S c,A O时1士；中正E角的结论是〈）A℃B.①③④C②＠④⑤ D.①＠⑤4.AD与BE是6ABC的角平分线，D,E分别在BC,AC上，若AD=AB,BE=BC，贝�L'.C=()Bc AA.69。

ωTRU900c.（τ3)° D.不能确定5.在四边形ABCD中，AD=DC=2，ζDAB＝ζDCB=90。

，BC,A D的延长线交于P，求AB•S i:.PAB的最小值pDBA6.着，1个等腰三角形的顶角a1、a2、…、an两两不等，它们的共同特点是：被一条直线分得的两个较小三角形也是等腰三角形，则a1+ a 2＋…＋an＝·fα－ 2b = m-7 7设。

、b分别是等腰三角形的两条边的长，m是这个三角形的周长，当。

、b、川满足方程t R Ja+b＝号＋2时，m的值是8.己知ID.ABC中，AB=AC,L'.BAC=90。

NB光轴直线光轴

3.98×104
35
7.37×104
将这些值代入表F-3的1式，
40
1.26×105
δmax=Pℓ 3C=0.31（mm）
50
3.07×105
2.54×10－8 8.03×10－9 3.29×10－9 1.59×10－9 5.03×10－10 2.06×10－10 9.91×10－11 7.22×10－11 4.06×10－11 3.14×10－11 1.29×10－11 5.27×10－12 2.54×10－12 1.37×10－12 8.03×10－13 3.29×10－13
弯曲变形角计算公式 i1＝0 i2＝ 16EI ＝3Pℓ2C
2 固定 ┃
固定
3 支持
┃ 支持 4 固定
┃ 固定
5 支持 ┃
支持
固定
固定 7 固定
┃ 自由
8 固定 ┃ 自由
9 支持 ┃
支持
10 固定 ┃
固定
δm
δmax
δmax
δma x 1
δma x 1
ax
δ
δmax
δmax
δ
R/2 P R
均匀负荷p
特征
高度的加工技术经过多年的加工技术的积累，从要求分段、螺钉、螺纹孔等简单加工，到主轴、高速旋转轴等的高度的加工技术，可进行广泛的高精度加工。另外还可进行较长物件的研磨、钻孔加工等。
具有优异的耐磨损性使用具有优异耐磨损性的高碳铬轴承钢（SUJ2）和马氏体系列不锈钢（相当于SUS440C）进行退火、淬火以及回火。利用NB优异的热处理技术，不论在圆周方向还是轴方向，均可实现均匀而平整的硬化层。 (参考照片）
等价

选择题

void swap( int *p, int *q );
int x, y;
A) swap( x, y );
B) swap( *x, *y );
C) swap( &x, &y );
D) swap( p, q );
窗体底端
9.
窗体顶端
以下字符串定义与赋值中，正确的是( )。
A) char s[80]; s = {'A', 'B', 'C'};
D) void hex2dec(char str);
窗体底端
30.
窗体顶端
若有变量定义int a; double b;要输入数据存放在a和b中，则下面正确的输入数据的语句为：
A. scanf("%d%f",a,b);
B. scanf("%d%f",&a,&b);
C. scanf("%d%lf",&a,&b);
(A)14
(B)3
(C)9
(D)字符串有非法字符，输出值不确定
窗体底端40.ຫໍສະໝຸດ 窗体顶端变量a与b分别初始为10与20，正确的语句是( )。
A) void fun_a (int x, int y)
{ int *p;
*p=x; x=y; y=*p;
}
B) void fun_b (int *x, int *y)
{ int *p;
*x=*y; *y=*x;
}
C) void fun_c (int *x, int *y)
{ *x=*x+*y;
*y=*x-*y;
窗体底端
32.

2024年湘教新版高一数学下册阶段测试试卷588

2024年湘教新版高一数学下册阶段测试试卷588考试试卷考试范围：全部知识点；考试时间：120分钟学校：______ 姓名：______ 班级：______ 考号：______总分栏题号一二三四五六总分得分评卷人得分一、选择题(共6题，共12分)1、【题文】已知函数的导函数为那么“”是“是函数的一个极值点”的（）A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件2、幂函数y=x a（α是常数）的图象（）A. 一定经过点（0，0）B. 一定经过点（1，1）C. 一定经过点（﹣1，1）D. 一定经过点（1，﹣1）3、不等式x2+ax+4＜0的解集不是空集，则实数a的取值范围是（）A. （﹣∞，﹣4）∪（4，+∞）B. （﹣4，4）C. （﹣∞，﹣4]∪[4，+∞）D. [﹣4，4]4、已知幂函数f（x）=x m-1（m∈Z，其中Z为整数集）是奇函数．则“m=4”是“f（x）在（0，+∞）上为单调递增函数”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件5、在△ABC中，若 O为△ABC的内心，且则λ+μ=（）A.B.C.D.6、设f(x)为定义在R上的奇函数，当x鈮�0时，f(x)=2x+2x鈭�b(b为常数)则f(鈭�1)=()A. 鈭�5B. 鈭�3C. 5D. 3评卷人得分二、填空题(共7题，共14分)7、已知不等式x2+px-6＜0的解集为{x|-3＜x＜2}，则p=____．8、如果函数在区间(5,20)不是单调函数，那么实数k的取值范围是____________________________.9、已知不等式ax2-5x+b>0的解集为{x|-3 <2}，则不等式bx 2-5x+a>0的解集为_________.10、【题文】某三棱锥P-ABC的正视图为如图所示边长为2的正三角形；俯视图为等腰直角三角形，则三棱锥的表面积是_______.11、【题文】函数的单调减区间为____.12、cos0°os2°-sin4°in2°的值等于 ______ ．13、化简+--=______ ．评卷人得分三、计算题(共5题，共10分)14、已知x=，y=，则x6+y6=____．15、若f（x）=，则方程f（4x）=x的根是____．16、Rt△ABC中，若∠C=90°，a=15，b=8，则 sinA+sinB=____．17、方程组的解为____．18、计算：① ﹣（）﹣（π+e）0+（）②2lg5+lg4+ln ．评卷人得分四、作图题(共3题，共30分)19、作出函数y=的图象．20、画出计算1+++ +的程序框图．21、已知简单组合体如图；试画出它的三视图（尺寸不做严格要求）评卷人得分五、解答题(共2题，共16分)22、【题文】某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)=x2+10x(万元).当年产量不小于80千件时,C(x)=51x+-1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式.(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?23、【题文】如果两个相交平面都垂直于第三个平面；那么它们的交线也垂直于这个平面。

高中数学必修第一册《一元二次函数、方程和不等式》期末复习专项训练(学生版+解析版)

高中数学必修第一册《一元二次函数、方程和不等式》期末复习专项训练一、单选题l. (2022·四川绵阳·高一期末〉下列结论正确的是（〉A.若的b，则。

c>bc c.若。

＞b，则。

＋c>b+cl I B.若α＞b，则－〉－a D D.着。

＞b，则。

2> b22.(2022·辽宁·新民市第一高级中学高一期末〉已知α＜b<O，则（〉A.a2 <abB.ab<b2C.a1 <b1D.a2 >b i3.(2022·陕西汉中·高一期末〉若关于工的不等式，咐2+2x+m>O的解集是R，则m的取值范围是（〉A.(I, +oo)B.(0, I〕C.( -J, I)D.(J, +oo)4.(2022·广东珠海高一期末〉不等式。

＋l)(x+3)<0的解集是（〉A.RB.②c.｛对－3<x<-I} D.{xi x<-3，或x>-l}5. (2022·四川甘孜·高一期末〉若不等式似2+bx-2<0的解集为｛xl-2<x<I｝，则。

÷b=( )A.-2B.OC.ID.26. (2022·湖北黄石·商一期末〉若关于X的不等式x2-ax’＋7＞。

在（2,7）上有实数解，则α的取值范围是（〉A.（唱，8)B.（叫8] c.（叫2./7) D.（斗）7.(2022·新疆乌市一中高一期末〉已知y=(x-m)(x-n)+2022(n> m），且α，β（α〈别是方程y=O的两实数根，则α，β，111,n的大小关系是（〉A.α＜m<n＜βC.m＜α〈β＜nB.m＜α＜n＜βD.α＜m＜β＜n8.(2022·浙江·杭州四中高一期末〉已失11函数y＝κ－4+...2....(x>-1），当x=a时，y取得最小值b，则。

温度传感器产品说明书

iiE -5: GYJ17.1060X(±t!!i.Jt: Obere Wank 1, 87484 Nesse Iwang, Germany)� -5 � � TMT142 *�UroJ ��;r-� ExdIICT4-T6GbIII�.$ UU -5 14 25 00 000GB 3836.1-2010, GB 3836.2-2010�� Wi � llt iiE 0* iiE � � � Wh 2017 � 2 � 22 B 3§: 2022 fF 2 � 21 B-fk 51 1. ��ffm)!�;rtnjlim*iiE�f!11i'f o2.iiE��%€*uxn.�F�A*��m ••• �. �.m*iiE�M�o3. �%��iJtajjm*iiE�f!11�o4. ��m*iiE�f!11�o5. *iiE�rii]ll1mmT!�.l�WT�wri.ffil.JJt f)(. (�#l) *��0'ii.l(±t!!t.il:: �#l.I�JJ!lm[R�!l!IIflIm465%) �Fßf,J��%F�ottf!:I:.It: »t3i: 1m 1 03-i5-JilB�: 200233 1XX.J:I:.It: Email:****************It!.ii!i: +8621 64368180fifa: +8621 64844580EXPLOSION PROTECTIONCERTIFICATE o F CONFORMITYCert NO.GYJ17.1060XThis is to certify that the productTemperature field transmittermanufactured by Endress + Hauser Wetzer GmbH + Co. KG(Address:Obere Wank 1,87484 Nesselwang, GerIllany)which model is TMT142 SedesEx marking Ex dUC T4�T6 Gbproduct standard /drawing number 142500000has been inspected and certified by NEPSI, and that it conformsto GB 3836.1-2010,GB 3836.2-2010This Approval shall remain in force until 2022.02.21Remarks l.Conditions for safe use are specified in the attachment(s) to this certificate.2.Symbol X placed after the certification lIumber denotes specific conditions of use,which are specified in the aHachment(s) to this certificate.3.Model designation is specified in the attachment(s) to this ccrtificate.4.lntrinsic safety parameters specified in the attachment(s) to this cert.ificate.5.Thi s certificate i also applicable for the product with the same type manufactured byEndress+Hauser Wetze I'(Suzhou) Co., Ltd. (address: Su Hong Zhong Lu No.465,S u z hou-S IP, China)DirectorIsslJed DateThis Certificate is valid for products compatible with the documents and sam p ies approved by NEPSI.103 C ao Bao Road Shanghai200233,China Email: **************.cnTel: +862164368180Fax: +8621 64844580Edition 05�*ätt�tt��.*��M National Supervision and Inspection Centre forExplosion Protection and Safety of Instrumentation(GYJ17.1060X) (Attachment I )EI3 }ß(1i&, JtIT + � ftJT -0 i§j 1:F (:11 T MT 142� �� 11fi'tJ1t 11!:�.f.�, � � % � 15( .f.HX. $: r�:lI:tc � 1lil �fft�ftft�(NEPSI);j§:�, r1:il-r ��fff-{jt:G83836.1-2010 mHfl l 7}: 15i:� jjfiffl�* G83836.2-201 0 :lItftl::E1�Jfi m2tfß7t: EI3 ��:J:I5'�)t "d" 1!-iHf' 811& �F J'b IlJJ :J:I fff-;=.t;Ex d II e T 4� T 6 Gb, �}j:ll il-*friiE -'%GY J 17.1 060Xo;2js:iiE �I� iA pJ 81 F Jf� lli -'% �.m*fr :im r :iTEMP HART TMT 142-30;!tr:I': 0$::1J\5'�%, �EJ.�.!F) I A�E\ m;:6:i!}:t:w., ii(; �FJjH.l\l�;fri�HJ.J 450-, F � ��-ß!!ffl *f 7'l�ftj:F�'bllh13il-*itiiE-'% )§� "X" 1J..1*�J?g:�llr:�R�.mil-®��.��F��%o=,F��fflY3:�.J.]lt1, Fn�:7�:Jti&�m!tJ1.ftIlij-=f, JtJ?tJ-=.��{fJi�Ui·m.PJ$m±-tl!.o2, FrI'b]*************:1v40Vdc o3, FR,d!tJfJ 31�J5i�\frßt�D11fi't }JUJHJ � 81*�:11ü\.]}t�JHJIjT 6 T 5 �1.t11ffi.J1t -40'C �+55'C -40'C�+70'C T4 -40'C �+85'C�ffffl��'i\1EUjti@J-=f 65'C, 4, F Jfb 81 Il!. �� 51 A D 5'Z �cffl � �}j:J:I;j§:� iA pT �, �{fil-G83836.1-201 O �II G83836.2-2010B1*J\!�, B.�}j:J:I��Ex d IIe Gba"J�>��JOJ\!*fr:1v1/2NPT (EI.x;M20X 1.5) B1tt!.��5I A'l& iI 0 7L� .EJ.�� 51 A D 5'Z*ffl �;§5'ZIlJJ :lI �� 05,FJfb��ffl.��m�"��§H�"��o6, ffl):Ct :f�� EI 1TI�!L��F Jfb 81 ftJ/=t-*t1'�1�:, m.� �1djj Uif�(rt1;t fPJfo zn';R:lE1T 9=t I±\��., ��.�IlJJ .tt��m��.��o(GY J17.1 060X) (Attachment I )7, F �,E11�9t, 1.l!!ffl*11�1Hf' e'Z1fD n,Jit'<i' FJjH�ffl �ryj �I];, G83836.13-2013 ";t�Hf.U:Jq� J5't m13tfß7t: if>(:�811Iir.lli,�11i, 11i�*I]�m" , G83836.15-2000 ":Ii�f.tl:4:1*:JqdJifflE@. l=t.&� m15$7t: mJfLthFf r4:!.4:�� CmWllil1l-) " , G83836.16-2006 ":Ii�tn4:1*�1:t ffl �4: -&�%16ttrl7t: C �Jffr�i�"') .&.G850257 -2014 "i4J.4:if;( ��9&I�.��*��4:9& ••1,F��r��mtt •• ��AF��ru��;2, tM Jilt r �, �1i1 JIli 1:ir tt: )10-N E P S l'lA 81 -x.1tJ: 'ti :t4 t" ;3, t" r.f b� il t! rp e'Z � Y � 3>-5 -F 31� i*J � :a)N EPS I-lAWJ:fj]\fit;b) F Jjt"ljj� :fj]\ fit;c) ll1J � ß-1:t'riiE -'%d ) 1!f: Ji=J � ±JUili't }j[ffil*�{)(�{)(��.1<�lI{t'l��M National Supervision and Inspection Centre forExplosion Proteetion and Safety of InstrumentationG YJ17.1060X) A ttachment I )Attachment I to GYJ17.1060X1. DescriptionTMT142 series Temperature field transmitter, manufactured by Endress+Hauser Wetzer GmbH + CO.I<G, has been certified by National Supervision and Inspection Center for Explosion Protection and Safety of Instrumentation (NEPSI). The product accords with following standards:G83836.1-2010 Explosive atmospheres-Part 1: Equipment-General requirementsG83836.2-2010 Explosive atmospheres-Part 2: Equipment protection by flameproof enclosure"d"The Ex marking is Ex d n C T 4-T6 Gb, its certificate number is GY J17.1 060X.Type approved in this certificate is shown as the following:iTEMP HART T M T142-3 0o indicates enclosure, cable entry, configuration connection and etc.Refer tü instruction manual for tl16 details.2. Special Conditions for Safe UseThe suffix "X" placed after the certificate number indicates that this product is subject to special conditions for safe use, that is:For information on the dimensions of the flameproof joints contact the manufacturer.3. Conditions for Safe Use3.1 The external earth connection facility of this product shall be connected reliably.3.2 Electrical data: 40 Vdc.3.3 The relationship between ambient temperature range and the temperature class is shown as foliows:Temperature class T6 T5 T4Ambient temperature range -40°C-+55°C -40°C-+ 70°C -40'C-+85°CUse the connection cable endurance to he a t at least 90°C when the ambient temperature is > 65°C.3.4 Suitable certified cable glands or blanking plugs for unused holes ('1/2 NPT or M20*1.5) approved by ExTL according to G83836.1-201 0 and G83836.2-2010 with Ex marking "Ex d II C Gb" shall be used and correctly installed. The cable glands and blanking plugs to be used shall suitable for the product working conditions.Page 1 of 2G Y J17.1 060X) A ttachment I )3.5 Any maintenance shall be performed only when the warning of "00 not open when energized" is obseNed.3.6 The user shall not change the configuration in order to maintain/ensure the explosion protection performance of the equipment. Any change may impair safety.3.7 For installation, use and maintenance of this product, the end user shall obseNe the instruction manual and the following standards:GB50257 -2014 "Code for construction and acceptance of electric device for explosion atmospheres and fire hazard electrical equipment installation engineering".GB3836.13-2013 "Explosive atmospheres-Part 13:Equipment repair, overhaul and reclamation".GB3836.15-2000 "Electrical apparatus for explosive gas atmospheres-Part 15:Electrical installations in hazardous area (other than mines)".GB3836.16-2006 "Electrical apparatus for explosive gas atmospheres-Part 16: I nspection and maintenance of electrical installation (other than mines)".4. Manufacturer's Responsibility4.1 Conditions for safe use, as specified above, should be included in the documentation the user is provided with ..4.2 Manufacturing shoulcl be done according to the documentation approved by NEPSI.4.3 Nameplate should include these contents listed below:1) NEPSl logo @2) Ex marking3) certificate number4) ambient temperature5) warning of "00 not open when energized"Page 2 of 2。

安徽省合肥市瑶海区2022-2023学年八年级下学期期末数学试卷(含解析)

安徽省合肥市瑶海区2022-2023学年八年级下学期期末数学试卷〈解析版〉一、选择题．〈本大题共10小题，每小题4分，满分40分〉每小题都给出A、B、C、D四个选项，其中只有一个是符合题目要求的．1.(4分〉下列式子中，是二次根式的是（A. '1/7 B飞/2 C.'\j-3 D. "Ix2.(4分〉若关于x的方程。

n+2):x2 -3x+ l =O是一元二次方程，则m的取值范剧是〈c.m丐丘·立 D.m>OA.m寻i:QB.111> -23.(4分）如图，在Rt6ABC中，L'.ACB=90。

，CD是AB J2l上的高，若AC=3,AB=5,则CD=(A. 2B.2.4 c.3 D.�4.(4分）如图，在口AMCN中，对角线AC、MN交子点。

，点B和点D分别在E OM、ON的延长线上．添加以下条件，不能说明四边形ABCD是平行四边形的是（�A.AB=ADB.ADI/BCC.BM=DND.LMAB=LNCD5.(4分）如图，为了了解某校学生的课外阅读情况，小明同学在全校随机抽取40名学生进行调查，并将统计数据汇总，整理绘制成学生每周课外阅读时间频数分布茧，方图，（每组含前一个边界倍，不含后一个边界值〉如图所示，若该校有学生2338入，估计阅读时民；不低于6小时的人数约有（）人．4事j数斗17105 。

A.351982 4 6 8 10时'f1可（小时）8.818 C.1052 D. 15206.(4分）如图，在0ABCD中，对角线AC、BD交子点o.若AB=2,AC=8, BD＝川，AD=n. 则化简：�＋占�的结果为（B DA.n+m -118.n-m-9 C.m-n+9 D.11-m-n7.(4分）菜商店对一利1商品进行库存消理，第一次降价30%，销量不佳；第二次又降价10%，销售大增，很快就清理了库存设两次降价的平均降价率为λ’，下面所列方程正确的是（A. 300+10% － -x28.(l -30%) (1 -10%) = (I -2x)C.(1-30%) (1-10%) =2 (1-x)D.(! -30%) (J -10%) = (! -x) 28.(4分）在矩形ABCD中，E是AD的中点，将l:::.ABE沿BE折叠后待J1JL:::.GB£，延长BG 交直线CD于点F，若CF=I,FD=2，则BC的长为〈〉A.纣飞8.3 c.'N6或纠言 D. '2:1/2成39.(4分〉如图，在l:::.ABC中，D是AC边上的中点，E在BC上，且£C=2町，y!I]且＝〈FEA.2B.3 c.4 D.5JO. (4分）若关于x的一元二次方程x2-2.x牛。

2019-2-20C#开发中常用加密解密方法解析

2019-2-20C#开发中常⽤加密解密⽅法解析C#开发中常⽤加密解密⽅法解析⼀、MD5加密算法我想这是⼤家都常听过的算法，可能也⽤的⽐较多。

MD5主要⽤途：1、对⼀段信息⽣成信息摘要，该摘要对该信息具有唯⼀性,可以作为数字签名。

2、⽤于验证⽂件的有效性(是否有丢失或损坏的数据),3、对⽤户密码的加密，4、在哈希函数中计算散列值从上边的主要⽤途中我们看到，由于算法的某些不可逆特征，在加密应⽤上有较好的安全性。

通过使⽤MD5加密算法，我们输⼊⼀个任意长度的字节串，都会⽣成⼀个128位的整数。

所以根据这⼀点MD5被⼴泛的⽤作密码加密。

下⾯我就像⼤家演⽰⼀下怎样进⾏密码加密。

先看下演⽰效果：具体代码如下：⾸先需要引⼊命名空间：using System.Security;using System.Security.Cryptography;private void btnmd5_Click(object sender, EventArgs e){MD5 md5 = new MD5CryptoServiceProvider();byte[] palindata = Encoding.Default.GetBytes(txtyuan.Text);//将要加密的字符串转换为字节数组byte[] encryptdata=puteHash(palindata);//将字符串加密后也转换为字符数组txtjiami.Text = Convert.ToBase64String(encryptdata);//将加密后的字节数组转换为加密字符串}这⾥我们需要注意的是，不论是在加密的过程中，加密前要将加密字符串转为字节数组，加密后也要⽣成密⽂的字节数据，然后再转化为密⽂。

王江《金融经济学》课后习题全部答案

U (c)
=
log
c0
+
1 2
(log
c1a
+
log
c1b)
�
�
U (c)
=
1 1−γ
c10−γ
+
1 2
1 1−γ
c11−a γ
+
1 1−γ
c11−b γ
U (c) = −e−ac0 − 1 �e−ac0 + e−ac0 �
2
证明它们满足�不满足性、连续性和凸性。
解. 在这里只证明第一个效用函数�可以类似地证明第二、第三个效用函数的性质。
+
(1
−
α)c1b)
≥
α(log(c0� )
+
1 2
log(c1� a)
+
1 2
log(c1� b))
+
(1
−
α)(log(c0)
+
1 2
log(c1a)
+
1 2
log(c1b))
= αU (C�) + (1 − α)U (C) > U (C�)
故凸性成立。
2.3
U
(c)
=
c
−
1 2
a
c2
是一可能的效用函数�其中
(b) 参与者的预算集是 {C ∈ R2+ : c0 = 100 − S, c1 = 1 + S(1 + rF ), S ∈ R}�如果
以当前消费为单位�他的总财富是
w
=
100
+
1 1+rF
。参与者的优化问题就是

第三篇数量关系与资料分析

推回库房。推车装满原材料和空车时，工人推车行走的速度分别为 72 米 / 分和 120
米 / 分，不计装卸材料的时间，累计 8 小时正好可以推车 30 个来回。问库房到厂房
的距离为多少米？（）
A� 480
B� 540
C� 720
D� 900
二、相对行程
【例 5】（2018 年天津）一小船顺流而下航行 36 公里到达目的地。已知小船
【例 3】（2018 年天津）A、B 两个盒子共有棋子 108 颗，先从 A 盒中取出 1 棋子 4
放入 B 盒，再从 B 盒中取出1棋子放入 A 盒，这时两盒的棋子数相等。问 A 盒中原 4
有棋子是多少？（）
A� 40 颗
B� 48 颗
C� 52 颗
D� 60 颗
【例 4】（2018 年联考）建筑公司租用吊车和叉车各若干辆，每日租金为 10 万元。已知
A� 64
B� 70
C� 72
D� 80
第五节行程问题
一、基础行程
【例 1】（2018 年马鞍山）飞行员前 4 分钟用半速飞行，后 4 分钟用全速飞行，在
8 分钟内一共飞行了 72 千米，则飞机全速飞行的时速是（）。
A� 360 千米
B� 540 千米
C� 720 千米
D� 840 千米
【例 2】（2019 年浙江）为响应绿色出行号召，小李决定步行上班。如果每分钟走
第四节工程问题
【例 1】（2019 年四川）录入员小张和小李需要合作完成一项录入任务，这项任务
小李一人需要 8 小时，小张一人需要 10 小时。两人在共同工作了 3 个小时后，小李
因故回了趟家，期间小张一直在工作，小李返回后，两个人又用了 1 个小时就完成了

STC15F2K60S2系列单片机总体介绍

STC15F2K60S2系列单片机总体介绍1.STC15F2K60S2系列单片机简介STC15F2K60S2系列单片机是STC 生产的单时钟/机器周期(1T)的单片机，是高速/高可靠/低功耗/超强抗干扰的新一代8051单片机，��代��技术，��，指�代��代��技术，��，指�代��指�代��容传统8051,但速度快8-12倍。

��高�度��高�度R/C 时钟(±0.3%)，±1%温飘(-40℃~+85℃)，常温下温飘±0.6%(-20℃~+65℃)，ISP 编程时5MHz~35MHz 宽范围可设置，可彻底省掉外�昂贵的晶振和外�复位电路(��已��高可靠复位电路，ISP 编程时8级复位门槛电压可选)。

3路CCP/PWM/PCA ，8路高速10位A/D 转换(30万次/秒)，�置2K 字节大容量SRAM ，2组超高速异步串行通信端口(UART1/UART2，可在5组管脚之间进行切换，分时复�可作5组串口使�)，1组高速同步串行通信端口SPI ，��串行口通信��串行口通信�串行口通信/电机控制/强干扰场合。

在 Ke�lC Ke�l C 开发环境中，选择 Intel 8052 编译，头文件包含<reg51.h>即可现STC15系列单片机��STC-Y5超高速CPU �核，在相同的时钟频率下，速度又比STC 早期的1T 系列单片机(如STC12系列/STC11系列/STC10系列)的速度快20%.1.增强型 8051 CPU ，1T ，单时钟/机器周期，速度比普通8051快8-12倍2.工作电压：STC15F2K60S2 系列工作电压：5.5V - 4.5V （5V 单片机）STC15L2K60S2 系列工作电压：3.6V - 2.4V （3V 单片机）3.8K/16K/24K/32K/40K/48K/56K/60K/61K/63.5K 字节片�Flash 程序存储器，可擦写次数10万次以上4.片�大容量�大容量2048字节的的SRAM ，包括常规的256字节RAM <�data> 和��扩展的1792字节XRAM <xdata>5.大容量片�EEPROM ，擦写次数10万次以上6.ISP/IAP ，在系统可编程/在应�可编程，�需编程器，�需仿真器7.共8通道10位高速ADC ，速度可达30万次/秒，3路PWM 还可当3路D/A 使�8.共3通道捕获/比较单元(CCP/PWM/PCA)----也可�来再实现3个定时器或3个外�中断(支持上升沿/下降沿中断)或3路D/A9.利�CCP/PCA高速脉冲输出功能可实现3路9 ~ 16位PWM (每通道占�系统时间小于0.6%)10.利�定时器T0、T1或T2的时钟输出功能可实现高�度的8 ~ 16位PWM (占�系统时间小于0.4%)11.��高可靠复位，ISP编程时8级复位门槛电压可选，可彻底省掉外�复位电路12.工作频率范围：0MHz ~ 28MHz，相当于普通8051的0MHz～336MHz13.��高�度R/C时钟(±0.3%)，±1%温飘(-40℃~+85℃)，常温下温飘±0.6%(-20℃~+65℃)，ISP编程时��时钟从5MHz~28MHz可设(5.5296MHz / 11.0592MHz / 22.1184MHz)14.不需外�晶振和外�复位，还可�外输出时钟和低电平复位信号15.两组超高速异步串行通信端口(可同时使�)，可在5组管脚之间进行切换，分时复�可当5组串口使�：串口1(RxD/P3.0, TxD/P3.1)可以切换到(RxD_2/P3.6, TxD_2/P3.7),还可以切换到(RxD_3/P1.6, TxD_3/P1.7)；串口2(RxD2/P1.0, TxD2/P1.1)可以切换到(RxD2_2/P4.6, TxD2_2/P4.7)注意：建议�户将串口1放在 P3.6/P3.7 或 P1.6/ P1.7 (P3.0/P3.1 作下载/仿真�)；若�户不想切换，坚持使� P3.0/P3.1 或作为串口1进行通信，则务必在下载程序时，在软件上勾选“下次冷启动时，P3.2/P3.3为0/0时才可以下载程序”。

对数函数试题及详细解答

4
C．[0，2) ）
3
D．（1，2）
10．（2011•宜阳县）设 a=log3π，b=log2√3，c=log3√2，则（ A．a＞b＞c B．a＞c＞b C．b＞a＞c
D．b＞c＞a ） D．c＞a＞b
11．（2011•天津）已知 a=log23.6，b=log43.2，c=log43.6 则（ A．a＞b＞c B．a＞c＞b 21 − x，x ≤ 1 1 −log2x , x＞1 ） C．b＞a＞c
2
15．（2011•番禺区）函数 y=loga（3x-2）（a＞0，a≠1）的图象过定点（ A．（0，3）
2
B．（1，0）
1 2 1 2
C．（0，1）） C．1＜x＜y
16．（2011•北京）如果 log x＜log y＜0 那么（ A．y＜x＜1 B．x＜y＜1
D．1＜y＜x ）
2
17．（2011•安徽）若点（a， b）在 y=lgx 图象上， a≠1，则下列点也在此图象上的是（ A．（�� ，b）
）
19．（2010•浙江）已知函数 f（x）=log2（x+1），若 f（α）=1，α=（ A．0 B．1 log2x，x＞0 log −x , x＜0
2 1
C．2
20．（2010•天津）若函数 f（x）=
若 f（a）＞f（-a），则实数 a 的取值范围是（
）
A．（-1，0）∪（0，1） B．（-∞，-1）∪（1，+∞）C．（-1，0）∪（1，+∞） D．（-∞，-1）∪（0，1）
1. 2. 3. 4. 5.
分析：利用 c=log25＞log24=2，2 ＞a=2 ＞2 =1，0＜b=0.3 ＜1 即可得到答案． D． -1 分析：由题意可知，y=f （x）必过点（0，1），从而可得答案．B 分析：先求出集合 M、N，再利用两个集合的交集的定义求出 M∩N．C 分析：分式的分母不为 0，对数的真数大于 0，被开方数非负，解出函数的定义域．B 分析：利用对数函数的图象和性质可判断 A 正确；利用幂函数的图象和性质可判断 B 错

AS3 正则表达式语句

正则表达式是一种通用的标准，大部分计算机语言都支持正则表达式，包括as3，这里转摘出了一些常用的正则表达式语句，大家用到的时候就不用自己写了。

^\d+$//匹配非负整数（正整数+ 0）^[0-9]*[1-9][0-9]*$//匹配正整数^((-\d+)|(0+))$//匹配非正整数（负整数+ 0）^-[0-9]*[1-9][0-9]*$//匹配负整数^-?\d+$//匹配整数^\d+(\.\d+)?$//匹配非负浮点数（正浮点数+ 0）^(([0-9]+\.[0-9]*[1-9][0-9]*)|([0-9]*[1-9][0-9]*\.[0-9]+)|([0-9]*[1-9][0-9]*))$//匹配正浮点数^((-\d+(\.\d+)?)|(0+(\.0+)?))$//匹配非正浮点数（负浮点数+ 0）^(-(([0-9]+\.[0-9]*[1-9][0-9]*)|([0-9]*[1-9][0-9]*\.[0-9]+)|([0-9]*[ 1-9][0-9]*)))$//匹配负浮点数^(-?\d+)(\.\d+)?$//匹配浮点数^[A-Za-z]+$//匹配由26个英文字母组成的字符串^[A-Z]+$//匹配由26个英文字母的大写组成的字符串^[a-z]+$//匹配由26个英文字母的小写组成的字符串^[A-Za-z0-9]+$//匹配由数字和26个英文字母组成的字符串^\w+$//匹配由数字、26个英文字母或者下划线组成的字符串^[\w-]+(\.[\w-]+)*@[\w-]+(\.[\w-]+)+$//匹配email地址^[a-zA-z]+://匹配(\w+(-\w+)*)(\.(\w+(-\w+)*))*(\?\S*)?$//匹配url匹配中文字符的正则表达式：[\一-\龥]匹配双字节字符(包括汉字在内)：[^\x00-\xff]匹配空行的正则表达式：\n[\s| ]*\r匹配HTML标记的正则表达式：/<(.*)>.*<\/>|<(.*) \/>/匹配首尾空格的正则表达式：(^\s*)|(\s*$)匹配Email地址的正则表达式：\w+([-+.]\w+)*@\w+([-.]\w+)*\.\w+([-.]\w+)*匹配网址URL的正则表达式：^[a-zA-z]+://(\w+(-\w+)*)(\.(\w+(-\w+)*))*(\?\S*)?$匹配帐号是否合法(字母开头，允许5-16字节，允许字母数字下划线)：^[a-zA-Z][a-zA-Z0-9_]{4,15}$匹配国内电话号码：(\d{3}-|\d{4}-)?(\d{8}|\d{7})?匹配腾讯QQ号：^[1-9]*[1-9][0-9]*$下表是元字符及其在正则表达式上下文中的行为的一个完整列表：\ 将下一个字符标记为一个特殊字符、或一个原义字符、或一个后向引用、或一个八进制转义符。

2023年福建省中考数学真题(学生版+解析版)

2023年福建省中考数学真题一、选择题z本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合要求的．l.下列实数中，最大的数是（〉A.-IB.0C. ID.22.下图是由一个长-;Jj＇体和一个圆柱组成的几何体，它的俯视图是（〉／主视方向c曰｜「0·10 I3.若某三角形的三边长分别为3,4, m，则m的值可以是（〉A.IB. 5C. 7D.94.党的二寸大报告指出，我国建成世界上规模最大的教育体系、社会保障体系、医疗卫生体系，教育普及水平实现历史性跨越，基本养老保险覆盖十亿四千万人，基本医疗保险参保旦在稳定在百分之九寸五、将数据1040000000用科学记数法表示为（〉A.104×107B.10.4xl085.下列计算正确的是（〉C.l.04xl09D.0.104×1010A (a2)3 ＝α。

B.a6÷a2 ＝α3 C.a3♂＝α12 D.a2 ＿α＝α6.根据福建省统计局数据，福建省2020年的地区生产总值为43903.89亿元，2022年的地区生产总值为53109.85亿元．设这两年福建省地区生产总值的年平均增长率为1，根据Jlfil意可列7日程（〉A.43佣3.89(1+x)= 53109.85C.43903.89x2 = 53109.857.阅读以下作图步骤：B.43903.89(1 + x)2 = 53109.85D.43佣3.89(l+x2）＝到09.85①在OA 和OB 上分别被取O C,OD ，佼OC=OD:②分别以C,D 为圆心，以大于.！＿CD 的长为半径作弧，两弧在：LAOB 内交于点M;2 ＠作射线OM ，连接C M,DM ，如图所示．根据以上作图，一定可以推得的结论是（A. LI＝ζ2且CM=DMC ζl＝ζ2且OD=DM B.L三1= L3llCM =DMD.L2=L3且OD=DM8.为贯彻落实教育部办公厅关于“保隙学生每夭校内、校夕｜、各l小时体育活动时间”的要求，：导：生每夫坚待体育锻炼．小亮记录了自己一周内每夭校外锻炼的时间〈单位：分钟〉，并制作了如1图所示的统计图．时间／分钟一二三四五六日星期根据统计图，下列关于小亮该周每天校外锻炼时间的描述，正确的是（）A.平均数为70分钟B众数为67分钟C中位数为67分钟D.方主主为。

编译原理及实现课后习题答案孙悦红 (1)

|xyz|=7 | (xy)3 |=12
2.3 设有文法 G[S]�S∷=SS*|SS+|a�写出符号串 aa+a*规范推导�并构造语法树。
S => SS* => Sa* => SS+a* => Sa+a* => aa+a*
S
S
S
*
SS+a
aa
2.4 已知文法 G[Z]�Z∷=U0∣V1 、 U∷=Z1∣1 、 V∷=Z0∣0 ,请写出全部由此文法描述的只含有四个符号的句子。
+i#
POP,NEXTSYM
18
#E’T
i#
POP,PUSH(T’F)
所用产生式 E→TE’ T→FT’ F→i
T’→ε E’→+TE’
T→FT’ F→i
T’→*FT’
F→i
T’→ε E’→+TE’
T→FT’
19 20 21 22 23 �2�i*(i+i+i) 步骤
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
N 错误
INPUTSYM=下一个符号
INPUTSYM=’b’ Y
N 出口
4.2 设有文法 G[Z]� Z∷=(A) , A∷=a|Bb , B∷=Aab 若采用递归下降分析方法�对此文法来说�在分析过程中�能否避免回溯�为什么�
解�若采用递归下降分析方法�对此文法来说�在分析过程中不能避免回朔。因为规则 A ∷=a|Bb 和规则 B∷=Aab 构成了间接左递归�不满足实现没有回溯的递归下降分析方法的条件�1��书 P67��且规则 A: := a|Bb�FIRST(a)={a}�FIRST(Bb)={a}�即此规则候选式的首符号集有相交�不满足实现没有回溯的递归下降分析方法的条件�2��书 P67��在分析过程中�将造成回溯。