四川省南充市白塔中学2019-2020学年度高二上期周考试题
四川省南充市白塔中学2019-2020学年度高二上学期第15周周考理科数学试题

在抽取的 2 份试卷中至少有1份优秀的概率为 P
9
3
.
15 5
18.(1)设 P x, y ,∵ x2 y2 4 ,∴ O 0, 0 , r 2 ,
∵ PA 2 3 ,∴ OP r2 PA 2 4 ,
∴
x2 x
2
y2 y
8
16, 0,
解得
x 0, y 4,
或
16.已知 F1 、 F2 分别为椭圆 C :
x2 a2
y2 b2
1(a
b
0) 的左、右焦点,点 F2 关于直线
y x 对称的点 Q 在椭圆上,则椭圆的离心率为______;若过 F1 且斜率为 k(k 0) 的
直线与椭圆相交于 AB 两点,且 AF1 3F1B ,则 k ______.
D. 以上三种情形都有可能
13.过点 M (1,1) 作斜率为
1 2
的直线与椭圆 C
:
x2 a2
y2 b2
1(a
b
0) 相交于
A, B ,
若 M 是线段 AB 的中点,则椭圆 C 的离心率为
2
14. 在平面直角坐标系 xOy 中,已知 ABC 顶点 A 1, 0 , B 1, 0 ,顶点 C 在椭圆
三、解答题 17. 2018 年,教育部发文确定新高考改革正式启动,湖南、广东、湖北等 8 省市开始实 行新高考制度,从 2018 年下学期的高一年级学生开始实行.为了适应新高考改革,某校 组织了一次新高考质量测评,在成绩统计分析中,高二某班的数学成绩的茎叶图和频率 分布直方图因故都受到不同程度的损坏,但可见部分如下,据此解答如下问题:
6
设 A x1, y1 , B x2, y2 , C x3, y3 , D x4, y4 ,
四川省南充市高坪区白塔中学2019_2020学年高二数学上学期期中试题文(含解析)

四川省南充市高坪区白塔中学2019-2020学年高二数学上学期期中试题 文(含解析)第Ⅰ卷(选择题共60分)一、选择题:(共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的一项).1.直线12,l l 方程分别为3420,220x y x y +-=++=,直线12,l l 倾斜角分别为12,αα,则( )A. 12αα>B. 12αα<C. 12αα=D. 不确定 【答案】A【解析】【分析】求出两条直线的斜率后可得它们的倾斜角的大小.【详解】直线1l 的斜率为134k =-,直线2l 的斜率为22k =-, 故13tan 4α=-,2tan 2α=-,因为21tan tan 0αα<<, 故212a παπ<<<,故选A.【点睛】对于直线方程()00Ax By C B ++=≠,其斜率为A k B =-,注意直线的倾斜角α与斜率的关系为:(1)当0,,22ππαπ⎡⎫⎛⎫∈⎪ ⎪⎢⎣⎭⎝⎭ 时,tan k α=;(2)当2πα=时,斜率不存在.2.我市修建经济适用房.已知我市顺庆、高坪、嘉陵三个区分别有低收入家庭360户、270户、180户,若首批经济适用房中有90套住房用于解决住房紧张问题,采用分层抽样的方法决定各区户数,则应从顺庆区中抽取低收入家庭的户数为( )A. 40B. 36C. 30D. 20 【答案】A【解析】【分析】先求出每个个体被抽到的概率,用顺庆区的低收入家庭数量乘以每个个体被抽到的概率,即得应从顺庆区中抽取低收入家庭的户数.【详解】顺庆、高坪、嘉陵三个区分别有低收入家庭360户、270户、180户,∴对应的户数比为:360:270:1804:3:2=,则应从顺庆区中抽取低收入家庭的户数为44909040 4329⨯=⨯=++.故选:A.【点睛】本题考查分层抽样的定义,属于基础题.3.执行所示程序后输出的结果是:A. -1B. 0C. 1D. 2 【答案】B【解析】当n=5,S=0时,满足进入循环的条件,执行完循环体后,S=5,n=4;当n=4,S=5时,满足进入循环的条件,执行完循环体后,S=9,n=3;当n=3,S=9时,满足进入循环的条件,执行完循环体后,S=12,n=2;当n=2,S=12时,满足进入循环条件,执行完循环体后,S=14,n=1;当n=1,S=14时,满足进入循环的条件,执行完循环体后,S=15,n=0;当n=0,S=15时,不满足进入循环的条件,退出循环体后,输出n=0故选B.4.阅读如图所示的程序框图,运行相应的程序,输出的i值等于A. 2B. 3C. 4D. 5【答案】C【解析】【详解】根据框图的循环结构依次可得:1=⨯===+=;a S i122,2,1122=⨯==+==+=;a S i228,2810,2133=⨯==+==+=,3224,102434,314a S ii=.故C正确.跳出循环,输出4【易错点晴】本题主要考查的是程序框图,属于容易题.解题时一定要抓住重要条件S>”,否则很容易出现错误.在给出程序框图求解输出结果的试题中只要按照程序“11框图规定的运算方法逐次计算,直到达到输出条件即可.5.某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如下图,则下面结论中错误..的一个是()A. 甲的极差是29B. 甲的中位数是24C. 甲罚球命中率比乙高D. 乙的众数是21【答案】B【解析】【分析】通过茎叶图找出甲的最大值及最小值求出极差判断出A 对;找出甲中间的两个数,求出这两个数的平均数即数据的中位数,判断出D 错;根据图的数据分布,判断出甲的平均值比乙的平均值大,判断出C 对.【详解】由茎叶图知甲的最大值为37,最小值为8,所以甲的极差为29,故A 对甲中间的两个数为22,24,所以甲的中位数为2224232+=故B 不对 甲的命中个数集中在20而乙的命中个数集中在10和20,所以甲的平均数大,故C 对 乙的数据中出现次数最多的是21,所以D 对故选:B .【点睛】茎叶图的优点是保留了原始数据,便于记录及表示,能反映数据在各段上的分布情况.茎叶图不能直接反映总体的分布情况,这就需要通过茎叶图给出的数据求出数据的数字特征,进一步估计总体情况.6.设点B 是点()2,3,5A -关于平面xOy 的对称点,则AB 等于( )B. 10 D. 38 【答案】B【解析】【分析】利用空间中的两个点关于xOy 平面对称时的坐标关系可求B 的坐标,再利用两点之间的距离公式可求AB .【详解】因为点B 是点()2,3,5A -关于平面xOy 的对称点,故()2,3,5B --,故10AB ==, 故选B.【点睛】本题考查空间中关于坐标平面对称的点的坐标关系,此类问题属于基础题.7.圆22(4)9x y -+=和圆22(3)4x y +-=的公切线有( )A. 1条B. 2条C. 3条D. 4条【答案】C【解析】【分析】 求出两圆的圆心和半径,根据两圆的圆心距小于半径之和,可得两圆相交,由此可得两圆的公切线的条数.【详解】解答:圆22(4)9x y -+=,表示以()4,0为圆心,半径等于3的圆。
四川省南充市白塔中学2019-2020学年度高二上学期第14周周考理科数学试题

13.已知椭圆的焦点在 x 轴上,焦距为 2,且经过点 (0, 2) ,则该椭圆的标准方程为
______.
14.设圆 (x 1)2 y2 36 的圆心为 C
是圆内一定点, Q 为圆周上任一点,线段
AQ 的垂直平分线与 CQ 的连线交于点 M ,则 M 的轨迹方程为________
15.若椭圆 C :
的 3 倍.
(1)求椭圆 C 的方程; (2)证明:直线 MN 恒过定点.
6
南充市白塔中学 2019-2020 学年度高二上期 14 周考
理科数学试题参考答案
1.A 2.A 3.D 4.B 5.A 6.B 7.D 8.C 9.B 10.B 11.B 12.C
13. x2 y2 1 54
14. x2 y2 1 98
∵ DO 平面 BCD ,平面 DBC 平面 ABC BC , 平面 BCD 平面 ABC , ∴ DO 平面 ABC , ∵ AE ⊥平面 ABC ,∴ AE ∕ ∕DO , 又 DO 2 AE , ∴四边形 AODE 是平行四边形,∴ ED ∕ ∕ AO , ∵ ABC 是等边三角形,∴ AO BC , ∵ AO 平面 ABC ,平面 BCD 平面 ABC BC ,平面 BCD 平面 ABC ,
2m
x2 2mx 2m 3 0 恒成立. (1)若“ q ”是真命题,求实数 m 的取值范围; (2)若“ p q ”为假命题,“ p q ”为真命题,求实数 m 的取值范围.
3
18.己知函数
f
(x)
2 cos
x
sin
x
3
.
(1)求函数
f
x
在区间
0,
4
上的取值范围;
(2)设 ABC 的三个内角 A , B , C 所对的边长分别为 a , b , c .若 A 为锐角,且
四川省南充市白塔中学2019 2020高二数学上学期期中试题理
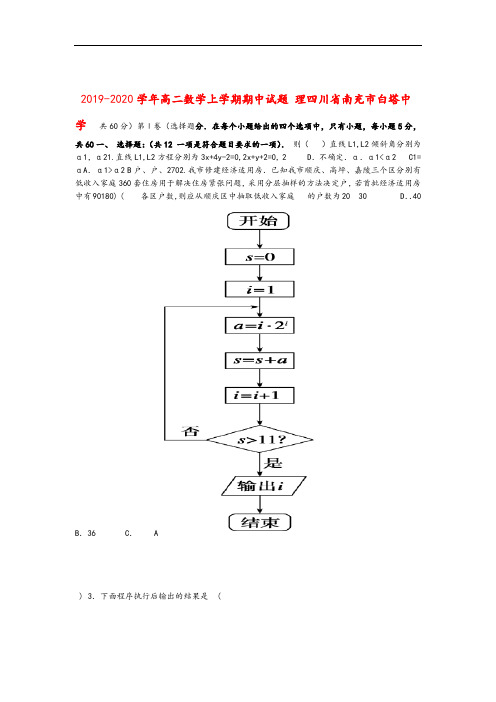
2019-2020学年高二数学上学期期中试题理四川省南充市白塔中学共60分)第Ⅰ卷(选择题分.在每个小题给出的四个选项中,只有小题,每小题5分,共60一、选择题:(共12 一项是符合题目要求的一项).则()直线L1,L2倾斜角分别为α1,α21.直线L1,L2方程分别为3x+4y-2=0,2x+y+2=0, 2 D.不确定.α.α1<α2 C1=αA.α1>α2 B户、户、2702.我市修建经济适用房.已知我市顺庆、高坪、嘉陵三个区分别有低收入家庭360套住房用于解决住房紧张问题,采用分层抽样的方法决定户,若首批经济适用房中有90180) ( 各区户数,则应从顺庆区中抽取低收入家庭的户数为20 30 D..40B.36 C. A) 3.下面程序执行后输出的结果是 (0 ..-1 B n=5 A 2.. S=01 D CWHILE S<15S=S+n n=n-1WEND PRINT nENDi) 值等于(4.阅读如右图所示的程序框图,运行相应的程序,则输出的54 D..3 C.A.2 B个.命中个数的茎叶40105.某篮球队甲、乙两名运动员练习罚球,每人练习组,每组罚球) 图如下图,则下面结论中错误的是(29 .甲的极差是A21 .乙的众数是B .甲罚球命中率比乙高C24.甲的中位数是D xOy( )等于的对称点,则B是点A(2,-3,5)关于平面|AB|6.设点381038 D. 10 C..A . B22)R?,(ab22OO1y???(xa1)(??2)?b4b?y?)ax(?()?,:.已知圆7,:21- 1 -那么两圆公切线的条数()A.0 B.1 C.2 D.38.从一批产品中取出三件产品,设A={三件产品全不是次品},B={三件产品全是次品},C= {三件产品至少有一件是次品},则下列结论正确的是()A.A与C互斥 B. A与B互为对立事件 C.B与C互斥 D.任何两个均互斥yx已知这组数据的平均,9.,105次上班途中所花的时间(单位:分钟)分别为,,119.某人yx) -的值为|数为10,方差为2,则|(4.2 C.3DA.1 B.10.已知过点A(-2,m)和B(m,4)的直线与直线2x+y-1=0平行,则m+6的值为()A.0 B.-8 C.-2 D.10?22,Mx?0?y???x?y??M,?所确定当约束条件M=311.时的平面区域内整点(横坐标纵坐标均为整?x?y?M.??数的点)的个数为(C )(A)9(B)13(C)16 (D)18l:x?4y?222C:x?y?1交于A、与圆B12..如图直线两点,O为坐标原点,若直线OA 、????cos?cos=( ) OB的倾斜角分别为,则、24D))17 ((B)13 ()(AC1717二、填空题:(共4小题,每小题5分,共20分).ABCDABCDAABD-则此动点在三棱锥中,13.在长方体-有一动点在此长方体内随机运动,11111内的概率为xy-2≤0-2??xy?+1≥0-zyxxy的最大值时最优解为.14.若=,满足约束条件3 +2,则??y≤022=4相切于A、B两点,则四边形xPBPA2x+y+10=015.P在直线上,、与圆+yPAOB面积的最小值为- 2 -????0B,?A10,1R?a0??:lax?y?1?0l:x?ay1,给出如已知直线,,,和两点,16.21下结论其中真命题的序号是all BA分别经过定点;①当和变化时, 与21all为何值时,都互相垂直;②不论与21MB?MA ll2M的最大值是交于点,则③如果;与21103PB?PA xy?2P为直线上的点,则④的最小值是.56小题,共70分。
四川省南充市白塔中学2019_2020学年高二物理上学期期中试题

四川省南充市白塔中学2019-2020学年高二物理上学期期中试题考试时间90分钟满分100分一、单选题(共8题,每题选对得3分,选错不得分,共计24分)1、关于电场强度与电势的关系,下面各种说法中正确的是( )A.电场强度大的地方,电势一定高 B.电场强度不变,电势也不变C.电场强度为零时,电势一定为零 D.电场强度的方向是电势降低最快的方向2、如图6所示的电路中,AB是两金属板构成的平行板电容器.先将电键K闭合,等电路稳定后再将K断开,然后将B板向下平移一小段距离,并且保持两板间的某点P与A板的距离不变.则下列说法错误的是( )A.电容器的电容变小B.电容器内部电场强度大小变大C.电容器内部电场强度大小不变D.P点电势升高图6 3、匀强电场的电场强度E随时间t变化的图像如图所示,在该匀强电场中,有一个带电粒子于t=0时刻由静止释放,若带电粒子只受电场力作用,则下列说法中正确的是()A.带电粒子只向一个方向运动;B. 0s~2s内,电场力的功等于0;C. 4s末带电粒子回到原出发点;D. 2.5s~4s内,电场力的冲量等于0。
4、如甲所示,x轴上固定两个点电荷Q1、Q2(Q2位于坐标原点O点),其上有M、N、P三点,间距MN=NP。
Q1、Q2在轴上产生的电势φ随x变化关系如图乙.则( )AB A.M点电场场强大小为零 B.N点电场场强大小为零C.M、N之间电场方向沿x轴负方向D.一正试探电荷从P移到M过程中,电场力做功|W PN|=|W NM|5、如图所示,质量为m,带电量为q的粒子,以初速度v0从A点竖直向上射入真空中的沿水平方向的匀强电场中,粒子通过电场中B点时,速率v B=2v0,方向与电场的方向一致,则A,B两点的电势差为( )6、如图所示,竖直平面内有一固定的光滑椭圆大环,其长轴长BD=4L、短轴长AC=2L.劲度系数为k的轻弹簧上端固定在大环的中心O,下端连接一个质量为m、电荷量为q、可视为质点的小环,小环刚好套在大环上且与大环及弹簧绝缘,整个装置处在水平向右的匀强电场中.将小环从A点由静止释放,小环运动到B点时速度恰好为0.已知小环在A,B两点时弹簧的形变量大小相等.则( )A.小环从A点运动到B点过程中,弹簧的弹性势能一直增大B.小环从A点运动到B点过程中,小环的电势能一直增大C.电场强度的大小E=mgqD .小环在A 点时受到大环对它的弹力大小F =mg +12kL 7、如图甲所示,一轻质弹簧的两端与质量分别为m1和m2的两物块A 、B 相连接,并静止在光滑的水平面上.现使A 瞬时获得水平向右的速度3m/s ,以此刻为计时起点,两物块的速度随时间变化的规律如图乙所示,从图象信息可得( )A .两物体的质量之比为m1:m2=2:1B .从t3到t4时刻弹簧由压缩状态恢复到原长C .在t1、t3时刻两物块达到共同速度1m/s ,弹簧分别处于压缩状态和拉伸状态D .在t2时刻A 和B 的动能之比为E K1: E K2=1:48、如图所示E 为电动势,r 为电源内阻,R1和R3均为定值电阻,R2为滑动变阻器.当R2的滑动触点在a 端时合上开关S ,此时三个电表A1、A2和V 的示数分别为I1、I2和U 。
四川省南充市2019-2020学年高二上学期期中数学试卷(理科)B卷

四川省南充市2019-2020学年高二上学期期中数学试卷(理科)B卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2016高二下·马山期末) 过点P(x,y)的直线分别与x轴和y轴的正半轴交于A,B两点,点Q与点P关于y轴对称,O为坐标原点,若且=1,则点P的轨迹方程是()A .B .C .D .2. (2分)下列命题中正确的个数是()①向量与是共线向量,则A、B、C、D必在同一直线上;②向量与向量平行,则方向相同或相反;③若下列向量、满足,且与同向,则;④若,则的长度相等且方向相同或相反;⑤由于零向量方向不确定,故不能与任何向量平行.A . 0B . 1C . 2D . 33. (2分)椭圆的焦点在y轴上,长轴长是短轴长的两倍,则m的值为()A .B .C . 2D . 44. (2分) (2015高二上·柳州期末) 如图,已知双曲线(a>0,b>0)的左、右焦点分别为F1、F2 , |F1F2|=8,P是双曲线右支上的一点,直线F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=2,则该双曲线的离心率为()A .B .C . 2D . 35. (2分) (2018高三上·静安期末) 已知椭圆抛物线焦点均在轴上,的中心和顶点均为原点,从每条曲线上各取两个点,将其坐标记录于表中,则的左焦点到的准线之间的距离为()A .B .C . 1D . 26. (2分) (2019高二上·德惠期中) 以为焦点的抛物线的准线与双曲线相交于两点,若为正三角形,则抛物线的标准方程为()A .B .C .D .7. (2分)已知F1 , F2是椭圆C1与双曲线C2的公共焦点,点P是C1与C2的公共点,若椭圆C1的离心率e1= ,∠F1PF2= ,则双曲线C2的离心率e2的值为()A .B .C .D .8. (2分)以原点为中心,焦点在y轴上的双曲线C的一个焦点为,一个顶点为,则双曲线C的方程为()A .B .C .9. (2分) (2018高二上·牡丹江期中) 已知椭圆,分别为其左、右焦点,椭圆上一点到的距离是2,是的中点,则的长为()A . 1B . 2C . 3D . 410. (2分)与椭圆共焦点且过点Q(2,1)的双曲线方程是()A .B .C .D .11. (2分) (2017高三上·甘肃开学考) 已知F1、F2分别是双曲线(a>0,b>0)的左、右焦点,P为双曲线上的一点,若∠F1PF2=90°,且△F1PF2的三边长成等差数列,则双曲线的离心率是()A . 2B . 3C . 4D . 512. (2分)中心在原点的双曲线,一个焦点为,一个焦点到最近顶点的距离是,则双曲线的方程是()B .C .D .二、填空题 (共4题;共4分)13. (1分) (2017高三上·南通期末) 已知点F是双曲线(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是________.14. (1分)(2017·淄博模拟) 设双曲线的右焦点是F,左、右顶点分别是A1 , A2 ,过F做x轴的垂线交双曲线于B,C两点,若A1B⊥A2C,则双曲线的离心率为________.15. (1分)已知三点,,,点Q在直线OP上运动,则当取得最小值时,Q点的坐标是________.16. (1分) (2017高二下·定州开学考) 已知双曲线 =1的准线经过椭圆(b>0)的焦点,则b=________.三、解答题 (共6题;共60分)17. (5分)平面内与两定点A1(﹣a,0),A2(a,0)(a>0)连线的斜率之积等于非零常数m的点的轨迹,加上A1、A2两点所在所面的曲线C可以是圆、椭圆或双曲线.求曲线C的方程,并讨论C的形状与m的位置关系.18. (15分) (2015高三上·天津期末) 已知四棱柱ABCD﹣A1B1C1D1的侧棱AA1⊥底面ABCD,ABCD是等腰梯形,AB∥DC,AB=2,AD=1,∠ABC=60°,E为A1C的中点(1)求证:D1E∥平面BB1C1C;(2)求证:BC⊥A1C;(3)若A1A=AB,求二面角A1﹣AC﹣B1的余弦值.19. (5分) (2017高二上·海淀期中) 如图所示,正方形与直角梯形所在平面互相垂直,,,.(I)求证:平面.(II)求证:平面.(III)求四面体的体积.20. (10分) (2015高二上·河北期末) 已知椭圆C:9x2+y2=m2(m>0),直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.(1)证明:直线OM的斜率与l的斜率的乘积为定值;(2)若l过点(,m),延长线段OM与C交于点P,四边形OAPB能否为平行四边形?若能,求此时l的斜率;若不能,说明理由.21. (15分)从椭圆E: + =1(a>b>0)上一点M向x轴作垂线,垂足恰为左焦点F1 ,点A、B 是椭圆与x轴正半轴、y轴正半轴的交点,且AB∥OM,|F1A|= .(1)求该椭圆的离心率;(2)若P是该椭圆上的动点,右焦点为F2,求• 的取值范围.(3)若直线y=kx+m与椭圆E有两个交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.22. (10分) (2015高一上·洛阳期末) 已知点A(6,2),B(3,2),动点M满足|MA|=2|MB|.(1)求点M的轨迹方程;(2)设M的轨迹与y轴的交点为P,过P作斜率为k的直线l与M的轨迹交于另一点Q,若C(1,2k+2),求△CPQ面积的最大值,并求出此时直线l的方程.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共60分) 17-1、18-1、18-2、18-3、19-1、20-1、20-2、21-1、21-2、21-3、22-1、22-2、。
2019~2020学年四川省南充市白塔中学高二上学期期中考试英语试卷及答案

绝密★启用前四川省南充市白塔中学2019~2020学年高二年级上学期期中考试英语试题(说明:考试时间120分钟,满分150分。
)卷Ⅰ(选择题共100分)第一部分听力理解(共两节,满分30分)第一节听下做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. When will the man pick up the woman?A. At 7:20.B. At 7:40.C. At 8:15.2. What does the man suggest doing?A. Taking the subway.B. Driving to the airport.C. Finding a cheap parking place.3. Where is Mimi probably?A. At home.B. At school.C. In a hospital.4. What is the conversation mainly about?A. The weather.B. A plan for tomorrow.C. The traffic.5. What will the woman probably do next?A. Help the old man.B. Ask the old man the time.C. Mend her watch.第二节听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
2019-2020学年四川省南充市白塔中学新校区高二数学文联考试题含解析

2019-2020学年四川省南充市白塔中学新校区高二数学文联考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. P: ,Q:,则“非P”是“非Q”的()A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分也不必要条件参考答案:B2. 江西省教育电视台做《一校一特色》访谈节目,分A,B,C三期播出,A期播出两所学校,B期,C期各播出1所学校,现从8所候选的重点中学中选出4所参与这三项任务,不同的安排方法共有()A. 140种B. 420种C. 840种D. 1680种参考答案:C【分析】将问题分两步解决,先计算从8所学校选择4所学校的选法;再计算将所选的4所学校安排到三期节目中的方法;根据分步乘法计数原理可求得结果.【详解】第一步:从8所学校选择4所学校参与任务,共有:种选法第二步:将所选的4所学校安排到三期节目中,共有:种方法由分步乘法计数原理可得,不同的安排方法共有:种本题正确选项:【点睛】本题考查分步乘法计数原理的应用,涉及到组合数的应用、分组分配问题的求解.3. 等差数列的前项和为,如果存在正整数和,使得,,则()A.的最小值为 B.的最大值为C.的最小值为 D.的最大值为参考答案:B4. 两条异面直线所成角为,则()A. B. C. D.参考答案:D略5. 在上定义运算:,若不等式对任意实数都成立,则的取值范围是____________。
参考答案:略6. 若圆(x-3)2+(y+5)2=r2上有且只有两个点到直线4x-3y-2=0距离等于1,则半径r 的取值范围是().A.(4,6) B.[4,6) C.(4,6] D.[4,6]参考答案:A7. 已知函数为R内的奇函数,且当时,,记,则a,b,c间的大小关系是()A. B.C. D.参考答案:D【分析】根据奇函数解得,设,求导计算单调性和奇偶性,根据性质判断大小得到答案.【详解】根据题意得,令.则为内的偶函数,当时,,所以在内单调递减又,故,选D. 【点睛】本题考查了函数的奇偶性单调性,比较大小,构造函数是解题的关键.8. 在平面直角坐标系中,若直线y=x与直线是参数,0≤θ<π)垂直,则θ=()A.B.C.D.参考答案:D【考点】参数方程化成普通方程.【分析】利用直线y=x与直线是参数,0≤θ<π)垂直,可得tanθ=﹣1,即可得出结论.【解答】解:∵直线y=x与直线是参数,0≤θ<π)垂直,∴tanθ=﹣1,∴θ=,故选D.9. 已知函数()在(0,1]上的最大值为3,则a=( )A. 2B. eC. 3D. e2参考答案:B【分析】对函数进行求导,得,,令,,对进行分类讨论,求出每种情况下的最大值,根据已知条件可以求出的值.【详解】解:,,令,,①当时,,,,在上单调递增,,即(舍去),②当时,,,;时,,,故在上单调递增,在上单调递减,,即,令(),,在上单调递减,且,,故选B.【点睛】本题考查了已知函数在区间上的最大值求参数问题,求导、进行分类讨论函数的单调性是解题的关键.10. ()参考答案:B二、填空题:本大题共7小题,每小题4分,共28分11. .参考答案:12. 设,则与的大小关系是_____________. 参考答案:A<1略13. 铁人中学欲将甲、乙、丙、丁四名大学毕业生安排到高一、高二、高三三个年级实习,每个年级至少一名毕业生,不同的分法有______种(结果用数字表示).参考答案:36【分析】由题得三个年级的分配人数为2、1、1,再利用排列组合列式求解.【详解】由题得三个年级的分配人数为2、1、1,所以不同的分法有.故答案为:36【点睛】本题主要考查排列组合的综合应用,意在考查学生对该知识的理解掌握水平和分析推理能力.14. 在如图所示的样本的频率分布直方图中,若样本容量为200,则数据落在[10,14]这组的频数为___ ▲ __.参考答案:7215. 已知函数,则=______________。
2019-2020学年四川省南充市白塔中学高二上学期期中考试数学(理)试卷

2019-2020学年四川省南充市白塔中学高二上学期期中考试数学(理)试卷★祝考试顺利★注意事项:1、答题前,请先将自己的姓名、准考证号用0.5毫米黑色签字笔填写在试题卷和答题卡上的相应位置,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B铅笔将答题卡上试卷类型A后的方框涂黑。
2、选择题的作答:每个小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非选择题答题区域的答案一律无效。
3、主观题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域的答案一律无效。
如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。
答案用0.5毫米黑色签字笔写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非选修题答题区域的答案一律无效。
5、保持卡面清洁,不折叠,不破损,不得使用涂改液、胶带纸、修正带等。
6、考试结束后,请将本试题卷、答题卡、草稿纸一并依序排列上交。
第Ⅰ卷(选择题共60分)一、选择题:(共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的一项).1.直线L1,L2方程分别为3x+4y-2=0,2x+y+2=0,直线L1,L2倾斜角分别为α1,α2则()A.α1>α2 B.错误!未找到引用源。
C.α1=α2错误!未找到引用源。
D.不确定错误!未找到引用源。
2.我市修建经济适用房.已知我市顺庆、高坪、嘉陵三个区分别有低收入家庭360户、270户、180户,若首批经济适用房中有90套住房用于解决住房紧张问题,采用分层抽样的方法决定各区户数,则应从顺庆区中抽取低收入家庭的户数为( )A.40 B.36 C. 30 D.203.下面程序执行后输出的结果是 ( )n=5 A.-1 B.0S=0 C.1 D.2WHILE S<15S=S+nn=n-1WENDPRINT nEND4.阅读如右图所示的程序框图,运行相应的程序,则输出的i值等于()A.2 B.3 C.4 D.55.某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如下图,则下面结论中错误的是( )A.甲的极差是29B.乙的众数是21C.甲罚球命中率比乙高D.甲的中位数是246.设点B是点A(2,-3,5)关于平面xOy的对称点,则|AB|等于( )A.10 B . 10 C.38 D.387.已知圆错误!未找到引用源。
四川省南充市白塔中学2019-2020高二物理上学期期中试题(含解析)

由牛顿第二定律可知,带电粒子在第1s内的加速度a1= ,为第2s内加速度a2= 的 ,因此先加速1s再减小0。5s速度为零,接下来的0.5s将反向加速,v——t图象如图所示,由对称关系可得,反向加速的距离使带电粒子刚回到减速开始的点,所以选项A错;0~2s内,带电粒子的初速度为零,但末速度不为零,由动能定理可知电场力所做的功不为零,选项B错误;由v——t图象中图线与坐标轴围成的图形的面积为物体的位移,由对称可以看出,前4s内的位移不为零,所以带电粒子不会回到原出发点,所以C错误;2。5s~4s内,电场力的冲量为 I=2qE0×0。5+(—qE0)×1=0,选项D正确.
Uq-mgh= —
解得,A、B两点电势差应为
故C正确,ABD错误。
6。如图所示,竖直平面内有一固定的光滑椭圆大环,其长轴长BD=4L、短轴长AC=2L。劲度系数为k的轻弹簧上端固定在大环的中心0,下端连接一个质量为m、电荷量为q、可视为质点的小环,小环刚好套在大环上且与大环及弹簧绝缘,整个装置处在水平向右的匀强电场中。将小环从A点由静止释放,小环运动到B点时速度恰好为O。已知小环在A、 B两点时弹簧的形变量大小相等。则( )
【详解】电场线密处,电场强度大,而电场线方向不确定,故无法判断电势高低,电势就不一定高,故A错误;在匀强电场中,电场强度不变,沿着电场线的方向,电势总是逐渐降低的,故B错误;电势为零,是人为选择的,电场强度为零的地方,电势不一定为零,故C错误;沿着电场方向电势降低最快,故D正确。
2。如图所示的电路中,AB是两金属板构成的平行板电容器.先将电键K闭合,等电路稳定后再将K断开,然后将B板向下平移一小段距离,并且保持两板间的某点P与A板的距离不变.则下列说法错误的是( )
A。 小环从A点运动到B点 过程中,弹簧的弹性势能一直增大
南充市高坪区白塔中学高二数学上学期期中试题文含解析

C。 甲罚球命中率比乙高D。 乙的众数是21
【答案】B
【解析】
【分析】
通过茎叶图找出甲的最大值及最小值求出极差判断出A对;找出甲中间的两个数,求出这两个数的平均数即数据的中位数,判断出D错;根据图的数据分布,判断出甲的平均值比乙的平均值大,判断出C对.
【详解】由茎叶图知
事件B与C能同时发生,故B与C不是互斥事件,故C错误;
由B与C不是互斥事件得D错误.
故选:A.
考点:互斥事件与对立事件.
9。 某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的平均数为10,方差为2,则|x﹣y|的值为( )
A。 1B. 2C. 3D。 4
【答案】D
故选:A。
【点睛】本题考查分层抽样的定义,属于基础题.
3.执行所示程序后输出的结果是:
A。 —1B. 0C。 1D。 2
【答案】B
【解析】
当n=5,S=0时,满足进入循环的条件,执行完循环体后,S=5,n=4;
当n=4,S=5时,满足进入循环的条件,执行完循环体后,S=9,n=3;
当n=3,S=9时,满足进入循环的条件,执行完循环体后,S=12,n=2;
16。设有一组圆 : .下列四个命题其中真命题的序号是____
①存在一条定直线与所有的圆均相切;
②存在一条定直线与所有的圆均相交;
③存在一条定直线与所有的圆均不相交;
④所有的圆均不经过原点.
【答案】②④
【解析】
分析】
由已知得圆心 ,由两圆的位置关系、圆心距、两圆的半径之差,即可判断出真命题个数.
【详解】根据题意得:圆心坐标为 ,
A。 B。 C. D.
四川省南充市白塔中学2019-2020学年高二12月月考数学(理)试题

白塔中学高二(上)期第四次考试 数学试题(理科)第Ⅰ卷(选择题 共60分)一.选择题:(共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的一项).1.在空间直角坐标系Oxyz 中,已知点A (2,1,﹣1),则与点A 关于原点对称的点A 1的坐标为( ) A . (﹣2,﹣1,1) B . (﹣2,1,﹣1) C . (2,﹣1,1) D . (﹣2,﹣1,﹣1)2.用系统抽样法从160名学生中抽取容量为20的样本,将160名学生从1~160编号.按编号顺序平均分成20组(1~8号,9~16号,…,153~160号),若第16组抽出的号码为125,则第2组中按此抽签方法确定的号码是 ( )A .15B .13C .12D .113.椭圆=1的焦距为2,则m 的值是( )A .6或2B .5C .1或9D .3或54.若某中学高二年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数是( )A .91.5B .92.5C .91D .925.若直线y =kx +1与椭圆x 25+y 2m =1总有公共点,则m 的取值范围是( )A .m>1B .m>0C .0<m<5且m≠1D .m ≥1且m≠56.已知,求z=的范围( )A .[,]B .[,]C .[,]D .[,]7.若直线l 1:x +ay +6=0与l 2:(a -2)x +3y +2a =0平行,则l 1与l 2之间的距离为( )A.423 B .4 2 C.823 D .2 28.椭圆C :x 225+y 216=1的左,右焦点分别为F 1,F 2,过F 2的直线交椭圆C 于A ,B 两点,则△F 1AB 的周长为( )A .12B .16C .20D .249.已知F 1,F 2是椭圆C 的两个焦点,P 是C 上的一点,若PF 1⊥PF 2,且∠PF 2F 1=60°,则C 的离心率为( )A .1-32B .2- 3 C.3-12 D.3-110.运行如图的程序框图,设输出数据构成的集合为A ,从集合A 中任取一个元素a ,,则取到的a 为非负数的概率为( )A .B .C .D .11.样本数据:﹣2,﹣1,0,1,2的标准差为( )A .B .2C .1D .2.512.在平面直角坐标系xOy 中,点A(0,3),直线l :y =2x -4,设圆C 的半径为1,圆心在l 上.若圆C 上存在点M ,使MA =2MO ,则圆心C 的横坐标a 的取值范围是( )A. [0,1] B .⎣⎢⎡⎦⎥⎤0,125 C.⎣⎢⎡⎦⎥⎤1,125 D.⎝ ⎛⎭⎪⎫0,125 二.填空题:(共4小题,每小题5分,共20分). 13. 直线3x+y +a =0的倾斜角为_______.14.用“除k 取余法”将十进制数2019转化为二进制数为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5
参考公式:回归直线 y bx a 中斜率和截距的最小二乘估计分别为
n
b
xi
i 1 n
x yi y
,
a
y bx
,相关系数 r
xi x 2
i 1
n
xi x yi y
i 1
n
n
④若 x x0 为函数 f x x2 x 2ln x ex 的零点,则 x0 2ln x0 0 .
其中正确的个数为( )
A. 0
B.1
C. 2
D. 3
9.已知函数 f x Asin x A 0, 0 的部分图象如图所示,则
f 1 f 2 f 3 f 105 的值等于( )
(2)分别从集合 P 和 Q 中随机取一个数 a 和 b 得到数对 a,b ,若 P x 1 x 3 , Q x 0 x 4,求函数 y f x 在区间1, 上是增函数的概率.
21.由于往届高三年级数学学科的学习方式大都是“刷题一讲题一再刷题”的模式,效果不理 想,某市一中的数学课堂教改采用了“记题型一刷题一检测效果”的模式,并记录了某学生的
③到 M 1, 0 , N 1, 0 两点的“折线距离”差的绝对值为 1 的点的集合是两条平行线;
④到 M 1, 0 , N 1, 0 两点的“折线距离”之和为 4 的点的集合是一个六边形.
3
其中正确的命题是______(写出所有正确的序号). 三、解答题
17.已知函数 f x x 3 2 的定义域是 A ,关于 x 的不等式 x2 a 3 x 3a 0 的
所以 P B
SA
24
1 21
2
7
.
S
24
8
21. (1)由题得 t 1 2 3 4 5 6 7 4 , 7
16 8 则没有零点的事件为 A ,
则 P A 1 P A 1 3 5 . 88
(2)要使 y f x 单调递增,所以 b 1即
2a
2a b , a,b 可看成是平面区域 a,b 1 a 3,0 b 4 中的所有点, 而满足条件是在平面区域 a,b 2a b,1 a 3, 0 b 4中的所有点,
2)
0
,解得
2
x
7
,
即 A 2,7,
由 : x A, : x B ,若 是 的必要不充分条件,
可得 B 是 A 的真子集, 则当 a 3时,则 a 2 ,即 2 a 3 ; 当 a 3时,显然满足题意; 当 a 3时,则 a 7 ,即 3 a 7 , 综上可知: 2 a 7 ,
这四个命题中,所有真命题的编号是( )
A.①③
B.①②
C.②③
D.③④
4.下列 4 个命题中,真命题是( )
A.如果 a 0 且 a 1,那么 loga f x loga g x 的充要条件是 a f x agx
B.如果 A 、 B 为 ABC 的两个内角,那么 A B 的充要条件是 sin A sin B
一、选择题
理科数学参考答案
1.B 2.A 3.A 4.B 5.B 6.B 7.A 8.C 9.A 10. D 11.B 12.D 二、填空题
13. 2047 14. [0, 3 ] 15. 3, 3 2
3
16.①②③④
3
三、解答题
17.解:(1)因为 x2 a 3 x 3a 0 ,所以 (x a)(x 3) 0 ,
14.已知实数 x、y 满足 x2 y 22 1,则
3 2
x
1 2
y
的取值范围
x2 y2
是_________.
15.已知直线 l : y k x 1 ,l 与圆 C : x 12 y2 3 相交于 A 、B 两
点, k 的取值范围为_____,弦长 AB 2 的概率为______.
故实数 a 的取值范围为2, 7 .
18.
(1)∵ sin( A B)
3 , sin( A B)
1
,
5
5
7
∴
sin sin
A A
cos cos
B B
cos cos
A A
sin sin
B B
3 5 1 5
,
解得
sin cos
A cos A sin
B B
2 5 1 5
.
则 sin Acos B 2cos Asin B ,故 tan A 2 tan B . (2)设 AB 边上的高为 CD ,则
11.素数指整数在一个大于 1 的自然数中,除了 1 和此整数自身外,不能被其他自然数整除
的数。我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果。哥德巴赫猜想是
“每个大于 2 的偶数可以表示为两个素数的和”,如10 3 7 。在不超过 15 的素数中,随机
选取两个不同的数,其和小于 18 的概率是( )
4
19.数列{an}中,a1=1,n≥2
时,其前
n
项的和
Sn
满足
Sn2=an(Sn﹣
1 2
)
(1)求 Sn 的表达式;
(2)设
bn=
Sn 2n
1
,数列{bn}的前
n
项和为
Tn,求
lim
n
Tn
.
20.已知函数 f x ax2 bx 1. (1)若 a , b 都是从集合0,1, 2,3 中任取的一个数,求函数 f x 没有零点的概率;
B
,整理得
2
tan2
B
4
tan
B
1
0
,解得
1 tan A tan B 4
tan B 0
tan B 2 6 . 2
则
3CD 2 6
3 ,解得 CD
2
6.
故 AB 边上的高为 2 6 .
19.
(1)n≥2,sn2=(sn﹣sn﹣1)(sn﹣
1 2
),∴sn=
Sn1 2Sn1 1
11
1
即 ﹣ =2(n≥2),所以数列{ } 是一个等差数列,
xi x 2 yi y 2
i 1
i 1
7
7
参考数据: y 4.3 , yi y 2 7.08 , ti t yi y 14 , 198.24 14.08
i 1
i 1
22.已知 M 为圆 O : x2 y2 1 上的动点,过点 M 作 x 轴、 y 轴的垂线,垂足分别为 A 、
当 a 3时, a x 3 ;当 a 3时,方程无解;当 a 3时, 3 x a ,
故当 a 3时,不等式的解集为 B a,3 ;
当 a 3时,不等式的解集为 B ;
当 a 3时,不等式的解集为 B 3, a .
(2)解不等式
x x
3 2
2
0
,即
x x
7 2
0 ,即
(x 7)(x x 2 0
A. 2
B. 2 2 2
C. 2 2
D. 2 2
10.根据如下样本数据得到的回归直线方程为 y bx a ,则()
x
2
3
4
5
6
y
4.0
2.5
-0.5
0.5
-2
2
A. b 0 , 0.9b a 4
B. b 0 , 4b a 0.9
C. a 0 , 0.9b a 4
D. a 0 , 4b a 0.9
2.若命题“ x R, ax2 4x a 2x2 1”是假命题,则实数 a 的取值范围是( )
A. , 2
B. , 2
C.2, 2
D. , 2
3.记不等式组
x 2
y x y
6
0
表示的平面区域为
D
,命题
p
:
(x,
y)
D,
2x
y
9 ;命题
q : (x, y) D, 2x y 12 .给出了四个命题:① p q ;② p q ;③ p q ;④ p q ,
南充市白塔中学 2019-2020 学年度第 12 周考试题
理科数学
一、选择题
1.下列关于命题的说法正确的是( )
A.命题“若 xy 0 ,则 x 0 ”的否命题是“若 xy 0 ,则 x 0 ”
B.命题“若 x y 0 ,则 x, y 互为相反数”的逆命题是真命题
C.命题“ x R, x2 2x 2 0 ”的否定是“ x R, x2 2x 2 0 ” D.命题“若 cos x cos y ,则 x y ”的逆否命题是真命题
A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既非充分又非必要条件
8.给出下列四个说法:
①命题“ x
0 ,都有
x
1 x
2
”的否定是“
x0
0,使得x源自1 x2 ”;②已知 a 、 b 0 ,命题“若 a b ,则 a b ”的逆否命题是真命题;
③ x 1是 x2 1的必要不充分条件;
Sn Sn1
Sn
∴
1 Sn
=2n﹣1,故
Sn
1 2n 1
.
(2)bn=
Sn 2n 1
=
(2n
1 1)(2n
1)
=
1 2
(
1 2n 1
1 2n 1
)
Tn=
1 2
(1﹣
1 3
+
1 3
1 5
+
1 5
1 7
+…+
1 2n 1
1 2n 1
)=
1 2
