高中数学逻辑思维导图 (河北衡水重点中学)
高中数学知识点思维导图--21张图梳理高中数学知识结构

高中数学知识点思维导图
----21张图理清高中数学知识结构
目录
一、集合与简易逻辑 (1)
二、函数与基本初等函数 (2)
三、导数及其应用 (3)
四、三角函数 (4)
五、解三角形与平面向量 (5)
六、数列 (6)
七、不等式 (7)
八、三视图与空间位置关系 (8)
九、立体几何 (9)
十、空间向量与立体几何 (10)
十一、直线的方程 (11)
十二、圆的方程 (12)
十三、直线系、圆系、直线与圆锥曲线关系 (13)
十四、圆锥曲线 (14)
十五、椭圆的定义与几何性质 (15)
十六、双曲线的定义与几何性质 (16)
十七、抛物线的定义与几何性质 (17)
十八、计数原理、二项式定理、推理与证明 (18)
十九、概率与统计 (20)
二十、复数 (21)
二十一、算法 (22)
一、集合与简易逻辑
二、函数与基本初等函数
三、导数及其应用
四、三角函数
五、解三角形与平面向量
六、数列
七、不等式
八、三视图与空间位置关系
九、立体几何
十、空间向量与立体几何
十一、直线的方程
十二、圆的方程
十三、直线系、圆系、直线与圆锥曲线关系
十四、圆锥曲线
十五、椭圆的定义与几何性质
十八、计数原理、二项式定理、推理与证明
十九、概率与统计
二十、复数
二十一、算法。
高中数学知识点最全思维导图(K12教育文档)

高中数学知识点最全思维导图(word版可编辑修改)
编辑整理:
尊敬的读者朋友们:
这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学知识点最全思维导图(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学知识点最全思维导图(word版可编辑修改)的全部内容。
高中数学知识点最全思维导图思维导图又叫心智图,是表达发射性思维的有效的图形思维工具,它简单却又极其有效,是一种革命性的思维工具。
高中中数学知识点思维导图,可以帮助同学做总结梳理,事半功倍,值得反思借鉴.。
高中数学知识框架思维导图(2019.3.21整理,14页)

两个原理
分类加法计算原理和分步乘法计算原理 排列数:������������ ������ = ������(������ − 1) ⋯ (������ − ������ + 1) = (������−������)!
������!
计算原理
排列与组合
������! m 组合数:C n = ������!(������−������)!
高考数学知识框架思维导图(2019.3.21 整理,14 页)
陈永清
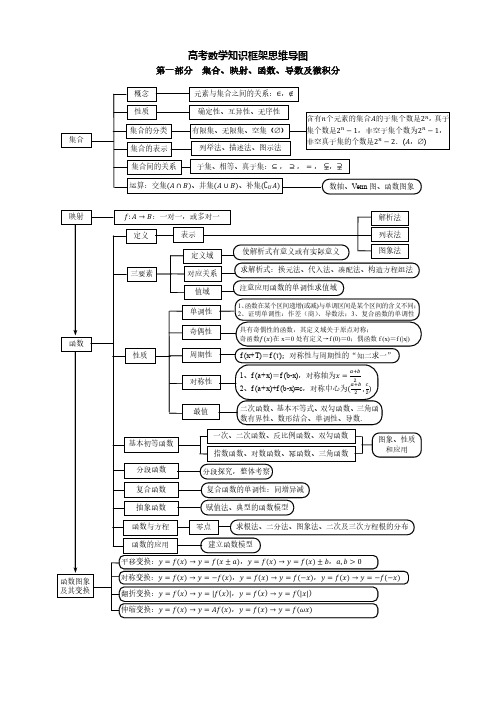
第一部分
集合、算法语言、简易逻辑、复数、推理与证明、排列组合
概念 性质 集合的分类 集合 集合的表示 集合间的关系
Hale Waihona Puke 元素与集合之间的关系:∈,∉ 确定性、互异性、无序性 有限集、无限集、空集() 列举法、描述法、图示法
求解(两个)集合中的参数值,注意检验: 1.是否违反互异性;2.是否违反其他条件 含有������个元素的集合������的子集个数是2������ , 真子 ������ ������ 集个数是2 − 1,非空子集个数为2 − 1, 非空真子集的个数是2������ − 2.(������,)
性质
C n =C n
m
m
n-m
Cn+1=C n +C
m
m-1 n
应用
捆绑法、插空法、优先法、隔板法、间接法、建模法、分类法、树状图
0 ������ ������ + ������ 1 ������ ������−1 ������ + ⋯ + ������ ������ ������ ������−������ ������ ������ + ⋯ + ������ ������−1 ������1 ������ ������−1 + ������ ������ ������ ������ (������∈N*). (������ + ������)������ = ������������ ������ ������ ������ ������
高中数学知识框架思维导图(整理版)
柯西不等式
第四部分
位置关系
截距
解析几何
斜率公式、倾斜角的变化与斜率的变化: = tan , =
倾斜角和斜率
重合
A1B2-A2B1=0,C1B2-C2B1=0
平行
A1B2-A2B1=0,C1B2-C2B1≠0
相交
A1B2-A2B1≠0
垂直
直线的方程
z 的几何意义:
过可行域内一点(, )
向直线 = , = 作
复合函数
函数与方程
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
基本初等函数
分段函数
, )
零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换: = () → = ( ± ), = () → = () ± ,, > 0
对称性
y=Asin(x+)+b
化简、求值、
证明(恒等变形)
)
值域
图象
对称轴(正切函数除外)经过函数图象
的最高(或低)点且垂直 x 轴的直线,
对称中心是正余弦函数图象的零点,正
切函数的对称中心为( ,0)(k∈Z).
最值
2
①图象可由正弦曲线经过平移、伸缩得到,但要注意先平移后伸缩与先伸缩后平移不同;
2.
3.
分组求和法
2
=
1
−
−1)(2+1 −1)
2 −1
+1
1 1
1
= (
2 (+2)2
(−1) ∙4
4 2
(2−1)(2+1)
1
2+1 −1
