高中数学思维导图全汇总
合集下载
高中数学知识框架思维导图(整理版)
基本初等函数 指数函数、对数函数、幂函数、三角函数 分段函数 复合函数 抽象函数 函数与方程 函数的应用 分段探究，整体考察 复合函数的单调性：同增异减 赋值法、典型的函数模型 零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换：������ = ������(������) → ������ = ������(������ ± ������)，������ = ������(������) → ������ = ������(������) ± ������，������, ������ > 0 函数图象 及其变换 对称变换：������ = ������(������) → ������ = −������(������)，������ = ������(������) → ������ = ������(−������)，������ = ������(������) → ������ = −������(−������) 翻折变换：������ = ������(������) → ������ = |������(������)|，������ = ������(������) → ������ = ������(|������|) 伸缩变换：������ = ������(������) → ������ = ������������(������)，������ = ������(������) → ������ = ������(������������)
������
第二部分
角的概念
三角函数与平面向量
弧长公式������ = ������������、扇形面积公式������ = ������������
2 1 π 2
高中数学知识框架思维导图
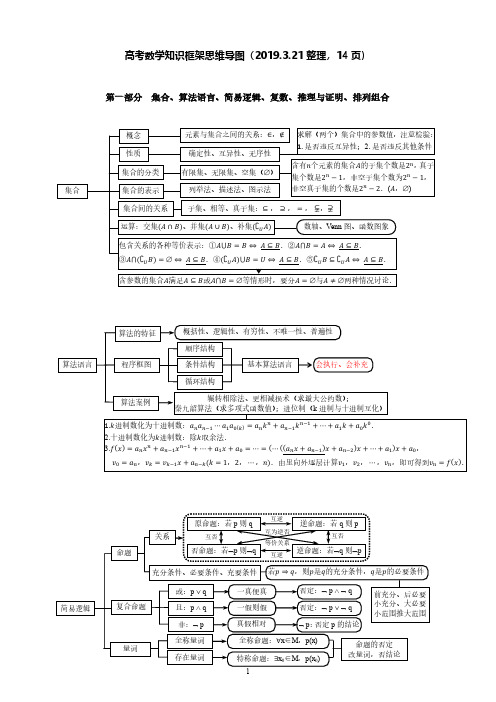
i．
①(1 ± i)2 = ±2i；
②1+i = i；1−i = −i；
1−i
1+i
③������ + ������i = i(������ − ������i)，
如3+4i = i(4−3i) = i；
4−3i 4−� = ������ + ������i、复平面内点 Z(������, ������)、向量���⃗⃗���⃗⃗���⃗��� = (������, ������)的一一对应关系； 复数模的几何意义：|������| = |������ + ������i| = √������2 + ������2 = |���⃗⃗���⃗⃗���⃗���|
2.对数的运算性质(������>0，且������ ≠1，������>0，������>0)：①log������(������ ∙ ������) = log������������ + log������������；
简易逻辑
命题
关系
原命题：若 p 则 q
互否
否命题：若p 则q
互逆
互为逆否 等价关系
互逆
逆命题：若 q 则 p
互否
逆命题：若q 则p
充分条件、必要条件、充要条件 若������ ⇒ ������，则������是������的充分条件，������是������的必要条件
复合命题 量词
或：p q 且：p q 非： p 全称量词 存在量词
2
映射
函数
函数图象 及其变换
第二部分 函数、导数及微积分
������: ������ → ������：一对一，或多对一
高中数学必修全思维导图
调性不同，则 y f [g(x)] 是减函数。
4、奇函数在对称区间上的单调性相同，偶函数在对称区间上的单调性相反。 5、常用函数的单调性解答：比较大小、求值域、求最值、解不等式、证不等式、作 函数图象。 六、函数奇偶性的常用结论：
1、如果一个奇函数在 x 0 处有定义，则 f (0) 0 ，如果一个函数 y f (x) 既是
高一数学必修 1 知识网络
集合
（ 1）元素与集合的关系：属于（）和不属于（）
集合与元素
（ 2）集合中元素的特性：确定性、互异性、无序性 （ 3）集合的分类：按集合中元素的个数多少分为：有限集、无限集、空集 （ 4）集合的表示方法：列举法、描述法（自然语言描述、特征性质描述）、图示法、区间法
C.
4、空集是任何集合的（真）子集。
集合
真子集：若A
B且A
B（即至少存在x0
B但x0
A），则A是B的真子集。
集合与集合
运算集并交合集集Ca相r定定性性d等(义义质质A：：：：：ABAAAA)BBBC且AAaArdAAxx，(，A//BxAxA) CAAa或且rAdxx(AB，B，)BB-AACarBdB(ABBBA)A，，AABBAA，, AABB
定义
按照某个对应关系f , y都有唯一确定的值和它对应。那么y就是x的函数。记作y f ( x ).
近代定义：函数是从一个数集到另一个数集的映射。
定义域 函数及其表示 函数的三要素 值域 对应法则
解析法
函数的表示方法 列表法
函数
几类不同的增长函数模型 函数模型及其应用 用已知函数模型解决问题 建立实际问题的函数模型
高中数学全套思维导图(高清版)
23／59
请关注微信公众号“名师伴你学”获取更多精品资源
24／59
请关注微信公众号“名师伴你学”获取更多精品资源
25／59
请关注微信公众号“名师伴你学”获取更多精品资源
26／59
请关注微信公众号“名师伴你学”获取更多精品资源
27／59
请关注微信公众号“名师伴你学”获取更多精品资源
28／59
56／59
请关注微信公众号“名师伴你学”获取更多精品资源
57／59
请关注微信公众号“名师伴你学”获取更多精品资源
58／59
请关注微信公众号“名师伴你学”获取更多精品资源
59／59
请关注微信公众号“名师伴你学”获取更多精品资源
29／59
请关注微信公众号“名师伴你学”获取更多精品资源
30／59
请关注微信公众号“名师伴你学”获取更多精品资源
31／59
请关注微信公众号“名师伴你学”获取更多精品资源
32／59
请关注微信公众号“名师伴你学”获取更多精品资源
33／59
请关注微信公众号“名师伴你学”获取更多精品资源
6／59
请关注微信公众号“名师伴你学”获取更多精品资源
7／59
请关注微信公众号“名师伴你学”获取更多精品资源
8／59
请关注微信公众号“名师伴你学”获取更多精品资源
9／59
请关注微信公众号“名师伴你学”获取更多精品资源
10／59
请关注微信公众号“名师伴你学”获取更多精品资源
11／59
请关注微信公众号“名师伴你学”获取更多精品资源
请关注微信公众号“名师伴你学”获取更多精品资源
18／59
请关注微信公众号“名师伴你学”获取更多精品资源
高中数学知识框架思维导图(整理版)
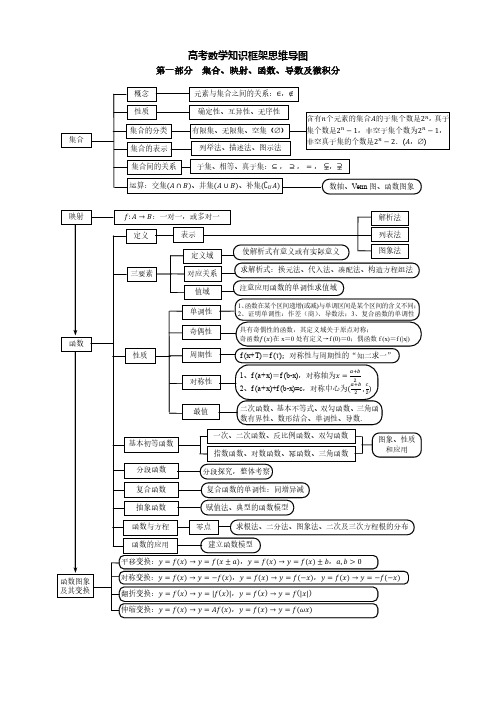
柯西不等式
第四部分
位置关系
截距
解析几何
斜率公式、倾斜角的变化与斜率的变化: = tan ， =
倾斜角和斜率
重合
A1B2－A2B1＝0，C1B2－C2B1＝0
平行
A1B2－A2B1＝0，C1B2－C2B1≠0
相交
A1B2－A2B1≠0
垂直
直线的方程
z 的几何意义：
过可行域内一点（, ）
向直线 = ， = 作
复合函数
函数与方程
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
基本初等函数
分段函数
, )
零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换： = () → = ( ± )， = () → = () ± ，, > 0
对称性
y＝Asin(x＋)＋b
化简、求值、
证明（恒等变形）
）
值域
图象
对称轴（正切函数除外）经过函数图象
的最高（或低）点且垂直 x 轴的直线，
对称中心是正余弦函数图象的零点，正
切函数的对称中心为( ，0)（k∈Z）.
最值
2
①图象可由正弦曲线经过平移、伸缩得到，但要注意先平移后伸缩与先伸缩后平移不同；
2.
3.
分组求和法
2
=
1
−
−1)(2+1 −1)
2 −1
+1
1 1
1
= (
2 (+2)2
(−1) ∙4
4 2
(2−1)(2+1)
1
2+1 −1
高中数学思维导图大全
国
｀截式： y ＝妇干 b
＇，两点式:� V-VI-＝－X-— X1 芍( :¢:X动 五） y?-P1 芬寸
！截距式: :＋责＝ l （吐 0,b#o)
注意（1)截距百 :，可负，也可
1彝为o. (2)方程
各种形式的变化 和适用范围
宜 线
一般式：Ax+By+ C = O(AB-:f:. o)
的
两直线 行
序性
组合的分类
＾集 卜巳渠合的表示一 口
列举法，特征性质描述法、Veen图法 性质
(2)A云小(3)则A�B则A.::B或4=， 凡 (4)若A�B, B竺C，则AGC; (5)含有11. '个元素的集合有2“ 个子无宇 有2片－i 个真丁采：
(6)E心；的区别�E表示元素与集合关系
已表示集合与集合关系； (7)屿｛叶区别· 一 般地，a表示元压 ｛叶表示只有 一 个元素tr的菜合：
咖
(
5 l， 万
L1 5 ｀ 为方向向泣｝
la•司 lal• 2直线与平面的夹角6cosO=
恒|
（a 为直线方向向址，行为平面法向盘｝
I· 杭I 面角0:cos_0·=� 匠．开介 1 枫
飞，h，．为两平面 向优）．
倾斜角与斜卒
倾斜伽「包18OO)和斜率K气na的变化
！点斜式：，V － y0 ＝沁－X。)
,p) +b
描点法（五点作阻法— ） I 斗几何作图法
对称轴．（正切函数 除外）经过函数图 象的蚊扁氓t低）
点且垂直x轴的直线
对称中心是正余弦函
＿佟］象的零点，正切 函数的对称中心为 （一 .k.2it ，．0) (kGZ)
碑象可由正千玄曲线经过平移、伸缩得到，但耍注意先平移后伸缩与先伸缩后平移不同：
高中数学思维导图(新课标)
c 0 c 为常数
'
f x 与 f x 0 的区别
vt S ， at vt
'
0 0
第 二 部 分 映 射 、 函 数 、 导 数 、 定 积 分 与 微 积 分
导 数
导数概念
运动的平均速度 曲线的割线的斜率
'
0
k f
'
'
x
0
' '
； x
n
nx 1 x
定
映
A中元素在B中都有唯一的象；可一对一 （一一映射），也可多对一，但不可一对多 定义 函数的概念 表示 定义域
列表法 解析法 图象法 使解析式有意义及实际意义
第 二 部 分 映 射 、 函 数 、 导 数 、 定 积 分 与 微 积 分
射
三要素
区间 单调性 奇偶性 周期性 对称性
对应关系 值域
常用换元法求解析式 观察法、判别式法、分离常数法、单调性法、最值法、 重要不等式、三角法、图象法、线性规划等
函数的 基本性质
函 数
函数常见的
最值
几种变换
基本初等函数 分段函数 复合函数 抽象函数 函数与方程 函数的应用
平移变换、对称变换 翻折变换、伸缩变换
三角函数 单调性：同增异减 赋值法，典型的函数 零点 建立函数模型 求根法、二分法、图象法；一元二次方程根的分布 退出 上一页
函数的平均变化率
函数的瞬时变化率 运动的瞬时速度 曲线的切线的斜率
第一部分 第二部分 第三部分 第四部分 第五部分 第六部分
集合与简易逻辑 映射、函数、导数、定积分与微积分 三角函数与平面向量 数列 不等式 立体几何与空间向量
'
f x 与 f x 0 的区别
vt S ， at vt
'
0 0
第 二 部 分 映 射 、 函 数 、 导 数 、 定 积 分 与 微 积 分
导 数
导数概念
运动的平均速度 曲线的割线的斜率
'
0
k f
'
'
x
0
' '
； x
n
nx 1 x
定
映
A中元素在B中都有唯一的象；可一对一 （一一映射），也可多对一，但不可一对多 定义 函数的概念 表示 定义域
列表法 解析法 图象法 使解析式有意义及实际意义
第 二 部 分 映 射 、 函 数 、 导 数 、 定 积 分 与 微 积 分
射
三要素
区间 单调性 奇偶性 周期性 对称性
对应关系 值域
常用换元法求解析式 观察法、判别式法、分离常数法、单调性法、最值法、 重要不等式、三角法、图象法、线性规划等
函数的 基本性质
函 数
函数常见的
最值
几种变换
基本初等函数 分段函数 复合函数 抽象函数 函数与方程 函数的应用
平移变换、对称变换 翻折变换、伸缩变换
三角函数 单调性：同增异减 赋值法，典型的函数 零点 建立函数模型 求根法、二分法、图象法；一元二次方程根的分布 退出 上一页
函数的平均变化率
函数的瞬时变化率 运动的瞬时速度 曲线的切线的斜率
第一部分 第二部分 第三部分 第四部分 第五部分 第六部分
集合与简易逻辑 映射、函数、导数、定积分与微积分 三角函数与平面向量 数列 不等式 立体几何与空间向量
人教版高中数学必修一章节思维导图全套
《3.1 函数的概念》思维导图
《3.2 函数的性质》思维导图
《3.3 幂函数》思维导图
《4.1 指数的运算》思维导图
《4.2指数函数》思维导图
《4.3 对数的运算》思维导图
《4.4 对数函数》思维导图
《4.5 函数的应用（二）》思维导图
《5.1 任意角和弧度制》思维导图
《5.2 三角函数的概念》思维导图
人教版高中数学必修一章节思维导图全套
《1.1集合的概念及特征》思维导图
《1.2 集合间的关系》思维导图
《1.3 集合的基本运算》思维导图
《1.4 充分、必要条件》思维导图
《1.5 全称量词与存在量词》思维导图
《2.1 等式与不等式的性质元二次方程、不等式》思维导图
《5.3 诱导公式》思维导图
《5.4 三角函数的图象与性质》思维导图
《5.5 三角恒等变换》思维导图
《5.6 函数 》思维导图
《5.7 三角函数的应用》思维导图
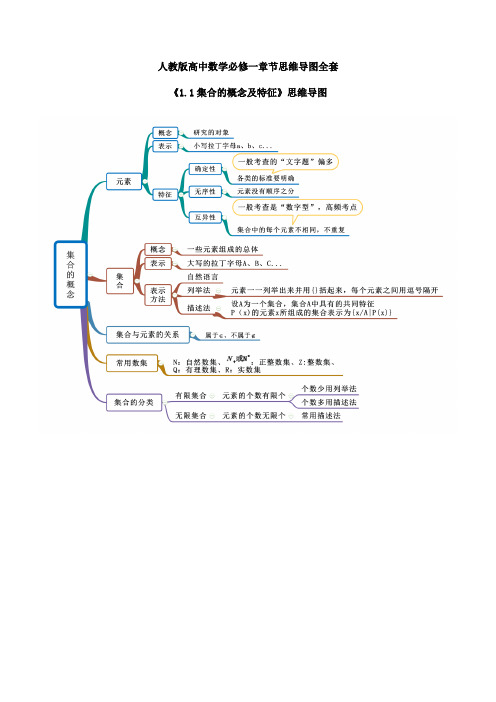
《3.2 函数的性质》思维导图
《3.3 幂函数》思维导图
《4.1 指数的运算》思维导图
《4.2指数函数》思维导图
《4.3 对数的运算》思维导图
《4.4 对数函数》思维导图
《4.5 函数的应用（二）》思维导图
《5.1 任意角和弧度制》思维导图
《5.2 三角函数的概念》思维导图
人教版高中数学必修一章节思维导图全套
《1.1集合的概念及特征》思维导图
《1.2 集合间的关系》思维导图
《1.3 集合的基本运算》思维导图
《1.4 充分、必要条件》思维导图
《1.5 全称量词与存在量词》思维导图
《2.1 等式与不等式的性质元二次方程、不等式》思维导图
《5.3 诱导公式》思维导图
《5.4 三角函数的图象与性质》思维导图
《5.5 三角恒等变换》思维导图
《5.6 函数 》思维导图
《5.7 三角函数的应用》思维导图
高中数学知识框架思维导图(整理版)
2 : 2 + 2 + 2 = 0.
点斜式：y－y0＝k(x－x0)
注意：截距可正、
可负，也可为 0.
2 −1
注意各种形式的转化和运用范围.
x y
截距式： ＋ ＝1
a b
两直线的交点
距离
一般式：Ax＋By＋C＝0
两点间的距离公式|1 2 | = √(1 − 2 )2 + (1 − 2 )2 ．
2.
3.
分组求和法
2
=
1
−
−1)(2+1 −1)
2 −1
+1
1 1
1
= (
2 (+2)2
(−1) ∙4
4 2
(2−1)(2+1)
1ቤተ መጻሕፍቲ ባይዱ
2+1 −1
− (+2)2 )
= (−1) (
1
2−1
+
错位相加法: = ( + )−1 → = ( + ) −
复合函数
函数与方程
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
基本初等函数
分段函数
, )
零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换： = () → = ( ± )， = () → = () ± ，, > 0
与 的关系
1 ，
= 1，
= {
− −1 ， ≥ 2．
构造等差数列
an＋1 p an
= · ＋1 转为③
qn q qn－1
⑤an + 1＝pan＋qn
点斜式：y－y0＝k(x－x0)
注意：截距可正、
可负，也可为 0.
2 −1
注意各种形式的转化和运用范围.
x y
截距式： ＋ ＝1
a b
两直线的交点
距离
一般式：Ax＋By＋C＝0
两点间的距离公式|1 2 | = √(1 − 2 )2 + (1 − 2 )2 ．
2.
3.
分组求和法
2
=
1
−
−1)(2+1 −1)
2 −1
+1
1 1
1
= (
2 (+2)2
(−1) ∙4
4 2
(2−1)(2+1)
1ቤተ መጻሕፍቲ ባይዱ
2+1 −1
− (+2)2 )
= (−1) (
1
2−1
+
错位相加法: = ( + )−1 → = ( + ) −
复合函数
函数与方程
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
基本初等函数
分段函数
, )
零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换： = () → = ( ± )， = () → = () ± ，, > 0
与 的关系
1 ，
= 1，
= {
− −1 ， ≥ 2．
构造等差数列
an＋1 p an
= · ＋1 转为③
qn q qn－1
⑤an + 1＝pan＋qn
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高中数学思维导图全汇总
确定性、互异性｀无序性(1)空集是任何非空集合的孔子果；
(2)A s;;; A:(3)贝归�B则A=B或cB:
(4)若A=B,B=C，则A.;;C,
(5)含有n个元素的集合有2“个子集，
有2忙1个兵子集；
(6)E．三的区别玉表示元术与菜合关系．三表示见合与集合关系，
(7)a与｛a区别一般地，a表示元素，｛a棒示只有一个元和的集合
(8){0办｝，心区别·{o}扒表示架合，
表示空集，小二{o}，小二｛rp}.
)A U A "'A, An A "'A,
AU心＝A,An少＝妒(2)A介B=A~ A乙B,
AUB""A�B�A
A n
B i;;;;A（如）已,1UB,
(3)AU(C己）＝u,An(c页）＝妒
C u(C u A)aa A:
(4)Cu(A匡）＝饥A)U忆B}
(5)分配伴：An(Buc),,,(A na)u (Anc}. Au (B nc)"'(A UB)n {A UC}
(6)结合律，加(Bnc)＝(AnB)nc:
U(BUC)"'(;l UB)UC:
若p.v.rE M, p（叶则-,p3x O EM, .... p伈）若p玉。
E M,p（一动；贝lJ.... p:沁xe M, -.p(x)
算法的概念算法的基本思想和程序框OO 符法特征：概括性、逻抗性、
有穷性、不唯一性、普迫性
一一一一一一一一一一一一一一、
, l l｀
I
I
I
'
I
I
算法的概念..... ｀ 飞直到型十
一一一一一一一一一一节i__ -✓
算法基本语旬
权伯语句
条件语句
循环语句
辗转相除法与
更相减损术
秦九韶钵法
示内容＇，：变
－内容”；表达式
I F条件T H E N
语句体
END IF
． ．
IF条件THEN
语句体1
ELSE
语句体2
END IF
循环体；循环体
LOOP U NTIL条件；WEN D
（直到型）i （当型）
1求最大公约数
f(x)＝，q,x" ＋ q,-I，产＋…＋矿＋a o
= （．．（亿x+a贮1)x+ a,,_2)x + · · · + a1)x + a0
求值时，从里到外计笲：v,=a,,x+a"一1.
V�=V1X+(1“2:v3 = v1x+ a，心…V n= V._,x+a。
戏制化十进制：气气，…a l a
o(k)＝ G“x k贮l+a同一1x /..，II-2 +…+a
1
x k + a。
.。