信息论中有关信源熵的不等式
信息论第二章(2)

若有两个消息xi,yj 同时出现,它们所带有的信息量, 称为联合自信息量
I ( xi y j ) log p( xi y j ) (bit)
6 条件自信息量:
事件xi在事件yj给定的条件下的自信息量,称为条件自 信息量
I ( xi y j ) log p( x|y j ) (bit) | i
i
j
1 H (( X ))=(p( xy) log p( xy) H XY H X | Y ) X ,Y
平均互信息与各类熵之间关系的集合图(维拉图)表示:
I(X;Y) = H(X) - H(X|Y) = H(Y) - H(Y|X) = H(X)+H(Y)-H(XY) 图中,左边的圆代表 H(XY)= H(X)+H(Y)- I(X;Y) 随机变量X的熵,右 边的圆代表随机变量 Y的熵,两个圆重叠 H(X|Y) 部分是平均互信息 H(Y|X) I(X;Y)。每个圆减去 =H(X)-I(X;Y) =H(Y)-I(X;Y) I(X;Y)后剩余的部分 代表两个条件熵。 I(X;Y)
i 1 i
n
★定义自信息的数学期望为平均自信息量H
n 1 H ( X ) E log p ( xi ) log p ( xi ) (bit/符号) p ( xi ) i 1
(X),称为信息熵:
★熵的含义:
① 熵是从整个集合的统计特性来考虑的,它从平均意义上来表征 信源的总体特征。 ② 在信源输出后,信息熵H(X)表示每个消息提供的平均信息量;
复习
3 离散信源的数学模型:
x2 x3 ... ... xn X x1 P ( x) P ( x ) P ( x ) P ( x ) ... ... P( x ) 1 2 3 n 要满足的条件: P ( xi ) 0,
信息理论与编码-期末试卷A及答案

信息理论与编码-期末试卷A及答案⼀、填空题(每空1分,共35分)1、1948年,美国数学家发表了题为“通信的数学理论”的长篇论⽂,从⽽创⽴了信息论。
信息论的基础理论是,它属于狭义信息论。
2、信号是的载体,消息是的载体。
3、某信源有五种符号}{,,,,a b c d e ,先验概率分别为5.0=a P ,25.0=b P ,125.0=c P ,0625.0==e d P P ,则符号“a ”的⾃信息量为 bit ,此信源的熵为 bit/符号。
4、某离散⽆记忆信源X ,其概率空间和重量空间分别为1234 0.50.250.1250.125X x x x x P =???和12340.5122X x x x x w=,则其信源熵和加权熵分别为和。
5、信源的剩余度主要来⾃两个⽅⾯,⼀是,⼆是。
6、平均互信息量与信息熵、联合熵的关系是。
7、信道的输出仅与信道当前输⼊有关,⽽与过去输⼊⽆关的信道称为信道。
8、马尔可夫信源需要满⾜两个条件:⼀、;⼆、。
9、若某信道矩阵为010001000001100,则该信道的信道容量C=__________。
10、根据是否允许失真,信源编码可分为和。
11、信源编码的概率匹配原则是:概率⼤的信源符号⽤,概率⼩的信源符号⽤。
(填短码或长码)12、在现代通信系统中,信源编码主要⽤于解决信息传输中的性,信道编码主要⽤于解决信息传输中的性,保密密编码主要⽤于解决信息传输中的安全性。
13、差错控制的基本⽅式⼤致可以分为、和混合纠错。
14、某线性分组码的最⼩汉明距dmin=4,则该码最多能检测出个随机错,最多能纠正个随机错。
15、码字1、0、1之间的最⼩汉明距离为。
16、对于密码系统安全性的评价,通常分为和两种标准。
17、单密钥体制是指。
18、现代数据加密体制主要分为和两种体制。
19、评价密码体制安全性有不同的途径,包括⽆条件安全性、和。
20、时间戳根据产⽣⽅式的不同分为两类:即和。
信息论与编码 第二章 信源与信息熵

现概率是它自身的先验概率。
无记忆信源
{发出符号序列的无记忆信源
发出单个符号的无记忆信源
{
离散 连续
2.1.1 无记忆信源
发出单个符号的离散无记忆信源
——指信源每次只发出一个符号代表一个消息, 且消息的取值个数是有限的(或可列无限多个)。 例如扔骰子,每次实验结果必然是1~6点中的某一 个面朝上。每次实验的结果不随实验次数变化,也 不与先前的实验结果相关,因而该信源是单符号离
p( X1 , X 2 , X l , X L ) p( X l ) [ p( X )]L
l 1
L
2.1.2 有记忆信源
有记忆信源——在不同时刻发出的符号是相互依赖的。 发出符号序列的有记忆信源 ——每次发出1组含2个以上符号的符号序列来代表一 个消息的信源,且各符号之间是相互依赖的。
I=-log2(1/2m)=m bit
2.2.1 自信息量
自信息量I (xi)的特性:
⑴ I (xi)是非负值
⑵ 当p(xi) = 1时, I (xi) = 0
⑶ 当p (xi) = 0时, I (xi) =∞
⑷ I (xi)是先验概率p (xi)的单调递减函数,即 当p (x1)>p (x2)时, I (x1) < I (x2) ⑸可加性 : 两个独立事件的联合信息量等于它们分别的信 息量之和。
发出符号序列的无记忆信源
——每次发出1组含2个以上符号的符号序列来代表一 个消息的信源,且各符号之间没有统计关联性。
需要用随机序列(或随机矢量) X =(X1, X2,…, Xl, …, XL)来描 述信源输出的消息,用联合概率分布p(X1, X2,…, Xl, …, XL)来表 示信源特性。 p (X 1 ) p (X 2 ) … p (X l ) … p (X L ) 若离散信源输出的每个符号是统计独立的,且具有相同的概 率空间,则该信源是离散平稳无记忆信源,亦称为独立同分布 (independently identical distribution,i. i. d.)信源。
信息论考试题(填空简答)

一.填空题(每空1分,共20分)1.香农信息论的三个基本概念分别为_______________ 、_____________ 、 ____________ 。
2•对离散无记忆信源来说,当信源呈_______________ 分布情况下,信源熵取最大值。
3•写出平均互信息的三种表达公式________________ 、_____________ 、 ____________ 。
4.若连续信源输出的平均功率和均值被限定,则其输出信号幅度的概率密度函数为______________ 时,信源具有最大熵值;若连续信源输出非负信号的均值受限,则其输出信号幅度呈____________ 分布时,信源具有最大熵值。
5. ________________________________ 信道容量是为了解决通信的_________________________ 问题,而信息率失真函数是为了解决通信的___________ 问题。
6. ______________________________________________________ 费诺编码比较适合于的信源。
7•无记忆编码信道的每一个二元符号输出可以用多个比特表示,理想情况下为实数,此时的无记忆二进制信道又称为__________________________ 。
&差错控制的4种基本方式是:_________________ 、_____________ 、 ____________ 、______________ 。
9 . (n,k)线性码能纠t个错误,并能发现I个错误(l>t),码的最小距离为:10.循环码码矢的i次循环移位等效于将码多项式乘___________________ 后再模______________ 。
二.简答题(每小题5分,共30分)1 •分别说明平均符号熵与极限熵的物理含义并写出它们的数学表达式。
2•写出二进制均匀信道的数学表达式,并画出信道容量C与信道转移概率 p的曲线图。
信息论与编码2-信源及信源熵1

信息论与编码-信源及信源熵
又例如对离散化的平面图像来说,从 空间上来看是一系列离散的符号,而空间 每一点的符号(灰度)又都是随机的,由此 形成了不同的图像.所以我们可以把一般 信源输出的消息看作为时间或空间上离 散的一系列随机变量,即随机矢量.这样,信 源 描的述输,其出中可N可用为N维有随限机正矢整量数(或x1,可x2,数…的xN)无来 限值.
25
信息论与编码-信源及信源熵
2.2.2 离散信源熵
前面定义的自信息是指某一信源发出某一消 息所含有的信息量.所发出的消息不同,它们所含 有的信息量也就不同.所以自信息I(ai) 是一个 随机变量,不能用它来作为整个信源的信息测度.
我们定义自信息的数学期望为信源的平均信 息量,即
H ( X ) E [ I ( X ) ]p ( x i) I ( x i) p ( x i) lo p ( x i) g
7
信息论与编码-信源及信源熵
离散信源的数学模型就是离散型的概率空间:
X P
x1
p(x1)
x2
xn
p(x2) p(xn)
其中概率p(xi)(i=1,2,…,n)称为符号xi的先验概 率,应满足∑p(xi)=1
它表示信源可能取的消息(符号)只有n 个:x1,x2,…xn,而且每次必定取其中一个.
当xi和yj相互独立时,有p(xi,yj)=p(xi)p(yj) 于是有
I(xi,yj)= I(xi)+ I(yj)
24
信息论与编码-信源及信源熵
条件自信息量: 当xi和yj相互联系时,在事件yj 出现的条件下,xi 的
自信息量称为条件自信息量,定义为 I(xi|yj)=-logp(xi|yj)
第二章基本信息论6_连续信源的熵

一、连续信源熵的定义
♦连续信源:输出在时间和取值上都是连续的信源 连续信源:
连续信源
采样
离散信源
求信源熵
若连续信源的频带受限, 若连续信源的频带受限,为W,则根据采样定理, ,则根据采样定理, 只要采样频率大于2W, 只要采样频率大于 ,则连续信源经采样离散 不损失任何信息。 后,不损失任何信息。 p( x ) 将连续信源离散化为离散 信源,其信源熵为: 信源,其信源熵为:
∞
1 λ1 −1 e = σ 2π ⇒ λ =− 1 2 2 2σ
− 2 1 得p ( x ) = e 2σ 为高斯分布 σ 2π
x2
P(x)
最大熵
H max ( X ) = − ∫ p ( x )log p( x )dx
−∞
x 1 − 2 = − ∫ p ( x )ln e 2σ −∞ σ 2π
H max ( X ) = − ∫
V2 −V1
V2
x
p ( x )log p ( x )dx = log(V1 + V2 )
2、输出平均功率受限的信源 、 设信源 ( X ) = − ∫ p( x )log p ( x )dx为极大值的p ( x )
−V
V
以及对应的最大熵H max ( X ), 其限制条件:
P( x )
1/ 2
0
1 dx1 3
x
P(x)
2
dx2
6 x
二、连续信源熵的性质
♦ 连续信源熵可正可负
H ( X ) = −∫
−∞
∞
p ( x )log p( x )dx
1 1 = − ∫ lb dx = −1比特/采样 3 2 2
2015秋.信息论.第2章离散信源与信息熵

第2章离散信源与信息熵信号 信号+干扰 消息干扰消息 信源 编码器 信道 译码器 信宿 噪声源通信系统模型信息2.1 信源的分类和描述信源是信息的发源地,可以是人、生物、机器或其他事物。
信源的输出是包含信息的消息。
消息的形式可以是离散的或连续的。
信源输出为连续信号形式(如语音),可用连续随机变量描述。
连续信源←→模拟通信系统信源输出是离散的消息符号(如书信),可用离散随机变量描述。
离散信源←→数字通信系统离散信源…X i…X j…离散无记忆信源:输出符号Xi Xj之间相互无影响;离散有记忆信源:输出符号Xi Xj之间彼此依存。
3离散信源无记忆有记忆发出单个符号发出符号序列马尔可夫信源非马尔可夫信源y j将一粒棋子随意地放在棋盘中的某列;棋子放置的位置是一个随机事件;可看做一个发出单个符号的离散信源。
x i1212,,...,(),(),...,()m m x x x X P p x p x p x ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦就数学意义来讲,信源就是一个概率场,可用概率空间来描述信源。
由离散随机变量X 表示棋子位置:10()1,()1m i ii p x p x =≤≤=∑i x 其中,代表随机事件的某一结果。
2.2离散信源的信息熵信息的可度量性是信息论建立的基础;香农的信息论用事件发生概率的对数来描述事件的不确定性,得到消息的信息量,建立熵的概念。
2.2.1自信息量–定义2.1 任意随机事件x i 的自信息量定义为:i i i 1(x )log log (x )(x )I P P ==-小概率事件所包含的不确定性大,自信息量大。
大概率事件所包含的不确定性小,自信息量小。
概率为1的确定性事件,自信息量为零。
i i i 1(x )log log (x )(x )I P P ==-信息量的单位与公式中的对数取底有关。
以2为底,单位比特(bit );以e 为底,单位奈特(nat );()22log log ,log log ln log c a c b b x e x a==⋅–例:棋盘共8列,甲随手一放,将一枚棋子放在了第3列。
信息论第3章信源及信息熵

举例
数学描述
离散信源 (数字信源)
连续信号
文字、数据、 离散化图象
离散随机变量 序列
跳远比赛的结果、语音 连续随机变量
信号抽样以后
序列
波形信源 (模拟信源)
语音、音乐、热噪声、 图形、图象
不常见
随机过程
表3.1 信源的分类
3.1 信源的分类及其数学模型
我们还可以根据各维随机变量的概率分布是否随时间的推移 而变化将信源分为平稳信源和非平稳信源,根据随机变量间 是否统计独立将信源分为有记忆信源和无记忆信源。
定义3.2 随机变量序列中,对前N个随机变量的联合熵求平
均:
HN
(X)
1 N
H ( X1X 2
XN)
称为平均符号熵。如果当N
时上式极限存在,则
lim
N
H
N
(X)
称为熵率,或称为极限熵,记为
def
H
lim
N
H
N
(
X
)
3.3.1 离散平稳无记忆信源
离散平稳无记忆信源输出的符号序列是平稳随机序列,并且
H(X ) H(X1X2 XN ) H ( X1) H ( X2 | X1) H ( X3 | X1X 2 ) H ( X N | X1X 2 X N1)
定理3.1 对于离散平稳信源,有以下几个结论:
(1)条件熵 H (X N | X1X 2 X N1) 随N的增加是递减的;
(2)N给定时平均符号熵大于等于条件熵,即
s1
si p(s j
| si )
s q
m
状态空间由所有状态及状态间的状态转移概率组成。通过引
入状态转移概率,可以将对马尔可夫信源的研究转化为对马 尔可夫链的研究。
信息论-信息论第7次课ch3--信源熵
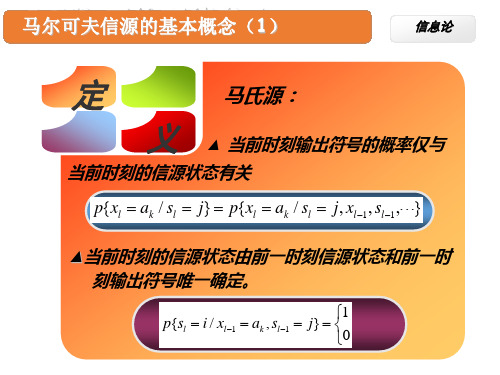
1) m阶马氏链的符号转移概率已给定:
p(xm1 / x1 xm )其中xi取自A {a1L an}
2) 做m长符号序列到信源状态的映射(x1 xm) s j ,
xi 取遍 A {a1L an} ,i=1,…,m; 状态取自 s j
Am {1,2,L nm} ,nm为状态数;
m§阶2马.1氏链自的信处息理和方互法信(2息)
H
() 3
0.918
比特/符号
H0 log 2 1 比特/符号
1 H 1 0.896 0.104
H0
信息论
本章 小结
1 离散信源X的N次扩展源的H熵(X N ) N H (X ) 源无记忆时等式成立;
,仅当信
离
散
信
源
X
的
N
次
H
扩
N展( X
)
源
1H
N的
(
XN)
平
H
均
(
X)
符
号
熵
,仅当信源无记忆时等式
信息信论息基论础
字母 空格
A B C D E F G H
概率 0.1859 0.0642 0.0127 0.0218 0.0317 0.1031 0.0208 0.0152 0.0467
字母 I J K L M N O P Q
概率 0.0575 0.0008 0.0049 0.0321 0.0198 0.0574 0.0632 0.0152 0.0008
1:0.7 11
0:0.4
1:0.6
p(0)
0.41
0.2 2
0.33
0.4 4
1 3
p(1) 1 p(0) 2 3
《信息论、编码与密码学》课后习题答案资料

《信息论、编码与密码学》课后习题答案第1章 信源编码1.1考虑一个信源概率为{0.30,0.25,0.20,0.15,0.10}的DMS 。
求信源熵H (X )。
解: 信源熵 ∑=-=512)(log )(k k k p p X HH(X)=-[0.30*(-1.737)+0.25*(-2)+0.2*(-2.322)+0.15*(-2.737)+0.1*(-3.322)]=[0.521+0.5+0.464+0.411+0.332] =2.228(bit)故得其信源熵H(X)为2.228bit1.2 证明一个离散信源在它的输出符号等概率的情况下其熵达到最大值。
解: 若二元离散信源的统计特性为P+Q=1 H(X)=-[P*log(P)+(1-P)*log(1-P)] 对H(X)求导求极值,由dH(X)/d(P)=0可得211101log ==-=-p ppp p可知当概率P=Q=1/2时,有信源熵)(1)(max bit X H =对于三元离散信源,当概率3/1321===P P P 时,信源熵)(585.1)(m ax bit X H =,此结论可以推广到N 元的离散信源。
1.3 证明不等式ln 1x x ≤-。
画出曲线1ln y x =和21y x =-的平面图以表明上述不等式的正确性。
证明:max ()ln 1(0)1()()01001()0()0ln 11ln 1ln 1f x x x x f x xf x x x x f x f x f x x x x x x x =-+>'=''==>∴<≤>≤=≤-≥≤-≤-令,又有时此时也即当时同理可得此时综上可得证毕绘制图形说明如下 可以很明确说明上述 不等式的正确性。
1.4 证明(;)0I X Y ≥。
在什么条件下等号成立?1111(,)(,)(,)(,)log()()n mi j i j i j n mi j i j i j i j I P x y I x y P x y P x y P x P y =====∑∑∑∑(X ;Y )=当和相互独立时等号成立。
信息论与编码第五章课后习题答案

第五章课后习题【5.1】某信源按43)0(=P ,41)1(=P 的概率产生统计独立的二元序列。
(1)试求0N ,使当0N N >时有01.005.0)()(≤≥−S H N I P i α 式中,)(S H 是信源的熵。
(2)试求当0N N =时典型序列集N G ε中含有的信源序列个数。
解:(1)该信源的信源熵为811.0)(log )()(=−=∑i i s p s p S H 比特/符号自信息的方差为4715.0811.04log 4134log 43)()]([)]([22222=−+=−=S H s I E s I D i i 根据等长码编码定理,我们知道δεα−≤≥−1)()(S H N I P i 根据给定条件可知,05.0=ε,99.0=δ。
而[]2)(εδN s I D i =因此[]5.19099.0*05.04715.0)(220==≥δεi s I D N 取1910=N 。
(2)ε典型序列中信源序列个数取值范围为:])([])([22)1(εεεδ+−<<−S H N N S H N G代入上述数值得451.164351.1452201.0<<×N G ε【5.2】有一信源,它有六个可能的输出,其概率分布如下表所示,表中给出了对应的码A 、B 、C 、D 、E 和F 。
表5.2消息 )(i a P A B C D E F 1a 1/2 000 0 0 0 0 0 2a 1/4 001 01 10 10 10 100 3a 1/16 010 011 110 110 1100 101 4a 1/16 011 0111 1110 1110 1101 110 5a 1/16 100 01111 11110 1011 1110 111 6a1/1610101111111111011011111011(1) 求这些码中哪些是惟一可译码; (2) 求哪些码是非延长码(即时码); (3) 求对所有惟一可译码求出其平均码长L 。
信息论研究中的不等式及应用分析

信息论研究中的不等式及应用分析信息论是一门研究信息量、信息传输、信息存储等方面的学科。
信息论中的不等式及其应用是信息论研究中的一个重要方面。
本文将从信息论中的不等式出发,从数学的角度探讨这些不等式的应用分析。
一、信息论中的不等式1. 马尔科夫不等式马尔科夫不等式是信息论中的一个基本不等式,它给出了一个随机变量非负函数的上界。
具体地,对于一个非负的随机变量X和正实数a,马尔科夫不等式表达为:P(X≥a) ≤E(X)/a其中,P(X≥a)为X≥a的概率,E(X)为随机变量X的期望。
马尔科夫不等式的应用非常广泛。
例如,在大数据分析中,常常需要计算某个变量大于某一阈值的概率,这时通过马尔科夫不等式可以快速地得到一个上界。
2. 切比雪夫不等式切比雪夫不等式是信息论中的另一个经典不等式,它给出了一个随机变量与其期望的偏离度的上界。
具体地,对于任意一个随机变量X,正实数a和其期望E(X),切比雪夫不等式表达为:P(|X-E(X)|≥a) ≤Var(X)/a²其中,P(|X-E(X)|≥a)为X与其期望的偏离超过a的概率,Var(X)为X的方差。
切比雪夫不等式的应用也非常广泛。
例如,在机器学习和数据挖掘中,常常需要评估模型预测结果的准确性,并给出相应的置信区间,这时可以使用切比雪夫不等式。
3. 卡方不等式卡方不等式是信息论中的另一个重要不等式,它给出了一个非负随机变量的期望的下界。
具体地,对于任意一个非负的随机变量X和正实数a,卡方不等式表达为:P(X≥a) ≤E(X²)/a²其中,P(X≥a)为X≥a的概率,E(X²)为随机变量X的平方的期望。
卡方不等式的应用也非常广泛。
例如,在统计学中,常常需要评估变量之间的相关性,这时可以使用卡方不等式。
二、信息论中不等式的应用分析信息论中的不等式具有广泛的应用,在各个领域都有着重要的作用。
常见的应用领域有机器学习、数据挖掘、信号处理、密码学、概率论和统计学等。
第2章信源熵-概念及单符号离散信源熵

表示
x2 xn X x1 P(X) P(x ) P( x ) P( x ) 1 2 n
其中,0 P( x i ) 1, i 1,2,, n且 P( x i ) 1
i 1
n
例1
6 X 1 2 P(X) 1/ 6 1 / 6 1/ 6
I(x 4 ) log P(x 4 ) log( 1/ 8) log 8 3(bit )
信源熵
3、熵
定义
信源各消息自信息量的数学期望为该信源的熵, 也叫无条件熵,用H(X)表示。
表示
H(X) E[I( x i )] P( x i )I( x i ) P( x i ) log P( x i )
i 1 i 1
n
n
同理, (1 )P2 ( x i ) log[ P1 ( x i ) (1 )P2 ( x i )]
i 1
n
(1 )P2 ( x i ) log P2 ( x i )
i 1
n
信源熵
[P1 ( x i ) (1 )P2 ( x i )] log[ P1 ( x i ) (1 )P2 ( x i )]
信源熵
2、自信息量
假设单符号离散信源发出消息xi、xj 的概率 P(xi) < P(xj),那条消息具有更大的信 息量, xi 还是xj ?
信源熵
根据香农信息的概念,消息中具有不确定 性的成分才是信息,不确定性的成分越大, 或者说概率越小,信息量就越大,从这个 意义判断,消息xi 具有更大的信息量。
信源熵
离散信源又可以细分为: (1)离散无记忆信源:所发出的各 个符号之间是相互独立的,发出 的符号序列中的各个符号之间没 有统计关联性,各个符号的出现 概率是它自身的先验概率。 (2)离散有记忆信源:发出的各个 符号之间不是相互独立的,各个 符号出现的概率是有关联的。
信息论与编码试卷及答案

一、(11')填空题(1)1948年,美国数学家香农发表了题为“通信的数学理论”的长篇论文,从而创立了信息论。
(2)必然事件的自信息是0 。
(3)离散平稳无记忆信源X的N次扩展信源的熵等于离散信源X的熵的N倍.(4)对于离散无记忆信源,当信源熵有最大值时,满足条件为__信源符号等概分布_。
(5)若一离散无记忆信源的信源熵H(X)等于2.5,对信源进行等长的无失真二进制编码,则编码长度至少为3 。
(6)对于香农编码、费诺编码和霍夫曼编码,编码方法惟一的是香农编码。
(7)已知某线性分组码的最小汉明距离为3,那么这组码最多能检测出_2_______个码元错误,最多能纠正___1__个码元错误。
(8)设有一离散无记忆平稳信道,其信道容量为C,只要待传送的信息传输率R__小于___C(大于、小于或者等于),则存在一种编码,当输入序列长度n足够大,使译码错误概率任意小。
(9)平均错误概率不仅与信道本身的统计特性有关,还与___译码规则____________和___编码方法___有关三、(5')居住在某地区的女孩中有25%是大学生,在女大学生中有75%是身高1。
6米以上的,而女孩中身高1。
6米以上的占总数的一半。
假如我们得知“身高1。
6米以上的某女孩是大学生”的消息,问获得多少信息量?解:设A表示“大学生”这一事件,B表示“身高1.60以上”这一事件,则P(A)=0。
25 p(B)=0.5 p(B|A)=0。
75 (2分)故 p(A|B)=p(AB)/p(B)=p(A)p(B|A)/p(B)=0.75*0。
25/0。
5=0。
375 (2分)I(A|B)=—log0.375=1。
42bit (1分)四、(5')证明:平均互信息量同信息熵之间满足I(X;Y)=H(X)+H(Y)—H(XY)证明:(2分)同理(1分)则因为(1分)故即(1分)五、(18')。
黑白气象传真图的消息只有黑色和白色两种,求:1)黑色出现的概率为0。
柯西不等式多维形式及其推论的证明

柯西不等式多维形式及其推论的证明柯西不等式是数学中一个重要的不等式,它可以表示为多维形式。
柯西不等式在很多领域都有广泛的应用,例如线性代数、凸优化、信息论等。
本文将介绍柯西不等式的多维形式,并且给出它的一些推论的证明。
1. 定义和形式化在数学中,柯西不等式是一个重要的不等式,它可以用来限制一个函数的行为。
柯西不等式的通用形式为:$$f(x\_1,x\_2,\dots,x\_n) \geqslant 0$$其中 $f$ 是一个实值函数,$x\_1,x\_2,\dots,x\_n$ 是 $n$ 个实数。
柯西不等式可以被用来限制一个多元函数的值域。
柯西不等式也可以表示为多维形式,即:$$f(\mathbf{x}) \geqslant 0$$其中 $\mathbf{x}$ 是一个 $n$ 维向量。
多维柯西不等式是柯西不等式的推广,它具有更广泛的应用。
在实际应用中,柯西不等式通常被用来限制一个函数的值域,使得该函数在某些条件下具有某些性质。
柯西不等式在很多领域都有广泛的应用,例如线性代数、凸优化、信息论等。
2. 多维柯西不等式的证明多维柯西不等式是柯西不等式的推广,它可以用来限制一个多元函数的值域。
多维柯西不等式的通用形式为:$$f(\mathbf{x}) \geqslant 0$$其中 $\mathbf{x}$ 是一个 $n$ 维向量,$f$ 是一个实值函数。
证明多维柯西不等式的方法有很多,具体方法取决于具体的函数 $f$ 以及所满足的条件。
在本文中,我们将介绍几种常见的证明方法。
首先,我们可以使用数学归纳法来证明多维柯西不等式。
这种方法适用于当 $f$ 满足一些递推关系时。
其次,我们可以使用数学归纳法的变形来证明多维柯西不等式。
这种方法适用于当$f$ 满足一些递推关系,但不能直接使用数学归纳法时。
第三,我们可以使用数学归纳法的变形来证明多维柯西不等式。
这种方法适用于当$f$ 满足一些递推关系,但不能直接使用数学归纳法时。
《信息论》—基础理论与应用(傅祖芸)课后答案

注意:消息中平均每个符号携带的信息量有别于离散平均无记忆信源平均每个符号携带的 信息量,后者是信息熵,可计算得 H ( X ) = − ∑ P( x) log P( x) = 1.91 比特/符号
【2.6】如有 6 行 8 列的棋型方格,若有二个质点 A 和 B,分别以等概率落入任一方格内, 且它们的坐标分别为(XA,YA)和(XB,YB) ,但 A 和 B 不能落入同一方格内。 (1) 若仅有质点 A,求 A 落入任一个格的平均自信息量是多少? (2) 若已知 A 已落入,求 B 落入的平均自信息量。 (3) 若 A、B 是可分辨的,求 A、B 同都落入的平均自信息量。 解: (1)求质点 A 落入任一格的平均自信息量,即求信息熵,首先得出质点 A 落入任一 格的概率空间为: a X 1 P = 1 48 平均自信息量为 H ( A) = log 48 = 5.58 比特/符号 (2)已知质点 A 已落入,求 B 落入的平均自信息量,即求 H ( B | A) 。 A 已落入,B 落入的格可能有 47 个,条件概率 P(b j | ai ) 均为
= −(1 − ε )∑ Pi log(1 − ε ) − (1 − ε )∑ Pi log Pi − ε ∑ Pi log ε − ε ∑ Pi log Pi
′ = p1 − ε , 【2.10】设有一概率空间,其概率分布为 { p1 , p 2 ,..., p q } ,并有 p1 > p 2 。若取 p1 ′ = p 2 + ε ,其中 0 < 2ε ≤ p1 − p 2 ,而其他概率值不变。试证明由此所得新的概率空间的 p2 熵是增加的,并用熵的物理意义加以解释。 解: 设新的信源为 X ′ ,新信源的熵为: H ( X ′) = −∑ pi log p i = −( p1 − ε ) log( p1 − ε ) − ( p 2 + ε ) log( p 2 + ε ) − L − p q log p q 原信源的熵 H ( X ) = − ∑ p i log pi = − p1 log p1 − p 2 log p 2 − L − p q log p q 因此有, H ( X ) − H ( X ′) = ( p1 − ε ) log( p1 − ε ) + ( p 2 + ε ) log( p 2 + ε ) − p1 log p1 − p 2 log p 2 p1 − p 2 令 f ( x ) = ( p1 − x) log( p1 − x ) + ( p 2 + x ) log( p 2 + x) , x ∈ 0, 2 ,则 f ′( x) = log p2 + x ≤0 p1 − x
信息熵的概念及其在信息论中的应用

信息熵的概念及其在信息论中的应用信息熵是信息论中一个重要的概念,它被用来衡量一段信息的不确定性或者说信息的平均编码长度。
熵的概念最早由克劳德·香农在1948年提出,对于信息的量化和信源编码具有重要的理论和实际应用。
本文将对信息熵的概念进行详细的介绍,并探讨其在信息论中的应用。
一、信息熵的定义信息熵可以看作是一个信源所产生的信息的不确定性度量。
当一个信源产生的符号具有均匀分布时,熵的值最大;而当信源的输出符号呈现高度集中的分布时,熵的值最小。
具体地,对于一个离散型信源,其熵的定义如下:H(X) = -Σp(x)log2p(x),其中,H(X)表示信源X的熵,p(x)表示信源X输出符号x出现的概率。
二、信息熵的解释信息熵可以理解为对信息的平均编码长度的期望。
在信息论中,我们可以通过霍夫曼编码等方法对信息进行编码,使得熵最小化,从而达到最高的编码效率。
假设信源X有n个符号,出现的概率分别为p1, p2, ..., pn,则信源X的平均编码长度L为:L = ΣpiLi,其中,Li为信源X的符号i的编码长度。
根据不等式关系log2(p1/p2) <= p1/p2,我们可以得到:H(X) = -Σp(x)log2p(x) <= Σp(x) * (-log2p(x)) = Σp(x)log2(1/p(x)) = Σp(x)log2n = log2n,即熵的值小于等于log2n,其中n为符号的个数。
当n个符号均匀分布时,熵的值达到最大,即log2n。
三、信息熵的应用信息熵在信息论中具有广泛的应用,下面将介绍几个常见的应用场景。
1. 数据压缩信息熵在数据压缩中起到重要的作用。
根据信息论的原理,我们可以利用数据的统计特性进行有损压缩。
对于频率出现较高的符号,我们可以分配较短的编码,而对于出现频率较低的符号,则分配较长的编码。
通过这种方式,我们可以大大减少数据的存储空间,提高传输效率。
2. 通信系统信息熵在通信系统中也有重要应用。
信息导论-第6讲-信源熵

信源熵的度量
03
熵的离散型度量
离散型熵
离散型熵是用于度量离散随机变量不确定性的量,其定义基于概率分布。对于一个离散随机变量X,其熵H(X)定 义为H(X)=−∑p(x)logp(x)text{H}(X) = -sum p(x) log p(x)H(X)=−∑p(x)logp(x),其中p(x)是随机变量取某个值 的概率。
深入研究信源熵与信息论其他概念,如互信息、相对熵等之间的联系,有助于更全面地 理解信息传递的本质。
扩展信源熵到多维和连续变量
目前信源熵主要应用于离散随机变量,未来研究可以探索将其扩展到多维和连续变量的 情况,以更好地描述复杂数据。
信源熵的量子化研究
随着量子信息理论的不断发展,探索信源熵在量子领域的表现和性质,有望为信息理论 带来新的突破。
条件熵
条件熵是在给定某个条件随机变量下,另一个随机变量的熵。条件熵H(X∣Y)表示在已知Y的条件下,X的不确定 性。
熵的连续型度量
连续型熵
对于连续随机变量,其熵的度量方式 略有不同。连续型熵通常使用概率密 度函数来定义,并涉及到积分运算。
条件连续型熵
与离散型条件熵类似,连续型条件熵 表示在给定某个连续随机变量条件下 ,另一个连续随机变量的不确定性。
03
通过信源熵的分析,可以帮助决策者更好地理解和 评估决策的风险,从而做出更明智的决策。
信源熵与其他信息论
05
概念的关联
与互信息的关系
互信息
互信息是描述两个随机变量之间相互依赖程度的概念,它表示一个随机变量中包含的关 于另一个随机变量的信息量。在信息论中,互信息用于度量两个信源之间的相互依赖程
度。
熵的极限性质
熵函数的连续性
信息论中的重要不等式

相对熵的性质
p( x) q( x) D ( p || q ) 0 ,等号成立 D ( p || q )是概率分布对 ( p , q ) 的凸函数
7
互信息
X 信源 P(X
Y 信宿 P (Y
x2 , , xi , , x n x1 , , p ( xi ) 1 ) p ( x1 ), p ( x 2 ), , p ( x i ), , p ( x n ) i
3.合写:
I ( X ;Y )
i j
p ( x i y j ) lo g 2
p ( xi y j )
p ( x i ) p ( y j ) H(X) + H(Y) – H(XY)
I (Y ; X )
18
平均互信息(物理意义)
1. I(X;Y)= H(X) – H(X/Y) (1) H(X)——信源熵:X的不确定度 H(X/Y)——已知Y时,对X仍剩的不确定度 [结论]―Y已知”使得对X的不确定度减小了, 即获得了I(X;Y) 的信息量 (2) H(X)——信源含有的平均信息量(有用总体) I(X/Y)——信宿收到的平均信息量(有用部分) [结论] H(X/Y)—因信道有扰而丢失的平均信息 19 量,故称损失熵
9
互信息
1. 互信息 (1) yj对xi的互信息 I(xi;yj) p ( xi / y j ) I ( x i ; y j ) lo g 即: I(xi;yj)= I(xi)- I(xi/yj) p ( xi ) p(xi) ——先验概率:信源发xi的概率 p(xi/yj)——后验概率:信宿收到yj后, 推测信源发xi的概率 [含义] 互信息I(xi;yj) =自信息I(xi) - 条件自信息I(xi/yj) *I(xi) __信宿收到yj之前,对信源发xi的不确定度 * I(xi/yj) __信宿收到yj之后,对信源发xi的不确定度 * I(xi;yj) __收到yj而得到(关于xi )的互信息 =不确定度的减少量 10
(完整版)信息论第五章答案

5.1 设信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡01.01.015.017.018.019.02.0)(7654321x x x x x x x X P X (1) 求信源熵H(X); (2) 编二进制香农码;(3) 计算平均码长和编码效率。
解: (1)symbolbit x p x p X H i i i /609.2)01.0log 01.01.0log 1.015.0log 15.017.0log 17.018.0log 18.019.0log 19.02.0log 2.0()(log )()(2222222712=⨯+⨯+⨯+⨯+⨯+⨯+⨯-=-=∑=%1.8314.3609.2)()(14.301.071.0415.0317.0318.0319.032.03)(=====⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑KX H R X H x p k K ii i η5.2 对信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡01.01.015.017.018.019.02.0)(7654321x x x x x x x X P X 编二进制费诺码,计算编码效率。
%2.9574.2609.2)()(74.201.041.0415.0317.0218.0319.032.02)(=====⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑KX H R X H x p k K ii i η5.3 对信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡01.01.015.017.018.019.02.0)(7654321x x x x x x x X P X 编二进制和三进制哈夫曼码,计算各自的平均码长和编码效率。
解:%9.9572.2609.2)()(72.201.041.0415.0317.0318.0319.022.02)(=====⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑KX H R X H x p k K ii i η%4.913log 8.1609.2log )()(8.1)01.01.015.017.018.019.0(22.01)(22=⨯====+++++⨯+⨯==∑m LK X H R X H x p k K ii i η5.4 设信源⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎥⎦⎤⎢⎣⎡12811281641321161814121)(87654321x x x x x x x x X P X (1) 求信源熵H(X);(2) 编二进制香农码和二进制费诺码;(3) 计算二进制香农码和二进制费诺码的平均码长和编码效率; (4) 编三进制费诺码;(5) 计算三进制费诺码的平均码长和编码效率;解: (1)symbolbit x p x p X H i i i /984.1128log 1281128log 128164log 64132log 32116log 1618log 814log 412log 21)(log )()(22222222812=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯=-=∑==127/64 bit/symbol (2)二进制费诺码:香农编码效率:%100984.1984.1)()(64/127984.17128171281664153214161381241121)(======⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑KX H R X H x p k K ii i η费诺编码效率:%100984.1984.1)()(984.17128171281664153214161381241121)(=====⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑KX H R X H x p k K ii i η(5)%3.943log 328.1984.1log )()(328.14128141281364133212161281141121)(22=⨯=⋅===⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑m K X H R X H x p k K ii i η5.5 设无记忆二进制信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡1.09.010)(X P X先把信源序列编成数字0,1,2,……,8,再替换成二进制变长码字,如下表所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
论文题目:信息论中有关各种熵之间关系的证明学院:数学科学学院专业:信息与计算科学姓名:周艳君学号:20071115158信息论中有关各种熵之间关系的证明07信息班 周艳君 20071115158 指导老师 王桂霞摘 要 根据信息量与熵的定义和重要定理以及主要公式,对各种熵之间的关系进行分析和证明.关键词 无条件熵 条件熵 联合熵 交互熵.⒈基本定义1.1信息就是对事物动态(或它的存在方式)的不确定性的一种描述.不确定 性及随机性,可以用研究随机现象的数学教具—概率论与随机过程来描述信息.1.2自信息量:一个随机事件发生某一结果后所带来的信息量称为自信息量,简称自信息.用)(i a I 来表示.1.3联合自信息量:自信息量是二维联合集XY 上元素j i b a 的联合概率)(j i b a p 数的负值,称为联合自信息量.用)(j i b a I 来表示.1.4条件自信息量:为条件概率对数的负值.用)/(j i b a I 来表示.1.5交互信息量:i a 后验概率与先验概率比值的对数为j b 对i a 的互信息量, 也称交互信息量(简称互信息).用);(j i b a I 来表示.1.6信源熵:信源各个离散消息的自信息量的数学期望(即概率加权的统计 平均值)为信源的平均自信息量,一般称为信源的信息熵,也叫信源熵或香农熵,记为)(X H .1.7条件熵:在联合符号集合XY 上的条件自信息量的数学期望.可以用)/(Y X H 表示.1.8联合熵:也叫共熵,是联和离散符号XY 上的每的元素j i b a 的联合自信息量的数学期望,用)(XY H 表示.2.基本公式2.1 自信息量:)(log )(2i i a p a I -=2.2 联合的自信息量:)(log )(2j i j i b a p b a I -= 当X 和Y 相互独立时,)()()(j i j i b p a p b a p =;则有:)()()(log )(log )()(log )(log )(2222j i j i j i j i j i b I a I b p a p b p a p b a p b a I +=--=-=-=2.3条件自信息量:)/(log )/(2j i j i b a p b a I -= 或 )/(log )/(2i j i j a b p a b I -= 2.4互信息量:)()/(log );(2i j i j i a p b a p b a I = ),,2,1;,,2,1(m j n i ==2.5信源熵:)(log )(])(1[log )]([)(212i ni i i i a p a p a p E a I E X H ∑=-=== 2.6条件熵:ⅰ:在已知随机变量Y 的条件下,随机变量X 的条件熵)/(Y X H 为:)/()()]/([)/(11j i mj ni j i j i b a I b a p b a I E Y X H ∑∑====)/(l o g )(211j i m j ni j i b a p b a p ∑∑==-=.ⅱ:在已知随机变量X 的条件下,随机变量Y 的条件熵)/(X Y H 为:)/()()]/([)/(11i j mj ni j i i j a b I b a p a b I E X Y H ∑∑====)/(l o g )(211i j m j ni j i a b p b a p ∑∑==-=.2.7联合熵:)(log )()()()(21111j i m j ni j i j i n i m j j i b a p b a p b a I b a p XY H ∑∑∑∑====-==.2.8有关概率的基本公式:1)(1=∑=n i i a p ,1)(1=∑=m j j b p ,1)/(1=∑=ni j i b a p ,1)/(1=∑=mj i ja bp ,1)(11=∑∑==m j ji n i b a p ,)()(1j n i j i b p b a p =∑=,)()(1imj j i a p b a p =∑=,)/()()/()()(j i j i j i j i b a p b p a b p a p b a p ==.3.各种熵之间的关系 3.1无条件熵3.1.2 )/();()/()(Y X H Y X I Y X H X H ≥+=. 证明:①)(log )()(21i ni i a p a p X H ∑=-=)/()/()(l o g )(211j i j i i m j ni j i b a p b a p a p b a p ∑∑==-=)/(l o g )()()/(l o g )(211211j i mj ni j i i j i mj ni j i b a p b a p a p b a p b a p ∑∑∑∑====-=)/();(Y X H Y X I +=.②)/(log )/()()/(2j i jij i j b a p b a p b p Y X H ∑∑-=])/(log )/([)(2∑∑-=ij i j i jj b a p b a p b p .由熵的极值性知:≤)/(Y X H ])(l o g )/([)(2∑∑-ii j i jj a p b a p b p∑∑-=ji j i j ia pb a p b p )(l o g )]/()([2)(X H =, 其中)()()/()(ijji jijja pb a p b a p b p ==∑∑.同理: )/();()/()(X Y H Y X I X Y H Y H ≥+=.3.1.2. )/()()(X Y H XY H X H -=.证明:)(log )()(2i ii a p a p X H ∑-=∑∑-=ji j j i j i j ia b p b a p b a p b p )/()(log )]/()([2)]/(log )([)(log )(22i j ijj i j i ijj i a b p b a p b a p b a p ∑∑∑∑---=)/()(X Y H XY H -=, 同理:)/()()(Y X H XY H Y H -=.3.2条件熵 );()()()()/(Y X I X H Y H XY H Y X H -=-=. 3.2.1 )()()/(Y H XY H Y X H -=. 证明:)/(Y X H )/(log)(211j i n i mj ji b a p b a p ∑∑==-=+-=∑∑==)(log )(211j i ni m j j i b a p b a p )(log])([211j m j ni ji b p b a p ∑∑==)(log )()(log )(21211j mj j j i ni mj j i b p b p b a p b a p ∑∑∑===+-=)()(Y H XY H -=, 其中:)()(1j ni j i b p b a p =∑=.3.2.2 );()()/(Y X I X H Y X H -= .证明:)/(log )()/(211j i ni mj j i b a p b a p Y X H ∑∑==-=)()()(l o g )(211i j i i n i mj j i a p b a p a p b a p ∑∑==-=)()/(l o g )()(l o g ])([211211i j i mj j i ni i ni mj j i a p b a p b a p a p b a p ∑∑∑∑====--=);()(Y X I X H -=, 其中:)()(1imj ji a p b a p =∑=.同理:);()()()()/(Y X I Y H X H XY H X Y H -=-=. 3.3联合熵 )()(YX H XY H =)/()()/()()(Y X H Y H X Y H X H XY H +=+=);()()(Y X I Y H X H -+= );()/()/(Y X I X Y H Y X H ++=.3.3.1)/()()/()()(Y X H Y H X Y H X H XY H +=+= . 证明:)(log )()(211j i ni mj j i b a p b a p XY H ∑∑==-=)/()(l o g )(211i j i n i mj j i a b p a p b a p ∑∑==-=)/()()(l o g ])([11211i j n i mj j i i ni mj j i a b p b a p a p b a p ∑∑∑∑====--=)/()(X Y H X H +=, 其中:)()(1i mj j i a p b a p =∑=.同理: )/()()(Y X H Y H XY H +=. 3.3.2 );()()()(Y X I Y H X H XY H -+= . 证明:)/()(log )()(211i j i ni mj j i a b p a p b a p XY H ∑∑==-=)()/()()(l o g )(211j i j j i n i mj j i b p a b p b p a p b a p ∑∑==-=)(l o g ])([)(l o g ])([211211jb p b a p a p b a p mj ni j i i ni mj j i ∑∑∑∑====--=)()/(l o g )(211j i j n i mj j i b p a b p b a p ∑∑==-);()()(Y X I Y H X H -+=.3.3.3 );()/()/()(Y X I X Y H Y X H XY H ++=. 证明:)/()(log )()(211i j i ni mj j i a b p a p b a p XY H ∑∑==-=)/()()/()/(l o g )(211j i i i j j i n i mj j i b a p a p a b p b a p b a p ∑∑==-=)/(l o g )(211j i ni mj j i b a p b a p ∑∑==-=)/(l o g )(211i j ni mj j i a b p b a p ∑∑==-)()/(l o g )(211i j i n i mj j i a p b a p b a p ∑∑==+);()/()/(Y X I X Y H Y X H ++= 3.4交互熵 );();(X Y I Y X I =)/()()/()();(X Y H Y H Y X H X H Y X I -=-=)()()()/()/()(XY H Y H X H X Y H Y X H XY H -+=--= . 3.4.1 )/()()/()();(X Y H Y H Y X H X H Y X I -=-= 证明:=);(Y X I )()/(log )(211i j i n i mj j i a p b a p b a p ∑∑==∑∑∑∑====+-=ni mj j i j i i ni mj j i b a p b a p a p b a p 112211)/(l o g )()(l o g ])([)/()(Y X H X H -=, 其中:)()(1i mj j i a p b a p =∑=.同理:)/()();(X Y H Y H Y X I -=. 3.4.2证明: )()/(log )();(211i j i ni mj j i a p b a p b a p Y X I ∑∑===)(1)/()/(log )(211j i i j j i n i mj j i b a p a b p b a p b a p ∑∑===)(log )(211j i ni mj j i b a p b a p ∑∑==-=)/(log )(211j i ni mj j i b a p b a p ∑∑==+)/(log )(211i j ni mj j i a b p b a p ∑∑==+)/()/()(X Y H Y X H XY H --=.3.4.3证明:)()/(log )();(211i j i n i mj j i a p b a p b a p Y X I ∑∑===)()()(l o g )(211j i j i n i mj j i b p a p b a p b a p ∑∑===)(l o g ])([211i ni mj j i a p b a p ∑∑==-=)(l o g ])([211j mj ni j i b p b a p ∑∑==-)(l o g )(211j i ni mj j i b a p b a p ∑∑==+)()()(XY H Y H X H -+=.其中:)()(1i m j j i a p b a p =∑=,)()(1j ni j i b p b a p =∑=.参考文献[1]傅祖芸,赵建中.信息论与编码.电子工业出版社,2006,4. [2]邓稼先,康耀红.信息论与编码.西安电子科技大学出版社,2007,5. [3]陈运.信息论与编码.电子工业出版社,2007,12.[4]贾世楼.信息论理论基础. 哈尔滨工业大学出版社,2002,6.。
