特征值模态
关于对模态概念的理解

第43卷第2期力学与实践2021年4月关于对模态概念的理解陈立群D(上海大学力学与工程科学学院力学系,上海200444)摘要通过分析模态的性质并与复模态和非线性模态比较以加强对模态概念的理解。
固有模态的基本性质是模态振动的同频性、对初始条件的不变性、模态的正交性和系统响应的叠加性。
复模态仍具有模态振动的 同频性,但没有对初始条件的不变性,正交性和叠加性仅在状态空间中成立。
非线性模态仅保留了同频性或不 变性,不具有正交性和叠加性。
关键词教学,模态,复模态,非线性模态,振动中图分类号:0312 文献标识码:Adoi: 10.6052/1000-0879-20-430ON THE CONCEPT OF MODESC H E N L i q u n 1)(D ep artm en t of M echanics, School of M echanics and Engineering Science, Shanghai University, Shanghai 200444, C hina)A b s t r a c t In order to better understand the concept of m o d e s , the characteristics of m o d e s are analyzed a n d c o m p a r e d with those of c o m p l e x m o d e s or nonlinear m o d e s . T h e connotation of a m o d e includes the synchronic - ity of the m o d a l vibrations , the invariance to the initial conditions , the orthogonality a m o n g m o d e s , a n d the superposition of the m o d a l vibrations into the response . A c o m p l e x m o d e concerns with the synchronicity but not the invariance , while the orthogonality a n d the superposition hold only in the state space . A nonlinear m o d e concerns bot h with the synchronicity a n d the invariance , but not the orthogonality nor the superposition .K e y w o r d s teaching , m o d e , c o m p l e x m o d e , nonlinear m o d e , vibration17世纪,人们开始对模态有所认识。
特征值和标准值

特征值和标准值特征值和标准值是数学和统计学中常用的概念,它们在数据分析和模型建立中起着重要的作用。
特征值是一个矩阵经过线性变换后,变换矩阵与原矩阵方向相同的非零向量所对应的实数λ,称为矩阵的特征值。
而标准值则是指在统计学中,将原始数据转化为具有特定均值和标准差的数值,以便进行比较和分析。
特征值和标准值在不同领域有着不同的应用,下面将分别对其进行详细介绍。
特征值在线性代数中有着重要的地位,它可以用来描述线性变换过程中的特征和性质。
在矩阵的特征值分解中,矩阵可以分解为特征向量和特征值的乘积形式,这种分解在很多数学和工程问题中都有着重要的应用。
例如,在物理学中,特征值可以用来描述量子力学中的物理量,它们是算符的本征值,可以用来描述量子态的性质和演化规律。
在工程学中,特征值可以用来描述振动系统的固有频率和振动模态,对于结构动力学和振动控制有着重要的应用。
在机器学习和模式识别中,特征值可以用来描述数据的特征和结构,是模型建立和数据分析的基础。
而标准值在统计学中有着广泛的应用,它可以用来对原始数据进行标准化处理,使得不同数据之间具有可比性。
在正态分布的情况下,标准值可以用来描述数据的相对位置和离散程度。
在质量管理和过程控制中,标准值可以用来描述产品质量和过程稳定性,是质量管理和过程改进的重要工具。
在心理学和教育学中,标准值可以用来描述测试成绩和学生表现,是评价和比较的基础。
在金融学和经济学中,标准值可以用来描述资产收益和风险水平,是投资决策和风险管理的重要指标。
总的来说,特征值和标准值在数学和统计学中有着重要的地位,它们是描述数据和模型的重要工具,对于理论研究和实际应用都具有重要的意义。
在实际问题中,我们需要根据具体情况选择合适的特征值和标准值,合理应用它们来描述和分析数据,从而得到准确的结论和有效的决策。
在实际应用中,我们需要注意特征值和标准值的计算方法和应用条件,避免盲目使用和错误解释。
特征值和标准值的选择和应用需要结合具体问题和数据特点,合理分析和判断,从而得到可靠的结果和有效的结论。
模态分析的目的和意义

模态分析的目的和意义模态分析是关于寻找特征值和特征向量。
特征值是关于知道对应于结构的一些基本振动模式的频率。
实践中,为了避开这些基频,防止共振,有时需要加强振动。
根据实际需要,基本固有频率可以给我们一个判断我们结构变形快慢的准则,基本固有频率也可以代表整个结构的刚度:频率低说明结构刚度很低(结构很软),反之频率高。
该结构的硬度根据需求而变化。
比如刚性的高层设计虽然不会晃动太大,但是不容易吸收地震能量。
相反,高层建筑的柔性设计往往可以吸收很多地震能量,虽然会晃动很多。
振动模式有什么实用价值?从振动状态的形状可以知道结构在某一固有共振频率下的变形趋势。
要加强结构的刚性,可以从这些薄弱部位加强。
举个例子,在高层建筑的设计中,如果模态分析显示最低频率的振动状态是在整个高层建筑的扭转方向,那就说明这个方向的刚度是首先要加强的部分。
模态截断理想情况下,我们希望得到结构的完整模态集,这在实际应用中既不可能也没有必要。
实际上,并非所有模式对响应的贡献都相同。
对于低频响应,高阶模态的影响较小。
就实际结构而言,我们往往对它的前几个或十几个模态感兴趣,高阶模态往往被丢弃。
虽然这样会造成一点误差,但是频响函数的矩阵阶次会大大降低,工作量也会大大减少。
这种处理方法称为模态截断。
实例解释模态分析简单地说,模态分析是根据用结构的固有特征,包括频率、阻尼和模态振型,这些动力学属性去描述结构的过程。
那只是一句总结性的语言,现在让我来解释模态分析到底是怎样的一个过程。
不涉及太多的技术方面的知识,我经常用一块平板的振动模式来简单地解释模态分析。
这个解释过程对于那些振动和模态分析的新手们通常是有用的。
考虑自由支撑的平板,在平板的一角施加一个常力,由静力学可知,一个静态力会引起平板的某种静态变形。
但是在这儿我要施加的是一个以正弦方式变化,且频率固定的振荡常力。
改变此力的振动频率,但是力的峰值保持不变,仅仅是改变力的振动频率。
同时在平板另一个角点安装一个加速度传感器,测量由此激励力引起的平板响应。
屈曲分析实例解析

屈曲分析屈曲分析- 分析内容屈曲分析主要用于研究结构在特定载荷下的稳定性以及确定结构失稳的临界载荷,屈曲分析包括:线性屈曲和非线性屈曲分析。
线弹性失稳分析又称特征值屈曲分析;线性屈曲分析可以考虑固定的预载荷,也可使用惯性释放;非线性屈曲分析包括几何非线性失稳分析,弹塑性失稳分析,非线性后屈曲(Snap-through)分析。
欧拉屈曲buckling结构丧失稳定性称作(结构)屈曲或欧拉屈曲。
L.Euler从一端固支另一端自由的受压理想柱出发.给出了压杆的临界载荷。
所谓理想柱,是指起初完全平直而且承受中心压力的受压杆。
设此柱是完全弹性的,且应力不超过比例极限,若轴向外载荷P小于它的临界值,此杆将保持直的状态而只承受轴向压缩。
如果一个扰动(如—横向力)作用于杆,使其有一小的挠曲,在这一扰动除去后。
挠度就消失,杆又恢复到平衡状态,此时杆的直的形式的弹性平衡是稳定的。
若轴向外载荷P大于它的临界值,柱的直的平衡状态变为不稳定,即任意扰动产生的挠曲在扰动除去后不仅不消失,而且还将继续扩大,直至达到远离直立状态的新的平衡位置为止,或者弯折。
此时,称此压杆失稳或屈曲(欧拉屈曲)。
屈曲分析- 分析分类线性屈曲:是以小位移小应变的线弹性理论为基础的,分析中不考虑结构在受载变形过程中结构构形的变化,也就是在外力施加的各个阶段,总是在结构初始构形上建立平衡方程。
当载荷达到某一临界值时,结构构形将突然跳到另一个随遇的平衡状态,称之为屈曲。
临界点之前称为前屈曲,临界点之后称为后屈曲。
侧扭屈曲:梁的截面一般都作成窄而高的形式,对截面两主轴惯性矩相差很大。
如梁跨度中部无侧向支承或侧向支承距离较大,在最大刚度主平面内承受横向荷载或弯矩作用时,荷裁达一定数值,梁截面可能产生侧向位移和扭转,导致丧失承载能力,这种现象叫做梁的侧向弯扭屈曲,简称侧扭屈曲。
理想轴向受压直杆的弹性弯曲屈曲:即假定压杆屈曲时不发生扭转,只是沿主轴弯曲。
但是对开口薄壁截面构件,在压力作用下有可能在扭转变形或弯扭变形的情况下丧失稳定,这种现象称为扭转屈曲或弯扭屈曲。
AMESim 线性分析
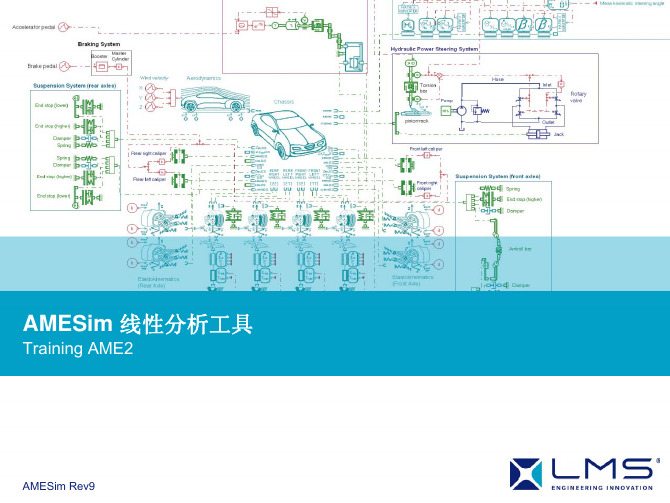
现在得到线性系统 :
k P k a பைடு நூலகம்k P P 1 2 1 3 S
with
k1
f B 2 1 1 Cq a10 a 20 P V ρ 2 Ps 0 P0 2 P0
k2
k3
f B 2 PSO P0 Cq u V ρ
f B 2 1 Cq a10 Ps V ρ 2 PSO PO
系统的自由响应 :
k P P 1
k1t
分析解:
Pt P0e
k1 = - 1/RC 为时间常数,由容积(C) 和阻力 (R) 构成
10 Copyright LMS Imagine - 2009
线性分析 – 第一个例子 : 一阶研究
线性分析 – 第一个例子 : 一阶研究
B Cq 2 a u P P a P P 1 s 2 V
与前一个表达式相关
代入 :
f P, u P
0 P
进行线性分析首先要找到平衡点,即是说
0
B 2 Cq a1 u Ps P a2 P V
6 Copyright LMS Imagine - 2009
线性分析 根轨迹:
根轨迹主要用来分析系统的稳定性并且代表了复数坐标下的特征 值
7 Copyright LMS Imagine - 2009
线性分析 – 第一个例子 : 一阶研究
例子 : 液阻 – 一个一阶系统
O1 Ps O2
Volume V Pression P
AMESim 线性分析工具
Training AME2
AMESim Rev9
内容
模态分析中的几个基本概念

模态分析中的几个基本概念物体按照某一阶固有频率振动时,物体上各个点偏离平衡位置的位移是满足一定的比例关系的,可以用一个向量表示,这个就称之为模态。
模态这个概念一般是在振动领域所用,你可以初步的理解为振动状态,我们都知道每个物体都具有自己的固有频率,在外力的激励作用下,物体会表现出不同的振动特性。
一阶模态是外力的激励频率与物体固有频率相等的时候出现的,此时物体的振动形态叫做一阶振型或主振型;二阶模态是外力的激励频率是物体固有频率的两倍时候出现,此时的振动外形叫做二阶振型,以依次类推。
一般来讲,外界激励的频率非常复杂,物体在这种复杂的外界激励下的振动反应是各阶振型的复合。
模态是结构的固有振动特性,每一个模态具有特定的固有频率、阻尼比和模态振型。
这些模态参数可以由计算或试验分析取得,这样一个计算或试验分析过程称为模态分析。
有限元中模态分析的本质是求矩阵的特征值问题,所以“阶数”就是指特征值的个数。
将特征值从小到大排列就是阶次。
实际的分析对象是无限维的,所以其模态具有无穷阶。
但是对于运动起主导作用的只是前面的几阶模态,所以计算时根据需要计算前几阶的。
一个物体有很多个固有振动频率(理论上无穷多个),按照从小到大顺序,第一个就叫第一阶固有频率,依次类推。
所以模态的阶数就是对应的固有频率的阶数。
振型是指体系的一种固有的特性。
它与固有频率相对应,即为对应固有频率体系自身振动的形态。
每一阶固有频率都对应一种振型。
振型与体系实际的振动形态不一定相同。
振型对应于频率而言,一个固有频率对应于一个振型。
按照频率从低到高的排列,来说第一振型,第二振型等等。
此处的振型就是指在该固有频率下结构的振动形态,频率越高则振动周期越小。
在实验中,我们就是通过用一定的频率对结构进行激振,观测相应点的位移状况,当观测点的位移达到最大时,此时频率即为固有频率。
实际结构的振动形态并不是一个规则的形状,而是各阶振型相叠加的结果。
模态扩展是为了是结果在后处理器中观察而设置的,原因如下:求解器的输出内容主要是固有频率,固有频率被写到输出文件Jobname.OUT及振型文件Jobnmae.MODE中,输出内容中也可以包含缩减的振型和参与因子表,这取决于对分析选项和输出控制的设置,由于振型现在还没有被写到数据库或结果文件中,因此不能对结果进行后处理,要进行后处理,必须对模态进行扩展。
模态相关概念

弹性力弹性物体因外力产生形变后的恢复力。
简称弹力。
形变也存在于物体内部,因此物体内部的各部分间都有弹性力相作用。
弹性力有各种名称:相互压缩时,称压力,垂直于物体表面的压力称法向压力;相互拉长时,称张力。
物体给平面或斜面的法向压力的反作用力,称支持力或反力,实质上也是压力。
一定范围内弹性力和变形程度成正比,这个范围称弹性限度。
在限度内,撤去外力,物体能恢复原状;超过这限度,变形程度不再和外力成正比,撤去外力后物体也不能恢复原状。
对弹簧来说,弹性力为F=-kx,x表示弹簧终端的位移,k 为弹性力和位移值之比,称刚度系数,负号表示弹性力的方向与位移的方向相反。
弹性力也是保守力,弹性力作功可用弹性势能表示,其值为,x为位移的值。
在外力作用下弹性物体形变后所产生的一种恢复力。
弹性力的特点是它在变形体上所做的功并不转化为热,但可转化为势能。
弹性力是一种保守力。
物体中任何两个质点相对位置的变化,称为物体变形。
当物体的形变很小时,弹性力F和物体中质点M开平衡位置时的位移成正比,其方向指向力图使质点复到平衡位置的方向。
固有振动固有振动是指物质系统在不受到与时间有关的外界作用而阻尼又可忽略的情况下所发生的振动。
又称自由振动、自然振动、本征振动(是天文学专有名词)。
固有振动的振幅决定于振动起始时系统所具有的能量。
固有振动的频率称为固有频率,只与振动系统的固有条件有关(如弹性和惯性,电容和电感等,见振动)。
物理系统(包括机械、电磁或其它类型的振动)从外界取得一定的能量开始振动以后,不再受外界作用而阻力又可忽略的情况下,仅在内部弹性力或准弹性力作用下,以固有频率而保持振幅恒定的振动状态叫“固有振动”。
固有振动的振幅决定于系统开始振动时所具有的能量,但频率则完全取决于系统本身的性质。
例如被击动后鼓膜的振动,弹簧振子偏离平衡位置后无外力作用下的振动等都是“自由振动”。
自由振动在外力使弹簧振子的小球和单摆的摆球偏离平衡位置后,它们就在系统内部的弹力或重力作用下振动起来,不再需要外力的推动,这种振动叫做自由振动。
模态阶数介绍

模态阶数物体按照某一阶固有频率振动时,物体上各个点偏离平衡位置的位移是满足一定的模式的,可以用一个整体模型的向量表示,这个就称之为对应于该固有频率的模态。
模态这个概念一般应用于振动领域,它代表一种振动状态。
每个物体都有自己的固有频率,在外力的激励作用下,物体会表现出不同的振动特性。
一阶模态是物体发生共振的最低频率,当外力激励的频率与该频率相等时发生,此时物体的振动模式叫做一阶振型或主振型;二阶模态是外力的激励频率等于物体最低共振频率的两倍时候出现,此时的振动模式叫做二阶振型,以依次类推。
一般来讲,外界激励的频率是非常复杂的,物体在这种复杂的外界激励下的振动反应是各阶振型的复合叠加。
模态属于结构的固有特性,每一个模态具有特定的固有频率、阻尼比和模态振型。
固有频率、阻尼比、振型可以由计算或试验分析取得,计算或试验分析过程被称为模态分析。
从原理上讲,数值计算中模态分析的本质是求矩阵的特征值问题,所以“阶数”就是指特征值的个数。
将特征值从小到大排列就是阶次,理论上一个矩阵是有无限个特征值的,所以其模态具有无穷阶。
但是对于运动起主导作用的只是前面的几阶模态,所以计算时根据需要只计算前几阶即可。
矩阵的特征值求解中,每个特征值都对应着一个特征向量,特征向量就是模态,因此特征值的阶数就是模态的阶数。
每个特征向量反应在实际物体上就代表着一种振型。
每一个特征值都对应着一个固有频率,每个特征频率都对应着一种振型。
此处的振型就是指在该固有频率下结构的振动模式,由矩阵的特征值求解可知,特征值越大,对应的特征向量就越小,因此,反应在实际物体上,频率越高则振动周期越小。
在模态分析的实验中,使用一定频率的激励施加在结构上,观测整个物体的位移情况,当物体的振动位移达到最大时,此时频率即为固有频率。
与数值计算不同的是,试验得到的振动模式并不完全是对应于该激励频率(对应于该激励频率对应的特征值)的特征向量,而是所有特征向量的叠加。
模态分析理论

模态分析指的是以振动理论为基础、以模态参数为目标的分析方法..首先建立结构的物理参数模型;即以质量、阻尼、刚度为参数的关于位移的振动微分方程;其次是研究其特征值问题;求得特征对特征值和特征矢量;进而得到模态参数模型;即系统的模态频率、模态矢量、模态阻尼比、模态质量、模态刚度等参数..特征根问题以图3所示的三自由度无阻尼系统为例;设123m =m =m =m ;123k =k =k =k ;图 1 三自由度系统其齐次运动方程为: 8其中分别为系统的质量矩阵和刚度矩阵;123m 00m 00m=0m 0=0m 000m 00m ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦;11212221k -k 0k -k 0k=-k k +k -k =-k 2k -k 0-k k 0-k k ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦;则运动方程展开式为:¨11¨22¨33z m 00k k 0z 00m 0z k 2k k z 000m 0k k z 0z ⎡⎤⎢⎥-⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+--=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦9定义主振型由于是无阻尼系统;因此系统守恒;系统存在振动主振型..主振型意味着各物理坐标振动的相位角不是同相相差0o 就是反相位相差180o ;即同时达到平衡位置和最大位置..主振型定义如下:()i ij ωt+i i sin ωt+=Im(e)φφi mi mi z =z z 10其中为第i 阶频率下;各自有度的位移矢量;为第i 个特征矢量;表示第i 阶固有频率下的振型;i ω为第i 阶频率下的第i 个特征值;i φ为初始相位..对于三自由度系统;在第i 阶频率下;等式可以写成1m1i 2m2i i i 3m3i z z z =z sin(ωt+)z z φ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦11mki z 表示第k 个自由度在第i 阶模态下的模态矩阵..特征值对式10二次求导;得2i i i =-ωsin(ω+)φ¨i mi z z 12代入齐次运动方程得13去除项化简得14以矩阵的形式展开得:2i 2i mi 2i k-ωm -k 0-k 2k-ωm -k z =00-k k-ωm ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦15 有非零解;则2i 2i 2i k-ωm -k 0-k 2k-ωm -k =00-k k-ωm ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦16即()234222ω-m ω+4km ω-3k m =0 17方程解如下:1ω=0;23k ω=m ±;3kω=m±..三个解对应该系统的前三阶固有频率;每一个特征根对应一个特征矢量;表示对应模态下该系统的振型..特征矢量由式得矩阵展开形式:2i m1i 2i m2i 2i m3i k-ωm -k 0z -k 2k-ωm -k z =00-k k-ωm z ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ 18 展开第一行和第二行;忽略下脚标m 和i;得()()2i1221i3k-ωm z -kz =0-kz 2k-ωm kz+-= 19得22i 124223ii21z k-ωm =z k z m ω-3km ω+k =z k 20如果设定了1z 值;则就可以求出三个特征根值下;2z 和3z 相对于1z 的位移..假设m=k=1;一阶模态;1ω=0:21z =1z ;31z =1z ;即;二阶模态;223k ω=m :21z =0z ;31z =-1z ;即;三阶模态;23kω=m :21z =-2z ;31z =1z ;即..模态矩阵所谓模态矩阵就是指各列由各阶模态特征矢量构成的矩阵;如图4所示..图 2 模态矩阵对于前面提到的三自由度系统;模态矩阵如下:运动方程的解耦对于一个复杂的系统;在物理坐标系统中建立的运动方程之间存在耦合关系;因此求解起来比较麻烦;因此需要进行坐标系转化;将耦合的运动方程变为非耦合的运动方程;再将求得的结果转化为物理坐标系下的结果;运动方程解耦过程如下图5:图 3 运动方程解耦过程在进行坐标变换之前需对刚度矩阵和质量矩阵进行归一化..任意上面的三自由度系统为例;由式得2122 对式21左乘得23 又因为因为系统对称所以;;则:24 对式24右乘25 则式23—式25得26 当时;则27 当;即;则可以为任何值;令28 则对质量矩阵和刚度矩阵的归一化结果如下:2930特征矢量的归一化由于特征矢量只是位移之比;而不是绝对振幅;因此可以对其进行归一化处理..令;其中3132对于对角质量矩阵33则三自由度系统:343m 2m 6m 326=003m 6m m 363m2m6m 326n z 35 则归一化的质量矩阵为100010001⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦Tn n n m =z mz 36 同理归一化后的刚度矩阵为000k =010m003⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦n k 37可以看出归一化后的刚度矩阵对角线上的各项就是各阶模态固有频率的平方..运动方程解耦将物理坐标系下的运动方程¨11¨22¨33z m 00k -k 0z 0 0m 0z +-k 2k -k z =000m 0-k k z 0z ⎡⎤⎢⎥⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦按照前面介绍的归一化方法转化为主坐标系下的运动方程;其结果如下:¨p1p1¨p2p2¨p3p30z 00z 0k 00z +-k z =0m 00z 03k z 0-km 001101⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦38 可以看出在主坐标系中的运动方程之间没有耦合关系;分别单独描述各阶模态的运动特性..初始条件和激励的坐标转换物理坐标系中的非齐次运动方程为..mz+kz =F 39做如下变形..T -1T -1Tnn nn n n n z mz z z+z kz z z =z F 40 其中T n n z mz ;Tn n z kz 就是前面介绍的质量和刚度矩阵的对角化.. 令Tp n n m =z mz ;主坐标质量矩阵;Tp n n k =z kz ;主坐标刚度矩阵; ....-1p nz z =z ;主坐标系加速度矢量;-1n p z z =z ;主坐标系位移矢量; T n p z F =F ;主坐标系激励矢量..同样的关系也适用于初始位移和速度:-1op n o ..-1op n o z =z z z =z z 42两种坐标系的对比物理坐标系主坐标系物理坐标系中的运动方程的变量是速度和位移;在主坐标系中的变量是各阶振动模态下的位移和速度..由主坐标系转变为物理坐标系前面介绍了物理坐标系与主坐标系之间的关系为-1n p z z =z 43对式41左乘n z ;变为=-1n n n p z z z =z z z 44同理p =..n z z z 45非参数模型传递函数传递函数由系统的本质特性所决定;与系统的输入输出无关..知道了系统的传递函数就可以根据输入求输出或根据输出求输入..以图2的单自由度粘性阻尼系统为例;图 4 单自由度系统则该系统的运动方程为:...m z +c z +kz=F 1其中m 为质量;c 为阻尼系数;k 为刚度系数;z;分别为位移、速度和加速度..对二阶微分方程进行拉普拉斯变换;其中二阶导数项的拉普拉斯变换为:2假设初始位移和速度都为零;则3则经过拉普拉斯变换后的运动方程为:4求解拉氏方程得传递函数:22z(s)11/m==c k F(s)ms +cs+k s +s+m m5 其中定义2n kω=m为非阻尼系统的固有频率;rad/sec ;cr c 2km =阻尼值;ζ为阻尼比;一般为阻尼与临界阻尼的比值;cr c =c ζ;则n c 2ω=mζ.. 则传递函数又可以写成:22n nz(s)1/m=F(s)s +2ωs+ωζ 6 频响函数FRF用“j ω”代替s;得系统的频响函数;其中j 是虚数项:()()22n n 22n n z(j ω)1/m=F(j ω)j ω+2ζωj ω+ω1/m=-ω+2ζωωj+ω 7其中n kω=m ;=2kmζ则频响函数可以写成2z(j ω)1=F(j ω)-m ω+j ωc+k8 质量、阻尼、刚度对FRF 的影响刚度增大导致共振频率的增大;并且降低FRF 在低频段的幅值..增加阻尼会使共振频率略微减小;但它的主要作用是减小频响函数在共振点的幅值;同时使相位的改变较为平缓..如果阻尼为零;在共振点振动振幅将趋于无穷大;相位会突变180o ..增大质量会降低共振频率;同时也降低FRF 在高频段的幅值..。
第9章 分析控制(Analysis)(新)(patran工程计算仿真)
Attach XDB
Object设成“attach XDB” 设成“ 设成 “Select Result File” 选“*.xdb”文件 文件 Apply
Attach后,Patran可在 后 可在 Result 或Insight中访问 中访问xdb 中访问 数据库进行图形后处理
Read Ouput2
Patran支持的 种分析类型 支持的10种分析类型 支持的
•线性静力(linear Static) 线性静力( 线性静力 ) •非线性静力(nonlinear Static) 非线性静力( 非线性静力 ) •自然模态(normal Modes) 自然模态( 自然模态 ) •屈曲分析(buckling) 屈曲分析( 屈曲分析 ) •复特征值模态(complex Eigenvalue) 复特征值模态( 复特征值模态 ) •频率响应(frequent Response) 频率响应( 频率响应 ) •瞬态响应(transient Response) 瞬态响应( 瞬态响应 ) •非线性瞬态响应(nonlinear Transient) 非线性瞬态响应( 非线性瞬态响应 ) •非线性冲击(implicit nonlinear) 非线性冲击( 非线性冲击 ) • (DDAM solution) )
patran支持的10种分析类型?线性静力linearstatic?非线性静力nonlinearstatic?自然模态normalmodes?屈曲分析buckling?复特征值模态complexeigenvalue?频率响应frequentresponse?瞬态响应transientresponse?非线性瞬态响应nonlineartransient?非线性冲击implicitnonlinearddamsolution除静力分析外其他分析类型都需进一步指定求解参数不同分析类型要求给定不同参数这些都在点solutionparameters按钮后出现的界面中指定
理解特征值、主振动和模态

理解特征值、主振动和模态陈奎孚中国农业大学应用力学系摘要 分析多自由度系统的主振动特性时,传统振动教材的某些处理方式值得进一步斟酌。
比如,用假设解的办法引入特征值概念,感觉比较生硬。
对模态振型的理解也比较突兀和抽象。
本文通过解耦方式引入特征值问题,在逻辑上比较自然。
而通过快照叠放图的方式引入振型则有助于直观理解模态的意义。
关键词 振动;特征值;模态;快照叠放图对N 自由度无阻尼线性系统或系统作微幅振动,最后都得到如下的振动微分方程组 []{}[]{}{0}M x K x += (1) 其中{}x 表征各自由度位移的1N ×向量,[][]M K 和均为N N ×的实对称矩阵,其中[]M 正定而[]K 半正定。
1. 传统处理中的问题为了分析上述方程和理解振动物理特性,在绝大多数教科书中都是通过如下的方式引入数学特征值的概念的。
即假定 {}{}sin()x X pt ϕ=+ (2) 其中{}X 为各自由度的振动幅度,p ϕ和分别为振动频率和初相位。
将式(2)代入方程(1)有2([][]){}sin(){0}p M K X pt ϕ−++=将sin()pt ϕ+约去可得2([][]){}{0}p M K X −+=或者[]{}[]{}M X K X λ= (3)其中2p λ=。
式(3)就是广义特征值问题。
式(2)的假设当然最终是正确的,但是从理解角度来讲,这种假定有生硬的感觉。
首先解为什么要假定为简谐函数的形式?难道就没有其他形式的解吗?其次,即使假定了简谐形式,为什么各个自由度规律都是以相同的频率振动?第三,为什么振动的初相位对各自由度也相同?怎样直观地理解主振动呢?对上述问题,教科书是避而不谈的。
本文将从对方程(1)解耦角度逻辑地过渡特征值问题(3)。
进一步采用了快照叠放图来实现对主振动的直观理解。
2. 方程解耦方程(1)建立后的下一步就是要求解该方程,但这组方程之间是耦合的([]M 或[]K 非对角)。
结构模态及频率响应分析与优化设计

结构模态及频率响应分析与优化设计结构模态及频率响应分析与优化设计是结构工程中的重要内容。
通过对结构的模态分析和频率响应分析,可以了解结构的振动特性和动态响应,并通过优化设计来改善结构的性能。
结构模态分析是指通过数值模拟和计算方法,计算结构在自由振动状态下的固有频率和振型。
固有频率是结构的固有特性,振型则是结构在特定频率下的振动形态。
通过模态分析,可以了解结构的固有频率分布情况,以及各个模态的振型特征。
模态分析的步骤主要包括:建立结构的有限元模型、求解结构的特征值问题、计算模态振型和固有频率。
有限元模型是通过离散化方法将结构划分为有限个单元,并根据单元的性质和连接关系构建刚度矩阵和质量矩阵。
求解特征值问题即求解结构的特征值和特征向量,通常采用迭代计算方法。
计算模态振型和固有频率则是根据特征值和特征向量计算得到的结果。
通过模态分析,可以得到结构的固有频率和振型信息,进而对结构的振动特性进行分析和评估。
例如,可以判断结构是否存在共振现象,即结构在某一频率下受到外力激励时,振动幅值会不断增大。
共振会引发结构的破坏和失稳,因此需要避免共振频率与外力频率相近的情况。
另外,模态分析还可以用于结构的设计优化,例如通过调整结构的几何形状、材料参数或支撑条件等,来改变结构的固有频率和振型,从而满足设计要求。
频率响应分析是指通过数值模拟和计算方法,计算结构在受到外力激励时的动态响应。
频率响应分析可以用于评估结构的动态性能和振动稳定性,以及分析结构在地震、风荷载等自然灾害下的响应情况。
频率响应分析的步骤主要包括:建立结构的有限元模型、施加外力激励、求解结构的动态响应。
有限元模型的建立和求解方法与模态分析类似,不同之处在于需要施加外力激励,即将结构在受力条件下进行分析。
外力激励可以是单点力、均布载荷、地震波等。
求解结构的动态响应则是通过数值计算方法,计算得到结构在不同频率下的振动幅值和相位。
通过频率响应分析,可以得到结构在不同频率下的振动响应情况,进而判断结构是否满足设计要求。
使用Matlab技术进行模态分析的基本步骤

使用Matlab技术进行模态分析的基本步骤引言:模态分析是一种有效的结构动力学分析方法,可以用来研究结构系统的固有振动特性,以及结构的响应模态。
Matlab作为一种强大的数值计算软件,提供了丰富的工具和函数,可以用于执行模态分析。
本文将介绍使用Matlab技术进行模态分析的基本步骤。
一、数据准备在进行模态分析之前,首先需要准备结构系统的数据。
这些数据包括结构的几何信息、材料参数、截面性能等。
在Matlab中,可以使用矩阵或数据文件的方式存储这些数据,并将其导入到Matlab工作环境中。
二、建立有限元模型建立结构的有限元模型是进行模态分析的基础。
在Matlab中,可以使用专门的有限元工具或编写自定义的有限元程序来建立结构的有限元模型。
根据结构的几何形状和边界条件,将结构划分为一系列的有限元单元,并建立单元之间的连接关系。
通过定义单元的材料属性和截面性能,可以完善有限元模型。
三、求解结构的特征值问题模态分析的核心是求解结构的特征值问题,即计算结构的固有频率和模态形态。
在Matlab中,可以使用特征值求解函数如“eig”或“eigs”来求解特征值问题。
将有限元模型转化为刚度矩阵和质量矩阵,并通过特征值求解函数计算特征值和对应的特征向量。
特征值代表结构的固有频率,特征向量代表结构的模态形态。
四、结果后处理通过求解特征值问题,可以得到结构的固有频率和模态形态。
在Matlab中,可以使用绘图函数如“plot3”或“mesh”来展示模态形态。
绘制出模态形态的空间图像,可以直观地观察结构的振动特性。
此外,还可以计算和分析结构的模态阻尼比和模态参与系数等参数,进一步分析结构的动态特性。
五、模态分析的应用模态分析在工程领域有着广泛的应用。
通过对结构的模态分析,可以识别结构的固有频率,了解结构的振动模态,为结构的设计和优化提供指导。
例如,在桥梁工程中,模态分析可以用来评估结构的动力特性,预测回响频率,判断结构的稳定性。
阻尼

阻 尼系统结构特征值和模态的求解是在无阻尼情况下得到的,而在动力学问题中,任意结构都应存在或大或小的阻尼,阻尼的大小对系统的动力学响应将产生一定的影响。
本章主要讨论在动力学分析中怎样应用ABAQUS 定义系统的阻尼特性。
引言当系统作无阻尼自由振动时,由于没有能量输入与输出,系统机械能守恒,系统的振幅为常数。
然而在实际结构中,这种无阻尼自由振动并不存在。
结构运动时能量耗散,振幅将逐渐减小直至停止振动,这种能量耗散被称为阻尼(damping)。
通常假定阻尼为粘性的,其大小正比于速度,方向与速度相反。
有阻尼结构系统的动力学方程可以写为:0MuI P +−=&& (4.1.1) I Ku Cu=+& (4.1.2) 其中, C 为结构的阻尼矩阵,u&为结构的速度。
能量耗散来源于几个因素,其中包括结构连接处的摩擦和局部材料的迟滞效应。
阻尼对于表征结构吸收能量是一个很方便的方法,它包含了重要的能量吸收过程,而不需要模拟耗能的具体机制。
阻尼在ABAQUS/Standard 中,特征模态的计算是从无阻尼系统中提取出的。
然而,大多数工程问题都包含某种阻尼,尽管阻尼可能很小。
对于每一模态,有阻尼固有频率和无阻尼固有频率之间的关系是:d ω= (4.2.1)其中d ω是有阻尼的固有频率;cc c ξ=为临界阻尼;c 是该模态的阻尼,0c 是该模态的临界阻尼。
当临界阻尼ξ取较小值(< 0.1ξ)时,有阻尼系统的特征频率和特征向量与无阻尼系统非常接近;随着ξ的增加,采用无阻尼系统求得的特征频率就会变得不太准确,当ξ接近1时,无阻尼特征频率和特征向量就失效了。
但是,大多数用线性动力学分析的结构问题只有很小的阻尼,因而可以采用无阻尼特征频率。
当结构处于临界阻尼即1ξ=时,施加一个扰动后,结构不会振荡,而是尽可能迅速地恢复到它的初始静止构形,如图4.2.1所示。
图4.2.1 阻尼在ABAQUS中定义阻尼在ABAQUS中阻尼可以应用在下面的动力学分析中:z非线性问题直接积分求解(显式分析或者隐式分析);z直接法或子空间法稳态动力学分析;z模态动力学分析(线性)。
模态中的特征值

模态中的特征值
在模态分析中,特征值是非常重要的概念,它们描述了系统的稳定性和性能。
特征值实部和虚部是反映系统特性的两个重要参数。
实部表示系统的稳定性,虚部表示系统的响应性能。
模态特征值可以通过系统模型获得。
例如,使用数学模型描述控制系统的行为,包括系统的输入、输出和内部动态,通过分析模型,可以获得系统的模态特征值。
总之,模态特征值是用来描述系统模态特性的一种方式,对于理解和分析系统的动态行为具有重要意义。
matlab复模态分解求解方程的特征值

Matlab复模态分解求解方程的特征值1. 简介复模态分解(Complex Modal Decomposition,CMD)是一种用于分解复杂信号的方法,可以将信号分解为一组复模态函数(Complex Modal Functions,CMFs)和相应的复模态系数(Complex Modal Coefficients,CMCs)。
CMD广泛应用于信号处理、图像处理、模式识别等领域。
本文将介绍如何使用Matlab进行复模态分解,并利用分解得到的复模态函数求解方程的特征值。
具体而言,我们将使用Matlab中的CMD工具箱,通过编写代码实现该功能。
2. 复模态分解2.1 复模态函数和复模态系数复模态分解将信号分解为一组复模态函数和相应的复模态系数。
复模态函数是一组基函数,可以描述信号的不同频率和振幅成分。
复模态系数是每个复模态函数的权重,用于表示信号中各个频率和振幅成分的贡献程度。
2.2 复模态分解的步骤复模态分解的过程可以简要描述如下:1.将信号进行Hilbert变换,得到解析信号。
2.对解析信号进行奇异值分解(Singular Value Decomposition,SVD),得到解析信号的模态函数和模态系数。
3.根据模态函数和模态系数重构信号。
2.3 Matlab中的CMD工具箱Matlab中有多个CMD工具箱可供选择,如Hilbert-Huang变换工具箱、Empirical Mode Decomposition工具箱等。
在本文中,我们将使用Hilbert-Huang变换工具箱进行复模态分解。
3. 求解方程的特征值3.1 求解特征值的方法求解方程的特征值是一种常见的问题,可以通过多种方法进行求解,如传统的特征值分解方法、数值计算方法等。
在本文中,我们将利用复模态函数来求解方程的特征值。
3.2 使用复模态函数求解特征值的步骤使用复模态函数求解特征值的步骤如下:1.将方程转化为矩阵形式。
2.对矩阵进行复模态分解,得到复模态函数和复模态系数。
模态计算

模态计算
分析原理
特征值是构件的一种固有属性,一个构件一旦制造出来,其特征值就是固定的。
与特征值相对应的是模态,模态对于的频率是共振频率。
模态实际上是有限元模型中各节点的位移的一种比例关系,在线性空间中,不同的模态之间是相互垂直的,它们构成了位移线性空间,并可以作为这个线性空间中的坐标轴。
问题描述
对该构件进行响应计算
边界条件
一端孔固定,一端孔施加随时间变化的载荷。
材料参数
材料为铁材,单元厚度T=0.2mm,集中力F=sin(360*200*t)N。
分析结果
第3阶119.6Hz 第9阶1031Hz
约束点
加载点网格模型
卡片控制
Load step(case)
SOL求解卡片设置(模态计算)
TIME求解时长设置
PARAM输出文件设置
CASE_UNSUPPORTED_CARDS
GLOBAL_OUTPUT_REQUEST输出数据控制。
屈曲模态特征值规范要求

屈曲模态特征值规范要求有着如下七条的规范要求:要求1、屈曲模态特征值是理想化的情况,现实结构中并不会发生。
所以对其数值模拟的准确性、可靠性较低,实用价值不高,不过对于均匀材质的结构,可以先计算其特征值屈曲,为以后的深入计算提供依据;2、屈曲模态特征值,仅考虑结构的线性行为。
所以,初学者们不要被名字吓倒。
至于有初始变形、残余应力等都不属于特征值屈曲考虑的范围之内;3、ansys的屈曲模态特征值分析中,计算结果得到的是屈曲荷载系数和屈曲模态,其中屈曲荷载系数更重要,因为将系数与外加荷载相乘,结果便是屈曲荷载;4、创建屈曲模态特征值模型的过程中,对于两点连一线的杆件,尽量考虑对其多划分几段网格,也就是说尽量不要把两点连线作为一个杆件单元,因为那样会使得计算结果不准确;5、必须激活屈曲模态特征值预应力选项——即便计算中不包含预应力效应。
因为只有激活该选项才能使得几何刚度矩阵保存下来;6、关于屈曲模态特征值恒载与活载。
结构可能会同时收到恒载与活载的作用,而得到的屈曲荷载系数将会对所有荷载进行缩放——不分恒载与活载。
这时候需要将二者区分开来,毕竟在多次试算过程中,恒载的作用效应是不应该变化的。
这时的操作方法就是:调整活载的数值,重新计算,目标是使得到的屈曲荷载系数为1、0(或者非常接近1、0)。
结果,屈曲荷载就等于“恒载+修正之后的活载”;7、有预应力存在情况下的考虑屈曲模态特征值。
在假设前提是“允许结构发生变形”之后,在施加预应力操作完成时,结构已经发了微小的变形,而这种变形又在一定程度上改变了原来的张拉力。
说白了,就是“一把张满的弓,松了一下,弦中的力会有变化”。
所以在施加预应力的时候要考虑这一点,从而把这段可能会被损失掉的张拉力算进最开始的预应力中,以保证屈曲分析过程中预应力与设计相符。
