平面切割圆锥PPT.ppt
合集下载
人教版中职数学9.4.4圆柱圆锥一ppt课件

什么样的几何体叫做圆柱,圆锥? 这些几何体分别是由什么平面图形旋转而成的?
以矩形的一边所在直 线为旋转轴,其余边旋转 形成的曲面所围成的几何 体叫做圆柱.
以直角三角形的一条直 角边所在直线为旋转轴,其 余两边旋转形成的曲面所围 成的几何体叫做圆锥.
旋转轴叫做它们的轴, 在轴上的这条边(或它的长度)分别 叫做它们的高, 垂直于轴的边旋转而成的圆面分 别叫做它们的底面, 不垂直于轴的边旋转而成的曲面 分别叫做它们的侧面, 无论旋转到什么位置,这条边都 叫做侧面的母线.
S
设圆锥的母线长为y,小圆锥底 面与圆锥底面半径分别是x,4x, 根据相似三角形的性质得
x y
3 x y 4x
所以y=12. 即圆锥母线长为12cm.
A 4x OO
B
证明:平行于圆锥底面的截面与底面的面积的比,等 于顶点到截面的距离与圆锥的高的平方比 .
r O
l
2r
O
c
圆柱的侧面展开图是矩形
S圆柱侧面积 cl =2rl
圆锥的侧面展开图是扇形
S圆锥侧面积
1 半径为3,母线长为6, 求该圆柱的全面积. 54
2 .已知圆锥的底面半径为2,母线长为4, 求该圆锥的全面积以及侧面展开图的圆心角. 12
圆柱
圆锥
以矩形的一边所在直线为 以直角三角形的一条直角
旋转轴,其余边旋转形成 边所在直线为旋转轴,其
轴 高 底面
母线 侧面
问题一 用一个平行于底面的 平面去截圆柱和圆锥,它们的截 面是什么形状? 问题二 过它们的轴的平面去 截圆柱和圆锥,所得截面分别是 什么形状?
圆柱、圆锥有下面的性质:
(1) 平行于底面的截面是圆;
(2)过轴的截面(轴截面)分别是矩形、等腰三角形.
以矩形的一边所在直 线为旋转轴,其余边旋转 形成的曲面所围成的几何 体叫做圆柱.
以直角三角形的一条直 角边所在直线为旋转轴,其 余两边旋转形成的曲面所围 成的几何体叫做圆锥.
旋转轴叫做它们的轴, 在轴上的这条边(或它的长度)分别 叫做它们的高, 垂直于轴的边旋转而成的圆面分 别叫做它们的底面, 不垂直于轴的边旋转而成的曲面 分别叫做它们的侧面, 无论旋转到什么位置,这条边都 叫做侧面的母线.
S
设圆锥的母线长为y,小圆锥底 面与圆锥底面半径分别是x,4x, 根据相似三角形的性质得
x y
3 x y 4x
所以y=12. 即圆锥母线长为12cm.
A 4x OO
B
证明:平行于圆锥底面的截面与底面的面积的比,等 于顶点到截面的距离与圆锥的高的平方比 .
r O
l
2r
O
c
圆柱的侧面展开图是矩形
S圆柱侧面积 cl =2rl
圆锥的侧面展开图是扇形
S圆锥侧面积
1 半径为3,母线长为6, 求该圆柱的全面积. 54
2 .已知圆锥的底面半径为2,母线长为4, 求该圆锥的全面积以及侧面展开图的圆心角. 12
圆柱
圆锥
以矩形的一边所在直线为 以直角三角形的一条直角
旋转轴,其余边旋转形成 边所在直线为旋转轴,其
轴 高 底面
母线 侧面
问题一 用一个平行于底面的 平面去截圆柱和圆锥,它们的截 面是什么形状? 问题二 过它们的轴的平面去 截圆柱和圆锥,所得截面分别是 什么形状?
圆柱、圆锥有下面的性质:
(1) 平行于底面的截面是圆;
(2)过轴的截面(轴截面)分别是矩形、等腰三角形.
3.1、3.2、3.3 平行射影 平面与圆柱面的截线 平面与圆锥面的截线 课件(人教A选修4-1)

6-2 2,
A′B2+A′C2-BC2 6- 3 cos ∠BA′C= = . 3 2A′B· A′C
[例2]
如图,在圆柱O1O2内嵌入双球,使它们
与圆柱面相切,切线分别为⊙O1和⊙O2,并且和圆 柱的斜截面相切,切点分别为F1、F2. 求证:斜截面与圆柱面的截线是以F1、F2为焦 点的椭圆.
[思路点拨]
线射影若是同一条直线,则两直线必共面,这与a、b异
面矛盾,所以③错,故正确答案:①②④.
答案:①②④
2.梯形ABCD中,AB∥CD,若梯形不在α内,则它在α 上的射影是____________. 解析:如果梯形ABCD所在平面平行于投影方向,则梯
形ABCD在α上的射影是一条线段.
如果梯形ABCD所在平面不平行于投影方向,则平行线 的射影仍是平行线,不平行的线的射影仍不平行,则梯 形ABCD在平面α上的射影仍是梯形. 答案:一条线段或梯形
知PF1=PK1,PF2=PK2,
所以PF1+PF2=PK1+PK2=K1K2. 由于K1K2为定值,故点P的轨迹是以F1、F2为焦点的椭圆.
(1)证明平面与圆柱面的截线是椭圆,利用Dandelin
双球确定椭圆的焦点,然后利用椭圆的定义判定曲线的
形状. (2)该题使用了切线长定理的空间推广 (从球外一点 引球的切线,切线长都相等).
为A沿l的方向在平面α上的平行射影.
一个图形上各点在平面α上的平行射影 所组成的图形,叫 做这个图形的平行射影.
3.正射影与平行射影的联系与区别 正射影与平行射影的投影光线与投影方向都是平行
的.因此,正射影也是平行射影,不同的是正射影的光
线与投影面垂直.而平行射影的投影光线与投影面斜 交.平面图形的正射影与原投影面积大小相等.而一般 平行射影的面积要小于原投影图形的面积.
识图与制图 3.3-曲面体及曲面切割体三视图的绘制与识读(2)(圆锥体)

基本体三视图的绘制 与识读
第三章 基本体三视图的绘制与识读
目录
contents
3.1 三视图及三视图的关系
3.2 平面体及平面切割体三视图的绘制与识读
3.3 曲面体及曲面切割体三视图的绘制与识读
3.4 相交两基本体的投影
3.5 基本体的尺寸标注
二、圆锥体
1、圆锥体的组成
由圆锥面和底面组成。
2、圆圆锥锥体面的是三由视直图线SA 绕与它相交的轴线OO1旋 转3、而轮成廓。线素线的投影与
1.空间分析 2.作图
求特殊点 求中间点 光滑连接 补轮廓线
三、圆球
1、圆球的形成
圆母线以它的 直径为轴旋转而成。
2、圆球的三视图
k
三个视图分别为三
个3、和圆轮球廓的线直的径投相影等的与曲 圆,它面们可分别见是性圆的球判三断
个方向轮廓线的投影。
4、圆球面上取点
k
辅助圆法
k
圆的半径?
5、圆球的截切
平面与圆球相交,截交线的形状都是圆, 但根据截平面与投影面的相对位置不同,其截交 线的投影可能为圆、椭圆或积聚成一条直线。
例3:求半球体截切后的俯视图和左视图。
两个侧平面截圆球的截交线 的投影,在侧视图上为部分 圆弧,在俯视图上积聚为直 线。
例3:求半球体截切后的俯视图和左视图。
两个侧平面截圆球的截交线 的投影,在侧视图上为部分 圆弧,在俯视图上积聚为直 线。
四、复合回转体的截切
例:求作顶尖的俯视图
●
●
●●
●
●●
●
●
●
●
● ●
● ●
●
首先分析复合回转体由哪些基本回转体组成以及它们 的连接关系,然后分别求出这些基本回转体的截交线,并 依次将其连接。
第三章 基本体三视图的绘制与识读
目录
contents
3.1 三视图及三视图的关系
3.2 平面体及平面切割体三视图的绘制与识读
3.3 曲面体及曲面切割体三视图的绘制与识读
3.4 相交两基本体的投影
3.5 基本体的尺寸标注
二、圆锥体
1、圆锥体的组成
由圆锥面和底面组成。
2、圆圆锥锥体面的是三由视直图线SA 绕与它相交的轴线OO1旋 转3、而轮成廓。线素线的投影与
1.空间分析 2.作图
求特殊点 求中间点 光滑连接 补轮廓线
三、圆球
1、圆球的形成
圆母线以它的 直径为轴旋转而成。
2、圆球的三视图
k
三个视图分别为三
个3、和圆轮球廓的线直的径投相影等的与曲 圆,它面们可分别见是性圆的球判三断
个方向轮廓线的投影。
4、圆球面上取点
k
辅助圆法
k
圆的半径?
5、圆球的截切
平面与圆球相交,截交线的形状都是圆, 但根据截平面与投影面的相对位置不同,其截交 线的投影可能为圆、椭圆或积聚成一条直线。
例3:求半球体截切后的俯视图和左视图。
两个侧平面截圆球的截交线 的投影,在侧视图上为部分 圆弧,在俯视图上积聚为直 线。
例3:求半球体截切后的俯视图和左视图。
两个侧平面截圆球的截交线 的投影,在侧视图上为部分 圆弧,在俯视图上积聚为直 线。
四、复合回转体的截切
例:求作顶尖的俯视图
●
●
●●
●
●●
●
●
●
●
● ●
● ●
●
首先分析复合回转体由哪些基本回转体组成以及它们 的连接关系,然后分别求出这些基本回转体的截交线,并 依次将其连接。
《机械制图》平面截切圆锥

平面截切圆锥
二、平面截切圆锥
1. 基本形式
规律: 1.随着平面的倾斜程度(即 平面与轴线的夹角θ)而变 化 2.呈现出五种形状:圆、椭 圆、抛物线、双曲线和直线 3.Ⅰ、Ⅱ的主视图中,截平 面与两条素线相交 4.Ⅲ、Ⅳ的主视图中,截平 面与一条素线相交 5.Ⅴ的主视图中,截平面把 一条素线切掉。
5
机械制图
MECHANICAL DRAWING
目录
CONTENTS
平面截切圆锥
平面截切圆锥 一、内容回顾
斜切横置圆柱 两侧切直立圆柱 中间切直立圆柱 侧切、中间切直立圆柱 中间切直立圆筒 圆柱综合切
由易到难
3
由浅入深
平面截切圆锥 二、平面截切圆锥
斜切圆锥
4
竖切圆锥
由易到难 由浅入深
圆锥的综合截切
1. 求特殊点; 2. 求一般位置的点; 3. 判断可见性; 4. 光滑连线。
通常采用纬圆法:在圆锥表面上取若 干个纬圆,并求出这些纬圆与截平面 的交点。
谢谢观看
Thanks for looking
Ⅵ Ⅳ Ⅷ
Ⅰ
Ⅱ
Ⅴ Ⅲ Ⅶ
平面截切圆锥
二、平面截切棱锥 3.竖切圆锥
纬圆法
a' c'
b'
b ca
7
求解步骤: 1.分析: 截平面为正平面,截 交线为双曲线;截交线的水平投 影和侧面投影为直线,正面投影
a" 为双曲线并反映实形;
2.求截交线上的特殊点A、B;
c" 3.求出一般点C;
4.光滑且顺次地连接各点,作 出截交线,并且判别可见性;
平面截切圆锥
二、平面截切棱锥
2.斜切圆锥 纬圆法
2.2-2.3 平面与圆柱面的截线 平面与圆锥面的截线 课件(人教A选修4-1)

曲线的形状,尤其是焦点的确定更加不容易,但可以采 用与上节中定理1的证明相同的方法,即Danelin双球法, 这时较容易确定椭圆的焦点,学生也容易入手证明,使 问题得到解决.
返回
[通一类] 2.在空间中,取直线l为轴,直线l′与l相交于O点,夹角
为α,l′围绕l旋转得到以O为顶点,l′为母线的圆锥面,任
取平面π,若它与轴l的交角为β(当π与l平行时,记β=0), 求证:β=α时,平面π与圆锥的交线是抛 物线.(如图)
返回
证明:如图,设平面 π 与圆锥内切球相切于点 F1,球与圆 锥的交线为圆 S,过该交线的平面为 π′,π 与 π′相交于 直线 m. 在平面 π 与圆锥的截线上任取一点 P,连接 PF1.过点 P 作 PA⊥m,交 m 于点 A,过点 P 作 π′的垂线,垂足为 B,连 接 AB,则 AB⊥m,∴∠PAB 是 π 与 π′所成二面角的平面 角.连接点 P 与圆锥的顶点,与 S 相交于点 Q1,连接 BQ1, 则∠BPQ1=α,∠APB=β. 在 Rt△APB 中,PB=PAcos β.
返回
[研一题] [例2] 证明:定理2的结论(1),即β>α时,平面π与圆 锥的交线为椭圆. 分析:本题考查平面与圆锥面的截线.解答本题需要 明确椭圆的定义,利用椭圆的定义证明.
返回
证明:如图,与定理1的证明相同,在圆锥内部嵌入 Dandelin双球,一个位于平面π的上方,一个位于平面π的 下方,并且与平面π及圆锥均相切.
所以PF1+PF2=PQ1+PQ2=Q1Q2. 由正圆锥的对称性,Q1Q2的长度等于两圆S1、S2所在平行平 面间的母线段的长度而与P的位置无关,由此我们可知在β>α时, 平面π与圆锥的交线是以F1、F2为焦点的椭圆.
返回
返回
[通一类] 2.在空间中,取直线l为轴,直线l′与l相交于O点,夹角
为α,l′围绕l旋转得到以O为顶点,l′为母线的圆锥面,任
取平面π,若它与轴l的交角为β(当π与l平行时,记β=0), 求证:β=α时,平面π与圆锥的交线是抛 物线.(如图)
返回
证明:如图,设平面 π 与圆锥内切球相切于点 F1,球与圆 锥的交线为圆 S,过该交线的平面为 π′,π 与 π′相交于 直线 m. 在平面 π 与圆锥的截线上任取一点 P,连接 PF1.过点 P 作 PA⊥m,交 m 于点 A,过点 P 作 π′的垂线,垂足为 B,连 接 AB,则 AB⊥m,∴∠PAB 是 π 与 π′所成二面角的平面 角.连接点 P 与圆锥的顶点,与 S 相交于点 Q1,连接 BQ1, 则∠BPQ1=α,∠APB=β. 在 Rt△APB 中,PB=PAcos β.
返回
[研一题] [例2] 证明:定理2的结论(1),即β>α时,平面π与圆 锥的交线为椭圆. 分析:本题考查平面与圆锥面的截线.解答本题需要 明确椭圆的定义,利用椭圆的定义证明.
返回
证明:如图,与定理1的证明相同,在圆锥内部嵌入 Dandelin双球,一个位于平面π的上方,一个位于平面π的 下方,并且与平面π及圆锥均相切.
所以PF1+PF2=PQ1+PQ2=Q1Q2. 由正圆锥的对称性,Q1Q2的长度等于两圆S1、S2所在平行平 面间的母线段的长度而与P的位置无关,由此我们可知在β>α时, 平面π与圆锥的交线是以F1、F2为焦点的椭圆.
返回
圆柱与圆锥的切割图

增加了2个三角形的面积三角形的底底面直径三角形的高圆锥的高感谢亲观看此幻灯片此课件部分内容来源于网络如有侵权请及时联系我们删除谢谢配合
圆柱与圆锥的切割图
本课件仅供大家学习学习家学习学习
学习完毕请自觉删除 谢谢
旋转出的圆柱与圆锥
圆柱与圆锥的切割图
增加了2个底面
增加了2个长方形的面, 长方形的长=底面直径, 长方形的宽=圆柱的高。
增加了2个圆的 面积,但不是底 面。
增加了2个三角形的面积, 三角形的底=底面直径, 三角形的高=圆锥的高
圆柱与圆锥的切割图
本课件仅供大家学习学习家学习学习
学习完毕请自觉删除 谢谢
旋转出的圆柱与圆锥
圆柱与圆锥的切割图
增加了2个底面
增加了2个长方形的面, 长方形的长=底面直径, 长方形的宽=圆柱的高。
增加了2个圆的 面积,但不是底 面。
增加了2个三角形的面积, 三角形的底=底面直径, 三角形的高=圆锥的高
圆锥曲线 课件

利用线性代数知识求解圆锥曲线问题
线性方程组
线性方程组是线性代数中的基础内容, 它可以用来求解与圆锥曲线相关的问题 。例如,通过解线性方程组,可以找到 满足特定条件的点的坐标。
VS
特征值与特征向量
特征值和特征向量在解析几何中也有广泛 应用。通过计算圆锥曲线的特征值和特征 向量,可以深入了解曲线的性质,从而更 好地解决相关问题。
椭圆离心率的范围是0<e<1,双曲线的离心率范围是e>1。
圆锥曲线的光学性质
01
光线经过圆锥曲线上的点时,其 方向会发生改变,这种现象叫做 圆锥曲线的光学性质。
02
光线经过椭圆时,会沿着椭圆的 主轴方向折射;经过双曲线时, 会沿着双曲线的副轴方向折射。
圆锥曲线的对称性
圆锥曲线具有对称性,即如果将圆锥 曲线沿其对称轴旋转180度,它仍然 与原来的曲线重合。
02 圆锥曲线的性质
焦点与准线
焦点
圆锥曲线上的点到曲线的两个焦 点的距离之和等于常数,这个常 数等于椭圆的长轴长,等于双曲 线的实轴长。
准线
与圆锥的母线平行的线,在平面 内与准线相交的直线与圆锥相切 于一点,这个点叫做切点。
离心率
离心率:是描述圆锥曲线形状的一个重要参数,它等于圆锥顶点到曲线的距离与 圆锥的半径之比。离心率越大,圆锥曲线越扁平,反之则越接近于球形。
双曲线的极坐标 方程
$frac{rho^2}{a^2} frac{rho^2}{b^2} = 1$
圆锥曲线在极坐 标下的表…
将圆锥曲线问题转化为极 坐标形式,便于理解和求 解。
利用极坐标求解圆锥曲线问题
利用极坐标求解圆锥曲线问题的步骤
首先将问题转化为极坐标形式,然后利用极坐标的性质和公式进行求解。
平面与圆柱面圆锥面的截面课件

创建自定义截面
提供创建自定义截面的工具或方法 ,以便用户根据自己的需要进行截 面设计。
修改自定义截面
允许用户修改自定义的截面形状, 以适应不同的设计需求。
截面的修整与编辑
调整截面轮廓
允许用户调整截面的轮廓,以使 其更加符合设计要求。
修整截面边缘
提供修整截面边缘的工具或方法 ,以使截面更加平滑或达到特定
中性面法
利用中性面(即与截面平行的平面)来求解截面 。
数值法求解截面
要点一
有限元法
使用有限元分析软件,对模型进行离散化处理,然后求解 截面。
要点二
边界元法
使用边界元分析方法,对模型进行离散化处理,然后求解 截面。
模拟法求解截面
物理模拟
通过物理模拟实验来求解截面。
数值模拟
通过数值模拟实验来求解截面。
如“径向标注 R10”,表示圆心到圆边缘的距离为10。
03
圆锥面截面
定义与性质
定义
圆锥面截面是指在平面与圆锥面相交的情况下,形成的交线或截面图形。
性质
圆锥面截面的形状和大小取决于平面与圆锥面的相对位置和角度。
截面类型
01
02
03
04
圆
当平面与圆锥面的轴线平行时 ,截面为一个圆。
椭圆
当平面与圆锥面的轴线斜交时 ,截面为一个椭圆。
02
圆柱面截面
定义与性质
定义
圆柱面是由一条直线围绕一条与之平行的直线旋转而成的曲 面。
性质
圆柱面的母线与旋转轴之间成一定的夹角,且每个截面都是 一个圆。
截面类型
横截面
与圆柱轴线垂直的截面。
纵截面
与圆柱轴线平行的截面。
圆锥ppt课件

在工程设计中的应用
圆锥在工程设计中也有着广泛的 应用,例如桥梁的设计、隧道的
设计等。
圆锥的形状和性质在工程设计中 有着重要的意义,例如圆锥的稳
定性、抗压性等。
圆锥在水利工程、土木工程等领 域也有着实际的应用,例如在设 计水坝、大坝等工程时,需要考
虑圆锥形的结构稳定性。
05
圆锥的相关公式与定理
圆锥的母线
利用手工绘制圆锥的草图
绘制底面
使用圆规和直尺,绘制出一个 圆形作为圆锥的底面。
连接底面和侧面
使用直尺或曲线板,将侧面与 底面平滑连接起来,得到圆锥 的草图。
准备工具
准备好纸、笔、圆规、直尺等 手工绘图工具。
绘制侧面
以底面圆心为顶点,用直尺绘 制出一个等腰三角形,作为圆 锥的侧面。
调整草图
可以使用橡皮等工具对草图进 行修改和调整,使其更加符合 要求。
圆锥的侧面积可以通过公式 S = πrl 来计算,其 中 r 是底面半径,l 是母线长度。
侧面积公式的推导
侧面积公式是由圆的周长公式和圆锥的侧面展开 图推导而来的。
3
侧面积的应用
圆锥的侧面积在几何学、工程、艺术等领域都有 广泛的应用。
圆锥的全面积
全面积公式
圆锥的全面积可以通过公式 S_total = πrl + πr² 来计算,其中 r 是底面半径,l 是母线长度。
06
圆锥的绘制方法
利用几何软件绘制圆锥
确定底面半径
首先需要确定圆锥的底面半径,可以使用几何软件中的测 量工具进行测量。
绘制圆
在几何软件中,选择画圆工具,并确定圆心和半径,绘制 出一个圆形。
绘制圆锥
选择画三角形工具,以圆心为顶点,绘制出一个等腰三角 形,然后选择“合并形状”工具,将三角形与圆形进行合 并,得到圆锥的侧面。
平面与圆锥面的截线 PPT

A.圆
B.椭圆
C.双曲线
D.抛物线
3.一平面截圆锥的截线为椭圆,椭圆的长轴为 8,长轴
的两端点到顶点的距离分别是 6 和 10,则椭圆的离心率为
(C )
A. 3
B. 4
5
5
ห้องสมุดไป่ตู้
C. 1
D. 2
2
2
4.用一个平面去截一个正圆锥,而且这个平面不通 过圆锥的顶点,则会出现四种情况:________、________、 ________和________.
如图所示,平面ABC是圆锥面的正截面,PAB 是圆锥的轴截面,已知∠APC=60°,∠BPC=90°,PA=4.
(1)求二面角A-PC-B的余弦值. (2)求正截面圆圆心O到平面PAC的距离.
解析:(1)∵∠APC=60,∴△APC 为等边三角形. 如图所示,分别取 PC、BC 的中点 D、E,连接 AD、DE, 则 AD⊥PC,DE∥PB. 又 PB⊥PC,∴DE⊥PC. 故∠ADE 为二面角 A-PC-B 的平面角. 连接 AE,在 Rt△ACE 中,求得 AE2=24.
在截口上任取一点P,连接PF1、PF2.过点P和圆锥的顶 点O作母线,分别与两个球相切于点Q1、Q2,则PF1=PQ1, PF2=PQ2,所以|PF1-PF2|=|PQ1-PQ2|=Q1Q2.
由于Q1Q2为两圆S1、S2所在平行平面之间的母线段长, 因此Q1Q2的长为定值.
由上述可知,双曲线的结构特点是:双曲线上任意一 点到两个定点(即双曲线的两个焦点)的距离之差的绝对值为 常数.
解析:设⊙O 的半径为 R,母线 VA=l,则侧面展开图的
中心角为 2πR = 2 ,∴圆锥的半顶角= π .
l
4
平面与圆锥面的截线
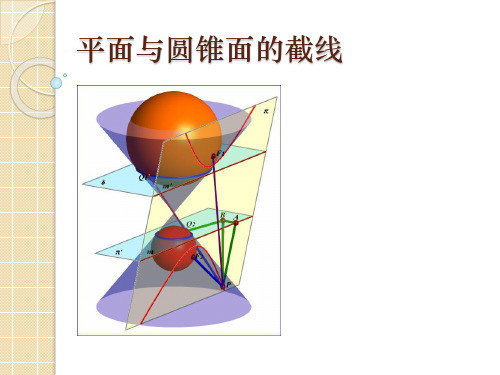
归纳提升:
定理 在空间中,取直线l为轴,直线l'与l 相交于O点,其夹角为α,l'围绕l旋转得到 以O为顶点,l'为母线的圆锥面,任取平面 π,若它与轴l交角为β(π与l平行,记作β =0),则: (1)β>α,平面π与圆锥的交线为椭圆; (2)β=α,平面π与圆锥的交线为抛物线; (3)β<α,平面π与圆锥的交线为双曲线。
平面与圆锥面的截线
观察平面截圆锥面的图形,截线 是什么图形?
改变平面的 位置,可得 到三种曲线, 它们统称为 圆锥曲线.
从平面图形入手,开始讨论一条 直线与等腰三角形的位置关系:
将等腰三角形拓 广为圆锥,直线 拓广为平面。如 果用一平面去截 一个正圆锥,而 且这个平面不通 过圆锥的顶点, 会出现哪些情况 呢?
证明结论:
利用Dandelin双球(这两个球位于圆锥的内部,一个位于平面的上方,一 个位于平面的下方,并且与平面及圆锥均相切)证明:β>α,平面与圆 锥的交线为椭圆.
利用切线长相等,容易证明 PF1+PF2=PQ1+PQ2=Q1Q2=定值.
证明:β=α时,平面与圆锥面的 交线曲线时 准线的 及离心 率:
换个角度 看图:
结论:
截得的圆锥曲线的离心率等于截面和圆 锥轴的夹角的余弦与圆锥顶角一半的余 弦之比. 三种曲线的丹迪林Dandelin双球图可以 在《几何图霸》中统一到一幅图中;
图片的制作可以使用软件《几何图霸》.
知识运用
图形制作(《几何图霸》)
圆锥曲线的发展历史ppt课件

;.
8
1600年,天才观察家第谷邀请开普勒(Kepler)称为他的助 手
两人经常争吵,同时多次和解,共事18个月,第谷去世,开普 勒接受了第谷一生所有的观测数据
开普勒凭借其过人的数学才能与坚忍不拔的毅力,经过多年的 艰苦探索后,提出了影响巨大的三个定律
;.
9
圆锥曲线与天文学
;.
10
圆锥曲线与天文学 开普勒被誉为“天空的立法者”。 通过对数据的整理而获得的,是否有更一般的定理? 1684年8月,哈雷访问牛顿,哈雷问:如果太阳的引力与行星
德国天文学家开普勒(Kepler,1571~1630)继承了哥白尼的日心说,揭 示出行星按椭圆轨道环绕太阳运行的事实;
意大利物理学家伽利略(Galileo,1564~1642)得出物体斜抛运动的轨道 是抛物线。人们发现圆锥曲线不仅是依附在圆锥面上的静态曲线,而且是 自然界物体运动的普遍形式。
;.
个山洞里,囚徒们多次密谋逃跑,但秘密的计划总是被 杰尼西亚所发现。起初,囚徒们以为狱友中有内奸,他 们互相指责、怀疑,但始终没有发现任何一个囚徒在告 密。 后来,又关进了个囚徒,这个囚徒有些数学知识,在囚 徒们又一次密谋逃跑时,这个数学家囚徒却劝告别白费 力气徒劳了,他告诉大家,这个囚禁囚徒的山洞有古怪, 洞壁是类椭球形的,囚徒们被关押在椭圆的一个焦点附 近,他们的密谋的话都被处于另一个焦点处的密探听到 而报告给上司,所以,没人能够逃出生天。于是,囚徒 们把这个山洞诅咒为“杰尼西亚的耳朵”。
1
圆锥曲线 北京市第十五中学 凌艺国
;.
2
圆锥曲线的形成 用一个平面截圆锥面所得的曲线形成圆锥曲线
;.
3
圆锥曲线的历史 两千多年前,古希腊数学家最先开始研究圆锥曲线,并获得了大量的成果。 古希腊数学家阿波罗尼(Apollonius)(约公元前262-前190)采用平面切割
8
1600年,天才观察家第谷邀请开普勒(Kepler)称为他的助 手
两人经常争吵,同时多次和解,共事18个月,第谷去世,开普 勒接受了第谷一生所有的观测数据
开普勒凭借其过人的数学才能与坚忍不拔的毅力,经过多年的 艰苦探索后,提出了影响巨大的三个定律
;.
9
圆锥曲线与天文学
;.
10
圆锥曲线与天文学 开普勒被誉为“天空的立法者”。 通过对数据的整理而获得的,是否有更一般的定理? 1684年8月,哈雷访问牛顿,哈雷问:如果太阳的引力与行星
德国天文学家开普勒(Kepler,1571~1630)继承了哥白尼的日心说,揭 示出行星按椭圆轨道环绕太阳运行的事实;
意大利物理学家伽利略(Galileo,1564~1642)得出物体斜抛运动的轨道 是抛物线。人们发现圆锥曲线不仅是依附在圆锥面上的静态曲线,而且是 自然界物体运动的普遍形式。
;.
个山洞里,囚徒们多次密谋逃跑,但秘密的计划总是被 杰尼西亚所发现。起初,囚徒们以为狱友中有内奸,他 们互相指责、怀疑,但始终没有发现任何一个囚徒在告 密。 后来,又关进了个囚徒,这个囚徒有些数学知识,在囚 徒们又一次密谋逃跑时,这个数学家囚徒却劝告别白费 力气徒劳了,他告诉大家,这个囚禁囚徒的山洞有古怪, 洞壁是类椭球形的,囚徒们被关押在椭圆的一个焦点附 近,他们的密谋的话都被处于另一个焦点处的密探听到 而报告给上司,所以,没人能够逃出生天。于是,囚徒 们把这个山洞诅咒为“杰尼西亚的耳朵”。
1
圆锥曲线 北京市第十五中学 凌艺国
;.
2
圆锥曲线的形成 用一个平面截圆锥面所得的曲线形成圆锥曲线
;.
3
圆锥曲线的历史 两千多年前,古希腊数学家最先开始研究圆锥曲线,并获得了大量的成果。 古希腊数学家阿波罗尼(Apollonius)(约公元前262-前190)采用平面切割
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
连接各点,作出截交线;
2”(3 5 整理轮廓线。 ”)
24
1 53
Ⅰ Ⅲ
Ⅱ
SUCCESS
THANK YOU
2020/1/11
Ⅰ Ⅲ
Ⅱ
练习:圆锥被水平面截切,求出截交线的水平投影。
3' 5' 1' 2”4” 3” 5” 1” (4') (2')
2
4 3
5 1
平面与圆锥相交
5
4
32
1
例3 求带缺口圆锥的水平投影和侧面投影。
5
24 ””
12 6 ” ”8
”
10 ”
31 ””
5 11” 7” ”
9”
练习:已知立体的正面投影,试完成H、W两面投影
1 (2')
(4) ' 3'
'
(8) (12) 5' ' 7' '11' (6)
'
9' (10) '
10 8
12 6
4 2
1 3
9
7 11
5
24 ””
12 ”6 8
””
10 ”
31 ””
工程制图
第三章 组合体
第二节 立体表面的交线
一、截交线
(二)平面切割回转体——圆柱、圆球、圆锥 3、平面切割圆锥
一、截交线
(二)平面切割回转体——圆柱、圆球、圆锥 3、平面切割圆锥
θ PV
θ = 90° 圆
过锥顶 相交直线
θ α
θ>α 椭圆
θ α
PV
θ=α
抛物线
α
θ= 0°<α
双曲线
复习:
5 11” 7” ”
9”
作业:
SUCCESS
THANK YOU
2020/1/11
7”
1”
(2)再作一般点。
(3)判别可见性,依次光滑连 接各点。
(4)补全侧面转向轮廓线。
4
8பைடு நூலகம்
6
1
2
7 35
Ⅳ Ⅰ
正垂线
Ⅱ Ⅲ
正平线
例2 补画正平面与圆锥截交线的正面投影。
1 分析:截交线的正面投 影为双曲线并反映实形;
1'
4' 5'
2'
3'
2 求出截交线上的特殊点 1” Ⅰ、Ⅱ、Ⅲ;
3 求出一般点ⅣⅤ ; 4”(5 ”) 4判别可见性并顺次光滑
1'
4'
2'(3')
6'(5 ')
1”
3”
2”
5” 4”
6”
4 1
5 3
2 6
练习:完成切割圆锥的俯视图和左视图。
练习:已知立体的正面投影,试完成H、W两面投影
1 (2')
(4) ' 3'
'
(8) (12) 5' ' 7' '11' (6)
'
9' (10) '
10 8
12 6
4 2
1 3
9
7 11
s'
s”
2' m'
3'
a'
b'
a2
s 3b
m
m”
d”
c”
V
m'
X
Z
W
m” M
m
Y
例1 圆锥被正垂面截切,求出截交线的另外两个投影。
分析:截交线的水平和侧面投 影为椭圆。
Ⅳ Ⅰ
正垂线
Ⅱ Ⅲ
正平线
具体步骤如下:
(1)先作出截交线上的特殊点。
2'
5'(6')
3'(4')
1' 7'(8')
6”
4”
8”
2” 5” 3”
2”(3 5 整理轮廓线。 ”)
24
1 53
Ⅰ Ⅲ
Ⅱ
SUCCESS
THANK YOU
2020/1/11
Ⅰ Ⅲ
Ⅱ
练习:圆锥被水平面截切,求出截交线的水平投影。
3' 5' 1' 2”4” 3” 5” 1” (4') (2')
2
4 3
5 1
平面与圆锥相交
5
4
32
1
例3 求带缺口圆锥的水平投影和侧面投影。
5
24 ””
12 6 ” ”8
”
10 ”
31 ””
5 11” 7” ”
9”
练习:已知立体的正面投影,试完成H、W两面投影
1 (2')
(4) ' 3'
'
(8) (12) 5' ' 7' '11' (6)
'
9' (10) '
10 8
12 6
4 2
1 3
9
7 11
5
24 ””
12 ”6 8
””
10 ”
31 ””
工程制图
第三章 组合体
第二节 立体表面的交线
一、截交线
(二)平面切割回转体——圆柱、圆球、圆锥 3、平面切割圆锥
一、截交线
(二)平面切割回转体——圆柱、圆球、圆锥 3、平面切割圆锥
θ PV
θ = 90° 圆
过锥顶 相交直线
θ α
θ>α 椭圆
θ α
PV
θ=α
抛物线
α
θ= 0°<α
双曲线
复习:
5 11” 7” ”
9”
作业:
SUCCESS
THANK YOU
2020/1/11
7”
1”
(2)再作一般点。
(3)判别可见性,依次光滑连 接各点。
(4)补全侧面转向轮廓线。
4
8பைடு நூலகம்
6
1
2
7 35
Ⅳ Ⅰ
正垂线
Ⅱ Ⅲ
正平线
例2 补画正平面与圆锥截交线的正面投影。
1 分析:截交线的正面投 影为双曲线并反映实形;
1'
4' 5'
2'
3'
2 求出截交线上的特殊点 1” Ⅰ、Ⅱ、Ⅲ;
3 求出一般点ⅣⅤ ; 4”(5 ”) 4判别可见性并顺次光滑
1'
4'
2'(3')
6'(5 ')
1”
3”
2”
5” 4”
6”
4 1
5 3
2 6
练习:完成切割圆锥的俯视图和左视图。
练习:已知立体的正面投影,试完成H、W两面投影
1 (2')
(4) ' 3'
'
(8) (12) 5' ' 7' '11' (6)
'
9' (10) '
10 8
12 6
4 2
1 3
9
7 11
s'
s”
2' m'
3'
a'
b'
a2
s 3b
m
m”
d”
c”
V
m'
X
Z
W
m” M
m
Y
例1 圆锥被正垂面截切,求出截交线的另外两个投影。
分析:截交线的水平和侧面投 影为椭圆。
Ⅳ Ⅰ
正垂线
Ⅱ Ⅲ
正平线
具体步骤如下:
(1)先作出截交线上的特殊点。
2'
5'(6')
3'(4')
1' 7'(8')
6”
4”
8”
2” 5” 3”
