北师大七年级下几何证明入门专项练习
北师大七年级下几何证明入门专项练习

几何证明题专项训练13、如图,Z 1二Z 2,AC 平分Z DAB 试说明:DC72,如图,AZ\/\ E ( 1 ) V Z ABD 二Z BDC (已 知), ••• //E( );(2):DBC Z ADB(已知),••• // ,( );(3):CBE Z DCB(已知),•••//,()(4 ) v Z CBE= Z A ,(已知),•••//();(5 ) v Z A+ Z ADC=180o (已知), 二//();(6 ) v Z A+ Z ABC=180o (已知),二//();,((4) vZ ADC # C=180o(已知),二 //(已知), );// —,(2)vZ 3二/ 4 (已知),二—//—, );(3)vZ 2二/ 5(已知),二 //,);1、( 1 ) ••• / 1= / A (②•••/ 3=Z 4 (已知), ______ // _____ ( )③ T Z FAD=Z FBC (已知),• ___________ // ____7、如图 2-57,直线 AB CD EF 被直线 GH 所截,Z 1 = 70出,Z2=110",Z 3=70 .求证:AB//CD .证明:TZ 1=70,Z 3=70 (已知),4,如图,/ ABC 玄ADC BF 和 DE 分另U 平分/ ABCDE// FB.5.如图 2-67,已知Z 1 = Z 2, 求Z 3+Z 4的度数. (两直线平行,内错角相等)• Z BCD+=80° (和 Z ADC / 1=Z 2,试说明:// AB.6、如图2-56 •••ZABC=①••• AB//CD (已知),• Z 1 = Z 3 ( )二___ // _____ (•••/ 2=110,/ 3=70 ( ),AB//CD ()•8. 如图2-58,①直线DE AC被第三条直线BA所截,则/ 1和/2是__________ ,如果/ 仁/2,则___//__其理由是().②/ 3和/ 4是直线、 ________被直线截,因此____//___ ./ 3 /4,其理由是().9. 如图2-59,已知AB//CD,BE平分/ ABC CE平分/BCD求证/ 1+Z 2=90 .证明:••• BE平分/ ABC(已知),•••/ 2= _________ ( )同理/ 1= _______________ ,• / 1+ / 2= -2又••• AB//CD (已知),・・ZABC+ ZBCD=()・・Z1 +Z2=O90()10、如图 2-60,E 、F 、G 分别是 AB AC BC 上 点.①如 果 Z B= Z FGC ,则// ,其 理 由 是()②ZBEG= Z EGF ,则// ,其 理 由 是()③如 果 Z AEG+Z EAF=180 ,则//■ ? 其理 由 是( )11.如图 2-61,已知 AB//CD , AB//DE ,求证:/ B+Z D 二/ BCF+Z DCF证明:T AB//CF (已知),•••Z _____ =Z (两直线平行,内错角相等)•••• AB//CF , AB//DE (已知), 二 CF//DE(•••Z图 2-<il・Z B+Z D=Z BCF+Z DCF (等式6U)性质).几何证明题专项训练21、如图,/ B 二/ C , AB// EF ,试说明:/ BGF M C 。
三角形全等几何模型5一线三等角专项练习20202021学年七年级数学下册基础知识专项讲练北师大版
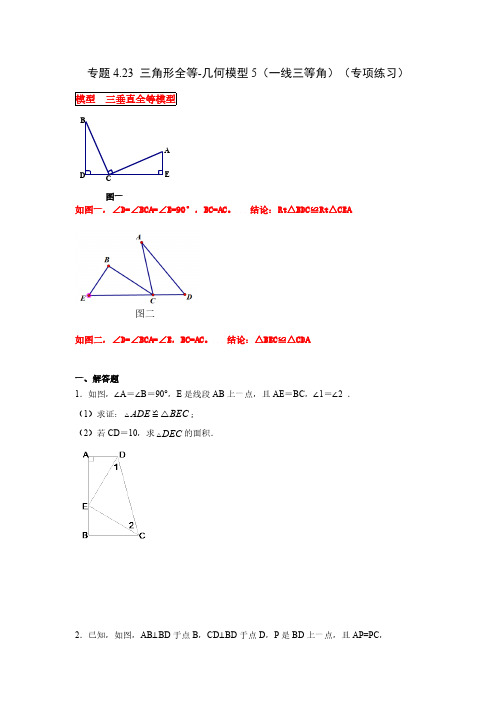
CD E BA专题4.23 三角形全等-几何模型5(一线三等角)(专项练习)模型 三垂直全等模型图一如图一,∠D=∠BCA=∠E=90°,BC=AC 。
结论:Rt △BDC ≌Rt △CEA图二如图二,∠D=∠BCA=∠E ,BC=AC 。
结论:△BEC ≌△CDA一、解答题1.如图,∠A =∠B =90°,E 是线段AB 上一点,且AE =BC ,∠1=∠2 .(1)求证:ADE V ≌BEC △;(2)若CD =10,求DEC V 的面积.2.已知,如图,AB ⊥BD 于点B ,CD ⊥BD 于点D,P 是BD 上一点,且AP=PC ,AP ⊥PC .(1)求证:△ABP ≌△PDC(2)若AB=3,CD=4,连接AC ,求AC 的长.3.如图,在ABC V 中,AB AC =,D 、A 、E 三点都在直线m 上,并且有BDA AEC BAC ÐÐÐ==,求证:DE BD CE =+.4.已知:如图,MS ⊥PS ,MN ⊥SN ,PQ ⊥SN ,垂足分别为S ,N ,Q ,MS =PS ,SN =4,MN =3.求NQ 的长.5.如图1,∠ACB =90°,AC =BC ,AD ⊥MN ,BE ⊥MN ,垂足分别为D 、E .(1)求证:△ADC ≌△CEB ;(2)猜想线段AD 、BE 、DE 之间具有怎样的数量关系,并说明理由;(3)题设条件不变,根据图2可得线段AD 、BE 、DE 之间的数量关系是 .6.如图,已知:ABC V 中,AB AC =,BAC 90Ð=°,分别过B ,C 向经过点A 的直线EF 作垂线,垂足为E ,F .(1)当EF 与斜边BC 不相交时,请证明EF BE CF(=+如图1);(2)如图2,当EF 与斜边BC 这样相交时,其他条件不变,证明:EF BE CF =-;7.如图,一条河流MN 旁边有两个村庄A ,B ,AD ⊥MN 于D .由于有山峰阻挡,村庄B 到河边MN 的距离不能直接测量,河边恰好有一个地点C 能到达A ,B 两个村庄,与A ,B 的连接夹角为90°,且与A ,B 的距离也相等,测量C ,D 的距离为150m ,请求出村庄B 到河边的距离.8.已知:AB BD ^,ED BD ^,AC CE =,BC DE =.(1)试猜想线段AC 与CE 的位置关系,并证明你的结论.(2)若将CD 沿CB 方向平移至图2情形,其余条件不变,结论12AC C E ^还成立吗?请说明理由.(3)若将CD 沿CB 方向平移至图3情形,其余条件不变,结论12AC C E ^还成立吗?请说明理由.9.如图,90ACB Ð=°,AC BC =,AD CE ^,BE CE ^,垂足分别为D ,E ,若9AD =,6DE =,求BE 的长.10.如图所示,A ,C ,E 三点在同一直线上,且ABC DAE △△≌.(1)求证:BC DE CE =+;(2)当ABC V 满足什么条件时,//BC DE ?11.已知:D ,A ,E 三点都在直线m 上,在直线m 的同一侧作ABC V ,使AB AC =,连接BD ,CE .(1)如图①,若90BAC Ð=°,BD m ^,CE m ^,求证ABD ACE @V V ;(2)如图②,若BDA AEC BAC Ð=Ð=Ð,请判断BD ,CE ,DE 三条线段之间的数量关系,并说明理由.12.如图,点C 在BE 上,AB ⊥BE ,DE ⊥BE ,且AB =CE ,AC =CD .判断AC 和CD 的关系并说明理由.13.直线CD 经过BCA Ð的顶点C ,CA=CB .E ,F 分别是直线CD 上两点,且BEC CFA a Ð=Ð=Ð.(1)(数学思考)若直线CD 经过BCA Ð的内部,且E ,F 在射线CD 上,请解决下面两个问题:①如图1,若90BCA Ð=°,90a Ð=°,求证:EF BE AF =-;②如图2,若090BCA °<Ð<°,当a Ð与BCA Ð之间满足________关系时,①中结论仍然成立,并给予证明.(2)(问题拓展)如图3,若直线CD 经过BCA Ð的外部,BCA a Ð=Ð,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.14.如图,已知在ABC V 中,AB AC =,90BAC Ð=°,别过B 、C 两点向过A 的直线作垂线,垂足分别为E 、F .求证:EF BE CF =+.15.在Rt ABC △中,90C Ð=°,8cm AC =,6cm BC =,点D 在AC 上,且6cm AD =,过点A 作射线AE AC ^(AE 与BC 在AC 同侧),若点P 从点A 出发,沿射线AE 匀速运动,运动速度为1cm/s ,设点P 运动时间为t 秒.连结PD 、BD .(1)如图①,当PD BD ^时,求证:PDA DBC △≌△;(2)如图②,当PD AB ^于点F 时,求此时t 的值.16.如图所示,△ABC 中,∠ACB=90°,AC=BC ,直线EF 经过点C ,BF ⊥EF 于点F ,AE ⊥EF于点E .(1)求证:△ACE ≌△CBF ;(2)如果AE 长12cm ,BF 长5cm ,求EF 的长.17.如图,90ACB Ð=°,AC BC =,AD CE ^,BE CE ^,垂足分别为D ,E ,2.5cm AD =,求1cm BE =,求DE 的长.18.已知AD ⊥AB 于A ,BE ⊥AB 于B ,点C 在线段AB 上,DC ⊥EC ,且DC=CE .(1)求证:AD+BE=AB ;(2)将△BEC 绕点C 逆时针旋转,使点B 落在AC 上,如图(2),试问:AD ,BE ,AB 又怎样的数量关系?说明理由.19.如图(1),已知ABC V 中,90BAC Ð=°,AB AC =;AE 是过A 的一条直线,且B ,C 在AE 的异侧,BD AE ^于D ,CE AE ^于E .(1)求证:BD DE CE =+;(2)若直线AE 绕A 点旋转到图(2)位置时(BD CE <),其余条件不变,问BD 与DE ,CE 的数量关系如何?请给予证明.(3)若直线AE 绕A 点旋转到图(3)位置时(BD CE >),其余条件不变,问BD 与DE ,CE 的数量关系如何?请直接写出结果,不需证明;(4)根据以上的讨论,请用简洁的语言表达直线AE 在不同位置时BD 与DE ,CE 的位置关系.20.如图,在ABC V 中,AB AC =,AB BC >,点D 在边BC 上,点E ,F 在线段AD 上,且2DF AF =,12BAC Ð=Ð=Ð.若BE 的长为5,求AD 的长.21.已知:如图,△ABC 中,∠BAC =90°,AB =AC ,l 是过点A 的一条直线,BD ⊥l ,CE ⊥l ,垂足分别为D 、E .(1) 如图(1),求证:DE =BD +CE ;(2) 若直线l 绕A 点旋转到图(2)位置时,其余条件不变,请把图形补充完整,写出BD 、CE 与DE 之间的数量关系,并证明你的结论.22.(1)如图1,已知OAB V 中,OA OB =,90AOB Ð=°,直线l 经过点O ,BC ⊥直线l ,AD ^ 直线l ,垂足分别为点C ,D .依题意补全图l ,并写出线段BC ,AD ,CD 之间的数量关系为______;(2)如图2,将(1)中的条件改为:在OAB V 中,OA OB =,C ,O ,D 三点都在直线l 上,并且有BCO ODA BOA Ð=Ð=Ð,请问(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;(3)如图3,在ABC V 中,AB AC =,90CAB Ð=°,点A 的坐标为(0,1),点C 的坐标为()3,2,请直接写出点B 的坐标.23.在△ABC 中,AC=BC ,直线MN 经过点C ,AD ⊥MN 于点D ,BE ⊥MN 于点E ,且AD=CE ;(1)当直线MN 绕点C 旋转到如图1的位置时,求证:AC ⊥BC .(2)判断AD 、BE 、DE 这三条线段之间的数量关系,并说明理由.(3)当直线MN 绕点C 旋转到如图2的位置时,线段DE 、AD 、BE 之间又有什么样的数量关系?请你直接写出这个数量关系,不必证明.24.如图1所示,在△ABC 中,∠ACB=90°,AC= BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E .(1)当直线MN 绕点C 旋转到图2(a)的位置,求证:①△ADC ≌△CEB;②DE=AD- BE .(2)当直线MN 绕点C 旋转到图2(b)的位置时,求证:DE= BE-AD .25.如图,90B C Ð=Ð=°,BAE CED Ð=Ð,且AB CE =.(1)试说明:ADE V 是等腰直角三角形;(2)若2CDE BAE Ð=Ð,求CDE Ð的度数.26.如图,已知在ABC V 中,AC BC AD ==,CDE B Ð=Ð,求证:ADE BCD △≌△.27.如图1,已知AB =AC ,AB ⊥AC .直线m 经过点A ,过点B 作BD ⊥m 于D , CE ⊥m 于E .我们把这种常见图形称为“K”字图.(1)悟空同学对图1进行一番探究后,得出结论:DE =BD +CE ,现请你替悟空同学完成证明过程.(2)悟空同学进一步对类似图形进行探究,在图2中,若AB =AC ,∠BAC =∠BDA =∠AEC ,则结论DE =BD +CE ,还成立吗?如果成立,请证明之.28.(1)如图①,已知:ABC V 中,90BAC Ð=°,AB AC =,直线m 经过点A ,BD m ^于D ,CE m ^于E ,请探索DE 、BD 、CE 三条线段之间的数量关系,直接写出结论;(2)拓展:如图2,将(1)中的条件改为:ABC V 中,AB AC =,D 、A 、E 三点都在直线m 上,并且BDA AEC BAC a Ð=Ð=Ð=,a 为任意锐角或钝角,请问(1)中结论是否还成立?如成立,请证明;若不成立,请说明理由;(3)应用:如图③,在ABC V 中,BAC Ð是钝角,AB AC =,BAD CAE ÐÐ>,BDA AEC BAC Ð=Ð=Ð,直线m 与BC 的延长线交于点F ,若2BC CF =,ABC V 的面积是16,求ABD △与CEF △的面积之和.29.如图(1)在△ABC 中,∠ACB =90°,AC =BC ,直线MN 经过点C ,且AD ⊥MN 于点D ,BE ⊥MN 于点E .(1)求证:①△ADC ≌△CEB ;②DE =AD +BE .(2)当直线MN 绕点C 旋转到图(2)的位置时,DE 、AD 、BE 又怎样的关系?并加以证明.30.如图,在ABC V 中,90ACB Ð=°,AC BC =,直线MN 经过点C ,且AD MN ^于点D ,BE MN ^于点E .(1)当直线MN 绕点C 旋转到图1的位置时,求证:①ADC CEB △≌△;②DE AD BE =+;(2)当直线MN 绕点C 旋转到如图2所示的位置时,求证:DE AD BE =-;(3)当直线MN 绕点C 旋转到如图3所示的位置时,试问DE ,AD ,BE 具有怎样的数量关系?请直接写出这个等量关系,不需要证明.31.已知:如图,在ABC D 中,90C Ð=°,点E 在AC 上,且AE BC =,ED AB ^于点D ,过A 点作AC 的垂线,交ED 的延长线于点F .求证:AB EF =.32.如图,两个形状、大小完全相同的含有30°、60°的直角三角板如图①放置,PA 、PB 与直线MN 重合,且三角板PAC 、三角板PBD 均可绕点P 逆时针旋转(1)试说明∠DPC=90°;(2)如图②,若三角板PBD 保持不动,三角板PAC 绕点P 逆时针旋转旋转一定角度,PF 平分∠APD ,PE 平分∠CPD ,求∠EPF ;(3)如图③.在图①基础上,若三角板PAC 开始绕点P 逆时针旋转,转速为5°/秒,同时三角板PBD 绕点P 逆时针旋转,转速为1°/秒,(当PA 转到与PM 重合时,两三角板都停止转动),在旋转过程中,PC 、PB 、PD 三条射线中,当其中一条射线平分另两条射线的夹角时,请求出旋转的时间.33.(1)如图1,∠MAN =90°,射线AE 在这个角的内部,点B 、C 在∠MAN 的边AM ,AN 上,且AB =AC ,CF ⊥AE 于点F ,BD ⊥AE 于点D .求证:ABD CAF @V V .(2)如图2,点B 、C 在∠MAN 的边AM 、AN 上,点E 、F 在∠MAN 内部射线AD 上,∠1,∠2分别是ABE △,CAF V 的外角,已知AB =AC ,∠1=∠2=∠BAC ,求证:ABE CAF @V V ;(3)如图3,在ABC V 中,AB =AC ,AB >BC ,点D 在边BC 上,CD =2BD ,点E 、F 在线段AD 上,12BAC Ð=Ð=Ð,若ABC V 的面积是15,则ACF V 与BDE V 的面积之和是_________.34.如图(1)AB=9cm ,AC ⊥AB ,AC=BD=7cm ,点P 在线段AB 上以2cm/s 的速度由点A 向点B 运动,同时,点Q 在线段BD 上由点B 向点D 运动,它们运动的时间为t (s ).(1)若点Q 的速度与点P 的速度相等,当t=1时.①求证:△ACP ≌△BPQ ;②判断此时PC 和PQ 的位置关系,并证明;(2)将图(1)中的“AC ⊥AB ,BD ⊥AB”,改为“∠CAB=∠DBA=70°”,得到图(2),其他条件不变.设点Q 的运动速度为x cm/s ,请问是否存在实数x ,使得△ACP 与△BPQ 全等?若存在,求出相应的x 和t 的值;若不存在,请说明理由.35.如图1,2OA =,4OB =,以A 点为顶点、AB 为腰在第三象限作等腰直角ABC D .(1)求点C 的坐标;(2)如图2,P 是y 轴负半轴上一个动点,当P 点向y 轴负半轴向下运动时,若以P 为直角顶点,PA 为腰作等腰直角APD D ,过点D 作DE x ^轴于点E ,求OP DE -的值;(3)如图3,已知点F 坐标为()3,3--,当G 在y 轴运动时,作等腰直角FGH D ,并始终保持90GFH Ð=°,FG 与y 轴交于点()0,G m ,FH 与x 轴交于点(),0H n ,求m 、n 满足的数量关系.36.已知:在ABC V 中,90BAC Ð=°,AB AC =,AE 是过点A 的一条直线,且BD AE ^于D ,CE AE ^于E .(1)当直线AE 处于如图①的位置时,有BD DE CE =+,请说明理由;(2)当直线AE 处于如图②的位置时,则BD 、DE 、CE 的关系如何?请说明理由.参考答案1.(1)证明见解析;(2)25【分析】(1)根据12Ð=Ð,∠A =∠B =90°,可得DE CE =,ADE V 和BEC △为直角三角形,利用“HL ”即可证明Rt ADE △≌Rt BEC △;(2)根据(1)中Rt ADE △≌Rt BEC △,则ADE BEC Ð=Ð,根据直角三角形的性质推出90AED BEC Ð+Ð=°,则可得DEC Ð为直角,又因为∠1=∠2,则可知DEC Ð为等腰直角三角形,进而通过等腰直角三角形的性质求出其面积.【详解】(1)∵12Ð=Ð,∴DE CE =,∵∠A =∠B =90°,在Rt ADE △和Rt BEC △中,DE EC AE BC =ìí=î,∴Rt ADE △≌Rt BEC △;(2)∵Rt ADE △≌Rt BEC △,∴ADE BEC Ð=Ð,∵90ADE AED Ð+Ð=°,∴90AED BEC Ð+Ð=°,∴90DEC Ð=°,∵12Ð=Ð,∴DE CE =,∴DEC V 为等腰直角三角形,∴其斜边CD 上的高为5,∴1105252DEC S =´´=△.【点拨】本题考查了直角三角形的判定和性质,全等三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题.2.(1)见解析;(2)【分析】(1)根据等角的余角相等证明BAP CPD Ð=Ð,继而证明()ABP PDC AAS @V V ;(2)根据全等三角形对应边相等性质及勾股定理解题.【详解】(1)证明:,AB BD CD BD^^Q 90B D \Ð=Ð=°90BAP APB \Ð+Ð=°AP PC^Q 90APB CPD \Ð+Ð=°BAP CPD\Ð=ÐAP PC=Q ()ABP PDC AAS \@V V ;(2)连接AC ,()ABP PDC AAS @QV V 3,4AB BP CD ===Q5AP \===在,5Rt APC AP PC ==VAC \==.【点拨】本题考查全等三角形的判定与性质、勾股定理等知识,是重要考点,难度较易,掌握相关知识是解题关键.3.见解析【分析】首先根据等量代换得出CAE ABD Ð=Ð,从而可证ADB CEA △≌△,最后利用全等三角形的性质即可得出结论.【详解】证明:设BDA BAC a Ð=Ð=,∴180-DBA BAD BAD CAE a Ð+Ð=Ð+Ð=°,∴CAE ABD Ð=Ð,∵在ADB △和CEA V 中ABD CAE BDA CEA AB AC Ð=ÐìïÐ=Ðíï=î,∴()ADB CEA AAS ≌△△,∴AE BD =,AD CE =,∴DE AE AD BD CE =+=+.【点拨】本题主要考查全等三角形的判定及性质,掌握全等三角形判定方法和性质是解题的关键.4.NQ =1.【分析】首先求出∠M=∠PSQ ,进而利用AAS 证明△MNS ≌△SQP ,所以MN=SQ 问题可解.解:,MS ,PS MN SN PQ SN ^^^Q ,90MSP N SQP \Ð=Ð=Ð=°,M MSN MSN PSQ \Ð+Ð=Ð+Ð,M PSQ \Ð=Ð,在MNS △和SQP V 中,M PSQ MNS SQP MS PS Ð=ÐìïÐ=Ðíï=î,()MNS SQP AAS \△≌△,SQ MN \=,∵SN =4,MN =3,431NQ SN SQ SN MN \=-=-=-= .【点拨】本题考查了全等三角形的判定和性质,垂直定义,根据条件证MNS SQP △≌△是解此题的关键.5.(1)见解析;(2)AD =BE +DE ,见解析;(3)DE =AD +BE【分析】(1)由已知推出∠CDA=∠BEC=90°,因为∠ACD+∠BCE=90°,∠ACD +∠DAC =90°,推出∠DAC=∠ECB ,根据AAS 即可得到△ADC ≌△CEB ;(2)由(1)得到AD=CE ,CD=BE ,即可求出答案;(3)与(1)证法类似可证出∠ACD=∠CBE ,能推出△ADC ≌△CEB ,得到AD=CE ,CD=BE ,即可得到DE 、AD 、BE 之间的等量关系.(1)证明:∵AD ⊥MN ,BE ⊥MN ,∴∠CDA =∠BEC =90°.∴∠ACD +∠DAC =90°.∵∠ACB =90°,∴∠ACD +∠BCE =90°.∴∠DAC =∠ECB .在△ADC 和△CEB 中,CDA BEC DAC ECB AC CB ÐÐìïÐÐíïî===,∴△ADC ≌△CEB .(2)AD =BE +DE .理由如下:由(1)知△ADC ≌△CEB .∴AD =CE ,CD =BE .∴AD =CE =CD +DE =BE +DE .(3)DE =AD +BE .理由:∵AD ⊥MN ,BE ⊥MN ,∴∠ADC=90°,∠BEC=90°,∴∠EBC+∠ECB=90°,∵∠ACB=90°,∴∠ECB+∠ACD=90°,∴∠ACD=∠CBE ,又∵∠ADC=∠CEB ,AC=CB ,∴△ADC ≌△CEB ,∴AD=CE ,CD=BE ,∵CD+CE=DE ,∴DE=AD+BE .【点拨】本题主要考查了余角的性质,直角三角形的两锐角互余,全等三角形的判定和性质等知识点,能根据已知证明△ADC ≌△CEBE 是解此题的关键,题型较好,综合性比较强.6.(1)见解析;(2)见解析.【分析】(1)根据已知条件容易证明△BEA ≌△AFC ,然后利用对应边相等就可以证明题目的结论;(2)根据(1)知道△BEA ≌△AFC 仍然成立,则BE=AF ,AE=CF ,就可以求出EF=BE-CF .解:(1)BE EA ^Q ,CF AF ^,BAC BEA CFE 90ÐÐÐ\===°,EAB CAF 90ÐÐ\+=°,EBA EAB 90ÐÐ+=°,CAF EBA ÐÐ\=,在ABE V 和CAF V 中,BEA AFC EBA FACAB AC Ð=ÐìïÐ=Ðíï=îBEA \V ≌()AFC AAS V ,EA FC \=,BE AF =,EF EA AF BE CF \=+=+.(2)BE EA ^Q ,CF AF ^,BAC BEA CFE 90ÐÐÐ\===°,EAB CAF 90ÐÐ\+=°,ABE EAB 90ÐÐ+=°,CAF ABE ÐÐ\=,在ABE V 和ACF V 中,EBA FAC BEA CFAAB AC Ð=ÐìïÐ=Ðíï=îBEA \V ≌()AFC AAS V ,EA FC \=,BE AF =,∵EF AF AE =-,∴EF BE CF=-【点拨】本题主要考查了全等三角形的性质与判定,利用它们解决问题,经常用全等来证线段和的问题.7.150米【分析】根据题意,判断出△ADC ≌△CEB 即可求解.解:如图,过点B 作BE ⊥MN 于点E ,∵∠ADC =∠ACB =90°,∴∠A =∠BCE (同角的余角相等).在△ADC 与△CEB 中,90ADC CEB A BCEAC CB Ð=Ð=°ìïÐ=Ðíï=î∴△ADC ≌△CEB (AAS ).∴BE =CD =150m .即村庄B 到河边的距离是150米.【点拨】本题主要考查的是全等三角形的实际应用,熟练掌握全等三角形的判定及性质是解答本题的关键.8.(1)AC CE ^,见解析;(2)成立,理由见解析;(3)成立,理由见解析【分析】(1)先用HL 判断出Rt Rt ABC CDE ≌△△,得出A DCE Ð=Ð,进而判断出90DCE ACB Ð+Ð=°,即可得出结论;(2)同(1)的方法,即可得出结论;(3)同(1)的方法,即可得出结论.【详解】解:(1)AC CE ^理由如下:∵AB BD ^,ED BD ^,∴90B D Ð=Ð=°在Rt ABC △和Rt CDE △中AC CE BC DE=ìí=î∴()Rt Rt HL ABC CDE △△≌,∴A DCEÐ=Ð∵90B Ð=°,∴90A ACB Ð+Ð=°,∴()18090ACE DCE ACB Ð=°-Ð+Ð=°,∴AC CE ^;(2)成立,理由如下:∵AB BD ^,ED BD ^,∴90B D Ð=Ð=°,在1Rt ABC V 和2Rt C DE △中121AC C E BC DE=ìí=î,∴()12Rt Rt HL ABC C DE ≌△△,∴2A C E D Ð=Ð,∵90B Ð=°,∴190B A AC Ð+Ð=°,∴2190DC E AC B Ð+Ð=°,在12C FC V 中,()122118090C FC DC E AC B Ð=°-Ð+Ð=°,∴12AC C E ^;(3)成立,理由如下:∵AB BD ^,ED BD ^,∴190ABC D Ð=Ð=°在1Rt ABC V 和2Rt C DE △中121AC C E BC DE =ìí=î,∴()12Rt Rt HL ABC C DE ≌△△,∴2A C E D Ð=Ð,∵190ABC Ð=°,∴190B A AC Ð+Ð=°,在12C FC V 中,()2112180=90C FC DC E AC B Ð=°-Ð+а,∴12AC C E ^.【点拨】此题是几何变换综合题,主要考查了全等三角形的判定和性质,直角三角形的性质,判断出12Rt Rt ABC C DE ≌△△是解本题的关键.9.3【分析】根据同角的余角相等可得EBC DCA Ð=Ð,根据“AAS”可证CEB △≌ADC V ,可得9AD CE ==,即可求BE 的长.解:∵BE CE ^,AD CE ^,∴90E ADC Ð=Ð=°,∴90EBC BCE Ð+Ð=°.∵90BCE ACD Ð+Ð=°,∴EBC DCA Ð=Ð.在CEB △和ADC V 中,E ADC EBC ACD BC AC Ð=ÐìïÐ=Ðíï=î,∴CEB △≌ADC V (AAS ),∴BE CD =,9AD CE ==,∴963BE CD CE DE ==-=-=.【点拨】本题考查了全等三角形的判定和性质,直角三角形的性质,熟练运用全等三角形的判定是本题的关键.10.(1)证明见解析;(2)ACB Ð为直角时,//BC DE【分析】(1)根据全等三角形的性质求出BD=AE ,AD=CE ,代入求出即可;2)根据全等三角形的性质求出∠E=∠BDA= 90°,推出∠BDE=90° ,根据平行线的判定求出即可.【详解】(1)证明:∵ABC DAE △△≌,∴AE=BC ,AC=DE ,又∵AE AC CE =+,∴BC DE CE =+.(2)若//BC DE ,则BCE E Ð=Ð,又∵ABC DAE △△≌,∴ACB E Ð=Ð,∴ACB BCE Ð=Ð,又∵180ACB BCE Ð+Ð=°,∴90ACB Ð=°,即当ABC V 满足ACB Ð为直角时,//BC DE .【点拨】本题考查全等三角形的性质和平行线的判定的应用,关键是通过三角形全等得出正确的结论.11.(1)见详解;(2)DE =BD +CE .理由见详解【分析】(1)根据BD ⊥直线m ,CE ⊥直线m 得∠BDA =∠CEA =90°,而∠BAC =90°,根据等角的余角相等,得∠CAE =∠ABD ,然后根据“AAS”可判断△ABD ≌△CAE ;(2)由∠BDA =∠AEC =∠BAC ,就可以求出∠BAD =∠ACE ,进而由ASA 就可以得出△ABD ≌△CAE ,就可以得出BD =AE ,DA =CE ,即可得出结论.【详解】(1)证明:如图①,∵D ,A ,E 三点都在直线m 上,∠BAC =90°,∴∠BAD +∠CAE =90°,∵BD ⊥m ,CE ⊥m ,∴∠ADB =∠CEA =90°,∴∠BAD +∠ABD =90°,∴∠ABD =∠CAE ,在△ABD 和△CAE 中,ADB AEC ABD CAE AB AC ÐÐìïÐÐíïî===,∴△ABD ≌△CAE (AAS );(2)DE =BD +CE .理由如下:如图②,∵∠BDA =∠AEC =∠BAC ,∴由三角形内角和及平角性质,得:∠BAD +∠ABD =∠BAD +∠CAE =∠CAE +∠ACE ,∴∠ABD =∠CAE ,∠BAD =∠ACE ,在△ABD 和△CAE 中,ABD CAE AB ACBAD ACE ÐÐìïíïÐÐî===,∴△ABD ≌△CAE (ASA ),∴BD =AE ,AD =CE ,∴DE =AD +AE =BD +CE .【点拨】本题考查了全等三角形的判定与性质以及三角形内角和定理的综合应用,解题的关键是熟练掌握全等三角形的判定方法,灵活运用所学知识解决问题.12.AC ⊥CD ,理由见解析【分析】根据条件证明△ABC ≌△CED 就得出∠ACD=90°,则可以得出AC ⊥CD .【详解】解:AC ⊥CD .理由:∵AB ⊥BE ,DE ⊥BE ,∴∠B =∠E =90°.在Rt △ABC 和Rt △CED 中,AB CE AC CD =ìí=î,∴Rt △ABC ≌Rt △CED (HL ),∴∠A =∠DCE ,∠ACB =∠D .∵∠A+∠ACB =90°,∴∠DCE+∠ACB =90°.∵∠DCE+∠ACB+∠ACD =180°,∴∠ACD =90°,∴AC ⊥CD .【点拨】本题考查了全等三角形的判定及性质的运用,垂直的判定及性质的运用,解答时证明三角形全等是关键.13.(1)证明见解析;(2)180ACB a Ð+Ð=°,证明见解析;(3)EF BE AF =+,证明见解析.【分析】(1)①求出∠BEC =∠AFC =90°,∠CBE =∠ACF ,根据AAS 证△BCE ≌△CAF ,推出BE =CF ,CE =AF 即可;②当∠α+∠ACB =180°,证明∠BEC =∠AFC ,∠CBE =∠ACF ,根据AAS 证△BCE ≌△CAF ,推出BE =CF ,CE =AF 即可;(2)求出∠BEC =∠AFC ,∠CBE =∠ACF ,根据AAS 证△BCE ≌△CAF ,推出BE =CF ,CE=AF 即可.【详解】(1)①在图1中,90BEC AFC Ð=Ð=°Q ,90ACB Ð=°,90BCE ACF Ð+Ð=°,90EBC BCE Ð+Ð=°,EBC ACF \Ð=Ð,在BCE V 和CAF V 中,EBC ACF BEC AFC BC AC Ð=ÐìïÐ=Ðíï=î,()BCE CAF AAS \@V V ,BE CF \=,CE AF =,EF CF CE BE AF \=-=-;②当180ACB a Ð+Ð=°时,①中结论仍然成立;证明:在图2中,BEC CFA a Ð=Ð=ÐQ ,180ACB a Ð+Ð=°,BCE ACF EBC BCE \Ð+Ð=Ð+Ð,EBC ACF \Ð=Ð,在BCE V 和CAF V 中,EBC ACF BEC AFC BC AC Ð=ÐìïÐ=Ðíï=î,()BCE CAF AAS \@V V ,BE CF \=,CE AF =,EF CF CE BE AF \=-=-.故答案为180ACB a Ð+Ð=°;(2)不成立,结论:EF BE AF =+.理由:在图3中,BEC CFA a Ð=Ð=ÐQ ,a BCA Ð=Ð,又180EBC BCE BEC +Ð+Ð=°Q ,180BCE ACF ACB Ð+Ð+Ð=°,EBC BCE BCE ACF \Ð+Ð=Ð+Ð,EBC ACF \Ð=Ð,在BEC △和CFA △中,EBC FCA BEC CFA BC CA Ð=ÐìïÐ=Ðíï=î,()BEC CFA AAS \@V V ,AF CE \=,BE CF =,EF CE CF =+Q ,EF BE AF \=+.【点拨】本题综合考查三角形综合题、全等三角形的判定和性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,注意这类题目图形发生变化,结论基本不变,证明方法完全类似,属于中考常考题型.14.见解析【分析】证明△BEA ≌△AFC ,得到AE=CF ,BE=AF ,即可得到结论.证明:BE EA ^Q ,CF AF ^,90BAC BEA AFC \Ð=Ð=Ð=°,90EAB CAF \Ð+Ð=°,90EBA EAB Ð+Ð=°,CAF EBA \Ð=Ð,在ABE △和AFC △中,BEA AFC EBA CAF AB AC Ð=ÐìïÐ=Ðíï=î,(AAS)BEA AFC \△≌△.AE CF ∴=,BE AF =.EF AF AE BE CF \=+=+..【点拨】此题考查全等三角形的判定及性质,熟记三角形的判定定理是解题的关键.15.(1)见解析;(2)8秒【分析】(1)根据垂直及角之间的关系证明出PDA CBD Ð=Ð,又有90PAD C Ð=Ð=°,=6AD BC =,根据三角形全等的判定定理则可证明PDA DBC △≌△.(2)根据垂直及角之间的关系证明APF DAF Ð=Ð,又因为90PAD C Ð=Ð=°,AD BC =,则可证明PAD ACB △≌△,所以8cm AP AC ==,即t=8秒.(1)证明:PD BD ^Q,90PDB \Ð=°,即90BDC PDA Ð+Ð=°又90C Ð=°Q ,90BDC CBD Ð+Ð=°PDA CBD\Ð=Ð又AE AC ^Q ,90PAD \Ð=°90PAD C \Ð=Ð=°又6cm BC =Q ,6cmAD =AD BC\=在PAD △和DCB V 中PAD C AD CBPDA DBC Ð=Ðìï=íïÐ=Ðî()PDA DBC ASA \△≌△(2)PD AB ^Q ,90AFD AFP \Ð=Ð=°,即90PAF APF Ð+Ð=°又AE AC ^Q ,90PAF DAF \Ð+Ð=°APF DAF\Ð=Ð又90PAD C Ð=Ð=°Q ,AD BC=在APD △和CAB △中APD CAB PAD CAD BC Ð=ÐìïÐ=Ðíï=î()PAD ACB AAS \△≌△8cmAP AC \==即8t =秒.【点拨】本题主要考查的是全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理,灵活运用角之间的关系是解题关键.16.(1)证明见解析;(2)EF=17cm .【分析】(1)根据垂直的定义可得∠AEC=∠CFB=90°,然后求出∠EAC=∠FCB ,再利用“角角边”证明即可;(2)由全等三角形的性质可得:AE=CF ,CE=BF ,再根据线段的和差求解即可.【详解】(1)证明:在Rt △ACB 中,∵∠ACB=90°,∴∠ACE+∠BCF=90°∵AE ⊥EF ,BF ⊥EF∴∠ACE+∠EAC=90°∴∠CAE=∠BCF又∵ AC=CB∴△ACE ≌△CBF(ASA)(2)由△ACE ≌△CBF 可得:AE=CF=12cm , EC=BF=5cm ,∴EF=EC+CF=12+5=17cm .【点拨】本题考查了全等三角形的判定与性质,同角的余角相等的性质,熟练掌握三角形全等的判断方法并找出全等的条件是解题的关键.17. 1.5cm DE =.【分析】根据垂直定义求出∠BEC =∠ACB =∠ADC ,根据等式性质求出∠ACD =∠CBE ,根据AAS 证明△BCE ≌△CAD ;根据全等三角形的对应边相等得到AD =CE ,BE =CD ,利用DE =CE−CD ,即可解答.【详解】AD CE ^Q ,BE CE^90ADC CEB \Ð=Ð=°90BCE CBE \Ð+Ð=°又90ACB Ð=°Q 90BCE ACD \Ð+Ð=°CBE ACD\=Ð在ACD △和CBE △中ADC CEB ACD CBEAC BC Ð=ÐìïÐ=Ðíï=î()AAS ACD CBE \△≌△CD BE \=,AD CE=又 2.5cm AD =Q ,1cmBE =2.5cm CE \=,1cm=CD 2.51 1.5cm DE CE CD \=-=-=.【点拨】本题考查了全等三角形的性质和判定,垂线的定义等知识点的应用,解此题的关键是推出证明ACD CBE \V V ≌的三个条件.18.(1)见解析;(2)BE= AB+AD ,理由见解析.【分析】(1)利用余角的性质得到∠ACD=∠BEC ,从而证明△ACD ≌△BEC ,得到AD=BC ,AC=BE ,从而得到结论;(2)根据△ACD ≌△BEC ,得到AD=BC ,AC=BE ,从而得到BE=AC=AB+BC=AB+AD .【详解】解:(1)∵BE ⊥AB ,∴∠BCE+∠BEC=90°,∵DC ⊥EC ,∴∠ACD+∠BCE=90°,∴∠ACD=∠BEC ,在△ACD 和△BEC 中,A B ACD BECCD CE Ð=ÐìïÐ=Ðíï=î∴△ACD ≌△BEC (AAS ),∴AD=BC ,AC=BE ,∴AD+BE=AC+BC=AB ;(2)由(1)可得:△ACD ≌△BEC ,∴AD=BC ,AC=BE ,∴BE=AC=AB+BC=AB+AD .【点拨】本题考查了全等三角形的判定与性质,找出条件,证明全等,利用全等的性质得到线段的数量关系是本题考查的内容.19.(1)见解析;(2)BD DE CE =-,见解析;(3)BD DE CE =-;(4)当B ,C 在AE 的同测时,BD DE CE =-;当B ,C 在AE 的异侧时,若BD CE >,则BD DE CE =+,若BD CE <,则BD CE DE=-【分析】(1)在直角三角形中,由题中条件可得∠ABD=EAC ,又有AB=AC ,则有一个角及斜边相等,则可判定△BAD ≌△AEC ,由三角形全等可得三角形对应边相等,进而通过线段之间的转化,可得出结论;(2)由题中条件同样可得出△BAD ≌△AEC ,得出对应线段相等,进而可得线段之间的关系;(3)同(2)的方法即可得出结论.(4)利用(1)(2)(3)即可得出结论.【详解】解:(1)∵BD ⊥AE ,CE ⊥AE∴∠ADB=∠CEA=90°∴∠ABD+∠BAD=90°又∵∠BAC=90°∴∠EAC+∠BAD=90°∴∠ABD=∠CAE在△ABD 与△ACE 中ADB CEA ABD CAEAB AC Ð=ÐìïÐ=Ðíï=î∴△ABD ≌△ACE∴BD=AE ,AD=EC ,∴BD=DE+CE(2)∵BD ⊥AE ,CE ⊥AE∴∠ADB=∠CEA=90°∴∠ABD+∠BAD=90°又∵∠BAC=90°∴∠EAC+∠BAD=90°∴∠ABD=∠CAE在△ABD 与△ACE 中ADB CEA ABD CAEAB AC Ð=ÐìïÐ=Ðíï=î∴△ABD ≌△ACE∴BD=AE ,AD=EC∴BD=DE-CE ,(3)∵∠BAC=90°,∴∠BAD+∠EAC=90°,又∵BD ⊥AE ,CE ⊥AE ,∴∠BDA=∠AEC=90°,∠BAD+∠ABD=90°,∴∠ABD=∠EAC ,在△ABD 与△CAE 中,BDA AEC ABD EACAB AC Ð=ÐìïÐ=Ðíï=î∴△ABD ≌△CAE ,∴BD=AE ,AD=CE ,∵DE=AD+AE=BD+CE ,∴BD=DE-CE .(4)归纳:由(1)(2)(3)可知:当B ,C 在AE 的同侧时,若BD> CE,则BD= DE +CE,若BD> CE,则BD= DE +CE,若BD< CE,则BD= CE- DE.【点拨】此题是几何变换综合题,主要考查了三角形全等的判定方法,余角的性质,线段的和差,熟练掌握全等三角形的判定和性质是解题的关键.20.15.【分析】解:由∠1=∠2=∠BAC ,得到∠BAE=∠ACF ,∠ABE=∠CAF 从而证明△ABE ≌△CAF(ASA).得到AF=BE ,再根据DF=2AF ,BE 的长为5,求得AD 的长.【详解】解:∵12BAC Ð=Ð=Ð,且1BAE ABE Ð=Ð+Ð,2CAF ACF Ð=Ð+Ð,∠BAC=∠BAE+∠CAF ,∴∠BAE=∠ACF ,∠ABE=∠CAF .在ABE △和CAF V 中,BAE ACF AB CAABE CAF Ð=Ðìï=íïÐ=Ðî∴()ABE CAF ASA ≌△△.∴AF BE=∵2DF AF =,BE 的长为5,∴10DF =,5AF BE ==,∴51015AD AF DF =+=+=.【点拨】本题考查了全等三角形的性质和判定,解题的关键是熟悉掌握全等三角形的性质和证明.21.(1)详见解析;(2)结论:DE =CE ﹣BD ,详见解析【分析】(1)利用已知得出∠CAE=∠ABD ,进而利用AAS 得出则△ABD ≌△CAE ,即可得出DE=BD+CE ;(2)利用已知得出∠CAE=∠ABD ,进而利用AAS 得出则△ABD ≌△CAE ,即可得出BD 、CE 与DE 之间的数量关系.【详解】解:(1)证明:∵BD ⊥l ,CE ⊥l ,∴∠BD A =∠AEC =90°又 ∵Rt ABC D ,∴∠BAD +∠CAE =90°,∠BAD +∠ABD =90°,∴∠CAE =∠ABD在△ABD 和△CAE 中=ABD CAE ADB CEAAB AC =ìïíï=î∠∠∠∠∴△ABD ≌ △CAE∴BD =AE ,AD =CE∵DE =AD +AE ,∴DE =CE +BD .(2) 如图②所示:结论:DE =CE ﹣BD证明:∵BD ⊥l ,CE ⊥l ,∴∠BD A =∠AEC = 90°∵∠BAD +∠CAE =90°,∠BAD +∠ABD =90°,∴∠CAE =∠ABD在△ABD 和△CAE 中==ABD CAE ADB CEAAB AC ìïíï=î∠∠∠∠∴△ABD ≌△CAE (AAS )∴BD =AE ,AD =CE∵DE =AD ﹣AE∴DE =CE ﹣BD【点拨】此题主要考查了全等三角形的判定与性质等知识,根据已知得出△ABD ≌△CAE 是解题关键.22.(1)补全如图所示见解析;CD BC AD =+;(2)成立,证明见解析;(3)点B 的坐标为()1,2-.【分析】(1)依题意补全图,易证△AOD ≌△OBC ,则有AD =CO ,OD =BC ,从而可得CD BC AD =+;(2)利用三角形内角和易证23ÐÐ=,再证明BCO ODA V V ≌,同(1)即可证明结论;(3)过B 、C 两点作y 轴垂线,构造如(1)图形,即可得三角形全等,再将线段关系即可求出点B 坐标.【详解】(1)补全图1如图所示,CD BC AD =+;证明:∵90AOB Ð=°,BC ⊥直线l ,AD ^ 直线l ,∴∠BCO =∠ODA =90°,∴∠BOC +∠OBC =90°,又∵90AOB Ð=°,∴∠BOC +∠AOD =90°,∴∠OBC =∠AOD ,在△AOD 和△OBC 中BCO ODA OBC AOD BO AO Ð=ÐìïÐ=Ðíï=î,∴△AOD ≌△OBC (AAS )∴AD =CO ,OD =BC ,∵CD OD CO =+,∴CD BC AD =+.(2)成立.证明:如图,∵12180BOA Ð+Ð=°-Ð,13180BOA Ð+Ð=°-Ð,BOA BCOÐ=Ð∴23ÐÐ=在BCO V 和ODA V中32BCO ODABO OA Ð=ÐìïÐ=Ðíï=î∴BCO ODA V V ≌(AAS )∴BC OD =,CO AD=∴CD CO OD AD BC=+=+(3)点B 的坐标为()1,2-.过程如下:过B 、C 两点作y 轴垂线,垂足分别为M 、N ,同理(1)可得,CN =AM ,AN =MB ,∵点A 的坐标为(0,1),点C 的坐标为()3,2,∴CN =AM =3,ON =2,OA =1,∴MB =AN =ON -OA =1,OM =AM -OA =2,∵点B 在第四象限,∴点B 坐标为:()1,2-.【点拨】主要考查了等腰直角三角形的性质,全等三角形的判定和性质、图形与坐标变换,构造出全等三角形是解本题的关键.23.(1)见解析;(2)DE =AD +BE ;见解析;(3)AD =DE +BE【分析】(1)利用垂直的定义得∠ADC =∠CEB =90°,再利用HL 证明Rt △ADC ≌Rt △CEB ,得到∠DAC =∠BCE ,再根据余角的定义得到∠ACD +∠BCE =∠ACB =90°,可得结论;(2)根据Rt △ADC ≌Rt △CEB 得到DC =BE ,从而利用等量代换得到DE =AD +BE ;(3)同理可证:Rt △ADC ≌Rt △CEB ,利用等量代换可得AD =DE +BE .【详解】解:(1)证明:∵AD ⊥MN ,BE ⊥MN ,∴∠ADC =∠CEB =90°,在Rt △ADC 和Rt △CEB 中,AC BC AD CE =ìí=î,∴Rt △ADC ≌Rt △CEB (HL ),∴∠DAC =∠BCE ,∵∠ADC =90°,即∠DAC +∠ACD =90°,∴∠ACD +∠BCE =90°,即∠ACB =90°,∴AC ⊥BC ;(2)DE =AD +BE ,理由如下:∵Rt △ADC ≌Rt △CEB ,∴DC =BE ,∵AD =CE ,∴DE =DC +CE =AD +BE ;(3)AD =DE +BE ,同理可证:Rt △ADC ≌Rt △CEB (HL ),∴CD =BE ,∴AD =CE =DE +CD =DE +BE ,∴即AD =DE +BE .【点拨】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS ”、“SAS ”、“ASA ”、“AAS ”、“HL ”;全等三角形的对应边、对应角相等.24.(1)①见解析;②见解析;(2)见解析.【分析】(1)①根据已知可利用AAS 证明△ADC ≌△CEB ;②由①证得△ADC ≌△CEB ,得出对应边相等,CE =AD ,CD =BE 由此可证DE =AD−BE ;(2)根据已知可利用AAS 证明△ADC ≌△CEB ,得出对应边相等,AD =CE ,CD =BE ,由此可证DE =BE−AD .【详解】证明:(1)①∵∠ADC =∠ACB =∠BEC =90°,∴∠CAD +∠ACD =90°,∠BCE +∠CBE =90°,∠ACD +∠BCE =90°.∴∠CAD =∠BCE .∵AC =BC ,∴△ADC ≌△CEB .②由①证得△ACD ≌△CBE .∴CE =AD ,CD =BE .∴DE =CE−CD =AD−BE .(2)∵∠ADC =∠CEB =∠ACB =90°,∴∠ACD =∠CBE ,又∵AC =BC ,∴△ACD ≌△CBE ,∴AD =CE ,CD =BE ,∴DE =CD−CE =BE−AD .【点拨】本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS 、ASA 、SAS 、SSS ,直角三角形可用HL 定理,但AAA 、SSA ,无法证明三角形全等,再根据全等三角形对应边相等得出结论.25.(1)见解析;(2)60°.【分析】(1)利用ASA 证明△BAE ≌△CED ,可证AE=DE ,后利用∠BAE+∠BEA=90°,证明∠BEA+∠CED=90°,问题得证;(2)利用直角三角形的两个锐角互余,求解即可.【详解】(1)∵90B C Ð=Ð=°,BAE CED Ð=Ð,且AB CE =,∴△BAE ≌△CED ,∴AE=DE ,∵∠BAE+∠BEA=90°,∴∠BEA+∠CED=90°,∴∠AED=90°,∴△AED 是等腰直角三角形;(2)∵2CDE BAE Ð=Ð,BAE CED Ð=Ð,∴2CDE CED Ð=Ð,∵∠CDE+∠CED=90°,∴∠CDE=60°.【点拨】本题考查了三角形的全等,等腰直角三角形的定义,直角三角形的锐角互余的性质,根据图形,结合条件选择对应判定方法,根据性质构造基本的计算等式是解题的关键.26.见解析.【分析】证明ADE BCD Ð=Ð,为三角形的全等提供条件即可.证明:ADE CDE B BCD Ð+Ð=Ð+ÐQ ,CDE B Ð=Ð,ADE BCD \Ð=Ð,AC BC =Q ,A B \Ð=Ð,在ADE V 和BCD △中A B AD BCADE BCD Ð=Ðìï=íïÐ=Ðî,ADE \V ≌BCD △(ASA) .【点拨】本题考查了ASA 证明三角形的全等,抓住题目的特点,补充全等需要的条件是解题的关键.27.(1)见解析;(2)成立,见解析【分析】(1)先证∠ABD=∠EAC ,再证△ABD ≌ △CAE (AAS )即可;(2)先证出∠ABD = ∠EAC ,再证△ABD ≌ △CAE (AAS )即可.证明:(1)∵AB ⊥AC,BD ⊥DE,CE ⊥DE,∴∠BDA=∠AEC=∠BAC=90°,∴∠DAB+∠ABD=∠EAC+∠DAB=90°,∴∠ABD=∠EAC,在△ABD 和 △CAE 中,ABD EAC BDA AEC AB AC Ð=ÐìïÐ=Ðíï=î,∴ △ABD ≌ △CAE (AAS ),∴ BD = AE ,AD = CE ,∴ DE = AE + DA ;(2)成立,理由如下:∵ ∠BAC + ∠BAD + ∠EAC = 180° ,∠ADB + ∠BAD + ∠ABD = 180°,∠BAC = ∠BDA ,∴∠ABD = ∠EAC ,在△ABD 和 △CAE 中,ABD EAC BDA AEC AB AC Ð=ÐìïÐ=Ðíï=î,∴ △ABD ≌ △CAE (AAS ),∴ BD = AE ,AD = CE ,∴ DE = AE + DA = BD + CE.【点拨】本题考查三角形全等的判定与性质,掌握三角形全等的判定与性质是解题关键.28.(1)DE BD CE =+;(2)成立,证明见详解;(3)8.【分析】(1)通过题中的直角和垂直条件,可得到CAE ABD Ð=Ð,然后证明△CAE ≌△ABD ,即得到BD AE =,AD CE =,然后通过等量代换即可得到结论;(2)同(1)中类似,先证明△CAE ≌△ABD 后得到对应边成比例即可;(3)证明△CAE ≌△ABD ,发现ABD △与CEF △的面积之和即为△ACF 的面积,然后根据2BC CF =即可得到答案.解:(1)DE BD CE =+,∵90BAC Ð=°,∴90BAD CAE Ð+Ð=°,∵BD m ^,CE m ^,∴90CEA BDA Ð=Ð=°,∴90BAD ABD Ð+Ð=°,∴CAE ABDÐ=Ð在△CAE 和△ABD 中,90CAE ABD AB ACCEA BDA Ð=Ð=Ð=Ð=°ìïíïî∴△CAE ≌△ABD ,∴BD AE =,AD CE =,∵DE AD AE =+,∴DE BD CE =+;(2)成立,∵BDA AEC BAC a Ð=Ð=Ð=,且180BAD BAC CAE Ð+Ð+Ð=°,∴180BAD CAE a Ð+Ð+=°,在△ABD 中,180BAD ABD BDA Ð+Ð+Ð=°,∴180BAD ABD a Ð+Ð+=°,∴CAE ABD Ð=Ð,在△CAE 和△ABD 中,。
七年级数学下册证明题专项训练(新版)北师大版

证明题专题训练1. 已知,在△ ABC中,DE// AB, FG// AC, BE=GC求证:DE=FB
2. 已知,AB=CD AB// CD BF=CE C, E,F,B 在一条直上,试问AF, DE的关系如何?并证明
3. 如图,AB=DE,BE=CF,A/ DE ,求证:
4. 已知,如图所示,AB=AC,BD=CD,DEL AB于点E , DF
点F ,求证:DE=DF
接叽猜想^ABC^ZACN有何数壘关系?并证明你的结论多
(2)类比操究
如團跖在等边△ A巩中,点N是巩延长绒上的任竜一点(不含端点,茸他条件不变,CD中的结论星否仍然成立?请说明理由.丄AC于
如團「在等边△加f中,点N罡阮上的任意一点.(不含端点占,C),连接AM,,以勰为边作菩边AM虬连
如蓟已知在込A肚中"AB=AC=10cm,肌Pcm,直D为細的中点,点P在找段肌上由E点向「直运动,同
时,点Q在线段CA上由点C向点A运动.
⑴ 如果直F、Q的速度均为3厘粉秒,经过1秒后,匕EFD与△CQF是否全諄?请
说明理由:
(2)若点P的运动速匱为2屋米秒,点Q的运动速度为2.51米严冥是否存在某一个
时刻,便得ABPD^ACQP全等?如果存在请求出这一时刻井证明;如果不存衽,请说
明現由.
7、已知;在厶ABC中,AB =BC / ABC90° .F为AB延长线上一点,点E在BC上,BE = BF,连接AE EF和CF ( 1)求证:AECF;
(2)若/ CAE=30°,求/ EFC的度数.
初中精品资料欢迎下载。
最新北师大版七年级下册三角形全等(SSS)的证明试题以及答案(共41道证明题)
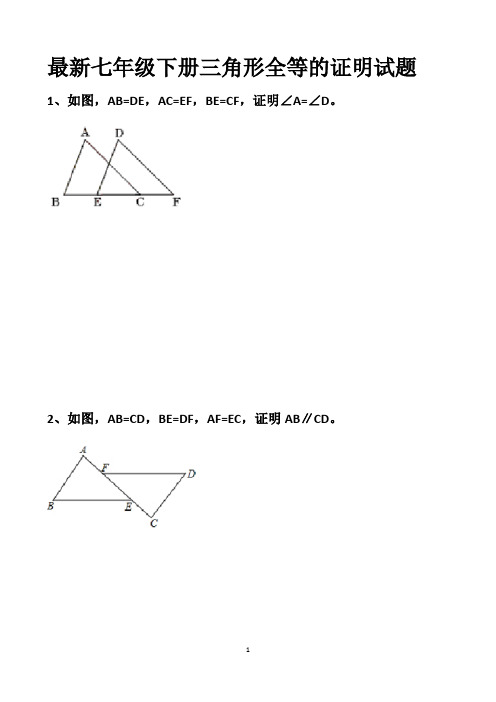
最新七年级下册三角形全等的证明试题1、如图,AB=DE,AC=EF,BE=CF,证明∠A=∠D。
2、如图,AB=CD,BE=DF,AF=EC,证明AB∥CD。
3、如图,AC=DF,EF=BC,AD=BE,证明∠F=∠C。
4、如图,AB=AC,AD=AE,BE=DC,证明∠ABD=∠AEC。
5、如图,AB=AD,AE=AC,BC=ED,证明∠ABE=∠ACD。
6、如图,AD=AB,DC=BC,证明∠B=∠D。
7、如图,AB=AC,BD=DC,证明∠1=∠2.8、如图,∠C=90°,AD=BD,DE=DC,AE=BC,说明AB和DE的关系。
9、如图,AB=DE,BC=EF,AF=CD,证明AB∥DE。
10、如图,AB=AC,D是BC的中点,证明AD⊥BC。
11、如图,AE=DF,AB=CD,CE=BF,证明AE∥DF。
12、如图,AB=AD,AE=AC,BC=DE,证明∠E=∠C。
13、如图,BC=BE,DE=DC,∠C=90°,证明(1)DE⊥AB(2)BD是∠ABC的角平分线。
14、如图,AB=EF,AD=CF,DE=BC,证明∠B=∠E。
15、如图,OA=OB,AC=BD,AD=BC,证明∠ACB=∠ADB。
16、如图,AD=BC,A0=OB,OC=OD,证明∠BAD=∠ABC。
17、如图,AD=BD,BE=AC,AD+DE=BC,AD⊥BC,证明BE⊥AC。
18、如图,AD=BC,AF=EC,DE=BF,证明DE∥BF,AD∥BC。
19、如图,AB=DC,AC=BD,AO=OD,证明∠B=∠C。
20、如图,AB=AD,AE=AC,BC=DE,证明∠1=∠2.21、如图,AC⊥CE,AC=CE,AB=CD,且AB+DE=BD,AB∥DE。
22、如图,AE=AB,AC=AF,EC=BF,证明∠BAE=∠CAF。
23、如图,AD=BC,AC=BD,证明∠ADO=∠BCO。
24、如图,AB=AC,BD=CE,AD=AE,证明∠ABC=∠ADE。
最新北师大版七年级下册三角形全等的证明练习题以及答案
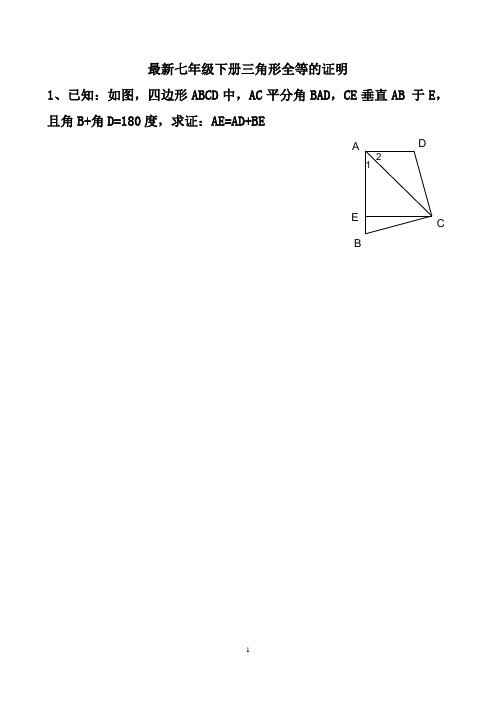
最新七年级下册三角形全等的证明1、已知:如图,四边形ABCD中,AC平分角BAD,CE垂直AB 于E,且角B+角D=180度,求证:AE=AD+BEA B DCE 122、已知,如图,AB=CD,DF⊥AC于F,BE⊥AC于E,DF=BE。
求证:AF=CE。
FE A CDB3、已知,如图,AB ⊥AC ,AB =AC ,AD ⊥AE ,AD =AE 。
求证:BE =CD 。
AEDC B4、如图,DE⊥AB,DF⊥AC,垂足分别为E、F,请你从下面三个条件中任选出两个作为已知条件,另一个为结论,推出一个正确的命题。
①AB=AC ②BD=CD ③BE=CFBD C5、如图,△ABC中,AB=AC,过A作GE∥BC,角平分线BD、CF 交于点H,它们的延长线分别交GE于E、G,试在图中找出三对全等三角形,并对其中一对给出证明。
E G6、如图,在△ABC中,点D在AB上,点E在BC上,BD=BE。
(1)请你再添加一个条件,使得△BEA≌△BDC,并给出证明。
你添加的条件是:________ ___(2)根据你添加的条件,再写出图中的一对全等三角形:______________(不再添加其他线段,不再标注或使用其他字母,不必写出证明过程)7、已知:如图,AB⊥BC,AD⊥DC,AB=AD,若E是AC上一点。
求证:EB=ED。
DA E CB8、已知:如图,AB、CD交于O点,CE//DF,CE=DF,AE=BF。
求证:∠ACE=∠BDF。
AB CDEFO9、已知:如图,△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,若BD=AD,DE=DC。
求证:BF⊥AC。
AE FDB C10、. 已知:如图,△ABC 和△A 'B 'C '中,∠BAC=∠B 'A 'C ',∠B=∠B ',AD 、A 'D '分别是∠BAC 、∠B 'A 'C '的平分线,且AD=A 'D '。
求证:△ABC ≌△A’B’C’。
北师大版七年级数学下册几何常见模型练习题(有答案)

全等三角形判定的三种类型已知一边一角型一次全等型1.已知,如图△ABC中,BD=DC,∠1=∠2,求证:AD平分∠BAC.2.如图,在△ABC中,D是BC边上的一点,连接AD,过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F,且BE=CF.求证:AD是△ABC的中线.两次全等型3.如图,已知,在四边形ABCD中,E是AC上一点,∠DAC=∠BAC,∠DCA=∠BCA.求证:∠DEC =∠BEC.4.如图,在△ABC中,AB=AC,∠BAC=90°,D为AC的中点,AE⊥BD于F交BC于E.(1)求证:∠ABD=∠CAE.(2)求证:∠ADB=∠CDE.(3)直接写出BD、AE、ED之间满足的数量关系.已知两边型一次全等型5.如图,点B,F,C,E在直线l上(点F,点C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.(1)求证:△ABC≌△DEF;(2)指出图中所有平行的线段,并说明理由.两次全等型6.如图所示,AB=CB,AD=CD,E是BD上任意一点,求证:AE=CE.7.如图:已知AE交BD于点C,∠DAC=∠EBC=∠BAC,AB=AC.试说明:DC与BE有怎样的数量关系.已知两角型一次全等型8.如图,已知∠BDC=∠CEB=90°,BE、CD交于点O,且AO平分∠BAC,求证:OB=OC.三角形中的四种常见说理类型说明相等关系1.如图,△ABC中,AB=AC,D是BC的中点,E、F分别是AB、AC上的点,且AE=AF,求证:DE=DF.说明位置关系说明平行关系2.已知△ABC为等边三角形,点P在AB上,以CP为边长作等边三角形△PCE.求证:AE∥BC.说明垂直关系3.如图,△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,且BD=CF,BE=CD,G是EF的中点,求证:DG⊥EF.说明倍分关系说明角的倍分关系4.如图,△ABC中,AB=AC,BD⊥AC于D.猜想:∠DBC与∠BAC之间的数量关系,并予以证明.说明线段的倍分关系5.如图,△ABC中,AB=AC,AD和BE是高,它们相交于H,且AE=BE.(1)求∠C的度数.(2)求证:AH=2BD.说明和、差关系6.如图,在△ABC中,∠ABC=2∠C,AD平分∠BAC,求证:AB+BD=AC.线段垂直平分线与角平分线的应用类型典例例1.已知:如图,△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,垂足分别是E、F.(1)求证:AE=BF;(2)求线段DG的长.利用线段垂直平分线的性质求线段的长1.如图,已知AB比AC长3cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14cm,求AB和AC的长.利用线段垂直平分线的性质求角的度数2.如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于D,连接AD.(1)若△ADC的周长为16,AB=12,求△ABC的周长;(2)若AD将∠CAB分成两个角,且∠CAD:∠DAB=2:5,求∠ADC的度数.利用线段垂直平分线的性质解决实际问题3.某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?利用线段垂直平分线的性质说明线段的数量关系4.如图,已知∠AOB=90°,OM是∠AOB的平分线,将三角尺的直角顶点P放在射线OM上,两直角边分别与OA,OB交于点C,D.(1)证明:PC=PD.(2)若OP=4,求OC+OD的长度.利用线段垂直平分线的性质说明线段的位置关系5.如图所示,AD为△ABC的角平分线,DE⊥AC于点E,DF⊥AB于点F,EF交AD于点M,求证:AM ⊥EF.全等三角形判定的三种类型1.证明:如右图所示,∵BD=DC,∴∠3=∠4,又∵∠1=∠2,∴∠1+∠3=∠2+∠4,即∠ABC=∠ACB,∴△ABC是等腰三角形,∴AB=AC,在△ABD和△ACD中,∴△ABD≌△ACD(SAS),∴∠BAD=∠CAD,∴AD平分∠BAC.2.证明:∵BE⊥AD,CF⊥AD,∴∠BED=∠F=90°,在△BED和△CFD中,,∴△BED≌△CFD,∴BD=CD,∴AD是△ABC的中线.3.证明:在△ACD和△ACB中,,∴△ACD≌△ACB,(ASA)∴BC=CD,在△DCE和△BCE中,,∴△DCE≌△BCE(ASA),∴∠DEC=∠BEC.4.(1)证明:∵AE⊥BD,∴∠AFB=∠BAC=90°,∴∠ABD+∠BAF=90°,∠BAF+∠CAE=90°,∴∠ABD=∠CAE.(2)证明:过C作CM⊥AC,交AE的延长线于M,则∠ACM=90°=∠BAC,∴CM∥AB,∴∠MCE=∠ABC=∠ACB,∵∠BAF=∠ADB,∠ADB+∠F AD=90°,∠ABD+∠BAF=90°,∴∠ABD=∠CAM,在△ABD和△CAM中,,∴△ABD≌△CAM(ASA),∴∠ADB=∠M,AD=CM,BD=AM,∵D为AC中点,∴AD=DC=CM,在△CDE和△CME中,,∴△CDE≌△CME(SAS),∴∠M=∠CDE,∴∠ADB=∠CDE.(3)解:结论:BD=AE+DE.理由:∵△CDE≌△CME,∴ME=DE,∵AM=AE+ME=AE+DE,∵BD=AM,∴BD=AE+DE.5.(1)证明:∵BF=CE,∴BF+FC=FC+CE,即BC=EF,在△ABC和△DEF中,,∴△ABC≌△DEF(SSS);(2)解:结论:AB∥DE,AC∥DF.理由:∵△ABC≌△DEF,∴∠ABC=∠DEF,∠ACB=∠DFE,∴AB∥DE,AC∥DF.6.证明:在△ABD与△CBD中,∴△ABD≌△CBD(SSS),∴∠ABD=∠CBD,在△ABE与△CBE中,△ABE≌△CBE(SAS),∴AE=CE.7.解:DC=BE,∵∠EBC=∠BAC,∠ACD=∠BAC+∠ABC,∠ABE=∠EBC+∠ABC,∴∠ACD=∠ABE,在△ACD和△ABE中,,∴△ACD≌△ABE(ASA),∴DC=BE.8.证明:∵∠BDC=∠CEB=90°,∴CD⊥AB,BE⊥AC,∵AO平分∠BAC,∴OD=OE,在△BDO和△CEO中∴△BDO≌△CEO(ASA),∴OB=OC.三角形中的四种常见说理类型1.证明:连接AD,∵AB=AC,D是BC的中点,∴∠EAD=∠F AD,在△AED和△AFD中,,∴△AED≌△AFD(SAS),∴DE=DF.2、证明:∵△ABC与△PCE为等边三角形,∴AC=BC,EC=PC,∠BCA=∠PCE=60°,∴∠BCP=∠ACE,在△BCP和△ACE中,,∴△CBP≌△CAE(SAS),∴∠CAE=∠B=60゜=∠ACB,∴AE∥BC.3.证明:连ED,DF,∵AB=AC,∴∠B=∠C,在△BED和△CDF中,,∴△BDE≌△CFD(SAS),∴DE=DF,∵G是EF的中点,∴DG⊥EF.4.解:∠DBC=∠BAC.设∠C=β,∵AB=AC,∴∠ABC=∠C=β,∴∠BAC=180°﹣2β,∠BAD=∠ABC+∠C=2β,∵BD⊥AC,∴∠ABD=90°﹣2β,∴∠DBC=90°﹣β,∴∠DBC=∠BAC.5.(1)解:∵AE=BE,BE⊥AC,∴∠BAE=45°,又∵AB=AC,∴∠C=(180°﹣∠BAE)=(180°﹣45°)=67.5°;(2)证明:∵AB=AC,AD⊥BC,∴BC=2BD,∠1+∠C=90°,∵BE⊥AC,∴∠2+∠C=90°,∴∠1=∠2,在△AEH和△BEC中,,∴△AEH≌△BEC(ASA),∴AH=BC,∴AH=2BD.6.证明:如图,在AC上截取AE=AB,∵AD平分∠BAC,∴∠CAD=∠BAD,在△ABD和△AED中,,∴△ABD≌△AED(SAS),∴DE=BD,∠AED=∠ABC,∵∠AED=∠C+∠CDE,∠ABC=2∠C,∴∠CDE=∠C,∴CE=DE,∵AE+CE=AC,∴AB+BD=AC.线段垂直平分线与角平分线的应用类型例1.(1)证明:连接AD、BD,∵AD是∠BCA的平分线,DE⊥AC,DF⊥BC,∴DE=DF,∵DG是AB边的垂直平分线,∴AD=DB,在Rt△AED和Rt△DFB中,,∴Rt△AED≌Rt△BFD(HL),∴AE=BF;(2)由(1)得:CE=CF==7,∴AE=EC﹣AC=1,∵∠ECD=∠EDC=45°,∴DE=CE=7,由题意可得:AG=BG=5,∴AD2=AE2+DE2=50,∴DG2=AD2﹣AG2=25,∴DG=5.1.解:∵DE是BC的垂直平分线,∴CD=BD,∴△ACD的周长=AC+AD+CD=AC+BD+AD=AC+AB,由题意得,,解得.∴AB和AC的长分别为8.5cm,5.5cm.2.解:(1)∵DE是AB的垂直平分线,∴AD=BD,又∵△ADC的周长为16,∴AD+CD+AC=16,即BD+CD+AC=BC+AC=16,又AB=12,∴AB+BC+AC=16+12=28,则△ABC的周长为28;(2)∵AD=BD,∴∠BAD=∠ABD,∵∠CAD:∠DAB=2:5,设一份为x,即∠CAD=2x,∠DAB=∠ABD=5x,又∠C=90°,∴∠ABD+∠BAC=90°,即2x+5x+5x=90°,解得:x=7.5°,∵∠ADC为△ABD的外角,∴∠ADC=∠DAB+∠ABD=5x+5x=10x=75°.3.解:如图,这所中学建在P点位置(点P为△ABC的外心).连结AB、BC、AC,作AB和BC的垂直平分线,两垂直平分线相交于点P,则点P到点A、B、C的距离相等.4.证明:(1)如图,过点P作PE⊥OA于点E,PF⊥OB于点F,∴∠PEC=∠PFD=90°.∵OM是∠AOB的平分线,∴PE=PF,∵∠AOB=90°,∠CPD=90°,∴∠PCE+∠PDO=360°﹣90°﹣90°=180°.而∠PDO+∠PDF=180°,∴∠PCE=∠PDF在△PCE和△PDF中∴△PCE≌△PDF(AAS)∴PC=PD;(2)∵∠AOB=90°,OM平分∠AOB,∴△POE与△POF为等腰直角三角形,∴OE=PE=PF=OF,∵OP=4,∴OE=2,由(1)知△PCE≌△PDF ∴CE=DF ∴OC+OD=OE+OF=2OE=4.5.证明:∵DE⊥AC于点E,DF⊥AB于点F,∴∠AED=∠AFD=90°,∵AD为三角形ABC的角平分线,∴∠EAD=∠F AD,而AD=AD,∴△AED≌△AFD∴ED=DF,AE=AF∴△AEF为等腰三角形,AM为∠BAC的平分线∴AM是△AEF的高,即AM⊥EF.。
北师大版七年级数学下册几何常见模型练习题(有答案)

全等三角形判定的三种类型已知一边一角型一次全等型1.已知,如图△ABC中,BD=DC,∠1=∠2,求证:AD平分∠BAC.2.如图,在△ABC中,D是BC边上的一点,连接AD,过点B作BE⊥AD于点E,过点C作CF⊥AD交AD的延长线于点F,且BE=CF.求证:AD是△ABC的中线.两次全等型3.如图,已知,在四边形ABCD中,E是AC上一点,∠DAC=∠BAC,∠DCA=∠BCA.求证:∠DEC =∠BEC.4.如图,在△ABC中,AB=AC,∠BAC=90°,D为AC的中点,AE⊥BD于F交BC于E.(1)求证:∠ABD=∠CAE.(2)求证:∠ADB=∠CDE.(3)直接写出BD、AE、ED之间满足的数量关系.已知两边型一次全等型5.如图,点B,F,C,E在直线l上(点F,点C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.(1)求证:△ABC≌△DEF;(2)指出图中所有平行的线段,并说明理由.两次全等型6.如图所示,AB=CB,AD=CD,E是BD上任意一点,求证:AE=CE.7.如图:已知AE交BD于点C,∠DAC=∠EBC=∠BAC,AB=AC.试说明:DC与BE有怎样的数量关系.已知两角型一次全等型8.如图,已知∠BDC=∠CEB=90°,BE、CD交于点O,且AO平分∠BAC,求证:OB=OC.三角形中的四种常见说理类型说明相等关系1.如图,△ABC中,AB=AC,D是BC的中点,E、F分别是AB、AC上的点,且AE=AF,求证:DE=DF.说明位置关系说明平行关系2.已知△ABC为等边三角形,点P在AB上,以CP为边长作等边三角形△PCE.求证:AE∥BC.说明垂直关系3.如图,△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,且BD=CF,BE=CD,G是EF的中点,求证:DG⊥EF.说明倍分关系说明角的倍分关系4.如图,△ABC中,AB=AC,BD⊥AC于D.猜想:∠DBC与∠BAC之间的数量关系,并予以证明.说明线段的倍分关系5.如图,△ABC中,AB=AC,AD和BE是高,它们相交于H,且AE=BE.(1)求∠C的度数.(2)求证:AH=2BD.说明和、差关系6.如图,在△ABC中,∠ABC=2∠C,AD平分∠BAC,求证:AB+BD=AC.线段垂直平分线与角平分线的应用类型典例例1.已知:如图,△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,垂足分别是E、F.(1)求证:AE=BF;(2)求线段DG的长.利用线段垂直平分线的性质求线段的长1.如图,已知AB比AC长3cm,BC的垂直平分线交AB于点D,交BC于点E,△ACD的周长是14cm,求AB和AC的长.利用线段垂直平分线的性质求角的度数2.如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于D,连接AD.(1)若△ADC的周长为16,AB=12,求△ABC的周长;(2)若AD将∠CAB分成两个角,且∠CAD:∠DAB=2:5,求∠ADC的度数.利用线段垂直平分线的性质解决实际问题3.某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等.请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?利用线段垂直平分线的性质说明线段的数量关系4.如图,已知∠AOB=90°,OM是∠AOB的平分线,将三角尺的直角顶点P放在射线OM上,两直角边分别与OA,OB交于点C,D.(1)证明:PC=PD.(2)若OP=4,求OC+OD的长度.利用线段垂直平分线的性质说明线段的位置关系5.如图所示,AD为△ABC的角平分线,DE⊥AC于点E,DF⊥AB于点F,EF交AD于点M,求证:AM ⊥EF.全等三角形判定的三种类型1.证明:如右图所示,∵BD=DC,∴∠3=∠4,又∵∠1=∠2,∴∠1+∠3=∠2+∠4,即∠ABC=∠ACB,∴△ABC是等腰三角形,∴AB=AC,在△ABD和△ACD中,∴△ABD≌△ACD(SAS),∴∠BAD=∠CAD,∴AD平分∠BAC.2.证明:∵BE⊥AD,CF⊥AD,∴∠BED=∠F=90°,在△BED和△CFD中,,∴△BED≌△CFD,∴BD=CD,∴AD是△ABC的中线.3.证明:在△ACD和△ACB中,,∴△ACD≌△ACB,(ASA)∴BC=CD,在△DCE和△BCE中,,∴△DCE≌△BCE(ASA),∴∠DEC=∠BEC.4.(1)证明:∵AE⊥BD,∴∠AFB=∠BAC=90°,∴∠ABD+∠BAF=90°,∠BAF+∠CAE=90°,∴∠ABD=∠CAE.(2)证明:过C作CM⊥AC,交AE的延长线于M,则∠ACM=90°=∠BAC,∴CM∥AB,∴∠MCE=∠ABC=∠ACB,∵∠BAF=∠ADB,∠ADB+∠F AD=90°,∠ABD+∠BAF=90°,∴∠ABD=∠CAM,在△ABD和△CAM中,,∴△ABD≌△CAM(ASA),∴∠ADB=∠M,AD=CM,BD=AM,∵D为AC中点,∴AD=DC=CM,在△CDE和△CME中,,∴△CDE≌△CME(SAS),∴∠M=∠CDE,∴∠ADB=∠CDE.(3)解:结论:BD=AE+DE.理由:∵△CDE≌△CME,∴ME=DE,∵AM=AE+ME=AE+DE,∵BD=AM,∴BD=AE+DE.5.(1)证明:∵BF=CE,∴BF+FC=FC+CE,即BC=EF,在△ABC和△DEF中,,∴△ABC≌△DEF(SSS);(2)解:结论:AB∥DE,AC∥DF.理由:∵△ABC≌△DEF,∴∠ABC=∠DEF,∠ACB=∠DFE,∴AB∥DE,AC∥DF.6.证明:在△ABD与△CBD中,∴△ABD≌△CBD(SSS),∴∠ABD=∠CBD,在△ABE与△CBE中,△ABE≌△CBE(SAS),∴AE=CE.7.解:DC=BE,∵∠EBC=∠BAC,∠ACD=∠BAC+∠ABC,∠ABE=∠EBC+∠ABC,∴∠ACD=∠ABE,在△ACD和△ABE中,,∴△ACD≌△ABE(ASA),∴DC=BE.8.证明:∵∠BDC=∠CEB=90°,∴CD⊥AB,BE⊥AC,∵AO平分∠BAC,∴OD=OE,在△BDO和△CEO中∴△BDO≌△CEO(ASA),∴OB=OC.三角形中的四种常见说理类型1.证明:连接AD,∵AB=AC,D是BC的中点,∴∠EAD=∠F AD,在△AED和△AFD中,,∴△AED≌△AFD(SAS),∴DE=DF.2、证明:∵△ABC与△PCE为等边三角形,∴AC=BC,EC=PC,∠BCA=∠PCE=60°,∴∠BCP=∠ACE,在△BCP和△ACE中,,∴△CBP≌△CAE(SAS),∴∠CAE=∠B=60゜=∠ACB,∴AE∥BC.3.证明:连ED,DF,∵AB=AC,∴∠B=∠C,在△BED和△CDF中,,∴△BDE≌△CFD(SAS),∴DE=DF,∵G是EF的中点,∴DG⊥EF.4.解:∠DBC=∠BAC.设∠C=β,∵AB=AC,∴∠ABC=∠C=β,∴∠BAC=180°﹣2β,∠BAD=∠ABC+∠C=2β,∵BD⊥AC,∴∠ABD=90°﹣2β,∴∠DBC=90°﹣β,∴∠DBC=∠BAC.5.(1)解:∵AE=BE,BE⊥AC,∴∠BAE=45°,又∵AB=AC,∴∠C=(180°﹣∠BAE)=(180°﹣45°)=67.5°;(2)证明:∵AB=AC,AD⊥BC,∴BC=2BD,∠1+∠C=90°,∵BE⊥AC,∴∠2+∠C=90°,∴∠1=∠2,在△AEH和△BEC中,,∴△AEH≌△BEC(ASA),∴AH=BC,∴AH=2BD.6.证明:如图,在AC上截取AE=AB,∵AD平分∠BAC,∴∠CAD=∠BAD,在△ABD和△AED中,,∴△ABD≌△AED(SAS),∴DE=BD,∠AED=∠ABC,∵∠AED=∠C+∠CDE,∠ABC=2∠C,∴∠CDE=∠C,∴CE=DE,∵AE+CE=AC,∴AB+BD=AC.线段垂直平分线与角平分线的应用类型例1.(1)证明:连接AD、BD,∵AD是∠BCA的平分线,DE⊥AC,DF⊥BC,∴DE=DF,∵DG是AB边的垂直平分线,∴AD=DB,在Rt△AED和Rt△DFB中,,∴Rt△AED≌Rt△BFD(HL),∴AE=BF;(2)由(1)得:CE=CF==7,∴AE=EC﹣AC=1,∵∠ECD=∠EDC=45°,∴DE=CE=7,由题意可得:AG=BG=5,∴AD2=AE2+DE2=50,∴DG2=AD2﹣AG2=25,∴DG=5.1.解:∵DE是BC的垂直平分线,∴CD=BD,∴△ACD的周长=AC+AD+CD=AC+BD+AD=AC+AB,由题意得,,解得.∴AB和AC的长分别为8.5cm,5.5cm.2.解:(1)∵DE是AB的垂直平分线,∴AD=BD,又∵△ADC的周长为16,∴AD+CD+AC=16,即BD+CD+AC=BC+AC=16,又AB=12,∴AB+BC+AC=16+12=28,则△ABC的周长为28;(2)∵AD=BD,∴∠BAD=∠ABD,∵∠CAD:∠DAB=2:5,设一份为x,即∠CAD=2x,∠DAB=∠ABD=5x,又∠C=90°,∴∠ABD+∠BAC=90°,即2x+5x+5x=90°,解得:x=7.5°,∵∠ADC为△ABD的外角,∴∠ADC=∠DAB+∠ABD=5x+5x=10x=75°.3.解:如图,这所中学建在P点位置(点P为△ABC的外心).连结AB、BC、AC,作AB和BC的垂直平分线,两垂直平分线相交于点P,则点P到点A、B、C的距离相等.4.证明:(1)如图,过点P作PE⊥OA于点E,PF⊥OB于点F,∴∠PEC=∠PFD=90°.∵OM是∠AOB的平分线,∴PE=PF,∵∠AOB=90°,∠CPD=90°,∴∠PCE+∠PDO=360°﹣90°﹣90°=180°.而∠PDO+∠PDF=180°,∴∠PCE=∠PDF在△PCE和△PDF中∴△PCE≌△PDF(AAS)∴PC=PD;(2)∵∠AOB=90°,OM平分∠AOB,∴△POE与△POF为等腰直角三角形,∴OE=PE=PF=OF,∵OP=4,∴OE=2,由(1)知△PCE≌△PDF ∴CE=DF ∴OC+OD=OE+OF=2OE=4.5.证明:∵DE⊥AC于点E,DF⊥AB于点F,∴∠AED=∠AFD=90°,∵AD为三角形ABC的角平分线,∴∠EAD=∠F AD,而AD=AD,∴△AED≌△AFD∴ED=DF,AE=AF∴△AEF为等腰三角形,AM为∠BAC的平分线∴AM是△AEF的高,即AM⊥EF.。
(完整版)北师大七年级下几何证明入门专项练习

几何证明题专项训练11、( 1)∵∠ 1=∠ A(已知),∴∥,();( 2)∵∠ 3=∠4(已知),∴∥,();( 3)∵∠ 2=∠5(已知),∴∥,();( 4)∵∠ ADC+∠ C=180o(已知),∴∥,();2,如图,( 1)∵∠ ABD=∠ BDC(已知),∴∥,();( 2)∵∠ DBC=∠ ADB(已知),∴∥,();( 3)∵∠ CBE=∠ DCB(已知),∴∥,();( 4)∵∠ CBE=∠ A,(已知),∴∥,();( 5)∵∠ A+∠ ADC=180o(已知),∴∥,();( 6)∵∠ A+∠ ABC=180o(已知),∴∥,();3、如图,∠ 1=∠ 2, AC均分∠ DAB,试说明: DC∥ AB.4,如图,∠ ABC=∠ ADC, BF 和 DE分别均分∠ ABC和∠ ADC,∠1=∠ 2,试说明: DE∥ FB.5.如图 2-67,已知∠ 1= ∠2,求∠ 3+∠ 4 的度数.6、如图 2-56①∵ AB//CD (已知),∴∠ ABC=_______ ()______=______ (两直线平行,内错角相等),∴∠ BCD+______= 180()②∵∠ 3=∠ 4(已知),∴ ______∥ _____()③∵∠ FAD= ∠ FBC(已知),∴ _____∥()7、如图 2-57,直线 AB ,CD,EF 被直线 GH 所截,∠ 1= 70,∠ 2=110,∠3= 70.求证: AB//CD .证明:∵∠ 1= 70,∠ 3= 70(已知),∴∠ 1=∠ 3()∴ ____∥ _____()∵∠ 2=110,∠ 3= 70(),∴______+_____=____,∴_____//______,∴ AB//CD ().8.如图 2-58,①直线 DE ,AC 被第三条直线BA 所截,则∠ 1 和∠ 2 是 ________,假如∠ 1= ∠ 2,则 ___//___,其原因是().②∠ 3 和∠ 4 是直线 __________ 、 __________ ,被直线 ____________所截,所以 ____//____ .∠ 3____∠ 4,其原因是().9.如图 2-59,已知 AB//CD ,BE 均分∠ ABC , CE 均分∠ BCD ,求证∠ 1+∠ 2= 90 .证明:∵BE 均分∠ ABC (已知),∴∠ 2=_________()同理∠ 1=_______________,∴∠1)1+∠2= ____________ (2又∵ AB//CD (已知),∴∠ ABC+ ∠ BCD=_____ ()∴∠ 1+ ∠2= 90()10、如图 2-60,E、 F、 G 分别是 AB 、 AC 、BC 上一点.①假如∠ B= ∠ FGC,则 ____//____, 其原因是()②∠ BEG= ∠EGF,则 _____//____ ,其原因是()③假如∠ AEG+ ∠ EAF= 180,则 ____//____ ,其原因是()11.如图2-61,已知AB//CD , AB//DE ,求证:∠ B+ ∠D= ∠BCF+∠DCF.证明:∵ AB//CF(已知),∴∠ ______=∠ ________(两直线平行,内错角相等).∵ AB//CF ,AB//DE (已知),∴ CF//DE ()∴∠ _________=∠ _________()∴∠ B+ ∠ D=∠ BCF+ ∠ DCF(等式性质).EA CGBD 图 7 F几何证明题专项训练 21、如图,∠ B=∠ C, AB ∥ EF,试说明:∠BGF= ∠ C。
最新北师大版七年级下册数学 全等三角形的证明专题

最新北师大版七年级下册数学 全等三角形的证明专题【温故而知新】全等三角形的判定:边边边 (SSS ) 【稳定性】角边角 (ASA ) 三角形全等的条件边角边(SAS )角角边 (AAS )1、判定三角形全等的条件一 边边边三边对应相等的两个三角形全等,简写为“边边边”或“SSS ”。
例题1)已知,如图AD=CB ,AB=CD ,试证明ΔABD ≌ΔCDB2)已知:如图,A 、B 、E 、F 在一条直线上,且AC=BD ,CE=DF ,AF=BE 。
求证: △ACE ≌△BDFDBD C B课堂练习1、已知:如图,B 、E 、C 、F 在一条直线上,且BE=CF ,AB=DE ,AC=DF 。
求证:△ABC ≌△DEF 。
2、已知:如图,AB=DC ,AD=BC ,求证:∠A=∠C 。
3、如图,△ABC 中,D 是BC 边的中点,AB=AC ,求证:∠B=∠C 。
2、判定三角形全等的条件二 角边角两角和它们的夹边对应相等的两个三角形全等,简写为“角边角”或“ASA ”。
例题1、如图,∠ABC=∠DCB ,∠ACB=∠DCB ,试说明△ABC ≌△DCB.A DB CFCEDCB DCB2、已知:如图,∠DAB=∠CAB,∠ABD=∠ABC。
求证:△ABD≌△ABC.DA B EC课堂练习1、如图:在△ABC和△DBC中,∠ABD=∠DCA,∠DBC=∠ACB,求证:AC=DB.A DB C2、如图,D、E分别在AB、AC上,且AB=AC,∠B=∠C,求证:△ABE≌△ACD.B3、已知:如图 , AB=AC , ∠B=∠C,BE、DC交于O点。
求证:BD=CE.AD EOB C4、图,已知:AE=CE ,∠A=∠C ,∠BED=∠AEC ,求证:△ABE ≌△CDE A EC B D3、判定三角形全等的条件三 边角边两边及它们的夹角对应相等的两个三角形全等,简写为“角边角”或“SAS ”。
例题1.已知如图,AE =AC,AB =AD,∠EAB =∠CAD,试说明:∠B =∠D2、如图,△ABC 中,AB =AC ,AD 平分∠BAC ,试说明△ABD ≌△ACD 。
北师大版七年级下册数学证明题练习

北师大版七年级下册数学证明题练习以下15题15分,第8题10分,其余的每小题5分。
1.如图,已知AB∥CD,EF交AB,CD于G, H, GM, HN分别平分EHDAGF∠∠,,试说明GM ∥HN.2.已知:如图,AD∥BC,∠BAD = ∠BCD,求证:AB∥CD。
3.如图,AB∥CD,P为AB,CD之间的一点,已知︒2,求BPC∠25∠∠32=1,︒=的度数。
4.已知AB∥CD,BC∥DE.试说明D∠.B∠=5.已知:,21,,,∠=∠⊥⊥⊥G AB FG AC BC E AC DE 于于求证:AB CD ⊥.6.在ABC ∆中,,D AB CD 于⊥AB FG ⊥于G ,ED ∥BC,试说明21∠=∠.7.已知:在△ABC 中,∠BAC=80°,∠B=60°,AD ⊥BC 于D ,AE 平分∠DAC ,求∠AEC8.如图,已知∠A=∠F ,AB ∥EF ,BC=DE ,请说明AD ∥CF.BA CDE CBEAD解:∵ BC=DE (已知) ∴ 在△ABD 与△FEC 中, ∴ BC+CD=DE+CD ( ) ∠A=∠F (已知) 即:_________=_________ _______=______(已证) 又∵AB ∥EF (已知)_______=______(已证) ∴ ________=_________ ∴△ABD ≌△FEC (________)∴∠ADB =∠FCE (_____________________) ∴ AD ∥CF (_________________________) 9.如图,AB=AD ,AC=AE ,∠BAE=∠DAC ,试说明∠C=∠E10.如图,已知OC=OE ,OD=OB ,试说明△ADE ≌△ABC.11.已知AO 是△ABC 中BC 边上的高,点D 、点E 是三角形外的两个点,且满足AD=AE ,DB =EC ,∠D =∠E ,试说明AO 平分∠BAC12.如图,在△ABC 中,BC=10,边BC 的垂直平分线分别交AB ,BC 于点E 和D ,BE=6, 求△BCE 的周长.ODEACBECBODA1.如图,已知在AB=AC ,DB=DC ,则AD ⊥BC ,为什么?14、在Rt △ABC 中,BD 是∠B 的平分线,DE ⊥AB 于E, 则DE = DC 吗?说明你的理由.15、如图,△ABC 中∠C = 900,沿过B 点的直线BE 折叠△ABC ,使点C 恰好落在AB 的中点D 处. (1)求∠A 的度数;(2)若CE = 2cm ,则求出ED 的长度;(3)若CB = 4cm ,则求出AB 的长度.16、如图,在△ABC 中,AB = AC ,D 是BC 的中点,E 在AD 上,BE = CE 吗?说明你的理由.(8分)ABD E ABC DE┌17、如图,△ABC中,AB=AC,D是AB边上的一点,DE垂直平分AC,∠A=040,求∠BDC的度数。
初一几何专项训练北师大深圳

初一几何专项训练北师大深圳几何学是数学中的一个重要分支,它研究的是形状、大小、相对位置和变换等概念。
对于初一学生来说,几何学的学习是基础而关键的,它不仅能够锻炼学生的空间想象能力,还能够帮助学生理解更高层次的数学概念。
以下是针对北师大深圳版初一几何专项训练的一些建议和练习题目。
一、几何基本概念1. 点、线、面:点是几何学中最基本的元素,线是由无数个点组成的,面是由无数条线组成的。
2. 角:由两条射线组成的图形,两条射线的公共端点称为角的顶点。
3. 平行线:在同一平面内,且永不相交的两条直线。
4. 垂直线:两条直线相交成90度角。
二、几何形状1. 三角形:由三条线段首尾相连组成的封闭图形。
2. 四边形:由四条线段首尾相连组成的封闭图形,如矩形、正方形、梯形等。
3. 圆:平面上所有与定点(圆心)距离相等的点的集合。
三、几何性质1. 等边三角形:三条边长度相等的三角形。
2. 等腰三角形:至少有两条边长度相等的三角形。
3. 直角三角形:有一个角为90度的三角形。
四、几何定理1. 勾股定理:直角三角形的斜边的平方等于两直角边的平方和。
2. 相似三角形:对应角相等,对应边成比例的两个三角形。
五、几何证明1. 全等三角形:通过SSS(边边边)、SAS(边角边)、ASA(角边角)、AAS(角角边)等方法证明两个三角形全等。
2. 平行线的性质:如平行线间的距离处处相等,平行线划分的角相等。
六、练习题目1. 题目一:在一个等腰三角形ABC中,AB=AC,∠A=70°,求∠B和∠C的度数。
2. 题目二:已知三角形DEF的三边DF=4cm,EF=5cm,DE=3cm,判断三角形DEF的形状。
3. 题目三:在一个直角三角形中,如果斜边的长度是13cm,一条直角边的长度是5cm,求另一条直角边的长度。
4. 题目四:如果两条平行线被第三条直线所截,求证截线与平行线所形成的同位角相等。
5. 题目五:在一个圆中,弦AB和弦CD相交于点E,求证∠AEC=∠BEC。
北师大版七年级下册第四章全等三角形推理训练(证明入门专题)无答案

初中七年级数学专题练习全等三角形一、知识点睛:1.三角形全等判定方法:(1)能够 的两个图形叫做全等形,能够 的两个三角形叫做全等三角形.(2)把两个全等的三角形重合到一起,重合的顶点叫做 ,重合的边叫做 ,重合的角叫做 .(3)全等三角形的 边相等,全等三角形的 角相等. (4) 对应相等的两个三角形全等(边边边或 ).(5)两边和它们的 对应相等的两个三角形全等(边角边或 ). (6)两角和它们的 对应相等的两个三角形全等(角边角或 ). (7)两角和其中一角的 对应相等的两个三角形全等(角角边或 ). 2.求证两条线段或两个角相等的方法:要善于把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等. 步骤:(1)根据所要求证的线段或角度,找出它们所在的两个三角形;(2)从已知条件入手,证明这两个三角形全等。
从四种证明全等的判定方法里找出最简单并且最合适的方法;(3)写出准确的证明过程。
找准两个三角形的对应角、对应线段和对应顶点。
(4)由三角形全等的性质得到所要求证的线段或角。
二、推理填空,完成下面的证明过程:1. 如图,OA =OC ,OB =OD. 求证:AB ∥DC.证明:在△ABO 和△CDO 中,OA OC ,AOB __________,OB OD ,⎧=⎪∠=⎨⎪=⎩∴△ABO ≌△CDO ( ).∴∠A = .∴AB ∥DC ( 相等,两直线平行).2. 如图,AB ∥DC ,AE ⊥BD ,CF ⊥BD ,BF =DE. 求证:△ABE ≌△CDF.证明:∵AB ∥DC ,( )ABC DO∴∠1= .( ) ∵AE ⊥BD ,CF ⊥BD ,( )∴∠AEB = = .( ) ∵BF =DE ,( ) ∴ BF- =DE-∴BE = .在△ABE 和△CDF 中,1______,BE ______,AEB _______,⎧∠=⎪=⎨⎪∠=⎩∴△ABE ≌△CDF ( ).3.如图,点B 、E 、C 、F 在同一直线上,且AB=DE ,AC=DF ,BE=CF ,求证:ΔABC ≌ΔDEF 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何证明题专项训练11、(1)∵∠1=∠A (已知), ∴ ∥ ,( ); (2)∵∠3=∠4(已知),∴ ∥ ,( ); (3)∵∠2=∠5(已知),∴ ∥ ,( ); (4)∵∠ADC+∠C=180º(已知),∴ ∥ ,( ); 2,如图,(1)∵∠ABD=∠BDC (已知),∴ ∥ ,( ); (2)∵∠DBC=∠ADB (已知),∴ ∥ ,( ); (3)∵∠CBE=∠DCB (已知),∴ ∥ ,( );(4)∵∠CBE=∠A ,(已知),∴ ∥ ,( ); (5)∵∠A+∠ADC=180º(已知),∴ ∥ ,( ); (6)∵∠A+∠ABC=180º(已知),∴ ∥ ,( ); 3、如图,∠1=∠2,AC 平分∠DAB ,试说明:DC ∥AB.4,如图,∠ABC=∠ADC ,BF 和DE 分别平分∠ABC 和∠ADC , ∠1=∠2,试说明:DE ∥FB.5.如图2-67,已知∠1=∠2,求∠3+∠4的度数.6、如图2-56①∵AB//CD (已知),∴∠ABC=_______( ) ______=______(两直线平行,错角相等),∴∠BCD+______=︒180( ) ②∵∠3=∠4(已知),∴______∥_____( ) ③∵∠FAD=∠FBC (已知),∴_____∥_____( )7、如图2-57,直线AB ,CD ,EF 被直线GH 所截,∠1=︒70,∠2=︒110,∠3=︒70.求证:AB//CD .证明:∵∠1=︒70,∠3=︒70(已知), ∴∠1=∠3( )∴ ____∥_____( )∵∠2=︒110,∠3=︒70( ),∴______+_____=____, ∴_____//______,∴AB//CD ( ).8.如图2-58,①直线DE ,AC 被第三条直线BA 所截,则∠1和∠2是________,如果∠1=∠2,则___//___, 其理由是( ). ②∠3和∠4是直线__________、__________, 被直线____________所截,因此____//____.∠3____∠4,其理由是( ). 9.如图2-59,已知AB//CD ,BE 平分∠ABC ,CE 平分∠BCD ,求证∠1+∠2=︒90.证明:∵ BE 平分∠ABC (已知),∴∠2=_________( ) 同理∠1=_______________,∴∠1+∠2=21____________( ) 又∵AB//CD (已知),∴∠ABC+∠BCD=_____( ) ∴∠1+∠2=︒90( )10、如图2-60,E 、F 、G 分别是AB 、AC 、BC 上一点.①如果∠B=∠FGC ,则____//____,其理由是( ) ②∠BEG=∠EGF ,则_____//____,其理由是( ) ③如果∠AEG+∠EAF=︒180,则____//____,其理由是( )11.如图2-61,已知AB//CD ,AB//DE ,求证:∠B+∠D=∠BCF+∠DCF .证明: ∵AB//CF (已知),∴∠______=∠________(两直线平行,错角相等). ∵AB//CF ,AB//DE (已知),∴CF//DE ( ) ∴∠_________=∠_________( )∴∠B+∠D=∠BCF+∠DCF (等式性质).几何证明题专项训练21、如图,∠B=∠C ,AB ∥EF ,试说明:∠BGF=∠C 。
(6分)解:∵ ∠B=∠C∴ AB ∥CD ( ) 又∵ AB ∥EF ( )∴ ∥ ( ) ∴ ∠BGF=∠C ( )2、如图,在△ABC 中,CD ⊥AB 于D ,FG ⊥AB 于G ,ED//BC ,试说明∠1=∠2,以下是证明过程,请填空:(8分) 解:∵CD ⊥AB ,FG ⊥AB∴∠CDB=∠ =90°( 垂直定义)∴_____//_____ ( ) ∴∠2=∠3 ( ) 又∵DE//BC∴∠ =∠3 ( ) ∴∠1=∠2 ( )3、已知:如图,∠1+∠2=180°,试判断AB 、CD 有何位置关系?并说明理由。
(8分)4、如图,AD 是∠EAC 的平分线,AD ∥BC ,∠B = 30°,你能算出∠EAD 、∠DAC 、∠C 的度数吗?(7分)5、如图,已知EF ∥AD ,∠1=∠2,∠BAC=70 o,求∠AGD 。
解:∵EF ∥AD (已知)∴∠2= ( )又∵∠1=∠2(已知)∴∠1=∠3(等量替换) ∴AB ∥ () ∴∠BAC+ =180 o()∵∠BAC=70 o(已知) ∴∠AGD= °6、如图,已知∠BED=∠B+∠D ,试说明AB 与CD 的位置关系。
解:AB ∥CD ,理由如下:过点E 作∠BEF=∠B∴AB ∥EF ()∵∠BED=∠B+∠D (已知)且∠BED=∠BEF+∠FED ∴∠FED=∠D ∴CD ∥EF ( ) ∴AB ∥CD ()7、 如图,AD 是∠EAC 的平分线,AD ∥BC ,∠B=30 o ,求∠EAD 、∠DAC 、∠C 的度数。
(6分)8、如图,EB ∥DC ,∠C=∠E ,请你说出∠A=∠ADE 的理由。
9、已知,如图,∠1=∠ABC=∠ADC ,∠3=∠5,∠2=∠4,∠ABC+∠BCD=180°.将下列推理过程补充完整:(1)∵∠1=∠ABC (已知),∴AD ∥______(_______________________________) (2)∵∠3=∠5(已知), ∴AB ∥______,(_______________________________)(3)∵∠ABC+∠BCD=180°(已知),∴_____∥______,(______________________)10、已知,如图14,∠1=∠ABC=∠ADC ,∠3=∠5,∠2=∠4,∠ABC+∠BCD=180°。
(1)∵∠1=∠ABC(已知)∴AD ∥ ( ) (2)∵∠3=∠5(已知) ∴AB ∥ ( ) (3)∵∠2=∠4(已知)∴ ∥ ( ) (4)∵∠1=∠ADC(已知)∴ ∥ ( )(5)∵∠ABC+∠BCD=180°(已知)∴ ∥ ( )A 12 345B CD图1411、如图15,(1)∵∠A= (已知)∴AC ∥ED ( )(2)∵∠2= (已知)∴AC ∥ED ( )(3)∵∠A+ =180°(已知) ∴AB ∥FD ( ) (4)∵AB ∥ (已知) ∴∠2+∠AED=180°( ) (5)∵AC ∥ (已知)∴∠C=∠1 ( )12、已知:如图15,AB ⊥BC 于B ,CD ⊥BC 于C ,∠1=∠2。
求证:BE ∥CF 。
证明:∵ AB ⊥BC ,CD ⊥BC (已知)∴ ∠1+∠3=90º,∠2+∠4=90º( ) 又∵ ∠1=∠2( )∵ ∠3=∠4( )∴ BE ∥CF ( )13、(9分)已知:如图16,AB ∥CD ,∠1=∠2, 求证:∠B =∠D 。
证明:∵ ∠1=∠2(已知)∴ ∥ ( ) ∴ ∠BAD +∠B = ( ) 又∵ AB ∥CD (已知)∴ + =180º( )∴ ∠B =∠D ( ) 14、在空格填上推理的理由(1)如图,已知AB//DE ,∠B=∠E ,求证:BC//EF 。
证明: AB//DE ( )∴ ∠B= ( )又 ∠B=∠E ( )∴ = (等量代换)∴ // ( )AEFD BC12 3图15BEADOFC(2)已知,如图,∠1=120°,∠2=120°,求证:AB//CD 。
证明: ∠1=120°,∠2=120°( ) ∴∠1=∠2( )又 = ( )∴∠1=∠3( )∴AB//CD ( )(3)已知,如图,AB//CD ,BC//AD ,∠3=∠4。
求证:∠1=∠2证明: AB//CD ( )∴ = ( )又 BC//AD ( )∴ = ( ) 又 ∠3=∠4( ) ∴∠1=∠2( )15、(1)如图12,根据图形填空:直线a 、b 被直线c 所截(即直线c 与直线a 、b 都相交),已知a ∥b ,若∠1=120°,则∠2的度数=__________, 若∠1=3∠2,则∠1的度数=___________;如图13中,已知a ∥b ,且∠1+2∠2=1500,则∠1+∠2=_________0 (2)如图14,根据图形填空: ∵∠B =∠______;∴AB ∥CD (________________); ∵∠DGF =______;∴CD ∥EF (________________________); ∵AB ∥EF ;∴∠B +______=180°(____________________);132A BC DBCD123 4 AA B C DGEF图14a bc12图13 a bc 1 2图12(3)已知:如图15,AB ⊥BC ,BC ⊥CD 且∠1=∠2,求证:BE ∥CF 。
证明:∵AB ⊥BC ,BC ⊥CD (已知) ∴ = =90°( ) ∵∠1=∠2(已知)∴ = (等式性质) ∴BE ∥CF ( )(4)已知:如图16,AC ⊥BC ,垂足为C ,∠BCD 是∠B 的余角。
求证:∠ACD=∠B 。
证明:∵AC ⊥BC (已知)( ) ∴∠ACB=90°∴∠BCD+∠DCA=900∵∠BCD 是∠B 的余角(已知)∴∠BCD+∠B=900∴∠ACD=∠B ( ) (5)已知,如图17,BCE 、AFE 是直线,AB ∥CD ,∠1=∠2,∠3=∠4。
求证:AD ∥BE 。
证明:∵AB ∥CD (已知)∴∠4=∠ ( ) ∵∠3=∠4(已知)∴∠3=∠ ( ) ∵∠1=∠2(已知)∴∠1+∠CAF=∠2+∠CAF ( )即∠ =∠∴∠3=∠ ( )∴AD ∥BE ( )16、已知,如图,∠1=∠2,∠A =∠F 。
求证:∠C =∠D 。
证明:∵∠1=∠2(已知)∠1=∠3( ) ∴∠2=∠ ( ) ∴BD ∥ ( ) ∴∠4=∠C ( ) 又∵∠A = (已知) ∴AC ∥ ( ) ∴ =∠D ( )∴∠C =∠D ( )C ABD EF 1 2 图15BDAC图16A D BCEF1234图1717、已知,如图,∠1=∠2,CF ⊥AB ,DE ⊥AB ,求证:FG ∥BC 。
证明:∵CF ⊥AB ,DE ⊥AB (已知)∴∠BED =900,∠BFC =900( ) ∴ = ( ) ∴ED ∥ ( ) ∴ =∠BCF ( )又∵∠1=∠2(已知)∴∠2= () ∴FG ∥BC ( )18.如图,已知CD AB //,CF AE //,求证:DCF BAE ∠=∠。
