1212轴对称图形的性质 (2)PPT课件
合集下载
《轴对称》 ppt课件

2.同样,我们把这条直线叫做_对__称_轴__.
3.折叠后重合的点是对应点,叫做_对__称_点__.
PPT课件
22
轴对称
对称点
D
A A′ D′
B C
B′ C′
23
PPT课件
八年级 数学
第十四章 轴对称
想一想:一辆汽车的车牌在水中的倒影如 图所示,你能确定该车车牌的号码吗?
PPT课件
24
轴对称
练习 :下列给出的每幅图形中的两个图案是轴 对称吗?如果是,试着找出它们的对称轴。
第十二章 轴对称
PPT课件
要 仔 细 观 察 哦!
6
八年级 数学
12.1 轴对称(1)
第十二章 轴对称
PPT课件
要 仔 细 观 察 哦!
7
定义
如果_一__个_图__形__沿一条直线折叠,直线两旁的部分
能够_互__相__重_合___,这个图形叫做__轴__对_称__图__形___.这条直
线就是它的__对__称_轴_____.
轴对称图形
两个图形成轴对称
27
PPT课件
比较归纳:
区别 联系
轴对称图形 一_个图形
两个图形成轴对称 _两 个图形
1.沿一条直线折叠,直线两旁的部分能够 _互_相_重合_.
2.都有_对_称_轴 _.
3.如果把一个轴对称图形沿对称轴分成 两个图形,那么这两个图形关于这条直线 _对_称_;如果把两个成轴对称的图形看成 一个图形,那么这个图形就是_轴_对称_图_形.PPTFra bibliotek件28
八年级 数学
12.1 轴对称(1)
第十二章 轴对称
做一做:
如图,△ABC与△DEF关于直线a对称,
3.折叠后重合的点是对应点,叫做_对__称_点__.
PPT课件
22
轴对称
对称点
D
A A′ D′
B C
B′ C′
23
PPT课件
八年级 数学
第十四章 轴对称
想一想:一辆汽车的车牌在水中的倒影如 图所示,你能确定该车车牌的号码吗?
PPT课件
24
轴对称
练习 :下列给出的每幅图形中的两个图案是轴 对称吗?如果是,试着找出它们的对称轴。
第十二章 轴对称
PPT课件
要 仔 细 观 察 哦!
6
八年级 数学
12.1 轴对称(1)
第十二章 轴对称
PPT课件
要 仔 细 观 察 哦!
7
定义
如果_一__个_图__形__沿一条直线折叠,直线两旁的部分
能够_互__相__重_合___,这个图形叫做__轴__对_称__图__形___.这条直
线就是它的__对__称_轴_____.
轴对称图形
两个图形成轴对称
27
PPT课件
比较归纳:
区别 联系
轴对称图形 一_个图形
两个图形成轴对称 _两 个图形
1.沿一条直线折叠,直线两旁的部分能够 _互_相_重合_.
2.都有_对_称_轴 _.
3.如果把一个轴对称图形沿对称轴分成 两个图形,那么这两个图形关于这条直线 _对_称_;如果把两个成轴对称的图形看成 一个图形,那么这个图形就是_轴_对称_图_形.PPTFra bibliotek件28
八年级 数学
12.1 轴对称(1)
第十二章 轴对称
做一做:
如图,△ABC与△DEF关于直线a对称,
《轴对称》PPT课件

关于这条直线对称, 简称轴对称,这条直线 叫对称轴
2. 两个图形中的对应点(即两图形 重合时互相重合的点)叫做关于这条 直线的对称点
注意:如果一点在对称轴上,它的对称点就是 它本身
1. △ABC和△A’ B ’ C ’是否关于直线l对称?为什么? 2. 线段AB与线段A ’ B ’否关于直线l对称?为什么?
练习:
一、判断 1. 轴对称图形必有对称轴
()
2. 轴对称图形至少有一条对称轴 ( )
3. 关于某直线成轴对称的两个图形必能互相重合( )
4. 两个完全互相重合的图形必是轴对称( )
二、选择 1. 符合下列哪个条件的图形是轴对称图形? ( D )
(A)能够互相重合的两个图形
(B)一个图形在某直线翻折,能与另一个图形重合
是
2条 对角线所在的直线
是
4条
两条邻边的中垂线和 对角线所在的直线
是
无数条 直径所在的直线
是
1条 一条底的中垂线
下列(1) (2)两个图形有什么区别?
(1)
(2)
两个图形 轴对称
一个图形 轴对称图形
二、轴对称和对称点的定义:
1. 平面上的两个图形,将其中一个图 形沿着某一条直线翻折过去,如果它能够 与另一个图形重合,那么就说这两个图形
BC与B ’ C ’ ,CA与C ’A ’呢? 3. 点A和B ’点关于直线l的对称点各是哪一点?
△ABC△ A ’ B ’ C ’关于直线l对称。 点A和点A ’,点B和点B ’ ,点C ’和点C ’分别是关于直线l的对称点
区别:
“轴对称图形”是指同一个图形的两部 分 沿某直线翻折时,两部分重合的图形。
线段是轴对称图形,它的对称轴是这条线段的垂直平分线 角是轴对称图形,它的对称轴是这个角的平分线所在的直线
2. 两个图形中的对应点(即两图形 重合时互相重合的点)叫做关于这条 直线的对称点
注意:如果一点在对称轴上,它的对称点就是 它本身
1. △ABC和△A’ B ’ C ’是否关于直线l对称?为什么? 2. 线段AB与线段A ’ B ’否关于直线l对称?为什么?
练习:
一、判断 1. 轴对称图形必有对称轴
()
2. 轴对称图形至少有一条对称轴 ( )
3. 关于某直线成轴对称的两个图形必能互相重合( )
4. 两个完全互相重合的图形必是轴对称( )
二、选择 1. 符合下列哪个条件的图形是轴对称图形? ( D )
(A)能够互相重合的两个图形
(B)一个图形在某直线翻折,能与另一个图形重合
是
2条 对角线所在的直线
是
4条
两条邻边的中垂线和 对角线所在的直线
是
无数条 直径所在的直线
是
1条 一条底的中垂线
下列(1) (2)两个图形有什么区别?
(1)
(2)
两个图形 轴对称
一个图形 轴对称图形
二、轴对称和对称点的定义:
1. 平面上的两个图形,将其中一个图 形沿着某一条直线翻折过去,如果它能够 与另一个图形重合,那么就说这两个图形
BC与B ’ C ’ ,CA与C ’A ’呢? 3. 点A和B ’点关于直线l的对称点各是哪一点?
△ABC△ A ’ B ’ C ’关于直线l对称。 点A和点A ’,点B和点B ’ ,点C ’和点C ’分别是关于直线l的对称点
区别:
“轴对称图形”是指同一个图形的两部 分 沿某直线翻折时,两部分重合的图形。
线段是轴对称图形,它的对称轴是这条线段的垂直平分线 角是轴对称图形,它的对称轴是这个角的平分线所在的直线
轴对称课件(60张PPT)

轴对称在解直角三角形中应用
在解直角三角形时,可以利用轴对称的 性质来构造全等或相似的直角三角形,
从而简化计算过程。
例如,如果一个直角三角形关于某条直 线对称,那么它的两个锐角相等,同时 它的两条直角边也相等。这样我们就可 以通过已知的一边和一角来求解其他未
知量。
另外,如果两个直角三角形关于某条直 线对称,那么它们一定是相似的。这样 我们就可以通过已知的相似比来求解未
知量。
05
绘制和分析轴对称图形方 法技巧
使用直尺和圆规绘制轴对称图形
确定对称轴
在平面上选择一条直线作为对 称轴。
找到对称点
使用直尺和圆规,按照轴对称 的定义,找到该点关于对称轴 的对称点。
选择一个点
在对称轴的一侧选择一个点。
绘制图形
连接原点和对称点,即可得到轴对 称图形的一部分。重复以上步骤,
可以得到完整的轴对称图形。
动物
一些动物的身体结构也具 有轴对称性,如蝴蝶的翅 膀、蜻蜓的复眼等。
晶体
晶体结构中的原子排列往 往呈现出轴对称性,如雪 花、钻石等。
科技产品中的轴对称设计
电子产品
手机、平板电脑等电子产品的外观设 计中,常采用轴对称元素,实现简洁、 时尚的视觉效果。
汽车设计
航空航天
飞机、火箭等航空航天器的设计中也 广泛应用轴对称性,以确保飞行稳定 性和安全性。
典型例题解析
解析
根据轴对称性质,我们知道 △ABC≌△A'B'C',所以 ∠BAC=∠B'A'C'。
例题2
已知点P(2,3)关于x轴对称的点为P', 求点P'的坐标。
解析
由于点P关于x轴对称,所以点P'的 横坐标不变,纵坐标取反。因此, 点P'的坐标为(2,-3)。
沪科版数学八年级上册15.1.2轴对称课件(共17张PPT)

创设情境
观察以上图形,有什么特点?
新知引入
知识点1 成轴对称
如果平面内两个图形在一条直线的两旁,如果沿着这条直线折叠,这两个图形能完全重合,那么称这两个图形成轴对称,这条直线就是对称轴. 折叠后重合的两点叫做对应点(也叫对称点).
思考: 轴对称图形与两个图形成轴对称有什么区别与联系?
第十五章 轴对称图形与等腰三角形
15.1 轴对称图形15.1.2 轴对称
学习目标
学习重难点
重点
难点
1.掌握成轴对称的概念,会找成轴对称图形的对应点;2.理解垂直平分线的相关知识,掌握轴对称的两个性质.
掌握成轴对称的概念,会找成轴对称图形的对应点.
理解垂直平分线的相关知识,掌握轴对称的两个性质.
轴对称的两个特性:
1、成轴对称的两个图形全等,但全等的两个图形不一定成轴对称; 2、轴对称是图形的一种全等变换.
1、定义:两个图形、一条直线、完全重合; 2、反面观察法:从纸的反面观察,若观察到的图形和正面一样,就是轴对称.
识别轴对称的方法:
创设情境
结论: (1)线段AA'、BB'、CC'都与MN垂直
D
归纳小结
二者有区别,但实质一样
经过线段的中点并且垂直于这条线段的直线
同学们再见!
授课老师:
时间:2024年9月1日
随堂练习
下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是( )
B
练习1
如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠ACD的度数是________.
65°
练习2
练习3
如图是一个风筝的图案,直线AF是它的对称轴,下列结论不一定成立的是( )A.△ABD≌△ACD B.AF垂直平分EGC.直线BG,CE的交点在AF上 D.AD=DF
观察以上图形,有什么特点?
新知引入
知识点1 成轴对称
如果平面内两个图形在一条直线的两旁,如果沿着这条直线折叠,这两个图形能完全重合,那么称这两个图形成轴对称,这条直线就是对称轴. 折叠后重合的两点叫做对应点(也叫对称点).
思考: 轴对称图形与两个图形成轴对称有什么区别与联系?
第十五章 轴对称图形与等腰三角形
15.1 轴对称图形15.1.2 轴对称
学习目标
学习重难点
重点
难点
1.掌握成轴对称的概念,会找成轴对称图形的对应点;2.理解垂直平分线的相关知识,掌握轴对称的两个性质.
掌握成轴对称的概念,会找成轴对称图形的对应点.
理解垂直平分线的相关知识,掌握轴对称的两个性质.
轴对称的两个特性:
1、成轴对称的两个图形全等,但全等的两个图形不一定成轴对称; 2、轴对称是图形的一种全等变换.
1、定义:两个图形、一条直线、完全重合; 2、反面观察法:从纸的反面观察,若观察到的图形和正面一样,就是轴对称.
识别轴对称的方法:
创设情境
结论: (1)线段AA'、BB'、CC'都与MN垂直
D
归纳小结
二者有区别,但实质一样
经过线段的中点并且垂直于这条线段的直线
同学们再见!
授课老师:
时间:2024年9月1日
随堂练习
下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是( )
B
练习1
如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠ACD的度数是________.
65°
练习2
练习3
如图是一个风筝的图案,直线AF是它的对称轴,下列结论不一定成立的是( )A.△ABD≌△ACD B.AF垂直平分EGC.直线BG,CE的交点在AF上 D.AD=DF
轴对称图形2优质课件PPT

B
轴对称垂直平分连结两个对称点之间的线段。
2021/02/02
11
例1 分别画出下列轴对称图形的对称轴:
m
n
F
A
B
EGБайду номын сангаас
E′
怎样找出点E和点F的对称点?
2021/02/02
12
例2 下面的一些虚线,哪些是图形的对称轴,哪些不是?
请分别举出哪些轴对称图形 只有一条对称轴、两条或两条以上 对称轴、无数条对称轴?
感谢您的观看!本教学内容具有更强的时代性和丰富性,更适合学习需要和特点。为了 方便学习和使用,本文档的下载后可以随意修改,调整和打印。欢迎下载!
2021/02/02
15
2021/02/02
2.1轴对称图形
1
2021/02/02
2
下面是国粹京剧脸谱:
2021/02/02
3
2021/02/02
4
把一个图形沿着某一条直线折叠,直线 两侧的部分能够互相重合,那么这个图形叫 做轴对称图形,这条直线叫做对称轴。
两个图形中的对应点(即两个图形重合 时互相重合的点)叫做对称点.
说一说:
1.请你在周围环境中找出轴 对称的物体和建筑物.
2021/02/02
5
2021/02/02
6
2021/02/02
7
找出图中的对称轴:
2021/02/02
8
我们所学过的哪些几何图形是轴对称图形?
1条对称轴
2条对称轴
4条对称轴
2021/02/02
无数条对称轴
9
观察下列各种图形,判断是不是轴对称图形.
2021/02/02
10
轴对称--完整版课件
BC=10cm,那么△BCD的周长是
_______cm.
26cm
A
E D
B
C
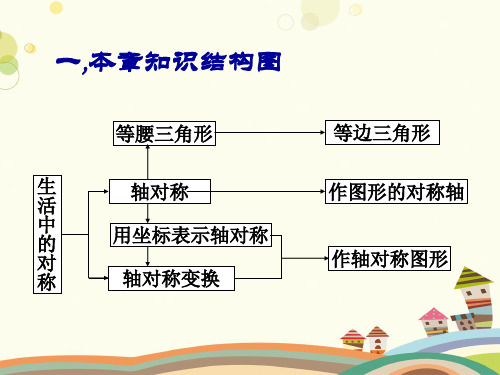
一,本章知识结构图
等腰三角形
等边三角形
生 活
轴对称
作图形的对称轴
中 的
用坐标表示轴对称
对
作轴对称图形
称
轴对称变换
轴对称的性质
•对应点所连的线段的中垂线就是 对称轴 •对应线段相等,对应角相等
轴对称变换
准确做图形对称轴的方法
因为对称轴垂直平分每对对应点所连接 的线段,所以只要找一对对应点,用圆规 作出对应点所连线段的垂直平分线即可。
8、已知,如图: AB=AC AD=DC=BC
则∠A=
Байду номын сангаас
360
A
D
B
C
9.在△ABC中,AB=AC,DE 为AB的垂直 A 平分线,D为垂足,交AC与E,若AB=8cm, △ABC的周长为21cm,求△BCE的周长.
D E
10.如图∠ ABC=70°, ∠ A=50°
B
C
AB的垂直平分线交AC于D,则∠DBC=___.
A
E
B
D
C
11 如图, ∠ABC、∠ACB的平分线相 交于F,过F作DE//BC交AB于D,交AC于E, 若AB=9cm, AC=8cm,则△ADE的周长是 多少? A
AB=AD+DB=AD+DF D F E AC=AE+EC=AE+EF
B
C
13、如图,在△ABC中,AB=AC=16cm,
AB的垂直平分线交AC于D,如果
利用轴对称变换作图1
作出三角形关于直线L对称的图形
《轴对称》PPT课件

∠A与∠___A_'____,∠B与∠____B_'___,∠C与∠___C_'____分
别是对应角.
知识要点
比较归纳
轴对称图形
两个图形成轴对称
图形
区别 联系
一个图形具有的特 殊形状
两个全等图形的特殊 的位置关系
1.都是沿着某条直线折叠后能重合. 2.可以互相转化.
想一想 (1)根据全等的意义,△ABC和△A'B'C'全等吗? 对应线段有怎样的数量关系?对应角呢?
△ABC≌△A'B'C' 对应线段相等 对应角相等
想一想 (2)对应角点的连线AA',BB',CC'分别与对称轴l
具有怎样和的位置关系?
AA'∥BB'∥CC'
AA'⊥l,BB'⊥l,CC'⊥l
轴对称图形的性质
如果两个图形关于某条直线成轴对称,那么,这两个图形 是全等形,它们的对应线段相等,对应角相等,对应点所连 的线段被对称轴垂直平分.
现在就让我们一起来认识这奇妙的轴对称吧!
讲授新课
一 轴对称图形与轴对称的概念
问题1 如图,观察这几张图片,它们是不是轴对称,可通过 什么方法进行说明?
√
√
×
a m
轴对称图形和对称轴 一般地,如果一个图形沿某条直线对折后,直线两旁的部
分能够完全重合,那么这个图形就叫做轴对称图形,这条直 线叫做对称轴.
当堂练习
1.你能找出这些图形的对称轴吗?
2.找出下列各图形中的对称轴,并说明哪一个图形的对称轴最多.
3.(1)整个图形是轴对称图形吗?对称轴是什么? (2)图中红色的三角形与哪些三角形成轴对称? (3)图形可以看作某两个图形成轴对称吗?
别是对应角.
知识要点
比较归纳
轴对称图形
两个图形成轴对称
图形
区别 联系
一个图形具有的特 殊形状
两个全等图形的特殊 的位置关系
1.都是沿着某条直线折叠后能重合. 2.可以互相转化.
想一想 (1)根据全等的意义,△ABC和△A'B'C'全等吗? 对应线段有怎样的数量关系?对应角呢?
△ABC≌△A'B'C' 对应线段相等 对应角相等
想一想 (2)对应角点的连线AA',BB',CC'分别与对称轴l
具有怎样和的位置关系?
AA'∥BB'∥CC'
AA'⊥l,BB'⊥l,CC'⊥l
轴对称图形的性质
如果两个图形关于某条直线成轴对称,那么,这两个图形 是全等形,它们的对应线段相等,对应角相等,对应点所连 的线段被对称轴垂直平分.
现在就让我们一起来认识这奇妙的轴对称吧!
讲授新课
一 轴对称图形与轴对称的概念
问题1 如图,观察这几张图片,它们是不是轴对称,可通过 什么方法进行说明?
√
√
×
a m
轴对称图形和对称轴 一般地,如果一个图形沿某条直线对折后,直线两旁的部
分能够完全重合,那么这个图形就叫做轴对称图形,这条直 线叫做对称轴.
当堂练习
1.你能找出这些图形的对称轴吗?
2.找出下列各图形中的对称轴,并说明哪一个图形的对称轴最多.
3.(1)整个图形是轴对称图形吗?对称轴是什么? (2)图中红色的三角形与哪些三角形成轴对称? (3)图形可以看作某两个图形成轴对称吗?
轴对称课件ppt

具之一。
THANKS
感谢观看
04
轴对称的作图
轴对称作图的方法和步骤
确定对称轴
首先确定图形关于哪条直线对称,即对称轴的位 置。
绘制对称图形
根据对称轴,绘制出与原图形对称的图形。
检查完整性
确保新绘制的图形与原图形完全一致,没有遗漏 或多余的部分。
轴对称作图的实例解析
矩形
以矩形为例,其对称轴为其对角线,沿对称轴折叠后,两侧图形 完全重合。
轴对称的两个图形也是全等的,它们的对应点关于对称轴对称,且每个点到对称轴的距离等 于它到对称点的距离。
轴对称与旋转对称的关系
旋转对称是指图形绕某一点旋转一定角度后与自身重合,而轴对称则是 图形关于某一直线对称。
旋转对称和轴对称可以同时存在于一个图形中,例如正三角形既具有旋 转对称性(绕中心点旋转120度与自身重合),又具有轴对称性(关于中
轴对称的几何意义
点关于对称轴的对称
对于直线上的任意一点,关于对称轴都有另一个点与之对称,且 两点连线与对称轴垂直。
直线关于对称轴的对称
对于直线上的任意一段线段,关于对称轴都有另一段线段与之对称 ,且两段线段平行于对称轴。
平面图形关于对称轴的对称
对于平面图形中的任意部分,关于对称轴都有另一部分与之对称, 且两部分形状和大小完全相同。
01
首先需要确定两个图形之间的对称轴。
寻找对应点
02
在两个图形上寻找关于对称轴对称的对应点。
判断是否满足判定定理
03
检查对应点连线是否被对称轴垂直平分,以及对应线段是否关
于对称轴对称。
判定轴对称的实例解析
01
02
03
等腰三角形
等腰三角形是轴对称的, 其对称为底边的中垂线 。
THANKS
感谢观看
04
轴对称的作图
轴对称作图的方法和步骤
确定对称轴
首先确定图形关于哪条直线对称,即对称轴的位 置。
绘制对称图形
根据对称轴,绘制出与原图形对称的图形。
检查完整性
确保新绘制的图形与原图形完全一致,没有遗漏 或多余的部分。
轴对称作图的实例解析
矩形
以矩形为例,其对称轴为其对角线,沿对称轴折叠后,两侧图形 完全重合。
轴对称的两个图形也是全等的,它们的对应点关于对称轴对称,且每个点到对称轴的距离等 于它到对称点的距离。
轴对称与旋转对称的关系
旋转对称是指图形绕某一点旋转一定角度后与自身重合,而轴对称则是 图形关于某一直线对称。
旋转对称和轴对称可以同时存在于一个图形中,例如正三角形既具有旋 转对称性(绕中心点旋转120度与自身重合),又具有轴对称性(关于中
轴对称的几何意义
点关于对称轴的对称
对于直线上的任意一点,关于对称轴都有另一个点与之对称,且 两点连线与对称轴垂直。
直线关于对称轴的对称
对于直线上的任意一段线段,关于对称轴都有另一段线段与之对称 ,且两段线段平行于对称轴。
平面图形关于对称轴的对称
对于平面图形中的任意部分,关于对称轴都有另一部分与之对称, 且两部分形状和大小完全相同。
01
首先需要确定两个图形之间的对称轴。
寻找对应点
02
在两个图形上寻找关于对称轴对称的对应点。
判断是否满足判定定理
03
检查对应点连线是否被对称轴垂直平分,以及对应线段是否关
于对称轴对称。
判定轴对称的实例解析
01
02
03
等腰三角形
等腰三角形是轴对称的, 其对称为底边的中垂线 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C.这直线上 D.这直线两旁或这直线上
2.轴对称图形沿对称轴对折后,对称轴两旁的 部分( A )
A.完全重合 C.两者都有
B.不完全重合
3. 已知互不平行的两条线段AB,CD关于直线L
对称,AB,CD所在直线交于点P,下列结论中:
①AB=CD;②点P在直线L上; ③若A,C是对称
点,则L垂直平分线段AC; ④若B,D是对称点,
A N
B M
C
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
12
结束语
当你尽了自己的最大努力时,失败也是伟大的, 所以不要放弃,坚持就是正确的。
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End 演讲人:XXXXXX 时 间:XX年XX月XX日
于( )。 A A.60° B.40° C.50° D.70°
m
ቤተ መጻሕፍቲ ባይዱ
A
B
E
C
D
2.如图所示,在△ABC中,AB=AC=10,DE
垂直平分AB, △BEC的周长为18,求BC的
长
A
D E
B
C
1 . 如图,已知点P是∠AOB内任意一点,
点P1,P关于OA对称,点P2,P关
于OB对称。连接P1P2,分别交OA,OB于
则PB=PD 其中正确的结论有( )D
A. 1个
B. 2个
C. 3个
D. 4个
4. 下面说法中正确的是(C )
A.点A,B关于直线MN对称,则AB垂 直平分MN。
B.如果△ABC≌△DEF,则一定存在一条 直线MN,使△ABC与△DEF关于MN 对称。
C.如果一个三角形是轴对称图形,且对称 轴不止一条,则它是等边三角形。
C, D。连接PC,PD。若P1P2=10cm,
则△PCD的. 周长为10cm
。
p1
A
C
.
O
.
p
B D
p2
2.如图2,AD⊥BC,BD=DC,点C在AE的垂 直平分线上,AB,AC,CE的长度有什么关 系?AB+BD与DE有什么关系?
A
B
C D
E
3.如图△ABC中,AC的垂直平分线交AC于N 点,交BC于M点,若△ABM的周长为12㎝, △ABC的周长为17㎝,则AC的长为__。
12.1 轴对称图形的性质
自学目标:
1、掌握轴对称图形的基本性质; 2、理解线段垂直平分线的概念,掌握它的 性质; 3、能利用所学知识解决轴对称的相关问题。
自学方法:
自学课本31页下面思考至33页探究之前的部分
1.根据31页的思考填空:AB_A’B’,BC _B’C’,
AC _A’C’.线段AA’、BB’、CC’与直线MN有什
D.两个图形关于MN对称,则这两个图形 分别在MN的两侧。
一、轴对称的性质: 1.对应点所连的线段被对称轴垂直平分 2.对应线段相等,对应角相等
二、线段垂直平分线的性质: 线段垂直平分线上的点与这条线段两个
端点的距离相等。
1.如图所示,如果直线m是多边形ABCDE的对称轴,
其中∠A=130°,∠E=110°,那么∠EDC的度数等
么关系?可以得出的结论是
。
2.经过线段_并且__这条线段的直线,叫做这条线 段的垂直平分线。
3.如果两个图形关于某条直线对称,那么对称轴是_ _______,类似的,轴对称图形的对称轴是_ _______。
4.线段垂直平分线上的点与这条线段两个端点的距离 __。
1.两个图形关于某直线对称,对称点一定 ( D) A.这直线的两旁 B.这直线的同旁
2.轴对称图形沿对称轴对折后,对称轴两旁的 部分( A )
A.完全重合 C.两者都有
B.不完全重合
3. 已知互不平行的两条线段AB,CD关于直线L
对称,AB,CD所在直线交于点P,下列结论中:
①AB=CD;②点P在直线L上; ③若A,C是对称
点,则L垂直平分线段AC; ④若B,D是对称点,
A N
B M
C
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
12
结束语
当你尽了自己的最大努力时,失败也是伟大的, 所以不要放弃,坚持就是正确的。
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End 演讲人:XXXXXX 时 间:XX年XX月XX日
于( )。 A A.60° B.40° C.50° D.70°
m
ቤተ መጻሕፍቲ ባይዱ
A
B
E
C
D
2.如图所示,在△ABC中,AB=AC=10,DE
垂直平分AB, △BEC的周长为18,求BC的
长
A
D E
B
C
1 . 如图,已知点P是∠AOB内任意一点,
点P1,P关于OA对称,点P2,P关
于OB对称。连接P1P2,分别交OA,OB于
则PB=PD 其中正确的结论有( )D
A. 1个
B. 2个
C. 3个
D. 4个
4. 下面说法中正确的是(C )
A.点A,B关于直线MN对称,则AB垂 直平分MN。
B.如果△ABC≌△DEF,则一定存在一条 直线MN,使△ABC与△DEF关于MN 对称。
C.如果一个三角形是轴对称图形,且对称 轴不止一条,则它是等边三角形。
C, D。连接PC,PD。若P1P2=10cm,
则△PCD的. 周长为10cm
。
p1
A
C
.
O
.
p
B D
p2
2.如图2,AD⊥BC,BD=DC,点C在AE的垂 直平分线上,AB,AC,CE的长度有什么关 系?AB+BD与DE有什么关系?
A
B
C D
E
3.如图△ABC中,AC的垂直平分线交AC于N 点,交BC于M点,若△ABM的周长为12㎝, △ABC的周长为17㎝,则AC的长为__。
12.1 轴对称图形的性质
自学目标:
1、掌握轴对称图形的基本性质; 2、理解线段垂直平分线的概念,掌握它的 性质; 3、能利用所学知识解决轴对称的相关问题。
自学方法:
自学课本31页下面思考至33页探究之前的部分
1.根据31页的思考填空:AB_A’B’,BC _B’C’,
AC _A’C’.线段AA’、BB’、CC’与直线MN有什
D.两个图形关于MN对称,则这两个图形 分别在MN的两侧。
一、轴对称的性质: 1.对应点所连的线段被对称轴垂直平分 2.对应线段相等,对应角相等
二、线段垂直平分线的性质: 线段垂直平分线上的点与这条线段两个
端点的距离相等。
1.如图所示,如果直线m是多边形ABCDE的对称轴,
其中∠A=130°,∠E=110°,那么∠EDC的度数等
么关系?可以得出的结论是
。
2.经过线段_并且__这条线段的直线,叫做这条线 段的垂直平分线。
3.如果两个图形关于某条直线对称,那么对称轴是_ _______,类似的,轴对称图形的对称轴是_ _______。
4.线段垂直平分线上的点与这条线段两个端点的距离 __。
1.两个图形关于某直线对称,对称点一定 ( D) A.这直线的两旁 B.这直线的同旁
