计算机图形学显示变换算法具体程序实现
计算机图形学

计算机图形学
——投影变换
姓名:
学号:
班级:一大班二小班
一、实现目标
将屏幕垂直划分为两部分,左半部分绘制三维坐标系和长方体,右半部分绘制二维坐标系及三视图。
首先设置成长方体,在绘制绘制三视图
二、算法设计
1. 在屏幕左半部分绘制三维坐标系。
2. 在屏幕右半部分绘制二维坐标系。
3. 读入长方体的三维顶点齐次坐标及其面坐标,并将三维顶点齐次坐标变换为相应的屏幕二维齐次坐标,并在屏幕左半部分绘制长方体。
4. 分别给主视图、俯视图和侧视图变换矩阵的非零元素赋值。
5. 将原始图形的顶点集合齐次坐标矩阵和三视图变换矩阵相乘,结果赋予变换后的三视图顶点集合齐次坐标矩阵。
其中,
主视图变换矩阵为:
俯视图变换矩阵为:
主视图变换矩阵为:
6. 根据变换后的顶点集合齐次坐标矩阵的元素绘制三视图。
三、源代码及注释
文件
lass CMygroup7View : public CView
{
protected:
#endif。
《计算机图形学》实验指导书

计算机图形学实验指导书袁科计算机技术实验中心目录实验一实现DDA、中点画线算法和Bresenham画线算法 (24)实验二实现Bezier曲线 (25)实验三实现B样条曲线 (26)实验四实现多边形填充的边界标志算法 (27)实验五实现裁剪多边形的Cohen-Sutherland算法 (28)实验六二维图形的基本几何变换 (30)实验七画图软件的编制 (31)实验一实现DDA、中点画线算法和Bresenham画线算法【实验目的】1、掌握直线的多种生成算法;2、掌握二维图形显示原理。
【实验环境】VC++6.0/ BC【实验性质及学时】验证性实验,2学时,必做实验【实验内容】利用任意的一个实验环境,编制源程序,分别实现直线的三种生成算法,即数字微分法(DDA)、中点画线法以及Bresenham画线算法。
【实验原理】1、数字微分法(Digital Differential Analyzer,DDA)算法思想:基于直线的微分方程来生成直线。
ε=1/max(|△x|,|△y|)max(|△x|,|△y|)=|△x|,即|k|≤1 的情况:max(|△x|,|△y|)=|△y|,此时|k|≥1:2、中点画线法算法思想:每次在最大位移方向上走一步,另一方向是否走步取决于误差项的判断。
3、Bresenham画线算法算法思想:其基本思想同中点算法一样,即每次在最大位移方向上走一步,而另一个方向是否走步取决于误差项的判断。
【实验要求】1.上交源程序;2.上交实验报告,实验报告内容如下:(1) 实验名称(2) 实验目的(3) 算法实现的设计方法及程序流程图(4) 程序结果分析【分析与思考】(1) 上述所阐述的三个算法,其基本算法只能适用于直线的斜率(|K|<=1) 的情形,如何将上述算法进行推广,使其能够处理任意斜率的直线?(2) 计算机显示屏幕的坐标圆心在哪里,与我们平时的习惯有什么差异,如何协调二者?实验二 实现Bezier 曲线【实验目的】1、掌握Bezier 曲线的定义;2、能编程实现N 次Bezier 曲线的绘制与显示。
计算机图形学几何变换算法具体程序实现

数学与软件科学学院实验报告学期: 2010 至 2011 第一学期 2010年 11月 3日课程名称: 计算机图形学专业:信息与计算科学班级 2007级5班实验编号: 05 实验项目: 几何变换指导教师庞朝阳姓名:学号:200706005 实验成绩:一、实验目的及要求图形变换时计算机图形学的重要内容,在图形的生成、处理和现实过程中发挥着关键性的作用,同时,变换本身也是描述图形的一个有力工具。
通过这次的实验,要理解计算机图形学中几何变换的概念和作用,掌握几何变换的过程。
二、实验内容1、整理和总结关于几何变换的概念和作用。
2、掌握基本几何变换3、掌握组合几何变换在齐次坐标下的应用。
三、具体实验内容:1、几何变换的概念和作用:几何变换提供了构造和修改图形的一种方法,图形在位置、方向、尺寸和形状方面的改变都可以通过几何变换来实现。
几何变换的基本方法是吧变换矩阵作为一个算子,作用到图形一系列顶点的位置矢量,从而得到这些顶点在几何变换后的新的顶点序列,连接新的顶点序列即可得到变换后的图形。
2、基本几何变换:假设)yP表示三维空间上一个未被变换的点,而该点经过某种变换后得x(z,,到新的点用)'P表示。
yx,','('z①平移变换:如果点)','(zyx,P在x轴,y轴和z轴分别移动x∆、y∆、y,'('zxP是由点),z∆距离得到的,则两点坐标关系为:='+x∆xxy y y ∆+=' z z z ∆+=' 则矢量形式为:T P P +=' 其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=''''z y x P , ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=z y x P , ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∆∆∆=z y x T ② 缩放变换:缩放变换改变物体的大小。
有坐标关系 x s x x =' y s y y =' z s z z ='其中,x s ,y s ,z s 分别为沿x ,y 和z 轴方向放大或缩小的比例。
计算机图形学 图形的几何变换的实现算法教程文件

计算机图形学图形的几何变换的实现算法实验二 图形的几何变换的实现算法班级 08信计 学号 59 姓名 分数一、实验目的和要求:1、掌握而为图形的基本几何变换,如平移,旋转,缩放,对称,错切变换;。
2、掌握OpenGL 中模型变换函数,实现简单的动画技术。
3、学习使用OpenGL 生成基本图形。
4、巩固所学理论知识,加深对二维变换的理解,加深理解利用变换矩阵可由简单图形得到复杂图形。
加深对变换矩阵算法的理解。
编制利用旋转变换绘制齿轮的程序。
编程实现变换矩阵算法,绘制给出形体的三视图。
调试程序及分析运行结果。
要求每位学生独立完成该实验,并上传实验报告。
二、实验原理和内容:. 原理:图像的几何变换包括:图像的空间平移、比例缩放、旋转、仿射变换和图像插值。
图像几何变换的实质:改变像素的空间位置,估算新空间位置上的像素值。
图像几何变换的一般表达式:[,][(,),(,)]u v X x y Y x y = ,其中,[,]u v 为变换后图像像素的笛卡尔坐标, [,]x y 为原始图像中像素的笛卡尔坐标。
这样就得到了原始图像与变换后图像的像素的对应关系。
平移变换:若图像像素点 (,)x y 平移到 00(,)x x y y ++,则变换函数为0(,)u X x y x x ==+,0(,)v Y x y y y ==+,写成矩阵表达式为:00x u x y v y ⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦其中,x 0和y 0分别为x 和y 的坐标平移量。
比例缩放:若图像坐标 (,)x y 缩放到( ,x y s s )倍,则变换函数为:00x y s u x s v y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 其中, ,x y s s 分别为x 和y 坐标的缩放因子,其大于1表示放大,小于1表示缩小。
旋转变换:将输入图像绕笛卡尔坐标系的原点逆时针旋转θ角度,则变换后图像坐标为:cos sin sin cos u x v y θ-θ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥θθ⎣⎦⎣⎦⎣⎦内容:1、对一个三角形分别实现平移,缩放旋转等变化。
计算机图形学二维图形变换

宁夏师范学院数学与计算机科学学院《计算机图形学》实验报告实验序号:7 实验项目名称:二维图形变换菜单菜单项ID值图形变换(&T)缩放(&Z)ID_TRANSFORM_SCALE图形变换(&T)旋转(&R)ID_TRANSFORM_ROTATE图形变换(&T)对称(&S)ID_TRANSFORM_SYMMETRY 4、在CTransView视图类中添加消息映射函数;对象消息函数ID_TRANSFORM_SCALE COMMAND OnFigureCirleID_TRANSFORM_ROTATE COMMAND OnFigureEllipseID_TRANSFORM_SYMMETRY COMMAND OnTransformSymmetry5、添加自定义的成员变量:CPoint Pt[3]; //三角形定点数组float dAngle; //每一次旋转的角度在视图类CPP文件的构造函数中初始化成员变量Pt[0].x = 540; Pt[0].y = 220;Pt[1].x = 670; Pt[1].y = 130;Pt[2].x = 560; Pt[2].y = 120;dAngle = 0;6、在视图类的OnDraw()函数中加入下列代码,实现视图绘图。
void CTransView::OnDraw(CDC* pDC){CTransDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);// TODO: add draw code for native data here//绘出以以(540,220)、(670,130)、(560,120)为顶点的三角形。
pDC->MoveTo(Pt[0]);pDC->LineTo(Pt[1]);三、运行结果变换前:对称变换:缩放变换:旋转变换:五、教师评语成绩签名:日期:年月日。
计算机图形学图形几何变换的实现

计算机图形学图形⼏何变换的实现实验五图形⼏何变换的实现班级 08信计2班学号 20080502053 姓名杨少卿分数⼀、实验⽬的和要求:1、掌握⼆维图形⼏何变换的基本原理及⼆维图形的⼏何算法。
2、巩固所学理论知识,加深对⼆维变换的理解,加深理解利⽤变换矩阵可⽤简单图形得到复杂图形的理解。
3、通过编程完成⼆维图形的⼏何变换动态过程。
4、观察改变图形的形状、⼤⼩、位置等,其关键是坐标的变换。
⼆、实验内容:1、将四边形以原点为中⼼,以10度为间隔做360度旋转。
2、齿轮的边缘轮廓⽣成的⼏何变换,编制利⽤旋转变换绘制齿轮的程序。
3、⼏何图形变换算法(缩放、旋转和平移),编程实现⼆维图形齐次坐标变换的算法和组合变换的算法。
三、实验步骤1、将四边形以原点为中⼼,以10度为间隔做360度旋转。
程序代码:#include#include#include#includedouble sin(),cos();double xmax=639.0,ymax=399.0;double f[3][3],xx,yy;scx(double xi){int x;x=(int)(xi+xmax/2);return(x);}scy(double yi){int y;y=ymax-(int)(yi+ymax/2);return(y);}parallel(double dx,double dy){f[0][0]=1.0;f[0][1]=0.0;f[0][2]=0.0;f[1][0]=0.0;f[1][1]=1.0;f[1][2]=0.0;f[2][0]=dx;f[2][1]=dy;f[2][2]=1.0;}rotate(double theta){double th=theta/180*3.1415627;f[0][0]=cos(th);f[0][1]=sin(th); f[0][2]=0.0; f[1][0]=-sin(th); f[1][1]=cos(th); f[1][2]=0.0; f[2][0]=0.0; f[2][1]=0.0;f[2][2]=1.0;}scale(double s){f[0][0]=s;f[0][1]=0.0;f[0][2]=0.0;f[1][0]=0.0;f[1][1]=s;f[1][2]=0.0;f[2][0]=0.0;f[2][1]=0.0;f[2][2]=1.0;}taishox(){f[0][0]=1.0;f[0][1]=0.0;f[0][2]=0.0;f[1][0]=0.0;f[1][1]=-1.0;f[1][2]=0.0;f[2][0]=0.0;f[2][1]=0.0;f[2][2]=1.0;}taishoy(){f[0][0]=-1.0;f[0][1]=0.0;f[0][2]=0.0;f[1][0]=0.0;f[1][1]=1.0;f[1][2]=0.0;f[2][0]=0.0;f[2][1]=0.0;f[2][2]=1.0;}taishoo(){f[0][0]=-1.0;f[0][1]=0.0;f[0][2]=0.0;f[1][0]=0.0;f[1][1]=-1.0;f[1][2]=0.0;f[2][0]=0.0;f[2][1]=0.0;f[2][2]=1.0;}taishoxy(){f[0][0]=0.0;f[0][1]=1.0;f[0][2]=0.0;f[1][0]=1.0;f[1][1]=0.0;f[1][2]=0.0;f[2][0]=0.0;f[2][1]=0.0;f[2][2]=1.0;}axis(){line(scx(0),scy(-ymax/2),scx(0),scy(ymax/2)); line(scx(-xmax/2),scy(0.0),scx(xmax/2),scy(0.0)); }tuoq(double a,double b){f[0][0]=1.0;f[0][1]=b;f[0][2]=1.0;f[1][0]=a;f[1][1]=1.0;f[1][2]=0.0;f[2][0]=0.0;f[2][1]=0.0;f[2][2]=1.0;}affinex(double x,double y,double d){xx=x*f[0][0]+y*f[1][0]+f[2][0];return(xx);}affiney(double x,double y,double d){yy=x*f[0][1]+y*f[1][1]+f[2][1];return(yy);}main(){int graphdriver=DETECT,graphmode;static double x1[]={0.0,10.0,100.0,110.0,0.0}; static double y1[]={0.0,50.0,50.0,0.0,0.0};static double x2[5];static double y2[5];int i;double r,xx,yy;initgraph(&graphdriver,&graphmode,"");srand((unsigned)time(NULL));for(r=0;r<=360;r=r+10){rotate(r);for(i=0;i<=4;i++){x2[i]=affinex(x1[i],y1[i],1.0);y2[i]=affiney(x1[i],y1[i],1.0);}setcolor(RGB(rand()%256,rand()%256,rand()%256)); Sleep(80);for(i=0;i<=3;i++){line(scx(x2[i]),scy(y2[i]),scx(x2[i+1]),scy(y2[i+1]));}}getch();closegraph();}运⾏结果:截图:2、齿轮的边缘轮廓⽣成的⼏何变换。
计算机图形学图形几何变换的实现

实验五图形几何变换的实现班级08信计2 学号89姓名徐阳分数一、实验目的和要求:1、掌握理解二维、三维变换的数学知识、变换原理、变换种类、变换方法;进一步理解采用齐次坐标进行二维、三维变换的必要性;利用Turboc实现二维、三维图形的基本变换和复合变换。
二、实验内容:1、理解采用齐次坐标进行图形变换的必要性——变换的连续性,使复合变换得以实现。
2、掌握二维、三维图形基本变换(平移、缩放、对称、旋转、错切)的原理及数学公式。
3、利用Turboc实现二维、三维图形的基本变换、复合变换,在屏幕上显示变换过程或变换结果。
三、实验结果分析:程序代码如下:/*二维图形(直线)平移变换*/#include<stdio.h>#include<graphics.h>#include<conio.h>main(){int x0,y0,x1,y1,i,j;int a[3][3];char key;for(i=0;i<3;i++)for(j=0;j<3;j++)a[i][j]=0;for(i=0;i<3;i++)a[i][i]=1;int graphdriver=DETECT;int graphmode=0;initgraph(&graphdriver,&graphmode," ");cleardevice();x0=250;y0=120;x1=350;y1=220;line(x0,y0,x1,y1);for( ; ;){outtextxy(100,400,"<-:left->:right^:up v:down Esc->exit");key=getch();switch(key){case 75: a[2][0]=-10;break;case 77: a[2][0]=10;break;case 72: a[2][1]=-10;break;case 80: a[2][1]=10;break;case 27: exit(0);break;}x0=x0*a[0][0]+y0*a[1][0]+a[2][0];y0=x0*a[0][1]+y0*a[1][1]+a[2][1];x1=x1*a[0][0]+y1*a[1][0]+a[2][0];y1=x1*a[0][1]+y1*a[1][1]+a[2][1];cleardevice();line(x0,y0,x1,y1);}closegraph();}2.三维图形(立方体)旋转和比例变换的算法:#include<stdio.h>#include<math.h>#include<graphics.h>#include<conio.h>#include<time.h>#include<ctype.h>#define ZOOM_IN 0.9#define ZOOM_OUT 1.1int turn1[3]; /* [0] rx,[1] ry,[3] zoom*/typedef struct{float x;float y;float z;}point;typedef struct{float x;float y;}point2d;typedef struct{float x;float y;float h;point biao[8];}fanti;void make_box(float x,float y,float h,fanti *p) {p->x=x;p->y=y;p->h=h;p->biao[0].x=x/2;p->biao[0].y=y/2;p->biao[0].z=h/2;p->biao[1].x=-x/2;p->biao[1].y=y/2;p->biao[1].z=h/2;p->biao[2].x=-x/2;p->biao[2].y=-y/2;p->biao[2].z=h/2;p->biao[3].x=x/2;p->biao[3].y=-y/2;p->biao[3].z=h/2;p->biao[4].x=x/2;p->biao[4].y=y/2;p->biao[4].z=-h/2;p->biao[5].x=-x/2;p->biao[5].y=y/2;p->biao[5].z=-h/2;p->biao[6].x=-x/2;p->biao[6].y=-y/2;p->biao[6].z=-h/2;p->biao[7].x=x/2;p->biao[7].y=-y/2;p->biao[7].z=-h/2;}void trun2d(point *p,point2d *q){q->x=p->x+p->z*cos(0.25);q->y=p->y+p->z*sin(0.25);}void initm(float mat[][4]){int count;for(count=0;count<4;count++){ mat[count][0]=0.;mat[count][1]=0.;mat[count][3]=0.;mat[count][count]=1.;}return;}void transfrom(point *p,point *q,float tm[][4]){float xu,yv,zw,h;xu=tm[0][0]*p->x+tm[1][0]*p->y+tm[2][0]*p->z+tm[3][0]; yv=tm[0][1]*p->x+tm[1][1]*p->y+tm[2][1]*p->z+tm[3][1]; zw=tm[0][2]*p->x+tm[1][2]*p->y+tm[2][2]*p->z+tm[3][2]; p->x=xu;p->y=yv;p->z=zw;return;}void rotationx(point *p,float alfa,float tm[][4]){float rad=0.0174532925;initm(tm);tm[1][1]=cos(rad*alfa);tm[1][2]=sin(rad*alfa);tm[2][1]=-tm[1][2];tm[2][2]=tm[1][1];return;}void rotationz(point *p,float alfa,float tm[][4]){float rad=0.0174532925;initm(tm);tm[0][0]=cos(rad*alfa);tm[0][1]=sin(rad*alfa);tm[1][0]=-tm[0][1];tm[1][1]=tm[0][0];return;}void rotationy(point *p,float alfa,float tm[][4]){float rad=0.0174532925;initm(tm);tm[0][0]=cos(rad*alfa);tm[2][0]=sin(rad*alfa);tm[0][2]=-tm[2][0];return;}void adjust(point *p,point *q) {float t[4][4];switch(turn1[0]){case 1:rotationy(p,2,t);transfrom(p,q,t);break;case -1:rotationy(p,-2,t);transfrom(p,q,t);break;default:break;}switch(turn1[1]){case 1:rotationz(p,2,t);transfrom(p,q,t);break;case -1:rotationz(p,-2,t);transfrom(p,q,t);break;default:break;}switch(turn1[2]){case 1:q->x=ZOOM_IN*p->x;q->y=ZOOM_IN*p->y;q->z=ZOOM_IN*p->z; break;case -1:q->x=ZOOM_OUT*p->x;q->y=ZOOM_OUT*p->y;q->z=ZOOM_OUT*p->z; break;default:break;}void drawbox(fanti *p){point2d fan2d[8];int i;for(i=0;i<=7;i++){adjust(&p->biao[i],&p->biao[i]);trun2d(&p->biao[i],&fan2d[i]);fan2d[i].x+=300;fan2d[i].y+=200;}cleardevice();setcolor(RGB(255,24,39));outtext(" ->:right <-:left ^:up v:down");moveto(0,20);outtext("page up:zoom in page down:zoom out space:redraw Esc:exit"); for(i=0;i<=3;i++){if(i==3){line(fan2d[i].x,fan2d[i].y,fan2d[0].x,fan2d[0].y);line(fan2d[i+4].x,fan2d[i+4].y,fan2d[4].x,fan2d[4].y);}else{line(fan2d[i].x,fan2d[i].y,fan2d[i+1].x,fan2d[i+1].y);line(fan2d[i+4].x,fan2d[i+4].y,fan2d[i+5].x,fan2d[i+5].y);}line(fan2d[i].x,fan2d[i].y,fan2d[i+4].x,fan2d[i+4].y);}}void main(){int gd=DETECT,gm,i,j;char key;float x,y,h;fanti a1;x=100;y=100;h=100;initgraph(&gd,&gm,"");make_box(x,y,h,&a1);drawbox(&a1);for(;;)turn1[0];turn1[1];turn1[2];key=getch();switch(key){case 77: turn1[0]=1;break; /*RIGHT*/case 75: turn1[0]=-1;break; /*LIFT*/case 72:turn1[1]=1;break; /*UP*/case 80:turn1[1]=-1;break; /*DOWN*/case 73:turn1[2]=1;break; /*ZOOM IN*/ case 81:turn1[2]=-1;break; /*ZOOM OUT*/ case 32:make_box(x,y,h,&a1);break; /*REDRAW*/case 27:exit(0);break; /*ESC*/default: key=0;break;}if(key!=0) drawbox(&a1);}closegraph();}。
计算机图形学 图形几何变换的实现

实验五图形几何变换的实现班级08信计2班学号20080502050姓名张玉凤分数一、实验目的和要求:1、掌握图形的旋转变换数学原理。
2、掌握一般图形旋转的基本算法。
二、实验内容:1、画一个正方形,并实现45度旋转,进一步可以使之动起来。
2、二维图形变换,包含了平移变换和旋转变换,比例变换。
三、实验步骤1、画一个正方形,并实现45度旋转,进一步可以使之动起来.程序源代码:#include "dos.h"#include "math.h"#include "graphics.h"#include "bios.h"#include "stdlib.h"#include "stdio.h"#define PI 3.1415962void Rotating(){int x1=150 , y1=150;int x2=x1 , y2=y1+100;int n=180;double i=0;int rx1,rx2,ry1,ry2;int wid=100,hei=100;while(!kbhit()){setcolor(RED);line(150,300,450,300);line(150,300,150,10);outtextxy(140,305,"0");outtextxy(140,10,"y");outtextxy(450,305,"x"); /*标出x,y轴*/setcolor(GREEN);rx1=x1+wid*sin(i*360/n*PI/180);ry1=y1+hei*cos(i*360/n*PI/180);rx2=rx1;ry2=ry1+100;line(x1,y1,x2,y2);line(x1,y1,rx1,ry1);line(x2,y2,rx2,ry2);line(rx1,ry1,rx2,ry2);sleep(1);delay(15000);setcolor(YELLOW); /*显示正方形旋转后的痕迹*/line(x1,y1,x2,y2);line(x1,y1,rx1,ry1);line(x2,y2,rx2,ry2);line(rx1,ry1,rx2,ry2);i+=22.5;}}main(){int driver =VGA, mode=VGAHI;initgraph(&driver,&mode,"");Rotating();getch();closegraph();}运行结果:2.二维图形变换,包含了平移变换和旋转变换。
计算机图形学的算法与实现

计算机图形学的算法与实现随着计算机技术的不断发展,计算机图形学逐渐成为了一个非常重要的领域。
在这个领域中,算法和实现是最为核心的两个方面。
本文主要介绍计算机图形学中的算法和实现,并探讨它们的应用和未来发展趋势。
一、计算机图形学的基本算法计算机图形学的基本算法包括三维坐标转换、光栅化和渲染。
其中,三维坐标转换主要负责将三维的对象转换成二维图像,光栅化则将图像转换成像素,在这个过程中生成显卡可以渲染的数据,而渲染则负责按照场景中的光照模型和材质对每个像素进行计算和着色。
这三个算法是计算机图形学的基础,任何其他高级算法和应用都有赖于这些基础算法。
1.三维坐标转换三维坐标转换包括了从世界坐标系转换到相机坐标系,从相机坐标系到裁剪坐标系,裁剪坐标系到屏幕坐标系等一系列转换过程。
这些过程一般由变换矩阵来描述,分别为世界变换,视图变换,投影变换和视口变换。
其中,世界变换和视图变换用于将世界中的点转换到相机坐标系中,投影变换则用于将相机坐标系中的点映射到裁剪坐标系中。
视口变换则是将裁剪坐标系中的点映射到屏幕坐标系中。
2.光栅化光栅化是将连续的几何图形转换成离散的像素点的过程。
这个过程中需要进行像素颜色的计算。
在计算像素颜色时,需要使用光照公式计算出每个顶点的颜色,然后根据三角形内的关系使用插值法得到每个像素的颜色值。
在图像中,我们个人感觉最难做的就是手工描色的细节,如果都能自动输出会好很多。
3.渲染渲染是将像素点着色成二维图像的过程。
在这个过程中,需要根据光照模型对每个像素进行着色和计算。
光照模型是指用于描述光线和材质之间相互作用的一种数学模型。
常用的光照模型有Phong模型、Blinn-Phong模型和Gouraud模型等。
二、计算机图形学的实现方式计算机图形学的实现方式包括软件渲染和硬件渲染。
在软件渲染中,图形数据由CPU处理,而在硬件渲染中,图形数据由显卡的GPU处理。
硬件渲染是目前最为流行的方式,因为它比软件渲染更快、更准确、更可靠。
计算机图形学图形变换
计算机图形学图形变换实验五:图形变换⼀、实验⽬的:1、掌握图形变换的基本⽅法。
2、初步掌握映射菜单消息和捕获键盘消息的⽅法。
⼆、实验内容及要求:1、以三⾓形为例,使⽤Visual C++实现⼆维图形的平移、旋转和缩放功能。
2、每⼈单独完成实验。
3、按要求撰写实验报告,写出实验⼼得,并在实验报告中附上程序的核⼼算法代码。
三、实验设备:微机,Visual C++6.0四、实验内容和步骤:1、打开VC,新建⼀个MFC Appwizard项⽬,选择创建单⽂档⼯程(SDI⼯程)。
假设⼯程名为Transform。
如图1和图2所⽰。
图1图22、在图2的界⾯上点击Finish,完成⼯程的创建。
3、在TransformView.h⽂件中,加⼊如下代码:public:CPoint Pt[3]; //存储三⾓形的三个顶点float dAngle; //存储三⾓形旋转的⾓度4、在类CTransformView的构造函数中定义三⾓形的三个顶点的初始坐标和dAngle的初值,代码如下;CTransformView::CTransformView(){// TODO: add construction code herePt[0].x = 200; Pt[0].y = 220;Pt[1].x = 260; Pt[1].y = 300;Pt[2].x = 360; Pt[2].y = 180;dAngle = 0.0;}5、在类CTransformView中添加成员函数void DrawTriangle(CDC *pDC),并实现该函数。
(该部分代码请同学们⾃⼰实现,为了简便编程,可以使⽤MoveTo和LineTo函数,也可以调⽤⾃⼰在实验2中编写的DDA或者Bresenham画线函数);6、在类CTransformView的OnDraw()函数中添加绘制三⾓形的代码;void CTransformView::OnDraw(CDC* pDC){CTransformDoc* pDoc = GetDocument();ASSERT_V ALID(pDoc);// TODO: add draw code for native data here}7、映射菜单消息,⽅法是打开ResourceView菜单,依次展开MENU \ IDR_MAINFRAME,添加“图形变换”主菜单项,在其下添加“平移”,如图3所⽰。
计算机图形学图形的几何变换的实现算法

实验二 图形的几何变换的实现算法班级 08信计 学号 59 姓名 分数一、实验目的和要求:1、掌握而为图形的基本几何变换,如平移,旋转,缩放,对称,错切变换;。
2、掌握OpenGL 中模型变换函数,实现简单的动画技术。
3、学习使用OpenGL 生成基本图形。
4、巩固所学理论知识,加深对二维变换的理解,加深理解利用变换矩阵可由简单图形得到复杂图形。
加深对变换矩阵算法的理解。
编制利用旋转变换绘制齿轮的程序。
编程实现变换矩阵算法,绘制给出形体的三视图。
调试程序及分析运行结果。
要求每位学生独立完成该实验,并上传实验报告。
二、实验原理和内容:. 原理:图像的几何变换包括:图像的空间平移、比例缩放、旋转、仿射变换和图像插值。
图像几何变换的实质:改变像素的空间位置,估算新空间位置上的像素值。
图像几何变换的一般表达式:[,][(,),(,)]u v X x y Y x y = ,其中,[,]u v 为变换后图像像素的笛卡尔坐标, [,]x y 为原始图像中像素的笛卡尔坐标。
这样就得到了原始图像与变换后图像的像素的对应关系。
平移变换:若图像像素点 (,)x y 平移到 00(,)x x y y ++,则变换函数为0(,)u X x y x x ==+,0(,)v Y x y y y ==+,写成矩阵表达式为:00x u x y v y ⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦其中,x 0和y 0分别为x 和y 的坐标平移量。
比例缩放:若图像坐标 (,)x y 缩放到( ,x y s s )倍,则变换函数为:00x y s u x s v y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 其中, ,x y s s 分别为x 和y 坐标的缩放因子,其大于1表示放大,小于1表示缩小。
旋转变换:将输入图像绕笛卡尔坐标系的原点逆时针旋转θ角度,则变换后图像坐标为: cos sin sin cos u x v y θ-θ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥θθ⎣⎦⎣⎦⎣⎦内容:1、对一个三角形分别实现平移,缩放旋转等变化。
计算机视觉空间几何变换流程

计算机视觉空间几何变换流程
计算机视觉空间中的几何变换流程主要包括以下步骤:
1. 坐标系转换:对于旋转和偏移,一般是以图像中心为原点,这涉及坐标系转换。
通常的图像坐标系是以图像左上角为原点,水平向右为X轴,垂直向下为Y轴。
而数学课本中常见的坐标系是以图像中心为原点,水平向右为X 轴,垂直向上为Y轴,这称为笛卡尔坐标系。
在图像中我们的坐标系通常是AB和AC方向的,原点为A,而笛卡尔直角坐标系是DE和DF方向的,原点为D。
2. 旋转计算:进行旋转计算。
旋转矩阵前面已经给出了。
3. 坐标转换回:将旋转后的图像的笛卡尔坐标转回图像坐标。
此外,了解图像形成过程的简化模型也是必要的。
这包括了解基本几何图元(点、线和平面)以及将这些3D量投影到2D图像特征的几何变换。
同时,还要了解光照、表面属性和相机光学如何相互作用以产生落在图像传感器上的颜色值。
以上信息仅供参考,如有需要建议查阅计算机视觉领域的专业书籍或咨询专业人士。
计算机图形学实验_简单动画的实现、三维图形变换

学号专业姓名实验日期2018.12.11 教师签字成绩实验报告【实验名称】简单动画的实现、三维图形变换【实验目的】(1)指定图形运动轨迹,实现物体的移动过程和移动速度控制;(2)理解并掌握形体的投影变换的原理;【实验原理】1)简单动画的原理:显示一个对象,然后把它抹去,把这个图形进行变换后,再在新位置予以显示.当上述过程重复执行时,在视觉上便产生了运动;了解getimage函数和 putimage函数、imagesize函数、malloc 函数、 cleardevice 函数的使用。
2)绘制一点透视图的变换矩阵:1 0 0 0T= 0 1 0 00 0 0 1/dL m n 1+n/d得变换后的点坐标为:x’=(x+l)/(d+(n+z)*d)y’=(y+m)/(d+(n+z)*d)z’=0一.设计思想(一)图形的移动分别画出一个六边形和一个三角形,用两个一维数组p和A来存放其各点坐标;运用putimage(x,y,p,op)函数将六边形不断地向三角形平移,直到到达三角形的边界位置为止。
用到的函数如下: getimage(x1,y1,x2,y2,p); 将屏幕左上角(x1,y1),右下角(x2,y2)的矩形区域内的图象存到指针P 所指向的内存区域中。
putimage(x,y,p,op);将p 所指向的内存区域的内容在屏幕上显示,左上角坐标(x,y)。
(二) 一点透视基本步骤如下:1. 将三维物体平移到适当位置(l,m,n);2. 令视点在z 轴,进行透视变换,变换矩阵如下:1000/110000100001d 3. 最后,向xOy 面作正投影变换,将结果变换到xOy 面上。
如此构造的一点透视变换矩阵为:d n n ml d/1/100000100001+ 则三维形体中任意一点(x,y,z )的一点透视变换的齐次坐标计算形式为:[x’,y’,z’,1]=10)/(*)()/(*)(z n d d m y z n d d l x ++++++;【实验内容】1.图形的移动显示两个图形,然后移动其中一个图形.当被移动的图形超出屏幕范围时,输 出错误信息“Coordinate out of range ”并结束。
C++3D图形变换(含源码,下载后可复制黏贴使用)

实验三 3D图形变换一.实验目的:掌握3D图像的变换,了解多数的3D变换,平移,旋转等几何变换,还有投影变换等知识。
二.实验原理:3D图像的移动,比例变化,旋转等几何变换算法原理及各种投影变换算法原理。
三.实验步骤:一.建立MFC单文档程序,用来编写3D变换。
二.建立Mainframe,并设计,添加相应的ID及映射函数。
三.实验的主要代码:1、设计3维图形平移变换算法的实现程序;void CMyView::OnTranslation(){m_Select=SEL_TS;m_str="平移";CBaseClass my1; //构造新的CBaseClass对象int i,j;for ( i=1;i<=4;++i){for ( j=1;j<=4;++j)my1.A[i][j]=0;}my1.A[1][1]=1;my1.A[2][2]=1;my1.A[4][4]=1;my1.A[3][3]=1;my1.A[4][1]=20; //x轴方向上平移my1.A[4][2]=28; //y轴方向上平移my1.A[4][3]=28; //z轴方向上平移my1.Draw();}2、设计3维图形缩放变换算法的实现程序;void CMyView::OnScalingS(){m_Select=SEL_MO;m_str="整体变比";CBaseClass my1; //构造新的CBaseClass对象int i,j;for ( i=1;i<=4;++i){for ( j=1;j<=4;++j)my1.A[i][j]=0;}my1.A[1][1]=1;my1.A[2][2]=1;my1.A[3][3]=1;my1.A[4][4]=0.5;my1.Draw();}void CMyView::OnScalingXyz(){m_Select=SEL_MO;m_str="XYZ变比";CBaseClass my1; //构造新的CBaseClass对象int i,j;for ( i=1;i<=4;++i){for ( j=1;j<=4;++j)my1.A[i][j]=0;}my1.A[1][1]=2; //x轴方向上比例my1.A[2][2]=1; //y轴方向上比例my1.A[3][3]=2; //z轴方向上比例my1.A[4][4]=1;my1.Draw();}3、设计3维图形旋转变换算法的实现程序。
图像变换实验报告

图像变换实验报告图像变换实验报告一、引言图像变换是计算机图形学中的重要研究方向,它涉及到将图像从一种形式转换为另一种形式,常见的变换包括旋转、缩放、镜像等。
本实验旨在通过实际操作,探索图像变换的原理和应用。
二、实验目的1. 了解图像变换的基本概念和原理;2. 掌握图像变换的常用算法和方法;3. 利用编程语言实现图像变换,并观察结果。
三、实验步骤1. 实验准备:a. 下载并安装图像处理软件;b. 准备一组测试图像。
2. 图像旋转变换:a. 打开图像处理软件,选择一张测试图像;b. 在软件中选择旋转变换功能,并设置旋转角度;c. 运行程序,观察图像旋转结果。
3. 图像缩放变换:a. 选择另一张测试图像;b. 在软件中选择缩放变换功能,并设置缩放比例;c. 运行程序,观察图像缩放结果。
4. 图像镜像变换:a. 选择第三张测试图像;b. 在软件中选择镜像变换功能,并选择水平或垂直镜像;c. 运行程序,观察图像镜像结果。
5. 图像变换算法比较:a. 将同一张测试图像分别使用不同的图像变换算法进行处理;b. 观察不同算法处理后的图像效果,并比较它们的差异。
四、实验结果与分析通过实验,我们成功实现了图像的旋转、缩放和镜像变换,并获得了相应的结果。
在图像旋转变换中,我们观察到图像按照指定角度旋转后,保持了原始图像的形状和内容,但位置发生了变化。
在图像缩放变换中,我们发现图像按照设定的比例进行缩放后,尺寸发生了变化,但整体结构和细节保持了一定的相似性。
在图像镜像变换中,我们发现图像在水平或垂直方向上翻转后,整体形状和内容发生了镜像对称的变化。
通过比较不同的图像变换算法,我们发现不同算法对于同一张图像可能会产生不同的效果。
这是因为不同算法对图像的处理方式和策略不同,导致最终的结果也有所差异。
因此,在实际应用中,我们需要根据具体需求选择适合的图像变换算法,以达到最佳的效果。
五、实验总结本实验通过实际操作,深入了解了图像变换的原理和应用。
计算机图形学 图形几何变换的实现

二.实验内容
(1) 理解采用齐次坐标进行图形变换的必要性——变换的连续性,使复合变换
得以ቤተ መጻሕፍቲ ባይዱ现。
(2) 掌握二维、三维图形基本变换的原理及数学公式。
三维几何变换:
(1) 比例变换:
??d1???h??l
beim
cfjn
p??? r??s?
?x1
y1
z11?=?x
yz
1?T3D=?x
yz
局部
(3) 利用VC++语言实现二维、三维图形的基本变换、复合变换,在屏幕上显
示变换过程或变换结果。
三.实验步骤
(1) 学习教材关于二维、三维图形变换的原理和方法。 (2) 使用VC++语言实现某一种或几种基本变换。 (3) 调试、编译、运行程序。
四.原理分析
源程序分别实现了对二维图形进行的平移变换—基本变换;对三维图形进行的绕某一个坐标轴旋转变换以及相对于立方体中心的比例变换—复合变换。
计算机图形变换流程三维数学表达式

计算机图形变换流程三维数学表达式下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor.I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!计算机图形变换的三维数学表达与流程解析在计算机图形学中,三维数学表达式扮演着至关重要的角色,它们是构建、操作和理解虚拟世界的基础。
计算机图形学中的三维变换与投影算法

计算机图形学中的三维变换与投影算法计算机图形学是研究计算机中图形的表示、生成、处理和显示的学科。
在计算机图形学中,三维变换和投影算法是非常重要的技术,它们可以用来对三维物体进行位置、姿态和尺寸的调整,并将其投影到二维画面上。
三维变换是指通过对三维物体的顶点进行一系列变换操作,来改变物体的位置、形状和方向。
常用的三维变换操作包括平移、旋转和缩放。
平移操作改变物体的位置,旋转操作改变物体的方向,而缩放操作改变物体的尺寸。
通过组合不同的变换操作,可以实现复杂的三维物体的变换。
平移是通过将物体的每个顶点按照指定的距离移动来改变物体的位置。
旋转是通过将物体的每个顶点绕着旋转中心按照指定的角度旋转来改变物体的方向。
缩放是通过将物体的每个顶点按照指定的比例因子进行缩放来改变物体的尺寸。
这些变换操作可以通过矩阵运算来进行计算,从而实现对三维物体的变换。
投影是将三维物体投影到二维画面上的操作。
在计算机图形学中,常用的投影算法有平行投影和透视投影。
平行投影是将物体的每个顶点沿着平行于视线的方向进行投影,得到二维画面上的对应点。
透视投影则考虑到物体离视点的距离,并根据投影面和视点的位置关系而调整投影结果。
通过投影操作,可以将三维物体在计算机屏幕上展示出来,从而实现真实感的图形显示。
在实际应用中,三维变换和投影算法被广泛应用于计算机游戏、虚拟现实、计算机辅助设计等领域。
通过三维变换,可以实现物体的动画效果,使得游戏或虚拟现实场景更加逼真。
而通过投影算法,可以实现对物体的观察和测量,帮助设计师更好地进行产品设计和展示。
总结来说,计算机图形学中的三维变换和投影算法是实现三维物体在计算机中显示和操作的关键技术。
通过对物体进行平移、旋转和缩放等变换操作,可以改变物体的位置、方向和尺寸;而通过投影操作,可以将三维物体投影到二维画面上展示出来。
这些技术在计算机游戏、虚拟现实和计算机辅助设计等领域发挥着重要的作用,推动了计算机图形学的发展。
计算机图形学实验五:图形变换
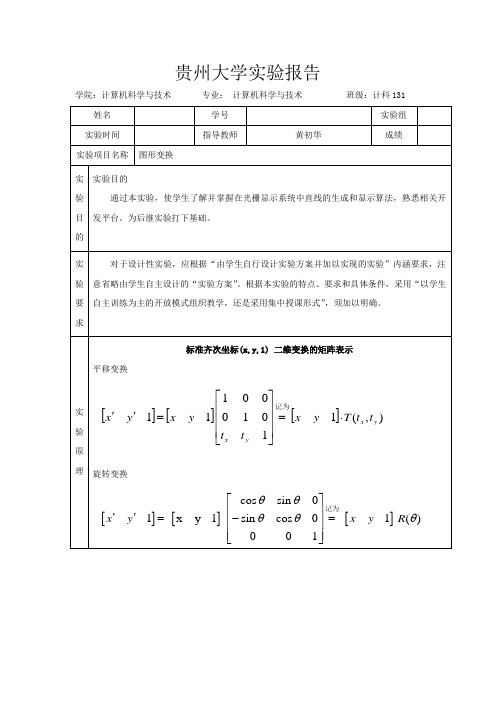
贵州大学实验报告学院:计算机科学与技术专业:计算机科学与技术班级:计科131实验内容#include"stdafx.h"#include<glut.h>#include<stdlib.h>#include<math.h>GLsizei winWidth = 600, winHeight = 600;GLfloat xwcMin = 0.0, xwcMax = 225.0;GLfloat ywcMin = 0.0, ywcMax = 225.0;class wcPt2D{public:GLfloat x, y;};typedef GLfloat Matrix3x3[3][3];Matrix3x3 matComposite;const GLdouble pi = 3.14159;void init(void){glClearColor(1.0, 1.0, 1.0, 0.0);}void matrix3x3SetIdentity(Matrix3x3matIdent3x3){GLint row, col;for (row = 0; row<3; row++)for (col = 0; col<3; col++)matIdent3x3[row][col] = (row == col);//生成{{1,0,0}{0,1,0}{0,0,1}}}void matrix3x3PreMultiply(Matrix3x3m1, Matrix3x3m2){GLint row, col;Matrix3x3 matTemp;for (row = 0; row<3; row++)for (col = 0; col<3; col++)matTemp[row][col] = m1[row][0] * m2[0][col] + m1[row][1] * m2[1][col] + m1[row][2] * m2[2][col];for (row = 0; row<3; row++)for (col = 0; col<3; col++)m2[row][col] = matTemp[row][col];}void translate2D(GLfloat tx, GLfloat ty)//平移{Matrix3x3 matTransl;matrix3x3SetIdentity(matTransl);matTransl[0][2] = tx;matTransl[1][2] = ty;matrix3x3PreMultiply(matTransl, matComposite);}void rotate2D(wcPt2D pivotPt, GLfloat theta)//旋转{Matrix3x3 matRot;matrix3x3SetIdentity(matRot);matRot[0][0] = cos(theta);matRot[0][1] = -sin(theta);matRot[0][2] = pivotPt.x*(1 - cos(theta)) + pivotPt.y*sin(theta);matRot[1][0] = sin(theta);matRot[1][1] = cos(theta);matRot[31][2] = pivotPt.x*(1 - cos(theta)) - pivotPt.y*sin(theta);matrix3x3PreMultiply(matRot, matComposite);}void scale2D(GLfloat sx, GLfloat sy, wcPt2D fixedPt)//缩放{Matrix3x3 matScale;matrix3x3SetIdentity(matScale);matScale[0][0] = sx;matScale[0][2] = (1 - sx)*fixedPt.x;matScale[1][1] = sy;matScale[1][2] = (1 - sy)*fixedPt.y;matrix3x3PreMultiply(matScale, matComposite);}void transformVerts2D(GLint nVerts, wcPt2D * verts)//组合变化后的矩阵{GLint k;GLfloat temp;for (k = 0; k<nVerts; k++){temp = matComposite[0][0] * verts[k].x + matComposite[0][1] * verts[k].y + matComposite[0][2];verts[k].y = matComposite[1][0] * verts[k].x + matComposite[1][1] *verts[k].y + matComposite[1][2];verts[k].x = temp;}}void triangle(wcPt2D*verts){GLint k;glBegin(GL_TRIANGLES);for (k = 0; k<3; k++)glVertex2f(verts[k].x, verts[k].y);glEnd();}void displayFcn(void){GLint nVerts = 3;wcPt2D verts[3] = { { 50.0, 25.0 }, { 150.0, 25.0 }, { 100.0, 100.0 } };wcPt2D centroidPt;GLint k, xSum = 0, ySum = 0;for (k = 0; k<nVerts; k++){xSum += verts[k].x;ySum += verts[k].y;}centroidPt.x = GLfloat(xSum) / GLfloat(nVerts);centroidPt.y = GLfloat(ySum) / GLfloat(nVerts);wcPt2D pivPt, fixedPt;pivPt = centroidPt;fixedPt = centroidPt;GLfloat tx = 0.0, ty = 100.0;GLfloat sx = 0.5, sy = 0.5;GLdouble theta = pi / 2.0;glClear(GL_COLOR_BUFFER_BIT);glColor3f(0.0, 0.0, 1.0);triangle(verts);//三角形matrix3x3SetIdentity(matComposite);scale2D(sx, sy, fixedPt);//缩小transformVerts2D(nVerts, verts);glColor3f(1.0, 0.0, 0.0);triangle(verts);matrix3x3SetIdentity(matComposite);rotate2D(pivPt, theta);//旋转90transformVerts2D(nVerts, verts);glColor3f(1.0, 0.0, 0.0);triangle(verts);matrix3x3SetIdentity(matComposite);translate2D(tx, ty);//平移transformVerts2D(nVerts, verts);glColor3f(1.0, 0.0, 0.0);实验结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学与软件科学学院实验报告学期:___2010 至_2011 第__一__ 学期2010年12月21日课程名称:____计算机图形学 _____ 专业:__信息与计算科学_ 2007级_5_班实验编号: 07 实验项目_____显示变换__指导教师__庞朝阳_ 姓名:学号: 20070605 __实验成绩:_____实验目的:(1) 了解掌握显示变换的相关知识,知道什么是平行投影和透视投影;实验内容:(1) 知道显示变换是什么;(2) 掌握平行投影变换;(3) 掌握透视投影变换;(4) 编写并执行简单的Prolog程序,并熟悉测试或调试的方法。
实验步骤:(1)显示变换三维空间中的物体要在二维的屏幕显示出来,必须通过投影的方式把三维物体转换成二维的平面图形。
投影的方式有平行投影,透视投影。
平行投影变换(2)平行投影变换平行投影可根据投影方向与投影面的夹角分为:正投影和斜投影。
当投影方向与投影面垂直时,为正投影;否则为斜投影。
A.正投影1.假设投影平面垂直于Z轴,且位于Z=Z0外,则在视坐标系中任意一点(X,Y,Z)的投影是过该点的投影线与投影平面的交点,如下图:P(x,y,z) p`(x`,y`,z`)Z0 Z则空间点的坐标与投影坐标间关系为:x`=x , y`=y , z`=z即```1xyz=000010000000001Z.1xyz2.```1x y z =1000010000000001 . 1x y z 即平面投影的变换矩阵为:Mz (平)=10000100000001同理可得:在y0z 平面的投影变换矩阵为:Mx(平) =0000010000000001 在x0z 平面的投影变换矩阵为:My(平) =10000000001002.斜投影 如下图求空间中任意一点D (x,y,z )在斜面ABC 上的投影。
Step1:确定一定Q,并过P 作斜面的法向量n 。
X ZYACBP由=(1,0,1)T ,=(0,1,-1)T及 = * =(1,1,1)T。
单位值得:=31⎪⎪⎪⎭⎫ ⎝⎛111。
P 点坐标为P (1/2,0,1/2)。
Step2:将过点的法向量n 平移到原点O ,记该平移变换为T P =⎪⎪⎪⎪⎪⎭⎫⎝⎛--10002/110000102/1001。
Step3:将平移后的法向量 (连同斜面)绕x 轴旋转α角度,使斜面与xOz 面垂直,则: cos α=22,则α=4/π , sin α=22,即: R x ()α=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-10000cos sin 00sin cos 00001αααα=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-100222200222200001Step4:记旋转后法向量为1n ,则有:1n = R x ()α*=31⎪⎪⎪⎪⎪⎭⎫⎝⎛0201记1n 与z 轴的夹角为β,则tan β =22,即sin β=31,cos β=32。
Step5:使1n 连同斜面)绕y 轴旋转-β角度后与z 轴重合,即斜面与xOy 面重合,则:R y ()β-=()()()()⎪⎪⎪⎪⎪⎭⎫⎝⎛-----10000cos 0sin 00100sin 0cos ββββ=⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-1000320310010031032 Step6:绕z 轴向xOy 面平行投影(正投影),则有:M ()平z =⎪⎪⎪⎪⎪⎭⎫⎝⎛1000000000100001 Step7:作一系列逆变换,使P 点还原到原来位置。
像上:对任意点D (x,y,z ),它在斜面ABC 上的投影记为D '(x ’,y ’,z ’,),则有⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1'''z y x =T 1-P *R ()α1-x *R ()β1-y * R y ()β-* R x ()α* T P *⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1z y x如原点(0,0,0)在斜面ABC 上的投影点为(1/3, 1/3, 1/3)②透视投影变换据投影定义,空间任意一点的透视投影是投影中心与空间点构成的投影线与投影平面的交点。
假设视点(投影中心)为E (0,0,d ),投影平面为xOy 面,空间中任意一点记为P (x ,y ,z ),求P 点在xOy 面上的像点P ’(x ’,y ’,z ’)及P 到P ’点的变换矩阵M ()透z 。
如下图所示:求解:利用三角形相似原理⎪⎩⎪⎨⎧=-=+=-=+=0)/(|)|/(/')/(|)|/(/'z z d d z d d y y z d d z d d x x −−−→−==d/1r 令⎪⎩⎪⎨⎧=+=+=0')1/(')1/('z rz y y rz x x 则有:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡H z y x '''=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1000000000100001*⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡100010000100001r *⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1z y x =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡100000000100001r *⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1z y x即M ()透z =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-1/10000000100001d。
若记为:(x ’,y ’,z ’,H )=(x,y,z,1)* M ()透z则M ()透z =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-1000/100000100001d 同理,若视点E 在y 轴上,即E (0,d ,0),且投影面为xOz 平面,则有:M ()透y =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-10/10010000000001d 或⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-10000100/10000001d 若视点E 在x 轴上,即E (d ,0,0),且投影面为yOz 平面,则有:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡H z y x '''=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-100/1010000100000d 或⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-100001000010/1000d ③视坐标系与视变换(斜方向投影)前面得到的是特殊情况下的透视和平行投影的变换矩阵,而实际情况往往需要在一般情况下进行投影变换。
首先根据场景要求建立一视坐标系(如下图),然后构建一个视平面(也称投影平面),使该平面与z v 轴垂直。
显示过程即是场景中物体从世界坐标转换成视坐标。
最后,把视坐标再投影到视平面。
Step1:建立视坐标系。
1.取视平面(投影平面)的法矢量为视坐标系的z 轴方向。
记为z vl 单位矢量。
2.记视平面中心P 0为视坐标系原点,P 0(x 0,y 0,z 0),则存在平移矢量OP =(x 0,y 0,z 0)T. 3.取y v ,使y v *z v =04.由x v = y v *z v 确定视坐标的x 轴,从而得到视坐标系(P 1,x 111,,v v v z y ). Step2:求世界坐标系(O,x w w w z y ,,)到视坐标(P, x v , y v ,z v )的变换。
x w =(1,0,0)T,y W =(0,1,0)T,z w =(0,0,1)T设x v =u x * x w +m x * y W +n x * z w y v =u y * x w +m y * y W +n y * z w z v =u z * x w +m z * y W +n z * z w 考虑到原点(平移变换),则有:(x v ,y v ,z v ,P )=(x w ,y W ,z w ,O )*M且:M=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡10000z n n n y m m m x u u u z y x z y xz y x Step3:求世界坐标中任意一点P (x,y,z )在视平面内的投影P ’(x ’,y ’,z ’)。
(p 在z v 的负向)。
则有:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1'''z y x = T ()透y *M*⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1z y x .其中:T ()透z =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1000/100000100001d 。
④.求侧面在xOy 面的投影 思路:R ()β-Y →R ⎪⎭⎫⎝⎛-απ2X →T ⎪⎪⎭⎫ ⎝⎛-22Z →P ()投Z 即:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1'''z y x =R()β--1Y*R⎪⎭⎫ ⎝⎛--απ21x*T ⎪⎪⎭⎫ ⎝⎛--221z*P z*T ⎪⎪⎭⎫⎝⎛-22Z * R ⎪⎭⎫⎝⎛-απ2X * R ()β-Y *⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1z y x⑤窗口到视区的变换。
由于在图形显示时往往只需要显示某一部分,这时可以在投影面上定义一个窗口, 只有在窗口内的图形才被显示,而窗口外的部分则不显示。
在屏幕上也可定义一个矩 形,称为视区。
经过窗口到视区的变换,窗口内的图形才能变换到视区中显示。
假设窗口的左下角顶点坐标为(WXL,WYB ),右下角顶点坐标为(WXR,WYT ) 视区左下角为(VXL,VYT ),右下角顶点为(VXR,VYT ),则要将窗口内的点(x w ,y w ),映射到视区内的点(x v ,y v ),则据相似原理有:VXL VXR VXL x v --=WXL WXR WXL x w -- , VYB VYT VTB y v --=WYBWYT WYBy w --由此可得:x v =VXL+( x w -WXL)*s x y v =VYB+( y w -VYB)*s y其中:s x =VXL VXR VXL VXR -- , s y =WYBWYT WYBVYT --上述窗口到视区变换,也可通过一系列变换的组合得到。
变换过程如下: Step1:将窗口左下角顶点(WXL,WYB )平移至窗口所在坐标T 1。
Step2:进行缩放变换,使窗口大小与视区相等T 2。
Step3:将窗口内的点映射到视区中,再进行反平移,将视区左下角移到后来的位置T 3。
即有:T窗视= T3* T2* T1=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1001001VYB VXL *⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100000y xs s *⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--1001001WYB WXL =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-100*0*0VYB s WYB s VXL s WXL s y y x x综上:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1v v y x =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-100*0*0VYB s WYB s VXL s WXL s y y x x*⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1w w y x。
