简单的三角恒等变换专题及答案

合集下载

专题12 简单的三角恒等变换（解析版）

于是 b + c = 2R (sinB + sinC )
=
43 3
sinB
+
sin
2 3
−
B
=
43 3
3 sinB + 2
3 2
cosB
=
4sin
B
+
6
.
因为 ABC 是锐角三角形且 A = ， 3
所以由 C
2
，得
2 3
−
B
2
，因此
B
的取值范围是
6
,
2
.
6/7
( 而由
；（2）
−
2 2
,1
.
【解析】（1）由正弦定理得： sinA = sinBcosC + sinCsinB
因为： sinA = sin ( B + C ) = sinBcosC + cosBsinC
故 cosBsinC = sinCsinB 因为 sinC 0 ，所以 cosB = sinB 因为 0 B ，所以 B =
2
2
∴ A .
6
4
) ∵
a
=
2
，∴
a sinA
2
2,4
.又 b + c = a ， sinB + sinC sinA
3/7
( ) ∴ b + c 2 2, 4 . sinB + sinC
( ) 故答案为 2 2, 4
7．（三角恒等变换在实际中的运用）如图，有一壁画，最高点 A 处离地面 6m，最低点 B 处离地面 3.5m.若从离地高 2m 的 C 处观赏它，则离墙______m 时，视角最大.

4.5 简单的三角恒等变换

点击此处进入作业手册
【例1】求证：】证明：法一：左端＝证明：证法一：左端＝＝sin α＋cos α＝右端则原恒等式成立．＋＝右端则原恒等式成立．证法二：设sin α＋cos α＝t，则左端＝证法二：＋＝，则左端＝＝t＝右端则原恒等式成立．＝右端则原恒等式成立．
＝sin α＋cos α. ＋
(2)f(θ)＝2sin2 ＝＝(1＋sin 2θ)－＋－＝2sin ∵θ∈ ∈ ∴2≤2sin 即当θ＝即当＝＋1≤3. ＋1.
cos 2θ＝＝ cos 2θ＝sin 2θ－＝－ cos 2θ＋1 ＋
cos 2θ
时，f(θ)max＝3；当θ＝；＝
时，f(θ)min＝2.
【分析点评】分析点评】
∴sin 2x＝－＝－ ∴原式＝原式＝
变式2.求变式求值：
解答：解答：原式＝
＝
＝
解决三角函数的图象与性质问题很大程度上可通过三角恒等变换将函数转化为y 解决三角函数的图象与性质问题很大程度上可通过三角恒等变换将函数转化为的形式，＝Asin(ωx＋φ)的形式，进而可解决函数的周期、奇偶性、单调性和作函数图象＋的形式进而可解决函数的周期、奇偶性、等问题．等问题．
4.5
简单的三角恒等变换
能运用同角三角函数的基本关系、诱导公式、能运用同角三角函数的基本关系、诱导公式、两角和与差三角函数公式进行简单的恒等变换
1．降幂公式． sin αcos α＝＝ 2．半角公式． sin 2α；sin2α＝；＝
3．Asin x＋Bcos x＝．＋＝ cos φ＝＝
【例3】已知函数】知函数f(x)＝sin ＝ x∈R(其中 ∈ 其中其中ω>0)．． (1)求函数的值域；求函数f(x)的值域的值域；求函数 (2)若对任意的 ∈R，函数＝f(x)，x∈(a，a＋π]的图象与直线＝－有且仅若对任意的a∈ ，函数y＝， ∈ ，＋的图象与直线＝－1有且仅的图象与直线y＝－若对任意的有两个不同的交点，试确定的值不必证明)，并求函数y＝， ∈ 的单的值(不必证明有两个不同的交点，试确定ω的值不必证明，并求函数＝f(x)，x∈R的单调增区间．调增区间．

三角恒等变换大题(含详细解答)

三角恒等变换1．已知0＜α＜π4，0＜β＜π4且3sin β＝sin(2α＋β),4tan α2＝1－tan 2α2，求α＋β的值． 2．化简：(1－sinα)(1－sinβ)－⎝⎛⎭⎫sin α＋β2－cos α－β2 2. 3．已知sin(2α－β)＝35，sinβ＝－1213，且α∈⎝⎛⎭⎫π2，π，β∈⎝⎛⎭⎫－π2，0，求sinα 4．若cos(α＋β)cos(α－β)＝13，求cos2α－sin2β 5．函数y ＝12sin2x ＋sin2x ，x ∈R ，求y 的值域 6．已知0＜α＜π4，0＜β＜π4且3sinβ＝sin(2α＋β),4tan α2＝1－tan2α2，求α＋β的值． 7．化简：(1－sinα)(1－sinβ)－⎝⎛⎭⎫sin α＋β2－cos α－β2 2. 8．已知函数()sin()cos()f x x x θθ=+++的定义域为R ，（1）当0θ=时，求()f x 的单调区间；（2）若(0,)θπ∈，且sin 0x ≠，当θ为何值时，()f x 为偶函数． 9 已知sin sin sin 0,cos cos cos 0,αβγαβγ++=++=求cos()βγ-的值 10 若,22sin sin =+βα求βαcos cos +的取值范围 11 求值：0010001cos 20sin10(tan 5tan 5)2sin 20-+-- 12 已知函数.,2cos 32sinR x x x y ∈+=（1）求y 取最大值时相应的x 的集合；（2）该函数的图象经过怎样的平移和伸变换可以得到)(sin R x x y ∈=的图象参考答案1. 解：由4tan α2＝1－tan 2α2得tan α＝2tan α21－tan 2α2＝12. 由3sin[(α＋β)－α]＝sin[(α＋β)＋α]，得3sin(α＋β)cos α－3cos(α＋β)sin α＝sin(α＋β)cos α＋cos(α＋β)sin α，∴2sin(α＋β)cos α＝4cos(α＋β)sin α.∴tan(α＋β)＝2tan α.∴tan(α＋β)＝1.又∵0＜α＜π4，0＜β＜π4，∴0＜α＋β＜π2，∴α＋β＝π4评析：首先由4tan α2＝1－tan 2α2的形式联想倍角公式求得tan α，再利用角的变换求tan(α＋β)，据α、β的范围确定角α＋β.求角的问题的关键是恰当地选择一个三角函数值，再依据范围求角，两步必不可少．2. 分析：本题由于α＋β2＋α－β2＝α，α＋β2－α－β2＝β，因此可以从统一角入手，考虑应用和差化积公式．解：原式＝1－(sin α＋sin β)＋sin αsin β－⎝⎛ sin 2α＋β2－⎭⎫2sin α＋β2cos α－β2＋cos 2α－β2 ＝1－2sin α＋β2cos α－β2＋sin αsin β－⎣⎡⎦⎤1－cos(α＋β)2＋1＋cos(α－β)2－2sin α＋β2cos α－β2 ＝sin αsin β＋12[cos(α＋β)－cos(α－β)]＝sin αsin β＋12·(－2)sin αsin β＝0. 评析：(1)必须是同名三角函数才能和差化积；(2)若是高次函数必须用降幂公式降为一次．3．解：∵π2<α<π，∴π<2α<2π.又－π2<β<0，∴0<－β<π2.∴π<2α－β<5π2.而sin(2α－β)＝35>0，∴2π<2α－β<5π2，cos (2α－β)＝45.又－π2<β<0且sin β＝－1213，∴cos β＝513， ∴cos2α＝cos[(2α－β)＋β]＝cos(2α－β)cos β－sin(2α－β)sin β＝45×513－35×⎝⎛⎭⎫－1213＝5665. 又cos2α＝1－2sin 2α，∴sin 2α＝9130，又α∈⎝⎛⎭⎫π2，π，∴sin α＝3130130. 评析：由sin(2α－β)求cos(2α－β)、由sin β求cos β，忽视2α－β、β的范围，结果会出现错误．另外，角度变换在三角函数化简求值中经常用到，如：α＝(α＋β)－β，2α＝(α－β)＋(α＋β)，⎝⎛⎭⎫π4＋α＋⎝⎛⎭⎫π4－α＝π2等． 4. 解析：∵cos(α＋β)cos(α－β)＝13， ∴12(cos2α＋cos2β)＝13， ∴12(2cos 2α－1＋1－2sin 2β)＝13， ∴cos 2α－sin 2β＝13. 5．解析：y ＝12sin2x ＋sin 2x ＝12sin2x －12cos2x ＋12＝22sin ⎝⎛⎭⎫2x －π4＋12 评析：本题是求有关三角函数的值域的一种通法，即将函数化为y ＝A sin(ωx ＋φ)＋b 或y ＝A cos(ωx ＋φ)＋b 的模式．一般地，a cos x ＋b sin x ＝a 2＋b 2⎝ ⎛⎭⎪⎫a a 2＋b 2cos x ＋b a 2＋b 2sin x ＝a 2＋b 2(sin φcos x ＋cos φsin x )＝a 2＋b 2sin(x ＋φ)，其中tan φ＝a b，也可以变换如下：a cos x ＋b sin x ＝a 2＋b 2(cos φcos x ＋sin φsin x )＝a 2＋b 2cos(x －φ)，其中tan φ＝b a. 6. 解：由4tan α2＝1－tan 2α2 得tan α＝2tan α21－tan 2α2＝12. 由3sin[(α＋β)－α]＝sin[(α＋β)＋α]，得3sin(α＋β)cos α－3cos(α＋β)sin α＝sin(α＋β)cos α＋cos(α＋β)sin α， ∴2sin(α＋β)cos α＝4cos(α＋β)sin α. ∴tan(α＋β)＝2tan α. ∴tan(α＋β)＝1.又∵0＜α＜π4，0＜β＜π4，∴0＜α＋β＜π2， ∴α＋β＝π4. 评析：首先由4tan α2＝1－tan 2α2的形式联想倍角公式求得tan α，再利用角的变换求tan(α＋β)，据α、β的范围确定角α＋β.求角的问题的关键是恰当地选择一个三角函数值，再依据范围求角，两步必不可少．7. 分析：本题由于α＋β2＋α－β2＝α，α＋β2－α－β2＝β，因此可以从统一角入手，考虑应用和差化积公式．解：原式＝1－(sin α＋sin β)＋sin αsin β－⎝⎛sin 2α＋β2－ ⎭⎫2sin α＋β2cos α－β2＋cos 2α－β2 ＝1－2sin α＋β2cos α－β2＋sin αsin β－ ⎣⎡⎦⎤1－cos(α＋β)2＋1＋cos(α－β)2－2sin α＋β2cos α－β2 ＝sin αsin β＋12[cos(α＋β)－cos(α－β)]＝sin αsin β＋12·(－2)sin αsin β＝0. 评析：(1)必须是同名三角函数才能和差化积；(2)若是高次函数必须用降幂公式降为一次．8. 解：（1）当0θ=时，()sin cos )4f x x x x π=+=+ 322,22,24244k x k k x k πππππππππ-≤+≤+-≤≤+()f x 为递增； 3522,22,24244k x k k x k πππππππππ+≤+≤++≤≤+()f x 为递减 ()f x ∴为递增区间为 3[2,2],44k k k Z ππππ-+∈； ()f x 为递减区间为5[2,2],44k k k Z ππππ++∈。

简单的三角恒等变换(含解析)

第六节简单的三角恒等变换[知识能否忆起]半角公式(不要求记忆)1．用cos α表示sin 2α2，cos 2α2，tan 2α2.sin 2α2＝1－cos α2；cos 2α2＝1＋cos α2；tan 2α2＝1－cos α1＋cos α. 2．用cos α表示sin α2，cos α2，tan α2.sin α2＝± 1－cos α2；cos α2＝± 1＋cos α2； tan α2＝± 1－cos α1＋cos α.3．用sin α，cos α表示tan α2.tan α2＝sin α1＋cos α＝1－cos αsin α. [小题能否全取]1．(教材习题改编)已知cos α＝13，α∈(π，2π)，则cos α2等于( )A.63 B ．－63 C.33D ．－33解析：选B ∵cos α＝13，α∈(π，2π)，∴α2∈⎝⎛⎭⎫π2，π， ∴cos α2＝－1＋cos α2＝－ 1＋132＝－63.2．已知函数f (x )＝cos 2⎝⎛⎭⎫π4＋x －cos 2⎝⎛⎭⎫π4－x ，则f ⎝⎛⎭⎫π12等于( ) A.12B ．－12C.32D ．－32解析：选B f (x )＝cos 2⎝⎛⎭⎫π4＋x －sin 2⎝⎛⎭⎫x ＋π4＝－sin 2x ，∴f ⎝⎛⎭⎫π12＝－sin π6＝－12. 3．已知tan α＝12，则cos 2α＋sin 2α＋1cos 2α等于( )A ．3B ．6C ．12D.32解析：选A cos 2α＋sin 2α＋1cos 2α＝2cos 2α＋2sin α·cos αcos 2α＝2＋2tan α＝3. 4.sin 20°cos 20°cos 50°＝________.解析：sin 20°cos 20°cos 50°＝12sin 40°cos 50°＝12sin 40°sin 40°＝12.答案：125．若1＋tan α1－tan α＝2 013，则1cos 2α＋tan 2α＝________.解析：1cos 2α＋tan 2α＝1＋sin 2αcos 2α＝(cos α＋sin α)2cos2α－sin2α＝cos α＋sin αcos α－sin α＝1＋tan α1－tan α＝2 013.答案：2 013三角恒等变换的常见形式三角恒等变换中常见的三种形式：一是化简；二是求值；三是三角恒等式的证明．(1)三角函数的化简常见的方法有切化弦、利用诱导公式、同角三角函数关系式及和、差、倍角公式进行转化求解．(2)三角函数求值分为给值求值(条件求值)与给角求值，对条件求值问题要充分利用条件进行转化求解．(3)三角恒等式的证明，要看左右两侧函数名、角之间的关系，不同名则化同名，不同角则化同角，利用公式求解变形即可．典题导入[例1] 化简2cos 4x －2cos 2x ＋122tan ⎝⎛⎭⎫π4－x sin 2⎝⎛⎭⎫π4＋x .[自主解答] 原式＝－2sin 2x cos 2x ＋122sin ⎝⎛⎭⎫π4－x cos 2⎝⎛⎭⎫π4－x cos ⎝⎛⎭⎫π4－x＝12(1－sin 22x )2sin ⎝⎛⎭⎫π4－x cos ⎝⎛⎭⎫π4－x ＝12cos 22x sin ⎝⎛⎭⎫π2－2x＝12cos 2x . 由题悟法三角函数式的化简要遵循“三看”原则(1)一看“角”，这是最重要的一环，通过看角之间的差别与联系，把角进行合理的拆分，从而正确使用公式；(2)二看“函数名称”，看函数名称之间的差异，从而确定使用的公式，常见的有“切化弦”；(3)三看“结构特征”，分析结构特征，可以帮助我们找到变形的方向，如“遇到分式要通分”等．以题试法1．化简⎝ ⎛⎭⎪⎫1tan α2－tan α2·⎝⎛⎭⎫1＋tan α·tan α2. 解：法一：原式＝⎝ ⎛⎭⎪⎫cos α2sin α2－sin α2cos α2·⎝ ⎛⎭⎪⎫1＋sin αcos α·sin α2cos α2＝cos 2α2－sin 2α2sin α2·cos α2·cos αcos α2＋sin αsinα2cos αcos α2＝2cos αsin α·cos ⎝⎛⎭⎫α－α2cos αcosα2 ＝2cos αsin α·cosα2cos αcosα2＝2sin α. 法二：原式＝1－tan 2α2tan α2·⎝ ⎛⎭⎪⎫1＋sin αsin α2cos αcos α2＝2tan α·cos αcos α2＋sin αsinα2cos αcosα2 ＝2cos αsin α·cos α2cos α·cosα2＝2sin α.典题导入[例2] (1)(2012·重庆高考)sin 47°－sin 17°cos 30°cos 17°＝( )A ．－32 B ．－12C.12D.32. (2)已知α、β为锐角，sin α＝35，cos ()α＋β＝－45，则2α＋β＝________.[自主解答] (1)原式＝sin (30°＋17°)－sin17°cos 30°cos 17°＝sin 30°cos 17°＋cos 30°sin 17°－sin 17°cos 30°cos 17°＝sin 30°cos 17°cos 17°＝sin 30°＝12.(2)∵sin α＝35，α∈⎝⎛⎭⎫0，π2， ∴cos α＝45，∵cos(α＋β)＝－45，α＋β∈(0，π)，∴sin(α＋β)＝35，∴sin(2α＋β)＝sin[α＋(α＋β)]＝sin αcos(α＋β)＋cos αsin(α＋β)＝35×⎝⎛⎭⎫－45＋45×35＝0. 又2α＋β∈⎝⎛⎭⎫0，3π2. ∴2α＋β＝π. [答案] (1)C (2)π由题悟法三角函数求值有三类(1)“给角求值”：一般所给出的角都是非特殊角，从表面上来看是很难的，但仔细观察非特殊角与特殊角总有一定关系，解题时，要利用观察得到的关系，结合公式转化为特殊角并且消除非特殊角的三角函数而得解．(2)“给值求值”：给出某些角的三角函数式的值，求另外一些角的三角函数值，解题关键在于“变角”，使其角相同或具有某种关系．(3)“给值求角”：实质是转化为“给值求值”，先求角的某一函数值，再求角的范围，确定角．以题试法2．(2012·广州一测)已知函数f (x )＝tan ⎝⎛⎭⎫3x ＋π4. (1)求f ⎝⎛⎭⎫π9的值；(2)设α∈⎝⎛⎭⎫π，3π2，若f ⎝⎛⎭⎫α3＋π4＝2，求cos ⎝⎛⎭⎫α－π4的值．解：(1)f ⎝⎛⎭⎫π9＝tan ⎝⎛⎭⎫π3＋π4＝tan π3＋tanπ41－tan π3tanπ4＝3＋11－3＝－2－ 3. (2)因为f ⎝⎛⎭⎫α3＋π4＝tan ⎝⎛⎭⎫α＋3π4＋π4＝tan(α＋π)＝tan α＝2，所以sin αcos α＝2，即sin α＝2cos α.①又sin 2α＋cos 2α＝1，② 由①②解得cos 2α＝15.因为α∈⎝⎛⎭⎫π，3π2，所以cos α＝－55，sin α＝－255. 所以cos ⎝⎛⎭⎫α－π4＝cos αcos π4＋sin αsin π4＝－55×22＋⎝⎛⎭⎫－255×22＝－31010.典题导入[例3] (2011·四川高考)已知函数f (x )＝sin ⎝⎛⎭⎫x ＋7π4＋cos ⎝⎛⎭⎫x －3π4，x ∈R . (1)求f (x )的最小正周期和最小值；(2)已知cos(β－α)＝45，cos(β＋α)＝－45，0＜α＜β≤π2，求证：[f (β)]2－2＝0.[自主解答] (1)∵f (x )＝sin ⎝⎛⎭⎫x ＋7π4－2π＋cos ⎝⎛⎭⎫x －π4－π2 ＝sin ⎝⎛⎭⎫x －π4＋sin ⎝⎛⎭⎫x －π4＝2sin ⎝⎛⎭⎫x －π4， ∴T ＝2π，f (x )的最小值为－2.(2)证明：由已知得cos βcos α＋sin βsin α＝45，cos βcos α－sin βsin α＝－45.两式相加得2cos βcos α＝0.∵0＜α＜β≤π2，∴β＝π2.∴[f (β)]2－2＝4sin 2π4－2＝0.在本例条件不变情况下，求函数f (x )的零点的集合．解：由(1)知f (x )＝2sin ⎝⎛⎭⎫x －π4， ∴sin ⎝⎛⎭⎫x －π4＝0，∴x －π4＝k π(k ∈Z )， ∴x ＝k π＋π4(k ∈Z )．故函数f (x )的零点的集合为⎩⎨⎧⎭⎬⎫x ⎪⎪x ＝k π＋π4，k ∈Z .由题悟法三角变换的综合应用主要是将三角变换与三角函数的性质相结合，通过变换把函数化为y ＝A sin(ωx ＋φ)的形式再研究性质，解题时注意观察角、名、结构等特征，注意利用整体思想解决相关问题．以题试法3．已知函数f (x )＝2cos x cos ⎝⎛⎭⎫x －π6－3sin 2x ＋sin x cos x . (1)求f (x )的最小正周期；(2)当α∈[0，π]时，若f (α)＝1，求α的值．解：(1)因为f (x )＝2cos x cos ⎝⎛⎭⎫x －π6－3sin 2x ＋sin x cos x ＝3cos 2 x ＋sin x cos x －3sin 2x ＋sin x cos x ＝3cos 2x ＋sin 2x ＝2sin ⎝⎛⎭⎫2x ＋π3，所以最小正周期T ＝π.(2)由f (α)＝1，得2sin ⎝⎛⎭⎫2α＋π3＝1，又α∈[0，π]，所以2α＋π3∈⎣⎡⎦⎤π3，7π3，所以2α＋π3＝5π6或2α＋π3＝13π6，故α＝π4或α＝11π12.1．在△ABC 中，tan B ＝－2，tan C ＝13，则A 等于( )A.π4 B.3π4 C.π3D.π6解析：选A tan A ＝tan [π－(B ＋C )]＝－tan(B ＋C )＝－tan B ＋tan C1－tan B tan C＝－－2＋131－(－2)×13＝1.故A ＝π4.2.sin (180°＋2α)1＋cos 2α·cos 2αcos (90°＋α)等于( )A ．－sin αB ．－cos αC ．sin αD ．cos α解析：选D 原式＝(－sin 2α)·cos 2α(1＋cos 2α)·(－sin α)＝2sin α·cos α·cos 2α2cos 2α·sin α＝cos α.3．(2013·深圳调研)已知直线l: x tan α－y －3tan β＝0的斜率为2，在y 轴上的截距为1，则tan(α＋β)＝( )A ．－73B.73C.57D ．1解析：选D 依题意得，tan α＝2，－3tan β＝1，即tan β＝－13，tan(α＋β)＝tan α＋tan β1－tan αtan β＝2－131＋23＝1.4．(2012·山东高考)若θ∈⎣⎡⎦⎤π4，π2，sin 2θ＝378，则sin θ＝( ) A.35B.45C.74D.34解析：选D 因为θ∈⎣⎡⎦⎤π4，π2，所以2θ∈⎣⎡⎦⎤π2，π，所以cos 2θ<0，所以cos 2θ＝－1－sin 22θ＝－18.又cos 2θ＝1－2sin 2θ＝－18，所以sin 2θ＝916，所以sin θ＝34.5．(2012·河北质检)计算tan ⎝⎛⎭⎫π4＋α·cos 2α2cos 2⎝⎛⎭⎫π4－α的值为( )A ．－2B ．2C ．－1D ．1解析：选D tan ⎝⎛⎭⎫π4＋α·cos 2α2cos 2⎝⎛⎭⎫π4－α＝sin ⎝⎛⎭⎫π4＋α·cos 2α2sin 2⎝⎛⎭⎫π4＋αcos ⎝⎛⎭⎫π4＋α＝cos 2α2sin ⎝⎛⎭⎫π4＋αcos ⎝⎛⎭⎫π4＋α＝cos 2αsin 2⎝⎛⎭⎫π4＋α ＝cos 2αsin ⎝⎛⎭⎫π2＋2α ＝cos 2αcos 2α＝1. 6．定义运算⎪⎪⎪⎪⎪⎪a b c d ＝ad －bc .若cos α＝17，⎪⎪⎪⎪⎪⎪sin α sin βcos α cos β＝3314，0<β<α<π2，则β等于( )A.π12 B.π6 C.π4D.π3解析：选D 依题意有sin αcos β－cos αsin β ＝sin(α－β)＝3314，又0<β<α<π2，∴0<α－β<π2，故cos(α－β)＝1－sin 2(α－β)＝1314，而cos α＝17，∴sin α＝437，于是sin β＝sin[α－(α－β)] ＝sin αcos(α－β)－cos αsin(α－β)＝437×1314－17×3314＝32. 故β＝π3.7．若tan ⎝⎛⎭⎫π4－θ＝3，则cos 2θ1＋sin 2θ＝________. 解析：∵tan ⎝⎛⎭⎫π4－θ＝1－tan θ1＋tan θ＝3， ∴tan θ＝－12.∴cos 2θ1＋sin 2θ＝cos 2θ－sin 2θsin 2θ＋2sin θcos θ＋cos 2θ＝1－tan 2θtan 2θ＋2tan θ＋1＝1－1414－1＋1＝3.答案：38．若锐角α、β满足(1＋3tan α)(1＋3tan β)＝4，则α＋β＝________. 解析：由(1＋3tan α)(1＋3tan β)＝4，可得tan α＋tan β1－tan αtan β＝3，即tan(α＋β)＝ 3.又α＋β∈(0，π)，所以α＋β＝π3.答案：π39．计算：cos 10°＋3sin 10°1－cos 80°＝________.解析：cos 10°＋3sin 10°1－cos 80°＝2(sin 30°cos 10°＋cos 30°sin 10°)2sin 240°＝2sin 40°2sin 40°＝ 2.答案： 210．已知函数f (x )＝sin x ＋cos x ，f ′(x )是f (x )的导函数． (1)求f ′(x )及函数y ＝f ′(x )的最小正周期；(2)当x ∈⎣⎡⎦⎤0，π2时，求函数F (x )＝f (x )f ′(x )＋f 2(x )的值域．解：(1)由题意可知，f ′(x )＝cos x －sin x ＝－2·sin ⎝⎛⎭⎫x －π4，所以y ＝f ′(x )的最小正周期为T ＝2π. (2)F (x )＝cos 2x －sin 2x ＋1＋2sin x cos x ＝1＋sin 2x ＋cos 2x ＝1＋2sin ⎝⎛⎭⎫2x ＋π4. ∵x ∈⎣⎡⎦⎤0，π2，∴2x ＋π4∈⎣⎡⎦⎤π4，5π4， ∴sin ⎝⎛⎭⎫2x ＋π4∈⎣⎡⎦⎤－22，1. ∴函数F (x )的值域为[0,1＋ 2 ]．11．已知0<α<π2<β<π，tan α2＝12，cos(β－α)＝210.(1)求sin α的值； (2)求β的值．解：(1)∵tan α2＝12，∴tan α＝2tanα21－tan 2α2＝2×121－⎝⎛⎭⎫122＝43，由⎩⎪⎨⎪⎧sin αcos α＝43，sin 2α＋cos 2α＝1，解得sin α＝45⎝⎛⎭⎫sin α＝－45舍去. (2)由(1)知cos α＝1－sin 2α ＝1－⎝⎛⎭⎫452＝35，又0<α<π2<β<π，∴β－α∈(0，π)，而cos(β－α)＝210， ∴sin(β－α)＝1－cos 2(β－α)＝ 1－⎝⎛⎭⎫2102＝7210，于是sin β＝sin[α＋(β－α)] ＝sin αcos(β－α)＋cos αsin(β－α) ＝45×210＋35×7210＝22. 又β∈⎝⎛⎭⎫π2，π，∴β＝3π4.12．已知sin(2α＋β)＝3sin β，设tan α＝x ，tan β＝y ，记y ＝f (x )． (1)求证：tan(α＋β)＝2tan α； (2)求f (x )的解析式．解：(1)证明：由sin(2α＋β)＝3sin β，得sin [(α＋β)＋α]＝3sin [(α＋β)－α]，即sin(α＋β)cos α＋cos(α＋β)sin α＝3sin(α＋β)cos α－3cos(α＋β)sin α， ∴sin(α＋β)cos α＝2cos(α＋β)sin α. ∴tan(α＋β)＝2tan α.(2)由(1)得tan α＋tan β1－tan αtan β＝2tan α，即x ＋y1－xy ＝2x ，∴y ＝x 1＋2x 2，即f (x )＝x1＋2x 2.1．(2012·郑州质检)已知曲线y ＝2sin ⎝⎛⎭⎫x ＋π4cos ⎝⎛⎭⎫π4－x 与直线y ＝12相交，若在y 轴右侧的交点自左向右依次记为P 1，P 2，P 3，…，则|15P P |等于( )A ．πB ．2πC ．3πD ．4π解析：选B 注意到y ＝2sin ⎝⎛⎭⎫x ＋π4cos ⎝⎛⎭⎫π4－x ＝2sin 2⎝⎛⎭⎫x ＋π4＝1－cos 2⎝⎛⎭⎫x ＋π4＝1＋sin 2x ，又函数y ＝1＋sin 2x 的最小正周期是2π2＝π，结合函数y ＝1＋sin 2x 的图象(如图所示)可知，|15P P |＝2π.2.3－sin 70°2－cos 210°等于( )A.12B.22 C ．2D.32解析：选C3－sin 70°2－cos 2 10°＝3－cos 20°2－cos 210°＝3－(2cos 210°－1)2－cos 210°＝2(2－cos 210°)2－cos 210°＝2.3．(2012·江西重点高中模拟)已知函数f (x )＝sin ⎝⎛⎭⎫2x ＋π3＋sin ⎝⎛⎭⎫2x －π3＋3cos 2x －m ，若f (x )的最大值为1.(1)求m 的值，并求f (x )的单调递增区间；(2)在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，若f (B )＝3－1，且3a ＝b ＋c ，试判断三角形的形状．解：(1)f (x )＝2sin 2x ·cos π3＋3cos 2x －m ＝sin 2x ＋3cos 2x －m ＝2sin ⎝⎛⎭⎫2x ＋π3－m . 又f (x )max ＝2－m ，所以2－m ＝1，得m ＝1. 由－π2＋2k π≤2x ＋π3≤π2＋2k π(k ∈Z )得到k π－5π12≤x ≤k π＋π12(k ∈Z )，所以f (x )的单调递增区间为⎣⎡⎦⎤k π－5π12，k π＋π12(k ∈Z )． (2)由f (B )＝3－1，得2sin ⎝⎛⎭⎫2B ＋π3－1＝3－1，所以B ＝π6.又3a ＝b ＋c ，则3sin A ＝sin B ＋sin C ， 3sin A ＝12＋sin ⎝⎛⎭⎫5π6－A ，即sin ⎝⎛⎭⎫A －π6＝12，所以A ＝π3，C ＝π2，故△ABC 为直角三角形．1．求证：tan α＋1tan ⎝⎛⎭⎫π4＋α2＝1cos α.证明：左边＝sin αcos α＋cos ⎝⎛⎭⎫π4＋α2sin ⎝⎛⎭⎫π4＋α2＝sin αsin ⎝⎛⎭⎫π4＋α2＋cos αcos ⎝⎛⎭⎫π4＋α2cos αsin ⎝⎛⎭⎫π4＋α2＝cos ⎝⎛⎭⎫π4＋α2－αcos αsin ⎝⎛⎭⎫π4＋α2＝cos ⎝⎛⎭⎫π4－α2cos αsin ⎝⎛⎭⎫π4＋α2＝sin ⎝⎛⎭⎫π4＋α2cos αsin ⎝⎛⎭⎫π4＋α2＝1cos α＝右边．故原式得证．2．已知f (x )＝⎝⎛⎭⎫1＋1tan x sin 2x －2sin ⎝⎛⎭⎫x ＋π4·sin ⎝⎛⎭⎫x －π4. (1)若tan α＝2，求f (α)的值；(2)若x ∈⎣⎡⎦⎤π12，π2，求f (x )的取值范围．解：(1)f (x )＝(sin 2x ＋sin x cos x )＋2sin ⎝⎛⎭⎫x ＋π4·cos ⎝⎛⎭⎫x ＋π4 ＝1－cos 2x 2＋12sin 2x ＋sin ⎝⎛⎭⎫2x ＋π2 ＝12＋12(sin 2x －cos 2x )＋cos 2x ＝12(sin 2x ＋cos 2x )＋12. 由tan α＝2，得sin 2α＝2sin αcos αsin 2α＋cos 2α＝2tan αtan 2α＋1＝45.cos 2α＝cos 2α－sin 2αsin 2α＋cos 2α＝1－tan 2α1＋tan 2α＝－35.所以f (α)＝12(sin 2α＋cos 2α)＋12＝35.(2)由(1)得f (x )＝12(sin 2x ＋cos 2x )＋12＝22sin ⎝⎛⎭⎫2x ＋π4＋12. 由x ∈⎣⎡⎦⎤π12，π2，得5π12≤2x ＋π4≤54π. 故－22≤sin ⎝⎛⎭⎫2x ＋π4≤1，则0≤f (x )≤2＋12，所以f (x )的取值范围是⎣⎢⎡⎦⎥⎤0，2＋12.。

考向13 简单的三角恒等变换(重点)-备战2023年高考数学一轮复习考点微专题(全国通用)(解析版)

考向13 简单的三角恒等变换1．【2022年新高考2卷第6题】角,αβ满足sin()cos()22)sin 4παβαβαβ+++=+，则A ．tan()1αβ+=B ．tan()1αβ+=-C ．tan()1αβ-=D ．tan()1αβ-=-【答案】D【解析】解法一：设0β=则sin cos 0αα+=，取34απ=，排除A ，C ；再取0α=则sin cos 2sin βββ+=，取4πβ=，排除B ；选D ．解法二：由sin()cos()2sin()2sin[()]44ππαβαβαβαβ+++=++=++2sin()cos 2cos()sin 44ππαβαβ=+++，故2sin()cos 2cos()sin 44ππαβαβ+=+，故sin()cos cos()sin 044ππαβαβ+-+=，即sin()04παβ+-=，故22sin()sin()cos()0422παβαβαβ-+=-+-=，故sin()cos()αβαβ-=--，故tan()1αβ-=-．故选D. 2.【2022年北京卷第5题】已知函数()cos sin f x x x =-，则（A ）()f x 在()26ππ--,上单调递减（B ）()f x 在()412ππ-,上单调递增（C ）()f x 在(0)3π,上单调递减（D ）()f x 在7()412ππ,上单调递增【答案】C【解析】因为()22cos sin cos2f x x x x =-=.对于A 选项，当26x ππ-<<-时，23x ππ-<<-，则()f x 在,26ππ⎛⎫-- ⎪⎝⎭上单调递增，A 错；对于B 选项，当412x ππ-<<时，226x ππ-<<，则()f x 在,412ππ⎛⎫-⎪⎝⎭上不单调，B 错；对于C 选项，当03x π<<时，2023x π<<，则()f x 在0,3π⎛⎫⎪⎝⎭上单调递减，C 对；对于D 选项，当7412x ππ<<时，7226x ππ<<，则()f x 在7,412ππ⎛⎫⎪⎝⎭上不单调，D 错.故选：C.3．【2022年浙江卷第13题】若3sin cos 10,2παβαβ-=+=，则sin α= ，cos 2β= ．【答案】3104,105【解析】由题3sin cos 10,2παβαβ-=+=，所以3sin cos 10αα-=，解得310sin 10α=．所以24cos 2cos(π2)cos 212cos 5βααα=-=-=-=．1.三角函数公式的应用策略(1)使用两角和、差及倍角公式，首先要记住公式的结构特征和符号变化规律．例如两角差的余弦公式可简记为：“同名相乘，符号反．”(2)使用公式求值，应注意与同角三角函数基本关系、诱导公式的综合应用． 2.三角函数公式活用技巧①逆用公式应准确找出所给式子与公式的异同，创造条件逆用公式；②tan αtan β，tan α＋tan β(或tan α－tan β)，tan(α＋β)(或tan(α－β))三者中可以知二求一，注意公式的正用、逆用和变形使用． 3.三角函数公式逆用和变形使用应注意的问题①公式逆用时一定要注意公式成立的条件和角之间的关系；②注意特殊角的应用，当式子中出现12，1，32，3等这些数值时，一定要考虑引入特殊角，把“值变角”以便构造适合公式的形式． 4.三角公式求值中变角的解题思路①当“已知角”有两个时，“所求角”一般表示为两个“已知角”的和或差的形式；②当“已知角”有一个时，此时应着眼于“所求角”与“已知角”的和或差的关系，再应用诱导公式把“所求角”变成“已知角”． 5.三角函数名的变换技巧明确各个三角函数名称之间的联系，常常用到同角关系、诱导公式，把正弦、余弦化为正切，或者把正切化为正弦、余弦．1.降幂公式：cos 2α＝1＋cos 2α2，sin 2α＝1－cos 2α2.2.升幂公式：1＋cos 2α＝2cos 2α，1－cos 2α＝2sin 2α.3.tan α±tan β＝tan(α±β)(1∓tan αtan β)， 1＋sin 2α＝(sin α＋cos α)2， 1－sin 2α＝(sin α－cos α)2， sin α±cos α＝2sin ⎝ ⎛⎭⎪⎫α±π4. 4.辅助角公式a sin x ＋b cos x ＝a 2＋b 2sin (x ＋φ)，其中tan φ＝ba .1.明确二倍角是相对的，如：α2是α4的2倍，3α是3α2的2倍．2.解题时注意观察角、名、结构等特征，注意利用整体思想解决相关问题．3.运用公式时要注意公式成立的条件，要注意和、差、倍角的相对性，要注意升幂、降幂的灵活运用，要注意“1”的各种变形．4.在三角求值时，往往要估计角的范围后再求值．特别是在(0，π)内，正弦值对应的角不唯一．1．sin 2⎝ ⎛⎭⎪⎫α－π6＋sin 2⎝ ⎛⎭⎪⎫α＋π6－sin 2α＝( )A ．－12B ．－32 C.12 D.32 【答案】C2．已知sin α＝35，α∈⎝ ⎛⎭⎪⎫π2，π，tan(π－β)＝12，则tan(α－β)的值为( )A ．－211 B.211 C.112 D ．－112A ．－1718B ．1718C ．－89D ．89 ⎝ ⎛⎭π4＋A ．13 B ．23 C ．－23 D ．－13A．2sin 67.5°cos 67.5°B．2cos2π12－1C．1－2sin215°D．2tan 22.5°1－tan222.5°A．∃x∈R，sin2x2＋cos2x2＝12B．∃x，y∈R，sin(x－y)＝sin x－sin yC．∀x∈[0，π], 1－cos 2x2＝sin xD．sin x＝cos y⇒x＋y＝π28．若cos α＝－45，α是第三象限的角，则sin ⎝ ⎛⎭⎪⎫α＋π4＝________．【答案】－7210【解析】因为α是第三象限角，所以sin α＝－1－cos 2α＝－35，所以sin ⎝ ⎛⎭⎪⎫α＋π4＝－35×22＋⎝ ⎛⎭⎪⎫－45×22＝－7210.9.已知α，β都是锐角，cos(α＋β)＝513，sin(α－β)＝35，则cos 2α＝________．【答案】－1665. 【解析】因为α，β都是锐角，所以0<α＋β<π，－π2<α－β<π2，又因为cos(α＋β)＝513，sin(α－β)＝35，所以sin(α＋β)＝1213，cos(α－β)＝45，则cos 2α＝cos[(α＋β)＋(α－β)]＝cos(α＋β)cos(α－β)－sin(α＋β)sin(α－β)＝513×45－1213×35＝－1665. 10．已知sin α＝－45，α∈⎣⎢⎡⎦⎥⎤3π2，2π，若sin （α＋β）cos β＝2，则tan(α＋β)＝________．【答案】613.【解析】因为sin α＝－45，α∈⎣⎢⎡⎦⎥⎤3π2，2π，所以cos α＝35. 又因为sin （α＋β）cos β＝2，所以sin(α＋β)＝2cos[(α＋β)－α]．展开并整理，得65cos(α＋β)＝135sin(α＋β)，所以tan(α＋β)＝613.一、单选题1．（2022·广西桂林·模拟预测（文））若1sin 72πα⎛⎫+= ⎪⎝⎭，则3sin 214πα⎛⎫-=⎪⎝⎭（） A ．35B ．12-C ．12D ．13【答案】Csin160tan203+=，则实数A．4B．C．23D)()2sin60cos20cos60sin20tan203cos20sin201sin20cos2018020sin402--==-40440=.A.3．（2022·湖北武汉·二模）设sin32k=，则1tan16tan16+=（）A．2kB．1kC．2k D．k4．（2022·陕西·西北工业大学附属中学模拟预测（理））已知不等式()2sin cos cos02x x x m m-++≥∈R对,43xππ⎡⎤∀∈-⎢⎥⎣⎦恒成立，则m的最小值为（）A B．12C．D5．（2022·福建省福州第一中学三模）若3sin 5α=-，且3ππ,2α⎛⎫∈ ⎪⎝⎭，则1tan21tan2α-=+（） A ．12B ．12-C ．2D ．-2在平面直角坐标系内，点(),P m n -为角α终边上任意一点，则()()sin 2g x x α=-的一个对称中心为（） A ．5,08⎛⎫- ⎪⎝⎭B ．3,02π⎛⎫-⎪⎝⎭C ．(),0π-D ．()0,0120cos 40cos802sin 20cos 20cos 40cos802sin 20=⨯111sin 40cos 40cos80sin80cos802sin 202sin 202⨯︒︒︒=⨯︒︒︒︒111sin160sin 201︒︒当0k =时，函数的一个对称中心是5,08⎛⎫- ⎪⎝⎭故选：A7．（2021·上海虹口·二模）在平面上，已知定点()2,0A ，动点()sin ,cos P αα.当α在区间,44ππ⎡⎤-⎢⎥⎣⎦上变化时，动线段AP 所形成图形的面积为（） A ．24π-B ．33π-C ．6πD ．4π 【答案】D【解析】因为22sin cos 1αα+=，所以点()sin ,cos P αα在单位圆221x y +=上，由于sin cos 2παα⎛⎫=- ⎪⎝⎭，cos sin 2παα⎛⎫=- ⎪⎝⎭，所以，cos ,sin 22P ππαα⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭是其与x 轴正方向的有向角为2AOP πα∠=-，,44ππα⎡⎤∈-⎢⎥⎣⎦，则3,244πππα⎡⎤-∈⎢⎥⎣⎦，记点22,22B ⎛⎫- ⎪ ⎪⎝⎭，22,22C ⎛⎫ ⎪ ⎪⎝⎭，所以，点P 的轨迹是劣弧CB ，所以，动线段AP 所形成图形为阴影部分区域，因为ABC OBC S S =△△，因此，阴影部分区域的面积为211144OBC S S ππ==⨯=扇形.故选：D.【点睛】关键点点睛：本题考查动线段运动轨迹图形的面积，解题的关键在于确定动点P 的轨迹图形，数形结合求出图形的面积.．（浙江绍兴模拟预测）已知，设函数1，2，若当12对[,]()∈<x m n m n 恒成立时，n m -的最大值为3π2，则（） A ．21a ≥ B ．21a ≤C ．22≥bD ．22≤b 【答案】A二、多选题9．（2022·全国·模拟预测）已知函数()223cos2xf x =-，则下列说法正确的有（） A ．函数()f x 的最大值为2B ．函数()f x 在区间2ππ,36⎡⎤--⎢⎥⎣⎦上单调递增C ．函数()f x 图像的一个对称中心为1π,2⎛⎫⎪⎝⎭D ．将函数()f x 的图像向左平移π2个单位长度得到函数()13sin 12y x =+的图像10．（2022·山东·肥城市教学研究中心模拟预测）向量22(sin ,cos ),sin (),cos ,0,242x a x x b ωπωωω⎛⎫==+> ⎪⎝⎭ 函数()f x a b =⋅，则下述结论正确的有（）A ．若()f x 的图像关于直线2x π=对称，则ω可能为12B ．周期T π=时，则()f x 的图像关于点3,08π⎛⎫⎪⎝⎭对称C ．若()f x 的图像向左平移3π个单位长度后得到一个偶函数，则ω的最小值为34D ．若()f x 在2,56ππ⎡⎤-⎢⎥⎣⎦上单调递增，则30,2ω⎛⎤∈ ⎥⎝⎦【解析】()sin f x =(1sin x ω⋅+选项，若f 时，1ω=，故三、填空题11．（2022·黑龙江·鸡东县第二中学二模）已知1cos 63πα⎛⎫ ⎪⎝=⎭+，则5cos 6πα⎛⎫- ⎪⎝⎭的值为______．形三个内角都小于23π时，费马点与三角形三个顶点的连线构成的三个角都为23π.已知点P 为ABC 的费马点，角A ，B ，C 的对边分别为a ，b ，c ，若cos 2sin cos 6A C B π⎛⎫=- ⎪⎝⎭，且22()6b a c =-+，则PA PB PB PC PA PC ⋅+⋅+⋅的值为__________.ABCS=PA PB ⋅故答案为：【点睛】三角恒等变换是化简已知条件常用的方法，13．（2022·全国·模拟预测）已知63α<<，sin 4sin cos tan 15315315αα⎛⎫⎛⎫-+-+= ⎪ ⎪⎝⎭⎝⎭α=______．面几何极值问题：“已知一个三角形，求作一点，使其与此三角形的三个顶点的距离之和最小．”费马问题中的所求点称为费马点，已知对于每个给定的三角形，都存在唯一的费马点，当ABC 的三个内角均小于120︒时，则使得120APB BPC CPA ∠=∠=∠=︒的点P 即为费马点．已知点P 为ABC 的费马点，且AC BC ⊥，若||||||PA PB PC λ+=，则实数λ的最小值为_________．为ABC 的费马点，ABC 的三个内角均小于120CPA =︒，所以在BCP 和ACP △中，,,3236CBP ACP CAP ACP ππππααα∠=-∠=-∠=-∠=-，且均为锐角，所以,63ππα⎛⎫∈ ⎪⎝⎭所以由正弦定理得：sin sin 3BPPC παα=⎛⎫- ⎪⎝⎭，sin sin 26PA PCππαα=⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，所以sin sin 3BP PC απα=⎛⎫- ⎪⎝⎭，sin 2sin 6PA PC παπα⎛⎫- ⎪⎝⎭=⎛⎫- ⎪⎝⎭，因为||||||PA PB PC λ+=所以333sin cos sin sin cos 44sin 2233sin sin sin cos sin cos 3644πααααααλππαααααα⎛⎫⎛⎫-- ⎪-- ⎪⎝⎭⎝⎭=+==⎛⎫⎛⎫---- ⎪ ⎪⎝⎭⎝⎭ 3341132sin 23sin cos 4ααα=-=---，因为,63ππα⎛⎫∈ ⎪⎝⎭，所以22,33ππα⎛⎫∈ ⎪⎝⎭，所以(2sin 230,23α⎤-∈-⎦，所以)31232,2sin 23α⎡-∈++∞⎣- 故实数λ的最小值为232+. 故答案为：232+【点睛】本题考查数学文化背景下的解三角形，三角恒等变换解决三角函数取值范围问题，考查运算求解能力，数学建模能力，化归转化思想，是难题.本题解题的关键在于根据题目背景，通过设PCB α∠=，进而建立解三角形的模型，再根据正弦定理及三角恒等变换化简求最值即可.1．（2021·北京高考真题）若点(cos ,sin )P θθ与点(cos(),sin())66Q ππθθ++关于y 轴对称，写出一个符合题意的θ=___．【答案】512π（满足5,12k k Z πθπ=+∈即可）【解析】(cos ,sin )P θθ与cos ,sin 66Q ππθθ⎛⎫⎛⎫⎛⎫++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭关于y 轴对称，即,6πθθ+关于y 轴对称， 2,6k k Z πθθππ++=+∈，则5,12k k Z πθπ=+∈，当0k =时，可取θ的一个值为512π.故答案为：512π（满足5,12k k Z πθπ=+∈即可）. 2．(2021年高考全国甲卷理科)若cos 0,,tan 222sin ααα⎛⎫∈= ⎪-⎝⎭，则tan α= ( ) A ．1515B 5C ．53D ．153【答案】A 【解析】cos tan 22sin ααα=-2sin 22sin cos cos tan 2cos 212sin 2sin αααααααα∴===--，0,2πα⎛⎫∈ ⎪⎝⎭，cos 0α∴≠，22sin 112sin 2sin ααα∴=--，解得1sin 4α=，215cos 1sin 4αα∴=-=，sin 15tan cos 15ααα∴==． A ．cos2α>0 B ．cos2α<0 C ．sin2α>0D ．sin2α<0【答案】D【解析】方法一：由α为第四象限角，可得3222,2k k k Z ππαππ+<<+∈，所以34244,k k k Z ππαππ+<<+∈此时2α的终边落在第三、四象限及y 轴的非正半轴上，所以sin 20α< 故选：D ．4．(2020年高考数学课标Ⅰ卷理科)已知，且，则 ( )A ．3B ．23C ．13D ．9又(0,απ∈故选：A ．5．(2020年高考数学课标Ⅲ卷理科)已知2tan θ–tan(θ+4)=7，则tan θ= ( )A ．–2B ．–1C ．1D ．2【答案】D 【解析】2tan θ-tan ,t θ=≠故选：D ．6．(2019年高考数学课标全国Ⅱ卷理科)已知0,2α⎛⎫∈ ⎪⎝⎭，2sin 2cos21αα=+，则sin α= ( )A ．1 B C D7．(2018年高考数学课标Ⅲ卷（理）)若sin 3α=，则cos2α= ( )A ．8 B ．7 C ．7-D ．8-a A ．πB ．π C ．3π D ．π9．(2016高考数学课标Ⅲ卷理科)若tan 4α=,则2cos 2sin 2αα+= ( )A ．6425B ．4825C ．1D ．162510．(2016高考数学课标Ⅱ卷理科)若π3cos 45α⎛⎫-=⎪⎝⎭，则sin 2α= ( ) A ．725 B ．15 C ．15-D ．725-。

三角恒等变换专题复习带答案

三角恒等变换专题复习教学目标：1、能利用单位圆中的三角函数线推导出 απαπ±±,2的正弦、余弦、正切的诱导公式；2、理解同角三角函数的基本关系式：；3、可熟练运用三角函数见的基本关系式解决各种问题; 教学重难点：可熟练运用三角函数见的基本关系式解决各种问题基础知识一、同角的三大关系：① 倒数关系 tan α•cot α=1 ② 商数关系 sin cos αα= tan α ； cos sin αα= cot α ③ 平方关系 22sin cos 1αα+=温馨提示：1求同角三角函数有知一求三规律,可以利用公式求解,最好的方法是利用画直角三角形速解;来源:学+科+网2利用上述公式求三角函数值时,注意开方时要结合角的范围正确取舍“±”号;二、诱导公式口诀：奇变偶不变,符号看象限用诱导公式化简,一般先把角化成,2k z α+∈的形式,然后利用诱导公式的口诀化简如果前面的角是90度的奇数倍,就是 “奇”,是90度的偶数倍,就是“偶”；符号看象限是,把α看作是锐角,判断角2k πα+在第几象限,在这个象限的前面三角函数的符号是 “+”还是“--”,就加在前面;用诱导公式计算时,一般是先将负角变成正角,再将正角变成区间0(0,360)的角,再变到区间00(0,180)的角,再变到区间00(0,90)的角计算;三、和角与差角公式：sin()sin cos cos sin αβαβαβ±=±; cos()cos cos sin sin αβαβαβ±=;tan tan tan()1tan tan αβαβαβ±±=变用 tan α±tan β=tan α±β1 tan αtan β四、二倍角公式：sin 2α= 2sin cos αα.2222cos 2cos sin 2cos 112sin ααααα=-=-=-.22tan tan 21tan ααα=-五、注意这些公式的来弄去脉这些公式都可以由公式cos()cos cos sin sin αβαβαβ±=推导出来;六、注意公式的顺用、逆用、变用;如：逆用sin cos cos sin sin()αβαβαβ±=± 1sin cos sin 22ααα=变用22cos 1cos 2αα+=22cos 1sin 2αα-= 21cos 4cos 22αα+= 七、合一变形辅助角公式把两个三角函数的和或差化为“一个三角函数,一个角,一次方”的 B x A y ++=)sin(ϕϖ形式;()22sin cos αααϕA +B =A +B +,其中tan ϕB=A．八、万能公式ααα2tan 1tan 22sin += ααα22tan 1tan 12cos +-= ααα2tan 1tan 22tan -=九、用αsin ,αcos 表示2tanααααααsin cos 1cos 1sin 2tan-=+=十、积化和差与和差化积积化和差 )]sin()[sin(cos sin βαβαβα-++=； )]sin()[sin(sin cos βαβαβα--+=；)]cos()[cos(cos cos βαβαβα-++=； )]cos()[cos(sin sin βαβαβα--+=.和差化积 2cos2sin2sin sin ϕθϕθϕθ-+=+2sin 2cos 2sin sin ϕθϕθϕθ-+=- 2cos 2cos 2cos cos ϕθϕθϕθ-+=+ 2sin 2sin 2cos cos ϕθϕθϕθ-+=-十一、方法总结1、三角恒等变换方法观察角、名、式→三变变角、变名、变式1 “变角”主要指把未知的角向已知的角转化,是变换的主线,如α=α+β－β=α－β+β, 2α=α+β+ α－β, 2α=β+α－β－α,α+β=2·错误! , 错误! = α－错误!－错误!－β等.2“变名”指的是切化弦正切余切化成正弦余弦sin cos tan ,cot cos sin αααααα==, 3“变式’指的是利用升幂公式和降幂公式升幂降幂,利用和角和差角公式、合一变形公式展开和合并等; 2、恒等式的证明方法灵活多样①从一边开始直接推证,得到另一边,一般地,如果所证等式一边比较繁而另一边比较简时多采用此法,即由繁到简.②左右归一法,即将所证恒等式左、右两边同时推导变形,直接推得左右两边都等于同一个式子. ③比较法, 即设法证明: "左边－右边=0" 或" 错误! =1";④分析法,从被证的等式出发,逐步探求使等式成立的充分条件,一直推到已知条件或显然成立的结论成立为止,则可以判断原等式成立.例题精讲例1 已知α为第四象限角,化简：ααααααcos 1cos 1sin sin 1sin 1cos +-++-解：1因为α为第四象限角所以原式=αααααα2222cos 1)cos 1(sin sin 1)sin 1(cos --+-- ()ααααααααααsin cos cos 1sin 1sin cos 1sin cos sin 1cos -=---=--+-=例2 已知360270<<α,化简α2cos 21212121++ 解：360270<<α,02cos,0cos <>∴αα所以原式2111cos211cos 22222αα++=+21cos cos cos 222ααα+===- 例3 tan20°+4sin20°解：tan20°+4sin20°=0020cos 40sin 220sin +=0sin(6040)2sin 40cos 20-+00003340sin 403cos 20223cos 20+=== 例4 05天津已知727sin()2425παα-==,求sin α及tan()3πα+．解：解法一：由题设条件,应用两角差的正弦公式得)cos (sin 22)4sin(1027ααπα-=-=,即57cos sin =-αα ①由题设条件,应用二倍角余弦公式得)sin (cos 57)sin )(cos sin (cos sin cos 2cos 25722ααααααααα+-=+-=-== 故51sin cos -=+αα ② 由①和②式得53sin =α,54cos -=α因此,43tan -=α,由两角和的正切公式11325483343344331433tan 313tan )3tan(-=+-=+-=-+=+ααπα 解法二：由题设条件,应用二倍角余弦公式得αα2sin 212cos 257-==, 解得 259sin 2=α,即53sin ±=α 由1027)4sin(=-πα可得57cos sin =-αα由于0cos 57sin >+=αα,且057sin cos <-=αα,故α在第二象限于是53sin =α,从而5457sin cos -=-=αα 以下同解法一小结：1、本题以三角函数的求值问题考查三角变换能力和运算能力,可从已知角和所求角的内在联系均含α进行转换得到．2、在求三角函数值时,必须灵活应用公式,注意隐含条件的使用,以防出现多解或漏解的情形．例 5 已知,,A B C 为锐角ABC ∆的三个内角,两向量(22sin ,cos sin )p A A A =-+,(sin cos ,q A A =-1sin )A +,若p 与q 是共线向量.1求A 的大小；2求函数232sin cos()2C By B -=+取最大值时,B 的大小. 解：122// 2(1)(1+)- p q sinA sinA sin A cos A ∴-=22220 120cos A cos A cos A ∴+=∴+= 1cos 2A 2∴=-0<2A<π,002A 120 A=60∴=∴200A=60 B+C=120∴ 2013y=2sin B+cos(602B)1cos 2B+cos 2B sin 2B 22-=-+31 =sin 2B cos 2B+1=sin(2B )1226π--+ , 2B B 623πππ-=当时，即=．小结：三角函数与向量之间的联系很紧密,解题时要时刻注意例6 设关于x 的方程sinx ＋3cosx ＋a ＝0在0, 2π内有相异二解α、β.1求α的取值范围; 2求tan α＋β的值. 解: 1∵sinx ＋3cosx ＝221sinx ＋23cosx ＝2 sinx ＋3π, ∴方程化为sinx ＋3π＝－2a.∵方程sinx ＋3cosx ＋a ＝0在0, 2π内有相异二解, ∴sinx ＋3π≠sin 3π＝23 .又sinx ＋3π≠±1 ∵当等于23和±1时仅有一解, ∴|－2a |<1 . 且－2a≠23. 即|a |<2且a ≠－3.∴ a 的取值范围是－2, －3∪－3, 2.2 ∵α、 β是方程的相异解, ∴sin α＋3cos α＋a ＝0 ①. sin β＋3cos β＋a ＝0 ②. ①－②得sin α－ sin β＋3 cos α－ cos β＝0. ∴ 2sin2βα-cos2βα+－23sin2βα+sin2βα-＝0, 又sin2βα+≠0, ∴tan2βα+＝33.∴tan α＋β＝2tan22tan22βαβα+-+＝3.小结：要注意三角函数实根个数与普通方程的区别,这里不能忘记0, 2π这一条件. 例7 已知函数()x x m x f cos sin 2-=在区间⎪⎭⎫⎝⎛2,0π上单调递减,试求实数m 的取值范围．解：已知条件实际上给出了一个在区间⎪⎭⎫⎝⎛2,0π上恒成立的不等式．任取∈21,x x ⎪⎭⎫⎝⎛2,0π,且21x x <,则不等式()()21x f x f >恒成立,即>-11cos sin 2x x m 22cos sin 2x x m -恒成立．化简得()()2112sin 2cos cos x x x x m ->- 由2021π<<<x x 可知：0cos cos 12<-x x ,所以()1221cos cos sin 2x x x x m --<上式恒成立的条件为：()上的最小值，在区间⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛--<20cos cos sin 21221πx x x x m . 由于()2sin 2cos 22sin 2sin 22cos 2sin4cos cos sin 22121212121211221x x x x x x x x x x x x x x x x +-=-+--=-- 2sin2cos 2cos 2sin 2sin 2sin 2cos 2cos 221212121x x x x x x x x +⎪⎭⎫ ⎝⎛+=2tan2tan 2tan 2tan 122121x x x x +⎪⎭⎫ ⎝⎛+=且当2021π<<<x x 时,42,2021π<<x x ,所以 12tan ,2tan 021<<x x , 从而 02tan 12tan 12tan 2tan 2tan 2tan1212121>⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+x x x x x x , 有 22tan2tan 2tan 2tan 122121>+⎪⎭⎫ ⎝⎛+x x x x , 故 m 的取值范围为]2,(-∞.基础精练1．已知α是锐角,且sin 错误!＝错误!,则sin 错误!的值等于A.错误! B ．－错误! C.错误! D ．－错误!2．若－2π＜α＜－错误!,则错误!的值是A ．sin 错误!B ．cos 错误!C ．－sin 错误!D ．－cos 错误!3.错误!·错误!等于A.－sinαB.－cosαC.sinαD.cosα4.已知角α在第一象限且cosα＝错误!,则错误!等于A.错误!B.错误!C.错误!D.－错误!5.定义运算错误!＝ad －bc.若cosα＝错误!,错误!＝错误!,0<β<α<错误!,则β等于A.错误!B.错误!C.错误!D.错误!6.已知tanα和tan 错误!－α是方程ax 2＋bx ＋c ＝0的两个根,则a 、b 、c 的关系是A.b ＝a ＋cB.2b ＝a ＋cC.c ＝b ＋aD.c ＝ab7.设a ＝错误!sin56°－cos56°,b ＝cos50°cos128°＋cos40°cos38°,c ＝错误!,d ＝错误!cos80°－2cos 250°＋1,则a,b,c,d 的大小关系为A.a ＞b ＞d ＞cB.b ＞a ＞d ＞cC.d ＞a ＞b ＞cD.c ＞a ＞d ＞b8．函数y ＝错误!sin2x ＋sin 2x,x ∈R 的值域是A.错误!B.错误!C.错误!D.错误!9.若锐角α、β满足1＋错误!tanα1＋错误!tanβ＝4,则α＋β＝ .10.设α是第二象限的角,tanα＝－错误!,且sin 错误!<cos 错误!,则cos 错误!＝ .11.已知sin-4πx=135,0<x<4π,求)4cos(2cos x x +π的值;12.若),0(,πβα∈,31tan ,507cos -=-=βα,求α+2β;拓展提高1、设函数fx ＝sin 错误!－错误!－2cos 2错误!＋11求fx 的最小正周期.2若函数y ＝gx 与y ＝fx 的图像关于直线x ＝1对称,求当x ∈0,错误!时y ＝gx 的最大值2.已知向量a ＝cosα,sinα,b ＝cosβ,sinβ,|a －b|＝错误!1求cosα－β的值；2若0<α<错误!,－错误!<β<0,且sinβ＝－错误!,求sinα.3、求证：αβαsin 2sin ）（+－2cos α+β=αβsin sin .基础精练参考答案4．C 解析原式＝错误!＝错误!＝错误!＝2×cosα＋sinα＝2×错误!＋错误!＝错误!. 5.D 解析依题设得：sinα·cosβ－cosα·sinβ＝sin α－β＝错误!.∵0<β<α<错误!,∴cosα－β＝错误!. 又∵cosα＝错误!,∴sinα＝错误!.sinβ＝sinα－α－β＝sinα·cosα－β－cosα·sinα－β ＝错误!×错误!－错误!×错误!＝错误!,∴β＝错误!.6.C 解析tan tan()4,tan tan(),4b a c a πααπαα⎧+-=-⎪⎪⎨⎪-=⎪⎩∴tan 错误!＝tan 错误!－α＋α＝错误!＝1,∴－错误!＝1－错误!,∴－b ＝a －c,∴c ＝a ＋b.7.B 解析a ＝sin56°－45°＝sin11°,b ＝－sin40°cos52°＋cos40°sin52°＝sin52°－40°＝sin12°,c ＝错误!＝cos81°＝sin9°,d ＝错误!2cos 240°－2sin 240°＝cos80°＝sin10°∴b ＞a ＞d ＞c.8.C 解析y ＝错误!sin2x ＋sin 2x ＝错误!sin2x －错误!cos2x ＋错误!＝错误!sin 错误!＋错误!,故选择C. 9. 错误!解析由1＋错误!tanα1＋错误!tanβ＝4,可得错误!＝错误!,即tanα＋β＝错误!. 又α＋β∈0,π,∴α＋β＝错误!.10. －错误!解析：∵α是第二象限的角,∴错误!可能在第一或第三象限,又sin 错误!<cos 错误!,∴错误!为第三象限的角, ∴cos 错误!<0.∵tanα＝－错误!,∴cosα＝－错误!,∴cos 错误!＝－错误!＝－错误!.12.解析∵),0(,πβα∈,507cos -=α∴),0,33(71tan -∈-=α),0,33(31tan -∈-=β∴),65(,ππβα∈,α+2β)3,25(ππ∈,又tan2β=43tan 1tan 22-=-ββ,12tan tan 12tan tan )2tan(-=-+=+βαβαβα,来源:Zxxk ∴α+2β=411π拓展提高参考答案1、解析 1fx ＝sin 错误!cos 错误!－cos 错误!sin 错误!－cos 错误!x ＝错误!sin 错误!x －错误!cos 错误!x＝错误!sin 错误!x －错误!,故fx 的最小正周期为T ＝错误!＝82法一：在y ＝g x 的图象上任取一点 x,gx,它关于x ＝1的对称点2－x,gx.由题设条件,点2－x ,gx 在y ＝fx 的图象上,从而gx ＝f2－x ＝错误!sin 错误!2－x －错误! ＝错误!sin 错误!－错误!x －错误!＝错误!cos 错误!x ＋错误!,当0≤x≤错误!时, 错误!≤错误!x ＋错误!≤错误!,因此y ＝gx 在区间0,错误!上的最大值为gx max ＝错误!cos 错误!＝错误!.法二：因区间0,错误!关于x ＝1的对称区间为错误!,2,且y ＝gx 与y ＝fx 的图象关于x ＝1对称,故y ＝gx 在0,错误!上的最大值为y ＝fx 在错误!,2上的最大值,由1知fx ＝错误!sin 错误!x －错误!, 当错误!≤x ≤2时,－错误!≤错误!x －错误!≤错误!,因此y ＝gx 在0,错误!上的最大值为gx max ＝错误!sin 错误!＝错误!.2、解析1∵a ＝cos α,sinα,b ＝cosβ,sinβ, ∴a －b ＝cosα－cosβ,sinα－sinβ. ∵|a －b|＝错误!,∴错误!＝错误!, 即2－2cosα－β＝错误!,∴cosα－β＝错误!.2∵0<α<错误!,－错误!<β<0,∴0<α－β<π,∵cosα－β＝错误!,∴sinα－β＝错误! ∵sin β＝－错误!,∴cosβ＝错误!,∴sinα＝sinα－β＋β＝sinα－βcosβ＋cosα－βsinβ＝错误!·错误!＋错误!·－错误!＝错误!。

高考数学专题《三角恒等变换》习题含答案解析

专题5.4 三角恒等变换1．（2021·四川德阳市·高三二模（文））在平面直角坐标系中，已知点()2cos80,2sin 80A ︒︒，()2cos 20,2sin 20B ︒︒，那么AB =（）A ．2B．C．D ．4【答案】A 【解析】利用利用两点间的距离公式求得AB .【详解】AB ==2====.故选：A2．（2018·全国高考真题（文））（2018年全国卷Ⅲ文）若sin α=13，则cos2α=（）A ．89 B ．79 C ．―79 D ．―89【答案】B 【解析】cos2α=1―2sin 2α=1―29=79故答案为B.3．（2021·商丘市第一高级中学高三月考（文））已知2sin 21sin 22πθθ⎛⎫-=+ ⎪⎝⎭，则tan θ的所有取值之和为（）A ．－5B ．－6C ．－3D ．2【答案】D练基础利用诱导公式和二倍角公式化简已知式，得到sin cos θθ=-或sin 3cos θθ=，即得tan θ的可能取值，求和即可.【详解】依题意得，2cos 21sin 2θθ-=+，即()()2222sincos sin cos θθθθ-=+，即()()()22sin cos sin cos sin cos θθθθθθ+-=+，故sin cos 0θθ+=或()2sin cos sin cos θθθθ-=+，所以sin cos θθ=-或sin 3cos θθ=，可得tan 1θ=-或tan 3θ=，所以tan θ的所有取值之和为2．故选：D.4．（2021·北京北大附中高三其他模拟）已知()0,απ∈，且1cos 23α=，则sin α=（）A B ．23C ．13D 【答案】A 【解析】由余弦的二倍角公式，先求出2sin α的值，结合角α的范围可得答案.【详解】由21cos 212sin 3αα=-=，可得21sin 3α=又()0,απ∈，则sin α=故选：A5．（2022·河南高三月考（理））若,2παπ⎛⎫∈ ⎪⎝⎭，且23cos sin 210αα-=，则tan α=（）A ．-7B ．13C ．17-D ．-7或13【答案】A 【解析】利用二倍角公式及同角三角函数的基本关系将弦化切，再解方程即可；解：因为23cos sin 210αα-=，所以2222cos sin 2cos 2sin cos 31sin cos 10ααααααα--==+，所以212tan 3tan 110αα-=+，得23tan 20tan 70αα+-=，则tan 7=-α或1tan 3α=，又,2παπ⎛⎫∈⎪⎝⎭，所以tan 7=-α.故选：A6．（2021·江苏淮安市·高三三模）设2sin 46a =︒，22cos 35sin 35b =︒-︒，2tan 321tan 32c ︒=-︒，则a ，b ，c 的大小关系为（）A ．b c a <<B ．c a b <<C ．a b c <<D ．b a c<<【答案】D 【解析】根据正弦函数的单调性，结合不等式性质，可得到a 的范围；利用二倍角公式化简b 、c ，结合函数单调性，可得到b 、c 的大致范围；从而，可以比较a 、b 、c 的大小.【详解】因为sin 45sin 46sin 60︒<︒<︒，所以有222sin 45sin 46sin 60︒<︒<︒，即222sin 46<︒<，所以1324a <<；因为222cos 35sin 3512sin 35︒-︒=-︒，而sin 30sin 35sin 45︒<︒<︒，所以有211sin 3542<︒<，所以21012sin 352<-︒<，即102b <<；因为22tan 3212tan 321tan 641tan 3221tan 322︒︒=⨯=︒-︒-︒，而tan 64tan 60︒>︒=所以c >显然，b a <，而22233(44c >=>，所以34c >，即c a>所以b a c <<故选：D7．（2020·河北高三其他模拟（文））已知函数()22sincos f x x x x ωωω=+(0>ω)的最小正周期为π，关于函数()f x 的性质，则下列命题不正确的是（）A ．1ω=B ．函数()f x 在R 上的值域为[]1,3-C ．函数()f x 在,63ππ⎡⎤-⎢⎥⎣⎦上单调递增D ．函数()f x 图象的对称轴方程为3x k ππ=+(k ∈Z )【答案】D 【解析】首先把函数的关系式进行恒等变换，把函数的关系式变形成正弦型函数，进一步利用函数的性质的应用求出结果.【详解】解：函数()22sincos f x x x xωωω=+1cos 222sin 216x x x πωωω⎛⎫=-+=-+ ⎪⎝⎭，由于函数()f x 的最小正周期为π，即22ππω=，所以1ω=，故A 正确；故()2sin 216f x x π⎛⎫=-+ ⎪⎝⎭.对于B ：由于x ∈R ，所以函数()f x 的最小值为1-，函数的最大值为3，故函数的值域为[]1,3-，故B 正确；对于C ：当,63x ππ⎡⎤∈-⎢⎥⎣⎦时，2,622πππ⎡⎤-∈-⎢⎥⎣⎦x ，故函数在该区间上单调递增，故C 正确；对于D ：当262x k πππ-=+，()k Z ∈时，整理得23k x ππ=+(k ∈Z )为函数的对称轴，故D 错误.故选：D .8.（2020·全国高考真题（文））若，则__________．【答案】【解析】.故答案为：.9．（2021·贵溪市实验中学高二期末）tan 42tan1842tan18︒+︒︒︒的值是___________.【解析】由()tan18tan 42tan 60tan 18421tan18tan 42︒+︒︒=︒+︒==-︒⋅︒进行转化，可得答案.【详解】解：由()tan18tan 42tan 60tan 18421tan18tan 42︒+︒︒=︒+︒==-︒⋅︒)tan18tan 421tan18tan 42∴︒+︒=-︒⋅︒tan18tan 42tan 42∴︒+︒︒⋅︒=.10．（2021·山东高三其他模拟）若tan()4πα-=，则3cos 22απ⎛⎫+ ⎪⎝⎭＝__________________．【答案】﹣817【解析】先用诱导公式化简，再根据二倍角及22sin cos 1a a +=变形，再求值即可.【详解】解：因为tan （π﹣α）＝﹣tan α＝4，2sin 3x =-cos 2x =1922281cos 212sin 12()1399x x =-=-⨯-=-=19所以tan α＝﹣4，则cos （2α＋32π）＝sin2α＝2sin αcos α＝222sin cos sin cos a a a a +＝22tan 1tan a a+＝﹣817．故答案为：﹣817．1．（2021·广东佛山市·高三其他模拟）(sin 40tan10-=（）A ．2B ．－2C ．1D ．－1【答案】D 【解析】利用切化弦，三角恒等变换，逆用两角差的正弦公式，二倍角公式，诱导公式化简求值.【详解】(sin 40tan10sin10=sin40(cos10sin 40sin 402(cos 60sin10sin 60cos10)sin 40cos102sin(1060)sin 40cos102sin 50sin 40cos102sin -︒︒⋅-︒==︒⋅︒-︒⋅︒=︒⋅︒︒-︒=︒⋅︒-︒=︒⋅︒-=⋅ 40cos 40cos10sin 80cos101︒⋅︒︒-︒=︒=-2．（2021·沈阳市·辽宁实验中学高三二模）攒尖是古代中国建筑中屋顶的一种结构形式，宋代称为撮尖，清代称攒尖．攒尖建筑的屋面在顶部交汇为一点，形成尖顶，依其平面有圆形攒尖、三角攒尖、四角攒尖、八角攒尖．也有单檐和重檐之分，多见于亭阁式建筑、园林建筑．辽宁省实验中学校园内的明心亭，为一个八角攒尖，它的主要部分的轮廓可近似看作一个正八棱锥，设正八棱锥的侧面等腰三角形的顶角为2θ，练提升它的侧棱与底面内切圆半径的长度之比为（）．ABCD【答案】A 【解析】分别用SA 和θ表示出AB 的一半，得出侧棱与底面边长的比，再根据正八边形的结构特征求出底面内切圆的半径与边长的关系，即可求出结果．【详解】设O 为正八棱锥S ABCDEFGH -底面内切圆的圆心，连接OA ，OB ，取AB 的中点M ，连接SM 、OM ，则OM 是底面内切圆半径R ，如图所示：设侧棱长为x ，底面边长为a ，由题意知2ASB θ∠=，ASM θ∠=，则12sin axθ=，解得2sin a x θ=；由底面为正八边形，其内切圆半径OM 是底面中心O 到各边的距离，AOB V 中，45AOB ∠=︒，所以22.5AOM ∠=︒，由22tan 22.5tan 4511tan 22.5︒︒==-︒，解得tan 22.51︒=，所以12tan 22.512aa R R==︒=-，所以2sin 12x R θ=-，解得x R =，．故选:A ．3.（2020·海南枫叶国际学校高一期中）若，则的值为( )3cos 22sin()4παα=-(,)2παπ∈sin 2αA ．B ．C ．D．【答案】C 【解析】因为，所以，，，因为，所以，所以所以，两边平方得，所以，故选：C4．（2019·江苏高考真题）已知，则的值是_____..【解析】由，得，解得，或.79-793cos 22sin()4παα=-3cos 22(sincos cossin )sin )44ππααααα=-=-223(cos sin )sin )αααα--3(cos sin )(cos sin )sin )αααααα+--(,)2παπ∈cos sin 0αα-≠3(cos sin )αα+cos sin αα+=212cos sin 9αα+=7sin 29α=-tan 2π3tan 4αα=-⎛⎫+ ⎪⎝⎭πsin 24α⎛⎫+ ⎪⎝⎭()tan 1tan tan tan 2tan 1tan 13tan 1tan 4αααααπααα-===-++⎛⎫+ ⎪-⎝⎭23tan 5tan 20αα--=tan 2α=1tan 3α=-，当时，上式当时，上式综上，5．（2021·全国高三其他模拟（理））已知函数2ππ()sin 6212x f x x ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭在[0,]m 上恰有10个零点，则m 的取值范围是________________．【答案】55π61π,66⎡⎫⎪⎢⎣⎭【解析】先用降幂公式和辅助角公式化简()f x ，再转化为图象与x 轴交点个数问题.【详解】∵()2ππππsin sin 1cos 621266x f x x x x ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+++=++-+ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦π2sin 6x ⎛⎫=- ⎪⎝⎭，∴π()02sin 06f x x ⎛⎫=⇔-= ⎪⎝⎭，∵()f x 在[0,]m 上恰有10个零点，sin 2sin 2cos cos 2sin444πππααα⎛⎫+=+ ⎪⎝⎭)22222sin cos cos sin sin 2cos 2=sin cos αααααααα⎫+-=+⎪+⎭222tan 1tan tan 1ααα⎫+-⎪+⎭tan 2α=22221221⎫⨯+-⎪+⎭1tan 3α=-22112133113⎛⎫⎛⎫⎛⎫⨯-+--⎪ ⎪ ⎪⎝⎭⎝⎭⎪⎪⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭sin 24πα⎛⎫+= ⎪⎝⎭∴πsin 06x ⎛⎫-= ⎪⎝⎭在[0,]m 上恰有10个解，∴π9π10π6m -<…，解得55π61π66m <…，故答案为：55π61π,66⎡⎫⎪⎢⎣⎭．6．（2021·上海复旦附中高三其他模拟）已知函数()3sin 24cos 2f x x x =+.若存在0x R ∈，对任意x ∈R ，都有()()0f x f x ≥成立.给出下列两个命题：（1）对任意x ∈R ，不等式()02f x f x π⎛⎫+⎪⎝⎭≤都成立.（2）存在512πθ>-，使得()f x 在005,12x x πθ⎛⎫-+ ⎪⎝⎭上单调递减.则其中真命题的序号是__________.（写出所有真命题的序号）【答案】（1）（2）【解析】由辅助角公式可得()5sin(2)f x x ϕ=+，由题意可得0x 是()f x 的最小值点，()f x 关于0x x =对称，由三角函数的性质逐个分析各个选项，即可求得结论．【详解】解：函数()3sin 24cos 25sin(2)f x x x x ϕ=+=+，其中ϕ为锐角，且3cos 5ϕ=，由题意，0x 是()f x 的最小值点，所以()f x 关于0x x =对称，因为()f x 的最小正周期22T ππ==，所以0()2f x π+为最大值，所以任意x ∈R ，0()(2f x f x π+…，故（1）正确；因为函数()f x 在()00,2x k x k k Z πππ⎛⎫-++∈ ⎪⎝⎭上单调递减，取4πθ=-，则00005,,1242x x x x πππ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭Ü，所以()f x 即在005,124x x ππ⎛⎫-- ⎪⎝⎭内单调递减，故（2）正确；故答案为：（1）（2）7．（2021·全国高三其他模拟（文））已知角0,4πα⎛⎫∈ ⎪⎝⎭，,2πβπ⎛⎫∈⎪⎝⎭，若3sin 35πα⎛⎫-=- ⎪⎝⎭，1cos 32πβ⎛⎫-=- ⎪⎝⎭，则()cos αβ-=___________.【答案】【解析】根据,αβ的范围确定,33ππαβ--的范围，然后求出cos 3πα⎛⎫- ⎪⎝⎭和sin 3πβ⎛⎫- ⎪⎝⎭，将()cos αβ-变形为cos 33ππαβ⎡⎤⎛⎫⎛⎫-++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，结合两角和的余弦公式即可求解.【详解】∵0,4πα⎛⎫∈ ⎪⎝⎭，,2πβπ⎛⎫∈ ⎪⎝⎭，∴3312πππα-<-<-，2336πππβ-<-<-，又3sin 35πα⎛⎫-=- ⎪⎝⎭，1cos 032πβ⎛⎫-=-< ⎪⎝⎭，∴2332πππβ-<-<-∴4cos 35πα⎛⎫-=== ⎪⎝⎭，sin 3πβ⎛⎫-=== ⎪⎝⎭∴()cos cos 33ππαβαβ⎡⎤⎛⎫⎛⎫-=-++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦cos cos sin sin 3333ππππαβαβ⎛⎫⎛⎫⎛⎫⎛⎫=----- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭413525⎛⎛⎫⎛⎫=⨯---⨯ ⎪ ⎪ ⎝⎭⎝⎭⎝=.故答案为：.8．（2021·江西新余市·高一期末（理））已知单位圆上第三象限内的一点P 沿圆周逆时针旋转4π到点Q ，若点Q 的横坐标为35，则点P 的横坐标为___________.【答案】【解析】首先设(cos ,sin )2P πθθπθ⎛⎫-<<- ⎪⎝⎭，根据题意得到cos ,sin 44ππθθ⎛⎫⎛⎫⎛⎫++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，从而得到3cos 45πθ⎛⎫+= ⎪⎝⎭，4sin 45πθ⎛⎫+=- ⎪⎝⎭，再根据cos cos 44ππθθ⎡⎤⎛⎫=+- ⎪⎢⎥⎝⎭⎣⎦求解即可.【详解】由题意设(cos ,sin )2P πθθπθ⎛⎫-<<-⎪⎝⎭，从而点P 沿圆周逆时针旋转4π到点Q ，即Q 点坐标为cos ,sin 44ππθθ⎛⎫⎛⎫⎛⎫++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以3cos 45πθ⎛⎫+= ⎪⎝⎭，3,444πππθ⎛⎫+∈-- ⎪⎝⎭，∵3cos 045πθ⎛⎫+=> ⎪⎝⎭，∴,424πππθ⎛⎫+∈-- ⎪⎝⎭，则4sin 45πθ⎛⎫+=- ⎪⎝⎭，所以cos cos cos cos sin sin 444444ππππππθθθθ⎡⎤⎛⎫⎛⎫⎛⎫=+-=+++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦3455=-=所以点P 的横坐标为故答案为：9.（2020·浙江吴兴�湖州中学高三其他）已知，，，则02πα<<4sin 5α=1tan()3αβ-=-tan β=_________.【答案】3 【解析】因为，，所以，所以，因为所以，，故答案为：3；.10．（2021·聊城市·山东聊城一中高三其他模拟）在①6x π=-是函数()f x 图象的一条对称轴，②12π是函数()f x 的一个零点，③函数()f x 在[],a b 上单调递增，且b a -的最大值为2π，这三个条件中任选一个，补充在下面问题中，并解答．已知函数1()2sin cos (02)62f x x x πωωω⎛⎫=--<< ⎪⎝⎭，__________，求()f x 在,22ππ⎡⎤-⎢⎥⎣⎦上的单调递减区间．注：如果选择多个条件分别解答，按第一个解答计分．【答案】选择见解析；单调递减区间为,26ππ⎡⎤--⎢⎥⎣⎦，,32ππ⎡⎤⎢⎥⎣⎦．【解析】利用三角函数恒等变换的应用化简函数解析式可得()sin(2)6f x x πω=-，=3202πα<<4sin 5α=3cos 5α===sin 4tan cos 3ααα==1tan()3αβ-=-tan tan()tan tan[()]1tan tan()ααββααβααβ--=--=+-415()33334151()339--===+⨯-sin tan 33cos sin 1tan 132βββββ---====---32若选①，利用正弦函数的对称性可得362k πωπππ--=+，k Z ∈，得32k ω=--，k Z ∈，又02ω<<，可得ω，可求()sin(26f x x π=-；若选②，由题意可得2126k ππωπ⨯-=，可得61k ω=+，k Z ∈，又02ω<<，可得ω，可求()sin(2)6f x x π=-；若选③，可求22T ππω==，可得1ω=，可得()sin(2)6f x x π=-，利用正弦函数的单调性，结合22x ππ-……，即可求解()f x 在[2π-，]2π上的单调递减区间．【详解】解：11()2sin cos 2sin cos cos sin sin 62662f x x x x x x πππωωωωω⎛⎫⎛⎫=--=+- ⎪ ⎪⎝⎭⎝⎭21sin sin 2x x x ωωω=+-12cos 22x x ωω=-sin x π⎛⎫=ω- ⎪⎝⎭26．①若6x π=-是函数()f x 图象的一条对称轴，则362k πωπππ--=+，k Z ∈，即233k πωππ-=+，k Z ∈，得32k ω=--，k Z ∈，又02ω<<，∴当1k =-时，1ω=，()sin 26f x x π⎛⎫=- ⎪⎝⎭．②若12π是函数()f x 的一个零点，则2126k ππωπ⨯-=，即66k ππωπ=+，k Z ∈，得61k ω=+，k Z ∈．又02ω<<，∴当0k =时，1ω=，所以，()sin 26f x x π⎛⎫=- ⎪⎝⎭．③若()f x 在[],a b 上单调递增，且b a -的最大值为2π．则22T ππω==，故1ω=，所以()sin 26f x x π⎛⎫=- ⎪⎝⎭．由3222262k x k πππππ+≤-≤+，k Z ∈，得536k x k ππππ+≤≤+，k Z ∈，令0k =，得536x ππ≤≤，令1k =-，得236k ππ-≤≤-，又22x ππ-≤≤，所以()f x 在,22ππ⎡⎤-⎢⎥⎣⎦上的单调递减区间为,26ππ⎡⎤--⎢⎥⎣⎦，,32ππ⎡⎤⎢⎥⎣⎦．1．（2021·全国高考真题（文））函数()sin cos 33x xf x =+的最小正周期和最大值分别是（）A ．3πB ．3π和2C ．6πD ．6π和2【答案】C 【解析】利用辅助角公式化简()f x ，结合三角函数最小正周期和最大值的求法确定正确选项.【详解】由题，()34x f x π⎛⎫=+ ⎪⎝⎭，所以()f x 的最小正周期为2613T pp ==.故选：C ．2．（2021·北京高考真题）函数()cos cos 2f x x x =-，试判断函数的奇偶性及最大值（）A ．奇函数，最大值为2B ．偶函数，最大值为2C ．奇函数，最大值为98D ．偶函数，最大值为98【答案】D 【解析】由函数奇偶性的定义结合三角函数的性质可判断奇偶性；利用二倍角公式结合二次函数的性质可判断最大值.【详解】练真题由题意，()()()()cos cos 2cos cos 2f x x x x x f x -=---=-=，所以该函数为偶函数，又2219()cos cos 22cos cos 12cos 48f x x x x x x ⎛⎫=-=-++=--+ ⎪⎝⎭，所以当1cos 4x =时，()f x 取最大值98.故选：D.3．（2019·全国高考真题（文））tan255°=（）A ．－2B ．－C ．2D ．【答案】D 【解析】=4．（2019·全国高考真题（文理））已知a ∈（0，），2sin2α=cos2α+1，则sinα=（）A ．BCD【答案】B 【解析】，．，又，，又，B ．5.（2020·全国高考真题（理））已知2tan θ–tan(θ+π4)=7，则tan θ=（）A ．–2B ．–1C ．1D ．2【答案】D000000tan 255tan(18075)tan 75tan(4530)=+==+000tan 45tan 3021tan 45tan 30+==+-π2152sin 2cos 21α=α+ 24sin cos 2cos .0,,cos 02π⎛⎫∴α⋅α=αα∈∴α> ⎪⎝⎭sin 0,2sin cos α>∴α=α22sin cos 1αα+=2215sin 1,sin 5∴α=α=sin 0α>sin α∴=【解析】2tan tan 74πθθ⎛⎫-+= ⎪⎝⎭，tan 12tan 71tan θθθ+∴-=-，令tan ,1t t θ=≠，则1271tt t+-=-，整理得2440t t -+=，解得2t =，即tan 2θ=.故选：D.6．（2020·全国高考真题（文））已知πsin sin =31θθ⎛⎫++ ⎪⎝⎭，则πsin =6θ⎛⎫+ ⎪⎝⎭（）A ．12B C ．23D 【答案】B 【解析】由题意可得：1sin sin 12θθθ++=，则：3sin 12θθ+=1cos 2θθ+=从而有：sin coscos sin66ππθθ+=，即sin 6πθ⎛⎫+= ⎪⎝⎭故选：B.。

专题12 三角恒等变换(纯答案)

专题12三角恒等变换答案例1、【答案】A【解析】3cos28cos 5αα-=，得26cos 8cos 80αα--=，即23cos 4cos 40αα--=，解得2cos 3α=-或cos 2α=（舍去），又(0,),sin 3αα∈π∴==. 故选：A ．变式1、【答案】35；13 【解析】2222222222cos sin 1tan 123cos 2cos sin cos sin 1tan 125θθθθθθθθθ---=-====-+++， tan 1211tan()41tan 123πθθθ---===++，故答案为：31,53- 变式2、【解析】由()tan 1tan tan tan 2tan 1πtan 13tan 1tan 4αααααααα-===-++⎛⎫+ ⎪-⎝⎭，得23tan 5tan 20αα--=，解得tan 2α=，或1tan 3α=-. πππsin 2sin 2cos cos 2sin 444ααα⎛⎫+=+ ⎪⎝⎭()22222sin cos cos sin sin 2cos 2=22sin cos αααααααα⎫+-=+⎪+⎝⎭222tan 1tan =2tan 1ααα⎛⎫+- ⎪+⎝⎭，当tan 2α=时，上式222212==22110⎛⎫⨯+- ⎪+⎝⎭ 当1tan 3α=-时，上式=22112()1()33[]=1210()13⨯-+---+综上，πsin 2410α⎛⎫+= ⎪⎝⎭ 变式3、【解析】 (1)因为cos 2β＝－35，cos 2β＝2cos 2β－1，所以 2cos 2β－1＝－35，解得cos 2β＝15.(2分) 因为β为钝角，所以cos β＝－55. 从而sin β＝1－cos 2β＝1－15＝255.(5分) 所以tan β＝sin βcos β＝255－55＝－2.(7分) (2)因为α为钝角，sin α＝35，所以cos α＝－1－sin 2α＝－2531⎪⎭⎫ ⎝⎛-＝－45. (9分) 所以 sin 2α＝2sin αcos α＝2×35×⎪⎭⎫ ⎝⎛-54＝－2425，cos 2α＝1－2sin 2α＝1－2×⎪⎭⎫ ⎝⎛532＝725. (11分) 从而cos (2α＋β)＝cos 2αcos β－sin 2αsin β＝725×⎪⎪⎭⎫ ⎝⎛-55－⎪⎭⎫ ⎝⎛-2524×255 ＝415125.(14分)题型二、变角问题例2、【答案】17【解析】因为sin cos 11cos 2ααα=-，所以2sin cos 2sin ααα=且cos 0α≠，所以1tan 2α=；又1tan()3αβ-=，所以()()()11tan tan 123tan tan 11tan tan 716ααββααβααβ---=--===⎡⎤⎣⎦+-+. 故答案为：17. 变式1、【解析】（1）因为4tan 3=α，sin tan cos =ααα，所以4sin cos 3=αα．因为22sin cos 1+=αα，所以29cos 25=α，因此，27cos 22cos 125=-=-αα．（2）因为,αβ为锐角，所以(0,)+∈παβ．又因为cos()+=αβ，所以sin()+==αβ，因此tan()2+=-αβ．因为4tan 3=α，所以22tan 24tan 21tan 7==--ααα，因此，tan 2tan()2tan()tan[2()]1tan 2tan()11-+-=-+==-++ααβαβααβααβ．变式2、【答案】A【解析】0,2πα⎛⎫∈ ⎪⎝⎭，,444πππα⎛⎫-∈- ⎪⎝⎭4cos 45πα⎛⎫-== ⎪⎝⎭， cos cos cos cos sin sin 444444ππππππαααα⎡⎤⎛⎫⎛⎫⎛⎫=-+=--- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦43525210=⨯-⨯=. 故选：A题型三、求角问题例3、【解析】 (1) 由cos α＝437，α∈⎪⎭⎫ ⎝⎛2,0π，得sin α＝1－cos 2α＝27341⎪⎪⎭⎫ ⎝⎛-＝17.(2分) 所以sin ⎪⎭⎫ ⎝⎛+απ4＝sin π4cos α＋cos π4sin α(4分) ＝22×437＋22×17＝46＋214.(6分) (2) 因为α，β∈⎪⎭⎫ ⎝⎛2,0π，所以α＋β∈(0，π)．又cos (α＋β)＝1114，则sin (α＋β)＝1－cos 2（α＋β）＝214111⎪⎭⎫ ⎝⎛-＝5314.(8分) 所以sin β＝sin (α＋β－α)＝sin (α＋β)cos α－cos (α＋β)sin α(10分)＝5314×437－1114×17＝12.(12分) 因为β∈⎪⎭⎫ ⎝⎛2,0π，所以β＝π6.(14分) 变式【解析】因为锐角α的终边与单位圆交于点A ，且点A 的横坐标是31010，所以由任意角的三角函数的定义可知cos α＝31010，从而sin α＝1－cos 2α＝1010.(2分) 因为钝角β的终边与单位圆交于点B ，且点B 的纵坐标是255，所以sin β＝255，从而cos β＝－1－sin 2β＝－55.(4分) (1) cos(α－β)＝cos αcos β＋sin αsin β＝31010×⎪⎪⎭⎫ ⎝⎛-55＋1010×255＝－210.(8分) (2) sin(α＋β)＝sin αcos β＋cos αsin β＝1010×⎪⎪⎭⎫ ⎝⎛-55＋31010×255＝22.(11分)因为α为锐角，β为钝角，所以α＋β∈⎪⎭⎫⎝⎛232ππ，，所以α＋β＝3π4.(14分) 易错警示求角的大小，经常会因为忽略角的取值范围而导致增解．另外，在求角的大小时，一般地，应首先确定所求角的范围，然后根据角的范围来确定求角的哪个三角函数，通常所选择的那个三角函数应该在范围内是单调的．1、【答案】B 【解析】2217cos 212sin 12()39αα=-=-⨯=. 故选B.2、【答案】D【解析】方法一：由α为第四象限角，可得3222,2k k k απ+π<<π+π∈Z ，所以34244,k k k απ+π<<π+π∈Z此时2α的终边落在第三、四象限及y 轴的非正半轴上，所以sin 20α<，故选：D ．方法二：当6απ=-时，cos 2cos 03απ⎛⎫=-> ⎪⎝⎭，选项B 错误；当3απ=-时，2cos 2cos 03απ⎛⎫=-< ⎪⎝⎭，选项A 错误；由α在第四象限可得：sin 0,cos 0αα<>，则sin 22sin cos 0ααα=<，选项C 错误，选项D 正确；故选：D ．3、【答案】D 【解析】2tan tan 74πθθ⎛⎫-+= ⎪⎝⎭，tan 12tan 71tan θθθ+∴-=-，令tan ,1t t θ=≠，则1271t t t+-=-，整理得2440t t -+=，解得2t =，即tan 2θ=. 故选：D ．4、【答案】B【解析】2sin 2cos21αα=+，24sin cos 2cos .0,,cos 02αααααπ⎛⎫∴⋅=∈∴> ⎪⎝⎭，sin 0,α>2sin cos αα∴=，又22sin cos 1αα+=，2215sin 1,sin 5αα∴==，又sin 0α>，sin 5α∴=，故选B ． 5、【答案】13【解析】221sin ())(1sin 2)42παααα+=+=+ 121(1sin 2)sin 2233αα∴+=∴= 故答案为：136、【答案】12- 【解析】因为sin cos 1+=αβ，cos sin 0+=αβ，所以()()221sin cos 1,-+-=αα所以11sin ,cos 22==αβ， ()22111111sin sin cos cos sin cos 1sin 1.224442+=+=⨯-=-+=-+=-αβαβαβαα7、【答案】【解析】由于1sin 4x =，x 为第二象限角，所以cos x ==所以1sin 22sin cos 2448x x x ⎛==⨯⨯-=- ⎝⎭.故答案为：8、【答案】A【解析】2π2π2πππcos 2cos π2cos 2cos 22sin 133333ααααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+=--=--=--=-- ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ 1721168=⨯-=-．故选A ．。

三角函数恒等变换练习题及答案详解

两角和与差的正弦、余弦、正切1.利用两角和与差的正弦、余弦、正切公式进行三角变换；2.利用三角变换讨论三角函数的图象和性质 2.1.牢记和差公式、倍角公式，把握公式特征；2.灵活使用(正用、逆用、变形用)两角和与差的正弦、余弦、正切公式进行三角变换，三角变换中角的变换技巧是解题的关键．知识点回顾1．两角和与差的余弦、正弦、正切公式cos(α－β)＝cos αcos β＋sin αsin β (C α－β) cos(α＋β)＝cos_αcos_β－sin_αsin_β (C α＋β) sin(α－β)＝sin_αcos_β－cos_αsin_β (S α－β) sin(α＋β)＝sin_αcos_β＋cos_αsin_β (S α＋β) tan(α－β)＝tan α－tan β1＋tan αtan β (T α－β)tan(α＋β)＝tan α＋tan β1－tan αtan β(T α＋β)2．二倍角公式sin 2α＝ααcos sin 2；cos 2α＝cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2α； tan 2α＝2tan α1－tan 2α.3．在准确熟练地记住公式的基础上，要灵活运用公式解决问题：如公式的正用、逆用和变形用等．如T α±β可变形为tan α±tan β＝tan(α±β)(1∓tan_αtan_β)， tan αtan β＝1－tan α＋tan βtan (α＋β)＝tan α－tan βtan (α－β)－1.4．函数f (α)＝a cos α＋b sin α(a ，b 为常数)，可以化为f (α)＝a 2＋b 2sin(α＋φ)或f (α)＝a 2＋b 2cos(α－φ)，其中φ可由a ，b 的值唯一确定． [难点正本疑点清源] 三角变换中的“三变”(1)变角：目的是沟通题设条件与结论中所涉及的角，其手法通常是“配凑”．(2)变名：通过变换函数名称达到减少函数种类的目的，其手法通常有“切化弦”、“升幂与降幂”等． (3)变式：根据式子的结构特征进行变形，使其更贴近某个公式或某个期待的目标，其手法通常有“常值代换”、“逆用变用公式”、“通分约分”、“分解与组合”、“配方与平方”等．热身训练1．已知sin(α＋β)＝23，sin(α－β)＝－15，则tan αtan β的值为_______．2．函数f (x )＝2sin x (sin x ＋cos x )的单调增区间为______________________．3． (2012·江苏)设α为锐角，若cos ⎪⎭⎫ ⎝⎛+6πα＝45，则 4． (2012·江西)若sin α＋cos αsin α－cos α＝12，则tan 2α等于( )A ．－34B.34C ．－43D.43 5． (2011·辽宁)设sin(π4＋θ)＝13，则sin 2θ等于( )A ．－79B ．－19C.19D.79典例分析题型一三角函数式的化简、求值问题例1 (1)化简：⎝ ⎛⎭⎪⎫1tan α2－tan α2·⎝⎛⎭⎫1＋tan α·tan α2； (2)求值：[2sin 50°＋sin 10°(1＋3tan 10°)]·2sin 280°.在△ABC 中，已知三个内角A ，B ，C 成等差数列，则tan A 2＋tan C 2＋3tan A 2tan C2的值为________．题型二三角函数的给角求值与给值求角问题例2 (1)已知0<β<π2<α<π，且cos ⎪⎭⎫ ⎝⎛-2πα＝－19，sin ⎪⎭⎫ ⎝⎛-βα2＝23，求cos(α＋β)的值；(2)已知α，β∈(0，π)，且tan(α－β)＝12，tan β＝－17，求2α－β的值．已知cos α＝17，cos(α－β)＝1314，且0<β<α<π2，求β.题型三三角变换的简单应用例3 已知f (x )＝⎪⎭⎫ ⎝⎛+x tan 11sin 2x －2sin ⎪⎭⎫ ⎝⎛+4πx ·sin ⎪⎭⎫ ⎝⎛-4πx (1)若tan α＝2，求f (α)的值；(2)若x ∈⎣⎡⎦⎤π12，π2，求f (x )的取值范围．已知函数f (x )＝3sin ⎪⎭⎫ ⎝⎛-62πx ＋2sin 2⎪⎭⎫ ⎝⎛-12πx (x ∈R )． (1)求函数f (x )的最小正周期；(2)求使函数f (x )取得最大值时x 的集合．利用三角变换研究三角函数的性质典例：(12分)(2011·北京)已知函数f (x )＝4cos x ·sin ⎪⎭⎫⎝⎛+6πx －1. (1)求f (x )的最小正周期； (2)求f (x )在区间⎥⎦⎤⎢⎣⎡-4,6ππ上的最大值和最小值．总结方法与技巧 1．巧用公式变形：和差角公式变形：tan x ±tan y ＝tan(x ±y )·(1∓tan x tan y )；倍角公式变形：降幂公式cos 2α＝1＋cos 2α2，sin 2α＝1－cos 2α2；配方变形：1±sin α＝⎝⎛⎭⎫sin α2±cos α22,1＋cos α＝2cos 2α2，1－cos α＝2sin 2α2. 2．利用辅助角公式求最值、单调区间、周期．由y ＝a sin α＋b cos α＝a 2＋b 2sin(α＋φ)(其中tan φ＝ba)有a 2＋b 2≥|y |.3．重视三角函数的“三变”：“三变”是指“变角、变名、变式”；变角：对角的分拆要尽可能化成同名、同角、特殊角；变名：尽可能减少函数名称；变式：对式子变形一般要尽可能有理化、整式化、降低次数等．在解决求值、化简、证明问题时，一般是观察角度、函数名、所求(或所证明)问题的整体形式中的差异，再选择适当的三角公式恒等变形．4．已知和角函数值，求单角或和角的三角函数值的技巧：把已知条件的和角进行加减或二倍角后再加减，观察是不是常数角，只要是常数角，就可以从此入手，给这个等式两边求某一函数值，可使所求的复杂问题简单化．5．熟悉三角公式的整体结构，灵活变换．本节要重视公式的推导，既要熟悉三角公式的代数结构，更要掌握公式中角和函数名称的特征，要体会公式间的联系，掌握常见的公式变形，倍角公式应用是重点，涉及倍角或半角的都可以利用倍角公式及其变形．失误与防范1．运用公式时要注意审查公式成立的条件，要注意和、差、倍角的相对性，要注意升次、降次的灵活运用，要注意“1”的各种变通． 2．在(0，π)范围内，sin(α＋β)＝22所对应的角α＋β不是唯一的． 3．在三角求值时，往往要估计角的范围后再求值．过手训练(时间：25分钟，满分：43分)一、选择题(每小题5分，共15分) 1． (2012·山东)若θ∈⎥⎦⎤⎢⎣⎡2,4ππ，sin 2θ＝378，则sin θ等于( )A.35B.45C.74D.342．已知tan(α＋β)＝25，tan ⎪⎭⎫ ⎝⎛-4πβ＝14，那么tan ⎪⎭⎫ ⎝⎛+4πα等于( )A.1318B.1322C.322D.163．当－π2≤x ≤π2时，函数f (x )＝sin x ＋3cos x 的( )A ．最大值是1，最小值是－1B ．最大值是1，最小值是－12C ．最大值是2，最小值是－2D ．最大值是2，最小值是－1二、填空题(每小题5分，共15分) 4．已知锐角α满足cos 2α＝cos ⎪⎭⎫⎝⎛-απ4，则sin 2α＝________. 5．已知cos ⎪⎭⎫⎝⎛-απ4＝1213，α∈⎪⎭⎫⎝⎛4,0π，则cos 2αsin ⎝⎛⎭⎫π4＋α＝________. 6．设x ∈⎪⎭⎫⎝⎛2,0π，则函数y ＝2sin 2x ＋1sin 2x的最小值为________．三、解答题7． (13分)(2012·广东)已知函数f (x )＝2cos ⎪⎭⎫⎝⎛+6πωx (其中ω>0，x ∈R )的最小正周期为10π. (1)求ω的值；(2)设α，β∈⎣⎡⎦⎤0，π2，f ⎝⎛⎭⎫5α＋53π＝－65，f ⎝⎛⎭⎫5β－56π＝1617，求cos(α＋β)的值．课后习题(时间：35分钟，满分：57分)一、选择题(每小题5分，共20分)1． (2012·江西)若tan θ＋1tan θ＝4，则sin 2θ等于( )A.15B.14C.13D.122． (2012·大纲全国)已知α为第二象限角，sin α＋cos α＝33，则cos 2α等于 ( )A ．－53B ．－59C.59D.533．已知α，β都是锐角，若sin α＝55，sin β＝1010，则α＋β等于( )A.π4B.3π4C.π4和3π4D ．－π4和－3π44． (2011·福建)若α∈⎪⎭⎫ ⎝⎛2,0π，且sin 2α＋cos 2α＝14，则tan α的值等于 ( )A.22B.33C. 2D. 3二、填空题(每小题5分，共15分)5． cos 275°＋cos 215°＋cos 75°cos 15°的值为________． 6.3tan 12°－3(4cos 212°－2)sin 12°＝________.7． sin α＝35，cos β＝35，其中α，β∈⎪⎭⎫⎝⎛2,0π，则α＋β＝____________.三、解答题(共22分) 8． (10分)已知1＋sin α1－sin α－1－sin α1＋sin α＝－2tan α，试确定使等式成立的α的取值集合．9． (12分)已知α∈⎪⎭⎫⎝⎛ππ，2，且sin α2＋cos α2＝62. (1)求cos α的值；(2)若sin(α－β)＝－35，β∈⎪⎭⎫⎝⎛ππ，2，求cos β的值．。

4.6简单的三角恒等变换

1.公式的常见变形(1)1＋cos α＝2cos 2α2； 1－cos α＝2sin 2α2. (2)1＋sin α＝(sin α2＋cos α2)2； 1－sin α＝(sin α2－cos α2)2. (3)tan α2＝sin α1＋cos α＝1－cos αsin α. 2.辅助角公式a sin x ＋b cos x ＝a 2＋b 2sin(x ＋φ)，其中sin φ＝b a 2＋b 2，cos φ＝a a 2＋b 2. 3.arcsin y 、arccos y 、arctan y 的意义arcsin y (|y |≤1)表示⎣⎡⎦⎤－π2，π2上正弦值等于y 的角；arccos y (|y |≤1)表示[0，π]上余弦值等于y 的角；arctan y 表示⎝⎛⎭⎫－π2，π2内正切值等于y 的角. 【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)y ＝3sin x ＋4cos x 的最大值是7.( × )(2)设α∈(π，2π)，则 1－cos (π＋α)2＝sin α2.( × ) (3)在非直角三角形中有：tan A ＋tan B ＋tan C ＝tan A tan B tan C .( √ )(4)设5π2<θ<3π，且|cos θ|＝15，那么sin θ2的值为155.( × )(5)公式a sin x ＋b cos x ＝a 2＋b 2sin(x ＋φ)中φ的取值与a ，b 的值无关.( × ) (6)arcsin 13表示正弦值等于13的角.( × )1.已知cos α＝13，α∈(π，2π)，则cos α2等于( ) A.63 B.－63 C.33 D.－33答案 B解析 ∵α2∈(π2，π)， ∴cos α2＝－ 1＋cos α2＝－23＝－63. 2.2sin 235°－1cos 10°－3sin 10°的值为( ) A.1B.－1C.12D.－12答案 D解析原式＝2sin 235°－12⎝⎛⎭⎫12cos 10°－32sin 10° ＝－cos 70°2sin 20°＝－12. 3.arccos ⎝⎛⎭⎫－32＝； arcsin ⎝⎛⎭⎫－22＝ . 答案 56π －π44.若f (x )＝2tan x －2sin 2 x 2－1sin x 2cos x 2，则f ⎝⎛⎭⎫π12的值为 . 答案 8解析 ∵f (x )＝2tan x ＋1－2sin 2 x 212sin x＝2tan x ＋2cos x sin x ＝2sin x cos x ＝4sin 2x， ∴f ⎝⎛⎭⎫π12＝4sin π6＝8. 5.若锐角α、β满足(1＋3tan α)(1＋3tan β)＝4，则α＋β＝ .答案 π3解析由(1＋3tan α)(1＋3tan β)＝4，可得tan α＋tan β1－tan αtan β＝3，即tan(α＋β)＝ 3. 又α＋β∈(0，π)，∴α＋β＝π3.题型一三角函数式的化简与求值例1 (1)化简：2cos 4x －2cos 2x ＋122tan ⎝⎛⎭⎫π4－x sin 2⎝⎛⎭⎫π4＋x ＝ . (2)已知α∈⎝⎛⎭⎫0，π2，且2sin 2α－sin α·cos α－3cos 2α＝0，则sin ⎝⎛⎭⎫α＋π4sin 2α＋cos 2α＋1＝ .答案 (1)12cos 2x (2)268解析 (1)原式＝12(4cos 4x －4cos 2x ＋1)2×sin ⎝⎛⎭⎫π4－x cos ⎝⎛⎭⎫π4－x ·cos 2⎝⎛⎭⎫π4－x ＝(2cos 2x －1)24sin ⎝⎛⎭⎫π4－x cos ⎝⎛⎭⎫π4－x ＝cos 22x 2sin ⎝⎛⎭⎫π2－2x ＝cos 22x 2cos 2x ＝12cos 2x . (2)∵α∈⎝⎛⎭⎫0，π2，且2sin 2α－sin α·cos α－3cos 2α＝0，则(2sin α－3cos α)·(sin α＋cos α)＝0，∴2sin α＝3cos α，又sin 2α＋cos 2α＝1，∴cos α＝213，sin α＝313， ∴sin ⎝⎛⎭⎫α＋π4sin 2α＋cos 2α＋1 ＝22(sin α＋cos α)(sin α＋cos α)2＋(cos 2α－sin 2α)＝268. 思维升华 (1)三角函数式的化简要遵循“三看”原则，一看角，二看名，三看式子结构与特征.(2)三角函数式化简要注意观察条件中角之间的联系(和、差、倍、互余、互补等)，寻找式子和三角函数公式之间的共同点.(1)cos π9·cos 2π9·cos ⎝⎛⎭⎫－23π9等于( ) A.－18B.－116C.116D.18 (2)若1＋cos 2αsin 2α＝12，则tan 2α等于( ) A.54 B.－54C.43D.－43 答案 (1)A (2)D 解析 (1)原式＝cos π9·cos 29π·cos(－3π＋49π) ＝－cos π9·cos 29π·cos 49π·sin π9sin π9＝－12sin 29π·cos 29π·cos 49πsin π9＝－18sin 89πsin π9＝－18. (2)1＋cos 2αsin 2α＝2cos 2α2sin αcos α＝cos αsin α＝12，∴tan α＝2，∴tan 2α＝2tan α1－tan 2α＝41－4＝－43. 题型二三角函数的求角问题例2 (1)已知锐角α，β满足sin α＝55，cos β＝31010，则α＋β等于( ) A.3π4 B.π4或3π4 C.π4 D.2k π＋π4(k ∈Z ) (2)已知方程x 2＋3ax ＋3a ＋1＝0(a ＞1)的两根分别为tan α、tan β，且α、β∈⎝⎛⎭⎫－π2，π2，则α＋β等于( ) A.π8B.－3π4C.π8或－3π8D.π4或－3π4答案 (1)C (2)B解析 (1)由sin α＝55，cos β＝31010且α，β为锐角，可知cos α＝255，sin β＝1010，故cos(α＋β)＝cos αcos β－sin αsin β ＝255×31010－55×1010＝22，又0<α＋β<π，故α＋β＝π4. (2)依题意有⎩⎪⎨⎪⎧tan α＋tan β＝－3a ，tan α·tan β＝3a ＋1， ∴tan(α＋β)＝tan α＋tan β1－tan α·tan β＝－3a 1－(3a ＋1)＝1. 又⎩⎪⎨⎪⎧tan α＋tan β＜0，tan α·tan β＞0， ∴tan α＜0且tan β＜0.∴－π2＜α＜0且－π2＜β＜0，即－π＜α＋β＜0，结合tan(α＋β)＝1，得α＋β＝－3π4. 思维升华通过求角的某种三角函数值来求角，在选取函数时，有以下原则：(1)已知正切函数值，则选正切函数.(2)已知正弦、余弦函数值，则选正弦或余弦函数.若角的范围是⎝⎛⎭⎫0，π2，则选正弦、余弦皆可；若角的范围是(0，π)，则选余弦较好；若角的范围为⎝⎛⎭⎫－π2，π2，则选正弦较好. (1)已知sin α＝55，sin(α－β)＝－1010，α，β均为锐角，则角β等于( ) A.5π12B.π3C.π4D.π6(2)在△ABC 中，tan A ＋tan B ＋3＝3tan A ·tan B ，则C 等于( )A.π3B.2π3C.π6D.π4 答案 (1)C (2)A解析 (1)∵α、β均为锐角，∴－π2<α－β<π2. 又sin(α－β)＝－1010，∴cos(α－β)＝31010. 又sin α＝55，∴cos α＝255， ∴sin β＝sin [α－(α－β)]＝sin αcos(α－β)－cos αsin(α－β)＝55×31010－255×(－1010)＝22. ∴β＝π4. (2)由已知可得tan A ＋tan B ＝3(tan A ·tan B －1)，∴tan(A ＋B )＝tan A ＋tan B 1－tan A tan B＝－3，又0<A ＋B <π，∴A ＋B ＝23π，∴C ＝π3. 题型三三角恒等变换的应用例3 已知函数f (x )＝sin(x ＋θ)＋a cos(x ＋2θ)，其中a ∈R ，θ∈⎝⎛⎭⎫－π2，π2. (1)当a ＝2，θ＝π4时，求f (x )在区间[0，π]上的最大值与最小值； (2)若f ⎝⎛⎭⎫π2＝0，f (π)＝1，求a ，θ的值.解 (1)f (x )＝sin ⎝⎛⎭⎫x ＋π4＋2cos ⎝⎛⎭⎫x ＋π2 ＝22(sin x ＋cos x )－2sin x＝22cos x －22sin x ＝sin ⎝⎛⎭⎫π4－x ，因为x ∈[0，π]，从而π4－x ∈⎣⎡⎦⎤－3π4，π4，故f (x )在[0，π]上的最大值为22，最小值为－1. (2)由⎩⎪⎨⎪⎧ f ⎝⎛⎭⎫π2＝0，f (π)＝1. 得⎩⎪⎨⎪⎧cos θ(1－2a sin θ)＝0，2a sin 2θ－sin θ－a ＝1，由θ∈⎝⎛⎭⎫－π2，π2知cos θ≠0，解得⎩⎪⎨⎪⎧ a ＝－1，θ＝－π6. 思维升华三角恒等变换的综合应用主要是将三角变换与三角函数的性质相结合，通过变换把函数化为y ＝A sin(ωx ＋φ)＋k 的形式再研究性质，解题时注意观察角、函数名、结构等特征.(1)(2014·课标全国Ⅱ)函数f (x )＝sin(x ＋φ)－2sin φcos x 的最大值为 .(2)函数f (x )＝sin(2x －π4)－22sin 2x 的最小正周期是 . 答案 (1)1 (2)π 解析 (1)因为f (x )＝sin(x ＋φ)－2sin φcos x＝sin x cos φ－cos x sin φ＝sin(x －φ)，－1≤sin(x －φ)≤1，所以f (x )的最大值为1.(2)f (x )＝22sin 2x －22cos 2x －2(1－cos 2x ) ＝22sin 2x ＋22cos 2x －2＝sin(2x ＋π4)－2， ∴T ＝2π2＝π.8.化归思想和整体代换思想在三角函数中的应用典例 (12分)(2015·重庆)已知函数f (x )＝sin ⎝⎛⎭⎫π2－x sin x －3cos 2x .(1)求f (x )的最小正周期和最大值；(2)讨论f (x )在⎣⎡⎦⎤π6，2π3上的单调性.思维点拨 (1)讨论形如y ＝a sin ωx ＋b cos ωx 型函数的性质，一律化成y ＝a 2＋b 2sin(ωx ＋φ)型的函数. (2)研究y ＝A sin(ωx ＋φ)型函数的最值、单调性，可将ωx ＋φ视为一个整体，换元后结合y ＝sin x 的图象解决.规范解答解 (1)f (x )＝sin ⎝⎛⎭⎫π2－x sin x －3cos 2x ＝cos x sin x －32(1＋cos 2x )＝12sin 2x －32cos 2x －32＝sin ⎝⎛⎭⎫2x －π3－32，[4分] 因此f (x )的最小正周期为π，最大值为2－32.[6分] (2)当x ∈⎣⎡⎦⎤π6，2π3时，0≤2x －π3≤π，[7分] 从而当0≤2x －π3≤π2，即π6≤x ≤5π12时，f (x )单调递增，[9分] 当π2≤2x －π3≤π，即5π12≤x ≤2π3时，f (x )单调递减.[11分] 综上可知，f (x )在⎣⎡⎦⎤π6，5π12上单调递增；在⎣⎡⎦⎤5π12，2π3上单调递减.[12分] 温馨提醒 (1)讨论三角函数的性质，要先利用三角变换化成y ＝A sin(ωx ＋φ)，φ的确定一定要准确.(2)将ωx ＋φ视为一个整体，设ωx ＋φ＝t ，可以借助y ＝sin t 的图象讨论函数的单调性、最值等.[方法与技巧]1.三角函数的求值与化简要注意观察角、函数名称、式子结构之间的联系，然后进行变换.2.利用三角函数值求角要考虑角的范围.3.与三角函数的图象与性质相结合的综合问题.借助三角恒等变换将已知条件中的函数解析式整理为f (x )＝A sin(ωx ＋φ)的形式，然后借助三角函数图象解决.[失误与防范]1.利用辅助角公式，a sin x ＋b cos x 转化时一定要严格对照和差公式，防止搞错辅助角.2.计算形如y ＝sin(ωx ＋φ), x ∈[a ，b ]形式的函数最值时，不要将ωx ＋φ的范围和x 的范围混淆.A 组专项基础训练(时间：35分钟)1.(2015·陕西)“sin α＝cos α”是“cos 2α＝0”的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件答案 A解析 sin α＝cos α⇒cos 2α＝cos 2α－sin 2α＝0； cos 2α＝0⇔cos α＝±sin αsin α＝cos α，故选A.2.已知sin 2α＝23，则cos 2⎝⎛⎭⎫α＋π4等于( )A.16B.13C.12D.23答案 A解析因为cos 2⎝⎛⎭⎫α＋π4＝1＋cos 2⎝⎛⎭⎫α＋π42＝1＋cos ⎝⎛⎭⎫2α＋π22＝1－sin 2α2，所以cos 2⎝⎛⎭⎫α＋π4＝1－sin 2α2＝1－232＝16，故选A.3.若α∈⎝⎛⎭⎫π2，π，且3cos 2α＝sin ⎝⎛⎭⎫π4－α，则sin 2α的值为( )A.118B.－118C.1718D.－1718答案 D解析 cos 2α＝sin ⎝⎛⎭⎫π2－2α＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫π4－α＝2sin ⎝⎛⎭⎫π4－αcos ⎝⎛⎭⎫π4－α，代入原式，得6sin ⎝⎛⎭⎫π4－αcos ⎝⎛⎭⎫π4－α＝sin ⎝⎛⎭⎫π4－α，∵α∈⎝⎛⎭⎫π2，π，∴cos ⎝⎛⎭⎫π4－α＝16，∴sin 2α＝cos ⎝⎛⎭⎫π2－2α＝2cos 2⎝⎛⎭⎫π4－α－1＝－1718.4.若sin 2α＝55，sin(β－α)＝1010，且α∈⎣⎡⎦⎤π4，π，β∈⎣⎡⎦⎤π，3π2，则α＋β的值是() A.7π4 B.9π4 C.5π4或7π4 D.5π4或9π4答案 A解析 ∵α∈⎣⎡⎦⎤π4，π，∴2α∈⎣⎡⎦⎤π2，2π.∵sin 2α＝55，∴2α∈⎣⎡⎦⎤π2，π，∴α∈⎣⎡⎦⎤π4，π2，cos 2α＝－255.∵β∈⎣⎡⎦⎤π，3π2，∴β－α∈⎣⎡⎦⎤π2，5π4，∴cos(β－α)＝－31010，∴cos(α＋β)＝cos [2α＋(β－α)]＝cos 2αcos(β－α)－sin 2αsin(β－α) ＝⎝⎛⎭⎫－255×⎝⎛⎭⎫－31010－55×1010＝22.又∵α＋β∈⎣⎡⎦⎤5π4，2π，∴α＋β＝7π4.5.函数f (x )＝sin(2x ＋θ)＋3cos(2x ＋θ)⎝⎛⎭⎫|θ|＜π2的图象关于点⎝⎛⎭⎫π6，0对称，则f (x )的单调递增区间为() A.⎣⎡⎦⎤π3＋k π，5π6＋k π，k ∈Z B.⎣⎡⎦⎤－π6＋k π，π3＋k π，k ∈Z C.⎣⎡⎦⎤－7π12＋k π，－π12＋k π，k ∈Z D.⎣⎡⎦⎤－π12＋k π，5π12＋k π，k ∈Z答案 C解析 ∵f (x )＝sin(2x ＋θ)＋3cos(2x ＋θ) ＝2sin ⎝⎛⎭⎫2x ＋θ＋π3，由题意知2×π6＋θ＋π3＝k π(k ∈Z )， ∴θ＝k π－23π(k ∈Z ).∵|θ|＜π2，∴θ＝π3.∴f (x )＝2sin ⎝⎛⎭⎫2x ＋23π.由2k π－π2≤2x ＋23π≤2k π＋π2(k ∈Z )，得k π－712π≤x ≤k π－π12(k ∈Z ).故选C.6.已知tan(π4＋θ)＝3，则sin 2θ－2cos 2θ的值为 . 答案－45解析 ∵tan(π4＋θ)＝3， ∴1＋tan θ1－tan θ＝3，解得tan θ＝12. ∵sin 2θ－2cos 2θ＝sin 2θ－cos 2θ－1＝2sin θcos θsin 2θ＋cos 2θ－cos 2θ－sin 2θsin 2θ＋cos 2θ－1 ＝2tan θ1＋tan 2θ－1－tan 2θ1＋tan 2θ－1 ＝45－35－1＝－45. 7.若tan α＋1tan α＝103，α∈(π4，π2)，则sin(2α＋π4)的值为 . 答案－210解析由tan α＋1tan α＝103得sin αcos α＋cos αsin α＝103， ∴1sin αcos α＝103，∴sin 2α＝35. ∵α∈(π4，π2)，∴2α∈(π2，π)， ∴cos 2α＝－45. ∴sin(2α＋π4)＝sin 2αcos π4＋cos 2αsin π4＝22×(35－45)＝－210. 8.若α、β是锐角，且sin α－sin β＝－12，cos α－cos β＝12，则tan(α－β)＝ . 答案－73解析 ∵sin α－sin β＝－12，cos α－cos β＝12，两式平方相加得：2－2cos αcos β－2sin αsin β＝12，即2－2cos(α－β)＝12，∴cos(α－β)＝34. ∵α、β是锐角，且sin α－sin β＝－12＜0，∴0＜α＜β＜π2，∴－π2＜α－β＜0. ∴sin(α－β)＝－1－cos 2(α－β)＝－74. ∴tan(α－β)＝sin (α－β)cos (α－β)＝－73. 9.已知函数f (x )＝2cos x (sin x ＋cos x ).(1)求f ⎝⎛⎭⎫5π4的值；(2)求函数f (x )的最小正周期及单调递增区间.解 (1)f ⎝⎛⎭⎫5π4＝2cos 5π4⎝⎛⎭⎫sin 5π4＋cos 5π4 ＝－2cos π4⎝⎛⎭⎫－sin π4－cos π4＝2. (2)因为f (x )＝2sin x cos x ＋2cos 2x＝sin 2x ＋cos 2x ＋1＝2sin ⎝⎛⎭⎫2x ＋π4＋1，所以T ＝2π2＝π，故函数f (x )的最小正周期为π. 由2k π－π2≤2x ＋π4≤2k π＋π2，k ∈Z ，得k π－3π8≤x ≤k π＋π8，k ∈Z . 所以f (x )的单调递增区间为⎣⎡⎦⎤k π－3π8，k π＋π8，k ∈Z . 10.已知函数f (x )＝sin ⎝⎛⎭⎫ωx ＋π6＋sin ⎝⎛⎭⎫ωx －π6－2cos 2 ωx 2，x ∈R (其中ω＞0). (1)求函数f (x )的值域；(2)若函数f (x )的图象与直线y ＝－1的两个相邻交点间的距离为π2，求函数f (x )的单调递增区间. 解 (1)f (x )＝32sin ωx ＋12cos ωx ＋32sin ωx －12cos ωx －(cos ωx ＋1) ＝2⎝⎛⎭⎫32sin ωx －12cos ωx －1 ＝2sin ⎝⎛⎭⎫ωx －π6－1. 由－1≤sin ⎝⎛⎭⎫ωx －π6≤1，得－3≤2sin ⎝⎛⎭⎫ωx －π6－1≤1，所以函数f (x )的值域为[－3,1].(2)由题设条件及三角函数的图象和性质可知，f (x )的周期为π，所以2πω＝π，即ω＝2.所以f (x )＝2sin ⎝⎛⎭⎫2x －π6－1，再由2k π－π2≤2x －π6≤2k π＋π2(k ∈Z )，解得k π－π6≤x ≤k π＋π3(k ∈Z ).所以函数f (x )的单调递增区间为⎣⎡⎦⎤k π－π6，k π＋π3(k ∈Z ).B 组专项能力提升(时间：25分钟)11.设α∈(0，π2)，β∈(0，π2)，且tan α＝1＋sin βcos β，则( )A.3α－β＝π2B.2α－β＝π2C.3α＋β＝π2D.2α＋β＝π2答案 B解析由tan α＝1＋sin βcos β得sin αcos α＝1＋sin βcos β，即sin αcos β＝cos α＋cos αsin β，∴sin(α－β)＝cos α＝sin(π2－α).∵α∈(0，π2)，β∈(0，π2)，∴α－β∈(－π2，π2)，π2－α∈(0，π2)，由sin(α－β)＝sin(π2－α)，得α－β＝π2－α，∴2α－β＝π2.12.定义运算⎪⎪⎪⎪⎪⎪a b c d ＝ad －bc ，若cos α＝17，⎪⎪⎪⎪⎪⎪sin α sin βcos α cos β＝3314，0<β<α<π2，则β等于() A.π12 B.π6C.π4 D.π3答案 D解析依题意有sin αcos β－cos αsin β＝sin(α－β)＝3314，又0<β<α<π2，∴0<α－β<π2，故cos(α－β)＝1－sin 2(α－β)＝1314，而cos α＝17，∴sin α＝437，于是sin β＝sin [α－(α－β)]＝sin αcos(α－β)－cos αsin(α－β) ＝437×1314－17×3314＝32，故β＝π3，故选D. 13.若f (x )＝3sin x －4cos x 的一条对称轴方程是x ＝a ，则a 的取值范围可以是( )A.⎝⎛⎭⎫0，π4 B.⎝⎛⎭⎫π4，π2 C.⎝⎛⎭⎫π2，3π4D.⎝⎛⎭⎫3π4，π答案 D解析因为f (x )＝3sin x －4cos x ＝5sin(x －φ)⎝⎛⎭⎫其中tan φ＝43且0＜φ＜π2，则sin(a －φ)＝±1，所以a －φ＝k π＋π2，k ∈Z ，即a ＝k π＋π2＋φ，k ∈Z ，而tan φ＝43且0＜φ＜π2，所以π4＜φ＜π2，所以k π＋3π4＜a ＜k π＋π，k ∈Z ，取k ＝0，此时a ∈⎝⎛⎭⎫3π4，π，故选D.14.设x ∈⎝⎛⎭⎫0，π2，则函数y ＝2sin 2x ＋1sin 2x的最小值为 . 答案 3 解析方法一因为y ＝2sin 2x ＋1sin 2x ＝2－cos 2x sin 2x，所以令k ＝2－cos 2x sin 2x.又x ∈⎝⎛⎭⎫0，π2，所以k 就是单位圆x 2＋y 2＝1的左半圆上的动点P (－sin 2x ，cos 2x )与定点Q (0,2)所成直线的斜率.又k min ＝tan 60°＝3，所以函数y ＝2sin 2x ＋1sin 2x的最小值为 3. 方法二 y ＝2sin 2x ＋1sin 2x ＝3sin 2x ＋cos 2x 2sin x cos x＝3tan 2x ＋12tan x ＝32tan x ＋12tan x. 因为x ∈(0，π2)，所以tan x >0.所以32tan x ＋12tan x≥232tan x ·12tan x ＝ 3. (当tan x ＝33，即x ＝π6时取等号) 即函数的最小值为 3.15.已知函数f (x )＝2cos 2ωx －1＋23cos ωx sin ωx (0＜ω＜1)，直线x ＝π3是f (x )图象的一条对称轴. (1)试求ω的值；(2)已知函数y ＝g (x )的图象是由y ＝f (x )图象上各点的横坐标伸长到原来的2倍，然后再向左平移2π3个单位长度得到的，若g ⎝⎛⎭⎫2α＋π3＝65，α∈⎝⎛⎭⎫0，π2，求sin α的值. 解 f (x )＝2cos 2ωx －1＋23cos ωx sin ωx＝cos 2ωx ＋3sin 2ωx＝2sin ⎝⎛⎭⎫2ωx ＋π6. (1)由于直线x ＝π3是函数f (x )＝2sin ⎝⎛⎭⎫2ωx ＋π6图象的一条对称轴， ∴sin ⎝⎛⎭⎫2π3ω＋π6＝±1. ∴2π3ω＋π6＝k π＋π2(k ∈Z )， ∴ω＝32k ＋12(k ∈Z ). 又0＜ω＜1，∴－13＜k ＜13. 又∵k ∈Z ，从而k ＝0，∴ω＝12. (2)由(1)知f (x )＝2sin ⎝⎛⎭⎫x ＋π6，由题意可得g (x )＝2sin ⎣⎡⎦⎤12⎝⎛⎭⎫x ＋2π3＋π6，即g (x )＝2cos 12x . ∵g ⎝⎛⎭⎫2α＋π3＝2cos ⎝⎛⎭⎫α＋π6＝65， ∴cos ⎝⎛⎭⎫α＋π6＝35. 又α∈⎝⎛⎭⎫0，π2， ∴π6＜α＋π6＜2π3，∴sin ⎝⎛⎭⎫α＋π6＝45. ∴sin α＝sin ⎣⎡⎦⎤⎝⎛⎭⎫α＋π6－π6 ＝sin ⎝⎛⎭⎫α＋π6cos π6－cos ⎝⎛⎭⎫α＋π6sin π6 ＝45×32－35×12＝43－310.。

简单的三角恒等变换

①当α是第一象限角时，sin . (2)求f(x)的单调递减区间.
2 2 又∵a∈(0,1),∴- <θ<0,∴tan θ∈(-1,0)，
1cos ∴tan θ= .
2
②对任意角α，都成立. tan 因为59°<60°<61°，所以sin 59°<sin 60°<sin 61°，
2 1cos ∴cos 2θ= .
所以cos
1cos
11 3
6.
2
2
23
3.化简 sin2cossin等于(
cos 2
A.-sin α
B.-cos α
) C.sin α
D.cos α
【解析】选C. s in2 c o s s in ＝ 2 s in c o s2 s in
c o s 2
c o s 2
＝ s in 2 c o s2 1＝ s in c o s2 ＝ s in .
1.利用三角公式进行化简后研究函数的性质是高考考
查的热点
考情播报
2.常与三角函数的性质、向量、解三角形的知识相结
合命题
3.题型以解答题为主,属中低档题
【知识梳理】 1.半角公式
2sin2α
2α
1 2sin 2 2
2cos2α
α
2cos2 1 2
1-cos 2
1+cos 2
1 cos 1+cos
的化又【图简∵解a象后题∈向研视(0左究点,1)平单】,∴移调(-1)性m利<(、θm用1<对＞0倍,称0∴角c)t个a性o2公n单s式θ位∈2化长 (简-1度, .0后)，c，o所s得2 到的[s图in象2关于y轴12(12sin2)]

三角恒等变换常考题(含答案)

三角恒等变换基础题型一．选择题（共20小题，每小题5分）时间60分钟4．已知sin2α=，则cos2（）=（）A．﹣B．C．﹣ D．5．若，则cos（π﹣2α）=（）A．B．C．D．6．已知sin（α+）+sinα=﹣，﹣＜α＜0，则cos（α+）等于（）A．﹣ B．﹣ C．D．7．若，则=（）A． B．C．D．8．已知cosα=，cos（α﹣β）=，且0＜β＜α＜，那么β=（）A．B．C．D．9．若α∈（，π），且3cos2α=sin（﹣α），则sin2α的值为（）A．B．C．D．10．若α，β为锐角，且满足cosα=，cos（α+β）=，则sinβ的值为（）A．B．C．D．12．已知sin（﹣α）﹣cosα=，则cos（2α+）=（）A．B．﹣C．D．﹣13．已知cosα=﹣，且α∈（，π），则tan（α+）等于（）A．﹣B．﹣7 C．D．715．已知，则sin2α的值为（）A．B．C．D．16．cos15°•cos105°﹣cos75°•sin105°的值为（）A．﹣ B．C．D．﹣17．若tanα=，则sin2α+cos2α的值是（）A．﹣B．C．5 D．﹣519．cos43°cos77°+sin43°cos167°的值是（）A． B．C．D．21．已知sinα+cosα=，则sin2α=（）A．﹣B．﹣ C．D．23．若tanα=，则cos2α+2sin2α=（）A．B．C．1 D．24．已知向量，且，则sin2θ+cos2θ的值为（）A．1 B．2 C．D．325．已知tan（α﹣）=，则的值为（）A．B．2 C．2 D．﹣226．已知，则tanα=（）A．﹣1 B．0 C．D．1三角恒等变换基础题型组卷参考答案与试题解析一．选择题（共30小题）4．（2017•泉州模拟）已知sin2α=，则cos2（）=（）A．﹣ B．C．﹣ D．【解答】解：==，由于：，所以：=，故选：D．5．（2017•焦作二模）若，则cos（π﹣2α）=（）A．B．C．D．【解答】解：由，可得：sinα=．∵cos（π﹣2α）=﹣cos2α=﹣（1﹣2sin2α）=2sin2α﹣1=．故选D6．（2017•衡水一模）已知sin（α+）+sinα=﹣，﹣＜α＜0，则cos（α+）等于（）A．﹣ B．﹣ C．D．【解答】解：∵sin（α+）+sinα=﹣，∴，∴，∴cos（α﹣）=，∴cos（α+）=cos[π+（α﹣）]=﹣cos（α﹣）=．故选C．7．（2017•商丘三模）若，则=（）A．B．C．D．【解答】解：∵=cos（α+），∴=cos[2（α+）]=2cos2（α+）﹣1=2×﹣1=﹣．故选：D．8．（2017•德州二模）已知cosα=，cos（α﹣β）=，且0＜β＜α＜，那么β=（）A．B．C．D．【解答】解：由0＜α＜β＜，得到0＜β﹣α＜，又cosα=，cos（α﹣β）=cos（β﹣α）=，所以sinα==，sin（β﹣α）=﹣sin（α﹣β）=﹣=﹣，则cosβ=cos[（β﹣α）+α]=cos（β﹣α）cosα﹣sin（β﹣α）sinα=×﹣（﹣）×=，所以β=．故选：C．9．（2017•青海模拟）若α∈（，π），且3cos2α=sin（﹣α），则sin2α的值为（）A．B．C．D．【解答】解：∵α∈（，π），∴sinα＞0，cosα＜0，∵3cos2α=sin（﹣α），∴3（cos2α﹣sin2α）=（cosα﹣sinα），∴co sα+sinα=，∴两边平方，可得：1+2sinαcosα=，∴sin2α=2sinαcosα=﹣．故选：D．10．（2017•大武口区校级四模）若α，β为锐角，且满足cosα=，cos（α+β）=，则sinβ的值为（）A．B．C．D．【解答】解：α，β为锐角，且满足cosα=，∴sinα==，sin（α+β）==，则sinβ=sin[（α+β）﹣α]=sin（α+β）cosα﹣cos（α+β）sinα=﹣×=，故选：C．12．（2017•腾冲县校级二模）已知sin（﹣α）﹣cosα=，则cos（2α+）=（）A．B．﹣C．D．﹣【解答】解：∵sin（﹣α）﹣cosα=cosα﹣sinα﹣cosα=﹣sin（α+）=，∴sin（α+）=﹣，则cos（2α+）=1﹣2sin2（α+）=，故选：C．13．（2017•榆林一模）已知cosα=﹣，且α∈（，π），则tan（α+）等于（）A．﹣ B．﹣7 C．D．7【解答】解析：由cosα=﹣且α∈（）得tanα=﹣，∴tan（α+）==，故选C．15．（2017•全国三模）已知，则sin2α的值为（）A．B．C．D．【解答】解：∵已知，则平方可得1﹣sin2α=，∴sin2α=，故选：C．16．（2017•山西一模）cos15°•cos105°﹣cos75°•sin105°的值为（）A．﹣ B．C．D．﹣【解答】解：cos15°•cos105°﹣cos75°•sin105°=cos15°•cos105°﹣sin15°•sin105°=cos（15°+105°）=cos120°=﹣．故选：A．17．（2017春•陆川县校级月考）若tanα=，则sin2α+cos2α的值是（）A．﹣ B．C．5 D．﹣5【解答】解：原式=．故选B．19．（2017春•福州期末）cos43°cos77°+sin43°cos167°的值是（）A．B．C．D．【解答】解：cos43°cos77°+sin43°cos167°=cos43°cos77°+sin43°cos（90°+77°）=cos43°cos77°﹣sin43°sin77°=cos（43°+77°）=cos120°=﹣cos60°=﹣．故选D．21．（2017春•荔城区校级期中）已知sinα+cosα=，则sin2α=（）A．﹣ B．﹣ C．D．【解答】解：∵sina+cosa=，∴（sina+cosa）2=，∴1+2sinacosa=，∴sin2a=﹣．故选：A．23．（2016•新课标Ⅲ）若tanα=，则cos2α+2sin2α=（）A．B．C．1 D．【解答】解：∵tanα=，∴cos2α+2sin2α====．故选：A．24．（2016•肃南裕县校级模拟）已知向量，且，则sin2θ+cos2θ的值为（）A．1 B．2 C．D．3【解答】解：由题意可得=sinθ﹣2cosθ=0，即tanθ=2．∴sin2θ+cos2θ===1，故选A．25．（2016•河南模拟）已知tan（α﹣）=，则的值为（）A．B．2 C．2 D．﹣2【解答】解：由tan（α﹣）==，得tanα=3．则=．故选：B．26．（2016•全国二模）已知，则tanα=（）A．﹣1 B．0 C．D．1【解答】解：∵，∴cosα﹣sinα=cosα﹣sinα，∴cosα=sinα，∴tanα===﹣1．故选：A．29．（2017•玉林一模）若3sinα+cosα=0，则的值为（）A．B．C．D．﹣2【解答】解：∵3sinα+cosα=0，∴tanα=﹣，∴===，故选：A．30．（2017•成都模拟）已知函数f（x）=cos（x+）sinx，则函数f（x）的图象（）A．最小正周期为T=2πB．关于点（，﹣）对称C．在区间（0，）上为减函数D．关于直线x=对称【解答】解：∵函数f（x）=cos（x+）sinx=（cosx﹣sinx）•sinx=sin2x﹣•=（sin2x+cos2x）﹣=sin（2x+）+，故它的最小正周期为=π，故A不正确；令x=，求得f（x）=+=，为函数f（x）的最大值，故函数f（x）的图象关于直线x=对称，且f（x）的图象不关于点（，）对称，故B不正确、D正确；在区间（0，）上，2x+∈（，），f（x）=sin（2x+）+为增函数，故C不正确，故选：D．。

简单的三角恒等变换

简单的三角恒等变换考点一三角函数式的化简[典例] (1)sin (180°＋2α)1＋cos 2α·cos 2αcos (90°＋α)等于( )A ．－sin αB ．－cos αC ．sin αD ．cos α(2)化简：sin (2α＋β)sin α－2cos(α＋β)．[解] (1)选D 原式＝－sin 2α·cos 2α2cos 2α(－sin α)＝－2sin αcos α·cos 2α2cos 2α(－sin α)＝cos α.(2)原式＝sin (2α＋β)－2sin αcos (α＋β)sin α＝sin[α＋(α＋β)]－2sin αcos (α＋β)sin α＝sin αcos (α＋β)＋cos αsin (α＋β)－2sin αcos (α＋β)sin α＝cos αsin (α＋β)－sin αcos (α＋β)sin α＝sin[(α＋β)－α]sin α＝sin βsin α.[解题技法] [题组训练]1．化简：sin 2α－2cos 2αsin ⎝⎛⎭⎫α－π4＝________.解析：原式＝2sin αcos α－2cos 2α22(sin α－cos α)＝22cos α.答案：22cos α2．化简：2cos 2α－12tan ⎝⎛⎭⎫π4－αcos 2⎝⎛⎭⎫π4－α.解：原式＝cos 2α2sin ⎝⎛⎭⎫π4－αcos ⎝⎛⎭⎫π4－α＝cos 2αsin ⎝⎛⎭⎫π2－2α＝cos 2αcos 2α＝1.考点二三角函数式的求值考法(一) 给角求值 [典例]cos 10°(1＋3tan 10°)cos 50°的值是________．[解析] 原式＝cos 10°＋3sin 10°cos 50°＝2sin (10°＋30°)cos 50°＝2sin 40°sin 40°＝2.[答案] 2[解题技法] 三角函数给角求值问题的解题策略一般所给出的角都是非特殊角，要观察所给角与特殊角间的关系，利用三角变换转化为求特殊角的三角函数值问题，另外此类问题也常通过代数变形(比如：正负项相消、分子分母相约等)的方式来求值．考法(二) 给值求值[典例] 已知sin ⎝⎛⎭⎫α＋π4＝210，α∈⎝⎛⎭⎫π2，π. 求：(1)cos α的值； (2)sin ⎝⎛⎭⎫2α－π4的值． [解] (1)由sin ⎝⎛⎭⎫α＋π4＝210，得sin αcos π4＋cos αsin π4＝210，化简得sin α＋cos α＝15，①又sin 2α＋cos 2α＝1，且α∈⎝⎛⎭⎫π2，π② 由①②解得cos α＝－35.(2)∵α∈⎝⎛⎭⎫π2，π，cos α＝－35，∴sin α＝45， ∴cos 2α＝1－2sin 2α＝－725，sin 2α＝2sin αcos α＝－2425，∴sin ⎝⎛⎭⎫2α－π4＝sin 2αcos π4－cos 2αsin π4＝－17250.[解题技法] 三角函数给值求值问题的基本步骤 (1)先化简所求式子或已知条件；(2)观察已知条件与所求式子之间的联系(从三角函数的名及角入手)； (3)将已知条件代入所求式子，化简求值．考法(三) 给值求角 [典例] 若sin 2α＝55，sin(β－α)＝1010，且α∈⎣⎡⎦⎤π4，π，β∈⎣⎡⎦⎤π，3π2，则α＋β的值是( ) A.7π4 B.9π4C.5π4或7π4D.5π4或9π4[解析] ∵α∈⎣⎡⎦⎤π4，π，∴2α∈⎣⎡⎦⎤π2，2π， ∵sin 2α＝55，∴2α∈⎣⎡⎦⎤π2，π. ∴α∈⎣⎡⎦⎤π4，π2且cos 2α＝－255. 又∵sin(β－α)＝1010，β∈⎣⎡⎦⎤π，3π2， ∴β－α∈⎣⎡⎦⎤π2，5π4，cos(β－α)＝－31010， ∴cos(α＋β)＝cos[(β－α)＋2α] ＝cos(β－α)cos 2α－sin(β－α)sin 2α ＝⎝⎛⎭⎫－31010×⎝⎛⎭⎫－255－1010×55＝22，又∵α＋β∈⎣⎡⎦⎤5π4，2π，∴α＋β＝7π4. [答案] A[解题技法] 三角函数给值求角问题的解题策略 (1)根据已知条件，选取合适的三角函数求值． ①已知正切函数值，选正切函数；②已知正、余弦函数值，选正弦或余弦函数．若角的范围是⎝⎛⎭⎫0，π2，选正、余弦函数皆可；若角的范围是(0，π)，选余弦函数较好；若角的范围是⎝⎛⎭⎫－π2，π2，选正弦函数较好． (2)注意讨论所求角的范围，及解题过程中角的范围．[题组训练]1．求值：cos 20°cos 35°1－sin 20°＝( )A ．1B ．2 C. 2D. 3解析：选C 原式＝cos 20°cos 35°|sin 10°－cos 10°|＝cos 210°－sin 210°cos 35°(cos 10°－sin 10°)＝cos 10°＋sin 10°cos 35°＝2⎝⎛⎭⎫22cos 10°＋22sin 10°cos 35°＝2cos (45°－10°)cos 35°＝2cos 35°cos 35°＝ 2.2．已知α为第二象限角，sin α＋cos α＝33，则cos 2α＝( ) A ．－53B ．－59C.59D.53解析：选A 法一：因为sin α＋cos α＝33，所以(sin α＋cos α)2＝13，即2sin αcos α＝－23，即sin 2α＝－23. 又因为α为第二象限角且sin α＋cos α＝33>0，所以sin α>0，cos α<0，cos α－sin α<0，cos 2α＝cos 2α－sin 2α＝(cos α＋sin α)(cos α－ sin α)<0.所以cos 2α＝－1－sin 22α＝－1－⎝⎛⎭⎫－232＝－53. 法二：由cos 2α＝cos 2α－sin 2α＝(cos α＋sin α)(cos α－sin α)，且α为第二象限角，得cos α－sin α<0，因为sin α＋cos α＝33，所以(sin α＋cos α)2＝13＝1＋2sin αcos α，得2sin αcos α＝－23，从而(cos α－sin α)2＝1－2sin αcos α＝53，则cos α－sin α＝－153，所以cos 2α＝33×⎝⎛⎭⎫－153＝－53.3．已知锐角α，β满足sin α＝55，cos β＝31010，则α＋β等于( ) A.3π4 B.π4或3π4C.π4D ．2k π＋π4(k ∈Z)解析：选C 由sin α＝55，cos β＝31010，且α，β为锐角，可知cos α＝255，sin β＝1010，故cos(α＋β)＝cos αcos β－sin αsin β＝255×31010－55×1010＝22，又0<α＋β<π，故α＋β＝π4.考点三三角恒等变换的综合应用[典例] (2018·北京高考)已知函数f (x )＝sin 2x ＋3sin x cos x . (1)求f (x )的最小正周期；(2)若f (x )在区间⎣⎡⎦⎤－π3，m 上的最大值为32，求m 的最小值． [解] (1)因为f (x )＝sin 2x ＋3sin x cos x ＝12－12cos 2x ＋32sin 2x ＝sin ⎝⎛⎭⎫2x －π6＋12，所以f (x )的最小正周期为T ＝2π2＝π. (2)由(1)知f (x )＝sin ⎝⎛⎭⎫2x －π6＋12. 由题意知－π3≤x ≤m ，所以－5π6≤2x －π6≤2m －π6.要使f (x )在区间⎣⎡⎦⎤－π3，m 上的最大值为32，即sin ⎝⎛⎭⎫2x －π6在区间⎣⎡⎦⎤－π3，m 上的最大值为1，所以2m －π6≥π2，即m ≥π3.所以m 的最小值为π3.[解题技法]三角恒等变换综合应用的解题思路(1)将f (x )化为a sin x ＋b cos x 的形式； (2)构造f (x )＝a 2＋b 2⎝⎛⎭⎪⎫a a 2＋b 2·sin x ＋b a 2＋b 2·cos x ； (3)和角公式逆用，得f (x )＝a 2＋b 2sin(x ＋φ)(其中φ为辅助角)； (4)利用f (x )＝a 2＋b 2sin(x ＋φ)研究三角函数的性质； (5)反思回顾，查看关键点、易错点和答题规范．[题组训练]1．已知ω>0，函数f (x )＝sin ωx cos ωx ＋3cos 2ωx －32的最小正周期为π，则下列结论正确的是( )A ．函数f (x )的图象关于直线x ＝π3对称B ．函数f (x )在区间⎣⎡⎦⎤π12，7π12上单调递增C ．将函数f (x )的图象向右平移π6个单位长度可得函数g (x )＝cos 2x 的图象D ．当x ∈⎣⎡⎦⎤0，π2时，函数f (x )的最大值为1，最小值为－32 解析：选D 因为f (x )＝sin ωx cos ωx ＋3cos 2ωx －32＝12sin 2ωx ＋32cos 2ωx ＝sin ⎝⎛⎭⎫2ωx ＋π3，所以T ＝2π2ω＝π，所以ω＝1，所以f (x )＝sin ⎝⎛⎭⎫2x ＋π3.对于A ，因为f ⎝⎛⎭⎫π3＝0，所以不正确；对于B ，当x ∈⎣⎡⎦⎤π12，7π12时，2x ＋π3∈⎣⎡⎦⎤π2，3π2，所以函数f (x )在区间⎣⎡⎦⎤π12，7π12上单调递减，故不正确；对于C ，将函数f (x )的图象向右平移π6个单位长度所得图象对应的函数y＝f ⎝⎛⎭⎫x －π6＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫x －π6＋π3＝sin 2x ，所以不正确；对于D ，当x ∈⎣⎡⎦⎤0，π2时，2x ＋π3∈⎣⎡⎦⎤π3，4π3，所以f (x )∈⎣⎡⎦⎤－32，1，故正确．故选D. 2．已知函数f (x )＝4sin x cos ⎝⎛⎭⎫x －π3－ 3. (1)求函数f (x )的单调区间；(2)求函数f (x )图象的对称轴和对称中心．解：(1)f (x )＝4sin x cos ⎝⎛⎭⎫x －π3－ 3 ＝4sin x ⎝⎛⎭⎫12cos x ＋32sin x － 3＝2sin x cos x ＋23sin 2x － 3 ＝sin 2x ＋3(1－cos 2x )－ 3 ＝sin 2x －3cos 2x ＝2sin ⎝⎛⎭⎫2x －π3. 令2k π－π2≤2x －π3≤2k π＋π2(k ∈Z)，得k π－π12≤x ≤k π＋5π12(k ∈Z)，所以函数f (x )的单调递增区间为⎣⎡⎦⎤k π－π12，k π＋5π12(k ∈Z)．令2k π＋π2≤2x －π3≤2k π＋3π2(k ∈Z)，得k π＋5π12≤x ≤k π＋11π12(k ∈Z)，所以函数f (x )的单调递减区间为⎣⎡⎦⎤k π＋5π12，k π＋11π12(k ∈Z)． (2)令2x －π3＝k π＋π2(k ∈Z)，得x ＝k π2＋5π12(k ∈Z)，所以函数f (x )的对称轴方程为x ＝k π2＋5π12(k ∈Z)．令2x －π3＝k π(k ∈Z)，得x ＝k π2＋π6(k ∈Z)，所以函数f (x )的对称中心为⎝⎛⎭⎫k π2＋π6，0(k ∈Z)．[课时跟踪检测]A 级1．已知sin ⎝⎛⎭⎫π6－α＝cos ⎝⎛⎭⎫π6＋α，则tan α＝( ) A ．1 B ．－1 C.12D ．0解析：选B ∵sin ⎝⎛⎭⎫π6－α＝cos ⎝⎛⎭⎫π6＋α， ∴12cos α－32sin α＝32cos α－12sin α，即⎝⎛⎭⎫32－12sin α＝⎝⎛⎭⎫12－32cos α，∴tan α＝sin αcos α＝－1.2．化简：cos 40°cos 25°1－sin 40°＝( )A ．1 B. 3 C. 2D ．2解析：选C 原式＝cos 220°－sin 220°cos 25°(cos 20°－sin 20°)＝cos 20°＋sin 20°cos 25°＝2cos 25°cos 25°＝ 2.3．(2018·唐山五校联考)已知α是第三象限的角，且tan α＝2，则sin ⎝⎛⎭⎫α＋π4＝( ) A ．－1010B.1010C ．－31010D.31010解析：选C 因为α是第三象限的角，tan α＝2，所以⎩⎨⎧sin αcos α＝2，2α＋cos 2α＝1，所以cos α＝－55，sin α＝－255，则sin ⎝⎛⎭⎫α＋π4＝sin αcos π4＋cos αsin π4＝－255×22－55×22＝－31010. 4．(2019·咸宁模拟)已知tan(α＋β)＝2，tan β＝3，则sin 2α＝( ) A.725 B.1425C ．－725D ．－1425解析：选C 由题意知tan α＝tan[(α＋β)－β]＝tan (α＋β)－tan β1＋tan (α＋β)tan β＝－17，所以sin 2α＝2sin αcos αsin 2α＋cos 2α＝2tan αtan 2α＋1＝－725.5．已知cos ⎝⎛⎭⎫2π3－2θ＝－79，则sin ⎝⎛⎭⎫π6＋θ的值为( ) A.13 B ．±13C ．－19D.19解析：选B ∵cos ⎝⎛⎭⎫2π3－2θ＝－79， ∴cos ⎣⎡⎦⎤π－⎝⎛⎭⎫π3＋2θ＝－cos ⎝⎛⎭⎫π3＋2θ ＝－cos ⎣⎡⎦⎤2⎝⎛⎭⎫π6＋θ＝－⎣⎡⎦⎤1－2sin 2⎝⎛⎭⎫π6＋θ＝－79，解得sin 2⎝⎛⎭⎫π6＋θ＝19，∴sin ⎝⎛⎭⎫π6＋θ＝±13. 6．若sin(α－β)sin β－cos(α－β)cos β＝45，且α为第二象限角，则tan ⎝⎛⎭⎫α＋π4＝( ) A ．7 B.17C ．－7D ．－17解析：选B ∵sin(α－β)sin β－cos(α－β)cos β＝45，即－cos(α－β＋β)＝－cos α＝45，∴cos α＝－45.又∵α为第二象限角，∴tan α＝－34，∴tan ⎝⎛⎭⎫α＋π4＝1＋tan α1－tan α＝17. 7．化简：2sin (π－α)＋sin 2αcos 2α2＝________.解析：2sin (π－α)＋sin 2αcos 2α2＝2sin α＋2sin αcos α12(1＋cos α)＝4sin α(1＋cos α)1＋cos α＝4sin α.答案：4sin α8．(2018·洛阳第一次统考)已知sin α＋cos α＝52，则cos 4α＝________. 解析：由sin α＋cos α＝52，得sin 2α＋cos 2α＋2sin αcos α＝1＋sin 2α＝54，所以sin 2α＝14，从而cos 4α＝1－2sin 22α＝1－2×⎝⎛⎭⎫142＝78. 答案：789．若锐角α，β满足tan α＋tan β＝3－3tan αtan β，则α＋β＝________. 解析：由已知可得tan α＋tan β1－tan αtan β＝3，即tan(α＋β)＝ 3.又因为α＋β∈(0，π)，所以α＋β＝π3.答案：π310．函数y ＝sin x cos ⎝⎛⎭⎫x ＋π3的最小正周期是________．解析：y ＝sin x cos ⎝⎛⎭⎫x ＋π3＝12sin x cos x －32sin 2x ＝14sin 2x －32·1－cos 2x 2＝12sin ⎝⎛⎭⎫2x ＋π3－34，故函数f (x )的最小正周期T ＝2π2＝π. 答案：π11．化简：(1)3tan 12°－3sin 12°(4cos 212°－2)； (2)cos 2α1tanα2－tan α2. 解：(1)原式＝3sin 12°cos 12°－32(2cos 212°－1)sin 12°＝3sin 12°－3cos 12°2sin 12°cos 12°cos 24°＝23(sin 12°cos 60°－cos 12°sin 60°)sin 24°cos 24°＝43sin (12°－60°)sin 48°＝－4 3.(2)法一：原式＝cos 2αcos α2sin α2－sin α2cos α2＝cos 2 αcos 2 α2－sin 2 α2sin α2cos α2＝cos 2αsin α2cos α2cos 2 α2－sin 2α2＝cos 2αsin α2cosα2cos α＝sin α2cos α2cos α＝12sin αcos α＝14sin 2α.法二：原式＝cos 2αtan α21－tan 2 α2＝12cos 2α·2tanα21－tan 2 α2＝12cos 2α·tan α＝12cos αsin α＝14sin 2α. 12．已知函数f (x )＝2sin x sin ⎝⎛⎭⎫x ＋π6. (1)求函数f (x )的最小正周期和单调递增区间；(2)当x ∈⎣⎡⎦⎤0，π2时，求函数f (x )的值域．解：(1)因为f (x )＝2sin x ⎝⎛⎭⎫32sin x ＋12cos x ＝3×1－cos 2x 2＋12sin 2x ＝sin ⎝⎛⎭⎫2x －π3＋32，所以函数f (x )的最小正周期为T ＝π. 由－π2＋2k π≤2x －π3≤π2＋2k π，k ∈Z ，解得－π12＋k π≤x ≤5π12＋k π，k ∈Z ，所以函数f (x )的单调递增区间是⎣⎡⎦⎤－π12＋k π，5π12＋k π，k ∈Z. (2)当x ∈⎣⎡⎦⎤0，π2时，2x －π3∈⎣⎡⎦⎤－π3，2π3， sin ⎝⎛⎭⎫2x －π3∈⎣⎡⎦⎤－32，1，f (x )∈⎣⎡⎦⎤0，1＋32. 故f (x )的值域为⎣⎡⎦⎤0，1＋32. B 级1．(2018·大庆中学期末)已知tan α，1tan α是关于x 的方程x 2－kx ＋k 2－3＝0的两个实根，且3π<α<7π2，则cos α＋sin α＝( )A. 3B. 2 C ．－ 2D ．－ 3解析：选C ∵tan α，1tan α是关于x 的方程x 2－kx ＋k 2－3＝0的两个实根，∴tan α＋1tan α＝k ，tan α·1tan α＝k 2－3.∵3π<α<7π2，∴k >0，∴k ＝2，∴tan α＝1，∴α＝3π＋π4，则cos α＝－22，sin α＝－22，∴cos α＋sin α＝－ 2. 2．在△ABC 中，sin(C －A )＝1，sin B ＝13，则sin A ＝________.解析：∵sin(C －A )＝1， ∴C －A ＝90°，即C ＝90°＋A ， ∵sin B ＝13，∴sin B ＝sin(A ＋C )＝sin(90°＋2A )＝cos 2A ＝13，即1－2sin 2A ＝13，∴sin A ＝33.答案：333．已知角α的顶点在坐标原点，始边与x 轴的正半轴重合，终边经过点P (－3，3)． (1)求sin 2α－tan α的值；(2)若函数f (x )＝cos(x －α)cos α－sin(x －α)sin α，求函数g (x )＝3f ⎝⎛⎭⎫π2－2x －2f 2(x )在区间⎣⎡⎦⎤0，2π3上的值域．解：(1)∵角α的终边经过点P (－3，3)， ∴sin α＝12，cos α＝－32，tan α＝－33.∴sin 2α－tan α＝2sin αcos α－tan α＝－32＋33＝－36. (2)∵f (x )＝cos(x －α)cos α－sin(x －α)sin α＝cos x ，∴g (x )＝3cos ⎝⎛⎭⎫π2－2x －2cos 2x ＝3sin 2x －1－cos 2x ＝2sin ⎝⎛⎭⎫2x －π6－1. ∵0≤x ≤2π3，∴－π6≤2x －π6≤7π6.∴－12≤sin ⎝⎛⎭⎫2x －π6≤1， ∴－2≤2sin ⎝⎛⎭⎫2x －π6－1≤1，故函数g (x )＝3f ⎝⎛⎭⎫π2－2x －2f 2(x )在区间⎣⎡⎦⎤0，2π3上的值域是[－2,1]．第七节正弦定理和余弦定理一、基础知识1．正弦定理a sin A ＝b sin B ＝c sin C＝2R (R 为△ABC 外接圆的半径)．正弦定理的常见变形(1)a ＝2R sin A ，b ＝2R sin B ，c ＝2R sin C ； (2)sin A ＝a 2R ，sin B ＝b 2R ，sin C ＝c 2R； (3)a ∶b ∶c ＝sin A ∶sin B ∶sin C ； (4)a ＋b ＋c sin A ＋sin B ＋sin C ＝a sin A. 2．余弦定理a 2＝b 2＋c 2－2bc cos A ； b 2＝c 2＋a 2－2ca cos B ； c 2＝a 2＋b 2－2ab cos C . 3．三角形的面积公式(1)S △ABC ＝12ah a (h a 为边a 上的高)；(2)S △ABC ＝12ab sin C ＝12bc sin A ＝12ac sin B ；(3)S ＝12r (a ＋b ＋c )(r 为三角形的内切圆半径)．二、常用结论汇总——规律多一点 1．三角形内角和定理在△ABC 中，A ＋B ＋C ＝π；变形：A ＋B 2＝π2－C2.2．三角形中的三角函数关系(1)sin(A ＋B )＝sin C ；(2)cos(A ＋B )＝－cos C ； (3)sin A ＋B 2＝cos C 2；(4)cos A ＋B 2＝sin C2.3．三角形中的射影定理在△ABC 中，a ＝b cos C ＋c cos B ；b ＝a cos C ＋c cos A ；c ＝b cos A ＋a cos B . 4．用余弦定理判断三角形的形状在△ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，当b 2＋c 2－a 2>0时，可知A 为锐角；当b 2＋c 2－a 2＝0时，可知A 为直角；当b 2＋c 2－a 2<0时，可知A 为钝角．第一课时正弦定理和余弦定理(一) 考点一利用正、余弦定理解三角形考法(一) 正弦定理解三角形[典例] (1)(2019·江西重点中学联考)在△ABC 中，a ＝3，b ＝2，A ＝30°，则cos B ＝________.(2)设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .若a ＝3，sin B ＝12，C ＝π6，则b＝________.[解析] (1)由正弦定理可得sin B ＝b sin A a ＝2×sin 30°3＝13，∵a ＝3>b ＝2，∴B <A ，即B为锐角，∴cos B ＝1－sin 2B ＝223. (2)∵sin B ＝12且B ∈(0，π)，∴B ＝π6或B ＝5π6，又∵C ＝π6，∴B ＝π6，A ＝π－B －C ＝2π3.又a ＝3，由正弦定理得a sin A ＝bsin B ，即3sin 2π3＝b sinπ6，解得b ＝1. [答案] (1)223 (2)1考法(二) 余弦定理解三角形[典例] (1)(2019·山西五校联考)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若b cos A ＋a cos B ＝c 2，a ＝b ＝2，则△ABC 的周长为( )A ．7.5B ．7C ．6D ．5(2)(2018·泰安二模)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且c －b2c －a＝sin Asin B ＋sin C，则角B ＝________.[解析] (1)∵b cos A ＋a cos B ＝c 2，∴由余弦定理可得b ·b 2＋c 2－a 22bc ＋a ·a 2＋c 2－b 22ac＝c 2，整理可得2c 2＝2c 3，解得c ＝1，则△ABC 的周长为a ＋b ＋c ＝2＋2＋1＝5.(2)由正弦定理可得c －b 2c －a ＝sin A sin B ＋sin C ＝ab ＋c， ∴c 2－b 2＝2ac －a 2，∴c 2＋a 2－b 2＝2ac ，∴cos B ＝a 2＋c 2－b 22ac ＝22，∵0<B <π，∴B ＝π4.[答案] (1)D (2)π4[题组训练]1.△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，若b 2＝ac ，c ＝2a ，则cos C ＝( ) A.24B ．－24C.34D ．－34解析：选B 由题意得，b 2＝ac ＝2a 2，即b ＝2a ，∴cos C ＝a 2＋b 2－c 22ab ＝a 2＋2a 2－4a 22a ×2a＝－24.2.△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知sin B ＋sin A (sin C －cos C )＝0，a ＝2，c ＝2，则C ＝( )A.π12 B.π6C.π4D.π3解析：选B 因为sin B ＋sin A (sin C －cos C )＝0，所以sin(A ＋C )＋sin A sin C －sin A cos C ＝0，所以sin A cos C ＋cos A sin C ＋sin A sin C －sin A cos C ＝0，整理得sin C (sin A ＋cos A )＝0.因为sin C ≠0，所以sin A ＋cos A ＝0，所以t a n A ＝－1，因为A ∈(0，π)，所以A ＝3π4，由正弦定理得sin C ＝c ·sin Aa ＝2×222＝12，又0＜C ＜π4，所以C ＝π6.3.在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，已知sin 2B ＋sin 2C ＝sin 2A ＋sin B sin C .(1)求角A 的大小；(2)若cos B ＝13，a ＝3，求c 的值．解：(1)由正弦定理可得b 2＋c 2＝a 2＋bc ，由余弦定理得cos A ＝b 2＋c 2－a 22bc ＝12，因为A ∈(0，π)，所以A ＝π3.(2)由(1)可知sin A ＝32，因为cos B ＝13，B 为△ABC 的内角，所以sin B ＝223，故sin C ＝sin(A ＋B )＝sin A cos B ＋cos A sin B ＝32×13＋12×223＝3＋226. 由正弦定理a sin A ＝c sin C得c ＝a sin C sin A ＝3×(3＋22)32×6＝1＋263.考点二判定三角形的形状[典例] (1)设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，若b cos C ＋c cos B ＝a sin A ，则△ABC 的形状为( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不确定(2)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若sin A sin B ＝ac ，(b ＋c ＋a )(b ＋c －a )＝3bc ，则△ABC 的形状为( )A ．直角三角形B ．等腰非等边三角形C ．等边三角形D ．钝角三角形[解析] (1)法一：因为b cos C ＋c cos B ＝a sin A ，由正弦定理知sin B cos C ＋sin C cos B ＝sin A sin A ，得sin(B ＋C )＝sin A sin A .又sin(B ＋C )＝sin A ，得sin A ＝1，即A ＝π2，因此△ABC 是直角三角形．法二：因为b cos C ＋c cos B ＝b ·a 2＋b 2－c 22ab ＋c ·a 2＋c 2－b 22ac ＝2a 22a＝a ，所以a sin A ＝a ，即sin A ＝1，故A ＝π2，因此△ABC 是直角三角形．(2)因为sin A sin B ＝a c ，所以a b ＝ac，所以b ＝c .又(b ＋c ＋a )(b ＋c －a )＝3bc ，所以b 2＋c 2－a 2＝bc ，所以cos A ＝b 2＋c 2－a 22bc ＝bc 2bc ＝12.因为A ∈(0，π)，所以A ＝π3，所以△ABC 是等边三角形．[答案] (1)B (2)C[变透练清]1.(变条件)若本例(1)条件改为“a sin A ＋b sin B <c sin C ”，那么△ABC 的形状为________．解析：根据正弦定理可得a 2＋b 2<c 2，由余弦定理得cos C ＝a 2＋b 2－c 22ab <0，故C 是钝角，所以△ABC 是钝角三角形．答案：钝角三角形2.(变条件)若本例(1)条件改为“c －a cos B ＝(2a －b )cos A ”，那么△ABC 的形状为________．解析：因为c －a cos B ＝(2a －b )cos A ， C ＝π－(A ＋B )，所以由正弦定理得sin C －sin A cos B ＝2sin A cos A －sin B ·cos A ，所以sin A cos B ＋cos A sin B －sin A cos B ＝2sin A cos A －sin B cos A ，所以cos A (sin B －sin A )＝0，所以cos A ＝0或sin B ＝sin A ，所以A ＝π2或B ＝A 或B ＝π－A (舍去)，所以△ABC 为等腰或直角三角形．答案：等腰或直角三角形3.(变条件)若本例(2)条件改为“cos A cos B ＝ba ＝2”，那么△ABC 的形状为________．解析：因为cos A cos B ＝b a ，由正弦定理得cos A cos B ＝sin B sin A ，所以sin 2A ＝sin 2B .由ba ＝2，可知a ≠b ，所以A ≠B .又因为A ，B ∈(0，π)，所以2A ＝π－2B ，即A ＋B ＝π2，所以C ＝π2，于是△ABC是直角三角形．答案：直角三角形[课时跟踪检测]A 级1．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c .若sin A a ＝cos Bb，则B 的大小为( ) A ．30° B ．45° C ．60°D ．90°解析：选B 由正弦定理知，sin A sin A ＝cos Bsin B ，∴sin B ＝cos B ，∴B ＝45°.2．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c .已知b ＝40，c ＝20，C ＝60°，则此三角形的解的情况是( )A ．有一解B ．有两解C ．无解D ．有解但解的个数不确定解析：选C 由正弦定理得b sin B ＝c sin C， ∴sin B ＝b sin Cc＝40×3220＝3>1.∴角B 不存在，即满足条件的三角形不存在．3．(2018·重庆六校联考)在△ABC 中，cos B ＝ac (a ，b ，c 分别为角A ，B ，C 的对边)，则△ABC 的形状为( )A ．直角三角形B ．等边三角形C ．等腰三角形D ．等腰三角形或直角三角形解析：选A 因为cos B ＝ac ，由余弦定理得a 2＋c 2－b 22ac ＝a c ，整理得b 2＋a 2＝c 2，即C 为直角，则△ABC 为直角三角形．4．在△ABC 中，a ，b ，c 分别是内角A ，B ，C 的对边．若b sin A ＝3c sin B ，a ＝3， cos B ＝23，则b ＝( )A ．14B ．6 C.14D. 6解析：选D ∵b sin A ＝3c sin B ⇒ab ＝3bc ⇒a ＝3c ⇒c ＝1，∴b 2＝a 2＋c 2－2ac cos B ＝9＋1－2×3×1×23＝6，∴b ＝ 6.5．(2019·莆田调研)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，若a sin B cos C＋c sin B cos A ＝12b ，且a >b ，则B ＝( )A.π6B.π3C.2π3D.5π6解析：选A ∵a sin B cos C ＋c sin B cos A ＝12b ，∴根据正弦定理可得sin A sin B cos C ＋sinC sin B cos A ＝12sin B ，即sin B (sin A cos C ＋sin C cos A )＝12sin B ．∵sin B ≠0，∴sin(A ＋C )＝12，即sin B ＝12.∵a >b ，∴A >B ，即B 为锐角，∴B ＝π6.6．(2019·山西大同联考)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若2(b cos A ＋a cos B )＝c 2，b ＝3,3cos A ＝1，则a ＝( )A. 5 B ．3 C.10D ．4解析：选B 由正弦定理可得2(sin B cos A ＋sin A cos B )＝c sin C ， ∵2(sin B cos A ＋sin A cos B )＝2sin(A ＋B )＝2sin C ，∴2sin C ＝c sin C ，∵sin C >0，∴c ＝2，由余弦定理得a 2＝b 2＋c 2－2bc cos A ＝32＋22－2×3×2×13＝9，∴a ＝3.7．在△ABC 中，AB ＝6，A ＝75°，B ＝45°，则AC ＝________. 解析：C ＝180°－75°－45°＝60°，由正弦定理得AB sin C ＝AC sin B ，即6sin 60°＝AC sin 45°，解得AC ＝2. 答案：28．设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且a ＝2，cos C ＝－14，3sin A ＝2sin B ，则c ＝________.解析：∵3sin A ＝2sin B ，∴3a ＝2b . 又∵a ＝2，∴b ＝3.由余弦定理可知c 2＝a 2＋b 2－2ab cos C ， ∴c 2＝22＋32－2×2×3×⎝⎛⎭⎫－14＝16，∴c ＝4. 答案：49．(2018·浙江高考)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c .若a ＝7，b ＝2，A ＝60°，则sinB ＝________，c ＝________.解析：由正弦定理a sin A ＝bsin B ，得sin B ＝b a ·sin A ＝27×32＝217.由余弦定理a 2＝b 2＋c 2－2bc cos A ，得7＝4＋c 2－4c ×cos 60°，即c 2－2c －3＝0，解得c ＝3或c ＝－1(舍去)．答案：2173 10．在△ABC 中，a ，b ，c 分别为角A ，B ，C 所对的边，sin A ，sin B ，sin C 成等差数列，且a ＝2c ，则cos A ＝________.解析：因为sin A ，sin B ，sin C 成等差数列，所以2sin B ＝sin A ＋sin C ．由正弦定理得a ＋c ＝2b ，又因为a ＝2c ，可得b ＝32c ，所以cos A ＝b 2＋c 2－a 22bc ＝94c 2＋c 2－4c 22×32c 2＝－14.答案：－1411．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且A ＝2B . (1)求证：a ＝2b cos B ； (2)若b ＝2，c ＝4，求B 的值．解：(1)证明：因为A ＝2B ，所以由正弦定理a sin A ＝b sin B ，得a sin 2B ＝bsin B ，所以a ＝2b cos B .(2)由余弦定理，a 2＝b 2＋c 2－2bc cos A ，因为b ＝2，c ＝4，A ＝2B ，所以16c os 2B ＝4＋16－16cos 2B ，所以c os 2B ＝34，因为A ＋B ＝2B ＋B <π，所以B <π3，所以cos B ＝32，所以B ＝π6.12．(2019·绵阳模拟)在△ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，且2a sin A ＝(2b ＋c )sin B ＋(2c ＋b )sin C .(1)求A 的大小；(2)若sin B ＋sin C ＝1，试判断△ABC 的形状．解：(1)由已知，结合正弦定理，得2a 2＝(2b ＋c )b ＋(2c ＋b )c ，即a 2＝b 2＋c 2＋bc . 又由余弦定理，得a 2＝b 2＋c 2－2bc cos A ，所以bc ＝－2bc cos A ，即cos A ＝－12.由于A 为△ABC 的内角，所以A ＝2π3.(2)由已知2a sin A ＝(2b ＋c )sin B ＋(2c ＋b )sin C ，结合正弦定理，得2sin 2A ＝(2sin B ＋sin C )sin B ＋(2sin C ＋sin B )sin C ，即sin 2A ＝sin 2B ＋sin 2C ＋sin B sin C ＝sin 22π3＝34.又由sin B ＋sin C ＝1，得sin 2B ＋sin 2C ＋2sin B sin C ＝1，所以sin B sin C ＝14，结合sin B ＋sin C ＝1，解得sin B ＝sin C ＝12.因为B ＋C ＝π－A ＝π3，所以B ＝C ＝π6，所以△ABC 是等腰三角形．B 级1．(2019·郑州质量预测)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c .若2c os 2A ＋B2－cos 2C ＝1,4sin B ＝3sin A ，a －b ＝1，则c 的值为( )A.13B.7C.37D ．6解析：选A 由2c os 2A ＋B2－cos 2C ＝1，得1＋c os(A ＋B )－(2c os 2C －1)＝2－2c os 2C －cos C ＝1，即2c os 2C ＋cos C －1＝0，解得cos C ＝12或cos C ＝－1(舍去)．由4sin B ＝3sin A及正弦定理，得4b ＝3a ，结合a －b ＝1，得a ＝4，b ＝3.由余弦定理，知c 2＝a 2＋b 2－2ab cos C ＝42＋32－2×4×3×12＝13，所以c ＝13.2．(2019·长春模拟)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，且c ＝3，2sin A a ＝t a n C c，若sin(A －B )＋sin C ＝2sin 2B ，则a ＋b ＝________. 解析：∵2sin A a ＝t a n C c ＝sin C c cos C ，且由正弦定理可得a ＝2R sin A ，c ＝2R sin C (R 为△ABC的外接圆的半径)，∴cos C ＝12.∵C ∈(0，π)，∴C ＝π3.∵sin(A －B )＋sin C ＝2sin 2B ，sin C ＝sin(A ＋B )，∴2sin A cos B ＝4sin B cos B ．当cos B ＝0时，B ＝π2，则A ＝π6，∵c ＝3， ∴a ＝1，b ＝2，则a ＋b ＝3.当cos B ≠0时，sin A ＝2sin B ，即a ＝2b .∵cos C ＝a 2＋b 2－c 22ab ＝12，∴b 2＝1，即b ＝1，∴a ＝2，则a ＋b ＝3.综上，a ＋b ＝3.答案：33．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且2a cos C －c ＝2b . (1)求角A 的大小；(2)若c ＝2，角B 的平分线BD ＝3，求a .解：(1)2a cos C －c ＝2b ⇒2sin A cos C －sin C ＝2sin B ⇒2sin A cos C －sin C ＝2sin(A ＋C )＝2sin A cos C ＋2cos A sin C ，∴－sin C ＝2cos A sin C ， ∵sin C ≠0，∴cos A ＝－12，又A ∈(0，π)，∴A ＝2π3.(2)在△ABD 中，由正弦定理得，AB sin ∠ADB ＝BDsin A ，∴sin ∠ADB ＝AB sin A BD ＝22.又∠ADB ∈(0，π)，A ＝2π3，∴∠ADB ＝π4，∴∠ABC ＝π6，∠ACB ＝π6，b ＝c ＝2，由余弦定理，得a 2＝c 2＋b 2－2c ·b ·cos A ＝(2)2＋(2)2－2×2×2c os 2π3＝6，∴a ＝ 6.第二课时正弦定理和余弦定理(二) 考点一有关三角形面积的计算[典例] (1)(2019·广州调研)△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，已知b ＝7，c ＝4，cos B ＝34，则△ABC 的面积等于( )A ．37 B.372C ．9D.92(2)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c .若△ABC 的面积为34(a 2＋c 2－b 2)，则B ＝________.[解析] (1)法一：由余弦定理b 2＝a 2＋c 2－2ac cos B ，代入数据，得a ＝3，又cos B ＝34，B ∈(0，π)，所以sin B ＝74，所以S △ABC ＝12ac sin B ＝372. 法二：由cos B ＝34，B ∈(0，π)，得sin B ＝74，由正弦定理b sin B ＝csin C 及b ＝7，c ＝4，可得sin C ＝1，所以C ＝π2，所以sin A ＝cos B ＝34，所以S △ABC ＝12bc sin A ＝372.(2)由余弦定理得cos B ＝a 2＋c 2－b 22ac ，∴a 2＋c 2－b 2＝2ac cos B . 又∵S ＝34(a 2＋c 2－b 2)，∴12ac sin B ＝34×2ac cos B ， ∴t a n B ＝3，∵B ∈()0，π，∴B ＝π3.[答案] (1)B (2)π3[变透练清]1.(变条件)本例(1)的条件变为：若c ＝4，sin C ＝2sin A ，sin B ＝154，则S △ABC ＝________. 解析：因为sin C ＝2sin A ，所以c ＝2a ，所以a ＝2，所以S △ABC ＝12ac sin B ＝12×2×4×154＝15.答案：152.(变结论)本例(2)的条件不变，则C 为钝角时，ca 的取值范围是________．解析：∵B ＝π3且C 为钝角，∴C ＝2π3－A >π2，∴0<A <π6.由正弦定理得ca ＝sin ⎝⎛⎭⎫2π3－A sin A＝32cos A ＋12sin A sin A ＝12＋32·1t a n A.∵0<t a n A <33，∴1t a n A>3， ∴c a >12＋32×3＝2，即ca >2. 答案：(2，＋∞)3．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，(2b －a )cos C ＝c cos A . (1)求角C 的大小；(2)若c ＝3，△ABC 的面积S ＝433，求△ABC 的周长．解：(1)由已知及正弦定理得(2sin B －sin A )cos C ＝sin C cos A ，即2sin B cos C ＝sin A cos C ＋sin C cos A ＝sin(A ＋C )＝sin B ， ∵B ∈(0，π)，∴sin B >0，∴cos C ＝12，∵C ∈(0，π)，∴C ＝π3.(2)由(1)知，C ＝π3，故S ＝12ab sin C ＝12ab sin π3＝433，解得ab ＝163.由余弦定理可得c 2＝a 2＋b 2－2ab cos C ＝a 2＋b 2－ab ＝(a ＋b )2－3ab ，又c ＝3，∴(a ＋b )2＝c 2＋3ab ＝32＋3×163＝25，得a ＋b ＝5.∴△ABC 的周长为a ＋b ＋c ＝5＋3＝8.[解题技法]1．求三角形面积的方法(1)若三角形中已知一个角(角的大小或该角的正、余弦值)，结合题意求解这个角的两边或该角的两边之积，代入公式求面积．(2)若已知三角形的三边，可先求其一个角的余弦值，再求其正弦值，代入公式求面积．总之，结合图形恰当选择面积公式是解题的关键．2．已知三角形面积求边、角的方法(1)若求角，就寻求夹这个角的两边的关系，利用面积公式列方程求解． (2)若求边，就寻求与该边(或两边)有关联的角，利用面积公式列方程求解．考点二平面图形中的计算问题[典例] (2018·广东佛山质检)如图，在平面四边形ABCD 中，∠ABC ＝3π4，AB ⊥AD ，AB ＝1. (1)若AC ＝5，求△ABC 的面积； (2)若∠ADC ＝π6，CD ＝4，求sin ∠CAD .[解] (1)在△ABC 中，由余弦定理得，AC 2＝AB 2＋BC 2－2AB ·BC ·c os ∠ABC ，即5＝1＋BC 2＋2BC ，解得BC ＝2，所以△ABC 的面积S △ABC ＝12AB ·BC ·sin ∠ABC ＝12×1×2×22＝12.(2)设∠CAD ＝θ，在△ACD 中，由正弦定理得AC sin ∠ADC ＝CDsin ∠CAD ，即AC sin π6＝4sin θ， ① 在△ABC 中，∠BAC ＝π2－θ，∠BCA ＝π－3π4－⎝⎛⎭⎫π2－θ＝θ－π4，由正弦定理得AC sin ∠ABC ＝ABsin ∠BCA ，即AC sin3π4＝1sin ⎝⎛⎭⎫θ－π4，② ①②两式相除，得sin 3π4sin π6＝4sin ⎝⎛⎭⎫θ－π4sin θ，即4⎝⎛⎭⎫22sin θ－22cos θ＝2sin θ，整理得sin θ＝2cos θ. 又因为sin 2θ＋c os 2θ＝1，所以sin θ＝255，即sin ∠CAD ＝255.[解题技法]与平面图形有关的解三角形问题的关键及思路求解平面图形中的计算问题，关键是梳理条件和所求问题的类型，然后将数据化归到三角形中，利用正弦定理或余弦定理建立已知和所求的关系．具体解题思路如下：(1)把所提供的平面图形拆分成若干个三角形，然后在各个三角形内利用正弦、余弦定理求解；(2)寻找各个三角形之间的联系，交叉使用公共条件，求出结果．[提醒] 做题过程中，要用到平面几何中的一些知识点，如相似三角形的边角关系、平行四边形的一些性质，要把这些性质与正弦、余弦定理有机结合，才能顺利解决问题．[题组训练]1.如图，在△ABC 中，D 是边AC 上的点，且AB ＝AD,2AB ＝3BD ，BC ＝2BD ，则sin C 的值为________．解析：设AB ＝a ，∵AB ＝AD,2AB ＝3BD ，BC ＝2BD ，∴AD ＝a ，BD ＝2a 3，BC ＝4a 3. 在△ABD 中，c os ∠ADB ＝a 2＋4a 23－a 22a ×2a 3＝33，∴sin ∠ADB ＝63，∴sin ∠BDC ＝63. 在△BDC 中，BD sin C ＝BCsin ∠BDC ，∴sin C ＝BD ·sin ∠BDC BC ＝66.答案：662.如图，在平面四边形ABCD 中，DA ⊥AB ，DE ＝1，EC ＝7，EA＝2，∠ADC ＝2π3，且∠CBE ，∠BEC ，∠BCE 成等差数列．(1)求sin ∠CED ； (2)求BE 的长．解：设∠CED ＝α.因为∠CBE ，∠BEC ，∠BCE 成等差数列，所以2∠BEC ＝∠CBE ＋∠BCE ，又∠CBE ＋∠BEC ＋∠BCE ＝π，所以∠BEC ＝π3.(1)在△CDE 中，由余弦定理得EC 2＝CD 2＋DE 2－2CD ·DE ·c os ∠EDC ，即7＝CD 2＋1＋CD ，即CD 2＋CD －6＝0，解得CD ＝2(CD ＝－3舍去)．在△CDE 中，由正弦定理得EC sin ∠EDC ＝CDsin α，于是sin α＝CD ·sin 2π3EC ＝2×327＝217，即sin ∠CED ＝217.(2)由题设知0<α<π3，由(1)知cos α＝1－sin 2α＝1－2149＝277，又∠AEB ＝π－∠BEC －α＝2π3－α，所以c os ∠AEB ＝c os ⎝⎛⎭⎫2π3－α＝c os 2π3cos α＋sin 2π3sin α＝－12×277＋32×217＝714. 在Rt △EAB 中，c os ∠AEB ＝EA BE ＝2BE ＝714，所以BE ＝47.考点三三角形中的最值、范围问题[典例] (1)在△ABC 中，内角A ，B ，C 对应的边分别为a ，b ，c ，A ≠π2，sin C ＋sin(B－A )＝2sin 2A ，则角A 的取值范围为( )A.⎝⎛⎦⎤0，π6 B.⎝⎛⎦⎤0，π4 C.⎣⎡⎦⎤π6，π4D.⎣⎡⎦⎤π6，π3(2)已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且cos 2A ＋cos 2B ＝2cos 2C ，则cos C 的最小值为( )A.32B.22C.12D ．－12[解析] (1)在△ABC 中，C ＝π－(A ＋B )，所以sin(A ＋B )＋sin(B －A )＝2sin 2A ，即2sin B cos A ＝22sin A cos A ，因为A ≠π2，所以cos A ≠0，所以sin B ＝2sin A ，由正弦定理得，b ＝2a ，所以A 为锐角．又因为sin B ＝2sin A ∈(0,1]，所以sin A ∈⎝⎛⎦⎤0，22，所以A ∈⎝⎛⎦⎤0，π4. (2)因为cos 2A ＋cos 2B ＝2cos 2C ，所以1－2sin 2A ＋1－2sin 2B ＝2－4sin 2C ，得a 2＋b 2＝2c 2，cos C ＝a 2＋b 2－c 22ab ＝a 2＋b 24ab ≥2ab 4ab ＝12，当且仅当a ＝b 时等号成立，故选C.[答案] (1)B (2)C[解题技法]1．三角形中的最值、范围问题的解题策略解与三角形中边角有关的量的取值范围时，主要是利用已知条件和有关定理，将所求的量用三角形的某个内角或某条边表示出来，结合三角形边角取值范围等求解即可．2．求解三角形中的最值、范围问题的注意点(1)涉及求范围的问题，一定要搞清已知变量的范围，利用已知的范围进行求解，已知边的范围求角的范围时可以利用余弦定理进行转化．(2)注意题目中的隐含条件，如A ＋B ＋C ＝π，0<A <π，b －c <a <b ＋c ，三角形中大边对大角等．[题组训练]1．在钝角△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，B 为钝角，若a cos A ＝ b sin A ，则sin A ＋sin C 的最大值为( )A. 2B.98C ．1D.78解析：选B ∵a cos A ＝b sin A ，由正弦定理可得，sin A cos A ＝sin B sin A ，∵sin A ≠0，∴cos A ＝sin B ，又B 为钝角，∴B ＝A ＋π2，sin A ＋sin C ＝sin A ＋sin(A ＋B )＝sin A ＋cos 2A＝sin A ＋1－2sin 2A ＝－2⎝⎛⎭⎫sin A －142＋98，∴sin A ＋sin C 的最大值为98. 2．(2018·哈尔滨三中二模)在△ABC 中，已知c ＝2，若sin 2A ＋sin 2B －sin A sin B ＝sin 2C ，则a ＋b 的取值范围为________．解析：∵sin 2A ＋sin 2B －sin A sin B ＝sin 2C ，∴a 2＋b 2－ab ＝c 2，∴cos C ＝a 2＋b 2－c 22ab ＝12，又∵C ∈(0，π)，∴C ＝π3.由正弦定理可得a sin A ＝b sin B ＝2sin π3＝433，∴a ＝433sin A ，b ＝433sin B ．又∵B ＝2π3－A ，∴a ＋b ＝433sin A ＋433sin B ＝433sin A ＋433sin ⎝⎛⎭⎫2π3－A ＝4sin ⎝⎛⎭⎫A ＋π6.又∵A ∈⎝⎛⎭⎫0，2π3，∴A ＋π6∈⎝⎛⎭⎫π6，5π6，∴sin ⎝⎛⎭⎫A ＋π6∈⎝⎛⎦⎤12，1，∴a ＋b ∈(2,4]．答案：(2,4]3．已知在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且cos B b ＋cos C c ＝sin A 3sin C .(1)求b 的值；(2)若cos B ＋3sin B ＝2，求△ABC 面积的最大值．解：(1)由题意及正、余弦定理得a 2＋c 2－b 22abc ＋a 2＋b 2－c 22abc ＝3a 3c ，整理得2a 22abc ＝3a3c ，所以b ＝ 3.(2)由题意得cos B ＋3sin B ＝2sin ⎝⎛⎭⎫B ＋π6＝2，所以sin ⎝⎛⎭⎫B ＋π6＝1，因为B ∈(0，π)，所以B ＋π6＝π2，所以B ＝π3.由余弦定理得b 2＝a 2＋c 2－2ac cos B ，所以3＝a 2＋c 2－ac ≥2ac －ac ＝ac ，即ac ≤3，当且仅当a ＝c ＝3时等号成立．所以△ABC 的面积S △ABC ＝12ac sin B ＝34ac ≤334，当且仅当a ＝c ＝3时等号成立．故△ABC 面积的最大值为334.考点四解三角形与三角函数的综合应用考法(一) 正、余弦定理与三角恒等变换[典例] (2018·天津高考)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c .已知 b sin A ＝ac os ⎝⎛⎭⎫B －π6. (1)求角B 的大小；(2)设a ＝2，c ＝3，求b 和sin(2A －B )的值． [解] (1)在△ABC 中，由正弦定理a sin A ＝b sin B ，可得b sin A ＝a sin B .又因为b sin A ＝ac os ⎝⎛⎭⎫B －π6，所以a sin B ＝ac os ⎝⎛⎭⎫B －π6，即sin B ＝32cos B ＋12sin B ，所以t a n B ＝ 3.因为B ∈(0，π)，所以B ＝π3.(2)在△ABC 中，由余弦定理及a ＝2，c ＝3，B ＝π3，得b 2＝a 2＋c 2－2ac cos B ＝7，故b ＝7. 由b sin A ＝ac os ⎝⎛⎭⎫B －π6，可得sin A ＝37. 因为a ＜c ，所以cos A ＝27. 所以sin 2A ＝2sin A cos A ＝437，cos 2A ＝2c os 2A －1＝17.所以sin(2A －B )＝sin 2A cos B －cos 2A sin B ＝437×12－17×32＝3314. 考法(二) 正、余弦定理与三角函数的性质[典例] (2018·辽宁五校联考)已知函数f (x )＝c os 2x ＋3sin(π－x )c os(π＋x )－12.(1)求函数f (x )在[0，π]上的单调递减区间；(2)在锐角△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，已知f (A )＝－1，a ＝2，b sin C ＝a sin A ，求△ABC 的面积．[解] (1)f (x )＝c os 2x －3sin x cos x －12＝1＋cos 2x 2－32sin 2x －12＝－sin ⎝⎛⎭⎫2x －π6，令2k π－π2≤2x －π6≤2k π＋π2，k ∈Z ，得k π－π6≤x ≤k π＋π3，k ∈Z ，又∵x ∈[0，π]，∴函数f (x )在[0，π]上的单调递减区间为⎣⎡⎦⎤0，π3和⎣⎡⎦⎤5π6，π. (2)由(1)知f (x )＝－sin ⎝⎛⎭⎫2x －π6， ∴f (A )＝－sin ⎝⎛⎭⎫2A －π6＝－1， ∵△ABC 为锐角三角形，∴0<A <π2，∴－π6<2A －π6<5π6，∴2A －π6＝π2，即A ＝π3.又∵b sin C ＝a sin A ，∴bc ＝a 2＝4， ∴S △ABC ＝12bc sin A ＝ 3.[对点训练]在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，(2a －c )cos B －b cos C ＝0. (1)求角B 的大小；(2)设函数f (x )＝2sin x cos x cos B －32cos 2x ，求函数f (x )的最大值及当f (x )取得最大值时x 的值．解：(1)因为(2a －c )cos B －b cos C ＝0，所以2a cos B －c cos B －b cos C ＝0，由正弦定理得2sin A cos B －sin C cos B －cos C sin B ＝0，即2sin A cos B －sin(C ＋B )＝0，又因为C ＋B ＝π－A ，所以sin(C ＋B )＝sin A . 所以sin A (2cos B －1)＝0.在△ABC 中，sin A ≠0，所以cos B ＝12，又因为B ∈(0，π)，所以B ＝π3.。

第六节简单的三角恒等变换

第六节
简单的三角恒等变换
结束
(2016· 沈阳质检)已知函数 f(x)＝2sin
π xsinx＋6 .
(1)求函数 f(x)的最小正周期和单调递增区间； (2)当
π x∈0， 2 时，求函数
f(x)的值域．
解析
栏目索引
课堂· 考点突破
课后· 三维演练
结束
“课后·三维演练”见“课时跟踪检测(二十二)”
栏目索引
课堂· 考点突破
课后· 三维演练
第六节
简单的三角恒等变换
结束
栏目索引
课堂· 考点突破
课后· 三维演练
第六节
简单的三角恒等变换
结束
π (2015· 天津高考)已知函数 f(x)＝sin x－sin x－6 ，x∈R.
2 2

(1)求 f(x)的最小正周期； (2)求
π π f(x)在区间－3 ， 4 上的最大值和最小值．
栏目索引
课堂· 考点突破课后· 三维演练
第六节
简单的三角恒等变换
结束
3．化简：sin 50°(1＋ 3tan 10°)＝________.
解析：sin 50°(1＋ 3tan 10°) ＝sin
50° 1＋
sin 10° 3· cos 10°
cos 10°＋ 3sin 10° ＝sin 50°× cos 10°
第六节
简单的三角恒等变换
结束
栏目索引
课堂· 考点突破
课后· 三维演练
第六节
简单的三角恒等变换
结束
研究三角函数式的求值，解题的关键都是找出条件中的角与结论中的角的联系，依据函数名称的变换特点，选择合适的公式求解．常见的命题角度有： (1)给值求值； (2)给角求值； (3)给值求角．

方法技巧专题19 三角恒等变换(解析版)

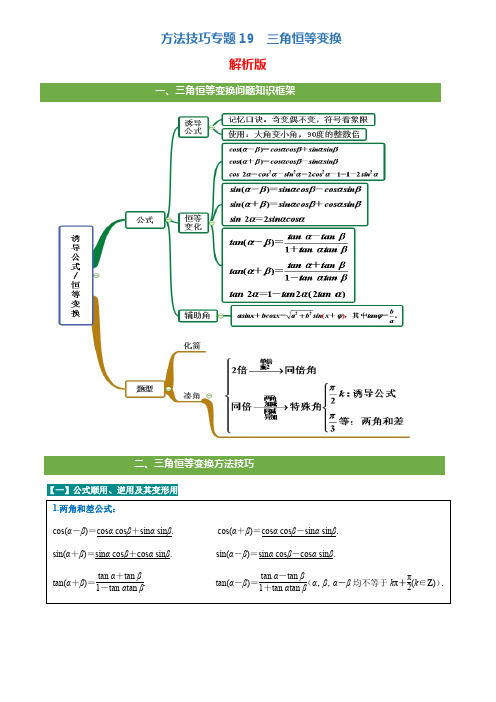
方法技巧专题19 三角恒等变换解析版一、三角恒等变换问题知识框架【一】公式顺用、逆用及其变形用1.例题【例1】计算：(1)cos(－15°)； (2)cos 15°cos 105°＋sin 15°sin 105°. 【解析】(1)方法一原式＝cos(30°－45°)＝cos 30°cos 45°＋sin 30°sin 45°＝32×22＋12×22＝6＋24. 方法二原式＝cos 15°＝cos(45°－30°)＝cos 45°cos 30°＋sin 45°sin 30°＝22×32＋22×12＝6＋24. (2)原式＝cos(15°－105°)＝cos(－90°)＝cos 90°＝0. 【例2】(1)计算：cos 2π12－sin 2π12；【解析】原式＝cos π6＝32.(2)计算：1－tan 275°tan 75°；【解析】 1－tan 275°tan 75°＝2·1－tan 275°2tan 75°＝2·1tan 150°＝－2 3.(3)计算：cos 20°cos 40°cos 80°.【解析】原式＝12sin 20°·2sin 20°cos 20°cos 40°cos 80°＝12sin 20°·sin 40°·cos 40°cos 80°＝122sin 20°sin 80°cos 80°＝123sin 20°·sin 160°＝sin 20°23sin 20°＝18.【例3】(1)1＋tan 15°1－tan 15°＝________.【解析】3 原式＝tan 45°＋tan 15°1－tan 45°tan 15°＝tan(45°＋15°)＝tan 60°＝ 3.(2)化简：tan 23°＋tan 37°＋3tan 23°tan 37°. 【解析】方法一 tan 23°＋tan 37°＋3tan 23°tan 37° ＝tan(23°＋37°)(1－tan 23°tan 37°)＋3tan 23°tan 37° ＝tan 60°(1－tan 23°tan 37°)＋3tan 23°tan 37°＝ 3. 方法二 ∵tan(23°＋37°)＝tan 23°＋tan 37°1－tan 23°tan 37°，∴3＝tan 23°＋tan 37°1－tan 23°tan 37°，∴3－3tan 23°tan 37°＝tan 23°＋tan 37°， ∴tan 23°＋tan 37°＋3tan 23°tan 37°＝ 3. （3）已知sin θ＝45，5π2＜θ＜3π，求cos θ2和tan θ2.【解析】 ∵sin θ＝45，且5π2＜θ＜3π，∴cos θ＝－1－sin 2θ＝－35.由cos θ＝2cos 2θ2－1，得cos 2θ2＝1＋cos θ2＝15.∵5π4＜θ2＜3π2，∴cos θ2＝－ 1＋cos θ2＝－55. tan θ2＝sin θ1＋cos θ＝2.2.巩固提升综合练习【练习1】化简cos 15°cos 45°＋cos 75°sin 45°的值为( )A.12B.32 C ．－12 D ．－32【解析】Bcos 15°cos 45°＋cos 75°sin 45°＝cos 15°cos 45°＋sin 15°sin 45°＝cos(15°－45°)＝cos(－30°)＝32.【练习2】1－3tan 75°3＋tan 75°＝________.【解析】－1原式＝33－tan 75°1＋33tan 75°＝tan 30°－tan 75°1＋tan 30°tan 75°＝tan(30°－75°)＝－tan 45°＝－1.【练习3】在△ABC 中，A ＋B ≠π2，且tan A ＋tan B ＋3＝3tan A tan B ，则角C 的值为( )A.π3B.2π3C.π6D.π4 【解析】A∵tan A ＋tan B ＋3＝3tan A tan B ⇔tan(A ＋B )·(1－tan A tan B )＝3(tan A tan B －1)．(*) 若1－tan A tan B ＝0，则cos A cos B －s in A sin B ＝0，即cos(A ＋B )＝0. ∵0<A ＋B <π，∴A ＋B ＝π2与题设矛盾．∴由(*)得tan(A ＋B )＝－3，即tan C ＝ 3.又∵0<C <π，∴C ＝π3.【练习4】若sin α＋cos α＝13，则sin 2α= .【解析】由题意，得(sin α＋cos α)2＝19，∴1＋2sin αcos α＝19，即1＋sin 2α＝19，∴sin 2α＝－89.1.例题【例1】已知31)3sin(=-πα，则)6cos(πα+ 的值为( ) A ．－13 B.13 C.223 D ．－223【答案】A 【解析】∵sin )3(πα-＝13，∴cos )6(πα+＝cos )]3(2[παπ-+＝－sin )3(πα-＝－13.【例2】已知角α的顶点与原点O 重合，始边与x 轴的非负半轴重合，它的终边过点⎪⎭⎫⎝⎛--54,53P . 若角β满足sin(α＋β)＝513，则cos β的值为________．【答案】－5665或1665【解析】由角α的终边过点⎪⎭⎫⎝⎛--54,53P ，得sin α＝－45，cos α＝－35. 由sin(α＋β)＝513，得cos(α＋β)＝±1213.由β＝(α＋β)－α，得cos β＝cos(α＋β)cos α＋sin(α＋β)sin α，所以cos β＝－5665或cos β＝1665.【例3】若1sin 63πα⎛⎫-= ⎪⎝⎭，则2cos 23πα⎛⎫+= ⎪⎝⎭（） A ．13 B ．13-C ．79D ．79-【答案】D 【解析】222πππcos 22cos 12cos 13326πααα⎡⎤⎛⎫⎛⎫⎛⎫+=+-=--- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦2π272sin 11699α⎛⎫=--=-=- ⎪⎝⎭2.巩固提升综合练习【练习1】已知33)6tan(=-απ，则=+)65tan(απ________. 【答案】－33【解析】tan )65(απ+＝tan )6(αππ+-＝tan )]6([αππ--＝－tan )6(απ-＝－33. 【练习2】若1027)4sin(=+πA ，A ∈),4(ππ，则sin A 的值为( ) A.35 B.45C.35或45D.34【答案】B 【解析】∵A ∈),4(ππ，∴A ＋π4∈)45,2(ππ， ∴cos （A ＋π4）＝－1－sin 2⎝⎛⎭⎫A ＋π4＝－210， ∴sin A ＝sin[（A ＋π4）- π4]＝sin （A ＋π4）cos π4－cos （A ＋π4）sin π4＝45.【练习3】已知sin(α−3π10)=35，则cos(α+π5)=（） A.−45 B.45C.−35D.35【答案】C【解析】因为sin(α−3π10)=35，则cos(α+π5)=cos[π2+(α−3π10)]=−sin(α−3π10)=−35．故应选C ．【练习4】若sin （3x π-）=23，则cos （23x π+）=（）A ．79B ．19C ．19-D ．79-【答案】C 【解析】令3x πθ=-，则223x ππθ+=-，所以()21cos 2cos 2cos 22sin 139x ππθθθ⎛⎫+=-=-=-=- ⎪⎝⎭，故选C ．【练习5】已知3sin 245x π⎛⎫-= ⎪⎝⎭，则sin 4x 的值为（） A ．1825B ．1825±C ．725D ．725±【答案】C【解析】由题意得：297cos 412sin 212242525x x ππ⎛⎫⎛⎫-=--=-⨯=⎪ ⎪⎝⎭⎝⎭7sin 4cos 4225x x π⎛⎫∴=-= ⎪⎝⎭本题正确选项：C1.例题【例1】已知02απ<<，cos()4απ+= （1）求tan()4απ+的值；（2）求sin(2)3απ+的值．【解析】（1）∵02απ<<，cos()4απ+= ∴sin()4απ+==， ∴sin()4tan()24cos()4αααπ+π+==π+．（2）∵tan 1tan()241tan αααπ++==-，∴1tan 3α=， ∴2222sin cos 2tan 3sin 2sin cos tan 15ααααααα===++，2222cos sin cos 2sin cos ααααα-=+221tan 4tan 15αα-==+，3sin(2)sin 2cos cos 2sin 33310αααπππ++=+=．【例2】已知△ABC 中,137cos sin -=+A A ,则tanA= . 【解析】解法一：列出方程组⎪⎩⎪⎨⎧=+-=+1cos sin 137cos sin 22A A A A由第一个方程得,A A sin 137cos --=,代入第二个方程得1)sin 137(sin 22=--+A A ，即016960sin 137sin 2=-+A A ，解得135sin =A 或1312sin -=A ，因为△ABC 中0<A<π, 所以sinA>0,135sin =A ，1312cos -=A ，所以125tan -=A . 答案:125-. 解法二：由已知得sinA>0, cosA<0, |sin A|<|cos A|, tanA>-1, 由137cos sin -=+A A 两边平方,整理得16960cos sin -=⋅A A ，即16960cos sin cos sin 22-=+⋅A A A A ，分子分母同除以A 2cos 得169601tan tan 2-=+A A ，解得125tan -=A .2.巩固提升综合练习【练习1】已知a ∈R ，sina +2cosa =√102，则tan2a =（）A ．−34或−35 B ．−34C ．34D ．−35【答案】B 【解析】因为sina +2cosa =√102，所以(sina +2cosa )2=52，所以sin 2a +4cos 2a +4sinacosa =52，所以sin 2a+4cos 2a+4sin acosasin 2a+cos 2a=52，即tan 2a+4+4tanatan 2a+1=52，解得tana =3或者tana =−13，当tana =3时，tan2a =2tana1−tan 2a =−34，当tana =−13时，tan2a =2tana 1−tan 2a =−34，综上所述，tan2a =−34，故选B 。

简单的三角恒等变换(基础知识+基本题型)(含解析)

5.5.2简单的三角恒等变换（基础知识+基本题型）知识点一半角公式 1.半角公式sin2α=；cos2α=tan2a =. 2.半角公式的推导(1)2cos212sin αα=-2αααα−−−−→代替2代替2cos 12sin sin22ααα=-→=； (2)222cos 22cos 1αααααα=-−−−−→代替代替2cos 2cos 1cos22ααα=-→=(3)sin2tan2cos 2ααα==【拓展】半角公式根号前符号的确定(1)当给出的角是某一象限的角时，可根据下表确定半角的函数值的符号(2)当给出角α的范围(即某一区间)时，可先求2的范围，再根据2的范围来确定各函数值的符号. (3)若没有给出确定符号的条件，则在根号前保留正、负两个符号. 3.半角公式的变形(1)sin sin2cos222tan2cos cos 2cos222ααααααα⋅==⋅2sin sin 1cos 2cos 2αααα==+；(2)sin 2sin sin 222tan2cos 2sincos222ααααααα⋅==⋅22sin 1cos 2sin sin αααα-==. 所以sin 1cos tan21cos sin ααααα-==+. 【提示】(1)重视得到结果的过程，从思考α与2α之间的关系入手，理解角的倍、半的相对性，思考cos α与2sin 2α之间的关系.(2)使用公式时要深刻体会α与2α的含义，如2α与α，αβ+与2αβ+等都可看成倍半关系.知识点二积化和差与和差化积公式 1.积化和差公式1cos cos [cos()cos()]2αβαβαβ=++-；1sin sin [cos()cos()]2αβαβαβ=-+--；1sin cos [sin()sin()]2αβαβαβ=++-；1cos sin [sin()sin()]2αβαβαβ=+--.2.积化和差公式的推导由sin()sin cos cos sin αβαβαβ+=+， sin()sin cos cos sin αβαβαβ-=-，得 1sin cos [sin()sin()]2αβαβαβ=++-，① 1cos sin [sin()sin()]2αβαβαβ=+--.②由cos()cos cos sin sin αβαβαβ+=-. cos()cos cos sin sin αβαβαβ-=+，得 1cos cos [cos()cos()]2αβαβαβ=++-，③1sin sin [cos()cos()]2αβαβαβ=-+--.④上面的①②③④四个式子统称为积化和差公式. 3.和差化积公式 sin sin 2sincos 22αβαβαβ+-+=； sin sin 2cossin22αβαβαβ+--=； cos cos 2coscos22αβαβαβ+-+=； cos cos 2sinsin22αβαβαβ+--=-.4.和差化积公式的推导在积化和差公式中，设,αβθαβϕ+=-=，则有2θϕα+=，2θϕβ-=，把,αβ代入①②③④，就得到sin sin 2sincos22θϕθϕθϕ+-+=； ⑤ sin sin 2cossin22θϕθϕθϕ+--=； ⑥ cos cos 2coscos22θϕθϕθϕ+-+=； ⑦ cos cos 2sinsin22θϕθϕθϕ+--=-.⑧上面的⑤⑥⑦⑧四个式子统称为和差化积公式. 注意公式推导过程中换元思想与方程思想的应用. 【提示】(1)积化和差公式的记忆口诀前角用和后角差，正余二分正弦和，余正二分正弦差，余余二分余弦和，正正负半余弦差. (2)和差化积公式的记忆口诀正加正，正在前；余加余，余并肩. 正减正，余在前；余减余，负正弦.考点一半角公式的应用【例1】已知角α为钝角,β为锐角,且4sin 5α=,12sin 13β=,求cos 2αβ-与tan 2αβ-的值.解:因为角α为钝角,β为锐角,且4sin 5α=,12sin 13β=,所以3cos 5α=-,5cos 13β=. 所以()cos cos cos sin sin αβαβαβ-=+35412513513⎛⎫=-⨯+⨯ ⎪⎝⎭3365=. 又因为2παπ<<,且02πβ<<,所以0αβπ<-<,即022αβπ-<<.所以cos2αβ-===. 方法1:由022αβπ-<<,得sin2αβ-==. 所以tan2αβ-sin2cos2αβαβ-=-47=. 方法2：由330,cos()65αβπαβ<-<-=，得 56sin()65αβ-==. 所以56sin()465tan .3321cos()7165αβαβαβ--===+-+对于含有半角的求值问题,一定要判断角的取值范围,以免产生增根. 考点二积化和差与和差化积公式的应用【例2】在ABC 中,A C >,且60B =,能否利用44log sin log sin 1A C +=-求出A 和C 的大小?若能,请求出;若不能,请说明理由.解:在ABC 中,因为60B =,所以120A C +=. 因为44log sin log sin 1A C +=-,所以1sin sin 4A C =. 因为()()1sin sin cos cos 2A C A C A C =--+⎡⎤⎣⎦, 所以()()11cos cos 24A C A C --+=⎡⎤⎣⎦. 所以()()11cos cos cos120022A C A C -=++=+=. 又因为0180A C <-<,所以90A C -=.由①②,得105,15A C ==. 考点三三角恒等式的证明【例3】在ABC 中,求证:222sin sin sin 2sin sin cos A B C A B C +-=. 证明:因为左边()21cos 21cos 2sin 22B CB C --=++-① ()()21sin cos 2cos 22B C C B =++- ()()()2sinsin sin B C B C B C =+++- ②()()()sin sin sin B C B C B C =+++-⎡⎤⎣⎦ ()sin 2sin cos B C B C =+• ③ 2sin sin cos A B C ==右边所以原命题成立.证明三角恒等式的基本思路:根据等式两端的特征,通过三角恒等变换,应用化繁为简、左右归一、变更论证等方法，使等式两端的“异”化为“同”，当分式不好证时，可变形为整式来证。

2024年高考数学专项三角恒等变换4种常见考法归类(解析版)

三角恒等变换4种常见考法归类高频考点考点一两角和与差的正弦、余弦和正切公式(一)给角求值(二)给值(式)求值(三)给值求角(四)三角函数式的化简(五)两角和与差的正弦、余弦、正切公式的综合应用考点二二倍角公式(一)给角求值(二)给值(式)求值(三)给值求角(四)与同角三角函数的基本关系综合(五)与诱导公式的综合(六)利用二倍角公式化简求值考点三辅助角公式的应用考点四简单的三角恒等变换(一)半角公式的应用(二)三角恒等式的证明(三) 三角恒等变换的综合问题解题策略1.两角和与差的正弦、余弦和正切公式(1)两角和与差的正弦、余弦和正切公式(和角、差角公式)C(α-β)cos(α-β)=cosαcosβ+sinαsinβC(α+β)cos(α+β)=cos_αcos_β-sin_αsin_β记忆口诀：1、余余正正符号反2、同名相乘、加减相反3、谐音：“吃吃睡睡，颠倒黑白”S(α-β)sin(α-β)=sin_αcos_β-cos_αsin_β(异名相乘、加减一致)S(α+β)sin(α+β)=sin_αcos_β+cos_αsin_β(异名相乘、加减一致)记忆口诀：1、正余余正符号同2、异名相乘、加减一致3、谐音：“上错厕所，一一对应”T (α-β)tan(α-β)=tanα-tanβ1+tanαtanβ；(两式相除、上同下异)．变形：①tanα-tanβ=tan(α-β)(1+tanαtanβ)②tanα·tanβ=tanα-tanβtan(α-β)-1 2024年高考数学专项三角恒等变换4种常见考法归类（解析版）T (α+β)tan (α+β)=tan α+tan β1-tan αtan β；(两式相除、上同下异)．变形：①tan α+tan β=tan (α+β)(1-tan αtan β)②tan α·tan β=1-tan α+tan βtan (α+β)(2)二倍角的正弦、余弦、正切公式(倍角公式)二倍角是相对的，如：α2是α4的2倍，3α是3α2的2倍.S 2αsin 2α=2sin _αcos _α；变形：sin αcos α=12sin2α，cos α=sin2α2sin α，⇒1±sin2α=sin 2α+cos 2α±2sin αcos α=(sin α±cos α)2C 2αcos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α；变形：cos 2α=1+cos2α2，sin 2α=1-cos2α2T 2αtan 2α=2tan α1-tan 2α(α≠k π+π2且α≠k π2+π4，k ∈Z )2.简单的三角恒等变换(1)降幂公式sin 2α=1-cos2α2.cos 2α=1+cos2α2.sin αcos α=12sin2α.(2)升幂公式1+cos α=2cos 2α2. 1-cos α=2sin 2α2. 1+sin α=sin α2+cos α2 2. 1-sin α=sin α2-cos α22.注：1+cos2α=2cos 2α；1−cos2α=2sin 2α；1+sin2α=(sin α+cos α)2；1−sin2α=(sin α−cos α)2(3)万能公式sin α=2tan α21+tan 2α2,cos α=1-tan 2α21+tan 2α2,tan α=2tan α21-tan 2α2(4)其他常用变式sin2α=2sin αcos αsin 2α+cos 2α=2tan α1+tan 2α；cos2α=cos 2α−sin 2αsin 2α+cos 2α=1−tan 2α1+tan 2α；cos 4x -sin 4x =(cos 2x +sin 2x )(cos 2x -sin 2x )=cos2x 3.辅助角公式(同角异名1次)a sin α+b cos α=a 2+b 2sin (α+φ)，其中cos φ=a a 2+b 2，sin φ=b a 2+b 2，或tan φ=ba . 其中φ称为辅助角，它的终边所在象限由点(a ，b )决定．4.半角的正弦、余弦、正切公式(1)sin α2=±1-cos α2.(2)cosα2=±1+cosα2.(3)tanα2=±1-cosα1+cosα=sinα1+cosα=1-cosαsinα.5.常用的拆角、拼角技巧(1)15°=45°-30°=60°-45°=30°2.(2)β=α-a-β，α=(α+β)-β=β-(β-α)，2α=(α+β)+(α-β)，α=12[(α+β)+(α-β)]β=α+β2-α-β2=(α+2β)-(α+β). α-β=(α-γ)+(γ-β)(3)π3-α=π2-π6+α，π6-α=π2-π3+α，π3+α=π-2π3-α，π4+α=π-3π4-α. π4+α=π2-π4-α6. 应用和、差、倍角公式化简求值的策略(1)首先要记住公式的结构特征和符号变化规律．例如两角差的余弦公式可简记为：“同名相乘，符号反”；(2)注意与同角三角函数基本关系、诱导公式的综合应用；(3)注意配方法、因式分解和整体代换思想的应用．　7. 和、差、倍角公式的逆用和变形用的应用技巧(1)逆用公式应准确找出所给式子与公式的异同，创造条件逆用公式；(2)和差角公式变形：sinαsinβ+cos(α+β)=cosαcosβ；cosαsinβ+sin(α-β)=sinαcosβ；tanα±tanβ=tan(α±β)·(1∓tanα·tanβ)；(3)倍角公式变形：降幂公式．(4)tanαtanβ，tanα+tanβ(或tanα-tanβ)，tan(α+β)(或tan(α-β))三者中可以知二求一，且常与一元二次方程根与系数的关系结合命题．　8. 解决非特殊角求值问题的基本思路有：①化非特殊角为特殊角；②化为正负相消的项，消去后求值；③化分子、分母使之出现公约数，进行约分求值；④当有α，2α，3α，4α同时出现在一个式子中时，一般将α向2α，3α(或4α)向2α转化，再求关于2α式子的值．9.三角函数式的化简要遵循“三看”原则注：三角函数式化简、求值的一般思路：异名三角函数化为同名三角函数，异角化为同角，异次化为同次，切化弦，特殊值与特殊角的三角函数互化等. 10. 给值(式)求值的解题策略(1)已知某些角的三角函数值，求另外一些角的三角函数值，要注意观察已知角与所求表达式中角的关系，即拆角与凑角．(2)由于和、差角与单角是相对的，因此解题过程中根据需要灵活地进行拆角或凑角的变换．常见角的变换有：①α=(α-β)+β；②α=α+β2+α-β2；③2α=(α+β)+(α-β)；④2β=(α+β)-(α-β)．(3)当“已知角”有两个时，“所求角”一般表示为两个“已知角”的和或差的形式．(4)当“已知角”有一个时，此时应着眼于“所求角”与“已知角”的和或差的关系，然后应用诱导公式把“所求角”变成“已知角”．(5)给值求值型恒等变换问题，重在对所给条件进行挖掘，如由某角正弦值可得其余弦、正切值，由所给值的符号判断角所在的象限等. 必要时还要进行估算，如锐角α的余弦值为35，由12<35<22，及余弦函数在0，π2上单调递减可知45°<α<60°，从而2α∈(90°，120°)，或3α∈(135°，180°)等. 另外，注意三种主要变换：①变角，通常是“配凑”，常用的角的拆拼有2α=(α+β)+(α-β)，α=(α+β)-β=(α-β)+β等；②变名，通过变换函数名称达到减少函数种类的目的，其手段通常有“切化弦”“升幂与降幂”等；③变式，根据式子的结构特征进行变形，使其更贴近某个公式或某个期待的目标，其手段通常有：“常值代换”如1=tan π4，1=sin 2α+cos 2α“逆用变换公式”“通分约分”“分解与组合”“配方与平方”等. 其中角的变换居核心地位.11. 已知三角函数值求角的解题步骤(1)界定角的范围，根据条件确定所求角的范围．(在给值求角时，一般地选择一个适当的三角函数，根据题设确定所求角的范围，利用三角函数的单调性求出角. 确定角的范围是关键，一定要使所选的函数在此范围内是单调的，必要时，还需根据已知三角函数值缩小角的范围.)(2)求所求角的某种三角函数值．为防止增解最好选取在范围内单调的三角函数(已知三角函数值求角，选三角函数时可按下列规则：(i )已知正切值，常选正切函数；(ii )已知正、余弦值，常选正弦或余弦函数；(iii )若角的范围是0，π2 ，π，3π2 ，常选正、余弦函数；(iv )若角的范围是π2，3π2 或-π2，π2 ，常选正弦函数；(v )若角的范围是(0，π)或(π，2π)，常选余弦函数. )(3)结合三角函数值及角的范围求角．12. 利用半角公式求值的思路(1)看角：若已知三角函数式中的角是待求三角函数式中角的两倍，则求解时常常借助半角公式求解．(2)明范围：由于半角公式求值常涉及符号问题，因此求解时务必依据角的范围，求出相应半角的范围．(3)选公式：涉及半角公式的正切值时，常用tan α2=sinα1+cosα=1-cosαsinα，其优点是计算时可避免因开方带来的求角的范围问题；涉及半角公式的正、余弦值时，常先利用sin2α2=1-cosα2，cos2α2=1+cosα2计算．13. 三角恒等式证明的常用方法(1)执因索果法：证明的形式一般是化繁为简．(2)左右归一法：证明左右两边都等于同一个式子．(3)拼凑法：针对题设和结论之间的差异，有针对性地变形，以消除它们之间的差异，简言之，即化异求同．(4)比较法：设法证明“左边-右边=0”或“左边/右边=1”．(5)分析法：从被证明的等式出发，逐步地探求使等式成立的条件，直到已知条件或明显的事实为止，就可以断定原等式成立．考点精析考点一两角和与差的正弦、余弦和正切公式(一)给角求值14(2023·全国·高三专题练习)cos-75°的值是A.6-22B.6+22C.6-24D.6+2415(2023·全国·模拟预测)sin20°cos40°+sin70°sin40°=()A.32B.12C.22D.116(2023·广东湛江·统考一模)cos70°-cos20°cos65°=．17(2023·全国·高三专题练习)sin220°-cos220°sin45°cos155°1-sin40°=.(二)给值(式)求值18(2023·江西九江·统考三模)已知0<α<π2<β<π，且sinα=23，cosβ=-75，则cos(α-β)=()A.-115B.-1315C.-41415D.2141519(江西省九江市2023届高三三模数学(理)试题)已知0<α<β<π，且cosα=13，cosα-β=223，则cosβ=()A.89B.79C.429D.020(2023·陕西榆林·统考模拟预测)若tanα+π4=15，则tanα=()A.-23B.23C.-13D.1321(山西省晋中市2023届高三三模数学试题(A卷))已知α，β为锐角，且tanα=2，sinα+β= 22，则cosβ=()A.-31010B.31010C.-1010D.101022(河南省名校青桐鸣2023届高三下学期4月联考文科数学试题)已知tanαtanβ=2，cosα+β=-15，则cosα-β=()A.35B.-35C.115D.-11523(2023·全国·高三专题练习)若α∈π2,3π4，cosα-π4=210，则sinα+π3=24【多选】(河北省承德市2023届高三下学期4月高考模拟数学试题)已知0<α<π2<β<π，sinα=13，cos(α+β)=-223，下列选项正确的有()A.sin(α+β)=±13B.cosβ=-79C.cos2β=-1781D.sin(α-β)=-232725(2023·陕西商洛·统考三模)已知tan(α+β)=3，tanα+π4=-3，则tanβ=()A.-15B.15C.-17D.1726(2023·江西上饶·校联考模拟预测)已知α、β均为锐角，且sinα=2sinβ，2cosα=cosβ，则sinα-β=.(三)给值求角27(2023·全国·高三专题练习)已知α,β都是锐角，cosα=17,cos(α+β)=-1114，则β=.28(2023·全国·高三专题练习)已知cosα=17，cos(α-β)=1314，若0<β<α<π2，则β=．29(2023·河南·校联考模拟预测)设tanα，tanβ是方程x2+33x+4=0的两根，且α,β∈-π2 ,π2，则α+β=( )．A.π3B.-2π3C.π3或-2π3D.2π330(2023·全国·高三专题练习)已知cosα=255，sinβ=1010，且α∈0,π2，β∈0,π2，则α+β的值是()A.3π4B.π4C.7π4D.5π431【多选】(2023·全国·高三专题练习)若tan α+tan β=3-3tan αtan β，则α+β的值可能为()A.π3 B.π6C.-2π3D.-5π632(2023·全国·高三专题练习)已知0<α<π2，cos α+π4 =13．(1)求sin α的值；(2)若-π2<β<0，cos β2-π4=33，求α-β的值．33(2023·全国·高三专题练习)已知角α为锐角，π2<β-α<π，且满足tan α2=13，sin β-α =7210(1)证明：0<α<π4；(2)求β.34(2023·全国·高三专题练习)已知sin π4-α=-55,sin 3π4+β =1010，且α∈π4,3π4,β∈0,π4，求α-β的值为．(四)三角函数式的化简35(2023·福建厦门·统考模拟预测)已知sin α+sin α+2π3=sin π3-α ，则sin α=()A.0B.±217C.±22D.±3236(2023春·山西·高三校联考阶段练习)已知2sin θ+π4 =3cos θ，则sin θsin θ-cos θ=.37(2023·湖北·校联考模拟预测)已知sin x +π4 =-35,3π4<x <5π4，则sin x 1-tan x =()A.21100B.-21100C.7280D.-728038(2023·全国·高三专题练习)已知θ≠k π+π4k ∈Z ，且cos2θcos 3π2-θ=cos θ-sin θ，则tan θ-π4-tan2π2-θ =()A.83B.53C.-13D.-13339(2023·湖南长沙·长郡中学校考一模)已知α,β∈0,π2,sin (2α+β)=2sin β ，则tan β的最大值为()A.12B.33C.22D.3240(河南省部分学校2023届高三高考仿真适应性测试理科数学试题)已知向量a=2cos75°,2sin75°，b =cos15°,-sin15° ，且(2a +b )⊥(a -λb )，则实数λ的值为()A.8B.-8C.4D.-441(2023·陕西·统考一模)在△ABC 中，点D 是边BC 上一点，且AB =4，BD =2.cos B =1116，cos C =64，则DC =.42【多选】(2023·江苏南通·模拟预测)重庆荣昌折扇是中国四大名扇之一，其精雅宜士人，其华灿宜艳女，深受各阶层人民喜爱.古人曾有诗赞曰：“开合清风纸半张，随机舒卷岂寻常；金环并束龙腰细，玉栅齐编凤翅长”.荣昌折扇平面图为下图的扇形COD ，其中∠COD =2π3，OC =3OA =3，动点P 在CD 上(含端点)，连结OP 交扇形OAB 的弧AB 于点Q ，且OQ =xOC +yOD，则下列说法正确的是()A.若y =x ，则x +y =23B.若y =2x ，则OA ⋅OP=0C.AB ⋅PQ≥-2D.PA ⋅PB ≥11243(广东省潮州市2023届高三二模数学试题)在锐角△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，已知3tan A tan C =tan A +tan C +3.(1)求角B 的大小；(2)求cos A +cos C 的取值范围.考点二二倍角公式(一)给角求值44【多选】(2023·全国·高三专题练习)下列等式成立的是()A.sin275°-cos275°=32B.12sin15°+32cos15°=22C.sin75°cos75°=14D.1-tan15°1+tan15°=3345(2023·河南开封·开封高中校考模拟预测)4sin40°-tan40°sin75°-cos75°sin75°+cos75°的值为()A.66B.12C.63D.146(2023·重庆·统考模拟预测)式子2sin18°3cos29°-sin29°-1cos6°+3sin6°化简的结果为()A.12B.1C.2sin9°D.247(2023·全国·高三专题练习)公元前6世纪，古希腊的毕达哥拉斯学派通过研究正五边形和正十边形的作图，发现了黄金分割值约为0.618，这一数值也可以表示为m=2sin18°，若m2+n=4，m n2cos227°-1 =.48(2023·全国·高三专题练习)若λsin160°+tan20°=3，则实数λ的值为()A.4B.43C.23D.433(二)给值(式)求值49【多选】(2023·山西·校联考模拟预测)已知sin x=35，其中x∈π2,π，则()A.tan x=-43B.cos x2=1010C.sin2x=-2425D.cos x-π4=-21050(2023·福建泉州·校考模拟预测)已知cosα=-35,π2≤α≤π，则cos2α+π4=．51(2023秋·湖南衡阳·高三衡阳市一中校考期中)已知sinα-cosα=-23，则sin2α=．52【多选】(2023·全国·高三专题练习)已知cosα+β=-55，cos2α=-45，其中α，β为锐角，则以下命题正确的是()A.sin2α=35B.cosα-β=-2255C.cosαcosβ=510D.tanαtanβ=1353(2023春·山西太原·高三山西大附中校考阶段练习)已知α∈0,π，cosα=-35，则cos2α2+π4=．54(2023秋·辽宁葫芦岛·高三统考期末)已知α∈0,π2，sin2α=cosπ4-α，则cos2α的值为()A.0B.12C.32D.-3255(2023·全国·高三专题练习)已知sinαsinπ3-α=3cosαsinα+π6，则cos2α+π3=()A.-32B.-1 C.12D.3256(2023·全国·高三专题练习)已知cos2π4+α=45，则sin2α=()A.35B.-35C.15D.-15(三)给值求角57(2023·全国·高三专题练习)已知tan α=13,tan β=-17,且α,β∈(0,π)，则2α-β=()A.π4B.-π4C.-3π4D.-3π4或π458(2023·全国·高三专题练习)若α∈0,π ，cos2α=sin 2α2-cos 2α2，则α=．(四)与同角三角函数的基本关系综合59(2023·全国·高三专题练习)已知α∈π4,π2，且sin2α=45，则3sin α-cos α4sin α+2cos α=60(2023·海南·校联考模拟预测)已知tan α=2，则1-3cos 2αsin2α=．61(2023秋·四川成都·高三四川省成都市玉林中学校考阶段练习)已知tan α=2，则sin2αsin 2α+sin αcos α-cos2α-1的值为()A.12B.1C.2D.-1(五)与诱导公式的综合62(2023春·江西南昌·高三统考开学考试)已知tan (π-α)=22，则sin2α=()A.429B.229C.-229D.-42963(2023·全国·高三专题练习)若cos π3-2x =-78，则sin x +π3的值为( ).A.14B.78C.±14D.±7864(2023·河北·统考模拟预测)已知sinα-π6=-25，则cos2α+5π3=()A.825B.1725C.255D.5565(2023·湖北武汉·统考二模)已知sinα+π3=35，则sin2α+π6=()A.2425B.-2425C.725D.-725(六)利用二倍角公式化简求值66(2023·全国·高三专题练习)已知tanα=3，则sinα-π4cosα+π4sin2α=．67(2023·全国·高三专题练习)若sinθ1-cosθ=2，则1+2sin2θ+3cos2θ1-2sin2θ+3cos2θ=()A.5B.43C.2D.468(2023·全国·高三专题练习)已知函数f x =sin2x+cos2x-2sinπ-xcosπ+xsin9π2-x-cos13π2+x．(1)求fπ12的值；(2)已知fα =23，求sin2α的值．考点三辅助角公式的应用69(2023·全国·高三专题练习)函数y =cos x +cos x -π3x ∈R 的最大值为，最小值为.70(2023·陕西铜川·统考二模)已知函数f x =cos x +π2 cos x +π4，若x ∈-π4,π4，则函数f x 的值域为.71(2023·山东泰安·统考二模)已知sin α+3cos α=233，则sin 5π6-2α =.72(2023·湖北荆门·荆门市龙泉中学校联考模拟预测)若sin 2α+π6+cos2α=-3，则tan α=.73(2023·辽宁丹东·统考二模)若cos α≠0,2(sin2α+5cos α)=1+cos2α，则tan2α=()A.-43B.-34C.34D.4374(2023秋·福建莆田·高三校考期中)已知函数f (x )=23sin x cos x -2cos 2x +1.(1)求函数f (x )的最小正周期及单调递增区间；(2)求函数f (x )在区间-5π12,π6的值域；考点四简单的三角恒等变换(一)半角公式的应用75(2023秋·河北石家庄·高三统考期末)已知1+cos θsin θ=33，则tan θ2=.76(2023·全国·高三专题练习)若α∈0,π2 ，sin α2-cos α=tan α2，则tan α=( )．A.33B.3C.34D.6277(2023·全国·高三专题练习)若cos α=-45，α是第三象限的角，则1-tan α21+tan α2=()A.2B.12C.-2D.-1278(2023·浙江·校联考二模)数学里有一种证明方法叫做Pr oofwithoutwords ，也被称为无字证明，是指仅用图象而无需文字解释就能不证自明的数学命题，由于这种证明方法的特殊性，无字证时被认为比严格的数学证明更为优雅与有条理.如下图，点C 为半圆O 上一点，CH ⊥AB ，垂足为H ，记∠COB =θ，则由tan ∠BCH =BHCH可以直接证明的三角函数公式是()A.tanθ2=sin θ1-cos θB.tanθ2=sin θ1+cos θC.tanθ2=1-cos θsin θD.tanθ2=1+cos θsin θ(二)三角恒等式的证明79(2023·全国·高三专题练习)已知α，β∈0,π2 ，且满足sin βsin α=cos α+β ．(1)证明：tan β=sin αcos α1+sin 2α；(2)求tan β的最大值．80(2023·高三课时练习)小明在一次研究性学习中发现，以下五个式子的值都等于同一个常数．①sin213°+cos217°-sin13°cos17°；②sin215°+cos215°-sin15°cos15°；③sin218°+cos212°-sin18°cos12°；④sin2-18°cos48°；+cos248°-sin-18°⑤sin2-25°+cos255°-sin-25°cos55°．(1)请依据②式求出这个常数；(2)相据(1)的计算结果，将小明的发现推广为三角恒等式，并证明你的结论．81(2023春·江苏宿迁·高三校考阶段练习)已知△ABC为斜三角形．(1)证明：tan A+tan B+tan C=tan A tan B tan C；(2)若△ABC为锐角三角形，sin C=2sin A sin B，求tan A+tan B+tan C的最小值．(三)三角恒等变换的综合问题82(2023春·北京·高三清华附中校考期中)已知函数f x =sin x +cos x 2-2sin 2x .(1)求函数f x 的最小正周期和单调递增区间；(2)求函数f x 在区间0,π2上的最大值和最小值，并求相应的x 的值.83(2023·上海浦东新·统考三模)已知向量a =3sin x ,cos x ，b =sin x +π2,cos x .设f x =a ⋅b .(1)求函数y =f x 的最小正周期；(2)在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c .若f A =1，b =4，三角形ABC 的面积为23，求边a 的长.84(2023·浙江绍兴·统考模拟预测)在△ABC 中，a ,b ,c 分别是角A ,B ,C 的对边，且满足a +b +c a +b -c =3ab .(1)求角C 的大小；(2)若△ABC 是锐角三角形，求a +2bc的取值范围.85(2023春·四川成都·高三成都外国语学校校考期中)已知向量a =sin x +π6,cos 2x ，b =cos x ,-1 ．设函数f x =2a ⋅b +12，x ∈R ．(1)求函数f x 的解析式及其单调减区间；(2)若将y =f x 的图像上的所有点向左平移π4个单位，再把所得图像上所有点的横坐标伸长为原来的2倍(纵坐标不变)，得到函数h x 的图像．当x ∈m ,m +π2(其中m ∈0,π2 )时，记函数h x 的最大值与最小值分别为h x max 与h x min ，设φm =h x max -h x min ，且使对∀m ∈0,π2都有k ≥φm 成立，求实数k 的最小值．86(2023春·四川成都·高三成都市锦江区嘉祥外国语高级中学校联考期中)嘉祥教育秉承“为生活美好､社会吉祥而努力”的企业理念及“坚韧不拔､创造第一”的企业精神，经过30年的发展和积累，目前已建设成为具有高度文明素质和良好社会信誉的综合性教育集团.某市有一块三角形地块，因发展所需，当地政府现划拨该地块为教育用地，希望嘉祥集团能帮助打造一所新的教育品牌学校.为更好地利用好这块土地，集团公司决定在高三年级学生中征集解决方案.如图所示，AB=BC=AC=2km,D是BC中点，E､F分别在AB､AC上，△CDF拟建成办公区，四边形AEDF拟建成教学区，△BDE拟建成生活区，DE和DF拟建成专用通道，∠EDF=90°，记∠CDF=θ.(1)若θ=30°，求教学区所在四边形AEDF的面积；(2)当θ取何值时，可使快速通道E-D-F的路程最短？最短路程是多少？三角恒等变换4种常见考法归类高频考点考点一两角和与差的正弦、余弦和正切公式(一)给角求值(二)给值(式)求值(三)给值求角(四)三角函数式的化简(五)两角和与差的正弦、余弦、正切公式的综合应用考点二二倍角公式(一)给角求值(二)给值(式)求值(三)给值求角(四)与同角三角函数的基本关系综合(五)与诱导公式的综合(六)利用二倍角公式化简求值考点三辅助角公式的应用考点四简单的三角恒等变换(一)半角公式的应用(二)三角恒等式的证明(三) 三角恒等变换的综合问题解题策略1.两角和与差的正弦、余弦和正切公式(1)两角和与差的正弦、余弦和正切公式(和角、差角公式)C(α-β)cos(α-β)=cosαcosβ+sinαsinβC(α+β)cos(α+β)=cos_αcos_β-sin_αsin_β记忆口诀：1、余余正正符号反2、同名相乘、加减相反3、谐音：“吃吃睡睡，颠倒黑白”S(α-β)sin(α-β)=sin_αcos_β-cos_αsin_β(异名相乘、加减一致)S(α+β)sin(α+β)=sin_αcos_β+cos_αsin_β(异名相乘、加减一致)记忆口诀：1、正余余正符号同2、异名相乘、加减一致3、谐音：“上错厕所，一一对应”T (α-β)tan(α-β)=tanα-tanβ1+tanαtanβ；(两式相除、上同下异)．变形：①tanα-tanβ=tan(α-β)(1+tanαtanβ)②tanα·tanβ=tanα-tanβtan(α-β)-1T (α+β)tan (α+β)=tan α+tan β1-tan αtan β；(两式相除、上同下异)．变形：①tan α+tan β=tan (α+β)(1-tan αtan β)②tan α·tan β=1-tan α+tan βtan (α+β)(2)二倍角的正弦、余弦、正切公式(倍角公式)二倍角是相对的，如：α2是α4的2倍，3α是3α2的2倍.S 2αsin 2α=2sin _αcos _α；变形：sin αcos α=12sin2α，cos α=sin2α2sin α，⇒1±sin2α=sin 2α+cos 2α±2sin αcos α=(sin α±cos α)2C 2αcos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α；变形：cos 2α=1+cos2α2，sin 2α=1-cos2α2T 2αtan 2α=2tan α1-tan 2α(α≠k π+π2且α≠k π2+π4，k ∈Z )2.简单的三角恒等变换(1)降幂公式sin 2α=1-cos2α2.cos 2α=1+cos2α2.sin αcos α=12sin2α.(2)升幂公式1+cos α=2cos 2α2. 1-cos α=2sin 2α2. 1+sin α=sin α2+cos α2 2. 1-sin α=sin α2-cos α22.注：1+cos2α=2cos 2α；1−cos2α=2sin 2α；1+sin2α=(sin α+cos α)2；1−sin2α=(sin α−cos α)2(3)万能公式sin α=2tan α21+tan 2α2,cos α=1-tan 2α21+tan 2α2,tan α=2tan α21-tan 2α2(4)其他常用变式sin2α=2sin αcos αsin 2α+cos 2α=2tan α1+tan 2α；cos2α=cos 2α−sin 2αsin 2α+cos 2α=1−tan 2α1+tan 2α；cos 4x -sin 4x =(cos 2x +sin 2x )(cos 2x -sin 2x )=cos2x 3.辅助角公式(同角异名1次)a sin α+b cos α=a 2+b 2sin (α+φ)，其中cos φ=a a 2+b 2，sin φ=b a 2+b 2，或tan φ=ba . 其中φ称为辅助角，它的终边所在象限由点(a ，b )决定．4.半角的正弦、余弦、正切公式(1)sin α2=±1-cos α2.(2)cosα2=±1+cosα2.(3)tanα2=±1-cosα1+cosα=sinα1+cosα=1-cosαsinα.5.常用的拆角、拼角技巧(1)15°=45°-30°=60°-45°=30°2.(2)β=α-a-β，α=(α+β)-β=β-(β-α)，2α=(α+β)+(α-β)，α=12[(α+β)+(α-β)]β=α+β2-α-β2=(α+2β)-(α+β). α-β=(α-γ)+(γ-β)(3)π3-α=π2-π6+α，π6-α=π2-π3+α，π3+α=π-2π3-α，π4+α=π-3π4-α. π4+α=π2-π4-α6. 应用和、差、倍角公式化简求值的策略(1)首先要记住公式的结构特征和符号变化规律．例如两角差的余弦公式可简记为：“同名相乘，符号反”；(2)注意与同角三角函数基本关系、诱导公式的综合应用；(3)注意配方法、因式分解和整体代换思想的应用．　7. 和、差、倍角公式的逆用和变形用的应用技巧(1)逆用公式应准确找出所给式子与公式的异同，创造条件逆用公式；(2)和差角公式变形：sinαsinβ+cos(α+β)=cosαcosβ；cosαsinβ+sin(α-β)=sinαcosβ；tanα±tanβ=tan(α±β)·(1∓tanα·tanβ)；(3)倍角公式变形：降幂公式．(4)tanαtanβ，tanα+tanβ(或tanα-tanβ)，tan(α+β)(或tan(α-β))三者中可以知二求一，且常与一元二次方程根与系数的关系结合命题．　8. 解决非特殊角求值问题的基本思路有：①化非特殊角为特殊角；②化为正负相消的项，消去后求值；③化分子、分母使之出现公约数，进行约分求值；④当有α，2α，3α，4α同时出现在一个式子中时，一般将α向2α，3α(或4α)向2α转化，再求关于2α式子的值．9.三角函数式的化简要遵循“三看”原则注：三角函数式化简、求值的一般思路：异名三角函数化为同名三角函数，异角化为同角，异次化为同次，切化弦，特殊值与特殊角的三角函数互化等. 10. 给值(式)求值的解题策略(1)已知某些角的三角函数值，求另外一些角的三角函数值，要注意观察已知角与所求表达式中角的关系，即拆角与凑角．(2)由于和、差角与单角是相对的，因此解题过程中根据需要灵活地进行拆角或凑角的变换．常见角的变换有：①α=(α-β)+β；②α=α+β2+α-β2；③2α=(α+β)+(α-β)；④2β=(α+β)-(α-β)．(3)当“已知角”有两个时，“所求角”一般表示为两个“已知角”的和或差的形式．(4)当“已知角”有一个时，此时应着眼于“所求角”与“已知角”的和或差的关系，然后应用诱导公式把“所求角”变成“已知角”．(5)给值求值型恒等变换问题，重在对所给条件进行挖掘，如由某角正弦值可得其余弦、正切值，由所给值的符号判断角所在的象限等. 必要时还要进行估算，如锐角α的余弦值为35，由12<35<22，及余弦函数在0，π2上单调递减可知45°<α<60°，从而2α∈(90°，120°)，或3α∈(135°，180°)等. 另外，注意三种主要变换：①变角，通常是“配凑”，常用的角的拆拼有2α=(α+β)+(α-β)，α=(α+β)-β=(α-β)+β等；②变名，通过变换函数名称达到减少函数种类的目的，其手段通常有“切化弦”“升幂与降幂”等；③变式，根据式子的结构特征进行变形，使其更贴近某个公式或某个期待的目标，其手段通常有：“常值代换”如1=tan π4，1=sin 2α+cos 2α“逆用变换公式”“通分约分”“分解与组合”“配方与平方”等. 其中角的变换居核心地位.11. 已知三角函数值求角的解题步骤(1)界定角的范围，根据条件确定所求角的范围．(在给值求角时，一般地选择一个适当的三角函数，根据题设确定所求角的范围，利用三角函数的单调性求出角. 确定角的范围是关键，一定要使所选的函数在此范围内是单调的，必要时，还需根据已知三角函数值缩小角的范围.)(2)求所求角的某种三角函数值．为防止增解最好选取在范围内单调的三角函数(已知三角函数值求角，选三角函数时可按下列规则：(i )已知正切值，常选正切函数；(ii )已知正、余弦值，常选正弦或余弦函数；(iii )若角的范围是0，π2 ，π，3π2 ，常选正、余弦函数；(iv )若角的范围是π2，3π2 或-π2，π2 ，常选正弦函数；(v )若角的范围是(0，π)或(π，2π)，常选余弦函数. )(3)结合三角函数值及角的范围求角．12. 利用半角公式求值的思路(1)看角：若已知三角函数式中的角是待求三角函数式中角的两倍，则求解时常常借助半角公式求解．(2)明范围：由于半角公式求值常涉及符号问题，因此求解时务必依据角的范围，求出相应半角的范围．(3)选公式：涉及半角公式的正切值时，常用tan α2=sin α1+cos α=1-cos αsin α，其优点是计算时可避免因开方带来的求角的范围问题；涉及半角公式的正、余弦值时，常先利用sin 2α2=1-cos α2，cos 2α2=1+cos α2计算．13. 三角恒等式证明的常用方法(1)执因索果法：证明的形式一般是化繁为简．(2)左右归一法：证明左右两边都等于同一个式子．(3)拼凑法：针对题设和结论之间的差异，有针对性地变形，以消除它们之间的差异，简言之，即化异求同．(4)比较法：设法证明“左边-右边=0”或“左边/右边=1”．(5)分析法：从被证明的等式出发，逐步地探求使等式成立的条件，直到已知条件或明显的事实为止，就可以断定原等式成立．考点精析考点一两角和与差的正弦、余弦和正切公式(一)给角求值14(2023·全国·高三专题练习)cos -75° 的值是A.6-22B.6+22C.6-24D.6+24【答案】C【解析】变形cos -75° =cos 45°-120° 后，根据两角差的余弦公式计算可得答案.【详解】cos -75° =cos 45°-120° =cos45°⋅cos120°+sin45°sin120°=22×-12+22×32=6-24，故选：C .【点睛】本题考查了两角差的余弦公式，属于基础题.15(2023·全国·模拟预测)sin20°cos40°+sin70°sin40°=()A.32B.12C.22D.1【答案】A【分析】根据诱导公式及三角恒等变换化简求值即可.【详解】已知可化为：sin20°cos40°+cos20°sin40°=sin 20°+40° =32.故选：A16(2023·广东湛江·统考一模)cos70°-cos20°cos65°=．【答案】-2【分析】根据三角函数的诱导公式和两角和的余弦公式，准确化简，即可求解.【详解】由三角函数的诱导公式和两角和的余弦公式，可得：cos70°-cos20°cos65°=cos (90°-20°)-cos20°cos65°=sin20°-cos20°cos 45°+20°=sin20°-cos20°cos45°cos20°-sin45°sin20°=- 2.故答案为：- 2.17(2023·全国·高三专题练习)sin 220°-cos 220°sin45°cos155°1-sin40°=.【答案】2【分析】根据三角恒等变换公式化简求值即可.【详解】因为sin 220°-cos 220°=sin20°-cos20° sin20°+cos20° ，cos155°=-cos25°=-cos 45°-20° ，1-sin40°=cos 220°+sin 220°-2sin20°cos20°=cos20°-sin20° =cos20°-sin20°，所以sin 220°-cos 220°sin45°cos155°1-sin40°=cos20°+sin20°22cos 45°-20° =cos20°+sin20°22×cos45°cos20°+sin45°sin20°=cos20°+sin20° 12cos20°+sin20°=2故答案为：2.(二)给值(式)求值18(2023·江西九江·统考三模)已知0<α<π2<β<π，且sin α=23，cos β=-75，则cos (α-β)=()A.-115B.-1315C.-41415D.21415【答案】A【分析】先根据0<α<π2<β<π，sin α=23，cos β=-75求出cos α，sin β，再利用两角差的余弦公式求cos (α-β)【详解】解析：∵0<α<π2<β<π，sin α=23，cos β=-75，∴cos α=1-sin 2α=1-29=73，sin β=1-cos 2β=1-725=325，∴cos (α-β)=cos αcos β+sin αsin β=73×-75 +23×325=-115，故选：A .19(江西省九江市2023届高三三模数学(理)试题)已知0<α<β<π，且cos α=13，cos α-β =223，则cos β=()A.89B.79C.429D.0【答案】D【分析】利用三角恒等变换计算即可，注意整体思想的运用.【详解】解法一：∵0<α<π，cos α=13，∴sin α=223，又-π<α-β<0,cos α-β =223⇒-π2<α-β<0，∴sin α-β =-13，∴cos β=cos α-α-β =cos αcos α-β +sin a sin α-β=13×223+223×-13 =0，故选：D ．解法二：∵0<α<π，cos α=13，∴sin α=223，∴cos α-β =sin α，即cos β-α =cos π2-α ∵0<β-α<π，0<π2-α<π2∴β-α=π2-α⇒β=π2,cos β=0，故选：D ．20(2023·陕西榆林·统考模拟预测)若tan α+π4 =15，则tan α=()A.-23B.23C.-13D.13【答案】A【分析】利用正切函数的和差公式即可得解.【详解】因为tan α+π4 =15，所以tan α=tan α+π4 -π4 =15-11+15×1=-23.故选：A .21(山西省晋中市2023届高三三模数学试题(A 卷))已知α，β为锐角，且tan α=2，sin α+β =22，则cos β=()A.-31010B.31010C.-1010D.1010【答案】D【分析】由条件，结合同角关系求sin α,cos α，再由特殊角三角函数值求α+β，再利用两角差的余弦公式求cos β.【详解】因为tan α=2，所以sin α=2cos α，又sin 2α+cos 2α=1，α为锐角，所以sin α=255，cos α=55，且α>π4．因为α，β为锐角，α>π4，所以π4<α+β<π，又sin (α+β)=22，所以α+β=3π4，故cos β=cos 3π4-α =cos 3π4cos α+sin 3π4sin α=1010．故选：D .22(河南省名校青桐鸣2023届高三下学期4月联考文科数学试题)已知tan αtan β=2，cos α+β =-15，则cos α-β =()A.35B.-35C.115D.-115【答案】A【分析】根据切化弦以及两角和差公式解出sin αsin β,cos αcos β，代入两角差的余弦公式即可.【详解】由题意可得tan αtan β=sin αsin βcos αcos β=2cos α+β =cos αcos β-sin αsin β=-15，即sin αsin β=2cos αcos βcos αcos β-sin αsin β=-15 ，sin αsin β=25cos αcos β=15，故cos α-β =cos αcos β+sin αsin β=35.故选：A .23(2023·全国·高三专题练习)若α∈π2,3π4，cos α-π4 =210，则sin α+π3=【答案】4-3310【分析】根据同角三角函数的基本关系求出sin α-π4，由cos α=cos π4+α-π4 求出cos α，从而求出sin α，再利用两角和的正弦公式计算可得.【详解】∵cos α-π4 =210，α∈π2,3π4 ，所以α-π4∈π4,π2，∴sin α-π4 =1-cos 2α-π4 =7210，∴cos α=cos π4+α-π4 =cos π4cos α-π4 -sin π4sin α-π4 =22×210-7210×22=-35，sin α=1-cos 2α=45，所以sin α+π3 =sin αcos π3+cos αsin π3=45×12-35×32=4-3310.故答案为：4-331024【多选】(河北省承德市2023届高三下学期4月高考模拟数学试题)已知0<α<π2<β<π，sin α=13，cos (α+β)=-223，下列选项正确的有()A.sin (α+β)=±13B.cos β=-79C.cos2β=-1781D.sin (α-β)=-2327【答案】BD【分析】根据同角关系以及诱导公式可得可得α+β=π-α，进而可判断A ，根据和差角公司以及二倍角公式即可代入求解BCD .【详解】由于0<α<π2且sin α=13，所以cos α=223，又α+β∈π2,3π2 ，cos (α+β)=-223=-cos α，故α+β=π-α或α+β=π+α，当α+β=π+α时，β=π显然不满足，故α+β=π-α，所以sin (α+β)=13，故A 错误，对于B ，cos β=cos α+β cos α+sin α+β sin α=-223×223+13×13=-79，故B 正确，对于C , cos2β=2cos 2β-1=2×-792-1=1781，故C 错误，对于D ，由B 可知sin β=1-cos 2β=429，所以sin (α-β)=sin αcos β-cos αsin β=13×-79-223×429=-2327，故D 正确，故选：BD25(2023·陕西商洛·统考三模)已知tan (α+β)=3，tan α+π4=-3，则tan β=()A.-15B.15C.-17D.17【答案】D【分析】由tan α+π4 =-3求得tan α，再使用凑配角由tan (α+β)=3求tan β.【详解】tan α+π4 =1+tan α1-tan α=-3，解得tan α=2，则tan β=tan [(α+β)-α]=tan (α+β)-tan α1+tan (α+β)tan β=17．故选：D 26(2023·江西上饶·校联考模拟预测)已知α、β均为锐角，且sin α=2sin β，2cos α=cos β，则sin α-β =.【答案】35/0.6【分析】利用题目信息以及平方关系分别计算得α、β角的正弦、余弦值，再利用两角差的正弦公式即可求得结果.【详解】因为sin α=2sin β，2cos α=cos β，即cos α=12cos β，所以sin 2α+cos 2α=4sin 2β+14cos 2β=1，又4sin 2β+14cos 2β=154sin 2β+14sin 2β+14cos 2β=1，即sin 2β=15，则cos 2β=45，又α、β均为锐角，所以sin β=55，cos β=255，所以sin α=255，cos α=55，所以sin α-β =sin αcos β-cos αsin β=255×255-55×55=35.故答案为：35(三)给值求角27(2023·全国·高三专题练习)已知α,β都是锐角，cos α=17,cos (α+β)=-1114，则β=.【答案】π3/60°【分析】要求β，先求cos β，结合已知可有cos β=cos [(α+β)-α]，利用两角差的余弦公式展开可求.【详解】∵α、β为锐角，∴0<α+β<π∵cos α=17，cos (α+β)=-1114∴sin α=1-cos 2α=437，sin (α+β)=1-cos 2α+β =5314∴cos β=cos [(α+β)-α]=cos (α+β)cos α+sin (α+β)sin α=-1114 ×17+5314×437=12由于β为锐角，∴β=π3故答案为：π328(2023·全国·高三专题练习)已知cos α=17，cos (α-β)=1314，若0<β<α<π2，则β=．【答案】π3【详解】因为cos α=17,0<α<π2,所以sin α=437,又因为0<α-β<π2,所以sin (α-β)=3314,所以sin β=sin [α-(α-β)]=sin αcos (α-β)-cos αsin (α-β)=437×1314-17×3314=32,又因为0<β<π2,所以β=π3.29(2023·河南·校联考模拟预测)设tan α，tan β是方程x 2+33x +4=0的两根，且α,β∈-π2,π2，则α+β=( )．A.π3B.-2π3C.π3或-2π3D.2π3【答案】B【分析】利用两角和的正切公式求解即可.【详解】因为tan α，tan β是方程x 2+33x +4=0的两根，所以tan α+tan β=-33,tan αtan β=4,所以tan (α+β)=tan α+tan β1-tan αtan β=3，因为tan α+tan β=-33,tan αtan β=4,所以tan α<0,tan β<0,且α,β∈-π2,π2，所以α,β∈-π2,0 ，所以α+β∈-π,0 ，所以α+β=-2π3，故选:B .30(2023·全国·高三专题练习)已知cos α=255，sin β=1010，且α∈0,π2 ，β∈0,π2，则α+β的值是()A.3π4B.π4C.7π4D.5π4。

简单的三角恒等变换专题及答案

简单的三角恒等变换专题及答案简单的三角恒等变换专题一、选择题1.已知sinα＝5115，则cos(π－2α)＝()。

答案：B。

通过sinα和cos(π－2α)的关系，可以得到cos(π－2α)＝－sinα＝－(1/5115)。

2.sin70°/(2cos10°－sin20°)的值是()。

答案：C。

通过三角函数的恒等变换，可以将sin70°/(2cos10°－sin20°)化简为sin70°/cos80°，再使用tan的定义式，得到tan70°=sin70°/cos70°=sin70°/sin10°cos80°=sin70°/sin10°sin10°=1/sin10°=3.3.若sin76°＝m，用含m的式子表示cos7°为()。

答案：B。

通过三角函数的恒等变换，可以得到cos(π/2－76°)＝sin76°＝m，即cos14°＝m，再通过三角函数的恒等变换，可以得到cos7°＝2cos2(7°)－1＝2cos2(14°)cos(π/2－14°)－1＝2(1－sin2(14°))－1＝1－2sin2(14°)＝1－2(cos14°)2＝1－2m2.4.若cos2α＝－2，则sinα＋cosα的值为sin(7π/4)()。

答案：B。

通过cos2α的值可以得到sin2α＝1－cos2α＝3，再通过三角函数的恒等变换，可以得到sinα＋cosα＝√2sin(π/4＋α)＝√2sin(π/4＋α－2π)＝√2sin(7π/4－α)。

5.已知f(x)＝2tanx－2/(x＋π/12)，则f(π/6)的值为()。

答案：D。

专题4.3 三角函数--简单的三角恒等变换(有详细答案)

专题4.3 三角函数---简单的三角恒等变换【考点定位】2020考纲解读和近几年考点分布一、简单的三角恒等变换（一）两角和与差的正弦、余弦和正切公式：⑴()cos cos cos sin sin αβαβαβ-=+；⑵()cos cos cos sin sin αβαβαβ+=-； ⑶()sin sin cos cos sin αβαβαβ-=-；⑷()sin sin cos cos sin αβαβαβ+=+； ⑸()tan tan tan 1tan tan αβαβαβ--=+ ⇒ （()()tan tan tan 1tan tan αβαβαβ-=-+）；⑹()tan tan tan 1tan tan αβαβαβ++=- ⇒ （()()tan tan tan 1tan tan αβαβαβ+=+-）．（二）二倍角的正弦、余弦和正切公式：⑴sin22sin cos ααα=．222)cos (sin cos sin 2cos sin 2sin 1ααααααα±=±+=±⇒ ⑵2222cos2cossin 2cos 112sin ααααα=-=-=-⇒升幂公式2sin 2cos 1,2cos 2cos 122αααα=-=+⇒降幂公式2cos 21cos 2αα+=，21cos 2sin 2αα-=． ⑶22tan tan 21tan ααα=-．（三）辅助角公式1、尝试：将以下各式化为只含有正弦的形式，即化为)sin(βα+A ()0A >的形式（11cos 2αα+ （2）sin αα 2、辅助角公式对于一般形式ααcos sin b a +（a 、b 不全为零），如何将表达式化简为只含有正弦的三角形式？sin cos ))a b αααααβ+==+其中辅助角β由cos sin ββ⎧=⎪⎪⎨⎪=⎪⎩β（通常πβ20<≤）的终边经过点(,)a b我们称上述公式为辅助角公式，其中角β为辅助角。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

简单的三角恒等变换专题一、选择题1．已知sin α＝23，则cos(π－2α)＝( )A ．－53B ．－19 C.19 D.532．2cos10°－sin20°sin70°的值是( )A.12B.32 C.3 D. 23．若sin76°＝m ，用含m 的式子表示cos7°为( )A.1＋m 2B.1－m 2 C ．±1＋m2 D.1＋m24．若cos2αsin ⎝ ⎛⎭⎪⎫α＋7π4＝－22，则sin α＋cos α的值为( )A ．－22B ．－12 C.12 D.725．已知f (x )＝2tan x －2sin 2x2－1sin x 2cos x 2，则f ⎝ ⎛⎭⎪⎫π12的值为( )A ．4 3 B.833C ．4D ．86．已知cos ⎝ ⎛⎭⎪⎫π6－α＋sin α＝45，则cos ⎝ ⎛⎭⎪⎫α＋2π3的值是( )A ．－25 B.25 C.4315 D ．－43157．已知α，β∈⎝ ⎛⎭⎪⎫0，π2，满足tan(α＋β)＝4tan β，则tan α的最大值是( )A.14B.34C.34 2D.328．已知tan α＝4，则1＋cos2α＋8sin 2αsin2α的值为( )A ．4 3 B.654 C ．4 D.2339．已知sin2α＝－2425，且α∈⎝ ⎛⎭⎪⎫3π4，π，则sin α＝( ) A.35 B.45 C ．－35 D ．－4510．已知α∈(0，π)，cos ⎝ ⎛⎭⎪⎫α＋π6＝22，则tan2α＝( )A.33 B ．－33C. 3 D ．－ 3二、填空题11． 3tan12°－3(4cos 212°－2)sin12°＝________.12．设α是第二象限角，tan α＝－43，且sin α2<cos α2，则cos α2＝________.13．设α为第四象限的角，若sin3αsin α＝135，则tan2α＝________.14．已知cos ⎝ ⎛⎭⎪⎫π4－α＝1213，α∈⎝ ⎛⎭⎪⎫0，π4，则cos2αsin ⎝ ⎛⎭⎪⎫π4＋α＝________.三、解答题15．已知cos ⎝ ⎛⎭⎪⎫π6＋α·cos ⎝ ⎛⎭⎪⎫π3－α＝－14，α∈⎝ ⎛⎭⎪⎫π3，π2. (1)求sin2α的值； (2)求tan α－1tan α的值．16．已知α，β∈(0，π)，f (α)＝3－2cos2α4sin α.(1)用sin α表示f (α)；(2)若f (α)＝sin β，求α及β的值．简单的三角恒等变换专题答案一、选择题1．已知sin α＝23，则cos(π－2α)＝( )A ．－53 B ．－19 C.19 D.53解析：依题意得cos(π－2α)＝－cos2α＝2sin 2α－1＝2×(23)2－1＝－19，选B.答案：B 2．2cos10°－sin20°sin70°的值是( )A.12B.32 C.3 D. 2 解析：原式＝2cos (30°－20°)－sin20°sin70°＝2(cos30°·cos20°＋sin30°·sin20°)－sin20°sin70°＝3cos20°cos20°＝ 3.答案：C3．若sin76°＝m ，用含m 的式子表示cos7°为( )A.1＋m 2 B.1－m2C ．±1＋m2D.1＋m2解析：∵sin76°＝cos14°＝2cos 27°－1＝m ， ∴cos 27°＝1＋m2，∴cos7°＝1＋m2. 答案：D 4．若cos2αsin ⎝ ⎛⎭⎪⎫α＋7π4＝－22，则sin α＋cos α的值为( ) A ．－22 B ．－12 C.12 D.72 解析：由已知三角等式得cos 2α－sin 2α22(sin α－cos α)＝－22，整理得sin α＋cos α＝12.答案：C5．已知f (x )＝2tan x －2sin 2x 2－1sin x 2cos x 2，则f ⎝ ⎛⎭⎪⎫π12的值为( )A ．4 3 B.833 C ．4 D ．8解析：∵f (x )＝2(tan x ＋cos x sin x )＝2×(sin x cos x ＋cos xsin x) ＝2×1cos x ·sin x ＝4sin2x ，∴f ⎝ ⎛⎭⎪⎫π12＝4sin π6＝8. 答案：D6．已知cos ⎝ ⎛⎭⎪⎫π6－α＋sin α＝45，则cos ⎝ ⎛⎭⎪⎫α＋2π3的值是( )A ．－25 B.25 C.4315 D ．－4315解析：由条件知cos ⎝ ⎛⎭⎪⎫π6－α＋sin α＝⎝ ⎛⎭⎪⎫32cos α＋12sin α＋sin α＝3⎝ ⎛⎭⎪⎫32sin α＋12cos α＝3sin ⎝ ⎛⎭⎪⎫α＋π6＝45，即sin ⎝ ⎛⎭⎪⎫α＋π6＝4315，故cos ⎝ ⎛⎭⎪⎫α＋2π3＝cos ⎝ ⎛⎭⎪⎫α＋π6＋π2＝－sin ⎝ ⎛⎭⎪⎫α＋π6＝－4315. 答案：D7．已知α，β∈⎝ ⎛⎭⎪⎫0，π2，满足tan(α＋β)＝4tan β，则tan α的最大值是( )A.14B.34C.34 2D.32解析：α，β∈⎝ ⎛⎭⎪⎫0，π2，故tan α，tan β>0.由tan(α＋β)＝tan α＋tan β1－tan αtan β＝4tan β得tan α＝3tan β1＋4tan 2β＝34tan β＋1tan β≤34，故选B. 答案：B8．已知tan α＝4，则1＋cos2α＋8sin 2αsin2α的值为( )A ．4 3 B.654 C ．4 D.233解析：1＋cos2α＋8sin 2αsin2α＝2cos 2α＋8sin 2α2sin αcos α＝2＋8tan 2α2tan α＝2＋8×422×4＝654.故选B.答案：B 9．已知sin2α＝－2425，且α∈⎝ ⎛⎭⎪⎫3π4，π，则sin α＝( ) A.35 B.45 C ．－35 D ．－45解析：∵α∈⎝ ⎛⎭⎪⎫3π4，π，∴cos α<0，sin α>0，且|cos α|>|sin α|，又(sin α＋cos α)2＝1＋sin2α＝1－2425＝125，∴sin α＋cos α＝－15，同理可得sin α－cos α＝75，∴sin α＝35，故选A. 答案：A10．已知α∈(0，π)，cos ⎝ ⎛⎭⎪⎫α＋π6＝22，则tan2α＝( )A.33 B ．－33C. 3 D ．－ 3解析：由α∈(0，π)，cos ⎝ ⎛⎭⎪⎫α＋π6＝22，所以α＋π6＝π4，即α＝π12，tan2α＝tan π6＝33，故选A.答案：A 二、填空题 11．3tan12°－3(4cos 212°－2)sin12°＝________.解析：原式＝3sin12°cos12°－32(2cos 212°－1)sin12°＝23⎝ ⎛⎭⎪⎫12sin12°－32cos12°cos12°2cos24°sin12°＝23sin (－48°)2cos24°sin12°cos12°＝－23sin48°sin24°cos24°＝－23sin48°12sin48°＝－4 3. 答案：－4 312．设α是第二象限角，tan α＝－43，且sin α2<cos α2，则cos α2＝________.解析：∵α是第二象限角，∴α2可能在第一或第三象限．又sin α2<cos α2，∴α2为第三象限角，∴cos α2<0，∵tan α＝－43，∴cos α＝－35，∴cos α2＝－1＋cos α2＝－55. 答案：－5513．设α为第四象限的角，若sin3αsin α＝135，则tan2α＝________. 解析：sin3αsin α＝sin (2α＋α)sin α＝sin2αcos α＋cos2αsin αsin α＝135.∴2cos 2α＋cos2α＝135，2cos 2α－1＋cos2α＝85. ∴cos2α＝45.∵2k π－π2<α<2k π，∴4k π－π<2α<4k π(k ∈Z)．又∵cos2α＝45>0，∴2α为第四象限的角，sin2α＝－1－cos 22α＝－35，∴tan2α＝－34.答案：－3414．已知cos ⎝ ⎛⎭⎪⎫π4－α＝1213，α∈⎝ ⎛⎭⎪⎫0，π4，则cos2αsin ⎝ ⎛⎭⎪⎫π4＋α＝________.解析：方法1：由cos ⎝ ⎛⎭⎪⎫π4－α＝1213，得sin α＋cos α＝12213，两边平方，得1＋2sin αcos α＝288169， ∴2sin αcos α＝119169， ∵α∈⎝ ⎛⎭⎪⎫0，π4，∴cos α>sin α，∴cos α－sin α>0，∴cos α－sin α＝(cos α－sin α)2 ＝1－2sin αcos α＝5213， ∴cos2αsin ⎝ ⎛⎭⎪⎫π4＋α＝cos 2α－sin 2α22sin α＋22cos α＝2(cos α－sin α)＝1013. 方法2：sin ⎝ ⎛⎭⎪⎫π4＋α＝sin ⎣⎢⎡⎦⎥⎤π2－⎝ ⎛⎭⎪⎫π4－α＝cos ⎝ ⎛⎭⎪⎫π4－α＝1213，∵α∈⎝ ⎛⎭⎪⎫0，π4，∴0<π4－α<π4，∴sin ⎝ ⎛⎭⎪⎫π4－α＝1－cos 2⎝ ⎛⎭⎪⎫π4－α＝513，∴cos2α＝sin ⎝ ⎛⎭⎪⎫π2－2α＝2sin ⎝ ⎛⎭⎪⎫π4－αcos ⎝ ⎛⎭⎪⎫π4－α＝120169，∴cos2αsin ⎝ ⎛⎭⎪⎫π4＋α＝1013. 答案：1013三、解答题15．已知cos ⎝ ⎛⎭⎪⎫π6＋α·cos ⎝ ⎛⎭⎪⎫π3－α＝－14，α∈⎝ ⎛⎭⎪⎫π3，π2.(1)求sin2α的值； (2)求tan α－1tan α的值．解：(1)cos ⎝ ⎛⎭⎪⎫π6＋α·cos ⎝ ⎛⎭⎪⎫π3－α ＝cos ⎝ ⎛⎭⎪⎫π6＋α·sin ⎝ ⎛⎭⎪⎫π6＋α＝12sin ⎝ ⎛⎭⎪⎫2α＋π3＝－14，即sin ⎝ ⎛⎭⎪⎫2α＋π3＝－12.∵α∈⎝ ⎛⎭⎪⎫π3，π2，∴2α＋π3∈⎝ ⎛⎭⎪⎫π，4π3， ∴cos ⎝ ⎛⎭⎪⎫2α＋π3＝－32，∴sin2α＝sin ⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫2α＋π3－π3 ＝sin ⎝ ⎛⎭⎪⎫2α＋π3cos π3－cos ⎝ ⎛⎭⎪⎫2α＋π3sin π3＝12.(2)∵α∈⎝ ⎛⎭⎪⎫π3，π2，∴2α∈⎝ ⎛⎭⎪⎫2π3，π.又由(1)知sin2α＝12，∴cos2α＝－32.∴tanα－1tanα＝sinαcosα－cosαsinα＝sin2α－cos2αsinαcosα＝－2cos2αsin2α＝－2×－3212＝2 3.16．已知α，β∈(0，π)，f(α)＝3－2cos2α4sinα.(1)用sinα表示f(α)；(2)若f(α)＝sinβ，求α及β的值．解：(1)f(α)＝3－2(1－2sin2α)4sinα＝1＋4sin2α4sinα.(2)∵0<α<π，∴sinα>0.∴f(α)＝sinα＋14sinα≥214＝1，当且仅当sinα＝1 4sinα即sinα＝12时，等号成立．又f(α)＝sinβ≤1，∴f(α)＝1.此时sinα＝14sinα，即sinα＝12，∴α＝π6或5π6.又∵0<β<π，0<sinβ≤1，f(α)≥1，所以f(α)＝sinβ＝1，所以β＝π2.综上可知α＝π6或5π6，β＝π2.。

简单的三角恒等变换专题及答案

专题12 简单的三角恒等变换（解析版）

4.5 简单的三角恒等变换

三角恒等变换大题(含详细解答)

简单的三角恒等变换(含解析)

考向13 简单的三角恒等变换(重点)-备战2023年高考数学一轮复习考点微专题(全国通用)(解析版)

三角恒等变换专题复习带答案

高考数学专题《三角恒等变换》习题含答案解析

专题12 三角恒等变换(纯答案)

三角函数恒等变换练习题及答案详解

4.6简单的三角恒等变换

简单的三角恒等变换

三角恒等变换常考题(含答案)

简单的三角恒等变换

第六节 简单的三角恒等变换

方法技巧专题19 三角恒等变换(解析版)

简单的三角恒等变换(基础知识+基本题型)(含解析)

2024年高考数学专项三角恒等变换4种常见考法归类(解析版)

简单的三角恒等变换专题及答案

专题4.3 三角函数--简单的三角恒等变换(有详细答案)

第六节简单的三角恒等变换