儿童数独入门(一)讲解学习
儿童数独入门一(共8张PPT)
32
24
2
4
3
2
四宫格数独
36
6 54 1
3
4
6
5
3 62 4
45
六宫格数独46832316
8
3
2
9
7
7
9
78 29
5
4
九宫格数独
青少年数独活动—香港
青少年数独活动—印度
儿童数独入门一
“数独”（sudoku）一词来自日语，意思是“单独的数字” 或“只出现一次的数字”。它就是一种填数字游戏，是十 八世纪瑞士数学家欧拉发明的。
第1列 第2列
第3列
第1行
第2行 第3行
“数独”（sudoku）一词来自日语，意思是“单独的数字”或“只出现一次的数字”。 “它数就独是”（一s种ud填ok数u）字一游词戏来，自是日十语八，世意纪思瑞是士“数单学独家的欧数拉字发”或明“只的出。现一次的数字”。 “它数就独是”（一s种ud填ok数u）字一游词戏来，自是日十语八，世意纪思瑞是士“数单学独家的欧数拉字发”或明“只的出。现一次的数字”。 它就是一种填数字游戏，是十八世纪瑞士数学家欧拉发明的。 “数独”（sudoku）一词来自日语，意思是“单独的数字”或“只出现一次的数字”。 它就是一种填数字游戏，是十八世纪瑞士数学家欧拉发明的。 “它数就独是”（一s种ud填ok数u）字一游词戏来，自是日十语八，世意纪思瑞是士“数单学独家的欧数拉字发”或明“只的出。现一次的数字”。 “它数就独是”（一s种ud填ok数u）字一游词戏来，自是日十语八，世意纪思瑞是士“数单学独家的欧数拉字发”或明“只的出。现一次的数字”。 “数独”（sudoku）一词来自日语，意思是“单独的数字”或“只出现一次的数字”。 “数独”（sudoku）一词来自日语，意思是“单独的数字”或“只出现一次的数字”。 它“数就独是”（一s种ud填ok数u）字一游词戏来，自是日十语八，世意纪思瑞是士“数单学独家的欧数拉字发”或明“只的出。现一次的数字”。 “数独”（sudoku）一词来自日语，意思是“单独的数字”或“只出现一次的数字”。 它“数就独是”（一s种ud填ok数u）字一游词戏来，自是日十语八，世意纪思瑞是士“数单学独家的欧数拉字发”或明“只的出。现一次的数字”。 “它数就独是”（一s种ud填ok数u）字一游词戏来，自是日十语八，世意纪思瑞是士“数单学独家的欧数拉字发”或明“只的出。现一次的数字”。 “数独”（sudoku）一词来自日语，意思是“单独的数字”或“只出现一次的数字”。 它“数就独是”（一s种ud填ok数u）字一游词戏来，自是日十语八，世意纪思瑞是士“数单学独家的欧数拉字发”或明“只的出。现一次的数字”。
《小学生数独》课件
区块摒除法
总结词
利用数独中数字的关联关系，将多个可能的数字组合成一个区块，然后排除掉其 他数字的解法。
详细描述
在解题过程中，通过观察和分析数独中数字的关联关系，将多个可能值相同的空 格组合成一个区块，然后利用这个区块排除掉其他数字的可能性。这种方法需要 一定的观察力和逻辑推理能力。
X-Wing法
总结词
简单规则，适合初学者
示例题目
在9x9的棋盘上，将数字1-9填入空格中， 使得每一行、每一列以及每一个3x3的小 方格都包含数字1-9，不重复。
详细描述
初级数独题目通常包含较少的数字，规则 较为简单，适合初学者熟悉数独的基本规 则和解题技巧。
解析
首先，按照基本规则，将数字1-9填入空 格中，然后通过排除法、唯一解法等技巧 解决剩余的空格。
高级题目及解析
高难度挑战，需要综合运用技巧
输入 标题
详细描述
高级数独题目难度较大，需要解题者综合运用各种解 题技巧和推理能力来解决。
总结词
示例题目
除了遵循基本规则和找出只出现一次的三个数字外， 还需要综合考虑其他线索和限制条件，运用多种解题
技巧来逐步解决空格。
解析
在9x9的棋盘上，将数字1-9填入空格中，使得每一行 、每一列以及每一个3x3的小方格都包含数字1-9，不 重复。其中，有三个数字只出现一次。
《小学生数独》ppt课 件
目录
• 数独简介 • 数独基本解法 • 数独题目及解析 • 数独练习和挑战 • 数独进阶技巧和策略
数独简介
01
数独的起源
18世纪欧式解法
全球风靡
数独起源于18世纪的欧式解法，最初 的形式是拉丁方块，是一种在当时流 行的数学游戏。
儿童数独入门(一)
儿童数独入门（一）
戎卫武
一、教学内容：
“数独”（英文名为 SU DOKU）（一）
二、教学目标：
知识与技能：
1、培养学生把握全局的能力。
2、培养学生的观察反应能力。
3、培养学生分析推理能力。
数学思考：通过数独游戏，可以益智，可以获得持久的脑力锻炼。
解决问题：培养学生用排除法思考问题，初步学会的推理分析问题，掌握解决问题的策略。
情感态度与价值观：既在同伴之间的交流与团结协作中，获得肯定，又在独立思考后，获得成就感。
三、教学重、难点：
培养学生的观察和推理能力。
四、教具和学具：
课件数独游戏题纸
五、教学过程：
1、激趣引新：
师：孩子们，你们喜欢玩游戏吗？老师也喜欢玩，今天老师将为你们介绍一款全世界的聪明人都在玩的数学游戏——“数独”游戏。
B、出示课件：回过头来再看看，怎样观察才能很快的开始呢？
小结：不仅要观察行，列，还要观察区。
而且找到提供信息最多的方位开始。
③第三关“画一画”
师：看来你们的本领掌握得很不错，老师对你们进入下一关很有信心，那你们自己呢？好，进入第三关画一画。
师：将圆形，三角形，长方形和五角星形画入方格中，每一行，每一列，每一区都不能重复。
要求：
这道题是画一画，请先思考三十秒后再小组内合作完成。
出示学具纸
一二三四。
小学生数独完整ppt课件
1
什么是九宫格数独
• 问题：观察一下， • 第一行有哪些数字？ • 第二行呢？ • 第三行呢？ • 每列呢？
一个小九宫格里有
一个小
哪些数字
九宫格 可编辑课件PPT
2
标准数独的规则： 在空格内填入数 字，使每行、每 列和每宫内都为 1-9，且不重复。
九宫格数独
可编辑课件PPT
3
四宫格数独
六宫格数独
17
可编辑课件PPT
18
此课件下载可自行编辑修改，此课件供参考！ 部分内容来源于网络，如有侵权请与我联系删除！感谢你的观看！
精选编辑ppt规则吗精选编辑ppt怎么填九宫格数独这一行填的是否重复精选编辑ppt是否重复精选编辑ppt精选编辑ppt10六宫格练习精选编辑ppt11九宫格数独精选编辑ppt12精选编辑ppt13精选编辑ppt14精选编辑ppt15创意数独精选编辑ppt16精选编辑ppt17精选编辑ppt18
可编辑课件PPT
8
试试吧
一找二看三填
六宫格数独
可编辑课件PPT
9
六宫格练习
可编辑课件PPT
10
一找二看三填
哪一行、列、 宫谁余下少
九宫格数独
可编辑课件PPT
11
可编辑课件PPT
12
创 意 数 独
可编辑课件PPT
13可编辑课Biblioteka PPT14创意数独
可编辑课件PPT
15
可编辑课件PPT
16
可编辑课件PPT
可编辑课件PPT
你能想到 四宫格和 六宫格的
规则吗
4
怎么填九宫格数独
这一行填的 数对吗？
28
2
可编辑课件PPT
数独方法及技巧(小图)
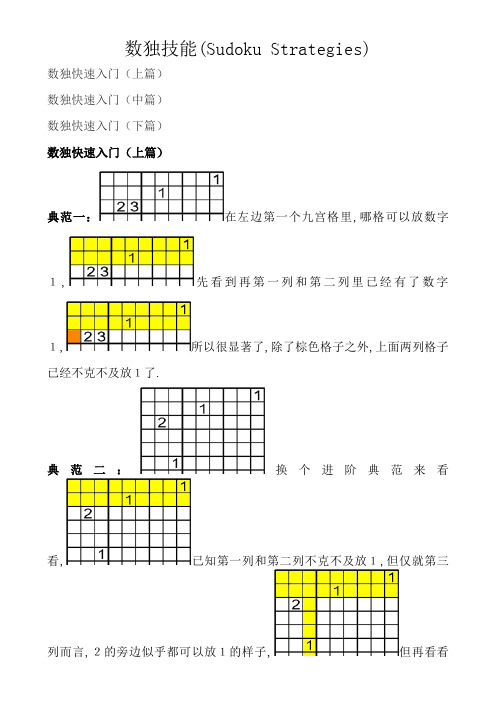
数独技能(Sudoku Strategies)数独快速入门（上篇）数独快速入门（中篇）数独快速入门（下篇）数独快速入门（上篇）典范一：在左边第一个九宫格里,哪格可以放数字１,先看到再第一列和第二列里已经有了数字１,所以很显著了,除了棕色格子之外,上面两列格子已经不克不及放１了.典范二：换个进阶典范来看看,已知第一列和第二列不克不及放１,但仅就第三列而言,２的旁边似乎都可以放１的样子,但再看看被色彩标示的第三行,看到第三行有１之后,就知道棕色格子应当放１.典范三：来个更进阶点的,想想左上角第一个九宫格里,哪一格可以放１,再看先看看前两列,应当不克不及放１,看被色彩标示的第二行与第三行,又是不克不及放１,很显然的,就只有棕色格子能放１.典范四：再看看这个主要典范,想想左上角第一个九宫格里,哪格可以放１,先看看被色彩标示的第二列,再看看被色彩标示的第二行,经由剖析后可知１要放在这棕色格子.典范五：换个轻松点的典范,看看第一列,数字有哪些,显而易见的就是缺１.数独快速入门（中篇）典范一：看看这个比上篇难的,想想１能放在哪里呢,被色彩标示起来的第一列和第一行已经不克不及放１了,就左上角的九宫格而言,在红色标示区域似乎是可以摆１的,但在这里而言,似乎无法决议１放在两格红色区域的哪一格,所以,可以先看看临近的九宫格,发明到棕色格子能放１喔,这时刻就不必疑惑立时写下１.典范二：看看这个有技巧性的,想想１能放在哪里,看到黄色的第一列已经有１,所以不克不及再放１了,就中心的九宫格而言,合理的推论,１必定是在第二列中心红色三格的个中之一了,既然知道第二列的情况,再斟酌黄色区域后,那么可以先肯定右方九宫格的１必定放在这棕色格子.典范三：由上篇的概念再进阶,斟酌这上面三个九宫格,看看可否决议１的地位,黄色标示的第三行已先被清除,就第一个九宫格而言,１必定在红色区域,就黄色标示区域来看,已不克不及再放１了,这时可以立时先决议右上九宫格里的棕色格子是能放１的啦.典范四：看到这左上方九宫格的第一列,就可以立时知道缺了哪两个数字,是不是已经看出红色格子不是１就是９了,但是又看到第二行有１,所以很轻松知道左上棕色格子必定是１,接下来９就肯定在红色格子了.典范五：先看看这第一列,左上方的九宫格里,第一列绝对有１.８.９,再斟酌到第一行黄色区域,看到有８和９,这下就可肯定１绝对放在左上角的棕色格子.数独快速入门（下篇）典范一：来看看这个高等进阶例子,可以先把眼光放在第一列和第一行,看到在黄色区域里都有２和３,所以此黄色区域已经不克不及再放２和３了,这时可以斟酌到左上九宫格里的红色格子能放２和３,再看到第一列和第三列的黄色区域,这黄色区域里已经不克不及放１,在左上九宫格里,能放１的只有红色与棕色格子,但红色格子将会被２和３所占领,所以能肯定棕色格子必定为１.典范二：看看左上方九宫格里,可否由些微线索决议１的地位,起首,看到第一列后先清除５.６.７,又因左上方九宫格里有２.３.４,再清除这三个数字,这下,在左上方九宫格的第一列,只剩下１.８.９可以填,然后,又看到第一行有８和９,所以,棕色格子必定不会是８和９,那么,就只剩下１可以填入啦！•直不雅法(Direct Elimination Techniques)•候选数法(Candidates Elimination Techniques)直不雅法(Direct Elimination Techniques)经常在报章杂志上看到的数独谜题,一般就算再难都可以用直不雅法来解决.它不须要象候选数法(Candidates Elimination Techniques)那样在每个空白的单元格顶用铅笔填上一大堆候选数.你只要有相对锋利的眼光和必定的逻辑剖析才能,就可以精确地把空余的数字逐个填出来.现实上,直不雅法就是对数独游戏规矩的充分应用.固然它其实不如候选数法(Candidates Elimination Techniques)那样壮大,但平日要想领会解决数独谜题的乐趣,应用直不雅法倒是不二之选.直不雅法(Direct Elimination Techniques)具有以下的特色：轻松上手.即等于数独新手,在拿到谜题的一刹那,就可以用直不雅法来解题了.无需帮助.在纸上解题时一般只须要一支钢笔就可以.因为是经由过程推理和逻辑剖析来肯定哪个格填哪个数,或是哪个数填在哪个格里,所以根本不须要猜测.轻易控制.对于直不雅法(Direct Elimination Techniques)中应用的各类算法,可以很快控制并应用于现实中.相对简略.比起候选数法(Candidates Elimination Techniques),它的算法比拟较较简略,当然能解决的谜题的庞杂度也相对要低.在直不雅法(Direct Elimination Techniques)中,经常应用的算法包含：1.单元独一法 ( Sole Position Technique )2.单元清除法 ( Basic Elimination Technique )3.区块清除法 ( Block Elimination Technique )4.独一余数法 ( Sole Number Technique )5.组合清除法 ( Combination Elimination Technique)6.矩形清除法 ( Rectangle Elimination Technique)1.单元独一法 ( Sole Position Technique )这应当算是直不雅法中最简略的办法了.根本上只须要看谜题,推理剖析一概都用不上,这是因为要应用它所需知足的前提十分显著.同样,也恰是因为它简略,所以只能处理很简略的谜题,或是在处理较庞杂谜题的后期才用得上.我们先来看一个例子：在上图中,不雅察行B,可以看到除了[B3]外,其他所有的单元格中都已有了数字,依据数独游戏的规矩,即每行,列或区块中不克不及有反复的数字,则[B3]中能填入的数字只能是行B中所未消失过的,也就是数字3.所以可以毫不迟疑地在[B3]中填入3.这就是单元独一法在行中的应用.这里的单元(Unit, or group),指的是行,列或区块.所以有三种情况：当某行有8个单元格中已稀有字,或当某列有8个单元格中已稀有字,或当某区块有8个单元格中已稀有字.无论是哪种情况,我们都可以很快地在该行,列或区块残剩的空格中填入该单元还未消失过的数字.下面是单元独一法在列中的应用：在第7列中,只有[F7]未填入数字,且这一列中数字8还未消失过.所以[F7] = 8.在区块中也是一样：在肇端于[D7]的区块中,只有[E7]还未填入数字,且这个区块中数字5还未消失过,所以可以立时在[E7]中填入5.单元独一法在解题初期应用的几率其实不高,而在解题后期,跟着越来越多的单元格填上了数字,使得应用这一办法的前提也逐渐得以知足.2.单元清除法 ( Basic Elimination Technique )单元清除法是直不雅法中最经常应用的办法,也是在平凡解决数独谜题时应用最频仍的办法.应用得当的话,甚至可以单独处理中等难度的谜题.应用单元清除法的目标就是要在某一单元（即行,列或区块）中找到能填入某一数字的独一地位,换句话说,就是把单元中其他的空白地位都清除掉落.它对应于候选数法中的隐式独一法.那么要若何清除其余的空格呢？当然照样不克不及忘了游戏规矩,即行,列或区块中不克不及有反复的数字.从另一个角度来懂得,就是假如某行中已经有了某一数字,则该行中的其他地位不成能再消失这一数字.假如某列中已经有了某一数字,则该列中的其他地位不成能再消失这一数字.假如某区块中已经有了某一数字,则该区块中的其他地位不成能再消失这一数字.单纯懂得上面的规矩照样缺乏以解题,但是在实践中这些规矩却可以交叉应用.在现实解题进程中,应用最多也最便利的是对区块的单元清除法,我们可以先看下面这个例子：对于肇端于[D1]的区块,其未填数字的空格有6个之多,假如不应用单元清除法,是很难为这一区块填入任何数字的.这时我们就可以应用行,列及区块的互相关系,即一个单元格既在某一行上,也同时在某一列上以及某一区块中的这种关系来解题.不雅察数字9在谜题中的地位,可以看到它出如今[B2],[A4],[C7],[D8],[I1]和[H9].而这些地位中,只有[B2],[D8]和[I1]与肇端于[D1]的区块有联系关系.因为[I1]=9,它地点的第1列上的其他单元格中不成能再消失9,而区块中的[D1]和[F1]正好也在第1列上,所以这两个单元格填入9的可能性被清除.同理,因为[B2]=9,它地点的第2列中的其他单元格不成能再填入9,而区块中的[D2]和[E2]也正好在第2列上,是以,这两个单元格填入9的可能性也被清除掉落了.再看行D,因为[D8]=9,所以该行上的[D1],[D2]和[D3]也不成能再填入9,而这些单元格正好也在肇端于[D1]的区块中.所以,这个区块中能填入数字9的地位就只剩下了[E3],如许就经由过程清除法找到了答案,即[E3]=9.下面再看一个在行中应用单元清除法的例子：在谜题中不雅察数字4和行H,在行H有5个空单元格无法肯定命字,但是[C3]地位上的4使得其地点的第3列中的其他单元格上不克不及再消失4,所以[H3]不克不及填入 4.[I4]上的4使得其地点的区块中也不克不及再填入4,它帮忙行H清除了两个单元格[H4]和[H6],而第8列上的[E8]中的数字4使得同样位于这一列上的[H8]也清除了填入4的可能.如许,行H中能填入4的地位就只剩下[H9]了.在列中也可以应用单元清除法：在第7列中,我们试图肯定能填入数字1的地位.在行B中,数字1已经出如今[B2]上,所以[B7]不成能再填入数字1了.而位于[D8]的数字1也使得[F7]清除了填入数字1的可能,因为它们位于统一区块中.如许,第7列上就只有[A7]能填入数字1了.经由过程上面的示例,可以看到,要对区块应用单元清除法,须要不雅察与该区块订交的行和列.要对行应用单元清除法,须要不雅察与该行订交的区块和列.要对列应用单元清除法,须要不雅察与该列订交的区块和行.在现实解题进程中,行,列和区块之间的关系其实不象上面这些图中所示的那么显著,所以须要必定的眼光和仔细不雅察.一般来说,先看哪个数字在谜题中消失得最多,就从哪个数字开端下手,找到还未填入这个数字的单元（行,列或区块）,应用已填入该数字的单元格与单元之间的关系,看能不克不及清除一些不成能填入该数字的地位,直到剩下独一的地位.假如畏惧搞不清已经处理过哪些数字的话,可以从数字1开端,从左上角的区块开端一向检讨到右下角的区块,看能不克不及在这些区块中应用单元清除法.然后测试数字2,以此类推.单元清除法是应用得最多的直不雅法,固然在实践中经常会因为粗心而漏掉落很多应用这一办法的机遇,但只要勤加演习,就可以应用自如.3.区块清除法 ( Block Elimination Technique )区块清除法是直不雅法中进阶的技法.固然它的应用规模不如单元清除法那样广泛,但用它可能找到用单元清除法无法找到的解.有时在碰到艰苦无法持续时,只要用一次区块清除法,接下去解题就会所向无敌了.区块清除法现实上是应用区块与行或列之间的关系来实现的,这一点与单元清除法颇为类似.然而,它现实上是一种隐约清除法,也就是说,它其实不象单元清除法那样应用谜题中现有的肯定命字对行,列或区块进行清除,而是在不肯定命字的具体地位的情况下进行清除的.这句话听起来似乎不好懂得,让我们先从一个例子入手,看看区块清除法是怎么应用的.对于上面这个谜题,用根本的单元清除法或是单元独一法都无法再找到解.这时可以测验测验应用区块清除法.我们先从填入数字最多的区块着手,也就是肇端于[G4]的区块,该区块中只有[H6]和[I5]为空,且残剩数字1和2还未填入.如许,我们可以想办法肯定这两个数字的地位.不雅察全局,可以看到[D2]=2,依据单元清除法,它地点的第2列上不克不及再消失数字2,所以[H2]和[I2]将不克不及填入2,这使得肇端于[G1]的区块中数字2可能消失的地位仅剩下[I1]和[I3],见下图：固然我们无法肯定2在肇端于[G1]的区块中的肯定地位,但荣幸的是,能填入2的地位正好都在行I上,也就是说,无论2在[I1]照样在[I3],行I的其他单元格中将不成能再消失数字2,所以可以毫不迟疑地清除在[I5]填入2的可能性,如许,对于肇端于[G4]的区块而言,能填入数字2的地位就只剩下[H6]了.所以[H6]=2.接下来,当然毫无疑问,应用单元独一法,在[I5]填入数字1.先小结一下上面的求解办法：解题时,现实上是在对目标区块（主区块）有影响的区块（帮助区块）中应用单元单元清除法,使帮助区块知足某些前提并能介入对主区块的数字清除.现实应用中,可能消失下面四种情况：当某数字在某个区块中可填入的地位正好都在统一行上,因为该区块中必须要有该数字,所以这一行中不在该区块内的单元格大将不克不及再消失该数字.当某数字在某个区块中可填入的地位正好都在统一列上,因为该区块中必须要有该数字,所以这一列中不在该区块内的单元格大将不克不及再消失该数字.当某数字在某行中可填入的地位正好都在统一区块上,因为该行中必须要有该数字,所以该区块中不在该行内的单元格大将不克不及再消失该数字.当某数字在某列中可填入的地位正好都在统一区块上,因为该列中必须要有该数字,所以该区块中不在该列内的单元格大将不克不及再消失该数字.个中1,2两种情况相对罕有,也比较轻易断定.上面的示例就是第1种情况.下面我们会看到第2种情况的例子：固然在肇端于[A7]的区块中,未填入数字的空单元格多达4个,但我们照样可以轻松地肯定命字5的地位.这是因为在肇端于[G7]的区块中,我们欣喜地发明数字5可能消失的地位正好都在第8列上,这时5的确实地位已经不主要了,因为它已经知足了上面介绍的第2种情况的前提,是以可以介入对肇端于[A7]的区块进行数字清除了.在它的影响下,[A8]和[B8]中填入数字5的可能性已经不消失,因为它们都在第8列上.如许,在肇端于[A7]的区块中,数字5能填入的地位只剩下[A9]和[C9]了.这时,我们再应用单元清除法,经由过程[A4]地位上的数字5再清除其地点行A上的[A9],最终得到能填入5的独一地位[C9].下面看几个比较少见的例子在行C上,数字3的地位可以经由过程下面的办法来肯定：先看行B,应用单元清除法,经由过程[H2]和[F3]地位上的3进行列清除,得到行B中能填入3的地位为[B4]和[B5].恰巧的是,这两个单元格都在肇端于[A4]的区块中,这时已经知足了上述情况3的前提.应用单元清除法的区块清除,则行C上的[C4]和[C5]都不克不及再填入3;再加上[F3]的列清除的配合尽力,最终肯定命字3在行C上的独一地位就是[C1].第4种情况的例子如下：在这个示例中,只是应用单元清除法和单元独一法到这一步就持续不下去了.要想求得数字8在第6列的地位,就必须要借助区块清除法.先看第4列,经由过程位于[C3]和[I8]的数字8的行清除,使8在第4列可能填入的地位只剩下[D4]和[F4],而这两个单元格正好都在肇端于[D4]的区块中.因为第4列不克不及没稀有字8,而数字8假如填在区块中的其他地位（如[D6],[E6]或[F6]）时将迫使[D4]和[F4]上不克不及再填入8,如许会导致第4列没稀有字8.是以,第6列中的[D6],[E6]和[F6]能填入数字8的可能性被清除.如许第6列中就只剩下[B6]能填入8了.现实解题进程中,还会碰着比较庞杂的情况,看下面的谜题：你能肯定命字3在肇端于[A1]的区块中的地位吗？先看位于[C5]的数字3,它不但清除了统一行中[C1]和[C3]中填入3的可能性,也同时清除了统一行中[C8]和[C9]填入3的可能性,这使得在肇端于[A7]的区块中,能填入3的地位只剩下[B8]和[B9],见下图：应用区块清除法,在肇端于[A7]的区块中,无论3在[B8]照样[B9],行B 中的其他地位都不克不及再填入3,所以[B1],[B2]和[B3]都被清除.于是,在肇端于[A1]的区块中,能填入3的地位仅剩下[A1]和[A2]了.但至此我们还无法肯定3的精确地位,这时我们还要借助于其他的帮助区块来进一步清除.不雅察肇端于[D1]的区块,应用[D7]地位上的3清除统一行的[D1],以及用[G3]地位上的3清除统一列的[E3]和[F3],使区块中可能填入3的地位只余[E2]和[F2],刚好这两个地位都在第2列中,相符上面介绍的第2种情况,于是可以把[A2]也清除掉落.最后,我们就可以很肯定地在[A1]中填入数字3了.这个例子同时应用了多个帮助区块同时介入清除.在现实应用中固然这种情况其实不罕有,但却也很多见.症结在于若何能精确辨认并适当应用区块清除法.信任经由过程大量的演习并勤于剖析思虑,这种办法就可以应用自如,得心应手.下面是其他的一些例子,可以帮忙更好地懂得并控制这种技法：4.独一余数法 ( Sole Number Technique )独一余数法是直不雅法中较不经常应用的办法.固然它很轻易被懂得,所以解释这个办法不须要很大篇辐,然而在实践中,却不轻易看出可以或许应用这个办法的前提是否得以知足,从而使这个办法的应用受到限制.与单元独一法比拟,独一余数法是肯定某个单元格能填什么数的办法,而单元独一法是肯定某个数能填在哪个单元格的办法.别的,应用单元独一法的前提十分简略,几乎一目了然.与候选数法比拟,独一余数法相当于显式独一法.固然显式独一法是候选数法中最简略且应用最轻易的办法,但在直不雅法中却正好相反.先看一个例子：对于单元格[G9]应当填入什么数字,就算你把前面介绍的所有直不雅技法都用上,也不得而知.然而,我们经由过程不雅察它地点的行,列和区块,可以发明除了数字2以外,1到9中其他的数字都消失了,个中行G中包含了7,6,9,5,3和8,第9列中包含了数字5,8,7和1,肇端于[G7]的单元格中包含了3,8,4,7,5和1.如许,假如[G9]不填入数字2,就必定会违背游戏“行,列或区块不克不及消失反复数字”的规矩.所以[G9]中的数字必定是2总结一下,就是假如某一单元格地点的行,列及区块中共消失了8个不合的数字,那么该单元格可以肯定地填入还未消失过的数字.怎么样,很简略吧,但在实践中却不那么轻易辨认.看下面的谜题：你能看出来对哪个单元格应用独一余数法吗？还有这个谜题：答案分离是[E6]=9和[I7]=9.一般来说,只有在应用根本的清除办法都掉效的情况下,才试着应用这个办法来解题.5.组合清除法 ( Combination Elimination Technique)组合清除法和区块清除法一样,都是直不雅法中进阶的技法,但它的应用规模要更小一点.一般情况下,根本没有机遇用到这种办法解题,所以要找到响应的例子也都很艰苦.当然,假如你愿望优先以这个技法来解题的话,照样能碰着很多能相符应用组合清除法前提的情况.组合清除法,顾名思义,要斟酌到某种组合.这里的组合既包含区块与区块的组合,也包含单元格与单元格的组合,应用组合的联系关系与排挤的关系而进行某种清除.它也是一种隐约清除法,同样是在不肯定命字的具体地位的情况下进行清除的.下面先看一个例子：对于上面这个谜题,你能肯定命字6在肇端于[G4]的区块中的地位吗？要想获得精确的答案初看起来有些艰苦.因为固然在[G9]和[H3]已经消失了两个6,但是应用它们只能行清除区块中的[G4]和[H6]两个单元格,照样无法肯定6到底是在[I4]照样在[I5]中.这时刻,组合清除法就派上用处了.如今撇开肇端于[G4]的区块,先看它上面的两个区块,即肇端于[A4]和[D4]的区块.这几个区块的配合特色是占领同样的几列,也就是第4列至第6列,是以它们之间的数字会互相直接影响.对于肇端于[A4]的区块,应用[A1]处已有的数字6进行行清除,可以得到这个区块中可能填入6的地位只剩下两个：[B5]和[C6].对于肇端于[D4]的区块,应用[E7]处已有的数字6进行行清除,可以得到这个区块中可能填入6的地位也剩下两个：[F5]和[F6].这时,我们仍无法肯定6在这两个区块中的确实地位.但无妨对可能消失的情况作一下剖析：假设在肇端于[A4]的区块中,[B5]=6,则统一区块中的[C6]必不为6,并且[B5]还将列清除[F5],如许在肇端于[D4]的区块中,只有[F6]=6.假设在肇端于[A4]的区块中,[C6]=6,则统一区块中的[B5]必不为6,并且[C6]还将列清除[F6],如许在肇端于[D4]的区块中,只有[F5]=6.简略地说,只有两种可能：[B5]=6且[F6]=6,或者[C6]=6且[F5]=6.决不会再消失其他的情况.但无论是个中哪一种情况,第5列和第6列都邑有肯定的6出如今这两个区块中,也就是说,第5列和第6列的其他地位不成能再消失数字 6.如许,本来无法肯定的6在肇端于[G4]区块中的地位,一会儿就变得明白了.应用肇端于[A4]和[D4]的区块对肇端于[G4]的区块进行列清除,可以把[I5]清除掉落,如许,就只剩下[I4]可以填入6了.小结一下,组合清除法的要知足的前提如下：假如在横向并行的两个区块中,某个数字可能填入的地位正好都分离占领雷同的两行,则这两行可以被用来对横向并行的另一区块做行清除.假如在纵向并行的两个区块中,某个数字可能填入的地位正好都分离占领雷同的两列,则这两列可以被用来对纵向并行的另一区块做列清除.让我们再看一个例子：要想肯定命字1在肇端于[D4]的单元格中的地位,我们将设法借助于其横向上相邻两个区块的帮忙.应用[I2]的列清除,我们可以把肇端于[D1]的区块中的[E2]和[F2]清除掉落,如许,这个区块中能填入1的地位剩下[D1],[D3]和[E1].应用[H7]的列清除,可以把肇端于[D7]的区块中的[E7]和[F7]清除掉落,再应用[A9]的列清除,可以把这个区块中[E9]和[F9]清除掉落,如许,这个区块中能填入1的地位只剩下[D8]和[E8].固然在肇端于[D1]的区块中,能填入1的地位多达3个,但是它们正好只散布在行D和行E上,并且在肇端于[D7]的区块中能填入1的地位所占领的也是这两行.最终1的地位只可能有三种情况：[D1]=1且[E8]=1;或者[D3]=1且[E8]=1;或者[E1]=1且[D8]=1.无论是哪种情况,行D和行E都邑有肯定的1出如今这两个区块中,也就是说,这两行的其他地位不会再消失 1.于是,借助于这两个区块的行清除,我们可以把肇端于[D4]的区块中的[D4]和[D6]清除掉落,再应用[G4]地位的列清除,最终肯定1的地位在[F6].下面是其他一些应用组合清除法的例子：在实践中,组合清除法的现实应用机遇不如区块清除法多.但是,控制这一技法无疑可以大大进步求解谜题的灵巧性,从而增长解题的乐趣.6.矩形清除法 ( Rectangle Elimination Technique)。
《小学生数独》课件
数独游戏还可以 帮助小学生提高 对数字的敏感度 和认识，增强他 们的数学素养和 解决问题的能力。
通过玩数独，小 学生可以逐渐培 养出对数学的兴 趣和爱好，为将 来的数学学习打 下坚实的基础。
数独游戏能够激发学生对数学 的兴趣
数独游戏能够培养学生的数学 思维和逻辑推理能力
数独游戏能够帮助学生提高数 学成绩和数学素养
总结回顾：在解题结束后，要及时总结回顾，分析错题原因，加深对数独解题方法和策略的理解和 掌握。
掌握基本规则：介绍数独的基本规则和解题技巧，帮助小学生熟悉数独 的基本玩法。
练习题目难度：根据小学生的认知水平，选择适当的数独题目进行练习， 逐步提高难度，帮助小学生逐步提高数独水平。
培养逻辑思维：数独需要具备一定的逻辑思维能力，因此，在帮助小学 生提高数独水平的同时，也要注重培养他们的逻辑思维能力。
PART SEVEN
互动性强：通过PPT的动画和 音效，使学习过程更加生动有 趣。
内容丰富：涵盖了数独的基本 规则、技巧和题目，适合小学 生学习。
易于理解：通过简单的语言和 形象的图片，帮助小学生更好
地理解数独。
拓展性强：可以作为数独爱好 者的入门教材，也可以作为提
高的练习册。
拓展数独教育的内容和形式：将数独教育纳入学校教育体系，增加数独教育的课程和教材，同时开 展线上和线下的数独教育活动，提高数独教育的普及度和影响力。
选择合适的数独题目：根据学生的年龄和水平选择适合的数独题目， 确保活动的难度适中。
制定活动计划：安排好活动的流程和时间，确保活动的顺利进行。
组织活动形式：可以采用个人或团队的形式进行数独比赛，增加活动 的趣味性和互动性。
做好活动总结：对活动进行总结和反思，总结经验教训，为今后的活 动提供参考。
儿童数独入门快速掌握技巧
儿童数独入门快速掌握技巧数独作为一种著名的益智游戏，不仅对大人有益处，对儿童的智力发展也有积极的影响。
通过数独游戏，儿童可以锻炼逻辑思维、推理能力和注意力等多种技能。
本文将介绍一些儿童数独入门的快速掌握技巧，帮助儿童更好地玩转数独。
一、数独基本规则在掌握数独的技巧之前，我们先来了解一下数独的基本规则。
数独是一个9x9的九宫格游戏，九宫格又划分为9个3x3的小方格。
每个小方格内都需要填入1至9的数字，保证每行、每列和每个小方格内的数字都不重复。
二、从已知数字入手在解决数独难题时，始终从已知数字入手是一个重要的技巧。
找到已经给出的数字，并且确定其位置对解题过程有很大的帮助。
先将已知数字填入相应的格子，然后再根据基本规则进行推理和判断。
三、行、列和九宫格的判断在填写数独时，我们需要根据基本规则来判断每个格子应该填入的数字。
行、列和九宫格的判断是一个重要的技巧。
首先，在同一行的其余格子中，我们要避免填写已经出现过的数字；其次，在同一列的其余格子中，也要避免填写已经出现过的数字；最后，在同一个九宫格的其余格子中，同样不能填写已经出现过的数字。
四、排除法排除法是解决数独难题中常用的一种技巧。
通过观察已填入数字的格子，我们可以排除其他数字的可能性，从而更快地解决难题。
例如，如果某个小方格已经填入了1、2和3，则可以排除该小方格中的其他数字。
同样地，如果某一行或列已经填入了1、2和3，则可以在该行或列中排除这些数字的其他位置。
五、试错法当遇到一些比较难的数独谜题时，试错法是另一种有效的解题技巧。
试错法就是通过尝试填入数字，不断进行推理和判断，直到找到正确解答。
在试错法中，我们需要具备耐心和细心的品质，不断尝试不同的数字组合，直到找到正确的答案。
六、不间断的练习除了上述的技巧之外，不间断的练习也是快速掌握数独技巧的关键。
不论是简单的数独还是复杂的数独，只有通过大量的练习，才能更加熟练地掌握解题方法和技巧。
建议儿童每天都能抽出一些时间来进行数独的练习，逐渐提高解题的速度和准确性。
幼儿数独的方法与技巧
幼儿数独的方法与技巧
幼儿数独是一种适合幼儿学习逻辑思维和数学的益智游戏。
以下是一些幼儿玩数独的方法与技巧：
1. 从简单开始：给幼儿选择一些简单的数独题目，每个题目中的数字不宜太多，让他们先体验一下填数字的乐趣。
2. 观察数字排列：教导幼儿观察数独格子中已经填入的数字，找出规律和关联，帮助他们更快地填写其他格子中的数字。
3. 试填数字：鼓励幼儿尝试在空格中填入数字，然后观察填入数字对其他格子的影响，这有助于培养他们的逻辑思维能力。
4. 尝试不同方法：让幼儿尝试不同的填数字方法，例如从1到9逐个尝试填入，或者根据已有的数字逆向思考，找到合适的数字填入空格。
5. 错误纠正：当幼儿填错数字时，及时纠正他们的错误，并告诉他们正确的填写方法，以避免形成错误的习惯。
6. 时间管理：对于较大的数独题目，可以适当设置一个时间限制，让幼儿在规定的时间内尽可能填写更多的数字，从而培养他们的时间管理能力。
总的来说，幼儿数独的方法与技巧需要注重启发幼儿的逻辑思维和观察力，同时在游戏中培养他们的耐心和毅力。
在玩数独的过程中，家长或老师应该给予适当的引导和帮助，让幼儿在游戏中获得快乐的学习体验。
数独入门到精通知识讲解
目录数独快速入门（上篇） (2)数独快速入门（中篇） (5)数独快速入门（下篇） (10)WXYZ形态匹配法（WXYZ-wing) (12)三链数删减法(Swordfish) (14)XYZ形态匹配法（XYZ-wing) (16)XY形态匹配法（XY-wing） (19)矩形对角线法(X-wing) (24)隐式四数集法(Hidden Quad) (25)隐式三数集法(Hidden Triplet) (27)隐式数对法(Hidden Pair) (29)显式四数集法(Naked Quad) (31)显式唯一法(Naked Single) (33)隐式唯一法(Hidden Single) (34)区块删减法(Intersection Removal) (36)显式数对法(Naked Pair) (38)显式三数集法(Naked Triplet) (40)数独快速入门（上篇）范例一：在左边第一个九宫格里，哪格可以放数字１，先看到再第一列和第二列里已经有了数字１，所以很明显了，除了棕色格子之外，上面两列格子已经不能放１了。
范例二：换个进阶范例来看看，已知第一列和第二列不能放１，但仅就第三列而言，２的旁边似乎都可以放１的样子，但再看看被颜色标示的第三行，看到第三行有１之后，就知道棕色格子应该放１。
范例三：来个更进阶点的，想想左上角第一个九宫格里，哪一格可以放１，再看先看看前两列，应该不能放１，看被颜色标示的第二行与第三行，又是不能放１，很显然的，就只有棕色格子能放１。
范例四：再看看这个重要范例，想想左上角第一个九宫格里，哪格可以放１，先看看被颜色标示的第二列，再看看被颜色标示的第二行，经过分析后可知１要放在这棕色格子。
范例五：换个轻松点的范例，看看第一列，数字有哪些，显而易见的就是缺１。
数独快速入门（中篇）范例一：看看这个比上篇难的，想想１能放在哪里呢，被颜色标示起来的第一列和第一行已经不能放１了，就左上角的九宫格而言，在红色标示区域似乎是可以摆１的，但在这里而言，似乎无法决定１放在两格红色区域的哪一格，所以，可以先看看邻近的九宫格，发现到棕色格子能放１喔，这时候就不用怀疑马上写下１。
数独启蒙四宫格入门及技巧
四宫格数独（32题）
笔者整理了一些四宫格基础数独（只看行列）以及含有宫的数独，难度递增，由入门到进阶。
附带教学方法。
适用于幼儿园以及一年级或者未接触过数独的朋友们。
一、只看行列的四宫格数独。
方法：
1、三个只缺一个能直接确定，能确定的先确定。
2、如果没有只空一个的，先选空格少的，比如说空两格的，行列一起看进行排除。
134
13 321 432124
14
3
412
1
312
32 143
13 241 12 34
34 21
3
431
1
241 143
2
42
41
4
24
34 41
12 2
2 3
4
4
2
2
1 2
二、行列宫都要看
方法：
1、行、列、宫内只差一个，可以先确定
2、如果没有只空一个的，先选空格少的，比如说空两格的，行列一起看进行排除。
3、行列一起排除不了还可以结合宫一起看。
小学生数独技巧从入门到精通(双色版)PPT模板
10 九六字（6×6）连体数独
九六字（6×6） 连体数独
一、六字连体数独规则 二、解题方法 本章练习题
1 标准数独
一、九字标准数独规则 二、解题方法 本章练习题
12 习题答案
习题答案
一、四字连体数独规则 二、解题方法 本章练习题
07 六五字（5×5）标准数独
六五字（5×5） 标准数独
一、五字标准数独规则 二、解题方法 本章练习题
08 七五字（5×5）异形数独
七五字（5×5） 异形数独
一、五字异形数独规则 二、解题方法 本章练习题
09 八六字（6×6）标准数独
八六字（6×6） 标准数独
04 三四字（4×4）对角线四宫 阵数独
三四字（4×4） 对角线四宫阵数独
一、四字对角线四宫阵数独规则 二、解题方法 本章练习题
05 四四字（4×4）异形四宫阵 数独
四四字（4×4） 异形四宫阵数独
一、四字异形四宫阵数独规则 二、解题方法 本章练习题
06 五四字（4×4）连体数独
五四字（4×4） 连体数独
01
一习题答案
02
二习题答案
03
三习题答案
04
四习题答案
05
五习题答案
06
六习题答案
单击此处添加标题
单击此处添加文本具体内 容，简明扼要的阐述您的 观点。根据需要可酌情增 减文字，以便观者准确的 理解您传达的思想。
习题答案
七习题答案 八习题答案 九习题答案 十习题答案
感谢聆听
202x
小学生数独技巧从入门 到精通（双色版）
演讲人
2 0 2 x - 11 - 11
数独启蒙-图形数字三宫格
幼儿数独启蒙——图形以及数字三宫格
数独游戏可以很好地锻炼孩子的观察能力、排除能力以及逻辑分析能力哦。
那今天这一篇主要是分享给3-5岁儿童或者从来没有接触过数独的朋友们。
刚开始学习数独的的时候，可以用图形来代替，增强数独的趣味性。
首先玩一玩图案三宫格，数字三宫格在末尾。
先来介绍规则，现在有黄小熊、棕小熊、粉
小熊。
每行每列不能出现相同颜色的小熊。
（小熊在末尾可打打印粘贴）
1、每行：还差什么颜色的小熊呢？
3、尝试玩简单的3宫格：三只小熊要回家，请你帮他们找到正确回家的路吧？
难度一：一行一行有序观察，再一列一列有序观察。
如果孩子不认识行列，可以用横竖来代替哦。
注意：看行确定不了，就先看列。
3个已知2个就能确定。
难度2：一行一行有序观察，再一列一列有序观察。
然后再一行一行一列一列的反复观察。
难度3：除了之前的行列，这次要行列结合起来一起看
指导思路：（以第一个为例）
只看行都确定不了，那么看列，第二列可以确定。
接着再看行，第一行可以确定。
剩下的，不论看行还是列都没有只空一个能唯一确定的。
那就行列都看看。
比如第二行第一空，列有黄小熊，行有棕小熊，就只能是粉小熊。
上述完成之后可以出相应的数字数独给孩子完成哦。
后续会出四宫格系列。
2
1231
1
3
2
33
1
1
3
3
2
1
小熊打印页。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
儿童数独入门(一)
儿童数独入门（一）
戎卫武
一、教学内容：
“数独”（英文名为 SU DOKU）（一）
二、教学目标：
知识与技能：
1、培养学生把握全局的能力。
2、培养学生的观察反应能力。
3、培养学生分析推理能力。
数学思考：通过数独游戏，可以益智，可以获得持久的脑力锻炼。
解决问题：培养学生用排除法思考问题，初步学会的推理分析问题，掌握解决问题的策略。
情感态度与价值观：既在同伴之间的交流与团结协作中，获得肯定，又在独立思考后，获得成就感。
三、教学重、难点：
培养学生的观察和推理能力。
四、教具和学具：
课件数独游戏题纸
五、教学过程：
1、激趣引新：
B、出示课件：回过头来再看看，怎样观察才能很快的开始呢？
小结：不仅要观察行，列，还要观察区。
而且找到提供信息最多的方位开始。
③第三关“画一画”。