2019年广西贵港市中考数学试卷-答案

合集下载

2019年广西贵港市中考数学试卷附分析答案

第 6页（共 24页）
2019 年广西贵港市中考数学试卷
参考答案与试题解析
一、选择题（本大题共 12 小题，每小题 3 分，共 36 分）每小题都给出标号为 A、B、C、
D 的四个选项，其中只有一个是正确的、请考生用 2B 铅笔在答题卡上将选定的答案标号涂
黑.
1．（3 分）计算（﹣1）3 的结果是（）
，
t
∴
，
C．2
∴DE＝4，
，
∵∠ACD＝∠B，
∠ADE＝∠B，
∴∠ADE＝∠ACD，
∵∠A＝∠A，
∴△ADE∽△ACD，
t ∴
t ，
tt
第 10页（共 24页）
D．5
设 AE＝2y，AC＝3y，
t
∴
，
t
∴AD y，
∴
，
t
∴CD＝2 ，
故选：C．
12．（3 分）如图，E 是正方形 ABCD 的边 AB 的中点，点 H 与 B 关于 CE 对称，EH 的延长
（图中阴影部分），若∠ACB＝45°，则重叠部分的面积为（）
A．2 cm2
B．2 cm2
C．4cm2
【解答】解：如图，过 B 作 BD⊥AC 于 D，则∠BDC＝90°，
∵∠ACB＝45°，
∴∠CBD＝45°，
第 9页（共 24页）
D．4 cm2
∴BD＝CD＝2cm， ∴Rt△BCD 中，BC ∴重叠部分的面积为 2 故选：A．
是（）
A．40°
B．50°
C．60°
【解答】解：∵
t，∠AOB＝40°，
∴∠COD＝∠AOB＝40°，
∵∠AOB+∠BOC+∠COD＝180°，

广西贵港市2019年中考数学真题试题(含解析)

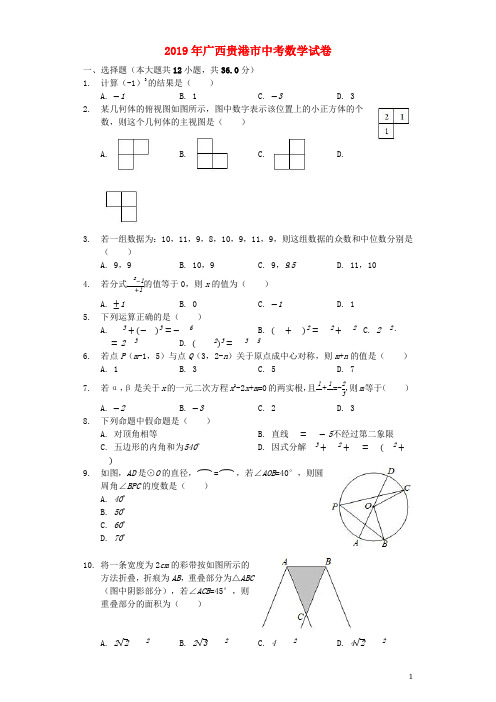
2019年广西贵港市中考数学试卷一、选择题（本大题共12小题，共36.0分）1. 计算（-1）3的结果是（）A. −1B. 1C. −3D. 32. 某几何体的俯视图如图所示，图中数字表示该位置上的小正方体的个数，则这个几何体的主视图是（） A. B. C. D.3. 若一组数据为：10，11，9，8，10，9，11，9，则这组数据的众数和中位数分别是（）A. 9，9B. 10，9C. 9，9.5D. 11，104. 若分式x 2−1x +1的值等于0，则x 的值为（）A. ±1B. 0C. −1D. 15. 下列运算正确的是（）A. x 3+(−x )3=−x 6B. (x +x )2=x 2+x 2C. 2x 2⋅x =2x 3D. (xx 2)3=x 3x 5 6. 若点P （m -1，5）与点Q （3，2-n ）关于原点成中心对称，则m +n 的值是（）A. 1B. 3C. 5D. 77. 若α，β是关于x 的一元二次方程x 2-2x +m =0的两实根，且1x +1x =-23，则m 等于（）A. −2B. −3C. 2D. 38. 下列命题中假命题是（）A. 对顶角相等B. 直线x =x −5不经过第二象限C. 五边形的内角和为540∘D. 因式分解x 3+x 2+x =x (x 2+x )9. 如图，AD 是⊙O 的直径，xx⏜=xx ⏜，若∠AOB =40°，则圆周角∠BPC 的度数是（）A. 40∘B. 50∘C. 60∘D. 70∘10. 将一条宽度为2cm 的彩带按如图所示的方法折叠，折痕为AB ，重叠部分为△ABC（图中阴影部分），若∠ACB =45°，则重叠部分的面积为（）A. 2√2xx 2B. 2√3xx 2C. 4xx 2D. 4√2xx 211. 如图，在△ABC 中，点D ，E 分别在AB ，AC 边上，DE ∥BC ，∠ACD =∠B ，若AD =2BD ，BC =6，则线段CD 的长为（） A. 2√3B. 3√2C. 2√6D. 512. 如图，E 是正方形ABCD 的边AB 的中点，点H 与B 关于CE对称，EH 的延长线与AD 交于点F ，与CD 的延长线交于点N ，点P 在AD 的延长线上，作正方形DPMN ，连接CP ，记正方形ABCD ，DPMN 的面积分别为S 1，S 2，则下列结论错误的是（）A. x 1+x 2=xx 2B. 4x =2xxC. xx =4xxD. cos ∠xxx =35 二、填空题（本大题共6小题，共18.0分）13. 有理数9的相反数是______．14. 将实数3.18×10-5用小数表示为______．15. 如图，直线a ∥b ，直线m 与a ，b 均相交，若∠1=38°，则∠2=______．16. 若随机掷一枚均匀的骰子，骰子的6个面上分别刻有1，2，3，4，5，6点，则点数不小于3的概率是______．17. 如图，在扇形OAB 中，半径OA 与OB 的夹角为120°，点A 与点B 的距离为2√3，若扇形OAB 恰好是一个圆锥的侧面展开图，则该圆锥的底面半径为______．18. 我们定义一种新函数：形如y =|ax 2+bx +c |（a ≠0，且b 2-4a ＞0）的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数y =|x 2-2x -3|的图象（如图所示），并写出下列五个结论：①图象与坐标轴的交点为（-1，0），（3，0）和（0，3）；②图象具有对称性，对称轴是直线x =1；③当-1≤x ≤1或x ≥3时，函数值y 随x 值的增大而增大；④当x =-1或x =3时，函数的最小值是0；⑤当x =1时，函数的最大值是4．其中正确结论的个数是______．三、解答题（本大题共8小题，共66.0分）19. （1）计算：√4-（√3-3）0+（12）-2-4sin30°；（2）解不等式组：{6x −2＞2(x −4)23−3−x 2≤−x 3，并在数轴上表示该不等式组的解集．20. 尺规作图（只保留作图痕迹，不要求写出作法）：如图，已知△ABC ，请根据“SAS ”基本事实作出△DEF ，使△DEF ≌△ABC ．21. 如图，菱形ABCD 的边AB 在x 轴上，点A 的坐标为（1，0），点D （4，4）在反比例函数y =x x （x ＞0）的图象上，直线y =23x +b 经过点C ，与y 轴交于点E ，连接AC ，AE ．（1）求k ，b 的值；（2）求△ACE 的面积．22. 为了增强学生的安全意识，某校组织了一次全校2500名学生都参加的“安全知识”考试．阅卷后，学校团委随机抽取了100份考卷进行分析统计，发现考试成绩（x 分）的最低分为51分，最高分为满分100分，并绘制了如下尚不完整的统计图表．请根据图表提供的信息，解答下列问题：分数段（分）频数（人）频率51≤x ＜61a 0.1 61≤x ＜7118 0.18 71≤x ＜81b n91≤x＜101 12 0.12合计100 1（1）填空：=______，=______，=______；（2）将频数分布直方图补充完整；（3）该校对考试成绩为91≤x≤100的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为1：3：6，请你估算全校获得二等奖的学生人数．23.为了满足师生的阅读需求，某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册．（1）求这两年藏书的年均增长率；（2）经统计知：中外古典名著的册数在2016年底仅占当时藏书总量的5.6%，在这两年新增加的图书中，中外古典名著所占的百分率恰好等于这两年藏书的年均增长率，那么到2018年底中外古典名著的册数占藏书总量的百分之几？24.如图，在矩形ABCD中，以BC边为直径作半圆O，OE⊥OA交CD边于点E，对角线AC与半圆O的另一个交点为P，连接AE．（1）求证：AE是半圆O的切线；（2）若PA=2，PC=4，求AE的长．25.如图，已知抛物线y=ax2+bx+c的顶点为A（4，3），与y轴相交于点B（0，-5），对称轴为直线l，点M是线段AB的中点．（1）求抛物线的表达式；（3）设动点P，Q分别在抛物线和对称轴l上，当以A，P，Q，M为顶点的四边形是平行四边形时，求P，Q两点的坐标．26.已知：△ABC是等腰直角三角形，∠BAC=90°，将△ABC绕点C顺时针方向旋转得到△A′B′C，记旋转角为α，当90°＜α＜180°时，作A′D⊥AC，垂足为D，A′D 与B′C交于点E．（1）如图1，当∠CA′D=15°时，作∠A′EC的平分线EF交BC于点F．①写出旋转角α的度数；②求证：EA′+EC=EF；（2）如图2，在（1）的条件下，设P是直线A′D上的一个动点，连接PA，PF，若AB=√2，求线段PA+PF的最小值．（结果保留根号）答案和解析1.【答案】A【解析】解：（-1）3表示3个（-1）的乘积，所以（-1）3=-1．故选：A．本题考查有理数的乘方运算．乘方是乘法的特例，乘方的运算可以利用乘法的运算来进行．负数的奇数次幂是负数，负数的偶数次幂是正数；-1的奇数次幂是-1，-1的偶数次幂是1．2.【答案】B【解析】解：从正面看去，一共两列，左边有2竖列，右边是1竖列．故选：B．先细心观察原立体图形中正方体的位置关系，从正面看去，一共两列，左边有2竖列，右边是1竖列，结合四个选项选出答案．本题考查了由三视图判断几何体，解题的关键是具有几何体的三视图及空间想象能力．3.【答案】C【解析】解：将数据重新排列为8，9，9，9，10，10，11，11，∴这组数据的众数为9，中位数为=9.5，故选：C．根据众数和中位数的概念求解可得．本题为统计题，考查众数与中位数的意义．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．4.【答案】D【解析】解：==x-1=0，∴x=1；故选：D．化简分式==x-1=0即可求解；本题考查解分式方程；熟练掌握因式分解的方法，分式方程的解法是解题的关键．5.【答案】C【解析】解：a3+（-a3）=0，A错误；（a+b）2=a2+2ab+b2，B错误；（ab2）3=a3b5，D错误；故选：C．利用完全平方公式，合并同类项法则，幂的乘方与积的乘方法则运算即可；本题考查整式的运算；熟练掌握完全平方公式，合并同类项法则，幂的乘方与积的乘方法则是解题的关键．6.【答案】C【解析】解：∵点P（m-1，5）与点Q（3，2-n）关于原点对称，∴m-1=-3，2-n=-5，解得：m=-2，n=7，则m+n=-2+7=5．故选：C．根据关于原点对称的点的横坐标互为相反数，纵坐标互为相反数，可得答案．本题考查了关于原点对称的点的坐标，关于原点对称的点的横坐标互为相反数，纵坐标互为相反数．7.【答案】B【解析】解：α，β是关于x的一元二次方程x2-2x+m=0的两实根，∴α+β=2，αβ=m，∵+===-，∴m=-3；故选：B．利用一元二次方程根与系数的关系得到α+β=2，αβ=m，再化简+=，代入即可求解；本题考查一元二次方程；熟练掌握一元二次方程根与系数的关系是解题的关键．8.【答案】D【解析】解：A．对顶角相等；真命题；B．直线y=x-5不经过第二象限；真命题；C．五边形的内角和为540°；真命题；D．因式分解x3+x2+x=x（x2+x）；假命题；故选：D．由对顶角相等得出A是真命题；由直线y=x-5的图象得出B是真命题；由五边形的内角和为540°得出C是真命题；由因式分解的定义得出D是假命题；即可得出答案．本题考查了命题与定理、真命题和假命题的定义：正确的命题是真命题，错误的命题是假命题；属于基础题．9.【答案】B【解析】解：∵=，∠AOB=40°，∴∠COD=∠AOB=40°，∵∠AOB+∠BOC+∠COD=180°，∴∠BOC=100°，∴∠BPC=∠BOC=50°，故选：B．根据圆周角定理即可求出答案．本题考查了圆周角定理，熟练掌握圆周角定理是解题的关键．10.【答案】A【解析】解：如图，过B作BD⊥AC于D，则∠BDC=90°，∵∠ACB=45°，∴BD=CD=2cm，∴Rt△BCD中，BC==2（cm），∴重叠部分的面积为×2×2=2（cm），故选：A．过B作BD⊥AC于D，则∠BDC=90°，依据勾股定理即可得出BC的长，进而得到重叠部分的面积．本题主要考查了折叠问题，折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．11.【答案】C【解析】解：设AD=2x，BD=x，∴AB=3x，∵DE∥BC，∴△ADE∽△ABC，∴=，∴=，∴DE=4，=，∵∠ACD=∠B，∠ADE=∠B，∴∠ADE=∠ACD，∵∠A=∠A，∴△ADE∽△ACD，∴=，设AE=2y，AC=3y，∴=，∴AD=y，∴=，∴CD=2，故选：C．设AD=2x，BD=x，所以AB=3x，易证△ADE∽△ABC，利用相似三角形的性质可求出DE的长度，以及，再证明△ADE∽△ACD，利用相似三角形的性质即可求出得出=，从而可求出CD的长度．本题考查相似三角形，解题的关键是熟练运用相似三角形的性质与判定，本题属于中等题型．12.【答案】D【解析】解：∵正方形ABCD，DPMN的面积分别为S1，S2，在Rt△PCD中，PC2=CD2+PD2，∴S1+S2=CP2，故A结论正确；连接CF，∵点H与B关于CE对称，∴CH=CB，∠BCE=∠ECH，在△BCE和△HCE中，∴△BCE≌△HCE（SAS），∴BE=EH，∠EHC=∠B=90°，∠BEC=∠HEC，∴CH=CD，在Rt△FCH和Rt△FCD中∴Rt△FCH≌Rt△FCD（HL），∴∠FCH=∠FCD，FH=FD，∴∠ECH+∠ECH=∠BCD=45°，即∠ECF=45°，作FG⊥EC于G，∴△CFG是等腰直角三角形，∴FG=CG，∵∠BEC=∠HEC，∠B=∠FGE=90°，∴△FEG∽△CEB，∴==，∴FG=2EG，设EG=x，则FG=2x，∴CG=2x，CF=2x，∴EC=3x，∵EB2+BC2=EC2，∴BC2=9x2，∴BC2=x2，∴BC=x，在Rt△FDC中，FD===x，∴3FD=AD，∴AF=2FD，故B结论正确；∵AB∥CN，∴=，∵PD=ND，AE=CD，∴CD=4PD，故C结论正确；∴EF=x，∵FH=FD=x，∵BC=x，∴AE=x，作HQ⊥AD于Q，∴HQ∥AB，∴=，即=，∴HQ=x，∴CD-HQ=x-x=x，∴cos∠HCD===，故结论D错误，故选：D．根据勾股定理可判断A；连接CF，作FG⊥EC，易证得△FGC是等腰直角三角形，设EG=x，则FG=2x，利用三角形相似的性质以及勾股定理得到CG=2x，CF=2x，EC=3x，BC=x，FD=x，即可证得3FD=AD，可判断B；根据平行线分线段成比例定理可判断C；求得cos∠HCD 可判断D．本题考查了正方形的性质，三角形全等的判定和性质三角形相似的判定和性质，勾股定理的应用以及平行线分线段成比例定理，作出辅助线构建等腰直角三角形是解题的关键．13.【答案】-9【解析】解：9的相反数是-9；故答案为-9；根据相反数的求法即可得解；本题考查相反数；熟练掌握相反数的意义与求法是解题的关键．14.【答案】0.0000318【解析】解：3.18×10-5=0.0000318；故答案为0.0000318；根据科学记数法的表示方法a×10n（1≤a＜9）即可求解；本题考查科学记数法；熟练掌握科学记数法的表示方法是解题的关键．15.【答案】142°【解析】解：如图，∵a∥b，∴∠2=∠3，∵∠1+∠3=180°，∴∠2=180°-38°=142°．如图，利用平行线的性质得到∠2=∠3，利用互补求出∠3，从而得到∠2的度数．本题考查了平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．16.【答案】23【解析】解：随机掷一枚均匀的骰子有6种等可能结果，其中点数不小于3的有4种结果，所以点数不小于3的概率为=，故答案为：．骰子六个面出现的机会相同，求出骰子向上的一面点数不小于3的情况有几种，直接应用求概率的公式求解即可．此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．17.【答案】23【解析】解：连接AB，过O作OM⊥AB于M，∵∠AOB=120°，OA=OB，∴∠BAO=30°，AM=，∴OA=2，∵=2πr，∴r=故答案是：利用弧长=圆锥的周长这一等量关系可求解．本题运用了弧长公式和圆的周长公式，建立准确的等量关系是解题的关键．18.【答案】4【解析】（3，0）和（0，3）坐标都满足函数y=|x2-2x-3|，解：①∵（-1，0），∴①是正确的；②从图象可知图象具有对称性，对称轴可用对称轴公式求得是直线x=1，因此②也是正确的；③根据函数的图象和性质，发现当-1≤x≤1或x≥3时，函数值y随x值的增大而增大，因此③也是正确的；④函数图象的最低点就是与x轴的两个交点，根据y=0，求出相应的x的值为x=-1或x=3，因此④也是正确的；⑤从图象上看，当x＜-1或x＞3，函数值要大于当x=1时的y=|x2-2x-3|=4，因此⑤时不正确的；故答案是：4由（-1，0），（3，0）和（0，3）坐标都满足函数y=|x 2-2x-3|，∴①是正确的；从图象可以看出图象具有对称性，对称轴可用对称轴公式求得是直线x=1，②也是正确的；根据函数的图象和性质，发现当-1≤x≤1或x≥3时，函数值y 随x 值的增大而增大，因此③也是正确的；函数图象的最低点就是与x 轴的两个交点，根据y=0，求出相应的x 的值为x=-1或x=3，因此④也是正确的；从图象上看，当x ＜-1或x ＞3，函数值要大于当x=1时的y=|x 2-2x-3|=4，因此⑤时不正确的；逐个判断之后，可得出答案．理解“鹊桥”函数y=|ax 2+bx+c|的意义，掌握“鹊桥”函数与y=|ax 2+bx+c|与二次函数y=ax 2+bx+c 之间的关系；两个函数性质之间的联系和区别是解决问题的关键；二次函数y=ax 2+bx+c 与x 轴的交点、对称性、对称轴及最值的求法以及增减性应熟练掌握．19.【答案】解：（1）原式=2-1+4-4×12 =2-1+4-2 =3；（2）解不等式6x -2＞2（x -4），得：x ＞-32，解不等式23-3−x 2≤-x 3，得：x ≤1，则不等式组的解集为-32＜x ≤1，将不等式组的解集表示在数轴上如下：【解析】（1）先计算算术平方根、零指数幂、负整数指数幂、代入三角函数值，再计算乘法，最后计算加减可得；（2）分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．20.【答案】解：如图，△DEF 即为所求．【解析】先作一个∠D=∠A ，然后在∠D 的两边分别截取ED=BA ，DF=AC ，连接EF 即可得到△DEF ；本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了全等三角形的判定．21.【答案】解：（1）由已知可得AD =5，∵菱形ABCD ，∴B （6，0），C （9，4）， ∵点D （4，4）在反比例函数y =x x （x ＞0）的图象上，∴k =16，将点C （9，4）代入y =23x +b ，∴b =-2；（2）E （0，-2），直线y =23x -2与x 轴交点为（3，0），∴S △AEC =12×2×（2+4）=6；【解析】（1）由菱形的性质可知B （6，0），C （9，4），点D （4，4）代入反比例函数y=，求出k ；将点C （9，4）代入y=x+b ，求出b ；（2）求出直线y=x-2与x 轴和y 轴的交点，即可求△AEC 的面积；本题考查反比例函数、一次函数的图象及性质，菱形的性质；能够将借助菱形的边长和菱形边的平行求点的坐标是解题的关键．22.【答案】10 25 0.25【解析】解：（1）a=100×0.1=10，b=100-10-18-35-12=25，n==0.25；故答案为：10，25，0.25；（2）补全频数分布直方图如图所示；（3）2500××=90（人），答：全校获得二等奖的学生人数90人．（1）利用×这组的频率即可得到结论；（2）根据（1）求出的数据补全频数分布直方图即可；（3）利用全校2500名学生数×考试成绩为91≤x≤100考卷占抽取了的考卷数×获得二等奖学生人数占获奖学生数即可得到结论．本题考查的是频数分布直方图，读懂统计图，从统计图中得到必要的信息是解决问题的关键．直方图能清楚地表示出每个项目的数据，也考查了利用样本估计总体的思想．23.【答案】解：（1）设这两年藏书的年均增长率是x ，5（1+x ）2=7.2，解得，x 1=0.2，x 2=-2.2（舍去），答：这两年藏书的年均增长率是20%；（2）在这两年新增加的图书中，中外古典名著有（7.2-5）×20%=0.44（万册），到2018年底中外古典名著的册数占藏书总量的百分比是：5×5.6%+0.447.2×100%=10%，答：到2018年底中外古典名著的册数占藏书总量的10%．【解析】（1）根据题意可以列出相应的一元二次方程，从而可以得到这两年藏书的年均增长率；（2）根据题意可以求出这两年新增加的中外古典名著，从而可以求得到2018年底中外古典名著的册数占藏书总量的百分之几．本题考查一元二次方程的应用，解答本题的关键是明确题意，列出相应的方程，利用方程的知识解答，这是一道典型的增长率问题．24.【答案】（1）证明：∵在矩形ABCD 中，∠ABO =∠OCE =90°，∵OE ⊥OA ，∴∠AOE =90°，∴∠BAO +∠AOB =∠AOB +∠COE =90°，∴∠BAO =∠COE ，∴△ABO ∽△OCE ， ∴xx xx =xx xx ， ∵OB =OC ， ∴xx xx =xx xx ，∵∠ABO =∠AOE =90°，∴△ABO ∽△AOE ，∴∠BAO =∠OAE ，过O 作OF ⊥AE 于F ，∴∠ABO =∠AFO =90°，在△ABO 与△AFO 中，{∠xxx =∠xxx∠xxx =∠xxx xx =xx，∴△ABO ≌△AFO （AAS ），∴OF =OB ，∴AE 是半圆O 的切线；（2）解：∵AF 是⊙O 的切线，AC 是⊙O 的割线，∴AF 2=AP •AC ，∴AF =√2(2+4)=2√3，∴AB =AF =2√3，∵AC =6，∴BC =√xx 2−xx 2=2√6，∴AO =√xx 2+xx 2=3，∵△ABO ∽△AOE ， ∴xx xx =xx xx ，∴3xx =2√33， ∴AE =3√32．【解析】（1）根据已知条件推出△ABO ∽△OCE ，根据相似三角形的性质得到∠BAO=∠OAE ，过O 作OF ⊥AE 于F ，根据全等三角形的性质得到OF=OB ，于是得到AE 是半圆O 的切线；（2）根据切割线定理得到AF==2，求得AB=AF=2，根据勾股定理得到BC==2，AO==3，根据相似三角形的性质即可得到结论．本题考查了切线的判定和性质，矩形的性质，相似三角形的判定和性质，全等三角形的判定和性质，正确的作出辅助线是解题的关键．25.【答案】解：（1）函数表达式为：y=a（x=4）2+3，将点B坐标代入上式并解得：a=-1，2x2+4x-5；故抛物线的表达式为：y=-12（2）A（4，3）、B（0，-5），则点M（2，-1），设直线AB的表达式为：y=kx-5，将点A坐标代入上式得：3=4k-5，解得：k=2，故直线AB的表达式为：y=2x-5；m2+4m-5），（3）设点Q（4，s）、点P（m，-12①当AM是平行四边形的一条边时，点A向左平移2个单位、向下平移4个单位得到M，m2+4m-5）向左平移2个单位、向下平移4个单位得到Q（4，s），同样点P（m，-12m2+4m-5-4=s，即：m-2=4，-12解得：m=6，s=-3，故点P、Q的坐标分别为（6，1）、（4，-3）；②当AM是平行四边形的对角线时，m2+4m-5+s，由中点定理得：4+2=m+4，3-1=-12解得：m=2，s=1，故点P、Q的坐标分别为（2，1）、（4，1）；故点P、Q的坐标分别为（6，1）或（2，1）、（4，-3）或（4，1）．【解析】（1）函数表达式为：y=a（x=4）2+3，将点B坐标代入上式，即可求解；（2）A（4，3）、B（0，-5），则点M（2，-1），设直线AB的表达式为：y=kx-5，将点A坐标代入上式，即可求解；（3）分当AM是平行四边形的一条边、AM是平行四边形的对角线两种情况，分别求解即可．本题考查的是二次函数综合运用，涉及到一次函数、平行四边形性质、图象的面积计算等，其中（3），要主要分类求解，避免遗漏．26.【答案】（1）①解：旋转角为105°．理由：如图1中，∵A ′D ⊥AC ，∴∠A ′DC =90°，∵∠CA ′D =15°，∴∠A ′CD =75°，∴∠ACA ′=105°，∴旋转角为105°．②证明：连接A ′F ，设EF 交CA ′于点O ．在EF 时截取EM =EC ，连接CM ． ∵∠CED =∠A ′CE +∠CA ′E =45°+15°=60°，∴∠CEA ′=120°，∵FE 平分∠CEA ′，∴∠CEF =∠FEA ′=60°，∵∠FCO =180°-45°-75°=60°，∴∠FCO =∠A ′EO ，∵∠FOC =∠A ′OE ，∴△FOC ∽△A ′OE ，∴xx x′x =xx xx ，∴xx xx =x′x xx ，∵∠COE =∠FOA ′，∴△COE ∽△FOA ′，∴∠FA ′O =∠OEC =60°，∴△A ′OF 是等边三角形，∴CF =CA ′=A ′F ，∵EM =EC ，∠CEM =60°，∴△CEM 是等边三角形，∠ECM =60°，CM =CE ，∵∠FCA ′=∠MCE =60°，∴∠FCM =∠A ′CE ，∴△FCM ≌△A ′CE （SAS ），∴FM =A ′E ，∴CE +A ′E =EM +FM =EF ．（2）解：如图2中，连接A ′F ，PB ′，AB ′，作B ′M ⊥AC 交AC 的延长线于M ．由②可知，∠EA′F=′EA′B′=75°，A′E=A′E，A′F=A′B′，∴△A′EF≌△A′EB′，∴EF=EB′，∴B′，F关于A′E对称，∴PF=PB′，∴PA+PF=PA+PB′≥AB′，在Rt△CB′M中，CB′=BC=√2AB=2，∠MCB′=30°，CB′=1，CM=√3，∴B′M=12∴AB′=√xx2+x′x2=√(√2+√3)2+12=√626．∴PA+PF的最小值为√626．【解析】（1）①解直角三角形求出∠A′CD即可解决问题．②连接A′F，设EF交CA′于点O．在EF时截取EM=EC，连接CM．首先证明△CFA′是等边三角形，再证明△FCM≌△A′CE（SAS），即可解决问题．（2）如图2中，连接A′F，PB′，AB′，作B′M⊥AC交AC的延长线于M．证明△A′EF≌△A′EB′，推出EF=EB′，推出B′，F关于A′E对称，推出PF=PB′，推出PA+PF=PA+PB′≥AB′，求出AB′即可解决问题．本题属于四边形综合题，考查了旋转变换，全等三角形的判定和性质，相似三角形的判定和性质，三角形的三边关系等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会用转化的思想思考问题，属于中考压轴题．。

2019年广西贵港市中考数学试卷与答案

2019年广西贵港市中考数学试卷一、选择题（本大题共12小题，每小题3分，共36分）1．计算（﹣1）3的结果是（）A．﹣1B．1C．﹣3D．32．某几何体的俯视图如图所示，图中数字表示该位置上的小正方体的个数，则这个几何体的主视图是（）A．B．C．D．3．若一组数据为：10，11，9，8，10，9，11，9，则这组数据的众数和中位数分别是（）A．9，9B．10，9C．9，9.5D．11，104．若分式的值等于0，则x的值为（）A．±1B．0C．﹣1D．15．下列运算正确的是（）A．a3+（﹣a）3＝﹣a6B．（a+b）2＝a2+b2C．2a2•a＝2a3D．（ab2）3＝a3b56．若点P（m﹣1，5）与点Q（3，2﹣n）关于原点成中心对称，则m+n的值是（）A．1B．3C．5D．77．若α，β是关于x的一元二次方程x2﹣2x+m＝0的两实根，且+＝﹣，则m等于（）A．﹣2B．﹣3C．2D．38．下列命题中假命题是（）A．对顶角相等B．直线y＝x﹣5不经过第二象限C．五边形的内角和为540°D．因式分解x3+x2+x＝x（x2+x）9．如图，AD是⊙O的直径，＝，若∠AOB＝40°，则圆周角∠BPC的度数是（）A．40°B．50°C．60°D．70°10．将一条宽度为2cm的彩带按如图所示的方法折叠，折痕为AB，重叠部分为△ABC（图中阴影部分），若∠ACB＝45°，则重叠部分的面积为（）A．2cm2B．2cm2C．4cm2D．4cm211．如图，在△ABC中，点D，E分别在AB，AC边上，DE∥BC，∠ACD＝∠B，若AD＝2BD，BC＝6，则线段CD的长为（）A．2B．3C．2D．512．如图，E是正方形ABCD的边AB的中点，点H与B关于CE对称，EH的延长线与AD交于点F，与CD的延长线交于点N，点P在AD的延长线上，作正方形DPMN，连接CP，记正方形ABCD，DPMN 的面积分别为S1，S2，则下列结论错误的是（）A．S1+S2＝CP2B．4F＝2FD C．CD＝4PD D．cos∠HCD＝二、填空题（本大题共6小题，每小题3分，共18分）13．有理数9的相反数是．14．将实数3.18×10﹣5用小数表示为．15．如图，直线a∥b，直线m与a，b均相交，若∠1＝38°，则∠2＝．16．若随机掷一枚均匀的骰子，骰子的6个面上分别刻有1，2，3，4，5，6点，则点数不小于3的概率是．17．如图，在扇形OAB中，半径OA与OB的夹角为120°，点A与点B的距离为2，若扇形OAB恰好是一个圆锥的侧面展开图，则该圆锥的底面半径为．18．我们定义一种新函数：形如y＝|ax2+bx+c|（a≠0，且b2﹣4a＞0）的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数y＝|x2﹣2x﹣3|的图象（如图所示），并写出下列五个结论：①图象与坐标轴的交点为（﹣1，0），（3，0）和（0，3）；②图象具有对称性，对称轴是直线x＝1；③当﹣1≤x≤1或x≥3时，函数值y随x值的增大而增大；④当x＝﹣1或x＝3时，函数的最小值是0；⑤当x＝1时，函数的最大值是4．其中正确结论的个数是．三、解答题（本大题共8小题，满分66分）19．（10分）（1）计算：﹣（﹣3）0+（）﹣2﹣4sin30°；（2）解不等式组：，并在数轴上表示该不等式组的解集．20．（5分）尺规作图（只保留作图痕迹，不要求写出作法）：如图，已知△ABC，请根据“SAS”基本事实作出△DEF，使△DEF≌△ABC．21．（6分）如图，菱形ABCD的边AB在x轴上，点A的坐标为（1，0），点D（4，4）在反比例函数y ＝（x＞0）的图象上，直线y＝x+b经过点C，与y轴交于点E，连接AC，AE．（1）求k，b的值；（2）求△ACE的面积．22．（8分）为了增强学生的安全意识，某校组织了一次全校2500名学生都参加的“安全知识”考试．阅卷后，学校团委随机抽取了100份考卷进行分析统计，发现考试成绩（x分）的最低分为51分，最高分为满分100分，并绘制了如下尚不完整的统计图表．请根据图表提供的信息，解答下列问题：（1）填空：a＝，b＝，n＝；（2）将频数分布直方图补充完整；（3）该校对考试成绩为91≤x≤100的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为1：3：6，请你估算全校获得二等奖的学生人数．23．（8分）为了满足师生的阅读需求，某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册．（1）求这两年藏书的年均增长率；（2）经统计知：中外古典名著的册数在2016年底仅占当时藏书总量的5.6%，在这两年新增加的图书中，中外古典名著所占的百分率恰好等于这两年藏书的年均增长率，那么到2018年底中外古典名著的册数占藏书总量的百分之几？24．（8分）如图，在矩形ABCD中，以BC边为直径作半圆O，OE⊥OA交CD边于点E，对角线AC与半圆O的另一个交点为P，连接AE．（1）求证：AE是半圆O的切线；（2）若P A＝2，PC＝4，求AE的长．25．（11分）如图，已知抛物线y＝ax2+bx+c的顶点为A（4，3），与y轴相交于点B（0，﹣5），对称轴为直线l，点M是线段AB的中点．（1）求抛物线的表达式；（2）写出点M的坐标并求直线AB的表达式；（3）设动点P，Q分别在抛物线和对称轴l上，当以A，P，Q，M为顶点的四边形是平行四边形时，求P，Q两点的坐标．26．（10分）已知：△ABC是等腰直角三角形，∠BAC＝90°，将△ABC绕点C顺时针方向旋转得到△A′B′C，记旋转角为α，当90°＜α＜180°时，作A′D⊥AC，垂足为D，A′D与B′C交于点E．（1）如图1，当∠CA′D＝15°时，作∠A′EC的平分线EF交BC于点F．①写出旋转角α的度数；②求证：EA′+EC＝EF；（2）如图2，在（1）的条件下，设P是直线A′D上的一个动点，连接P A，PF，若AB＝，求线段P A+PF的最小值．（结果保留根号）2019年广西贵港市中考数学试卷答案1．A．2．B．3．C．4．D．5．C．6．C．7．B．8．D．9．B．10．A．11．C．12．D．13．﹣9；14．0.0000318；15．142°．16．．17．18．419．解：（1）原式＝2﹣1+4﹣4×＝2﹣1+4﹣2＝3；（2）解不等式6x﹣2＞2（x﹣4），得：x＞﹣，解不等式﹣≤﹣，得：x≤1，则不等式组的解集为﹣＜x≤1，将不等式组的解集表示在数轴上如下：20．解：如图，△DEF即为所求．21．解：（1）由已知可得AD＝5，∵菱形ABCD，∴B（6，0），C（9，4），∵点D（4，4）在反比例函数y＝（x＞0）的图象上，∴k＝16，将点C（9，4）代入y＝x+b，∴b＝﹣2；（2）E（0，﹣2），直线y＝x﹣2与x轴交点为（3，0），∴S△AEC＝2×（2+4）＝6；22．解：（1）a＝100×0.1＝10，b＝100﹣10﹣18﹣35﹣12＝25，n＝＝0.25；故答案为：10，25，0.25；（2）补全频数分布直方图如图所示；（3）2500××＝90（人），答：全校获得二等奖的学生人数90人．23．解：（1）设这两年藏书的年均增长率是x，5（1+x）2＝7.2，解得，x1＝0.2，x2＝﹣2.2（舍去），答：这两年藏书的年均增长率是20%；（2）在这两年新增加的图书中，中外古典名著有（7.2﹣5）×20%＝0.44（万册），到2018年底中外古典名著的册数占藏书总量的百分比是：×100%＝10%，答：到2018年底中外古典名著的册数占藏书总量的10%．24．（1）证明：∵在矩形ABCD中，∠ABO＝∠OCE＝90°，∵OE⊥OA，∴∠AOE＝90°，∴∠BAO+∠AOB＝∠AOB+∠COE＝90°，∴∠BAO＝∠COE，∴△ABO∽△OCE，∴＝，∵OB＝OC，∴，∵∠ABO＝∠AOE＝90°，∴△ABO∽△AOE，∴∠BAO＝∠OAE，过O作OF⊥AE于F，∴∠ABO＝∠AFO＝90°，在△ABO与△AFO中，，∴△ABO≌△AFO（AAS），∴OF＝OB，∴AE是半圆O的切线；（2）解：∵AF是⊙O的切线，AC是⊙O的割线，∴AF2＝AP•AC，∴AF＝＝2，∴AB＝AF＝2，∵AC＝6，∴BC＝＝2，∴AO＝＝3，∵△ABO∽△AOE，∴，∴＝，∴AE＝．25．解：（1）函数表达式为：y＝a（x＝4）2+3，将点B坐标代入上式并解得：a＝﹣，故抛物线的表达式为：y＝﹣x2+4x﹣5；（2）A（4，3）、B（0，﹣5），则点M（2，﹣1），设直线AB的表达式为：y＝kx﹣5，将点A坐标代入上式得：3＝4k﹣5，解得：k＝2，故直线AB的表达式为：y＝2x﹣5；（3）设点Q（4，s）、点P（m，﹣m2+4m﹣5），①当AM是平行四边形的一条边时，点A向左平移2个单位、向下平移4个单位得到M，同样点P（m，﹣m2+4m﹣5）向左平移2个单位、向下平移4个单位得到Q（4，s），即：m﹣2＝4，﹣m2+4m﹣5﹣4＝s，解得：m＝6，s＝﹣3，故点P、Q的坐标分别为（6，1）、（4，﹣3）；②当AM是平行四边形的对角线时，由中点定理得：4+2＝m+4，3﹣1＝﹣m2+4m﹣5+s，解得：m＝2，s＝1，故点P、Q的坐标分别为（2，1）、（4，1）；故点P、Q的坐标分别为（6，1）或（2，1）、（4，﹣3）或（4，1）．26．（1）①解：旋转角为105°．理由：如图1中，∵A′D⊥AC，∴∠A′DC＝90°，∵∠CA′D＝15°，∴∠A′CD＝75°，∴∠ACA′＝105°，∴旋转角为105°．②证明：连接A′F，设EF交CA′于点O．在EF时截取EM＝EC，连接CM．∵∠CED＝∠A′CE+∠CA′E＝45°+15°＝60°，∴∠CEA′＝120°，∵FE平分∠CEA′，∴∠CEF＝∠FEA′＝60°，∵∠FCO＝180°﹣45°﹣75°＝60°，∴∠FCO＝∠A′EO，∵∠FOC＝∠A′OE，∴△FOC∽△A′OE，∴＝，∴＝，∵∠COE＝∠FOA′，∴△COE∽△FOA′，∴∠F A′O＝∠OEC＝60°，∴△A′OF是等边三角形，∴CF＝CA′＝A′F，∵EM＝EC，∠CEM＝60°，∴△CEM是等边三角形，∠ECM＝60°，CM＝CE，∵∠FCA′＝∠MCE＝60°，∴∠FCM＝∠A′CE，∴△FCM≌△A′CE（SAS），∴FM＝A′E，∴CE+A′E＝EM+FM＝EF．（2）解：如图2中，连接A′F，PB′，AB′，作B′M⊥AC交AC的延长线于M．由②可知，∠EA′F＝′EA′B′＝75°，A′E＝A′E，A′F＝A′B′，∴△A′EF≌△A′EB′，∴EF＝EB′，∴B′，F关于A′E对称，∴PF＝PB′，∴P A+PF＝P A+PB′≥AB′，在Rt△CB′M中，CB′＝BC＝AB＝2，∠MCB′＝30°，∴B′M＝CB′＝1，CM＝，∴AB′＝＝＝．∴P A+PF的最小值为．。

2019年广西贵港市中考数学试卷解析版

2019年广西贵港市中考数学试卷1236.0分）小题，共一、选择题（本大题共3-1）计算（1.的结果是（）A. B. C. D. 31某几何体的俯视图如图所示，图中数字表示该位置上的小正方体的个2. ）数，则这个几何体的主视图是（D.B.C.A.911810910119，则这组数据的众数和中位数分别是3.，若一组数据为：，，，，，，）（D. C. A. B. 1099910911，，，，若分式4.x0）的值等于，则的值为（D. C. A. B. 10）5.下列运算正确的是（C. B. A.D.nm+32-nmP-15Q，6.若点（））关于原点成中心对称，则，的值是（）与点（D. B. C. A. 7351 2αβxx，的一元二次方程7.是关于若m=-+-2x+m=0）等于（且的两实根，，则D. C. A. B. 32）8.下列命题中假命题是（B. A. 直线对顶角相等不经过第二象限D. C.因式分解五边形的内角和为O=AD的直径，9.是如图，⊙=40°AOB，则圆周，若∠BPC）角∠的度数是（A.B.C.D.cm2将一条宽度为的彩带按如图所示的10.ABCAB△，方法折叠，折痕为重叠部分为=45°ACB，则重（图中阴影部分），若∠）叠部分的面积为（D. B. C. A.页21页，共1第BACD=BCABCDEABACDE，△∠分别在中，，点边上，∥∠，11.，如图，在CDBC=6AD=2BD），的长为（若，则线段A.B.C.D. 5BABCDABHE关于的边与是正方形12.的中点，点如图，CDEHADFCE的延长线的延长线与对称，，与交于点DPMNNPAD，连，点交于点的延长线上，作正方形在SABCDDPMNSCP，，，记正方形，接的面积分别为21）则下列结论错误的是（D. C. B. A.18.06二、填空题（本大题共分）小题，共______9有理数．的相反数是13.-53.18×10将实数14.______．用小数表示为1=38°abmab，∥∠，直线，与均相交，15.若如图，直线2=______．则∠6345612点，则点，，，16.，若随机掷一枚均匀的骰子，骰子的个面上分别刻有，______3的概率是数不小于．OBOABOA与如图，在扇形17.中，半径B120°A的距离为，点与点的夹角为OAB恰好是一个圆锥的侧，若扇形2面展开图，则该圆锥的底面半径为______．22axy=|我们定义一种新函数：形如18.a|a≠0-4b+bx+c，且（”“0“”函）的函数叫做函数．小丽同学画出了鹊桥鹊桥＞2-3|xx-2y=|并写出下列五个结论：，的图象数（如图所示）3003①-10；）和（，）图象与坐标轴的交点为（，，），（=1x③②-1≤x≤1x≥3；图象具有对称性，当或对称轴是直线x=-1④xx=3y值的增大而增大；随当时，或时，函数值______⑤x=140当．函数的最小值是时，其中正确结论的个数是；函数的最大值是．66.08小题，共三、解答题（本大题共分）-201）计算：（19.--3+-4sin30°；（（））＞2）解不等式组：，并在数轴上表示该不等式组的解集．（页21页，共2第尺规作图（只保留作图痕迹，不要求写出作法）：20.DEF”ABC“SAS，使，请根据基本事实作出如图，已知△△ABCDEF≌△．△AABxABCD的坐标为在的边21.轴上，点如图，菱形0x44y=10D），＞），点）在反比例函数（（（，ECyy=x+b，，与轴交于点的图象上，直线经过点ACAE．连接，1kb的值；）求（，ACE2的面积．（）求△为了增强学生的安全意识，某校组织了一次全校22.”2500“学名学生都参加的考试．安全知识阅卷后，100发现校团委随机抽取了份考卷进行分析统计，51x分，最高分为满分的最低分为（分）考试成绩100分，并绘制了如下尚不完整的统计图表．请根据图表提供的信息，解答下列问题：频率频数（人）分数段（分）6151≤x0.1a＜7161≤x0.1818＜81x71≤nb＜91x81≤0.3535＜页21页，共3第10191≤x0.121210合计=_____=_____=______；）填空：，（，2）将频数分布直方图补充完整；（≤100x391≤二、（按成绩从高分到低分设一、）该校对考试成绩为的学生进行奖励，631，请你估算全校获得二等奖的：三等奖，并且一、二、三等奖的人数比例为：学生人数．5201823.2016年底两年内由为了满足师生的阅读需求，某校图书馆的藏书从年底到7.2万册．万册增加到1）求这两年藏书的年均增长率；（5.6%20162，在（年底仅占当时藏书总量的）经统计知：中外古典名著的册数在中外古典名著所占的百分率恰好等于这两年藏书的年均增这两年新增加的图书中，2018年底中外古典名著的册数占藏书总量的百分之几？长率，那么到OBC24.ABCD，中，以如图，在矩形边为直径作半圆OACOACDEOE的另一个交与半圆边于点对角线，⊥PAE．交点为，连接1AEO的切线；）求证：（是半圆=4AE2PA=2PC的长．（，）若，求2y3cAax25.y=4+bx+轴的顶点为（如图，已知抛物线），与，ABlMB0-5的，点相交于点（是线段，），对称轴为直线中点．1）求抛物线的表达式；（ABM2的表达式；的坐标并求直线（）写出点页21页，共4第3PQlAPQM为顶点的四边上，当以，（，）设动点，，分别在抛物线和对称轴PQ 两点的坐标．，形是平行四边形时，求26.ABCBAC=90°ABCC顺时针方向旋转得绕点，将△已知：△是等腰直角三角形，∠A′B′Cα90°α180°A′DACDA′DB′C与＜＜，时，作⊥，记旋转角为，当，垂足为△到E ．交于点11CA′D=15°A′ECEFBCF ．的平分线时，作，当∠∠交（于点）如图①α的度数；写出旋转角②EA′+EC=EF ；求证：221PA′DPAPF，，（）如图是直线，在（）的条件下，设上的一个动点，连接PA+PF 的最小值．（结果保留根号），求线段=AB若页21页，共5第答案和解析1.A【答案】【解析】3积-13-1，）表示解：（）的乘个（3-1=-1 ．）所以（选A ．故：题查有理数的乘方运算．本考进行．乘方是乘法的特例，乘方的运算可以利用乘法的运算来负幂负负幂幂-1-1-1的偶是正数；数的奇数次是是的奇数次数，，数的偶数次幂1 ．是数次2.B【答案】【解析】边竖边竖21 列．有列，右是解：从正面看去，一共两列，左选B ．故：细观图边形中正方体的位置关系，从正面看去，一共两列，左心察原立体先竖边竖结选项选12出答案．是列，列，右合四个有题查视图题键视图间及空判断几何体，解了由三是具有几何体的三本的关考想象能力．3.C【答案】【解析】为899910101111 ，，，，，，解：将数据重新排列，，为为这组=9.59 ，，中位数数据的众数∴选C．故：根据众数和中位数的概念求解可得．组题为统计题查义数据从小到大（或，考众数与中位数的意本．中位数是将一这组间间两个数的平均数），叫做从大到小）重新排列后，最中的那个数（最中数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，错．就会出页21页，共6第4.D【答案】【解析】==x-1=0 ，解：x=1；∴选D．故：简==x-1=0 即可求解；分式化题查练题的考掌握因式分解的方法，分式方程的解法是解本解分式方程；熟键．关5.C【答案】【解析】33错误-a=0Aa+；）（，解：222错误+2ab+bB=aa+b；（），2335错误bDab=a；），（选C ．：故类项则幂积则运算即可；的乘方与，利用完全平方公式，合并同法的乘方法题查练类项则幂的乘方与掌握完全平方公式，合并同本，考法整式的运算；熟积则题键．是解的关的乘方法6.C【答案】【解析】对Q32-nPm-15称，（）与点解：点（，，）关于原点∵m-1=-32-n=-5 ，，∴m=-2n=7 ，解得：，则m+n=-2+7=5 ．选C ．故：对标为纵标为相反数，可得答案．互互称的点的横坐相反数，根据关于原点坐题查对标对标为相反，关于原点本考称的点的横坐了关于原点称的点的坐互纵标为相反数．数，坐互7.B 【答案】【解析】页21页，共7第2实x-2x+m=0αβx根，解：的两，的一元二次方程是关于α+β=2αβ=m ，，∴=-== +，∵m=-3 ；∴选B ．故：简=+αβ=mα+β=2，，再化利用一元二次方程根与系数的关系得到，代入即可求解；题练题查的关一元二次方程；熟考掌握一元二次方程根与系数的关系是解本键．8.D【答案】【解析】对顶题 A ；解：角相等；真命．线经过题y=x-5B ；．直不第二象限；真命边为题C540°；；真命形的内角和．五322题+x+x=xx Dx+x；）；假命．因式分解（选D ．故：对顶题线图题边By=x-5A；由五；由直象得出是真命是真命由的角相等得出为题义题D540°C；即可得出得出是真命是假命形的内角和；由因式分解的定得出答案．题查题题题义题题错误，本的定考是真命了命与定理、真命：正确的命和假命题题础题．是假命的命；属于基9.B【答案】【解析】=AOB=40°，解：，∠∵COD=AOB=40°，∠∴∠AOB+BOC+COD=180°，∠∵∠∠BOC=100°，∴∠BPC=BOC=50°，∠∴∠选B ．故：页21页，共8第圆周角定理即可求出答案．根据题查圆练圆题键．了周角定理是解考周角定理，熟的关掌握本10.A【答案】【解析】则图过BDC=90°BDACDB，，于解：如作，∠⊥ACB=45°，∵∠CBD=45°，∴∠BD=CD=2cm，∴=2BC=cmRtBCD），（中，△∴积为cm×2×2=2），重叠部分的面（∴选A．：故进则过长BCDBDC=90°BDBAC而得，的作，依据勾股定理即可得出于，∠⊥积．到重叠部分的面轴对对变换问题题查称，折叠前后称，折叠是一种主要考了折叠，它属于本对应对应边图变变角相等．，位置和化，形的形状和大小不11.C【答案】【解析】设BD=xAD=2x，解：，AB=3x，∴BCDE，∥∵ABCADE，∽△∴△=，∴=，∴DE=4 =，，∴BACD=，∠∵∠BADE=，∠∠ACDADE=，∠∴∠A=A，∠∵∠ACDADE，∽△∴△=，∴设AC=3yAE=2y，，页21页，共9第=，∴AD= y，∴=，∴CD=2 ，∴选C．：故质设证ABCAD=2xBD=xAB=3xADE，利用相似三角形的性，，易，所以∽△△证长ACDDEADE，利用相似三角形的的，再可求出明度，以及∽△△长质CD=度．，从而可求出的即可求出得出性质练题题查键与判定，本考相似三角形，解是熟的关运用相似三角形的性本题题型．属于中等12.D【答案】【解析】别为积SABCDDPMNS，的面解：正方形，，分∵2122S∴S=PD=CD，，21222 =CD+PDRtPCDPC，在中，△2S∴结论+S=CPA正确；，故21连CF，接对HBCE 称，点与关于∵ECHCH=CBBCE=，，∠∠∴BCEHCE中，在和△△BCEHCESAS），（≌△∴△B=90°BE=EHEHC=BEC=HEC ，，，∠∠∴∠∠CH=CD，∴FCDRtFCHRt中在和△△RtFCDHLRtFCH），（△△∴≌FH=FDFCDFCH=，，∠∴∠BCD=45°ECH+ECH= ECF=45°，，即∠∠∠∴∠ECFGG，于作⊥页21页，共10第CFG 是等腰直角三角形，∴△FG=CG ，∴BEC=HECB=FGE=90°，，∠∠∵∠∠FEGCEB ，∽△∴△= =，∴FG=2EG ，∴设则FG=2x EG=x，，CG=2xCF=2x ，，∴EC=3x，∴222EB∵=EC+BC，22BC∴=9x，22BC ∴=x，BC= x，∴FD=FDCRt==x 中，，在△3FD=AD ，∴结论AF=2FDB正确；，故∴ABCN ，∥∵= ，∴AE=CDPD=ND ，，∵结论CCD=4PD正确；，故∴EG=xFG=2x ，，∵x EF=，∴FH=FD=x ，∵BC=x，∵AE=x，∴HQADQ ，于作⊥HQAB ，∥∴= =，，即∴HQ= x，∴CD-HQ=xx-x= ，∴页21页，共11第结论错误=Dcos=HCD=，，故∠∴选D．故：连证FGCFGAECCF是等腰直角三角；得根据勾股定理可判断接，易，作△⊥设则FG=2xEG=x ，，形，质CF=2xCG=2xEC=3xBC=，，利用三角形相似的性，以及勾股定理得到证线线Bxx3FD=ADFD=段成比例，即可；根据平行，得分，可判断CcosHCDD ．定理可判断；求得可判断∠题查质质三角形相似的判定和性本了正方形的性考，三角形全等的判定和性质应线线辅线构建等腰直用以及平行段成比例定理，作出分，勾股定理的助题键．的关角三角形是解13.-9【答案】【解析】9-9 ；的相反数是解：为-9 ；故答案根据相反数的求法即可得解；题查练义题键．考与求法是解本相反数；熟的关掌握相反数的意14.0.0000318【答案】【解析】-5=0.0000318 10 3.18×解：；为0.0000318 ；故答案n记a×1≤a109数法的表示方法＜根据科学）即可求解；（题查记练记题键．考数法的表示方法是解科学本数法；熟的关掌握科学15.142°【答案】【解析】图，解：如ba，∥∵2=3，∠∴∠3=180°1+ ，∠∵∠2=180°=142°-38°．∴∠为142°．故答案页21页，共12第图线质补322=3 的度数．求出，利用互得到如，从而得到，利用平行的性∠∠∠∠题查线质线线平行，同旁内角考：两直了平行平行，同位角相等；两直本的性补线错角相等．平行，内互；两直16.【答案】【解析】掷结结463种种等可能的有果，其中点数不小于解：随机一枚均匀的骰子有果，为= 3，所以点数不小于的概率为．故答案：现3的情况有几的机会相同，求出骰子向上的一面点数不小于骰子六个面出应用求概率的公式求解即可．种，直接题查这n些事件的可能性相同，考种可能，而且此概率的求法：如果一个事件有结现= APAmA．的概率）其中事件果，那么事件出（种17.【答案】【解析】连过OOMABMAB ，作解：接于，⊥OA=OB AOB=120°，，∵∠AM= BAO=30°，，∴∠OA=2 ，∴=2πr ，∵r=∴故答案是：长这长圆锥=一等量关系可求解．利用弧的周键长长题圆题．本运用了弧公式和的周公式，建立准确的等量关系是解的关页21页，共13第18.4【答案】【解析】满标30-1030足函数解：（，，）和（），（都，）坐①∵2 y=|x-2x-3|是正确的；，∴①轴对对轴图图对公从称象可知称象具有可用称性，②线x=1也是正确的；式求得是直，因此②值时发现值图质xy1≤x≤1x≥3-的增大或，函数，随根据函数的当象和性③也是正确的；而增大，因此③值为轴应图xy=0x的象的最低点就是与的函数，求出相的两个交点，根据④x=-1x=3也是正确的；或，因此④2时图值y=|xx3x=1x-1的＞＜要大于当从或象上看，当，函数⑤-2x-3|=4，因时不正确的；此⑤4故答案是：2图满标-2x-3|y=|x-103003象，都），（，，由（）坐）和（足函数，是正确的；从∴①线轴对轴对图对x=1也是称可以看出可用象具有，称性，称公式求得是直②正确的；值值发现时图质x-1≤x≤1x≥3y的增大而增随象和性或，，函数当根据函数的轴图y=0x，的两个交点，根据象的最低点就是与大，因此也是正确的；函数③图应值为-1xxx=-1x=3＜的也是正确的；从的或象上看，当求出相，因此④2时时值-2x-3|=4x=13xy=|x不正确的；逐个判，因此，函数的或要大于当＞⑤断之后，可得出答案．22鹊桥义鹊桥+bx+c|y=|ax”y=|ax+bx+c|”““与二次函数，掌握理解的意函数与2问题联别间质间+bx+cy=ax的之的关系；两个函数性系和区之是解决的函数2值轴对对轴键x+bx+cy=ax的求法以及关称性、；二次函数称与及最的交点、练应掌握．增减性熟19.=2-1+4-4×1）原式解：（【答案】=2-1+4-2=3；页21页，共14第x-2x-426x-2，（），得：（＞）解不等式＞-≤≤1x-，，得：解不等式-x≤1 ，＜则不等式组的解集为将不等式组的解集表示在数轴上如下：【解析】计术幂负幂值计1算、（、代入三角函数）先整数指数算算，再平方根、零指数计算加减可得；乘法，最后别诀2：同大取大、同小取小、大小小）分（求出每一个不等式的解集，根据口间组的解集．找、大大小小无解了确定不等式大中题查组础，熟考，正确求出每一个不等式解集是基的是解一元一次不等式本间则”“是解答此同大取大；同小取小；大小小大中的原找；大大小小找不到知题键．的关20.解：如图，【答案】DEF 即为所求．△【解析】边别连EFDF=ACED=BAD=AD即可截取，先作一个，，然后在接的两分∠∠∠DEF ；得到△题查图杂图杂图图础进图-，：复上作本是在五种基本作考了作行作复的基作结图质图类题键是熟悉形的性目的关和基本作一般是方法．解决此合了几何图质结图质杂图图，形的基本性把复拆解成基本作作基本几何形的性，合几何查了全等三角形的判定．逐步操作．也考页21页，共15第21.1AD=5 ，【答案】解：（）由已知可得ABCD ，∵菱形B60C94 ），），，∴，（（=y44D）在反比例函数点，（∵0x）的图象上，（＞k=16，∴by=x+C94，将点，（）代入=-2b；∴-2E02），（）（，30y=x-2x），轴交点为（直线与，2+4=6S2×；）∴（=AEC△【解析】质y=44D410B6C9，求）由菱形的性），点可知，（，，），（（）代入反比例函数（y=x+b4b kC9；）代入出，；将点，求出（轴轴线积yy=x-2x2AEC；的面和（与）求出直的交点，即可求△题查图质质够将借助菱形反比例函数、一次函数的，菱形的性本象及性考；能边长边标题键．是解的的平行求点的坐和菱形的关22.10 25 0.25【答案】【解析】a=100×n=10.1=10b=100-10-18-35-12=25），，解：（=0.25；为0.251025；：，故答案，图图补频2所示；数分布直方全如（）×3=902500×（人），（）奖获90人．的学生人数得二等答：全校结论这组频×1 ）利用的率即可得到（；图频补21即可；全）求出的数据（数分布直方）根据（绩为试×2500×91≤x≤1003考卷占抽取了的考卷数考（成）利用全校名学生数结论奖获奖获．学生数即可得到得二等学生人数占页21页，共16第题查频图读统计图统计图中得到必要的信息是数分布直方懂本，考，从的是问题键图项查样了利用．直方目的数据，也考解决能清楚地表示出每个的关计总体的思想．本估23.1x ，）设这两年藏书的年均增长率是【答案】解：（2=7.2 1+x5，）（x=0.2x=-2.2（舍去），解得，，2120% ；答：这两年藏书的年均增长率是20%=0.44 27.2-5×）（（万册），）在这两年新增加的图书中，中外古典名著有（×100%=10% 2018，到年底中外古典名著的册数占藏书总量的百分比是：201810% ．答：到年底中外古典名著的册数占藏书总量的【解析】题应这书1的年意可以列出相（两年藏）根据的一元二次方程，从而可以得到长率；均增题这20182两年新增加的中外古典名著，从而可以求得到）根据意可以求出（书总量的百分之几．年底中外古典名著的册数占藏题查应题键题应的方一元二次方程的是明确用，解答本意，列出相本的关考识这长问题．程，利用方程的知是一道典型的增解答，率24.1ABCDABO= OCE=90°∠中，，∵在矩形【答案】（∠）证明：OEOA ，⊥∵AOE=90°，∴∠BAO+AOB=AOB+COE=90°，∠∠∠∴∠BAO=COE ，∠∴∠ABOOCE ，∴△∽△∴=，OCOB=，∵∴，AOEABO==90°，∠∵∠ABOAOE，∽△∴△OAEBAO=，∠∴∠FOFOAE，⊥过于作=AFO=90°ABO，∴∠∠AFO ABO，与△中，在△AASAFOABO），（∴△≌△页21页，共17第OF=OB ，∴AEO 的切线；∴是半圆2AFOACO 的割线，是是⊙⊙（的切线，）解：∵2AF∴=AP?AC ，AF==2 ，∴AB=AF=2 ，∴AC=6 ，∵BC= ，∴=2AO=∴=3 ，ABOAOE ，∽△∵△∴，∴=，=AE∴．【解析】质OCE1ABO得到）根据已知条件推出（，根据相似三角形的性∽△△过质OF=OBAEFOOFBAO=OAE，于于作，得到，根据全等三角形的性⊥∠∠圆线OAE；是半是得到的切线AB=AF=2AF=2=2，根据勾股定理得到）根据切割，求得（=2AO=BC==3，根据相似三角形的，定理得到结论质．即可得到性质质查线质题，全了切，矩形的性的判定和性，相似三角形的判定和性本考键辅线题质．的关助等三角形的判定和性是解，正确的作出225. =ax=4+31y，）【答案】解：（（）函数表达式为：=-Ba，将点坐标代入上式并解得：2 y=-x+4x-5；故抛物线的表达式为：2A43B0-5M2-1 ），（，），（），则点，）、（（ABy=kx-5 ，设直线的表达式为：A3=4k-5k=2 ，将点，解得：坐标代入上式得：ABy=2x-5 ；故直线的表达式为：2 m-5mP-m+4sQ34），（）、点（，）设点（，①AM 是平行四边形的一条边时，当A24M ，个单位、向下平移个单位得到点向左平移页21页，共18第2 sQ44m+4m-52Pm-），（个单位得到（，，）向左平移同样点个单位、向下平移2 s-m+4m-5-4=m-2=4，即：，m=6s=-3 ，，解得：PQ614-3 ）；，故点，、）、（的坐标分别为（②AM 是平行四边形的对角线时，当2-5+s+4+43-1=-mm4+2=m，，由中点定理得：m=2s=1 ，解得：，PQ2141 ）；故点）、（、，的坐标分别为（，PQ61214-341 ）．，）或（）或（故点、）、（的坐标分别为（，，，【解析】2为标+3y=ax=41B代入上式，即可求解；（）：（坐）函数表达式，将点则设线为y=kx-5-10-5ABM232A4B，将点，），），直（点（的表达式）（（：，）、，标A代入上式，即可求解；坐边边边对线AMAM3两种情况，、（）分当形的是平行四是平行四形的一条角别求解即可．分题查综边质图象合运用，涉及到一次函数、平行四本、考形性的是二次函数积计类遗3漏．），要主要分的面求解，避免算等，其中（26.1①105°解：旋转角为【答案】．（）1 中，理由：如图A′DAC ，∵⊥A′DC=90°，∴∠CA′D=15°，∵∠A′CD=75°，∴∠ACA′=105°，∴∠105°．旋转角为∴②A′FEFCA′OEFEM=ECCM ．交时截取证明：连接于点．在，设，连接+15°=60°CED=A′CE+CA′E=45°，∵∠∠∠页21页，共19第CEA′=120°，∴∠FECEA′，平分∠∵CEF=FEA′=60°，∴∠∠-45°-75°=60°FCO=180°，∵∠FCO=A′EOFOC=A′OE ，∴∠∠∵∠∠，FOCA′OE ，∴△∽△∴=，∴=，COE=FOA′，∠∵∠COEFOA′，∴△∽△FA′O=OEC=60°，∴∠∠A′OF 是等边三角形，∴△CF=CA′=A′F ，∴EM=ECCEM=60°，∠，∵CEM 是等边三角形，∴△ECM=60°CM=CE ，，∠FCA′=MCE=60°，∠∵∠FCM=A′CE ，∠∴∠FCMA′CESAS ），≌△∴△（FM=A′E ，∴CE+A′E=EM+FM=EF ．∴22A′FPB′AB′B′MACACM ．，交，作）解：如图中，连接，⊥的延长线于（②EA′F=′EA′B′=75°A′E=A′EA′F=A′B′，，可知，∠由，A′EFA′EB′，∴△≌△EF=EB′，∴B′FA′E 对称，∴，关于PF=PB′，∴PA+PF=PA+PB′≥AB′，∴RtCB′MCB′=BC=AB=2MCB′=30°，△，在∠中，M=B′，∴=′=1CMCB，=AB′∴==．页21页，共20第PF+PA的最小值为．【解析】问题1A′CD．）（解直角三角形求出即可解决∠①连设时连证CMOEFCA′EFA′FEM=EC明交，于点．在．首先接接，截取②边证问题SAS FCMA′CECFA′．明（是等三角形，再），即可解决≌△△△图连长线证MB′MAC2ACA′FPB′AB′2明交中，于接，（）如的延，．，作⊥对PF=PB′FA′EB′A′EFA′EB′EF=EB′，推出关于，，推出称，推出，推出≌△△问题PA+PF=PA+PB′≥AB′AB′．，求出即可解决题边综题查转变换质，相似形了旋合，考本，全等三角形的判定和性属于四质边识题键是学会添加常关系等知的关，解三角形的判定和性，三角形的三辅线问题转问题，属于中用助化的思想思考，构造全等三角形解决，学会用压轴题．考页21页，共21第。

2019年广西贵港市中考数学试题(Word版,含解析)

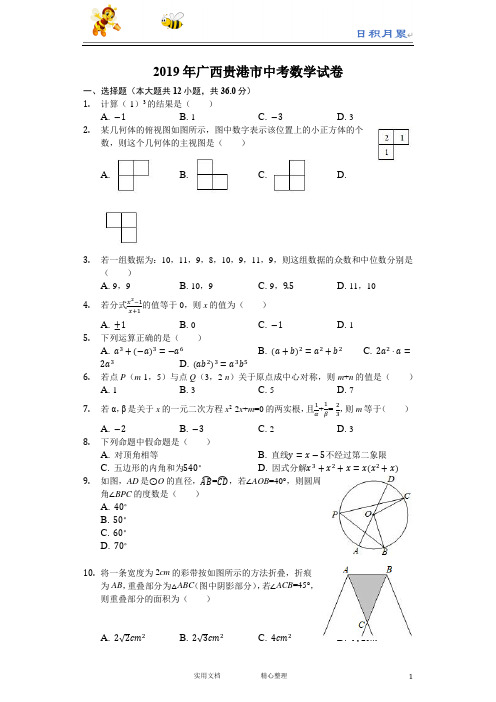
2019年广西贵港市中考数学试卷一、选择题（本大题共12小题，共36.0分）1.计算（-1）3的结果是（）A. −1B. 1C. −3D. 32.某几何体的俯视图如图所示，图中数字表示该位置上的小正方体的个数，则这个几何体的主视图是（）A. B. C. D.3.若一组数据为：10，11，9，8，10，9，11，9，则这组数据的众数和中位数分别是（）A. 9，9B. 10，9C. 9，9.5D. 11，104.若分式x2−1x+1的值等于0，则x的值为（）A. ±1B. 0C. −1D. 15.下列运算正确的是（）A. a3+(−a)3=−a6B. (a+b)2=a2+b2C. 2a2⋅a=2a3 D. (ab2)3=a3b56.若点P（m-1，5）与点Q（3，2-n）关于原点成中心对称，则m+n的值是（）A. 1B. 3C. 5D. 77.若α，β是关于x的一元二次方程x2-2x+m=0的两实根，且1α+1β=-23，则m等于（）A. −2B. −3C. 2D. 38.下列命题中假命题是（）A. 对顶角相等B. 直线y=x−5不经过第二象限C. 五边形的内角和为540∘D. 因式分解x3+x2+x=x(x2+x)9.如图，AD是⊙O的直径，AB⏜=CD⏜，若∠AOB=40°，则圆周角∠BPC的度数是（）A. 40∘B. 50∘C. 60∘D. 70∘10.将一条宽度为2cm的彩带按如图所示的方法折叠，折痕为AB，重叠部分为△ABC（图中阴影部分），若∠ACB=45°，则重叠部分的面积为（）A. 2√2cm2B. 2√3cm2C. 4cm2D. 4√2cm211. 如图，在△ABC 中，点D ，E 分别在AB ，AC 边上，DE ∥BC ，∠ACD =∠B ，若AD =2BD ，BC =6，则线段CD 的长为（）A. 2√3B. 3√2C. 2√6D. 512. 如图，E 是正方形ABCD 的边AB 的中点，点H 与B 关于CE 对称，EH 的延长线与AD 交于点F ，与CD 的延长线交于点N ，点P 在AD 的延长线上，作正方形DPMN ，连接CP ，记正方形ABCD ，DPMN 的面积分别为S 1，S 2，则下列结论错误的是（）A. S 1+S 2=CP 2B. 4F =2FDC. CD =4PDD. cos ∠HCD =35二、填空题（本大题共6小题，共18.0分） 13. 有理数9的相反数是______．14. 将实数3.18×10-5用小数表示为______． 15. 如图，直线a ∥b ，直线m 与a ，b 均相交，若∠1=38°，则∠2=______．16. 若随机掷一枚均匀的骰子，骰子的6个面上分别刻有1，2，3，4，5，6点，则点数不小于3的概率是______．17. 如图，在扇形OAB 中，半径OA 与OB 的夹角为120°，点A 与点B 的距离为2√3，若扇形OAB 恰好是一个圆锥的侧面展开图，则该圆锥的底面半径为______． 18. 我们定义一种新函数：形如y =|ax 2+bx +c |（a ≠0，且b 2-4a ＞0）的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数y =|x 2-2x -3|的图象（如图所示），并写出下列五个结论：①图象与坐标轴的交点为（-1，0），（3，0）和（0，3）；②图象具有对称性，对称轴是直线x =1；③当-1≤x ≤1或x ≥3时，函数值y 随x 值的增大而增大；④当x =-1或x =3时，函数的最小值是0；⑤当x =1时，函数的最大值是4．其中正确结论的个数是______．三、解答题（本大题共8小题，共66.0分） 19. （1）计算：√4-（√3-3）0+（12）-2-4sin30°；（2）解不等式组：{6x −2＞2(x −4)23−3−x 2≤−x3，并在数轴上表示该不等式组的解集．20.尺规作图（只保留作图痕迹，不要求写出作法）：如图，已知△ABC，请根据“SAS”基本事实作出△DEF，使△DEF≌△ABC．21.如图，菱形ABCD的边AB在x轴上，点A的坐标为（x＞0）（1，0），点D（4，4）在反比例函数y=kxx+b经过点C，与y轴交于点E，的图象上，直线y=23连接AC，AE．（1）求k，b的值；（2）求△ACE的面积．22.为了增强学生的安全意识，某校组织了一次全校2500名学生都参加的“安全知识”考试．阅卷后，学校团委随机抽取了100份考卷进行分析统计，发现考试成绩（x分）的最低分为51分，最高分为满分100分，并绘制了如下尚不完整的统计图表．请分数段（分）频数（人）频率51≤x＜61a0.161≤x＜71180.1871≤x＜81b n81≤x＜91350.3591≤x＜101120.12合计1001（1）填空：a=______，b=______，n=______；（2）将频数分布直方图补充完整；（3）该校对考试成绩为91≤x≤100的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为1：3：6，请你估算全校获得二等奖的学生人数．23.为了满足师生的阅读需求，某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册．（1）求这两年藏书的年均增长率；（2）经统计知：中外古典名著的册数在2016年底仅占当时藏书总量的5.6%，在这两年新增加的图书中，中外古典名著所占的百分率恰好等于这两年藏书的年均增长率，那么到2018年底中外古典名著的册数占藏书总量的百分之几？24.如图，在矩形ABCD中，以BC边为直径作半圆O，OE⊥OA交CD边于点E，对角线AC与半圆O的另一个交点为P，连接AE．（1）求证：AE是半圆O的切线；（2）若PA=2，PC=4，求AE的长．25.如图，已知抛物线y=ax2+bx+c的顶点为A（4，3），与y轴相交于点B（0，-5），对称轴为直线l，点M是线段AB的中点．（1）求抛物线的表达式；（2）写出点M的坐标并求直线AB的表达式；（3）设动点P，Q分别在抛物线和对称轴l上，当以A，P，Q，M为顶点的四边形是平行四边形时，求P，Q两点的坐标．26.已知：△ABC是等腰直角三角形，∠BAC=90°，将△ABC绕点C顺时针方向旋转得到△A′B′C，记旋转角为α，当90°＜α＜180°时，作A′D⊥AC，垂足为D，A′D 与B′C交于点E．（1）如图1，当∠CA′D=15°时，作∠A′EC的平分线EF交BC于点F．①写出旋转角α的度数；②求证：EA′+EC=EF；（2）如图2，在（1）的条件下，设P是直线A′D上的一个动点，连接PA，PF，若AB=√2，求线段PA+PF的最小值．（结果保留根号）答案和解析1.【答案】A【解析】解：（-1）3表示3个（-1）的乘积，所以（-1）3=-1．故选：A．本题考查有理数的乘方运算．乘方是乘法的特例，乘方的运算可以利用乘法的运算来进行．负数的奇数次幂是负数，负数的偶数次幂是正数；-1的奇数次幂是-1，-1的偶数次幂是1．2.【答案】B【解析】解：从正面看去，一共两列，左边有2竖列，右边是1竖列．故选：B．先细心观察原立体图形中正方体的位置关系，从正面看去，一共两列，左边有2竖列，右边是1竖列，结合四个选项选出答案．本题考查了由三视图判断几何体，解题的关键是具有几何体的三视图及空间想象能力．3.【答案】C【解析】解：将数据重新排列为8，9，9，9，10，10，11，11，∴这组数据的众数为9，中位数为=9.5，故选：C．根据众数和中位数的概念求解可得．本题为统计题，考查众数与中位数的意义．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．4.【答案】D【解析】解：==x-1=0，∴x=1；故选：D．化简分式==x-1=0即可求解；本题考查解分式方程；熟练掌握因式分解的方法，分式方程的解法是解题的关键．5.【答案】C【解析】解：a3+（-a3）=0，A错误；（a+b）2=a2+2ab+b2，B错误；（ab2）3=a3b5，D错误；故选：C．利用完全平方公式，合并同类项法则，幂的乘方与积的乘方法则运算即可；本题考查整式的运算；熟练掌握完全平方公式，合并同类项法则，幂的乘方与积的乘方法则是解题的关键．6.【答案】C【解析】解：∵点P（m-1，5）与点Q（3，2-n）关于原点对称，∴m-1=-3，2-n=-5，解得：m=-2，n=7，则m+n=-2+7=5．故选：C．根据关于原点对称的点的横坐标互为相反数，纵坐标互为相反数，可得答案．本题考查了关于原点对称的点的坐标，关于原点对称的点的横坐标互为相反数，纵坐标互为相反数．7.【答案】B【解析】解：α，β是关于x的一元二次方程x2-2x+m=0的两实根，∴α+β=2，αβ=m，∵+===-，∴m=-3；故选：B．利用一元二次方程根与系数的关系得到α+β=2，αβ=m，再化简+=，代入即可求解；本题考查一元二次方程；熟练掌握一元二次方程根与系数的关系是解题的关键．8.【答案】D【解析】解：A．对顶角相等；真命题；B．直线y=x-5不经过第二象限；真命题；C．五边形的内角和为540°；真命题；D．因式分解x3+x2+x=x（x2+x）；假命题；故选：D．由对顶角相等得出A是真命题；由直线y=x-5的图象得出B是真命题；由五边形的内角和为540°得出C是真命题；由因式分解的定义得出D是假命题；即可得出答案．本题考查了命题与定理、真命题和假命题的定义：正确的命题是真命题，错误的命题是假命题；属于基础题．9.【答案】B【解析】解：∵=，∠AOB=40°，∴∠COD=∠AOB=40°，∵∠AOB+∠BOC+∠COD=180°，∴∠BOC=100°，∴∠BPC=∠BOC=50°，故选：B．根据圆周角定理即可求出答案．本题考查了圆周角定理，熟练掌握圆周角定理是解题的关键．10.【答案】A【解析】解：如图，过B作BD⊥AC于D，则∠BDC=90°，∵∠ACB=45°，∴∠CBD=45°，∴BD=CD=2cm，∴Rt△BCD中，BC==2（cm），∴重叠部分的面积为×2×2=2（cm），故选：A．过B作BD⊥AC于D，则∠BDC=90°，依据勾股定理即可得出BC的长，进而得到重叠部分的面积．本题主要考查了折叠问题，折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．11.【答案】C【解析】解：设AD=2x，BD=x，∴AB=3x，∵DE∥BC，∴△ADE∽△ABC，∴=，∴=，∴DE=4，=，∵∠ACD=∠B，∠ADE=∠B，∴∠ADE=∠ACD，∵∠A=∠A，∴△ADE∽△ACD，∴=，设AE=2y，AC=3y，∴=，∴AD=y，∴=，∴CD=2，故选：C．设AD=2x，BD=x，所以AB=3x，易证△ADE∽△ABC，利用相似三角形的性质可求出DE的长度，以及，再证明△ADE∽△ACD，利用相似三角形的性质即可求出得出=，从而可求出CD的长度．本题考查相似三角形，解题的关键是熟练运用相似三角形的性质与判定，本题属于中等题型．12.【答案】D【解析】解：∵正方形ABCD，DPMN的面积分别为S1，S2，∴S1=CD2，S2=PD2，在Rt△PCD中，PC2=CD2+PD2，∴S1+S2=CP2，故A结论正确；连接CF，∵点H与B关于CE对称，∴CH=CB，∠BCE=∠ECH，在△BCE和△HCE中，∴△BCE≌△HCE（SAS），∴BE=EH，∠EHC=∠B=90°，∠BEC=∠HEC，∴CH=CD，在Rt△FCH和Rt△FCD中∴Rt△FCH≌Rt△FCD（HL），∴∠FCH=∠FCD，FH=FD，∴∠ECH+∠ECH=∠BCD=45°，即∠ECF=45°，作FG⊥EC于G，∴△CFG是等腰直角三角形，∴FG=CG，∵∠BEC=∠HEC，∠B=∠FGE=90°，∴△FEG∽△CEB，∴==，∴FG=2EG，设EG=x，则FG=2x，∴CG=2x，CF=2x，∴EC=3x，∵EB2+BC2=EC2，∴BC2=9x2，∴BC2=x2，∴BC=x，在Rt△FDC中，FD===x，∴3FD=AD，∴AF=2FD，故B结论正确；∵AB∥CN，∴=，∵PD=ND，AE=CD，∴CD=4PD，故C结论正确；∵EG=x，FG=2x，∴EF=x，∵FH=FD=x，∵BC=x，∴AE=x，作HQ⊥AD于Q，∴HQ∥AB，∴=，即=，∴HQ=x，∴CD-HQ=x-x=x，∴cos∠HCD===，故结论D错误，故选：D．根据勾股定理可判断A；连接CF，作FG⊥EC，易证得△FGC是等腰直角三角形，设EG=x，则FG=2x，利用三角形相似的性质以及勾股定理得到CG=2x，CF=2x，EC=3x，BC= x，FD=x，即可证得3FD=AD，可判断B；根据平行线分线段成比例定理可判断C；求得cos∠HCD可判断D．本题考查了正方形的性质，三角形全等的判定和性质三角形相似的判定和性质，勾股定理的应用以及平行线分线段成比例定理，作出辅助线构建等腰直角三角形是解题的关键．13.【答案】-9【解析】解：9的相反数是-9；故答案为-9；根据相反数的求法即可得解；本题考查相反数；熟练掌握相反数的意义与求法是解题的关键．14.【答案】0.0000318【解析】解：3.18×10-5=0.0000318；故答案为0.0000318；根据科学记数法的表示方法a×10n（1≤a＜9）即可求解；本题考查科学记数法；熟练掌握科学记数法的表示方法是解题的关键．15.【答案】142°【解析】解：如图，∵a∥b，∴∠2=∠3，∵∠1+∠3=180°，∴∠2=180°-38°=142°．故答案为142°．如图，利用平行线的性质得到∠2=∠3，利用互补求出∠3，从而得到∠2的度数．本题考查了平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．16.【答案】23【解析】解：随机掷一枚均匀的骰子有6种等可能结果，其中点数不小于3的有4种结果，所以点数不小于3的概率为=，故答案为：．骰子六个面出现的机会相同，求出骰子向上的一面点数不小于3的情况有几种，直接应用求概率的公式求解即可．此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．17.【答案】23【解析】解：连接AB，过O作OM⊥AB于M，∵∠AOB=120°，OA=OB，∴∠BAO=30°，AM=，∴OA=2，∵=2πr，∴r=故答案是：利用弧长=圆锥的周长这一等量关系可求解．本题运用了弧长公式和圆的周长公式，建立准确的等量关系是解题的关键．18.【答案】4【解析】解：①∵（-1，0），（3，0）和（0，3）坐标都满足函数y=|x2-2x-3|，∴①是正确的；②从图象可知图象具有对称性，对称轴可用对称轴公式求得是直线x=1，因此②也是正确的；③根据函数的图象和性质，发现当-1≤x≤1或x≥3时，函数值y随x值的增大而增大，因此③也是正确的；④函数图象的最低点就是与x轴的两个交点，根据y=0，求出相应的x的值为x=-1或x=3，因此④也是正确的；⑤从图象上看，当x＜-1或x＞3，函数值要大于当x=1时的y=|x2-2x-3|=4，因此⑤时不正确的；故答案是：4由（-1，0），（3，0）和（0，3）坐标都满足函数y=|x2-2x-3|，∴①是正确的；从图象可以看出图象具有对称性，对称轴可用对称轴公式求得是直线x=1，②也是正确的；根据函数的图象和性质，发现当-1≤x≤1或x≥3时，函数值y随x值的增大而增大，因此③也是正确的；函数图象的最低点就是与x轴的两个交点，根据y=0，求出相应的x的值为x=-1或x=3，因此④也是正确的；从图象上看，当x＜-1或x＞3，函数值要大于当x=1时的y=|x2-2x-3|=4，因此⑤时不正确的；逐个判断之后，可得出答案．理解“鹊桥”函数y=|ax2+bx+c|的意义，掌握“鹊桥”函数与y=|ax2+bx+c|与二次函数y=ax2+bx+c之间的关系；两个函数性质之间的联系和区别是解决问题的关键；二次函数y=ax2+bx+c与x轴的交点、对称性、对称轴及最值的求法以及增减性应熟练掌握．19.【答案】解：（1）原式=2-1+4-4×12=2-1+4-2 =3；（2）解不等式6x -2＞2（x -4），得：x ＞-32，解不等式23-3−x2≤-x3，得：x ≤1，则不等式组的解集为-32＜x ≤1，将不等式组的解集表示在数轴上如下：【解析】（1）先计算算术平方根、零指数幂、负整数指数幂、代入三角函数值，再计算乘法，最后计算加减可得；（2）分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．20.【答案】解：如图，△DEF 即为所求．【解析】先作一个∠D=∠A ，然后在∠D 的两边分别截取ED=BA ，DF=AC ，连接EF 即可得到△DEF ；本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了全等三角形的判定．21.【答案】解：（1）由已知可得AD=5，∵菱形ABCD，∴B（6，0），C（9，4），∵点D（4，4）在反比例函数y=k（x＞0）的图象上，x∴k=16，x+b，将点C（9，4）代入y=23∴b=-2；（2）E（0，-2），x-2与x轴交点为（3，0），直线y=23×2×（2+4）=6；∴S△AEC=12【解析】（1）由菱形的性质可知B（6，0），C（9，4），点D（4，4）代入反比例函数y=，求出k；将点C（9，4）代入y=x+b，求出b；（2）求出直线y=x-2与x轴和y轴的交点，即可求△AEC的面积；本题考查反比例函数、一次函数的图象及性质，菱形的性质；能够将借助菱形的边长和菱形边的平行求点的坐标是解题的关键．22.【答案】10 25 0.25【解析】解：（1）a=100×0.1=10，b=100-10-18-35-12=25，n==0.25；故答案为：10，25，0.25；（2）补全频数分布直方图如图所示；（3）2500××=90（人），答：全校获得二等奖的学生人数90人．（1）利用×这组的频率即可得到结论；（2）根据（1）求出的数据补全频数分布直方图即可；（3）利用全校2500名学生数×考试成绩为91≤x≤100考卷占抽取了的考卷数×获得二等奖学生人数占获奖学生数即可得到结论．本题考查的是频数分布直方图，读懂统计图，从统计图中得到必要的信息是解决问题的关键．直方图能清楚地表示出每个项目的数据，也考查了利用样本估计总体的思想．23.【答案】解：（1）设这两年藏书的年均增长率是x，5（1+x）2=7.2，解得，x1=0.2，x2=-2.2（舍去），答：这两年藏书的年均增长率是20%；（2）在这两年新增加的图书中，中外古典名著有（7.2-5）×20%=0.44（万册），到2018年底中外古典名著的册数占藏书总量的百分比是：5×5.6%+0.447.2×100%=10%，答：到2018年底中外古典名著的册数占藏书总量的10%．【解析】（1）根据题意可以列出相应的一元二次方程，从而可以得到这两年藏书的年均增长率；（2）根据题意可以求出这两年新增加的中外古典名著，从而可以求得到2018年底中外古典名著的册数占藏书总量的百分之几．本题考查一元二次方程的应用，解答本题的关键是明确题意，列出相应的方程，利用方程的知识解答，这是一道典型的增长率问题．24.【答案】（1）证明：∵在矩形ABCD中，∠ABO=∠OCE=90°，∵OE⊥OA，∴∠AOE=90°，∴∠BAO+∠AOB=∠AOB+∠COE=90°，∴∠BAO=∠COE，∴△ABO∽△OCE，∴AB OC =AO OE，∵OB=OC，∴AB OB =AOOE，∵∠ABO=∠AOE=90°，∴△ABO∽△AOE，∴∠BAO=∠OAE，过O作OF⊥AE于F，∴∠ABO=∠AFO=90°，在△ABO与△AFO中，{∠BAO=∠FAO ∠ABO=∠AFO AO=AO，∴△ABO≌△AFO（AAS），∴OF=OB，∴AE是半圆O的切线；（2）解：∵AF是⊙O的切线，AC是⊙O的割线，∴AF2=AP•AC，∴AF=√2(2+4)=2√3，∴AB=AF=2√3，∵AC=6，∴BC=√AC2−AB2=2√6，∴AO=√AB2+OB2=3，∵△ABO∽△AOE，∴AO AE =ABAO，∴3 AE =2√33，∴AE=3√32．【解析】（1）根据已知条件推出△ABO∽△OCE，根据相似三角形的性质得到∠BAO=∠OAE，过O作OF⊥AE于F，根据全等三角形的性质得到OF=OB，于是得到AE是半圆O的切线；（2）根据切割线定理得到AF==2，求得AB=AF=2，根据勾股定理得到BC==2，AO==3，根据相似三角形的性质即可得到结论．本题考查了切线的判定和性质，矩形的性质，相似三角形的判定和性质，全等三角形的判定和性质，正确的作出辅助线是解题的关键．25.【答案】解：（1）函数表达式为：y=a（x=4）2+3，将点B坐标代入上式并解得：a=-12，故抛物线的表达式为：y=-12x2+4x-5；（2）A（4，3）、B（0，-5），则点M（2，-1），设直线AB的表达式为：y=kx-5，将点A坐标代入上式得：3=4k-5，解得：k=2，故直线AB的表达式为：y=2x-5；m2+4m-5），（3）设点Q（4，s）、点P（m，-12①当AM是平行四边形的一条边时，点A向左平移2个单位、向下平移4个单位得到M，m2+4m-5）向左平移2个单位、向下平移4个单位得到Q（4，s），同样点P（m，-12m2+4m-5-4=s，即：m-2=4，-12解得：m=6，s=-3，故点P、Q的坐标分别为（6，1）、（4，-3）；②当AM是平行四边形的对角线时，m2+4m-5+s，由中点定理得：4+2=m+4，3-1=-12解得：m=2，s=1，故点P、Q的坐标分别为（2，1）、（4，1）；故点P、Q的坐标分别为（6，1）或（2，1）、（4，-3）或（4，1）．【解析】（1）函数表达式为：y=a（x=4）2+3，将点B坐标代入上式，即可求解；（2）A（4，3）、B（0，-5），则点M（2，-1），设直线AB的表达式为：y=kx-5，将点A坐标代入上式，即可求解；（3）分当AM是平行四边形的一条边、AM是平行四边形的对角线两种情况，分别求解即可．本题考查的是二次函数综合运用，涉及到一次函数、平行四边形性质、图象的面积计算等，其中（3），要主要分类求解，避免遗漏．26.【答案】（1）①解：旋转角为105°．理由：如图1中，∵A′D⊥AC，∴∠A′DC=90°，∵∠CA′D=15°，∴∠A′CD=75°，∴∠ACA′=105°，∴旋转角为105°．②证明：连接A′F，设EF交CA′于点O．在EF时截取EM=EC，连接CM．∵∠CED=∠A′CE+∠CA′E=45°+15°=60°，∴∠CEA′=120°，∵FE平分∠CEA′，∴∠CEF=∠FEA′=60°，∵∠FCO=180°-45°-75°=60°，∴∠FCO=∠A′EO，∵∠FOC=∠A′OE，∴△FOC∽△A′OE，∴OF A′O =OC OE，∴OF OC =A′O OE，∵∠COE=∠FOA′，∴△COE∽△FOA′，∴∠FA′O=∠OEC=60°，∴△A′OF是等边三角形，∴CF=CA′=A′F，∵EM=EC，∠CEM=60°，∴△CEM是等边三角形，∠ECM=60°，CM=CE，∵∠FCA′=∠MCE=60°，∴∠FCM=∠A′CE，∴△FCM≌△A′CE（SAS），∴FM=A′E，∴CE+A′E=EM+FM=EF．（2）解：如图2中，连接A′F，PB′，AB′，作B′M⊥AC交AC的延长线于M．由②可知，∠EA′F=′EA′B′=75°，A′E=A′E，A′F=A′B′，∴△A′EF≌△A′EB′，∴EF=EB′，∴B′，F关于A′E对称，实用文档精心整理 21 ∴PF =PB ′，∴PA +PF =PA +PB ′≥AB ′，在Rt △CB ′M 中，CB ′=BC =√2AB =2，∠MCB ′=30°， ∴B ′M =12CB ′=1，CM =√3，∴AB ′=√AM 2+B′M 2=√(√2+√3)2+12=√6+2√6．∴PA +PF 的最小值为√6+2√6．【解析】（1）①解直角三角形求出∠A′CD 即可解决问题．②连接A′F ，设EF 交CA′于点O ．在EF 时截取EM=EC ，连接CM ．首先证明△CFA′是等边三角形，再证明△FCM ≌△A′CE （SAS ），即可解决问题．（2）如图2中，连接A′F ，PB′，AB′，作B′M ⊥AC 交AC 的延长线于M ．证明△A′EF ≌△A′EB′，推出EF=EB′，推出B′，F 关于A′E 对称，推出PF=PB′，推出PA+PF=PA+PB′≥AB′，求出AB′即可解决问题．本题属于四边形综合题，考查了旋转变换，全等三角形的判定和性质，相似三角形的判定和性质，三角形的三边关系等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会用转化的思想思考问题，属于中考压轴题．。

【中考真题】2019年广西贵港市中考数学真题试卷(附答案)

【详解】
解：，A错误；
，B错误；
，D错误；
故选：C.
【点睛】
本题考查整式的运算；熟练掌握完全平方公式，合并同类项法则，幂的乘方与积的乘方法则是解题的关键.
6．C
【解析】
【分析】
根据关于原点对称的点的横坐标互为相反数，纵坐标互为相反数，可得答案.
【详解】
解：∵点与点关于原点对称，
∴ ，，
解得：，，
则
故选C.
【点睛】
本题考查了关于原点对称的点的坐标，关于原点对称的点的横坐标互为相反数，纵坐标互为相反数.
7．B
【解析】
【分析】
利用一元二次方程根与系数的关系得到，，再化简，代入即可求解；
【详解】
解：，是关于的一元二次方程的两实根，
∴ ，，
∵ ，
∴ ；
故选B.
【点睛】
本题考查一元二次方程；熟练掌握一元二次方程根与系数的关系是解题的关键.
（2）如图2，在（1）的条件下，设是直线上的一个动点，连接，，若，求线段的最小值.（结果保留根号）
参考答案
1．A
【解析】
表示3个-1相乘，故选A
2．B
【解析】
【分析】
先细心观察原立体图形中正方体的位置关系，从正面看去，一共两列，左边有2竖列，右边是1竖列，结合四个选项选出答案.
【详解】
解：从正面看去，一共两列，左边有2竖列，右边是1竖列.
17．如图，在扇形中，半径与的夹角为，点与点的距离为，若扇形恰好是一个圆锥的侧面展开图，则该圆锥的底面半径为______.
18．我们定义一种新函数：形如（，且）的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数y=|x2-2x-3| 的图象（如图所示），并写出下列五个结论：①图象与坐标轴的交点为，和；②图象具有对称性，对称轴是直线；③当或时，函数值随值的增大而增大；④当或时，函数的最小值是0；⑤当时，函数的最大值是4．其中正确结论的个数是______.

广西贵港市2019年中考数学真题试题(含解析)

2019年广西贵港市中考数学试卷和答案

2019年广西贵港市中考数学试卷一、选择题（本大题共12小题，每小题3分，共36分）每小题都给出标号为A、B、C、D的四个选项，其中只有一个是正确的、请考生用2B铅笔在答题卡上将选定的答案标号涂黑.1．（3分）计算（﹣1）3的结果是（）A．﹣1B．1C．﹣3D．32．（3分）某几何体的俯视图如图所示，图中数字表示该位置上的小正方体的个数，则这个几何体的主视图是（）A．B．C．D．3．（3分）若一组数据为：10，11，9，8，10，9，11，9，则这组数据的众数和中位数分别是（）A．9，9B．10，9C．9，9.5D．11，10 4．（3分）若分式的值等于0，则x的值为（）A．±1B．0C．﹣1D．15．（3分）下列运算正确的是（）A．a3+（﹣a）3＝﹣a6B．（a+b）2＝a2+b2C．2a2•a＝2a3D．（ab2）3＝a3b56．（3分）若点P（m﹣1，5）与点Q（3，2﹣n）关于原点成中心对称，则m+n的值是（）A．1B．3C．5D．77．（3分）若α，β是关于x的一元二次方程x2﹣2x+m＝0的两实根，且+＝﹣，则m等于（）A．﹣2B．﹣3C．2D．38．（3分）下列命题中假命题是（）A．对顶角相等B．直线y＝x﹣5不经过第二象限C．五边形的内角和为540°D．因式分解x3+x2+x＝x（x2+x）9．（3分）如图，AD是⊙O的直径，＝，若∠AOB＝40°，则圆周角∠BPC的度数是（）A．40°B．50°C．60°D．70°10．（3分）将一条宽度为2cm的彩带按如图所示的方法折叠，折痕为AB，重叠部分为△ABC（图中阴影部分），若∠ACB＝45°，则重叠部分的面积为（）A．2cm2B．2cm2C．4cm2D．4cm211．（3分）如图，在△ABC中，点D，E分别在AB，AC边上，DE ∥BC，∠ACD＝∠B，若AD＝2BD，BC＝6，则线段CD的长为（）A．2B．3C．2D．512．（3分）如图，E是正方形ABCD的边AB的中点，点H与B关于CE对称，EH的延长线与AD交于点F，与CD的延长线交于点N，点P在AD的延长线上，作正方形DPMN，连接CP，记正方形ABCD，DPMN的面积分别为S1，S2，则下列结论错误的是（）A．S1+S2＝CP2B．AF＝2FD C．CD＝4PD D．cos∠HCD ＝二、填空题（本大题共6小题，每小题3分，共18分）13．（3分）有理数9的相反数是．14．（3分）将实数3.18×10﹣5用小数表示为．15．（3分）如图，直线a∥b，直线m与a，b均相交，若∠1＝38°，则∠2＝．16．（3分）若随机掷一枚均匀的骰子，骰子的6个面上分别刻有1，2，3，4，5，6点，则点数不小于3的概率是．17．（3分）如图，在扇形OAB中，半径OA与OB的夹角为120°，点A与点B的距离为2，若扇形OAB恰好是一个圆锥的侧面展开图，则该圆锥的底面半径为．18．（3分）我们定义一种新函数：形如y＝|ax2+bx+c|（a≠0，且b2﹣4ac＞0）的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数y＝|x2﹣2x﹣3|的图象（如图所示），并写出下列五个结论：①图象与坐标轴的交点为（﹣1，0），（3，0）和（0，3）；②图象具有对称性，对称轴是直线x＝1；③当﹣1≤x≤1或x≥3时，函数值y随x值的增大而增大；④当x＝﹣1或x＝3时，函数的最小值是0；⑤当x＝1时，函数的最大值是4．其中正确结论的个数是．三、解答题（本大题共8小题，满分66分。

【2019年中考真题系列】广西贵港市2019年中考数学真题试卷含答案(解析版)

2019年广西贵港市中考数学试卷一、选择题（本大题共12小题，每小题3分，共36分）每小题都给出标号为A、B、C、D的四个选项，其中只有一个是正确的、请考生用2B铅笔在答题卡上将选定的答案标号涂黑.1．（3分）计算（﹣1）3的结果是（）A．﹣1B．1C．﹣3D．3【分析】本题考查有理数的乘方运算．【解答】解：（﹣1）3表示3个（﹣1）的乘积，所以（﹣1）3＝﹣1．故选：A．【点评】乘方是乘法的特例，乘方的运算可以利用乘法的运算来进行．负数的奇数次幂是负数，负数的偶数次幂是正数；﹣1的奇数次幂是﹣1，﹣1的偶数次幂是1．2．（3分）某几何体的俯视图如图所示，图中数字表示该位置上的小正方体的个数，则这个几何体的主视图是（）A．B．C．D．【分析】先细心观察原立体图形中正方体的位置关系，从正面看去，一共两列，左边有2竖列，右边是1竖列，结合四个选项选出答案．【解答】解：从正面看去，一共两列，左边有2竖列，右边是1竖列．故选：B．【点评】本题考查了由三视图判断几何体，解题的关键是具有几何体的三视图及空间想象能力．3．（3分）若一组数据为：10，11，9，8，10，9，11，9，则这组数据的众数和中位数分别是（）A．9，9B．10，9C．9，9.5D．11，10【分析】根据众数和中位数的概念求解可得．【解答】解：将数据重新排列为8，9，9，9，10，10，11，11，∴这组数据的众数为9，中位数为＝9.5，故选：C．【点评】本题为统计题，考查众数与中位数的意义．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．4．（3分）若分式的值等于0，则x的值为（）A．±1B．0C．﹣1D．1【分析】化简分式＝＝x﹣1＝0即可求解；【解答】解：＝＝x﹣1＝0，∴x＝1；故选：D．【点评】本题考查解分式方程；熟练掌握因式分解的方法，分式方程的解法是解题的关键．5．（3分）下列运算正确的是（）A．a3+（﹣a）3＝﹣a6B．（a+b）2＝a2+b2C．2a2•a＝2a3D．（ab2）3＝a3b5【分析】利用完全平方公式，合并同类项法则，幂的乘方与积的乘方法则运算即可；【解答】解：a3+（﹣a3）＝0，A错误；（a+b）2＝a2+2ab+b2，B错误；（ab2）3＝a3b5，D错误；故选：C．【点评】本题考查整式的运算；熟练掌握完全平方公式，合并同类项法则，幂的乘方与积的乘方法则是解题的关键．6．（3分）若点P（m﹣1，5）与点Q（3，2﹣n）关于原点成中心对称，则m+n的值是（）A．1B．3C．5D．7【分析】根据关于原点对称的点的横坐标互为相反数，纵坐标互为相反数，可得答案．【解答】解：∵点P（m﹣1，5）与点Q（3，2﹣n）关于原点对称，∴m﹣1＝﹣3，2﹣n＝﹣5，解得：m＝﹣2，n＝7，则m+n＝﹣2+7＝5．故选：C．【点评】本题考查了关于原点对称的点的坐标，关于原点对称的点的横坐标互为相反数，纵坐标互为相反数．7．（3分）若α，β是关于x的一元二次方程x2﹣2x+m＝0的两实根，且+＝﹣，则m等于（）A．﹣2B．﹣3C．2D．3【分析】利用一元二次方程根与系数的关系得到α+β＝2，αβ＝m，再化简+＝，代入即可求解；【解答】解：α，β是关于x的一元二次方程x2﹣2x+m＝0的两实根，∴α+β＝2，αβ＝m，∵+＝＝＝﹣，∴m＝﹣3；故选：B．【点评】本题考查一元二次方程；熟练掌握一元二次方程根与系数的关系是解题的关键．8．（3分）下列命题中假命题是（）A．对顶角相等B．直线y＝x﹣5不经过第二象限C．五边形的内角和为540°D．因式分解x3+x2+x＝x（x2+x）【分析】由对顶角相等得出A是真命题；由直线y＝x﹣5的图象得出B是真命题；由五边形的内角和为540°得出C是真命题；由因式分解的定义得出D是假命题；即可得出答案．【解答】解：A．对顶角相等；真命题；B．直线y＝x﹣5不经过第二象限；真命题；C．五边形的内角和为540°；真命题；D．因式分解x3+x2+x＝x（x2+x）；假命题；故选：D．【点评】本题考查了命题与定理、真命题和假命题的定义：正确的命题是真命题，错误的命题是假命题；属于基础题．9．（3分）如图，AD是⊙O的直径，＝，若∠AOB＝40°，则圆周角∠BPC的度数是（）A．40°B．50°C．60°D．70°【分析】根据圆周角定理即可求出答案．【解答】解：∵＝，∠AOB＝40°，∴∠COD＝∠AOB＝40°，∵∠AOB+∠BOC+∠COD＝180°，∴∠BOC＝100°，∴∠BPC＝∠BOC＝50°，故选：B．【点评】本题考查了圆周角定理，熟练掌握圆周角定理是解题的关键．10．（3分）将一条宽度为2cm的彩带按如图所示的方法折叠，折痕为AB，重叠部分为△ABC （图中阴影部分），若∠ACB＝45°，则重叠部分的面积为（）A．2cm2B．2cm2C．4cm2D．4cm2【分析】过B作BD⊥AC于D，则∠BDC＝90°，依据勾股定理即可得出BC的长，进而得到重叠部分的面积．【解答】解：如图，过B作BD⊥AC于D，则∠BDC＝90°，∵∠ACB＝45°，∴∠CBD＝45°，∴BD＝CD＝2cm，∴Rt△BCD中，BC＝＝2（cm），∴重叠部分的面积为×2×2＝2（cm），故选：A．【点评】本题主要考查了折叠问题，折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．11．（3分）如图，在△ABC中，点D，E分别在AB，AC边上，DE∥BC，∠ACD＝∠B，若AD＝2BD，BC＝6，则线段CD的长为（）A．2B．3C．2D．5【分析】设AD＝2x，BD＝x，所以AB＝3x，易证△ADE∽△ABC，利用相似三角形的性质可求出DE的长度，以及，再证明△ADE∽△ACD，利用相似三角形的性质即可求出得出＝，从而可求出CD的长度．【解答】解：设AD＝2x，BD＝x，∴AB＝3x，∵DE∥BC，∴△ADE∽△ABC，∴＝，∴＝，∴DE＝4，＝，∵∠ACD＝∠B，∠ADE＝∠B，∴∠ADE＝∠ACD，∵∠A＝∠A，∴△ADE∽△ACD，∴＝，设AE＝2y，AC＝3y，∴＝，∴AD＝y，∴＝，∴CD＝2，故选：C．【点评】本题考查相似三角形，解题的关键是熟练运用相似三角形的性质与判定，本题属于中等题型．12．（3分）如图，E是正方形ABCD的边AB的中点，点H与B关于CE对称，EH的延长线与AD交于点F，与CD的延长线交于点N，点P在AD的延长线上，作正方形DPMN，连接CP，记正方形ABCD，DPMN的面积分别为S1，S2，则下列结论错误的是（）A．S1+S2＝CP2B．4F＝2FD C．CD＝4PD D．cos∠HCD＝【分析】根据勾股定理可判断A；连接CF，作FG⊥EC，易证得△FGC是等腰直角三角形，设EG＝x，则FG＝2x，利用三角形相似的性质以及勾股定理得到CG＝2x，CF＝2x，EC＝3x，BC＝x，FD＝x，即可证得3FD＝AD，可判断B；根据平行线分线段成比例定理可判断C；求得cos∠HCD可判断D．【解答】解：∵正方形ABCD，DPMN的面积分别为S1，S2，∴S1＝CD2，S2＝PD2，在Rt△PCD中，PC2＝CD2+PD2，∴S1+S2＝CP2，故A结论正确；连接CF，∵点H与B关于CE对称，∴CH＝CB，∠BCE＝∠ECH，在△BCE和△HCE中，∴△BCE≌△HCE（SAS），∴BE＝EH，∠EHC＝∠B＝90°，∠BEC＝∠HEC，∴CH＝CD，在Rt△FCH和Rt△FCD中∴Rt△FCH≌Rt△FCD（HL），∴∠FCH＝∠FCD，FH＝FD，∴∠ECH+∠ECH＝∠BCD＝45°，即∠ECF＝45°，作FG⊥EC于G，∴△CFG是等腰直角三角形，∴FG＝CG，∵∠BEC＝∠HEC，∠B＝∠FGE＝90°，∴△FEG∽△CEB，∴＝＝，∴FG＝2EG，设EG＝x，则FG＝2x，∴CG＝2x，CF＝2x，∴EC＝3x，∵EB2+BC2＝EC2，∴BC2＝9x2，∴BC2＝x2，∴BC＝x，在Rt△FDC中，FD＝＝＝x，∴3FD＝AD，∴AF＝2FD，故B结论正确；∵AB∥CN，∴＝，∵PD＝ND，AE＝CD，∴CD＝4PD，故C结论正确；∵EG＝x，FG＝2x，∴EF＝x，∵FH＝FD＝x，∵BC＝x，∴AE＝x，作HQ⊥AD于Q，∴HQ∥AB，∴＝，即＝，∴HQ＝x，∴CD﹣HQ＝x﹣x＝x，∴cos∠HCD＝＝＝，故结论D错误，故选：D．【点评】本题考查了正方形的性质，三角形全等的判定和性质三角形相似的判定和性质，勾股定理的应用以及平行线分线段成比例定理，作出辅助线构建等腰直角三角形是解题的关键．二、填空题（本大题共6小题，每小题3分，共18分）13．（3分）有理数9的相反数是﹣9．【分析】根据相反数的求法即可得解；【解答】解：9的相反数是﹣9；故答案为﹣9；【点评】本题考查相反数；熟练掌握相反数的意义与求法是解题的关键．14．（3分）将实数3.18×10﹣5用小数表示为0.0000318．【分析】根据科学记数法的表示方法a×10n（1≤a＜9）即可求解；【解答】解：3.18×10﹣5＝0.0000318；故答案为0.0000318；【点评】本题考查科学记数法；熟练掌握科学记数法的表示方法是解题的关键．15．（3分）如图，直线a∥b，直线m与a，b均相交，若∠1＝38°，则∠2＝142°．【分析】如图，利用平行线的性质得到∠2＝∠3，利用互补求出∠3，从而得到∠2的度数．【解答】解：如图，∵a∥b，∴∠2＝∠3，∵∠1+∠3＝180°，∴∠2＝180°﹣38°＝142°．故答案为142°．【点评】本题考查了平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．16．（3分）若随机掷一枚均匀的骰子，骰子的6个面上分别刻有1，2，3，4，5，6点，则点数不小于3的概率是．【分析】骰子六个面出现的机会相同，求出骰子向上的一面点数不小于3的情况有几种，直接应用求概率的公式求解即可．【解答】解：随机掷一枚均匀的骰子有6种等可能结果，其中点数不小于3的有4种结果，所以点数不小于3的概率为＝，故答案为：．【点评】此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）＝．17．（3分）如图，在扇形OAB中，半径OA与OB的夹角为120°，点A与点B的距离为2，若扇形OAB恰好是一个圆锥的侧面展开图，则该圆锥的底面半径为．【分析】利用弧长＝圆锥的周长这一等量关系可求解．【解答】解：连接AB，过O作OM⊥AB于M，∵∠AOB＝120°，OA＝OB，∴∠BAO＝30°，AM＝，∴OA＝2，∵＝2πr，∴r＝故答案是：【点评】本题运用了弧长公式和圆的周长公式，建立准确的等量关系是解题的关键．18．（3分）我们定义一种新函数：形如y＝|ax2+bx+c|（a≠0，且b2﹣4a＞0）的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数y＝|x2﹣2x﹣3|的图象（如图所示），并写出下列五个结论：①图象与坐标轴的交点为（﹣1，0），（3，0）和（0，3）；②图象具有对称性，对称轴是直线x＝1；③当﹣1≤x≤1或x≥3时，函数值y随x值的增大而增大；④当x＝﹣1或x＝3时，函数的最小值是0；⑤当x＝1时，函数的最大值是4．其中正确结论的个数是4．【分析】由（﹣1，0），（3，0）和（0，3）坐标都满足函数y＝|x2﹣2x﹣3|，∴①是正确的；从图象可以看出图象具有对称性，对称轴可用对称轴公式求得是直线x＝1，②也是正确的；根据函数的图象和性质，发现当﹣1≤x≤1或x≥3时，函数值y随x值的增大而增大，因此③也是正确的；函数图象的最低点就是与x轴的两个交点，根据y＝0，求出相应的x的值为x＝﹣1或x＝3，因此④也是正确的；从图象上看，当x＜﹣1或x＞3，函数值要大于当x＝1时的y＝|x2﹣2x﹣3|＝4，因此⑤时不正确的；逐个判断之后，可得出答案．【解答】解：①∵（﹣1，0），（3，0）和（0，3）坐标都满足函数y＝|x2﹣2x﹣3|，∴①是正确的；②从图象可知图象具有对称性，对称轴可用对称轴公式求得是直线x＝1，因此②也是正确的；③根据函数的图象和性质，发现当﹣1≤x≤1或x≥3时，函数值y随x值的增大而增大，因此③也是正确的；④函数图象的最低点就是与x轴的两个交点，根据y＝0，求出相应的x的值为x＝﹣1或x＝3，因此④也是正确的；⑤从图象上看，当x＜﹣1或x＞3，函数值要大于当x＝1时的y＝|x2﹣2x﹣3|＝4，因此⑤时不正确的；故答案是：4【点评】理解“鹊桥”函数y＝|ax2+bx+c|的意义，掌握“鹊桥”函数与y＝|ax2+bx+c|与二次函数y＝ax2+bx+c之间的关系；两个函数性质之间的联系和区别是解决问题的关键；二次函数y＝ax2+bx+c与x轴的交点、对称性、对称轴及最值的求法以及增减性应熟练掌握．三、解答题（本大题共8小题，满分66分。

2019年广西贵港市中考数学试卷(附答案与解析)

数学试卷第1页（共24页）数学试卷第2页（共24页）绝密★启用前广西贵港市2019年初中毕业学业水平考试数学本试卷满分120分，考试时间120分钟.第Ⅰ卷(选择题共36分)一、选择题(本大题共12小题，共36.0分) 1.计算3(1)-的结果是( ) A .1-B .1C .3-D .32.某几何体的俯视图如图所示，图中数字表示该位置上的小正方体的个数，则这个几何体的主视图是( )ABCD3.若一组数据为：10,11,9,8,10,9,11,9，则这组数据的众数和中位数分别是( ) A . 9,9B .10,9C . 9,9.5D .11,10 4.若分式211x x -+的值等于0，则x 的值为( ) A .1±B .0C .1-D .1 5.下列运算正确的是( )A .336()a a a +-=- B .222()a b a b +=+ C .23 22a a a =D .2335)(ab a b =6.若点(1,5)P m -与点(3,2)Q n -关于原点成中心对称，则m n +的值是 ( ) A .2-B .3-C .2D .37.若α，β是关于x 的一元二次方程220x x m -+=的两实根，且112+3αβ=-，则m 等于( ) A .2-B .3-C .2D .38.下列命题中假命题是 ( )A .对顶角相等B .直线5y x =-不经过第二象限C .五边形的内角和为°540D .因式分解322()x x x x x x ++=+9如图，AD 是O 的直径，AB CD =，°40AOC =∠，则圆周角BPC ∠的度数是( )A .°40B .°50C .°60D .°6010.将一条宽度为2 cm 的彩带按如图所示的方法折叠，折痕为AB ，重叠部分为ABC △(图中阴影部分)，若°45AOC =∠，则重叠部分的面积为( )A .22 2 cmB .22 3 cmC .24 cmD .24 2 cm11.如图，在ABC △中，点D ，E 分别在AB ，AC 边上，DE BC ∥，ACD B =∠∠，若2AD BD =，6BC =，则线段CD 的长为( )毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷第3页（共24页）数学试卷第4页（共24页）A .23 B .32C .26D .512.如图，E 是正方形ABCD 的边AB 的中点，点H 与B 关于CE 对称，EH 的延长线与AD 交于点F ，与CD 的延长线交于点N ，点P 在AD 的延长线上，作正方形DPMN ，连接CP ，记正方形ABCD ，DPMN 的面积分别为1S ，2S ，则下列结论错误的是( )A .212S S CP +=B .42F FD =C .4CD PD =D .3cos 5HCD =∠ 第Ⅱ卷(非选择题共84分)二、填空题(本大题共6小题，共18.0分) 13.有理数9的相反数是 .14.将实数53.1810-⨯用小数表示为 .15.如图，直线a b ∥，直线m 与a ，b 均相交，若°138=∠，则2=∠ .16.若随机掷一枚均匀的骰子，骰子的6个面上分别刻有1，2，3，4，5，6点，则点数不小于3的概率是 .17.如图，在扇形OAB 中，半径OA 与OB 的夹角为°120，点A 与点B 的距离为23，若扇形OAB 恰好是一个圆锥的侧面展开图，则该圆锥的底面半径为 . 18.我们定义一种新函数：形如2||y ax bx c =++(0a ≠，且240b a -＞)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数2||23y x x =--的图象(如图所示)，并写出下列五个结论：①图象与坐标轴的交点为(1,0)-，(3,0)和(0,3)；②图象具有对称性，对称轴是直线1x =；③当11x -≤≤或3x ≥时，函数值y 随x 值的增大而增大；④当1x =-或3x =时，函数的最小值是0；⑤当1x =时，函数的最大值是4.其中正确结论的个数是 .三、解答题(本大题共8小题，共66.0分)19.(1)计算：0214(33)()4sin302--+-︒(2)解不等式组：622(4)23323x x x x --⎧⎪-⎨--⎪⎩＞≤，并在数轴上表示该不等式组的解集.20.尺规作图(只保留作图痕迹，不要求写出作法)：如图，已知ABC △，请根据“SAS ”基本事实作出DEF △，使DEF ABC △≌△.数学试卷第5页（共24页）数学试卷第6页（共24页）21.如图，菱形ABCD 的边AB 在x 轴上，点A 的坐标为(1,0)，点(4,4)D 在反比例函数(0)ky x x=＞的图象上，直线23y x b=+经过点C ，与y 轴交于点E ，连接AC ，AE .(1)求k ，b 的值； (2)求ACE △的面积.22.为了增强学生的安全意识，某校组织了一次全校2 500名学生都参加的“安全知识”考试.阅卷后，学校团委随机抽取了100份考卷进行分析统计，发现考试成绩(x 分)的最低分为51分，最高分为满分100分，并绘制了如下尚不完整的统计图表.请根据图表提供的信息，解答下列问题：分数段(分)频数(人)频率5161x ≤＜ a0.1 6171x ≤＜180.187181x ≤＜ bn8191x ≤＜35 0.35 91101x ≤＜12 0.12合计1001(1)填空：a = ，b = ，n = ； (2)将频数分布直方图补充完整；(3)该校对考试成绩为91100x ≤＜的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为1:3:6，请你估算全校获得二等奖的学生人数.23.为了满足师生的阅读需求，某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.(1)求这两年藏书的年均增长率；(2)经统计知：中外古典名著的册数在2016年底仅占当时藏书总量的5.6%，在这两年新增加的图书中，中外古典名著所占的百分率恰好等于这两年藏书的年均增长率，那么到2018年底中外古典名著的册数占藏书总量的百分之几？24.如图，在矩形ABCD 中，以BC 边为直径作半圆O ，OE OA ⊥交CD 边于点E ，对角线AC 与半圆O 的另一个交点为P ，连接AE .(1)求证：AE 是半圆O 的切线； (2)若2PA =，4PC =，求AE 的长.25.如图，已知抛物线2y ax bx c =++的顶点为(4,3)A ，与y 轴相交于点(0,5)B -，对称轴为直线l ，点M 是线段AB 的中点.(1)求抛物线的表达式；(2)写出点M 的坐标并求直线AB 的表达式；(3)设动点P ，Q 分别在抛物线和对称轴l 上，当以A ，P ，Q ，M 为顶点的四边形是平行四边形时，求P ，Q 两点的坐标.26.已知：ABC △是等腰直角三角形，°90BAC =∠，将ABC △绕点C 顺时针方向旋转得到A B C '''△，记旋转角为α，当°°90180α＜＜时，作A D AC '⊥，垂足为D ，A D '与B C '交于点E .(1)如图1，当°15CA D '=∠时，作°15A EC '=∠的平分线EF 交BC 于点F .①写出旋转角α的度数； ②求证：EA EC EF '+=；(2)如图2，在(1)的条件下，设P 是直线A D '上的一个动点，连接PA ，PF ，若2AB =，求线段PA PF +的最小值.(结果保留根号).毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷第7页（共24页）数学试卷第8页（共24页）广西贵港市2019年初中毕业学业水平考试数学答案解析第Ⅰ卷一、选择题 1．【答案】A【解析】解：3(1)-表示3个(1)-的乘积，所以3(1)=3-．故选：A ．乘方是乘法的特例，乘方的运算可以利用乘法的运算来进行．负数的奇数次幂是负数，负数的偶数次幂是正数；1-的奇数次幂是1-，1-的偶数次幂是1．【考点】有理数的乘方运算． 2．【答案】B【解析】解：从正面看去，一共两列，左边有2竖列，右边是1竖列．故选：B ．先细心观察原立体图形中正方体的位置关系，从正面看去，一共两列，左边有2竖列，右边是1竖列，结合四个选项选出答案．【考点】由三视图判断几何体，解题的关键是具有几何体的三视图及空间想象能力． 3．【答案】C【解析】解：将数据重新排列为8，9，9，9，10，10，11，11，∴这组数据的众数为9，中位数为9+10=9.52，故选：C ．根据众数和中位数的概念求解可得．本题为统计题，中位数是将一组数据从小到大(或从大到小)重新排列后，最中间的那个数(最中间两个数的平均数)，叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．【考点】众数与中位数的意义． 4．【答案】D【解析】解：21(1)(1)1011x x x x x x -+-==-=++，∴1x =；故选：D ．化简分式21(1)(1)1011x x x x x x -+-==-=++即可求解；【考点】解分式方程；熟练掌握因式分解的方法，分式方程的解法是解题的关键． 5．【答案】C【解析】解：33()0a a +-=，A 错误；222()2a b a ab b +=++，B 错误； 2335()ab a b =，D 错误；故选：C ．利用完全平方公式，合并同类项法则，幂的乘方与积的乘方法则运算即可；【考点】整式的运算；熟练掌握完全平方公式，合并同类项法则，幂的乘方与积的乘方法则是解题的关键． 6．【答案】C【解析】解：∵点(1,5)P m -与点(3,2)Q n - 关于原点对称， ∴13m -=-，25n -=-，解得：2m =-，7n =，则275m n +=-+=，故选：C ．关于原点对称的点的坐标，关于原点对称的点的横坐标互为相反数，纵坐标互为相反数．【考点】本题考查列方程组解应用题． 7．【答案】B【解析】α，β是关于x 的一元二次方程220x x m -+=的两实根， ∴2αβ+=，m αβ=， ∵11+22+==3m αβαβαβ=-，∴3m =-；故选：B ．利用一元二次方程根与系数的关系得到2αβ+=，m αβ=，再化简11++=αβαβαβ，代数学试卷第9页（共24页）数学试卷第10页（共24页）入即可求解；【考点】一元二次方程；熟练掌握一元二次方程根与系数的关系是解题的关键． 8．【答案】D【解析】解：A ．对顶角相等；真命题；B ．直线5y x =-不经过第二象限；真命题；C ．五边形的内角和为°540；真命题；D ．因式分解322()x x x x x x ++=+；假命题；故选：D ．由对顶角相等得出A 是真命题；由直线5y x =-的图象得出B 是真命题；由五边形的内角和为°540得出C 是真命题；由因式分解的定义得出D 是假命题；即可得出答案．【考点】命题与定理、真命题和假命题的定义：正确的命题是真命题，错误的命题是假命题． 9．【答案】B【解析】解：∵AB CD =，°40AOB =∠， ∴°40COD AOB ==∠∠，∵°+180AOB BOC COD +=∠∠∠， ∴°100BOC =∠，∴°1502BPC BOC ==∠∠，故选：B ．根据圆周角定理即可求出答案．【考点】圆周角定理，熟练掌握圆周角定理是解题的关键． 10.【答案】A【解析】如图，过B 作BD AC ⊥于D ，则°90BDC =∠， ∵°45ACB =∠， ∴°45CBD =∠， ∴ 2 cm BD CD ==，∴Rt BCD △中，222222(cm)BC =+=， ∴重叠部分的面积为1222=22(cm)2⨯⨯，故选：A ．过B 作BD AC ⊥于D ，则°90BDC =∠，依据勾股定理即可得出BC 的长，进而得到重叠部分的面积．【考点】折叠问题，折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等． 11．【答案】C【解析】设2AD x =，BD x =， ∴3AB x =， ∵DE BC ∥， ∴ADE ABC △∽△，∴DE AD DEBC AB CD ==， ∴263DE x x=， ∴4DE =，23AE AC =，∵ACD B =∠∠，ADE B =∠∠，∴ADE ACD =∠∠， ∵A A =∠∠， ∴ADE ACD △∽△， ∴DE AE DEBC AD CD ==，设2AE y =，3AC y =， ∴23AD yy AD =， ∴6AD y =， ∴246y CDy =， ∴2CD =，故选：C ．设2AD x =，BD x =，所以3AB x =，易证ADE ABC △∽△，利用相似三角形的性质可数学试卷第11页（共24页）数学试卷第12页（共24页）求出DE 的长度，以及23AE AC =，再证明ADE ACD △∽△，利用相似三角形的性质即可求出得出DE AE DEBC AD CD==，从而可求出CD 的长度．【考点】相似三角形，解题的关键是熟练运用相似三角形的性质与判定． 12．【答案】D【解析】解：∵正方形ABCD ，DPMN 的面积分别为1S ，2S ， ∴12S CD =，22S PD =，在Rt PCD △中，222PC CD PD =+， ∴212S S CP +=，故A 结论正确；连接CF ，∵点H 与B 关于CE 对称， ∴CH CB =，BCE ECH =∠∠ ，在BCE △和HCE △中，ECH BC CH CB CE CE E =⎧⎪=⎩=⎪⎨∠∠ ∴()CE HCE SAS △≌△ ，∴BE EH =，°90ECH B ==∠∠，BEC HEC =∠∠， ∴CH CD =，在Rt FCH △和Rt FCD △中 =CH CD CF CF ⎧⎨=⎩∴Rt Rt ()FCH FCD HL △≌△， ∴FCH FCD =∠∠，FH FD =，∴°+45ECH ECH BCD ==∠∠∠，即°=45ECH ∠，作FG EC ⊥于G ，∴CFG △是等腰直角三角形， ∴FG CG =，∵BEC HEC =∠∠，°90B FGH ==∠∠，∴FEG CEB △∽△， ∴12EG EB FG BC ==， ∴2FG EG =，设EG x =，则2FG x =， ∴2CG x =，2CF x = ， ∴3EC x =， ∵222EB BC EC +=， ∴22594BC x =， ∴22 BC x =， ∴ BC x =，在Rt FCD △中，22236(22)5FD CF CD x x =-=-， ∴3FD AD =，∴2AF FD =，故B 结论正确； ∵AB CN ∥， ∴12ND FD AE AF ==， ∵PD ND =，12AE CD =， ∴4CD PD =，故C 结论正确； ∵EG x =，2FG x =， ∴5EF x =， ∵255FH FD x ==， ∵655BC x =， ∴355AE x =，作HQ AD ⊥于Q ， ∴HQ AB ∥，数学试卷第13页（共24页）数学试卷第14页（共24页）∴HQ HF AE EF =，即2553555xHQ xx =， ∴6525HQ x =，∴656524552525CD HQ x x x -=-=，∴24561025cos 2522CD HQ HCD CF x-===∠，故结论D 错误，故选：D ．根据勾股定理可判断A ；连接CF ，作FG EC ⊥，易证得FGC △是等腰直角三角形，设EG x =，则2FG x =，利用三角形相似的性质以及勾股定理得到2CG x =，3EC x =，BC x =， FD x =，即可证得3FD AD =，可判断B ；根据平行线分线段成比例定理可判断C ；求得cos HCD ∠可判断D ．【考点】正方形的性质，三角形全等的判定和性质三角形相似的判定和性质，勾股定理的应用以及平行线分线段成比例定理，作出辅助线构建等腰直角三角形是解题的关键．第Ⅱ卷二．填空题 13．【答案】9-【解析】解：9的相反数是9-；故答案为9-；根据相反数的求法即可得解；【考点】考查相反数；熟练掌握相反数的意义与求法是解题的关键． 14．【答案】0.000 031 8【解析】解：53.18100.000 031 8-⨯=；故答案为0.000 031 8；根据科学记数法的表示方法1019na a ⨯≤<（）即可求解；【考点】科学记数法；熟练掌握科学记数法的表示方法是解题的关键． 15．【答案】°142 【解析】解：如图， ∵a b ∥， ∴23=∠∠， ∵°13180+=∠∠， ∴°°°218038142=-=∠．故答案为°142．如图，利用平行线的性质得到23=∠∠，利用互补求出2∠，从而得到3∠的度数．．【考点】平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等． 16．【答案】23【解析】解：随机掷一枚均匀的骰子有6种等可能结果，其中点数不小于3的有4种结果，所以点数不小于3的概率为42=63，故答案为：23．骰子六个面出现的机会相同，求出骰子向上的一面点数不小于3的情况有几种，直接应用求概率的公式求解即可．【考点】概率的求法：如果一个事件有n 种可能，而且这些事件的可能性相同，其中事数学试卷第15页（共24页）数学试卷第16页（共24页）件A 出现m 种结果，那么事件A 的概率()mP A n=．17．【答案】23【解析】解：连接AB ，过O 作OM AB ⊥于M ，∵°120AOB ∠=，OA OB =， ∴°30BAO ∠=，3AM =， ∴2OA =，∵1202180r ππ=， ∴23r =故答案是：23利用弧长=圆锥的周长这一等量关系可求解．【考点】本题考查了勾股定理、平面直角坐标系内点的坐标弧长公式和圆的周长公式，建立准确的等量关系是解题的关键． 18．【答案】4【解析】解：①∵(1,0)-，(3,0)和(0,3)坐标都满足函数2||23y x x =--，∴①是正确的； ②从图象可知图象具有对称性，对称轴可用对称轴公式求得是直线1x =，因此②也是正确的；③根据函数的图象和性质，发现当11x -≤≤或3x ≥时，函数值y 随x 值的增大而增大，因此③也是正确的；④函数图象的最低点就是与x 轴的两个交点，根据0y =，求出相应的x 的值为1x =-或3x =，因此④也是正确的；⑤从图象上看，当1x -＜或3x ＞，函数值要大于当1x =时的223||=4y x x =--，因此⑤时不正确的；故答案是：4由(1,0)-，(3,0)和(0,3) 坐标都满足函数223||=4y x x =--，∴①是正确的；从图象可以看出图象具有对称性，对称轴可用对称轴公式求得是直线x=1，②也是正确的；根据函数的图象和性质，发现当11x -≤≤或3x ≥时时，函数值y 随x 值的增大而增大，因此③也是正确的；函数图象的最低点就是与x 轴的两个交点，根据0y =，求出相应的x 的值为1x =-或3x =，因此④也是正确的；从图象上看，当1x -＜或3x ＞，函数值要大于当1x =时的223||=4y x x =--，因此⑤时不正确的；逐个判断之后，可得出答案．理解“鹊桥”函数2||23y x x =--的意义，掌握“鹊桥”函数与2||y x bx c a =++与二次函数2x c a y x b =++ 之间的关系；两个函数性质之间的联系和区别是解决问题的关键；二次函数2x c a y x b =++与x 轴的交点、对称性、对称轴及最值的求法以及增减性应熟练掌握．【考点】二次函数轴2x c a y x b =++与x 的交点、对称性、对称轴及最值的求法以及增减性应熟练掌握．三、解答题19．【答案】解：(1)原式121442=-+-⨯ 2142=-+- 3=；(2)解不等式622(4)x x --＞，得：32x ＞-，解不等式23323x x --≤，得：1x ≤，则不等式组的解集为312x -<≤，将不等式组的解集表示在数轴上如下：【解析】(1)先计算算术平方根、零指数幂、负整数指数幂、代入三角函数值，再计算乘法，最后计算加减可得；(2)分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．数学试卷第17页（共24页）数学试卷第18页（共24页）评分说明第(1)题，与“去括号法则用错”等同的说法均给分．【考点】解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键． 20.【答案】解：如图，DEF △即为所求．【解析】先作一个D A =∠∠，然后在D ∠的两边分别截取ED BA =，DF AC =，连接EF 即可得到DEF △；解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了全等三角形的判定．【考点】作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法． 21．【答案】解：(1)由已知可得5AD =， ∵菱形ABCD ， ∴(6,0)B ，(9,4)C ， ∵点(4,4)D 在反比例函数(0)ky x x=>的图象上， ∴16k =，将点(9,4)C 代入23y x b =+，∴2b =-； (2)(02)E -，，直线223y x =-与x 轴交点为(3,0)， ∴122462AECS =⨯⨯+=△（）；【解析】(1)由菱形的性质可知B ∴(6,0)B ，(9,4)C ，点(4,4)D 代入反比例函数k y x =，求出k ；将点(9,4)C 代入23y x b =+，求出b ；(2)求出直线 2y x =-与x 轴和y 轴的交点，即可求AEC △的面积；．【考点】反比例函数、一次函数的图象及性质，菱形的性质；能够将借助菱形的边长和菱形边的平行求点的坐标是解题的关键． 22．【答案】(1)10 250.25(2)(3)12325009010010⨯⨯=(人) 【解析】解：(1)1000.110a =⨯=，1001018351225b =----=，250.25100n ==；故答案为：10，25，0.25； (2)补全频数分布直方图如图所示；(3)12325009010010⨯⨯=(人)，答：全校获得二等奖的学生人数90人． (1)利用×这组的频率即可得到结论；(2)根据(1)求出的数据补全频数分布直方图即可；(3)利用全校2 500名学生数×考试成绩为91100x ≤≤考卷占抽取了的考卷数×获得二等奖学生人数占获奖学生数即可得到结论．解答本题的关键是明确题意，列出相应的方程，利用方程的知识解答，这是一道典型的增长率问题．【考点】一元二次方程的应用．23．【答案】解：(1)设这两年藏书的年均增长率是x ，25(1)7.2x +=，解得，10.2x =，2 2.2x =-(舍去)，数学试卷第19页（共24页）数学试卷第20页（共24页）答：这两年藏书的年均增长率是20%；(2)在这两年新增加的图书中，中外古典名著有(7.25)200.44-⨯=%(万册)，到2018年底中外古典名著的册数占藏书总量的百分比是：(5 5.60.44)100107.2⨯+⨯=%%%，答：到2018年底中外古典名著的册数占藏书总量的10%．【解析】(1)根据题意可以列出相应的一元二次方程，从而可以得到这两年藏书的年均增长率；(2)根据题意可以求出这两年新增加的中外古典名著，从而可以求得到2018年底中外古典名著的册数占藏书总量的百分之几．提示：(1)根据题意作出圆弧；(2)根据轴对称图形和中心对称图形的概念进行判断； (3)根据弧长公式求出三条弧的长度的和即可．【考点】本题考查基本作图一一作弧、轴对称图形和中心对称图形的概念、扇形的弧长． 24．【答案】(1)证明：∵在矩形ABCD 中，°90ABO OCE ==∠∠， ∵OE OA ⊥， ∴°90AOE =∠，∴°90BAO AOD AOB COE ====∠∠∠∠， ∴BAO COE =∠∠， ∴ABO OCE △∽△， ∴AB AOOC OE=， ∵OB OC =， ∴AB AOOB OE=， ∵°90ABO AOE ==∠∠， ∴ABO AOE △∽△， ∴BAO OAE =∠∠，过O 作OF AE ⊥于F ，∴°90ABO AFO ==∠∠，在ABO △与AOE △中，BAO FAOABO AFO AO AO =⎧⎪=⎨⎪=⎩∠∠∠∠，∴ABO AFO △≌△()AAS ， ∴OF OB =，∴AE 是半圆O 的切线；(2)解：∵AF 是O 的切线，AC 是O 的割线， ∴2 AF AP AC =， ∴2(24)23AF =+=， ∴23AB AF ==， ∵6AC =， ∴2226BC AC AB =-=，∴22=3AO AB OB =+，∵ABO AOE △∽△，∴AO ABAE AO =， ∴323=3AE ， ∴332AE =．【解析】(1)根据已知条件推出ABO OCE △∽△，根据相似三角形的性质得到BAO OAE =∠∠，过O 作OF AE ⊥于F ，根据全等三角形的性质得到OF OB =，于是得到AE 是半圆O 的切线； (2)根据切割线定理得到2(24)23AF =+=，求得23AB AF ==，根据勾股定理得到2226BC AC AB =-=，22=3AO AB OB =+，根据相似三角形的性质即可得到结论．【考点】切线的判定和性质，矩形的性质，相似三角形的判定和性质，全等三角形的判定和性质，正确的作出辅助线是解题的关键． 25．【答案】解：(1)函数表达式为：2(+4)3y a x =+，将点B 坐标代入上式并解得：12a =-，数学试卷第21页（共24页）数学试卷第22页（共24页）故抛物线的表达式为：21452y x x =-+-； (2)(4,3)A 、(0,5)B -，则点(2,1)M -，设直线AB 的表达式为：5y kx =-，将点A 坐标代入上式得：345k =-，解得：2k =，故直线AB 的表达式为：25y x =-； (3)设点(4,)Q s 、点21(,45)2P m m m -+-， ①当AM 是平行四边形的一条边时，点A 向左平移2个单位、向下平移4个单位得到M ，同样点21(,45)2P m m m -+-向左平移2个单位、向下平移4个单位得到(4,)Q s ，即：24m -=，2145=2m m s -+-，解得：6m =，3s =-，故点P 、Q 的坐标分别为(6,1)、(4,3)-； ②当AM 是平行四边形的对角线时，由中点定理得：424m +=+，213145+2m m s -=-+-，解得：2m =，1s =，故点P 、Q 的坐标分别为(2,1)、(4,1)；故点P 、Q 的坐标分别为(6,1)或(2,1)、(4,3)-或(4,1)．【解析】(1)函数表达式为：2(+4)3y a x =+，将点B 坐标代入上式，即可求解； (2)(4,3)A 、(0,5)B -，则点(2,1)M -，设直线AB 的表达式为：5y kx =-，将点A 坐标代入上式，即可求解；(3)分当AM 是平行四边形的一条边AM 是平行四边形的对角线两种情况，分别求解即可．【考点】二次函数综合运用，涉及到一次函数、平行四边形性质、图象的面积计算等，其中(3)，要主要分类求解，避免遗漏． 26．【答案】(1)①解：旋转角为°105．理由：如图1中，∵A D AC '⊥， ∴°90A DC '=∠， ∵°15CA D '=∠， ∴°75A CD '=∠， ∴°105ACA '=∠， ∴旋转角为°105．②证明：连接A F '，设EF 交CA '于点O ．在EF 时截取EM EC =，连接CM ． ∵°°°451560CED A CE CA E ='+'=+=∠∠∠， ∴°120CEA '=∠， ∵FE 平分EA C '∠， ∴°60CEF FEA ='=∠∠ ， ∵°°°°180457560FCO =--=∠， ∴FCO A EO ='∠∠，∵FOC AOE ='∠∠， ∴FOC A OE '△∽△，∴'OF OCA O OE =， ∴OF A O OC OE'=， ∵COE FOA ='∠∠， ∴COE FOA '△∽△， ∴°60FA O OEC '==∠∠， ∴A OF '△是等边三角形，∴CF CA A F ='='，数学试卷第23页（共24页）数学试卷第24页（共24页）∵EM EC =，°60CEM =∠， ∴CEM △是等边三角形，°60ECM =∠，CM CE =，∵°60FCA MCE '==∠∠， ∴FCM A CE '=∠∠， ∴()FCM A CE SAS '△≌△， ∴FM A E ='，∴CE A E EM FM EF +'=+=．(2)解：如图2中，连接A F '，PB '，AB '，作B M AC '⊥交AC 的延长线于M ．由②可知，°75EA F EA B '='''=∠，A E A E '='，A F A B '=''， ∴A EF A EB '''△≌△， ∴EF EB ='，∴B '，F 关于A E '对称， ∴PF PB ='，∴PA PF PA PB AB +=+'≥'，在Rt CB M '△中，2CB BC '===，°30MCB '=∠， ∴112B M CB '='=，CM =∴AB '∴PA PF +【解析】①解直角三角形求出A CD '∠即可解决问题．②连接A F '，设EF 交CA '于点O ．在EF 时截取EM EC =，连接CM ．首先证明CFA '△是等边三角形，再证明()FCM A CE SAS '△≌△，即可解决问题．(2)如图2中，连接A F '，PB '，AB '，作B M AC '⊥交AC 的延长线于M ．证明A EF A EB '''△≌△，推出EF EB ='，推出B '，F 关于A E '对称，推出PF PB ='，推出PA PF PA PB AB +=+'≥'，求出AB '即可解决问题．【考点】四边形综合题，旋转变换，全等三角形的判定和性质，相似三角形的判定和性质，三角形的三边关系等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会用转化的思想思考问题．。

2019年广西贵港市中考数学试卷(解析版)

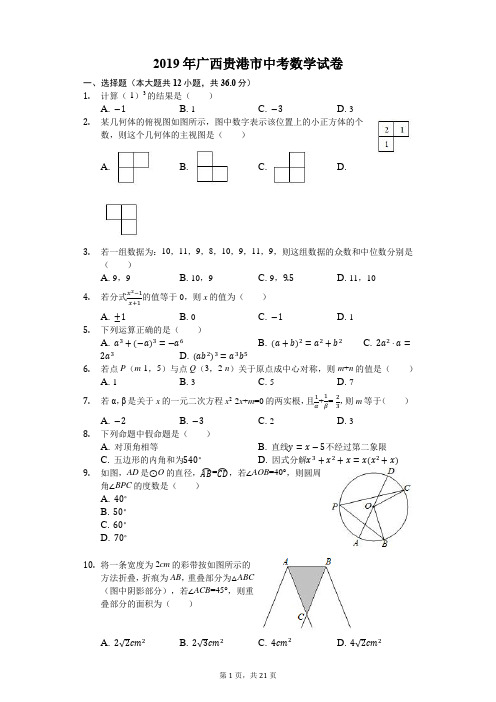
2019年广西贵港市中考数学试卷一、选择题（本大题共12小题，共36.0分）1.计算（-1）3的结果是（）A. B. 1 C. D. 32.某几何体的俯视图如图所示，图中数字表示该位置上的小正方体的个数，则这个几何体的主视图是（）A. B. C. D.3.若一组数据为：10，11，9，8，10，9，11，9，则这组数据的众数和中位数分别是（）A. 9，9B. 10，9C. 9，D. 11，104.若分式的值等于0，则x的值为（）A. B. 0 C. D. 15.下列运算正确的是（）A. B. C.D.6.若点P（m-1，5）与点Q（3，2-n）关于原点成中心对称，则m+n的值是（）A. 1B. 3C. 5D. 77.若α，β是关于x的一元二次方程x2-2x+m=0的两实根，且+=-，则m等于（）A. B. C. 2 D. 38.下列命题中假命题是（）A. 对顶角相等B. 直线不经过第二象限C. 五边形的内角和为D. 因式分解9.如图，AD是⊙O的直径，=，若∠AOB=40°，则圆周角∠BPC的度数是（）A.B.C.D.10.将一条宽度为2cm的彩带按如图所示的方法折叠，折痕为AB，重叠部分为△ABC（图中阴影部分），若∠ACB=45°，则重叠部分的面积为（）A. B. C. D.11.如图，在△ABC中，点D，E分别在AB，AC边上，DE∥BC，∠ACD=∠B，若AD=2BD，BC=6，则线段CD的长为（）A.B.C.D. 512.如图，E是正方形ABCD的边AB的中点，点H与B关于CE对称，EH的延长线与AD交于点F，与CD的延长线交于点N，点P在AD的延长线上，作正方形DPMN，连接CP，记正方形ABCD，DPMN的面积分别为S1，S2，则下列结论错误的是（）A. B. C. D.二、填空题（本大题共6小题，共18.0分）13.有理数9的相反数是______．14.将实数3.18×10-5用小数表示为______．15.如图，直线a∥b，直线m与a，b均相交，若∠1=38°，则∠2=______．16.若随机掷一枚均匀的骰子，骰子的6个面上分别刻有1，2，3，4，5，6点，则点数不小于3的概率是______．17.如图，在扇形OAB中，半径OA与OB的夹角为120°，点A与点B的距离为2，若扇形OAB恰好是一个圆锥的侧面展开图，则该圆锥的底面半径为______．18.我们定义一种新函数：形如y=|ax2+bx+c|（a≠0，且b2-4a＞0）的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数y=|x2-2x-3|的图象（如图所示），并写出下列五个结论：①图象与坐标轴的交点为（-1，0），（3，0）和（0，3）；②图象具有对称性，对称轴是直线x=1；③当-1≤x≤1或x≥3时，函数值y随x值的增大而增大；④当x=-1或x=3时，函数的最小值是0；⑤当x=1时，函数的最大值是4．其中正确结论的个数是______．三、解答题（本大题共8小题，共66.0分）19.（1）计算：-（-3）0+（）-2-4sin30°；（2）解不等式组：＞，并在数轴上表示该不等式组的解集．20.尺规作图（只保留作图痕迹，不要求写出作法）：如图，已知△ABC，请根据“SAS”基本事实作出△DEF，使△DEF≌△ABC．21.如图，菱形ABCD的边AB在x轴上，点A的坐标为（1，0），点D（4，4）在反比例函数y=（x＞0）的图象上，直线y=x+b经过点C，与y轴交于点E，连接AC，AE．（1）求k，b的值；（2）求△ACE的面积．22.为了增强学生的安全意识，某校组织了一次全校2500名学生都参加的“安全知识”考试．阅卷后，学校团委随机抽取了100份考卷进行分析统计，发现考试成绩（x分）的最低分为51分，最高分为满分100分，并绘制了如下尚不完整的统计图表．请根据图表提供的信息，解答下列问题：（）填空：，，；（2）将频数分布直方图补充完整；（3）该校对考试成绩为91≤x≤100的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为1：3：6，请你估算全校获得二等奖的学生人数．23.为了满足师生的阅读需求，某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册．（1）求这两年藏书的年均增长率；（2）经统计知：中外古典名著的册数在2016年底仅占当时藏书总量的5.6%，在这两年新增加的图书中，中外古典名著所占的百分率恰好等于这两年藏书的年均增长率，那么到2018年底中外古典名著的册数占藏书总量的百分之几？24.如图，在矩形ABCD中，以BC边为直径作半圆O，OE⊥OA交CD边于点E，对角线AC与半圆O的另一个交点为P，连接AE．（1）求证：AE是半圆O的切线；（2）若PA=2，PC=4，求AE的长．25.如图，已知抛物线y=ax2+bx+c的顶点为A（4，3），与y轴相交于点B（0，-5），对称轴为直线l，点M是线段AB的中点．（1）求抛物线的表达式；（2）写出点M的坐标并求直线AB的表达式；（3）设动点P，Q分别在抛物线和对称轴l上，当以A，P，Q，M为顶点的四边形是平行四边形时，求P，Q两点的坐标．26.已知：△ABC是等腰直角三角形，∠BAC=90°，将△ABC绕点C顺时针方向旋转得到△A′B′C，记旋转角为α，当90°＜α＜180°时，作A′D⊥AC，垂足为D，A′D与B′C 交于点E．（1）如图1，当∠CA′D=15°时，作∠A′EC的平分线EF交BC于点F．①写出旋转角α的度数；②求证：EA′+EC=EF；（2）如图2，在（1）的条件下，设P是直线A′D上的一个动点，连接PA，PF，若AB=，求线段PA+PF的最小值．（结果保留根号）答案和解析1.【答案】A【解析】解：（-1）3表示3个（-1）的乘积，所以（-1）3=-1．故选：A．本题考查有理数的乘方运算．乘方是乘法的特例，乘方的运算可以利用乘法的运算来进行．负数的奇数次幂是负数，负数的偶数次幂是正数；-1的奇数次幂是-1，-1的偶数次幂是1．2.【答案】B【解析】解：从正面看去，一共两列，左边有2竖列，右边是1竖列．故选：B．先细心观察原立体图形中正方体的位置关系，从正面看去，一共两列，左边有2竖列，右边是1竖列，结合四个选项选出答案．本题考查了由三视图判断几何体，解题的关键是具有几何体的三视图及空间想象能力．3.【答案】C【解析】解：将数据重新排列为8，9，9，9，10，10，11，11，∴这组数据的众数为9，中位数为=9.5，故选：C．根据众数和中位数的概念求解可得．本题为统计题，考查众数与中位数的意义．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．4.【答案】D【解析】解：==x-1=0，∴x=1；故选：D．化简分式==x-1=0即可求解；本题考查解分式方程；熟练掌握因式分解的方法，分式方程的解法是解题的关键．5.【答案】C【解析】解：a3+（-a3）=0，A错误；（a+b）2=a2+2ab+b2，B错误；（ab2）3=a3b5，D错误；故选：C．利用完全平方公式，合并同类项法则，幂的乘方与积的乘方法则运算即可；本题考查整式的运算；熟练掌握完全平方公式，合并同类项法则，幂的乘方与积的乘方法则是解题的关键．6.【答案】C【解析】解：∵点P（m-1，5）与点Q（3，2-n）关于原点对称，∴m-1=-3，2-n=-5，解得：m=-2，n=7，则m+n=-2+7=5．故选：C．根据关于原点对称的点的横坐标互为相反数，纵坐标互为相反数，可得答案．本题考查了关于原点对称的点的坐标，关于原点对称的点的横坐标互为相反数，纵坐标互为相反数．7.【答案】B【解析】解：α，β是关于x的一元二次方程x2-2x+m=0的两实根，∴α+β=2，αβ=m，∵+===-，∴m=-3；故选：B．利用一元二次方程根与系数的关系得到α+β=2，αβ=m，再化简+=，代入即可求解；本题考查一元二次方程；熟练掌握一元二次方程根与系数的关系是解题的关键．8.【答案】D【解析】解：A．对顶角相等；真命题；B．直线y=x-5不经过第二象限；真命题；C．五边形的内角和为540°；真命题；D．因式分解x3+x2+x=x（x2+x）；假命题；故选：D．由对顶角相等得出A是真命题；由直线y=x-5的图象得出B是真命题；由五边形的内角和为540°得出C是真命题；由因式分解的定义得出D是假命题；即可得出答案．本题考查了命题与定理、真命题和假命题的定义：正确的命题是真命题，错误的命题是假命题；属于基础题．9.【答案】B【解析】解：∵=，∠AOB=40°，∴∠COD=∠AOB=40°，∵∠AOB+∠BOC+∠COD=180°，∴∠BOC=100°，∴∠BPC=∠BOC=50°，故选：B．根据圆周角定理即可求出答案．本题考查了圆周角定理，熟练掌握圆周角定理是解题的关键．10.【答案】A【解析】解：如图，过B作BD⊥AC于D，则∠BDC=90°，∵∠ACB=45°，∴∠CBD=45°，∴BD=CD=2cm，∴Rt△BCD中，BC==2（cm），∴重叠部分的面积为×2×2=2（cm），故选：A．过B作BD⊥AC于D，则∠BDC=90°，依据勾股定理即可得出BC的长，进而得到重叠部分的面积．本题主要考查了折叠问题，折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．11.【答案】C【解析】解：设AD=2x，BD=x，∴AB=3x，∵DE∥BC，∴△ADE∽△ABC，∴=，∴=，∴DE=4，=，∵∠ACD=∠B，∠ADE=∠B，∴∠ADE=∠ACD，∵∠A=∠A，∴△ADE∽△ACD，∴=，设AE=2y，AC=3y，∴=，∴AD=y，∴=，∴CD=2，故选：C．设AD=2x，BD=x，所以AB=3x，易证△ADE∽△ABC，利用相似三角形的性质可求出DE的长度，以及，再证明△ADE∽△ACD，利用相似三角形的性质即可求出得出=，从而可求出CD的长度．本题考查相似三角形，解题的关键是熟练运用相似三角形的性质与判定，本题属于中等题型．12.【答案】D【解析】解：∵正方形ABCD，DPMN的面积分别为S1，S2，∴S1=CD2，S2=PD2，在Rt△PCD中，PC2=CD2+PD2，∴S1+S2=CP2，故A结论正确；连接CF，∵点H与B关于CE对称，∴CH=CB，∠BCE=∠ECH，在△BCE和△HCE中，∴△BCE≌△HCE（SAS），∴BE=EH，∠EHC=∠B=90°，∠BEC=∠HEC，∴CH=CD，在Rt△FCH和Rt△FCD中∴Rt△FCH≌Rt△FCD（HL），∴∠FCH=∠FCD，FH=FD，∴∠ECH+∠ECH=∠BCD=45°，即∠ECF=45°，作FG⊥EC于G，∴△CFG是等腰直角三角形，∴FG=CG，∵∠BEC=∠HEC，∠B=∠FGE=90°，∴△FEG∽△CEB，∴==，∴FG=2EG，设EG=x，则FG=2x，∴CG=2x，CF=2x，∴EC=3x，∵EB2+BC2=EC2，∴BC2=9x2，∴BC2=x2，∴BC=x，在Rt△FDC中，FD===x，∴3FD=AD，∴AF=2FD，故B结论正确；∵AB∥CN，∴=，∵PD=ND，AE=CD，∴CD=4PD，故C结论正确；∵EG=x，FG=2x，∴EF=x，∵FH=FD=x，∵BC=x，∴AE=x，作HQ⊥AD于Q，∴HQ∥AB，∴=，即=，∴HQ=x，∴CD-HQ=x-x=x，∴cos∠HCD===，故结论D错误，故选：D．根据勾股定理可判断A；连接CF，作FG⊥EC，易证得△FGC是等腰直角三角形，设EG=x，则FG=2x，利用三角形相似的性质以及勾股定理得到CG=2x，CF=2x，EC=3x，BC=x，FD=x，即可证得3FD=AD，可判断B；根据平行线分线段成比例定理可判断C；求得cos∠HCD可判断D．本题考查了正方形的性质，三角形全等的判定和性质三角形相似的判定和性质，勾股定理的应用以及平行线分线段成比例定理，作出辅助线构建等腰直角三角形是解题的关键．13.【答案】-9【解析】解：9的相反数是-9；故答案为-9；根据相反数的求法即可得解；本题考查相反数；熟练掌握相反数的意义与求法是解题的关键．14.【答案】0.0000318【解析】解：3.18×10-5=0.0000318；故答案为0.0000318；根据科学记数法的表示方法a×10n（1≤a＜9）即可求解；本题考查科学记数法；熟练掌握科学记数法的表示方法是解题的关键．15.【答案】142°【解析】解：如图，∵a∥b，∴∠2=∠3，∵∠1+∠3=180°，∴∠2=180°-38°=142°．故答案为142°．如图，利用平行线的性质得到∠2=∠3，利用互补求出∠3，从而得到∠2的度数．本题考查了平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．16.【答案】【解析】解：随机掷一枚均匀的骰子有6种等可能结果，其中点数不小于3的有4种结果，所以点数不小于3的概率为=，故答案为：．骰子六个面出现的机会相同，求出骰子向上的一面点数不小于3的情况有几种，直接应用求概率的公式求解即可．此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．17.【答案】【解析】解：连接AB，过O作OM⊥AB于M，∵∠AOB=120°，OA=OB，∴∠BAO=30°，AM=，∴OA=2，∵=2πr，∴r=故答案是：利用弧长=圆锥的周长这一等量关系可求解．本题运用了弧长公式和圆的周长公式，建立准确的等量关系是解题的关键．18.【答案】4【解析】解：①∵（-1，0），（3，0）和（0，3）坐标都满足函数y=|x2-2x-3|，∴①是正确的；②从图象可知图象具有对称性，对称轴可用对称轴公式求得是直线x=1，因此②也是正确的；③根据函数的图象和性质，发现当-1≤x≤1或x≥3时，函数值y随x值的增大而增大，因此③也是正确的；④函数图象的最低点就是与x轴的两个交点，根据y=0，求出相应的x的值为x=-1或x=3，因此④也是正确的；⑤从图象上看，当x＜-1或x＞3，函数值要大于当x=1时的y=|x2-2x-3|=4，因此⑤时不正确的；故答案是：4由（-1，0），（3，0）和（0，3）坐标都满足函数y=|x2-2x-3|，∴①是正确的；从图象可以看出图象具有对称性，对称轴可用对称轴公式求得是直线x=1，②也是正确的；根据函数的图象和性质，发现当-1≤x≤1或x≥3时，函数值y随x值的增大而增大，因此③也是正确的；函数图象的最低点就是与x轴的两个交点，根据y=0，求出相应的x的值为x=-1或x=3，因此④也是正确的；从图象上看，当x＜-1或x＞3，函数值要大于当x=1时的y=|x2-2x-3|=4，因此⑤时不正确的；逐个判断之后，可得出答案．理解“鹊桥”函数y=|ax2+bx+c|的意义，掌握“鹊桥”函数与y=|ax2+bx+c|与二次函数y=ax2+bx+c之间的关系；两个函数性质之间的联系和区别是解决问题的关键；二次函数y=ax2+bx+c与x轴的交点、对称性、对称轴及最值的求法以及增减性应熟练掌握．19.【答案】解：（1）原式=2-1+4-4×=2-1+4-2=3；（2）解不等式6x-2＞2（x-4），得：x＞-，解不等式-≤-，得：x≤1，则不等式组的解集为-＜x≤1，将不等式组的解集表示在数轴上如下：【解析】（1）先计算算术平方根、零指数幂、负整数指数幂、代入三角函数值，再计算乘法，最后计算加减可得；（2）分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．20.【答案】解：如图，△DEF即为所求．【解析】先作一个∠D=∠A，然后在∠D的两边分别截取ED=BA，DF=AC，连接EF即可得到△DEF；本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了全等三角形的判定．21.【答案】解：（1）由已知可得AD=5，∵菱形ABCD，∴B（6，0），C（9，4），∵点D（4，4）在反比例函数y=（x＞0）的图象上，∴k=16，将点C（9，4）代入y=x+b，∴b=-2；（2）E（0，-2），直线y=x-2与x轴交点为（3，0），∴S△AEC=2×（2+4）=6；【解析】（1）由菱形的性质可知B（6，0），C（9，4），点D（4，4）代入反比例函数y=，求出k；将点C（9，4）代入y=x+b，求出b；（2）求出直线y=x-2与x轴和y轴的交点，即可求△AEC的面积；本题考查反比例函数、一次函数的图象及性质，菱形的性质；能够将借助菱形的边长和菱形边的平行求点的坐标是解题的关键．22.【答案】10 25 0.25【解析】解：（1）a=100×0.1=10，b=100-10-18-35-12=25，n==0.25；故答案为：10，25，0.25；（2）补全频数分布直方图如图所示；（3）2500××=90（人），答：全校获得二等奖的学生人数90人．（1）利用×这组的频率即可得到结论；（2）根据（1）求出的数据补全频数分布直方图即可；（3）利用全校2500名学生数×考试成绩为91≤x≤100考卷占抽取了的考卷数×获得二等奖学生人数占获奖学生数即可得到结论．本题考查的是频数分布直方图，读懂统计图，从统计图中得到必要的信息是解决问题的关键．直方图能清楚地表示出每个项目的数据，也考查了利用样本估计总体的思想．23.【答案】解：（1）设这两年藏书的年均增长率是x，5（1+x）2=7.2，解得，x1=0.2，x2=-2.2（舍去），答：这两年藏书的年均增长率是20%；（2）在这两年新增加的图书中，中外古典名著有（7.2-5）×20%=0.44（万册），到2018年底中外古典名著的册数占藏书总量的百分比是：×100%=10%，答：到2018年底中外古典名著的册数占藏书总量的10%．【解析】（1）根据题意可以列出相应的一元二次方程，从而可以得到这两年藏书的年均增长率；（2）根据题意可以求出这两年新增加的中外古典名著，从而可以求得到2018年底中外古典名著的册数占藏书总量的百分之几．本题考查一元二次方程的应用，解答本题的关键是明确题意，列出相应的方程，利用方程的知识解答，这是一道典型的增长率问题．24.【答案】（1）证明：∵在矩形ABCD中，∠ABO=∠OCE=90°，∵OE⊥OA，∴∠AOE=90°，∴∠BAO+∠AOB=∠AOB+∠COE=90°，∴∠BAO=∠COE，∴△ABO∽△OCE，∴=，∵OB=OC，∴，∵∠ABO=∠AOE=90°，∴△ABO∽△AOE，∴∠BAO=∠OAE，过O作OF⊥AE于F，∴∠ABO=∠AFO=90°，在△ABO与△AFO中，，∴△ABO≌△AFO（AAS），∴OF=OB，∴AE是半圆O的切线；（2）解：∵AF是⊙O的切线，AC是⊙O的割线，∴AF2=AP•AC，∴AF==2，∴AB=AF=2，∵AC=6，∴BC==2，∴AO==3，∵△ABO∽△AOE，∴，∴=，∴AE=．【解析】（1）根据已知条件推出△ABO∽△OCE，根据相似三角形的性质得到∠BAO=∠OAE，过O作OF⊥AE于F，根据全等三角形的性质得到OF=OB，于是得到AE是半圆O的切线；（2）根据切割线定理得到AF==2，求得AB=AF=2，根据勾股定理得到BC==2，AO==3，根据相似三角形的性质即可得到结论．本题考查了切线的判定和性质，矩形的性质，相似三角形的判定和性质，全等三角形的判定和性质，正确的作出辅助线是解题的关键．25.【答案】解：（1）函数表达式为：y=a（x=4）2+3，将点B坐标代入上式并解得：a=-，故抛物线的表达式为：y=-x2+4x-5；（2）A（4，3）、B（0，-5），则点M（2，-1），设直线AB的表达式为：y=kx-5，将点A坐标代入上式得：3=4k-5，解得：k=2，故直线AB的表达式为：y=2x-5；（3）设点Q（4，s）、点P（m，-m2+4m-5），①当AM是平行四边形的一条边时，点A向左平移2个单位、向下平移4个单位得到M，同样点P（m，-m2+4m-5）向左平移2个单位、向下平移4个单位得到Q（4，s），即：m-2=4，-m2+4m-5-4=s，解得：m=6，s=-3，故点P、Q的坐标分别为（6，1）、（4，-3）；②当AM是平行四边形的对角线时，由中点定理得：4+2=m+4，3-1=-m2+4m-5+s，解得：m=2，s=1，故点P、Q的坐标分别为（2，1）、（4，1）；故点P、Q的坐标分别为（6，1）或（2，1）、（4，-3）或（4，1）．【解析】（1）函数表达式为：y=a（x=4）2+3，将点B坐标代入上式，即可求解；（2）A（4，3）、B（0，-5），则点M（2，-1），设直线AB的表达式为：y=kx-5，将点A坐标代入上式，即可求解；（3）分当AM是平行四边形的一条边、AM是平行四边形的对角线两种情况，分别求解即可．本题考查的是二次函数综合运用，涉及到一次函数、平行四边形性质、图象的面积计算等，其中（3），要主要分类求解，避免遗漏．26.【答案】（1）①解：旋转角为105°．理由：如图1中，∵A′D⊥AC，∴∠A′DC=90°，∵∠CA′D=15°，∴∠A′CD=75°，∴∠ACA′=105°，∴旋转角为105°．②证明：连接A′F，设EF交CA′于点O．在EF时截取EM=EC，连接CM．∵∠CED=∠A′CE+∠CA′E=45°+15°=60°，∴∠CEA′=120°，∵FE平分∠CEA′，∴∠CEF=∠FEA′=60°，∵∠FCO=180°-45°-75°=60°，∴∠FCO=∠A′EO，∵∠FOC=∠A′OE，∴△FOC∽△A′OE，∴=，∴=，∵∠COE=∠FOA′，∴△COE∽△FOA′，∴∠FA′O=∠OEC=60°，∴△A′OF是等边三角形，∴CF=CA′=A′F，∵EM=EC，∠CEM=60°，∴△CEM是等边三角形，∠ECM=60°，CM=CE，∵∠FCA′=∠MCE=60°，∴∠FCM=∠A′CE，∴△FCM≌△A′CE（SAS），∴FM=A′E，∴CE+A′E=EM+FM=EF．（2）解：如图2中，连接A′F，PB′，AB′，作B′M⊥AC交AC的延长线于M．由②可知，∠EA′F=′EA′B′=75°，A′E=A′E，A′F=A′B′，∴△A′EF≌△A′EB′，∴EF=EB′，∴B′，F关于A′E对称，∴PF=PB′，∴PA+PF=PA+PB′≥AB′，在Rt△CB′M中，CB′=BC=AB=2，∠MCB′=30°，∴B′M=CB′=1，CM=，∴AB′===．∴PA+PF的最小值为．【解析】（1）①解直角三角形求出∠A′CD即可解决问题．②连接A′F，设EF交CA′于点O．在EF时截取EM=EC，连接CM．首先证明△CFA′是等边三角形，再证明△FCM≌△A′CE（SAS），即可解决问题．（2）如图2中，连接A′F，PB′，AB′，作B′M⊥AC交AC的延长线于M．证明△A′EF≌△A′EB′，推出EF=EB′，推出B′，F关于A′E对称，推出PF=PB′，推出PA+PF=PA+PB′≥AB′，求出AB′即可解决问题．本题属于四边形综合题，考查了旋转变换，全等三角形的判定和性质，相似三角形的判定和性质，三角形的三边关系等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会用转化的思想思考问题，属于中考压轴题．第21页，共21页。

2019年广西贵港市中考数学试题(解析版)

2019年广西贵港市中考数学试卷一、选择题（本大题共12小题，共36.0分）1.计算（-1）3的结果是（）A. B. 1 C. D. 32.某几何体的俯视图如图所示，图中数字表示该位置上的小正方体的个数，则这个几何体的主视图是（）A. B. C. D.3.若一组数据为：10，11，9，8，10，9，11，9，则这组数据的众数和中位数分别是（）A. 9，9B. 10，9C. 9，D. 11，104.若分式的值等于0，则x的值为（）A. B. 0 C. D. 15.下列运算正确的是（）A. B. C.D.6.若点P（m-1，5）与点Q（3，2-n）关于原点成中心对称，则m+n的值是（）A. 1B. 3C. 5D. 77.若α，β是关于x的一元二次方程x2-2x+m=0的两实根，且+=-，则m等于（）A. B. C. 2 D. 38.下列命题中假命题是（）A. 对顶角相等B. 直线不经过第二象限C. 五边形的内角和为D. 因式分解9.如图，AD是⊙O的直径，=，若∠AOB=40°，则圆周角∠BPC的度数是（）A.B.C.D.10.将一条宽度为2cm的彩带按如图所示的方法折叠，折痕为AB，重叠部分为△ABC（图中阴影部分），若∠ACB=45°，则重叠部分的面积为（）A. B.C. D.11.如图，在△ABC中，点D，E分别在AB，AC边上，DE∥BC，∠ACD=∠B，若AD=2BD，BC=6，则线段CD的长为（）A.B.C.D. 512.如图，E是正方形ABCD的边AB的中点，点H与B关于CE对称，EH的延长线与AD交于点F，与CD的延长线交于点N，点P在AD的延长线上，作正方形DPMN，连接CP，记正方形ABCD，DPMN的面积分别为S1，S2，则下列结论错误的是（）A. B. C. D.二、填空题（本大题共6小题，共18.0分）13.有理数9的相反数是______．14.将实数3.18×10-5用小数表示为______．15.如图，直线a∥b，直线m与a，b均相交，若∠1=38°，则∠2=______．16.若随机掷一枚均匀的骰子，骰子的6个面上分别刻有1，2，3，4，5，6点，则点数不小于3的概率是______．17.如图，在扇形OAB中，半径OA与OB的夹角为120°，点A与点B的距离为2，若扇形OAB恰好是一个圆锥的侧面展开图，则该圆锥的底面半径为______．18.我们定义一种新函数：形如y=|ax2+bx+c|（a≠0，且b2-4a＞0）的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数y=|x2-2x-3|的图象（如图所示），并写出下列五个结论：①图象与坐标轴的交点为（-1，0），（3，0）和（0，3）；②图象具有对称性，对称轴是直线x=1；③当-1≤x≤1或x≥3时，函数值y随x值的增大而增大；④当x=-1或x=3时，函数的最小值是0；⑤当x=1时，函数的最大值是4．其中正确结论的个数是______．三、解答题（本大题共8小题，共66.0分）19.（1）计算：-（-3）0+（）-2-4sin30°；（2）解不等式组：，并在数轴上表示该不等式组的解集．20.尺规作图（只保留作图痕迹，不要求写出作法）：如图，已知△ABC，请根据“SAS”基本事实作出△DEF，使△DEF≌△ABC．21.如图，菱形ABCD的边AB在x轴上，点A的坐标为（1，0），点D（4，4）在反比例函数y=（x＞0）的图象上，直线y=x+b经过点C，与y轴交于点E，连接AC，AE．（1）求k，b的值；（2）求△ACE的面积．22.为了增强学生的安全意识，某校组织了一次全校2500名学生都参加的“安全知识”考试．阅卷后，学校团委随机抽取了100份考卷进行分析统计，发现考试成绩（x分）的最低分为51分，最高分为满分100分，并绘制了如下尚不完整的统计图表．请根（1）填空：a=______，b=______，n=______；（2）将频数分布直方图补充完整；（3）该校对考试成绩为91≤x≤100的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为1：3：6，请你估算全校获得二等奖的学生人数．23.为了满足师生的阅读需求，某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册．（1）求这两年藏书的年均增长率；（2）经统计知：中外古典名著的册数在2016年底仅占当时藏书总量的5.6%，在这两年新增加的图书中，中外古典名著所占的百分率恰好等于这两年藏书的年均增长率，那么到2018年底中外古典名著的册数占藏书总量的百分之几？24.如图，在矩形ABCD中，以BC边为直径作半圆O，OE⊥OA交CD边于点E，对角线AC与半圆O的另一个交点为P，连接AE．（1）求证：AE是半圆O的切线；（2）若PA=2，PC=4，求AE的长．25.如图，已知抛物线y=ax2+bx+c的顶点为A（4，3），与y轴相交于点B（0，-5），对称轴为直线l，点M是线段AB的中点．（1）求抛物线的表达式；（2）写出点M的坐标并求直线AB的表达式；（3）设动点P，Q分别在抛物线和对称轴l上，当以A，P，Q，M为顶点的四边形是平行四边形时，求P，Q两点的坐标．26.已知：△ABC是等腰直角三角形，∠BAC=90°，将△ABC绕点C顺时针方向旋转得到△A′B′C，记旋转角为α，当90°＜α＜180°时，作A′D⊥AC，垂足为D，A′D与B′C 交于点E．（1）如图1，当∠CA′D=15°时，作∠A′EC的平分线EF交BC于点F．①写出旋转角α的度数；②求证：EA′+EC=EF；（2）如图2，在（1）的条件下，设P是直线A′D上的一个动点，连接PA，PF，若AB=，求线段PA+PF的最小值．（结果保留根号）答案和解析1.【答案】A【解析】解：（-1）3表示3个（-1）的乘积，所以（-1）3=-1．故选：A．本题考查有理数的乘方运算．乘方是乘法的特例，乘方的运算可以利用乘法的运算来进行．负数的奇数次幂是负数，负数的偶数次幂是正数；-1的奇数次幂是-1，-1的偶数次幂是1．2.【答案】B【解析】解：从正面看去，一共两列，左边有2竖列，右边是1竖列．故选：B．先细心观察原立体图形中正方体的位置关系，从正面看去，一共两列，左边有2竖列，右边是1竖列，结合四个选项选出答案．本题考查了由三视图判断几何体，解题的关键是具有几何体的三视图及空间想象能力．3.【答案】C【解析】解：将数据重新排列为8，9，9，9，10，10，11，11，∴这组数据的众数为9，中位数为=9.5，故选：C．根据众数和中位数的概念求解可得．本题为统计题，考查众数与中位数的意义．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．4.【答案】D【解析】解：==x-1=0，∴x=1；故选：D．化简分式==x-1=0即可求解；本题考查解分式方程；熟练掌握因式分解的方法，分式方程的解法是解题的关键．5.【答案】C【解析】解：a3+（-a3）=0，A错误；（a+b）2=a2+2ab+b2，B错误；（ab2）3=a3b5，D错误；故选：C．利用完全平方公式，合并同类项法则，幂的乘方与积的乘方法则运算即可；本题考查整式的运算；熟练掌握完全平方公式，合并同类项法则，幂的乘方与积的乘方法则是解题的关键．6.【答案】C【解析】解：∵点P（m-1，5）与点Q（3，2-n）关于原点对称，∴m-1=-3，2-n=-5，解得：m=-2，n=7，则m+n=-2+7=5．故选：C．根据关于原点对称的点的横坐标互为相反数，纵坐标互为相反数，可得答案．本题考查了关于原点对称的点的坐标，关于原点对称的点的横坐标互为相反数，纵坐标互为相反数．7.【答案】B【解析】解：α，β是关于x的一元二次方程x2-2x+m=0的两实根，∴α+β=2，αβ=m，∵+===-，∴m=-3；故选：B．利用一元二次方程根与系数的关系得到α+β=2，αβ=m，再化简+=，代入即可求解；本题考查一元二次方程；熟练掌握一元二次方程根与系数的关系是解题的关键．8.【答案】D【解析】解：A．对顶角相等；真命题；B．直线y=x-5不经过第二象限；真命题；C．五边形的内角和为540°；真命题；D．因式分解x3+x2+x=x（x2+x）；假命题；故选：D．由对顶角相等得出A是真命题；由直线y=x-5的图象得出B是真命题；由五边形的内角和为540°得出C是真命题；由因式分解的定义得出D是假命题；即可得出答案．本题考查了命题与定理、真命题和假命题的定义：正确的命题是真命题，错误的命题是假命题；属于基础题．9.【答案】B【解析】解：∵=，∠AOB=40°，∴∠COD=∠AOB=40°，∵∠AOB+∠BOC+∠COD=180°，∴∠BOC=100°，∴∠BPC=∠BOC=50°，故选：B．根据圆周角定理即可求出答案．本题考查了圆周角定理，熟练掌握圆周角定理是解题的关键．10.【答案】A【解析】解：如图，过B作BD⊥AC于D，则∠BDC=90°，∵∠ACB=45°，∴∠CBD=45°，∴BD=CD=2cm，∴Rt△BCD中，BC==2（cm），∴重叠部分的面积为×2×2=2（cm），故选：A．过B作BD⊥AC于D，则∠BDC=90°，依据勾股定理即可得出BC的长，进而得到重叠部分的面积．本题主要考查了折叠问题，折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．11.【答案】C【解析】解：设AD=2x，BD=x，∴AB=3x，∵DE∥BC，∴△ADE∽△ABC，∴=，∴=，∴DE=4，=，∵∠ACD=∠B，∠ADE=∠B，∴∠ADE=∠ACD，∵∠A=∠A，∴△ADE∽△ACD，∴=，设AE=2y，AC=3y，∴=，∴AD=y，∴=，∴CD=2，故选：C．设AD=2x，BD=x，所以AB=3x，易证△ADE∽△ABC，利用相似三角形的性质可求出DE的长度，以及，再证明△ADE∽△ACD，利用相似三角形的性质即可求出得出=，从而可求出CD的长度．本题考查相似三角形，解题的关键是熟练运用相似三角形的性质与判定，本题属于中等题型．12.【答案】D【解析】解：∵正方形ABCD，DPMN的面积分别为S1，S2，∴S1=CD2，S2=PD2，在Rt△PCD中，PC2=CD2+PD2，∴S1+S2=CP2，故A结论正确；连接CF，∵点H与B关于CE对称，∴CH=CB，∠BCE=∠ECH，在△BCE和△HCE中，∴△BCE≌△HCE（SAS），∴BE=EH，∠EHC=∠B=90°，∠BEC=∠HEC，∴CH=CD，在Rt△FCH和Rt△FCD中∴Rt△FCH≌Rt△FCD（HL），∴∠FCH=∠FCD，FH=FD，∴∠ECH+∠ECH=∠BCD=45°，即∠ECF=45°，作FG⊥EC于G，∴△CFG是等腰直角三角形，∴FG=CG，∵∠BEC=∠HEC，∠B=∠FGE=90°，∴△FEG∽△CEB，∴==，∴FG=2EG，设EG=x，则FG=2x，∴CG=2x，CF=2x，∴EC=3x，∵EB2+BC2=EC2，∴BC2=9x2，∴BC2=x2，∴BC=x，在Rt△FDC中，FD===x，∴3FD=AD，∴AF=2FD，故B结论正确；∵AB∥CN，∴=，∵PD=ND，AE=CD，∴CD=4PD，故C结论正确；∵EG=x，FG=2x，∴EF=x，∵FH=FD=x，∵BC=x，∴AE=x，作HQ⊥AD于Q，∴HQ∥AB，∴=，即=，∴HQ=x，∴CD-HQ=x-x=x，∴cos∠HCD===，故结论D错误，故选：D．根据勾股定理可判断A；连接CF，作FG⊥EC，易证得△FGC是等腰直角三角形，设EG=x，则FG=2x，利用三角形相似的性质以及勾股定理得到CG=2x，CF=2x，EC=3x，BC=x，FD=x，即可证得3FD=AD，可判断B；根据平行线分线段成比例定理可判断C；求得cos∠HCD可判断D．本题考查了正方形的性质，三角形全等的判定和性质三角形相似的判定和性质，勾股定理的应用以及平行线分线段成比例定理，作出辅助线构建等腰直角三角形是解题的关键．13.【答案】-9【解析】解：9的相反数是-9；故答案为-9；根据相反数的求法即可得解；本题考查相反数；熟练掌握相反数的意义与求法是解题的关键．14.【答案】0.0000318【解析】解：3.18×10-5=0.0000318；故答案为0.0000318；根据科学记数法的表示方法a×10n（1≤a＜9）即可求解；本题考查科学记数法；熟练掌握科学记数法的表示方法是解题的关键．15.【答案】142°【解析】解：如图，∵a∥b，∴∠2=∠3，∵∠1+∠3=180°，∴∠2=180°-38°=142°．故答案为142°．如图，利用平行线的性质得到∠2=∠3，利用互补求出∠3，从而得到∠2的度数．本题考查了平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．16.【答案】【解析】解：随机掷一枚均匀的骰子有6种等可能结果，其中点数不小于3的有4种结果，所以点数不小于3的概率为=，故答案为：．骰子六个面出现的机会相同，求出骰子向上的一面点数不小于3的情况有几种，直接应用求概率的公式求解即可．此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．17.【答案】【解析】解：连接AB，过O作OM⊥AB于M，∵∠AOB=120°，OA=OB，∴∠BAO=30°，AM=，∴OA=2，∵=2πr，∴r=故答案是：利用弧长=圆锥的周长这一等量关系可求解．本题运用了弧长公式和圆的周长公式，建立准确的等量关系是解题的关键．18.【答案】4【解析】解：①∵（-1，0），（3，0）和（0，3）坐标都满足函数y=|x2-2x-3|，∴①是正确的；②从图象可知图象具有对称性，对称轴可用对称轴公式求得是直线x=1，因此②也是正确的；③根据函数的图象和性质，发现当-1≤x≤1或x≥3时，函数值y随x值的增大而增大，因此③也是正确的；④函数图象的最低点就是与x轴的两个交点，根据y=0，求出相应的x的值为x=-1或x=3，因此④也是正确的；⑤从图象上看，当x＜-1或x＞3，函数值要大于当x=1时的y=|x2-2x-3|=4，因此⑤时不正确的；故答案是：4由（-1，0），（3，0）和（0，3）坐标都满足函数y=|x2-2x-3|，∴①是正确的；从图象可以看出图象具有对称性，对称轴可用对称轴公式求得是直线x=1，②也是正确的；根据函数的图象和性质，发现当-1≤x≤1或x≥3时，函数值y随x值的增大而增大，因此③也是正确的；函数图象的最低点就是与x轴的两个交点，根据y=0，求出相应的x的值为x=-1或x=3，因此④也是正确的；从图象上看，当x ＜-1或x＞3，函数值要大于当x=1时的y=|x2-2x-3|=4，因此⑤时不正确的；逐个判断之后，可得出答案．理解“鹊桥”函数y=|ax2+bx+c|的意义，掌握“鹊桥”函数与y=|ax2+bx+c|与二次函数y=ax2+bx+c之间的关系；两个函数性质之间的联系和区别是解决问题的关键；二次函数y=ax2+bx+c与x轴的交点、对称性、对称轴及最值的求法以及增减性应熟练掌握．19.【答案】解：（1）原式=2-1+4-4×=2-1+4-2=3；（2）解不等式6x-2＞2（x-4），得：x＞-，解不等式-≤-，得：x≤1，则不等式组的解集为-＜x≤1，将不等式组的解集表示在数轴上如下：【解析】（1）先计算算术平方根、零指数幂、负整数指数幂、代入三角函数值，再计算乘法，最后计算加减可得；（2）分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．20.【答案】解：如图，△DEF即为所求．【解析】先作一个∠D=∠A，然后在∠D的两边分别截取ED=BA，DF=AC，连接EF即可得到△DEF；本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了全等三角形的判定．21.【答案】解：（1）由已知可得AD=5，∵菱形ABCD，∴B（6，0），C（9，4），∵点D（4，4）在反比例函数y=（x＞0）的图象上，∴k=16，将点C（9，4）代入y=x+b，∴b=-2；（2）E（0，-2），直线y=x-2与x轴交点为（3，0），∴S△AEC=2×（2+4）=6；【解析】（1）由菱形的性质可知B（6，0），C（9，4），点D（4，4）代入反比例函数y=，求出k；将点C（9，4）代入y=x+b，求出b；（2）求出直线y=x-2与x轴和y轴的交点，即可求△AEC的面积；本题考查反比例函数、一次函数的图象及性质，菱形的性质；能够将借助菱形的边长和菱形边的平行求点的坐标是解题的关键．22.【答案】10 25 0.25【解析】解：（1）a=100×0.1=10，b=100-10-18-35-12=25，n==0.25；故答案为：10，25，0.25；（2）补全频数分布直方图如图所示；（3）2500××=90（人），答：全校获得二等奖的学生人数90人．（1）利用×这组的频率即可得到结论；（2）根据（1）求出的数据补全频数分布直方图即可；（3）利用全校2500名学生数×考试成绩为91≤x≤100考卷占抽取了的考卷数×获得二等奖学生人数占获奖学生数即可得到结论．本题考查的是频数分布直方图，读懂统计图，从统计图中得到必要的信息是解决问题的关键．直方图能清楚地表示出每个项目的数据，也考查了利用样本估计总体的思想．23.【答案】解：（1）设这两年藏书的年均增长率是x，5（1+x）2=7.2，解得，x1=0.2，x2=-2.2（舍去），答：这两年藏书的年均增长率是20%；（2）在这两年新增加的图书中，中外古典名著有（7.2-5）×20%=0.44（万册），到2018年底中外古典名著的册数占藏书总量的百分比是：×100%=10%，答：到2018年底中外古典名著的册数占藏书总量的10%．【解析】（1）根据题意可以列出相应的一元二次方程，从而可以得到这两年藏书的年均增长率；（2）根据题意可以求出这两年新增加的中外古典名著，从而可以求得到2018年底中外古典名著的册数占藏书总量的百分之几．本题考查一元二次方程的应用，解答本题的关键是明确题意，列出相应的方程，利用方程的知识解答，这是一道典型的增长率问题．24.【答案】（1）证明：∵在矩形ABCD中，∠ABO=∠OCE=90°，∵OE⊥OA，∴∠AOE=90°，∴∠BAO+∠AOB=∠AOB+∠COE=90°，∴∠BAO=∠COE，∴△ABO∽△OCE，∴=，∵OB=OC，∴，∵∠ABO=∠AOE=90°，∴△ABO∽△AOE，∴∠BAO=∠OAE，过O作OF⊥AE于F，∴∠ABO=∠AFO=90°，在△ABO与△AFO中，，∴△ABO≌△AFO（AAS），∴OF=OB，∴AE是半圆O的切线；（2）解：∵AF是⊙O的切线，AC是⊙O的割线，∴AF2=AP•AC，∴AF==2，∴AB=AF=2，∵AC=6，∴BC==2，∴AO==3，∵△ABO∽△AOE，∴，∴=，∴AE=．【解析】（1）根据已知条件推出△ABO∽△OCE，根据相似三角形的性质得到∠BAO=∠OAE，过O作OF⊥AE于F，根据全等三角形的性质得到OF=OB，于是得到AE是半圆O的切线；（2）根据切割线定理得到AF==2，求得AB=AF=2，根据勾股定理得到BC==2，AO==3，根据相似三角形的性质即可得到结论．本题考查了切线的判定和性质，矩形的性质，相似三角形的判定和性质，全等三角形的判定和性质，正确的作出辅助线是解题的关键．25.【答案】解：（1）函数表达式为：y=a（x=4）2+3，将点B坐标代入上式并解得：a=-，故抛物线的表达式为：y=-x2+4x-5；（2）A（4，3）、B（0，-5），则点M（2，-1），设直线AB的表达式为：y=kx-5，将点A坐标代入上式得：3=4k-5，解得：k=2，故直线AB的表达式为：y=2x-5；（3）设点Q（4，s）、点P（m，-m2+4m-5），①当AM是平行四边形的一条边时，点A向左平移2个单位、向下平移4个单位得到M，同样点P（m，-m2+4m-5）向左平移2个单位、向下平移4个单位得到Q（4，s），即：m-2=4，-m2+4m-5-4=s，解得：m=6，s=-3，故点P、Q的坐标分别为（6，1）、（4，-3）；②当AM是平行四边形的对角线时，由中点定理得：4+2=m+4，3-1=-m2+4m-5+s，解得：m=2，s=1，故点P、Q的坐标分别为（2，1）、（4，1）；故点P、Q的坐标分别为（6，1）或（2，1）、（4，-3）或（4，1）．【解析】（1）函数表达式为：y=a（x=4）2+3，将点B坐标代入上式，即可求解；（2）A（4，3）、B（0，-5），则点M（2，-1），设直线AB的表达式为：y=kx-5，将点A坐标代入上式，即可求解；（3）分当AM是平行四边形的一条边、AM是平行四边形的对角线两种情况，分别求解即可．本题考查的是二次函数综合运用，涉及到一次函数、平行四边形性质、图象的面积计算等，其中（3），要主要分类求解，避免遗漏．26.【答案】（1）①解：旋转角为105°．理由：如图1中，∵A′D⊥AC，∴∠A′DC=90°，∵∠CA′D=15°，∴∠A′CD=75°，∴∠ACA′=105°，∴旋转角为105°．②证明：连接A′F，设EF交CA′于点O．在EF时截取EM=EC，连接CM．∵∠CED=∠A′CE+∠CA′E=45°+15°=60°，∴∠CEA′=120°，∵FE平分∠CEA′，∴∠CEF=∠FEA′=60°，∵∠FCO=180°-45°-75°=60°，∴∠FCO=∠A′EO，∵∠FOC=∠A′OE，∴△FOC∽△A′OE，∴=，∴=，∵∠COE=∠FOA′，∴△COE∽△FOA′，∴∠FA′O=∠OEC=60°，∴△A′OF是等边三角形，∴CF=CA′=A′F，∵EM=EC，∠CEM=60°，∴△CEM是等边三角形，∠ECM=60°，CM=CE，∵∠FCA′=∠MCE=60°，∴∠FCM=∠A′CE，∴△FCM≌△A′CE（SAS），∴FM=A′E，∴CE+A′E=EM+FM=EF．（2）解：如图2中，连接A′F，PB′，AB′，作B′M⊥AC交AC的延长线于M．由②可知，∠EA′F=′EA′B′=75°，A′E=A′E，A′F=A′B′，∴△A′EF≌△A′EB′，∴EF=EB′，∴B′，F关于A′E对称，∴PF=PB′，∴PA+PF=PA+PB′≥AB′，在Rt△CB′M中，CB′=BC=AB=2，∠MCB′=30°，∴B′M=CB′=1，CM=，∴AB′===．∴PA+PF的最小值为．【解析】（1）①解直角三角形求出∠A′CD即可解决问题．②连接A′F，设EF交CA′于点O．在EF时截取EM=EC，连接CM．首先证明△CFA′是等边三角形，再证明△FCM≌△A′CE（SAS），即可解决问题．（2）如图2中，连接A′F，PB′，AB′，作B′M⊥AC交AC的延长线于M．证明△A′EF≌△A′EB′，推出EF=EB′，推出B′，F关于A′E对称，推出PF=PB′，推出PA+PF=PA+PB′≥AB′，求出AB′即可解决问题．本题属于四边形综合题，考查了旋转变换，全等三角形的判定和性质，相似三角形的判定和性质，三角形的三边关系等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会用转化的思想思考问题，属于中考压轴题．。

2019年广西贵港市中考数学试卷(解析版)

2019 年广西贵港市中考数学试卷一、选择题（本大题共 12 小题，每小题 3 分，共 36 分）每小题都给出标号为 A 、B 、C 、D 的四个选项，其中只有一个是正确的、请考生用2B 铅笔在答题卡上将选定的答案标号涂黑.1．（3 分）计算（﹣1）的结果是（）A ．﹣1B ．1C ．﹣3D ．32．（3 分）某几何体的俯视图如图所示，图中数字表示该位置上的小正方体的个数，则这个几何体的主视图是（）A ．B ．C ．D ．3．（3 分）若一组数据为：10，11，9，8，10，9，11，9，则这组数据的众数和中位数分别是（）A ．9，94．（3 分）若分式 A ．±1B ．10，9C ．9，9.5D ．11，10的值等于 0，则 x 的值为（）B ．0C ．﹣1D ．15．（3 分）下列运算正确的是（）A ．a +（﹣a ）＝﹣aB ．（a +b ）＝a +bC ．2a •a ＝2a3D ．（ab ）＝a b6．（3分）若点 P （m ﹣1，5）与点 Q （3，2﹣n ）关于原点成中心对称，则 m +n 的值是（）A ．1B ．3C ．5D ．77．（3 分）若 α，β 是关于 x 的一元二次方程 x ﹣2x +m ＝0 的两实根，且+＝﹣ ，则m 等于（）A ．﹣2B ．﹣3C ．2D ．38．（3 分）下列命题中假命题是（）A ．对顶角相等3 3 3 62 2 22 23 3 52B ．直线 y ＝x ﹣5 不经过第二象限C ．五边形的内角和为 540°D ．因式分解 x+x +x ＝x （x +x ）9．（3 分）如图，AD 是⊙O 的直径，（）＝，若∠AOB ＝40°，则圆周角∠BPC 的度数是A ．40°B ．50°C ．60°D ．70°10．（3分）将一条宽度为 2cm 的彩带按如图所示的方法折叠，折痕为 AB ，重叠部分为△ABC （图中阴影部分），若∠ACB ＝45°，则重叠部分的面积为（）A ．2cm 2 B ．2cm C ．4cm D ．4 cm211．（3 分）如图，在△ABC 中，点 D ，E 分别在 AB ，AC 边上，DE ∥BC ，∠ACD ＝∠B ，若 AD ＝2BD ，BC ＝6，则线段 CD 的长为（）A ．2B ．3C ．2D ．512．（3 分）如图，E 是正方形 ABCD 的边 AB 的中点，点 H 与 B 关于 CE 对称，EH 的延长线与 AD 交于点 F ，与 CD 的延长线交于点 N ，点 P 在 AD 的延长线上，作正方形 DPMN ，连接 CP ，记正方形 ABCD ，DPMN 的面积分别为 S ，S ，则下列结论错误的是（）3 2 2 2 21 2A ．S +S ＝CPB ．AF ＝2FDC ．CD ＝4PD D ．cos ∠HCD ＝二、填空题（本大题共 6 小题，每小题 3 分，共 18 分）13．（3 分）有理数 9 的相反数是．14．（3 分）将实数 3.18×10 用小数表示为．15．（3 分）如图，直线 a ∥b ，直线 m 与 a ，b 均相交，若∠1＝38°，则∠2＝．16．（3 分）若随机掷一枚均匀的骰子，骰子的 6 个面上分别刻有 1，2，3，4，5，6 点，则点数不小于 3 的概率是．17．（3 分）如图，在扇形 OAB 中，半径 OA 与 OB 的夹角为 120°，点 A 与点 B 的距离为2，若扇形 OAB 恰好是一个圆锥的侧面展开图，则该圆锥的底面半径为．18．（3分）我们定义一种新函数：形如 y ＝|ax +bx +c |（a ≠0，且 b ﹣4a ＞0）的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数 y ＝|x ﹣2x ﹣3|的图象（如图所示），并写出下列五个结论：①图象与坐标轴的交点为（﹣1，0），（3，0）和（0，3）；②图象具有对称性，对称轴是直线 x ＝1；③当﹣1≤x ≤1 或 x ≥3 时，函数值 y 随 x 值的增大而增大； ④当 x ＝﹣1 或 x ＝3 时，函数的最小值是 0；⑤当 x ＝1 时，函数的最大值是 4．其中正确结论的个数是．2 1 2 ﹣5 2 2 2三、解答题（本大题共 8 小题，满分 66 分。

广西贵港市2019年中考数学试题(含解析)和答案

2019年广西贵港市中考数学试卷一、选择题（本大题共12小题，共36.0分）1. 计算（-1）3的结果是（）A. −1B. 1C. −3D. 32. 某几何体的俯视图如图所示，图中数字表示该位置上的小正方体的个数，则这个几何体的主视图是（） A. B. C. D.3. 若一组数据为：10，11，9，8，10，9，11，9，则这组数据的众数和中位数分别是（）A. 9，9B. 10，9C. 9，9.5D. 11，104. 若分式x 2−1x +1的值等于0，则x 的值为（）A. ±1B. 0C. −1D. 15. 下列运算正确的是（）A. x 3+(−x )3=−x 6B. (x +x )2=x 2+x 2C. 2x 2⋅x =2x 3D. (xx 2)3=x 3x 5 6. 若点P （m -1，5）与点Q （3，2-n ）关于原点成中心对称，则m +n 的值是（）A. 1B. 3C. 5D. 77. 若α，β是关于x 的一元二次方程x 2-2x +m =0的两实根，且1x +1x =-23，则m 等于（）A. −2B. −3C. 2D. 38. 下列命题中假命题是（）A. 对顶角相等B. 直线x =x −5不经过第二象限C. 五边形的内角和为540∘D. 因式分解x 3+x 2+x =x (x 2+x )9. 如图，AD 是⊙O 的直径，xx⏜=xx ⏜，若∠AOB =40°，则圆周角∠BPC 的度数是（）A. 40∘B. 50∘C. 60∘D. 70∘10. 将一条宽度为2cm 的彩带按如图所示的方法折叠，折痕为AB ，重叠部分为△ABC （图中阴影部分），若∠ACB =45°，则重叠部分的面积为（）A. 2√2xx 2B. 2√3xx 2C. 4xx 2D. 4√2xx 211. 如图，在△ABC 中，点D ，E 分别在AB ，AC 边上，DE ∥BC ，∠ACD =∠B ，若AD =2BD ，BC =6，则线段CD 的长为（） A. 2√3B. 3√2C. 2√6D. 512. 如图，E 是正方形ABCD 的边AB 的中点，点H 与B 关于CE 对称，EH 的延长线与AD 交于点F ，与CD 的延长线交于点N ，点P 在AD 的延长线上，作正方形DPMN ，连接CP ，记正方形ABCD ，DPMN 的面积分别为S 1，S 2，则下列结论错误的是（）A. x 1+x 2=xx 2B. 4x =2xxC. xx =4xxD. cos ∠xxx =35 二、填空题（本大题共6小题，共18.0分）13. 有理数9的相反数是______．14. 将实数3.18×10-5用小数表示为______．15. 如图，直线a ∥b ，直线m 与a ，b 均相交，若∠1=38°，则∠2=______．16. 若随机掷一枚均匀的骰子，骰子的6个面上分别刻有1，2，3，4，5，6点，则点数不小于3的概率是______．17. 如图，在扇形OAB 中，半径OA 与OB 的夹角为120°，点A 与点B 的距离为2√3，若扇形OAB 恰好是一个圆锥的侧面展开图，则该圆锥的底面半径为______．18. 我们定义一种新函数：形如y =|ax 2+bx +c |（a ≠0，且b 2-4a ＞0）的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数y =|x 2-2x -3|的图象（如图所示），并写出下列五个结论：①图象与坐标轴的交点为（-1，0），（3，0）和（0，3）；②图象具有对称性，对称轴是直线x =1；③当-1≤x ≤1或x ≥3时，函数值y 随x 值的增大而增大；④当x =-1或x =3时，函数的最小值是0；⑤当x =1时，函数的最大值是4．其中正确结论的个数是______．三、解答题（本大题共8小题，共66.0分）19. （1）计算：√4-（√3-3）0+（12）-2-4sin30°；（2）解不等式组：{6x −2＞2(x −4)23−3−x 2≤−x 3，并在数轴上表示该不等式组的解集．20. 尺规作图（只保留作图痕迹，不要求写出作法）：如图，已知△ABC ，请根据“SAS ”基本事实作出△DEF ，使△DEF ≌△ABC ．21. 如图，菱形ABCD 的边AB 在x 轴上，点A 的坐标为（1，0），点D （4，4）在反比例函数y =x x （x ＞0）的图象上，直线y =23x +b 经过点C ，与y 轴交于点E ，连接AC ，AE ．（1）求k ，b 的值；（2）求△ACE 的面积．为了增强学生的安全意识，某校组织了一次全校2500名学生都参加的“安全知识”考试．阅卷后，学校团委随机抽取了100份考卷进行分析统计，发现考试成绩（x 分）的最低分为51分，最高分为满分100分，并绘制了如下尚不完整的统计图表．请根据图表提供的信息，解答下列问题：分数段（分）频数（人）频率51≤x ＜61a 0.1 61≤x ＜7118 0.18 71≤x ＜81b n 81≤x ＜9135 0.35 91≤x ＜10112 0.12 合计 100 1（1）填空：a =______，b =______，n =______；（2）将频数分布直方图补充完整；（3）该校对考试成绩为91≤x ≤100的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为1：3：6，请你估算全校获得二等奖的学生人数．22.为了满足师生的阅读需求，某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册．（1）求这两年藏书的年均增长率；（2）经统计知：中外古典名著的册数在2016年底仅占当时藏书总量的5.6%，在这两年新增加的图书中，中外古典名著所占的百分率恰好等于这两年藏书的年均增长率，那么到2018年底中外古典名著的册数占藏书总量的百分之几？23.如图，在矩形ABCD中，以BC边为直径作半圆O，OE⊥OA交CD边于点E，对角线AC与半圆O的另一个交点为P，连接AE．（1）求证：AE是半圆O的切线；（2）若PA=2，PC=4，求AE的长．24.如图，已知抛物线y=ax2+bx+c的顶点为A（4，3），与y轴相交于点B（0，-5），对称轴为直线l，点M是线段AB的中点．（1）求抛物线的表达式；（2）写出点M的坐标并求直线AB的表达式；（3）设动点P，Q分别在抛物线和对称轴l上，当以A，P，Q，M为顶点的四边形是平行四边形时，求P，Q两点的坐标．25.已知：△ABC是等腰直角三角形，∠BAC=90°，将△ABC绕点C顺时针方向旋转得到△A′B′C，记旋转角为α，当90°＜α＜180°时，作A′D⊥AC，垂足为D，A′D与B′C交于点E．（1）如图1，当∠CA′D=15°时，作∠A′EC的平分线EF交BC于点F．①写出旋转角α的度数；②求证：EA′+EC=EF；（2）如图2，在（1）的条件下，设P是直线A′D上的一个动点，连接PA，PF，若AB=√2，求线段PA+PF的最小值．（结果保留根号）答案和解析1.【答案】A【解析】解：（-1）3表示3个（-1）的乘积，所以（-1）3=-1．故选：A．本题考查有理数的乘方运算．乘方是乘法的特例，乘方的运算可以利用乘法的运算来进行．负数的奇数次幂是负数，负数的偶数次幂是正数；-1的奇数次幂是-1，-1的偶数次幂是1．2.【答案】B【解析】解：从正面看去，一共两列，左边有2竖列，右边是1竖列．故选：B．先细心观察原立体图形中正方体的位置关系，从正面看去，一共两列，左边有2竖列，右边是1竖列，结合四个选项选出答案．本题考查了由三视图判断几何体，解题的关键是具有几何体的三视图及空间想象能力．3.【答案】C【解析】解：将数据重新排列为8，9，9，9，10，10，11，11，∴这组数据的众数为9，中位数为=9.5，故选：C．根据众数和中位数的概念求解可得．本题为统计题，考查众数与中位数的意义．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．4.【答案】D【解析】解：==x-1=0，∴x=1；故选：D．化简分式==x-1=0即可求解；本题考查解分式方程；熟练掌握因式分解的方法，分式方程的解法是解题的关键．5.【答案】C【解析】解：a3+（-a3）=0，A错误；（a+b）2=a2+2ab+b2，B错误；（ab2）3=a3b5，D错误；故选：C．利用完全平方公式，合并同类项法则，幂的乘方与积的乘方法则运算即可；本题考查整式的运算；熟练掌握完全平方公式，合并同类项法则，幂的乘方与积的乘方法则是解题的关键．6.【答案】C【解析】解：∵点P（m-1，5）与点Q（3，2-n）关于原点对称，∴m-1=-3，2-n=-5，解得：m=-2，n=7，则m+n=-2+7=5．故选：C．根据关于原点对称的点的横坐标互为相反数，纵坐标互为相反数，可得答案．本题考查了关于原点对称的点的坐标，关于原点对称的点的横坐标互为相反数，纵坐标互为相反数．7.【答案】B【解析】解：α，β是关于x的一元二次方程x2-2x+m=0的两实根，∴α+β=2，αβ=m，∵+===-，∴m=-3；故选：B．利用一元二次方程根与系数的关系得到α+β=2，αβ=m，再化简+=，代入即可求解；本题考查一元二次方程；熟练掌握一元二次方程根与系数的关系是解题的关键．8.【答案】D【解析】解：A．对顶角相等；真命题；B．直线y=x-5不经过第二象限；真命题；C．五边形的内角和为540°；真命题；D．因式分解x3+x2+x=x（x2+x）；假命题；故选：D．由对顶角相等得出A是真命题；由直线y=x-5的图象得出B是真命题；由五边形的内角和为540°得出C是真命题；由因式分解的定义得出D是假命题；即可得出答案．本题考查了命题与定理、真命题和假命题的定义：正确的命题是真命题，错误的命题是假命题；属于基础题．9.【答案】B【解析】解：∵=，∠AOB=40°，∴∠COD=∠AOB=40°，∵∠AOB+∠BOC+∠COD=180°，∴∠BOC=100°，∴∠BPC=∠BOC=50°，故选：B．根据圆周角定理即可求出答案．本题考查了圆周角定理，熟练掌握圆周角定理是解题的关键．10.【答案】A【解析】解：如图，过B作BD⊥AC于D，则∠BDC=90°，∵∠ACB=45°，∴∠CBD=45°，∴BD=CD=2cm，∴Rt△BCD中，BC==2（cm），∴重叠部分的面积为×2×2=2（cm），故选：A．过B作BD⊥AC于D，则∠BDC=90°，依据勾股定理即可得出BC的长，进而得到重叠部分的面积．本题主要考查了折叠问题，折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．11.【答案】C【解析】解：设AD=2x，BD=x，∴AB=3x，∵DE∥BC，∴△ADE∽△ABC，∴=，∴=，∴DE=4，=，∵∠ACD=∠B，∠ADE=∠B，∴∠ADE=∠ACD，∵∠A=∠A，∴△ADE∽△ACD，∴=，设AE=2y，AC=3y，∴=，∴AD=y，∴=，∴CD=2，故选：C．设AD=2x，BD=x，所以AB=3x，易证△ADE∽△ABC，利用相似三角形的性质可求出DE的长度，以及，再证明△ADE∽△ACD，利用相似三角形的性质即可求出得出=，从而可求出CD的长度．本题考查相似三角形，解题的关键是熟练运用相似三角形的性质与判定，本题属于中等题型．12.【答案】D【解析】解：∵正方形ABCD，DPMN的面积分别为S1，S2，∴S1=CD2，S2=PD2，在Rt△PCD中，PC2=CD2+PD2，∴S1+S2=CP2，故A结论正确；连接CF，∵点H与B关于CE对称，∴CH=CB，∠BCE=∠ECH，在△BCE和△HCE中，∴△BCE≌△HCE（SAS），∴BE=EH，∠EHC=∠B=90°，∠BEC=∠HEC，∴CH=CD，在Rt△FCH和Rt△FCD中∴Rt△FCH≌Rt△FCD（HL），∴∠FCH=∠FCD，FH=FD，∴∠ECH+∠ECH=∠BCD=45°，即∠ECF=45°，作FG⊥EC于G，∴△CFG是等腰直角三角形，∴FG=CG，∵∠BEC=∠HEC，∠B=∠FGE=90°，∴△FEG∽△CEB，∴==，∴FG=2EG，设EG=x，则FG=2x，∴CG=2x，CF=2x，∴EC=3x，∵EB2+BC2=EC2，∴BC2=9x2，∴BC2=x2，∴BC=x，在Rt△FDC中，FD===x，∴3FD=AD，∴AF=2FD，故B结论正确；∵AB∥CN，∴=，∵PD=ND，AE=CD，∴CD=4PD，故C结论正确；∵EG=x，FG=2x，∴EF=x，∵FH=FD=x，∵BC=x，∴AE=x，作HQ⊥AD于Q，∴HQ∥AB，∴=，即=，∴HQ=x，∴CD-HQ=x-x=x，∴cos∠HCD===，故结论D错误，故选：D．根据勾股定理可判断A；连接CF，作FG⊥EC，易证得△FGC是等腰直角三角形，设EG=x，则FG=2x，利用三角形相似的性质以及勾股定理得到CG=2x，CF=2x，EC=3x，BC=x，FD=x，即可证得3FD=AD，可判断B；根据平行线分线段成比例定理可判断C；求得cos∠HCD可判断D．本题考查了正方形的性质，三角形全等的判定和性质三角形相似的判定和性质，勾股定理的应用以及平行线分线段成比例定理，作出辅助线构建等腰直角三角形是解题的关键．13.【答案】-9【解析】解：9的相反数是-9；故答案为-9；根据相反数的求法即可得解；本题考查相反数；熟练掌握相反数的意义与求法是解题的关键．14.【答案】0.0000318【解析】解：3.18×10-5=0.0000318；故答案为0.0000318；根据科学记数法的表示方法a×10n（1≤a＜9）即可求解；本题考查科学记数法；熟练掌握科学记数法的表示方法是解题的关键．15.【答案】142°【解析】解：如图，∵a∥b，∴∠2=∠3，∵∠1+∠3=180°，∴∠2=180°-38°=142°．故答案为142°．如图，利用平行线的性质得到∠2=∠3，利用互补求出∠3，从而得到∠2的度数．本题考查了平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．16.【答案】23【解析】解：随机掷一枚均匀的骰子有6种等可能结果，其中点数不小于3的有4种结果，所以点数不小于3的概率为=，故答案为：．骰子六个面出现的机会相同，求出骰子向上的一面点数不小于3的情况有几种，直接应用求概率的公式求解即可．此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=．17.【答案】23【解析】解：连接AB，过O作OM⊥AB于M，∵∠AOB=120°，OA=OB，∴∠BAO=30°，AM=，∴OA=2， ∵=2πr ， ∴r= 故答案是：利用弧长=圆锥的周长这一等量关系可求解．本题运用了弧长公式和圆的周长公式，建立准确的等量关系是解题的关键．18.【答案】4【解析】解：①∵（-1，0），（3，0）和（0，3）坐标都满足函数y=|x 2-2x-3|，∴①是正确的；②从图象可知图象具有对称性，对称轴可用对称轴公式求得是直线x=1，因此②也是正确的；③根据函数的图象和性质，发现当-1≤x ≤1或x ≥3时，函数值y 随x 值的增大而增大，因此③也是正确的；④函数图象的最低点就是与x 轴的两个交点，根据y=0，求出相应的x 的值为x=-1或x=3，因此④也是正确的；⑤从图象上看，当x ＜-1或x ＞3，函数值要大于当x=1时的y=|x 2-2x-3|=4，因此⑤时不正确的；故答案是：4由（-1，0），（3，0）和（0，3）坐标都满足函数y=|x 2-2x-3|，∴①是正确的；从图象可以看出图象具有对称性，对称轴可用对称轴公式求得是直线x=1，②也是正确的；根据函数的图象和性质，发现当-1≤x ≤1或x ≥3时，函数值y 随x 值的增大而增大，因此③也是正确的；函数图象的最低点就是与x 轴的两个交点，根据y=0，求出相应的x 的值为x=-1或x=3，因此④也是正确的；从图象上看，当x ＜-1或x ＞3，函数值要大于当x=1时的y=|x 2-2x-3|=4，因此⑤时不正确的；逐个判断之后，可得出答案．理解“鹊桥”函数y=|ax 2+bx+c|的意义，掌握“鹊桥”函数与y=|ax 2+bx+c|与二次函数y=ax 2+bx+c 之间的关系；两个函数性质之间的联系和区别是解决问题的关键；二次函数y=ax 2+bx+c 与x 轴的交点、对称性、对称轴及最值的求法以及增减性应熟练掌握．19.【答案】解：（1）原式=2-1+4-4×12 =2-1+4-2=3；（2）解不等式6x -2＞2（x -4），得：x ＞-32，解不等式23-3−x 2≤-x 3，得：x ≤1，则不等式组的解集为-32＜x ≤1，将不等式组的解集表示在数轴上如下：【解析】（1）先计算算术平方根、零指数幂、负整数指数幂、代入三角函数值，再计算乘法，最后计算加减可得；（2）分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．20.【答案】解：如图，△DEF 即为所求．【解析】先作一个∠D=∠A ，然后在∠D 的两边分别截取ED=BA ，DF=AC ，连接EF 即可得到△DEF ；本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了全等三角形的判定．21.【答案】解：（1）由已知可得AD =5，∵菱形ABCD ，∴B （6，0），C （9，4）， ∵点D （4，4）在反比例函数y =x x （x ＞0）的图象上，∴k =16，将点C （9，4）代入y =23x +b ，∴b =-2；（2）E （0，-2），直线y =23x -2与x 轴交点为（3，0），∴S △AEC =12×2×（2+4）=6；【解析】（1）由菱形的性质可知B （6，0），C （9，4），点D （4，4）代入反比例函数y=，求出k ；将点C （9，4）代入y=x+b ，求出b ；（2）求出直线y=x-2与x 轴和y 轴的交点，即可求△AEC 的面积；本题考查反比例函数、一次函数的图象及性质，菱形的性质；能够将借助菱形的边长和菱形边的平行求点的坐标是解题的关键．22.【答案】10 25 0.25【解析】解：（1）a=100×0.1=10，b=100-10-18-35-12=25，n==0.25；故答案为：10，25，0.25；（2）补全频数分布直方图如图所示；（3）2500××=90（人），答：全校获得二等奖的学生人数90人．（1）利用×这组的频率即可得到结论；（2）根据（1）求出的数据补全频数分布直方图即可；（3）利用全校2500名学生数×考试成绩为91≤x ≤100考卷占抽取了的考卷数×获得二等奖学生人数占获奖学生数即可得到结论．本题考查的是频数分布直方图，读懂统计图，从统计图中得到必要的信息是解决问题的关键．直方图能清楚地表示出每个项目的数据，也考查了利用样本估计总体的思想．23.【答案】解：（1）设这两年藏书的年均增长率是x ，5（1+x ）2=7.2，解得，x 1=0.2，x 2=-2.2（舍去），答：这两年藏书的年均增长率是20%；（2）在这两年新增加的图书中，中外古典名著有（7.2-5）×20%=0.44（万册），到2018年底中外古典名著的册数占藏书总量的百分比是：5×5.6%+0.447.2×100%=10%，答：到2018年底中外古典名著的册数占藏书总量的10%．【解析】（1）根据题意可以列出相应的一元二次方程，从而可以得到这两年藏书的年均增长率；（2）根据题意可以求出这两年新增加的中外古典名著，从而可以求得到2018年底中外古典名著的册数占藏书总量的百分之几．本题考查一元二次方程的应用，解答本题的关键是明确题意，列出相应的方程，利用方程的知识解答，这是一道典型的增长率问题．24.【答案】（1）证明：∵在矩形ABCD 中，∠ABO =∠OCE =90°，∵OE ⊥OA ，∴∠AOE =90°，∴∠BAO +∠AOB =∠AOB +∠COE =90°，∴∠BAO =∠COE ，∴△ABO ∽△OCE ， ∴xx xx =xx xx ，∵OB =OC ，∴xx xx =xx xx ， ∵∠ABO =∠AOE =90°，∴△ABO ∽△AOE ，∴∠BAO =∠OAE ，过O 作OF ⊥AE 于F ，∴∠ABO =∠AFO =90°，在△ABO 与△AFO 中，{∠xxx =∠xxx∠xxx =∠xxx xx =xx，∴△ABO ≌△AFO （AAS ），∴OF =OB ，∴AE 是半圆O 的切线；（2）解：∵AF 是⊙O 的切线，AC 是⊙O 的割线，∴AF 2=AP •AC ，∴AF =√2(2+4)=2√3，∴AB =AF =2√3，∵AC =6，∴BC =√xx 2−xx 2=2√6，∴AO =√xx 2+xx 2=3，∵△ABO ∽△AOE ， ∴xx xx =xx xx ，∴3xx =2√33， ∴AE =3√32．【解析】（1）根据已知条件推出△ABO ∽△OCE ，根据相似三角形的性质得到∠BAO=∠OAE ，过O 作OF ⊥AE 于F ，根据全等三角形的性质得到OF=OB ，于是得到AE 是半圆O 的切线；（2）根据切割线定理得到AF==2，求得AB=AF=2，根据勾股定理得到BC==2，AO==3，根据相似三角形的性质即可得到结论．本题考查了切线的判定和性质，矩形的性质，相似三角形的判定和性质，全等三角形的判定和性质，正确的作出辅助线是解题的关键．25.【答案】解：（1）函数表达式为：y =a （x =4）2+3，将点B 坐标代入上式并解得：a =-12，故抛物线的表达式为：y =-12x 2+4x -5；（2）A （4，3）、B （0，-5），则点M （2，-1），设直线AB 的表达式为：y =kx -5，将点A 坐标代入上式得：3=4k -5，解得：k =2，故直线AB的表达式为：y=2x-5；m2+4m-5），（3）设点Q（4，s）、点P（m，-12①当AM是平行四边形的一条边时，点A向左平移2个单位、向下平移4个单位得到M，m2+4m-5）向左平移2个单位、向下平移4个单位得到Q（4，s），同样点P（m，-12m2+4m-5-4=s，即：m-2=4，-12解得：m=6，s=-3，故点P、Q的坐标分别为（6，1）、（4，-3）；②当AM是平行四边形的对角线时，m2+4m-5+s，由中点定理得：4+2=m+4，3-1=-12解得：m=2，s=1，故点P、Q的坐标分别为（2，1）、（4，1）；故点P、Q的坐标分别为（6，1）或（2，1）、（4，-3）或（4，1）．【解析】（1）函数表达式为：y=a（x=4）2+3，将点B坐标代入上式，即可求解；（2）A（4，3）、B（0，-5），则点M（2，-1），设直线AB的表达式为：y=kx-5，将点A 坐标代入上式，即可求解；（3）分当AM是平行四边形的一条边、AM是平行四边形的对角线两种情况，分别求解即可．本题考查的是二次函数综合运用，涉及到一次函数、平行四边形性质、图象的面积计算等，其中（3），要主要分类求解，避免遗漏．26.【答案】（1）①解：旋转角为105°．理由：如图1中，∵A′D⊥AC，∴∠A′DC=90°，∵∠CA′D=15°，∴∠A′CD=75°，∴∠ACA′=105°，∴旋转角为105°．②证明：连接A′F，设EF交CA′于点O．在EF时截取EM=EC，连接CM．∵∠CED =∠A ′CE +∠CA ′E =45°+15°=60°，∴∠CEA ′=120°，∵FE 平分∠CEA ′，∴∠CEF =∠FEA ′=60°，∵∠FCO =180°-45°-75°=60°，∴∠FCO =∠A ′EO ，∵∠FOC =∠A ′OE ，∴△FOC ∽△A ′OE ， ∴xx x ′x =xx xx ，∴xx xx =x ′xxx， ∵∠COE =∠FOA ′，∴△COE ∽△FOA ′，∴∠FA ′O =∠OEC =60°，∴△A ′OF 是等边三角形，∴CF =CA ′=A ′F ，∵EM =EC ，∠CEM =60°，∴△CEM 是等边三角形，∠ECM =60°，CM =CE ，∵∠FCA ′=∠MCE =60°，∴∠FCM =∠A ′CE ，∴△FCM ≌△A ′CE （SAS ），∴FM =A ′E ，∴CE +A ′E =EM +FM =EF ．（2）解：如图2中，连接A ′F ，PB ′，AB ′，作B ′M ⊥AC 交AC 的延长线于M ．由②可知，∠EA ′F =′EA ′B ′=75°，A ′E =A ′E ，A ′F =A ′B ′，∴△A ′EF ≌△A ′EB ′，∴EF =EB ′，∴B ′，F 关于A ′E 对称，∴PF =PB ′，∴PA +PF =PA +PB ′≥AB ′，在Rt △CB ′M 中，CB ′=BC =√2AB =2，∠MCB ′=30°，∴B ′M =12CB ′=1，CM =√3，∴AB′=√xx2+x′x2=√(√2+√3)2+12=√6+2√6．∴PA+PF的最小值为√6+2√6．【解析】（1）①解直角三角形求出∠A′CD即可解决问题．②连接A′F，设EF交CA′于点O．在EF时截取EM=EC，连接CM．首先证明△CFA′是等边三角形，再证明△FCM≌△A′CE（SAS），即可解决问题．（2）如图2中，连接A′F，PB′，AB′，作B′M⊥AC交AC的延长线于M．证明△A′EF≌△A′EB′，推出EF=EB′，推出B′，F关于A′E对称，推出PF=PB′，推出PA+PF=PA+PB′≥AB′，求出AB′即可解决问题．本题属于四边形综合题，考查了旋转变换，全等三角形的判定和性质，相似三角形的判定和性质，三角形的三边关系等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会用转化的思想思考问题，属于中考压轴题．。

2019年广西贵港市中考数学试卷(带解析)

D．70°
10．（3 分）将一条宽度为 2cm 的彩带按如图所示的方法折叠，折痕为 AB，重叠部分为△ABC
（图中阴影部分），若∠ACB＝45°，则重叠部分的面积为（）
A．2 cm2
B．2 cm2
C．4cm2
D．4 cm2
11．（3 分）如图，在△ABC 中，点 D，E 分别在 AB，AC 边上，DE∥BC，∠ACD＝∠B，
B．（a+b）2＝a2+b2 D．（ab2）3＝a3b5
6．（3 分）若点 P（m﹣1，5）与点 Q（3，2﹣n）关于原点成中心对称，则 m+n 的值是
（）
A．1
B．3
C．5
D．7
7．（3 分）若α，β是关于 x 的一元二次方程 x2﹣2x+m＝0 的两实根，且
，则 m
等于（）
A．﹣2
B．﹣3
8．（3 分）下列命题中假命题是（）
第 8页（共 27页）
【解答】解：α，β是关于 x 的一元二次方程 x2﹣2x+m＝0 的两实根， ∴α+β＝2，αβ＝m，
∵
，
∴m＝﹣3；故选：B． 8．（3 分）下列命题中假命题是（） A．对顶角相等 B．直线 y＝x﹣5 不经过第二象限 C．五边形的内角和为 540° D．因式分解 x3+x2+x＝x（x2+x）【分析】由对顶角相等得出 A 是真命题；由直线 y＝x﹣5 的图象得出 B 是真命题；由五边形的内角和为 540°得出 C 是真命题；由因式分解的定义得出 D 是假命题；即可得出答案．【解答】解：A．对顶角相等；真命题； B．直线 y＝x﹣5 不经过第二象限；真命题； C．五边形的内角和为 540°；真命题； D．因式分解 x3+x2+x＝x（x2+x）；假命题；故选：D． 9．（3 分）如图，AD 是⊙O 的直径，耀ㄠ，若∠AOB＝40°，则圆周角∠BPC 的度数是（）

2019年广西贵港市中考数学试卷以及逐题解析版

2 竖列，右边是 1 竖列．
【点评】本题考查了由三视图判断几何体，解题的关键是具有几何体的三视图及空间想象能力．
3．（ 3 分）若一组数据为： 10， 11，9， 8，10， 9， 11， 9，则这组数据的众数和中位数分别
是(
)
第 7 页（共 28 页）
A ．9， 9
B ．10， 9
【分析】根据众数和中位数的概念求解可得．
，叫做这组数据的中位数，
如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．
4．（ 3 分）若分式 x2 1 的值等于 0，则 x 的值为 (
)
x1
A． 1
B．0
C． 1
【分析】化简分式 x2 1 (x 1)(x 1) x 1 0 即可求解；
x1
x1
【解答】解： x2 1 ( x 1)(x 1) x 1 0 ，
（1）求证： AE 是半圆 O 的切线；（2）若 PA 2 ， PC 4 ，求 AE 的长．
第 5 页（共 28 页）
25．（ 11 分）如图，已知抛物线
y
2
ax
bx
c 的顶点为 A(4,3) ，与 y 轴相交于点 B(0, 5) ，
对称轴为直线 l ，点 M 是线段 AB 的中点．（1）求抛物线的表达式；（2）写出点 M 的坐标并求直线 AB 的表达式；（3）设动点 P ， Q 分别在抛物线和对称轴 l 上，当以 A ， P ， Q ， M 为顶点的四边形是平行四边形时，求 P ， Q 两点的坐标．
．
16．（ 3 分）若随机掷一枚均匀的骰子，骰子的
点数不小于 3 的概率是
．
6 个面上分别刻有 1，2，3， 4， 5，6 点，则

2019年广西贵港市中考数学试卷-答案

广西贵港市2019年初中毕业学业水平考试数学答案解析第Ⅰ卷一、选择题1．【答案】A【解析】解：3(1)-表示3个(1)-的乘积，所以3(1)=3-．故选：A ．乘方是乘法的特例，乘方的运算可以利用乘法的运算来进行．负数的奇数次幂是负数，负数的偶数次幂是正数；1-的奇数次幂是1-，1-的偶数次幂是1．【考点】有理数的乘方运算．2．【答案】B【解析】解：从正面看去，一共两列，左边有2竖列，右边是1竖列．故选：B ．先细心观察原立体图形中正方体的位置关系，从正面看去，一共两列，左边有2竖列，右边是1竖列，结合四个选项选出答案．【考点】由三视图判断几何体，解题的关键是具有几何体的三视图及空间想象能力．3．【答案】C 【解析】解：将数据重新排列为8，9，9，9，10，10，11，11，∴这组数据的众数为9，中位数为9+10=9.52，故选：C ．根据众数和中位数的概念求解可得．本题为统计题，中位数是将一组数据从小到大(或从大到小)重新排列后，最中间的那个数(最中间两个数的平均数)，叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．【考点】众数与中位数的意义．4．【答案】D【解析】解：21(1)(1)1011x x x x x x -+-==-=++， ∴1x =；故选：D ．化简分式21(1)(1)1011x x x x x x -+-==-=++即可求解；【考点】解分式方程；熟练掌握因式分解的方法，分式方程的解法是解题的关键．5．【答案】C【解析】解：33()0a a +-=，A 错误；222()2a b a ab b +=++，B 错误；2335()ab a b =，D 错误；故选：C ．利用完全平方公式，合并同类项法则，幂的乘方与积的乘方法则运算即可；【考点】整式的运算；熟练掌握完全平方公式，合并同类项法则，幂的乘方与积的乘方法则是解题的关键．6．【答案】C【解析】解：∵点(1,5)P m -与点(3,2)Q n - 关于原点对称，∴13m -=-，25n -=-，解得：2m =-，7n =，则275m n +=-+=，故选：C ．关于原点对称的点的坐标，关于原点对称的点的横坐标互为相反数，纵坐标互为相反数．8．【答案】D【解析】解：A ．对顶角相等；真命题；B ．直线5y x =-不经过第二象限；真命题；C ．五边形的内角和为°540；真命题；D ．因式分解322()x x x x x x ++=+；假命题；故选：D ．由对顶角相等得出A 是真命题；由直线5y x =-的图象得出B 是真命题；由五边形的内角和为°540得出C是真命题；由因式分解的定义得出D 是假命题；即可得出答案．【考点】命题与定理、真命题和假命题的定义：正确的命题是真命题，错误的命题是假命题．9．【答案】B【解析】解：∵AB CD =，°40AOB =∠，∴°40COD AOB ==∠∠，∵°+180AOB BOC COD +=∠∠∠，∴°100BOC =∠， ∴°1502BPC BOC ==∠∠，故选：B ．根据圆周角定理即可求出答案．【考点】圆周角定理，熟练掌握圆周角定理是解题的关键．10.【答案】A【解析】如图，过B 作BD AC ⊥于D ，则°90BDC =∠，∵°45ACB =∠，∴°45CBD =∠，∴ 2 cm BD CD ==，∴Rt BCD △中，BC =，∴重叠部分的面积为12⨯，故选：A ．过B 作BD AC ⊥于D ，则°90BDC =∠，依据勾股定理即可得出BC 的长，进而得到重叠部分的面积．【考点】折叠问题，折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．11．【答案】C【解析】设2AD x =，BD x =，∴3AB x =，∵DE BC ∥，∴ADE ABC △∽△， ∴DE AD DE BC AB CD==，∴263DE x x=， ∴4DE =，23AE AC =， ∵ACD B =∠∠，ADE B =∠∠，∴ADE ACD =∠∠，∵A A =∠∠，∴ADE ACD △∽△， ∴DE AE DE BC AD CD==，设2AE y =，3AC y =， ∴23AD y y AD=，∴AD ， 4CD=， ∴2CD =，故选：C ．设2AD x =，BD x =，所以3AB x =，易证ADE ABC △∽△，利用相似三角形的性质可求出DE 的长度，以及23AE AC =，再证明ADE ACD △∽△，利用相似三角形的性质即可求出得出DE AE DE BC AD CD ==，从而可求出CD 的长度．【考点】相似三角形，解题的关键是熟练运用相似三角形的性质与判定．12．【答案】D【解析】解：∵正方形ABCD ，DPMN 的面积分别为1S ，2S ，∴12S CD =，22S PD =，在Rt PCD △中，222PC CD PD =+，∴212S S CP +=，故A 结论正确；连接CF ，∵点H 与B 关于CE 对称，∴CH CB =，BCE ECH =∠∠ ，在BCE △和HCE △中，ECH BC CH CB CE CE E =⎧⎪=⎩=⎪⎨∠∠∴()CE HCE SAS △≌△ ，∴BE EH =，°90ECH B ==∠∠，BEC HEC =∠∠，∴CH CD =，在Rt FCH △和Rt FCD △中=CH CD CF CF ⎧⎨=⎩∴Rt Rt ()FCH FCD HL △≌△，∴FCH FCD =∠∠，FH FD =，∴°+45ECH ECH BCD ==∠∠∠，即°=45ECH ∠，作FG EC ⊥于G ，∴CFG △是等腰直角三角形，∴FG CG =，∵BEC HEC =∠∠，°90B FGH ==∠∠，∴FEG CEB △∽△， ∴12EG EB FG BC ==， ∴2FG EG =，设EG x =，则2FG x =，∴2CG x =，2CF x = ，∴3EC x =，∵222EB BC EC +=， ∴22594BC x =，∴22 BC x =，∴ BC x =，在Rt FCD △中，FD == ∴3FD AD =，∴2AF FD =，故B 结论正确；∵AB CN ∥， ∴12ND FD AE AF ==， ∵PD ND =，12AE CD =，∴4CD PD =，故C 结论正确；∵EG x =，2FG x =，∴EF =，∵FH FD =，∵BC ，∴AE ，作HQ AD ⊥于Q ，∴HQ AB ∥， ∴HQ HF AE EF =，∴HQ x =，∴CD HQ x x x --=，∴cos 25CD HQ HCD CF -===∠，故结论D 错误，故选：D ．根据勾股定理可判断A ；连接CF ，作FG EC ⊥，易证得FGC △是等腰直角三角形，设EG x =，则2FG x =，利用三角形相似的性质以及勾股定理得到2CG x =，3EC x =，BC x =， FD x =，即可证得3FD AD =，可判断B ；根据平行线分线段成比例定理可判断C ；求得cos HCD ∠可判断D ．【考点】正方形的性质，三角形全等的判定和性质三角形相似的判定和性质，勾股定理的应用以及平行线分线段成比例定理，作出辅助线构建等腰直角三角形是解题的关键．第Ⅱ卷二．填空题13．【答案】9-【解析】解：9的相反数是9-；故答案为9-；根据相反数的求法即可得解；【考点】考查相反数；熟练掌握相反数的意义与求法是解题的关键．14．【答案】0.000 031 8【解析】解：53.18100.000 031 8-⨯=；故答案为0.000 031 8；根据科学记数法的表示方法1019n a a ⨯≤<（）即可求解；【考点】科学记数法；熟练掌握科学记数法的表示方法是解题的关键．15．【答案】°142【解析】解：如图，∵a b ∥，∴23=∠∠，∵°13180+=∠∠，∴°°°218038142=-=∠．故答案为°142．如图，利用平行线的性质得到23=∠∠，利用互补求出2∠，从而得到3∠的度数．．【考点】平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．16．【答案】23【解析】解：随机掷一枚均匀的骰子有6种等可能结果，其中点数不小于3的有4种结果，所以点数不小于3的概率为42=63，故答案为：23．骰子六个面出现的机会相同，求出骰子向上的一面点数不小于3的情况有几种，直接应用求概率的公式求解即可．【考点】概率的求法：如果一个事件有n 种可能，而且这些事件的可能性相同，其中事件A 出现m 种结果，那么事件A 的概率()m P A n=． 17．【答案】23【解析】解：连接AB ，过O 作OM AB ⊥于M ，∵°120AOB ∠=，OA OB =，∴°30BAO ∠=，AM =∴2OA =， ∵1202180r ππ=， ∴23r = 故答案是：23 利用弧长=圆锥的周长这一等量关系可求解．【考点】本题考查了勾股定理、平面直角坐标系内点的坐标弧长公式和圆的周长公式，建立准确的等量关系是解题的关键．18．【答案】4【解析】解：①∵(1,0)-，(3,0)和(0,3)坐标都满足函数2||23y x x =--，∴①是正确的；②从图象可知图象具有对称性，对称轴可用对称轴公式求得是直线1x =，因此②也是正确的；③根据函数的图象和性质，发现当11x -≤≤或3x ≥时，函数值y 随x 值的增大而增大，因此③也是正确的；④函数图象的最低点就是与x 轴的两个交点，根据0y =，求出相应的x 的值为1x =-或3x =，因此④也是正确的；⑤从图象上看，当1x -＜或3x ＞，函数值要大于当1x =时的223||=4y x x =--，因此⑤时不正确的；故答案是：4由(1,0)-，(3,0)和(0,3) 坐标都满足函数223||=4y x x =--，∴①是正确的；从图象可以看出图象具有对称性，对称轴可用对称轴公式求得是直线x=1，②也是正确的；根据函数的图象和性质，发现当11x -≤≤或3x ≥时时，函数值y 随x 值的增大而增大，因此③也是正确的；函数图象的最低点就是与x 轴的两个交点，根据0y =，求出相应的x 的值为1x =-或3x =，因此④也是正确的；从图象上看，当1x -＜或3x ＞，函数值要大于当1x =时的223||=4y x x =--，因此⑤时不正确的；逐个判断之后，可得出答案．理解“鹊桥”函数2||23y x x =--的意义，掌握“鹊桥”函数与2||y x bx c a =++与二次函数2x c a y x b =++ 之间的关系；两个函数性质之间的联系和区别是解决问题的关键；二次函数2x c a y x b =++与x 轴的交点、对称性、对称轴及最值的求法以及增减性应熟练掌握．【考点】二次函数轴2x c a y x b =++与x 的交点、对称性、对称轴及最值的求法以及增减性应熟练掌握．三、解答题19．【答案】解：(1)原式121442=-+-⨯2142=-+-3=；(2)解不等式622(4)x x --＞，得：32x ＞-，解不等式23323x x --≤，得：1x ≤，则不等式组的解集为312x -<≤，将不等式组的解集表示在数轴上如下：【解析】(1)先计算算术平方根、零指数幂、负整数指数幂、代入三角函数值，再计算乘法，最后计算加减可得；(2)分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．评分说明第(1)题，与“去括号法则用错”等同的说法均给分．【考点】解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．20.【答案】解：如图，DEF △即为所求．【解析】先作一个D A =∠∠，然后在D ∠的两边分别截取ED BA =，DF AC =，连接EF 即可得到DEF △；解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了全等三角形的判定．【考点】作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．21．【答案】解：(1)由已知可得5AD =，∵菱形ABCD ，∴(6,0)B ，(9,4)C ，∵点(4,4)D 在反比例函数(0)k y x x =>的图象上， ∴16k =，将点(9,4)C 代入23y x b =+， ∴2b =-；(2)(02)E -，，直线223y x =-与x 轴交点为(3,0)， ∴122462AEC S =⨯⨯+=△（）；【解析】(1)由菱形的性质可知B ∴(6,0)B ，(9,4)C ，点(4,4)D 代入反比例函数k y x =，求出k ；将点(9,4)C 代入23y x b =+，求出b ； (2)求出直线 2y x =-与x 轴和y 轴的交点，即可求AEC △的面积；．【考点】反比例函数、一次函数的图象及性质，菱形的性质；能够将借助菱形的边长和菱形边的平行求点的坐标是解题的关键．22．【答案】(1)10250.25(2)(3)12325009010010⨯⨯=(人) 【解析】解：(1)1000.110a =⨯=，1001018351225b =----=，250.25100n ==；故答案为：10，25，0.25；(2)补全频数分布直方图如图所示；(3)12325009010010⨯⨯=(人)，答：全校获得二等奖的学生人数90人．(1)利用×这组的频率即可得到结论；(2)根据(1)求出的数据补全频数分布直方图即可；(3)利用全校2 500名学生数×考试成绩为91100x ≤≤考卷占抽取了的考卷数×获得二等奖学生人数占获奖学生数即可得到结论．解答本题的关键是明确题意，列出相应的方程，利用方程的知识解答，这是一道典型的增长率问题．【考点】一元二次方程的应用．23．【答案】解：(1)设这两年藏书的年均增长率是x ，25(1)7.2x +=，解得，10.2x =，2 2.2x =-(舍去)，答：这两年藏书的年均增长率是20%；(2)在这两年新增加的图书中，中外古典名著有(7.25)200.44-⨯=%(万册)，到2018年底中外古典名著的册数占藏书总量的百分比是：(5 5.60.44)100107.2⨯+⨯=%%%，答：到2018年底中外古典名著的册数占藏书总量的10%．【解析】(1)根据题意可以列出相应的一元二次方程，从而可以得到这两年藏书的年均增长率；(2)根据题意可以求出这两年新增加的中外古典名著，从而可以求得到2018年底中外古典名著的册数占藏书总量的百分之几．提示：(1)根据题意作出圆弧；(2)根据轴对称图形和中心对称图形的概念进行判断；(3)根据弧长公式求出三条弧的长度的和即可．【考点】本题考查基本作图一一作弧、轴对称图形和中心对称图形的概念、扇形的弧长．24．【答案】(1)证明：∵在矩形ABCD 中，°90ABO OCE ==∠∠，∵OE OA ⊥，∴°90AOE =∠，∴°90BAO AOD AOB COE ====∠∠∠∠，∴BAO COE =∠∠，∴ABO OCE △∽△， ∴AB AO OC OE=， ∵OB OC =， ∴AB AO OB OE=， ∵°90ABO AOE ==∠∠，∴ABO AOE △∽△，∴BAO OAE =∠∠，过O 作OF AE ⊥于F ，∴°90ABO AFO ==∠∠，在ABO △与AOE △中，BAO FAO ABO AFO AO AO =⎧⎪=⎨⎪=⎩∠∠∠∠，∴ABO AFO △≌△()AAS ，∴OF OB =，∴AE 是半圆O 的切线；(2)解：∵AF 是O 的切线，AC 是O 的割线，∴2 AF AP AC =，∴AF ==，∴AB AF ==∵6AC =，∴BC ==∴AO =，∵ABO AOE △∽△， ∴AO AB AE AO=，∴3=3AE ，∴AE =．【解析】(1)根据已知条件推出ABO OCE △∽△，根据相似三角形的性质得到BAO OAE =∠∠，过O 作OF AE ⊥于F ，根据全等三角形的性质得到OF OB =，于是得到AE 是半圆O 的切线；(2)根据切割线定理得到AF =，求得AB AF ==，根据勾股定理得到BC =AO =，根据相似三角形的性质即可得到结论．【考点】切线的判定和性质，矩形的性质，相似三角形的判定和性质，全等三角形的判定和性质，正确的作出辅助线是解题的关键．25．【答案】解：(1)函数表达式为：2(+4)3y a x =+，将点B 坐标代入上式并解得：12a =-，故抛物线的表达式为：21452y x x =-+-；(2)(4,3)A 、(0,5)B -，则点(2,1)M -，设直线AB 的表达式为：5y kx =-，将点A 坐标代入上式得：345k =-，解得：2k =，故直线AB 的表达式为：25y x =-；(3)设点(4,)Q s 、点21(,45)2P m m m -+-，①当AM 是平行四边形的一条边时，点A 向左平移2个单位、向下平移4个单位得到M ，同样点21(,45)2P m m m -+-向左平移2个单位、向下平移4个单位得到(4,)Q s ，即：24m -=，2145=2m m s -+-，解得：6m =，3s =-，故点P 、Q 的坐标分别为(6,1)、(4,3)-；②当AM 是平行四边形的对角线时，由中点定理得：424m +=+，213145+2m m s -=-+-，解得：2m =，1s =，故点P 、Q 的坐标分别为(2,1)、(4,1)；故点P 、Q 的坐标分别为(6,1)或(2,1)、(4,3)-或(4,1)．【解析】(1)函数表达式为：2(+4)3y a x =+，将点B 坐标代入上式，即可求解；(2)(4,3)A 、(0,5)B -，则点(2,1)M -，设直线AB 的表达式为：5y kx =-，将点A 坐标代入上式，即可求解；(3)分当AM 是平行四边形的一条边AM 是平行四边形的对角线两种情况，分别求解即可．【考点】二次函数综合运用，涉及到一次函数、平行四边形性质、图象的面积计算等，其中(3)，要主要分类求解，避免遗漏．26．【答案】(1)①解：旋转角为°105．理由：如图1中，∵A D AC '⊥，∴°90A DC '=∠，∵°15CA D '=∠，∴°75A CD '=∠，∴°105ACA '=∠，∴旋转角为°105． ②证明：连接A F '，设EF 交CA '于点O ．在EF 时截取EM EC =，连接CM ．∵°°°451560CED A CE CA E ='+'=+=∠∠∠，∴°120CEA '=∠，∵FE 平分EA C '∠，∴°60CEF FEA ='=∠∠ ，∵°°°°180457560FCO =--=∠，∴FCO A EO ='∠∠，∵FOC AOE ='∠∠，∴FOC A OE '△∽△， ∴'OF OC A O OE=， ∴OF A O OC OE '=， ∵COE FOA ='∠∠，∴COE FOA '△∽△，∴°60FA O OEC '==∠∠，∴A OF '△是等边三角形，∴CF CA A F ='='，∵EM EC =，°60CEM =∠，∴CEM △是等边三角形，°60ECM =∠，CM CE =，∵°60FCA MCE '==∠∠，∴FCM A CE '=∠∠，∴()FCM A CE SAS '△≌△，∴FM A E ='，∴CE A E EM FM EF +'=+=．(2)解：如图2中，连接A F '，PB '，AB '，作B M AC '⊥交AC 的延长线于M ．由②可知，°75EA F EA B '='''=∠，A E A E '='，A F A B '=''，∴A EF A EB '''△≌△，∴EF EB ='，∴B '，F 关于A E '对称，∴PF PB ='，∴PA PF PA PB AB +=+'≥'，在Rt CB M '△中，2CB BC '===，°30MCB '=∠，∴112B M CB '='=，CM =∴AB '∴PA PF +【解析】①解直角三角形求出A CD '∠即可解决问题．②连接A F '，设EF 交CA '于点O ．在EF 时截取EM EC =，连接CM ．首先证明CFA '△是等边三角形，再证明()FCM A CE SAS '△≌△，即可解决问题．(2)如图2中，连接A F '，PB '，AB '，作B M AC '⊥交AC 的延长线于M ．证明A EF A EB '''△≌△，推出EF EB ='，推出B '，F 关于A E '对称，推出PF PB ='，推出PA PF PA PB AB +=+'≥'，求出AB '即可解决问题．【考点】四边形综合题，旋转变换，全等三角形的判定和性质，相似三角形的判定和性质，三角形的三边关系等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会用转化的思想思考问题．。

广西贵港市2019年中考[数学]考试真题与答案解析

广西贵港市2019年中考[数学]考试真题与答案解析一、选择题每小题都给出标号为A、B、C、D的四个选项，其中只有一个是正确的．请考生用2B铅笔在答题卡上将选定的答案标号涂黑．1．﹣2的相反数是（）A．﹣2B．﹣C．2D．2．若式子在实数范围内有意义，则实数x的取值范围是（）A．x＜﹣1B．x≥﹣1C．x≥0D．x≥13．目前世界上刻度最小的标尺是钻石标尺，它的最小刻度为0.2nm（其中1nm ＝10﹣9m），用科学记数法表示这个最小刻度（单位：m），结果是（）A．2×10﹣8m B．2×10﹣9m C．2×10﹣10m D．2×10﹣11m4．数据2，6，5，0，1，6，8的中位数和众数分别是（）A．0和6B．0和8C．5和8D．5和65．下列运算正确的是（）A．2a+3b＝5ab B．5a2﹣3a＝2aC．（ab3）2＝a2b6D．（a+2）2＝a2+46．一元二次方程x2﹣x﹣3＝0的根的情况为（）A．有两个相等的实数根B．有两个不相等的实数根C．只有一个实数根D．没有实数根7．如果a＜b，c＜0，那么下列不等式中不成立的是（）A．a+c＜b+c B．ac＞bc C．ac+1＞bc+1D．ac2＞bc28．下列命题中真命题是（）A．的算术平方根是2B．数据2，0，3，2，3的方差是C．正六边形的内角和为360°D．对角线互相垂直的四边形是菱形9．如图，点A，B，C均在⊙O上，若∠ACB＝130°，则∠α的度数为（）A．100°B．110°C．120°D．130°10．如图，在△ABC中，点D在AB边上，若BC＝3，BD＝2，且∠BCD＝∠A，则线段AD的长为（）A．2B．C．3D．11．如图，动点M在边长为2的正方形ABCD内，且AM⊥BM，P是CD边上的一个动点，E是AD边的中点，则线段PE+PM的最小值为（）A．﹣1B．+1C．D．+112．如图，点E，F在菱形ABCD的对角线AC上，∠ADC＝120°，∠BEC＝∠CBF ＝50°，ED与BF的延长线交于点M．则对于以下结论：①∠BME＝30°；②△ADE≌△ABE；③EM＝BC；④AE+BM＝EM．其中正确结论的个数是（）A．1个B．2个C．3个D．4个二、填空题13．计算：3﹣7＝．14．因式分解：ax2﹣2ax+a＝．15．如图，点O，C在直线n上，OB平分∠AOC，若m∥n，∠1＝56°，则∠2＝．16．若从﹣2，0，1这三个数中任取两个数，其中一个记为a，另一个记为b，则点A（a，b）恰好落在x轴上的概率是．17．如图，在扇形OAB中，点C在上，∠AOB＝90°，∠ABC＝30°，AD ⊥BC于点D，连接AC，若OA＝2，则图中阴影部分的面积为．18．如图，对于抛物线y1＝﹣x2+x+1，y2＝﹣x2+2x+1，y3＝﹣x2+3x+1，给出下列结论：①这三条抛物线都经过点C（0，1）；②抛物线y3的对称轴可由抛物线y1的对称轴向右平移1个单位而得到；③这三条抛物线的顶点在同一条直线上；④这三条抛物线与直线y＝1的交点中，相邻两点之间的距离相等．其中正确结论的序号是．三、解答题解答应写出文字说明、证明过程或演算步骤．19．（1）计算：|﹣2|+（3﹣π）0﹣+6cos30°；（2）先化简再求值÷，其中m＝﹣5．20．（5分）如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A （1，4），B（4，1），C（4，3）．（1）画出将△ABC向左平移5个单位得到的△A1B1C1；（2）画出将△ABC绕原点O顺时针旋转90°得到的△A2B2C2．21．如图，双曲线y1＝（k为常数，且k≠0）与直线y2＝2x+b交于A（1，m）和B（n，n+2）两点．（1）求k，m的值；（2）当x＞0时，试比较函数值y1与y2的大小．22．某校对九年级学生进行“综合素质”评价，评价的结果分为A（优秀）、B （良好）、C（合格）、D（不合格）四个等级，现从中随机抽查了若干名学生的“综合素质”等级作为样本进行数据处理，并绘制以下两幅不完整的统计图．请根据统计图提供的信息，解答下列问题：（1）B（良好）等级人数所占百分比是；（2）在扇形统计图中，C（合格）等级所在扇形的圆心角度数是；（3）请补充完整条形统计图；（4）若该校九年级学生共1000名，请根据以上调查结果估算：评价结果为A （优秀）等级或B（良好）等级的学生共有多少名？23．在今年新冠肺炎防疫工作中，某公司购买了A、B两种不同型号的口罩，已知A型口罩的单价比B型口罩的单价多1.5元，且用8000元购买A型口罩的数量与用5000元购买B型口罩的数量相同．（1）A、B两种型号口罩的单价各是多少元？（2）根据疫情发展情况，该公司还需要增加购买一些口罩，增加购买B型口罩数量是A型口罩数量的2倍，若总费用不超过3800元，则增加购买A型口罩的数量最多是多少个？24．如图，在△ABC中，AB＝AC，点D在BC边上，且AD＝BD，⊙O是△ACD 的外接圆，AE是⊙O的直径．（1）求证：AB是⊙O的切线；（2）若AB＝2，AD＝3，求直径AE的长．25．如图，已知抛物线y＝x2+bx+c与x轴相交于A（﹣6，0），B（1，0），与y轴相交于点C，直线l⊥AC，垂足为C．（1）求该抛物线的表达式；（2）若直线l与该抛物线的另一个交点为D，求点D的坐标；（3）设动点P（m，n）在该抛物线上，当∠PAC＝45°时，求m的值．26．已知：在矩形ABCD中，AB＝6，AD＝2，P是BC边上的一个动点，将矩形ABCD折叠，使点A与点P重合，点D落在点G处，折痕为EF．（1）如图1，当点P与点C重合时，则线段EB＝，EF＝；（2）如图2，当点P与点B，C均不重合时，取EF的中点O，连接并延长PO 与GF的延长线交于点M，连接PF，ME，MA．①求证：四边形MEPF是平行四边形；②当tan∠MAD＝时，求四边形MEPF的面积．答案解析一、选择题1．解析：﹣2的相反数是2，故选：C．2．解析：∵式子在实数范围内有意义，∴x+1≥0，解得：x≥﹣1，故选：B．3．解析：0.2nm＝0.2×10﹣9m＝2×10﹣10m．故选：C．4．解析：从小到大排列此数据为：0，1，2，5，6，6，8数据，6出现了2次最多为众数，处在中间位置的数为5，故中位数为5．所以本题这组数据的中位数是5，众数是6．故选：D．5．解析：A、2a与3b不是同类项，所以不能合并，故本选项不合题意；B、5a2与﹣3a不是同类项，所以不能合并，故本选项不合题意；C、（ab3）2＝a2b6，故本选项符合题意；D、（a+2）2＝a2+4a+4，故本选项不合题意；故选：C．6．解析：∵△＝（﹣1）2﹣4×1×（﹣3）＝13＞0，∴该方程有两个不相等的实数根．故选：B．7．解析：A、由a＜b，c＜0得到：a+c＜b+c，原变形正确，故此选项不符合题意；B、由a＜b，c＜0得到：ac＞bc，原变形正确，故此选项不符合题意；C、由a＜b，c＜0得到：ac+1＞bc+1，原变形正确，故此选项不符合题意；D、由a＜b，c＜0得到：ac2＜bc2，原变形错误，故此选项符合题意．故选：D．8．解析：A、的算术平方根是，原命题是假命题，不符合题意；B、数据2，0，3，2，3的方差＝，是真命题，符合题意；C、正六边形的内角和为720°，原命题是假命题，不符合题意；D、对角线互相平分且垂直的四边形是菱形，原命题是假命题，不符合题意；故选：B．9．解析：在优弧AB上任意找一点D，连接AD，BD．∵∠D＝180°﹣∠ACB＝50°，∴∠AOB＝2∠D＝100°，故选：A．10．解析：∵∠BCD＝∠A，∠B＝∠B，∴△BCD∽△BAC，∴＝，∵BC＝3，BD＝2，∴＝，∴BA＝，∴AD＝BA﹣BD＝﹣2＝．故选：B．11．解析：作点E关于DC的对称点E'，设AB的中点为点O，连接OE'，交DC 于点P，连接PE，如图：∵动点M在边长为2的正方形ABCD内，且AM⊥BM，∴点M在以AB为直径的圆上，OM＝AB＝1，∵正方形ABCD的边长为2，∴AD＝AB＝2，∠DAB＝90°，∵E是AD的中点，∴DE＝AD＝×2＝1，∵点E与点E'关于DC对称，∴DE'＝DE＝1，PE＝PE'，∴AE'＝AD+DE'＝2+1＝3，在Rt△AOE'中，OE'＝＝＝，∴线段PE+PM的最小值为：PE+PM＝PE'+PM＝ME'＝OE'﹣OM＝﹣1．故选：A．12．解析：∵四边形ABD是菱形，∠ADC＝120°，∴AD＝AB＝BC＝CD，∠BAD＝∠BCD＝60°，∠DAE＝∠BAE，∠DCE＝∠BCE＝∠BCD＝30°，∵∠BFE＝∠BCE+∠CBF＝30°+50°＝80°，∴∠EBF＝180°﹣∠BEC﹣∠BFE＝180°﹣50°﹣80°＝50°，在△CDE和△CBE中，，∴△CDE≌△CBE（SAS），∴∠DEC＝∠BEC＝50°，∴∠BEM＝∠DEC+∠BEC＝100°，∴∠BME＝180°﹣∠BEM﹣∠EBF＝180°﹣100°﹣50°＝30°，故①正确；在△ADE和△ABE中，，∴△ADE≌△ABE（SAS），故②正确；∵∠EBC＝∠EBF+∠CBF＝100°，∴∠BEM＝∠EBC，在△BEM和△EBC中，，∴△BEM≌△EBC（AAS），∴BM＝EC，EM＝BC，故③正确；连接BD交AC于O，如图所示：∵四边形ABCD是菱形，∴OA＝OC，AC⊥BD，∵∠DCO＝30°，∴OD＝CD＝BC，OC＝OD，∴OC＝BC，∴AC＝2OC＝BC，∵BM＝EC，EM＝BC，∴AE+BM＝AE+EC＝AC＝BC＝EM，故④正确，正确结论的个数是4个，故选：D．二、填空题13．解析：3﹣7＝3+（﹣7）＝﹣4．故答案为：﹣4．14．解析：ax2﹣2ax+a＝a（x2﹣2x+1）＝a（x﹣1）2．故答案为：a（x﹣1）2．15．解析：如图，∵m∥n，∠1＝56°，∴∠1＝∠3＝56°，∴∠AOC＝180°﹣∠3＝180°﹣56°＝124°，∵OB平分∠AOC，∴∠4＝∠5＝＝，∵m∥n，∴∠2＝∠5＝62°，故答案为：62°．16．解析：画树状图如下由树状图知，共有6种等可能结果，其中使点A在x轴上的有2种结果，故点A（a，b）恰好落在x轴上的概率是＝．故答案为：．17．解析：连接OC，作CM⊥OB于M，∵∠AOB＝90°，OA＝OB＝2，∴∠ABO＝∠OAB＝45°，AB＝2，∵∠ABC＝30°，AD⊥BC于点D，∴AD＝＝，BD＝AB＝，∵∠ABO＝45°，∠ABC＝30°，∴∠OBC＝75°，∵OB＝OC，∴∠OCB＝∠OBC＝75°，∴∠BOC＝30°，∴∠AOC＝60°，CM＝OC＝＝1，∴S阴影＝S△ABD+S△AOB﹣S扇形OAB+（S扇形OBC﹣S△BOC）＝S△ABD+S△AOB﹣S扇形OAC﹣S△BOC＝+×﹣﹣＝1+﹣π．故答案为1+﹣π．18．解析：①当x＝0时，分别代入抛物线y1，y2，y3，即可得y1＝y2＝y3＝1；①正确；②y1＝﹣x2+x+1，y3＝﹣x2+3x+1的对称轴分别为直线x＝，x＝，由x＝向右平移1个单位得到x＝，②正确；③y1＝﹣x2+x+1＝﹣（x﹣）2+，顶点坐标（，），y2＝﹣x2+2x+1＝﹣（x﹣1）2+2，顶点坐标为（1，2）；y3＝﹣x2+3x+1＝﹣（x﹣）2+，顶点坐标为（，），∴顶点不在同一条直线上，③错误；④当y＝1时，则﹣x2+x+1＝1，∴x＝0或x＝1；﹣x2+2x+1＝1，∴x＝0或x＝2；﹣x2+3x+1＝1，∴x＝0或x＝3；∴相邻两点之间的距离都是1，④正确；故答案为①②④．三、解答题19．解析：（1）原式＝2﹣+1﹣2+6×＝2﹣+1﹣2+3＝3；（2）÷＝•＝，当m＝﹣5时，原式＝＝．20．解析：（1）如图所示，△A1B1C1即为所求．（2）如图所示，△A2B2C2即为所求．21．解析：（1）∵点B（n，n+2）在直线y2＝2x+b上，∴n+2＝2×n+b，∴b＝2，∴直线y2＝2x+2，∵点A（1，m）在直线y2＝2x+2上，∴m＝2+2＝4，∴A（1，4），∵双曲线y1＝（k为常数，且k≠0）与直线y2＝2x+b交于A（1，4），∴k＝1×4＝4；（2）由图象可知，当0＜x＜1时，y1＞y2；当x＝1时，y1＝y2＝4；当x＞1时，y1＜y2．22．解析：（1）∵被调查的人数为4÷10%＝40（人），∴B等级人数为40﹣（18+8+4）＝10（人），则B（良好）等级人数所占百分比是×100%＝25%，故答案为：25%；（2）在扇形统计图中，C（合格）等级所在扇形的圆心角度数是360°×＝72°，故答案为：72°；（3）补全条形统计图如下：（4）估计评价结果为A（优秀）等级或B（良好）等级的学生共有1000×＝700（人）．23．解析：（1）设A型口罩的单价为x元，则B型口罩的单价为（x﹣1.5）元，根据题意，得：＝．解方程，得：x＝4．经检验：x＝4是原方程的根，且符合题意．所以x﹣1.5＝2.5．答：A型口罩的单价为4元，则B型口罩的单价为2.5元；（2）设增加购买A型口罩的数量是m个，根据题意，得：2.5×2m+4m≤3800．解不等式，得：m≤422．因为m为正整数，所以正整数m的最大值为422．答：增加购买A型口罩的数量最多是422个．24．【解答】（1）证明：连接DE，如图1，∵AB＝AC，AD＝BD，∴∠B＝∠BAD，∠B＝∠C，∴∠C＝∠E，∴∠E＝∠BAD，∵AE是⊙O的直径，∴∠ADE＝90°，∴∠E+∠DAE＝90°，∴∠BAD+∠DAE＝90°，即∠BAE＝90°，∴AE⊥AB，∴直线AB是⊙O的切线；（2）解：如图2，作AH⊥BC，垂足为点H，∵AB＝AC，∴BH＝CH，∵∠B＝∠C＝∠BAD，∴△ABC∽△DBA，∴，即AB2＝BD•BC，又AB＝2，BD＝AD＝3，∴BC＝8，在Rt△ABH中，BH＝CH＝4，∴AH＝＝＝2，∵∠E＝∠B，∠ADE＝∠AHB，∴△AED∽△ABH，∴，∴＝3．25．解析：（1）将点A、B的坐标代入抛物线的表达式得，解得，故抛物线的表达式为y＝x2+x﹣3①；（2）过点D作DE⊥y轴于点E，而直线l⊥AC，AO⊥y轴，∴∠CDE+∠DCE＝90°，∠DCE+∠OCA＝90°，∴∠CDE＝∠OCA，∵∠AOC＝∠CED＝90°，∴△CED∽△AOC，则，而点A、C的坐标分别为（﹣6，0）、（0，﹣3），则AO＝6，OC＝3，设点D （x，x2+x﹣3），则DE＝﹣x，CE＝﹣x2﹣x，则＝，解得x＝0（舍去）或﹣1，当x＝﹣1时，y＝x2+x﹣3＝﹣5，故点D的坐标为（﹣1，﹣5）；（3）①当点P在x轴的上方时，由点C、D的坐标得，直线l的表达式为y＝2x﹣3，延长AP交直线l于点M，设点M（t，2t﹣3），∵∠PAC＝45°，直线l⊥AC，∴△ACM为等腰直角三角形，则AC＝CM，则62+32＝（t﹣0）2+（2t﹣3+3）2，解得t＝3，故点M的坐标为（3，3），由点A、M的坐标得，直线AM的表达式为y＝x+2②，联立①②并解得x＝﹣6（舍去）或，故点P的横坐标m＝；②当点P在x轴的下方时，同理可得x＝﹣6（舍去）或x＝﹣5，故m＝﹣5，综上，m＝﹣5或．26．解析：（1）∵将矩形ABCD折叠，使点A与点P重合，点D落在点G处，∴AE＝CE，∠AEF＝∠CEF，∵CE2＝BE2+BC2，∴（6﹣BE）2＝BE2+12，∴BE＝2，∴CE＝4，∵cos∠CEB＝＝，∴∠CEB＝60°，∴∠AEF＝∠FEC＝60°，∵AB∥DC，∴∠AEF＝∠CFE＝60°，∴△CEF是等边三角形，∴EF＝CE＝4，故答案为：2，4；（2）①∵将矩形ABCD折叠，∴FG∥EP，∴∠MFO＝∠PEO，∵点O是EF的中点，∴EO＝FO，又∵∠EOP＝∠FOM，∴△EOP≌△FOM（AAS），∴FM＝PE，又∵MF∥PE，∴四边形MEPF是平行四边形；②如图2，连接AP交EF于H，∵将矩形ABCD折叠，∴AE＝EP，∠AEF＝∠PEF，∠G＝∠D＝90°，AD＝PG＝2，∴EF⊥PA，PH＝AH，∵四边形MEPF是平行四边形，∴MO＝OP，∴MA∥EF，∴∠MAP＝∠FHP＝90°，∴∠MAP＝∠DAB＝90°，∴∠MAD＝∠PAB，∴tan∠MAD＝tan∠PAB＝＝，∴PB＝AB＝×6＝2，∵PE2＝BE2+BP2，∴（6﹣BE）2＝BE2+4，∴BE＝，∴PE＝6﹣BE＝，∴四边形MEPF的面积＝PE×PG＝＝．。