自动控制原理实验教程第2章
合集下载
《自动控制原理》第2章 线性系统的传递函数

+
anc(t)
=
b0
dm dtm
r(t)
+
b1
d m−1 d t m −1
r(t)
++
bm−1
d dt
r(t)
+
bmr(t)
(m n)
设r(t), c(t)及各阶导数在t=0时的值均为零(零初始条件), 则对方程两端求拉氏变换,可得系统的传递函数
Ch2 控制系统的数学模型
◼ 传递函数的一般形式:
Ch2 控制系统的数学模型
第二章 控制系统的数学模型
Ch2 控制系统的数学模型
本章内容
❖ 引言 ❖ 物理系统的微分方程 ❖ 拉氏变换与拉氏反变换 ❖ 线性系统的传递函数 ❖ 方框图及其等效变换 ❖ 信号流图与Mason公式*
Ch2 控制系统的数学模型
2.3 线性系统的传递函数
一. 传递函数的定义
Ux(s) =
I
(s) − I2(s) sC1
(2)
I 2 (s)
=
Ux
(s) −Uo(s) R2
(3)
U o (s)
=
I 2 (s) sC2
(4)
Ch2 控制系统的数学模型
I (s) = Ui (s) −U x (s) (1) R1
Ui _
I
1/R1
Ux
Ux(s) =
I
(s) − I2(s) sC1
Uo (s)
Ui (s) (b)
I(s) Uo (s)
Ch2 控制系统的数学模型
I(s)
(c)
Uo (s)
Ui (s)
I(s)
- Uo (s) (d)
自动控制原理第2章

自动控制理论
电气信息学院
任课教师: 高秀梅
1
第二章 控制系统的数学模型
§2-1 微分方程 §2-2 传递函数 §2-3 动态结构图 §2-4 信号流图 §2-5 梅逊(Mason)公式 §2-6 自动控制系统的传递函数
2
一、什么是数学模型? 二、为什么要建立数学模型? 三、建立数学模型的方法? 四、数学模型的形式有哪些?
2) . 比例定理: f (t ) Kf1 (t ), L[ f1 (t )] F1 (s) 若 则 st
0
L[ f (t )] Kf1 (t )e dt KF1 ( s)
1)和2)为拉氏变换的线性特性。 3). 微分定理: 若 L df (t ) df (t ) e at dt sF (s) f (0 ) dt dt 0 则
1、系统输入量: F(t) 输出量: y(t) 2、列写方程组:
F(t)
k m f y(t)
11
§2-1 微分方程
3、消去中间变量并写成标准形式:
m d y (t ) f dy ( t ) 1 y (t ) F (t ) 2 k k dt k dt
令T
2 2
2
m f 1 , , K k k 2 mk
有
T
d y (t ) dt 2
dy ( t ) 2 T y ( t ) KF ( t ) dt
12
§2-1 微分方程
例3 求下图的微分方程
i1
i1
i
i2
13
§2-1 微分方程 二、线性微分方程式的求解
工程实践中常采用拉氏变换法求解线 性常微分方程。 拉氏变换法求解微分方程的基本思路:
电气信息学院
任课教师: 高秀梅
1
第二章 控制系统的数学模型
§2-1 微分方程 §2-2 传递函数 §2-3 动态结构图 §2-4 信号流图 §2-5 梅逊(Mason)公式 §2-6 自动控制系统的传递函数
2
一、什么是数学模型? 二、为什么要建立数学模型? 三、建立数学模型的方法? 四、数学模型的形式有哪些?
2) . 比例定理: f (t ) Kf1 (t ), L[ f1 (t )] F1 (s) 若 则 st
0
L[ f (t )] Kf1 (t )e dt KF1 ( s)
1)和2)为拉氏变换的线性特性。 3). 微分定理: 若 L df (t ) df (t ) e at dt sF (s) f (0 ) dt dt 0 则
1、系统输入量: F(t) 输出量: y(t) 2、列写方程组:
F(t)
k m f y(t)
11
§2-1 微分方程
3、消去中间变量并写成标准形式:
m d y (t ) f dy ( t ) 1 y (t ) F (t ) 2 k k dt k dt
令T
2 2
2
m f 1 , , K k k 2 mk
有
T
d y (t ) dt 2
dy ( t ) 2 T y ( t ) KF ( t ) dt
12
§2-1 微分方程
例3 求下图的微分方程
i1
i1
i
i2
13
§2-1 微分方程 二、线性微分方程式的求解
工程实践中常采用拉氏变换法求解线 性常微分方程。 拉氏变换法求解微分方程的基本思路:
自动控制原理实验教程

Ui(S )
TS
(3) 阶跃响应: Uo(t) = K + 1 t
T
(t ≥ 0)
(4) 模拟电路图:如图 1.1-6 所示。
其中 K = R1 / R0 ; T = R0C
4
自动控制原理
第 1 章 线性系统的时域分析
比例积分环节
R1
C
Ui
R0
_
10K
信号输入端
反相器
10K _
R0 = R1 = 200K; C = 1uF 或 2uF
Ui(S)
1
Uo(S)
TS
(2) 传递函数: Uo(S) = 1
Ui(S) TS
(3) 阶跃响应: Uo(t) = 1 t (t ≥ 0)
T
(4) 模拟电路图:如图 1.1-4 所示。
图 1.1-3
其中 T = R0C
Ui
R0
信号输入端
积分环节 C
_
反相器
10K
10K
_
Uo
输出测量端
R0 = 200K; C = 1uF 或 2uF
图 1.1-4 3
自动控制原理
(5) 理想与实际阶跃响应曲线对照: ① 取 R0 = 200K;C = 1uF。
理想阶跃响应曲线
Uo 无穷
Uo(t)
1 Ui(t)
0 0.2s
t
② 取 R0 = 200K;C = 2uF。
第 1 章 线性系统的时域分析
实测阶跃响应曲线
Uo
10V
Uo(t)
1 Ui(t)
(5) 理想与实际阶跃响应曲线对照: ① 取 R0 = R1 = 200K;C = 1uF。
图 1.1-6
《自动控制原理》课件第二章

Cen idRd
Ld
d id dt
ud
(2-4)
当略去电动机的负载力矩和粘性摩擦力矩时,机械运动
微分方程式为
M GD2 d n 375 d t
(2-5)
式中,M为电动机的转矩(N·m); GD2为电动机的飞轮矩
(N·m2)。当电动机的励磁不变时,电动机的转矩与电枢电
流成正比,即电动机转矩为
M=Cmid
称为相似量。如式(2-1)中的变量ui、uo分别与式(2-3)中的变
量f(t)、y(t)为对应的相似量。
2.1.2 线性定常微分方程求解及系统运动的模态 当系统微分方程列写出来后,只要给定输入量和初始条
件,便可对微分方程求解,并由此了解系统输出量随时间变 化的特性。
若线性定常连续系统的微分方程模型的一般表示形式为 y(n)(t)+a1y(n-1)(t)+···+any(t)=b0u(m)(t)+b1u(m-1)(t)+…+bmu(t)
x0
( x x0 )2
当增量x-x0很小时,略去其高次幂项,则有
y
y0
f (x)
f (x0)
d f (x) dx
x0
(x x0)
令Δy=y-y0=f(x)-f(x0),Δx=x-x0,K=(df(x)/dx)|x0,则线性
化方程可简记为Δy=KΔx。这样,便得到函数y=f(x)在工作
点A附近的线性化方程为y=Kx。
图2-4 小偏差线性化示意图
对于有两个自变量x1、x2的非线性函数f(x1,x2),同样 可在某工作点(x10,x20)附近用泰勒级数展开为
y
f (x1 ,x2 )
f
自控原理cp2第二章

23
叠加原理
叠加原理含有两重含义,即可叠加性和均匀性(或 叫齐次性)。
例: 设线性微分方程式为
d 2c(t) dc(t) c(t) r(t) dt dt
若 r(t) r1(t) 时,方程有解 c1(t),而 r(t) r2(t)时,
方程有解 c2(t) ,分别代入上式且将两式相加,则显 然有,当 r(t) r1(t) +r2 (t) 时,必存在解 为 c(t) c1(t) c2(t) ,即为可叠加性。
ur
8
• 例3. 设有一弹簧•质 量• 阻尼动力系统如 图所示,当外力F(t)作 用于系统时,系统将
产生运动,试写出外 力F(t)与质量块的位移 y(t)之间的动态方程。 其中弹簧的弹性系数 为k,阻尼器的阻尼系 数为f,质量块的质量 为m。
F(t) f
k M y(t)
解:分析质量块m受力,有
基本步骤: 分析各元件工作原理,明确输入、输 出量 建立输入、输出量的动态联系 消去中间变量 标准化微分方程
4
列写微分方程的一般方法
• 例1. 列写如图所示RC网络的微分方程。 R
i
ur
C
uc
5
解:由基尔霍夫定律得:
ur
Ri
1 C
idt
uc
1 C
idt
i=C duC dt
1 C2s
(1 R1C1s)(1 R2C2 s)
Ur (s)
1 R1 C1s
R1C1C2 s 2
R1
1 C1s
(c)
R2
1 Cs
Uc
(s)
R2
自控控制原理第2章课件

第一节 列写系统微分方程
人们常将描述系统工作状态的各物理量随时间变化的规律 用数学表达式或图形表示出来,这种描述系统各个物理量之间 关系的数学表达式或图形称为系统的数学模型。
建立数学模型有两种方法:机理分析法和实验辨识法。机 理分析法是通过理论推导得出,这种方法是根据各环节所遵循 的物理规律来编写;实验辨识法是由实验求取,即根据实验数 据通过整理编写出来。
Ld Rd
Tm
GD2 375
Rd cmce
则得
TmTd
d 2n dt 2
Tm
dn dt
n
ud ce
6
列写系统微分方程
以上两例中的物理部件(环节)不尽相同,但它们的数学 模型却是相同的。我们把具有相同数学模型的不同物理系统称 之为相似系统。在相似系统中,占据相应位置的物理量称为相 似量。
对于同一个物理系统,当输入量、输出量改变时,所求出 的数学模型却是不同的。利用相似系统的概念,我们可以用一 个易于实现的系统来研究与其相似的复杂系统,并根据相似系 统的理论出现了仿真研究法。
C
R
uo
C
11
列写系统微分方程
方法一:从第一个电容、电阻网络环节列出微分方程:
RC
duo dt
uo
uo1
从第二个电容、电阻网络环节列出微分方程:
RC
duo1 dt
uo1
ui
代入上式中得:
(RC)2
d 2uo dt 2
2RC
duo dt
uo
ui
但实际上第一个网络和第二个网络之间存在负载效应(耦合),因此 它们不能划分为独立的两个环节。
di ed id Rd Ld dt ud ed cen
根据电动机力矩平衡原理列微分方程
人们常将描述系统工作状态的各物理量随时间变化的规律 用数学表达式或图形表示出来,这种描述系统各个物理量之间 关系的数学表达式或图形称为系统的数学模型。
建立数学模型有两种方法:机理分析法和实验辨识法。机 理分析法是通过理论推导得出,这种方法是根据各环节所遵循 的物理规律来编写;实验辨识法是由实验求取,即根据实验数 据通过整理编写出来。
Ld Rd
Tm
GD2 375
Rd cmce
则得
TmTd
d 2n dt 2
Tm
dn dt
n
ud ce
6
列写系统微分方程
以上两例中的物理部件(环节)不尽相同,但它们的数学 模型却是相同的。我们把具有相同数学模型的不同物理系统称 之为相似系统。在相似系统中,占据相应位置的物理量称为相 似量。
对于同一个物理系统,当输入量、输出量改变时,所求出 的数学模型却是不同的。利用相似系统的概念,我们可以用一 个易于实现的系统来研究与其相似的复杂系统,并根据相似系 统的理论出现了仿真研究法。
C
R
uo
C
11
列写系统微分方程
方法一:从第一个电容、电阻网络环节列出微分方程:
RC
duo dt
uo
uo1
从第二个电容、电阻网络环节列出微分方程:
RC
duo1 dt
uo1
ui
代入上式中得:
(RC)2
d 2uo dt 2
2RC
duo dt
uo
ui
但实际上第一个网络和第二个网络之间存在负载效应(耦合),因此 它们不能划分为独立的两个环节。
di ed id Rd Ld dt ud ed cen
根据电动机力矩平衡原理列微分方程
自动控制原理第2章课后习题及解答
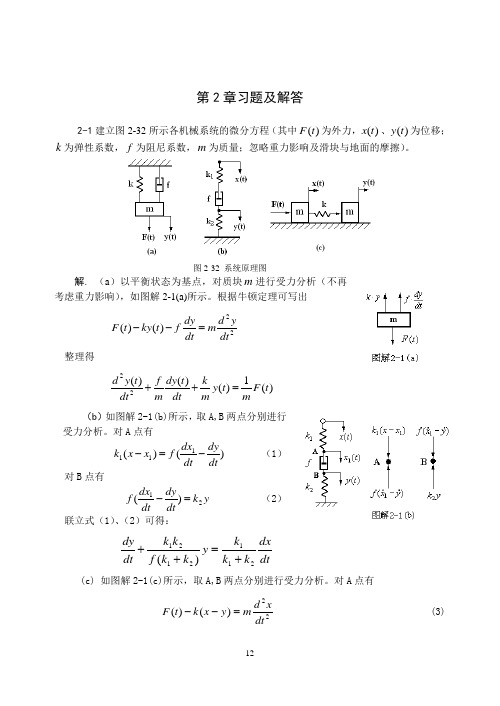
uc
= R1RL2C ur
2-3 证明图 2-34 (a) 所示的力学系统和图 2-34 (b) 所示的电路系统是相似系统(即 有相同形式的数学模型)。
图 2-34 系统原理图
解
(a) 取A、B两点分别进行受力分析,如图解2-3(a)所示。对A点有
k2 (x − y) + f 2 (x − y) = f1 ( y − y1 )
9
- 17 -
(3)
X (s) =
1
s(s + 2)3 (s + 3)
(4) X (s) =
s +1
s(s 2 + 2s + 2)
解
(1) x(t) = et−1
(2)
原式
=
2 3
⋅
s
2
3 + 32
x(t) = 2 sin 3t 3
(3)
原式 = −1 + 1 − 3 + 1 + 1 2(s + 2)3 4(s + 2)2 8(s + 2) 24s 3(s + 3)
+
1 C2R2
uc
=
du
2 r
dt 2
+
2 CR
dur dt
+
1 C2R2
ur
(c) 由图解 2-2(c)可写出
Ur (= s) R1 [I1(s) + I2 (s)] + (Ls + R2 )I2 (s) (6)
1 Cs
I1
(s)
=
(Ls
+
R2
)I2
(s)
(7)
自动控制原理第2章

拉普拉斯变换
因果
t f1 (t) f (t)e
s jw
象函数
( jw )t w F1 ( ) f (t )e dt
0
正LT
F(s) f (t)e dt
st
0
原函数 逆LT
1 jw st f (t ) F ( s )e ds w 2j j
d 2 y (t ) F (t ) mg Fk (t ) Ff (t ) m dt 2 由虎克定律:
Fk (t ) k[ y(t ) y0 ]
其中ky0 mg
摩擦力和速度成正比:
非重根系数的计算
cr +1 ,...,cn按式2-12或2-13计算获得;
重根系数的计算 cr ,cr -1 ,...,c1按下式计算:
cr lim( s - s1 ) r F ( s) d cr -1 lim [( s - s1 ) r F ( s )] s s1 ds ... cr - j ... 1 d (r-1) r c1 = [( s s ) 1 F ( s )] lim j (r -1)! s s1 ds1 1 d (j) lim j [( s - s1 ) r F ( s )] j! s s1 ds1
无量纲化
可用数学模型
标准化
标准数学模型
数学模型的分类
按输入输出的表达形式
微分方程(时间域)
传递函数(复数域)
动态结构图(各元件传函的连接关系) 响应曲线(step、pulse) 频率特性(bode图、nyquist图、nichols图)
状态变量形式
• 静态数学模型 • 动态数学模型
自动控制原理第2章

传递函数是在拉氏变换基础上的复域中的数学模型。
※传递函数不仅可以表征系统的动态特性,而且可以
用来研究系统的结构或参数变化对系统性能的影响。
微分方程 t (时域)
L
L
1
F
F 1
系统
传递函数
s j
j
频率特性
s
(复域)
s
(频域)
2.3.1拉氏变换相关知识
2.3.2传递函数的定义
线性定常系统在零初始条件下,输出量的拉氏变换
②两个自变量: y=f(x1, x2) 静态工作点: y0=f(x10, x20) 在y0=f(x10, x20) 附近展开成泰勒级数,即
f 1 2 f f 2 f 2 f 2 ( x1 x10 ) 2 y f ( x10 , x20 ) ( x1 x10 ) ( x2 x20 ) ( x1 x10 )(x2 x20 ) 2 ( x2 x20 ) 2 x 2! x x2 x1x2 x2 1 1
例2.5试建立如图2.4所示系 统的微分方程。
R1
解:根据克希霍夫电压定律, 可写出下列方程组
u1
R2
ur
i1
C1 图2.4
i2
C2
uc
1 ur R1i1 C (i1 i2 )dt 1 1 1 (i1 i2 )dt R2i2 i2 dt C2 C1 1 uc i2 dt C2
用台劳级数展开为
df ( x) 1 d 2 f ( x) y f ( x) f ( x0 ) ( ) x 0 ( x x0 ) ( ) x 0 ( x x0 ) 2 ... dx 2! dx 2
※传递函数不仅可以表征系统的动态特性,而且可以
用来研究系统的结构或参数变化对系统性能的影响。
微分方程 t (时域)
L
L
1
F
F 1
系统
传递函数
s j
j
频率特性
s
(复域)
s
(频域)
2.3.1拉氏变换相关知识
2.3.2传递函数的定义
线性定常系统在零初始条件下,输出量的拉氏变换
②两个自变量: y=f(x1, x2) 静态工作点: y0=f(x10, x20) 在y0=f(x10, x20) 附近展开成泰勒级数,即
f 1 2 f f 2 f 2 f 2 ( x1 x10 ) 2 y f ( x10 , x20 ) ( x1 x10 ) ( x2 x20 ) ( x1 x10 )(x2 x20 ) 2 ( x2 x20 ) 2 x 2! x x2 x1x2 x2 1 1
例2.5试建立如图2.4所示系 统的微分方程。
R1
解:根据克希霍夫电压定律, 可写出下列方程组
u1
R2
ur
i1
C1 图2.4
i2
C2
uc
1 ur R1i1 C (i1 i2 )dt 1 1 1 (i1 i2 )dt R2i2 i2 dt C2 C1 1 uc i2 dt C2
用台劳级数展开为
df ( x) 1 d 2 f ( x) y f ( x) f ( x0 ) ( ) x 0 ( x x0 ) ( ) x 0 ( x x0 ) 2 ... dx 2! dx 2
自动控制原理第2章

第三节 传递函数
4.微分环节
理想微分环节数学模型: C(s) dr(t) G(s) = R(s) = Ts c (t) = T dt T — 微分时间常数
R(S) C(S) Ts
微分环节方框图
单位阶跃响应函数: c(t) =Tδ(t)
第三节 传递函数
单位阶跃响应曲线
r(t) c(t)
c(t)
0
r(t)
第二章 自动控制系统的数学模型
第二章自动控制系统的数学模型
第一节 控制系统的微分方程 第二节 数学模型的线性化 第三节 传递函数 第四节 动态结构图
第五节 反馈控制系统的传递函数
第二章 自动控制系统的数学模型
第一节 控制系统的微分方程
一、建立微分方程的一般步骤
二、常见环节和系统的微分 方程的建立
三、 线性微分方程式的求解
1
r(t) t
c(t)
0
由于微分环节的输出量反映输入量的变化,而不反 映输入本身的大小,有些场合不能单独使用,故常用 比例微分环节。 C(s) 其传递函数: = K (Ts + 1) G(s) =
R(s)
比例微分环节的单位阶跃响应:
c(t) r(t)
c(t) = KTδ(t) +K = K [Tδ(t) + 1]
c(t) = e –t sin t= 0 r(t) =δ(t), c(0) = c'(0)
第一节 控制系统的微分方程
输出响应曲线
r(t) c(t)
0
r(t)
c(t)
t
第二章 自动控制系统的数学模型
第二节 数学模型的线性化(自学)
绝大多数物理系统在参数某些范围 内呈现出线性特性。当参数范围不加限 制时,所有的物理系统都是非线性的。 对每个系统都应研究其线性特性和相 应的线性工作范围。
自动控制原理:第2章-控制系统的数学模型可编辑全文

下图所示为三个环节串联的例子。图中,每个环节的方框图为:
*
上式表明,三个环节的串联可以用一个等效环节来代替。这种情况可以推广到有限个环节串联(各环节之间无负载效应)的情况,等效环节的传递函数等于各个串联环节的传递函数的乘积,如有n个环节串联则等效传递函数可表示为:
*
2. 环节的并联
环节并联的特点是各环节的输入信号相同,输出信号相加(或相减)。
2.7 闭环系统的传递函数
一.闭环系统
*
(3)开环传递函数: 假设N(s)=0,主反馈信号B(s)与误差信号E(s)之比。
(2)反馈回路传递函数:假设N(s)=0,主反馈信号B(s)与输出信号C(s)之比。
*
(4)闭环传递函数 Closed-loop Transfer Function 假设N(s)=0 输出信号C(s)与输入信号R(s)之比。
复习拉普拉斯变换有关内容(6)
(3)积分定理
零初始条件下有:
进一步有:
例4 求 L[t]=?
解.
例5 求
解.
复习拉普拉斯变换有关内容(7)
(4)实位移定理
证明:
例6
解:
令
复习拉普拉斯变换有关内容(8)
(5)复位移定理
证明:
令
例7
例8
例9
复习拉普拉斯变换有关内容(9)
负反馈:反馈信号与给定输入信号符号相反的反馈。
正反馈:反馈信号与给定输入信号符号相同的反馈。
*
上述三种基本变换是进行方框图等效变换的基础。对于较复杂的系统,例如当系统具有信号交叉或反馈环交叉时,仅靠这三种方法是不够的。
(二)信号相加点和信号分支点的等效变换
对于一般系统的方框图,系统中常常出现信号或反馈环相互交叉的现象,此时可将信号相加点(汇合点)或信号分支点(引出点)作适当的等效移动,先消除各种形式的交叉,再进行等效变换即可。
*
上式表明,三个环节的串联可以用一个等效环节来代替。这种情况可以推广到有限个环节串联(各环节之间无负载效应)的情况,等效环节的传递函数等于各个串联环节的传递函数的乘积,如有n个环节串联则等效传递函数可表示为:
*
2. 环节的并联
环节并联的特点是各环节的输入信号相同,输出信号相加(或相减)。
2.7 闭环系统的传递函数
一.闭环系统
*
(3)开环传递函数: 假设N(s)=0,主反馈信号B(s)与误差信号E(s)之比。
(2)反馈回路传递函数:假设N(s)=0,主反馈信号B(s)与输出信号C(s)之比。
*
(4)闭环传递函数 Closed-loop Transfer Function 假设N(s)=0 输出信号C(s)与输入信号R(s)之比。
复习拉普拉斯变换有关内容(6)
(3)积分定理
零初始条件下有:
进一步有:
例4 求 L[t]=?
解.
例5 求
解.
复习拉普拉斯变换有关内容(7)
(4)实位移定理
证明:
例6
解:
令
复习拉普拉斯变换有关内容(8)
(5)复位移定理
证明:
令
例7
例8
例9
复习拉普拉斯变换有关内容(9)
负反馈:反馈信号与给定输入信号符号相反的反馈。
正反馈:反馈信号与给定输入信号符号相同的反馈。
*
上述三种基本变换是进行方框图等效变换的基础。对于较复杂的系统,例如当系统具有信号交叉或反馈环交叉时,仅靠这三种方法是不够的。
(二)信号相加点和信号分支点的等效变换
对于一般系统的方框图,系统中常常出现信号或反馈环相互交叉的现象,此时可将信号相加点(汇合点)或信号分支点(引出点)作适当的等效移动,先消除各种形式的交叉,再进行等效变换即可。
自动控制原理(王万良)第二章
18
考察单位脉冲输入信号下系统的输出
单位脉冲输入信号的拉氏变换为1
U (s) = L{δ (t)} = 1
U(s) 系统G(s) Y(s)
单位脉冲输入信号下系统的输出的拉氏变换为
Y(s) = G(s)
1 系统G(s) Y(s)
单位脉冲输入信号下系统的输出为
g(t) = L−1{Y(s)} = L−1{G(s)} δ(t)
2
2.1 系统数学模型的概念
自控理论方法是先将系统抽象完数学模型,然后用数学的方法处理。 控制系统的数学模型是描述系统内部各物理量(或变量) 之间关系的数学表达式或图形表达式或数字表达式。
F(t)
m
f
X(t)
d 2 X (t) m
+
f
dX (t)
+ kX (t)
=
F (t)
dt 2
dt
+ ur(t) -
相应的传递函数为: G (s) = C (s) = 3s 2 + 5s + 1 R(s) s3 + s2 + 4s
练习2
已知某系统传递函数为:
G(s) = C(s) = 3s2 + 2s +1 R(s) s3 + 4s +1
相应的微分方程为: c (t) + 4c(t) + c(t) = 3r(t) + 2r(t) + r(t)
惯性环节: 从输入开始时刻就已有输出,仅由于惯性,输出要经过一段
时间之后才接近所要求的输出值;
延迟环节: 从输入开始后在0-τ时间内没有输出,在t =τ之后,才有输出。
r(t) c(t)
0τ
24
精品课件-自动控制原理-第2章

1 sn
F(s)
n
(2.15)
第二章 线性系统的数学描述
4) 初值定理 函数f(t)在t=0时的函数值可以通过f(t)的拉氏变换F(s)乘 以s取s→∞时的极限而得到, 即
lim f (t) f (0) lim sF(s)
t 0
s
(2.16)
第二章 线性系统的数学描述
5) 终值定理 函数f(t)在t→+∞时的函数值(即稳定值)可以通过F(s)的 拉氏变换F(s)乘以s取s→0 时的极限而得到, 即
c(0) c(0) c(0) c(n1) (0) 0 r(0) r(0) r(0) r(m1) (0) 0
则根据拉氏变换的定义和性质,对式(2.18)进行拉氏变换, 并令 C(s)=L[c(t)], R(s)=L[r(t)],可得
[a0sn a1sn1 an1s an ]C(s) [b0sm b1sm1 bm1s bm ]R(s)
第二章 线性系统的数学描述
2.1.1 电气系统
电气系统中最常见的装置是由电阻、电容、运算放大器等元 件组成的电路, 又称电气网络。我们将电阻、电感和电容等本身 不含有电源的器件称为无源器件,而将运算放大器这样本身包含 电源的器件称为有源器件。仅由无源器件构成的电气网络称为无 源网络;如果电气网络中含有有源器件或电源, 就称之为有源网 络。
第二章 线性系统的数学描述
2.1.2 机械系统
【例 2-3】 图2-3表示一个含有弹簧、运动部件、阻尼器 的机械位移装置。其中k是弹簧系数,m是运动部件质量,μ是阻 尼器的阻尼系数;外力f(t)是系统的输入量,位移y(t)是系统的 输出量。试确定系统的微分方程。
解 根据牛顿运动定律, 运动部件在外力作用下克服弹簧拉
自动控制原理第二章

1 ui (t ) 1(t ), U i ( s) s Ui 0.1s 0.2 1 1 u0 (t ) L [U 0 ( s )] L [ 2 2 ] s s 1 s s 1 1 0.1s 0.2 1 L [ 2 ] 2 s ( s s 1) s s 1
m=10, f=1, k=1
m=10, f=1, k=5
输入: Fi 1(t )
m=10, f=1, k=1
m=10, f=1, k=5
相似系统
RLC无源网络和弹簧-质量-阻尼器机械系 统的数学模型均是二阶微分方程,为相似 系统。 相似系统便于用一个简单系统去研究与其 相似的复杂系统,也便于控制系统的计算 机数字仿真。
化的过程。
4、线性系统的基本特性 叠加性:系统在几个输入信号同时作用 下的总响应,等于这几个输入信号单独 作用的响应之和。
如果元件输入为: r1(t)、r2(t)、r(t) ,
对应的输出为: c1(t)、c2(t)、c(t) 。
如果 r(t)=r1(t)+r2(t) 时, c(t)=c1(t)+c2(t) 满足叠加性。
满足齐次性。
满足叠加性和齐次性的元件才是线性元件
例如 y=kx 是线性元件
输入 x1 输出 y1=kx1 x2 输入x1 +x2 C为常数, Cx1 y2=kx2 y1 + y2 满足迭加性 Cy1 满足齐次性
所表示的元件 为线性元件
线性方程不一定满足迭加性和齐次性
y=kx+b(b为常数 0)线性方程,所表示的元件不是 线性元件 . 输入 x1y1 输出 y1= kx1+b x2 y2 y2 =kx2+b 输入 x1 + x2 输出 y=k(x1 + x2)+b =k x1 +kx2+b y1 +y2 不满足迭加性 k为常数 :kx1输出y=k(kx1)+b=k2x1+b ky1=k(kx1+b)= k2x1+kb yky1 不满足齐次方程。 所表示的元件不是线性元件。
孙炳达版 《自动控制原理》第2章 线性连续系统的数学模型-1

自动控制原理
第二章 线性连续系统的数学模型 2.1 动态微分方程的编写
2.1 动态微分方程的编写
分析和设计任何一个控制系统,首要任务是建 立系统的数学模型。 控制系统的数学模型,就是描述系统输入、输 出以及内部变量之间动态关系的数学表达式,也 称为动态数学模型。 常用的动态数学模型有: 微分方程 传递函数 动态结构图 信号流图
2.1 动态微分方程的编写
例 建立直流调速系统的微分方程
2.1 动态微分方程的编写
(1)确定输入量为控制电压Ug; 输出量为电动机转速n。
(2)编写各环节的微分方程。根据系统框图,把 系统划分为4个环节,分别为: 比较和电压放大器环节; 功率放大环节; 直流电动机环节; 反馈环节。
R R
ui
i1
C
i2
C
uo
消除中间变量, 可以解得:
d uo duo ( RC ) 3RC uo ui 2 dt dt
2
2
2.1 动态微分方程的编写
方法二:从第一个电容、电阻网络环节列出微分方程
duo RC uo uo1 dt
从第二个电容、电阻网络环节列出微分方程
duo1 RC uo1 ui dt
其中
K k1k s
为正向通道电压放大系数
k1k s a Kk 为系统开环放大系数 Ce
2.1 动态微分方程的编写
三、负载效应与系统(或环节)的相似性
在建立系统微分方程时,若在部件(环节)划 分时没有考虑负载效应,即部件(环节)间存在 的耦合关系,将不能得到系统正确的微分方程。 例 建立电容、电阻网络的微分方程,其中u i 为 输入电压,欲求以电容两端电压 uo 为输出的微分 方程。
第二章 线性连续系统的数学模型 2.1 动态微分方程的编写
2.1 动态微分方程的编写
分析和设计任何一个控制系统,首要任务是建 立系统的数学模型。 控制系统的数学模型,就是描述系统输入、输 出以及内部变量之间动态关系的数学表达式,也 称为动态数学模型。 常用的动态数学模型有: 微分方程 传递函数 动态结构图 信号流图
2.1 动态微分方程的编写
例 建立直流调速系统的微分方程
2.1 动态微分方程的编写
(1)确定输入量为控制电压Ug; 输出量为电动机转速n。
(2)编写各环节的微分方程。根据系统框图,把 系统划分为4个环节,分别为: 比较和电压放大器环节; 功率放大环节; 直流电动机环节; 反馈环节。
R R
ui
i1
C
i2
C
uo
消除中间变量, 可以解得:
d uo duo ( RC ) 3RC uo ui 2 dt dt
2
2
2.1 动态微分方程的编写
方法二:从第一个电容、电阻网络环节列出微分方程
duo RC uo uo1 dt
从第二个电容、电阻网络环节列出微分方程
duo1 RC uo1 ui dt
其中
K k1k s
为正向通道电压放大系数
k1k s a Kk 为系统开环放大系数 Ce
2.1 动态微分方程的编写
三、负载效应与系统(或环节)的相似性
在建立系统微分方程时,若在部件(环节)划 分时没有考虑负载效应,即部件(环节)间存在 的耦合关系,将不能得到系统正确的微分方程。 例 建立电容、电阻网络的微分方程,其中u i 为 输入电压,欲求以电容两端电压 uo 为输出的微分 方程。
自动控制原理_第2章_5

前向通路中各支路传输的乘积,称为前向通路增益, 相当于方框图中的前向通道传递函数。
6
2.4.2 控制系统的信号流图
控制系统的信号流图可以根据系统运动方程的 拉氏变换式所构成的代数方程来绘制。
7
控制系统方框图与信号流图的对照
R( s )
G ( s)
Y ( s)
R( s )
G ( s)
Y ( s)
R( s ) ( s)
L7 G2G8 H3
41
该信号流图含有每两个互不接触的回路增益乘积:
G8
G7
R( s) G1
G9 G3 G4 G5 G6
1 1 1 Y ( s)
G2
H1 H3
H2
L1L2 G4G6 H1H 2 L1L7 G2G4G8 H1H3 L2 L7 G2G6G8 H2 H3
42
该信号流图含有每三个互不接触的回路增益乘积:
G2
H1 H3
H2
L6 G7G4G9G6 H3
39
第7条回路
G8
G7
R( s) G1
G9 G3 G4 G5 G6
1 1 1 Y ( s)
G2
H1 H3
H2
L7 G2G8 H3
40
即
L1 G4 H1 L2 G6 H 2
L3 G2G3G4G5G6 H3 L4 G2G3G4G9G6 H3 L5 G7G4G5G6 H3 L6 G7G4G9G6 H3
G3 (s)
R( s )
1
E ( s) G1 ( s)
1
G2 (s)
Y ( s)
1
Y ( s)
E (s)
1
《自动控制原理》第2章自动控制系统的数学模型

dt
t 0
[
d
nf dt
(t
n
)
]
snF(s)
sn1
f
(0)
sn2
f
(1) (0)...
f
(n1) (0)
定理4 积分定理
2021年2月
t
[
f ( )d ] F (s)
0
s
自动控制原理
定理6 初值定理
设F(s)为f(t)的拉氏变换,且
lim
s
sF
(s)
存在
lim f (t) lim sF(s)
实验求取
2021年2月
自动控制原理
例2-1试列写图2-1所示电路
输入量 u r (t) 与输出量 u c (t) 的微分方程。
1. 确定输入、输出量 2. 列写与输入、输出有
关的微分方程
L
di(t) dt
Ri(t)
u
c
(t)
u
r
(t)
i(t) C du c (t)
dt
3. 消去中间变量
LC
d
2u c (t) dt 2
G(s) Ks1 Ks2 ... Ksn
s s1 s s2
s sn
且
Ks1 [(s
….
si )G(s)]ss1
(s2
Q( s1 ) s1)(s3 s1)...(sn
s1)
2021年2月
自动控制原理
例:已知函数
1 设因式展开为 G(s) s(s 1)3 (s 2)
G(s) K1 K2 K3 K4 K5 s s 2 s 1 (s 1)2 (s 1)3
u(c’t)
+
自动控制原理实验教程第2章

R2
C(t)
r(t) R1 D / A1
R0
c(t) K
A/ D1 0
G(s) L[c(t)] R2 K L[r(t)] R1
5 10 15 t
比例环节的特性参数为比例增益K,表征比例 环节的输出量能够无失真、无滞后地按比例复 现输入量。
2020/2/18
自动控制原理实验教程
(2)惯性环节
运算放大器的同相端接地电阻r0均为100输入阶跃信号幅值设置为1201249自动控制原理实验教程1比例环节p比例环节的特性参数为比例增益k表征比例环节的输出量能够无失真无滞后地按比例复现输入量
第2章 控制系统的数学模型
实验一 基于MATLAB/Simulink建立控制系统数学模型
1. 实验目的
(1)熟悉MATLAB实验环境,掌握MATLAB命令窗口的基本操作。 (2)掌握MATLAB建立控制系统数学模型的命令及模型相互转换的 方法。 (3)掌握使用MATLAB命令化简模型基本连接的方法。 (4)学会使用Simulink模型结构图化简复杂控制系统模型的方法。
6. 实验能力要求
(1)能够设计各典型环节的模拟电路,并且推导出传递函数。 (2)能够由实测的阶跃响应曲线建立环节传递函数,与机理推导的
传递函数比较,分析误差产生的原因。
(3)总结各环节的特性,能够由典型环节构造复合控制系统。
7. 拓展与思考
2020/2/18
自动控制原理实验教程
若G(s)为闭环前向通道的传递函数sys1,H (s)为反馈函数的传递函数sys2,
则feedback()函数调用格式为:
sys = feedback(sys1, sys2, sign)
其中sign是反馈极性,sign缺省时,默认为 负反馈,sign=-1;正反馈时,sign=1, 单位反馈时,sys2=1,且不能省略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020/2/18
自动控制原理实验教程
【范例2-8】已知系统,。求负反馈闭环传递函数。
G(s)
2s2 5s 1 s2 2s 3
H (s) 5(s 2) s 10
【自我实践2-6】已知系统,求它的单位负反馈闭环传递函 数。
G(s) 2s 1 s2 2s 3
2020/2/18
2020/2/18
自动控制原理实验教程
【范例2-3】已知系统传递函数
G(s)
10 s 5
(s 0.5)(s 2)(s 3)
【自我实践2-2】建立控制系统的零极点模型:
G(s) 8(s 1 j)(s 1 j) s 2 (s 5)(s 6)(s 2 1)
2020/2/18
自动控制原理实验教程
2. 实验原理 动态特性可采用阶跃响应或脉冲响应测量法,即给被测对 象施加阶跃输入信号或脉冲输入信号,利用示波器或记录 仪测量被测对象的输出响应,如图所示。
阶跃信号 或
脉冲信号
被测对象
uc
超低频示波器 或
数字示波器
ur
2020/2/18
自动控制原理实验教程
G(s) b0sm b1sm1 ... bm num(s) , a0sn a1s n1 ... an den(s)
nm
在MATLAB中用分子、分母多项式系数按s的降幂次序构 成两个向量: num = [ b0 , b1 ,…, bm ] ,den = [ a0 , a1 ,…, an]。
第2章 控制系统的数学模型
实验一 基于MATLAB/Simulink建立控制系统数学模型
1. 实验目的
(1)熟悉MATLAB实验环境,掌握MATLAB命令窗口的基本操作。 (2)掌握MATLAB建立控制系统数学模型的命令及模型相互转换的 方法。 (3)掌握使用MATLAB命令化简模型基本连接的方法。 (4)学会使用Simulink模型结构图化简复杂控制系统模型的方法。
自动控制原理实验教程
(4)用系统Simulink模型结构图化简控制系统模型 【范例2-9】已知系统结构图,求系统闭环传递函数 。
1
5
1
1
s+1
s+2
R(s)
C(s)
G1
G2
2020/2/18
自动控制原理实验教程
3. 实验能力要求
(1)熟练使用各种函数命令建立控制系统数学模型。 (2)完成实验的范例题和自我实践,并记录结果。
2020/2/18
自动控制原理实验教程
用函数tf ( ) 来建立控制系统的传递函数模型, 用函数printsys ( ) 来输出控制系统的函数, 其命令调用格式为:
sys = tf ( num , den ) 和printsys ( num , den )
Tips:对于已知的多项式模型传递函数,其分子、分母多 项式系数两个向量可分别用sys.num{1}与sys.den{1}命令 求出。
2020/2/18
自动控制原理实验教程
实验二 典型环节模拟电路及其数学模型
1. 实验目的 (1)掌握典型环节模拟电路的构成,学会运用模拟电子 组件构造控制系统。 (2)观察和分析各典型环节的单位阶跃响应曲线,掌握 它们各自的特性。 (3)掌握各典型环节的特征参数的测量方法,并根据阶 跃响应曲线建立传递函数。
若G(s)为闭环前向通道的传递函数sys1,H (s)为反馈函数的传递函数sys2,
则feedback()函数调用格式为:
sys = feedback(sys1, sys2, sign)
其中sign是反馈极性,sign缺省时,默认为 负反馈,sign=-1;正反馈时,sign=1, 单位反馈时,sys2=1,且不能省略。
G(s)
s2 5s 6 s3 2s2 s
【自我实践2-4】建立控制系统的多项式模 型。
G(s) 8(s 1)(s 2) s(s 5)(s 6)(s 3)
2020/2/18
自动控制原理实验教程
(3)控制系统反馈连接之后的等效传递函数
两个环节反馈连接后,其等效传递函数可用 feedback ( ) 函数求得。
5 1)(s2
4s
4)
2020/2/18
自动控制原理实验教程
2)零极点增益模型
零极点模型是是分别对原传递函数的分子、分母进行因式 分解,以获得系统的零点和极点的表示形式。
G(s) K (s z1 )(s z2 ) (s zm ) (s p1 )(s p2 ) (s pn )
式中,K为系统增益,z1,z2,…,zm为系统零点,p1, p2,…,pn为系统极点。 在MATLAB中,用向量z,p,k构成矢量组 [ z, p, k ] 表示 系统。即 z = [ z1, z2 ,…,zm ] ,p = [ p1, p2,…, pn ] ,k = [ k ] 用函数命令zpk ( ) 来建立系统的零极点增益模型,其函数 调用格式为: sys = zpk ( z, p, k )
2020/2/18
自动控制原理实验教程
2. 实验内容
(1)控制系统模型的建立 控制系统常用的数学模型有四种:传递函数模型(tf对 象)、零极点增益模型(zpk对象)、结构框图模型和状 态空间模型(ss对象)。经典控制理论中数学模型一般 使用前三种模型,状态空间模型属于现代控制理论范畴。
1)传递函数模型(也称为多项式模型) 连续系统的传递函数模型为:
【范例2-1】已知系统传递函数
G(s)
s3
s 3 2s2 2s
1
2020/2/18
自动控制原理实验教程
【范例2-2】已知系统传递函数
G(s)
5(s 2)2 (s1)
【自我实践2-1】建立控制系统的传递函数模型:
G(s)
s(s
(2)控制系统模型间的相互转换 [num , den] = zp2tf ( z, p, k ) 零极点模型转换为多项式模型 [z , p , k] = tf2zp ( num, den ) 多项式模型转化为零极点模型
2020/2/18
自动控制原理实验教程
【范例2-6】已知系统传递函数 ,求其等效
的零极点模型。
