中科大算法第二章近似算法--黄刘生(调整后适合打印版)
简并微扰论的二级近似公式

(0) n′ l′
) 〉 ]= ∆( n l, n ′ l′
( 17)
其次, 对于 Κ ≠0 情形, { n l} 的正交归一条件应当与 Κ具体取值无关 (0) (1) (0) (1) 2 (2) 2 (2) 利用: n l = Υn l + Κ = Υn ′ + Κ + Κ + … Υn l + Κ Υn l + … n ′ l′ l′ Υn ′ l′ Υn ′ l′ ) ( 〈 n l n′ 〉 = ′ ′ l′ ∆ n l, n l (0) (0) (0) (0) (1) (0) (1) (1) (0) (2) 2 )+ Κ ) ( Υn(1) ( Υn(2) 〈 [ Υn l Υn ′ 〉 + Κ Υn ′ 〉 +〈Υn l Υn ′ 〉 Υn ′ 〉 +〈Υn l Υn ′ 〉 +〈Υn l Υn ′ 〉 〈 〈 l′ l l′ l′ l l′ l′ l′ (3) (0) 3 ) ( Υn l Υn ′ + Κ〈 〉 + …) + … ]= ∆( n l, n ′ l′ l′ (0) (0) ) , 因此要求: ( 由于上式右边第二项为 〈Υn l Υn ′ 〉 = l′ ∆ n l, n ′ l′ (1) (0) (0) (1) 〈Υn l Υn ′ 〉 +〈Υn l Υn ′ 〉 = 0 l′ l′ (2) (0) (1) (1) (0) (2) 〈Υn l Υn ′ 〉 +〈Υn l Υn ′ 〉 +〈Υn l Υn ′ 〉 = 0 l′ l′ l′
∑Ε Υ 〈Υ ∑ (E - E
n″ l″ (1) nl n″ l″ n″ l″ (0) n″ (1) nl n l′
中国科学技术大学程序设计1995真题.doc

中国科学技术大学一九九五年招收硕士学位研究生入学考试试题试题名称:程序设计.选择题1.一颗深度为6的平衡二叉树,其每个非终端节点的平衡因子均为1,则该树共有个节点.(2分)a) 14; b) 16; c) 18; d) 20; e) 22; f) 242.一个有28条边的非连通无向图,至少应有个节点.(2分)a) 6; b)7; c) 8; d) 9; e) 10; f) 113.一颗124个叶节点的完全二叉树,最多有—个节点.(2分)a) 247; b) 248; c) 249; d) 250; e) 2514.按锦标赛排序的方法,决定出8位运动员之间的名次顺序排列,至少需编排场次的比赛.(考虑最坏情况)(2分)a) 13; b) 14; c) 15; d) 16; e) 175.已知Head(Tail([Head(S),Head(Tail(Tail(S)))]))=[a],广义表S 满足上式,则S为.(其中,方括号表示广义表,圆括号表示函数,如[a,b]表示由a,b构成的广义表,而Head。
表示取广义表的头部.)(2分)a) [[a,b],b,a] b)[[b,a],[a],[b]]c) [[a],[a,b],[b]] d)[b,[a],[a,b]]e) [[a],[b],[b,a]] f)[[b],[b,a],[a]]6.在下列三种次序的线索二叉树中,—对查找指定节点在该次序下的后继效果较差.(2分)a)前序线索树b)中序线索树c)后序线索树7.有二叉树的前序和后序遍历序列唯一的确定这颗二叉树.(2分)a)能b)不能8.在下列两种求图的最小生成树的算法中,—算法适合于求边稀疏的网的最小生成树.(2分)a) Prim; b) Kruskal9.下列无向图的存储结构中,在对无向图的边进行操作时(如删除一条边)存储结构更为合适a)邻接表b)邻接多重表10.在下述几中树中,—可以表示静态查找表.(2分)a)次优查找树;b)二叉排序树;c)B-树d)平衡二叉树11.答案写在填空的字母后面1)在文件“局部有序”或文件长度较小的情况下,最佳内部排序的方法是A2)快速排序在最坏情况下,时间复杂度是,比的性能差3)就平均时间而言, 最佳 (共4分)c) 0( W) C: a )堆排序;D: a )堆排序;A: a )直接插入排序;b )起泡排序;c )简单选择排序;B: a) O(n log n);b )起泡排序;c )选择排序 b )快速排序;c )归并排序12. 一程序规定的职能是:“输入三个整 数作为三边的边长构成三角形,判别 是等腰三角形,等边三角形,或是一 般三角形,再做计算....... ”.若用等价 类划分方法对该程序做功能测试,至 少应对该程序的输入数据考虑 A 个等价类,其中包括—个有效等 价和C 个无效等价类.,B,C:(答案写在填空的字母后面)1)3; 2)5; 3)7; 4) 12;5) 15; 6) 18; 7)21; 8) 259) 33; 10) 40二叉树如图所示给出先序遍历的节点问顺序; __________出中序遍历的节点问顺序; __________出后序遍历的节点问顺序; __________用二叉链表作为存储结构,将出现多少个空指针(nil )域?(共4分)13. 下列函数 (6分) function calc(x,y:integer): integer; beginif y=l then calc := xelse calc := calc ( x, y-1 ) + x end;a,b 均为正整数,则calc (a,b) =1) a*(b-l); 2) a*b; 3) a + b 4) a+a14. 程序段read (a,b);c := 3.0 * a + b;if c=0 then a := 1else a := 1.0 + 1.0 / c + 1.0 / b保证该程序段运行不出错的必要条件是:. (4分)1) b>0 2) a>0 and b>03)boO 4)bo0 and cAO二.程序改错与填空1.指出下列程序段中的错误位置,对错误编号,说明理由:程序段一:(8分)label 1;const max=50;type day = { Mon , Tue, Wed, Thu, Fri, Sat, Sun);var date:day;N: integer;begina: N:=N-ord('0');b: for date :=Mon to Sund oN := ord(succ(date)) 一c: for n := 1 to 10dobegin1:语句; end;goto 1;end.箜. 口. _________________________________________程一(8^)program type(input,output);var R:real;procedure print(var x:integer, y:real); var z:real;procedure sum(x:integer, y:real);var k:real;beginz:= x+y; k:= 3*z;x:= x+y;end; {sum)beginsum(x,y);writeln(x,y,z,k)end; (print}begin {主程序} readln(R); print(15,R);print(R,R)end.答: ______________________________________________________2.阅读下列程序,填空使之成为一个完整的程序.该程序输出N个元素的全排列.例如N=3时,程序输出为:1 2 32 1 33 2 12 3 11 3 23 1 2 (12分)程序:program pic(input,output);const n=10;var A:array[l..n] of integer;i,k: integer;procedure output 1;beginfor i := 1 to n do write(A[i]:3);writein;end; {output 1)procedure permute(k: integer);var i,t: integer;beginif k=l then output 1else beginfor i:=l to do begint:=A[k];A[k]:=A[i];A[i]:=t;------------- , t:=; A[k]:=:--------------- , end {for) end {else) end; { permute }begink:=n;for i:=l to k do A[i]:=i;permute(k)end.三.编程题:(语言可任选,要求思路清晰,书写工整)1.编写程序将一个循环队列的内容倒置,该循环队列存储在一个数组A[l..n] 中,例如图a 中为倒置前的队列,图b 中为倒置后的队列.要求倒置后的队列 从数组的第一个元素开始存储,整个程序的运行时间为0(n ). (15分)2.设计一个程序,使输入的句子按如下方式改造之后输出: 1) 单词之间只留一个空格做间隔; 2) 句子结束后必须紧跟句号;3) 如果把句子的单词从左到右依次编号为1,2,3,…则对于第奇数个 单词,只要直接复制就行了,而对于第偶数个单词,应按反序打 印.(15分)例如:输入句子是:this u u u is u u 3. u u silly u u u u program ——;改造后的输出是:this u si u a u yllis u program. (a )(b )。
中科大2023年843科目试题

中科大2023年843科目试题全文共四篇示例,供读者参考第一篇示例:中科大2023年843科目试题中科大2023年843科目试题在学术界引起了广泛的争议和讨论。
这份试题共包含了各类不同科目的考题,涉及了数理、工程、人文、社会等多个领域。
下面我们将逐一介绍其中的一部分试题内容。
数学试题:1. 计算\int_0^1 \frac{1}{x+1} dx;2. 证明勾股定理:a^2 + b^2 = c^2;3. 解方程组:\begin{cases} x + y = 5 \\ 2x - y = 3\end{cases};4. 求解微分方程:\frac{dy}{dx} = 2x;5. 计算\lim_{x \to 0} \frac{\sin x}{x}。
物理试题:1. 将一个质量为m的物体从高度为h的斜面顶端滑下,求其最终速度;2. 已知一个光滑水平面上有一质量为m的物体,初速度为v_0,求它在t 时间后的位移;3. 在空气中自由落体的重力加速度约为g = 9.8 m/s^2,已知一个物体自由落体t秒后的速度v,求它的高度;4. 将一个质量为m的物体用力水平拉动,求它的加速度;5. 用牛顿第二定律推导匀加速直线运动的位移公式。
化学试题:1. 用化学方程式表示硫酸与氢氧化钠中和的反应过程;2. 已知一个反应的生成物为氧气和氢氧化钠,求该反应的方程式;3. 用化学式表示乙醇的结构;4. 硝酸铜与氢氧化钠反应得到什么产物?写出反应式;5. 用分子式表示氧化铁的结构。
工程试题:1. 设计一个简单的小车,使其能够在水平地面上行走;2. 制作一个简易的电路,包括电源、开关和LED灯;3. 根据给定材料设计一个简单的风筝;4. 利用简单材料制作一个可以测量温度的仪器;5. 设计一个简易的太阳能发电设备。
以上仅仅是中科大2023年843科目试题中的一小部分内容,试题种类繁多,覆盖了多个学科领域,旨在全面考核学生的综合能力和学识水平。
中科大软件学院算法复习概念综合题
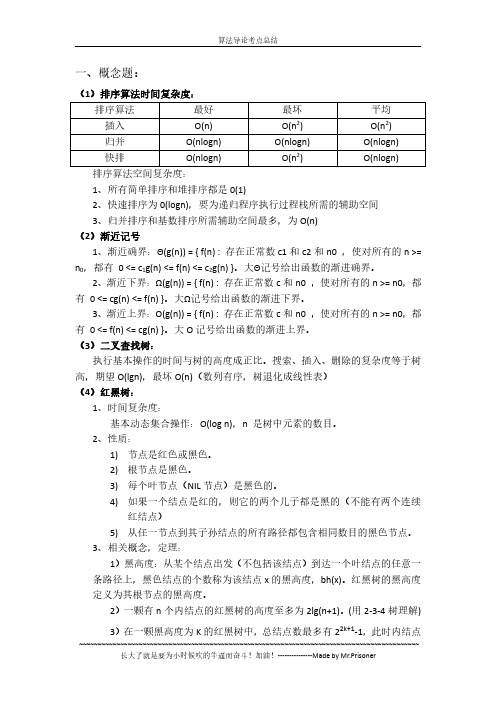
一、概念题:(1)排序算法时间复杂度:排序算法最好最坏平均插入O(n)O(n2)O(n2)归并O(nlogn)O(nlogn)O(nlogn)快排O(nlogn)O(n2)O(nlogn)排序算法空间复杂度:1、所有简单排序和堆排序都是0(1)2、快速排序为0(logn),要为递归程序执行过程栈所需的辅助空间3、归并排序和基数排序所需辅助空间最多,为O(n)(2)渐近记号1、渐近确界:Θ(g(n))={f(n):存在正常数c1和c2和n0,使对所有的n>= n0,都有0<=c1g(n)<=f(n)<=c2g(n)}。
大Θ记号给出函数的渐进确界。
2、渐近下界:Ω(g(n))={f(n):存在正常数c和n0,使对所有的n>=n0,都有0<=cg(n)<=f(n)}。
大Ω记号给出函数的渐进下界。
3、渐近上界:O(g(n))={f(n):存在正常数c和n0,使对所有的n>=n0,都有0<=f(n)<=cg(n)}。
大O记号给出函数的渐进上界。
(3)二叉查找树:执行基本操作的时间与树的高度成正比。
搜索、插入、删除的复杂度等于树高,期望O(lgn),最坏O(n)(数列有序,树退化成线性表)(4)红黑树:1、时间复杂度:基本动态集合操作:O(log n),n是树中元素的数目。
2、性质:1)节点是红色或黑色。
2)根节点是黑色。
3)每个叶节点(NIL节点)是黑色的。
4)如果一个结点是红的,则它的两个儿子都是黑的(不能有两个连续红结点)5)从任一节点到其子孙结点的所有路径都包含相同数目的黑色节点。
3、相关概念,定理:1)黑高度:从某个结点出发(不包括该结点)到达一个叶结点的任意一条路径上,黑色结点的个数称为该结点x的黑高度,bh(x)。
红黑树的黑高度定义为其根节点的黑高度。
2)一颗有n个内结点的红黑树的高度至多为2lg(n+1)。
(用2-3-4树理解)3)在一颗黑高度为K的红黑树中,总结点数最多有22k+1-1,此时内结点最多为22k-1(满二叉树,红黑交替),内结点最少有2k-14)RB-INSERT-FIXUP操作所作的旋转不超过两次,RB-DELETE-FIXUP所作的操作至多三次旋转(5)动态规划:1、装配线调度:FASTEST-WAY时间复杂度O(n)2、矩阵链乘法:MATRIX-CHAIN-ORDER时间复杂度O(n3)3、最长公共子序列:LCS-LENGTH时间复杂度为O(mn),m、n为序列的长度4、最优二叉查找树:OPTIMAL-BST时间复杂度为O(n3)(6)贪心算法:1、活动选择问题:初试时活动已按结束时间排序,O(n),否则可在O(nlgn)内排序2、哈夫曼编码:Q用最小二叉堆实现,运行时间在O(nlgn)3、任务调度问题:时间复杂度为O(n2),因为算法中O(n)次独立性检查中每一次都有花O(n)的时间(7)二项堆:1、可合并堆时间复杂度过程二叉堆(最坏)二项堆(最坏)Fibonacci(平摊)MAKE-HEAPΘ(1)Θ(1)Θ(1)INSERTΘ(lgn)Ω(lgn)Θ(1)MINIMUMΘ(1)Ω(lgn)Θ(1) EXTRACT-MINΘ(lgn)Θ(lgn)O(lgn) UNIONΘ(n)Θ(lgn)Θ(1) DECREASE-KEYΘ(lgn)Θ(lgn)Θ(1) DELETEΘ(lgn)Θ(lgn)O(lgn)2、二项树B k是一种递归定义的树,由两颗B k-1连接而成,其中一颗树的根是另一颗树的根的最左孩子性质:1)共有2k个结点2)树的高度为k3)在深度i处恰有(上k,下i)(因此叫二项树)个结点,其中i=0,...,k;4)根的度数为k,它大于任何其他结点的度数,并且,如果对根的子女从左到右编号为k-1,k-2,...,0,子女i是子树Bi的根。
中国科技大学编译原理课程PDF精讲课件合辑(共1289页)

第二章 词法分析
记号(token) 源程序 词法分析器 取下一个记号 符号表 语法分析器
本章内容
– 词法分析器:把构成源程序的字符流翻译成 记号流,还完成和用户接口的一些任务 – 围绕词法分析器的自动生成展开 – 介绍正规式、状态转换图和有限自动机概念
2.1 词法记号及属性
2.1.1 词法记号、模式、词法单元
三地址中间代码
1.1 编译器概述
t1 = id3 * 60.0 id1 = id2 + t1 代码生成器 MOVF id3, R2 MULF #60.0, R2 MOVF id2, R1 ADDF R2, R1 MOVF R1, id1
三地址中间代码
符 号 表 1 position . . . ... 2 initial ... 3 rate
1.2 编译器技术的应用
• 新计算机体系结构的设计
– 现在计算机系统的性能不仅仅取决于它的原始速 度,还取决于编译器是否能生成充分利用其特征 的代码 – 在现代计算机体系结构的研究中,在处理器的设 计阶段就开发编译器,并将编译生成的代码在模 拟器上运行,以评价拟采用体系结构的特征 – 编译器技术影响计算机体系结构设计的一个著名 例子是精简指令集计算机(RISC)的发明
60
语法树
= id, 1
1.1 编译器概述
+
id, 2 id, 3 语义分析器 = +
语法树
60 符 号 表 1 position . . . ... 2 initial ... 3 rate
id, 1
id, 2 语法树 inttofloat id, 3 60
1.2 编译器技术的应用
• 针对计算机体系结构的优化
黄宇《算法设计与分析》课后习题解析(二)精选全文

黄宇《算法设计与分析》课后习题解析(⼆)第2章:从算法的视⾓重新审视数学的概念2.1:(向下取整)题⽬:请计算满⾜下⾯两个条件的实数的区间解析:根据向下取整的含义,令,讨论a的取值范围即可解答:令,则可得:即:故的取值区间为:2.2: (取整函数)题⽬:证明:对于任意整数,(提⽰:将n划分为)。
解析:根据提⽰将n进⾏划分,根据取整函数的定义⽤k表⽰取整函数,即可证明;证明如下:因为对于任意整数,可划分为,则:① ;② ;综上:对于任意整数,, 得证;2.3: (斐波拉契数列)对于斐波拉契数列,请证明:1)题⽬:是偶数当且仅当n能被3整除解析:由斐波拉契数列的递归定义式,容易联想到数学归纳法;证明如下:(采⽤数学归纳法)i)当n = 1,2,3时,依次为1,1,2,符合命题;ii)假设当(k>=1)时命题均成⽴,则:① 当n = 3k+1时,是奇数,成⽴;② 当n = 3k+2时,是奇数,成⽴;③ 当 n = 3(k+1)时,是偶数,成⽴;综上:归纳可得为偶数当且仅当,得证;2)题⽬:x x =1+a (0<a <1)x =1+a (0<a <1)⌊x ⌋=1⇒⌊x ⌋=21⌊x ⌋=2⌊1+a +22a ⌋=1a +22a <1⇒0<a <−21⇒1<a +1<⇒21<x <2x (1,)2n ≥1⌈log (n +1)⌉=⌊logn ⌋+12≤k n ≤2−k +11n ≥12≤k n ≤2−k +11k +1=⌈log (2+k 1)⌉≤⌈log (n +1)⌉≤⌈log (2)⌉=k +1k +1=>⌈log (n +1)⌉=k +1k =⌊log (2)⌋≤k ⌊logn ⌋≤⌊log (2−k +11)⌋=k =>⌊logn ⌋=k n ≥1⌈log (n +1)⌉=k +1=⌊logn ⌋+1F n F n n ≤3k F =n F +n −1F =n −2F +3k F =3k −1>F 3k +1F =n F +3k +1F =3k >F 3k +2F =n F +3k +2F =3k +1>F 3k +3F n 3∣n F −n 2F F =n +1n −1(−1)n +1解析:同1)理,容易联想到数学归纳法证明如下:(采⽤数学归纳法)i)当n = 2时,, 易知成⽴;ii)假设当 n = k 时命题成⽴,① 若k = 2m, 则,当n = k+1 = 2m+1时,要证命题成⽴,即证: => ,代⼊递推式, 得:, 易知是恒等式,故命题成⽴;②当 k=2m+1时,同①理可证命题成⽴;综上:归纳可得,得证;2.4:(完美⼆叉树)给定⼀棵完美⼆叉树,记其节点数为,⾼度为,叶节点数为,内部节点数为1)题⽬:给定上述4个量中的任意⼀个,请推导出其他3个量解析:根据完美⼆叉树的结构特点易得解答:(仅以已知⾼度h推导其他三个量为例,其余同理)已知⾼度为h,可得:节点数:叶节点数:内部节点数:2)题⽬:请计算完美⼆叉树任意⼀层的节点个数:① 如果任意指定深度为的⼀层节点,请计算该层节点个数;② 如果任意指定⾼度为的⼀层节点,请计算该层节点个数;解析:根据完美⼆叉树的结构特点易得(注意节点深度和节点⾼度是互补的,相加为树⾼)解答:① ; ② ;2.5: (⼆叉树的性质)对于⼀棵⾮空的⼆叉树T,记其中叶节点的个数为,有1个⼦节点的节点个数为,有两个⼦节点的节点个数为1)题⽬:如果T是⼀棵2-tree,请证明。
近似算法

装箱问题有四种算法
方法一 首次适宜(FF)算法 首次适宜(FF)算法
把箱子按 下标 1 , 2 , , k , 标记,所有的箱子初始化 为空; 按物体 u 1 , u 2 , , u n 顺序装入箱子. 装入过程 如下: 把第 一个物体 u 1 装入第一个箱子 b1 , 如果 b1 还容纳得下第二个物体,继续把第二个 物体 u 2 装入 b1 ; 否则 ,把 u 2 装入 b 2 . 一般 地,为了装入物体 u i ,先找出能容纳得下
a
b
c
d
e
f
a
b
c
d
e
f
g
h
i
g
h
i
j
k (a)
l
m
j
k (b)
l
m
a
b
c
d
e
f
a
b
c
d
e
f
g
h
i
g
h
i
j
k (c)
l
m
j
k (d)
l
m
a
b
c
d
e
f
a
b
c
d
e
f
g
h
i
g
h
i
j
k (e)
l
m
j
k (f)
l
m
a
b
c
d
e
f
a
b
c
d
e
f
g
h
i
g
h
j
k (g)
l
m
j
k (h)
l
m
中科院 国科大 黄庆明 模式识别与机器学习 期末考点 复习

SVR:一般形式及其对偶问题 Multi-class SVM:一对多。 VC dimension:一般而言, VC 维 越大, 学习能力就 越强,学习也越复杂;可以通过 VC 维 计算学习风 险的上界
概念 K-means:形式化,思想 高斯混合模型及EM算法(思想,步骤)
模式识别系统的基本构成
数据 获取 预处理
分类器设 计
特征提取和 选择
分类决 策
机器学习的基本构成
环境 学习 知识库 执行与评价
数据聚类 统计分类 结构模式识别 神经网络 监督学习 无监督学习 半监督学习 集成学习 增强学习 深度学习
在贝叶斯分类器中,构造分类器需要知道类概率密 度函数。
流形学习
◦ ◦ ◦ ◦ ◦ Multidimensional Scaling(MDS): 点对距离 Kernel PCA Isomap:保持内在几何结构(测地距离) LLE:映射到低维空间时要保持局部线性结构 LPP:保持局部结构
半监督学习 假设:平滑假设 Disagreement-based 方法:Co-training Low-density separation方法:transductive SVM Graph-based SSL:加入不同的正则项得到不同的 方法
分类方法
◦ 感知器算法:
perceptron criterion 随机梯度下降求解 缺点
分类方法
◦ Logistic regression
MLE+SGD求解 多类logistic regression: Cross Entropy Loss Function
WKB近似-中国科学技术大学

Vp~r ` ~q « Vp~rq;
|~|
„
ℏ a2mrE ´
Vp~rqs
这正是把 WKB 方法称为半经典近似的理由1.
1对于经典力学体系而言,ℏ „ 0,德布罗意波长趋于零,WKB 方法对于势 场缓慢变化的要求先天性满足.
2 / 41
WKB 方法的一般程式:
假设量子力学粒子在不含时的势场 Vp~rq 中运动,体系的定态波 函数 Ep~rq 满足薛定谔方程:
H ℏ2
A
2A
使其近似为:
H H H H p Sq2 “ 2mrE ´ Vp~rqs; 2p Aq ¨ p Sq ` A 2S “ 0:
对于一维量子力学体系,上式简化为:
ˆ dS ˙2 dx
“
2mrE
´
Vpxqs;
2
dA dx
dS dx
`
A
d2S dx2
“
0:
2WKB 的理由是此项正比于 ℏ2. 对于经典力学体系而言,ℏ „ 0.
5 / 41
定义:
ppxq “ a2mrE ´ Vpxqs
上式又可以表为:
dS dx
“
˘ppxq;
2
ˆd dx
ln
˙ A
ppxq
`
d dx
ppxq
“
0:
即:
dS dx
“
˘ppxq;
d dx
r2
ln
Apxq
`
ln
ppxqs
“
0:
容易求出此方程组的一次积分,结果是:
ż
S˘pxq “ ˘ ppxqdx;
H ℏ2
´ 2m
2 Ep~rq ` Vp~rq Ep~rq “ E Ep~rq
中科大-组合数学复习知识点

中科⼤-组合数学复习知识点⼀、鸽巢原理定理:n+1个物品放⼊n个盒⼦中,那⾄少有 1 个盒⼦中⾄少有 2 个物品。
解题思路:构造部分和序列正整数a i=2s i×r i,s i为⾮负整数,r i为奇数加强形式:m个物品放⼊n个盒⼦中,⾄少有 1 个盒⼦中⾄少有mn个物品。
若物品数与盒⼦数相等,则⾄少 1 个盒⼦中⾄少有 1 个物品。
若m=n+1,则⾄少 1 ⼀个盒⼦中⾄少有 2 个物品。
解题思路:递增⼦序列问题:构造{m k},m k表⽰从a k开始的最长递增⼦序列长度将集合分成 n 部分,使⽤加强形式取余⼆、排列与组合2.1 集合的排列组合r排列=P(n,r)=A rn =n! (n−r)!r圆排列=1r P(n,r)=1r A rn=n!r(n−r)!r组合数=nr=C rn=n!r!(n−r)!定理:(n0)+(n1)+⋯+(nn)=2n解题思路:能被 3 整除的数,各位数字之和也要能被 3 整除2.2 多重集合定理:多重集合M={∞⋅a1,∞⋅a2,⋯,∞⋅a k}的r排列数为k r.定理:多重集合M={k1⋅a1,k2⋅a2,⋯,k n⋅a n}的全排列数为(k1+k2+⋯+k n)!k1!k2!⋯k n!.只适⽤全排列,如果 k 排列,则⽤指数型⽣成函数。
定理:多重集合M={∞⋅a1,∞⋅a2,⋯,∞⋅a k}的r组合数为(k+r−1r)=C rk+r−1.证明⽅法:对应求⾮负整数解⽅案数x1+x2+⋯+x k=r =>r 个相同的球放⼊ k 个不同的盒⼦中定理:多重集合M={∞⋅a1,∞⋅a2,⋯,∞⋅a k},要求各元素⾄少出现⼀次的r组合数为(r−1k−1)=C k−1r−1.证明⽅法:对应求满⾜⼀定条件的整数解⽅案数x1+x2+⋯+x k=r,x i≥1例题:求⽅程x1+x2+x3+x4=18满⾜条件x1≥3,x2≥1,x3≥4,x4≥2的整数解数⽬。
解:令y1=x1−3,y2=x2−1,y3=x3−4.y4=x4−2,则原⽅程变为y1+y2+y3+y4=8的⾮负整数解数⽬,(8+4−1 8)⌈⌉()课后习题 13,不穿过直线y=x课后习题 13,不穿过直线y=x的⾮降路径数?三、⼆项式系数⼆项式定理:(x+y)n=x n+(n1)x n−1y+(n2)x n−1y2+⋯+y n=∑ni=0(ni)x n−i y i⽜顿⼆项式定理:(1+x)α=∑∞r=0(αr)x r,(αr)=α(α−1)⋯(α−r+1)r!,α为⼀切实数,|x|<1α=−n 时,有(αr)=(−1)r(n+r−1r)(1+x)−n=∑∞r=0(−1)r(n+r−1 r)x r(1−x)−n=∑∞r=0(n+r−1 r)x r(1+x)−1=1−x+x2−x3+⋯(1−x)−1=1+x+x2+x3+⋯α=12时,有(αr)=(−1)r−11r22r−1(2r−2r−1)(1+x)12=∑∞r=1(−1)r−11r22r−1(2r−2r−1)x r,Catalan数基本性质:对称关系:(nr)=(nn−r)递推关系:(nr)=(n−1r)+(n−1r−1)=C rn−1+C r−1n−1组合恒等式:C1 n +2C2n+3C3n+⋯+nC nn=n2n−1C k 0+C k1+C k2+⋯+C kn=C k+1n+1∑n i=0(C in)2=C n2n∑r i=0C imC r−in=C rm+n,Vandermonde恒等式∑m i=0C imC r+in=C m+rm+n多项式定理:(x1+x2+⋯+x t)n=∑(nn1n2⋯n t)x n11x n22⋯x n tt,(nn1n2⋯n t)=n!n1!n2!⋯n t!例题:展开 (2x1−3x2+5x3)6,则 x31x2x23系数为解:6!3!1!2!23(−3)52多项式定理性质:展开式项数为n1+n2+⋯+n t=n的⾮负整数解个数,为(n+t−1 n)∑(nn1n2⋯n t)=t n,令所有xi都为1四、容斥原理定理:|¯A1∩¯A2∩⋯∩¯A m|=|S|−∑|Ai|+∑|A i∩A j|+⋯+(−1)m|A1∩A2∩⋯∩A m|推论:|A1∪A2∪⋯∪A m|=|S|−|¯A1∩¯A2∩⋯∩¯A m|欧拉函数的证明欧拉函数表⽰⼩于 n 且与 n 互素的整数的个数n =p i 11p i 12⋯p iq q 记 A i ={x |x ≤n 且p i |x} ,表⽰与 p i 成倍数的那些数那么 φ(n)=|¯A 1∩¯A 2∩⋯∩¯A q |=n ∏q i=1(1−1p i )定义:N (P i 1,P i 2,⋯,P i k ) 表⽰ S 中具有性质 P i 1,P i 2,⋯,P i k的元素个数ω(k )=∑N (P i 1,P i 2,⋯,P i k) 表⽰具备 k 个性质的元素计数,其中⼀个元素会被多次计数。
中科大算法分析课件分布式算法

具体:对各种分布式情况发生的问题进行抽象,精确地陈述 这些问题,设计和分析有效算法解决这些问题,证明这些算 法的最优性。
计算模型:
通信:计算实体间msg传递还是共享变量? 哪些计时信息和行为是可用的? 容许哪些错误
复杂性度量标准
时间,空间
通信成本:msg的个数,共享变量的大小及个数 故障和非故障的数目
模拟在信道上传输的msgs
11
§2.1.1 系统
初始状态:
Qi包含一个特殊的初始状态子集:每个inbufi[l]必 须为空,但outbufi[l]未必为空。
转换函数(transition):
处理器pi的转换函数(实际上是一个局部程序) 输入:pi可访问的状态 输出:对每个信道l ,至多产生一个msg输出 转换函数使输入缓冲区(1≤l≤r)清空。
4
§1.2 分布式计算的理论
否定结果、下界和不可能的结果
常常要证明在一个特定的分布式系统中,某个特定问 题的不可解性。
就像NP-完全问题一样,表示我们不应该总花精力去 求解这些问题。 当然,可以改变规则,在一种较弱的情况下去求解问 题。
我们侧重研究:
可计算性:问题是否可解?
计算复杂性:求解问题的代价是什么?
5
§1.3 理论和实际之关系
主要的分布式系统的种类,分布式计算理论中常用 的形式模型之间的关系 种类
中科大黄刘生算法第一次作业
算法实验报告Ex.1 若将y ← uniform(0, 1) 改为 y ← x, 则上述的算法估计的值是什么?实验结果如下:可见结果趋近于2*sqrt(2) Ex.2 在机器上用2041x dx -⎰估计π值,给出不同的n 值及精度。
计算方法就采用课上讲到的HitorMiss 算法,伪代码如下: f ←sqrt(1 – x*x) HitorMiss (f, n) { k ← 0;for i ← 1 to n do { x ← uniform(0, 1); y ← uniform(0, 1);if y ≤ f(x) then k++;}//endfor return 4*k/n;}实验结果如下:从总的趋势来看,n的值越大,给出的pai的精度越高。
但对应到两次实验结果未必n 大的精度一定高,这是概率算法的特点。
EX.3 采用算法类似HitorMiss算法,不过加入了一些特殊处理,以便能够正确计算穿越x 轴、周期函数等的积分。
算法伪代码如下:f ← x^2 / - sqrt(x) / sin(x)MyCalc(f , minx, maxx, miny, maxy, n){k ← 0;for i ← 1 to n do {x ← uniform(minx, maxx);y ← uniform(miny, maxy);if f(x) >= 0//函数在x轴上方,积分是f与x轴之间的部分,积分值为正then if y <= f(x) && y >=0k++;else//函数在x轴下方,积分是f与x轴之间的部分,积分值为负if y >= f(x) && y <= 0k--;}//endforif miny > 0//函数在x轴上方then return k / n * (maxx - minx) * (maxy - miny) + miny * (maxx - minx));else if maxy < 0//函数在x轴下方then return k / n * (maxx - minx) * (maxy - miny) + maxy * (maxx - minx);else//函数穿越x轴then return k / n * (maxx - minx) * (maxy - miny);}运行结果如下:可见程序运行结果还是很准确的,能正常处理在x轴单侧、穿越x轴的连续函数积分。
国科大中科院算法 近似算法

8
-近似旅行商问题是NP难问题
• 假定存在一个多项式时间算法A求解-近似旅行商问题。对于 Hamilton问题实例I, 其图为G=(V,E),构造一个新的图G1=(V,E1) 它是一个完全图,各边赋权如下:
若(u,v)E, w(u,v)=1 ; 否则 w(u,v)=k。 其中,k=(1+)n, n是G的顶点数,得到旅行商问题实例I'。 可见,图G有Hamilton回路当且仅当图G1有长为n的环游路线。 因为算法A能够求得旅行商问题的-近似解,由 F(I’)-F*(I’)F*(I’), 得F(I’)(1+)F*(I’)F*(I’)k/n 如果F(I’)>n,则由图G1的构造,必有F(I’)n-1+k,结合上式得 F*(I’)n+(n-1)n/k>n,说明G1没有长为n的环游,因而G没有Hamil ton回路;如果F(I’)n,则由G1的构造,必有F(I’)=n,G1有长为n环 游,因而G有Hamilton回路.说明算法A能够求解Hamilton问题.因 为Hamilton回路问题是NPC问题,故-近似旅行商问题是NP难问题9 .
F*(I)=r, F(I)=2, |F*(I)–F(I)|=r–2
4
绝对近似算法(2)
• 最多程序存储问题:两个容量为L的磁盘,n个程序需要的存 储空间分别是:l1, l2, …, ln,求存入磁盘的程序的最大个数。
• 最多程序存储问题存在1-绝对近似的多项式时间算法。
• 算法:将程序按照所需存储空间由小到大编号,然后逐一向 第一个磁盘存储,第一个磁盘不能存储时,再将剩下的程序逐 一向第二个磁盘存储,直至第二个磁盘也不能存储为止。 • 如果考虑将这n个程序向一个容量为2L的磁盘存储,则上述算 法会得到最优解,不妨设为k个。因而,将n个程序向两个容量 各为L的磁盘存储时,存储的最大个数不会超过k。即F*(I)k。 按照上述算法假设第一个磁盘存储了k1个程序,第二个磁盘存储 k2个程序,则k1+k2+1k,即F(I)k-1,于是|F*(I)–F(I)|1。
中科院计算机算法分析与设计_习题1-2_答案精品PPT课件

{(E,A),(B,C),(A,B)}
7. 对图的另一种检索方法是 D-Search。该方法与 BFS 的不同 之处在于将队列换成栈,即下一个要检测的结点是最新加到未 检测结点表的那个结点。 1)写一个D-Search算法; 2)证明由结点v开始的D-Search能够访问v可到达的所有结点; 3)你的算法的时、空复杂度是什么?
Tmax
*
t0 64
t
3* 2n
*t0
可解决的最大时间复杂度为
Tmax 192 * 2n ,(n为原始的输入规模)。
因为 T (n) 8 Tmax ,且为常数不随输入规模n变化,
所以任意规模的问题都可在t秒内解决。
8. Fibonacci数有递推关系:
1,
n0
F(n)
1,
n 1
F (n 1) F (n 2), n 1
}
}
return true;
return true;
}
}
最好,最坏,平均比较次数都是 2*(n-1) 最坏2*(n-1) 最好 n-1, 平均 3(n 1)
2
6. 按照渐进阶从低到高的顺序排列以下表达式:
4n2 , log n, 3n , 20n, n2 / 3 , n!
log n n2/3 20n 4n2 3n n!
template<class T>
bool MinMax(T a[], int n, int& Min, int& Max) bool MinMax(T a[], int n, int& Min, int& Max)
{ if(n<1) return false;
{ if(n<1) return false;
计算物理学(刘金远)第-3-章-函数近似方法(课后习题及答案)

第3章函数近似方法(习题及答案)§3.1插值法【3.1.1】已知sin()x 在030,45,60的值分别为1/2,分别用一次插值和二次插值求0sin(50)近似值。
【3.1.2】误差函数的数据表:x 0.460.470.480.49…f(x)0.48465550.49374520.50274980.5116683…利用二次插值计算:(1)(0.472)f ;(2)()0.5,?f x x ==【3.1.3】【3.1.4】已知列表函数x -101y-15-5-3给出二次插值函数【解】0(0)(1)1()(1)(10)(11)2x x l x x x --==-----;1(1)(1)()(1)(1)(01)(01)x x l x x x +-==--++-2(1)(0)1()(1)(11)(10)2x x l x x x +-==++-2153()(1)5(1)(1)(1)22L x x x x x x x =--+-+--【3.1.5】已知,3)9(,2)4(==f f 用线性插值计算)5(f ,并估计误差。
【解】取插值节点014, 9x x ==,两个插值基函数分别为)9(51)(1010--=--=x x x x x x l )4(51)(0101-=--=x x x x x x l 故有565)4(53)9(52)()()(11001+=-+--=+=x x x y x l y x l x L 2.25655)5()5(1=+=»L f 误差为)(2)95)(45(!2)()5(2x x f f R ¢¢-=--¢¢=【3.1.6】已知(1)2,(1)1,(2)1f f f -===,求()f x 的二次拉格郎日插值多项式【解】22(1)(2)(1)(2)(1)(1)()21(11)(12)(11)(12)(21)(21)1(38)6x x x x x x L x x x --+-+-=++----+-+-=-+【3.1.7】求经过(0,1),(1,2),(2,3)A B C 三点的二次拉格郎日插值多项式【解】22(1)(2)(0)(2)(0)(1)()123(01)(02)(10)(12)(20)(21)1(343)2x x x x x x L x x x ------=++------=-+【3.1.8】编写拉格朗日三点插值程序,绘出)cos(x y =在[p ,0]区间的插值曲线,将[p ,0]区间8等份(9个插值点),由插值函数取25个点绘出插值曲线。
中科大算法设计与分析分布式算法部分作业部分答案

1. 分析在同步和异步模型下汇集算法的复杂性。 分析在同步和异步模型下பைடு நூலகம்集算法的复杂性。
解:与广播算法分析时间复杂性的步骤一致,一两句的说明 与广播算法分析时间复杂性的步骤一致, 不是分析。 不是分析。 <1> 同步模型 引理:在汇集算法的每个容许执行里, 引理:在汇集算法的每个容许执行里,树中每个高为 t 轮里收到所有孩子的msg。 子树根结点在第 t 轮里收到所有孩子的msg。 归纳证明。。。 归纳证明。。。 定理:当生成树高为 d 时,存在一个时间复杂度为O(d)的 定理: 存在一个时间复杂度为O(d)的 同步汇集算法。 同步汇集算法。 <2> 异步模型 引理:在汇集算法的每个容许的执行里, 引理:在汇集算法的每个容许的执行里,树中每个高为 t 收到所有孩子的msg。 的子树根结点在时刻 t 收到所有孩子的msg。 归纳证明。。。 归纳证明。。。 定理: 存在一个时间复杂度为O(d)的 定理:当生成树高为 d 时,存在一个时间复杂度为O(d)的 异步汇集算法。 异步汇集算法。
6.
证明同步环上不存在匿名的、 证明同步环上不存在匿名的、一致性的 Leader选举算法 Leader选举算法。 选举算法。
解:由Lemma3.1可得。 解:由Lemma3.1可得。 假设R是大小为n>1的环(非均匀),A 假设R是大小为n>1的环(非均匀),A是其上的一 个匿名算法,它选中某处理器为leader。因为环是 个匿名算法,它选中某处理器为leader。因为环是 同步的且只有一种初始配置,故在R 同步的且只有一种初始配置,故在R上A只有唯一的 合法执行。 Lemma3.1: 在环R上算法A Lemma3.1: 在环R上算法A的容许执行里,对于每 轮k,所有处理器的状态在第k轮结束时是相同的。 ,所有处理器的状态在第k Note:每个处理器同时宣布自己是Leader! Note:每个处理器同时宣布自己是Leader!
一个快速的RSA方幂模算法

一个快速的RSA方幂模算法
罗永龙;黄刘生
【期刊名称】《小型微型计算机系统》
【年(卷),期】2004(025)001
【摘要】RSA中最主要的运算是执行方幂模(ae mod N),传统的方幂模算法按指数e的二进制重复迭代计算;文[1]引入2k进制的算法缩短了序列的长度,从而减少迭代次数;本文介绍了一种基于2k进制的改进算法,分析比较了相关算法的效率;实验结果表明,改进后的算法是高效的.
【总页数】3页(P76-78)
【作者】罗永龙;黄刘生
【作者单位】中国科学技术大学,计算机系,安徽,合肥,230027;安徽师范大学,计算机系,安徽,芜湖,241000;中国科学技术大学,计算机系,安徽,合肥,230027
【正文语种】中文
【中图分类】TP301
【相关文献】
1.几种方幂模快速算法的加法链一致性分析 [J], 董付国;厉玉蓉
2.一种高效率的RSA模幂算法的研究 [J], 饶进平;冯登国
3.RSA方幂模算法研究 [J], 李天志;梁家荣;徐凤生
4.RSA算法中方幂模快速算法的证明与实现 [J], 鲁世银
5.抵御简单功耗分析的RSA模幂算法实现 [J], 范黎恒;陈开颜;张鹏;赵强
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
NP-完全性理论
Karp的贡献
理查德·卡普(Richard Karp , 1935- ) 1972 年论文 ”Reducibility among Combinatorial Problems” 发 展和加强了由库克提出的“NP完全性”理论。 尤其是库 克仅证明了命题演算的可满足问题是NP完全的,而卡普则证明了从 组合优化中引出的大多数经典问题(背包问题、覆盖问题、匹配问 题、分区问题、路径问题、调度问题等)都是NP完全问题。只要证 明其中任一个问题是属于P类的,就可解决计算复杂性理论中最大 的一个难题,即P=?NP。
SAT∈P当且仅当P=NP
Cook 于1961 年获 Michigan 大学学士学位, 1962 和 1966年分获哈佛 大学硕士与博士学位。 1966-1970 ,他在 UC Berkeley 担任助教授; 1970年加盟多伦多大学,现为该校CS 和数学系教授,他的论文开启 了NP完备性的研究,令该领域于之后的十年成为计算机科学中最活 跃和重要的研究。因其在计算复杂性理论方面的贡献,尤其是在奠 定NP完全性理论基础上的突出贡献而荣获1982年度的图灵奖。
9
P、NP及NPC类问题
NP=?P
∵确定型图灵机是非确定型图灵机的特例,∴P⊆NP 是否有NP⊆P?即是否NP=P?
美国麻省的Clay数学研究所于2000年5月24日在巴黎法兰西学院宣 布:对七个“千年数学难题”中的每一个均悬赏 100 万美元,而 问题NP=?P位列其首:
1.P问题对NP问题 2.霍奇猜想 3. 庞加莱猜想 (2002.11-2003.7 ,俄罗斯数学家佩雷尔曼在 3 篇 论文预印本中证明了几何化猜想,2006被授予菲尔兹奖) 4.黎曼假设 5.杨-米尔斯存在性和质量缺口 6.纳维叶-斯托克斯方程的存在性与光滑性 7.贝赫和斯维讷通-戴尔猜想
p L m L 1 2
8
P、NP及NPC类问题
NPC问题:对于一个(判定性)问题q,若
(1)q∈NP (2)NP中任一问题均可多项式时间多一归约到q
则称问题q为NP-完全的(NP-complete,NPC)
NP-hard问题:若问题q仅满足条件(2)而不一定满足条件(1),则 问题q称为NP-难的(NP-hard,NPH)。显然:NPC⊆NP-hard NPC和NP-hard关系 NP-hard问题至少跟NPC问题一样难。 NPC问题肯定是NP-hard的,但反之不一定 例:停机问题是NP-hard而非NPC的。 ∵该问题不可判定,即无任何算法(无论何复杂度)求解该问题 ∴该问题∉NP。但是 可满足问题SAT≤p停机问题
18
Ch.1导论
优化问题近似解分类
1)容易近似 Knapsack,Scheduling,Bin Packing等 2)中等难度 Vertex Cover , Euclidean TSP , Steiner Trees 等 3)难于近似 Graph Coloring,TSP,Clique等 这类问题即使找到很差的近似解也是NP-hard
典型情况是问题Π1是问题Π2的判定版本。若Π2是最大值 问题,则Π1的形式为: “是否存在σ ∊D(I),使得f(σ) ≥k?”
4
停机问题
停机问题:能否写一个程序正确判定输入给它的任何一个程序 是否会停机? 设程序halts(P,X)总是正确地判定程序P在其输入X上是否停机:若 停机,则返回yes;否则死循环,返回no。设另有一程序:
diagonal(Y){ a: if halts(Y,Y) then goto a; else halt; } 功能:若 halts 断定当程 序Y用其自身Y作为输入时 Y 停 机 , 则 diagonal(Y) 死 循环;否则它停机
7
P、NP及NPC类问题
多一归约 假设 L1 和 L2 是两个判定问题, f 将 L1 的每个实例 I 变换成 L2 的实例f(I)。若对L1的每个实例I,I的答案为“是”当且仅 当f(I)是L2的答案为“是”的实例,则称f是从L1到L2的多 一归约,记作: L1≤mL2(传递关系) 直观意义:将求解L1的问题转换为求解L2的问题,而问题 L1不会难于L2 多项式时间多一归约:若 f是多项式时间可计算,则上述 归约称为多项式时间多一归约,也称多项式时间变换。记 作:
17
Ch.1导论
2.启发式概率分析 不再要求问题的解满足所有的输入实例。在某些应用 中,有可能输入实例的类被严格限制,对这些受限实例 易于找到其有效算法。而这种结果往往归功于对输入实 例约束的概率模型。 缺点:选取一个特殊的输入分布往往是不易的。 3.近似算法 不再要求总是找到最优解。在实际应用中有时很难确定 一个最优解和近似最优解(次优解)之间的差别,因问题 的输入实例数据本身就可能是近似的。 设计一个算法能够求出所有情况下的次优解来解 NPhard问题往往是真正有效的手段。
14
NP完全问题的求解 减少搜索量 简单算法是穷举搜索,时间为指数 减少搜索量:分枝限界法,隐枚举法、动态规划等 可以提高效率,但时间复杂度不变 优化问题 降低优化要求,求近似解,以得到一个多项式时间的算 法。即:找寻在容许的时间内得到容许精度的近似最优 解的算法
15
2
近似算法
16 16 | Presentation Title | Month 2010
难解问题与易解问题之相似性 1)最短/最长简单路径 单源最短路径问题:对有向图G,时间O(VE),P问题 两点间最长路径:NPC问题,即使所有边上权为1 2)欧拉环/哈密尔顿圈(G为无向图或有向图) 欧拉环:G中有通过每条边恰好一次的环?P,多项式时间可解 哈氏圈:G中有通过每个顶恰好1次的圈?NPC
近似算法
黄刘生
2013年9月16日
目录
Part1 NP-完全性理论
Part2 近似算法
1
NP-完全性理论
3 | Presentation Title | Month 2010
计算机科学的局限性
可解性:问题及其可解性可用函数和可计算性来代替 可计算性理论:研究计算的一般性质的数学理论,它 通过建立计算的数学模型(例如抽象计算机),精确 区分哪些是可计算的,哪些是不可计算的。 可计算函数:能够在抽象计算机上编出程序计算其值 的函数。这样就可以讨论哪些函数是可计算的,哪些 函数是不可计算的。 Church-Turing论题:若一函数在某个合理的计算模型 上可计算,则它在图灵机上也是可计算的。 不可计算性:很多问题和函数是无法用具有有穷描述 的过程完成计算
有限状态控制器
依据控制器的状态和读写头所读字符,决定执行以下3个操 作之一、之二或全部: 1)改变有限状态控制器中的状态; 2)读写头在相应的方格中写一符号; 3)读写头左、右移一格或不动。 确定型图灵机DTM:若对任一个状态和符号,要执行的动作 都是唯一的 非确定型图灵机NTM:若执行的动作是有穷多个可供选择
jBi
j
21
§1.1 预备知识和基本定义
约定 1)f的值域和I里的所有数是整数 易于扩展至有理数 2 )对任何 σ ∈ S(I) , f(σ) 受囿于多项式 ( 对 I 中数的 size) 只讨论 NP 完全的优化问题,因为它易被转换为判定问 题 Def1.2 若一个NPH判定问题Π1是多项式可归约为计算一 个优化问题Π2的解,则是Π2 NPH的 。
10
P、NP及NPC类问题
P、NP、NPC和NP-hard之关系
NPC是NP中最难的问题,但是NP-hard至少与NPC一样难
如何证明问题q是NP-hard或是NPC的? 若已知q’∊NPC或q’∊NPH,且q’≤pq,则q∊NPH;若进一步有q∊NP ,则q∊NPC。 即:要证q是NPH的,只要找到1个已知的NPC或NPH问题q‘,然 后将q’多项式归约到q即可。若还能验证q ∊NP,则q是NPC的。 ∵ NP中任意问题均可多项式归约到q’,由于≤p有传递性 ∴他们也都能多项式归约到q,由定义可知q是NPH的
S (I ), f ( ) f ( )
I opt
此最优解的值称为OPT(I),即: OPT ( I ) 有时不太严格地可称其为最优解
20
I f ( opt )
§1.1预备知识和基本定义
装箱问题(BP) 非形式地,给定一个 size 在 0,1 之间的项的集合,要求 将其放入单位size的箱子中,使得所用的箱子数目最少 。故有最小优化问题: 1)实例: I={s1, s2, „ , sn}, 满足∀i, si∈[0,1] 2)解: σ={B1, B2, „ ,Bk}是I的一个不相交的划分, 使得 S 1 ∀i, Bi⊂I 且 3)解的值:使用的箱子数,即f(σ)=│σ│=k 最小优化问题是求最小的k
Karp于1955、1956和1959年分别获哈佛大学文学学士、理学硕士和应用 数学博士学位,现任UC Berkeley计算机科学讲座教授,美国科学院、美 国工程院、美国艺术与科学院、欧洲科学院院士。因其在计算机科学领域 的基础贡献曾获图灵奖(1985)、冯诺依曼奖、美国国家科学勋章、哈佛大 学百年奖章等奖项.
19
§1.1预备知识和基本定义
Def1.1 一个优化问题∏由三部分构成: 实例集D:输入实例的集合 解集S(I):输入实例I∊D的所有可行解的集合 解的值函数f:给每个解赋一个值,f:S(I)→R 一个最大值优化问题∏是: I 对于给定的I∊D,找一个解 opt S (I ) 使得:
diagonal(diagonal)是否停机? 不可判定 它停机当且仅当halts(diagonal,diagonal)返回否,也就是: diagonal停机当且仅当它自己不停机,矛盾! 即:halts(P,X)并不存在,停机问题是不可解的!
5
图灵机
输入带
„„ 无限长
读写头
有单带、多带等变 种,计算能力等价
