集合概念与符号_图文
合集下载
苏教版(2019)必修第一册 1-1 集合的概念与表示 课件(37张)

(1)确定性:给定的集合,它的元素必须是确定的,也就是说,给定一个集合,那么任何一个元素在不在
这个集合中就确定了.
(2)互异性:一个给定集合中的元素是互不相同的,也就是说,集合中的元素是不重复出现的.任何两个
相同的对象在同一个集合中,只能算作这个集合的一个元素.
(3)无序性:集合中的元素无先后顺序之分.
些对象的全体,而非个别对象.
【示例】中国古代四大发明组成一个集合,那么集合的元素就是造纸术、指南针、火药、印刷术.
二十一世纪中国有新四大发明:高铁、移动支付、共享单车和网购.这四大发明就组成了一个集合.
即时巩固
[多选题]下列所给对象能构成集合的是(AD)
A.平面直角坐标系内到原点的距离等于1的点
B.《高中数学必修第一册》课本上的所有难题
两个集合相等,记作A=B.
【提示】(1)两个集合相等时,其元素个数一定相等.
(2)当两个集合相等时,其元素不一定依次对应相同.
如:集合{1,2,3}与集合{3,2,1}相等.
(3)两个集合是否相等,不能只看形式.
如:不等式0<x<1的解集与不等式 0<y<1的解集是两个相等的集合.
三、集合的表示方法
,即
∈{
}.
2.常用数集及其记法(要牢记)
数学中一些常用的数集及其记法:
全体自然数组成的集合,叫作自然数集,记作N;
全体正整数组成的集合,叫作正整数集,记作N*或N+;
全体整数组成的集合,叫作整数集,记作Z;
全体有理数组成的集合,叫作有理数集,记作Q;
全体实数组成的集合,叫作实数集,记作R.
【提示】(1)N比N*(或N+)多一个元素0;(2)N*中*在右上角,N+中+在右下角.
这个集合中就确定了.
(2)互异性:一个给定集合中的元素是互不相同的,也就是说,集合中的元素是不重复出现的.任何两个
相同的对象在同一个集合中,只能算作这个集合的一个元素.
(3)无序性:集合中的元素无先后顺序之分.
些对象的全体,而非个别对象.
【示例】中国古代四大发明组成一个集合,那么集合的元素就是造纸术、指南针、火药、印刷术.
二十一世纪中国有新四大发明:高铁、移动支付、共享单车和网购.这四大发明就组成了一个集合.
即时巩固
[多选题]下列所给对象能构成集合的是(AD)
A.平面直角坐标系内到原点的距离等于1的点
B.《高中数学必修第一册》课本上的所有难题
两个集合相等,记作A=B.
【提示】(1)两个集合相等时,其元素个数一定相等.
(2)当两个集合相等时,其元素不一定依次对应相同.
如:集合{1,2,3}与集合{3,2,1}相等.
(3)两个集合是否相等,不能只看形式.
如:不等式0<x<1的解集与不等式 0<y<1的解集是两个相等的集合.
三、集合的表示方法
,即
∈{
}.
2.常用数集及其记法(要牢记)
数学中一些常用的数集及其记法:
全体自然数组成的集合,叫作自然数集,记作N;
全体正整数组成的集合,叫作正整数集,记作N*或N+;
全体整数组成的集合,叫作整数集,记作Z;
全体有理数组成的集合,叫作有理数集,记作Q;
全体实数组成的集合,叫作实数集,记作R.
【提示】(1)N比N*(或N+)多一个元素0;(2)N*中*在右上角,N+中+在右下角.
第1章 集合、映射与关系

������
≜
{������ ∶ ������, ������ ∈ ������}称为������形成的关于������的等价类或以������为代
例 : 设 ������ = {������, ������, ������, ������, ������} , ������ 上 的 一 个 等 价 关 系 ������ =
• 补集运算(余集运算)
基本集合:限制在一定范围内的研究对象的全体形成 的集合称为基本集合(全集). 补集(余集):给定基本集合������及其子集������ (⊂ ������), 称 差集������\������为集������的补集(余集), 记������������ = ������\������.
第1章 集合、映射与关系
1.1 集合
1、集合的概念
• 若干个 (有限或无限) 确定的事物的全体叫做一个集合, 通常用大写字母������, ������, ������, ⋯ 表示集合. • 组成一个集合的事物叫做这个集合的元素, 用小写字 母 ������, ������, ������, ⋯表示集合的元素.
① 元������与元������有关系������即(������, ������) ∈ ������时, 简记为������������������.
② 若������, ������ 之间的二元关系������ 具有性质∀������ ∈ ������, ∃! ������ ∈ ������ , 使得������������������, 则关系������决定了������到������的一个映射. 因此, 二元关系是映射概念的推广.
• 多个集合的直积(笛卡尔积) ������1 × ������2 × · · ·× ������������ = { ������1 , ������2 , ⋯ , ������������ ∶ ������������ ∈ ������������ , ������ = 1, 2, ⋯ , ������}
≜
{������ ∶ ������, ������ ∈ ������}称为������形成的关于������的等价类或以������为代
例 : 设 ������ = {������, ������, ������, ������, ������} , ������ 上 的 一 个 等 价 关 系 ������ =
• 补集运算(余集运算)
基本集合:限制在一定范围内的研究对象的全体形成 的集合称为基本集合(全集). 补集(余集):给定基本集合������及其子集������ (⊂ ������), 称 差集������\������为集������的补集(余集), 记������������ = ������\������.
第1章 集合、映射与关系
1.1 集合
1、集合的概念
• 若干个 (有限或无限) 确定的事物的全体叫做一个集合, 通常用大写字母������, ������, ������, ⋯ 表示集合. • 组成一个集合的事物叫做这个集合的元素, 用小写字 母 ������, ������, ������, ⋯表示集合的元素.
① 元������与元������有关系������即(������, ������) ∈ ������时, 简记为������������������.
② 若������, ������ 之间的二元关系������ 具有性质∀������ ∈ ������, ∃! ������ ∈ ������ , 使得������������������, 则关系������决定了������到������的一个映射. 因此, 二元关系是映射概念的推广.
• 多个集合的直积(笛卡尔积) ������1 × ������2 × · · ·× ������������ = { ������1 , ������2 , ⋯ , ������������ ∶ ������������ ∈ ������������ , ������ = 1, 2, ⋯ , ������}
高一数学集合的概念PPT课件 图文

-P4回答下列问题 • 1.集合的概念 • 2.集合的表示法 • 3.元素和集合之间的关系 • 4.元素的性质 • 5.重要数集
观察下列对象:
(1) 2,4,6,8,10,12; (2)我校的篮球队员; (3)满足x-3>2 的实数; (4)我国古代四大发明; (5)抛物线y=x2上的点.
A={2,4成,6,8,10}, 其中集合中的2元,素4为,8,10
(2)所有直角三角形,可表示为 A={x/x是直角三角形}
注:“{}”本身包含“所有”“全体” 的意义,在{}内元素应去除“所 有”“全体”的字样.
33..集元合素元与集素合的之性间质的:关系
如果a是集合A的元素,就说a
属于集合A,记作a ∈ A;
1. 定 义
一般地, 把一些能够确定的 不同对象看成一个整体, 就说这个整体是由这些对 象的全体构成的 集合.
集合中每个对象叫做这个
集合的元素.
2. 集合的表示法
集合常用大写字母A,B, C...表示,且用“{}” 括起来.
元素则常用小写字母a,b, c,...表示.
例如 (1)2,4,6,8,10可表示
如果a不是集合A的元素,就
说a不属于集合A,记作a A.
例如:A={1,3,5,7},则
1∈ A,3∈ A,2 A
4.集合中元素的性质 (1)确定性:集合中的元素必须是 确定的.
(2)互异性:集合中的元素必须
是互不相同的.
(3)无序性:集合中的元素是无 先后顺序的. 集合中的任何两个 元素都可以交换位置.
例:判断下列说法是否正确
× 1.著名的科学家构成一个集合 × 2.很小的数构成一个集合 √ 3.身高超过1.80米的学生构成一个集合 × 4.{1,2,2,3}集合中有4个元素
观察下列对象:
(1) 2,4,6,8,10,12; (2)我校的篮球队员; (3)满足x-3>2 的实数; (4)我国古代四大发明; (5)抛物线y=x2上的点.
A={2,4成,6,8,10}, 其中集合中的2元,素4为,8,10
(2)所有直角三角形,可表示为 A={x/x是直角三角形}
注:“{}”本身包含“所有”“全体” 的意义,在{}内元素应去除“所 有”“全体”的字样.
33..集元合素元与集素合的之性间质的:关系
如果a是集合A的元素,就说a
属于集合A,记作a ∈ A;
1. 定 义
一般地, 把一些能够确定的 不同对象看成一个整体, 就说这个整体是由这些对 象的全体构成的 集合.
集合中每个对象叫做这个
集合的元素.
2. 集合的表示法
集合常用大写字母A,B, C...表示,且用“{}” 括起来.
元素则常用小写字母a,b, c,...表示.
例如 (1)2,4,6,8,10可表示
如果a不是集合A的元素,就
说a不属于集合A,记作a A.
例如:A={1,3,5,7},则
1∈ A,3∈ A,2 A
4.集合中元素的性质 (1)确定性:集合中的元素必须是 确定的.
(2)互异性:集合中的元素必须
是互不相同的.
(3)无序性:集合中的元素是无 先后顺序的. 集合中的任何两个 元素都可以交换位置.
例:判断下列说法是否正确
× 1.著名的科学家构成一个集合 × 2.很小的数构成一个集合 √ 3.身高超过1.80米的学生构成一个集合 × 4.{1,2,2,3}集合中有4个元素
集合的概念ppt课件

04
差集的应用举例:在数据筛选中,可以使用差集运算找出满足某一条 件但不满足另一条件的记录。
补集及其运算
补集的定义:对于全集U 和它的一个子集A,由全 集U中所有不属于A的元 素组成的集合称为A的补 集,记作∁UA或~A。
补集的运算性质:满足德 摩根定律,即 ∁U(A∩B)=(∁UA)∪(∁UB) , ∁U(A∪B)=(∁UA)∩(∁UB) 。
集合的包含关系
01
集合包含的定义
对于两个集合A和B,如果集合A的每一个元素都是集合B的元素,则称
集合B包含集合A。
02
集合包含的性质
如果集合B包含集合A,则A是B的子集,即A⊆B。
03
集合包含的符号表示
B⊇A表示集合B包含集合A。
04
集合的应用
集合在数学中的应用
01
02
03
描述数学对象
集合论是数学的基础,用 于描述各种数学对象及其 性质,如数、点、线、面 等。
偏序集的概念
偏序集的定义
偏序集是一种具有部分顺序关系的集合,其中元素之间的比较不是完全的,而是部分的。 偏序关系通常表示为≤。
偏序集的性质
偏序集具有一些重要的性质,如自反性、反对称性和传递性。此外,偏序集还可以有最大 元、最小元、上界和下界等概念。
偏序集的应用
偏序集在数学、计算机科学、经济学等领域有着广泛的应用,如用于描述数据结构中的排 序问题、经济学中的偏好关系等。
THANKS FOR WATCHING
感谢您的观看
似,但要考虑隶属度的影响。
幂集的概念
幂集的定义
给定集合A,由A的所有 子集(包括空集和A本 身)组成的集合称为A 的幂集,记作P(A)。
幂集的性质
差集的应用举例:在数据筛选中,可以使用差集运算找出满足某一条 件但不满足另一条件的记录。
补集及其运算
补集的定义:对于全集U 和它的一个子集A,由全 集U中所有不属于A的元 素组成的集合称为A的补 集,记作∁UA或~A。
补集的运算性质:满足德 摩根定律,即 ∁U(A∩B)=(∁UA)∪(∁UB) , ∁U(A∪B)=(∁UA)∩(∁UB) 。
集合的包含关系
01
集合包含的定义
对于两个集合A和B,如果集合A的每一个元素都是集合B的元素,则称
集合B包含集合A。
02
集合包含的性质
如果集合B包含集合A,则A是B的子集,即A⊆B。
03
集合包含的符号表示
B⊇A表示集合B包含集合A。
04
集合的应用
集合在数学中的应用
01
02
03
描述数学对象
集合论是数学的基础,用 于描述各种数学对象及其 性质,如数、点、线、面 等。
偏序集的概念
偏序集的定义
偏序集是一种具有部分顺序关系的集合,其中元素之间的比较不是完全的,而是部分的。 偏序关系通常表示为≤。
偏序集的性质
偏序集具有一些重要的性质,如自反性、反对称性和传递性。此外,偏序集还可以有最大 元、最小元、上界和下界等概念。
偏序集的应用
偏序集在数学、计算机科学、经济学等领域有着广泛的应用,如用于描述数据结构中的排 序问题、经济学中的偏好关系等。
THANKS FOR WATCHING
感谢您的观看
似,但要考虑隶属度的影响。
幂集的概念
幂集的定义
给定集合A,由A的所有 子集(包括空集和A本 身)组成的集合称为A 的幂集,记作P(A)。
幂集的性质
集合的概念与表示ppt课件

由此能总结出集合元素有什么特性?
互异性 一个集合中的任何两个元素都互不相同。
也就是说,集合中的元素互不相同
探究3: 将某学校高一(1)班全体学生组成的集合记为集合A, 改变这个班同学的座次,集合A是否发生改变?
集合A不发生改变,即不管班里的学生怎么改变座次,学生改 变座次后的集合仍然还是学生改变座次之前的集合.
描述法 通过描述元素满足的条件表示集合的方法叫作描述法。
一般地可将集合表示为{x及x的范围|x满足的条件}
例如,集合 D={x∈R|x<10}也可表示为D={x|x<10}; 集合E={x∈Z|x=2k+1,k∈Z}也可表示为E={x|x=2k+1,k∈Z}.
思考:你能用列举法表示不等式 x-7<3的解集吗?
如上述思考中不等式x-7<3的解是x<10,因为满足x<10的实数 有无数个,所以x-7<3的解集无法用列举法表示,
但是,我们可以利用解集中元素的共同特征,即:x是实数, 且x<10,因此把解集表示为{x|x<10}.
整数集Z可以分为奇数集和偶数集。 对于每一个x∈Z,如果它能表示为x=2k+1(k∈Z)的形式,那么它 是一个奇数;反之,如果x是一个奇数,那么它能表示为x=2k+1(k∈Z) 的形式。 所以,x=2k+1(k∈Z)是所有奇数的一个共同特征,于是奇数集可 以表示为:{x|x=2k+1,k∈Z}.
5、集合的表示方法
思考:从上面的例子看到,我们可以用自然语言描述一个集合。 除此之外,还可以用什么方式表示集合呢? 列举法 把集合的所有元素一一列举出来,并用花括号“{ }”括起来 表示集合的方法叫做列举法。
“地球上的四大洋”组成的集合可以表示为{太平洋,大西洋, 印度洋,北冰洋}; “方程x2-3x+2=0的所有实数根”组成的集合可以表示为{1,2}.
互异性 一个集合中的任何两个元素都互不相同。
也就是说,集合中的元素互不相同
探究3: 将某学校高一(1)班全体学生组成的集合记为集合A, 改变这个班同学的座次,集合A是否发生改变?
集合A不发生改变,即不管班里的学生怎么改变座次,学生改 变座次后的集合仍然还是学生改变座次之前的集合.
描述法 通过描述元素满足的条件表示集合的方法叫作描述法。
一般地可将集合表示为{x及x的范围|x满足的条件}
例如,集合 D={x∈R|x<10}也可表示为D={x|x<10}; 集合E={x∈Z|x=2k+1,k∈Z}也可表示为E={x|x=2k+1,k∈Z}.
思考:你能用列举法表示不等式 x-7<3的解集吗?
如上述思考中不等式x-7<3的解是x<10,因为满足x<10的实数 有无数个,所以x-7<3的解集无法用列举法表示,
但是,我们可以利用解集中元素的共同特征,即:x是实数, 且x<10,因此把解集表示为{x|x<10}.
整数集Z可以分为奇数集和偶数集。 对于每一个x∈Z,如果它能表示为x=2k+1(k∈Z)的形式,那么它 是一个奇数;反之,如果x是一个奇数,那么它能表示为x=2k+1(k∈Z) 的形式。 所以,x=2k+1(k∈Z)是所有奇数的一个共同特征,于是奇数集可 以表示为:{x|x=2k+1,k∈Z}.
5、集合的表示方法
思考:从上面的例子看到,我们可以用自然语言描述一个集合。 除此之外,还可以用什么方式表示集合呢? 列举法 把集合的所有元素一一列举出来,并用花括号“{ }”括起来 表示集合的方法叫做列举法。
“地球上的四大洋”组成的集合可以表示为{太平洋,大西洋, 印度洋,北冰洋}; “方程x2-3x+2=0的所有实数根”组成的集合可以表示为{1,2}.
集合的概念与表示方法ppt课件

③互异性,即同一集合中的元素是互不相同的.
能够确定的不同的对象所构成的整体叫做集合(简称集)。
练习1
1、下列说法中,正确的有______.(填序号)
2
①单词 book 的所有字母组成的集合的元素共有 4 个;
②集合 M 中有 3 个元素 a,b,c,其中 a,b,c 是△ABC 的三
边长,则△ABC不可能是等腰三角形;
5
∉
A
集合与元素的关系
集合与元素的关系:
①属于,如果 a 是集合 A 的元素,就说 a 属于集合 A,记作a∈A
;
②不属于,如果 a 不是集合 A 中的元素,就说 a 不属于集合 A,记
作 a∉A.
0
∉
Ф
集合的三大特性
集合三要素:
①确定性,即同一集合中的元素必须是确定的;
②无序性,即同一集合中的元素之间不考虑顺序;
4
6
习题:
能正确表示集合 M={x∈R|0≤x≤2}和集合 N={x∈R|x2-x=0}
关系的Venn 图是(B)。
总结
集合
THANK YOU
习题:
1、被 3 除余 2 的正整数集合;
解:(1)
{x|x=3n+2,n∈N}
2、平面直角坐标系中坐标轴上的点组成的集合.
(2)
{(x,y)|xy=0}
三、韦恩图:用平面上封闭曲线的内部代表集合,这种图称
为韦恩图,一般画成椭圆或矩形.
问题3 使用韦恩图表示中0-10之间的偶数集合。
0
10
2
8ቤተ መጻሕፍቲ ባይዱ
集合
集合的概念与表示方法
你眼中的
集合
你眼中的
集合
高一数学课件:1.1 集合的含义与表示(新人教版必修1)

6.如果在集合I中,属于集合A的任意一个元素x都具有性质p(x), 而不属于集合A的元素都不具有性质p(x),则性质p(x)叫做集合 特征性质 A的 . 7.描述法的表示形式为 {x∈I|p(x)} .
返回
学点一 集合的概念 下列各组对象能否组成集合. (1)小于10的自然数:0,1,2,3,…,9; (2)满足3x-2>x+3的全体实数; (3)所有直角三角形;
所以x∈R且x≠±1且x≠0.
【评析】解决这类问题的主要依据是集合元素的性质特征—
互异性,列出两两元素的关系式求解,通常要用到分类讨论.
返回
集合{3,x,x2-2x}中,x应满足的条件是 【解析】 x≠3且x≠0且x≠-1根据构成集合的元素的 互异性,x应满足
.
x3 2 x 2x 3 x 2 2x x
(5)直角坐标平面上在直线x=1和x=-1的两侧的点所组成
的集合.
返回
(1)由
2 x 3 y 14 3x 2 y 8
得
x4 y 2
方程组的解集为{(4,-2)}. (2)1 000以内被3除余2的正整数可以表示为x=3k+2,k∈N的 形式. 故所求的集合为{x|x=3k+2,k∈N,且x<1 000}.
③因为N中最小元素为0,故当a∈N,b∈N时,a+b的最小值为0,故 错误.
返回
学点三
集合中元素的性质
已知由1,x,x2三个实数构成一个集合,求x应满足的条件. 【分析】1,x,x2是集合中的三个元素,则它们是互不相等的. 【解析】根据集合中元素的互异性,得
x 1 2 x 1 x x 2
1 1 1 1 a
集合的概念ppt课件

A.中央电视台著名节目主持人
B.我市跑得快的汽车
C.上海市所有的中学生
D.香港的高楼
(
)
C
)
3.若以方程x2-3x+2=0和x2-5x+6=0的所有解为元素组成集合A,则A中元素的
个数为
(
A.1
B.2
C.3
D.4
C )
解析: 方程x2 - 3x +2=0的解为1,2,方程x2 -5x+6=0的解为2,3由于两方程有相
借助判别式的符号求解.
素养形成
典例 已知集合A是由方程ax2+2x+1=0(a∈R)的实数解作为元素构成的集合.
(1)1是A中的一个元素,求集合A中的其他元素;
(2)若A中有且仅有一个元素,求a的值组成的集合B中元素的个数;
(3)若A中至多有一个元素,试求a的值.
【规范答题】
解 (1)若1是A中的一个元素,则只需a+2+1=0,
于不确定的概念,因此“2020年高考数学难题”不能构成集合;由于任意给一
个数都能判断是否为有理数,故能构成集合;小于π的正整数分别为1,2,3,能
够组成集合.故选B.
探究二
元素与集合的关系
例2. (1)已知不等式2x-5<0的解集为M,则以下表示方法正确的是(
A.0∈M,3∈M
B.0∉M,3∈M
√
可能只含有一个元素.
素养形成
利用分类讨论思想求解一类关于x的方程ax2+bx+c=0的解集
一般地,形如ax2+bx+c=0是关于x的方程,当a≠0时,该方程是关于x的一元
二次方程,当a=0,b≠0时是关于x的一元一次方程,求解此类方程的解集问题,
B.我市跑得快的汽车
C.上海市所有的中学生
D.香港的高楼
(
)
C
)
3.若以方程x2-3x+2=0和x2-5x+6=0的所有解为元素组成集合A,则A中元素的
个数为
(
A.1
B.2
C.3
D.4
C )
解析: 方程x2 - 3x +2=0的解为1,2,方程x2 -5x+6=0的解为2,3由于两方程有相
借助判别式的符号求解.
素养形成
典例 已知集合A是由方程ax2+2x+1=0(a∈R)的实数解作为元素构成的集合.
(1)1是A中的一个元素,求集合A中的其他元素;
(2)若A中有且仅有一个元素,求a的值组成的集合B中元素的个数;
(3)若A中至多有一个元素,试求a的值.
【规范答题】
解 (1)若1是A中的一个元素,则只需a+2+1=0,
于不确定的概念,因此“2020年高考数学难题”不能构成集合;由于任意给一
个数都能判断是否为有理数,故能构成集合;小于π的正整数分别为1,2,3,能
够组成集合.故选B.
探究二
元素与集合的关系
例2. (1)已知不等式2x-5<0的解集为M,则以下表示方法正确的是(
A.0∈M,3∈M
B.0∉M,3∈M
√
可能只含有一个元素.
素养形成
利用分类讨论思想求解一类关于x的方程ax2+bx+c=0的解集
一般地,形如ax2+bx+c=0是关于x的方程,当a≠0时,该方程是关于x的一元
二次方程,当a=0,b≠0时是关于x的一元一次方程,求解此类方程的解集问题,
集合的概念ppt课件

(2) 设x B, 则x是整数,则x Z,且10 x 20. 因此, 用描述法表示为: B { x Z | 10 x 20}
因此,用列举法表示为 B {11, 12, 13, 14, 15, 16, 17, 18, 19}.
学习新知
我们约定, 如果从上下文的关系看, x R, x Z 是明确的, 那么, x R, x Z 可以省略, 只写其元素x.
学习新知
在初中,我们已经接触过一些集合,你能举出一些集合的例子吗?如:
自然数的集合
有理数的集合
不等式的解的集合
到一个定点的距离 等于定长的点的集合
到一条线段的两个端点 距离相等的点的集合
......
学习新知
观察下列实例:
1 1~10以内的所有奇数 2 方程x2-9=0的实数根 3 小于8的素数
集合
设A是一个集合,我们把集合A中,所有具有共同特征P(x)的元素x所组成的
集合表示为:
x A P(x)
我们称这种方法为描述法。
x为该集合的代表元素
P(x)表示该集合中的元素x所具有的性质
学习新知
例如,实数集R 中,有限小数和无限循环小数都具有 q ( p, q Z, p 0) 的 p
形式,这些数组成有理数集,我们将它表示为:
{0}.
(4) b
{a,b,c}.
【总结提升】求解此类问题必须要做到以下两点: ①熟记常见的数集的符号; ②正确理解元素与集合之间的“属于”关系。
总结新知 判断元素与集合关系的两种方法
直接法:
如果集合中的元素是直接给出的,只要判断该元素在已知集合中是否 出现即可,此时应先明确集合是由哪些元素构成的。
总结新知 思考:除字母表示法和自然语言之外,还能用什么方法表示集合?
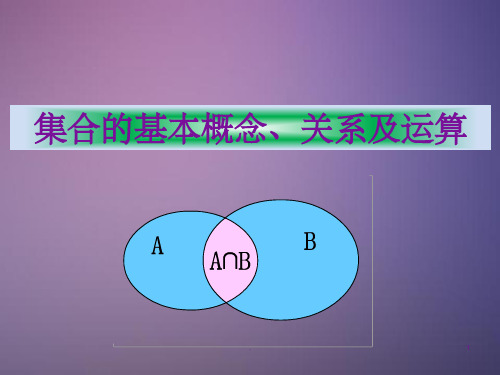
集合的基本概念、关系及运算
2020/9/23
.
37
(2)当B A时,又可分为: (a) B≠时,即B ={0},或B ={-4}, Δ = 4(a+1)2 -4(a2 -1) = 0,解得a = -1 B ={0}满足条件; (b)B = 时,Δ = 4(a+1)2 -4(a2 -1) < 0,解得a < -1 综合(1)、(2)知,所求实数a的值a -1,或a =1.
AC
(3)对于两个集合A,B,如果A B 且 B A ,那么
A=B (4)空集是任何集合的子集,是任何非空集合的真 子集,即 Φ A
2020/9/23
.
24
例 写出集合{ a , b }的所有子集,并指出哪些是它的
真子集.
解:集合{ a , b }的所有子集为 ,{a},{b},{a,b}.
2020/9/23
.
19
知识要 点
3.集合相等与真子集的概念
如 果 集 合 A是 集 合 B的 子 集 (AB), 且 集 合 B是 集 合 A的 子 集 ( BA) , 此 时 , 集 合 A与 集 合 B中 的 元 素 是 一 样 的 , 因 此 , 集 合 A与 集 合 B相 等 . 记 作 A= B
2020/9/23
.
16
2.在数学中,经常用平面上的封闭曲线的 内部代表集合,这种图称为Venn图.
A B用Venn图表示如下:(有两种情况)
A
B
A(B)
思考1
包含关系{a} A与属于关系 a A有什么区别吗?
2020/9/23
.
17
注意
与 的区别:前者表示集合与集合之间的关系;
后者表示元素与集合之间的关系.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
幂集合
• 空集的幂集合是什么?集合{Φ }的幂集 合是什么? • P(Φ )={Φ } P({Φ })={Φ ,{Φ }} • 如果一个集合有n个元素,那么它的幂集 合有2n个元素。
2. 笛卡尔积
• 定义7 有序n元组(a1,a2,…,an)是以a1为第 一个元素,a2为第2个元素,…,an为第n 个元素的有序组。 • 2元组特称为有序偶。 • 集合A和B的笛卡尔积C=AB表示所有有 序偶(a,b)的集合, 其中aA, bB. 也就是 AB={(a,b) | aA且 bB}
• 由此原发许多数学家哲学家为克服这些矛盾而建立了 各种公理化集合论体系,其中尤以本世纪初、中期的 ZFS(E . Zermelo, A . Fraenkel, T . Skolem)和NBG(Von Neurnann, P . Bernavs, K . Gö del)公理化体系最为流行. 到 20世纪 60年代,P . L . Cohen发明了强制方法而得 到了关于连续统与选择公理的独立性成果,尔后的研 究结果推陈出新,大量涌现.在同一时代,美国数学 家 L . A.Zadeh提出了Fuzzy集理论, 以及 20世纪80年 代波兰数学家Z . Pawlak发表了Rough集理论,这两种 理论区别于以往的集合论, 是一种新的模糊集理论, 受到了学术界的重视和青睐,取得了喜人成果.还有 多位著名学者也为集合论的发展作出了重要贡献.
集合论
1. 集合概念与符号
• • • • 集合(直观描述) 集合相等和子集合 子集的表示方式和全集 常用数学符号和常用集合记号
起源
• 集合论(Set Theory)是现代数学的基础.它的起源可追 溯到16世纪末,主要是对数集进行卓有成效的研 究.但集合论实际发展是由 19世纪 70年代德国数学家 康托尔(G . Cantor) 在无穷序列和分析的有关课题的理 论研究中创立的.康托尔对具有任意特性的无穷集合 进入了深入的探讨,提出了关于基数、序数、超穷数 和良序集等理论,奠定了集合论的深厚基础.因此, 康托尔被誉为集合论的创始人.但随着集合论的发展, 以及它与数学哲学密切联系所作的讨论,在本世纪初, 出现了许多似是而非、自相矛盾的悖论,如著名的罗 素(B . A . W . Russell)悖论,有力冲击了或者说动摇了 集合论的发展.
集合的基数
• 定义4 令S为集合。若S中恰有n个不同元 素,n是非负整数,就说S是有限集合, 而n是集合S的基数,用| S |表示。 • 例 令A为小于10的正奇数集合,则| A | = 5 • 空集Φ 没有元素,所以| Φ | = 0 • 定义5 如果一个集合不是有限的,就说 它是无限的。
幂集合
笛卡尔积
• 定义9 集合A1, A2,…,An的笛卡儿积用 A1×A2×…×An表示,这是有序n元组 (a1,a2,…,an)的集合,其中对于i=1,2,…,n, ai∈Ai。 • 什么是笛卡儿积A×B×C,其中 A={0,1},B={1,2},C={0,1,2}?
笛卡尔积
• 什么是笛卡儿积A×B×C,其中 A={0,1},B={1,2},C={0,1,2}?
• 集合论在计算机科学、人工智能领域、逻辑学及语言 学等方面都有着重要的应用.对子从事计算机科学的 工作者来说,集合论是不可缺少的理论知识,熟悉和 掌握它是十分必要的.
集合(直观描述)
• 具有某种属性的对象总体(通常用大写字 母表示,如A,B等),这些对象称为其元 素 (通常用小写字母表示,如x,y等). • x是A的元素记为: xA (读作x属于A) • x不是A的元素记为: xA (读作x不属于A) • 集合的基本特性是,对于给定的集合A, 任何对象x, xA与xA中有且只有一个 成立.
• 解: A×B×C={(0,1,0),(01,1),(0,1,2),(0,2,0),(0, 2,1),(0,2,2),(1,1,0),(1,1,1),(1,1,2),(1,2,0),(1, 2,1),(1,2,2)}
• 小于10的正奇数集合A={1, 3, 5, 7, 9} • 表面看起w Jerseg} • 集合B={x | x是小于10的正奇数} • 上例中集合A=B
集合相等和子集合
• 集合相等:如果两个集合A和B有同样的 元素组成,就说集合A和B相等,记作A= B或B=A. • 子集合: 如果集合B的元素都是集合A的 元素,B叫做A的子集合(简称子集). 记作 BA (读作B包含于A),或AB (读作A包 含B). • 命题: A= B当且仅当AB且AB.
• 很多问题都要检查一个集合的元素的所 有可能的组合,看它们是否具有某种性 质。为了考虑集合元素所有可能的组合, 我们构造一个新集合,它以S的所有子集 作为它的元素。
幂集合
• 定义6 已知集合S, S的幂集合是集合S所 有子集的集合,用P(S)表示。 • 例 集合{0, 1, 2}的幂集合是 P({0,1,2}={Φ ,{0},{1},{2},{0,1},{0,2 },{1,2},{0,1,2}}。 • 空集的幂集合是什么?集合{Φ }的幂集 合是什么?
子集的表示方式和全集
• 设A是一个集合,其子集B通常用下面的形 式表示:B={xA | P(x)}, 其中P(x)表示x 在B中所要满足的条件 • 空集:不含任何元素的集合叫做空集,用 符号表示,空集是任何集合的子集: ={xA | x x} • 在数学的讨论中,常常涉及到的是某个 固定集合的子集,例如,实数的子集. 这 个固定集合叫做全集. 一般用E表示.
笛卡尔积
• 例 令A为某大学所有学生的集合,B表示 该大学开设的所有课程的集合。A和B的 笛卡儿积A×B是什么? • 解:笛卡儿积A×B由形为(a, b)的所有有 序偶组成,其中a是学生,而b是该校开 的一门课。集合A×B可以用来表示该校 学生选课的所有可能情况。
笛卡尔积
• 例 A={1,2}, B={a, b, c}, A×B=? • 上例中A×B是否等于B×A
