初一数学练习册

合集下载

七上数学练习册及答案电子

七上数学练习册及答案电子### 七年级上册数学练习册及答案#### 第一章：数的认识练习一：整数的认识1. 填空题：请填写下列数的绝对值。

- |-3| = 3- |+5| = 5- |-8| = 82. 选择题：以下哪个数是负数？- A. -3- B. 5- C. 0- D. 9答案： A3. 计算题：计算下列各数的和。

- 3 + (-5) + 7 = 5练习二：有理数的运算1. 填空题：计算下列有理数的乘积。

- (-2) × 3 = -6- (-3) × (-4) = 122. 选择题：下列哪个表达式的结果为正数？- A. (-2) × (-3)- B. 4 × (-5)- C. (-1) × (-1)- D. 3 × (-2)答案： A, C3. 计算题：计算下列有理数的除法。

- 18 ÷ (-3) = -6#### 第二章：代数基础练习一：代数式1. 填空题：将下列代数式简化。

- 3x + 2y - 5x = -2x + 2y2. 选择题：以下哪个代数式是二次的？- A. x + 2- B. x^2 + 3x + 1- C. 4y - 2- D. 5z答案： B3. 计算题：计算下列代数式的值。

- 当 x = 2, y = 3 时，2x + 3y = 2 × 2 + 3 × 3 = 4 + 9 = 13练习二：方程的解法1. 填空题：解下列方程。

- 3x - 5 = 10- 3x = 15- x = 52. 选择题：下列哪个方程的解是 x = 2？- A. x + 3 = 5- B. 2x - 1 = 3- C. 3x + 4 = 10- D. 4x - 2 = 6答案： A3. 计算题：解下列方程组。

- \begin{cases}x + y = 5 \\x - y = 1\end{cases}解得：x = 3, y = 2#### 第三章：几何初步练习一：线段、射线、直线1. 填空题：线段的两个端点是 A 和 B，可以表示为线段 __AB__。

初中数学练习册七年级

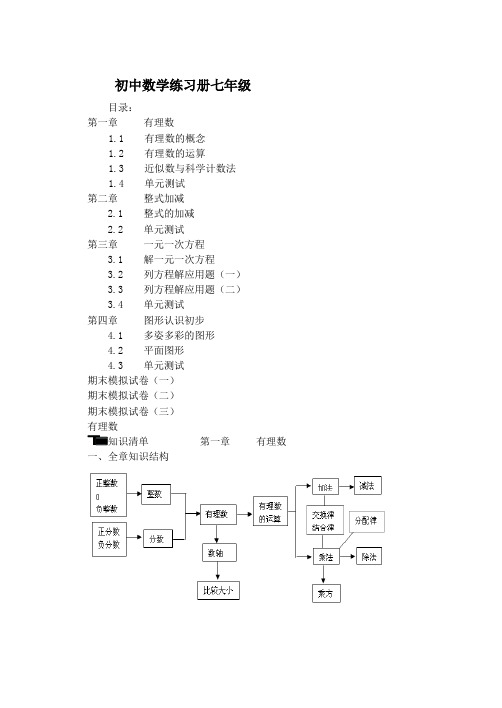
初中数学练习册七年级目录：第一章有理数1.1 有理数的概念1.2 有理数的运算1.3 近似数与科学计数法1.4 单元测试第二章整式加减2.1 整式的加减2.2 单元测试第三章一元一次方程3.1 解一元一次方程3.2 列方程解应用题（一）3.3 列方程解应用题（二）3.4 单元测试第四章图形认识初步4.1 多姿多彩的图形4.2 平面图形4.3 单元测试期末模拟试卷（一）期末模拟试卷（二）期末模拟试卷（三）有理数第一章有理数一、全章知识结构二、回顾正数、负数的意义及表示方法 1、正数的表示方法：a>0， 2、负数的表示方法：a<0三、有理数的分类定义：整数和分数统称为有理数有限小数和无限循环小数都是有理数而无限不循环小数却不是有理数1、按整数分数分类2、按数的正负性分类⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数负整数负数零正分数正整数正数有理数. 3、在数轴上分类数轴：规定了原点，正方向和单位长度的直线叫做数轴。

数轴的作用：（1）用数轴上的点表示有理数；（2）在数轴上比较有理数的大小；（3）可用数轴揭示一个数的绝对值和互为相反数的几何意义；（4）在数轴上可求任意两点间的距离：两点间的距离=|x －y|=|y －x|四、有理数中具有特殊意义的数：相反数、倒数、绝对值、非负数1、相反数：（1）几何意义：在数轴上表示一对相反数的两个点与原点的距离相等。

⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数..（2）代数意义：只有符号不同的两个数。

（3）互为相反数的特性：a+b=0，0的相反数是0。

（4）会求一个数的相反数：a 的相反数为 a-b 的相反数为 2、倒数:（1）乘积是1的两个数互为倒数（2）互为倒数的特性: ab=1, （3）0没有倒数（4）互为负倒数: 乘积是－1的两个数互为负倒数; ab=－13、非负数：（1）就是大于或等于0的数：a ≥0（2）数轴上，在原点的右边包括原点的点表示的数（3）任何数的平方数都是非负数（4）非正数：就是小于或等于0的数：a ≤0（5）数轴上，在原点的左边包括原点的点表示的数4、绝对值：（学生演示）（1）几何意义：一个数的绝对值就是它到原点的距离。

初一数学练习册及答案

初一数学练习册及答案### 初一数学练习册及答案#### 第一章：数的认识1. 正数与负数- 正数表示数量的增加或温度的升高，负数则相反。

- 例如：+5°C表示气温比零度高5度，-5°C表示气温比零度低5度。

2. 有理数的加减法- 加法：同号相加，取相同符号，绝对值相加。

- 减法：减去一个数等于加上这个数的相反数。

3. 有理数的乘除法- 乘法：同号得正，异号得负，绝对值相乘。

- 除法：除以一个数等于乘以这个数的倒数。

#### 第二章：代数基础1. 代数式- 代数式是由数字、字母和运算符组成的式子。

2. 等式与不等式- 等式表示两个代数式相等，不等式表示两个代数式不相等。

3. 解一元一次方程- 移项、合并同类项、系数化为1是解方程的基本步骤。

#### 第三章：几何初步1. 线段、射线和直线- 线段是有限长度的直线，射线有一端有端点，另一端无限延伸，直线没有端点。

2. 角度的分类- 锐角、直角、钝角、平角和周角是角度的基本分类。

3. 平行线的性质- 平行线永不相交，且它们之间的距离处处相等。

#### 第四章：数据的收集与处理1. 数据的收集- 数据收集是统计分析的第一步。

2. 数据的整理- 整理数据包括分类、排序等。

3. 图表的制作- 条形图、折线图和饼图是常见的数据可视化方式。

#### 练习题及答案1. 练习题：计算下列有理数的和：$ -3 + 2 + 5 - 1 $。

- 答案：$ -3 + 2 + 5 - 1 = 3 $。

2. 练习题：解一元一次方程 $ 3x - 7 = 11 $。

- 答案：首先移项得 $ 3x = 11 + 7 $，然后合并同类项得$ 3x = 18 $，最后系数化为1得 $ x = 6 $。

3. 练习题：判断两条直线 $ y = 2x + 3 $ 和 $ y = -2x + 5 $ 是否平行。

- 答案：两条直线的斜率分别为2和-2，斜率不同，所以不平行。

初一数学练习册答案人教版上册

初一数学练习册答案人教版上册【第一章：有理数】1. 判断题：- 有理数包括整数和分数。

（√）- 0是最小的有理数。

（×）2. 选择题：- 下列哪个数是有理数？A. πB. √2C. 1/2D. -3答案：C, D3. 填空题：- 绝对值是其本身的数是______。

答案：非负数4. 计算题：- 计算下列各数的和：-3, 5, -1, 2答案：3【第二章：代数式】1. 判断题：- 代数式中的字母可以代表任何数。

（√）- 代数式2x + 3y是二次代数式。

（×）2. 选择题：- 代数式3a - 2b的值是：A. 3aB. 2bC. 3a - 2bD. 无法确定答案：D3. 填空题：- 如果3x + 2 = 11，那么x的值为______。

答案：34. 计算题：- 计算下列代数式的值：2(3x - 1)，当x = 2时。

答案：10【第三章：方程】1. 判断题：- 方程是含有未知数的等式。

（√）- 所有等式都是方程。

（×）2. 选择题：- 下列哪个是一元一次方程？A. x + y = 5B. 2x + 3 = 7C. x^2 = 4D. 3x - 5y = 0答案：B3. 填空题：- 解方程2x - 3 = 7，得到x = ______。

答案：54. 应用题：- 一个数的三倍加上5等于23，求这个数。

答案：x = (23 - 5) / 3 = 6【结束语】本练习册答案仅供参考，希望同学们在做完练习后，能够认真核对答案，理解解题过程，提高自己的数学能力。

数学学习是一个不断探索和思考的过程，希望每位同学都能在数学的世界里找到乐趣。

结束。

七年级数学上册练习册及答案

七年级数学上册练习册及答案### 七年级数学上册练习册及答案#### 第一章：数与式##### 1.1 整数练习题：1. 计算下列各题：- $ 37 + 42 $- $ 85 - 59 $- $ 45 \times 2 $- $ 98 ÷ 14 $答案：1. $ 37 + 42 = 79 $- $ 85 - 59 = 26 $- $ 45 \times 2 = 90 $- $ 98 ÷ 14 = 7 $##### 1.2 分数和小数练习题：1. 将下列分数化为小数：- $ \frac{3}{4} $- $ \frac{7}{8} $答案：1. $ \frac{3}{4} = 0.75 $- $ \frac{7}{8} = 0.875 $##### 1.3 代数式练习题：1. 简化下列代数式：- $ 3x + 2y + 5x - 3y $答案：1. $ 3x + 2y + 5x - 3y = 8x - y $#### 第二章：方程与不等式##### 2.1 一元一次方程练习题：1. 解下列方程：- $ 2x + 5 = 11 $- $ 3x - 7 = 2x + 10 $答案：1. $ 2x + 5 = 11 $ 解得 $ x = 3 $- $ 3x - 7 = 2x + 10 $ 解得 $ x = 17 $##### 2.2 不等式练习题：1. 解下列不等式：- $ 5x - 3 > 2x + 4 $答案：1. $ 5x - 3 > 2x + 4 $ 解得 $ x > \frac{7}{3} $#### 第三章：几何初步##### 3.1 线段、射线、直线练习题：1. 判断下列说法是否正确：- 线段是直线的一部分。

- 射线有一个端点。

答案：1. 正确，线段是直线的一部分。

初一数学练习册

目录第一章丰富的图形世界 1 第二章有理数及其运算 11 第三章整式及其加减 31 第四章基本平面图形43 第五章一元一次方程 51 第六章生活中的数据 63第一章丰富的图形世界1 生活中的立体图形（第一课时）【知识梳理】1.我们学的几何体，主要有___________________________________________。

2.棱柱与圆柱的相同点是_____________________________________________________，不同点是________________________________________________________________.一、仔细选一选1.下列各物体的形状是圆柱体的物体是（）A．火力发电厂的烟囱B．打足气的自行车内胎C．没有使用的，上下两个面是圆形的铅笔D．体育用品标枪2.如图所示的图形中都是柱体的是（）二、细心填一填3．在乒乓球、橄榄球、足球、羽毛球、冰球中，其形状是球体的有____________．4．一个直角三角形绕其一条直角边旋转得到的几何体是___________．5．一个长方形绕其一边旋转得到的几何体是____________．三、认真做一做6．将下图中的几何体进行分类，并说明理由．1 生活中的立体图形（第二课时）【知识梳理】1.图形是由________________________构成的.2.点动成_________，______ 动成面，面动成_____________.3.棱柱的特性：（1）棱柱的上、下底面形状________________；（2）棱柱的所有侧棱长___________________；（3）棱柱侧面的形状都是________________,个数与底面多边形的边数____________.一、仔细选一选1．下列立体图形①圆柱，②圆锥，③正方体，④四棱柱，其中面数相同的是（）A．①② B．①③ C．②③ D．③④2．下列说法错误的是（）A．长方体是多面体 B．圆柱的上下底面可以不同C．正六棱柱的侧面不是六边形 D．球仅有一个曲面3.下列说法不正确的是（）A．长方体与正方体都有六个面 B．圆锥的底面是圆C．棱柱的上下底面是完全相同的图形 D．三棱柱有三个面，三条棱二、细心填一填4.笔尖在纸上快速滑动写出了一个又一个的英文字母，这说明了；车轮旋转时，看起来像一个整体的圆面，这说明了；直角三角形绕它的直角边旋转一周，形成一个圆锥体，这说明了；5.圆柱的侧面和底面相交成条线，它们是线；6.正方体有个面，个顶点，经过每个顶点有条棱.这些棱的长度__________________（填相同或不同）.棱长为acm的正方体的表面积为 cm2.7.长方体有个顶点，条棱，个面.8.五棱柱是由个面围成的，它有个顶点，有条棱.9.一个六棱柱共有条棱，如果六棱柱的底面边长都是2cm，侧棱长都是4cm，那么它所有棱长的和是 cm.三、认真做一做10.下图中的棱柱、圆柱、圆锥分别是由几个面围成的？它们是平的还是曲的？2 展开与折叠（第一课时）【知识梳理】1.圆柱的表面展开图是_________作底面和______________作侧面．2.圆锥的表面展开图是___________作底面和_______________作侧面．一、仔细选一选1.下面图形不能围成一个长方体的是（）2.如下图，哪个是正方体的展开图（）二、细心填一填3．七棱柱有____个顶点，有____条棱，有______个侧面．4．请自己动手用硬纸板剪一个三边都相等的三角形，再用这个三角形围成一个几何体。

七年级上数学练习册及答案

七年级上数学练习册及答案### 七年级上数学练习册及答案#### 第一章：数的认识练习一：整数的分类与运算1. 将下列整数按照正数和负数进行分类。

- 3, -5, 0, 12, -8, 72. 计算下列各组整数的和。

- 3 + (-5) + 12- -8 + 7 + 5答案解析：1. 正数：3, 12, 7负数：-5, -82. 3 + (-5) + 12 = 10-8 + 7 + 5 = 4#### 第二章：分数和小数练习二：分数的加减法1. 计算下列分数的和。

- 3/4 + 2/52. 计算下列分数的差。

- 5/6 - 1/3答案解析：1. 首先找到通分母，即20。

然后将分数转换为相同的分母：- $ \frac{3}{4} + \frac{2}{5} = \frac{15}{20} +\frac{8}{20} = \frac{23}{20} $2. 同样地，找到通分母，即6：- $ \frac{5}{6} - \frac{1}{3} = \frac{5}{6} - \frac{2}{6} = \frac{3}{6} = \frac{1}{2} $#### 第三章：几何初步练习三：线段、射线和直线1. 描述线段、射线和直线的特点。

2. 给出一个实际生活中的例子，说明线段的应用。

答案解析：1. 线段是两点之间的有限直线部分，有两个端点；射线是从一个端点开始，无限延伸的直线；直线是无限延伸的，没有端点。

2. 例如，教室黑板的边缘可以看作是一条线段。

#### 第四章：代数基础练习四：代数表达式1. 简化下列代数表达式。

- $ 3x + 2y - 5x + y $2. 解下列方程。

- $ 2x + 5 = 3x - 1 $答案解析：1. 合并同类项：- $ 3x - 5x + 2y + y = -2x + 3y $2. 解方程：- 将 $ x $ 项移到一边，常数项移到另一边： - $ 2x - 3x = -1 - 5 $- $ -x = -6 $- $ x = 6 $#### 第五章：数据的收集与处理练习五：统计图表1. 根据下列数据，绘制条形统计图。

7年级数学练习册答案(热门19篇)

7年级数学练习册答案(热门19篇）7年级数学练习册答案（1）基础达标1、整式：-3x+2/5m;a+3b/5;m-4/4;1/π(x+y)分式：x+1/x+2;1+3/x;m-3/m;4/3-2x;2/2x+12、x=-2;x=2/3;x≠2;x≠1且x≠-23、x>1;x+y≠04、1/a-b5、(1)-2/3x(2)1/y(3)-2/ab(4)5+y/x6、B7、A8、D9、C10、D综合提升11、a+1=3,a=2a+1=1,a=0a+1=-3,a=-4a+1=-1,a=-212、5-x/x2>0x2(5-x)0x-5<0x<5,且x≠013、(1)6x+4y/3x-4y(2)10x+4y/10y-5x14、p/(a/m+b/n)=pmn/an+bm(天)15、P1=MP/(1-35%)M=20/13P16、解：kda2/m27年级数学练习册答案（2）第1节认识分式答案基础达标1、整式：-3x+2/5m;a+3b/5;m-4/4;1/π(x+y) 分式：x+1/x+2;1+3/x;m-3/m;4/3-2x;2/2x+12、x=-2;x=2/3;x≠2;x≠1且x≠-23、x>1;x+y≠04、1/a-b5、(1)-2/3x(2)1/y(3)-2/ab(4)5+y/x6、B7、A8、D9、C10、D综合提升11、a+1=3,a=2a+1=1,a=0a+1=-3,a=-4a+1=-1,a=-212、5-x/x2>0x2(5-x)0x-5<0x<5,且x≠013、(1)6x+4y/3x-4y(2)10x+4y/10y-5x14、p/(a/m+b/n)=pmn/an+bm(天)15、P1=MP/(1-35%)M=20/13P16、解：kda2/m27年级数学练习册答案（3）第4节分式方程答案基础达标1、B2、D3、A4、C5、(1)解：x/2x-5-5/2x-5=1x-5/2x-5=1x-5=2x-5x=0(2)解：5x-4/2x-4=2x+5/3x-6-1/2 15x-12/6x-12-4x+10/6x-12=-1/2 11x-22=-1/2(6x-12)11x-22=-3x+614x=28x=26、2x+a/x-2=12x+a/x-2+1=02x+a+x-2/x-2=03x+a-2/x-2=03x+a-2=03x=a-2x=2-a/3>0a<2且a≠-47、1/x-1=-1/28、解：2/x+1+5/1-x=m/x2-12(x-1)-5(1+x)=m2x-2-5-5x=m-3x-7=m当x=1时，m=-10当x=-1时，m=-49、(1)通分(2)②(3)移项变号10、解：设慢车的速度是x，快车的速度是X=50慢车速度50km/h11、解：设第一批的进价是x元。

七年级上册数学练习册 (3)

七年级上册数学练习册第一章：整数1.1 整数的概念与比较整数是由正整数、零和负整数组成的数集。

在数轴上，我们可以用负数表示左侧的点，用正数表示右侧的点。

0位于正数和负数之间。

例题：在以下数中，哪个数是最大的？-1，2，0，-3，5解答：最大的数是5。

1.2 整数的加法和减法在整数的加法和减法中，有以下规律：•两个正数相加，结果为正数；•两个负数相加，结果为负数；•正数和负数相加，结果的符号取决于绝对值较大的数的符号。

例题：计算下列整数的和或差：1.(-5) + (-3)2.7 - (-4)3.12 + (-9)4.8 - 14解答： 1. (-5) + (-3) = -8 2. 7 - (-4) = 7 + 4 = 11 3. 12 + (-9) = 12 - 9 = 3 4. 8 - 14 = -61.3 整数的乘法和除法整数的乘法和除法同样存在一些规律：•两个正数相乘或相除，结果为正数；•两个负数相乘或相除，结果为正数；•正数和负数相乘或相除，结果为负数。

例题：计算下列整数的积或商：1.(-4) × 32.(-6) ÷ 23.8 × (-2)4.15 ÷ (-5)解答： 1. (-4) × 3 = -12 2. (-6) ÷ 2 = -3 3. 8 × (-2) = -16 4. 15 ÷ (-5) = -3第二章：分数2.1 分数的概念与表示分数是用两个整数表示一个数的形式。

其中，上方的整数称为分子，下方的整数称为分母。

例题：用分数表示下列图形中阴影部分所占的面积：image解答：阴影部分所占的面积可以表示为 $\\frac{3}{4}$。

2.2 分数的加法和减法在分数的加法和减法中，需要找到相同的分母，然后分别对分子进行加法或减法运算。

例题：计算下列分数的和或差：1.$\\frac{1}{3}$ + $\\frac{2}{3}$2.$\\frac{4}{5}$ - $\\frac{1}{5}$3.$\\frac{7}{8}$ + $\\frac{1}{4}$4.$\\frac{5}{6}$ - $\\frac{3}{4}$解答： 1. $\\frac{1}{3}$ + $\\frac{2}{3}$ =$\\frac{3}{3}$ = 1 2. $\\frac{4}{5}$ - $\\frac{1}{5}$ =$\\frac{3}{5}$ 3. $\\frac{7}{8}$ + $\\frac{1}{4}$ =$\\frac{7}{8}$ + $\\frac{2}{8}$ = $\\frac{9}{8}$ =1$\\frac{1}{8}$ 4. $\\frac{5}{6}$ - $\\frac{3}{4}$ =$\\frac{10}{12}$ - $\\frac{9}{12}$ = $\\frac{1}{12}$2.3 分数的乘法和除法分数的乘法和除法的操作相对简单：•两个分数相乘，将分子相乘得到新的分子，分母相乘得到新的分母；•两个分数相除，将被除数乘以除数的倒数。

七年级上册数学练习册及答案

七年级上册数学练习册及答案# 七年级上册数学练习册及答案## 第一章：数的认识### 1.1 数的分类- 整数：包括正整数、负整数和零。

- 分数：表示整体被等分后的一份或几份。

- 小数：一种表示分数的方法，使用小数点来表示。

### 1.2 数的运算- 加法：结合数的和。

- 减法：求差的过程。

- 乘法：求积的过程。

- 除法：求商的过程。

### 1.3 数的比较- 大小比较：比较两个数的大小。

- 绝对值：一个数距离零点的距离。

## 第二章：代数基础### 2.1 代数式- 单项式：只含有一个变量的代数式。

- 多项式：含有多个项的代数式。

### 2.2 代数方程- 一元一次方程：只含有一个未知数，且未知数的最高次数为1的方程。

### 2.3 代数表达式的简化- 合并同类项：将含有相同变量的项合并。

## 第三章：几何初步### 3.1 点、线、面- 点：几何图形的基本元素。

- 线：由无数点组成的一维对象。

- 面：由无数线组成的二维对象。

### 3.2 角的概念- 锐角：小于90度的角。

- 直角：等于90度的角。

- 钝角：大于90度但小于180度的角。

### 3.3 几何图形的性质- 三角形：由三条线段首尾相连组成的封闭图形。

- 四边形：由四条线段首尾相连组成的封闭图形。

## 第四章：数据的收集与处理### 4.1 数据的收集- 调查法：通过问卷或访谈收集数据。

- 观察法：直接观察现象收集数据。

### 4.2 数据的整理- 分类：将数据按照一定标准进行分组。

- 排序：将数据按照大小或其他标准进行排列。

### 4.3 数据的描述- 图表：使用图形或表格来展示数据。

- 统计量：如平均数、中位数、众数等。

## 练习题及答案### 练习题1：数的运算- 题目：计算下列各数的和：3, -5, 7, 2- 答案：3 + (-5) + 7 + 2 = 7### 练习题2：代数方程求解- 题目：解一元一次方程：2x - 5 = 9- 答案：2x = 14，x = 7### 练习题3：几何图形的性质- 题目：一个三角形的三个内角之和是多少？- 答案：180度### 练习题4：数据的描述- 题目：给定一组数据：1, 2, 3, 4, 5，求这组数据的平均数。

初一数学练习册上册及答案

初一数学练习册上册及答案【练习一：有理数的加减法】1. 计算下列各题：- (1) 3 + (-2)- (2) (-5) + 4- (3) (-3) + (-2)2. 根据题目1的结果，判断以下说法是否正确：- (1) 正数加负数，和一定是负数。

- (2) 负数加正数，和一定是正数。

【练习二：有理数的乘除法】1. 计算下列各题：- (1) (-3) × 5- (2) (-4) ÷ (-2)- (3) 0 × 92. 解释有理数乘除法的规则。

【练习三：绝对值】1. 求下列数的绝对值：- (1) |-7|- (2) |5|- (3) |-12|2. 根据题目1的结果，判断以下说法是否正确： - (1) 一个数的绝对值总是正数或零。

- (2) 正数的绝对值是它本身。

【练习四：解一元一次方程】1. 解下列方程：- (1) 2x + 5 = 11- (2) 3x - 7 = 82. 说明解一元一次方程的一般步骤。

【练习五：几何图形的初步认识】1. 根据题目要求，画出以下图形：- (1) 一个正方形- (2) 一个等边三角形2. 解释正方形和等边三角形的性质。

【答案】【练习一】1. (1) 1(2) -1(3) -52. (1) 错误，例如：3 + (-2) = 1(2) 错误，例如：(-5) + 4 = -1【练习二】1. (1) -15(2) 2(3) 02. 有理数乘除法规则：同号得正，异号得负，绝对值相乘或相除。

【练习三】1. (1) 7(2) 5(3) 122. (1) 正确(2) 正确【练习四】1. (1) x = 3(2) x = 52. 解一元一次方程的一般步骤：去分母，去括号，移项，合并同类项，系数化为1。

【练习五】1. 根据题目要求画出图形。

2. 正方形的性质：四边相等，四角都是直角。

等边三角形的性质：三边相等，三个内角都是60度。

结束语：通过本练习册的练习，同学们应该能够掌握初一数学的基础知识和基本技能，为进一步学习打下坚实的基础。

初一数学练习册答案28页

初一数学练习册答案28页【问题1】题目：某工厂计划在一个月内生产一批零件，已知前10天平均每天生产100个零件，后20天平均每天生产150个零件。

求这个月工厂总共生产了多少个零件？答案：首先，我们计算前10天生产的零件总数，即100个零件/天× 10天= 1000个零件。

接着，计算后20天生产的零件总数，即150个零件/天× 20天 = 3000个零件。

最后，将两个阶段的零件总数相加，得到这个月工厂总共生产的零件数：1000 + 3000 = 4000个零件。

【问题2】题目：一个长方形的长是宽的两倍，如果长增加2米，宽增加1米，面积将增加18平方米。

求原长方形的长和宽。

答案：设原长方形的宽为x米，那么长就是2x米。

根据题意，我们可以得到以下等式：(2x + 2) * (x + 1) - 2x * x = 18化简后得到：2x^2 + 2x + 2x + 2 - 2x^2 = 18进一步化简得到：4x + 2 = 18解得：4x = 16x = 4所以原长方形的宽是4米，长是2 * 4 = 8米。

【问题3】题目：一个数的平方加上这个数的两倍等于这个数的3倍，求这个数。

答案：设这个数为a，根据题意，我们有以下等式：a^2 + 2a = 3a将等式化简得到：a^2 - a = 0提取公因式a，得到：a(a - 1) = 0解得：a = 0 或 a = 1【问题4】题目：一个班级有40名学生，其中1/3是男生，2/3是女生。

如果班级中新增了5名男生，班级的总人数变为45人，现在班级中男生和女生的比例是多少？答案：首先，计算原班级中男生的人数：40 × 1/3 = 13.33（向下取整为13人）。

女生的人数为：40 - 13 = 27人。

新增5名男生后，男生人数变为：13 + 5 = 18人。

女生人数不变，仍为27人。

现在班级中男生和女生的比例为：18 : 27，简化比例为：2 : 3。

初一数学最全最经典习题册

第一章走进数学世界略第二章有理数单元测试题一．判断题：1．有理数可分为正有理数与负有理数． ( × ) 2．两个有理数的和是负数，它们的积是正数，则这两个数都是负数． ( √ ) 3．两个有理数的差一定小于被减数． ( ) 4．任何有理数的绝对值总是不小于它本身． ()5．若0<ab ，则b a b a -=+；若0>ab ，则b a b a +=+ ．（）二．填空题：1．最小的正整数是，最大的负整数是，绝对值最小的数是． 2．绝对值等于2)4(-的数是，平方等于34的数是，立方等于28-的数是．3．相反数等于本身的数是，倒数等于本身的数是，绝对值等于本身的数是，立方等于本身的数是． 4．已知a 的倒数的相反数是715，则a = ；b 的绝对值的倒数是312，则b = ．5．数轴上A 、B 两点离开原点的距离分别为2和3，则AB 两点间的距离为． 6．若222)32(,)32(,32⨯-=⨯-=⨯-=c b a ，用“<”连接a ，b ，c 三数：．7．绝对值不大于10的所有负整数的和等于；绝对值小于2002的所有整数的积等于．三．选择题：1．若a ≤0，则2++a a 等于 ( )A ．2a +2B ．2C ．2―2aD ．2a ―22．已知a 、b 互为相反数，c 、d 互为倒数，m 的绝对值为1， p 是数轴到原点距离为1的数，那么122000++++-m abcdba cd p的值是 ( )． A ．3 B ．2 C ．1 D ．0 3．若01<<-a ，则2,1,a aa 的大小关系是 ( )．A ．21a aa <<B ．21a a a<< C ．a a a<<21D ．aa a 12<<4．下列说法中正确的是 ( )． A. 若,0>+b a 则.0,0>>b a B. 若,0<+b a 则.0,0<<b a C. 若,a b a >+则.b b a >+ D. 若b a =，则b a =或.0=+b a 5．ccb b a a ++的值是 ( ) A ．3± B ．1± C ．3±或1± D ．3或16．设n 是正整数，则n)1(1--的值是 ( )A ．0或1B ．1或2C ．0或2D ．0，1或2 四．计算题 1．[]24)3(2611--⨯-- 2．23.013.0)211653(1⨯⎥⎦⎤⎢⎣⎡+--÷3．%).25()215(5.2425.0)41()370(-⨯-+⨯+-⨯-4．223200120013)21(24)23(3)5.0(292)1(-⨯÷-÷⎥⎦⎤⎢⎣⎡-⨯--⨯+÷-五、2++b a 与4)12(-ab 互为相反数，求代数式++-+ba abab b a 33)(21的值．六、 a 是有理数，试比较2a a 与的大小．七．32－12＝8×1 52－32＝8×2 72－52＝8×3 92－72＝8×4…… 观察上面的一系列等式，你能发现什么规律？用代数式表示这个规律，并用这个规律计算20012－19992的值．第三章整式的加减单元测试题（一）一、填空题:(每小题3分,共24分) 1.代数式-7,x,-m,x 2y,2x y +, -5ab 2c 3, 1y 中,单项式有______个,其中系数为1 的有_____.系数为-1的有_____,次数是1的有________.2.把4x 2y 3,-3x 2y 4,2x,-7y 3,5 这几个单项式按次数由高到低的顺序写出是_________. 3.当5-│x+1│取得最大值时,x=_____,这时的最大值是_______.4.不改变2-xy+3x 2y-4xy 2的值,把前面两项放在前面带有“+”号的括号里, 后面两项放在前面带有“-”号的括号里,得_______.5.五个连续奇数中,中间的一个为2n+1,则这五个数的和是_________.6.某音像社对外出租光盘的收费方法是:每张光盘在租出后的头两天每天收0. 8元,以后每天收0.5元,那么一张光盘在租出的第n 天(n 是大于2的自然数),应收租金______元.7.如果m-n=50,则n-m=_____,5-m+n=______,70+2m-2n=________.8.设M=3a 3-10a 2-5,N=-2a 3+5-10a,P=7-5a-2a 2,那么M+2n-3P=_________.M-3N+2P=_______. 二、选择题:(每小题3分,共24分) 9.下列判断中,正确的个数是( )①在等式x+8=8+x 中,x 可以是任何数;②在代数式18x +中,x 可以是任何数; ③代数式x+8的值一定大于8;④代数式x+8的相反数是x-8 A.0个 B.1个 C.2个 D.3个10.一种商品单价为a 元,先按原价提高5%,再按新价降低5%,得到单价b 元,则a 、b 的大小关系为( )A.a>bB.a=bC.a<bD.无法确定11.若x<y<z,则│x-y │+│y-z │+│z-x │的值为( ) A.2x-2z B.0 C.2x-2y D.2z-2x12.对于单项式-23x 2y 2z 的系数、次数说法正确的是( ) A.系数为-2,次数为8 B.系数为-8,次数为5 C.系数为-23,次数为4 D.系数为-2,次数为7 13.下列说法正确的有( )①-1999与2000是同类项 ②4a 2b 与-ba 2不是同类项 ③-5x 6与-6x 5是同类项 ④-3(a-b)2与(b-a)2可以看作同类项 A.1个 B.2个 C.3个 D.4个14.已知x 是两数,y 是一位数,那么把y 放在x 的左边所得的三位数是( ) A.yx B.x+y C.10y+x D.100y+x15.如果m 是三次多项式,n 是三次多项式,则m+n 一定是( ) A.六次多项式 B.次数不高于三的整式 C.三次多项式 D.次数不低于三的多项式 16.若2ax 2-3b x+2=-4x 2-x+2对任何x 都成立,则a+b 的值为( ) A.-2 B.-1 C.0 D.1 三、解答题:(共52分) 17.如果单项式2amx y 与235a nx y --是关于x 、y 的单项式,且它们是同类项.(1)求2002(722)a -的值.(2)若2amx y 235a nx y --=0,且xy ≠0,求2003(25)m n -的值.(8分)18.先化简再求值(12分)(1)5x-{2y-3x+[5x-2(y-2x)+3y]},其中x=11,26y -=-.(2)已知A=x2+4x-7,B=-12x2-3x+5,计算3A-2B.(3)已知m2+3mn=5,求5m2-[+5m2-(2m2-mn)-7mn-5]的值.(4)若3x2-x=1,求6x3+7x2-5x+1994的值.19.某同学做一道数学题,误将求“A-B”看成求“A+B”, 结果求出的答案是3x2-2x+5.已知A=4x2-3x-6,请正确求出A-B.(8分)20.探索规律(8分)(1)计算并观察下列每组算式:88____55____1212____,,79____46____1113____⨯=⨯=⨯=⎧⎧⎧⎨⎨⎨⨯=⨯=⨯=⎩⎩⎩(2)已知25×25=625,那么24×26=__________.(3)从以上的过程中,你发现了什么规律,你能用语言叙述这个规律吗?你能用代数式表示设这个规律吗?21. (8分)有理数a、b、c在数轴上对应点为A、B、C,其位置如图所示, 试去掉绝对值符号并合并同类项: │c│-│c+b│+│a-c│+│b+a│.22.某移动通讯公司开设了两种通讯业务:“全球通”使用者缴50元月租费, 然后每通话1分钟再付话费0.4元;“快捷通”不缴月租费,每通话1分钟,付话费0,6 元(本题的通话均指市内通话).若一个月内通话x分钟,两种方式的费用分别为y1 元和y2元.(8分)(1)用含x的代数式分别表示y1和y2,则y1=________,y2=________.(2)某人估计一个月内通话300分钟,应选择哪种移动通讯合算些?第三章整式的加减单元测试题（二）一、选择题（20分）1．下列说法中正确的是（）．A ．单项式223x y -的系数是－2，次数是2B ．单项式a 的系数是0，次数也是0C ．532ab c 的系数是1，次数是10D ．单项式27a b -的系数是17-，次数是32．若单项式421m a b -+与272m m a b +-是同类项，则m 的值为（）．A ．4B ．2或－2C ．2D ．－23．计算（3a 2－2a ＋1）－（2a 2＋3a －5）的结果是（）．A ．a 2－5a ＋6B ．7a 2－5a －4C ．a 2＋a －4D ．a 2＋a ＋64．当23,32a b ==时，代数式2[3(2)1]b a a --+的值为（）．A ．269B ．1113C ．2123D ．135．如果长方形周长为4a ，一边长为a ＋b,，则另一边长为（）． A ．3a －b B ．2a －2b C ．a －b D ．a －3b6．一个两位数，十位数字是a ，个位数字是b ，则这个两位数可表示为（）． A ．ab B ．10a +b C ．10b +a D ．a +b7．观察右图给出的四个点阵，s 表示每个点阵中的点的个数，按照图形中的点的个数变化规律，猜想第n 个点阵中的点的个数s 为（）．（）．A ．3n －2B ．3n －1C ．4n ＋1D ．4n －3 8. 长方形的一边长为2a+b,另一边比它大a －b ，则周长为( ) A.10a+2b B.5a+b C.7a+b D.10a －b 9. 两个同类项的和是（）A.单项式B.多项式C.可能是单项式也可能是多项式D.以上都不对10、如果A 是3次多项式，B 也是3次多项式，那么A ＋B 一定是（）（A ）6次多项式。

初一数学练习册答案

初一数学练习册答案第一章：整数集的基础1.以下数中，哪一个是正整数？A. -5B. 0C. 3/4D. √2答案：B. 02.将以下数从小到大排列：-3, 0, 5/4, -2, 1答案：-3, -2, 0, 1, 5/43.计算：（-2） + 5/3 * 4答案：(-2) + (5/3 * 4) = -2 + 20/3 = (-2) + (6 + 2/3) = 4 + 2/3 = 14/3第二章：正数的运算1.计算：15 - 7 + 3 * 4答案：15 - 7 + 3 * 4 = 15 - 7 + 12 = 202.计算：15 + 7 - 3 * 4答案：15 + 7 - 3 * 4 = 15 + 7 - 12 = 22 - 12 = 103.将以下两个式子计算得到的结果从大到小排列：A. 4 + 5 * 2B. 3 * 6 - 12答案：B. 3 * 6 - 12 = 18 - 12 = 6A. 4 + 5 * 2 = 4 + 10 = 14排序结果：B. 6, A. 14第三章：小数的运算1.计算：0.5 + 0.3答案：0.5 + 0.3 = 0.82.计算：1.2 - 0.6答案：1.2 - 0.6 = 0.63.计算：0.4 * 0.2答案：0.4 * 0.2 = 0.08第四章：分数的运算1.计算：3/4 + 1/2答案：3/4 + 1/2 = 6/8 + 4/8 = 10/8 = 5/42.计算：5/6 - 1/3答案：5/6 - 1/3 = 10/12 - 4/12 = 6/12 = 1/23.计算：2/3 * 4/5答案：2/3 * 4/5 = 8/15第五章：算式的应用1.计算：6 + 8 * 2 - 5 * 3答案：6 + 8 * 2 - 5 * 3 = 6 + 16 - 15 = 72.将以下式子化简到最简形式：(1 + 2) * 3 - 4 / 2答案：(1 + 2) * 3 - 4 / 2 = 3 * 3 - 4 / 2 = 9 - 2 = 73.在计算8 * (24 - 23)时，如何处理括号内算式的?答案：括号内的算式先计算，8 * (24 - 23) = 8 * 1 = 8以上是初一数学练习册的答案。

初一数学同步练习册及答案

初一数学同步练习册及答案### 初一数学同步练习册及答案#### 第一章：数的认识1. 整数加减法- 练习题：计算下列各题，并写出结果。

- 35 + 42 = ?- 78 - 26 = ?- 答案：- 35 + 42 = 77- 78 - 26 = 522. 小数的四则运算- 练习题：完成以下小数的加法和减法。

- 0.75 + 1.2 = ?- 2.3 - 0.85 = ?- 答案：- 0.75 + 1.2 = 1.95- 2.3 - 0.85 = 1.453. 分数的加减法- 练习题：计算下列分数的和。

- 2/3 + 1/4 = ?- 3/5 - 1/6 = ?- 答案：- 2/3 + 1/4 = 11/12- 3/5 - 1/6 = 7/30#### 第二章：代数基础1. 字母表示数- 练习题：用字母表示下列表达式。

- 爸爸的年龄比小明大30岁，如果小明今年x岁，爸爸的年龄是多少？- 一个数的两倍加上5等于15，求这个数。

- 答案：- 爸爸的年龄 = x + 30- 设这个数为y，则 2y + 5 = 152. 简单的代数方程- 练习题：解下列方程。

- 2x - 3 = 7- x + 4 = 10- 答案：- 2x - 3 = 7 → 2x = 10 → x = 5- x + 4 = 10 → x = 63. 代数式的简化- 练习题：简化下列代数式。

- 3x + 5x - 2- 4y^2 - 3y + 1 - 2y^2 + y- 答案：- 3x + 5x - 2 = 8x - 2- 4y^2 - 3y + 1 - 2y^2 + y = 2y^2 - 2y + 1#### 第三章：几何初步1. 线段、射线和直线- 练习题：判断下列说法是否正确，并给出理由。

- 线段有两个端点。

- 射线有一个端点。

- 直线没有端点。

- 答案：- 正确，线段是有限的，所以有两个端点。

- 正确，射线从一个端点开始，无限延伸。

(完整版)人教版七年级数学下册练习册

第一章数的基本运算一、选择题1.计算：（）A.8+5=13B.8-5=3C.8×5=40D.8÷5=1.62.计算：（）A.34+5=39B.34-5=29C.34×5=170D.34÷5=6.83.计算：（）A.97+12=109B.97-12=85C.97×12=1164D.97÷12=8.084.计算：（）A.23+54=77B.23-54=-31C.23×54=1242D.23÷54=0.45.计算：（）A.98+25=123B.98-25=73C.98×25=2450D.98÷25=3.92二、填空题1.计算：38+26=＿＿答案：642.计算：45-17=＿＿答案：283.计算：51×7=＿＿答案：3574.计算：72÷6=＿＿答案：125.计算：65÷5=＿＿答案：13三、解答题1.计算：（7+3）×6答案：（7+3）×6=60 2.计算：（53-18）÷6答案：（53-18）÷6=7 3.计算：（78+45）÷7答案：（78+45）÷7=154.计算：（23+54）×2答案：（23+54）×2=1565.计算：（98-45）÷7答案：（98-45）÷7=9第二章分数一、选择题1.将2/5表示为小数，正确的是（）A.0.2B.0.25C.2.5D.0.022.将3/4表示为小数，正确的是（）A.0.3B.0.4C.3.4D.0.343.将5/8表示为小数，正确的是（）A.0.5B.0.8C.5.8D.0.584.将7/9表示为小数，正确的是（）A.0.7B.0.9C.7.9D.0.795.将1/3表示为小数，正确的是（）A.0.1B.0.3C.1.3D.0.13二、填空题1.将2/3表示为小数，答案是＿＿答案：0.662.将4/5表示为小数，答案是＿＿答案：0.83.将5/6表示为小数，答案是＿＿答案：0.834.将7/8表示为小数，答案是＿＿答案：0.885.将9/10表示为小数，答案是＿＿答案：0.9三、解答题1.将3/5表示为小数答案：3/5=0.62.将7/10表示为小数答案：7/10=0.73.将4/7表示为小数答案：4/7=0.574.将8/9表示为小数答案：8/9=0.885.将6/11表示为小数答案：6/11=0.54。

初中初一数学必刷题练习册

初中初一数学必刷题练习册一、选择题1. 下列哪个选项是最小的正整数？A. 0B. 1C. -1D. 22. 如果一个数的立方等于它本身，那么这个数可能是：A. 0B. 1C. -1D. 23. 一个数的平方根是它本身，这个数可以是：A. 0B. 1C. -1D. 24. 一个数的绝对值是它本身，这个数是：A. 负数B. 正数C. 0D. 任意实数5. 以下哪个表达式等于0？A. 3 + 2B. 5 - 5C. 4 × 0D. 2 / 2二、填空题6. 一个数的相反数是-8，这个数是______。

7. 一个数的绝对值是5，这个数可以是______。

8. 如果一个数的平方等于9，那么这个数可以是______。

9. 一个数的立方等于27，这个数是______。

10. 一个数的平方根是3，这个数是______。

三、计算题11. 计算下列各题，并写出计算过程：- (-2) × (-3)- √16- |-5|12. 解下列方程，并写出解法：- 3x + 5 = 14- 2y - 4 = 6四、解答题13. 一个班级有40名学生，如果每名学生平均分得5本练习册，那么这个班级总共需要多少本练习册？14. 如果一个圆的半径是7厘米，那么这个圆的面积是多少平方厘米？五、应用题15. 某商店进了一批货物，每件货物的成本是20元，标价是30元，如果商店卖出了50件货物，那么商店的总利润是多少？16. 一个长方形的长是12厘米，宽是8厘米，求这个长方形的面积和周长。

结束语：通过本练习册的习题练习，同学们可以巩固和加深对初一数学知识点的理解和应用。

希望同学们能够认真完成每一道题目，不断提高自己的数学能力。

数学是一门需要不断练习和思考的学科，只有通过不断的练习，才能更好地掌握数学知识，解决实际问题。

祝同学们学习进步，数学成绩优异！【答案】1. B2. B, C3. A, B4. B, C5. B, C6. 87. ±58. ±39. 310. 911. (-2) × (-3) = 6；√16 = 4；|-5| = 512. 3x + 5 = 14 → x = 3；2y - 4 = 6 → y = 513. 40 × 5 = 200本14. 面积= π × 7² = 153.94平方厘米；周长= 2 × (7 × 2) = 28厘米15. 利润 = (30 - 20) × 50 = 500元16. 面积= 12 × 8 = 96平方厘米；周长= 2 × (12 + 8) = 40厘米。

七年级数学练习册

七年级数学练习册篇一：七年级下册数学练习册答案篇二：七年级下册数学练习册答案篇三：七年级数学练习册答案《新课程课堂同步练习册·数学(人教版七年级上)》参考答案第一章有理数1.1正数和负数（一）一、1. D2. B3. C二、1. 5米 2. -8℃3. 正西面600米 4. 90 三、1. 正数有:1,2.3,68,+123;负数有:-5.5,?13,-112.记作-3毫米,有1张不合格3. 一月份超额完成计划的吨数是-20, 二月份超额完成计划的吨数是0, 三月份超额完成计划的吨数是+102.1.1正数和负数（二）一、1. B2. C 3. B二、1. 3℃ 2. 3℃3. -2米4. -18m三、1.最大不超过9.05cm, 最小不小于8.95cm；2.甲地最高,丙地最低,最高的地方比最低的地方高50米3. 70分1.2.1有理数一、1. D2. C3. D二、1. 02. 1,-13. 0,1,2,34. -10三、1.自然数的集合：｛6,0,+5,+10…｝整数集合：｛-30,6,0,+5,-302,+10…｝负整数集合：｛-30,-302… ｝分数集合：｛?负分数集合：｛?121223,0.02,-7.2,2,?1011,2.1…｝,-7.2, ?1011… ｝非负有理数集合：｛0.02, 223,6,0,2.1,+5,+10…｝；1102. 有31人可以达到引体向上的标准3. (1) ?1.2.2数轴一、1. D2. C 3. C二、1. 右5左32.?412(2)120093. -34. 10三、1. 略2.(1)依次是-3,-1,2.5,4 (2)13. ±1，±31.2.3相反数一、1. B2. C3. D二、1. 3,-72. 非正数3. 34. -9三、1.(1) -3 (2) -4 (3) 2.5 (4) -62. -33. 提示:原式=12(x?2y?12z)?3=12(x?2y?4y?12z)?3?31.2.4绝对值一、1. A2. D3. D二、1. ?62. ?a3. 7 4. ±4三、1. 2x?1 2. 203. (1)|0|一、1. C2. B3. C二、1. -72.这个数3. 74. -3,-3. 三、1. (1)2 (2) -35(3) - 3.1(4) ?2.(1)197889>?16(5) -2(6) -2.75；(2) 190.1.3.1有理数的加法(二)一、1. D2. B3. C二、1. -11.762. 2 3. -6 4. 7,0三、1. (1) 10 (2) 63(3) ?16(4) -2.52. 在东边距A处40dm 480dm3. 0或?6. 1.3.2有理数的减法(一)一、1. A2. D3. A.二、1. -5 2.-200-(-30)3.互为相反数4.-8. 三、1. (1) -12 (2) 12 (3) -4.3(4) ?61.3.2有理数的减法(二)一、1. A2. D3. D.二、1. 82. -2.53. 7+8-4.2-5.34. 7或-5. 三、1.3.52.盈452(万元)3. 160cm.1.4.1有理数的乘法(一) 一、1. B 2. A 3. D二、1. 102. -103.3.63.6?三、1. (1) 0(2)10(3) 1(4)2.当m=1时,12665162. (1) 256(2) 85184. 15当m=-1时,4123.-16°C.1.4.1有理数的乘法(二)一、1. D2. B3. C二、1. 992. 0 3.负数4. 0三、1. (1) ?53(2) -77 (3) 0 (4)39942. 1073. 这四个数分别是±1和±5，其和为01.4.2有理数的除法(一) 一、1. C2. B3. B二、1. 72. 03. ?三、1. (1)-3(2) ?131544.12,?356.(3) 64(4) -42. 43.平均每月盈利0.35万元.1.4.2有理数的除法(二)一、1. D2. D3. C二、1. ?542. ?1，3. -54. 0,13100三、1. (1) 15 (2) -1(3) 1.5.1乘方一、1. A2. D3. A. 二、1. 162. ?12(4) 22. 8.853. 0或-2,53. ?4,-44. 0或1.254三、1. (1) -32 (2) 1.5.2科学记数法(3) -53(4) -152. 643. 8，6，2n一、1. B2. D3. C二、1.9.59696?10平方米2.(n+1)3.130 000 0004.-9.37×106. 三、1.(1)6.808?10(2) -4.012×107(3) -3.72109×103 (4)3.24?10;2.(1) 203000(2) -6120(3) -50030 (4) 11 000 0003.2.16?10. 1.5.3近似数一、1. C2. B3. B二、1.5.7×1042.2,4和0,万分3.百分,64.2.2?10. 三、1.(1)个位3(2)十分位,3(3)千万位,2(4)万位,36452.(1)?2.365(2)?2.54?10(3)?2.1?10(4)9.55?10.54576第二章整式加减2.1整式（一）一、1. C2. B3. B 二、1. 15x元2.3，33. 三、1. ah24. 1.05a2. 6h3. 任意一个偶数可表示为：２n，任意一个奇数可表示为：2n+1．4. 每件售价为：a(1?40%)?1.4a（元）;现售价为：80%(1?40%)a?1.12a （元）;盈利：80%(1?40%)a?a?0.12a（元）2.1整式（二）一、1. D2. D3. A二、1. 5a+72. 四，三-1，-5；3、-7，?x2，a?b，m?n44.（2m+10）三、1. ①5-2χ ②16?4y③15?2xy④19.2 14.22. 依题意可知：九年级有a名学生，八年级有443a名学生，七年级有?4a?50?名学??3??生，所以七至九年级共有a??11?a?50?=1810??3??4??11?a??a?50???a?50?3?3??3?2名学生，当a=480时，名．3. (a?b)2??a?b??4ab2.2整式加减（一）一、1. C2. B3. D二、1.（答案不唯一），如7ab22. 3x2与-6x2，-7x与5x ，-4与13. 2，24.（答案不唯一）如：3xy.2222三、1. 3xy与?4xy，-2与3，4m与－m，5xy与?6xy，?ab与ba22. ①④是同类项;②③不是同类项，因为不符合同类项的条件：相同的字母的指数相同；3、(1)-a，(2)4x2y．2.2整式加减（二）一、1. D2. C3. A.二、1. ?2a2b2、3x与-x , -2xy与2xy,2x+y 3. ?2x3?3x2?5x?14. 8三、1. (1)原式??3x?4x????2y?3y??1??x?y?1(2)解：原式??a2?2a2???4a?3a?a??3?1=(a—２a)＝?a2＋２2. 原式?(3a2b?5a2b)?(?4ab2?4b2a)?（5?3）?8 a2b?212222当a??，b=3时，原式?8 ab?2?8???1??3?2?8???2?23.（1）?a?2?(2) ?a?n?1?（3）若a＝20，n＝26，则礼堂可容纳人数为：(2a?n?1)n2=(2?20?26?1)?262=845（人）2.2整式加减（三）一、1. C2. D3. A.二、1. ①4a?2b?3c,②?x?2?3y?15z2. ?2x2?2y23.13a4. 6x-3三、1.(1)原式?4n?6m?2m?3n??4n?3n??(?6m?2m)?7n?8m(2)原式?x?2y?1?6x?3y?6??5x?y?72.-1 3. 原式=3x2-y+2y2-x2-x2-2y2 =(3x2- x2- x2)+(2 y2-2 y2)-y= x2-y当x＝1，y＝－2时，原式=x?y?1?(?2)?3 2.2整式加减（四）一、1. C2. C3. B.二、1. (8a-8) 2. 63. 24. 1三、1. A-2B=（x?2xy?6y）?2（x?xy?3y）= x?2xy?6y-2x?2xy?6y=-x 2. 依题意有：（ab?3bc?4ac）-2（2ab?3bc?ac）=ab?3bc?4ac?4ab?6bc?2ac?a?c3. m=-4?(ab?4ab)?(?3bc?6bc)?(4ac?2c3ab?3bc?6a 2222222222。

初一数学练习册答案北师版

初一数学练习册答案北师版【练习一：有理数的加减法】1. 计算下列各题：- (1) 3 + (-2) = 1- (2) (-4) + 5 = 1- (3) 8 + (-7) = 12. 判断下列各题的正负：- (1) 6 - 9 = -3，结果为负数。

- (2) 7 + (-5) = 2，结果为正数。

3. 解决实际问题：- 某商店一天的收入为500元，支出为300元，求净收入。

净收入 = 500 - 300 = 200元。

【练习二：有理数的乘除法】1. 计算下列各题：- (1) (-3) × 5 = -15- (2) 4 × (-6) = -24- (3) (-2) × (-1) = 22. 判断下列各题的正负：- (1) (-3) × (-4) = 12，结果为正数。

- (2) 5 × (-2) = -10，结果为负数。

3. 解决实际问题：- 某工厂原计划生产零件800个，实际生产了1200个，求超产的百分比。

超产百分比 = (1200 - 800) / 800 × 100% = 50%。

【练习三：有理数的混合运算】1. 计算下列各题：- (1) 21 ÷ (-7) - 3 × 2 = -3 - 6 = -9- (2) 4 + 8 ÷ (-2) = 4 - 4 = 02. 解决实际问题：- 某学生原计划每天学习4小时，实际每天学习了6小时，求实际学习时间比计划多的百分比。

多出的百分比 = (6 - 4) / 4 × 100% = 50%。

【练习四：代数式】1. 根据题目所给的代数式，求值：- 代数式：3x + 2y- 已知 x = 2, y = 3- 代入求值：3 × 2 + 2 × 3 = 6 + 6 = 122. 解决实际问题：- 某商品原价为100元，打8折后的售价是多少？- 售价= 100 × 0.8 = 80元。

初中数学七年级上册练习册(精品)

初中数学七年级上册练习册初中数学练习册七年级（上）人教版目录：第一章有理数1。

１有理数的概念1。

２有理数的运算1.３近似数与科学计数法1。

４单元测试第二章整式加减2.1 整式的加减２.2 单元测试第三章一元一次方程3．1 解一元一次方程3.２列方程解应用题(一）３。

３列方程解应用题（二) 3．4 单元测试第四章图形认识初步4.1 多姿多彩的图形4。

２平面图形4.3 单元测试期末模拟试卷(一)期末模拟试卷（二)期末模拟试卷（三)第一章有理数知识清单一、全章知识结构二、回顾正数、负数的意义及表示方法1、正数的表示方法:a>0,2、负数的表示方法：a<0三、有理数的分类定义：整数和分数统称为有理数有限小数和无限循环小数都是有理数而无限不循环小数却不是有理数1、按整数分数分类2、按数的正负性分类⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数负整数负数零正分数正整数正数有理数.3、在数轴上分类数轴：规定了原点，正方向和单位长度的直线叫做数轴。

数轴的作用：（１）用数轴上的点表示有理数；(2）在数轴上比较有理数的大小;⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数..（3）可用数轴揭示一个数的绝对值和互为相反数的几何意义;（4)在数轴上可求任意两点间的距离：两点间的距离=｜ｘ—ｙ|=｜ｙ－x｜四、有理数中具有特殊意义的数：相反数、倒数、绝对值、非负数1、相反数:（1）几何意义：在数轴上表示一对相反数的两个点与原点的距离相等。

（２）代数意义：只有符号不同的两个数。

（3)互为相反数的特性：a＋b=０,0的相反数是0.（4）会求一个数的相反数：a的相反数为a-b的相反数为2、倒数:（1)乘积是１的两个数互为倒数（2)互为倒数的特性: ab＝１，（3)0没有倒数（４）互为负倒数：乘积是－1的两个数互为负倒数; ab=-13、非负数：(1）就是大于或等于0的数：a 0（2）数轴上，在原点的右边包括原点的点表示的数(3）任何数的平方数都是非负数（4）非正数：就是小于或等于０的数：ａ≤0 （5）数轴上，在原点的左边包括原点的点表示的数4、绝对值：(学生演示) (1）几何意义：一个数的绝对值就是它到原点的距离。