太阳黑子周期matlab仿真
-Lyapunov指数的计算方法

【总结】Lyapunov指数的计算方法非线性理论近期为了把计算LE的一些问题弄清楚,看了有7~9本书!下面以吕金虎《混沌时间序列分析及其应用》、马军海《复杂非线性系统的重构技术》为主线,把目前已有的LE计算方法做一个汇总!1. 关于连续系统Lyapunov指数的计算方法连续系统LE的计算方法主要有定义方法、Jacobian方法、QR分解方法、奇异值分解方法,或者通过求解系统的微分方程,得到微分方程解的时间序列,然后利用时间序列(即离散系统)的LE求解方法来计算得到。
关于连续系统LE的计算,主要以定义方法、Jacobian方法做主要介绍内容。
(1)定义法定义法求解Lyapunov指数.JPG关于定义法求解的程序,和matlab板块的“连续系统LE求解程序”差不多。
以Rossler系统为例Rossler系统微分方程定义程序function dX = Rossler_ly(t,X)% Rossler吸引子,用来计算Lyapunov指数% a=0.15,b=0.20,c=10.0% dx/dt = -y-z,% dy/dt = x+ay,% dz/dt = b+z(x-c),a = 0.15;b = 0.20;c = 10.0;x=X(1); y=X(2); z=X(3);% Y的三个列向量为相互正交的单位向量Y = [X(4), X(7), X(10);X(5), X(8), X(11);X(6), X(9), X(12)];% 输出向量的初始化,必不可少dX = zeros(12,1);% Rossler吸引子dX(1) = -y-z;dX(2) = x+a*y;dX(3) = b+z*(x-c);% Rossler吸引子的Jacobi矩阵Jaco = [0 -1 -1;1 a 0;z 0 x-c];dX(4:12) = Jaco*Y;求解LE代码:% 计算Rossler吸引子的Lyapunov指数clear;yinit = [1,1,1];orthmatrix = [1 0 0;0 1 0;0 0 1];a = 0.15;b = 0.20;c = 10.0;y = zeros(12,1);% 初始化输入y(1:3) = yinit;y(4:12) = orthmatrix;tstart = 0; % 时间初始值tstep = 1e-3; % 时间步长wholetimes = 1e5; % 总的循环次数steps = 10; % 每次演化的步数iteratetimes = wholetimes/steps; % 演化的次数mod = zeros(3,1);lp = zeros(3,1);% 初始化三个Lyapunov指数Lyapunov1 = zeros(iteratetimes,1); Lyapunov2 = zeros(iteratetimes,1); Lyapunov3 = zeros(iteratetimes,1);for i=1:iteratetimestspan = tstart:tstep:(tstart + tstep*steps); [T,Y] = ode45('Rossler_ly', tspan, y);% 取积分得到的最后一个时刻的值y = Y(size(Y,1),:);% 重新定义起始时刻tstart = tstart + tstep*steps;y0 = [y(4) y(7) y(10);y(5) y(8) y(11);y(6) y(9) y(12)];%正交化y0 = ThreeGS(y0);% 取三个向量的模mod(1) = sqrt(y0(:,1)'*y0(:,1));mod(2) = sqrt(y0(:,2)'*y0(:,2));mod(3) = sqrt(y0(:,3)'*y0(:,3));y0(:,1) = y0(:,1)/mod(1);y0(:,2) = y0(:,2)/mod(2);y0(:,3) = y0(:,3)/mod(3);lp = lp+log(abs(mod));%三个Lyapunov指数Lyapunov1(i) = lp(1)/(tstart);Lyapunov2(i) = lp(2)/(tstart);Lyapunov3(i) = lp(3)/(tstart);y(4:12) = y0';end% 作Lyapunov指数谱图i = 1:iteratetimes;plot(i,Lyapunov1,i,Lyapunov2,i,Lyapunov3)程序中用到的ThreeGS程序如下:%G-S正交化function A = ThreeGS(V) % V 为3*3向量v1 = V(:,1);v2 = V(:,2);v3 = V(:,3);a1 = zeros(3,1);a2 = zeros(3,1);a3 = zeros(3,1);a1 = v1;a2 = v2-((a1'*v2)/(a1'*a1))*a1;a3 = v3-((a1'*v3)/(a1'*a1))*a1-((a2'*v3)/(a2'*a2))*a2;A = [a1,a2,a3];计算得到的Rossler系统的LE为———— 0.063231 0.092635 -9.8924Wolf文章中计算得到的Rossler系统的LE为————0.09 0 -9.77需要注意的是——定义法求解的精度有限,对有些系统的计算往往出现计果和理论值有偏差的现象。
基于MATLAB的太阳黑子时间序列与仿真

2012.326 基于MATLAB 的太阳黑子时间序列分析与仿真周园 肖洪祥 董俊飞桂林理工大学信息科学与工程学院 广西 541004摘要:本文研究了时间序列的分析方法,具体分析了基于最大Lyapunov 指数的方法在太阳黑子时间序列分析中的应用。
介绍利用MATLAB 对太阳黑子时间序列进行分析与仿真的方法,并给出相关的流程、程序和相应的仿真结果。
最终证明太阳黑子时间序列是一个混沌时间序列。
关键词:混沌时间序列;最大Lyapunov 指数;太阳黑子数;仿真0 引言在非线性系统中,初始条件的微小变化,往往会导致结果以指数级的大小发生分离,这时我们称这个系统存在混沌。
时间序列是非线性动力系统的一种模型。
如果时间序列对初始条件敏感,采用传统线性时间序列分析方法将很难予以分析,因此传统时间序列预测模型对混沌时间序列的拟合和预测准确度都很差。
经过混沌学的发展,可以使用序列本身的规律对其进行预测。
Lyapunov 指数法即是其中之一。
通过最大Lyapunov 指数的数值,可以判断一个时间序列是否是混沌时间序列,亦即该非线性系统中是否存在着混沌。
本文对太阳黑子序列进行分析,证明其是一个混沌时间序列。
1 基于Lyapunov 指数的时间序列分析方法对时间序列进行分析,首先必须进行相空间重构。
根据有限的数据重构吸引子以研究系统动力行为的方法即是相空间重构。
主要思想为:系统中每个分量的演化皆是由与之联系的其他分量所决定的,相关分量的信息隐含在任意其他分量的变化过程中,即是运用系统的任何一个观察量可以重构出整个系统的模型。
设时间序列为{}t x ,其中1,2,...,t N =。
重构相空间mR 的元素组为:(1)(,,)(,,...,),T=1,2,3,...,T T T T m X m N X X X p τττ++-= (1)其中,N 为重构相空间维数;τ为延迟时间间隔数,且为正整数;(1)p N m τ=--为时间序列嵌入相空间的向量数,N 为时间序列的数据点数。
MATLAB太阳黑子活动周期

2021/10/10
6
• 1、将望远镜极轴大致对准北极,镜筒指向太阳,观察 镜筒的影子,当影子最小时,说明太阳已经大致对好。
• !!!请注意,千万不能用眼睛通过望远镜直接寻找太 阳,寻星镜也最好不要加装。
• 2、记录透明度、宁静度、云量、描图开始时间等观测 背景数据。关于宁静度和透明度的规定是这样的:范围 是0-5最好是5,最差是0,一般都要在2.5以上才可以观 测。宁静度与风有关,一般4级以下可以定为3。透明度 与污染等有关,取值看经验了。
2021/10/10
19
2021/10/10
20
(3) 功率与频率的关系曲线则被定义为周期图。 用周期图法对Wolfer数进行功率谱密度分析。 程序:figure n=length(Y);%取FFT结果长度为n power = abs(Y(1:n/2)).^2; %取前n/2个数据求其 功率
nyquist = 1/2; %取最大频率为0.5 freq = (1:n/2)/(n/2)*nyquist; %将FFT转换为DTFT
title('Sunb Data') %标注横纵坐标和标题
• pause
2021/10/10
15
2021/10/10
16
• 为清楚起见,画出部分时间段(如实验中采 取最近50年)的Wolfer 图进行观察。程序 如下:
• figure
• plot(year(261:311),wolfer(261:311),'b .-'); %用进50年数据做图
text(period(index)+2,power(index),['Period = ',mainPeriodStr]);%文字标注该点 hold off;
基于Matlab的光学实验仿真

基于Matlab的光学实验仿真一、本文概述随着科技的快速发展,计算机仿真技术已成为科学研究、教学实验以及工程应用等领域中不可或缺的一部分。
在光学实验中,仿真技术能够模拟出真实的光学现象,帮助研究者深入理解光学原理,优化实验设计,提高实验效率。
本文旨在探讨基于Matlab的光学实验仿真方法,分析Matlab在光学实验仿真中的优势和应用,并通过具体案例展示其在光学实验仿真中的实际应用效果。
通过本文的阐述,读者将能够了解Matlab在光学实验仿真中的重要作用,掌握基于Matlab的光学实验仿真方法,从而更好地应用仿真技术服务于光学研究和实验。
二、Matlab基础知识Matlab,全称为Matrix Laboratory,是一款由美国MathWorks公司出品的商业数学软件,主要用于算法开发、数据可视化、数据分析以及数值计算等领域。
Matlab以其强大的矩阵计算能力和丰富的函数库,在光学实验仿真领域具有广泛的应用。
Matlab中的变量无需预先声明,可以直接使用。
变量的命名规则相对简单,以字母开头,后面可以跟字母、数字或下划线。
Matlab支持多种数据类型,包括数值型(整数和浮点数)、字符型、逻辑型、结构体、单元数组和元胞数组等。
Matlab的核心是矩阵运算,它支持多维数组和矩阵的创建和操作。
用户可以使用方括号 [] 来创建数组或矩阵,通过索引访问和修改数组元素。
Matlab还提供了大量用于矩阵运算的函数,如矩阵乘法、矩阵转置、矩阵求逆等。
Matlab具有强大的数据可视化功能,可以绘制各种二维和三维图形。
在光学实验仿真中,常用的图形包括曲线图、散点图、柱状图、表面图和体积图等。
用户可以使用plot、scatter、bar、surf和volume 等函数来创建这些图形。
Matlab支持多种控制流结构,如条件语句(if-else)、循环语句(for、while)和开关语句(switch)。
这些控制流结构可以帮助用户编写复杂的算法和程序。
太阳黑子MATLAB

附参考程序:装载太阳黑子的数据程序如下:load sunspot.dat; %这组数据记录了在过去的288年(1700-1987年)间每年太阳黑子出现的数量和大小的观测数据。
绘制Wolfer图的程序如下:year=sunspot(:,1); wolfer=sunspot(:,2);plot(year,wolfer);xlabel('Years');ylabel(' Sunspot Data ')title('Sunspot Data')求Wolfer数的FFT程序如下:Y = fft(wolfer);在复平面上绘制由Y给出的傅立叶系数的分布图程序如下:Y(1)=[ ];plot(Y,'ro')title('Fourier Coefficients in the Complex Plane');xlabel('Real Axis');ylabel('Imaginary Axis');set(gca,'YTick',[],'XTick',[]);Wolfer数的周期图程序如下:n=length(Y);power = abs(Y(1:n/2)).^2;nyquist = 1/2;freq = (1:n/2)/(n/2)*nyquist;plot(freq,power)xlabel('cycles/year')title('Periodogram')% 加载.据load sunspot.datyear=sunspot(:,1);relNums=sunspot(:,2);plot(year,relNums)title(‘太阳黑子wolfer图’)xlabel(‘年份’);ylabel(‘太阳黑子数量’ );year=sunspot(:,1);%从数据中读取年份的相关信息wolfer=sunspot(:,2);%从数据中读取关于黑子出现数量的相关信息plot(year,wolfer,'-c');%绘制太阳黑子Wolfer图title('太阳黑子Wolfer图');grid on;hold on;% 前五⼗十年的数据figure(1);plot(year(1:50),relNums(1:50),'c.-');xlabel('Year')hold on;% 将头⼗一个Y的值省略Y = fft(relNums);Y(1)=[];%在复平⼗面中进.行复平⼗面figure(2);plot(Y,'bo')title('在复平⼗面傅里叶系数’);xlabel('Real Axis');ylabel('Imaginary Axis');hold on;Y = fft(wolfer);Y(1)=[ ];%去掉Y的第一个数据plot(Y,'yo')%在复平面上绘制由Y给出的傅立叶系数的分布图 title('傅里叶系数分布图');xlabel('实数轴');ylabel('虚数轴');set(gca,'YTick',[],'XTick',[]);%将功率⼗比频率定义为”preiodogram”,也就是周期图,并显示。
matlab仿真实验报告

matlab仿真实验报告Matlab仿真实验报告引言:Matlab是一种广泛应用于科学和工程领域的数值计算软件,它提供了强大的数学和图形处理功能,可用于解决各种实际问题。
本文将通过一个具体的Matlab 仿真实验来展示其在工程领域中的应用。
实验背景:本次实验的目标是通过Matlab仿真分析一个电路的性能。
该电路是一个简单的放大器电路,由一个输入电阻、一个输出电阻和一个放大倍数组成。
我们将通过Matlab对该电路进行仿真,以了解其放大性能。
实验步骤:1. 定义电路参数:首先,我们需要定义电路的各个参数,包括输入电阻、输出电阻和放大倍数。
这些参数将作为Matlab仿真的输入。
2. 构建电路模型:接下来,我们需要在Matlab中构建电路模型。
可以使用电路元件的模型来表示电路的行为,并使用Matlab的电路分析工具进行仿真。
3. 仿真分析:在电路模型构建完成后,我们可以通过Matlab进行仿真分析。
可以通过输入不同的信号波形,观察电路的输出响应,并计算放大倍数。
4. 结果可视化:为了更直观地观察仿真结果,我们可以使用Matlab的图形处理功能将仿真结果可视化。
可以绘制输入信号波形、输出信号波形和放大倍数的变化曲线图。
实验结果:通过仿真分析,我们得到了以下实验结果:1. 输入信号波形与输出信号波形的对比图:通过绘制输入信号波形和输出信号波形的变化曲线,我们可以观察到电路的放大效果。
可以看到输出信号的幅度大于输入信号,说明电路具有放大功能。
2. 放大倍数的计算结果:通过对输出信号和输入信号的幅度进行计算,我们可以得到电路的放大倍数。
通过比较不同输入信号幅度下的输出信号幅度,可以得到放大倍数的变化情况。
讨论与分析:通过对实验结果的讨论和分析,我们可以得出以下结论:1. 电路的放大性能:根据实验结果,我们可以评估电路的放大性能。
通过观察输出信号的幅度和输入信号的幅度之间的比值,可以判断电路的放大效果是否符合设计要求。
(完整版)光伏发电的MATLAB仿真

(完整版)光伏发电的MATLAB仿真⼀、实验过程记录1.画出实验接线图图1 实验接线图图2 光伏电池板图3 实验接线实物图2.实验过程记录与分析(1)给出实验的详细步骤○1实验前根据指导书要求完成预习报告○2按预习报告设计的实习步骤,利⽤MATLAB建⽴光伏数学模型,如下图4所⽰。
图4 光伏电池模型其中PV Array模块⾥⼦模块如下图5所⽰。
图5 PV Array模型其中Iph,Uoc,Io,Vt⼦模块如下图6-9所⽰。
图6Iph⼦模块图7Uoc⼦模块图8 Io⼦模块图9Vt⼦模块○3在光伏电池建模的基础上,输⼊实际光伏电池参数值,研究不同光照强度下、不同温度下光伏电池的I-V、P-V特性曲线,并得出结论。
○4设计光伏电池测试平台,在不同光照、温度情况下测试光伏电池输出电压、输出电流值,对实测数据进⾏处理并加以分析,记录实际光伏电池的I-V、P-V特性曲线,与仿真结果进⾏对⽐,得出有意义的结论。
○5确定电⼒变换电路拓扑结构,设计电路中的相关参数值,通过MATLAB搭建电路并仿真分析,搭建电路如图10所⽰。
图10离⽹型光伏发电系统○6确定系统MPPT控制策略,建⽴MPPT模块仿真模型,并仿真分析。
系统联调,调节离⽹型光伏发电系统的电路和控制参数值,仿真并分析最⼤功率跟踪控制效果。
(2)记录实验数据表1当T=290K时S=1305W/m2时的测试数据表2当T=287K时S=1305W/m2时的测试数据表3当T=287K时S=1278W/m2时的测试数据⼆、实验结果处理与分析1.实验数据的整理和选择使⽤MATLAB软件其中的simulink⼯具进⾏模型的搭建。
再对其进⾏仿真,得到仿真曲线。
使⽤Excel表格输⼊实验所测得U、I、P,在对其⾃动⽣成I-V,P-V曲线。
2.绘制不同光照强度下、不同温度下光伏电池的I-V、P-V特性曲线;图11 I-V曲线图12 P-V曲线当T=290K时S=1305W/m2时的测拟合曲线图13 I-V曲线图14 P-V曲线当T=287K时S=1305W/m2时的拟合曲线图15 I-V曲线图16 P-V曲线当T=287K时S=1278W/m2时的拟合曲线3.所得实验数值和预习所得理论值⽐较,进⾏实验结果的误差分析所得实验数值和预习所得理论值⽐较,仿真波形开路电压均⽐实验所得的开路电压⼤,仿真波形最⼤功率也⽐实验所得最⼤功率⼤,所取得最⼤功率值对应的电压值也是仿真时⽐实验时的⼤,造成这个现象的原因有以下⼏点:(1)由于天⽓原因,真实测试环境的光照强度有些不稳定,前后变化幅度明显,这也导致了⼀部分的误差。
matlab仿真实验总结

matlab仿真实验总结摘要:本文旨在介绍基于Matlab的仿真实验,从基本的Matlab 代码编写开始,到分析参数变化的影响,再到定量分析实验结果。
实验结果表明,通过Matlab的仿真实验,可以很容易地理解模型的参数变化对模型性能的影响,并对模型调整做出科学决策。
关键词:Matlab;仿真实验;参数变化;定量分析Matlab仿真实验总结一、实验目标1、掌握Matlab基本的语法、操作和使用;2、掌握利用Matlab进行模型仿真及参数调优的基本方法;3、熟悉Matlab程序运行过程,熟悉Matlab调试程序的基本方法;4、通过程序仿真实验,了解系统及模型的基本特性,定性分析及定量分析系统特性;二、实验内容1、基于Matlab的程序编写:(1)建立Matlab编辑器环境,熟悉编辑环境基本操作;(2)了解Matlab程序编写的基本方法,熟悉调试Matlab程序的基本方法;(3)编写模型仿真程序。
2、Matlab仿真实验:(1)分析仿真实验结果,收集数据;(2)定性分析实验结果,观察参数变化对结果的影响;(3)计算参数变化后的结果,定量分析实验结果;(4)将实验结果以图形的形式展示,完成Matlab仿真实验报告。
三、实验结果通过本次Matlab仿真实验,可以得出:1、通过Matlab的仿真实验,可以很容易地理解模型的参数变化对模型性能的影响,从而有效地进行模型调整;2、可以定量分析实验结果,从而更好地进行科学决策;3、Matlab操作安全,程序编写简单实用,可以有效地减少实验工时。
四、实验总结本次Matlab仿真实验对于掌握Matlab程序编写及仿真实验的基本方法,了解实验结果的定性及定量分析等方面有着很大的帮助,为今后更深入的Matlab程序及仿真研究打下了基础。
MATLAB仿真与建模中常见问题与解决方法

MATLAB仿真与建模中常见问题与解决方法引言MATLAB作为一种功能强大的数学软件平台,被广泛应用于科学研究、工程设计等领域。
然而,在进行MATLAB仿真和建模过程中,常常会遇到一些问题和困惑。
本文将针对这些常见问题,提供一些解决方法和建议,帮助读者更好地应对挑战。
1. 数据处理问题在仿真和建模过程中,数据处理是一个常见的问题。
首先,当我们从实验中获得大量数据时,如何进行处理和分析就成为一个关键问题。
MATLAB提供了各种强大的数据处理函数,例如mean、std、histogram等,可以帮助我们对数据进行统计和可视化分析。
此外,MATLAB还提供了数据拟合函数和插值函数,可以对数据进行拟合和补全。
另一个常见的数据处理问题是数据噪声的处理。
在实际应用中,测量数据常常存在噪声,这会对仿真和建模结果产生影响。
为了解决这个问题,我们可以使用滤波器函数来降低噪声的影响。
MATLAB中常用的滤波器函数有移动平均滤波器和中值滤波器等。
2. 优化问题在一些实际应用中,我们需要对模型进行优化,以找到最优解。
MATLAB提供了一些优化算法和工具箱,可以帮助我们解决这个问题。
一种常见的优化算法是遗传算法,它模拟了自然界的进化过程,通过遗传操作来搜索最优解。
MATLAB中的Global Optimization Toolbox提供了遗传算法的实现。
此外,MATLAB还提供了其他优化算法,如线性规划、非线性规划和整数规划等。
通过选择合适的算法和设置适当的优化目标,我们可以得到满意的优化结果。
3. 建模问题在建模过程中,我们常常需要选择适当的模型和参数来描述系统。
这需要一定的经验和技巧。
MATLAB提供了一些建模工具和函数,可以帮助我们更好地处理这个问题。
首先,MATLAB中的Curve Fitting Toolbox提供了各种曲线拟合函数,如线性拟合、多项式拟合和非线性拟合等。
通过选择合适的模型和调整参数,我们可以将实验数据拟合成理想的曲线。
利用Matlab仿真波动光学实验

利用Matlab仿真波动光学实验∗李珏璇;蓝海江【摘要】通过干涉、衍射实验实例,探讨利用 Matlab 仿真波动光学实验的方法及其仿真结果在教学中的作用。
实践表明,在波动光学教学过程中,适当地穿插一些利用Matlab仿真的实验及其结果,能让学生快速地观察到细微复杂而且不易操作和控制的实验现象,对教学质量的提高能起到事半功倍的效果。
%Through the examples of interference and diffraction experiments,we mainly discuss the meth-ods of simulations for the wave optics experiments using Matlab and the teaching effects by using these sim-ulation results.The practice shows that,in the teaching of wave optics,if we use some simulation experi-ments using Matlab and its results properly,the students will observe the experiment phenomenon which is not only tiny,complex but also difficult to handle and control very fast,so it will get half the work with double results of the improvement of teaching qualities.【期刊名称】《湘潭大学自然科学学报》【年(卷),期】2014(000)004【总页数】5页(P90-94)【关键词】波动光学;干涉实验;衍射实验;Matlab;仿真【作者】李珏璇;蓝海江【作者单位】广西师范大学物理科学与技术学院,广西桂林 541004; 柳州师范高等专科学校物理与信息科学系,广西柳州 545004;柳州师范高等专科学校物理与信息科学系,广西柳州 545004【正文语种】中文【中图分类】TP391.41两束电磁波的干涉是彼此振动的电场强度矢量叠加的结果,光的干涉是光子自身的几率幅叠加的结果,两列或几列光波在空间相遇时相互叠加,在一些区域始终加强,在另一些区域则始终削弱,形成稳定的强弱分布的现象,在现实生活中是可见到的,例如:阳光下五彩缤纷的肥皂泡,雨后公路边水面上漂浮的薄层油膜的彩色条纹,高温处理后的金属表面呈现的美丽蓝色.而光的衍射是指光在空间传播遇到障碍物时,光的直线传播定律、反射定律和折射定律不再成立,光进入几何阴影区,并在屏幕上出现弥漫的光强不均匀分布的现象.一切波都能发生衍射,但在现实生活中光的衍射现象是不明显的,通常情况下不易为人们所觉察.干涉、衍射是波的特有现象.由于受到实验仪器、时间和场地等条件的限制,在传统的光学教学与实验中,部分理论知识的实验没有明显的现象,有些理论知识甚至难以在实验中得到真实地再现[1],而利用一些软件进行仿真,则可真实地再现这些实验现象.大量的实践证明,在波动光学教学中,利用软件对光的干涉、衍射现象进行仿真,能为了解、认识、研究光的波动现象、光的性质提供良好的平台[2~7],而且在自然条件下,产生干涉、衍射的光大部分都是白光,所以用白光进行仿真更接近自然.我们的工作就是利用Matlab软件通过建模和编程对白光等色光的干涉、衍射现象进行仿真,以获得实际实验不易实现的各种光学现象.1 运用定量分析法研究实验参数对仿真结果的影响1.1 经典白光干涉、衍射实验的Matlab仿真在经典的干涉、衍射实验的仿真中,多数作者[8,9]采用单色光,少数作者[10]采用非单色光进行仿真,但其仿真的结果不尽人意.我们把日光分割成2 000份色光,然后利用Matlab软件对经典的干涉、衍射现象进行仿真.1.1.1 日光圆孔衍射实验的Matlab仿真夫琅和费圆孔衍射实验衍射屏上任一点P(x,y)的光强为I(P)=I0[J1(2m)/m]2,(1)式中I0为衍射屏中心点P0的光强,J1(s)为一阶贝塞尔函数,m=(πRsin θ)/λ,R 为衍射孔的半径,为透镜的焦距,λ为色光的波长.依据式(1)即可仿真日光夫琅和费圆孔衍射实验,仿真结果如图1所示[11].1.1.2 日光单缝衍射实验的Matlab仿真夫琅和费单缝衍射实验的衍射屏上任一点P(x,y)的光强为I(P)=I0((sin α)/α)2,(2)式中α=πasin θ/λ,a为单缝宽度,sin θ≈x/f.依据式(2)即可仿真日光夫琅和费单缝衍射实验,仿真结果如图2所示.1.1.3 日光杨氏双缝干涉实验若两束色光的光强相等,则双缝干涉实验的干涉屏上任一点P(x,y)的光强为I(P)=4I0cos2(φ/2),(3)式中,I0为单缝的光强;φ=2πdsin θ/λ,为两缝光源的相位差;d为双缝的间距;sin θ≈x/D,x轴与缝的方向垂直,D为双缝到干涉屏的距离.依据式(3)即可仿真日光双缝干涉实验,仿真结果如图3所示[11].1.1.4 日光光栅衍射实验的Matlab仿真设平面光栅有N个单元,每个单元的透光缝宽为a,光栅常数为d,则夫琅和费光栅衍射实验的衍射屏上任一点P(x,y)的光强为(4)式中I0为单缝衍射情况下P0点的光强;α=πasin θ/λ,φ=πdsin θ/λ.依据式(4)即可仿真日光夫琅和费光栅衍射实验,仿真结果如图4所示[12].从图1~图4可知:在仿真实验中,由于仿真光源是2 000份色光,所以仿真图像体现出可见光波段波长连续变化的干涉、衍射现象,并且图像细腻、逼真.1.2 影响仿真结果的参数利用Matlab仿真波动光学实验,可便捷地调节各种实验参数.分别调小夫琅和费圆孔衍射实验的透光孔、夫琅和费单缝衍射实验的透光缝、杨氏双缝干涉实验透光缝的间距,可得到如图1(b)、图2(b)的仿真图像;而调小光栅衍射实验透光的缝宽、光栅常数和光栅的单元数,则可得到如图3(b)、(c)、(d)所示的仿真图像.从以上图像可知:在波长不变的情况下,夫琅和费圆孔衍射实验的透光孔、单缝衍射实验的透光缝变小,杨氏双缝干涉实验透光缝的间距变小时,中央明条纹的光强变弱,但明条纹的宽度增加.在光栅衍射实验中,当光栅透光的缝宽变小时,次级衍射条纹变亮;而当光栅常数变小时,彩色的衍射明条纹会变宽.为了更直观地了解波长对仿真实验的影响,可采用不同的单色光作为光源.以杨氏双缝干涉实验为例,在缝间距不变时,用红光和蓝光进行仿真,图像如图5所示. 由图5可知:当缝宽不变时,波长越长,干涉条纹及条纹的间距越宽.2 巧用仿真图像展现波动光学的特殊现象2.1 光栅衍射中的缺级现象在光栅衍射光强分布中,同时存在干涉因子和衍射因子.在衍射图像中,干涉形成明纹的条件为:dsin θ=±kλ,k=1,2,3… .(5)衍射形成暗纹的条件为:asin θ=±k′λ ,k′=1,2,3….(6)衍射角相同时,若干涉明纹的位置恰好与衍射暗纹的位置重合,则会发生缺级现象,即对应级次的干涉主极大缺失.由式(5)和式(6)可得k/k′=d/a.(7)若光栅常数d是缝宽a的3倍,当k′=1时,k=3,即第3级干涉主极大缺失;当k′=2时,k=6,即第6级干涉主极大缺失.图6为黄光(λ=570 nm)光栅衍射实验缺级现象的仿真结果.结果与理论一致.2.2 可见光谱的互补色现象在可见光中,色彩中的互补色有红色与绿色互补、蓝色与橙色互补、紫色与黄色互补等.要观察光的互补色现象,可通过等厚干涉现象仿真实验图像进行研究.图7为在平凸透镜的半径不变(R=4 m)的情况下,白光透、反射光牛顿环干涉实验的仿真结果.为了便于比较,我们把透射光的牛顿环干涉仿真图(图7(a))和反射光的牛顿环干涉仿真图(图7(b)),各取一半放在一起组合成为一个图,如图7(c)所示[13].由图7可知,在离接触点O为中心、半径为r的同心圆中,透射光和反射光的牛顿环干涉条纹的颜色完全不同,白环与黑环对应,红环与青环对应,蓝环与黄环对应,绿环与品红环对应,由此证实了光谱的色光互补原则:蓝光+黄光=白光,绿光+品红光=白光,红光+青光=白光,即蓝光与黄光互补,绿光与品红光互补,红光与青光互补.2.3 研究光的干涉与衍射现象的联系与区别光的干涉和衍射现象都是光波所特有的现象,都表现为光在遇到障碍物之后出现光的强度或明暗的稳定分布现象,但如何区分它们从理论上不易理解,可以以双缝衍射和双缝干涉为例,利用Matlab仿真实验进行讨论.以绿光(λ=550 nm)为光源,双缝衍射实验的仿真结果如图8所示,双缝干涉实验的仿真结果如图9所示.由图8和图9可知:双缝衍射实验衍射条纹与双缝干涉实验的干涉条纹是不同的,衍射条纹是中央亮纹最亮,两侧亮纹具有对称性而且亮度逐渐变暗;干涉条纹是等间距明暗相间的均匀条纹.图8为双缝干涉受单缝衍射调制现象.图9为纯双缝干涉现象,是透光缝宽变为无限窄(此时,透过干涉屏的光束的衍射效应可忽略)时,由衍射变为干涉的现象,因此,干涉是衍射的特殊情况.在多数实验中干涉和衍射是同时存在的,衍射对干涉的调制主要反映在光强的分布上,这就是干涉和衍射的联系与区别.3 不同衍射孔衍射实验的仿真3.1 夫琅和费双矩孔衍射实验仿真夫琅和费双矩孔衍射的光强分布.夫琅和费双矩孔衍射观察屏上任一点P(x,y)的光强为[6~8]I(P)=I0(sin α/α)2(sin β/β)2cos2(γ),(8)式中I0为观察屏中心点P0的光强,α=πasin θx/λ,β=πbsin θy/λ,γ=πcsin θx/λ.a、b分别为矩孔的宽(平行于x轴,x轴为双矩孔的排列方向)和高(平行于y 轴),c为双矩孔中心的间距,λ为光波的波长.在傍轴近似条件下,sin θx≈x/f,sin θy≈y/f,f为透镜的焦距.根据式(8)即可得到夫琅和费双矩孔衍射的仿真图像,如图10所示[9].3.2 夫琅和费单矩孔衍射实验仿真若矩孔长为a(沿x方向)、宽为b(沿y方向),矩孔后面的会聚透镜的焦距为f,有一波长为λ的平行光正入射到矩孔上,衍射屏上任一点p(x,y)的光强为I(x,y)=I0(sin α/α)2(sin β/β)2 ,(9)式中α≈(axπ)/(λf),β≈(byπ)/(λf).根据式(9)即可得到夫琅和费单矩孔衍射的衍射图像,如图11所示[15].从光强分布公式(8)、(9)以及图10、11的仿真结果可知,双矩孔衍射的光强为单矩孔衍射的光强与双光束干涉因子(cos2(γ))的乘积,单矩孔衍射是双矩孔衍射的一个特例. 3.3 日光双孔干涉实验的仿真设两束色光的光强相等,则双孔干涉实验的干涉屏上任一点P(x,y)的光强为[8](10)式中,I0为单孔的光强;轴与双孔的连线平行,d为双孔的间距,D为双孔到干涉屏的距离;波数k=2π/λ,λ为色光的波长.依据式(10)即可得到如图12所示的仿真结果 (仿真参数d=10 μm,D=0.25 m).4 结论利用Matlab仿真光的干涉和衍射等波动光学实验,可真实地再现实验室较难完成甚至不能完成的实验,而且大大地节约时间和经费;在仿真实验中,通过调节实验参数,就可得到不同的实验图像,可运用这种方法研究各实验参数对仿真实验的影响;同时,巧妙运用不同的仿真图像,可认识波动光学的一些特殊现象,即可用最简单的图像方法描述抽象的光现象.参考文献[1] 翟海瑛,李玉春,杨瑞,等.光学虚拟实验系统研究[J].光学技术,2012,38(4):447-450.[2] 唐锋意,张翼,赵瑞,等.大学物理仿真实验在民族医学院校中的应用浅谈[J].物理实验,2011,30(2):31-33.[3] 吕太国.干涉和衍射的联系与区别[J].物理与工程,2010,20(1):19-20.[4] 李多,景红梅,平澄,等.六角孔的夫琅禾费衍射场的实验演示[J].物理实验,2010,30(6):5-7.[5] 杨磊,王志兰,刘杰,等.基于光的波粒二象性猜想的数学建模与仿真[J].数学的实践与认识,2012,42(14):108-117.[6] 刘中亮,李一辰,刘洪,等.光的波粒二象性探索[J].数学的实践与认识,2012,42(14):98-105.[7] 郝忠秀,赵亚军,李立功,等.基于MATLAB的矩孔夫琅和费衍射场模拟计算[J].河北大学学报(自然科学版),2009, 29(3):266-269.[8] 王亚伟,刘莹,卜敏.数字虚拟仿真技术在大学物理学光学教学中的应用[J].南通大学学报(教育科学版),2009, 25(1):83-85.[9] 胡颖舒,吴先球,廖文,等.基于Origin的光学实验计算机仿真[J].实验室研究与探索,2007,26(8):11-13.[10] 符运良.MATLAB在光学教学中的应用[J].华南热带农业大学学报,2004,10(3):55-57.[11] 蓝海江.日光干涉与衍射典型实验的Matlab仿真[J].安徽农业科学,2010,38(27):15 396-15 397.[12] 蓝海江.白光干涉、衍射实验的计算机仿真[J].实验室研究与探索,2009,28(12):16-19.[13] 李珏璇,蓝海江.利用七色光仿真白光牛顿环干涉实验 [J].实验室科学,2012,15 (2):65-67.[14] 陆朝华,蓝海江.日光夫琅和费双矩衍射的计算机仿真[J].安徽农业科学,2012,40(5):2 966-2 967.[15] 李珏璇,蓝海江,张学科.日光夫琅和费矩孔衍射实验的计算机仿真[J].软件导刊,2011,10 (10):47-48.。
【研究】MATLAB论文利用MATLAB研究黑体辐射规律

【关键字】研究《MATLAB语言》课程论文利用MATLAB研究黑体辐射规律姓名:陈清源学号:专业:电子信息工程班级:2010级1班指导老师:汤全武学院:物理电气信息学院完成日期:2011年12月10日利用MATLAB研究黑体辐射规律(陈清源2010级1班)[摘要]黑体是一种完全的温度辐射体,其辐射能力只与温度有关。
与黑体相联系的温度称为色温。
任何非黑体所发射的辐射通量都小于同温度下的黑体发射的辐射通量。
[关键词]黑体辐射MATLAB语言图形绘制一.问题的提出MATLAB 语言是当今国际上科学界最具影响力和活力的软件。
它提供了强大的科学运算、灵活的程序设计流程、高质量的图形可视化与界面设计、便捷的与其他程序和语言接口的功能。
MATLAB 语言在各国高校与研究单位起着重大的作用,它集数值计算、符号运算、可视化建模、仿真和图形处理等多种功能于一体的仿真软件。
所以我们就可以利用matlab进行一些物理或者数学方面实验的仿真或是规律的研究。
在此我利用matlab这款软件对黑体辐射的规律进行了一些研究。
黑体辐射:所谓黑体是指入射的电磁波全部被吸收,既没有反射,也没有透射(当然黑体仍然要向外辐射)。
显然自然界不存在真正的黑体,但许多地物是较好的黑体近似(在某些波段上)。
在自然界中,人们似乎见不到黑体这种东西,但是任何物体都具有不断辐射、吸收、发射电磁波的本领。
辐射出去的电磁波在各个波段是不同的,也就是具有一定的谱分布。
基尔霍夫辐射定律(Kirchhoff),在热平衡状态的物体所辐射的能量与吸收的能量之比与物体本身物性无关,只与波长和温度有关。
按照基尔霍夫辐射定律,在一定温度下,黑体必然是辐射本领最大的物体,可叫作完全辐射体。
这种谱分布与物体本身的特性及其温度有关,因而被称之为热辐射。
为了研究不依赖于物质具体物性的热辐射规律,物理学家们定义了一种理想物体——黑体(black body),以此作为热辐射研究的标准物体。
基于MATLAB仿真的太阳影子定位模型

Computer Science and Application 计算机科学与应用, 2019, 9(4), 790-801Published Online April 2019 in Hans. /journal/csahttps:///10.12677/csa.2019.94090Sun Shadow Positioning Model Basedon MATLAB SimulationZhe Wang, Jifa Zhang, Zhuang WangSchool of Electronic Information, Qingdao University, Qingdao ShandongReceived: Apr. 9th, 2019; accepted: Apr. 19th, 2019; published: Apr. 26th, 2019AbstractIn this paper, aiming at the problem of sun shadow localization, by analyzing and calculating the parameters affecting the shadow length of the object, the rod length optimization model based on multi-parameter hierarchical search is established with the aim of inversion of the rod length, and the MATLAB simulation is used to realize the sun shadow positioning technology. Firstly, a straight-line shadow length variation model based on the change of solar height angle is estab-lished, and the relationship between the straight shadow length and the declination angle and the time angle is obtained. Secondly, the control variable is used to analyze the length of the straight rod. Using the method of control variable to analyze the variation rule of longitude, latitude, mea-surement date and measurement time and the curve of the straight shadow length from 9:00 to 15:00 (Beijing time), it is found that the shadow length decreases first and then increases at 11:45.The minimum value obtained is about 2.1. Finally, the model is tested by the actual measurement method, the error of the model result relative to the actual measured value is about 1.732%, and the model has higher precision. For the shadow localization problem, the relationship between the straight shadow length and the shadow vertex coordinate value is obtained through the geometric relationship. For the case where the straight rod location is unknown, this paper applies the long length of the shadow length and the solar elevation angle inversion at the same place. Based on the principle of the parameter, the pole length optimization model based on parameter hierarchical search is established, and the range of the poles in the same group is approximated to zero. The MATLAB is used to perform rough search and fine search on the longitude and latitude. The feasi-ble longitude and latitude values are (108.4566˚E, 19.2771˚N) and (103.1670˚E, 3.2552˚S). The first group of latitude and longitude corresponds to the offshore area of Hainan Province, and its longitude and longitude error of Hainan Province is 1.256%. Therefore, the first location is desig-nated as Hainan Province within the error tolerance. The second group of latitude and longitude corresponds to Indonesia.KeywordsMATLAB Simulation, Sun Shadow Localization, Hierarchical Search, Single Target Optimization基于MATLAB仿真的太阳影子定位模型王者,张吉发,王壮王者 等青岛大学电子信息学院,山东 青岛收稿日期:2019年4月9日;录用日期:2019年4月19日;发布日期:2019年4月26日摘 要 本文针对太阳影子定位问题,通过对影响物体影长的各个参数进行分析计算,以反演杆长最优为目标建立基于多参数分层搜索的杆长优化模型,利用MATLAB 仿真从而实现太阳影子定位技术。
MATLAB控制系统的仿真
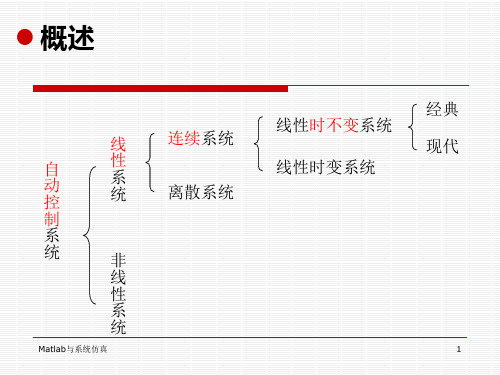
C R
x1 x2
0 1
L
u
L
y [1
0]
x1 x2
[0]u
•
x Ax bu
y CT x du
• 没有良好的计算工具前:系统建立、变换、分析、设 计、绘图等相当复杂。
• MATLAB控制系统软件包以面向对象的数据结构为基 础,提供了大量的控制工程计算、设计库函数,可以 方便地用于控制系统设计、分析和建模。
Transfer function:
s+1 ------------s^2 + 5 s + 6
Matlab与系统仿真
22
应用——系统稳定性判断
系统稳定性判据: 对于连续时间系统,如果闭环极点全部在S平面左半平面,
则系统是稳定的;
若连续时间系统的全部零/极点都位于S左半平面, 则系统是——最小相位系统。
Matlab与系统仿真
38
4.2 动态特性和时域分析函数
(一)动态特性和时域分析函数表 (二)常用函数说明 (三)例子
Matlab与系统仿真
39
(一)动态特性和时域分析函数表 ——与系统的零极点有关的函数
表8.6前部分p263
Matlab与系统仿真
40
——与系统的时域分析有关的函数
Matlab与系统仿真
Matlab与系统仿真
8
4.1 控制工具箱中的LTI对象
Linear Time Invariable
(一)控制系统模型的建立 (二)模型的简单组合 (三)连续系统和采样系统变换(*略)
Matlab与系统仿真
9
(一)控制系统模型的建立
➢ MATLAB规定3种LTI子对象:
• Tf 对象—— 传递函数模型 • zpk 对象—— 零极增益模型 • ss 对象—— 状态空间模型
matlab仿真实验

matlab仿真实验实验一典型环节的MATLAB 仿真一、实验目的1.熟悉MATLAB 桌面和命令窗口,初步了解SIMULINK 功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK 的使用MATLAB 中SIMULINK 是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK 功能模块可以快速的建立控制系统的模型,进行仿真和调试。
1.运行MATLAB 软件,在命令窗口栏“>>”提示符下键入simulink 命令,按Enter 键或在工具栏单击按钮,即可进入如图1-1所示的SIMULINK 仿真环境下。
2.选择File 菜单下New 下的Model 命令,新建一个simulink 仿真环境常规模板。
3.在simulink 仿真环境下,创建所需要的系统。
以图1-2所示的系统为例,说明基本设计步骤如下:1)进入线性系统模块库,构建传递函数。
点击simulink 下的“Continuous ”,再将右边窗口中“Transfer Fen ”的图标用左键拖至新建的“untitled ”窗口。
2)改变模块参数。
在simulink 仿真环境“untitled ”窗口中双击该图标,即可改变传递函数。
其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数,数字之间用空格隔开;设置完成后,选择OK ,即完成该模块的设置。
图1-1 SIMULINK 仿真界面图1-2 系统方框图3)建立其它传递函数模块。
按照上述方法,在不同的simulink 的模块库中,建立系统所需的传递函数模块。
例:比例环节用“Math ”右边窗口“Gain ”的图标。
4)选取阶跃信号输入函数。
用鼠标点击simulink 下的“Source ”,将右边窗口中“Step ”图标用左键拖至新建的“untitled ”窗口,形成一个阶跃函数输入模块。
(完整版)光伏发电的MATLAB仿真

一、实验过程记录1.画出实验接线图图1 实验接线图图2 光伏电池板图3 实验接线实物图2.实验过程记录与分析(1)给出实验的详细步骤○1实验前根据指导书要求完成预习报告○2按预习报告设计的实习步骤,利用MATLAB建立光伏数学模型,如下图4所示。
图4 光伏电池模型其中PV Array模块里子模块如下图5所示。
图5 PV Array模型其中Iph,Uoc,Io,Vt子模块如下图6-9所示。
图6Iph子模块图7Uoc子模块图8 Io子模块图9Vt子模块○3在光伏电池建模的基础上,输入实际光伏电池参数值,研究不同光照强度下、不同温度下光伏电池的I-V、P-V特性曲线,并得出结论。
○4设计光伏电池测试平台,在不同光照、温度情况下测试光伏电池输出电压、输出电流值,对实测数据进行处理并加以分析,记录实际光伏电池的I-V、P-V特性曲线,与仿真结果进行对比,得出有意义的结论。
○5确定电力变换电路拓扑结构,设计电路中的相关参数值,通过MATLAB搭建电路并仿真分析,搭建电路如图10所示。
图10离网型光伏发电系统○6确定系统MPPT控制策略,建立MPPT模块仿真模型,并仿真分析。
系统联调,调节离网型光伏发电系统的电路和控制参数值,仿真并分析最大功率跟踪控制效果。
(2)记录实验数据表1当T=290K时S=1305W/m2时的测试数据表2当T=287K时S=1305W/m2时的测试数据表3当T=287K时S=1278W/m2时的测试数据二、实验结果处理与分析1.实验数据的整理和选择使用MATLAB软件其中的simulink工具进行模型的搭建。
再对其进行仿真,得到仿真曲线。
使用Excel表格输入实验所测得U、I、P,在对其自动生成I-V,P-V曲线。
2.绘制不同光照强度下、不同温度下光伏电池的I-V、P-V特性曲线;图11 I-V曲线图12 P-V曲线当T=290K时S=1305W/m2时的测拟合曲线图13 I-V曲线图14 P-V曲线当T=287K时S=1305W/m2时的拟合曲线图15 I-V曲线图16 P-V曲线当T=287K时S=1278W/m2时的拟合曲线3.所得实验数值和预习所得理论值比较,进行实验结果的误差分析所得实验数值和预习所得理论值比较,仿真波形开路电压均比实验所得的开路电压大,仿真波形最大功率也比实验所得最大功率大,所取得最大功率值对应的电压值也是仿真时比实验时的大,造成这个现象的原因有以下几点:(1)由于天气原因,真实测试环境的光照强度有些不稳定,前后变化幅度明显,这也导致了一部分的误差。
经典功率谱估计及其仿真

量 , 因此 , 求数学期望是必要的 , 也就是说 , 对 R( m) 作
Fourier 变换后 , S (ω) 不具有各态历经性 , 所以 , 真实谱
S (ω) 应在总集意义上求 。另外 ,如果没有求数学期望运
160
算 ,式(4) 的求极限运算在任何统计意义上都不会收敛。
而式 (1) 与式(5) 相比 ,既无求均值计算 ,也无求极限运算 ,
谱估计质量下降 ;由 R^ ( m) 得到的 S^ (ω) 不一定为正值 ,从
而可能失去功率谱的物理意义 。
4 经典谱估计方法的改进
4. 1 经典谱估计性能分析 平稳随机信号 X ( n) 的自相关函数为 :
R ( n) = E[ X ( n) X ( n + m) ]
( 2)
功率谱为 :
∞
变换 ,可见 S^ (ω) 不是 S (ω) 的一致估计 ;随着 N 的增大 ,谱
估计起伏增大 , N → ∞时 , var ( S^ (ω) ) λ S2 (ω) 。
(3) 估计的分辨率 :数据窗为长度为 N 的矩形窗时 ,
Re s{ S (ω) } = 0. 89 2π, N 增大时 , 分辨率提高 , 但会使 N
1 N
|
x ( n) e - jωn | 2
n=0
(1)
主要性能指标有 :
(1) 估计的均值 :
E[ S^ (ω) ] = 2π1 S (ω) 3 W (ω) W (ω) 是 窗 函 数 ω( n) 的 Fourier 变 换 。当 N → ∞ 时 , E[ S^ (ω) ] → S (ω) , 是无偏估计 ; N 是有限值时 ,是有偏估 计 ,偏差为 :
SON G Ning , GUAN Hua
matlab仿真教程

前言MA TLAB的简介MATLAB是一种适用于工程应用的各领域分析设计与复杂计算的科学计算软件,由美国Mathworks公司于1984年正式推出,1988年退出3.X(DOS)版本,19992年推出4.X(Windows)版本;19997年腿5.1(Windows)版本,2000年下半年,Mathworks公司推出了他们的最新产品MATLAB6.0(R12)试用版,并于2001年初推出了正式版。
随着版本的升级,内容不断扩充,功能更加强大。
近几年来,Mathworks公司将推出MATLAB语言运用于系统仿真和实时运行等方面,取得了很多成绩,更扩大了它的应用前景。
MATLAB已成为美国和其他发达国家大学教学和科学研究中最常见而且必不可少的工具。
MATLAB是“矩阵实验室”(Matrix Laboratory)的缩写,它是一种以矩阵运算为基础的交互式程序语言,着重针对科学计算、工程计算和绘图的需要。
在MATLAB中,每个变量代表一个矩阵,可以有n*m个元素,每个元素都被看做复数摸索有的运算都对矩阵和复数有效,输入算式立即可得结果,无需编译。
MATLAB强大而简易的做图功能,能根据输入数据自动确定坐标绘图,能自定义多种坐标系(极坐标系、对数坐标系等),讷讷感绘制三维坐标中的曲线和曲面,可设置不同的颜色、线形、视角等。
如果数据齐全,MATLAB通常只需要一条命令即可做图,功能丰富,可扩展性强。
MATLAB软件包括基本部分和专业扩展部分,基本部分包括矩阵的运算和各种变换、代数和超越方程的求解、数据处理和傅立叶变换及数值积分风,可以满足大学理工科学生的计算需要,扩展部分称为工具箱,它实际上使用MATLAB的基本语句编成的各种子程序集,用于解决某一方面的问题,或实现某一类的新算法。
现在已经有控制系统、信号处理、图象处理、系统辨识、模糊集合、神经元网络及小波分析等多种工具箱,并且向公式推倒、系统仿真和实时运行等领域发展。
基于MATLAB的太阳辐照模型仿真分析

基于MATLAB的太阳辐照模型仿真分析作者:李宏燕,何建国,李明滨来源:《湖北农业科学》 2014年第24期李宏燕a,b,何建国c,李明滨d(宁夏大学,a.土木与水利工程学院;b.机械学院;c.农学院;d.新能源研究中心,银川750021)摘要:太阳辐照模型是工农业及建筑节能领域开发利用太阳能的基础,不同地理位置的地区,其水平面上所能接收到的太阳辐照度随着季节、纬度、经度以及海拔高度等条件的不同而变化。
在建立太阳辐照模型的基础上,利用MATLAB仿真软件模拟了不同条件下的太阳辐照度,分析了辐照度随一年中的典型季节、纬度、经度及海拔高度的变化趋势。
结果表明,太阳辐照度随不同季节发生明显变化,夏季辐照度高,冬季辐照度低;而随纬度、经度及海拔高度则变化较小,为太阳能的开发利用提供理论依据。
关键词:太阳辐照;MATLAB;模型;仿真中图分类号:TK519文献标识码:A文章编号:0439-8114(2014)24-6128-03DOI:10.14088/j.cnki.issn0439-8114.2014.24.060收稿日期:2014-07-10基金项目:宁夏自然科学基金项目(NZ14027)作者简介:李宏燕(1976-),女,宁夏银川人,副教授,博士,主要从事太阳能热利用技术方面的研究,(电话)18295187269(电子信箱)lhy-208@163.com。
随着世界能源消耗的日益增长和能源储量的不断下降,能源与环境之间的矛盾日益严峻。
研究开发清洁能源和可再生能源成为21世纪世界各国研究人员普遍关注的问题之一[1]。
太阳能具有取之不尽、用之不竭的特点,已成为工农业及建筑等领域节能降耗最具开发前景的清洁可再生能源[2]。
在太阳能开发利用领域中,太阳辐照度的计算是确定太阳辐射模型的基础,也是对太阳能光热、光电利用效率进行理论分析的依据[3]。
不同地理位置的地区,其水平面上所能接收到的太阳辐照度随着季节、纬度、经度以及海拔高度等条件的不同而变化[4-6]。
Lyapunov指数的计算方法

【总结】Lyapunov指数的计算方法非线性理论近期为了把计算LE的一些问题弄清楚,看了有7~9本书!下面以吕金虎《混沌时间序列分析及其应用》、马军海《复杂非线性系统的重构技术》为主线,把目前已有的LE计算方法做一个汇总!1. 关于连续系统Lyapunov指数的计算方法连续系统LE的计算方法主要有定义方法、Jacobian方法、QR分解方法、奇异值分解方法,或者通过求解系统的微分方程,得到微分方程解的时间序列,然后利用时间序列(即离散系统)的LE 求解方法来计算得到。
关于连续系统LE的计算,主要以定义方法、Jacobian方法做主要介绍内容。
(1)定义法定义法求解Lyapunov指数.JPG关于定义法求解的程序,和matlab板块的“连续系统LE求解程序”差不多。
以Rossler系统为例Rossler系统微分方程定义程序function dX = Rossler_ly(t,X)% Rossler吸引子,用来计算Lyapunov指数% a=,b=,c=% dx/dt = -y-z,% dy/dt = x+ay,% dz/dt = b+z(x-c),a = ;b = ;c = ;x=X(1); y=X(2); z=X(3);% Y的三个列向量为相互正交的单位向量Y = [X(4), X(7), X(10);X(5), X(8), X(11);X(6), X(9), X(12)];% 输出向量的初始化,必不可少dX = zeros(12,1);% Rossler吸引子dX(1) = -y-z;dX(2) = x+a*y;dX(3) = b+z*(x-c);% Rossler吸引子的Jacobi矩阵Jaco = [0 -1 -1;1 a 0;z 0 x-c];dX(4:12) = Jaco*Y;求解LE代码:% 计算Rossler吸引子的Lyapunov指数clear;yinit = [1,1,1];orthmatrix = [1 0 0;0 1 0;0 0 1];a = ;b = ;c = ;y = zeros(12,1);% 初始化输入y(1:3) = yinit;y(4:12) = orthmatrix;tstart = 0; % 时间初始值tstep = 1e-3; % 时间步长wholetimes = 1e5; % 总的循环次数steps = 10; % 每次演化的步数iteratetimes = wholetimes/steps; % 演化的次数mod = zeros(3,1);lp = zeros(3,1);% 初始化三个Lyapunov指数Lyapunov1 = zeros(iteratetimes,1);Lyapunov2 = zeros(iteratetimes,1);Lyapunov3 = zeros(iteratetimes,1);for i=1:iteratetimestspan = tstart:tstep:(tstart + tstep*steps);[T,Y] = ode45('Rossler_ly', tspan, y);% 取积分得到的最后一个时刻的值y = Y(size(Y,1),:);% 重新定义起始时刻tstart = tstart + tstep*steps;y0 = [y(4) y(7) y(10);y(5) y(8) y(11);y(6) y(9) y(12)];%正交化y0 = ThreeGS(y0);% 取三个向量的模mod(1) = sqrt(y0(:,1)'*y0(:,1));mod(2) = sqrt(y0(:,2)'*y0(:,2));mod(3) = sqrt(y0(:,3)'*y0(:,3));y0(:,1) = y0(:,1)/mod(1);y0(:,2) = y0(:,2)/mod(2);y0(:,3) = y0(:,3)/mod(3);lp = lp+log(abs(mod));%三个Lyapunov指数Lyapunov1(i) = lp(1)/(tstart);Lyapunov2(i) = lp(2)/(tstart);Lyapunov3(i) = lp(3)/(tstart);y(4:12) = y0';end% 作Lyapunov指数谱图i = 1:iteratetimes;plot(i,Lyapunov1,i,Lyapunov2,i,Lyapunov3)程序中用到的ThreeGS程序如下:%G-S正交化function A = ThreeGS(V) % V 为3*3向量v1 = V(:,1);v2 = V(:,2);v3 = V(:,3);a1 = zeros(3,1);a2 = zeros(3,1);a3 = zeros(3,1);a1 = v1;a2 = v2-((a1'*v2)/(a1'*a1))*a1;a3 = v3-((a1'*v3)/(a1'*a1))*a1-((a2'*v3)/(a2'*a2))*a2;A = [a1,a2,a3];计算得到的Rossler系统的LE为————Wolf文章中计算得到的Rossler系统的LE为————0需要注意的是——定义法求解的精度有限,对有些系统的计算往往出现计果和理论值有偏差的现象。
