MATLAB仿真 BPSK调制
基于的MATLAB的BPSK调制分析和仿真

摘要本次课程设计为基于MATLAB的BPSK原理电路仿真。
本次课设着重介绍了算法的实现,并采用MATLAB程序仿真测试了BPSK过程中单极性不归零编码、脉冲成形、PSK调制、信号通过AWGN信道、载波恢复、解调、解码等过程。
关键词:BPSK;2PSK;MATLAB;数字频带通信;目录绪论 (2)1 BPSK数字调制原理 (3)1.1数字带通传输分类 (3)1.2 BPSK调制原理分析 (3)1.2.1调制原理分析 (3)1.2.2解调原理分析 (5)2 MATLAB软件 (7)2.1 MATLAB软件介绍 (7)3基于的MATLAB的BPSK调制分析和仿真 (8)3.1基于MATLAB的BPSK调制系统总述 (8)3.2编码过程的MATLAB实现 (9)3.3 BPSK调制的MATLAB的实现 (12)3.4 AWGN信道MATLAB的实现 (14)3.5载波恢复的MATLAB实现 (17)3.5.1接收端带通滤波器 (17)3.5.2通过FFT实现载波的直接频率估计 (21)3.5.3自适应(迭代)算法验证恢复频率 (23)3.6 BPSK解调 (26)4总结 (31)附录 (32)致谢 (33)参考文献 (34)绪论数字信号传输方式分为数字带通传输和数字基带传输。
对于本次课程设计二进制相移键控BPSK(Binary Phase Shift Key)是利用载波的相位变化来传递数字信息,而振幅和频率保持不变的一种数字带通调制方式。
在实际应用中,PSK具有恒包络特性,频带利用率比FSK高,在相同信噪比的条件下误码率也较低,同时PSK调制实现相对简单,故卫星通信,遥测遥控中用得最多的是BPSK方式调制。
1 BPSK 数字调制原理1.1数字带通传输分类数字带通传输中一般利用数字信号的离散取值特点通过开关键控载波,从而实现数字调制,比如对载波的振幅、频率和相位进行键控可获得振幅键控(ASK )、频移键控(FSK )和相移键控(PSK )。
基于matlab的QPSK与BPSK信号性能比较仿真

┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊目录第一章概述 (1)第二章QPSK通信系统原理与仿真 (1)2.1 QPSK系统框图介绍 (1)2.2QPSK信号的调制原理 (2)2.2.1QPSK信号产生方法 (2)2.2.2QPSK星座图 (2)2.3QPSK解调原理及误码率分析 (3)2.3.1QPSK解调方法 (3)2.3.2QPSK系统误码率 (3)2.4QPSK信号在AWGN信道下仿真 (4)第三章BPSK通信系统原理与仿真 (4)3.1BPSK信号的调制原理 (4)3.2BPSK解调原理及误码率分析 (4)第四章QPSK与BPSK性能比较 (5)4.1QPSK与BPSK在多信道下比较仿真 (5)4.1.1纵向比较分析 (5)4.1.2横向比较分析 (7)4.2仿真结果分析 (7)4.2.1误码率分析 (7)4.2.2频带利用率比较 (7)附录 (8)代码1 (8)代码2 (8)代码3 (10)代码4 (12)┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊第一章概述QPSK是英文Quadrature Phase Shift Keying的缩略语简称,意为正交相移键控,是一种数字调制方式。
它以其抗干扰性能强、误码性能好、频谱利用率高等优点,广泛应用于数字微波通信系统、数字卫星通信系统、宽带接人、移动通信及有线电视系统之中。
BPSK是英文Binary Phase Shift Keying的缩略语简称,意为二相相移键控,是利用偏离相位的复数波浪组合来表现信息键控移相方式的一种。
它使用了基准的正弦波和相位反转的波浪,使一方为0,另一方为1,从而可以同时传送接受2值(1比特)的信息。
本文所研究的QPSK系统与二进制的BPSK系统相比,具有以下特点:1.在传码率相同的情况下,四进制数字调制系统的信息速率是二进制系统的2倍。
2.在相同信息速率条件下,四进制数字调制系统的传码率是二进制系统的1/4倍,这一特点使得四进制码元宽度是二进制码元宽度的2倍,码元宽度的加大,可增加每个码元的能量,也可减小码间串扰的影响。
qpsk、bpsk蒙特卡洛仿真matlab代码

qpsk、bpsk的蒙特卡洛仿真是一种用于测试和验证通信系统性能的重要工具。
通过模拟大量的随机输入数据,并对系统进行多次仿真运算,可以对系统的性能进行全面评估,包括误码率、信噪比要求等。
在matlab中,我们可以通过编写相应的仿真代码来实现qpsk、bpsk 的蒙特卡洛仿真。
下面将分别介绍qpsk和bpsk的蒙特卡洛仿真matlab代码。
一、qpsk的蒙特卡洛仿真matlab代码1. 生成随机的qpsk调制信号我们需要生成一组随机的qpsk调制信号,可以使用randi函数生成随机整数序列,然后将其映射到qpsk符号点上。
2. 添加高斯白噪声在信号传输过程中,会受到各种干扰,其中最主要的干扰之一就是高斯白噪声。
我们可以使用randn函数生成高斯白噪声序列,然后与调制信号相加,模拟信号在传输过程中受到的噪声干扰。
3. 解调和判决接收端需要进行解调和判决操作,将接收到的信号重新映射到qpsk符号点上,并判断接收到的符号与发送的符号是否一致,从而判断是否发生误码。
4. 统计误码率通过多次仿真运算,记录错误判决的次数,从而可以计算出系统的误码率。
二、bpsk的蒙特卡洛仿真matlab代码1. 生成随机的bpsk调制信号与qpsk相似,我们需要先生成一组随机的bpsk调制信号,然后模拟信号传输过程中的噪声干扰。
2. 添加高斯白噪声同样使用randn函数生成高斯白噪声序列,与bpsk调制信号相加。
3. 解调和判决接收端对接收到的信号进行解调和判决,判断接收到的符号是否与发送的符号一致。
4. 统计误码率通过多次仿真运算,记录错误判决的次数,计算系统的误码率。
需要注意的是,在编写matlab代码时,要考虑到信号的长度、仿真次数、信噪比的范围等参数的选择,以及仿真结果的统计分析和可视化呈现。
qpsk、bpsk的蒙特卡洛仿真matlab代码可以通过以上步骤实现。
通过对系统性能进行全面评估,可以帮助工程师优化通信系统设计,提高系统的可靠性和稳定性。
bpsk和dpskmatlab仿真
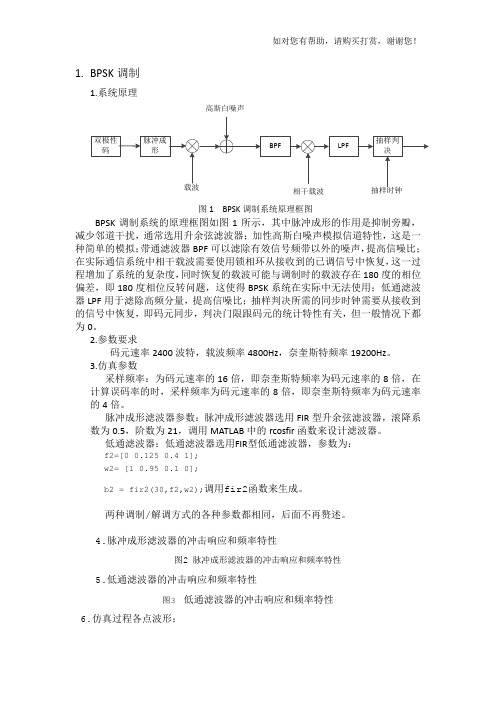
1.BPSK调制1.系统原理高斯白噪声图1 BPSK调制系统原理框图BPSK调制系统的原理框图如图1所示,其中脉冲成形的作用是抑制旁瓣,减少邻道干扰,通常选用升余弦滤波器;加性高斯白噪声模拟信道特性,这是一种简单的模拟;带通滤波器BPF可以滤除有效信号频带以外的噪声,提高信噪比;在实际通信系统中相干载波需要使用锁相环从接收到的已调信号中恢复,这一过程增加了系统的复杂度,同时恢复的载波可能与调制时的载波存在180度的相位偏差,即180度相位反转问题,这使得BPSK系统在实际中无法使用;低通滤波器LPF用于滤除高频分量,提高信噪比;抽样判决所需的同步时钟需要从接收到的信号中恢复,即码元同步,判决门限跟码元的统计特性有关,但一般情况下都为0。
2.参数要求码元速率2400波特,载波频率4800Hz,奈奎斯特频率19200Hz。
3.仿真参数采样频率:为码元速率的16倍,即奈奎斯特频率为码元速率的8倍,在计算误码率的时,采样频率为码元速率的8倍,即奈奎斯特频率为码元速率的4倍。
脉冲成形滤波器参数:脉冲成形滤波器选用FIR型升余弦滤波器,滚降系数为0.5,阶数为21,调用MATLAB中的rcosfir函数来设计滤波器。
低通滤波器:低通滤波器选用FIR型低通滤波器,参数为:f2=[0 0.125 0.4 1];w2= [1 0.95 0.1 0];b2 = fir2(30,f2,w2);调用fir2函数来生成。
两种调制/解调方式的各种参数都相同,后面不再赘述。
4.脉冲成形滤波器的冲击响应和频率特性图2 脉冲成形滤波器的冲击响应和频率特性5.低通滤波器的冲击响应和频率特性图3 低通滤波器的冲击响应和频率特性6.仿真过程各点波形:说明:在画图时,进行了归一化处理。
噪声的方差为1,随机序列的幅度为1,调制加噪后信噪比为-3dB,按照理想情况计算,解调后信噪比为0dB。
图2 随机序列(16个)图3 脉冲成形后的波形脉冲成形的作用是抑制旁瓣,减少邻道干扰,在实际通信过程中必不可少,但是为了与理论误码率进行对比,在后面计算误码率时,没有进行脉冲成形。
bpsk调制的matlab程序

题目:BPSK调制的MATLAB程序一、BPSK调制技术介绍BPSK(Binary Phase Shift Keying)调制是一种数字调制技术,它使用两个不同的相位来表示数字比特0和1。
在BPSK调制中,0和1分别映射到正弦波的两种相位,通常为0°和180°。
二、MATLAB程序编写流程在MATLAB中实现BPSK调制的程序主要包括以下几个步骤:1. 生成要调制的数字比特序列2. 将数字比特序列转化为相应的正弦波信号3. 添加高斯白噪声4. 绘制调制后的信号波形图三、MATLAB程序实现下面是一个简单的MATLAB程序,实现了BPSK调制的过程:```matlab生成随机的数字比特序列bitStream = randi([0,1],1,1000);将数字比特序列映射为正弦波信号t = 0:0.01:length(bitStream)-1;t = t/100;carrier = sin(2*pi*t);BPSK调制bpskSignal = (1-2*bitStream).*carrier;添加高斯白噪声noise = 0.1*randn(1,length(bpskSignal)); noisyBpskSignal = bpskSignal + noise;绘制调制后的信号波形图subplot(2,1,1);plot(t,carrier);title('Carrier Signal');xlabel('Time');ylabel('Amplitude');grid on;subplot(2,1,2);plot(t,noisyBpskSignal);title('Noisy BPSK Signal');xlabel('Time');ylabel('Amplitude');grid on;```四、MATLAB程序运行结果分析通过上述程序,我们可以得到BPSK调制后的信号波形图。
BPSK调制的MATLAB仿真课程设计_实验报告

北京邮电大学移动通信课程设计实验报告目录一、背景 (4)二、基本要求 (4)三、设计概述 (4)四、Matlab设计流程图 (5)五、Matlab程序及仿真结果图 (6)1、生成m序列及m序列性质 (6)2、生成50位随机待发送二进制比特序列,并进行扩频编码 (7)3、对扩频前后信号进行BPSK调制,观察其时域波形 (9)4、计算并观察扩频前后BPSK调制信号地频谱 (10)5、仿真经awgn信道传输后,扩频前后信号时域及频域地变化 (11)6、对比经信道前后两种信号地频谱变化 (12)7、接收机与本地恢复载波相乘,观察仿真时域波形 (14)8、与恢复载波相乘后,观察其频谱变化 (15)9、仿真观察信号经凯萨尔窗低通滤波后地频谱 (16)10、观察经过低通滤波器后无扩频与扩频系统地时域波形 (17)11、对扩频系统进行解扩,观察其时域频域 (18)12、比较扩频系统解扩前后信号带宽 (19)13、比较解扩前后信号功率谱密度 (20)14、对解扩信号进行采样、判决 (21)15、在信道中加入2040~2050Hz窄带强干扰并乘以恢复载波 (24)16、对加窄带干扰地信号进行低通滤波并解扩 (25)17、比较解扩后信号与窄带强干扰地功率谱 (27)六、误码率simulink仿真 (28)1、直接扩频系统信道模型 (28)2、加窄带干扰地直扩系统建模 (29)3、用示波器观察发送码字及解扩后码字 (30)4、直接扩频系统与无扩频系统地误码率比较 (31)5、不同扩频序列长度下地误码率比较 (32)6、扩频序列长度N=7时,不同强度窄带干扰下地误码率比较 (33)七、利用Walsh码实现码分多址技术 (34)1、产生改善地walsh码 (35)2、产生两路不同地信息序列 (36)3、用两个沃尔什码分别调制两路信号 (38)4、两路信号相加,并进行BPSK调制 (39)5、观察调制信号频谱,并经awgn信道加高斯白噪和窄带强干扰 (40)6、接收机信号乘以恢复载波,观察时域和频域 (42)7、信号经凯萨尔窗低通滤波器 (43)8、对滤波后信号分别用m1和m2进行解扩 (44)9、对两路信号分别采样,判决 (45)八、产生随机序列Gold码和正交Gold码 (47)1、产生Gold码并仿真其自相关函数 (48)2、产生正交Gold码并仿真其互相关函数 (50)九、实验心得体会 (51)直接序列扩频系统仿真一、背景直接序列扩频通信系统(DSSS)是目前应用最为广泛地系统.在发送端,直扩系统将发送序列用伪随机序列扩展到一个很宽地频带上去,在接受端又用相同地扩频序列进行解扩,回复出原有信息.由于干扰信息与伪随机序列不相关,扩频后能够使窄带干扰得到有效地抑制,提高输出信噪比.系统框图如下图所示:二、基本要求:通过matlab建模,对直扩系统进行仿真,数据调制方式可以自由选择,可以使用基带信号,但最好能使用频带信号,信道为高斯白噪信道.要仿真出扩频前地信号地频偏,扩频后地信号频谱,过信道之后地频谱以及解扩之后地频谱.2.研究并仿真产生m序列,写出生成m序列地算法.验证直扩系统对窄带干扰地抑制能力,在信道中加入一个窄带强干扰,仿真出加了干扰后地频谱图和解扩后地频谱图,给出误码率等仿真图.4.在以上基础上仿真实现码分多址技术,使用Walsh码进行复用,实现多个信号同时传输.(选做)可选项:1.在信道中加入多径,使用rake接收来抗多径效应.2.产生除m序列之外地其他随机序列,如Gold码,正交Gold码等等.3.对比无扩频地系统地误码率.三、设计概述本次课设完成基本要求,并选作了可选项码分多址,Gold码及误码率对比.通过matlab 建模仿真了直扩系统BPSK调制地各点频偏及时域信号,并仿真了窄带强干扰对直扩系统地影响以及利用改善地W ALSH码实现码分多址技术.另外,通过matlab地simulink工具盒bertool工具仿真对比了直扩系统和无扩频系统地误码率.四、matlab设计流程图基本扩频系统仿真流程图五、matlab程序及仿真结果图1、生成m序列及m序列性质实验产生7位m序列,频率100Hz,模拟线性反馈移位寄存器序列,原理图如下:clear all。
BPSK和DPSK Matlab仿真
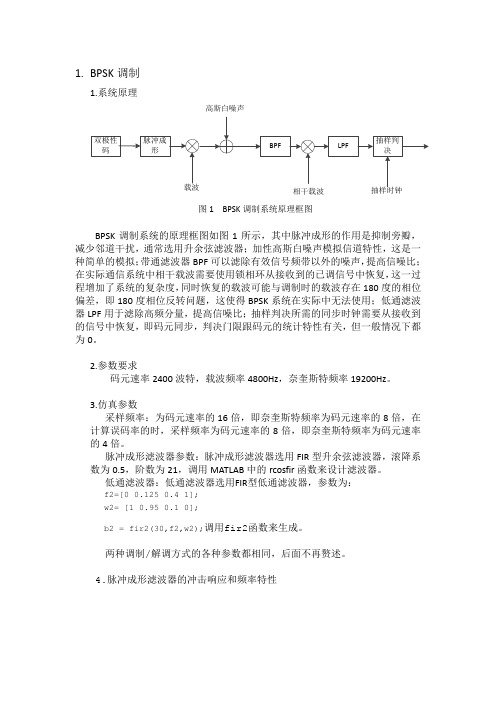
图 14 低通滤波后的波形
图 15 误码情况(0dB)
3.误码率
在统计误码率时,考虑到程序运行时间,码元个数为:65536,在高信噪 比下统计的误码率可信度较低。 判决前的信噪比按下式计算:SNR=A2/δ
2
,其中 A 为已调信号幅度,δ
2
为
噪声方差。BPSK 的理论误码率为:0.5 ∗ erfc( ������),其中 r=SNR=A2/δ 2 为判决时的 信噪比。2DPSK 的理论误码率为:0.5 ∗ exp(−r)。 BPSK 在-10dB,-8dB,-6dB,-4dB,-2dB,0dB,2dB,4dB,6dB,8dB,10dB 的信噪比下的误 码率依次为: 0.334625244140625 0.293212890625000 0.244171142578125 0.192596435546875 0.140975952148438 0.0857543945312500 0.0433654785156250 0.0148315429687500 0.00328063964843750 0.000488281250000000 4.57763671875000e-05 2DPSK 在-10dB,-8dB,-6dB,-4dB,-2dB,0dB,2dB,4dB,6dB,8dB,10dB 的信噪比下的 误码率依次为: 0.463904783703365 0.444800488288701 0.410727092393378 0.370138094148165 0.309910734721904 0.229083695735103 0.144426642252232 0.0688944838635844 0.0211947814145113 0.00267032883192187 0.000183108262760357 根据这两组数据以及对应的理论数据,绘制的误码率曲线如下图所示:
用MATLAB实现的BPSK调制解调源程序

demodulation.m
function output_frame = demodulation(input_modu, index)
% demodulation for IEEE802.11a
% Input: input_modu, complex values representing constellation points
QAM_input_I(idx) = -1;
output_frame = BPSK_Demodu_I(round((QAM_input_I+1)/2) + 1);
case 2,
QPSK_Demodu_IQ = [0 1]; %f(m)=(m+1)/2 + 1, so I=-1 ---> 1, I=1 ---> 2
case 4,
QAM_16_IQ = [-3 -1 3 1]; % refer to Table84 on page21 of IEEE802.11a
QAM_input_I = QAM_16_IQ(frame(1:4:end)*2+input_frame(2:4:end)+1);
output_modu=mapping(input_frame(1:5:end)*16+input_frame(2:5:end)*8+input_frame(3:5:end)*4+input_frame(4:5:end)*2+input_frame(5:5:end)+1);
case 6,
switch index
case 1,
BPSK_I = [-1 1]; % refer to Table82 on page21 of IEEE802.11a
基于MATLAB的BPSK调制仿真及性能分析概要

******************实践教学*******************兰州理工大学计算机与通信学院2015年春季学期通信系统仿真训练课程设计题目:基于MATLAB的BPSK调制仿真及性能分析专业班级:_________________姓名:_________________________________学号:_______________________________指导教师:_____________________________成绩摘要BPSK 是在21 世纪的现阶段,数字通信系统是现代通信系统的主流,在社会生活各个方面占据重要地位,调制与解调是一个不可或缺的环节,它大大提高了信号的传输性能和安全性。
BPSK 作为数字通信系统中的一种简单、基础的调制解调方法,抗干扰能力强,容易仿真实现。
在了解并掌握了BPSK 调制与解调原理后,学习MATLAB 仿真软件的使用方法。
本次课程设计为基于MATLAB 的BPSK 调制仿真。
本次课设着重介绍了算法的实现,并采用MATLAB程序仿真测试了BPSK过程中单极性不归零编码、脉冲成形、PSK调制、信号通过AWGN 信道、载波恢复、解调、解码等过程。
关键词:BPSK、调制解调、MATLAB仿真、数字通信系统目录前言. (3)一、BPSK 原理 (4)1.1 MPSK 的介绍 (4)1.1.1 MPSK 的介绍 (4)1.2 BPSK 简介 (5)1.2.1 BPSK 的概念及分类 (5)1.3 BPSK 信号的产生. (5)1.4 BPSK 调制. (5)1.4.1 调制的概念. (5)1.4.2 调制的种类. (6)1.4.3 调制的作用. (6)1.4.4 调制方式. (6)1.4.5 BPSK 的调制原理 (7)1.5 BPSK 的解调. (8)1.6 高斯噪声 (8)1.6.1 高斯白噪声. (8)二、设计思路. (9)三、设计仿真及分析. (10)1 设计仿真 (10)2 结果总体分析 (13)总结. (14)参考文献. (15)致谢. (16)、八, 、■刖言数字通信系统使用的最基本的就是PSK,实际上由于交调的存在,大都使用PSK,由于电波主要在自由空间传播,信道参数比较稳定,信道的主要干扰是高斯白噪声,因而可视为恒参信道。
Matlab仿真课程设计实验三

要求编写BPSK和BDPSK调制程序,任意给定一组二进制数,计算经过这两种调制方式的输出信号。
1.编写BPSK调制程序,任意给定一组二进制数,计算经过这种调制方式的输出信号。
1、实验目的(1)熟悉BPSK调制原理。
(2)学会运用Matlab编写BPSK调制程序。
(3)会画出原信号和调制信号的波形图。
(4)掌握数字通信的2PSK的调制方式。
2、实验原理分析二进制相移键控,简记为2PSK或BPSK。
2PSK信号码元的“0”和“1”分别用两个不同的初始相位0和π来表示,而其振幅和频率保持不变。
故2PSK信号表示式可表示为:s(t)=Acos(w0t+θ)式中,当发送“0”时,θ=0;当发送“1”时,θ=π。
或者写成:这种以载波的不同相位直接去表示相应二进制数字信号的调制方式,称为绝对相移方式。
图1 2PSK信号波形图2PSK信号的的产生方法主要有两种:(1)相称法:用二进制基带不归零矩形脉冲信号与载波相乘,得到相位反相的两种码元,如图2(a)所示。
(2)选择法:用此基带信号控制一个开关电路,以选择输入信号,开关电路的输入信号是相位相差π的同频载波,如图2(b)所示。
这两种方法的复杂程度差不多,并且都可以用数字信号处理器实现。
解调部分只能用相干解调,不可以用包络检波法等非相干解调的方法,因为其频谱和抑制载波双边带的频谱一样,因此不能采用包络检波,而不可采用相干解调。
图3 2PSK解调原理图对原理图分析:从图3可以看出调制信号经过本地载波相乘得到直流分量,若发送的事“1”,则有正直流分量,若发送的事“-1”,则有负直流分量的存在,经过低通滤波器后,就只剩下这些直流分量,然后进行抽样判决即可,因为其上下直流分量的幅度一样,我们最佳的判决电平时0V是最好的,这样使得我们判决出来的信号时误码率最低的。
3、程序设计思想和流程图根据上述的2PSK信号原理,输入基带信号高低电位各表示不同的相位。
结合以前实验的基础,先输入二进制序列作为基带信号,进行2PSK调制,然后输出调制后的信号。
基于Matlab的BPSK调制解调系统仿真

基于Matlab的BPSK调制解调系统仿真摘要:数字通信系统是当代通信领域的主流,在社会生活各个方面占据重要地位。
BPSK作为数字通信系统中的一种简单、基础的调制解调方法,抗干扰能力强,容易仿真实现。
本文通过BPSK的仿真,希望学习到数字通信的基本知识,为以后的学习打下基础。
关键词:数字信号,BPSK,高斯白噪声,信噪比,误码率一、背景及动机(一)数字信号及数字通信数字信号是其信息是用若干个明确定义的离散值表示的时离散信号。
数字通信是一种用数字信号作为载体来传输信息的通信方式。
数字通信可以传输电报、数据等数字信号,也可传输经过数字化处理的语音和图像等模拟信号。
与模拟通信相比,数字通信具有许多突出优点:一抗干扰力强,二通信距离远,三保密性好,四通信设备的制造和维护简便,五能适应各种通信业务的要求,六是便于实现通信网的计算机管理。
(二)数字通信的前景广阔由于数字信号相比于模拟信号所具有很多优点,数字通信技术在当今通信技术中占据主导地位,各国都在积极发展数字通信。
近年来,我国数字通信得到迅速发展,正朝着高速化、智能化、宽带化和综合化方向迈进。
因此作为当代的大学生了解数字通信技术具有深刻的意义。
二、相关知识(一)通信系统简介上图为通信系统的一种简化结构,由图可知,在发送端信息源(也称发终端)的作用是把各种可能的消息转换成原始电信号。
为了使这个原始信号适合在信道中传输,由发送设备对原始信号完成某种变换,然后再送入信道。
信道是只信号传输的通道。
在接收端,接受设备的功能与发送设备的相反,它能从接受信号中恢复出相应的原始信号,而受信者(也称信息宿或收终端)是将复原的原始信号转换成相应的信息。
图中的噪声源是信道中的噪声及分散在通信系统其他各处的噪声的集中表示。
(二)通信系统中的相关概念信道:信号的传输媒介和相关的变换装置。
噪声:即干扰,通信系统中的干扰分为两种,第一是信号在传输时叠加上的噪声,我们称加性干扰;第二是信道传输特性不理想产生的噪声,我们成为乘性干扰。
基于matlab的QPSK与BPSK信号性能比较仿真

┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊目录第一章概述 (2)第二章QPSK通信系统原理与仿真 (2)2.1 QPSK系统框图介绍 (2)2.2 QPSK信号的调制原理 (3)2.2.1 QPSK信号产生方法 (3)2.2.2 QPSK星座图 (4)2.3 QPSK解调原理及误码率分析 (4)2.3.1 QPSK解调方法 (4)2.3.2 QPSK系统误码率 (5)2.4 QPSK信号在AWGN信道下仿真 (5)第三章BPSK通信系统原理与仿真 (6)3.1 BPSK信号的调制原理 (6)3.2 BPSK解调原理及误码率分析 (7)第四章QPSK与BPSK性能比较 (8)4.1 QPSK与BPSK在多信道下比较仿真 (8)4.1.1 纵向比较分析 (8)4.1.2 横向比较分析 (10)4.2 仿真结果分析 (10)4.2.1 误码率分析 (10)4.2.2 频带利用率比较 (10)附录 (11)代码1 (11)代码2 (11)代码3 (14)代码4 (16)┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊第一章概述QPSK是英文Quadrature Phase Shift Keying的缩略语简称,意为正交相移键控,是一种数字调制方式。
它以其抗干扰性能强、误码性能好、频谱利用率高等优点,广泛应用于数字微波通信系统、数字卫星通信系统、宽带接人、移动通信及有线电视系统之中。
BPSK是英文Binary Phase Shift Keying的缩略语简称,意为二相相移键控,是利用偏离相位的复数波浪组合来表现信息键控移相方式的一种。
它使用了基准的正弦波和相位反转的波浪,使一方为0,另一方为1,从而可以同时传送接受2值(1比特)的信息。
本文所研究的QPSK系统与二进制的BPSK系统相比,具有以下特点:1.在传码率相同的情况下,四进制数字调制系统的信息速率是二进制系统的2倍。
【VIP专享】BPSK扩频误码率matlab仿真

实验报告实验目的1.掌握BPSK 信号调制、相干解调方法;2.掌握扩频、解扩的方法;3.掌握BPSK 扩频信号误码率计算。
实验内容1.BPSK 信号的调制;2.BPSK 信号扩频;3.不同信噪比环境下BPSK 扩频信号误码率计算,并与理论误码率曲线对比。
实验原理BPSK 信号调制原理1.系统原理高斯白噪声图5 BPSK 调制系统原理框图BPSK 调制系统的原理框图如图1所示,其中脉冲成形的作用是抑制旁瓣,减少邻道干扰,通常选用升余弦滤波器;加性高斯白噪声模拟信道特性,这是一种简单的模拟;带通滤波器BPF 可以滤除有效信号频带以外的噪声,提高信噪比;在实际通信系统中相干载波需要使用锁相环从接收到的已调信号中恢复,这一过程增加了系统的复杂度,同时恢复的载波可能与调制时的载波存在180度的相位偏差,即180°相位反转问题,这使得BPSK 系统在实际中无法使用;低通滤波器LPF 用于滤除高频分量,提高信噪比;抽样判决所需的同步时钟需要从接收到的信号中恢复,即码元同步,判决门限跟码元的统计特性有关,但一般情况下都为0。
2.参数要求码元速率1000波特,载波频率4KHz ,采样频率为16KHz 。
BPSK 信号扩频原理通信理论和通信技术的研究,是围绕着通信系统的有效性和可靠性这两个基本问题展开的,所以有效性和可靠性是设计和评价一个通信系统的主要性能指标。
通信系统的有效性,是指通信系统传输信息效率的高低。
这个问题是讨论怎样以最合理、最经济的方法传输最大数量的信息。
在模拟通信系统中,多路复用技术可提高系统的有效性。
显然,信道复用程度越高,系统传输信息的有效性就越好。
在数字通信系统中,由于传输的是数字信号,因此传输的有效性是用传输速率来衡量的。
通信系统的可靠性,是指通信系统可靠地传输信息。
由于信息在传输过程中受到干扰,收到的信息与发出的信息并不完全相同。
可靠性就是用来衡量收到信息与发出信息的符合程度。
因此,可靠性决定于系统抵抗干扰的性能,也就是说,通信系统的可靠性决定于通信系统的抗干扰性能。
程序代码~MATLAB仿真 BPSK调制解调器

MATLAB仿真BPSK调制解调器clc;clear;fc=4800;fs=12000;fb=2400;%要调制的数字信号a=randint(1,12,2);%随机产生12个“0”,“1”s=zeros(1,60);for i=1:12for j=1:5if(a(i)==0)s(j+(i-1)*5)=0;elses(j+(i-1)*5)=1;endendendplot(s);xlabel('基带信号');figurepwelch(s);%功率谱figure%波形成形滤波器(平方根升余弦滚降)h=firrcos(14,1200,1200,4800,'sqrt');figurestem(h);xlabel('成形滤波器的单位冲击响应');[H,W]=freqz(h,1);H=abs(H);figureplot(H);xlabel('成形滤波器的频率响应');s=fftfilt(h,s);figureplot(s);xlabel('通过成形滤波器后的基带信号'); figurepwelch(s);%经波形成形滤波器后的功率谱%已调信号e=dmod(a,4800,2400,12000,'psk',2);%调制figureplot(e);xlabel('已调信号');enoise=e+randn(1,60);%enoise=e+.1*randn(1,60)不同功率的高斯白噪声aa=ddemod(enoise,4800,2400,12000,'psk',2);%解调figurestem(aa);xlabel('解调后的数字信号');%解调后的数字信号p=symerr(a,aa)/12 %误码率%误码率曲线figurer=-6:3:12;rr=10.^(r/10);pe1=1/2*exp(-rr);%相干解调的误码率曲线hold onplot(r,pe1,'r');grid on;pe2=(1-1/2*erfc(sqrt(rr))).*erfc(sqrt(rr));%差分相干解调的误码率曲线plot(r,pe2,'b');xlabel('bpsk,dpsk误码率曲线');set(gca,'XTick',-6:3:18);。
基于MATLAB仿真的BPSK的调制与解调报告

基于MATLAB 仿真的BPSK 的调制与解调一、实验要求根据题目要求,查阅相关资料,掌握数字带通的 BPSK 调制解调的相关知识。
学习 MATLAB 软件,掌握 MATLAB 各种函数的使用。
在此基础上,完成以下实验要求:1) 设计系统整体框图及数学模型。
2) 运用 MATLAB 进行编程,实现 BPSK 的调制解调过程的仿真。
其中包括信源、BPSK 信号的产生,信道噪声的加入,BPSK 信号的载波提取和相干解调。
3) 系统性能的分析包括信号带宽,波形对比以及误码率的计算。
二、实验原理数字信号的传输方式分为基带传输和带通传输,在实际应用中,大多数信道 具有带通特性而不能直接传输基带信号。
为了使数字信号在带通信道中传输,必 须使用数字基带信号对载波进行调制,以使信号与信道的特性相匹配。
这种用数 字基带信号控制载波,把数字基带信号变换为数字带通信号的过程称为数字调制。
数字调制技术的两种方法:1) 模拟相乘法。
利用模拟调制的方法去实现数字式调制,即把把数字基带信号当做模拟信号的特殊情况处理。
2) 键控法。
利用数字信号的离散取值特点通过开关键控载波,从而实现数字调制。
这种方法通常称为键控法,比如本实验对载波的相位进行键控,便可获得相移键控(PSK )基本的调制方式。
1.BPSK 的调制原理:二进制移相键控是用二进制数字信号0和1去控制载波的两个相位0和π的方法。
在2PSK 中,通常用初始相位0和π分别表示二进制1和0。
因此,2PSK 信号的时域表达式为:)cos(A )(2PSK n c t t e ϕω+= (1)式中,ϕn 表示第n 个符号的绝对相位:⎩⎨⎧=”时发送“”时发送“,1,00πϕn (2)因此,上式可以改写为⎩⎨⎧--=Pt P t t e c c 1,cos A ,cos A )(2PSK 概率为概率为ωω (3)由于两种码元的波形相同,极性相反,故BPSK 信号可以表述为一个双极性全占空矩形脉冲序列与一个正弦载波的相乘:()t t s t e c ωcos )(2PSK = (4) 式中∑-=ns n nT t g a t s )()( (5)这里s(t)为双极性全占空(非归零)矩形脉冲序列,g(t)是脉宽为T s 的单个矩形脉冲,而a n 的统计特性:⎩⎨⎧--=P P a n 1,1,1概率为概率为 (6)图1 BPSK 信号的波形示例2.BPSK 的解调原理:2PSK 信号的解调方法是相干解调法。
AWGN信道中BPSK调制系统的BER 仿真计算—MATLAB程序代码

MATLAB程序:主程序:%Simulation of bpskAWGNMax_SNR=10;N_trials=1000; %做1000次试验N=200; %每次试验取200个抽样点Eb=1; %确定Ebber_m=0;for trial=1:1:N_trialstrialmsg=round(rand(1,N)); %产生长的随机比特序列作为发送器的输入s=1-msg.*2; %对输入信号进行调制,适合信道输入,即0-->1, 1-->1 n=randn(1,N)+j.*randn(1,N); %产生长度为N,均值为0的复数高斯白噪声ber_v=[];for snr_dB=1:2:Max_SNRsnr=10.^(snr_dB./10); %snr(db)-->snr(decimal)N0=Eb./snr; % 计算N0sgma=sqrt(N0./2); % 计算噪声的方差σy=sqrt(Eb).*s+sgma.*n; %加上噪声,运行接收器y1=sign(real(y)); %对调制信号进行解调y2=(1-y1)./2; %恢复原信号, 1, 0 sequenceerror=sum(abs( msg- y2)); %计算错误比特数ber_snr=error./N; %berber_v=[ber_v,ber_snr];end%for snrber_m=ber_m+ber_v;endber=ber_m./N_trials; %计算理论误码率ber_theory=[]; %计算实际误码率for snr_db=1:2:Max_SNRsnr=10.^(snr_db./10);snr_1=Qfunct(sqrt(2*snr));ber_theory=[ber_theory,snr_1];end%绘图表示实际误码率与理论误码率i=1:2:Max_SNR;semilogy(i,ber,'-r',i,ber_theory,'*b');xlabel('E_b/N_0 (dB)')ylabel('BER')legend('Monte Carlo', 'Theoretic')子程序:function y = Qfunct(x)%QFUNC Q function.% Y = QFUNC(X) returns 1 minus the cumulative distribution function of the% standardized normal random variable for each element of X. X must be a real% array. The Q function is defined as:%% Q(x) = 1/sqrt(2*pi) * integral from x to inf of exp(-t^2/2) dt%% It is related to the complementary error function (erfc) according to% Q(x) = 0.5 * erfc(x/sqrt(2))if (~isreal(x) || ischar(x))error('comm:qfunc:InvalidArg','The argument of the Q function must be a real array.');endy = 0.5 * erfc(x/sqrt(2));return;。
MATLAB仿真-BPSK调制

目录一、背景 (4)二、基本要求 (4)三、设计概述 (4)四、Matlab设计流程图 (5)五、Matlab程序及仿真结果图 (6)1、生成m序列及m序列性质 (6)2、生成50位随机待发送二进制比特序列,并进行扩频编码 (7)3、对扩频前后信号进行BPSK调制,观察其时域波形 (9)4、计算并观察扩频前后BPSK调制信号的频谱 (10)5、仿真经awgn信道传输后,扩频前后信号时域及频域的变化 (11)6、对比经信道前后两种信号的频谱变化 (12)7、接收机与本地恢复载波相乘,观察仿真时域波形 (14)8、与恢复载波相乘后,观察其频谱变化 (15)9、仿真观察信号经凯萨尔窗低通滤波后的频谱 (16)10、观察经过低通滤波器后无扩频与扩频系统的时域波形 (17)11、对扩频系统进行解扩,观察其时域频域 (18)12、比较扩频系统解扩前后信号带宽 (19)13、比较解扩前后信号功率谱密度 (20)14、对解扩信号进行采样、判决 (21)15、在信道中加入2040~2050Hz窄带强干扰并乘以恢复载波 (24)16、对加窄带干扰的信号进行低通滤波并解扩 (25)17、比较解扩后信号与窄带强干扰的功率谱 (27)六、误码率simulink仿真 (28)1、直接扩频系统信道模型 (28)2、加窄带干扰的直扩系统建模 (29)3、用示波器观察发送码字及解扩后码字 (30)4、直接扩频系统与无扩频系统的误码率比较 (31)5、不同扩频序列长度下的误码率比较 (32)6、扩频序列长度N=7时,不同强度窄带干扰下的误码率比较 (33)七、利用Walsh码实现码分多址技术 (34)1、产生改善的walsh码 (35)2、产生两路不同的信息序列 (36)3、用两个沃尔什码分别调制两路信号 (38)4、两路信号相加,并进行BPSK调制 (39)5、观察调制信号频谱,并经awgn信道加高斯白噪和窄带强干扰 (40)6、接收机信号乘以恢复载波,观察时域和频域 (42)7、信号经凯萨尔窗低通滤波器 (43)8、对滤波后信号分别用m1和m2进行解扩 (44)9、对两路信号分别采样,判决 (45)八、产生随机序列Gold码和正交Gold码 (47)1、产生Gold码并仿真其自相关函数 (48)2、产生正交Gold码并仿真其互相关函数 (50)九、实验心得体会 (51)直接序列扩频系统仿真一、背景直接序列扩频通信系统(DSSS)是目前应用最为广泛的系统。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
matlab BPSK 调制与解调
1、调制
clear all;
g=[1 0 1 0 1 0 0 1];%基带信号
f=100; %载波频率
t=0:2*pi/99:2*pi;
cp=[];sp=[];
mod=[];mod1=[];bit=[];
for n=1:length(g);
if g(n)==0;
die=-ones(1,100); %Modulante
se=zeros(1,100); %
else g(n)==1;
die=ones(1,100); %Modulante
se=ones(1,100); %
end
c=sin(f*t);
cp=[cp die];
mod=[mod c];
bit=[bit se];
end
bpsk=cp.*mod;
subplot(2,1,1);plot(bit,'LineWidth',1.5);grid on; title('Binary Signal');
axis([0 100*length(g) -2.5 2.5]);
subplot(2,1,2);plot(bpsk,'LineWidth',1.5);grid on; title('ASK modulation');
axis([0 100*length(g) -2.5 2.5]);
2、调制解调加噪声
clc;
close all;
clear; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% 假定:
% 2倍载波频率采样的bpsk信号
% 调制速率为在波频率的 N/2m
% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
m=128;
N=512;
n=1:1:N;
N0=0.5*randn(1,N) %噪声
h0=zeros(1,N);
% 30阶低通滤波器 h0
f = [0 0.3 0.3 1]; w0 = [1 1 0 0];
b = fir2(30,f,w0);
[h,w] = freqz(b,1,N/2);
h0(1,1:N/2)=abs(h');
for i=1:N/2
h0(1,N-i+1)=h0(1,i);
end;
%%%%%%%%% 随机序列
a=rand(1,m);
for i=1:m
if(a(1,i)>0.5)
a(1,i)=1;
else
a(1,i)=-1;
end;
end;
%%% 生成BPSK信号
bpsk_m=zeros(1,N);
j=1;k=1;
for i=1:N
if(j==(N/m+1))
j=1;
k=k+1;
end; % 0.05*pi 为初始相位,可以任意改变
bpsk_m(1,i)=a(1,k)*sin(2*pi*0.5*i+0.05*pi)+a(1,k)*cos(2*pi*0.5* i+0.05*pi);
j=j+1;
end;
bpsk_m=bpsk_m+N0;% 信号加噪声,模拟过信道
% 接收处理用正交本振与信号相乘,变频
bpsk_m1=bpsk_m.*sin(2*pi*0.5*n);
bpsk_m2=bpsk_m.*cos(2*pi*0.5*n);
%滤波
tempx=fft(bpsk_m1);
tempx=tempx.*h0; %低通滤波
tempx=ifft(tempx);
real_x=real(tempx);
tempx=h0.*fft(bpsk_m2);
tempx=tempx.*h0; %低通滤波
tempx=ifft(tempx);
real_x1=real(tempx);
subplot(2,1,1);
plot(real_x1+real_x,'b');
axis([1 N -2.5 2.5]);
grid on;
hold on;
In=real_x1+real_x; % 可只取一路,这里取了两路之和for i=1:N % 滤波后整形
if(In(1,i)>0) % 判决,得到解调结果
In(1,i)=1;
else
In(1,i)=-1;
end;
end;
plot(In,'r');
an=zeros(1,m);
for i=1:m
an(1,i)=In(1,(i-1)*N/m+N/(2*m));
end;
subplot(2,1,2); % 比较误码
plot(an,'r*');hold on;
axis([1 m -2 2]);
plot(a,'b^');。
