一模专题:圆锥曲线静安闸北寒暑假高中补习班
静安闸北恒高一对一高暑假中英语补习班

1
Anthony Lee 作文指导 S
SELS Summer English Courses
English course Total Hours of Study Total Hours of Part-time Job 6-week course 8-week course 90 120 No Job but Tour Instead 48
English course Total Hours of Study Total Hours of Part-time Job 6-week course 8-week course 90 120 No Job but Tour Instead 48
Date July 1 —Aug 15 July 1—Aug 30
Date July 1 —Aug 15 July 1—Aug 30
Cost 15,000 yuan 25,000 yuan
信中必须包括:1.简单介绍你的情况; 2.你的选择及理由; 3.对该课程的要求和建议。 ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ _______ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ (120) ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ ________ (150)
静安闸北高中寒暑假补习班-朱老师教学计划

2017高二秋季班-静安新王牌第一课:数列的极限
第二课:向量的基本运算
第三课:向量的数量积
第四课:平面向量的分解定理
第五课:向量的应用
第六课:矩阵与行列式
第七课:直线的方程
第八课:直线的斜率和倾斜角
第九课:两直线的夹角
第十课:两直线的距离公式
第十一课:期中复习
第十二课:求动点轨迹方程
第十三课:圆的方程
第十四课:圆的性质研究,点,直线,圆的位置关系
第十五课:椭圆的方程
第十六课:椭圆的方程和性质研究
第十七课:双曲线的方程和性质研究
第十八课:抛物线的方程和性质研究
第十九课:圆锥曲线与直线相交问题
第二十课:期末复习课
高中数学朱yz老师。
高中化学张S老师2018年暑假静安闸北高三恒高一对一补习班

化学张S老师暑假教学安排-静安新王牌教学理念:以《上海市高中化学学科教学基本要求》为教学目标导向,落实“目标—教学—评价”的内在一致性,有效开展基于标准的教学,帮助学生按照自己的特点开展学习,促进每一位学生都得到发展。
教学风格:以生活中学生喜闻乐见的化学新闻或经验来创设真实的化学问题情境,以风趣机智的语言吸引学生注意,用严谨细致的教学内容让学生感受到化学学习的成就感,借助多媒体实验视频来提高学生学习化学的兴趣。
高三化学教学计划高三暑假学习的重要性:经过高中两年的学习,大多数同学都已经把高中的知识要点学习过一遍,此时如果能充分利用假期时间在老师的指导下对整个高中阶段的知识进行系统性梳理,建立清晰的高中知识网络,将可以让自己在高三总复习时更加具有主动性和前瞻性。
这个暑假会是同学们人生中最忙最累的,高三一年流的汗以后十年都流不出来。
只有含泪播种的人,才能含笑收获,相信傻叉一样的坚持一定会获得牛叉一样的结果。
下述安排是预设教学计划,可能会根据实际情况做调整。
以下几个板块内容是高考必考知识点,占到大约40分左右,其中化学平衡的内容是大多数学生感觉很难的,希望张老师的真情付出能够为大家的高三化学学习打开另一扇窗,引领大家攻克难关,让大家学有所思、学有所获。
第1次课:各类化学用语的区别(包括核外电子排布、电子轨道式书写、电子式、结构式、结构简式等)、离子键讲解第2次课:配套练习巩固第3次课:共价键、金属键第4次课:配套练习巩固第5次课:化学反应速率第6次课:配套练习巩固第7次课:化学平衡讲解第8次课:配套练习巩固第9次课:化学平衡移动(包括勒夏特列原理)讲解第10次课:配套练习巩固第11次课:化学平衡图像讲解第12次课:配套练习巩固第14次课:电离平衡讲解及配套练习巩固第15次课:各种离子方程式的书写讲解第16次课:水的电离平衡及pH计算第17次课:配套练习巩固第18次课:各种盐的水解实质及规律讲解第19次课:三大守恒及配套练习巩固第20次课:氧化还原反应讲解第21次课:配套练习巩固。
上海市高三数学一模试卷静安高考补习班新王牌.doc
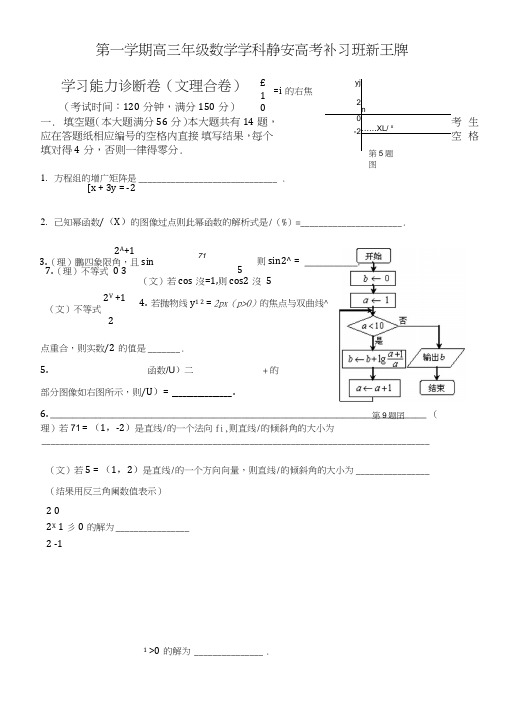
第一学期高三年级数学学科静安高考补习班新王牌学习能力诊断卷(文理合卷) (考试时间:120分钟,满分150分) 一. 填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接 填写结果,每个空格填对得4分,否则一律得零分.1. 方程组的增广矩阵是 ______________________________ .[x + 3y = -22. 己知幂函数/(X )的图像过点则此幂函数的解析式是/(%)=______________________ .(文)若cos 沒=1,则cos2沒 54. 若抛物线y 1 2 = 2px (p>0)的焦点与双曲线^一6点重合,则实数/2的值是 _______ .5.函数/U )二 + 的部分图像如右图所示,则/U )= ________________ .6. ___________________________________________________________________ (理)若71 = (1,-2)是直线/的一个法向fi,则直线/的倾斜角的大小为____________________________________________________________________________________ (文)若5 = (1,2)是直线/的一个方向向量,则直线/的倾斜角的大小为 ________________ (结果用反三角阑数值表示)2 02X 1彡0的解为 ________________ 2 -11 >0的解为 _______________ .yj2n 0-2……XL/ x£ 10 =i 的右焦 第5题图2A +17.(理)不等式 0 3 2V +1(文)不等式2第9题囝3.(理)鵬四象限角,且sin 71则sin2^ =5q 的収值范围是./?(/? +1)limS/;—>oo11.(理)若平面向量冗满足 |5| = 1(/ = 1,2,3,4)且5.&>0(,. = 1,2,3),则值有.(文)边长为1的正方形ABCZ )中,M 为BC 的中点,£在线段AB 上运动,则的取值范围12 53 4■垂l ■ ■ ■ ■ i ■ I ■Ao A] A2 A3 A4 A5 Ag A7 Ag A9 A JQ第14题囝二. 选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案,考生应在 答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.15. 下列排列数中,等于(n —5)(zi — 6)."(n —12) (z?> 13,ne A^)的是 ( )(A )<_12(B ) P^_5(C ).(D ) <1216. 在MSC 小,“cos 欠+ sin/l = cosB + sinB ” 是 “ZC = 9O 0” 的()(A )充分非必要条件 (B )必要非充分条件 (C )充要条件(D )既不充分也不必要条件17. 若函数/(x ) = ^_在(0,+00)上单调递增,那么实数6/的取值范围是( )X(A )tz>0(B )CZ >0(C )6Z<O(D ) a<018. (理)对于直角坐标平面沁>,内的点4(x ,y )(不是原点),A 的“对偶点” B 是指:满足|OA||Ofi| =l 且 在射线OA 上的那个点.若p ,(2,尺,S 是在同一直线上的四个不同的点(都不是原点),则它们的“对偶10.(理)已知等比数列{人}的首项% =1,公比为g (《〉0),前n 项和为S,,,若lim• ^n+l1,则公比(文)数列{a n }的通项公式a n =<(HE N f),前n 项和为,则可能的■个.点” P,Q,R,S()(A)一定共线(B)—定共圆(C)要么共线,要么共圆(D)既不共线,也不共圆(文)对于直角坐标平面xOy内的点A(x,y)(不是原点),A的“对偶点” B是指:.满足|OA||O6| = 1且在射线04上的那个点.则圆心在原点的圆的对偶图形()(A)一定为圆(B)—定为椭圆(C)可能为圆,也可能为椭圆(D)既不是圆,也不是椭圆三.解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.19.(本题满分12分)已知集合A = {x\^<0},实数6/使得集合B = {x\(x-6/)(X-5)>0}满足4求6Z的取值范围.2().(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.X+ 1已知函数/(x) = log,-一.• X-1(1)判断函数/(X)的奇偶性,并证明;⑵求/(X)的反函数厂\x),并求使得函数=厂1 U)-Iog2々有零点的实数々的取值范围.21.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.(理)某种型号汽车叫个轮胎半径相同,均为R = 40cm,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为I = 280cm(假定四个轮胎中心构成一个矩形).当该型号汽车开上一段上坡路ABC (如图(1)所示,其屮ZABC = a(-7r<a<7r)},且前轮£己在BC段上时,后轮中心在F位置;若前轮中心到达G处时, 4后轮中心在H处(假定该汽车能顺利驶上该上坡路).设前轮中心在£和6处时与地面的接触点分别为S 和且fiS = 60cm, ST = 100cm.(其它因素忽略不计)(1)如图(2)所示,77/和的延长线交于点0,(Y求证:= 40cot —+ 60(cm);(2)当6Z二时,后轮中心从F处移动到W处实际移动了多少厘米?(精确到lcm) 6(文)某种型号汽车的四个轮胎半径相同,均为/? = 40cm,该车的底盘与轮胎中心在同一水平而上.该车的涉水安全要求是:水而不能超过它的底盘岛度.如阁所示:某处有一“坑形”地而,.其中坑/U5C形成顶角为120()的等腰三角形,且= = 如果地面上有/?(^)(//<40)高的积水(此吋坑内全是水,其它因素忽略不计).(1)当轮胎与Afi、SC同时接触时,求证:此轮胎露在水而外的高度(从轮胎最上部到水而的距离)(2)假定该汽车能顺利通过这个坑(指汽车在过此坑时,符合寧本萃•牟睪率〉,求/?的最大伉. (精确到lcm).22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分.第3小题满分6分.22(理)已知椭圆c:久+4 = 1 0〉/2〉o)的一个焦点为尸(1,0),点(一1,1)在椭圆c上,点r满a~ b~2——a2—足OT=,OF(其中O为坐标原点),过点F作一直线交椭圆于尸、0两点.yja2 -b2(1)求椭圆C的方程;(2)求而积的最大值;(3)设点/为点P关于x轴的对称点,判断@与。
上海市2021届高考数学一轮复习 专题突破训练 圆锥曲线 文

上海市2021届高考数学一轮复习专题突破训练圆锥曲线文上海市2021届高考数学一轮复习专题突破训练圆锥曲线文上海2022所高中数学与文学复读专项突破训练圆锥曲线一、选择题并填空1、(2021年高考)抛物线y2?2px(p?0)上的动点q到焦点的距离的最小值为1,则Px2y2??如果1的右焦点重合,抛物线的拟线性平方是2,(2022年高考)抛物线y?2px的焦点和椭圆952程为.3.(2022年高考)让AB为椭圆?点C的长轴在哪里?上,然后呢?中国篮球协会两个焦点之间的距离是多少?4.如果AB=4,BC=2,那么?46.34,(奉贤区2022高三第二模拟考试)抛物线Y2?4x的焦点F是圆的中心,与抛物线的拟直线相切的圆的标准方程为____5、(虹口区2021届高三二模)已知抛物线y2?2px(p?0)的焦点在圆(x?1)2?y2?4上,则p________x2y2?1(a?0)的一个焦6、(黄浦区2021届高三二模)已知抛物线y?16x的焦点与双曲线2?a122点重合,则双曲线的渐近线方程是7,(静安、青浦和宝山区2022个高水平的第二模拟考试),已知的抛物线Y?2px的拟线性方程是x??2.那么2p?.8,浦东新区2022中学的第二次模拟考试是AX?通过3.0和圆x?Y3.没有公共点,所以设置一个P点坐下22x2y2??1的公共点的个数为(c)标(a,b),则过点p的一条直线与椭圆43(a)0(b)19,(普陀区2022高级2022的第一次模拟考试)如果方程2, 2)(3,+无穷大)。
10、(闸北区2021届高三一模)关于曲线c:①曲线c是椭圆;② 关于坐标原点的中心对称性;1(c)二,(d)1或2+=1表示双曲线,则实数k的取值范围为(=1,给出下列四个结论:③ 关于y=x轴对称线;④ 如果封闭图形区域小于8,则正确结论的序列号为② ④. (注:填写你认为正确的命题序号)11、(长宁、嘉定区2021届高三二模)抛物线x2?8y的焦点到准线的距离是_____________12、(崇明县2021届高三一模)已知双曲线k2x2?y2?1(k?0)的一条渐近线的法向量是(1,2),那么k?x2y2??1中有两点a?1,3?, B3013.已知椭圆?,P是椭圆上的一个点,那么Pa?Pb的最大值为2516____x2y214、若双曲线c:2?2?1的焦距为10,点p(2,1)在c的渐近线上,则c的方程为_________.Ab15。
闸北高中补习班高考冲刺补习-秋季新王牌课程高一数学-函数概念与性质

高一数学(寒假) 第一讲 函数概念与性质【例题解析】1、下列各函数解析式中,满足)(21)1(x f x f =+的是 ( ) (A) 2x (B)21+x (C) x -2 (D)21x + 2、已知32)121(+=-x x f ,且 6)(=m f ,则m 等于 ( ) (A) 41- (B)41 (C) 23 (D)23- 3、已知1)1(+=+x x f ,则函数)(x f 的解析式为 ( )(A )2)(x x f = (B ))1(1)(2≥+=x x x f (C ))1(22)(2≥+-=x x x x f (D ))1(2)(2≥-=x x x x f 4、设函数))((R x x f ∈为奇函数,),2()()2(,21)1(f x f x f f +=+=则=)5(f ( )(A)0 (B)23 (C)25 (D)23- 5、已知)(x f y =是偶函数,当0>x 时,x x x f 4)(+=,且当]1,3[--∈x 时,m x f n ≤≤)( 恒成立,则n m -的最小值是( ) (A)31 (B)32 (C)1 (D)34 11、已知)(x f y =是定义在R 上的单调函数,实数21x x ≠,,1,121λλλ++=-≠x x a λλβ++=112x x ,若|)()(||)()(|21βαf f x f x f -<-,则( ) (A)0<λ (B)0=λ(C)10<<λ (D)1≥λ12、设函数{2,0,()2,0.x bx c x f x x ++≤=>若(4)(0)f f -=,(2)2f -=-,则关于x 的方程x x f =)(的解的个数为 ( )(A)1 (B)2 (C)3 (D)4对于上题,解不等式()f x x >的解为 。
13、设函数()y f x =的定义域为R ,则函数(1)y f x =-与(1)y f x =-的图象关于( )(A)直线0y =对称 (B)直线0x =对称 (C)直线1y =对称 (D)直线1x =对称14、设定义在[-2, 2]上的偶函数()f x 在区间[0, 2]上单调递减,若(1)()f m f m -<,实数m 的取值范围是 。
静安闸北高中英语暑假补习班-名师课堂

静安新王牌*一模英语试题(A)Don't Take the Fun Out of Youth SportsWhen I joined a private football league a few years ago, the sport meant everything to me. My coach said I had lots of potential, and I became captain of my team. That was before all the fun (25)_______(take) out of playing.At first, everyone on the team got equal playing time. Then the team moved up to the top division after winning all its games, and the pressure started. Some parents, who (26)_____(pay) the coach extra (27)_____return for their daughters' private one-on-one training, got angry when she didn't give them more playing time. The coach was replaced. The new coach, however, took all the fun out of the game: All we did during practice was run. We ran so much that, afterwards, we had trouble (28) ______(breathe).Younger people shouldn't be doing exercises(29)______ (design) for 18-year-olds.I was thin before I started football, but as a member of this team I wouldn't eat much, because I thought to (30) _____ that I was afraid of being too full to run. Finally, I ended up leaving the football team. Four other girls did the same, two of (31)______stopped playing football completely.That's sad because they had so much potential. They were just burned-out with all the pressure they felt from the coach or their parents.I continued playing football at school and rediscovered my love for it. I joined a private team and the coach told me I needed to relax because I looked nervous. After I calmed down, I played better. When you enjoy something, it is a lot (32)______(easy) to do it well.(B)How to Be a WinnerSteven Redgrave---Winner of 5 Olympic Gold Medals"In 2012 I was found to have developed lung disease. (33)______ (believe) my career was over, I felt extremely low. Then one of the specialists said there was no reason why I should stop training and competing. That was it----the encouragement I needed. I could still be a winner (34) ______ _______ _______I believed in myself. I am not saying that it isn't difficult sometimes. But I wanted to prove to myself that hard (35) ______the condition was, I wasn't finished yet. Nothing is to stand in my way."Karen Pickering-Swimming World Champion"I swim 4 hours a day, 6 days a week. I manage that sort of workload by putting it on top of my diary. This is the key to success--- you (36) ____ not bear following a career in any field without being well-organized. List (37) _____ you believe you can achieve. Trust yourself, write down your goals for the day, however small they are, and you'll be a step closer to achieving them."Kirsten Best-Poet &Writer"When things are getting hard, a voice inside my head tells me I can't achieve something. Then, there are other influencing factors, such as family or hobbies. The key is to concentrate, (38) _____ helps a lot to repeat words such as ‘calm’, ‘peace’or ‘focus’, either out loud or silently in my mind when I feel tense. It makes me (39)_______( feel) more in control and increases my confidence. This is a habit that can become second nature quite easily and is(40)______powerful psychological tool."(C)The Problem with Top-Schools ListsThere are around 4,000 accredited universities and other higher education institutions in the United States. They offer an immense range of educational experiences, (25)________ largeresearch universities to small, friendly liberal arts colleges. This helps explain (26)______the United States attracts more international students than any other country, says Allan E. Goodman, president of the Institute of International Education, (27)_____non-profit group promoting student exchanges to and from America."While elite(精英)U.S. programs are among the top ten in the world," Goodman says, "the unique strength of the U.S. higher education system is diversity."There is no official ranking system to indicate which institutions are better than others, (28)_______several unofficial rankings are listed by magazines and associations. However, educators urge caution in using a ranking table and emphasize that (29)_____(good) choice for one student may be very different for another.Institutions of all types (30) ______ (spread) across the United States. Some students want a campus that will give them the excitement and rich cultural life of a big city such as New York, Chicago, or Los Angeles. (31)_____value the peace and beauty of a rural setting, whether the quiet forests and snowy winters of the Northeast, subtropical Florida, the dry expanses of the West, or the Pacific coast with its seashore and nearby mountainsMany institutions have particular strengths in certain academic areas, (32)______ (make) them a good choice for students interested in those fields.(D)An evolving gameAsia has already become a center of the women's professional game, and much of the growth in participation across the world is coming from women's golf.Family-friendly facilities (33)_____(develop) for a new golfing demographic(人群)in the following years, (34)____ more women are playing the game and men and women are increasingly spending their leisure time together.Children's engagement with the game will increase. In China, golf is recognized as a game (35)______teaches children important life principles. Free golf training is offered to kinder-gartners and some parents are now prepared to spend up to 300,000 yuan ($43,940) a year on lessons for their children."Asia will play an increasingly vital role in the future development of golf," say top players past and present.More top events will be add to the schedule in China and other places in Asia, (36)______the game is becoming more popular. Back-to-back Open Champion Padraig Harrington agrees: "You only (37)_______ ________ look at the European Tour's schedule and see how many tournaments are now being hosted by Asia, whether in the Middle East or Far East," he says."Change is the price of survival," says golf legend Gary Player, one of a handful of players(38)______ (achieve) the Career Grand Slam(大满贯)."With the eyes of the sport now firmly(39)_____(focus) on Asia, I can see several of the world's Top 10 coming from Asia and several more global tournaments hosted there by 2020."The game will also become more technologically engaged. Advances in digital technology will change the face of (40)_____(coach) with "smart clubs" which memorize golfers' grip and swing, allowing them to analyze their performance and learn from their mistakes.John Nash, a Nobel Prize winner and mathematical genius whose struggle with mental illness was documented in the Oscar-winning film "A Beautiful Mind", was killed in a car accident on Saturday. He was 86. The accident ___41___ when the taxi Nash was traveling in ran into another car on the New Jersey Turnpike. Neither of the two drivers involved in the accident underwent life-___42___ injuries.At Princeton, Nash published a 27-page essay about the field of game theory, which led to ___43___ in economics, international politics, and evolutionary biology. His signature solution found that competition among two opponents is not necessarily governed by zero-sum logic. Two opponents can, for instance, each achieve their maximum ___44___ through cooperating with the other, or gain nothing at all by refusing to cooperate. This simple understanding is now regarded as one of the most important social science ideas in the 20th century, and a proof to his almost unique ___45___ gifts.But in the late 1950s, Nash began a slide into mental illness and each therapy failed to cure him, and for much of the next three decades, Nash ___46___ freely on the Princeton campus, scratching his hands on empty blackboards and staring blankly ahead in the library. Robert Wright remembers Nash as “some math genius that went crazy” who wore colorful shoes and quietly watched people. His mental illness removed him ___47___ from his work. By the time Nash was awarded the Nobel Prize in Economics in 1994, he hadn’t published a paper in 36 years.But like a child cured of a terrible dream by the switch of a light, Nash recovered from his illness seemingly by choosing not to be sick anymore. Five years later, the ___48___ of the film “A Beautiful Mind”, based on Sylvia Nasar’s 1998 book of the same name, expanded Nash’s ___49___ life story to an international audience. He continued to work, travel, and speak at conferences for the rest of his life.It’s tempting to wonder w hat Nash might have ___50___, had mental illness not robbed him of so many productive years. “Because the ideas I had about super natural beings came to me the same way that my mathemat ical ideas did,” said Nash. “So I took them seriously.”Chinese traders were recorded as making voyages to the north coast of Australia from the 1750s, but were probably visiting Australia long before. Chinese men arrived in Australia in small numbers after the 1788 British settlement as free settlers and criminals. A small population grew rapidly after 1848 under a system of indentured (契约的labour, after China had __41__ its ports to foreign trade in 1842. They worked in rural New South Wales as cooks,farm labours and etc.Indentured Chinese __42__ worked in all colonies variously as station hands,plantationworkers, miners, on public works, cabinet makers, personal servants and in laundries. Most camefrom the south-eastern provinces of Guangdong and Fujian.Due to labour __43__ in west Australia ,the colonial government organized Chinesecontract labour between 1847 and 1898,most working as labourers, cooks and gardeners. ManyChinese came from rural backgrounds and brought with them __44__ and water managementskills. By 1885, there were 54 Chinese market gardens in Sydney. By 1901, 67% of the New SouthWales market gardeners were Chinese.Gold rushes in Victoria in the 1850s and New South Wales in the 1860s significantly __45__the population of Chinese immigrants in Australia;about 45,000 prospectors arrived in Victoriaalone in 1854-58. Numbers continued to increase as gold and other __46__ were discovered inQueensland, North Territory and Tasmania.When mining became less __47__,many Chinese people worked successfully to providegoods and services such as furniture making,market gardening, fishing and, particularly,store-keeping including the import and export of goods from overseas. Chinese goods,especiallytea,silk,vegetables, herbs and other spices were highly sought after items of trade bynon-Chinese people. Tea rooms, importing and selling many varieties of tea,were very popular.Chinese silk was turned into __48___ evening wear and cloaks by Chinese tailors andseamstresses.Today there is a culturally diverse Chinese __49___ in Australia with links to south-eastern China as well as Vietnam and Hong Kong. The Chinese communities in Australia are brought together every day by __50 __of Lunar New Year.The most exciting kind of education is also the most personal. Nothing is beyond the joy of discovering for yourself something that is a big ___51___ to you! It may be an idea or a bit of information you come across accidentally or a sudden understanding, fitting together pieces of information or working through a problem. Such personal ___52___ are the "payoff" in education. A teacher may direct you to learning and even ___53___ you in it-but no teacher can make the excitement or the joy happen. That is ___54___ you.A research paper, assigned in a course and perhaps checked at ___55___ stages by an instructor, leads you beyond classrooms, beyond the texts for classes and into a ___56___ where the joy of discovery and learning can come to you many times. Preparing the research paper is an active and individual process, and ___57___ learning process. It provides a structure within which you can make exciting discoveries, of knowledge and of self, which are basic to education. The research paper also gives you a chance to individualize a school assignment, to ___58___ a piece of work to your own interests and abilities, to show others what you can do. Writing a research paper is ___59___ just a classroom exercise. It is an experience in searching out, understanding and synthesizing (综合), which forms the ___60___ of many skills applicable to both academic and nonacademic tasks. It is, in the fullest sense, a discovery, an education. So, to produce a good research paper is both a useful and a ___61___ satisfying experience!To some, the thought of having to write an ___62___ number of pages, often more than ever produced before, is disturbing. To others, the very idea of having to work independently is ___63___. But there is no need to approach paper assignment with ___64___, and nobody should view the research paper as an obstacle to overcome. ___65___, consider it a goal to accomplish, a goal within reach if you find great pleasure in it.51. A. mistake B. deal C. plan D. challenge52. A. behaviours B. opportunities C. encounters D. entertainments53. A. encourage B. assess C. emphasize D. affect54. A. familiar to B. suitable for C. considerate of D. dependent on55. A. similar B. unbelievable C. flexible D. various56. A. outcome B. process C. achievement D. position57. A. ideal B. complicated C. competitive D. causal58. A. devote B. lead C. suit D. adopt59. A. no more than B. less than C. none other than D. more than60. A. evidence B. basis C. impression D. experience61. A. hardly B. skillfully C. thoroughly D. vividly62. A. assigned B. limited C. established D. fixed63. A. inspiring B. rewarding C. frightening D. threatening64. A. anxiety B. interest C. excitement D. embarrassment65. A. Furthermore B. Instead C. However D. ThereforeDigital fingerprinting, fluctuations(波动)in the dollar exchange rate, and a mass of online information are some of the ways making travel to the United Nations in 2010 a different ___51___ for international visitors than it was earlier in the 21st century.These ___52___ are evident before the visitor leaves his or her country.In 2004, the U.S. Department of Homeland Security(DHS)——a department of the federal government established by laws and regulations in late 2002, after the September 11, 2001, terrorist attacks——established a new series of security ___53___ for the international visitors holding non-U.S. passports or visas.___54___ when these visitors apply for a visa, the officer ___55___ them reviews their application and supporting papers and collects both digital fingerprints and a digital photograph.Recently, the waiting time for these interviews has been significantly ___56___. According to Geoff Freeman, a senior vice president of public affairs of U.S. Travel, the trade organization for the U.S. travel industry, many prospective visa applicants now wait fewer than 30 days for an interview, ___57___ more than 100 days in the past.The Visa Waiter Program(VWP)—which ___58___ citizens from countries that meet various security and other requirements from obtaining a visa for visits to the United States of 90 days or fewer for business or pleasure— ___59___ 36 countries such as Australia, Austria, Belgium and so on.A traveler from a country ___60___ in the VWP must obtain an Electronic System for Travel Authorization(ESTA), an online travel authorization, established by DHS. ESTA determines, before the traveler boards a flight, whether the traveler is ___61___ to travel to the United States under the VWP and whether such travel poses any law implementation or security risks.When an international traveler arrives in the United States, he or she must subject one of the two ___62___ to the U.S. Customs and Boarder Protection(CBP)officer: either a white Form I-94, if the traveler has a visa, or a green Form I-94W, if the traveler is a VWP participant. The CBP officer asks the traveler questions about his or her stay, scans the traveler’s fingerprints, and takes a digital photograph. ___63___, VWP travelers, who are not required to obtain a visa, will soon need to pay a fee. The travelers keeps a portion of the I-94 or I-94W form after the CBP ___64___ and returns it to CBP upon departure from the United States.In 2007 Congress authorized the consumption of $40 million on a “Model Ports of Entry”program, designed to improve the ___65___ procedures of foreign travelers at the 20 U.S. airports with the highest number of international visitors. The program aims to improve staffing, queue management, signage, and infrastructure at the top 20 U.S. international airports and to hire at least 200 new CBP officers.51. A. experiment B. examination C. experience D. excursion52. A. changes B. fluctuations C. fingerprints D. communications53. A. explanations B. registrations C. applications D. procedures54. A. Surprisingly B. Specifically C. Hopefully D. Occasionally55. A. inspecting B. instructing C. interviewing D. investigating56. A. reduced B. resolved C. reviewed D. released57. A. owing to B. compared to C. according to D. added up to58. A. protects B. stimulates C. promises D. relieves59. A. leads to B. applies to C. depends on D. makes up60. A. persevering B. previewing C. participating D. promoting61. A. accessible B. acceptable C. available D. adaptable62. A. participants B. decisions C. documents D. photographs63. A. For instance B. As a result C. In addition D. On the contrary64. A. check B. project C. design D. proposal65. A. queue B. program C. arrival D. departure。
闸北高中补习班 秋季新王牌 高考冲刺补习 直线与圆锥曲线高二

直线与圆锥曲线一、填空题:1.方程01)1()(22=--++y a x a a 表示直线的充要条件是__________________.2.已知直线l :x ―y ―1=0,l 1:2x ―y ―2=0.若直线l 2与l 1关于l 对称,则l 2的方程是__________.3.抛物线2ax y =的准线方程为1-=y ,则实数a 的值是__________.4.双曲线116922=-y x 的焦距是 .5.若经过点)0,1(P 的直线与圆042422=+-++y x y x 相切,则此直线与y 轴的夹角为 .6.若已知点)2,3(A ,且1=,则点B 的轨迹方程是____________________.7.椭圆5522=-ky x 的一个焦点是)2,0(,那么=k ___________.8.已知直线l 过点)1,2(P ,且与x 轴、y 轴的正半轴分别交于B A 、两点,O 为坐标原点,则三角形OAB 面积的最小值为 .9.抛物线x y 82=上的点),(00y x 到抛物线焦点的距离为3,则|y 0|= .10.若m <-1,则曲线11222=+--m x m y 的焦点坐标为 . 11.若直线mx +y +2=0与线段AB 有交点,其中A(-2, 3),B(3,2),则实数m 的取值范围是________________________.12.在抛物线x y 42=上有点M ,它到直线x y =的距离为24,如果点M 的坐标为()b a ,,+∈R b a ,,则b a的值为_____________.13.过椭圆22ax +22b y =1(0<b<a )中心的直线与椭圆交于A 、B 两点,右焦点为F 2(c,0), 则△ABF 2的最大面积是___________.14.分别以椭圆1162522=+y x 的焦点和顶点为双曲线的顶点和焦点的双曲线的标准方程是________________________.15.已知双曲线的一条渐近线方程是02=-y x ,若双曲线经过点)1,52(M ,则双曲线的标准方程为__________________________.16.中心在原点,焦点坐标为(0, ±52)的椭圆被直线3x -y -2=0截得的弦的中点的横坐标为21,则椭圆方程为__________________.17.某桥的桥洞呈抛物线形,桥下水面宽16米,当水面上涨2米后达到警戒水位,水面宽变为12米,此时桥洞顶部距水面高度约为 米(精确到0.1米)18.已知椭圆m x 2+ny 2=1与双曲线p x 2-q y 2=1(m ,n ,p ,q ∈{x |x 是正实数})有共同的焦点F 1、F 2,P 是椭圆和双曲线的一个交点,则|PF 1|·|PF 2|= .19.若直线y =kx -1与双曲线122=-y x 的左支交于A ,B 两点,则实数k 的取值范围________.20.已知圆M :(x +cos θ)2+(y -sin θ)2=1,直线l :y =kx ,下面四个命题: ①任意实数k 与θ,直线l 和圆M 相切;②对任意实数k 与θ,直线l 和圆M 有公共点;③对任意实数θ,必存在实数k ,使得直线l 与和圆M 相切;④对任意实数k ,必存在实数θ,使得直线l 与和圆M 相切.其中真命题的代号是______________(写出所有真命题的代号)二、选择题:1.如果直线01=++by ax 平行于x 轴,则有( )A .00≠≠b a ,B .00==b a ,C .00=≠b a ,D .00≠=b a ,2.设0>m ,则直线01)(2=+++m y x 与圆m y x =+22的位置关系为( )A .相切B .相交C .相切或相离D .相交或相切3.已知方程1||2-m x +my -22=1表示焦点在y 轴上的椭圆,则m 的取值范围是( )A .m <2B .1<m <2C .m <-1或1<m <2D .m <-1或1<m <23 4.已知两个观察站A 、B 相距1千米.一炮弹在某处C 爆炸,在A 处听到爆炸声的时间比B 处快2秒钟,则C 点一定在( )A. 以A 、B 为焦点的双曲线的左半支上B. 以A 、B 为焦点的双曲线的右半支上C. 以A 、B 为焦点的椭圆上D. 在向量BA 的延长线上5.设b a ,是非零实数,则方程ab ay bx =+22及0=+by ax 所表示的图形可能是( )6.若一条曲线既是轴对称图形,又是中心对称图形,则我们称此曲线为双重对称曲线,有下列曲线:①1162522=+y x ;②y=x 2+2x -1;③)32s i n (2π+=x y ;④y =x +1. 其中双重对称曲线的条数为( )A 、1B 、2C 、3D 、4三、解答题:1.已知椭圆C 的焦点分别为F 1(-22,0)和F 2(22,0),长轴长为6,设直线y=x +2交椭圆C 于A 、B 两点,求线段AB 的中点坐标.2.已知倾斜角为︒45的直线l 过点)2,1(-A 和点B ,B 在第一象限,23||=AB .(1) 求点B 的坐标; (2)若直线l 与双曲线1:222=-y ax C )0(>a 相交于E 、F 两点,且线段EF 的中点坐标为)1,4(,求a 的值.3.设坐标原点为O ,抛物线)0(22≠=p py x 与过焦点的直线交于AB 两点.试求向量与的数量积.4.已知椭圆的一个顶点为A(0,-1),焦点在x 轴上,其右焦点到直线x -y +22=0的距离为3,(1)求椭圆方程;(2)椭圆与直线y =kx +m (k ≠0)相交于不同的两点M 、N ,当|AM|=|AN|时,求m 的取值范围.5.已知曲线C:x 2-y 2=1及直线L:y =kx -1,曲线C ′与C 关于直线L 对称.(1)当k =1时,求曲线C ′的方程;(2)求证:不论实数k 为何值,C 与C ′恒有公共点.6.设椭圆C 1的方程为)0(12222>>=+b a b y a x ,曲线C 2的方程为xy 1=,且C 1与C 2在第一象限内只有一个公共点P.(1)用a 表示点P 的坐标;(2)已知A 、B 是椭圆C 1的两个焦点,当a 变化时,求△ABP 的面积函数)(a S 的值域;(3)记min{y 1,y 2,…y n }为y 1,y 2,…y n 中最小的一个,设)(a g 是以椭圆C 1的半焦距为边长的正方形的面积,试求函数)}(),(m in{)(a S a g a f =的表达式.。
数形结合静安闸北高中数学寒暑假补习班

第五课:数形结合-静安新王牌1,设函数2()min{1,1,1}f x x x x =-+-+,其中min{,,}x y z 表示,,x y z 中的最小者. 若(2)()f a f a +>,则实数a 的取值范围为…………( ). .A ()1,0-; .B []2,0-; .C ()(),21,0-∞-- ; .D [)2,-+∞,2,已知函数()f x =2(4,0l 3)3og (1)1,0ax a x a x x x ⎧+<⎨++≥-+⎩,(01)a a >≠且在R 上单调递减,且关于x 的方程|()|2f x x =-恰好有两个不相等的实数解,则a 的取值范围是( ). (A )(0,23] (B )[23,34] (C )123[,]{}334⋃ (D )123[,){}334⋃3,关于x 的不等式)(43432b a b x x a <≤+-≤的解集是[]b a ,,则a+b 的值为_______4,设函数)0()(2<++=a c bx ax x f 的定义域为D ,若所有点),))((,(D t s t f s ∈构成一个正方形区域,则a 的值为________5,在平面直角坐标系中,把位于直线y k =与直线y l =(k l ,均为常数,且k l <)之间 的点所组成区域(含直线y k =、直线y l =)称为“k l ⊕型带状区域”.设()f x 为二次函数,三点(2(2)2)f --+,、(0(0)2)f +,、(2(2)2)f +,均位于“04⊕型带状区域”,如果点(1)t t +,位于“13-⊕型带状区域”,那么,函数()y f t =的最大值为 ( ) (A )72 (B )3 (C )52(D )26,当实数,x y 满足221x y +=时,232x y a x y +++--的取值与,x y 均无关,则实数a 的取范围是 .7,已知)(x g y =与)(x h y =都是定义在),0()0,(+∞-∞ 上的奇函数,且当0>x 时,⎩⎨⎧>-≤<=.1),1(,10,)(2x x g x x x g ,x k x h 2log )(=(0>x ),若)()(x h x g y -=恰有4个零点,则正实数k 的取值范围是 【 】A .]1,21[;B .]1,21(; C .]2log ,21(3; D .]2log ,21[3.8,已知b a x f x -=)(0(>a 且1≠a ,R ∈b ),1)(+=x x g ,若对任意实数x 均有0)()(≤⋅x g x f ,则ba 41+的最小值为________.9,已知定义域为R 的函数)(x f y =满足)()2(x f x f =+,且11<≤-x 时,21)(x x f -=;函数⎩⎨⎧=≠=.0,1,0,lg )(x x x x g ,若)()()(x g x f x F -=,则[]10,5-∈x ,函数)(x F 零点的个数是 .10,已知函数13()283x x f x x ≤≤=->⎪⎩,若()()F x f x kx =-在其定义域内有3个零点,则实数k ∈ ▲ .11,已知实数x 、y 满足方程()()22111x a y -++-=,当0y b ≤≤(b R ∈)时,由此方程可以确定一个偶函数()y f x =,则抛物线212y x =-的焦点F 到点(,)a b 的轨迹上点的距离最大值为________.12,已知点(,)M a b 与点(0,1)N -在直线3450x y -+=的两侧,给出以下结论: ①3450a b -+>;②当0a >时,a b +有最小值,无最大值;③221a b +>; ④当0a >且1a ≠时,11b a +-的取值范围是93(,)(,)44-∞-+∞ . 正确的个数是( ).A 1 .B 2 .C 3 .D 413,已知函数⎪⎩⎪⎨⎧≤≤⎪⎭⎫ ⎝⎛<<=,153,6sin ,30,|log |)(3x x x x x f π 若存在实数1x ,2x ,3x ,4x 满足 )()()()(4321x f x f x f x f ===,其中4321x x x x <<<,则4321x x x x 的取值范围是(A ))96,60( (B ))72,45( (C ))48,30( (D ))24,15(14,已知函数()f x 是定义在[)1,+∞上的函数,且123,12()11,222x x f x f x x ⎧--<⎪=⎨⎛⎫ ⎪⎪⎝⎭⎩≤≥,则函数2()3y x f x =-在区间(1,2016)上的零点个数为 .15,若函数()lg[sin()sin(2)sin(3)sin(4)]f x x x x x =π⋅π⋅π⋅π的定义域与区间[0,1]的交集由n个开区间组成,则n 的值为[答] ( ).A .2B .3C .4D .516,定义在R 上的奇函数(),f x 当0x ≥时,[)[)12log (1),0,1,()13,1,,x x f x x x ⎧+∈⎪=⎨⎪--∈+∞⎩则关于x 的函数()()(01)F x f x a a =-<<的所有零点之和为________________(结果用a 表示).17,若关于x 的方程5445x x m x x⎛⎫+--= ⎪⎝⎭在(0,)+∞内恰有三个相异实根,则实数m 的取值范围为 .18,关于x 的方程11sin 211x x π=--在[]2016,2016-上解的个数是 .19,关于函数||()|||1|x f x x =-,给出以下四个命题:①当0x >时,()y f x =单调递减且没 有最值;②方程()f x kx b =+(0k ≠)一定有实数解;③如果方程()f x m =(m 为常数)有解,则解的个数一定是偶数;④()y f x =是偶函数且有最小值;其中假命题的序号是20,定义在R 上的函数()f x 满足2201()4210x x x f x x -⎧+≤<=⎨--≤<⎩,且(1)(1)f x f x -=+,则 函数35()()2x g x f x x -=--在区间[1,5]-上的所有零点之和为( ) A. 4 B. 5 C. 7 D. 821,已知13a >,函数()lg(||1)f x x a =-+在区间[0,31]a -上有最小值为0且最大值为 lg(1)a +,则实数a 的取值范围是22,已知函数122|1|log (1)1()23x x x n f x n x m ----≤≤⎧⎪=⎨⎪-<≤⎩(n m <)的值域是[1,1]-,有下列结论:① 当0n =时,(0,2]m ∈;② 当12n =时,1(,2]2m ∈;③ 当1[0,)2n ∈时,[1,2]m ∈; ④ 当1[0,)2n ∈时,(,2]m n ∈; 其中结论正确的所有的序号是( )A. ①②B. ③④C. ②③D. ②④。
著名机构高三数学暑假班讲义第9讲.圆锥曲线的几何性质.尖子班

本讲分三小节,分别为第一定义与焦点三角形、第二定义与相似三角形、第三定义,建议用时2—3课时.由于这一讲主要介绍圆锥曲线的重要且常用的几何性质,而这些性质在之前的学习中并没有系统的介绍过,可以作为新课进行讲授.对于尖子班的学生,以介绍及证明性质为主要教学目标;对于目标班学生,以性质的灵活应用为主要教学目标.第一小节为第一定义与焦点三角形,共3道例题.其中例1主要讲解椭圆的焦点三角形的周长问题;例2主要讲解椭圆的焦点三角形的面积问题;例3主要讲解双曲线的焦点三角形的面积问题.第二小节为第二定义与相似三角形,在知识梳理时通过探索铺垫题的形式给出非圆圆锥曲线的第二定义,例题部分共2道,其中例4主要讲解第二定义与方程;例5主要讲解利用椭圆的第二定义构造相似三角形解过焦点的弦的相关问题;第三小节为第三定义,在知识梳理时通过探索铺垫题的形式给出有心圆锥曲线的第三定义,例题部分共2道,其中例5主要讲解椭圆的第三定义;例6主要讲解双曲线的第三定义.知识结构图第9讲圆锥曲线的几何性质93第9讲·教师版94第9讲·教师版椭圆22221x y a b +=(0a b >>)或双曲线22221x y a b-=上一点P (不在x 轴上)与两个焦点1F 、2F 形成的三角形称为焦点三角形.F 1yO x PF 2 F 2yO xPF 1焦点三角形与椭圆、双曲线的第一定义联系密切,因此解焦点三角形的问题是圆锥曲线问题中的重点问题.在解焦点三角形时,由于已知一边及另外两边的和(差),因此只需要再加一个条件就可以求解.考点:椭圆的焦点三角形【例1】 ⑴点P 是椭圆22221x y a b+=(0a b >>)上一点,12,F F 是椭圆的两个焦点,则12F PF △的周长为 .⑵点P 是椭圆2212516x y +=上一点,12,F F 是椭圆的两个焦点,且12PF F △ 的内切圆半径为1,当P 在第一象限时,P 点的纵坐标为 .⑶点P 是椭圆22221x y a b+=(0a b >>)上一点,12,F F 是椭圆的两个焦点,过1F 作直线l 交椭圆于点A 、点B ,则2F AB △的周长为 .⑷如图,ABC △是椭圆内接等腰直角三角形,斜边2BC =.C 是椭圆的右焦点,椭圆的左焦点在边AB 上,则椭圆的长轴长为 .【解析】 ⑴ 22a c +.⑵ 83.⑶ 4a .⑷ 22+.【拓1】 ⑴ (2012年福建理)椭圆E :22221x y a b+=(0a b >>)的经典精讲知识梳理9.1第一定义与焦点三角形CBA xOy95第9讲·教师版左焦点为1F ,右焦点为2F ,离心率12e =.过1F 的直线交椭圆于A 、B 两点,且2ABF △的周长为8.则椭圆E 的方程为 .⑵ 椭圆221169x y +=的左、右焦点分别为1F ,2F ,过焦点1F 的直线交椭圆于A 、B 两点,2ABF △的周长为_________;若A 、B 两点的坐标分别为()11,x y 和()22,x y ,且2ABF △的面积是4,则21y y -的值为___________.【解析】 ⑴ 22143x y +=.⑵ 16,477.【教师备案】椭圆焦点三角形面积公式及其推导对于椭圆22221x y a b +=(0a b >>),设1PF m =,2PF n =,则2m n a +=,()222122cos 2m n c F PF mn+-∠=221b mn=-,∴21221cos b mn F PF =+∠ 于是1222121212sin 1sin tan 21cos 2F PF b F PF S mn F PF b F PF θ⋅∠=∠==+∠△.【例2】 ⑴已知椭圆E :22221x y a b+=(0a b >>),()1,0F c -、()2,0F c 分别为椭圆的左、右焦点,动点P E ∈,连接1PF 、2PF 形成12PF F △.① 12PF F △面积的取值范围是 ; ② 设12F PF θ∠=,则12F PF △的面积为 ;③ 综合①②,可知当P 点位于 位置时,12F PF ∠取得最大值. ④ 当椭圆离心率e 增大时,12F PF ∠的最大值 .(填增大或减小)⑵已知点P 为椭圆22143x y +=上一点,1F 、2F 分别为椭圆的左、右焦点,若12π3F PF ∠=,则点P 到x 轴的距离为 .⑶已知椭圆22221x y a b+=,焦点为12,F F ,在椭圆上存在点P ,使得12PF PF ⊥,则椭圆的离心率e 的取值范围为________.【追问】若将条件“12PF PF ⊥”改为“122π3F PF ∠=”,则离心率的取值范围是多少?【解析】 ⑴ ① (]0,bc ;② 2tan2b θ;③ 上顶点或下顶点;④ 增大.⑵3⑶ 21⎫⎪⎪⎣⎭. 【追问】31⎫⎪⎪⎣⎭. 【拓2】 ⑴ 1F 、2F 是椭圆C :22184x y +=的焦点,在C 上满足12PF PF ⊥的点P 的个数为 .⑵ 设1F 、2F 分别为椭圆2214832x y +=的左右焦点,且点P 是椭圆上的一点.若12PF F △是直角96第9讲·教师版三角形,则点P 到x 轴的距离为 .【解析】 ⑴ 2;⑵833;【拓3】 在ABC △中,A 、B 、C 所对的边分别为a 、b 、c ,若2b c a +≥,求证:π3A ≤. 【解析】 如图以B 、C 为焦点2a 为长轴长构造椭圆,则∵2b c a +≥,∴点A 在椭圆上或椭圆外. 如图,容易证明π3A ≤,当且仅当A 为椭圆的上(下)顶点时取得等号. O yxAC B考点:双曲线的焦点三角形【教师备案】双曲线焦点三角形面积公式及其推导对于双曲线22221x y a b -=,设1PF m =,2PF n =,则2m n a -=,()222122cos 2m n c F PF mn+-∠=221b mn=-,∴21221cos b mn F PF =-∠ 于是1222121212sin 1sin cot 21cos 2F PF b F PF S mn F PF b F PF θ⋅∠=∠==-∠△.【例3】 ⑴已知双曲线E :22221x y a b-=(0a >,0b >),()1,0F c -、()2,0F c 分别为双曲线的左、右焦点,动点P E ∈,连接1PF 、2PF 形成12PF F △,设12F PF θ∠=.① 12F PF △的面积为 ; ② θ的取值范围为 . ⑵(2010年全国卷Ⅰ)已知1F 、2F 为双曲线C :221x y -=的左、右焦点,点P 在C 上,1260F PF ∠=︒,则P 到x 轴的距离为 .⑶设1F 、2F 为双曲线2211620x y -=的两个焦点,点P 在双曲线上满足1290F PF ∠=︒,则P 的坐标为 . ⑷(2011年华约)已知双曲线C :22221x y a b-=(,0a b >),1F 、2F 分别为C 的左右焦点,97第9讲·教师版P 为C 右支上一点且使12π3F PF ∠=,又12F PF △的面积为233a .则C 的离心率e = . 【解析】 ⑴ ① 2cot 2b θ;② ()0,π.⑵6.⑶ 4101433⎛⎫±± ⎪⎝⎭,;⑷ 2.【备注】本铺垫的目的是通过推导焦半径公式,引入圆锥曲线的第二定义.【铺垫】已知(),0F c 为椭圆22221x y a b+=的右焦点,点P 为椭圆上一点,若P 点的横坐标为0x .⑴ 求证:P 点到右焦点的距离为0a ex -,其中e 为椭圆的离心率;⑵ ⑴的结论即20a PF e x c ⎛⎫=- ⎪⎝⎭,指出20a x c -的几何意义;⑶ 指出⑵中等式的意义,并思考当题干中的右焦点F 改为左焦点时相应的结论变化.⑷ 结合抛物线的定义,试给出椭圆的第二定义,并思考该定义是否可以推广到双曲线.【解析】 ⑴ 利用两点间的距离公式即可推得;⑵ 20a x c -的几何意义时点P 到直线2a x c=的距离; ⑶ 椭圆上的点到右焦点与到直线2a x c =的距离之比为离心率e ,我们称直线2a x c =为椭圆的右准线.当右焦点变为左焦点时,右准线2a x c =也相应变为左准线2a x c =-.⑷ 平面上到定点与到定直线的距离之比为常数e (01e <<)的点的轨迹为椭圆; 该定义可以推广到双曲线:平面上到定点与到定直线的距离之比为常数e (1e >)的点的轨迹为双曲线.【教师备案】本组拓展题是关于焦半径公式的应用的,教师可以根据情况选用.焦半径公式:已知离心率为e ,长半轴长为a 的椭圆上一点P 的横坐标为0x ,则P 到左焦点的距离为0a ex +,P 到右焦点的距离为0a ex -.(可以利用“左加右减”记忆)已知离心率为e ,实半轴长为a 的双曲线左支上一点P 的横坐标为0x ,则P 到左焦点的距离9.2第二定义与相似三角形知识梳理98第9讲·教师版为()0ex a -+,P 到右焦点的距离为()0ex a --;已知离心率为e ,实半轴长为a 的双曲线右支上一点P 的横坐标为0x ,则P 到左焦点的距离为0ex a +,P 到右焦点的距离为0ex a -.【拓4】 ⑴ 椭圆221259x y +=上三个不同的点()11,A x y 、94,5B ⎛⎫ ⎪⎝⎭、()22,C x y 到右焦点的距离成等差数列,则12x x +的值为 .⑵ 已知椭圆22143x y +=,1F 、2F 为其两个焦点,则椭圆C 上 (填“存在”或“不存在”)点M ,使得点M 到左准线的距离MN 是1MF 与2MF 的等比中项.⑶(2010年江苏)在平面直角坐标系xOy 中,已知双曲线221412x y -=上一点M 的横坐标是3,则M 到双曲线右焦点的距离为 .⑷(2010年江西)点()00A x y ,在双曲线221432x y -=的右支上,若点A 到右焦点的距离等于02x ,则0x = .【解析】 ⑴ 8;⑵ 不存在⑶ 4.⑷ 2.由此例题可以引出非圆圆锥曲线的统一定义:圆锥曲线上的点到焦点距离与到准线距离的比为常数,且该常数即为离心率e .如下图所示:考点:椭圆、双曲线的第二定义与方程【例4】 ⑴(2012年全国大纲卷理)椭圆的中心在原点,焦距为4,一条准线为4x =-,则该椭圆的方程为 .⑵(2009年北京)已知双曲线C :22221x y a b -=(,0a b >)的离心率为3,右准线方程为3x =,则双曲线的方程为 . 经典精讲99第9讲·教师版⑶(2010年四川)已知()2,0F ,定直线l :12x =,动点P 到点F 的距离是它到直线l 的距离的2倍.则点P 的轨迹为 .【解析】 ⑴22184x y +=;⑵2212y x -=;⑶2213y x -=;考点:利用椭圆的第二定义构造相似三角形解过焦点的弦的相关问题【例5】 ⑴(2011年四中高二期中)已知椭圆C :22221x y a b+=(0a b >>)的左焦点为()1,0F c -.过点1F 且倾斜角为π3的直线与椭圆相交所得的弦被1F 分为2:1的两段,则椭圆C 的离心率为 .⑵已知A 、B 为过椭圆22221x y a b+=(0a b >>)的左焦点F 的直线与椭圆的交点,判断11FA FB+是否为定值,并说明理由. ⑶已知椭圆C :2212x y +=的右焦点为F ,右准线为l ,点A l ∈,线段AF 交C 于点B .若3FA FB =u u u r u u u r ,则AF =u u u r.【解析】 ⑴23. ⑵ 如图,作椭圆的左准线,设直线AB 与左准线交于点P ,过A 、F 、B 引左准线的垂线,垂足分别为M 、Q 、N ,则Q N MPOyxBA F根据椭圆的第二定义,AF BF e AMBM ==∵PMA PQF PNB △∽△∽△,∴AM FQ BN PAPFPB==于是设AM m =,BN n =,FQ p =,PF t =则AF me =,BF ne =,m p nt me t t ne==-+ 取倒数t t t e e m p n -==+,∴2t t t m n p +=,即112m n p +=∴11112AF BF me ne ep +=+=为定值,其中ce a=,22a b p c c c =-=100第9讲·教师版∴11FA FB +为定值22ab. 【备注】该结论可以推广到对于椭圆、双曲线、抛物线均适用的112FA FB ep+=.事实上ep 为圆锥曲 线的半通径长度.因此这个结论的文字叙述为:圆锥曲线焦点分过焦点的弦所得的两条线段的调和平均数为半通径长度. 例如:(2012年重庆理)过抛物线22y x =的焦点F 作直线交抛物线于A 、B 两点,若2512AB =,AF BF <,则AF =56. ⑶2.【铺垫】(2011年湖北)平面内与两定点()1,0A a -、()2,0A a (0a >)连线的斜率之积等于非零常数m 的点的轨迹,加上1A 、2A 两点所成的曲线C 可以是圆、椭圆或双曲线.求曲线C 的方程,并讨论C 的形状及离心率与m 值的关系.【解析】 设动点的坐标为(),x y ,那么y ym x a x a⋅=+-()222y m x a =-,222mx y ma -=,22221x y a ma -= 当0m >时,曲线C 是焦点在x 轴上的双曲线,离心率为1m +;当10m -<<时,曲线C 是焦点在x 上的椭圆,离心率为1m +; 当1m =-时,曲线C 是圆;当1m <-时,曲线C 是焦点在y 轴上的椭圆,离心率为11m+. A 2A 1Oyxm<-1m=-1-1<m<0m>0这个例题可以拓展出去,即A 、B 可以是坐标平面上关于原点对称的任意两点()00,A x y 、9.3“第三定义”知识梳理101第9讲·教师版()00,B x y --,此时所得的轨迹中心为原点,对称轴与x 、y 轴平行.由此引出有心圆锥曲线的统一定义:当0m >时,轨迹方程22221x y a b -=(0x x ≠±),其中22b m a=,2200221x y a b -=;当10m -<<时,轨迹方程为22221x y a b +=(0x x ≠±),其中22b m a=-,2200221x y a b +=;当1m =-时,轨迹方程为222x y r +=(0x x ≠±),其中22200x y r +=. 我们称此为有心圆锥曲线的第三定义.于是立即有设A 、B 为椭圆22221x y a b+=上关于原点对称的两点,P 为椭圆上任意一点(P 点的横坐标与A 、B 点的横坐标均不相同),则直线PA 与直线PB 连线的斜率乘积为定值22b a-;设A 、B 为双曲线22221x ya b-=上关于原点对称的两点,P 为双曲线上任意一点(P 点的横坐标与A 、B点的横坐标均不相同),则直线PA 与直线PB 连线的斜率乘积为定值22b a.考点:椭圆的第三定义 【例6】 ⑴(2010年北京)在平面直角坐标系xOy 中,点B 与点A ()1,1-关于原点O 对称,P 是动点,且直线AP 与BP 的斜率之积等于13-.则动点P 的轨迹方程为 .⑵(2011年东城高三期末)设A 、B 分别为椭圆2214x y +=的左、右顶点,P 为直线4x =上不同于点()4,0的任意一点,若直线AP 与椭圆相交于异于A 的点M .证明:MBP △为钝角三角形.OyxMPBA【解析】 ⑴ 2234x y +=(1x ≠±).⑵ 只需要证明0BM BP ⋅<u u u u r u u u r即可.设点(),M x y ,()4,P m 则 ()()2,2,24BM BP x y m x my ⋅=-⋅=-+u u u u r u u u r…… ①由于M 在椭圆上等价于1264MA MB y m k k x ⋅=⋅=--,∴332my x =-+ …… ② 经典精讲102第9讲·教师版将②代入①,有3243122xBM BP x x ⋅=--+=-u u u u r u u u r由于2x <,∴0BM BP ⋅<u u u u r u u u r,因此MBP △为钝角三角形.【拓5】 (2009年海淀一模)椭圆方程为22142x y +=,A 、B 为长轴端点,M 为直线2x =上任意一点,连接AM 交椭圆于P 点.⑴ 求证:OP OM ⋅u u u r u u u u r为定值;⑵ 是否存在x 轴上的定点Q 使得以MP 为直径的圆恒通过MQ 与BP 的交点.MQPB AOyx【解析】 ⑴ 设()2,M m ,(),P x y ,则2142AP BP k k ⋅=-=-于是1242y m x ⋅=--,整理有24my x +=.而24OP OM my x ⋅=+=u u u r u u u u r 为定值∴原命题成立.⑵ 假设存在定点Q ,设()2,M m ,(),P x y ,(),0Q n 则由以MP 为直径的圆通过MQ 与BP的交点有0MQ BP ⋅=u u u u r u u u r.∴()()2,2,n m x y --⋅-224nx n x my =--+-0= ……①.而2142AP BP k k ⋅=-=-,于是1422m y x ⋅=--,整理有24my x += ……②将②代入①,有()20n x -=,解得0n =.∴存在x 轴上的定点()0,0Q ,使得以MP 为直径的圆恒通过MQ 与BP 的交点.考点:双曲线的第三定义 【例7】 ⑴已知点P 在双曲线222x y a -=(0a >)的右支上(P 与2A 不重合),1A 、2A 分别为双曲线的左、右顶点,且21122A PA PA A ∠=∠,则12PA A ∠=( ) A .30︒ B .27.5︒ C .25︒ D .22.5︒⑵(2011年江西)()00,P x y (0x a ≠±)是双曲线E :22221x y a b-=(,0a b >)上一点,M 、N 分别是双曲线E 的左、右顶点,直线PM 、PN 的斜率之积为15,则双曲线的离心率为 ;【解析】 ⑴ D .103第9讲·教师版⑵305.1、设1F 、2F 为椭圆2214x y +=的左、右焦点,过椭圆中心任作一直线与椭圆交于P 、Q 两点,当四边形12PFQF 的面积最大时,12PFPF ⋅u u u r u u u u r的值等于 . 【解析】 2-. 2、已知椭圆22221x y a b+=的左焦点、右焦点分别为1F 、2F ,且椭圆上存在两点P 、Q ,使得12120F PF ∠=︒,1260FQF ∠=︒,则椭圆离心率的取值范围为 ,12F PF △的面积与12F QF △的面积之比为 .【解析】 3,12⎡⎫⎪⎢⎪⎣⎭,3:1.3、设1F 、2F 分别是双曲线2219y x -=的左、右焦点,若点P 在双曲线上,且120PF PF ⋅=u u u r u u u u r ,则12PF F △的面积为 ,12PF PF +=u u u r u u u u r.【解析】 9;210. 4、设1F 、2F 分别为椭圆2213x y +=的左、右焦点,点A 、B 在椭圆上.若125F A F B =u u u r u u u u r ,则1F A .【解析】 3. 5、(2009年福建)已知椭圆C :2214x y +=的左、右顶点分别为A 、B .点S 是椭圆C 上位于x 轴上方的动点,直线AS 、BS 与直线l :103x =分别交于M 、N 两点.求线段MN 的长度的最小值.DA SNB My x O【解析】 83.课后习题104第9讲·教师版6、 已知A 、B 是椭圆22221x y a b+=(0a b >>)的左、右顶点,P 是椭圆上异于A 、B 的动点.试证明:当P 为椭圆的上顶点或下顶点时APB ∠最大.【解析】 设直线PA 、PB 的斜率分别为1k 、2k ,则2122b k k a=-.注意到APB ∠为钝角,于是2122212112221212tan 11b k k k a k a b APB k b k k c a k a+⎛⎫-=-=-=-⋅+ ⎪ ⎪+⋅⎝⎭-∠ 于是当且仅当1bk a=时APB ∠最大,即原命题得证.。
高中语文于J暑假计划静安闸北恒高一对一补习班

次数
1 2 3 4 5 6 塘月色》——诗歌中的意象和意境 诗歌的题材和体裁 诗歌的表现手法和审题 诗词鉴赏小结巩固1 诗词鉴赏小结巩固2 文言文《秦晋崤之战》的讲解及实词用法、古今异义,含翻译 文言文《秦晋崤之战》的讲解及虚词用法、活用,含翻译 文言文《苏武传》的讲解及手法的使用 文言文断句和特殊句式 文言文人物传记中人物性格的把握 文言文阅读人物传记的小结巩固1 文言文人物传记及事件的小结巩固2
备注
1.高三进行专题讲 解,授课过程中遇 到的新课(高三 上)会在专题中涉 及、讲解。 2.注重高考语文脉 络的把握和思路的 培养。
高中数学(暑假)静安闸北恒高一对一数学补习班

高一数学教学安排对即将步入高中学习的新生而言,当务之急要了解高中数学与初中数学的差异,暑假课程将结合初中生数学学习的方法和高中数学学习方法展开,从学习过程中,学生逐步体验初中数学与高中数学之间差异,培养良好的数学学习习惯。
结合高考数学和综合评价数学考试的要求,针对学生学习特点,暑期课程涉及到集合、不等式、函数等知识点,重点在于培养学生高中数学的学习方法和高中数学的学习技巧。
具体课程安排如下表:时间安排专题第一讲集合概念及运算第二讲集合运算——交集并集第三讲命题及简易逻辑第四讲集合与命题习题课第五讲解一元二次不等式和绝对值不等式第六讲求解其它类型不等式第七讲不等式性质及证明第八讲基本不等式第九讲不等式习题课第十讲集合不等式综合第十一讲函数概念第十二讲函数性质以上只是初步的安排,根据学生的实际学习情况,课程安排会做适当的调整。
高三数学教学安排步入高三学习的学生,已经学习了高中数学所有的知识。
对高中数学知识框架有初步的知识,学生知识点分布较零散,缺乏系统性整理。
结合高考数学和综合评价数学考试的要求,针对学生学习特点,暑期课程将高中数学内容进行重新组合、整理,知识点各个击破,提升学生对高中数学知识点理解高度,培养学生良好的解题能力。
暑期课程将重点复习函数、数列、解析几何内容,这三块是高三学生返校摸底考的重点内容,更为重要的是这三块内容占据高考总分的70%-85%。
除了函数、数列、解析几何,还其中穿插复习集合、不等式、三角、向量等知识点。
立体几何和排列组合概率是高二下学期高学习的内容,暑期课程不做重点复习。
暑期课程具体课程安排如下表:时间安排专题第1讲集合及简易逻辑第2讲不等式及其应用第3讲函数的概念第4讲函数的性质(一)第5讲函数的性质(二)第6讲幂指对函数图像与性质第7讲函数图像与方程第8讲函数综合第9讲三角化简第10讲解斜三角形第11讲三角函数第12讲数列概念等差等比数列第13讲数列通项与求和(一)第14讲数列通项与求和(二)第15讲数学归纳法及数列极限第16讲数列综合(一)第17讲数列综合(二)第18讲向量第19讲直线第20讲圆第21讲椭圆与双曲线以上只是初步的安排,根据学生的实际学习情况,课程安排会做适当的调整。
文言文实词(三)静安闸北补习班

文言文实词(三)静安闸北补习班新王牌61、去:①离开;②距,距离;③除掉,去掉。
例句:⑴项王军在鸿门下,沛公军在霸上,相去()四十里。
(《鸿门宴》)⑵欲呼张良与俱去()。
(《鸿门宴》)⑶而庭阶寂寂,小鸟时来啄食,人至不去()。
《项脊轩志》)⑷比去(),以手阖门,自语曰:“……”(《项脊轩志》)⑸当横行天下,为汉家除残去()秽。
(《赤壁之战》)⑹登斯楼也,则有去()国怀乡,忧谗畏讥(《岳阳楼记》)答案:⑴距,距离;⑵离开;⑶离开;⑷离开;⑸除掉;⑹离开。
62、劝:①勉励,鼓励;②勤勉,勤奋;③劝说。
例句:⑴且举世而誉之而不加劝(),举世而非之而不加沮。
(《逍遥游》)⑵劝()君更尽一杯酒,西出阳关无故人。
(王维《送元二使安西》)⑶荀子《劝()学》答案:⑴勤勉,勤奋;⑵劝说;⑶勉励,鼓励。
63、却:①退,后退;②使…退,击退;③推却,不接受。
例句:⑴乃使蒙恬北筑长城而守藩篱,却()匈奴七百余里。
(《过秦论》)⑵却()与小姑别,泪落连珠子。
(《孔雀东南飞》)⑶感我此言良久立,却()坐促弦弦转急。
(《琵琶行》)⑷相如因持璧却()立,倚柱,怒发上冲冠。
(《史记·廉颇蔺相如列传》)⑸成语“盛情难却()”“却()之不恭”答案:⑴使…退,击退;⑵退,后退;⑶退,后退;⑷退,后退;⑸推却/推却。
64、如:①到……去;②像,如同;③遵从,按照;④连词,假如,如果;⑤及,比得上。
例句:⑴沛公默然,曰:“固不如()也。
且为之奈何?”(《鸿门宴》)⑵今人有大功而击之,不义也。
不如()因善遇之。
(《鸿门宴》)⑶杀人如()不能举,刑人如()恐不胜(《鸿门宴》)⑷坐须臾,沛公起如()厕,因招樊哙出。
(《鸿门宴》)⑸是故弟子不必不如()师,师不必贤于弟子(《师说》)⑹纵一苇之所如(),凌万顷之茫然。
(《赤壁赋》)⑺母如()其言,附舟诣谭。
(06广东卷《杜环小传》)⑻成语“如()法炮制”“如()期举行”“如()丧考妣”“如()日中天”“如()胶似膝”“如()鸟兽散”“如()数家珍”“如()汤沃雪”“如()蚁附膻”“如()火如荼”“如()出一辙”“如()雷贯耳”“如()坐针毡”答案:⑴及,比得上;⑵及,比得上;⑶像,如同;⑷到……去;⑸及,比得上;⑹到;⑺遵从,按照;⑻遵从,按照/遵从,按照/其余都是“像,如同”。
闸北高中补习班 秋季新王牌 历年上海高考冲刺补习立体几何题
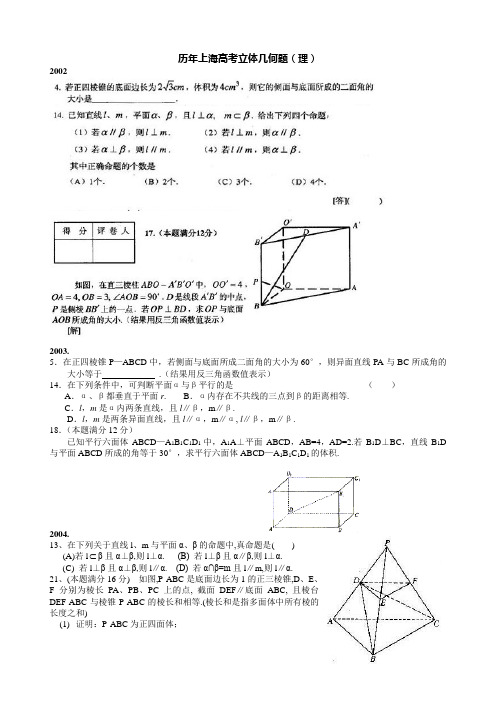
历年上海高考立体几何题(理)20022003.5.在正四棱锥P —ABCD 中,若侧面与底面所成二面角的大小为60°,则异面直线PA 与BC 所成角的大小等于 .(结果用反三角函数值表示) 14.在下列条件中,可判断平面α与β平行的是 ( ) A .α、β都垂直于平面r . B .α内存在不共线的三点到β的距离相等. C .l ,m 是α内两条直线,且l ∥β,m ∥β.D .l ,m 是两条异面直线,且l ∥α,m ∥α, l ∥β,m ∥β. 18.(本题满分12分)已知平行六面体ABCD —A 1B 1C 1D 1中,A 1A ⊥平面ABCD ,AB=4,AD=2.若B 1D ⊥BC ,直线B 1D 与平面ABCD 所成的角等于30°,求平行六面体ABCD —A 1B 1C 1D 1的体积.2004.13、在下列关于直线l 、m 与平面α、β的命题中,真命题是( ) (A)若l β且α⊥β,则l ⊥α. (B) 若l ⊥β且α∥β,则l ⊥α. (C) 若l ⊥β且α⊥β,则l ∥α. (D) 若α∩β=m 且l ∥m,则l ∥α.21、(本题满分16分) 如图,P-ABC 是底面边长为1的正三棱锥,D 、E 、F 分别为棱长PA 、PB 、PC 上的点, 截面DEF ∥底面ABC, 且棱台DEF-ABC 与棱锥P-ABC 的棱长和相等.(棱长和是指多面体中所有棱的长度之和)(1) 证明:P-ABC 为正四面体; (2) 若PD=21PA, 求二面角D-BC-A 的CB1C 1B1AA大小;(结果用反三角函数值表示)(3) 设棱台DEF-ABC 的体积为V , 是否存在体积为V 且各棱长均相等的直 平行六面体,使得它与棱台DEF-ABC 有相同的棱长和? 若存在,请具体构造 出这样的一个直平行六面体,并给出证明;若不存在,请说明理由.2005.11.有两个相同的直三棱柱,高为a2,底面三角形的三边长分别为)0(5,4,3>a a a a 。
闸北高中补习班 秋季高考新王牌冲刺补习 曲线运动

第六章 曲线运动1:平抛运动:水平方向匀速直线运动和竖直方向自由落体运动的合运动水平分运动:水平位移: x= v o t 水平分速度:v x = v o竖直分运动:竖直位移: y =21g t 2竖直分速度:v y = g t (注解:以下有一些推论不过重要性不大仅作参考)tg θ= V V yo V y = V o tg θ V o =V y ctg θ V = 22y o V V + V o = Vcos θ V y = Vsin θ时间由y =221gt 得t =gy 2(由下落的高度y 决定)(注解:解题时题目当然比较灵活,竖直和水平直线运动的共同点是时间相同,所以无论那个运动出的了时间都可以)2:斜抛运动斜抛运动是将物体以一定的初速度和与水平方向成一定角度抛出,在重力作用下,物体作匀变速曲线运动,它的运动轨迹是抛物线,这种运动叫做“斜抛运动”。
属匀变速曲线运动。
(注解:将初速度分解,得到水平为初速度Vx=Vcos θ 竖直方向初速度V y = Vsin θ,那么斜抛运动由2个分运动组成,水平方向初速度为V o =Vcos θ的匀速直线,竖直方向为初速度V y = Vsin θ的竖直上抛运动合成)3:其他更复杂的曲线运动(注解:任何复杂运动都一定可以分解成2个相互垂直的直线分运动,这是解此类题唯一的方法,或者说,任意两个相互直线运动也能合成一个曲线运动,这个曲线运动可能远远比平抛,斜抛复杂的多,甚至复杂到无法描述的地步,但只要从两个直线分运动去解释,一切都变得简单易行,因为对直线运动的处理我们已经很拿手,但需要注意的是,运动轨迹的切线方向是合速度方向)试举两例:例1:初速度水平,竖直方向受到力的作用使物体在竖直方向以某一加速度a 1初速度静止开始加速时间t 后,再以另一加速度a 2加速t 后返回原高度例2:4、匀速圆周运动质点沿圆周运动,如果在相等的时间里通过的圆弧长度相等,这种运动就叫做匀速圆周运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三课:一模专题:圆锥曲线
1,(2018杨浦一模20)设直线l 与抛物线2:4y x Ω=相交于不同两点A 、B ,O 为坐标原点.
(1)求抛物线Ω的焦点到准线的距离;
(2)若直线l 又与圆22:(5)16C x y -+=相切于点M ,且M 为线段AB 的中点,求直线l 的方程;
(3)若0OA OB ⋅= ,点Q 在线段AB 上,满足OQ AB ⊥,求点Q 的轨迹方程.
2,(2018松江一模20)已知椭圆2222:1x y E a b +=(0a b >>)经过点3(1,),其左焦点为
(F ,过F 点的直线l 交椭圆于A 、B 两点,交y 轴的正半轴于点M .
(1)求椭圆E 的方程;
(2)过点F 且与l 垂直的直线交椭圆于C 、D 两点,
若四边形ACBD 的面积为
43,求直线l 的方程; (3)设1MA AF λ= ,2MB BF λ= ,求证:12λλ+为定值.
3,(2018虹口一模20)已知平面内的定点F到定直线l的距离等于p(0
p>),动圆M过点F且与直线l相切,记圆心M的轨迹为曲线C,在曲线C上任取一点A,过A作l的垂线,垂足为E.
(1)求曲线C的轨迹方程;
(2)记点A到直线l的距离为d,且34
43
p p
d
≤≤,求EAF
∠的取值范围;
(3)判断EAF
∠的平分线所在的直线与曲线的交点个数,并说明理由.
4,(2018金山一模20)给出定理:在圆锥曲线中,AB 是抛物线2:2y px Γ=(0p >)的一条弦,C 是AB 的中点,过点C 且平行于x 轴的直线与抛物线的交点为D ,若A 、B 两点纵坐标之差的绝对值||A B y y a -=(0a >),则ADB ∆的面积316ADB
a S p ∆=,试运用上述定理求解以下各题:
(1)若2p =,AB 所在直线的方程为24y x =-,C 是AB 的中点,过C 且平行于x 轴的 直线与抛物线Γ的交点为D ,求ADB S ∆;
(2)已知AB 是抛物线2:2y px Γ=(0p >)的一条弦,C 是AB 的中点,过点C 且平行于x 轴的直线与抛物线的交点为D ,E 、F 分别为AD 和BD 的中点,过E 、F 且平行于x 轴的直线与抛物线2:2y px Γ=(0p >)分别交于点M 、N ,若A 、B 两点纵坐标之差的绝对值||A B y y a -=(0a >),求AMD S ∆和BND S ∆;
(3)请你在上述问题的启发下,设计一种方法求抛物线:22y px =(0p >)与弦AB 围成的“弓形”的面积,并求出相应面积.
5,(2018普陀一模20)设点1F 、2F 分别是椭圆22
22:12x y C t t
+=(0t >)的左、右焦点,
且椭圆C 上的点到点2F 的距离的最小值为2,点M 、N 是椭圆C 上位于x 轴上方的两点,且向量1F M 与向量2F N 平行.
(1)求椭圆C 的方程;
(2)当120
F N F N ⋅= 时,求1F MN ∆的面积;
(3)当21||||F N F M -= 2F N 的方程.
6,(2018徐汇一模20)已知椭圆22
22:1x y a b
Γ+=(0a b >>)的左、右焦点分别为1F 、2F ,
且1F 、2F 与短轴的一个端点Q 构成一个等腰直角三角形,点P 在椭圆Γ上,过点2F 作互相垂直且
与x 轴不重合的两直线AB 、CD 分别交椭圆Γ于A 、B 、C 、D ,且M 、N 分别是弦AB 、 CD 的中点.
(1)求椭圆Γ的标准方程;
(2)求证:直线MB 过定点2(,0)3
R ;
(3)求2MNF ∆面积的最大值.
7,(2018年宝山一模20)设椭圆22
22:1x y C a b
+=(0a b >>)过点(2,0)-,且直线510x y -+=过C 的左焦点.
(1)求C 的方程;
(2)设()x 为C 上的任一点,记动点(,)x y 的轨迹为Γ,Γ与x 轴的负半轴、y 轴的正半轴分别交于点G 、H ,C 的短轴端点关于直线y x =的对称点分别为1F 、2F ,当点P 在直线GH 上运动时,求12PF PF ⋅
的最小值;
(3)如图,直线l 经过C 的右焦点F ,并交C 于A 、B 两点,且A 、B 在直线4x =上的射影依次为D 、E ,当l 绕F 转动时,直线AE 与BD 是否相交于定点?若是,求出定点的坐标,否则,请说明理由.
8,(2018浦东一模20)已知椭圆22
22:1x y a b
Γ+=(0a b >>)的左、右焦点分别为1F 、2F ,
设点(0,)A b ,在12AF F ∆中,1223
F AF π∠=,周长为4+(1)求椭圆Γ的方程;
(2)设不经过点A 的直线l 与椭圆Γ相交于B 、C 两点,若直线AB 与AC 的斜率之和为 1-,求证:直线l 过定点,并求出该定点的坐标;
(3)记第(2)问所求的定点为E ,点P 为椭圆Γ上的一个动点,试根据AEP ∆面积S 的 不同取值范围,讨论AEP ∆存在的个数,并说明理由.
9,(2018闵行一模20)已知椭圆22
1109
x y +=的右焦点是抛物线2:2y px Γ=的焦点,直线l 与Γ相交于不同的两点11(,)A x y 、22(,)B x y .
(1)求Γ的方程;
(2)若直线l 经过点(2,0)P ,求OAB ∆的面积的最小值(O 为坐标原点);
(3)已知点(1,2)C ,直线l 经过点(5,2)Q -,D 为线段AB 的中点,求证:||2||AB CD =.
10,(2018年崇明一模)在平面直角坐标系中,已知椭圆2
22:1x C y a
+=(0a >,1a ≠)的两个焦点分别是1F 、
2F ,直线:l y kx m =+(,k m R ∈)与椭圆交于A 、B 两点.
(1)若M 为椭圆短轴上的一个顶点,且12MF F ∆是直角三角形,求a 的值;
(2)若1k =,且OAB ∆是以O 为直角顶点的直角三角形,求a 与m 满足的关系;
(3)若2a =,且14
OA OB k k ⋅=-,求证:OAB ∆的面积为定值.
点00(,)P x y M ∈,M 表示的曲线是C ,N 表示的曲线是1C ,1C 的渐近线为1l 和2l .
(1)判断M 和N 的关系并说明理由;
(2)设01x ≠±,1(1,0)A -,2(1,0)A ,直线1PA 的斜率是1k ,直线2PA 的斜率是2k ,求12k k 的取值范围;
(3)过P 点作1l 和2l 的平行线分别交曲线C 的另外两点于Q 、R ,求证:PQR ∆的面积为定值.
00(,)P x y M ∈,M 表示的曲线是C ,N 表示的曲线是1C ,1C 的渐近线为1l 和2l .
(1)判断M 和N 的关系并说明理由;
(2)设01x ≠±,1(1,0)A -,2(1,0)A ,直线1PA 的斜率是1k ,直线2PA 的斜率是2k ,求12k k 的取值范围;
(3)过P 点作1l 和2l 的平行线分别交曲线C 的另外两点于Q 、R ,求证:PQR ∆的面积为定值.。
