MATLAB模型预测控制工具箱函数
使用MATLAB进行数据预测和预测

使用MATLAB进行数据预测和预测引言:数据预测和预测在许多领域中都具有重要的应用价值。
它们可以帮助我们预测未来的发展趋势,做出合理的决策,并在经营和决策中提供有力的支持。
在这一过程中,MATLAB作为一种功能强大的编程语言和数据分析工具,为我们提供了一个强大的工具箱,可以进行数据预测和预测。
数据预处理:在开始数据预测和预测之前,我们首先需要对数据进行预处理。
预处理包括数据清洗、数据归一化、特征选择等步骤。
通过这些步骤,我们可以提高数据的质量,减少噪声的影响,并使数据更适合于预测模型的建立。
数据清洗是指删除或修复数据中的错误值、缺失值和异常值。
在MATLAB中,我们可以使用一些函数和工具箱来处理这些问题。
例如,我们可以使用`isnan`函数来检测缺失值,并使用`fillmissing`函数来填充缺失值。
对于异常值,我们可以使用一些统计方法,如3σ原则或箱线图来识别和处理。
数据归一化是将不同尺度的数据映射到统一的尺度上。
这是因为不同尺度的数据可能对预测模型的训练和预测产生不利影响。
在MATLAB中,有许多方法可以实现数据归一化,如MinMax归一化、Z-score归一化等。
我们可以使用`mapminmax`函数来实现MinMax归一化,并使用`zscore`函数来实现Z-score归一化。
特征选择是从原始数据中选择最相关的特征,以降低数据维度并提高预测模型的准确性。
在MATLAB中,我们可以使用一些算法和函数来实现特征选择。
例如,我们可以使用`fsrnca`函数(基于相关系数的特征选择)或`sequentialfs`函数(基于逐步搜索的特征选择)来选择最佳特征子集。
在完成数据预处理后,我们可以使用各种算法和方法进行数据预测。
在MATLAB中,有许多经典的预测算法和函数可供选择。
以下是几个常用的预测方法。
1. 线性回归:线性回归是一种基本的预测方法,它使用线性模型来建立输入变量和输出变量之间的关系。
模型预测控制matlab工具箱实例

模型预测控制matlab工具箱实例模型预测控制(MPC)是一种广泛应用于工业过程控制的高级控制策略。
Matlab提供了用于设计和实施MPC的工具箱。
本实例演示了如何使用Matlab MPC工具箱执行MPC控制。
1. 创建一个MPC对象首先,我们需要创建一个MPC对象。
使用mpc对象构造函数可以创建MPC对象。
例如:```mpcobj = mpc(object func, sample time, prediction horizon, control horizon);```其中,object func是被控制系统的离散时间状态空间模型的函数句柄;sample time是采样时间,prediction horizon是预测时域长度,control horizon是控制时域长度。
2. 配置MPC对象接下来,我们需要配置MPC对象。
可以使用MPC对象的属性来进行配置。
例如:```mpcobj.Model.Plant = ss(A,B,C,D);mpcobj.Model.Noise = 'Custom';mpcobj.Model.Disturbance = 'Custom';mpcobj.PredictionHorizon = 10;mpcobj.ControlHorizon = 2;mpcobj.Weights.OV = 1;mpcobj.Weights.MV = 0.1;mpcobj.Weights.ECR = [0.1 0.2];mpcobj.MV = struct('Min',-10,'Max',10);```上述代码中,我们设置了被控制系统的动态模型,噪声模型和干扰模型的类型。
我们还设置了预测时域长度,控制时域长度和权重。
3. 模拟仿真现在,我们可以使用MPC对象进行控制。
首先,我们需要对系统进行模拟仿真以生成实验数据。
可以使用sim函数进行仿真。
MATLAB的常用函数和工具介绍

MATLAB的常用函数和工具介绍MATLAB是一款被广泛应用于科学计算和工程设计的软件,它提供了丰富的函数库和工具箱,能够帮助用户进行数据分析、模拟仿真、图像处理、信号处理等多种任务。
本文将介绍一些MATLAB常用的函数和工具,帮助读者更好地利用MATLAB进行编程和数据处理。
一、MATLAB函数介绍1. plot函数:该函数用于绘制二维图形,如折线图、曲线图等。
通过输入数据点的坐标,plot函数可以帮助用户快速可视化数据分布,同时支持自定义线型、颜色和标注等功能。
2. imread函数:该函数用于读取图像文件,支持常见的图像格式,如JPEG、PNG等。
通过imread函数,用户可以方便地加载图像数据进行后续的处理和分析。
3. fft函数:该函数用于进行快速傅里叶变换,可以将时域信号转换为频域信号。
傅里叶变换在信号处理中广泛应用,通过fft函数,用户可以快速计算信号的频谱信息。
4. solve函数:该函数用于求解方程组,支持线性方程和非线性方程的求解。
用户只需输入方程组的表达式,solve函数会自动求解变量的值,帮助用户解决复杂的数学问题。
5. mean函数:该函数用于计算数据的平均值。
mean函数支持数组、矩阵和向量等多种数据类型,可以方便地对数据进行统计分析。
6. importdata函数:该函数用于导入外部数据文件,如文本文件、CSV文件等。
通过importdata函数,用户可以将外部数据加载到MATLAB中,进行后续的数据处理和分析。
二、MATLAB工具介绍1. MATLAB Editor:这是MATLAB自带的编辑器,可以用于编写和调试MATLAB代码。
它提供了代码高亮、自动缩进和代码片段等功能,能够提高编程效率和代码可读性。
2. Simulink:这是MATLAB的一个强大的仿真工具,用于建立动态系统的模型并进行仿真。
Simulink支持直观的图形化建模界面,用户可以通过拖拽元件和线条来搭建系统模型,进而进行仿真和系统分析。
预测控制matlab工具箱
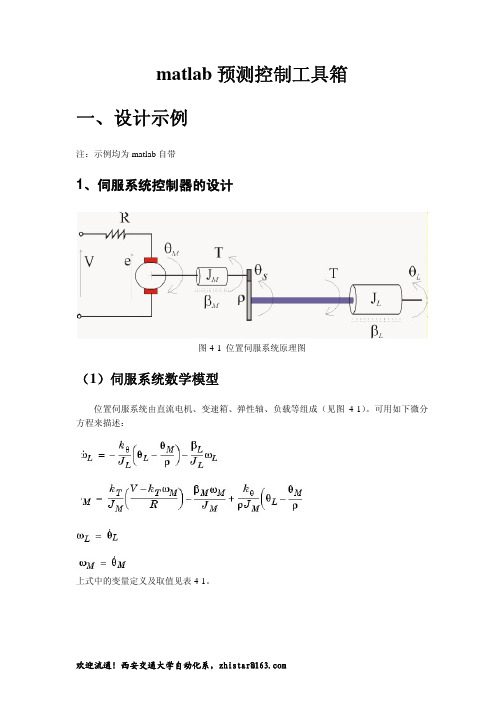
matlab预测控制工具箱一、设计示例注:示例均为matlab自带1、伺服系统控制器的设计图4-1 位置伺服系统原理图(1)伺服系统数学模型位置伺服系统由直流电机、变速箱、弹性轴、负载等组成(见图4-1)。
可用如下微分方程来描述:上式中的变量定义及取值见表4-1。
将上述微分方程写成状态方程形式,有其中,。
(2)控制目标及约束控制目标:在电压V的控制下,使过载角位置跟踪指定值。
输出量仅有可观测。
弹性轴承受的强度有一定的限制,因此对输出力矩T的赋值作一定约束:对输入电压的约束:该系统有一个输入V,两个输出:(可测量)和T(不可测量)。
(3)在matlab中定义该系统的状态空间模型首先需要在matlab中对系统的数学模型进行定义。
可以直接在命令行输入mpcmotormodel(建议做法),也可以在命令行中输入下列命令:% DC-motor with elastic shaft%%Parameters (MKS)%-----------------------------------------------------------Lshaft=1.0; %Shaft lengthdshaft=0.02; %Shaft diametershaftrho=7850; %Shaft specific weight (Carbon steel)G=81500*1e6; %Modulus of rigiditytauam=50*1e6; %Shear strengthMmotor=100; %Rotor massRmotor=.1; %Rotor radiusJmotor=.5*Mmotor*Rmotor^2; %Rotor axial moment of inertia Bmotor=0.1; %Rotor viscous friction coefficient (A CASO)R=20; %Resistance of armatureKt=10; %Motor constantgear=20; %Gear ratioJload=50*Jmotor; %Load inertiaBload=25; %Load viscous friction coefficientIp=pi/32*dshaft^4; %Polar momentum of shaft(circular) sectionKth=G*Ip/Lshaft; %Torsional rigidity(Torque/angle)Vshaft=pi*(dshaft^2)/4*Lshaft; %Shaft volumeMshaft=shaftrho*Vshaft; %Shaft massJshaft=Mshaft*.5*(dshaft^2/4); %Shaft moment of inertiaJM=Jmotor;JL=Jload+Jshaft;Vmax=tauam*pi*dshaft^3/16; %Maximum admissible torqueVmin=-Vmax;%Input/State/Output continuous time form%----------------------------------------------------------AA=[0 1 0 0;-Kth/JL -Bload/JL Kth/(gear*JL) 0;0 0 0 1;Kth/(JM*gear) 0 -Kth/(JM*gear^2)-(Bmotor+Kt^2/R)/JM];BB=[0;0;0;Kt/(R*JM)];Hyd=[1 0 0 0];Hvd=[Kth 0 -Kth/gear 0];Dyd=0;Dvd=0;% Define the LTI state-space modelsys=ss(AA,BB,[Hyd;Hvd],[Dyd;Dvd]);(4)利用MPCTOOL界面设计控制器第一步:导入模型在命令行窗口中输入mpctool,工具箱界面出来后点击Imort Plant…,此时界面如4-2所示。
MATLAB常用工具箱与函数库介绍

MATLAB常用工具箱与函数库介绍1. 统计与机器学习工具箱(Statistics and Machine Learning Toolbox):该工具箱提供了各种统计分析和机器学习算法的函数,包括描述统计、概率分布、假设检验、回归分析、分类与聚类等。
可以用于进行数据探索和建模分析。
2. 信号处理工具箱(Signal Processing Toolbox):该工具箱提供了一系列信号处理的函数和算法,包括滤波、谱分析、信号生成与重构、时频分析等。
可以用于音频处理、图像处理、通信系统设计等领域。
3. 控制系统工具箱(Control System Toolbox):该工具箱提供了控制系统设计与分析的函数和算法,包括系统建模、根轨迹设计、频域分析、状态空间分析等。
可以用于控制系统的设计和仿真。
4. 优化工具箱(Optimization Toolbox):该工具箱提供了各种数学优化算法,包括线性规划、非线性规划、整数规划、最优化等。
可以用于寻找最优解或最优化问题。
5. 图像处理工具箱(Image Processing Toolbox):该工具箱提供了图像处理和分析的函数和算法,包括图像滤波、边缘检测、图像分割、图像拼接等。
可以用于计算机视觉、医学影像处理等领域。
6. 神经网络工具箱(Neural Network Toolbox):该工具箱提供了神经网络的建模和训练工具,包括感知机、多层前馈神经网络、循环神经网络等。
可以用于模式识别、数据挖掘等领域。
7. 控制系统设计工具箱(Robust Control Toolbox):该工具箱提供了鲁棒控制系统设计与分析的函数和算法,可以处理不确定性和干扰的控制系统设计问题。
8. 信号系统工具箱(Signal Systems Toolbox):该工具箱提供了分析、设计和模拟线性时不变系统的函数和算法。
可以用于信号处理、通信系统设计等领域。
9. 符号计算工具箱(Symbolic Math Toolbox):该工具箱提供了符号计算的功能,可以进行符号表达式的运算、求解方程、求解微分方程等。
matlab的mpc函数

在MATLAB中,MPC(模型预测控制)函数可用于实现模型预测控制(MPC)算法。
MPC是一种先进的控制策略,用于处理具有预测模型的连续或离散时间线性系统。
它通过优化性能指标并限制未来的行为,实现对系统的控制。
要使用MATLAB的MPC函数,您需要遵循以下步骤:
1. 定义模型:首先,您需要定义系统的模型。
这可以是一个线性时不变(LTI)系统,也可以是一个非线性系统。
您可以使用MATLAB 的控制系统工具箱中的函数(如`tf`,`ss`等)来定义模型。
2. 定义优化问题:接下来,您需要定义优化问题。
优化问题应包括预测模型、性能指标和约束条件。
在MPC中,预测模型通常是一个预测矩阵,用于预测未来的系统状态。
性能指标可以是控制变量的权重或状态变量的权重。
约束条件可以是控制变量的限制或状态变量的限制。
3. 调用MPC函数:一旦您定义了模型和优化问题,您可以使用MATLAB的MPC函数来求解优化问题并生成控制序列。
常用的MPC函数包括`mpcmin`和`mpcmove`。
4. 应用控制序列:最后,您需要将生成的control sequence应用于系统。
这可以通过使用一个数字或模拟控制器来实现。
这些步骤是使用MATLAB的MPC函数进行模型预测控制的一般流程。
但是,请注意,具体的实现方法可能会因应用而异。
建议查阅MATLAB的官方文档以获取更详细的信息和使用示例。
MATLAB中的模型预测控制算法实现方法

MATLAB中的模型预测控制算法实现方法1. 引言模型预测控制(Model Predictive Control,MPC)是一种广泛应用于工业过程控制的先进控制策略。
它基于数学模型对系统未来行为进行预测,并通过优化算法计算出最优控制输入,以实现对系统的稳定控制和性能优化。
在MATLAB中,实现MPC算法可以借助一些工具箱和函数,本文将介绍其中一种典型方法。
2. MPC算法的基本原理MPC算法通过建立系统的数学模型,预测系统未来的行为。
在每个控制时刻,MPC算法根据已知的系统状态和控制目标,计算出最优的控制输入,并将其应用于系统中。
这个优化问题可以通过求解一个多目标优化问题来完成。
3. MATLAB中的MPC工具箱MATLAB的Control System Toolbox提供了一个用于设计和实现MPC控制器的工具箱。
首先,我们需要使用命令"mpc"创建一个空白的MPC对象。
然后,我们可以通过指定MPC对象的属性来定义系统模型、控制目标、约束条件等。
4. 构建系统模型在MPC算法中,必须先构建系统的数学模型。
在MATLAB中,可以使用State Space工具箱中的ss或tf函数构建系统模型。
我们可以根据实际系统的特点选择不同的模型结构。
例如,对于连续时间系统,可以使用连续时间状态空间模型或传递函数模型;对于离散时间系统,可以使用离散时间状态空间模型或传递函数模型。
5. 设置MPC对象属性创建MPC对象后,我们需要设置一些重要的属性。
其中,PredictionHorizon属性定义了预测时间窗口的长度,即MPC算法根据模型预测未来的时长;ControlHorizon属性定义了控制时间窗口的长度,即MPC算法计算最优控制输入的时间长度。
一般来说,预测时间窗口应大于控制时间窗口。
6. 设定控制目标与约束条件MPC算法的目标是使系统的输出尽可能地接近控制目标,并同时满足一定的约束条件。
MATLAB环境下的模型预测控制理论的应用

MATLAB环境下的模型预测控制理论的应用丛爽邓娟(中国科学技术大学自动化系,合肥230027)E-mail:scong@ustc.edu.cn摘要从模型预测控制的原理出发。
介绍利用MA7ⅡAB模型预测控制工具箱进行模型预测控制器设计的全过程。
就被控对象的不同模型。
以及备类模型形式之间的转换做了具体的系统的阐述。
在控刺器的设计过程中,给出不同情况下的控制器的设计方法,并且对控制器设计申的参数选择对系统控制性能的影响进行了分析与总结。
最后通过数值实例说明了如何进行了模型预测控制器的设计。
关键词模型预测控制模型辨识阶跃响应模型系统仿真文章编号l002—8331一(2005)16-0196—03文献标识码A中圈分类号TPl3ModelPredictiveControlTheoryandApplicationunderMATLABEnvironment(Dept.ofAutomation,UniversityofScience&TechnologyofChina,Hefei230027)Abstract:Basedtheprincipleofmodelpredictivecontrol,thepaperintroducesthewholeprocessofmodelpredic—fivecontrollerdesignwithmodelpredictivecontroltoolboxinMATLAB.Systematicallyrepresentthedifferentmodelsofcontrolledplant,aswellastheconversionsofthosemodels.Intheprocedureofthecontrollerdesign,differentcontrollerdesignmethodsintroduced.Atthe8alTletime,theanalysesandconclusionofeffectstosystemcontrolperformanceintheaspectofparametersselection啪done.Atlast.annumericalexampleofthemodelpredictivecontrollerdesignisgiven.Keywords:modelpredictivecontrol,modelidentification,stepresponsemodel,systemsimulation1引言以状态空间法为基础的现代控制理论从20世纪60年代提出到70年代在理论上日趋完善,并且在许多方面得到了成功的运用。
Matlab控制系统工具箱的高级应用教程

Matlab控制系统工具箱的高级应用教程Matlab是一种强大的数学软件,广泛应用于科学研究和工程领域。
控制系统工具箱(Control System Toolbox)是Matlab中一个重要的工具包,提供了许多用于设计、分析和模拟控制系统的函数和工具。
在这篇文章中,我将介绍一些Matlab控制系统工具箱的高级应用,以帮助读者更好地利用这个工具包。
首先,让我们从控制系统的建模开始。
控制系统的建模是设计和分析控制系统的第一步。
在Matlab中,你可以使用Transfer Function模型(传递函数模型)或State Space模型(状态空间模型)来描述控制系统。
对于简单的系统,你可以使用Transfer Function模型,它是用输入和输出之间的传递函数来表示系统的模型。
对于更复杂的系统,你可以使用State Space模型,它是用系统的状态变量和它们之间的关系来表示系统的模型。
使用这两种模型,你可以方便地进行控制系统的分析和设计。
一旦你得到了控制系统的模型,你可以使用Matlab控制系统工具箱中提供的函数来进行控制系统的分析。
例如,你可以使用"step"函数来绘制控制系统的阶跃响应,从而判断系统的稳定性和性能。
你也可以使用"bode"函数来绘制系统的频率响应曲线,从而分析系统的幅频特性和相频特性。
此外,你还可以使用"Sensitivity"函数来分析系统对参数的敏感性,以评估系统的鲁棒性。
除了控制系统的分析,Matlab控制系统工具箱还提供了许多函数和工具来进行控制系统的设计。
例如,你可以使用"LQG"函数来设计线性二次高斯(LQG)控制器,它是一种常用的最优控制器设计方法。
你也可以使用"H∞"函数来设计H∞控制器,它是一种用于鲁棒控制的设计方法。
此外,你还可以使用"PID Tuner"工具箱来进行PID控制器的调参,以满足控制系统的性能要求。
MATLAB模型预测控制工具箱函数

MATLAB模型预测控制工具箱函数8.2 系统模型建立与转换函数前面读者论坛了利用系统输入/输出数据进行系统模型辨识的有关函数及使用方法,为时行模型预测控制器的设计,需要对系统模型进行进一步的处理和转换。
MATLAB的模型预测控制工具箱中提供了一系列函数完成多种模型转换和复杂系统模型的建立功能。
在模型预测控制工具箱中使用了两种专用的系统模型格式,即MPC状态空间模型和MPC传递函数模型。
这两种模型格式分别是状态空间模型和传递函数模型在模型预测控制工具箱中的特殊表达形式。
这种模型格式化可以同时支持连续和离散系统模型的表达,在MPC传递函数模型中还增加了对纯时延的支持。
表8-2列出了模型预测控制工具箱的模型建立与转换函数。
表8-2 模型建立与转换函数8.2.1 模型转换在MATLAB模型预测工具箱中支持多种系统模型格式。
这些模型格式包括:①通用状态空间模型;②通用传递函数模型;③MPC阶跃响应模型;④MPC状态空间模型;⑤ MPC 传递函数模型。
在上述5种模型格式中,前两种模型格式是MATLAB 通用的模型格式,在其他控制类工具箱中,如控制系统工具箱、鲁棒控制工具等都予以支持;而后三种模型格式化则是模型预测控制工具箱特有的。
其中,MPC 状态空间模型和MPC 传递函数模型是通用的状态空间模型和传递函数模型在模型预测控制工具箱中采用的增广格式。
模型预测控制工具箱提供了若干函数,用于完成上述模型格式间的转换功能。
下面对这些函数的用法加以介绍。
1.通用状态空间模型与MPC 状态空间模型之间的转换MPC 状态空间模型在通用状态空间模型的基础上增加了对系统输入/输出扰动和采样周期的描述信息,函数ss2mod ()和mod2ss ()用于实现这两种模型格式之间的转换。
1)通用状态空间模型转换为MPC 状态空间模型函数ss2mod ()该函数的调用格式为pmod= ss2mod (A,B,C,D)pmod = ss2mod (A,B,C,D,minfo)pmod = ss2mod (A,B,C,D,minfo,x0,u0,y0,f0)式中,A, B, C, D 为通用状态空间矩阵;minfo 为构成MPC 状态空间模型的其他描述信息,为7个元素的向量,各元素分别定义为:◆ minfo(1)=dt ,系统采样周期,默认值为1;◆ minfo(2)=n ,系统阶次,默认值为系统矩阵A 的阶次;◆ minfo(3)=nu ,受控输入的个数,默认值为系统输入的维数;◆ minfo(4)=nd ,测量扰的数目,默认值为0;◆ minfo(5)=nw ,未测量扰动的数目,默认值为0;◆ minfo(6)=nym ,测量输出的数目,默认值系统输出的维数;◆ minfo(7)=nyu ,未测量输出的数目,默认值为0;注:如果在输入参数中没有指定m i n f o ,则取默认值。
matlab机器人工具箱函数

matlab机器人工具箱函数使用Matlab机器人工具箱进行轨迹规划和控制Matlab机器人工具箱是一个常用的用于机器人建模、仿真、控制和运动规划的工具箱。
其中包含了众多函数,能够帮助用户快速完成机器人任务的规划和控制。
本文将介绍Matlab机器人工具箱的一些常用函数,包括轨迹规划、控制和运动学分析等方面。
1. 轨迹规划轨迹规划是机器人控制中的一个重要环节。
Matlab机器人工具箱中内置了许多轨迹规划函数,其中最常用的是trapezoidal和cubic spline函数。
Trapezoidal函数是一种基于梯形速度剖面的轨迹规划方法,能够保证机器人在规定的时间内从起始点到达终点,并且经过指定的路线。
使用该函数时需要指定起始点、终点、时间和最大速度等参数,例如:traj = trapveltraj(q0,qf,t,vmax,amax);其中,q0和qf是起始点和终点的位置,t是规定的时间,vmax和amax是机器人的最大速度和加速度。
Cubic spline函数是一种基于三次多项式的轨迹规划方法,能够实现平滑的轨迹规划。
该函数能够自动选择合适的多项式系数,以满足起始点、终点和速度等限制条件。
使用该函数时需要指定起始点、终点、时间和边界条件等参数,例如:[q,qd,qdd] = cubicpolytraj(q0,qf,t,qd0,qdf);其中,q0和qf是起始点和终点的位置,t是规定的时间,qd0和qdf是起始点和终点的速度。
2. 控制控制是机器人控制中的核心内容之一。
Matlab机器人工具箱中提供了许多控制函数,包括PID控制器、模型预测控制器和自适应控制器等。
PID控制器是一种基于比例、积分和微分三个控制分量的控制方法,能够实现快速响应和稳定性能。
使用该函数时需要指定比例、积分和微分系数,例如:Kp = 1; Ki = 0.1; Kd = 0.01;pidController = pid(Kp,Ki,Kd);Model Predictive Control(MPC)是一种基于模型的控制方法,能够预测机器人的未来状态,并基于预测结果进行控制。
模型预测控制及其MATLAB实现

模型预测控制及其MATLAB实现模型预测控制(Model Predictive Control, MPC)是一种先进的控制算法,用于处理动态系统的控制问题。
MPC通过在未来的时间范围内优化控制动作序列,以使系统的性能指标最小化,从而实现对系统的优化控制。
MPC的核心思想是建立一个系统模型,然后使用该模型来预测系统的行为,并根据预测结果进行优化控制决策。
具体而言,MPC首先使用系统模型对未来的状态和输出进行预测,然后根据预测结果计算出最优的控制动作序列。
接下来,仅施加最优的第一个控制动作,并在下一个采样时刻重复该过程。
这种迭代优化的过程可以使系统在每个采样时刻都能够进行最优的控制。
MPC的优势在于它可以处理多变量、非线性和时变系统,并且可以轻松地加入约束条件。
此外,MPC还能够在面对不确定性和扰动时提供鲁棒性,以确保控制系统的稳定性和性能。
因此,MPC在多个领域中都得到了广泛的应用,例如化工、能源、机械等。
在MATLAB中,有多种方法可以实现MPC控制算法。
最简单的方法是使用MPC工具箱,该工具箱提供了一套全面的函数和工具,用于建立系统模型、设定控制参数、优化控制决策等。
使用MPC工具箱,可以通过以下几个步骤来实现MPC控制:1.建立系统模型:使用MATLAB的系统建模工具箱,建立系统的状态空间模型或传递函数模型。
2.设定控制参数:根据系统的性能指标和控制目标,设定MPC控制的参数,例如控制时域、控制权重和约束条件等。
3.优化控制决策:使用MPC工具箱提供的优化函数,根据系统模型和控制参数,计算最优的控制动作序列。
4.实施控制动作:根据最优的控制动作序列,施加最优的第一个控制动作,并等待下一个采样时刻。
5.重复步骤3和4:在每个采样时刻,重复步骤3和4,以实现迭代优化控制。
请注意,MPC控制算法的实现还可能涉及其他细节,例如状态估计、鲁棒性设计和性能评估等。
因此,在具体应用中,可能需要根据系统的特点和需求进行相应的调整和扩展。
利用Matlab进行模型预测控制的技术方法

利用Matlab进行模型预测控制的技术方法引言在工业控制过程中,模型预测控制(Model Predictive Control,MPC)是一种有效的控制策略,它基于对系统建立的数学模型进行预测,并通过优化目标来产生最优的控制动作。
在过去的几十年中,MPC已经得到了广泛的应用,并且在各个领域都取得了显著的成果。
本文将介绍利用Matlab进行MPC的技术方法,包括建立系统模型、设置优化问题、解决优化问题以及实时控制实现等方面。
一、建立系统模型在进行MPC控制之前,首先需要建立系统的数学模型。
系统模型可以是连续时间的,也可以是离散时间的。
对于连续时间系统,可以采用常微分方程描述,而对于离散时间系统,可以采用差分方程描述。
在Matlab中,可以使用符号计算工具箱进行方程的推导和求解,得到系统的数学模型表达式。
以一个简单的控制系统为例,假设系统的控制目标是使温度保持在某一设定值附近。
我们可以基于物理原理建立一个温度控制的数学模型:```dx/dt = -a*x + b*uy = c*x```其中,x表示温度,u表示控制输入,y表示控制输出,a、b和c为系统的系数。
通过符号计算工具箱,可以推导出描述系统演化的微分方程,并将其转化为离散时间的差分方程。
二、设置优化问题在MPC中,需要设置一个优化问题来求解最优控制动作。
通常,优化目标包括使系统的输出误差最小化、使控制信号的变化量最小化等。
同时,还需要考虑系统的约束条件,如输入变量的限制、输出变量的限制等。
在Matlab中,可以使用优化工具箱来设置和求解优化问题。
对于上述温度控制系统,优化问题可以设置为最小化输出误差的平方和,并且限制控制输入的取值范围:```minimize J = ∑ (y_ref - y)^2subject to u_min ≤ u ≤ u_max```其中,J表示优化目标,y_ref表示参考输出,u_min和u_max表示控制输入的最小和最大取值。
Matlab中的系统辨识与模型预测控制技术

Matlab中的系统辨识与模型预测控制技术引言Matlab是一种广泛应用于工程和科学领域的高级计算环境和编程语言。
它提供了丰富的工具箱和函数,使工程师和科学家能够进行数据分析、模拟和建模。
本文将探讨Matlab中的系统辨识与模型预测控制(Model Predictive Control, MPC)技术,并介绍其基本原理、应用和优势。
一、系统辨识的基本原理系统辨识是指通过对系统输入和输出数据的分析和处理,来获得对系统动态行为的理解和描述的过程。
在Matlab中,系统辨识工具箱提供了一系列方法和算法来实现系统辨识,其中最常用的方法是基于数据的系统辨识方法。
这些方法根据系统输入和输出的数据样本,通过参数估计和模型拟合来获取系统模型。
在系统辨识中,常用的模型包括线性模型、非线性模型和时变模型等。
线性模型是最简单和最常用的模型类型,它假设系统的行为是线性的,具有参数可调整的特点。
非线性模型考虑了系统的非线性特性,能更准确地描述系统的行为,但参数估计和模型拟合的复杂性也相应增加。
时变模型是指系统参数会随时间变化的模型,能更好地描述实际系统动态行为的变化。
在Matlab中,可以使用系统辨识工具箱中的命令和函数来进行参数估计和模型拟合。
通过对实际系统的输入和输出数据进行采样和记录,然后使用这些数据来拟合和评估系统模型,可以有效地了解和预测系统的行为。
这些模型可以用于系统控制的设计和优化,为工程师和科学家提供决策支持和指导。
二、模型预测控制的基本原理模型预测控制是一种先进的控制技术,它通过预测系统的未来行为来生成控制策略,并根据实际系统的反馈信息进行修正和优化。
在Matlab中,模型预测控制工具箱提供了一系列函数和工具,使工程师和科学家能够轻松地设计和实现模型预测控制算法。
模型预测控制的基本原理是通过建立一个系统模型来预测系统未来的行为,并根据这些预测结果生成相应的控制策略。
通常,系统模型可以使用系统辨识技术获得,也可以采用已知的数学模型。
MATLAB常用工具箱及常用函数

常用工具箱MATLAB包括拥有数百个内部函数的主包和三十几种工具包。
工具包又可以分为功能性工具包和学科工具包。
功能工具包用来扩充MATLAB的符号计算,可视化建模仿真,文字处理及实时控制等功能。
学科工具包是专业性比较强的工具包,控制工具包,信号处理工具包,通信工具包等都属于此类。
开放性使MATLAB广受用户欢迎。
除内部函数外,所有MATLAB主包文件和各种工具包都是可读可修改的文件,用户通过对源程序的修改或加入自己编写程序构造新的专用工具包。
Matlab Main Toolbox——matlab主工具箱Control System Toolbox——控制系统工具箱Communication Toolbox——通讯工具箱Financial Toolbox——财政金融工具箱System Identification Toolbox——系统辨识工具箱FuzzyLogic Toolbox——模糊逻辑工具箱Higher-Order Spectral Analysis Toolbox——高阶谱分析工具箱Image Processing Toolbox——图象处理工具箱computer vision systemtoolbox----计算机视觉工具箱LMI Control Toolbox——线性矩阵不等式工具箱Model predictive Control Toolbox——模型预测控制工具箱μ-Analysis and Synthesis Toolbox——μ分析工具箱Neural Network Toolbox——神经网络工具箱Optimization Toolbox——优化工具箱Partial Differential Toolbox——偏微分方程工具箱Robust Control Toolbox——鲁棒控制工具箱Signal Processing Toolbox——信号处理工具箱 Spline Toolbox——样条工具箱Statistics Toolbox——统计工具箱Symbolic Math Toolbox——符号数学工具箱Simulink Toolbox——动态仿真工具箱Wavele Toolbox——小波工具箱DSP systemtoolbox-----DSP处理工具箱常用函数Matlab内部常数[2]eps:浮点相对精度exp:自然对数的底数ei 或j:基本虚数单位inf 或Inf:无限大, 例如1/0nan或NaN:非数值(Not a number),例如0/0 pi:圆周率p(= 3.1415926...)realmax:系统所能表示的最大数值realmin:系统所能表示的最小数值nargin: 函数的输入引数个数nargout: 函数的输出引数个数lasterr:存放最新的错误信息lastwarn:存放最新的警告信息MATLAB常用基本数学函数abs(x):纯量的绝对值或向量的长度angle(z):复数z的相角(Phase angle)sqrt(x):开平方real(z):复数z的实部imag(z):复数z的虚部conj(z):复数z的共轭复数round(x):四舍五入至最近整数fix(x):无论正负,舍去小数至最近整数floor(x):下取整,即舍去正小数至最近整数ceil(x):上取整,即加入正小数至最近整数rat(x):将实数x化为多项分数展开rats(x):将实数x化为分数表示sign(x):符号函数(Signum function)。
模型预测控制 matlab

模型预测控制 matlab
模型预测控制(MPC)是一种在控制系统中应用较多的高级控制方法,它可以考虑多个控制因素对系统的影响,并对其进行优化控制。
MPC在工
业自动化、化工、电力、航空等领域得到广泛应用。
在 MATLAB 中,可以使用“Control System Toolbox”工具箱来实现MPC控制。
主要步骤如下:
1.建立控制系统的动态模型:使用系统辨识或物理建模等方法,得到
系统的传递函数或状态空间模型;
2.确定控制目标和约束条件:确定系统需要达到的目标,以及控制输
入和输出的约束条件;
3.设计MPC控制器:使用MPC设计工具箱中的函数,设计MPC控制器
参数,并将其与动态模型和控制目标一起合成成为MPC控制器对象;
4.设置控制器参数:设置MPC控制器的采样周期、预测时域、控制输
入和输出约束、惩罚矩阵等参数;
5.进行仿真和实验:使用MATLAB进行仿真和实验验证MPC控制器的
性能。
需要注意的是,MPC控制器设计的好坏很大程度上依赖于系统模型的
准确性,因此在建立系统模型时需要认真考虑各种因素对系统的影响,并
进行准确的建模。
利用Matlab进行模型预测控制算法实现

利用Matlab进行模型预测控制算法实现引言:在现代控制领域,模型预测控制(Model Predictive Control,MPC)算法是一种非常重要的控制方法,其适用于多种工艺过程和系统控制。
本文将重点介绍如何利用Matlab实现模型预测控制算法。
第一部分:MPC算法简介模型预测控制算法是一种根据系统的数学模型进行控制的方法。
它不仅可以考虑系统的当前状态,还可以预测未来一段时间的状态,并优化控制器的输入,从而实现更好的控制效果。
MPC算法主要包括三个步骤:建模、预测和优化。
第二部分:MPC算法的建模在建立MPC控制模型之前,首先需要对控制对象进行数学建模。
一般来说,可以使用传统的物理建模方法或者数据驱动的建模方法。
在Matlab中,可以利用系统辨识工具箱或者曲线拟合工具箱等功能进行模型建立。
建模的目的是获取系统的状态方程和输出方程,用于后续的预测和优化。
第三部分:MPC算法的预测预测是MPC算法的核心步骤,它通过对系统的当前状态进行预测,得到未来一段时间内的状态和输出。
在Matlab中,可以利用预测模型对未来状态和输出进行计算,并得到一个预测轨迹。
预测模型可以在建模过程中得到,也可以根据实时数据进行在线更新。
第四部分:MPC算法的优化在预测的基础上,MPC算法通过优化控制器的输入信号,使得系统的输出符合预期的性能指标。
这个优化问题一般可以表示为一个多目标优化或者约束优化的问题。
在Matlab中,可以使用优化工具箱中的函数进行优化操作。
通过迭代计算,可以得到最优控制输入信号,从而实现更好的控制效果。
第五部分:MPC算法的实现在Matlab中,可以利用Control System Toolbox和Optimization Toolbox等工具箱来实现MPC算法。
首先,需要将系统的数学模型导入Matlab环境,并进行参数设置。
然后,可以使用MPC对象进行建模、预测和优化等操作。
最后,将MPC控制器与实际的控制系统进行连接,实现闭环控制。
在Matlab中使用机器学习工具箱进行模型训练和预测

在Matlab中使用机器学习工具箱进行模型训练和预测引言:随着人工智能的快速发展,机器学习在各个领域中得到了广泛的应用。
而Matlab作为一款功能强大的数值计算软件,其机器学习工具箱为用户提供了便捷的模型训练和预测功能。
本文将介绍在Matlab中如何使用机器学习工具箱进行模型训练和预测,并结合实例加以说明。
一、数据准备在进行模型训练和预测之前,首先需要准备训练和测试所需的数据集。
Matlab中的机器学习工具箱提供了丰富的数据导入和处理函数,可以直接读取常见的数据格式,如CSV和Excel文件。
同时,也可以通过代码生成或手动输入数据。
数据准备包括数据清洗、预处理、特征选择等步骤,这些步骤的目的是为了提高后续模型训练和预测的准确性和效果。
二、选择合适的算法在进行机器学习任务之前,需要先选择合适的算法。
Matlab的机器学习工具箱提供了各类经典的机器学习算法,如线性回归、逻辑回归、决策树、支持向量机等。
在选择算法时,需要根据任务的特点和数据的性质来决定。
比如要进行分类任务,可以选择逻辑回归或支持向量机;要进行回归任务,可以选择线性回归或决策树。
算法的选择直接影响了后续模型的性能和效果,因此需要慎重考虑。
三、模型训练选择好算法之后,就可以进行模型训练了。
在Matlab中,只需要简单几行代码就可以完成模型的训练过程。
以线性回归为例,首先需要定义一个线性回归模型对象,然后使用训练数据对模型进行训练。
训练过程中可以设置一些参数,如迭代次数、学习率等。
训练完成后,可以通过评估指标来评价模型的性能,如均方误差(MSE)和决定系数(R-squared)。
四、模型预测模型训练完成后,就可以使用该模型进行预测了。
Matlab提供了预测函数,可以将测试数据输入模型,得到预测结果。
预测结果可以通过可视化的方式呈现,以便于观察。
同时,也可以计算预测结果与真实标签之间的误差,以评估模型的预测能力。
五、模型调优在模型训练和预测的过程中,有时候会出现性能不佳的情况。
如何使用Matlab进行模型预测控制

如何使用Matlab进行模型预测控制在现代控制系统中,模型预测控制(Model Predictive Control, MPC)被广泛应用于工业自动化领域。
它是一种基于数学模型的控制算法,通过对系统行为进行预测,优化控制过程以实现最佳控制效果。
在本文中,我们将探讨如何使用Matlab 进行模型预测控制。
1. 简介模型预测控制是一种基于数学模型的的控制策略,它通过预测系统的未来行为来选择最佳的控制输入。
与传统的控制方法相比,MPC在处理多变量、受约束的控制问题上具有明显的优势。
它不仅可以优化系统的追踪性能,还可以有效地处理输入和输出约束。
2. 建立系统模型在使用MPC进行控制前,我们首先需要建立系统的数学模型。
这个模型描述了系统的动态行为,并用于预测系统的未来响应。
通常情况下,我们可以使用传统的物理建模方法来建立系统的数学模型,例如使用微分方程或差分方程描述系统的动态行为。
3. 参数辨识为了建立准确的系统模型,我们需要对模型中的参数进行辨识。
参数辨识是通过实验数据来确定系统模型中未知参数的过程。
在Matlab中,我们可以使用系统辨识工具箱中的函数来进行参数辨识,例如使用最小二乘法拟合实验数据以估计模型参数。
4. 模型预测在控制过程中,模型预测是MPC的核心部分。
它通过对系统的数学模型进行迭代计算来预测未来的系统响应。
在Matlab中,我们可以使用控制系统工具箱中的函数来实现模型预测。
例如,可以使用step函数对模型进行步响应分析,或者使用impulse函数对模型进行冲激响应分析。
5. 优化控制在模型预测控制中,优化控制是为了选择最佳的控制输入而进行的。
通常情况下,我们需要定义一个性能指标来衡量控制系统的性能,并通过优化算法来选择最佳的控制输入。
在Matlab中,我们可以使用优化工具箱中的函数来进行优化控制,例如使用fmincon函数来求解非线性约束优化问题。
6. 约束处理与传统的控制方法不同,MPC能够有效地处理输入和输出的约束。
Matlab中的模型预测控制方法介绍

Matlab中的模型预测控制方法介绍一、引言在控制系统领域,模型预测控制(Model Predictive Control,简称MPC)是一种经典且高效的控制方法。
它基于数学模型的预测能力,通过优化控制变量序列,实现对系统状态的最优化调节。
在Matlab中,MPC方法得到了广泛应用,并通过Matlab的建模和优化工具箱实现了方便的开发和调试环境。
二、MPC方法的基本原理MPC方法的核心思想是通过预测系统未来的动态行为,来优化控制策略。
在MPC中,首先需要建立数学模型描述系统的动态行为,并将其转化为离散形式。
然后,根据模型预测出系统未来一段时间的状态和输出,通过对控制变量序列进行优化,得到最优的控制策略。
最后,根据所得到的控制策略实施控制动作,并反馈实际的系统输出,用于调整下一次的控制策略。
三、Matlab中的MPC建模工具箱为了方便用户使用MPC方法,MathWorks公司开发了专门的MPC工具箱。
MPC工具箱提供了一系列用于建模、仿真和优化的函数和工具,使得使用MPC方法更加简单和高效。
通过MPC工具箱可以方便地导入系统模型、设置控制目标、调节控制权重和约束条件,并进行模拟和优化。
四、MPC建模实例下面我们通过一个实例来介绍如何在Matlab中使用MPC方法进行建模和控制设计。
假设我们需要设计一个MPC控制器来控制一个加热系统的温度。
首先,我们需要获取加热系统的数学模型,并将其离散化得到离散时间步长的动态方程。
然后,通过MPC工具箱中的函数将模型导入Matlab环境中。
在导入模型后,我们需要设置控制目标和约束条件。
例如,我们可以设置目标温度为30摄氏度,并限制加热功率不超过100瓦特。
此外,我们还可以设置对温度变化率的约束,以确保系统动态响应的稳定性。
在设置好目标和约束后,我们可以使用MPC工具箱中的仿真函数模拟系统的响应,并通过图形界面直观地观察温度的变化趋势。
最后,我们需要调节控制权重以求得最优的控制策略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB模型预测控制工具箱函数8.2 系统模型建立与转换函数前面读者论坛了利用系统输入/输出数据进行系统模型辨识的有关函数及使用方法,为时行模型预测控制器的设计,需要对系统模型进行进一步的处理和转换。
MATLAB的模型预测控制工具箱中提供了一系列函数完成多种模型转换和复杂系统模型的建立功能。
在模型预测控制工具箱中使用了两种专用的系统模型格式,即MPC状态空间模型和MPC传递函数模型。
这两种模型格式分别是状态空间模型和传递函数模型在模型预测控制工具箱中的特殊表达形式。
这种模型格式化可以同时支持连续和离散系统模型的表达,在MPC传递函数模型中还增加了对纯时延的支持。
表8-2列出了模型预测控制工具箱的模型建立与转换函数。
表8-2 模型建立与转换函数8.2.1 模型转换在MATLAB模型预测工具箱中支持多种系统模型格式。
这些模型格式包括:①通用状态空间模型;②通用传递函数模型;③MPC阶跃响应模型;④MPC状态空间模型;⑤ MPC 传递函数模型。
在上述5种模型格式中,前两种模型格式是MATLAB 通用的模型格式,在其他控制类工具箱中,如控制系统工具箱、鲁棒控制工具等都予以支持;而后三种模型格式化则是模型预测控制工具箱特有的。
其中,MPC 状态空间模型和MPC 传递函数模型是通用的状态空间模型和传递函数模型在模型预测控制工具箱中采用的增广格式。
模型预测控制工具箱提供了若干函数,用于完成上述模型格式间的转换功能。
下面对这些函数的用法加以介绍。
1.通用状态空间模型与MPC 状态空间模型之间的转换MPC 状态空间模型在通用状态空间模型的基础上增加了对系统输入/输出扰动和采样周期的描述信息,函数ss2mod ()和mod2ss ()用于实现这两种模型格式之间的转换。
1)通用状态空间模型转换为MPC 状态空间模型函数ss2mod ()该函数的调用格式为pmod= ss2mod (A,B,C,D)pmod = ss2mod (A,B,C,D,minfo)pmod = ss2mod (A,B,C,D,minfo,x0,u0,y0,f0)式中,A, B, C, D 为通用状态空间矩阵;minfo 为构成MPC 状态空间模型的其他描述信息,为7个元素的向量,各元素分别定义为:◆ minfo(1)=dt ,系统采样周期,默认值为1;◆ minfo(2)=n ,系统阶次,默认值为系统矩阵A 的阶次;◆ minfo(3)=nu ,受控输入的个数,默认值为系统输入的维数;◆ minfo(4)=nd ,测量扰的数目,默认值为0;◆ minfo(5)=nw ,未测量扰动的数目,默认值为0;◆ minfo(6)=nym ,测量输出的数目,默认值系统输出的维数;◆ minfo(7)=nyu ,未测量输出的数目,默认值为0;注:如果在输入参数中没有指定m i n f o ,则取默认值。
x0, u0, y0, f0为线性化条件,默认值均为0;pmod 为系统的MPC 状态空间模型格式。
例8-5 将如下以传递函数表示的系统模型转换为MPC 状态空间模型。
12213)(232+++++=s s s s s s G 解:MATLAB 命令如下:其输出结果为: pmod =1 3 1 0 0 1 0NaN -2 -2 -1 1 0 00 1 0 0 0 0 00 0 1 0 0 0 00 1 3 1 0 0 02)MPC 状态空间模型转换为通用状态空间模型函数mod2ss ()该函数的调用格式为[A, B, C, D]= mod2ss(pmod)[A, B, C, D, minfo]= mod2ss(pmod)[A,B,C,D,minfo,x0,u0,y0,f0]= mod2ss(pmod)式中,pmod 为系统的MPC 状态空间模型格式;A,B,C,D 为通用状态空间矩阵;minfo 为构成MPC 状态空间模型的其他描述信息,其说明参见函数ss2mod ()。
2.通用传递函数模型转换为MPC 传递函数模型通用传递函数模型与MPC 传递函数模型的转换函数poly2tfd ()的调用格式为g=poly2tfd (num,den,delt,delay)式中,num 为通用传递函数模型的分子多项式系数向量;den 为通用传递函数模型的分母多项式系数向量;delt 为采样周期,对连续系统,该参数为0;delay 为系统纯时延,对于离散系统,纯时延为采样时间周期的整数倍;g 为被控对象的MPC 传递函数模型。
例8-6 考虑如下的纯时延二阶对象,并将其转换为MPC 传递函数模型。
44)1()(25.0+++=-s s s e s G s 解:MATLAB 命令如下:>> num=[1 1];den=[1 4 4];>> g=poly2tfd(num,den,0,0.5)结果显示:g =0 1.0000 1.00001.0000 4.0000 4.00000 0.5000 03.MPC传递函数模型转换为MPC状态空间模型函数tfd2mod()该函数的调用格式为pmod=tfd2mod(delt,ny,g1,g2,……,g25)式中,delt为采样时间;ny为输出个数;g1,g2,……为SISO传递函数,对应多变量系统传递函数矩阵的各个元素按行向量顺序排序构成的向量,其最大个数限制为25;pmod为系统的MPC状态空间模型。
4.MPC阶跃响应模型与其他模型格式之间的转换函数mod2step()、tfd2step()和ss2step()分别用于将MPC状态空间模型、MPC 传递函数模型和通用状态空间模型转换为MPC阶跃响应模型。
下面对这个三函数的用法进行说明。
1)MPC状态空间模型转换为MPC阶跃响应模型函数mod2step()plant=mod2step(pmod,tfinal)[plant, dplant]=mod2step(pmod,tfinal,delt,nout)式中,pmod为系统的MPC状态空间模型;tfinal为阶跃响应模型的截断时间;delt为采样周期,默认值由MPC状态空间模型的参数minfo(1)决定;nout为输出稳定性向量,用于指定输出的稳定性。
对于稳定的系统,nout等于输出的个数;对于具有一个或多个积怨分输出的系统,nout为一个长度等于输出个数的向量,该向量对应积分输出的分量为0,其余分量为1;plant为对象在受控变量作用下的阶跃响应系数矩阵;dplant为对象在扰动作用下阶跃响应矩阵。
2)MPC传递函数模型转换为MPC阶跃响应模型函数tfd2step()该函数的调用格式为plant=tfd2step(tfinal,delt,nout,g1)plant=tfd2step(tfinal,delt,nout,g1,……,g25)式中,tfinal为阶跃响应的截断时间;delt为采样周期;nout为输出稳定性向量,参见函数mod2step()的有关说明;g1,……,g25为SISO传递函数,对应多变量系统传递函数矩阵的各个元素按行向量顺序排列构成的向量,其最大个数限制为25;plant为对象的阶跃响应系统矩阵。
例8-8设系统传递函数为132)(2+++=s s s s G 将其转换为阶跃响应模型。
解:MATLAB 命令如下:>> num=[1 2];den=[1 3 1];>> tf1=poly2tfd(num,den,0,0);>> plant=tfd2step(5,0.1,1,tf1);>> plotstep(plant) 由阶跃响应模型绘制的系统阶跃响应曲线如图8-5所示。
图8-5 系统阶跃响应曲线8.4 基于阶跃响应模型的控制器设计与仿真函数基于系统的阶跃响应模型进行模型预测控制器设计的方法称为动态矩阵控制方法。
该方法是采用工程上易于获取的对象阶跃响应模型,算法较为简单,计算量较少,鲁棒性较强,适用于纯时迟、开环渐近稳定的非最小相位系统,在工业过程控制中得到成功应用。
MATLAB 的模型预测控制工具箱提供了对动态矩阵控制方法的支持,有关的函数能够基于阶跃响应模型的模型预测控制器设计与仿真,见表8-3。
表8-3 动态矩阵控制设计与仿真函数例8-12 考虑如下的双输入输出纯时延对象,其传递函数矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-+-++=----14.144.1910.219.1819.106.617.168.12)(3371s e s e s e s e s G s ss s解:MATLAB 程序如下:闭环系统的输出和控制量变化曲线如图1所示。
图1 闭环系统的输出和控制量变化曲线8.4 基于状态空间模型的预测控制器设计函数在MATLAB模型预测控制工具箱中,除了提供基于阶跃响应模型的预测控制器设计功能外,还提供了MPC状态空间模型的预测控制器设计功能。
有关的函数参见表8-4。
表8-4 基于MPC状态空间模型的预测控制器设计函数8.4.1 输入/输出有约束的状态空间模型预测控制器设计函数scmpc()用于进行输入/输出有约束条件下的状态空间模型预测控制器设计,该函数的调用格式为[y, u, ym]=scmpc(pmod, imod, ywt, uwt, M, P, tend, r, ulim, ylim, kest, z, v, w, wu) 式中,pmod为MPC状态空间模型格式的对象状态空间模型,用于仿真;imod为MPC状态空间模型格式的对象内部模型,用于预测控制器设计;ywt为二次型性能指标的输出误差加权矩阵;uwt为二次型性能指标的控制量加权矩阵;M为控制时域长度;P为预测时域长度;tend为仿真的结束时间;r为输入设定值或参考轨迹;ulim=[ulow uhigh delu],式中,ulow为控制变量的下界,uhigh为控制变量的上界,delu为控制变量的变化率约束;ylim=[ylow yhigh],式中,ylow为输出的下界,yhigh为输出的上界;kest为估计器的增益矩阵;z为测量噪声;v为测量扰动;w为输出未测量扰动;wu为施加到控制输入的未测量扰动;y为系统响应;u为控制变量;ym为模型预测输出。
例8-15 考虑如下的双输入输出纯时延对象,其传递函数矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-+-++=----14.144.1910.219.1819.106.617.168.12)(3371s e s e s e s e s G s ss s解:MATLAB 程序如下:[1] 李国勇. 智能控制及其MATLAB实现[M]. 北京:电子工业出版社, 2005.。
