MA AB模型预测控制工具箱函数
MA AB 回归预测模型

MATLAB---回归预测模型Matlab统计工具箱用命令regress实现多元线性回归,用的方法是最小二乘法,用法是:b=regress(Y,X)[b,bint,r,rint,stats]=regress(Y,X,alpha)Y,X为提供的X和Y数组,alpha为显着性水平(缺省时设定为0.05),b,bint为回归系数估计值和它们的置信区间,r,rint为残差(向量)及其置信区间,stats 是用于检验回归模型的统计量,有四个数值,第一个是R2,第二个是F,第三个是与F对应的概率 p ,p <α拒绝 H0,回归模型成立,第四个是残差的方差 s2 。
残差及其置信区间可以用 rcoplot(r,rint)画图。
例1合金的强度y与其中的碳含量x有比较密切的关系,今从生产中收集了一批数据如下表 1。
先画出散点图如下:x=0.1:0.01:0.18;y=[42,41.5,45.0,45.5,45.0,47.5,49.0,55.0,50.0];plot(x,y,'+')可知 y 与 x 大致上为线性关系。
设回归模型为y =β0+β1x用regress 和rcoplot 编程如下:clc,clearx1=[0.1:0.01:0.18]';y=[42,41.5,45.0,45.5,45.0,47.5,49.0,55.0,50.0]'; x=[ones(9,1),x1];[b,bint,r,rint,stats]=regress(y,x);b,bint,stats,rcoplot(r,rint)得到 b =27.4722 137.5000bint =18.6851 36.259475.7755 199.2245stats =0.7985 27.7469 0.0012 4.0883即β0=27.4722 β1=137.5000β的置信区间是[18.6851,36.2594],β1的置信区间是[75.7755,199.2245];R2= 0.7985 , F = 27.7469 , p = 0.0012 , s2 =4.0883 。
模型预测控制matlab工具箱实例

模型预测控制matlab工具箱实例模型预测控制(MPC)是一种广泛应用于工业过程控制的高级控制策略。
Matlab提供了用于设计和实施MPC的工具箱。
本实例演示了如何使用Matlab MPC工具箱执行MPC控制。
1. 创建一个MPC对象首先,我们需要创建一个MPC对象。
使用mpc对象构造函数可以创建MPC对象。
例如:```mpcobj = mpc(object func, sample time, prediction horizon, control horizon);```其中,object func是被控制系统的离散时间状态空间模型的函数句柄;sample time是采样时间,prediction horizon是预测时域长度,control horizon是控制时域长度。
2. 配置MPC对象接下来,我们需要配置MPC对象。
可以使用MPC对象的属性来进行配置。
例如:```mpcobj.Model.Plant = ss(A,B,C,D);mpcobj.Model.Noise = 'Custom';mpcobj.Model.Disturbance = 'Custom';mpcobj.PredictionHorizon = 10;mpcobj.ControlHorizon = 2;mpcobj.Weights.OV = 1;mpcobj.Weights.MV = 0.1;mpcobj.Weights.ECR = [0.1 0.2];mpcobj.MV = struct('Min',-10,'Max',10);```上述代码中,我们设置了被控制系统的动态模型,噪声模型和干扰模型的类型。
我们还设置了预测时域长度,控制时域长度和权重。
3. 模拟仿真现在,我们可以使用MPC对象进行控制。
首先,我们需要对系统进行模拟仿真以生成实验数据。
可以使用sim函数进行仿真。
Matlab金融工具箱的使用指南

Matlab金融工具箱的使用指南随着信息时代的到来,金融数据的处理和分析变得越来越重要。
为了满足金融领域的需求,MathWorks推出了Matlab金融工具箱。
本文将为您介绍这个工具箱的基本功能和如何使用它来进行金融数据的分析和建模。
1. 引言金融工具箱是Matlab的一个扩展模块,专门用于金融数据的处理和分析。
它提供了一系列函数和工具,能够帮助用户进行金融数据的可视化、建模和风险管理等工作。
下面我们将详细介绍该工具箱的主要功能和常用函数。
2. 金融数据的导入和导出金融数据通常以电子表格或文本文件的形式存储。
Matlab金融工具箱提供了多种函数,可以方便地将这些数据导入到Matlab中进行处理。
同时,用户也可以将处理后的数据导出到电子表格或文本文件中。
这些函数包括readtable、writetable、readmatrix、writematrix等。
3. 金融时间序列分析金融数据通常是按照时间顺序排列的,因此时间序列分析是金融数据分析的重要组成部分。
Matlab金融工具箱提供了一系列函数,可以方便地进行时间序列的建模和分析。
其中包括acf(自相关函数)、pacf(偏自相关函数)、arma(自回归移动平均模型)等。
4. 金融数据的可视化可视化是金融数据分析的重要工具。
Matlab金融工具箱提供了多种函数,可以帮助用户将金融数据可视化展示。
其中包括plot(绘制折线图)、bar(绘制柱状图)、histogram(绘制直方图)等。
用户可以根据自己的需求选择适当的函数进行数据可视化。
5. 金融数据的建模和预测建模和预测是金融数据分析的核心工作。
Matlab金融工具箱提供了多种经典的建模和预测方法,帮助用户进行金融数据的建模和预测。
其中包括线性回归模型、ARMA模型、GARCH模型等。
用户可以使用这些函数来分析和预测金融市场的走势。
6. 风险管理与投资组合优化风险管理对于金融机构和投资者至关重要。
Matlab金融工具箱提供了一系列函数和工具,可以帮助用户进行风险管理和投资组合优化。
预测控制matlab工具箱
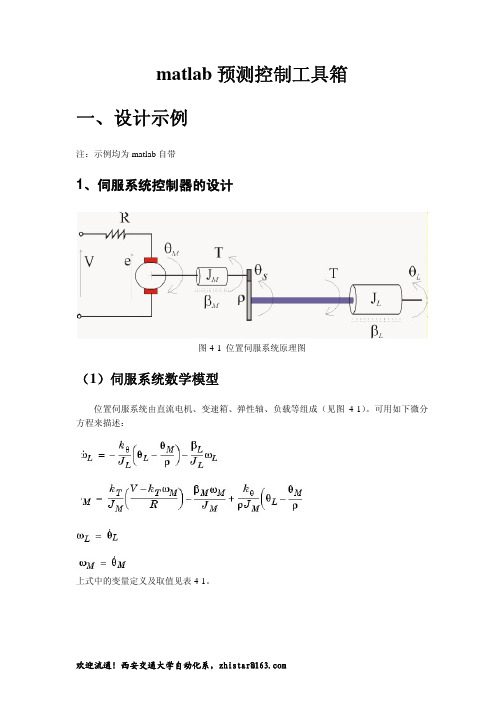
matlab预测控制工具箱一、设计示例注:示例均为matlab自带1、伺服系统控制器的设计图4-1 位置伺服系统原理图(1)伺服系统数学模型位置伺服系统由直流电机、变速箱、弹性轴、负载等组成(见图4-1)。
可用如下微分方程来描述:上式中的变量定义及取值见表4-1。
将上述微分方程写成状态方程形式,有其中,。
(2)控制目标及约束控制目标:在电压V的控制下,使过载角位置跟踪指定值。
输出量仅有可观测。
弹性轴承受的强度有一定的限制,因此对输出力矩T的赋值作一定约束:对输入电压的约束:该系统有一个输入V,两个输出:(可测量)和T(不可测量)。
(3)在matlab中定义该系统的状态空间模型首先需要在matlab中对系统的数学模型进行定义。
可以直接在命令行输入mpcmotormodel(建议做法),也可以在命令行中输入下列命令:% DC-motor with elastic shaft%%Parameters (MKS)%-----------------------------------------------------------Lshaft=1.0; %Shaft lengthdshaft=0.02; %Shaft diametershaftrho=7850; %Shaft specific weight (Carbon steel)G=81500*1e6; %Modulus of rigiditytauam=50*1e6; %Shear strengthMmotor=100; %Rotor massRmotor=.1; %Rotor radiusJmotor=.5*Mmotor*Rmotor^2; %Rotor axial moment of inertia Bmotor=0.1; %Rotor viscous friction coefficient (A CASO)R=20; %Resistance of armatureKt=10; %Motor constantgear=20; %Gear ratioJload=50*Jmotor; %Load inertiaBload=25; %Load viscous friction coefficientIp=pi/32*dshaft^4; %Polar momentum of shaft(circular) sectionKth=G*Ip/Lshaft; %Torsional rigidity(Torque/angle)Vshaft=pi*(dshaft^2)/4*Lshaft; %Shaft volumeMshaft=shaftrho*Vshaft; %Shaft massJshaft=Mshaft*.5*(dshaft^2/4); %Shaft moment of inertiaJM=Jmotor;JL=Jload+Jshaft;Vmax=tauam*pi*dshaft^3/16; %Maximum admissible torqueVmin=-Vmax;%Input/State/Output continuous time form%----------------------------------------------------------AA=[0 1 0 0;-Kth/JL -Bload/JL Kth/(gear*JL) 0;0 0 0 1;Kth/(JM*gear) 0 -Kth/(JM*gear^2)-(Bmotor+Kt^2/R)/JM];BB=[0;0;0;Kt/(R*JM)];Hyd=[1 0 0 0];Hvd=[Kth 0 -Kth/gear 0];Dyd=0;Dvd=0;% Define the LTI state-space modelsys=ss(AA,BB,[Hyd;Hvd],[Dyd;Dvd]);(4)利用MPCTOOL界面设计控制器第一步:导入模型在命令行窗口中输入mpctool,工具箱界面出来后点击Imort Plant…,此时界面如4-2所示。
Matlab灰色预测工具箱

Matlab灰色预测工具箱——走过数模2009-07-02 23:05灰色预测几乎是每年数模培训必不可少的内容,相对来说也是比较简单,这里写了四个函数,方便在Matlab里面调用,分1),新陈代谢GM(1,1),Verhust自己写得难免有所疏忽,需要的朋友自己找本书本来试验一下。
Gm(1,1)function [px0,ab,rel]=gm11(x0,number)%[px0,ab,rel]=gm11(x0,number)%px0为预测数列,rel为平均相对误差,rel为平均相对误差(为百分比)%默认的number参数为原数组大小if nargin==1number=max(size(x0));endn=max(size(x0));x1=zeros(size(x0));for k=1:nfor i=1:kx1(k)=x1(k)+x0(i);endendz=zeros(size(x0));for k=2:nz(k)=0.5*(x1(k)+x1(k-1));endy=x0';y(1)=[];b(:,1)=-z';b(:,2)=1;b(1,:)=[];ab=inv(b'*b)*b'*y;a=ab(1);b=ab(2);px0(1)=x0(1);%求还原值系列for k=1:number-1px0(k+1)=(1-exp(a)) * ( x0(1)-b/a ) * exp(-a*k);endtemp=px0(1:n);x0;temp=(temp-x0)./x0; %相对误差temp(1)=[]; %删除第一个为零的误差temp=abs(temp);rel=sum(temp)/(n-1)*100;残差Gm(1,1)function [px0,ab,rel]=ccgm11(x0,number)%[px0,ab,rel]=gm11(x0,number)%px0为残差预测数列,ab为求得的系数,rel为平均相对误差(为百分比) %默认的number参数为原数组大小if nargin==1number=max(size(x0));endn=max(size(x0)); %数组大小..[px0,ab,rel]=gm11(x0,number);wucha=x0-px0(1:n);i=n;%求后面的同号的数目.while(wucha(i)*wucha(i-1)>0 & i>=2)i=i-1;endstart=i;length=n-i+1;new=wucha(start:n);if length>=4pwucha=gm11(new);px0(start:n)=px0(start:n)+pwuchaclear wucha;wucha=px0-x0;wucha=wucha./x0; %相对误差wucha=abs(wucha);rel=sum(wucha)/(n-1)*100;endverhustfunction [px0,ab,rel]=verhust(x1,number)%[px0,ab,rel]=verhust(x0,number)%px0为预测数列,rel为平均相对误差,rel为平均相对误差(为百分比) %默认的number参数为原数组大小if nargin==1number=max(size(x1));endn=max(size(x1));x0(1)=x1(1);for k=2:nx0(k)=x1(k)-x1(k-1);z(k)=0.5*(x1(k)+x1(k-1));endx0;z;B=[-(z(2:n))' (z(2:n).^2)'];B;Y=(x0(2:n))';Y;ab=inv(B'*B)*B'*Y;a=ab(1);b=ab(2);for k=1:numberpx0(k)=(a*x1(1))/(b*x1(1)+(a-b*x1(1)).*exp(a*(k-1)));endtemp=px0(1:n);x1;temp=(temp-x1)./x1; %相对误差temp(1)=[]; %删除第一个为零的误差temp=abs(temp);rel=sum(temp)/(n-1)*100;新陈代谢Gm(1,1)function [px0,ab,rel]=xcdxgm11(x0,number,step)%[px0,ab,rel]=xcdxgm11(x0,number,step)%x0为原系列,number为要预测的数目,step为基本步长%px0为预测数列,rel为平均相对误差,rel为平均相对误差(为百分比) %默认的number参数为原数组大小%模型假设预测的数据和原始数据都要大于等于5if nargin==1number=max(size(x0));step=max(size(x0));endif nargin==2step=max(size(x0));endn=max(size(x0));if n<step | n<5error('此模型要求至少有五个原始数据,并且原始数据个数要大于新陈代谢的步长.'); end[px0,ab,rel]=gm11(x0,n);last=n;x0;px0;while last<numberbegin=last-step+1;temp=px0(begin:last);temp=gm11(temp,step+1);last=last+1;px0(last)=temp(step+1);end。
MATLAB环境下的模型预测控制理论的应用

MATLAB环境下的模型预测控制理论的应用丛爽邓娟(中国科学技术大学自动化系,合肥230027)E-mail:scong@ustc.edu.cn摘要从模型预测控制的原理出发。
介绍利用MA7ⅡAB模型预测控制工具箱进行模型预测控制器设计的全过程。
就被控对象的不同模型。
以及备类模型形式之间的转换做了具体的系统的阐述。
在控刺器的设计过程中,给出不同情况下的控制器的设计方法,并且对控制器设计申的参数选择对系统控制性能的影响进行了分析与总结。
最后通过数值实例说明了如何进行了模型预测控制器的设计。
关键词模型预测控制模型辨识阶跃响应模型系统仿真文章编号l002—8331一(2005)16-0196—03文献标识码A中圈分类号TPl3ModelPredictiveControlTheoryandApplicationunderMATLABEnvironment(Dept.ofAutomation,UniversityofScience&TechnologyofChina,Hefei230027)Abstract:Basedtheprincipleofmodelpredictivecontrol,thepaperintroducesthewholeprocessofmodelpredic—fivecontrollerdesignwithmodelpredictivecontroltoolboxinMATLAB.Systematicallyrepresentthedifferentmodelsofcontrolledplant,aswellastheconversionsofthosemodels.Intheprocedureofthecontrollerdesign,differentcontrollerdesignmethodsintroduced.Atthe8alTletime,theanalysesandconclusionofeffectstosystemcontrolperformanceintheaspectofparametersselection啪done.Atlast.annumericalexampleofthemodelpredictivecontrollerdesignisgiven.Keywords:modelpredictivecontrol,modelidentification,stepresponsemodel,systemsimulation1引言以状态空间法为基础的现代控制理论从20世纪60年代提出到70年代在理论上日趋完善,并且在许多方面得到了成功的运用。
Matlab常用工具箱及常用函数

Matlab常用工具箱MATLAB包括拥有数百个内部函数的主包和三十几种工具包.工具包又可以分为功能性工具包和学科工具包.功能工具包用来扩充MATLAB的符号计算,可视化建模仿真,文字处理及实时控制等功能.学科工具包是专业性比较强的工具包,控制工具包,信号处理工具包,通信工具包等都属于此类.开放性使MATLAB广受用户欢迎.除内部函数外,所有MATLAB主包文件和各种工具包都是可读可修改的文件,用户通过对源程序的修改或加入自己编写程序构造新的专用工具包.Matlab Main Toolbox——matlab主工具箱Control System Toolbox——控制系统工具箱Communication Toolbox——通讯工具箱Financial Toolbox——财政金融工具箱System Identification Toolbox——系统辨识工具箱Fuzzy Logic Toolbox——模糊逻辑工具箱Higher-Order Spectral Analysis Toolbox——高阶谱分析工具箱Image Processing Toolbox——图象处理工具箱LMI Control Toolbox——线性矩阵不等式工具箱Model predictive Control Toolbox——模型预测控制工具箱μ-Analysis and Synthesis Toolbox——μ分析工具箱Neural Network Toolbox——神经网络工具箱Optimization Toolbox——优化工具箱Partial Differential Toolbox——偏微分方程工具箱Robust Control Toolbox——鲁棒控制工具箱Signal Processing Toolbox——信号处理工具箱Spline Toolbox——样条工具箱Statistics Toolbox——统计工具箱Symbolic Math Toolbox——符号数学工具箱Simulink Toolbox——动态仿真工具箱Wavele Toolbox——小波工具箱常用函数Matlab内部常数[3]eps:浮点相对精度exp:自然对数的底数ei 或 j:基本虚数单位inf 或 Inf:无限大, 例如1/0nan或NaN:非数值(Not a number),例如0/0pi:圆周率 p(= 3.1415926...)realmax:系统所能表示的最大数值realmin:系统所能表示的最小数值nargin: 函数的输入引数个数nargout: 函数的输出引数个数lasterr:存放最新的错误信息lastwarn:存放最新的警告信息MATLAB常用基本数学函数abs(x):纯量的绝对值或向量的长度angle(z):复数z的相角(Phase angle)sqrt(x):开平方real(z):复数z的实部imag(z):复数z的虚部conj(z):复数z的共轭复数round(x):四舍五入至最近整数fix(x):无论正负,舍去小数至最近整数floor(x):地板函数,即舍去正小数至最近整数ceil(x):天花板函数,即加入正小数至最近整数rat(x):将实数x化为分数表示rats(x):将实数x化为多项分数展开sign(x):符号函数 (Signum function).当x0时,sign(x)=1.rem(x,y):求x除以y的馀数gcd(x,y):整数x和y的最大公因数lcm(x,y):整数x和y的最小公倍数exp(x) :自然指数pow2(x):2的指数log(x):以e为底的对数,即自然对数或log2(x):以2为底的对数log10(x):以10为底的对数MATLAB常用三角函数sin(x):正弦函数cos(x):余弦函数tan(x):正切函数asin(x):反正弦函数acos(x):反余弦函数atan(x):反正切函数atan2(x,y):四象限的反正切函数sinh(x):双曲正弦函数cosh(x):双曲余弦函数tanh(x):双曲正切函数asinh(x):反双曲正弦函数acosh(x):反双曲余弦函数atanh(x):反双曲正切函数适用于向量的常用函数有min(x): 向量x的元素的最小值max(x): 向量x的元素的最大值mean(x): 向量x的元素的平均值median(x): 向量x的元素的中位数std(x): 向量x的元素的标准差diff(x): 向量x的相邻元素的差sort(x): 对向量x的元素进行排序(Sorting)length(x): 向量x的元素个数norm(x): 向量x的欧氏(Euclidean)长度sum(x): 向量x的元素总和prod(x): 向量x的元素总乘积cumsum(x): 向量x的累计元素总和cumprod(x): 向量x的累计元素总乘积dot(x, y): 向量x和y的内积cross(x, y): 向量x和y的外积MATLAB基本绘图函数plot: x轴和y轴均为线性刻度(Linear scale)loglog: x轴和y轴均为对数刻度(Logarithmic scale)semilogx: x轴为对数刻度,y轴为线性刻度semilogy: x轴为线性刻度,y轴为对数刻度matlab插值和样条plot绘图函数的参数字元颜色字元图线型态y 黄色 . 点k 黑色 o 圆w 白色 x xb 蓝色 + +g 绿色 * *r 红色 - 实线c 亮青色 : 点线m 锰紫色 -. 点虚线-- 虚线注解xlabel('Input Value'); % x轴注解ylabel('Function Value'); % y轴注解title('Two Trigonometric Functions'); % 图形标题legend('y = sin(x)','y = cos(x)'); % 图形注解grid on; % 显示格线二维绘图函数bar 长条图errorbar 图形加上误差范围fplot 较精确的函数图形polar 极座标图hist 累计图rose 极座标累计图stairs 阶梯图stem 针状图fill 实心图feather 羽毛图compass 罗盘图quiver 向量场图[4]Welcome To Download !!!欢迎您的下载,资料仅供参考!。
Matlabyalmip工具编写自动驾驶模型预测控制(MPC)代码

Matlabyalmip⼯具编写⾃动驾驶模型预测控制(MPC)代码⽬录前⾔在⽆⼈驾驶的运动控制中,模型预测控制(MPC)算法得到了⼴泛使⽤,龚建伟的《⽆⼈驾驶车辆模型预测控制》⼀书对MPC算法进⾏了细致的讲解,并提供了代码,⾮常值得参考和学习。
但书中各系数矩阵的推导对于初学者来说极难理解,代码结构也过于复杂,改动代码容易报错。
采⽤yalmip⼯具可以很⼤程度简化代码,利于初学者对应理解MPC公式与代码,代码修改起来也⾮常容易。
⼀、yalmip简介yalmip是由Lofberg开发的⼀种免费的优化求解⼯具。
它是⼀个建模⼯具,甚⾄可以称为⼀种“语⾔”,通过这种“语⾔”来描述模型,然后再调⽤其他求解器(如quadprog、gurobi、fmincon等)来求解模型。
其最⼤特⾊在于集成许多外部的优化求解器,形成⼀种统⼀的建模求解语⾔,提供了Matlab的调⽤API,减少学习者学习成本。
⼆、车辆模型1.车辆运动学模型2.离散化3.线性化这⾥使⽤针对状态轨迹的线性化⽅法(《⽆⼈驾驶车辆模型预测控制》(第⼆版)第五章代码所使⽤的⽅法),与第三、四章的存在参考系统的性线化⽅法略有不同,本质上区别不⼤,具体可以参考《⽆⼈驾驶车辆模型预测控制》(第⼀版)的介绍。
若使⽤较复杂的模型,可借助jacobian函数求解雅可⽐矩阵A,B三、MPC 优化问题定义程序⽬标是对轨迹进⾏跟踪,设计成本函数第⼀项:状态量与参考轨迹误差的平⽅,第⼆项:控制量的平⽅。
约束依次为初始状态约束,车辆运动学模型,控制量约束,控制增量约束。
优化问题如下所⽰:四、Matlab 代码本⽂编写的代码主要为了对标《⽆⼈驾驶车辆模型预测控制》(第⼆版)第四章的代码,主体参照S函数形式编写,便于结合Carsim 使⽤。
以下主要介绍yalmip编写的MPC计算函数:1.函数输⼊1syms x y phi delta v L T 2%x :横坐标;y :纵坐标;phi:航向⾓;delta :前轮偏⾓;3%v :速度;L :轴距;T :离散时间4kesi=[v*cos(phi);v*sin(phi);v*tan(delta)/L]*T+[x;y;phi];%离散化⽅程5X=[x,y,phi];%状态量6u=[v,delta];%控制量7A=jacobian(kesi,X)8B=jacobian(kesi,u)A,B:模型(系统)矩阵;Q,R:权重矩阵;N:控制步长;kesi:当前状态量和控制量;state_k1:下⼀时刻状态量;umin,umax,delta_min,delta_max:控制量和控制增量约束矩阵;Ref: 参考轨迹;MPC_solver:求解器。
Matlab的m_map工具箱函数说明

Matlab的m_map工具箱函数说明%---------------------------------------地磁坐标%lat=[25*ones(1,100) 50*ones(1,100) 25];%lon=[-99:0 0:-1:-99 -99];%clf%subplot(121);%m_coord('IGRF2000-geomagnetic'); % Treat all lat/longs as geomagnetic(地磁坐标)%m_proj('stereographic'); %立体投影%m_coast;%m_grid;%m_line(lon,lat,'color','r'); % "lat/ln" assumed geomagnetic on the geomagnetic map %m_coord('geographic'); % Switch to assuming geographic(地理坐标)%m_line(lon,lat,'color','c'); % Now they are treated as geographic%subplot(122);%m_coord('geographic'); % Define all in geographic%m_proj('stereographic');%m_coast;%m_grid;%m_line(lon,lat,'color','c');%m_coord('IGRF2000-geomagnetic'); % Now assume that values are in geomagnetic%m_line(lon,lat,'color','r');%---------------------------------------------------画轨迹线%m_proj('UTM','long',[-72 -68],'lat',[40 44]);%m_gshhs_i('color','k');%m_grid('box','fancy','tickdir','out');% fake up a trackline%lons=[-71:.1:-67];%lats=60*cos((lons+115)*pi/180);%dates=datenum(1997,10,23,15,1:41,zeros(1,41));%m_track(lons,lats,dates,'ticks',0,'times',4,'dates',8,...% 'clip','off','color','r','orient','upright');%--------------------------------------------------改变坐标%[X,Y]=m_ll2xy(LONG,LAT, ...optional clipping arguments )%[LONG,LAT]=m_xy2ll(X,Y)%DIST=m_lldist([20 30],[44 45]) %计算两点之间的距离%--------------------------------------------------以某点为中心画半径%m_proj('lambert','long',[-160 -40],'lat',[30 80]);%m_coast;%m_range_ring(-123,49,[1e3:1e3:10e3],'color','r');%m_ungrid range_ring%m_range_ring(-123,49,[200:200:2000],'color','r');%------------------------------------------------自定义海岸线%Adding your own coastlinesmatla地图投影有关函数(2007-03-11 22:52:34)转载function [ output_args ] = Untitled1( input_args )%UNTITLED1 Summary of this function goes here% Detailed explanation goes here%---------------------海岸线%m_coast('patch',[.7 .7 .7],'edgecolor','none');%m_grid('xlabeldir','end','fontsize',10);%m_line(-129,48.5,'marker','square','markersize',4,'color','r');%m_text(-129,48.5,' M5','vertical','top');%---------------------------------------椭圆型投影%m_proj('mollweide');%m_coast('patch','r');%m_grid('xaxislocation','middle');%m_proj('stereographic'); % Example for stereographic projection(立体投影)%m_coast;%m_grid;load coast.datm_line(coast(:,1),coast(:,2));Filled coastlines will require more work. You should first read theinstructions there on joining the coastline data into continuous segments.If you are lucky, (i.e. no lakes or anything else), you may achieve success with load coast.dat[X,Y]=m_ll2xy(coast(:,1),coast(:,2),'clip','patch');k=[find(isnan(X(:,1)))];for i=1:length(k)-1,x=coast([k(i)+1:(k(i+1)-1) k(i)+1],1);y=coast([k(i)+1:(k(i+1)-1) k(i)+1],2);patch(x,y,'r');end;%-----------------------------------------------toolbox contents 中各文件的描述Contents.m - toolbox contentsm_demo.m - demonstrates a few maps.User-callable functionsm_proj.m - initializes projectionm_coord - geomagnstic to geographic coordsm_grid.m - draws gridsm_scale.m - forces map to a given scalem_ungrid.m - erases map elements (if you want to change parameters)m_coast.m - draws a coastlinem_elev.m - draws elevation datam_tbase.m - draws elevation data from high-resolution databasem_etopo2.m - draws elevation data from (another) high-resolution databasem_gshhs_c.m - draws coastline from GSHHS crude databasem_gshhs_l.m - draws coastline from GSHHS low-resolution databasem_gshhs_i.m - draws coastline from GSHHS intermediate-resolution database m_gshhs_h.m - draws coastline from GSHHS high-resolution databasem_gshhs_f.m - draws coastline from GSHHS full resolution databasem_plotbndry.m - draws a political boundary from the DCWm_usercoast.m - draws a coastline using a user-specified subset database.m_plot.m - draws line data in map coordsm_line.m - draws line data in map coordsm_text.m - adds text data in map coordsm_legend.m - Draw a legend boxm_patch.m - adds patch data in map coordsm_pcolor - draws pcolor surfacem_quiver - draws arrows for vector datam_contour - draws contour lines for gridded datam_contourf - draws filled contoursm_track - draws annotated tracklinesm_range_ring - draws range ringsm_ll2xy.m - converts from long/lat to map coordinatesm_xy2ll.m - converts from map coordinates to long/latm_geo2mag - converts from magnetic to geographic coordsm_mag2geo - the reversem_lldist - distance between long/lat pointsm_xydist - distance between map coordinate pointsm_fdist - location of point at given range/bearing along ellipsoidal earthm_idist - range/bearings between points on ellipsoidal earthm_geodesic - points on geodesics between given points on ellipsoidal earthm_tba2b.m - used in installing high-resolution elevation database.m_vec.m - fancy arrowsInternal functions (not meant to be user-callable)private/mp_azim.m - azimuthal projectionsprivate/mp_cyl.m - cylindrical projections (equatorial)private/mp_conic.m - conic projectionsprivate/mp_tmerc.m - transverse cylindrical projectionsprivate/mp_utm.m - elliptical universal transverse cylindrical projectionsprivate/mp_omerc.m - oblique cylindrical projectionprivate/mu_util.m - various utility routinesprivate/mu_coast.m - routines to handle coastlines.private/mc_coords - coordinate conversion.private/clabel.m - patched version of clabel (matlab v5.1 version does not contain capabilities for different text properties).private/m_coasts.mat - coastline dataHTML Documentationmap.html - documentation introprivate/mapug.html - users guidevarious .gif - examples.。
MATLAB中的模型预测控制算法实现方法

MATLAB中的模型预测控制算法实现方法1. 引言模型预测控制(Model Predictive Control,MPC)是一种广泛应用于工业过程控制的先进控制策略。
它基于数学模型对系统未来行为进行预测,并通过优化算法计算出最优控制输入,以实现对系统的稳定控制和性能优化。
在MATLAB中,实现MPC算法可以借助一些工具箱和函数,本文将介绍其中一种典型方法。
2. MPC算法的基本原理MPC算法通过建立系统的数学模型,预测系统未来的行为。
在每个控制时刻,MPC算法根据已知的系统状态和控制目标,计算出最优的控制输入,并将其应用于系统中。
这个优化问题可以通过求解一个多目标优化问题来完成。
3. MATLAB中的MPC工具箱MATLAB的Control System Toolbox提供了一个用于设计和实现MPC控制器的工具箱。
首先,我们需要使用命令"mpc"创建一个空白的MPC对象。
然后,我们可以通过指定MPC对象的属性来定义系统模型、控制目标、约束条件等。
4. 构建系统模型在MPC算法中,必须先构建系统的数学模型。
在MATLAB中,可以使用State Space工具箱中的ss或tf函数构建系统模型。
我们可以根据实际系统的特点选择不同的模型结构。
例如,对于连续时间系统,可以使用连续时间状态空间模型或传递函数模型;对于离散时间系统,可以使用离散时间状态空间模型或传递函数模型。
5. 设置MPC对象属性创建MPC对象后,我们需要设置一些重要的属性。
其中,PredictionHorizon属性定义了预测时间窗口的长度,即MPC算法根据模型预测未来的时长;ControlHorizon属性定义了控制时间窗口的长度,即MPC算法计算最优控制输入的时间长度。
一般来说,预测时间窗口应大于控制时间窗口。
6. 设定控制目标与约束条件MPC算法的目标是使系统的输出尽可能地接近控制目标,并同时满足一定的约束条件。
利用Matlab进行模型预测控制算法实现

利用Matlab进行模型预测控制算法实现引言:在现代控制领域,模型预测控制(Model Predictive Control,MPC)算法是一种非常重要的控制方法,其适用于多种工艺过程和系统控制。
本文将重点介绍如何利用Matlab实现模型预测控制算法。
第一部分:MPC算法简介模型预测控制算法是一种根据系统的数学模型进行控制的方法。
它不仅可以考虑系统的当前状态,还可以预测未来一段时间的状态,并优化控制器的输入,从而实现更好的控制效果。
MPC算法主要包括三个步骤:建模、预测和优化。
第二部分:MPC算法的建模在建立MPC控制模型之前,首先需要对控制对象进行数学建模。
一般来说,可以使用传统的物理建模方法或者数据驱动的建模方法。
在Matlab中,可以利用系统辨识工具箱或者曲线拟合工具箱等功能进行模型建立。
建模的目的是获取系统的状态方程和输出方程,用于后续的预测和优化。
第三部分:MPC算法的预测预测是MPC算法的核心步骤,它通过对系统的当前状态进行预测,得到未来一段时间内的状态和输出。
在Matlab中,可以利用预测模型对未来状态和输出进行计算,并得到一个预测轨迹。
预测模型可以在建模过程中得到,也可以根据实时数据进行在线更新。
第四部分:MPC算法的优化在预测的基础上,MPC算法通过优化控制器的输入信号,使得系统的输出符合预期的性能指标。
这个优化问题一般可以表示为一个多目标优化或者约束优化的问题。
在Matlab中,可以使用优化工具箱中的函数进行优化操作。
通过迭代计算,可以得到最优控制输入信号,从而实现更好的控制效果。
第五部分:MPC算法的实现在Matlab中,可以利用Control System Toolbox和Optimization Toolbox等工具箱来实现MPC算法。
首先,需要将系统的数学模型导入Matlab环境,并进行参数设置。
然后,可以使用MPC对象进行建模、预测和优化等操作。
最后,将MPC控制器与实际的控制系统进行连接,实现闭环控制。
模型预测控制 matlab

模型预测控制 matlab
模型预测控制(MPC)是一种在控制系统中应用较多的高级控制方法,它可以考虑多个控制因素对系统的影响,并对其进行优化控制。
MPC在工
业自动化、化工、电力、航空等领域得到广泛应用。
在 MATLAB 中,可以使用“Control System Toolbox”工具箱来实现MPC控制。
主要步骤如下:
1.建立控制系统的动态模型:使用系统辨识或物理建模等方法,得到
系统的传递函数或状态空间模型;
2.确定控制目标和约束条件:确定系统需要达到的目标,以及控制输
入和输出的约束条件;
3.设计MPC控制器:使用MPC设计工具箱中的函数,设计MPC控制器
参数,并将其与动态模型和控制目标一起合成成为MPC控制器对象;
4.设置控制器参数:设置MPC控制器的采样周期、预测时域、控制输
入和输出约束、惩罚矩阵等参数;
5.进行仿真和实验:使用MATLAB进行仿真和实验验证MPC控制器的
性能。
需要注意的是,MPC控制器设计的好坏很大程度上依赖于系统模型的
准确性,因此在建立系统模型时需要认真考虑各种因素对系统的影响,并
进行准确的建模。
MATLAB模型预测控制工具箱函数..

MATLAB模型预测控制工具箱函数8.2 系统模型建立与转换函数前面读者论坛了利用系统输入/输出数据进行系统模型辨识的有关函数及使用方法,为时行模型预测控制器的设计,需要对系统模型进行进一步的处理和转换。
MATLAB的模型预测控制工具箱中提供了一系列函数完成多种模型转换和复杂系统模型的建立功能。
在模型预测控制工具箱中使用了两种专用的系统模型格式,即MPC状态空间模型和MPC传递函数模型。
这两种模型格式分别是状态空间模型和传递函数模型在模型预测控制工具箱中的特殊表达形式。
这种模型格式化可以同时支持连续和离散系统模型的表达,在MPC传递函数模型中还增加了对纯时延的支持。
表8-2列出了模型预测控制工具箱的模型建立与转换函数。
表8-2 模型建立与转换函数8.2.1 模型转换在MATLAB模型预测工具箱中支持多种系统模型格式。
这些模型格式包括:①通用状态空间模型;②通用传递函数模型;③MPC阶跃响应模型;④MPC状态空间模型;⑤ MPC 传递函数模型。
在上述5种模型格式中,前两种模型格式是MATLAB 通用的模型格式,在其他控制类工具箱中,如控制系统工具箱、鲁棒控制工具等都予以支持;而后三种模型格式化则是模型预测控制工具箱特有的。
其中,MPC 状态空间模型和MPC 传递函数模型是通用的状态空间模型和传递函数模型在模型预测控制工具箱中采用的增广格式。
模型预测控制工具箱提供了若干函数,用于完成上述模型格式间的转换功能。
下面对这些函数的用法加以介绍。
1.通用状态空间模型与MPC 状态空间模型之间的转换MPC 状态空间模型在通用状态空间模型的基础上增加了对系统输入/输出扰动和采样周期的描述信息,函数ss2mod ()和mod2ss ()用于实现这两种模型格式之间的转换。
1)通用状态空间模型转换为MPC 状态空间模型函数ss2mod ()该函数的调用格式为pmod= ss2mod (A,B,C,D)pmod = ss2mod (A,B,C,D,minfo)pmod = ss2mod (A,B,C,D,minfo,x0,u0,y0,f0)式中,A, B, C, D 为通用状态空间矩阵;minfo 为构成MPC 状态空间模型的其他描述信息,为7个元素的向量,各元素分别定义为:◆ minfo(1)=dt ,系统采样周期,默认值为1;◆ minfo(2)=n ,系统阶次,默认值为系统矩阵A 的阶次;◆ minfo(3)=nu ,受控输入的个数,默认值为系统输入的维数;◆ minfo(4)=nd ,测量扰的数目,默认值为0;◆ minfo(5)=nw ,未测量扰动的数目,默认值为0;◆ minfo(6)=nym ,测量输出的数目,默认值系统输出的维数;◆ minfo(7)=nyu ,未测量输出的数目,默认值为0;注:如果在输入参数中没有指定m i n f o ,则取默认值。
MA AB在时间序列建模预测及程序代码

at = yt
yt−1 = yt − bt
yt−2 = yt − 2bt
…
所以
yt−N+1 = yt − (N −1)bt
M (1) t
=
yt
+
yt−1 + L + N
yt−N +1
=
yt
+ ( yt
− bt ) + L + [ yt N
− (N
−1)bt ]
=
Nyt
− [1+ 2 + L + (N N
似的波动。 (4)不规则变动。通常它分为突然变动和随机变动。
通常用 Tt 表示长期趋势项,St 表示季节变动趋势项,Ct 表示循环变动趋势项,Rt
表示随机干扰项。常见的时间序列模型有以下几种类型: (1)加法模型
yt = Tt + St + Ct + Rt
(2)乘法模型
yt = Tt ⋅ St ⋅ Ct ⋅ Rt
的概率分布与时间 t 无关,则称该序列为严格的(狭义的)平稳时间序列。如果序列的 一、二阶矩存在,而且对任意时刻 t 满足:
(1)均值为常数
(2)协方差为时间间隔τ 的函数。
则称该序列为宽平稳时间序列,也叫广义平稳时间序列。我们以后所研究的时间序列主 要是宽平稳时间序列。
4.按时间序列的分布规律来分,有高斯型时间序列和非高斯型时间序列。
§2 移动平均法 移动平均法是根据时间序列资料逐渐推移,依次计算包含一定项数的时序平均数,
以反映长期趋势的方法。当时间序列的数值由于受周期变动和不规则变动的影响,起伏 较大,不易显示出发展趋势时,可用移动平均法,消除这些因素的影响,分析、预测序
matlab预测控制工具箱函数精品

MATLAB预测控制工具箱函数1通用的传递函数转变为MPC传递函数模型 (1)2MPC传递函数模型转换为MPC阶跃响应模型 (1)3基于阶跃响应模型的控制器设计和仿真函数 (2)MATLAB的模型预测控制工具箱提供了一系列用于模型预测控制的分析、设计和仿真的函数。
这些函数的类型主要有:①系统模型辨识函数:主要功能包括通过多变量线性回归方法计算MISO脉冲响应模型和阶跃响应模型及测量数据的归一化等。
②模型建立和转换函数:主要功能包括建立模型预测控制工具箱使用的MPC状态空间模型及状态空间模型与MPC状态空间模型、阶跃响应模型、脉冲响应模型之间的转换。
③模型预测控制器设计和仿真工具主要功能包括面向阶跃响应模型的预测控制器设计与仿真函数和面向MPC状态空间模型的设计和仿真函数两类。
④系统分析工具主要功能包括计算模型预测控制系统频率响应、极点和奇异值的有关函数。
⑤其他功能函数主要功能包括绘图和矩阵计算函数等。
1通用的传递函数转变为MPC传递函数模型转换函数为2()ploy tfd的调用格式为=(21)2(,,,)g ploy tfd num den delt delay式中num为通用传递函数模型的分子多项式系数向量;den为通用传递函数模型的分母多项式系数向量;delt为采样周期,对连续系统,该参数为0;delay为系统纯时延。
2MPC传递函数模型转换为MPC阶跃响应模型该函数的调用格式为=(22)2(,,,)plant tfd step tfinal delt nout gl式中final为阶跃响应的截断时间;delt为采样周期;nout为输出稳定性向量。
3基于阶跃响应模型的控制器设计和仿真函数基于阶跃响应模型的预测控制器设计的方法称为动态矩阵控制方法。
①输入/输出有约束的模型预测控制器设计与仿真:输入输出有约束就是要求满足一定的上界和下界要求。
函数的调用格式为=y u ym cmpc plant el ywt uwt M P tend r u y tflter dplant d el dstep [,,](,mod,,,,,,,lim,lim,,,mod,)(23)式中plant为开环对象的实际阶跃响应模型;mod el为辨识得到的开环对象阶跃响应模型;ywt为二次型性能指标的输出误差加权矩阵;uwt为二次型性能指标的控制量加权矩阵;M为控制时域长度;P为输出设定时域长度;tend仿真的结束时间;r输出设定值。
Matlab中的模型预测控制方法介绍

Matlab中的模型预测控制方法介绍一、引言在控制系统领域,模型预测控制(Model Predictive Control,简称MPC)是一种经典且高效的控制方法。
它基于数学模型的预测能力,通过优化控制变量序列,实现对系统状态的最优化调节。
在Matlab中,MPC方法得到了广泛应用,并通过Matlab的建模和优化工具箱实现了方便的开发和调试环境。
二、MPC方法的基本原理MPC方法的核心思想是通过预测系统未来的动态行为,来优化控制策略。
在MPC中,首先需要建立数学模型描述系统的动态行为,并将其转化为离散形式。
然后,根据模型预测出系统未来一段时间的状态和输出,通过对控制变量序列进行优化,得到最优的控制策略。
最后,根据所得到的控制策略实施控制动作,并反馈实际的系统输出,用于调整下一次的控制策略。
三、Matlab中的MPC建模工具箱为了方便用户使用MPC方法,MathWorks公司开发了专门的MPC工具箱。
MPC工具箱提供了一系列用于建模、仿真和优化的函数和工具,使得使用MPC方法更加简单和高效。
通过MPC工具箱可以方便地导入系统模型、设置控制目标、调节控制权重和约束条件,并进行模拟和优化。
四、MPC建模实例下面我们通过一个实例来介绍如何在Matlab中使用MPC方法进行建模和控制设计。
假设我们需要设计一个MPC控制器来控制一个加热系统的温度。
首先,我们需要获取加热系统的数学模型,并将其离散化得到离散时间步长的动态方程。
然后,通过MPC工具箱中的函数将模型导入Matlab环境中。
在导入模型后,我们需要设置控制目标和约束条件。
例如,我们可以设置目标温度为30摄氏度,并限制加热功率不超过100瓦特。
此外,我们还可以设置对温度变化率的约束,以确保系统动态响应的稳定性。
在设置好目标和约束后,我们可以使用MPC工具箱中的仿真函数模拟系统的响应,并通过图形界面直观地观察温度的变化趋势。
最后,我们需要调节控制权重以求得最优的控制策略。
ma模型自相关函数

ma模型自相关函数MA模型是一种常用的时间序列分析方法,用于描述数据中的自相关关系。
在统计学中,自相关函数是一种衡量时间序列数据之间相关性的工具。
它可以帮助我们判断数据是否存在周期性、趋势性等特征,并为我们提供预测未来数据的依据。
自相关函数是对时间序列数据与其自身滞后版本之间的相关性进行测量的一种方法。
在MA模型中,自相关函数是一个重要的指标,用于描述数据之间的相关性。
自相关函数通常用ACF表示,假设时间序列数据为{X1, X2, ..., Xn},则ACF定义为:ACF(k) = (1/n) * Σ(Xt - Xbar)(Xt-k - Xbar)其中,Xt表示时间t的数据点,Xbar表示数据的均值,k表示滞后期。
ACF(k)表示在滞后期为k的情况下,时间序列数据与其滞后版本之间的相关性。
通过计算ACF,我们可以得到不同滞后期的自相关系数。
当滞后期为0时,自相关系数为1,表示数据与自身完全正相关。
当滞后期为正数时,自相关系数表示数据与过去滞后期时间点的相关性。
当滞后期为负数时,自相关系数表示数据与未来滞后期时间点的相关性。
在MA模型中,自相关函数的特点是在滞后期为0之后,自相关系数迅速衰减至0。
这意味着时间序列数据之间的相关性主要存在于近期,而随着时间的推移,相关性逐渐减弱。
这是因为MA模型假设数据之间的相关性只存在于滞后期为k的情况下,而在其他滞后期,数据之间的相关性为0。
通过对自相关函数进行分析,我们可以判断数据是否存在周期性、趋势性等特征。
如果自相关函数在某个滞后期之后仍然持续地保持正相关或负相关,那么数据很可能存在周期性。
如果自相关函数在某个滞后期之后迅速衰减至0,那么数据很可能不存在周期性。
此外,我们还可以通过观察自相关函数的衰减速度来判断数据是否存在趋势性。
如果自相关函数的衰减速度较慢,那么数据很可能存在趋势性;如果自相关函数的衰减速度较快,那么数据很可能不存在趋势性。
除了分析自相关函数,我们还可以利用自相关函数来进行预测。
MA AB基础知识

一、1、数学建模基础知识及常用命令一、界面窗口介绍:1 命令窗口(command window),窗口中输入命令,回车实现计算或绘图功能。
2 工作空间窗口(work space)运行matlab命令时所产生的变量都被加入到工作空间,该窗口可以显示命令窗口中已输入的变量的名称,数值等。
3 命令历史窗口(command history)显示所有执行过的命令,选定某个命令时可以双击或按F9执行。
4 当前目录窗口(Current folder)显示当下目录下的文件信息。
二、常用运算1、算术运算符加 + 减 - 乘 * 左除 / 右除 \ 乘方 ^注意:在普通的数值运算中,左除为我们常用的除法形式,左除右除结果比较像逆运算,如1/2 和1\2结果互为倒数,但在矩阵的运算中,结果完全不一样,类似于左乘和右乘结果一般会不一样。
运算的优先级:从左到右,幂运算最高优先级,乘除法具有相同次优先级,加减法具有相同的低优先级,括号可以用来改变优先次序。
大家可以进行几个普通计算(练习10分钟)1、325+47⨯÷ 2、4 59+986-2.7+55-1033.5+20⨯()29()2、数据显示格式默认情况下,matlab显示小数点后4位小数,可以利用format命令改变显示格式(一般写在要改变的数值的命令前):format short 小数点后4位format long 小数点后15位format bank 小数点后2位(以上为三个常用的)format rat 最接近的有理数如以 为例:>> pi= 3.1416>> format long>> pi>> format rat>> pians =355/113>> format bank>> pians =3.14>> format short>> pians =3.1416三、matlab变量1、变量赋值形式变量=表达式(数值)或表达式(数值)其中,“=”为赋值符号,将右边表达式的值赋给左边变量(上面左的含义),当不指定输出变量时,matlab将表达式的值赋给临时变量ans(右的含义)。
ma模型基本原理

ma模型基本原理MA模型是一种常用的时间序列预测模型,其基本原理是利用过去若干期的数据来预测未来的趋势。
MA模型的全称为Moving Average Model,中文名为移动平均模型。
MA模型的核心思想是通过计算时间序列数据在不同时间点上的平均值来预测未来的值。
这里的移动平均指的是对过去若干期的数据进行平均处理,而不是对整个时间序列的数据进行平均。
具体来说,MA模型可以表示为:yt = μ + et + θ1 * et-1 + θ2 * et-2 + ... + θq * et-q其中,yt代表时间序列在t时刻的值,μ代表时间序列的均值,et 代表时间序列在t时刻的误差,θ1、θ2、...、θq代表模型参数,q代表模型的阶数。
MA模型的基本原理是通过不同阶数的误差项的加权和来预测未来的值。
每个误差项都有一个对应的权重参数,这些参数反映了不同时间点的误差对于未来值的影响程度。
当模型参数确定后,可以通过对过去的误差项进行加权求和,得到对未来值的预测。
为了确定MA模型的参数,需要进行模型的参数估计。
常用的方法是最小二乘法,即通过最小化误差的平方和来确定模型的参数。
通过最小二乘法可以找到使得预测值与实际观测值误差最小的参数组合,从而得到较为准确的预测结果。
在实际应用中,MA模型可以用于对时间序列数据的未来走势进行预测。
通过对历史数据的分析,可以确定合适的模型参数,从而得到对未来值的预测。
这对于许多领域的决策和规划具有重要的参考价值。
然而,需要注意的是,MA模型有一些前提条件。
首先,时间序列数据要具有平稳性,即均值和方差在不同时间点上保持不变。
其次,模型的参数要满足一定的条件,例如参数要小于1,以保证模型的稳定性。
MA模型也有一些局限性。
首先,MA模型只考虑了过去若干期的数据,忽略了其他可能的影响因素。
其次,模型参数的确定需要依赖于历史数据,对于长期预测来说可能存在一定的不确定性。
MA模型是一种基于移动平均的时间序列预测模型,通过对过去若干期的数据进行加权平均来预测未来的值。
ma模型参数计算

ma模型参数计算MA模型是一种常用的时间序列分析模型,用于预测未来的数据趋势和变化。
它是基于过去一段时间的数据来预测未来的数据,主要使用移动平均方法来计算预测值。
在这篇文章中,我们将介绍MA 模型的参数计算方法以及如何应用它进行数据预测。
MA模型的参数计算主要涉及到确定移动平均的阶数。
移动平均是通过计算一定时间范围内的平均值来预测未来的数据。
在MA模型中,移动平均的阶数表示计算平均值时使用的时间范围。
例如,MA(1)表示使用过去一个时间点的数据来计算移动平均值。
确定移动平均的阶数是一个关键步骤,它直接影响到预测结果的准确性。
一般来说,我们可以通过观察自相关图和偏自相关图来确定移动平均的阶数。
自相关图是用来观察时间序列数据的自相关性,而偏自相关图则是用来观察时间序列数据的偏自相关性。
在自相关图中,如果自相关系数在某个阶数后趋于零,那么这个阶数就是移动平均的阶数。
类似地,在偏自相关图中,如果偏自相关系数在某个阶数后趋于零,那么这个阶数也是移动平均的阶数。
除了观察自相关图和偏自相关图外,还可以使用信息准则来确定移动平均的阶数。
常用的信息准则有赤池信息准则(AIC)和贝叶斯信息准则(BIC)。
这些信息准则可以通过计算模型的拟合优度和模型的参数数量来衡量模型的优劣,从而确定移动平均的阶数。
确定了移动平均的阶数之后,我们可以使用移动平均方法来计算预测值。
移动平均的计算公式为:预测值 = 历史数据的移动平均值 + 白噪声。
其中,历史数据的移动平均值是通过计算过去一段时间的数据的平均值得到的,白噪声是一个随机项,用来表示模型中未能解释的随机波动。
在实际应用中,我们可以使用各种编程语言或统计软件来进行MA 模型的参数计算和数据预测。
例如,Python中的statsmodels库提供了MA模型的参数估计和预测功能,可以方便地进行相关分析和预测。
MA模型是一种常用的时间序列分析模型,通过移动平均方法来计算预测值。
确定移动平均的阶数是关键步骤,可以通过观察自相关图和偏自相关图以及使用信息准则来确定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M A T L A B模型预测控制工具箱函数
8.2系统模型建立与转换函数
前面读者论坛了利用系统输入/输出数据进行系统模型辨识的有关函数及使用方法,为时行模型预测控制器的设计,需要对系统模型进行进一步的处理和转换。
MATLAB的模型预测控制工具箱中提供了一系列函数完成多种模型转换和复杂系统模型的建立功能。
在模型预测控制工具箱中使用了两种专用的系统模型格式,即MPC状态空间模型和MPC传递函数模型。
这两种模型格式分别是状态空间模型和传递函数模型在模型预测控制工具箱中的特殊表达形式。
这种模型格式化可以同时支持连续和离散系统模型的表达,在MPC传递函数模型中还增加了对纯时延的支持。
表8-2列出了模型预测控制工具箱的模型建立与转换函数。
表8-2模型建立与转换函数
8.2.1模型转换
在MATLAB模型预测工具箱中支持多种系统模型格式。
这些模型格式包括:
①通用状态空间模型;
②通用传递函数模型;
③MPC阶跃响应模型;
④MPC状态空间模型;
⑤MPC传递函数模型。
在上述5种模型格式中,前两种模型格式是MATLAB通用的模型格式,在其他控制类工具箱中,如控制系统工具箱、鲁棒控制工具等都予以支持;而后三种模型格式化则是模型预测控制工具箱特有的。
其中,MPC状态空间模型和MPC传递函数模型是通用的状态空间模型和传递函数模型在模型预测控制工具箱中采用的增广格式。
模型预测控制工具箱提供了若干函数,用于完成上述模型格式间的转换功能。
下面对这些函数的用法加以介绍。
1.通用状态空间模型与MPC状态空间模型之间的转换
MPC状态空间模型在通用状态空间模型的基础上增加了对系统输入/输出扰动
和采样周期的描述信息,函数ss2mod()和mod2ss()用于实现这两种模型格式之间的转换。
1)通用状态空间模型转换为MPC状态空间模型函数ss2mod()
该函数的调用格式为
pmod=ss2mod(A,B,C,D)
pmod=ss2mod(A,B,C,D,minfo)
pmod=ss2mod(A,B,C,D,minfo,x0,u0,y0,f0)
式中,A,B,C,D为通用状态空间矩阵;
minfo为构成MPC状态空间模型的其他描述信息,为7个元素的向量,各元素分别定义为:
◆minfo(1)=dt,系统采样周期,默认值为1;
◆minfo(2)=n,系统阶次,默认值为系统矩阵A的阶次;
◆minfo(3)=nu,受控输入的个数,默认值为系统输入的维数;
◆minfo(4)=nd,测量扰的数目,默认值为0;
◆minfo(5)=nw,未测量扰动的数目,默认值为0;
◆minfo(6)=nym,测量输出的数目,默认值系统输出的维数;
◆minfo(7)=nyu,未测量输出的数目,默认值为0;
注:如果在输入参数中没有指定m i n f o,则取默认值。
x0,u0,y0,f0为线性化条件,默认值均为0;
pmod为系统的MPC状态空间模型格式。
例8-5将如下以传递函数表示的系统模型转换为MPC状态空间模型。
解:MATLAB命令如下:
0100000
0010000
0131000
2)MPC状态空间模型转换为通用状态空间模型函数mod2ss()
该函数的调用格式为
[A,B,C,D]=mod2ss(pmod)
[A,B,C,D,minfo]=mod2ss(pmod)
[A,B,C,D,minfo,x0,u0,y0,f0]=mod2ss(pmod) 式中,pmod为系统的MPC状态空间模型格式;A,B,C,D为通用状态空间矩阵;minfo为构成MPC状态空间模型的其他描述信息,其说明参见函数ss2mod()。
2.通用传递函数模型转换为MPC传递函数模型
通用传递函数模型与MPC传递函数模型的转换函数poly2tfd()的调用格式为
g=poly2tfd(num,den,delt,delay)
式中,num为通用传递函数模型的分子多项式系数向量;
den为通用传递函数模型的分母多项式系数向量;
delt为采样周期,对连续系统,该参数为0;
delay为系统纯时延,对于离散系统,纯时延为采样时间周期的整数倍;
g为被控对象的MPC传递函数模型。
例8-6考虑如下的纯时延二阶对象,并将其转换为MPC传递函数模型。
解:MATLAB命令如下:
>>num=[11];den=[144];
>>g=poly2tfd(num,den,0,0.5)
结果显示:
g=
01.00001.0000
1.00004.00004.0000
00.50000
3.MPC传递函数模型转换为MPC状态空间模型函数tfd2mod()
该函数的调用格式为
pmod=tfd2mod(delt,ny,g1,g2,……,g25)
式中,delt为采样时间;
ny为输出个数;
g1,g2,……为SISO传递函数,对应多变量系统传递函数矩阵的各个元素按行向量顺序排序构成的向量,其最大个数限制为25;
pmod为系统的MPC状态空间模型。
4.MPC阶跃响应模型与其他模型格式之间的转换
函数mod2step()、tfd2step()和ss2step()分别用于将MPC状态空间模型、MPC 传递函数模型和通用状态空间模型转换为MPC阶跃响应模型。
下面对这个三函数的用法进行说明。
1)MPC状态空间模型转换为MPC阶跃响应模型函数mod2step()
plant=mod2step(pmod,tfinal)
[plant,dplant]=mod2step(pmod,tfinal,delt,nout)
式中,pmod为系统的MPC状态空间模型;
tfinal为阶跃响应模型的截断时间;
delt为采样周期,默认值由MPC状态空间模型的参数minfo(1)决定;
nout为输出稳定性向量,用于指定输出的稳定性。
对于稳定的系统,nout等于输出的个数;对于具有一个或多个积怨分输出的系统,nout为一个长度等于输出个数的向量,该向量对应积分输出的分量为0,其余分量为1;
plant为对象在受控变量作用下的阶跃响应系数矩阵;
dplant为对象在扰动作用下阶跃响应矩阵。
2)MPC传递函数模型转换为MPC阶跃响应模型函数tfd2step()
该函数的调用格式为
plant=tfd2step(tfinal,delt,nout,g1)
plant=tfd2step(tfinal,delt,nout,g1,……,g25)
式中,tfinal为阶跃响应的截断时间;
delt为采样周期;
nout为输出稳定性向量,参见函数mod2step()的有关说明;
g1,……,g25为SISO传递函数,对应多变量系统传递函数矩阵的各个元素按行向量顺序排列构成的向量,其最大个数限制为25;
plant为对象的阶跃响应系统矩阵。
例8-8设系统传递函数为
将其转换为阶跃响应模型。
解:MATLAB命令如下:
>>num=[12];den=[131];
>>tf1=poly2tfd(num,den,0,0);
>>plant=tfd2step(5,0.1,1,tf1);
>>plotstep(plant)
由阶跃响应模型绘制的系统阶跃响应曲线如图8-5所示。
图8-5系统阶跃响应曲线
8.4基于阶跃响应模型的控制器设计与仿真函数
基于系统的阶跃响应模型进行模型预测控制器设计的方法称为动态矩阵控制方法。
该方法是采用工程上易于获取的对象阶跃响应模型,算法较为简单,计算量较少,鲁棒性较强,适用于纯时迟、开环渐近稳定的非最小相位系统,在工业过程控制中得到成功应用。
MATLAB的模型预测控制工具箱提供了对动态矩阵控制方法的支持,有关的函数能够基于阶跃响应模型的模型预测控制器设计与仿真,见表8-3。
表8-3动态矩阵控制设计与仿真函数
例8-12考虑如下的双输入输出纯时延对象,其传递函数矩阵为
解:MATLAB程序如下:
ywt为二次型性能指标的输出误差加权矩阵;
uwt为二次型性能指标的控制量加权矩阵;
M为控制时域长度;
P为预测时域长度;
tend为仿真的结束时间;
r为输入设定值或参考轨迹;
ulim=[ulowuhighdelu],式中,ulow为控制变量的下界,uhigh为控制变量的上界,delu为控制变量的变化率约束;
ylim=[ylowyhigh],式中,ylow为输出的下界,yhigh为输出的上界;
kest为估计器的增益矩阵;
z为测量噪声;v为测量扰动;w为输出未测量扰动;wu为施加到控制输入的未测量扰动;
y为系统响应;u为控制变量;ym为模型预测输出。
例8-15考虑如下的双输入输出纯时延对象,其传递函数矩阵为解:MATLAB程序如下:。
