MATLAB作业5 作业本
MATLAB语言基础与应用(第二版)第5章 习题答案

第5章习题与答案5.1用矩阵三角分解方法解方程组123123123214453186920x x x x x x x x x +-=⎧⎪-+=⎨⎪+-=⎩ 解答:>>A=[2 1 -1;4 -1 3;6 9 -1] A =2 1 -1 4 -13 6 9 -1 >>b=[14 18 20]; b =14 18 20 >> [L, U, P]=lu(A) L =1.0000 0 0 0.6667 1.0000 0 0.3333 0.2857 1.0000 U =6.0000 9.0000 -1.0000 0 -7.0000 3.6667 0 0 -1.7143 P =0 0 1 0 1 0 1 0 0 >> y=backsub(L,P*b’) y =20.0000 4.6667 6.0000 >> x=backsub(U,y) x =6.5000 -2.5000 -3.5000 5.2 Cholesky 分解方法解方程组123121332352233127x x x x x x x ++=⎧⎪+=⎨⎪+=⎩ 解答:>> A=[3 2 3;2 2 0;3 0 12] A =3 2 32 2 03 0 12>> b=[5;3;7]b =537>> L=chol(A)L =1.7321 1.1547 1.73210 0.8165 -2.44950 0 1.7321>> y=backsub(L,b)y =-11.6871 15.7986 4.0415>> x=backsub(L',y)x =-6.7475 28.8917 49.93995.3解答:观察数据点图形>> x=0:0.5:2.5x =0 0.5000 1.0000 1.5000 2.0000 2.5000 >> y=[2.0 1.1 0.9 0.6 0.4 0.3]y =2.0000 1.1000 0.9000 0.6000 0.4000 0.3000 >> plot(x,y)图5.1 离散点分布示意图从图5.1观察数据点分布,用二次曲线拟合。
MATLAB第五章作业

第五章作业1.选择题(1)if结构的开始是“if”命令,结束是C命令。
A. End ifB. endC. EndD. else(2)下面的switch结构,正确的是C。
A. >>switch a case a>1B. >>switch acase a=1C. >>switch acase 1D. >>switch acase =1(3)运行以下命令:>>a=eye(5);>>for n=a(2:end,:)则for循环的循环次数是B。
A. 5B. 4C. 3D. 1(4)运行以下命令,则for循环的循环次数是C。
>>x=0:10;>>for n=xif n==5continueendendA. 10B. 5C. 11D. 10(5)运行以下命令则B。
>>a=[1 2 3]>>keyboardK>>a=[1 2 4];K>>returnA. a=[1 2 3]B. a=[1 2 4]C. 命令窗口的提示符为“K>>”D. 出错(6)关于主函数,以下说法正确的是D。
A. 主函数名必须与文件名相同B. 主函数的工作空间与子函数的工作空间是嵌套的C. 主函数中不能定义其他函数D. 每个函数文件中都必须有主函数(7)当在命令窗口中输入“sin(a)”时,则对“a”的搜索顺序是D。
A. 是否内部函数→是否变量→是否私有函数B. 是否内部函数→是否搜索路径中函数→是否私有函数C. 是否内部函数→是否搜索路径中函数→是否当前路径中函数D. 是否变量→是否私有函数→是否当前路径中函数2.求分段函数2226,0356,0<5231x x x xy x x x x xx x⎧+-<≠-⎪=-+≠≠⎨⎪--⎩且≤且及,其他的值。
用if语句实现,分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y值。
Matlab上机作业部分参考答案.ppt

[rank(A), rank([A B])]
ans =
34 由得出的结果看,A, [A;B] 两个矩阵的秩不同,故方程是
矛盾方程,没有解。
5. 试求下面齐次方程的基础解系
7. 建立如下一个元胞数组,现在要求计算第一个元胞第4行第 2列加上第二个元胞+第三个元胞里的第二个元素+最后一个元 胞的第二个元素。
a={pascal(4),'hello';17.3500,7:2:100}
解: >> a={pascal(4),'hello';17.3500,7:2:100} a=
[ 173/34, 151/34]
6. 求解方程组的通解
x1 2x2 4x3 6x4 3x5 2x6 4 2x1 4x2 4x3 5x4 x5 5x6 3
3x1 6x2 2x3 5x5 9x6 1 2x1 3x2 4x4 x6 8
4x2
5x3
2x4
x5
参考答案: (1) >> limit(sym('(tan(x) - sin(x))/(1cos(2*x))')) ans = 0 (2) >> y = sym('x^3 - 2*x^2 + sin(x)'); >> diff(y) ans = 3*x^2-4*x+cos(x) (3) >> f = x*y*log(x+y); >> fx = diff(f,x) fx = y*log(x+y)+x*y/(x+y)
学生实验作业matlab

实验报告(MATLAB课后作业练习题)学院电子信息学院班级学号姓名任课教师目录实验作业1 (3)第一题、一阶电路 (3)实验作业2 (7)第一题Waterfall Scope(瀑布显示图) (7)Chirp Signal扫频信号源 (7)Uniform Random Number信号源下 (8)Band-Limited White Noise信号源 (8)第二题:设计一个编程开关仿真系统框图 (9)仿真实验作业3 (10)第一题 (10)第二题 (13)仿真实验作业4 (14)第一题 (14)第二题 (16)仿真实验作业5 (19)仿真实验作业6 (21)仿真实验作业7 (23)仿真实验作业8 (26)实验作业1第一题、一阶电路(1)、电路图如下,R=1.4欧,L=2亨,C=0.32法,初始状态:电感电流为零,电容电压为0.5V ,t=0时刻接入1V 的电压,求0<t<15s 时,i (t),v o (t)的值,并且用Simulink 仿真画出R=1.4、R=5和 R=9的电流与电容电压的关系曲线。
还可以进一步修改信号源参数,使用三角波、正弦波等作为激励信号,观察输出信号的情况。
function xdot=funcforexl23(t,x,~,R,L,C)xdot=zeros(2,1); %矩阵初始化 xdot(1)=-R/L*x(1)-1/L*x(2)+1/L* f(t); %方程1 xdot(2)=1/C * x(1); %方程2 function in=f(t) %输入信号 in=(t>0)*1; %阶跃信号%filename ex123.mL=2; %电感值 C=0.32; %电容值for R=[1.4 5 9] %仿真电阻值分别为1.5, 3, 5欧姆的情况[t,x]=ode45('funcforexl23',[0,15],[0;0.5],[],R,L,C); %也可采用ode23, ode15s 等求解figure(1);plot(t,x(:,1));hold on ; xlabel('time sec'); text(2,0.07,'\leftarrow i_L(t)');grid;figure(2);plot(t,x(:,2));hold on ;xlabel('time sec'); text(2.1,0.75,'\leftarrow u_C(t)');grid; End输入输出的传递函数:11)()()(2++==RCs LCs s F s U s H c① R=1.4时:1448.064.01)(2++=s s s H ±Vs=1Vt=0R L C +-)(t i )(t v o② R=5时:16.164.01)(2++=s s s H③ R=9时:188.264.01)(2++=s s s H连续系统的传递函数如下:借助多项式乘法函数conv 来处理:两个向量分别用num 和den 表示。
MATLAB练习

3,
z 10 * sin* ( / 3) * cos( / 3)
答案:
10*sin(pi/3)...cos(pi/3) 4, x 求
sin( 223 / 3), y x 2 , z y 10 ; x 2 y 5z
z1 2 7i, z 2 2i, z 3 5e 2 i , 计 算 z
f ( x ) e sin
3
x
的数值积分 s
f ( x )dx ,并请采用符号计算尝试复算。
fun=inline('exp((sin(x)).^3)');y1=quad(fun,0,pi); 3.绘 制 出 正 态 分 布 N(-1,1) 的 概 率 密 度 函 数 和 分 布 函 数 曲 线 x=(-5:pi/100:5);y=normpdf(x,0,1),plot(x,y)
x=1,f1=(x^3-2*x^2+x-6.3)/(x^2+0.05*x-3.14), x=2,f2=(x^3-2*x^2+x-6.3)/(x^2+0.05*x-3.14), x=3,f3=(x^3-2*x^2+x-6.3)/(x^2+0.05*x-3.14),f1*f2+f3^2
MATLAB 练习 2
1、要求在闭区间[0,2π ]上产生 50 个等距采样的一维数组。试用两种不同的指令实现。 1:A=linspace[0,2*pi,50]; 2:A=[0:2*pi/49:2*pi] 2.说出 MATLAB 指令 A(3,1,2,:)=1:4 所产生数组的维数、大小和长度;然后对 A 进行降维处 理;最后指出降维后 A 中所有非零元素的“单下标”和“全下标”的位置。 A(3,1,2,:)=1:4,ndims(A),size(A),length(A),A(:), A (6) =1=A (3,1,2,1) ; A (12) =2=A (3,1,2,2) ; A(18)=3=A(3,1,2,3) ;A(24)=4=A(3,1,2,4) 3. 写出使以下这段文字成为字符串的 MATLAB 程序。注意保持这段文字的格式。 In GB usage quotation marks are usually single:’Fire!’. S1=char('In GB usage quotation marks are usually single:’Fire!’.') 4. 请建立下列 4×3 的元胞数组 A,如表所示。 张惠妹 周华健 王杰 孙燕姿 听海 花心 一场游戏一场梦 超快感 1998 1992 1988 2000
《MATLAB及应用》实验指导书“作业”

《MATLAB及应⽤》实验指导书“作业”《MATLAB及应⽤》实验指导书班级:姓名:学号:总评成绩:汽车⼯程系电测与汽车数字应⽤中⼼⽬录实验04051001 MATLAB语⾔基础 (3)实验04051002 MATLAB科学计算及绘图 (12)实验04051001 MATLAB语⾔基础实验⽬的1)熟悉MATLAB的运⾏环境2)掌握MATLAB的矩阵和数组的运算3)掌握MATLAB符号表达式的创建4)熟悉符号⽅程的求解实验内容(任选6题)1.利⽤rand等函数产⽣下列矩阵:产⽣⼀个均匀分布在(-5,5)之间的随机阵(50×2),要求显⽰精度为精确到⼩数点后⼀位(精度控制指令为format)。
format banka=-5; b=5;r = a + (b-a).* rand(50,2)r =3.15 -2.244.06 1.80-3.73 1.554.13 -3.371.32 -3.81-4.02 -0.02-2.22 4.600.47 -1.604.58 0.854.57 0.06 -0.15 1.99 3.00 3.91 -3.58 4.59 -0.78 0.47 4.16 -3.612.92 -3.514.59 -2.42 1.56 3.41 -4.64 -2.463.49 3.144.34 -2.56 2.58 -1.502.43 -3.03-1.08 -2.49 1.55 1.16 -3.29 -0.27 2.06 -1.48 -4.68 3.31 -2.23 0.85 -4.54 0.50 -4.03 4.17 3.23 -2.141.952.57-1.83 2.54 4.50 -1.20 -4.66 0.68 -0.61 -4.24 -1.18 -4.46-0.10 -3.70-0.54 0.691.46 -0.312.09 -4.882.55 -1.632.在⼀个已知的测量矩阵T(100×100)中,删除整⾏数据全为0的⾏,删除整列数据全为0的列(判断某列元素是否为0⽅法:检查T(: , i) .* (T(: , i))是否为0)。
matlab综合大作业(附详细答案)

m a t l a b综合大作业(附详细答案)-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII《MATLAB语言及应用》期末大作业报告1.数组的创建和访问(20分,每小题2分):1)利用randn函数生成均值为1,方差为4的5*5矩阵A;实验程序:A=1+sqrt(4)*randn(5)实验结果:A =0.1349 3.3818 0.6266 1.2279 1.5888-2.3312 3.3783 2.4516 3.1335 -1.67241.2507 0.9247 -0.1766 1.11862.42861.5754 1.6546 5.3664 0.8087 4.2471-1.2929 1.3493 0.7272 -0.6647 -0.38362)将矩阵A按列拉长得到矩阵B;实验程序:B=A(:)实验结果:B =0.1349-2.33121.25071.5754-1.29293.38183.37830.92471.65461.34930.62662.4516-0.17665.36640.72721.22793.13351.11860.8087-0.66471.5888-1.67242.42864.2471-0.38363)提取矩阵A的第2行、第3行、第2列和第4列元素组成2*2的矩阵C;实验程序:C=[A(2,2),A(2,4);A(3,2),A(3,4)]实验结果:C =3.3783 3.13350.9247 1.11864)寻找矩阵A中大于0的元素;]实验程序:G=A(find(A>0))实验结果:G =0.13491.25071.57543.38183.37830.92471.65461.34930.62662.45165.36640.72721.22793.13351.11860.80871.58882.42864.24715)求矩阵A的转置矩阵D;实验程序:D=A'实验结果:D =0.1349 -2.3312 1.2507 1.5754 -1.29293.3818 3.3783 0.9247 1.6546 1.34930.6266 2.4516 -0.1766 5.3664 0.72721.2279 3.1335 1.1186 0.8087 -0.66471.5888 -1.67242.4286 4.2471 -0.38366)对矩阵A进行上下对称交换后进行左右对称交换得到矩阵E;实验程序:E=flipud(fliplr(A))实验结果:E =-0.3836 -0.6647 0.7272 1.3493 -1.29294.2471 0.80875.3664 1.6546 1.57542.4286 1.1186 -0.1766 0.9247 1.2507-1.6724 3.1335 2.4516 3.3783 -2.33121.5888 1.2279 0.6266 3.3818 0.13497)删除矩阵A的第2列和第4列得到矩阵F;实验程序:F=A;F(:,[2,4])=[]实验结果:F =0.1349 0.6266 1.5888-2.3312 2.4516 -1.67241.2507 -0.17662.42861.5754 5.3664 4.2471-1.2929 0.7272 -0.38368)求矩阵A的特征值和特征向量;实验程序:[Av,Ad]=eig(A)实验结果:特征向量Av =-0.4777 0.1090 + 0.3829i 0.1090 - 0.3829i -0.7900 -0.2579 -0.5651 -0.5944 -0.5944 -0.3439 -0.1272-0.2862 0.2779 + 0.0196i 0.2779 - 0.0196i -0.0612 -0.5682 -0.6087 0.5042 - 0.2283i 0.5042 + 0.2283i 0.0343 0.6786 0.0080 -0.1028 + 0.3059i -0.1028 - 0.3059i 0.5026 0.3660 特征值Ad =6.0481 0 0 0 00 -0.2877 + 3.4850i 0 0 00 0 -0.2877 - 3.4850i 0 00 0 0 0.5915 00 0 0 0 -2.30249)求矩阵A的每一列的和值;实验程序:lieSUM=sum(A)实验结果:lieSUM =-0.6632 10.6888 8.9951 5.6240 6.208710)求矩阵A的每一列的平均值;实验程序:average=mean(A)实验结果:average =-0.1326 2.1378 1.7990 1.1248 1.24172.符号计算(10分,每小题5分):1)求方程组20,0++=++=关于,y z的解;uy vz w y z w实验程序:S = solve('u*y^2 + v*z+w=0', 'y+z+w=0','y,z');y= S. y, z=S. z实验结果:y =[ -1/2/u*(-2*u*w-v+(4*u*w*v+v^2-4*u*w)^(1/2))-w] [ -1/2/u*(-2*u*w-v-(4*u*w*v+v^2-4*u*w)^(1/2))-w] z =[ 1/2/u*(-2*u*w-v+(4*u*w*v+v^2-4*u*w)^(1/2))] [ 1/2/u*(-2*u*w-v-(4*u*w*v+v^2-4*u*w)^(1/2))]2)利用dsolve 求解偏微分方程,dx dyy x dt dt==-的解; 实验程序:[x,y]=dsolve('Dx=y','Dy=-x')实验结果:x =-C1*cos(t)+C2*sin(t)y = C1*sin(t)+C2*cos(t)3.数据和函数的可视化(20分,每小题5分):1)二维图形绘制:绘制方程2222125x y a a +=-表示的一组椭圆,其中0.5:0.5:4.5a =;实验程序:t=0:0.01*pi:2*pi; for a=0.5:0.5:4.5; x=a*cos(t); y=sqrt(25-a^2)*sin(t); plot(x,y) hold on end实验结果:2) 利用plotyy 指令在同一张图上绘制sin y x =和10x y =在[0,4]x ∈上的曲线;实验程序:x=0:0.1:4; y1=sin(x); y2=10.^x;[ax,h1,h2]=plotyy(x,y1,x,y2); set(h1,'LineStyle','.','color','r'); set(h2,'LineStyle','-','color','g'); legend([h1,h2],{'y=sinx';'y=10^x'});实验结果:3)用曲面图表示函数22z x y =+;实验程序:x=-3:0.1:3; y=-3:0.1:3; [X,Y]=meshgrid(x,y); Z=X.^2+Y.^2; surf(X,Y,Z)实验结果:4)用stem 函数绘制对函数cos 4y t π=的采样序列;实验程序:t=-8:0.1:8;y=cos(pi.*t/4); stem(y)实验结果:4. 设采样频率为Fs = 1000 Hz ,已知原始信号为)150π2sin(2)80π2sin(t t x ⨯+⨯=,由于某一原因,原始信号被白噪声污染,实际获得的信号为))((ˆt size randn x x+=,要求设计出一个FIR 滤波器恢复出原始信号。
DSP Matlab作业(第5~10章)
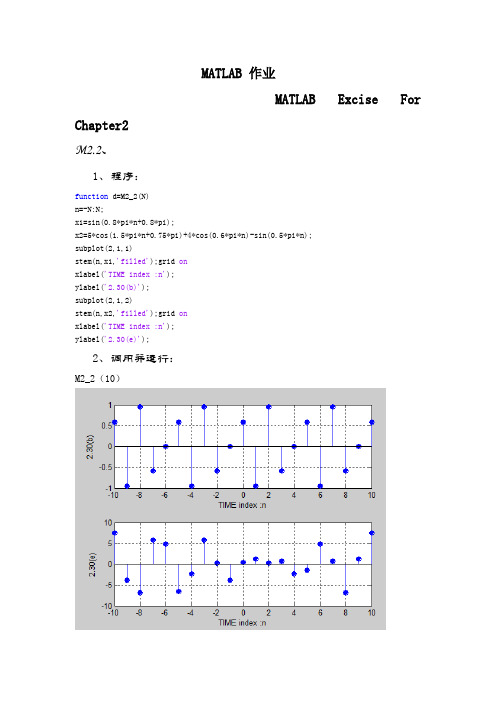
MATLAB 作业MATLAB Excise For Chapter2M2.2、1、程序:function d=M2_2(N)n=-N:N;x1=sin(0.8*pi*n+0.8*pi);x2=5*cos(1.5*pi*n+0.75*pi)+4*cos(0.6*pi*n)-sin(0.5*pi*n);subplot(2,1,1)stem(n,x1,'filled');grid onxlabel('TIME index :n');ylabel('2.30(b)');subplot(2,1,2)stem(n,x2,'filled');grid onxlabel('TIME index :n');ylabel('2.30(e)');2、调用并运行:M2_2(10)M2.3、1、程序:function s=M2_3(A,omega,fai,N)n=0:N;x=A*sin(omega*n+fai);stem(n,x,'fill');grid onaxis([0,N,-2,2]);xlabel('Time index n');ylabel('Amplitude');2、调用并运行(a)、M2_3(1.5,0,pi/2,40)、M2_3(1.5,0.1*pi,pi/2,40)、M2_3(1.5,0.2*pi,pi/2,40)、M2_3(1.5,0.8*pi,pi/2,40)、M2_3(1.5,0.9*pi,pi/2,40)、M2_3(1.5,pi,pi/2,40)、M2_3(1.5,1.1*pi,pi/2,40)、M2_3(1.5,1.2*pi,pi/2,40)(b)、(1)omega=0.6*pi周期T=10;理论上:T=10 (2)omega=0.28*pi周期T=50;;理论上:T=50;(3)omega=0.45*pi周期T=40;理论上:T=40;(4)omega=0.55*pi周期T=40;理论上:T=40;(4)omega=0.65*pi周期T=40;理论上:T=40;M2.9、MATLAB Excise For Chapter3M3.3、调用程序program 3-1运行M3_3Number of frequency points = [1000]Numerator coefficients = 0.2418*[1 0.139 -0.3519 0.139 1] Denominator coefficients = [1 0.2386 0.8258 0.1393 0.4153]The plot of the program are shown in below:运行M3_3Number of frequency points = [1000]Numerator coefficients = 0.1397*[1 -0.0911 0.0911 -1] Denominator coefficients = [1 1.1454 0.7275 0.1205]The plot of the program are shown in below:M3.7、h=input('Type in the target sequence= ');%输入要计算群延时的序列N=input('Type in the group delay frequency point=');%输入要计算的群延时点n=0:(length(h)-1);H=fft(h,N);K=fft(n.*h,N);tao=real(K./H)运行M3-7M3_7Type in the target sequence= [1 1 2 0 0 6 3]Type in the group delay frequency point=8tao =4.0769 7.7221 4.6923 4.0556 9.0000 4.05564.6923 7.7221MATLAB Excise For Chapter5 M5.11、程序function d=M5_1(N)k1=-N:N;x1=ones(1,2*N+1);omega=0:pi/500:2*pi;X1=freqz(x1,1,omega);X1dft=fft(x1);n1=0:1:2*N;figure(1),plot(omega/pi,abs(X1),2*n1/(2*N+1),abs(X1dft),'ro') xlabel('\omega/\pi'),ylabel('Amplitude');k2=0:N;x2=ones(1,N+1);X2=freqz(x2,1,omega);X2dft=fft(x2);n2=0:1:N;figure(2),plot(omega/pi,abs(X2),2*n2/(N+1),abs(X2dft),'ro') xlabel('\omega/\pi'),ylabel('Amplitude');k3=k1;x3=1-(abs(k3)/N);X3=freqz(x3,1,omega);X3dft=fft(x3);n3=n1;figure(3),plot(omega/pi,abs(X3),2*n3/(2*N+1),abs(X3dft),'ro') xlabel('\omega/\pi'),ylabel('Amplitude');x4=N+1-abs(k3);X4=freqz(x4,1,omega);X4dft=fft(x4);figure(4),plot(omega/pi,abs(X4),2*n3/(2*N+1),abs(X4dft),'ro') xlabel('\omega/\pi'),ylabel('Amplitude');x5=cos(pi*k3/(2*N));X5=freqz(x5,1,omega);X5dft=fft(x5);figure(5),plot(omega/pi,abs(X5),2*n3/(2*N+1),abs(X5dft),'ro') xlabel('\omega/\pi'),ylabel('Amplitude');实现了problem3.19中5个序列的求DTFT和DFT2、调用程序运行结果M5_1(8)The red circles denote the DFT samples.当N=8时序列y1的DTFT和DFT采样当N=8时序列y2的DTFT和DFT采样当N=8时序列y3的DTFT和DFT采样当N=8时序列y4的DTFT和DFT采样当N=8时序列y5的DTFT和DFT采样M5.21、程序x=input('the sequence one to convolution;');y=input('the sequence two to convolution;');X=fft(x);Y=fft(y);S=X.*Y;s=ifft(S)2、调用程序M5_2the sequence one to convolution;[5,-2,2,0,4,3]the sequence two to convolution;[3,1,-2,2,4,4]s =10.0000 9.0000 16.0000 44.0000 36.0000 29.0000 M5_2M5_2the sequence one to convolution;[2-j,-1-j*3,4-j*3,1+j*2,3+j*2] the sequence two to convolution;[-3,2+j*4,-1+j*4,4+j*2,-3+j]s =11.0000 +25.0000i -9.0000 +48.0000i 3.0000 +17.0000i 29.0000 + 0.0000i -10.0000 +12.0000iProgram for (c)N=4;n=0:1:N;x=cos(pi*n/2);y=3.^n;X=fft(x);Y=fft(y);S=X.*Y;s=ifft(S)s =-23.0000 -69.0000 35.0000 105.0000 73.0000M5.81、程序X=[11 8-j*2 1-j*12 6+j*3 -3+j*2 2+j 15];k=8:12;XR(k)=conj(X(mod(-k+2,12)));XC=[X XR(k)];x=ifft(XC);n=0:1:11;x1=exp(i*2*pi*n/3);y=x1.*x;output=[x(1) x(7) sum(x) sum(y)];disp(output)disp(sum(x.*x))2、调用程序M5_84.5000 -0.8333 11.0000 -3.0000 - 2.0000i 74.8333MATLAB Excise For Chapter6M6.1(a)、The output of program6_1 by input the coefficient of problem (a)Numerator factors1.00000000000000 -2.10000000000000 5.000000000000001.00000000000000 -0.40000000000000 0.90000000000000Denominator factors1.000000000000002.00000000000000 4.999999999999991.00000000000000 -0.20000000000000 0.40000000000001Gain constant0.50000000000000Then ,The pole-zero plot of is given below:There are 3 ROCs associated with :R1,|z|<;R2,<|z|<; R3,|z|>The inverse –transform corresponding to the ROC is a left-sided sequence, the inverse–transform corresponding to the ROC is a two-sided sequence, and the inverse –transform corresponding to the ROC is a right-sided sequence.(b)、The output of program6_1 by input the coefficient of problem (b)Numerator factors1.00000000000000 1.20000000000000 3.999999999999991.00000000000000 -0.50000000000000 0.90000000000001Denominator factors1.000000000000002.10000000000000 4.000000000000011.00000000000000 0.60000000000003 01.00000000000000 0.39999999999997 0Gain constant1Then ,The pole-zero plot of is given below:There are 4 ROCs associated with :R1,|z|<R2,<|z|<; R3,<|z|<; R4,|z|>The inverse –transform corresponding to the ROC is a left-sided sequence, the inverse–transform corresponding to the ROC is a two-sided sequence, and the inverse –transform corresponding to the ROC is a right-sided sequence.M6.3The output of programme6_4 by type in:(a)M6_3Type in the residues = [-0.8,-7/6]Type in the poles = [-0.2,-1/6]Type in the constants = 3The output is as following:Numerator polynomial coefficients1.0333 0.7333 0.1000Denominator polynomial coefficients1.0000 0.3667 0.0333Hence(b)Rewrite X2(z)asM6_3Type in the residues = [3,-0.7+j*0.6454972243679,-0.7-j*0.6454972243679] Type in the poles = [-0.4,j*0.774596669,-j*0.774596669]Type in the constants = -2.5The output is as following:Numerator polynomial coefficients-0.9000 -2.5600 -0.1000 -0.6000Denominator polynomial coefficients1.0000 0.4000 0.6000 0.2400Hence,(c)M6_3Type in the residues = [5,1.5,-0.25]Type in the poles = [-0.64,-0.5,-0.5]Type in the constants = 0The output is as following:Numerator polynomial coefficients6.2500 6.5500 1.7300 0Denominator polynomial coefficients1.0000 1.6400 0.8900 0.1600Hence,(d)Rewrite X4(z)asM6_3Type in the residues = [-0.75,-0.375+j*0.2905,-0.375-j*0.2905] Type in the poles = [0.5,-j*0.4303,j*0.4303]Type in the constants = -5The output is as following:Numerator polynomial coefficients-4.5000 -6.8750 -3.6375 -0.8438Denominator polynomial coefficients1.0000 1.5000 0.7875 0.1688MATLAB Excise For Chapter7M7.31、程序k = input('Number of frequency points = ');num = input('Numerator coefficients = ');den = input('Denominator coefficients = ');w = 0:pi/(k-1):pi;h = freqz(num, den, w);plot (w,20*log10(abs(h)));gridxlabel('Normalized frequency'); ylabel('Gain, dB');2、调用M7_3运行结果如下M7_3Number of frequency points = 1000Numerator coefficients = [0,1,-2,1]Denominator coefficients = [1,-1.28,0.61+0.4*0.88,-(0.4*0.61)]From the gain response of the transfer function we can get that when the frequency become high and stable then we can conclude that this has a high pass responseM7.51、程序k = input('Number of frequency points = ');num = input('Numerator coefficients = ');den = input('Denominator coefficients = ');w = 0:pi/(k-1):pi;h = freqz(num, den, w);figure(1),plot(w/pi,abs(h));grid ontitle('Magnitude Spectrum')xlabel('\omega/\pi'); ylabel('Magnitude')figure(2),plot(w/pi,angle(h));grid ontitle('Phase Spectrum')xlabel('\omega/\pi'); ylabel('Phase, radians')2、调用M7_5运行结果如下M7_5Number of frequency points = 1000Numerator coefficients = 0.2031*[1,-(1+0.2743),1+0.2743,-1]Denominator coefficients =[1,0.487+0.1532,0.8351+0.83+0.1532*0.487+0.84,0.1532*0.84+0.487*0.8352,0.84*0.8351]Fro m the magnitude response plot given above it can be seen that represents a highpass filter. The difference equation representation of is given byy[n]+0.7074y[n-1]+0.7976y[n-2]+0.2004y[n-3]=0.2031x[n]-0.2588x[n-1]+0.2588x[n-2]-0.2031x[n-3]MATLAB Excise For Chapter9M9.21、程序Fp = input('Passband edge frequency in Hz = ');Fs = input('Stopband edge frequency in Hz = ');FT = input('Sampling frequency in Hz = ');Rp = input('Passband ripple in dB = ');Rs = input('Stopband minimum attenuation in dB = ');Wp = 2*Fp/FTWs = 2*Fs/FT[N, Wn] = buttord(Wp, Ws, Rp, Rs)[b, a] = butter(N, Wn);disp('Numerator polynomial');disp(b)disp('Denominator polynomial');disp(a)[h, w] = freqz(b, a, 512);figure(1),plot(w/pi, 20*log10(abs(h))); grid axis([0 1 -60 5]);xlabel('\omega/\pi'); ylabel('Magnitude, dB'); figure(2),plot(w/pi, unwrap(angle(h))); grid axis([0 1 -8 1]);xlabel('\omega/\pi'); ylabel('Phase, radians');2、调用M9_2运行结果如下M9_2Passband edge frequency in Hz = 10000Stopband edge frequency in Hz = 30000Sampling frequency in Hz = 100000Passband ripple in dB = 0.4Stopband minimum attenuation in dB = 50Wp =0.2000Ws =0.6000N =5Wn =0.2613Numerator polynomial0.0039 0.0197 0.0394 0.0394 0.0197 0.0039Denominator polynomial1.0000 -2.3611 2.6131 -1.5486 0.4864-0.0636M9.111、(a)TF=9kHZ,1pF=1.2kHZ,2pF=2.2kHZ,1sF=650HZ,2sF=3kHZ pα=0.8dB,sα=31dBThenTpp FF112πω==0.8378,Tpp FF222πω==1.536,Tss FF112πω==0.4538,Tss FF222πω==2.094According to bilinear transformation method :)2tan(11ppω=ΩΛ=0.445,)2tan(22ppω=ΩΛ=0.996,)2tan(11ssω=ΩΛ=0.231,)2tan(22s s ω=ΩΛ=1.731. ωB =2p ΛΩ—1p ΛΩ=0.521,s Ω=3.13程序[N, Wn] = cheb1ord(1, 3.13, 0.8, 31, 's');[B, A] = cheby1(N, 0.8, Wn, 's');[BT, AT] = lp2bp(B, A, sqrt(0.43), 0.521);[num, den] = bilinear(BT, AT, 0.5);[h, omega] = freqz(num, den, 256);plot(omega/pi, 20*log10(abs(h)));grid;xlabel('\omega/\pi'); ylabel('Gain,in dB');title('Chebyshev I Bandpass Filter');axis([0 1 -60 5]);2、调用M9_11运行结果如下MATLAB Excise For Chapter10M10.11、程序M1= input('M1= ');M2= input('M2= ');n1=-M1:0.5:M1;n2=-M2:0.5:M2;num1=-0.4*sinc(0.4*n1);num2=-0.4*sinc(0.4*n2);num1(M1+1)=0.6;num2(M2+1)=0.6;w1= 0:pi/(4*M1):pi;w2= 0:pi/(4*M2):pi;h1= freqz(num1, 1, w1);h2= freqz(num2, 1, w2);plot(w1/pi,abs(h1),w2/pi,abs(h2));grid ontitle('Magnitude Spectrum')xlabel('\omega/\pi'); ylabel('Magnitude')2、调用程序运行结果M10.51、程序N = 36;fc = 0.2*pi;M = N/2;n = -M:1:M;t = fc*n;lp = fc*sinc(t);b = 2*[lp(1:M) (lp(M+1) - 0.5) lp((M+2):N+1)]; bw = b.*hamming(N+1)';[h2, w] = freqz(bw, 1, 512);plot(w/pi, abs(h2));axis([0 1 0 1.2]);xlabel('\omega/\pi');ylabel('Magnitude');title(['\omega_c = ', num2str(fc), ', N = ', num2str(N)]);grid on 2、运行结果M10.81、程序wp = 4*(2*pi)/18;ws = 6*(2*pi)/18;wc = (wp + ws)/2;dw = ws - wp;% HammingM = ceil(3.32*pi/dw);N = 2*M+1;n = -M:M;num = (6/18)*sinc(6*n/18);wh = hamming(N)';b = num.*wh;figure(1);k=0:2*M;stem(k,b);title('Impulse Response Coefficients');xlabel('Time index n'); ylabel('Amplitude');figure(2);[h, w] = freqz(b,1,512);plot(w/pi, 20*log10(abs(h))); grid;xlabel('\omega/\pi'); ylabel('Gain, in dB');title('Lowpass filter designed using Hamming window');axis([0 1 -80 10]);% HannM = ceil(3.11*pi/dw);N = 2*M+1;n = -M:M;num = (6/18)*sinc(6*n/18);wh = hann(N)';b = num.*wh;figure(3);k=0:2*M;stem(k,b);title('Impulse Response Coefficients');xlabel('Time index n'); ylabel('Amplitude');figure(4);[h, w] = freqz(b,1,512);plot(w/pi, 20*log10(abs(h)));grid;xlabel('\omega/\pi');ylabel('Gain, in dB');title('Lowpass filter designed using Hann window'); axis([0 1 -80 10]);% BlackmanM = ceil(5.56*pi/dw);N = 2*M+1;n = -M:M;num = (6/18)*sinc(6*n/18);wh = blackman(N)';b = num.*wh;figure(5);k=0:2*M;stem(k,b);title('Impulse Response Coefficients');xlabel('Time index n'); ylabel('Amplitude');figure(6);[h, w] = freqz(b,1,512);plot(w/pi, 20*log10(abs(h)));grid;xlabel('\omega/\pi');ylabel('Gain, in dB');title('Lowpass filter designed using Blackman window'); axis([0 1 -80 10]);2、运行结果M10.91、程序beta = 3.631;N = 44;n = -N/2:N/2;num = (6/18)*sinc(6*n/18);wh = kaiser(N+1,beta)';b = num.*wh;figure(1);stem(b);title('Impulse Response Coefficients');xlabel('Time index n');ylabel('Amplitude')figure(2);[h, w] = freqz(b,1,512);plot(w/pi, 20*log10(abs(h)));grid;xlabel('\omega/\pi');ylabel('Gain, in dB');title('Lowpass filter designed using Kaiser window'); axis([0 1 -80 10]);2、运行结果。
matlab1-5练习

1. 请生成从0到10间隔为0.1的列向量。
A=0:0.1:102. 矩阵A 为5×5的魔方矩阵,请从A 中提取8和16产生新的列向量B 。
a=magic(5) b=(a[1 2],[4 5])已知A =1 2 3 45 6 7 89 1 2 34 5 6 7⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦请通过矩阵变换,由A 生成B= 4 2 3 18 6 7 53 1 2 97 5 6 4⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦A=[1 2 3 4;5 6 7 8;9 1 2 3;4 5 6 7]; B=A(:,[4 2 3 1])3. 写出产生序列[100π,1002π,1003π,…π]的程序。
A=pi/100:pi/100:pi4. 下列变量名中, 属于合法变量名的是 ____A___ ______。
A. flower2 B. 2flower C. _what D. who's_it5. 矩阵M=[11 27 33; 29 57 12; 73 45 37] 则M(2,3)= ____A ___ ______。
A. 12B. 29C. 37D. 456. 表达式')sin(35-43517o2÷⨯+=a '的执行结果是 _____B__ ______。
A. a = 38.18 B. a = 293.18 C. a = 292.18 D. a = 37.567. 某同学设计了一个程序文件myprogram.m ,并将其保存到了c:\mydocument中,但在命令窗口中输入文件名>>myprogram 后,MATLAB 系统提示: Undefined function or variable ‘myprogram ’ 试分析产生错误的原因并给出解决办法。
没有修改路径;file-set path-add Folder8. MATLAB 语句后,加上___A__ ____,则运行时不显示中间结果。
MATLAB作业

zhangjiangwei4_1clcclearclear;x=1:10;y=[11,12,13,14,15,16,17,18];[x,y]=fexch(x,y)% fexch.m文件function[a,b]=exch(a,b)c=a;a=b;b=c;zhangjiangwei4_2clccleara=input('a=?');b=input('b=?');c=input('c=?');d=b*b-4*a*c;x=[(-b+sqrt(d))/(2*a),(-b-sqrt(d))/(2*a)];disp(['x1=',num2str(x(1)),',x2=',num2str(x(2))]); %zhangjiangwei 4_3clcclearx=input('ÇëÊäÈëxµÄÖµ£º');if x==10y=cos(x+1)+sqrt(x*x+1);elsey=x*sqrt(x*sqrt(x));endy%zhangjiangwei 4_4clcclearc=input('ÇëÊäÈëÒ»¸ö×Ö·û','s');if c>='A'&c<='Z'disp(setstr(abs(c)+abs('a')-abs('A')));elseif c>='a'&c<='z'disp(setstr(abs(c)-abs('a')+abs('A')));elseif c>='0'&c<='9'disp(abs(c)-abs('0'));elsedisp(c)end%zhangjiangwei 4_5clcclearprice=input('¼Û¸ñ');switch fix(price/100)case{0,1}rate=0;case{2,3,4}rate=3/100;case num2cell(5:9)rate=5/100;case num2cell(10:24)rate=8/100;case num2cell(25:49)rate=10/100;otherwiserate=14/100endprice=price*(1-rate)%zhangjiangwei 4_6clcclearA=[1,2,3;4,5,6];B=[7,8,9;10,11,12];tryC=A*B;catchC=A.*B;endCLasterr%zhangjiangwei 4_7clcclearfor m=100:999m1=fix(m/100);m2=rem(fix(m/10),10);m3=rem(m,10);if m==m1*m1*m1+m2*m2*m2+m3*m3*m3 disp(m)endend%zhangjiangwei 4_8clccleary=0;n=100;for i=1:ny=y+1/i/i;endy%chenjiaxin4_9clccleara=0;b=3*pi;n=1000;h=(b-a)/n;x=a;s=0;f0=exp(-0.5*x)*sin(x+pi/6);for i=1:nx=x+h;f1=exp(-0.5*x)*sin(x+pi/6);s=s+(f0+f1)*h/2;f0=f1;endsZhangjiangwei5—1clcclearx1=0:pi/100:2*pi;y1=2*exp(-0.5*x1).*sin(2*pi*x1); subplot(2,2,1);plot(x1,y1)t=-pi:pi/100:pi;x2=t.*cos(3*t);y2=t.*sin(t).*sin(t);subplot(2,2,2);plot(x2,y2)x3=linspace(0,2*pi,100);y3=[sin(x3);cos(x3)];subplot(2,2,3);plot(x3,y3)t1=linspace(0,2*pi,100);x4=[t1;t1]';y4=[sin(t1);cos(t1)]';subplot(2,2,4);plot(x4,y4)Zhangjiangwei5—4clccleart1=0:pi/100:2*pi;x1=exp(i*t1);subplot(2,2,1);plot(x1)t2=0:0.01:2*pi;x2=exp(i*t2);y2=[x2;2*x2;3*x2]';subplot(2,2,2);plot(y2)x=(0:pi/100:2*pi)';y1=2*exp(-0.5*x)*[1,-1];y2=2*exp(-0.5*x).*sin(2*pi*x);x1=(0:12)/2;y3=2*exp(-0.5*x1).*sin(2*pi*x1); subplot(2,2,3);plot(x,y1,'k:',x,y2,'b--',x1,y3,'rp') x1=0:pi/100:2*pi;x2=0:pi/100:3*pi;y1=exp(-0.5*x1).*sin(2*pi*x1);y2=1.5*exp(-0.1*x2).*sin(x2);subplot(2,2,4);plot(x1,y1,x2,y2)Zhangjiangwei5—5clcclearx=linspace(0,10,100);y=[];for(x0=x)if(x0>=8)y=[y,1];elseif(x0>=6)y=[y,5-x0/2];elseif(x0>=4)y=[y,2];elseif(x0>=0)y=[y,sqrt(x0)];endendplot(x,y)axis([0 10 0 2.5])title('·Ö¶Îº¯ÊýÇúÏß')xlabel('Variable X')ylabel('Variable Y')text(2,1.3,'y=x{1/2}')text(4.5,1.9,'y=2')text(7.3,1.5,'y=5-x/2')text(8.5,0.9,'y=1')zhangjiangwei5_6clcclearx=(0:pi/100:2*pi)';y1=2*exp(-0.5*x)*[-1,1];y2=2*exp(-0.5*x).*sin(2*pi*x);plot(x,y1,'b:')axis([0,2*pi,-2,2]);hold on;plot(x,y2,'k');legend('°üÂçÏß','°üÂçÏß','ÇúÏßy'); hold off;grid5-7(1)clcclearx=linspace(0,2*pi,60);z=cos(x);y=sin(x);t=sin(x)./(cos(x)+eps);ct=cos(x)./(sin(x)+eps);subplot(2,2,1);plot(x,y)title('sin(x)');axis([0,2*pi,-1,1]);subplot(2,2,2);plot(x,z)title('cos(x)');axis([0,2*pi,-1,1]);subplot(2,2,3);plot(x,t)title('tangent(x)');axis([0,2*pi,-40,40]); subplot(2,2,4);plot(x,ct)title('contangent(x)'); axis([0,2*pi,-40,40]);5-7(2)clcclearx=linspace(0,2*pi,60);z=cos(x);y=sin(x);t=sin(x)./(cos(x)+eps);ct=cos(x)./(sin(x)+eps); subplot(2,2,1);stairs(x,y)title('sin(x)-1');axis([0,2*pi,-1,1]); subplot(2,1,2);stem(x,y)title('sin(x)-2');axis([0,2*pi,-1,1]); subplot(4,4,3);plot(x,y)title('sin(x)');axis([0,2*pi,-1,1]); subplot(4,4,4);plot(x,z)title('cos(x)');axis([0,2*pi,-1,1]); subplot(4,4,7);plot(x,t)title('tangent(x)');axis([0,2*pi,-40,40]); subplot(4,4,8);plot(x,ct)title('contangent(x)'); axis([0,2*pi,-40,40]);5-8clcclearx=0:0.35:7;y=2*exp(-0.5*x);subplot(2,2,1);bar(x,y,'g')title('bar(x,y,"g")'); axis([0,7,0,2]);subplot(2,2,2);stairs(x,y,'r')title('stairs(x,y,"r")'); axis([0,7,0,2]);subplot(2,2,3);stem(x,y,'b')title('stem(x,y,"b")'); axis([0,7,0,2]);subplot(2,2,4);fill(x,y,'k')title('fill(x,y,"k")');axis([0,7,0,2]);5-9clccleartheta=0:0.01:2*pi;rho=sin(2*theta).*cos(2*theta);polar(theta,rho,'k')5-10clcclearx=0:0.01:10;y=10*x.*x;subplot(2,2,1);plot(x,y);title('plot(x,y)');grid on;subplot(2,2,2);semilogx(x,y)title('semilogx(x,y)');grid on;subplot(2,2,3);semilogy(x,y)title('semilogy(x,y)');grid on;subplot(2,2,4);loglog(x,y)title('loglog(x,y)');grid on;5-12clcclearsubplot(2,1,2);fplot('cos(tan(pi*x))',[-0.4,1.4],1e-4) subplot(2,2,1);pie([7,17,23,19,5])title('饼图');legend('优秀','良好','中等','及格','不及格'); subplot(2,2,2);compass([3+2i,5.5-i,-1.5+5i])title('相量图‘);5-13clccleart=0:pi/50:2*pi;x=8*cos(t);y=4*sqrt(2)*sin(t);z=-4*sqrt(2)*sin(t);plot3(x,y,z,'p')title('Line in 3-D Space');text(0,0,0,'origin');xlable('X'),ylable('Y'),zlable('Z');grid on;5-14clcx=7:29;y=16:35;[x,y]=meshgrid(x,y);z=2*x+5*y;k=find(z==126);x(k)',y(k)'5-15(1)clcclearx=0:0.1:2*pi;[x,y]=meshgrid(x);z=sin(y).*cos(x);mesh(x,y,z)xlable('x-axis'),ylable('y-axis'),zlable('z-axis'); title('mesh');(2)clcclearx=0:0.1:2*pi;[x,y]=meshgrid(x);z=sin(y).*cos(x);surf(x,y,z)xlable('x-axis'),ylable('y-axis'),zlable('z-axis'); title('surf');(3)clcclearx=0:0.1:2*pi;[x,y]=meshgrid(x);z=sin(y).*cos(x);plot3(x,y,z)xlable('x-axis'),ylable('y-axis'),zlable('z-axis'); title('plot3-1');5-16clcclearm=30;z=1.2*(0:m)/m;r=ones(size(z));theta=(0:m)/m*2*pi;x1=r'*cos(theta);y1=r'*sin(theta);z1=z'*ones(1,1+m);x=(-m:2:m)/m;x2=x'*ones(1,m+1);y2=r'*cos(theta);z2=r'*sin(theta);surf(x1,y1,z1)axis equal,axis offhold onsurf(x2,y2,z2);axis equal,axis offtitle('Á½¸öµÈÖ±¾¶¹ÜµÄ½»Ïß');zhangjiangwei_17clcclear[x,y]=meshgrid(-10:0.2:10);z1=(x^2-2*y^2)+eps;a=input('a=?');z2=a*ones(size(x));subplot(1,2,1);mesh(x,y,z1)hold on;mesh(x,y,z2)v=[-10,10,-10,10,-100,100];axis(v);grid;hold off;r0=abs(z1-z2)<=1;xx=r0.*x;yy=r0.*y;zz=r0.*z2;subplot(1,2,2);plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'*')axis(v);grid;zhangjiangwei_18clcclear[x,y]=meshgrid(-8:0.5:8);z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2+eps); subplot(2,2,1);meshc(x,y,z)title('meshc(x,y,z)');subplot(2,2,2);meshz(x,y,z)title('meshz(x,y,z)');subplot(2,2,3);surfc(x,y,z)title('surfc(x,y,z)');subplot(2,2,4);surfl(x,y,z)title('surfl(x,y,z)');zhangjiangwei_19clccleart=0:pi/20:2*pi;[x,y,z]=cylinder(2+sin(t),30);subplot(2,2,1);surf(x,y,z)subplot(2,2,2);[x,y,z]=sphere(100);surf(x,y,z)subplot(2,2,3);[x,y,z]=peaks(30);meshz(x,y,z)subplot(2,2,4);bar3(magic(4))zhangjiangwei_20clcclearsubplot(2,2,1);[x,y,z]=peaks(100);meshc(x,y,z)subplot(2,2,2);y=2*sin(0:pi/10:2*pi);stem3(x,'b')subplot(2,2,3);pie([2347,1827,2043,3025])subplot(2,2,4);fill(rand(3,5),rand(3,5),rand(3,5)) zhangjiangwei_22clcclearsubplot(2,2,1);mesh(peaks(30))view(-37.5,30);title('azmiuth=-37.5,elevation=30') subplot(2,2,2);mesh(peaks(30))view(0,90);title('azmiuth=0,elevation=90') subplot(2,2,3);mesh(peaks(30))view(90,0);title('azmiuth=90,elevation=0') subplot(2,2,4);mesh(peaks(30))view(-7,-10);title('azmiuth=-7,elevation=-10') zhangjiangwei_23clcclearsubplot(2,2,1);[x,y,z]=peaks(100);waterfall(x,y,z)subplot(2,2,2);contour3(x,y,z,12)z=peaks(50);colormap(copper);subplot(2,2,3);surf(z)subplot(2,2,4);surf(z)shading interp;Zhangjiangwei5——24clcclear[x,y,z]=sphere(20);z1=z;z1(:,1:4)=NaN;c1=ones(size(z1));surf(3*x,3*y,3*z1,c1);hold on;z2=z;c2=2*ones(size(z2));c2(:,1:4)=2*ones(size(c2(:,1:4))); surf(1.5*x,1.5*y,1.5*z2,c2); colormap([0,1,0;0.5,0,0;1,0,0]) grid onhold off第五章习题:P1371.(1)clcclearx=-10:0.01:10;y=100./(1+x.^2);plot(x,y)(2)clcclearx=-2*pi:pi/100:2*pi;y=(1./2*pi).*exp(-x.*x./2);plot(x,y)(3)clcclearezplot('x^2+y^2=1',[-2*pi,2*pi])(4)clccleart=-2*pi:pi/100:2*pi;x=t.*t;y=5.*t.*t.*t;plot(x,y)P1383(1)clccleart=-2*pi:pi/100:2*pi;x=cos(t);y=sin(t);z=t;plot3(x,y,z)(2)clcclearu=-2*pi:pi/100:2*pi;v=-2*pi:pi/100:2*pi;x=(1+cos(u)).*cos(v);y=(1+cos(u)).*cos(v);z=sin(u);plot3(x,y,z)(3)clcclearx=-10:0.01:10;y=-10:0.01:10;z=5*ones(size(x));plot3(x,y,z)(4)clcclear[x,y,z]=sphere(10);surf(x,y,z)6(1)clcclearx=linspace(-10,10,100);y=[];for x0=xif x0>0y=[y,x0.^2+(1+x0).^(1/4)+5];elseif x0==0y=[y,0];elseif x0<0y=[y,x0.*x0.*x0+(1-x0)^(1/2)-5]; endendplot(x,y)(2)clcclearfplot('x0.^2+(1+x0).^(1/4)+5',[0,1])fplot('x0.*x0.*x0+(1-x0)^(1/2)-5',[-1,0]) fplot('0',0)zhangjiangwei6_1clcclearA=[13,-56,78;25,63,-235;78,25,563;1,0,-1]; y1=max(A,[],1)y2=min(A,[],2)y3=max(A)y4=min(A)y5=max(max(A))y6=min(min(A))zhangjiangwei6_2clcclearA=[1,2,3,4;5,6,7,8;9,10,11,12];X=[1,5,9];x1=mean(A)y1=mean(A,2)x2=mean(X)y2=mean(A,1)x3=median(A)y3=median(A,2)x4=median(X)y4=median(A,1)S=prod(A,2)S1=sum(A,1)Zhangjiangwei6_6clcclearx=[4,5,6;1,4,8];y1=std(x,0,1)y2=std(x,1,1)M=randn(10000,5);S=mean(M)D=std(M)R=corrcoef(M)A=[1,-8,5;-8,12,7;5,6,-13];sort(A)sort(A,2,'descend')Zhangjiangwei6_7clcclearx=0.46:0.01:0.49;f=[0.4846555,0.4937542,0.5027498,0.5116683]; format longinterp1(x,f,0.472)interp1(x,f,0.472,'nearest')Zhangjiangwei6-10clcclearx=0:0.1:1;y=0:0.2:2;[X,Y]=meshgrid(x,y);Z=X.^2+Y.^2;interp2(x,y,Z,[0.5 0.6],0.4)x=0:2.5:10;h=[0:30:60]';T=[95,14,0,0,0;88,48,32,12,6;67,64,54,48,41]; xi=[0:0.5:10];hi=[0:10:60]';temps=interp2(x,h,T,xi,hi,'cubic')mesh(xi,hi,temps)Zhangjiangwei6-11clcclearX=linspace(0,2*pi,50);Y=sin(X);P=polyfit(X,Y,3)X=linspace(0,2*pi,20);Y=sin(X);Y1=polyval(P,X);plot(X,Y,':b',X,Y1,'-*r')习题P1892(2)clcclearN=[1,4,9,16,25,36,49,64,81,100];Y=N.^0.5;p=polyfit(N,Y,3)N=[1,4,9,16,25,36,49,64,81,100];interp1(N,Y,[1,4,9,16,25,36,49,64,81,100]) N=[1,4,9,16,25,36,49,64,81,100];Y=N.^0.5;interp1(N,Y,18.2654,'cubic')拟合曲线clcclearN=[1,4,9,16,25,36,49,64,81,100];Y=N.^0.5;p=polyfit(N,Y,8)pk=poly2str(p,'x')N=[1,4,9,16,25,36,49,64,81,100];Y=N.^0.5;Y1=polyval(p,N);plot(N,Y,':b',N,Y1,'-*r')3clcclearx=[165,123,150,123,141];y=[187,126,172,125,148];p=polyfit(x,y,6)y1=polyval(p,x);plot(x,y,':b',x,y1,'-*r')zhangjiangwei7_2clcclearsyms a m x;f=(x^(1/m)-a^(1/m))/(x-a);limit(f,x,a)f=(sin(x+a)-sin(x-a))/x;limit(f)f=x*(sqrt(x^2+1)-x);limit(f,x,inf,'left')f=(sqrt(x)-sqrt(a)-sqrt(x-a))/sqrt(x*x-a*a);limit(f,x,a,'right')zhangjiangwei7_3clcclearsyms a b t x y z;f=sqrt(1+exp(x));diff(f)f=x*cos(x);diff(y,x,2)diff(y,x,3)f1=a*cos(t);f2=a*sin(t);diff(f2)/diff(f1)(diff(f1)*diff(f2,2)-diff(f1,2)*diff(f2))/(diff(f1))^3;f=x*exp(y)/y^2;diff(f,x)diff(f,y)f=x^2+y^2+z^2-a^2;zx=-diff(f,x)/diff(f,z)zy=-diff(f,y)/diff(f,z) zhangjiangwei7_4clcclearsyms x;f=x^3+3*x-2;h=diff(f,x);g=h-4;solve(g) zhangjiangwei7_5clcclearsyms x;f=(3-x^2)^3;int(f)f=(sin(x))^2,int(f)syms alpha t;f=exp(alpha*t);int(f)f=(5*x*t)/(1+x^2);int(f)zhangjiangwei7_6clcclearsyms x t;f=abs(1-x);int(f,1,2)f=1/(1+x^2);int(f,-inf,inf)f=x^3/(x-1)^10;I=int(f,2,3)double(I)f=4*x/t;int(f,t,2,sin(x)) zhangjiangwei7_7clcclearsyms a b c z;f=pi*a*b*(c^2-z^2)/c^2; V=int(f,z,-c,c) Zhangjiangwei7_8 clcclearsyms t;x=3*t;y=3*t^2;z=2*t^3;f=diff([x,y,z],t); g=sqrt(f*f');l=int(g,t,0,1)Zhangjiangwei7_16clcclearsyms xy;y=dsolve('Dy-(x^2+y^2)/x^2/2','x')y1=dsolve('Dy*x^2+2*x*y-exp(x)','x')y2=dsolve('Dy-x^2/(1+y^2)','y(2)=1','x')[x,y]=dsolve('Dx=4*x-2*y','Dy=2*x-y','t')[x,y]=dsolve('D2y-y','D2y+x','t')P190(1)clcclear[x,y,z]=solve('2*x+3*y+5*z=10','3*x+7*y+4*z=3','x-7*y+z=5','x,y,z') A=[2,3,5;3,7,4;1,-7,1];b=[10,3,5]';x=A\bP2139:clcclearx0=solve('a*x^2+b*x+c=0','x')x=solve('sin(x)-sqrt(3)*cos(x)=sqrt(2)','x')x2=solve('2*sin(3*x-pi/4)','x')x3=solve('x^2+10*(x-1)*sqrt(x)+14*x+1','x')Zhangjiangwei7_9clcclearsyms xt;y=abs(x);Ft=fourier(y,x,t)fx=ifourier(Ft,t,x)Zhangjiangwei7_10clcclearsyms xt;y=x^2;Ft=laplace(y,x,t)fx=ilaplace(Ft,t,x)Zhangjiangwei7_11clcclearsyms nz;fn=exp(-n);Fz=ztrans(fn,n,z)f=iztrans(Fz,z,n)Zhangjiangwei7_12clcclearsyms n;s1=symsum(1/2^n,n,1,inf)s2=symsum((-1)^(n+1)/n,1,inf)s3=symsum(n*x^n,n,1,inf)s4=symsum(n^2,1,100)Zhangjiangwei7_13clcclearsyms x;f1=sqrt(1-2*x+x^3)-(1-3*x+x^2)^(1/3);f2=(1+x+x^2)/(1-x+x^2);taylor(f1,x,5)taylor(f2,6,1)Zhangjiangwei7_14clcclearx=solve('1/(x+2)+4*x/(x^2-4)=1+2/(x-2)','x')f=solve('x-(x^3-4*x-7)^(1/3)','x')x=solve('2*sin(3*x-pi/4)=1','x')x=solve('x+x*exp(x)-10','x')Zhangjiangwei7_15clcclear[x,y]=solve('1/x^3+1/y^3=28','1/x+1/y=4','x,y')[x,y]=solve('x+y=98','x^(1/3)+y^(1/3)=2','x,y')[u,v]=solve('u^3+v^3=98','u+v=2','u,v')实验一1.(1)clcclearz1=(2*sin(85*pi/180))/(1+exp(2))(2)clcclearx=[2,1+2*i;-0.45,5];z2=0.5*log(x+sqrt(1+x^2))(3)clccleara=-3.0:0.1:3.0;z3=((exp(0.3*a)-exp(-0.3*a))/2).*sin(a+0.3)+log((0.3+a)/2) 2:clcclearA=[12,34,-4;34,7,87;3,65,7];B=[1,3,-1;2,0,3;3,-2,7];I=[1,1,1;1,1,1;1,1,1];x1=A+6*Bx2=A-B+I %未定义单位矩阵,导致无法算出x2,对I进行了定义x3=A*Bx4=A.*Bx5=A^3x6=A.*3x7=A/Bx8=B\Ax9=[A,B]x10=[A([1,3],:);B^2]实验二5(1)clcclearA=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6];B=[0.95,0.67,0.52]';x=A\Bx=inv(A)*B(2)clcclearA=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6]; B=[0.95,0.67,0.52]';B1=[0.95,0.67,0.53]';x=A\By=A\B1实验三2:(1)第一种方法:clcclearx=input('ÇëÊäÈë³É¼¨xµÄÖµ£º');if(x>=90)y='A'elseif(x>=80&x<90)y='B'elseif(x>=70&x<80)y='C'elseif(x>=60&x<70)y='D'elseif(x<60)y='E'end第二种方法:clcclearx=input(‘请输入成绩x:’);switch floor(x/10)case {9,10}t='A';case 8t='B';case 7t='C';case 6t='D';case {0,1,2,3,4,5}t='E';otherwisedisp('Invalid score')enddisp(t)(2)clcclearx=input(‘请输入成绩x:’);if(x>=60)‘成绩合格’else‘成绩不合格’end实验四:2(1)clcclearsyms ny;y=1;n=1;while(y<3)y=y+1/(2*n-1);n=n+1;endn(2)clcclearsyms ny;n=input('Enter a number:');y=1;for i=1:ny=y+1/(2*i-1);endy实验五1function [y] = f(s)s=2*i;y1=exp(s)y2=log(s)y3=cos(s)y4=sin(s)end实验六1.clcclearx=0:2*pi/100:2*pi;y=(0.5+3.*sin(x)./(1+x.^2)).*cos(x); plot(x,y)2.(1)clcclearx=0:pi/100:2*pi;y1=x.^2;subplot(1,2,1);plot(x,y1)y2=cos(2*x);subplot(2,2,2);plot(x,y2)y3=x.^2.*cos(2.*x); subplot(2,2,4)plot(x,y3)(2)A:clcclearx=0:pi/100:2*pi;y1=x.^2;plot(x,y1)B:clcclearx=0:pi/100:2*pi;y2=cos(2*x);plot(x,y2)C:clcclearx=0:pi/100:2*pi;y3=x.^2.*cos(2.*x); plot(x,y3)(3)A:clcclearx=0:pi/100:2*pi;y1=x.^2;subplot(2,2,1);bar(x,y1)subplot(2,2,2);stairs(x,y1)subplot(2,2,3)stem(x,y1)subplot(2,2,4);fill(rand(1,3),rand(1,3),'y')B:clcclearx=0:pi/100:2*pi;y2=cos(2*x);subplot(2,2,1);bar(x,y2)subplot(2,2,2);stairs(x,y2)subplot(2,2,3)stem(x,y2)subplot(2,2,4);fill(rand(1,3),rand(1,3),'y')C:clcclearx=0:pi/100:2*pi;y3=x.^2.*cos(2.*x);subplot(2,2,1);bar(x,y3)subplot(2,2,2);stairs(x,y3)subplot(2,2,3)stem(x,y3)subplot(2,2,4);fill(rand(1,3),rand(1,3),'y')3.clcclearx=-5:0.1:5;if(x<=0)y=(x+sqrt(pi))/exp(2);plot(x,y)elsey=0.5.*log(x+sqrt(1+x.^2)); plot(x,y)end4.clccleara=input('a=');b=input('b=');n=input('n=');theta=-2*pi:pi/100:2*pi;rho=a.*sin(b+n.*theta);polar(theta,rho)[a=2;b=5;n=6][a=20;b=50;n=60][a=200;b=500;n=600]5.(未解决)clcclearx=-5:0.5:5;y=0:1/3:10;z=cos(x).*cos(y).*exp(-sqrt(x.^2+y.^2)./4); subplot(2,1,1);surf(x,y,z)title('surf');subplot(2,1,2);contour3(x,y,z)title('contour3');6clcclears=0:pi/100:pi/2;t=0:3*pi/100:3*pi/2;x=cos(s).*cos(t);y=cos(s).*sin(t);z=sin(s);plot3(x,y,z,':b')。
MATLAB编程作业

《Matlab编程训练》作业专业学生姓名班级学号指导教师完成日期实训一 MATLAB 语言介绍和数值计算1.先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存变量。
122sin 851z e =+.2. 已知 1234413134787,2033657327A B --⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦,求下列表达式的值:(1) A+6*B 和A-B+I (其中I 为单位矩阵) A+6*B:A-B+I:(2)A*B和A.*BA*B程序:A=[12 34 -4;34 7 87;3 65 7]B=[1 3 -1;2 0 3;3 -2 7]c=A*B结果:A.*B程序:A=[12 34 -4;34 7 87;3 65 7]B=[1 3 -1;2 0 3;3 -2 7]D=A.*B结果:(3)A^3和A.^3A^3程序:A=[12 34 -4;34 7 87;3 65 7]E=A^3结果:A.^3程序:A=[12 34 -4;34 7 87;3 65 7]C=A.^3(4)A/B及B\AA/B程序:A=[12 34 -4;34 7 87;3 65 7]B=[1 3 -1;2 0 3;3 -2 7]C=A/B结果:B\A程序:A=[12 34 -4;34 7 87;3 65 7]B=[1 3 -1;2 0 3;3 -2 7]D=B\A结果:(5)将矩阵C=B\A的右下角2*2子矩阵赋给D, 并(3)保存变量(mat文件)程序:A=[12 34 -4;34 7 87;3 65 7];B=[1 3 -1;2 0 3;3 -2 7];C=B*inv(A);D=C(2:3,2:3)结果:3. 求得矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=34157864653434533145A 的每行最大元素所在的位置?(至少两种方法) 第一种:A=[5 14 33;45 43 3;65 4 6;78 15 34][RowMax Order]=max(A')结果:第二种:A=[5 14 33;45 43 3;65 4 6;78 15 34][Max_num,index]=max(A,[],2)结果:实训二 MATLAB 编程基础1. 求[25,1258]之间能被15整除的数的个数。
清华大学MATLAB数学实验作业参考
数学实验内容及目的(作业参考)实验1 一元函数的图形实验目的1.学习 matlab一元函数绘图命令.2.进一步理解函数概念.实验内容1.学习matlab命令.matlab绘图命令比较多,我们选编一些常用命令,并简单说明其作用,这些命令的调用格式,可参阅例题及使用帮助help查找.表1.1 二维绘图函数表1.2 基本线型和颜色表1.3 二维绘图工具表1.4 axis 命令linspace 创建数组命令,调用格式为:x=linspace(x1,x2,n),创建了x 1到x2之间有n 个数据的数组.funtool 函数工具,在matlab 指令窗键入funtool 可打开“函数计算器”图形用户界面.2.绘制函数图形举例. 例1.1.画出x y sin =的图形解:首先建立点的坐标,然后用plot 命令将这些点绘出并用直线连接起来,采用中学五点作图法,选取五点)0,0(、)1,2(π、)0,(π、)1,23(-π、)0,2(π.输入命令:x=[0,pi/2,pi ,3*pi/2,2*pi];y=sin(x);plot(x ,y) 这里分号表示该命令执行结果不显示.可以想象,随点数增加,图形越来越接近x y sin =的图象.例如,在0到π2之间取30个数据点,绘出的图形与x y sin =的图象已经非常接近了. x=linspace(0,2*pi ,30);y=sin(x);plot(x ,y) 也可以如下建立该图形.x=0:0.1:2*pi ;y=sin(x);plot(x ,y) 还可以给图形加标记、格栅线. x=0:0.1:2*pi ; y=sin(x);plot(x ,y ,’r—‘) title(‘正弦曲线’) xlabel(‘自变量 x’) ylabel(‘函数y=sinx’) text(5.5,0,’y=sinx’) grid 上述命令第三行选择了红色虚线,第四行给图加标题“正弦曲线”,第五行给x 轴加标题“自变量x ”,第六行给y 轴加标题“函数x y sin =”,第七行在点)0,5.5(处放置文本“x y sin =”,第八行给图形加格栅线.例1.2.画出xy 2=和xy )2/1(=的图象.解:输入命令:x=-4:0.1:4;y1=2.^x ;y2=(1/2).^x ;plot(x ,y1,x ,y2); axis([-4,4,0,8])matlab 允许在一个图形中画多条曲线.plot(x1,y1,x2,y2,x3,y3)指令绘制)2(2),1(1x f y x f y ==等多条曲线.matlab 自动给这些曲线以不同颜色.例1.3.画出arctgx y =的图象. 解: 输入命令:x=-20:0.1:20;y=atan(x);plot(x ,y ,[-20,20],[pi/2,pi/2],[-20,20],[-pi/2,-pi/2]) grid从图上看,arctgx y =是有界函数,2π±=y 是其水平渐近线. 例1.4.在同一坐标系中画出tgx y x y x y ===,,sin 的图象.解:输入命令:x=-pi/2:0.1:pi/2;y1=sin(x);y2=tan(x); plot(x ,x ,x ,y1,x ,y2) axis equalaxis([-pi/2,pi/2,-3,3]) grid从图上看,当0>x 时,tgx x x <<sin ,当0<x 时,tgx x x >>sin ,x y =是x y sin =和tgx y =在原点的切线,因此,当1<<x 时,x tgx x x ≈≈,sin .例1.5.画出110-=xy 及)1lg(+=x y 的图形.解:输入命令:x1=-1:0.1:2;y1=10.^x1-1;x2=-0.99:0.1:2;y2=log10(x2+1); plot(x1,y1,x2,y2)从图上看,这两条曲线与我们所知的图象相差很远,这是因为坐标轴长度单位不一样的缘故.110-=xy 与)1lg(+=x y 互为反函数,图象关于x y =对称,为更清楚看出这一点,我们再画出x y =的图象. hold onx=-1:0.01:2;y=x ;plot(x ,y ,’r’) axis([-1,2,-1,2]) axis square ;hold offplot 语句清除当前图形并绘出新图形,hold on 语句保持当前图形.例1.6.画出心形线)cos 1(3a r +=的图象. 解:输入命令:x=-2*pi:0.1:2*pi ;r=3*(1+cos(x));polar(x ,r)例1.7.画出星形线t y t x 33sin 3,cos 3==的图象. 解:这是参数方程,可化为极坐标方程.233232)sin (cos 3a a r +=输入命令:x=0:0.01:2*pi ;r=3./(((cos(x)).^2).^(1/3)+((sin(x)).^2).^(1/3)).^(3/2); polar(x ,r)注意,如果建立r 与t 的关系,此时t 只是参数,不是极坐标系下的极角.实验2 函数极限实验目的1.理解极限概念.2.掌握用matlab 软件求函数极限的方法.实验内容1.学习matlab 命令.matlab 求极限命令可列表如下:表2.1matlab 代数方程求解命令solve 调用格式. solve (函数)(x f ) 给出0)(=x f 的根.2.理解极限概念.数列}{n x 收敛或有极限是指当n 无限增大时,n x 与某常数无限接近或n x 趋向于某一定值,就图形而言,也就是其点列以某一平行与y 轴的直线为渐近线.例2.1.观察数列}1{+n n 当∞→n 时的变化趋势.解:输入命令:n=1:100;xn=n./(n+1)得到该数列的前100项,从这前100项看出,随n 的增大,1+n n与1非常接近,画出nx 的图形.stem(n ,xn) 或for i=1:100;plot(n(i),xn(i),’r’) hold on end其中for … end 语句是循环语句,循环体内的语句被执行100次,n(i)表示n 的第i 个分量.由图可看出,随n 的增大,点列与直线1=y 无限接近,因此可得结论:1lim+∞→n nn =1.对函数的极限概念,也可用上述方法理解.例2.2.分析函数x x x f 1sin )(=,当0→x 时的变化趋势. 解:画出函数)(x f 在]1,1[-上的图形.x=-1:0.01:1;y=x.*sin(1./x);plot(x ,y)从图上看,x x 1sin 随着x 的减小,振幅越来越小趋近于0,频率越来越高作无限次振荡.作出x y ±=的图象.hold on ;plot(x ,x ,x ,-x)例2.3.分析函数x x f 1sin )(=当0→x 时的变化趋势. 解:输入命令:x=-1:0.01:1;y=sin(1./x);plot(x ,y)从图上看,当0→x 时,x 1sin 在-1和1之间无限次振荡,极限不存在.仔细观察该图象,发现图象的某些峰值不是1和-1,而我们知道正弦曲线的峰值是1和-1,这是由于自变量的数据点选取未必使x 1sin 取到1和-1的缘故,读者可试增加数据点,比较它们的结果. 例2.4.考察函数x xx f sin )(=当0→x 时的变化趋势. 解:输入命令:x=linspace(-2*pi ,2*pi ,100);y=sin(x)./x ;plot(x ,y)从图上看,x xsin 在0=x 附近连续变化,其值与1无限接近,可见x xx sin lim 0→=1.例2.5.考察xx x f )11()(+=当∞→x 时的变化趋势. 解:输入命令:x=1:20:1000;y=(1+1./x).^x ;plot(x ,y)从图上看,当∞→x 时,函数值与某常数无限接近,我们知道,这个常数就是e . 3.求函数极限例2.6.求)1311(lim 31+-+-→x x x .解:输入命令:syms x ;f=1/(x+1)-3/(x^3+1);limit(f ,x ,-1) 得结果ans=-1.画出函数图形.ezplot(f);hold on ;plot(-1,-1,’r.’)例2.7.求30sin limx xtgx x -→.解:输入命令:limit((tan(x)-sin(x))/x^3) 得结果:ans=1/2例2.8.求xx x x )11(lim -+∞→.解:输入命令:limit(((x+1)/(x-1))^x ,inf) 得结果:ans=exp(2)例2.9.求xx x +→0lim . 解:输入命令:limit(x^x ,x ,0,’right’) 得结果:ans =1 例2.10.求x ctgx 10)(lim+→.解:输入命令:limit((cot(x))^(1/log(x)),x ,0,’right’) 得结果:ans=exp(-1)4.求方程的解. 例2.11.解方程02=++c bx ax . 解:输入命令:syms a b c x ;f=a*x^2+b*x+c ;solve(f) 得结果:ans=[ 1/2/a*(-b+(b^2-4*a*c)^(1/2))] [ 1/2/a*(-b-(b^2-4*a*c)^(1/2))]如果不指明自变量,系统默认为x ,也可指定自变量,比如指定b 为自变量. solve(f ,b)得结果:ans=-(a*x^2+c)/x例2.12.解方程0155=--x x . 解:输入命令:f=x^5-5*x-1;solve(f) 得结果:ans=[ -1.4405003973415600893186320629653] [ -.20006410262997539129073370075959] [.49456407933505360591791681140791e-1 -1.4994413672391491358223492788056*i] [.49456407933505360591791681140791e-1 +1.4994413672391491358223492788056*i] [ 1.5416516841045247594257824014433] 画出图象ezplot(f ,[-2,2]);hold on ;plot([-2,2],[0,0])实验3 导数及偏导数计算实验目的1.进一步理解导数概念及其几何意义. 2.学习matlab 的求导命令与求导法.实验内容1.学习matlab 命令.建立符号变量命令sym 和syms 调用格式: x=sym(`x `), 建立符号变量x ;syms x y z , 建立多个符号变量x ,y ,z ; matlab 求导命令diff 调用格式:diff (函数)(x f ) , 求)(x f 的一阶导数)(x f '; diff (函数)(x f , n ) , 求)(x f 的n 阶导数)()(x fn (n 是具体整数);diff (函数),(y x f ,变量名x ), 求),(y x f 对x 的偏导数x f∂∂;diff (函数),(y x f , 变量名x ,n ) ,求),(y x f 对x 的n 阶偏导数n n x f∂∂;matlab 求雅可比矩阵命令jacobian ,调用格式:jacobian ([函数),,(z y x f ;函数),,(z y x g ; 函数),,(z y x h ], [z y x ,,])给出矩阵:⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂z h yh xh z g y g x g z f y f x f2.导数概念.导数是函数的变化率,几何意义是曲线在一点处的切线斜率. (1)点导数是一个极限值.例3.1.设xe xf =)(,用定义计算)0(f '.解:)(x f 在某一点0x 的导数定义为极限:x x f x x f x ∆-∆+→∆)()(lim000我们记x h ∆=,输入命令:syms h ;limit((exp(0+h)-exp(0))/h ,h ,0) 得结果:ans=1.可知1)0(='f(2)导数的几何意义是曲线的切线斜率.例3.2.画出xe xf =)(在0=x 处()1,0(P )的切线及若干条割线,观察割线的变化趋势.解:在曲线x e y =上另取一点),(he h M ,则PM 的方程是:011--=--h e x y h .即 11+-=x h e y h取01.0,1.0,1,2,3=h ,分别作出几条割线.h=[3,2,1,0.1,0.01];a=(exp(h)-1)./h ;x=-1:0.1:3; plot(x ,exp(x),’r’);hold on for i=1:5;plot(h(i),exp(h(i)),’r.’) plot(x ,a(i)*x+1) endaxis square作出xe y =在0=x 处的切线1+=x yplot(x ,x+1,’r’)从图上看,随着M 与P 越来越接近,割线PM 越来越接近曲线的割线. 3.求一元函数的导数.(1))(x f y =的一阶导数.例3.3.求x x y )sin(=的导数.解:打开matlab 指令窗,输入指令:dy_dx=diff(sin(x)/x). 得结果:dy_dx=cos(x)/x-sin(x)/x^2.matlab 的函数名允许使用字母、空格、下划线及数字,不允许使用其他字符,在这里我们用dy_dx 表示x y '. 例3.4.求)ln(sin x y =的导数.解: 输入命令:dy_dx=diff(log(sin(x))). 得结果:dy_dx=cos(x)/sin(x).在matlab 中,函数x ln 用log(x)表示,而log10(x)表示x lg . 例3.5.求202)2(x x y +=的导数.解: 输入命令:dy_dx=diff((x^2+2*x)^20). 得结果:dy_dx=20*(x^2+2*x)^19*(2*x+2).注意x 2输入时应为2*x.例3.6.求xx y =的导数. 解: 输入命令:dy_dx=diff(x^x). 得结果:dy_dx =x^x*(log(x)+1).利用matlab 命令diff 一次可以求出若干个函数的导数. 例3.7.求下列函数的导数:1.5221+-=x x y .2.x x y 2cos 2cos 22+=. 3.xy sin 34=.4.x y ln ln 4=. 解: 输入命令:a=diff([sqrt(x^2- 2*x+5),cos(x^2)+2*cos(2*x),4^(sin(x)), log(log(x))]). 得结果: a=[1/2/(x^2-2*x+5)^(1/2)*(2*x-2),-2*sin(x^2)*x-4*sin(2*x), 4^sin(x)*cos(x)*log(4), 1/x/log(x)]. dy1_dx=a(1)↵.dy1_dx=1/2/(x^2-2*x+5)^(1/2)*(2*x-2). dy2_dx=a(2)↵.dy2_dx=-2*sin(x^2)*x-4*sin(2*x). dy3_dx=a(3)↵.dy3_dx=4^sin(x)*cos(x)*log(4).dy4_dx=a(4)↵.dy4_dx=1/x/log(x).由本例可以看出,matlab 函数是对矩阵或向量进行操作的,a(i)表示向量a 的第i 个分量.(2)参数方程所确定的函数的导数.设参数方程⎩⎨⎧==)()(t y y t x x 确定函数)(x f y =,则y 的导数)()(t x t y dx dy ''=. 例3.8.设⎩⎨⎧-=-=)cos 1()sin (t a y t t a x ,求dx dy .解: 输入命令:dx_dt=diff(a*(t-sin(t)));dy_dt=diff(a*(1-cos(t))); dy_dx=dy_dt/dx_dt. 得结果:dy_dx=sin(t)/(1-cos(t)). 其中分号的作用是不显示结果. 4.求多元函数的偏导数.例3.9.设 u=222z y x ++求 u 的一阶偏导数.解: 输入命令:diff((x^2+y^2+z^2)^(1/2), x). 得结果:ans=1/(x^2+y^2+z^2)^(1/2)*x. 在命令中将末尾的x 换成y 将给出y 的偏导数:ans=1/(x^2+y^2+z^2)^(1/2)*y. 也可以输入命令:jacobian((x^2+y^2+z^2)^(1/2),[x y]). 得结果:ans=[1/(x^2+y^2+z^2)^(1/2)*x , 1/(x^2+y^2+z^2)^(1/2)*y]给出矩阵⎪⎭⎫ ⎝⎛∂∂∂∂y u x u ,.例3.10.求下列函数的偏导数:1.)(1x yarctg z =. 2.yx z =2.解: 输入命令:diff(atan(y/x). 得结果:ans=-y/x^2/(1+y^2/x^2). 输入命令:diff(atan(y/x), y). 得结果:ans=1/x/(1+y^2/x^2). 输入命令:diff(x^y , x). 得结果:ans=x^y*y/x . 输入命令:diff(x^y , y). 得结果:ans=x^y*log(x).使用jacobian 命令求偏导数更为方便. 输入命令:jacobian([atan(y/x),x^y],[x ,y]). 得结果:ans=[ -y/x^2/(1+y^2/x^2), 1/x/(1+y^2/x^2)] [ x^y*y/x , x^y*log(x)]. 5.求高阶导数或高阶偏导数.例3.11.设xe x xf 22)(=,求)()20(x f.解:输入指令:diff(x^2*exp(2*x),x ,20). 得结果: ans =99614720*exp(2*x)+20971520*x*exp(2*x)+1048576*x^2*exp(2*x)例3.12.设224623y x y x z +-=,求y x z y z x z ∂∂∂∂∂∂∂22222,,.解:输入命令:diff(x^6-3*y^4+2*x^2*y^2,x ,2)可得到22x z ∂∂:ans=30*x^4+4*y^2.将命令中最后一个x 换为y 得22y z ∂∂:ans=-36*y^2+4*x^2. 输入命令:diff(diff(x^6-3*y^4+2*x^2*y^2,x),y)可得y x z ∂∂∂2:ans=8*x*y同学们可自己计算x y z∂∂∂2比较它们的结果.注意命令:diff(x^6-3*y^4+2*x^2*y^2,x ,y),是对y 求偏导数,不是求y x z∂∂∂2.6.求隐函数所确定函数的导数或偏导数 例3.13.设e e x xy =+-ln ,求dx dy解:e ex y x F xy -+=-ln ),(,先求x F ',再求y F '. 输入命令:df_dx=diff(log(x)+exp(-y/x)-exp(1),x)得到x F ':df_dx=1/x+y/x^2*exp(-y/x). 输入命令:df_dy=diff(log(x)+exp(-y/x)-exp(1),y) 得到y F ':df_dy=-1/x*exp(-y/x) 输入命令:dy_dx=-df_dx/df_dy 可得所求结果:dy_dx=-(-1/x-y/x^2*exp(-y/x))*x/exp(-y/x).例3.14.设0)()cos()sin(=++xz tg yz xy ,求y zx z ∂∂∂∂,解:)()cos()sin()(xz tg yz xy x F ++=输入命令:a=jacobian(sin(x*y)+cos(y*z)+tan(z*x),[x ,y ,z])可得矩阵()z y x F F F ''',,a=[cos(x*y)*y+(1+tan(z*x)^2)*z ,cos(x*y)*x-sin(y*z)*z , -sin(y*z)*y+(1+tan(z*x)^2)*x]. 输入命令:dz_dx=-a(1)/a(3) 得:dz_dx=(-cos(x*y)*y-(1+tan(z*x)^2)*z)/(-sin(y*z)*y+(1+tan(z*x)^2)*x) 输入命令:dz_dy=-a(2)/a(3) 得:dz_dy=(-cos(x*y)*x+sin(y*z)*z)/(-sin(y*z)*y+(1+tan(z*x)^2)*x)实验4 积分计算实验目的1.通过本实验加深理解积分理论中分割、近似、求和、取极限的思想方法. 2.学习并掌握用matlab 求不定积分、定积分、二重积分、曲线积分的方法. 3.学习matlab 命令sum 、symsum 与int . 实验内容1.学习matlab 命令(1)求和命令sum 调用格式.sum(x),给出向量x 的各个元素的累加和,如果x 是矩阵,则sum(x)是一个元素为x 的每列列和的行向量.例4.1.x=[1,2,3,4,5,6,7,8,9,10];↵ sum(x)↵ ans=55例4.2.x=[1,2,3;4,5,6;7,8,9]↵ x=1 2 3 4 5 6 7 8 9 sum(x)↵ans=12 15 18(2)求和命令symsum 调用格式.symsum(s ,n), 求∑nssymsum(s ,k ,m ,n),求∑=nm k s当x 的元素很有规律,比如为表达式是)(k s 的数列时,可用symsum 求得x 的各项和,即 symsum ),1),((n k s =)()2()1(n s s s +++symsum )()1()(),,),((n s m s m s n m k k s ++++= 例4.3.syms k n ↵ symsum(k ,1,10)↵ ans=55symsum(k^2,k ,1,n)↵ans=1/3*(n+1)^3-1/2*(n+1)^2+1/6*n+1/6 (3)matlab 积分命令int 调用格式int (函数)(x f ) 计算不定积分⎰dx x f )(int (函数),(y x f ,变量名x ) 计算不定积分⎰dx y x f ),(int (函数b a x f ,),() 计算定积分⎰badxx f )(int (函数),,(y x f 变量名b a x ,,) 计算定积分⎰badxy x f ),(2.计算不定积分 例4.4.计算xdxx ln 2⎰解:输入命令:int(x^2*log(x)) 可得结果:ans=1/3*x^3*log(x)-1/9*x^3 注意设置符号变量.例4.5.计算下列不定积分: 1.dxx a ⎰-222.⎰++dx x x 31313.⎰xdxx arcsin 2解:首先建立函数向量. syms xsyms a realy=[sqrt(a^2-x^2),(x-1)/(3*x-1)^(1/3),x^2*asin(x)]; 然后对y 积分可得对y 的每个分量积分的结果.int(y ,x)↵ ans =[1/2*x*(a^2-x^2)^(1/2)+1/2*a^2*asin((1/a^2)^(1/2)*x), -1/3*(3*x-1)^(2/3)+1/15*(3*x-1)^(5/3),1/3*x^3*asin(x)+1/9*x^2*(1-x^2)^(1/2)+2/9*(1-x^2)^(1/2)] 3.定积分的概念.定积分是一个和的极限.取xe xf =)(,积分区间为]1,0[,等距划分为20个子区间. x=linspace(0,1,21);选取每个子区间的端点,并计算端点处的函数值. y=exp(x);取区间的左端点乘以区间长度全部加起来. y1=y(1:20);s1=sum(y1)/20 s1=1.6757s1可作为⎰10dx e x 的近似值.若选取右端点:y2=y(2:21);s2=sum(y2)/20 s2=1.7616s2也可以作为⎰10dx e x 的近似值.下面我们画出图象.plot(x ,y);hold onfor i=1:20 fill([x(i),x(i+1),x(i+1),x(i),x(i)],[0,0,y(i),y(i),0],’b’)end如果选取右端点,则可画出图象. for i=1:20; fill([x(i),x(i+1),x(i+1),x(i),x(i)],[0,0,y(i+1),y(i+1),0],’b’) hold on endplot(x ,y ,’r’)在上边的语句中,for … end 是循环语句,执行语句体内的命令20次,fill 命令可以填充多边形,在本例中,用的是兰色(blue)填充.从图上看211s dx e s x <<⎰,当分点逐渐增多时,12s s -的值越来越小,读者可试取50个子区间看一看结果怎样.下面按等分区间计算∑∑=∞→=∞→=∆ξn i n i n ni i n n ex f 111lim)(limsyms k ns=symsum(exp(k/n)/n ,k ,1,n); limit(s ,n ,inf) 得结果ans=exp(1)-14.计算定积分和广义积分.例4.6.计算⎰10dx e x .解:输入命令:int(exp(x),0,1)得结果ans=exp(1)-1.这与我们上面的运算结果是一致的. 例4.7.计算⎰-201dxx解:输入命令:int(abs(x-1),0,2)得结果ans =1.本例用mathematica 软件不能直接求解. 例4.8.判别广义积分⎰+∞11dx x p 、⎰+∞∞--πdx e x 2221与⎰-202)1(1dx x 的敛散性,收敛时计算积分值.解:对第一个积分输入命令:syms p real ;int(1/x^p ,x ,1,inf)得结果ans =limit(-1/(p-1)*x^(-p+1)+1/(p-1),x = inf).由结果看出当1<p 时,x^(-p+1)为无穷,当1>p 时,ans=1/(p-1),这与课本例题是一致的.对第二个积分输入命令:int(1/(2*pi)^(1/2)*exp(-x^2/2),-inf ,inf) 得结果:ans=7186705221432913/18014398509481984*2^(1/2)*pi^(1/2) 由输出结果看出这两个积分收敛.对后一个积分输入命令:int(1/(1-x)^2,0,2)结果得ans=inf .说明这个积分是无穷大不收敛. 例4.9.求积分⎰t dxxx 0sin解:输入命令:int(sin(x)/x ,0,t),可得结果sinint(t),通过查帮助(help sinint )可知sinint(t)=⎰t dxxx 0sin,结果相当于没求!实际上matlab 求出的只是形式上的结果,因为这类积分无法用初等函数或其值来表示.尽管如此,我们可以得到该函数的函数值.输入vpa(sinint(0.5))可得sinint(0.5)的值.5.二重积分计算 例4.10.求二次积分⎰⎰+12102x x xydydx解:输入命令:int(int(x*y ,y ,2*x ,x^2+1),x ,0,1) 得结果ans=1/12. 例4.11.求⎰⎰≤++π12222))(sin(y x dxdyy x解:积分区域用不等式可以表示成2211,11x y x x -≤≤--≤≤-,二重积分可化为二次积分⎰⎰----+π22112211)(sin(x x dyy x dx,输入命令:int(int(sin(pi*(x^2+y^2)),y ,-sqrt(1-x^2),sqrt(1-x^2)),x ,-1,1) 由输出结果可以看出,结果中仍带有int ,表明matlab 求不出这一积分的值.采用极坐标可化为二次积分⎰⎰ππ20102)sin(drr r da ,输入命令:int(int(r*sin(pi*r^2),r ,0,1),a ,0,2*pi) 可得结果为ans=2.6.曲线积分例4.12.求曲线积分⎰L xyds ,其中L 为曲线122=+y x 在第一象限内的一段.解:曲线的参数方程是)20(,sin ,cos π≤≤==t t y t x 曲线积分可以化为⎰π⋅0s i n c o s t d tt .输入命令:int(cos(t)*sin(t),0,pi/2) 执行后即可求出曲线积分结果1/2.实验5 matlab 自定义函数与导数应用实验目的1.学习matlab 自定义函数.2.加深理解罗必塔法则、极值、最值、单调性. 实验内容1.学习matlab 自定义函数及求函数最小值命令.函数关系是指变量之间的对应法则,这种对应法则需要我们告诉计算机,这样,当我们输入自变量时,计算机才会给出函数值,matlab 软件包含了大量的函数,比如常用的正弦、余弦函数等.matlab 允许用户自定义函数,即允许用户将自己的新函数加到已存在的matlab 函数库中,显然这为matlab 提供了扩展的功能,无庸置疑,这也正是matlab 的精髓所在.因为matlab 的强大功能就源于这种为解决用户特殊问题的需要而创建新函数的能力.matlab 自定义函数是一个指令集合,第一行必须以单词function 作为引导词,存为具有扩展名“.m ”的文件,故称之为函数M -文件.函数M -文件的定义格式为:function 输出参数=函数名(输入参数) 函数体 …… 函数体一旦函数被定义,就必须将其存为M -文件,以便今后可随时调用.比如我们希望建立函数12)(2++=x x x f ,在matlab 工作区中输入命令:syms x ;y=x^2+2*x+1;不能建立函数关系,只建立了一个变量名为y 的符号表达式,当我们调用y 时,将返回这一表达式.y ↵y=x^2+2*x+1当给出x 的值时,matlab 不能给出相应的函数值来. x=3;y ↵y=x^2+2*x+1 如果我们先给x 赋值.x=3;y=x^2+2*x+1 得结果:y=16若希望得出2|=x y 的值,输入: x=2;y ↵得结果:y=16,不是2=x 时的值.读者从这里已经领悟到在matlab 工作区中输入命令:y=x^2+2*x+1不能建立函数关系,如何建立函数关系呢?我们可以点选菜单Fill\New\M-fill 打开matlab 文本编辑器,输入: function y=f1(x) y=x^2+2*x+1;存为f1.m .调用该函数时,输入: syms x ;y=f1(x)↵ 得结果:y= x^2+2*x+1.输入: y1=f1(3)↵ 得结果:y1=16matlab 求最小值命令fmin 调用格式:fmin(‘fun’,a ,b) 给出)(x f 在),(b a 上的最小值点. 2.自定义函数例5.1.建立正态分布的密度函数22)(21),.,(μ--σπ=μσx e x f解:打开文本编辑器,输入:function y=zhengtai(x ,a ,b)y=1/sqrt(2*pi)/a*exp(-(x-b).^2/2/a^2); 存为zhengtai.m .调用时可输入命令: y=zhengtai(1,1,0)得结果:y=0.2420.此即)0,1,1(f 的值.如果想画出标准正态分布的密度函数的图象,输入: ezplot(zhengtai(x ,1,0))例5.2.解一元二次方程02=++c bx ax .解:我们希望当输入c b a ,,的值时,计算机能给出方程的两个根.在文本编辑器中建立名为rootquad.m 的文件.function [x1,x2]=rootquad(a ,b ,c) d=b*b-4*a*c ;x1=(-b+sqrt(d))/(2*a) x2=(-b-sqrt(d))/(2*a) 比如求方程07322=-+x x 的根,可用语句: [r1,r2]=rootquad(2,3,-7)得结果:r1=1.2656 r2=-2.76562.验证罗必塔法则.罗必塔法则是指在求00及∞∞的极限时,可用导数之比的极限来计算(如果导数之比的极限存在或∞)例5.3.以x ba xx x -→0lim 为例验证罗必塔法则.解:这是00型极限f=a^x-b^x ;g=x ;L=limit(f/g ,x ,0)得结果:L=log(a)-log(b)df=diff(f ,x);dg=diff(g ,x);L1=limit(df/dg ,x ,0) 得结果:L1=log(a)-log(b) 从结果看出:L=L1,即x b a x x x -→0lim=x b a x x x '-→'0)(lim4.函数的单调性与极值.例5.4.求函数396)(23++-=x x x x f 的单调区间与极值.解:求可导函数的单调区间与极值,就是求导函数的正负区间与正负区间的分界点,利用matlab 解决该问题,我们可以先求出导函数的零点,再画出函数图象,根据图象可以直观看出函数的单调区间与极值.输入命令:f=x^3-6*x^2+9*x+3;df=diff(f ,x);s=solve(df) 得结果:ans=[1,3],画出函数图象. ezplot(f ,[0,4])从图上看,)(x f 的单调增区间为)1,(-∞、),1(+∞,单调减区间是)3,1(,极大值7)1(=f ,极小值3)3(=f .我们可以建立一个名为dandiao.m 的M —文件,用来求求函数的单调区间. disp(‘输入函数(自变量为x )’) syms xf=input('函数f(x)=') df=diff(f); s=solve(df) a=[];for i=1:size(s); a(i)=s(i); endezplot(f ,[min(a)-1,max(a)+1])要求函数)1ln(x x y +-=的单调区间与极值,可调用dandiao.m .输入: dandiao ↵在matlab 工作区出现以下提示: 输入函数(自变量为x ) 函数f(x)=在光标处输入:x-log(1+x),可得结果s=0.从图上看,)(x f 的单调增区间为),0(+∞,单调减区间是)0,(-∞,极小值0)0(=f . 5.函数的最值调用求函数最小值命令fmin 时,可得出函数的最小值点,为求最小值,必须建立函数M —文件.例5.5.求函数1)3()(2--=x x f 在区间)5,0(上的最小值. 解:我们可以建立一个名为f.m 的函数M -文件. function y=f(x) y=(x-3).^2-1; 并且调用fminx=fmin((‘f’,0,5)得:x=3,)(x f 在最小值点处的值(函数最小值)是1)3(-=f .求最大值时可用x=fmin(‘-f(x)’,a ,b)实验6 matab 矩阵运算与数组运算实验目的:1.理解矩阵及数组概念.2.掌握matlab 对矩阵及数组的操作命令.实验内容:1.矩阵与数组的输入. 对于较小较简单的矩阵,从键盘上直接输入矩阵是最常用的数值矩阵创建方法.用这种方法输入矩阵时注意以下三点:(1)整个输入矩阵以方括号“[ ]”为其首尾; (2)矩阵的元素必须以逗号“,”或空格分隔; (3)矩阵的行与行之间必须用分号“;”或回车键隔离. 例1:下面的指令可以建立一个3行4列的矩阵 a . a=[1 2 3 4;5 6 7 8;9 10 11 12] (下面是屏幕的显示结果) a =1 2 3 4 5 6 7 8 9 10 11 12 分号“;”有三个作用:(1)在“[ ]”方括号内时它是矩阵行间的分隔符.例子如上. (2)它可用作指令与指令间的分隔符.(3)当它存在于赋值指令后时,该指令执行后的结果将不显示在屏幕上. 例如,输入指令:b=[1 2 0 0;0 1 0 0;1 1 1 1];矩阵b 将不被显示,但b 已存放在matlab 的工作内存中,可随时被以后的指令所调用或显示.例如,输入指令: b得结果: b =1 2 0 0 0 1 0 0 1 1 1 1数值矩阵的创建还可由其他方法实现.如:利用matlab 函数和语句创建数值矩阵;利用m 文件创建数值矩阵;从其他文件获取数值矩阵.有兴趣的读者可参阅其他参考书.数组可以看成特殊的矩阵,即1行n列的矩阵,数组的输入可以采用上面矩阵的输入方法.例2:输入以下指令以建立数组c.c=[1 2 3 4 5 6 7 8]c =1 2 3 4 5 6 7 8另外还有两种方法输入数组.请看下面两个例子.例3:在0和2中间每隔0.1一个数据建立数组d.解:输入指令:d=0:0.1:2d =Columns 1 through 70 0.1000 0.2000 0.3000 0.4000 0.50000.6000Columns 8 through 140.7000 0.8000 0.9000 1.0000 1.1000 1.20001.3000Columns 15 through 211.4000 1.5000 1.6000 1.7000 1.8000 1.90002.0000注意“:”的使用方法.例4:在0和2之间等分地插入一些分点,建立具有10个数据点的数组e.解:输入指令:e=linspace(0,2,10)e =Columns 1 through 70 0.2222 0.4444 0.6667 0.8889 1.11111.3333Columns 8 through 101.5556 1.77782.0000linspace(a,b,n)将建立从a到b有n个数据点的数组.2.常用矩阵的生成.matlab为方便编程和运算,提供了一些常用矩阵的生成指令:n⨯单位矩阵eye(n) nn⨯全1矩阵ones(n) nn⨯零矩阵zeros(n) nm⨯标准型矩阵eye(m,n) nm⨯全1矩阵ones(m,n) nm⨯零矩阵zeros(m,n) neye(size(A)) 与A同型的标准型矩阵ones(size(A)) 与A同型的全1矩阵zeros(size(A))与A同型的零矩阵其中指令size(A)给出矩阵A的行数和列数.例5:生成以下矩阵.3⨯零矩阵.(1)33 全1矩阵.(2)6(3)与例1中矩阵a同型的标准型矩阵.解:输入下面指令:d=zeros(3)d =0 0 00 0 00 0 0e=ones(3,6)e =1 1 1 1 1 11 1 1 1 1 11 1 1 1 1 1f=eye(size(a))f =1 0 0 00 1 0 00 0 1 03.矩阵元素的标识矩阵的元素、子矩阵可以通过标量、向量、冒号的标识来援引和赋值.(1)矩阵元素的标识方式A(ni,nj).ni,nj都是标量.若它们不是整数,则在调用格式中会自动圆整到最临近整数.ni指定元素的行位置,nj指定元素的列位置.(2)子矩阵的序号向量标识方式A(v,w).v,w是向量,v,w中的任意一个可以是冒号“:”,他表示取全部行(在v位置)或全部列(在w位置).v,w中所用序号必须大于等于1且小于等于矩阵的行列数.例6:元素和矩阵的标识a=[1 2 3 4;5 6 7 8;9 10 11 12]a =1 2 3 45 6 7 89 10 11 12a24=a(2,4)a24 =8a1=a([1,2],[2,3,4])a1 =2 3 46 7 8a2=a([1,2],[2,3,1])a2 =2 3 16 7 5a3=a([3,1],:)a3 =9 10 11 121 2 3 4a([1,3],[2,4])=zeros(2)a =1 0 3 05 6 7 89 0 11 04.矩阵运算和数组运算.矩阵运算的指令和意义如下:A' 矩阵A的共轭转置矩阵,当A是实矩阵时,A'是A的转置矩阵.A+B 两个同型矩阵A与B相加.A-B 两个同型矩阵A与B相减.A*B 矩阵A与矩阵B相乘,要求A的列数等于B的行数.s+B 标量和矩阵相加(matlab约定的特殊运算,等于s加B的每一个分量).s-B B-s 标量和矩阵相减(matlab约定的特殊运算,含意同上).s*A 数与矩阵A相乘.例7:a=[1 2 3;4 5 6]a =1 2 34 5 6b=[-1 0 1;3 1 2]b =-1 0 13 1 2a'ans =1 42 53 6a+bans =0 2 47 6 8a-bans =2 2 21 4 41+aans =2 3 45 6 7a-1ans =0 1 23 4 52*bans =-2 0 26 2 4c=[2 4;1 3;0 1]c =2 41 30 1a*cans =4 1313 37数组可以看成特殊矩阵即一行n列的矩阵,矩阵运算的指令和含意同样适用于数组运算.如果在运算符前加“.”,含意将有所不同.A.*B 同维数组或同型矩阵对应元素相乘.A./B A的元素被B的元素对应除.A.^n A的每个元素n次方.p.^A 以p为底,分别以A的元素为指数求幂.例8:a=[1 2 3;4 5 6]a =1 2 34 5 6b=[-1 0 1;3 1 2]b =-1 0 13 1 2a.*bans =-1 0 312 5 12a./bWarning: Divide by zero.ans =-1.0000 Inf 3.00001.3333 5.0000 3.0000a.^2ans =1 4 916 25 362.^aans =2 4 816 32 64实验7矩阵与线性方程组实验目的:1.掌握matlab求矩阵的秩命令.2.掌握matlab求方阵的行列式命令.3.理解逆矩阵概念,掌握matlab求逆矩阵命令.4.会用matlab求解线性方程组.实验内容:1.矩阵的秩.指令rank(A)将给出矩阵A的秩.例1:a=[3 2 -1 -3 -2;2 -1 3 1 -3;7 0 5 -1 -8]a =3 2 -1 -3 -22 -13 1 -37 0 5 -1 -8rank(a)ans =22.方阵的行列式.指令det(A)给出方阵A的行列式.例2:b=[1 2 3 4;2 3 4 1;3 4 1 2;4 1 2 3];det(b)ans =160det(b')ans =160c=b;c(:,1)=2*b(:,1);det(c)ans =320det(b(:,[3 2 1 4]))ans =-160d=b;d(2,:);det(d)ans =160你能解释上例中的运算结果吗?在这里我们实际上验证了行列式的性质.3.逆矩阵指令inv(A)给出方阵A的逆矩阵,如果A不可逆,则inv(A)给出的矩阵的元素都是Inf.例3:设⎪⎪⎪⎭⎫⎝⎛=343122321A,求A的逆矩阵.解:输入指令:A=[1 2 3;2 2 1;3 4 3];B=inv(A)B =1.0000 3.0000 -2.0000-1.5000 -3.0000 2.50001.0000 1.0000 -1.0000还可以用伴随矩阵求逆矩阵,打开m 文件编辑器,建立一个名为companm 的M-文件文件内容为:function y=companm(x)[n,m]=size(x);y=[];for j=1:n;a=[];for i=1:n;x1=det(x([1:i-1,i+1:n],[1:j-1,j+1:n]))*(-1)^(i+j);a=[a,x1];endy=[y;a];end利用该函数可以求出一个矩阵的伴随矩阵.输入命令:C=1/det(A)*companm(A)C =1.0000 3.0000 -2.0000-1.5000 -3.0000 2.50001.0000 1.0000 -1.0000利用初等变换也可以求出逆矩阵,构造n 行2n 列的矩阵(A E),并进行行初等变换,当把A 变为单位矩阵时,E 就变成了A 的逆矩阵.利用matlab 命令rref 可以求出矩阵的行简化阶梯形.输入命令:D=[A,eye(3)]D =1 2 3 1 0 02 2 1 0 1 03 4 3 0 0 1rref(D)ans =1.0000 0 0 1.0000 3.0000 -2.0000 0 1.0000 0 -1.5000 -3.0000 2.5000 0 0 1.0000 1.0000 1.0000 -1.0000n m ⨯线性方程组B AX =的求解是用矩阵除来完成的,B A X \=,当n m =且A 可逆时,给出唯一解.这时矩阵除B A \相当于B A inv *)(;当m n >时,矩阵除给出方程的最小二乘解;当m n <时,矩阵除给出方程的最小范数解.例4:解方程组:⎪⎪⎩⎪⎪⎨⎧=-+=++=+-+=++-12121243132143214321x x x x x x x x x x x x x x 解:输入命令:a=[1 -1 1 2;1 1 -2 1;1 1 1 0;1 0 1 -1];b=[1;1;2;1];x=a\bx =0.83330.75000.41670.2500输入命令:z=inv(a)*bz =0.83330.75000.41670.2500例5:解方程组:⎪⎩⎪⎨⎧=-++-=-++-=--++8343242222543215432154321x x x x x x x x x x x x x x x解:方程的个数和未知数不相等,用消去法,将增广矩阵化为行简化阶梯形,如果系数矩阵的秩不等于增广矩阵的秩,则方程组无解;如果系数矩阵的秩等于增广矩阵的秩,则方程组有解,方程组的解就是行简化阶梯形所对应的方程组的解.输入命令:a=[2 1 1 -1 -2 2;1 -1 2 1 -1 4;2 -3 4 3 -1 8];rref(a)ans =1 0 0 0 0 00 1 0 -1 -1 00 0 1 0 -1 2由结果看出,4x ,5x 为自由未知量,方程组的解为:01=x542x x x +=532x x +=例6:解方程组:⎪⎪⎩⎪⎪⎨⎧=+--=--=-+-=+--0320030432142143214321x x x x x x x x x x x x x x x解:输入命令:a=[1 -1 -1 1;1 -1 1 -3;1 -1 0 -1;1 -1 -2 3];rref(a)ans =1 -1 0 -10 0 1 -20 0 0 00 0 0 0由结果看出,2x ,4x 为自由未知量,方程组的解为:421x x x +=432x x =实验8 常微分方程与级数实验目的:1.学习用matlab求解微分方程命令dsolve.2.学习matlab泰勒级数展开命令.3.巩固幂级数的收敛半径、和等概念.实验内容:1.学习matlab命令.matlab求解微分方程命令dsolve,调用格式为:dsolve(‘微分方程’)给出微分方程的解析解,表示为t的函数.dsolve(‘微分方程’,‘初始条件’)给出微分方程初值问题的解,表示为t的函数.dsolve(‘微分方程’,‘变量x’)给出微分方程的解析解,表示为x的函数.dsolve(‘微分方程’,‘初始条件’,‘变量x’)给出微分方程初值问题的解,表示为x的函数.求已知函数的taylor展开式taylor命令,调用格式为:taylor(函数f(x)) f(x)的5次taylor多项式.taylor(函数f(x),n) f(x)的n-1次taylor多项式.taylor(函数f(x),a) f(x)在a点的taylor多项式.求级数的和命令symsum调用格式为:symsum(S,n),求∑n Ssymsum(S,k,m,n),求∑=nmkSmatlab求极限命令limit调用格式为:limit(函数f(x),变量x,自变量的趋向值)2.求解一阶微分方程.微分方程在输入时,y'应输入Dy,y''应输入D2y等,D应大写.例1:求微分方程22xxexydxdy-=+的通解.解:输入命令:dsolve('Dy+2*x*y=x*exp(-x^2)')结果为ans =1/2*(1+2*exp(-2*x*t)*C1*exp(x^2))/exp(x^2)系统默认的自变量是t,显然系统把x当作常数,把y当作t的函数求解.输入命令:dsolve('Dy+2*x*y=x*exp(-x^2)','x')得正确结果:ans =1/2*(x^2+2*C1)/exp(x^2)例2:求微分方程0=-+'x e y y x 在初始条件e y x 21==下的特解.解:输入命令:dsolve('x*Dy+y-exp(x)=0','y(1)=2*exp(1)','x')得结果为:ans =1/x*(exp(x)+exp(1))例3:求微分方程0cos 2)1(2=-+-x xy dx dy x 在初始条件10==x y 下的特解.解:输入命令:dsolve('(x^2-1)*Dy+2*x*y-cos(x)=0','y(0)=1','x')得结果为ans =1/(x^2-1)*(sin(x)-1)3.求解二阶微分方程.例4:求03=+'+''x e y y 的通解.解:输入命令:dsolve('D2y+3*Dy+exp(x)=0','x')得结果:ans =-1/4*exp(x)+C1+C2*exp(-3*x)例5:求解微分方程.02='-''y e y y 解:输入命令:dsolve('D2y-exp(2*y)*Dy=0','x')得结果:ans =1/2*log(-2*C1/(-1+exp(2*x*C1+2*C2*C1)))+x*C1+C2*C14.taylor 展开式.例6:求函数y=cosx 在x=0点处的5阶taylor 展开式及在3π=x 处的6阶taylor 展开式.解:输入命令:syms x;taylor(cos(x))得结果:ans =1-1/2*x^2+1/24*x^4输入命令:taylor(cos(x),pi/3,7)得结果:ans =1/2-1/2*3^(1/2)*(x-1/3*pi)-1/4*(x-1/3*pi)^2+1/12*3^(1/2)*(x- 1/3*pi)^3+1/48*(x-1/3*pi)^4-1/240*3^(1/2)*(x-1/3*pi)^5-1/1440*(x-1/3*pi)^6 5.级数求和.例7:求∑∞=121n n .解:输入命令:syms n;symsum(1/2^n,1,inf) 得结果:ans =1例8:求幂级数∑∞=⨯12nnnnx的和函数.解:输入命令:symsum(x^n/(n*2^n),n,1,inf) 得结果ans =-log(1-1/2*x)例9:求幂级数∑∞=1nnnx的和函数.解:输入命令:symsum(n*x^n,n,1,inf) 得结果:ans =x/(x-1)^26.判别级数敛散性.例10:判断数项级数∑∞=+1)1(1nnn的收敛性.解:输入求和命令:symsum(1/(n*(n+1)),n,1,inf) 得结果:ans =1求和得是1,说明该级数收敛.例11:判别级数∑∞=+1)1(sinnnnπ的敛散性.解:输入命令:symsum(sin(pi/(n*(n+1))),1,inf)得结果:ans =sum(sin(pi/n/(n+1)),pi = 1 .. inf)由执行结果看出仍含有sum,说明用matlab不能求出其和,可采用比较判别法,取比较级数为P级数∑∞=121nn,取二者通项比值的极限.输入命令:limit(sin(pi/(n*(n+1)))/(1/n^2),n,inf)得结果:ans =pi得值为pi,由所取P级数收敛,得知所要判别的级数也收敛.例12:判别级数∑∞=⎪⎭⎫⎝⎛143nnn的敛散性.解:用比值判别法,输入命令:limit((n+1)*(3/4)^(n+1)/(n*(3/4)^n),n,inf)得结果:ans =3/4极限值小于1,由比值判别法知级数收敛.实际上输入求和命令:symsum(n*(3/4)^n,n,1,inf)得结果:ans =12。
matlab作业五

作业五1.在一天24小时内,从零点开始每隔2个小时测得的环境温度分别为:12,9,9,10,18,24,28,27,25,20,18,15,13,推测中午一点时的温度。
2. 画你自己的手的形状,以执行下面的命令为开始:figure('position', get(0,'screensize'));axes('position',[0 0 1 1]);[x,y]=ginput;将你的手掌张开放在计算机的屏幕上,然后使用计算机鼠标选取一系列点勾勒出手的轮廓。
按回车键结束ginput过程。
现在从点的x和y坐标值看作是两个独立变量的函数,这个独立变量的取值从1到记录的点的数目。
下面可以在变量取值更密的集合上对这两个函数进行插值,并画出结果。
n=length(x);s=(1:n)';t=(1:0.05:n)';u=interp1(s,x,t,'spline');v=interp1(s,y,t,'spline');clf resetplot(x,y,'.',u,v,'-');3. 曲线拟合图形界面操作。
(1) 建立如下的M文件:x=1:10;y=[0.09,0.95,0.9 2.4 2.5 3 5 6.4 8 10.3];plot(x,y,'ro');(2) 运行M文件,打开图形窗口中“TOOL”的“Basic Fitting”命令。
展开对话框,选择数据拟合的类型,同时在图形中显示拟合的结果方程:在“Check to display fits on figure”选择“cubic”,则原始图形显示拟合曲线;选中“show equation”选项。
选中“plot residuals”和“show norm of residuals”。
(3) 进行数据预测:进一步展开对话框,在”enter value”面板中输入”7.5”,单击”Evaluate”,选中”plot evaluated results”。
matlab作业

第一题求解线性方程组AX=B 其中20900836215.87333223107445.06.307925.11---=A ,1652043-=B程序:a=[1 1.5 2 9 7;0 3.6 0.5 -4 4;7 10 -3 22 33;3 7 8.5 21 6;3 8 090 -20];b=[3 -4 20 5 16]'; A=det(a); for i=1:5 D=a;D(:,i)=b;x(i)=det(D)/A; end x运行结果:第二题x (x<1) 计算函数值 2x-1 (1<x<10) 3x-11 (x>=10) 程序:display('第二题') x=input('输入x=') if x<1 xelseif x<10 2*x-1 else3*x-11End运行结果:第三题求一元二次方程02=++c bx ax程序:a=input('a=');b=input('b='); c=input('c='); d=b*b-4*a*c;x=[(-b+sqrt(d))/(2*a),(-b-sqrt(d))/(2*a)];disp(['x1=',num2str(x(1)),',x2=',num2str(x(2))]);x = 3.5653 -0.9255 -0.2695 0.1435 0.0101第二题 输入x=2 x = 2 ans = 3运行结果:第四题输入三角形的三条边,求面积。
程序:disp('请输入三角形的三条边') a=input('a='); b=input('b='); c=input('c=');if a+b>c & b+c>a & c+a>b d=(a+b+c)/2;s=sqrt(d*(d-a)*(d-b)*(d-c)); disp(['三角形的面积是:',num2str(s)]) else a+b<=c|b+c<=a|c+a<=bdisp('不能构成三角形') end运行结果:第五题输入20个数,求其中最大数和最小数。
MATLAB作业南京理工大学

MATLAB作业南京理工大学MATLAB软件语言及程序设计课程论文任课教师:张登峰一、问答题1. MATLAB 、Toolboxes 、Complier2. ans:如果用户未定义变量名,系统用于计算结果存储的默认变量名pi :圆周率i 或j :虚数单位nargin :函数输入参数个数nargout :函数输出参数个数lasterr :存放最新的错误信息 lastwarn :存放最新的警告信息 3. 不会,会得到ans = 1.6180 + 1.1756i ;solve('t^5+32') %计算全部方根 ans =-2 -1/2*5^(1/2)+1/2-1/2*i*2^(1/2)*(5+5^(1/2))^(1/2) 1/2*5^(1/2)+1/2-1/2*i*2^(1/2)*(5-5^(1/2))^(1/2)1/2*5^(1/2)+1/2+1/2*i*2^(1/2)*(5-5^(1/2))^(1/2) -1/2*5^(1/2)+1/2+1/2*i*2^(1/2)*(5+5^(1/2))^(1/2)4. 空格和逗号都能起到分隔符的作用,逗号可作为函数分割符,也可用于区分行,现实运算结果,当然不加标点也显示运算结果,而在大多数情况下,MATLAB 对空格不予处理。
矩阵中空格与逗号相同一些固定的函数调用中,如solve 、subplot 等括号中的逗号不能替代为空格一般MATLAB 对空格不予处理,这些地方可以用空格,却不能用逗号,如表达式中,加空格不影响结果,但是加逗号就是错的;还有如“syms x y z ”,字母间的空格不能替代为逗号。
5. 实数数组: 8字节字符串数组:与字符数的个数有关,每个占2字节单元数组:与cell 中的数据类型有关,一般是在68字节的基础上加上数据所占的内存结构数组:具体字节数不确定,和结构所含的域的个数和数据有关。
每一个域用124个字节,每个字母用2字节,数字用8字节。
MATLAB及应用参考答案

《MATLAB及应用》上机作业学院名称:机械工程学院专业班级:测控1201学生姓名:学生学号:201 年 4 月《MATLAB及应用》上机作业要求及规范一、作业提交方式:word文档打印后提交。
二、作业要求:1.封面:按要求填写学院、班级、姓名、学号,不要改变封面原有字体及大小。
2.内容:只需解答过程(结果为图形输出的可加上图形输出结果),不需原题目;为便于批阅,题与题之间应空出一行;每题答案只需直接将调试正确后的M文件内容复制到word 中(不要更改字体及大小),如下所示:%作业1_1clcA=[1 2 3 4;2 3 5 7;1 3 5 7;3 2 3 9;1 8 9 4];B=[1+4*i 4 3 6 7 7;2 3 3 5 5 4+2*i;2 6+7*i 5 3 4 2;1 8 9 5 4 3];C=A*BD=C(4:5,4:6)三、大作业评分标准:1.提交的打印文档是否符合要求;2.作业题的解答过程是否完整和正确;3.答辩过程中阐述是否清楚,问题是否回答正确;4.作业应独立完成,严禁直接拷贝别人的电子文档,发现雷同者都以无成绩论处。
作业11、用MATLAB 可以识别的格式输入下面两个矩阵12342357135732391894A ⎛⎫⎪⎪ ⎪= ⎪⎪ ⎪⎝⎭,144367723355422675342189543i i B i +⎛⎫⎪+⎪= ⎪+ ⎪⎪⎝⎭再求出它们的乘积矩阵C ,并将C 矩阵的右下角23⨯子矩阵赋给D 矩阵。
赋值完成后,调用相应的命令查看MATLAB 工作空间的占有情况。
解:A=[1 2 3 4;2 3 5 7;1 3 5 7 ;3 2 3 9 ;1 8 9 4;]B=[1+4i 4 3 6 7 7;2 3 3 5 5 4+2i;2 6+7i 5 3 4 2;1 8 9 5 4 3;] B=[1+4i 4 3 6 7 7;2 3 3 5 5 4+2i;2 6+7i 5 3 4 2;1 8 9 5 4 3;] C=A*B D=C(4:5,4:6);2、设矩阵16231351110897612414152⎛⎫⎪⎪ ⎪ ⎪⎝⎭,求A ,1A -,3A ,12A A -+,1'3A A --,并求矩阵A 的特征值和特征向量。
matlab作业

a=imread('d:\abc.jpg');a1=imcrop(a,[80,120,100,50]); subplot(1,2,1),imshow(a);subplot(1,2,2),imshow(a1);----------------------------------------------- c=imread('d:\abc.jpg');c1=imresize(c,0.5);c2=imresize(c,[100,100]);subplot(1,2,1),imshow(c1);subplot(1,2,2),imshow(c2);------------------------------------------------- b=imread('d:\abc.jpg');b1=imadjust(b,[0.2,0.5],[0,1]); imshow(b1);-----------------------------------b=imread('d:\abc.jpg');b1=rgb2gray(b);imshow(b1,16);-------------------------------------RGB = imread('d:\abc.jpg');G = RGB(:,:,2);BW = dither(G);figure, imagesc(G), colormap(gray) figure, image(BW), colormap(gray(2))---------------------------------------------I = imread('d:\123.jpg');J = histeq(I);figure, imshow(I), figure, imshow(J)------------------------------------------------- load treesBW = im2bw(X,map,0.4);figure, imshow(X,map), figure, imshow(BW)------------------------------------------BW1 = imread('circbw.tif');BW2 = bwperim(BW1,8);figure, imshow(BW1)figure, imshow(BW2)--------------------------------------------- I = imread('d:\123.jpg');BW1 = edge(I,'prewitt');BW2 = edge(I,'canny');figure, imshow(BW1)figure, imshow(BW2)-------------------------------------------------1. Make a 3-D binary image containing two overlapping spheres.center1 = -10;center2 = -center1;dist = sqrt(3*(2*center1)^2);radius = dist/2 * 1.4;lims = [floor(center1-1.2*radius) ceil(center2+1.2*radius)];[x,y,z] = meshgrid(lims(1):lims(2));bw1 = sqrt((x-center1).^2 + (y-center1).^2 + ...(z-center1).^2) <= radius;bw2 = sqrt((x-center2).^2 + (y-center2).^2 + ...(z-center2).^2) <= radius;bw = bw1 | bw2;figure, isosurface(x,y,z,bw,0.5), axis equal, title('BW')xlabel x, ylabel y, zlabel zxlim(lims), ylim(lims), zlim(lims)view(3), camlight, lighting gouraud-----------------------------------------------------watershed10202f2.jpg2. Compute the distance transform of the complement of the binaryimage.D = bwdist(~bw);figure, imshow(D,[],'InitialMagnification','fit')title('Distance transform of ~bw')----------------------------------------------watershed10203f3.jpgCompute the watershed transform, and display the resulting label matrix as an RGB image.L = watershed(D);rgb = label2rgb(L,'jet',[.5 .5 .5]);figure, imshow(rgb,'InitialMagnification','fit')title('Watershed transform of D')----------------------------------------------------- watershed10205f1.jpgD = bwdist(~bw);figure, isosurface(x,y,z,D,radius/2), axis equaltitle('Isosurface of distance transform')xlabel x, ylabel y, zlabel zxlim(lims), ylim(lims), zlim(lims)view(3), camlight, lighting gouraud-------------------------------------------------- watershed10206f1.jpgD = -D;D(~bw) = -Inf;L = watershed(D);figure, isosurface(x,y,z,L==2,0.5), axis equaltitle('Segmented object')xlabel x, ylabel y, zlabel zxlim(lims), ylim(lims), zlim(lims)view(3), camlight, lighting gouraudfigure, isosurface(x,y,z,L==3,0.5), axis equaltitle('Segmented object')xlabel x, ylabel y, zlabel zxlim(lims), ylim(lims), zlim(lims)view(3), camlight, lighting gouraud。
MATLAB练习作业(已做)2021

MATLAB练习作业(已做)2021说明:如在测试时请将程序中的中文字符改为西文(部分程序为手写,并未经matlab验证)2021年春《matlab基础》第一次上机练习与作业练1:脚本文件建立一个文件名为helloworld的脚本文件,运行该文件时显示出如下文字:helloworld!iamgoingtolearnmatlab提示:用disp显示字符串,将要显示的字符号串用单引号引起来。
如'thisisastring'练2:变量获取并保存当前的日期与时间用函数clock分解成一个变量,变量名叫start用size查看start的维数,它是一个行向量还是一个列向量??start包含什么内容?用helpclock查看用函数datestr将向量start转换成字符串,获得代莱变量,名叫startstring?将start与startstring留存为mat文件,文件名为starttime在练习1建立的脚本文件helloworld.m文件中,用load函数导入变量starttime,并显示如下文字:istartedlearningmatlabon*startdateandtime*练习3:标量你将要以指数快速增长的速度去自学matlab,将如下内容嵌入至helloworld.m文件中?假设你的自学时间就是一个常量,为1.5days,将此时间用秒则表示,参数值变量tau?假设课程持续时间为5days.将这个时间单位切换为秒,留存在变量endofclass中?将学到的知识描述为t的函数,函数方程为:用函数datestr将向量start转换成字符串,获得代莱变量startstring在课程结束时间endofclass,你将学到多少知识?用变量knowledgeatend表示(指数函数exp)用变量knowledgeatend,表明如下语句:attheendofthematlabclass,iwillknowx%ofmatlab提示:将数转换成字符串,用num2str练4:向量运算计算从课程开始到现在经过的时间,用秒表示.在helloworld.m中,创建一系列变量,局部变量分别为:secpermin,secperhour,secperday,secpermonth(假设每个月30.5天),以及secperyear.将变量按次序secperyear,secpermonth,secperday,secperhour,secpermin,1排序,二重成一个行向量,命名为secconversion??用时钟函数clock生成一个向量currenttime排序经过的时间elapsedtime,用currenttime与start相乘.?通过向量secondconversion与elapsedtime的数量内积运算排序时间t,显示当前的时间水平,用变量currentknowledge表示.()表明如下语句:atthistime,iknowx%ofmatlab练5:向量函数计算你的学习轨迹.在helloworld.m中,创建线性时间向量tvec,涵盖从0至endofclass的10000个样本点.计算在每个时间点处对应的知识值,仍然用函数练6:向量串行什么时候你将学到50%的matlab知识?.在向量knowledgevec中,搜寻最吻合0.5的元素所在的边线.?用halftime留存对应的时间?表明如下语句:iwillknowhalfofmatlabafterxdays要将halftime用secperday转换成天数练7:绘图画出学习的轨迹图?.在helloworld.m中,关上一个代莱图形窗口(figure)用向量tvec与knowledgevec画出知识轨迹,画图时,将时间单位转换为天?用图形窗口中的zoomin查看halftime,与前面计算结果相比较.clear,clc;disp('helloworld!');disp('iamgoingtolearnmatlab');start=clock;[startx,starty]=size(start);ifstartx>startydisp('一个行向量')elsedisp('一个列向量');endstartstring=datestr(start);savestarttime.matstartstartstring;waittime=input('为并使程序达至较好的继续执行效果,恳请输出程序须要暂停时间(秒):');state=0;h=waitbar(0,'恳请等候...','name','进度条','createcancelbtn',...'state=1;delete(h);clearh');h1=findall(h,'style','pushb utton');set(h1,'string','中止','fontsize',10)fori=1:100waitbar(i/100,h,['已暂停时间百分比'num2str(i)'%']);pause(waittime/100);ifstatebreakendendifexist('h')==1delete(h);endloadstarttimedisp('istartedlearningmatlabon*startdateandtime*');tau=1.5*24*3600;endofclass=5*24*3600;knowledgeatend=1-exp(-tau/endofclass);disp(['attheendofthematlabclass,iwillknow',num2str(knowledgeatend*100),'%ofmat lab']);secpermin=60;secperhour=3600;secperday=24*secperhour;secpermonth=30.5*secperday;secperyear=12*secpermonth;secondconversion=[secperyear,secpermonth,secperday,secperhour,secpermin,1];cur renttime=clock;elapsedtime=currenttime-start;elapsedtime=elapsedtime.*secondconversion;currentknowledge=1-exp(-elapsedtime/endofclass);disp(['atthistime,iknow',num2str(sum(currentknowledge)*100),'%ofmatlab']);tvec =linspace(0,endofclass,1000);knowledgevec=1-exp(-tvec./endofclass);halftimeindex=find(abs(knowledgevec-0.5)<1e-3);halftime=sum(tvec(halftimeindex))/length(halftimeindex)/secperday;disp(['iwill knowhalfofmatlabafter',num2str(halftime),'days']);plot(tvec/secperday,knowledg evec);xlabel('day');2021年春《matlab基础》第二次上机练与作业练习1:函数文件创建一个文件名为plotsin的函数文件,建议:?函数声明为:functonplotsin(f1)该函数用作图画出来频率为的正弦波在区间上的图像.每个周期含有16个数据点functionplotsin(f1)xnum=16*f1;x=linspace(0,2*pi,xnum);plot(x,sin(f1*x));练2:条件语句修改函数plotsin(f1)使之有两个输入变量,形式为plotsin(f1,f2)如果输出的变量个数为1,继续执行以前写下的绘图命令.否则表明文字'twoinputsweregiven'?提示信息:输出变量的数目用内置局部变量:narginfunctionplotsin(f1,f2)ifnargin==1xnum=16*f1;x=linspace(0,2*pi,xnum);plot(x,sin(f1*x));elseerror('twoinputsweregiven');end练3:绘图命令修改plotsin中的绘图命令,将数据点类型改为正方形,线形改为红色虚线,线宽为2.设置数据点填充色为黑色(属性名叫:linewidth,markerfacecolor)如果有2个输入变量,新开一个绘图窗口,上下排列,并且激活上面图形窗口plotsin(6)plotsin(2,3)functionplotsin(f1,f2)ifnargin==1h1=figure(1);xnum=16*f1;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB
作业5
1、 试求解下面微分方程的通解以及满足(0)1,()2,(0)0x x y π===条件下的解析解。
66()5()4()3()sin(4)2()()4()6()cos(4)
t t x t x t x t y t e t y t y t x t x t e t --⎧+++=⎨+++=⎩ 解:
>> syms t x y;
>>[x,y]=dsolve('D2x+5*Dx+4*x+3*y=exp(-6*t)*sin(4*t)',
'2*Dy+y+4*Dx+6*x=exp(-6*t)*cos(4*t)','x(0)=1','x(pi)=2','y(0)=0');vpa(x,20)
ans =
.24816266536011758942e-1*exp(-6.*t)*cos(4.*t)-.16682998530132288094e-1*exp(-6.*t)*sin(4.*t)+.85861668591377882749e-1*exp(t)-.57658489325155296910e-1*exp(-5.1374586088176874243*t)+.94698055419776565523*exp(-1.3625413911823125757*t)
>>vpa(y,20)
ans =
-.10607545320921117099*exp(-6.*t)*cos(4.*t)+.68348848603625673689e-1*exp(-6.*t)*sin(4.*t)-.28620556197125960916*exp(t)+.90450561852315609427e-1*exp(-5.1374586088176874243*t)+.30183045332815517077*exp(-1.3625413911823125757*t)
2、 Lotka-Volterra 扑食模型方程为()4()2()()()()()3()
x t x t x t y t y t x t y t y t =-⎧⎨=-⎩,且初值为(0)2,(0)3x y ==,
试求解该微分方程,并绘制相应的曲线。
解:
>>syms x y t;
>> f=inline('[4*x(1)-2*x(1)*x(2); x(1)*x(2)-3*x(2)]','t','x');
>> [t,x]=ode45(f,[0,10],[2;3]);plot(t,x)
3、 是给出求解下面微分方程的MA TLAB 命令,
(3)22,(0)2,(0)(0)0ty y tyy t yy e y y y -++====
并绘制出()y t 曲线。
试问该方程存在解析解吗?选择四阶定步长Runge-Kutta 算法求解该方程时,步长选择多少可以得出较好的精度,MATLAB 语言给出的现成函数在速度、精度上进行比较。
解:
>> f=inline('[x(2); x(3); -t^2*x(1)*x(2)-t^2*x(2)*x(1)^2+exp(-t*x(1))]','t','x');
[t,x]=ode45(f,[0,10],[2;0;0]); >> plot(t,x)
4、 试用解析解和数值解的方法求解下面的微分方程组
5()2()3(),(0)1,(0)2()2()3()4()4()sin ,(0)3,(0)4t x t x t x t e x x y t x t y t x t y t t y y -⎧=--+==⎨=----==⎩
解:
解析解:
>> syms t x y;
[x,y]=dsolve('D2x=-2*x-3*Dx+exp(-5*t)','D2y=2*x-3*y-4*Dx-4*Dy-sin(t)','x(0)=1','Dx(0)=2','y(0)=3','Dy(0)=4')
x =
1/12*exp(-5*t)-10/3*exp(-2*t)+17/4*exp(-t)
y =
-265/16*exp(-t)-71/5*exp(-3*t)+11/48*exp(-5*t)+100/3*exp(-2*t)+51/4*exp(-t)*t+1/5*cos(t)-1/10*sin(t)
数值解:
>> f=inline('[x(2); -2*x(1)-3*x(2)+exp(-5*t); x(4); 2*x(1)-3*x(3)-4*x(2)-4*x(4)-sin(t)]','t','x');
[t1,x1]=ode45(f,[0,10],[1;2;3;4]);
ezplot(x,[0,10]), line(t1,x1(:,1)) figure; ezplot(y,[0,10]), line(t1,x1(:,3))
5、 下面的方程在传统微分方程教程中经常被认为是刚性微分方程。
使用常规微分方程解法和刚性微分方程解法分别求解这个微分方程的数值解,并求出解析解,用状态变量曲线比较数值求解的精度。
11212122119245cos sin ,(0)331224519cos sin ,(0)33
y y y t t y y y y t t y ⎧=++-=⎪⎪⎨⎪=---+=⎪⎩ 解:
>> syms t y1 y2;
>>
[y1,y2]=dsolve('Dy1=9*y1+24*y2+5*cos(t)-1/3*sin(t)','Dy2=-24*y1-51*y2-9*cos(t)+1/3*sin(t)','y1(0)=1/3','y2(0)=2/3')
y1 =2/(3*exp(3*t)) - 2/(3*exp(39*t)) + cos(t)/3
y2 =4/(3*exp(39*t)) - 1/(3*exp(3*t)) - cos(t)/3
6、试用数值方法求解偏微分方程
22
22
0,00,0
1,0
0,0
x y y x
u u
x y
u u
x y
=>=≥
⎧∂∂
+=
⎪∂∂
⎪⎪
==
⎨
⎪
>>
⎪
⎪⎩
,并绘制出u函数曲面。
