《系统工程》第四版习题解答资料
《系统工程》第四版习题解答

V
V
A
A
A
V
V
A
V
V
V
A
V
V
(A)
A
V
(V)
V
V
V
A
V
(V)
V
绘制多级递阶有向图:
23.已知下面的系统可适矩阵,分别用规范方法与实用方法建立其递阶结构模型。
(1) (2)
解:(1)规范方法:
①区域划分
1
1,5,7
1
1
2
2
2,4
2
2
3
3,5,6
3,6
3,6
4
2,4
4
4
5
5
1,3,5,6,7
5
5
6
3,5,6
系统工程第四版习题解答
第三章
21.给定描述系统基本结构的有向图,如图3-16a、b所示。要求:
(1)写出系统要素集合 及 上的二元关系集合 。
(2)建立邻接矩阵 、可达矩阵 及缩减矩阵 。
解:(2)3-16a:
规范方法:
, ,
①区域划分
1
1,2,3,4,5
1
1
2
2,3,4
1,2,5
2
3
3,4
1,2,3,5
。
②级位划分
要素集合
1
2
3
4
5
6
7
8
1
1,4
1,3
1
3
1,3,4
3
3
4
4
1,3,4,5,6,7
4
4
5
4,5
5,6,7
5
6
4,5,6,7
系统工程第四版第三章课后题答案

系统工程第三章作业02613102 徐晗P80.21. 给定描述系统基本结构的有向图,如图3-16a 、b 所示。
要求:(1)写出系统要素集合S 及S 上的二元关系集合Rb 。
(2)建立邻接矩阵A 、可达矩阵M 及缩减矩阵M ’。
解:(a) (1) 51234{S ,,,,}S S S S S =55551212334234{(S ,),(,),(,),(,),(,),(,),(,S )}b R S S S S S S S S S S S S =(2)010********00100000001110A ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦=1100101100001100001001111A I ⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎣⎦231111101110()()001100001001110A I A I M ⎡⎤⎢⎥⎢⎥⎢⎥+==+=⎢⎥⎢⎥⎢⎥⎣⎦'M M =(b)(1){1,2,3,4,5,6}S ={(1,3),(1,5),(2,4),(4,2),(4,6),(5,2),(5,1)}b R =(2) 0010*********00000010001110000000000A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦101010010100001000010101110010000001A I ⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦2111010010101001000()01010111111000001A I ⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦3411111111111001000()()0000001010101010111A I A I M ⎡⎤⎢⎥⎢⎥⎢⎥+==+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦11110101'00100001M ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦22. 请依据图3-171P9解:1P9123456789110000001120101000113101000011400010001151001110116000001011711110111180000000119000000001P P P P P P P P P P P P P M P P P P P ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦23. 已知下面的系统可达矩阵,分别用规范方法与实用方法建立其递阶结构模型。
系统工程第四版第三章课后题答案
对应的先行课
1
高等数学
2
大学物理
1
3
C++程序设计
4
几何与代数
5
概率论与数理统计
1,2
6
应用统计学
1,5
7
运筹学
1,4
8
管理学
9
质量控制
1,4,5
10
系统工程
4,7,8
11
计算方法
1,3,4
(2)用方格图判断课程间的“支持”关系
V
(V)
V
V
V
V
V
V
V
(V)
(V)
V
2
V
3
V
V
V
V
4
V
V
5
6
V
7
V
8
толькодля людей, которые используются для обучения, исследований и не должны использоваться в коммерческих целях.
以下无正文
①区域划分
1
1,5,7
1
1
2
2
2,4
2
2
3
3,5,6
3,6
3,6
4
2,4
4
4
5
5
1,3,5,6,7
5
5
6
3,5,6
3,6
3,6
7
5,7
1,7
7
所以系统可划分为两个相互独立的区域,即 。
②级位划分
要素集合
2
2
2,4
2
2
系统工程第四版第三章课后题答案

系统工程第四版第三章课后题答案-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII系统工程第三章作业02613102 徐晗P80.21. 给定描述系统基本结构的有向图,如图3-16a 、b 所示。
要求:(1)写出系统要素集合S 及S 上的二元关系集合Rb 。
For personal use only in study and research; not for commercial use(2)建立邻接矩阵A 、可达矩阵M 及缩减矩阵M ’。
解:(a) (1)51234{S ,,,,}S S S S S =55551212334234{(S ,),(,),(,),(,),(,),(,),(,S )}b R S S S S S S S S S S S S =(2)0100100100000100000001110A ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦=1100101100001100001001111A I ⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎣⎦231111101110()()001100001001110A I A I M ⎡⎤⎢⎥⎢⎥⎢⎥+==+=⎢⎥⎢⎥⎢⎥⎣⎦'M M =(b)(1) {1,2,3,4,5,6}S ={(1,3),(1,5),(2,4),(4,2),(4,6),(5,2),(5,1)}b R =(2) 0010*********00000010001110000000000A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦101010010100001000010101110010000001A I ⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦2111010010101001000()010101111110000001A I ⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦34111111*********00()()0000001010101010111A I A I M ⎡⎤⎢⎥⎢⎥⎢⎥+==+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦11110101'00100001M ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦22. 请依据图1P9解:1P9123456789110000001120101000113101000011400010001151001110116000001011711110111180000000119000000001P P P P P P P P P P P P P M P P P P P ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦23. 已知下面的系统可达矩阵,分别用规范方法与实用方法建立其递阶结构模型。
《系统工程》第四版习题解答doc资料

7
1
1
1
1
1
③提取骨架矩阵
,
④绘制多级递阶有向图
(2)规范方法:
①区域划分
1
1,2,4
1,3
1
2
2
1,2,3,4,5,6,7
2
2
3
1,2,3,4
3
3
4
2,4
1,3,4,5,6,7
4
5
2,4,5
5,6,7
5
6
2,4,5,6,7,8
6
6
7
2,4,5,7,8
6,7
7
8
8
6,7,8
8
8
所以系统不能划分为两个或两个以上相互独立的区域,即
1,5
1,5
6
6
1,2,4,5,6
6
6
1
1,2,4,5
1,5
1,5
2
2,4
1,2,4,5
2,4
2
4
2,4
1,2,4,5
2,4
4
5
1,2,4,5
1,5
1,5
1
1,5
1,5
1,5
1
5
1,5
1,5
1,5
5
③提取骨架矩阵
,
④绘制多级递阶有向图
实用方法:
缩减矩阵
,
绘制多级递阶有向图:
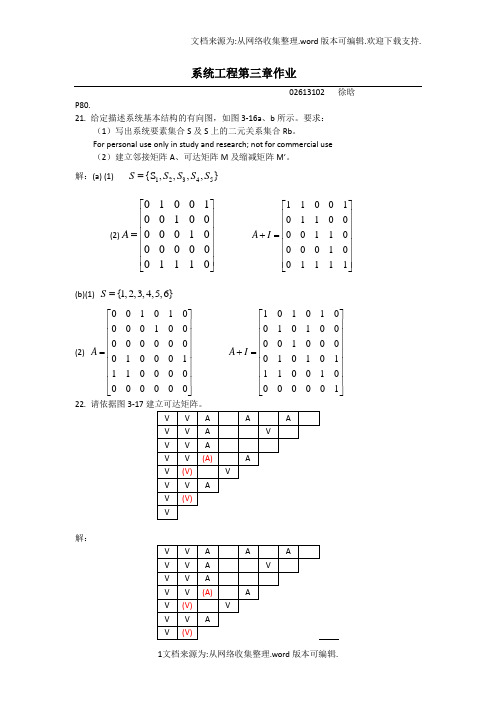
22.请依据图3-17建立可达矩阵,并用简化方法建立其递阶结构模型。
2
3
3
1,2,3,5
3
3
5
2,3,5
1,5
5
1
1,2,5
1
1
2
《系统工程》第四版习题解答

系统工程第四版习题解答第三章 系统模型与模型化21. 给定描述系统基本结构的有向图,如图3-16a 、b 所示。
要求: (1)写出系统要素集合S 及S 上的二元关系集合b R 。
(2)建立邻接矩阵A 、可达矩阵M 及缩减矩阵M '。
解:(2)3-16a : 规方法:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=0111000000010000010010010A ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=11110010011000111011111M ,M M ='}5,4,3,2,1{)(==∏P S 。
⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=11110010000110001110111115432154321)(P M}1{},5{},2{},3{},4{,,,,)(54321==∏L L L L L P⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=11111011110011100011000011523415234)(54321L L L L L L M ③提取骨架矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=''1100011000011000011000011523415234)(54321L L L L L L M ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=-''='01000001000001000001000001523415234)(54321L L L L L I L M A ④绘制多级递阶有向图实用方法:缩减矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=='11110010000110001110111115432154321M M⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡='11111011110011100011000011523415234)(54321L L L L L L M3-16b :规方法:⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=000000000011100010000000001000010100A ,⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=100000111111101010000100101010111111Mφ≠=⋂=⋂}5,1{}6,5,4,2,1{}5,3,1{)()(63S A S A所以系统无法划分为两个或两个以上相互独立的区域,即}6,5,4,3,2,1{)(==∏P S 。
(完整版)系统工程第四版习题解答
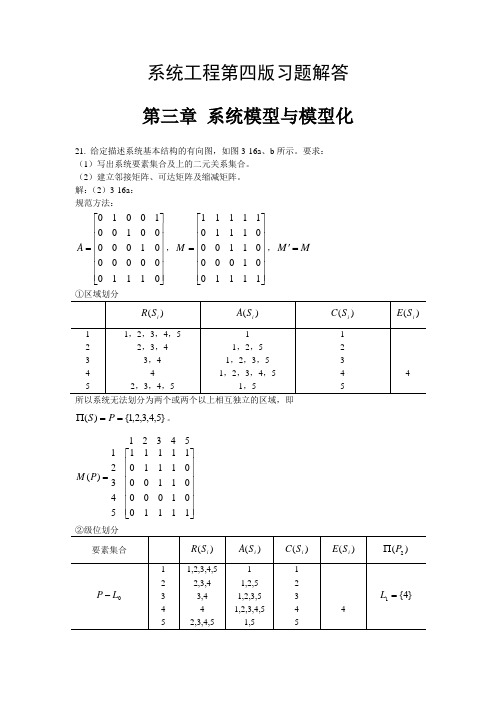
系统工程第四版习题解答 第三章 系统模型与模型化21. 给定描述系统基本结构的有向图,如图3-16a 、b 所示。
要求: (1)写出系统要素集合及上的二元关系集合。
(2)建立邻接矩阵、可达矩阵及缩减矩阵。
解:(2)3-16a : 规范方法:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=0111000000010000010010010A ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=1111001000011000111011111M ,M M ='所以系统无法划分为两个或两个以上相互独立的区域,即}5,4,3,2,1{)(==∏P S 。
⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=11110010000110001110111115432154321)(P M ②级位划分}1{},5{},2{},3{},4{,,,,)(54321==∏L L L L L P⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=11111011110011100011000011523415234)(54321L L L L L L M ③提取骨架矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=''1100011000011000011000011523415234)(54321L L L L L L M ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=-''='01000001000001000001000001523415234)(54321L L L L L I L M A ④绘制多级递阶有向图实用方法:缩减矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=='11110010000110001110111115432154321M M⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡='11111011110011100011000011523415234)(54321L L L L L L M3-16b :规范方法:⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=000000000011100010000000001000010100A ,⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=100000111111101010000100101010111111Mφ≠=⋂=⋂}5,1{}6,5,4,2,1{}5,3,1{)()(63S A S A所以系统无法划分为两个或两个以上相互独立的区域,即}6,5,4,3,2,1{)(==∏P S 。
系统工程第四版第三章课后题答案

系统工程第三章作业02613102 徐晗P80.21. 给定描述系统基本结构的有向图,如图3-16a 、b 所示。
要求:(1)写出系统要素集合S 及S 上的二元关系集合Rb 。
(2)建立邻接矩阵A 、可达矩阵M 及缩减矩阵M ’。
解:(a) (1) 51234{S ,,,,}S S S S S =55551212334234{(S ,),(,),(,),(,),(,),(,),(,S )}b R S S S S S S S S S S S S =(2)010********00100000001110A ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦=1100101100001100001001111A I ⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎣⎦231111101110()()001100001001110A I A I M ⎡⎤⎢⎥⎢⎥⎢⎥+==+=⎢⎥⎢⎥⎢⎥⎣⎦'M M =(b)(1){1,2,3,4,5,6}S ={(1,3),(1,5),(2,4),(4,2),(4,6),(5,2),(5,1)}b R =(2) 0010*********00000010001110000000000A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦101010010100001000010101110010000001A I ⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦2111010010101001000()01010111111000001A I ⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦3411111111111001000()()0000001010101010111A I A I M ⎡⎤⎢⎥⎢⎥⎢⎥+==+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦11110101'00100001M ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦22. 请依据图3-171P9解:1P9123456789110000001120101000113101000011400010001151001110116000001011711110111180000000119000000001P P P P P P P P P P P P P M P P P P P ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦23. 已知下面的系统可达矩阵,分别用规范方法与实用方法建立其递阶结构模型。
《系统工程》第四版习题解答 (3)
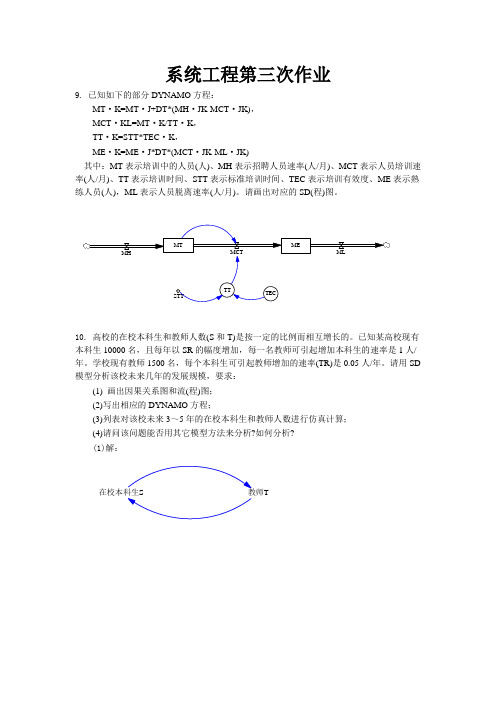
系统工程第三次作业9. 已知如下的部分DYNAMO方程:MT·K=MT·J+DT*(MH·JK-MCT·JK),MCT·KL=MT·K/TT·K,TT·K=STT*TEC·K,ME·K=ME·J*DT*(MCT·JK-ML·JK)其中:MT表示培训中的人员(人)、MH表示招聘人员速率(人/月)、MCT表示人员培训速率(人/月)、TT表示培训时间、STT表示标准培训时间、TEC表示培训有效度、ME表示熟练人员(人),ML表示人员脱离速率(人/月)。
请画出对应的SD(程)图。
10. 高校的在校本科生和教师人数(S和T)是按一定的比例而相互增长的。
已知某高校现有本科生10000名,且每年以SR的幅度增加,每一名教师可引起增加本科生的速率是1人/年。
学校现有教师1500名,每个本科生可引起教师增加的速率(TR)是0.05人/年。
请用SD 模型分析该校未来几年的发展规模,要求:(1) 画出因果关系图和流(程)图;(2)写出相应的DYNAMO方程;(3)列表对该校未来3~5年的在校本科生和教师人数进行仿真计算;(4)请问该问题能否用其它模型方法来分析?如何分析?(1)解:T(2)、解:L S.K=S.J+SR.JK*DTN S=10000R SR.KL=T.K*TSRC TSR=1L T.K=T.J+TR.JK*DTN T=1500R TR.KL=S.K*STRC STR=0.05(3)解:(4)11.某城市国营和集体服务网点的规模可用SD来研究。
现给出描述该问题的DYNAMO方程及其变量说明。
要求:(1)绘制相应的SD流(程)图(绘图时可不考虑仿真控制变量);(2)说明其中的因果反馈回路及其性质。
L S·K=S·J+DT*NS·JKN S=90R NS·KL=SD·K*P·K/(LENGTH-TIME·K)A SD·K=SE-SP·KC SE=2A SP·K=SR·K/P·KA SR·K=SX+S·KC SX=60L P·K=P·J+DT*NP·JKN P=100R NP·KL=I*P·KC I=0.02其中:LENGTH为仿真终止时间、TIME为当前仿真时刻,均为仿真控制变量;S为个体服务网点数(个)、NS为年新增个体服务网点数(个/年)、SD为实际千人均服务网点与期望差(个/千人)、SE为期望的千人均网点数、SP为的千人均网点数(个/千人)、SX为非个体服务网点数(个)、SR为该城市实际拥有的服务网点数(个)、P为城市人口数(千人)、NP为年新增人口数(千人/年)、I为人口的年自然增长率。
最新《系统工程》第四版习题解答-(3)

精品资料《系统工程》第四版习题解答-(3)........................................系统工程第三次作业9. 已知如下的部分DYNAMO方程:MT·K=MT·J+DT*(MH·JK-MCT·JK),MCT·KL=MT·K/TT·K,TT·K=STT*TEC·K,ME·K=ME·J*DT*(MCT·JK-ML·JK)其中:MT表示培训中的人员(人)、MH表示招聘人员速率(人/月)、MCT表示人员培训速率(人/月)、TT表示培训时间、STT表示标准培训时间、TEC表示培训有效度、ME表示熟练人员(人),ML表示人员脱离速率(人/月)。
请画出对应的SD(程)图。
10. 高校的在校本科生和教师人数(S和T)是按一定的比例而相互增长的。
已知某高校现有本科生10000名,且每年以SR的幅度增加,每一名教师可引起增加本科生的速率是1人/年。
学校现有教师1500名,每个本科生可引起教师增加的速率(TR)是0.05人/年。
请用SD 模型分析该校未来几年的发展规模,要求:(1) 画出因果关系图和流(程)图;(2)写出相应的DYNAMO方程;(3)列表对该校未来3~5年的在校本科生和教师人数进行仿真计算;(4)请问该问题能否用其它模型方法来分析?如何分析?(1)解:T(2)、解:L S.K=S.J+SR.JK*DTN S=10000R SR.KL=T.K*TSRC TSR=1L T.K=T.J+TR.JK*DTN T=1500R TR.KL=S.K*STRC STR=0.05(3)解:11.某城市国营和集体服务网点的规模可用SD来研究。
现给出描述该问题的DYNAMO方程及其变量说明。
要求:(1)绘制相应的SD流(程)图(绘图时可不考虑仿真控制变量);(2)说明其中的因果反馈回路及其性质。
系统工程第四版第三章课后题答案

系统工程第三章作业02613102 徐晗P80.21. 给定描述系统基本结构的有向图,如图3-16a 、b 所示。
要求:(1)写出系统要素集合S 及S 上的二元关系集合Rb 。
(2)建立邻接矩阵A 、可达矩阵M 及缩减矩阵M ’。
解:(a) (1) 51234{S ,,,,}S S S S S =55551212334234{(S ,),(,),(,),(,),(,),(,),(,S )}b R S S S S S S S S S S S S =(2)010********00100000001110A ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦=1100101100001100001001111A I ⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎣⎦231111101110()()001100001001110A I A I M ⎡⎤⎢⎥⎢⎥⎢⎥+==+=⎢⎥⎢⎥⎢⎥⎣⎦'M M =(b)(1) {1,2,3,4,5,6}S ={(1,3),(1,5),(2,4),(4,2),(4,6),(5,2),(5,1)}b R =(2) 0010*********00000010001110000000000A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦101010010100001000010101110010000001A I ⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦2111010010101001000()010101111110000001A I ⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦3411111111111001000()()0000001010101010111A I A I M ⎡⎤⎢⎥⎢⎥⎢⎥+==+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦11110101'00100001M ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦22. 请依据图3-17建立可达矩阵。
1P9解:3P9123456789110000001120101000113101000011400010001151001110116000001011711110111180000000119000000001P P P P P P P P P P P P P M P P P P P ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦23. 已知下面的系统可达矩阵,分别用规范方法与实用方法建立其递阶结构模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7
5,7
1,7
7
所以系统可划分为两个相互独立的区域,即 。
②级位划分
要素集合
2
2
2,4
2
2
4
2,4
4
4
4
4
4
4
4
要素集合
1
1,5,7
1
1
3
3,5,6
3,6
3,6
5
5
1,3,5,6,7
5
5
6
3,5,6
3,6
3,6
7
5,7
1,7
7
1
1,7
1
1
3
3,6
3,6
3,6
3
6
3,6
3,6
3,6
6
7
7
1,7
7
4
4
5
2,3,4,5
1,5
5
所以系统无法划分为两个或两个以上相互独立的区域,即
。
②级位划分
要素集合
1
1,2,3,4,5
1
1
2
2,3,4
1,2,5
2
3
3,4
1,2,3,5
3
4
4
1,2,3,4,5ቤተ መጻሕፍቲ ባይዱ
4
4
5
2,3,4,5
1,5
5
1
1,2,3,5
1
1
2
2,3
1,2,5
2
3
3
1,2,3,5
3
3
5
2,3,5
1,5
解:设市场畅销为 ,市场滞销为 ;设产品预测畅销为 ,产品预测滞销为 ,则由已知条件: , , ,
有: ,
, , ,
,
, , ,
贝叶斯行动:如果市场预测结果为畅销,应该选择经营该高科技产品;若市场预测结果为滞销,则不经营。
由决策树可知,咨询公司提供信息的价值为1.13-1.1=0.03万元,因此要价超过300元不应聘请。
第三章
21.给定描述系统基本结构的有向图,如图3-16a、b所示。要求:
(1)写出系统要素集合 及 上的二元关系集合 。
(2)建立邻接矩阵 、可达矩阵 及缩减矩阵 。
解:(2)3-16a:
规范方法:
, ,
①区域划分
1
1,2,3,4,5
1
1
2
2,3,4
1,2,5
2
3
3,4
1,2,3,5
3
4
4
1,2,3,4,5
1,5
1,5
2
2,4
1,2,4,5
2,4
2
4
2,4
1,2,4,5
2,4
4
5
1,2,4,5
1,5
1,5
1
1,5
1,5
1,5
1
5
1,5
1,5
1,5
5
③提取骨架矩阵
,
④绘制多级递阶有向图
实用方法:
缩减矩阵 ,
绘制多级递阶有向图:
22.请依据图3-17建立可达矩阵,并用简化方法建立其递阶结构模型。
解:
V
V
A
TIME
0
1
2
3
4
5
S
10,000
11,500
13,500
16,075
19,325
23,378
T
1,500
2,000
2,575
3,250
4,053
5,020
11.
12.
(1)
(2) 15.
第六章决策分析
补充题1某商店拟经营一种高科技产品,若市场畅销,可以获利1万5千元;若市场滞销,将亏损5千元;若不经营,则不亏不赚。根据收集的市场销售资料,该产品畅销的概率为0.8,滞销的概率为0.2。为了降低风险,可以聘请某咨询公司进行市场调查和分析,该咨询公司对该产品畅销预测的准确率为0.95,滞销预测的准确率为0.90。画出该决策问题的决策树,并进行决策分析。
1,5
1,5
6
6
1,2,4,5,6
6
6
所以系统无法划分为两个或两个以上相互独立的区域,即
。
②级位划分
要素集合
1
1,2,3,4,5,6
1,5
1,5
2
2,4,6
1,2,4,5
2,4
3
3
1,3,5
3
3
4
2,4,6
1,2,4,5
2,4
5
1,2,3,4,5,6
1,5
1,5
6
6
1,2,4,5,6
6
6
1
1,2,4,5
0.57
1.00
进一步有,
x1
x2
x3
θ1
0.7273
0.1905
0.0000
θ2
0.2727
0.5714
0.2105
θ3
0.0000
0.2381
0.7895
决策树为:
贝叶斯行动:如果试销结果为差,则不改变包装;如果试销结果为一般,则改变包装;如果试销结果为好,则改变包装。
由决策树可知,试销的价值为(抽样信息的价值)298.4-292=6.4万元,因此如果试销费用大于6.4万元则不试销,如果试销费用小于6.4万元时试销。
补充题2某公司拟改变产品的包装,改变包装后产品的销路不能确定,公司经理的估计是:
销路差θ1
销路一般θ2
销路好θ3
概率P
0.2
0.3
0.5
销路与收益的关系如下表:
θ1
θ2
θ3
改变包装
-40
0
600
包装不变
0
0
0
为了对销路的估计更有把握,公司先在某个地区试销改变了包装的产品。根据以往的经验,试销的结果与产品在将来的实际销路中有如下关系(x1、x2、x3分别为试销为差、一般和好的事件):
7
1
1
1
1
1
③提取骨架矩阵
,
④绘制多级递阶有向图
(2)规范方法:
①区域划分
1
1,2,4
1,3
1
2
2
1,2,3,4,5,6,7
2
2
3
1,2,3,4
3
3
4
2,4
1,3,4,5,6,7
4
5
2,4,5
5,6,7
5
6
2,4,5,6,7,8
6
6
7
2,4,5,7,8
6,7
7
8
8
6,7,8
8
8
所以系统不能划分为两个或两个以上相互独立的区域,即
A
A
V
V
A
V
V
V
A
V
V
(A)
A
V
(V)
V
V
V
A
V
(V)
V
绘制多级递阶有向图:
23.已知下面的系统可适矩阵,分别用规范方法与实用方法建立其递阶结构模型。
(1) (2)
解:(1)规范方法:
①区域划分
1
1,5,7
1
1
2
2
2,4
2
2
3
3,5,6
3,6
3,6
4
2,4
4
4
5
5
1,3,5,6,7
5
5
6
3,5,6
3,6
5
1
1,2,5
1
1
2
2
1,2,5
2
2
5
2,5
1,5
5
1
1,5
1
1
5
5
1,5
5
5
1
1
1
1
1
③提取骨架矩阵
④绘制多级递阶有向图
实用方法:
缩减矩阵
3-16b:
规范方法:
,
①区域划分
1
1,2,3,4,5,6
1,5
1,5
2
2,4,6
1,2,4,5
2,4
3
3
1,3,5
3
3
4
2,4,6
1,2,4,5
2,4
5
1,2,3,4,5,6
。
②级位划分
要素集合
1
2
3
4
5
6
7
8
1
1,4
1,3
1
3
1,3,4
3
3
4
4
1,3,4,5,6,7
4
4
5
4,5
5,6,7
5
6
4,5,6,7
6
6
7
4,5,7
6,7
7
1
1
1,3
1
1
3
1,3
3
3
5
5
5,6,7
5
5
6
5,6,7
6
6
7
5,7
6,7
7
3
3
3
3
3
6
6,7
6
6
7
7
6,7
7
7
6
6
6
6
6
③提取骨架矩阵
④绘制多级递阶有向图
(1)实用方法:
缩减矩阵
(2)实用方法:
第四章
9.已知如下的部分DYNAMO方程:
请画出对应的SD流(程)图。
