山东省德州市经济技术开发区太阳城中学2020-2021学年九年级上学期第一次检测化学试题
山东省德州市陵城区2023-2024学年九年级上学期期中考试物理试题(含答案)

2023-2024学年义务教育学业质量素养监测(九年级物理)注意事项:1.全卷共4页,满分100分,考试时间为90分钟.2.答卷前,考生务必用0.5毫米黑色签字笔将学校、姓名、准考证号填写在试题和答题卡规定的位置上.3.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号.4.非选择题必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.一、选择题:本大题包括12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.废物利用是节约资源的重要手段.下列废物再加工后,最适合做电工钳柄外套的是()A .废铜B .废铁C .废橡胶D .废纸壳2.我国幅员辽阔,人文自然资源丰富,下列分析正确的是( )A .新疆吐鲁番的火焰山昼夜温差大,是因为火焰山沙石比热容大B .云南大理的蝴蝶泉边花香四溢,是因为分子不停地做无规则运动C .黑龙江哈尔滨寒冷的冰雕不易融化,是因为冰雕没有内能D .山东潍坊的潍柴内燃机工作时,将机械能转化成内能3.下列关于热和能的说法正确的是()A .温度高的物体,内能一定大B .热量总是从内能大的物体向内能小的物体传递C .物体的温度不变,它的内能一定不变D .物体的内能增加,可能是从外界吸收了热量4.质量均为的水和另一种液体在相同时间内放出的热量相等,它们温度随时间变化的关系如图所示.已知水的比热容,.下列说法中()0.5kg ()34.210J /kg c =⨯⋅水℃c c >水液①甲物质是水②乙温度降低了③甲放出了的热量④乙物质的比热容为A .只有①②正确B .只有②④正确C .只有①③正确D .只有①④正确5.汽车是现代生活中最常见的一种交通工具,如图甲、乙分别是某汽油机的某冲程及能量流向图.下列有关说法正确的是( )A .甲图是排气冲程B .由乙图可知该汽油机的效率是C .汽车尾气中的“汽油味”越浓燃料燃烧得越不充分,这会降低燃料的热值D .图乙的过程遵守能量守恒定律6.以下说法正确的是()A .根据可知:物体吸热越多,它的比热容就越大B .根据可知:导体的电阻跟它两端的电压成正比,跟电流成反比C .根据可知:燃料的质量越大,其热值就越小D .根据可知:有用功占燃料完全燃烧放出热量的比例越大,热机效率就越大7.用毛皮摩擦过的橡胶棒接触不带电的验电器金属球后,金属箔张角如图甲所示;接着用毛皮摩擦过的气球再接触金属球,金属箔张角变大,如图乙所示;然后用短波紫外光照射但不接触金属球,金属箔张角如图丙所示,此时金属球中的某种电荷“逃”到了空气中.下列推断错误的是( )012min ~20℃012min ~48.410J ⨯()32.110J /kg ⨯⋅℃30%ΔQ c m t=U R I=Q q m=W Q η=放A .甲图中瞬间电流方向是由验电器到橡胶棒B .乙图中摩擦过的气球带负电C .丙图中金属箔张角变小是因为它们相互吸引D .丙图中从金属球“逃”出的是电子8.在如图所示的电路中,下列说法正确的是( )A .当只闭合开关时,并联B .当闭合开关时,电源短路C .当只闭合开关时,串联D .当只闭合开关时,串联9.如图所示电路的电源电压为,电阻的阻值为,闭合开关后,电流表的示数为,则()A .通过的电流大于B .电阻和是并联的C .电压表的示数为D .电阻的阻值为10.为了交通安全,驾驶员必须使用安全带.某汽车厂家为了提醒驾驶员系好安全带,做了如下设计:驾驶员坐上驾驶座位未系安全带时,开关闭合,提示灯亮;系上安全带后,开关也闭合,提示灯灭.如图所示12S S 、12L L 、123S S S 、、23S S 、12L L 、13S S 、12L L 、1.5V 1R 2Ω0.3A 1R 0.3A 1R 2R 0.9V 2R 3Ω1S 2S的四个选项中,符合电路设计要求的是( )A .B .C .D .11.如图甲所示,将三个规格相同的小灯泡接入电路,用电压表测量其中一个小灯泡两端的电压示数如图乙所示,则下列说法错误的是( )A .A 端导线应与电源的负极相连B .电流从D 接线柱流入电压表“3”接线柱C .若CD 间的小灯泡从灯座上旋下来,电压表示数为零D .AF 两接线柱间电压为12.如图所示,电源电压保持不变,是定值电阻,R 是光敏电阻,其阻值随光照的增强而减小.闭合开关,逐渐减小R 的光照强度,电表示数的变化情况是( )A .电流表和电压表示数均变B .电流和电压表示数均变小C .电流表示数变大,电压表示数变小D .电流表示数变小,电压表示数变大二、填空题:本大题包括6个小题,每个空1分,共14分.13.在中国空间站中,王亚平老师往一个水球中注入适量的蓝色颜料,观察到整个水球很快就变蓝了,这是_________现象,水的温度越高,变色越_________(选填“快”或“慢”).组成水球的水分子没有四处散开,是因为分子间存在_________.14.如图,是我国古代的一种取暖用具——黑漆描金手炉.在手炉中装满热水后抱在怀中,便可取暖,这是利用了_________的方式改变内能,手炉中装热水,是利用了水的_________较大.6V0R15.在水果中平行插入两片不同金属制成的极板,就组成了一个水果电池.如图甲所示,几个水果电池提供的电力足以点亮一排发光二极管.(1)图甲中的“水果”在这里扮演了电源的角色,它为发光二极管提供了_________;(2)如图乙所示,将电压表接在西红柿电池两端,指针向右偏转一定角度,则金属片B 是这个电池的_________极.16.手机移动电源(俗称充电宝)有两个输出端,可以单独为一部手机或同时为两部手机充电,这两个输出端的连接方式是_________联;给充电宝充电时,充电宝相当于电路中的_________.17.小灯泡的图象如图甲所示,将它与定值电阻R 接入图乙所示的电路中.只闭合开关,电流表的示数为;再闭合开关时,电流表的示数为.则电源电压为_________V ;只闭合开关时,电阻R 两端的电压为_________V .18.图甲所示电路的电源电压为,闭合开关后,两电流表的指针偏转均如图乙所示,则电路的总电阻为_________;电阻,的阻值为_________;断开开关后,电阻的阻值为_________.I U -1S 0.2A 2S 0.25A 1S 3V Ω1R Ω2R Ω三、作图与实验题:本大题包括6个小题,共26分.19.(2分)请将如图实际电路对应的电路图画在方框里.20.(2分)甲为测定油箱内油量的装置,把电流表刻度盘改为相应的油量体积数,就可以直接读出油箱中的油量,当油箱中的油量减少时,浮子就会带动滑杆使电流表的示数变小.现将电流表换成电压表,请把乙图电路连接完整,使油箱中的油量消耗到最少时,电压表的示数减小到零.21.(4分)为了比较水和煤油吸热本领的大小,某同学做了如图所示的实验,在两个相同的烧杯中,分别装有水和煤油,用相同的电热器分别对它们加热相同的时间.物质初温/末温/加热时间/水20456煤油20706(1)实验中应保证水和煤油的初温与_________(选填“质量”或“体积”)都相同.(2)实验中选用相同的电热器对水和煤油加热相同的时间,水吸收的热量_________(选填“大于”、“等于”或“小于”)煤油吸收的热量.(3)本实验是通过比较_________(选填“升高的温度”或“加热时间”)来反映水和煤油吸热能力的强弱;实验表明,_________(选填“水”或“煤油”)的吸热能力更强.22.(6分)小宁在做探究并联电路电流规律的实验,如图甲是实验的电路图.(1)在连接电路前发现,电流表的指针在图乙的位置,是因为没有_________.纠正后继续接好电路,闭合开℃℃min关,指针又偏到图乙的位置,是因为_________.(2)他在测量A 处的电流时,电流表的示数如图丙所示,则电流表的示数为_________A .(3)在解决了以上问题后,将电流表分别接入A 、B 、C 三点处,闭合开关,测出了一组电流并记录在表格中,得出了并联电路的电流规律.请你指出他们实验应改进的方法是_________.(4)实验结束后,小宁又利用器材换个电源连接了如图丁所示的电路图,当开关S 由断开到闭合时,电流表的示数_________(选填“变大”“变小”或“不变”).灯亮度_________.23.(5分)某学习小组在“探究影响导体电阻大小的因素”实验时,设计了如图所示的实验装置,实验中分别将A 、B 、C 、D 四根导体接入电路,四根导体的材料规格如下表所示.(1)为比较A 、B 、C 、D 四根导体电阻的大小,可通过观察_________来判断.(2)要探究导体电阻大小与长度的关系,应选用_________两根导体进行实验.(3)将A 、C 两根导体分别接入电路中进行实验,可得出:当导体的长度和材料相同时,横截面积越大,电阻越_________.(4)将A 、D 两根导体分别接入电路中进行实验,可探究导体电阻大小与_________的关系.(5)实验中采用的研究方法是_________.导体代号长度/m 横截面积/材料电流表示数/A A1.00.4锰铜 1.4B0.50.4锰铜 2.7C1.00.6锰铜2.0D 1.00.4镍铬合金0.624.(7分)某实验小组用图甲所示电路进行“探究电流与电压的关系”实验.(1)请用笔画线代替导线将图甲电路连接完整,要求滑动变阻器滑片P 向左移动时电阻变大,导线不交2A 1L 2mm叉.(2)连接电路时,开关应该_________.闭合开关前,滑动变阻器滑片P 应该位于_________(选填“A ”或“B ”)端.(3)闭合开关,同学们发现电流表没有示数,电压表示数接近电源电压,原因可能是_________.(4)排除故障后,根据实验数据绘制出定值电阻R 的图象如图乙所示.由图象可得:当导体的电阻一定时,通过导体的电流与导体两端的电压成_________.(5)同学们利用完整的图甲电路进一步“探究电流与电阻的关系”,测得实验数据如下表所示.实验时,将的电阻换上的电阻后,应将滑片P 向_________(选填“A ”或“B ”)端移动,保持电压表的示数为_________V 不变.实验次数123455101520250.400.200.130.100.08四、计算题:本大题包括3小题,共24分.解答时应写出必要的文字说明、公式和重要的演算步骤,只写出最后答案的不能得分.25.(9分)氢燃料新能源公交车已经投入使用,如图所示.氢燃料具有清洁无污染、效率高等优点.请完成下列问题.(1)质量为的氢燃料完全燃烧放出的热量是多少?(2)若这些热量全部被质量为、温度为的水吸收,水升高的温度是多少?(3)若某氢能源公交车以的恒定功率匀速行驶,的氢燃料完全燃烧释放的能量能使该公交车匀速行驶,则氢能源公交车动力系统的效率是多少?26.(6分)如图所示电路,电阻的阻值为,闭合开关后,电流表示数为.I U -5Ω10ΩR /ΩI /A()384.210J /kg ; 1.410J /kg c q ⎡⎤=⨯⋅=⨯⎣⎦水氢℃0.3kg 200kg 15℃140kW 0.3kg 3min 1R 10Ω 1.2A(1)求电源电压U ;(2)若在电路中串联接入一个电阻,使得接入前后电流表的示数变化,求的阻值.27.(9分)随着我国经济的发展,人民生活水平日益提高,我国出现了越来越多的潜水爱好者.为了保障安全,潜水员潜水时会佩戴图甲所示的水压表和深度表.图乙是某深度表的工作原理简化电路图,电源电压(且恒定不变,定值电阻,电压表量程为(是阻值随水深度变化的电阻,其变化关系图象如图丙所示,允许通过的最大电流为.求:(1)深度表在水面上时,电路中的电流(计算结果保留1位小数);(2)电压表示数为时,潜水员下潜的深度;(3)在保证电路安全的情况下,该深度表能浸入水中的最大深度.物理试题参考答案及评分标准一、选择题:每小题3分,共36分.123456789101112C B D D D D C B D A C D二、填空题:每空1分,共14分.13.扩散 快 引力14.热传递 比热容 15.(1)电能 (2)正16.并 用电器 17.2.5 1 18.2 10 2.5三、作图与实验题(共26分)19.20.21.(1)质量 (2)等于 (3)升高的温度 水2R 0.4A 2R 6V U =015ΩR =P 03V,R ~P R 0.24A 2V22.(1)调零电流表的正负接线柱接反了 (2)0.24(3)换用不同规格的灯泡进行多次实验 (4)变大 不变23.(1)电流表示数大小 (2)A 、B (3)小 (4)材料 (5)控制变量法(或转换法)24.(1)(2)断开A (3)定值电阻R 断路 (4)正比 (5)A 2四、计算题(共24分)25.解:(1)质量为的氢燃料完全燃烧放出的热量:(2)由题可知水吸收的热量:,由可知水升高的温度:(3)已知公交车的功率,行驶时间,则公交车的机械能为:则公交车的效率:26.解:(1)电路为只有的简单电路,电阻的阻值为,闭合开关后,电流表示数为,则电源电压:(2)将串联在电路中,电路中电流应减小,此时电路中电流为:电路中总电阻为:的阻值为:.27.解:(1)由图乙可知,该电路为和的串联电路,电压表测两端的电压;深度表在水面上时,即时,由图丙可知,此时,由串联电路的电阻特点和欧姆定律可知电路中的电流为0.3kg 871.410J /kg 0.3kg 4.210JQ q m ==⨯⨯=⨯放氢74.210J Q Q ==⨯吸放ΔQ c m t ='吸水()734.210J Δ504.210J /kg 200kgQ t c m ⨯===⨯⋅⨯'吸水℃℃5140kW 1.410W P ==⨯3min 180s t ==571.410W 180s 2.5210JW Pt ==⨯⨯=⨯772.5210J 60%4.210JW Q η⨯===⨯放1R 1R 10Ω 1.2A 11 1.2A 10Ω12VU I R ==⨯=2R 0.4A 10.4A 1.2A 0.4A 0.8AI I =-=-=串12V 15Ω0.8AU R I ===总串2R 2115Ω10Ω5ΩR R R =-=-=总0R P R 0R 0m h =P R 40Ω=(2)电压表示数为时,即两端的电压为,电路中的电流为由串联电路的电压特点可知两端的电压为则此时的阻值为由图丙可知,此时潜水员下潜的深度为.(3)由电压表量程可知两端的电压最大为,此时电路中电流为所以为保护电路,电路中允许通过的最大电流为,此时电路总电阻为由串联电路的电阻特点可知电阻的阻值为由图丙可知,此时下潜的深度为,即该深度表能浸入水中的最大深度为.06V 0.1A 15Ω40Ωp U U I R R R ===≈++总2V 0R 02V U =002V 2A 15Ω15U I R ==='p R 06V 2V 4V p U U U =-=-=p R 4V 30Ω2A 15p p U R I '=='=10m 0R 3V 0max 03V 0.2A 0.24A 15ΩU I R ===<0.2A 6V 30Ω0.2A U R I ===总大p R 030Ω15Ω15Ωp R R R =-=-=总40m 40m。
山东省济南地区2020-2021学年上学期九年级英语第一次月考试试卷汇编:单项选择(无答案)

山东省济南地区2020-2021学年上学期九年级英语第一次月考试试卷汇编:单项选择2020-2021济南市高新区中学九年级英语10月月考试题III. 选择填空从每题A、B、C、D四个选项中,选出一个最佳答案。
(20分)26 If you read an article for one more time, you will have _________better understanding of itA. theB. aC. anD. /27. --____do you study for a test? -By working with friends.A. WhenB. HowC. WhyD. What28. After a 4-week winter vacation, students usually _____a few kilos when they return to school.A. put awayB. put upC. put inD. put on29. If you don't know the words, _______________in a dictionary.A. give it upB. look up itC. look them upD. give up30. --The Dragon Boat races are so exciting, but our boat is still behind.-- Don't worry. I believe ____________our team will win.A. ifB. thatC. whetherD. why31. —Han Li has improved her English a lot since she joined the English club.—How _____________she chose to join it at first!A. quicklyB. suddenlyC. simplyD. wisely32. Tina used to_________ in the village, but now she's used to ______________in the city.A. live, liveB. live, livingC. living, liveD. living, living33. I decide to ______________ exercise to keep healthy.A. take upB. cheer upC. keep upD. give up34. -______________ fine day! Shall e go for a walk? - That sounds great!A. WhatB. HowC. What aD. How35. If you don't hear someone clearly, you should say "_____. "A. Me tooB. Pardon meC. Excuse meD. Help me36. -- I think you should _________what you need to learn ____________your interest.-- That's a good idea.A. connect, withB. communicate, withC. end, upD. explain, to37. —Would you like to watch Transformer 4 in the MAX theater with me?—I’d love to, ________I have watched it twice. The movie is really a treat to eyes.A. ifB. sinceC. becauseD. even though38. Our teachers often tell us "The _______ careful you are, the ______mistakes you will make.A. more, lessB. much; lessC. more. fewerD. much, fewer39. ________you meet, you should try to be polite to them.A. WheneverB. HoweverC. Whoever D Wherever40. The reading room for children is____________ the ________________floor.A. on, secondB. on , twoC. in, twoD. in, second41. Excuse me, do you know ______there's a hotel near here?A. whereB. howC. whenD. if42. In summer, food will go bad quickly ___________we put it into a fridge.A. unlessB. ifC. untilD. while43. There isn't ________________in the movie.A. something excitedB. anything excitedC. Anything excitedD. exciting something44. - It's dangerous to swim in this lake.--Yes, you are right. The government has _____________people not to swim in it.A. encourageB. ledC. warnedD. promise45. -- Can you spare time to come to our Thanksgiving party?-- Well, I don't know___________.A. that I can finish my work by then.B. if can I finish the work by thenC, whether I can finish the work by then D. that can I finish the work by then2020-2021学年济南市甸柳一中九年级英语10月月考试题II. 选择填空(30分)6. China is ________Asian country.A. anB. theC. aD. /7. When you meet new words in reading, you needn't __________in a dictionary at once.A. Look up themB. look them upC. look up itD. look it up8. He was ______weak ________________stand up.A. enough; toB. such; thatC. too; toD. so; that9. —What do you usually do in your free time?-I often practice______________ English.A. speakB. to speakC. speakingD. speaks10. He has done ________to improve his English.A. something usefulB. anything usefulC. useful nothingD. useful anything11. ___________you take exercise, ____________ you will be.A. Much; healthyB. The more; the healthyC. The more; the healthierD. More; the healthier12. At last, the poor little girl was ____________on a winter night in the street.A. diedB. deadC. deathD. dying13. —Will you go to net bars with me?-Sorry. My brother advised me ___________there. We are allowed to play computer games at home at weekends.A. not goB. goC. not to goD. to go14. -Could you tell me where I can get a dictionary?—Sure. Go along the street, and there's a ________on your right.A. bankB. bookstoreC. museumD. restaurant15 Which of the following pictures is he most traditional Chinese food?16. We will have two family parties this autumn. One is at Halloween and __________is at Thanksgiving.A. otherB. the otherC. anotherD. the others17. He worked hard and ___________ as the general manager of the company.A. got upB. ended upC. put upD. set up18. ___________ the boss didn't understand what the foreigner was saying, he knew what he wanted to buy. They used body language to communicate.A. UnlessB. No materC. Even thoughD. Because19. It's impolite ___________ information directly when asking for help.A. askB. askingC. askedD. to ask20. I'm not sure whether he will come here, because it ________his feeling.A. cares forB. depends onC. lives onD. agrees with21. ____Rita ___________her mother knows my address. They often come to visit me.A. Neither; norB. Both; andC. Either; orD. Not only; but also22. My brother is too young to go to school. He is only a ________________boy.A. five-year-oldB. five-years-oldC. five year oldD. five years old23. —A number of tourists _________in Jinan for vacation on October 1st,2017.—It's said that the number of the tourist ____________about over 8 million.A. were; wasB. were; wereC. was; wereD. was; was24. She used __________ate. But now she is used ________________early.B. to get up, to getting upC. to getting up, to get upD. to getting up, to getting up25. -Did you watch the movie The Little Prince last weekend?—Yes. _____fantastic movie!A. What anB. How anC. What aD. How26. He is an honest man. ________ what he said, we will believe him without doubt.A. Even thoughB. Depend onC. No matterD. It seems that27. Mary is very shy. She _________goes out and she has few friends.A. oftenB. alwaysC. seldomD. usually28. Edison was a great __________. He ________over 1,000 __________ during his life.A. invent, invented, inventionsB. inventor, invented, inventionC. inventor, invented, inventionsD. inventor, invents, inventions29. He found _________ interesting that so many products in the local shops were made in China.A. thatB. itC. whenD. where30. Students _________not to use mobile phones in our school now.A. askB. askedC. are askedD. were asked31. -Your new bike is so cool.-Thank you! In fact, I have________________ it for two months.A. boughtB. buyC. hadD. has32. Mary went abroad three years ago. She didn't return home __________this year.A. unlessB. untilC. whenD. since33. -What are the shoes with lights used for?-They are used ______________in the dark.A. seeB. seeingC. for seeingD. to seeing34. — Will we have dinner at the Hope Restaurant?---Maybe. We'll go there if the show_____before6. But I don't know if there ___any free tables then.A. will end; wereB. will end; will beC. ends; wereD. ends; will be35. -Could you tell us____?-It starts at 8:00p. m.A. where I can get some medicineB. when the band starts playing this eveningC. when does the band start playing this eveningD. how I can get to the library山东省济南市五中2020-2021学年九年级上学期英语10月月考试题Ⅱ. 选择填空从每题AR. C、D四个选项中, 选出一个最佳答案。
2020-2021学年山东省德州九中九年级(上)第一次月考数学试卷(10月份)(附答案详解)

2020-2021学年山东省德州九中九年级(上)第一次月考数学试卷(10月份)一、选择题(本大题共12小题,共48.0分)1.下列方程中,是一元二次方程的是()A. ax2+2x=1B. x+1x−1=0C. 3(x+2)2=3x2−4x+1D. 3x2−12=x+232.下列抛物线中,与抛物线y=x2−2x+4具有相同对称轴的是()A. y=4x2+2x+1B. y=2x2−4x+1C. y=2x2−x+4D. y=x2−4x+23.若x=2是关于x的一元二次方程x2−mx+8=0的一个解.则m的值是()A. 6B. 5C. 2D. −64.用配方法解方程x2+10x+9=0,配方后可得()A. (x+5)2=16B. (x+5)2=1C. (x+10)2=91D. (x+10)2=1095.某树主干长出若干数目的支干,每个支干又长出同样数目小分支,主干、支干和小分支总数共31.若设主干长出x个支干,则可列方程是()A. (1+x)2=31B. 1+x+x2=31C. (1+x)x=31D. 1+x+2x=316.已知点A(−3,y1),B(−1,y2),C(2,y3)在函数y=−x2−2x+b的图象上,则y1、y2、y3的大小关系为()A. y1<y3<y2B. y3<y1<y2C. y3<y2<y1D. y2<y1<y37.设a,b是方程x2+x−2020=0的两个实数根,则a2+2a+b的值是()A. 2021B. 2020C. 2019D. 20188.二次函数y=−2x2+4x+1的图象如何平移可得到y=−2x2的图象()A. 向左平移1个单位,向上平移3个单位B. 向右平移1个单位,向上平移3个单位C. 向左平移1个单位,向下平移3个单位D. 向右平移1个单位,向下平移3个单位9.在平面直角坐标系中,将抛物线y=x2−(m−1)x+m(m>1)沿y轴向下平移3个单位.则平移后得到的抛物线的顶点一定在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限10.在同一平面直角坐标系内,二次函数y=ax2+bx+b(a≠0)与一次函数y=ax+b的图象可能是()A. B.C. D.11.已知抛物线y=x2+bx+c的对称轴为x=1,且它与x轴交于A、B两点.若AB的长是6,则该抛物线的顶点坐标为()A. (1,9)B. (1,8)C. (1,−9)D. (1,−8)12.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(−1,0)和B,与y轴交于点C.下列结论:①abc<0,②2a+b<0,③4a−2b+c>0,④3a+c>0,其中正确的结论个数为()A. 1个B. 2个C. 3个D. 4个二、填空题(本大题共6小题,共24.0分)13.方程x2=2x的根为______.14.篮球联赛实行单循环赛制,即每两个球队之间进行一场比赛,计划一共打36场比赛,设一共有x个球队参赛,根据题意,所列方程为______.15.抛物线y=ax2+bx+c的部分图象如图所示,则当y>0时,x的取值范围是______16.若二次函数y=(k−2)x2+2x+1的图象与x轴有交点,则k的取值范围是______.17.抛物线y=12x2+mx+m+12经过定点的坐标是______18.平面直角坐标系中,将抛物线y=−x2平移得到抛物线C,如图所示,且抛物线C经过点A(−1,0)和B(0,3),点P是抛物线C上第一象限内一动点,过点P作x轴的垂线,垂足为Q,则OQ+PQ的最大值为______.三、解答题(本大题共7小题,共78.0分)19.解方程:(1)2x2+5x=−1;(2)2(x−3)2=x2−9.20.已知关于x的一元二次方程x2+(4m+1)x+2m−1=0,(1)求证:不论m任何实数,方程总有两个不相等的实数根;(2)若方程的两根为x1、x2且满足1x1+1x2=−12,求m的值.21.我市某楼盘原计划以每平方米5000元的均价对外销售,由于国家“限购”政策出台,购房者持币观望,房产商为了加快资金周转,对该楼盘价格经过两次下调后,决定以每平方米4050元的均价开盘销售.(1)求两次下调的平均百分率;(2)对开盘当天购房的客户,房产商在开盘均价的基础上,还给予以下两种优惠方案供选择:①打9.9折销售;②不打折,一次性送装修费每平方米40元,某客户在开盘当天购买了该楼盘的一套120平方米的商品房,试问该客户选择哪种方案购房更优惠一些?x2+bx+c经过点A(3√3,0)和点B(0,3),且这个抛物线的对称轴为22.抛物线y=−13直线l,顶点为C.(1)求抛物线的解析式;(2)连接AB、AC、BC,求△ABC的面积.23.如图,要设计一幅宽20cm,长30cm的图案,其中有两横两竖的彩条,横竖彩条的宽度比为2:1,如果要使彩条所占的面积是图案面积的19,则竖彩条宽度为多少?7524.商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.设每件商品降价x元.据此规律,请回答:(1)商场日销售量增加______件,每件商品盈利______元(用含x的代数式表示).(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?(3)在上述条件不变、销售正常情况下,商场日盈利可以达到2200元吗?如果可以,请求出x,如果不行,请说明理由.25.已知直线l:y=−2,抛物线C:y=ax2−1经过点(2,0)(1)求a的值;(2)如图①,点P是抛物线C上任意一点,过点P作直线l的垂线,垂足为Q.求证:PO=PQ;(3)请你参考(2)中的结论解决下列问题1.如图②,过原点作直线交抛物线C于A,B两点,过此两点作直线l的垂线,垂足分别为M,N,连接ON,OM,求证:OM⊥ON;2.如图③,点D(1,1),使探究在抛物线C上是否存在点F,使得FD+FO取得最小值?若存在,求出点F的坐标,若不存在,请说明理由.答案和解析1.【答案】D【解析】【分析】本题考查一元二次方程的概念,一元二次方程未知数的最高次数是2,为整式方程,并且二次项系数不为0.找到化简后未知数的最高次数是2,二次项系数不为0的整式方程的选项即可.【解答】解:A、a有可能为0,不符合题意;B、为分式方程,不符合题意;C、化简后为一元一次方程,不符合题意;D、未知数的最高次数是2,二次项系数不为0,是一元二次方程,符合题意;故选D.2.【答案】B【解析】解:抛物线y=x2−2x+4的对称轴为x=1;A、y=4x2+2x+1的对称轴为x=−1,不符合题意;4B、y=2x2−4x+1的对称轴为x=1,符合题意;C、y=2x2−x+4的对称轴为x=1,不符合题意;4D、y=x2−4x+2的对称轴为x=2,不符合题意,故选B.根据对称轴方程分别确定各个抛物线的对称轴后即可作出判断.此题考查了二次函数的性质,牢记对称轴方程公式是解答本题的关键,难度不大.3.【答案】A【解析】【分析】本题考查了一元二次方程的解,此题比较简单,易于掌握.先把x的值代入方程即可得到一个关于m的方程,解一元一次方程即可.【解答】解:把x=2代入方程得:4−2m+8=0,解得m=6.故选:A.4.【答案】A【解析】解:方程x2+10x+9=0,整理得:x2+10x=−9,配方得:x2+10x+25=16,即(x+5)2=16,故选A.方程移项,利用完全平方公式化简得到结果即可.此题考查了解一元二次方程−配方法,熟练掌握完全平方公式是解本题的关键.5.【答案】B【解析】解:设主干长出x个支干,根据题意列方程得:x2+x+1=31.故选:B.由题意设主干长出x个支干,每个支干又长出x个小分支,则又长出x2个小分支,则共有x2+x+1个分支,即可列方程.此题考查了由实际问题抽象出一元二次方程,要根据题意分别表示主干、支干、小分支的数目,找到关键描述语,找到等量关系是解决问题的关键.6.【答案】B【解析】【分析】本题考查二次函数的性质,解题的关键是明确二次函数的性质,找出所求问题需要的条件.根据二次函数图象具有对称性和二次函数的增减性,可以判断y1、y2、y3的大小,从而可以解答本题.【解答】解:∵y=−x2−2x+b,∴函数y =−x 2−2x +b 的对称轴为直线x =−1,开口向下,当x <−1时,y 随x 的增大而增大,当x >−1时,y 随x 的增大而减小, ∵−1−(−3)=2,−1−(−1)=0,2−(−1)=3, ∴y 3<y 1<y 2, 故选B .7.【答案】C【解析】解:∵a ,b 是方程x 2+x −2020=0的两个实数根, ∴a 2+a =2020,a +b =−1,∴a 2+2a +b =(a 2+a)+(a +b)=2020−1=2019. 故选:C .根据一元二次方程的解及根与系数的关系可得出a 2+a =2020、a +b =−1,将其代入a 2+2a +b =(a 2+a)+(a +b)中即可求出结论.本题考查了根与系数的关系以及一元二次方程的解,根据一元二次方程的解及根与系数的关系找出a 2+a =2020、a +b =−1是解题的关键.8.【答案】C【解析】解:二次函数y =−2x 2+4x +1的顶点坐标为(1,3),y =−2x 2的顶点坐标为(0,0),只需将函数y =−2x 2+4x +1的图象向左移动1个单位,向下移动3个单位即可. 故选:C .根据配方法,可得顶点式解析式,根据右移减,上移加,可得答案.本题考查函数的图象变换,讨论两个二次函数的图象的平移问题,只需看顶点坐标是如何平移得到的即可.9.【答案】D【解析】解:∵y =x 2−(m −1)x +m =(x −m−12)2+m −(m−1)24,∴该抛物线顶点坐标是(m−12,m −(m−1)24),∴将其沿y 轴向下平移3个单位后得到的抛物线的顶点坐标是(m−12,m −(m−1)24−3),∵m>1,∴m−1>0,∴m−12>0,∵m−(m−1)24−3=4m−(m2−2m+1)−124=−(m−3)2−44=−(m−3)24−1<0,∴点(m−12,m−(m−1)24−3)在第四象限;故选:D.根据平移规律得到平移后抛物线的顶点坐标,然后结合m的取值范围判断新抛物线的顶点所在的象限即可.本题考查了二次函数的图象与性质、平移的性质、抛物线的顶点坐标等知识;熟练掌握二次函数的图象和性质,求出抛物线的顶点坐标是解题的关键.10.【答案】C【解析】【分析】本题考查了二次函数的图象以及一次函数图象与系数的关系,根据a、b的正负确定一次函数图象经过的象限是解题的关键.根据二次函数图象的开口以及对称轴与y轴的关系即可得出a、b的正负,由此即可得出一次函数图象经过的象限,再与函数图象进行对比即可得出结论.【解答】解:A.二次函数图象开口向上,对称轴在y轴右侧,∴a>0,b<0,∴一次函数图象应该过第一、三、四象限,且与二次函数交于y轴负半轴的同一点,故A错误;B.∵二次函数图象开口向下,对称轴在y轴左侧,∴a<0,b<0,∴一次函数图象应该过第二、三、四象限,且与二次函数交于y轴负半轴的同一点,故B错误;C.二次函数图象开口向上,对称轴在y轴右侧,∴a>0,b<0,∴一次函数图象应该过第一、三、四象限,且与二次函数交于y轴负半轴的同一点,故C 正确;∵D.二次函数图象开口向上,对称轴在y 轴右侧,∴a >0,b <0,∴一次函数图象应该过第一、三、四象限,且与二次函数交于y 轴负半轴的同一点, 故D 错误;故选C .11.【答案】C【解析】解:∵抛物线y =x 2+bx +c 的对称轴为x =1,且它与x 轴交于A 、B 两点.AB 的长是6,∴点A 的坐标为(−2,0),点B 的坐标为(4,0)或点A 的坐标为(4,0),点B 的坐标为(−2,0), ∴{−b 2×1=14−2b +c =0, 得{b =−2c =−8, ∴y =x 2−2x −8=(x −1)2−9,∴该抛物线的顶点坐标为(1,−9),故选:C .根据题意可以得到点A 和点B 的坐标,然后根据对称轴为x =1可以求得b 、c 的值,然后将函数解析式化为顶点式即可解答本题.本题考查抛物线与x 轴的交点、二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答.12.【答案】B【解析】解:①∵由抛物线的开口向上知a >0,∵对称轴位于y 轴的右侧,∴b <0.∵抛物线与y 轴交于负半轴,∴c <0,∴abc >0;故错误;<1,得2a>−b,即2a+b>0,②对称轴为x=−b2a故错误;③如图,当x=−2时,y>0,4a−2b+c>0,故正确;④∵当x=−1时,y=0,∴0=a−b+c<a+2a+c=3a+c,即3a+c>0.故正确.综上所述,有2个结论正确.故选:B.由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴求出2a与b的关系.本题主要考查抛物线与x轴的交点坐标,二次函数图象与函数系数之间的关系,解题的关键是掌握数形结合思想的应用,注意掌握二次函数图象与系数的关系.13.【答案】x1=0,x2=2【解析】解:x2=2x,x2−2x=0,x(x−2)=0,x=0,或x−2=0,x1=0,x2=2,故答案为:x1=0,x2=2.移项后分解因式,即可得出两个一元一次方程,求出方程的解即可.本题考查了解一元二次方程−因式分解法,因式分解法解一元二次方程的一般步骤:①移项,使方程的右边化为零;②将方程的左边分解为两个一次因式的乘积;③令每个因式分别为零,得到两个一元一次方程;④解这两个一元一次方程,它们的解就都是原方程的解.14.【答案】12x(x −1)=36【解析】解:设一共有x 个球队参赛,每个队都要赛(x −1)场,但两队之间只有一场比赛,由题意得:12x(x −1)=36,故答案为12x(x −1)=36.赛制为单循环形式(每两队之间都赛一场),x 个球队比赛总场数为x(x−1)2,即可列方程.本题考查了由实际问题抽象出一元二次方程,解决本题的关键是读懂题意,得到总场数的等量关系.15.【答案】−1<x <3【解析】解:抛物线的对称轴为直线x =1,而抛物线与x 轴的一个交点坐标为(−1,0),所以抛物线与x 轴的另一个交点坐标为(3,0),所以当−1<x <3时,y >0.故答案为−1<x <3.利用抛物线的对称性得到抛物线与x 轴的另一个交点坐标为(3,0),然后写出抛物线在x 轴上方所对应的自变量的范围即可.本题考查了抛物线与x 轴的交点:把求二次函数y =ax 2+bx +c(a,b ,c 是常数,a ≠0)与x 轴的交点坐标问题转化解.关于x 的一元二次方程即可求得交点横坐标.也考查了二次函数的性质.16.【答案】k ≤3且k ≠2【解析】解:∵二次函数y =(k −2)x 2+2x +1的图象与x 轴有交点,∴一元二次方程(k −2)x 2+2x +1=0有解,∴{k −2≠0△=22−4(k −2)=12−4k ≥0, 解得:k ≤3且k ≠2.故答案为:k ≤3且k ≠2.根据二次函数图象与x 轴有交点可得出关于x 的一元二次方程有解,根据根的判别式结合二次项系数非零即可得出关于k 的一元一次不等式组,解不等式组即可得出结论. 本题考查了抛物线与x 轴的交点、根的判别式以及解一元一次不等式组,根据根的判别式△≥0结合二次项系数非零找出关于k 的一元一次不等式组是解题的关键.17.【答案】(−1,1)【解析】解:∵y =12x 2+(x +1)m +12,∵抛物线经过定点,∴x +1=0,∴x =−1,y =1,∴定点坐标为(−1,1),故答案为(−1,1)由y =12x 2+(x +1)m +12,抛物线经过定点,可得x +1=0,由此即可解决问题; 本题考查二次函数图象上的点的坐标特征,定点问题等知识,解题的关键是学会用转化的思想思考问题,属于中考常考题型.18.【答案】214【解析】解:设平移后的解析式为y =−x 2+bx +c ,∵抛物线C 经过点A(−1,0)和B(0,3),∴{−1−b +c =0c =3,解得{b =2c =3, ∴抛物线C 的解析式为y =−x 2+2x +3,设Q(x,0),则P(x,−x 2+2x +3),∵点P 是抛物线C 上第一象限内一动点,∴OQ +PQ =x +(−x 2+2x +3)=−x 2+3x +3=−(x −32)2+214,∴OQ +PQ 的最大值为214,故答案为214.求得抛物线C 的解析式,设Q(x,0),则P(x,−x 2+2x +3),即可得出OQ +PQ =x +(−x 2+2x +3)=−(x −32)2+214,根据二次函数的性质即可求得.本题考查了二次函数的性质,二次函数图象与几何变换,根据题意得出OQ +PQ =−x 2+3x +3是解题的关键.19.【答案】解:(1)2x 2+5x +1=0,∵a =2,b =5,c =1,∴b 2−4ac =52−4×2×1=17,∴x =−b±√b 2−4ac 2a=−5±√172,, ∴x 1=−5+√172,x 2=−5−√172;(2)2(x −3)2=x 2−9,2(x −3)2−(x −3)(x +3)=0,(x −3)(2x −6−x −3)=0,∴x −3=0或x −9=0,∴x 1=3,x 2=9.【解析】(1)先把方程化为一般式,然后利用公式法解方程;(2)先把方程变形为2(x −3)2−(x −3)(x +3)=0,然后利用因式分解法解方程. 本题考查了解一元二次方程−因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.也考查了公式法解一元二次方程.20.【答案】解:(1)证明:Δ=(4m +1)2−4(2m −1)=16m 2+8m +1−8m +4=16m 2+5>0,∴不论m 为任何实数,方程总有两个不相等的实数根;(2)∵1x 1+1x 2=−12,即x 1+x 2x 1x 2=−12, ∴由根与系数的关系可得−4m−12m−1=−12,解得 m =−12,经检验得出m =−12是原方程的根,即m的值为−12.【解析】本题考查一元二次方程根与系数的关系,熟练掌握一元二次方程的根的情况与判别式Δ的符号的关系,把求未知系数的范围问题转化为解不等式的问题,体现了转化的数学思想.(1)要证明方程总有两个不相等的实数根,那么只要证明Δ>0即可;(2)因为1x1+1x2=x1+x2x1x2=−12,所以由根与系数的关系可得−4m−12m−1=−12,解方程可得m的值.21.【答案】解:(1)设两次下调的平均百分率为x,根据题意得:5000(1−x)2=4050,解得:x1=0.1=10%,x2=1.9(舍去),答:两次下调的平均百分率为10%.(2)∵方案①可优惠4050×120×(1−0.99)=4860(元),方案②可优惠400×120=4800(元),且4860>4800,∴方案①更优惠.【解析】(1)根据每次的均价等于上一次的价格乘以(1−x)(x为平均每次下调的百分率),可列出一个一元二次方程,解此方程可得平均每次下调的百分率;(2)根据优惠方案先分别求出方案①和方案②的优惠钱数,再进行比较即可得出答案.本题主要考查一元二次方程在实际中的应用:解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.22.【答案】解:(1)∵抛物线y=−13x2+bx+c经过A(3√3,0)、B(0,3),∴{−9+3√3b+c=0 c=3由上两式解得b=2√33,∴抛物线的解析式为:y=−13x2+2√33x+3;(2)由(1)抛物线对称轴为直线x=√3,把x=√3代入,y=−13x2+2√33x+3得y=4,则点C坐标为(√3,4),设线段AB所在直线为:y=kx+b,解得AB解析式为:y=−√33x+3,∵线段AB所在直线经过点A(3√3,0)、B(0,3),抛物线的对称轴l与直线AB交于点D,∴设点D的坐标为D(√3,m),将点D(√3,m)代入y=−√33x+3,解得m=2,∴点D坐标为(√3,2),∴CD=CE−DE=2过点B作BF⊥l于点F,∴BF=OE=√3,∵BF+AE=OE+AE=OA=3√3,∴S△ABC=S△BCD+S△ACD=12CD⋅BF+12CD⋅AE,∴S△ABC=12CD(BF+AE)=12×2×3√3=3√3.【解析】本题考查的是待定系数法求二次函数的解析式、待定系数法求一次函数的解析式,用割补法求三角形面积,二次函数的图象和性质,解答时注意数形结合.(1)利用待定系数法求抛物线解析式;(2)利用割补法求ABC的面积.23.【答案】解:设竖彩条的宽为xcm,则横彩条的宽为2xcm,则(30−2x)(20−4x)=30×20×(1−1975),整理得:x2−20x+19=0,解得:x1=1,x2=19(不合题意,舍去).答:竖彩条的宽度为1cm.【解析】可设竖彩条的宽是xcm,则横彩条的宽是2xcm,根据彩条所占面积是图案面积的19,可列方程求解.75本题考查的是一元二次方程的应用,设出横竖条的宽,以面积做为等量关系列方程求解.24.【答案】2x(50−x)【解析】解:(1)商场日销售量增加2x件,每件商品盈利(50−x)元,故答案为:2x、(50−x);(2)根据题意可得(30+2x)(50−x)=2100,解得:x=15或x=20,∵该商场为了尽快减少库存,∴降的越多,越吸引顾客,∴选x=20,答:每件商品降价20元,商场日盈利可达2100元.(3)根据题意可得(30+2x)(50−x)=2200,整理得到:x2−35x+350=0.由于△=b2−4ac=1225−1400=−175<0,所以该方程无解.故商场日盈利不可以达到2200元.(1)降价1元,可多售出2件,降价x元,可多售出2x件,盈利的钱数=原来的盈利−降低的钱数;(2)(3)根据日盈利=每件商品盈利的钱数×(原来每天销售的商品件数30+2×降价的钱数),列出方程求解即可.此题主要考查了一元二次方程的应用;得到日盈利的等量关系是解决本题的关键.25.【答案】解:(1)∵抛物线C:y=ax2−1经过点(2,0),∴0=4a−1,∴a=14;(2)∵a=14,∴抛物线解析式:y=14x2−1,设点P(a,14a2−1),∴PO=√(a−0)2+(14a2−1) 2=14a2+1,PQ=14a2−1−(−2)=14a2+1,∴PO=PQ;(3)1.由(2)可得OA=AM,OB=BN,∴∠BON=∠BNO,∠AOM=∠AMO,∵AM⊥MN,BN⊥MN,∴AM//BN,∴∠ABN+∠BAM=180°,∵∠ABN+∠BON+∠BNO=180°,∠AOM+∠AMO+∠BAM=180°,∴∠ABN+∠BON+∠BNO+∠AOM+∠AMO+∠BAM=360°,∴∠BON+∠AOM=90°,∴∠MON=90°,∴OM⊥ON;2.如图:过点F作EF⊥直线l,由(2)可得OF=EF,∵OF+DF=EF+DF,∴当点D,点F,点E三点共线时,OF+DF的值最小.即此时DE⊥直线l,∴OF+DF的最小值为DE=1+2=3.【解析】本题考查了二次函数综合题,待定系数法求解析式,两点距离公式,三角形内角和定理,最短路径问题,利用数形思想解决问题是本题的关键.(1)利用待定系数法可求a的值;a2−1),根据两点距离公式可求PQ,PO的长度,即可证PQ=PO;(2)设点P(a,14(3)1.由(2)可得OB=BN,AM=AO,即可求∠BON=∠BNO,∠AOM=∠AMO,根据三角形内角和定理可求OM⊥ON;2.过点F作EF⊥直线l,由(2)得OF=EF,当点D,点F,点E三点共线时,OF+DF的值最小,此时DE⊥直线l,即可求FD+FO的最小值.。
2020-2021学年九年级上学期第一次月考语文试题 (含答案)

2020-2021学年第一次月考语文试题一、积累与运用(共24分)1.根据拼音写汉字。
(2分)我感到一种bùkěmíng zhuàng(不可名状)的恐惧,一种同亲人隔绝、同大地分离的孤独感yóu rán ér shēng(油然而生)。
2.表述有误的一项是(2分)( c )A.《我的叔叔于勒》一文中,以我的视角叙说事件的进展,这篇小说有两条线索:明线是菲利普夫妇对于勒态度的变化,暗线是于勒经济状况的变化。
B.《故乡》《我的叔叔于勒》《孤独之旅》的作者分别是鲁迅、莫泊桑、曹文轩。
C.成语“百废具兴”“气象万千”“心旷神怡”“觥筹交错”都是出自《岳阳楼记》。
D.《沁园春雪》是一首词,“沁园春”是词牌名,“雪”是题目。
3.判断题(正确的打“√”,错误的打“×”)(2分)①“风骚”本指《楚辞》里的《国风》和《诗经》里的《离骚》,后泛指文章辞藻。
(×)②我们学过鲁迅的《从百草园到三味书屋》《阿长与山海经》《社戏》均选自他的散文集《朝花夕拾》。
(×)4.按要求答题。
(2分)“每天进步一点点,三年语文灿年华。
”三年初中生活里,你一定学会了一些阅读积累的方法。
从下列名言中任选一句进行积累,并说明理由。
①书山有路勤为径,学海无涯苦作舟。
——韩愈②读过一本好书,像交了一个益友。
——臧克家③鸟欲高飞先振翅,人求上进先读书。
——李苦禅④书犹药也,善读可以医愚。
——刘向我选择第___句理由__________________________________________________5.按要求填空。
(16分)①江山如此多娇,引无数英雄竞折腰。
(毛泽东《沁园春雪》)②欲为圣明除弊事,肯将衰朽惜残年。
(韩愈《左迁至蓝关示侄孙湘》)③起舞弄清影,___何似在人间__。
(苏轼《水调歌头》)④戍鼓断人行,边秋一雁声。
(杜甫《月夜忆舍弟》)⑤叙说诗人获罪原因的诗句:“一封朝奏九重天,夕贬潮州路八千。
2020-2021学年九年级第一学期期中考试考试物理试题(附解答)

2020-2021学年九年级第一学期期中考试考试物理试题本试卷分为A卷和B卷两部分,共8页。
A卷共100分,B卷共35分,全卷满分135分。
注意事项:1.答题前请仔细阅读答题卡上的注意事项。
2.所有试题的答案必须按题号填写在答题卡相应的位置上,在试卷上、草稿纸上答题无效。
3.考试结束后,监考人员将答题卡收回,试卷由学生自己保管好。
A卷(共100分)一、选择题(本大题共12小题,每小题4分,共48分。
每个小题只有—个选项是符合题目要求的。
)1、分子是保持物质化学性质的最小微粒.首先提出分子概念的科学家是( )A、阿伏伽德罗B、道尔顿C、卢瑟福D、汤姆生2、下面四个实验现象中,能够说明分子在不停地运动的是 ( )3、初春培育水稻秧苗时,为了不使秧苗受冻,下列做法中正确的是 ( ) A.早晨多排水,傍晚多灌水 B.早晨多灌水,傍晚多排水C.早晨和傍晚都要多灌水 D.早晨和傍晚都不要灌水4、做功和热传递在改变物体的内能上是等效的,下图不属于做功改变物体内能的是()5、如图所示的滑动变阻器的四种接法中,当滑片P 向右移动时使电路的电阻变小的接法是( )6、关于热机的效率,下列说法正确的是()A、蒸汽机的效率通常高于喷气发动机;B、热机的效率一定小于100%;C、汽车排放的尾气,是城市环境污染的重要来源。
目前有一些新型燃料汽车,实现了“零排放”,它们的效率达到了100%;D、在完全无摩擦的道路上,汽车发动机的效率可达到100%。
7、如图所示,在探究并联电路中的电流关系时,小明同学用电流表测出A.B.C三处的电流分别为IA =0.5A,IB=0.3A,IC=0.2A,在表格中记录数据后,下一步首先应该做的是:()A.整理器材,结束实验;B.换用不同规格的小灯泡,再测出几组电流值C.分析数据,得出结论;D.换用电流表的另一量程,再测出一组电流值8、在一本用电常识的书中,列出了使用白炽电灯的常见故障与检修,其中一项故障现象如下:从电路的组成来看,上述故障现象可以概括成一个原因:()A、开路;B、通路;C、短路;D、以上都不对。
山东省德州市德州经济技术开发区太阳城中学2024年数学九上开学综合测试试题【含答案】

山东省德州市德州经济技术开发区太阳城中学2024年数学九上开学综合测试试题题号一二三四五总分得分A 卷(100分)一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、(4分)若分式23x +有意义,则x 的取值范围是()A .3x ≠-B .3x ≠C .3x >-D .3x <-2、(4分)如图,在四边形ABCD 中,AB =BC =2,且∠B =∠D =90°,连接AC ,那么四边形ABCD 的最大面积是()A .B .4C .D .83、(4分)能判定一个四边形是平行四边形的条件是()A .一组对角相等B .两条对角线互相平分C .一组对边相等D .两条对角线互相垂直4、(4分)下列命题,①4的平方根是2;②有两边和一角相等的两个三角形全等;③等腰三角形的底角必为锐角;④两组对角分别相等的四边形是平行四边形.其中真命题有()A .4个B .3个C .2个D .1个5、(4分)一次函数y =ax +1与y =bx -2的图象交于x 轴上同一个点,那么a ∶b 的值为()A .1∶2B .-1∶2C .3∶2D .以上都不对6、(4分)如果分式13a -有意义,则a 的取值范围是()A .a 为任意实数出B .a =3C .a ≠0D .a ≠37、(4分)正方形ABCD 在坐标系中的位置如图所示,将正方形ABCD 绕D 点顺时针方向旋转90°后,C 点的坐标为()A .(﹣1,2)B .(2,0)C .(2,1)D .(2,﹣1)8、(4分)要了解全校学生的课外作业负担情况,你认为以下抽样方法中比较合理的是()A .调查九年级全体学生B .调查七、八、九年级各30名学生C .调查全体女生D .调查全体男生二、填空题(本大题共5个小题,每小题4分,共20分)9、(4分)把多项式n (n ﹣2)+m (2﹣n )分解因式的结果是_____.10、(4分)关于x 的不等式组2131xa x +>⎧⎨->⎩的解集为1<x <3,则a 的值为____.11、(4分)直线y =2x +1经过点(a ,0),则a =________.12、(4分)如图,已知函数y =kx +2与函数y =mx -4的图象交于点A ,根据图象可知不等式kx +2<mx -4的解集是__________.13、(4分)在平面直角坐标系xOy 中,点A 、B 的坐标分别为(3,m )、(3,m +2),若线段AB 与x 轴有交点,则m 的取值范围是_____.三、解答题(本大题共5个小题,共48分)14、(12分)如图,在矩形ABCD 中,4,5==AB BC .(1)请用尺规作图法,在矩形ABCD 中作出以BD 为对角线的菱形EBFD ,且点E F 、分别在AD BC 、上.(不要求写作法,保留作图痕迹)(2)在(1)的条件下,求菱形EBFD 的边长.15、(8分)如图,在平行四边形ABCD 中,对角线AC 与BD 相交于点O ,AB =5,AD =3,E 是AB 上的一点,F 是AD 上的一点,连接BO 和FO .(1)当点E 为AB 中点时,求EO 的长度;(2)求线段AO 的取值范围;(3)当EO ⊥FO 时,连接EF .求证:BE +DF >EF .16、(8分)在正方形ABCD 中,点F 是BC 延长线上一点,过点B 作BE ⊥DF 于点E ,交CD 于点G ,连接CE.(1)若正方形ABCD 边长为3,DF=4,求CG 的长;(2)求证:EF+EG=CE.17、(10分)如图,▱ABCD 的对角线AC ,BD 相交于点O ,△OAB 是等边三角形.(1)求证:▱ABCD 为矩形;(2)若AB =4,求▱ABCD 的面积.18、(10分)4月23日是世界读书日,总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读,该校文学社为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:min ):3060815044110130146801006080120140758110308192课外阅读时间()min x 040x ≤<4080x ≤<80120x ≤<120160x ≤<等级D C B A 人数3a 8b 平均数中位数众数80c 81四、得出结论:①表格中的数据:a =,b =,c =;②用样本中的统计量估计该校学生每周用于课外阅读时间的等级为;③如果该校现有学生400人,估计等级为“B ”的学生有人;④假设平均阅读一本课外书的时间为320分钟,请你用样本平均数估计该校学生每人一年(按52周计算)平均阅读本课外书.B 卷(50分)一、填空题(本大题共5个小题,每小题4分,共20分)19、(4分)如图,把菱形ABCD 沿AH 折叠,使点B 落在BC 上的E 点处,若70B ︒∠=,则EDC ∠的大小为_____________.20、(4分)如果n 边形的每一个内角都相等,并且是它外角的3倍,那么n =______21、(4分)如图,△ABC 中,AB =BC =12cm ,D 、E 、F 分别是BC 、AC 、AB 边上的中点,则四边形BDEF 的周长是__________cm .22、(4分)如图,在平行四边形ABCD 中,4AB =,7BC =.以点B 为圆心,适当长为半径画弧,交BA 于点E ,交BC 于点F ,再分别以点E ,F 为圆心,大于12EF 的长为半径画弧,两弧相交于点G ,射线BG 交CD 的延长线于点H ,则DH 的长是____________.23、(4分)如图,菱形ABCD 的面积为24cm 2,正方形ABCF 的面积为18cm 2,则菱形的边长为_____.二、解答题(本大题共3个小题,共30分)24、(8分)解方程()21450x x +-=;()()()23222x x x -=-.25、(10分)我国是世界上严重缺水的国家之一,2011年春季以来,我省遭受了严重的旱情,某校为了组织“节约用水从我做起”活动,随机调查了本校120名同学家庭月人均用水量和节水措施情况,如图1、图2是根据调查结果做出的统计图的一部分.请根据信息解答下列问题:(1)图1中淘米水浇花所占的百分比为;(2)图1中安装节水设备所在的扇形的圆心角度数为;(3)补全图2;(4)如果全校学生家庭总人数为3000人,根据这120名同学家庭月人均用水量,估计全校学生家庭月用水总量是多少吨?26、(12分)如图,在正方形ABCD 中,点M 在CD 边上,点N 在正方形ABCD 外部,且满足∠CMN =90°,CM =MN .连接AN ,CN ,取AN 的中点E ,连接BE ,AC ,交于F 点.(1)①依题意补全图形;②求证:BE ⊥AC .(2)请探究线段BE ,AD ,CN 所满足的等量关系,并证明你的结论.(3)设AB =1,若点M 沿着线段CD 从点C 运动到点D ,则在该运动过程中,线段EN 所扫过的面积为______________(直接写出答案).参考答案与详细解析一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)1、A【解析】直接利用分式有意义的条件即分母不为零,进而得出答案.【详解】解:分式23x+有意义,30x∴+≠,解得:3x≠-.故选:A.此题主要考查了分式有意义的条件,正确把握定义是解题关键.2、B【解析】等腰直角三角形△ABC的面积一定,要使四边形ABCD的面积最大,只要△ACD面积最大即可,当点D在AC的中垂线上时,△ACD面积最大,此时ABCD是正方形,即可求出面积,做出选择即可.【详解】解:∵∠B=90°,AB=BC=2,∵△ABC是等腰直角三角形,要使四边形ABCD的面积最大,只要△ACD面积最大即可,当点D在AC的中垂线上时,△ACD面积最大,此时ABCD是正方形,面积为2×2=4,故选:B.此题考查正方形的性质,直角三角形的性质,线段的中垂线的性质,何时面积最大是正确解题的关键.3、B【解析】【详解】A.两组对角分别相等的四边形是平行四边形,故本选项错误;B.两条对角线互相平分的四边形是平行四边形,故本选项正确;C.两组对边分别相等的四边形是平行四边形,故本选项错误;D.对角线互相平分的四边形才是平行四边形,而对角线互相垂直的四边形不一定是平行四边形,故本选项错误.故选B.本题考查平行四边形的判定,定理有:①两组对角分别相等的四边形是平行四边形,②两组对边分别相等的四边形是平行四边形,③对角线互相平分的四边形是平行四边形,④有一组对边相等且平行的四边形是平行四边形.4、C【解析】根据平方根的定义对①进行判断;根据全等三角形的判定方法对②进行判断;根据等腰三角形的性质和平行四边形的判定方法对③④进行判断.【详解】解:①4的平方根是±2,是假命题;②有两边和其夹角相等的两个三角形全等,是假命题;③等腰三角形的底角必为锐角,是真命题;④两组对角分别相等的四边形是平行四边形是真命题;故选:C.本题考查命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.5、B【解析】试题分析:先根据x轴上的点的横坐标相等表示出x的值,再根据相交于同一个点,则x 值相等,列式整理即可得解.解:∵两个函数图象相交于x轴上同一个点,∴y=ax+1=bx ﹣1=0,解得x=﹣=,所以=﹣,即a :b=(﹣1):1.故选B .6、D 【解析】直接利用分式的分母不等于0,进而得出答案.【详解】解:分式13a -有意义,则30a -≠,解得:3a ≠.故选:D .此题主要考查了分式有意义的条件,正确把握定义是解题关键.7、D 【解析】利用网格特点和旋转的性质画出正方形ABCD 绕D 点顺时针方向旋转90°后所得的正方形CEFD ,则可得到C 点的对应点的坐标.【详解】如图,正方形ABCD 绕D 点顺时针方向旋转90°后得到正方形CEFD ,则C 点旋转后的对应点为F (2,﹣1),故选D .本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.【解析】【分析】如果抽取的样本得当,就能很好地反映总体的情况,否则抽样调查的结果会偏离总体情况.要抽出具有代表性的调查样本.【详解】A.只调查九年级全体学生,没有代表性;B.调查七、八、九年级各30名学生,属于分层抽样,有代表性;C.只调查全体女生,没有代表性;D.只调查全体男生,没有代表性.故选B.【点睛】本题考核知识点:抽样调查.解题关键点:要了解全校学生的课外作业负担情况,抽取的样本一定要具有代表性.二、填空题(本大题共5个小题,每小题4分,共20分)9、(n﹣2)(n﹣m).【解析】用提取公因式法分解因式即可.【详解】n(n﹣2)+m(2﹣n)=n(n﹣2)-m(n-2)=(n﹣2)(n﹣m).故答案为(n﹣2)(n﹣m).本题考查了用提公因式法进行因式分解;一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.10、4【解析】解:解不等式2x+1>3可得x>1,解不等式a-x>1,可得x<a-1,然后根据不等式组的解集为1<x<3,可知a-1=3,解得a=4.故答案为4.此题主要考查了不等式组的解,解题关键是根据不等式组的解集和求出不等式的解集的特点,求解即可.11、1 2-【解析】代入点的坐标,求出a的值即可.【详解】将(a,0)代入直线方程得:2a+1=0解得,a=1 2-,故答案1 2-.本题考查了直线方程问题,考查函数代入求值,是一道常规题.12、x<-2【解析】观察函数图象得到当x<-2时,y=kx+2的图象位于y=mx-1的下方,即kx+2<mx-1.【详解】解:∵观察图象知当<>-2时,y=kx+2的图象位于y=mx-1的下方,根据图象可知不等式kx+2<mx-1的解集是x<-2,故答案为:x<-2.本题考查一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.13、﹣2≤m≤1【解析】由点的坐标特征得出线段AB∥y轴,当直线y=1经过点A时,得出m=1;当直线y=1经过点B时,得出m=﹣2;即可得出答案.【详解】解:∵点A、B的坐标分别为(3,m)、(3,m+2),∴线段AB∥y轴,当直线y=1经过点A时,则m=1,当直线y=1经过点B时,m+2=1,则m=﹣2;∴直线y=1与线段AB有交点,则m的取值范围为﹣2≤m≤1;故答案为﹣2≤m≤1.本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.三、解答题(本大题共5个小题,共48分)14、(1)见解析;(2)菱形EBFD 的边长为4110.【解析】(1)连接BD ,作BD 的垂直平分线交AD 、BC 与E 、F ,点E 、F 即为所求的点;(2)设ED=x ,则BE=x ,AE=5-x ,在Rt △ABE 中利用勾股定理可以算出x 的值即可.【详解】(1)连接BD ,作BD 的垂直平分线交AD 、BC 与E 、F ,连接BE ,DF 即可,如图,菱形EBFD 即为所求.(2)设ED 的长为x ,∵,5===BE ED AD BC ,∴5,=-=AE x BE x ,∴在∆Rt ABE 中,222AB AE BE +=,即()22245+-=x x ,解得4110=x ,即菱形EBFD 的边长为4110.此题主要考查了菱形的判定与性质,以及勾股定理的应用,关键是正确画出图形,熟练掌握菱形的判定方法.15、(1)32;(2)1<AO <4;(3)见解析.【解析】(1)O 是中点,E 是中点,所以OE =12BC =32;(2)在△ACD 中利用三角形的第三边长小于两边之和,大于两边只差;(3)延长FO 交BC 于G 点,就可以将BE,FD,EF 放在一个三角形中,利用三角形两边之和大于第三边即可.【详解】(1)解:∵四边形ABCD 为平行四边形,∴BC =AD =3,OA =OC ,∵点E 为AB 中点,∴OE 为△ABC 的中位线,∴OE =12BC =32;(2)解:在△ABC 中,∵AB ﹣BC <AC <AB +BC ,而OA =OC ,∴5﹣3<2AO <5+3,∴1<AO <4;(3)证明:延长FO 交BC 于G 点,连接EG ,如图,∵四边形ABCD 为平行四边形,∴OB =OD ,BC ∥AD ,∴∠OBG =∠ODF ,在△OBG 和△ODF 中OBG ODF OB OD BOG DOF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△OBG ≌△ODF ,∴BG =DF ,OG =OF ,∵EO ⊥OF ,∴EG =EF ,在△BEG 中,BE +BG >EG ,∴BE +FD >EF .本题主要考查中位线的性质,以及通过构造新的全等三角形,应用三角形两边之和大于第三边性质来比较线段的关系.16、;(2)证明见解析.【解析】(1)根据正方形的性质可得∠BCG=∠DCB=∠DCF=90°,BC=DC ,再根据同角的余角相等求出∠CBG=∠CDF ,然后利用“角边角”证明△CBG 和△CDF 全等,根据全等三角形对应边相等可得BG=DF ,再利用勾股定理列式计算即可得解;(2)过点过点C 作CM ⊥CE 交BE 于点M ,根据全等三角形对应边相等可得CG=CF ,全等三角形对应角相等可得∠F=∠CGB ,再利用同角的余角相等求出∠MCG=∠ECF ,然后利用“角边角”证明△MCG 和△ECF 全等,根据全等三角形对应边相等可得MG=EF ,CM=CE ,从而判断出△CME 是等腰直角三角形,再根据等腰直角三角形的性质证明即可.【详解】(1)解:∵四边形ABCD 是正方形,∴∠BCG=∠DCB=∠DCF=90°,BC=DC ,∵BE ⊥DF ,∴∠CBG+∠F=∠CDF+∠F ,∴∠CBG=∠CDF ,在△CBG 和△CDF 中,90{BCG DCF BC CD CBG CDF∠=∠=︒=∠=∠,∴△CBG ≌△CDF (ASA ),∴BG=DF=4,∴在Rt △BCG 中,CG 2+BC 2=BG 2,∴;(2)证明:如图,过点C 作CM ⊥CE 交BE 于点M ,∵△CBG ≌△CDF ,∴CG=CF,∠F=∠CGB ,∵∠MCG+∠DCE=∠ECF+∠DCE=90°,∴∠MCG=∠ECF ,在△MCG 和△ECF 中,MCG ECF CG CF F CGB ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△MCG ≌△ECF (SAS ),∴MG=EF ,CM=CE ,∴△CME 是等腰直角三角形,∴ME=CE ,又∵ME=MG+EG=EF+EG ,∴CE .本题考查了正方形的性质;全等三角形的判定与性质;勾股定理;等腰直角三角形,熟练掌握性质定理是解题的关键.17、(1)见解析;(2).【解析】(1)根据题意可求OA =OB =DO ,∠AOB =60°,可得∠BAD =90°,即结论可得;(2)根据勾股定理可求AD 的长,即可求▱ABCD 的面积.【详解】解(1)∵△AOB 为等边三角形∴∠BAO =60°=∠AOB ,OA =OB ∵四边形ABCD 是平行四边形∴OB =OD ,∴OA =OD ∴∠OAD =30°,∴∠BAD =30°+60°=90°∴平行四边形ABCD 为矩形;(2)在Rt △ABC 中,∠ACB =30°,∴AB =4,BC AB =∴▱ABCD 的面积==本题考查了矩形的性质和判定,等边三角形的性质,灵活运用这些性质解决问题是本题的关键.18、①5、4、80.5;②B ;③160;④1.【解析】①根据已知数据和中位数的概念可得;②由样本中位数和众数、平均数都是B 等级可得答案;③利用样本估计总体思想求解可得;④用没有阅读书籍的平均时间乘以一年的周数,再除以阅读每本书所需时间即可得.【详解】①由已知数据知5a =,4b =,第10、11个数据分别为80、81,∴中位数808180.52c +==,故答案为:5、4、80.5;②用样本中的统计量估计该校学生每周用于课外阅读时间的等级为B ,故答案为:B ;③估计等级为“B ”的学生有840016020⨯=(人),故答案为:160;④估计该校学生每人一年(按52周计算)平均阅读课外书805213320⨯=(本),故答案为:1.此题主要考查数据的统计和分析的知识.准确把握三数(平均数、中位数、众数)和理解样本和总体的关系是关键.一、填空题(本大题共5个小题,每小题4分,共20分)19、15︒【解析】根据菱形性质,得到∠ADC=∠B=70°,从而得出∠AED=∠ADE,又因为AD∥BC,得到∠DAE=∠AEB,进而求出∠ADE=∠AED=55°,从而得到∠EDC【详解】∵四边形ABCD为菱形,∴∠ADC=∠B=70°,AD∥BC,AD=AB∵AD=AB=AE,∴∠AED=∠ADE∵AD∥BC,∴∠DAE=∠AEB=70°∴∠ADE=∠AED=(180°-∠DAE)÷2=55°∴∠EDC=70°-∠ADE=70°-55°=15°本题主要考查菱形的基本性质,在计算过程中综合运用了等边对等角,三角形内角和定理等知识点20、8【解析】根据多边形内角和公式可知n边形的内角和为(n-2)·180º,n边形的外角和为360,再根据n边形的每个内角都等于其外角的3倍列出关于n的方程,求出n的值即可.【详解】解:∵n边形的内角和为(n-2)·180º,外角和为360,n边形的每个内角都等于其外角的3倍,∴(n-2)·180º=360×3,解得:n=8.故答案为:8.本题考查的是多边形的内角与外角的关系的应用,明确多边形一个内角与外角互补和外角和的特征是解题的关键.21、24【解析】根据中点的性质求出BF、BD,根据中位线的性质求出DE、FE,从而求出四边形BDEF的周长.【详解】∵D、E、F分别是BC、AC、AB边上的中点,∴11,22BF AB BD BC==,1//2DE AB,1//2FE BC,∵AB=BC=12cm∴BF=DE=BD=BF=6cm∴四边形BDEF的周长为24cm.本题考查线段的中点、三角形中位线定理.解决本题的关键是利用三角形的中位线平行于第三边并且等于第三边的一半求出DE和FE.22、3【解析】根据角平分线的作图和平行四边形的性质以及等腰三角形的判定和性质解答即可.【详解】由作图可知:BH是∠ABC的角平分线,∴∠ABG=∠GBC,∵平行四边形ABCD,∴AD∥BC,∴∠AGB=∠GBC,∴∠ABG=∠AGB,∴AG=AB=4,∴GD=AD=AG=7-4=3,∵平行四边形ABCD ,∴AB ∥CD ,∴∠H=∠ABH=∠AGB ,∵∠AGB=∠HGD ,∴∠H=∠HGD ,∴DH=GD=3,故答案为:3.此题考查角平分线的做法,平行四边形的性质,熟练根据角平分线的性质得出∠ABG=∠GBC 是解题关键.23、5cm 【解析】根据正方形的面积可用对角线进行计算解答即可.【详解】解:因为正方形AECF 的面积为18cm 2,所以AC ==6cm ,因为菱形ABCD 的面积为24cm 2,所以BD =2246⨯=8cm ,=5cm .故答案为:5cm .此题考查正方形的性质,关键是根据正方形和菱形的面积进行解答.二、解答题(本大题共3个小题,共30分)24、(1)1x 5=-,2x 1=;(2)1x 2=,22x 3=.【解析】根据解一元二次方程的方法-因式分解法解方程即可.【详解】解:()1因式分解得()()x 5x 10+-=,x 50∴+=或x 10-=,1x 5∴=-,2x 1=;()()()23x x 22x 20---=,()()x 23x 20--=,x 20∴-=或3x 20-=,1x 2∴=,22x 3=.本题考查了解一元二次方程-因式分解法,熟练掌握因式分解法是解题的关键.25、【解】(1)15﹪;(2)108°;(3)见解析;(4)全校学生家庭月用水总量是9600吨【解析】(1)根据扇形统计图的特点可知,用1减去其他3种节水措施所占的百分比即可解答.(2)用安装节水设备所在的扇形的百分比乘360度,即可得出正确答案.(3)根据随机调查了本校120名同学家庭可知总数为120,减去其他4组的户数得出答案,再画图即可解答.(4)先求出这120名同学家庭月人均用水量,再用样本估计总体的方法即可解答.【详解】(1)淘米水浇花所占的百分比为1-30%-44%-11%=15%.(2)安装节水设备所在的扇形的圆心角度数为360°×30%=108°.(3)如图(4)(1×10+2×42+3×20+4×32+5×16)÷120×3000=9100吨.即全校学生家庭月用水总量是9100吨.考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.26、(1)①补图见解析;②证明见解析;(2)2BE AD +CN ,证明见解析;(3)34.【解析】分析:(1)①依照题意补全图形即可;②连接CE ,由正方形以及等腰直角三角形的性质可得出∠ACD=∠MCN=45°,从而得出∠ACN=90°,再根据直角三角形的性质以及点E 为AN 的中点即可得出AE=CE ,由此即可得出B 、E 在线段AC 的垂直平分线上,由此即可证得BE ⊥AC ;(2)BE=2AD+12CN .根据正方形的性质可得出BF=2AD ,再结合三角形的中位线性质可得出EF=12CN ,由线段间的关系即可证出结论;(3)找出EN 所扫过的图形为四边形DFCN .根据正方形以及等腰直角三角形的性质可得出BD ∥CN ,由此得出四边形DFCN 为梯形,再由AB=1,可算出线段CF 、DF 、CN 的长度,利用梯形的面积公式即可得出结论.详解:(1)①依题意补全图形,如图1所示.②证明:连接CE ,如图2所示.∵四边形ABCD 是正方形,∴∠BCD=90°,AB=BC ,∴∠ACB=∠ACD=12∠BCD=45°,∵∠CMN=90°,CM=MN ,∴∠MCN=45°,∴∠ACN=∠ACD+∠MCN=90°.∵在Rt △ACN 中,点E 是AN 中点,∴AE=CE=12AN .∵AE=CE ,AB=CB ,∴点B ,E 在AC 的垂直平分线上,∴BE 垂直平分AC ,∴BE ⊥AC .(2)BE=2AD+12CN .证明:∵AB=BC ,∠ABE=∠CBE ,∴AF=FC .∵点E 是AN 中点,∴AE=EN ,∴FE 是△ACN 的中位线.∴FE=12CN .∵BE ⊥AC ,∴∠BFC=90°,∴∠FBC+∠FCB=90°.∵∠FCB=45°,∴∠FBC=45°,∴∠FCB=∠FBC ,∴BF=CF .在Rt △BCF 中,BF 2+CF 2=BC 2,∴BF=2BC .∵四边形ABCD 是正方形,∴BC=AD ,∴BF=2AD .∵BE=BF+FE ,∴BE=2AD+12CN .(3)在点M 沿着线段CD 从点C 运动到点D 的过程中,线段EN 所扫过的图形为四边形DFCN .∵∠BDC=45°,∠DCN=45°,∴BD ∥CN ,∴四边形DFCN 为梯形.∵AB=1,∴CF=DF=12BD=2,,∴S 梯形DFCN =12(DF+CN )•CF=12(22)×22=34.点睛:本题考查了正方形的性质、等腰直角三角形的性质、平行线的性质以及梯形的面积公式,解题的关键是:(1)根据垂直平分线上点的性质证出垂直;(2)用AD 表示出EF 、BF 的长度;(3)找出EN 所扫过的图形.本题属于中档题,难度不小,解决该题型题目时,根据题意画出图形,利用数形结合解决问题是关键.。
山东省德州市某校2021-2022学年-有答案-九年级上学期期中英语试题

山东省德州市某校2021-2022学年九年级上学期期中英语试题一、阅读单选1. Home Alone is a very funny 1990 American film. It tells us a story about a boy who is accidentally left alone at home.One night before Christmas, McAlister family meet at their house. They are planning to fly to Paris for the holiday and are busy getting ready. Eight-year-old Kevin is the youngest child and is fighting with his brothers, sisters and cousins. When he goes to bed, he is so angry that he wishes all his family would go away. In the morning, everyone wakes up very late. They are all in a hurry to get to the airport, so they forget Kevin and he is left alone at home by accident.Although Kevin is alone, he is very happy at first. His terrible family have gone —his wish has come true. He watches TV, eats lots of fast food and plays games. He has a good time. But later on, he goes out and hears two bad men called Harry and Mary planning to steal from his house. He goes home and plans some very funny ways to catch Harry and Marv. Many things in the house get broken as Kevin tries to stop them. Finally, the police come and the men are taken away.The house is now in a mess, so Kevin tidies it up and waits for his parents. They get back from Paris and are very happy to find that Kevin is safe.(1)According to the passage, Home Alone is ______.A.a bookB.a filmC.a playD.a song(2)Why does Kevin think his family are “terrible” at first?A.Because his family are busy preparing for the holiday.B.Because he is angry with his brothers, sisters and cousins.C.Because his family wake up late.D.Because he is left alone at home.(3)What doesn’t Kevin do when he is alone at home?A.Go to the police station.B.Eat fast food.C.Play games.D.Stop the thieves stealing.(4)When Kevin's family come home, they find ______.A.the house is in a messB.two bad men are at their homeC.Kevin is safeD.Kevin is gone(5)From the passage we can infer (推断) that ______.A.Kevin is not clever or braveB.Kevin can't do houseworkC.Kevin loves his familyD.Kevin doesn’t want to go for the holiday2. Passage 1Lisa’s GymKeep fit! Lose weight!Play basketball, do yoga(瑜伽), dance and meet many new friends!Price:¥40/hourOpen time: Saturdays and SundaysTe1: 2133730A Concert(1)You can ______ at Lisa’s Gym.A.watch a movieB.find a jobC.listen to a concertD.play basketball(2)Mr. and Mrs. Smith and their 14-year-old son want to go to the concert, they have to pay __for the tickets.A.¥120B.¥180C.¥300D.¥240(3)Star Wars is the name of ______.A.a cinemaB.a movieC.a clubD.a gym(4)Linda wants to find a job during her summer holiday, she can ______ for more information.A.call 8124697B.call LisaC.call 2133730D.go to the Children’s Palace(5)Which of the following is TRUE?A.Lisa’s Gym is open every day.B.You have to work late as a waiter in the restaurant.C.You and your friend should pay 80 yuan for the movie.D.The movie will be on for a week.3. Willow Shields is an American film and television actress. She was born on Junelst, 2000 in Albuquerque, New Mexico. She has a twin sister and an elderbrother. Willow is a very beautiful girl. She has golden hair, big eyes and sweet smiles. Willow got her first job in 2008 and she acted in a 7minute short film with her sister. In it, she plays the role of a little girl watching a gun fight. Her most famous role is Primrose in the movie The Hunger Games. She worked hard for the movie and she read the book carefully before acting. Willow did so well that the director said, " It's so exciting to find an amazing young actress like her. We're very lucky to have her. "Willow continued in her role until November, 2015, when the final of the four movies in the Hunger Games series came out.Because Willow is always busy, she is homeschooled. She makes use of every chance to enrich herself. She especially loves reading. Besides, she is warmhearted. In her free time, she often volunteers to send out food to homeless people.(1)Willow Shields acted in her first film with________.A. her twin sisterB. her directorC. her brotherD. her best friend.(2)From the director's words, we know that________.A. Willow Shields is a lucky girlB. the director is pleased with WillowC. Willow Shields is a television actressD. Willow Shields is a girl from New Mexico.(3)Willow Shields often________in her free time.A. goes to an amusement parkB. goes abroad with her friendsC. helps some homeless peopleD. hangs out in a shopping mall.(4)Which of the following is TRUE about Willow Shields?________A. She has a brother and two sisters.B. She gets to school every weekday.C. She played a role in Harry Potter V in 2008.D. She acted in a film for the first time when she was 8..4.There was a player named Jerry in the soccer team; his father died. Returning from the funeral(葬礼),an important match was going to begin.He found the coach atonce, asking to attend the match.Jerry was not good at the skill, so the coach should not allow him to attend the match.But now, as he relented, he agreed to let Jerry play for three minutes.When the time was up, Jerry would be changed by others.On the court, Jerry played very well.Three minutes passed.The coach made Jerry keep staying on the court.Jerry played an important role, leading the team to win the match.The coach said excitedly, "Kid, you have never been so fast, so strong and so skilled.What happened? " Jerry said, "My father is blind, so he has never watched my match.Now, he has gone to the heaven(天堂)and finally can watch my match.As soon as I think of my father watching me, I have everything…"The coach understood: Love can drive everything!(1)Why didn't the coach want Jerry to attend the match at first? ________A.Because his father died.B.Because he wasn't interested in the match.C.Because he wasn't good at the skill.D.Because he was a bad boy.(2)How long did the coach agree to let Jerry play? ________A.For 3 minutes.B.For 5 minutes.C.For 10 minutes.D.For 15 minutes.(3)Who made Jerry keep staying on the court? ________A.His coach.B.His father.C.His friend.D.His teacher.(4)Jerry felt that he had everything because of ________ .A.his coach's wordsB.other players' helpC.his friends' supportD.his father's love(5)What's the best title of the passage? ________A.A Soccer TeamB.Three Minutes' MatchC.A Clever BoyD.Jerry's Idea二、补全短文6选5请阅读下面短文,根据短文内容,从方框内所给的选项中选出能填入空白处的最佳选项,使短文意思通顺。
2020-2021学年度上学期九年级语文第一次月考试卷及答案

2020-2021学年上学期九年级语文第一次月考测评试题(A)(时间:90分钟分值:120分)班级: 姓名:成绩:一、诗文积累(28分):(一)经典诗文积累(14分)1、《沁园春雪》中写景与议论之间过渡的句子是:,。
2、为什么我的眼里常含泪水?。
3、《醉翁亭记》一文中微露主旨(为后人传诵)的句子是:,。
4、《岳阳楼记》中从时间上表现景象的千变万化的句子是:,。
描述古仁人阔达胸襟的句子是:,。
5、雾凇沆砀,,,湖上影子,、、、舟中人两三粒而已。
(二)阅读下面的词,完成下面的问题(14分)《沁园春长沙》独立寒秋,湘江北去,橘子洲头。
看万山红遍,层林尽染;漫江碧透,百舸争流。
鹰击长空,鱼翔浅底,万类霜天竞自由。
怅寥廓,问苍茫大地,谁主沉浮?携来百侣曾游,忆往昔峥嵘岁月稠。
恰同学少年,风华正茂;书生意气,挥斥方遒。
指点江山,激扬文字,粪土当年万户侯。
曾记否,到中流击水,浪遏飞舟?6、旧体诗词讲究押韵,而且有些地方还讲究对偶,请从词中找出三组对偶的句子。
(6分)(1),。
(2),。
(2),。
7、“看”字统领了哪几句?描绘了一幅什么样的图画?(4)8、文学作品中的秋景一般都是萧条、肃杀的,本词的秋景具有怎样的特色?为什么?(4)二、阅读理解(42分):(一)阅读甲乙两文,完成9—12题。
(14分)[甲]至若春和景明,波澜不惊,上下天光,一碧万顷;沙鸥翔集,锦鳞游泳;岸芷汀兰,郁郁青青。
而或长烟一空,皓月千里,浮光跃金,静影沉璧,渔歌互答,此乐何极!登斯楼也,则有心旷神怡,宠辱偕忘,把酒临风,其喜洋洋者矣。
嗟夫!予尝求古仁人之心,或异二者之为,何哉?不以物喜,不以己悲;居庙堂之高则忧其民;处江湖之远则忧其君。
是进亦忧,退亦忧。
然则何时而乐耶?其必曰“先天下之忧而忧,后天下之乐而乐”乎。
噫!微斯人,吾谁与归?[乙]滕子京负大才,为众忌疾,自庆阳帅谪巴陵,愤郁颇见辞色。
文正与之同年,友善,爱其才,恐后贻(遗留)祸。
山东省德州五中2021-2022学年九年级上学期期中数学试卷(解析版) (1)

山东省德州五中2021-2022学年九年级上学期期中数学试卷(解析版)一、选择题(每题4分,共48分)1.下列图形,可以看作中心对称图形的是()A.B.C.D.2.若矩形的长和宽是关于x的方程2x2﹣8x+m=0的两根,则矩形的周长为()A.8B.4C.2D.63.已知⊙O的半径是一元二次方程x2﹣3x﹣4=0的一个根,圆心O到直线l的距离d=6.则直线l与⊙O的位置关系是()A.相离B.相切C.相交D.无法判断4.如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线P A交OC的延长线于点P.则P A的长为()A.2B.C.D.5.已知A(﹣1,y1),B(1,y2),C(4,y3)三点都在二次函数y=﹣(x﹣3)2+k的图象上,则y1,y2,y3的大小关系为()A.y1<y2<y3B.y1<y3<y2C.y3<y1<y2D.y3<y2<y1 6.下列说法中正确的有()个.①相等的圆心角所对的弧相等:②三点可以确定一个圆:③在同圆中,相等的弦所对的弧相等:④圆的每一条直径都是它的对称轴;⑤在同圆或等圆中,垂直于弦的直径平分弦.A.0个B.1个C.2个D.3个7.如图,把抛物线y=x2沿直线y=x平移2个单位长度后,其顶点在直线上的点A处,则平移后抛物线的解析式是()A.y=(x+1)2﹣1B.y=(x+)2+C.y=(x﹣)2+D.y=(x﹣1)2﹣18.如图,两边平行的刻度尺在圆上移动,当刻度尺的边与直径为10cm的圆相切时,另边与圆两个交点处的读数恰好为“4“”和“12“(单位:cm),则刻度尺的宽为()cm.A.1B.2C.4D.89.如图,四边形ABCD为⊙O的内接四边形,已知∠BCD为120°,则∠BOD的度数为()A.100°B.110°C.120°D.130°10.某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为29米的篱笆围成,已知墙长为18米,为方便进入,在墙的对面留出1米宽的门(如图所示),设这个苗圃园垂直于墙的一边长为x米,苗圃园的面积为100平方米,根据题意正确的是()A.x(29﹣2x+1)=100B.x(29﹣2x﹣1)=100C.x(29﹣2x+1)=100D.x(29﹣2x﹣1)=10011.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B,0分别落在点B1,C1处,点B在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x 轴上,依次进行下去..若点A(,0).B(0,2).则点B2021的坐标为()A.(4042,2)B.(4042,0)C.(6064,2)D.(6064,0)12.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中正确的有()A.①②③B.②④C.②⑤D.②③⑤二、填空题(每小题4分,共24分)13.已知抛物线y=x2﹣3x+m与x轴只有一个公共点,则m=.14.一条排水管的截面如图所示,已知排水管的半径OA=2m,水面宽AB=2.4m.某天下雨后,水管水面上升后的水面宽度为3.2m,则排水管水面上升了m.15.如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式y<0的解集是.16.有一长、宽分别为4cm,3cm的矩形ABCD,以A为圆心作圆,若B、C、D三点中至少有一点在圆内,且至少有一点在圆外,则⊙O的半径r的取值范围是.17.汽车刹车后行驶的距离s(单位:m)关于行驶的时间(单位:)的函数解析式是s=15t ﹣6t2,汽车刹车后到停下来前进了米.18.如图,正方形ABCD中,AB=3cm,以B为圆心,1cm长为半径画⊙B,点P在⊙B上移动,连接AP,并将AP绕点A逆时针旋转90°至AP′.连接BP′.在点P移动的过程中,BP′长度的最小值为cm.三、解答题(共78分)19.(8分)用适当的方法解下列方程:(1)(2x﹣1)2=6x﹣3;(2)5(x+1)2=3(x+1).20.(10分)如图,△ABC三个顶点的坐标分别为A(3,6),B(2,2),C(7,1).(1)请画出△ABC关于原点对称的△A1B1C1,并写出对应坐标;(2)请画出△ABC绕原点顺时针旋转90°后的△A2B2C2;(3)已知△ABC绕点P旋转后的三角形为△DEF(点A与点D重合,点B与点E重合),其中D(﹣8,5),E(﹣4,4),F(﹣3,9).直接写出点P的坐标.21.(10分)如图,AB是⊙O的直径,F为⊙O上一点,AC平分∠F AB交⊙O于点C.过点C作CD⊥AF交AF的延长线于点D.(1)求证:CD是⊙O的切线.(2)若DC=3,AD=9,求⊙O半径.22.(12分)某商场要经营一种新上市的文具,进价为20元/件试营销阶段发现:当销售单价是30元时,每天的销售量为300件:销售单价每上涨1元,每天的销售量就减少10件.(1)写出商场销售这种文具每天所得的销售利润W(元)与销售单价x(元)之间的函数关系;(2)该文具每天的销售总利润为3750元,求销售单价是多少元;(3)为尽快减少库存,商场规定每天的销售量不得低于240件.求销售单价为多少元时,该文具每天的销售利润最大?最大利润是多少?23.(12分)如图所示,⊙O的直径AB=10cm,弦AC=6cm,∠ACB的平分线交⊙O于点D,(1)求证:△ABD是等腰三角形;(2)求CD的长.24.(12分)问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连接AG,先证明△ABE ≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由;实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.25.(14分)如图,抛物线y=ax2+bx+2与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C.(1)求该抛物线的解析式;(2)在抛物线的对称轴1上是否存在一点M,使MA+MC的值最小?若存在,求出点M 的坐标:若不存在,请说明理由.(3)若点D是抛物线上的一点,且位于直线BC上方,连接CD、BD、AC.当四边形ABDC的面积有最大值时,求点D的坐标及四边形ABDC的面积.参考答案与试题解析一、选择题(每题4分,共48分)1.下列图形,可以看作中心对称图形的是()A.B.C.D.【分析】根据中心对称图形的概念对各选项分析判断即可得解.【解答】解:A、不是中心对称图形,故本选项不符合题意;B、是中心对称图形,故本选项符合题意;C、不是中心对称图形,故本选项不符合题意;D、不是中心对称图形,故本选项不符合题意.故选:B.【点评】本题考查了中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后两部分重合.2.若矩形的长和宽是关于x的方程2x2﹣8x+m=0的两根,则矩形的周长为()A.8B.4C.2D.6【分析】设矩形的长为a,宽为b,根据一元二次方程根与系数的关系可得a+b=4,即可得到答案.【解答】解:设矩形的长为a,宽为b,∵矩形的长和宽是关于x的方程2x2﹣8x+m=0的两根,∴a+b=﹣=4,∴矩形的周长为2(a+b)=2×4=8,故选:A.【点评】本题考查一元二次方程根与系数的关系和矩形的性质,解题的关键是掌握一元二次方程根与系数的关系.3.已知⊙O的半径是一元二次方程x2﹣3x﹣4=0的一个根,圆心O到直线l的距离d=6.则直线l与⊙O的位置关系是()A.相离B.相切C.相交D.无法判断【分析】先求方程的根,可得r的值,由直线与圆的位置关系的判断方法可求解.【解答】解:∵x2﹣3x﹣4=0,∴x1=﹣1,x2=4,∵⊙O的半径为一元二次方程x2﹣3x﹣4=0的根,∴r=4,∵d>r∴直线l与⊙O的位置关系是相离,故选:A.【点评】本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d 与圆半径大小关系完成判定.4.如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线P A交OC的延长线于点P.则P A的长为()A.2B.C.D.【分析】连接OA,根据圆周角定理求出∠AOP,根据切线的性质求出∠OAP=90°,解直角三角形求出AP即可.【解答】解:连接OA,∵∠ABC=30°,∴∠AOC=2∠ABC=60°,∵AP是⊙O的切线,∴∠OAP=90°,∵OA=OC=1,∴AP=OA tan60°=1×,故答案为:B.【点评】本题考查了切线的性质和圆周角定理、解直角三角形等知识点,能熟记切线的性质是解此题的关键,注意:圆的切线垂直于过切点的半径.5.已知A(﹣1,y1),B(1,y2),C(4,y3)三点都在二次函数y=﹣(x﹣3)2+k的图象上,则y1,y2,y3的大小关系为()A.y1<y2<y3B.y1<y3<y2C.y3<y1<y2D.y3<y2<y1【分析】根据二次函数的性质可以判断y1,y2,y3的大小关系,从而可以解答本题.【解答】解:∵y=﹣(x﹣3)2+k,﹣1<0,∴当x<3时,y随x的增大而增大,当x>3时,y随x的增大而减小,∵抛物线y=﹣(x﹣3)2+k的图象上有三个点A(﹣1,y1),B(1,y2),C(4,y3),|﹣1﹣3|=4,|1﹣3|=2,|4﹣3|=1,∴y1<y2<y3,故选:A.【点评】本题考查了二次函数图象上点的坐标特征和二次函数的性质,能熟记二次函数的性质是解此题的关键.6.下列说法中正确的有()个.①相等的圆心角所对的弧相等:②三点可以确定一个圆:③在同圆中,相等的弦所对的弧相等:④圆的每一条直径都是它的对称轴;⑤在同圆或等圆中,垂直于弦的直径平分弦.A.0个B.1个C.2个D.3个【分析】根据确定圆的条件、垂径定理、圆周角定理判断即可.【解答】解:①在同圆或等圆中,相等的圆心角所对的弧相等,说法不正确;②不在同一直线上的三点可以确定一个圆,说法不正确;③在同圆中,相等的弦所对的弧不一定相等,说法不正确;④圆的每一条直径所在直线都是它的对称轴,说法不正确;⑤在同圆或等圆中,垂直于弦的直径平分弦,符合垂径定理,说法正确.其中正确的有1个.故选:B.【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理.7.如图,把抛物线y=x2沿直线y=x平移2个单位长度后,其顶点在直线上的点A处,则平移后抛物线的解析式是()A.y=(x+1)2﹣1B.y=(x+)2+C.y=(x﹣)2+D.y=(x﹣1)2﹣1【分析】首先根据A点所在位置设出A点坐标为(m,m),再根据AO=2,利用勾股定理求出m的值,然后根据抛物线平移的性质:左加右减,上加下减可得解析式.【解答】解:∵A在直线y=x上,∴设A(m,m),∵OA=2,∴m2+m2=22,解得:m=±(m=﹣舍去),∴m=,∴A(,),∴抛物线解析式为:y=(x﹣)2+,故选:C.【点评】此题主要考查了二次函数图象的几何变换,关键是求出A点坐标,掌握抛物线平移的性质:左加右减,上加下减.8.如图,两边平行的刻度尺在圆上移动,当刻度尺的边与直径为10cm的圆相切时,另边与圆两个交点处的读数恰好为“4“”和“12“(单位:cm),则刻度尺的宽为()cm.A.1B.2C.4D.8【分析】根据垂径定理得BE的长,再根据勾股定理列方程求解即可.【解答】解:作OE垂直AB于E交⊙O与D,根据垂径定理,BE=AB=4,根据题意列方程得:(5﹣DE)2+16=52,解得DE=2,∴该直尺的宽度为2cm.故选:B.【点评】此题主要考查了垂径定理的应用,此题很巧妙,将垂径定理和勾股定理不露痕迹的镶嵌在实际问题中,考查了同学们的转化能力.9.如图,四边形ABCD为⊙O的内接四边形,已知∠BCD为120°,则∠BOD的度数为()A.100°B.110°C.120°D.130°【分析】根据圆内接四边形的性质求出∠A,根据圆周角定理计算,得到答案.【解答】解:∵四边形ABCD是⊙O的内接四边形,∴∠A=180°﹣∠BCD=60°,由圆周角定理得,∠BOD=2∠A=120°,故选:C.【点评】本题考查的是圆内接四边形的性质,掌握圆内接四边形的对角互补是解题的关键.10.某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为29米的篱笆围成,已知墙长为18米,为方便进入,在墙的对面留出1米宽的门(如图所示),设这个苗圃园垂直于墙的一边长为x米,苗圃园的面积为100平方米,根据题意正确的是()A.x(29﹣2x+1)=100B.x(29﹣2x﹣1)=100C.x(29﹣2x+1)=100D.x(29﹣2x﹣1)=100【分析】设这个苗圃园垂直于墙的一边长为x米,则这个苗圃园平行于墙的一边长为(29﹣2x+1)米,根据矩形的面积公式结合苗圃园的面积为100平方米,即可得出关于x的一元二次方程.【解答】解:设这个苗圃园垂直于墙的一边长为x米,则这个苗圃园平行于墙的一边长为(29﹣2x+1)米,根据题意得:x(29﹣2x+1)=100,故选:A.【点评】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.11.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B,0分别落在点B1,C1处,点B在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x 轴上,依次进行下去..若点A(,0).B(0,2).则点B2021的坐标为()A.(4042,2)B.(4042,0)C.(6064,2)D.(6064,0)【分析】首先根据已知求出三角形三边长度,然后通过旋转发现,B、B1、B3…,由图象可知点B2021在x轴上,B1B3=6,根据这个规律可以求得B2021的坐标.【解答】解:由图象可知点B2021在x轴上,∵OA=,OB=2,∠AOB=90°,∴AB===,∴B1(4,0),B3(10,0),B5(16,0),…,∴B1B3=B3B5=6,∵2021÷2=1010……1,∴1010×6=6060,6060+4=6064,∴B2021(6064,0).故选:D.【点评】本题考查坐标与图形的变化﹣旋转、勾股定理等知识,解题的关键是从特殊到一般探究规律,发现规律,利用规律解决问题,属于中考常考题型.12.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中正确的有()A.①②③B.②④C.②⑤D.②③⑤【分析】根据抛物线开口方向得a<0,由抛物线对称轴为直线x=﹣=1,得到b=﹣2a>0,即2a+b=0,由抛物线与y轴的交点位置得到c>0,所以abc<0;根据二次函数的性质得当x=1时,函数有最大值a+b+c,则当m≠1时,a+b+c>am2+bm+c,即a+b >am2+bm;根据抛物线的对称性得到抛物线与x轴的另一个交点在(﹣1,0)的右侧,则当x=﹣1时,y<0,所以a﹣b+c<0;把ax12+bx1=ax22+bx2先移项,再分解因式得到(x1﹣x2)[a(x1+x2)+b]=0,而x1≠x2,则a(x1+x2)+b=0,即x1+x2=﹣,然后把b=﹣2a代入计算得到x1+x2=2.【解答】解:∵抛物线开口向下,∴a<0,∵抛物线对称轴为直线x=﹣=1,∴b=﹣2a>0,即2a+b=0,所以②正确;∵抛物线与y轴的交点在x轴上方,∴c>0,∴abc<0,所以①错误;∵抛物线对称轴为直线x=1,∴函数的最大值为a+b+c,∴当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm,所以③错误;∵抛物线与x轴的一个交点在(3,0)的左侧,而对称轴为直线x=1,∴抛物线与x轴的另一个交点在(﹣1,0)的右侧∴当x=﹣1时,y<0,∴a﹣b+c<0,所以④错误;∵ax12+bx1=ax22+bx2,∴ax12+bx1﹣ax22﹣bx2=0,∴a(x1+x2)(x1﹣x2)+b(x1﹣x2)=0,∴(x1﹣x2)[a(x1+x2)+b]=0,而x1≠x2,∴a(x1+x2)+b=0,即x1+x2=﹣,∵b=﹣2a,∴x1+x2=2,所以⑤正确.综上所述,正确的有②⑤.故选:C.【点评】本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线开口向上;当a<0时,抛物线开口向下;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左侧;当a与b异号时(即ab<0),对称轴在y轴右侧;常数项c决定抛物线与y轴交点.抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定,Δ=b2﹣4ac>0时,抛物线与x轴有2个交点;Δ=b2﹣4ac=0时,抛物线与x 轴有1个交点;Δ=b2﹣4ac<0时,抛物线与x轴没有交点.二、填空题(每小题4分,共24分)13.已知抛物线y=x2﹣3x+m与x轴只有一个公共点,则m=.【分析】令y=0,则关于x的一元二次方程x2﹣x+m=0的根的判别式Δ=0,据此列出关于m的新方程,通过解新方程即可求得m的值.【解答】解:令y=0,则当抛物线y=x2﹣3x+m与x轴只有一个公共点时,关于x的一元二次方程x2﹣3x+m=0的根的判别式Δ=0,即(﹣3)2﹣4m=0,解得:m=.故答案是:.【点评】本题考查了抛物线与x轴的交点.解题时,运用“二次函数y=ax2+bx+c与x 轴的交点个数与系数的关系:当b2﹣4ac=0时,只有一个交点”求解即可.14.一条排水管的截面如图所示,已知排水管的半径OA=2m,水面宽AB=2.4m.某天下雨后,水管水面上升后的水面宽度为3.2m,则排水管水面上升了0.4或2.8m.【分析】过O作OE⊥AB于E,交CD于F,连接OC,由垂径定理得AE=BE=AB=1.2(m),CF=DF=CD,在Rt△OAE中,由勾股定理得OE=1.6(m),OF=1.2(m),然后再分两种情况,根据EF=OE﹣OF可求解.【解答】解:过O作OE⊥AB于E,交CD于F,连接OC,如图所示:则AE=BE=AB=1.2(m),OF⊥CD,∴CF=DF=CD,∵OA=2m,∴OE==1.6(m),∵CD=2CF=3.2m,∴CF=1.6m,∵OC=OA=2m,∴OF=(m),当水面没过圆心O时,EF=OE﹣OF=1.6﹣1.2=0.4(m),当水面超过圆心O时,EF=OE+OF=1.6+1.2=2.8(m)即水管水面上升了0.4m或2.8m,故答案为:0.4或2.8.【点评】本题考查的是垂径定理的应用以及勾股定理等知识;熟练掌握垂径定理和勾股定理是解题的关键.15.如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式y<0的解集是x<﹣1或x>5.【分析】根据抛物线的对称轴及与x轴的交点求出抛物线与x轴的另一个交点,通过图象即可求解.【解答】解:∵抛物线经过点(5,0),对称轴为直线x=2,∴抛物线与x轴的另一个交点为(﹣1,0),∵y>0,∴对应抛物线在x轴下方,即在(﹣1,0)点的左侧或(5,0)点的右侧.∴x<﹣1或x>5.故答案为:x<﹣1或x>5.【点评】本题考查二次函数和不等式,将y<0转化为抛物线在x轴的下方是求解是解决问题的关键.16.有一长、宽分别为4cm,3cm的矩形ABCD,以A为圆心作圆,若B、C、D三点中至少有一点在圆内,且至少有一点在圆外,则⊙O的半径r的取值范围是3<r<5.【分析】根据点与圆的位置关系,与点A相邻的点且宽的另一个端点在圆内,与点A不相邻的顶点在圆外,求得矩形的对角线,再确定⊙O的半径r的取值范围.【解答】解:∵矩形ABCD的长、宽分别为4cm,3cm,∴矩形的对角线为5cm,∵B、C、D三点中至少有一点在圆内,且至少有一点在圆外,∴⊙O的半径r的取值范围是3<r<5.【点评】本题考查的知识点:勾股定理和点与圆的位置关系:①点P在⊙O上;②点P 在⊙O内;③点P在⊙O外.17.汽车刹车后行驶的距离s(单位:m)关于行驶的时间(单位:)的函数解析式是s=15t ﹣6t2,汽车刹车后到停下来前进了米.【分析】根据二次函数的解析式找出其顶点式,再利用二次函数的性质求出s的最大值即可得出结论.【解答】解:∵s=15t﹣6t2=﹣6(t﹣)2+,∴汽车刹车后到停下来前进了米.故答案为:.【点评】本题考查了二次函数的应用,利用配方法,找出二次函数的顶点式是解题的关键.18.如图,正方形ABCD中,AB=3cm,以B为圆心,1cm长为半径画⊙B,点P在⊙B上移动,连接AP,并将AP绕点A逆时针旋转90°至AP′.连接BP′.在点P移动的过程中,BP′长度的最小值为(3﹣1)cm.【分析】通过画图发现,点P′的运动路线为以D为圆心,以1为半径的圆,可知:当P′在对角线BD上时,BP′最小,先证明△P AB≌△P′AD,则P′D=PB=1,再利用勾股定理求对角线BD的长,则得出BP′的长.【解答】解:如图,当P′在对角线BD上时,BP′最小,连接BP,由旋转得:AP=AP′,∠P AP′=90°,∴∠P AB+∠BAP′=90°,∵四边形ABCD为正方形,∴AB=AD,∠BAD=90°,∴∠BAP′+∠DAP′=90°,∴∠P AB=∠DAP′,∴△P AB≌△P′AD,∴P′D=PB=1,在Rt△ABD中,∵AB=AD=3,由勾股定理得:BD==3,∴BP′=BD﹣P′D=3﹣1,即BP′长度的最小值为(3﹣1)cm.故答案为:(3﹣1).【点评】本题考查了正方形的性质、旋转的性质和最小值问题,寻找点P′的运动轨迹是本题的关键,通过证明两三角形全等求出BP′长度的最小值.三、解答题(共78分)19.(8分)用适当的方法解下列方程:(1)(2x﹣1)2=6x﹣3;(2)5(x+1)2=3(x+1).【分析】(1)根据因式分解法可以解答此方程;(2)根据因式分解法可以解答此方程.【解答】解:(1)移项得(2x﹣1)2﹣(6x﹣3)=0,因式分解得(2x﹣1)(2x﹣4)=0,2x﹣1=0或2x﹣4=0,解得,x1=,x2=2;(2)移项得5(x+1)2﹣3(x+1)=0.把方程左边进行因式分解得(x+1)(5x+2)=0.∴x+1=0或5x+2=0.∴x1=﹣1,x2=﹣.【点评】本题考查一元二次方程,解题的关键是熟练运用一元二次方程的解法,本题属于基础题型.20.(10分)如图,△ABC三个顶点的坐标分别为A(3,6),B(2,2),C(7,1).(1)请画出△ABC关于原点对称的△A1B1C1,并写出对应坐标;(2)请画出△ABC绕原点顺时针旋转90°后的△A2B2C2;(3)已知△ABC绕点P旋转后的三角形为△DEF(点A与点D重合,点B与点E重合),其中D(﹣8,5),E(﹣4,4),F(﹣3,9).直接写出点P的坐标.【分析】(1)利用中心对称不会的性质分别作出A,B,C的对应点A1,B1,C1即可;(2)利用旋转变换的性质分别作出A,B,C的对应点A2,B2,C2即可;(3)对应点连线的垂直平分线的交点即为旋转中心.【解答】解:(1)如图,△A1B1C1即为所求,A1(﹣3,﹣6),B1(﹣2,﹣2),C1(﹣7,﹣1);(2)如图,△A2B2C2即为所求;(3)如图,点P即为所求,点P的坐标(﹣2,0).【点评】本题考查作图﹣旋转变换,中心对称变换等知识,解题的关键是掌握旋转变换的性质,属于中考常考题型.21.(10分)如图,AB是⊙O的直径,F为⊙O上一点,AC平分∠F AB交⊙O于点C.过点C作CD⊥AF交AF的延长线于点D.(1)求证:CD是⊙O的切线.(2)若DC=3,AD=9,求⊙O半径.【分析】(1)根据角平分线的定义和平行线的判定和性质以及切线的判定定理即可得到结论;(2)过点O作OE⊥AF于E,证明四边形OEDC为矩形,设设⊙O的半径为r,由勾股定理列出方程求解.【解答】(1)证明:连接OC,∵AC平分∠F AB,∴∠F AC=∠CAO,∵AO=CO,∴∠ACO=∠CAO,∴∠F AC=∠ACO,∴AD∥OC,∵CD⊥AF,∴CD⊥OC,∵OC为半径,∴CD是⊙O的切线;(2)解:过点O作OE⊥AF于E,∴AE=EF=,∠OED=∠EDC=∠OCD=90°,∴四边形OEDC为矩形,∴CD=OE=3,DE=OC,设⊙O的半径为r,则OA=OC=DE=r,∴AE=9﹣r,∵OAOA2﹣AE2=OE2,∴r2﹣(9﹣r)2=32,解得r=5.∴⊙O半径为5.【点评】本题主要考查了切线的判定,矩形的性质与判定,构造直角三角形是解题的关键.22.(12分)某商场要经营一种新上市的文具,进价为20元/件试营销阶段发现:当销售单价是30元时,每天的销售量为300件:销售单价每上涨1元,每天的销售量就减少10件.(1)写出商场销售这种文具每天所得的销售利润W(元)与销售单价x(元)之间的函数关系;(2)该文具每天的销售总利润为3750元,求销售单价是多少元;(3)为尽快减少库存,商场规定每天的销售量不得低于240件.求销售单价为多少元时,该文具每天的销售利润最大?最大利润是多少?【分析】(1)根据利润=(销售单价﹣进价)×销售量,列出函数关系式即可;(2)根据(1)式列出的函数关系式,运用配方法求最大值;(3)根据题意列函数解析式,根据二次函数的性质即可得到结论.【解答】解:(1)由题意得,销售量=300﹣10(x﹣30)=﹣10x+600,则w=(x﹣20)(﹣10x+600)=﹣10x2+800x﹣12000;(2)根据题意得,(x﹣20)(﹣10x+600)=3750,解得x1=45,x2=35,答:该文具每天的销售总利润为3750元,销售单价是45元或35元;(3)w=﹣10x2+800x﹣12000=﹣10(x﹣40)2+4000.∵﹣10<0,∴函数图象开口向下,w有最大值,∵商场规定每天的销售量不得低于240件,∴﹣10x+600≥240,解得x≤36,∴当x=36时,w最大=3840,故当单价为36元时,该文具每天的利润最大,最大利润是3840元.【点评】本题考查了二次函数的应用,难度较大,最大销售利润的问题常利用函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.其中要注意应该在自变量的取值范围内求最大值(或最小值).23.(12分)如图所示,⊙O的直径AB=10cm,弦AC=6cm,∠ACB的平分线交⊙O于点D,(1)求证:△ABD是等腰三角形;(2)求CD的长.【分析】(1)连接OD,根据角平分线的定义得到∠ACD=∠BCD,根据圆周角定理,等腰三角形的定义证明;(2)作AE⊥CD于E,根据等腰直角三角形的性质求出AD,根据勾股定理求出AE、CE,DE,结合图形计算,得到答案.【解答】(1)证明:连接OD,∵AB为⊙O的直径,∴∠ACB=90°,∵CD是∠ACB的平分线,∴∠ACD=∠BCD=45°,由圆周角定理得,∠AOD=2∠ACD,∠BOD=2∠BCD,∴∠AOD=∠BOD,∴DA=DB,即△ABD是等腰三角形;(2)解:作AE⊥CD于E,∵AB为⊙O的直径,∴∠ADB=90°,∴AD=AB=5,∵AE⊥CD,∠ACE=45°,∴AE=CE=AC=3,在Rt△AED中,DE==4,∴CD=CE+DE=3+4=7.【点评】本题考查的是圆周角定理,勾股定理,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解题的关键.24.(12分)问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连接AG,先证明△ABE ≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是EF=BE+FD;探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由;实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.【分析】问题背景中,根据小亮的设计可以得到所要的结论;探索延伸中,先判断结论是否成立,然后根据图形和题目中条件,作出合适的辅助线,进行说明即可;在实际应用中,根据题目中的条件进行合理的推导,只要能说明符合探索延伸的条件,即可解答本题.【解答】解:问题背景:∵小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连接AG,先证明△ABE ≌△ADG,再证明△AEF≌△AGF,∴EF=FG,FG=FD+DG=FD+BE,∴EF=BE+FD,故答案为:EF=BE+FD;探索延伸:上述结论EF=BE+FD成立,理由:如图2,延长FD到点G,使得DG=BE,连接AG,∵∠B+∠ADC=180°,∠ADG+∠ADC=180°,∴∠B=∠ADG,∵AB=AD,∴△ABE≌△ADG(SAS),∴AE=AG,∠BAE=∠DAG,∵∠EAF=∠BAD,∴∠GAF=∠DAG+∠DAF=∠DAF+∠BAE=∠BAD﹣∠EAF=∠BAD,∴∠GAF=∠EAF,又∵AG=AE,AF=AF,∴△AFG≌△AFE(SAS),∴EF=GF,∵GF=DF+DG=DF+BE,∴EF=BE+FD;实际应用:如图3,连接EF,延长AE、BF相交于点C,在四边形AOBC中,∵∠AOB=30°+90°+(90°﹣70°)=140°,∠FOE=70°=,又∵OA=OB,∠OAC+∠OBC=(90°﹣30°)+(70°+50°)=60°+120°=180°,∴图3符合探索延伸的条件,∴EF=AE+FB=1.5×(60+80)=210(海里),即此时两舰艇之间的距离210海里.【点评】本题考查三角形综合题,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想进行解答.25.(14分)如图,抛物线y=ax2+bx+2与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C.(1)求该抛物线的解析式;(2)在抛物线的对称轴1上是否存在一点M,使MA+MC的值最小?若存在,求出点M 的坐标:若不存在,请说明理由.(3)若点D是抛物线上的一点,且位于直线BC上方,连接CD、BD、AC.当四边形ABDC的面积有最大值时,求点D的坐标及四边形ABDC的面积.【分析】(1)用待定系数法求函数的解析式即可;(2)BC与直线l的交点即为点M,求出直线BC的解析式,当x=时,即可求M(,);(3)过D点作DE∥y轴交BC于点E,设D(t,﹣t2+t+2),则E(﹣t+2),则S=﹣t2+4t,从而得到S四边形ABCD﹣(t﹣2)2+9,当t=2时,四边形ABDC的面积有△BCD最大值9,此时D(2,3).【解答】解:(1)将A(﹣1,0),B(4,0)代入y=ax2+bx+2,∴,解得,∴y=﹣x2+x+2;(2)存在点M,使MA+MC的值最小,理由如下:∵点A与点B关于对称轴l对称,∴BC与直线l的交点即为点M,∵MA=BM,∴MA+MC=MB+MC≥BC,当B、C、M三点共线时,MA+MC的值最小,令x=0,则y=2,∴C(0,2),设直线BC的解析式为y=kx+b,∴,解得,∴y=﹣x+2,∵y=﹣x2+x+2=﹣(x﹣)2+,∴抛物线的对称轴为直线x=,当x=时,y=﹣×+2=,∴M(,);(3)∵A(﹣1,0),B(4,0),C(0,2),∴AB=5,OC=2,∴S△ABC=5×2=5,过D点作DE∥y轴交BC于点E,设D(t,﹣t2+t+2),则E(﹣t+2),∴DE=﹣t2+2t,∴S△BCD=4×(﹣t2+2t)=﹣t2+4t,∴S四边形ABDC=﹣t2+4t+5=﹣(t﹣2)2+9,∴当t=2时,四边形ABDC的面积有最大值9,此时D(2,3).【点评】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,轴对称求最短距离的方法,铅锤法求三角形面积的方法是解题的关键.。
2019-2020学年度山东省德州市太阳城中学七年级上数学第一次月考试题(含答案)

-2019-2020学年第一学期第一次月考七年级数学试题注意事项:1. 本试题共三个大题,26个小题,全卷满分150分,考试时间为120分钟。
2. 请将所有题目的答案答在答题纸上,答在本试卷上一律无效。
一、选择题(每题4分,共48分)1.如果收入500元记作500元,那么支出237元,应记作( )A .-500元B 。
-237元C 。
237元D 。
500元2. 13-的绝对值的相反数是( )A .-3 B.3 C.-13 D.133. 如果□+2=0,那么“□”内应填的有理数是( )A .-2B .21-C .21±D .214.下列各数中互为倒数的是( ) A .-2与2 B 。
-2与12 C 。
-2与12- D.-2与2- 5.下列语句正确的有( )个①所有整数都是正数;②所有正数都是整数;③小学学过的数都是正数;④奇数都是正数;⑤分数是有理数;⑥在有理数中不是负数就是正数A.0B.1C.2D.3 6.若x 的相反数是3,│y│=5,则x +y 的值为( )A .-8B .2C .-8或2D .8或-27.对于实数a ,b ,如果a>0,b<0,且|a|<|b|,那么下列等式成立的是( )A.a+b=|a|+|b|B.a+b=-(|a|+|b|)C.a+b=-(|a|-|b|)D.a+b=-(|b|-|a|) 8、如图a ,b 是有理数,它们在数轴上的对应点的位置如图所示:把a ,-a ,b ,-b 按照从小到大的顺序排列______. A 、-b <-a <a <b B 、a <-b <b <-a C 、-b <a <-a <b D 、a <-b <-a <b .9.绝对值大于3,而小于6的所有负整数的和是( ) A .9 B.-9 C.0 D.1 10.若ab <0,则ab的值是( ) A .正数 B 。
负数 C 。
非正数 D 。
非负数 11.一个数在数轴上所对应的点向右移动8个单位长度后,得到它的相反数的对应点,则这个数为( ) A.8 B.-8 C.-4 D.412.正整数按如图的规律排列.请写出第20行,第21列的数字是( )-A.400B.420C.440D.460 二、填空题(每小题4分,共24分)13. -2的倒数是 ,相反数是 . 14. 比较大小:(1)。
山东省德州市某校2021-2022学年-有答案-九年级上学期期中语文试题

山东省德州市某校2021-2022学年九年级上学期期中语文试题一、选择题1. 结合语境,选出下列语段中字音、字形全对的一项是()清晨读书,耳根清净,书卷在握,清风徐来,舒适qiè()意。
沉浸()书里,或吮指注目,或凝神屏()息;看到妙处,或拍案叫绝,或手舞足蹈;读到悲情,双目红润,泪眼婆娑;读到谐处,仰天大笑,喜上眉shāo()。
A.惬 qìn píng 梢B.惬 jìn bǐng梢C.挈 jìn bǐng稍D.挈 qìn píng 稍2. 加点词语使用正确的一项是()A.凳子凌驾在桌子上,被褥堆在床上,碗也没洗,苍蝇乱飞,屋内一片狼藉。
B.少一点置之度外,多一点温暖关怀,体现文明进步,善待我们身边的流浪动物。
C.站在李老师左边的是一位英俊的解放军战士,右边是一位文弱的莘莘学子。
D.各国争端不少,按下葫芦起了瓢。
解决争端,一味示强施压不行,武力干预更要不得。
3. 下列说法有误的一项是()A.八年级学生小芳想与志趣相投的同龄学友建个微信群,最适合的群名选“豆蔻年华”。
B.“桃李”“烽烟”“巾帼”“丝竹”“布衣”分别指学生、战争、妇女、音乐、百姓。
C.小玲向同学小明询问他母亲的姓氏,按照古代的礼仪应这么问:“家母贵姓?”D.农历九月初九重阳节,晓风应该陪家里的老人一起登高望远,赏菊吟诗,遍插茱萸。
4. 下列句子,没有语病的一项是()A.中国不仅是“一带一路”建设的倡议者,更是负责任的参与者、有担当的行动者。
B.通过参加这次活动,使我对中国博大精深的书法艺术产生了浓厚的兴趣。
C.《大鱼海棠》在影片质感和人物情节方面突破了一大步的跨越。
D.防止校园欺凌事件不再发生是个系统工程,需要多方面、多领域齐心协力完成。
二、句子默写默写①溪云初起日沉阁,________。
________________,蝉鸣黄叶汉宫秋。
②杜甫《春望》中“烽火连三月,家书抵万金”与他的《月夜忆舍弟》一诗中“________________,________________ ”一句表达的意思相近。
山东省德州市第十中学2024-2025学年九年级上学期10月月考数学试卷

山东省德州市第十中学2024-2025学年九年级上学期10月月考数学试卷一、单选题1.若方程2(1)90a x x +++=是关于x 的一元二次方程,则a 的取值范围是( ) A .1a > B .1a ≠- C .0a = D .1a ≥- 2.抛物线22y x =-+的对称轴是( )A.直线2x = B .直线2x =- C .直线x =D .y 轴3.与抛物线y=﹣x 2+1的顶点相同、形状相同且开口方向相反的抛物线所对应的函数表达式为( )A .y=﹣x 2B .y=x 2﹣1C .y=﹣x 2﹣1D .y=x 2+1 4.用配方法解一元二次方程28100x x -+=配方后得到的方程是( )A .()2854x +=B .()2854x -= C .()246x += D .()246x -= 5.著名数学家华罗庚说过:“数缺形时少直觉,形缺数时难入微.数形结合百般好,隔离分家万事非.”寥窖数语,把图形之妙趣说的淋漓尽致.如图是函数2y ax bx c =++的图象,那么无论x 为何值,函数值y 永远为负的条件是( )A .0a >,240b ac ->B .0a >,240b ac -<C .a<0,240b ac ->D .a<0,240b ac -<6.如表是一组二次函数2y x bx c =++的自变量和函数值的关系,那么方程20x bx c ++=的一个近似根是( )A .1.2B .2.3C .3.4D .4.57.已知点()14,A y -,()21,B y -,()35,C y 都在二次函数()2250y ax ax a =-+<的图象上,则1y ,2y ,3y 的大小关系用“<”表示为( )A .231y y y <<B .132y y y <<C .213y y y <<D .321y y y << 8.关于x 的方程2210x kx +-=的根的情况描述正确的是( )A .k 为任何实数,方程都没有实数根B .k 为任何实数,方程都有两个不相等的实数根C .k 为任何实数,方程都有两个相等的实数根D .根据k 的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种9.已知二次函数23y x bx =++满足当1x <时,y 随x 的增大而减小,当1x >时,y 随x 的增大而增大,则当2x =时,y 的值为( )A .0B .3C .8D .1110.已知关于x 的一元二次方程260x x -=■,其中一次项系数被墨迹污染了.若这个方程的一个根为2-,则一次项系数为( )A .2-B .3-C .1-D .6-11.已知二次函数()2211y x x x t =--≤≤-,当=1x -时,函数取得最大值;当1x =时,函数取得最小值,则t 的取值范围是( )A .02t <≤B .04t <≤C .24t ≤≤D .2t ≥12.如图,已知抛物线2y ax bx c =++(a 、b 、c 为常数,且0a ≠)的对称轴为直线=1x -,且该抛物线与x 轴交于点()1,0A ,与y 轴的交点B 在()0,2-,()0,3-之间(不含端点),则下列结论正确的有多少个( )①0abc >;②930a b c -+≥; ③213a <<; ④若方程21ax bx c x +=++两根为(),m n m n <,则31m n -<<<.A .1B .2C .3D .4二、填空题13.将二次函数()234y x =-+-的图象先向右平移2个单位长度,再向上平移5个单位长度,侧平移后的二次函数解析式为.(写为顶点式即可)14.小明设计了一个魔术盒,当任意实数对(a ,b )进入其中时,会得到一个新的实数a 2+2b-3.例如把(2,-5)放入其中就会得到22+2×(-5)-3=-9.现将实数对(m ,-3m )放入其中,得到实数4,则m =.15.如图是某停车场的平面示意图,停车场外围的长为30米,宽为18米.停车场内车道的宽都相等.停车位总占地面积为288平方米.设车道的宽为x 米,可列方程为.16.二次函数()20y ax bx c a =++≠图象经过点()1,2-,且图象对称轴为直线2x =,则方程()2200ax bx c a +++=≠的解为.17.若关于x 的一元二次方程2230x kx k -+-=的两个实数根分别是1x ,2x ,且满足()12122x x x x +=.则k 的值为.18.已知抛物线234y x x =--的图象如图①所示,先将抛物线在x 轴下方的部分沿x 轴翻折,图象其余部分不变,得到一个新图象如图②,当直线y x b =+与图象②恰有两个公共点时,则b 的取值范围为.三、解答题19.解方程:(1)()2321108x +=;(2)()3122x x x -=-;(3)29103x x +=;(4)()()2312x x --=.20.已知二次函数245y x x =--+.(1)用配方法求函数的顶点坐标;(2)补全表格,并在平面直角坐标系中用描点法画出该二次函数的图象.(3)根据图象回答下列问题:①当x ________时,y 随x 的增大而减小;②当x ________时,函数y 有最________值,是________;③当0y >时,x 的取值范围是________;④当5x 0-<<时,y 的取值范围是________.21.请阅读下列材料,并完成相应的任务.如果关于x 的一元二次方程()200ax bx c a ++=≠有一个根是1,那么我们称这个方程为“方正方程”.(1)判断一元二次方程23520x x -+=是否为“方正方程”,请说明理由.(2)已知关于x 的一元二次方程250x bx c -+=是“方正方程”,求22b c -的最小值.22.每年5月的第三个星期日为全国助残日,今年的主题是“科技助残,共享美好生活”,康宁公司新研发了一批便携式轮椅计划在该月销售,根据市场调查,每辆轮椅盈利200元时,每天可售出60辆;单价每降低10元,每天可多售出4辆.公司决定在成本不变的情况下降价销售,但每辆轮椅的利润不低于180元,设每辆轮椅降价x 元,每天的销售利润为y 元.(1)求y 与x 的函数关系式;每辆轮椅降价多少元时,每天的销售利润最大?最大利润为多少元?(2)全国助残日当天,公司共获得销售利润12160元,请问这天售出了多少辆轮椅? 23.如图,在直角坐标系中,二次函数212y x bx c =++的图象与x 轴相交于点A −2,0 和点()6,0B ,与y 轴交于点C .(1)求b 、c 的值;(2)若点P 是抛物线BC 段上的一点,当PBC △的面积最大时求出点P 的坐标,并求出PBC △面积的最大值.。
2023年山东省德州市德城区中考一模数学试题(含答案解析)

2023年山东省德州市德城区中考一模数学试题学校:___________姓名:___________班级:___________考号:___________.温州博物馆.西藏博物馆C博物馆D.湖北博物馆.一块直角三角板和一把直尺如图摆放,直尺的一边DEA.100︒B.1204.与115+最接近的整数是(A.3B.45.某小组在“用频率估计概率示的折线图,那么符合这一结果的实验最有可能的是(A.袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是B .掷一枚质地均匀的硬币,落地时结果是“正面向上”C .掷一个质地均匀的正六面体骰子,落地时面朝上的点数是2D .从一副扑克牌中随机抽取一张,抽到的牌是梅花6.幻方历史悠久,传说最早出现在夏禹时代的“洛书”.洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图1),将9个数填在33⨯的方格中,如果满足每行、每列,每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图2的主格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则n m 的值为()A .0B .1C .3D .67.某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m 个人共同完成需n 天,选取6组数对(),m n ,在坐标系中进行描点,则正确的是()A .B .C .D .8.关于x ,y 的方程组2232x y k x y k-=-⎧⎨-=⎩的解中x 与y 的和不小于5,则k 的取值范围为()A .8k ≥B .8k >C .8k ≤D .8k <9.如图,在ABC 中,AB AC BC =>.小丽按照下列方法作图:①作BAC ∠的角平分线AD ,交BC 于点D ;②作AC 的垂直平分线,交AD 于点E .A .()cos 1cos θθ+C .()sin 1sin θθ+二、填空题13.分解因式:2242a a -+=_____.16.在Rt ABC △中,90C ∠=︒旋转1周,得到圆锥,则该圆锥的侧面积最大值为17.二次函数2y ax bx c =++的部分对应值列表如下:x (3)-013y…78-9-5-则一元二次方程2(21)(2a x b -+18.我国古代数学家刘徽利用圆内接正多边形创立了等分构造出2个矩形和1个正方形(如图)三、解答题19.先化简,再求值:23x ⎛- -⎝的整数解.20.为庆祝建党100周年,让同学们进一步了解中国科技的快速发展,长沙市某中学九(1)班团支部组织了一次手抄报比赛,C .“夸父一号”;D .题的频数,绘制不完整的统计图,请根据统计图中的信息解答下列问题:(1)九(1)班共有___________名学生;(2)请以九(1)班的统计数据估计全校2000名学生大约有多少人选择(3)D主题所对应扇形圆心角的大小为___________;(4)甲和乙从A、B、C、D四个主题中任选一个主题,请用画树状图的方法求出他们选(1)任务一:两次测量,A,B(2)任务二:根据以上测量结果,请你帮助该综合实践小组求出学校旗杆︒≈,cos(参考数据:sin25.70.43︒≈)tan310.6022.【调查活动】小峰同学为了完成老师布置的社会活动作业:了A市的甲、乙两所初中,收集到如下信息:①甲、乙两校图书室各藏书18000②甲校比乙校人均图书册数多(1)求证:MN 是半圆的切线;(2)已知弧AC 的中点D ,要求过(3)若4BC =,6AB =,求AE .24.(1)【实验】如图①,点O 为线段时,四边形PMQN 的形状为________A .矩形B .菱形C .正方形其理论依据是________.(2)【探究】如图②,在平行四边形交边CD 于点F ,连接AF ,试猜想证明.(3)【应用】如图③,在ABC 中,求ABC 的面积.25.如图,抛物线222433y x x =-++与坐标轴分别交于内抛物线上的一点且横坐标为m .(1)A ,B ,C 三点的坐标为____________,____________(2)连接AP ,交线段BC 于点D ,①当CP 与x 轴平行时,求PDDA的值;②当CP 与x 轴不平行时,求PDDA的最大值;参考答案:1.D【分析】相反数的定义是:如果两个数只有符号不同,我们称其中一个数为另一个数的相反数,特别地,0的相反数还是0.【详解】根据相反数的定义可得:-3的相反数是3,故选D .【点睛】本题考查相反数,题目简单,熟记定义是关键.2.A【分析】根据轴对称图形和中心对称图形的定义解答即可.【详解】解:A :既是中心对称图形,又是轴对称图形,故此选项符合题意;B :不是中心对称图形,是轴对称图形,故此选项不合题意;C :不是中心对称图形,也不是轴对称图形,故此选项不合题意;D :不是中心对称图形,是轴对称图形,故此选项不合题意;故选:A .【点睛】本题主要考查中心对称图形和轴对称图形的概念,轴对称图形:在同一平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形;中心对称图形:在同一平面内,如果把一个图形绕某一点旋转180度,旋转后的图形和原图完全重合,那么这个图形就叫做中心图形.3.B【分析】根据30BAC ∠=︒,求出903060B ∠=-=°°°,根据平行线的性质,求出180120DAB B =︒-=︒∠∠即可.【详解】解:∵30BAC ∠=︒,∴903060B ∠=-=°°°,∵DE BC ∥,∴180120DAB B =︒-=︒∠∠,故B 正确.故选:B .【点睛】本题主要考查了平行线的性质,解题的关键是熟练掌握平行线的性质,两直线平行,同位角相等;两直线平行内错角相等;两直线平行,同旁内角互补.4.C【分析】由于91516<<,由此根据算术平方根的概念可以找到10接近的两个完全平方数,由圆的对称性可知,点A 13601203AOD ∴∠=⨯︒=︒在Rt AOM △中,2OA =112OM OA ∴==,AM =在Rt BOM △中,BOM ∠1BM OM ∴==,31AB AM BM ∴=-=-8∴个阴影三角形的面积和为:故答案为:1683-.【点睛】本题考查正多边形和圆,算的方法是正确解答的前提.共有16种等可能的结果,甲和乙选择相同主题的结果有∴甲和乙选择相同主题的概率为41 164=.(3)解:如图,连接OD 交AC 点D 为 AC 的中点,OD AC ∴⊥,AH CH =,122OH BC ∴==,在OAH △和ODE 中,90OHA OED AOH DOE OA OD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,()AAS OAH ODE ∴ ≌,2OE OH ∴==,AB 是直径,132OA AB ∴==,321AE OA OE ∴=-=-=.【点睛】本题考查了切线的判定,垂线的作法,圆周角定理,全等三角形的判定与性质,垂径定理,熟练掌握知识点并正确作出辅助线是解题的关键.24.(1)D ;对角线相互平分的四边形是平行四边形;ABC 的面积为23【分析】(1)根据平行四边形的判定∵四边形ABCD 为平行四边形,点∴AB CD ∥,BE CE =,∴HBE FCE∠=∠又∵BEH CEF ∠=∠,∴(ASA)BEH CEF ≌,∴CF BH =,HE FE =,又∵AE HF ⊥,∴AF AH =,∵AH AB BH AB CF =+=+,∴AF AB CF =+;(3)如图,作DE AB ∥,∴CE CD AE BD=,∵点D 为BC 的中点,即CD BD =,∴AE CE =,∴DE 为ABC 的中位线,∴11922AE AC ==,∵DE AB ∥,∴90ADE BAD ∠=∠=︒,∴在Rt ADE △中,2232DE AE AD =-=,∴23AB DE ==,∴1132322ABD S AB AD =⋅=⨯⨯=△,∵ABD △与ACD 等底等高,=+ y k x b∵290BCO BCP ∠+∠=︒,在性等相关内容,解本题的关键是求抛物线解析式,确定点P的坐标.。
2024-2025学年山东省德州市初三上学期期末道德与法治试卷及解答参考

2024-2025学年山东省德州市道德与法治初三上学期期末自测试卷(答案在后面)一、单项选择题(本大题有12小题,每小题4分,共48分)1、新中国第一部《中华人民共和国宪法》诞生于哪一年?A、1949年B、1954年C、1978年D、1982年2、下列行为中,不属于违法行为的是?A、在校期间多次违反校规校纪,受到学校纪律处分B、故意破坏公共设施C、捡到他人遗失的财物,据为己有D、帮助同学复习功课3、下面哪个选项体现了法治精神的核心?A、有法可依B、执法必严C、违法必究D、以德治国4、在道德与法治的学习过程中,我们强调“法无授权不可为”,这句话体现了法律的哪一项基本原则?A、法律面前人人平等B、依法行使权力C、依法享受权利D、依法履行义务5、下列哪个选项体现了依法治国的基本要求之一?A、国家机关及其工作人员必须依法行使权力B、每个公民都享有无条件的言论自由C、只要求国家机关及其工作人员遵守法律D、公民个人可以忽略遵守相关法律法规6、在社会生活中,调解是一种重要的解决纠纷方式。
以下哪种情况最适合采用调解?A、李某和王某因合同条款存在争议诉至法院B、赵某与邻居张某晚上因音响声音过大而发生争吵C、孙某和刘某在公开场合发生了激烈的打斗事件D、周某和田某在下班回家的路上因琐事引起肢体冲突7、下列哪项行为体现了公民的基本道德规范和法治意识?A、在公交车上主动为老人让座B、在公安机关发现有人企图逃避法律制裁时选择视而不见C、随意在网络上散布他人的隐私信息D、为了逃避罚款故意提供虚假信息8、按照我国法律,未成年人享有特殊保护。
在此背景下,下列哪一选项正确体现了对未成年人法律保护的原则?A、任何情况下,未成年人不允许单独生活B、商家向未成年人出售烟草制品是合法的C、未成年人的行为一律不应受到行政处罚D、学校应当对未成年人进行法制教育,提高其自我保护意识和能力9、我国宪法宣誓制度在哪一年由全国人大常委会正式确立?A、2012年B、2013年C、2014年D、2015年 10、以下哪项不属于我国公民的基本权利?A、政治权利B、经济权利C、社会文化权利D、自由权利11、在我国的法律体系中,具有最高法律效力的是()A.宪法B.刑法C.民法D.行政法12、在日常生活中,当遇到违法犯罪行为时,我们应该怎么办?A.直接与违法犯罪分子进行搏斗B.尽量避开,防止自己受到伤害C.利用智慧和意识,及时报警或寻求周围安全的帮助D.默默忍受,事后向有关部门投诉二、非选择题(本大题有5小题,第5小题12分,其他每题10分,共52分)第一题(一) 阅读下面的文章,并根据文章内容回答问题。
2024届山东省德州市第一中学化学九年级第一学期期中综合测试试题含解析
2024届山东省德州市第一中学化学九年级第一学期期中综合测试试题注意事项:1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
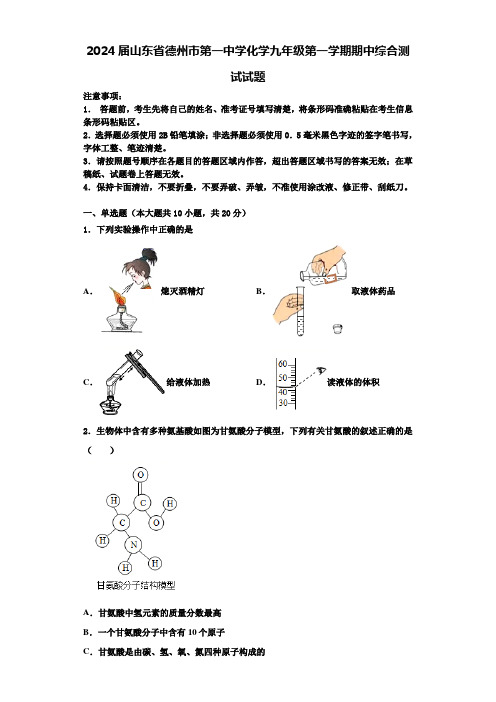
一、单选题(本大题共10小题,共20分)1.下列实验操作中正确的是A.熄灭酒精灯B.取液体药品C.给液体加热D.读液体的体积2.生物体中含有多种氨基酸如图为甘氨酸分子模型,下列有关甘氨酸的叙述正确的是()A.甘氨酸中氢元素的质量分数最高B.一个甘氨酸分子中含有10个原子C.甘氨酸是由碳、氢、氧、氮四种原子构成的D.甘氨酸中碳元素与氧元素的质量比为2:13.元素周期表是学习和研究化学的重要工具。
如图是元素周期表中氯元素的示意图,下列说法不正确的是()A.氯元素符号为ClB.氯原子的核内质子数为17C.氯元素为金属元素D.氯元素的相对原子质量为35.454.下列事实的微观解释不.正确的是A.干冰升华——分子空隙变大B.水烧开后把壶盖顶开——分子数目变多C.通过气味辨别酒精和水——分子不断运动,不同分子的性质不同D.湿衣服晾在太阳底下干得快—分子运动速率变快5.下图是微信热传的“苯宝宝表情包”,苯(化学式为C6H6)是一种重要的化工原料。
下列有关苯的说法正确的是( )A.苯的相对分子质量为78gB.苯由6个碳原子和6个氢原子构成C.苯由碳、氢两种元素组成D.苯中碳、氢两种元素的质量比为1∶16.能保持氢气化学性质的微粒是A.B.C.D.7.古诗词是中华民族的文化瑰宝,下列古诗词中对划线对象变化的表述属于化学变化的是()A.日照香炉生紫烟,遥看瀑布挂前川B.河上姹女,灵而最神,得火则飞,不见埃尘C.臣心一片磁针石,不指南方不肯休D.落红不是无情物,化作春泥更护花8.引起酸雨的主要物质是( )A.二氧化硫B.氧气C.氮气D.氦气9.如图是气体粒子的示意图,其中表示单质的是()A.B.C.D.10.学习完“原子的构成”之后,小李同学形成了以下认识,其中错误的是()A.原子由居于中心的原子核和核外电子构成B.任何原子核都是由质子和中子构成的C.原子的质量主要集中在原子核上D.原子核的体积与整个原子的体积相比要小很多二、填空题(本大题共1小题,共4分)11.下列是四种粒子的结构示意图:用序号填空:A B C D(1)电子层排布相同的是___;(2)属于同种元素的是______;(3)表示阳离子的是____;(4)表示阴离子的是____;(5)具有相似化学性质的是________。
2020-2021学年山东省德州市禹城市九年级(上)期末数学试卷(含解析)

2020-2021学年山东省德州市禹城市九年级第一学期期末数学试卷一、选择题(共12小题).1.下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.2.下列事件为不可能事件的是()A.某射击运动员射击一次,命中靶心B.掷一次骰子,向上的一面是5点C.找到一个三角形,其内角和为360°D.经过城市中某一有交通信号灯的路口,遇到红灯3.关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根0,则a值为()A.1B.﹣1C.±1D.04.如图,放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为()A.6cm B.12cm C.18cm D.24cm5.便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足y=﹣2(x﹣20)2+1558,由于某种原因,价格只能15≤x≤22,那么一周可获得最大利润是()A.20B.1508C.1550D.15586.将抛物线y=x2﹣2x﹣3的图象先向右平移1个单位,再向下平移4个单位,所得图象的函数解析式为()A.y=x2﹣3x﹣7B.y=x2﹣x﹣7C.y=x2﹣3x+1D.y=x2﹣4x﹣4 7.如图,点O是△ABC的内心,∠A=62°,则∠BOC=()A.59°B.31°C.124°D.121°8.一次函数y1=k1x+b和反比例函数y2=(k1•k2≠0)的图象如图所示,若y1>y2,则x 的取值范围是()A.﹣2<x<0或x>1B.﹣2<x<1C.x<﹣2或x>1D.x<﹣2或0<x<19.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=1 cm,扇形的圆心角θ=120°,则该圆锥的母线长l为()cm.A.1B.12C.3D.610.如图所示,⊙O是正方形ABCD的外接圆,P是⊙O上不与A、B重合的任意一点,则∠APB等于()A.45°B.60°C.45°或135°D.60°或120°11.如图,直线AB与⊙O相切于点A,弦CD∥AB,E,F为圆上的两点,且∠CDE=∠ADF.若⊙O的半径为,CD=4,则弦EF的长为()A.4B.2C.5D.612.二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.其中正确的结论有()A.1个B.2个C.3个D.4个二、填空题(共6小题,每小题4分,共24分)13.已知△ABC∽△DEF,若△ABC与△DEF的面积比为9:16,则△ABC与△DEF的相似比为.14.如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=50°,则∠CAD=.15.如图,矩形ABCD的长AB=6cm,宽AD=3cm.O是AB的中点,OP⊥AB,两半圆的直径分别为AO与OB.抛物线y=ax2经过C、D两点,则图中阴影部分的面积是cm2.16.如图,已知双曲线经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为.17.如图所示,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(﹣3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为.18.如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则的值为.三、解答题(本题共7小题,共78分,解答时应写出必要的文字说明、证明过程或演算步骤)19.解下列方程:(1)3x(x﹣2)=2(x﹣2);(2)2x2﹣7x+6=0.20.某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;(2)求销售单价为多少元时,该文具每天的销售利润最大;(3)商场的营销部结合上述情况,提出了A、B两种营销方案:方案A:该文具的销售单价高于进价且不超过30元;方案B:每天销售量不少于10件,且每件文具的利润至少为25元请比较哪种方案的最大利润更高,并说明理由.21.小明和小亮玩一种游戏:三张大小,质地都相同的卡片上分别标有数字1,2,3,现将标有数字的一面朝下,小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和,如果和为奇数,则小明胜,若和为偶数则小亮胜.(1)用列表或画树状图等方法,列出小明和小亮抽得的数字之和所有可能出现的情况.(2)请判断该游戏对双方是否公平?并说明理由.22.如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,﹣3),反比例函数y=的图象经过点C,一次函数y=ax+b的图象经过点A、C,(1)求反比例函数与一次函数的解析式;(2)求点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.23.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).(1)若△ABC和△A1B1C1关于原点O成中心对称,写出△A1B1C1的各顶点的坐标;(2)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标;(3)若△ABC和△A2B2C2关于点(﹣1,1)位似,位似比为1:2,画出△A2B2C2(在位似中心另一侧)并写出△A2B2C2各顶点的坐标.24.如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.(1)求证:EF是⊙O的切线;(2)求证:AC2=AD•AB;(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.25.如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求二次函数的表达式;(2)在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P的坐标;(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N 从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.参考答案一、选择题(共12小题,每题4分,共48分)1.下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.解:A、既是轴对称图形,是中心对称图形,故此选项正确;B、不是轴对称图形,是中心对称图形,故此选项错误;C、是轴对称图形,不是中心对称图形,故此选项正确;D、是轴对称图形,不是中心对称图形,故此选项错误;故选:A.2.下列事件为不可能事件的是()A.某射击运动员射击一次,命中靶心B.掷一次骰子,向上的一面是5点C.找到一个三角形,其内角和为360°D.经过城市中某一有交通信号灯的路口,遇到红灯解:A、某射击运动员射击一次,命中靶心可能发生,也可能不发生,属于随机事件,不符合题意;B、掷一次骰子,向上的一面是5点可能发生,也可能不发生,属于随机事件,不符合题意;C、在找到一个三角形,其内角和为360°,是不可能发生的事件,符合题意;D、经过城市中某一有交通信号灯的路口,遇到红灯是随机事件,不符合题意.故选:C.3.关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根0,则a值为()A.1B.﹣1C.±1D.0解:把x=0代入方程得:a2﹣1=0,解得:a=±1,∵(a﹣1)x2+x+a2﹣1=0是关于x的一元二次方程,∴a﹣1≠0,即a≠1,∴a的值是﹣1.故选:B.4.如图,放映幻灯片时,通过光源把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为()A.6cm B.12cm C.18cm D.24cm解:∵DE∥BC,∴△AED∽△ACB∴,设屏幕上的小树高是x,则,解得x=18cm.故选:C.5.便民商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足y=﹣2(x﹣20)2+1558,由于某种原因,价格只能15≤x≤22,那么一周可获得最大利润是()A.20B.1508C.1550D.1558解:∵一周利润y(元)与每件销售价x(元)之间的关系满足y=﹣2(x﹣20)2+1558,且15≤x≤22,∴当x=20时,y最大值=1558.故选:D.6.将抛物线y=x2﹣2x﹣3的图象先向右平移1个单位,再向下平移4个单位,所得图象的函数解析式为()A.y=x2﹣3x﹣7B.y=x2﹣x﹣7C.y=x2﹣3x+1D.y=x2﹣4x﹣4解:∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴将抛物线y=x2﹣2x﹣3的图象先向右平移1个单位,再向下平移4个单位,所得图象的函数y=(x﹣1﹣1)2﹣4﹣4,即y=(x﹣2)2﹣8=x2﹣4x﹣4.故选:D.7.如图,点O是△ABC的内心,∠A=62°,则∠BOC=()A.59°B.31°C.124°D.121°解:∵∠BAC=62°,∴∠ABC+∠ACB=180°﹣62°=118°,∵点O是△ABC的内心,∴∠OBC=∠ABC,∠OCB=∠ACB,∴∠OBC+∠OCB=(∠ABC+∠ACB)=×118°=59°,∴∠BOC=180°﹣59°=121°.故选:D.8.一次函数y1=k1x+b和反比例函数y2=(k1•k2≠0)的图象如图所示,若y1>y2,则x 的取值范围是()A.﹣2<x<0或x>1B.﹣2<x<1C.x<﹣2或x>1D.x<﹣2或0<x<1解:如图所示:若y1>y2,则x的取值范围是:x<﹣2或0<x<1.故选:D.9.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=1 cm,扇形的圆心角θ=120°,则该圆锥的母线长l为()cm.A.1B.12C.3D.6解:圆锥的底面周长=2π×1=2πcm,设圆锥的母线长为R,则:=2π,解得R=3.故选:C.10.如图所示,⊙O是正方形ABCD的外接圆,P是⊙O上不与A、B重合的任意一点,则∠APB等于()A.45°B.60°C.45°或135°D.60°或120°解:连接OA,OB,∵⊙O是正方形ABCD的外接圆,∴∠AOB=90°,若点P在优弧ADB上,则∠APB=∠AOB=45°;若点P在劣弧AB上,则∠APB=180°﹣45°=135°.∴∠APB=45°或135°.故选:C.11.如图,直线AB与⊙O相切于点A,弦CD∥AB,E,F为圆上的两点,且∠CDE=∠ADF.若⊙O的半径为,CD=4,则弦EF的长为()A.4B.2C.5D.6解:连接OA,并反向延长交CD于点H,连接OC,∵直线AB与⊙O相切于点A,∴OA⊥AB,∵弦CD∥AB,∴AH⊥CD,∴CH=CD=×4=2,∵⊙O的半径为,∴OA=OC=,∴OH==,∴AH=OA+OH=+=4,∴AC==2.∵∠CDE=∠ADF,∴=,∴=,∴EF=AC=2.故选:B.12.二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.其中正确的结论有()A.1个B.2个C.3个D.4个解:∵抛物线的对称轴为直线x=﹣=2,∴b=﹣4a,即4a+b=0,(故①正确);∵当x=﹣3时,y<0,∴9a﹣3b+c<0,即9a+c<3b,(故②错误);∵抛物线与x轴的一个交点为(﹣1,0),∴a﹣b+c=0,而b=﹣4a,∴a+4a+c=0,即c=﹣5a,∴8a+7b+2c=8a﹣28a﹣10a=﹣30a,∵抛物线开口向下,∴a<0,∴8a+7b+2c>0,(故③正确);∵对称轴为直线x=2,∴当﹣1<x<2时,y的值随x值的增大而增大,当x>2时,y随x的增大而减小,(故④错误).故选:B.二、填空题(本大题共6小题,每小题4分,共24分)13.已知△ABC∽△DEF,若△ABC与△DEF的面积比为9:16,则△ABC与△DEF的相似比为3:4.解:∵△ABC∽△DEF,△ABC与△DEF的面积之比为9:16,∴△ABC与△DEF的相似比为3:4,故答案为:3:4.14.如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=50°,则∠CAD=40°.解:连接CD,∵AD是⊙O的直径,∴∠ACD=90°,∵∠D=∠ABC=50°,∴∠CAD=90°﹣∠D=40°.故答案为:40°.15.如图,矩形ABCD的长AB=6cm,宽AD=3cm.O是AB的中点,OP⊥AB,两半圆的直径分别为AO与OB.抛物线y=ax2经过C、D两点,则图中阴影部分的面积是cm2.解:由题意,得:S阴影=S半圆=π()2=π(cm2).16.如图,已知双曲线经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣6,4),则△AOC的面积为9.解:∵点D为△OAB斜边OA的中点,且点A的坐标(﹣6,4),∴点D的坐标为(﹣3,2),把(﹣3,2)代入双曲线,可得k=﹣6,即双曲线解析式为y=﹣,∵AB⊥OB,且点A的坐标(﹣6,4),∴C点的横坐标为﹣6,代入解析式y=﹣,y=1,即点C坐标为(﹣6,1),∴AC=3,又∵OB=6,∴S△AOC=×AC×OB=9.故答案为:9.17.如图所示,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(﹣3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为1或5.解:当⊙P位于y轴的左侧且与y轴相切时,平移的距离为1;当⊙P位于y轴的右侧且与y轴相切时,平移的距离为5.故答案为:1或5.18.如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则的值为.解:∵矩形沿直线AC折叠,点B落在点E处,∴∠BAC=∠EAC,AE=AB=CD,∵矩形ABCD的对边AB∥CD,∴∠DCA=∠BAC,∴∠EAC=∠DCA,设AE与CD相交于F,则AF=CF,即DF=EF,∴=,又∵∠AFC=∠EFD,∴△ACF∽△EDF,∴==,设DF=3x,FC=5x,则AF=5x,在Rt△ADF中,AD===4x,又∵AB=CD=DF+FC=3x+5x=8x,∴==.故答案为:.三、解答题(本题共7小题,共78分,解答时应写出必要的文字说明、证明过程或演算步骤)19.解下列方程:(1)3x(x﹣2)=2(x﹣2);(2)2x2﹣7x+6=0.【解答】解:(1)∵3x(x﹣2)=2(x﹣2),∴3x(x﹣2)﹣2(x﹣2)=0,∴(3x﹣2)(x﹣2)=0,∴3x﹣2=0或x﹣2=0,解得:x1=,x2=2.(2)∵2x2﹣7x+6=0,∴(x﹣2)(2x﹣3)=0,解得x1=2,x2=.20.某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;(2)求销售单价为多少元时,该文具每天的销售利润最大;(3)商场的营销部结合上述情况,提出了A、B两种营销方案:方案A:该文具的销售单价高于进价且不超过30元;方案B:每天销售量不少于10件,且每件文具的利润至少为25元请比较哪种方案的最大利润更高,并说明理由.解:(1)由题意得,销售量=250﹣10(x﹣25)=﹣10x+500,则w=(x﹣20)(﹣10x+500)=﹣10x2+700x﹣10000;(2)w=﹣10x2+700x﹣10000=﹣10(x﹣35)2+2250.∵﹣10<0,∴函数图象开口向下,w有最大值,当x=35时,w最大=2250,故当单价为35元时,该文具每天的利润最大;(3)A方案利润高.理由如下:A方案中:20<x≤30,故当x=30时,w有最大值,此时w A=2000;B方案中:,故x的取值范围为:45≤x≤49,∵函数w=﹣10(x﹣35)2+2250,对称轴为直线x=35,∴当x=45时,w有最大值,此时w B=1250,∵w A>w B,∴A方案利润更高.21.小明和小亮玩一种游戏:三张大小,质地都相同的卡片上分别标有数字1,2,3,现将标有数字的一面朝下,小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和,如果和为奇数,则小明胜,若和为偶数则小亮胜.(1)用列表或画树状图等方法,列出小明和小亮抽得的数字之和所有可能出现的情况.(2)请判断该游戏对双方是否公平?并说明理由.解:法一,列表法二,画树形图(1)从上面表中(树形图)可看出小明和小亮抽得的数字之和可能有是:2,3,4,5,6;(2)因为和为偶数有5次,和为奇数有4次,所以P(小明胜)=,P(小亮胜)=,所以:此游戏对双方不公平.22.如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,﹣3),反比例函数y=的图象经过点C,一次函数y=ax+b的图象经过点A、C,(1)求反比例函数与一次函数的解析式;(2)求点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.解:(1)∵点A的坐标为(0,2),点B的坐标为(0,﹣3),∴AB=5,∵四边形ABCD为正方形,∴点C的坐标为(5,﹣3).∵反比例函数y=的图象经过点C,∴﹣3=,解得k=﹣15,∴反比例函数的解析式为y=﹣;∵一次函数y=ax+b的图象经过点A,C,∴,解得,∴一次函数的解析式为y=﹣x+2;(2)设P点的坐标为(x,y).∵△OAP的面积恰好等于正方形ABCD的面积,∴×OA•|x|=52,∴×2•|x|=25,解得x=±25.当x=25时,y=﹣=﹣;当x=﹣25时,y=﹣=.∴P点的坐标为(25,﹣)或(﹣25,).23.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).(1)若△ABC和△A1B1C1关于原点O成中心对称,写出△A1B1C1的各顶点的坐标;(2)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标;(3)若△ABC和△A2B2C2关于点(﹣1,1)位似,位似比为1:2,画出△A2B2C2(在位似中心另一侧)并写出△A2B2C2各顶点的坐标.解:(1)如图所示,△A1B1C1即为所求,由图知A1(3,﹣5),B1(2,﹣1),C1(1,﹣3).(2)如图,△PAB即为所求,点A关于x轴的对称点A′的坐标为(﹣3,﹣5),设BA′的解析式为y=kx+b,把A′(﹣3,﹣5),B(﹣2,1)代入得,解得∴BA′的解析式为y=6x+13,当y=0时,6x+13=0,解得x=﹣,∴点P(﹣,0);(3)如图所示,△A2B2C2即为所求,A2(3,﹣7),B2(1,1),C2(﹣1,﹣3).24.如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.(1)求证:EF是⊙O的切线;(2)求证:AC2=AD•AB;(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.【解答】(1)证明:连接OC,∵OA=OC,∴∠BAC=∠OCA,∵∠DAC=∠BAC,∴∠OCA=∠DAC,∴OC∥AD,∵AD⊥EF,∴OC⊥EF,∵OC为半径,∴EF是⊙O的切线.(2)证明:连接BC,∵AB为⊙O直径,AD⊥EF,∴∠BCA=∠ADC=90°,∵∠DAC=∠BAC,∴△ACB∽△ADC,∴=,∴AC2=AD•AB.(3)解:∵∠ACD=30°,∠OCD=90°,∴∠OCA=60°,∵OC=OA,∴△OAC是等边三角形,∴AC=OA=OC=2,∠AOC=60°,∵在Rt△ACD中,AD=AC=×2=1,由勾股定理得:DC=,∴阴影部分的面积是S=S梯形OCDA﹣S扇形OCA=×(2+1)×﹣=﹣π.25.如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求二次函数的表达式;(2)在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P的坐标;(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N 从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.解:(1)把A(1,0)和C(0,3)代入y=x2+bx+c,解得:b=﹣4,c=3,∴二次函数的表达式为:y=x2﹣4x+3;(2)令y=0,则x2﹣4x+3=0,解得:x=1或x=3,∴B(3,0),∴BC=3,点P在y轴上,当△PBC为等腰三角形时分三种情况进行讨论:如图1,①当CP=CB时,PC=3,∴OP=OC+PC=3+3或OP=PC﹣OC=3﹣3∴P1(0,3+3),P2(0,3﹣3);②当BP=BC时,OP=OC=3,∴P3(0,﹣3);③当PB=PC时,∵OC=OB=3∴此时P与O重合,∴P4(0,0);综上所述,点P的坐标为:(0,3+3)或(0,3﹣3)或(0,﹣3)或(0,0);(3)如图2,设A运动时间为t,由AB=2,得BM=2﹣t,则DN=2t,∴S△MNB=×(2﹣t)×2t=﹣t2+2t=﹣(t﹣1)2+1,即当M(2,0)、N(2,2)或(2,﹣2)时△MNB面积最大,最大面积是1.。
2020-2021学年德州九中八年级上学期第一次月考数学试卷(含解析)

2020-2021学年德州九中八年级上学期第一次月考数学试卷一、选择题(本大题共12小题,共48.0分)1.如图,直线AB//CD,直线EF分别交AB,CD于点M,N,过点N的直线GH交AB于点P,下列结论错误的是()A. ∠DNG=∠AMEB. ∠BMN=∠MNCC. ∠CNH=∠BPGD. ∠EMB=∠END2.如图:△ABC≌△BAD,则图中相等的线段有()对A. 5B. 4C. 3D. 23.下列三条线段能组成三角形的是()A. 2,5,4B. 14,22,7C. 22,9,7D. 1,1,√54.若|−5+a|=|−5|+|a|,则a是()A. 任意一个有理数B. 任意一个负数或0C. 任意一个非负数D. 任意一个不小于5的数5.下列说法正确的是()A. 有两条边和一个角对应相等的两个三角形全等B. 正方形既是轴对称图形又是中心对称图形C. 矩形的对角线互相垂直平分D. 六边形的内角和是540°6.已知AB是半径为1的圆O的一条弦,且AB=a<1,以AB为一边在圆O内作正△ABC,点D为圆O上不同于点A的一点,且DB=AB=a,DC的延长线交圆O于点E,则AE的长为()A. √5a2B. 1C. √32D. a7.与算式23+23+23的运算结果相等的是()A. 23B. 29C. 3×23D. 3×68.如图,∠1=∠2=65°,∠3=35°,则下列结论错误的是()A. AB//CDB. ∠B=30°C. ∠C+∠2=∠EFCD. CG>FG9.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果BC=3cm,AB=5那么AE+DE等于()A. 2cmB. 3cmC. 4cmD. 5cm10.如图,在△ABC中,点D为BC边上的一点,且AD=AB=4,AD⊥AB,过点D作DE⊥AD,DE交AC于点E,若DE=2,则△ABC的面积为()A. 8B. 8√5C. 16D. 16√211.如图,在△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,BC=8,BD=5,那么点D到AB的距离是()A. 3B. 4C. 5D. 612.若两个多边形的内角和的差是540°,则它们的边数之差等于()A. 4B. 3C. 2D. 1二、填空题(本大题共6小题,共24.0分)13.如图,AD=BC,要使△ABC≌△BAD,还需添加的个条件是______(填一个即可).14.已知△ABC≌△DEF,∠B=120°,∠F=35°.则∠D=______度.15.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,AE=3ED,如果AC=12cm,那么DE的长为______cm.16.如图,△ABC中,∠BAC的平分线交BC于点D,过点D作DE⊥AC于E,DE=4,AB=6,则△ABD面积是______.17.如图,CE平分∠ACD,∠A=40°,∠B=30°,∠D=104°,则∠BEC=____.18.如图,下面是按照一定规律画出的“树形图”,经观察可以发现:图A2比图A1多出2个“树枝”,图A3比图A2多出4个“树枝”,图A4比图A3多出8个“树枝”,…,照此规律,图A6比图A2多出______ 个“树枝”.三、解答题(本大题共5小题,共48.0分)19.如图,点A、B、C、D依次在同一条直线上,点E、F分别在直线AD的两侧,已知BE//CF,∠A=∠D,AE=DF.(1)求证:四边形BFCE是平行四边形;(2)填空:若AD=7,AB=2.5,∠EBD=60°,当四边形BFCE是菱形时,菱形BFCE的面积是______.20.一个多边形,它的内角和比外角和的5倍多180°,求这个多边形的边数及内角和度数.21.如图,小正方形的边长为1,△ABC为格点三角形.(1)如图①,△ABC的面积为______;(2)在图②中画出所有与△ABC全等,且只有一条公共边的格点三角形.22.如图,点F是△ABC的边BC的延长线上一点,FD⊥AB于点D.∠A=30°,∠F=40°,求∠ACB的度数.23.已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处(Ⅰ)如图1,已知折痕与边BC交于点O,连接AP、OP、OA.若△OCP与△PDA的面积比为1:4,求边CD的长.(Ⅱ)如图2,在(Ⅰ)的条件下,擦去折痕AO、线段OP,连接BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问当动点M、N在移动的过程中,线段EF的长度是否发生变化?若变化,说明变化规律.若不变,求出线段EF的长度.【答案与解析】1.答案:A解析:解:A、∠DNG与∠AME没有关系,无法判定其是否相等.B、∵AB//CD,∴∠BMN=∠MNC(两直线平行,内错角相等);C、∵AB//CD,∴∠CNH=∠MPN(两直线平行,同位角相等),∵∠MPN=∠BPG(对顶角),∴∠CNH=∠BPG(等量代换);D、∵AB//CD,∴∠EMB=∠END(两直线平行,同位角相等);故选:A.根据平行线的性质,找出各相等的角,再去对照四个选项即可得出结论.本题考查了平行线的性质,解题的关键是结合平行线的性质来对照四个选择.解决该题型题目时,根据平行线的性质找出相等(或互补)的角是关键.2.答案:A解析:因为△ABC≌△BAD所以AB=BA,AC=DB,BC=AD,∠DAB=∠CBA所以AE=BE因为CE=BC−BE,DE=AD−AE所以CE=DE故选A.3.答案:A解析:解:A.2+4>5,能组成三角形,故此选项正确;B.14+7<22,不能组成三角形,故此选项错误;C.7+9<22,不能组成三角形,故此选项错误;D.1+1<√5,不能组成三角形,故此选项错误;故选A.根据三角形两边之和大于第三边可得答案.此题主要考查了三角形的三边关系,关键是掌握在运用三角形三边关系,判定三条线段能否构成三角形时,并不一定要列出三个不等式,只要两条较短的线段长度之和大于第三条线段的长度,即可判定这三条线段能构成一个三角形.4.答案:B解析:解:由|−5+a|=|−5|+|a|,得|−5+a|=5+|a|,故a≤0,即a是任意一个负数或0.故选:B.先把等式变形,根据绝对值的非负性即可求出a的取值范围.本题考查了绝对值与不等式的综合运用,切记不要忘掉0.5.答案:B解析:解:A、有两条边和一个角对应相等的两个三角形全等,错误,必须是两边及其夹角分别对应相等的两个三角形全等;B、正方形既是轴对称图形又是中心对称图形,正确;C、矩形的对角线相等且互相平分,故此选项错误;D、六边形的内角和是720°,故此选项错误.故选:B.直接利用全等三角形的判定以及矩形、菱形的性质和多边形内角和定理.此题主要考查了全等三角形的判定以及矩形、菱形的性质和多边形内角和定理,正确把握相关性质是解题关键.6.答案:B解析:解:∵△ABC是等边三角形,∴AB=BC=AC=BD=a,∠CAB=∠ACB=60°;∵AB=BD,∴AB⏜=BD⏜,∴∠AED=∠AOB;∵BC=AB=BD,∴∠D=∠BCD;∵四边形EABD内接于⊙O,∴∠EAB+∠D=180°,即∠EAC+60°+∠D=180°;又∵∠ECA+60°+∠BCD=180°,∴∠ECA=∠EAC,即△EAC是等腰三角形;在等腰△EAC和等腰△OAB中,∠AEC=∠AOB,∵AC=AB,∴△EAC≌△OAB;∴AE=OA=1.故选:B.此题可通过证△EAC≌△OAB,得AE=OA,从而求出EA的长;△EAC和△OAB中,已知的条件只有AB=AC;由AB=BD,得AB⏜=BD⏜,可得∠AED=∠AOB;四边形ABDE内角于⊙O,则∠EAB+∠D=180°,即∠EAC=180°−60°−∠D=120°−∠D;而∠ECA=180°−∠ACB−∠BCD=120°−∠BCD,上述两个式子中,由BD=AB=BC,易证得∠D=∠BCD,则∠ECA=∠EAC,即△EAC、△OAB都是等腰三角形,而两个等腰三角形的顶角相等,且底边AC=AB,易证得两个三角形全等,由此得解.此题考查了圆心角、弧、弦的关系,等边三角形的性质,圆内接四边形的性质,全等三角形的判定和性质等知识,综合性强,难度较大;能够发现并证得△EAC≌△OAB是解答此题的关键.7.答案:C解析:解:23+23+23=3×23,故选C利用乘法的意义变形,即可作出判断.此题考查了有理数的混合运算,熟练掌握乘法的意义是解本题的关键.8.答案:C解析:解:∵∠1=∠2=65°,∴AB//CD,故A选项正确,又∵∠3=35°,∴∠C=65°−35°=30°,∴∠B=∠C=30°,故B选项正确,∵∠EFC是△CGF的外角,∴∠EFC=∠C+∠CGF,故C选项错误,∵∠3>∠C,∴CG>FG,故D选项正确,故选:C.依据平行线的判定与性质,以及三角形外角性质,即可得出结论.本题主要考查了平行线的判定与性质,以及三角形外角性质,解题时注意:两条直线被第三条所截,如果内错角相等,那么这两条直线平行.9.答案:C解析:试题分析:根据角平分线上的点到角的两边距离相等可得DE=CE,然后求出AE+DE=AC,然后利用勾股定理列式计算即可得解.∵BE平分∠ABC,DE⊥AB,∠ACB=90°,∴DE=CE,∴AE+DE=AC,∵BC=3cm,AB=5,∴AC=√AB2−BC2=√52−32=4cm,∴AE+DE=4cm.故选C.10.答案:C解析:解:∵AB⊥AD,AD⊥DE,∴∠BAD=∠ADE=90°,∴DE//AB,∴∠CED=∠CAB,∵∠C=∠C,∴△CED∽△CAB,∵DE=2,AB=4,即DE:AB=1:2,∴S△DEC:S△ACB=1:4,∴S四边形ABDE:S△ACB=3:4,∵S四边形ABDE =S△ABD+S△ADE=12×4×4+12×2×4=8+4=12,∴S△ACB=16,故选:C.由题意得到三角形DEC与三角形ABC相似,由相似三角形面积之比等于相似比的平方两三角形面积之比,进而求出四边形ABDE与三角形ABC面积之比,求出四边形ABDE面积,即可确定出三角形ABC面积.此题考查了相似三角形的判定与性质,以及等腰直角三角形,熟练掌握相似三角形的判定与性质是解本题的关键.11.答案:A解析:试题分析:根据角平分线的性质可得,DE=DC,根据BD=5,BC=8,求得CD即可求解.∵∠C=90°,AD是△ABC中∠CAB的角平分线,DE⊥AB于E,∴DE=DC,∴BD=5,BC=8,∴DC=BC−CD=8−5=3,∴DE=3.故选A.12.答案:B解析:解:设两个多边形的边数分别为x,y,由题意得,(x−2)⋅180°−(y−2)⋅180°=540°,∴x−y=3,∴它们的边数之差等于3,故选:B.根据多边形的内角和即可得到结论.本题考查了多边形的内角和,熟记多边形的内角和公式是解题的关键.13.答案:AC=BD或∠ABC=∠BAD解析:解:∵AB=BA,AD=BC,∴当AC=BD时,利用“SSS”可判断△ABC≌△BAD;当∠ABC=∠BAD时,利用“SAS”可判断△ABC≌△BAD.故答案为AC=BD或∠ABC=∠BAD.故答案为AC=BD或∠ABC=∠BAD.由于AB=BA,AD=BC,则根据“SSS”和“SAS”添加条件.题考查了全等三角形的判定:熟练掌握全等三角形的5种判定方法.14.答案:25解析:解:∵△ABC≌△DEF,∴∠E=∠B=120°,∵∠F=35°,∴∠D=180°−∠E−∠F=25°,故答案为25.根据全等三角形的性质得出∠E=∠B=120°,再根据三角形的内角和定理求出∠D的度数即可.本题考查了全等三角形的性质和三角形的内角和定理的应用,注意:全等三角形的对应角相等,对应边相等.15.答案:3解析:解:∵∠ACB=90°,BE平分∠ABC,DE⊥AB,∴CE=DE,∵AE=3ED,如果AC=12cm,∴AE=3EC,∴CE=DE=3cm,∵故答案为:3.根据角平分线上的点到角的两边距离相等可得CE=DE.本题考查了角平分线上的点到角的两边距离相等的性质,是基础题,熟记性质是解题的关键.16.答案:12解析:解:如图,过D作DF⊥AB于F,∵AD平分∠BAC,DE⊥AC,∴DF=DE=4,又∵AB=6,∴△ABD面积=12×AB×DF=12×6×4=12,故答案为:12.过D作DF⊥AB于F,依据角平分线的性质,即可得到DF=DE=4,再根据三角形的面积公式列式进行计算得出△ABD的面积.本题主要考查了角平分线上的点到角的两边的距离相等的性质,三角形的面积,熟记性质并作出辅助线是解题的关键.17.答案:57°解析:本题考查的是三角形的外角性质、角平分线的定义,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.延长CD交AB于F,根据三角形的外角性质求出∠BFD、∠ACF,根据角平分线的定义求出∠ECA,根据三角形的外角性质计算即可.解:延长CD交AB于F,∠BDC是△BDF的一个外角,则∠BFD=∠BDC−∠B=104°−30°=74°,同理,∠ACF=∠BFD−∠A=74°−40°=34°,∵CE平分∠ACD,∠ACF=17°,∴∠ECA=12∴∠BEC=∠A+∠ECA=40°+17°=57°,故答案为57°.18.答案:60解析:解:∵图A2比图A1多出2个“树枝”,图A3比图A2多出4个“树枝”,图A4比图A3多出8个“树枝”,…,∴图形从第2个开始后一个与前一个的差依次是:2¹,22,…,2n−1.∴第5个树枝为15+24=31,第6个树枝为:31+25=63,∴第(6)个图比第(2)个图多63−3=60个.故答案为:60.根据所给图形得到后面图形比前面图形多的“树枝”的个数用底数为2的幂表示的形式,代入求值即可.此题主要考查了图形的变化规律;得到后面图形比前面图形多的“树枝”的个数用底数为2的幂表示的形式与n的关系是解决本题的关键.19.答案:(1)证明:∵BE//CF,∴∠EBC=∠FCB,∴∠EBA=∠FCD,在△ABE和△DCF中,{∠A=∠D∠EBA=∠FCDAE=DF,∴△ABE≌△DCF(AAS),∴BE=CF,AB=CD,∴四边形BFCE是平行四边形.(2)2√3解析:(1)见答案(2)解:连接EF交BC于O,如图所示:∵AD=7,AB=DC=2.5,∴BC=AD−AB−DC=2,∵四边形BFCE是菱形,∠EBD=60°,EF⊥BC,OB=12BC=1,OE=OF,∴△CBE是等边三角形,∠BEO=30°,∴BC=EC=2,∴OE=√3OB=√3,∴EF=2√3,∴菱形BFCE的面积=12BC×EF=12×2×2√3=2√3;故答案为:2√3.(1)想办法证明BE=CF即可解决问题.(2)利用全等三角形的性质证明AB=CD,由菱形的性质求出EF的长,即可解决问题.本题考查菱形的性质,全等三角形的判定和性质,平行四边形的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.20.答案:解:根据题意,得(n−2)⋅180=1980,解得:n=13.则这个多边形的边数是11,内角和度数是1980°.解析:多边形的内角和比外角和的5倍多180°,而多边形的外角和是360°,则内角和是1980度.n 边形的内角和可以表示成(n−2)⋅180°,设这个多边形的边数是n,就得到方程,从而求出边数.本题考查了多边形的内角与外角,此题比较简单,只要结合多边形的内角和公式寻求等量关系,构建方程即可求解.21.答案:6解析:解:(1)S△ABC=4×4−12×2×2−12×2×4−12×2×4=16−2−4−4=6,故答案为6.(2)如图,△ABE,△ACF,△BCH即为所求.(1)利用分割法求解即可.(2)有三种情形分别画出图形即可.本题考查作图−应用与设计,三角形的面积,全等三角形的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.22.答案:解:在△DFB中,∵FD⊥AB,∴∠FDB=90°,∵∠F=40°,∠F+∠B=90°,∴∠B=90°−40°=50°.在△ABC中,∵∠A=30°,∠B=50°,∴∠ACB=180°−∠A−∠B=180°−30°−50°=100°.解析:先根据直角三角形两锐角互余求出∠B,再根据三角形内角和定理即可得出答案.本题考查了三角形的内角和定理以及直角三角形的性质;熟练掌握直角三角形的性质,熟记三角形内角和定理并准确识图是解题的关键.23.答案:解:(1)如图1,∵四边形ABCD是矩形,∴∠C=∠D=90°,∴∠1+∠3=90°,∵由折叠可得∠APO=∠B=90°,∴∠1+∠2=90°,∴∠2=∠3,又∵∠D=∠C,∴△OCP∽△PDA;∵△OCP与△PDA的面积比为1:4,∴OPPA =CPDA=√14=12,∴CP=12AD=4,设OP=x,则CO=8−x,在Rt△PCO中,∠C=90°,由勾股定理得x2=(8−x)2+42,解得:x=5,∴AB=AP=2OP=10,∴边CD的长为10;(2)作MQ//AN,交PB于点Q,如图2,∵AP=AB,MQ//AN,∴∠APB=∠ABP=∠MQP.∴MP=MQ,∵BN=PM,∴BN=QM.∵MP=MQ,ME⊥PQ,∴EQ=12PQ.∵MQ//AN,∴∠QMF=∠BNF,在△MFQ和△NFB中,{∠QFM=∠NFB ∠QMF=∠BNF MQ=BN,∴△MFQ≌△NFB(AAS).∴QF=12QB,∴EF=EQ+QF=12PQ+12QB=12PB,由(1)中的结论可得:PC=4,BC=8,∠C=90°,∴PB=√82+42=4√5,∴EF=12PB=2√5,∴在(1)的条件下,当点M、N在移动过程中,线段EF的长度不变,它的长度为2√5.解析:(1)先证出∠C=∠D=90°,再根据∠1+∠3=90°,∠1+∠2=90°,得出∠2=∠3,即可证出△OCP∽△PDA;根据△OCP与△PDA的面积比为1:4,得出CP=12AD=4,设OP=x,则CO=8−x,由勾股定理得x2=(8−x)2+42,求出x,最后根据AB=2OP即可求出边AB的长;(2)作MQ//AN,交PB于点Q,求出MP=MQ,BN=QM,得出MP=MQ,根据ME⊥PQ,得出EQ=12PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF=12QB,再求出EF=12PB,由(1)中的结论求出PB=√82+42=4√5,最后代入EF=12PB即可得出线段EF的长度不变此题考查了相似形综合,用到的知识点是相似三角形的判定与性质、全等三角形的判定与性质、勾股定理、等腰三角形的性质,关键是做出辅助线,找出全等和相似的三角形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省德州市经济技术开发区太阳城中学【最新】九年级上学期第一次检测化学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.发现了元素周期律并编制出元素周期表的科学家是( )A.拉瓦锡B.卢瑟福 C.门捷列夫D.道尔顿2.下列物质的用途,既利用物质的物理性质又利用物质化学性质的是()A.用氧气抢救危重病人B.用氦气填充飞艇C.用氮气做保护气填充食品包装袋D.稀有气体通电发出各色的光3.我们生活在不断变化的物质世界中,下列属于化学变化的是A.铁水铸锅B.冰雪消融C.粮食酿酒D.酒精挥发4.下列图示实验操作中,正确的是()A.点燃酒精灯B.称量固体C.液体加热D . 量取液体5.如图图示的实验装置或操作正确的是( )A .镁条在空气中燃烧B .细铁丝在氧气中燃烧C .收集氧气D .测量空气中氧气的体积分数6.“物质是由分子和原子构成的.”据此说明化学变化的基础是( )A .原子的破裂B .分子的破裂C .分子中原子的重新组合D .分子、原子同时破裂,重新组合成新的分子和原子7.下列关于催化剂的说法中,正确的是( )A .加入催化剂一定使化学反应的速率加快B .不使用催化剂物质就不能发生化学反应C .使用催化剂可增加生成物的量D .催化剂的化学性质及质量在化学反应前后保持不变8.下列反应中,既属于氧化反应,又属于化合反应的是①磷+氧气 −−−−→点燃五氧化二磷 ②乙炔+氧气−−−−→点燃二氧化碳+水 ③硫+氧气 −−−−→点燃二氧化硫 ④氢气+氧气−−−−→点燃水 ⑤高锰酸钾 −−−→加热锰酸钾+二氧化锰+氧气A.①②③B.①③④C.①②③④D.①②③④⑤9.下列有关空气成分的说法不正确的是( )A.稀有气体可用于制作霓虹灯B.氮气充入食品包装中可以防腐C.二氧化碳是一种空气污染物D.氧气主要来源于植物的光合作用10.冰熔化成水的过程中,一定发生变化的是( )A.质量B.分子结构C.温度D.分子间隔11.科学家发现,水在﹣157℃超低温、正常压力或真空条件下仍呈液态,比蜂蜜还粘稠,称为“高密度液态水”.下列关于这种“高密度液态水”的说法正确的是()A.化学性质与水不同B.分子间的间隔比普通的液态水(0~100℃)的大C.分子不再运动D.氢、氧两种原子的个数比为2:112.下列物质中属于纯净物的是A.洁净的食盐水B.冰水共存物C.净化后的空气D.高锰酸钾完全分解后的产物13.下列各图中和分别表示不同元素的原子,则其中表示化合物的是() A.B.C.D.14.从分子的角度分析,下列解释错误的是A.吹胀气球——气体分子间的间隔变大B.缉毒犬能根据气味发现毒品——分子在不断地运动C.液氧和氧气都能助燃——同种分子化学性质相同D.水电解生成氢气和氧气——分子分成原子,原子重新结合成分子15.下列说法完全正确的是( )A.地壳中含量最多元素—O 硅的元素符号—Si 2个氮原子—2NB.决定元素种类—核外电子数决定元素的化学性质—最外层电子数决定相对原质量的是—质子数和中子数C.铁—由分子构成二氧化碳—由原子构成氯化钠—由离子构成D.分子—化学变化中的最小粒子原子—保持物质化学性质的最小粒子离子—带电的原子16.下列关于分子、原子的说法错误的是( )A.分子是构成物质的一种粒子B.原子是化学变化中的最小粒子C.分子都是由两个原子构成的D.原子是由原子核和核外电子构成的17.下列说法正确的是( )A.铝原子和铝离子是同种元素B.Cl 的质子数比电子数多1C.原子都由质子、中子、电子构成D.保持水化学性质的最小粒子是氢原子和氧原子18.当下“共享单车”进入市区,方便了市民的绿色出行:但随着夏季气温的升高,“共享单车”的充气轮胎容易发生爆炸,其主要原因是()A.分子停止运动B.分子质量变大C.分子本身的体积变大,分子运动速率减慢D.分子间隔变大,分子运动速率加快19.下列是五种粒子的结构示意图,关于这五种粒子的说法正确的是( )A.它们表示五种元素B.④表示的粒子在化学反应中易失电子C.②③⑤都是稳定结构,都属于阳离子D.①表示的粒子为金属原子20.亚硒酸钠(Na2SeO3)可用于提升人体免疫力,硒元素在元素周期表中的部分信息及原子结构示意图如图所示,下列说法正确的是()A.Na2SeO3中Se的化合价为+3 B.Se是一种金属元素C.n的值为6 D.Se相对原子质量为78.96g二、填空题21.阅读下列短文,将符合题意的编号填入题后的横线上:①酒精是一种无色透明的、具有特殊气味的液体;②易挥发;③能与水以任意比例互溶,并能溶解碘、酚酞等多种物质;④酒精易燃烧;⑤因此,常被用做酒精灯和内燃机中的燃料,是一种绿色能源;⑥当点燃酒精灯时,酒精在灯芯上汽化;⑦且边汽化边燃烧,生成水和二氧化碳。
(1)酒精的物理性质有______;(2)酒精的化学性质有______;(3)酒精发生的物理变化有______;(4)酒精发生的化学变化有______;(5)文中描述酒精用途的是______。
22.请用化学符号或名称表示(1)3个氧分子__________;2个钠离子__________;13号元素__________;2个铁原子__________(2)生物体中含量最多的金属元素_____(填元素符号)(3)保持水化学性质的最小粒子是___________(填名称)23.如图是几种原子或离子的结构示意图.(1)A--E共表示______ 种元素。
(2)属于原子的有______(填序号,下同),其中属于金属元素的原子是______ ,属于非金属元素的原子是______ ,属于稀有气体元素的原子是______ 。
(3)属于阳离子的是______ ,属于阴离子的是______。
三、实验题24.测定空气中氧气体积分数的实验装置如图所示,在集气瓶内加入少量的水,并五等.用弹簧夹夹紧乳胶管,点燃燃烧匙内稍过量的红磷后,分水面以上的容积,做上记号立即伸入瓶中并把塞子塞紧,①看到的现象是______ ;②待红磷熄灭并冷却后,打开弹簧夹,观察到烧杯中的水进入集气瓶,瓶内水面最终上升约至1刻度处,由此可知氧气约占空气总体积的______ ;③红磷熄灭后,集气瓶内剩下的气体主要是______ ,该气体______ (填“支持”或“不支持”)燃烧;④实验中红磷需稍过量,目的是______ ;⑤小梅同学探究了空气中氧气的含量的试验之后,又设计了如甲装置所示的实验,红磷和木炭均为足量,分别把A、B两瓶中的红磷和木炭点燃,将燃烧完毕冷却至室温后,打开C、D两处的夹子,想一想.()1她将看到甲装置的烧杯中的水进入______ 瓶,原因是______ .()2如果将甲装置改装成乙装置,反应完毕后冷却至室温后,打开弹簧夹,观察到的现象是______ .25.实验室中,利用下列装置可以制取某些气体,请回答下列问题。
(1)写出上述标号仪器的名称①______ ② ______ 。
(2)向气体发生装置内加入药品前,应该进行的操作是______ 。
(3)林月用高锰酸钾制取氧气,她选择上述装置中的A作为发生装置,你认为A装置中还缺少______。
(4)若实验时用过氧化氢代替高锰酸钾加热制氧气,优点是______ (填序号)。
A生成物中只有氧气 B不需加热 C需加热(5)实验室若用氯酸钾和二氧化锰制取氧气,选择的发生装置是______ ;用双氧水制氧气,选择的发生装置是______ 。
(6)收集氧气的装置可以选用______ ;若选用E装置收集氧气,实验结束时,应______ 。
参考答案1.C【详解】A、拉瓦锡首先通过实验得出空气是由氮气和氧气组成的结论,故A不正确;B、卢瑟福通过α粒子散射实验发现了质子并预言了中子的存在,故B不正确;C、1869年,门捷列夫发现了元素周期律,并编制出元素周期表,故C正确;D、道尔顿在化学上的主要贡献是提出了原子学说,故D不正确。
故选C。
2.B【详解】A、用氧气抢救危重病人,是利用了氧气能供给呼吸的性质,需要发生化学变化才能表现出来,是利用了其化学性质,故选项错误;B、用氦气填充飞艇即利用了氦气化学性质的稳定性,又利用了氦气密度比空气小的物理性质,故选项正确;C、用氮气做保护气填充食品包装袋,是利用了氮气化学性质很不活泼、无毒的性质,需要发生化学变化才能表现出来,是利用了其化学性质,故选项错误;D、稀有气体通电发出各色的光,不需要发生化学变化就能表现出来,是利用了其物理性质,故选项错误。
故选B。
3.C【详解】A、铁水铸锅没有新物质生成,属于物理变化,选项错误;B、冰雪消融没有新物质生成,属于物理变化,选项错误;C、粮食酿酒有新物质生成,属于化学变化,选项正确;D、酒精挥发没有新物质生成,属于物理变化,选项错误。
故本题选C。
4.C【详解】A、点燃酒精灯,应该用火柴点燃,用燃着的酒精灯引燃另一只,易引发灯内酒精着火,甚至酒精灯爆炸,操作错误;B、用天平称量一定量的固体时,只能精确到0.1g,错误;C、加热试管中的液体时,液体的量不能超过试管容积的三分之一,且要用外焰加热,先均匀加热,后对准药品固定加热。
试管口向上倾斜,与桌面呈45°角,操作正确;D、量取一定量液体时,被量液体的体积应略小于量筒的量程,应该选用10毫升量筒,错误。
故选C。
5.C【详解】A、镁条应该用坩埚钳夹持,故A不正确;B、做铁丝在氧气中燃烧的实验时,集气瓶内应装入少量的水或铺上一层细沙,故B不正确;C、收集氧气可用向上排空气法,玻璃导管应该伸到集气瓶的底部,故C正确;D、测定空气中氧气的含量的实验不能用木炭,木炭燃烧产生二氧化碳气体,玻璃罩内压强变化很小,故D不正确。
故选C。
6.C【详解】A、原子的破裂只能说明原子的构成问题,不能说明物质是由分子和原子构成的,故A错误;B、分子的破裂只能说明分子的构成问题,不能说明物质是由分子和原子构成的,故B错误;C、分子中原子的重新组合,是化学变化的基础,故C正确;D、化学变化中原子不变,故D错误。
故选C。
7.D【详解】A、催化剂可以改变化学反应速率,可以加快反应速率,也可以减缓反应速率;故选项错误;B、物质是否反应与催化剂无关;故选项错误;C、催化剂不能增加生成物的产量;故选项错误;D、催化剂的化学性质及质量在化学反应前后保持不变;故选D。
8.B【分析】氧化反应是指物质与氧发生的化学反应,化合反应指的是由两种或两种以上的物质反应生成一种新物质的反应。
【详解】①磷和氧气点燃生成五氧化二磷,符合多变一,既属于氧化反应,又属于化合反应,故正确;②乙炔和氧气点燃二氧化碳和水,不符合多变一,不属于化合反应,故不正确;③硫和氧气点燃生成二氧化硫,符合多变一,既属于氧化反应,又属于化合反应,故正确;④氢气和氧气点燃水,符合多变一,既属于氧化反应,又属于化合反应,故正确;⑤高锰酸钾加热生成锰酸钾和二氧化锰和氧气,符和一变多,属于分解反应,故不正确;故选B。
