广告牌杆件计算

合集下载

广告牌钢结构部分计算书

—--—- 钢柱设计信息———-—钢材等级：235柱高（m):15.000柱截面：空心圆管截面：D*T=1000*12柱平面内计算长度系数：1。

000柱平面外计算长度：0.000强度计算净截面系数：1.000截面塑性发展:考虑构件所属结构类别：独立柱设计内力：绕X轴弯矩设计值Mx （kN。

m)：1600.000绕Y轴弯矩设计值My (kN.m）：0.000轴力设计值N (kN）：180。

000-————设计依据——-——《钢结构设计规范》（GB 50017—2003）—-———柱构件设计——-——1、截面特性计算A =4.9461e-002; Xc =5.0000e-001；Yc =5。

0000e—001;Ix =5。

9895e-003; Iy =5。

9895e—003;ix =3.4799e-001; iy =3.4799e—001;W1x=1.1979e-002; W2x=1.1979e—002;W1y=1.1979e—002; W2y=1。

1979e-002；2、柱构件强度验算结果截面塑性发展系数：γx=1.150柱构件强度计算最大应力(N/mm2）：119.784 < f=215。

000柱构件强度验算满足.3、柱构件平面内稳定验算结果平面内计算长度(m)：15。

000平面内长细比λx：43.105对x轴截面分类：b 类轴心受压稳定系数φx：0。

886等效弯矩系数βmx：1。

000计算参数Nex'（KN)：49201。

949柱平面内长细比：λx=43。

105 〈[λ]= 150。

000柱构件平面内稳定计算最大应力（N/mm2）: 120.593 〈f=215。

000柱构件平面内验算满足。

4、柱构件平面外稳定验算结果平面外计算长度（m）：0.000平面外长细比λy：0。

000对y轴截面分类：b 类轴心受压稳定系数φy：1。

000受弯整体稳定系数φbx:1。

000等效弯矩系数βtx：1.000闭口截面影响系数：η=0。

4.5m和6.5m信号灯杆件计算

Fwb=γ0·γQ·(0.5×ρ·C1·v²)·(wb·hb)
2.085 kN
横梁的风荷载
Fwh=n·γ0·γQ·(0.5×ρ·C2·v²)·(wh·hh)
0.500 kN
立柱的风荷载
Fwp=1.7×γ0·γQ·(0.5×ρ·C2·v²)·(wp·hp)
2.206 kN
Fhv=Gb/n
0.699 kN
判别：
ℎ
1
0.015 m
立柱顶部水平位移
∙ ℎ
1
∙
0 ∙ ∙
f=fhh+fp+θ·(wb+wh)
判别：
f/hp<1/50，满足要求
立柱顶部的扭转角
=
0.00976 rad
0.121 m
wb
标志板宽度
1.5 [m]
g
hb
标志板高度
1.5 [m]
ρ
ρb
标志板重度
24 [kg/m²]
ℎ ² + ℎℎ ²
判别：
fh<(wb+wh)/75=80，满足要求
56.8 mm
立柱的设计计算：
1、强度验算
立柱竖向荷载
Np=G
7.220 kN
立柱水平荷载
Hp=Fwb+Fwh+Fwp
4.791 kN
立柱根部由永久荷载引起的弯
矩
Mpy=n·Mhv
8.045 kN.m
由风荷载引起的弯矩
Mpx=(Fwb+Fwh)·(hp-hb/2)+Fwp·hp/2
γ0
wh
横梁露出部分的宽度
4.5 [m]
γG
hh

屋顶钢结构广告牌计算书

屋顶钢结构广告牌计算书一、计算模型：1.恒荷载：LED光源+大字铝板+大字龙骨荷载取0.5KN/㎡2.风荷载：风洞试验数据：㎡正风最大值2.17KN/雅居乐中心，“雅”字受荷载面积最大为60%正风（考虑1.1放大系数）：2.17KN/㎡*60%*1.1=1.43KN/㎡负风（考虑1.1放大系数）：-3.14KN/㎡*60%*1.1=-2.1KN/㎡㎡侧风（考虑1.1放大系数）：-3.14KN/㎡*60%*1.1=-2.1KN/正风侧风3.检修荷载：加载到梁单元检修荷载按照0.5KN/m4.地震荷载：当地地震荷载为7度设防，计算按照9度设防5.荷载组合：1gLCB1激活相加0工况(1.350)+1工况(0.980)2gLCB2激活相加0工况(1.200)+1工况(1.400)3gLCB3激活相加0工况(1.000)+1工况(1.400)4gLCB4激活相加0工况(1.200)+2工况(1.400)5gLCB5激活相加0工况(1.200)+3工况(1.400)6gLCB6激活相加0工况(1.200)+4工况(1.400)7gLCB7激活相加0工况(1.200)+2工况(-1.400)8gLCB8激活相加0工况(1.200)+3工况(-1.400)9gLCB9激活相加0工况(1.200)+4工况(-1.400)10gLCB10激活相加0工况(1.000)+2工况(1.400)11gLCB11激活相加0工况(1.000)+3工况(1.400)12gLCB12激活相加0工况(1.000)+4工况(1.400)13gLCB13激活相加0工况(1.000)+2工况(-1.400)14gLCB14激活相加0工况(1.000)+3工况(-1.400)15gLCB15激活相加0工况(1.000)+4工况(-1.400)16gLCB16激活相加0工况(1.200)+1工况(1.400)+2工况(0.840) 17gLCB17激活相加0工况(1.200)+1工况(1.400)+3工况(0.840) 18gLCB18激活相加0工况(1.200)+1工况(1.400)+4工况(0.840) 19gLCB19激活相加0工况(1.200)+1工况(1.400)+2工况(-0.840) 20gLCB20激活相加0工况(1.200)+1工况(1.400)+3工况(-0.840) 21gLCB21激活相加0工况(1.200)+1工况(1.400)+4工况(-0.840)0工况(1.000)+1工况(1.400)+2工况(0.840) 23gLCB23激活相加0工况(1.000)+1工况(1.400)+3工况(0.840) 24gLCB24激活相加0工况(1.000)+1工况(1.400)+4工况(0.840) 25gLCB25激活相加0工况(1.000)+1工况(1.400)+2工况(-0.840) 26gLCB26激活相加0工况(1.000)+1工况(1.400)+3工况(-0.840) 27gLCB27激活相加0工况(1.000)+1工况(1.400)+4工况(-0.840) 28gLCB28激活相加0工况(1.200)+1工况(0.980)+2工况(1.400) 29gLCB29激活相加0工况(1.200)+1工况(0.980)+3工况(1.400) 30gLCB30激活相加0工况(1.200)+1工况(0.980)+4工况(1.400) 31gLCB31激活相加0工况(1.200)+1工况(0.980)+2工况(-1.400) 32gLCB32激活相加0工况(1.200)+1工况(0.980)+3工况(-1.400) 33gLCB33激活相加0工况(1.200)+1工况(0.980)+4工况(-1.400) 34gLCB34激活相加0工况(1.000)+1工况(0.980)+2工况(1.400) 35gLCB35激活相加0工况(1.000)+1工况(0.980)+3工况(1.400) 36gLCB36激活相加0工况(1.000)+1工况(0.980)+4工况(1.400) 37gLCB37激活相加0工况(1.000)+1工况(0.980)+2工况(-1.400) 38gLCB38激活相加0工况(1.000)+1工况(0.980)+3工况(-1.400) 39gLCB39激活相加0工况(1.000)+1工况(0.980)+4工况(-1.400) 40gLCB40激活相加0工况(1.200)+1工况(0.600)+Rx(1.300) 41gLCB41激活相加0工况(1.200)+1工况(0.600)+Ry(1.300) 42gLCB42激活相加0工况(1.200)+1工况(0.600)+Rx(-1.300) 43gLCB43激活相加0工况(1.200)+1工况(0.600)+Ry(-1.300)0工况(1.000)+1工况(0.500)+Rx(1.300) 45gLCB45激活相加0工况(1.000)+1工况(0.500)+Ry(1.300) 46gLCB46激活相加0工况(1.000)+1工况(0.500)+Rx(-1.300) 47gLCB47激活相加0工况(1.000)+1工况(0.500)+Ry(-1.300)四、结构分析：内力1.轴力包络图剪力2包络图2.强度分析：应力比最大为0.89，满足规范要求位移分析：3.经计算，最大位移为20mm。

道路交通标志杆厂家分析价格算法

在购买道路交通标志杆的时候，消费者一般会问到商家这样一个问题：它的价格是是怎么计算的。

想必这也是大家比较关心的问题之一。

今天，就针对这个问题给大家讲解一下。

一般计算的方法有三种。

其一就是根据米进行计算，一米多少钱。

一般一米的价格在150元-300元之间。

其二是根据数量进行计算，一根多少钱。

一般一根的价格在650元-2700元之间。

其三就是根据配置进行计算。

配置相对好一些的，其价格在900元以上；
配置相对一般的，其价格在750元以上。

以上就是今天分享的全部内容，感谢大家的阅读与支持。

广告牌荷载计算

广告牌荷载计算1.1广告牌的荷载作用说明：广告牌承受的荷载包括：自重、风荷载、雪荷载以及活荷载。

(1)自重：包括广告布、杆件、连接件、附件等的自重，可以按照400N/m2估算：(2)风荷载：是垂直作用于广告牌表面的荷载，按GB50009采用；(3)雪荷载：是指广告牌水平投影面上的雪荷载，按GB50009采用；(4)活荷载：是指广告牌水平投影面上的活荷载，按GB50009，可按500N/m2采用；在实际工程的广告牌结构计算中，对上面的几种荷载，考虑最不利组合，有下面几种方式，取用其最大值：A：考虑正风压时：a.当永久荷载起控制作用的时候，按下面公式进行荷载组合：Sk+=1.35Gk+0.6×1.4wk+0.7×1.4Sk(或Qk)b.当永久荷载不起控制作用的时候，按下面公式进行荷载组合：Sk+=1.2Gk+1.4×wk+0.7×1.4Sk(或Qk)B：考虑负风压时：按下面公式进行荷载组合：Sk-=1.0Gk+1.4wk1.2风荷载标准值计算：按建筑结构荷载规范(GB50009-2001)计算：wk+=βgzμzμs1+w……7.1.1-2[GB50009-2001 2006年版]wk-=βgzμzμs1-w上式中：wk+：正风压下作用在广告牌上的风荷载标准值(MPa)；wk-：负风压下作用在广告牌上的风荷载标准值(MPa)；Z：计算点标高：3m；βgz：瞬时风压的阵风系数；根据不同场地类型,按以下公式计算(高度不足5m按5m计算)：βgz =K(1+2μf)其中K为地面粗糙度调整系数，μf为脉动系数A类场地：βgz =0.92×(1+2μf) 其中：μf=0.387×(Z/10)-0.12B类场地：βgz =0.89×(1+2μf) 其中：μf=0.5(Z/10)-0.16C类场地：βgz =0.85×(1+2μf) 其中：μf=0.734(Z/10)-0.22D类场地：βgz =0.80×(1+2μf) 其中：μf=1.2248(Z/10)-0.3对于B类地形，3m高度处瞬时风压的阵风系数：βgz=0.89×(1+2×(0.5(Z/10)-0.16))=1.9691μz：风压高度变化系数；根据不同场地类型,按以下公式计算：A类场地：μz=1.379×(Z/10)0.24当Z>300m时，取Z=300m，当Z<5m时，取Z=5m；B类场地：μz=(Z/10)0.32当Z>350m时，取Z=350m，当Z<10m时，取Z=10m；C类场地：μz=0.616×(Z/10)0.44当Z>400m时，取Z=400m，当Z<15m时，取Z=15m；D类场地：μz=0.318×(Z/10)0.60当Z>450m时，取Z=450m，当Z<30m时，取Z=30m；对于B类地形，3m高度处风压高度变化系数：μz=1.000×(Z/10)0.32=1μs1：局部风压体型系数，对于广告牌结构，按规范，计算正风压时，取μs1+=1.3；计算负风压时，取μs1-=-2.0；另注：上述的局部体型系数μs1(1)是适用于围护构件的从属面积A小于或等于1m2的情况，当围护构件的从属面积A大于或等于10m2时，局部风压体型系数μs1(10)可乘以折减系数0.8，当构件的从属面积小于10m2而大于1m2时，局部风压体型系数μs1(A)可按面积的对数线性插值，即：μs1(A)=μs1(1)+[μs1(10)-μs1(1)]logA在上式中：当A≥10m2时取A=10m2；当A≤1m2时取A=1m2；w：基本风压值(MPa)，根据现行<<建筑结构荷载规范>>GB50009-2001附表D.4(全国基本风压分布图)中数值采用，按重现期50年，福州地区取0.0007MPa；(1)计算龙骨构件的风荷载标准值：龙骨构件的从属面积：A=3×1.5=4.5m2LogA=0.653μsA1+(A)=μs1+(1)+[μs1+(10)-μs1+(1)]logA=1.13μsA1-(A)=μs1-(1)+[μs1-(10)-μs1-(1)]logA=1.739wkA+=βgzμzμsA1+w=1.9691×1×1.13×0.0007 =0.001558MPawkA-=βgzμzμsA1-w=1.9691×1×1.739×0.0007 =0.002397MPa(2)计算广告布部分的风荷载标准值：广告布构件的从属面积：A=1.5×1.5=2.25m2LogA=0.352μsB1+(A)=μs1+(1)+[μs1+(10)-μs1+(1)]logA=1.208μsB1-(A)=μs1-(1)+[μs1-(10)-μs1-(1)]logA=1.859wkB+=βgzμzμsB1+w=1.9691×1×1.208×0.0007 =0.001665MPawkB-=βgzμzμsB1-w=1.9691×1×1.859×0.0007 =0.002562MPa1.3风荷载设计值计算：wA+：正风压作用下作用在广告牌龙骨上的风荷载设计值(MPa)；wkA+：正风压作用下作用在广告牌龙骨上的风荷载标准值(MPa)；wA-：负风压作用下作用在广告牌龙骨上的风荷载设计值(MPa)；wkA-：负风压作用下作用在广告牌龙骨上的风荷载标准值(MPa)；wA+=1.4×wkA+=1.4×0.001558 =0.002181MPawA-=1.4×wkA-=1.4×0.002397=0.003356MPawB+：正风压作用下作用在广告牌广告布上的风荷载设计值(MPa)；wkB+：正风压作用下作用在广告牌广告布上的风荷载标准值(MPa)；wB-：负风压作用下作用在广告牌广告布上的风荷载设计值(MPa)；wkB-：负风压作用下作用在广告牌广告布上的风荷载标准值(MPa)；wB+=1.4×wkB+=1.4×0.001665 =0.002331MPawB-=1.4×wkB-=1.4×0.002562=0.003587MPa1.4雪荷载标准值计算：Sk：作用在广告牌上的雪荷载标准值(MPa)S：基本雪压，根据现行<<建筑结构荷载规范>>GB50009-2001取值，福州地区50年一遇最大积雪的自重：0MPa.μr：屋面积雪分布系数，按表6.2.1[GB50009-2001]，为2.0。

广告牌构件计算

广告牌构件计算一计算依据《建筑结构荷载规范》 GB50009—2001《钢结构社机规范》 GB50017-2003二计算参数2.1 Ø*1203.5钢管截面积 A=1280mm2回转半径 r=41.2mm2。

2 40＊3角钢截面系数 W=1230mm32.3 Q235钢抗弯设计强度 f=215N/mm2三构件计算3。

1 风荷载标准值广告牌高7.50m，总高H=14m，地面粗糙度按C类W k=βz·μs·μz·r w·W0式中βz-高度Z处风振系数取1.14～1。

36（计算附后）μs—风载体型系数取0.07（计算附后）μz-风压高度变化系数15m以内,0。

74r w-风载分项系数取1.4W k=βz·μs·μz·K·W0=1.14(1.36)×0.07×1×1.4×2。

64=0.295（0.35)KN/m2如取3.8m宽板带计算线荷载分别为q1=0。

295×3.8=1。

12KN/mq2=0.35×3。

8=1.33KN/ma 集中荷载P=7.5×（1.12+1。

33）/2=9.2KN b为安全计集中力作用于顶部节点，计算简图如图2c 支座反力A支座：水平反力27。

6KN竖向反力11.5KNB支座：水平反力18。

4KN竖向反力7.7KN3。

2.2 Ø120×3。

5钢管强度验算a 按绗架计算各杆内力系数注于图2内。

b 计算Ø120×3.5钢管应力，按最大压力及最长杆件计算,取大值.最大压力σ=N/ØA 其中N=KPλ=L/r=3905/41.2=95 查GB50010—2003附录C得Ø=0.676σ=N/ØA=2。

328×9.2/(0.676×1280）=24。

广告牌结构计算

一、风荷载计算1、标高为:Z=10M处风荷载计算(1). 风荷载标准值计算:W k: 作用在幕墙上的风荷载标准值(kN/m2): Zm高处阵风系数(按B类区计算):βgzμf=0.5×(Z/10)-0.16＝0.50βgz=0.89×(1+2μf)= 1.78μz: Z(m)高处风压高度变化系数(按B类区计算): (GB50009-2001)μz=(Z/10)0.32 = 1.00 风荷载体型系数μs= 1.2W k=βgz×μz×μs×W0 (GB50009-2001) =1.60kN/m2(2). 风荷载设计值:W: 风荷载设计值: kN/m2r w: 风荷载作用效应的分项系数: 1.4按《建筑结构荷载规范》GB50009-2001 3.2.5 规定采用W=r w×W k= 2.24kN/m2二.内力结构计算: (中横向ZHL)整体结构梁受力计算:荷载:(1) G(#2Ak)平均重力: 1.00kN/m^2(2).W 风荷载设计值: 2.24kN/m^2M(#1G): 平均自重下组合梁弯矩(kN.m)q(#1G):荷载集度设计值:(kN/m)a(#4sjcg):计算跨度: 14mB: 计算单元宽: 6.5mq(#1G)=1.4×G(#2Ak)×B=1.4×0.5×1.0=9.1 kN/mM(#1G)=q(#1G)×a(#4sjcg)^2/8=222.95kN.m垂直于平面的分布水平地震作用:α(#3max)= q(#3EAk): 垂直于平面的分布水平地震作用 (kN/m)q(#3EAk)=5×α(#3max)×G(#2Ak) (JGJ102-96 5.2.4) =0.8 kN/mγ(#1E): 地震作用分项系数: 1.3q(#2EA)=1.3×q(#3EAk)=1.04 kN/mq(#1E)：水平地震作用线分布最大荷载集度设计值(矩形分布)q(#1E)=q(#2EA)×B=6.76 kN/mM1=M(#1G)+0.6×M(#1E)=289.20kN.m风荷载线分布最大荷载集度设计值(矩形分布)q(#1w): 风荷载线分布最大荷载集度设计值(kN/m)r(#1w): 风荷载作用效应的分项系数： 1.4W(#1k): 风荷载标准值: 1.60kN/m2B: 计算单元宽: 1q(#1w)=1.4×W(#1k)×B= 2.24k N/mq(#1w): 风荷载线分布最大荷载集度设计值: 2.24 a’(#4sjcg):计算跨度:14mM(#1w)=q(#1w)×a’(#4sjcg)^2/8=54.95 kN.mN(#1w): 风荷载对横梁端的集中力设计值(kN)N(#1w)= q(#1w)×a’(#4sjcg)/2=61.62k N钢管（￠500×12）横梁强度校核1．刚度计算:A: D500X12钢管截面积: d=D-t=48.8=45.97cm^2γ: 塑性发展系数: 1.0i: 回转半径: I=0.35d=17.08 cm λ: 构件细长比L0: 钢管杆计算长度:7.00mλ=L0×100/i40.98<[λ]=150刚度满足.σ: 计算强度(N/mm2)(为拉弯构件)N: 受力设计值:61.62kNA: 立柱型材截面积: 45.97cm2M: 弯矩: 54.95kN·mW x1: 立柱截面抗弯矩:2191cm3γ: 塑性发展系数: 1.05σ=N×10/A+M×103/1.05/W x1=37.29≤ｆa=215N/mm2钢管梁强度可以满足钢管（￠1200×14）立柱强度校核1．刚度计算:A: D1200X14钢管截面积: d=D-t=118.6=111.72cm^2γ: 塑性发展系数: 1.0i: 回转半径: I=0.35d=41.51 cm λ: 构件细长比L0: 钢管杆计算长度:16.00mλ=L0×100/i38.54<[λ]=150刚度满足.σ: 计算强度(N/mm2)(为拉弯构件)Nw: 受风力设计值:61.62kNA: 立柱型材截面积: 111.72cm2M: 弯矩: 985.91kN·mW x1: 立柱截面抗弯矩:15280cm3γ: 塑性发展系数: 1.05σ=N×10/A+M×103/1.05/W x1=66.96≤ｆa=215N/mm2钢管立柱强度可以满足基础整体稳定验算：M1=985.91kN·mN=280KN*************************************************************************************************计算项目: 承载力计算-1************************************************************************************************[计算条件]1、基础信息基础埋深 d = 2.00 m基础宽 B = 4.50 m基础长 L = 9.00 m基础底标高 Bg = -2.00 m2、土层信息N= 280地下水标高 = -2.20 m 顶层土标高 = 0.00 m 土层数 = 3土层号厚度(m) 重度(MPa) 承载力深度修正相对密度孔隙比压缩模量土层 1 -5 18 130 1 2.7 0.8 7.5 土层 2 -10 18 130 1 2.7 0.8 7.5 土层 3 -15 18 130 1 2.7 0.8 7.5 3、荷载信息荷载标准值 N = 280.00 kn Mx = 1300.00 kn*m My = 130.00 kn*m单位面积的基础及覆土重 γ`h = 20.00 kPa[计算结果]计算根据：中华人民共和国国家标准GB50007-2002 --综合法4、底板反力 (kPa):平均 p= 26.914 最大 pmax= 52.593 最小 pmin= 1.235 角点 p1 = 1.235 p2 = 9.794 p3 = 52.593 p4 = 44.0335、承载力计算地基(抗震)承载力设计值 = 202.400地基承载力验算满足0.000-15.000-10.000-5.000剖面图1-N= 2804.50221)5.0()3(-+-+=d b f f m d b ak a γηγηak f p <ak f p 2.1max <6、下卧层承载力计算基底下土层号土层厚承载力特征值全压应力扩散角土层 2 5.00 207.86 56.43 0.00 土层 3 5.00 259.82 102.71 0.00四．预埋件计算: (第1处) 本工程预埋件受拉力和剪力(拉杆节点）V: 剪力设计值:Vc=61619.4NV=1.2*Vc=73943.2NN: 法向力设计值:Nd=616194NN=1.2*Nd=739432.3N Me=M1=985909761N·mmN(#3um1): 锚筋根数:20根锚筋层数:1层K(#1r): 锚筋层数影响系数: 1.000 关于混凝土：混凝土标号C30混凝土强度设计值:f(#1c)=15.000N/mm^2按现行国家标准≤混凝土结构设计规范≥ GBJ10采用。

杆件及节点计算

耳板 fc= 305 N/mm
2
Φ 20 Q 235
fv=
140 N/mm2
插板侧焊缝长度： 100 mm 插板侧焊缝高度： 5 mm
2.杆件实际受力：杆件轴力： -30 KN (受压为负，受拉为正)
3.杆件计算：截面积：每米重量：转动惯量：转动半径：长细比：稳定系数：应力值： A= g= I= i= λ = υ= σ＝ 577 mm2 4.53 kg/m 390269 mm4 26.0 mm 173 < 200 0.241 215.74 N/mm
第1页
杆件及节点计算
1.构件参数：杆件长度：杆件尺寸：杆件材质：插板厚度：插板垫板厚度：插板片数：插板材质： 4.5 m
Φ 76 x 2.5 Q 235
12 mm 0 mm 1片
f=
215 N/mm2 杆件
Q 235
8 mm 0 mm 2片 235
fc=Βιβλιοθήκη 305 N/mm2
插板耳板厚度：耳板垫板厚度：耳板片数：耳板材质： Q 插销大小：插销材质：
2
OK
> 215
λ n= 1.86
FALL
2014-10-14
第2页
4.插销计算：剪切面数：剪切类型：插销截面积：剪切计算： τ ＝ 2 双剪 314 mm2 47.75 N/mm2 < 140
OK
5.连接板局部承压计算：连接板计算厚度：连接板局部承压强度：局部承压计算： fc= σ C＝ t= 12 mm 305 N/mm2 125 N/mm2 < fc
OK
6.插板侧焊缝计算：角焊缝抗剪强度：角焊缝抗剪强度计算： ff= f= 160 N/mm2 22.56 N/mm2 < ff

各类杆件长度计算公式

各类杆件长度计算公式在工程设计和建筑施工中，各类杆件的长度计算是非常重要的一环。

不同类型的杆件，如钢管、钢筋、木材等，其长度计算公式也各不相同。

本文将针对不同类型的杆件，分别介绍其长度计算公式及相关知识。

一、钢管长度计算公式。

1. 直线钢管长度计算公式。

直线钢管的长度计算公式为，L = π D N。

其中，L为钢管的长度，π为圆周率（取3.14），D为钢管的直径，N为钢管的数量。

2. 弯曲钢管长度计算公式。

弯曲钢管的长度计算公式为，L = π D N + (2 R π N)。

其中，L为钢管的长度，π为圆周率，D为钢管的直径，N为钢管的数量，R 为钢管的弯曲半径。

二、钢筋长度计算公式。

钢筋长度计算公式主要根据构件的尺寸和形状来确定。

一般情况下，可以根据以下公式进行计算：1. 直线钢筋长度计算公式。

直线钢筋的长度计算公式为，L = √(X^2 + Y^2 + Z^2)。

其中，L为钢筋的长度，X、Y、Z分别为构件的三个尺寸。

2. 弯曲钢筋长度计算公式。

弯曲钢筋的长度计算公式为，L = √(X^2 + Y^2 + Z^2) + (2 R π)。

其中，L为钢筋的长度，X、Y、Z分别为构件的三个尺寸，R为钢筋的弯曲半径。

三、木材长度计算公式。

木材长度计算公式与其形状和用途有关，一般可根据以下公式进行计算：1. 直线木材长度计算公式。

直线木材的长度计算公式为，L = √(X^2 + Y^2 + Z^2)。

其中，L为木材的长度，X、Y、Z分别为木材的三个尺寸。

2. 弯曲木材长度计算公式。

弯曲木材的长度计算公式为，L = √(X^2 + Y^2 + Z^2) + (2 R π)。

其中，L为木材的长度，X、Y、Z分别为木材的三个尺寸，R为木材的弯曲半径。

以上是针对不同类型杆件长度计算公式的介绍，希望能对工程设计和建筑施工有所帮助。

在实际应用中，除了掌握计算公式外，还需根据具体情况进行合理的调整和计算，以确保杆件的精准使用和安全施工。

广场广告牌钢结构设计计算书

广场广告牌钢结构设计计算书设计单位：xxx设计工作室设计项目：广场广告牌钢结构设计计算书一、设计依据本设计计算书根据《国家建筑设计规范》、《钢结构设计规范》、《地震设计规范》等相关规范进行设计计算，并结合项目具体要求进行综合设计。

二、设计参数1. 广告牌总高度：H = 10m2. 广告牌宽度：W = 5m3. 流线型钢结构横截面形状：矩形4. 钢结构材料：Q2355. 风载荷设计等级：3级6. 设计基准风速：V = 45m/s7. 基本风压：Pb = 0.5kN/m²三、荷载计算1. 风载荷计算：风压力计算公式：P = Pb * Cpe * Cg * Cp其中，Cpe为风压力系数，取1.2；Cg为结构高度修正系数，通过计算得到；Cp为构件位置修正系数，取1.0。

风载荷计算公式：F = P * A其中，A为广告牌面积，取H * W。

2. 结构自重计算：自重计算公式：G = ρ * A其中，ρ为钢结构材料的密度，取7.85g/cm³；A为广告牌体积，取H * W * t。

t为钢结构板厚，根据实际情况确定。

3. 地震荷载计算：根据地震设计规范计算得到地震荷载，并进行相应的结构响应分析。

四、钢结构设计1. 主梁设计：依据强度设计准则计算主梁截面面积，并选择合适的热轧压型钢材料进行设计。

2. 柱腿设计：依据强度设计准则计算柱腿截面面积，并选择合适的热轧压型钢材料进行设计。

3. 铰接设计：根据结构拓扑形状和荷载分析，在适当位置设置合理的铰接连接，并对连接部位进行剪力、扭矩等设计计算。

4. 结构稳定性设计：进行整体结构稳定性计算，包括抗侧稳定、抗翻转稳定、抗滚动稳定等。

五、验算结果设计计算书提供结构各主要构件的设计验算结果，包括截面尺寸、受力状态、应力情况等。

六、结论本设计计算书综合考虑了风荷载、结构自重、地震荷载等多种荷载因素，并进行了相应的设计计算。

根据结果，确定了适合的钢结构型号和尺寸，保证了广场广告牌钢结构的安全可靠性。

广告牌结构计算

一、风荷载计算1、标高为:Z=16M处风荷载计算(1). 风荷载标准值计算:W k: 作用在幕墙上的风荷载标准值(kN/m2): Zm高处阵风系数(按B类区计算):βgzμf=0.5×(Z/10)-0.16＝0.46βgz=0.89×(1+2μf)= 1.72μz: Z(m)高处风压高度变化系数(按B类区计算): (GB50009-2001)μz=(Z/10)0.32 = 1.16 风荷载体型系数μs= 1.2W k=βgz×μz×μs×W0 (GB50009-2001) =1.79kN/m2(2). 风荷载设计值:W: 风荷载设计值: kN/m2r w: 风荷载作用效应的分项系数: 1.4按《建筑结构荷载规范》GB50009-2001 3.2.5 规定采用W=r w×W k= 2.51kN/m2二.内力结构计算: (中横向ZHL)整体结构梁受力计算:荷载:(1) G(#2Ak)平均重力: 1.00kN/m^2(2).W 风荷载设计值: 2.51kN/m^2M(#1G): 平均自重下组合梁弯矩(kN.m)q(#1G):荷载集度设计值:(kN/m)a(#4sjcg):计算跨度: 14mB: 计算单元宽: 6.5mq(#1G)=1.4×G(#2Ak)×B=1.4×0.5×1.0=9.1 kN/mM(#1G)=q(#1G)×a(#4sjcg)^2/8=222.95kN.m垂直于平面的分布水平地震作用:α(#3max)= q(#3EAk): 垂直于平面的分布水平地震作用 (kN/m)q(#3EAk)=5×α(#3max)×G(#2Ak) (JGJ102-96 5.2.4) =0.8 kN/mγ(#1E): 地震作用分项系数: 1.3q(#2EA)=1.3×q(#3EAk)=1.04 kN/mq(#1E)：水平地震作用线分布最大荷载集度设计值(矩形分布)q(#1E)=q(#2EA)×B=6.76 kN/mM1=M(#1G)+0.6×M(#1E)=289.20kN.m风荷载线分布最大荷载集度设计值(矩形分布)q(#1w): 风荷载线分布最大荷载集度设计值(kN/m)r(#1w): 风荷载作用效应的分项系数： 1.4W(#1k): 风荷载标准值: 1.79kN/m2B: 计算单元宽: 1q(#1w)=1.4×W(#1k)×B= 2.51k N/mq(#1w): 风荷载线分布最大荷载集度设计值: 2.51 a’(#4sjcg):计算跨度:14mM(#1w)=q(#1w)×a’(#4sjcg)^2/8=61.55 kN.mN(#1w): 风荷载对横梁端的集中力设计值(kN)N(#1w)= q(#1w)×a’(#4sjcg)/2=77.32k N钢管（￠500×12）横梁强度校核1．刚度计算:A: D500X12钢管截面积: d=D-t=48.8=45.97cm^2γ: 塑性发展系数: 1.0i: 回转半径: I=0.35d=17.08 cm λ: 构件细长比L0: 钢管杆计算长度:7.00mλ=L0×100/i40.98<[λ]=150刚度满足.σ: 计算强度(N/mm2)(为拉弯构件)N: 受力设计值:77.32kNA: 立柱型材截面积: 45.97cm2M: 弯矩: 61.55kN·mW x1: 立柱截面抗弯矩:2191cm3γ: 塑性发展系数: 1.05σ=N×10/A+M×103/1.05/W x1=43.58≤ｆa=215N/mm2钢管梁强度可以满足钢管（￠1200×14）立柱强度校核1．刚度计算:A: D1200X14钢管截面积: d=D-t=118.6=111.72cm^2γ: 塑性发展系数: 1.0i: 回转半径: I=0.35d=41.51 cm λ: 构件细长比L0: 钢管杆计算长度:16.00mλ=L0×100/i38.54<[λ]=150刚度满足.σ: 计算强度(N/mm2)(为拉弯构件)Nw: 受风力设计值:77.32kNA: 立柱型材截面积: 111.72cm2M: 弯矩: 1237.17kN·mW x1: 立柱截面抗弯矩:15280cm3γ: 塑性发展系数: 1.05σ=N×10/A+M×103/1.05/W x1=84.03≤ｆa=215N/mm2钢管立柱强度可以满足基础整体稳定验算：M1=1237.17kN·mN=280KN*************************************************************************************************计算项目: 承载力计算-1************************************************************************************************[计算条件]1、基础信息基础埋深 d = 2.00 m基础宽 B = 4.50 m基础长 L = 9.00 m基础底标高 Bg = -2.00 mN= 2802、土层信息地下水标高 = -2.20 m 顶层土标高 = 0.00 m 土层数 = 3土层号厚度(m) 重度(MPa) 承载力深度修正相对密度孔隙比压缩模量土层 1 -5 18 130 1 2.7 0.8 7.5 土层 2 -10 18 130 1 2.7 0.8 7.5 土层 3 -15 18 130 1 2.7 0.8 7.5 3、荷载信息荷载标准值 N = 280.00 kn Mx = 1300.00 kn*m My = 130.00 kn*m单位面积的基础及覆土重 γ`h = 20.00 kPa[计算结果]计算根据：中华人民共和国国家标准GB50007-2002 --综合法4、底板反力 (kPa):平均 p= 26.914 最大 pmax= 52.593 最小 pmin= 1.235 角点 p1 = 1.235 p2 = 9.794 p3 = 52.593 p4 = 44.0335、承载力计算地基(抗震)承载力设计值 = 202.400地基承载力验算满足0.000-15.000-10.000-5.000剖面图1-N= 2804.50221)5.0()3(-+-+=d b f f m d b ak a γηγηak f p <ak f p 2.1m ax <6、下卧层承载力计算基底下土层号土层厚承载力特征值全压应力扩散角土层 2 5.00 207.86 56.43 0.00 土层 3 5.00 259.82 102.71 0.00四．预埋件计算: (第1处) 本工程预埋件受拉力和剪力(拉杆节点）V: 剪力设计值:Vc=77323.0NV=1.2*Vc=92787.6NN: 法向力设计值:Nd=773230NN=1.2*Nd=927875.9N Me=M1=1237167808N·mmN(#3um1): 锚筋根数:20根锚筋层数:1层K(#1r): 锚筋层数影响系数: 1.000 关于混凝土：混凝土标号C30混凝土强度设计值:f(#1c)=15.000N/mm^2按现行国家标准≤混凝土结构设计规范≥ GBJ10采用。

3-4米广告牌支撑计算书

3-4米广告牌支撑计算书
1. 引言
本文档旨在提供计算3-4米广告牌支撑结构的相关参数和设计要求。

通过合理的计算和设计，确保广告牌的稳定性和安全性。

2. 设计要求
- 广告牌高度：3-4米
- 风压：根据当地附近地区的最大风速，选择合适的安全系数进行计算。

- 材料：根据设计要求，可选择合适的材料（如钢材等）。

3. 支撑结构设计计算
3.1 广告牌的重力计算
根据广告牌的高度和自身重量计算，可得到广告牌的重力。

重力计算公式如下：
重力 = 高度 ×单位长度的广告牌重量
3.2 广告牌受到的风力计算
根据广告牌的高度、风压和风力作用面积，可以计算得到广告牌受到的风力。

风力计算公式如下：
风力 = 风压 ×广告牌的风力作用面积
3.3 支撑结构的稳定性计算
为了保证广告牌的稳定性，需要计算支撑结构的稳定性。

支撑结构的稳定性计算公式如下：
稳定性 = 广告牌的重力 - 广告牌受到的风力
3.4 结构材料的选择
根据计算得到的支撑结构稳定性参数，选择合适的结构材料。

根据结构材料的强度和稳定性，计算出结构材料的截面尺寸和长度。

4. 结论
根据上述计算，我们能够得出3-4米广告牌支撑结构的相关参
数和设计要求。

根据计算结果，选择合适的结构材料和尺寸，能够
确保广告牌的稳定性和安全性。

> 注意：以上计算仅供参考，具体的设计和选材还需要根据实
际情况进行综合考虑。

为保证广告牌的安全性，建议寻求专业结构
工程师的意见和指导。

以上是关于3-4米广告牌支撑计算的文档。

广告牌钢结构设计计算书

广告牌钢结构设计计算书1 基本参数1.1广告牌所在地区：福州地区；1.2地面粗糙度分类等级：按《建筑结构荷载规范》(GB50009-2001)A类：指近海海面和海岛、海岸、湖岸及沙漠地区；B类：指田野、乡村、丛林、丘陵以及房屋比较稀疏的乡镇和城市郊区； C类：指有密集建筑群的城市市区；D类：指有密集建筑群且房屋较高的城市市区；依照上面分类标准，本工程按B类地形考虑。

2 广告牌荷载计算2.1广告布广告牌的荷载作用说明：广告牌承受的荷载包括：自重、风荷载、雪荷载以及活荷载。

(1)自重：包括广告布、杆件、连接件、附件等的自重，可以按照400N/m2估算：(2)风荷载：是垂直作用于广告牌表面的荷载，按GB50009采用；(3)雪荷载：是指广告牌水平投影面上的雪荷载，按GB50009采用；(4)活荷载：是指广告牌水平投影面上的活荷载，按GB50009，可按500N/m2采用；在实际工程的广告牌结构计算中，对上面的几种荷载，考虑最不利组合，有下面几种方式，取用其最大值：A：考虑正风压时：a.当永久荷载起控制作用的时候，按下面公式进行荷载组合：Sk+=1.35Gk+0.6×1.4wk+0.7×1.4Sk(或Qk)b.当永久荷载不起控制作用的时候，按下面公式进行荷载组合：Sk+=1.2Gk+1.4×wk+0.7×1.4Sk(或Qk)B：考虑负风压时：按下面公式进行荷载组合：Sk-=1.0Gk+1.4wk2.2风荷载标准值计算：按建筑结构荷载规范(GB50009-2001)计算：wk+=βgzμzμs1+w……7.1.1-2[GB50009-2001 2006年版]wk-=βgzμzμs1-w上式中：wk+：正风压下作用在广告牌上的风荷载标准值(MPa)；wk-：负风压下作用在广告牌上的风荷载标准值(MPa)；Z：计算点标高：6m；βgz：瞬时风压的阵风系数；根据不同场地类型,按以下公式计算(高度不足5m按5m计算)：βgz =K(1+2μf)其中K为地面粗糙度调整系数，μf为脉动系数A类场地：βgz =0.92×(1+2μf) 其中：μf=0.387×(Z/10)-0.12B类场地：βgz =0.89×(1+2μf) 其中：μf=0.5(Z/10)-0.16C类场地：βgz =0.85×(1+2μf) 其中：μf=0.734(Z/10)-0.22D类场地：βgz =0.80×(1+2μf) 其中：μf=1.2248(Z/10)-0.3对于B类地形，6m高度处瞬时风压的阵风系数：βgz=0.89×(1+2×(0.5(Z/10)-0.16))=1.8558μz：风压高度变化系数；根据不同场地类型,按以下公式计算：A类场地：μz=1.379×(Z/10)0.24当Z>300m时，取Z=300m，当Z<5m时，取Z=5m；B类场地：μz=(Z/10)0.32当Z>350m时，取Z=350m，当Z<10m时，取Z=10m；C类场地：μz=0.616×(Z/10)0.44当Z>400m时，取Z=400m，当Z<15m时，取Z=15m；D类场地：μz=0.318×(Z/10)0.60当Z>450m时，取Z=450m，当Z<30m时，取Z=30m；对于B类地形，6m高度处风压高度变化系数：μz=1.000×(Z/10)0.32=1μs1：局部风压体型系数，对于广告牌结构，按规范，计算正风压时，取μs1+=1.3；计算负风压时，取μs1-=-2.0；另注：上述的局部体型系数μs1(1)是适用于围护构件的从属面积A小于或等于1m2的情况，当围护构件的从属面积A大于或等于10m2时，局部风压体型系数μs1(10)可乘以折减系数0.8，当构件的从属面积小于10m2而大于1m2时，局部风压体型系数μs1(A)可按面积的对数线性插值，即：μs1(A)=μs1(1)+[μs1(10)-μs1(1)]logA在上式中：当A≥10m2时取A=10m2；当A≤1m2时取A=1m2；w：基本风压值(MPa)，根据现行<<建筑结构荷载规范>>GB50009-2001附表D.4(全国基本风压分布图)中数值采用，按重现期50年，福州地区取0.0007MPa；(1)计算龙骨构件的风荷载标准值：龙骨构件的从属面积：A=6×1.5=9m2LogA=0.954μsA1+(A)=μs1+(1)+[μs1+(10)-μs1+(1)]logA=1.052μsA1-(A)=μs1-(1)+[μs1-(10)-μs1-(1)]logA=1.618wkA+=βgzμzμsA1+w=1.8558×1×1.052×0.0007 =0.001367MPawkA-=βgzμzμsA1-w=1.8558×1×1.618×0.0007 =0.002102MPa(2)计算广告布部分的风荷载标准值：广告布构件的从属面积：A=1.5×1.5=2.25m2LogA=0.352μsB1+(A)=μs1+(1)+[μs1+(10)-μs1+(1)]logA=1.208μsB1-(A)=μs1-(1)+[μs1-(10)-μs1-(1)]logA=1.859wkB+=βgzμzμsB1+w=1.8558×1×1.208×0.0007 =0.001569MPawkB-=βgzμzμsB1-w=1.8558×1×1.859×0.0007=0.002415MPa2.3风荷载设计值计算：wA+：正风压作用下作用在广告牌龙骨上的风荷载设计值(MPa)；wkA+：正风压作用下作用在广告牌龙骨上的风荷载标准值(MPa)；wA-：负风压作用下作用在广告牌龙骨上的风荷载设计值(MPa)；wkA-：负风压作用下作用在广告牌龙骨上的风荷载标准值(MPa)；wA+=1.4×wkA+=1.4×0.001367 =0.001914MPawA-=1.4×wkA-=1.4×0.002102=0.002943MPawB+：正风压作用下作用在广告牌广告布上的风荷载设计值(MPa)；wkB+：正风压作用下作用在广告牌广告布上的风荷载标准值(MPa)；wB-：负风压作用下作用在广告牌广告布上的风荷载设计值(MPa)；wkB-：负风压作用下作用在广告牌广告布上的风荷载标准值(MPa)；wB+=1.4×wkB+=1.4×0.001569 =0.002197MPawB-=1.4×wkB-=1.4×0.002415=0.003381MPa2.4雪荷载标准值计算：Sk：作用在广告牌上的雪荷载标准值(MPa)S：基本雪压，根据现行<<建筑结构荷载规范>>GB50009-2001取值，福州地区50年一遇最大积雪的自重：0MPa.μr：屋面积雪分布系数，按表6.2.1[GB50009-2001]，为2.0。

广告牌计算程序

m m m kN/m2
kN/m kN.m
2
数据输入
钢管柱外径d (mm) 管壁厚度t (mm) 钢材抗压强度设计值f (N/mm2) 钢材屈服强度值fy (N/mm2) 2 钢材弹性模量E (N/mm ) 1350 12.0 315 325 2.06E+05 轴心压力N (KN) 最大弯矩Mx (KN·m) 计算长度l0x (mm) 计算长度l0y (mm) 等效弯矩系数βm
二、径厚比验算
验算 d/t ≤ 100*(235/fy)
三、刚度验算
构件容许长细比[λ] 150 刚度验算 Max[λx,λy]<[λ]
四、强度验算强度验算
N/A+M/γW (N/mm2) 258.11 验算 N/A+M/γW ≤ f
五、稳定性验算
⒈弯矩平面内 0.321 构件所属的截面类型系数α2 0.600 0.300 欧拉临界力NEx=π2EA/λx2 (KN) 当λx'＞0.215时，稳定系数ψx={(α2+α3λx'+λx'2)-[(α2+α3λx'+λx'2)2-4λx'2]1/2}/2λx'2 当λx'≤0.215时，稳定系数ψx=1-α1λx'2 局部稳定系数φ=1 （d/t≤60时）；φ=1.64-0.23*(d/t)1/4 （d/t>60时） N/ψxA+βmMx/γW(1-0.8N/NEx) (N/mm2) 验算 N/ψxA+βmMx/γW(1-0.8N/NEx) ≤ φf λx'=(fy/E)1/2*λx/π 系数α1 系数α3
1/2
5939.48 2699.56 12000 12000 1.0

广告牌工程量计算(钢材部分)

单位重量长度或面积总重量56525943357288216628135648底部钢板007128559548横管529818m18504412201612m570169圆形钢板146025两块657193003001240050012437086003001627119槽钢868248灯支架763安全网支架2664角位爬梯6782下部钢爬梯50865两面之间槽钢7205041624104角钢45454镀锌板08mm三角形32块2三角形24块1212059kgm40根每根18米长方管4545角钢5050572米每米37kg角钢4545424米角钢4545418米40根每根18米长
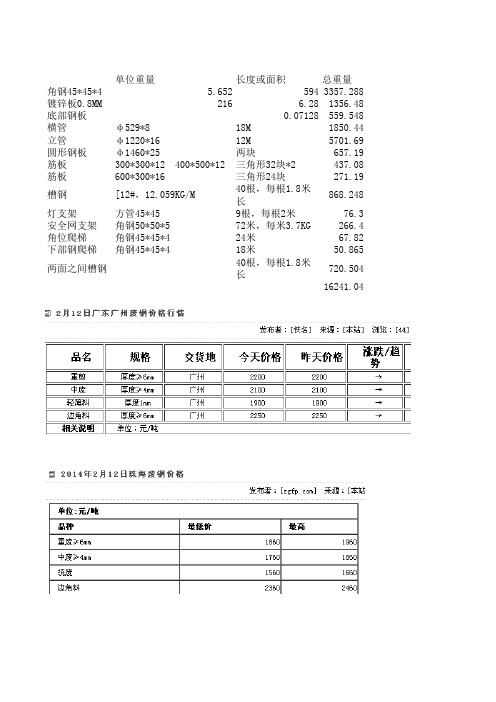
总重量角钢45*45*4 5.652 594 3357.288 镀锌板0.8MM 216 6.28 1356.48 底部钢板 0.07128 559.548 横管 φ 529*8 18M 1850.44 立管 φ 1220*16 12M 5701.69 圆形钢板 φ 1460*25 两块 657.19 筋板 300*300*12 400*500*12 三角形32块*2 437.08 筋板 600*300*16 三角形24块 271.19 槽钢 [12#，12.059KG/M 40根，每根1.8米长 868.248 灯支架方管45*45 9根，每根2米 76.3 安全网支架角钢50*50*5 72米，每米3.7KG 266.4 角位爬梯角钢45*45*4 24米 67.82 下部钢爬梯角钢45*45*4 18米 50.865 两面之间槽钢 40根，每根1.8米长 720.504 16241.04
单位重量长度或面积来自

杆件的强度计算公式

杆件的强度计算公式1.应力：应力是杆件内部单位面积上的力，通常以帕斯卡（Pa）为单位。

应力被定义为负载除以横截面积。

在强度计算中，应力是一个重要的参数，用于评估杆件是否能够承受给定的负载。

2.截面形状：截面形状指的是杆件横截面的形状，如圆形、矩形、梯形等。

截面形状对杆件的强度计算有很大影响，因为不同的形状在承载能力方面具有不同的特点。

3.材料性质：杆件的材料性质包括弹性模量、屈服强度、抗拉强度等。

这些参数用于计算杆件在受力情况下的应力和应变，并评估其强度。

根据杆件的受力类型和计算方法的不同，强度计算公式可以有很多种形式。

以下是几个常见的强度计算公式示例：1.杆件的拉伸强度计算公式：拉伸强度=屈服强度/安全系数这个公式适用于纯拉伸情况下的杆件强度计算。

通常，设计中会采用一个安全系数，以确保杆件在实际应用中不会超过其屈服强度。

2.杆件的压缩强度计算公式：压缩强度=屈服强度/安全系数这个公式适用于纯压缩情况下的杆件强度计算。

与拉伸情况类似，设计中也会采用一个安全系数。

3.杆件的弯曲强度计算公式：弯曲强度=弯矩/抗弯矩弯曲强度计算涉及到杆件的几何形状和截面惯性矩等参数，以及杆件的材料性质。

通过计算弯矩和抗弯矩的比值，可以评估杆件在受弯应力作用下的强度。

此外，还有一些特殊情况下的杆件强度计算公式，如扭转、剪切、冲击等。

这些公式通常相对复杂，需要更详细的材料性质和截面形状参数。

需要注意的是，强度计算公式只是一种初步评估杆件承载能力的方法，它没有考虑杆件的缺陷、损伤和非均匀加载等因素。

因此，在实际工程中，还需要进行更为详细的强度分析和安全性评估，以确保杆件的可靠性和安全性。