图形面积的计算 专题
初中数学培优专题学习专题25 图形面积的计算
专题25 图形面积的计算阅读与思考计算图形的面积是平面几何中常见的基本问题之一,它包括两种主要类型: 1.常见图形面积的计算由于一些常见图形有计算面积的公式,所以,常见图形面积一般用公式来解. 2.非常规图形面积的计算非常规图形面积的计算通常转化为常见图形面积的计算,解题的关键是将非常规图形面积用常规图形面积的和或差来表示.计算图形的面积还常常用到以下知识:(1)等底等高的两个三角形面积相等.(2)等底的两个三角形面积的比等于对应高的比. (3)等高的两个三角形面积的比等于对应底的比. (4)等腰三角形底边上的高平分这个三角形的面积. (5)三角形一边上的中线平分这个三角形的面积. (6)平行四边形的对角线平分它的面积. 熟悉如下基本图形:S 3S 4S 3S 4S 1S 2S 1S 2S 1S 2S 1S 2S 1S 2S 2S 1l 2l 1例题与求解【例1】 如图,在直角△ABC 的两直角边AC ,BC 上分别作正方形ACDE 和CBFG .AF 交BC 于W ,连接GW ,若AC =14,BC =28,则S △AGW =______________.(2013年“希望杯”全国数学邀请赛试题)解题思路:△AGW 的面积可以看做△AGF 和△GWF 的面积之差.WFGEDCBA【例2】 如图,已知△ABC 中的面积为24,点D 在线段AC 上,点F 在线段BC 的延长线上,且BC =4CF .四边形BDCE 是平行四边形,则图中阴影部分的面积为( )A .3B .4C .5D .6(2013年全国初中数学竞赛广东试题)解题思路:设△ABC 底边BC 上的高为h .本例关键是通过适当变形找出h 和DE 之间的关系.FC BDEA【例3】 如图,平行四边形ABCD 的面积为30cm 2,E 为AD 边延长线上的一点,EB 与DC 交于F 点,已知三角形FBC 的面积比三角形DEF 的面积大9cm 2,AD =5cm ,求DE 长.(北京市“迎春杯”竞赛试题)解题思路:由面积求相关线段,是一个逆向思维的过程,解题的关键是把条件中图形面积用DE 及其它线段表示.BACFDE【例4】 如图,四边形ABCD 被AC 与DB 分成甲、乙、丙、丁4个三角形,已知BE =80 cm ,CE =60 cm ,DE =40 cm ,AE =30 cm ,问:丙、丁两个三角形面积之和是甲、乙两个三角形面积之和的多少倍?(“华罗庚杯”竞赛决赛试题)解题思路:甲、乙、丙、丁四个三角形面积可通过线段的比而建立联系,找出这种联系是解本例的突破口.丁乙丙甲E BCDA【例5】 如图,△ABC 的面积为1,D ,E 为BC 的三等分点,F ,G 为CA 的三等分点,求四边形PECF 的面积.解题思路:连CP ,设S △PFC =x ,S △PEC =y ,建立x ,y 的二元一次方程组.QP F GEDCBA【例6】如图,E ,F 分别是四边形ABCD 的边AB ,BC 的中点, DE 与AF 交于点P ,点Q 在线段DE 上,且AQ ∥PC .求梯形APCQ 的面积与平行四边形ABCD 的面积的比值.(2013年”希望杯“数学邀请赛试题)解题思路:连接EF ,DF ,AC ,PB ,设S □ABCD =a ,求得△APQ 和△CPQ 的面积.FEPQDCBA能力训练A 级1.如图,边长为1的正方形ABCD 的对角线相交于点O .过点O 的直线分别交AD ,BC 于E ,F ,则阴影部分面积是______.FOEDCB A(海南省竞赛试题)2.如图,在长方形ABCD 中,E 是AD 的中点,F 是CE 的中点,若△BDF 的面积为6平方厘米,则长方形ABCD 的面积是_____________平方厘米.EFDCBA(“希望杯”邀请赛试题)3.如图,ABCD 是边长为a 的正方形,以AB ,BC ,CD ,DA 分别为直径画半圆,则这四个半圆弧所围成的阴影部分的面积是____________.DCBA(安徽省中考试题)4.如图,已知AB ,CD 分别为梯形ABCD 的上底、下底,阴影部分总面积为5平方厘米,△AOB 的面积是0.625平方厘米,则梯形ABCD 的面积是_________平方厘米.DOCBA(“祖冲之杯”邀请赛试题)5.如图,长方形ABCD 中,E 是AB 的中点,F 是BC 上的一点,且CF =BC 31,则长方形ABCD的面积是阴影部分面积的( )倍.A .2B . 3C . 4D .5DF CBEA6.如图,是一个长为a ,宽为b 的长方形,两个阴影图形都是一对长为c 的底边在长方形对边上的平行四边形,则长方形中未涂阴影部分的面积为( ).A .c b a ab )(+-B . c b a ab )(--C .))((c b c a --D .))((c b c a +-cccc7.如图,线段AB =CD =10cm ,BC 和DA 是弧长与半径都相等的圆弧,曲边三角形BCD 的面积是以D 为圆心、DC 为半径的圆面积的41,则阴影部分的面积是( ). A .25π B . 100 C .50π D .200CBD A(“五羊杯”竞赛试题)8.如图,一个大长方形被两条线段AB 、CD 中分成四个小长方形,如果其中图形Ⅰ,Ⅱ,Ⅲ的面积分别为8,6,5,那么阴影部分的面积为( ). A .29 B .27 C .310 D .815 ⅢⅡⅠCBDA9.如图,长方形ABCD 中,E ,F 分别为AD ,BC 边上的任一点,△ABG ,△DCH 的面积分别为15和20,求阴影部分的面积.HGEDCF B A(五城市联赛试题)10.如图,正方形ABCD ,正方形BEFG 和正方形RKPF 的位置如图所示,点G 在线段DK 上,已知正方形BEFG 的边长为4,求△DEK 的面积.RKP GF EC B AD(广西壮族自治区省南宁市中考试题)B 级1.如果图中4个圆的半径都为a ,那么阴影部分的面积为_____________.(江苏省竞赛试题)2.如图,在长方形ABCD 中,E 是BC 上的一点,F 是CD 上的一点,若三角形ABE 的面积是长方形ABCD 面积的31,三角形ADF 的面积是长方形ABCD 面积的52,三角形CEF 的面积为4cm 2,那么长方形ABCD 的面积是_________cm 2.DCFE BA(北京市“迎春杯”邀请赛试题)3.如图,边长为3厘米与5厘米的两个正方形并排放在一起,在大正方形中画一段以它的一个顶点为圆心,边长为半径的圆弧,则阴影部分的面积为___________________.(“希望杯”邀请赛试题)4.如图,若正方形APHM ,BNHP ,CQHN 的面积分别为7,4,6,则阴影部分的面积是_____.CMNDQPB A(“五羊杯”竞赛试题)5.如图,把等边三角形每边三等分,使其向外长出一个边长为原来的31的小等边三角形,称为一次“生长”,在得到的多边上类似“生长”,一共“生长”三次后,得到的多边形的边数=________,面积是原三角形面积的______倍.第2次生长第1次生长原图(“五羊杯”竞赛试题)6.如图,在长方形ABCD 中,AE =BG =BF =21AD =31AB =2,E ,H ,G 在同一条直线上,则阴影部分的面积等于( ).A .8B .12C .16D .20F BGCHDE A7.如图,边长分别为8cm 和6cm 的两个正方形,ABCD 与BEFG 并排放在一起,连接EG 并延长交AC 于K ,则△AKE 的面积是( ).A .48cm 2B .49cm 2C .50cm 2D .51cm 2KGFEC B A D(2013年“希望杯”邀请赛试题)8.在一个由8×8个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆经过的所有小方格的圆内部分的面积之和记为S 1,把圆周经过的所有小方格的圆外部分的面积之和记为S 2,则21S S 的整数部分是( ).A .0B .1C .2D .3(全国初中数学联赛试题)9.如图,△ABC 中,点D ,E ,F 分别在三边上,E 是AC 的中点,AD ,BE ,CF 交于一点G ,BD =2DC ,S △GEC =3,S △GDC =4,则△ABC 的面积是( ).A .25B .30C .35D .40GFE CBDA10.已知O (0,0),A (2,2),B (1,a ),求a 为何值时,S △ABO =5?11.如图,已知正方形ABCD 的面积为1,M 为AB 的中点,求图中阴影部分的面积.GCBMAD(湖北省武汉市竞赛试题)12.如图,△ABC 中,21===FA FB EC EA DB DC .求的面积△的面积△ABC GHI 的值. G IHEDCBFA(“华罗庚金杯”邀请赛试题)。
小学五年级数学解析:几何图形的面积计算

小学五年级数学解析:几何图形的面积计算一、常见几何图形的面积公式1. 长方形的面积公式:长方形的面积 = 长×宽。
例题解析:例题1:一个长方形的长为8米,宽为5米,求其面积。
解答:面积 = 8米× 5米 = 40平方米。
2. 正方形的面积公式:正方形的面积 = 边长×边长。
例题解析:例题2:一个正方形的边长为6厘米,求其面积。
解答:面积 = 6厘米× 6厘米 = 36平方厘米。
3. 三角形的面积公式:三角形的面积 = 底×高÷ 2。
例题解析:例题3:一个三角形的底为10米,高为4米,求其面积。
解答:面积 = 10米× 4米÷ 2 = 20平方米。
4. 平行四边形的面积公式:平行四边形的面积 = 底×高。
例题解析:例题4:一个平行四边形的底为9米,高为5米,求其面积。
解答:面积 = 9米× 5米 = 45平方米。
5. 梯形的面积公式:梯形的面积 = (上底 + 下底)×高÷ 2。
例题解析:例题5:一个梯形的上底为6米,下底为10米,高为4米,求其面积。
解答:面积 = (6米 + 10米)× 4米÷ 2 = 32平方米。
6. 圆的面积公式:圆的面积 = π×半径²。
例题解析:例题6:一个圆的半径为3厘米,求其面积。
解答:面积 = π× 3²厘米²≈ 3.14 × 9厘米² = 28.26平方厘米。
二、复合图形的分割与面积计算1. 复合图形的定义与分割方法定义:复合图形是由多个简单图形组合而成的图形。
要计算复合图形的面积,可以将其分割成多个简单图形,然后分别计算面积,再将这些面积相加。
例题解析:例题1:计算一个由两个长方形组合而成的L形图形的面积。
解答:将L形图形分割为两个长方形,分别计算面积,再将两部分面积相加。
中考数学专题---图形的面积

中考数学专题---面积问题计算图中阴影部分面积是多少平方厘米?(圆的半径r =10厘米)如图,ABCG和CDEF都是正方形,DC等于12厘米,CB等于10厘米。
求阴影的面积。
如图,以小正方形四角的顶点为圆心,边长的一半为半径,作4个圆,在4个圆外作一正方形,每边都与其中两个圆各有一个接触点,求阴影部分的面积。
如图,图中是黄鹤楼公司某产品的商品图案,若每个小长方形的都是1,则阴影部分的面积为如图,正方形ABCD边长为1,E、F、G、H分别为其各边的中点,则图中阴影面积为_____ 在□ABCD中,E是AD的中点,若S□ABCD=1,则图中的阴影面积为已知,如图,正方形ABCD的面积为25,菱形PQCB的面积为20,则阴影部分的面积为.如图,E、F分别是矩形ABCD边AD、BC上的点,且△ABG,△DCH的面积分别为15和20,则图中的阴影部分面积为(2012安徽)为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为()A.22aB. 32aC. 42aD.52a(2012安徽)如图,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:①S1+S2=S3+S4②S2+S4= S1+ S3③若S3=2 S1,则S4=2 S2④若S1= S2,则P点在矩形的对角线上。
其中正确的结论的序号是_________________(把所有正确结论的序号都填在横线上).(2012广东)如图,在□ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是(结果保留π).(2012恩施州)如图,菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是()A.B.2 C.3 D.(2012天门)如图,在Rt △ABC 中,∠C =90°,∠A =30°,AC =6cm ,CD ⊥AB 于D ,以C 为圆心,CD 为半径画弧,交BC 于E ,则图中阴影部分的面积为( )A. ﹣B.﹣C.﹣D.﹣(2012天门)如图,线段AC =n+1(其中n 为正整数),点B 在线段AC 上,在线段AC 同侧作正方形ABMN 及正方形BCEF ,连接AM 、ME 、EA 得到△AME .当AB =1时,△AME 的面积记为S 1;当AB =2时,△AME 的面积记为S 2;当AB=3时,△AME 的面积记为S 3;…;当AB=n 时,△AME 的面积记为S n .当n ≥2时,S n ﹣S n ﹣1=_________.(2012娄底)如图,正方形MNEF 的四个顶点在直径为4的大圆上,小圆与正方形各边都相切,AB 与CD 是大圆的直径,AB ⊥CD ,CD ⊥MN ,则图中阴影部分的面积是( ) A . 4π B . 3π C . 2πD .π(2012黄石)如图(2)所示,扇形AOB 的圆心角为120°,半径为2,则图中阴影部分的面积为( )A.43π43π-432π- D. 43π(2012临沂)如图,AB 是⊙O 的直径,点E 为BC 的中点,AB =4,∠BED =120°,则图中阴影部分的面积之和为( )A .1B .2C D .(2012烟台)如图,⊙O 1,⊙O ,⊙O 2的半径均为2cm ,⊙O 3,⊙O 4的半径均为1cm ,⊙O 与其他4个圆均相外切,图形既关于O 1O 2所在直线对称,又关于O 3O 4所在直线对称,则四边形O 1O 4O 2O 3的面积为( )A .12cm 2B .24cm 2C .36cm 2D .48cm 2(2012四川广安)如图,把抛物线y=x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=x2交于点Q,则图中阴影部分的面积为.(2012攀枝花)如图,以BC为直径的⊙O1与⊙O2外切,⊙O1与⊙O2的外公切线交于点D,且∠ADC=60°,过B点的⊙O1的切线交其中一条外公切线于点A.若⊙O2的面积为π,则四边形ABCD的面积是.(2011福建泉州)如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B’,则图中阴影部分的面积是().A. 3πB. 6πC. 5πD. 4π(2011山东潍坊)如图,半径为1的小圆在半径为9 的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为()A . 17πB . 32πC . 49πD . 80π(2011浙江台州)如图,CD是⊙O的直径,弦AB⊥CD,垂足为点M,AB=20,分别以DM,CM为直径作两个大小不同的⊙O1和⊙O2,则图中所示的阴影部分面积为______ (结果保留π)(2011福建泉州)如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.那么剪下的扇形ABC (阴影部分)的面积为 ;用此剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径r= .( 2011重庆江津)如图,点A 、B 、C 在直径为32的⊙O 上,∠BAC =45º,则图中阴影的面积等于______________,(结果中保留π).(2011安徽芜湖)如图,在正方形ABCD 内有一折线段,其中AE ⊥EF ,EF ⊥FC ,并且AE =6,EF =8,FC=10,则正方形与其外接圆之间形成的阴影部分的面积为___________.如图,在Rt △ABC 中,∠ABC = 900, AB = 8cm , BC = 6cm , 分别以A,C 为圆心,以2AC的长为半径作圆, 将 Rt △ABC 截去两个扇形,则剩余(阴影)部分的面积为 cm 2(结果保留π)第19题图(第17题)(2011贵州安顺)如图,在Rt △ABC 中,∠C =90°,CA =CB =4,分别以A 、B 、C 为圆心,以21AC 为半径画弧,三条弧与边AB 所围成的阴影部分的面积是 .8. (2011福建福州)如图,在ABC ∆中,90A ∠=o ,O 是BC 边上一点,以O 为圆心的半圆分别与AB 、AC 边相切于D 、E 两点,连接OD .已知2BD =,3AD =.图中两部分阴影面积的和.(2011山东枣庄,23,8分)如图,点D 在O ⊙的直径AB 的延长线上,点C 在O ⊙上,且AC =CD ,∠ACD =120°,若O ⊙的半径为2,求图中阴影部分的面积.(2011山东东营,21,9分)(本题满分9分)如图,已知点A 、B 、C 、D 均在已知圆上,AD ∥BC ,BD 平分∠ABC ,∠BAD=120,四边形ABCD 的周长为15.B图9第18题图第15题求图中阴影部分的面积。
专题10 面积计算(组合图形的面积)(原卷)

2022-2023学年小学六年级思维拓展举一反三精编讲义专题10 面积计算(组合图形的面积)对于一些比较复杂的组合图形,有时直接分解有一定的困难,这时,可以通过把其中的部分图形进行平移、翻折或旋转,化难为易。
有些图形可以根据“容斥问题“的原理来解答。
在圆的半径r用小学知识无法求出时,可以把“r2”整体地代入面积公式求面积。
【典例分析01】如图20-1所示,求图中阴影部分的面积。
【思路导航】解法一:阴影部分的一半,可以看做是扇形中减去一个等腰直角三角形(如图20-2),等腰直角三角形的斜边等于圆的半径,斜边上的高等于斜边的一半,圆的半径为20÷2=10厘米【3.14×102×14-10×(10÷2)】×2=107(平方厘米)答:阴影部分的面积是107平方厘米。
解法二:以等腰三角形底的中点为中心点。
把图的右半部分向下旋转90度后,阴影部分的面积就变为从半径为10厘米的半圆面积中,减去两直角边为10厘米的等腰直角三角形的面积所得的差。
(20÷2)2×12-(20÷2)2×12=107(平方厘米)知识精讲典例分析【典例分析02】如图20-6所示,求图中阴影部分的面积(单位:厘米)。
【思路导航】解法一:先用长方形的面积减去小扇形的面积,得空白部分(a )的面积,再用大扇形的面积减去空白部分(a )的面积。
如图20-7所示。
3.14×62×14 -(6×4-3.14×42×14 )=16.82(平方厘米)解法二:把阴影部分看作(1)和(2)两部分如图20-8所示。
把大、小两个扇形面积相加,刚好多计算了空白部分和阴影(1)的面积,即长方形的面积。
3.14×42×14 +3.14×62×14 -4×6=16.28(平方厘米) 答:阴影部分的面积是16.82平方厘米。
算出图形的面积的题

算出图形的面积的题圆是小学六年级所要学习的内容,通过圆的学习,我们还能更好的解决实际生活中与圆有关系的问题。
解决问题类型一:【例1】、把一个圆平均分成若干偶数等份,再拼成一个近似长方形,已知圆的半径是4厘米,那么长方形的长是多少?【例2】、把一个圆平均分成若干偶数等份,再拼成一个近似长方形。
量出长方形的长是12.56 厘米,这个圆的面积是多少平方厘米?【例3】、在推导圆的面积公式时,将圆等分成若干份,拼成一个近似的长方形,已知长方形的长比宽多6.42厘米,圆的面积是多少平方厘米?【例4】、把一个圆平均分成若干份,拼成一个近似的长方形,拼成的长方形的周长比圆的周长多8厘米,这个圆的面积是多少平方厘米?【例5】、把一个圆平均分成若干份,拼成一个近似长方形。
若圆的面积是50.24平方厘米,阴影部分的面积是()平方厘米。
【提示】、这类题型要把握好圆的面积公式推导过程中,圆和长方形之间的关联,解题就非常简单。
当然,先算出圆的半价,再计算长方形的面积也可以,只不过过程比较麻烦。
类型二、圆的面积与实际问题相结合【例6】、一个圆形花坛,直径是20米,在它的外围修一条宽2米的石子小路,这条小路的面积是多少平方米?【例7】、有一个环形铁片,它的内圆周长是62.8厘米,外圆周长是94.2厘米,这个铁片的面积是多少平方厘米?【例8】、将一个半径5厘米的圆形铁片,加工成半径为4厘米的圆形铁片零件,铁片的面积减少了多少平方厘米?类型三、求圆的阴影面积【例题1】已知阴影部分的面积是20平方厘米,圆的面积是多少?【例题2】求下图中阴影部分的面积。
(单位:厘米)【例题3】图中的4个圆的圆心恰好是正方形的4个顶点,如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?。
2019中考数学《面积的计算》专题复习考点讲解(含答案)

面积的计算考点图解技法透析面积法是一种重要方法,计算图形面积是平面几何中最常见的基本问题之一,与面积相关的知识有:(1)常见图形的面积计算公式:正方形面积=边长×边长;矩形的面积=长×宽;平行四边形面积=底×高;三角形面积=底×高÷2;梯形面积=(上底+下底)×高÷2;圆的面积=×半径的平方;扇形面积=2360n r(n为圆心角,r为半径)(2)计算面积常常用到以下结论:①等底等高的两个三角形的面积相等;②等底的两个三角形的面积比等于对应高的比;③等高的两个三角形的面积比等于对应底的比;④三角形一边上的中线平分这个三角形的面积.(3)面积计算常用到以下方法:①和差法:把所求图形的面积转化为常见图形面积的和、差表示,运用常见图形的面积公式;②等积法:找出与所求图形面积相等的或者关联的特殊图形,通过代换转化来求出图形的面积;③运动法:通过平移、旋转、割补等方式,将图形中的部分图形运动起来,把图形转化为容易观察或解决的形状;④代数法:通过寻求图形面积之间的关系列方程(组);把几何问题转化为代数问题.(4)非常规图形的面积计算往往采用“等积变换”,所谓“等积变换”就是不改变几何图形的面积,而是把它的形状改变成能够直接求出面积的图形,等积变换的主要目的,是把复杂的图形变成简单的图形,把不规则的图形变成规则的图形.(5)“等积变换”的方法①公式法,即运用某些图形的面积公式及其有关推论.②分割法,即把一个图形分割成熟知的若干部分图形.③割补法,即把一个图形的某一部分分割出来,然后用与其等积图形填补到某一位置.名题精讲考点1 用面积公式计算常规图形面积例1 如图,将直角三角形BC 沿着斜边AC 的方向平移到 △DEF 的位置(A 、D 、C 、F 四点在同一条直线上).直角边DE 交BC 于点G .如果BG =4,EF =12,△BEG 的面积等于4,那 么梯形ABGD 的面积是 ( )A .16B .20C .24D .28【切题技巧】【规范解答】 B【借题发挥】 把不能直接求出面积的图形通过转化或找出与它面积相等的特殊图形,从而能够求解.【同类拓展】 1.如图所示,A 是斜边长为m 的等腰直角三角形,B ,C ,D 都是正方形,则A ,B ,C ,D 的面积的和等于 ( )A .94m 2B .52m 2C .114m 2D .3m 2考点2 用面积的和、差计算非常规图形有面积例2 如图,P 是平行四边形ABCD 内一点,且S △PAB =5, S △PAD =2,请你求出S △PAC (即阴影部分的面积).【切题技巧】 △APC 的底与高显然无法求,则应用已知三角 形的面积的和或差来计算△APC 的面积.【规范解答】【借题发挥】 对于不能直接求的图形可以把图形进行分解和组合,通过图形的面积和或差进行计算.【同类拓展】 2.如图,长方形ABCD 中,△ABP 的面积为a , △CDG 的面积为b ,则阴影四边形的面积等于 ( )A .a +bB .a -bC .2a bD .无法确定考点3 列方程(组)求面积例3 如图所示,△ABC 的面积是1cm 2.AD =DE =EC , BG =GF =FC ,求阴影四边形的面积.【切题技巧】条件中有两组等分点,易知△BCE,△ACF的面积为13,但仍然不能求阴影部分面积,因此,只要求出△BCE中另两块面积即可,【规范解答】如图,设AG与BE交于N,AF与BE交于P,连接NC,ND,PC,PD.设△NGB的面积为x,△NDE的面积为y,则有△NCG的面积为2x,△NEA的面积为2y.因为△ABC的面积是1cm2,且AD=AE=EC,BG=GF=FC.【借题发挥】求一些关系复杂的图形面积,列方程是一个重要方法,它不但可以使我们熟悉列方程和了解方程在几何中的应用,而且能清晰地表明图形面积之间的关系,从而可以化解或降低解题的难度.【同类拓展】3.如图,正方形ABCD中,E、F分别是BC、CD边上的点,AE、DE、BF、AF把正方形分成8小块,各小块的面积分别为S1、S2、…、S8,试比较S3与S2+S7+S8的大小,并说明理由.考点4 面积比与线段比的转化例4 如图所示,凸四边形ABCD中,对角线AC、BD相交于O点,若△AOD的面积是2,△COD的面积是1,△COB的面积是4,则四边形ABCD的面积是 ( )A.16 B.15 C.14 D.13【切题技巧】分析△AOD,△DOC,△AOB,△COB四个三角形的面积,只有通过线段比联系起来,相邻两个三角形的面积都存在着一种比例关系.【规范解答】【借题发挥】 两三角形的高相等时,面积比等于对应底之比,则可以将面积比与对应线段比相互转化,这是.解答面积问题、线段比等问题的常用技巧.【同类拓展】 4.如图,点E 、F 分别是矩形ABCD 的边AB 、BC 的中点,连AF 、CE 交于点G ,则AGCD ABCDS S 四边形矩形等于 ( )A .56B .45C .34D .23考点5例5 如图所示,在四边形ABCD 中,AM =MN =ND , BE =EF =FC ,四边形ABEM 、MEFN 、NFCD 的面积分别记为S 1,S 2和S 3.求213?S S S =+【切题技巧】 把四边形分割成多个三角形,运用三角形等积变换定理即可求出,【规范解答】 连接A .E 、EN 、PC 和AC .【借题发挥】 等积变形的题目中,常将多边形面积转化为三角形面积,再运用等底同高来进行等积代换,因此,在转化时只要抓住题设中的等分点,就可以将多边形面积进行等积变换了.【同类拓展】 5.如图,张大爷家有一块四边形的菜地,在A 处有一口井,张大爷欲想从A 处引一条笔直的水渠,且这条笔直的水 渠将四边形菜地分成面积相等的两部分,请你为张大爷设计一种引水 渠的方案,画出图形并说明理由. 考点6 格点多边形的面积例6 如图,五边形ABCDE 的面积为多少?我们把方格纸上两组互相平行且垂直的直线的交点叫格点. 顶点在格点上的多边形叫格点多边形.可以通过图形的分割,转化为规则图形,再求面积.【规范解答】如图,标上字母F 、G 、H 、I 、J 点,使得△ABF , △BCG ,△CDH ,△DEI ,△EAJ 为直角三角形,【借题发挥】 格点多边形面积有如下计算规律:格点多边形的面积等于其所包含有格点个数,加上由其边界上的格点的个数之半,再减去1.此规律对凹多边形也适用.即:若格点多边形的面积为S ,格点多边形内部有且只有n 个格点,它各边上格点的个数和为x .则S =12x +n -1. 【同类拓展】 6.如图,在一个由4×4个小正方形组成的正方形 格中,阴影部分面积与正方形ABCD 面积的比是 ( ) A . 3:4 B .5:8 C .9:16 D .1:2 参考答案1.A 2.A 3.S 3=S 2+S 7+S 8. 4.D 5.S △ABF =S 四边形AFCD . 6.B2019-2020学年数学中考模拟试卷一、选择题1.如图,小明书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是()A.SSS B.SAS C.ASA D.AAS2.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1.5小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距40千米时,t=32或t=72,其中正确的结论有()A.1个B.2个C.3个D.4个3.点P(﹣3,m+1)在第二象限,则m的取值范围在数轴上表示正确的是()A. B.C. D.4.如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,AB长为半径画弧,交边AD于点F;②再分别以B,F为圆心画弧,两弧交于平行四边形ABCD内部的点G处;③连接AG并延长交BC于点E,连接BF,若3BF=, 2.5AB=,则AE的长为( )A.2B.4C.8D.55.如图,点是边长为1的菱形对角线上的一个动点,点,分别是边,的中点,则的最小值是( )A. B.1 C. D.26.方程组的解是( )A.B. C. D.7.多项式4x-x 3分解因式的结果是( ) A .()2x 4x-B .()()x 2x 2x -+C .()()x x 2x 2-+D .2x(2x)-8.一几何体的三视图如图所示,这个几何体是( )A .四棱锥B .圆锥C .三棱柱D .四棱柱9.如图,水平的讲台上放置的圆柱笔筒和长方体形粉笔盒,它的俯视图是( )A.B. C.D.10.从甲,乙,丙三人中任选一名代表,甲被选中的可能性是A.12B.1C.23D.1311.分解因式3a2b﹣6ab+3b的结果是()A.3b(a2﹣2a)B.b(3a2﹣6a+1)C.3(a2b﹣2ab)D.3b(a﹣1)212.在整数范围内,有被除数=除数×商+余数,即a=bq+r(a≥b,且b≠0,0≤r<b),若被除数a和除数b确定,则商q和余数r也唯一确定,如:a=11,b=2,则11=2×5+1此时q=5,r=1.在实数范围中,也有a=bq+r(a≥b且b≠0,商q为整数,余数r满足:0≤r<b),若被除数是,除数是2,则q与r的和( )A.﹣4 B.﹣6 C.-4 D.-2二、填空题13.如图,矩形ABCD中,AB=6,AD=,点E是BC的中点,点F在AB上,FB=2,P是矩形上一动点.若点P从点F出发,沿F→A→D→C的路线运动,当∠FPE=30°时,FP的长为_____.14.计算:(﹣12)2=_____.15.如图,扇形纸扇完全打开后,∠BAC=120°,AB=AC=30厘米,则BC的长为_____厘米.(结果保留π)16.若关于x 的一元二次方程2230x x m -+-=有两个相等的实数根,则m 的值是______________.17.如图,已知△ABC 的周长是21,OB ,OC 分别平分∠ABC 和∠ACB ,OD ⊥BC 于D ,且OD =4,△ABC 的面积是_____.18.计算:(a+b )(2a ﹣2b )=_____. 三、解答题19.已知:△ABC 的两边AB 、BC 的长是关于x 的一元二次方程x 2﹣(2k+2)x+k 2+2k =0的两个实数根,第三边长为10.问当k 为何值时,△ABC 是等腰三角形?20.如图,已知⊙O 是等边三角形ABC 的外接圆,点D 在圆上,过A 作AE ∥BC 交CD 延长线于E.(1)求证:EA 是⊙O 的切线;(2)若BD 经过圆心O ,其它条件不变,则△ADE 与圆重合部分的面积为_____.(在备用图中画图后,用阴影标出所求面积)21.小张在网上销售一种成本为20元/件的T 恤衫,销售过程中的其他各种费用(不再含T 恤衫成本)总计40(百元),若销售价格为x(元/件),销售量为y(百件),当30≤x≤50时,y 与x 之间满足一次函数关系,且当x =30时,y =5,有关销售量y(百件)与销售价格x(元/件)的相关信息如下:(1)请在表格中直接写出当30≤x≤50时,y与x的函数关系式;(2)求销售这种T恤衫的纯利润w(百元)与销售价格x(元/件)的函数关系式;(3)销售价格定为多少元/件时,获得的利润最大?最大利润是多少?22.如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,点O在AB上,以点O为圆心,OB 为半径的圆经过点D,交BC于点E(1)求证:AC是⊙O的切线;(2)若OB=2,CD留π).23.为考察甲、乙两种农作物的长势,研究人员分别抽取了6株苗,测得它们的高度(单位:cm)如下:甲:98,102,100,100,101,99;乙:100,103,101,97,100,99.(1)你认为哪种农作物长得高一些?说明理由;(2)你认为哪种农作物长得更整齐一些?说明理由.24.如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,过C作CF∥AB交DE延长线于点F,连接AF、DC.求证:(1)DE=FE;(2)四边形ADCF是菱形.25.已知,抛物线C1:y=- 12x2+mx+m+12(1)①当m=1时,抛物线与x轴的交点坐标为_______;②当m=2时,抛物线与x轴的交点坐标为________;(2)①无论m取何值,抛物线经过定点P________;②随着m的取值的变化,顶点M(x,y)随之变化,y是x的函数,记为函数C2,则函数C2的关系式为:________ ;(3)如图,若抛物线C1与x轴仅有一个公共点时,①直接写出此时抛物线C1的函数关系式;②请在图中画出顶点M满足的函数C2的大致图象,在x轴上任取一点C,过点C作平行于y轴的直线l分别交C1、C2于点A、B,若△PAB为等腰直角三角形,求点C的坐标;(4)二次函数的图象C2与y轴交于点N,连接PN,若二次函数的图象C1与线段PN有两个交点,直接写出m的取值范围.【参考答案】***一、选择题二、填空题14.415.20π16.417.4218.2a 2﹣2b 2三、解答题19.k =8或10【解析】【分析】因为方程有两个实根,所以△>0,从而用k 的式子表示方程的解,根据△ABC 是等腰三角形,分AB =AC ,BC =AC ,两种情况讨论,得出k 的值.【详解】∵△=[﹣(2k+2)]2﹣4(k 2+2k)=4k 2+8k+4﹣4k 2﹣8k=4>0,∴x =()222k --+⎡⎤⎣⎦,∴x 1=k+2,x 2=k ,设AB =k+2,BC =k ,显然AB≠BC,而△ABC 的第三边长AC 为10,(1)若AB =AC ,则k+2=10,得k =8,即k =8时,△ABC 为等腰三角形;(2)若BC =AC ,则k =10,即k =10时.△ABC 为等腰三角形.【点睛】本题考查了一元二次方程的根,公式法,解本题要充分利用条件,选择适当的方法求解k 的值,从而证得△ABC 为等腰三角形.20.(1)见解析;(2)23π.【解析】【分析】(1)根据等边三角形的性质可得:∠OAC=30°,∠BCA=60°,证明∠O AE=90°,可得:AE 是⊙O 的切线;(2)如备用图,根据等边三角形的性质得到BD ⊥AC ,∠ABD=∠CBD=30°,∠BAD=∠BCD=90°,根据平行线的性质得到∠AED=∠BCD=90°,解直角三角形得到AD=2,连接OA ,根据扇形和三角形的面积公式即可得到结论.(1)证明:如图1,连接OA,∵⊙O是等边三角形ABC的外接圆,∴∠OAC=30°,∠BCA=60°,∵AE∥BC,∴∠EAC=∠BCA=60°,∴∠OAE=∠OAC+∠EAC=30°+60°=90°,∴AE是⊙O的切线;(2)如备用图,∵△ABC是等边三角形,BD经过圆心O,∴BD⊥AC,∠ABD=∠CBD=30°,∠BAD=∠BCD=90°,∵EA是⊙O的切线,∴∠EAD=30°,∵AE∥BC,∴∠AED=∠BCD=90°,∵∴AD=2,∵OA=OB ,∴∠OAB=OBA=30°,∴∠AOD=60°,∴△ADE 与圆重合部分的面积=S 扇形AOD -S △AOD=260212236023ππ⋅⨯-⨯=故答案为:23π【点睛】本题考查了作图-复杂作图,切线的判定和性质,扇形的面积计算,正确的作出图形是解题的关键.21.(1)y =﹣110x+8;(2)见解析;(3)销售价格定为60元/件时,获得的利润最大,最大利润是60百元.【解析】【分析】(1)把x =50代入y =150x得y =3,设y 与x 的函数关系式为:y =kx+b ,把x =30,y =5;x =50,y =3,代入解方程组即可得到结论;(2)根据x 的范围分类讨论,由“总利润=单件利润×销售量”可得函数解析式;(3)结合(1)中两个函数解析式,分别依据二次函数的性质和反比例函数的性质求其最值即可.【详解】(1)把x =50代入y =150x得y =3, 设y 与x 的函数关系式为:y =kx+b ,∵当x =30时,y =5,当x =50时,y =3,∴530350k b k b =+⎧⎨=+⎩, 解得:1k 10b 8⎧=-⎪⎨⎪=⎩,∴y 与x 的函数关系式为:y =﹣1x+8;故答案为:y =﹣110x+8; (2)当30≤x≤60时,w =(x ﹣20)(﹣0.1x+8)﹣40=﹣0.1x 2+10x ﹣200;当60<x≤80时,w =(x ﹣20)• 150x ﹣40=﹣3000x+110; (3)当30≤x≤60时,w =﹣0.1x 2+10x ﹣200=﹣0.1(x ﹣50)2+50,∴当x =50时,w 取得最大值50(百元);当60<x≤80时,w =﹣3000x +110, ∵﹣3000<0,∴w 随x 的增大而增大,当x =60时,w 最大=60(百元),答:销售价格定为60元/件时,获得的利润最大,最大利润是60百元.【点睛】本题主要考查二次函数和反比例函数的应用,理解题意依据相等关系列出函数解析式,并熟练掌握二次函数和反比例函数的性质是解题的关键.22.(1)见解析;(2)23π-【解析】【分析】(1)欲证明AC 是⊙O 的切线,只要证明OD ⊥AC 即可.(2)证明△OBE 是等边三角形即可解决问题.【详解】(1)证明:连接OD ,如图,∵BD 为∠ABC 平分线,∴∠1=∠2,∵OB =OD ,∴∠1=∠3,∴∠2=∠3,∵∠C =90°,∴∠ODA =90°,∴OD ⊥AC ,∴AC 是⊙O 的切线.(2)过O 作OG ⊥BC ,连接OE ,则四边形ODCG 为矩形,∴GC =OD =OB =2,OG =CD ,在Rt △OBG 中,利用勾股定理得:BG =1,∴BE =2,则△OBE 是等边三角形,∴阴影部分面积为260?2360π⨯﹣12=23π- 【点睛】本题考查切线的判定和性质,等边三角形的判定和性质,思想的面积公式等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.23.甲组数据的平均数为100cm ;乙组数据的平均数为100cm ;(2)甲种农作物长得比较整齐.【解析】【分析】(1)根据平均数的计算公式分别把这6株农作物的高度加起来,再除以6即可;(2)先算出甲与乙的方差,再进行比较,方差越小的,农作物长势越整齐,即可得出答案.【详解】(1)甲组数据的平均数=16×(98+102+100+100+101+99)=100(cm ); 乙组数据的平均数=16×(100+103+101+97+100+99)=100(cm ); (2)s 2甲=16×[(98﹣100)2+(102﹣100)2+…+(99﹣100)2]=53; s 2乙=16×[(100﹣100)2+(103﹣100)2+…+(100﹣99)2]=103. s 2甲<s 2乙.所以甲种农作物长得比较整齐.【点睛】本题考查了平均数与方差,一般地设n 个数据,x 1,x 2,…x n 的平均数为x ,则方差大,波动性越大,反之也成立.24.(1)详见解析;(2)详见解析.【解析】【分析】(1)由“AAS ”可证AED CEF ∆≅∆,可得DE EF =;(2)由直角三角形的性质可得CD AD =,由对角线互相平分的四边形是平行四边形可证四边形ADCF 是平行四边形,即可证四边形ADCF 是菱形.【详解】(1)证明:∵CF AB ∥ ,∴DAC ACF ∠∠=,又∵AE EC AED CEF ∠∠=,= ,∴AED CEF AAS ≌(), ∴DE EF =.(2)∵90ACB ∠︒=,D 是AB 的中点,∴CD AD =∵DE EF AE EC =,=∴四边形ADCF 是平行边形又∵AD CD =∴四边形ADCF 是菱形.【点睛】本题考查了菱形的判定和性质,全等三角形的判定和性质,直角三角形的性质,灵活运用这些性质进行推理是本题的关键.25.(1)(﹣1,0)(3,0);(﹣1,0)(5,0);(2)(-1,0); y=12 (x+1);(3)点C 的坐标为(1,0)或(-3,0);(4)-12<m≤0 【解析】【分析】(1)①把m=1,y=0分别代入抛物线C1,得到一个一元二次方程,解方程即可求出交点横坐标。
图形面积的计算(通用版)(含答案)

图形面积的计算(通用版)试卷简介:检查学生对于面积问题的处理思路,公式法和割补法常常借助于特殊角,构造直角三角形来进行计算,转化法常常利用等(同)底、等(同)高模型来转化面积进行计算,需要学生能够辨识图形特点,选择合适的方法。
一、单选题(共8道,每道8分)1.由7个形状、大小完全相同的正六边形组成的网格如图所示,正六边形的顶点称为格点.已知每个正六边形的边长均为1,△ABC的顶点都在格点上,则△ABC的面积为( )A.2B.C. D.答案:B解题思路:如图,过点C作CD⊥AB于点D.可求得,,.试题难度:三颗星知识点:三角形面积问题2.如图,边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积为( )A. B.C. D.答案:D解题思路:如图,设BC与交于点E,连接AC.由题意得,,∴点在正方形的对角线AC上,∴.∵,∴为等腰直角三角形,∴.易得,∴这两个正方形重叠部分的面积为试题难度:三颗星知识点:割补求面积3.如图,四边形ABCD中,AB=2,CD=1,∠A=60°,∠B=∠D=90°,则四边形ABCD的面积为( )A. B.C. D.答案:D解题思路:考虑求面积的三种处理思路:①公式法;②割补法;③转化法.显然若求四边形ABCD的面积,可以利用割补法求面积.若采用分割求和求面积,无论是连接AC还是BD,分割出来的三角形并不能直接求出其面积,所以分割求和行不通,采用补形作差求面积.如图,延长AD,BC交于点E,∵∠A=60°,∠B=90°,∴∠E=30°.在Rt△EAB中,AB=2,∴.在Rt△EDC中,CD=1,∴,∴△EAB的面积为,△EDC的面积为,∴四边形ABCD的面积为.试题难度:三颗星知识点:割补求面积4.如图,菱形ABCD和菱形EFGD的边长分别为4和6,∠A=120°,则图中阴影部分的面积为( )A. B.C. D.答案:A解题思路:阴影部分是一个三角形,首先想到三角形面积公式,但是我们发现底或者高并不好求,那么考虑转化—借助于菱形的边和对角线.如图,连接BD,过点D作DM⊥EG,垂足为点M.易知EG∥DB,则(同底等高),在△EDM中,∵ED=6,∠MED=30°,∴,,∴,则.试题难度:三颗星知识点:同底等高模型转化面积5.正方形ABCD,正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,且G为BC的三等分点,R为EF中点.若正方形BEFG的边长为4,则△DEK的面积为( )A.12B.16C.20D.24答案:B解题思路:如图,连接DB,GE,FK,则DB∥GE∥FK,由题意,得.∴.试题难度:三颗星知识点:转化法(等底或等高)求面积6.如图,将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到,点B经过的路径为弧.若∠BAC=60°,AC=1,则图中阴影部分的面积为( )A. B.C. D.答案:A解题思路:阴影部分的面积=,根据扇形面积公式可以求得.试题难度:三颗星知识点:扇形面积的计算7.如图,在矩形ABCD中,AB=4cm,BC=3cm,点P是AB上除A,B外任一点,对角线AC,BD相交于点O,DP,CP分别交AC,BD于点E,F.若△ADE和△BCF的面积之和为,则四边形PEOF的面积为( )A. B.C. D.答案:A解题思路:∵四边形ABCD为矩形,∴AD=BC=3cm,AD⊥AP,BC⊥BP,∴.∵,,∴.∵,∴.试题难度:三颗星知识点:矩形的性质8.如图,在中,是斜边的中点,过作于,连接交于;过作于,连接交于;过作于,连接交于;…;如此继续.若分别记,,,…,的面积为,则( )A. B.C. D.答案:D解题思路:易知,∴△与△同底等高,面积相等,依次类推,,,…,的面积都可以转化为,,…,的面积,且,,…,都与原△ABC相似.∵,∴;∵,∴,∴,∵,∴,∴;…∴.试题难度:三颗星知识点:相似三角形的判定与性质二、填空题(共4道,每道9分)9.如图,在△ABC中,已知点D,E,F分别为BC,AD,CE的中点,若,则阴影部分的面积为____.答案:2解题思路:∵D是BC的中点,∴.∵E是AD的中点,∴,∴.∵F是EC的中点,∴,∴,即阴影部分的面积为2.试题难度:知识点:转化法(等底或等高)求面积10.如图为△ABC与△DEC重叠的情形,其中点E在BC上,AC与DE交于点F,且AB∥DE.若△ABC与△DEC的面积相等,且EF=9,AB=12,则DF=____.答案:7解题思路:易知△CEF∽△CBA,∵,∴S△CEF:S△CBA,∴DF=7.试题难度:知识点:三角形的面积11.如图,在矩形ABCD中,E是AD的中点,F是CE的中点,若△BDF的面积为6,则矩形ABCD的面积为____.答案:48解题思路:如图,延长DF交BC于点G,易证△DEF≌△GCF,∴,,∴,.∵E是AD的中点,即,∴CG=BG,,∴,,∴.试题难度:知识点:转化法(等底或等高)求面积12.如图,已知正方形ABCD的面积为120,E是AB的中点,F是BC的中点,EC分别交BD,DF于点G,H.则四边形BGHF的面积为____.答案:14解题思路:如图,连接GF.∵E是AB的中点,F是BC的中点,∴,.易证△GBE≌△GBF,∴.设,由得,,∴x=4.∴.试题难度:知识点:割补求面积。
五年级数学思维《平面图形面积计算》专题训练

五年级数学思维《平面图形面积计算》专题训练一、选择题(每小题6分,共60分)1 平行四边形的底扩大到原来的3倍,高扩大到原来的3倍,它的面积().(A)扩大到原来的3倍(B)扩大到原来的9倍(C)扩大到原来的6倍(D)不变2 一个梯形的上、下底各扩大到原来的5倍,它的面积扩大到原来的()倍.(A)5 (B)10 (C)25 (D)不一定3 如图,梯形中两个阴影部分的大小关系是().(A)①=②(B)①>②(C)①<②(D)无法比较4 一批钢管整齐地堆放在一起,最上层有5根,最下层有16根,每两层柜差1根.这批钢管共有()根.(A)120 (B)126 (C)231 (D)2525 一个梯形,高是4m,若上底和下底不变,高增加2m后,面积增加8㎡,那么原来梯形的面积是()㎡.(A)42 (B)16 (C)21 (D)326 如图,甲、乙两点分别为长方形宽的中点,那么图中面积相等的所有三角形是().(A)A、B和C (B)D和E (C)A和B (D)B和C7 如图,两个正方形的阴影部分的面积是26cm2,那么大正方形内的空白部分面积是()cm2.(A)25 (B)15 (C)12.5 (D)108 如图,平行线间的三个图形,比较它们的面积是().(A)平行四边形大(B)三角形大(C)梯形大(D)相等9 牧羊人用15段每段长2米的篱笆,一面靠墙围成一个正方形或长方形羊圈,则羊圈的最大面积是()平方米.(A)100 (B)108 (C)112 (D)122 10 如图,每个小方格面积为1,那么△ABC面积为().(A)10(B)11(C)12(D)11.5二、解答题(每题12分,共60分)11 如图,正方形的一组对边中,一条边增加17cm,另一条边减少10cm,这样就变成梯形,这时梯形的下底长是上底长的4倍.问:这个梯形的面积是多少?12 如图,将一个长方形分成一个三角形和一个梯形,其中三角形的面积比梯形的面积小60cm2,问:梯形的面积是多少?13 如图,正方形ABCD的边长为4cm,△BCF的面积比△DEF的面积多2cm2,求DE的长度.14 如图,已知△ABC的面积等于梯形BCDE的面积,求BC的长.(单位:cm)15 如图,已知长方形ABCD的长BC=l2厘米,宽DC=8厘米,并且BF=CG,三角形EFC的面积是32平方厘米,那么线段HG的长度是多少厘米?。
五年级数学上册图形面积(一)专题练习题

五年级数学上册图形面积(一)专题练习题一,填空题A,三角形1、两个完全一样的三角形可以拼成一个(),一个三角形的面积是这个()形的(),所以三角形的面积=(),字母表示()。
2、一个三角形的底是7分米,是高的2倍,它的面积是()平方厘米。
3、一个直角三角形,它的两条直角边分别是6cm和8cm,它的面积是()4、一个三角形的底是4分米,高是30厘米,面积是()平方分米。
5、两个完全一样的三角形能拼()所以三角形的面积等于()。
用字母表示是()。
6、一个三角形底是5cm,高是7cm,面积是()。
7、一个三角形和一个平行四边形面积相等,高也相等,则三角形的底是平行四边形底的()。
一个三角形的面积是30平方厘米,底是6厘米,高是()厘米。
8、一个三角形的高是7分米,底是8分米,和它等底等高的平行四边形的面积是()平方分米。
9、一个三角形的面积是4.8平方米,与它等底等高的平行四边形的面积是()10、一个三角形的面积比它等底等高的平行四边形的面积少12.5平方分米,平行四边形的面积是()平方分米,三角形的面积()平方分米。
11、一个三角形和一个平行四边形的面积相等,底也相等,如果三角形的高是10米,那么平行四边形的高是()米;如果平行四边形的高是10米,那么三角形的高是()米。
B,平行四边形1、一个平行四边形,沿它的一条高剪开,通过平移拼成长方形。
这个长方形的长与原来平行四边形的()相等;原平行四边形的高与长方形的()相等。
2、一个平行四边形的面积是20平方米,高是4米,它的底是(),与它等底等高的三角形面积是()平方米。
3、一个平行四边形的面积是48厘米2 ,高是6厘米,底是()厘米。
4、一个平行四边形的面积是48平方分米,与它等底等高的三角形的面积是()平方分米。
5、两个完全一样的三角形可以拼成一个平行四边形,这个平行四边形的底就是(),这个平行四边形的高也就是(),因为平行四边形的面积等于(),所以三角形的面积等于()。
图形的面积计算公式

图形的面积计算公式1、长方形的周长=(长+宽)×2C=(a+b)×22、正方形的周长=边长×4C=4a3、长方形的面积=长×宽S=ab4、正方形的面积=边长×边长S=a.a5、三角形的面积=底×高÷2S=ah÷26、平行四边形的面积=底×高S=ah7、梯形的面积=(上底+下底)×高÷2S=(a+b)h÷28、圆形直径=半径×2 圆形半径=直径÷2d=2r r= d÷29、圆的周长=圆周率×直径=圆周率×半径×2c=πd =2πr10、圆的面积=圆周率×半径×半径S=πr ^211、长方体的表面积=(长×宽+长×高+宽×高)×2S=(ab+bc+ca)×212、长方体的体积=长×宽×高V =abh13、正方体的表面积=棱长×棱长×6S =6a14、正方体的体积=棱长×棱长×棱长V=a.a.a15、圆柱的侧面积=底面圆的周长×高S=ch16、圆柱的表面积=上下底面面积+侧面积S=2πr +2πrh=2π(d÷2)+2π(d÷2)h=2π(C÷2÷π) +Ch17、圆柱的体积=底面积×高V=ShV=πrh=π(d÷2)h=π(C÷2÷π)h18、圆锥的体积=底面积×高÷3V=Sh÷3=πr h÷3=π(d÷2)h÷3=π(C÷2÷π)h÷319、长方体(正方体、圆柱体)的体积=底面积×高V=Sh。
专题05平面直角坐标系中求图形面积(解析版)

专题05平面直角坐标系中求图形面积类型一、直接用公式求面积例1.如图,在平面直角坐标系中,点()0,4A b 为y 轴正半轴上一点,点()3,0B b 是x 轴正半轴上一点,其中b 满足()316b +=.(1)求点A ,B 的坐标.(2)点C 为x 轴上一点,且ABC 的面积为12,求C 点的坐标.【答案】(1)()0,4A ,()3,0B ;(2)点C 的坐标为()3,0-或()9,0【解析】(1)由()316b +=得1b =,∴()04A ,,()30B ,.(2)设点C 的坐标为()0x ,,则3BC x =-,由1()可知4OA =,∴1432ABC S x =⨯⨯-= 12,解得:9x =或3-.∴点C 的坐标为()30-,或()90,.【变式训练1】在平面直角坐标系中,已知点(),0A a ,(),0B b ,a 、b 满足方程组24a b a b +=-⎧⎨-=-⎩,(1)求A 、B 两点的坐标;(2)C 为y 轴正半轴上一点,且6ABC S = ,请求出C 的坐标.【答案】(1)A (-3,0),B (1,0);(2)C (0,3)【解析】(1)解方程组24a b a b +=-⎧⎨-=-⎩,解得:31a b =-⎧⎨=⎩,∴A (-3,0),B (1,0);(2)由(1)可知:AB =4,∵S △ABC =12AB •OC =6,∴12×4×OC =6,解得OC =3,∴C (0,3).故答案为:(1)A (-3,0),B (1,0);(2)C (0,3)类型二、割补法求面积例1.如图,三角形ABC 的面积等于()A .12B .1122C .13D .1132【答案】D【解析】过点A 作AD x ⊥轴于D ,如图所示:由题意可得,3BO =,3OC =,6AD =,3CD =,∴6OD =,∴ABC BOC ACDBODA S S S S ∆∆∆=--梯形111()222BO AD OD BO OC CD AD=+⋅-⋅⋅-⋅⋅111(36)63336222=+⨯-⨯⨯-⨯⨯54918222=--272=,即272ABC S ∆=,故选:D .【变式训练1】如图,连接AB 、BC 、AC ,则△ABC 的面积是()A .312B .3C .212D .2【答案】C【解析】长方形AGDE 的面积为:3×2=6,AGC 的面积:3×1÷2=1.5,CDB △的面积:2×1÷2=1,ABE △的面积:2×1÷2=1,故ABC 的面积为:6-1.5-1-1=2.5,故答案为:C ;【变式训练2】如图,三角形ABO 中,()2,3A --,()2,1B -,A B O ''' 是ABO 平移之后得到的图形,并且O 的对应点O '的坐标为()5,4.(1)作出ABO 平移之后的图形A B O ''' ,并写出A '、B '两点的坐标分别为A '______,B '_____;(2)()00,P x y 为ABO 中任意一点,则平移后对应点P 的坐标为______.(3)求ABO 的面积;【解析】(1)如图,△A 'B 'O '即为所求,A '、B '两点的坐标分别(3,1),(7,3).故答案为:(3,1),(7,3).(2)点P '的坐标为(x 0+5,y 0+4).故答案为:(x 0+5,y 0+4).(3)S △ABO =3×4-12×2×3-12×1×2-12×4×2=4.【变式训练3】在平面直角坐标系xoy 中,△ABC 的位置如图所示,点A ,B ,C 都在格点上.(1)分别写出下列顶点的坐标:A ________;B ________;(2)请在图中画出△ABC 关于y 轴对称的图形△A ′B ′C ′;(3)计算出△ABC 的面积.【答案】(1)(-1,6),(-2,0);(2)见解析;(3)152【解析】(1)由图知,点A 的坐标为(-1,6),点B 的坐标为(-2,0),故答案为:(-1,6),(-2,0)(2)由图得,点C 的坐标为(-4,3),则点A 、B 、C 关于y 轴的对称点A ′,B ′,C ′坐标分别为(1,6),(2,0),(4,3),依次连接A ′,B ′,C ′,即得△A ′B ′C ′,所得图形如图所示(3)过A 、C 作x 轴的垂线,垂足分别为D 、E则ABC AOD CED ADEC S S S S =-- 梯形111(36)31623222=⨯+⨯-⨯⨯-⨯⨯152=类型三、点的存在性问题例1.如图,在平面直角坐标系中,点B ,C 的坐标分别为(),2a a -、()3,2a a ,其中0a >,点A 为BC 的中点,若4BC =,解决下列问题:(1)BC 所在直线与x 轴的位置关系是;(2)求出a 的值,并写出点A ,C 的坐标;(3)在y 轴上是否存在一点P ,使得三角形PAC 的面积等于5?若存在,求出点P 的坐标;若不存在,请说明理由.【答案】(1)平行;(2)()1,2A ,()3,2C ;(3)存在,P 点坐标为()0,3-或()0,7【解析】(1)∵点B ,C 的坐标分别为(),2a a -、()3,2a a ,∴BC 所在直线与x 轴的位置关系是平行.故答案为:平行.(2)∵4BC =,∴()34a a --=,∴1a =,∴B (-1,2),C (3,2),∵A 为BC 的中点,∴()1,2A .(3)存在点P .设()0,P m ,∵2AC =,∴12252m ⨯⨯-=,∴3m =-或7.∴P 为()0,3-或()0,7.【变式训练1】如图,在直角坐标系中,已知()0,2A ,()3,0B ,()3,4C 三点.(1)求四边形AOBC 的面积;(2)是否存在点()0.5P x x ,,使2ABC AOBC S S = 四边形?若存在,求出点P 的坐标.若不存在,请说明理由.【答案】(1)9;(2)存在,()189P --,或(18,9)【解析】如图,∵34C (,),∴33CD ==.∵()34C ,,30B (,),∴404CB =-=,∴4312DCBO S =⨯=四边形.∵()04D ,,()02A ,,∴422DA =-=,∴11236322DCA S =⨯⨯=⨯= .∵DCA AOBC DCBO S S S =- 四边形四边形,∴1239AOBC S =-=四边形.(2)由(1)得1239AOBC S =-=四边形设存在点()0.5P x x ,,使△AOP 的面积为四边形AOBC 的面积的两倍.∵△AOP 的面积=122x x ⨯⨯=,∴29x =⨯,∴18x =±∴存在点P (18,9)或(-18,-9),使△AOP 的面积为四边形AOBC 的面积的两倍.【变式训练2】如图,A (0,3)是直角坐标系y 轴上一点,动点P 从原点O 出发,沿x 轴正半轴运动,速度为每秒2个单位长度,以P 为直角顶点在第一象限内作等腰Rt △APB .设P 点的运动时间为t 秒.(1)若AB ∥x 轴,求t 的值;(2)如图2,当t =2时,坐标平面内有一点M (不与A 重合)使得以M 、P 、B 为顶点的三角形和△ABP 全等,请直接写出点M 的坐标.【答案】(1)t 的值为1.5;(2)点M 的坐标为(3,7),(8,﹣3),(11,1).【解析】(1)过点B 作BC ⊥x 轴于点C ,如图所示.∵AO⊥x轴,BC⊥x轴,且AB∥x轴,∴四边形ABCO为矩形,∴AO=BC=3,∵△APB为等腰直角三角形,∴AP=BP,∠PAB=∠PBA=45°,∴∠OAP=90°-∠PAB=45°,∴△AOP为等腰直角三角形,∴OA=OP=3,∴t=3÷2=1.5(秒),故t的值为1.5;(2)当t=2时,OP=4,①如图3,若△ABP≌△MBP,则AP=PM,过点M作MD⊥OP于点D,∵∠AOP=∠PDM,∠APO=∠DPM,∴△AOP≌△MDP(AAS),∴OA=DM=3,OP=PD=4,∴M(8,-3);②如图,若△ABP≌△MPB,连接AM,则AP=PB=BM,∠APB=∠MBP=90︒,∴AP∥MB,且AP=MB,∴四边形APBM是平行四边形,y轴于点E,又∠APB=∠MBP=90︒,∴四边形APBM是正方形,∴AP=AM,过点M作ME⊥同理可证△AOP≌△MEA(AAS),∴OA=EM=3,OP=AE=4,∴M(3,7);③如图,若△ABP≌△MPB,则AP=BP=BM,过点M 、B 分别作x 轴的垂线,垂足分别为点F 、G ,过点M 作MH ⊥BF 于点H ,∴四边形FGMH 是矩形,∴MH =FG ,MG =HF ,同理可证△AOP ≌△PFB ≌△BHM (AAS ),∴OA =PF =BH =3,OP =BF =MH =4,∴MG =HF =BF -BH =1,OG =OP +PF +FG =11,∴M (11,1);综合以上可得点M 的坐标为(3,7),(8,-3),(11,1).【变式训练3】在平面直角坐标系中,正方形ABCD 的位置如图所示,点A 的坐标为()1,0,点D 的坐标为()0,2.延长CB 交x 轴于点1A ,作第1个正方形111A B C C ;延长11C B 交x 轴于点2A ,作第2个正方形2221A B C C ,…,按这样的规律进行下去,第2021个正方形的面积是______.【答案】404235(2⨯【解析】()()1,0,0,2,A D 正方形ABCD ,1,2OA OD ∴==,,AD AB ===190,DAO ADO DAO BAA ∠+∠=︒=∠+∠1,ADO BAA ∴∠=∠190,DOA ABA ∠=∠=︒ 1,AOD A BA ∴ ∽1,AO OD A B AB ∴=15,2AO AB A B OD ∴== 正方形111A B C C,1113222A B A C ∴====⨯同理可得:22232442A B ⎛⎫=+==⨯ ⎪⎝⎭33332A B ⎛⎫= ⎪⎝⎭······20212021202132A B ⎛⎫= ⎪⎝⎭所以第2021个正方形的面积是22021404233=5.22⎡⎛⎫⎛⎫⨯⎢ ⎪ ⎪⎝⎭⎝⎭⎢⎣⎦故答案为:404235.2⎛⎫⨯ ⎪⎝⎭。
图形面积

【专题精华】【教材深化】 题1 一个长方形打谷场,长60米,宽40米,现在将它的长增加30米,宽增加20米,求增加的面积。
敏捷思维 这道题可以从多个角度来思考。
例如:可以先计算原来的面积,再计算增加后的面积,两者比较求出增加部分的面积;又或者直接计算增加部分的面积等。
全解 解法一:先求原来打谷场的面积: 60×40=2400(平方米) 再求增加后的面积: (60+30)×(40+20)=5400(平方米) 所以面积增加了5400-2400=3000(平方米)。
解法二:直接计算增加部分的面积,可以分成三部分来求(如下图)其中(1)的面积为30×40=1200(平方米);(2)的面积为60×20=1200(平方米);(3)的面积为30×20=600(平方米);所以增加的面积为1200+1200+600= 3000(平方米)。
答:增加的面积是3000平方米。
拓展探究 解决这道题由于思考的角度不同,就产生了不同的解决方法,例如求变化前后相差的方法,割补的方法等,我们可以从类似的题目中运用灵活多样的思考方法来解决问题。
(当然,我们还能从上面这道题里思考出更多的办法,不妨试试) 1.中山路小学操场长90米,宽45米,改造后长增加10米,宽增加5米。
现在操场面积比原来增加多少平方米?2.一个长方形,如果宽不变,长增加6米,那么它的面积增加54平方米;如果长不变,宽减少3米,那么它的面积减小36平方米。
这个长方形原来的面积是多少平方米?(1)(2) (3)60米 30米20米 40米第19讲 图形面积长方形和正方形的面积公式有: 长方形的面积=长×宽 正方形的面积=边长×边长 正方形的面积=对角线×对角线÷2 如果遇到不规则的多边形,我们可以考虑将图形通过平移、割补等方法转变成长方形或正方形,运用长方形的相关知识来解决问题。
专题28 求几何图形面积及面积法解题的问题(解析版)

专题28 求几何图形面积及面积法解题的问题一、几何图形面积公式1.三角形的面积:设三角形底边长为a ,底边对应的高为h ,则面积S=ah/22.平行四边形的面积:设平行四边形的底边长为a ,高为h ,则面积S=ah3.矩形的面积:设矩形的长为a ,宽为b ,则面积S=ab4.正方形的面积:设正方形边长为a ,对角线长为b ,则面积S=222b a = 5.菱形的面积:设菱形的底边长为a ,高为h ,则面积S=ah若菱形的两条对角线长分别为m 、n ,则面积S=mn/2也就是说菱形的面积等于两条对角线乘积的一半。
6.梯形的面积:设梯形的上底长为a,下底长为b ,高为h ,则面积S=(a+b )h/27.圆的面积:设圆的半径为r,则面积S=πr 28.扇形面积计算公式9.圆柱侧面积和表面积公式(1)圆柱的侧面积公式S 侧=2πrh2360r n s π⋅=lr s 21=或(2)圆柱的表面积公式:S 表=2S 底+S 侧=2πr 2+2πrh10.圆锥侧面积公式从右图中可以看出,圆锥的母线L 即为扇形的半径,而圆锥底面的周长是扇形的弧长2πr ,这样,圆锥侧面积计算公式:S 圆锥侧=S 扇形=πrL注意:有时中考题还经常考查圆的周长、扇形的弧长的公式的应用。
(1)圆的周长计算公式为:C=2πr(2)扇形弧长的计算公式为:(3)其他几何图形周长容易计算,不直接给出。
二、用面积法解题的理论知识1.面积方法:运用面积关系来证明或计算平面几何题的方法,称为面积方法,它是几何中的一种常用方法。
2.面积法解题的特点:把已知量和未知量用面积公式联系起来,通过运算达到求证的结果。
所以用面积法来解几何题,几何元素之间关系变成数量之间的关系,只需要计算,有时可以不添置补助线,即使需要添置辅助线,也很容易考虑到。
三、面积方法问题主要涉及以下两部分内容1.证明面积相等的理论依据(1)三角形的中线把三角形分成两个面积相等的部分。
面积专题答案版

专题三组合图形的面积计算1.一个量可以用它的等量来代替;被减数和减数都增加(或减少)同一个数,它们的差不变。
前者是等量公理,后者是减法的差不变性质。
这两个性质在解几何题时有很重要的作用,它能将求一个图形的面积转化为求另一个图形的面积,或将两个图形的面积差转化为另两个图形的面积差,从而使隐蔽的关系明朗化,找到解题思路。
例1小两个正方形组成下图所示的组合图形。
已知组合图形的周长是52厘米,DG=4厘米,求阴影部分的面积。
分析与解:组合图形的周长并不等于两个正方形的周长之和,因为CG部分重合了。
用组合图形的周长减去DG,就得到大、小正方形边长之和的三倍,所以两个正方形的边长之和等于(52-4)÷3=16(厘米)。
又由两个正方形的边长之差是4厘米,可求出大正方形边长=(16+4)÷2=10(厘米),小正方形边长=(16-4)÷2=6(厘米)。
两个正方形的面积之和减去三角形ABD与三角形BEF的面积,就得到阴影部分的面积。
102+62-(10×10÷2)-(10+6)×6÷2=38(厘米2)。
例2两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积。
分析与解:阴影部分是一个高为3厘米的直角梯形,然而它的上底与下底都不知道,因而不能直接求出它的面积。
因为三角形ABC与三角形DEF完全相同,都减去三角形DOC后,根据差不变性质,差应相等,即阴影部分与直角梯形OEFC面积相等,所以求阴影部分的面积就转化为求直角梯形OEFC的面积。
直角梯形OEFC的上底为10-3=7(厘米),面积为(7+10)×2÷2=17(厘米2)。
所以,阴影部分的面积是17厘米2。
例3 下页上图中,ABCD是7×4的长方形,DEFG是10×2的长方形,求三角形BCO与三角形EFO的面积之差。
分析:直接求出三角形BCO与三角形EFO的面积之差,不太容易做到。
图形的面积计算
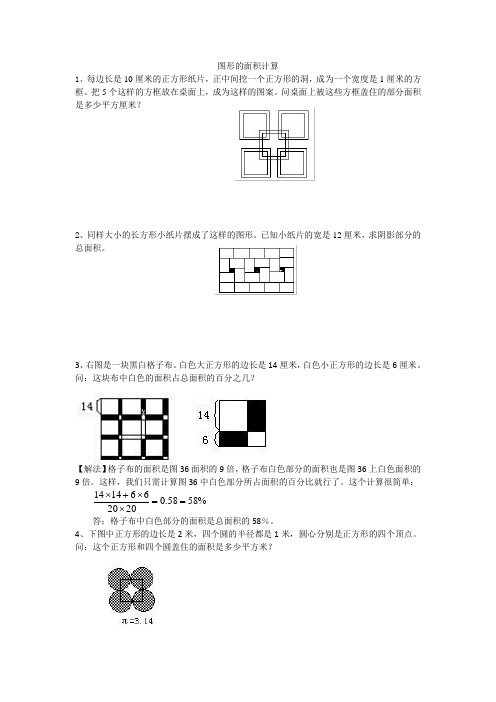
图形的面积计算1、每边长是10厘米的正方形纸片,正中间挖一个正方形的洞,成为一个宽度是1厘米的方框。
把5个这样的方框放在桌面上,成为这样的图案。
问桌面上被这些方框盖住的部分面积是多少平方厘米?2、同样大小的长方形小纸片摆成了这样的图形。
已知小纸片的宽是12厘米,求阴影部分的总面积。
3、右图是一块黑白格子布。
白色大正方形的边长是14厘米,白色小正方形的边长是6厘米。
问:这块布中白色的面积占总面积的百分之几?【解法】格子布的面积是图36面积的9倍,格子布白色部分的面积也是图36上白色面积的9倍。
这样,我们只需计算图36中白色部分所占面积的百分比就行了。
这个计算很简单: %5858.02020661414==⨯⨯+⨯ 答:格子布中白色部分的面积是总面积的58%。
4、下图中正方形的边长是2米,四个圆的半径都是1米,圆心分别是正方形的四个顶点。
问:这个正方形和四个圆盖住的面积是多少平方米?【解法】每个圆和正方形的公共部分是一个扇形,它的面积是圆的面积的四分之一。
因此,整个图形的面积等于正方形的面积加上四块四分之三个圆的面积。
而四块四分之三个圆的面积等于圆面积的三倍。
因此,整个图形的面积等于正方形的面积加上圆面积的三倍,也就是2×2+π×1×1×3≈13.42(平方米)。
答:这个正方形和四个圆盖住的面积约是13.42平方米。
5、有三条线段A、B、C,A长2.12米,B长2.71米,C长3.53米,以它们作为上底、下底和高,可以作出三个不同的梯形。
问:第几个梯形的面积最大?【解法】首先注意,梯形的面积=(上底+下底)×高÷2。
但我们现在是比较三个梯形面积的大小,所以不妨把它们的面积都乘以2,这样只须比较(上底+下底)×高的大小就行了。
我们用乘法分配律:第一个梯形的面积的2倍是:(2.12+3.53)×2.71=2.12×2.17+3.53×2.71第二个:(2.71+3.53)×2.12=2.71×2.12+3.53×2.12第三个:(2.12+2.71)×3.53=2.12×3.53+2.71×3.53先比较第一个和第二个。
基本图形的面积计算方法

基本图形的面积计算方法面积是研究几何学中的一个重要概念,它描述了一个物体或图形所占据的平面范围的大小。
在几何学中,面积的计算方法与图形的形状有关,在本文中,我将介绍一些常见基本图形的面积计算方法。
一、三角形的面积计算方法三角形是最简单的平面图形之一,其面积计算公式为:面积 = 底边长度 ×高 / 2其中,底边长度是指三角形的底边的长度,高是指从底边到与之平行的顶点的垂直距离。
二、矩形的面积计算方法矩形是一个拥有四个直角的四边形,其面积计算公式为:面积 = 长 ×宽其中,长代表矩形的长边的长度,宽代表矩形的短边的长度。
三、正方形的面积计算方法正方形是一种特殊的矩形,其四条边相等,且都是直角形成的。
正方形的面积计算公式为:面积 = 边长 ×边长其中,边长指正方形的任意一条边的长度。
四、圆的面积计算方法圆是一个几何学中重要的图形,其面积计算公式为:面积= π × 半径 ×半径其中,π是一个无理数,可以近似取为3.14或22/7,半径代表圆的半径长度。
五、椭圆的面积计算方法椭圆是一个具有两个焦点的几何图形,其面积计算公式为:面积= π × 长半径 ×短半径其中,长半径代表椭圆的长轴的一半长度,短半径代表椭圆的短轴的一半长度。
六、正多边形的面积计算方法正多边形是一个具有相等边长和相等内角的多边形,例如正三角形、正四边形等。
对于正多边形的面积计算,我们可以使用以下公式:面积 = (边长 ×边长) × (边数/ 4 × tan(π / 边数))其中,边长代表正多边形的任意一条边的长度,边数代表正多边形的边的数量。
通过以上的介绍,我们可以看到不同基本图形的面积计算方法是不同的,但都可以通过找到合适的公式来求解。
掌握这些方法对于几何学的学习和实际应用都具有重要意义。
最后,需要注意的是,在应用这些面积计算方法时,要确保所使用的长度单位一致,以求得准确的面积值。
专题 多乘多与图形面积(学生版)

专题2多乘多与图形面积1.如图,正方形卡片A 类,B 类和长方形卡片C 类若干张,如果要拼一个长为(a +2b ),宽为(3a +b )的大长方形,则需要C 类卡片()张.A .5B .6C .7D .82.如图可以通过不同的方法计算图形的面积,可以得到一个数学等式.这个大正方形边长为a +b +c ,用()2a b c ++可求得其面积.同时,大正方形的面积也等于6个长方形和3个正方形的面积之和;已知a +b +c =8,22226a b c ++=,则ab +bc +ac 的值是()A .34B .23C .20D .193.通过计算比较图1,图2中阴影部分的面积,可以验证的计算式子是()A .a (b -x )=ab -axB .b (a -x )=ab -bxC .(a -x )(b -x )=ab -ax -bx D .(a -x )(b -x )=ab -ax -bx +x 24.挪威数学家阿贝尔,年轻时就利用阶梯形,发现了一个重要的恒等式——阿贝尔公式:如图是一个简单的阶梯形,可用两种方法把图形分割成为三个长方形.利用它们之间的面积关系,可以得到:112233a b a b a b ++=()A .()()()()12312121233a b b a a b b a a a b -++-+++B .()()()()11212121232a b b a a b b a a a b -++-+++C .()()()()11212231233a b b a a b b a a a b -++-+++D .()()()()12312231232a b b a a b b a a a b -++-+++5.“数形结合”思想是一种常用的数学思想,其中“以形助数”是借助图形来理解和记忆数学公式.例如,根据图1的面积可以说明多项式的乘法运算(2a+b)(a+b)=2a2+3ab+b2,那么根据图2的面积可以说明多项式的乘法运算是()A.(a+3b)(a+b)=a2+4ab+3b2B.(a+3b)(a+b)=a2+3b2C.(b+3a)(b+a)=b2+4ab+3a2D.(a+3b)(a﹣b)=a2+2ab﹣3b26.如图,甲、乙、丙、丁四位同学给出了四种表示最大长方形面积的方法:①(2a+b)(m+n);②2a(m+n)+b(m+n);③m(2a+b)+n(2a+b);④2am+2an+bm+bn.你认为其中正确的个数有()A.1个B.2个C.3个D.4个7.用如图的正方形和长方形卡片若干张,拼成一个长为2a+b,宽为(a+b)的矩形,需要B类卡片_____张.8.如图,大正方形ABCD的边长为a,小正方形CEFG的边长为b,则阴影部分的面积是_____;9.如图(图中长度单位:m )阴影部分的面积是_____m 2(用含x 的式子表示),面积表达式是_____次三项式.10.如图,现有正方形卡片A 类、B 类和长方形卡片C 类各若干张,如果要拼一个长为()3a b +,宽为()32a b +的大长方形,那么需要C 类卡片的张数是___________;11.通过计算几何图形的面积可以得到一些恒等式,根据如图的长方形面积写出的恒等式为______.12.如图,甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式:①2(a+b )(m+n );②2a (m+n )+b (m+n );③m (2a+b )+n (2a+b );④2am+2mn+bm+bn ,你认为其中正确的有______13.如图,某市修建了一个大正方形休闲场所,在大正方形内规划了一个正方形活动区,连接绿地到大正方形四边的笔直小路如图所示.已知大正方形休闲场所的边长为6a 米,四条小路的长与宽都为b 米和2b米.阴影区域铺设草坪,草坪的造价为每平米30元.(1)用含a 、b 的代数式表示草坪(阴影)面积并化简.(2)若a =6,b =6,计算草坪的造价.14.小明计划用三种拼图将长为(520)a b +米,宽为(315)a b +米的客厅铺上一层漂亮的图案.其中A 和B 两种拼图为正方形,C 为长方形,边长如图所示.如果拼图不允许切割,请你帮助小明计算一下:(1)分别需要A ,B 和C 三种拼图多少块?(2)若A ,B 和C 三种拼图的单价分别为5元,3元,2元,且购买任意一种拼图的数量超过100块时,这种拼图的价格按照八折优惠,求小明的总花费.15.如图,在长为3a +2,宽为2b -1的长方形铁片上,挖去长为2a +4,宽为b 的小长方形铁片(1)求剩余部分面积.(2)求出当a =3,b =2时的面积.16.如图,将一个边长为a b +的正方形图形分割成四部分(两个正方形和两个长方形),请认真观察图形.解答下列问题:(1)根据图中条件.试通过两种方法求出该图形的总面积,并用公式的形式将两种关系表达出来;(2)当图中的(),0a b a b >>满足2257a b +=,12ab =.求a b +的值.17.(1)已知三个连续的奇数,若中间那个为n,求这三个奇数的积.(2)求图中阴影部分的面积.18.如图,请用两种不同的方法求阴影部分的面积.19.某学校教学楼前有一块长为(62)a b +米,宽为(42)a b +米的长方形空地要铺地砖,如图所示,空白的A 、B 两正方形区域是草坪,不需要铺地砖.两正方形区域的边长均为()a b +米.请你求出要铺地砖的面积是多少?20.当我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式,例如,由图1,可得等式:(a +2b )(a +b )=a 2﹣3ab +2b 2.(1)由图2,可得等式:.(2)利用(1)中所得到的结论,解决下面的问题:已知a +b +c =12,ab +bc +ac =28,求a 2+b 2+c 2的值;(3)计算(2a +b )(a +3b )=.利用图3中的纸片(足够多),画出一种拼图,使该拼图可用来验证上面的等式(要求图中有长度和面积的标识)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题23 面积的计算
○阅 ○读 ○与 ○思 ○考
计算图形的面积是几何问题中一种重要题型,计算图形的面积必须掌握如下与面积有关的重要知识:
1.常见图形的面积公式;
2.等积定理:等底等高的两个三角形面积相等; 3.等比定理:
(1) 同底(或等底)的两个三角形面积之比等于等于对应高之比;同高(或等高)的两个三角形面积之比等于等于对应底之比.
(2) 相似三角形的面积之比等于对应线段之比的平方. 熟悉下列基本图形、基本结论:
例 题 与 求 解
【例1】如图,△ABC 内三个三角形的面积分别为5,8,10,四边形AEFD 的面积为x ,
则x =________. (黄冈市竞赛试题)
解题思路:图中有多对小三角形共高,所以可将面积比转化为线段之比作为解题突破口.
【例2】如图,在△ABC 中,已知BD 和CE 分别是两边上的中线,并且BD ⊥CE ,BD =4,CE =6,那么△ABC 的面积等于 ( ) (全国初中数学联赛)
A .12
B .14
C .16
D .18 解题思路:由中点想到三角形中位线,这样△ABC 与四边形BCD
E 面积存在一定的关系.
例1图
C
【例3】如图,依次延长四边形ABCD 的边AB ,BC ,CD ,DA 至E ,F ,G ,H ,使BE AB =CF
BC =DG CD =AH
DA =m ,若S 四边形EFGH =2S 四边形ABCD ,求m
的值.
解题思路:添加辅助线将四边形分割成三角形,充分找出图形面积比与线段比之间的关系,建立关于m 的方程.
【例4】如图,P ,Q 是矩形ABCD 的边BC 和CD 延长线上的两点,PA 与CQ 相交于点E ,
且∠PAD =∠QAD ,求证:S 矩形ABCD =S △APQ .
解题思路:图形含全等三角形、相似三角形,能得到相等的线段、等积式,将它们与相应图形联系起来,促使问题的转化.
【例5】如图,在Rt △ABC 中,∠A =90°,AB =8,AC =6,若动点D 从点B 出发,沿线段BA 运动到点A 为止,移动速度为每秒2个单位长度. 过点D 作DE ∥BC 交AC 于点E ,设动点D 运动的时间为x 秒,AE 的长为y .
(1) 求出y 关于x 的函数关系式,并写出自变量x 的取值范围;
(2) 当x 为何值时,△BDE 的面积S 有最大值,最大值为多少? (江西省中考试题)
解题思路:对于(1)利用△ADE ∽△ABC 可得y 与x 的关系式;对于(2)先写出S 关于x 的函
例2图
C
例3图
例4图
数关系式,再求最大值.
【例6】如图,设P 为△ABC 内任意一点,直线AP ,BP ,CP 交BC ,CA ,AB 于点D ,E ,F .
求证:(1) PD AD +PE BE +PF
CF =1;
(2)PA AD +PB BE +PC CF =2
解题思路:过点A ,P 分别作BC 的垂线,这样既可得到平行线,产生比例线段,又可以
与面积联系起来,把PA
AD 转化为面积比,利用面积法证明.
○能 ○力 ○训 ○练
A 级
1.如图, ABCD 中,AE ∶BE =1∶2,S △AEF =6cm 2,则S △CDF 的值为________. (济南市中考试题)
2.如图,正六边形ABCDEF 的边长为23cm ,P 为正六边形内任一点,则点P 到各边距
例5图
C
例6图
D
离之和为_______.
3.如图,P 是边长为8的正方形ABCD 外一点,PB =PC ,△PBD 的面积等于48,则△PBC 的面积为_____________. (北京市竞赛试题)
4.如图,已知△BOF ,△AOF ,△BOD ,△COE 的面积分别为30,40,35,84,则△ABC 的
面积为________. (浙江省竞赛试题)
5.如图,已知AD 是Rt △ABC 斜边BC 上的高,DE 是Rt △ADC 斜边上的高,如果DC ∶AD =1∶2, S △DCE =a ,那么S △ABC 等于 ( ) (金华市中考试题)
A .4a
B .9a
C .16a
D .25a
6.如图,已知M 是 ABCD 边AB 的中点,CM 交BD 于点E ,则图中阴影部分面积与 ABCD 的面积之比为( ) (山西省中考试题)
A .16
B .14
C .13
D .512
7.如图,在△ABC 中,DE ∥BC ,DE 分别交AB ,AC 于点D ,E ,若S △ADE =2S △DCE ,则
S
△ADE S
△ABC
第5题图
C
第2题图
C
F
第1题图
第3题图
P
第4题图
D
第6题图
C
等于( )
(浙江省宁波市中考试题)
A .14
B .12
C .23
D .4
9 8.如图,△ABC 是边长为6cm 的等边三角形,被一平行于BC 的矩形所截,AB 被截成
三等分,则图中阴影部分面积面积为( )cm 2. (广东省竞赛试题)
A .4
B .2 3
C .3 3
D .4 3
9.如图,平面上有两个边长相等的正方形ABCD 和 A ′B ′C ′D ′,且正方形A ′B ′C ′D ′的顶点A ′
在正方形ABCD 的中心,当正方形A ′B ′C ′D ′绕A ′ 转动时,两个正方形重合部分的面积必然是一个
定
值
.
这
个
结
论
对
吗
?
证
明
你
的
判
断
.
(“希望杯”邀请赛试题)
10.如图,设凸四边形ABCD 的一组对边AB ,CD 的中点分别为K ,M .求证:S 四边形ABCD =S △ABM +S △DCK..
第8题图
第7
题图
C
第9题图
C'
11.如图1,AB ,CD 是两条线段,M 是AB 的中点,S △DMC ,S △DAC ,S △DBC 分别表示△DMC ,
△DAC ,△DBC 的面积,当AB ∥CD 时,有S △DMC =
S
△DAC +S △DBC
2
………..①.
(1) 如图2,若图1中AB 与CD 不平行时,①式是否成立?请说明理由.
(2) 如图3,若图1中AB 与CD 相交于点O 时, 问S △DMC 与S △DAC 和S △DBC 有何相等关系?试证明你的结论. (安徽省中考试题)
图2
图1
图3
12.如图,在△ABC 中,∠ACB =90°,∠ABC =30°,将△ABC 绕顶点C 顺时针旋转,旋转角为θ(0°<θ<180°),得到△A ′B ′C ′.
(1) 如图1,当AB ∥CB ′时,设A ′B ′与CB 相交于点D ,证明:△A ′CD 是等边三角形; (2) 如图2,连接A ′A ,B ′B ,设△ACA ′和△BCB ′的面积分别为S △ACA ′和S △BCB ′.求证:S △ACA ′∶S △BCB ′=1∶3.
(3) 如图3,设AC 的中点为E ,A ′B ′的中点为P ,AC =a ,连接EP ,当θ=_____时,EP 长度最大,最大值是____________.
(安徽省中考试题)
第10题图
图2
图1
图3
B'
B 级
1.如图,A 在线段BG 上,ABCD 和DEFG 都是正方形,面积分别为7cm 2和11cm 2,则△CDE 的面积等于___________cm 2. (武汉市竞赛试题)
2.如图,P 为正方形ABCD 内一点,PA =PB =10,并且P 到CD 边的距离也等于10,那么
正
方
形
ABCD
的
面
积
是
_______________.
(北京市竞赛试题)
3.如图,四边形ABCD 中,点E ,F 分别在BC ,DC 上,DF FC =1,CE
BE =2,若△ADF 的面积为m ,四边形AECF 的面积为n (n >m ),则四边形ABCD 的面积为___________. (全国初中数学联赛试题)
4.如图,图形ABCD 中,AB ∥CD ,AC 和BD 相交于点O ,若AC =5,BD =12,中位线长为13
2,△AOB 的面积为S 1,△OCD 的面积为S 2,则S 1+S 2=_________. (山东省竞赛试题)
5.如图,分别延长△ABC 的三边AB ,BC ,CA 至A ′,B ′,C ′,使得AA ′=3AB ,BB ′=3BC ,CC ′=3AC ,若S △ABC =1,则S △A ′B ′C ′等于 ( ).
A .18
B .19
C .24
D .27
(
山东省竞赛试题)
第4题图
第3题图
B
第
2题图
第1题图
F。
