河南中考第22题和23题练习附答案
2023年河南洛阳中考英语真题及答案

2023年河南洛阳中考英语真题及答案注意事项:1.本试卷共10页,六个大题,满分120分,考试时间100分钟。
2.本试卷上不要答题,请按答题卡上注意事项的要求直接把答案填写在答题卡上,答在试卷上的答案无效。
一、听力理解(20小题,每小题1分,共20分)第一节听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳答案。
每段对话读两遍。
1.Which club will the boy join?A.A music club.B.A painting club.C.A chess club.2.What will the weather be like this afternoon?A.Sunny.B.Cloudy.C.Windy.3.What’s the possible relationship between the two speakers?A.Father and daughter.B.Doctor and patient.C.Waiter and customer.4.Who likes jiaozi best?A.The man.B.The woman.C.Their friend5.What happened to Kevin?A.He lost the game.B.He left the team.C.He hurt his arm.第二节听下面几段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳答案。
每段对话或独白读两遍。
听下面一段对话,回答第6至第7两个小题。
6.When will the girl give a speech?A.Next Monday.B.Next Wednesday.C.Next Friday.7.What is the girl going to talk about?A.Environmental protection.nguage learning.C.Traditional culture.听下面一段对话,回答第8至第9两个小题。
2023年河南中考数学真题及答案

2023年河南中考数学真题及答案一、选择题1. 下列各数中,最小的数是( )A. -lB. 0C. 1 2. 北宋时期的汝官窑天蓝釉刻花鹅颈瓶是河南博物院九大镇院之宝之一,具有极高的历史价值、文化价值.如图所示,关于它的三视图,下列说法正确的是( )A. 主视图与左视图相同B. 主视图与俯视图相同C. 左视图与俯视图相同D. 三种视图都相同3. 2022年河南省出版的4.59亿册图书,为贯彻落实党的二十大关于深化全民阅读活动的重要精神,建设学习型社会提供了丰富的图书资源.数据“4.59亿”用科学记数法表示为( )A. B. C. D.74.5910⨯845.910⨯84.5910⨯90.45910⨯4. 如图,直线,相交于点O ,若,,则的度数为( )AB CD 180∠=︒230∠=︒AOE ∠A.B. C. D. 30︒50︒60︒80︒5. 化简的结果是( ) 11a a a -+A. 0 B. 1 C. a D.2a -6. 如图,点A ,B ,C 在上,若,则的度数为( )O 55C ∠=︒AOB ∠A. 95°B. 100°C. 105°D. 110°7. 关于x 的一元二次方程的根的情况是( )280x mx +-=A. 有两个不相等的实数根B. 有两个相等的实数根C. 只有一个实数根D. 没有实数根8. 为落实教育部办公厅、中共中央宣传部办公厅关于《第41批向全国中小学生推荐优秀影片片目》的通知精神,某校七、八年级分别从如图所示的三部影片中随机选择一部组织本年级学生观看,则这两个年级选择的影片相同的概率为( )A. B. C. D. 121316199. 二次函数的图象如图所示,则一次函数的图象一定不经过( ) 2y ax bx =+y x b =+A. 第一象限B. 第二象限C. 第三象限D. 第四象限10. 如图1,点P 从等边三角形的顶点A 出发,沿直线运动到三角形内部一点,再从该点沿直线运动ABC 到顶点B .设点P 运动的路程为x ,,图2是点P 运动时y 随x 变化的关系图象,则等边三角形PB y PC=的边长为( )ABCA. 6B. 3C.D. 二、填空题 11. 某校计划给每个年级配发n 套劳动工具,则3个年级共需配发______套劳动工具.12. 方程组的解为______. 35,37x y x y +=⎧⎨+=⎩13. 某林木良种繁育试验基地为全面掌握“无絮杨”品种苗的生长规律,定期对培育的1000棵该品种苗进行抽测.如图是某次随机抽测该品种苗的高度x (cm )的统计图,则此时该基地高度不低于的“无300cm 絮杨”品种苗约有______棵.14. 如图,与相切于点A ,交于点B ,点C 在上,且.若,PA O PO O PA CB CA =5OA =,则的长为______.12PA =CA15. 矩形中,M 为对角线的中点,点N 在边上,且.当以点D ,M ,N 为顶点ABCD BD AD 1AN AB ==的三角形是直角三角形时,的长为______.AD 三、解答题16. (1)计算:;135---+(2)化简:.()()224x y x x y ---17. 蓬勃发展的快递业,为全国各地的新鲜水果及时走进千家万户提供了极大便利.不同的快递公司在配送、服务、收费和投递范围等方面各具优势.樱桃种植户小丽经过初步了解,打算从甲、乙两家快递公司中选择一家合作,为此,小丽收集了10家樱桃种植户对两家公司的相关评价,并整理、描述、分析如下:a .配送速度得分(满分10分):甲:6 6 7 7 7 8 9 9 9 10乙:6 7 7 8 8 8 8 9 9 10b .服务质量得分统计图(满分10分):c .配送速度和服务质量得分统计表: 配送速度得分 服务质量得分项目统计量快递公司 平均数 中位数 平均数 方差 甲 7.8 m 72s 甲乙 8 8 72s 乙根据以上信息,回答下列问题:(1)表格中的______;______(填“>”“=”或“<”). m =2s 甲2s 乙(2)综合上表中的统计量,你认为小丽应选择哪家公司?请说明理由.(3)为了从甲、乙两家公司中选出更合适的公司,你认为还应收集什么信息(列出一条即可)?18. 如图,中,点D 在边上,且.ABC AC AD AB =(1)请用无刻度的直尺和圆规作出的平分线(保留作图痕迹,不写作法).A ∠(2)若(1)中所作的角平分线与边交于点E ,连接.求证:.BC DE DE BE =19. 小军借助反比例函数图象设计“鱼形”图案,如图,在平面直角坐标系中,以反比例函数图象k y x =上的点和点B 为顶点,分别作菱形和菱形,点D ,E 在x 轴上,以点O 为圆心,)A AOCD OBEF 长为半径作,连接.OA AC BF(1)求k 的值;(2)求扇形的半径及圆心角的度数;AOC (3)请直接写出图中阴影部分面积之和.20. 综合实践活动中,某小组用木板自制了一个测高仪测量树高,测高仪为正方形,ABCD 30cm AB =,顶点A 处挂了一个铅锤M .如图是测量树高的示意图,测高仪上的点D ,A 与树顶E 在一条直线上,铅垂线交于点H .经测量,点A 距地面,到树的距离,.求树AM BC 1.8m EG 11m AF =20cm BH =EG 的高度(结果精确到). 0.1m21. 某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种.活动一:所购商品按原价打八折;活动二:所购商品按原价每满300元减80元.(如:所购商品原价为300元,可减80元,需付款220元;所购商品原价为770元,可减160元,需付款610元)(1)购买一件原价为450元的健身器材时,选择哪种活动更合算?请说明理由.(2)购买一件原价在500元以下的健身器材时,若选择活动一和选择活动二的付款金额相等,求一件这种健身器材的原价.(3)购买一件原价在900元以下的健身器材时,原价在什么范围内,选择活动二比选择活动一更合算?设一件这种健身器材的原价为a 元,请直接写出a 的取值范围.22. 小林同学不仅是一名羽毛球运动爱好者,还喜欢运用数学知识对羽毛球比赛进行技术分析,下面是他对击球线路的分析.如图,在平面直角坐标系中,点A ,C 在x 轴上,球网与y 轴的水平距离,,击球AB 3m OA =2m CA =点P 在y 轴上.若选择扣球,羽毛球的飞行高度与水平距离近似满足一次函数关系()m y ()m x ;若选择吊球,羽毛球的飞行高度与水平距离近似满足二次函数关系0.4 2.8y x =-+()m y ()m x . ()21 3.2y a x =-+(1)求点P 的坐标和a 的值.(2)小林分析发现,上面两种击球方式均能使球过网.要使球的落地点到C 点的距离更近,请通过计算判断应选择哪种击球方式.23. 李老师善于通过合适的主题整合教学内容,帮助同学们用整体的、联系的、发展的眼光看问题,形成科学的思维习惯.下面是李老师在“图形的变化”主题下设计的问题,请你解答.(1)观察发现:如图1,在平面直角坐标系中,过点的直线轴,作关于轴对称的()4,0M l y ABC y 图形,再分别作关于轴和直线对称的图形和,则可以111A B C △111A B C △x l 222A B C △333A B C △222A B C △看作是绕点顺时针旋转得到的,旋转角的度数为______;可以看作是向右平移ABC O 333A B C △ABC 得到的,平移距离为______个单位长度.(2)探究迁移:如图,中,,为直线下方一点,作点关2ABCD Y ()090BAD αα∠=︒<<︒P AB P 于直线的对称点,再分别作点关于直线和直线的对称点和,连接,,请AB 1P 1P AD CD 2P 3P AP 2AP 仅就图的情形解决以下问题:2①若,请判断与的数量关系,并说明理由;2PAP β∠=βα②若,求,两点间的距离.AD m =P 3P(3)拓展应用:在(2)的条件下,若,,,连接.当与60α=︒AD =15PAB ∠=︒23P P 23P P 的边平行时,请直接写出的长.ABCD Y AP参考答案一、选择题【1题答案】A【2题答案】A【3题答案】C【4题答案】B【5题答案】B【6题答案】D【7题答案】A【8题答案】B【9题答案】D【10题答案】A二、填空题【11题答案】【答案】3n 【12题答案】【答案】12x y =⎧⎨=⎩【13题答案】【答案】280【14题答案】 【答案】103【15题答案】【答案】21三、解答题【16题答案】 【答案】(1);1524y【17题答案】【答案】(1)7.5; <(2)甲公司,理由见解析(3)还应收集甲、乙两家公司的收费情况.(答案不唯一,言之有理即可)【18题答案】【答案】(1)见解析 (2)见解析【19题答案】【答案】(1(2)60︒(3) 23π-【20题答案】【答案】树的高度为EG 9.1m 【21题答案】【答案】(1)活动一更合算(2)400元 (3)当或时,活动二更合算300400a ≤<600800a ≤<【22题答案】【答案】(1),,()0,2.8P 0.4a =-(2)选择吊球,使球的落地点到C 点的距离更近【23题答案】【答案】(1),.180︒8(2)①,理由见解析;②2βα=2sin m α(3)或。
2024、2024、2024年河南省中考物理试题(word版含答案)

2024年河南省一般中学招生考试试卷物理留意事项:1.本试卷共6页,五大题,22小题,满分70分,考试时间60分钟。
请用蓝、黑色水笔或圆珠笔干脆答在试卷上。
2.答卷前请将密封线内的项目填写清晰。
一、填空题(每空1分,共14分)1.物理是以试验为基础的学科,试验时测量工具必不行少。
请写出一种测量工具及其测量的物理量名称。
测量工具:;物理量名称:。
2.教室的楼道上张贴有如图l所示的标记,提倡同学们不要大声喧哗,养成轻声讲话的文明习惯。
从声音的特性分析,“大声”和“轻声”均是指声音的大小;从限制噪声的角度分析,这是从处减弱噪声。
3.如图2所示,小红和小明都能看到掉在地上的课本,这是由于太阳光射到课本上时发生了现象。
太阳能属于(选填“可再生”或“不行再生”)能源。
4.图3是小聪为拉船靠岸而设计的甲、乙两种方案,若拉船的力须要很大,则应选用方案(选填“甲”或“乙”),因为采纳这种方案可以。
(不计机械的自重及摩擦)5.信阳“毛尖”深受人们宠爱,在制茶过程中,通过加热能使簇新茶叶中的水分快速(填物态变更名称),这便是制茶工序中的“杀青”。
用高温开水能很快泡出茶香、茶色,这是因为温度越高,越猛烈。
6.图4是某款电热水龙头的电路原理图。
R1、R2为电热丝,通过旋转手柄可使扇形开关S同时接触两个相邻触点,实现冷水、温水、热水挡之间的切换。
当开关同时接触2、3触点时,水龙头放出的是水(选填“冷”、“温”或“热”)。
若R2=2R1,水龙头在温水挡正常工作时电功率为2000W,则它在热水挡正常工作1min消耗的电能为J。
7.如图5所示,物体在重力、支持力和摩擦力作用下,沿足够长的水平面对右做减速直线运动。
假设物体运动时,重力突然消逝,请推断物体的运动状况将是:,简要说明你的推理过程:。
二、选择题(每小题2分,共16分)在每个小题的选项中,只有一个选项符合题目要求,请将其字母代号填在题后的括号内。
8.2024年3月,我国胜利将首颗新一代北斗导航卫星放射升空,标记着我国北斗卫星导航系统由区域运行向全球拓展。
2020年河南省中考数学试卷(附答案)

河南省中考数学试卷(满分120 分,考试时间100 分钟)一、选择题:1. 下列运算正确的是()A . 3 ﹣ 1 = ﹣ 3B .= ± 3C .( 2 2 ) 3 =64D . 5 6 ÷ 5 ³=252 、已知平面直角坐标系内一点A(2 ,3) ,把点 A 沿x 轴向左平移3 个单位长度,再以O 点为旋转中心旋转180 °,然后以y 轴为对称轴得到点A' ,这A' 点的坐标为()A .(-2 ,-3)B .(-1 ,-3)C .(-3 ,1)D .(-2 ,3)3 、环境空气质量问题已经成为人们日常生活所关心的重要问题,我国新修订的《环境空气质量标准》中增加了PM2.5 检测指标,“ PM2.5 ”是指大气中危害健康的直径小于或等于 2.5 微米的颗粒物, 2.5 微米即0.0000025 米.用科学记数法表示0.0000025 为()A . 2.5 × 10 ﹣ 5B . 2.5 × 10 5C 2.5 × 10 ﹣ 6D . 2.5 × 10 64 .如图,把三角板的直角顶点放在直尺的一边上,若∠1=30 °,则∠ 2 的度数为()A .60 °B .50 °C .40 °D .30 °5 、某通讯公司提供了两种移动电话收费方式:方式 1 ,收月基本费20 元,再以每分钟0.1 元的价格按通话时间计费;方式 2 ,收月基本费20 元,送80 分钟通话时间,超过80 分钟的部分,以每分钟0.15 元的价格计费.下列结论:①如图描述的是方式 1 的收费方法;②若月通话时间少于240 分钟,选择方式 2 省钱;③若月通讯费为50 元,则方式 1 比方式 2 的通话时间多;④若方式 1 比方式 2 的通讯费多10 元,则方式 1 比方式 2 的通话时间多100 分钟.其中正确的是()A .只有①②B .只有③④C .只有①②③D .①②③④6 .如图所示的图形是由7 个完全相同的小正方体组成的立体图形,则下面四个平面图形中不是这个立体图形的三视图的是()A .B .C .D .7 .为了大力宣传节约用电,某小区随机抽查了10 户家庭的月用电量情况,统计如下表.关于这10 户家庭的月用电量说法正确的是()月用电量(度)25 30 40 50 60户数 1 4 2 2 1A .平均数是38.5B .众数是 4C .中位数是40D .极差是 38. 如图,在第 1 个△ A 1 BC 中,∠ B =30 °,A 1B = CB ;在边 A 1 B 上任取一点 D ,延长CA 1 到 A 2 ,使 A 1 A 2 = A1 D ,得到第2 个△ A 1 A 2 D ;在边 A 2 D 上任取一点 E ,延长 A 1 A 2到 A 3 ,使 A 2 A 3 = A 2 E ,得到第 3 个△ A 2 A 3 E ,…按此做法继续下去,则第n 个三角形中以 A n 为顶点的内角度数是()A .()n • 75 °B .()n ﹣ 1 • 65 °C .()n ﹣1 • 75 ° D .()n • 85 °二、填空题:9 .如图,在△ ABC 中,AB = AC ,AD ⊥ BC 于点 D ,若AB =6 ,CD =4 ,则△ ABC 的周长是.10 .已知圆锥的母线长为 6 cm ,底面圆的半径为 3 cm ,则此圆锥侧面展开图的圆心角是。
2024年河南省中考数学真题试卷及答案
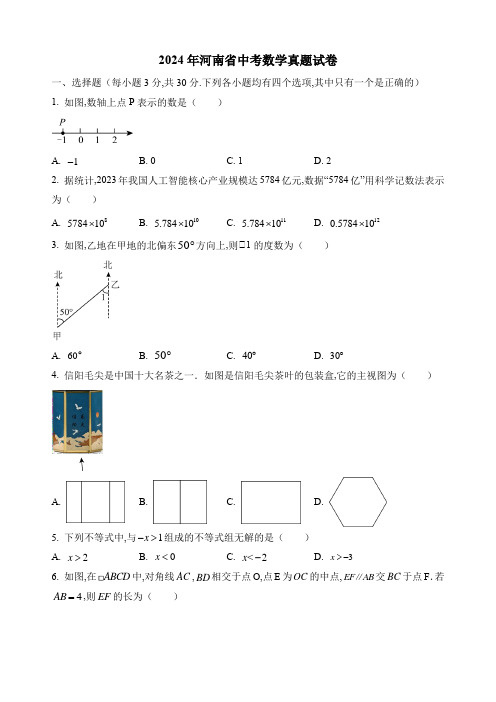
2024年河南省中考数学真题试卷一、选择题(每小题3分,共30分.下列各小题均有四个选项,其中只有一个是正确的) 1. 如图,数轴上点P 表示的数是( )A. 1-B. 0C. 1D. 22. 据统计,2023年我国人工智能核心产业规模达5784亿元,数据“5784亿”用科学记数法表示为( )A. 8578410⨯B. 105.78410⨯C. 115.78410⨯D. 120.578410⨯ 3. 如图,乙地在甲地的北偏东50︒方向上,则∠1的度数为( )A. 60︒B. 50︒C. 40︒D. 30︒4. 信阳毛尖是中国十大名茶之一.如图是信阳毛尖茶叶的包装盒,它的主视图为( )A. B. C. D. 5. 下列不等式中,与1x ->组成的不等式组无解的是( )A. 2x >B. 0x <C. <2x -D. 3x >-6. 如图,在ABCD 中,对角线AC ,BD 相交于点O,点E 为OC 的中点,EF AB ∥交BC 于点F .若4AB =,则EF 的长为( )A. 12 B. 1 C. 43 D. 27. 计算3()a a a a a ⋅⋅⋅个的结果是( )A. 5aB. 6aC. 3a a +D. 3a a 8. 豫剧是国家级非物质文化遗产,因其雅俗共赏,深受大众喜爱.正面印有豫剧经典剧目人物的三张卡片如图所示,它们除正面外完全相同.把这三张卡片背面朝上洗匀,从中随机抽取一张,放回洗匀后,再从中随机抽取一张,两次抽取的卡片正面相同的概率为( )A. 19B. 16C. 15D. 139. 如图,O 是边长为ABC 的外接圆,点D 是BC 的中点,连接BD ,CD .以点D 为圆心,BD 的长为半径在O 内画弧,则阴影部分的面积为( )A. 8π3B. 4πC. 16π3D. 16π10. 把多个用电器连接在同一个插线板上,同时使用一段时间后,插线板的电源线会明显发热,存在安全隐患.数学兴趣小组对这种现象进行研究,得到时长一定时,插线板电源线中的电流I 与使用电器的总功率P 的函数图象(如图1),插线板电源线产生的热量Q 与I 的函数图象(如图2).下列结论中错误的是( )A. 当440W P =时,2A I =B. Q 随I 的增大而增大C. I 每增加1A,Q 的增加量相同D. P 越大,插线板电源线产生的热量Q 越多二、填空题(每小题3分,共15分) 11. 请写出2m 的一个同类项:_______.12. 2024年3月是第8个全国近视防控宣传教育月,其主题是“有效减少近视发生,共同守护光明未来”.某校组织各班围绕这个主题开展板报宣传活动,并对各班的宣传板报进行评分,得分情况如图,则得分的众数为___________分.13. 若关于x 的方程2102x x c -+=有两个相等的实数根,则c 的值为___________. 14. 如图,在平面直角坐标系中,正方形ABCD 的边AB 在x 轴上,点A 的坐标为()20-,,点E 在边CD 上.将BCE 沿BE 折叠,点C 落在点F 处.若点F 的坐标为()06,,则点E 的坐标为___________.15. 如图,在Rt ABC △中,90ACB ∠=︒,3CA CB ==,线段CD 绕点C 在平面内旋转,过点B 作AD 的垂线,交射线AD 于点E .若1CD =,则AE 的最大值为_________,最小值为_________.三、解答题(本大题共8个小题,共75分)16. (1)计算(01 (2)化简:231124a a a +⎛⎫+÷ ⎪--⎝⎭. 17. 为提升学生体质健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中,甲、乙两名队员表现优异,他们在近六场比赛中关于得分、篮板和失误三个方面的统计结果如下.技术统计表根据以上信息,回答下列问题.(1)这六场比赛中,得分更稳定的队员是_________(填“甲”或“乙”);甲队员得分的中位数为27.5分,乙队员得分的中位数为________分.(2)请从得分方面分析:这六场比赛中,甲、乙两名队员谁的表现更好.(3)规定“综合得分”为:平均每场得分×1+平均每场篮板×1.5+平均每场失误()1⨯-,且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中甲、乙两名队员谁的表现更好. 18. 如图,矩形ABCD 的四个顶点都在格点(网格线的交点)上,对角线AC ,BD 相交于点E,反比例函数()0k y x x=>的图象经过点A .(1)求这个反比例函数的表达式.(2)请先描出这个反比例函数图象上不同于点A 的三个格点,再画出反比例函数的图象. (3)将矩形ABCD 向左平移,当点E 落在这个反比例函数的图象上时,平移的距离为________.19. 如图,在Rt ABC △中,CD 是斜边AB 上的中线,∥BE DC 交AC 的延长线于点E .(1)请用无刻度的直尺和圆规作ECM ∠,使ECM A ∠=∠,且射线CM 交BE 于点F (保留作图痕迹,不写作法).(2)证明(1)中得到的四边形CDBF 是菱形20. 如图1,塑像AB 在底座BC 上,点D 是人眼所在的位置.当点B 高于人的水平视线DE 时,由远及近看塑像,会在某处感觉看到的塑像最大,此时视角最大.数学家研究发现:当经过A,B 两点的圆与水平视线DE 相切时(如图2),在切点P 处感觉看到的塑像最大,此时APB ∠为最大视角.图1 图2(1)请仅就图2的情形证明APB ADB ∠>∠.(2)经测量,最大视角APB ∠为30︒,在点P 处看塑像顶部点A 的仰角APE ∠为60︒,点P 到塑像的水平距离PH 为6m .求塑像AB 的高(结果精确到0.1m .参考数据 1.73≈). 21. 为响应“全民植树增绿,共建美丽中国”的号召,学校组织学生到郊外参加义务植树活动,并准备了A,B 两种食品作为午餐.这两种食品每包质量均为50g ,营养成分表如下.(1)若要从这两种食品中摄入4600kJ 热量和70g 蛋白质,应选用A,B 两种食品各多少包? (2)运动量大的人或青少年对蛋白质的摄入量应更多.若每份午餐选用这两种食品共7包,要使每份午餐中的蛋白质含量不低于90g ,且热量最低,应如何选用这两种食品? 22. 从地面竖直向上发射的物体离地面的高度()m h 满足关系式205h t v t =-+,其中()s t 是物体运动的时间,()0m /s v 是物体被发射时的速度.社团活动时,科学小组在实验楼前从地面竖直向上发射小球.(1)小球被发射后_________s 时离地面的高度最大(用含0v 的式子表示).(2)若小球离地面的最大高度为20m ,求小球被发射时的速度.(3)按(2)中的速度发射小球,小球离地面的高度有两次与实验楼的高度相同.小明说:“这两次间隔的时间为3s .”已知实验楼高15m ,请判断他的说法是否正确,并说明理由. 23. 综合与实践在学习特殊四边形的过程中,我们积累了一定的研究经验,请运用已有经验,对“邻等对补四边形”进行研究定义:至少有一组邻边相等且对角互补的四边形叫做邻等对补四边形.(1)操作判断用分别含有30︒和45︒角的直角三角形纸板拼出如图1所示的4个四边形,其中是邻等对补四边形的有________(填序号).(2)性质探究根据定义可得出邻等对补四边形的边、角的性质.下面研究与对角线相关的性质. 如图2,四边形ABCD 是邻等对补四边形,AB AD =,AC 是它的一条对角线.∠写出图中相等的角,并说明理由∠若BC m =,DC n =,2BCD θ∠=,求AC 的长(用含m,n,θ的式子表示).(3)拓展应用如图3,在Rt ABC △中,90B ,3AB =,4BC =,分别在边BC ,AC 上取点M,N,使四边形ABMN 是邻等对补四边形.当该邻等对补四边形仅有一组邻边相等时,请直接写出BN 的长.2024年河南省中考数学真题试卷答案一、选择题(每小题3分,共30分.下列各小题均有四个选项,其中只有一个是正确的) 1. 【答案】A2. 【答案】C3. 【答案】B4. 【答案】A5. 【答案】A6. 【答案】B7. 【答案】D8. 【答案】D9. 【答案】C10. 【答案】C【解析】解∠根据图1知:当440W P =时,2A I =,故选项A 正确,但不符合题意 根据图2知:Q 随I 的增大而增大,故选项B 正确,但不符合题意根据图2知:Q 随I 的增大而增大,但前小半段增加的幅度小,后面增加的幅度大,故选项C 错误,符合题意根据图1知:I 随P 的增大而增大,又Q 随I 的增大而增大,则P 越大,插线板电源线产生的热量Q 越多,故选项D 正确,但不符合题意故选:C .二、填空题(每小题3分,共15分)11. 【答案】m (答案不唯一)12. 【答案】913. 【答案】1214. 【答案】()3,1015.【答案】 ∠. 1 ∠. 1【解析】解:∠90ACB ∠=︒,3CA CB == ∠190452BAC ABC ∠=∠=⨯︒=︒∠线段CD 绕点C 在平面内旋转,1CD =∠点D 在以点C 为圆心,1为半径的圆上∠BE AE ⊥∠90AEB ∠=︒∠点E 在以AB 为直径的圆上在Rt ABE △中,cos AE AB BAE =⋅∠∠AB 为定值∠当cos BAE ∠最大时,AE 最大,cos BAE ∠最小时,AE 最小 ∠当AE 与C 相切于点D,且点D 在ABC 内部时,BAE ∠最小,AE 最大,连接CD ,CE ,如图所示:则CD AE ⊥∠90ADE CDE ∠=∠=︒∠AD ==∠AC AC =∠45CED ABC ==︒∠∠∠90CDE ∠=︒∠CDE 为等腰直角三角形∠1DE CD ==∠1AE AD DE =+=+即AE 的最大值为1当AE 与C 相切于点D,且点D 在ABC 外部时,BAE ∠最大,AE 最小,连接CD ,CE ,如图所示:则CD AE ⊥∠90CDE ∠=︒∠AD ==∠四边形ABCE 为圆内接四边形 ∠180135CEA ABC =︒-=︒∠∠∠18045CED CEA =︒-=︒∠∠∠90CDE ∠=︒∠CDE 为等腰直角三角形∠1DE CD ==∠1AE AD DE =-=-即AE 的最小值为1故答案为:1;1.三、解答题(本大题共8个小题,共75分) 16. 【答案】(1)9(2)2a +17. 【答案】(1)甲 29(2)甲 (3)乙队员表现更好 18. 【答案】(1)6y x= (2)见解析 (3)92【小问1详解】解:反比例函数k y x =的图象经过点()3,2A ∠23k = ∠6k = ∠这个反比例函数的表达式为6y x =【小问2详解】解:当1x =时,6y =当2x =时,3y =当6x =时,1y =∠反比例函数6y x=的图象经过()1,6,()2,3,()6,1 画图如下:【小问3详解】解:∠()6,4E 向左平移后,E 在反比例函数的图象上∠平移后点E 对应点的纵坐标为4当4y =时,64x=解得32x = ∠平移距离为39622-=.故答案为:92.19. 【答案】(1)见解析(2)见解析【小问1详解】解:如图【小问2详解】证明:∠ECM A∠=∠∠CM AB∥∠∥BE DC∠四边形CDBF是平行四边形∠在Rt ABC△中,CD是斜边AB上的中线∠12 CD BD AB ==∠平行四边形CDBF是菱形.20. 【答案】(1)见解析(2)塑像AB的高约为6.9m 【小问1详解】证明:如图,连接BM.则AMB APB∠=∠.∠AMB ADB∠>∠∠APB ADB ∠>∠.【小问2详解】解:在Rt AHP 中,60APH ∠=︒,6PH =. ∠tan AH APH PH∠=∠tan 606AH PH =⋅︒==∠30APB ∠=︒∠603030BPH APH APB ∠=∠-∠=︒-︒=︒.在Rt BHP △中,tan BH BPH PH ∠=∠tan 306BH PH =⋅︒==∠()4 1.73 6.9m AB AH BH =-==≈⨯≈.答:塑像AB 的高约为6.9m .21. 【答案】(1)选用A 种食品4包,B 种食品2包(2)选用A 种食品3包,B 种食品4包【小问1详解】解:设选用A 种食品x 包,B 种食品y 包根据题意,得7009004600,101570.x y x y +=⎧⎨+=⎩解方程组,得4,2.x y =⎧⎨=⎩答:选用A 种食品4包,B 种食品2包.【小问2详解】解:设选用A 种食品a 包,则选用B 种食品()7-a 包根据题意,得()1015790a a +-≥.∠3a ≤.设总热量为kJ w ,则()70090072006300w a a a =+-=-+.∠2000-<∠w 随a 的增大而减小.∠当3a =时,w 最小.∠7734a -=-=.答:选用A 种食品3包,B 种食品4包.22. 【答案】(1)010v (2)()20m /s(3)小明的说法不正确,理由见解析【小问1详解】解:205h t v t =-+220051020v v t ⎛⎫=--+ ⎪⎝⎭ ∠当010v t =时,h 最大 故答案为:010v 【小问2详解】解:根据题意,得 当010v t =时,20h = ∠20005201010v v v ⎛⎫-⨯+⨯= ⎪⎝⎭∠()020m /s v =(负值舍去)【小问3详解】解:小明的说法不正确.理由如下:由(2),得2520h t t =-+当15h =时,215520t t =-+解方程,得11t =,23t =∠两次间隔的时间为312s -=∠小明的说法不正确.23. 【答案】(1)∠∠ (2)∠ACD ACB ∠=∠.理由见解析;∠2cos m n θ+(3)5或7 【小问1详解】解:观察图知,图∠和图∠中不存在对角互补,图2和图4中存在对角互补且邻边相等 故图∠和图∠中四边形是邻等对补四边形故答案为:∠∠【小问2详解】解:∠ACD ACB ∠=∠,理由:延长CB 至点E,使BE DC =,连接AE∠四边形ABCD 是邻等对补四边形∠180ABC D ∠+∠=︒∠180ABC ABE ∠+∠=︒∠ABE D ∠=∠∠AB AD =∠()SAS ABE ADC ≌∠E ACD ∠=∠,AE AC =∠E ACB ∠=∠∠ACD ACB ∠=∠∠过A 作AF EC ⊥于F∠AE AC = ∠()()1112222m n CF CE BC BE BC DC +==+=+= ∠2BCD θ∠=∠ACD ACB θ∠=∠=在Rt AFC △中,cos CF θAC= ∠cos 2cos CF m n AC θθ+== 【小问3详解】解:∠90B ,3AB =,4BC =∠5AC∠四边形ABMN 是邻等对补四边形 ∠180ANM B ∠+∠=︒∠90ANM =︒当AB BM =时,如图,连接AM ,过N 作NH BC ⊥于H∠22218AM AB BM =+=在Rt AMN 中222218MN AM AN AN =-=- 在Rt CMN 中()()22222435MN CM CN AN =-=--- ∠()()22218435AN AN -=--- 解得 4.2AN = ∠45CN = ∠90NHC ABC ∠=∠=︒,C C ∠=∠ ∠NHC ABC ∽534∠1225NH =,1625CH = ∠8425BH =∠BN ==当AN AB =时,如图,连接AM∠AM AM =∠Rt Rt ABM ANM ≌ ∠BM NM =,故不符合题意,舍去 当AN MN =时,连接AM ,过N 作NH BC ⊥于H∠90MNC ABC ∠=∠=︒,C C ∠=∠ ∠CMN CAB ∽△△ ∠CN MN BC AB =,即543CN CN -= 解得207CN =∠90NHC ABC ∠=∠=︒,C C ∠=∠ ∠NHC ABC ∽534∠127NH =,167CH = ∠127BH =∠BN ==当BM MN =时,如图,连接AM∠AM AM =∠Rt Rt ABM ANM ≌ ∠AN AB =,故不符合题意,舍去综上,BN 的长为5或7.。
【中考真题】河南省2024年普通高中招生考试历史真题试卷 附解析

【中考真题】河南省2024年普通高中招生考试历史试卷20小题,20分)下列每小题列出的四个选项中,只有一1.《史记》记载商纣王封周文王为西伯时,赐他“弓矢斧钺,使得征伐”;在描绘周武王指挥牧野之战时,“左杖黄钺,右秉白旄(máo)以麾”。
据此推测,下图玉钺在当时可能是()河南偃师二里头出土的玉钺A.最高祭祀权的代表B.高级生产工具C.军事统帅权的象征D.诸侯国的徽标2.战国时期的这些农具(见下图)虽貌不惊人,但其锋利已经悄无声息地划开了一个崭新的时代。
这里的“锋利”可以理解为()河南辉县出土的铁犁头河北易县出土的铁镰刀河南辉县出土的铁锤口A.较高生产力水平B.频繁的兼并战争C.新兴的小农经济D.宽松的社会氛围3.早在西周就已出现的瓦当,到西汉时一改原来的简单、朴素,变得纹饰繁多,构思奇巧,集绘画、浮雕、工艺美术和书法于一身。
材料强调了西汉瓦当()A.建筑用途广泛B.史料价值突出C.艺术价值较高D.材料来源丰富4.曹魏建立后,百姓购买物品、计算物价皆普遍使用布帛或谷物。
北魏孝文帝时,北方很多地方“犹以他物交易,钱略不入市”。
该现象从本质上反映了这一时期北方()A.铸币金属匮乏B.币制较为混乱C.农业技术落后D.商品经济衰退5.宋朝时,雕版印刷术使用更加普遍,“转相摹刻,诸子百家之书,日传万纸”,对文化发展是一个明显推动。
这主要说明宋朝时期()A.儒家思想备受推崇B.技术推动文化发展C.活字印刷普遍使用D.文化助力技术创新6.元朝汪大渊《岛夷志略》记载,澎湖“隶泉州晋江县,至元(忽必烈年号)间立巡检司”,巡检司负责管辖澎湖和琉球,每年征收盐税中统钞十锭二十五两。
元朝此举()A.完成了全国统一B.加强了边疆管理C.进行了赋税改革D.推行了行省制度7.1608年,徐光启从福建引来甘薯种在上海栽种,取得成功;后又写成《甘薯疏》,指出甘薯的优点,介绍其种植方法。
材料体现出他()A.关注科学理论B.得到百姓的支持C.重视数据分析D.注重实践与总结8.太平天国严禁鸦片贸易,不承认西方列强强加于中国的不平等条约,多次拒绝外国提出的侵略要求。
初中数学精品试题:中考专项第21、22、23题训练(1)

1.有一组互不全等的三角形,它们的边长均为整数,每个三角形有两条边的长分别为5和7.(1)请写出其中一个三角形的第三边的长;(2)设组中最多有n个三角形,求n的值;(3)当这组三角形个数最多时,从中任取一个,求该三角形周长为偶数的概率.2.在平面直角坐标系内,反比例函数和二次函数y=k(x2+x﹣1)的图象交于点A(1,k)和点B(﹣1,﹣k).(1)当k=﹣2时,求反比例函数的解析式;(2)要使反比例函数和二次函数都是y随着x的增大而增大,求k应满足的条件以及x的取值范围;(3)设二次函数的图象的顶点为Q,当△ABQ是以AB为斜边的直角三角形时,求k的值.3.已知,如图,在梯形ABCD中,AD∥BC,DA=DC,以点D为圆心,DA长为半径的⊙D与AB相切于A,与BC交于点F,过点D作DE⊥BC,垂足为E.(1)求证:四边形ABED为矩形;(2)若AB=4,AD3BC4,求CF的长.4.为进一步建设秀美、宜居的生态环境,某村欲购买甲、乙、丙三种树美化村庄,已知甲、乙丙三种树的价格之比为2:2:3,甲种树每棵200元,现计划用210000元资金,购买这三种树共1000棵.(1)求乙、丙两种树每棵各多少元?(2)若购买甲种树的棵树是乙种树的2倍,恰好用完计划资金,求这三种树各能购买多少棵?(3)若又增加了10120元的购树款,在购买总棵树不变的前提下,求丙种树最多可以购买多少棵?5.如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=.(1)求边AB的长;(2)求反比例函数的解析式和n的值;(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.6.某汽车租赁公司拥有20辆汽车.据统计,当每辆车的日租金为400元时,可全部租出;当每辆车的日租金每增加50元,未租出的车将增加1辆;公司平均每日的各项支出共4800元.设公司每日租出工辆车时,日收益为y元.(日收益=日租金收入一平均每日各项支出)(1)公司每日租出x辆车时,每辆车的日租金为元(用含x的代数式表示);(2)当每日租出多少辆时,租赁公司日收益最大?最大是多少元?(3)当每日租出多少辆时,租赁公司的日收益不盈也不亏?7.将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].(1)如图①,对△ABC作变换[60°,]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线B′C′所夹的锐角为度;(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;(4)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.8.周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.(1)求小明骑车的速度和在甲地游玩的时间;(2)小明从家出发多少小时后被妈妈追上?此时离家多远?(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.9.如图,一次函数y1=kx+b的图象与反比例函数y2=的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).(1)求这两个函数的解析式;(2)当x取何值时,y1>y2.10.为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.如表是该市居民“一户一表”生活用水及提示计费价格表的部分信息:自来水销售价格污水处理价格每户每月用水量单价:元/吨单价:元/吨17吨以下a0.80超过17吨但不超过30吨的部分b0.80超过30吨的部分 6.00 0.80(说明:①每户产生的污水量等于该户自来水用水量;②水费=自来水费用+污水处理费用)已知小王家2012年4月份用水20吨,交水费66元;5月份用水25吨,交水费91元.(1)求a、b的值;(2)随着夏天的到来,用水量将增加.为了节省开支,小王计划把6月份的水费控制在不超过家庭月收入的2%.若小王家的月收入为9200元,则小王家6月份最多能用水多少吨?11.在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;(2)如图2,连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积;(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值.12.如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=kx(k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.(1)求该双曲线所表示的函数解析式;(2)求等边△AEF的边长.13.小明参加班长竞选,需进行演讲答辩与民主测评,民主测评时一人一票,按“优秀、良好、一般”三选一投票.如图是7位评委对小明“演讲答辩”的评分统计图及全班50位同学民主测评票数统计图.(1)求评委给小明演讲答辩分数的众数,以及民主测评为“良好”票数的扇形圆心角度数;(2)求小明的综合得分是多少?(3)在竞选中,小亮的民主测评得分为82分,如果他的综合得分不小于小明的综合得分,他的演讲答辩得分至少要多少分?14.如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.(1)求证:AC是⊙O的切线;(2)已知sinA=,⊙O的半径为4,求图中阴影部分的面积.15.在直角坐标系中,点A是抛物线y=x2在第二象限上的点,连接OA,过点O作OB⊥OA,交抛物线于点B,以OA、OB为边构造矩形AOBC.(1)如图1,当点A的横坐标为时,矩形AOBC是正方形;(2)如图2,当点A的横坐标为12时,①求点B的坐标;②将抛物线y=x2作关于x轴的轴对称变换得到抛物线y=-x2,试判断抛物线y=-x2经过平移交换后,能否经过A,B,C三点?如果可以,说出变换的过程;如果不可以,请说明理由.16.邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图1,▱ABCD中,若AB=1,BC=2,则▱ABCD为1阶准菱形.(1)判断与推理:①邻边长分别为2和3的平行四边形是_________阶准菱形;②小明为了剪去一个菱形,进行了如下操作:如图2,把▱ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F,得到四边形ABFE.请证明四边形ABFE是菱形.(2)操作、探究与计算:①已知▱ABCD的邻边长分别为1,a(a>1),且是3阶准菱形,请画出▱ABCD及裁剪线的示意图,并在图形下方写出a的值;②已知▱ABCD的邻边长分别为a,b(a>b),满足a=6b+r,b=5r,请写出▱ABCD是几阶准菱形.参考答案:1.解:(1)设三角形的第三边为x,∵每个三角形有两条边的长分别为5和7,∴7﹣5<x<5+7,∴2<x<12,∴其中一个三角形的第三边的长可以为10.(2)∵2<x<12,它们的边长均为整数,∴x=3,4,5,6,7,8,9,10,11,∴组中最多有9个三角形,∴n=9;(3)∵当x=4,6,8,10时,该三角形周长为偶数,∴该三角形周长为偶数的概率是.2.解:(1)当k=﹣2时,A(1,﹣2),∵A在反比例函数图象上,∴设反比例函数的解析式为:y=,代入A(1,﹣2)得:﹣2=,解得:m=﹣2,∴反比例函数的解析式为:y=﹣;(2)∵要使反比例函数和二次函数都是y随着x的增大而增大,∴k<0,∵二次函数y=k(x2+x﹣1)=k(x+)2﹣k,的对称轴为:直线x=﹣,要使二次函数y=k(x2+x﹣1)满足上述条件,在k<0的情况下,x必须在对称轴的左边,即x<﹣时,才能使得y随着x的增大而增大,∴综上所述,k<0且x<﹣;(3)由(2)可得:Q(﹣,k),∵△ABQ是以AB为斜边的直角三角形,A点与B点关于原点对称,(如图是其中的一种情况)∴原点O平分AB,∴OQ=OA=OB,作AD⊥OC,QC⊥OC,∴OQ==,∵OA==,∴=,解得:k=±.3.(1)证明:∵⊙D与AB相切于点A,∴AB⊥AD。
2020年河南省中考数学试题(含答案解析)

2020年河南省中考数学试卷(共23题,满分120分)一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个是正确的.1.2的相反数是()A.﹣2B.C.D.22.如图摆放的几何体中,主视图与左视图有可能不同的是()A.B.C.D.3.要调查下列问题,适合采用全面调查(普查)的是()A.中央电视台《开学第一课》的收视率B.某城市居民6月份人均网上购物的次数C.即将发射的气象卫星的零部件质量D.某品牌新能源汽车的最大续航里程4.如图,l1∥l2,l3∥l4,若∠1=70°,则∠2的度数为()A.100°B.110°C.120°D.130°5.电子文件的大小常用B,KB,MB,GB等作为单位,其中1GB=210MB,1MB=210KB,1KB=210B.某视频文件的大小约为1GB,1GB等于()A.230B B.830B C.8×1010B D.2×1030B6.若点A(﹣1,y1),B(2,y2),C(3,y3)在反比例函数y的图象上,则y1,y2,y3的大小关系是()A.y1>y2>y3B.y2>y3>y1C.y1>y3>y2D.y3>y2>y17.定义运算:m☆n=mn2﹣mn﹣1.例如:4☆2=4×22﹣4×2﹣1=7.则方程1☆x =0的根的情况为()A.有两个不相等的实数根B.有两个相等的实数根C.无实数根D.只有一个实数根8.国家统计局统计数据显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x,则可列方程为()A.500(1+2x)=7500B.5000×2(1+x)=7500C.5000(1+x)2=7500D.5000+5000(1+x)+5000(1+x)2=75009.如图,在△ABC中,∠ACB=90°,边BC在x轴上,顶点A,B的坐标分别为(﹣2,6)和(7,0).将正方形OCDE沿x轴向右平移,当点E落在AB边上时,点D的坐标为()A.(,2)B.(2,2)C.(,2)D.(4,2)10.如图,在△ABC中,AB=BC,∠BAC=30°,分别以点A,C为圆心,AC 的长为半径作弧,两弧交于点D,连接DA,DC,则四边形ABCD的面积为()A.6B.9C.6D.3二、填空题(每小题3分,共15分)11.请写出一个大于1且小于2的无理数.12.已知关于x的不等式组其中a,b在数轴上的对应点如图所示,则这个不等式组的解集为.13.如图所示的转盘,被分成面积相等的四个扇形,分别涂有红、黄、蓝、绿四种颜色.固定指针,自由转动转盘两次,每次停止后,记下指针所指区域(指针指向区域分界线时,忽略不计)的颜色,则两次颜色相同的概率是.14.如图,在边长为2的正方形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为.15.如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交于点D,点E为半径OB上一动点.若OB=2,则阴影部分周长的最小值为.三、解答题(本大题共8个小题,满分75分)16.(8分)先化简,再求值:(1),其中a1.17.(9分)为发展乡村经济,某村根据本地特色,创办了山药粉加工厂.该厂需购置一台分装机,计划从商家推荐试用的甲、乙两台不同品牌的分装机中选择.试用时,设定分装的标准质量为每袋500g,与之相差大于10g为不合格.为检验分装效果,工厂对这两台机器分装的成品进行了抽样和分析,过程如下:[收集数据]从甲、乙两台机器分装的成品中各随机抽取20袋,测得实际质量(单位:g)如下:甲:501 497 498 502 513 489 506 490 505 486 502 503 498 497 491 500 505 502 504 505乙:505 499 502 491 487 506 493 505 499 498 502 503 501 490 501 502 511 499 499 501[整理数据]整理以上数据,得到每袋质量x(g)的频数分布表.质量频数机器485≤x<490490≤x<495495≤x<500500≤x<505505≤x<510510≤x<515甲224741乙135731 [分析数据]根据以上数据,得到以下统计量.统计量机器平均数中位数方差不合格率甲499.7501.542.01b乙499.7a31.8110%根据以上信息,回答下列问题:(1)表格中的a=,b=;(2)综合上表中的统计量,判断工厂应迭购哪一台分装机,并说明理由.18.(9分)位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6m.(1)求观星台最高点A距离地面的高度(结果精确到0.1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40, 1.41);(2)“景点简介”显示,观星台的高度为12.6m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.19.(9分)暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.设某学生暑期健身x(次),按照方案一所需费用为y1(元),且y1=k1x+b;按照方案二所需费用为y2(元),且y2=k2x.其函数图象如图所示.(1)求k1和b的值,并说明它们的实际意义;(2)求打折前的每次健身费用和k2的值;(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.20.(9分)我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具﹣﹣三分角器.图1是它的示意图,其中AB与半圆O的直径BC在同一直线上,且AB的长度与半圆的半径相等;DB与AC垂直于点B,DB足够长.使用方法如图2所示,若要把∠MEN三等分,只需适当放置三分角器,使DB经过∠MEN的顶点E,点A落在边EM上,半圆O与另一边EN恰好相切,切点为F,则EB,EO就把∠MEN三等分了.为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.已知:如图2,点A,B,O,C在同一直线上,EB⊥AC,垂足为点B,.求证:.21.(10分)如图,抛物线y=﹣x2+2x+c与x轴正半轴,y轴正半轴分别交于点A,B,且OA=OB,点G为抛物线的顶点.(1)求抛物线的解析式及点G的坐标;(2)点M,N为抛物线上两点(点M在点N的左侧),且到对称轴的距离分别为3个单位长度和5个单位长度,点Q为抛物线上点M,N之间(含点M,N)的一个动点,求点Q的纵坐标y Q的取值范围.22.(10分)小亮在学习中遇到这样一个问题:如图,点D是上一动点,线段BC=8cm,点A是线段BC的中点,过点C 作CF∥BD,交DA的延长线于点F.当△DCF为等腰三角形时,求线段BD的长度.小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题.请将下面的探究过程补充完整:(1)根据点D在上的不同位置,画出相应的图形,测量线段BD,CD,FD的长度,得到下表的几组对应值.BD/cm0 1.0 2.0 3.0 4.0 5.0 6.07.08.0 CD/cm8.07.77.2 6.6 5.9a 3.9 2.40 FD/cm8.07.4 6.9 6.5 6.1 6.0 6.2 6.78.0操作中发现:①“当点D为的中点时,BD=5.0cm”.则上表中a的值是;②“线段CF的长度无需测量即可得到”.请简要说明理由.(2)将线段BD的长度作为自变量x,CD和FD的长度都是x的函数,分别记为y CD和y FD,并在平面直角坐标系xOy中画出了函数y FD的图象,如图所示.请在同一坐标系中画出函数y CD的图象;(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当△DCF为等腰三角形时,线段BD长度的近似值(结果保留一位小数).23.(11分)将正方形ABCD的边AB绕点A逆时针旋转至AB′,记旋转角为α,连接BB′,过点D作DE垂直于直线BB′,垂足为点E,连接DB′,CE.(1)如图1,当α=60°时,△DEB′的形状为,连接BD,可求出的值为;(2)当0°<α<360°且α≠90°时,①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;②当以点B′,E,C,D为顶点的四边形是平行四边形时,请直接写出的值.2020年河南省中考数学试卷答案解析一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个是正确的.1.2的相反数是()A.﹣2B.C.D.2【解答】解:2的相反数是﹣2.故选:A.2.如图摆放的几何体中,主视图与左视图有可能不同的是()A.B.C.D.【解答】解:A、主视图和左视图是长方形,一定相同,故本选项不合题意题意;B、主视图和左视图都是等腰三角形,一定相同,故选项不符合题意;C、主视图和左视图都是圆,一定相同,故选项不符合题意;D、主视图是长方形,左视图是正方形,故本选项符合题意;故选:D.3.要调查下列问题,适合采用全面调查(普查)的是()A.中央电视台《开学第一课》的收视率B.某城市居民6月份人均网上购物的次数C.即将发射的气象卫星的零部件质量D.某品牌新能源汽车的最大续航里程【解答】解:A、调查中央电视台《开学第一课》的收视率,适合抽查,故本选项不合题意;B、调查某城市居民6月份人均网上购物的次数,适合抽查,故本选项不合题意;C、调查即将发射的气象卫星的零部件质量,适合采用全面调查(普查),故本选项符合题意;D、调查某品牌新能源汽车的最大续航里程,适合抽查,故本选项不合题意.故选:C.4.如图,l1∥l2,l3∥l4,若∠1=70°,则∠2的度数为()A.100°B.110°C.120°D.130°【解答】解:∵l1∥l2,∠1=70°,∴∠3=∠1=70°,∵l3∥l4,∴∠2=180°﹣∠3=180°﹣70°=110°,故选:B.5.电子文件的大小常用B,KB,MB,GB等作为单位,其中1GB=210MB,1MB=210KB,1KB=210B.某视频文件的大小约为1GB,1GB等于()A.230B B.830B C.8×1010B D.2×1030B 【解答】解:由题意得:210×210×210B=210+10+10=230B,故选:A.6.若点A(﹣1,y1),B(2,y2),C(3,y3)在反比例函数y的图象上,则y1,y2,y3的大小关系是()A.y1>y2>y3B.y2>y3>y1C.y1>y3>y2D.y3>y2>y1【解答】解:∵点A(﹣1,y1)、B(2,y2)、C(3,y3)在反比例函数y 的图象上,∴y16,y23,y32,又∵﹣3<﹣2<6,∴y1>y3>y2.故选:C.7.定义运算:m☆n=mn2﹣mn﹣1.例如:4☆2=4×22﹣4×2﹣1=7.则方程1☆x =0的根的情况为()A.有两个不相等的实数根B.有两个相等的实数根C.无实数根D.只有一个实数根【解答】解:由题意可知:1☆x=x2﹣x﹣1=0,∴△=1﹣4×1×(﹣1)=5>0,故选:A.8.国家统计局统计数据显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x,则可列方程为()A.500(1+2x)=7500B.5000×2(1+x)=7500C.5000(1+x)2=7500D.5000+5000(1+x)+5000(1+x)2=7500【解答】解:设我国2017年至2019年快递业务收入的年平均增长率为x,由题意得:5000(1+x)2=7500,故选:C.9.如图,在△ABC中,∠ACB=90°,边BC在x轴上,顶点A,B的坐标分别为(﹣2,6)和(7,0).将正方形OCDE沿x轴向右平移,当点E落在AB边上时,点D的坐标为()A.(,2)B.(2,2)C.(,2)D.(4,2)【解答】解:如图,设正方形D′C′O′E′是正方形OCDE沿x轴向右平移后的正方形,∵顶点A,B的坐标分别为(﹣2,6)和(7,0),∴AC=6,OC=2,OB=7,∴BC=9,∵四边形OCDE是正方形,∴DE=OC=OE=2,∴O′E′=O′C′=2,∵E′O′⊥BC,∴∠BO′E′=∠BCA=90°,∴E′O′∥AC,∴△BO′E′∽△BCA,∴,∴,∴BO′=3,∴OC′=7﹣2﹣3=2,∴当点E落在AB边上时,点D的坐标为(2,2),故选:B.10.如图,在△ABC中,AB=BC,∠BAC=30°,分别以点A,C为圆心,AC 的长为半径作弧,两弧交于点D,连接DA,DC,则四边形ABCD的面积为()A.6B.9C.6D.3【解答】解:连接BD交AC于O,∵AD=CD,AB=BC,∴BD垂直平分AC,∴BD⊥AC,AO=CO,∵AB=BC,∴∠ACB=∠BAC=30°,∵AC=AD=CD,∴△ACD是等边三角形,∴∠DAC=∠DCA=60°,∴∠BAD=∠BCD=90°,∠ADB=∠CDB=30°,∵AB=BC,∴AD=CD AB=3,∴四边形ABCD的面积=23,故选:D.二、填空题(每小题3分,共15分)11.请写出一个大于1且小于2的无理数.【解答】解:大于1且小于2的无理数是,答案不唯一.故答案为:.12.已知关于x的不等式组其中a,b在数轴上的对应点如图所示,则这个不等式组的解集为x>a.【解答】解:∵b<0<a,∴关于x的不等式组的解集为:x>a,故答案为:x>a.13.如图所示的转盘,被分成面积相等的四个扇形,分别涂有红、黄、蓝、绿四种颜色.固定指针,自由转动转盘两次,每次停止后,记下指针所指区域(指针指向区域分界线时,忽略不计)的颜色,则两次颜色相同的概率是.【解答】解:自由转动转盘两次,指针所指区域所有可能出现的情况如下:共有16种可能出现的结果,其中两次颜色相同的有4种,∴P(两次颜色相同),故答案为:.14.如图,在边长为2的正方形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为1.【解答】解:设DF,CE交于O,∵四边形ABCD是正方形,∴∠B=∠DCF=90°,BC=CD=AB,∵点E,F分别是边AB,BC的中点,∴BE=CF,∴△CBE≌△DCF(SAS),∴CE=DF,∠BCE=∠CDF,∵∠CDF+∠CFD=90°,∴∠BCE+∠CFD=90°,∴∠COF=90°,∴DF⊥CE,∴CE=DF,∵点G,H分别是EC,FD的中点,∴CG=FH,∵∠DCF=90°,CO⊥DF,∴CF2=OF•DF,∴OF,∴OH,OD,∵OC2=OF•OD,∴OC,∴OG=CG﹣OC,∴HG1,故答案为:1.15.如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交于点D,点E为半径OB上一动点.若OB=2,则阴影部分周长的最小值为.【解答】解:如图,作点D关于OB的对称点D′,连接D′C交OB于点E′,连接E′D、OD′,此时E′C+E′C最小,即:E′C+E′C=CD′,由题意得,∠COD=∠DOB=∠BOD′=30°,∴∠COD′=90°,∴CD′2,的长l,∴阴影部分周长的最小值为2.故答案为:.三、解答题(本大题共8个小题,满分75分)16.(8分)先化简,再求值:(1),其中a1.【解答】解:=a﹣1,把a1代入a﹣11﹣1.17.(9分)为发展乡村经济,某村根据本地特色,创办了山药粉加工厂.该厂需购置一台分装机,计划从商家推荐试用的甲、乙两台不同品牌的分装机中选择.试用时,设定分装的标准质量为每袋500g,与之相差大于10g为不合格.为检验分装效果,工厂对这两台机器分装的成品进行了抽样和分析,过程如下:[收集数据]从甲、乙两台机器分装的成品中各随机抽取20袋,测得实际质量(单位:g)如下:甲:501 497 498 502 513 489 506 490 505 486 502 503 498 497 491 500 505 502 504 505乙:505 499 502 491 487 506 493 505 499 498502 503 501 490 501 502 511 499 499 501[整理数据]整理以上数据,得到每袋质量x(g)的频数分布表.质量频数机器485≤x<490490≤x<495495≤x<500500≤x<505505≤x<510510≤x<515甲224741乙135731 [分析数据]根据以上数据,得到以下统计量.统计量机器平均数中位数方差不合格率甲499.7501.542.01b乙499.7a31.8110%根据以上信息,回答下列问题:(1)表格中的a=501,b=15%;(2)综合上表中的统计量,判断工厂应迭购哪一台分装机,并说明理由.【解答】解:(1)将乙的成绩从小到大排列后,处在中间位置的两个数都是501,因此中位数是501,b=3➗20=15%,故答案为:501,15%;(2)选择乙机器,理由:乙的不合格率较小,18.(9分)位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6m.(1)求观星台最高点A距离地面的高度(结果精确到0.1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40, 1.41);(2)“景点简介”显示,观星台的高度为12.6m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.【解答】解:(1)过A作AD⊥PM于D,延长BC交AD于E,则四边形BMNC,四边形BMDE是矩形,∴BC=MN=16m,DE=CN=BM=1.6m,∵∠AED=90°,∠ACE=45°,∴△ACE是等腰直角三角形,∴CE=AE,设AE=CE=x,∴BE=16+x,∵∠ABE=22°,∴tan22°0.40,∴x≈10.7(m),∴AD=10.7+1.6=12.3(m),答:观星台最高点A距离地面的高度约为12.3m;(2)∵“景点简介”显示,观星台的高度为12.6m,∴本次测量结果的误差为12.6﹣12.3=0.3m,减小误差的合理化建议为:为了减小误差可以通过多次测量取平均值的方法.19.(9分)暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.设某学生暑期健身x(次),按照方案一所需费用为y1(元),且y1=k1x+b;按照方案二所需费用为y2(元),且y2=k2x.其函数图象如图所示.(1)求k1和b的值,并说明它们的实际意义;(2)求打折前的每次健身费用和k2的值;(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.【解答】解:(1)∵y1=k1x+b过点(0,30),(10,180),∴,解得,k1=15表示的实际意义是:购买一张学生暑期专享卡后每次健身费用为15元,b=30表示的实际意义是:购买一张学生暑期专享卡的费用为30元;(2)由题意可得,打折前的每次健身费用为15÷0.6=25(元),则k2=25×0.8=20;(3)选择方案一所需费用更少.理由如下:由题意可知,y1=15x+30,y2=20x.当健身8次时,选择方案一所需费用:y1=15×8+30=150(元),选择方案二所需费用:y2=20×8=160(元),∵150<160,∴选择方案一所需费用更少.20.(9分)我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具﹣﹣三分角器.图1是它的示意图,其中AB与半圆O的直径BC在同一直线上,且AB的长度与半圆的半径相等;DB与AC垂直于点B,DB足够长.使用方法如图2所示,若要把∠MEN三等分,只需适当放置三分角器,使DB经过∠MEN的顶点E,点A落在边EM上,半圆O与另一边EN恰好相切,切点为F,则EB,EO就把∠MEN三等分了.为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.已知:如图2,点A,B,O,C在同一直线上,EB⊥AC,垂足为点B,AB =OB,EN切半圆O于F.求证:EB,EO就把∠MEN三等分.【解答】解:已知:如图2,点A,B,O,C在同一直线上,EB⊥AC,垂足为点B,AB=OB,EN切半圆O于F.求证:EB,EO就把∠MEN三等分,证明:∵EB⊥AC,∴∠ABE=∠OBE=90°,∵AB=OB,BE=BE,∴△ABE≌△OBE(SAS),∴∠1=∠2,∵BE⊥OB,∴BE是⊙E的切线,∵EN切半圆O于F,∴∠2=∠3,∴∠1=∠2=∠3,∴EB,EO就把∠MEN三等分.故答案为:AB=OB,EN切半圆O于F;EB,EO就把∠MEN三等分.21.(10分)如图,抛物线y=﹣x2+2x+c与x轴正半轴,y轴正半轴分别交于点A,B,且OA=OB,点G为抛物线的顶点.(1)求抛物线的解析式及点G的坐标;(2)点M,N为抛物线上两点(点M在点N的左侧),且到对称轴的距离分别为3个单位长度和5个单位长度,点Q为抛物线上点M,N之间(含点M,N)的一个动点,求点Q的纵坐标y Q的取值范围.【解答】解:(1)∵抛物线y=﹣x2+2x+c与y轴正半轴分别交于点B,∴点B(0,c),∵OA=OB=c,∴点A(c,0),∴0=﹣c2+2c+c,∴c=3或0(舍去),∴抛物线解析式为:y=﹣x2+2x+3,∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点G为(1,4);(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴对称轴为直线x=1,∵点M,N为抛物线上两点(点M在点N的左侧),且到对称轴的距离分别为3个单位长度和5个单位长度,∴点M的横坐标为﹣2或4,点N的横坐标为6,∴点M坐标为(﹣2,﹣5)或(4,﹣5),点N坐标(6,﹣21),∵点Q为抛物线上点M,N之间(含点M,N)的一个动点,∴﹣21≤y Q≤4或﹣21≤y Q≤﹣5.22.(10分)小亮在学习中遇到这样一个问题:如图,点D是上一动点,线段BC=8cm,点A是线段BC的中点,过点C 作CF∥BD,交DA的延长线于点F.当△DCF为等腰三角形时,求线段BD的长度.小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题.请将下面的探究过程补充完整:(1)根据点D 在上的不同位置,画出相应的图形,测量线段BD,CD,FD的长度,得到下表的几组对应值.0 1.0 2.0 3.0 4.0 5.0 6.07.08.0BD/cmC8.07.77.2 6.6 5.9a 3.9 2.40 D/cm8.07.4 6.9 6.5 6.1 6.0 6.2 6.78.0FD/cm操作中发现:①“当点D 为的中点时,BD=5.0cm”.则上表中a的值是5;②“线段CF的长度无需测量即可得到”.请简要说明理由.(2)将线段BD的长度作为自变量x,CD和FD的长度都是x的函数,分别记为y CD和y FD,并在平面直角坐标系xOy中画出了函数y FD的图象,如图所示.请在同一坐标系中画出函数y CD的图象;(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当△DCF为等腰三角形时,线段BD长度的近似值(结果保留一位小数).【解答】解:(1)∵点D为的中点,∴,∴BD=CD=a=5cm,故答案为:5;(2)∵点A是线段BC的中点,∴AB=AC,∵CF∥BD,∴∠F=∠BDA,又∵∠BAD=∠CAF,∴△BAD≌△CAF(AAS),∴BD=CF,∴线段CF的长度无需测量即可得到;(3)由题意可得:(4)由题意画出函数y CF的图象;由图象可得:BD=3.8cm或5cm或6.2cm时,△DCF为等腰三角形.23.(11分)将正方形ABCD的边AB绕点A逆时针旋转至AB′,记旋转角为α,连接BB′,过点D作DE垂直于直线BB′,垂足为点E,连接DB′,CE.(1)如图1,当α=60°时,△DEB′的形状为等腰直角三角形,连接BD,可求出的值为;(2)当0°<α<360°且α≠90°时,①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;②当以点B′,E,C,D为顶点的四边形是平行四边形时,请直接写出的值.【解答】解:(1)∵AB绕点A逆时针旋转至AB′,∴AB=AB',∠BAB'=60°,∴△ABB'是等边三角形,∴∠BB'A=60°,∴∠DAB'=∠BAD﹣∠BAB'=90°﹣60°=30°,∵AB'=AB=AD,∴∠AB'D=∠ADB',∴∠AB'D75°,∴∠DB'E=180°﹣60°﹣75°=45°,∵DE⊥B'E,∴∠B'DE=90°﹣45°=45°,∴△DEB'是等腰直角三角形.∵四边形ABCD是正方形,∴∠BDC=45°,∴,同理,∴,∵∠BDB'+∠B'DC=45°,∠EDC+∠B'DC=45°,∴BDB'=∠EDC,∴△BDB'∽△CDE,∴.故答案为:等腰直角三角形,.(2)①两结论仍然成立.证明:连接BD,∵AB=AB',∠BAB'=α,∴∠AB'B=90°,∵∠B'AD=α﹣90°,AD=AB',∴∠AB'D=135°,∴∠EB'D=∠AB'D﹣∠AB'B=135°45°,∵DE⊥BB',∴∠EDB'=∠EB'D=45°,∴△DEB'是等腰直角三角形,∴,∵四边形ABCD是正方形,∴,∠BDC=45°,∴,∵∠EDB'=∠BDC,∴∠EDB'+∠EDB=∠BDC+∠EDB,即∠B'DB=∠EDC,∴△B'DB∽△EDC,∴.②3或1.若CD为平行四边形的对角线,点B'在以A为圆心,AB为半径的圆上,取CD的中点.连接BO交⊙A于点B',过点D作DE⊥BB'交BB'的延长线于点E,由(1)可知△B'ED是等腰直角三角形,∴B'D B'E,由(2)①可知△BDB'∽△CDE,且BB'CE.∴1111=3.若CD为平行四边形的一边,如图3,点E与点A重合,∴1.综合以上可得3或1.。
2019河南省中招考试数学试题【含答案】

2019年河南省中招考试题(满分120分,考试时间100分钟)一、选择题(每小题3分,共30分)的绝对值是 ( ) B.C.2D.-22.成人每天维生素D 的摄入量约为0.0000046克.数据 “0.0000046”用科学记数法表示为 ( )A.46×10-7B.4.6×10-7C.4.6×10-6D.0.46×10-5 3.如图, AB//CD,ZB=75°,ZE=27°,则ZD 的度数为 ( ) A.45° B.48° C.50° D.58°4.下列计算正确的是 ( ) A.2a+3a=6a B.(-3a)²=6a² C.(x-y)²=x²-y² D.3√2-√2=2√25.如图(1)是由大小相同的小正方体搭成的几何体,将上层的小正方体平移后得到图(2).关于平移前后几何体的三 视图,下列说法正确的是 ( )图(1) 图(2)A. 主视图相同B. 左视图相同C. 俯视图相同D. 三种视图都不相同 6.一元二次方程(x+1)(x- 1)=2x+3的根的情况是( ) A. 有两个不相等的实数根B.有两个相等的实数根C. 只有一个实数根D.没有实数根 7.某超市销售A,B,C,D 四种矿泉水,它们 的单价依次是5元、3元、2元、1元.某天 的销售情况如图所示,则这天销售的矿泉 水的平均单价是 ( ) A . 1 . 95元 B . 2 . 15元 C . 2 . 25元 D . 2 . 75元8.已知抛物线y =-x²+bx+4经过(-2,n )和(4,n)两点, 则n 的值为 ( ) A.-2 B.-4 C.2 D.49.如图,在四边形ABCD 中, AD//BC,ZD=90°,AD=4, BC=3.分别以点A,C 为圆心、大于的长为半径作弧,两弧交于点E ,作射线BE 交AD 于点F ,交AC 于点 0.若点0是AC 的中点,则CD 的长为 ( ) A.2√2 B.4 C.3 D.√ 10(第10题)10.如图,在△OAB 中,顶点0(0,0),A(-3,4),B(3,4).将△OAB 与正方形ABCD 组成的图形绕点0顺时针旋转, 每次旋转90°,则第70次旋转结束时,点D 的坐标为( )A.(10,3)B.(-3,10)C.(10,-3)D.(3,- 10) 二、填空题(每小题3分,共15分)11.计算:/4-2-1=12. 不等式丝的解集是13.现有两个不透明的袋子, 一个装有2个红球、1个白球, 另一个装有1个黄球、2个红球,这些球除颜色外完全相 同.从两个袋子中各随机摸出1个球,摸出的2个球颜 色相同的概率是14.如图,在扇形AOB 中,ZAOB =120°,半径0C 交弦AB于点D,且0C10A.若0A=2 √ 3,则阴影部分的面积为(第15题)15.如图,在矩形ABCD 中, AB=1,BC=a,点E 在边BC 上, 且.连接AE,将△ABE 沿AE 折叠,若点B 的对应点B'落在矩形ABCD 的边上,则a 的值为(第14题)( 第 9 题 )三、解答题(本大题共8个小题,满分75分)16. (8分)先化简,再求值;,其中x=/3.(每组包含最小值,不包含最大值)b. 七年级成绩在70≤x<80这一组的是:17 . (9分)如图,在△ABC 中,BA=BC,ZABC=90°, 以AB为直径的半圆0交AC于点D,点E是BD上不与点B,D重合的任意一点,连接AE交BD于点F,连接BE并延长交AC于点G.(1)求证:△ADF一△BDG;(2)填空:①若AB=4.且点E是BD的中点,则DF的长为②取正的中点H,连接EH,OH,当ZEAB的度数为时,四边形OBEH为菱形.根据以上信息,回答下列问题:(1)在这次测试中,七年级在80分以上(含80分)的有人;(2)表中m的值为;(3)在这次测试中,七年级学生甲与八年级学生乙的成绩都是78分,请判断两位学生在各自年级的排名谁更靠前,并说明理由;(4)该校七年级学生有400人,假设全部参加此次测试,请估计七年级成绩超过平均数76.9分的人数. 18. (9分)某校为了解七、八年级学生对“防溺水”安全知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理、描述和分析.部分信息如下:a.七年级成绩频数分布直方图:70 72 74 75 76 76 77 77 77 78 79c.七、八年级成绩的平均数、中位数(单位:分)如下:年级平均数七中位数76.9八m79.2 79.5◆2019河南省中招试题◆19. (9分)数学兴趣小组到黄河风景名胜区测量炎帝塑像(塑像中高者)的高度.如图所示,炎帝塑像DE在高55 m 的小山EC上,在A处测得塑像底部E的仰角为34°,再沿AC方向前进21 m到达B处,测得塑像顶部D的仰角为60°,求炎帝塑像DE的高度. (精确到1 m.参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67,√3≈1.73)20. (9分)学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品共需120元;购买5 个A奖品和4个B奖品共需210元.(1)求A,B两种奖品的单价;(2)学校准备购买A,B两种奖品共30个,且A奖品的数量不少于B奖品数量的.请设计出最省钱的购买方案,并说明理由.◆2019河南省中招试题◆21. (10分)模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:(1)建立函数模型设矩形相邻两边的长分别为x,y,由矩形的面积为4,得xy=4,民;由周长为m,得2(x+y)=m,满足要求的(x,y)应是两个函数图象在第象限内交点的坐标.(2)画出函数图象函数的图象如图所示,函数y=- ×+的图象可由直线y=-x平移得到.请在同一直角坐标系中直接画出直线y=-x.(3)平移直线y=-x,观察函数图象①当直线平移到与函的图象有唯一交点(2,2)时,周长m的值为 ;②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.(4)得出结论若能生产出面积为4的矩形模具,则周长m的取值范围为◆2019河南省中招试题◆22 . (10分)在△ABC 中, CA=CB,ZACB =α .点P 是平面内不与点A,C 重合的任意一点,连接AP,将线段AP 绕 点P 逆时针旋转α得到线段DP,连接AD,BD,CP.(1)观察猜想如图(1),当α=60°时,的值是 ,直线BD 与直线CP 相交所成的较小角的度数是(2)类比探究当α=90°时,请写出的值及直线BD 与直线CP相交所成的较小角的度数,并就图(2)的情形说明理由. (3)解决问题当α=90°时,若点E,F 分别是CA,CB 的中点,点P 在直线EF 上,请直接写出点C,P,D 在同一直线上值.图(1)备用图图(2)◆2019河南省中招试题◆23. (11分)如图,抛物线交x轴于A,B两点,交y轴于点C.直线经过点A,C.(1)求抛物线的解析式;(2)点P是抛物线上一动点,过点P作x轴的垂线,交直线AC于点M,设点P的横坐标为m.①连接PC,当△PCM是直角三角形时,求点P的坐标;②作点B关于点C的对称点B',则平面内存在直线l,使点M,B,B'到该直线的距离都相等,当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线I:y=hx+b的解析式. (k,b可用含m的式子表示)备用图48 不等式姓 数体米米间水姓 ,》6,可小8解集*>6<*<*无都◆2019河南省中招试题◆藻2019年河南省普通高中招生考试2.C 【解析】 0.0000046=4.6×10-*,故选C3.B 【素养落地】 本题考查平行线的性质,体现了逻辑推理的核 心素养.技法1 求不等式解集公共部分的两种方法中所有不等式解集的公共部分,找1数赫法巡不等式组中所有不等式的解集在间一条数轴上表苏出来,利用 数形结合用燃,自观北得到公共部分,两个一元一次不等式所级 减故不美式湖的剂集有以巴种类(设4<6):【解析】 如图,∵AB//CD,:21=2B=75°,又∵Z1=ZD+ZE, . . 2D=Z1 - ZE=75° - 27°=48°,故选B .4.D 【素养落地】 本题考查了整式的运算、二次根式的运算,体现了数学运算的核心素养.【解析】 2a+3a=(2+3)a=5a,故A 项错误; ( - 3a)²= ( - 3)²a²=9a²,故B 项错误; (x - y)²=x² - 2y+y²,故C 项错误;3、/2- √Z=2 √2,故D 项正确.5.C 【素养落地】 本题考查几何体的三视图,体现了直观想象的口使法 遂用口状”大大取夜大,小小取教小;大小小大中同找,大大小 能不了”来殊定13. 【素养落地】 本题考查用列举法求事件的概率,体现了数据分析的核心素养.【解析】 根据题意列表如下:核心素养.【解析】 根据俯视图的定义,可知平移前后几何体的俯视图相同,均如图所示,故选C.6.A 【解析】 把该方程变形为一般形式,为x²-2x-4=0,由一元二次方程根的判别式△=b²-4ac=(-2)²-4×1×(-4)=20> 0,可知该方程有两个不相等的实数根.故选A. 7.C 【素养落地】本题考查扇形统计图的识图能力及平均数的求解方法,体现了数据分析的核心素养,【解析】 5×10%+3×15%+2×55%+1×20%=2.25(元),故这天销售的矿泉水的平均单价为2.25元. 8.B 【素养落地】 本题考查二次函数的图象与性质,体现了逻辑推理的核心素养,【解析】 根据该抛物线经过(-2,n)和(4,n)两点,可知这条抛 物线的对称轴是直线,”,解得b=2,:该抛物线的解析式为y=-z²+2x+4,把x=4或x=-2代入, 得y =-4,即n =-4 .9.A 【素养落地】 本题考查尺规作图、垂直平分线的判定与性质、勾股定理等,体现了逻辑推理的核心素养. 【解析】 由作图可知,点E 在线段AC 的垂直平分线上,又点0是AC 的中点, .直线BE 是线段AC 的垂直平分线,AB=BC=3.过点B 作BM 工AD 于点M,则四边形BMDC 为矩形, .BM=CD, DM=BC=3 . :4M=1 .根据勾股定理,可得BM= √AB -AM=√ 3²-1⁷=2/2,即CD=2 √ 2.故选A.10.D 【素养落地】 本题考查旋转的性质,体现了直观想象、逻辑推理的核心素养.【解析】 根据题意,易知在旋转过程中,组合图形每4次一循环,而70÷4=17……2,.第70次旋转结東时,组合图形的位置如图所示,延长DA 交x 轴于点E, 易知AEIx 轴,则0E=3,AE=4,:AD=AB=20E=6,:DE=AD+AE=10,故点D 的坐标 为(3,-10),故选D. 11. 【解析】 Ⅱ12.x≤-2 【素养落地】 本题考查不等式组的解法,体现了数学 运算的核心素养. 【解析】 解不等;,得x≤-2,解不等式-x+7>4,得红 , 红2白 黄 (红,,黄) (红2,黄) (白,黄) 红 , (红,,红;) (红2,红,) (白,红,) 红4 (红,红4) (红2,红) (白,红4) 由表格可知,共有9种等可能的结果,其中摸出的2个球颜色相 同的结果有4种,故所求概率为 · 高分技法 14. π+J3【素养落地】本题考查不规 则图形面积的计算,体现了逻辑推理、 数学运算的核心素养. 【解析】 :0A=0B,ZAOB=120°, :.Z0AB=Z0BA=30° . ∵0C10A, : .ZBOC=120° - 90°=30°=Z0BA,,OD=BD .如图,过点0 作OELAB 于点E,在Rt △AOE 中, 0E=0A · sinZOAE=2/3× sin30°=√3.在Rt △AOD 中, 0D=0A ·tanZ0AD=25×tan 30°= 2.".BD=2," 2+15.【素养落地】 本题考查折叠的性质及分类讨论思想,体现了逻辑推理、直观想象的核心素养.技法2列举法求概率的解题通法时(则是表北或用西引树表状法图近)法一;数下一散适用于两步只不更不源地川半出改有下能出见的结笑,并到断每种结装出 现的可能性是香然茶;48公式户4)=拉求事件以发你的概③1定开有可已现的结是有不及所家事件A 出现的结果疗 m ; 混半问通,消好状图法适用于再与及两步以上泉敬率问题; 1.B 【解析】 根据负数的绝对值等于它的相反数,可高分技法◆2019河南省中招试题◆则四边形ABEB'是正方形, .BE=AB=1,即 · , ; ②当点B'落在边CD 上时,如图(2),易证△ECB '~~△B'DA,,即,”. ,<a=AD=√BA² B'D=.综上可知,a 的值)图(2)高分技法16. 【素养落地】本题考查了分式的化简求值,体现了数学运算的核心素养.【参考答案及评分标准】(4分) (6分)当x=\3时,(8分)17. 【素养落地】本题以圆为背景,考查了圆的相关性质、全等三角形的判定与性质、菱形的性质等,体现了逻辑推理的核心素养 【参考答案及评分标准】 (1)证明:∵BA=BC,ZABC=90°, .LCAB=ZC=45° .∵AB 为半圆0的直径, :ZADF=ZBDG=90°, :ZDBA=ZDAB=45°, .:AD=BD.∵ZDAF 和ZDBG 都是充所对的圆周角, :LDAF=ZDBG, . △ADF △BDG. (2)①4-2 √/2 2300解法提示:①:AB为半圆0的直径, ZAEB=90°,AEIBG. .ZAEG=90° · · 点E 是丽的中点, .ZGAE=ZBAE, 又AE=AE,:△AEB=△AEG, ..AG=AB=4...DG=AG-AD=4-2√2. :DF=DG=4-2√2. ∵四边形0BEH 是菱形, ..0B=BE, 又0B=OE,..△0BE是等边三角形, :2EOB=60°,:ZEAB=30° ·分析的核心素养.【参考答案及评分标准】(1)23 (2分) 解法提示:由七年级成绩频数分布直方图可知,80分以上(含80 分)的有15+8=23(人).(2)77.5 (4分) 解法提示:(3)七年级学生甲在本年级的排名更靠前. (5分) 理由:七年级学生甲的成绩大于七年级抽测成绩的中位数,而八 年级学生乙的成绩小于八年级抽测成绩的中位数.' ( 6 分 )答:估计七年级成绩超过平均数76.9分的人数为224人,(9分)19. 【素养落地】“本题以实际生活为背景,考查解直角三角形的实 际应用,体现了逻辑推理、数学抽象、数学建模的核心素养.【参考答案及评分标准】在Rt △ACE 中,∵ZA =34°,CE=55,1,:BC=AC-AB=82.1-21=61.1. 在Rt △BCD 中,∵2CBD=60°, :CD=BC ·tan60°≈61. 1×1.73≈105.7, :.DE=CD-CE=105.7-55≈51.鼓炎帝塑像DE 的高度约为51 m.(4分) (7分) (9分)圜高分技法20.【素养落地】本题材料来源于生活,通过构建一次函数、方程组、不等式模型解决实际问题,体现了数学抽象、数学建模、数学 运算的核心素养.【参考答案及评分标准】(1)设A 奖品的单价为x 元,B 奖品的 单价为y 元, (1分) 根据题意,得 ’解得故A 奖品的单价为30元,B 奖品的单价为15元. (4分) (2)最省钱的购买方案:A 奖品8个,B 奖品22个. ( 5 分 ) 理由:设购买A 奖品a 个,则购买B 奖品(30-a)个,共需w 元, 根据题意,得w=30a+15(30-a)=15a+450. (6分) :15>0,:当a 取最小值时,w 取最小值.:.a≥7.5,又a 为正整数,:当a=8时,w 取得最小值. 30-8=22.故当购买A 奖品8个,B 奖品22个时最省钱. 21. 【参考答案及评分标准】(1) 一(2)画直线y=-x 如图所示:(3)①8 (4分) ②直线与函数 的图象交点还有两种情况: 技法4解直角三角形的实际应用题目的解题通法(1)心用“解直角三角形”时党型解央问过,关健是把已知角或 特株角放在自角二角形中,当两卜直角三尚形有公共边时,公共劲是联系两个直角三角形的汛管,通常要水出这条公共边的长 度,进而解决问题,(2)当图形中设有直单三角形洲,则需要根据实际情况构造直角三角形.(3)运用“解直角一角形”的模型解决实际问题的步骤:①审题, 报据题干,弄明白图形中哪些是已知量,哪些是米知量;②将已知条件转化到示意图中,把实际问巡转化为解直角三角形的问题;③选择置当的关系式解直角三有形技法3解决折叠间题的方法掌器折叠的性成;直战对称;②公千浙泉两假的保形(指脊后变合的测形)合等,对放议角,线段,例长,百长多均相务,③对原点的徙线改浙报从在真线垂直平分;2.我出隐全的折叠前后的位置关系(平行或垂直)和数量关累 (相筹);3.一服运甲全等三角形,匀没是理,据似三僧形等知识及方程思 想,设出恰当的未和效,解方栓米求线设长,幻辽于折痕两侧的因形(进管后重台的周形)失于析很所在 (3分)(5分) (7分) (9分)(9分) (1分) (3分)②连接OE,图(1)由(1)知△ADF≥△BDG,◆2019河南省中招试题◆当有2个交点时,周长m 的取值范围是m>8. (8分)(4)m≥8 (10分)22.【素养落地】 本题是几何图形的类比探究题,主要考查了等腰 三角形的性质、等腰直角三角形的性质、全等三角形的判定与性质、相似三角形的判定与性质及分类讨论思想的运用等,体现了 逻辑推理、直观想象的核心素养.【解题思路】 (1)利用“SAS”证得△ACPm △ABD,可得CP= BD,ZACP=ZABD,继而可得直线BD 与直线CP 相交所成的较 小角等于ZBAC. (2)根据(1)中的思路,可以证明△DAB △PAC,直线BD 与直线CP 相交所成的较小角仍然等于ZBAC. (3)分点P 在线段CD 上和点P 在线段CD 延长线上两种情况进 行讨论即可.【参考答案及评分标准】(1)160° (2分)解法提示:∵AC=BC,ZACB=60°, △ABC是等边三角形, ..ZCAB=60°,AC=AB. 由旋转可得ZAPD=60°,AP=PD, △APD是等边三角形,.ZPAD=60°=ZCAB,AP=AD, ZCAP=ZBAD, :△ACP=△ABD,:CP=BD,ZACP= ZABD,如图(1),延长CP,BD 交于点M ,CM 与AB 交于点N,在△ANC 和△BNM 中,ZACN=ZMBN,ZCN=ZBNM, ZM=ZCAN=60° · ,直线BD 与直线CP 相交所成的较小角的度数为45° · (4分)理由如下:∵ZACB=90°,CA=CB, .ZCAB=45°,同理可得,23. 【解题思路】(1)根据直线AC 的解析式求出点A,C 的坐标,再 △PCM 是直角三角形, ZCMP<90°,可知分ZPCM=90°和ZMPC=90°两种情况进行讨论,据此求解即可;②易知满足条件的直线1即为△MBB'的三条中位线所在的直线,故先求出点B,B',M 的坐标,再求出线段BM,B'M 的中点坐标,即可求得直 线1的解析式.【参考答案及评分标准】 (1)∵直线经过点A,C,:A(-4,0),C(0,-2).∵抛物线经过点A,C,故抛物线的解析式为 (3分)(2)①:点P 的横坐标为m, :点P 的坐标为(m,当△PCM是直角三角形时,因ZPMC<90°,故分以下两种情况 讨论(i)当ZCPM=90° 时, PC//x 轴,则· 解得m;=0(舍去),mz=-2.:点P 的坐标为(-2,-2). (5分)(i)方法一:当ZPCM=90°时,如图,过点P 作PNly 轴于点N,ZCAB+ZDAC=ZPAD+ZDAC, 即ZDAB=ZPAC,:. △DAB △PAC, (6分)。
河南人教版中考英语基础教材过关练习 第22课时 九年级(全) Units 13~14

第22课时九年级(全)Units 13~14一、单项选择1.(2018湖南长沙)—Is the man over there Adam?—It be him. He has gone to Hong Kong on vacation.A.mustB.can’tC.mustn’t2.(2018上海)Catherine has two cousins. One is quiet, and is noisy.A.anotherB.the otherC.otherD.others3.(2018甘肃兰州)—times have you visited Gansu Science Museum?—Only once.A.How oftenB.How manyC.How longD.How soon4.(2018河南实验中学二模)When you leave the classroom, please turn off the light energy.A.saveB.savingC.savedD.to save5.(2018河南平顶山二模)Which of the following sentences is correct?A.We needn’t worry about they.B.Jim father teaches in a middle school.C.Mary looks young than before.D.He as well as I wants to go skating.6.(2017浙江温州)Simon looks worried because he a writing competition and now he’s waiting for the result.A.entersB.enteredC.will enterD.is entering7.(原创)No free plastic bags in the supermarkets can help to white pollution.A.reduceB.removeC.provideD.produce8.(原创)They had to walk back because they a taxi.A.couldn’t afford to takeB.couldn’t afford takingC.can afford to takeD.couldn’t afford take9.(原创)I have to prepare well for the math test tomorrow because it30% of the final exam.A.sets upB.puts upes upD.makes up10.(原创),he raised $150,000.A.In firstB.At the end ofC.In the endD.At the first11.—What did you do on Earth Day this year?—We a show to spread the messages about protecting the environment.A.put awayB.put upC.put onD.put off12.The Internet is used information for people,but still lots of people are used information from books.A.to get;to gettingB.to get;to getC.to getting;to gettingD.to getting;to get13.—Excuse me, sir. You’re driving so. I have to get to the airport in five minutes.—I’m sorry, but it’s the rush hour.A.quicklyB.slowlyC.clearlyD.sadly14.—Your shoes are beautiful!—Thank you. They are the present my mom bought me last month.A.thatB.whoC.whatD.where15.It’s cruel to sharks’ fins. We must stop people from doing that.A.cut downB.cut offC.take downD.take off二、完形填空Do you ever watch old movies?Maybe you will see one with Carole Lombard.She was a famous1in the 1930s.She died when she was only 34.In her2life she made 70 movies!Lombard’s real name was Jane Alice Peters.In 1921,she was playing baseball in the3near her home.A movie director4her and decided to put her in a movie.She was only 13 at the time.The movie was one of the last silent movies.She acted(表演)so well that she5the hearts of some people.At 16,she left school to act.In 1925,she had an agreement with a6studio,20th Century Fox.The studio gave7 a new name,and she acted in several films.Then,at age 18,she was in a bad car accident.The accident left scars(伤疤)on her face.The studio broke the agreement,but she did not8.She continued to act.It was Paramount Studio that made Lombard a9.She made many movies for the studio.She also married two of their stars.Lombard was married to actor William Powell for only 23 months.10seven years later,she married the great love of her life,actor Clark Gable.It was a great Hollywood love story.1.A.nurse B.actress C.doctor D.teacher2.A.short zy C.long D.humorous3.A.kitchen B.classroom C.cinema D.street4.A.forgot B.saw C.hurt D.pushed5.A.broke B.avoided C.won D.treated6.A.dance B.film C.music D.school7.A.me B.it C.her D.him8.A.give up B.have a try C.make sure D.lift up9.A.scientist B.writer C.driver D.star10.A.But B.Before C.Since D.As三、阅读理解(2018河南安阳二模)We don’t meet people by accident. Every person you meet will play a role in your life, whether it is big or small. Some will help you grow, some will hurt you, and some will encourage you to do better. At the same time, you are playing a role in their lives as well. We should know that paths cross for a reason.The best teachers are those who don’t tell you how to get there but show you the way.There is no better joy than helping people see something for themselves, seeing them go to higher levels that they could never have imagined on their own. But that doesn’t mean you have to fix them or enable them to do something. Instead, guide them to the source of their own power. Offer them support to help them find their own way and show you what they’re able to do. All you have to do is to believe in them.Never look down on someone. We like to think much of great people, so it’s easy to look down on someone who isn’t as successful or well educated as you are. But you have no idea how far that person has already climbed or where they will end up. Time could easily change your positions, so be sure you treat everyone with dignity(尊严).Appreciate those who have supported you, forgive those who have hurt you, help those who need you. Treat all people, including yourself, with love and compassion, and you can’t go wrong. Treat people the way you want to be treated and your life will get better soon.1.According to the passage, the people we meet will not us.A.helpB.hurtC.changeD.encourage2.According to the passage, who are the best teachers?A.The teachers who show you the way there.B.The teachers who are kind to the students.C.The teachers who tell you how to get there.D.The teachers who help you get good grades.3.The writer thinks that we should treat all people with if we don’t want to go wrong.A.a lot of moneyB.good thingsC.candies and fruitD.love and compassion4.Which of the following is true according to the passage?A.We shouldn’t forgive those who have hurt us.B.We have to fix people or enable them to do something.C.We have to guide people to the source of their own power.D.There is better joy than helping people see something for themselves.5.What can we learn from the passage?A.We should treat other people kindly.B.We should cherish the people we meet.C.We should thank those who help and support us.D.We should try to help the people who are in trouble.四、任务型阅读(2018河南洛阳二模)Since two years ago, city streets around China have seen colorful shared bikes. 1To reduce traffic jams and air pollution, many cities have offered shared bikes. But sometimes, dreams can turn sour(坏的).As shared bikes become more popular, problems keep showing up. 2When people are using the bike, some of them just throw it onto streets and even into ditches(水沟). Some bikes are stolen. Recently, a man in Shanghai was fined(罚款) 1,000 yuan for stealing a shared bike.Besides, the damage to the QR codes on the bikes has brought huge losses(损失) to bike-sharing companies, like Mobike. 3It can take several hundred yuan for the company workers to find a lost bike and get it repaired.Mobike has 100 credit(信用) scores for each user. 4Once the score drops to below 80, bike rental will go up to five yuan per 30 minutes.5Bike sharing services will work well if people follow the rules and show respect for the bikes and other users.根据材料内容,从下面五个选项中选出能填入文中空缺处的最佳选项,使短文意思通顺,内容完整。
2023年河南洛阳中考历史真题及答案

2023年河南洛阳中考历史真题及答案注意事项:1.本试卷共6页,分为选择题和非选择题,满分50分,考试时间50分钟。
2.开卷考试,可查阅参考资料,但应独立答题,禁止交流资料。
3.本试卷上不要答题,请按答题卡上注意事项的要求直接把答案填写在答题卡上。
答在试卷上的答案无效。
选择题(共20小题,20分)下列每小题列出的四个选项中,只有一个选项是最符合题目要求的。
请将正确选项的字母代号涂写在答题卡相应位置上。
1.有学者说,在我国史前时期的各个文化区当中,中原有“居天下之中”的地理优势,扮演了中华文明大熔炉的角色。
该学者肯定了中原文化区在中华文明形成过程中()A.产生时间最早B.居于核心地位C.发展相对独立D.体系最为完备2.殷墟出土了大量的贝,商朝时期的一些文字都含“贝”字(如下表)。
据此判断,贝在商朝应该是()甲骨文对应汉字贝买贯宝A.货币B.礼器C.食器D.酒具3.考古发现的战国中后期的铁器,出土范围遍及秦、齐、燕、楚等七国境内,器类包括农具、手工业工具、兵器和杂器。
这表明当时铁器()A.象征贵族身份B.制作工艺精良C.实行官营专卖D.得到广泛使用4.汉武帝分别设置《诗》《书》《易》《礼》《春秋》博士,让他们专心传经讲学,后来,博士又演变为国家学术教育机关的学官。
这有利于()A.儒学地位提高B.科举制度完善C.人民负担减轻D.经济管理强化5.唐三彩是盛唐气象的一个缩影,它延续了秦汉以来彩塑的写实风格,又创造性地运用了低温铅釉的绚丽、斑斓色彩和略带夸张的手法。
这折射出唐朝注重()A.传承与创新B.交流与传播C.改进与推广D.开放与互鉴6.宋朝在泉州、广州等地都设有“蕃市”“蕃坊”“蕃学”。
这是由于当时()A.市民阶层壮大B.海外贸易兴盛C.民族交往频繁D.文化教育发展7.秦汉至唐主要依据自然界限来划分行政区划,而元代不惜打破自然地理界限,人为地造成区划边界处于犬牙交错的格局,使地方丧失扼险而守的地理条件。
河南省2022年中考[数学]考试真题与答案解析
![河南省2022年中考[数学]考试真题与答案解析](https://img.taocdn.com/s3/m/cfd27ad6710abb68a98271fe910ef12d2af9a9aa.png)
河南省2022年中考[数学]考试真题与答案解析一、选择题下列各小题均有四个选项,其中只有一个是正确的.1. 的相反数是( )12-A. B. 2 C. D. 2-12-122. 2022年北京冬奥会的奖牌“同心”表达了“天地合·人心同”的中华文化内涵,将这六个汉字分别写在某正方体的表面上,如图是它的一种展开图,则在原正方体中,与“地”字所在面相对的面上的汉字是()同 C. 心 D. 人3. 如图,直线AB ,CD 相交于点O ,EO ⊥CD ,垂足为O .若∠1=54°,则∠2的度数为( )A. 26°B. 36°C. 44°D. 54°4. 下列运算正确的是( )A. B. 2-=()2211a a +=+C. D. ()325a a =2322a a a ⋅=5. 如图,在菱形ABCD 中,对角线AC ,BD 相交于点O ,点E 为CD 的中点.若OE =3,则菱形ABCD 的周长为( )A. 6B. 12C. 24D. 486. 一元二次方程的根的情况是()210x x +-=A. 有两个不相等的实数根B. 没有实数根C. 有两个相等的实数根D. 只有一个实数根7. 如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况(满分5分),则所打分数的众数为( )A. 5分B. 4分C. 3分D. 45%8. 《孙子算经》中记载:“凡大数之法,万万曰亿,万万亿曰兆.”说明了大数之间的关系:1亿=1万×1万,1兆=1万×1万×1亿,则1兆等于()A. B. 8101210C. D. 161024109. 如图,在平面直角坐标系中,边长为2的正六边形ABCDEF 的中心与原点O 重合,AB x∥轴,交y 轴于点P .将△OAP 绕点O 顺时针旋转,每次旋转90°,则第2022次旋转结束时,点A 的坐标为()A. B. C.D. )1-(1,-()1-(10. 呼气式酒精测试仪中装有酒精气体传感器,可用于检测驾驶员是否酒后驾车.酒精气体传感器是一种气敏电阻(图1中的),的阻值随呼气酒精浓度K 的变化而变化(如图2),1R 1R 血液酒精浓度M 与呼气酒精浓度K 的关系见图3.下列说法不正确的是()A. 呼气酒精浓度K 越大,的阻值越小B. 当K =0时,的阻值为1001R 1RC. 当K =10时,该驾驶员为非酒驾状态D. 当时,该驾驶员为醉驾状态120=R 二、填空题11. 请写出一个随增大而增大的一次函数表达式_________.y x 12. 不等式组的解集为______.30,12x x -≤⎧⎪⎨>⎪⎩13. 为开展“喜迎二十大、永远跟党走、奋进新征程”主题教育宣讲活动,某单位从甲、乙、丙、丁四名宣讲员中随机选取两名进行宣讲,则恰好选中甲和丙的概率为______.14. 如图,将扇形AOB 沿OB 方向平移,使点O 移到OB 的中点处,得到扇形.若O 'A O B '''∠O =90°,OA =2,则阴影部分的面积为______.15. 如图,在Rt△ABC 中,∠ACB =90°,,点D 为AB 的中点,点P 在AC AC BC ==上,且CP =1,将CP 绕点C 在平面内旋转,点P 的对应点为点Q ,连接AQ ,DQ .当∠ADQ =90°时,AQ 的长为______.三、解答题16. (1;(2)化简:.01123-⎛⎫-+ ⎪⎝⎭2111x x x -⎛⎫÷- ⎪⎝⎭17. 2022年3月23日下午,“天宫课堂”第二课在中国空间站开讲,神舟十三号乘组航天员翟志刚、王亚平、叶光富相互配合进行授课,这是中国空间站的第二次太空授课,被许多中小学生称为“最牛网课”.某中学为了解学生对“航空航天知识”的掌握情况,随机抽取50名学生进行测试,并对成绩(百分制)进行整理,信息如下:a .成绩频数分布表:成绩x (分)5060x ≤<6070x ≤<7080x ≤<8090x ≤<90100x ≤≤频数7912166b .成绩在这一组的是(单位:分):7080x ≤<70 71 72 72 74 77 78 78 78 79 79 79根据以上信息,回答下列问题:(1)在这次测试中,成绩的中位数是______分,成绩不低于80分的人数占测试人数的百分比为______.(2)这次测试成绩的平均数是76.4分,甲的测试成绩是77分.乙说:“甲的成绩高于平均数,所以甲的成绩高于一半学生的成绩.”你认为乙的说法正确吗?请说明理由.(3)请对该校学生“航空航天知识”的掌握情况作出合理的评价.18. 如图,反比例函数的图像经过点和点,点在点的下方,平分()0ky x x =>()2,4A B B A AC ,交轴于点.OAB ∠x C(1)求反比例函数的表达式.(2)请用无刻度的直尺和圆规作出线段的垂直平分线.(要求:不写作法,保留作图痕迹,AC 使用2B 铅笔作图)(3)线段与(2)中所作的垂直平分线相交于点,连接.求证:.OA D CD CD AB ∥19. 开封清明上河园是依照北宋著名画家张择端的《清明上河图》建造的,拂云阁是园内最高的建筑.某数学小组测量拂云阁DC 的高度,如图,在A 处用测角仪测得拂云阁顶端D 的仰角为34°,沿AC 方向前进15m 到达B 处,又测得拂云阁顶端D 的仰角为45°.已知测角仪的高度为1.5m ,测量点A ,B 与拂云阁DC 的底部C 在同一水平线上,求拂云阁DC 的高度(结果精确到1m .参考数据:,,).sin 340.56︒≈cos340.83︒≈tan 340.67︒≈20. 近日,教育部印发《义务教育课程方案》和课程标准(2022年版),将劳动从原来的综合实践活动课程中独立出来.某中学为了让学生体验农耕劳动,开辟了一处耕种园,需要采购一批菜苗开展种植活动.据了解,市场上每捆A 种菜苗的价格是菜苗基地的倍,用300元在54市场上购买的A 种菜苗比在菜苗基地购买的少3捆.(1)求菜苗基地每捆A 种菜苗的价格.(2)菜苗基地每捆B 种菜苗的价格是30元.学校决定在菜苗基地购买A ,B 两种菜苗共100捆,且A 种菜苗的捆数不超过B 种菜苗的捆数.菜苗基地为支持该校活动,对A ,B 两种菜苗均提供九折优惠.求本次购买最少花费多少钱.21. 红看到一处喷水景观,喷出的水柱呈抛物线形状,她对此展开研究:测得喷水头P 距地面0.7m ,水柱在距喷水头P 水平距离5m 处达到最高,最高点距地面3.2m ;建立如图所示的平面直角坐标系,并设抛物线的表达式为,其中x (m )是水柱距喷水头的水平()2y a x h k =-+距离,y (m )是水柱距地面的高度.(1)求抛物线的表达式.(2)爸爸站在水柱正下方,且距喷水头P 水平距离3m ,身高1.6m 的小红在水柱下方走动,当她的头顶恰好接触到水柱时,求她与爸爸的水平距离.22. 为弘扬民族传统体育文化,某校将传统游戏“滚铁环”列入了校运动会的比赛项目.滚铁环器材由铁环和推杆组成.小明对滚铁环的启动阶段进行了研究,如图,滚铁环时,铁环⊙O 与水平地面相切于点C ,推杆AB 与铅垂线AD 的夹角为∠BAD ,点O ,A ,B ,C ,D 在同一平面内.当推杆AB 与铁环⊙O 相切于点B 时,手上的力量通过切点B 传递到铁环上,会有较好的启动效果.(1)求证:∠BOC +∠BAD =90°.(2)实践中发现,切点B 只有在铁环上一定区域内时,才能保证铁环平稳启动.图中点B 是该区域内最低位置,此时点A 距地面的距离AD 最小,测得.已知铁环⊙O 的3cos 5BAD ∠=半经为25cm ,推杆AB 的长为75cm ,求此时AD 的长.23. 综合与实践综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.(1)操作判断操作一:对折矩形纸片ABCD ,使AD 与BC 重合,得到折痕EF ,把纸片展平;操作二:在AD 上选一点P ,沿BP 折叠,使点A 落在矩形内部点M 处,把纸片展平,连接PM ,BM .根据以上操作,当点M 在EF 上时,写出图1中一个30°的角:______.(2)迁移探究小华将矩形纸片换成正方形纸片,继续探究,过程如下:将正方形纸片ABCD 按照(1)中的方式操作,并延长PM 交CD 于点Q ,连接BQ .①如图2,当点M 在EF 上时,∠MBQ =______°,∠CBQ =______°;②改变点P 在AD 上的位置(点P 不与点A ,D 重合),如图3,判断∠MBQ 与∠CBQ 的数量关系,并说明理由.(3)拓展应用在(2)的探究中,已知正方形纸片ABCD 的边长为8cm ,当FQ =1cm 时,直接写出AP 的长.答案解析一、选择题1.D2.D3.B4.D5.C6.A7.B8.C9.B 10.C二、填空题11.(答案不唯一)y x =12.23x <≤13.1614.3π+三、解答题16.(1);(2)521x +17.(1),(2)不正确.理由见解析(3)见解析78.544%18.(1)(2)图见解析部分(3)证明见解析8y x=19.拂云阁DC 的高度约为32m20.(1)20元(2)2250元21.(1)(2)2或6m()20.15 3.2y x =--+22.(1)见解析(2)50 cm23.(1)或或或(2)①15,15;②,理由见解析BME ∠ABP ∠PBM ∠MBC ∠MBQ CBQ ∠=∠(3)cm 4011AP =。
2023年河南中考语文试题(含答案)

⑫两个月后,他老母亲看见一个风尘仆仆的人牵着一匹马站在门前。她惊喜地认出了儿子!他抱着瘦小的母亲,“妈,我回来了。你看,咱们又有一匹‘白头心儿’了!”
4.小豫想为下面幻灯片中的文字选配一幅插图。A、B两幅备选图中,你建议选择哪一幅,请简述理由。
【当代奇迹】河南有一个水利奇迹——红旗渠,它是林县(今林州市)人民历时十年在悬崖陡壁上修建的人工天河,解决了当地55万人的饮水难题和54万亩耕地的浇灌问题。过去的林县“十年九旱,水贵如油”;红旗渠建成后,“旱涝都不怕,年年保丰收”。修建红旗渠异常艰辛,其中“青年洞”的开凿尤为不易,300多名壮小伙儿组成突击队,一锤一钎打了17个月,才凿出了长616米、宽6.2米、高2米的“青年洞”。
5.小豫想用一组排比句为班会作总结,请你仿照画波浪线的语句帮他续写一句话。要求:语意连贯,句式、修辞一致。
同学们,河南文化如万里长河,我们今天掬起的不过是几朵浪花;河南文化如鸿篇巨制,我们今天欣赏的不过是几个片段;河南文化如____________,____________。希望同学们读万卷书,行万里路,更全面地了解河南,更深刻地理解河南文化。
③DNA竟然可以存储壁画?其实,这并不奇怪。自有生命以来,大自然一直用DNA来存储信息。纷繁复杂的人类基因组信息,就是记录在比细胞还小得多的DNA上,一代代遗传下来的。通过一根头发附带的DNA信息,就能复原生命体的所有遗传信息。DNA存储了亿万年来无数生物的遗传信息,可谓大自然中最好的存储器。如果能把海量的信息“写”到小小的DNA上存储起来,岂不便利?
2020年河南省中考数学试卷及答案解析

2020年河南省中考数学试卷一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个是正确的.1.(3分)2的相反数是()A.﹣2B.−12C.12D.22.(3分)如图摆放的几何体中,主视图与左视图有可能不同的是()A.B.C.D.3.(3分)要调查下列问题,适合采用全面调查(普查)的是()A.中央电视台《开学第一课》的收视率B.某城市居民6月份人均网上购物的次数C.即将发射的气象卫星的零部件质量D.某品牌新能源汽车的最大续航里程4.(3分)如图,l1∥l2,l3∥l4,若∠1=70°,则∠2的度数为()A.100°B.110°C.120°D.130°5.(3分)电子文件的大小常用B,KB,MB,GB等作为单位,其中1GB=210MB,1MB=210KB,1KB=210B.某视频文件的大小约为1GB,1GB等于()A.230B B.830B C.8×1010B D.2×1030B6.(3分)若点A(﹣1,y1),B(2,y2),C(3,y3)在反比例函数y=−6x的图象上,则y1,y2,y3的大小关系是()A.y1>y2>y3B.y2>y3>y1C.y1>y3>y2D.y3>y2>y1 7.(3分)定义运算:m☆n=mn2﹣mn﹣1.例如:4☆2=4×22﹣4×2﹣1=7.则方程1☆x =0的根的情况为()A.有两个不相等的实数根B.有两个相等的实数根C .无实数根D .只有一个实数根8.(3分)国家统计局统计数据显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x ,则可列方程为( ) A .500(1+2x )=7500 B .5000×2(1+x )=7500 C .5000(1+x )2=7500D .5000+5000(1+x )+5000(1+x )2=75009.(3分)如图,在△ABC 中,∠ACB =90°,边BC 在x 轴上,顶点A ,B 的坐标分别为(﹣2,6)和(7,0).将正方形OCDE 沿x 轴向右平移,当点E 落在AB 边上时,点D 的坐标为( )A .(32,2)B .(2,2)C .(114,2) D .(4,2)10.(3分)如图,在△ABC 中,AB =BC =√3,∠BAC =30°,分别以点A ,C 为圆心,AC 的长为半径作弧,两弧交于点D ,连接DA ,DC ,则四边形ABCD 的面积为( )A .6√3B .9C .6D .3√3二、填空题(每小题3分,共15分)11.(3分)请写出一个大于1且小于2的无理数 . 12.(3分)已知关于x 的不等式组{x >a ,x >b ,其中a ,b 在数轴上的对应点如图所示,则这个不等式组的解集为 .13.(3分)如图所示的转盘,被分成面积相等的四个扇形,分别涂有红、黄、蓝、绿四种颜色.固定指针,自由转动转盘两次,每次停止后,记下指针所指区域(指针指向区域分界线时,忽略不计)的颜色,则两次颜色相同的概率是.14.(3分)如图,在边长为2√2的正方形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为.15.(3分)如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交BĈ于点D,点E为半径OB上一动点.若OB=2,则阴影部分周长的最小值为.三、解答题(本大题共8个小题,满分75分)16.(8分)先化简,再求值:(1−1a+1)÷aa2−1,其中a=√5+1.17.(9分)为发展乡村经济,某村根据本地特色,创办了山药粉加工厂.该厂需购置一台分装机,计划从商家推荐试用的甲、乙两台不同品牌的分装机中选择.试用时,设定分装的标准质量为每袋500g,与之相差大于10g为不合格.为检验分装效果,工厂对这两台机器分装的成品进行了抽样和分析,过程如下:[收集数据]从甲、乙两台机器分装的成品中各随机抽取20袋,测得实际质量(单位:g)如下:甲:501 497 498 502 513 489 506 490 505 486502 503 498 497 491 500 505 502 504 505乙:505 499 502 491 487 506 493 505 499 498502 503 501 490 501 502 511 499 499 501[整理数据]整理以上数据,得到每袋质量x(g)的频数分布表.质量频数机器485≤x<490490≤x<495495≤x<500500≤x<505505≤x<510510≤x<515甲224741乙135731 [分析数据]根据以上数据,得到以下统计量.统计量机器平均数中位数方差不合格率甲499.7501.542.01b乙499.7a31.8110%根据以上信息,回答下列问题:(1)表格中的a=,b=;(2)综合上表中的统计量,判断工厂应迭购哪一台分装机,并说明理由.18.(9分)位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6m.(1)求观星台最高点A距离地面的高度(结果精确到0.1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,√2≈1.41);(2)“景点简介”显示,观星台的高度为12.6m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.19.(9分)暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.设某学生暑期健身x(次),按照方案一所需费用为y1(元),且y1=k1x+b;按照方案二所需费用为y2(元),且y2=k2x.其函数图象如图所示.(1)求k1和b的值,并说明它们的实际意义;(2)求打折前的每次健身费用和k2的值;(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.20.(9分)我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具﹣﹣三分角器.图1是它的示意图,其中AB与半圆O的直径BC在同一直线上,且AB的长度与半圆的半径相等;DB与AC垂直于点B,DB足够长.使用方法如图2所示,若要把∠MEN三等分,只需适当放置三分角器,使DB经过∠MEN 的顶点E,点A落在边EM上,半圆O与另一边EN恰好相切,切点为F,则EB,EO 就把∠MEN三等分了.为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.已知:如图2,点A,B,O,C在同一直线上,EB⊥AC,垂足为点B,.求证:.21.(10分)如图,抛物线y=﹣x2+2x+c与x轴正半轴,y轴正半轴分别交于点A,B,且OA=OB,点G为抛物线的顶点.(1)求抛物线的解析式及点G的坐标;(2)点M,N为抛物线上两点(点M在点N的左侧),且到对称轴的距离分别为3个单位长度和5个单位长度,点Q为抛物线上点M,N之间(含点M,N)的一个动点,求点Q的纵坐标y Q的取值范围.22.(10分)小亮在学习中遇到这样一个问题:̂上一动点,线段BC=8cm,点A是线段BC的中点,过点C作CF∥BD,如图,点D是BC交DA的延长线于点F.当△DCF为等腰三角形时,求线段BD的长度.小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题.请将下面的探究过程补充完整:̂上的不同位置,画出相应的图形,测量线段BD,CD,FD的长度,(1)根据点D在BC得到下表的几组对应值.BD/cm0 1.0 2.0 3.0 4.0 5.0 6.07.08.0 CD/cm8.07.77.2 6.6 5.9a 3.9 2.40 FD/cm8.07.4 6.9 6.5 6.1 6.0 6.2 6.78.0操作中发现:①“当点D为BĈ的中点时,BD=5.0cm”.则上表中a的值是;②“线段CF的长度无需测量即可得到”.请简要说明理由.(2)将线段BD的长度作为自变量x,CD和FD的长度都是x的函数,分别记为y CD和y FD,并在平面直角坐标系xOy中画出了函数y FD的图象,如图所示.请在同一坐标系中画出函数y CD的图象;(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当△DCF为等腰三角形时,线段BD长度的近似值(结果保留一位小数).23.(11分)将正方形ABCD的边AB绕点A逆时针旋转至AB′,记旋转角为α,连接BB′,过点D作DE垂直于直线BB′,垂足为点E,连接DB′,CE.(1)如图1,当α=60°时,△DEB′的形状为,连接BD,可求出BB′CE的值为;(2)当0°<α<360°且α≠90°时,①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;②当以点B′,E,C,D为顶点的四边形是平行四边形时,请直接写出BEB′E的值.2020年河南省中考数学试卷参考答案与试题解析一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个是正确的.1.(3分)2的相反数是()A.﹣2B.−12C.12D.2【解答】解:2的相反数是﹣2.故选:A.2.(3分)如图摆放的几何体中,主视图与左视图有可能不同的是()A.B.C.D.【解答】解:A、主视图和左视图是长方形,一定相同,故本选项不合题意题意;B、主视图和左视图都是等腰三角形,一定相同,故选项不符合题意;C、主视图和左视图都是圆,一定相同,故选项不符合题意;D、主视图是长方形,左视图是正方形,故本选项符合题意;故选:D.3.(3分)要调查下列问题,适合采用全面调查(普查)的是()A.中央电视台《开学第一课》的收视率B.某城市居民6月份人均网上购物的次数C.即将发射的气象卫星的零部件质量D.某品牌新能源汽车的最大续航里程【解答】解:A、调查中央电视台《开学第一课》的收视率,适合抽查,故本选项不合题意;B、调查某城市居民6月份人均网上购物的次数,适合抽查,故本选项不合题意;C、调查即将发射的气象卫星的零部件质量,适合采用全面调查(普查),故本选项符合题意;D、调查某品牌新能源汽车的最大续航里程,适合抽查,故本选项不合题意.故选:C.4.(3分)如图,l1∥l2,l3∥l4,若∠1=70°,则∠2的度数为()A.100°B.110°C.120°D.130°【解答】解:∵l1∥l2,∠1=70°,∴∠3=∠1=70°,∵l3∥l4,∴∠2=180°﹣∠3=180°﹣70°=110°,故选:B.5.(3分)电子文件的大小常用B,KB,MB,GB等作为单位,其中1GB=210MB,1MB=210KB,1KB=210B.某视频文件的大小约为1GB,1GB等于()A.230B B.830B C.8×1010B D.2×1030B【解答】解:由题意得:210×210×210B=210+10+10=230B,故选:A.6.(3分)若点A(﹣1,y1),B(2,y2),C(3,y3)在反比例函数y=−6x的图象上,则y1,y2,y3的大小关系是()A.y1>y2>y3B.y2>y3>y1C.y1>y3>y2D.y3>y2>y1【解答】解:∵点A(﹣1,y1)、B(2,y2)、C(3,y3)在反比例函数y=−6x的图象上,∴y1=−6−1=6,y2=−62=−3,y3=−63=−2,又∵﹣3<﹣2<6,∴y1>y3>y2.故选:C.7.(3分)定义运算:m☆n=mn2﹣mn﹣1.例如:4☆2=4×22﹣4×2﹣1=7.则方程1☆x=0的根的情况为( ) A .有两个不相等的实数根 B .有两个相等的实数根 C .无实数根D .只有一个实数根【解答】解:由题意可知:1☆x =x 2﹣x ﹣1=0, ∴△=1﹣4×1×(﹣1)=5>0, 故选:A .8.(3分)国家统计局统计数据显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x ,则可列方程为( ) A .500(1+2x )=7500 B .5000×2(1+x )=7500 C .5000(1+x )2=7500D .5000+5000(1+x )+5000(1+x )2=7500【解答】解:设我国2017年至2019年快递业务收入的年平均增长率为x , 由题意得:5000(1+x )2=7500, 故选:C .9.(3分)如图,在△ABC 中,∠ACB =90°,边BC 在x 轴上,顶点A ,B 的坐标分别为(﹣2,6)和(7,0).将正方形OCDE 沿x 轴向右平移,当点E 落在AB 边上时,点D 的坐标为( )A .(32,2)B .(2,2)C .(114,2) D .(4,2)【解答】解:如图,设正方形D ′C ′O ′E ′是正方形OCDE 沿x 轴向右平移后的正方形,∵顶点A ,B 的坐标分别为(﹣2,6)和(7,0), ∴AC =6,OC =2,OB =7, ∴BC =9,∵四边形OCDE 是正方形, ∴DE =OC =OE =2, ∴O ′E ′=O ′C ′=2, ∵E ′O ′⊥BC ,∴∠BO ′E ′=∠BCA =90°, ∴E ′O ′∥AC , ∴△BO ′E ′∽△BCA , ∴E′O′AC =BO′BC,∴26=BO′9,∴BO ′=3,∴OC ′=7﹣2﹣3=2,∴当点E 落在AB 边上时,点D 的坐标为(2,2), 故选:B .10.(3分)如图,在△ABC 中,AB =BC =√3,∠BAC =30°,分别以点A ,C 为圆心,AC 的长为半径作弧,两弧交于点D ,连接DA ,DC ,则四边形ABCD 的面积为( )A .6√3B .9C .6D .3√3【解答】解:连接BD 交AC 于O , ∵AD =CD ,AB =BC , ∴BD 垂直平分AC , ∴BD ⊥AC ,AO =CO ,∵AB=BC,∴∠ACB=∠BAC=30°,∵AC=AD=CD,∴△ACD是等边三角形,∴∠DAC=∠DCA=60°,∴∠BAD=∠BCD=90°,∠ADB=∠CDB=30°,∵AB=BC=√3,∴AD=CD=√3AB=3,∴四边形ABCD的面积=2×12×3×√3=3√3,故选:D.二、填空题(每小题3分,共15分)11.(3分)请写出一个大于1且小于2的无理数√3.【解答】解:大于1且小于2的无理数是√3,答案不唯一.故答案为:√3.12.(3分)已知关于x的不等式组{x>a,x>b,其中a,b在数轴上的对应点如图所示,则这个不等式组的解集为x>a.【解答】解:∵b<0<a,∴关于x的不等式组{x>a,x>b,的解集为:x>a,故答案为:x>a.13.(3分)如图所示的转盘,被分成面积相等的四个扇形,分别涂有红、黄、蓝、绿四种颜色.固定指针,自由转动转盘两次,每次停止后,记下指针所指区域(指针指向区域分界线时,忽略不计)的颜色,则两次颜色相同的概率是14.【解答】解:自由转动转盘两次,指针所指区域所有可能出现的情况如下:共有16种可能出现的结果,其中两次颜色相同的有4种, ∴P (两次颜色相同)=416=14, 故答案为:14.14.(3分)如图,在边长为2√2的正方形ABCD 中,点E ,F 分别是边AB ,BC 的中点,连接EC ,FD ,点G ,H 分别是EC ,FD 的中点,连接GH ,则GH 的长度为 1 .【解答】解:设DF ,CE 交于O , ∵四边形ABCD 是正方形,∴∠B =∠DCF =90°,BC =CD =AB , ∵点E ,F 分别是边AB ,BC 的中点, ∴BE =CF ,∴△CBE ≌△DCF (SAS ), ∴CE =DF ,∠BCE =∠CDF , ∵∠CDF +∠CFD =90°, ∴∠BCE +∠CFD =90°, ∴∠COF =90°,∴DF⊥CE,∴CE=DF=√(2√2)2+(√2)2=√10,∵点G,H分别是EC,FD的中点,∴CG=FH=√10 2,∵∠DCF=90°,CO⊥DF,∴CF2=OF•DF,∴OF=CF2DF=√2)210=√105,∴OH=3√1010,OD=4√105,∵OC2=OF•OD,∴OC=√105×4105=2√105,∴OG=CG﹣OC=√102−2√105=√1010,∴HG=√OG2+OH2=√110+910=1,故答案为:1.15.(3分)如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交BĈ于点D,点E为半径OB上一动点.若OB=2,则阴影部分周长的最小值为6√2+π3.【解答】解:如图,作点D关于OB的对称点D′,连接D′C交OB于点E′,连接E′D、OD′,此时E′C+E′C最小,即:E′C+E′C=CD′,由题意得,∠COD=∠DOB=∠BOD′=30°,∴∠COD′=90°,∴CD′=√OC2+OD′2=√22+22=2√2,CD̂的长l =30π×2180=π3, ∴阴影部分周长的最小值为2√2+π3=6√2+π3. 故答案为:6√2+π3.三、解答题(本大题共8个小题,满分75分) 16.(8分)先化简,再求值:(1−1a+1)÷aa 2−1,其中a =√5+1. 【解答】解:(1−1a+1)÷aa 2−1=a+1−1a+1×(a−1)(a+1)a=a ﹣1,把a =√5+1代入a ﹣1=√5+1﹣1=√5.17.(9分)为发展乡村经济,某村根据本地特色,创办了山药粉加工厂.该厂需购置一台分装机,计划从商家推荐试用的甲、乙两台不同品牌的分装机中选择.试用时,设定分装的标准质量为每袋500g ,与之相差大于10g 为不合格.为检验分装效果,工厂对这两台机器分装的成品进行了抽样和分析,过程如下:[收集数据]从甲、乙两台机器分装的成品中各随机抽取20袋,测得实际质量(单位:g )如下:甲:501 497 498 502 513 489 506 490 505 486 502 503 498 497 491 500 505 502 504 505 乙:505 499 502 491 487 506 493 505 499 498 502 503 501 490 501 502 511 499 499 501 [整理数据]整理以上数据,得到每袋质量x (g )的频数分布表.质量485≤x <490≤x <495≤x <500≤x <505≤x <510≤x <频数 机器 490 495 500 505 510 515甲 2 2 4 7 4 1 乙135731[分析数据]根据以上数据,得到以下统计量. 统计量 机器 平均数中位数方差不合格率甲 499.7 501.5 42.01 b 乙499.7a31.8110%根据以上信息,回答下列问题:(1)表格中的a = 501 ,b = 15% ;(2)综合上表中的统计量,判断工厂应迭购哪一台分装机,并说明理由.【解答】解:(1)将乙的成绩从小到大排列后,处在中间位置的两个数都是501,因此中位数是501, b =3➗20=15%, 故答案为:501,15%;(2)选择乙机器,理由:乙的不合格率较小,18.(9分)位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP 上架设测角仪,先在点M 处测得观星台最高点A 的仰角为22°,然后沿MP 方向前进16m 到达点N 处,测得点A 的仰角为45°.测角仪的高度为1.6m . (1)求观星台最高点A 距离地面的高度(结果精确到0.1m .参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,√2≈1.41);(2)“景点简介”显示,观星台的高度为12.6m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.【解答】解:(1)过A作AD⊥PM于D,延长BC交AD于E,则四边形BMNC,四边形BMDE是矩形,∴BC=MN=16m,DE=CN=BM=1.6m,∵∠AED=90°,∠ACE=45°,∴△ACE是等腰直角三角形,∴CE=AE,设AE=CE=x,∴BE=16+x,∵∠ABE=22°,∴tan22°=AEBE=x16+x=0.40,∴x≈10.7(m),∴AD=10.7+1.6=12.3(m),答:观星台最高点A距离地面的高度约为12.3m;(2)∵“景点简介”显示,观星台的高度为12.6m,∴本次测量结果的误差为12.6﹣12.3=0.3m,减小误差的合理化建议为:为了减小误差可以通过多次测量取平均值的方法.19.(9分)暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.设某学生暑期健身x(次),按照方案一所需费用为y1(元),且y1=k1x+b;按照方案二所需费用为y2(元),且y2=k2x.其函数图象如图所示.(1)求k1和b的值,并说明它们的实际意义;(2)求打折前的每次健身费用和k2的值;(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.【解答】解:(1)∵y 1=k 1x +b 过点(0,30),(10,180), ∴{b =3010k 1+b =180,解得{k 1=15b =30, k 1=15表示的实际意义是:购买一张学生暑期专享卡后每次健身费用为15元, b =30表示的实际意义是:购买一张学生暑期专享卡的费用为30元;(2)由题意可得,打折前的每次健身费用为15÷0.6=25(元), 则k 2=25×0.8=20;(3)选择方案一所需费用更少.理由如下: 由题意可知,y 1=15x +30,y 2=20x . 当健身8次时,选择方案一所需费用:y 1=15×8+30=150(元), 选择方案二所需费用:y 2=20×8=160(元), ∵150<160,∴选择方案一所需费用更少.20.(9分)我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具﹣﹣三分角器.图1是它的示意图,其中AB 与半圆O 的直径BC 在同一直线上,且AB 的长度与半圆的半径相等;DB 与AC 垂直于点B ,DB 足够长.使用方法如图2所示,若要把∠MEN三等分,只需适当放置三分角器,使DB经过∠MEN 的顶点E,点A落在边EM上,半圆O与另一边EN恰好相切,切点为F,则EB,EO 就把∠MEN三等分了.为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.已知:如图2,点A,B,O,C在同一直线上,EB⊥AC,垂足为点B,AB=OB,EN 切半圆O于F.求证:EB,EO就把∠MEN三等分.【解答】解:已知:如图2,点A,B,O,C在同一直线上,EB⊥AC,垂足为点B,AB =OB,EN切半圆O于F.求证:EB,EO就把∠MEN三等分,证明:∵EB⊥AC,∴∠ABE=∠OBE=90°,∵AB=OB,BE=BE,∴△ABE≌△OBE(SAS),∴∠1=∠2,∵BE⊥OB,∴BE是⊙E的切线,∵EN切半圆O于F,∴∠2=∠3,∴∠1=∠2=∠3,∴EB,EO就把∠MEN三等分.故答案为:AB=OB,EN切半圆O于F;EB,EO就把∠MEN三等分.21.(10分)如图,抛物线y=﹣x2+2x+c与x轴正半轴,y轴正半轴分别交于点A,B,且OA=OB,点G为抛物线的顶点.(1)求抛物线的解析式及点G的坐标;(2)点M,N为抛物线上两点(点M在点N的左侧),且到对称轴的距离分别为3个单位长度和5个单位长度,点Q为抛物线上点M,N之间(含点M,N)的一个动点,求点Q的纵坐标y Q的取值范围.【解答】解:(1)∵抛物线y=﹣x2+2x+c与y轴正半轴分别交于点B,∴点B(0,c),∵OA=OB=c,∴点A(c,0),∴0=﹣c2+2c+c,∴c=3或0(舍去),∴抛物线解析式为:y=﹣x2+2x+3,∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点G为(1,4);(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴对称轴为直线x=1,∵点M,N为抛物线上两点(点M在点N的左侧),且到对称轴的距离分别为3个单位长度和5个单位长度,∴点M的横坐标为﹣2或4,点N的横坐标为6,∴点M坐标为(﹣2,﹣5)或(4,﹣5),点N坐标(6,﹣21),∵点Q为抛物线上点M,N之间(含点M,N)的一个动点,∴﹣21≤y Q≤4或﹣21≤y Q≤﹣5.22.(10分)小亮在学习中遇到这样一个问题:̂上一动点,线段BC=8cm,点A是线段BC的中点,过点C作CF∥BD,如图,点D是BC交DA的延长线于点F.当△DCF为等腰三角形时,求线段BD的长度.小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题.请将下面的探究过程补充完整:̂上的不同位置,画出相应的图形,测量线段BD,CD,FD的长度,(1)根据点D在BC得到下表的几组对应值.BD/cm0 1.0 2.0 3.0 4.0 5.0 6.07.08.0 CD/cm8.07.77.2 6.6 5.9a 3.9 2.40FD/cm8.07.4 6.9 6.5 6.1 6.0 6.2 6.78.0操作中发现:①“当点D为BĈ的中点时,BD=5.0cm”.则上表中a的值是5;②“线段CF的长度无需测量即可得到”.请简要说明理由.(2)将线段BD的长度作为自变量x,CD和FD的长度都是x的函数,分别记为y CD和y FD,并在平面直角坐标系xOy中画出了函数y FD的图象,如图所示.请在同一坐标系中画出函数y CD的图象;(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当△DCF为等腰三角形时,线段BD长度的近似值(结果保留一位小数).̂的中点,【解答】解:(1)∵点D为BĈ=CD̂,∴BD∴BD=CD=a=5cm,故答案为:5;(2)∵点A是线段BC的中点,∴AB=AC,∵CF∥BD,∴∠F=∠BDA,又∵∠BAD=∠CAF,∴△BAD≌△CAF(AAS),∴BD=CF,∴线段CF的长度无需测量即可得到;(3)由题意可得:(4)由题意画出函数y CF的图象;由图象可得:BD=3.8cm或5cm或6.2cm时,△DCF为等腰三角形.23.(11分)将正方形ABCD 的边AB 绕点A 逆时针旋转至AB ′,记旋转角为α,连接BB ′,过点D 作DE 垂直于直线BB ′,垂足为点E ,连接DB ′,CE .(1)如图1,当α=60°时,△DEB ′的形状为 等腰直角三角形 ,连接BD ,可求出BB′CE的值为 √2 ;(2)当0°<α<360°且α≠90°时,①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;②当以点B ′,E ,C ,D 为顶点的四边形是平行四边形时,请直接写出BE B′E的值.【解答】解:(1)∵AB 绕点A 逆时针旋转至AB ′, ∴AB =AB ',∠BAB '=60°, ∴△ABB '是等边三角形, ∴∠BB 'A =60°,∴∠DAB '=∠BAD ﹣∠BAB '=90°﹣60°=30°, ∵AB '=AB =AD , ∴∠AB 'D =∠ADB ', ∴∠AB 'D =180°−30°2=75°, ∴∠DB 'E =180°﹣60°﹣75°=45°, ∵DE ⊥B 'E ,∴∠B 'DE =90°﹣45°=45°, ∴△DEB '是等腰直角三角形. ∵四边形ABCD 是正方形, ∴∠BDC =45°, ∴BD DC=√2,同理B′D DE=√2,∴BD DC=B′D DE,∵∠BDB '+∠B 'DC =45°,∠EDC +∠B 'DC =45°, ∴BDB '=∠EDC , ∴△BDB '∽△CDE , ∴BB′CE=BD DC=√2.故答案为:等腰直角三角形,BB′CE=√2.(2)①两结论仍然成立. 证明:连接BD ,∵AB =AB ',∠BAB '=α, ∴∠AB 'B =90°−α2,∵∠B 'AD =α﹣90°,AD =AB ', ∴∠AB 'D =135°−α2,∴∠EB 'D =∠AB 'D ﹣∠AB 'B =135°−α2−(90°−α2)=45°, ∵DE ⊥BB ',∴∠EDB '=∠EB 'D =45°, ∴△DEB '是等腰直角三角形, ∴DB′DE=√2,∵四边形ABCD 是正方形, ∴BD CD =√2,∠BDC =45°,∴BD CD=DB′DE,∵∠EDB '=∠BDC ,∴∠EDB '+∠EDB =∠BDC +∠EDB , 即∠B 'DB =∠EDC , ∴△B 'DB ∽△EDC , ∴BB′CE =BD CD=√2.②BE B′E=3或1.若CD 为平行四边形的对角线,点B '在以A 为圆心,AB 为半径的圆上,取CD 的中点.连接BO 交⊙A 于点B ', 过点D 作DE ⊥BB '交BB '的延长线于点E ,由(1)可知△B 'ED 是等腰直角三角形, ∴B 'D =√2B 'E ,由(2)①可知△BDB '∽△CDE ,且BB '=√2CE . ∴BE B′E=B′B+B′E B′E=BB′B′E+1=√2CEB′E+1=√2B′DB′E+1=√2×√2+1=3.若CD 为平行四边形的一边,如图3,点E与点A重合,∴BEB′E=1.综合以上可得BEB′E =3或1.。
河南中考22题集锦

河北中考22题集锦之阳早格格创做1. (2009年)如图,正在Rt △ABC 中,∠ACB =90°, ∠B=60°,BC =2.面0是AC 的中面,过面0的曲线l 从与AC 沉合的位子启初,绕面0做顺时针转动,接AB 边于面D .过面C 做CE ∥AB 接曲线l 于面E ,设曲线l 的转动角为α.(1)①当α=________度时,四边形EDBC 是等腰梯形,此时AD 的少为_________;②当α=________度时,四边形EDBC 是曲角梯形,此时AD 的少为_________;(2) 当α=90°时,推断四边形EDBC 是可为菱形,并道明缘由.2.(2010年)(1)支配创制如图,矩形ABCD 中,E 是AD 的中面,将△AB E 沿BE 合叠后得到△GBE ,且面G 正在矩形ABCD 里里.小明将BG 延少接DC 于面F ,认为GF =DF ,您共意吗?道明缘由.(2)问题办理脆持(1)中的条件没有变,若DC =2DF ,供AB AD 的值;脆持(1)中条件没有变,若DC=nDF3、(2011年)如图,正在Rt△ABC中,∠B=90°,BC C=30°.面D从面C出收沿CA目标以每秒2个单位少的速度背面A匀速疏通,共时面E从面A出收沿AB 目标以每秒1个单位少的速度背面BD、E疏通的时间是t 秒(t>0).过面D做DF⊥BC于面F,对接DE、EF.(1)供证:AE=DF;(2)四边形AEFD不妨成为菱形吗?如果能,供出相映的t值;如果没有克没有及,道明缘由.(3)当t为何值时,△DEF为曲角三角形?请道明缘由.22、(2012河北)类比、转移、从特殊到普遍等思维要领,正在数教教习战钻研中经时常使用到,如下是一个案例,请补充完备.本题:如图1E是BC边上的中面,面F是线段AE上一面,BF的延少线接射线CD于面G.(1)测验考查商量BG于面H,则AB正在图1中,过面E战EH的数量闭系是,CG战EH如图2,正在本题的条件下,若(0)AF m m EF =>,则CD CG 的值是(用含m 的代数式表示),试写出解问历程.(3)拓展迁移如图3,梯形ABCD 中,DC ∥AB ,面E 是BC 延少线上一面,AE战BD 相接于面F ,若,(0,0)AB BC a b a b CD BE ==>>,则AF EF 的值是(用含,a b 的代数式表示).22.(2013年河北)如图1,将二个实足相共的三角形纸片ABC 战DEC 沉合搁置,其中∠C =90°,∠B =∠E =30°.(1)支配创制如图2,牢固△ABC ,使△DEC 绕面C 转动,当面D 恰佳降正在AB 边上时,挖空:①线段DE 与AC 的位子闭系是_________;②设△BDC 的里积为S 1,△AEC 的里积为S 2,则S 1与S 2的数量闭系是_________________.(2)预测论证当△DEC 绕面C 转动到图3所示的位子时,小明预测(1)中S 1与S 2的数量闭系仍旧创制,并测验考查分别做出了△BDC 战△AEC 中BC 、CE 边上的下,请您道明小明的预测.(3)拓展商量已知∠ABC =60°,面D 是其角仄分线上一面,BD =CD =4,DE //AB 接BC 于面E (如图4).若正在射线BA 上存留面F ,使S△DCF =S △BDE ,请间接写出相映的BF 的少.22.(2014河北)(1)问题创制如图1,△ACB 战△DCE 均为等边三角形,面A 、D 、E 正在共背来线上,对接BE挖空:(1)∠AEB 的度数为;(2)线段AD 、BE 之间的数量闭系是.(2)拓展商量如图2,△ACB 战△DCE 均为等腰曲角三角形,∠ACB=∠DCE=900, 面A 、D 、E正在共背来线上,CM 为△DCE 中DE 边上的下,对接BE.请推断∠AEB 的度数及线段CM 、AE 、BE 之间的数量闭系,并 D A 图4道明缘由.(3)办理问题如图3,正在正圆形ABCD中,CD=2.若面P谦脚PD=1,且∠BPD=900,请间接写出面A到BP的距离.22.(2015河北)如图1,正在Rt△ABC中,∠B=900,BC=2,AB=8,面D,E分别是边BC,AC的中面,连DE,将△EDC绕面C按顺时针目标转动,记转动角为α.(1)问题创制①当α=00时,AEBD=;②当α=1800时,AEBD=.(2)拓展商量试推断:当00≤α≤3600时,AEBD的大小有无变更?请仅便图2的情形给出道明.(3)办理问题当△EDC转动至A,D,E三面共线时,间接写出线段BD 的少.22.(2016河北)(1)问题如图1,面A为线段BC中一动面,且BC=a,AB=b.挖空:当面A位于时线段AC的图1baAB C少博得最大值,且最大值为(用含a ,b 的式子表示)(2)应用面A 为线段BC 中一动面,且BC=3,AB=1.如图2所示,分别以AB ,AC 为边,做等边三角形ABD战等边三角形ACE ,对接CD,BE. ①请找出图中与BE 相等的线段,并道明缘由②间接写出线段BE 少的最大值.(3)拓展如图3,正在仄里曲角坐标系中,面A 的坐标为(2,0),面B 的坐标为(5,0),面P 为线段AB 中一动面,且PA=2,PM=PB ,∠BPM=900.请间接写出线段AM 少的最大值及此时面P 的坐标.解:(1)CB 的延少线上,a+b ;………………………………………2分(2)①DC=BE,缘由如下∵△ABD 战△ACE 皆是等边三角形,∴AD=AB,AC=AE,∠BAD=∠CAE=600,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB, ……………5分∴△CAD ≌△EAB (SAS ),∴图2CDDC=BE ………………………………6分②BE少的最大值是4. …………………………………………………8分(3)AM的最大值为P的坐标为(10分【提示】如图3,构制△BNP≌△MAP,则NB=AM,由(1)知,当面N正在BA的延少线上时,NB有最大值(如备用图).易得△APN是等腰曲角三角形,AP=2,∴过面P做PE⊥x轴于面E,又A(2,0)∴P(1.(2017河北)如图1.图1________,位(2)商量道明2的位子,对接(3)拓展蔓延在仄里内自由转动,。
2022年河南中招考试真题及答案word版

2022年河南省普通高中招生考试试卷一、听力理解(20小题,每小题1分,共20分)第一节听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳答案。
每段对话读两遍。
1.How is the weather now?A. Sunny.B. Windy.C. Rainy.2. When does the boy usually go to bed?A. At 8:00 p.m.B. At 9:00 p.m.C. At 10:00 p.m.3.What will the girl do?A. Draw a picture.B. Sing a song.C. Play the piano.4.How will the speakers go to the Forest Park?A. On foot.B. By bike.C. By bus.5. Where did the boy go?A. To a zoo.B. To a library.C. To a theatre.第二节听下面几段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳答案。
每段对话或独白读两遍。
听下面一段对话,回答第6至第7两个小题。
6.Where will the speakers have a picnic?A. On the mountain.B. By the river.C. Near the lake.7.What will the boy take with him?A. A bag.B. A coat.C. A camera.听下面一段对话,回答第8至第9两个小题。
8.When is the mother's birthday?A. On July 5.B. On July 6.C. On July 7.9. What will the two speakers buy?A. A hat.B. A dress.C. A scarf.听下面一段独白,回答第10至第12三个小题。
河南中招数学22、23题总结

18.(2008)(9分)复习“全等三角形”的知识时,老师布置了一道作业题:“如图①,已知在△ABC 中,AB =AC ,P 是△ABC 内部任意一点,将AP 绕A 顺时针旋转至AQ ,使∠QAP =∠BAC ,连接 BQ 、CP ,则BQ =CP .”小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ ≌△ACP ,从而证得BQ =CP 之后,将点P 移到等腰三角形ABC 之外,原题中的条件不变,发现“BQ =CP ”仍然成立,请你就图②给出证明.23.(2008)(12分)如图,直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ,点A 的坐标是(-2,0). (1)试说明△ABC 是等腰三角形;(2)动点M 从A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M 运动t 秒时,△MON 的面积为S . ① 求S 与t 的函数关系式;② 设点M 在线段OB 上运动时,是否存在S =4的情形?若存在,求出对应的t 值;若不存在请说明理由; ③在运动过程中,当△MON 为直角三角形时,求t 的值.21.(2009) (10分)如图,在Rt △ABC 中,∠ACB =90°, ∠B =60°,BC =2.点0是AC 的中点,过点0的直线L 从与AC 重合的位置开始,绕点0作逆时针旋转,交AB 边于点D .过点C 作C E ∥A B 交直线l 于点E ,设直线L 的旋转角为α.(1)①当α=________度时,四边形EDBC 是等腰梯形,此时AD 的长为_________; ②当α=________度时,四边形EDBC 是直角梯形,此时AD 的长为_________; (2)当α=90°时,判断四边形EDBC 是否为菱形,并说明理由.图①QPCBAAQBPC图②23.(2009)(11分)如图,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (4,0)、C (8,0)、D (8,8).抛物线y =ax 2+bx 过A 、C 两点.(1)直接写出点A 的坐标,并求出抛物线的解析式;(2)动点P 从点A 出发.沿线段AB 向终点B 运动,同时点Q 从点C 出发,沿线段CD 向终点D 运动.速度均为每秒1个单位长度,运动时间为t 秒.过点P 作PE ⊥AB 交A C 于点E ①过点E 作EF ⊥AD 于点F ,交抛物线于点G .当t 为何值时,线段EG 最长?②连接EQ .在点P 、Q 运动的过程中,判断有几个时刻使得△CEQ 是等腰三角形? 请直接写出相应的t 值.22.(2010)(10分) (1)操作发现如图,矩形ABCD 中,E 是AD 的中点,将△AB E 沿BE 折叠后得到△GBE ,且点G 在矩行ABCD 内部.小明将BG 延长交DC 于点F ,认为GF =DF ,你同意吗?说明理由.(2)问题解决保持(1)中的条件不变,若DC =2DF ,求ABAD的值; (3)类比探求保持(1)中条件不变,若DC =nDF ,求AB AD的值.GABCD EG23.(2010)(11分)在平面直角坐标系中,已知抛物线经过A )0,4(-,B )4,0(-,C )0,2(三点. (1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S .求S 关于m 的函数关系式,并求出S 的最大值.(3)若点P 是抛物线上的动点,点Q 是直线x y -=上的动点,判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.22. (2011)(10分)如图,在Rt △ABC 中,∠B =90°,BC =53,∠C =30°.点D 从点C 出发沿CA 方向以每秒2个单位长的速度向点A 匀速运动,同时点E 从点A 出发沿AB 方向以每秒1个单位长的速度向点B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D 、E 运动的时间是t 秒(t >0).过点D 作DF ⊥BC 于点F ,连接DE 、EF .(1)求证:AE =DF ;(2)四边形AEFD 能够成为菱形吗?如果能,求出相应的t 值;如果不能,说明理由. (3)当t 为何值时,△DEF 为直角三角形?请说明理由.第22题图 23.(2011)(11分)如图,在平面直角坐标系中,直线3342y x =-与抛物线214y x bx c =-++交于A 、B 两点,点A 在x 轴上,点B 的横坐标为-8.求:(1)求该抛物线的解析式;(2)点P 是直线AB 上方..的抛物线上一动点(不与点A 、B 重合),过点P 作x 轴的垂线,垂足为C ,交直线AB 于点D ,作PE ⊥AB 于点E .①设△PDE 的周长为l ,点P 的横坐标为x ,求l 关于x 的函数关系式,并求出l 的最大值;MC BA Oxy②连接PA ,以PA 为边作图示一侧的正方形APFG .随着点P 的运动,正方形的大小、位置也随之改变.当顶点F 或G 恰好落在y 轴上时,直接写出对应的点P 的坐标.22.(2012)(10分)类比转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整。
2024年河南郑州中考生物试题及答案

2024年河南郑州中考生物学试题及答案注意事项:1.本试卷共6页,分为选择题和非选择题,满分50分,考试时间50分钟。
2.本试卷上不要答题,请按答题卡上注意事项的要求,直接把答案填写在答题卡上。
答在试卷上的答案无效。
选择题(共20小题,20分)下列每小题列出的四个选项中,只有一个选项是最符合题目要求的。
请将正确选项的英文字母代号涂写在答题卡相应位置上。
1. 黄河落天走东海,万里写入胸怀间。
今日黄河,岸高林密,鱼跃鸟鸣,岁岁安澜。
下列选项中,属于生命现象的是( )A. 鲤鱼戏水B. 波光鄰鄰C. 层峦叠嶂D. 云蒸霞蔚2. 人们对微观世界的认识离不开显微镜。
光学显微镜的结构如图甲所示,植物细胞的结构如图乙所示。
下列相关叙述正确的是( )A. 光线暗时可用①的平面镜B. 具有放大功能的结构是③C. ⑤具有支持和保护的作用D. 营养物质主要储存在⑦中3. 水杉和镇海林蛙都是我国的特有物种。
下列选项不属于两者共有的结构层次是( )A. 系统B. 器官C. 组织D. 细胞4. 生物生长发育离不开细胞的分裂和分化。
在细胞分化过程中,不发生改变的是( )A. 形态B. 结构C. 遗传物质D. 生理功能5. 郑州市西流湖公园已建设成为集生态文明、休闲游憩、历史文化传承于一体的城市公园。
园内生物种类众多,形成了多条食物链。
下列选项中,正确表示食物链的是( )A. 昆虫→青蛙→蛇B.草→昆虫→食虫鸟的C. 鲫鱼→水蚤→藻类D. 阳光→藻类→鲢鱼6. 绿化祖国要扩绿、兴绿、护绿并举。
下列关于绿色植物在生物圈中作用的叙述,错误的是( )A. 制造有机物B. 降低大气湿度C. 参与水循环D. 养育其他生物7. 孟德尔通过豌豆杂交实验,为我们揭示了遗传的奥秘。
豌豆花的结构如图所示,下列叙述正确的是( )A. 杂交时需将花粉涂在①上B. ②是能够产生花粉花药C. ③能够发育成豌豆的种皮D. ④能够发育成豌豆的种子8. 养料由母体运给胎儿的途径是:母体子宫内膜→P→脐带→胎儿。
