异方差性与自相关性
多重共线性-异方差-内生性-自相关总结对照表
六、怀特检验
七、布殊-帕甘检验
一、RESET检验
二、豪斯曼检验
一、图示检验法
二、解释变量严格外生条件下,误差项一阶自相关检验。
ut=ut-1+vt
三、古典假定下,误差项一阶自相关的DW检验
四、自变量非严格外生条件下,误差项一阶自相关检验。
五、误差项高阶自相关的布殊-戈弗雷检验BG检验
处理
3.因变量的预测精度降低。
检验
一、直观判断法
1、散点图法。
2、简单相关系数法。
3.经验判断法。
4.“经典”判断法。
5. Klein判别法。
二、辅助回归法vif
三、特征值与病态指数
四、法勒—格劳伯(Farrar—Glauber)检验
一、图示法
二、斯皮尔曼等级(秩)相关检验
三、戈德菲尔德-匡特检验
四、帕克检验
3、基于DW统计量的估计
4、基于残差的回归估计
5、科克伦-奥克特迭代法
三、非线性回归方法
四、尼威-威斯特(Newey-West)方法
3、原始数据的处理变换
4、经济变量的惯性作用
5、误差项本身存在自相关
后果
近似多重共线性并不违反回归假定。无偏的、有效的、一致的参数估计量仍可以得出,其标准误也仍将被正确估计。
1、估计结果不好解释
2、参数估计值的方差增大
3、参数估计的置信区间变大
4、假设检验容易作出错误的判断
1、最小二乘估计量仍然是线性无偏的与一致的,但不再
一、增加样本观测值
二、删去不重要的解释变量
三、利用“先验”信息
四、变量变换
五、变换模型的形式
六、逐步回归法
一、加权最小二乘法
计量经济学重点整理

一、含义:多重共线性:对于解释变量 ,如果存在不全为0的数 ,使得 则称解释变量 之间存在着完全的多重共线性。
或者 异方差性:如果对于模型中随机误差项Ui 有: 则称Ui 具有异方差性。
自相关:是指总体回归模型的随机误差项之间存在相关关系。
即不同观测点上的误差项彼此相关。
可以表示为:造成的后果:不完全的多重共线性:(1)OLS 估计量仍保持BLUE 的性质(2)假设检验容易作出错误的判断(3)可能造成可决系数较高,但对各个参数单独的 t 检验却可能不显著,甚至可能使估计的回归系数符号相反,得出完全错误的结论。
异方差性和自相关:(1)OLS 估计量仍然是线性无偏的,但不再是有效的,即方差不再是最小的。
(2) T 检验和F 检验失效。
检验方法:多重共线性:(1)简单相关系数检验法(如果每两个解释变量的简单相关系数比较高,如果大于0.8则可以认为存在着严重的多重共线性.但此种方法只是充分条件而不是必要条件,也需要同时检查偏相关系数) (2)方差扩大(膨胀)因子法(3)直观判断法(当增加一个或者剔除一个解释变量改变一个观测值时,回归参数的估计值发生较大变化;从定性分析一些重要的解释变量的回归系数的标准误差较大,在回归方程没有通过显著性检验;有些解释变量回归系数所带正负号与定性结果违背时;相关矩阵种自变量之间的相关系数较大时都可能存在多重共线性一些重要的解释变量在回归方程中没有通过显著性检验,同时R2很高(或F 检验显著),即t 检验和F 检验的结果相矛盾,或解释变量的回归系数所带正负号与定性分析结果违背时,模型可能存在严重的多重共线性。
(4)逐步回归法。
异方差性:(1)图示检验法(2)Goldfeld-Quanadt 检验作用:检验递增性(或递减性)异方差。
(3)White 检验检验步骤1)提出假设2)构造辅助回归方程 3)构造统计量并计算统计量的值,构造并计算统计量nR ²。
R ²为辅助回归的可决系数,n 为样本容量。
异方差与自相关

七、 异方差与自相关一、背景我们讨论如果古典假定中的同方差和无自相关假定不能得到满足,会引起什么样的估计问题呢?另一方面,如何发现问题,也就是发现和检验异方差以及自相关的存在性也是一个重要的方面,这个部分就是就这个问题进行讨论。
二、知识要点1、引起异方差的原因及其对参数估计的影响2、异方差的检验(发现异方差)3、异方差问题的解决办法4、引起自相关的原因及其对参数估计的影响5、自相关的检验(发现自相关)6、自相关问题的解决办法 (时间序列部分讲解) 三、要点细纲1、引起异方差的原因及其对参数估计的影响原因:引起异方差的众多原因中,我们讨论两个主要的原因,一是模型的设定偏误,主要指的是遗漏变量的影响。
这样,遗漏的变量就进入了模型的残差项中。
当省略的变量与回归方程中的变量有相关关系的时候,不仅会引起内生性问题,还会引起异方差。
二是截面数据中总体各单位的差异。
后果:异方差对参数估计的影响主要是对参数估计有效性的影响。
在存在异方差的情况下,OLS 方法得到的参数估计仍然是无偏的,但是已经不具备最小方差性质。
一般而言,异方差会引起真实方差的低估,从而夸大参数估计的显著性,即是参数估计的t 统计量偏大,使得本应该被接受的原假设被错误的拒绝。
2、异方差的检验 (1)图示检验法由于异方差通常被认为是由于残差的大小随自变量的大小而变化,因此,可以通过散点图的方式来简单的判断是否存在异方差。
具体的做法是,以回归的残差的平方2i e 为纵坐标,回归式中的某个解释变量i x 为横坐标,画散点图。
如果散点图表现出一定的趋势,则可以判断存在异方差。
(2)Goldfeld-Quandt 检验Goldfeld-Quandt 检验又称为样本分段法、集团法,由Goldfeld 和Quandt 1965年提出。
这种检验的思想是以引起异方差的解释变量的大小为顺序,去掉中间若干个值,从而把整个样本分为两个子样本。
用两个子样本分别进行回归,并计算残差平方和。
异方差、自相关、多重共线性比较(计量经济学)

基本思想:
由OLS法得到残差e,取e的绝对值,然后将此绝对值对某个解释变量X回归,根部回归模型的显著性和拟合优度来判断是否存在异方差。
操作步骤:
1.根据样本数据建立回归模型,并求残差序列e.
2.用残差绝对值对X进行回归,由于|e|与X的真实函数形式并不知道,可用各种函数形式去试验,从中选择最佳形式。
2.quick/equation estimation输入“e2 c e2(-1) e2(-2) e2(-3) e2(-4) e2(-5) e2(-6)”
3.view/residual diagnostics/heteroskedasticity tests,选择arch。
2.Quick/graph,在series list对话框中输入“e(-1) e”,选择scatter’,得到e(-1)与e的散点图。
方法二:1.用OLS估计Resid→e。
2.Quick/graph,在series list对话框中输入“e”,得到e随时间t的变化图示。
操作思想
操作步骤
适用性
软件操作
实际检验中可逐次向更高阶检验,并结合辅助回归中滞后项参数的显著性去帮助判断自相关的阶数。
ห้องสมุดไป่ตู้DW检验
操作思想:
DW与ρ的关系:DW≈2(1-ρ)
ρ的取值范围0≤DW≤4.
根据样
本容量n和解释变量的数目k'(不包括常数项),查DW分布表,可得临界值dl和du,
DW取值范围
自相关状态
[0,dl]
正自相关
(dl,du]
5.判断。给定显著性水平α,查F分布表,得临界值。 > ,拒绝 ,反之不拒绝 。
适用性:
该方法得到的F分布是近似的,而且只是对异方差是否存在进行判断,在多个解释变量的情况下,对判断是哪一个变量引起异方差还存在局限。此检验方法也可将样本分为多个组,从中任选两个组进行检验。
第五讲-多重共线性、异方差、自相关

表 4.3.3 中国粮食生产与相关投入资料
农业化肥施 粮食播种面 受灾面积 农业机械总
用量 X 1
(万公斤)
积X 2
(千公顷)
X3
(公顷)
动力X 4
(万千瓦)
1659.8
114047 16209.3
18022
1739.8
11288பைடு நூலகம் 15264.0
19497
1775.8
108845 22705.3
20913
0.9752 1.53
t值
0.85
19.6 3.35 -3.57
Y=f(X1,X2,X3,X4) -13056 6.17 0.42 -0.17 -0.09
0.9775 1.80
t值
-0.97 9.61 3.57 -3.09 -1.55
Y=f(X1,X3,X4,X5) -12690 5.22 0.40 -0.20
含义:解释变量的样本向量近似线性相关。
多重共线性来源:
(1)解释变量x受到同一个因素的影响; 例如:政治事件对很多变量都产生影响,这些变量同时上升 或同时下降。
(2)解释变量x自己的当期和滞后期;
(3)错误设定。
二、多重共线性的后果
1、完全共线性下参数估计量不存在
Y X
的OLS估计量为: βˆ (XX) 1 XY
1、检验多重共线性是否存在
(1)对两个解释变量的模型,采用简单相关系数法 求出X1与X2的简单相关系数r,若|r|接近1,则说
明两变量存在较强的多重共线性。
(2)对多个解释变量的模型,采用综合统计检验法
若 在OLS法下:R2与F值较大,但t检验值较小, 说明各解释变量对Y的联合线性作用显著,但各解 释变量间存在共线性而使得它们对Y的独立作用不 能分辨,故t检验不显著。
统计分析与方法-第七章 回归分析2-异方差与自相关

1.000 . 15 .443 .098 15 .721** .002 15
**. Correlation is significant at the 0.01 level (2-tailed).
因此选取注册资本构造权函数
最优权数的幂指数确定
Source variable.. 注册资本 Dependent variable.. 销销收收 Log-likelihood Function = -125.581891 POWER value = -2.000 Log-likelihood Function = -122.148284 POWER value = -1.500 Log-likelihood Function = -118.756247 POWER value = -1.000 Log-likelihood Function = -115.440464 POWER value = -.500 Log-likelihood Function = -112.257523 POWER value = .000 Log-likelihood Function = -109.297553 POWER value = .500 Log-likelihood Function = -106.695645 POWER value = 1.000 Log-likelihood Function = -104.627066 POWER value = 1.500 Log-likelihood Function = -103.261903 POWER value = 2.000 Log-likelihood Function = -102.682848 POWER value = 2.500 Log-likelihood Function = -102.833168 POWER value = 3.000 The Value of POWER Maximizing Log-likelihood Function = 2.500
eviews异方差、自相关检验与解决办法

eviews异方差、自相关检验与解决办法一、异方差检验:1.相关图检验法LS Y C X 对模型进行参数估计GENR E=RESID 求出残差序列GENR E2=E^2 求出残差的平方序列SORT X 对解释变量X排序SCAT X E2 画出残差平方与解释变量X的相关图2.戈德菲尔德——匡特检验已知样本容量n=26,去掉中间6个样本点(即约n/4),形成两个样本容量均为10的子样本。
SORT X 将样本数据关于X排序SMPL 1 10 确定子样本1LS Y C X 求出子样本1的回归平方和RSS1SMPL 17 26 确定子样本2LS Y C X 求出子样本2的回归平方和RSS2计算F统计量并做出判断。
解决办法3.加权最小二乘法LS Y C X 最小二乘法估计,得到残差序列GRNR E1=ABS(RESID) 生成残差绝对值序列LS(W=1/E1) Y C X 以E1为权数进行加权最小二成估计二、自相关1.图示法检验LS Y C X 最小二乘法估计,得到残差序列GENR E=RESID 生成残差序列SCAT E(-1) E et—et-1的散点图PLOT E 还可绘制et的趋势图2.广义差分法LS Y C X AR(1) AR(2)首先,你要对广义差分法熟悉,不是了解,如果你是外行,我奉劝你还是用eviews来做就行了,其实我想老师要你用spss无非是想看你是否掌握广义差分,好了,废话不多说了。
接着,使用spss16来解决自相关。
第一步,输入变量,做线性回归,注意在Liner Regression 中的Statistics中勾上DW,在save中勾Standardized,查看结果,显然肯定是有自相关的(看dw值)。
第二步,做滞后一期的残差,直接COPY数据(别告诉我不会啊),然后将残差和滞后一期的残差做回归,记下它们之间的B指(就是斜率)。
第三步,再做滞后一期的X1和Y1,即自变量和因变量的滞后一期的值,也是直接COPY。
多重共线性-异方差-内生性-自相关总结对照表

一、加权最小二乘法 二、怀特异方差-稳健程序。 三、解释变量的代数变换
解释变量内生性 cov(x ji , ui ) 0 解 释 变 量 与随机误差项之间往往存 在某种程度的相关性。与 随机误差项相关的解释变 量称为内生解释变量。 1、遗漏变量 2、测量误差 3、错误的函数形式 4、联立性
1、解释变量的遗漏或省 略 2、模型函数形式设定错 误 3、原始数据的处理变换 4、经济变量的惯性作用 5、误差项本身存在自相 关 1.斜率系数 Bj 依然是线 性的和无偏的。
E(ˆj ) j
2、最小二乘估计量的方 差估计是有偏的。 3. 因 变 量 的 预 测 精 度 降低。
一、图示检验法 二、解释变量严格外生 条件下,误差项一阶自 相关检验。 ut=ut-1+vt 三、古典假定下,误差 项一阶自相关的 DW 检验 四、自变量非严格外生 条件下,误差项一阶自 相关检验。 五、误差项高阶自相关 的布殊-戈弗雷检验 BG 检验
定义 原因 后果 检验
处理
多重共线性 如果存在某解释变量是其他解释变量 的线性组合,则称为存在完全多重共线
性。 0 1x1 k xk 0
它们之间存在高度的线性相关性,称模 型存在近似(不完全)多重共线性。 0 1x1 k xk v 0 1.经济变量之间具有共同变化趋势。 2.变量之间存在经济联系。 3.模型中包含滞后变量。 4、样本数据自身原因。
异方差
var(u
|
xi )
2
i
常数
则称随机误差项 u 具有异方差性
1.模型中省略的解释变量。 2. 测量误差。 3、截面数据中总体各单位的差 异。 4、模型函数形式设定错误。 5、异常观测
异方差、自相关检验
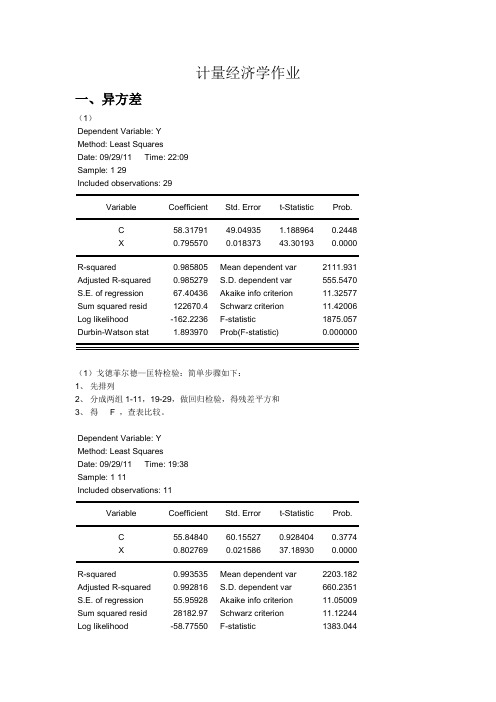
计量经济学作业一、异方差(1)Dependent Variable: YMethod: Least SquaresDate: 09/29/11 Time: 22:09Sample: 1 29Included observations: 29Variable Coefficient Std. Error t-Statistic Prob.C 58.31791 49.04935 1.188964 0.2448X 0.795570 0.018373 43.30193 0.0000R-squared 0.985805 Mean dependent var 2111.931 Adjusted R-squared 0.985279 S.D. dependent var 555.5470 S.E. of regression 67.40436 Akaike info criterion 11.32577 Sum squared resid 122670.4 Schwarz criterion 11.42006 Log likelihood -162.2236 F-statistic 1875.057 Durbin-Watson stat 1.893970 Prob(F-statistic) 0.000000(1)戈徳菲尔德—匡特检验:简单步骤如下:1、先排列2、分成两组1-11,19-29,做回归检验,得残差平方和3、得 F ,查表比较。
Dependent Variable: YMethod: Least SquaresDate: 09/29/11 Time: 19:38Sample: 1 11Included observations: 11Variable Coefficient Std. Error t-Statistic Prob.C 55.84840 60.15527 0.928404 0.3774X 0.802769 0.021586 37.18930 0.0000R-squared 0.993535 Mean dependent var 2203.182 Adjusted R-squared 0.992816 S.D. dependent var 660.2351 S.E. of regression 55.95928 Akaike info criterion 11.05009 Sum squared resid 28182.97 Schwarz criterion 11.12244 Log likelihood -58.77550 F-statistic 1383.044Durbin-Watson stat 1.657950 Prob(F-statistic) 0.000000第一组:Sum squared resid(残差平方和)=28182.97Dependent Variable: YMethod: Least SquaresDate: 09/29/11 Time: 19:39Sample: 19 29Included observations: 11Variable Coefficient Std. Error t-Statistic Prob.C 92.44615 96.01293 0.962851 0.3608X 0.782281 0.035369 22.11798 0.0000R-squared 0.981935 Mean dependent var 2141.455Adjusted R-squared 0.979928 S.D. dependent var 590.5276S.E. of regression 83.66352 Akaike info criterion 11.85445Sum squared resid 62996.26 Schwarz criterion 11.92679Log likelihood -63.19947 F-statistic 489.2051Durbin-Watson stat 1.770865 Prob(F-statistic) 0.000000第二组:Sum squared resid(残差平方和)=62996.26F=62996.26/28182.97=2.23526,给定显著性水平a=0.05查F分布临界值表可得临界值F0.05(11,11)=2.85,所以统计量F< F0.05(11,11),支出模型不存在异方差。
【总结】计量经济学异方差性、多重共线性、自相关的联系与区别知识总结

《计量经济学》中多重共线性、异方差性、自相关三者之间的联系与区别首先我们先来回顾一下经典线性回归模型的基本假设:1、为什么会出现异方差性我们可以从一下两方面来分析:第一,因为随即误差项包括了测量误差和模型中被省略的一些因素对因变量的影响;第二,来自不同抽样单元的因变量观察值之间可能差别很大。
因此,异方差性多出现在截面样本之中。
至于时间序列,则由于因变量观察值来自不同时期的同一样本单元,通常因变量的不同观察值之间的差别不是很大,所以异方差性一般不明显。
含义及影响:y=X β+ε,var(εi )var(εj ), ij ,E(ε)=0,或者记为212200['|]0000n E X σεεσσ⎛⎫⎪=Ω= ⎪ ⎪⎝⎭即违背假设3。
用OLS 估计,所得b 是无偏的,但不是有效的。
111(')'(')'()(')'b X X X y X X X X X X X βεβε---==+=+由于E(ε)=0,所以有E(b )=β。
即满足无偏性。
但是,b 的方差为1111121var(|)[()()'][(')''(')|] (')'['|](') (')'()(')b X E b b E X X X X X X X X X X E X X X X X X X X X X ββεεεεσ------=--===Ω其中212200['|]0000n E X σεεσσ⎛⎫⎪=Ω= ⎪ ⎪⎝⎭2、自相关产生的原因:(1)、经济数据的固有的惯性带来的相关 (2)、模型设定误差带来的相关 (3)、数据的加工带来的相关 含义及影响:cov(,)0,i j i j εε≠≠影响:和异方差一样,系数的ls 估计是无偏的,但不是有效的。
D -W 检验(Durbin -Watson )221212222121212222112112122211221122121()()()2()()222222(1)n i i i n i i n n n i i i i i i i n i i n n n i i i i i i i n n i i n i i i nn n i i i i nn i ie e d e e e e e e e e e e e e e e e e e e e e e e ρρ=-===-=-====-==-===∑-=∑∑+∑-∑=∑∑+∑-∑--=∑∑+=--∑∑+=--∑≈-其中2121n i i i n i ie e e ρ=-=∑=∑是样本一阶自相关函数。
异方差性、自相关以及广义最小二乘(GLS)

G是J×K矩阵,其中第j行是第j个函数关于b的导数。利用(4-21)的斯拉茨基(Slutsky)定理,
并且
,
于是
(0)
实际上,渐近协方差矩阵的估计量是
如果某个函数是非线性的,则b的无偏的性质不会传给f(b)。不过从(0)中可得f(b)是f(β)的一致估计量,而且渐近协方差矩阵很容易获得。对f(β)的检验也很容易。
可行的最小二乘ቤተ መጻሕፍቲ ባይዱ计(FGLS)
具有代表性的问题涉及到一小组参数 ,满足 。例如, 只有一个未知数 ,其常见的表达形式是
,
其中,也只有一个附加的未知参数。一个也只包含一个新参数的异方差模型是
接下来,假定 是 的一致估计量(如果我们知道如何求得这样的估计量)为了使GLS估计可行,我们将使用
替代真正的 。我们所考虑的问题是利用 是否要求我们改变上节的某些结果。
三)可行的最小二乘估计(FGLS)
上一节的结果是基于Ω必须是已知的条件基础上的。如果Ω含有必须估计的未知参数,则GLS是不可行的。但在无约束的情况下, 中有n(n+1)/2个附加参数。这对于用n个观测值来估计这么多的参数是不现实的。只有当模型中需要估计的参数较少时,即模型中Ω某种结构要简化,才可以找到求解的方法。
这些是必须逐个情况进行核实的条件。但在大多数情况中,它们的确成立。如果我们假设它们成立,基于 的FGLS估计量与GLS估计量具有同样的渐近性质。这是一个相当有用的结果。特别地,注意以下结论:
1、一个渐近有效的FLGS估计量不要求我们有 的有效估计量,只需要一个一致估计量。
2、除了最简单的情况,FGLS估计量的有限样本性质和精确分布是未知的。FGLS估计量的渐近有效性在小样本的情况下可能不再成立,这是因为由估计的 引入的易变性。对于异方差情况的一些分析由泰勒(1977年)给出。自相关的模型由格涅里切斯和拉奥(1969年)做了分析。在这两项研究中,他们发现对于许多类型的参数,FGLS比最小二乘更为有效。但是,如果偏离古典假设不太严重,在小样本情况下最小二乘可能比FGLS更有效。
自相关和异方差处理顺序

自相关和异方差处理顺序在统计学和计量经济学中,自相关和异方差是两个常见的问题,需要进行相应的处理才能保证模型的准确性和可靠性。
本文将以人类的视角,采用准确的中文进行描述,详细介绍自相关和异方差的处理顺序及其重要性。
一、自相关处理自相关是指时间序列数据中观测值之间存在的相关性。
当序列中的观测值之间存在一定的相关性时,会导致统计模型的参数估计不准确,假设检验无效,预测结果不可靠。
因此,需要进行自相关的处理。
自相关处理的一种常见方法是使用自相关函数(ACF)和偏自相关函数(PACF)进行分析。
ACF表示观测值与不同滞后期的观测值之间的相关性,PACF表示观测值与滞后期观测值之间的相关性,探究观测值之间的相关性结构。
在进行自相关处理时,可以采取以下步骤:1. 绘制时间序列图,观察序列的趋势和波动性。
2. 进行序列的平稳性检验,确保序列满足平稳性的要求。
3. 绘制ACF和PACF图,分析观测值之间的相关性结构。
4. 根据ACF和PACF的图形特征,选择合适的自回归移动平均模型(ARMA模型)。
5. 估计模型参数,进行模型拟合。
6. 检验模型的残差序列是否存在自相关,如果存在,则返回第3步,重新选择模型。
通过以上步骤,可以有效地处理自相关问题,提高模型的准确性和可靠性。
二、异方差处理异方差是指随着自变量的变化,因变量的方差也发生变化。
当存在异方差时,会导致模型的参数估计不准确,假设检验无效,预测结果不可靠。
因此,需要进行异方差的处理。
异方差处理的一种常见方法是使用加权最小二乘法(Weighted Least Squares, WLS)。
WLS是一种在回归分析中常用的方法,通过对误差项进行加权,降低异方差对回归结果的影响。
在进行异方差处理时,可以采取以下步骤:1. 绘制残差图,观察残差的分布特征。
2. 进行异方差检验,判断是否存在异方差。
3. 如果存在异方差,可以使用加权最小二乘法进行回归估计。
4. 根据异方差的特点,选择合适的加权函数,对误差项进行加权。
异方差与自相关广义线性模型

第三章 异方差与自相关广义线性模型本章继续讨论线性模型Y =X β+ε, E (ε)=0 (3.0.1)所不同在于以前的关于误差方差的假定是Var(ε)=σ2I n (3.0.2)这一章逐次推广讨论。
第一节讨论异方差的存在与检验,尤其是在经济模型资料中的存在与影响,第二节讨论的是n i d i a g V a r i n ,,1,),,,()(2221 ==σσσε已知(3.0.3) 2221222222212121,),,,,,,,,,()(σσσσσσσσε diag Var =未知 (3.0.4) )e x p (),,,()(2221ασσσεi i n Z diag Var '== ,α未知(3.0.5)这些都是误差方差为对角阵的模型。
第三节讨论自相关线性模型。
首先讨论的是残差一阶自回归线性模型,它的残差满足i i i υρεε+=-1(3.0.6) )(,0)(,)(,0)(22j i E E E j i i i ≠===υυσυυ(3.0.7)此时残差εi 的方差虽不为对角阵,但只含一个参数。
接着我们介绍自回归条件异方差(ARCH)模型,它的误差假设是i p i p i i υεαεααε++++=--221102(3.0.8) )(,0)(,)(,0)(22j i E E E j i i i ≠===υυσυυ(3.0.9)因为模型计算中用到了广义矩估计方法(GMM),我们在第四节又介绍了GMM 。
第五节讨论的是22 ,0)(σσε>=M V a r 未知,M 已知(3.0.10)第六节讨论的是22,0)(σσε≥=M Var 未知,M 已知(3.0.11)所讨论的内容还是各种回归模型、算法及性质。
第一节 异方差的存在与检验一、异方差的存在与影响前面介绍的线性回归模型,都是假定随机误差项εi独立同分布,有相同的方差(Homoscedasticity)2)( ,0)(σεε==i i Var E(3.1.1)但是实际抽样很难保证这一点。
自相关和异方差处理顺序

自相关和异方差处理顺序自相关和异方差是统计学中常见的两个问题,它们在数据分析和建模中起着重要的作用。
在本文中,我们将讨论自相关和异方差的处理顺序,并介绍一些常用的方法和技巧。
一、自相关的处理自相关是指同一时间序列数据中不同时间点之间的相关性。
在时间序列分析中,我们经常会遇到自相关的问题,这会影响到模型的准确性和可靠性。
为了解决自相关问题,我们可以采取以下几种方法:1. 平稳化处理:对于非平稳的时间序列数据,我们可以通过差分、对数变换或者其他方法来使其变得平稳。
平稳化后的数据能够更好地满足模型的假设条件,从而减小自相关的影响。
2. 引入滞后项:在建立模型时,我们可以引入滞后项来考虑时间序列数据中不同时间点之间的相关性。
常用的方法有自回归(AR)模型和移动平均(MA)模型等。
3. 模型诊断:在建立模型后,我们需要对模型进行诊断,检验是否存在自相关。
常用的方法有自相关图和部分自相关图等。
如果发现存在自相关,我们可以进一步调整模型的参数或者引入其他变量来解决自相关问题。
二、异方差的处理异方差是指同一时间序列数据中不同时间点之间方差不相等的现象。
异方差会导致模型的预测结果不准确,因此需要进行处理。
以下是一些处理异方差的方法:1. 变换方法:对于存在异方差的数据,我们可以通过对数变换、平方根变换或者倒数变换等方法来使其变得更加稳定。
变换后的数据能够更好地满足模型的假设条件,从而减小异方差的影响。
2. 加权最小二乘法:在建立模型时,我们可以采用加权最小二乘法来解决异方差问题。
加权最小二乘法能够根据不同时间点的方差大小来调整模型的参数,从而减小异方差的影响。
3. 残差诊断:在建立模型后,我们需要对模型的残差进行诊断,检验是否存在异方差。
常用的方法有残差图和方差稳定性检验等。
如果发现存在异方差,我们可以进一步调整模型的参数或者引入其他变量来解决异方差问题。
自相关和异方差是统计学中常见的问题,它们在数据分析和建模中起着重要的作用。
第五讲 异方差和自相关.

2。利用广义最小二乘法(GLS)
广义最小二乘法是对原模型加权,使之变成一个新 的不存在异方差性的模型,然后采用普通最小二乘 法估计其参数。 其含义为 Var(b) =σ2 (X'X)-1(X'Σ X) (X'X)-1 通过加权使得Σ =I 因此,GLS和WLS要求Σ 已知。
加权最小二乘法(WLS):
4-DL
4
经验上DW值1.8---2.2之间接受原假设, 不存在一阶自相关。 DW值接近于0或者接近于4,拒绝原假 设,存在一阶自相关。
4。Q检验和Bartlett检验 reg D.rs LD.r20 predict e2,res wntestq e2 wntestq e2,lag(2) wntestb e2
r 20t 1 r 20t 1 r 20t 2
rst rst rst 1
回归方程为: use ukrates,clear tsset month reg D.rs LD.r20
自相关的检验
1。图形法:自相关系数和偏自相关系数 predict e1,res ac e1 pac e1 corrgram e1,lag(10)
3。DW检验:只能检验一阶自相关的序列相 关形式,并且要求解释变量严格外生。
根据样本个数和自由度查表得到DL和DU,并 且构造不同的区域。
reg D.rs LD.r20 dwstat
Reject H0
Uncertainty
Accept H0
Uncertainty
Reject H0
0
DL
DU
4-DU
0 . 0
2 1
0
2 2
. 0
0 0 ... . 2 ... n .. ...
异方差、自相关检验及修正

异方差、自相关的检验与修正实验目的:通过对模型的检验掌握异方差性问题和自相关问题的检验方法及修正的原理,以及相关的Eviews 操作方法。
模型设定:εβββ+++=23121i i i X X YYi----人均消费支出X1--从事农业经营的纯收入X2--其他来源的纯收入 中国内地2006年各地区农村居民家庭人均纯收入与消费支出 单位:元 城市 y x1 x2 城市 y x1 x2 北京 5724.5 958.3 7317.2 湖北 2732.5 1934.6 1484.8 天津 3341.1 1738.9 4489 湖南 3013.3 1342.6 2047 河北 2495.3 1607.1 2194.7 广东 3886 1313.9 3765.9 山西 2253.3 1188.2 1992.7 广西 2413.9 1596.9 1173.6 内蒙古 2772 2560.8 781.1 海南 2232.2 2213.2 1042.3 辽宁 3066.9 2026.1 2064.3 重庆 2205.2 1234.1 1639.7 吉林 2700.7 2623.2 1017.9 四川 2395 1405 1597.4 黑龙江 2618.2 2622.9 929.5 贵州 1627.1 961.4 1023.2 上海 8006 532 8606.7 云南 2195.6 1570.3 680.2 江苏 4135.2 1497.9 4315.3 西藏 2002.2 1399.1 1035.9 浙江 6057.2 1403.1 5931.7 陕西 2181 1070.4 1189.8 安徽 2420.9 1472.8 1496.3 甘肃 1855.5 1167.9 966.2 福建 3591.4 1691.4 3143.4 青海 2179 1274.3 1084.1 江西 2676.6 1609.2 1850.3 宁夏 2247 1535.7 1224.4 山东 3143.8 1948.2 2420.1 新疆 2032.4 2267.4 469.9 河南 2229.3 1844.6 1416.4 数据来源:《中国农村住户调查年鉴(2007)》、《中国统计年鉴(2007)》参数估计:估计结果如下:2709030.01402097.01402.728X X Y ++=Λ(2.218) (2.438) (16.999) 922173.02=R D.W.=1.4289 F=165.8853 SE=395.2538实验步骤:一、检查模型是否存在异方差1.图形分析检验(1)散点相关图分析分别做出X1和Y 、X2和Y 的散点相关图,观察相关图可以看出,随着X1、X2的增加,Y 也增加,但离散程度逐步扩大,尤其表现在X1和Y .这说明变量之间可能存在递增的异方差性。
零条件均值假定不成立的情况

零条件均值假定不成立的情况
1. 异方差性,当因变量的残差在自变量的不同取值下具有不同的方差时,就会出现异方差性。
这种情况下,零条件均值假定不成立,因为残差的方差并不相等。
2. 自相关,自相关指的是因变量的残差之间存在相关性,也就是说,残差在时间序列或者空间数据中并不是相互独立的。
在存在自相关的情况下,零条件均值假定也会受到影响。
3. 遗漏变量,如果模型中存在未考虑的重要自变量,那么这些遗漏变量可能会对因变量产生影响,导致因变量的残差在不同自变量取值下具有不同的均值。
4. 非线性关系,当自变量和因变量之间的关系不是简单的线性关系时,也会导致零条件均值假定不成立。
在这种情况下,模型可能会出现残差的均值随着自变量取值的变化而发生变化。
5. 模型设定错误,如果所选择的模型并不符合真实的数据生成过程,那么零条件均值假定也可能不成立。
例如,使用了错误的函数形式或者错误的函数参数。
在实际数据分析中,我们需要对这些情况进行仔细的检验和处理,以确保所建立的模型符合零条件均值假定,或者采用一些修正的方法来处理假定不成立的情况,以确保模型的准确性和可靠性。
