2018年考研数学三真题与解析

合集下载

2018考研数学(三)真题

代入已知条件
f x dx 0, 得
0
1
2 1 1 f 1 1 0 f f x x dx 0 2 2 2 2 2 1 2 2 1 f x 1 1 1 x f f x dx 2 2 2 2 2 0 0 2 1 2 1 1 1 f f x dx 2 2 0 2 2 1 f 1 1 f x dx, 0 2 2 2
1 1 0 （5）下列矩阵中，与矩阵 0 1 1 相似的为 0 0 1 1 1 1 (A) 0 1 1 . 0 0 1 1 0 1 (B) 0 1 1 . 0 0 1
【
】
1 1 1 (C) 0 1 0 . 0 0 1
x
lim
0 x
x
2 x
2
0,
f 0 lim
x 0
cos x 1 lim x 0 x
x
2 x
2
1 , 2
f 0 lim
x 0
cos x 1 lim x 0 x

x 2 x

2
lim
1 ，Y 服从参数为的泊松 2
设总体 X 的概率密度为 f x;
1 e , 其中 0, 为未知参数， X1 , X 2 X n 为来自总体 2
x
X 的简单随机样本，记的最大似然估计量为 .
（Ι ）求；（Ⅱ）求 E 和 D .
1 , 则 P AC A B 2

考研数学三模拟题2018年(13)_真题(含答案与解析)-交互

考研数学三模拟题2018年(13)(总分100, 做题时间90分钟)一、填空题1.设且存在三阶非零矩阵B，使得AB=O，则a=______，b=______．SSS_FILL分值: 12 1[解析] 因为AB=O，所以r(A)+r(B)≤3，又B≠O，于是r(B)≥1，故r(A)≤2，从而a=2，b=1．2.设η为非零向量，η为方程组AX=0的解，则a=______，方程组的通解为______．SSS_FILL分值: 13 k(-3，1，2) T [解析] AX=0有非零解，所以|A|=0，解得a=3，于是方程组AX=0的通解为k(-3，1，2) T．二、选择题1.设A是m×s矩阵，B为s×n矩阵，则方程组BX=0与ABX=0同解的充分条件是______．SSS_SINGLE_SELA r(A)=sB r(A)=mC r(B)=sD r(B)=n分值: 1答案:A[解析] 设r(A)=s，显然方程组BX=0的解一定为方程组ABX=0的解，反之，若ABX=0。

因为r(A)=s，所以方程组AY=0只有零解，故BX=0，即方程组BX=0与方程组ABX=0同解，选A．2.设n阶矩阵A的伴随矩阵A *≠O，且非齐次线性方程组AX=b有两个不同解η1，η2，则下列命题正确的是______．A．AX=b的通解为k1η1+k2η2B．η1+η2为AX=b的解C．方程组AX=0的通解为k(η1 -η2)D．AX=b的通解为SSS_SIMPLE_SINA B C D分值: 1答案:C[解析] 因为非齐次线性方程组AX=b的解不唯一，所以r(A)＜n，又因为A *≠O，所以r(A)=n-1，η2 -η1为齐次线性方程组AX=0的基础解系，选C．3.设有方程组AX=0与BX=0，其中A，B都是m×n矩阵，下列四个命题：(1)若AX=0的解都是BX=0的解，则r(A)≥r(B)(2)若r(A)≥r(B)，则AX=0的解都是BX=0的解(3)若AX=0与BX=0同解，则r(A)=r(B)(4)若r(A)=r(B)，则AX=0与BX=0同解以上命题正确的是______．SSS_SINGLE_SELA (1)(2)B (1)(3)C (2)(4)D (3)(4)分值: 1答案:B[解析] 若方程组AX=0的解都是方程组BX=0的解，则n-r(A)≤n-r(B)，从而r(A)≥r(B)，(1)为正确的命题；显然(2)不正确；因为同解方程组系数矩阵的秩相等，但反之不对，所以(3)是正确的，(4)是错误的，选B．4.设A是m×n矩阵，B是n×m矩阵，则______．SSS_SINGLE_SELA 当m＞n时，线性齐次方程组ABX=0有非零解B 当m＞n时，线性齐次方程组ABX=0只有零解C 当n＞m时，线性齐次方程组ABX=0有非零解D 当n＞m时，线性齐次方程组ABX=0只有零解分值: 1答案:A[解析] AB为m阶方阵，当m＞n时，因为r(A)≤n，r(B)≤n且r(AB)≤min{r(A)，r(B)}，所以r(AB)＜m，于是方程组ABX=0有非零解，选A．5.设A为m×n阶矩阵，则方程组AX=b有唯一解的充分必要条件是______．SSS_SINGLE_SELA r(A)=mB r(A)=nC A为可逆矩阵D r(A)=n且b可由A的列向量组线性表示分值: 1答案:D[解析] 方程组AX=b有解的充分必要条件是b可由矩阵A的列向量组线性表示，在方程组AX=b有解的情形下，其有唯一解的充分必要条件是r(A)=n，故选D．三、解答题1.设向量组α1，α2，…，αn-1为n维线性无关的列向量组，且与非零向量β1，β2正交．证明：β1，β2线性相关．SSS_TEXT_QUSTI分值: 5[证明] 令因为α1，α2，…，αn-1与β1，β2正交，所以Aβ1 =0，Aβ2=0，即β1，β2为方程组AX=0的两个非零解，因为r(A)=n-1，所以方程组AX=0的基础解系含有一个线性无关的解向量，所以β1，β2线性相关．2.设齐次线性方程组其中ab≠0，n≥2．讨论a，b取何值时，方程组只有零解、有无穷多个解?在有无穷多个解时求出其通解．SSS_TEXT_QUSTI分值: 5[解](1)当a≠b，a≠(1-n)b时，方程组只有零解；(2)当a=b时，方程组的同解方程组为x1 +x2+…+xn=0，其通解为X=k1(-1，1，0，…，0) T +k2 (-1，0，1，…，0) T+…+kn-1(-1，0，…，0，1) T(k1，k2，…，kn-1为任意常数)；(3)令当a=(1-n)b时，r(A)=n-1，显然(1，1，…，1) T为方程组的一个解，故方程组的通解为k(1，1，…，1) T (k为任意常数)．3.设A为三阶矩阵，A的第一行元素为a，b，c且不全为零，又且AB=O，求方程组AX=0的通解．SSS_TEXT_QUSTI分值: 5[解] 由AB=O得r(A)+r(B)≤3且r(A)≥1．(1)当k≠9时，因为r(B)=2，所以r(A)=1，方程组AX=0的基础解系含有两个线性无关的解向量，显然基础解系可取B的第1、3两列，故通解为(2)当k=9时，r(B)=1，1≤r(A)≤2，当r(A)=2时，方程组AX=0的通解为当r(A)=1时，A的任意两行都成比例，不妨设a≠0，由得通解为4.a，b取何值时，方程组有解?SSS_TEXT_QUSTI分值: 5[解](1)a≠1时，唯一解为(2)a=1，b≠-1时，r(A)≠ ，因此方程组无解；(3)a=1，b=-1时，通解为X=k1 (1，-2，1，0) T +k2(1，-2，0，1) T +(-1，1，0，0) T (k1，k2为任意常数)．5.A，B为n阶矩阵且r(A)+r(B)＜n．证明：方程组AX=0与BX=0有公共的非零解．SSS_TEXT_QUSTI分值: 5[证明] 方程组的解即为方程组AX=0与BX=0的公共解．因为所以方程组有非零解，故方程组AX=0与BX=0有公共的非零解．设(Ⅰ) α1，α2，α3，α4为四元非齐次线性方程组BX=b的四个解，其中α1=SSS_TEXT_QUSTI 6.求方程组(Ⅰ)的基础解系；分值: 2[解] 方程组(Ⅰ)的基础解系为SSS_TEXT_QUSTI7.求方程组(Ⅱ)BX=0的基础解系；分值: 2[解] 因为r(B)=2，所以方程组(Ⅱ)的基础解系含有两个线性无关的解向量，为方程组(Ⅱ)的基础解系；SSS_TEXT_QUSTI8.(Ⅰ)与(Ⅱ)是否有公共的非零解?若有公共解求出其公共解．分值: 2[解] 方程组(Ⅰ)的通解为方程组(Ⅱ)的通解为=k，则方程组(Ⅰ)与方程组(Ⅱ)的公共解为k(-1，令，则有取k21，1，1) T (其中k为任意常数)．设(Ⅰ)(Ⅱ)SSS_TEXT_QUSTI9.求(Ⅰ)，(Ⅱ)的基础解系；分值: 3[解] 的基础解系为的基础解系为SSS_TEXT_QUSTI10.求(Ⅰ)，(Ⅱ)的公共解．分值: 3[解] 方法一(Ⅰ)，(Ⅱ)公共解即为的解，(Ⅰ)，(Ⅱ)的公共解为方法二(Ⅰ)的通解代入(Ⅱ) =2k2，故(Ⅰ)，(Ⅱ)的公共解为(-k，k，2k，k) T =k(-1，1，2，1) T (k为任意常数)．方法三(Ⅰ)的通解为(Ⅱ)的通解为令∴(Ⅰ)，(Ⅱ)的公共解为11.问a，b，c取何值时，(Ⅰ)，(Ⅱ)为同解方程组?SSS_TEXT_QUSTI分值: 5[解] 方法一的通解为把(Ⅱ)的通解代入(Ⅰ)，得方法二因为(Ⅰ)，(Ⅱ)同解，所以它们的增广矩阵有等价的行向量组，(Ⅱ)的增广矩阵为阶梯阵，其行向量组线性无关．α1可由β1，β2，β3唯一线性表出，α1=-2β1+β2+aβ2a=-1，α2可由β1，β2，β3唯一线性表出，α2=β1+β2-β3b=-2，α3可由β1，β2，β3唯一线性表出，α3=3β1+β2+β3c=4．12.证明线性方程组(Ⅰ)有解的充分必要条件是方程组(Ⅲ)是同解方程组．SSS_TEXT_QUSTI分值: 5[证明] 令方程组(Ⅰ)可写为AX=b，方程组(Ⅱ)、(Ⅲ)可分别写为A TY=0及若方程组(Ⅰ)有解，则r(A)=r( )，从而又因为(Ⅲ)的解一定为(Ⅱ)的解，所以(Ⅱ)与(Ⅲ)同解；反之，若(Ⅱ)与(Ⅲ)同解，则从而r(A)=r( )，故方程组(Ⅰ)有解．13.设的一个基础解系为写出的通解并说明理由．SSS_TEXT_QUSTI分值: 5[解] 令则(Ⅰ)可写为AX=0，令其中则(Ⅱ)可写为BY=0，因为β1，β2，…，βn为(Ⅰ)的基础解系，因此r(A)=n，β1，β2，…，βn线性无关，．α1T，α2T，…，αn T为BY=0的一组解，而r(B)=n，α1T，α2T，…，αnT线性无关，因此α1T，α2T，…，αnT为BY=0的一个基础解系．14.设A是m×s矩阵，B是s×n矩阵，且r(B)=r(AB)．证明：方程组BX=0与ABX=0是同解方程组．SSS_TEXT_QUSTI分值: 5[证明] 首先，方程组BX=0的解一定是方程组ABX=0的解．令r(B)=r且ξ1，ξ2，…，ξn-r是方程组BX=0的基础解系，现设方程组ABX=0有一个解η0不是方程组BX=0的解，即Bη≠0，显然ξ1，ξ2，…，ξn-r，η0线性无关，若ξ1，ξ2，…，ξn-r，η线性相关，则存在不全为零的常数k1，k2，…，kn-r，k，使得k1ξ1+k2ξ2+…+kn-rξn-r +kη=0，若k=0，则k1ξ1+k2ξ2+…+kn-rξn-r+kη=0，因为ξ1，ξ2，…，ξn-r线性无关，所以k1=k2=…=kn-r=0，从而ξ1，ξ2，…，ξn-r，η线性无关，所以k≠0，故η可由ξ1，ξ2，…，ξn-r线性表示，由齐次线性方程组解的结构，有Bη=0，矛盾，所以ξ1，ξ2，…，ξn-r，η线性无关，且为方程组ABX=0的解，从而n-r(AB)≥n-r+1，r(AB)≤r-1，这与r(B)=r(AB)矛盾，故方程组BX=0与ABX=0同解．设A，B，C，D都是n阶矩阵，r(CA+DB)=n．SSS_TEXT_QUSTI15.证明分值: 3[证明] 因为n=r(CA+DB)=所以SSS_TEXT_QUSTI16.设ξ1，ξ2，…，ξr与η1，η2，…，ηs分别为方程组Ax=0与BX=0的基础解系，证明：ξ1，ξ2，…，ξr，η1，η2，…，ηs线性无关．分值: 3[证明] 因为所以方程组只有零解，从而方程组AX=0与BX=0没有非零的公共解，故ξ1，ξ2，…，ξr与η1，η2，…，ηs线性无关．17.设A为n阶矩阵，A11≠0．证明：非齐次线性方程组AX=b有无穷多个解的充分必要条件是A * b=0．SSS_TEXT_QUSTI分值: 5[证明] 设非齐次线性方程组AX=b有无穷多个解，则r(A)＜n，从而|A|=0，于是A * b=A * AX=|A|X=0．反之，设A * b=0，因为b≠0，所以方程组A * X=0有非零解，从而r(A * )＜n，又A11≠0，所以r(A * )=1，且r(A)=n-1．因为r(A * )=1，所以方程组A * X=0的基础解系含有n-1个线性无关的解向量，而A * A=0，所以A的列向量组α1，α2，…，αn为方程组A * X=0的一组解向量．由A11≠0，得α2，…，αn线性无关，所以α2，…，αn是方程组A* X=0的基础解系．因为A * b=0，所以b可由α2，…，αn线性表示，也可由α1，α2，…，αn线性表示，故r(A)= =n-1＜n，即方程组AX=b有无穷多个解．18.证明：r(AB)≤min{r(A)，r(B)}．SSS_TEXT_QUSTI分值: 5[证明] 令r(B)=r，BX=0的基础解系含有n-r个线性无关的解向量，因为BX=0的解一定是ABX=0的解，所以ABX=0的基础解系所含的线性无关的解向量的个数不少于BX=0的基础解系所含的线性无关的解向量的个数，即n-r(AB)≥n-r(B)，r(AB)≤r(B)；又因为r[(AB) T ]=r(AB)=r(B T A T)≤r(A T )=r(A)，所以r(AB)≤min{r(A)，r(B)}．19.证明：r(A)=r(A T A)．SSS_TEXT_QUSTI分值: 5[证明] 只需证明AX=0与A T AX=0为同解方程组即可．若AX0 =0，则A T AX=0．反之，若A T AX0 =0，则XT A T AX=0 (AX) T (AX)=0 AX=0，所以AX=0与A T AX=0为同解方程组，从而r(A)=r(A T A)．20.设A是m×n矩阵，且非齐次线性方程组AX=b满足．证明：方程组AX=b 的线性无关的解向量的个数最多是n-r+1个．SSS_TEXT_QUSTI分值: 5[证明] 因为r(A)=r＜n，所以齐次线性方程组AX=0的基础解系含有n-r个线性无关的解向量，设为ξ1，ξ2，…，ξn-r．设η为方程组AX=b的一个特解，令β0=η，β1=ξ1+η，β2=ξ2+η…，βn-r=ξn-r+η0，显然β，β1，β2，…，βn-r为方程组AX=b的一组解．令k0β+k1β1+…+kn-rβn-r=0，即(k0 +k1+…+kn-r)η+k1β1+k2β2+…+kn-rβn-r=0，上式两边左乘A得(k0 +k1+…+kn-r)b=0，因为b为非零列向量，所以k0 +k1+…+kn-r=0，于是k1ξ1+k2ξ2+…+kn-rξn-r=0，注意到ξ1，ξ2，…，ξn-r线性无关，所以k1=k2=…=kn-r=0，故β0，ξ1，ξ2，…，ξn-r线性无关，即方程组AX=b存在由n-r+1个线性无关的解向量构成的向量组．设ξ1，ξ2，…，ξn-r+2为方程组AX=b的一组线性无关解，令γ1=β2-β1，γ2=β3-β1，…，γn-r+1=βn-r+2-β1，根据定义，易证γ1，γ2，…，γn-r+1线性无关，又γ1，γ2，…，γn-r+1为齐次线性方程组AX=0的一组解，即方程组AX=0含有n-r+1个线性无关的解，矛盾，所以AX=b的任意n-r+2个解向量都是线性相关的，所以AX=b的线性无关的解向量的个数最多为n-r+1个．21.讨论方程组的解的情况，在方程组有解时求出其解，其中a，b为常数．SSS_TEXT_QUSTI分值: 5[解](1)当a≠-1，b≠-2时．因为D≠0，所以方程组有唯一解，由克拉默法则得(2)当a=-1，b≠-2时，当b≠-1时，方程组无解当b=-1时，方程组的通解为(3)当a≠-1，b=-2时，当a=1时，方程组的通解为当a≠1时，显然r(A)=2≠ =3，方程组元解．22.设问a，b，c为何值时，矩阵方程AX=B有解?有解时求出全部解．SSS_TEXT_QUSTI分值: 5[解] 令X=(X1，X2，X3)，B=(β1，β2，β3)，方程组AX=B等价于则AX=B有解的充分必要条件是r(A)=r( )，由r(A)=r( )得a=1，b=2，c=-2，此时AX1=β1的通解为AX2=β2的通解为AX 3 =β 3 的通解为则其中k 1 ，k 2 ，k 3 为任意常数． 1。

2018考研数学三试题及答案解析

2018年全国硕士研究生入学统一考试数学（三）试题及答案解析一、选择题:1 8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的.(1)下列函数中，在0x =处不可导的是（）(A)()sin f x x x =(B)()sin f x x =(C)()cos f x x =(D)()f x =【答案】（D）【解析】根据导数的定义：（A）sin limlim0,x x x x x x →→== 可导；（B）0,x x →→==可导；（C）1cos 12limlim0,x x xx x→→--==可导；（D）000122limlim,x x x xx x→→→-==极限不存在，故选D。

(2)()[]()10,10,f x f x dx =⎰设函数在上二阶可导，且则（）(A)1()0,()02f x f '<<当时(B)1()0,()02f x f ''<<当时(C)1()0,()02f x f '><当时(D)1()0,(02f x f ''><当时【答案】（D ）【解析】2111()11()()()()(,2222!22f f x f f x x x ξξ'''=+-+-介于，之间，故1111220000120111()11()10=()()(()((2222!222!2()11()0()0,()0..2!22f f f x dx f f x dx x dx f x dxf f x x dx f D ξξξ'''''=+-+-=+-''''>⇒-><⎰⎰⎰⎰⎰由于所以，应选(3)设()(2222222211,,1,1x x xM dx N dx K dx x e ππππππ---++===++⎰⎰⎰则（）(A)M N K >>(B)M K N >>(C)K M N >>(D)K N M>>【答案】（C）【解析】22222222222(1)122=(1).111x x x x M dx dx dx x x x πππππππ---+++==+=+++⎰⎰⎰22222111(0)11xxxxx e x N dx dx Mee πππππ--+++<≠⇒<⇒=<=<⎰⎰2222=11K dx dx M πππππ-->==⎰⎰（,K M N >>故应选C 。

考研数学三历年真题答案与解析-模拟试题

考研数学三历年真题答案与解析|模拟试题展开全文第一部分历年真题及详解2008年全国硕士研究生入学统一考试考研数学三真题及详解2009年全国硕士研究生入学统一考试考研数学三真题及详解2010年全国硕士研究生入学统一考试考研数学三真题及详解2011年全国硕士研究生入学统一考试考研数学三真题及详解详解2013年全国硕士研究生入学统一考试考研数学三真题及详解2014年全国硕士研究生入学统一考试考研数学三真题及详解2015年全国硕士研究生招生考试考研数学三真题及详解2016年全国硕士研究生招生考试考研数学三真题及详解2017年全国硕士研究生招生考试考研数学三真题及详解2018年全国硕士研究生招生考试考研数学三真题及详解2019年全国硕士研究生招生考试考研数学三真题及详解（2）模拟试题及详解部分：精选了3套模拟试题，且附有详尽解析。

考生可通过模拟试题部分的练习，掌握最新考试动态，提前感受考场实战。

第二部分模拟试题及详解全国硕士研究生招生考试考研数学三模拟试题及详解（一）全国硕士研究生招生考试考研数学三模拟试题及详解（二）全国硕士研究生招生考试考研数学三模拟试题及详解（三）第一部分历年真题及详解解一、选择题（1～8小题，每小题4分，共32分。

下列每题给出的四个选项中，只有一个选项符合题目要求。

）1设函数f（x）在区间[－1，1]上连续，则x＝0是函数的（）。

A．跳跃间断点B．可去间断点C．无穷间断点D．振荡间断点【答案】B查看答案【考点】函数间断点的类型【解析】首先利用间断点的定义确定该点为间断点，然后利用如下的间断点的类型进行判断。

第一类间断点：x＝x0为函数f（x）的间断点，且与均存在，则称x＝x0为函数f（x）的第一类间断点，其中：①跳跃型间断点：②可去型间断点：第二类间断点：x＝x0为函数f（x）的间断点，且与之中至少有一个不存在，则称x＝x0为函数f（x）的第二类间断点，其中：①无穷型间断点：与至少有一个为∞；②振荡型间断点：或为振荡型，极限不存在。

2018年考研数学三真题及答案解析(完整版)

(C) f x cos x
(D) f x cos x
【答案】（D）
【解析】根据导数的定义：
x sin x
x
lim
lim
x 0,可导；
（A） x0 x
x0 x
x sin x
x
lim
lim
x 0,可导；
（B） x0
x
x0 x
cos lim
x
1

lim

1 2
t 0
t 0
2= lim (1 bt)et 1 lim et 1 lim btet 1 b,
t 0
t
t t 0
t t 0
从而b 1.
综上，a 1,b 1.
(16)(本题满分 10 分)
设平面区域D由曲线y 3 1 x2 与直线y 3x及y轴围成, 计算二重积分 x2dxdy.
2018 年全国硕士研究生入学统一考试数学（三）试题及答案解析
一、选择题:1 8 小题,每小题 4 分,共 32 分.下列每题给出的四个选项中,只有一个选项符合题目要求的.
(1) 下列函数中，在 x 0 处不可导的是（）
(A) f x x sin x
(B) f x x sin x
x
x
x 0时，可得f (x) 2xf (x) f (x) 2xf (x) 0.
由公式得：f (x) Ce(2x)dx =Cex2 , f (0) 2 C 2. 故f (x)=2ex2 f (1) 2e.
(13) 设A为3阶矩阵, a1, a2, a3是线性无关的向量组,若Aa1 a1 a2, Aa2 a2 a3, Aa3 a1 a3,

2018年考研数学三试题与答案解析(完整版)

M 2 (1
2

2x ) dx 22 1dx 1 x2
x - , 时， 1 cos x 1, 所以K M 2 2 令f ( x) 1 x e x , f (0) 0, f ( x) 1 e x 当x 0, 时，f ( x ) 0; 当x , 0 时，f ( x ) 0 2 2 1 x 所以x - , 时，有f ( x ) 0，从可有 x 1，由比较定理得N<M, 故选C e 2 2
B. f ( x ) x sin( D. f ( x ) cos(
x) x)
f - 0 lim
x 0
x sin x x x sin x x
lim
x 0
x sin x x sin x x sin x 0 lim 0, f lim 0 x 0 x 0 x x x x sin x x sin x x sin x 0 lim 0, f lim 0 x 0 x 0 x x x
0 2
B. r ( A BA) r ( A). D. r ( A B ) r ( A B ).
T T
【解析】特殊值法：由已知可将 f ( x ) 看成随机变量 X N 1, 布的对称性， P X 0 0.2

2
的概率密度，根据正态分
1 n Xi ， n i 1
Born to win
2018 年考研数学三试题与答案解析（完整版)
——跨考教育数学教研室
一、选择题：1～8 小题，每小题 4 分，共 32 分，下列每小题给出的四个选项中，只有一项符合题目要求的，请将所选项前的字母填在答题纸指定位置上. ．．． 1. 下列函数中，在 x 0 处不可导的是（ A. f ( x ) x sin( x ) C. f x cos( x ) 【答案】D 【解析】 A 可导：）。

2018考研数学三真题及答案

2018考研数学三真题及答案一、选择题1.下列函数中,在 0x =处不可导的是()().sin A f x x x = ().B f x x =().?C f x cos x = ().D f x =答案:() D 解析:方法一:()()()000sin 0limlim lim sin 0,x x x x x x f x f x x xx A →→→-===可导 ()()()0000limlim 0,x x x x f x f x x B →→→-===可导()()()20001cos 102limlim lim 0,x x x x x f x f x x C x→→→---===可导 ()()()000102limlim x x x x f f x xD x →→→--==不存在,不可导应选()D . 方法二:因为()(1)0f f x ==()()000102lim limx x x x f x f x x→→→--==不存在 ()f x ∴在0x =处不可导,选()D对()():?A f x xsinx =在 0x =处可导对()()32:~?B f x x x =在 0x =处可导对()():x x C f cos =在 0x =处可导. 2.设函数()f x 在[0,1]上二阶可导,且()10,f x dx =⎰则()()1'0,02A f x f ⎛⎫<<⎪⎝⎭当时 ()()1''0,02B f x f ⎛⎫<< ⎪⎝⎭当时 ()()1'0,02C f x f ⎛⎫><⎪⎝⎭当时 ()()1''0,02D f x f ⎛⎫>< ⎪⎝⎭当时答案()D【解析】将函数()f x 在12处展开可得()()()()()222111000''1111',22222''1111111''',22222222f f x f f x x f f x dx ff x x dx f f x dx ξξξ⎛⎫⎛⎫⎛⎫⎛⎫=+-+- ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+-+-=+-⎢⎥ ⎪ ⎪⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦⎰⎰⎰故当''()0f x >时,()111.0.22f x dx f f⎛⎫⎛⎫>< ⎪ ⎪⎝⎭⎝⎭⎰从而有选()D 。

2018年考研数学一二三真题解析及点评(史上最强版)

证明数列收敛只有唯一的方法：证明数列单调有界。《金讲》17页予以重要说明并给出两道难度高于本题的同型例题详解，本题再不济，直接用第一问的结论求出第二问的结果应该是一丝难度都没有。
数一第20题数三第20题数二第22题
《金讲》403-405页不仅给出了通用性齐次方程组的详细解题过程，还给予具体具体方程解析示例，详细程度超越市面任何一本数学参考书，足以解答任何复杂齐次方程组。
本质一样
数一第18题
(Ⅰ)是简单一阶微分方程求解，直接套公式即得，送分题；(Ⅱ)不定积分函数与变现积分函数的灵活转换，需要对两者关系有较深度地掌握方可轻易转换，稍有难度，本题完整证明出来的同学应该不超过万分之一。
较难题
考查不等式的证明，具有天然的难题属性。但《金讲》在142页对这类题型设了一个专题给予了本质性的总结，任何不等式证明本质都可以归结到两类情况，每类情况的证明有唯一思路，因此，不等式证明对于《金讲》读者不太可能成为难题，但《金讲》以外，没有任何参考书做过这种深度总结，因此本道题对于有些人是难题。
数二第18题
数三第18题
简单函数的级数展开并求通项。展开部分直接套公式，属于送分。求通项虽偶有难度，但任何求通项都可以通过适当展开进行归纳这一万能方法，在《金讲》中有强调，所以也属于半送分。《金讲》 254页至259页用了一个重点专题予以详解本考点，足以解决任何函数的展开式。
数一第19题数三第19题数二第21题
数二第20题
考查微分的基本应用，将题目内容用数学式子表示出来，问题就转化为了最简单的微分或积分问题，本题几乎是《金讲》配套暑期集训讲义中的原题。
数一第11题
考查旋度公式的记忆，直接用旋度公式计算即得答案。旋度公式的详细计算公式参见《金讲》288页，属送分题。

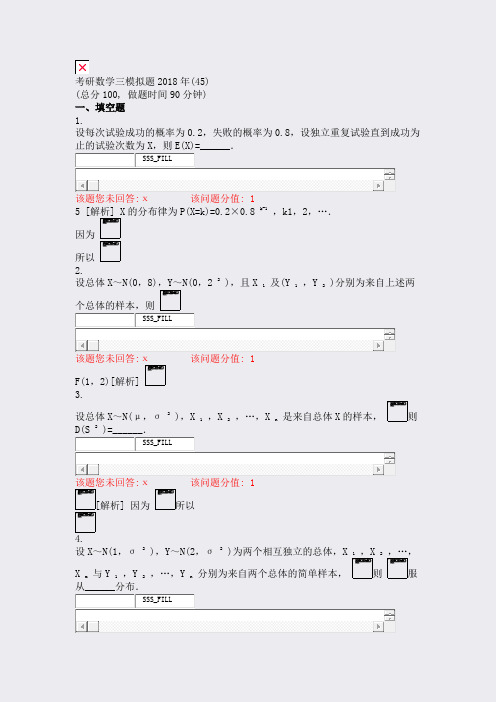
考研数学三模拟题2018年(45)_真题(含答案与解析)-交互

考研数学三模拟题2018年(45)(总分100, 做题时间90分钟)一、填空题1.设每次试验成功的概率为0.2，失败的概率为0.8，设独立重复试验直到成功为止的试验次数为X，则E(X)=______．SSS_FILL该题您未回答:х该问题分值: 15 [解析] X的分布律为P(X=k)=0.2×0.8 k-1，k1，2，…．因为所以2.设总体X～N(0，8)，Y～N(0，2 2 )，且X1及(Y1，Y2)分别为来自上述两个总体的样本，则SSS_FILL该题您未回答:х该问题分值: 1F(1，2)[解析]3.设总体X～N(μ，σ 2 )，X1，X2，…，Xn是来自总体X的样本，则D(S 2 )=______．SSS_FILL该题您未回答:х该问题分值: 1 [解析] 因为所以4.设X～N(1，σ 2 )，Y～N(2，σ 2 )为两个相互独立的总体，X1，X2，…，Xm 与Y1，Y2，…，Yn分别为来自两个总体的简单样本，则服从______分布．SSS_FILL该题您未回答:х该问题分值: 1[解析]且相互独立，则5.设X～N(μ，σ 2 )，其中σ 2已知，μ为未知参数．从总体X中抽取容量为16的简单随机样本．且μ的置信度为0.95的置信区间中的最小长度为0.588，则σ 2 =______．SSS_FILL该题您未回答:х该问题分值: 1** [解析] 在σ 2 已知的情况下，μ的置信区间为 /其中 /于是有 /二、选择题1.对于随机变量X1，X2，…，Xn，下列说法不正确的是______．A．若X1，X2，…，Xn两两不相关，则B．若X1，X2，…，Xn相互独立，则D(X1+X2+…+Xn)=D(X1)+D(X2)+…+D(Xn)C．若X1，X2，…，Xn相互独立同分布，服从N(0，σ 2 )，则D．若D(X1 +X2+…+Xn)=D(X1)+D(X2)+…+D(Xn)，则X1+X2+…+Xn两两不相关SSS_SIMPLE_SINA B C D该题您未回答:х该问题分值: 1答案:D[解析] 若X1 +X2+…+Xn相互独立，则B，C是正确的，若X1+X2+…+Xn两两不相关，则A是正确的，选．2.设(X，Y)服从二维正态分布，其边缘分布为X～N(1，1)，Y～N(2，4)，X，Y的相关系数为ρXY=-0.5，且P(aX+by≤1)=0.5，则______．A．B．C．D．SSS_SIMPLE_SINA B C D该题您未回答:х该问题分值: 1答案:D[解析] 因为(X，Y)服从二维正态分布，所以aX+bY服从正态分布，E(aX+bY)=a+2b，D(aX+by)=a 2 +4b 2 +2abCov(X，Y)=a 2 +4b 2 -2ab，即aX+bY～N(a+2b，a 2 +4b 2 -2ab)，由P(aX+by≤1)=0.5得a+2b=1，所以选D．3.设X1，X2，…，Xn是来自正态总体X～N(μ，σ 2 )的简单随机样本，记则服从t(n-1)分布的随机变量是______．A．B．C．D．SSS_SIMPLE_SINA B C D该题您未回答:х该问题分值: 1答案:D[解析] 即选D．4.设X～t(n)，则下列结论正确的是______．A．X 2～F(1，n)B．C．X 2～χ 2 (n)D．X 2～χ 2 (n-1)SSS_SIMPLE_SINA B C D该题您未回答:х该问题分值: 1答案:A[解析] 由X～t(n)，得其中U～N(0，1)，V～χ 2 (n)，且U，V相互独立，于是选A．5.从正态总体X～N(0，σ 2 )中抽取简单随机样本X1，X2，…，Xn，则可作为参数σ 2的无偏估计量的是______．A．B．C．D．SSS_SIMPLE_SINA B C D该题您未回答:х该问题分值: 1答案:A[解析] 因为所以为σ 2的无偏估计量，选A．三、解答题1.设总体X～N(0，σ 2 )，X1，X2，…，Xn为来自总体X的简单随机样本，S 2 = 求所服从的分布．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 6 [解] 又且相互独立，则即设X1，X2，…，Xn(n＞2)是来自总体X～N(0，1)的简单随机样本，记Yi=Xi- (i=1，2，…，n)．求：SSS_TEXT_QUSTI2.D(Yi)；该题您未回答:х该问题分值: 3[解] 由得SSS_TEXT_QUSTI3.Cov(Y1，Yn)．该题您未回答:х该问题分值: 3[解] 因为X 1 ，X 2 ，…，X n (n ＞2)相互独立，所以由得4.设总体X ～N(μ，σ 2 )，X 1 ，X 2 ，…，X n 是来自总体X 的样本，令求E(X 1 T)．SSS_TEXT_QUSTI该题您未回答:х 该问题分值: 6[解] 因为X 1 ，X 2 ，…，X n 独立同分布，所以有E(X 1 T)=E(X 2 T)=…=E(X n T)5.设总体X 服从正态分布N(μ，σ 2 )(σ＞0)，X 1 ，X 2 ，…，X n 为来自总体X 的简单随机样本，令求Y 的数学期望与方差．SSS_TEXT_QUSTI该题您未回答:х 该问题分值: 6 [解]而于是 6.设总体X 服从正态分布N(μ，σ 2 )(σ＞0)．从该总体中抽取简单随机样本X1，X 2 ，…，X 2n (n ＞2)．令求统计量的数学期望．SSS_TEXT_QUSTI该题您未回答:х 该问题分值: 6[解] 令Y i =X i +X n+i (i=1，2，…，n)，则Y 1 ，Y 2 ，…，Y n 为正态总体N(2μ，2σ 2 )的简单随机样本，=(n-1)S 2 ，其中S 2 为样本Y 1 ，Y2，…，Y n 的方差，而E(S 2 )=2σ 2 ，所以统计量U= 的数学期望为E(U)=E[(n-1)S 2 ]=2(n-1)σ 2 ． 7.设总体且X，Y相互独立，来自总体X，Y的样本均值为，样本方差为记求统计量的数学期望．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 6[解] 由相互独立，可知a，b与相互独立，显然a+b=1．E(U)=μ[E(a)+E(b)]=μE(a+b)=μE(1)=μ．8.设总体X～N(μ，σ 2 )，X1，X2，…，Xn+1为总体X的简单随机样本，记求统计量服从的分布．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 6[解] 因为Xn+1～N(μ，σ 2 )，且它们相互独立，所以又相互独立，所以由t分布的定义，有9.设总体X的概率分布为X 0 1 2 3p θ 2 2θ(1-θ) θ 2 1-2θ是未知参数．用样本值3，1，3，0，3，1，2，3求θ的矩估计值和最大似然估计值．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 6[解] E(X)=0×θ 2+1×2θ(1-θ)+2×θ 2+3×(1-2θ)=3-4θ，令得参数θ的矩估计值为L(θ)=θ 2×[2θ(1-θ)] 2×θ 2×(1-2θ) 4=4θ 6 (1-θ) 2 (1-2θ) 4，lnL(θ)=ln4+6lnθ+2ln(1-θ)+4ln(1-2θ)，令得参数θ的最大似然估计值为10.设总体样本值为1，1，3，2，1，2，3，3，求θ的矩估计和最大似然估计．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 7[解] (1)X为离散型随机变量，其分布律为E(X)=3-3θ．今3-3θ=2得θ的矩估计值为(2)L(1，1，3，2，1，2，3，3；θ)=P(X=1)P(X=1)…P(X=3)=θ 3×θ 2×(1-2θ) 3，lnL(θ)=5lnθ+3ln(1-2θ)，令得θ的最大似然估计值为11.设总体X～U[0，θ]，其中θ＞0，求θ的极大似然估计量，判断其是否是θ的无偏估计量．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 7[解] 总体X的密度函数和分布函数分别为设x1，x2，…，xθ为总体X的样本观察值，似然函数为(i=1，2，…，n)．当0＜xi＜θ(i=1，2，…，n)时，且当θ越小时L(θ)越大，所以θ的最大似然估计值为=max{x1，x2，…，xn}，θ的最大似然估计量为=max{X1，X2，…，Xn}．因为=max{X1，X2，…，Xn}的分布函数为则的概率密度为所以=max{X1，X2，…，Xn}不是θ的无偏估计量．12.设总体X的密度函数为θ＞0为未知参数，a＞0为已知参数，求θ的极大似然估计量．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 7[解]令得参数θ的极大似然估计量为13.设总体X～U(θ1，θ2)，X1，X2，…，Xn是来自总体X的样本，求θ1，θ2的矩估计和最大似然估计．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 7 [解] (1)令(2)lnL(θ1，θ2)=-nln(θ2-θ1)，而因为lnL(θ1，θ2)是θ1的单调增函数，是θ2的单调减函数，所以14.设总体X在区间(0，θ)内服从均匀分布，X1，X2，X3是来自总体的简单随机样本．证明：都是参数θ的无偏估计量，试比较其有效性．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 7[解] 因为总体X在区间(0，θ)内服从均匀分布，所以分布函数为令则则U，V的密度函数分别为因为所以都是参数θ的无偏估计量．因为所以更有效．15.设总体X，Y相互独立且都服从N(μ，σ 2 )分布，(X1，X2，…，Xm)与(Y1，Y2，…，Yn)分别为来自总体X，Y的简单随机样本．证明：为参数σ 2的无偏估计量．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 7[证明] 令因为所以于是即为参数σ 2的无偏估计量．1。

2018年数学三考研真题及解析

2018年全国硕士研究生入学统一考试数学三试题解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求的，请将所选项前的字母填在答题纸．．．指定位置上. 1. 下列函数中，在0x =错误!未找到引用源。

处不可导的是（）。

A. ()sin()f x x x =B. ()f x x =C. ()cos()f x x =D. ()f x =【答案】D 【解析】 A 可导：()()()()-0000sin sin sin sin 0lim lim 0,0lim lim 0x x x x x x x x x x x xf f x x x x--+++→→→→⋅⋅''====== B 可导：()()-0000sin 0lim lim 0,0lim lim 0x x x x x x f f x x--+++→→→→-⋅⋅''======C 可导：()()22-000011cos -1cos -1220lim lim 0,0lim lim 0x x x x x x x x f f x x x x--+++→→→→--''====== D 不可导：()()()()()-000-11-11220lim lim ,0lim lim -2200x x x x x x f f x x f f --+++→→→→+--''======''≠2 .已知函数()f x 在[]0,1上二阶可导，且()10,=⎰f x dx 则A.当()0'<f x 时，102⎛⎫<⎪⎝⎭f B. 当()0''<f x 时，102⎛⎫< ⎪⎝⎭f C. 当()0'>f x 时，102⎛⎫< ⎪⎝⎭f D. 当()0''>f x 时，102⎛⎫< ⎪⎝⎭f 【答案】D 【解析】A 错误：()()()11000,10111,2,022f x f x dx dx f x x f x ⎛⎫'===-< ⎪⎛⎫=-+-+= ⎝⎝⎭⎪⎭⎰⎰B 错误：()()()100212111111,033243120,20,f x dx dx f x x f f x x ⎛⎫''==⎛⎫=-+-+=-+=-< ⎪⎝⎭=> ⎪⎝⎭⎰⎰C 错误：()()()1100111,0220,10,2f x d f x x x f x dx f x ⎛⎫=-⎛⎫'-===> ⎪⎝⎭= ⎪⎝⎭⎰⎰D 正确：方法1：由()0f x ''>可知函数是凸函数，故由凸函数图像性质即可得出102f ⎛⎫< ⎪⎝⎭方法2：21112200011111()()()()()(),22222111111()()()()()()()()()02222221()0,()0.2f x f f x f x x f x dx f f x f x dx f f x dx f x f ξξξξ'''=+-+-'''''=+-+-=+-=''><⎰⎰⎰介于和之间,又故 3.设()(2222222211,,1,1ππππππ---++===++⎰⎰⎰x x xM dx N dx K dx x e 则 A.>>M N K B.>>M K NC.>>K M ND.>>K N M 【答案】C 【解析】222222(1)11-,11,22()1,(0)0,()10,()0;,0()0221-,()01N<M,C22x xx xM dx dx x x K Mf x x e f f x e x f x x f x x x f x e ππππππππππ--=+=+⎡⎤∈≥>⎢⎥⎣⎦'=+-==-⎡⎤⎡⎤''∈<∈->⎢⎥⎢⎥⎣⎦⎣⎦+⎡⎤∈≤≤⎢⎥⎣⎦⎰⎰时，所以令当时，当时，所以时，有，从可有，由比较定理得故选4. 设某产品的成本函数()C Q 可导，其中Q 为产量，若产量为0Q 时平均成本最小，则( ) A. ()00C Q '= B.()()00C Q C Q '= C.()()000C Q Q C Q '= D. ()()000Q C Q C Q '= 【答案】D【解析】根据平均成本()C Q C Q=，根据若产量为0Q 时平均成本最小，则有 ()()()()()()()0000000220Q Q Q QC Q Q C Q C Q Q C Q C C Q Q C Q Q Q ==''--''===⇒=5.下列矩阵中，与矩阵110011001⎛⎫ ⎪ ⎪ ⎪⎝⎭相似的为 A. 111011001-⎛⎫⎪⎪ ⎪⎝⎭ B.101011001-⎛⎫ ⎪ ⎪ ⎪⎝⎭ C. 111010001-⎛⎫ ⎪⎪ ⎪⎝⎭D.101010001-⎛⎫ ⎪ ⎪ ⎪⎝⎭【答案】A【解析】方法一：排除法令110011001Q ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，特征值为1,1,1，()2r E Q -= 选项A ：令111011001A -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，A 的特征值为1,1,1，()0110012000r E A r -⎡⎤⎢⎥-=-=⎢⎥⎢⎥⎣⎦ 选项B ：令101011001B -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，B 的特征值为1,1,1，()0010011000r E B r ⎡⎤⎢⎥-=-=⎢⎥⎢⎥⎣⎦ 选项C ：令111010001C -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，C 的特征值为1,1,1，()0110001000r E C r -⎡⎤⎢⎥-==⎢⎥⎢⎥⎣⎦选项B ：令101010001D -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，D 的特征值为1,1,1，()0010001000r E D r ⎡⎤⎢⎥-==⎢⎥⎢⎥⎣⎦若矩阵Q 与J 相似，则矩阵E Q -与E J -相似，从而()()r E Q r E J -=-，故选（A ）方法二：构造法（利用初等矩阵的性质）令110010001P ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，1110010001P --⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦1110111011011001001P P --⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ ，所以110111011011001001-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦与相似故选（A ）6.设,A B 为n 阶矩阵，记()r X 为矩阵X 的秩，(,)X Y 表示分块矩阵，则 A.()().r A AB r A = B.()().r A BA r A = C.()max{()()}.r A B r A r B =， D.()().T T r A B r A B = 【答案】（A ）【解析】(,)(,)[(,)]()r E B n r A AB r A E B r A =⇒== 故选（A ）7.设()f x 为某分布的概率密度函数，(1)(1)f x f x +=-，()200.6f x dx =⎰，则{0}P X <=A.0.2 B.0.3 C.0.4 D.0.6 【答案】A【解析】特殊值法：由已知可将()f x 看成随机变量()21,X N σ的概率密度，根据正态分布的对称性，()00.2P X <= 8.已知12,,,n X X X 为来自总体2~(,)X N μσ的简单随即样本，11ni i X X n ==∑，*S S ==A.()~()X t n S μ- B.()~(1)X t n S μ--C.*)~()X t n Sμ-D. *)~(1)X t n Sμ-- 【答案】B 【解析】2,XN n σμ⎛⎫⎪⎝⎭()()()22211,0,1n SX N n χσ--，又2X S 与相互独立，所以)()1X t n Sμ--，故选项B 正确，而A 错.()()()*22210,1,n S X Nn μχσσ--，2X S *与相互独立 ()n X t n μ-，故选项C ，D 错。

考研数学三模拟题2018年(4)_真题(含答案与解析)-交互

考研数学三模拟题2018年(4) (总分100, 做题时间90分钟) 解答题 1.若随机变量序列X 1 ，X 2 ，…，X n ，…满足条件证明：{X n }服从大数定律．SSS_TEXT_QUSTI该题您未回答:х 该问题分值: 1.5 【证】由切比雪夫不等式，对任意的ε＞0有所以对任意的ε＞0，故{X n }服从大数定律． 2.某计算机系统有100个终端，每个终端有20%的时间在使用，若各个终端使用与否相互独立，试求有10个或更多个终端在使用的概率．SSS_TEXT_QUSTI该题您未回答:х 该问题分值: 1.5【解】设则同时使用的终端数所求概率为3.设X 1 ，X 2 ，…，X n 为总体X 的一个样本，EX=μ，DX=σ 2 ＜∞，求SSS_TEXT_QUSTI该题您未回答:х 该问题分值: 1.5【解】进而有从装有1个白球，2个黑球的罐子里有放回地取球，记这样连续取5次得样本X 1 ，X 2 ，X 3 ，X 4 ，X 5 ．记Y=X 1 +X 2 +…+X 5 ，求：SSS_TEXT_QUSTI4.Y的分布律，EY，E(Y 2 )；该题您未回答:х该问题分值: 1.75【解】Y是连续5次取球中取得黑球的个数，所以从而SSS_TEXT_QUSTI5.，E(S 2 )(其中，S 2分别为样本X1，X2，…，X5的均值与方差)．该题您未回答:х该问题分值: 1.75【解】由于X的分布律为所以6.若X～χ 2 (n)，证明：EX=n，DX=2n．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】因X～χ 2 (n)，所以X可表示为其中X1，X2，…，Xn相互独立，且均服从N(0，1)，于是7.已知X～t(n)，求证：X 2～F(1，n)．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】X～t(n)，则X可表示为其中Z～N(0，1)，Y～χ 2 (n)且Z，Y相互独立，又Z 2～χ 2 (1)，于是8.设X1，X2，…，Xm，Y1，Y2，…，Yn独立．Xi～N(a，σ 2 )，i=1，2，…，m，Yi～N(b，σ 2 )，i=1，2，…，n，而α，β为常数．试求的分布．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】由于Xi ～N(a，σ 2 )，i=1，2，…，m，Yi～N(b，σ 2 )，i=1，2，…，n，且X1，X2，…，Xm，Y1，Y2，…，Yn相互独立，则也服从正态分布．所以9.一个罐子里装有黑球和白球，黑、白球数之比为a:1．现有放回的一个接一个地抽球，直至抽到黑球为止，记X为所抽到的白球个数．这样做了n次以后，获得一组样本：X1，X2，…，Xn基于此，求未知参数a的矩估计和最大似然估计．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】由题意知，随机变量X的分布律为令解得对于给定的样本X1，X2，…，Xn，似然函数为取对数，得令得解得10.罐中有N个硬币，其中有θ个是普通硬币(掷出正面与反面的概率各为0.5)，其余N-θ个硬币两面都是正面，从罐中随机取出一个硬币，把它连掷两次，记下结果，但不去查看它属于哪种硬币，如此重复n次，若掷出0次、1次、2次正面的次数分别为n0，n1，n2，利用(1)矩法；(2)最大似然法，求参数θ的估计量．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】设X为“连掷两次正面出现的次数”，A={取出的硬币为普通硬币}，则即X的分布为(1) 解得θ=N(2-μ1)，θ的矩估计为(2)解得θ的最大似然估计11.设总体X的概率密度为又设X1，X2，…，Xn是来自X的一个简单随机样本，求未知参数θ的矩估计量SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】X的数学期望为用样本均值代替①中的EX得此方程的解即为θ的矩估计量12.设总体X的概率密度为试用样本X1，X2，…，Xn求参数α的矩估计和最大似然估计．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】先求矩估计：解得所以α的矩估计为再求极大似然估计：解得α的极大似然估计：13.设X1，X2，…，Xn是来自对数级数分布的一个样本，求p的矩估计．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】因为p很难解出来，所以再求总体的二阶原点矩①÷②得所以所以得p的矩估计14.设总体X服从参数为N和p的二项分布，X1，X2，Xn为取自X的样本，试求参数N和p的矩估计．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】解之得N=μ1/p，即所以N和p的矩估计为15.设总体X的分布列为截尾几何分布P{X=k}=θk-1(1-θ)， k=1，2，…，r，P{X=r+1}=θr，从中抽得样本X1，X2，…，Xn，其中有m个取值为r+1，求θ的极大似然估计．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】解似然方程得θ的极大似然估计设总体X服从正态分布N(μ，σ 2 )，X1，X2，…，Xn是其样本．SSS_TEXT_QUSTI16.求C使得是σ 2的无偏估计量；该题您未回答:х该问题分值: 2【解】可见当是σ 2的无偏估计量．SSS_TEXT_QUSTI17.求k使得为σ的无偏估计量．该题您未回答:х该问题分值: 2【解】18.设X1，X2，…，Xn是来自总体X的一个样本，是θ的一个估计量，若θ+kn，试证：是θ的相合(一致)估计量．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】由切比雪夫不等式，对任意的ε＞0有于是即依概率收敛于θ，故是θ的相合(一致)估计量．19.设X1，X2，…，Xn是取自均匀分布在[0，θ]上的一个样本，试证：Tn=max{X1，X2，…，Xn}是θ的相合估计．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】Tn =X(n)的分布函数为Tn的密度为所以由切比雪夫不等式有当n→∞时，故Tn是θ的相合估计．20.已知X具有概率密度X1，X2，…，Xn为X的简单随机样本．求未知参数α的矩估计和最大似然估计．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】先求矩估计．故再求最大似然估计得α的最大似然估计21.设总体X～N(μ，σ 2 )，X1，X2，X3是来自X的样本，证明：估计量都是μ的无偏估计，并指出它们中哪一个最有效．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】故都是μ的无偏估计．所以最有效．22.设X1，X2，…，Xn为总体X的一个样本，设EX=μ，DX=σ 2，试确定常数C，使为μ 2的无偏估计．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】由题意知：23.设总体服从U[0，θ]，X1，X2，…，Xn为总体的样本，证明：为θ的一致估计．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】由切比雪夫不等式有：因此得为θ的一致估计．24.设从均值为μ，方差为σ 2＞0的总体中分别抽取容量为n1，n2的两个独立样本，样本均值分别为证明：对于任何满足条件a+b=1的常数a，b，是μ的无偏估计量，并确定常数a，b，使得方差DT达到最小．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】由题意得：所以故T是μ的无偏估计量．又令对a求导并解方程如下：得到所以处取得极小值，此时方差DT达到最小．25.设X1，X2，…，Xn独立同分布，X2的取值有四种可能，其概率分布分别为：p1 =1-θ，p2=θ-θ 2，p3=θ 2 -θ 3，p4=θ 3，记N，为X1，X2，…，Xn中出现各种可能的结果的次数，N1+N2+N3+N4=n．确定a1，a2，a3，a4使为θ的无偏估计．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】由于Ni ～B(n，pi)，i=1，2，3，4，所以E(Ni)=npi，从而有：若使T是θ的无偏估计，即要求解之得：即是θ的无偏估计．设总体X～N(μ1，σ 2 )，Y～N(μ2，σ 2 )．从总体X，Y中独立地抽取两个容量为m，n的样本X1，…，Xm和Y1，…，Yn．记样本均值分别为若是σ 2的无偏估计．求：SSS_TEXT_QUSTI26.C；该题您未回答:х该问题分值: 2【解】同理故则SSS_TEXT_QUSTI27.Z 的方差DZ ．该题您未回答:х 该问题分值: 2 【解】因故则有28.设有k 台仪器，已知用第i 台仪器测量时，测定值总体的标准差为σ i ，i=1，2，…，k ，用这些仪器独立地对某一物理量θ各观察一次，分别得到X 1 ，X 2 ，…，X k ，设仪器都没有系统误差，即E(X i )=θ，i=1，2，…，k ，试求：a 1 ，a 2 ，…，a k 应取何值，使用估计θ时，是无偏的，并且最小?SSS_TEXT_QUSTI该题您未回答:х 该问题分值: 2 【解】(1)即当是无偏的．(2)令函数问题归结为求多元函数g(a 1 ，a 2 ，…，a k )在条件之下的最小值．作拉格朗日函数：G(a 1 ,a 2 ,…,a k ，λ)=g(a 1 ,a 2 ,…,a k )+λ(a 1 +a 2 +…+a k -1)．29.设{X n }是一随机变量序列，X n 的密度函数为：试证：SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】对任意给定的ε＞0，由于30.设X1，X2， (X)n，…是独立同分布的随机变量序列，EXi=μ，DXi=σ2，i=1，2，…，令证明：随机变量序列{Yn}依概率收敛于μ．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】由切比雪夫不等式得：所以31.一生产线生产的产品成箱包装，每箱的重量是随机的，假设每箱平均重量50千克，标准差为5千克，若用最大载重为5吨的汽车承运，试用中心极限定理说明每辆车最多可装多少箱，才能保障不超载的概率大于0.977(Φ(2)=0.977)．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】设Xi是“装运的第i箱的重量”，n表示装运箱数．则EXi =50，DXi=5 2 =25，且装运的总重量Y=X1 +X2+…+Xn，{Xn}独立同分布，EY=50n，DY=25n．由列维—林德伯格中心极限定理知Y～N(50n，25n)．于是故也就是最多可以装98箱．32.用概率论方法证明：SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】设{Xn }为一独立同分布随机变量序列，每个Xk服从参数为1的泊松分布，则EXk =1，DXk=1，服从参数为n的泊松分布．故有由列维—林德伯格中心极限定理知：33.截至2010年10月25日，上海世博会参观人数超过了7000万人．游园最大的痛苦就是人太多．假设游客到达中国馆有三条路径，沿第一条路径走3个小时可到达；沿第二条路径走5个小时又回到原处；沿第三条路径走7个小时也回到原处．假定游客总是等可能地在三条路径中选择一个，试求他平均要用多少时间才能到达中国馆．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】设游客需要X小时到达中国馆，则X的可能取值为3，5+3，7+3，5+5+3，5+7+3，7+7+3，…要写出X的分布律很困难，所以无法直接求EX．为此令Y={第一次所选的路径}，即{Y=i}表示“选择第i条路径”．则因为E(X|Y=1)=3，E(X|Y=2)=5+EX，E(X|Y=3)=7+EX，所以故EX=15，即该游客平均要15个小时才能到达中国馆．34.设X1，X2， (X)n为一列独立同分布的随机变量，随机变量N只取正整数且N与{Xn}独立，求证：SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】35.假设你是参加某卫视“相亲节目”的男嘉宾，现有n位女嘉宾在你面前自左到右排在一条直线上，每两位相邻的女嘉宾的距离为a(米)．假设每位女嘉宾举手时你必须和她去握手，每位女嘉宾举手的概率均为，且相互独立，若Z 表示你和一位女嘉宾握手后到另一位举手的女嘉宾处所走的路程，求EZ．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】设按从左到右的顺序将女嘉宾编号为1，2，…，n．X为“已经握手的女嘉宾的编号”，Y表示“将要去握手的女嘉宾的编号”，则于是36.对于任意二事件A1，A2，考虑二随机变量试证明：随机变量X1和X2独立的充分必要条件是事件A1和A2相互独立．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】记pi =P(Ai)(i=1，2)，p12=P(A1A2)，而ρ是X1和X2的相关系数．易见，随机变量X1和X2都服从0—1分布，并且(1)必要性．设随机变量X1和X2独立，则P(A1 A2)=P{X1=1，X2=1}=P{X1=1}P{X2=1}=P(A1)P(A2)．从而，事件A1和A2相互独立．(2)充分性．设事件A1和A2相互独立，则也都独立，故从而，随机变量X1和X2相互独立．37.假设有四张同样卡片，其中三张上分别只印有a1，a2，a3，而另一张上同时印有a1，a2，a3．现在随意抽取一张卡片，令Ak={卡片上印有ak }．证明：事件A1，A2，A3两两独立但不相互独立．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】由于对任意k，j=1，2，3且k≠j，有可见事件A1，A2，A3两两独立．但是，由于可见事件A1，A2，A3不相互独立．38.某商品一周的需求量X是随机变量，已知其概率密度为假设各周的需求量相互独立，以Uk表示k周的总需求量，试求：(1)U2和U3的概率密度fk(x)(k=2，3)；(2)接连三周中的周最大需求量的概率密度f(3)(x)．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】以Xi (i=1，2，3)表示“第i周的需求量”，则Xi的概率密度均为而U2 =X1+X2，U3=U2+X3．三周中周最大需求量为X(3)=max{X1，X2，X3}．(1)当x≤0时，显然f2 (x)=f3(x)=0；对于x＞0，有于是，两周和三周的总需求量U2和U3的概率密度(2)设F(x)是随机变量X的分布函数．由题意知连续三周中的周最大需求量X(3)的分布函数为G(x)=[F(x)] 3．于是，有39.设X和Y相互独立都服从0-1分布：P{X=1}=P{Y=1}=0.6，试证明：U=X+Y，V=X-Y不相关，但是不独立．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2由协方差的定义和性质，以及X和Y相互独立，可见Cov(U，V)=E(UV)-EUEV=E(X 2 -Y 2 )-E(X+Y)E(X-Y)=E(X 2 )-E(Y 2 )=0．于是，U=X+Y，V=X-Y不相关．(2)现在证明U=X+Y，V=X-Y不独立．事实上，由P{U=0}=P{X=0，Y=0}=P{X=0}P{Y=0}=0.16，P{V=0}=P{X=0，Y=0}+P{X=1，Y=1}=P{X=0}P{Y=0}+P{X=1}P{Y=1}=0.52，P{U=0，V=0}=P{X=0，Y=0}=P{X=0}P{Y=0}=0.16≠0.16×0.52=P{U=0}P{V=0}，可见U和V不独立．40.假设G={(x，y)|x 2 +y 2≤r 2 }是以原点为圆心，半径为r的圆形区域，而随机变量X和Y的联合分布是在网G上的均匀分布．试确定随机变量X和Y的独立性和相关性．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】(1)X和Y的联合密度为那么，X的密度函数f1 (x)和Y的密度函数f2(y)相应为由于f(x，y)≠f1 (x)f2(y)，可见随机变量X和Y不独立．(2)证明X和Y不相关，即X和Y的相关系数ρ=0．因此，有于是，X和Y的相关系数ρ=0．这样，X和Y虽然不相关，但是不独立．41.假设某季节性商品，适时地售出1千克可以获利s元，季后销售每千克净亏损t元．假设一家商店在季节内该商品的销售量X(千克)是一随机变量，并且在区间(a，b)内均匀分布．问季初应安排多少这种商品，可以使期望销售利润最大?SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】根据条件随机变量X的概率密度为以Y=P(h)表示“销售利润”，它与季初应安排商品的数量h有关．由条件知为求使期望利润最大的h，我们计算销售利润Y=P(h)的数学期望．为此，首先注意到：a＜h＜b，销售利润Y=P(h)的数学期望为对h求导并令其等于0，得于是，季初安排h千克商品，可以使期望销售利润最大．42.独立地重复进行某项试验，直到成功为止，每次试验成功的概率为p．假设前5次试验每次的试验费用为10元，从第6次起每次的试验费用为5元．试求这项试验的总费用的期望值a．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】以X表示“试验的总次数”，首先求X的概率分布．设Ak={第k次试验成功}(k=1，2，…)，则P(Ak)=p，X的概率分布为其中q=1-p．于是试验的总次数X服从参数为p的几何分布．现在求试验的总费用的期望值a．由条件知，试验的总费用为该项试验的总费用Y是一随机变量，其期望值为例如，设p=0.8，q=0.2，得a=12.498元；设p=q=0.5，得a=19.6875元；设p=0.2，q=0.8，得a=41.808元；设p=0.1，q=0.9，得a=70.4755元．43.利用列维—林德伯格定理，证明：棣莫弗—拉普拉斯定理．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】设随机变量X1，X2，…，Xn相互独立，同服从0—1分布；EXi =p，DXi=pq (i=1，2，…，n)，Sn =X1+X2+…+Xn，ESn=np，DSn=npq，其中q=1-p．X1，X2，…，Xn满足列维—林德伯格定理的条件：X1，X2，…，Xn独立同分布且数学期望和方差存在，当n充分大时近似地Sn～N(np，npq)．44.某保险公司接受了10000辆电动自行车的保险，每辆车每年的保费为12元．若车丢失，则赔偿车主1000元．假设车的丢失率为0.006，对于此项业务，试利用中心极限定理，求保险公司：(1)亏损的概率α；(2)一年获利润不少于40000元的概率β；(3)一年获利润不少于60000元的概率γ．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】设X为“需要赔偿的车主人数”，则需要赔偿的金额为Y=0.1X(万元)；保费总收入C=12万元．易见，随机变量X服从参数为n，p的二项分布，其中n=10000，p=0.006；EX=np=60，DX=np(1-p)=59.64．由棣莫弗—拉普拉斯定理知，随机变量X近似服从正态分布N(60，59，64)，随机变量Y近似服从正态分布N(6，0.5964)．(1)保险公司亏损的概率(2)保险公司一年获利润不少于4万元的概率(3)保险公司一年获利润不少于6万元的概率45.将n个观测数据相加时，首先对小数部分按“四舍五入”舍去小数位后化为整数．试利用中心极限定理估计：(1)试当n=1500时求舍位误差之和的绝对值大于15的概率；(2)估计数据个数n满足何条件时，以不小于90%的概率，使舍位误差之和的绝对值小于10的数据个数n．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】设Xi 是“第i个数据的舍位误差”，由条件可以认为Xi独立且都在区间[-0.5，0.5]上服从均匀分布，从而EXi =0，DXi=1/12．记Sn =X1+X2+…+Xn，为n个数据的舍位误差之和，则ESn =0，DSn=n/12．根据列维—林德伯格中心极限定理，当n充分大时Sn近似服从N(0，n/12)．记Φ(x)为N(0，1)的分布函数．(1)由于近似服从标准正态分布，且n=1500，可见(2)数据个数n应满足条件：由于近似服从N(0，1)，可见于是，当n＞721时，才能使误差之和的绝对值小于10的概率不小于90%．46.设X是任一非负(离散型或连续型)随机变量，已知的数学期望存在，而ε＞0是任意实数．证明：不等式SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【证】(1)设X是离散型随机变量，其一切可能值为{xi}，则(2)设X是连续型随机变量，其概率密度为f(x)，则47.设事件A出现的概率为p=0.5，试利用切比雪夫不等式，估计在1000次独立重复试验中事件A出现的次数在450到550次之间的概率α．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】设vn是“1000次独立重复试验中事件A出现的次数”，则vn～B(1000，0.5)，EX=1000×0.5=500，DX=1000×0.5 2 =250．利用切比雪夫不等式，知设来自总体X的简单随机样本X1，X2，…，Xn，总体X的概率分布为其中0＜θ＜1．分别以v1，v2表示X1，X2，…，Xn中1，2出现的次数，试求SSS_TEXT_QUSTI48.未知参数θ的最大似然估计量；该题您未回答:х该问题分值: 2【解】求参数θ的最大似然估计量．样本X1，X2，…，Xn中1，2和3出现的次数分别为v1，v2和n-v1-v2，则似然函数和似然方程为似然方程的唯一解就是参数θ的最大似然估计量SSS_TEXT_QUSTI49.未知参数θ的矩估计量；该题您未回答:х该问题分值: 2【解】求参数θ的矩估计量．总体X的数学期望为EX=θ 2+4θ(1-θ)+3(1-θ) 2．在上式中用样本均值估计数学期望EX，可得θ的矩估计量SSS_TEXT_QUSTI50.当样本值为1，1，2，1，3，2时的最大似然估计值和矩估计值．该题您未回答:х该问题分值: 2【解】对于样本值1，1，2，1，3，2，由上面得到的一般公式，可得最大似然估计值矩估计值51.假设一批产品的不合格品数与合格品数之比为R(未知常数)．现在按还原抽样方式随意抽取的n件中发现k件不合格品．试求R的最大似然估计值．SSS_TEXT_QUSTI该题您未回答:х该问题分值: 2【解】设a是这批产品中不合格品的件数，b是合格品的件数．从而，a=Rb，合格品率为设X是“随意抽取的一件产品中不合格品的件数”，则X服从参数为p的0-1分布．对于来自总体X的简单随机样本X1，X2，…，Xn，记vn=X1+X2+…+Xn，则似然函数和似然方程为由条件知vn =X1+X2+…+Xn=k，于是似然方程的唯一解即是R的最大似然估计值．1。

2018年考研数学三真题与答案解析

2018年考研数学三真题及答案解析一、选择题（4分）1 •下列函数中在e = oil：不可导的是（）扎f⑵-\x\sin. |x|B. = |a|siii y/\^\G f @）= CM |zD、J⑵=roe \/|r|【麻】D2谡團數在［0 J「上二阶可导.且力血=0 ■则（〉化当< 0时0B.当严go时」点心D、Sf ff（T）>0【答臺】DJT 空离1C王设Af =丄玉£［斗必,N= /_¥吕^忑-K = /_刍1 + idr，则（）久N> K艮M>K >NJ K > M>N匕K>N> M【答室】C4：殳某士品的5&本囲故G（Q）可导.具中Q九产量・若产量为班时平均成本最小.则（）&"Q D）- 0氐C\Q Q）= QQa）G 仪（QJ - Qo^（<?o）P Q0缶-叽）【蒔塞］D^1 1 0'5.下列拒氏中,空阵0 1 1梧似的为（）-0 0 1 _■1 1 -1'人 0 1 L0 0 1 ■1 0 -110 1 10 0 1ri 1 -rC.0 1 0_0 0 14 o -i iD、0 1 0 I0 0 1d al【答室】A匕设4 D知阶袒阵，记伪矩肚X的枝「(&幻表示甘埃矩隹，则()人r^A, AB) = T(J4)BS 3A) = r(A)J r(A?B) = max{r(4)?r(B)}D, r(A,3) = r(A T,B T)［答案】A了蛙随机豈量工的惑養厦f 0)淒定几1 +刃=/(1 - X).且k f (工问=0』，则P{X< 0}=()入0.2B、03C x 0.4D、05【希A&设Xl.Xd，…，X n(n> 2)为来自总脚仏/脸A0)的筲单随机样本<,令天■扌f J 土丈的一那.b■侶f 因-G 侧();-1 »1-1 » t-i【答套］8二、填空题(4分)虫曲㈱=/ +型”在具拐点处的切巻方程为_________【答却V=4®-310.J*E T arcsjin. 二店血=________【答案】e1 arrsiji v 1 - e Ha一讥一严 + C口■羞分方程-轴-5凶通解是倍臺】u, = e ■ 2T+1 - 5.12＞画数汛z)萬卫甲(h 4- Az)—归⑹—2Z^(B)A S十o(A*)g? T O)fi^(O) = 2 ,则就1) = _____【答棄】网=加1 窑盂^为” Ol.0!* 巧方誌向fi® * 若Afl] = dR + flg .A HJ =+ fls Aij =01+03 二#1 = __________【軽】214随匚事件儿乩牒互独立’且-P(3)-P[C)- i .则P(AC\A LIB}-【答垂】扌三解答题(10分)1王已知宾数仏b」満足1血匸一0险足+ b)E：—彳=2 »求仏b【答秦】叙-号可得皿s*包牡1. 2其中lim t^)+ 仏岬-J 吟十 lim t^)+ 时=l™t^)+ 远”十b可那吋亠4 吟=2 —齐而臺使得压叫卫* 吟存在,必须有■血=1.1W ,有Km匕T* o^1- L - 2- b. St&-1_踪上(a = 1^ & = 1【咎秦】稅分区域口凰17将长为2m 的铁丝分成三段,依次围成HR 正方形与正三角形,三个圏形的面积之和是否存在最小值？若存在.求出最小值.r 则有总+ J ； +之=2及乂,彭2 >^y 2 r 正三甬形的面积为気= 器H 「则问题擴化为在祭件a +y + z=2.x 隼/的最小值&令資”+ A(i +y + z- 2) f a? +A = 0 2+入r =咗血心n工曲=妒 r (vs (i-i 1)--占2 /少1二内滋-声丘2 x 3dx rV 』具于对于/ V3(l-z a)dz . * =血片可化为屮僻r?g 丿应=芈圧血也⑺)=半•彳=徐「而v 综上"昌一黒』喙一习0 J 圆前面积为糾，总面积，爲之> OF .求 x-v ■鬲f'M 西+9_再9v^ir+4v ■存+9 r忑=—更—【答秦】设分成的三段分别为头闵 Si = ^x 2 t 正方形的面积为隔二 $=討+討函数吉丞+壽/ “討+討 / QL 呢dL则有 M j 布—店龙十忍鮫“+护+ ” 该点的囲数彳直即为最A 值,*解得唯n 牛极值点为〈二 0 2 = 0最小值为^/X切卄 i = （一 1产日（刼 +2）=2n+2,n=O,l,2r -;口陥=需卢+ （一 1严刊（加十1）=气黑一（加+ l ）.n = 0J …Ui 益数列｛%”蒿足：4 >0^X B+1三『程-l （n = 1,2^-）.证明｛%｝收鈣I 「并求】叽十入【答臺】由题意可和斗屮.=血吩严「首先证阴&讣的有界性：证明跖j >■ 0 ;当n = 1时山1 > 0』斷=恵时「盹> 0 ,则孔+1 =加气詈,其中 e Jfc-1 > i fc ,可知用1 > B L 1 = 0 r 因此对于任息的U ,有弓> 0.再证明｛工讣的星疆性：JJ 因为才时]—£Xn=芒比」一已珈=e In-l-J n e Tng %令f （z ） = e* — 1 — xe^ t 则f （H ）=—詔 f f （H ）= —ze E< 0（x > 0） r 故当n > 0 时，fb ） < /（□） = 0 ,从而严羅一丹< 0 ”記却.一险C 0 ”可知｛唧单调递痰综上「｛%｝为单希谨减有下界的憩列f 可知｛%｝收巍。

2018考研数学三真题最强解析及点评,给你2019考研数学最科学的指导

送分题
半送分题
初等变换不改变矩阵的秩，这是（Ⅰ）唯一必然的解题路径，《金讲》356页不仅对这一重点结论给予说明，还给出超越任何参考书的通俗解释，足以解答任何此类问题。（Ⅱ）中在《金讲》406页有几乎是完全征计算的关键掌握公式的使用。《金讲》在随机变量的数字特征这一章给出了每个公式的详细推导及通俗解释，足以应对任何本章的考题。问题2中求复合随机变量问题，《金讲》给出了同型例题的详细过程，足以化解这方面的任何问题。
唯一最严谨的解析
半送分题
可能是大部分同学卷面遇上的第二道难题，考查矩阵秩性质的应用，是大部分考生恐惧的问题。但《金讲》中有超越任何一本参考书的全面总结，尤其是满秩矩阵性质的说明，并给出了7道同型例题详解，也是暑期集训重点解析内容，稍加把握，瞬间即得答案为A，如果没有这方面的知识把握，本题较难。线代中简单而应用最频繁的性质
送分题
难题
可能是大部分同学卷面遇上的第一道难题，本题区别一般矩阵相似性的判断，一般相似性判断是通过求其共同相似于一个对角矩阵，但这里矩阵不能相似对角化，超出常规试题的判断范围，增加了难度。《金讲》 518页有对相似性性质有最全面的归纳和对定义的超倍辨析，如果学习不疏忽这部分内容，本题判断并不难。不管矩阵多复杂的相似性判断，首先必然从求特征值入手，然后进一步用必要条件判断，本题亦不难，但没有这种本质的思维习惯，本题难度较大。
考差分方程定义的简单理解。见《金讲》289-291页。
送分题
考微分定义的简单理解及简单微分方程公式的使用。见《金讲》57页及273页公式。
送分题
送分题
送分题
考矩阵特征向量的简单应用。出现多组矩阵与特征向量乘积结构的必须将其转化为矩阵运算形式，这是《金讲》中再三强调的技能，见《金讲》 451页例 2.5.25。