第四章习题解题过程和参考答案
现代通信原理答案WORD版( 罗新民) 指导书 第四章 信号设计导论 习题详解

4-10设有一个 的线性移位寄存器反馈系统,当 、 及 时,分别画出其状态转换图及写出相应的输出序列的一个周期。指出以上哪种 的组合能产生m序列?
解: 时,可得到三个周期均为5的周期序列,其状态(依次)分别为:
1111,0111,1011,1101,1110(输出序列的一个周期为11110);
不可能出现8个连“1”。
分析:见教材图4.17。设当连续9个连“1”码出现在系统的9个移位寄存器处时,除去 ,在 中若有奇数个1,则下一个码 ,与最多9个连“1”矛盾,故 中一定有偶数个1。
那么,当连续8个“1”码出现在系统的 8个移位寄存器处时, 一个为“1”,一个为“0”。其余 全为1。这时下一个码元 ,不可能为0。因此,不可能出现8个 “1”的连码。
①求此 序列的周期;
② 序列中连续出现“1”的最多个数为多少?是否有8个“1”的连码?为什么?
③该序列中出现最长连“0”的游程长度是多少?
④该序列中游程的总个数是多少?
解:①此 序列的周期为
②该 序列中连续出现“1”的最多个数为 。
分析:如果出现连续10个1,即 ,由于 ,说明序列前9个1决定了第10个元素仍为1,这样依次递推下去就有 ,则系统一直保持全1状态,系统静止。
举例:矩形信号通过匹配滤波器后输出为一三角形脉冲(其自相关函数)。
4-2设高斯脉冲信号为
试计算对该信号匹配的滤波器的传输函数和输出最大信噪比(设滤波器输入端的白噪声功率谱密度为 )。
解:由习题2-15的结论可以得到,
故匹配滤波器的传输函数为
由于信号能量为
,
所以输出最大信噪比为
4-3已知信号 和 如图E 4.1所示。试分别画出对信号 和 匹配的滤波器的冲激响应及输出响应波形,并且标出关键点的值(峰值及波形宽度等)。
第四章习题解答

0)
(
1 e
1 e2
)
(1
1)
1 e2
1 1 ; e e2
E[(
X1
X
2
)2
]
(0
0)2
(1
1) e
(0
1)2
0
(1
0)2
(
1 e
1 e2
)
(1
1) 2
1 e2
1 e
3 e2
;
D( X1
X2)
1 e
3 e2
(1 e
1 e2
)2
1 e
2 e2
2 e3
1 e4
.
解法二 由⑴可求得 X1 X 2
44 32
44
16
P{X
2}
C42 (C42 C21C41 ) 44
21 ,P{X 64
3}
C43 44
1 64
,即
X
0 1 2 3
3 32
9 21 1 16 64 64
,
所以
EX 0 3 1 9 2 21 3 1 81 . 32 16 64 64 64
又 E( X 2 ) 02 3 12 9 22 21 32 1 129 ,所以
i j, i, j 1, 2,
i j,
, n .所以
Байду номын сангаас
C
ov( X1,Y )
C ov( X1,
1 n
n i 1
Xi)
1 n
n i 1
C ov( X1,
Xi)
2 n
,选(A).
同理可计算得
D( X1
Y
)
n
人教版七年级上第四章几何图形初步点、线、面、体同步练习题含答案

【分析】利用雨刷可看成线,扇面是面,即可求出答案.
【详解】汽车的雨刷在挡风玻璃上画出一个扇面,这说明线动成面的数学原理.
故答案为:线动成面.
【点睛】本题考查了点,线,面、体,此题较简单,解题时要灵活应用点、线、面、体之间的关系.
12.②
【分析】易得此几何体为两个底面相同且相连的圆锥的组合体,主视图是从几何体正面看到的图形.
8.由4个面围成;面与面相交形成6条线,直线有5条,曲线有1条.
【分析】由题意直接根据立体图形的基本知识结合图形进行分析即可得出答案.
【详解】解:由图可知,该几何体由4个面围成;
面与面相交形成6条线,直线有5条,曲线有1条.
【点睛】本题考查认识立体图形的知识,比较简单,注意基本知识的掌握.
9.见解析.
12.将图所示的Rt△ABC绕AB旋转一周所得的几何体的主视图是图中的________(只填序号).
参考答案:
1.C
【分析】观察截面形状可发现,长方体内部的圆自上而下由大圆逐渐变成小圆、点,符合圆锥截面的性质.
【详解】解:观察截面形状可知,这个长方体的内部构造是长方体中间有一圆锥状空洞,
故选:C.
【点睛】本题考查了截一个几何体,解答的关键是熟悉常见的几何体的截面,由截面的形状想象复杂几何体的组成.
【详解】解:Rt△ABC绕斜边AB旋转一周所得的几何体是两个底面相等相连的圆锥,圆锥的主视图是等腰三角形,所以该几何体的左视图是两个底边相等的等腰三角形相连,并且上面的等腰三角形较大,故为图②.
故答案为②.
【点睛】本题考查了空间想象能力及几何体的三视图;发挥空间想象能力,确定旋转一周所得的几何体形状是关键.
【分析】根据生活中常见的几何体的特征进行求解即可得到答案.
第四章习题
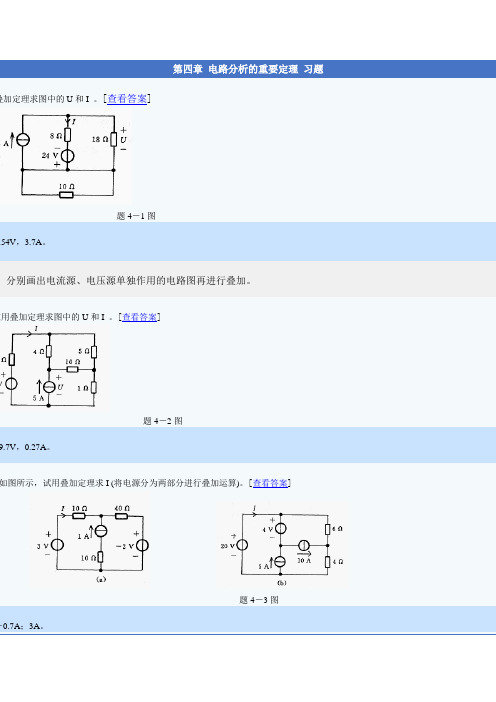
第四章电路分析的重要定理习题叠加定理求图中的U和I 。
[查看答案]题4-1图.54V,3.7A。
:分别画出电流源、电压源单独作用的电路图再进行叠加。
应用叠加定理求图中的U和I 。
[查看答案]题4-2图9.7V,0.27A。
如图所示,试用叠加定理求I (将电源分为两部分进行叠加运算)。
[查看答案]题4-3图-0.7A;3A。
电路如图所示。
若48 V压源突然降为24 V,试求电流I2 有多大变化。
[查看答案]题4-4图.324A:电压源由48V降为24V,相当于一个48V电压源和一个-24V电压源一起作用。
I2=I2原+△I2路如图所示,试用叠加定理求U。
[查看答案]题4-5图5V电路如图所示,N R为线性电阻网络。
已知:当Us=5 V、Is=2 A时,I2=1 A;I S=4 A时,I2=2 A。
求当Us=1 V、Is=1 A时,I2=? [查看答案]题4-6图.5A。
:设I2=αUs+βIs,由已知有5α+2β=12α+4β=2可以得α=0,β=1/2如图所示,N R为线性电阻网络。
当电流源i s和电压源u Sl反向时(u S2不变),电压u ab是原来的0.5倍;向时(u Sl不变),u ab为原来的0.3倍。
问:仅i s反向时(u Sl、u S2均不变),u ab为原来的多少倍?题4-7图.8。
路如图所示。
已知I=1 A,试用替代定理求图(a)中Us和图(b)中R的值。
[查看答案]题4-8图V;4Ω。
电路中,N R为线性电阻网络。
已知:R=R1时,I1=5 A、I2=2 A;4 A、I2=1 A。
求:R=时,I1=? [查看答案]4-9图3A。
图所示各含源二端网络的戴维南等效电路。
[查看答案]题4-10图4—10答案:6V,12.6Ω;-2V,6Ω;14V,2.5Ω;13.3V,2.07kΩ;25V,0.67kΩ;43V,3.1kΩ;14.17V,120.8Ω;;16V,10.67Ω;55V,13.75Ω。
数电习题解答_杨志忠_第四章练习题_部分

教材:数字电子技术基础(“十五”国家级规划教材) 杨志忠 卫桦林 郭顺华 编著高等教育出版社2009年7月第2版; 2010年1月 北京 第2次印刷;第四章 组合逻辑电路(部分练习题答案)练习题P172【4.1】、试分析图P4.1所示电路的逻辑功能。
解题思路:根据逻辑图依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。
(b )、Y AB AB A B =+=:;(同或功能) 真值表略; 【4.2】、试分析图P4.2所示电路的逻辑功能。
解题思路:根据逻辑图依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。
(a )、Y AB AB AB AB A B =⋅=+=⊕;(异或功能) 真值表略; 【4.3】、试分析图P4.3所示电路的逻辑功能。
解题思路:根据逻辑图从输入到输出逐级依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。
(a )、()Y ABC A ABC B ABC C ABC A B C ABC ABC =⋅+⋅+⋅=⋅++=+; 真值表略; 【4.4】、试分析图P4.4所示电路的逻辑功能。
解题思路:根据逻辑图从输入到输出逐级依次写出函数表达式、化简表达式、列写真值表、分析逻辑功能。
解:12 Y A B C Y AB A B C AB A B C =⊕⊕=⋅⊕⋅=+⊕⋅;该逻辑电路实现一位全加运算。
Y1表示本位和数,Y2是进位输出。
mi A B C Y1 Y2 0 0 0 0 0 0 1 0 0 1 1 02 0 1 0 1 03 0 1 1 0 14 1 0 0 1 05 1 0 1 0 16 1 1 0 0 17 1 1 1 1 1【4.6】、写出图P4.6所示电路的逻辑函数表达式,并且把它化成最简与或表达式。
解题思路:变量译码器实现逻辑函数是把逻辑变量输入译码器地址码,译码器输出i i m Y =,再用与非门(输出低电平有效)变换就可以得到所需的逻辑函数,输出函数具有下列的表达形式:(,,)0356m(0,3,5,6)A B C F Y Y Y Y ==∑。
马克思主义哲学原理第四章习题及答案(二)

马克思主义哲学原理第四章习题及答案(二)一、选择题Ⅰ1.【答案】B【解题思路】本题考查认识的本质。
辩证唯物主义在认识本质上的根本观点是能动的反映论,反映论是所有唯物主义在认识论中的共同的观点,而形而上学唯物主义是消极被动的反映论,辩证唯物主义是能动的反映论。
本题中"建构论"、"内省论"、"选择论"作为认识的本质均是唯心主义的。
在这里,承认认识有建构、内省和选择的能动作用,这是辩证唯物主义的观点,但把认识的本质归结为建构、内省、选择,就变成了唯心主义的观点了。
2.【答案】B【解题思路】本题考查对实践对认识决定作用的具体理解。
陆游的诗句反映了正确的认识要来自于实践即"躬行"。
选项A本身表述是错误的。
C、D是正确的,但与本题题干内容无关。
3.【答案】A【解题思路】本题考查考生对实践是检验真理标准问题的准确理解。
实践标准是确定的又是不确定的,它的确定性是因为实践标准是客观的,不以人的意志为转移的,它的不确定性是因为实践是具体的历史的,是不断发展的。
依据对实践标准确定性和不确定性的认识,所以本题选A。
4.【答案】A【解题思路】本题考查真理的含义与特征。
所谓客观真理指的是真理的客观性,真理是人对事物的正确认识,真理的客观性指的是人的正确认识中的客观内容,所以本题选A。
5.【答案】C【解题思路】本题考查真理的含义与特征。
真理具有三个特性,即客观性、绝对性、相对性,所以我们又说绝对真理、相对真理和客观真理,这样的表述不能理解为有三个真理,真理只有一个。
就真理的绝对性我们说有绝对真理,就真理的相对性我们说有相对真理,就真理的客观性我们说有客观真理。
所以本题选择命题C,即凡真理都是客观真理。
6.【答案】B【解题思路】本题考查考生对认识的主体特征的把握。
认识的主体是指一定社会中从事认识和实践的人,它具有社会物质性、自觉能动性、社会历史性,其中认识的主体性原则指的就是主体的能动性原则。
形式逻辑(第5版)课后练习参考答案 第4章

《形式逻辑》课后习题参考答案第四章简单命题及其推理(下)一、指出下列三段论的格和式,并指出其中的大项、中项和小项,以及大前提、小前提和结论。
1.第一格AAA式。
大项:一定要胜利的;中项:正义的事业;小项:我们的事业。
大前提:一切正义的事业都是一定要胜利的;小前提:我们的事业是正义的事业;结论:我们的事业是一定要胜利的。
2.第三格AAI式。
大项:能导电;中项:石墨;小项:非金属。
大前提:石墨能导电;小前提:石墨是非金属;结论:有的非金属能导电。
3.第二格AEE式。
大项:文学作品;中项:需要创造艺术形象;小项:学术论文。
大前提:一切文学作品都需要创造艺术形象;小前提:学术论文不需要创造艺术形象;结论:学术论文不是文学作品。
4.第二格AEE式。
大项:鱼;中项:用鳃呼吸;小项:鲸。
大前提:鱼都是用鳃呼吸的;小前提:鲸不是用鳃呼吸的;结论:鲸不是鱼。
二、下列三段论是否正确?如果不正确,违反了什么规则?1.不正确。
大项扩张(大项“青年”在前提中不周延,但在结论中周延。
注:按照对当关系,并非所有的青年工人都是共青团员=有的青年不是共青团员)。
2.不正确。
中项两次不周延。
3.不正确。
四概念错误(大小前提中的两个“物质”不是一个概念)4.不正确。
两前提都是特称命题,或者中项两次不周延。
5.不正确。
中项两次不周延(不是快车是不带邮件的=带邮件的是快车)6.不正确。
中项两次不周延。
三、在下列括号内填入适当的符号,构成一个正确的三段论,并写出解题过程。
1.它的限制条件少,很多三段论都满足要求,第一格的有AAA, AAI, AII,第二格的有AEE, AEO, AOO,第三格的有AAI, AII,第四格的有AAI,AEE。
例如,对于第一格的AAA式,即MAP, SAM/SAP,假设结论为SAP,那么S在结论中是周延的。
根据三段论规则3,S在前提中也必须周延。
按照规则4,前提不能出现否定。
所以,小前提为SAM。
此时,中项M不周延。
人教版数学七年级上册第四章复习题带答案

4.1几何图形一.选择题1.一个长方体音箱,长是宽的2倍,宽和高相等,它的体积是54000cm3,则这个音箱的长是()A.30cm B.60cm C.300cm D.600cm2.某正方体每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“厉”字所在面相对的面上的汉字是()A.国B.了C.的D.我3.如图是一个正方体纸盒的表面展开图,折成正方体后,相对面上的两个数互为相反数,则A、B、C表示的数分别为()A.0,﹣5,3B.0,3,﹣5C.3,0,﹣5D.﹣5,3,04.如图,是一个正方体的展开图,把展开图折叠成正方体后有“水”字一面的相对面上的字是()A.共B.山C.绿D.建5.如图,是一个正方体的平面展开图,把展开图折叠成正方体后,与“美”字相对的面上的字是()A.的B.利C.川D.市6.一圆柱形桶内装满了水,已知桶的底面直径和高都为m,另一长方体形容器的长为m,宽为m,若把圆柱形桶中的水倒入长方体形容器中刚好倒满,则长方体形容器的高为()A.2mπB.mπC.mπD.4mπ7.将一个棱长为m(m>2且m为正整数)的正方体木块的表面染上红色,然后切成m3个棱长为1的小正方体,发现只有一个表面染有红色的小正方体的数量是恰有两个表面染有红色的小正方体的数量的12倍,则m等于()A.16B.18C.26D.328.下列图形中能折叠成棱柱的是()A.B.C.D.9.下面四个图形中,经过折叠能围成如图所示的几何图形的是()A.B.C.D.10.如图,将下面的平面图形绕直线l旋转一周,得到的立体图形是()A.B.C.D.二.填空题11.将一个直角三角形ABC绕它的一边旋转,旋转后所得的几何体可能是下面图中的哪个.12.用一个平面去截长方体,三棱柱,圆柱,和圆锥,其中不能截出三角形的几何体是.13.若如图的平面展开图折叠成正方体后,相对面上两个数都互为相反数,则a+b=.14.如图,将硬纸片沿虚线折起来,便可做成一个正方体,这个正方体的2号面的对面是号面.15.如图,在长方体ABCD﹣A1B1C1D1中,已知AB=4,AD=3,AA1=2.则三棱锥C1﹣A1DB的体积为.三.解答题16.把一个长方形绕它的一条边所在的直线旋转一周能得到一个圆柱体,那么把一个长为4cm,宽为3cm的长方形绕它的一条边所在的直线旋转一周后,得到的圆柱体的体积是多少?(结果保留π)17.求下列图形中阴影部分的面积.(用字母表示)18.(1)三棱锥有6条棱,4个面,四棱锥有条棱,个面;(2)棱锥有30条棱;(3)有没有一个多棱锥,其棱数是2006,若有求出有多少个面;若没有,说明理由.19.如图所示,图①~图④都是平面图形(1)每个图中各有多少个顶点?多少条边?这些边围出多少个区域?请将结果填入表格中.(2)根据(1)中的结论,推断出一个平面图形的顶点数、边数、区域数之间有什么关系.图序顶点数边数区域数①463②③④参考答案与试题解析一.选择题1.【解答】解:设长方体的宽为xcm,则高是xcm,长是2xcm,根据题意,得2x3=54000,x3=27000,x=30,所以这个音箱的长是60cm.故选:B.2.【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“的”与“害”是相对面,“了”与“厉”是相对面,“我”与“国”是相对面;故选:B.3.【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,∴A与0是相对面,B与5是相对面,C与﹣3是相对面,∵折成正方体后相对的面上的两个数互为相反数,∴A=0,B=﹣5,C=3.故选:A.4.【解答】解:∵正方体的表面展开图,相对的面之间一定相隔一个正方形,∴有“水”字一面的相对面上的字是“建”.故选:D.5.【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,与“美”字相对的面上的字是市.故选:D.6.【解答】解:==.所以长方体形容器的高为.故选:B.7.【解答】解:将一个棱长为m(m>2且m为正整数)的正方体木块的表面染上红色,然后切成m3个棱长为1的小正方体,则只有一个表面染有红色的小正方体的数量为6(m﹣2)2,恰有两个表面染有红色的小正方体的数量12(m﹣2),∵只有一个表面染有红色的小正方体的数量是恰有两个表面染有红色的小正方体的数量的12倍,∴6(m﹣2)2=12×12(m﹣2),解得m1=26,m2=2(舍去),故选:C.8.【解答】解:A、不能折叠成棱柱,缺少一个侧面,故A不符合题意;B、能折叠成四棱柱,故B符合题意;C、不能折叠成四棱柱,有两个面重叠,故C不符合题意;D、不能折叠成六棱柱,底面缺少一条边,故D不符合题意;故选:B.9.【解答】解:三角形图案的顶点应与圆形的图案相对,而选项A与此不符,所以错误;三角形图案所在的面应与正方形的图案所在的面相邻,而选项C与此也不符,三角形图案所在的面应与圆形的图案所在的面相邻,而选项D与此也不符,正确的是B.故选:B.10.【解答】解:面动成体,直角三角形绕直角边旋转一周可得圆锥,长方形绕一边旋转一周可得圆柱,那么所求的图形是下面是圆锥,上面是圆柱的组合图形.故选:D.二.填空题(共5小题)11.【解答】解:以AC边所在的直线为轴,旋转一周所形成的图(2)的圆锥体,以BC边所在的直线为轴,旋转一周所形成的图(3)的圆锥体,以AB边所在的直线为轴,旋转一周所形成的图(4)的圆锥体,故答案为:(2)(3)(4).12.【解答】解:长方体沿体面对角线截几何体可以截出三角形,三棱柱沿顶点截几何体可以截得三角形,圆柱不能截出三角形,圆锥沿顶点可以截出三角形,故不能截出三角形的几何体是圆柱.13.【解答】解:这是一个正方体的平面展开图,共有六个面,其中面“a”与面“1”相对,面“b”与面“3”相对,“2”与面“﹣2”相对.因为相对面上两个数都互为相反数,所以a=﹣1,b=﹣3,故a+b=﹣4.14.【解答】解:这是一个正方体的平面展开图,共有六个面,其中面“1”与面“4”相对,面“3”与面“5”相对,“2”与面“6”相对.故填6.15.【解答】解:在长方体ABCD﹣A1B1C1D1中,三棱锥C1﹣A1DB的体积V=V﹣(V+V+V+V)=V﹣(S△ABD ×AA1+S△CBD×CC1+S×BB1+S×DD1)=S ABCD×AA1﹣(S ABCD×AA1+S×AA1)=S ABCD×AA1=V=×AB×AD×AA1=×4×3×2=8.∴三棱锥C1﹣A1DB的体积为8;故答案为:8.三.解答题(共4小题)16.【解答】解:绕长所在的直线旋转一周得到圆柱体积为:π×32×4=36π(cm3),绕宽所在的直线旋转一周得到圆柱体积为:π×42×3=48π(cm3),答:得到的圆柱体的体积是36πcm3或者48πcm3.17.【解答】解:左图:阴影部分的长为(a﹣x),宽为b,因此S=b(a﹣x)=ab﹣阴影部分bx,=R2﹣=.右图:S阴影部分18.【解答】解:(1)四棱锥有8条棱,5个面;(2)十五棱锥有30条棱;(3)一个多棱锥的棱数是2006,则这个多面体的面数是2006÷2+1=1004.故有1004个面.故答案为:8,5;十五.19.【解答】解:(1)填表如下:图序顶点数边数区域数①463②8125③694④10156(2)由(1)中的结论得:边数﹣顶点数+1=区域数.4.2直线射线线段一、选择题1.下列说法中正确的是A. 延长射线OA到点BB. 线段AB为直线AB的一部分C. 射线OM与射线MO表示同一条射线D. 一条直线由两条射线组成2.如图,在下列说法中,错误的是A. 点P为直线AB外一点B. 直线AB不经过点PC. 直线AB与直线BA是同一条直线D. 点P在直线AB上3.如图,对于直线AB,线段CD,射线EF,其中能相交的是A. B.C. D.4.如图,点B,C,D依次在射线AP上,则下列线段长度错误的是A. B. C. D.5.小红家分了一套住房,她想在自己的房间的墙上钉一根细木条,挂上自己喜欢的装饰物,那么小红至少需要几根钉子使细木条固定A. 1根B. 2根C. 3根D. 4根6.如图,C是线段AB的中点,D是线段BC的中点,下列等式不正确的是A. B.C. D.7.有三个点A,B,C,过其中每两个点画直线,可以画出直线A. 1条B. 2条C. 1条或3条D. 无法确定8.如图所示,C是线段AB的中点,D在线段CB上,,,则A. 20B. 12C. 10D. 89.在线段MN的延长线上取一点P,使,再在MN的延长线上截取,那么线段MP的长是线段NQ的长的A. B. C. D.10.将一根绳子对折以后用线段AB表示,现从一点P处将绳子剪断,剪断后的各段绳子中最长的一段为60cm,若AP PB,则这条绳子的原长为A. 100cmB. 150cmC. 100cm或150cmD. 120cm或150cm二、填空题(本大题共6小题,共18.0分)11.把一条弯曲的公路改成直道,可以缩短路程.用几何知识解释其道理是______.12.如图,A,B,C是直线l上的三个点,图中共有条线段.13.如图,已知C、D是AB上两点,且,,M是AD的中点,N是BC的中点,则线段MN的长为_______________.14.线段,点C在线段AB上,且,M为BC的中点,则AM的长为______cm.15.如图,数轴上A、B两点之间的距离,有一根木棒MN,MN在数轴上移动,当N移动到与A、B其中一个端点重合时,点M所对应的数为9,当N移动到线段AB的中点时,点M所对应的数为.16.线段,是AB的中点,是的中点,是的中点,是的中点,依此类推,线段的长为_____.三、计算题(本大题共2小题,共12.0分)17.如图,已知线段,M为AB的中点,P在MB上,N为PB的中点,且,求MB的长;求PB的长;求PM的长.18.已知:如图,点C、D是线段AB上的两点,线段AC:CD::3:4,点E、F分别是线段AC、DB的中点,且线段,求线段AB的长.四、解答题(本大题共4小题,共32.0分)19.如图,在平面内有A,B,C三点.画直线AC,线段BC,射线AB;在线段BC上任取一点不同于B,,连接线段AD;请直接写出图中的线段条数.20.已知,点C在直线AB上,如果,D是线段AC的中点,求线段BD的长度.下面是马小虎同学的解题过程:解:根据题意可画出如图所示的图形.由图可得.因为D是线段AC的中点,所以.所以.若你是老师,会判马小虎满分吗若会,请说明理由若不会,请将马小虎的错误指出,并给出你认为正确的解法.21.A,B两点在数轴上的位置如图所示,其中点A表示的有理数为,且点P从点A出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为秒.当时,AP的长为,点P表示的有理数为.当时,求t的值.为线段AP的中点,N为线段PB的中点在点P运动的过程中,线段MN 的长度是否发生变化若发生变化,请说明理由若不发生变化,请你画出图形,并求出线段MN的长.22.如图,在射线OM上有三点A、B、C,满足,,如图所示,点P从点O出发,沿OM方向以的速度匀速运动,点Q从点C出发在线段CO上向点O以的速度匀速运动点Q运动到点O时停止运动,两点同时出发.若关于m、n的单项式与的和仍为单项式,请直接写出:_____,_____;当,时,点Q运动到的位置恰好是线段AB的三等分点,求点Q的运动速度;点E、F分别是线段OA、OC的中点,当AB以的速度向右运动t秒时,是否存在某一时刻恰好点F是线段BE的中点?若存在,请求出t的值;若不存在,请说明理由.答案和解析1.【答案】B【解析】【分析】本题主要考查的是直线,射线,线段的有关知识,利用直线、射线、线段的特征判定即可.【解答】解:延长射线OA到点B,射线OA是无限延伸的,故选项错误;B.线段AB为直线AB的一部分是正确的;C.射线OM与射线MO表示两条射线,故选项错误;D.一条直线不一定由两条射线组成,故选项错误.故选B.2.【答案】D【解析】【分析】考查直线、射线和线段的意义.注意图形结合的解题思想结合图形,对选项一一分析,选出正确答案.【解答】解:A、点P为直线AB外一点,符合图形描述,选项正确;B、直线AB不经过点P,符合图形描述,选项正确;C、直线AB与直线BA是同一条直线,符合图形描述,选项正确;D、点P在直线AB上应改为点P在直线AB外一点,选项错误.故选D.3.【答案】B【解析】【分析】本题考查了直线、射线、线段,熟记定义并准确识图是解题的关键,根据直线、射线、线段的定义对各选项分析判断利用排除法求解.【解答】解:A、直线AB与线段CD不能相交,故本选项错误;B、直线AB与射线EF能够相交,故本选项正确;C、射线EF与线段CD不能相交,故本选项错误;D、直线AB与射线EF不能相交,故本选项错误.故选B.4.【答案】C【解析】【分析】本题主要考查的是两点间的距离的有关知识,直接根据数轴结合两点间的距离公式对给出的各个选项进行逐一分析即可.【解答】解:,,故本选项正确;B.,,,故本选项正确;C.由图示可知,,故本选项错误;D.,,,故本选项正确.故选C.5.【答案】B【解析】【分析】本题考查直线的性质.经过两点有一条直线,并且只有一条直线,即两点确定一条直线.根据直线的性质求解,判定正确选项.【解答】解:根据直线的性质,小红至少需要2根钉子使细木条固定.只有B符合.故选B.6.【答案】D【解析】【分析】此题主要考查线段的中点定义及线段和差问题,根据线段的中点定义求解【解答】解:是线段AB的中点,D是线段BC的中点,,故A选项正确,,故B选项正确,故C选项正确,故D选项错误故选D7.【答案】C【解析】【分析】此题考查直线的基本性质:两点确定一条直线,分当三点在同一条直线上时,当三点不在同一条直线上时讨论求解即可.【解答】解:当三点在同一条直线上时,只能画一条;当三点不在同一条直线上时可以画3条;故选C.8.【答案】D【解析】【分析】此题考查的知识点是线段的和差,由已知得,又由C是线段AB的中点可求出,从而求得.【解答】解:,是线段AB的中点,,.故选D.9.【答案】C【解析】【分析】本题主要考查了两点间的距离和线段的和差.根据题意设,则,,,然后得到,进而得到MP:::4,问题得到解决.【解答】解:线段MN的延长线上取一点P,,如图,设,则,,,,,MP :::4,故选C.10.【答案】C【解析】【分析】本题考查了两点间的距离,分类讨论是解题关键.根据绳子对折以后用线段AB表示,可得绳长是AB的2倍,分类讨论,PB的2倍最长,可得PB,AP的2倍最长,可得AP的长,再根据线段间的比例关系,可得答案.【解答】解:当PB的2倍最长时,得,,,这条绳子的原长为;当AP的2倍最长时,得,,,,这条绳子的原长为.故选C.11.【答案】两点之间线段最短【解析】解:把一条弯曲的公路改成直道,可以缩短路程.用几何知识解释其道理是两点之间线段最短,故答案为:两点之间线段最短.根据线段的性质,可得答案.本题考查了线段的性质,熟记线段的性质是解题关键.12.【答案】3【解析】【分析】本题考查了线段,记住线段是直线上两点及其之间的部分是解题的关键,写出所有的线段,然后再计算条数【解答】解:图中线段有:线段AB、线段AC、线段BC,共三条.故答案为3.13.【答案】7cm【解析】【试题解析】【分析】本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.设,则,再用x表示出各线段的长度,再根据即可得出结论.【解答】解:,,,设,则,是AD的中点,N是BC的中点,,,,,.故答案为7cm.14.【答案】【解析】解:如图,点C在线段AB上,,即,即为BC的中点,.故答案为.根据点C在线段AB上,且,可得,再根据M为BC的中点,即可求得AM的长.本题考查了两点间的距离,解决本题的关键是利用线段中点定义.15.【答案】21或【解析】【分析】本题主要考查了数轴与分类讨论思想的综合,关键是要运用分类讨论思想的方法设MN的长度为m,根据点M对应的数据利用分类讨论思想得出结果.【解答】解:设MN的长度为m.当点N与点A重合时,此时点M对应的数为9,则点N对应的数为.当点N到AB中点时,点N此时对应的数为,则点M对应的数为当点N与点B重合时,同理可得点M对应的数为.故答案为21或.16.【答案】【解析】【试题解析】【分析】本题主要考查了线段中点的概念,图形的变化规律,有理数乘方的意义解答本题的关键是发现图形的变化规律首先根据线段中点的概念得出线段的长,然后根据线段AB的长,求出的长,即可求解.【解答】解:,是AB的中点,是的中点,是的中点,是的中点,,,,,,.故答案为.17.【答案】解:是AB的中点,;为PB的中点,且,;,,.【解析】【试题解析】本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.根据线段,M为AB的中点可直接得出结论;根据N为PB的中点,且可直接得出PB的长;根据MB与PB的长可直接得出结论.18.【答案】解:设,则线段,,、F分别是线段AC、DB的中点,,,,,.【解析】【试题解析】首先设,则线段,,然后根据E、F分别是线段AC、DB的中点,分别用x表示出EC、DF,根据,求出x的值,即可求出线段AB的长是多少.此题主要考查了两点间的距离的求法,以及线段的中点的特征和应用,要熟练掌握.19.【答案】解:如图,直线AC,线段BC,射线AB即为所求;如图,线段AD即为所求;图中的线段条数为6.【解析】本题主要考查了直线、射线、线段的定义,线段和直线的关系:线段是直线的一部分,用一个小写字母表示,如线段a;用两个表示端点的字母表示,如:线段或线段.依据直线、射线、线段的定义,即可得到直线AC,线段BC,射线AB;依据在线段BC上任取一点不同于B,,连接线段AD即可;根据图中的线段为AB,AC,AD,BD,CD,BC,即可得到图中线段的条数.20.【答案】解:不会判马小虎同学满分点C可能在线段AB的延长线上,也可能在线段AB 上,有两种情况,而马小虎只考虑了一种情况.应分两种情况讨论:第一种情况同马小虎同学的解题过程,可求得第二种情况根据题意画图如下:由图可得.因为D是线段AC的中点,所以.所以.综上可得,线段BD的长度为3cm或7cm.【解析】本题主要考查了线段的和差、线段的中点的定义等知识,需要注意的是不要将“点C在直线AB上”与“点C在线段AB上”混为一谈.由于,点C在直线AB上,因此可分点C在线段AB上、点C在线段AB的延长线上两种情况讨论,只需把BD转化为DC 与BC的和或差,就可解决问题.21.【答案】解:,;当点P在点B左侧时,,,,由题意得:,解得:;当点P在点B右侧时,由题意可得,解得:;综上,或6;如图1,当点P在线段AB上时,;如图2,当点P在AB延长线上时,;综上所述,线段MN的长度不发生变化,其值为5.【解析】【分析】本题考查了一元一次方程的应用和数轴,解题关键是根据题目给出的条件,找出合适的等量关系列出方程,再求解.根据题意知,点P表示的有理数为,将代入即可求得;由、知,根据得出关于t的方程,解之即可得;分类讨论:当点P在点A、B两点之间运动时,当点P运动到点B的左侧时,利用中点的定义和线段的和差易求出MN.【解答】解:设运动时间为t秒,则,点P表示的有理数为,当时,,点P表示的有理数为,故答案为:2,;见答案;见答案.22.【答案】;2;以O未原点,以OM方向为正方向,以作单位长度建立数轴,则O:0,A:20,B:80,C:100,设ts时有,Q为AB的三等分点,:2t,,,,由,即,当时,,得舍去,当时,,得,当时,,得,的三等分点为40或60,当时,或,解得:或;当时,或,解得:或;由建立数轴,A:,B:,O:0,,为OC的中点,,即F表示50,为OA的中点,,当t秒时,F为BE的中点,即,解得:.【解析】【试题解析】【分析】本题主要考查了合并同类项的定义,线段的和差,解题的关键是注意分情况讨论.根据同类项的定义进行解答即可;根据,当P在AB上和P在AB延长线上时,求出它的运动时间,即是点Q的运动时间,点Q运动到的位置恰好是线段AB的三等分点,这里的三等分点是两个点,分别是时,时,由此就可求出它的速度;需要正确找准点F随AB的移动而移动,得出BE、BF的大小即可解决.【解答】解:单项式与的和仍为单项式,,,故答案为1;2;见答案;见答案.4.3《角》一、选择题:1、下列说法中,正确的是( )A.两条射线组成的图形叫做角B.有公共端点的两条线段组成的图形叫做角C.角可以看作是由一条射线绕着它的端点旋转而形成的图形D.角可以看作是由一条线段绕着它的端点旋转而形成的图形2、如图,点O在直线AB上,则在此图中小于平角的角有( )A.4个B.5个C.6个D.7个3、∠ACB的两边是()A.射线AC、BCB.射线CA、CBC.线段AC、BCD.线段CA、CB4、用量角器量∠MON 的度数,下列操作正确的是( )A B C D5、下列各式中,角度互化正确的是( )A.63.5°=63°50″B.23°12′36″=25.48°C.18°18′18″=3.33°D.22.25°=22°15′6、下列说法错误的是()A.角的大小与角的边画出部分的长短无关B.角的大小与它们度数的大小是一致的C.角的平分线是一条线段D.角的和、差、倍、分的度数与它们度数的和、差、倍、分相等7、若∠A+∠B=180°,∠A与∠C互补,则∠B与∠C的关系是()A.相等B.互补C.互余D.不能确定8、如图,∠1=∠2,∠3=∠4,则下列结论正确的有( )①AD平分∠BAE;②AF平分∠EAC;③AE平分∠DAF;④AF平分∠BAC;⑤AE平分∠BAC. A.4个B.3个C.2个D.1个二、填空题:9、如图,∠1,∠2表示的角可分别用大写字母表示为 , ;∠A也可表示为,还可以表示为 .10、把15°30′化成度的形式,则15°30′=度.11、8点整,时针与分针之间的夹角是 .12、如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,则∠AOB的度数为 .13、一个角补角比它的余角的2倍多30°,则这个角的度数为.14、如图,将一副三角板叠放在一起,使直角的顶点重合于O,则∠AOC+∠DOB= .三、解答题:15、计算:(1)153°29′42″+26°40′32″(2)110°36′-90°37′32″16、如图,写出符合下列条件的角(图中所有的角均指小于平角的角).(1)能用一个大写字母表示的角;(2)以点A为顶点的角;(3)图中所有的角(可用简便方法表示).17、如图,∠AOB=124°,OC是∠AOB的平分线,∠1与∠2互余,求∠1和∠BOD的度数.18、如图1所示,将一副三角尺的直角顶点重合在点O处.(1)①∠AOD和∠BOC相等吗?说明理由;②∠AOC和∠BOD在数量上有何关系?说明理由;(2)若将等腰的三角尺绕点O旋转到如图2的位置.①∠AOD和∠BOC相等吗?说明理由;②∠AOC和∠BOD的以上关系还成立吗?说明理由.参考答案一、选择题:1、C2、B3、 B4、C5、D6、C7、A8、C二、填空题:9、∠ABC,∠BCN ∠BAC ∠MAN.10、15.511、120°12、28°13、30°14、180°三、解答题:15、(1)180°10′14″(2)19°58′32″16、(1)∠B,∠C.(2)∠CAD,∠BAD,∠BAC.(3)∠C,∠B,∠1,∠2,∠3,∠4,∠CAB.17、∠1=28°.∠BOD=34°18、(1)①∠AOD=∠BOC.②∠AOC和∠BOD互补.(2)①∠AOD=∠BOC.②∠AOC和∠BOD互补.4.2直线、射线、线段一.选择题1.如图,点C在线段AB上,点D是AC的中点,如果CD=3,AB=10,那么BC长度为()A.3B.3.5C.4.5D.42.已知线段AB,在AB的延长线上取一点C,使BC=2AB,若AC=9cm,则线段AB的长度为()A.4.5cm B.4cm C.3cm D.2cm3.如图,已知AB=10cm,M是AB中点,N在AB的延长线上,若NB=MB,则MN的长为()A.7.5cm B.10cm C.5cm D.6cm4.已知线段AB=6cm,点C在直线AB上,且线段AC=1cm,则线段BC的长为()A.5cm B.7cm C.5cm或7cm D.以上均不对5.如图,下列说法错误的是()A.直线AC与射线BD相交于点AB.BC是线段C.直线AC经过点AD.点D在直线AB上6.如图,小明同学用剪刀沿着虚线将一张圆形纸片剪掉一部分,发现剩下纸片的周长比原来的周长要小,能正确解释这一现象的数学知识是()A.两点之间,直线最短B.经过一点,有无数条直线C.两点确定一条直线D.两点之间,线段最短7.已知点C在线段AB上,下列各式中:①AC=AB;②AC=CB;③AB=2AC;④AC+CB=AB,能说明点C是线段AB中点的有()A.①B.①②C.①②③D.①②③④8.如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在()A.点A B.点B C.AB之间D.BC之间9.判断下列语句,①一根拉紧的细线就是直线;②点A一定在直线AB上;③过三点可以画三条直线;④两点之间,线段最短.正确的有几个()A.1B.2C.3D.410.如图,建筑工人砌墙时,经常用细绳在墙的两端之间拉一条参照线,使砌的每一层砖在一条直线上,这样做的依据是()A.直线比曲线短B.两点之间,线段最短C.两点确定一条直线D.垂线段最短二.填空题11.点M是线段AB上一点,且AM:MB=2:3,MB比AM长2cm,则AB长为.12.把一根木条钉在墙上使其固定,至少需要个钉子,其理由是.13.如图已知线段AD=16cm,线段AC=BD=10cm,E,F分别是AB,CD的中点,则EF 长为cm.14.如图,射击运动员在瞄准时,总是用一只眼瞄准准星和目标,这种现象用数学知识解释为.15.已知A、B、C三站在一条东西走向的马路边,小马现在A站,小虎现在B站,两人分别从A、B两站同时出发,约定在C站会面商议事宜.若小马的行驶速度是小虎的行驶速度的,两人同时到达C站,且A、B两站之间的距离为8km,求C站与A、B两站之间的距离之和是.三.解答题16.如图,点C是线段AB上一点,点M、N、P分别是线段AC、BC、AB的中点,AC=3cm,CP=1cm,求:(1)线段AM的长;(2)线段PN的长.17.如图,点P是线段AB上的一点,点M、N分别是线段AP、PB的中点.(1)如图1,若点P是线段AB的中点,且MP=4cm,求线段AB的长;(2)如图2,若点P是线段AB上的任一点,且AB=12cm,求线段MN的长.18.已知:四点A、B、C、D的位置如图所示,根据下列语句,画出图形.(1)画直线AD、直线BC相交于点O;(2)画射线AB.19.如图,已知线段AB=60,点C、D分别是线段AB上的两点,且满足AC:CD:DB=3:4:5,点K是线段CD的中点,求线段KB的长.解:设AC=3x,则CD=4x,DB=,∵AB=AC+CD+DB=60∴AB=(用含x的代数式表示)=60.∴x=.∵点K是线段CD的中点.∴KD==.∴KB=KD+DB=.参考答案与试题解析一.选择题(共10小题)1.【解答】解:∵点D是AC的中点,∴AC=2CD=2×3=6,∴BC=AB﹣AC=10﹣6=4.故选:D.2.【解答】解:如图,∵BC=2AB、AC=9cm,∴AB=AC=3cm,故选:C.3.【解答】解:∵AB=10cm、M为AB的中点,∴AM=MB=AB=5cm,又∵NB=MB,∴NB=2.5cm,则MN=MB+BN=5+2.5=7.5(cm),故选:A.4.【解答】解:①点C在A、B中间时,BC=AB﹣AC=6﹣1=5(cm).②点C在点A的左边时,BC=AB+AC=6+1=7(cm).∴线段BC的长为5cm或7cm.故选:C.5.【解答】解:A、直线AC与射线BD相交于点A,说法正确,故本选项错误;B、B、C是两个端点,则BC是线段,说法正确,故本选项错误;C、直线AC经过点A,说法正确,故本选项错误;D、如图所示,点D在射线BD上,说法错误,故本选项正确.。
04化工原理第四章习题答案

4-1、燃烧炉的平壁由下列三种材料构成: 耐火砖的热导率为,K m W 05.111--⋅⋅=λ 厚度 mm 230=b ;绝热砖的热导率为11K m W 151.0--⋅⋅=λ;普通砖的热导率为11K m W 93.0--⋅⋅=λ。
若耐火砖内侧温度为C 10000, 耐火砖与绝热砖接触面最高温度为C 9400 ,绝热砖与普通砖间的最高温度不超过C 1300 (假设每两种砖之间接触良好界面上的温度相等) 。
试求:(1)绝热砖的厚度。
绝热砖的尺寸为:mm 230mm 113mm 65⨯⨯; (2) 普通砖外测的温度。
普通砖的尺寸为:mm 240mm 1200mm 5⨯⨯。
(答: ⑴m 460.02=b ;⑵C 6.344︒=t )解:⑴第一层:1121λb t t AQ -=第二层:2232λb t t AQ -=⇒()()32222111t t b t t b -=-λλ⇒()()130940151.0940100023.005.12-=-b⇒m 446.02=b因为绝热砖尺寸厚度为mm 230,故绝热砖层厚度2b 取m 460.0, 校核:()()3940460.0151.0940100023.005.1t -=-⇒C 3.1053︒=t ; ⑵()()43332111t t b t t b -=-λλ⇒C 6.344︒=t 。
4-2、某工厂用mm 5mm 170⨯φ的无缝钢管输送水蒸气。
为了减少沿途的热损失,在管外包两层绝热材料:第一层为厚mm 30的矿渣棉,其热导率为11K m 0.065W --⋅⋅ ;第二层为厚mm 30的石棉灰,其热导率为11K m 0.21W --⋅⋅。
管内壁温度为C 3000,保温层外表面温度为C 400。
管道长m 50。
试求该管道的散热量。
(答:kW 2.14=Q )解:已知:11棉Km 0.065W --⋅⋅=λ,11灰Km0.21W --⋅⋅=λ查表得:11Km W 54--⋅⋅=钢λ()34323212141ln1ln1ln 12d d d d d d t t l Q λλλπ++-=其中:0606.016.017.0ln ln 12==d d , 302.017.023.0ln ln 23==d d , 231.023.029.0lnln34==d d()1mW 28421.0231.0065.0302.0450606.0403002-⋅=++-=πlQ ,kW 2.14W 1042.1502844=⨯=⨯=Q 。
(完整版)概率论第四章答案

习题4-11. 设随机变量X求()E X ;E (2-3 X );2()E X ;2(35)E X +.解 由定义和数学期望的性质知2.03.023.004.0)2()(-=⨯+⨯+⨯-=X E ; (23)23()23(0.2) 2.6E X E X -=-=-⨯-=; 8.23.023.004.0)2()(2222=⨯+⨯+⨯-=X E ; 4.1358.235)(3)53(22=+⨯=+=+X E X E . 2. 设随机变量X 的概率密度为,0,()0,0.xe xf x x -⎧>⎪=⎨⎪⎩≤求Xe Z X Y 22-==和的数学期望.解()(2)2()22x E Y E X E X x x ∞-====⎰e d ,2201()()3Xx x E Z E ee e dx ∞---==⋅=⎰. 3. 游客乘电梯从底层到电视塔顶观光, 电梯于每个整点的第5分钟、第25分钟和第55分钟从底层起行. 假设一游客在早八点的第X 分钟到达底层侯梯处, 且X 在区间[0, 60]上服从均匀分布. 求该游客等候电梯时间的数学期望. 解已知X 在[0,60]上服从均匀分布, 其概率密度为1,060,()600,.x f x =⎧⎪⎨⎪⎩≤≤其它记Y 为游客等候电梯的时间,则5,05,25,525,()55,2555,65,5560.X X X X Y g X X X X X -<-<==-<-<⎧⎪⎪⎨⎪⎪⎩≤≤≤≤因此, 6001()[()]()()()60E Y E g X g x f x dx g x dx ∞-∞===⎰⎰()5255560525551(5)(25)(55)(65)60x dx x dx x dx x dx =-+-+-+-⎰⎰⎰⎰=11.67(分钟)..14. 某保险公司规定, 如果在一年内顾客的投保事件A 发生, 该公司就赔偿顾客a 元. 若一年内事件A 发生的概率为p , 为使该公司受益的期望值等于a 的10%, 该公司应该要求顾客交多少保险费?解 设保险公司要求顾客交保费c 元. 引入随机变量⎩⎨⎧=.A ,0,A 1不发生事件发生事件,X 则{1},{0}1P X p P X p ====-. 保险公司的受益值1,,0.c a X Y c X -=⎧=⎨=⎩, 于是 ()(){1}{0}E Y c a P X c P X ap c =-⨯=+⨯==-+. 据题意有10%ap c a -+=⨯, 因此应要求顾客角保费(0.1)c p a =+.习题4-21. 选择题(1) 已知(1,(3))E D X X =-= 则2[3(2)]()E X-=.(A) 9. (B) 6. (C) 30. (D) 36. 解22[3(2)]3(44)E X E X X -=-+23[()4()4]E X E X =-+23{()[()]4()4}D X E X E X =+-+ 3(3144)36=⨯+++=.可见,应选(D).(2) 设~(,),(6,( 3.6))B n p E D X X X ==, 则有( ).(A)10, 0.6n p ==. (B) 20, 0.3n p ==. (C) 15, 0.4n p ==. (D) 12, 0.5n p ==.解 因为~(,),B n p X 所以E (X )=n p,D (X )=np (1-p ), 得到np =6, np (1-p )=3.6 . 解之,n=15 , p =0.4 . 可见,应选(C).(3) 设X 与Y 相互独立,且都服从2(,)N μσ, 则有( ).(A) ()()()E X Y E X E Y -=+. (B) ()2E X Y μ-=.(C)()()()D X Y D X D Y -=-. (D) 2()2D X Y σ-=.解 注意到0)()()(=-=-Y E X E Y XE .由于X 与Y 相互独立,所以22)()()(σ=+=-Y D X D Y X D . 选(D).(4) 在下列结论中, 错误的是( ).(A) 若~(,),().X B n p E X np =则(B) 若()~1,1X U -,则()0D X =. (C) 若X 服从泊松分布, 则()()D X E X =.(D) 若2~(,),X N μσ 则~(0,1)X N μσ-.解)1,1(~-U X , 则3112212)()(22==-=a b X D . 选(B). 2. 已知X , Y 独立, E (X )= E (Y )=2, E (X 2)= E (Y 2)=5, 求E (3X -2Y ),D (3X -2Y ).解 由数学期望和方差的性质有E (3X -2Y )= 3E (X )-2 E (Y )=3×2-2×2=2,(32)9()4()D X Y D X D Y -=+})]([)({4})]([)({92222Y E Y E X E X E -⨯+-⨯=13)45(4)45(9=-⨯+-⨯=.3. 设随机变量X 1, X 2, X 3相互独立, 其中X 1服从区间[0, 6]上的均匀分布,22~0,2X N (), 3~3X P (), 记12323Y X X X =-+, 求E (Y )和D (Y ) .解 由题设知21122(60)()3,()3,()0,()4,12E X D X E X D X -=====3321111(),()39E X D X λλ====.由期望的性质可得123123()(23)()2()3()13203 4.3E Y E X X X E X E X E X =-+=-+=-⨯+⨯=又123,,X X X 相互独立, 所以123123()(23)()4()9()1344920.9D Y D X X X D X D X D X =-+=++=+⨯+⨯=4. 设两个随机变量X 和Y 相互独立, 且都服从均值为0, 方差为12的正态分布, 求||X Y -的的期望和方差.解 记UX Y =-. 由于11~(0,),~(0,)22X N Y N , 所以()()()0,E U E X E Y =-= ()()()1D U D X D Y =+=.由此~(0,1)U N . 进而2222220 (||)(||)||x x xE X Y E U x dx xe dx e+∞---+∞+∞-∞-====⎰2222(||)()()[()]101E U E U D U E U==+=+=.故而2222 (||)(||)(||)[(||)]11D X Y D UE U E Uπ-==-=-=-.5. 设随机变量]2,1[~-UX, 随机变量⎪⎩⎪⎨⎧<-=>=.0,1,0,0,0,1XXXY求期望()E Y和方差)(YD.解因为X的概率密度为1,12,()30,.Xxf x-=⎧⎪⎨⎪⎩≤≤其它于是Y的分布率为00--11{1}{0}31()d d3XP Y P X f x x x∞=-=<===⎰⎰,{0}{0}0P Y P X====,+2002{1}{0}31()d d3XP Y P X f x x x∞==>===⎰⎰.因此121()1001333E Y=-⨯+⨯+⨯=,222212()(1)001133E Y=-⨯+⨯+⨯=.故有2218()()[()]199D YE Y E Y=-=-=.6. 设随机变量U在区间[-2, 2]上服从均匀分布, 随机变量1,1,1, 1.UXU--=>-⎧⎨⎩若≤若1,1,1, 1.UYU-=>⎧⎨⎩若≤若求E(X+Y), D(X+Y).解(1) 随机变量(X, Y)的可能取值为(-1,-1),(-1,1),(1,-1),(1,1).{1,1}{P X Y P U =-=-=≤1,U -≤-1-211}{1}41d 4P U x =-==⋅⎰≤, {1,1}{P X Y P U =-==≤1,U -1}0>=, {1,1}{1P X Y P U ==-=>-,U ≤1111}21d 4x -==⋅⎰, 211{1,1}{1,1}41d 4P X Y P U U x ===>->==⋅⎰.于是得X 和Y 的联合密度分布为(2) Y X +和)(Y X +的概率分布分别为由此可见22()044E X Y +=-+=;2()[()]2D X Y E X Y +=+=.习题4-31. 选择题(1) 在下列结论中, ( )不是随机变量X 与Y 不相关的充分必要条件(A) E (XY )=E (X )E (Y ). (B) D (X +Y )=D (X )+D (Y ). (C) Cov(X ,Y )=0. (D) X 与 Y 相互独立.解 X 与 Y 相互独立是随机变量X 与Y 不相关的充分条件,而非必要条件. 选(D).(2) 设随机变量X 和Y 都服从正态分布, 且它们不相关, 则下列结论中不正确的是( ).(A) X 与Y 一定独立. (B) (X , Y )服从二维正态分布. (C) X 与Y 未必独立. (D) X +Y 服从一维正态分布.解 对于正态分布不相关和独立是等价的. 选(A).(3) 设(X , Y )服从二元正态分布, 则下列说法中错误的是( ).(A) (X , Y )的边缘分布仍然是正态分布.(B) X 与Y 相互独立等价于X 与Y 不相关. (C) (X , Y )是二维连续型随机变量.(D)由(X , Y )的边缘分布可完全确定(X , Y )的联合分布. 解 仅仅由(X , Y )的边缘分布不能完全确定(X , Y )的联合分布. 选(D)2 设D (X )=4, D (Y )=6, ρXY =0.6, 求D (3X -2Y ) .解(32)9()4()12Cov(,)D X Y D X D Y X Y -=+-)()(126449Y D X D XY ⨯⨯-⨯+⨯=ρ727.24626.0122436≈⨯⨯⨯-+=.3. 设随机变量X , Y 的相关系数为5.0, ,0)()(==Y E X E 22()()2E X E Y ==,求2[()]E XY +.解222[()]()2()()42[Cov(,)()()]E X Y E X E XY E Y X Y E X E Y +=++=++42420.526.ρ=+=+⨯⨯=4. 设随机变量(X , Y )若E (XY )=0.8, 求常数a ,b 解 首先由∑∑∞=∞==111i j ijp得4.0=+b a . 其次由0.8()100.420110.2210.22E XY a b b ==⨯⨯+⨯⨯+⨯⨯+⨯⨯=+ 得3.0=b . 进而1.0=a . 由此可得边缘分布律于是 , . 故 Cov(,)()()()0.8 1.40.50.1X Y E XY E X E Y =-=-⨯=.5. 已知随机变量(,)~(0.5,4;0.1,9;0)X Y N , Z =2X -Y , 试求方差D (Z ), 协方差Cov(,)X Z , 相关系数ρXZ .解 由于X ,Y 的相关系数为零, 所以X 和Y 相互独立(因X 和Y 服从正态分布). 因此25944)()(4)2()(=+⨯=+=-=Y D X D Y X D Z D ,Cov(,)Cov(,2)2Cov(,)Cov(,)2()08X Z X X Y X X X Y D X =-=-=-=.因此80.825XZ ρ===⨯. 6. 设随机变量(X , Y )服从二维正态分布: 2~(1,3)X N , 2~(0,4)Y N ; X 与Y 的相关系数1,232XYX YZ ρ=-=+. 求: (1) E (Z ), D (Z ); (2) X 与Z 的相关系数ρXZ ; (3)问X 与Z 是否相互独立?为什么?解 (1) 由于)3,1(~2N X , )4,0(~2N Y , 所以16)(,0)(,9)(,1)(====Y D Y E X D X E ,而1Cov(,)3462XY X Y ρ==-⨯⨯=-.因此 31021131)(21)(31)23()(=⨯+⨯=+=+=Y E X E Y X E Z E ,1111()()()()2Cov(,)329432X Y D Z D D X D Y X Y =+=++111916Cov(,)943X Y =⨯+⨯+3)6(3141=-⨯++=.(2) 由于1111Cov(,)Cov(,)()Cov(,)9(6)0,323232XY X Z X D X X Y =+=+=⨯+⨯-= 所以0XZ ρ==.(3) 由0=XZ ρ知X 与Z 不相关, 又X 与Z 均服从正态分布, 故知X 与Z 相互独立.7.证明: 对随机变量(X , Y ), E (XY )=E (X )E (Y )或者D (X ±Y )=D (X )+D (Y )的充要条件是X与Y 不相关.证 首先我们来证明)()()(Y E X E XY E =和()()()D X Y D X D Y ±=+是等价的.事实上, 注意到()()()2Cov(,)D X Y D X D Y X Y ±=+±.因此()()()D X Y D X D Y ±=+Cov(,)0()()()X Y E XY E X E Y ⇔=⇔=.其次证明必要性. 假设E (XY )=E (X )E (Y ), 则Cov(,)()()()0X Y E XY E X E Y =-=.进而0XYρ==, 即X 与Y 不相关.最后证明充分性. 假设X 与Y 不相关, 即0=XYρ, 则Cov(,)0X Y =. 由此知)()()(Y E X E XY E =.总习题四1. 设X 和Y 是相互独立且服从同一分布的两个随机变量, 已知X 的分布律为1{},1,2,33P X i i ===. 又设max{,},min{,}U X Y V X Y ==.(1) 写出二维随机变量(U , V )的分布律; (2) 求()E U .解 (1) 下面实际计算一下{1,3}P UV ==.注意到max{,},min{,}U X Y V X Y ==, 因此{1,3}{1,3}{3,1}P U V P X Y P X Y =====+=={1}{3}{3}{1}P X P Y P X P Y ===+==9231313131=⨯+⨯=.(2) 由(,)U V 的分布律可得关于U 的边缘分布律所以13522()1239999E U =⨯+⨯+⨯=. 2. 从学校乘汽车到火车站的途中有3个交通岗. 假设在各个交通岗遇到红灯的事件是相互独立的, 并且概率是25. 设X 为途中遇到红灯的次数, 求随机变量X 的分布律、分布函数和数学期望.解 令X 表示途中遇到红灯的次数, 由题设知2~(3,)XB . 即X 的分布律为从而3127543686(){}01231251251251255k E X kP X k ====⨯+⨯+⨯+⨯=∑. 3. 设随机变量),(Y X 的概率密度为212,01,(,)0,.y y x f x y ⎧⎪=⎨⎪⎩≤≤≤其它求22(),(),(),()E X E Y E XY E X Y +.解 112404()(,)1245xE X xf x y dxdy dx x y dy x dx ∞∞-∞-∞==⋅==⎰⎰⎰⎰⎰. 11240003()(,)1235xE X yf x y dxdy dx y y dy x dx ∞∞-∞-∞==⋅==⎰⎰⎰⎰⎰.112500031()(,)12362x E XY xyf x y dxdy dx xy y dy x dx ∞∞-∞-∞==⋅===⎰⎰⎰⎰⎰.122222220()()(,)()12xE X Y x y f x y dxdy dx x y y dy ∞∞-∞-∞+=+=+⋅⎰⎰⎰⎰155012423216(4)5653015x x dx =+=+==⎰. 4. 设随机变量(X ,Y )的概率密度为1sin(),0,0,222(,)0,.≤≤≤≤其它ππx y x y f x y ⎧+⎪=⎨⎪⎩求E (X ),D (X ),E (Y ),D (Y ),E (XY )和 Cov(X ,Y ).解22001()(,)sin()24E X xf x y dxdy x x y dxdy πππ+∞+∞-∞-∞==+=⎰⎰⎰⎰.22222200()(,)1sin() 2.282E X x f x y dxdyx x y dxdy ππππ+∞+∞-∞-∞==+=+-⎰⎰⎰⎰于是有2216)]([)()(222-+=-=ππX E X E X D . 利用对称性,有2216)(,4)(2-+==πππY D Y E .又()(,)E XY xyf x y dxdy +∞+∞-∞-∞=⎰⎰22001sin()2xy x y dxdy ππ=+⎰⎰220022001sin()21[sin cos cos sin ]2xdx y x y dyxdx y x y x y dyππππ=+=+⎰⎰⎰⎰12-=π.所以协方差2Cov(,)()()()1216X Y E XY E X E Y ππ=-=--.5. 设随机变量X 与Y 独立, 同服从正态分布1(0,)2N , 求(1)();()E X Y D X Y --;(2) (max{,});(min{,})E X Y E X Y .解 (1) 记Y X -=ξ.由于)21,0(~),21,0(~N Y N X ,所以,0)()()(=-=Y E X E E ξ 1)()()(=+=Y D X D D ξ.由此)1,0(~N ξ. 所以2222(||)(||)||x x E X Y E x dx xedx ξ+∞+∞---∞-==⎰22x e+∞-==101)]([)()()|(|2222=+=+==ξξξξE D E E .故而ππξξξ2121|)](|[)|(||)(||)(|222-=⎪⎪⎭⎫ ⎝⎛-=-==-E E D Y X D .(2) 注意到2||)(),max(Y X Y X Y X -++=, 2||),min(Y X Y X Y X --+=.所以ππ21221|]}[|)()({21)],[max(==-++=Y X E Y E X E Y X E ,ππ21221|]}[|)()({21)],[min(-=-=--+=Y X E Y E X E Y X E .6. 设随机变量),(Y X 的联合概率密度为,02,02,8(,)0,.x yx y f x y +⎧⎪=⎨⎪⎩≤≤≤≤其它求: E (X ), E (Y ), Cov(X ,Y ), ρXY , D (X+Y ).解 注意到),(y x f 只在区域2≤≤0,2≤≤0:y x G 上不为零, 所以()(,)8Gx yE X xf x y dxdy x x y ∞∞-∞-∞+==⎰⎰⎰⎰d d222000117()(1)846dx x x y dy x x dx =+=+=⎰⎰⎰,22()(,)E Xx f x y dxdy ∞∞-∞-∞=⎰⎰222232000115()()843dx x x y dy x x dx =+=+=⎰⎰⎰, 因而 36116735)]([)()(2222=-=-=X E X E X D .又()(,)E XY xyf x y dxdy ∞∞-∞-∞=⎰⎰22220001144()()8433dx xy x y dy x x dx =+=+=⎰⎰⎰. 由对称性知2275()(),()()63E Y E X E Y E X ====, 3611)()(==X D Y D . 这样,4491Cov(,)()()()33636X Y E XY E X E Y =-=-=-, 111XY ρ==-,5()()()2Cov(,)9D X Y D X D Y X Y +=++=.7. 设A , B 为随机事件, 且111(),(|),(|)432P A P B A P A B ===, 令 10A X A =⎧⎨⎩,发生,,不发生, 10B Y B =⎧⎨⎩,发生,,不发生.求: (1) 二维随机变量(X , Y )的概率分布; (2) X 与Y 的相关系数XY ρ.解 由1()(|)3()P AB P B A P A ==得1111()()33412P AB P A ==⨯=, 进而由1(|)2P A B = ()()P AB P B =得1()2()6P B P AB ==. 在此基础上可以求得(1)1{1,1}()12P X Y P AB ====,111{0,1}()()()61212P X Y P AB P B P AB ====-=-=,111{1,0}()()()4126P X Y P AB P A P AB ====-=-=,{0,0}()1()1[()()()]P X Y P AB P A B P A P B P AB ====-=-+-U 11121[]46123=-+-=.故(X , Y )的概率分布为(2) 由(1)因此211(),(),44E X E X ==22113()()[()]41616D XE X E X =-=-=, 22211115(),(),()()[()]6663636E Y E Y D Y E Y E Y ===-=-=. 又由(X , Y )的分布律可得21111()00011011312121212E XY =⨯⨯+⨯⨯+⨯⨯+⨯⨯=. 故11115XYρ-⨯===.。
高数课本大连理工第四章习题答案

高数课本大连理工第四章习题答案在高等数学的学习过程中,解决课本习题是巩固知识点和提高解题能力的重要环节。
以下是大连理工大学出版的高等数学教材第四章习题的一些参考答案,请注意,这些答案仅供参考,解题思路和方法才是学习的关键。
第一章:极限与连续1. 求极限:对于函数f(x),当x趋近于某一点a时,如果存在一个确定的实数L,使得f(x)的值无限接近于L,则称L为f(x)在x=a处的极限。
2. 极限存在准则:如果函数f(x)在x=a的邻域内连续,那么f(x)在x=a处的极限存在。
3. 连续性:如果函数f(x)在x=a处的极限与f(a)相等,则称f(x)在x=a处连续。
第二章:导数与微分1. 导数的定义:函数f(x)在x=a处的导数定义为极限\[ \lim_{h \to 0} \frac{f(a+h)-f(a)}{h} \],如果该极限存在,则称f(x)在x=a处可导。
2. 基本导数公式:例如,\( (x^n)' = nx^{n-1} \),\( (\sin x)' = \cos x \),\( (\ln x)' = \frac{1}{x} \) 等。
3. 复合函数的导数:链式法则的应用,\( (f(g(x)))' = f'(g(x))\cdot g'(x) \)。
第三章:微分中值定理及其应用1. 罗尔定理:如果函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且f(a)=f(b),则至少存在一点c在开区间(a,b)内,使得f'(c)=0。
2. 拉格朗日中值定理:如果函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,则至少存在一点c在开区间(a,b)内,使得\( f'(c)= \frac{f(b)-f(a)}{b-a} \)。
3. 柯西中值定理:如果函数f(x)和g(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且g'(x)不为0,则存在一点c在开区间(a,b)内,使得\( \frac{f'(c)}{g'(c)} = \frac{f(b)-f(a)}{g(b)-g(a)} \)。
小学数学新西师版一年级上册第四单元《10—20的认识》课本练习题解析(解题思路+参考答案)

第四单元 10—20的认识练习九1.【解题思路】先想一想学习的相关知识,再填空。
【参考答案】2.【解题思路】先圈10,再数。
【参考答案】15颗 12颗 20颗3.【解题思路】先看图中有几个十和几个一,再写数。
【参考答案】17 15 204.【解题思路】想数的排列顺序填空。
【参考答案】5.【解题思路】想几和几组成10或10可以分成几个几填空。
【参考答案】3+7=10 10-6=4 1+9=10(答案不唯一)6.【解题思路】先想一想学习的相关知识,再填空。
【参考答案】7.【解题思路】想数的排列顺序填空。
【参考答案】8.【解题思路】比18少,在2和16中选择,少一些,选择16。
【参考答案】16根。
9.【解题思路】想数的组成比较大小。
【参考答案】8>6 9<10 17>16 13<18 19<20 14>12 11<17 19>1510.【解题思路】想数的组成分解计算。
【参考答案】10-1=9 10+10=20 5+5=10 19-9=10 17-7=10 2+8=10 16-10=64+10=14练习十1.【解题思路】想不进位加法和不退位减法计算方法解题。
【参考答案】14+2=16 16-2=14 15+3=18 18-3=15 13+3=16 17-4=132.【解题思路】想不进位加法和不退位减法计算方法解题。
【参考答案】12+6=18 11+5=16 2+16=18 14+5=19 17-2=15 20-10=10 18-5=13 14-3=113.【解题思路】先说图意,再按图意列式计算。
【参考答案】15-3=12(本) 13+6=19(颗)4.【解题思路】把红花分成两部分,去掉与黄花同样多的红花,剩下的红花就是红花比黄花多的红花,也是黄花比红花少的朵数。
【参考答案】16-4=12(朵)5.【解题思路】按把两部分合起来、两部分比多少的思路分别列式计算。
(完整word版)高等数学课后习题及参考答案第四章

高等数学课后习题及参考答案(第四章)习题4-11. 求下列不定积分:(1)⎰dx x 21;解 C x C x dx x dx x +-=++-==+--⎰⎰112111222.(2)⎰dx x x ; 解 C x x C x dx x dx x x +=++==+⎰⎰212323521231.(3)⎰dx x1;解C x C x dx xdx x+=++-==+--⎰⎰21211112121. (4)⎰dx x x 32; 解 C x x C x dx x dx x x+=++==+⎰⎰3313737321031371. (5)⎰dx x x 21; 解C x x C x dx xdx xx +⋅-=++-==+--⎰⎰12312511125252. (6)dx x m n ⎰; 解C x mn mC x mn dx x dx x mn m m n m nmn++=++==++⎰⎰111.(7)⎰dx x 35;解 C x dx x dx x +==⎰⎰4334555.(8)⎰+-dx x x )23(2;解 C x x x dx dx x dx x dx x x ++-=+-=+-⎰⎰⎰⎰2233123)23(2322.(9)⎰ghdh 2(g 是常数);解C ghC h gdh hgghdh +=+⋅==⎰⎰-22212122121. (10)⎰-dx x 2)2(;解 C x x x dx dx x dx x dx x x dx x ++-=+-=+-=-⎰⎰⎰⎰⎰423144)44()2(23222.(11)⎰+dx x 22)1(;解 C x x x dx dx x dx x dx x x dx x +++=++=++=+⎰⎰⎰⎰⎰3524242232512)12()1(.(12)dx x x ⎰-+)1)(1(3;解 ⎰⎰⎰⎰⎰⎰-+-=-+-=-+dx dx x dx x dx x dx x x x dx x x 23212323)1()1)(1(C x x x x +-+-=25233523231.(13)⎰-dx x x 2)1(;解C x x x dx x x xdx xx x dx xx ++-=+-=+-=-⎰⎰⎰-2523212321212252342)2(21)1(. (14)⎰+++dx x x x 1133224; 解 C x x dx x x dx x x x ++=++=+++⎰⎰arctan )113(1133322224. (15)⎰+dx x x 221;解⎰⎰⎰+-=+-=+-+=+C x x dx xdx xx dx x x arctan )111(111122222.(16)⎰+dx xe x )32(;解 C x e dx xdx e dx x e x x x ++=+=+⎰⎰⎰||ln 32132)32(.(17)⎰--+dx xx )1213(22;解 ⎰⎰⎰+-=--+=--+C x x dx xdx x dx xx arcsin 2arctan 3112113)1213(2222.(18)dx x e e x x⎰--)1(;解 C x edx xe dx xe e xxx x+-=-=-⎰⎰--21212)()1(.(19)⎰dx e x x 3;解 C e C e e dx e dx e xx x xxx++=+==⎰⎰13ln 3)3ln()3()3(3.(20)⎰⋅-⋅dx xxx 32532;解 C x C x dx dx x xx xxx+--=+-=-=⋅-⋅⎰⎰)32(3ln 2ln 5232ln )32(52])32(52[32532. (21)⎰-dx x x x )tan (sec sec ;解 ⎰⎰+-=-=-C x x dx x x x dx x x x sec tan )tan sec (sec )tan (sec sec 2.(22)⎰dx x2cos 2;解 C x x dx x dx x dx x ++=+=+=⎰⎰⎰)sin (21)cos 1(212cos 12cos 2.(23)⎰+dx x 2cos 11;解 ⎰⎰+==+C x dx xdx x tan 21cos 212cos 112.(24)⎰-dx xx xsin cos 2cos ;解 ⎰⎰⎰+-=+=--=-C x x dx x x dx xx xx dx x x x cos sin )sin (cos sin cos sin cos sin cos 2cos 22.(25)⎰dx x x x22sin cos 2cos ; 解 ⎰⎰⎰+--=-=-=C x x dx xx dx x x x x dx x x x tan cot )cos 1sin 1(sin cos sin cos sin cos 2cos 22222222.(26)⎰-dx x x x)11(2;解 ⎰⎪⎭⎫ ⎝⎛-dx x x x 211⎰++=-=--C x x dx x x 41474543474)(.2. 一曲线通过点(e 2, 3), 且在任一点处的切线的斜率等于该点横坐标的倒数, 求该曲线的方程.解 设该曲线的方程为y =f (x ), 则由题意得xx f y 1)(='=',所以 C x dx xy +==⎰||ln 1.又因为曲线通过点(e 2, 3), 所以有=3-2=1 3=f (e 2)=ln|e 2|+C =2+C , C =3-2=1. 于是所求曲线的方程为y =ln|x |+1.3. 一物体由静止开始运动, 经t 秒后的速度是3t 2(m/s ), 问 (1)在3秒后物体离开出发点的距离是多少? (2)物体走完360m 需要多少时间?解 设位移函数为s =s (t ), 则s '=v =3 t 2, C t dt t s +==⎰323. 因为当t =0时, s =0, 所以C =0. 因此位移函数为s =t 3. (1)在3秒后物体离开出发点的距离是s =s (3)=33=27.(2)由t 3=360, 得物体走完360m 所需的时间11.73603≈=t s. 4. 证明函数x e 221, e x sh x 和e xch x 都是x x e x sh ch -的原函数.证明 x x xx x x x x x e ee e e e e e x x e 222sh ch ==--+=----. 因为x x e e 22)21(=', 所以x e 221是x x e xsh ch -的原函数.因为(e x sh x )'=e x sh x +e x ch x =e x (sh x +ch x )x x x x x x e e e e e e 2)22(=++-=--, 所以e x sh x 是xx e xsh ch -的原函数.因为(e x ch x )'=e x ch x +e x sh x =e x (ch x +sh x )x x x x x x e e e e e e 2)22(=-++=--, 所以e xch x 是xx e x sh ch -的原函数.习题4-21. 在下列各式等号右端的空白处填入适当的系数, 使等式成立(例如: )74(41+=x d dx :(1) dx = d (ax );解dx = a 1d (ax ).(2) dx = d (7x -3);解dx = 71d (7x -3).(3) xdx = d (x 2); 解xdx = 21 d (x 2).(4) x d x = d (5x 2);解x d x = 101d (5x 2).(5))1( 2x d xdx -=;解 )1( 212x d xdx --=.(6)x 3dx = d (3x 4-2);解x 3dx = 121d (3x 4-2).(7)e 2x dx = d (e 2x ); 解e 2x dx = 21 d (e 2x ).(8))1( 22x x ed dxe --+=;解 )1( 2 22x x e d dx e --+-=.(9))23(cos 23sin x d xdx =;解 )23(cos 32 23sin x d xdx -=.(10)|)|ln 5( x d xdx=; 解 |)|ln 5( 51x d x dx =. (11)|)|ln 53( x d xdx-=; 解|)|ln 53( 51x d x dx --=. (12))3(arctan 912x d x dx=+; 解 )3(arctan 31912x d x dx =+. (13))arctan 1( 12x d xdx -=-;解)arctan 1( )1( 12x d xdx --=-.(14))1( 122x d x xdx -=-.解)1( )1( 122x d x xdx --=-.2. 求下列不定积分(其中a , b , ω, ϕ均为常数): (1)⎰dt e t 5; 解 C e x d e dt e xx t +==⎰⎰55551551. (2)⎰-dx x 3)23(; 解 C x x d x dx x +--=---=-⎰⎰433)23(81)23()23(21)23(. (3)⎰-dx x 211; 解C x x d x dx x +--=---=-⎰⎰|21|ln 21)21(21121211.(4)⎰-332x dx ;解C x C x x d x xdx+--=+-⋅-=---=-⎰⎰-3232313)32(21)32(2331)32()32(3132. (5)⎰-dx e ax bx)(sin ;解C be ax ab x d e b ax d ax a dx e ax b xb xbx+--=-=-⎰⎰⎰cos 1)()(sin 1)(sin .(6)⎰dt tt sin ;解⎰⎰+-==C t t d t dt tt cos 2sin 2sin .(7)⎰⋅xdx x 210sec tan ;解 ⎰⋅xdx x 210sec tan C x x xd +==⎰1110tan 111tan tan . (8)⎰xx x dxln ln ln ;解C x x d x x d x x x x x dx +===⎰⎰⎰|ln ln |ln ln ln ln ln 1ln ln ln ln 1ln ln ln .(9)⎰+⋅+dx xx x 2211tan ;解 ⎰+⋅+dx x x x 2211tan 2222211cos 1sin 11tan x d x x x d x +++=++=⎰⎰C x x d x ++-=++-=⎰|1cos |ln 1cos 1cos 1222.(10)⎰xx dxcos sin ;解 C x x d x dx x x x x dx +===⎰⎰⎰|tan |ln tan tan 1tan sec cos sin 2.(11)⎰-+dx ee x x 1;解 ⎰-+dx e e xx 1C e de edx e e x x xx x +=+=+=⎰⎰arctan 11122.(12)⎰-dx xe x 2; 解 .21)(212222C e x d e dx xe x x x +-=--=---⎰⎰ (13)⎰⋅dx x x )cos(2;解 C x x d x dx x x +==⋅⎰⎰)sin(21)()cos(21)cos(2222. (14)⎰-dx xx 232;解C x C x x d x dx x x+--=+--=---=-⎰⎰-2212221223231)32(31)32()32(6132.(15)⎰-dx xx 4313; 解⎰⎰+--=---=-C x x d x dx x x |1|ln 43)1(11431344443.(16)⎰++dt t t ))sin((cos 2ϕωϕω; 解 C t t d t dt t t ++-=++-=++⎰⎰)(cos 31)cos()(cos 1)sin()(cos 322ϕωωϕωϕωωϕωϕω. (17)⎰dx x x3cos sin ; 解 C x C x x xd dx xx +=+=-=--⎰⎰2233sec 21cos 21cos cos cos sin . (18)⎰-+dx x x xx 3cos sin cos sin ;解 )sin cos (cos sin 1cos sin cos sin 33x x d xx dx x x x x +--=-+⎰⎰C x x x x d x x +-=--=⎰-3231)cos (sin 23)cos (sin )cos (sin .(19)⎰--dx xx 2491;解dx xx dx xdx xx ⎰⎰⎰---=--22249491491)49(49181)32()32(1121222x d x x d x --+-=⎰⎰C x x +-+=2494132arcsin 21.(20)⎰+dx x x 239;解 C x x x d xx d x x dx x x ++-=+-=+=+⎰⎰⎰)]9ln(9[21)()991(21)(9219222222223. (21)⎰-dx x 1212;解⎰⎰⎰+--=+-=-dx x x dx x x dx x )121121(21)12)(12(11212 ⎰⎰++---=)12(121221)12(121221x d x x d x C x x C x x ++-=++--=|1212|ln 221|12|ln 221|12|ln 221.(22)⎰-+dx x x )2)(1(1;解C x x C x x dx x x dx x x ++-=++--=+--=-+⎰⎰|12|ln 31|1|ln |2|(ln 31)1121(31)2)(1(1. (23)⎰xdx 3cos ;解 C x x x d x x d x xdx +-=-==⎰⎰⎰3223sin 31sin sin )sin 1(sin cos cos .(24)⎰+dt t )(cos 2ϕω; 解 C t t dt t dt t +++=++=+⎰⎰)(2sin 4121)](2cos 1[21)(cos 2ϕωωϕωϕω. (25)⎰xdx x 3cos 2sin ; 解 ⎰xdx x 3cos 2sin C x x dx x x ++-=-=⎰cos 215cos 101)sin 5(sin 21. (26)⎰dx xx 2cos cos ;解 C x x dx x x dx x x ++=+=⎰⎰21sin 23sin 31)21cos 23(cos 212cos cos .(27)⎰xdx x 7sin 5sin ; 解 C x x dx x x xdx x ++-=--=⎰⎰2sin 4112sin 241)2cos 12(cos 217sin 5sin . (28)⎰xdx x sec tan 3;解 x d x xdx x x xdx x sec tan tan sec tan sec tan 223⎰⎰⎰=⋅=C x x x d x +-=-=⎰sec sec 31sec )1(sec 32.(29)⎰-dx xx2arccos 2110;解C x d x d dx xx xxx+-=-=-=-⎰⎰⎰10ln 210)arccos 2(1021arccos 10110arccos 2arccos 2arccos 22arccos 2.(30)⎰+dx x x x )1(arctan ;解C x x d x x d x xdx x x x +==+=+⎰⎰⎰2)(arctan arctan arctan 2)1(arctan 2)1(arctan .(31)⎰-221)(arcsin xx dx;解C xx d x x x dx+-==-⎰⎰arcsin 1arcsin )(arcsin 11)(arcsin 222.(32)⎰+dx x x x 2)ln (ln 1; 解C xx x x d x x dx x x x+-==+⎰⎰ln 1)ln ()ln (1)ln (ln 122. (33)⎰dx xx xsin cos tan ln ;解⎰⎰⎰=⋅=x d x x xdx x x dx x x x tan tan tan ln sec tan tan ln sin cos tan ln 2C x x d x +==⎰2)tan (ln 21tan ln tan ln .(34)⎰-dx x a x 222(a >0);解⎰⎰⎰⎰-===-dt t a dt t a tdt a t a t a t a x dx xa x 22cos 1sin cos cos sin sin 22222222令, C x a x a x a C t a t a +--=+-=222222arcsin 22sin 421.(35)⎰-12x x dx ;解C x C t dt tdt t t t tx x x dx +=+==⋅⋅=-⎰⎰⎰1arccos tan sec tan sec 1sec 12令.或C x x d x dx xx x x dx +=--=-=-⎰⎰⎰1arccos 111111112222.(36)⎰+32)1(x dx ;解C t tdt t d t tx x dx +==+=+⎰⎰⎰sin cos tan )1(tan 1tan )1(3232令C x x ++=12.(37)⎰-dx xx 92; 解⎰⎰⎰=-=-tdt t d tt t x dx x x 222tan 3)sec 3(sec 39sec 9sec 39令 C x x C t t dt t+--=+-=-=⎰3arccos 393tan 3)1cos 1(322.(38)⎰+x dx 21; 解C x x C t t dt t tdt t tx xdx ++-=++-=+-=+=+⎰⎰⎰)21ln(2)1ln()111(11221令.(39)⎰-+211x dx ;解⎰⎰⎰⎰-=+-=+=-+dt tdt t tdt t tx x dx)2sec211()cos 111(cos cos 11sin 1122令 C xxx C t t t C t t +-+-=++-=+-=211arcsin cos 1sin 2tan .(40)⎰-+21x x dx .解⎰⎰⎰+-++=⋅+=-+dt tt tt t t tdt t t tx x x dx cos sin sin cos sin cos 21cos cos sin 1sin 12令C t t t t t d t t dt +++=+++=⎰⎰|cos sin |ln 2121)cos (sin cos sin 12121 C x x x ++-+=|1|ln 21arcsin 212.习题4-3求下列不定积分: 1. ⎰xdx x sin ; 解C x x x xdx x x x xd xdx x ++-=+-=-=⎰⎰⎰sin cos cos cos cos sin .2. ⎰xdx ln ;解 C x x x dx x x x xd x x xdx +-=-=-=⎰⎰⎰ln ln ln ln ln . 3. ⎰xdx arcsin ;解 ⎰⎰-=x xd x x xdx arcsin arcsin arcsin ⎰--=dx xx x x 21arcsinC x x x +-+=21arcsin . 4. ⎰-dx xe x ;解 ⎰⎰⎰----+-=-=dx e xe xde dx xe x x x x C x e C e xe x x x ++-=+--=---)1(. 5. ⎰xdx x ln 2; 解 ⎰⎰⎰-==x d x x x xdx xdx x ln 31ln 31ln 31ln 3332 C x x x dx x x x +-=-=⎰332391ln 3131ln 31.6. ⎰-xdx e x cos ; 解 因为⎰⎰⎰⎰------+=-==xdx e x e xde x e x d e xdx e x x x x x x sin sin sin sin sin cos ⎰⎰-----+-=-=x x x x x xde x e x e x d e x e cos cos sin cos sin⎰-----=xdx e x e x e x x x cos cos sin ,所以 C x x e C x e x e xdx e x x x x +-=+-=----⎰)cos (sin 21)cos sin (21cos .7. ⎰-dx xe x 2sin 2;解 因为⎰⎰⎰-----==x x x x de xx e x d e dx x e 22222cos 22cos 22cos 22sin⎰⎰----+=+=2sin 82cos 22cos 42cos 22222xd e x e dx x e x e x x x x⎰----+=x x x de xx e x e 2222sin 82sin 82cos 2⎰---++=dx xe x e x e x x x 2sin 162sin 82cos 2222,所以 C xx e dx x e x x ++-=--⎰)2sin 42(cos 1722sin 22.8. ⎰dx xx 2cos ;解 C xx x dx x x x x xd dx x x ++=-==⎰⎰⎰2cos 42sin 22sin 22sin 22sin 22cos .9. ⎰xdx x arctan 2; 解 ⎰⎰⎰+⋅-==dx x x x x xdx xdx x 233321131arctan 31arctan 31arctan ⎰⎰+--=+-=2232223)111(61arctan 31161arctan 31dx xx x dx x x x x C x x x x +++-=)1ln(6161arctan 31223.10. ⎰xdx x 2tan解 ⎰⎰⎰⎰⎰+-=-=-=x xd x xdx xdx x dx x x xdx x tan 21sec )1(sec tan 2222C x x x x xdx x x x +++-=-+-=⎰|cos |ln tan 21tan tan 2122.11. ⎰xdx x cos 2;解 ⎰⎰⎰⎰+=⋅-==x xd x x xdx x x x x d x xdx x cos 2sin 2sin sin sin cos 2222C x x x x x xdx x x x x +-+=-+=⎰sin 2cos 2sin cos 2cos 2sin 22. 12. ⎰-dt te t 2;解 ⎰⎰⎰----+-=-=dt e te tde dt te t t tt 2222212121 C t e C e te t t t ++-=+--=---)21(214121222.13. ⎰xdx 2ln ;解 ⎰⎰⎰-=⋅⋅-=xdx x x dx xx x x x xdx ln 2ln 1ln 2ln ln 222C x x x x x dx x x x x x x ++-=⋅+-=⎰2ln 2ln 12ln 2ln 22.14. ⎰xdx x x cos sin ; 解 ⎰⎰⎰⎰+-=-==xdx x x x xd xdx x xdx x x 2cos 412cos 412cos 412sin 21cos sin C x x x ++-=2sin 812cos 41.15. ⎰dx xx 2cos 22; 解 ⎰⎰⎰⎰-+=+=+=xdx x x x x x d x x dx x x dx x x sin sin 2161sin 2161)cos 1(212cos 2323222⎰⎰-++=++=xdx x x x x x x xd x x x cos cos sin 2161cos sin 21612323C x x x x x x +-++=sin cos sin 216123.16. ⎰-dx x x )1ln(; 解 ⎰⎰⎰-⋅--=-=-dx x x x x dx x dx x x 1121)1ln(21)1ln(21)1ln(222 ⎰-⋅++--=dx x x x x )111(21)1ln(212C x x x x x +-----=)1ln(212141)1ln(2122.17. ⎰-xdx x 2sin )1(2;解 ⎰⎰⎰⋅+--=--=-xdx x x x x d x xdx x 22cos 212cos )1(212cos )1(212sin )1(222 ⎰+--=x xd x x 2sin 212cos )1(212⎰-+--=xdx x x x x 2sin 212sin 212cos )1(212C x x x x x +++--=2cos 412sin 212cos )1(212.18. ⎰dx x x23ln ;解⎰⎰⎰⎰+-=+-=-=xdx xx x x d x x x x xd dx x x22333323ln 13ln 1ln 1ln 11ln ln⎰⎰+--=--=x d x x x x x x xd x x 22323ln 13ln 3ln 11ln 3ln 1⎰⎰---=+--=x xd x x x x dx x xx x x x 1ln 6ln 3ln 1ln 16ln 3ln 123223⎰+---=dx xx x x x x x 22316ln 6ln 3ln 1C x x x x x x x +----=6ln 6ln 3ln 123.19. ⎰dx e x3;解 ⎰⎰⎰==t t xde t dt e t t x dx e223333令⎰⎰-=-=t t t t tde e t dt te e t 636322 ⎰+-=dt e te e t t t t 6632 C e te e t t t t ++-=6632 C x x ex ++-=)22(33323.20. ⎰xdx ln cos ; 解 因为⎰⎰⋅⋅+=dx xx x x x xdx 1ln sin ln cos ln cosdx xx x x x x x xdx x x 1ln cos ln sin ln cos ln sin ln cos ⋅⋅-+=+=⎰⎰⎰-+=xdx x x x x ln cos ln sin ln cos , 所以 C x x xxdx ++=⎰)ln sin ln (cos 2ln cos .21. ⎰dx x 2)(arcsin ;解 ⎰⎰-⋅⋅-=dx xx x x x dx x 22211arcsin 2)(arcsin )(arcsin⎰-+=221arcsin 2)(arcsin x xd x x ⎰--+=dx x x x x 2arcsin 12)(arcsin 22 C x x x x x +--+=2arcsin 12)(arcsin 22. 22. ⎰xdx e x 2sin . 解 ⎰⎰⎰-=-=xdx e e dx x e xdx e xx x x 2cos 2121)2cos 1(21sin 2, 而 dx x e x e xde xdx e x x x x ⎰⎰⎰+==2sin 22cos 2cos 2cos⎰⎰-+=+=xdx e x e x e de x x e x x x x x 2cos 42sin 22cos 2sin 22cos ,C x x e xdx e x x ++=⎰)2sin 22(cos 512cos ,所以 C x x e e xdx e x x x ++-=⎰)2sin 22(cos 10121sin 2.习题4-4求下列不定积分:1. dx x x ⎰+33;解 dx x x x x dx x x dx x x ⎰⎰⎰+-+-+=+-+=+327)93)(3(327273233⎰⎰+-+-=dx x dx x x 3127)93(2C x x x x ++-+-=|3|ln 279233123.2. ⎰-++dx x x x 103322;解 C x x x x d x x dx x x x +-+=-+-+=-++⎰⎰|103|ln )103(1031103322222.3. ⎰--+dx xx x x 3458;解 ⎰⎰⎰--++++=--+dx x x x x dx x x dx x x x x 3223458)1(8⎰⎰⎰--+-+++=dx x dx x dx x x x x 13148213123C x x x x x x +--+-+++=|1|ln 3|1|ln 4||ln 8213123.4. ⎰+dx x 133;解⎰⎰⎰+-⋅++--⋅-+=+-+-++=+dx x x x x x x dx x x x x dx x )11231122111()1211(132223⎰⎰-+-++-+--+=)21()23()21(123)1(1121|1|ln 2222x d x x x d x x xC x x x x +-++-+=312arctan31|1|ln2. 5. ⎰+++)3)(2)(1(x x x xdx;解dx x x x x x x xdx )331124(21)3)(2)(1(+-+-+=+++⎰⎰C x x x ++-+-+=|)1|ln |3|ln 3|2|(ln 21.6. ⎰-++dx x x x )1()1(122;解 ⎰⎰+--⋅++⋅=-++dx x x x dx x x x ])1(111211121[)1()1(1222 C x x x +++-+-=11|1|ln 21|1|ln 21C x x +++-=11|1|ln 212.7. dx x x )1(12+⎰; 解 C x x dx x x x dx x x ++-=+-=+⎰⎰)1ln(21||ln )11()1(1222. 8. ⎰++))(1(22x x x dx;解⎰⎰+⋅-++⋅-=++dx x x x x x x x dx )112111211())(1(222⎰++-+-=dx x x x x 1121|1|ln 21||ln 2⎰⎰+-+-+-=dx x dx x x x x 11211241|1|ln 21||ln 22C x x x x +-+-+-=arctan 21)1ln(41|1|ln 21||ln 2.9. ⎰+++)1)(1(22x x x dx; 解dx x xx x x x x x dx )111()1)(1(2222⎰⎰+-+++=+++)1ln(21112111221222+-++++++=⎰⎰x dx x x x x x ⎰++++-++=dx x x x x x 1121)1ln(21|1|ln 21222C x x x x ++++-++=312arctan 33)1ln(21|1|ln 2122. 10. ⎰+dx x 114;解dx x x x x dx x ⎰⎰+-++=+)12)(12(111224⎰⎰+-+-++++=dx x x x dx x x x 12214212214222⎰⎰+----++++=dx x x x dx x x x 1222)22(21421222)22(214222 )1212(41]12)12(12)12([82222222⎰⎰⎰⎰+-+++++-+--++++=x x dxx x dx x x x x d x x x x d C x x x x x x +-++++-++=)12arctan(42)12arctan(42|1212|ln 8222. 11. ⎰++--dx x x x 222)1(2; 解 ⎰⎰⎰++-++-=++--dx x x dx x x x dx x x x 11)1(1)1(2222222 ⎰⎰⎰++-++-+++=dx x x dx x x dx x x x 11)1(123)1(122122222 ⎰⎰++-++-++⋅-=dx x x dx x x x x 11)1(12311212222, 因为)312arctan(32)312()312(11321122+=+++=++⎰⎰x x d x dx x x , 而⎰⎰++=++dx x dx x x 22222])23()21[(1)1(1由递推公式 ⎰⎰--+-++-=+])()32()([)1(21)(122122222n n n a x dxn a x x n a a x dx ,得⎰⎰++=++dx x dx x x 22222])23()21[(1)1(1312arctan 323211231)1121()23(212222+⋅++++⋅=++++++=⎰x x x x x x dx x x x , 所以 ⎰++--dx x x x 222)1(2C x x x x x x x ++-+-+++-++⋅-=312arctan 32312arctan 3211221112122C x x x x ++-+++-=312arctan34112.12. ⎰+x dx2sin 3;解⎰⎰⎰+=-=+x d x dx x x dx tan 3tan 41cos 41sin 3222C x x d x +=+=⎰3tan 2arctan321tan )23(tan 14122.13.⎰+dx x cos 31;解 ⎰⎰⎰+=+=+)2sec 1(2cos )2(2cos 121cos 31222x x x d x dx dx x ⎰+=+=C x x x d 22tanarctan 212tan 22tan 2. 或⎰⎰+⋅++=+du u u u x u dxx 221212312tancos 31令 C xC u du u +=+=+=⎰22tan arctan212arctan21)2(122. 14.⎰+dx x sin 21;解 ⎰⎰⎰+=+=+)2cot 2(csc 2sin )2(2cos 2sin 22sin 2122x x x x d x x dx dx x⎰⎰+++-=++-=222)23()212(cot )212(cot 12cot 2cot )2(cot x x d x x x dC x ++-=312cot 2arctan 32. 或⎰⎰+⋅++=+du u u u x u dxx 221212212tansin 21令 ⎰⎰++=++=du u du u u 222)23()21(111C xC u ++=++=312tan 2arctan 32312arctan 32. 15.⎰++x x dxcos sin 1;解 ⎰⎰⎰+=+=+=++C x x xd x x dx x x dx |2tan |ln 2tan1)2(tan )2tan 1(2cos 21cos sin 12. 或⎰⎰+⋅+-+++=++du u u u u ux u xx dx2222121112112tancos sin 1令C xC u du u ++=++=+=⎰|12tan |ln |1|ln 11. 16.⎰+-5cos sin 2x x dx; 解⎰⎰⎰++=+⋅++--+=+-du u u du u u u u ux u x x dx2231125111412tan5cos sin 222222令C xC u du u ++=++=++=⎰512tan 3arctan 51513arctan 51)35()31(13122. 或⎰⎰+⋅++--+=+-du uu uu u x u x x dx2222125111412tan5cos sin 2令⎰⎰++=++=du u du u u 222)35()31(1312231C xC u ++=++=512tan 3arctan 51513arctan 51. 17. ⎰++dx x 3111;解⎰⎰⎰++-=⋅+=+=++du uu du uu ux dx x )111(33111111233令 C x x x C u u u +++++-+=+++-=)11ln(313)1(23|1|ln 332333322.18.⎰++dx x x 11)(3;解C x x x dx x x dx x x ++-=+-=++⎰⎰232233221]1)[(11)(.19.⎰++-+dx x x 1111;解 ⎰⎰⎰++-=⋅+-=+++-+du u u udu u u u x dxx x )122(221111111令C u u u +++-=|)1|ln 2221(22C x x x +++++-+=)11ln(414)1(. 20.⎰+4x x dx ;解⎰⎰⋅+=+du uu u u x xx dx 324441令C u u u du uu +++-=++-=⎰|1|ln 442)111(42 C x x x +++-=)1ln(4244.21.⎰+-xdxx x 11;解 令u x x=+-11, 则2211u u x +-=, du u u dx 22)1(4+-=,⎰⎰⎰++-=+-⋅-+⋅=+-du uu du u u u u u x dx x x )1111(2)1(41111222222 C u u u +++-=arctan 2|11|ln C xxx x x x ++-+++-+--=11arctan2|1111|ln . 22.⎰-+342)1()1(x x dx.解 令u x x =-+311, 则1133-+=u u x , 232)1(6--=u u dx , 代入得C x x C u du x x dx +-+-=+-=-=-+⎰⎰334211232323)1()1(.总习题四求下列不定积分(其中a , b 为常数):1. ⎰--x x e e dx;解 C e e de e dx e e e e dxx x xx x xxx ++-=---=-⎰⎰⎰-|11|ln 2111122.2. dx x x ⎰-3)1(; 解C x x dx x dx x dx x x+-⋅+-=----=-⎰⎰⎰2323)1(12111)1(1)1(1)1(. 3. ⎰-dx xa x 662(a >0);解 C ax a x a x d x a dx x a x +-+=-=-⎰⎰||ln 61)()()(1313333332323662. 4. ⎰++dx x x xsin cos 1;解 C x x x x d x x dx x x x ++=++=++⎰⎰|sin |ln )sin (sin 1sin cos 1.5. ⎰dx xxln ln ; 解C x x x dx x x x x x x xd dx x x +-⋅=⋅⋅-⋅==⎰⎰⎰ln ln ln ln 1ln 1ln ln ln ln ln ln ln ln ln . 6. ⎰+dx x xx 4sin 1cos sin ; 解 C x x d x x d xx dx x x x +=+=+=+⎰⎰⎰222244sin arctan 21)(sin )(sin 1121sin sin 1sin sin 1cos sin . 7. ⎰xdx 4tan ; 解 xxd x x d xx xdx tan sin tan tan cos sin tan 22244⎰⎰⎰==⎰⎰++-=+=x d x x x d x x tan )1tan 11(tan tan 1tan tan 2224c x x x c x x x ++-=++-=tan tan 31tan arctan tan tan 3133.8. ⎰xdx x x 3sin 2sin sin ; 解 ⎰⎰--=xdx x x xdx x x 3sin )cos 3(cos 213sin 2sin sin ⎰⎰+-=xdx x xdx x 3sin cos 213sin 3cos 21 ⎰⎰++=dx x x x xd )2sin 4(sin 41)3(cos 3cos 61 C x x x +--=2cos 814cos 1613cos 1212. 9. ⎰+)4(6x x dx;解 C x x dx x x x x x dx++-=+-=+⎰⎰)4ln(241||ln 41)41(41)4(6656.10.)0(>-+⎰a dx xa xa ; 解⎰⎰⎰⎰-+-=-+=-+dx xa xdx x a a du x a x a dx x a x a 2222221C x a a xa +--=22arcsin .11.⎰+)1(x x dx ;解C x x C x x x d x x x dx +++=+++=+=+⎰⎰)1ln(2))(1ln(2)(112)1(22.12. ⎰xdx x 2cos ; 解 ⎰⎰⎰+=+=x xd x dx x x x xdx x 2sin 4141)2cos (21cos 22 C x x x x xdx x x x +++=-+=⎰2cos 812sin 41412sin 412sin 414122.13. ⎰bxdx e ax cos ; 解 因为dx bx e a b bx e a bxde a bxdx e ax axax ax ⎰⎰⎰+==sin cos 1cos 1cos dx bx e ab bx e a b bx e a de bx a b bx e a ax ax axax ax ⎰⎰-+=+=cos sin cos 1sin cos 12222,所以 C bx e ab bx e a b a a bxdx e axax ax+++=⎰)sin cos 1(cos 2222C bx b bx a e b a ax +++=)sin cos (122.14.⎰+xedx 1;解⎰⎰⎰⎰+--=-=-=++du u u du u u d u u e e dxx x)1111(112)1ln(11122令.c e e c u u x x +++-+=++-=1111ln |11|ln .15.⎰-122x xdx ;解C t tdt tdt t t t tx x xdx+==⋅⋅=-⎰⎰⎰sin cos tan sec tan sec 1sec 1222令C xx +-=12. 16.⎰-2/522)(x a dx;解⎰⎰⋅=-tdt a t a ta x x a dx cos )cos (1sin )(52/522令⎰⎰+==t d t adt ta tan )1(tan1cos 112444C t at a ++=tan 1tan 31434C xa x a x a x a+-+-⋅=224322341)(31.17.⎰+241x xdx;解tdt t t tx x xdx2424secsec tan 1tan 1⋅⋅=+⎰⎰令⎰⎰==t d t tdt t tsin sin cos sin cos 4243 C t tt d t t ++-=-=⎰sin 1sin 31sin )sin 1sin 1(324 C xx x x ++++-=233213)1(.18.⎰dx x x sin ;解⎰⎰⎰=⋅=tdt t tdt t t t x dx x x sin 22sin sin 2令⎰⎰⋅+-=-=tdt t t t t d t 2cos 2cos 2cos 222⎰⎰-+-=+-=tdt t t t t t td t t sin 4sin 4cos 2sin 4cos 222 C t t t t t +++-=cos 4sin 4cos 22C x x x x x +++-=cos 4sin 4cos 2. 19. ⎰+dx x )1ln(2;解 ⎰⎰+⋅-+=+dx xx x x x dx x 22212)1ln()1ln(⎰+--+=dx x x x )111(2)1ln(22C x x x x ++-+=arctan 22)1ln(2. 20.⎰dx x x32cos sin ;解 x d x xx x d x x dx x xtan )1tan tan (tan tan cos sin cos sin 2232⎰⎰⎰+-== C x x ++-=)1ln(tan 21tan 2122.21. ⎰dx x arctan ;解 x d xx x x dx x ⎰⎰+⋅-=11arctan arctan x d xx x ⎰+⋅--=)111(arctan C x x x x ++-=arctan arctan C x x x +-+=arctan )1(. 22.dx xx⎰+sin cos 1;解C x x x d x dx x x xdx x x +-===+⎰⎰⎰|2cot 2csc |ln 222csc 22cos2sin 22cos2sin cos 1. 23.⎰+dx x x 283)1(;解 C x x x dx x dx x x +++⋅=+=+⎰⎰]arctan 1[2141)1(141)1(484428283. 提示: 已知递推公式⎰⎰--+-++-=+])()32()([)1(21)(122122222n n n a x dxn a x x n a a x dx .24. ⎰++dx x x x 234811; 解 ⎰⎰⎰++=++=++dt t t t t x dx x x x dx x x x 234123412322444884811令 ⎰⎰+++-=+++-=dt t t dt t t t )11241(41)23231(412 C t t t ++++-=|1|ln 41|2|ln 41C x x x ++++=21ln 414444. 25.⎰-416x dx; 解⎰⎰⎰++-=+-=-dx xx dx x x x dx)4141(81)4)(4(11622224C xx x ++-+=)2arctan 21|22|ln 41(81C x x x ++-+=2arctan 161|22|ln 321. 26.dx x x⎰+sin 1sin ;解 ⎰⎰⎰-=--=+dx xxx dx x x x dx x x 222cos sin sin sin 1)sin 1(sin sin 1sinC x x x dx x x x++-=+-=⎰tan sec )cos 11cos sin (22.27. dx x xx ⎰++cos 1sin ;解⎰⎰⎰⎰+=+=++dx x xdx x x dx x x x dx x x x 2cossin 212cos 212cos 2sin cos 1sin 222 ⎰⎰+=dx xx xd 2tan 2tanC xx dx x dx x x x +=+-=⎰⎰2tan 2tan 2tan 2tan .28. ⎰-dx x x x x ex23sin cos sin cos ;解 ⎰⎰⎰⋅⋅-⋅⋅=-xdx x e xdx e x dx xx x x e x x xsec tan cos cos sin cos sin sin 23sin⎰⎰-=x d e x d xe x x sec sin sin sin ⎰⎰+⋅-=x x x xde e x xde sin sin sin sec sec⎰⎰⋅⋅+⋅--=xdx e x e x dx e xe x x x x cos sec sec sin sin sin sin C e x xe x x +⋅-=sin sin sec .29.⎰+dx x x x x)(33;解dt t t dt t t t t t t x dxx x x x)111(66)()(52362633+-=⋅+=+⎰⎰⎰令C x xC t t ++=++=66)1(ln 1ln6. 30.⎰+2)1(x e dx;解⎰⎰⎰---=-⋅=++dt t t t dt t tt e e dxx x )1111(1111)1(222令 C tt t ++--=1ln )1ln(C e e x xx ++++-=11)1ln(.31. ⎰+-+dx e e e e x x xx 1243;解)()(1111222243x xx x x x xx x x x x e ed e e dx e e e e dx e e e e ------+=+-+=+-+⎰⎰⎰C e e x x +-=-)arctan( C x +=)sh 2arctan(. 32.⎰+dx e xe xx 2)1(;解⎰⎰⎰+-=++=+11)1()1()1(22x x x x xe xde d e x dx e xe⎰⎰+++-=+++-=x x x x x x de e e e x dx e e x )1(11111⎰+-++-=x x xx de e e e x )111(1C e e e x x x x ++-++-=)1ln(ln 1C e e xe x x x ++-+=)1ln(1.33. ⎰++dx x x )1(ln 22;解 dx x x x x x x dx x x ])1([ln )1(ln )1(ln 222222'++⋅-++=++⎰⎰ ⎰+⋅++-++=dx xx x x x x x 22221)1ln(2)1(ln⎰+++-++=22221)1ln(2)1(ln x d x x x x x⎰'++⋅+++++-++=dx x x x x x x x x x ])1[ln(12)1ln(12)1(ln 222222 ⎰++++-++=dx x x x x x x 2)1ln(12)1(ln 2222 C x x x x x x x +++++-++=2)1ln(12)1(ln 2222.34.⎰+dx x x2/32)1(ln ; 解 因为⎰⎰⎰++=+==⋅=+C xx C t tdt tdt t tx dx x 2232/321sin cos secsec 1tan )1(1令,所以⎰⎰⎰⋅+-+=+=+dx xx xx x x x x xd dx x x111ln )1(ln )1(ln 2222/32 C x x x x x +++-+=)1ln(1ln 22.35. ⎰-xdx x arcsin 12;解⎰⎰⎰+=⋅=-dt t t t tdt t t x xdx x )2cos (21cos sin arcsin 122令 ⎰⎰-+=+=tdt t t t t t t 2sin 412sin 41412sin 414122C t t t t +++=2cos 812sin 41412122241arcsin 121)(arcsin 41C x x x x x +--+=.36.⎰-dx xx x 231arccos ;解⎰⎰⎰--=-⋅=-2222231arccos 1arccos 1arccos x xd x dx x x x x dx x x x⎰'⋅-+--=dx x x x x x x )arccos (1arccos 12222 ⎰-⋅-⋅-+--=dx xx x x x x x x )11arccos 2(1arccos 122222⎰⎰-⋅-+--=dx x xdx x x x x x 2222arccos 12arccos 1⎰-----=32322)1(arccos 3231arccos 1x xd x x x x⎰-------=dx x x x x x x x )1(32arccos )1(3231arccos 1232322。
《基础会计》练习题及参考答案与指导 04第四章 应用练习题参考答案与指导

第四章复式记账方法及其应用练习题参考答案与指导一、判断题答题要求:根据各题给出的说法判断正误,你认为正确的,在题后的括号中打“√”,你认为错误的打“×”。
1.复式记账是指对交易或事项分别在总账与其所属明细账中记录的方法。
( ×) 解题指导:复式记账是指对交易或事项分别在有关总账账户中记录的方法,而不是分别在总账与其所属明细账中记录的方法。
2.对交易或事项在三个或三个以上的账户中登记的做法不属于复式记账。
( ×) 解题指导:根据复式记账原理,对交易或事项在两个或两个以上相互联系的账户中进行登记即为复式记账,在三个或三个以上的账户中登记的做法当然应属于复式记账。
3.借贷记账法的记账符号“借”只表示增加,“贷”只表示减少。
( ×)解题指导:借贷记账法的记账符号“借”、“贷”在不同类别的账户中分别表示增加或减少。
例如对于资产类账户,“借”表示增加,“贷”表示减少;而对于负债类账户,“贷”表示增加,“借”表示减少。
每个记账符号都具有双重含义,并不是简单的“借”只表示增加,“贷”只表示减少。
4.在借贷记账法下设置的账户中,每一账户的左边均为借方,右边均为贷方。
( √) 解题指导:尽管借贷记账法的记账符号“借”、“贷”对不同类别的账户有着不同的增减含义,但在账户结构的设置上,各类账户却是一致的。
即每一账户的左边均为借方,右边均为贷方。
不能因为账户类别的不同而设计账户的不同结构。
5.所有账户在会计期末一定都有余额。
( ×)解题指导:有些账户在会计期末不一定有余额。
如收入类、费用类账户在期末结转后就不会再有余额;另外,有的账户在一定会计期间其增加额和减少额相等,期末时也不会再有余额。
6.所有账户期末余额的方向都是固定不变的。
( ×)解题指导:对于绝大多数账户来说,期末余额的方向是固定不变的。
但有的账户期末余额的方向在期末时可能会发生变化。
例如,“本年利润”账户在企业实现利润(即本期收入对于本期费用)的情况下为贷方余额,而当本期发生的费用大于实现的收入发生亏损时,就会出现借方余额;又如,“应交税费”账户属于负债类账户,正常情况下应当是贷方余额,但是,当这个账户本月只有借方发生额,或者借方发生额大于贷方发生额的时候,其余额就会出现在借方。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4-1 设单位反馈系统的开环传递函数为:10()1G s s =+。
当系统作用有下列输入信号时:()sin(30)r t t =+︒,试求系统的稳态输出。
解:系统的闭环传递函数为:10()()11()()1()111C s G s s s R s G s Φ===++这是一个一阶系统。
系统增益为:1011K =,时间常数为:111T =其幅频特性为:()A ω=其相频特性为:()arctan T ϕωω=-当输入为()sin(30)r t t =+︒,即信号幅值为:1A =,信号频率为:1ω=,初始相角为:030ϕ=︒。
代入幅频特性和相频特性,有:1(1)A ====11(1)arctan arctan5.1911T ωϕω==-=-=-︒ 所以,系统的稳态输出为:[]()(1)sin 30(1)24.81)c t A A t t ϕ=⋅⋅+︒+=+︒4-2 已知系统的单位阶跃响应为:49()1 1.80.8(0)ttc t e e t --=-+≥。
试求系统的幅频特性和相频特性。
解:对输出表达式两边拉氏变换:1 1.80.8361()49(4)(9)(1)(1)49C s s s s s s s s s s =-+==++++++ 由于()()()C s s R s =Φ,且有1()R s s=(单位阶跃)。
所以系统的闭环传递函数为: 1()(1)(1)49s s s Φ=++可知,这是由两个一阶环节构成的系统,时间常数分别为:1211,49T T ==系统的幅频特性为二个一阶环节幅频特性之积,相频特性为二个一阶环节相频特性之和:12()()()A A Aωωω===1212()()()arctan arctan arctan arctan49T Tωωϕωϕωϕωωω=+=--=--4-3 已知系统开环传递函数如下,试概略绘出奈氏图。
(1)1()10.01G ss=+(2)1()(10.1)G ss s=+(3))1008()1(1000)(2+++=sssssG(4)250(0.61)()(41)sG ss s+=+解:手工绘制奈氏图,只能做到概略绘制,很难做到精确。
所谓“概略”,即计算与判断奈氏曲线的起点、终点、曲线与坐标轴的交点、相角变化范围等,这就可以绘制出奈氏曲线的大致形状。
对一些不太复杂的系统,已经可以从曲线中读出系统的部分基本性能指标了。
除做到上述要求外,若再多取若干点(如6-8点),并将各点光滑连线。
这就一定程度上弥补了要求A的精度不足的弱点。
但因为要进行函数计算,例如求出实虚频率特性表格,工作量要大些。
在本题解答中,作如下处理:小题(1):简单的一阶惯性系统,教材中已经研究得比较详细了。
解题中只是简单套用。
小题(2):示范绘制奈氏图的完整过程。
小题(3)、小题(4):示范概略绘制奈氏图方法。
4-3(1)1()10.01G ss=+这是一个一阶惯性(环节)系统,例4-3中已详细示范过(当T=0.5时),奈氏曲线是一个半圆。
而表4-2给出了任意时间常数T下的实虚频率特性数据。
可以套用至本题。
①系统参数:0型,一阶,时间常数0.01T=②起终点奈氏曲线的起点:(1,0),正实轴奈氏曲线的终点:(0,0),原点奈氏曲线的相角变化范围:(0,-90°),第IV象限③求频率特性。
据式(4-29)已知:实频特性:221()1PTωω=+虚频特性:22()1TQTωωω=-+⑤绘图:4-3(2)1()(10.1)G s s s =+示范绘制奈氏图的完整过程。
这是一个由一个积分环节和一个一阶惯性环节组成的二阶系统。
①系统参数:1型系统,n=2, m=0 ②起终点奈氏曲线的起点:查表4-7,1型系统起点为负虚轴无穷远处; 奈氏曲线的终点:n-m=2>0,查表4-7知终点为原点,入射角为-180°; 奈氏曲线的相角变化范围:(-90°,-180°),第III 象限 ③求频率特性:21(0.1)()(10.1)(10.01)j G j j j ωωωωωω-+==++实频特性:20.1()10.01P ωω-=+ 虚频特性:21()(10.01)Q ωωω-=+ 当0ω=时,实频曲线有渐近线为-0.1。
⑤绘图:4-3(3))1008()1(1000)(2+++=s s s s s G示范概略绘制奈氏图方法。
①系统参数:1型系统,n=3, m=1 ②起终点奈氏曲线的起点:查表4-7,1型系统起点为负虚轴无穷远处; 奈氏曲线的终点:n-m=2>0,查表4-7知终点为原点,入射角为-180°; 奈氏曲线的相角变化范围:(-90°,-180°); ③绘图:4-3(4)250(0.61)()(41)s G s s s +=+示范概略绘制奈氏图方法。
①系统参数:2型系统,n=3, m=1 ②起终点奈氏曲线的起点:查表4-7,2型系统起点为负实轴无穷远处; 奈氏曲线的终点:n-m=2>0,查表4-7知终点为原点,入射角为-180°; 奈氏曲线的相角变化范围:(-180°,-180°); ③绘图:4-4 试画出下列传递函数的波德图。
(1))18)(12(2)()(++=s s s H s G(2)2200()()(1)(101)G s H s s s s =++(3)2250()()(1)(101)G s H s s s s s =+++(4)210(0.2)()()(0.1)s G s H s s s +=+(5)228(0.1)()()(1)(425)s G s H s s s s s s +=++++ 解:绘制波德图要按照教材P134-135中的10步,既规范也不易出错。
4-4(1))18)(12(2)()(++=s s s H s G(1) 开环传递函数已如式(4-41)标准化;(2) 计算开环增益K ,计算)(lg 20dB K ;得系统型别ν,确定低频段斜率;开环增益K =2, 20lg 20lg 26()K dB == 0型系统,低频段斜率为0;(3) 求各转折频率,并从小到大按顺序标为 ,,,321ωωω,同时还要在转折频率旁注明对应的斜率;①110.1258ω==,惯性环节,斜率-20; ②210.52ω==,惯性环节,斜率-20;(4) 绘制波德图坐标。
横坐标从0.1到10二个十倍频程。
见图; (5) 绘制低频段幅频渐近线,为水平线;(6) 在10.125ω=,斜率变为-20;在20.5ω=,斜率变为-40;标注斜率见图;(7) 幅频渐近线的修正。
在10.125ω=处修正-3dB ,在0.06,0.25ω=处修正-1dB ;在0.5ω=处修正-3dB ,在0.5,1ω=处修正-1dB ;注意在0.5ω=处有两个-1dB 修正量,共修正-2dB ;(8) 绘制两个惯性环节的相频曲线;(9) 环节相频曲线叠加,形成系统相频曲线; (10) 检查幅频渐近线、转折频率、相频起终点的正确性。
4-4(2)2200()()(1)(101)G s H s s s s =++(1) 开环传递函数已如式(4-41)标准化;(2) 计算开环增益K ,计算)(lg 20dB K ;得系统型别ν,确定低频段斜率;开环增益K =200, 20lg 20lg 20046()K dB == 2型系统,低频段斜率为-40; (3) 求各转折频率:①110.110ω==,惯性环节,斜率-20; ②21ω=,惯性环节,斜率-20;(4) 以下文字略,见绘图;4-4(3)2250()()(1)(101)G s H s s s s s =+++ (1) 开环传递函数标准化:2250()()(20.511)(101)G s H s s s s s =+⨯⨯++(2) 计算开环增益K ,计算)(lg 20dB K ;得系统型别ν,确定低频段斜率;开环增益K =50, 20lg 20lg5034()K dB ==2型系统,低频段斜率为-40; (3) 求各转折频率:①110.110ω==,惯性环节,斜率-20; ②21ω=,二阶振荡环节,阻尼比0.5ζ=,斜率-40;(4) 其它:二阶振荡环节在转折频率处要按实际阻尼比按图4-17修正。
见绘图;4-4(4)210(0.2)()()(0.1)s G s H s s s +=+ (1) 开环传递函数标准化:2220(1)10(0.2)0.2()()(0.1)(1)0.1ss G s H s s s s s ++==++ (2) 计算开环增益K ,计算)(lg 20dB K ;得系统型别ν,确定低频段斜率;开环增益K =20, 20lg 20lg 2026()K dB ==2型系统,低频段斜率为-40; (3) 求各转折频率:①10.1ω=,惯性环节,斜率-20; ②20.2ω=,一阶微分环节,斜率+20; (4) 其它见绘图;4-4(5)228(0.1)()()(1)(425)s G s H s s s s s s +=++++ (1) 开环传递函数标准化:22220.0325(1)0.1()()(20.511)(20.455)sG s H s s s s s s ⨯+=+⨯⨯++⨯⨯+ (2) 计算开环增益K ,计算)(lg 20dB K ;得系统型别ν,确定低频段斜率;开环增益K =0.032, 20lg 20lg0.03230()K dB ==-1型系统,低频段斜率为-20; (3) 求各转折频率:①10.1ω=,一阶微分环节,斜率+20;②21ω=,二阶振荡环节,阻尼比0.5ζ=,斜率-40; ③35ω=,二阶振荡环节,阻尼比0.4ζ=,斜率-40; (4) 其它见绘图;4-5 根据下列给定的最小相位系统对数幅频特性曲线图写出相应的传递函数。
解:4-5(a)(1)求结构从图中看出,低频段斜率为0,是0型系统,由渐近线的斜率变化: 第1个转折频率处斜率变化20/dB dec -,是一阶惯性环节; 第2个转折频率处斜率变化也是20/dB dec -,也是一阶惯性环节; 因此传递函数结构为12()(1)(1)KG s T s T s =++(2)求参数从图中看出,低频段与零分贝线水平重合,因此1K =对第1个一阶惯性环节,转折频率11ω=,则:1111T ω==对第2个一阶惯性环节,转折频率24ω=,则:22110.254T ω=== 综合得:()(1)(0.251)KG s s s =++解:4-5(b)(1)求结构从图中看出,低频段斜率为20/dB dec -,是1型系统,由渐近线的斜率变化: 第1个转折频率处斜率变化20/dB dec -,是一阶惯性环节; 第2个转折频率处斜率变化也是20/dB dec -,也是一阶惯性环节; 因此传递函数结构为12()(1)(1)KG s s T s T s =++(2)求参数从图中看出,低频段延长线与零分贝线交点频率:0100ω=,因为是1型系统,由式(4-67)100K =对第1个一阶惯性环节,转折频率10.01ω=,则:11111000.01T ω=== 对第2个一阶惯性环节,转折频率2100ω=,则:22110.01100T ω=== 综合得:12100()(1)(1)(1001)(0.011)K G s s T s T s s s s ==++++解:4-5(c)(1)求结构从图中看出,低频段斜率为0,是0型系统,由渐近线的斜率变化: 第1个转折频率处斜率变化20/dB dec -,是一阶惯性环节; 第2个转折频率处斜率变化也是20/dB dec -,也是一阶惯性环节; 第3个转折频率处斜率变化也是20/dB dec -,也是一阶惯性环节; 因此传递函数结构为123()(1)(1)(1)KG s T s T s T s =+++(2)求参数从图中看出,低频段为水平线,幅值为48k L dB =。
