立体几何中常见模型总结归纳精编版
(完整版)立体几何知识点总结完整版

立体几何知识点【考纲解读】1、平面的概念及平面的表示法,理解三个公理及三个推论的内容及作用,初步掌握性质与推论的简单应用。
2、 空间两条直线的三种位置关系,并会判定。
3、 平行公理、等角定理及其推论,了解它们的作用,会用它们来证明简单的几何问题,掌握证明空间两直线 平行及角相等的方法。
4、 异面直线所成角的定义,异面直线垂直的概念,会用图形来表示两条异面直线,掌握异面直线所成角的范 围,会求异面直线的所成角。
5•理解空间向量的概念,掌握空间向量的加法、减法和数乘;了解空间向量的基本定理,理解空间向量坐标的概念,掌握空间向量的坐标运算 ;掌握空间向量的数量积的定义及其性质,掌握用直角坐标计算空间向量数量积公式.6•了解多面体、凸多面体、正多面体、棱柱、棱锥、球的概念•掌握棱柱,棱锥的性质,并会灵活应用,掌握球的表面积、体积公式;能画出简单空间图形的三视图, 能识别上述的三视图所表示的立体模型, 会用斜二测法画出它们的直观图•7•空间平行与垂直关系的论证 •8.掌握直线与平面所成角、二面角的计算方法,掌握三垂线定理及其逆定理,并能熟练解决有关问题 ,进一步掌握异面直线所成角的求解方法,熟练解决有关问题9•理解点到平面、直线和直线、直线和平面、平面和平面距离的概念会用求距离的常用方法(如:直接法、转 化法、向量法)•对异面直线的距离只要求学生掌握作出公垂线段或用向量表示的情况)和距离公式计算距离。
【知识络构建】<— 翅MJL 何体的峯构特征一袞间几何怀的表面锲和体枳 —I 吩间儿何体的三视图和吒现图 空何向話的槪念线性运算空间向园数呈积理和坐标运算【重点知识整合】1. 空间几何体的三视图专间儿何体空问点仁n线、平面ft置关系宀VIHI向虽与<体儿何(1) 正视图:光线从几何体的前面向后面正投影得到的投影图;(2) 侧视图:光线从几何体的左面向右面正投影得到的投影图;(3) 俯视图:光线从几何体的上面向下面正投影得到的投影图.几何体的正视图、侧视图和俯视图统称为几何体的三视图.2. 斜二测画水平放置的平面图形的基本步骤(1) 建立直角坐标系,在已知水平放置的平面图形中取互相垂直的Ox, Oy,建立直角坐标系;(2) 画出斜坐标系,在画直观图的纸上(平面上)画出对应的Ox', Oy',使/ x Oy = 45。
立体几何的知识点总结

立体几何的知识点总结篇1:高中立体几何知识点总结高中立体几何知识点总结1.棱柱、棱锥、棱(圆)台的本质特征⑴棱柱:①有两个互相平行的面(即底面平行且全等),②其余各面(即侧面)每相邻两个面的公共边都互相平行(即侧棱都平行且相等)。
⑵棱锥:①有一个面(即底面)是多边形,②其余各面(即侧面)是有一个公共顶点的三角形。
⑶棱台:①每条侧棱延长后交于同一点,②两底面是平行且相似的多边形。
⑷圆台:①平行于底面的截面都是圆,②过轴的截面都是全等的等腰梯形,③母线长都相等,每条母线延长后都与轴交于同一点。
2.圆柱、圆锥、圆台的展开图、表面积和体积的计算公式3.线线平行常用方法总结(1)定义:在同一平面内没有公共点的两条直线是平行直线。
(2)公理:在空间中平行于同一条直线的两条直线互相平行。
(3)线面平行的性质:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和两平面的交线平行。
么两直线平行。
(5)面面平行的性质:若两个平行平面同时与第三个平面相交,那么两条交线平行。
4.线面平行的判定方法。
(1)定义:直线和平面没有公共点。
(2)判定定理:若不在平面内的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行。
(3)面面平行的性质:两个平面平行,其中一个平面内的任何一条直线必平行于另一个平面。
(4)线面垂直的性质:平面外于已知平面的垂线垂直的直线平行于已知平面。
5.判定两平面平行的方法。
(1)依定义采用反证法;(2)利用判定定理:如果一个平面内有两条相交直线平行于另一个平面,那么这两个平面平行。
(3)利用判定定理的推论:如果一个平面内有两条相交直线平行于另一个平面内的两条直线,则这两平面平行。
(4)垂直于同一条直线的两个平面平行。
(5)平行于同一个平面的两个平面平行。
6.证明线线垂直的方法(1)利用定义。
条直线垂直于这个平面的任何一条直线。
7.证明线面垂直的方法(1)线面垂直的定义。
立体几何四个重要模型

立体几何四个重要模型广州市第六十五中学朱星如模型1:在棱长为a 的正面体ABCD 中:1.求证它是一个正三棱锥。
证明:即证顶点A 在底面BCD 的中心H 的连线与底面垂直。
取BC 的中点E,BD 的中点F,连CF,DE 相交于点H,则H 是三角形BCD 的中心,且H 是CF,DE 的一个三等分点,连AH,由BC ⊥DE,BC ⊥AE,AE 交DE=E,AE,DE 的平面AED 内,得BC ⊥平面AED,由此得BC ⊥AH,即AH ⊥BC。
(1)同理:AH ⊥BD。
(2)由BC 交BD=B,BC,BD 在平面BCD 内及(1)(2)得:AH ⊥平面BCD。
所以四面体ABCD 是正三棱锥。
2.设E、F、S、T 分别是BC、BD、AD、AC 的中点,求证:四边形EFST 是正方形。
证明:由于E、F、S、T 分别是BC、BD、AD、AC 的中点,故有ST 12DC EF,ST EF,所四边形EFST 是平行四边形。
同理:SF 12AB TE ,DC=AB ,所以四边形EFST 是菱形。
仿题1可证DC ⊥平面ABH,故DC ⊥AB,故有四边形EFST 是正方形。
注;由此可得到相对的两棱所成角为90o 。
3.设E、S 分别是BC、AD 的中点,求证:ES ⊥BC,ES ⊥AD,并求ES 的长。
证明:可证BC ⊥平面AED,从而BC ⊥ES;可得AD ⊥平面BCS,从而AD ⊥ES。
在直角三角形SBE 中,SB=32a,BE=12a,从而,2222ES SB BE =-=4.求任何一条棱与它相交的面所成角的正弦值。
解:只要求AB 与平面BCD 所成的角。
AH ⊥平面BCD,∴AB 与平面BCD 所成的角是ABH ∠。
22333323BH DE ==⨯=,在直角三角形ABH 中,2263AH AB BH =-=,故6sin 3AH ABH AB ∠==。
5.求相邻两个面的夹角的余弦值。
解:只要求二面角A-BD-C 的平面的余弦值。
高中数学立体几何知识点归纳总结

高中数学立体几何知识点归纳总结一、立体几何知识点归纳 第一章 空间几何体(一)空间几何体的结构特征(1)多面体——由若干个平面多边形围成的几何体.围成多面体的各个多边形叫叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做顶点。
旋转体——把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。
其中,这条定直线称为旋转体的轴。
(2)柱,锥,台,球的结构特征 1.棱柱1.1棱柱——有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
1.2相关棱柱几何体系列(棱柱、斜棱柱、直棱柱、正棱柱)的关系:①⎧⎪⎧−−−−−→⎨⎪−−−−−→⎨⎪⎪⎩底面是正多形棱垂直于底面斜棱柱棱柱正棱柱直棱柱其他棱柱 底面为矩形侧棱与底面边长相等1.3①侧棱都相等,侧面是平行四边形;②两个底面与平行于底面的截面是全等的多边形; ③过不相邻的两条侧棱的截面是平行四边形;④直棱柱的侧棱长与高相等,侧面与对角面是矩形。
1.4长方体的性质:①长方体一条对角线长的平方等于一个顶点上三条棱的平方和;【如图】222211AC AB AD AA =++②(了解)长方体的一条对角线1AC 与过顶点A 的三条棱所成的角分别是αβγ,,,那么222cos cos cos 1αβγ++=,222sin sin sin 2αβγ++=;③(了解)长方体的一条对角线1AC 与过顶点A 的相邻三个面所成的角分别是αβγ,,,则222cos cos cos 2αβγ++=,222sin sin sin 1αβγ++=.1.5侧面展开图:正n 棱柱的侧面展开图是由n 个全等矩形组成的以底面周长和侧棱长为邻边的矩形.1.6面积、体积公式:2S c hS c h S S h=⋅=⋅+=⋅直棱柱侧直棱柱全底棱柱底,V (其中c 为底面周长,h为棱柱的高) 2.圆柱2.1圆柱——以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱. 2.2圆柱的性质:上、下底及平行于底面的截面都是等圆;过轴的截面(轴截面)是全等的矩形. 2.3侧面展开图:圆柱的侧面展开图是以底面周长和母线长为邻边的矩形. 2.4面积、体积公式:S 圆柱侧=2rh π;S 圆柱全=222rh r ππ+,V 圆柱=S 底h=2r h π(其中r 为底面半径,h 为圆柱高) 3.棱锥3.1棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
高考立体几何知识点总结(详细)
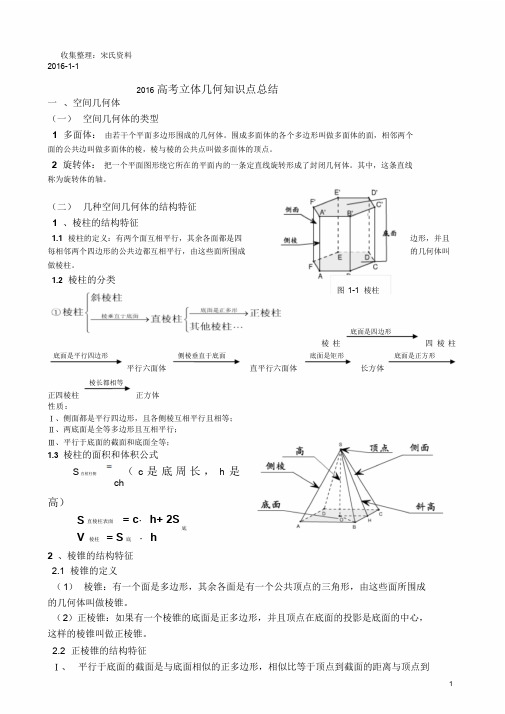
收集整理:宋氏资料2016-1-12016 高考立体几何知识点总结一、空间几何体(一)空间几何体的类型1 多面体:由若干个平面多边形围成的几何体。
围成多面体的各个多边形叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点。
2 旋转体:把一个平面图形绕它所在的平面内的一条定直线旋转形成了封闭几何体。
其中,这条直线称为旋转体的轴。
(二)几种空间几何体的结构特征1 、棱柱的结构特征1.1 棱柱的定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
1.2棱柱的分类图1-1 棱柱底面是四边形棱柱四棱柱底面是平行四边形侧棱垂直于底面底面是矩形底面是正方形平行六面体直平行六面体长方体棱长都相等正四棱柱正方体性质:Ⅰ、侧面都是平行四边形,且各侧棱互相平行且相等;Ⅱ、两底面是全等多边形且互相平行;Ⅲ、平行于底面的截面和底面全等;1.3棱柱的面积和体积公式S直棱柱侧(c 是底周长,h 是ch高)S 直棱柱表面= c·h+ 2S底V 棱柱= S 底·h2 、棱锥的结构特征2.1 棱锥的定义(1)棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
(2)正棱锥:如果有一个棱锥的底面是正多边形,并且顶点在底面的投影是底面的中心,这样的棱锥叫做正棱锥。
2.2 正棱锥的结构特征Ⅰ、平行于底面的截面是与底面相似的正多边形,相似比等于顶点到截面的距离与顶点到1底面的距离之比;它们面积的比等于截得的棱锥的高与原棱锥的高的平方比;截得的棱锥的体积与原棱锥的体积的比等于截得的棱锥的高与原棱锥的高的立方比;Ⅱ、正棱锥的各侧棱相等,各侧面是全等的等腰三角形;正棱锥侧面积:1S正棱椎ch (c为底周长,h'为斜高)'2P体积:1V棱椎Sh(S为底面积,h 为高)3D CO H正四面体:A B2对于棱长为a正四面体的问题可将它补成一个边长为 a的正方体问题。
立体几何初步知识点全总结

立体几何初步知识点全总结一、空间几何体的结构。
1. 棱柱。
- 定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。
- 分类:- 按底面多边形的边数分为三棱柱、四棱柱、五棱柱等。
- 直棱柱:侧棱垂直于底面的棱柱。
正棱柱:底面是正多边形的直棱柱。
- 性质:- 侧棱都相等,侧面是平行四边形。
- 两个底面与平行于底面的截面是全等的多边形。
- 过不相邻的两条侧棱的截面(对角面)是平行四边形。
2. 棱锥。
- 定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。
- 分类:- 按底面多边形的边数分为三棱锥、四棱锥、五棱锥等。
- 正棱锥:底面是正多边形,且顶点在底面的射影是底面正多边形的中心的棱锥。
- 性质:- 正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高)。
- 棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形;棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形。
3. 棱台。
- 定义:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫做棱台。
- 分类:由三棱锥、四棱锥、五棱锥等截得的棱台分别叫做三棱台、四棱台、五棱台等。
- 性质:- 棱台的各侧棱延长后交于一点。
- 棱台的上下底面是相似多边形,侧面是梯形。
4. 圆柱。
- 定义:以矩形的一边所在直线为轴旋转,其余三边旋转所成的曲面所围成的几何体叫做圆柱。
- 性质:- 圆柱的轴截面是矩形。
- 平行于底面的截面是与底面全等的圆。
5. 圆锥。
- 定义:以直角三角形的一条直角边所在直线为轴旋转,其余两边旋转所成的曲面所围成的几何体叫做圆锥。
- 性质:- 圆锥的轴截面是等腰三角形。
- 平行于底面的截面是圆,截面半径与底面半径之比等于顶点到截面距离与圆锥高之比。
6. 圆台。
- 定义:用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台。
立体几何知识点归纳

一、空间几何体(一)空间几何体的结构:1、几何体:2、多面体:3、旋转体:4、棱柱:5、棱锥:6、棱台:7、圆柱:8、圆锥:9、圆台:10、球:(二)简单几何体的构成:1、2、(三)三视图:1、投影:2、投影类型:3、三视图:(1)正视图(2)侧视图:(3)俯视图:(三)直观图:(1)直观图:(2)斜二测画法规则:(四)体积面积公式:1、柱体体积:2、锥体体积:3、台体体积:4、球体体积:球体表面积:5、祖暅原理:二、平面的性质与直线的位置关系1、平面意义:(1)空间图形是由点、线、面组成的(2)平面图形与空间图形的概念:如果一个图形的所有点都在同一个平面内,则称这个图形为平面图形,否则称为空间图形(3)平面的两个特征:①无限延展 ②平的(没有厚度) 平面是没有厚薄的,可以无限延伸,这是平面最基本的属性一个平面把空间分成两部分,一条直线把平面分成两部分 2 平面的基本性质公理1 如果一条直线的两点在一个平面内,那么这条直线上的所有点都在这个平面内推理模式:A AB B ααα∈⎫⇒⊂⎬∈⎭. 如图示: 或者:∵,A B αα∈∈,∴AB α⊂ 应用:①判定直线在平面内;②判定点在平面内模式:a A A aαα⊂⎧⇒∈⎨∈⎩.公理2如果两个不重合平面有一个公共点,那么它们有且只有一条过该点的公共直线。
推理模式:A A l A ααββ∈⎫⇒∈=⎬∈⎭ 如图示:或者:∵,A A αβ∈∈,∴,l A l αβ=∈ 应用:①确定两相交平面的交线位置;②判定点在直线上公理3 经过不在同一条直线上的三点,有且只有一个平面推理模式:,, ,,,,A B C A B C A B C ααβ⎫⎪∈⇒⎬⎪∈⎭不共线与β重合或者:∵,,A B C 不共线,∴存在唯一的平面α,使得,,A B C α∈.应用:①确定平面;②证明两个平面重合“有且只有一个”的含义分两部分理解,“有”说明图形存在,但不唯一,“只有一个”说明图形如果有顶多只有一个,但不保证符合条件的图形存在,“有且只有一个”既保证了图形的存在性,又保证了图形的唯一性.在数学语言的叙述中,“确定一个”,“可以作且只能作一个”与“有且只有一个”是同义词,因此,在证明有关这类语句的命题时,要从“存在性”和“唯一性”两方面来论证.推论1:推论2:推论3:3、 空间两直线的位置关系(1)相交——有且只有一个公共点;(2)平行——在同一平面内,没有公共点;(3)异面——不同在任何..一个平面内,没有公共点; 4、平线直线:(1)公理4 :平行于同一条直线的两条直线互相平行(空间平行线的传递性)推理模式://,////a b b c a c ⇒.(2)空间四边形:顺次连结不共面的四点A,B,C,D 所组成的四边形叫空间四边形,相对顶点的连线AC,BD 叫空间四边形的对角线(3)等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等(4)等角定理的推论:如果两条相交直线和另两条相交直线分别平行,那么这两条直线所成的锐角(或直角)相等.指出:等角定理及其推论,说明了空间角通过任意平行移动具有保值性,因而成为异面直线所成角的基础.5、异面直线:不同在任何..一个平面内,没有公共点 (1).空间两条异面直线的画法a b1A CA(2)异面直线判定定理:连结平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线推理模式:,,,A B l B l ααα∉∈⊂∉⇒AB 与l 是异面直线(3)异面直线判定方法:判定定理、反证法。
生活中的立体几何(一)精编版

5
6
6
8
7
10
8
12
9
14
n+2
2n
侧棱数 总棱数
3
9
4
12
5
15
6
18
7
21
n
3n
3、棱柱可以分为直棱柱和斜棱柱。
本书只 讨论直 棱柱简 称棱柱
注意:直棱柱的侧面是长方形,斜棱柱的侧面是平行四边形。
(五)
棱柱与圆柱的相同点与不同点?
相同点:都有上、下两个底面,都有侧面 不同点:
(1)棱柱的底面是形状和大小完全相同的 多边形,圆柱的底面是圆
3、下列几何体中,面数相同的是( D )
A、圆柱和圆锥 C、圆锥和正方体
B、圆柱和正方体 D、正方体和四棱柱
4、下列有六个面的几何体的个数是( C )
长方体 、 圆柱、 四棱柱 、 正方体 、三棱柱、 四棱锥
A、1个
B、2个 C、3个 D、4个
5、下列几何体属于棱柱的是( A )
A、正方体 B、球 C、圆锥 D、棱台
(2)棱柱的侧面是长方形,圆柱的侧面是 曲面
(3)棱柱有顶点,圆柱没有顶点
(六)巩固练习:
1、下列说法中,正确的是( C)
A、六角螺母的形状类似于圆柱 B、电视机的形状类似于球体
C、数学课本的形状类似于长方体 D、鸡蛋的形状类似于圆锥
2、下列几何体中,每个面都由同一种图形组成的是( D)
A、圆柱 B、圆锥 C、三棱柱 D、正方体
11、若一个四棱柱的12条棱都相等,且它们的和为24cm,则这 个棱柱的体积是___8___cm3
12、如图所示是一个正六棱柱,它的底面边长是3cm,高是 6cm.
(完整版)空间立体几何知识点归纳,推荐文档

与平面无任何公共点)⎭平行;a ba a a ⊂ A性质Ⅰ:如果一个平面与两平行平面都相交,那么它αα性质Ⅱ:平行于同一平面的两平面平行;11、线面垂直:⑵判定:一条直线与一个平面内的两条相交直⑴定义:两个平面相交,如果它们所成的二面角是直二面角,就说这两个l l αα空间角及空间距离的计算1.异面直线所成角:使异面直线平移后相交形成的夹角,通常在两异面直线中的一条上取一点,过该点作另一条直线平行线,2. 斜线与平面成成的角:斜线与它在平面上的射影成的角。
如图:PA 是平面的一α条斜线,A 为斜足,O 为垂足,OA 叫斜线PA 在平面上射影,为线αPAO ∠面角。
3.二面角:从一条直线出发的两个半平面形成的图形,如图为二面角,二l αβ--面角的大小指的是二面角的平面角的大小。
二面角的平面角分别在两个半平面内且角的两边与二面角的棱垂直用二面角的平面角的定义求二面角的大小的关键点是:①确构成二面角两个半平面和棱;②明确二面角的平面角是哪个?而要想明确二面角的平面角,关键是看该角的两边是否都和棱垂直。
(求空间角的三个步骤是“一找”、“二证”、“三计算”)5.点到平面的距离:指该点与它在平面上的射影的连线段的长度。
如图:O 为P 在平面上的射影,α线段OP 的长度为点P 到平面的距离求法通常有:定义法和等体积法α等体积法:就是将点到平面的距离看成是三棱锥的一个高。
如图在三棱锥V ABC-中有:S ABCA SBCB SAC C SABV V V V ----===----,,l OA OB l OA l OB l AOBαβαβαβ⊂⊂⊥⊥∠如图:在二面角中,O 棱上一点,,,的平面角。
且则为二面角 a b ''︒︒如图:直线a 与b 异面,b//b ,直线a 与直线b 的夹角为两异面直线与所成的角,异面直线所成角取值范围是(0,90]。
常用几何模型总结

常用几何模型总结全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型:说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明:通过对称进行等量代换,转换成两点间距离及点到直线距离。
立体几何解答题常考模型归纳总结(九大题型)(原卷版)-高中数学

立体几何解答题常考模型归纳总结 高考立体几何解答题常考模型主要包括柱体、锥体、球体、旋转体、多面体等。
这些模型常涉及体积、表面积的计算,截面问题,以及与其他几何体的组合或相交问题。
此外,空间位置关系,如平行、垂直的判断与证明,也是常考内容。
空间角的计算,包括异面直线所成的角、直线与平面所成的角、二面角等,同样是高考立体几何的重要考点。
最后,空间距离的计算,如点到平面的距离、两平行平面间的距离等,也是解答题中常见的考查点。
掌握这些模型的基本性质和解题方法,对于提高高考立体几何的解题能力至关重要。
题型一:非常规空间几何体为载体【典例1-1】(2024·河南濮阳·模拟预测)如图,侧面11BCC B 水平放置的正三棱台11111,24ABC A B C AB A B -==(1)求证:1AA ^平面11BCC B ;(2)求直线AB 和平面1ACB 所成角的正弦值.【典例1-2】(2024·云南昆明·三模)如图,在三棱台111ABC A B C -中,上、下底面是边长分别为2和4的正三角形,1AA ^平面ABC ,设平面11AB C I 平面=ABC l ,点,E F 分别在直线l 和直线1BB 上,且满足EF l ^,1EF BB ^.(1)证明:^EF 平面11BCC B ;(2)若直线EF 和平面ABC 【变式1-1】(2024·天津和平·二模)如图,三棱台111ABC A B C -中,ABC V 为等边三角形,1124AB A B ==,1AA ^平面ABC ,点M ,N ,D 分别为AB ,AC ,BC 的中点,11A B AC ^.(1)证明:1CC ∥平面1A MN ;(2)求直线1A D 与平面1A MN 所成角的正弦值;(3)求点D 到平面1A MN 的距离.【变式1-2】(2024·河南周口·模拟预测)如图,平行六面体1111ABCD A B C D -中,底面ABCD 与平面11ABC D 都是边长为2的菱形,11120BCD BC D °Ð=Ð=,侧面11BCC B(1)求平行六面体1111ABCD A B C D -的体积;(2)求平面11BCC B 与平面11CDD C 的夹角的余弦值.题型二:立体几何存在与探索性问题【典例2-1】如图1,ABC V 是边长为3的等边三角形,点,D E 分别在线段,AC AB 上,且1,2AE AD ==,沿DE 将ADE V 翻折到PDE △的位置,使得PB 2.(1)求证:平面PDE ^平面BCDE ;(2)在线段PB 上是否存在点M ,使得//EM 平面PCD ,若存在,求出PM MB的值;若不存在,请说明理由.【典例2-2】(2024·广东·一模)如图所示,四边形ABCD 是圆柱底面的内接四边形,AC 是圆柱的底面直径,PC 是圆柱的母线,E 是AC 与BD 的交点,608AB AD BAD AC Ð===o ,,.(1)记圆柱的体积为1V ,四棱锥P ABCD -的体积为 2V ,求 12V V ;(2)设点F 在线段AP 上,且存在一个正整数k ,使得PA kPF PC kCE ==,,若已知平面FCD 与平面PCDk 的值.【变式2-1】在ABC V 中,90ABC Ð=°,6AB BC ==,D 为边AB 上一点,2AD =,E 为AC 上一点,//DE BC ,将ADE V 沿DE 翻折,使A 到A ¢处,90DA B ¢Ð=°.(1)证明:A B ¢^平面A DE ¢;(2)若射线DE 上存在点M ,使l =uuuu r uuu r DM DE ,且MC 与平面A EC ¢所成角的正弦值为15,求λ.【变式2-2】(2024·甘肃张掖·模拟预测)如图,在四棱锥P ABCD -中,底面四边形ABCD为菱形,且60,DAB PAD Ð=o V 是边长为2的等边三角形,且平面PAD ^平面,ABCD O 为AD 中点.(1)求证:OB ^平面PAD ;(2)在线段PC 上是否存在点M ,使二面角M BO C --的大小为60o ,若存在,求PM PC的值,若不存在,请说明理由.题型三:立体几何折叠问题【典例3-1】(2024·湖北武汉·模拟预测)如图1,在矩形ABCD 中,2AB =,BC =ABD △沿矩形的对角线BD 进行翻折,得到如图2所示的三棱锥A BCD -,且AB CD ^.(1)求翻折后线段AC 的长;(2)点M 满足2AM MD =uuuu r uuuu r ,求CM 与平面ABD 所成角的正弦值.【典例3-2】(2024·山东·模拟预测)如图,在菱形ABCD 中,60BAD Ð=°,E 是AD 的中点,将ABE V沿直线BE 翻折使点A 到达点1A 的位置,F 为线段1AC 的中点.(1)求证:DF ∥平面1A BE ;(2)若平面1A BE ^平面BCDE ,求直线1A E 与平面1A BC 所成角的大小.【变式3-1】(2024·河南驻马店·二模)在如图①所示的平面图形中,四边形ACDE 为菱形,现沿AC 进行翻折,使得AB ^平面ACDE ,过点E 作//EF AB ,且12EF AB =,连接,,FD FB BD ,所得图形如图②所示,其中G 为线段BD 的中点,连接FG .(1)求证:FG ^平面ABD ;(2)若2AC AD ==,直线FG 与平面BCD ,求AB 的值.【变式3-2】在等腰梯形ABCD 中,//AB CD ,2AB =,2AD BC ==,60DAB Ð=°,M 为AB 中点,将AMD V ,BMC △沿MD ,MC 翻折,使A ,B 重合于点E ,得到三棱锥M CDE -.(1)求ME 与平面CDE 所成角的大小;(2)求二面角M DE C --的余弦值.题型四:立体几何作图问题【典例4-1】(2024·河南信阳·模拟预测)长方体1111ABCD A B C D -中,123,2AB AA AD CE ED ===uuu r uuu r .(1)过E 、B 作一个截面,使得该截面平分长方体的表面积和体积.写出作图过程及其理由.(2)记(1)中截面为a ,若a 与(1)中过D 点的长方体的三个表面成二面角分别为,,q j w ,求222cos cos cos q j w ++的值.【典例4-2】(2024·高三·河北承德·期中)如图,在四棱锥P ABCD -中,底面ABCD 是正方形,,,O E F 分别是,,BD PA BC 的中点.(1)证明://OE 平面PBC ;(2)若平面a 经过点,,F D E ,且与棱PB 交于点H .请作图画出H 在棱PB 上的位置,并求出PH HB的值.【变式4-1】(2024·辽宁大连·一模)如图多面体ABCDEF 中,面FAB ^面ABCD ,FAB V 为等边三角形,四边形ABCD 为正方形,EF BC ∥,且334EF BC ==,H ,G 分别为CE ,CD 的中点.(1)证明:BF AD ^;(2)求平面BCEF 与平面FGH 所成角的余弦值;(3)作平面FHG 与平面ABCD 的交线,记该交线与直线AD 交点为P ,写出AP AD的值(不需要说明理由,保留作图痕迹).【变式4-2】如图,已知底面为平行四边形的四棱锥P ABCD -中,平面MNGH 与直线PB 和直线AC 平行,点E 为PD 的中点,点F 在CD 上,且:1:2DF FC =.(1)求证:四边形MNGH 是平行四边形;(2)求作过EF 作四棱锥P ABCD -的截面,使PB 与截面平行(写出作图过程,不要求证明).截面的定义:用一个平面去截一个几何体,平面与几何体的表面的交线围成的平面图形.【变式4-3】(2024·北京·三模)四棱锥P ABCD -中,底面ABCD 是边长为2的菱形,23DAB p Ð=.AC BD O =I ,且^PO 平面ABCD ,PO =,点,F G 分别是线段.PB PD 上的中点,E 在PA 上.且3PA PE =.(Ⅰ)求证://BD 平面EFG ;(Ⅱ)求直线AB 与平面EFG 的成角的正弦值;(Ⅲ)请画出平面EFG 与四棱锥的表面的交线,并写出作图的步骤.题型五:立体几何建系繁琐问题【典例5-1】(2024·山东淄博·二模)已知直角梯形ABCD ,90ADC Ð=°,//AB CD ,2AB CD AD ===M 为对角线AC 与BD 的交点.现以AC 为折痕把ADC V 折起,使点D 到达点P 的位置,点Q 为PB 的中点,如图所示:(1)证明:AC ^平面PBM ;(2)求三棱锥P ACQ -体积的最大值;(3)当三棱锥P ACQ -的体积最大时,求直线AB 与平面PBC 所成角的正弦值.【典例5-2】(2024·贵州黔东南·二模)如图,在四棱台1111ABCD A B C D -中,O 为AC 的中点,1111122AA A C C C AC ====.(1)证明:1//OC 平面11AA D D ;(2)若平面ABCD ^平面11ACC A ,AB BC ^,当四棱锥11B AA C C -的体积最大时,求1CC 与平面11AA B B 夹角的正弦值.【变式5-1】(2024·重庆·三模)如图所示的几何体是一个半圆柱和一个三棱锥的组合体.11,BB CC 是半圆柱的母线,1,O O 分别是底面直径BC 和11B C 的中点,11114,2,BC B C BB CC A ====是半圆O 上一动点,1A 是半圆1O 上的动点,1AA 是圆柱的母线,延长1A A 至P 点使得A 为1A P 的中点,连接PB ,PC 构成三棱锥P ABC -.(1)证明:1AC BA ^;(2)当三棱锥P ABC -的体积最大时,求平面1ABA 与平面1BA C 的夹角.【变式5-2】已知平面四边形ABCD ,2AB AD ==,60BAD Ð=°,30BCD Ð=°,现将ABD D 沿BD 边折起,使得平面ABD ^平面BCD ,此时AD CD ^,点P 为线段AD 的中点.(1)求证:BP ^平面ACD ;(2)若M 为CD 的中点①求MP 与平面BPC 所成角的正弦值;②求二面角P BM D --的平面角的余弦值.题型六:两角相等(构造全等)的立体几何问题【典例6-1】(2024·河南·模拟预测)如图,在三棱锥A BCD -中,ABC V 是等边三角形,90BAD BCD Ð=Ð=°,点P 是AC 的中点,连接,BP DP .(1)证明:平面ACD ^平面BDP ;(2)若BD =,且二面角A BD C --为120°,求直线AD 与平面BCD 所成角的正弦值.【典例6-2】(2024·广西桂林·二模)如图,四棱锥F ABCD -中,底面ABCD 为边长是2的正方形,E ,G 分别是CD ,AF 的中点,4AF =,FAE BAE Ð=Ð,且二面角F AE B --的大小为90°.(1) 求证:AE BG ^;(2) 求二面角B AF E --的余弦值.【变式6-1】(2024·安徽合肥·模拟预测)如图,四棱锥E ABCD -中,四边形ABCD 是边长为2的菱形,45DAE BAE °Ð=Ð=,60DAB Ð=°.(1)证明:平面ADE ^平面ABE ;(2)当直线DE 与平面ABE 所成的角为30°时,求平面DCE 与平面ABE 所成锐二面角的余弦值.【变式6-2】(2024·辽宁沈阳·模拟预测)如图,四棱锥E ABCD -中,四边形ABCD 是边长为2的菱形45DAE BAE Ð=Ð=°,60DAB Ð=°(1)证明:平面ADE ^平面ABE ;(2)当平面DCE 与平面ABE DE 与平面ABE 所成角正弦值.题型七:利用传统方法找几何关系建系【典例7-1】(2024·江苏南京·二模)如图,//AD BC ,AD AB ^,点E 、F 在平面ABCD 的同侧,//CF AE ,1AD =,2AB BC ==,平面ACFE ^平面ABCD ,EA EC ==(1)求证://BF 平面ADE ;(2)若直线EC 与平面FBD ,求线段CF 的长.【典例7-2】斜三棱柱ABC -A 1B 1C 1上,侧面AA 1C 1C ⊥平面ABC ,侧面AA 1C 1C 是菱形,∠A 1AC =60°,A 1C =AC AB =2,为BB 1的中点.(1)求二面角C -A 1D -C 1的余弦值;(2)记△ABC 的外接圆上有一动点P ,若二面角P -AA 1-C 与二面角C -A 1D -C 1相等,求AP 的长.【变式7-1】如图,已知四棱锥P ABCE -中,PA ^平面ABCE ,平面PAB ^平面PBC ,且1AB =,2BC =,BE =,点A 在平面PCE 内的射影恰为PCE V 的重心G .(1)证明:BC AB ^;(2)求直线CG 与平面PBC 所成角的正弦值.【变式7-2】如图所示,圆锥的高2PO =,底面圆O 的半径为R ,延长直径AB 到点C ,使得BC R =,分别过点A ,C 作底面圆O 的切线,两切线相交于点E ,点D 是切线CE 与圆O 的切点.(1)证明:平面PDE ^平面POD ;(2)若直线PE 与平面PBD ,求点A 到平面PED 的距离.题型八:空间中的点不好求【典例8-1】(2024·山东日照·三模)在五面体ABCDEF 中,CD ADE ^平面,EF ADE ^平面.(1)求证:AB CD ∥;(2)若222AB AD EF ===,3CD =,90ADE Ð=°,点D 到平面ABFE A BC F --的余弦值.【典例8-2】(2024·全国·校联考模拟预测)已知三棱锥ABCD ,D 在面ABC 上的投影为O ,O 恰好为△ABC 的外心.4AC AB ==,2BC =.(1)证明:BC ⊥AD ;(2)E 为AD 上靠近A 的四等分点,若三棱锥A-BCD 的体积为1,求二面角E CO B --的余弦值.【变式8-1】(2024·河南·校联考模拟预测)如图,在四棱锥P ABCD -中,AB BC ==AD CD AC ===E ,F 分别为AC ,CD 的中点,点G 在PF 上,且G 为三角形PCD 的重心.(1)证明://GE 平面PBC ;(2)若PA PC =,PA CD ^,四棱锥P ABCD -的体积为GE 与平面PCD 所成角的正弦值.【变式8-2】(2024·湖北武汉·华中师大一附中校考模拟预测)如图,平行六面体1111ABCD A B C D -中,点P 在对角线1BD 上,AC BD O =I ,平面ACP ∥平面11AC D .(1)求证:O ,P ,1B 三点共线;(2)若四边形ABCD 是边长为2的菱形,11π3BAD BAA DAA =ÐÐ==Ð,13AA =,求二面角P AB C --大小的余弦值.【变式8-3】(2024·全国·模拟预测)已知菱形ABCD 中,1AB BD ==,四边形BDEF 为正方形,满足2π3ABF Ð=,连接AE ,AF ,CE ,CF .(1)证明:CF AE ^;(2)求直线AE 与平面BDEF 所成角的正弦值.题型九:数学文化与新定义问题【典例9-1】(2024·高三·山东青岛·期中)某校积极开展社团活动,在一次社团活动过程中,一个数学兴趣小组发现《九章算术》中提到了“刍薨”这个五面体,于是他们仿照该模型设计了一道数学探究题,如图1,E 、F 、G 分别是边长为4的正方形的三边AB CD AD 、、的中点,先沿着虚线段FG 将等腰直角三角形FDG 裁掉,再将剩下的五边形ABCFG 沿着线段EF 折起,连接AB CG 、就得到了一个“刍甍” (如图2)。
立体几何知识点总结(全)

立体几何知识点总结(全)垂直直线:相交成直角的直线。
三.点与平面的位置关系点在平面上:点在平面内部;点在平面外:点在平面的一侧;点在平面上方或下方:只有在三维空间中才有,点在平面上方或下方的判断需要借助向量的概念。
四.直线与平面的位置关系直线在平面上:直线的每一个点都在平面上;直线与平面相交:有且只有一个交点;直线与平面平行:没有交点,且方向与平面的法向量垂直;直线与平面垂直:直线方向与平面的法向量相同或相反。
五.平面与平面的位置关系两个平面相交:有且只有一条公共直线;两个平面平行:没有公共直线;两个平面重合:所有点都相同。
改写:一。
空间几何体的三视图在空间几何体中,正视图是指光线从几何体的前面向后面正投影得到的投影图,反映了物体的高度和长度。
侧视图是指光线从几何体的左面向右面正投影得到的投影图,反映了物体的高度和宽度。
俯视图是指光线从几何体的上面向下面正投影得到的投影图,反映了物体的长度和宽度。
三视图中反应的长、宽、高的特点有“长对正”,“高平齐”,“宽相等”。
二。
空间几何体的直观图斜二测画法的基本步骤包括建立适当的直角坐标系xOy (尽可能使更多的点在坐标轴上)、建立斜坐标系x'O'y',使x'O'y'=45(或135)以及画对应图形。
在已知图形平行于X轴的线段,在直观图中画成平行于X‘轴,且长度保持不变;在已知图形平行于Y轴的线段,在直观图中画成平行于Y‘轴,且长度变为原来的一半。
直观图与原图形的面积关系为S直观图= S原图/4.三。
空间几何体的表面积与体积圆柱侧面积为S侧面=2πr×l,圆锥侧面积为S侧面=πr×l,圆台侧面积为S侧面=πr×l+πR×l。
柱体的体积为V柱体=S×h,锥体的体积为V锥体=S×h/3,台体的体积为V台体=S上+S下+√S上×S下×h/3.球的表面积和体积分别为S=4πR2和V球=4πR3/3.正三棱锥是底面是等边三角形,三个侧面是全等的等腰三角形的三棱锥,正四面体是每个面都是全等的等边三角形的三棱锥。
(完整word)高考立体几何知识点总结(详细),推荐文档

高考立体几何知识点总结一 、空间几何体 (一) 空间几何体的类型1 多面体:由若干个平面多边形围成的几何体。
围成多面体的各个多边形叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点。
2 旋转体:把一个平面图形绕它所在的平面内的一条定直线旋转形成了封闭几何体。
其中,这条直线称为旋转体的轴。
(二) 几种空间几何体的结构特征 1 、棱柱的结构特征1.1 棱柱的定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
1.2 棱柱的分类棱柱四棱柱平行六面体直平行六面体长方体正四棱柱正方体 性质:Ⅰ、侧面都是平行四边形,且各侧棱互相平行且相等; Ⅱ、两底面是全等多边形且互相平行; Ⅲ、平行于底面的截面和底面全等;1.3 棱柱的面积和体积公式ch S 直棱柱侧(c 是底周长,h 是高)S 直棱柱表面 = c ·h+ 2S 底 V 棱柱 = S 底 ·h2 、棱锥的结构特征2.1 棱锥的定义(1) 棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
(2)正棱锥:如果有一个棱锥的底面是正多边形,并且顶点在底面的投影是底棱长都相等底面是正方形底面是矩形侧棱垂直于底面底面是平行四边形底面是四边形图1-1 棱柱面的中心,这样的棱锥叫做正棱锥。
2.2 正棱锥的结构特征Ⅰ、 平行于底面的截面是与底面相似的正多边形,相似比等于顶点到截面的距离与顶点到底面的距离之比;它们面积的比等于截得的棱锥的高与原棱锥的高的平方比;截得的棱锥的体积与原棱锥的体积的比等于截得的棱锥的高与原棱锥的高的立方比;Ⅱ、 正棱锥的各侧棱相等,各侧面是全等的等腰三角形;正棱锥侧面积:1'2S ch =正棱椎(c 为底周长,'h 为斜高) 体积:13V Sh =棱椎(S 为底面积,h 为高)正四面体:对于棱长为a 正四面体的问题可将它补成一个边长为a 22的正方体问题。
立体几何中常见模型总结归纳

正方体中包含了丰富的线面关系
A
C
B
D
A1
C1
B1
D1
观察图中的线面垂直关系
正方体中包含了丰富的线面关系
A
C
B
D
A1
C1
B1
D1
观察图中的线面垂直关系
正方体中包含了丰富的线面关系
A
C
B
D
A1
C1
B1
D1
观察图中的线面垂直关系
观察图中的线面垂直关系
A
C
B
D
A1
C1
B1
D1
正方体中包含了丰富的线面关系
常见模型归纳
Annual Work Summary Report
C
B
D
C1
B1
观察图中的线面垂直关系
01
单击添加内容标题
02
单击添加内容标题
03
单击添加内容标题
正方体中包含了丰富的线面关系
A
C
B
D
A1
C1
B1
D1
观察图中的线面垂直关系
正方体中包含了丰富的线面关系
A
C
B
D
A1
C1
B1
D1
观察图中的线面垂直关系
A
C
B
D
A1
C1
B1
D1
正方体中包含了丰富的线面关系
A
C
B
D
A1
C1
B1
D1
观察图中的不变的线面关系源自ACBD
B1
A1
C1
D1
观察图中的不变的线面关系
正方体中包含了其他几何模型
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 正方体中包含了丰富的线面关系
观察图中的线面垂直关系
D1 A1
D A
C1 B1C B•正方体中包含了丰富的线面关系观察图中的线面垂直关系
D1 A1
C1 B1
D A
C B
• 正方体中包含了丰富的线面关系
观察图中的线面垂直关系
D1 A1
C1 B1
D A
C B
• 正方体中包含了丰富的线面关系
观察图中的线面垂直关系
D1 A1
C1 B1
D1 A1
C1 B1
D A
C
D
B
A
C B
• 正方体中包含了丰富的线面关系
观察图中的不变的线面关系
D1 A1
D
C1 B1
C
AB 侧 面ADD1A1 BC 侧 面DCC 1D1
所 以 四 棱 锥D ABCD 中 的 四 个 三 角 形 都 是 直 角 三角 形
A
B
• 正方体中包含了其他几何模型 观察图中的不变的线面关系
D1 A1
D
C1 B1
C
A
B
常见模型归纳
桓台一中 高一数学组
尹朔
• 正方体中包含了丰富的线面关系
观察图中的线面垂直关系
D1 A1
C1 B1
D A
C B
• 正方体中包含了丰富的线面关系
观察图中的线面垂直关系
D1 A1
C1 B1
D A
C B
• 正方体中包含了丰富的线面关系
观察图中的线面垂直关系
D1 A1
C1 B1
D A
C B
