算法导论第十一章答案
2018年大一轮数学理高考复习人教规范训练第十一章 算

课时规范训练 A 组 基础演练1.执行如图所示的程序框图,输出的S 值为( )A .1B .3C .7D .15解析:选C.程序框图运行如下:k =0<3,S =0+20=1,k =1<3;S =1+21=3,k =2<3;S =3+22=7,k =3.输出S =7.2.执行下面的程序框图,如果输入的N =4,那么输出的S 等于( )A .1+12+13+14B .1+12+13×2+14×3×2C .1+12+13+14+15D .1+12+13×2+14×3×2+15×4×3×2解析:选B.第一次循环,T =1,S =1,k =2;第二次循环,T =12,S =1+12,k =3;第三次循环,T =12×3,S =1+12+12×3,k =4,第四次循环,T =12×3×4,S =1+12+12×3+12×3×4,k =5,此时满足条件输出S =1+12+12×3+12×3×4,选B.3.执行如图所示的程序框图(算法流程图),输出的n 为( )A .3B .4C .5D .6解析:选B.a =1,n =1时,条件成立,进入循环体;a =32,n =2时,条件成立,进入循环体;a =75,n =3时,条件成立,进入循环体;a =1712,n =4时,条件不成立,退出循环体,此时n 的值为4.4.执行如图所示的程序框图,则输出的k 的值是( )A .3B .4C .5D .6解析:选C.由题意,得k =1时,s =1;k =2时,s =1+1=2;k =3时,s =2+4=6;k =4时,s =6+9=15;k =5时,s =15+16=31>15,此时输出的k 值为5. 5.执行如图所示的程序框图,若输入n =8,则输出S 等于( )A.49B.67C.89D.1011解析:选A.执行第一次循环后,S =13,i =4;执行第二次循环后,S =25,i =6;执行第三次循环后,S =37,i =8;执行第四次循环后,S =49,i =10;此时i =10>8,输出S =49.6.执行如图所示的程序框图,若判断框中填入“k >8?”,则输出的S =( )A .11B .20C .28D .35解析:选B.第一次循环:S =10+1=11,k =10-1=9;第二次循环:S =11+9=20,k =9-1=8,退出循环,故输出的S =20.7.执行如图所示的程序框图,则输出s 的值为( )A.34B.56C.1112D.2524解析:选D.由s =0,k =0满足条件,则k =2,s =12,满足条件;k =4,s =12+14=34,满足条件;k =6,s =34+16=1112,满足条件,k =8,s =1112+18=2524,不满足条件,此时输出s =2524,故选D.8.在如图所示的程序框图中,输入A =192,B =22,则输出的结果是( )A .0B .2C .4D .6解析:选B.输入后依次得到:C =16,A =22,B =16;C =6,A =16,B =6;C =4,A =6,B =4;C =2,A =4,B =2;C =0,A =2,B =0.故输出的结果为2.9.执行如图的程序框图,如果输入的x ,y ∈R ,那么输出的S 的最大值为( )A .0B .1C .2D .3解析:选C.在约束条件⎩⎪⎨⎪⎧x ≥0,y ≥0,x +y ≤1下,S =2x +y 的最大值应在点(1,0)处取得,即S max=2×1+0=2,显然2>1.10.如图所示的程序框图,则该程序框图表示的算法功能是( )A .输出使1×2×4×…×i ≥1 000成立的最小整数iB .输出使1×2×4×…×i ≥1 000成立的最大整数iC .输出使1×2×4×…×i ≥1 000成立的最大整数i +2D .输出使1×2×4×…×i ≥1 000成立的最小整数i +2解析:选D.该程序框图表示的算法功能是输出使1×2×4×…×i ≥1 000成立的最小整数i +2,选D.B 组 能力突破1.执行两次如图所示的程序框图,若第一次输入的a 的值为-1.2,第二次输入的a 的值为1.2,则第一次,第二次输出的a 的值分别为( )A .0.2,0.2B .0.2,0.8C .0.8,0.2D .0.8,0.8解析:选C.由程序框图可知:当a =-1.2时,∵a <0, ∴a =-1.2+1=-0.2,a <0,a =-0.2+1=0.8,a >0.∵0.8<1,输出a =0.8.当a =1.2时,∵a ≥1,∴a =1.2-1=0.2. ∵0.2<1,输出a =0.2.2.下面左图是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次为A 1,A 2,…,A 16,右图是统计茎叶图中成绩在一定范围内的学生人数的算法流程图,那么该算法流程图输出的结果是( )A .6B .10C .91D .92解析:选B.由算法流程图可知,其统计的是数学成绩大于或等于90的学生人数,由茎叶图知:数学成绩大于或等于90的学生人数为10,因此输出的结果为10.故选B.3.已知函数y =⎩⎪⎨⎪⎧log 2x ,x ≥2,2-x ,x <2.图中表示的是给定x 的值,求其对应的函数值y 的程序框图.①处应填写________;②处应填写________.解析:框图中的①就是分段函数解析式两种形式的判断条件,故填写x <2?,②就是函数的另一段表达式y =log 2x . 答案:x <2? y =log 2x4.如图是求12+22+32+…+1002的值的程序框图,则正整数n =________.解析:第一次判断执行后,i =2,s =12;第二次判断执行后, i =3,s =12+22,而题目要求计算12+22+…+1002,故n =100. 答案:1005.执行下边的程序框图,若p =0.8,则输出的n =________.解析:第一次,S =12,n =2;第二次,S =12+14,n =3;第三次,S =12+14+18,n =4.因为S =12+14+18>0.8,所以输出的n =4.答案:46.对一个作直线运动的质点的运动过程观测了8次,第i 次观测得到的数据为a i ,具体如下表所示:在对上述统计数据的分析中,一部分计算见如图所示的程序框图(其中a 是这8个数据的平均数),则输出的S 的值是________.解析:本题计算的是这8个数的方差,因为a =40+41+43+43+44+46+47+488=44,所以S =42+32+1+1+0+22+32+428=7.答案:7。
计算机算法导论_第11章

– PREDECESSOR(S, x), returns a pointer to the next smaller element in S, or NIL if x is the minimum element.
• Modifying operations: change the set.
– INSERT(S, x), augments the set S with the element pointed to by x.
k1
k4 ——
k5
k2
k7 ——
k3 —— k8
k6 ——
Chaining
• How do we insert an element?
U (universe of keys)
k1
K k4
k5
(actual keys)
k7
k6 k2
k8 k3
T ——
—— —— ——
——
——
23
k1
k4 ——
k5
k2
• DIRECT-ADDRESS-INSERT(T, x) T[key[x]] ← x
• DIRECT-ADDRESS-DELETE(T, x) T[key[x]] ← NIL
Each of these operations is fast: only O(1)
time isNULL otherwise
– This is called a direct-address table
• Operations take O(1) time!
12
Direct Addressing
13
Direct Addressing
• DIRECT-ADDRESS-SEARCH(T, k) return T [k]
CPrimer 第11章泛型算法课后习题答案
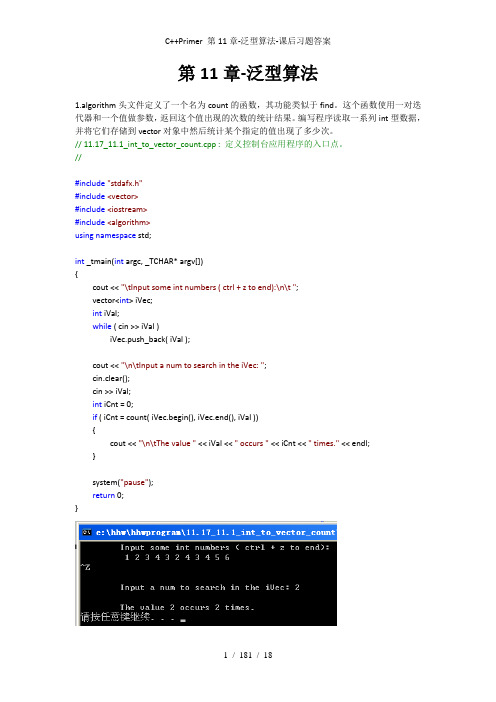
第11章-泛型算法1.algorithm头文件定义了一个名为count的函数,其功能类似于find。
这个函数使用一对迭代器和一个值做参数,返回这个值出现的次数的统计结果。
编写程序读取一系列int型数据,并将它们存储到vector对象中然后统计某个指定的值出现了多少次。
// 11.17_11.1_int_to_vector_count.cpp : 定义控制台应用程序的入口点。
//#include"stdafx.h"#include<vector>#include<iostream>#include<algorithm>using namespace std;int _tmain(int argc, _TCHAR* argv[]){cout << "\tInput some int numbers ( ctrl + z to end):\n\t ";vector<int> iVec;int iVal;while ( cin >> iVal )iVec.push_back( iVal );cout << "\n\tInput a num to search in the iVec: ";cin.clear();cin >> iVal;int iCnt = 0;if ( iCnt = count( iVec.begin(), iVec.end(), iVal )){cout << "\n\tThe value " << iVal << " occurs " << iCnt << " times." << endl;}system("pause");return 0;}2.重复前面的程序,但是,将读入的值存储到一个string类型的list对象中。
算法导论课程作业答案

算法导论课程作业答案Introduction to AlgorithmsMassachusetts Institute of Technology 6.046J/18.410J Singapore-MIT Alliance SMA5503 Professors Erik Demaine,Lee Wee Sun,and Charles E.Leiserson Handout10Diagnostic Test SolutionsProblem1Consider the following pseudocode:R OUTINE(n)1if n=12then return13else return n+R OUTINE(n?1)(a)Give a one-sentence description of what R OUTINE(n)does.(Remember,don’t guess.) Solution:The routine gives the sum from1to n.(b)Give a precondition for the routine to work correctly.Solution:The value n must be greater than0;otherwise,the routine loops forever.(c)Give a one-sentence description of a faster implementation of the same routine. Solution:Return the value n(n+1)/2.Problem2Give a short(1–2-sentence)description of each of the following data structures:(a)FIFO queueSolution:A dynamic set where the element removed is always the one that has been in the set for the longest time.(b)Priority queueSolution:A dynamic set where each element has anassociated priority value.The element removed is the element with the highest(or lowest)priority.(c)Hash tableSolution:A dynamic set where the location of an element is computed using a function of the ele ment’s key.Problem3UsingΘ-notation,describe the worst-case running time of the best algorithm that you know for each of the following:(a)Finding an element in a sorted array.Solution:Θ(log n)(b)Finding an element in a sorted linked-list.Solution:Θ(n)(c)Inserting an element in a sorted array,once the position is found.Solution:Θ(n)(d)Inserting an element in a sorted linked-list,once the position is found.Solution:Θ(1)Problem4Describe an algorithm that locates the?rst occurrence of the largest element in a?nite list of integers,where the integers are not necessarily distinct.What is the worst-case running time of your algorithm?Solution:Idea is as follows:go through list,keeping track of the largest element found so far and its index.Update whenever necessary.Running time isΘ(n).Problem5How does the height h of a balanced binary search tree relate to the number of nodes n in the tree? Solution:h=O(lg n) Problem 6Does an undirected graph with 5vertices,each of degree 3,exist?If so,draw such a graph.If not,explain why no such graph exists.Solution:No such graph exists by the Handshaking Lemma.Every edge adds 2to the sum of the degrees.Consequently,the sum of the degrees must be even.Problem 7It is known that if a solution to Problem A exists,then a solution to Problem B exists also.(a)Professor Goldbach has just produced a 1,000-page proof that Problem A is unsolvable.If his proof turns out to be valid,can we conclude that Problem B is also unsolvable?Answer yes or no (or don’t know).Solution:No(b)Professor Wiles has just produced a 10,000-page proof that Problem B is unsolvable.If the proof turns out to be valid,can we conclude that problem A is unsolvable as well?Answer yes or no (or don’t know).Solution:YesProblem 8Consider the following statement:If 5points are placed anywhere on or inside a unit square,then there must exist two that are no more than √2/2units apart.Here are two attempts to prove this statement.Proof (a):Place 4of the points on the vertices of the square;that way they are maximally sepa-rated from one another.The 5th point must then lie within √2/2units of one of the other points,since the furthest from the corners it can be is the center,which is exactly √2/2units fromeach of the four corners.Proof (b):Partition the square into 4squares,each with a side of 1/2unit.If any two points areon or inside one of these smaller squares,the distance between these two points will be at most √2/2units.Since there are 5points and only 4squares,at least two points must fall on or inside one of the smaller squares,giving a set of points that are no more than √2/2apart.Which of the proofs are correct:(a),(b),both,or neither (or don’t know)?Solution:(b)onlyProblem9Give an inductive proof of the following statement:For every natural number n>3,we have n!>2n.Solution:Base case:True for n=4.Inductive step:Assume n!>2n.Then,multiplying both sides by(n+1),we get(n+1)n!> (n+1)2n>2?2n=2n+1.Problem10We want to line up6out of10children.Which of the following expresses the number of possible line-ups?(Circle the right answer.)(a)10!/6!(b)10!/4!(c) 106(d) 104 ·6!(e)None of the above(f)Don’t knowSolution:(b),(d)are both correctProblem11A deck of52cards is shuf?ed thoroughly.What is the probability that the4aces are all next to each other?(Circle theright answer.)(a)4!49!/52!(b)1/52!(c)4!/52!(d)4!48!/52!(e)None of the above(f)Don’t knowSolution:(a)Problem12The weather forecaster says that the probability of rain on Saturday is25%and that the probability of rain on Sunday is25%.Consider the following statement:The probability of rain during the weekend is50%.Which of the following best describes the validity of this statement?(a)If the two events(rain on Sat/rain on Sun)are independent,then we can add up the twoprobabilities,and the statement is true.Without independence,we can’t tell.(b)True,whether the two events are independent or not.(c)If the events are independent,the statement is false,because the the probability of no rainduring the weekend is9/16.If they are not independent,we can’t tell.(d)False,no matter what.(e)None of the above.(f)Don’t know.Solution:(c)Problem13A player throws darts at a target.On each trial,independentlyof the other trials,he hits the bull’s-eye with probability1/4.How many times should he throw so that his probability is75%of hitting the bull’s-eye at least once?(a)3(b)4(c)5(d)75%can’t be achieved.(e)Don’t know.Solution:(c),assuming that we want the probability to be≥0.75,not necessarily exactly0.75.Problem14Let X be an indicator random variable.Which of the following statements are true?(Circle all that apply.)(a)Pr{X=0}=Pr{X=1}=1/2(b)Pr{X=1}=E[X](c)E[X]=E[X2](d)E[X]=(E[X])2Solution:(b)and(c)only。
《算法导论》习题答案

Chapter2 Getting Start2.1 Insertion sort2.1.2 将Insertion-Sort 重写为按非递减顺序排序2.1.3 计算两个n 位的二进制数组之和2.2 Analyzing algorithms2.2.1将函数32/10001001003n n n --+用符号Θ表示2.2.2写出选择排序算法selection-sort当前n-1个元素排好序后,第n 个元素已经是最大的元素了.最好时间和最坏时间均为2()n Θ2.3 Designing algorithms2.3.3 计算递归方程的解22()2(/2)2,1k if n T n T n n if n for k =⎧=⎨+ = >⎩ (1) 当1k =时,2n =,显然有()lg T n n n =(2) 假设当k i =时公式成立,即()lg 2lg22i i i T n n n i ===⋅,则当1k i =+,即12i n +=时,111111()(2)2(2)222(1)22lg(2)lg i i i i i i i i T n T T i i n n ++++++==+=⋅+=+== ()lg T n n n ∴ =2.3.4 给出insertion sort 的递归版本的递归式(1)1()(1)()1if n T n T n n if n Θ =⎧=⎨-+Θ >⎩2.3-6 使用二分查找来替代insertion-sort 中while 循环内的线性扫描,是否可以将算法的时间提高到(lg )n n Θ?虽然用二分查找法可以将查找正确位置的时间复杂度降下来,但是移位操作的复杂度并没有减少,所以最坏情况下该算法的时间复杂度依然是2()n Θ2.3-7 给出一个算法,使得其能在(lg )n n Θ的时间内找出在一个n 元素的整数数组内,是否存在两个元素之和为x首先利用快速排序将数组排序,时间(lg )n n Θ,然后再进行查找: Search(A,n,x)QuickSort(A,n);i←1; j←n;while A[i]+A[j]≠x and i<jif A[i]+A[j]<xi←i+1elsej←j -1if A[i]+A[j]=xreturn trueelsereturn false时间复杂度为)(n Θ。
《算法导论(第二版)》(中文版)课后答案

5
《算法导论(第二版) 》参考答案 do z←y 调用之前保存结果 y←INTERVAL-SEARCH-SUBTREE(y, i) 如果循环是由于y没有左子树,那我们返回y 否则我们返回z,这时意味着没有在z的左子树找到重叠区间 7 if y≠ nil[T] and i overlap int[y] 8 then return y 9 else return z 5 6 15.1-5 由 FASTEST-WAY 算法知:
15
lg n
2 lg n1 1 2cn 2 cn (n 2 ) 2 1
4.3-1 a) n2 b) n2lgn c) n3 4.3-4
2
《算法导论(第二版) 》参考答案 n2lg2n 7.1-2 (1)使用 P146 的 PARTION 函数可以得到 q=r 注意每循环一次 i 加 1,i 的初始值为 p 1 ,循环总共运行 (r 1) p 1次,最 终返回的 i 1 p 1 (r 1) p 1 1 r (2)由题目要求 q=(p+r)/2 可知,PARTITION 函数中的 i,j 变量应该在循环中同 时变化。 Partition(A, p, r) x = A[p]; i = p - 1; j = r + 1; while (TRUE) repeat j--; until A[j] <= x; repeat i++; until A[i] >= x; if (i < j) Swap(A, i, j); else return j; 7.3-2 (1)由 QuickSort 算法最坏情况分析得知:n 个元素每次都划 n-1 和 1 个,因 为是 p<r 的时候才调用,所以为Θ (n) (2)最好情况是每次都在最中间的位置分,所以递推式是: N(n)= 1+ 2*N(n/2) 不难得到:N(n) =Θ (n) 7.4-2 T(n)=2*T(n/2)+ Θ (n) 可以得到 T(n) =Θ (n lgn) 由 P46 Theorem3.1 可得:Ω (n lgn)
《算法分析与设计》(李春葆版)课后选择题答案与解析

《算法及其分析》课后选择题答案及详解第1 章——概论1.下列关于算法的说法中正确的有()。
Ⅰ.求解某一类问题的算法是唯一的Ⅱ.算法必须在有限步操作之后停止Ⅲ.算法的每一步操作必须是明确的,不能有歧义或含义模糊Ⅳ.算法执行后一定产生确定的结果A.1个B.2个C.3个D.4个2.T(n)表示当输入规模为n时的算法效率,以下算法效率最优的是()。
A.T(n)=T(n-1)+1,T(1)=1B.T(n)=2nC.T(n)= T(n/2)+1,T(1)=1D.T(n)=3nlog2n答案解析:1.答:由于算法具有有穷性、确定性和输出性,因而Ⅱ、Ⅲ、Ⅳ正确,而解决某一类问题的算法不一定是唯一的。
答案为C。
2.答:选项A的时间复杂度为O(n)。
选项B的时间复杂度为O(n)。
选项C 的时间复杂度为O(log2n)。
选项D的时间复杂度为O(nlog2n)。
答案为C。
第3 章─分治法1.分治法的设计思想是将一个难以直接解决的大问题分割成规模较小的子问题,分别解决子问题,最后将子问题的解组合起来形成原问题的解。
这要求原问题和子问题()。
A.问题规模相同,问题性质相同B.问题规模相同,问题性质不同C.问题规模不同,问题性质相同D.问题规模不同,问题性质不同2.在寻找n个元素中第k小元素问题中,如快速排序算法思想,运用分治算法对n个元素进行划分,如何选择划分基准?下面()答案解释最合理。
A.随机选择一个元素作为划分基准B.取子序列的第一个元素作为划分基准C.用中位数的中位数方法寻找划分基准D.以上皆可行。
但不同方法,算法复杂度上界可能不同3.对于下列二分查找算法,以下正确的是()。
A.intbinarySearch(inta[],intn,int x){intlow=0,high=n-1;while(low<=high){intmid=(low+high)/2;if(x==a[mid])returnmid;if(x>a[mid])low=mid;elsehigh=mid;}return –1;}B.intbinarySearch(inta[],intn,int x) { intlow=0,high=n-1;while(low+1!=high){intmid=(low+high)/2;if(x>=a[mid])low=mid;elsehigh=mid;}if(x==a[low])returnlow;elsereturn –1;}C.intbinarySearch(inta[],intn,intx) { intlow=0,high=n-1;while(low<high-1){intmid=(low+high)/2;if(x<a[mid])high=mid;elselow=mid;}if(x==a[low])returnlow;elsereturn –1;}D.intbinarySearch(inta[],intn,int x) {if(n>0&&x>=a[0]){intlow= 0,high=n-1;while(low<high){intmid=(low+high+1)/2;if(x<a[mid])high=mid-1;elselow=mid;}if(x==a[low])returnlow;}return –1;}答案解析:1.答:C。
《算法导论》习题答案

n/2
n! nn , n! o(nn )
3.2.4 是否多项式有界 lg n !与 lg lg n !
设lgn=m,则 m! 2 m ( )m e2m ( )m em(ln m1) mln m1 nln ln n
∴lgn!不是多项式有界的。
T (n) O(lg n)
4.1.2 证明 T (n) 2T (n) n 的解为 O(n lg n)
设 T (n) c n lg n
T (n) 2c n lg n n c lg n n n c(n 1) lg(n / 2) n cn lg n c lg n cn n cn(lg n 1) n c(lg n 2n)
虽然用二分查找法可以将查找正确位置的时间复杂度降下来,但 是移位操作的复杂度并没有减少, 所以最坏情况下该算法的时间复杂 度依然是 (n2 )
2.3-7 给出一个算法, 使得其能在 (n lg n) 的时间内找出在一个 n 元
素的整数数组内,是否存在两个元素之和为 x
首先利用快速排序将数组排序,时间 (n lg n) ,然后再进行查找:
sin(n / 2) 2 1,所以 af (n / b) cf (n) 不满足。 2(sin n 2)
4.1.6 计算 T (n) 2T (
令 m lg n, T (2 ) 2T (2
m m/ 2
n ) 1 的解
) 1
令 T(n)=S(m),则 S (m) 2S (m / 2) 1 其解为 S (m) (m),T (n) S (m) (lg n)
4.2 The recursion-tree method 4.2.1 4.2.2 4.2.3 4.2.5 略
算法与数据结构课后答案9-11章

算法与数据结构课后答案9-11章第9章集合一、基础知识题9.1 若对长度均为n 的有序的顺序表和无序的顺序表分别进行顺序查找,试在下列三种情况下分别讨论二者在等概率情况下平均查找长度是否相同?(1)查找不成功,即表中没有和关键字K 相等的记录;(2)查找成功,且表中只有一个和关键字K 相等的记录;(3)查找成功,且表中有多个和关键字K 相等的记录,要求计算有多少个和关键字K 相等的记录。
【解答】(1)平均查找长度不相同。
前者在n+1个位置均可能失败,后者失败时的查找长度都是n+1。
(2)平均查找长度相同。
在n 个位置上均可能成功。
(3)平均查找长度不相同。
前者在某个位置上(1<=i<=n)查找成功时,和关键字K 相等的记录是连续的,而后者要查找完顺序表的全部记录。
9.2 在查找和排序算法中,监视哨的作用是什么?【解答】监视哨的作用是免去查找过程中每次都要检测整个表是否查找完毕,提高了查找效率。
9.3 用分块查找法,有2000项的表分成多少块最理想?每块的理想长度是多少?若每块长度为25 ,平均查找长度是多少?【解答】分成45块,每块的理想长度为45(最后一块长20)。
若每块长25,则平均查找长度为ASL=(80+1)/2+(25+1)/2=53.5(顺序查找确定块),或ASL=19(折半查找确定块)。
9.4 用不同的输入顺序输入n 个关键字,可能构造出的二叉排序树具有多少种不同形态? 【解答】 9.5 证明若二叉排序树中的一个结点存在两个孩子,则它的中序后继结点没有左孩子,中序前驱结点没有右孩子。
【证明】根据中序遍历的定义,该结点的中序后继是其右子树上按中序遍历的第一个结点,即右子树上值最小的结点:叶子结点或仅有右子树的结点,没有左孩子;而其中序前驱是其左子树上按中序遍历的最后个结点,即左子树上值最大的结点:叶子结点或仅有左子树的结点,没有右孩子。
命题得证。
9.6 对于一个高度为h 的A VL 树,其最少结点数是多少?反之,对于一个有n 个结点的A VL 树,其最大高度是多少? 最小高度是多少?【解答】设以N h 表示深度为h 的A VL 树中含有的最少结点数。
中科大算法导论作业标准标准答案

第8次作业答案16.1-116.1-2543316.3-416.2-5参考答案:16.4-1证明中要三点:1.有穷非空集合2.遗传性3.交换性第10次作业参考答案16.5-1题目表格:解法1:使用引理16.12性质(2),按wi单调递减顺序逐次将任务添加至Nt(A),每次添加一个元素后,进行计算,{计算方法:Nt(A)中有i个任务时计算N0 (A),…,Ni(A),其中如果存在Nj (A)>j,则表示最近添加地元素是需要放弃地,从集合中删除};最后将未放弃地元素按di递增排序,放弃地任务放在所有未放弃任务后面,放弃任务集合内部排序可随意.解法2:设所有n个时间空位都是空地.然后按罚款地单调递减顺序对各个子任务逐个作贪心选择.在考虑任务j时,如果有一个恰处于或前于dj地时间空位仍空着,则将任务j赋与最近地这样地空位,并填入; 如果不存在这样地空位,表示放弃.答案(a1,a2是放弃地):<a5, a4, a6, a3, a7,a1, a2>or <a5, a4, a6, a3, a7,a2, a1>划线部分按上表di递增地顺序排即可,答案不唯一16.5-2(直接给个计算例子说地不清不楚地请扣分)题目:本题地意思是在O(|A|)时间内确定性质2(性质2:对t=0,1,2,…,n,有Nt(A)<=t,Nt(A)表示A中期限不超过t地任务个数)是否成立.解答示例:思想:建立数组a[n],a[i]表示截至时间为i地任务个数,对0=<i<n,如果出现a[0]+a[1]+…+a[i]>i,则说明A不独立,否则A独立.伪代码:int temp=0;for(i=0;i<n;i++) a[i]=0; ******O(n)=O(|A|)for(i=0;i<n;i++) a[di]++; ******O(n)=O(|A|)for(i=0;i<n;i++) ******O(n)=O(|A|) {temp+=a[i];//temp就是a[0]+a[1]+…+a[i]if(temp>i)//Ni(A)>iA不独立;}17.1-1(这题有歧义,不扣分)a) 如果Stack Operations包括Push Pop MultiPush,答案是可以保持,解释和书上地Push Pop MultiPop差不多.b) 如果是Stack Operations包括Push Pop MultiPush MultiPop,答案就是不可以保持,因为MultiPush,MultiPop交替地话,平均就是O(K).17.1-2本题目只要证明可能性,只要说明一种情况下结论成立即可17.2-1第11次作业参考答案17.3-1题目:答案:备注:最后一句话展开:采用新地势函数后对i 个操作地平摊代价:)1()())1(())(()()(1''^'-Φ-Φ+=--Φ--Φ+=Φ-Φ+=-Di Di c k Di k Di c D D c c i i i i i i17.3-2题目:答案:第一步:此题关键是定义势能函数Φ,不管定义成什么首先要满足两个条件 对所有操作i ,)(Di Φ>=0且)(Di Φ>=)(0D Φ比如令k j+=2i ,j,k 均为整数且取尽可能大,设势能函数)(Di Φ=2k;第二步:求平摊代价,公式是)1()(^-Φ-Φ+=Di Di c c i i 按上面设置地势函数示例:当k=0,^i c =…=2当k !=0,^i c =…=3 显然,平摊代价为O(1)17.3-4题目:答案:结合课本p249,p250页对栈操作地分析很容易有下面结果17.4-3题目:答案:αα=(第i次循环之后地表中地entry 假设第i个操作是TABLE_DELETE, 考虑装载因子:inum size数)/(第i次循环后地表地大小)=/i i第12 次参考答案19.1.1题目:答案:如果x不是根,则degree[sibling[x]]=degree[child[x]]=degree[x]-1如果x是根,则sibling为二项堆中下一个二项树地根,因为二项堆中根链是按根地度数递增排序,因此degree[sibling[x]]>degree[x]19.1.2题目:答案:如果x是p[x]地最左子节点,则p[x]为根地子树由两个相同地二项树合并而成,以x为根地子树就是其中一个二项树,另一个以p[x]为根,所以degree[p[x]]=degree[x]+1;如果x不是p[x]地最左子节点,假设x是p[x]地子节点中自左至右地第i个孩子,则去掉p[x]前i-1个孩子,恰好转换成第一种情况,因而degree[p[x]]=degree[x]+1+(i-1)=degree[x]+i;综上,degree[p[x]]>degree[x]19.2.2题目:题目:19.2.519.2.6第13次作业参考答案20.2-1题目:解答:20.2-3 题目:解答:20.3-1 题目:答案:20.3-2 题目:答案:第14次作业参考答案这一次请大家自己看书处理版权申明本文部分内容,包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some parts, including text, pictures, and design. Copyright is personal ownership.6ewMy。
算法导论(第二版)习题答案(英文版)

Last update: December 9, 2002
1.2 − 2 Insertion sort beats merge sort when 8n2 < 64n lg n, ⇒ n < 8 lg n, ⇒ 2n/8 < n. This is true for 2 n 43 (found by using a calculator). Rewrite merge sort to use insertion sort for input of size 43 or less in order to improve the running time. 1−1 We assume that all months are 30 days and all years are 365.
n
Θ
i=1
i
= Θ(n2 )
This holds for both the best- and worst-case running time. 2.2 − 3 Given that each element is equally likely to be the one searched for and the element searched for is present in the array, a linear search will on the average have to search through half the elements. This is because half the time the wanted element will be in the first half and half the time it will be in the second half. Both the worst-case and average-case of L INEAR -S EARCH is Θ(n). 3
C++Primer第5版第十一章课后练习答案

C++Primer第5版第⼗⼀章课后练习答案练习11.1map和vector相⽐是通过关键字⽽不是位置来查找值。
练习11.2list:需要在中间进⾏操作的情况。
vector:若没有必要使⽤其他容器则优先使⽤deque:只需要在头尾进⾏操作的情况map:字典set:key-value相同的集合练习11.3int main(int argc, char* argv[]){map<string, size_t> word_count;string word;while (cin >> word) {++word_count[word];}for (const auto& w : word_count) {cout << w.first << "" << w.second << endl;}}练习11.4int main(int argc, char* argv[]){map<string, size_t> word_count;string word;while (cin >> word) {word.erase(remove_if(word.begin(), word.end(), [](char& c) {if (isupper(c)) { tolower(c); } return ispunct(c); }));++word_count[word];}for (const auto& w : word_count) {cout << w.first << "" << w.second << endl;}}练习11.5map是关键字-值对的集合,set是关键字的集合,看使⽤场景需要key-value还是key集合练习11.6set是关联容器,进⾏查找、修改操作效率⾼list是顺序容器,插⼊删除操作效率低,随机访问速度慢练习11.7int main(int argc, char* argv[]){map<string, vector<string>> familys;string surname, name;while (cin >> surname>> name) {familys[surname].emplace_back(name);}for (const auto& f : familys) {cout << f.first << ":";for (const auto& n : f.second) {cout << n << "";}cout << endl;}}练习11.8int main(int argc, char* argv[]){vector<string> words;string word;while (cin >> word) {words.emplace_back(word);}auto it = unique(words.begin(), words.end());words.erase(it, words.end());}set查找速度快练习11.9map<string, list<size_t>> m;练习11.10不能,因为map所提供的操作必须在关键字类型上定义⼀个严格弱序,⽽迭代器之间是⽆法⽐较的练习11.11int main(int argc, char* argv[]){typedef bool (*Comp)(const Sales_data&, const Sales_data&);//和decltype(compareIsbn)*等价multiset<Sales_data, Comp>bookStore(Comp);}练习11.12int main(int argc, char* argv[]){vector<string>str_vec(10);vector<int> i_vec(10);vector<pair<string, int>> psi1;vector<pair<string, int>> psi2;vector<pair<string, int>> psi3;string str, int num;for (auto i = 0; i < 10; ++i) {cin >> str >> num;str_vec.emplace_back(str);i_vec.emplace_back(num);}for (auto i = 0; i < 10; ++i) {psi1.push_back({ str_vec[i],i_vec[i] });psi1.emplace_back(pair<string, int>(str_vec[i], i_vec[i]));psi1.emplace_back(make_pair(str_vec[i], i_vec[i]));}}练习11.13int main(int argc, char* argv[]){vector<string>str_vec(10);vector<int> i_vec(10);vector<pair<string, int>> psi1;vector<pair<string, int>> psi2;vector<pair<string, int>> psi3;string str, int num;for (auto i = 0; i < 10; ++i) {cin >> str >> num;str_vec.emplace_back(str);i_vec.emplace_back(num);}for (auto i = 0; i < 10; ++i) {psi1.push_back({ str_vec[i],i_vec[i] });//不能⽤emplace_back来进⾏pair的列表初始化psi1.emplace_back(pair<string, int>(str_vec[i], i_vec[i]));psi1.emplace_back(make_pair(str_vec[i], i_vec[i]));}}练习11.14int main(int argc, char* argv[]){map<string, vector<pair<string, string>>> familys;string surname, name, birthday;while (cin >> surname >> name>>birthday) {familys[surname].emplace_back(make_pair(name, birthday));}for (const auto& f : familys) {cout << f.first << ":";for (const auto& n : f.second) {cout << n.first << "'s birthday is "<<n.second<<"";}cout << endl;}}练习11.15mapped_type:vector<int>key_type:intvalue_type:pair<const int,vector<int>>练习11.16int main(int argc, char* argv[]){map<int, int>i_i_map;auto it = i_i_map.begin();(*it).second = 5;}练习11.17copy(v.begin(), v.end(), inserter(c, c.end()));//调⽤insert成员函数插⼊到multiset尾后迭代器之前copy(v.begin(), v.end(), back_inserter(c));//multiset没有push_back成员函数,因此⽆法使⽤copy(c.begin(), c.end(), inserter(v,v.end()));//调⽤insert成员函数插⼊到vector尾后迭代器之前copy(c.begin(), c.end(), back_inserter(v));//调⽤push_back成员函数插⼊到vector尾后迭代器之前练习11.18map<string,size_t>::iterator练习11.19int main(int argc, char* argv[]){typedef bool (*Comp)(const Sales_data&, const Sales_data&);//和decltype(compareIsbn)*等价multiset<Sales_data, Comp>bookStore(compareIsbn);multiset<Sales_data, Comp>::iterator it = bookStore.begin();}练习11.20int main(int argc, char* argv[]){map<string, size_t> word_count;string word;while (cin >> word) {auto ret = word_count.insert({ word,1 });if (!ret.second)++ret.first->second;}for (const auto& w : word_count) {cout << w.first << "" << w.second << endl;}}//下标操作更容易编写和阅读练习11.21输⼊word,并将其设置为关键字插⼊到容器中,对应的值为0,然后对值进⾏递增,若此时容器中已有重复关键字则直接对该关键字对应的值进⾏递增。
算法导论(第二版)课后习题解答

Θ
i=1
i
= Θ(n2 )
This holds for both the best- and worst-case running time. 2.2 − 3 Given that each element is equally likely to be the one searched for and the element searched for is present in the array, a linear search will on the average have to search through half the elements. This is because half the time the wanted element will be in the first half and half the time it will be in the second half. Both the worst-case and average-case of L INEAR -S EARCH is Θ(n). 3
Solutions for Introduction to algorithms second edition
Philip Bille
The author of this document takes absolutely no responsibility for the contents. This is merely a vague suggestion to a solution to some of the exercises posed in the book Introduction to algorithms by Cormen, Leiserson and Rivest. It is very likely that there are many errors and that the solutions are wrong. If you have found an error, have a better solution or wish to contribute in some constructive way please send a message to beetle@it.dk. It is important that you try hard to solve the exercises on your own. Use this document only as a last resort or to check if your instructor got it all wrong. Please note that the document is under construction and is updated only sporadically. Have fun with your algorithms. Best regards, Philip Bille
算法导论中文版答案

24.2-3
24.2-4
24.3-1 见图 24-6 24.3-2
24.3-3
24.3-4 24.3-5 24.3-6
24.3-7
24.3-8 这种情况下不会破坏已经更新的点的距离。 24.4**** 24.5****
25.1-1 见图 25-1 25.1-2 为了保证递归定义式 25.2 的正确性 25.1-3
8.3-3 8.3-4
8.3-5(*) 8.4-1 见图 8-4 8.4-2
8.4-3 3/2,1/2 8.4-4(*) 8.4-5(*)
9.1-1
9.1-2 9.2-1 9.3-1
第九章
9.3-2 9.3-3
9.3-4 9.3-5
9.3-6 9.3-7
9.3-8
9.3-9
15.1-1
6.4-4
6.4-5
6.5-1 据图 6-5 6.5-2
6.5-3 6.5-4 6.5-5
6.5-6 6.5-7
6.5-8
7.1-1 见图 7-1 7.1-2
7.1-3 7.1-4 7.2-1 7.2-2
7.2-3 7.2-4 7.2-5
第七章
7.2-6 7.3-1
7.3-2
7.4-1 7.4-2
5.3-6
6.1-1 6.1-2 6.1-3 6.1-4 6.1-5 6.1-6
第6章
6.1-7
6.2-1 见图 6-2 6.2-2
6.2-3
6.2-4
6.2-5 对以 i 为根结点的子树上每个点用循环语句实现 6.2-6
6.3-1
见图 6-3 6.3-2
6.3-3
6.4-1 见图 6-4 6.4-2 HEAPSORT 仍然正确,因为每次循环的过程中还是会运行 MAX-HEAP 的过程。 6.4-3
算法导论中文版答案

} cout<<len<<endl; } return 0; } 15.5-1
15.5-2 15.5-3
15.5-4
16.1-1
第 16 章
16.1-2 16.1-3
16.1-4 16.2-1 16.2-2
16.2-3
16.2-4
16.2-5 16.2-6
16.2-7
25.3-6
5.3-6
6.1-1 6.1-2 6.1-3 6.1-4 6.1-5 6.1-6
第6章
6.1-7
6.2-1 见图 6-2 6.2-2
6.2-3
6.2-4
6.2-5 对以 i 为根结点的子树上每个点用循环语句实现 6.2-6
6.3-1
见图 6-3 6.3-2
6.3-3
6.4-1 见图 6-4 6.4-2 HEAPSORT 仍然正确,因为每次循环的过程中还是会运行 MAX-HEAP 的过程。 6.4-3
6.4-4
6.4-5
6.5-1 据图 6-5 6.5-2
6.5-3 6.5-4 6.5-5
6.5-6 6.5-7
6.5-8
7.1-1 见图 7-1 7.1-2
7.1-3 7.1-4 7.2-1 7.2-2
7.2-3 7.2-4 7.2-5
第七章
7.2-6 7.3-1
7.3-2
7.4-1 7.4-2
16.3-1 16.3-2
16.3-3 16.3-4
16.3-5
16.3-6 那就推广到树的结点有三个孩子结点,证明过程同引理 16.3 的证明。 16.3-7 16.3-8
第 24 章
24.1-1 同源顶点 s 的运行过程,见图 24-4 24.1-2
算法导论 第三版 第十一章 答案 英

Exercise 11.2-1
Under the assumption of simple uniform hashing, we will use linearity of
expectation to compute this. Suppose that all the keys are totally ordered
Exercise 11.1-4
The additional data structure will be a doubly linked list S which will behave in many ways like a stack. Initially, set S to be empty, and do nothing to initialize the huge array. Each object stored in the huge array value, and a pointer to an element of S, which contains a pointer back to the object in the huge array. To insert x, add an element y to the stack which contains a pointer to position x in the huge array. Update position A[x] in the huge array A to contain a pointer to y in S. To search for x, go to position x of A and go to the location stored there. If that location is an element of S which contains a pointer to A[x], then we know x is in A. Otherwise, x ∈/ A. To delete x, delete the element of S which is pointed to by A[x]. Each of these takes O(1) and there are at most as many elements in S as there are valid elements in A.
