复习全程测评卷
h子甲全程测评试卷八年级下册语文第一部分专项复习试卷(三)名

h子甲全程测评试卷八年级下册语文第一部分专项复习试卷(三)名一、现代文阅读(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1~3题。
中华文明源远流长,从诗书礼乐到钟鼎彝器,博大精深的古典文化,素来为国人所津津乐道。
然而一到谈及传统建筑,多数人不是一脸茫然,便是心怀遗憾。
保存下来的古建筑本就不多,往往还被岁月剥去了光彩,有几分“土里土气”,相形之下,欧洲古建筑遍地开花,如风光片里古堡的坚固伟岸、教堂的华丽炫酷,让人如何与之一较高下?此言差矣。
以中西古建筑最显著的对比,即材料上的土木和砖石为例。
乍看之下,木质建筑简朴,易朽,扁平,似乎很难与巍峨高耸的石头教堂一争高下。
有人把这归咎于古人的技术不行,或材料短缺。
但事实上,中华大地并不缺石材,古代冶金技术的世界领先,石料开采加工的器具也更先进。
同时,老祖宗们并非完全不用石料修筑,譬如陵墓,在他们看来,才是该用石头堆砌的。
而从秦汉陵墓的空间布局、工程结构之精妙来看,早在那个时代,我们的砖石建筑就已经达到了相当高的水准。
因此,对于砖石建筑,古人“非不能也,乃不为也”。
就像中国传统绘画对散点透视的情有独钟一个样,形式和质料上的偏好,其实是一种文化选择。
追根溯源,审美偏好的出发点,还取决于人与环境的相处方式。
欧洲建筑多以石砌,呈竖向耸立之势,以求“飞升天国”的不朽。
而中国建筑的外部形态,基本是横平舒展,寄寓着华夏先民对土地的依恋。
在中国古人心中,石头冰冷坚硬,缺乏生气,太过疏离自然,至于寻常起居,则一定要置身于“生生之气”的土木之中,以求“天人合一”的居住理想。
中西建筑在文化体系中的“地位”也不尽相同。
在西方,建筑是主要的文化载体,法国作家雨果就曾说过,“建筑是石头的史书”,一切艺术门类都须为建筑服务,绘画之,雕刻之,咏叹之,摹写之,以图将其打造为“高大上”的永恒纪念碑。
而古老的东方中国就不这么看了:文字才是千古之承载,不朽之盛事。
相比于文字上的“理想主义”,中国人在对待建筑上体现出了充分的“实用主义”态度。
新人教版六年级数学下册总复习测试卷(三)含答案

新⼈教版六年级数学下册总复习测试卷(三)含答案总复习测试卷(三)⼀、填空题。
侮题3分,共30分)1 .扇形统计图可以清楚地表⽰出()和()之间的关系;()统计图不但可以表⽰出数量的多少,⽽且可以清楚地表⽰出数量增减变化的情况。
2. —个盒⼦⾥有8个红球,4个蓝球,2个⽩球,它们的⼤⼩、形状⼀样,从中任意摸⼀个球,摸到()球的可能性最⼤,摸到()球的可能性最⼩。
3. 右图是六(1)班图书⾓藏书情况统计图。
(1)童话书占图书总数的()%。
(2)如果科技书有150本,那么作⽂书有()本。
4. 在⼀个条形统计图⾥,若⽤1.5厘⽶⾼的直条表⽰10吨,则⽤()厘⽶⾼的直条表⽰40吨,⽤9厘⽶⾼的直条表⽰()吨。
5. ⼝袋⾥有9张数字卡⽚,从中任意摸出1张。
[1[6[3[9[2[5[8[7^(1)()摸到⾃然数,()摸到⼩数。
(填⼀定”可能”或不可能”)⑵摸到()的可能性⼤,摸到()的可能性⼩。
(填奇数”或偶数”)⑶摸到()、()和()的可能性相等。
(填奇数”偶数”质数”或合数”)6. 亮亮前⼏次英语测试的平均成绩为84分,这次考试要得100分,才能把这⼏次英语测试的平均成绩提到86分,这是第()次测试。
7. 在学校组织的校园舞⽐赛中,七位评委⽼师给六(2)班的评分分别是:9.45、9.47、9.38、9.55、9.24、9.35、9.40。
去掉⼀个最⾼分和⼀个最低分,六(2)班最终平均得分是()。
&有三张数字卡⽚[4 , 15 , |_6,任意选两个组成两位数,两位数是奇数的⼩芳赢,两位数是偶数的⼩玲赢,她们两⼈中()赢的可能性⼤。
9. 要统计学校各社团⼈数,应绘制()统计图;要统计午餐各种营养成分所占的百分⽐,应绘制()统计图;要统计⽂⽂6-12 岁体重变化情况,应绘制()统计图。
10. 跳绳⽐赛前,采⽤⽯头”剪⼑”布”的游戏⽅法确定谁先跳,这种游戏规则是()的。
(填公平”或不公平”)⼆、判断题。
2023-2024新北师大版小学5五年级数学下册全册全程测评卷(附答案)

第一单元测试卷(满分:100分时间:90分钟)姓名:得分:一、认真思考,细心填写。
(每空1分,共31分)1.43+65,因为这两个加数的分母不同,也就是()不同,所以不能直接相加。
2.计算21+31时可以这样想,21是()个61,31是()个61,21+31就是()个61加()个61,等于()个61,也就是)()(。
3.53的分数单位是)()(,与85的分数单位相差)()(。
4.32比1少(),31米比61米多(),比54米长203米的是()米。
5.分数单位是151的最大真分数和分数单位是61的最小假分数的和是()。
6.在○里填上“>”“<”或“=”。
43○0.8 1.8○5961+31+0.5○185-31○2143-52○1031-132○2161+92○3243+41○51+5481-(41-81)○81-41+817.一块花圃,其中61种月季,32种郁金香,月季和郁金香一共占这块地的)()(。
8.一根木头,用去32米,还剩2119米,这根木头原来长()米。
9.一根长6米的绳子,用去21米,还剩()米。
10.一堆煤重8吨,如果用去总量的41,那么还剩下这堆煤的)()(。
如果用去41吨,那么还剩下()吨。
11.一根铁丝长54米,比另一根铁丝短41米,两根铁丝一共长()米。
五年级数学(下)(BS 版)12.把一块饼平均切成8块,妈妈吃了21块,小明吃了2块,还剩下)()(块。
13.一批化肥,第一天运走了它的31,第二天运走了它的52,还剩这批化肥的)()(没有运。
14.三个分数的和是1213,它们的分子都是l,分母是相邻的三个自然数,这三个分数是()。
二、火眼金睛,准确判断。
(每题1分,共7分)1.计算31+43,先通分再相加,是为了统一它们的分数单位。
()2.分数加减混合运算的运算顺序,和整数加减混合运算的运算顺序相同。
()3.整数加法的交换律、结合律对分数加法不适用。
()4.95+83-95+83=0()5.一根电线用去41,还剩下43米。
全程测评卷难度系数

全程测评卷难度系数【引言】作为一名职业写手,我经常收到同学们关于全程测评卷难度系数的问题。
为了帮助大家更好地应对这类考试,本文将详细分析全程测评卷的难度系数,并提供相应的应对策略。
【全程测评卷难度的具体分析】一、题目设置全程测评卷的题目设置通常包括基础题、提高题和拓展题三部分。
其中,基础题占比较大,考查学生对基本知识的掌握程度;提高题和拓展题则考查学生的综合运用能力和创新能力。
在全程测评卷中,题目设置会有一定程度的难度分布,以保证考试的区分度。
二、试题分布全程测评卷的试题分布通常遵循以下原则:重点知识重点考查,难点知识适当考查,基本知识全面考查。
这样可以保证考试的全面性和针对性。
此外,试卷还会设置一定数量的拔高题,以考查学生的应变能力和学科素养。
三、考查范围全程测评卷的考查范围较广,涵盖课程标准要求的所有知识点。
因此,在备考过程中,同学们要确保对各个知识点都有所了解,避免在考试中因为某个知识点的遗漏而失分。
【应对策略】一、备考方法1.制定合理的学习计划,确保各个知识点的学习时间分配;2.依据教材和课程标准,系统梳理各学科知识点;3.针对薄弱环节,进行有针对性的复习和强化训练。
二、考试技巧1.先易后难,合理分配答题时间;2.审题要认真,避免因为理解偏差而失分;3.答题要有条理,论述清晰;4.注重学科素养的展现,提高得分概率。
三、心理调适1.保持良好的作息,确保充足的睡眠;2.调整心态,避免过度紧张;3.增强信心,相信自己的能力。
【总结】全程测评卷难度系数较高,但只要同学们掌握正确的备考方法、考试技巧和心理调适策略,完全有能力在考试中取得好成绩。
2023-2024人教版小学5五年级数学下册全册全程测评卷(附答案)
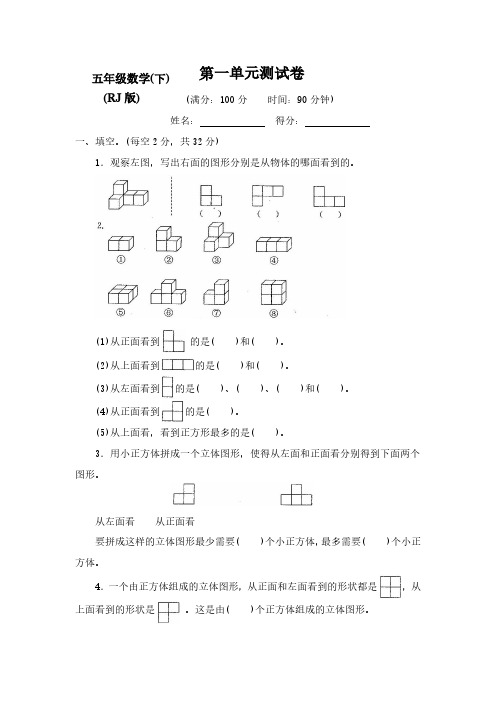
第一单元测试卷(满分:100分时间:90分钟)姓名:得分:一、填空。
(每空2分,共32分)1.观察左图,写出右面的图形分别是从物体的哪面看到的。
(1)从正面看到的是()和()。
(2)从上面看到的是()和()。
(3)从左面看到的是()、()、()和()。
(4)从正面看到的是()。
(5)从上面看,看到正方形最多的是()。
3.用小正方体拼成一个立体图形,使得从左面和正面看分别得到下面两个图形。
从左面看从正面看要拼成这样的立体图形最少需要()个小正方体,最多需要()个小正方体。
4.一个由正方体组成的立体图形,从正面和左面看到的形状都是,从上面看到的形状是。
这是由()个正方体组成的立体图形。
五年级数学(下)(RJ 版)二、判断。
(正确的画“√”,错误的画“×”)(每题2分,共10分)1.从上面看到的形状是。
()2.从正面、左面、上面看到的形状都相同。
()3.根据“横看成岭侧成峰”这句诗可以知道,诗人是从两个方向看庐山的。
()4.用4个完全相同的正方体能拼成一个更大的正方体。
()5.从左面看是。
()三、选择。
(将正确答案的序号填在括号里)(每题2分,共10分)1.()从正面看到的形状是,从左面看到的形状是。
2.从的左面看,能看到()个正方形。
①5②3③43.一个由正方体组成的立体图形,从不同方向观察得到的图形如下图,这是由()个正方体组成的立体图形。
从正面看从左面看从上面看①9②6③34.去掉一个小正方体后,从左面看不可能是()。
5.如果用□表示1个正方体,用表示2个同样大小的正方体叠加,用■表示3个同样大小的正方体叠加,那么右图是由6个同样大小的正方体叠加的几何体,从上面观察,可画出的平面图形是()。
四、连一连。
(每题6分,共18分)从左面看从正面看从上面看2.正方体的六个面都按相同的规律标有A、B、C、D、E、F六个字母,请你仔细观察已有的字母,判断A、B、C的对面各是什么字母?A的对面B的对面C的对面D E F从左面看从正面看五、下面的立体图形从正面、左面和上面看到的形状分别是什么?请你画一画。
全程测评试卷六年级下数学

1. 下列各数中,哪个数是质数?A. 25B. 29C. 24D. 352. 一个长方形的长是6厘米,宽是4厘米,它的周长是多少厘米?A. 20厘米B. 24厘米C. 30厘米D. 36厘米3. 小明有12个苹果,他给了小红6个,小红又给了小刚2个,现在小明还剩多少个苹果?A. 4个B. 6个C. 8个D. 10个4. 下列哪个图形是轴对称图形?A. 长方形B. 正方形C. 三角形D. 圆形5. 一个数的因数有1、2、3、4、6,这个数可能是:A. 10B. 12C. 15D. 186. 一个平行四边形的底是8厘米,高是5厘米,它的面积是多少平方厘米?A. 40平方厘米B. 42平方厘米C. 44平方厘米D. 46平方厘米7. 小华的年龄是小明的3倍,小明的年龄是小红的2倍,如果小红12岁,那么小华的年龄是多少岁?A. 24岁B. 18岁C. 15岁D. 12岁8. 一个圆的半径是5厘米,它的直径是多少厘米?A. 10厘米B. 15厘米C. 20厘米D. 25厘米9. 下列哪个数是奇数?A. 18B. 20C. 22D. 2410. 一个长方体的长、宽、高分别是3厘米、4厘米、5厘米,它的体积是多少立方厘米?A. 60立方厘米B. 72立方厘米C. 90立方厘米D. 108立方厘米11. 0.5 + 0.25 = _______12. 8 - 3.2 = _______13. 9 × 6 = _______14. 36 ÷ 4 = _______15. 5 + 7 + 9 = _______16. 12 - 8 ÷ 2 = _______17. 0.3 × 0.5 = _______18. 2.5 × 4 = _______19. 7 ÷ 0.7 = _______20. 0.2 + 0.8 = _______三、解答题(每题10分,共40分)21. 用简便方法计算下列各题:(1) 8.5 + 1.5 + 2.5(2) 12.3 - 4.5 - 2.8(3) 6.7 × 0.3(4)0.8 ÷ 0.222. 小明家离学校有300米,他每天骑自行车上学,速度是每分钟200米,他骑自行车上学需要多少分钟?23. 一个正方形的周长是24厘米,求它的面积。
【推荐】新人教版小学6六年级数学下册全册全程测评试卷

人教版六年级数学下册全套试卷(新教材)特别说明:本试卷为最新人教版教材(新版)配套试卷。
全套试卷共22 份(含答案)。
试卷内容如下:1.第一单元测评卷12.分类测评卷(三)2.第二单元测评卷13.阶段测评卷(四)3.第三单元测评卷14.分类测评卷(五)4.阶段测评卷15.分类测评卷(六)5.第四单元测评卷16.分类测评卷(七)6.期中测评卷(一)17.期末测评卷(一)7.期中测评卷(二)18.期末测评卷(二)8.期中测评卷(三)19.期末测评卷(三)9.第五单元测评卷20.期末测评卷(四)10.分类测评卷(一)21.期末测评卷(五)11.分类测评卷(二) 22.期末测评卷(六)附:参考答案六年级数学(下) (RJ 版)一、填空。
(28 分)第一单元测评卷(满分:100 分 时间:90 分钟) 姓名:得分:1.像-3,-2.4,- 2……这样的数叫做( ),像+15,23,1600……这样 3的数叫做(),其中- 2读作(),+15 读作( )。
32. 在直线上表示数时,所有的负数都在 0 的( )边,所有的正数都在0的( )边。
3.一个数既不是正数,也不是负数,这个数是( )。
4.所有的负数都比 0( ),所有的正数都比 0( ),负数都比正数 ( )。
5.写出点 A 、B 、C 、D 、O 、M 所表示的数。
点 A 表示(),点 B 表示( ),点 C 表示( ),点 D 表示(),点O 表示( ) , 点 M 表示( ) 。
这些数按从大到小的顺序排列为 ()。
6.大于-1 小于+2 的整数有( )个,它们分别是()。
7.写出下面温度计上表示的度数。
( )℃ ( )℃ ( )℃8. 某农村信用合作社在国庆期间吸纳存款 150 万元,记作( )万元,支出现金 60 万元,记作( )万元。
9.如果用+88 表示股指上涨 88 个点,那么下跌 29 个点应记作( ),下跌 95 个点应记作( )。
新版人教版小学2二年级数学上册全程测评卷全套【含答案】
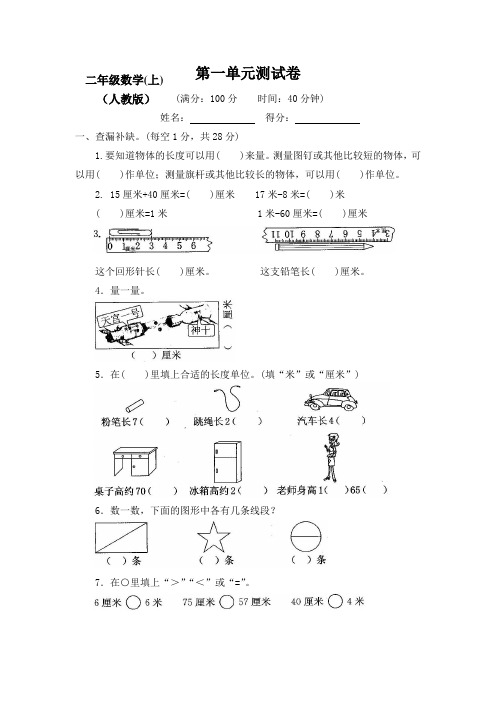
第一单元测试卷(满分:100分 时间:40分钟) 姓名: 得分: 一、查漏补缺。
(每空1分,共28分)1.要知道物体的长度可以用( )来量。
测量图钉或其他比较短的物体,可以用( )作单位;测量旗杆或其他比较长的物体,可以用( )作单位。
2. 15厘米+40厘米=( )厘米 17米-8米=( )米 ( )厘米=1米 1米-60厘米=( )厘米这个回形针长( )厘米。
这支铅笔长( )厘米。
4.量一量。
5.在( )里填上合适的长度单位。
(填“米”或“厘米”)6.数一数,下面的图形中各有几条线段?7.在○里填上“>”“<”或“=”。
二年级数学(上)(人教版)8. 1根竹竿长12米,插入水中一截后,露在水面外的部分长4米,水中部分长( )米。
二、火眼金睛。
(对的画“√”,错的画“×’’)(10分)1.米和厘米都是长度单位。
( ) 2.数学课本封面较长的一条边长约20米。
( ) 3.每条线段都是直的,都可以量出长度。
( )4. 1米长的铁丝比100厘米长的绳子短。
( )5.右图中有2条线段。
( ) 三、珠海拾贝。
(将正确答案的序号填在括号里)(10分)1.下面三条线中,( )是线段。
2.比38厘米短10厘米的是( )。
①48厘米②38厘米③28厘米3.下图中,测量方法正确的是( )。
4.下面长度最接近1米的是( )。
①教室的长②一个小朋友伸开两臂的长③一支铅笔的长5.两只小动物各画了一条线段,这两条线段中,( )。
①小熊画的长②小兔画的长③一样长四、动手操作我最棒。
(共12分)1.画一条4厘米长的线段。
(2分)2.画一条比下面的线段短3厘米的线段。
(3分)3.小老鼠的新家刚刚建成,为了自己出入方便,它想在家里的粮仓、卧室、厨房和卫生间每两个房间之间修通道。
小老鼠最多能修几条通道呢?请你帮它设计一下吧。
(7分)五、圈出合适的答案。
(16分)六、解决问题。
(共24分)(1)一只山羊比一只鸡高多少厘米?(3分)(2)一只山羊和一只鸡的身高一共是多少米?(3分)2.比身高,请你选一选,填一填。
【新】人教版小学2二年级数学下册全程测评试卷(全册)【附答案】

人教版二年级数学下册全套试卷
(新教材)
特别说明:本试卷为最新人教版教材(新版)配套试卷。
全套试卷共22份(含答案)。
试卷内容如下:
1. 第一单元测评卷1
2.第八、九单元测评卷
2. 第二单元测评卷1
3.分类测评卷(一)
3. 阶段测评卷(一)1
4.分类测评卷(二)
4. 第三单元测评卷1
5.分类测评卷(三)
5. 第四单元测评卷1
6.分类测评卷(四)
6. 第五单元测评卷1
7.期末测评卷(一)
7. 期中测评卷(一)18.期末测评卷(二)
8. 期中测评卷(二)19.期末测评卷(三)
9. 第六单元测评卷20.期末测评卷(四)
10.第七单元测评卷21.期末测评卷(五)
11.阶段测评卷(二)22.期末测评卷(六)附:参考答案。
2023-2024人教版小学3三年级数学下册全册全程测评卷(附答案)

第一单元测试卷(满分:100分时间:60分钟)姓名:得分:一、填空。
(每空1分,共24分)1.完成下面的方位示意图。
2.地图通常是按上()下(),左()右()绘制的。
3.当你面向西时,你背对着的方向一定是()。
4.我面向太阳升起的方向是(),背对的方向是(),左手指的方向是(),右手指的方向是()。
5.小红上学的时候向东走了60米,回家的时候向()走()米。
6.利用大自然也能辨别方向。
早晨,太阳从()方升起;傍晚,太阳从()方落下。
冬天下雪后,屋顶上()面的雪先融化,()面的雪后融化。
7.如果莉莉家在学校的西南方向,那么学校在莉莉家的()方向。
8.放学时,小明站在学校门口面向南面,之后他向左转走回家,他家在学校的()面。
二、判断。
(每题2分,共10分)1.小华面向东,他背对着的方向是北。
()2.一阵东风把树叶吹得向西飘去。
()3.早上,小明的影子在他的前面,那么他的后面是西方。
()4.小军上学时往东南方向走,那么他放学回家时一定往东北方向走。
()5.小力家在学校的西面,小明家在学校的东面,那么小明家在小力家的东面。
()三年级数学(下)(RJ 版)三、选择。
(每题2分,共8分)1.东南方与()方相对。
①西②东北③西南④西北2.早上国旗飘向太阳升起的方向,这时吹的是()。
①东风②南风③西风④北风3.小华家在学校的南面,小明家在学校的北面,上学时,小华和小明()而行。
放学时,小华和小明()而行。
①同向②相向③反向4.小明面向南方,先向后转,再向左转,这时小明面向()方。
①东②南③西④北四、根据地图判断正误,画“√”或“×”。
(每题2分,共16分)1.宝岛台湾在我国的东南方向。
() 2.乌鲁木齐在我国的西北方向,兰州也在我国的西北方向。
() 3.昆明在我国的东南方向,长沙在我国的西南方向。
() 4.南宁在我国的最下方。
() 5.上海在西安的东面,西安在上海的西面。
() 6.北京在广州的北面,广州在北京的南面。
六年级全程评价试卷数学

一、选择题(每题2分,共20分)1. 下列各数中,最小的质数是()A. 2B. 3C. 4D. 52. 下列各数中,最大的合数是()A. 8B. 9C. 10D. 113. 下列各数中,是两位数的是()A. 123B. 12C. 112D. 12344. 下列各数中,是三位数的是()A. 98B. 109C. 99D. 10005. 下列各数中,是正数的是()A. -5B. 0C. 3D. -86. 下列各数中,是负数的是()A. 5B. -3C. 0D. 77. 下列各数中,是偶数的是()A. 7B. 8C. 9D. 108. 下列各数中,是奇数的是()A. 4B. 5C. 6D. 79. 下列各数中,是整数的是()A. 1.2B. 3.5C. 2D. 1.110. 下列各数中,是小数的是()A. 2B. 1.5C. 0.6D. 1二、填空题(每题2分,共20分)11. 0.25的小数点向右移动两位后是______。
12. 0.6乘以100后是______。
13. 2.5除以0.5的商是______。
14. 0.3加上0.7的和是______。
15. 1.2减去0.9的差是______。
16. 4.5乘以3再除以2的商是______。
17. 7.8加上2.2再减去3.4的和是______。
18. 0.8乘以25再除以5的商是______。
19. 1.5除以0.3的商是______。
20. 0.2乘以100再减去50的差是______。
三、计算题(每题5分,共20分)21. 计算下列各题:(1)8.5 + 3.2 - 1.7(2)12.4 ÷ 1.2(3)4.6 × 2.5(4)6.8 - 3.1 + 1.922. 计算下列各题:(1)5.3 × 4.2(2)9.6 ÷ 1.2(3)7.5 + 2.4 - 3.8(4)8.1 × 0.6四、应用题(每题10分,共20分)23. 小明有20元钱,他想买一本故事书,这本书的价格是18元,他还剩下多少钱?24. 一辆汽车以每小时60千米的速度行驶,它行驶了3小时,它一共行驶了多少千米?五、解答题(每题10分,共20分)25. 请写出10个整数,并分别判断它们是正数、负数、零、奇数还是偶数。
全程测评试卷期中语文二上

一、选择题(每题2分,共20分)1. 下列词语中,加点字注音完全正确的一项是()A. 沉默(mò)沉思(chén)沉重(zhòng)B. 淘气(táo)淘汰(tāo)淘金(táo)C. 恋恋不舍(liàn)恋家(liàn)恋情(liàn)D. 漫步(màn)漫画(màn)漫不经心(màn)2. 下列句子中,没有语病的一项是()A. 他虽然成绩优秀,但从不骄傲自满。
B. 这本书不仅内容丰富,而且插图精美。
C. 我们要努力学习,争取早日实现我们的梦想。
D. 小明因为生病,所以没有参加这次比赛。
3. 下列词语中,字形、字音、字义完全正确的一项是()A. 稳如泰山(wěn)比喻非常坚固,不可动摇。
B. 水滴石穿(chuān)比喻力量虽小,只要坚持不懈,事情就能成功。
C. 雪中送炭(tàn)比喻在别人急需时给予帮助。
D. 狐假虎威(wēi)比喻依仗别人的势力来欺压人。
4. 下列句子中,使用了修辞手法的一项是()A. 这本书真好看,我一口气就读完了。
B. 天上的星星好像在向我眨眼。
C. 这个花园里的花真多,红的、黄的、蓝的,五颜六色。
D. 我们要努力学习,争取早日实现我们的梦想。
5. 下列诗句中,描写春天景色的一项是()A. 窗含西岭千秋雪,门泊东吴万里船。
B. 红酥手,黄藤酒,满城春色宫墙柳。
C. 桃花潭水深千尺,不及汪伦送我情。
D. 两情若是久长时,又岂在朝朝暮暮。
二、填空题(每空2分,共20分)6. 《游子吟》中,“谁言寸草心,报得三春晖”一句表达了诗人对母爱的赞美。
7. 《两小儿辩日》中,孔子对两个小孩的辩论态度是______。
8. 《小石潭记》中,作者通过描写小石潭的景色,抒发了对自然美景的______。
9. 《古诗两首》中,《泊船瓜洲》中“春风又绿江南岸”一句,表达了诗人对家乡的______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复习全程测评卷测试时间:120分钟满分:150分第Ⅰ卷(选择题,共60分)一、选择题(本题共12小题,每小题5分,共60分,每小题只有一个选项符合题意)1.[2016·成都诊断考试]已知集合A={x|y=4x-x2},B={x||x|≤2},则A∪B=()A.[-2,2] B.[-2,4]C.[0,2] D.[0,4]答案 B解析A={x|0≤x≤4},B={x|-2≤x≤2},故A∪B={x|-2≤x ≤4},故选B.2.[2017·重庆统考]函数y =e |x |-x 3的大致图象是( )答案 A解析 易知函数y =e |x |-x 3为非奇非偶函数,排除B ;当x <0时,y >0,排除C ;当x =2时,y =e 2-8<0,排除D ,故选A.3.[2017·呼和浩特调研]设直线y =kx 与椭圆x 24+y 23=1相交于A ,B 两点,分别过A ,B 向x 轴作垂线,若垂足恰好为椭圆的两个焦点,则k 等于( )A.32 B .±32 C .±12 D.12答案 B解析 由题意可得c =1,a =2,b =3,不妨取A 点坐标为⎝ ⎛⎭⎪⎫1,±32,则直线的斜率k =±32.4.[2016·洛阳第一次联考]如果圆x 2+y 2=n 2至少覆盖曲线f (x )=3sin πxn (x ∈R)的一个最高点和一个最低点,则正整数n 的最小值为( )A .1B .2C .3D .4答案 B解析 最小范围内的至高点坐标为⎝ ⎛⎭⎪⎫n 2,3,原点到至高点距离为半径,即n 2=n24+3⇒n =2,故选B.5.[2016·长春质量检测]运行如图所示的程序框图,则输出的S 值为( )A.29-129B.29+129C.210-1210D.210210+1 答案 A解析 由程序框图可知,输出的结果是首项为12,公比也为12的等比数列的前9项和,即29-129,故选A.6.[2017·广州调研]如图,在矩形ABCD 中,M 是BC 的中点,N 是CD 的中点,若AC →=λAM →+μBN →,则λ+μ=( )A.25B.45 C.65 D.85答案 D解析 ∵AC →=λAM →+μBN →=λ(AB →+BM →)+μ(BC →+CN →)=λ⎝ ⎛⎭⎪⎪⎫AB →+12AD →+μ⎝ ⎛⎭⎪⎪⎫AD →-12AB →=⎝ ⎛⎭⎪⎫λ-12μAB →+⎝ ⎛⎭⎪⎫12λ+μAD →,又AC →=AB →+AD →,∴⎩⎪⎨⎪⎧λ-12μ=1,12λ+μ=1,解得⎩⎪⎨⎪⎧λ=65,μ=25,∴λ+μ=85.7.[2017·贵阳检测]已知a =2- 13,b =(2log 23)- 12,c =cos50°·cos10°+cos140°sin170°,则实数a ,b ,c 的大小关系是( )A .a >c >bB .b >a >cC .a >b >cD .c >b >a答案 C解析 因为a =2- 13=⎝ ⎛⎭⎪⎫12 13 =⎝ ⎛⎭⎪⎫14 16 ,b =(2 log 23) - 12 =3- 12=⎝ ⎛⎭⎪⎫13 12=⎝⎛⎭⎪⎫127 16,所以a >b ,排除B 、D ;c =cos50°·cos10°+cos140°sin170°=sin40°cos10°-cos40°sin10°=sin30°=12=⎝ ⎛⎭⎪⎫14 12,所以b >c ,所以a >b >c ,故选C.8.[2016·浙江高考]在平面上,过点P 作直线l 的垂线所得的垂足称为点P 在直线l 上的投影.由区域⎩⎪⎨⎪⎧x -2≤0,x +y ≥0,x -3y +4≥0中的点在直线x +y -2=0上的投影构成的线段记为AB ,则|AB |=( )A .2 2B .4C .3 2D .6答案 C解析 作出不等式组所表示的平面区域如图中阴影部分所示,过点C ,D 分别作直线x +y -2=0的垂线,垂足分别为A ,B ,则四边形ABDC 为矩形,又C (2,-2),D (-1,1),所以|AB |=|CD |=(2+1)2+(-2-1)2=3 2.故选C.9.[2017·广西质检]某几何体的三视图如图所示,则该几何体的表面积为()A.24+6π B.12πC.24+12π D.16π答案 A解析由三视图可知,该几何体是由一个棱长为2的正方体与6个半径为1的半球构成的组合体,该组合体的表面由6个半球的表面(除去半球底面圆)、正方体的6个表面正方形挖去半球底面圆构成,所以6个半球的表面(除去半球底面圆)的面积之和S1等于3个球的表面积,即S1=3×4π×12=12π;正方体的6个表面正方形挖去半球底面圆的面积之和为S2=6(22-π×12)=24-6π.所以该组合体的表面积为S=S1+S2=12π+(24-6π)=24+6π.10.[2016·南京模拟]已知四面体P-ABC中,P A=4,AC=27,PB=BC=23,P A⊥平面PBC,则四面体P-ABC的外接球半径为()A.2 2 B.2 3C.4 2 D.4 3答案 A解析 P A ⊥平面PBC ,AC =27,P A =4,∴PC =23,∴△PBC 为等边三角形,设其外接圆半径为r ,则r =2,∴外接球半径为2 2.故选A.11.[2017·桂林联考]已知抛物线y 2=4x 的准线与x 轴相交于点P ,过点P 且斜率为k (k >0)的直线l 与抛物线交于A ,B 两点,F 为抛物线的焦点,若|FB |=2|F A |,则AB 的长度为( )A.32 B .2 C.172 D.17答案 C解析 依题意知P (-1,0),F (1,0),设A (x 1,y 1),B (x 2,y 2),由|FB |=2|F A |,得x 2+1=2(x 1+1),即x 2=2x 1+1 ①,∵P (-1,0),则AB 的方程为y =kx +k ,与y 2=4x 联立,得k 2x 2+(2k 2-4)x +k 2=0,则Δ=(2k 2-4)2-4k 4>0,即k 2<1,x 1x 2=1 ②,由①②得x 1=12,则A ⎝ ⎛⎭⎪⎫12,2,∴k =2-012-(-1)=223,∴x 1+x 2=52, |AB |=⎝⎛⎭⎪⎫1+89[](x 1+x 2)2-4x 1x 2=172,选C.12.[2017·河南郑州检测]已知点F 2、P 分别为双曲线x 2a 2-y 2b 2=1(a >0,b >0)的右焦点与右支上的一点,O 为坐标原点,若OM →=12(OP →+OF 2→),OF 2→2=F 2M →2,且2OF 2→·F 2M →=a 2+b 2,则该双曲线的离心率为( )A.3+12 B.32 C.3 D .2 3答案 A解析 设双曲线的左焦点为F 1,依题意知,|PF 2|=2c ,因为OM →=12(OP →+OF 2→),所以点M 为线段PF 2的中点.因为2OF 2→·F 2M →=a 2+b 2,所以OF 2→·F 2M →=c 22,所以c ×c ×cos ∠PF 2x =12c 2,所以cos ∠PF 2x =12,所以∠PF 2x =60°,所以∠PF 2F 1=120°,从而|PF 1|=23c ,根据双曲线的定义,得|PF 1|-|PF 2|=2a ,所以23c -2c =2a ,所以e =c a =13-1=3+12,故选A.第Ⅱ卷 (非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)13.[2016·北京高考]双曲线x 2a 2-y 2b 2=1(a >0,b >0)的渐近线为正方形OABC 的边OA ,OC 所在的直线,点B 为该双曲线的焦点.若正方形OABC 的边长为2,则a =________.答案 2解析 由OA 、OC 所在直线为渐近线,且OA ⊥OC ,知两条渐近线的夹角为90°,从而双曲线为等轴双曲线,则其方程为x 2-y 2=a 2.OB是正方形的对角线,且点B 是双曲线的焦点,则c =22,根据c 2=2a 2可得a =2.14.[2017·云南检测]若函数f (x )=4sin5ax -43cos5ax 的图象的相邻两条对称轴之间的距离为π3,则实数a 的值为________.答案 ±35解析 因为f (x )=8sin ⎝ ⎛⎭⎪⎫5ax -π3,依题意有,T 2=π3,所以T =2π3,又因为T =2π5|a |,所以2π5|a |=2π3,解得a =±35.15.[2017·山西怀仁期末]已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1、F 2,焦距为2c ,直线y =33(x +c )与双曲线的一个交点P 满足∠PF 2F 1=2∠PF 1F 2,则双曲线的离心率e 为________.答案3+1解析 ∵直线y =33(x +c )过左焦点F 1,且其倾斜角为30°,∴∠PF 1F 2=30°,∠PF 2F 1=60°,∴∠F 2PF 1=90°,即F 1P ⊥F 2P .∴|PF 2|=12|F 1F 2|=c ,|PF 1|=|F 1F 2|·sin60°=3c ,由双曲线的定义得2a =|PF 1|-|PF 2|=3c -c ,∴双曲线C 的离心率e =c a =c3c -c 2=3+1. 16.[2017·成都诊断]已知函数f (x )= ⎩⎪⎨⎪⎧2a -x -4x -3,x ∈(-∞,a ),x -4x -3,x ∈[a ,+∞)(a >0)有且只有3个不同的零点x 1,x 2,x 3(x 1<x 2<x 3),且2x 2=x 1+x 3,则a =________.答案 1+332解析f (x )=⎩⎪⎨⎪⎧2a -x -4x -3,x ∈(-∞,a ),x -4x -3,x ∈[a ,+∞),则当x ≥a 时,令f (x )=0,解得x =-1或x =4.①当0<a ≤4时,x 3=4,由题意知x 1,x 2是2a -x -4x -3=0,即方程x 2-(2a -3)x +4=0的两个解,所以⎩⎪⎨⎪⎧x 1+x 2=2a -3,x 1·x 2=4,2x 2=x 1+4,得a =1+332或a =1-332(舍去);②当a >4时,f (x )=0最多有两个解,不满足题意. 综上,a =1+332.三、解答题(共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.[2016·河南六市联考](本小题满分12分)如图,在一条海防警戒线上的点A 、B 、C 处各有一个水声监测点,B 、C 两点到A 的距离分别为20千米和50千米,某时刻,B 收到发自静止目标P 的一个声波信号,8秒后A 、C 同时接收到该声波信号,已知声波在水中的传播速度是1.5千米/秒.(1)设A 到P 的距离为x 千米,用x 表示B 、C 到P 的距离,并求x 的值;(2)求P 到海防警戒线AC 的距离.解 (1)依题意,有P A =PC =x ,PB =x -1.5×8=x -12.(2分)在△P AB 中,AB =20,cos ∠P AB =P A 2+AB 2-PB 22P A ·AB=x 2+202-(x -12)22x ·20=3x +325x , 同理,在△P AC 中,AC =50,cos ∠P AC =P A 2+AC 2-PC 22P A ·AC =x 2+502-x 22x ·50=25x .(4分)∵cos ∠P AB =cos ∠P AC ,∴3x +325x =25x ,解得x =31.(6分)(2)作PD ⊥AC 于点D ,在△ADP 中,由cos ∠P AD =2531,得sin ∠P AD =1-cos 2∠P AD =42131,(9分) ∴PD =P A sin ∠P AD =31×42131=421.故静止目标P 到海防警戒线AC 的距离为421千米.(12分)18.[2017·重庆八中质检](本小题满分12分)某蛋糕店每天制作生日蛋糕若干个,每个生日蛋糕的成本为50元,然后以每个100元的价格出售,如果当天卖不完,剩下的蛋糕作垃圾处理,现搜集并整理了100天生日蛋糕的日需求量(单位:个),得到如图所示的柱状图.以100天记录的各需求量的频率作为每天各需求量发生的概率.若蛋糕店一天制作17个生日蛋糕.(1)求当天的利润y (单位:元)关于当天需求量n (单位:个,n ∈N)的函数解析式;(2)求当天的利润不低于750元的概率.解 (1)当n ≥17时,y =17×(100-50)=850;当n ≤16时,y =50n -50(17-n )=100n -850.得y =⎩⎪⎨⎪⎧100n -850(n ≤16),850(n ≥17)(n ∈N).(7分) (2)设当天的利润不低于750元为事件A ,由(1)得“利润不低于750元”等价于“需求量不低于16个”,P (A )=1-10+20100=0.7.(12分)19.[2017·河北五校联考](本小题满分12分)在如图所示的三棱锥D -ABC 中,AD ⊥DC ,AB =4,AD =CD =2,∠BAC =45°,平面ACD ⊥平面ABC ,E ,F 分别在BD ,BC 上,且BE =2ED ,BC =2BF .(1)求证:BC⊥AD;(2)求平面AEF将三棱锥D-ABC分成的四棱锥A-EFCD与三棱锥E-ABF的体积之比.解(1)证明:∵AD=CD=2,AD⊥DC,∴△ACD是等腰直角三角形,AC=22,如图,取AC的中点O,连接OD,则OD⊥AC.(2分)∵平面ACD⊥平面ABC,∴OD⊥平面ABC,则OD⊥BC.∵AB=4,∠BAC=45°,∴BC=22,(4分)即△ACB是等腰直角三角形,且BC⊥AC.∵OD∩AC=O,∴BC⊥平面ACD.∵AD⊂平面ACD,∴BC⊥AD.(6分)(2)解法一:由(1)得OD =2,过E 作EH ⊥平面ABC 交OB 于点H ,则EH OD =BE BD .∵BE =2ED ,∴BE BD =23,则EH OD =BE BD =23,则EH =23OD =223.(8分)∵BC =2BF ,∴F 是BC 的中点,则BF =12BC =12×22=2,则△ABF 的面积S =12BF ×AC =12×2×22=2,则三棱锥D -ABC 的体积V =13×12AC ×BC ×OD =13×12×22×22×2=423,三棱锥E -ABF 的体积V 1=13×2×223=429,则四棱锥A -EFCD 的体积V 2=423-429=1229-429=829,则平面AEF 将三棱锥D -ABC 分成的四棱锥A -EFCD 与三棱锥E -ABF 的体积之比为829∶429=2∶1.(12分)解法二:∵V E -ABF =V A -BEF ,∴V A -EFCD ∶V E -ABF =V A -EFCD ∶V A -BEF =S 四边形EFCD ∶S △BEF .(8分)又S △BEF =12×BE ×BF sin ∠EBF , S △BCD =12×BC ×BD sin ∠CBD=12×2BF ×32BE sin ∠EBF ,∴S 四边形EFCE =S △BCD -S △BEF =BE ×BF sin ∠EBF ,∴S 四边形EFCD ∶S △BEF =2∶1, (11分)即平面AEF 将三棱锥D -ABC 分成的四棱锥A -EFCD 与三棱锥E -ABF 的体积之比为2∶1.(12分)20.[2016·全国卷Ⅲ](本小题满分12分)已知抛物线C :y 2=2x 的焦点为F ,平行于x 轴的两条直线l 1,l 2分别交C 于A ,B 两点,交C 的准线于P ,Q 两点.(1)若F 在线段AB 上,R 是PQ 的中点,证明AR ∥FQ ;(2)若△PQF 的面积是△ABF 的面积的两倍,求AB 中点的轨迹方程.解 由题知F ⎝ ⎛⎭⎪⎫12,0.设l 1:y =a ,l 2:y =b ,则ab ≠0, 且A ⎝ ⎛⎭⎪⎫a 22,a ,B ⎝ ⎛⎭⎪⎫b 22,b ,P ⎝ ⎛⎭⎪⎫-12,a ,Q ⎝ ⎛⎭⎪⎫-12,b , R ⎝ ⎛ -12,⎭⎪⎫a +b 2. 记过A ,B 两点的直线为l ,则l 的方程为2x -(a +b )y +ab =0.(3分)(1)证明:由于F 在线段AB 上,故1+ab =0.记AR 的斜率为k 1,FQ 的斜率为k 2,则k 1=a -b 1+a 2=a -b a 2-ab =1a=-ab a =-b =k 2, 所以AR ∥FQ .(5分)(2)设l 与x 轴的交点为D (x 1,0),则S △ABF =12|b -a |·|FD |=12|b -a |⎪⎪⎪⎪⎪⎪x 1-12,S △PQF =|a -b |2. 则题设可得|b -a |⎪⎪⎪⎪⎪⎪x 1-12=|a -b |2,所以x 1=0(舍去)或x 1=1. 设满足条件的AB 的中点为E (x ,y ).当AB 与x 轴不垂直时,由k AB =k DE 可得2a +b =y x -1(x ≠1),而a +b 2=y ,所以y 2=x -1(x ≠1).当AB 与x 轴垂直时,E 与D 重合,此时E 点坐标为(1,0),满足方程y 2=x -1.所以,所求轨迹方程为y 2=x -1.(12分)21.[2016·湖北八校联考](本小题满分12分)如图,在三棱柱ABC -A 1B 1C 1中,△ABC 是等边三角形,BC =CC 1=4,D 是A 1C 1中点.(1)求证:A 1B ∥平面B 1CD ;(2)当三棱锥C -B 1C 1D 体积最大时,求点B 到平面B 1CD 的距离. 解 (1)证明:连接BC 1交B 1C 于O ,连接DO .在三棱柱ABC -A 1B 1C 1中,四边形BB 1C 1C 为平行四边形,则BO =OC 1,又D 是A 1C 1中点,∴DO ∥A 1B ,而DO ⊂平面B 1CD ,A 1B ⊄平面B 1CD ,∴A 1B ∥平面B 1CD .(4分)(2)设点C 到平面A 1B 1C 1的距离是h ,则V C -B 1C 1D =13S △B 1C 1D h =233h ,而h ≤CC 1=4,故当三棱锥C -B 1C 1D 体积最大时,h =CC 1=4,即CC 1⊥平面A 1B 1C 1.(6分)由(1)知BO =OC 1,所以B 到平面B 1CD 的距离与C 1到平面B 1CD 的距离相等.∵CC 1⊥平面A 1B 1C 1,B 1D ⊂平面A 1B 1C 1,∴CC 1⊥B 1D .∵△ABC 是等边三角形,D 是A 1C 1中点,∴A 1C 1⊥B 1D ,又CC 1∩A 1C 1=C 1,CC 1⊂平面AA 1C 1C ,A 1C 1⊂平面AA 1C 1C ,∴B 1D ⊥平面AA 1C 1C ,∴B 1D ⊥CD ,由计算得:B 1D =23,CD=25,所以S △B 1CD =215,(8分)设C 1到平面B 1CD 的距离为h ′,由V C -B 1C 1D =V C 1-B 1CD ,得233×4=13S △B 1CD h ′⇒h ′=455,所以B 到平面B 1CD 的距离是455.(12分)22.[2016·兰州质检](本小题满分12分)已知椭圆C 的焦点坐标是F 1(-1,0)、F 2(1,0),过点F 2垂直于长轴的直线l 交椭圆C 于B 、D 两点,且|BD |=3.(1)求椭圆C 的方程;(2)是否存在过点P (2,1)的直线l 1与椭圆C 相交于不同的两点M 、N ,且满足PM →·PN →=54?若存在,求出直线l 1的方程;若不存在,请说明理由.解 (1)设椭圆的方程是x 2a 2+y 2b 2=1(a >b >0),则c =1,∵|BD |=3,∴2b 2a =3,又a 2-b 2=1,∴a =2,b =3, ∴椭圆C 的方程为x 24+y 23=1.(4分)(2)假设存在直线l 1且由题意得斜率存在,设满足条件的方程为y =k (x -2)+1,由⎩⎨⎧ y =k (x -2)+1,x 24+y 23=1,得(3+4k 2)x 2-8k (2k -1)x +16k 2-16k -8=0, 因为直线l 1与椭圆C 相交于不同的两点M 、N ,设M (x 1,y 1)、N (x 2,y 2),所以Δ=[-8k (2k -1)]2-4(3+4k 2)(16k 2-16k -8)>0,所以k >-12.又x 1+x 2=8k (2k -1)3+4k 2,x 1x 2=16k 2-16k -83+4k 2,(8分)因为PM →·PN →=(x 1-2)(x 2-2)+(y 1-1)(y 2-1)=54,所以(x 1-2)(x 2-2)(1+k 2)=54,即[x 1x 2-2(x 1+x 2)+4](1+k 2)=54, 所以⎣⎢⎡⎦⎥⎤16k 2-16k -83+4k 2-2·8k (2k -1)3+4k 2+4(1+k 2)=4+4k 23+4k 2=54. 解得k =±12,因为k >-12,所以k =12.故存在直线l 1满足条件,其方程为y =12x .(12分)。
