1-5 极坐标系中质点运动描述
质点运动的坐标系

r
y
1
位置矢量可表示为
r xi yj zk
j 其中 i 、和 k 分别是x、y和z方向的单位矢量。
位矢大小 r r x 2 y 2 z 2
可用方向余弦来表示位置矢量方向。
y x cos , cos , r r
z cos r
小球的加速度可表示为 :
a ut 2 u
2
由上式可以看到, 径向加速度是时间的线性函
数, 横向加速度则为常量。
22
三、自然坐标系 (natural coordinates) 沿着质点的运动轨道所建立的坐标系。 取轨道上一固定点为原点, 规定两个随质点位置
变化而改变方向的单位矢量, 一个是指向质点运动
ˆ d
dt
dt dt
dt dt
dt
dt dt
a [
d2
d d ˆ ˆ ( ) ] [ 2 2 ] 2 dt dt dt dt dt
2
d
d 2
ˆ ˆ a a a
18
a
d2 dt 2
d d d 2 d 2 ( ) , a 2 2 dt dt dt dt
分别称为径向加速度和横向加速度。
质点直线运动, 取该直线为极径,极角为常量:
d2 a 2 , a 0 dt
质点圆周运动, 极径是圆周半径, 为常量, 有
d 2 d 2 a ( ) , a 2 dt dt
19
2 d 2 d 2 1 v 继续推算 a ( ) ( ) dt dt
方向的切向单位矢量, 用 表示, 另一个是垂直于
质点运动的描述

质点运动的描述质点运动是经典力学中的基本概念,它描述了一个物体在空间中运动的方式。
质点被定义为一个没有体积的点,它具有质量和位置。
在质点运动的描述中,我们通常关注的是质点的位置、速度和加速度,以及与时间的关系。
I. 位置的描述质点的位置可以用坐标来描述。
在二维情况下,我们可以用笛卡尔坐标系或极坐标系来表示质点的位置。
在三维情况下,我们通常使用笛卡尔坐标系。
质点在空间中的位置可以用一个向量来表示,该向量以质点所处位置为终点,以参考点为起点。
II. 速度的描述质点的速度是指单位时间内质点位置的变化率。
在一维情况下,我们可以用标量表示质点的速度。
在二维或三维情况下,我们需要使用向量表示质点的速度。
质点的速度可以通过位置对时间的导数来计算,即速度等于位置关于时间的导数。
III. 加速度的描述质点的加速度是指单位时间内质点速度的变化率。
加速度表示了质点运动的变化情况。
在一维情况下,我们可以用标量表示质点的加速度。
在二维或三维情况下,我们需要使用向量表示质点的加速度。
质点的加速度可以通过速度对时间的导数来计算,即加速度等于速度关于时间的导数。
IV. 运动方程的描述运动方程是描述质点运动的基本方程。
对于匀速直线运动,质点的运动方程可以表示为x = x0 + vt,其中x为质点的位置,x0为初始位置,v为速度,t为时间。
对于匀加速直线运动,质点的运动方程可以表示为x = x0 + vt + 0.5at^2,其中a为加速度。
在二维或三维情况下,我们可以将位置、速度和加速度的每个分量分别表示,并分别应用相应的运动方程。
V. 质点运动的特殊情况在质点运动中,还存在一些特殊情况。
例如,匀速圆周运动中,质点沿着一个固定半径的圆周以恒定速度运动。
在这种情况下,质点的位置可以用极坐标来表示,并且质点的速度与加速度垂直于运动方向。
VI. 质点运动的描述与分析质点运动的描述和分析对于理解物体运动的基本规律和设计运动轨迹具有重要意义。
质点在极坐标系中的运动分析

质点在极坐标系中的运动分析在物理学中,质点在极坐标系中的运动是一种常见的运动形式。
极坐标系是一种由径向和角度两个坐标轴组成的坐标系,对于描述圆形或者旋转运动的物体非常有用。
在本文中,我们将探讨质点在极坐标系中的运动特点以及相关的物理概念。
首先,我们来介绍一下极坐标系的基本概念。
在极坐标系中,一个质点的位置可以由径向距离和角度来确定。
径向距离表示质点与原点之间的距离,而角度则表示质点所在位置相对于参考方向的角度。
这种坐标系的特点是能够直观地描述物体的旋转和径向运动。
接下来,我们将讨论质点在极坐标系中的运动方程。
对于质点在极坐标系中的运动,我们可以通过径向速度和角速度来描述。
径向速度表示质点沿着径向的运动速度,而角速度则表示质点绕原点旋转的速度。
根据牛顿第二定律,我们可以得到质点在极坐标系中的运动方程:质点的径向加速度等于质点的径向力除以质量,即:a_r = F_r / m质点的角加速度等于质点的角力矩除以质量,即:α = τ / I其中,F_r表示径向力,m表示质量,τ表示角力矩,I表示转动惯量。
在质点的运动过程中,我们还需要考虑到质点的角动量和角动量守恒定律。
角动量表示质点绕原点旋转的动量,可以用以下公式表示:L = Iω其中,L表示角动量,I表示转动惯量,ω表示角速度。
根据角动量守恒定律,当质点在极坐标系中的运动过程中没有外力或者外力矩作用时,质点的角动量保持不变。
这意味着质点的转动惯量和角速度的乘积保持不变。
此外,我们还需要了解质点在极坐标系中的运动特点。
质点在极坐标系中的运动可以是径向运动、角度运动,或者同时具有径向和角度运动。
径向运动表示质点沿着径向方向的运动,可以是向内或者向外的运动。
角度运动表示质点绕原点旋转的运动,可以是顺时针或者逆时针的运动。
质点的运动轨迹可以是圆形、椭圆形或者其他形状,取决于质点的运动方程和初始条件。
最后,我们来看一个实例来更好地理解质点在极坐标系中的运动分析。
第1章-质点运动学

位移
rrrBArxBxBAii
rA
yA
yB
j j
y
yB A r
r y A A
rB
B
yB yA
(xB xA)i ( yB yA) j
xi yj
o
xA
xB x
xB xA
若质点r 在 (三x维B 空x间A中)i运动( yB
yA)
j
(zB
z A )k
位移的大小为 r x2 y2 z2
23
1-2 求解运动学问题举例
例3 有 一个球体在某液体中竖直下落, 其初速度
为 v0 10 j , 它的加速度为 a 1.0v j. 问:(1)经
过多少时间后可以认为小球已停止运动, (2)此球体
在停止运动前经历的路程有多长?
解:由加速度定义
v dv 1.0
t
dt
,
v v0
0
a dv 1.0v dt
v v2
位矢量
t
0,
t 0
0,
tv
rv
a
dv dt
v2 r
en
2ren
法向单 位矢量
vB
r
o
en
v
vB
vA et r
vA
31
1-3 圆周运动
三alitlami tm 变00速litdmdv圆vvvt0tt周nt运vtavt动dvdttrev2ttleeit切mntv向a0nn加aaevn速tntneen度t 和法向v加2v速tove度2vnrevtv1vn1
一 圆周运动的角速度和角加速度
角坐标 (t)
角速度 (t) d (t)
dt
速率
质点运动的描述,自然坐标系
结论:
z K
r
R
z K P
r
o
y
o x
y
运动目标
(船)
绝
相
牵 动系 (水)
对
对
对
静系 (岸)
对
对
对
对
对
对
人骑车以速率
向正西行驶
遇到从北向南刮的风 , 速率也是
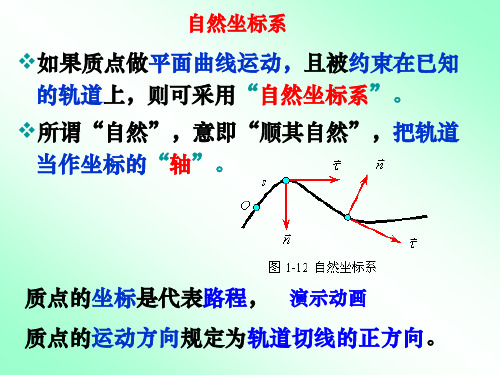
自然坐标系
如果质点做平面曲线运动,且被约束在已知 的轨道上,则可采用“自然坐标系”。
所谓“自然”,意即“顺其自然”,把轨道 当作坐标的“轴”。
质点的坐标是代表路程, 演示动画 质点的运动方向规定为轨道切线的正方向。
自然坐标系的建立
O
ˆ n
s
ˆ n
ˆ
将此轨道曲线作为一维坐标的轴线,在其上任意选一 点O作为坐标原点。 质点在轨道上的位置可以用从原点O算起的弧长 度s 来表示,s 称为弧坐标。 运动方程:s s (t ) 自然坐标系是建立在物体运动的轨迹上的。 在质点上建立两个的坐标轴:切向坐标和法向坐标。 •切向坐标 沿运动轨迹的切线并指向质点运动的方向;
x R cost , y R sin t
x2 y 2 R2
o
P2 v1 R an P 1 t x
dr v (R sin t )i (R cost ) j dt
2 2
r ( R cost )i ( R sin t ) j
a ( R cost )i ( R sin t ) j r
此处的 d
质点运动学

例1-1 已知质点在xy平面内运动,其运动方程是 x R cost ,y R sin t 。 式中R、 均为正常数。求(1)质点的轨迹方程;(2)质点在任意时刻的位矢、 速度和加速度;(3)质点在 t1 0 到 t2 3 2 时间内的位移。
解:(1) 由运动方程消去时间参量,可得质点轨迹方程
O
y
x
s
p2
p1
r
r1 r2
| r | p1p2 | r2 r1 |
s : 路程即弧线 p1p 2
路程s是标量
| r |
|r| || r2| |r1| |
图中 s | r | |r|
平均速度
平均速率
r v t
v2
2 ac tan
vy vx
(3)求加速度 a
3 y
2 1 a a
dv d a (2 i 2t j ) 2 j dt dt
a
2
-1
-2 -3
a
4
x
沿y轴负方向 矢量有两个重要特征: 大小 方向
a a
例1-2 汽车在半径 R 300.0m 的轨道上加速运动,其路程与时间的关系是 s 5.0t 2 0.1t 3 m ,求时 t 1.0s ,汽车的加速度大小。
(
v x i v y j vz k
dt
dt
( xi yj zk )
dt
i
dt
j
dt
k
r (t )
O
v
v | v |
2 2 2 vx v y vz
大学物理第1章质点运动学的描述
t0
0 2 4
t 2s 4
2
t 2s
x/m
6
-6 -4 -2
例3 如图所示, A、B 两物体由一长为 l 的刚性 细杆相连, A、B 两物体可在光滑轨道上滑行.如物体 A以恒定的速率 v 向左滑行, 当 60 时, 物体B的 速率为多少? 解 建立坐标系如图, 物体A 的速度
1. 5 arctan 56.3 1
(2) 运动方程
x(t ) (1m s )t 2m
y(t ) ( m s )t 2m
1 4 2 2
1
由运动方程消去参数
1 -1 2 y ( m ) x x 3m 4
轨迹图
t 4s
6
t 可得轨迹方程为
y/m
三、位置变化的快慢——速度
速度是描写质点位置变化快慢和方向的物理量,是矢量。
速率是描写质点运动路程随时间变化快慢的物理量,是标量。 1 平均速度 在t 时间内, 质点从点 A 运动到点 B, 其位移为
B
y
r r (t t) r (t)
r (t t)
s r
质点是经过科学抽象而形成的理想化的物理模 型 . 目的是为了突出研究对象的主要性质 , 暂不考 虑一些次要的因素 .
二、位置矢量、运动方程、位移
1 位置矢量
确定质点P某一时刻在 坐标系里的位置的物理量称 . 位置矢量, 简称位矢 r
y
y j
r xi yj zk
j k 式中 i 、 、 分别为x、y、z
xA xB xB x A
yB y A
o
x
经过时间间隔 t 后, 质点位置矢量发生变化, 由 始点 A 指向终点 B 的有向线段 AB 称为点 A 到 B 的 位移矢量 r . 位移矢量也简称位移.
极坐标下的质点运动

rer r e
a
dv dt
d dt
(rer
r e
)
rer
2r e
r e
r
d e dt
d e lim e d t t0 t
1 d
dt
(erd
dt
d dt
(re
r e
)
rer
2r e
dt
r e
r e
re(err) 2er
对于匀速圆周运动, ,是一常量,所以, 0
由此得: v re (切线方向)
a r 2er (向心方向)
4
d er dt
er
e
d e dt
e
(er )
例 质点的圆周运动问题
解:在某时刻,设质点运动图所示位置,
选取极坐标系,对于固定的圆,r 是常数,于是有,
r rer
v
dr dt
d(rer )
dt
rer
rer 0 r e
a
dv dt
d (r e )
极坐标下的质点运动
——曲线运动问题
极坐标系下表示
r
rer
v=
d r = d(rer )= dt dt
d d
r t
er
+
r
d er dt
d er lim er d t t0 t
1 d
dt
e
e
由此整理得:
v dr dt
= d(rer ) dt
dr dt
哈里德大学物理学第一章

vB
运动到B, 速度改变为:
v v B v A 用 v t 可粗略描述
质点速度改变的快慢和方 向, 称为平均加速度 。
Δv 表示为: a Δt
Δv 用平均加速度 a Δt
只能粗略地描述质点速度改变的快慢和方向, 瞬时加速度 —— 当△t 趋于 0 时,求得平均加速度的
2 x 2 y
2
t 2 s v 2 2 5 4.47 m s -1
解一错误, 解二正确!
判 断 正 误 并 说 明 理 由
§1-4 加速度矢量 描述质点速度大小、方向变化的快慢 质点在A ,B 两点的速度分别
是 v A ,vB ,
在△t 时间内从A
vA
vA
A
v
r (t ) v , a
第二类:已知加速度(或速度)及初始条件,求
质点任一时刻的速度和运动方程(积分法)
a (t ) , (t 0时 r0 , v0 ) v (t ) , r (t )
r (t )
微分 积分
v(t )
微分 积分
a (t )
一、直线运动
t 时间内位置变化的净效果:
A
rA
r
B
rB
AB rB rA r
位移 矢量
末 位 矢 初 位 矢 位矢 增量
O
直角坐标表示(以二维情况为例):
rA x A i y A j rB x B i y B j r ( xB x A ) i ( yB y A ) j x i y j
dr ds dr v dt dt dt
大学物理11质点运动的描述

位置 位置随时间的变化 位置随时间变化的快慢---速度 速度随时间的变化快慢
直角坐标系中的四个物理量 位矢,位移,速度,加速度
自然坐标系中的四个物理量 位置,路程,速度,加速度(切向、法向)
极坐标系中的四个物理量 角位置,角位移,角速度,角加速度
一、位置矢量
1.位置矢量
确定质点P某一时刻在坐标
v2-v02 2a(x x0 )
这就是中学学过的匀变速运动的基本公式。
例2 已知加速度表达式
a
3i
2tj
以及
初始条件:当t=0时, r0 0, v0 0 ,求速度
方程及运动方程
解:a 是t 的函数,由相应的公式得:
ax
dvx dt
,
dvx axdt,
vx
t
dvx 3dt,
vx0
0
12
j
r
62 122
180
r
2t
2i
4t
2
j
r2 8i 16 j
r2
82 162
320
r1 2i 4 j r1 22 42 20
r 320 20
三、速度
1. 速度
y
在 时t间内, 质点从点A 运
动到点 B, 其位移 为
rA
r rB rA
o
t 时间内,质点的平均速度
从1秒末到2秒末的位移
r
(8
2)i
(16
4)
j
6i
12
j
讨论 1) 位移确切反映物体在空间位置的变化, 与路径 无关,只决定于质点的始末位置.
位移与路程有区别
y
s'
欧拉动力学方程一、欧拉动力学方程...

第一章 质点运动学§1-1 质点运动的矢量描述与直角坐标描述一、参考系和坐标系有一定大小且不变形的物体, 或几个相对位置保持不变的物体, 都可以作为参考系. 一个点不能作参考系!坐标系可以看成是由坐标曲线组成的带有标度的空间网格.各种坐标系的坐标曲线都在它们的交点处互相正交, 都属于正交曲线坐标系.沿质点所在位置的坐标曲线切线方向建立的一组单位矢量称为坐标系的基矢. 直角坐标系Oxyz (坐标曲线321,,c z c y c x ===),基矢为单位矢量k j i ,,, 按惯例我们使用的坐标系 全是右手正交系, 其基矢满足如下关系: k j i =× 0=⋅=⋅=⋅i k k j j i 若坐标系的空间网格相对参考系固定不动, 则该坐标系相对参考系固定不动, 这时我们称该 坐标系与参考系固连.二、自由度我们称确定力学系统位置所需要的独立坐标 数为系统的自由度, 自由度记为s .三、运动学方程和轨道图中我们用直角坐标系Oxyz 代表参考系, 位置矢量(简称位矢)r e r r = )(t r r =称为质点的运动学方程, 它包括了质点运动的全 部信息. 质点运动的轨道即为位置矢量r 的矢端曲线.在直角坐标系Oxyz 中 k z j y i x r ++=运动学方程的分量形式为)(),(),(t z z t y y t x x ===由式中消去时间t , 则得到轨道方程.四、位移和路程位移是质点位置矢量的增量, )()Δ(Δt r t t r r −+=路程是质点沿轨道走过的长度, 为一恒正标 量, 记为s ∆,AB s =∆弧长.注意s r ΔΔ≠s r ΔΔ≠r r ΔΔ≠但当0Δ→t 时,B A ,间弦长与弧长相等, s r ∆→∆ , 或记为s r d d =五、速度瞬时速度矢量简称为速度, 被定义为位置矢量对时间的导数,r t r t r v t ==∆∆=→∆d d lim 0 速度的方向沿轨道 (即r 的矢端曲线) 的切线指向运动的前方, 它的大小为速率v ,s ts t rt r v v t ===∆∆==→∆d d d d lim0 在直角坐标系Oxyz 中, k z j y i x v ++=.六、加速度瞬时加速度矢量简称加速度, 定义为速度对时间的导数,r t r v t v t v a t ====∆∆=→∆220d d d d lim 加速度a 一定指向轨道的凹侧. 若将不同时刻的速度矢量的矢尾集中于一点, 则可得出速度矢量v 的矢端曲线即速端曲线. 加速度a 沿速端曲线切线方向并指向v 的矢端沿速端曲线运动的前方, 加速度的大小a 等于v 的矢端沿速端曲线运动的速率.任意矢量A 对时间的导数A 的方向沿A 的矢端曲线的切线, 其指向与A 的矢端沿矢端曲线的运动方向一致; A 的大小即A 的矢端沿矢端曲线运动的速率.在直角坐标系Oxyz 中, k zj y i x k v j v i v a z y x ++=++=§1-2 质点运动的平面极坐标描述当质点被限制在一个平面上运动时, 其自由度2=s , 我们建立与参考系固连的极坐标系. 质点P 的位置由坐标量r 和θ确定, 要明确极角θ的正方向 (即θ的增加方向)!平面极坐标系是正交曲线坐标系, 其平面坐标网格由一组同心圆(1c r =)及一组放射状半直线(2c =θ)组成.平面极坐标系的基矢为r e 和θe .0=⋅θe e r .r e 的方向为径向, θe 的方向为横向.)(θr r e e = ,)(θθθe e =. 我们把矢量沿质点所在位置的基矢 “就地” 进行正交分解.在极坐标系中, 质点的运动学方程为[])()(t e t r r r θ =标量形式)(),(t t r r θθ==消去时间t , 则得到轨道方程0),(=θr f .根据速度的定义, 把[])()(t e t r r r θ = 对时间求导数, 得到 t e r e t r t r v r r d d d d d d +==下面求单位矢量r e 的时间 导数t e r d d ,t e t t e t t e t e r t r r t r ∆∆=∆−∆+=→∆→∆ 00lim )()(lim d d 当0→∆t 时,0→∆θ. 注意到由r e 及r e ∆组成的矢量三角形为腰长为1的等腰三角形, 所以当0→∆t 时r e ∆与r e 垂直, 且θ∆⋅=∆1r e . 由于0→∆θ且0Δ>θ时r e ∆与θe 方向相同, 所以0→∆t 时θθe e r ⋅∆=∆, 故 θθθθe e tt e t r ⋅=∆∆=→∆0lim d d于是得到极坐标系中的速度表达式,θθe r e rv r += rv r =称为径向速度, θθ r v =称为横向速度. 根据加速度的定义,得)(d d d d θθe r e r tt v a r +==t e r e r e r e r e r r d d θθθθθθθθ ++++=下面改换一个方法求t e d d θ . 由于θe 为单位矢量, 故θe 的矢端曲线为半径为1的单位圆. 0Δ>θ 时, θe 的矢端沿其矢端曲线运动的速率为θ ⋅1, t e d d θ 的方向沿矢端曲线切线, 其指向如图所示,故可知 r e te θθ−=d d 同样,θθe t e r =d d于是得到极坐标系中加速度的表达式θθθθe r r e r r a r )2()(2++−=2θ r r a r −=和θθθ r r a 2+=分别称为径向加速度和横向加速度.矢量的变化为矢量大小的变化及矢量方向的变化二者产生效果的叠加, 请读者试用这种观点分析式中各项是如何产生的. 还可用运动分解和合成的观点理解式中各项的意义.例题1半径为R 的铁圈上套一小环P , 直杆OA 穿过小环P 并绕铁圈上O 点以匀角速度ω转动. 求小环P 的运动方程、 轨道方程、 速度和加速度.解 如图所示建立极坐标系,设0=t 时0θθ=, 则运动学方程为+=+=00)cos(2θωθθωt t R r 轨道方程为θcos 2R r =速度和加速度为 θθe r e r v r += θθωωθωωe t R e t R r )cos(2)sin(200+++−= θθθθe r r e r r a r )2()(2++−= θθωωθωωe t R e t R r )sin(4)cos(40202+−+−=本例题也可用图中直角坐标系xyz O 2求解, 由读者自行完成. 请读者另行验证:(1) 不同方法中a v ,表达式不同, 但它们对描述P点运动是等价的;(2) 不同方法中a v ,的大小和方向是惟一确定的.例题1是运动学正问题, 即先写出运动学方程,通过求导数运算求出v 和a . 运动学逆问题是已知速度或加速度及初条件求运动学方程, 使用的数学方法是积分或解微分方程, 和正问题比较要复杂一些, 但只要把握解题的方向也是不难解决的.例题2 已知一质点做平面运动, 其速率为常量c ,其位置矢量转动的角速度亦为常量0ω,试求质点的运动学方程及轨道方程. 设0=t 时,0=r , 0=θ.解 由已知条件ωθ= (1) 2222c r r =+θ (2) 把(1)是式化为t d d 0ωθ=,积分并由0=t 时0=θ定积分常数,可得t 0ωθ= (3)把(1)式代入(2)式,分离变量得t r c r d d 2202±=−ω 积分并以0=t 时0=r 定积分常数,得t c r 00sin ωω±= (4) (3)(4)二式即为运动学方程=±=t t c r 000sin ωθωω 消去t 得轨道方程θωsin 0c r ±= 轨道为两个圆,如图所示.柱坐标系可以看成是由Oxy 平面内的极坐标系 (坐标量为ρ和θ) 及z 轴构成的三维空间坐标系. 其空间坐标网格由1c =ρ的圆柱面、 2c =θ的放射状半平面和3c z =的平面3组曲面相交形成的曲线所组成. 质点位置由坐标量z ,,θρ确定. 柱坐标系的基矢为单位矢量θρe e ,和k . 柱坐标系为右手正交系, 其基矢满足如下关系:k e e =×θρ质点的运动学方程为 []k t z t e t t r r )()()()(+==θρρ速度和加速度的表达式为 k z e e v ++=θρθρρk z e e a +++−=θρθρθρθρρ)2()(2 推导请仿照§1-2自己完成.球坐标系如图所示, 质点P 的位置由坐标量ϕθ,,r 确定. 球坐标系的空间坐标网格由1c r =的球面、 2c =θ的圆锥面和3c =ϕ的放射状半平面3组曲面相交形成的曲线所组成.球坐标系的基矢为r e ,θe ,ϕe .r e 沿位矢r 的方向, θe 和ϕe 的指向与θ和ϕ的正方向一致. 球坐标系为右手正交系, 其基矢满足如下关系:ϕθe e e r =×0=⋅=⋅=⋅r r e e e e e e ϕϕθθ球坐标系中的θ亦称为极角、 ϕ称为方位角. 球坐标系中的基矢不是常矢量, 其中r e 为θ和ϕ的函数. 我们把矢量沿质点所处位置的基矢r e ,θe 和ϕe “就地”进行正交分解.质点的运动学方程为 [])(),()()(t t e t r t r r r ϕθ ==下面我们从速度的定义导出球坐标系中的速度表达 式. 将r ∆沿t 时刻质点所在位置的基矢正交分解, 得到ϕθe s e s e s r r 321∆+∆+∆=∆当0→∆t 时, r s ∆→∆1,2s ∆和3s ∆可用坐标曲线上的弧长来表示, 即θ∆→∆r s 2和ϕθ∆⋅→∆sin 3r s 于是可知 t e r e r e r t r t r v r t t ∆∆⋅+∆+∆=∆∆==→∆→∆ϕθϕθθ sin lim lim d d 00 ϕθθϕθe r e r e rr sin ++= 球坐标系中的加速度公式可按矢量导数定义求导得出, 但比较复杂, 我们将在后面用分析力学的方法导出.§1-5 质点运动的自然坐标描述利用质点运动轨道本身的几何特性 (如切线、法线方向等)来描述质点的运动. 这种方法称为自然坐标法.一、弧长方程在轨道上取一点作原点O , 规定沿轨道的某一方向为弧长的正方向, 质点位置可由原点O 到质点间的一段弧长s 来确定, s 称为弧坐标.)(t s s =上式称为弧长方程. 弧长方程和轨道方程一起与质点的运动学方程等价.弧坐标s 为可正可负的标量, 与恒正的路程是不同的.二、相关的微分几何知识轨道上无限接近的两个点所决定的直线称为切线. 定义切向单位矢量t e 沿切线, 其指向与弧长正方向一致. 沿t e 的方向称为切向.轨道上无限接近的3个点确定的平面, 即无限接近的两条切线所确定的平面, 称为密切面.密切面取向的改变反映了曲线的挠曲情况.轨道曲线上无限接近的3个点所决定的圆称为曲率圆, 曲率圆在密切面内. 曲率圆的圆心称为曲率中心, 曲率圆的半径ρ称为曲率半径, 曲率半径的倒数ρκ1=称为曲率.设弧长s P P d =′, 显然s d d 1ϕρκ==, 曲率κ越大则曲线弯曲程度越大. 当轨道为平面曲线)(x y y =时, 可利用数学分析中的公式 []23222)d d (1d d 1x y x y +==ρκ求曲率κ及曲率半径ρ.过轨道上一点, 与切线垂直的线称为法线. 法线有无限多条,它们组成的平面称为法平面.密切面内的法线称为主法线, 定义主法向单位矢量n e 沿主法线指向曲率中心. 沿n e 的方向称主法向, n e 指向轨道凹侧.垂直于密切面的法线称为副法线. 定义副法向单位矢量b e 沿副法线, 指向n t e e ×的方向.n t b e e e ×=沿b e 的方向为副法向.单位矢量b n t ,,e e e 两两互相垂直, 并成右手螺旋关系.三、速度和加速度表达式把质点的速度和加速度沿质点所在处的单位矢量b n t ,,e e e “就地”正交分解, 进而导出质点的速度和加速度表达式.速度沿切线指向运动的前方, 所以0b n ==v v . 考虑到0>s 时v 与t e 同向, 故 t t t e se v v == 速度的大小sv v v ===t . 由加速度的定义 t e s e s e s t t v a d d )(d d d d t t t +===当ϕ的正向与弧长s 正向一致时, ϕρd d =s ,故ρρϕt v s == . 所以 n n n t d d 1d d e s e e t t e ρϕϕ==⋅=因此 n t e s e s a ρ2+=s v a ==t t 称为切向加速度, 是由于速度t t e v v =的大小改变而产生的. ρρ22n s v a ==称为法向加速度, 是由于速度的方向改变而产生的. 由于n a 恒正, 故a 一定指向轨道凹侧, 与§1-1中结论一致. 0b ≡a 说明对任何空间曲线运动,加速度a 必在密切面内, 这是加速度和密切面定义导致的必然结果.注意原点O 的选定和弧长正方向的规定! 在自然坐标描述中, 需要已知质点运动的轨道, 而对轨道的数学描述又需要一个坐标系, 所以必须掌握自然坐标描述中的物理量与其他坐标系中的物理量之间的联系. 建立这个联系的基本依据是: 速度v 和加速度a 在不同的描述方法中有不同的表达形式, 但它们的大小和方向是惟一确定的.例题1半径为R 的铁圈上套一小环P , 直杆OA 穿过小环P 并绕铁圈上O 点以匀角速度ω转动. 求小环P 的运动方程、 轨道方程、 速度和加速度.解 曾用如图所示建立极坐标系求解.此例题也可用自然坐标法求解: 以1O 为原点,规定弧长正方向如图所示.轨道已知,弧长方程为)(20θω+=t R s速度和加速度为 t e R e s v ω2t == n 2n 2t 4)(e R e s e sa ωρ=+= 比其它方法简单!自然坐标描述并不是自然坐标系中的描述.请读者验证: (1) 不同方法中a v ,表达式不同, 但它们对描述P点运动是等价的; (2) 不同方法中a v ,的大小和方向是惟一确定的.例题3 已知质点的运动学方程为t R x ωcos = t R y ωsin = t h z ωπ2= (h R ,,ω为常量)试分析质点的运动,求切向加速度、法向加速度及轨道的曲率半径。
极坐标系中质点运动描述

二、角量和线量的关系:
o
ds rd
Q
ds
d r
P
x (极轴)
ds r d
dt dt
dv r d
dt dt
an
v2 r
r
2
v r
a r
an r 2
位置
线 量r
位移
角 速度
量 与
加速度
vΔarddrrv//ddr0tt
线
量 切线加速度
的
比 较
法向加速度a dv /dFra bibliotek an v 2/r
解 (1) 由运动学方程可得
d 12t 2
dt an rω2 230.4(m/s2 )
d2
dt 2
24t
aτ r 4.8(m/s2 )
a an2 aτ 2 230.5(m/s2 )
(2) 设 t´ 时刻, 质点的加速度与半径成45o角, 则
t' : aτ an
rω2 r
(12t'2 )2 24t'
144t'4 24t' t' 0.55(s) 2 4t'3 2.67(rad)
例
质点沿半径为R的圆周按
v0、b为常量。
s
v
0t
运 动b t,2 式中s为自然坐标, 2
求 (1) 质点的加速度;
(2) 质点的角速度、角加速度;
(3) 法向加速度和切向加速度数值相等前,质点运动的时间。
解 (1) 本题是自然坐标的第一类问题。
先求出速率
v
ds dt
v0
bt
at
dv dt
b
an
v2 R
第一章质点运动学

3v 1.73v, y 轴正向 沿
作业:习题1-7,1-9
练习:习题1-6
提示:1-1题为第一类质点运动学问题,即 运动方程 加速度
速度 加速度
1-2题为第二类质点运动学问题,即
速度 运动方程
§1-3
圆周运动
y
y
平面极坐标 质点在A点的位置由 (r,θ)来确定. 以(r,θ)为坐标的 坐标系称为平面极坐标系
x x(t ) 分量式 y y (t ) z z(t )
—参数方程
2.运动方程
y
y (t )
r (t )
P
x(t )
从上式中消去参数 t ,可 z (t ) z 得质点运动的轨迹方程:
o
x
f ( x, y, z) 0
选择题.已知一质点位置矢量的表达式为 : r 2i 5 j 37k ,则该质点作 (A) 匀速直线运动。 (B) 静止。 (C) 抛物线运动。 (D)一般曲线运动。
物 理 学
第一章
质点运动学
§1-1
质点运动的描述
一 参考系 质点 1.参考系 为描述物体运动而选定的标准物,称 为参考系。 参考系选取的不同,物体运动的描 述不同,即对物体运动的描述具有相 对性。 2.质点 忽略物体的体积与形状,将其抽象为 具有同等质量的点,称为质点. 质点是理想模型.
二 位置矢量
x(t ) 1.0t 2.0, (2)运动方程 2 y(t ) 0.25t 2.0, 则有 t x 2 ,带入 y 中可消去参数 t ,
可得轨迹方程为
轨迹图
t 4 s
6
y 0.25x x 3.0
2
y/m
第一章 质点运动学

六. 单位 本课程采用国际单位制( ), ),其中 本课程采用国际单位制(SI),其中 长度单位 时间单位 速度单位 加速度单位 米(符号 m) ) 秒(符号 s) ) 米每秒( 米每秒(符号 m/s ) 米每二次方秒( 米每二次方秒(符号 m/s2 )
例题1-4 已知质点作匀加速直线运动,加速度 已知质点作匀加速直线运动, 例题 求这质点的运动方程。 为 a ,求这质点的运动方程。 dv = a 常量),积分得 ),积分得 解 由定义 (常量), dt
∆r = r1 − r
即等于质点位矢在∆t O 即等于质点位矢在∆ 时间内的增量。 时间内的增量。且有
r
r ∆t 时间内位移 1
t +∆t 时刻位矢 ∆
x
∆r = x1i + y1 j − xi − yj = ( x1 − x )i + ( y1 − y ) j
时间内质点通过的路程 为标量 路程∆ 为标量, ∆t 时间内质点通过的路程∆s为标量,仅当 ∆t→0时,位移的大小 时 lim ∆r = ∆s
d 2 x dv x ax = 2 = = −ω 2 R cos ω t dt dt d 2 y dv y ay = 2 = = −ω 2 R sin ω t dt dt
由此得加速度的大小
v a = ω R cos ωt + sin ωt = ω R = R
2 2 2 2
2
如果把加速度写成矢量式, 如果把加速度写成矢量式,则有
本课程中只讨论平面内的运动问题, 本课程中只讨论平面内的运动问题,常用坐标 系有平面直角坐标系 极坐标系和自然坐标系。 平面直角坐标系、 系有平面直角坐标系、极坐标系和自然坐标系。
二. 质点 一般情况下, 一般情况下,运动物体的形状和大小都可能变化
质点运动的数学描述

质点运动的数学描述质点运动是物理学的一个重要概念,用数学语言进行描述可以帮助我们更好地理解和分析运动的规律。
在本文中,我们将探讨质点运动的数学描述,并以一些例子来说明。
一、位置、位移和坐标系质点的位置可以用坐标系来描述,一般使用直角坐标系或极坐标系。
在直角坐标系中,质点的位置可以由其在x、y、z轴上的坐标来表示;而在极坐标系中,质点的位置可以由其距离原点的距离和与参考方向的夹角来表示。
质点的位移是指其位置发生变化的差值,可以用Δx、Δy、Δz或Δr、Δθ来表示。
其中,Δx、Δy、Δz表示质点在直角坐标系中的位移量,Δr、Δθ表示质点在极坐标系中的位移量。
二、速度和加速度质点的速度是指其单位时间内位移的瞬时变化率,可用速度矢量来表示。
在直角坐标系中,质点的速度可以表示为v = (vx, vy, vz),其中vx、vy、vz为质点在x、y、z轴上的速度分量。
在极坐标系中,质点的速度可以表示为v = (vr, vθ),其中vr为质点沿径向的速度分量,vθ为质点沿角度方向的速度分量。
质点的加速度是指其单位时间内速度的瞬时变化率,可用加速度矢量来表示。
在直角坐标系中,质点的加速度可以表示为a = (ax, ay, az),其中ax、ay、az为质点在x、y、z轴上的加速度分量。
在极坐标系中,质点的加速度可以表示为a = (ar, aθ),其中ar为质点沿径向的加速度分量,aθ为质点沿角度方向的加速度分量。
三、运动方程通过对质点的位置、速度和加速度的描述,我们可以得到质点的运动方程。
对于一维运动,质点的运动方程可以表示为x = x0 + v0t +(1/2)at^2,其中x0为初始位置,v0为初始速度,a为加速度,t为时间。
对于二维或三维运动,质点的运动方程需要根据具体情况进行推导和描述。
四、曲线运动对于曲线运动,质点的运动方程可以更为复杂。
在直角坐标系中,质点的曲线运动可以通过参数方程来描述,例如x = f(t),y = g(t),z =h(t);在极坐标系中,质点的曲线运动可以通过参数方程r = f(t),θ =g(t)来描述。
极坐标质点运动方程

极坐标质点运动方程
极坐标质点运动方程描述了质点在极坐标系中的运动规律。
极坐标系由极径r和极角θ组成。
极坐标质点运动方程可以用以下形式表示:
r = r(t)
θ = θ(t)
其中,r(t)和θ(t)分别表示质点的极径和极角与时间的函数。
根据牛顿力学定律,质点的运动可以由质点所受的力来描述。
在极坐标系中,质点的速度和加速度可以用以下形式表示:
v = dr/dt (极径的变化率)
a = d²r/dt² - r(d²θ/dt²) (极径的二阶变化率)
根据动力学原理,可以获得质点的运动方程。
根据欧拉公式,可以将极坐标运动方程与直角坐标运动方程相互转换。
极坐标与直角坐标之间的转换关系为:
x = r*cos(θ)
y = r*sin(θ)
其中,x和y分别表示质点在直角坐标系中的坐标。
通过这种转换,可以将直角坐标系的运动方程转换为极坐标系的运动方程,或者反过来。
综上所述,极坐标质点运动方程是根据质点所受的力和质点在极坐标系中的速度、加速度之间的关系得出的。
具体的极坐标质点运动方程可以根据具体问题的条件和假设来确定。
质点运动的平面极坐标描述
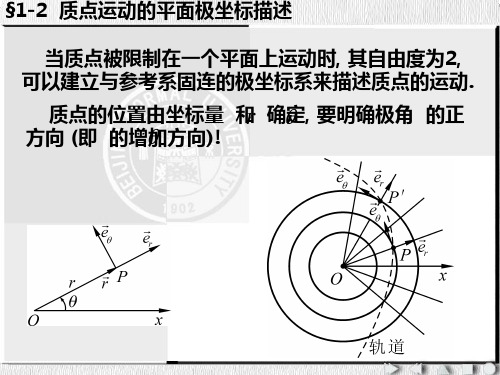
e e ( )
与直角坐标系不同的是,矢量沿质点所在位置的基 矢 “就地” 进行正交分解. 在极坐标系中, 质点的运动学方程为
r r (t )er (t )
r r (t ), (t )
根据速度的定义
f (r , ) 0源自§1-2质点运动的平面极坐标描述
§1-2
质点运动的平面极坐标描述
当质点被限制在一个平面上运动时, 其自由度为2, 可以建立与参考系固连的极坐标系来描述质点的运动 . 质点的位置由坐标量 r 和 确定, 要明确极角 的正方向 (即 的增加方向)!
§1-2
质点运动的平面极坐标描述
平面极坐标系的基矢为极角的函数
er er ( )
径向加速度
横向加速度
2 r )er (r 2r )e a ( r
dr dr der v er r dt dt dt der er (t t ) er (t ) lim d t t 0 t er lim lim e e t 0 t t 0 t
径向速度 横向速度
er re v r
§1-2
质点运动的平面极坐标描述
矢量的变 化为矢量 大小的变 化及矢量 方向的变 化二者产 生效果的 叠加!
dv d er re ) a (r dt dt
de e r e re r rer r dt de e r dt
第一章质点运动的描述_大学物理(工科)

Oxy
,则该物体以恒定加速度
a = g 作斜抛运动。设在 t = 0 时,该物体位于原点 O ,其
位矢 r0 = 0 。于是由曲线运动方程矢量式(1-9),有
r = v 0t +
1 2 gt 2 (1-10a)
上式的物理意义可以这样来理解:
从上图中可以看出,在时间 t 内,该物体从原点 O 到点 P 的位移 r 是
有一个具有恒定加速度( a =恒矢量)的质点,在平面上作曲线运动。此恒定加速度 a 在 Ox 轴 和
Oy
轴上的分量也是一定的。
v 0 x 和v 0 y
设 t = 0 时,质点的初始速度为 v 0 ,它在坐标轴上的分量为 可得
,于是,由加速度定义,
∫v
解得
v
0
dv = ∫ adt
0
t
v = v 0 + at
v 0t
1 2 gt 与2 这两个位移
矢量之和。显然,我们是把斜抛运动看成由沿着与 Ox 轴成 α 角的匀速直线运动和沿 加速直线运动这两个运动的叠加而成。 抛体运动的叠加性,可用 枪打靶的演示来验证。 扩充内容:枪打落靶的演示
Oy 轴的匀
枪打落靶演示
猎人举起枪直接瞄准树上吊挂的靶子,靶子在枪击同时自由落下,子弹总是可以击中靶子, 这是真的吗? 如果枪口水平瞄准靶子,子弹能击中靶子吗?请看! 如果枪口斜向下瞄准靶子,子弹能击中靶子吗?请看!
(1)求 t = 3s 时的速度。 (2)作出质点的运动轨迹图。 解 这是已知运动方程求运动状态的一类运动学问题,可以通过求导数的方法求出。 (1)由题意可得速度分量分别为
vx = dx dy 1 = 1m ⋅ s −1 , v y = = ( m ⋅ s − 2 )t dt dt 2
大学物理学C基本内容

《大学物理学C 》课程基本内容第一章 质点的运动1.直角坐标系、极坐标系、自然坐标系※2.质点运动的描述:位置矢量r 、位移矢量r ∆=)()(t r t t r-∆+、运动方程)(t r r =。
在直角坐标系中,k t z j t y i t x t r)()()()(++=速度:t rv d d=; 加速度:22d d d d t r t v a == 在直角坐标系中,速度k v j v i v v z y x ++=,加速度k a j a i a a z y x++=自然坐标系中,速度 τ v v ==τts d d ,加速度t n a a a +==n r v t v 2d d +τ 在极坐标系中,角量的描述:角速度t d d θω=,角加速度22d d d d t t θωα==3.运动学的两类基本问题:第一类问题:已知运动方程求速度、加速度等。
此类问题的基本解法是根据各量定义求导数。
第二类问题:已知速度函数(或加速度函数)及初始条件求运动方程。
此类问题的基本解法是根据各量之间的关系求积分。
例如据txv d d =,可写出积分式⎰x d =⎰t v d .由此求出运动方程)(t x x =。
4.相对运动:位移:t u r r ∆+'∆=∆ ,速度:u v v+'=,加速度:0a a a +'=第七章 气体动理论1.对“物质的微观模型”的认识;对“理想气体”的理解。
※2.理想气体的压强公式23132v n p k ρε==,其中221v m k =ε※理想气体物态方程:RT MmpV =或 nkT p =理解压强与微观什么有关,即压强的物理含义是什么.※3.理想气体分子的平均平动动能与温度的关系:kT k 23=ε 理解温度与微观什么有关,即温度的物理含义。
※4.能量均分定理:气体处于平衡态时,分子每个自由度上的平均能量均为2kT概念:自由度※理想气体内能公式:RT iM m E 2=5.麦克斯韦气体分子速率分布律 ※麦克斯韦气体分子速率分布函数:定义:vNN v f d d 1)(=函数:22232π2π4)(v v v kTm ekT m f -⎪⎭⎫⎝⎛= 以及v v f NNd )(d =;v v Nf N d )(d =;⎰21d )(v v v v Nf ;⎰21d )(v v v v f 等表示的物理含义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
rω2 r
o
(12t '2 ) 2 24t '
t ' 0.55(s)
2 4t '3 2.67(rad)
b 2 例 质点沿半径为R的圆周按 s v 0t t 运动,式中s为自然 2 坐标,v 、b为常量。
0
求 (1) 质点的加速度; (2) 质点的角速度、角加速度; (3) 法向加速度和切向加速度数值相等前,质点运动的时间。 解 (1) 本题是自然坐标的第一类问题。 先求出速率
ds v v 0 bt dt dv at b dt
v (v 0 bt ) an R R
2
2
1 a an a t R 2b 2 (v 0 bt ) 4 R
2 2
(v 0 bt ) 2 tan Rb (2) 根据线量和角量关系,写出用角量描述的运动方程θ (t )
线 位置 位移
量
角 量 加速度 与 线 量 切线加速度 的 比 法向加速度 较
匀速直线运动
速度
v dr/dt a dv/dt
a dv /dt
a n v 2 /r
Δr r r0
r
角 角位置 角位移 角速度 角加速度
量
线量和角量的关系
θ
Δθ θ θ0
§ 1.5 极坐标系中质点运动描述
主要内容:
1. 圆周运动的角量描述 2.角量和线量的关系
一、圆周运动的角量描述 角位置 角位移 方向:
B s
A
沿逆时针转动, 为正; 沿顺时针转动, 为负。
角量表示运动方程
R
o
x
(t )
角速度
角加速度
Δ d lim Δt 0 Δt dt Δ d () lim t 0 Δt dt
解:由: 0 t 由: 2 02 2
0 8 0 2 得: t 4 2 rad / s
2 (rad) 得: 2 16
R =R = R 50 16 40 n 20 圈 R 20 2
用角量表示匀变速圆周运动的基本方程: 0 t 1 2 0 0 t t 2 2 0 2 2 0
Q
二、角量和线量的关系:
ds rd
o
v r
a r
an r
2
ds d P r
x( 极轴)
ds d r dt dt dv d r dt dt v2 an r 2 r
0 0 t t 2
2 0 2 2 ( 0 )
1 2
解题思路 极坐标中质点运动学问题也分为两类问题。
求导
积分
求导 积分
质点的圆周运动可用线量描述也可用角量描述。
例 一质点作半径为0.1m 的圆周运动,已知运动学方 3 2 4 t (rad) 程为 求 (1) 当t =2s时,质点运动的an 和 aτ 以及 a 的大小 o (2) 当 =? 时,质点的加速度与半径成45 角? 解 (1) 由运动学方程可得
d 12t 2 dt an rω2 230.4(m/s 2 )
2
d 2 2 24t dt
aτ r 4.8(m/s 2 )
2
a an aτ 230.5(m/s 2 )
(2) 设 t´ 时刻, 质点的加速度与半径成45 角, 则
t' : aτ an
s v0 b 2 t t R R 2R
d v 0 b t dt R R
d b dt R
(3) 由 at an 可得
(v 0 bt ) 2 b R
解出
v0 R t b b
例 半径为20cm的主动轮与半径为50cm的从动轮,用无相对 滑动的皮带连接。主动轮从静止开始作匀角加速转动,在4s 内从动轮角速度达 8rad / s。求在这4s内主动轮转过多少圈。
ω dθ/dt
v r
a r
an r 2
β dω/dt
Δx vΔt
匀速圆周运动
t
匀变速直线运动
匀变速圆周运动
1 x x0 v 0t at 2 2 2 2 v v 0 2a( x x0 )
v v 0 at
0 t
