传输原理课后习题答案
传输原理课后习题答案
传输原理课后习题答案)(196034Pa P P -==)(7644)(g 4545Pa h h P P =--=ρ2-6两个容器A 、B 充满水，高度差为a 0为测量它们之间的压强差，用顶部充满油的倒U 形管将两容器相连，如图2.24所示。
已知油的密度ρ油=900kg／m 3，h ＝0.1m ，a ＝0.1m 。
求两容器中的压强差。
解：记AB 中心高度差为a ，连接器油面高度差为h ，B 球中心与油面高度差为b ；由流体静力学公式知：ghg 42油水ρρ-=-P h P b)a g 2++=（水ρP P Agb 4水ρ+=P P B Paga P P P P P B A 1.107942=+-=-=∆水ρ 2-8一水压机如图2.26所示。
已知大活塞直径D ＝11.785cm ，小活塞直径d=5cm ，杠杆臂长a ＝15cm ，b ＝7.5cm ，活塞高度差h ＝1m 。
当施力F1＝98N 时，求大活塞所能克服的载荷F2。
22232D F 2d F ⎪⎭⎫ ⎝⎛=+⎪⎭⎫ ⎝⎛πρπgh解：由杠杆原理知小活塞上受的力为F 3：a F b F *=*3由流体静力学公式知：2223)2/()2/(D F gh d F πρπ=+∴F 2=1195.82N2-10水池的侧壁上，装有一根直径d＝0.6m 的圆管，圆管内口切成a ＝45°的倾角，并在这切口上装了一块可以绕上端铰链旋转的盖板，h=2m ，如图2.28所示。
如果不计盖板自重以及盖板与铰链间的摩擦力，问开起盖板的力T 为若干?(椭圆形面积的J C =πa 3b/4)解：建立如图所示坐标系oxy ，o 点在自由液面上，y 轴沿着盖板壁面斜向下，盖板面为椭圆面，在面上取微元面dA,纵坐标为y ，淹深为h=y * sin θ,微元面受力为A gy A gh F d sin d d θρρ==板受到的总压力为A h A y g A g F c c AA γθρθρ====⎰⎰sin yd sin d F盖板中心在液面下的高度为h c =d/2+h 0=2.3m,y c =a+h 0/sin45°盖板受的静止液体压力为F=γh c A=9810*2.3*πab压力中心距铰链轴的距离为 ：X=d=0.6m,由理论力学平衡理论知，当闸门刚刚转动时，力F 和T 对铰链的力矩代数和为零，即：0=-=∑Tx l F M故T=6609.5N2-14有如图2.32所示的曲管AOB 。
(完整版)移动通信原理与系统课后习题答案
第一章概述1・1简述移动通信的特点^tfl①移动通信利用无後电沁行信息传衛②移动也fims干扰I不境下工⑦通信吝呈有用，©逋億癡纷宾杂丿⑤対移动台的要求高。
】・2移动台主夢受坯些干扰彭响？坯总千吒是埠同系统所特有的？答，①互谓干扰，②邻说干拣③同倾干扰■(蛉宵毎艸所特有吊)©多址干执.1.，旬注妊淇式移功連伯旳犬匡万史・说明善代话功週百东统旳柿魚：S.策一代(1G)以横拟式軽窩网为左養待征.是20也SP年代束的坪优初就幵怕商用的。
其中最有代表性的是的AMPS (Advanced Mohle Phone System J 以渭的TACS (lota! Access Communicatoa System)两大系扯・另外述有龙殴的NMT艮日本的HCMTS系统執从技术特色上看・1G以解决两个內态性中瑕基本的用戸这一莖幼态協核"F渲当老虑到姜二至信道动态性。
王要是擋施是乘用炽分多址fDMA方式翊对用户的动态寻址坊违：.并以妹窝丈网络结构和预车规划痢m敢再用方式.达到扩大走需无苓范国和帚足用户数苛烤他京札在信总动态特性匹配上.适当采用了性彼优良的橫猷涸頻方式.并刑用茶站二ixfB)分集方式抿抗之碗杼性袞轧第二代(20)以数字化为主要特征.构翩孚式蛭黑移动谢信系统它干20曲己90年代初正式去向侖用.耳*昂具有代表性的有欧洲的时分多址(TDMA) GSM (GSM Group Special Mobile, 19S9年以gar>3 Global System for Mobile CommuxucidoQ).北姜曲田分多址(CDHA)的IS-9S 两大郭克.男外还有0*05 PDC 系统轨从技木持色上音.它杲以坟字化为荟趾牧全血地誉庭了信型5用户的二生动态特性艮湖应的匹記猎施，主要扌:丄山揑Wg：才匸TDXfA i.GSX：.K CDX<A (IS^5)方氏实观对用户的动态寻址功能.#以數字丈蜂宮闷络结杓和頡率(相位)规划冥奴戲顼(相位〉芳用方就.从麵扩大老盖般务范劇和滙足用P數殳旁上的磅求.在对信追动态特性的匹配上釆取了下面一系列抬施，(1)采甲杭干批性館优良的訣字式调制I GMSK(GSM). QPSKC1S 95).性能优良的拭干扰纠榕编码，肯枳真(GSM. (S-95K矩联码<0SM)i⑵ 彳用功率校制衣TIE抗罢京转和远近效应・这1疔CDMA方求的IS・9$尤为或負(3)采用R适应畑j (GSM)和Rake檢收(IS 95)杭坝李选摄怡衰蒂与多径干状■(4)釆用值2定肘(码如竦用恼间交织方式(GS\D和块交织方罠(1S-9S)曲加性秤罷据三代.(3G)以纟圾U业务为主翌缚征・它于*世圮初和M投人裔业化迄岀有代表性的有北芙的CDMA2000.欧汕和E*的UCDMA及我国握岀的TD SCDMA三尺系疝另外还有欧制的DECT及北美的UMC-B6.从技术上看.3G是住2G系扰适配信追与用户二垂功态約性的基瑞上又引入了业务用动态也即在3G 系统中.用户业务既可以是单一的倍音、细职国悅也可以是多嫖洌1务，且用户适择业务是幢机的，这个是第三运渤态性的引人忡禺貌大大复卒化。
计算机组成原理课后习题-参考答案
习题参考答案
5-2：计算机为什么要设置时序部件？ 周期、节拍、脉冲三级时序关系如何 表示？
一条指令运行的各种操作控制信号在时间上有严格 的定时关系， 的定时关系，时序部件用以控制时序以保证指令 的正确执行。 的正确执行。 将指令周期划分为几个不同的阶段， 将指令周期划分为几个不同的阶段，每个阶段称为 一个机器周期。 一个机器周期。 一个机器周期又分为若干个相等的时间段， 一个机器周期又分为若干个相等的时间段，每个时 时间段称为一个时钟周期（节拍）。 时间段称为一个时钟周期（节拍）。 在一个时钟周期（节拍）内可设置几个工作脉冲， 在一个时钟周期（节拍）内可设置几个工作脉冲， 用于寄存器的清除、接收数据等工作。 用于寄存器的清除、接收数据等工作。
9
习题什么特点？
依据控制器中的时序控制部件和微操作控制信号形 成部件的具体组成与运行原理不同，通常把控制 成部件的具体组成与运行原理不同， 器区分为微程序控制器和硬布线控制器两大类。 器区分为微程序控制器和硬布线控制器两大类。 微程序控制方式是用一个ROM做为控制信号产生 微程序控制方式是用一个 做为控制信号产生 的载体， 中存储着一系列的微程序， 的载体，ROM中存储着一系列的微程序，组成微 中存储着一系列的微程序 程序的微指令代码产生相应的操作控制信号， 程序的微指令代码产生相应的操作控制信号，这 是一种存储逻辑型的控制器。方便修改和扩充， 是一种存储逻辑型的控制器。方便修改和扩充， 但指令执行速度较慢。 但指令执行速度较慢。 硬布线控制方式采用组合逻辑电路实现各种控制功 在制造完成后， 能，在制造完成后，其逻辑电路之间的连接关系 就固定下来，不易改动。其运行速度快， 就固定下来，不易改动。其运行速度快，但构成 复杂。 复杂。
13
习题参考答案
北邮版通信原理课后习题的答案第四章
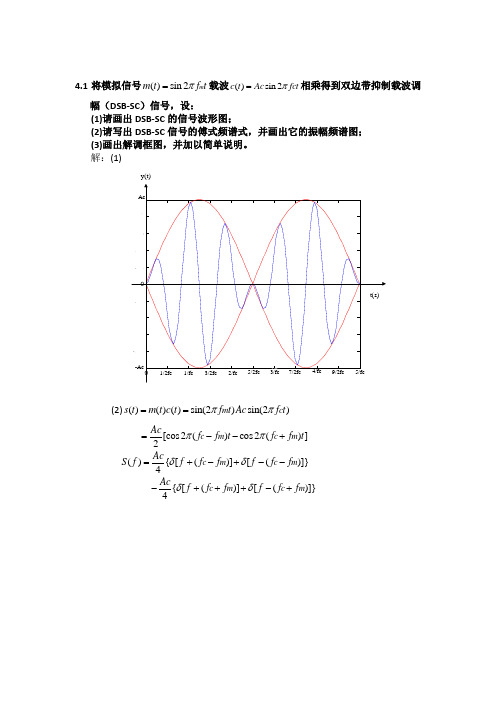
4.1将模拟信号()sin 2m m t f t π=载波()sin 2c c c t A f t π=相乘得到双边带抑制载波调幅（DSB-SC ）信号，设：(1)请画出DSB-SC 的信号波形图；(2)请写出DSB-SC 信号的傅式频谱式，并画出它的振幅频谱图； (3)画出解调框图，并加以简单说明。
解：(1)y(t)(2)()()()sin(2)sin(2)m c s t m t c t f t Ac f t ππ==[cos 2()cos 2()]2c m c m Acf f t f f t ππ=--+ (){[()][()]}4c m c m AcS f f f f f f f δδ=+-+--{[()][()]}4c m c m Acf f f f f f δδ-+++-+(3)相干解调相干解调：将接收信号与载波信号sin(2)fct π相乘，得到()sin(2)()sin(2)sin(2)c c c c r t f t A m t f t f t πππ=()[1cos(4)]2cc A m t f t π=- 通过低通滤波器抑制载频的二倍频分量，得到解调信号为0()()2cA y t m t =4.2已知某调幅波的展开式为：444)4cos()cos(2 1.210)()cos(2102 1.110t t t s t πππ++=⨯⨯⨯⨯⨯ (1)求调幅系数和调制信号频率；(2)写出该信号的傅式频谱式，画出它的振幅频谱图； (3)画出该信号的解调框图。
解：(1)444)4cos()cos(2 1.210)()cos(2102 1.110t t t s t πππ++=⨯⨯⨯⨯⨯ 444cos(2 1.110)[10.5cos(20.110)]t t ππ=+⨯⨯⨯⨯调制系数是a=0.5; 信号频率是f=1000Hz(2)44441()[(10)(10)]2[( 1.110)( 1.110)]2S f f f f f δδδδ=++-+++-⨯⨯441[( 1.210)( 1.210)]2f f δδ+++-⨯⨯(3)4.3现有一振幅调制信号： ()(1cos )cos m c s t A t t ωω=+其中调制信号的频率fm=5KHz ，载频 fc=100KHz ，常数A=15。
光纤通信课后习题解答-第2章习题参考答案
第二章 光纤和光缆1．光纤是由哪几部分组成的？各部分有何作用？答：光纤是由折射率较高的纤芯、折射率较低的包层和外面的涂覆层组成的。
纤芯和包层是为满足导光的要求；涂覆层的作用是保护光纤不受水汽的侵蚀和机械擦伤，同时增加光纤的柔韧性。
2．光纤是如何分类的？阶跃型光纤和渐变型光纤的折射率分布是如何表示的？答：（1）按照截面上折射率分布的不同可以将光纤分为阶跃型光纤和渐变型光纤；按光纤中传输的模式数量，可以将光纤分为多模光纤和单模光纤；按光纤的工作波长可以将光纤分为短波长光纤、长波长光纤和超长波长光纤；按照ITU-T 关于光纤类型的建议，可以将光纤分为G .651光纤（渐变型多模光纤）、G.652光纤（常规单模光纤）、G.653光纤（色散位移光纤）、G.654光纤（截止波长光纤）和G.655（非零色散位移光纤）光纤；按套塑（二次涂覆层）可以将光纤分为松套光纤和紧套光纤。
（2）阶跃型光纤的折射率分布 () 21⎩⎨⎧≥<=ar n ar n r n 渐变型光纤的折射率分布 () 2121⎪⎩⎪⎨⎧≥<⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛∆-=ar n a r a r n r n cm α 3．阶跃型光纤和渐变型光纤的数值孔径NA 是如何定义的？两者有何区别？它是用来衡量光纤什么的物理量？答：阶跃型光纤的数值孔径 2sin 10∆==n NA φ渐变型光纤的数值孔径 ()() 20-0s i n220∆===n n n NA c φ两者区别：阶跃型光纤的数值孔径是与纤芯和包层的折射率有关；而渐变型光纤的数值孔径只与纤芯内最大的折射率和包层的折射率有关。
数值孔径是衡量光纤的集光能力，即凡是入射到圆锥角φ0以内的所有光线都可以满足全反射条件，在芯包界面上发生全反射，从而将光线束缚在纤芯中沿轴向传播。
4．简述光纤的导光原理。
答：光纤之所以能够导光就是利用纤芯折射率略高于包层折射率的特点，使落于数值孔径角)内的光线都能收集在光纤中，并在芯包边界以内形成全反射，从而将光线限制在光纤中传播。
通信原理教程(第2版)课后答案12-9
解：由题意， t =120 次/秒， =12.5 ms。 （1） P t 120 12.5 10 3 1.5 。 （2） P0 e t e 1.5 0.223 。
37
kh
课
当 p 最大时，有：
p e 2 P 2 Pe 2 P 0 P
解：由题意， t 6000 30 / 3600 50 次/秒， 500 s ，则系统的归一化总业 务量为
w.
习题 9.10
ww
和重发。每次发送需占用一个 12.5 ms 的时隙。试问： （1） 系统的归一化总业务量等于多少？ （2） 第一次发送就成功的概率等于多少？ （3） 在一次成功发送前，刚好有两次碰撞的概率等于多少？
ww
w.
最多站数。
答： R-ALOHA。 因为纯 ALOHA 与 S-ALOHA 的最大通过量分别为 0.18 和 0.37。 习题 9.6 在一个纯 ALOHA 系统中， 信道容量为 64kb/s， 每个站平均每 10s 发送
一个分组，即使前一分组尚未发出（因碰撞留在缓存器中） ，后一分组也照常产生。 每个分组包含 3000b。若各站发送的分组按泊松分布到达系统，试问该系统能容纳的 解：对于纯的 ALOHA，可用的带宽为： 0.18 64 11.52 kb/s。
P=-ln(0.2)=1.61 p Pe P 1.61 e 1.61 1.61 0.2 0.322
因为 P>1，所有系统过载。
习题 9.12 设一个令牌环形网中的令牌由 10 个码元组成，信号发送速率为 10 多少米？当网中只有 3 个站工作（其他站都关闭）时，需要的最小的电缆总长度为多 解：信号发送速率为 10 Mb/s，则延迟 1 码元的时间为 1/10 us信原理》习题第九章
冶金传输原理课后习题答案
冶金传输原理课后习题答案【篇一：冶金传输原理课后答案(朱光俊版,第一章)】/m3 10001?273prtprtprt1-16 , r=(1) (2)1-21 dvxdy65010.5?0.0012dvx dy=vd1-23,,o=vx=hdy0.181.3?0.001=0.1385?1000 1/sdvx dy=1.011?1030.1385?107.2 pa.s【篇二：《冶金传输原理》吴铿编质量传输习题参考答案】s=txt>1. 解：（1）?ch4?ych4mch4ych4mch4?yc2h6mc2h6?yc3h8mc3h8?yco2mco2?90.27%（2）?ych4mch4?yc2h6mc2h6?yc3h8mc3h8?yco2mco2?16.82 （3）pch4?ych4p?9.62?104pa2. 解：dab?1/3b1/3pva?v?1.56?10?5m2/s3. 解：ch4的扩散体积24.42，h2的扩散体积7.07dab?1/3b1/3pva?v?3.19?10-5m2/s4. 解：（1）v??co2vco2??o2vo2??h2ovh2o??n2vn2?3.91m/s （2）vm?yco2vco2?yo2vo2?yh2ovh2o?yn2vn2?4.07m/s （3）jco2??co2?co2?????mco2pco2rtpco2rt??co2????0.212kg/?m2?s? ?（4）jco2?cco2?co2??m?????co2??m??5.33mol/?m2?s? ?5. 解：（1）21% （2）21%pvm?15.46kg （3）m?nm?rtm（4）?o2??0.117kg/m3vm（5）?n2??0.378kg/m3vm（6）?空气??0.515kg/m3v（7）c空气??空气m?17.4mol/m3（8）29.6g/mol（9）pn2?yn2p?7.9?104pa6. 证明：?a?manamaxama??mnama?nbmbxama?xbmb得证。
通信原理各章习题集的答案
第一章 通信系统概论一 填空选择题1.数字通信系统的主要优点是 __抗干扰能力强噪声不积累 、差错可控、容易加密_、可实现综合化（便于集成）等_。
2.通信系统的主要质量指标通常用_有效性_和可靠性_衡量， FSK 系统指标具体用_传输速率（传码率、传信率）和_差错率（误码率、误信率）_衡量，FM/PM 系统具体指标用_有效传输频带 和_信噪比_衡量。
3.已知二进制数字信号在2分钟内共传送72000个码元，0、1码等概率出现，则码元速率为600B ，信息速率为600b/s ；传送1小时后，接收到的错码为216个，其误码率为10-4；若保持码元速率不变，变换为8进制传输，每个码元所含信息量为3 ，信息速率为1800b/s 。
4.通信是指消息由一地向另一地进行＿＿＿＿＿＿，主要质量指标是＿＿＿＿＿和＿＿＿＿＿,它们在数字通信系统中具体为＿＿＿＿＿和＿＿＿＿＿。
5.在码元速率相同的条件下，16进制数字调制系统的信息速率是二进制的4 倍。
6.按传输媒介，通信系统可分为有线通信系统、无线通信系统。
7.数字通信系统的有效性指标包括 ( D )A.信息传输速率B.符号传输速率C.频带利用率D.以上都包括8.在码元速率相同条件下，m 进制数字调制系统的信息速率是二进制的 log 2m 倍。
9．通信系统按其传输信号形式分可分为模拟通信系统和数字通信系统 。
10.通信系统按信道中传输的信号不同分为模拟通信系统 和 数字通信系统11.衡量通信系统主要指标是有效性和可靠性，前者主要是消息传输速率问题，而后者是指消息传输的 质量问题。
12．设有四个信息A 、B 、C 、D 分别以概率1/4、1/8、1/8、1/2传送，每个消息出现是相互独立的，其平均信息量H=__1.75b/符号__。
13.设有4个消息符号，其出现概率是21、41、81、81各消息符号出现是相对独立的，该符号集的平均信息量为 1.75b/符号 。
14.某四元制信源，各符号对应的概率分别为21、41、81、1，则该信源符号的平均信息量为 1.75b/符号 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章 流体静力学（吉泽升版）2-1作用在流体上的力有哪两类，各有什么特点?解:作用在流体上的力分为质量力和表面力两种。
质量力是作用在流体内部任何质点上的力，大小与质量成正比，由加速度产生，与质点外的流体无关。
而表面力是指作用在流体表面上的力，大小与面积成正比，由与流体接触的相邻流体或固体的作用而产生。
2-2什么是流体的静压强，静止流体中压强的分布规律如何? 解： 流体静压强指单位面积上流体的静压力。
静止流体中任意一点的静压强值只由该店坐标位置决定，即作用于一点的各个方向的静压强是等值的。
2-3写出流体静力学基本方程式，并说明其能量意义和几何意义。
解:流体静力学基本方程为：h P h P P P Z P Z γργγ+=+=+=+002211g 或同一静止液体中单位重量液体的比位能 可以不等，比压强也可以不等，但比位 能和比压强可以互换，比势能总是相等的。
2-4如图2-22所示，一圆柱体d ＝0.1m ，质量M ＝50kg ．在外力F ＝520N 的作用下压进容器中，当h=0.5m 时达到平衡状态。
求测压管中水柱高度H ＝? 解：由平衡状态可知：)()2/()mg 2h H g d F +=+ρπ（ 代入数据得H=12.62m2.5盛水容器形状如图2.23所示。
已知hl ＝0.9m ，h2＝0.4m ，h3＝1.1m ，h4＝0.75m ，h5＝1.33m 。
求各点的表压强。
解：表压强是指：实际压强与大气压强的差值。
)(01Pa P =)(4900)(g 2112Pa h h P P =-+=ρ )(1960)(g 1313Pa h h P P -=--=ρ )(196034Pa P P -==)(7644)(g 4545Pa h h P P =--=ρ2-6两个容器A 、B 充满水，高度差为a 0为测量它们之间的压强差，用顶部充满油的倒U 形管将两容器相连，如图2.24所示。
已知油的密度ρ油=900kg ／m 3，h ＝0.1m ，a ＝0.1m 。
求两容器中的压强差。
解：记AB 中心高度差为a ，连接器油面高度差为h ，B 球中心与油面高度差为b ；由流体静力学公式知：gh g 42油水ρρ-=-P h P b)a g 2++=（水ρP P A gb 4水ρ+=P P BPa ga P P P P P B A 1.107942=+-=-=∆水ρ2-8一水压机如图 2.26所示。
已知大活塞直径D ＝11.785cm ，小活塞直径d=5cm ，杠杆臂长a ＝15cm ，b ＝7.5cm ，活塞高度差h ＝1m 。
当施力F1＝98N 时，求大活塞所能克服的载荷F2。
解：由杠杆原理知小活塞上受的力为F 3：a F b F *=*3 由流体静力学公式知：2223)2/()2/(D F gh d F πρπ=+∴F 2=1195.82N2-10水池的侧壁上，装有一根直径d ＝0.6m 的圆管，圆管内口切成a ＝45°的倾角，并在这切口上装了一块可以绕上端铰链旋转的盖板，h=2m ，如图2.28所示。
如果不计盖板自重以及盖板与铰链间的摩擦力，问开起盖板的力T 为若干?(椭圆形面积的J C =πa 3b/4)解：建立如图所示坐标系oxy ，o 点在自由液面上，y 轴沿着盖板壁面斜向下，盖板面为椭圆面，在面上取微元面dA,纵坐标为y ，淹深为h=y * sin θ,微元面受力为A gy A gh F d sin d d θρρ==22232D F 2d F ⎪⎭⎫ ⎝⎛=+⎪⎭⎫⎝⎛πρπgh板受到的总压力为A h A y g A g F c c AAγθρθρ====⎰⎰sin yd sin d F盖板中心在液面下的高度为 h c =d/2+h 0=2.3m,y c =a+h 0/sin45° 盖板受的静止液体压力为F=γh c A=9810*2.3*πab 压力中心距铰链轴的距离为 ：X=d=0.6m,由理论力学平衡理论知，当闸门刚刚转动时，力F 和T 对铰链的力矩代数和为零，即：0=-=∑Tx l F M故T=6609.5N2-14有如图2.32所示的曲管AOB 。
OB 段长L1＝0.3m ，∠AOB=45°，AO 垂直放置，B 端封闭，管中盛水，其液面到O 点的距离L2＝0.23m ，此管绕AO 轴旋转。
问转速为多少时，B 点的压强与O 点的压强相同?OB 段中最低的压强是多少?位于何处?解：盛有液体的圆筒形容器绕其中心轴以等角速度ω旋转时，其管内相对静止液体压强分布为：z r P P γωρ-+=2220以A 点为原点，OA 为Z 轴建立坐标系 O 点处面压强为20gl P P a ρ+= B 处的面压强为gZ P P a B ρωρ-+=2r 22其中：Pa 为大气压。
21145cos ,45s L L Z in L r -︒=︒= 当PB=PO 时ω=9.6rad/s OB 中的任意一点的压强为⎥⎦⎤⎢⎣⎡--+=)(2r 222L r g P P a ωρ对上式求P 对r 的一阶导数并另其为0得到，2ωgr =即OB 中压强最低点距O 处m rL 15.045sin =︒='代入数据得最低压强为P min =103060Pa第三章习题（吉泽升版）3.1已知某流场速度分布为，试求过点(3，1，4)的流线。
解：由此流场速度分布可知该流场为稳定流，流线与迹线重合，此流场流线微分方程为：即：求解微分方程得过点(3,1,4)的流线方程为：3.2试判断下列平面流场是否连续?解：由不可压缩流体流动的空间连续性方程（3-19，20）知： ，44.045sin 0445sin 1245sin h A J 30c =⎪⎭⎫ ⎝⎛︒++︒=︒-+=abh a ba d y y l c c ππ3,3,2-=-=-=z u y u x u z y x ⎪⎩⎪⎨⎧=-=-1)3(1)2(33y z y x y x u y x y x cos 3,sin u 33==当x=0，1，或y=k π （k=0，1，2，……）时连续。
3.4三段管路串联如图3.27所示，直径d 1=100 cm ，d 2=50cm ，d 3＝25cm ，已知断面平均速度v 3＝10m/s ，求v 1,v 2，和质量流量(流体为水)。
解：可压缩流体稳定流时沿程质量流保持不变， 故：质量流量为：3.5水从铅直圆管向下流出，如图3.28所示。
已知管直径d 1＝10 cm ，管口处的水流速度v I ＝1.8m/s ，试求管口下方h ＝2m 处的水流速度v 2，和直径d 2。
解：以下出口为基准面，不计损失，建立上出口和下出口面伯努利方程：代入数据得：v2=6.52m/s 由 得:d2=5.3cm3.6水箱侧壁接出一直径D ＝0.15m 的管路，如图3.29所示。
已知h1＝2.1m ，h2=3.0m,不计任何损失，求下列两种情况下A 的压强。
(1)管路末端安一喷嘴，出口直径d=0.075m ；(2)管路末端没有喷嘴。
解：以A 面为基准面建立水平面和A 面的伯努利方程：以B 面为基准，建立A,B 面伯努利方程：（1）当下端接喷嘴时，解得va=2.54m/s, PA=119.4KPa（2）当下端不接喷嘴时，解得PA=71.13KPa 3.7如图3.30所示，用毕托管测量气体管道轴线上的流速Umax ，毕托管与倾斜(酒精)微压计相连。
已知d=200mm ，sin α=0.2，L=75mm ，酒精密度ρ1=800kg／m3，气体密度ρ2＝1.66Kg/m 3；Umax=1.2v(v为平均速度)，求气体质量流量。
解：此装置由毕托管和测压管组合而成，沿轴线取两点，A(总压测点），测静压点为B ，过AB 两点的断面建立伯努利方程有：其中ZA=ZB, vA=0,此时A 点测得 的是总压记为PA*，静压为PB 不计水头损失，化简得 由测压管知：()yx y y y xxx x y x sin 13sin sin 32323-=-=∂∂+∂∂νν332211Q A v A v A v vA ====s m A A v /625.0v 1331==m/s 5.22332==A Av v ()s A /Kg 490v Q M 33==•=水ρρgv P g vP h a a2022221++=++γγ2211v A v A =gvP P h a A a 2002D 21++=+++γγγγab A a P g v Pg v h ++=+++2022D 222b b a a Av A v =b a v v =gg v 2vP Z 2P Z 2AA A 2max BB ++=++气气γγ2max B *A 21P -P v 气ρ=()agL cos P -P B *A 气酒精ρρ-=由于气体密度相对于酒精很小，可忽略不计。
由此可得气体质量流量:代入数据得3.9如图3.32所示，一变直径的管段AB ，直径dA=0.2m，dB=0.4m，高差h=1.0m ，用压强表测得PA ＝7x104Pa ，PB ＝4x104Pa ，用流量计测得管中流量Q=12m 3/min ，试判断水在管段中流动的方向，并求损失水头。
解:由于水在管道内流动具有粘性，沿着流向总水头必然降低，故比较A和B点总水头可知管内水的流动方向。
即：管内水由A 向B 流动。
以过A 的过水断面为基准，建立A 到B 的伯努利方程有：代入数据得，水头损失为hw=4m第九章 导 热1. 对正在凝固的铸件来说，其凝固成固体部分的两侧分别为砂型（无气隙）及固液分界面，试列出两侧的边界条件。
解：有砂型的一侧热流密度为 常数，故为第二类边界条件， 即τ＞0时),,,(nt z y x q T=∂∂λ固液界面处的边界温度为常数， 故为第一类边界条件，即 τ＞0时Τw =f(τ)注：实际铸件凝固时有气隙形成，边界条件复杂，常采用第三类边界条件3. 用一平底锅烧开水，锅底已有厚度为3mm 的水垢，其热导率λ为1W/(m · ℃)。
已知与水相接触的水垢层表面温度为111 ℃。
通过锅底的热流密度q 为42400W/m 2，试求金属锅底的最高温度。
解：热量从金属锅底通过水垢向水传导的过程可看成单层壁导热，由公式（9-11）知C q T 032.127110342400=⨯⨯==∆-λδ=∆T -=-121t t t 111℃， 得 1t =238.2℃4. 有一厚度为20mm 的平面墙，其热导率λ为1.3W/(m·℃)。
为使墙的每平方米热损失不超过1500W ，在外侧表面覆盖了一层λ为0.1W/(m·℃)的隔热材料，已知复合壁两侧表面温 度分布750 ℃和55 ℃，试确定隔热层的厚度。